(完整版)六年级圆柱表面积练习题(附答案)
六年级数学下册典型例题系列之第三单元:圆柱表面积的三种增减变化方式专项练习(含答案)人教版

加油!有志者事竟成答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好! 经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!1六年级数学下册典型例题系列之第三单元:圆柱表面积的三种增减变化方式专项练习(解析版)1.一个底面积为x平方厘米、高为h厘米的圆柱切成若干个小圆柱。
每切1次,表面积都增加( )平方厘米,切5次表面积增加( )平方厘米。
【解析】一个圆柱每切1次表面积就增加2个截面的面积,切5次表面积增加(2×5)个截面的面积,截面面积为x平方厘米。
一个底面积为x平方厘米、高为h厘米的圆柱切成若干个小圆柱。
每切1次,表面积都增加( 2x )平方厘米,切5次表面积增加( 10x )平方厘米。
部编新人教版小学六年级数学下册《圆柱的表面积》学霸作业及答案
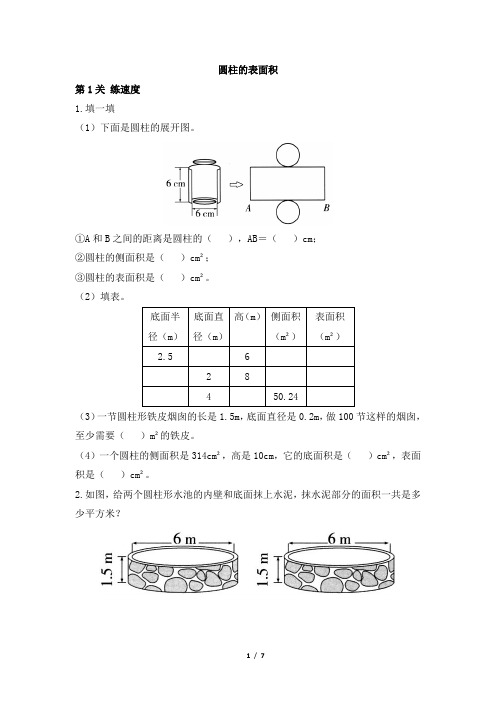
圆柱的表面积第1关练速度1.填一填(1)下面是圆柱的展开图。
①A和B之间的距离是圆柱的(),AB=()cm;②圆柱的侧面积是()cm²;③圆柱的表面积是()cm²。
(2)填表。
底面半径(m)底面直径(m)高(m)侧面积(m²)表面积(m²)2.5 62 84 50.24(3)一节圆柱形铁皮烟囱的长是1.5m,底面直径是0.2m,做100节这样的烟囱,至少需要()m²的铁皮。
(4)一个圆柱的侧面积是314cm²,高是10cm,它的底面积是()cm²,表面积是()cm²。
2.如图,给两个圆柱形水池的内壁和底面抹上水泥,抹水泥部分的面积一共是多少平方米?3.压路机的滚筒是一个圆柱,它的轮宽是2m,横截面直径是1.2m。
如果滚筒每分钟滚动5周,那么1小时可压路多少平方米?4.如图的“博士帽”是用灰色卡纸做成的,上面是边长为30cm的正方形,下面是底面直径为l6cm、高为10cm的无底无盖的圆柱。
制作20顶这样的“博士帽”,至少需要多少平方分米的灰色卡纸?第2关练准确率5.环卫工人用铁皮做了一个圆柱形的垃圾桶,它的上面留有一个直径为60cm的口(如图),做这个垃圾桶大约要用铁皮多少平方分米?6.一根长5m、横截面直径是20cm的木头浮在水面上,小红发现它正好有一半露出水面。
这根木头与水接触的面积是多少平方米?(得数保留一位小数)7.一根圆柱形木棒,木匠师傅将其锯成3段相同的小圆柱,木棒的表面积比原来增加了125.6cm²,如果锯成8段相同的小圆柱,那么木棒的表面积将增加多少平方厘米?8.如图,一个圆柱的高被截去5cm后,圆柱的表面积减少了31.4cm²,原来圆柱的表面积是多少?9.如图,把一个正方体木块削成一个体积最大的圆柱,如果圆柱的侧面积是314cm²,正方体木块的表面积是多少平方厘米?10.有一张长方形铁皮,如图,剪下阴影部分围成一个圆柱,求这个圆柱的表面积。
六年级下册数学圆柱表面积专项典型试题训练5(含答案)

六年级下册数学圆柱表面积专项典型试题训练一、单选题(共6题;共12分)1.圆柱体的底面半径扩大3倍,高不变,体积扩大()A. 3倍B. 9倍C. 6倍2.一个圆柱的底面半径扩大5倍,高不变,它的体积扩大()倍。
A. 5B. 10C. 15D. 253.用铁皮做5节同样长的通风管,每节长8分米,底面直径1分米,至少共需要铁皮()A. 125.6平方分米B. 25.12平方分米C. 26.69平方分米D. 250.12平方分米4.做一个无盖的圆柱形油箱,求至少要用多少铁皮就是求油箱的()A. 底面积B. 侧面积+一个底面积C. 表面积5.计算一节圆柱形通风管的铁皮用量,就是求圆柱的()A. 侧面积B. 表面积C. 侧面积加一个底面积6.把一个圆柱切拼成一个近似的长方体,体积与表面积()A. 都变了B. 都没变C. 体积变了,表面积没变D. 体积没变,表面积变了二、判断题(共5题;共10分)7.判断对错。
圆柱的表面积用“底面周长×高”来计算。
8.在棱长是6分米的正方体中,削一个最大的圆柱,这个圆柱的底面直径和高都是6分米.(判断对错)9.判断对错圆柱体的底面半径扩大2倍,它的侧面积就扩大4倍.10.如果两个圆柱体的体积相等,那么它们的侧面积也相等。
11.圆柱体的高扩大3倍,体积就扩大3倍.(判断对错)三、填空题(共13题;共16分)12.圆柱的________加上________就是圆柱的表面积。
13.一个圆柱体的侧面积是188.4平方分米,底面半径是3分米,它的高是________分米.14.一个圆柱的侧面积是62.8 ,高是4cm,底面半径是________ cm.15.制作下面圆柱体的物体,至少要用________平方米的铁皮?16.把一个圆柱体削成一个最大的圆锥体,体积减少了120立方厘米,这个圆锥的体积是________立方厘米。
17.如图是一个圆柱体的侧面展开图,原来这个圆柱的体积可能是________或________ cm3.18.圆柱的表面积=________+________.19.一台压路机的滚筒宽2米,直径为1.5米.如果它滚动100周,压路的面积是________平方米?20.求下面圆柱的表面积是________平方厘米?.(列出算式后,可以用计算器计算)(图中单位:厘米)21.一节圆柱形状的铁皮的烟囱,长1米,底面直径12厘米.做20节这样的铁皮烟囱,至少需要多大的铁皮?________22.一个圆柱的底面半径为4厘米,侧面展开后正好是一个正方形,这个圆柱的体积是________立方厘米。
六年级数学下册圆柱的表面积考试题与答案

六年级数学下册圆柱的表面积考试题与答案1. 圆柱的侧面展开后一定是长方形。
[判断题] *对错√2. 6立方厘米比5平方厘米显然要大。
[判断题] *对错√3. 一个物体上、下两个面是相等的圆面,那么,它一定是圆柱形物体。
[判断题] *对错√答案解析:中间的形状,大小不一定4. 把两张相同的长方形纸,分别卷成两个形状不同的圆柱筒,并装上两个底面,那么制的圆柱的高、侧面积、表面积一定相等。
[判断题] *对错√5. 圆柱体的表面积=底面积×2+底面积×高。
[判断题] *对错√6. 圆柱体的表面积一定比它的侧面积大。
[判断题] *对√错7. 圆柱体的高越长,它的侧面积就越大。
[判断题] *对错√答案解析:前提是底周长一定8. 一个圆柱体,底面周长是94.2厘米,高是25厘米,它的侧面积是()平方厘米。
[填空题] *_________________________________(答案:2355)9. 一个圆柱体,底面半径是2厘米,高是6厘米,它的侧面积是()平方厘米。
[填空题] *_________________________________(答案:75.36)10. 一个圆柱体的侧面积是12.56平方厘米,底面半径是2分米,它的高是()厘米。
[填空题] *_________________________________(答案:0.1)11. 把一张长8分米,宽5分米的白纸,围成一个圆柱形纸筒,这个纸筒的侧面积是()平方分米。
[填空题] *_________________________________(答案:40)12. 一个圆柱形木棒,底面半径2厘米,高3厘米,沿底面直径纵剖后,表面积之和增加()平方厘米。
[填空题] *_________________________________(答案:24)13. 做一个无盖的圆柱体的水桶,需要的铁皮的面积是()[单选题] *侧面积+一个底面积√(侧面积+底面积)×2侧面积+两个底面积14. 一个圆柱的底面直径是10厘米,高是4分米,它的侧面积是()平方厘米。
圆柱的表面积练习题答案

圆柱的表面积练习题答案圆柱是一种常见的几何图形,它具有特殊的形状和特点。
在计算圆柱的表面积时,我们需要考虑其底面积和侧面积。
下面是一些圆柱表面积的练习题及其答案。
练习题1:已知一个圆柱的高度为8cm,底面半径为4cm,求其表面积。
解答:首先,我们需要计算圆柱的底面积和侧面积,然后将它们相加得到表面积。
底面积= π * r^2 = 3.14 * 4^2 = 3.14 * 16 ≈ 50.24(平方厘米)侧面积 = 周长 * 高度= 2 * π * r * h = 2 * 3.14 * 4 * 8 = 3.14 * 32 ≈ 100.48(平方厘米)表面积 = 底面积 + 侧面积 = 50.24 + 100.48 = 150.72(平方厘米)因此,该圆柱的表面积约为150.72平方厘米。
练习题2:一个圆柱的高度为12cm,表面积为180π平方厘米,求其底面半径。
解答:我们已知该圆柱的表面积,可以利用这一信息来求解底面半径。
表面积 = 底面积 + 侧面积已知表面积为180π平方厘米,将其代入公式中:180π = π * r^2 + 2π * r * h由于高度已知为12cm,将其代入公式中:180π = π * r^2 + 2π * r * 12化简公式:180 = r^2 + 24r移项并整理:r^2 + 24r - 180 = 0我们可以将上述二次方程进行因式分解或者使用求根公式求解出r 的值。
通过解方程,得到底面半径r ≈ 6cm 或r ≈ -30cm,由于半径不可能为负值,所以底面半径约为6cm。
练习题3:一个圆柱的底面积为20π平方厘米,侧面积为60π平方厘米,求其高度和底面半径。
解答:我们已知该圆柱的底面积和侧面积,可以通过这些信息来求解其高度和底面半径。
底面积= π * r^2 = 20π解方程,得到底面半径r ≈ 2.83cm侧面积 = 周长 * 高度= 2 * π * r * h = 60π解方程,得到高度h ≈ 5cm因此,该圆柱的底面半径约为2.83cm,高度约为5cm。
人教版六年级下册数学《圆柱的表面积》同步轻松达标练(含参考答案)

人教版六年级下册数学《圆柱的表面积》同步轻松达标练一、单选题1.把圆柱的侧面展开后不可能得到一个()。
A.正方形B.长方形C.平行四边形D.梯形2.如图,把一个底面积为8cm2、高6cm的圆柱切成4个小圆柱,它的表面积增加了()cm2。
A.16 B.24 C.32 D.483.用一张长15厘米,宽8厘米的长方形纸围成一个圆柱,这个圆柱的侧面积是()平方厘米。
A.120 B.60 C.376.8 D.47.14.一根长为5分米,横截面是直径为20厘米的圆形木材,沿直径垂直切成同样大的两半,表面积增加了()A.100平方厘米B.10平方分米C.20平方分米D.628平方厘米5.如有下图,一个长方形长为a,宽为b。
分别以长为轴、宽为轴旋转,产生了两个圆柱甲、乙。
判断甲、乙两个圆柱侧面积的大小关系()。
A.甲>乙B.甲<乙C.甲=乙D.无法比较二、判断题6.圆柱的底面周长与高相等时,沿着某一条高剪开,它的侧面展开图是一个正方形。
()7.“压路机的滚轮转动一周能压多少路面”是指滚轮的表面积。
()8.圆柱的侧面展开图是一个半圆形。
()9.把一个圆柱切成两部分,它的表面积不变。
()10.侧面积相等的两个圆柱,表面积也一定相等。
()三、填空题11.圆柱的侧面积展开成一个长方形,它的长是圆柱,它的宽是圆柱的。
12.把一个圆柱形纸盒沿高线剪开,侧面展开图是一个,它的一条边就等于圆柱的,另一条边就等于圆柱的。
13.做无盖的铁皮水桶需要的铁皮,是求它的。
14.将底面周长为62.8cm,高为20cm的圆柱沿直径切开,表面积增加。
15.某工厂计划用钢板制一个高10米,底面周长是18.84米的圆柱形储油罐,大约需要钢板平方米?16.一个圆柱的侧面展开图是个正方形,这个圆柱的高是底面直径的倍。
17.下图是一个圆柱的14,其中两个截面都是正方形,每个正方形的面积是10cm2。
这个14圆柱的侧面积是cm²。
四、解答题18.如图是一个底面半径为1厘米,高为4厘米的圆柱.(1)如果沿着圆柱侧面虚线剪开,请准确画出这个圆柱侧面展开图,并标注所画图形的相关长度.(取3为π的近似值计算)(2)计算所画图形的面积.19.一个圆柱形蛋糕盒,底面半径是20厘米,高是25厘米。
圆柱体表面积练习题含答案

圆柱体表面积练习题含答案圆柱体表面积练习题含答案圆柱体是我们在日常生活中经常遇到的几何体之一,它具有很多有趣的特性。
其中一个重要的特性就是它的表面积。
在本文中,我们将介绍一些关于圆柱体表面积的练习题,并提供答案供大家参考。
练习题1:一个圆柱体的底面半径为5cm,高为10cm,求其表面积是多少?解答:首先,我们需要计算出圆柱体的侧面积和底面积,然后将它们相加。
底面积可以通过公式πr²来计算,其中r为底面半径。
所以底面积为π × 5² = 25π cm²。
侧面积可以通过公式2πrh来计算,其中r为底面半径,h为圆柱体的高。
所以侧面积为2π × 5 × 10 = 100π cm²。
最后,将底面积和侧面积相加得到总表面积。
总表面积为25π + 100π = 125π cm²。
练习题2:一个圆柱体的底面积为50π cm²,高为8cm,求其表面积是多少?解答:首先,我们需要计算出圆柱体的侧面积和底面积,然后将它们相加。
已知底面积为50π cm²,可以通过公式πr²来计算。
所以,50π = πr²,解得r² = 50,即r = √50 ≈ 7.07 cm。
侧面积可以通过公式2πrh来计算,其中r为底面半径,h为圆柱体的高。
所以侧面积为2π × 7.07 × 8 ≈ 112.8π cm²。
最后,将底面积和侧面积相加得到总表面积。
总表面积为50π + 112.8π ≈ 162.8π cm²。
练习题3:一个圆柱体的总表面积为300π cm²,高为12cm,求其底面半径是多少?解答:已知总表面积为300π cm²,可以通过公式计算出侧面积和底面积的和。
侧面积可以通过公式2πrh来计算,其中r为底面半径,h为圆柱体的高。
所以侧面积为2πrh。
人教版六年级数学下册《圆柱的表面积》练习题(含答案)
人教版六年级数学下册3.1《圆柱的表面积》练习题(含答案)一、选择题1.把一个圆柱体的侧面沿一条高线剪开,可能是()。
A.长方形B.长方形或正方形C.平行四边形D.长方形、正方形、平行四边形或不规则图形2.请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
你选择的材料是()号和()号。
A.B.C.D.3.用铁皮制作5节通风管,每节长1m,底面半径是10cm,至少需要()2m的铁皮。
A.0.628 B.3.14 C.6.28 D.31.44.数学家阿基米德以圆柱容球实验(如图),发现并证明了球的体积公式是V球=43πr3。
他发现,当圆柱容球时,球的体积正好是圆柱体积的23,球的表面积也是圆柱表面积的23。
那么,球的表面积是()A.3πr2B.4πr2C.5πr2D.6πr2 5.压路机的前轮转动一周能压多少路面是指()。
A.前轮的体积B.前轮的表面积C.前轮的侧面积D.前轮一个侧面积和一个底面积二、填空题6.700平方厘米=( )平方分米20000公顷=( )平方千米5平方米=( )平方分米 2.04千克=( )克3小时15分=( )小时9080平方米=( )公顷320立方厘米=( )立方分米7.相邻两个面积单位间的进率是( ),相邻两个体积单位间的进率是( ).8.一个长方体水箱从里面量底面积是25cm2,水深1.6m,这个水箱能装水( )立方米。
9.一个圆柱的侧面积是188.4平方米,高是1米,它的底面直径是( )米。
10.把一个长4米的长方体木料切成两段,表面积增加了100平方分米,这根木料的体积是( )立方分米。
三、判断题11.两个圆柱的底面周长相等,它们的侧面积也相等。
( )12.圆柱的侧面展开图只能是长方形或正方形。
( )13.两个圆柱的底面积相等,那么它们的侧面积也一定相等。
( )14.压路机滚筒在地面上滚动一周所压路面面积正好是压路机滚筒的侧面积。
( ) 15.棱长是1 m的正方体可以切成1000个棱长是1 cm 的小正方体.( )四、连线题16.小兔拔萝卜.(连一连)五、解决问题17.一个无盖的圆柱形铁皮水桶,底面直径是30厘米,高是45厘米,做一个这样的水桶要用多少平方厘米铁皮?18.一个圆柱形铁皮水桶(无盖),高20dm,底面半径是2dm,做这个水桶需要用多少平方分米的铁皮?(接头处不计)19.建一个圆形池塘,池底直径是20米,深度是5米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱表面积练习题
1、求下列各图侧面积和表面积
二、应用题
1、把一个圆柱体的侧面展开,得到一个长31.4厘米,宽10厘米的长方形,这个圆柱体的侧面积是多少平方厘米?表面积是多少平方厘米?
2、一个圆柱体的底面直径是5分米,高也是5分米,这个圆柱体的表面积是多少平方分米?
3、把一根底面直径是4分米,高是10分米的圆柱形木材,沿着直径对半锯开,每块木材的表面积是多少?表面积增加了多少平方分米?
4、有铁皮30平方米,最多能做底面直径和高都是3分米的无盖水桶多少个?(得数保留整数)
5、公园的凉亭有6根圆柱形柱子,每根柱子底面半径是4分米,高是5分米,要油漆这些柱子,每平方米用油漆0.3千克,共需要油漆多少千克?下底面不漆,得数保留两位小数)
6、一个无盖的圆柱形铁皮水桶,底面直径是30厘米,高是45厘米。
做这样一对水桶,至少需用铁皮多少平方厘米?
7、一个圆柱,侧面展开后是一个边长9.42分米的正方形。
这个圆柱的底面直径是多少分米?
8、一个圆柱,它的高增加1厘米,它的侧面积就增加50.24平方厘米,这个圆柱的底面半径是多少厘米?
9、把一根直径是20厘米,长是2米的圆柱形木材锯成同样的3段,表面积增加了多少平方厘米?
10、一个无盖的圆柱形铁皮水桶, 高50厘米, 底面直径30厘米, 做这个水桶大约需用多少铁皮? (得数保留整数)
11、一个圆柱形蓄水池,底面周长25.12米,高4米,沿着这个蓄水池的四周及底部抹水泥。
如果平方米用水泥20千克,一共需多少千克水泥?
12、一节铁皮烟囱长1.5米,直径是0.2米,做这样的烟囱500节,至少要用铁皮多少平方米?
13、有一张长方形铁皮,剪下两个园及一个长方形,正好可以做成一个圆柱,这个圆柱的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?
14、一台压路机的滚筒是一个圆柱体,宽1.2米,直径是0.8米,如果它滚动10
周,压路的面积是多少?
15、下面是一张长方形纸板,按图示剪下阴影部分刚好能做成一个圆柱体,求
做好的圆柱体的表面积。
16、一个圆柱的侧面积是188.4平方分米,底面半径是3分米,它的高是多少分米?
17、下图是一个圆柱体从中间劈开后得到的图形,这个图形的表面积是多少?
(单位:厘米)
18、一根高为20分米的圆柱形木块截下5分米后,表面积减少了31.4平方分米,原来圆柱形木块的表面积是多少平方分米?
19、一个圆柱沿着底面直径纵向切成相等的两部分后,表面积比原来增加了80平方厘米,圆柱的侧面是多少平方厘米?
20、工人师傅要在一个零件的表面涂一层防锈材料。
这个零件是由两个圆柱构成的,小圆柱的直径是4厘米,高2厘米,大圆柱的直径是6厘米,高5厘米。
这个零件涂防锈材料的面积是多少平方厘米?
参考答案:
1、求圆柱的表面积
(1)、25.12(平方厘米)50.24(平方厘米)
(2)、125.6(平方分米)150.72(平方分米)
(3)、1.256(平方分米) 1.6485(平方分米)
2、应用题
1、3.14×10=314(平方厘米)(31.4÷3.14÷2)2×314=471(平方厘米)
2、117.75(平方分米)
3、每块木材表面积:【3.14×10+3.14×(4÷2)】÷2=115.36(平方分米)
表面积增加:4×10×2=80(平方分米)
4、84(个)
5、【3.14×42+3.14×(4×2)×5】×6÷100×0.3=3.17(千克)
6、【3.14×30×45+3.14×(30÷2)2】×2=9891平方厘米
7、3分米
8、50.24÷1÷3.14÷2=8(厘米)
9、3.14×(20÷2)2×4=1256(平方厘米)
10、5417(平方厘米)
11、【3.14×(25.12÷3.14÷2)2+25.12×4】×20=3014.4(千克)
12、3.14×0.2×1.5×500=471(平方米)
13、长:10×2×2+3.14×10×2=102.8(厘米)
宽:10×2=20(厘米)
面积:102.8×20=2056(平方厘米)
14、3.14×10.8×1.2×10=30.144(平方米)
15、解:设圆柱底面半径为x厘米。
4X+2X=41.12
X=4
3.14×42×2+(41.12—4×4)×8=301.44(平方厘米)
16、188.4÷(2×3.14×3)=10(分米)
17、【3.14×8×16+3.14×(8÷2)2】÷2+16×8=379.2(平方厘米)
18、底面半径:r=31.4÷5÷3.14÷2=1(分米)
表面积:S=3.14×12×2+3.14×1×2×20=131.88(平方分米)
19、80÷2×3.14=125.6(平方厘米)
20、3.14×(6÷2)2×2+3.14×6×5+3.14×4×2=175.84(平方厘米)。
