(完整版)2018年人教版七年级数学下《压轴题培优》期末复习专题含答案,推荐文档
(完整版)人教版七年级数学下册期末复习压轴题-解答题试卷及答案

(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案一、解答题1. 仔细阅读下列解题过程:若 , 求 的值.解:2222690a ab b b ++-+=222222690()(3)003033a ab b b b a b b a b b a b ∴+++-+=∴++-=∴+=-=∴=-=,, 根据以上解题过程, 试探究下列问题:(1)已知 , 求 的值;(2)已知 , 求 的值;(3)若 , 求 的值.2. 启秀中学初一年级组计划将 本书奖励给本次期中考试中取得优异成绩的 名同学, 如果每人分 本, 那么还剩下 本;如果每人分 本, 那么最后一人分得的书不足 本, 但不少于 本. 最终, 年级组讨论后决定, 给 名同学每人发 本书, 那么将剩余多少本书?3.在南通市中小学标准化建设工程中, 某校计划购进一批电脑和电子白板, 经过市场考察得知, 购买 台电脑和 台电子白板需要 万元, 购买 台电脑和 台电子白板需要 万元.(1)求每台电脑、每台电子白板各多少万元;(2)根据学校实际, 需购进电脑和电子白板共 台, 若总费用不超过 万元, 则至多购买电子白板多少台?4.已知关于 , 的二元一次方程组 它的解是正数.(1)求m 的取值范围;(2)化简: ;5. 已知 , , 求 的平方根.6. 定义: 若实数x, y 满足 , , 且x ≠y, 则称点M(x, y)为“好点”. 例如, 点(0, -2)和 (-2, 0)是“好点”. 已知: 在直角坐标系xOy 中, 点P(m, n).(1)P1(3, 1)和P2(-3, 1)两点中, 点________________是“好点”.(2)若点P(m, n)是“好点”, 求m+n 的值.(3)若点P 是“好点”, 用含t 的代数式表示mn, 并求t 的取值范围.7. 已知有理数 满足: , 且 , 求 的值.8. 如图, 在方格纸内将 水平向右平移4个单位得到 .(1)补全 , 利用网格点和直尺画图;(2)图中 与 的位置关系是: ;(3)画出ABC ∆中AB 边上的中线CE ;(4)平移过程中, 线段 扫过的面积是: .9. 如图所示, A(2, 0), 点 B 在 y 轴上, 将三角形 OAB 沿 x 轴负方向平移, 平移后的图形为三角形 DEC, 且点 C 的坐标为(-6, 4) .(1)直接写出点E 的坐标;(2)在四边形 ABCD 中, 点 P 从点 B 出发, 沿“BC→CD”移动. 若点 P 的速度为每秒 2 个单位长度, 运动时间为 t 秒, 回答下列问题:①求点 P 在运动过程中的坐标, (用含 t 的式子表示, 写出过程);②当 3 秒<t<5 秒时, 设∠CBP=x°, ∠PAD=y°, ∠BPA=z°, 试问 x, y, z 之间的数量关系能否确定?若能, 请用含 x, y 的式子表示 z, 写出过程;若不能, 说明理由.10. 问题1: 现有一张△ABC纸片, 点D.E分别是△ABC边上两点, 若沿直线DE折叠. (1)探究1: 如果折成图①的形状, 使A点落在CE上, 则∠1与∠A的数量关系是;(2)探究2: 如果折成图②的形状, 猜想∠1+∠2和∠A的数量关系是;(3)探究3:如果折成图③的形状, 猜想∠1、∠2和∠A的数量关系, 并说明理由.(4)问题2: 将问题1推广, 如图④, 将四边形ABCD纸片沿EF折叠, 使点A.B落在四边形EFCD的内部时, ∠1+∠2与∠A.∠B之间的数量关系是 .11.已知a +b=5, ab=-2.求下列代数式的值:(1) ;(2) .12.如图, 在方格纸内将 水平向右平移4个单位得到△ .(1)画出△; (2)画出边上的中线和高线;(利用网格点和直尺画图)(3) 的面积为 .13. 如果ac =b, 那么我们规定(a, b )=c. 例如;因为23=8, 所以(2, 8)=3.(1)根据上述规定填空: (3, 27)= , (4, 1)= , (2, 0.25)= ;(2)记(3, 5)=a, (3, 6)=b, (3, 30)=c. 判断a, b, c 之间的等量关系, 并说明理由.14. 先化简, 再求值:(x ﹣2y )(x +2y )﹣(x ﹣2y )2, 其中x =3, y =﹣1.15.已知: , .求下列代数式的的值.(1)xy ;(2)224x xy y ++;(3) . 16. 装饰公司为小明家设计电视背景墙时需要A.B 型板材若干块, A型板材规格是a(b, B 型板材规格是b(b.现只能购得规格是150(b 的标准板材.(单位: cm )(1)若设a(60cm, 裁法一 裁法二 裁法三b(30cm.一张标准板材尽可能多的裁出A型、B型板材,共有下表三种裁法, 下图是裁法一的裁剪示意图.A型板材块数120B型板材块数3m n则上表中, m=___________, n=__________;(2)为了装修的需要, 小明家又购买了若干C型板材, 其规格是a(a, 并做成如下图的背景墙.请写出下图中所表示的等式:__________;(3)若给定一个二次三项式2a2(5ab(3b2, 试用拼图的方式将其因式分解. (请仿照(2)在几何图形中标上有关数量)17.已知关于x、y的方程组与有相同的解, 求a、b的值.18. 计算:(1)(12)﹣3﹣20160﹣|﹣5|;(2)(3a2)2﹣a2•2a2+(﹣2a3)2+a2;(3)(x+5)2﹣(x﹣2)(x﹣3);(4)(2x+y ﹣2)(2x+y+2).19. 已知关于 、 的二元一次方程组 (k 为常数).(1)求这个二元一次方程组的解(用含k 的代数式表示);(2)若 , 求k 的值;(3)若 , 设 , 且m 为正整数, 求m 的值.20. 解下列方程组或不等式组(1)24231x y x y +=⎧⎨-=⎩ (2)()211113x x x x ⎧--≤⎪⎨+>-⎪⎩【参考答案】***试卷处理标记, 请不要删除一、解答题1. (1) ;(2) ;(3) .【分析】(1)首先把第3项 裂项, 拆成 , 再用完全平方公式因式分解, 利用非负数的性质求得 代入求得数值;(2)首先把第2项 裂项, 拆成 , 再用完全平方公式因式分解, 利用非负数的性质求得 代入求得数值;(3)先把 代入 , 得到关于 和 的式子, 再仿照(1)(2)题.【详解】解: (1)2222210x xy y y y ∴-++-+=22()(1)0x y y ∴-+-=010x y y ∴-=-=,,11x y ∴==,,23x y ∴+=;(2)2254210a b ab b +--+=22244210a b ab b b ∴+-+-+=22(2)(1)0a b b ∴-+-=2010a b b ∴-=-=,21a b ∴==,;(3)4m n =+,2(4)8200n n t t ∴++-+=22448160n n t t ∴+++-+=22(2)(4)0n t ∴++-=2040n t ∴+=-=,24n t ∴=-=,42m n ∴=+=20(2)1m t n -∴=-=【点睛】本题考查的分组分解法、配方法和非负数的性质, 对于项数较多的多项式因式分解, 分组分解法是一个常用的方法.首先要观察各项特征, 寻找熟悉的式子, 熟练掌握平方差公式和完全平方公式是基础.2.38本【分析】先表示书的总量, 利用不等关系列不等式组, 求不等式组的正整数解即可得到答案.【详解】解: 由题意得:由①得:由②得:不等式组的解集是:为正整数,20,n ∴=478158,m n ∴=+=15820638.∴-⨯=答: 剩下 本书.【点睛】本题考查的是不等式组的应用, 掌握利用不等关系列不等式组是解题的关键.3.(1)电脑 万元, 电子白板 万元;(2) 台【分析】(1)设每台电脑 元, 每台电子白板 元, 根据题意列出方程组, 解方程组即可;(2)设购进电子白板 台, 则购进电脑 台, 根据总费用不超过 万元, 列出不等式, 根据 实际意义即可求解.【详解】(1)设每台电脑 元, 每台电子白板 元, 则 , 解得故每台电脑 万元, 每台电子白板 万元;(2)设购进电子白板 台, 则购进电脑 台, 由题意得1.50.5(31)30m m +-≤解得 , 又因为 是正整数, 则 , 故至多购买电子白板 台.【点睛】本题考查了二元一次方程组应用, 一元一次不等式应用, 综合性较强, 难度不大, 根据题意列出二元一次方程组、一元一次不等式是解题关键.4. (1)(2)m -【分析】(1)先解方程组, 用含m 的式子表示出x 、y, 再根据方程组的解时一对正数列出关于m 的不等式组, 解之可得;(2)根据m 的取值范围判断出m-2<0、m+1>0,m-1<0, 再根据绝对值性质去绝对值符号、合并同类项即可得.【详解】解: (1)解方程组 ,得321x m y m =+⎧⎨=-⎩因为解为正数, 则 , 解得 ;(2)原式2(1)(1)m m m m =--+--=-.【点睛】本题考查了二元一次方程组及解法、一元一次不等式组及解法. 解题的关键是根据题意列出关于m 的不等式组及绝对值的性质.5.【分析】根据题意得到三元一次方程组, 解方程组, 求出 , 最后求平方根即可.【详解】∵ , ,∴ , ,∴2113024010y x x y z -+-=⎧⎪-+=⎨⎪-=⎩,解得231x y z =⎧⎪=⎨⎪=⎩,则6x y z ++=,∴ 平方根为 .【点睛】本题考查相反数的意义, 非负数的表达, 解三元一次方程组, 求平方根等知识, 综合性较强, 解题关键是根据题意列出三元一次方程组.6. (1) ;(2) ;(3)【分析】(1)将P1(3, 1)和P2(-3, 1)分别代入等式即可得出结果;(2)将点P(m, n)代入等式即可得出m+n 的值;(3)根据“好点”的定义, 将P 点代入即可得到关于m 和n 的等式, 将两个等式结合即可得出结果.【详解】解: (1)对于 , ,对于 , , , 所以 是“好点”(2)∵点 是好点,∴222,2m n t n m t =+=+, 222()m n n m -=-,∴2m n +=-(3)∵ ,2222m n n t m t -=+--①,2222m n m t n t +=+++②,得()()2()0m n m n m n -++-=,即()(2)0m n m n -++=,由题知, ,由②得 ,∴4242,4mn t mn t -=-+=-,∵ , ∴ ,∴2()40m n mn +->,∴44(4)0t -->,所以3t >,【点睛】本题主要考查的是新定义“好点”, 正确的掌握整式的乘法解题的关键.7. 【分析】利用 将 整理求出 的值, 然后将 利用完全平方公式变形, 将各自的值代入计算即可求出值.【详解】∵221x y , ∴化简得: ,∵1x y -=,∴ 可化为: ,即有: ,∴2222313516x xy y x y xy .【点睛】此题考查了整式的混合运算 化简求值, 熟练掌握运算法则是解本题的关键.8. (1)图见详解;(2)平行且相等;(3)图见详解;(4)28.【分析】(1)根据图形平移的性质画出△A B C '''即可;(2)根据平移的性质可得出AC 与A C ''的关系;(3)先取 的中点 , 再连接 即可;(4)线段 扫过的面积为平行四边形 的面积, 根据平行四边形的底为4, 高为7, 可得线段 扫过的面积.【详解】解: (1)如图所示, △ 即为所求;(2)由平移的性质可得, 与 的关系是平行且相等;故答案为: 平行且相等;(3)如图所示, 线段 即为所求;(4)如图所示, 连接 , , 则线段 扫过的面积为平行四边形 的面积,由图可得, 线段 扫过的面积 .故答案为:28.【点睛】本题主要考查了利用平移变换进行作图, 作图时要先找到图形的关键点, 分别把这几个关键点按照平移的方向和距离确定对应点后, 再顺次连接对应点即可得到平移后的图形.9.(1) (2)1)点P 在线段BC 上时, , 2)点P 在线段CD 上时, ;(3)能确定, , 证明见解析【分析】(1)根据平移的性质即可得到结论;(2)①分两种情况: 1)点P 在线段BC 上时, 2)点P 在线段CD 上时;②如图, 作P 作 交于AB 于E, 则 , 根据平行线的性质即可得到结论.【详解】(1)∵点B 的横坐标为0, 点C 的横坐标为-6,∴将A(2, 0)向左平移6个单位长度得到点E∴()4,0E -;(2)①∵6,4BC CD ==∴1)点P 在线段BC 上时,(),4P t -;2)点P 在线段CD 上时,()6,10P t --;②能确定如图, 作P 作 交于AB 于E, 则∴1,2CBP x DAP y ==︒==︒∠∠∠∠ ∴1+2BPA x y z ==︒+︒=︒∠∠∠ ∴z x y =+.【点睛】本题考查了平行线的问题, 掌握平移的性质、代数式的用法、平行线的性质以及判定定理是解题的关键.10. (1) ;(2) ;(3)见解析;(4)【分析】(1)根据三角形外角性质可得;(2)在四边形 中, 内角和为360°, ∠BDA=∠CEA=180°, 利用这两个条件, 进行角度转化可得关系式;(3)如下图, 根据(1)可得∠1=2∠ , ∠2=2∠ , 从而推导出关系式;(4)根据平角的定义以及四边形的内角和定理, 与(2)类似思路探讨, 可得关系式.【详解】(1)∵△'EDA 是△EDA 折叠得到∴∠A=∠A '∵∠1是△'ADA 的外角∴∠1=∠A+∠A '∴12A ∠=∠;(2)∵在四边形 中, 内角和为360°∴∠A+A '+∠A DA '+∠A EA '=360°同理, ∠A=∠∴2∠A+∠A DA '+∠A EA '=360°∵∠BDA=∠CEA=180∴∠1+∠A DA '+∠A EA '+∠2=360°∴122A ∠+∠=∠ ;(3)数量关系:理由:如下图, 连接由(1)可知: ∠1=2∠ , ∠2=2∠∴212()2EAA DAA DAE ∠-∠=∠-=∠'∠';(4)由折叠性质知: ∠2=180°-2∠AEF, ∠1=180°-2∠BFE相加得: .【点睛】本题考查角度之间的关系, (4)问的解题思路是相同的, 主要运用三角形的内角和定理和四边形的内角和定理进行角度转换.11. (1)29;(2)64.【分析】(1)根据完全平方公式得到 , 然后整体代入计算即可;(2)根据完全平方公式得到 , 然后整体代入计算即可.【详解】解: (1) ;(2) .【点睛】本题考查了代数式求值, 完全平方公式和整体代入的思想, 熟练掌握完全平方公式是解题的关键.12. (1)见解析; (2) 见解析;(3) 4.【解析】【分析】(1)根据图形平移的性质画出△A′B′C′即可;(2)先取AB 的中点D, 再连接CD 即可;过点C 作CD ⊥AB 交AB 的延长线于点E, CE 即为所求;(3)利用割补法计算△ABC 的面积.【详解】(1)如图所示:(2)如图所示;(3)S△BCD=20-5-1-10=4.13. (1)3, 0, ﹣2;(2)a+b=c, 理由见解析.【分析】(1)直接根据新定义求解即可;(2)先根据新定义得出关于a, b, c的等式, 然后根据幂的运算法则求解即可.【详解】(1)∵33=27,∴(3, 27)=3,∵40=1,∴(4, 1)=0,∵2﹣2=,∴(2, 0. 25)=﹣2.故答案为: 3, 0, ﹣2;(2)a+b=c.理由: ∵(3, 5)=a, (3, 6)=b, (3, 30)=c,∴3a=5, 3b=6, 3c=30,∴3a×3b=5×6=3c=30,∴3a×3b=3c,∴a+b=c.【点睛】本题考查了新定义运算, 明确新定义的运算方法是解答本题的关键, 本题也考查了有理数的乘方、同底数幂的乘法运算.14.4xy﹣8y2, ﹣20【分析】先根据整式的乘法法则和乘法公式算乘法, 再合并同类项, 最后代入求出即可.【详解】(x﹣2y)(x+2y)﹣(x﹣2y)2=x2﹣4y2﹣(x2﹣4xy+4y2)=x2﹣4y2﹣x2+4xy﹣4y2=4xy﹣8y2,当x=3, y=﹣1时,原式=4×3×(﹣1)﹣8×(﹣1)2=﹣20.【点睛】本题考查整式的化简求值, 涉及平方差公式、完全平方公式、合并同类项等知识, 熟练掌握整式的乘法运算法则和乘法公式的运用是解答的关键.15. (1)3;(2)31;(3)25.【分析】(1)把多项式乘积展开, 再将已知 代入, 即可求解;(2)根据(1)得到 , 再利用完全平方公式, 即可求解;(3)根据 将 用 来表示, 再代入 , 合并同类项即可求解.【详解】解: (1)∵ , 而 ,∴ ()=324=3254=3xy x y -++--+⨯-.故答案为 .(2)由(1)知 ,∴ ()22224=2=523=31x xy y x y xy +++++⨯. 故答案为 .(3)∵ , 得 ,则()()22225=55525105525x xy y y y y y y y y y y ++-+-+=-++-+=. 故答案为 .【点睛】本题目考查整式的乘法, 难度一般, 是常考知识点, 熟练掌握代数式之间的转化是顺利解题的关键.16.(1)m(1, n(5;(2)(a(2b )2(a2(4ab(4b2;(3)2a2(5ab(3b2((a(b)(2a(3b), 详见解析【分析】(1)结合图形和条件分析可以得出按裁法二裁剪时, 可以裁出B 型板1块, 按裁法三裁剪时, 可以裁出5块B 型板;(2)看图即可得出所求的式子;(3)通过画图能更好的理解题意, 从而得出结果. 由于构成的是长方形, 它的面积等于所给图片的面积之和, 从而因式分解.【详解】(1)按裁法二裁剪时, 2块A 型板材块的长为120cm, 150-120=30, 所以可裁出B 型板1块, 按裁法三裁剪时, 全部裁出B 型板, 150÷30=5, 所以可裁出5块B 型板; ∴m=1, n=5.故答案为:1, 5;(2)如下图:发现的等式为: (a(2b )2(a2(4ab(4b2;故答案为: (a(2b )2(a2(4ab(4b2.(3)按题意画图如下:∵构成的长方形面积等于所给图片的面积之和,∴2a 2+5ab +3b 2=(a +b )(2a +3b ).【点睛】本题考查了完全平方公式和几何图形的应用及一元一次方程的应用, 关键是根据学生的画图能力, 计算能力来解答.17.149299a b ⎧=⎪⎪⎨⎪=⎪⎩【分析】因为两个方程组有相同的解, 故只需把两个方程组中不含未知数和含未知数的方程分别组成方程组, 求出未知数的值, 再代入另一组方程组即可.【详解】354526x y ax by -=⎧⎨+=-⎩①③ 和2348x y ax by +=-⎧⎨-=⎩②④ 解: 联立①②得:解得:12x y =⎧⎨=-⎩将 代入③④得: 解得:149299a b ⎧=⎪⎪⎨⎪=⎪⎩【点睛】此题考查了二元一次方程组的解, 方程组的解即为能使方程组中两方程都成立的未知数的值.18. (1)2;(2)7a4+4a6+a2;(3)15x+19;(4)4x2+4xy+y2﹣4【分析】(1)首先利用负整数指数幂的性质、零次幂的性质、绝对值的性质进行计算, 再算加减即可;(2)首先利用积的乘方的计算法则、单项式乘以单项式计算法则计算, 再合并同类项即可;(3)首先利用完全平方公式、多项式乘以多项式计算法则计算, 再合并同类项即可;(4)首先利用平方差计算, 再利用完全平方公式进行计算即可.【详解】解: (1)原式=8﹣1﹣5=2;(2)原式=9a4﹣2a4+4a6+a2,=7a4+4a6+a2;(3)原式=x2+10x+25﹣(x2﹣3x﹣2x+6),=x2+10x+25﹣x2+3x+2x﹣6,=15x+19;(4)原式=(2x+y)2﹣4,=4x2+4xy+y2﹣4.【点睛】本题考查的是实数的运算, 幂的运算及合并同类项, 整式的混合运算, 掌握以上知识点是解题的关键.19. (1);(2)或;(3)1或2.【分析】(1)根据题意直接利用加减消元法进行计算求解即可;(2)由题意根据和以及(n为整数)得到三个关于k的方程, 求出k即可;(3)根据题意用含m的代数式表示出k, 根据, 确定m的取值范围, 由m为正整数, 求得m的值即可.【详解】解: (1),①+②得: , 解得: ,①-②得:, 解得:,∴二元一次方程组的解为: .(2)∵, ,∴, 即, 解得: ;∵, ,∴, 即, 解得: ;∵(n为正整数), ,∴为偶数, 即, 解得: ;当时, , 为奇数, 不合题意, 故舍去.综上52k=或12k=-.(3)∵, 即,∴2114mk-=,∵14k≤,∴, 解得,∵m为正整数,∴m=1或2.【点睛】本题考查解二元一次方程组以及解一元一次不等式, 根据题意列出不等式是解题的关键.20. (1)(2)【分析】(1)运用加减消元法先消除x, 求y的值后代入方程②求x得解;(2)先分别解每个不等式, 然后求公共部分, 确定不等式组的解集.【详解】解: (1)①×2-②, 得 7y=7,∴y=1.把y=1代入②, 得 x=2.∴21 xy=⎧⎨=⎩.(2)解不等式得.解不等式得.∴不等式组的解集为.【点睛】此题考查解方程组和不等式组, 属常规基础题, 难度不大.。
(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案doc

(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案doc一、解答题1.从边长为a 的正方形中剪掉一个边长为b 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是 .(请选择正确的选项) A .a 2﹣b 2=(a +b )(a ﹣b )B .a 2﹣2ab +b 2=(a ﹣b )2C .a 2+ab =a (a +b )(2)若x 2﹣y 2=16,x +y =8,求x ﹣y 的值;(3)计算:(1﹣212)(1﹣213)(1﹣214)…(1﹣212019)(1﹣212020). 2.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1,可以得到222()2a b a ab b +=++这个等式,请解答下列问题:(1)写出图2中所表示的数学等式 .(2)根据整式乘法的运算法则,通过计算验证上述等式.(3)利用(1)中得到的结论,解决下面的问题:若10a b c ++=,35ab ac bc ++=,则222a b c ++= .(4)小明同学用图3中x 张边长为a 的正方形,y 张边长为b 的正方形,z 张长宽分别为a 、b 的长方形纸片拼出一个面积为2)(4)a b a b ++(的长方形,则x y z ++= . 3.已知有理数,x y 满足:1x y -=,且221xy ,求22x xy y ++的值. 4.先化简,再求值(x-2)2+2(x+2)(x-4)-(x-3)(x+3);其中x=1.5.因式分解:(1)3a x y y x ; (2)()222416x x +-.6.因式分解:(1)()()36x m n y n m ---;(2)()222936x x +-7.已知△ABC中,∠A =60°,∠ACB =40°,D 为BC 边延长线上一点,BM 平分∠ABC ,E 为射线BM 上一点.(1)如图1,连接CE ,①若CE ∥AB ,求∠BEC 的度数;②若CE 平分∠ACD ,求∠BEC 的度数.(2)若直线CE 垂直于△ABC 的一边,请直接写出∠BEC 的度数.8.先化简,再求值:(2a +b )2﹣(2a +3b )(2a ﹣3b ),其中a =12,b =﹣2. 9.利用多项式乘法法则计算:(1)()()22+-+a b a ab b = ;()()22a b a ab b -++ = .在多项式的乘法公式中,除了平方差公式,完全平方公式之外,如果把上面计算结果作为结论逆运用,则成为因式分解中的立方和与立方差公式.已知2,1a b ab -==,利用自己所学的数学知识,以及立方和与立方差公式,解决下列问题:(2)22a b += ;(直接写出答案)(3)33a b -= ;(直接写出答案)(4)66a b += ;(写出解题过程)10.如图,已知AB ∥CD ,∠1=∠2,求证:AE ∥DF .11.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC 的三个顶点的位置如图所示.现将△ABC 平移,使点C 变换为点D ,点A 、B 的对应点分别是点E 、F . (1)在图中请画出△ABC 平移后得到的△EFD ;(2)在图中画出△ABC 的AB 边上的高CH ;(3)△ABC 的面积为_______.12.如图,D 、E 、F 分别在ΔABC 的三条边上,DE//AB ,∠1+∠2=180º.(1)试说明:DF//AC ;(2)若∠1=120º,DF 平分∠BDE ,则∠C=______º.13.分解因式(1)321025a a a ++;(2)(1)(2)6t t ++- .14.计算:(1)()()122012514--⎛⎫+-⨯-- ⎪⎝⎭; (2)52342322)(a a a a a +÷-. 15.对于多项式x 3﹣5x 2+x +10,我们把x =2代入此多项式,发现x =2能使多项式x 3﹣5x 2+x +10的值为0,由此可以断定多项式x 3﹣5x 2+x +10中有因式(x ﹣2),(注:把x =a 代入多项式,能使多项式的值为0,则多项式一定含有因式(x ﹣a )),于是我们可以把多项式写成:x 3﹣5x 2+x +10=(x ﹣2)(x 2+mx +n ),分别求出m 、n 后再代入x 3﹣5x 2+x +10=(x ﹣2)(x 2+mx +n ),就可以把多项式x 3﹣5x 2+x +10因式分解.(1)求式子中m 、n 的值;(2)以上这种因式分解的方法叫“试根法”,用“试根法”分解多项式x 3+5x 2+8x +4.16.把几个图形拼成一个新的图形,再通过两种不同的方式计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2.(1)由图2,可得等式;(2)利用(1)所得等式,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.(3)如图3,将两个边长为a、b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF,若这两个正方形的边长a、b如图标注,且满足a+b=10,ab=20.请求出阴影部分的面积.(4)图4中给出了边长分别为a、b的小正方形纸片和两边长分别为a、b的长方形纸片,现有足量的这三种纸片.①请在下面的方框中用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形,并仿照图1、图2画出拼法并标注a、b;②研究①拼图发现,可以分解因式2a2+5ab+2b2=.17.解方程组(1)24 31 y xx y=-⎧⎨+=⎩(2)121632(1)13(2)x yx y--⎧-=⎪⎨⎪-=-+⎩.18.如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,若∠A=65°,∠B=45°,求∠AGD的度数.19.(1)如图,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有x、y的等式表示) ;(2)若2(32)5x y -=,2(32)9x y +=,求xy 的值;(3)若25,2x y xy +==,求2x y -的值.20.计算:(1)1021(3)(4)5π-⎛⎫---- ⎪⎝⎭(2)3()6m m n mn -+(3)4(2)(2)x x -+-(4)2(2)(2)a b a a b ---【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)A ;(2)2;(3)20214040 【分析】(1)由题意直接根据拼接前后的面积相等进行分析计算即可得出答案;(2)根据题意可知x 2﹣y 2=16,即(x +y )(x ﹣y )=16,又x +y =8,可求出x ﹣y 的值;(3)根据题意利用平方差公式将算式转化为分数的乘积的形式,根据数据规律得出答案.【详解】解:(1)图1的剩余面积为a 2﹣b 2,图2拼接得到的图形面积为(a +b )(a ﹣b ) 因此有,a 2﹣b 2=(a +b )(a ﹣b ),故答案为:A.(2)∵x 2﹣y 2=(x +y )(x ﹣y )=16,又∵x +y =8,∴x ﹣y =16÷8=2;(3)(1﹣212)(1﹣213)(1﹣214)…(1﹣212019)(1﹣212020)=(1﹣12)(1+12)(1﹣13)(1+13)(1﹣14)(1+14)……(1﹣12019)(1+12019)(1﹣12020)(1+12020) =12×32×23×43×34×54×……×20182019×20202019×20192020×20212020 =12×20212020 =20214040. 【点睛】本题考查平方差公式的几何意义及应用,掌握公式的结构特征是正确应用的前提,利用公式进行适当的变形是解题的关键.2.(1) ()2222222.a b c a b c ab ac bc ++=+++++(2)证明见解析;(3) 30; (4) 15.【分析】(1)依据正方形的面积=()2a b c ++ ;正方形的面积=222a +b +c +2ab+2ac+2bc.,可得等式;(2)运用多项式乘多项式进行计算即可;(3)依据()2222a b +c a b c -2ab-2ac-2bc,+=++ 进行计算即可;(4)依据所拼图形的面积为:22xa yb zab ++ , 而()()222224284249a b a b a ab ab b a b ab ++=+++=++ ,即可得到x, y, z 的值,即可求解.【详解】解: (1) 正方形的面积=()2a b c ++ ;大正方形的面积=222a +b +c +2ab+2ac+2bc. 故答案为:()2222222.a b c a b c ab ac bc ++=+++++(2)证明: (a+b+c) (a+b+c) ,=222a ab ac ab b bc ac bc c ++++++++ ,=222222a b c ab ac bc +++++ .(3)()2222222,a b c a b c ab ac bc ++=++---=()2102ab ac bc -++ , =100235-⨯ ,=30.故答案为: 30;(4)由题可知,所拼图形的面积为:22xa yb zab ++ ,(2a+b) (a+4b)=222a 8ab ab 4b ,+++=222a 4b 9ab,++∴x=2,y=4, z=9.∴x+y+z=2+4+9=15.故答案为: 15.【点睛】本题考查了完全平方公式的几何背景,根据矩形的面积公式分整体与部分两种思路表示出面积,然后再根据同一个图形的面积相等即可解答.3.【分析】利用1x y -=将221x y 整理求出xy 的值,然后将22x xy y ++利用完全平方公式变形,将各自的值代入计算即可求出值.【详解】∵221x y , ∴化简得:241xy x y , ∵1x y -=,∴241xy x y 可化为:241xy ,即有:5xy =,∴2222313516x xy y x y xy .【点睛】此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.4.2x 2-8x-3;-9.【解析】【分析】根据整式的乘法运算法则即可化简求值.【详解】解:原式=x 2-4x+4+2(x 2-2x-8)-(x 2-9)=x 2-4x+4+2x 2-4x-16-x 2+9=2x 2-8x-3当x=1时,原式=2-8-3=-9【点睛】此题主要考查整式的化简求值,解题的关键是熟知整式的运算法则.5.(1)3xy a ;(2)()()2222x x -+.【分析】(1)原式先提取负号,再按提取公因式分解即可;(2)原式利用平方差公式分解因式,再利用完全平方分解因式即可;【详解】(1)3a xy y x 3a x y x y3x y a ;(2)()222416x x +-()()224444x x x x =+-++2222x x .【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.6.(1)3()(2)m n x y -+;(2)22(3)(3)x x +-.【分析】(1)原式变形后,提取公因式即可;(2)原式先利用平方差公式进行因式分解,再利用完全平方公式分解即可.【详解】(1)原式3()6()x m n y m n =-+-3()3()2m n x m n y =-⋅+-⋅3()(2)m n x y =-+(2)原式()2229(6)x x =+-()()229696x x x x =+++-22(3)(3)x x =+-【点睛】此题考查了提公因式与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.7.(1)①40°;②30°;(2)50°,130°,10°【解析】试题分析:(1)①根据三角形的内角和得到∠ABC =80°,由角平分线的定义得到∠ABE =12∠ABC =40°,根据平行线的性质即可得到结论;②根据邻补角的定义得到∠ACD =180°-∠ACB =140°,根据角平分线的定义得到∠CBE=12∠ABC =40°,∠ECD =12∠ACD=70°,根据三角形的外角的性质即可得到结论;(2)①如图1,当CE ⊥BC 时,②如图2,当CE ⊥AB 于F 时,③如图3,当CE ⊥AC 时,根据垂直的定义和三角形的内角和即可得到结论.试题解析:(1)①∵∠A =60°,∠ACB =40°,∴∠ABC =80°,∵BM 平分∠ABC ,∴∠ABE =12∠ABC =40°, ∵CE ∥AB ,∴∠BEC=∠ABE=40°;②∵∠A=60°,∠ACB=40°,∴∠ABC=80°,∠ACD=180°-∠ACB=140°,∵BM平分∠ABC,CE平分∠ACD,∴∠CBE=12∠ABC=40°,∠ECD=12∠ACD=70°,∴∠BEC=∠ECD-∠CBE=30°;(2)①如图1,当CE⊥BC时,∵∠CBE=40°,∴∠BEC=50°;②如图2,当CE⊥AB于F时,∵∠ABE=40°,∴∠BEC=90°+40°=130°,③如图3,当CE⊥AC时,∵∠CBE=40°,∠ACB=40°,∴∠BEC=180°-40°-40°-90°=10°.【点睛】本题考查了平行线的性质,角平分线的定义,垂直的定义,三角形的内角和,三角形的外角的性质,正确的画出图形是解题的关键.8.4ab+10b2;36.【解析】【分析】先利用完全平方公式和平方差公式计算,再去括号、合并同类项即可化简原式,继而将a,b的值代入计算可得.【详解】原式=4a2+4ab+b2﹣(4a2﹣9b2)=4a2+4ab+b2﹣4a2+9b2=4ab+10b2当a12=,b=﹣2时,原式=412⨯⨯(﹣2)+10×(﹣2)2=﹣4+10×4=﹣4+40=36.【点睛】本题考查了整式的混合运算﹣化简求值,涉及的知识有:完全平方公式,平方差公式,去括号法则,以及合并同类项法则,熟练掌握运算法则是解答本题的关键.9.(1)33+a b ,33a b -;(2)6;(3)14;(4)198【分析】(1)根据整式的混合运算法则展开计算即可;(2)利用完全平方公式变形,再代入求值;(3)利用立方差公式和完全平方公式变形,再代入求值;(4)利用立方差公式和完全平方公式变形,再代入求值;【详解】解:(1)()()22+-+a b a ab b=322223a a b ab a b ab b -++-+=33+a b()()22a b a ab b -++=322223a a b ab a b ab b ++---=33a b -,故答案为:33+a b ,33a b -;(2)22a b +=()22a b ab -+=2221+⨯=6;(3)33a b -=()()22a b a ab b -++=()()23a b a b ab ⎡⎤--+⎣⎦ =()22231⨯+⨯=14;(4)66a b +=()()224224a b a a b b +-+=()()22222223a b ab a b a b ⎡⎤⎡⎤-++-⎢⎥⎣⎦⎣⎦=()()2222163+⨯-=198【点睛】本题考查了因式分解-运用公式法,正确的理解已知条件中的公式是解题的关键.10.见解析.【分析】首先根据直线平行得到∠CDA=∠DAB ,结合题干条件得到∠FDA=∠DAE ,进而得到结论.【详解】证明:∵AB∥CD,∴∠CDA=∠DAB,∵∠1=∠2,∴∠CDA﹣∠1=∠DAB﹣∠2,∴∠FDA=∠DAE,∴AE∥DF.【点睛】本题主要考查了平行线的判断与性质,解题的关键是掌握两直线平行,内错角相等,此题比较简单.11.(1)见详解;(2)见详解;(3)152.【分析】(1)按要求作图即可;(2)按要求作图即可;(3)根据勾股定理求出AB和CH的长即可得出面积.【详解】(1)△EFD如图所示,;(2)CH如图所示,;(3)根据勾股定理可得:223+635221+25∴S△ABC=12×AB×CH=12×355152.【点睛】本题考查了平移作图,勾股定理,掌握知识点是解题关键.12.(1)见解析;(2)60.【分析】(1)根据平行线的性质得出∠A=∠2,求出∠1+∠A=180°,根据平行线的判定得出即可.(2)根据平行线的性质解答即可.【详解】证明:(1)∵DE ∥AB ,∴∠A=∠2,∵∠1+∠2=180°.∴∠1+∠A=180°,∴DF ∥AC ;(2)∵DE ∥AB ,∠1=120°,∴∠FDE=60°,∵DF 平分∠BDE ,∴∠FDB=60°,∵DF ∥AC ,∴∠C=∠FDB=60°【点睛】本题考查了平行线的性质和判定定理,解题的关键是能灵活运用平行线的判定和性质定理进行推理.13.(1)()25a a +;(2)()()41t t +-. 【分析】(1)首先利用提公因式法,提出a ,再利用公式法,即可分解因式;(2)首先将两个多项式的乘积展开,合并同类项后,再利用十字相乘法即可分解因式.【详解】解:(1)()()23221025=10255a a a a a a a a ++++=+; (2)()()22(1)(2)6=3263441t t t t t t t t ++-++-=+-=+-. 【点睛】本题考查因式分解,难度不大,是中考的常考点,熟练掌握分解因式的方法是顺利解题的关键.14.(1)7;(2)55a .【分析】(1)直接利用负整数指数幂的性质、零指数幂的性质分别化简得出答案;(2)直接利用积的乘方运算法则、整式的除法运算法则计算得出答案.【详解】解:(1)(14)﹣1+(﹣2)2×50﹣(﹣1)﹣2;=4+4×1﹣1=4+4﹣1=7;(2)2a 5﹣a 2•a 3+(2a 4)2÷a 3=2a 5﹣a 5+4a 8÷a 3=2a 5﹣a 5+4a 5=5a 5.【点睛】此题主要考查了整式乘除和乘法运算,以及有理数乘方的运算,熟练掌握运算法则是解本题的关键.15.(1)m =﹣3,n =﹣5;(2)x 3+5x 2+8x +4=(x +1)(x +2)2.【解析】【分析】(1)根据x 3﹣5x 2+x+10=(x ﹣2)(x 2+mx+n ),得出有关m ,n 的方程组求出即可; (2)由把x =﹣1代入x 3+5x 2+8x+4,得其值为0,则多项式可分解为(x+1)(x 2+ax+b )的形式,进而将多项式分解得出答案.【详解】(1)在等式x 3﹣5x 2+x+10=(x ﹣2)(x 2+mx+n ),中,分别令x =0,x =1,即可求出:m =﹣3,n =﹣5(2)把x =﹣1代入x 3+5x 2+8x+4,得其值为0,则多项式可分解为(x+1)(x 2+ax+b )的形式,用上述方法可求得:a =4,b =4,所以x 3+5x 2+8x+4=(x+1)(x 2+4x+4),=(x+1)(x+2)2.【点睛】本题主要考查了因式分解的应用,根据已知获取正确的信息,是近几年中考中热点题型同学们应熟练掌握获取正确信息的方法.16.(1)2222()222a b c a b c ab bc ac ++=+++++;(2)45;(3)20;(4)①见解析,②(2)(2)a b a b ++.【分析】(1)根据面积的不同求解方法,可得到不同的表示方法.一种可以是3个正方形的面积和6个矩形的面积;另一种是直接利用正方形的面积公式计算,由此即可得出答案; (2)利用(1)中的等式直接代入即可求得答案;(3)根据阴影部分的面积等于两个正方形的面积之和减去两个直角三角形的面积即可得; (4)①依照前面的拼图方法,画出图形即可;②参照题(1)的方法,根据面积的不同求解方法即可得出答案.【详解】(1)由题意得:2222()222a b c a b c ab bc ac ++=+++++故答案为:2222()222a b c a b c ab bc ac ++=+++++;(2)11,38a b c ab bc ac ++=++=∴2222()(222)a b c a b c ab bc ac ++++=-++2)2(()a b c ab ac bc -+=+++211238=-⨯45=;(3)四边形ABCD 、四边形ECGF 为正方形,且边长分别为a 、b90A G ∴∠=∠=︒,AB AD BC a ===,FG CG b ==,BG BC CG a b =+=+ ∵10,20a b ab +==∴ABCD ECGF ABD BFG S S S S S =+--阴影221122AB CG AB AD FG BG =+-⋅-⋅ 2211()22a b a a b a b =+-⋅-⋅+ 22111222a b ab =+- 213()22a b ab =+- 213102022=⨯-⨯ 20=;(4)①根据题意,作出图形如下:②根据面积的不同求解方法得:22(2522)(2)a ab b a b a b ++=++故答案为:(2)(2)a b a b ++.【点睛】本题考查了因式分解的几何应用、完全平方公式的几何应用,掌握因式分解的相关知识是解题关键. 17.(1)12x y =⎧⎨=-⎩;(2)53x y =⎧⎨=⎩【分析】(1)方程组利用代入消元法求出解即可;(2)方程组整理后,利用加减消元法求出解即可.【详解】解:(1)2431y xx y=-⎧⎨+=⎩①②,把①代入②得:3x+2x﹣4=1,解得:x=1,把x=1代入①得:y=﹣2,则方程组的解为12 xy=⎧⎨=-⎩;(2)121632(1)13(2) x yx y--⎧-=⎪⎨⎪-=-+⎩方程组整理得:211 213x yx y+=⎧⎨+=⎩①②,①×2﹣②得:3y=9,解得:y=3,把y=3代入②得:x=5,则方程组的解为53 xy=⎧⎨=⎩.【点睛】本题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法,要根据方程特点选择合适的方法简化运算.18.70°【分析】由CD⊥AB,EF⊥AB可得出∠CDF=∠EFB=90°,利用“同位角相等,两直线平行”可得出CD∥EF,利用“两直线平行,同位角相等”可得出∠DCB=∠1,结合∠1=∠2可得出∠DCB=∠2,利用“内错角相等,两直线平行”可得出DG∥BC,利用“两直线平行,同位角相等”可得出∠ADG的度数,在△ADG中,利用三角形内角和定理即可求出∠AGD的度数.【详解】解:∵CD⊥AB,EF⊥AB,∴∠CDF=∠EFB=90°,∴CD∥EF,∴∠DCB=∠1.∵∠1=∠2,∴∠DCB=∠2,∴DG∥BC,∴∠ADG=∠B=45°.又∵在△ADG 中,∠A =65°,∠ADG =45°,∴∠AGD =180°﹣∠A ﹣∠ADG =70°【点睛】本题考查了平行线的判定与性质以及三角形内角和定理,利用平行线的性质求出∠ADG 的度数是解题的关键.19.(1)224()()xy x y x y =+--;(2)16xy =;(3)23x y -=±. 【分析】(1)阴影部分的面积可以由边长为x+y 的大正方形的面积减去边长为x-y 的小正方形面积求出,也可以由4个长为x ,宽为y 的矩形面积之和求出,表示出即可;(2)先利用完全平方公式展开,然后两个式子相减,即可求出答案;(3)利用完全平方变形求值,即可得到答案.【详解】解:(1)图中阴影部分的面积为: 224()()xy x y x y =+--;故答案为:224()()xy x y x y =+--;(2)∵2(32)5x y -=, ∴2291245x xy y -+=①,∵2(32)9x y +=,∴2291249x xy y ++=②,∴由②-①,得 24954xy =-=, ∴16xy =; (3)∵25,2x y xy +==, ∴222(2)4425x y x xy y +=++=,∴224254217x y +=-⨯=,∴222(2)4417429x y x y xy -=+-=-⨯=;∴23x y -=±;【点睛】本题考查了完全平方公式的几何背景,准确识图,以及完全平方公式变形求值,根据阴影部分的面积的两种不同表示方法得到的代数式的值相等列式是解题的关键.20.(1)12;(2)233m mn +;(3)28x -;(4)224ab b -+.【分析】(1)直接利用零指数幂的性质以及负指数幂的性质分别化简得出答案;(2)先做单项式乘多项式,再合并同类项即可得出答案;(3)先利用平方差公式计算,再合并同类项即可得出答案;(4)先利用完全平方公式以及单项式乘多项式计算,再合并同类项即可得出答案.【详解】解:(1)1021(3)(4)5π-⎛⎫---- ⎪⎝⎭5116=--12=-;(2)3()6m m n mn -+2336m mn mn =-+233m mn =+;(3)4(2)(2)x x -+-()244x =--244x ==-+28x =-;(4)()()222a b a a b --- ()()222442a ab b a ab =-+--222442a ab b a ab =-+-+224ab b +=-.【点睛】此题主要考查了平方差公式以及完全平方公式、实数运算,正确应用公式是解题关键.。
(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案

(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案一、解答题1.仔细阅读下列解题过程:若2222690a ab b b ++-+=,求a b 、的值.解:2222690a ab b b ++-+=222222690()(3)003033a ab b b b a b b a b b a b ∴+++-+=∴++-=∴+=-=∴=-=,,根据以上解题过程,试探究下列问题:(1)已知2222210x xy y y -+-+=,求2x y +的值;(2)已知2254210a b ab b +--+=,求a b 、的值;(3)若248200m n mn t t =++-+=,,求2m t n -的值.2.启秀中学初一年级组计划将m 本书奖励给本次期中考试中取得优异成绩的n 名同学,如果每人分4本,那么还剩下78本;如果每人分8本,那么最后一人分得的书不足8本,但不少于4本.最终,年级组讨论后决定,给n 名同学每人发6本书,那么将剩余多少本书?3.在南通市中小学标准化建设工程中,某校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)求每台电脑、每台电子白板各多少万元;(2)根据学校实际,需购进电脑和电子白板共31台,若总费用不超过30万元,则至多购买电子白板多少台?4.已知关于x ,y 的二元一次方程组233741x y m x y m +=+⎧⎨-=+⎩它的解是正数. (1)求m 的取值范围;(2)化简:2|2|m --5.0=,|1|z -=,求x y z ++的平方根.6.定义:若实数x ,y 满足22x y t =+,22y x t =+,且x ≠y ,则称点M (x ,y )为“好点”.例如,点(0,-2)和 (-2,0)是“好点”.已知:在直角坐标系xOy 中,点P (m ,n ).(1)P 1(3,1)和P 2(-3,1)两点中,点________________是“好点”.(2)若点P (m ,n )是“好点”,求m +n 的值.(3)若点P 是“好点”,用含t 的代数式表示mn ,并求t 的取值范围.7.已知有理数,x y 满足:1x y -=,且221x y ,求22x xy y ++的值. 8.如图,在方格纸内将ABC ∆水平向右平移4个单位得到'''A B C ∆.(1)补全'''A B C ∆,利用网格点和直尺画图;(2)图中AC 与''A C 的位置关系是: ;(3)画出ABC ∆中AB 边上的中线CE ;(4)平移过程中,线段AC 扫过的面积是: .9.如图所示,A (2,0),点 B 在 y 轴上,将三角形 OAB 沿 x 轴负方向平移,平移后的图形为三角形 DEC ,且点 C 的坐标为(-6,4) .(1)直接写出点 E 的坐标 ;(2)在四边形 ABCD 中,点 P 从点 B 出发,沿“BC →CD ”移动.若点 P 的速度为每秒 2 个单位长度, 运动时间为 t 秒,回答下列问题:①求点 P 在运动过程中的坐标,(用含 t 的式子表示,写出过程);②当 3 秒<t <5 秒时,设∠CBP =x °,∠PAD =y °,∠BPA =z °,试问 x ,y ,z 之间的数量关系能否确定?若能,请用含 x ,y 的式子表示 z ,写出过程;若不能,说明理由.10.问题1:现有一张△ABC 纸片,点D 、E 分别是△ABC 边上两点,若沿直线DE 折叠. (1)探究1:如果折成图①的形状,使A 点落在CE 上,则∠1与∠A 的数量关系是 ;(2)探究2:如果折成图②的形状,猜想∠1+∠2和∠A 的数量关系是 ; (3)探究3:如果折成图③的形状,猜想∠1、∠2和∠A 的数量关系,并说明理由.(4)问题2:将问题1推广,如图④,将四边形ABCD 纸片沿EF 折叠,使点A 、B 落在四边形EFCD 的内部时,∠1+∠2与∠A 、∠B 之间的数量关系是 .11.已知a +b =5,ab =-2.求下列代数式的值:(1)22a b +;(2)22232a ab b -+.12.如图,在方格纸内将水平向右平移4个单位得到△.(1)画出△; (2)画出边上的中线和高线;(利用网格点和直尺画图) (3)的面积为 .13.如果a c =b ,那么我们规定(a ,b )=c .例如;因为23=8,所以(2,8)=3. (1)根据上述规定填空:(3,27)= ,(4,1)= ,(2,0.25)= ; (2)记(3,5)=a ,(3,6)=b ,(3,30)=c .判断a ,b ,c 之间的等量关系,并说明理由.14.先化简,再求值:(x ﹣2y )(x +2y )﹣(x ﹣2y )2,其中x =3,y =﹣1.15.已知:5x y +=,(2)(2)3x y --=-.求下列代数式的的值.(1)xy ;(2)224x xy y ++;(3)25x xy y ++.16.装饰公司为小明家设计电视背景墙时需要A 、B 型板材若干块,A 型板材规格是a ⨯b ,B 型板材规格是b ⨯b .现只能购得规格是150⨯b 的标准板材.(单位:cm )(1)若设a =60cm ,b =30cm .一张标准板材尽可能多的裁出A 型、B 型板材,共有下表三种裁法,下图是裁法一的裁剪示意图.裁法一 裁法二 裁法三A 型板材块数1 2 0B 型板材块数 3 m n则上表中, m =___________, n =__________;(2)为了装修的需要,小明家又购买了若干C 型板材,其规格是a ⨯a ,并做成如下图的背景墙.请写出下图中所表示的等式:__________;(3)若给定一个二次三项式2a 2+5ab +3b 2,试用拼图的方式将其因式分解.(请仿照(2)在几何图形中标上有关数量)17.已知关于x 、y 的方程组354526x y ax by -=⎧⎨+=-⎩与2348x y ax by +=-⎧⎨-=⎩有相同的解,求a 、b 的值.18.计算:(1)(12)﹣3﹣20160﹣|﹣5|; (2)(3a 2)2﹣a 2•2a 2+(﹣2a 3)2+a 2;(3)(x+5)2﹣(x ﹣2)(x ﹣3);(4)(2x+y ﹣2)(2x+y+2).19.已知关于x 、y 的二元一次方程组21322x y x y k +=⎧⎪⎨-=-⎪⎩(k 为常数). (1)求这个二元一次方程组的解(用含k 的代数式表示);(2)若()2421y x +=,求k 的值;(3)若14k ≤,设364m x y =+,且m 为正整数,求m 的值. 20.解下列方程组或不等式组(1)24231x y x y +=⎧⎨-=⎩ (2)()211113x x x x ⎧--≤⎪⎨+>-⎪⎩【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)23x y +=;(2)21a b ==,;(3)21m t n -=.【分析】(1)首先把第3项22y 裂项,拆成22y y +,再用完全平方公式因式分解,利用非负数的性质求得x y 、代入求得数值;(2)首先把第2项25b 裂项,拆成224b b +,再用完全平方公式因式分解,利用非负数的性质求得a b 、代入求得数值;(3)先把4m n =+代入28200mn t t +-+=,得到关于n 和 t 的式子,再仿照(1)(2)题.【详解】解:(1)2222210x xy y y -+-+=2222210x xy y y y ∴-++-+=22()(1)0x y y ∴-+-=010x y y ∴-=-=,,11x y ∴==,,23x y ∴+=;(2)2254210a b ab b +--+=22244210a b ab b b ∴+-+-+=22(2)(1)0a b b ∴-+-=2010a b b ∴-=-=,21a b ∴==,;(3)4m n =+,2(4)8200n n t t ∴++-+=22448160n n t t ∴+++-+=22(2)(4)0n t ∴++-=2040n t ∴+=-=,24n t ∴=-=,42m n ∴=+=20(2)1m t n -∴=-=【点睛】本题考查的分组分解法、配方法和非负数的性质,对于项数较多的多项式因式分解,分组分解法是一个常用的方法. 首先要观察各项特征,寻找熟悉的式子,熟练掌握平方差公式和完全平方公式是基础.2.38本【分析】先表示书的总量,利用不等关系列不等式组,求不等式组的正整数解即可得到答案.【详解】解:由题意得:4788(1)84788(1)4n n n n +--⎧⎨+--≥⎩< ①②由①得:12n >19 由②得:1202n ≤ ∴ 不等式组的解集是:111922≤<n 20 n 为正整数,20,n ∴=478158,m n ∴=+=15820638.∴-⨯=答:剩下38本书.【点睛】本题考查的是不等式组的应用,掌握利用不等关系列不等式组是解题的关键.3.(1)电脑0.5万元,电子白板1.5万元;(2)14台【分析】(1)设每台电脑x 元,每台电子白板y 元,根据题意列出方程组,解方程组即可;(2)设购进电子白板m 台,则购进电脑()31m -台,根据总费用不超过30万元,列出不等式,根据m 实际意义即可求解.【详解】(1)设每台电脑x 元,每台电子白板y 元,则2 3.52 2.5x y x y +=⎧⎨+=⎩,解得0.51.5x y =⎧⎨=⎩故每台电脑0.5万元,每台电子白板1.5万元;(2)设购进电子白板m 台,则购进电脑()31m -台,由题意得1.50.5(31)30m m +-≤解得14.5m ≤,又因为m 是正整数,则14m ≤,故至多购买电子白板14台.【点睛】本题考查了二元一次方程组应用,一元一次不等式应用,综合性较强,难度不大,根据题意列出二元一次方程组、一元一次不等式是解题关键.4.(1)213m -<< (2)m -【分析】(1)先解方程组,用含m 的式子表示出x 、y ,再根据方程组的解时一对正数列出关于m 的不等式组,解之可得;(2)根据m 的取值范围判断出m-2<0、m+1>0,m-1<0,再根据绝对值性质去绝对值符号、合并同类项即可得.【详解】解:(1)解方程组233741x y m x y m +=+⎧⎨-=+⎩, 得321x m y m =+⎧⎨=-⎩因为解为正数,则32010m m +>⎧⎨->⎩,解得213m -<<; (2)原式2(1)(1)m m m m =--+--=-.【点睛】本题考查了二元一次方程组及解法、一元一次不等式组及解法.解题的关键是根据题意列出关于m 的不等式组及绝对值的性质.5.【分析】根据题意得到三元一次方程组,解方程组,求出x y z ++,最后求平方根即可.【详解】0=,|1|z -=,=|1|0z -=,∴2113024010y x x y z -+-=⎧⎪-+=⎨⎪-=⎩,解得231x y z =⎧⎪=⎨⎪=⎩,则6x y z ++=,∴x y z ++平方根为.【点睛】本题考查相反数的意义,非负数的表达,解三元一次方程组,求平方根等知识,综合性较强,解题关键是根据题意列出三元一次方程组.6.(1)2P ;(2)2-;(3)3t >【分析】(1)将P 1(3,1)和P 2(-3,1)分别代入等式即可得出结果;(2)将点P (m ,n )代入等式即可得出m+n 的值;(3)根据“好点”的定义,将P 点代入即可得到关于m 和n 的等式,将两个等式结合即可得出结果.【详解】解:(1)对于1(3,1)P ,2321,7t t =⨯+=,2123,5t t =⨯+=-对于2(3,1)P -,2(3)21,7t t -=⨯+=,212(3),7t t =⨯-+=,所以2P 是“好点” (2)∵点(,)P m n 是好点,∴222,2m n t n m t =+=+, 222()m n n m -=-,∴2m n +=-(3)∵222,2m n t n m t =+=+,2222m n n t m t -=+--①,2222m n m t n t +=+++②,得()()2()0m n m n m n -++-=,即()(2)0m n m n -++=,由题知,,2m n m n ≠∴+=-,由②得2()22()2m n mn m n t +-=++,∴4242,4mn t mn t -=-+=-,∵m n ≠,∴2()0m n ->,∴2()40m n mn +->,∴44(4)0t -->,所以3t >,【点睛】本题主要考查的是新定义“好点”,正确的掌握整式的乘法解题的关键.7.【分析】利用1x y -=将221x y 整理求出xy 的值,然后将22x xy y ++利用完全平方公式变形,将各自的值代入计算即可求出值. 【详解】∵221x y ,∴化简得:241xy x y , ∵1x y -=,∴241xy x y 可化为:241xy ,即有:5xy =,∴2222313516x xy y x y xy .【点睛】此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.8.(1)图见详解;(2)平行且相等;(3)图见详解;(4)28.【分析】(1)根据图形平移的性质画出△A B C '''即可;(2)根据平移的性质可得出AC 与A C ''的关系;(3)先取AB 的中点E ,再连接CE 即可;(4)线段AC 扫过的面积为平行四边形AA C C ''的面积,根据平行四边形的底为4,高为7,可得线段AC 扫过的面积.【详解】解:(1)如图所示,△A B C '''即为所求;(2)由平移的性质可得,AC 与A C ''的关系是平行且相等;故答案为:平行且相等;(3)如图所示,线段CE 即为所求;(4)如图所示,连接AA ',CC ',则线段AC 扫过的面积为平行四边形AA C C ''的面积,由图可得,线段AC 扫过的面积4728=⨯=.故答案为:28.【点睛】本题主要考查了利用平移变换进行作图,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.9.(1)()4,0- (2)1)点P 在线段BC 上时, (),4P t -,2)点P 在线段CD 上时, ()6,10P t --; (3)能确定,z x y =+,证明见解析【分析】(1)根据平移的性质即可得到结论;(2)①分两种情况:1)点P 在线段BC 上时,2)点P 在线段CD 上时;②如图,作P 作//PE BC 交于AB 于E ,则//PE AD ,根据平行线的性质即可得到结论.【详解】(1)∵点B 的横坐标为0,点C 的横坐标为-6,∴将A (2,0)向左平移6个单位长度得到点E∴()4,0E -;(2)①∵6,4BC CD ==∴1)点P 在线段BC 上时,PB t =(),4P t -;2)点P 在线段CD 上时,()4610PD t t =--=-()6,10P t --;②能确定如图,作P 作//PE BC 交于AB 于E ,则//PE AD∴1,2CBP x DAP y ==︒==︒∠∠∠∠ ∴1+2BPA x y z ==︒+︒=︒∠∠∠ ∴z x y =+.【点睛】本题考查了平行线的问题,掌握平移的性质、代数式的用法、平行线的性质以及判定定理是解题的关键.10.(1)12A ∠=∠;(2)122A ∠+∠=∠;(3)见解析;(4)1222360A B ∠+∠=∠+∠-︒【分析】(1)根据三角形外角性质可得;(2)在四边形A EAD '中,内角和为360°,∠BDA=∠CEA=180°,利用这两个条件,进行角度转化可得关系式;(3)如下图,根据(1)可得∠1=2∠DAA ',∠2=2∠EAA ',从而推导出关系式; (4)根据平角的定义以及四边形的内角和定理,与(2)类似思路探讨,可得关系式.【详解】(1)∵△'EDA 是△EDA 折叠得到∴∠A=∠A '∵∠1是△'ADA 的外角∴∠1=∠A+∠A '∴12A ∠=∠;(2)∵在四边形A EAD '中,内角和为360°∴∠A+A '+∠A DA '+∠A EA '=360°同理,∠A=∠A '∴2∠A+∠A DA '+∠A EA '=360°∵∠BDA=∠CEA=180∴∠1+∠A DA '+∠A EA '+∠2=360°∴122A ∠+∠=∠ ;(3)数量关系:212A ∠-∠=∠理由:如下图,连接AA '由(1)可知:∠1=2∠DAA ',∠2=2∠EAA '∴212()2EAA DAA DAE ∠-∠=∠-=∠'∠';(4)由折叠性质知:∠2=180°-2∠AEF ,∠1=180°-2∠BFE相加得:123602(360)22360A B A B ∠+∠=︒-︒-∠-∠=∠+∠-︒.【点睛】本题考查角度之间的关系,(4)问的解题思路是相同的,主要运用三角形的内角和定理和四边形的内角和定理进行角度转换.11.(1)29;(2)64.【分析】(1)根据完全平方公式得到()2222a b a b ab +=+-,然后整体代入计算即可; (2)根据完全平方公式得到()22223227a ab b a b ab -+=+-,然后整体代入计算即可.【详解】解:(1)()()2222252229a b a b b a =+-=-⨯-=+;(2)()()222222232242727257264a ab b a ab b ab a b ab -+=++-=+-=⨯-⨯-=.【点睛】本题考查了代数式求值,完全平方公式和整体代入的思想,熟练掌握完全平方公式是解题的关键.12.(1)见解析; (2) 见解析;(3) 4.【解析】【分析】(1)根据图形平移的性质画出△A′B′C′即可;(2)先取AB 的中点D ,再连接CD 即可;过点C 作CD ⊥AB 交AB 的延长线于点E ,CE 即为所求;(3)利用割补法计算△ABC 的面积.【详解】(1)如图所示:(2)如图所示;(3)S △BCD =20-5-1-10=4.13.(1)3,0,﹣2;(2)a +b =c ,理由见解析.【分析】(1)直接根据新定义求解即可;(2)先根据新定义得出关于a ,b ,c 的等式,然后根据幂的运算法则求解即可.【详解】(1)∵33=27,∴(3,27)=3,∵40=1,∴(4,1)=0,∵2﹣2=14, ∴(2,0.25)=﹣2.故答案为:3,0,﹣2;(2)a +b =c .理由:∵(3,5)=a ,(3,6)=b ,(3,30)=c ,∴3a =5,3b =6,3c =30,∴3a ×3b =5×6=3c =30,∴3a ×3b =3c ,∴a +b =c .【点睛】本题考查了新定义运算,明确新定义的运算方法是解答本题的关键,本题也考查了有理数的乘方、同底数幂的乘法运算.14.4xy ﹣8y 2,﹣20【分析】先根据整式的乘法法则和乘法公式算乘法,再合并同类项,最后代入求出即可.【详解】(x ﹣2y )(x +2y )﹣(x ﹣2y )2=x 2﹣4y 2﹣(x 2﹣4xy +4y 2)=x 2﹣4y 2﹣x 2+4xy ﹣4y 2=4xy ﹣8y 2,当x =3,y =﹣1时,原式=4×3×(﹣1)﹣8×(﹣1)2=﹣20.【点睛】本题考查整式的化简求值,涉及平方差公式、完全平方公式、合并同类项等知识,熟练掌握整式的乘法运算法则和乘法公式的运用是解答的关键.15.(1)3;(2)31;(3)25.【分析】(1)把多项式乘积展开,再将已知5x y +=代入,即可求解;(2)根据(1)得到3xy =,再利用完全平方公式,即可求解;(3)根据5x y +=将x 用y 来表示,再代入25x xy y ++,合并同类项即可求解.【详解】解:(1)∵()(2)(2)22424=3x y xy x y xy x y --=--+=-++-,而5x y +=, ∴ ()=324=3254=3xy x y -++--+⨯-.故答案为3.(2)由(1)知3xy =,∴ ()22224=2=523=31x xy y x y xy +++++⨯. 故答案为31.(3)∵5x y +=,得5x y =-,则()()22225=55525105525x xy y y y y y y y y y y ++-+-+=-++-+=. 故答案为25.本题目考查整式的乘法,难度一般,是常考知识点,熟练掌握代数式之间的转化是顺利解题的关键.16.(1)m=1,n=5;(2)(a+2b)2=a2+4ab+4b2;(3)2a2+5ab+3b2=(a+b)(2a+3b),详见解析【分析】(1)结合图形和条件分析可以得出按裁法二裁剪时,可以裁出B型板1块,按裁法三裁剪时,可以裁出5块B型板;(2)看图即可得出所求的式子;(3)通过画图能更好的理解题意,从而得出结果.由于构成的是长方形,它的面积等于所给图片的面积之和,从而因式分解.【详解】(1)按裁法二裁剪时,2块A型板材块的长为120cm,150-120=30,所以可裁出B型板1块,按裁法三裁剪时,全部裁出B型板,150÷30=5,所以可裁出5块B型板;∴m=1,n=5.故答案为:1,5;(2)如下图:发现的等式为:(a+2b)2=a2+4ab+4b2;故答案为:(a+2b)2=a2+4ab+4b2.(3)按题意画图如下:∵构成的长方形面积等于所给图片的面积之和,∴2a2+5ab+3b2=(a+b)(2a+3b).【点睛】本题考查了完全平方公式和几何图形的应用及一元一次方程的应用,关键是根据学生的画图能力,计算能力来解答.17.149299 ab⎧=⎪⎪⎨⎪=⎪⎩因为两个方程组有相同的解,故只需把两个方程组中不含未知数和含未知数的方程分别组成方程组,求出未知数的值,再代入另一组方程组即可.【详解】354526x y ax by -=⎧⎨+=-⎩①③ 和2348x y ax by +=-⎧⎨-=⎩②④ 解:联立①②得:35234x y x y -=⎧⎨+=-⎩解得:12x y =⎧⎨=-⎩将12x y =⎧⎨=-⎩代入③④得:4102628a b a b -=-⎧⎨+=⎩解得:149299a b ⎧=⎪⎪⎨⎪=⎪⎩【点睛】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.18.(1)2;(2)7a 4+4a 6+a 2;(3)15x+19;(4)4x 2+4xy+y 2﹣4【分析】(1)首先利用负整数指数幂的性质、零次幂的性质、绝对值的性质进行计算,再算加减即可;(2)首先利用积的乘方的计算法则、单项式乘以单项式计算法则计算,再合并同类项即可;(3)首先利用完全平方公式、多项式乘以多项式计算法则计算,再合并同类项即可; (4)首先利用平方差计算,再利用完全平方公式进行计算即可.【详解】解:(1)原式=8﹣1﹣5=2;(2)原式=9a 4﹣2a 4+4a 6+a 2,=7a 4+4a 6+a 2;(3)原式=x 2+10x+25﹣(x 2﹣3x ﹣2x+6),=x 2+10x+25﹣x 2+3x+2x ﹣6,=15x+19;(4)原式=(2x+y )2﹣4,=4x 2+4xy+y 2﹣4.本题考查的是实数的运算,幂的运算及合并同类项,整式的混合运算,掌握以上知识点是解题的关键.19.(1)218524k x ky -⎧=⎪⎪⎨-⎪=⎪⎩;(2)52k =或12k =-;(3)1或2. 【分析】(1)根据题意直接利用加减消元法进行计算求解即可;(2)由题意根据01(0)a a =≠和11n =以及2(1)1n -=(n 为整数)得到三个关于k 的方程,求出k 即可;(3)根据题意用含m 的代数式表示出k ,根据14k ≤,确定m 的取值范围,由m 为正整数,求得m 的值即可.【详解】 解:(1)21322x y x y k ⎧+=⎪⎪⎨⎪-=-⎪⎩①②, ①+②得:3412x k =+-,解得:218k x -=, ①-②得:3212y k =-+,解得:524k y -=, ∴二元一次方程组的解为:218524k x ky -⎧=⎪⎪⎨-⎪=⎪⎩. (2)∵01(0)a a =≠,2(42)1y x +=,∴20y =,即52204k -⨯=,解得:52k =; ∵11n =,2(42)1y x +=,∴421x +=,即214218k -⨯+=,解得:12k =-; ∵2(1)1n -=(n 为正整数),2(42)1y x +=, ∴4212x y +=-,为偶数,即214218k -⨯+=-,解得:52k =-; 当52k =-时,3532115222y k =-+=++=,为奇数,不合题意,故舍去.综上52k =或12k =-. (3)∵215213643647842k k m x y k --=+=⨯+⨯=+,即172m k =+, ∴2114m k -=, ∵14k ≤, ∴211144m k -=≤,解得94m ≤, ∵m 为正整数,∴m=1或2.【点睛】本题考查解二元一次方程组以及解一元一次不等式,根据题意列出不等式是解题的关键.20.(1)21x y =⎧⎨=⎩(2)12x ≤< 【分析】(1)运用加减消元法先消除x ,求y 的值后代入方程②求x 得解;(2)先分别解每个不等式,然后求公共部分,确定不等式组的解集.【详解】解:(1)24231x y x y +=⎧⎨-=⎩①② ①×2-②,得 7y=7,∴y=1.把y=1代入②,得 x=2.∴21x y =⎧⎨=⎩. (2)解不等式 ()211x x --≤得 1x ≥. 解不等式113x x +>- 得 2x <. ∴不等式组的解集为12x ≤<.【点睛】此题考查解方程组和不等式组,属常规基础题,难度不大.。
(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案

(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案一、解答题1.已知a +a 1-=3, 求(1)a 2+21a (2)a 4+41a2.在平面直角坐标系中,点A 、B 的坐标分别为(),0a ,()0,b ,其中a ,b 满足218|273|0a b a b +-+--=.将点B 向右平移15个单位长度得到点C ,如图所示.(1)求点A ,B ,C 的坐标;(2)动点M 从点C 出发,沿着线段CB 、线段BO 以1.5个单位长度/秒的速度运动,同时点N 从点O 出发沿着线段OA 以1个单位长度秒的速度运动,设运动时间为t 秒()012t <<.当BM AN <时,求t 的取值范围;是否存在一段时间,使得OACM OCN S S ≤四边形三角形?若存在,求出t 的取值范围;若不存在,说明理由.3.如图,甲长方形的两边长分别为1m +,7m +;乙长方形的两边长分别为2m +,4m +.(其中..m 为正整数....)(1)图中的甲长方形的面积1S ,乙长方形的面积2S ,比较: 1S 2S (填“<”、“=”或“>”);(2)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积S 与图中的甲长方形面积1S 的差(即1S S -)是一个常数,求出这个常数;(3)在(1)的条件下,若某个图形的面积介于1S 、2S 之间(不包括1S 、2S )并且面积为整数,这样的整数值有且只有16个,求m 的值. 4.先化简,再求值(x-2)2+2(x+2)(x-4)-(x-3)(x+3);其中x=1.5.某口罩加工厂有,A B 两组工人共150人,A 组工人每人每小时可加工口罩70只,B 组工人每小时可加工口罩50只,,A B 两组工人每小时一共可加工口罩9300只. (1)求A B 、两组工人各有多少人?(2)由于疫情加重,A B 、两组工人均提高了工作效率,一名A 组工人和一名B 组工人每小时共可生产口罩200只,若A B 、两组工人每小时至少加工15000只口罩,那么A 组工人每人每小时至少加工多少只口罩?6.问题1:现有一张△ABC 纸片,点D 、E 分别是△ABC 边上两点,若沿直线DE 折叠. (1)探究1:如果折成图①的形状,使A 点落在CE 上,则∠1与∠A 的数量关系是;(2)探究2:如果折成图②的形状,猜想∠1+∠2和∠A 的数量关系是 ; (3)探究3:如果折成图③的形状,猜想∠1、∠2和∠A 的数量关系,并说明理由.(4)问题2:将问题1推广,如图④,将四边形ABCD 纸片沿EF 折叠,使点A 、B 落在四边形EFCD 的内部时,∠1+∠2与∠A 、∠B 之间的数量关系是 . 7.因式分解: (1)16x 2-9y 2 (2)(x 2+y 2)2-4x 2y 2 8.仔细阅读下列解题过程:若2222690a ab b b ++-+=,求a b 、的值. 解:2222690a ab b b ++-+=222222690()(3)003033a ab b b b a b b a b b a b ∴+++-+=∴++-=∴+=-=∴=-=,,根据以上解题过程,试探究下列问题:(1)已知2222210x xy y y -+-+=,求2x y +的值;(2)已知2254210a b ab b +--+=,求a b 、的值; (3)若248200m n mn t t =++-+=,,求2m t n -的值.9.南山植物园中现有A ,B 两个园区.已知A 园区为长方形,长为(x +y)米,宽为(x -y)米;B 园区为正方形,边长为(x +3y)米.(1)请用代数式表示A ,B 两园区的面积之和并化简.(2)现根据实际需要对A 园区进行整改,长增加(11x -y)米,宽减少(x -2y)米,整改后A 园区的长比宽多350米,且整改后两园区的周长之和为980米. ①求x ,y 的值;②若A 园区全部种植C 种花,B 园区全部种植D 种花,且C ,D 两种花投入的费用与吸引游客的收益如下表:C D 投入(元/米2) 12 16 收益(元/米2)1826求整改后A ,B 两园区旅游的净收益之和.(净收益=收益-投入)10.如图,有一块长为(3)a b +米,宽为(2)a b +米的长方形空地,计划修筑东西、南北走向的两条道路,其余进行绿化(阴影部分),已知道路宽为a 米,东西走向的道路与空地北边界相距1米,则绿化的面积是多少平方米?并求出当a =3,b =2时的绿化面积.11.计算:(1)2201(2)3()3----÷- (2)22(21)(21)x x -+12.先化简后求值:224(2)(2)(2)x x y x y y x --+---,其中1x =-,2y =-. 13.观察下列式子:2×4+1=9;4×6+1=25;6×8+1=49;… (1)请你根据上面式子的规律直接写出第4个式子: ; (2)探索以上式子的规律,试写出第n 个等式,并说明等式成立的理由. 14.已知关于x,y 的方程组260250x y x y mx +-=⎧⎨-++=⎩(1)请直接写出方程260x y +-=的所有正整数解 (2)若方程组的解满足x+y=0,求m 的值(3)无论实数m 取何值,方程x -2y+mx+5=0总有一个固定的解,请直接写出这个解? 15.装饰公司为小明家设计电视背景墙时需要A 、B 型板材若干块,A 型板材规格是a ⨯b ,B 型板材规格是b ⨯b .现只能购得规格是150⨯b 的标准板材.(单位:cm )(1)若设a =60cm ,b =30cm .一张标准板材尽可能多的裁出A 型、B 型板材,共有下表三种裁法,下图是裁法一的裁剪示意图.裁法一 裁法二 裁法三 A 型板材块数 1 2 0 B 型板材块数3mn则上表中,m=___________,n=__________;(2)为了装修的需要,小明家又购买了若干C型板材,其规格是a⨯a,并做成如下图的背景墙.请写出下图中所表示的等式:__________;(3)若给定一个二次三项式2a2+5ab+3b2,试用拼图的方式将其因式分解.(请仿照(2)在几何图形中标上有关数量)16.先化简,再求值:(3x+2)(3x-2)-5x(x+1)-(x-1)2,其中x2-x-10=0.17.如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,若∠A=65°,∠B=45°,求∠AGD的度数.18.如图,边长为1的正方形ABCD被两条与边平行的线段EF,GH分割成四个小长方形,EF与GH交于点P,设BF长为a,BG长为b,△GBF的周长为m,(1)①用含a,b,m的式子表示GF的长为;②用含a,b的式子表示长方形EPHD的面积为;(2)已知直角三角形两直角边的平方和等于斜边的平方, 例如在图1,△ABC 中,∠ABC=900,则222AB BC AC +=, 请用上述知识解决下列问题:①写出a ,b ,m满足的等式; ②若m=1,求长方形EPHD 的面积;③当m 满足什么条件时,长方形EPHD 的面积是一个常数?19.已知关于x 、y 的二元一次方程组21322x y x y k +=⎧⎪⎨-=-⎪⎩(k 为常数).(1)求这个二元一次方程组的解(用含k 的代数式表示); (2)若()2421yx +=,求k 的值;(3)若14k ≤,设364m x y =+,且m 为正整数,求m 的值. 20.如图,点D 、E 、F 分别是△ABC 三边上的点,DF ∥AC ,∠BFD=∠CED ,请写出∠B 与∠CDE 之间的数量关系,并说明理由.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)7;(2)47. 【分析】(1)根据13a a -+=得出13a a +=,进而得出219a a ⎛⎫+= ⎪⎝⎭,从而可得出结论;(2)根据(1)中的结论可知2217a a +=,故2221()49a a +=,从而得出441a a +的值. 【详解】解:(1)∵13a a -+=, ∴13a a+=, ∴21()9a a +=,即:22129a a++=,∴2217a a+=; (2)由(1)知:2217a a +=, ∴2221()49a a +=,即:441249a a++=, ∴44147a a +=. 【点睛】本题主要考查的是负整数指数幂和分式的运算,解题的关键是熟练掌握完全平方公式的灵活应用.2.(1)(12,0)A (0,3)B (15,3)C(2)610.8t <<;存在,02t <≤或11.612t ≤< 【分析】(1)根据题意构造方程组21802730a b a b +-=⎧⎨--=⎩,解方程组,问题得解;(2)①当010t <≤时,15 1.5BM t =-,12AN t =-,根据BM AN <构造不等式,求出t ,当1012t <<时, 1.515BM t =-,12AN t =-,根据BM AN <构造不等式,求出t ,二者结合,问题得解;②分别表示出BCN S 三角形、 OACB S 四边形,分010t <≤,1012t <<两种情况讨论,问题得解.【详解】解:(1)由题意得21802730a b a b +-=⎧⎨--=⎩,解得123a b =⎧⎨=⎩,∴(12,0)A ,(0,3)B ,(15,3)C(2)①当010t <≤时,15 1.5BM t =-,12AN t =-,BM AN <得15 1.512t t -<-,解得6t >则610t <≤;当1012t <<时, 1.515BM t =-,12AN t =-,BM AN <得1.51512t t -<-,解得10.8t <,则1010.8t <<, 综上,610.8t <<; ②1145153222BCN S BC OB =⨯⨯=⨯⨯=三角形 1181()(1215)3222OACBS OA BC OB =⨯+⨯=⨯+⨯=四边形 当010t <≤时, 81145(15 1.5)3222OACM OACB BMO S S S t =-=-⨯-⨯≤四边形四边形三角形 解得2t ≤,则02t <≤;当1012t <<时, 81145(1.515)15222OACM OACB BMC S S S t =-=-⨯-⨯≤四边形四边形三角形 解得11.6t ≥,则11.612t ≤<, 综上02t <≤或11.612t ≤<. 【点睛】本题考查了非负数的表达、平面直角坐标系中图形面积表示,不等式,方程组、分类讨论等知识,综合性较强.根据题意,分类讨论是解题关键. 3.(1)>;(2)9;(3)9. 【分析】(1)根据矩形的面积公式计算即可;(2)根据矩形和正方形的周长和面积公式即可得到结论; (3)根据题意列出不等式,然后求解即可得到结论. 【详解】解:(1)图①中长方形的面积21(7)(1)87S m m m m,图②中长方形的面积22(4)(2)68S mmm m,1221S S m ,m 为正整数,m 最小为1,2110m ,12S S ∴>;(2)依题意得,正方形的边长为:2(71)44m m m;则:221(4)(87)9SS mm m,是一个定值;(3)由(1)得,1221S S m ,根据某个图形的面积介于1S 、2S 之间(不包括1S 、2S )并且面积为整数,这样的整数值有且只有16个,∴当162117m 时,∴1792m,m 为正整数,9m ∴=.【点睛】本题考查了完全平方方公式的几何背景,多项式的乘法,整式的混合运算,一元一次不等式,熟记相关运算法则是解题的关键. 4.2x 2-8x-3;-9. 【解析】 【分析】根据整式的乘法运算法则即可化简求值. 【详解】解:原式=x 2-4x+4+2(x 2-2x-8)-(x 2-9) =x 2-4x+4+2x 2-4x-16-x 2+9 =2x 2-8x-3当x=1时,原式=2-8-3=-9 【点睛】此题主要考查整式的化简求值,解题的关键是熟知整式的运算法则.5.(1)A 组工人有90人、B 组工人有60人(2)A 组工人每人每小时至少加工100只口罩 【分析】(1)设A 组工人有x 人、B 组工人有(150−x )人,根据题意列方程健康得到结论; (2)设A 组工人每人每小时加工a 只口罩,则B 组工人每人每小时加工(200−a )只口罩;根据题意列不等式健康得到结论. 【详解】(1)设A 组工人有x 人、B 组工人有(150−x )人, 根据题意得,70x +50(150−x )=9300, 解得:x =90,150−x =60,答:A 组工人有90人、B 组工人有60人;(2)设A 组工人每人每小时加工a 只口罩,则B 组工人每人每小时加工(200−a )只口罩;根据题意得,90a +60(200−a )≥15000, 解得:a ≥100,答:A 组工人每人每小时至少加工100只口罩. 【点睛】本题考查了一元一次方程的应用,一元一次不等式的应用,正确的理解题意是解题的关键.6.(1)12A ∠=∠;(2)122A ∠+∠=∠;(3)见解析;(4)1222360A B ∠+∠=∠+∠-︒ 【分析】(1)根据三角形外角性质可得;(2)在四边形A EAD '中,内角和为360°,∠BDA=∠CEA=180°,利用这两个条件,进行角度转化可得关系式;(3)如下图,根据(1)可得∠1=2∠DAA ',∠2=2∠EAA ',从而推导出关系式;(4)根据平角的定义以及四边形的内角和定理,与(2)类似思路探讨,可得关系式.【详解】(1)∵△'EDA 是△EDA 折叠得到 ∴∠A=∠A '∵∠1是△'ADA 的外角 ∴∠1=∠A+∠A ' ∴12A ∠=∠;(2)∵在四边形A EAD '中,内角和为360° ∴∠A+A '+∠A DA '+∠A EA '=360° 同理,∠A=∠A '∴2∠A+∠A DA '+∠A EA '=360° ∵∠BDA=∠CEA=180∴∠1+∠A DA '+∠A EA '+∠2=360° ∴122A ∠+∠=∠ ;(3)数量关系:212A ∠-∠=∠ 理由:如下图,连接AA '由(1)可知:∠1=2∠DAA ',∠2=2∠EAA '∴212()2EAA DAA DAE ∠-∠=∠-=∠'∠'; (4)由折叠性质知:∠2=180°-2∠AEF ,∠1=180°-2∠BFE相加得:123602(360)22360A B A B ∠+∠=︒-︒-∠-∠=∠+∠-︒. 【点睛】本题考查角度之间的关系,(4)问的解题思路是相同的,主要运用三角形的内角和定理和四边形的内角和定理进行角度转换.7.(1)(43)(4-3)x y x y +;(2)22()(-y)x y x +. 【分析】(1)直接利用平方差公式22()()a b a b a b +-=-分解即可;(2)先利用平方差公式,再利用完全平方公式222()2a b a ab b ±=±+即可.【详解】(1)原式2243))((x y =-(43)(43)x y x y =+-;(2)原式2222)()(2x y xy =-+2222(2)(2)x y x y xy y x ++=+-22()()x y x y =+-.【点睛】本题考查了利用平方差公式和完全平方公式进行因式分解,熟记公式是解题关键. 8.(1)23x y +=;(2)21a b ==,;(3)21m t n -=. 【分析】(1)首先把第3项22y 裂项,拆成22y y +,再用完全平方公式因式分解,利用非负数的性质求得x y 、代入求得数值;(2)首先把第2项25b 裂项,拆成224b b +,再用完全平方公式因式分解,利用非负数的性质求得a b 、代入求得数值;(3)先把4m n =+代入28200mn t t +-+=,得到关于n 和 t 的式子,再仿照(1)(2)题. 【详解】 解:(1)2222210x xy y y -+-+=2222210x xy y y y ∴-++-+= 22()(1)0x y y ∴-+-= 010x y y ∴-=-=,, 11x y ∴==,,23x y ∴+=;(2)2254210a b ab b +--+=22244210a b ab b b ∴+-+-+=22(2)(1)0a b b ∴-+-=2010a b b ∴-=-=, 21a b ∴==,;(3)4m n =+,2(4)8200n n t t ∴++-+= 22448160n n t t ∴+++-+=22(2)(4)0n t ∴++-=2040n t ∴+=-=, 24n t ∴=-=, 42m n ∴=+=20(2)1m t n -∴=-=【点睛】本题考查的分组分解法、配方法和非负数的性质,对于项数较多的多项式因式分解,分组分解法是一个常用的方法. 首先要观察各项特征,寻找熟悉的式子,熟练掌握平方差公式和完全平方公式是基础.9.(1)2x 2+6xy+8y 2;(2)①3010x y =⎧⎨=⎩②57600元; 【分析】(1)根据长方形的面积公式和正方形的面积公式分别计算A 、B 两园区的面积,再相加即可求解;(2)①根据等量关系:整改后A 区的长比宽多350米;整改后两园区的周长之和为980米;列出方程组求出x ,y 的值;②代入数值得到整改后A 、B 两园区的面积之和,再根据净收益=收益﹣投入,列式计算即可求解.【详解】解:(1)(x+y )(x ﹣y )+(x+3y )(x+3y )=x 2﹣y 2+x 2+6xy+9y 2=2x 2+6xy+8y 2(平方米)答:A 、B 两园区的面积之和为(2x 2+6xy )平方米;(2)(x+y )+(11x ﹣y )=x+y+11x ﹣y=12x (米),(x ﹣y )﹣(x ﹣2y )=x ﹣y ﹣x+2y=y (米),依题意有: 123502(12)4(3)980x y x y x y -=⎧⎨+++=⎩, 解得3010x y =⎧⎨=⎩9. 12xy=12×30×10=3600(平方米),(x+3y )(x+3y )=x 2+6xy+9y 2=900+1800+900=3600(平方米),(18﹣12)×3600+(26﹣16)×3600=6×3600+10×3600=57600(元).答:整改后A 、B 两园区旅游的净收益之和为57600元.考点:整式的混合运算.10.()2223a ab b ++平方米;40平方米. 【分析】(1)根据平移的原理,四块绿化面积可拼成一个长方形,其边长为原边长减去再减去道路宽为a 米,由此即可求绿化的面积的代数式;然后利用多项式乘多项式法则计算,去括号合并得到最简结果,将a 与b 的值代入计算即可求出值.【详解】解:根据题意得:22(3)(2)(2)()23a b a a b a a b a b a ab b +-+-=++=++(平方米).则绿化的面积是()2223a ab b ++平方米; 当3a =,2b =时,原式2223233240=⨯+⨯⨯+=(平方米).故当a =3,b =2时,绿化面积为40平方米.答:绿化的面积是()2223a ab b ++平方米;当a =3,b =2时,绿化面积为40平方米. 【点睛】此题考查整式的混合运算与代数式求值,掌握长方形的面积计算方法是解决问题的关键.11.(1)374-.(2)16x 4−8x 2+1. 【分析】(1)原式利用负整数指数幂,零指数幂、平方的计算法则得到1914--÷,再计算即可得到结果;(2)原式逆用积的乘方运算法则变形,再利用平方差公式及完全平方公式化简即可得到结果.【详解】(1)2201(2)3()3----÷-= 1914--÷=374-. (2)原式=[(2x−1)(2x +1)]2=(4x 2−1)2=16x 4−8x 2+1.【点睛】本题考查零指数幂、负整数指数幂 、平方差公式及完全平方公式,熟练掌握运算法则是解本题的关键.12.2243x xy y -++,19【分析】根据整式的乘法运算法则,将多项式乘积展开,再合并同类项,即可化简,再代入x ,y 即可求值.【详解】解:原式2222222=44424243x x xy y xy x y xy x xy y -+---++=-++,将1x =-,2y =-代入,则原代数式的值为: 2243=x xy y -++()()()()22141232=1812=19--+⋅-⋅-+⋅--++.【点睛】本题考查整式的乘法,难度一般,是中考的常考点,熟练掌握多项式与多项式相乘的法则,即可顺利解题.13.(1)8×10+1=81;(2)2n(2n+1)+1=(2n+1)2,理由见解析.【分析】(1)根据上面式子的规律即可写出第4个式子;(2)探索以上式子的规律,结合(1)即可写出第n个等式.【详解】解:观察下列式子:2×4+1=9=32;4×6+1=25=52:6×8+1=49=72;…(1)发现规律:第4个式子:8×10+1=81=92;故答案为:8×10+1=81;(2)第n个等式为:2n(2n+1)+1=(2n+1)2,理由:2n(2n+1)+1=4n2+4n+1=(2n+1)2.【点睛】本题考查了规律型-数字的变化类,解决本题的关键是根据数字的变化寻找规律,总结规律.14.(1)24,21x xy y==⎧⎧⎨⎨==⎩⎩(2)-136(3)2.5xy=⎧⎨=⎩【解析】分析:(1)先对方程变形为x=6-2y,然后可带入数值求解;(2)把已知的x+y=0和方程x+2y-6=0组合成方程组,求解方程组的解,然后代入方程x-2y+mx+5=0即可求m的值;(3)方程整理后,根据无论m如何变化,二元一次方程组总有一个固定的解,列出方程组,解方程组即可;详解:(1)∵x+2y-6=0∴x=6-2y当y=1时,x=4,当y=2时,x=2∴24,21 x xy y==⎧⎧⎨⎨==⎩⎩(2)根据题意,把x+y=6和x+2y-6=0构成方程组为:6260 x yx y+=⎧⎨+-=⎩和解得66 xy=-⎧⎨=⎩把66xy=-⎧⎨=⎩代入x-2y+mx+5=0,解得m=13 6 -(3)∵无论实数m取何值,方程x-2y+mx+5=0总有一个固定的解,∴x=0时,m的值与题目无关∴y=2.5∴2.5 xy=⎧⎨=⎩点睛:此题主要考查了二元一次方程组的应用,对方程组中的方程灵活变形,构成可解方程是解题关键,有一定的难度,合理选择加减消元法和代入消元法解题是关键. 15.(1)m=1,n=5;(2)(a+2b)2=a2+4ab+4b2;(3)2a2+5ab+3b2=(a+b)(2a+3b),详见解析【分析】(1)结合图形和条件分析可以得出按裁法二裁剪时,可以裁出B型板1块,按裁法三裁剪时,可以裁出5块B型板;(2)看图即可得出所求的式子;(3)通过画图能更好的理解题意,从而得出结果.由于构成的是长方形,它的面积等于所给图片的面积之和,从而因式分解.【详解】(1)按裁法二裁剪时,2块A型板材块的长为120cm,150-120=30,所以可裁出B型板1块,按裁法三裁剪时,全部裁出B型板,150÷30=5,所以可裁出5块B型板;∴m=1,n=5.故答案为:1,5;(2)如下图:发现的等式为:(a+2b)2=a2+4ab+4b2;故答案为:(a+2b)2=a2+4ab+4b2.(3)按题意画图如下:∵构成的长方形面积等于所给图片的面积之和,∴2a2+5ab+3b2=(a+b)(2a+3b).【点睛】本题考查了完全平方公式和几何图形的应用及一元一次方程的应用,关键是根据学生的画图能力,计算能力来解答.16.3x2-3x-5,25【分析】原式第一项利用平方差公式化简,第二项利用单项式乘以多项式法则计算,最后一项利用完全平方公式展开,去括号合并得到最简结果,将已知的方程变形后代入即可求值.【详解】原式=()222945521x x x x x -----+=222945521x x x x x ----+-=2335x x --,当2100x x =--,即210x x =-时,原式=()235310525x x -=⨯-=-【点睛】本题考查整式的混合运算-化简求值,涉及的知识点有:完全平方公式、平方差公式、去括号法则及合并同类项法则,熟练掌握以上公式及法则是解题的关键.17.70°【分析】由CD ⊥AB ,EF ⊥AB 可得出∠CDF=∠EFB=90°,利用“同位角相等,两直线平行”可得出CD ∥EF ,利用“两直线平行,同位角相等”可得出∠DCB=∠1,结合∠1=∠2可得出∠DCB=∠2,利用“内错角相等,两直线平行”可得出DG ∥BC ,利用“两直线平行,同位角相等”可得出∠ADG 的度数,在△ADG 中,利用三角形内角和定理即可求出∠AGD 的度数.【详解】解:∵CD ⊥AB ,EF ⊥AB ,∴∠CDF =∠EFB =90°,∴CD ∥EF ,∴∠DCB =∠1.∵∠1=∠2,∴∠DCB =∠2,∴DG ∥BC ,∴∠ADG =∠B =45°.又∵在△ADG 中,∠A =65°,∠ADG =45°,∴∠AGD =180°﹣∠A ﹣∠ADG =70°【点睛】本题考查了平行线的判定与性质以及三角形内角和定理,利用平行线的性质求出∠ADG 的度数是解题的关键.18.(1)①m a b --;②1a b ab --+;(2)①22220m ma mb ab --+=;②12;③m=1 【分析】(1)①直接根据三角形的周长公式即可;②根据BF 长为a ,BG 长为b ,表示出EP ,PH 的长,根据求长方形EPHD 的面积;(2)①直接根据直角三角形两直角边的平方和等于斜边的平方,表示出a ,b ,m 之间的关系式;②根据线段之间的关系利用勾股定理求出长方形EPHD 的面积的值;③结合①的结论和②的作法即可求解.【详解】(1)①∵BF 长为a ,BG 长为b ,△GBF 的周长为m ,∴GF m a b =--,故答案为:m a b --;②∵正方形ABCD 的边长为1 ,∴AB=BC=1,∵BF 长为a ,BG 长为b ,∴AG=1-b ,FC=1-a ,∴EP=AG=1-b ,PH=FC=1-a ,∴长方形EPHD 的面积为:(1)(1)1a b a b ab --=--+,故答案为:1a b ab --+;(2)①△ABC 中,∠ABC=90°,则222AB BC AC +=,∴在△GBF 中, GF m a b =--,∴()222m a b a b --=+, 化简得,22220m ma mb ab --+=故答案为:22220m ma mb ab --+=;②∵BF=a ,GB=b ,∴FC=1-a ,AG=1-b ,在Rt △GBF 中,22222GF BF BG a b ==+=+,∵Rt △GBF 的周长为1, ∴1BF BG GF a b ++=+=即1a b =--,即222212(()b a b a b a +=-+++),整理得12220a b ab --+= ∴12a b ab +-=, ∴矩形EPHD 的面积••S PH EP FC AG ==()()11a b =--1a b ab =--+11122=-=. ③由①得: 22220m ma mb ab --+=,∴212ab ma mb m =+-. ∴矩形EPHD 的面积••S PH EP FC AG == ()()11a b =--1a b ab =--+2112ma mb a m b +-=--+ ()()211121m a m m b =--+-+, ∴要使长方形EPHD 的面积是一个常数,只有m=1.【点睛】本题考查了正方形的特殊性质和勾股定理,根据正方形的特殊性质和勾股定理推出22220m ma mb ab --+=是解题的关键.19.(1)218524k x ky -⎧=⎪⎪⎨-⎪=⎪⎩;(2)52k =或12k =-;(3)1或2. 【分析】(1)根据题意直接利用加减消元法进行计算求解即可;(2)由题意根据01(0)a a =≠和11n =以及2(1)1n -=(n 为整数)得到三个关于k 的方程,求出k 即可;(3)根据题意用含m 的代数式表示出k ,根据14k ≤,确定m 的取值范围,由m 为正整数,求得m 的值即可.【详解】 解:(1)21322x y x y k ⎧+=⎪⎪⎨⎪-=-⎪⎩①②, ①+②得:3412x k =+-,解得:218k x -=, ①-②得:3212y k =-+,解得:524k y -=, ∴二元一次方程组的解为:218524k x k y -⎧=⎪⎪⎨-⎪=⎪⎩. (2)∵01(0)a a =≠,2(42)1y x +=,∴20y =,即52204k -⨯=,解得:52k =; ∵11n =,2(42)1y x +=,∴421x +=,即214218k -⨯+=,解得:12k =-; ∵2(1)1n -=(n 为正整数),2(42)1y x +=,∴4212x y +=-,为偶数,即214218k -⨯+=-,解得:52k =-; 当52k =-时,3532115222y k =-+=++=,为奇数,不合题意,故舍去. 综上52k =或12k =-. (3)∵215213643647842k k m x y k --=+=⨯+⨯=+,即172m k =+, ∴2114m k -=, ∵14k ≤, ∴211144m k -=≤,解得94m ≤, ∵m 为正整数,∴m=1或2.【点睛】本题考查解二元一次方程组以及解一元一次不等式,根据题意列出不等式是解题的关键.20.见解析【分析】由DF ∥AC ,得到∠BFD=∠A,再结合∠BFD=∠CED ,有等量代换得到∠A=∠CED ,从而可得DE ∥AB ,则由平行线的性质即可得到∠B=∠CDE.【详解】解:∠B=∠CDE,理由如下:∵ DF ∥AC ,∴∠BFD=∠A.∵∠BFD=∠CED ,∴∠A=∠CED.∴DE ∥AB ,∴∠B=∠CDE.【点睛】本题考查了平行线的判定与性质,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.。
人教版七年级数学下压轴题培优期末复习专题含答案精编版

人教版七年级数学下压轴题培优期末复习专题含答案精编版MQS system office room 【MQS16H-TTMS2A-MQSS8Q8-MQSH16898】人教版2018年七年级数学期末复习专题--压轴题培优已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)如图1,直接写出∠A和∠C之间的数量关系?? ;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.如图,已知两条射线OM∥CN,动线段AB的两个端点A.B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.(1)请在图中找出与∠AOC相等的角,并说明理由;(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.已知AB∥CD,线段EF分别与AB、CD相交于点E、F.(1)如图①,当∠A=25°,∠APC=70°时,求∠C的度数;(2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A.∠APC与∠C之间有什么确定的相等关系?试证明你的结论.(3)如图③,当点P在线段FE的延长线上运动时,(2)中的结论还成立吗?如果成立,说明理由;如果不成立,试探究它们之间新的相等关系并证明.如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB=16.⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC(1)求C点坐标;(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.已知BC∥OA,∠B=∠A=100°.试回答下列问题:(1)如图1所示,求证:OB∥AC;(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数;(3)在(2)的条件下,若平行移动AC,如图3,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值。
(完整版)人教版初一下册数学期末压轴题试题培优试题

一、解答题1.如图,A 点的坐标为(0,3),B 点的坐标为(﹣3,0),D 为x 轴上的一个动点且不与B ,O 重合,将线段AD 绕点A 逆时针旋转90°得线段AE ,使得AE ⊥AD ,且AE =AD ,连接BE 交y 轴于点M .(1)如图,当点D 在线段OB 的延长线上时, ①若D 点的坐标为(﹣5,0),求点E 的坐标. ②求证:M 为BE 的中点. ③探究:若在点D 运动的过程中,OMBD的值是否是定值?如果是,请求出这个定值;如果不是,请说明理由.(2)请直接写出三条线段AO ,DO ,AM 之间的数量关系(不需要说明理由).2.已知AB ∥CD ,∠ABE 与∠CDE 的角分线相交于点F .(1)如图1,若BM 、DM 分别是∠ABF 和∠CDF 的角平分线,且∠BED =100°,求∠M 的度数;(2)如图2,若∠ABM =13∠ABF ,∠CDM =13∠CDF ,∠BED =α°,求∠M 的度数;(3)若∠ABM =1n ∠ABF ,∠CDM =1n∠CDF ,请直接写出∠M 与∠BED 之间的数量关系3.已知//AM CN ,点B 为平面内一点,AB BC 于B .(1)如图1,求证:90A C ∠+∠=︒;(2)如图2,过点B 作BD MA ⊥的延长线于点D ,求证:ABD C ∠=∠;(3)如图3,在(2)问的条件下,点E 、F 在DM 上,连接BE 、BF 、CF ,且BF 平分DBC ∠,BE 平分ABD ∠,若AFC BCF ∠=∠,3BFC DBE ∠=∠,求EBC ∠的度数.4.点A ,C ,E 在直线l 上,点B 不在直线l 上,把线段AB 沿直线l 向右平移得到线段CD .(1)如图1,若点E 在线段AC 上,求证:∠B +∠D =∠BED ;(2)若点E 不在线段AC 上,试猜想并证明∠B ,∠D ,∠BED 之间的等量关系; (3)在(1)的条件下,如图2所示,过点B 作PB //ED ,在直线BP ,ED 之间有点M ,使得∠ABE =∠EBM ,∠CDE =∠EDM ,同时点F 使得∠ABE =n ∠EBF ,∠CDE =n ∠EDF ,其中n ≥1,设∠BMD =m ,利用(1)中的结论求∠BFD 的度数(用含m ,n 的代数式表示). 5.如图1,已知直线m ∥n ,AB 是一个平面镜,光线从直线m 上的点O 射出,在平面镜AB 上经点P 反射后,到达直线n 上的点Q .我们称OP 为入射光线,PQ 为反射光线,镜面反射有如下性质:入射光线与平面镜的夹角等于反射光线与平面镜的夹角,即∠OPA=∠QPB .(1)如图1,若∠OPQ =82°,求∠OPA 的度数;(2)如图2,若∠AOP =43°,∠BQP =49°,求∠OPA 的度数;(3)如图3,再放置3块平面镜,其中两块平面镜在直线m 和n 上,另一块在两直线之间,四块平面镜构成四边形ABCD ,光线从点O 以适当的角度射出后,其传播路径为O→P→Q→R→O→P→…试判断∠OPQ 和∠ORQ 的数量关系,并说明理由. 6.已知,//AE BD ,A D ∠=∠. (1)如图1,求证://AB CD ;(2)如图2,作BAE ∠的平分线交CD 于点F ,点G 为AB 上一点,连接FG ,若CFG ∠的平分线交线段AG 于点H ,连接AC ,若ACE BAC BGM ∠=∠+∠,过点H 作HM FH ⊥交FG 的延长线于点M ,且3518E AFH ∠-∠=︒,求EAF GMH ∠+∠的度数.7.阅读下面文字:对于5231591736342⎛⎫⎛⎫⎛⎫-+-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭可以如下计算:原式()()()5231591736342⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-+++-+- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦()()()5231591736342⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-+-+-++-⎡⎤ ⎪ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎝⎭⎣⎦ 1014⎛⎫=+- ⎪⎝⎭114=-上面这种方法叫拆项法,你看懂了吗? 仿照上面的方法,计算: (1)115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭(2)235120192018201720163462⎛⎫⎛⎫-++-+ ⎪ ⎪⎝⎭⎝⎭8.下列等式:111122=-⨯,1112323=-⨯,1113434=-⨯,将以上三个等式两边分别相加得:1111111113111223342233444++=-+-+-=-=⨯⨯⨯. (1)观察发现:1n(1)n =+__________1111122334n(1)n ++++=⨯⨯⨯+ . (2)初步应用:利用(1)的结论,解决以下问题“①把112拆成两个分子为1的正的真分数之差,即112= ;②把112拆成两个分子为1的正的真分数之和,即112= ; ( 3 )定义“⊗”是一种新的运算,若1112126⊗=+,11113261220⊗=++,111114*********⊗=+++,求193⊗的值.9.我们知道,任意一个正整数x 都可以进行这样的分解:x m n =⨯(m ,n 是正整数,且m n ≤),在x 的所有这种分解中,如果m ,n 两因数之差的绝对值最小,我们就称m n⨯是x 的最佳分解,并规定:()=nf x m.例如:18可分解成118⨯,29⨯或36⨯,因为1819263->->-,所以36⨯是18的最佳分解,所以()311862f == (1)填空:()6f = ;()16=f ;(2)一个两位正整数t (10t a b =+,19a b ≤≤≤,a ,b 为正整数),交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为54,求出所有的两位正整数;并求()f t 的最大值; (3)填空:①()22357f ⨯⨯⨯= ;②()42357f ⨯⨯⨯= ;10.a 是不为1的有理数,我们把11a-称为a 的差倒数.如:2的差倒数是1112=--,现已知a 1=12,a 2是a 1的差倒数,a 3是a 2的差倒数,a 4是a 3的差倒数,… (1)求a 2,a 3,a 4的值;(2)根据(1)的计算结果,请猜想并写出a 2016•a 2017•a 2018的值; (3)计算:a 33+a 66+a 99+…+a 9999的值. 11.探究与应用: 观察下列各式: 1+3= 2 1+3+5= 2 1+3+5+7= 2 1+3+5+7+9= 2 ……问题:(1)在横线上填上适当的数; (2)写出一个能反映此计算一般规律的式子;(3)根据规律计算:(﹣1)+(﹣3)+(﹣5)+(﹣7)+…+(﹣2019).(结果用科学记数法表示)12.对非负实数x “四舍五入”到各位的值记为x <>.即:当n 为非负整数时,如果12n x -≤<1n 2+,则x n <>=;反之,当n 为非负整数时,如果x n <>=,则1122n x n -<+≤.例如: 00.480<>=<>=,0.64 1.491, 3.5 4.124<>=<>=<>=<>=. (1)计算: 1.87<>= ;π= ; (2)①求满足12x <->=的实数x 的取值范围, ②求满足43x x <>=的所有非负实数x 的值; (3)若关于x 的方程21122a x x -<>+-=-有正整数解,求非负实数a 的取值范围. 13.如图1,在平面直角坐标系中,A (a ,0)是x 轴正半轴上一点,C 是第四象限内一点,CB ⊥y 轴交y 轴负半轴于B (0,b ),且|a ﹣3|+(b+4)2=0,S 四边形AOBC =16.(1)求点C 的坐标.(2)如图2,设D 为线段OB 上一动点,当AD ⊥AC 时,∠ODA 的角平分线与∠CAE 的角平分线的反向延长线交于点P ,求∠APD 的度数;(点E 在x 轴的正半轴).(3)如图3,当点D 在线段OB 上运动时,作DM ⊥AD 交BC 于M 点,∠BMD 、∠DAO 的平分线交于N 点,则点D 在运动过程中,∠N 的大小是否会发生变化?若不变化,求出其值;若变化,请说明理由.14.如图,//MN GH ,点A 、B 分别在直线MN 、GH 上,点O 在直线MN 、GH 之间,若116NAO ∠=︒,144OBH ∠=︒.(1)AOB ∠= ︒;(2)如图2,点C 、D 是NAO ∠、GBO ∠角平分线上的两点,且35CDB ∠=︒,求ACD ∠ 的度数;(3)如图3,点F 是平面上的一点,连结FA 、FB ,E 是射线FA 上的一点,若MAE ∠=n OAE ∠,HBF n OBF ∠=∠,且60AFB ∠=︒,求n 的值.15.如图1,C 点是第二象限内一点, CB y ⊥轴于B ,且()0,B b 是y 轴正半轴上一点,(),0A a 是x 轴负半x 轴上一点,且()2230, 9AOBC a b S ++-==四边形.(1)A( ),B ( )(2)如图2,设D 为线段OB 上一动点,当AD AC ⊥时,ODA ∠的角平分线与CAE ∠的角平分线的反向延长线交于点P ,求APD ∠的度数: (注: 三角形三个内角的和为180) (3)如图3,当D 点在线段OB 上运动时,作DM AD ⊥交CB 于,,M BMD DAO ∠∠的平分线交于N ,当D 点在运动的过程中,N ∠的大小是否变化?若不变,求出其值;若变化,请说明理由.16.如图,数轴上两点A 、B 对应的数分别是﹣1,1,点P 是线段AB 上一动点,给出如下定义:如果在数轴上存在动点Q ,满足|PQ |=2,那么我们把这样的点Q 表示的数称为连动数,特别地,当点Q 表示的数是整数时我们称为连动整数.(1)﹣3,0,2.5是连动数的是 ;(2)关于x 的方程2x ﹣m =x +1的解满足是连动数,求m 的取值范围 ;(3)当不等式组11212()3x x a +⎧>-⎪⎨⎪+-⎩的解集中恰好有4个解是连动整数时,求a 的取值范围.17.在平面直角坐标系中,(,1)A a ,(,3)B b 满足()2120a b ++-=. (1)直接写出a 、b 的值:a = ;b = ;(2)如图1,若点(3,)P n 满足ABP △的面积等于6,求n 的值;(3)设线段AB 交y 轴于C ,动点E 从点C 出发,在y 轴上以每秒1个单位长度的速度向下运动,动点F 从点(8,0)-出发,在x 轴上以每秒2个单位长度的速度向右运动,若它们同时出发,运动时间为t 秒,问t 为何值时,有2ABEABFSS=?请求出t 的值.18.如图所示,在直角坐标系xoy 中,已知()6,0A ,()8,6B ,将线段OA 平移至CB ,连接OC 、AB 、CD 、BD ,且//OC AB ,点D 在x 轴上移动(不与点O 、A 重合).(1)直接写出点C 的坐标;(2)点D 在运动过程中,是否存在ODC △的面积是ABD △的面积的3倍,如果存在请求出点D 的坐标,如果不存在请说明理由;(3)点D 在运动过程中,请写出OCD ∠、ABD ∠、BDC ∠三者之间存在怎样的数量关系,并说明理由.19.历史上的数学巨人欧拉最先把关于x 的多项式用记号f(x)来表示.例如f(x)=x 2+3x -5,把x =某数时多项式的值用f(某数)来表示.例如x =-1时多项式x 2+3x -5的值记为f(-1)=(-1)2+3×(-1)-5=-7.(1)已知g(x)=-2x 2-3x +1,分别求出g(-1)和g(-2);(2)已知h(x)=ax 3+2x 2-ax -6,当h(12)=a ,求a 的值;(3)已知f(x)=2+3kx a -6x bk --2(a ,b 为常数),当k 无论为何值,总有f(1)=0,求a ,b 的值.20.某公园的门票价格如下表所示:某中学七年级(1)、(2)两个班计划去游览该公园,其中(I)班的人数较少,不足 50 人;(2) 班人数略多,有 50 多人.如果两个班都以班为单位分别购票,则一共应付 1172 元,如 果两个班联合起来,作为一个团体购票,则需付 1078 元. (1)列方程求出两个班各有多少学生;(2)如果两个班联合起来买票,是否可以买单价为 9 元的票?你有什么省钱的方法来帮 他们买票呢?请给出最省钱的方案.21.如图,//CD EF ,AE 是CAB ∠的平分线,α∠和β∠的度数满足方程组2250(1)3100(2)αβαβ∠+∠=︒⎧⎨∠-∠=︒⎩,(1)求α∠和β∠的度数; (2)求证://AB CD . (3)求C ∠的度数.22.数轴上有两个动点M ,N ,如果点M 始终在点N 的左侧,我们称作点M 是点N 的“追赶点”.如图,数轴上有2个点A ,B ,它们表示的数分别为-3,1,已知点M 是点N 的“追赶点”,且M ,N 表示的数分别为m ,n .(1)由题意得:点A 是点B 的“追赶点”,AB =1-(-3)=4(AB 表示线段AB 的长,以下相同);类似的,MN =____________.(2)在A ,M ,N 三点中,若其中一个点是另外两个点所构成线段的中点,请用含m 的代数式来表示n .(3)若AM =BN ,MN =43BM ,求m 和n 值.23.如果3个数位相同的自然数m ,n ,k 满足:m +n =k ,且k 各数位上的数字全部相同,则称数m 和数n 是一对“黄金搭档数”.例如:因为25,63,88都是两位数,且25+63=88,则25和63是一对“黄金搭档数”.再如:因为152,514,666都是三位数,且152+514=666,则152和514是一对“黄金搭档数”.(1)分别判断87和12,62和49是否是一对“黄金搭档数”,并说明理由;(2)已知两位数s 和两位数t 的十位数字相同,若s 和t 是一对“黄金搭档数”,并且s 与t 的和能被7整除,求出满足题意的s .24.在平面直角坐标系xOy 中,把线段AB 先向右平移h 个单位,再向下平移1个单位得到线段CD (点A 对应点C ),其中()(),,,A a b B m n 分别是第三象限与第二象限内的点.(1)若|3|10,2a b h ++=,求C 点的坐标;(2)若1b n =-,连接AD ,过点B 作AD 的垂线l ①判断直线l 与x 轴的位置关系,并说明理由;②已知E 是直线l 上一点,连接DE ,且DE 的最小值为1,若点B ,D 及点(),s t 都是关于x ,y 的二元一次方程(0)px qy k pq +=≠的解(),x y 为坐标的点,试判断()()s m t n -+-是正数、负数还是0?并说明理由.25.某小区准备新建60个停车位,以解决小区停车难的问题.已知新建2个地上停车位和3个地下停车位共需1.7万元:新建4个地上停车位和2个地下停车位共需1.4万元, (1)该小区新建1个地上停车位和1个地下停车位各需多少万元?(2)若该小区新建车位的投资金额超过14万元而不超过15万元,问共有几种建造方案? (3)对(2)中的几种建造方案中,哪种方案的投资最少?并求出最少投资金额. 26.阅读材料:关于x ,y 的二元一次方程ax+by=c 有一组整数解00x x y y =⎧⎨=⎩,则方程ax+by=c 的全部整数解可表示为00x x bty y at =-⎧⎨=+⎩(t 为整数).问题:求方程7x+19y=213的所有正整数解.小明参考阅读材料,解决该问题如下:解:该方程一组整数解为0069x y =⎧⎨=⎩,则全部整数解可表示为61997x ty t =-⎧⎨=+⎩(t 为整数).因为61909+70.t t ->⎧⎨>⎩,解得96719t -<<.因为t 为整数,所以t =0或-1.所以该方程的正整数解为69x y =⎧⎨=⎩和252x y =⎧⎨=⎩. (1)方程3x-5y=11的全部整数解表示为:253x ty t θ=+⎧⎨=+⎩(t 为整数),则θ= ;(2)请你参考小明的解题方法,求方程2x+3y=24的全部正整数解; (3)方程19x+8y=1908的正整数解有多少组? 请直接写出答案.27.在平面直角坐标系xOy 中,已知点M (a ,b ).如果存在点N (a ′,b ′),满足a ′=|a +b |,b ′=|a ﹣b |,则称点N 为点M 的“控变点”. (1)点A (﹣1,2)的“控变点”B 的坐标为 ;(2)已知点C (m ,﹣1)的“控变点”D 的坐标为(4,n ),求m ,n 的值;(3)长方形EFGH 的顶点坐标分别为(1,1),(5,1),(5,4),(1,4).如果点P (x ,﹣2x )的“控变点”Q 在长方形EFGH 的内部,直接写出x 的取值范围.28.请阅读求绝对值不等式3x <和3x >的解的过程.对于绝对值不等式3x <,从图1的数轴上看:大于3-而小于3的数的绝对值小于3,所以3x <的解为33x -<<;对于绝对值不等式3x >,从图2的数轴上看:小于3-或大于3的数的绝对值大于3,所以3x >的解为3x <-或3x >.(1)求绝对值不等式32x ->的解(2)已知绝对值不等式21x a -<的解为3b x <<,求2a b -的值(3)已知关于x ,y 的二元一次方程组234461x y m x y m -=-⎧⎨+=-+⎩的解满足2x y +≤,其中m 是负整数,求m 的值.29.阅读理解:定义:A ,B ,C 为数轴上三点,若点C 到点A 的距离是它到点B 的时距离的n (n 为大于1的常数)倍,则称点C 是(),A B 的n 倍点,且当C 是(),A B 的n 倍点或(),B A 的n 倍点时,我们也称C 是A 和B 两点的n 倍点.例如,在图1中,点C 是(),A B 的2倍点,但点C 不是(),B A 的2倍点.(1)特值尝试.①若2n =,图1中,点______是(),D C 的2倍点.(填A 或B )②若3n =,如图2,M ,N 为数轴上两个点,点M 表示的数是2-,点N 表示的数是4,数______表示的点是(),M N 的3倍点.(2)周密思考:图2中,一动点P 从N 出发,以每秒2个单位的速度沿数轴向左运动t 秒,若P 恰好是M 和N 两点的n 倍点,求所有符合条件的t 的值.(用含n 的式子表示)(3)拓展应用数轴上两点间的距离不超过30个单位长度时,称这两点处于“可视距离”.若(2)中满足条件的M 和N 两点的所有n 倍点P 均处于点N 的“可视距离”内,请直接写出n 的取值范围.(不必写出解答过程)30.在平面直角坐标系中,点A ,B 的坐标分别为(﹣1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD .(1)求点C ,D 的坐标及四边形ABDC 的面积S 四边形ABDC ;(2)在y 轴上是否存在一点P ,连接PA ,PB ,使S △PAB =S 四边形ABDC ?若存在这样一点,求出点P 的坐标;若不存在,试说明理由;(3)点P 是直线BD 上一个动点,连接PC 、PO ,当点P 在直线BD 上运动时,请直接写出∠OPC 与∠PCD 、∠POB 的数量关系【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)①E (3,﹣2)②见解析;③12OM BD =,理由见解析;(2)OD+OA =2AM 或OA ﹣OD =2AM【分析】(1)①过点E 作EH ⊥y 轴于H .证明△DOA ≌△AHE (AAS )可得结论.②证明△BOM ≌△EHM (AAS )可得结论.③是定值,证明△BOM ≌△EHM 可得结论.(2)根据点D 在点B 左侧和右侧分类讨论,分别画出对应的图形,根据全等三角形的判定及性质即可分别求出结论.【详解】解:(1)①过点E作EH⊥y轴于H.∵A(0,3),B(﹣3,0),D(﹣5,0),∴OA=OB=3,OD=5,∵∠AOD=∠AHE=∠DAE=90°,∴∠DAO+∠EAH=90°,∠EAH+∠AEH=90°,∴∠DAO=∠AEH,∴△DOA≌△AHE(AAS),∴AH=OD=5,EH=OA=3,∴OH=AH﹣OA=2,∴E(3,﹣2).②∵EH⊥y轴,∴∠EHO=∠BOH=90°,∵∠BMO=∠EMH,OB=EH=3,∴△BOM≌△EHM(AAS),∴BM=EM.③结论:OMBD=12.理由:∵△DOA≌△AHE,∴OD=AH,∵OA=OB,∴BD=OH,∵△BOM≌△EHM,∴OM=MH,∴OM=12OH=12BD.(2)结论:OA+OD=2AM或OA﹣OD=2AM.理由:当点D在点B左侧时,∵△BOM≌△EHM,△DOA≌△AHE∴OM=MH,OD=AH∴OH=2OM,OD-OB=AH-OA∴BD=OH∴BD=2OM,∴OD ﹣OA =2(AM ﹣AO ),∴OD+OA =2AM .当点D 在点B 右侧时,过点E 作EH ⊥y 轴于点H∵∠AOD =∠AHE =∠DAE =90°,∴∠DAO+∠EAH =90°,∠EAH+∠AEH =90°,∴∠DAO =∠AEH ,∵AD=AE∴△DOA ≌△AHE (AAS ),∴EH=AO=3=OB ,OD=AH∴∠EHO =∠BOH =90°,∵∠BMO =∠EMH ,OB =EH =3,∴△BOM ≌△EHM (AAS ),∴OM =MH∴OA +OD= OA +AH=OH=OM +MH=2MH=2(AM +AH )=2(AM +OD )整理可得OA ﹣OD =2AM .综上:OA+OD =2AM 或OA ﹣OD =2AM .【点睛】此题考查的是全等三角形的判定及性质、旋转的性质和平面直角坐标系,掌握全等三角形的判定及性质、旋转的性质和点的坐标与线段长度的关系是解决此题的关键.2.(1)65°;(2)3606α︒-︒;(3)2n ∠M +∠BED =360° 【分析】(1)首先作EG ∥AB ,FH ∥AB ,连结MF ,利用平行线的性质可得∠ABE +∠CDE =260°,再利用角平分线的定义得到∠ABF +∠CDF =130°,从而得到∠BFD 的度数,再根据角平分线的定义和三角形外角的性质可求∠M 的度数;(2)先由已知得到∠ABE =6∠ABM ,∠CDE =6∠CDM ,由(1)得∠ABE +∠CDE =360°-∠BED ,∠M =∠ABM +∠CDM ,等量代换即可求解;(3)由(2)的方法可得到2n ∠M +∠BED =360°.【详解】解:(1)如图1,作//EG AB ,//FH AB ,连结MF ,//AB CD ,//////EG AB FH CD ∴,ABF BFH ∴∠=∠,CDF DFH ∠=∠,180ABE BEG ∠+∠=︒,180GED CDE ∠+∠=︒, 360ABE BEG GED CDE ∴∠+∠+∠+∠=︒,100BED BEG DEG ∠=∠+∠=︒,260ABE CDE ∴∠+∠=︒,ABE ∠和CDE ∠的角平分线相交于E ,130ABF CDF ∴∠+∠=︒,130BFD BFH DFH ∴∠=∠+∠=︒, BM 、DM 分别是ABF ∠和CDF ∠的角平分线,12MBF ABF ∴∠=∠,12MDF CDF ∠=∠, 65MBF MDF ∴∠+∠=︒,1306565BMD ∴∠=︒-︒=︒;(2)如图1,13ABM ABF ∠=∠,13CDM CDF ∠=∠, 3ABF ABM ∴∠=∠,3CDF CDM ∠=∠,ABE ∠与CDE ∠两个角的角平分线相交于点F ,6ABE ABM ∴∠=∠,6CDE CDM ∠=∠,66360ABM CDM BED ∴∠+∠+∠=︒,BMD ABM CDM ∠=∠+∠,6360BMD BED ∴∠+∠=︒,3606BMD α︒-︒∴∠=; (3)由(2)结论可得,22360n ABM n CDM E ∠+∠+∠=︒,M ABM CDM ∠=∠+∠, 则2360n M BED ∠+∠=︒.【点睛】本题主要考查了平行线的性质和四边形的内角和,关键在于掌握两直线平行同位角相等,内错角相等,同旁内角互补的性质.3.(1)见解析;(2)见解析;(3)︒=∠105EBC .【分析】(1)先根据平行线的性质得到C BDA ∠=∠,然后结合AB BC ⊥即可证明;(2)过B 作//BH DM ,先说明ABD CBH ∠=∠,然后再说明//BH NC 得到CBH C ∠=∠,最后运用等量代换解答即可;(3)设∠DBE =a ,则∠BFC =3a ,根据角平分线的定义可得∠ABD =∠C =2a ,∠FBC =12∠DBC =a +45°,根据三角形内角和可得∠BFC +∠FBC +∠BCF =180°,可得∠AFC =∠BCF 的度数表达式,再根据平行的性质可得∠AFC +∠NCF =180°,代入即可算出a 的度数,进而完成解答.【详解】(1)证明:∵//AM CN ,∴C BDA ∠=∠,∵AB BC ⊥于B , ∴90B ∠=︒,∴90A BDA ∠+∠=︒,∴90A C ∠+∠=︒;(2)证明:过B 作//BH DM ,∵BD MA ⊥,∴90ABD ABH ∠+∠=︒,又∵AB BC ⊥,∴90ABH CBH ∠+∠=︒,∴ABD CBH ∠=∠,∵//BH DM ,//AM CN∴//BH NC ,∴CBH C ∠=∠,∴ABD C ∠=∠;(3)设∠DBE =a ,则∠BFC =3a ,∵BE 平分∠ABD ,∴∠ABD =∠C =2a ,又∵AB ⊥BC ,BF 平分∠DBC ,∴∠DBC =∠ABD +∠ABC =2a +90,即:∠FBC =12∠DBC =a +45°又∵∠BFC +∠FBC +∠BCF =180°,即:3a +a +45°+∠BCF =180°∴∠BCF =135°-4a ,∴∠AFC =∠BCF =135°-4a ,又∵AM//CN,∴∠AFC+∠NCF=180°,即:∠AFC+∠BCN+∠BCF=180°,∴135°-4a+135°-4a+2a=180,解得a=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.【点睛】本题主要考查了平行线的性质、角平分线的性质及角的计算,熟练应用平行线的性质、角平分线的性质是解答本题的关键.4.(1)见解析;(2)当点E在CA的延长线上时,∠BED=∠D-∠B;当点E在AC的延长线上时,∠BED=∠BET-∠DET=∠B-∠D;(3)()12m nn-【分析】(1)如图1中,过点E作ET∥A B.利用平行线的性质解决问题.(2)分两种情形:如图2-1中,当点E在CA的延长线上时,如图2-2中,当点E在AC的延长线上时,构造平行线,利用平行线的性质求解即可.(3)利用(1)中结论,可得∠BMD=∠ABM+∠CDM,∠BFD=∠ABF+∠CDF,由此解决问题即可.【详解】解:(1)证明:如图1中,过点E作ET∥A B.由平移可得AB∥CD,∵AB∥ET,AB∥CD,∴ET∥CD∥AB,∴∠B=∠BET,∠TED=∠D,∴∠BED=∠BET+∠DET=∠B+∠D.(2)如图2-1中,当点E在CA的延长线上时,过点E作ET∥A B.∵AB∥ET,AB∥CD,∴ET∥CD∥AB,∴∠B=∠BET,∠TED=∠D,∴∠BED=∠DET-∠BET=∠D-∠B.如图2-2中,当点E在AC的延长线上时,过点E作ET∥A B.∵AB ∥ET ,AB ∥CD ,∴ET ∥CD ∥AB ,∴∠B =∠BET ,∠TED =∠D ,∴∠BED =∠BET -∠DET =∠B -∠D .(3)如图,设∠ABE =∠EBM =x ,∠CDE =∠EDM =y ,∵AB ∥CD ,∴∠BMD =∠ABM +∠CDM ,∴m =2x +2y ,∴x +y =12m ,∵∠BFD =∠ABF +∠CDF ,∠ABE =n ∠EBF ,∠CDE =n ∠EDF ,∴∠BFD =()111n n n x y x y n n n ---+=+=112n m n -⨯=()12m n n-. 【点睛】本题属于几何变换综合题,考查了平行线的性质,角平分线的定义等知识,解题的关键是学会条件常用辅助线,构造平行线解决问题,属于中考常考题型.5.(1)49°,(2)44°,(3)∠OPQ =∠ORQ【分析】(1)根据∠OPA =∠QP B .可求出∠OPA 的度数;(2)由∠AOP =43°,∠BQP =49°可求出∠OPQ 的度数,转化为(1)来解决问题; (3)由(2)推理可知:∠OPQ =∠AOP +∠BQP ,∠ORQ =∠DOR +∠RQC ,从而∠OPQ =∠ORQ .【详解】解:(1)∵∠OPA =∠QPB ,∠OPQ =82°,∴∠OPA =(180°-∠OPQ )×12=(180°-82°)×12=49°,(2)作PC ∥m ,∵m ∥n ,∴m ∥PC ∥n ,∴∠AOP =∠OPC =43°,∠BQP =∠QPC =49°,∴∠OPQ =∠OPC +∠QPC =43°+49°=92°,∴∠OPA =(180°-∠OPQ )×12=(180°-92°)×1244°,(3)∠OPQ =∠ORQ .理由如下:由(2)可知:∠OPQ =∠AOP +∠BQP ,∠ORQ =∠DOR +∠RQC ,∵入射光线与平面镜的夹角等于反射光线与平面镜的夹角,∴∠AOP =∠DOR ,∠BQP =∠RQC ,∴∠OPQ =∠ORQ .【点睛】本题主要考查了平行线的性质和入射角等于反射角的规定,解决本题的关键是注意问题的设置环环相扣、前为后用的设置目的.6.(1)见解析;(2)72︒【分析】(1)根据平行线的性质得出180A B ∠+∠=︒,再根据等量代换可得180B D ∠+∠=︒,最后根据平行线的判定即可得证;(2)过点E 作//EP CD ,延长DC 至Q ,过点M 作//MN AB ,根据平行线的性质及等量代换可得出ECQ BGM DFG ∠=∠=∠,再根据平角的含义得出ECF CFG ∠=∠,然后根据平行线的性质及角平分线的定义可推出,BHF CFH CFA FAB ∠=∠∠=∠;设,FAB CFH αβ∠=∠=,根据角的和差可得出2AEC AFH ∠=∠,结合已知条件35180AEC AFH ∠-∠=︒可求得18AFH ∠=︒,最后根据垂线的含义及平行线的性质,即可得出答案.【详解】(1)证明://AE BD180A B ∴∠+∠=︒A D ∠=∠180B D ∴∠+∠=︒//AB CD ∴;(2)过点E 作//EP CD ,延长DC 至Q ,过点M 作//MN AB//AB CDQCA CAB ∴∠=∠,BGM DFG ∠=∠,CFH BHF ∠=∠,CFA FAG ∠=ACE BAC BGM ∠=∠+∠ECQ QCA BAC BGM ∴∠+∠=∠+∠ECQ BGM DFG ∴∠=∠=∠180,180ECQ ECD DFG CFG ∠+=︒∠+=︒ECF CFG ∴∠=∠//AB CD//AB EP ∴,PEA EAB PEC ECF ∴∠=∠∠=∠AEC PEC PEA ∠=∠-∠AEC ECF EAB ∴∠=∠-∠ECF AEC EAB ∴∠=∠+∠AF 平分BAE ∠12EAF FAB EAB ∴∠=∠=∠ FH 平分CFG ∠12CFH HFG CFG ∴∠=∠=∠ //CD AB,BHF CFH CFA FAB ∴∠=∠∠=∠设,FAB CFH αβ∠=∠=AFH CFH CFA CFH FAB ∠=∠-∠=∠-∠AFH βα∴∠=-,BHF CFH β∠=∠=222ECF AFH AEC EAB AFH AEC β∴∠+∠=∠+∠+∠=∠+22ECF AFH E BHF ∴∠+∠=∠+∠2AEC AFH ∴∠=∠35180AEC AFH ∠-∠=︒18AFH ∴∠=︒FH HM ⊥90FHM ∴∠=︒90GHM β∴∠=︒-180CFM NMF ∠+∠=︒90HMB HMN β∴∠=∠=︒-EAF FAB ∠=∠18EAF CFA CFH AFH β∴∠=∠=∠-∠=-︒189072EAF GMH ββ∴∠+∠=-︒+︒-=︒72EAF GMH ∴∠+∠=︒.【点睛】本题考查了平行线的判定及性质,角平分线的定义,能灵活根据平行线的性质和判定进行推理是解此题的关键.7.(1)14-(2)124- 【分析】(1)根据例子将每项的整数部分相加,分数部分相加即可解答;(2)根据例子将每项的整数部分相加,分数部分相加即可解答.【详解】(1)115112744362⎛⎫⎛⎫-+-++- ⎪ ⎪⎝⎭⎝⎭()115112744362⎛⎫=--+-+--+- ⎪⎝⎭ 104⎛⎫=+- ⎪⎝⎭ 14=- (2)原式()235120192018201720163462⎛⎫=-+-++-+-+ ⎪⎝⎭ 124⎛⎫=-+- ⎪⎝⎭ 124=- 【点睛】此题考察新计算方法,正确理解题意是解题的关键,根据例子即可仿照计算.8.(1)111n n -+;1n n +;(2)①1341-;②112424+;( 3 )14. 【分析】(1)利用材料中的“拆项法”解答即可;(2)①先变形为111234=⨯,再利用(1)中的规律解题;②先变形为121224=,再逆用分数的加法法则即可分解;(3)按照定义“⊗”法则表示出193⊗,再利用(1)中的规律解题即可. 【详解】解:(1)观察发现:()11n n =+111n n -+, 1111122334(1)n n ++++⨯⨯⨯+ =11111111223341n n -+-+-+⋯+-+ =111n -+ =1n n +; 故答案是:111n n -+;1n n +. (2)初步应用: ①111234=⨯=1134-; ②121112242424==+; 故答案是:1134-;112424+. ( 3 )由定义可知:193⊗=11111111112203042567290110132++++++++ =455111111611311412-+-+-+⋯+- =13211- =14. 故193⊗的值为14. 【点睛】考查了有理数运算中的规律型问题:数字的变化规律,有理数的混合运算.本题是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.9.(1)23,1;(2)两位正整数为39,28,17,()f t 的最大值为47;(3)①2021;②2021【分析】(1)仿照样例进行计算即可;(2)由题设可以看出交换前原数的十位上数字为a ,个位上数字为b ,则原数可以表示为10a+b ,交换后十位上数字为b ,个位上数字为a ,则交换后数字可以表示为10b+a ,根据“交换其个位上的数字与十位上的数字得到的新数减去原数所得的差为54”确定出a 与b 的关系式,进而求出所有的两位数,然后求解确定出()f t 的最大值即可;(3)根据样例分解计算即可.【详解】解:(1)61623=⨯=⨯,∵6132->-,∴()263f =; 161162844=⨯=⨯=⨯∵1618244->->-,∴()161f =, 故答案为:23;1; (2)由题意可得:交换后的数减去交换前的数的差为:10109()54b a a b b a +--=-=,∴6b a -=,∵19a b ≤≤≤,∴93b a ==,或82b a ==,或71b a ==,,∴t 为39,28,17;∵39=1×39=3×13,∴()33913f =; 28=1×28=2×14=4×7,∴()28f =47; 17=1×17,∴()11717f =; ∴()f t 的最大值47. (3)①∵223572021⨯⨯⨯=⨯∴()220235721f ⨯⨯⨯=; ②423574042⨯⨯⨯=⨯∴()4402023574221f⨯⨯⨯==;故答案为:2021;2021【点睛】本题主要考查了有理数的运算,理解最佳分解的定义,并将其转化为有理数的运算是解题的关键.10.(1)a2=2,a3=-1,a4=1 2(2)a2016•a2017•a2018= -1(3)a33+a66+a99+…+a9999=-1【分析】(1)将a1=12代入11a-中即可求出a2,再将a2代入求出a3,同样求出a4即可.(2)从(1)的计算结果可以看出,从a1开始,每三个数一循环,而2016÷3=672,则a2016=-1,a2017=12,a2018=2然后计算a2016•a2017•a2018的值;(3)观察可得a3、a6、a9、…a99,都等于-1,将-1代入,即可求出结果.【详解】(1)将a1=12,代入11a-,得21=211-2a=;将a2=2,代入11a-,得31=-11-2a=;将a3=-1,代入11a-,得411=1--12a=().(2)根据(1)的计算结果,从a1开始,每三个数一循环,而2016÷3=672,则a2016=-1,a2017=12,a2018=2所以,a2016•a2017•a2018=(-1)×12×2= -1(3)观察可得a3、a6、a9、…a99,都等于-1,将-1代入,a33+a66+a99+…+a9999=(-1)3+(-1)6+(-1)9+…+(-1)99=(-1)+1+(-1)+…(-1)=-1【点睛】此类问题考查了数字类的变化规律,解题的关键是要严格根据定义进行解答,同时注意分析循环的规律.11.(1)2、3、4、5;(2)第n个等式为1+3+5+7+…+(2n+1)=n2;(3)﹣1.008016×106.【分析】(1) 根据从1开始连续n 各奇数的和等于奇数的个数的平方即可得到.(2) 根据规律写出即可.(3) 先提取符号,再用规律解题.【详解】解:(1)1+3=221+3+5=321+3+5+7=421+3+5+7+9=52……故答案为:2、3、4、5;(2)第n 个等式为1+3+5+7+…+(2n+1)=2(1)n +(3)原式=﹣(1+3+5+7+9+ (2019)=﹣10102=﹣1.0201×106.【点睛】本题考查数字变化规律,解题的关键是找到第一个的规律,然后加以运用即可.12.(1)2,3 (2)①5722x ≤<②330,,42 (3)00.5a ≤< 【分析】(1)根据新定义的运算规则进行计算即可;(2)①根据新定义的运算规则即可求出实数x 的取值范围;②根据新定义的运算规则和43x 为整数,即可求出所有非负实数x 的值; (3)先解方程求得22x a =-<>,再根据方程的解是正整数解,即可求出非负实数a 的取值范围.【详解】 (1) 1.87<>=2;π=3;(2)①∵12x <->= ∴1121222x --<+≤ 解得5722x ≤<; ②∵43x x <>=∴41413232x x x -<+≤ 解得3322x -<≤ ∵43x 为整数∴333,0,,442x =- 故所有非负实数x 的值有330,,42; (3)21122a x x -<>+-=- 1241a x x -<>+-=-22x a =-<>∵方程的解为正整数∴21a -<>=或2①当21a -<>=时,2x =是方程的增根,舍去②当22a -<>=时,00.5a ≤<.【点睛】本题考查了新定义下的运算问题,掌握新定义下的运算规则是解题的关键.13.(1) C (5,﹣4);(2)90°;(3)见解析.【详解】分析:(1)利用非负数的和为零,各项分别为零,求出a ,b 即可;(2)用同角的余角相等和角平分线的意义即可;(3)利用角平分线的意义和互余两角的关系简单计算证明即可.详解:(1)∵(a ﹣3)2+|b+4|=0,∴a ﹣3=0,b+4=0,∴a=3,b=﹣4,∴A (3,0),B (0,﹣4),∴OA=3,OB=4,∵S 四边形AOBC =16.∴0.5(OA+BC )×OB=16,∴0.5(3+BC )×4=16,∴BC=5,∵C 是第四象限一点,CB ⊥y 轴,∴C (5,﹣4);(2)如图,延长CA ,∵AF 是∠CAE 的角平分线,∴∠CAF=0.5∠CAE ,∵∠CAE=∠OAG ,∴∠CAF=0.5∠OAG,∵AD⊥AC,∴∠DAO+∠OAG=∠PAD+∠PAG=90°,∵∠AOD=90°,∴∠DAO+∠ADO=90°,∴∠ADO=∠OAG,∴∠CAF=0.5∠ADO,∵DP是∠ODA的角平分线,∴∠ADO=2∠ADP,∴∠CAF=∠ADP,∵∠CAF=∠PAG,∴∠PAG=∠ADP,∴∠APD=180°﹣(∠ADP+∠PAD)=180°﹣(∠PAG+∠PAD)=180°﹣90°=90°即:∠APD=90°(3)不变,∠ANM=45°理由:如图,∵∠AOD=90°,∴∠ADO+∠DAO=90°,∵DM⊥AD,∴∠ADO+∠BDM=90°,∴∠DAO=∠BDM,∵NA是∠OAD的平分线,∴∠DAN=0.5∠DAO=0.5∠BDM,∵CB⊥y轴,∴∠BDM+∠BMD=90°,∴∠DAN=0.5(90°﹣∠BMD),∵MN是∠BMD的角平分线,∴∠DMN=0.5∠BMD,∴∠DAN+∠DMN=0.5(90°﹣∠BMD)+0.5∠BMD=45°在△DAM中,∠ADM=90°,∴∠DAM+∠DMA=90°,在△AMN中,∠ANM=180°﹣(∠NAM+∠NMA)=180°﹣(∠DAN+∠DAM+∠DMN+∠DMA)=180°﹣[(∠DAN+DMN)+(∠DAM+∠DMA)] =180°﹣(45°+90°)=45°,∴D点在运动过程中,∠N的大小不变,求出其值为45°点睛:此题是四边形综合题,主要考查了非负数的性质,四边形面积的计算方法,角平分线的意义,解本题的关键是用整体的思想解决问题,也是本题的难点.14.(1)100;(2)75°;(3)n =3.【分析】(1)如图:过O 作OP //MN ,由MN //OP //GH 得∠NAO +∠POA =180°,∠POB +∠OBH =180°,即∠NAO +∠AOB +∠OBH =360°,即可求出∠AOB ;(2)如图:分别延长AC 、CD 交GH 于点E 、F ,先根据角平分线求得58NAC ∠=︒,再根据平行线的性质得到58CEF ∠=︒;进一步求得18DBF ∠=︒,17DFB ∠=︒,然后根据三角形外角的性质解答即可;(3)设BF 交MN 于K ,由∠NAO =116°,得∠MAO =64°,故∠MAE =641n n ︒⨯+,同理∠OBH =144°,∠HBF =n ∠OBF ,得∠FBH =1441n n ︒⨯+,从而=n BKA FBH n ∠∠=⨯︒+1441,又∠FKN =∠F +∠FAK ,得144606411n n n n ︒︒︒⨯=+⨯++,即可求n . 【详解】解:(1)如图:过O 作OP //MN ,∵MN //GHl∴MN //OP //GH∴∠NAO +∠POA =180°,∠POB +∠OBH =180°∴∠NAO +∠AOB +∠OBH =360°∵∠NAO =116°,∠OBH =144°∴∠AOB =360°-116°-144°=100°;(2)分别延长AC 、CD 交GH 于点E 、F ,∵AC 平分NAO ∠且116NAO ∠=︒,∴58NAC ∠=︒,又∵MN //GH ,∴58CEF ∠=︒;∵144OBH ∠=︒,36OBG ∠=︒∵BD 平分OBG ∠,∴18DBF ∠=︒,又∵,CDB ∠=︒35∴351817DFB CDB DBF ∠=∠-∠=-=︒;∴175875ACD DFB AEF ∠=∠+∠=︒+︒=︒;(3)设FB 交MN 于K ,∵116NAO ∠=︒,则MAO ∠=︒64; ∴641n MAE n ∠=⨯︒+ ∵144OBH ∠=︒, ∴+1n FBH n ∠=⨯︒144,=n BKA FBH n ∠∠=⨯︒+1441, 在△FAK 中,64601n BKA FKA F n ∠=∠+∠=⨯︒+︒+, ∴144646011n n n n ⨯︒=⨯︒+︒++, ∴3n =.经检验:3n =是原方程的根,且符合题意.【点睛】本题主要考查平行线的性质及应用,正确作出辅助线、构造平行线、再利用平行线性质进行求解是解答本题的关键.15.(1)A (-2,0)、B (0,3);(2)∠APD=90°;(3)∠N 的大小不变,∠N=45°【分析】(1)利用非负数的和为零,各项分别为零,求出a ,b 的值;(2)如图,作DM ∥x 轴,结合题意可设∠ADP=∠OAP=x ,∠EAF=∠CAF=∠OAP=y ,根据平角的定义可知∠OAD=90°-2y ,由平行线的性质可得∠OAD+∠ADM=180°,即90-2y+2x+90°=180°,进而可得出x=y ,再结合图形即可得出∠APD 的度数;(3)∠N 的大小不变,∠N=45°,如图,过D 作DE ∥BC ,过N 作NF ∥BC ,根据平行线的性质可知∠BMD+∠OAD=∠ADM=90°,然后根据角平分线的定义和平行线的性质,可得∠ANM=12∠BMD+12∠OAD ,据此即可得到结论. 【详解】(1)由()2230a b ++-=,可得20a 和230b ,解得2,3a b =-=∴A 的坐标是(-2,0)、B 的坐标是(0,3);(2)如图,作DM ∥x 轴根据题意,设∠ADP=∠OAP=x,∠EAF=∠CAF=∠OAP=y,∵∠CAD=90°,∴∠CAE+∠OAD=90°,∴2y+∠OAD=90°,∴∠OAD=90°-2y,∵DM∥x轴,∴∠OAD+∠ADM=180°,∴90-2y+2x+90°=180°,∴x=y,∴∠APD=180°-(∠PAD+∠ADP)=180°-(y+90°-2y+x)=180°-90°=90°(3)∠N的大小不变,∠N=45°理由:如图,过D作DE∥BC,过N作NF∥BC.∵BC∥x轴,∴DE∥BC∥x轴,NF∥BC∥x轴,∴∠EDM=∠BMD,∠EDA=∠OAD,∵DM⊥AD,∴∠ADM=90°,∴∠BMD+∠OAD=∠EDM+∠EDA=∠ADM=90°,∵MN平分∠BMD,AN平分∠DAO,∴∠BMN=12∠BMD,∠OAN=12∠OAD,∴∠ANM=∠BMN+∠OAN=12∠BMD+12∠OAD=12×90°=45°.【点睛】本题考查了坐标与图形性质:利用点的坐标计算出相应的线段的长和判断线段与坐标轴的位置关系.也考查了三角形内角和定理和三角形外角性质.16.(1)﹣3,2.5;(2)﹣4<m <﹣2或0<m <2;(3)1≤a <2.【分析】(1)根据连动数的定义逐一判断即得答案;(2)先求得方程的解,再根据连动数的定义得出相应的不等式组,解不等式组即可求出结果;(3)先解不等式组中的每个不等式,再根据连动整数的概念得到关于a 的不等式组,解不等式组即可求得答案.【详解】解:(1)设点P 表示的数是x ,则11x -≤≤,若点Q 表示的数是﹣3,由2PQ =可得()32x --=,解得:x =﹣1或﹣5,所以﹣3是连动数;若点Q 表示的数是0,由2PQ =可得02x -=,解得:x =2或﹣2,所以0不是连动数; 若点Q 表示的数是2.5,由2PQ =可得 2.52x -=,解得:x =﹣0.5或4.5,所以2.5是连动数;所以﹣3,0,2.5是连动数的是﹣3,2.5,故答案为:﹣3,2.5;(2)解关于x 的方程2x ﹣m =x +1得:x =m +1,∵关于x 的方程2x ﹣m =x +1的解满足是连动数,∴112112m m ---<⎧⎨-->⎩或112112m m +-<⎧⎨++>⎩, 解得:﹣4<m <﹣2或0<m <2;故答案为:﹣4<m <﹣2或0<m <2;(3)()112123x x a +⎧>-⎪⎨⎪+-≤⎩①②, 解不等式①,得x >﹣3,解不等式②,得x ≤1+a ,∵不等式组()112123x x a +⎧>-⎪⎨⎪+-≤⎩的解集中恰好有4个解是连动整数, ∴四个连动整数解为﹣2,﹣1,1,2,∴2≤1+a <3,解得:1≤a <2,∴a 的取值范围是1≤a <2.【点睛】本题是新定义试题,以数轴为载体,主要考查了一元一次不等式组,正确理解连动数与连动整数、列出相应的不等式组是解题的关键.17.(1)1-,2;(2)233n =或13-;(3)225t =或2。
(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案doc

(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案doc一、解答题1.先化简,再求值:(a -1)(2a +1)+(1+a )(1-a ),其中a =2.2.已知:如图EF ∥CD ,∠1+∠2=180°.(1)试说明GD ∥CA ;(2)若CD 平分∠ACB ,DG 平分∠CDB ,且∠A =40°,求∠ACB 的度数.3.已知:方程组2325x y a x y +=-⎧⎨+=⎩,是关于x 、y 的二元一次方程组. (1)求该方程组的解(用含a 的代数式表示);(2)若方程组的解满足0x <,0y >,求a 的取值范围.4.因式分解:(1)16x 2-9y 2(2)(x 2+y 2)2-4x 2y 25.如图,△ABC 的顶点都在方格纸的格点上,将△ABC 向下平移3格,再向右平移4格.(1)请在图中画出平移后的△A′B′C′;(2)在图中画出△A′B′C′的高C′D′.6.疫情初期,武汉物资告急,全国一心,各地纷纷运送物资到武汉.已知3辆大货车与2辆小货车可以一次运货17吨,5辆大货车与4辆小货车可以一次运货29吨,则2辆大货车与1辆小货车可以一次运货多少吨?7.计算(1)(π-3.14)0-|-3|+(12)1--(-1)2012 (2) (-2a 2)3+(a 2)3-4a .a 5(3)x (x+7)-(x-3)(x+2)(4)(a-2b-c )(a+2b-c )8.阅读下列各式:(a•b )2=a 2b 2,(a•b )3=a 3b 3,(a•b )4=a 4b 4…回答下列三个问题:(1)验证:(2×12)100= ,2100×(12)100= ; (2)通过上述验证,归纳得出:(a•b )n = ; (abc )n = .(3)请应用上述性质计算:(﹣0.125)2017×22016×42015.9.在南通市中小学标准化建设工程中,某校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)求每台电脑、每台电子白板各多少万元;(2)根据学校实际,需购进电脑和电子白板共31台,若总费用不超过30万元,则至多购买电子白板多少台?10.如图,在边长为1个单位长度的小正方形网格中,ΔABC 经过平移后得到ΔA B C ''',图中标出了点B 的对应点B ',点A '、C '分别是A 、C 的对应点.(1)画出平移后的ΔA B C ''';(2)连接BB '、CC ',那么线段BB '与CC '的关系是_________;(3)四边形BCC B ''的面积为_______.11.计算:(1)2201(2)3()3----÷- (2)22(21)(21)x x -+ 12.如图1是一个长为 4a ,宽为 b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).(1)图2中的阴影部分的面积为 ;(2)观察图2请你写出 ()2a b +,()2a b -,ab 之间的等量关系是 ;(3)根据(2)中的结论,若 6x y +=,114x y ⋅=,则 x y -= ;(4)实际上我们可以用图形的面积表示许多恒等式,下面请你设计一个几何图形来表示恒等式()()2222252a b a b a ab b ++=++.在图形上把每一部分的面积标写清楚. 13.(问题背景)(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B =∠C+∠D(简单应用)(2)如图2,AP 、CP 分别平分∠BAD 、∠BCD ,若∠ABC =28°,∠ADC =20°,求∠P 的度数(可直接使用问题(1)中的结论)(问题探究)(3)如图3,直线BP 平分∠ABC 的外角∠FBC ,DP 平分∠ADC 的外角∠ADE ,若∠A =30°,∠C =18°,则∠P 的度数为(拓展延伸)(4)在图4中,若设∠C =x ,∠B =y ,∠CAP =14∠CAB ,∠CDP =14∠CDB ,试问∠P 与∠C 、∠B 之间的数量关系为 (用x 、y 表示∠P )(5)在图5中,BP平分∠ABC,DP平分∠ADC的外角∠ADE,猜想∠P与∠A、∠C的关系,直接写出结论.14.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)(1)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是;(2)根据(1)中的结论,若x+y=5,x•y=94,则x﹣y=;(3)拓展应用:若(2019﹣m)2+(m﹣2020)2=15,求(2019﹣m)(m﹣2020)的值.15.(类比学习)小明同学类比除法240÷16=15的竖式计算,想到对二次三项式x2+3x+2进行因式分解的方法:15 162401 680802221322222xx x xx xxx+++++++即(x 2+3x +2)÷(x +1)=x +2,所以x 2+3x +2=(x +1)(x +2).(初步应用)小明看到了这样一道被墨水污染的因式分解题:x 2+□x +6=(x +2)(x +☆),(其中□、☆代表两个被污染的系数),他列出了下列竖式: 22262 (2)62 0x x x x x x x x +++++-++☆☆☆ 得出□=___________,☆=_________.(深入研究)小明用这种方法对多项式x 2+2x 2-x -2进行因式分解,进行到了:x 3+2x 2-x -2=(x +2)(*).(*代表一个多项式),请你利用前面的方法,列出竖式,将多项式x 3+2x 2-x -2因式分解.16.已知关于x 、y 的方程组354526x y ax by -=⎧⎨+=-⎩与2348x y ax by +=-⎧⎨-=⎩有相同的解,求a 、b 的值.17.先化简,再计算:(2a +b )(b -2a )-(a -b )2,其中a =-1,b =-218.计算:(1)(12)﹣3﹣20160﹣|﹣5|; (2)(3a 2)2﹣a 2•2a 2+(﹣2a 3)2+a 2;(3)(x+5)2﹣(x ﹣2)(x ﹣3);(4)(2x+y ﹣2)(2x+y+2).19.如图,边长为1的正方形ABCD 被两条与边平行的线段EF ,GH 分割成四个小长方形,EF 与GH 交于点P ,设BF 长为a ,BG 长为b ,△GBF 的周长为m ,(1)①用含a ,b ,m 的式子表示GF 的长为 ;②用含a ,b 的式子表示长方形EPHD 的面积为 ;(2)已知直角三角形两直角边的平方和等于斜边的平方,例如在图1,△ABC 中,∠ABC=900,则222AB BC AC +=,请用上述知识解决下列问题:①写出a,b,m满足的等式;②若m=1,求长方形EPHD的面积;③当m满足什么条件时,长方形EPHD的面积是一个常数?20.水果商贩老徐上水果批发市场进货,他了解到草莓的批发价格是每箱60元,苹果的批发价格是每箱40元.老徐购得草莓和苹果共60箱,刚好花费3100元.(1)问草莓、苹果各购买了多少箱?(2)老徐有甲、乙两家店铺,每出售一箱草莓或苹果,甲店分别获利15元和20元,乙店分别获利12元和16元.设老徐将购进的60箱水果分配给甲店草莓a箱,苹果b箱,其余均分配给乙店,由于他口碑良好,两家店都很快卖完了这批水果.①若老徐在甲店获利600元,则他在乙店获利多少元?+=?②若老徐希望获得总利润为1000元,则a b【参考答案】***试卷处理标记,请不要删除一、解答题1.a2-a,2【分析】分别根据多项式的乘法法则和平方差公式计算每一项,再合并同类项,然后把a的值代入化简后的式子计算即可.【详解】解:(a-1)(2a+1)+(1+a)(1-a)=2a2-a-1+1-a2= a2-a,当a=2时,原式=22-2=2.【点睛】本题考查了整式的混合运算和代数式求值,属于基本题型,熟练掌握多项式的乘法法则是解题的关键.2.(1)见解析;(2)∠ACB=80°【分析】(1)利用同旁内角互补,说明GD∥CA;(2)由GD∥CA,得∠A=∠GDB=∠2=40°=∠ACD,由角平分线的性质可求得∠ACB的度数.【详解】解:(1)∵EF ∥CD∴∠1+∠ECD =180°又∵∠1+∠2=180°∴∠2=∠ECD∴GD ∥CA ;(2)由(1)得:GD ∥CA ,∴∠BDG =∠A =40°,∠ACD =∠2,∵DG 平分∠CDB ,∴∠2=∠BDG =40°,∴∠ACD =∠2=40°,∵CD 平分∠ACB ,∴∠ACB =2∠ACD =80°.【点睛】本题考查了角平分线的性质和平行线的性质.解决本题的关键熟练利用所学的性质进行解题.3.(1)1213x a y a=+⎧⎨=-⎩;(2)12a <- 【分析】(1)利用加减消元法求解可得;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【详解】(1)①2⨯,得 2242x y a +=-.③②-③,得12x a =+把12x a =+代入①,得13y a =-所以原方程组的解是1213x a y a =+⎧⎨=-⎩(2)根据题意,得 120130a a +<⎧⎨->⎩解不等式组,得,12a <- 所以a 的取值范围是:12a <-. 【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.4.(1)(43)(4-3)x y x y +;(2)22()(-y)x y x +.【分析】(1)直接利用平方差公式22()()a b a b a b +-=-分解即可; (2)先利用平方差公式,再利用完全平方公式222()2a b a ab b ±=±+即可.【详解】(1)原式2243))((x y =-(43)(43)x y x y =+-;(2)原式2222)()(2x y xy =-+2222(2)(2)x y x y xy y x ++=+-22()()x y x y =+-.【点睛】本题考查了利用平方差公式和完全平方公式进行因式分解,熟记公式是解题关键.5.(1)图见解析;(2)图见解析.【详解】解:(1)△A′B′C′如下图;(2)高C′D′如下图.6.2辆大货车与1辆小货车可以一次运货11吨【分析】设1辆大货车一次运货x 吨,1辆小货车一次运货y 吨,根据“3辆大货车与2辆小货车可以一次运货17吨,5辆大货车与4辆小货车可以一次运货29吨”,即可得出关于x ,y 的二元一次方程组,解之即可得出x ,y 的值,将其代入(2)x y +中即可求出结论.【详解】设1辆大货车一次运货x 吨,1辆小货车一次运货y 吨由题意得:32175429x y x y +=⎧⎨+=⎩解得:51x y =⎧⎨=⎩则225111x y +=⨯+=答:2辆大货车与1辆小货车可以一次运货11吨.【点睛】本题考查了二元一次方程组的实际应用,理解题意,正确列出方程组是解题关键.7.(1)-1;(2)611a -;(3)86x +;(4)222a ac c -+ -24b【分析】(1)直接利用零指数幂,绝对值,负指数幂,乘方法则运算.(2)先利用幂的运算法则,再合并同类项.(3)利用整式的乘法法则进行运算.(4)利用平方差公式进行运算.【详解】解:(1)原式=1-3+2-1=-1(2)原式=68a - +6a -64a =611a -(3)原式=27x x + -()26x x -- =27x x +26x x -++ =86x +(4)原式=()2a c - -()22b =222a ac c -+ -24b【点睛】本题主要考查了数的计算,整式的加减与乘法,解题的关键要对零指数幂,绝对值,负指数幂以及幂的运算和整式的乘法法则熟悉.8.(1)1, 1, (2)a n b n , a n b n c n ,(3)132-. 【解析】【分析】(1)先算括号内的乘法,再算乘方;先乘方,再算乘法;(2)根据有理数乘方的定义求出即可;(3)根据同底数幂的乘法计算,再根据积的乘方计算,即可得出答案.【详解】 解:(1)(2×12)100=1,2100×(12)100=1; (2)(a•b )n =a n b n ,(abc )n =a n b n c n , (3)原式=(﹣0.125)2015×22015×42015×[(﹣0.125)×(﹣0.125)×2]=(﹣0.125×2×4)2015×132 =(﹣1)2015×132 =﹣1×132=﹣132. 【点睛】 本题主要考查了同底数幂的乘法和积的乘方,掌握运算法则是解答此题的关键.9.(1)电脑0.5万元,电子白板1.5万元;(2)14台【分析】(1)设每台电脑x 元,每台电子白板y 元,根据题意列出方程组,解方程组即可;(2)设购进电子白板m 台,则购进电脑()31m -台,根据总费用不超过30万元,列出不等式,根据m 实际意义即可求解.【详解】(1)设每台电脑x 元,每台电子白板y 元,则2 3.52 2.5x y x y +=⎧⎨+=⎩,解得0.51.5x y =⎧⎨=⎩故每台电脑0.5万元,每台电子白板1.5万元;(2)设购进电子白板m 台,则购进电脑()31m -台,由题意得 1.50.5(31)30m m +-≤解得14.5m ≤,又因为m 是正整数,则14m ≤,故至多购买电子白板14台.【点睛】本题考查了二元一次方程组应用,一元一次不等式应用,综合性较强,难度不大,根据题意列出二元一次方程组、一元一次不等式是解题关键.10.(1)见解析;(2)平行且相等;(3)28【分析】(1)根据平移的性质画出点A 、C 平移后的对应点A '、C '即可画出平移后的△A B C '''; (2)根据平移的性质解答即可;(3)根据平行四边形的面积解答即可.【详解】解:(1)如图,ΔA B C '''即为所求;(2)根据平移的性质可得:BB '与CC '的关系是平行且相等;故答案为:平行且相等;(3)四边形BCC B ''的面积为4×7=28.故答案为:28.【点睛】本题主要考查了平移的性质和平移作图,属于常考题型,熟练掌握平移的性质是解题关键.11.(1)374-.(2)16x 4−8x 2+1. 【分析】(1)原式利用负整数指数幂,零指数幂、平方的计算法则得到1914--÷,再计算即可得到结果;(2)原式逆用积的乘方运算法则变形,再利用平方差公式及完全平方公式化简即可得到结果.【详解】(1)2201(2)3()3----÷-= 1914--÷=374-. (2)原式=[(2x−1)(2x +1)]2=(4x 2−1)2=16x 4−8x 2+1.【点睛】本题考查零指数幂、负整数指数幂 、平方差公式及完全平方公式,熟练掌握运算法则是解本题的关键.12.(1)2()b a -;(2)22()()4a b a b ab +=-+;(3)±5;(4)详见解析 【分析】(1)表示出阴影部分正方形的边长,然后根据正方形的面积公式列式即可;(2)根据大正方形的面积减去小正方形的面积等于四个小长方形的面积列式即可; (3)将(x -y )2变形为(x +y )2—4xy ,再代入求值即可;(4)由已知的恒等式,画出相应的图形,如图所示.【详解】解:(1)阴影部分为一个正方形,其边长为b -a ,∴其面积为:2()b a -,故答案为:2()b a -;(2)大正方形面积为:()2a b +小正方形面积为:2()b a -=2()a b -, 四周四个长方形的面积为:4ab ,∴22()()4a b a b ab +=-+,故答案为:22()()4a b a b ab +=-+;(3)由(2)知,22()()4x y x y xy +=-+, ∴22()()4x y x y xy -=+-,∴x y -=5=±,故答案为:±5;(4)符合等式()()2222252a b a b a ab b ++=++的图形如图所示,【点睛】本题考查了完全平方公式的几何背景,此类题目关键在于同一个图形的面积用两种不同的方法表示.13.(1)证明见解析;(2)24°;(3)24°;(4)∠P=34x+14y ;(5)∠P=180()2A C ︒-∠+∠ 【分析】 (1)根据三角形内角和为180°,对顶角相等,即可证得∠A+∠B=∠C+∠D(2)由(1)的结论得:∠BCP+∠P=∠BAP+∠ABC ①,∠PAD+∠P=∠PCD+∠ADC ②,将两个式子相加,已知AP 、CP 分别平分∠BAD 、∠BCD ,可得∠BAP=∠PAD ,∠BCP=∠PCD ,可证得∠P=12(∠ABC+∠ADC),即可求出∠P 度数. (3)已知直线BP 平分∠ABC 的外角∠FBC ,DP 平分∠ADC 的外角∠ADE ,可得∠1=∠2,∠3=∠4,由(1)的结论得:∠C+180°-∠3=∠P+180°-∠1,∠A+∠4=∠P+∠2,两式相加即可求出∠P 的度数.(4)由(1)的结论得:14∠CAB+∠C=∠P+14∠CDB ,34∠CAB+∠P=∠B+34∠CDB ,第一个式子乘以3,得到的式子减去第二个式子即可得出用x 、y 表示∠P (5)延长AB 交DP 于点F ,标注出∠1,∠2,∠3,∠4,由(1)的结论得:∠A+2∠1=∠C+180°-2∠3,其中根据对顶角相等,三角形内角和,以及外角的性质即可得到∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P ,代入∠A+2∠1=∠C+180°-2∠3,即可得出∠P 与∠A 、∠C 的关系.【详解】(1)如图1,∠A+∠B+∠AOB=∠C+∠D+∠COD=180°∵∠AOB=∠COD∴∠A+∠B=∠C+∠D(2)∵AP、CP分别平分∠BAD、∠BCD∴∠BAP=∠PAD,∠BCP=∠PCD,由(1)的结论得:∠BCP+∠P=∠BAP+∠ABC①,∠PAD+∠P=∠PCD+∠ADC②①+②,得2∠P+∠PAD+∠BCP=∠BAP+∠ABC +∠PCD+∠ADC∴∠P=12(∠ABC+∠ADC)∴∠ABC=28°,∠ADC=20°∴∠P=12(28°+20°)∴∠P=24°故答案为:24°(3)∵如图3,直线BP平分∠ABC的外角∠FBC,DP平分∠ADC的外角∠ADE,∴∠1=∠2,∠3=∠4由(1)的结论得:∠C+180°-∠3=∠P+180°-∠1①,∠A+∠4=∠P+∠2②①+②,得∠C+180°-∠3+∠A+∠4=∠P+180°-∠1+∠P+∠2∴30°+18°=2∠P∴∠P=24°故答案为:24°(4)由(1)的结论得:14∠CAB+∠C=∠P+14∠CDB①,34∠CAB+∠P=∠B+34∠CDB②①×3,得34∠CAB+3∠C=3∠P+34∠CDB③②-③,得∠P-3x=y-3∠P∴∠P=34x+14y故答案为:∠P=34x+14y(5)如图5所示,延长AB交DP于点F由(1)的结论得:∠A+2∠1=∠C+180°-2∠3∵∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P ∴∠A+360°-2∠A-2∠3-2∠P=∠C+180°-2∠3解得:∠P=180()2A C︒-∠+∠故答案为:∠P=180()2A C︒-∠+∠【点睛】本题是考查了角平分线性质及三角形内角和定理,对顶角相等,三角形任一外角等于不相邻的两个内角和等知识点,本题是典型的拓展延伸题,一般第一问得出基本结论,后面的问题将基本结论作为解题基础,进行拓展延伸.14.(1)(a+b)2-(a-b)2=4ab;(2)±4;(3)-7【分析】(1)由图可知,图1的面积为4ab,图2中白色部分的面积为(a+b)2-(b-a)2=(a+b)2-(a-b)2,图1的面积和图2中白色部分的面积相等即可求解.(2)由(1)知,(x+y)2-(x-y)2=4xy,将x+y=5,x•y=94代入(x+y)2-(x-y)2=4xy,即可求得x-y的值(3)因为(2019﹣m)+(m﹣2020)=-1,等号两边同时平方,已知(2019﹣m)2+(m﹣2020)2=15,即可求解.【详解】(1)由图可知,图1的面积为4ab,图2中白色部分的面积为(a+b)2-(b-a)2=(a+b)2-(a-b)2∵图1的面积和图2中白色部分的面积相等∴(a+b)2-(a-b)2=4ab故答案为:(a+b)2-(a-b)2=4ab(2)由(1)知,(x+y)2-(x-y)2=4xy∵x+y=5,x•y=9 4∴52-(x-y)2=4×9 4∴(x-y)2=16∴x-y=±4故答案为:±4(3)∵(2019﹣m)+(m﹣2020)=-1∴[(2019﹣m)+(m﹣2020)]2=1∴(2019﹣m)2+2(2019﹣m)(m﹣2020)+ (m﹣2020)2=1∵(2019﹣m)2+(m﹣2020)2=15∴2(2019﹣m)(m﹣2020)=1-15=-14∴(2019﹣m)(m﹣2020)=-7故答案为:-7【点睛】本题考查了完全平方公式的几何背景,运用几何直观理解、解决完全平方公式的推导过程,通过几何图形之间的数量关系对完全平方公式做出几何解释.15.[初步应用]5,3;[深入研究]x3+2x2-x-2=(x+2)(x+1)(x-1);详见解析;【分析】[初步应用]列出竖式结合已知可得:2☆-6=0,2-=☆,求出□与☆即可.[深入研究]列出竖式可得x 3+2x 2-x -2÷(x +2),即可将多项式x 3+2x 2-x -2因式分解.【详解】[初步应用]∵多项式x 2+□x +6能被x +2整除,∴2☆-6=0,2-=☆,∴☆= 3,□=5,故答案为:5,3;[深入研究]∵2323212222 22 0x x x x x x x x x -++--+----, ∴()()()()()3222221211x x x x x x x x +--=+-=++-. 【点睛】本题考查整式的除法;理解题意,仿照整数的除法列出竖式进行运算是解题的关键.16.149299a b ⎧=⎪⎪⎨⎪=⎪⎩【分析】因为两个方程组有相同的解,故只需把两个方程组中不含未知数和含未知数的方程分别组成方程组,求出未知数的值,再代入另一组方程组即可.【详解】354526x y ax by -=⎧⎨+=-⎩①③ 和2348x y ax by +=-⎧⎨-=⎩②④ 解:联立①②得:35234x y x y -=⎧⎨+=-⎩解得:12x y =⎧⎨=-⎩将12x y =⎧⎨=-⎩代入③④得:4102628a b a b -=-⎧⎨+=⎩解得:149299a b ⎧=⎪⎪⎨⎪=⎪⎩【点睛】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.17.-5a 2+2ab ,-1【分析】先利用平方差公式和完全平方公式进行计算,然和合并同类项,最后把a ,b 的值代入即可.【详解】()()()22222()=4222b a a a b b a ab b a b --++----2222=42b a a b ab ---+252a ab =-+,当a =-1,b =-2时,原式=-1.【点睛】本题考查了整式的化简求值,解题的关键是熟练掌握混合运算的顺序和整式的乘法公式.18.(1)2;(2)7a 4+4a 6+a 2;(3)15x+19;(4)4x 2+4xy+y 2﹣4【分析】(1)首先利用负整数指数幂的性质、零次幂的性质、绝对值的性质进行计算,再算加减即可;(2)首先利用积的乘方的计算法则、单项式乘以单项式计算法则计算,再合并同类项即可;(3)首先利用完全平方公式、多项式乘以多项式计算法则计算,再合并同类项即可; (4)首先利用平方差计算,再利用完全平方公式进行计算即可.【详解】解:(1)原式=8﹣1﹣5=2;(2)原式=9a 4﹣2a 4+4a 6+a 2,=7a 4+4a 6+a 2;(3)原式=x 2+10x+25﹣(x 2﹣3x ﹣2x+6),=x 2+10x+25﹣x 2+3x+2x ﹣6,=15x+19;(4)原式=(2x+y )2﹣4,=4x 2+4xy+y 2﹣4.【点睛】本题考查的是实数的运算,幂的运算及合并同类项,整式的混合运算,掌握以上知识点是解题的关键.19.(1)①m a b --;②1a b ab --+;(2)①22220m ma mb ab --+=;②12;③m=1 【分析】(1)①直接根据三角形的周长公式即可;②根据BF 长为a ,BG 长为b ,表示出EP ,PH 的长,根据求长方形EPHD 的面积;(2)①直接根据直角三角形两直角边的平方和等于斜边的平方,表示出a ,b ,m 之间的关系式;②根据线段之间的关系利用勾股定理求出长方形EPHD 的面积的值;③结合①的结论和②的作法即可求解.【详解】(1)①∵BF 长为a ,BG 长为b ,△GBF 的周长为m ,∴GF m a b =--,故答案为:m a b --;②∵正方形ABCD 的边长为1 ,∴AB=BC=1,∵BF 长为a ,BG 长为b ,∴AG=1-b ,FC=1-a ,∴EP=AG=1-b ,PH=FC=1-a ,∴长方形EPHD 的面积为:(1)(1)1a b a b ab --=--+,故答案为:1a b ab --+;(2)①△ABC 中,∠ABC=90°,则222AB BC AC +=,∴在△GBF 中, GF m a b =--,∴()222m a b a b --=+, 化简得,22220m ma mb ab --+=故答案为:22220m ma mb ab --+=;②∵BF=a ,GB=b ,∴FC=1-a ,AG=1-b ,在Rt △GBF 中,22222GF BF BG a b ==+=+,∵Rt △GBF 的周长为1, ∴1BF BG GF a b ++=+=即1a b =--,即222212(()b a b a b a +=-+++),整理得12220a b ab --+= ∴12a b ab +-=, ∴矩形EPHD 的面积••S PH EP FC AG ==()()11a b =--1a b ab =--+11122=-=.③由①得: 22220m ma mb ab --+=, ∴212ab ma mb m =+-. ∴矩形EPHD 的面积••S PH EP FC AG ==()()11a b =--1a b ab =--+2112ma mb a m b +-=--+ ()()211121m a m m b =--+-+, ∴要使长方形EPHD 的面积是一个常数,只有m=1.【点睛】本题考查了正方形的特殊性质和勾股定理,根据正方形的特殊性质和勾股定理推出22220m ma mb ab --+=是解题的关键.20.(1)草莓35箱,苹果25箱;(2)①340元,②53或52【分析】(1)抓住题中关键的已知条件,老徐购得草莓和苹果共60箱,刚好花费3100元,设未知数列方程组,求解方程即可;(2)①由题意列二元一次方程,可得到34120a b +=,列式求出他在乙店获利;②根据老徐希望获得总利润为1000元,建立关于a 、b 的二元一次方程,整理可得18034a b -=,再根据a 、b 的取值范围及a 一定是4的整数倍,即可求出结果; 【详解】 (1)解:设草莓购买了x 箱,苹果购买了y 箱,根据题意得:6060403100x y x y ⎧+=⎨+=⎩, 解得3525x y ⎧=⎨=⎩.答:草莓购买了35箱,苹果购买了25箱;(2)解:①若老徐在甲店获利600元,则1520600ab +=, 整理得:34120a b +=,他在乙店的获利为:()()12351625a b -+-, =()820434a b -+,=820-4120⨯,=340元;②根据题意得:()()1520123516251000a b a b ++-+-=,整理得:34180ab +=, 得到18034ab -=,∵a、b 均为正整数,∴a 一定是4的倍数,∴a 可能是0,4,8…,∵035a ≤≤,025b ≤≤, ∴当且仅当a=32,b=21或a=25,b=24时34180a b +=成立, ∴322153a b +=+=或28+24=52. 故答案为340元;53或52.【点睛】本题主要考查了二元一次方程组的应用,根据题意列式是解题的关键.。
(完整版)人教版七年级数学下《压轴题培优》期末复习专题含答案,推荐文档

°.
B.如图 4, 点 B 在点 A 的右侧 , 且 AB< CD, AD<BC.若∠ ABC=n°,则∠ BED度数为
°.(用含 n
的代数式表示)
8. 已知 A(0 ,a) , B(b , 0) ,a、 b 满足
.
( 1)求 a、 b 的值; ( 2)在坐标轴上找一点 D,使三角形 ABD的面积等于三角形 OAB面积的一半,求 ( 3)做∠ BAO平分线与∠ AOC平分线 BE 的反向延长线交于 P 点,求∠ P的度数 .
时间为 t 秒,回答下列问题:
①当 t=
秒时,点 P 的横坐标与纵坐标互为相反数;
②求点 P 在运动过程中的坐标, (用含 t 的式子表示,写出过程) ;
③当 3 秒< t < 5 秒时,设∠ CBP=x°,∠ PAD=y°,∠ BPA=z°,试问 x , y, z 之间的数量关系能否确
定?若能,请用含 x, y 的式子表示 z,写出过程;若不能,说明理由.
P的坐标 .
1. 解:
参考答案
2. 解:
3. ⑴∠ C=45°分⑵∠ C=∠ APC-∠ A(证明略)⑶不成立,新的相等关系为∠
C=∠APC+∠ A(证明略)
4. 解:(
2
1)∵( a﹣ 3) +|b+4|=0
,∴
a﹣3=0, b+4=0,
∴ a=3, b=﹣ 4,∴ A( 3,0), B(0,﹣ 4),∴ OA=3, OB=4, ∵ S 四边形 AOBC=16.∴ 0.5 ( OA+BC)× OB=16,∴ 0.5 ( 3+BC)× 4=16,∴ BC=5, ∵ C 是第四象限一点, CB⊥ y 轴,∴ C( 5,﹣ 4) ( 2)如图,
(完整版)人教版初一数学下册期末压轴题试题(带答案) (一)
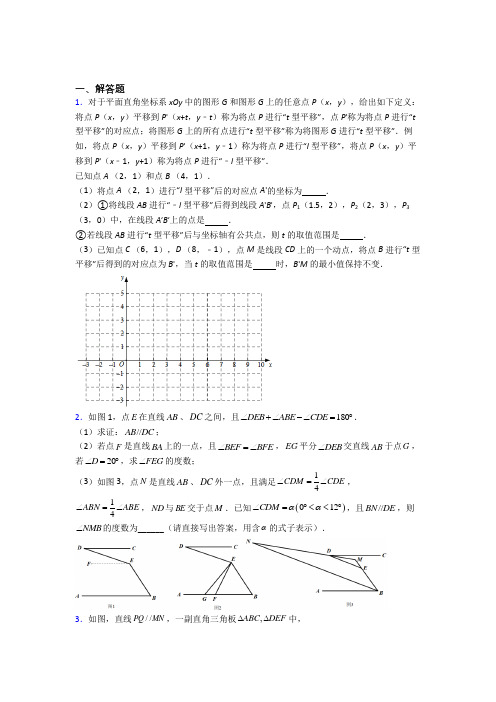
一、解答题1.对于平面直角坐标系xOy 中的图形G 和图形G 上的任意点P (x ,y ),给出如下定义: 将点P (x ,y )平移到P '(x +t ,y ﹣t )称为将点P 进行“t 型平移”,点P '称为将点P 进行“t 型平移”的对应点;将图形G 上的所有点进行“t 型平移”称为将图形G 进行“t 型平移”.例如,将点P (x ,y )平移到P '(x +1,y ﹣1)称为将点P 进行“l 型平移”,将点P (x ,y )平移到P '(x ﹣1,y +1)称为将点P 进行“﹣l 型平移”.已知点A (2,1)和点B (4,1).(1)将点A (2,1)进行“l 型平移”后的对应点A '的坐标为 .(2)①将线段AB 进行“﹣l 型平移”后得到线段A 'B ',点P 1(1.5,2),P 2(2,3),P 3(3,0)中,在线段A ′B ′上的点是 .②若线段AB 进行“t 型平移”后与坐标轴有公共点,则t 的取值范围是 .(3)已知点C (6,1),D (8,﹣1),点M 是线段CD 上的一个动点,将点B 进行“t 型平移”后得到的对应点为B ',当t 的取值范围是 时,B 'M 的最小值保持不变.2.如图1,点E 在直线AB 、DC 之间,且180DEB ABE CDE ∠+∠-∠=︒.(1)求证://AB DC ;(2)若点F 是直线BA 上的一点,且BEF BFE ∠=∠,EG 平分DEB ∠交直线AB 于点G ,若20D ∠=︒,求FEG ∠的度数;(3)如图3,点N 是直线AB 、DC 外一点,且满足14CDM CDE ∠=∠,14ABN ABE ∠=∠,ND 与BE 交于点M .已知()012CDM αα∠=︒<<︒,且//BN DE ,则NMB ∠的度数为______(请直接写出答案,用含α的式子表示).3.如图,直线//PQ MN ,一副直角三角板,ABC DEF ∆∆中,90,45,30,60ACB EDF ABC BAC DFE DEF ︒︒︒︒∠=∠=∠=∠=∠=∠=.(1)若DEF ∆如图1摆放,当ED 平分PEF ∠时,证明:FD 平分EFM ∠.(2)若,ABC DEF ∆∆如图2摆放时,则PDE ∠=(3)若图2中ABC ∆固定,将DEF ∆沿着AC 方向平移,边DF 与直线PQ 相交于点G ,作FGQ ∠和GFA ∠的角平分线GH FH 、相交于点H (如图3),求GHF ∠的度数.(4)若图2中DEF ∆的周长35,5cm AF cm =,现将ABC ∆固定,将DEF ∆沿着CA 方向平移至点F 与A 重合,平移后的得到''D E A ∆,点D E 、的对应点分别是''D E 、,请直接写出四边形'DEAD 的周长.(5)若图2中DEF ∆固定,(如图4)将ABC ∆绕点A 顺时针旋转,1分钟转半圈,旋转至AC 与直线AN 首次重合的过程中,当线段BC 与DEF ∆的一条边平行时,请直接写出旋转的时间.4.如图,∠EBF =50°,点C 是∠EBF 的边BF 上一点.动点A 从点B 出发在∠EBF 的边BE 上,沿BE 方向运动,在动点A 运动的过程中,始终有过点A 的射线AD ∥BC .(1)在动点A 运动的过程中, (填“是”或“否”)存在某一时刻,使得AD 平分∠EAC ? (2)假设存在AD 平分∠EAC ,在此情形下,你能猜想∠B 和∠ACB 之间有何数量关系?并请说明理由;(3)当AC ⊥BC 时,直接写出∠BAC 的度数和此时AD 与AC 之间的位置关系.5.已知,//AE BD ,A D ∠=∠.(1)如图1,求证://AB CD ;(2)如图2,作BAE ∠的平分线交CD 于点F ,点G 为AB 上一点,连接FG ,若CFG ∠的平分线交线段AG 于点H ,连接AC ,若ACE BAC BGM ∠=∠+∠,过点H 作HM FH ⊥交FG 的延长线于点M ,且3518E AFH ∠-∠=︒,求EAF GMH ∠+∠的度数.6.如图,直线HD //GE ,点A 在直线HD 上,点C 在直线GE 上,点B 在直线HD 、GE 之间,∠DAB =120°.(1)如图1,若∠BCG =40°,求∠ABC 的度数;(2)如图2,AF 平分∠HAB ,BC 平分∠FCG ,∠BCG =20°,比较∠B ,∠F 的大小; (3)如图3,点P 是线段AB 上一点,PN 平分∠APC ,CN 平分∠PCE ,探究∠HAP 和∠N 的数量关系,并说明理由.7.请观察下列等式,找出规律并回答以下问题.111122=-⨯,1112323=-⨯,1113434=-⨯,1114545=-⨯,…… (1)按照这个规律写下去,第5个等式是:______;第n 个等式是:______. (2)①计算:11111223344950⨯⨯⨯⨯++++. ②若a 30b -=,求:()()()()()()()()111111122339797ab a b a b a b a b +++++++++++++. 8.阅读理解:计算1111234⎛⎫+++ ⎪⎝⎭×11112345+++⎛⎫ ⎪⎝⎭﹣111112345⎛⎫++++ ⎪⎝⎭×111234++⎛⎫ ⎪⎝⎭时,若把11112345+++⎛⎫ ⎪⎝⎭与111234++⎛⎫ ⎪⎝⎭分别各看着一个整体,再利用分配律进行运算,可以大大简化难度.过程如下:解:设111234++⎛⎫ ⎪⎝⎭为A ,11112345+++⎛⎫ ⎪⎝⎭为B , 则原式=B (1+A )﹣A (1+B )=B+AB ﹣A ﹣AB=B ﹣A=15.请用上面方法计算: ①11111123456⎛⎫+++++ ⎪⎝⎭×111111234567⎛⎫+++++ ⎪⎝⎭-1111111234567⎛⎫++++++ ⎪⎝⎭×1111123456⎛⎫++++ ⎪⎝⎭②111123n ⎛⎫++++ ⎪⎝⎭111231n ⎛⎫+++ ⎪+⎝⎭-1111231n ⎛⎫++++ ⎪+⎝⎭11123n ⎛⎫+++ ⎪⎝⎭. 9.如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.(1)图2中A 、B 两点表示的数分别为___________,____________;(2)请你参照上面的方法:①把图3中51⨯的长方形进行剪裁,并拼成一个大正方形.在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长a=___________.(注:小正方形边长都为1,拼接不重叠也无空隙)②在①的基础上,参照图2的画法,在数轴上分别用点M、N表示数a以及3a-.(图中标出必要线段的长)10.我们知道,任意一个正整数n都可以进行这样的分解:n p q=⨯(p,q是正整数,且p q≤),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:()pF nq=.例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=31 62 =.(1)F(13)=,F(24)=;(2)如果一个两位正整数t,其个位数字是a,十位数字为1b-,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;(3)在(2)所得“和谐数”中,求F(t)的最大值.11.如果有一列数,从这列数的第2个数开始,每一个数与它的前一个数的比等于同一个非零的常数,这样的一列数就叫做等比数列(Geometric Sequences).这个常数叫做等比数列的公比,通常用字母q表示(q≠0).(1)观察一个等比列数1,1111,,,24816,…,它的公比q=;如果a n(n为正整数)表示这个等比数列的第n项,那么a18=,a n=;(2)如果欲求1+2+4+8+16+…+230的值,可以按照如下步骤进行:令S=1+2+4+8+16+…+230…①等式两边同时乘以2,得2S=2+4+8+16++32+…+231…②由② ﹣①式,得2S﹣S=231﹣1即(2﹣1)S=231﹣1所以3131212121S-==--请根据以上的解答过程,求3+32+33+…+323的值;(3)用由特殊到一般的方法探索:若数列a1,a2,a3,…,a n,从第二项开始每一项与前一项之比的常数为q,请用含a1,q,n的代数式表示a n;如果这个常数q≠1,请用含a1,q,n的代数式表示a1+a2+a3+…+a n.12.阅读下列材料:小明为了计算22019202012222+++++的值,采用以下方法:设22019202012222s=+++++①则22020202122222s=++++②②-①得,2021221s s s-==-请仿照小明的方法解决以下问题:(1)291222++++=________;(2)220333+++=_________;(3)求231na a a a++++的和(1a>,n是正整数,请写出计算过程).13.如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.(1)直接写出点C的坐标.(2)在y轴上是否存在点P,使得S△POB=23S△ABC若存在,求出点P的坐标;若不存在,请说明理由.(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.14.已知点C在射线OA上.(1)如图①,CD//OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD 与∠BO′E′的关系(用含α的代数式表示)(3)在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.15.在平面直角坐标系xOy 中,如图正方形ABCD 的顶点A ,B 坐标分别为()1,0A -,()3,0B ,点E ,F 坐标分别为(),0E m ,()3,0F m ,且12m -<≤,以EF 为边作正方形EFGH .设正方形EFGH 与正方形ABCD 重叠部分面积为S .(1)①当点F 与点B 重合时,m 的值为______;②当点F 与点A 重合时,m 的值为______.(2)请用含m 的式子表示S ,并直接写出m 的取值范围.16.阅读下列材料:我们知道||x 的几何意义是在数轴上数x 对应的点与原点的距离,即|||0|x x =-,也就是说,12||x x -表示在数轴上数1x 与数2x 对应的点之间的距离;例 1.解方程||2x =,因为在数轴上到原点的距离为2的点对应的数为2±,所以方程||2x =的解为2x =±.例 2.解不等式|1|2x ->,在数轴上找出|1|2x -=的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为1-或3,所以方程|1|2x -=的解为1x =-或3x =,因此不等式|1|2x ->的解集为1x <-或3x >.参考阅读材料,解答下列问题:(1)方程|3|5x +=的解为 ;(2)解不等式:|2|3x -≤;(3)解不等式:428x x -++>.17.在如图所示的平面直角坐标系中,A(1,3),B(3,1),将线段A平移至CD,C (m,-1),D(1,n)(1)m=_____,n=______(2)点P的坐标是(c,0)①设∠ABP=α,请写出∠BPD和∠PDC之间的数量关系(用含α的式子表示,若有多种数量关系,选择一种加以说明)②当三角形PAB的面积不小于3且不大于10,求点p的横坐标C的取值范围(直接写出答案即可)18.如图1,已知,点A(1,a),AH⊥x轴,垂足为H,将线段AO平移至线段BC,点B(b,0),其中点A与点B对应,点O与点C对应,a、b满足24(3)0a b-+-=.(1)填空:①直接写出A、B、C三点的坐标A(________)、B(________)、C(________);②直接写出三角形AOH的面积________.(2)如图1,若点D(m,n)在线段OA上,证明:4m=n.(3)如图2,连OC,动点P从点B开始在x轴上以每秒2个单位的速度向左运动,同时点Q从点O开始在y轴上以每秒1个单位的速度向下运动.若经过t秒,三角形AOP与三角形COQ的面积相等,试求t的值及点P的坐标.19.题目:满足方程组3512332x y kx y k+=+⎧⎨+=-⎩的x与y的值的和是2,求k的值.按照常规方法,顺着题目思路解关于x,y的二元一次方程组,分别求出xy的值(含有字母k),再由x+y=2,构造关于k的方程求解,从而得出k值.(1)某数学兴趣小组对本题的解法又进行了探究利用整体思想,对于方程组中每个方程变形得到“x+y”这个整体,或者对方程组的两个方程进行加减变形得到“x+y”整体值,从而求出k值请你运用这种整体思想的方法,完成题目的解答过程.(2)小勇同学的解答是:观察方程①,令3x=k,5y=1解得y=15,3x+y=2,∴x=95∴k=3×95=275把x=95,y=15代入方程②得k=﹣35所以k的值为275或﹣35.请诊断分析并评价“小勇同学的解答”.20.某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G 型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)21.(1)阅读下列材料并填空:对于二元一次方程组4354{336x yx y+=+=,我们可以将x,y的系数和相应的常数项排成一个数表4354 () 1336,求得的一次方程组的解{x ay b==,用数表可表示为10)01ab(.用数表可以简化表达解一次方程组的过程如下,请补全其中的空白:从而得到该方程组的解为x=,y=.(2)仿照(1)中数表的书写格式写出解方程组236{2x yx y+=+=的过程.22.在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+b﹣2|25a b-+0,现同时将点A,B分别向右平移1个单位,再向上平移2个单位,分别得到点A,B的对应点为C,D.(1)请直接写出A、B、C、D四点的坐标.(2)点E在坐标轴上,且S△BCE=S四边形ABDC,求满足条件的点E的坐标.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在线段BD 上移动时(不与B ,D 重合)求:DCP BOP CPO∠+∠∠的值.23.某校为了丰富同学们的课外活动,决定给全校20个班每班配4副乒乓球拍和若干乒乓球,两家体育用品商店对同一款乒乓球拍和乒乓球推出让利活动,甲商店买一副乒乓球拍送10个乒乓球,乙商店所有商品均打九折(按标价的90%)销售,已知2副乒乓球拍和10个乒乓球110元,3副乒乓球拍和20个乒乓球170元。
(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案

(完整版)人教版七年级数学下册期末复习压轴题 解答题试卷及答案一、解答题1.解方程或不等式(组)(1)24231x y x y +=⎧⎨-=⎩ (2)2151132x x -+-≥ (3)312(2)15233x x x x +<+⎧⎪⎨-≤+⎪⎩ 2.利用多项式乘法法则计算:(1)()()22+-+a b a ab b = ;()()22a b a ab b -++ = .在多项式的乘法公式中,除了平方差公式,完全平方公式之外,如果把上面计算结果作为结论逆运用,则成为因式分解中的立方和与立方差公式.已知2,1a b ab -==,利用自己所学的数学知识,以及立方和与立方差公式,解决下列问题:(2)22a b += ;(直接写出答案)(3)33a b -= ;(直接写出答案)(4)66a b += ;(写出解题过程)3.先化简,再求值(x-2)2+2(x+2)(x-4)-(x-3)(x+3);其中x=1.4.解方程组(1)21325x y x y +=⎧⎨-=⎩ (2)111231233x y x y ⎧-=⎪⎪⎨⎪--=⎪⎩ 5.某口罩加工厂有,A B 两组工人共150人,A 组工人每人每小时可加工口罩70只,B 组工人每小时可加工口罩50只,,A B 两组工人每小时一共可加工口罩9300只.(1)求A B 、两组工人各有多少人?(2)由于疫情加重,A B 、两组工人均提高了工作效率,一名A 组工人和一名B 组工人每小时共可生产口罩200只,若A B 、两组工人每小时至少加工15000只口罩,那么A 组工人每人每小时至少加工多少只口罩?6.因式分解:(1)()()36x m n y n m ---;(2)()222936x x +-7.解下列方程组 (1)29321x y x y +=⎧⎨-=-⎩.(2)34332(1)11x y x y ⎧+=⎪⎨⎪--=⎩.8.阅读下列各式:(a•b )2=a 2b 2,(a•b )3=a 3b 3,(a•b )4=a 4b 4…回答下列三个问题:(1)验证:(2×12)100= ,2100×(12)100= ; (2)通过上述验证,归纳得出:(a•b )n = ; (abc )n = .(3)请应用上述性质计算:(﹣0.125)2017×22016×42015. 9.解下列方程组:(1)32316x y x y -=⎧⎨+=⎩ (2)234229x y z x y z ⎧==⎪⎨⎪-+=-⎩ 10.如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,三角形ABC 的三个顶点均在格点上.(1)将三角形ABC 先向右平移6个单位长度,再向上平移3个单位长度,得到三角形A 1B 1C 1,画出平移后的三角形A 1B 1C 1;(2)建立适当的平面直角坐标系,使得点A 的坐标为(-4,3),并直接写出点A 1的坐标; (3)求三角形ABC 的面积.11.已知关于x 、y 的二元一次方程组21322x y x y k +=⎧⎪⎨-=-⎪⎩(k 为常数). (1)求这个二元一次方程组的解(用含k 的代数式表示);(2)若()2421y x +=,求k 的值; (3)若14k ≤,设364m x y =+,且m 为正整数,求m 的值. 12.疫情初期,武汉物资告急,全国一心,各地纷纷运送物资到武汉。
2018年人教版七年级数学下《压轴题培优》期末复习专题含问题详解
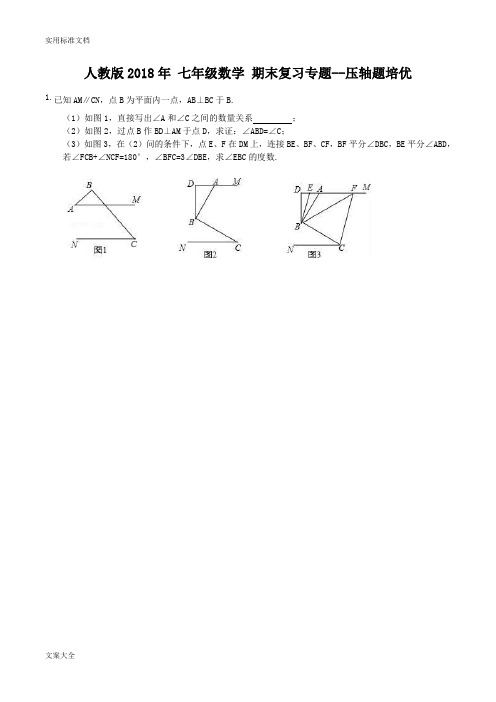
人教版2018年七年级数学期末复习专题--压轴题培优1.已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图3,在(2)问的条件下,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.2.如图,已知两条射线OM∥CN,动线段AB的两个端点A.B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.(1)请在图中找出与∠AOC相等的角,并说明理由;(2)若平行移动AB,那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.3.已知AB∥CD,线段EF分别与AB、CD相交于点E、F.(1)如图①,当∠A=25°,∠APC=70°时,求∠C的度数;(2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A.∠APC与∠C之间有什么确定的相等关系?试证明你的结论.(3)如图③,当点P在线段FE的延长线上运动时,(2)中的结论还成立吗?如果成立,说明理由;如果不成立,试探究它们之间新的相等关系并证明.4.如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.(1)求C点坐标;(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.5.已知BC∥OA,∠B=∠A=100°.试回答下列问题:(1)如图1所示,求证:OB∥AC;(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数;(3)在(2)的条件下,若平行移动AC,如图3,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值。
(完整版)七年级数学下册期末压轴题试卷及答案(一)培优试题

一、解答题1.如图,A 点的坐标为(0,3),B 点的坐标为(﹣3,0),D 为x 轴上的一个动点且不与B ,O 重合,将线段AD 绕点A 逆时针旋转90°得线段AE ,使得AE ⊥AD ,且AE =AD ,连接BE 交y 轴于点M .(1)如图,当点D 在线段OB 的延长线上时,①若D 点的坐标为(﹣5,0),求点E 的坐标.②求证:M 为BE 的中点.③探究:若在点D 运动的过程中,OM BD的值是否是定值?如果是,请求出这个定值;如果不是,请说明理由.(2)请直接写出三条线段AO ,DO ,AM 之间的数量关系(不需要说明理由).2.已知点C 在射线OA 上.(1)如图①,CD //OE ,若∠AOB =90°,∠OCD =120°,求∠BOE 的度数;(2)在①中,将射线OE 沿射线OB 平移得O ′E '(如图②),若∠AOB =α,探究∠OCD 与∠BO ′E ′的关系(用含α的代数式表示)(3)在②中,过点O ′作OB 的垂线,与∠OCD 的平分线交于点P (如图③),若∠CPO ′=90°,探究∠AOB 与∠BO ′E ′的关系.3.已知,如图:射线PE 分别与直线AB 、CD 相交于E 、F 两点,PFD ∠的角平分线与直线AB 相交于点M ,射线PM 交CD 于点N ,设PFM α∠=︒,EMF β∠=︒且()2350αβα-+-=.(1)α=________,β=________;直线AB 与CD 的位置关系是______;(2)如图,若点G 是射线MA 上任意一点,且MGH PNF ∠=∠,试找出FMN ∠与GHF ∠之间存在一个什么确定的数量关系?并证明你的结论.(3)若将图中的射线PM 绕着端点P 逆时针方向旋转(如图)分别与AB 、CD 相交于点1M 和点1N 时,作1PM B ∠的角平分线1M Q 与射线FM 相交于点Q ,问在旋转的过程中1FPN Q ∠∠的值变不变?若不变,请求出其值;若变化,请说明理由.4.已知,AB ∥CD .点M 在AB 上,点N 在CD 上.(1)如图1中,∠BME 、∠E 、∠END 的数量关系为: ;(不需要证明) 如图2中,∠BMF 、∠F 、∠FND 的数量关系为: ;(不需要证明)(2)如图3中,NE 平分∠FND ,MB 平分∠FME ,且2∠E +∠F =180°,求∠FME 的度数;(3)如图4中,∠BME =60°,EF 平分∠MEN ,NP 平分∠END ,且EQ ∥NP ,则∠FEQ 的大小是否发生变化,若变化,请说明理由,若不变化,求出∠FEQ 的度数.5.已知,如图1,射线PE 分别与直线AB ,CD 相交于E 、F 两点,∠PFD 的平分线与直线AB 相交于点M ,射线PM 交CD 于点N ,设∠PFM =α°,∠EMF =β°,且(40﹣2α)2+|β﹣20|=0(1)α= ,β= ;直线AB 与CD 的位置关系是 ;(2)如图2,若点G 、H 分别在射线MA 和线段MF 上,且∠MGH =∠PNF ,试找出∠FMN 与∠GHF 之间存在的数量关系,并证明你的结论;(3)若将图中的射线PM 绕着端点P 逆时针方向旋转(如图3),分别与AB 、CD 相交于点M 1和点N 1时,作∠PM 1B 的角平分线M 1Q 与射线FM 相交于点Q ,问在旋转的过程中1FPN Q∠∠的值是否改变?若不变,请求出其值;若变化,请说明理由. 6.已知:如图(1)直线AB 、CD 被直线MN 所截,∠1=∠2.(1)求证:AB //CD ;(2)如图(2),点E 在AB ,CD 之间的直线MN 上,P 、Q 分别在直线AB 、CD 上,连接PE 、EQ ,PF 平分∠BPE ,QF 平分∠EQD ,则∠PEQ 和∠PFQ 之间有什么数量关系,请直接写出你的结论;(3)如图(3),在(2)的条件下,过P 点作PH //EQ 交CD 于点H ,连接PQ ,若PQ 平分∠EPH ,∠QPF :∠EQF =1:5,求∠PHQ 的度数.7.请观察下列等式,找出规律并回答以下问题.111122=-⨯,1112323=-⨯,1113434=-⨯,1114545=-⨯,…… (1)按照这个规律写下去,第5个等式是:______;第n 个等式是:______. (2)①计算:11111223344950⨯⨯⨯⨯++++. ②若a 30b -=,求:()()()()()()()()111111122339797ab a b a b a b a b +++++++++++++. 8.阅读材料:求1+2+22+23+24+…+22017的值.解:设S=1+2+22+23+24+ (22017)将等式两边同时乘以2得:2S=2+22+23+24+…+22017+22018将下式减去上式得2S-S=22018-1即S=22018-1即1+2+22+23+24+…+22017=22018-1请你仿照此法计算:(1)1+2+22+23+…+29=_____;(2)1+5+52+53+54+…+5n(其中n为正整数);(3)1+2×2+3×22+4×23+…+9×28+10×29.9.若一个四位数t的前两位数字相同且各位数字均不为0,则称这个数为“前介数”;若把这个数的个位数字放到前三位数字组成的数的前面组成一个新的四位数,则称这个新的四位数为“中介数”;记一个“前介数”t与它的“中介数”的差为P(t).例如,5536前两位数字相同,所以5536为“前介数”;则6553就为它的“中介数”,P(5536)=5536﹣6553=-1017.(1)P(2215)=,P(6655)=.(2)求证:任意一个“前介数”t,P(t)一定能被9整除.(3)若一个千位数字为2的“前介数”t能被6整除,它的“中介数”能被2整除,请求出满足条件的P(t)的最大值.10.a是不为1的有理数,我们把11a-称为a的差倒数.如:2的差倒数是1112=--,现已知a1=12,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…(1)求a2,a3,a4的值;(2)根据(1)的计算结果,请猜想并写出a2016•a2017•a2018的值;(3)计算:a33+a66+a99+…+a9999的值.11.观察下列各式:(x-1)(x+1)=x2-1(x-1)(x2+x+1)=x3-1(x-1)(x3+x2+x+1)=x4-1……(1)根据以上规律,则(x-1)(x6+x5+x4+x3+x2+x+1)=__________________.(2)你能否由此归纳出一般性规律(x-1)(x n+x n-1+x n-2+…+x+1)=____________.(3)根据以上规律求1+3+32+…+349+350的结果.12.规律探究,观察下列等式:第1个等式:11111 1434a⎛⎫==⨯-⎪⨯⎝⎭第2个等式:21111 47347a⎛⎫==⨯-⎪⨯⎝⎭第3个等式:31111 7103710a⎛⎫==⨯-⎪⨯⎝⎭第4个等式:41111 101331013a⎛⎫==⨯-⎪⨯⎝⎭请回答下列问题:(1)按以上规律写出第5个等式:= ___________ = ___________(2)用含n 的式子表示第n 个等式:= ___________ = ___________(n 为正整数) (3)求1234100a a a a a +++++13.如图所示,A (1,0),点B 在y 轴上,将三角形OAB 沿x 轴负方向平移,平移后的图形为三角形DEC ,点C 的坐标为(﹣3,2).(1)直接写出点E 的坐标 ;(2)在四边形ABCD 中,点P 从点O 出发,沿OB →BC →CD 移动,若点P 的速度为每秒1个单位长度,运动时间为t 秒,请解决以下问题;①当t 为多少秒时,点P 的横坐标与纵坐标互为相反数;②当t 为多少秒时,三角形PEA 的面积为2,求此时P 的坐标14.如图,已知AM //BN ,点P 是射线AM 上一动点(与点A 不重合),BC BD 、分别平分ABP ∠和PBN ∠,分别交射线AM 于点,C D .(1)当60A ∠=︒时,ABN ∠的度数是_______;(2)当A x ∠=︒,求CBD ∠的度数(用x 的代数式表示);(3)当点P 运动时,ADB ∠与APB ∠的度数之比是否随点P 的运动而发生变化?若不变化,请求出这个比值;若变化,请写出变化规律.(4)当点P 运动到使ACB ABD =∠∠时,请直接写出14DBN A +∠∠的度数.15.如图1,在平面直角坐标系中,A (a ,0),C (b ,2),且满足2(a 2)b 20+-,过C 作CB x ⊥轴于B ,(1)求a ,b 的值;(2)在y 轴上是否存在点P ,使得△ABC 和△OCP 的面积相等,若存在,求出点P 坐标,若不存在,试说明理由.(3)若过B 作BD ∥AC 交y 轴于D ,且AE ,DE 分别平分∠CAB ,∠ODB ,如图2,图3, ①求:∠CAB +∠ODB 的度数;②求:∠AED 的度数.16.中国传统节日“端午节”期间,某商场开展了“欢度端午,回馈顾客”的让利促销活动,对部分品牌的粽子进行了打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折.已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买5盒甲品牌粽子和4盒乙品牌粽子需520元.(1)打折前,每盒甲、乙品牌粽子分别为多少元?(2)在商场让利促销活动期间,某敬老院准备购买甲、乙两种品牌粽子共40盒,总费用不超过2300元,问敬老院最多可购买多少盒乙品牌粽子?17.如图1,已知,点A (1,a ),AH ⊥x 轴,垂足为H ,将线段AO 平移至线段BC ,点B (b ,0),其中点A 与点B 对应,点O 与点C 对应,a 、b 满足24(3)0a b -+-=.(1)填空:①直接写出A 、B 、C 三点的坐标A (________)、B (________)、C (________); ②直接写出三角形AOH 的面积________.(2)如图1,若点D (m ,n )在线段OA 上,证明:4m =n .(3)如图2,连OC ,动点P 从点B 开始在x 轴上以每秒2个单位的速度向左运动,同时点Q 从点O 开始在y 轴上以每秒1个单位的速度向下运动.若经过t 秒,三角形AOP 与三角形COQ 的面积相等,试求t 的值及点P 的坐标.18.在平面直角坐标系中,点A ,B 的坐标分别为()2,0,()2,0-,现将线段AB 先向上平移3个单位,再向右平移1个单位,得到线段DC ,连接AD ,BC .(1)如图1,求点C ,D 的坐标及四边形ABCD 的面积;图1(2)如图1,在y 轴上是否存在点P ,连接PA ,PB ,使PAB ABCD S S =△四边形?若存在这样的点,求出点P 的坐标;若不存在,试说明理由;(3)如图2,在直线CD 上是否存在点Q ,连接QB ,使14QCB ABCDS S =△四边形?若存在这样的点,直接写出点Q 的坐标;若不存在,试说明理由.图2(4)在坐标平面内是否存在点M ,使23MAB ABCDS S =△四边形?若存在这样的点M ,直接写出点M 的坐标的规律;若不存在,请说明理由. 19.数学活动课上,小新和小葵各自拿着不同的长方形纸片在做数学问题探究.(1)小新经过测量和计算得到长方形纸片的长宽之比为3:2,面积为30,请求出该长方形纸片的长和宽;(2)小葵在长方形内画出边长为a ,b 的两个正方形(如图所示),其中小正方形的一条边在大正方形的一条边上,她经过测量和计算得到长方形纸片的周长为50,阴影部分两个长方形的周长之和为30,由此她判断大正方形的面积为100,间小葵的判断正确吗?请说明理由.20.每年的6月5日为世界环保日,为提倡低碳环保,某公司决定购买10台节省能源的新机器,现有甲、乙两种型号的机器可选,其中每台的价格、产量如下表:甲型机器 乙型机器价格(万元/台)a b产量(吨/月)240180经调查:购买一台甲型机器比购买一台乙型机器多12万元,购买2台甲型机器比购买3台乙型机器多6万元.(1)求a、b的值;(2)若该公司购买新机器的资金不超过216万元,请问该公司有哪几种购买方案?(3)在(2)的条件下,若公司要求每月的产量不低于1890吨,请你为该公司设计一种最省钱的购买方案.21.数轴上有两个动点M,N,如果点M始终在点N的左侧,我们称作点M是点N的“追赶点”.如图,数轴上有2个点A,B,它们表示的数分别为-3,1,已知点M是点N的“追赶点”,且M,N表示的数分别为m,n.(1)由题意得:点A是点B的“追赶点”,AB=1-(-3)=4(AB表示线段AB的长,以下相同);类似的,MN=____________.(2)在A,M,N三点中,若其中一个点是另外两个点所构成线段的中点,请用含m的代数式来表示n.(3)若AM=BN,MN=43BM,求m和n值.22.平面直角坐标系中,A(a,0),B(0,b),a,b满足2(25)220a b a b++++-=,将线段AB平移得到CD,A,B的对应点分别为C,D,其中点C在y轴负半轴上.(1)求A,B两点的坐标;(2)如图1,连AD交BC于点E,若点E在y轴正半轴上,求BE OEOC-的值;(3)如图2,点F,G分别在CD,BD的延长线上,连结FG,∠BAC的角平分线与∠DFG 的角平分线交于点H,求∠G与∠H之间的数量关系.23.在平面直角坐标系中,若点P(x,y)的坐标满足x﹣2y+3=0,则我们称点P为“健康点”:若点Q(x,y)的坐标满足x+y﹣6=0,则我们称点Q为“快乐点”.(1)若点A既是“健康点”又是“快乐点”,则点A的坐标为;(2)在(1)的条件下,若B 是x 轴上的“健康点”,C 是y 轴上的“快乐点”,求△ABC 的面积;(3)在(2)的条件下,若P 为x 轴上一点,且△BPC 与△ABC 面积相等,直接写出点P 的坐标.24.阅读感悟:有些关于方程组的问题,要求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:已知实数x 、y 满足35x y -=①,237x y +=②,求4x y -和75x y +的值.本题常规思路是将①②两式联立组成方程组,解得x 、y 的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①-②可得42x y -=-,由①+②×2可得7519x y +=.这样的解题思想就是通常所说的“整体思想”.解决问题:(1)已知二元一次方程组2728x y x y +=⎧⎨+=⎩,则x y -=_______,x y +=_______; (2)某班级组织活动购买小奖品,买20支水笔、3块橡皮、2本记事本共需35元,买39支水笔、5块橡皮、3本记事本工序62元,则购买6支水笔、6块橡皮、6本记事本共需多少元?(3)对于实数x 、y ,定义新运算:*x y ax by c =++,其中a 、b 、c 是常数,等式右边是通常的加法和乘法运算.已知3*515=,4*728=,那么1*1=_______.25.某治污公司决定购买10台污水处理设备.现有甲、乙两种型号的设备可供选择,其中每台的价格与月处理污水量如下表:甲型 乙型 价格(万元/台)x y 处理污水量(吨/月) 300 260经调查:购买一台甲型设备比购买一台乙型设备多2万元,购买3台甲型设备比购买4台乙型设备少2万元.(1)求x ,y 的值;(2)如果治污公司购买污水处理设备的资金不超过91万元,求该治污公司有哪几种购买方案;(3)在(2)的条件下,如果月处理污水量不低于2750吨,为了节约资金,请为该公司设计一种最省钱的购买方案.26.某数码专营店销售A ,B 两种品牌智能手机,这两种手机的进价和售价如表所示:(1)该店销售记录显示,三月份销售A 、B 两种手机共34部,且销售A 种手机的利润恰好是销售B 种手机利润的2倍,求该店三月份售出A 种手机和B 种手机各多少部?(2)根据市场调研,该店四月份计划购进这两种手机共40部,要求购进B 种手机数不低于A 种手机数的35,用于购买这两种手机的资金低于140000元,请通过计算设计所有可能的进货方案.27.某体育拓展中心的门票每张10元,一次性使用考虑到人们的不同需求,也为了吸引更多的顾客,该拓展中心除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法.年票分A 、B 两类:A 类年票每张120元,持票者可不限次进入中心,且无需再购买门票;B 类年票每张60元,持票者进入中心时,需再购买门票,每次2元.(1)小丽计划在一年中花费80元在该中心的门票上,如果只能选择一种购买门票的方式,她怎样购票比较合算?(2)小亮每年进入该中心的次数约20次,他采取哪种购票方式比较合算?(3)小明根据自己进入拓展中心的次数,购买了A 类年票,请问他一年中进入该中心不低于多少次?28.在平面直角坐标系中,点A ,B ,C 的坐标分别为(),0a ,()2,4-,(),0c ,且a ,c 满足方程()243240c a a x y ---+=为二元一次方程.(1)求A ,C 的坐标.(2)若点D 为y 轴正半轴上的一个动点.①如图1,当//AD BC 时,ADO ∠与ACB ∠的平分线交于点P ,求P ∠的度数;②如图2,连接BD ,交x 轴于点E .若ADE BCE S S ≤△△成立.设动点D 的坐标为()0,d ,求d 的取值范围.29.若关于x 的方程ax +b =0(a ≠0)的解与关于y 的方程cy +d =0(c ≠0)的解满足﹣1≤x ﹣y ≤1,则称方程ax +b =0(a ≠0)与方程cy +d =0(c ≠0)是“友好方程”.例如:方程2x ﹣1=0的解是x =0.5,方程y ﹣1=0的解是y =1,因为﹣1≤x ﹣y ≤1,方程2x ﹣1=0与方程y ﹣1=0是“友好方程”.(1)请通过计算判断方程2x ﹣9=5x ﹣2与方程5(y ﹣1)﹣2(1﹣y )=﹣34﹣2y 是不是“友好方程”.(2)若关于x 的方程3x ﹣3+4(x ﹣1)=0与关于y 的方程32y k++y =2k +1是“友好方程”,请你求出k 的最大值和最小值.30.如图1,在平面直角坐标系中,A (a ,0)是x 轴正半轴上一点,C 是第四象限内一点,CB ⊥y 轴交y 轴负半轴于B (0,b ),且|a ﹣3|+(b+4)2=0,S 四边形AOBC =16.(1)求点C 的坐标.(2)如图2,设D 为线段OB 上一动点,当AD ⊥AC 时,∠ODA 的角平分线与∠CAE 的角平分线的反向延长线交于点P ,求∠APD 的度数;(点E 在x 轴的正半轴).(3)如图3,当点D 在线段OB 上运动时,作DM ⊥AD 交BC 于M 点,∠BMD 、∠DAO 的平分线交于N 点,则点D 在运动过程中,∠N 的大小是否会发生变化?若不变化,求出其值;若变化,请说明理由.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)①E(3,﹣2)②见解析;③12OMBD,理由见解析;(2)OD+OA=2AM或OA﹣OD=2AM【分析】(1)①过点E作EH⊥y轴于H.证明△DOA≌△AHE(AAS)可得结论.②证明△BOM≌△EHM(AAS)可得结论.③是定值,证明△BOM≌△EHM可得结论.(2)根据点D在点B左侧和右侧分类讨论,分别画出对应的图形,根据全等三角形的判定及性质即可分别求出结论.【详解】解:(1)①过点E作EH⊥y轴于H.∵A(0,3),B(﹣3,0),D(﹣5,0),∴OA=OB=3,OD=5,∵∠AOD=∠AHE=∠DAE=90°,∴∠DAO+∠EAH=90°,∠EAH+∠AEH=90°,∴∠DAO=∠AEH,∴△DOA≌△AHE(AAS),∴AH=OD=5,EH=OA=3,∴OH=AH﹣OA=2,∴E(3,﹣2).②∵EH⊥y轴,∴∠EHO=∠BOH=90°,∵∠BMO=∠EMH,OB=EH=3,∴△BOM≌△EHM(AAS),∴BM=EM.③结论:OMBD=12.理由:∵△DOA≌△AHE,∴OD=AH,∵OA=OB,∴BD=OH,∵△BOM≌△EHM,∴OM=MH,∴OM=12OH=12BD.(2)结论:OA+OD=2AM或OA﹣OD=2AM.理由:当点D在点B左侧时,∵△BOM≌△EHM,△DOA≌△AHE∴OM=MH,OD=AH∴OH=2OM,OD-OB=AH-OA∴BD=OH∴BD=2OM,∴OD﹣OA=2(AM﹣AO),∴OD+OA=2AM.当点D在点B右侧时,过点E作EH⊥y轴于点H∵∠AOD=∠AHE=∠DAE=90°,∴∠DAO+∠EAH=90°,∠EAH+∠AEH=90°,∴∠DAO=∠AEH,∵AD=AE∴△DOA≌△AHE(AAS),∴EH=AO=3=OB,OD=AH∴∠EHO=∠BOH=90°,∵∠BMO=∠EMH,OB=EH=3,∴△BOM≌△EHM(AAS),∴OM=MH∴OA+OD= OA+AH=OH=OM+MH=2MH=2(AM+AH)=2(AM+OD)整理可得OA﹣OD=2AM.综上:OA+OD=2AM或OA﹣OD=2AM.【点睛】此题考查的是全等三角形的判定及性质、旋转的性质和平面直角坐标系,掌握全等三角形的判定及性质、旋转的性质和点的坐标与线段长度的关系是解决此题的关键.2.(1)150°;(2)∠OCD+∠BO′E′=360°-α;(3)∠AOB=∠BO′E′【分析】(1)先根据平行线的性质得到∠AOE的度数,再根据直角、周角的定义即可求得∠BOE的度数;(2)如图②,过O点作OF∥CD,根据平行线的判定和性质可得∠OCD、∠BO′E′的数量关系;(3)由已知推出CP∥OB,得到∠AOB+∠PCO=180°,结合角平分线的定义可推出∠OCD=2∠PCO=360°-2∠AOB,根据(2)∠OCD+∠BO′E′=360°-∠AOB,进而推出∠AOB=∠BO′E′.【详解】解:(1)∵CD∥OE,∴∠AOE=∠OCD=120°,∴∠BOE=360°-∠AOE-∠AOB=360°-90°-120°=150°;(2)∠OCD+∠BO′E′=360°-α.证明:如图②,过O点作OF∥CD,∵CD∥O′E′,∴OF∥O′E′,∴∠AOF=180°-∠OCD,∠BOF=∠E′O′O=180°-∠BO′E′,∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO′E′=360°-(∠OCD+∠BO′E′)=α,∴∠OCD+∠BO′E′=360°-α;(3)∠AOB=∠BO′E′.证明:∵∠CPO′=90°,∴PO′⊥CP,∵PO′⊥OB,∴CP∥OB,∴∠PCO+∠AOB=180°,∴2∠PCO=360°-2∠AOB,∵CP是∠OCD的平分线,∴∠OCD =2∠PCO =360°-2∠AOB ,∵由(2)知,∠OCD +∠BO ′E ′=360°-α=360°-∠AOB , ∴360°-2∠AOB +∠BO ′E ′=360°-∠AOB , ∴∠AOB =∠BO ′E ′. 【点睛】此题考查了平行线的判定和性质,平移的性质,直角的定义,角平分线的定义,正确作出辅助线是解决问题的关键.3.(1)35,35,平行;(2)∠FMN +∠GHF =180°,证明见解析;(3)不变,2 【分析】(1)根据(α-35)2+|β-α|=0,即可计算α和β的值,再根据内错角相等可证AB ∥CD ; (2)先根据内错角相等证GH ∥PN ,再根据同旁内角互补和等量代换得出∠FMN +∠GHF =180°;(3)作∠PEM 1的平分线交M 1Q 的延长线于R ,先根据同位角相等证ER ∥FQ ,得∠FQM 1=∠R ,设∠PER =∠REB =x ,∠PM 1R =∠RM 1B =y ,得出∠EPM 1=2∠R ,即可得1FPN Q∠∠=2. 【详解】解:(1)∵(α-35)2+|β-α|=0, ∴α=β=35,∴∠PFM =∠MFN =35°,∠EMF =35°, ∴∠EMF =∠MFN , ∴AB ∥CD ;(2)∠FMN +∠GHF =180°; 理由:由(1)得AB ∥CD , ∴∠MNF =∠PME , ∵∠MGH =∠MNF , ∴∠PME =∠MGH , ∴GH ∥PN , ∴∠GHM =∠FMN , ∵∠GHF +∠GHM =180°, ∴∠FMN +∠GHF =180°; (3)1FPN Q∠∠的值不变,为2, 理由:如图3中,作∠PEM 1的平分线交M 1Q 的延长线于R , ∵AB ∥CD , ∴∠PEM 1=∠PFN ,∵∠PER =12∠PEM 1,∠PFQ =12∠PFN , ∴∠PER =∠PFQ , ∴ER ∥FQ ,∴∠FQM 1=∠R ,设∠PER =∠REB =x ,∠PM 1R =∠RM 1B =y , 则有:122y x Ry x EPM ⎧⎨⎩=+∠=+∠,可得∠EPM 1=2∠R , ∴∠EPM 1=2∠FQM 1, ∴11EPM FQM ∠∠=1FPN Q∠∠=2.【点睛】本题主要考查平行线的判定与性质,熟练掌握内错角相等证平行,平行线同旁内角互补等知识是解题的关键.4.(1)∠BME =∠MEN ﹣∠END ;∠BMF =∠MFN +∠FND ;(2)120°;(3)不变,30° 【分析】(1)过E 作EH ∥AB ,易得EH ∥AB ∥CD ,根据平行线的性质可求解;过F 作FH ∥AB ,易得FH ∥AB ∥CD ,根据平行线的性质可求解;(2)根据(1)的结论及角平分线的定义可得2(∠BME +∠END )+∠BMF -∠FND =180°,可求解∠BMF =60°,进而可求解;(3)根据平行线的性质及角平分线的定义可推知∠FEQ =12∠BME ,进而可求解. 【详解】解:(1)过E 作EH ∥AB ,如图1,∴∠BME =∠MEH , ∵AB ∥CD , ∴HE ∥CD , ∴∠END =∠HEN ,∴∠MEN =∠MEH +∠HEN =∠BME +∠END , 即∠BME =∠MEN ﹣∠END .如图2,过F 作FH ∥AB , ∴∠BMF =∠MFK , ∵AB ∥CD , ∴FH ∥CD , ∴∠FND =∠KFN ,∴∠MFN =∠MFK ﹣∠KFN =∠BMF ﹣∠FND , 即:∠BMF =∠MFN +∠FND .故答案为∠BME =∠MEN ﹣∠END ;∠BMF =∠MFN +∠FND . (2)由(1)得∠BME =∠MEN ﹣∠END ;∠BMF =∠MFN +∠FND . ∵NE 平分∠FND ,MB 平分∠FME ,∴∠FME =∠BME +∠BMF ,∠FND =∠FNE +∠END , ∵2∠MEN +∠MFN =180°,∴2(∠BME +∠END )+∠BMF ﹣∠FND =180°, ∴2∠BME +2∠END +∠BMF ﹣∠FND =180°, 即2∠BMF +∠FND +∠BMF ﹣∠FND =180°, 解得∠BMF =60°, ∴∠FME =2∠BMF =120°;(3)∠FEQ 的大小没发生变化,∠FEQ =30°. 由(1)知:∠MEN =∠BME +∠END , ∵EF 平分∠MEN ,NP 平分∠END ,∴∠FEN =12∠MEN =12(∠BME +∠END ),∠ENP =12∠END , ∵EQ ∥NP , ∴∠NEQ =∠ENP ,∴∠FEQ =∠FEN ﹣∠NEQ =12(∠BME +∠END )﹣12∠END =12∠BME , ∵∠BME =60°, ∴∠FEQ =12×60°=30°. 【点睛】本题主要考查平行线的性质及角平分线的定义,作平行线的辅助线是解题的关键. 5.(1)20,20,//AB CD ;(2)180FMN GHF ∠+∠=︒;(3)1FPN Q∠∠的值不变,12FPN Q=∠∠ 【分析】(1)根据2(402)|20|0αβ-+-=,即可计算α和β的值,再根据内错角相等可证//AB CD ; (2)先根据内错角相等证//GH PN ,再根据同旁内角互补和等量代换得出180FMN GHF ∠+∠=︒;(3)作1PEM ∠的平分线交1M Q 的延长线于R ,先根据同位角相等证//ER FQ ,得1FQM R =∠∠,设PER REB x ==∠∠,11PM R RM B y ==∠∠,得出12EPM R ∠=∠,即可得12FPN Q=∠∠. 【详解】解:(1)2(402)|20|0αβ-+-=,4020α∴-=,200β-=,20αβ∴==,20PFM MFN ∴∠=∠=︒,20EMF ∠=︒, EMF MFN ∴∠=∠,//AB CD ∴;故答案为:20、20,//AB CD ; (2)180FMN GHF ∠+∠=︒; 理由:由(1)得//AB CD ,MNF PME ∴∠=∠, MGH MNF ∠=∠, PME MGH ∴∠=∠,//GH PN ∴, GHM FMN ∴∠=∠, 180GHF GHM ∠+∠=︒,180FMN GHF ∴∠+∠=︒;(3)1FPN Q ∠∠的值不变,12FPN Q=∠∠; 理由:如图3中,作1PEM ∠的平分线交1M Q 的延长线于R ,//AB CD ,1PEM PFN ∴∠=∠,112PER PEM ∠=∠,12PFQ PFN =∠∠,PER PFQ ∴∠=∠, //ER FQ ∴,1FQM R ∴∠=∠,设PER REB x ==∠∠,11PM R RM B y ==∠∠,则有:122y x Ry x EPM =+∠⎧⎨=+∠⎩,可得12EPM R ∠=∠,112EPM FQM ∴∠=∠,∴112EPM FQM ∠=∠. 【点睛】本题主要考查平行线的判定与性质,熟练掌握内错角相等证平行,平行线同旁内角互补等知识是解题的关键.6.(1)见解析;(2)∠PEQ +2∠PFQ =360°;(3)30° 【分析】(1)首先证明∠1=∠3,易证得AB //CD ;(2)如图2中,∠PEQ +2∠PFQ =360°.作EH //AB .理由平行线的性质即可证明; (3)如图3中,设∠QPF =y ,∠PHQ =x .∠EPQ =z ,则∠EQF =∠FQH =5y ,想办法构建方程即可解决问题; 【详解】 (1)如图1中,∵∠2=∠3,∠1=∠2, ∴∠1=∠3, ∴AB //CD .(2)结论:如图2中,∠PEQ +2∠PFQ =360°. 理由:作EH //AB .∵AB//CD,EH//AB,∴EH//CD,∴∠1=∠2,∠3=∠4,∴∠2+∠3=∠1+∠4,∴∠PEQ=∠1+∠4,同法可证:∠PFQ=∠BPF+∠FQD,∵∠BPE=2∠BPF,∠EQD=2∠FQD,∠1+∠BPE=180°,∠4+∠EQD=180°,∴∠1+∠4+∠EQD+∠BPE=2×180°,即∠PEQ+2(∠FQD+∠BPF)=360°,∴∠PEQ+2∠PFQ=360°.(3)如图3中,设∠QPF=y,∠PHQ=x.∠EPQ=z,则∠EQF=∠FQH=5y,∵EQ//PH,∴∠EQC=∠PHQ=x,∴x+10y=180°,∵AB//CD,∴∠BPH=∠PHQ=x,∵PF平分∠BPE,∴∠EPQ+∠FPQ=∠FPH+∠BPH,∴∠FPH=y+z﹣x,∵PQ平分∠EPH,∴Z=y+y+z﹣x,∴x=2y,∴12y=180°,∴y=15°,∴x=30°,∴∠PHQ=30°.【点睛】本题考查了平行线的判定与性质,角平分线的定义等知识.(2)中能正确作出辅助线是解题的关键;(3)中能熟练掌握相关性质,找到角度之间的关系是解题的关键. 7.(1)1115656=-⨯,()11111n n n n =-⨯++;(2)①4950;②1465119800【分析】(1)根据规律可得第5个算式;根据规律可得第n 个算式;(2)①根据运算规律可得结果.②利用非负数的性质求出a 与b 的值,代入原式后拆项变形,抵消即可得到结果.【详解】(1)根据规律得:第5个等式是1115656=-⨯,第n 个等式是()11111n n n n =-⨯++; (2)①11111223344950⨯⨯⨯⨯++++, 111111111223344950=-+-+-++-, 1150=-, 4950=;②a 0=,1a ,3b =,原式111111324354698100=+++++⨯⨯⨯⨯⨯, 11111111111111(1)()()+()()23224235246298100=⨯-+⨯-+⨯-⨯-++⨯-, 1111111111(1)2324354698100=⨯-+-+-+-++-, 1111(1)2299100=⨯+--, 1465119800=. 【点睛】本题主要考查了数字的变化规律,发现规律,运用规律是解答此题的关键.8.(1)210-1;(2)n 1514+-;(3)9×210+1. 【分析】(1)根据题目中材料可以得到用类比的方法得到1+2+22+23+…+29的值;(2)根据题目中材料可以得到用类比的方法得到1+5+52+53+54+…+5n 的值.(3)根据题目中的信息,运用类比的数学思想可以解答本题.【详解】解:(1)设S=1+2+22+23+ (29)将等式两边同时乘以2得:2S=2+22+23+24+…+29+210,将下式减去上式得2S-S=210-1,即S=210-1,即1+2+22+23+…+29=210-1.故答案为210-1;(2)设S=1+5+52+53+54+…+5n ,将等式两边同时乘以5得:5S=5+52+53+54+55+…+5n +5n+1,将下式减去上式得5S-S=5n+1-1,即S=n 1514+-, 即1+5+52+53+54+…+5n =n 1514+-; (3)设S=1+2×2+3×22+4×23+…+9×28+10×29,将等式两边同时乘以2得:2S=2+2×22+3×23+4×24+…+9×29+10×210,将上式减去下式得-S=1+2+22+23+…+29+10×210,-S=210-1-10×210,S=9×210+1,即1+2×2+3×22+4×23+…+9×28+10×29=9×210+1.【点睛】本题考查有理数的混合运算、数字的变化类,解题的关键是明确题意,发现数字的变化规律.9.(1)-3006,990;(2)见解析;(3)P (t )的最大值是P (2262)=36.【分析】(1)根据“前介数”t 与它的“中介数”的差为P (t )的定义求解即可;(2)设“前介数”为t aabc =且a 、b 、c 均不为0的整数,即1≤a 、b 、c 9≤,根据定义得到P (t )=()9110111aabc caab a b c -=+-,则P (t )一定能被9整除;(3)设“前介数”为22220010t ab a b ==++,根据题意得到4a b ++能被3整除,且b 只能取2,4,6,8中的其中一个数;t 对应的“中介数”是221000220b a b a =++,得到a 只能取2,4,6,8中的其中一个数,计算P (t )19809999a b =+-,推出要求P (t )的最大值,即a 要尽量的大,b 要尽量的小,再分类讨论即可求解.【详解】(1)解:2215是“前介数”,其对应的“中介数”是5221,∴P (2215)=2215-5221=-3006;6655是“前介数”,其对应的“中介数”是5665,∴P (6655)=6655-5665=990;故答案为:-3006,990;(2)证明:设“前介数”为t aabc =且a 、b 、c 均为不为0的整数,即1≤a 、b 、c 9≤, ∴100010010110010t a a b c a b c =+++=++,又t 对应的“中介数”是1000100101000110caab c a a b c a b =+++=++,∴P (t )=()1100101000110aabc caab a b c c a b -=++-++1100101000110a b c c a b =++---9909999a b c =+-()9110111a b c =+-,∵a 、b 、c 均不为0的整数,∴110111a b c +-为整数,∴P (t )一定能被9整除;(3)证明:设“前介数”为22t ab =且即1≤a 、b 9≤,a 、b 均为不为0的整数, ∴200020010220010t a b a b =+++=++,∵t 能被6整除,∴t 能被2整除,也能被3整除,∴b 为偶数,且224a b a b +++=++能被3整除,又19b ≤≤,∴b 只能取2,4,6,8中的其中一个数,又t 对应的“中介数”是221000200201000220b a b a b a =+++=++,且该“中介数”能被2整除,∴a 为偶数,又19a ≤≤,∴a 只能取2,4,6,8中的其中一个数,∴P (t )=()22222200101000220ab b a a b b a -=++-++2200101000220a b b a =++---19809999a b =+-,要求P (t )的最大值,即a 要尽量的大,b 要尽量的小,①a 的最大值为8,b 的最小值为2,但此时414a b ++=,且14不能被3整除,不符合题意,舍去;②a 的最大值为6,b 的最小值仍为2,但此时412a b ++=,能被3整除,且P (t )=2262-2226=36;③a 的最大值仍为8,b 的最小值为4,但此时416a b ++=,且16不能被3整除,不符合题意,舍去;其他情况,a 减少,b 增大,则P (t )减少,∴满足条件的P (t )的最大值是P (2262)=36.【点睛】本题考查用新定义解题,根据新定义,表示出“前介数”,与其对应的“中介数”是求解本题的关键.本题中运用到的分类讨论思想是重要一种数学解题思想方法.10.(1)a 2=2,a 3=-1,a 4=12(2)a 2016•a 2017•a 2018= -1(3)a33+a66+a99+…+a9999=-1【分析】(1)将a1=12代入11a-中即可求出a2,再将a2代入求出a3,同样求出a4即可.(2)从(1)的计算结果可以看出,从a1开始,每三个数一循环,而2016÷3=672,则a2016=-1,a2017=12,a2018=2然后计算a2016•a2017•a2018的值;(3)观察可得a3、a6、a9、…a99,都等于-1,将-1代入,即可求出结果.【详解】(1)将a1=12,代入11a-,得21=211-2a=;将a2=2,代入11a-,得31=-11-2a=;将a3=-1,代入11a-,得411=1--12a=().(2)根据(1)的计算结果,从a1开始,每三个数一循环,而2016÷3=672,则a2016=-1,a2017=12,a2018=2所以,a2016•a2017•a2018=(-1)×12×2= -1(3)观察可得a3、a6、a9、…a99,都等于-1,将-1代入,a33+a66+a99+…+a9999=(-1)3+(-1)6+(-1)9+…+(-1)99=(-1)+1+(-1)+…(-1)=-1【点睛】此类问题考查了数字类的变化规律,解题的关键是要严格根据定义进行解答,同时注意分析循环的规律.11.(1)x7-1;(2)x n+1-1;(3)51312-.【分析】(1)仿照已知等式写出答案即可;(2)先归纳总结出规律,然后按规律解答即可;(3)先利用得出规律的变形,然后利用规律解答即可.【详解】解:(1)根据题意得:(x-1)(x6+x5+x4+x3+x2+x+1)=x7-1;(2)根据题意得:(x-1)(x"+x"-1+.…+x+1)=x"+1-1;(3)原式=12×(3-1)(1+3+32+···+349+350)=12×(x50+1-1)=51312-故答案为:(1)x7-1;(2)x n+1-1;(3)51312-.【点睛】本题考查了平方差公式以及规律型问题,弄清题意、发现数字的变化规律是解答本题的关键.12.(1)11316⨯;11131316⎛⎫⨯- ⎪⎝⎭;(2)[]13(1)(131)n n +-⋅+;13(3111311)n n ⎡⎤--+⎢⎣+⎥⎦;(3)100301. 【分析】(1)观察前4个等式的分母先得出第5个式子的分母,再依照前4个等式即可得出答案;(2)根据前4个等式归纳类推出一般规律即可;(3)利用题(2)的结论,先写出1234100a a a a a +++++中各数的值,然后通过提取公因式、有理数加减法、乘法运算计算即可.【详解】(1)观察前4个等式的分母可知,第5个式子的分母为1316⨯则第5个式子为:51111131631316a ⎛⎫==⨯- ⎪⨯⎝⎭ 故应填:11316⨯;11131316⎛⎫⨯- ⎪⎝⎭; (2)第1个等式的分母为:14(130)(131)⨯=+⨯⨯+⨯第2个等式的分母为:47(131)(132)⨯=+⨯⨯+⨯第3个等式的分母为:710(132)(133)⨯=+⨯⨯+⨯第4个等式的分母为:1013(133)(134)⨯=+⨯⨯+⨯归纳类推得,第n 个等式的分母为:[]13(1)(13)n n +-⋅+则第n 个等式为:[]1111313(1)(13)13(1)13n a n n n n +-⋅++⎡⎤==-⎢⎥⎣-⎦+(n 为正整数) 故应填:[]13(1)(131)n n +-⋅+;13(3111311)n n ⎡⎤--+⎢⎣+⎥⎦; (3)由(2)的结论得:[]10013(1001)(13100)298301311111329801a ⎛⎫==+⨯-⨯+⨯⨯=⨯- ⎪⎝⎭ 则1234100a a a a a +++++ 1111144771010132983011+++++⨯⨯⨯⨯⨯= 111111111111343473711132981031013301⎛⎫⎛⎫⎛⎫⎛⎫⨯-+⨯-+⨯-+⨯-++ ⎪ ⎪ ⎛⎫=⨯-⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ ⎪⎝⎭ 111111111++++344771*********3018=-⎛⎫⨯-+--- ⎪⎝⎭1330111⎛=⨯-⎫ ⎪⎝⎭30130103⨯= 110030=. 【点睛】本题考查了有理数运算的规律类问题,依据已知等式归纳总结出等式的一般规律是解题关键.13.(1)(-2,0);(2)①4秒;②(0,43)或(-3,43) 【分析】(1)根据BC =AE =3,OA =1,推出OE =2,可得结论.(2)①判断出PB =CD ,即可得出结论;②根据△PEA 的面积以及AE 求出点P 到AE 的距离,结合点P 的路线可得坐标.【详解】解:(1)∵C (-3,2),A (1,0),∴BC =3,OA =1,∵BC =AE =3,∴OE =AE -AO =2,∴E (-2,0);(2)①∵点C 的坐标为(-3,2)∴BC =3,CD =2,∵点P 的横坐标与纵坐标互为相反数;∴点P 在线段BC 上,∴PB =CD =2,即t =(2+2)÷1=4;∴当t =4秒时,点P 的横坐标与纵坐标互为相反数;②∵△PEA 的面积为2,A (1,0),E (-2,0),∴AE =3,设点P 到AE 的距离为h ∴1322h ⨯⨯=, ∴h =43, 即点P 到AE 的距离为43, ∴点P 的坐标为(0,43)或(-3,43). 【点睛】本题考查坐标与图形变化-平移,三角形的面积等知识,解本题的关键是由线段和部分点的坐标,得出其它点的坐标.14.(1)120°;(2)90°-12x°;(3)不变,12;(4)45°【分析】(1)由平行线的性质:两直线平行同旁内角互补可得;(2)由平行线的性质可得∠ABN=180°-x°,根据角平分线的定义知∠ABP=2∠CBP、∠PBN=2∠DBP,可得2∠CBP+2∠DBP=180°-x°,即∠CBD=∠CBP+∠DBP=90°-12x°;(3)由AM∥BN得∠APB=∠PBN、∠ADB=∠DBN,根据BD平分∠PBN知∠PBN=2∠DBN,从而可得∠APB:∠ADB=2:1;(4)由AM∥BN得∠ACB=∠CBN,当∠ACB=∠ABD时有∠CBN=∠ABD,得∠ABC+∠CBD=∠CBD+∠DBN,即∠ABC=∠DBN,根据角平分线的定义可得∠ABP=∠PBN=12∠ABN=2∠DBN,由平行线的性质可得12∠A+12∠ABN=90°,即可得出答案.【详解】解:(1)∵AM∥BN,∠A=60°,∴∠A+∠ABN=180°,∴∠ABN=120°;(2)∵AM∥BN,∴∠ABN+∠A=180°,∴∠ABN=180°-x°,∴∠ABP+∠PBN=180°-x°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=180°-x°,∴∠CBD=∠CBP+∠DBP=12(180°-x°)=90°-12x°;(3)不变,∠ADB:∠APB=12.∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1,∴∠ADB:∠APB=12;(4)∵AM∥BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD=∠CBD+∠DBN,∴∠ABC=∠DBN,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠ABC,∠PBN=2∠DBN,∴∠ABP=∠PBN=2∠DBN=12∠ABN,∵AM∥BN,∴∠A+∠ABN=180°,∴12∠A+12∠ABN=90°,∴12∠A+2∠DBN=90°,∴14∠A+∠DBN=12(12∠A+2∠DBN)=45°.【点睛】本题主要考查平行线的性质和角平分线的定义,熟练掌握平行线的性质是解题的关键.15.(1)a=-2,b=2;(2)P(0,-4)或(0,4);(3)①∠CAB+∠ODB=90°;②∠AED=45°.【分析】(1)根据非负数的性质即可求得a、b的值;(2)先求得S△ABC=4,设P(0,t),根据S△OPC=12OP×2=12×t ×2=4求得t值,即可求得点P的坐标;(3)①已知BD∥AC,根据两直线平行,内错角相等可得∠CAB=∠OBD,由∠OBD+∠ODB=90°,即可得∠CAB+∠ODB=90°;②根据角平分线的定义及①中的结论,可求得∠3+∠4=45°;过点E作EF∥AC,即可得EF∥BD∥AC,根据平行线的性质可得∠3=∠1,∠2=∠4,由此求得∠AED=∠1+∠2=∠4+∠3=45°.【详解】(1)∵()220a+=,∴a+2=0,b-2=0,∴a=-2,b=2;(2)∵a=-2,b=2,∴A(-2,0),C(2,2),∴S△ABC=12AB•BC=12×4×2=4;设P(0,t),∴S△OPC=12OP×2=12×t ×2=t=4;∴t=4或t=-4,∴P(0,-4)或(0,4).(3)①∵BD∥AC,∴∠CAB=∠OBD,∵∠OBD+∠ODB=90°,∴∠CAB+∠ODB=90°;②∵AE,DE分别平分∠CAB,∠ODB,∴∠3=12CAB∠,∠4=12ODB∠,∵∠CAB+∠ODB=90°,。
2018年人版七年级数学下《压轴题培优》期末复习专题含答案
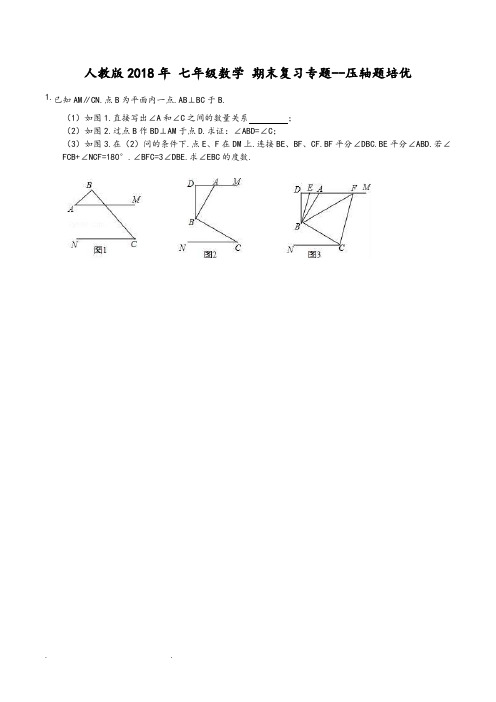
人教版2018年七年级数学期末复习专题--压轴题培优1.已知AM∥CN.点B为平面内一点.AB⊥BC于B.(1)如图1.直接写出∠A和∠C之间的数量关系;(2)如图2.过点B作BD⊥AM于点D.求证:∠ABD=∠C;(3)如图3.在(2)问的条件下.点E、F在DM上.连接BE、BF、CF.BF平分∠DBC.BE平分∠ABD.若∠FCB+∠NCF=180°.∠BFC=3∠DBE.求∠EBC的度数.2.如图.已知两条射线OM∥CN.动线段AB的两个端点A.B分别在射线OM、CN上.且∠C=∠OAB=108°.F在线段CB上.OB平分∠AOF.OE平分∠COF.(1)请在图中找出与∠AOC相等的角.并说明理由;(2)若平行移动AB.那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化?若变化.找出变化规律;若不变.求出这个比值;(3)在平行移动AB的过程中.是否存在某种情况.使∠OEC=2∠OBA?若存在.请求出∠OBA度数;若不存在.说明理由.3.已知AB∥CD.线段EF分别与AB、CD相交于点E、F.(1)如图①.当∠A=25°,∠APC=70°时.求∠C的度数;(2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A.∠APC与∠C之间有什么确定的相等关系?试证明你的结论.(3)如图③.当点P在线段FE的延长线上运动时,(2)中的结论还成立吗?如果成立,说明理由;如果不成立.试探究它们之间新的相等关系并证明.4.如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.(1)求C点坐标;(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.5.已知BC∥OA,∠B=∠A=100°.试回答下列问题:(1)如图1所示,求证:OB∥AC;(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC.并且OE平分∠BOF.试求∠EOC的度数;(3)在(2)的条件下.若平行移动AC.如图3.那么∠OCB:∠OFB的值是否随之发生变化?若变化.试说明理由;若不变.求出这个比值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版 2018 年七年级数学期末复习专题--压轴题培优i)已知AM∥CN,点B 为平面内一点,AB⊥BC于B.(1)如图 1,直接写出∠A和∠C之间的数量关系 ?? ;(2)如图 2,过点 B 作BD⊥AM于点D,求证:∠ABD=∠C;(3)如图 3,在(2)问的条件下,点 E、F 在DM 上,连接 BE、BF、CF,BF 平分∠DBC,BE 平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.ii)如图,已知两条射线OM∥CN,动线段 AB 的两个端点 A.B 分别在射线 OM、CN 上,且∠C=∠OAB=108°,F 在线段 CB 上,OB 平分∠AOF,OE 平分∠COF.(1)请在图中找出与∠AOC相等的角,并说明理由;(2)若平行移动 AB,那么∠OBC与∠OFC的度数比是否随着 AB 位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值;(3)在平行移动 AB 的过程中,是否存在某种情况,使∠OEC=2∠OBA?若存在,请求出∠OBA度数;若不存在,说明理由.iii)已知AB∥CD,线段EF分别与AB、CD相交于点E、F.(1)如图①,当∠A=25°,∠APC=70°时,求∠C的度数;(2)如图②,当点P在线段EF上运动时(不包括E、F两点),∠A.∠APC与∠C之间有什么确定的相等关系?试证明你的结论.(3)如图③,当点P在线段FE的延长线上运动时,(2)中的结论还成立吗?如果成立,说明理由;如果不成立,试探究它们之间新的相等关系并证明.iv)如图 1,在平面直角坐标系中,A(a,0)是x 轴正半轴上一点,C 是第四象限一点,CB⊥y轴,交 y=16.轴负半轴于 B(0,b),且(a-3)2+|b+4|=0,S 四边形AOBC(1)求C 点坐标;(2)如图 2,设D 为线段 OB 上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点 P,求∠APD的度数.(3)如图 3,当D 点在线段 OB 上运动时,作DM⊥AD交BC 于M 点,∠BMD、∠DAO的平分线交于 N 点,则D 点在运动过程中,∠N 的大小是否变化?若不变,求出其值,若变化,说明理由.v)已知BC∥OA,∠B=∠A=100°.试回答下列问题:(1)如图 1 所示,求证:OB∥AC;(2)如图 2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数;(3)在(2)的条件下,若平行移动AC,如图 3,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值。
vi)如图,已知 AM//BN,∠A=600.点 P 是射线 AM 上一动点(与点 A 不重合),BC、BD 分别平分∠ABP 和∠PBN,分别交射线 AM 于点 C,D. (1)①∠ABN 的度数是;②∵AM//BN,∴∠ACB=∠;(2)求∠CBD 的度数;(3)当点 P 运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.(4)当点 P 运动到使∠ACB=∠APD时,∠ABC的度数是.vii) 课题学习:平行线的“等角转化”功能.阅读理解:如图 1,已知点 A 是 BC 外一点,连接 AB,AC.求∠BAC+∠B+∠C 的度数.(1)阅读并补充下面推理过程.解:过点 A 作ED∥BC,所以∠B=,∠C=.又因为∠EAB+∠BAC+∠DAC=180°.所以∠B+∠BAC+∠C=180°.解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.方法运用:(2)如图 2,已知AB∥ED,求∠B+∠BCD+∠D的度数.深化拓展:(3)已知AB∥CD,点C 在点D 的右侧,∠ADC=70°,BE 平分∠ABC,DE 平分∠ADC,BE,DE 所在的直线交于点 E,点E 在AB 与CD 两条平行线之间.请从下面的 A,B 两题中任选一题解答,我选择题.A.如图 3,点B 在点A 的左侧,若∠ABC=60°,则∠BED的度数为°.B.如图 4,点B 在点A 的右侧,且 AB<CD,AD<BC.若∠ABC=n°,则∠BED度数为°.(用含n 的代数式表示)viii)已知A(0,a),B(b,0),a、b 满足.(1)求a、b 的值;(2)在坐标轴上找一点 D,使三角形 ABD 的面积等于三角形 OAB 面积的一半,求 D 点坐标;(3)做∠BAO平分线与∠AOC平分线 BE 的反向延长线交于 P 点,求∠P的度数.ix)如图 1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+b-2=0,过C 作CB⊥x轴于B.(1)求△ABC的面积.(2)若过 B 作BD∥AC 交y 轴于D,且AE,DE 分别平分∠CAB,∠ODB,如图 2,求∠AED的度数.(3)在y 轴上是否存在点 P,使得△ABC和△ACP的面积相等?若存在,求出 P 点坐标;若不存在,请说明理由.x)如图 1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,C(0,a),D(b,a),其中a,b满足关系式:|a+3|+(b-a+1)2=0.(1)a=,b=,△BCD的面积为;(2)如图 2,若AC⊥BC,点P线段OC上一点,连接BP,延长BP交AC于点Q,当∠CPQ=∠CQP时,求证:BP平分∠ABC;(3)如图 3,若AC⊥BC,点E是点A与点B之间一动点,连接CE,CB始终平分∠ECF,当点E在点A与点B之间运动时,的值是否变化?若不变,求出其值;若变化,请说明理由.xi)如图 1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+|a- b+6|=0,线段 AB 交y 轴于 F 点.(1)求点 A.B 的坐标.(2)点D 为y 轴正半轴上一点,若ED∥AB,且AM,DM 分别平分∠CAB,∠ODE,如图 2,求∠AMD的度数.(3)如图 3,(也可以利用图 1)①求点 F 的坐标;②点 P 为坐标轴上一点,若△ABP 的三角形和△ABC 的面积相等?若存在,求出 P 点坐标.xii)如图所示,A(1,0),点B 在y 轴上,将三角形 OAB 沿x 轴负方向平移,平移后的图形为三角形DEC,且点 C 的坐标为(-3,2).(1)直接写出点 E 的坐标;(2)在四边形 ABCD 中,点 P 从点B 出发,沿“BC→CD”移动.若点 P 的速度为每秒 1 个单位长度,运动时间为 t 秒,回答下列问题:①当 t=秒时,点 P 的横坐标与纵坐标互为相反数;②求点 P 在运动过程中的坐标,(用含 t 的式子表示,写出过程);③当 3 秒<t<5 秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z 之间的数量关系能否确定?若能,请用含 x,y 的式子表示 z,写出过程;若不能,说明理由.xiii)如图,已知平面直角坐标系内A(2a-1,4),B(-3,3b+1),A.B;两点关于y轴对称.(1)求A.B的坐标;(2)动点P、Q分别从A点、B点同时出发,沿直线AB向右运动,同向而行,点的速度是每秒 2 个单位长度,Q点的速度是每秒 4 个单位长度,设P、Q的运时间为t秒,用含t的代数式表示三角形OPQ的面积S,并写出t的取值范围;(3)在平面直角坐标系中存在一点M,点M的横纵坐标相等,且满足S△PQM:S△OPQ=3:2,求出点M=15 时,三角形OPQ的面积.的坐标,并求出当S△AQMxiv)如图,在平面直角坐标系中,O为原点,点A(0,8),点B(m,0),且m>0.把△AOB绕点A逆时针旋转90°,得△ACD,点O,B旋转后的对应点为C,D.(1)点C的坐标为;(2)①设△BCD的面积为S,用含m的式子表示S,并写出m的取值范围;②当S=6 时,求点B的坐标(直接写出结果即可).xv)如图,已知在平面直角坐标系中,△ABO的面积为 8,OA=OB,BC=12,点P的坐标是(a,6).(1)求△ABC三个顶点A,B,C的坐标;(2)若点P坐标为(1,6),连接PA,PB,则△PAB的面积为;(3)是否存在点P,使△PAB的面积等于△ABC的面积?如果存在,请求出点P的坐标.参考答案i)解:ii)解:iii)⑴∠C=45°分⑵∠C=∠APC-∠A(证明略)⑶不成立,新的相等关系为∠C=∠APC+∠A(证明略)iv)解:(1)∵(a﹣3)2+|b+4|=0,∴a﹣3=0,b+4=0,∴a=3,b=﹣4,∴A(3,0),B(0,﹣4),∴OA=3,OB=4,∵S 四边形=16.∴0.5(OA+BC)×OB=16,∴0.5(3+BC)×4=16,∴BC=5,AOBC∵C 是第四象限一点,CB⊥y 轴,∴C(5,﹣4)(2)如图,延长 CA,∵AF 是∠CAE 的角平分线,∴∠CAF=0.5∠CAE,∵∠CAE=∠OAG,∴∠CAF=0.5∠OAG,∵AD⊥AC,∴∠DAO+∠OAG=∠PAD+∠PAG=90°,∵∠AOD=90°,∴∠DAO+∠ADO=90°,∴∠ADO=∠OAG,∴∠CAF=0.5∠ADO,∵DP 是∠ODA 的角平分线∴∠ADO=2∠ADP,∴∠CAF=∠ADP,∵∠CAF=∠PAG,∴∠PAG=∠ADP,∴∠APD=180°﹣(∠ADP+∠PAD)=180°﹣(∠PAG+∠PAD)=180°﹣90°=90°即:∠APD=90°(3)不变,∠ANM=45°理由:如图,∵∠AOD=90°,∴∠ADO+∠DAO=90°,∵DM⊥AD,∴∠ADO+∠BDM=90°,∴∠DAO=∠BDM,∵N A 是∠OAD 的平分线,∴∠DAN=0.5∠DAO=0.5∠BDM,∵CB⊥y 轴,∴∠BDM+∠BMD=90°,∴∠DAN=0.5(90°﹣∠BMD),∵MN 是∠BMD 的角平分线,∴∠DMN=0.5∠BMD,∴∠DAN+∠DMN=0.5(90°﹣∠BMD)+0.5∠BMD=45°在△DAM 中,∠ADM=90°,∴∠DAM+∠DMA=90°,在△AMN 中,∠ANM=180°﹣(∠NAM+∠NMA)=180°﹣(∠DAN+∠DAM+∠DMN+∠DMA)=180°﹣[(∠DAN+DMN)+(∠DAM+∠DMA)]=180°﹣(45°+90°)=45°,∴D点在运动过程中,∠N的大小不变,求出其值为45°v)略vi)解:(1)120°;∠CBN(2)∵AM∥BN,∴∠ABN+∠A=180°,∴∠ABN=180°-60°=120°,∴∠ABP+∠PBN=120°,∵BC 平分∠ABP,BD 平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=120°,∴∠CBD=∠CBP+∠DBP=60°;(3)不变,∠APB:∠ADB=2:1.∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD 平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1;(4)∵AM∥BN,∴∠ACB=∠CBN,当∠ACB=∠ABD 时,则有∠CBN=∠ABD,∴∠ABC+∠CBD=∠CBD+∠DBN,∴∠ABC=∠DBN,由(1)可知∠ABN=120°,∠CBD=60°,∴∠ABC+∠DBN=60°,∴∠ABC=30°.vii)解:(1)∵ED∥BC,∴∠B=∠EAD,∠C=∠DAE,故答案为:∠EAD,∠DAE;(2)过 C 作CF∥AB,∵AB∥DE,∴CF∥DE,∴∠D=∠FCD,∵CF∥AB,∴∠B=∠BCF,∵∠BCF+∠BCD+∠DCF=360°,∴∠B+∠BCD+∠D=360°,(3)A.如图 2,过点 E 作EF∥AB,∵AB∥CD,∴AB∥CD∥EF,∴∠ABE=∠BEF,∠CDE=∠DEF,∵BE 平分∠ABC,DE 平分∠ADC,∠ABC=60°,∠ADC=70°,∴∠ABE=∠ABC=30°,∠CDE=∠ADC=35°,∴∠BED=∠BEF+∠DEF=30°+35°=65°;故答案为:65;B、如图 3,过点 E 作EF∥AB,∵BE 平分∠ABC,DE 平分∠ADC,∠ABC=n°,∠ADC=70°∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°∵AB∥CD,∴AB∥CD∥EF,∴∠BEF=180°﹣∠ABE=180°﹣n°,∠CDE=∠DEF=35°,∴∠BED=∠BEF+∠DEF=180°﹣n°+35°=215°﹣n°.故答案为:215°﹣n. viii)解:(1)a=-4,b=8;(2)D(-6,0),(-2,0),(0,4),(0,12);(3)45°.ix)解:x)解:xi)解:xii)解:(1)根据题意,可得三角形 OAB 沿x 轴负方向平移 3 个单位得到三角形 DEC,∵点 A 的坐标是(1,0),∴点 E 的坐标是(-2,0);故答案为:(-2,0);(2)①∵点C 的坐标为(-3,2).∴BC=3,CD=2,∵点 P 的横坐标与纵坐标互为相反数;∴点 P 在线段 BC 上,∴PB=CD,即 t=2;∴当 t=2 秒时,点 P 的横坐标与纵坐标互为相反数;故答案为:2;②当点 P 在线段 BC 上时,点 P 的坐标(-t,2),当点 P 在线段 CD 上时,点 P 的坐标(-3,5-t);③能确定,如图,过 P 作PE∥BC 交 AB 于E,则PE∥AD,∴∠1=∠CBP=x°,∠2=∠DAP=y°,∴∠BPA=∠1+∠2=x°+y°=z°,∴z=x+y.xiii)解:xiv)解:(1)∵点A(0,8),∴AO=8,∵△AOB绕点A逆时针旋转90°得△ACD,∴AC=AO=8,∠OAC=90°,∴C(8,8),故答案为:(8,8);(2)①延长DC交x轴于点E,∵点B(m,0),∴OB=m,∵△AOB绕点A逆时针旋转90°得△ACD,∴DC=OB=m,∠ACD=∠AOB=90°,∠OAC=90°,∴∠ACE=90°,∴四边形OACE是矩形,∴DE⊥x主,OE=AC=8,分三种情况:a、当点B在线段OE的延长线上时,如图 1 所示:则BE=OB﹣OE=m﹣8,∴S=0.5DC?BE=0.5m(m﹣8),即S=0.5m2﹣4m(m>8);b、当点B在线段OE上(点B不与O,E重合)时,如图 2 所示:则BE=OE﹣OB=8﹣m,∴S=0.5DC?BE=0.5m(8﹣m),即S=﹣0.5m2+4m(0<m<8);c、当点B与E重合时,即m=8,△BCD不存在;综上所述,S=0.5m2﹣4m(m>8),或S=﹣0.5m2+4m(0<m<8);②当S=6,m>8 时,0.5m2﹣4m=6,解得:m=4±2(负值舍去),∴m=4+2 ;当S=6,0<m<8 时,﹣0.5m2+4m=6,解得:m=2 或m=6,∴点B的坐标为(4+2 ,0)或(2,0)或(6,0).“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
