小波变换 mallat
mallat分解方法

mallat分解方法1. 简介mallat分解方法是一种在信号处理中常用的技术,用于将信号分解成不同尺度的频带。
这种方法基于小波变换,通过对信号进行多级分解,可以得到信号在不同频率范围内的表示。
mallat分解方法由Stephane Mallat于1989年提出,是一种基于多尺度分析的信号处理方法。
它在许多领域中得到广泛应用,如图像处理、音频处理、压缩等。
mallat分解方法的核心思想是使用小波函数作为基函数进行信号分解。
小波函数具有时域和频域上的局部性质,可以有效地捕捉信号的局部特征。
mallat分解方法通过对小波函数进行缩放和平移操作,构建了一组具有不同尺度和位置的小波函数族。
2. mallat算法步骤mallat算法主要包括两个步骤:分解和重构。
2.1 分解•将原始信号进行低通滤波和高通滤波得到近似系数和细节系数。
•低通滤波器将原始信号中的低频部分保留下来,并且去除了高频部分。
•高通滤波器将原始信号中的高频部分保留下来,并且去除了低频部分。
•重复上述步骤,将近似系数作为输入,继续进行低通滤波和高通滤波,直到达到设定的分解层数。
2.2 重构•将分解得到的近似系数和细节系数进行逆变换,得到重构信号。
•逆变换过程是对分解过程的逆操作,通过将每一级的近似系数和细节系数进行上采样、滤波和加权求和,得到重构信号。
3. mallat分解方法的应用mallat分解方法在信号处理领域有广泛的应用。
3.1 图像处理mallat分解方法可以用于图像压缩、去噪等方面。
通过对图像进行mallat分解,可以得到不同尺度上的图像信息。
根据不同尺度的重要性,可以选择保留部分系数,从而实现图像压缩。
同时,在mallat分解域中对图像进行去噪处理也是一种常见的应用。
3.2 音频处理mallat分解方法可以用于音频信号降噪、特征提取等方面。
通过对音频信号进行mallat分解,可以得到不同尺度上的音频信息。
在降噪方面,可以根据不同尺度的能量分布来选择保留或去除部分系数,从而实现降噪效果。
小波学习之一(单层一维离散小波变换DWT的Mallat算法C++和MATLAB实现)

⼩波学习之⼀(单层⼀维离散⼩波变换DWT的Mallat算法C++和MATLAB实现)1 Mallat算法离散序列的Mallat算法分解公式如下:其中,H(n)、G(n)分别表⽰所选取的⼩波函数对应的低通和⾼通滤波器的抽头系数序列。
从Mallat算法的分解原理可知,分解后的序列就是原序列与滤波器序列的卷积再进⾏隔点抽取⽽来。
离散序列的Mallat算法重构公式如下:其中,h(n)、g(n)分别表⽰所选取的⼩波函数对应的低通和⾼通滤波器的抽头系数序列。
2 ⼩波变换实现过程(C/C++)2.1 ⼩波变换结果序列长度⼩波的Mallat算法分解后的序列长度由原序列长SoureLen和滤波器长FilterLen决定。
从Mallat算法的分解原理可知,分解后的序列就是原序列与滤波器序列的卷积再进⾏隔点抽取⽽来。
即分解抽取的结果长度为(SoureLen+FilterLen-1)/2。
2.2 获取滤波器组对于⼀些通⽤的⼩波函数,简单起见,可以通过Matlab的wfilters(‘wavename’)获取4个滤波器;特殊的⼩波函数需要⾃⾏构造获得。
下⾯以db1⼩波函数(Haar⼩波)为例,其变换与重构滤波器组的结果如下://matlab输⼊获取命令>> [Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('db1')//获取的结果Lo_D =0.7071 0.7071Hi_D =-0.7071 0.7071Lo_R =0.7071 0.7071Hi_R =0.7071 -0.70712.3 信号边界延拓在Mallat算法中,假定输⼊序列是⽆限长的,⽽实际应⽤中输⼊的信号是有限的采样序列,这就会出现信号边界处理问题。
对于边界信号的延拓⼀般有3种⽅法,即零延拓、对称延拓和周期延拓。
3种延拓⽅法⽐较情况如下:对于正交⼩波变换来说,前两种延拓⽅法实现起来⽐较简单,但重建时会产⽣边界效应,⽽且分解的层数越多,产⽣的边界效应越显著。
小波变换发展史

小波变换发展史传统的信号理论,是建立在Fourier分析基础上的,而Fourier变换作为一种全局性的变化,其有一定的局限性。
在实际应用中人们开始对Fourier变换进行各种改进,小波分析由此产生了。
小波分析是一种新兴的数学分支,它是泛函数、Fourier分析、调和分析、数值分析的最完美的结晶;在应用领域,特别是在信号处理、图像处理、语音处理以及众多非线性科学领域,它被认为是继Fourier分析之后的又一有效的时频分析方法。
小波变换与Fourier变换相比,是一个时间和频域的局域变换因而能有效地从信号中提取信息,通过伸缩和平移等运算功能对函数或信号进行多尺(Multiscale Analysis),解决了Fourier变换不能解决的许多困难问题。
1.从傅立叶分析到小波分析1807年,法国学者Fourier指出任何周期函数都可以用一系列正弦波来表示,开创了傅立分析。
傅立叶分析揭示了时域与频域之间内在的联系,反映了“整个”时间范围内信号的“全部”频谱成分,是研究信号的周期现象不可缺少的工具。
建立在傅立叶分析基础上的采样定理和FFT技术奠定了现代数字化技术的理论基础。
尽管傅立叶变换具有很强的频域局域化能力,但是它明显的缺点,那就是无法反映非平稳信号在局部区域的频域特征及其对应关系,即FT在时域没有任何分辨率,无法确定信号奇异性的位置。
为了研究信号在局部时间范围内的频谱特征,1946年,Gabor提出了短时傅立叶变换(Short Time Fourier Transform,STFT),但是STFT的窗口宽度是固定的(和频率无关),这使得它无法同时兼顾信号的低频和高频特征,在分析时变信号时也有一定的局限性。
另外,STFT的窗口函数或核函数不能提供一组离散正交基,所以给数值计算带来了不便,这也是导致STFT 没有得到广泛应用的重要原因。
从傅立叶分析演变而来的小波分析的优点恰恰可以弥补傅立叶变换中存在的不足之处。
模极大值去噪方法

3.2 基于小波变换模极大值去噪方法的研究目前利用小波变换消除噪声的方法很多,但总结起来,比较成熟的是Mallat 提出的一种多尺度小波变换模极大值的去噪方法。
3.2.1 小波变换模极大值的定义定义在尺度s 下,若0x x d " ,()()0,,Wf s x Wf s x £成立,则0x 称为模极大值点,()0,Wf s x 称为模极大值。
小波变换极大模是由信号中奇异点和噪声产生的。
根据理论分析,知道以平滑函数的一阶导数为母小波作小波变换,其小波变换在各个尺度下的模极大值对应于信号突变点的位置。
小波分析尺度越小,平滑函数的平滑区域小,小波系数模极大值点与突变点位置的对应就越准确。
但是小尺度下小波变换随噪声影响非常大,产生许多伪极值点,往往只凭一个尺度不能定位突变点的位置。
相反,在大尺度下对噪声进行了一定的平滑,极值点相对稳定,但由于平滑作用使其定位又产生了偏差。
同时,只有在适当尺度下各突变点引起的小波变换才能避免交迭干扰。
因此,在用小波变换模极大值法判断信号突变点时,需要把多尺度结合起来综合观察。
下面由小波变换模极大值在多尺度上的变化规律来表征信号突变点的性质。
在许多情况下,小波变换并不要求保留所有的连续尺度a ,为了实现快速算法,选择尺度按二进制变化,即二进制变换。
信号的突变点在不同尺度2j 上都会产生对应的模极大值。
在任意尺度2j 上模极大值对应于信号在2j 尺度上平滑后的该点一阶导数大小。
小波理论表明,模极大值的幅值随着尺度的变化规律是由信号在该突变点的局部李氏指数(Lipschitzexponent)决定的。
3.2.2 模极大值随着尺度的变化规律李氏指数的定义为,设函数在0t 附近具有下述特征:()()00,1n x t h p t h A h n n aa +-+?<+ (3-1)则称()x t 在0t 处的李氏指数为a 。
式中h 是一个充分小量,()n p t 是过()0x t 点的n 次多项式()n Z Î。
小波变换
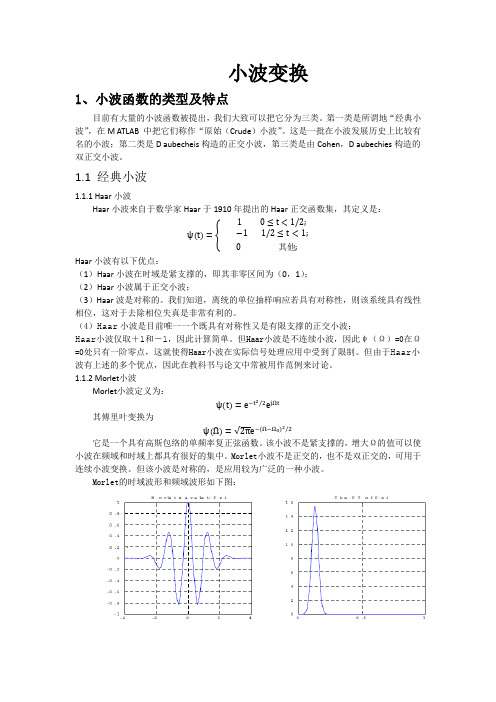
小波变换1、小波函数的类型及特点目前有大量的小波函数被提出,我们大致可以把它分为三类。
第一类是所谓地“经典小波”,在M ATLAB 中把它们称作“原始(Crude)小波”。
这是一批在小波发展历史上比较有名的小波;第二类是D aubecheis构造的正交小波,第三类是由Cohen,D aubechies构造的双正交小波。
1.1 经典小波1.1.1 Haar小波Haar小波来自于数学家Haar于1910年提出的Haar正交函数集,其定义是:ψt= 1 0≤t<1/2;−1 1/2≤t<1;0 其他;Haar小波有以下优点:(1)Haar小波在时域是紧支撑的,即其非零区间为(0,1);(2)Haar小波属于正交小波;(3)Haar波是对称的。
我们知道,离统的单位抽样响应若具有对称性,则该系统具有线性相位,这对于去除相位失真是非常有利的。
(4)Haar小波是目前唯一一个既具有对称性又是有限支撑的正交小波;Haar小波仅取+1和-1,因此计算简单。
但Haar小波是不连续小波,因此ψ(Ω)=0在Ω=0处只有一阶零点,这就使得Haar小波在实际信号处理应用中受到了限制。
但由于Haar小波有上述的多个优点,因此在教科书与论文中常被用作范例来讨论。
1.1.2 Morlet小波Morlet小波定义为:ψt=e−t2/2e jΩt其傅里叶变换为ψΩ=2πe−(Ω−Ω0)2/2它是一个具有高斯包络的单频率复正弦函数。
该小波不是紧支撑的,增大Ω的值可以使小波在频域和时域上都具有很好的集中。
Morlet小波不是正交的,也不是双正交的,可用于连续小波变换。
但该小波是对称的,是应用较为广泛的一种小波。
Morlet的时域波形和频域波形如下图:1.1.3 Mexican hat小波该小波的中文名字为“墨西哥草帽”小波,又称Marr小波。
它定义为:ψt=c1−t2e t2/21/4,其傅里叶变换为式中c=3ψΩ=2πcΩ2e−Ω2/2该小波是由一高斯函数的二阶导数所得到的,它沿着中心轴旋转一周所得到的三维图形犹如一顶草帽,故由此而得名。
小波变换(内附奇异值分析matlab程序)

2、算法及其应用实例
小波在信号的奇异性检测中的应用举例 信号的突变点和奇异点等不规则部分通常包含重要信息,一般信号 的奇异性分为两种情况: (1)信号在某一时刻其幅值发生突变,引起信号的非连续,这种类 型的突变称为第一类型的间断点; (2)信号在外观上很光滑,幅值没有发生突变,但是信号的一阶微 分有突变发生且一阶微分不连续,这种类型的突变称为第二类型的间 断点。 应用小波分析可以检测出信号中的突变点的位置、类型以及变 化的幅度。
程序代码
load nearbrk; x=nearbrk; %使用db4对信号进行2层分解 [c,l]=wavedec(x,2,‘db4’); subplot(411); subplot(4,1,i+2); plot(x); plot(d); ylabel('x'); ylabel(['d',num2str(3-i)]); %对分解的第六层低频系数进行重构 end a=wrcoef('a',c,l,'db4',2); subplot(412); plot(a); ylabel('a2'); for i=1:2 %对分解的第2层到第1层的高频系数 进行重构 a=wrcoef('a',c,l,'db4',3-i);
3、小波分析的优缺点
小波变换与Fourier变换相比,是一个时间和频域的局域变换因而能 有效地从信号中提取信息,通过伸缩和平移等运算功能对函数或信号进 行多尺度细化分析(Multiscale Analysis),解决了Fourier变换不能 解决的许多困难问题。 小波变换存在以下几个优点: 小波变换存在以下几个优点: (1)小波分解可以覆盖整个频域(提供了一个数学上完备的描述) (2)小波变换通过选取合适的滤波器,可以极大的减小或去除所提取得不 同特征之间的相关性 (3)小波变换具有“变焦”特性,在低频段可用高频率分辨率和低时间分 辨率(宽分析窗口),在高频段,可用低频率分辨率和高时间分辨率(窄分 析窗口) 。 (4)小波变换实现上有快速算法(Mallat小波分解算法)。
小波变换基本原理

第五章 小波变换基本原理问题①小波变换如何实现时频分析?其频率轴刻度如何标定? —尺度 ②小波发展史③小波变换与短时傅里叶变换比较a .适用领域不同 b.STFT 任意窗函数 WT (要容许性条件) ④小波相关概念,数值实现算法多分辨率分析(哈尔小波为例) Daubechies 正交小波构造 MRA 的滤波器实现⑤小波的历史地位仍不如FT ,并不是万能的5.1 连续小波变换一.CWT 与时频分析 1.概念:⎰+∞∞--ψ=dt abt t S ab a CWT )(*)(1),( 2.小波变换与STFT 用于时频分析的区别小波 构造?1910 Harr 小波80年代初兴起 Meyer —小波解析形式80年代末 Mallat 多分辨率分析—WT 无须尺度和小波函数—滤波器组实现90年代初 Daubechies 正交小波变换90年代中后期 Sweblews 第二代小波变换3.WT 与STFT 对比举例(Fig 5–6, Fig 5–7) 二.WT 几个注意的问题1.WT 与)(t ψ选择有关 — 应用信号分析还是信号复原2.母小波)(t ψ必须满足容许性条件 ∞<ψ=⎰∞+∞-ψdw ww C 2)(①隐含要求 )(,0)0(t ψ=ψ即具有带通特性 ②利用ψC 可推出反变换表达式⎰⎰+∞∞-+∞∞-ψ-ψ=dadb ab t b a CWT a C t S )(),(11)(23.CWT 高度冗余(与CSTFT 相似)4.二进小波变换(对平移量b 和尺度进行离散化) )2(2)()(1)(2,22,,n t t a b t at n b a m mn m b a mm-ψ=ψ⇒-ψ=⇒•==--ψdt t t S n CWT d n m m m n m )(*)()2,2(,,⎰+∞∞---ψ=•=5.小波变换具有时移不变性),()(),()(00b b a CWT b t S b a CWT t S -↔-↔6.用小波重构信号 ∑∑∑∑+∞-∞=+∞-∞=+∞-∞=+∞-∞=ψψ=m n m n nm nm nm n m t dt d t S )(ˆ)(ˆ)(,,,,正交小波 中心问题:如何构建对偶框架{}n m ,ˆψ如何构建正交小波?5.2 分段逼近P1. =)(t φ逼近函数)2(2)(n t n t -→-φφ)2(2)()()(S ,1,0n t C t S n t C t nn nn -≈⇒-≈∑∑φφ 尺度21=a ⇒一般式:∑-=-≈nm m nm m a n t Ct S 2)2(2)(,2尺度φ)(,0,τS a m 逼近收敛于→∞→ 0,,0→∞→→逼近a m2.两尺度函数间关系 )12()2()(-+=t t t φφφ①张成空间满足10V V ⊂ ②两尺度空间差异在哪? 3.表征细节的小波变换的引入很显然采样率越高,s T 越小, 逼近误差越小,采样率∞→无误差发现2)()()12(2)()()2(t t t t t t ϕφφϕφφ-=-+=⇒∑-≈⇒nn n t C S )2(2)t (,1φ 12,2+=m m n⎥⎦⎤⎢⎣⎡--+-∑∑+m m m m m t C m t C )122()22(212,12,1φφ⎥⎦⎤⎢⎣⎡---+-+-=∑∑+m m m m m t m t C m t m t C 2)()(2)()(212,12,1ϕφϕφ ∑∑-•-+-•+→++nn n mn n n t C C n t C C n m )(2)(212,12,112,12,1ϕφ001W V V ⊕=⇒ 4.推广⇓⊕⊕⊕⊕⊕=⊕⊕=⊕=⇒----012011011W W W W V W W V W V V m m0121W W W V V ⊕⊕⊕=--∞- ↑⊕⊕⊕=---m W W W V m m m m ,123,lim ,1012=↓↓⊕⊕⊕⊕⊕==↑↑∞---∞→∞V m W W W W V V m m m 逼近精度逼近精度⎭⎬⎫⎩-)2(22n t m m ϕ包含信息量决定 →形成最简单的MRA尺 度2V二.分段逼近与小波变换(哈尔小波) 1.信号的尺度逼近与小波表示 尺度逼近 ∑→-nm nm m t S n t C)()2(2,2φ 小波表示 ∑∑+∞-∞=+∞-∞=-=m n m mnm n t dt S )2(2)(2,ϕ Harr 小波2.Harr 小波特性①同一尺度平移正交性:⎰+∞∞-'-='--)()(*)(n n dt n t n t δϕϕ②尺度,平移均正交 ⎰∞+∞-''''+''='-->=<n n m m m m m m n m n m dt n t n t t t ,,2)(,,)2(*)2(2)(),(δδϕϕϕϕ ⇒⎭⎬⎫⎩⎨⎧-⇒形成正交基)2(22n t mm ϕ⎰∞+∞--=dt n t t S d mm n m )2(*)(22,ϕ影即为小波系数信号在正交基函数上投 分段逼近的推广—MRA 一.多分辨率分析含义①由内空间 ⊂⊂⊂⊂+-110m m m V V V 组成②若0V 空间尺度函数)(t ϕ平移正交:⎰+∞∞-=-)()(*)(n n t t δφφ则)(t ϕ为0V 空间尺度函数,任一函数S(t)可用表示)(t φ③成立当且仅当1)2()(+∈∈m m V t S V t S ④{}00=m mm V V 交集为⑤平方可积空间即为并集逼近m V )(lim 2R L V m m =∞→ 问题:Harr 小波构成最简单MRA⇓同尺度m 也满足⎰+∞∞-''-=)()(*)(,,n n dt t t n m n m δϕϕ 作变量替换即可证明⎰∑∞+∞--=-=dtn t t S C n t C t S n nn )(*)()()(φφ如何构造选其它具体的MRA 体系 二.正交小波函数的系统构造 1.两尺度方程引入 ①低通滤波器与尺度关系Harr 小波满足 ⎥⎦⎤⎢⎣⎡-+=-+=)12(21)2(212)12()2()(t t t t t φφφφφ∑-=⎥⎦⎤⎢⎣⎡=nn t n h th 卷积关系满足)()(2)2(212100φφ②频域反映令 )2(2)2()()()()(00w tw t w H n h φφφφ↔⇒↔↔)()(00w w H h φφ↔*⇒)()()2()()(2)2(200w w H w w w H w φφφφ==⇒即③含义a. LPF n h H 为)(,1)0(00=b .根据MRA ,∏∞==Φ=Φ100)0()2()2()2()(k k wH w w H w φc.1)0(=Φ 2.QMF 的引入①)(t φ的尺度正交关系的频域反映⎰+∞∞-=-)()(*)(n n t t δφφ⇒↔--)()(w e n t jnw φφ 频域也正交⎰∑+∞∞-=njnw n dw e w w )()(*)(21δφφπ两边对n 求和 ⎰∑+∞∞-=⇒ninw dw e w w 1)(*)(21φφπ利用泊松求和公式∑∑+=-nnjnwn w F en f )2()(π(令)(2)(,1)(w w F n f πδ==则) 有 ∑∑+=-nnjnwn w e)2(2πδπ∑∑-=⇒nnjnwn w e)2(21πδπ⎰∑+∞∞-=-⇒ndw n w w w 1)2()(*)(πδφφ∑⎰+∞∞-=-ndw n w w 1)2()(2πδφ即:∑∑=+⇒=-knk w n w 1)2(1)2(22πφπφ② QMF 正交镜像滤波器组的导出 利用两尺度关系∑=++k k wH k w 1)2()2(20ππφ对k 分奇偶讨论1))12(2())12(2()22()22(2020=+++++++⇒∑∑nn n wn w H n w n w H πφππφπ1))12(2()2()22()2(22220=+++++∑∑nnn ww H n w wH πφππφ 1)2()2(2020=++⇒πwH w H1)2(*)()(*)()()(00002020=+++=++⇒πππw H w H w H w H w H w H ③含义a.镜像为)()(,1)(1)0(0000w H w H H H ππ+=⇒=b.功率互补条件—半带条件 )(*)()(00w H w H w P =20)(π+w H1π20)(w H3.正交小波滤波器满足的条件 ①频域关系根据0)(),(=-k x x φϕ可推出0)(*)()(*)(1010=+++ππw H w H w H w H 上式的解为 )(*)(01π+-=-w H e w H jw ②时域关系 令 ∑-=↔↔njnw e n h w H w H n h w H n h )()()()()()(0011根据)(*)1()1()()(*)1()1()(*)()1()(*)(0010010000πππ+↔--=+↔--+↔--↔-⇒---w H e n h n h w H en h w H n h w H n h jw n jwn n③易证 QMF w H 也为)(1④小波滤波器同样满足两尺度关系∏∑∞==Φ=-=20111)2()2()2()2()()2()(2)(k k kwH w H w w H w k t k h t ϕφϕ4.尺度与小波滤波器频域关系的矩阵表示⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡++1001)()()()()(*)()()(11001010ππππw H w H w H w H W H w H w H w H 5.{}{}解释的与MRA t t n m n m )()(,,φϕ{}{}m nm mnm V t W t →→)()(,,φϕ 正交补 112+-⊕⊕⊕=⇒m m m W W W L⎰∑∑∞+∞-+∞-∞=+∞-∞===dtt t S d t dt S n m n m m n m n nm )(*)()()(,,,,ϕϕ例:求Harr 小波的频域尺度函数和小波函数⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=2121212110h h 解: 2)2()2()2()(11210w w Sin e w Cos e w H w k k w j k w j k •===Φ∏∏∞=∞=-+- ∑⋅⋅=-==---nwj jwjnww Sin e j e e n h w H )2()1(21)()(211 4)4()()2()2()(21w w Sin w w w H w =⇒=Φ=ϕϕ 其频域幅值图如Fig 5–13所示可发现其缺陷在于波纹太大 (原因—时域紧支撑) 例:理想LPF 也构成正交小波⎪⎩⎪⎨⎧≤=其它021)(0πw w H解:[]())1()1(2)()(00n n Sin w H IFT n h --==ππ 小波函数Sinc Sinc →•)( 三.有关小波函数的一些概念 1.小波消失矩 (vanishing moment ) 满足 阶消失矩具有则称N t N k dt t t k m k )(1,1,0,0)()(1ϕϕ-===⎰+∞∞-①母小波)(t ϕ平滑度由消失矩决定,消失矩越大,则)(w ϕ频域衰减越快)(t ϕ越平滑②消失矩越大,小波振荡程度越高 2.小波正则度(regularity ) ①定义:小波)(t ϕ的连续可导次数②正则度为n 的小波)(t ϕ具有(n +1)阶消失矩(必要条件) 四.问题讨论1.根据MRA 理论①小波和尺度函数均可由无穷频域次乘积得出,最终由)(0n h 决定 ②不关心其解析表达式2.MRA 理论 离散小波的数值实现5.4 小波变换与数字滤波器组一.时间离散小波变换的实现途径 1.不能直接对定义式离散化实现)2(2),()(),(2,,n t t S t t S d m mn m n m -==ϕϕ 令 )(采样周期→=T kT l 当m 较小时,n t m -2不为整数2.第一代小波变换:根据MRA 理论,由数字滤波器组实现3.第二代小波变换:Swelden 算法 由预测和更新滤波器进行交替提升实现 二.Mallat 算法 1.两个近似假设①∑∑∑-=+=nn m k nkn nk n m n m t dt C t S t S 1,000)()()()(ϕφ似由某一尺度空间函数近②n m C ,由采样数据直接近似 ⎰∞+∞--=dt n t t S C m m n m )2(*)(22,φm m w jnm jnw w e n t w e n t w t m----•↔-⇒↔-⇒↔2)2()2()()()()(2φφφφφφ滤波器组(Mallat 算法) (根据尺度函数和小波函数))2(2)2(2222w en t m wjn m mm m -⋅⋅---↔-⇒φφ⎰∞+∞---⋅=⇒dw e w w S C w nj m mnm m 22,)2(*)(221φπ当分辨率m 足够高时 0)2(*→-w m φnt m m m nwj mn m m mt S n S dwe w S C --=---∞+∞--==⋅≈⇒⎰22222,)(2)2(2)(212π故可直接用样本数据取代 2.Mallat 算法 ①分解算法 a.推导⎰⎰⎰∞+∞--∞+∞-∞+∞-----=-==-dtn t t S dtn t t S dt t t S C m m m m n m n m )222(*)(2)2(*)(2)()(1121*,1,1φφφ两尺度关系 ⎰∑∞+∞--+-⋅im m dt i n t i h t S ))2(2(*)(2)(2021φ∑∑∑⎰++∞+∞->=<⋅=+-=iiin m i n m im m C i h t t S i h dti n t t S i h 2,02,020)(2)(),()(2))2(2(*2)()(φφ∑-+='i i m C n i h in i ,0)2(22同理-=-i m n m C n i h d ,1,1)2(2②重构算法a.推导(由两尺度关系,正交关系,及奇偶讨论可导出)⎪⎭⎫⎝⎛-+-=∑∑--i i i m i m n m d i n h C i n h C ,11,10,)2()2(2b.滤波器组实现(上采样+滤波)5.5 小波变换的应用一.小波地位小波曾火热一时,但小波不是万能的,在某些应用场合特别适用 小波无法求解微分方程纯数字和物理地位不如FT 二.信号检测方面应用 发动机声音中的撞击声检测傅里叶分析:时间平均作用模糊了信号局部特性 Gabor 变换 :仍需长窗去包含振荡波形 小波变换 : 小波基可任意窄 三.降噪应用 1.适用场合经典滤波:要求信号与噪声频率足够窄且不重合 高斯类噪声和脉冲噪声 → 宽带噪声 → 小波去噪 2.滤波效果①经典滤波:丢失波形尖锐处信息②小波降噪:基本保留波形尖锐处信息(与小波基选择有关) 3.滤波手段①传统方法:Prony 参数建模法②小波降噪b.可证明其统计最优性c.阈值比较(阈值T 可基于信号标准差得出) 硬阈值:比较n m d ,软阈值:考虑n m d ,符号,及其其它系数相关性 4.小波基选择:小波基应与主体信号量相近相似度越高,主小波系数越大,噪声系数则越小 NI 信号处理工具箱分解重构。
mallat算法原理

mallat算法原理Mallat算法,又称Wavelet Transform,是一种基于小波函数的数据分析和处理方法,它将信号或图像分解成一系列小波频带,然后进行变换和重构以完成特定的分析或处理任务。
这种算法的优点在于具有时间和频率上的局部性、多分辨率分析和灵活的压缩性能等。
Mallat算法基于小波函数的变换,这些小波函数是一系列的正交函数(如Haar、Daubechies、Coiflet等),它们具有时频局部性质,可以捕捉信号的局部特征,如短暂的信号脉冲和边缘等。
这些小波函数都是由一个母小波函数通过平移、缩放、反转等操作得到的。
Mallat算法的基本过程分为分解、重构和逆变换三个步骤。
1. 分解:将原始信号或图像分解成一系列小波频带。
这个过程是由多层的低通和高通滤波器完成的,其中低通滤波器用于提取信号的低频成分,高通滤波器则用于提取信号的高频成分。
在每一层分解过程中,低频部分进一步分解,高频部分则用作下一层分解的输入。
这样就得到了一系列不同频段的小波系数,代表了原始信号或图像的局部特征。
2. 重构:将得到的小波系数重构成原始信号或图像。
这个过程是由多个逆滤波器和逆上采样操作完成的,逆滤波器用于将小波系数进行逆变换,同时逆上采样操作将分辨率恢复到原来的大小。
通过这种方式,可以从分解后的小波系数重构出与原始信号或图像相似的结果。
Mallat算法的应用范围很广,可以应用到信号和图像处理、数据压缩、模式识别、图像分割等领域。
其核心在于通过小波分析将信号和图像分解成不同频段的小波系数,通过对这些小波系数的变换和重构完成特定的分析或处理任务。
毕业设计221图像小波变换实现及EZW编码理论研究

论文题目:图像小波变换实现及EZW编码理论研究专业班级:学号:学生:签名:指导教师:签名:摘要21世纪,人类已进入信息化时代,其中图像信息是人类获得外界信息的主要来源,因此对图像的处理变得更为重要。
而小波变换以其良好的空间——频域局部特性,能对图像进行有效的处理。
本文研究的是小波变换在数字图像处理中的应用,文中介绍了数字图像处理的基本概念和小波变换的基本理论。
基于图像小波理论,对图像小波变换的实现技术——Mallat算法进行了分析,并根据Mallat算法应用VC++编程实现了图像小波变换。
Mallat算法是将计算小波系数与信号处理中滤波器相结合,构成塔式分解算法,大大简化了小波系数的计算。
嵌入式小波零树系数编码(EZW)是将小波变换的各子带系数表示为零树结构。
EZW是一种简单而有效的图像编码算法。
使用这种算法,编码者可在任一点结束编码,所以允许精确达到一个目标比率,而这时仍能产生同样的图像。
【关键词】图像处理、小波变换、压缩编码、EZW【论文类型】软件设计与理论研究Title:The Realization of Image Wavelet Transformation and The Coding Theory Research of EZW Major: Electronic information of science and technology Name: Signature:Name: Signature:ABSTRACTIn the 21st, man being steps into an era of information.In which image information become the main origin of obtain information from outside. So processing image information become more important. Wavelet transform has wonderful space and frequency, so it can deal with the image effectively.The main topic article discuss is wavelet transform the application of image processing. In the article introduces the basic conception of data image processing and the basic theory of wavelet transform. Based on the image wavelet transform theory, the realize of the image wavelet transform technology——analysis on Mallat algorithm, and basis on Mallat algorithm that use the software of VC++ realize of the image wavelet transform. Mallat algorithm is using the wavelet coefficients and the filter of signal processing, so it greatly simplified the computing of wavelet coefficients algorithm. EZW code is the structure which is a simple and effective image coding algorithm with which an encoder can terminate the encoding at any point ther eby allowing a target rate or distortion metric to be met exactly.【Key words】image process, wavelet transform,image compression, EZW【Type of Thesis】software design and theory research前言现在人类已经进入信息化时代,而人类从自然界获取信息中,其中图像信息是人类获得外界信息的主要来源,因为大约有70%的信息是通过人眼获得的,而人眼获得的都是图像信息。
第4章小波变换1

4.3.3 连续小波变换 1 .小波
形如下式的函数称之为小波。
a,b(t) 1atab
(5)
其中a为尺度参数,b是定位参数。
21
若a>1,函数 a,b (t) 具有伸展作用,
若0<a<1,函数 a,b (t) 具有收缩作用。而其
Fourier变换 ( ) 则恰好相反。伸缩参数a对 小波 a,b (t) 的影响见下图。小波
f 2f
4f
8f
频率
图 4 Gabor)变换特性(a)和小波滤波特性(b) 35
图4显示了Gabor变换与小波变换的滤波特 性。由图可见Gabor滤波是恒定带宽滤波, 而小波滤波随着中心频率增加而带宽加大。
36
3. 几种典型的一维小波 小波的选择是灵活的,凡能满足条件的函数均 可作为小波函数,这里仅介绍几种具有代表性的 小波以供参考。
13
3.4.2 小波变换
小波的概念是由法国的从事石油勘测信号处理的地 球物理学家J.Morlet于1984年提出的。他在分析地 震波的时频局部特性时,希望使用在高频处时窗变窄, 低频处频窗变窄的自适应变换。但Fourier变换很难 能满足这一要求,随后他引用了高斯余弦调制函数, 将其伸缩和平移得到一组函数系,它后来被称之为 “Morlet小波基”。
提高时域分辨率,反之亦然。
26
小波 (t ) 的选择既不是唯一的,也不是任意的。 这里 (t ) 是归一化的具有单位能量的解析函数, 它应满足如下几个条件: (1)定义域应是紧支撑的(Compact Support),换句 话说就是在一个很小的区间之外,函数为零,也就 是函数应有速降特性。
27
14
Morlet这一根据经验建立的公式当时并未得到数 学家的认可,幸运的是A.Caldron的发现、Hardy 空间原子分解的深入研究已为小波变换的诞生作 了理论上的准备。
小波变换

第五章 小波变换 Wavelet Transform小波理论是20世纪80年代后期发展起来的一门新兴应用数学分支,在法国学者莫列特(J.morlet )马莱特(S.Mallat )杜比垂丝(I.Daubechies )努力下,小波理论及其在工程中的应用迅猛发展,打破了积分变换领域长期以来付氏变换一统天下的格局,开创了一个划时代的局面。
小波变换被认为是信号分析工具和方法上的重大突破。
由于小波变换可看成是傅氏变换的发展,所以与傅氏变换一样具有极广的应用面。
目前,在通信、图像、语言、地震、雷达、声纳、机械振动分析、信号检测、特征提取、故障诊断、滤波、数据压缩等多方面都得到了应用。
小波变换的应用研究正方兴未艾。
小波变换之所以有如此好的局面,源于它具有的多分辨特性——多尺度特征,可以把小波变换看成是一组品质因数相同具有良好选频特性的带通滤波器,通过适当地选择尺度因子和平移因子和基本小波,可以得到一个伸缩窗使得小波变换在时域和频域都具有表征信号局部特征的能力——称为数学显微镜本章不对小波变换进行完整的数学讲述。
只从信号处理的角度对小波变换的基本理论和方法作一简单的介绍。
突出其定性的概念,建立起对小波的一点概念和兴趣,为今后的应用研究打下基础。
主要讲:连续小波变换、多分辨分析、Mallat 算法、小波包分析。
5.1 傅立叶变换到小波变换5.1.1傅立叶变换的局限性傅立叶变换: ()()j t x j x t e dt ωω∞--∞=⎰ (5-1) ()()12j t x t x e d ωωωπ∞-∞=⎰ (5-2)一个信号可表示成一系列正弦和余弦函数之和,叫做傅立叶展开式1.揭示了时间函数与频谱函数之间的内在联系(时域 频域)2.反映了信号在“整个”时间范围内的“全部”频谱成分。
注解:(1)积分区间都是无穷的,所以傅氏变换是对无穷区间函数的分析。
注解:(2)用傅氏变换的方法是提取信号频谱时,需要利用信号的全部时域信号。
小波变换简介PPT课件

47
X = waverec2(C,S,'wname')
reconstructs the matrix X based on the multi-level wavelet decomposition structure [C,S]
10
幅度
频率
时间窗
时间
时域加窗分析
时间
时频平面划分示意图
11
窗口傅立叶变换
12
窗口傅立叶变换
另一个缺点是:无论怎样离散化,都不能 使Gabor变换成为一组正交基;
而傅立叶变换经离散化后可得到按正交函 数展开的傅立叶级数。
13
1909: Alfred Haar
Alfred Haar对在函数空间中寻找一个与傅立叶类似 的基非常感兴趣。1909年他发现并使用了小波, 后来被命名为哈尔小波(Haar wavelets)
C 0
Wf
(a,b)a,b(t)dbda2a
a,b(t)
1 (t b)
aa
28
小波系数的意义
Wf (a,b)表示信号与尺度为a小波的相关程 度。小波系数越大,二者越相似。
F() f(t)ejtdt
W f(a,b)f(t) a,b(t)dt
29
连续小波变换的简单步骤
选择尺度为a确定的小波,与信号开始的 一段比较;
A = appcoef2(C,S,'wname',N)
小波变换的本质

为了应付老板的的一个任务而收集了几篇相关文章!我是搞电力系统故障波形分析的,正上研二,导师定的方向是用小波变换进行信号的消噪及波形奇异点检测. 出于研究方向的需要从去年年底开始接触小波.毕竟是工科出身,学起小波来觉得难度很大.不夸张地说常有学不下去的感觉.硬着头皮看了一段时间,终于觉得有点眉目,现将我从信号奇异性方面的理解写出来,请各位同仁批评指正,并希望能对刚接触小波的朋友有点帮助!1学习小波变换所需的基础知识由于小波变换的知识涵盖了调和分析,实变函数论,泛函分析及矩阵论,所以没有一定的数学基础很难学好小波变换. 但是对于我们工科学生来说,重要的是能利用这门知识来分析所遇到的问题. 所以个人认为并不需要去详细学习调和分析,实变函数论,泛函分析及矩阵论等数学知识.最重要是的理解小波变换的思想!从这个意义上说付立叶变换这一关必需得过!因为小波变换的基础知识在付立叶变换中均有提及,我觉得这也就是很多小波变换的书都将付立叶分析作为其重要内容的原因.所以我认为学习小波应从V数字信号处理〉中的付立叶分析开始.当然也可从V信号与系统〉这本书开始. 然后再看杨福生老师的小波变换书.个人觉得他的书最能为工科学生所接受.2信号的分解付立叶级数将周期信号分解为了一个个倍频分量的叠加,基函数是正交的,也就是通常所说的标准正交基.通过分解我们就能将特定的频率成分提取出来而实现特定的各种需要,如滤波,消噪等.付立叶变换则将倍频谱转换为了连续谱,其意义差不多.小波变换也是一种信号分解思想:只不过它是将信号分解为一个个频带信号的叠加. 其中的低频部分作为信号的近似,高频部分作为信号的细节.所谓的细节部分就是一组组小波分量的叠加,也就是常说的小波级数.3小波变换的时频分析思想付立叶变换将信号从时域变换到了频域,从整体上看待信号所包含的频率成分.对于某个局部时间点或时间段上信号的频谱分析就无能为力了,对于我们从事信号的奇异性检测的人来说,付立叶变换就失去了意义(包括加窗付立叶变换).因为我们要找的是信号的奇异点(时域方面)和奇异点处所包含的频带(频域方面)也就是说需要一种时频分析方法.当然能有纯时域的分析方法更好!(据说数学形态学能达到这种效果).小波变换之所以可以检测信号的奇异点,正在于它的"小".因为用小的波去近似奇异信号要比正弦波要好的多.4小波变换的实质小波变换的公式有内积形式和卷积形式,两种形式的实质都是一样的.它要求的就是一个个小波分量的系数也就是"权" .其直观意义就是首先用一个时窗最窄,频窗最宽的小波作为尺子去一步步地" 量"信号,也就是去比较信号与小波的相似程度. 信号局部与小波越相似,则小波变换的值越大,否则越小!当一步比较完成后,再将尺子拉长一倍,又去一步步地比较,从而得出一组组数据. 如此这般循环,最后得出的就是信号的小波分解(小波级数).当然这只是一种粗略的解释. 5连续小波变换,二进小波变换与离散小波变换的关系当尺度及位移均作连续变化时,可以理解必将产生一大堆数据,作实际应用时并不需要这么多的数据,因此就产生了离散的思想.将尺度作二进离散就得到二进小波变换,同时也将信号的频带作了二进离散.当觉得二进离散数据量仍显大时,同时将位移也作离散就得到了离散小波变换!6 MALLAT算法的意义想必大家都注意到,小波变换是以内积或卷积的形式实现的,这给数值计算带来了不利之处,因为用计算机作数值积分其计算量大.MALLAT算法则解决了这一问题,它不涉及小波的具体形式,只是对系数进行操作!其计算也就是用高通及低通滤波系数与小波系数作卷积.因为作信号处理时,我们往往并不关心小皮的具体形式,更为关心小波系数.需提出的是该算法仅适用于正交小波如果小波不是正交的(如E样条小波)则算法失效!7小波变换的模极大值及其意义对于我们搞信号奇异性检测的人来说,小波变换最重要的应用就是用模极大值定值奇异点.我觉得模极大值可以从两个方面去理解:第一, 从直观角度,上文已说明小波变换的实质就是一种度量波形相似程度的方法.信号与小波越相似,则小波系数越大.这也就可理解为出现了小波变换的模极大值.因为当信号出现奇异点时,或是间断点,或是一阶导数不连续点,其在各个尺度下都将必然出现大的小波系数.从而可以定位奇异点!第二个方面从小波的取法来看,当小波取为光滑函数一阶导数或二阶导数时,从公式可以推导出小波变换将出现模极大值点或是过零点.也就是很多书上说的模极大值检测和零交叉检测.这些可以查书看!我只谈谈连续小波变换,对于离散的也有同样的 argument 。
Mallat小波的s手工编程算法说明(原创)

Mallat 算法及问题Mallat 算法在小波多分辨率分析中具有极其重要的地位。
Mallat 算法中,与尺度函数)(t φ相联系的是低通滤波器)(n h ,与小波函数)(t ψ相联系的是高通滤波器)(n g 。
分解后得到离散逼近信号)(n a j [又称:尺度系数],和离散细节信号)(n d j [又称:离散小波系数]。
本文以《小波分析及其应用》为主要参考书。
未指明情况下,均指该书。
1. 由滤波器系数h 计算滤波器系数g尺度滤波器(低通滤波器))(n h 是核心,小波滤波器)(n g 可由)(n h 计算得到。
计算公式为)1()1()(1n h n g n --=-。
该公式的含义为:将)(n h 以0=n 翻转,得到)(n h -,再将序列右移1位,即得到)1(n h -。
再乘上符号n --1)1(,即得到)(n g 。
如图所示:可见,实现方法为:对)(n h 倒序,然后在对该序列的适当位置添加负号。
如最后(从左到右)1位乘以1-(因为其0=n ,1)1(1-=--n ),倒数第2位保持原数(因为其1-=n ,1)1(1+=--n ),以此类推。
特别注意,以上序列索引从1=n 开始(Matlab 中就是如此),而以0=n 点为中心翻转。
如果序列从0=n 开始索引,则需要作调整,原乘以1-改为乘以1+,原乘以1+的改为乘以1-。
在Matlab 中,用Orthfilt( )函数可得到各种正交小波的滤波器系数Lo_D (低频分解滤波器)和Hi_D (高频分解滤波器),另外,Lo_R 和Hi_R 分别为低频重构滤波器和高频重构滤波器。
特别注意的是,Lo_R 为Lo_D 的倒序:Lo_D = wrev(Lo_R);Hi_R 为Hi_D 的倒序:Hi_D = wrev(Hi_R)。
wrev 即矢量倒序。
另,Wfilters( )函数可得到各种小波的滤波器系数,不限于正交小波。
Matlab 中,分解是按照公式 3.2.6(即 3.4.9)和 3.2.18(即 3.4.10),即:∑∑-=-=++k j j kj j k a n k g n d k a n k h n a )()2()()()2()(11进行的,其对应的抽取图为图3.1,即滤波器为分解滤波器h 和g 。
mallat分解方法

mallat分解方法
Mallat分解方法是一种基于小波变换的信号分析方法,它可以将信号分解成不同频率的小波系数,从而实现信号的多尺度分析。
Mallat分解方法具有计算速度快、精度高、适用范围广等优点,因此在信号处理、图像处理、模式识别等领域得到了广泛应用。
Mallat分解方法的基本思想是将信号分解成不同频率的小波系数,然后通过对小波系数的处理来实现信号的分析和处理。
具体来说,Mallat分解方法将信号分解成多个尺度的小波系数,每个尺度的小波系数对应着不同频率的信号成分。
这些小波系数可以通过离散小波变换(DWT)来计算得到,DWT是一种基于滤波器组的算法,它可以将信号分解成多个尺度的小波系数。
Mallat分解方法的具体步骤如下:
1. 对信号进行离散小波变换,得到多个尺度的小波系数。
2. 对小波系数进行阈值处理,将小于某个阈值的小波系数置为0,从而实现信号的稀疏表示。
3. 对稀疏表示的小波系数进行逆小波变换,得到重构信号。
Mallat分解方法的优点在于它可以将信号分解成多个尺度的小波系数,从而实现信号的多尺度分析。
这种多尺度分析可以帮助我们更好地理
解信号的特征和结构,从而实现信号的分类、识别、去噪等处理。
此外,Mallat分解方法还具有计算速度快、精度高、适用范围广等优点,因此在信号处理、图像处理、模式识别等领域得到了广泛应用。
总之,Mallat分解方法是一种基于小波变换的信号分析方法,它可以
将信号分解成不同频率的小波系数,从而实现信号的多尺度分析。
Mallat分解方法具有计算速度快、精度高、适用范围广等优点,因此
在信号处理、图像处理、模式识别等领域得到了广泛应用。
小波变换(内附奇异值分析matlab程序)

a6
0 0 0
100 100 100
200 200 200
300 300 300
400 400 400
500 500 500
600 600 600
700 700 700
800 800 800
900 900 900
1000 1000 1000
0.5 0 -0.5 0.5 0 -0.5 2 0 -2
d4
4、应用及与以后研究的结合
(1)小波的应用
小波分析作为一个新的数学分支,它是泛函分析、Fourier分析、样 调分析、数值分析的完美结晶。被广泛用于数学领域的许多学科;信号分 析、图象处理;量子力学、理论物理;军事电子对抗与武器的智能化;计 算机分类与识别;音乐与语言的人工合成;医学成像与诊断;地震勘探数 据处理;大型机械的故障诊断等方面; 比如用在故障诊断中的应用 小波分析在故障诊断中的应用已取得了极大的成功,小波分析不仅 可以在低信噪比的信号中检测到故障信号, 而且可以滤去噪声恢复原信 号,它可以用于边界的处理与滤波、时域分析、信噪分离与提取弱信号、 求分形指数、信号的识别与诊断以及多尺度边缘检测等。
程序代码
load nearbrk; x=nearbrk; %使用db4对信号进行2层分解 [c,l]=wavedec(x,2,‘db4’); subplot(411); subplot(4,1,i+2); plot(x); plot(d); ylabel('x'); ylabel(['d',num2str(3-i)]); %对分解的第六层低频系数进行重构 end a=wrcoef('a',c,l,'db4',2); subplot(412); plot(a); ylabel('a2'); for i=1:2 %对分解的第2层到第1层的高频系数 进行重构 a=wrcoef('a',c,l,'db4',3-i);
基于小波变换的图像去噪方法研究报告附MATLAB程序

2.小波变换概述
2.1 小波变化去噪技术研究现状
上个世纪八十年代 Mallet 提出了 MRA(Multi_Resolution Analysis),并首先把 小波理论运用于信号和图像的分解与重构,利用小波变换模极大值原理进行信号 的奇异性检测,提出了交替投影算法用于信号重构,为小波变换用于图像处理奠 定了基础[1]。后来,人们根据信号与噪声在小波变换下模极大值在各尺度上的不 同传播特性,提出了基于模极大值去噪的基本思想。1992 年,Donoho 和 Johnstone 提出了“小波收缩”,它较传统的去噪方法效率更高。“小波收缩”被 Donoho 和 Johnstone 证明是在极小化极大风险中最优的去噪方法,但在这种方法中最重要 的就是确定阈值。1995 年,Stanford 大学的学者 D.L.Donoho 和 I.M.Johnstone 提 出了通过对小波系数进行非线性阈值处理来降低信号中的噪声[2]。从这之后的小 波去噪方法也就转移到从阈值函数的选择或最优小波基的选择出发来提高去噪 的 效 果 。 影 响 比 较 大 的 方 法 有 以 下 这 么 几 种 : Eero P.Semoncelli 和 Edward H.Adelson 提出的基于最大后验概率的贝叶斯估计准则确定小波阈值的方法[3]; Elwood T.Olsen 等在处理断层图像时提出了三种基于小波相位的去噪方法:边缘 跟踪法、局部相位方差阈值法以及尺度相位变动阈值法;学者 Kozaitis 结合小波 变换 和高阶 统计量 的特点 提出了 基于高 阶统计 量的小 波阈值 去噪方 法[4]; G.P.Nason 等 利 用 原 图 像 和 小 波 变 换 域 中 图 像 的 相 关 性 用 GCV(general crossvalidation)法对图像进行去噪;Hang.X 和 Woolsey 等人提出结合维纳滤波器和小 波阈值的方法对信号进行去噪处理[5],Vasily Strela 等人将一类新的特性良好的小 波(约束对)应用于图像去噪的方法[6];同时,在 19 世纪 60 年代发展的隐马尔科 夫模型(Hidden Markov Model),是通过对小波系数建立模型以得到不同的系数处 理方法;后又有人提出了双变量模型方法[7],它是利用观察相邻尺度间父系数与 子系数的统计联合分布来选择一种与之匹配的二维概率密度函数。这些方法均取 得了较好的效果,对小波去噪的理论和应用奠定了一定的基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验目的:通过编程实现离散快速小波变换Mallat 算法,从而加深理解二维小波变换的分解与合成,同时,提高编程能力和matlab 的应用,为以后的学习打下基础。
实验原理:1、Mallat 快速算法本实验使用离散快速小波变换快速算法Mallat 算法,算法原理如下(1)1(2)j j k n nc h n k c -=-∑(2)1(2)j j k n nd g n k c -=-∑重构算法:(3)1(2)(2)j j j n k k nnc h n k c g n kd -=-+-∑∑对于(1)、(2)等效于经过冲击响应为和的数字滤波器,然后再分别进1j n c -[]h n -[]g n -行“二抽取”,Mallat 分解算法的滤波器表示形式如下图C j-1d j (k)C j (k)用滤波器表示如下图d jC j C j-1(k)2、255*25510lgPSNR MSE='211()*MNijij i j ff MSE M N==-=∑∑ 分别表示原始图像和重建后的图像,。
{}ij f '{}ij f 1,1i M j N ≤≤≤≤3、边界延拓方法有零延拓、周期延拓、对称周期延拓、常数连续延拓等,本实验采用以上四种方法进行原图像的1/8延拓,并进行重构,各种延拓方法所对应的函数为yan0(x)、yancir (x )、yan(x)、yanc(x),在主程序中,需要某种延拓,便调用某种函数。
实验编程思路:为使程序易于理解,在不考虑算法复杂度的情况下,分解程序采用简洁的循环计算出下一级的分解系数,程序采用的编程思想如下[][][]11100[0][1][2][3][4][5]001[1]00[0][1][2][3]00[1][2][3][4][5]00[0][1]12j j j j j j c c h h h h h h c c h h h h n c n h h h h h h c ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥--⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦LL M M MM M M M M O O M L 以上矩阵等式左面是进行二抽样的结果,是分解的低频部分。
同理,对[0][1]2j j nc c -L j 于分解的高频部分有如下矩阵形式:j [][][]11100[0][1][2][3][4][5]001[1]00[0][1][2][3]00[1][2][3][4][5]00[0][1]12j j j j j d d g g g g g g d d g g g g n d n g g g g g g d ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥--⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦L L M M MM M M M M O OM L 分解程序: lenx=size(x,2);%x 为一维向量lenh=size(h,2);h=[h,zeros(1,(lenx-lenh))];g=[g,zeros(1,(lenx-lenh))];r1(1)=sum(h.*x);r2(1)=sum(g.*x);for k=1:1:(lenx/2-1) %循环求出下一级低频和高频分量h=[h(end-1:end),h(1:(end-2))];r1(k+1)=sum(h.*x);g=[g(end-1:end),g(1:1:(end-2))];r2(k+1)=sum(g.*x);end y=[r1,r2];对于重构算法,其等效形式为[][][]1(2)(2)j j j nnc n h n k c k g n kd k -=-+-∑∑上式等号右边部分实质上是对变量的数字卷积运算,程序采用频域相乘代替卷积,重建程k 序为 y=ifft(fft(c3,lenx).*fft(h,lenx))+ ifft(fft(d3,lenx).*fft(g,lenx));实验结果及分析:1、多尺度分解与重构图像二维小波变换采用小波采用db3,其峰值信噪比PNSR=230.13db,并对三级分解图像进行归一化,求出0的个数为37626,其所占的百分比为57.41%。
2、延拓重建图像延拓方法周期延拓对称周期延拓零延拓常数连续延拓PNSR230.18db230.48db229.80db230.13db 从PNSR结果可知,在各种延拓中,对称周期延拓的重建图像结果最好,相比之下零延拓图像效果不如其他方法延拓。
3、不同小波下重构图像的性质用不同小波进行图像重构,所得的重构图像能量分布如下用各种小波进行重构后的图像的均值方差如下表。
小波db1db2db3db4均值124.0309124.0509124.0509124.0509方差2272227222722272附录:1、主函数程序clc;clear;X=imread('LENA.bmp');%路径X=double(X);% S=yancir(X);A=mallatdec2(X,'db3', 3);image(abs(A));colormap(gray(255));title('3级多尺度分解图像');Y=mallatrec2(A,'db3',3);Y=real(Y);figure(2);subplot(1,2,1);image(X);colormap(gray(255));title('原始图像');subplot(1,2,2);image(Y);colormap(gray(255));title('重建图像');zerosn=numberzeros(A);% Y=Y(33:288,33:288); %当调用延拓图像时,从延拓的重建图像进行截取csize=size(X);sr=csize(1);sc=csize(2);mse=sum(sum( (Y-X).^2,1))/(sr*sc);psnr=10*log(255*255/mse)/log(10)2、分解程序function Y=mallatdec2(X,wname,level)%输入:X 载入的二维图像像数值;% level 小波分解次(级)数设定值(如果设定值超过最高可分解次数,按最高分解次数分% wname 小波名字wavelet name%输出:Y 多极小波分解后的小波系数矩阵[h,g]=wfilters(wname,'d'); %h,g 分别为低通和高通滤波器X=double(X);t=1;[hh,ll]=size(X);while t<=level%先进行行小波变换for row=1:hhY(row,1:ll)=mdec1(X(row,1:ll),h,g) ;end%再进行列小波变换for col=1:lltemp=mdec1( Y(1:hh,col)',h,g);Y(1:hh,col)=temp';endt=t+1;hh=hh/2;ll=ll/2;X=Y;endfunction y=mdec1(x,h,g)%输入:x 行数组% h 为低通滤波器% g 为高通滤波器%输出: y 进行一级小波分解后的系数lenx=size(x,2);lenh=size(h,2);h=[h,zeros(1,(lenx-lenh))];g=[g,zeros(1,(lenx-lenh))];r1(1)=sum(h.*x);r2(1)=sum(g.*x);for k=1:1:(lenx/2-1)h=[h(end-1:end),h(1:(end-2))];r1(k+1)=sum(h.*x);g=[g(end-1:end),g(1:1:(end-2))];r2(k+1)=sum(g.*x);endy=[r1,r2];3、重建程序function Y=mallatrec2(X,wname,level)%输入:X 载入的小波系数矩阵;% level 小波分解次(级)数设定值(如果设定值超过最高可分解次数,按最高分解次数% wname 小波名字wavelet name%输出:Y 重构图像矩阵[h,g]=wfilters(wname,'d'); %h,g 分别为重构低通滤波器和重构高通滤波器hz=size(X,2);h1=hz/(2^(level-1));while h1<=hz% 对列变换for col=1:h1temp=mrec1(X(1:h1,col)',h,g)';X(1:h1,col)=temp;end%再对行变换for row=1:h1temp=mrec1(X(row,1:h1),h,g);X(row,1:h1)=temp;endh1=h1*2;endY=X;function y=mrec1(x,h,g)%输入:x 行数组% h 为低通滤波器% g 为高通滤波器%输出: y 进行一级小波重构后值lenx=size(x,2);lenh=size(h,2);h=[h,zeros(1,(lenx-lenh))];g=[g,zeros(1,(lenx-lenh))];;c3=dyadup(x(1,1:lenx*0.5),0,lenx); %内插零use para 0d3=dyadup(x(1,(lenx*0.5+1):lenx),0,lenx); %use para 0y=ifft(fft(c3,lenx).*fft(h,lenx))+ ifft(fft(d3,lenx).*fft(g,lenx));4、延拓程序%零延拓程序function T=yan0(x)[r0,c0]=size(x);for s=1:r0a(s,:)=[zeros(1,c0/8),x(s,:),zeros(1,c0/8)];endc0=c0+c0/4;for t=1:c0T(:,t)=[zeros(r0/8,1)',a(:,t)',zeros(r0/8,1)']';End%连续常数延拓程序function T=yanc(x)[r0,c0]=size(x);for s=1:r0r1(1:c0/8)=x(s,1);r2(1:c0/8)=x(s,c0);a(s,:)=[r1,x(s,:),r2];endc0=c0+c0/4;for t=1:c0c1(1:r0/8)=a(1,t);c2(1:r0/8)=a(r0,t);T(:,t)=[c1,a(:,t)',c2]';end%对称周期延拓程序function T=yancir(x)[r0,c0]=size(x);for s=1:r0a(s,:)=[x(s,end-(c0/8-1):1:end),x(s,:),x(s,1:1:c0/8)];endc0=c0+c0/4;for t=1:c0T(:,t)=[a(end-(r0/8-1):1:end,t)',a(:,t)',a(1:1:r0/8,t)']'; end%周期延拓程序function T=yan(x)[r0,c0]=size(x);for s=1:r0a(s,:)=[x(s,c0/8:-1:1),x(s,:),x(s,end:-1:end-(c0/8-1))];endc0=c0+c0/4;for t=1:c0T(:,t)=[a(r0/8:-1:1,t)',a(:,t)',a(end:-1:end-(r0/8-1),t)']'; end。
