证明圆的切线的两种类型训练
圆切线的两种常考证明方法

圆切线的两种常考证明方法类型一、已知公共点(证明方法:有切点、连半径、证垂直)例.如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.(1)求证:CE是⊙O的切线:(2)连接BE,若⊙O的半径长为5,OF=3,求EF的长,1.如图,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在边AC上取一点D,使得DE=AD,连接OD、OE.(1)求证:①△AOD≌△EOD;②DE是⊙O的切线;(2)当BC=5,AD=2时,求⊙O的半径.2.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E、F.(1)试判断直线BC与OD的位置关系,并说明理由.(2)若BD=33BF=3,求⊙O的半径.3.如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.(1)求证:CP是⊙O的切线;(2)若M是弧AB的中点,CM交AB于点N,若AB=6,求MC•MN的值.DG BC,DG交线段AC于点G,交4.如图,△ABC内接于⊙O,AB是⊙O的直径,过⊙O外一点D作//AB于点E,交⊙O于点F,连接DB,CF,∠A=∠D.(1)求证:BD与⊙O相切;(2)若AE=OE,CF平分∠ACB,BD=12,求DE的长.5.如图,点E为正方形ABCD的边BC上的一点,O是ABE△的外接圆,与AD交于点F,G是CD上一∠=∠.点,且DGF AEB(1)求证:FG是O的切线;DG=,求半径OA的长.(2)若4AB=,16.如图,在Rt△ABC中,∠ABC=90∘,以AB为直径作半圆O,交AC于点D,E为BC的中点,连接DE.(1) 求证:DE是半圆O的切线;(2) 若∠C=60∘,DE=2,求AD的长.7.如图,AB为⊙O的直径,AD,BD是⊙O的弦,BC与⊙O相切于点B,OC∥AD,BA,CD的延长线相交于点E.(1) 求证:DC是⊙O的切线;(2) 若AE=1,ED=3,求⊙O的半径.8.如图,在Rt△ABC中,∠ACB=90∘,以斜边AB上的中线CD为直径作⊙O,与AC,BC分别交于点M,N,与AB的另一个交点为E.过点N作NF⊥AB,垂足为F.(1) 求证:NF是⊙O的切线;(2) 若NF=2,DF=1,求弦ED的长.类型二、未知公共点(证明方法:无切点、作垂直、证相等)例.如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.(1)求证:CD是⊙O的切线;(2)若AD=4,BC=9,求OD的长.1.如图,四边形ABCD中,AB∥CD,AE⊥CD于E,∠ABC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点D,交CD于点F.(1)求证:B C与⊙O相切;(2)若OB∥AD,DF=6,M E3OB的长度及阴影部分的面积.(结果保留π)2.如图,在Rt △ABC 中,∠ABC =90°,∠BAC 的平分线交BC 于点O ,D 为AB 上的一点,OD =OC ,以O 为圆心,OB 的长为半径作⊙O .(1)求证:AC 是⊙O 的切线;(2)若AB =6,BD =2,求线段AC 的长.3.如图,在四边形ABCD 中,AD BC ∥,90BAD ∠=︒,CB CD =,连接BD ,以点B 为圆心,BA 长为半径作B ,交BD 于点E .(1)求证:CD 是B 的切线;(2)若23AB =60BCD ∠=︒,求图中阴影部分的面积.4.如图,△ABC 为等腰三角形,O 是底边BC 的中点,腰AB 与⊙O 相切于点D ,OB 与⊙O 相交于点E .(1)求证:AC 是⊙O 的切线;(2)若BD =√3,BE =1.求阴影部分的面积.【课后练习】1.如图,在ABC 中,90ACB ∠=︒,点O 为BC 边上一点,以OB 为半径的⊙O 与边AB 、BC 交于点D 、E ,连接DC 、DE ,AC DC =.(1)求证:DC 为⊙O 切线;(2)若60A ∠=︒,⊙O 的半径为1,则DEC 的面积为.2.如图,Rt ABC 中,90ACB ∠=︒,以BC 为直径作半圆O 交AB 于点D ,点E 为AC 的中点,连接DE DC ,.(1)求证:DE 是半圆O 的切线;(2)若604BAC DE ∠=︒=,,求BD 的长.3.如图,ABC 中,90ACB ∠=︒,D 是边AB 上的一点,且2A DCB ∠=∠,E 是BC 上的一点,以EC 为直径的O 经过点D .(1)求证:AB 是O 的切线;(2)若圆心O 到弦CD 的距离为1,30DCB ∠=︒,求BD 的长.Math唐老师。
证明圆的切线方法

证明圆的切线方法我们学习了直线和圆的位置关系,就出现了新的一类习题,就是证明一直线是圆的切线•在我们所学的知识范围内,证明圆的切线常用的方法有:、若直线I过0 0上某一点A,证明I是0 0的切线,只需连0A,证明0A丄1就行了,简称“连半径,证垂直”,难点在于如何证明两线垂直例1如图,在"ABC中,AB二AC ,以AB为直径的0 0交BC于D,交AC于E,B为切点的切线交0D延长线于F.求证:EF与0 0相切.证明:连结OE, AD.••• AB是0 0的直径,…AD丄BC.又…AB=BC ,••• mD二DE , / 1 二 / 2・又…OB=OE , OF=OF , •••△ BOF NEOF ( SAS).•••/ OBF= / OEF.••• BF与0 0相切,• OB 丄BF.•••/ OEF=9O°.••• EF与0 0相切.说明:此题是通过证明三角形全等证明垂直的例2如图,AD是/ BAC 的平分线,求证:PA与0 0相切.P为BC延长线上一点,且PA=PD. OA, OE.•••/ DAB二 / DAC.•/ PA=PD,•••/ 2= / 1+ / DAC.•// 2= / B+ / DAB ,•/ AE是0 0的直径,…AC 丄EC, / E+ /EAC=90 ・•••/ 1 + / EAC=90 °.即0A丄PA.••• PA与0 0相切.证明二:延长AD交0 0于E,连结••• AD是Z BAC的平分线,• • •BE=CE ,••• 0E 丄BC.•••/ E+Z BDE二90 °,• • •9^/1・•/ PA=PD,•••/ PAD= / PDA. 又•••/ PDA= / BDE,•/ OA=OD ,•••/ 1 + / PAD二90°即0A丄PA.• • • PA与0 0相切说明:此题是通过证明两角互余,证明垂直的,解题中要注意知识的综合运用如图,AB二AC , AB是0 0的直径,0 0交BC于D, DM丄AC于M 求证:DM与0 0相切.证明一:连结0D.•/ AB二AC ,•/ 0B二0D ,•••0D // AC.•/ DM 丄AC ,…DM丄OD.••• DM与0 0相切证明二:连结0D , AD.••• AB是0 0的直径,…AD丄BC.又…AB=AC,•/ DM 丄AC ,•••/ 2+/4 二90°•••/ 3+/4=90°・•/ 0A=0D ,•证明二是通过证两角互余证明垂直的, 3证即0D 丄DM. ••• DM 是0 0的切线 说明:证明一是通过证平行来证明垂直的 解题屮注意充分利用已知及图上已知例4如图,已知:AB 是0 0的直径,D 在AB 的延长线上. 求证: DC 是0 0的切线 证明: 连结0C 、BC. •/ OA=OC ,•••/ A 二 / 1二 / 30° ・ •••/ BOC= / A+ / 1=60° ・ 又…OC=OB , •••△ OBC 是等边三角形. ••• OB=BC. •/ OB=BD , ••• OB=BC=BD ・ ••• 0C 丄 CD. ••• DC 是0 0的切线. 说明:此题是根据圆周角定理的推论如图,AB 是0 0的直径,CD 丄AB,且OA-OD - 0P. 求证:PC 是0 0的切线. 证明:连结0C•/ 0A 2二0D • OP, 0A 二0C ,2…0C 2=0D • 0P,0C,证明CE 丄0C 即可得解.OC OPOD 〃OC•••/ OCP 二 / ODC.•/ CD 丄 AB ,o•••/ OCP 二90 .••• PC 是0 0的切线.说明:此题是通过证三角形相似证明垂直的如图,ABCD 是正方形,G 是BC 延长线上一点,AG 交BD 于E,交CD 于求证:CE 与"CFG 的外接圆相切.分析:此题图上没有画出△ CFG 的外接圆,但厶CFG 是直角三角形,圆心在斜边 FG 的屮点,为此我们取FG 的屮点0,连结 证明:取FG 屮点0,连结0C.••• ABCD 是正方形,••• BC ± CD , △ CFG 是RtA•/ 0是FG 的中点,• 0是RtA CFG 的外心.•/ 0C 二0G ,•/ AD //BC,•/ AD=CD , DE=DE ,/ ADE= / CDE 二45° ,•••△ ADE CDE (SAS)•••/ 4= / 1,/ 1 = /3.•••/ 2+ /3=90° ,•••/ 1 + /2=90°・即CE丄0C.…CE与八CFG的外接圆相切二、若直线I与0 0没有已知的公共点,又要证明I是0 0的切线,只需作OA丄1,A为垂足,证明OA是0 0的半径就行了,简称:“作垂直;证半径” 例7如图,AB二AC , D 为BC中点,0 D与AB切于E点.求证:AC与0 D相切.证明一:连结DE,作DF丄AC, F是垂足.••• AB是0 D的切线,••• DE 丄AB.•/ DF 丄AC ,•••/ DEB二 / DFC=90°.•/ AB=AC ,•••/ B二 /C.又…BD=CD ,•••△ BDE CDF (AAS )DF=DE.••• F 在0 D 上.••• AC是0 D的切线证明二连结DE , AD,作DF丄AC , F是垂足.••• AB 与0 D 相切,•••DE 丄AB.•/ AB=AC , BD=CD ,•/ DE 丄AB , DF 丄AC ,DE 二DF・••• F 在0 D 上.••• AC 与0 D 相说明:证明一是爲过证明三角形全等证明DF二DE的,证明二是利用角平分线的性质证明DF=DE的,这类习题多数与角平分线有关例8已知:如图,AC, BD与0 0切于A、B,且AC // BD,若/ C0D=90°.求证:CD是0 0的切线.证明一:连结0A , 0B,作0E丄CD , E为垂足.••• AC , BD 与0 0 相切,••• AC 丄0A , BD 丄0B.•/ AC //BD , o•••/ 1 + / 2+ / 3+ /4 谢°COD 二90:•••/ 2+ / 3=90° ,/ 1 + /4=90°・•••/ 4+ /5=90°.••• RtA AOC s RtABDO AC OCOB 0D•/ OA=OB ,AC OC0A 0D又…/ CAO= / C0D=90°,又••• 0A 丄AC , 0E 丄CD,…OE=OA.••• E点在0 0上.••• CD是0 0的切线.证明二连结创,0B,作0E丄CD于E,延长DO交CA延长线于F.V AC , BD与0 0相切,Fu/.AC 丄OA, BD 丄OB.•/ AC II BD ,F=Z BDO.又••• OA=OB ,/.A AOF^ABOD (AAS)••• OF=OD.•// COD=90 °,••• CF=CD, / 1= / 2.又••• OA 丄AC , OE 丄CD , …OE=OA・••• E点在0 0上.••• CD是0 0的切线.证明三:连结A0并延长,作0E丄CD于E,取CD屮点F,连结OF.•/ AC与0 0相切,…AC丄A0.•/ AC // BD ,…AO丄BD.…BD与0 0相切于B,••• A啲延长线必经过点B.••• A琨0 0的直径./ AC// BD , OA=OB , CF二DF ,••• OF // AC , •••/ 仁/COF.•••/ COD二90 °, CF=DF ,••• OF 二—CD =CF ・2•••/ 2=/ COF.•/ OA 丄AC , OE 丄CD, ••• OE=OA・••• E点在0 0上.••• CD是0 0的切线说明:证明一是利用相似三角形证明/ 1 = / 2,证明二是利用等腰三角形三线合一证明/ 1二/ 2•证明三是利用梯形的性质证明/ 1二/ 2,这种方法必需先证明三点共线.此题较难,需要同学们利用所学过的知识综合求解以上介绍的是证明圆的切线常用的两种方法供同学们参考。
专题 证明圆的切线的常用方法(六大题型)(解析版)
(苏科版)九年级上册数学《第2章对称图形---圆》专题证明圆的切线的常用的方法★★★方法指引:证明一条直线是圆的切线的方法及辅助线作法:1、有交点:连半径、证垂直:当直线和圆有一个公共点时,把圆心和这个公共点连接起来,然后证明直线垂直于这条半径,简称:“有交点,连半径,证垂直”.2、无交点:作垂直、证半径:当直线和圆的公共点没有明确时,可以过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称:“无交点,作垂直,证半径”.类型一:有公共点:连半径,证垂直●●【典例一】(2022•雁塔区校级模拟)如图,AB 是⊙O 的直径,点D 在直径AB 上(D 与A ,B 不重合),CD ⊥AB ,且CD =AB ,连接CB ,与⊙O 交于点F ,在CD 上取一点E ,使得EF =EC .求证:EF 是⊙O 的切线;【分析】连接OF ,根据垂直定义可得∠CDB =90°,从而可得∠B +∠C =90°,然后利用等腰三角形的性质可得∠B =∠OFB ,∠C =∠EFC ,从而可得∠OFB +∠EFC =90°,最后利用平角定义可得∠OFE =90°,即可解答;【解答】证明:连接OF ,∵CD ⊥AB ,∴∠CDB =90°,∴∠B +∠C =90°,∵OB =OF ,EF =EC ,∴∠B =∠OFB ,∠C =∠EFC,∴∠OFB+∠EFC=90°,∴∠OFE=180°﹣(∠OFB+∠EFC)=90°,∵OF是⊙O的半径,∴EF是⊙O的切线:【点评】本题考查了切线的判定与性质,勾股定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.【变式1-1】(2022•澄城县三模)如图,AB是△ABC外接圆⊙O的直径,过⊙O外一点D作BC的平行线分别交AC,AB于点G,E,交⊙O于点F,连接DB,CF,∠BAC=∠D.求证:BD是⊙O的切线;【分析】证明∠ABD=90°,根据切线的判定可得BD与⊙O相切;【解答】证明:∵AB是⊙O的直径,∴∠ACB=90°,∵DG∥BC,∴∠AGE=∠ACB=90°,∴∠A+∠AEG=90°,又∵∠A=∠D,∠AEG=∠DEB,∴∠D+∠DEB=90°,∴∠DBE=90°,∴AB⊥BD,∵AB为直径,∴BD与⊙O相切;【点评】此题考查了切线的判定,垂径定理,解答本题需要我们熟练掌握切线的判定.【变式1-2】如图,AB是⊙O的直径,点C是圆上一点,CD⊥AB于点D,点E是圆外一点,CA平分∠ECD.求证:CE是⊙O的切线.【分析】利用切线的判定定理证明∠OCE=90°即可得出结论.【解答】证明:∵CA平分∠ECD,∴∠ECA=∠DCA.∵CD⊥AB,∴∠CAD+∠DCA=90°,∴∠ECA+∠CAD=90°.∵OA=OC,∴∠CAD=∠ACO,∴∠ECA+∠ACO=90°,即∠OCE=90°,∴OC⊥EC,∵OC是⊙O的半径,∴CE是⊙O的切线.【点评】本题主要考查了圆的切线的判定,熟练应用圆的切线的判定定理是解题的关键.【变式1-3】(2022秋•阳谷县校级期末)如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.(1)求证:MN是半圆的切线.(2)求证:FD=FG.【分析】(1)欲证明MN是半圆的切线,只需证得∠MAB=90°,即MA⊥AB即可;(2)根据圆周角定理推论得到∠ACB=90°,由DE⊥AB得到∠DEB=90°,则∠1+∠5=90°,∠3+∠4=90°,又D是弧AC的中点,即弧CD=弧DA,得到∠3=∠5,于是∠1=∠4,利用对顶角相等易得∠1=∠2,则有FD=FG.【解答】证明:(1)如图,∵AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°.又∵∠MAC=∠ABC,∴∠MAC+∠CAB=90°,即∠MAB=90°,∴MA⊥AB.∴MN是半圆的切线.(2)∵AB为直径,∴∠ACB=90°,而DE⊥AB,∴∠DEB=90°,∴∠1+∠5=90°,∠3+∠4=90°,∵D是弧AC的中点,即弧CD=弧DA,∴∠3=∠5,∴∠1=∠4,而∠2=∠4,∴∠1=∠2,∴FD=FG.【点评】本题考查了切线的判定:经过半径的外端点,并且与半径垂直的直线是圆的切线.也考查了圆周角定理及其推论、三角形外角的性质以及等腰三角形的判定.【变式1-4】如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接OC,PB,已知PB=6,DB=8,∠EDB=∠EPB.(1)求证:PB是⊙O的切线;(2)求⊙O的半径.(3)连接BE,求BE的长.【分析】(1)由已知角相等及直角三角形的性质得到∠OBP为直角,即可得证;(2)在直角三角形PBD中,由PB与DB的长,利用勾股定理求出PD的长,由切线长定理得到PC=PB =6,由PD﹣PC求出CD的长,在直角三角形OCD中,设OC=r,则有OD=8﹣r,利用勾股定理列出关于r的方程,求出方程的解得到r的值,即为圆的半径.(3)延长PB、DE相交于点F,证明△PED≌△PEF(ASA),由全等三角形的性质得出PD=PF=10,DE =EF,求出DF的长,则可得出答案.【解答】(1)证明:∵DE⊥PE,∴∠DEO=90°,∵∠EDB=∠EPB,∠BOE=∠EDB+∠DEO,∠BOE=∠EPB+∠OBP,∴∠OBP=∠DEO=90°,∴OB⊥PB,∴PB为⊙O的切线;(2)解:在Rt△PBD中,PB=6,DB=8,根据勾股定理得:PD=10,∵PD与PB都为⊙O的切线,∴PC=PB=6,∴DC=PD﹣PC=10﹣6=4;在Rt△CDO中,设OC=r,则有OD=8﹣r,根据勾股定理得:(8﹣r)2=r2+42,解得:r=3,则圆的半径为3.(3)延长PB、DE相交于点F,∵PD与PB都为⊙O的切线,∴OP平分∠CPB,∴∠DPE=∠FPE,∵PE⊥DF,∴∠PED=∠PEF=90°,又∵PE=PE,∴△PED ≌△PEF (ASA ),∴PD =PF =10,DE =EF ,∴BF =PF ﹣PB =10﹣6=4,在Rt △DBF 中,DF==∴BE =12DF =【点评】本题考查了切线的判定和性质,勾股定理,平行线的性质,全等三角形的判定和性质,熟练掌握性质定理是解题的关键.●●【典例二】 如图,△ABC 是直角三角形,点O 是线段AC 上的一点,以点O 为圆心,OA 为半径作圆.O 交线段AB 于点D ,作线段BD 的垂直平分线EF ,EF 交线段BC 于点.(1)若∠B =30°,求∠COD 的度数;(2)证明:ED 是⊙O 的切线.【分析】(1)根据三角形的内角和定理得到∠A =60°,根据等腰三角形的性质得到∠ODA =∠A =60°,于是得到∠COD =∠ODA +∠A =120°;(2)根据线段垂直平分线的性质得到∠EDB =∠B =30°,求得ED ⊥DO ,根据切线的判定定理即可得到结论.【解答】(1)解:∵∠C =90°,∠B =30°,∴∠A =60°,∵OD =OA,∴∠COD=∠ODA+∠A=120°;(2)证明:∵EF垂直平分BD,∴∠EDB=∠B=30°,∴∠EDO=180°﹣∠EDB﹣∠ODA=180°﹣30°﹣60°=90°,∴ED⊥DO,∵OD是⊙O的半径,∴ED是⊙O的切线.【点评】本题考查了切线的判定,等腰三角形的性质,线段垂直平分线的性质,熟练掌握切线的判定定理是解题的关键.【变式2-1】如图,AB为⊙O的直径,点C,D在⊙O上,AC=CD=DB,DE⊥AC.求证:DE是⊙O的切线.【分析】连接OD,根据已知条件得到∠BOD=13×180°=60°,求得∠EAD=∠DAB=12∠BOD=30°,根据等腰三角形的性质得到∠ADO=∠DAB=30°,求得∠EDA=60°,根据切线的判定定理即可得到结论.【解答】证明:连接OD,∵AC=CD=DB,∴∠BOD=13×180°=60°,∵CD=DB,∴∠EAD=∠DAB=12∠BOD=30°,∵OA=OD,∴∠ADO=∠DAB=30°,∵DE⊥AC,∴∠E=90°,∴∠EDA=60°,∴∠EDO=∠EDA+∠ADO=90°,∴OD⊥DE,∵OD是⊙O的半径,∴DE是⊙O的切线.【点评】本题考查了切线的判定,等腰三角形的性质,正确的作出辅助线是解题的关键.【变式2-2】如图,AC是⊙O的直径,B在⊙O上,BD平分∠ABC交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.求证:DE是⊙O的切线.【分析】连接OD,根据圆周角定理的推论得到∠ABC=90°,根据角平分线的性质求出∠DBE=45°,根据圆周角定理得到∠DOC,根据平行线的性质求出∠ODE=90°,根据切线的判定定理证明结论;【解答】证明:连接OD,∵AC是⊙O的直径,∴∠ABC=90°,∵BD平分∠ABC,∴∠DBE=45°,∴∠DOC=2∠DBE=90°,∵DE∥AC,∴∠ODE=∠DOC=90°,∴DE是⊙O的切线;【点评】本题考查的是切线的判定定理、圆周角定理以及正方形的判定和性质,掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.【变式2-3】(2023•鼓楼区校级模拟)如图,在⊙O中,AB为⊙O的直径,AC为弦,OC=4,∠OAC=60°.(1)求∠AOC的度数;(2)在图(1)中,P为直径BA的延长线上一点,且S△PAC=PC为⊙O的切线;【分析】(1)根据等腰三角形中有一角为60度时是等边三角形得到△ACO是等边三角形,则∠AOC=60°;(2)由等边三角形的性质以及勾股定理得出CD的长,再利用三角形外角的性质以及等腰三角形的性质得出∠PCA=30°,进而得出答案;【解答】(1)解:在△OAC中,∵OA=OC=4,∠OAC=60°,∴△OAC是等边三角形,∴∠AOC=60°;(2)证明:过点C作CD⊥AO于点D,∵△AOC是等边三角形,CD⊥AO,∴AD=DO=12OA=2,∠ACO=60°,∴CD∵S △PAC =∴12PA •CD =∴PA =4,∴PA =AC ,∴∠P =∠PCA =12∠OAC =30°,∴∠PCO =∠PCA +∠ACO =30°+60°=90°,∴OC ⊥PC ,∵OC 是⊙O 的半径,∴PC 为⊙O 的切线.【点评】本题考查了等边三角形的判定和性质,切线的判定,熟练掌握相关的性质和判定是解决问题的关键.【变式2-4】(2023•门头沟区二模)如图,AB 是⊙O 直径,弦CD ⊥AB 于E ,点F 在CD 上,且AF =DF ,连接AD ,BC .(1)求证:∠FAD =∠B(2)延长FA 到P ,使FP =FC ,作直线CP .如果AF ∥BC .求证:直线CP 为⊙O 的切线.【分析】(1)根据垂径定理、圆周角定理可得∠ACD =∠ACD =∠B ,根据等腰三角形的性质可得∠FAD=∠FDA,进而可得∠FAD=∠B;(2)根据平行线的性质以及三角形内角和定理可得∠FAB=∠FAD=∠FDA=30°,进而得到∠CFP=60°,再利用等边三角形的性质可得∠PCO=60°+30°=90°,由切线的判定方法可得结论.【解答】证明:(1)如图,连接AC,∵AB是⊙O直径,弦CD⊥AB,∴AC=AD,∴∠ACD=∠ACD=∠B,∵AF=FD,∴∠FAD=∠FDA,∴∠FAD=∠B;(2)如图,连接OC,∵AF∥BC,∴∠FAB=∠B,∴∠FAB=∠FAD=∠FDA,∵∠AED=90°,∴∠FAB=∠FAD=∠FDA=30°,∴∠CFP=60°,∵FP=FC,∴△CFP是等边三角形,∴∠PCF=60°,∵OB=OC,∴∠B=∠OCB=30°,∴∠OCD=30°,∴∠PCO=60°+30°=90°,即OC⊥PC,∵OC是半径,∴PC是⊙O的切线.【点评】本题考查切线的判定,圆周角定理、平行线的性质以及三角形内角和定理,掌握切线的判定方法,圆周角定理是正确解答的前提.●●【典例三】如图,四边形ABCD 内接于⊙O ,AB 为⊙O 的直径,过点C 作CE ⊥AD 交AD 的延长线于点E ,延长EC ,AB 交于点F ,∠ECD =∠BCF .求证:CE 为⊙O 的切线;【分析】连接OC ,BD ,可推出EF ∥BD ,进而可证CD =BC ,进而得出CE 为⊙O 的切线;【解答】证明:如图1,连接OC ,BD ,∵AB 是⊙O 的直径,∴∠ADB =90°,∵CE ⊥AE,∴∠E=∠ADB,∴EF∥BD,∴∠ECD=∠CDB,∠BCF=∠CBD,∵∠ECD=∠BCF,∴∠CDB=∠CBD,∴CD=BC,∴半径OC⊥EF,∴CE为⊙O的切线;【点评】本题考查了圆周角定理及其推论,圆的切线判定,解决问题的关键是作合适的辅助线.【变式3-1】(2022秋•阿瓦提县校级期末)已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连结AC,过点D作DE⊥AC,垂足为E.求证:DE为⊙O的切线.【分析】连接OD,根据OA=OB,CD=BD,得出OD∥AC,∠ODE=∠CED,再根据DE⊥AC,即可证出OD⊥DE,从而得出答案.【解答】证明:如图,连接OD.∵AB是⊙O的直径,∴∠ADB=90°,∴CD=BD,∵OA=OB,∴OD∥AC.∴∠ODE=∠CED.∵DE⊥AC,∴∠CED=90°.∴∠ODE=90°,∴OD⊥DE,∵OD是⊙O的半径,∴DE是⊙O的切线.【点评】本题考查了切线的判定与性质,解决本题的关键是掌握圆周角定理的推论、线段垂直平分线的性质以及等边三角形的判定,是一道常考题型.【变式3-2】已知,如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.(1)求证:点D是AB的中点;(2)判断DE与⊙O的位置关系,并证明你的结论.【分析】(1)连接CD,如图,根据圆周角定理,由BC为直径得到∠BDC=90°,然后根据等腰三角形的性质得AD=BD;(2)连接OD,先得到OD为△ABC的中位线,再根据三角形中位线性质得OD∥AC,而DE⊥AC,则DE⊥OD,然后根据切线的判定定理可得DE为⊙O的切线.【解答】(1)证明:连接CD,如图,∵BC为直径,∴∠BDC=90°,∴CD⊥AB,∵AC=BC,∴AD=BD,即点D是AB的中点;(2)解:DE与⊙O相切.理由如下:连接OD,∵AD=BD,OC=OB,∴OD为△ABC的中位线,∴OD∥AC,而DE⊥AC,∴DE⊥OD,∴DE为⊙O的切线.【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.【变式3-3】如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.(1)求证:BC是⊙O的切线;(2)已知∠B=30°,CD=4,求线段AB的长.【分析】(1)连接OD,根据角平分线的定义得到∠BAD=∠CAD,而∠OAD=∠ODA,则∠ODA=∠CAD,于是判断OD∥AC,由于∠C=90°,所以∠ODB=90°,然后根据切线的判定定理即可得到结论;(2)由∠B=30°得到∠BAC=60°,则∠CAD=30°,在Rt△ADC中,根据含30度的直角三角形三边的关系得到AC=Rt△ABC中,根据含30度的直角三角形三边的关系可得到AB=【解答】(1)证明:连接OD,如图,∵∠BAC的平分线交BC于点D,∴∠BAD=∠CAD,∵OA=OD,∴∠OAD=∠ODA,∴∠ODA=∠CAD,∴OD∥AC,∵∠C=90°,∴∠ODB=90°,∴OD⊥BC,∴BC是⊙O的切线;(2)解:∵∠B=30°,∴∠BAC=60°,∴∠CAD=30°,在Rt△ADC中,DC=4,∴AC==在Rt△ABC中,∠B=30°,∴AB=2AC=【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了含30度的直角三角形三边的关系.【变式3-4】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.(1)求证:AE是⊙O的切线;(2)若∠DBC=30°,DE=1cm,求BD的长.【分析】(1)连接OA,根据角之间的互余关系可得∠OAE=∠DEA=90°,故AE⊥OA,即AE是⊙O的切线;(2)根据圆周角定理,可得在Rt△AED中,∠AED=90°,∠EAD=30°,有AD=2DE;在Rt△ABD中,∠BAD=90°,∠ABD=30°,有BD=2AD=4DE,即可得出答案.【解答】(1)证明:连接OA,∵DA平分∠BDE,∴∠BDA=∠EDA.∵OA=OD,∴∠ODA=∠OAD,∴∠OAD=∠EDA,∴OA∥CE.∵AE⊥CE,∴AE⊥OA.∴AE是⊙O的切线.(2)解:∵BD是直径,∴∠BCD=∠BAD=90°.∵∠DBC=30°,∠BDC=60°,∴∠BDE=120°.∵DA平分∠BDE,∴∠BDA=∠EDA=60°.∴∠ABD=∠EAD=30°.∵在Rt△AED中,∠AED=90°,∠EAD=30°,∴AD=2DE.∵在Rt△ABD中,∠BAD=90°,∠ABD=30°,∴BD=2AD=4DE.∵DE的长是1cm,∴BD的长是4cm.【点评】此题主要考查了切线的判定,角平分线的性质,含30°的直角三角形的性质,勾股定理,矩形的判定和性质,构造出直角三角形是解本题的关键,是一道中等难度的中考常考题.●●【典例四】(2022•城关区一模)如图,C是⊙O上一点,点P在直径AB的延长线上,⊙O的半径为6,PB=4,PC=8.求证:PC是⊙O的切线;【分析】可以证明OC2+PC2=OP2得△OCP是直角三角形,即OC⊥PC,PC是⊙O的切线;【解答】解:如图,连接OC、BC,∵⊙O的半径为6,PB=4,PC=8.∴OC=OB=6,OP=OB+BP=6+4=10,∴OC2+PC2=62+82=100,OP2=102=100,∴OC2+PC2=OP2,∴△OCP是直角三角形,∴OC⊥PC,∴PC是⊙O的切线;【点评】本题考查圆的切线的判定和勾股定理逆定理,利用勾股定理的逆定理证明垂直是解决问题的关键.【变式4-1】如图,AD, BD是⊙O的弦,AD⊥BD,且BD=2AD=8 ,点C是BD的延长线上的一点,CD=2,求证:AC是⊙O的切线.【分析】先由勾股定理的逆定理证明垂直,再由切线的判断进行解答即可.【解答】证明:连接AB,∵AD⊥BD,且BD=2AD=8 ,∴AB为直径,AB2 =82+42 =80,∵CD=2,AD=4 ,∴AC2 =22 +42=20,∵CD=2,BD=8,∴BC=102=100,∴AC2+AB2=CB2,∴∠BAC=90° ,∴AC是⊙O的切线【点评】本题考查切线的判定,圆周角定理的推论,勾股定理的逆定理,解题关键是作出辅助线构造直角三角形.【变式4-2】如图,AD,BD是⊙O的弦,AD⊥BD,且BD=2AD=8,点C是BD的延长线上的一点,CD=2,求证:AC是⊙O的切线.【分析】先根据圆周角定理得到AB为⊙O的直径,再利用勾股定理计算出AB、AC,接着利用勾股定理的逆定理证明△ABC为直角三角形,∠BAC=90°,所以AC⊥AB,然后根据切线的判定定理得到结论.【解答】证明:∵AD⊥BD,∴∠ADB=90°,∴AB为⊙O的直径,∵BD =2AD =8,∴AD =4,在Rt △ADB 中,AB 2=AD 2+BD 2=42+82=80,在Rt △ADC 中,AC 2=AD 2+CD 2=42+22=20,∵BC 2=(2+8)2=10,∴AC 2+AB 2=BC 2,∴△ABC 为直角三角形,∠BAC =90°,∴AC ⊥AB ,∵AB 为直径,∴AC 是⊙O 的切线.【点评】本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理、勾股定理和勾股定理的逆定理.●●【典例五】(2022•鄞州区校级开学)如图,AB 为⊙O 的直径,点C 和点D 是⊙O 上的两点,连接BC ,DC ,BC =CD ,CE ⊥DA 交DA 的延长线于点E .求证:CE 是⊙O 的切线;【分析】连接OD ,OC ,证得△COD ≌△COB ,可得∠OCD =∠BCO ,从而得到∠ADC =∠DCO ,进而得到DA ∥CO ,利用切线的判定定理即可求证;【解答】证明:连接OD ,OC,如图,在△COD和△COB中,OD=OBOC=OC,CD=CB∴△COD≌△COB(SSS),∴∠OCD=∠BCO,∵CO=BO,∴∠B=∠BCO,∵∠B=∠ADC,∴∠ADC=∠DCO.∴DA∥CO,∴∠E+∠ECO=180°.∵CE⊥EA,∴∠E=90°.∴∠ECO=90°,∴EC⊥CO,∵CO是⊙O的半径,∴EC是⊙O的切线;【点评】本题主要考查了切线的判定,圆周角定理等知识,熟练掌握切线的判定,相似三角形的判定和性质,圆周角定理等知识是解题的关键.【变式5-1】如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.求证:CD是⊙O的切线;【分析】连接OD,利用SAS得到三角形COD与三角形COB全等,利用全等三角形的对应角相等得到∠ODC 为直角,即可得证;【解答】证明:如图,连接OD.∵AD∥OC,∴∠DAO=∠COB,∠ADO=∠COD,又∵OA=OD,∴∠DAO=∠ADO,∴∠COD=∠COB,在△COD和△COB中,OC=OC∠COD=∠COB,OD=OB∴△COD≌△COB(SAS),∴∠CDO=∠CBO=90°,∵OD是⊙O的半径,∴CD是⊙O的切线;【点评】此题考查了切线的判定和性质,以及全等三角形的判定与性质,熟练掌握各自的性质是解本题的关键.【变式5-2】(2022秋•新抚区期末)如图,AB为⊙O的直径,四边形OBCD是矩形,连接AD,延长AD 交⊙O于E,连接CE.求证:CE为⊙O的切线.【分析】连接OC、BE,根据矩形性质和圆半径相等,推出∠CDE=∠AEO,进而得到OP=CP,然后根据OB∥CD,可以推出∠COE=∠BOC,最后通过证明△BOC≌△EOC即可求解.【解答】证明:如图:连接OC、BE,OE,CD交于点P,∵四边形OBCD是矩形,∴OB∥CD,∠OBC=90°,OB=CD,∵OB∥CD,∴∠A=∠CDE,∵在⊙O中,OA=OB=OE,∴OE=CD,∵OA=OE,∴∠A=∠AEO,∴∠CDE=∠AEO,∴DP=PE,∵OE=CD,∴OP=CP,∴∠COE=∠DCO,∵OB∥CD,∴∠DCO=∠BOC,∴∠COE=∠BOC,在△BOC和△EOC中,OB=OECO=CO,∠BOC=∠COE∴△BOC≌△EOC(SAS),∴∠CEO=∠OBC=90°,∴CE⊥OE,又∵OE为⊙O的半径,∴CE为⊙O的切线.【点评】本题考查圆周角定理,全等三角形的判定和性质,矩形的性质等众多知识点,熟悉掌握以上知识点是解题关键.【变式5-3】(2022•建邺区二模)如图,四边形ABCD是菱形,以AB为直径作⊙O,交CB于点F,点E在CD上,且CE=CF,连接AE.(1)求证:AE是⊙O的切线;(2)连接AC交⊙O于点P,若AP BF=1,求⊙O的半径.【分析】(1)连接AF,根据菱形的性质得到∠ACF=∠ACE,根据全等三角形的性质得到∠AFC=∠AEC,推出OA⊥AE,根据切线的判定定理即可得到结论;(2)连接BP,根据圆周角定理得到∠APB=90°,求得AC=2AP=【解答】(1)证明:连接AF,∵四边形ABCD为菱形,∴∠ACF=∠ACE,在△ACF与△ACE中,CF=CE∠ACF=∠ACEAC=AC,∴△ACF≌△ACE(SAS),∴∠AFC=∠AEC,∵AB是⊙O的直径,∴∠AFB=∠AFC=90°,∴∠AEC=90°,∵AB∥DC,∴∠BAE+∠AEC=90°,∴∠BAE=90°,∴OA⊥AE,∵OA是⊙O的半径,∴AE是⊙O的切线;(2)解:连接BP,∵AB是⊙O的直径,∴∠APB=90°,∵AB=CB,AP=∴AC=2AP=设⊙O的半径为R,∵AC2﹣CF2=AF2,AB2﹣BF2=AF2,∴2−(2R−1)2=(2R)2−12,∴R=32(负值舍去),∴⊙O的半径为3 2.【点评】本题考查了切线的判定和性质,圆周角定理,菱形的性质,三角形全等的性质和判定,勾股定理等知识,解答本题的关键是根据勾股定理列方程解决问题.类型二:无公共点:作垂直,证半径●●【典例六】如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.求证:AC是⊙O的切线.【分析】过点O作OE⊥AC于点E,连接OD,OA,根据切线的性质得出AB⊥OD,根据等腰三角形三线合一的性质得出AO是∠BAC的平分线,根据角平分线的性质得出OE=OD,从而证得结论.【解答】证明:过点O作OE⊥AC于点E,连接OD,OA,∵AB与⊙O相切于点D,∴AB⊥OD,∵△ABC为等腰三角形,O是底边BC的中点,∴AO是∠BAC的平分线,∴OE=OD,即OE是⊙O的半径,∵圆心到直线的距离等于半径,∴AC是⊙O的切线.【点评】本题考查了切线的判定和性质,等腰三角形的性质,角平分线的性质,熟练掌握性质定理是解题的关键.【变式6-1】如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M.求证:CD与⊙O相切.【分析】利用正方形的性质得出AC平分角∠BCD,再利用角平分线的性质得出OM=ON,即可得出答案.【解答】证明:如图所示,连接OM,过点O作ON⊥CD于点N,∵⊙O与BC相切于点M,∴OM⊥BC,又∵ON⊥CD,O为正方形ABCD对角线AC上一点,∴OM=ON,∴ON为⊙O的半径,∴CD与⊙O相切.【点评】此题主要考查了正方形的性质以及角平分线的性质,得出OM=ON是解题关键.【变式6-2】如图,OC平分∠AOB,D是OC上任意一点,⊙D和OA相切于点E,连接CE.(1)求证:OB与⊙D相切;(2)若OE=4,⊙D的半径为3,求CE的长.【分析】(1)过点D作DF⊥OB于点F,先由切线的性质得DE⊥OA,则由角平分线的性质得DF=DE,即可证得结论;(2)过E作EG⊥OD于G,先由勾股定理求出OD=5,再由面积法求出EG=125,然后由勾股定理求出DG=95,最后由勾股定理求出CE即可.【解答】(1)证明:连接DE,过点D作DF⊥OB于点F,如图所示:∵⊙D与OA相切于点E,∴DE⊥OA,∵OC平分∠AOB,∴DF=DE,又∵DF⊥OB,∴OB与⊙D相切;(2)解:过E作EG⊥OD于G,如图所示:由(1)得:DE⊥OA,∴∠OED=90°,∵OE=4,DE=3,∴OD=5,∵EG⊥OD,∴12OD×EG=12OE×DE,∴EG=OE×DEOD=4×35=125,∴DG===9 5,∴CG=CD+DG=3+95=245,∴CE=【点评】此题考查了切线的判定与性质、勾股定理以及角平分线的性质等知识,解题的关键是准确作出辅助线.【变式6-3】如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.(1)求证:CD是⊙O的切线;(2)若AD=4,BC=9,求⊙O的半径R.【分析】(1)过O点作OE⊥CD于点E,通过角平分线的性质得出OE=OA即可证得结论.(2)过点D作DF⊥BC于点F,根据切线的性质可得出DC的长度,继而在Rt△DFC中利用勾股定理可得出DF的长,继而可得出半径.【解答】(1)证明:过O点作OE⊥CD于点E,∵AM切⊙O于点A,∴OA⊥AD,又∵DO平分∠ADC,∴OE=OA,∵OA为⊙O的半径,∴OE是⊙O的半径,且OE⊥DC,∴CD是⊙O的切线.(2)解:过点D作DF⊥BC于点F,∵AM,BN分别切⊙O于点A,B,∴AB⊥AD,AB⊥BC,∴四边形ABFD是矩形,∴AD=BF,AB=DF,又∵AD=4,BC=9,∴FC=9﹣4=5,∵AM,BN,DC分别切⊙O于点A,B,E,∴DA=DE,CB=CE,∴DC=AD+BC=4+9=13,在Rt△DFC中,DC2=DF2+FC2,∴DF=12,∴AB=12,∴⊙O的半径R是6.【点评】此题考查了切线的性质、角平分线的性质及勾股定理的知识,证明第一问关键是掌握切线的判定定理,解答第二问关键是熟练切线的性质.【变式6-4】(2022秋•清原县期末)如图,在△ABC中,∠ACB=90°,点D是AB边的中点,点O在AC边上,⊙O 经过点C 且与AB 边相切于点E ,∠FAC =12∠BDC .(1)求证:AF 是⊙O 的切线;(2)若BC =6,AB =10,求⊙O 的半径长.【分析】(1)作OH ⊥FA ,垂足为点H ,连接OE ,证明AC 是∠FAB 的平分线,进而根据OH =OE ,OE ⊥AB ,可得AF 是⊙O 的切线;(2)勾股定理得出AC ,设⊙O 的半径为r ,则OC =OE =r ,进而根据切线的性质,在Rt △OEA 中,勾股定理即可求解.【解答】(1)证明:如图,作OH ⊥FA ,垂足为点H ,连接OE ,∵∠ACB =90°,D 是AB 的中点,∴CD =AD =12AB ,∴∠CAD =∠ACD ,∵∠BDC =∠CAD +∠ACD =2∠CAD ,又∵∠FAC =12∠BDC ,∴∠FAC =∠CAD ,即AC 是∠FAB 的平分线,∵点O 在AC 上,⊙O 与AB 相切于点E ,∴OE ⊥AB ,且OE 是⊙O 的半径,∴OH =OE ,OH 是⊙O 的半径,∴AF 是⊙O 的切线;(2)解:如图,在△ABC中,∠ACB=90°,BC=6,AB=10,∴AC==8,∵BE,BC是⊙O的切线,∴BC=BE=6,∴AE=10﹣6=4设⊙O的半径为r,则OC=OE=r,在Rt△OEA中,由勾股定理得:OE2+AE2=OA2,∴16+r2=(8﹣r)2,∴r=3.∴⊙O的半径长为3.【点评】本题考查了切线的性质与判定,勾股定理,熟练掌握切线的性质与判定是解题的关键.1.如图,已知AB是⊙O的直径,AB=BE,点P在BA的延长线上,连接AE交⊙O于点D,过点D作PC⊥BE垂足为点C.求证:PC与⊙O相切;【分析】连接OD,根据等腰三角形的性质得到∠BAE=∠BEA,∠BAE=∠ODA,等量代换得到∠ODA=∠BEA,证明OD∥BE,根据平行线的性质得到PC⊥OD,根据切线的判定定理证明结论;【解答】证明:连接OD,∵AB=BE,∴∠BAE=∠BEA,∵OA=OD,∴∠BAE=∠ODA,∴∠ODA=∠BEA,∴OD∥BE,∵PC⊥BE,∴PC⊥OD,∵OD是⊙O的半径,∴PC与⊙O相切;【点评】本题考查的是切线的判定、解直角三角形,掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.2.如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,点D是BC的中点,DE∥BC交AC的延长线于点E.(1)求证:直线DE与⊙O相切;(2)若⊙O的直径是10,∠A=45°,求CE的长.【分析】(1)连接OD,如图,先利用垂径定理得到OD⊥BC,再根据平行线的性质得到OD⊥DE,然后根据切线的判定方法得到结论;(2)先根据圆周角定理得到∠B=90°,则∠ACB=45°,再根据平行线的性质得到∠E=45°,则可判断△ODE 为等腰直角三角形,于是可求出OE,然后计算OE﹣OC即可.【解答】(1)证明:连接OD,如图,∵点D是BC的中点,∴OD⊥BC,∵DE∥BC,∴OD⊥DE,∴直线DE与⊙O相切;(2)解:∵AC是⊙O的直径,∴∠B=90°,∵∠A=45°,∴∠ACB=45°,∵BC∥DE,∴∠E=45°,而∠ODE=90°,∴△ODE为等腰直角三角形,∴OE==∴CE=OE﹣OC=5.【点评】本题考查了切线的性质与判定:圆的切线垂直于经过切点的半径.也考查了垂径定理、圆周角定理和等腰直角三角形的性质.3.(2023•东城区校级模拟)如图,⊙O的半径OC与弦AB垂直于点D,连接BC,OB.(1)求证:2∠ABC+∠OBA=90°;(2)分别延长BO、CO交⊙O于点E、F,连接AF,交BE于G,过点A作AM⊥BC,交BC延长线于点M,若G是AF的中点,求证:AM是⊙O的切线.【分析】(1)先根据垂径定理得到AC=BC,再根据圆周角定理得到∠BOC=2∠ABC,然后利用互余关系得∠BOD+∠OBD=90°,从而得到结论;(2)如图,连接OA,根据垂径定理得到BE⊥AF,再根据圆周角定理得到∠CAF=90°,则可判断BE ∥AC,所以∠ABE=∠BAC,接着证明∠BAO=∠CBA得到OA∥BC,根据平行线的性质得到AM⊥OA,然后根据切线的判断方法得到结论.【解答】证明:(1)∵OD⊥AB,∴AC=BC,∠ODB=90°,∴∠BOC=2∠ABC,∵∠BOD+∠OBD=90°,∴2∠ABC+∠OBA=90°;(2)如图,连接OA,∵G是AF的中点,∴BE⊥AF,∵CF为直径,∴∠CAF=90°,∴CA⊥AF,∴BE∥AC,∴∠ABE=∠BAC,∴AC=BC,∴∠CAB=∠CBA,∵OA=OB,∴∠BAO=∠ABO,∴∠BAO=∠CBA,∴OA∥BC,∵AM⊥BC,∴AM⊥OA,而OA为⊙O的半径,∴AM是⊙O的切线.【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理、垂径定理.4.(2022•思明区校级二模)如图,四边形ABCD是⊙O的内接四边形,AC是⊙O直径,BE∥AD交DC 延长线于点E,若BC平分∠ACE.(1)求证:BE是⊙O的切线;(2)若BE=3,CD=2,求⊙O的半径.【分析】(1)连接OB,由条件可以证明OB∥DE,从而证明OB⊥BE;(2)由垂径定理求出AD长,从而由勾股定理可求AC长.【解答】(1)证明:连接OB,∵″OB=OC,∴∠OBC=∠OCB,∵∠BCE=∠OCB,∴∠OBC=∠BCE,∴OB∥DE,∵AC是⊙O直径,∴AD⊥DE,∵BE∥AD,∴BE⊥DE,∴OB⊥BE,∵OB是⊙O半径,∴BE是⊙O切线;(2)解:延长BO交AD于F,∵∠D=∠DEB=∠EBF=90°,∴四边形BEDF是矩形,∴BF⊥AD,DF=BE=3,∴AD=2DF=6,∵AC2=AD2+CD2,∴AC2=62+22=40,∴AC=∴⊙O【点评】本题考查切线的判定,矩形的判定和性质,垂径定理,勾股定理,用到的知识点较多,关键是熟练掌握知识点,并能灵活应用.5.(2023•封开县一模)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)当AB=5,BC=6时,求DE的长.【分析】(1)连接OD,由AC=AB,根据等边对等角得到一对角相等,再由OD=OB,根据等边对等角得到又一对角相等,等量代换可得一对同位角相等,根据同位角相等两直线平行可得OD与AC平行,又EF垂直于AC,根据垂直于两平行线中的一条,与另一条也垂直,得到EF与OD也垂直,可得EF为圆O的切线;(2)连接AD,由AB为圆的直径,根据直径所对的圆周角为直角可得∠ADB=90°,即AD与BC垂直,又AC=AB,根据三线合一得到D为BC中点,由BC求出CD的长,再由AC的长,利用勾股定理求出AD的长,三角形ACD的面积有两种求法,AC乘以DE除以2,或CD乘以AD除以2,列出两个关系式,两关系式相等可求出DE的长.【解答】(1)证明:连接OD,∵AB=AC,∴∠C=∠OBD,∵OD=OB,∴∠1=∠OBD,∴∠1=∠C,∴OD∥AC,∵EF⊥AC,∴EF⊥OD,∴EF是⊙O的切线;(2)连接AD,∵AB为⊙O的直径,∴∠ADB=90°,又∵AB=AC,且BC=6,∴CD=BD=12BC=3,在Rt△ACD中,AC=AB=5,CD=3,根据勾股定理得:AD=4,又S△ACD =12AC•ED=12AD•CD,即12×5×ED=12×4×3,∴ED=12 5.【点评】此题考查了等腰三角形的性质,圆周角定理,平行线的性质,勾股定理,三角形面积的求法,以及切线的判定,其中证明切线的方法为:有点连接圆心与此点,证垂直;无点过圆心作垂线,证明垂线段长等于圆的半径.本题利用的是第一种方法.6.(2023•宁德模拟)如图,OM 为⊙O 的半径,且OM =3,点G 为OM 的中点,过点G 作AB ⊥OM 交⊙O 于点A ,B ,点D 在优弧AB 上运动,将AB 沿AD 方向平移得到DC ;连接BD ,BC .(1)求∠ADB 的度数;(2)如图2,当点D 在MO 延长线上时,求证:BC 是⊙O 的切线.【分析】(1)连接AO ,BO ,先根据特殊角的正弦值可得∠OAG =30°,再根据等腰三角形的性质可得∠OAG =∠OBG =30°,从而可得∠AOB =120°,然后根据圆周角定理即可得;(2)连接AO ,BO ,CO ,先证出四边形ABCD 是平行四边形,再根据等边三角形的判定与性质可得AB =AD ,根据菱形的判定可得四边形ABCD 是菱形,根据菱形的性质可得CB =CD ,然后根据SSS 定理证出△COB ≌△COD ,根据全等三角形的性质可得∠OBC =∠ODC =90°,最后根据圆的切线的判定即可得证.【解答】(1)解:如图1,连接AO ,BO .∵点G 为OM 的中点,且OM =3,∴OG =12OM =32,OA =OB =OM =3,∵AB ⊥OM ,在Rt △AOG 中,OG =12OA .∴∠OAG =30°,又∵OA =OB ,∴∠OAG=∠OBG=30°,∴∠AOB=120°,∴∠ADB=12∠AOB=60°.(2)证明:如图2,连接AO,BO,CO,由平移得:AB=DC,AB∥DC,∴四边形ABCD是平行四边形,∵OM⊥AB,点D在MO延长线上,∴DM⊥CD,∵OA=OB,AB⊥OM,∴AG=BG,∴DM垂直平分AB,∴AD=BD,∵∠ADB=60°,∴△ABD为等边三角形,∴AB=AD,∴平行四边形ABCD是菱形,∴CB=CD,在△COB和△COD中,CB=CDOB=ODOC=OC,∴△COB≌△COD(SSS),∴∠OBC=∠ODC=90°,又∵OB是⊙O的半径,。
2023年中考九年级数学高频考点拔高训练-圆的切线的证明

2023年中考九年级数学高频考点拔高训练-圆的切线的证明1.如图,△ABD是△O的内接三角形,E是弦BD的中点,点C是△O外一点,且△DBC=△A=60°,连接OE并延长与△O相交于点F,与BC相交于点C.(1)求证:BC是△O的切线;(2)若△O的半径为6cm,求弦BD的长.2.如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)如果∠BAC=60°,AE=4√3,求AC长.3.如图,AC与△O相切,切点为C,点B在CO的延长线上,BD△AO,垂足为D,△ABD=△BO D.(1)求证:AB为△O的切线;(2)若BC=4,AC=3,求BD的长.4.如图,AB 是△O 的直径,点E 在△O 上,连接AE 和BE ,BC 平分△ABE 交△O 于点C ,过点C 作CD△BE ,交BE 的延长线于点D ,连接CE .(1)请判断直线CD 与△O 的位置关系,并说明理由;(2)若sin△ECD =35,CE =5,求△O 的半径. 5.如图,AB 为△O 的直径,C 、D 为△O 上不同于A 、B 的两点,△ABD =2△BAC ,连接CD ,过点C 作CE△DB ,垂足为E ,直径AB 与CE 的延长线相交于F 点.(1)求证:CF 是△O 的切线;(2)当BD = 185 ,sinF = 35时,求OF 的长. 6.如图,线段AB 经过圆心O ,交△O 于点A 、C ,点D 为△O 上一点,连结AD 、OD 、BD ,△A =△B =30°.(1)求证:BD 是△O 的切线.(2)若OA =5,求OA 、OD 与AD 围成的扇形的面积.7.如图,在Rt△ABC 中,△ACB =90°,CD 是斜边AB 上的中线,以CD 为直径的△O 分别交AC 、BC 于点M 、N ,过点N 作NE△AB ,垂足为E(1)若△O的半径为52,AC=6,求BN的长;(2)求证:NE与△O相切.8.如图,AB是△O的弦,OP△OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.(1)求证:BC是△O的切线;(2)若△O的半径为√5,OP=1,求BC的长.9.如图,AB是△O的直径,点C在AB的延长线上,AD平分△CAE交△O于点D,且AE△CD,垂足为点E.(1)求证:直线CE是△O的切线.(2)若BC=3,CD=3 √2,求弦AD的长.10.如图,AB为圆的直径,C是△O上一点,过点C的直线交AB的延长线于点M.作AD△MC,垂足为D,已知AC平分△MAD .(1)求证:MC是△O的切线:(2)若AB=BM=4,求tan△MAC的值11.如图,AB是△O的直径,点C在△O上,BD平分∠ABC交△O于点D,过点D作DE⊥BC,垂足为E.(1)求证:DE与△O相切;(2)若AB=10,AD=6,求DE的长.12.如图,点O在△APB的平分线上,△O与PA相切于点C.(1)求证:直线PB与△O相切;(2)PO的延长线与△O交于点E.若△O的半径为3,PC=4.求弦CE的长.13.如图,已知A(﹣5,0)、B(﹣3,0),点C在y轴的正半轴上,△CBO=45°,CD△AB,△CDA=90°点,P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时间ts.(1)求点C的坐标;(2)当△BCP=15°时,且△OPC中最长边是最短边的2倍,求t的值;(3)以点P为圆心,PC为半径的△P随点P的运动而变化,当△P与四边形ABCD的边(或边所在的直线)相切时,求t的值.14.已知AB为⊙O的直径,C为⊙O上一动点,连接AC,BC,在BA的延长线上取一点D,连接CD,使CD=CB.(1)如图1,若AC=AD,求证:CD是⊙O的切线;(2)如图2,延长DC交⊙O于点E,连接AE.①若⊙O的直径为√10,sinB=√10,求AD的长;10②若CD=2CE,求cosB的值.15.如图,AB、AC分别是△O的直径和弦,OD△AC于点D,过点A作△O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.(1)求证:PC是△O的切线;(2)若△ABC=60°,AB=10,求线段CF的长,16.如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,△BCD=60°,点E是AB上一点,AE=3EB,△P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.(1)求抛物线的解析式;(2)求证:ED是△P的切线;(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.答案解析部分1.【答案】(1)证明:连接OB ,如图所示:∵E 是弦BD 的中点,∴BE =DE ,OE△BD , BF ⌢=12BD ⌢ , ∴△BOE =△A ,△OBE+△BOE =90°,∵△DBC =△A ,∴△BOE =△DBC ,∴△OBE+△DBC =90°,∴△OBC =90°,即BC△OB ,∴BC 是△O 的切线;(2)解:∵OB =6,△DBC =△A =60°,BC△OB , ∴OC =12,∵△OBC 的面积= 12 OC•BE = 12OB•BC , ∴BE = OB×BC OC =6×6√312=3√3 , ∴BD =2BE =6 √3 ,即弦BD 的长为6 √3 .2.【答案】(1)证明:连接 OD ,如图,∵∠BAC 的平分线 AD 交 ⊙O 于点 D ,∴∠BAD=∠DAC,∵OA=OD,∴∠OAD=∠ODA,∴∠ODA=∠DAC,∴OD//AE,∵DE⊥AE,∴DE⊥OD,OD为半径,∴DE是⊙O的切线(2)解:作OF⊥AC于F∵∠BAC=60°,∴∠DAE=30°,在RtΔADE中,DE=AE⋅tan30°=4四边形ODEF为矩形,∴OF=DE=4,在RtΔOAF中,∵∠OAF=60°∴AF=√3=4√33∴AC=2AF=8√3 33.【答案】(1)证明:作OH△AB,垂足为H∵AC与△O相切,切点为C,∴△ACO=90°∴△OAC+△AOC=90°又BD△AO∴△BDO=90°∴△BOD+△DBO=90°,△BAD+△ABD=90°又△BOD=△AOC,△ABD=△BOD∴△OAC=△BAD∴OH=OC又OC为△O半径∴AB为△O的切线(2)解:在Rt△BOH和Rt△BAC中AB=√BC2+AC2=5sin∠ABC=OHOB=ACAB=354−OB OB=35,解得OB=52,OC=32,OA=√OC2+AC2=32√5∵△AOC=△BOD,△C=△D=90°∴△AOC△△BOD∴OAOB=ACBD∴32√552=3BD,解得:BD=√5.4.【答案】(1)解:结论:CD是△O的切线.理由:连接OC.∵OC=OB,∴△OCB=△OBC,∵BC平分△ABD,∴△OBC=△CBE,∴△OCB=△CBE,∴OC//BD ,∵CD△BD ,∴CD△OC ,∵OC 是半径,∴CD 是△O 的切线;(2)解:设OA =OC =r ,设AE 交OC 于点J .∵AB 是直径,∴△AEB =90°,∵OC△DC ,CD△DB ,∴△D =△DCJ =△DEJ =90°,∴四边形CDEJ 是矩形,∴△CJE =90°,CD =EJ ,CJ =DE ,∴OC△AE ,∴AJ =EJ ,∵sin△ECD =DE CE =35,CE =5, ∴DE =3,CD =4,∴AJ =EJ =CD =4,CJ =DE =3,在Rt△AJO 中,r 2=(r ﹣3)2+42,∴r =256, ∴△O 的半径为256. 5.【答案】(1)解:连接OC .如图1所示:∵OA=OC,∴△1=△2.又∵△3=△1+△2,∴△3=2△1.又∵△4=2△1,∴△4=△3,∴OC△DB.∵CE△DB,∴OC△CF.又∵OC为△O的半径,∴CF为△O的切线;(2)解:连接AD.如图2所示:∵AB是直径,∴△D=90°,∴CF△AD,∴△BAD=△F,∴sin△BAD=sinF=BDAB=35,∴AB=53BD=6,∴OB=OC=3,∵OC△CF,∴△OCF=90°,∴sinF=OCOF=35,解得:OF=5.6.【答案】(1)证明:∵△ADO=△BAD=30°,∴△DOB=60°∵△ABD=30°,∴△ODB=90°∴OD△BD.∵点D为△O上一点,∴BD是△O的切线.(2)解:∵△DOB=60°,∴△AOD=120°.∵OA=5,∴OA、OD与AD围成的扇形的面积为120·π·52360=253π.7.【答案】(1)解:∵ △O 的半径为52,则CD=5,AB=10,BC=√AB2−AC2=√100−36=8CD为直径,得DN△BC,D为AB的中点,则BD=CD,则△BDC为等腰三角形,由三线合一知,BN=NC=12BC=4。
证明圆的切线的七种常用方法

证明圆的切线的七种常用方法类型1、有公共点:连半径,证垂直方法1、勾股定理逆定理法证垂直1.如图,⊙O的直径AB=12,点P是AB延长线上一点,且PB=4,点C是⊙O上一点,PC=8. 求证:PC是⊙O的切线.方法2、特殊角计算法证垂直2. 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.(1)求证:P A是⊙O的切线;(2)若PD =5,求⊙O 的直径.方法3、等角代换法证垂直3.如图,在Rt△ABC中,∠C=90°,D为BC 的中点,以AC 为直径的⊙O交AB于点E . 求证:DE是⊙O 的切线.方法4、平行线性质法证垂直4.如图,已知四边形OABC的三个顶点A ,B ,C在以O为圆心的半圆上,过点C 作CD ⊥AB,分别交AB,AO 的延长线于点D,E,AE交半圆O于点F,连接CF,且∠E=30°,点B是︵AC的中点.(1)判断直线DE与半圆O的位置关系,并说明理由;(2)求证:CF=OC;(3)若⊙O的半径是6,求DC的长.AB POCACBPD OAEBDOCA O F ECDB方法5、全等三角形法证垂直5.如图,AB 是⊙O 的直径,点C ,D 在⊙O 上,且四边形AOCD 是平行四边形,过点D 作⊙O 的切线,交OC 的延长线于点F ,连接BF .求证:BF 是⊙O 的切线.类型2、无公共点:作垂直,证半径方法6、角平分线性质法证半径6.如图,在Rt △ABC 中,∠B =90°,∠BAC 的平分线交BC 于点D ,E 是AB 上一点,DE =DC ,以点D 为圆心,BD 长为半径作OD ,AB =5,EB =2. (1)求证:AC 是OD 的切线;(2)求线段AC 的长.方法7、全等三角形法证半径7.如图,四边形ABCD 中,∠A =∠ABC =90°,AD +BC =CD ,以AB 为直径作⊙O . 求证:⊙O 与边CD 相切.A OBCD F A B C D EA OB C D。
专题训练(七) 证明圆的切线的两种类型

在 Rt△OFB 中,OB2=BF2+(OB-AF)2,∴OB=4,∴BD=8,∴在 Rt△ABD 中,AD=
BD2-AB2= 64-8=2 14
4.如图,在△OAB中,OA=OB,以点O为圆心的⊙O经过AB的中点C,连接OC,直线 AO与⊙O相交于点E,D,OB交⊙O于点F,P是的中点,连接CE,CF,BP. (1)求证:AB是⊙O的切线; (2)若OA=4,则 ①当AC=____时,四边形OECF是菱形; ②当AC=____时,四边形OCBP是正方形.
专题训练(七) 证明圆的切线的两种 类型
类型之一 已知直线与圆的交点 1.如图,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DM⊥AC于点M. 求证:DM与⊙O相切.
证明:方法一:连接OD.∵AB=AC,∴∠B=∠C. ∵OB=OD,∴∠BDO=∠B,∴∠BDO=∠C,∴OD∥AC. ∵DM⊥AC,∴DM⊥OD.∴DM与⊙O相切. 方法二:连接OD,AD.∵AB是⊙O的直径,∴AD⊥BC. ∵AB=AC,∴∠BAD=∠CAD.∵DM⊥AC,∴∠CAD+∠ADM=90° ∵OA=OD,∴∠BAD=∠ODA.∴∠ODA+∠ADM=90°, 即OD⊥DM,∴DM是⊙O的切线
2.如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP=2,弦AB垂直平分OC. (1)求BC的长; (2)求证:PB是⊙O的切线.
解:(1)连接OB.∵弦AB垂直平分OC,∴OB=BC. 又∵OB=OC,∴△OBC是正三角形.∴BC=OC=2 (2)证明:∵BC=CP,∴∠CBP=∠CPB. ∵△OBC是正三角形,∴∠OBC=∠OCB=60°. ∴∠CBP=30°,∴∠OBP=∠CBP+∠OBC=90°, 即OB⊥BP.∵点B在⊙O上,∴PB是⊙O的切线
圆切线练习题(含答案)

圆切线练习题(含答案)XXX∠OAD,又∠OAD=90°,∴∠XXX°。
又因为CD与半径OD重合,∴CD垂直于过切点D的半径,即CD是⊙O的切线。
例5.证明:由点悟可知,须证OD=OA。
XXX是⊙O的直径,∴∠OAB=90°,又∠XXX°,因此O、B、D三点共线。
OBD是直角三角形,∴OD=OB×sin∠OBD=r×sin∠OAB=OA。
又因为OD是⊙O的半径,∴OD=r。
OA=r,即AC与⊙O相切。
例6.证明:如图所示。
OA⊥OB,∴∠XXX°,又∠OAD=∠DPB,∴∠DPB=90°。
CD是⊙O的切线,∴PC=CD。
例7.解:如图所示。
O是内心,∴∠BOC=2∠A=140°。
答案:∠BOC=140°。
题目:证明在一个圆中,若一条直径的一端点与圆上一点相连,且与该点相连的两条切线分别与直径所在直线交于不同点,则这两个交点和圆上的该点构成一个等腰三角形。
证明:连接直径的另一端点和圆上的该点,得到三角形ACD。
由于OA=OD,所以∠ODA=∠OAD,从而∠COB=∠COD。
又因为OD=OB,所以三角形COB≌三角形COD,从而∠B=∠XXX。
由于BC是切线,而AB是直径,所以∠B=90°,∠ODC=90°,因此CD是圆的切线。
在证明中,我们先利用“切线的性质定理”和“全等三角形”的基本图形,构造辅助线OD。
然后利用切线的判定定理,得到CD是圆的切线。
这样就证明了∠COB=∠COD和CD是圆的切线。
接下来,我们连接直径的另一端点和圆上的该点,得到三角形ACD。
由于OA=OD,所以∠ODA=∠OAD,从而∠COB=∠COD。
又因为OD=OB,所以三角形COB≌三角形COD,从而∠B=∠XXX。
由于BC是切线,而AB是直径,所以∠B=90°,∠ODC=90°,因此CD是圆的切线。
2022年中考数学大题圆证明切线的两种常用方法及专项练习题汇总

2022中考数学圆综合大题证明切线的两种常用方法类型1直线与圆有交点方法归纳:直线过圆上某一点,证明直线是圆的切线时,只需“连半径,证垂直,得切线”.“证垂直”时通常利用圆中的关系得到90°的角,如直径所对的圆周角等于90°等.【例1】如图,AB=AC,AB是⊙O的直径,⊙O交BC于D,DM⊥AC于M.求证:DM与⊙O相切.1.(朝阳中考)如图,AB是⊙O的弦,OA⊥OD,AB,OD交于点C,且CD=BD.(1)判断BD与⊙O的位置关系,并证明你的结论;(2)当OA=3,OC=1时,求线段BD的长.2.(德州中考)如图,已知⊙O的半径为1,DE是⊙O的直径,过D作⊙O的切线,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.(1)求AD的长;(2)BC是⊙O的切线吗?若是,给出证明,若不是,说明理由.3.(毕节中考)如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.(1)求证:AC是⊙O的切线;(2)已知圆的半径R=5,EF=3,求DF的长.类型2不确定直线与圆是否有公共点方法归纳:直线与圆没有已知的公共点时,通常“作垂直,证半径,得切线”.证明垂线段的长等于半径常用的方法是利用三角形全等或者利用角平分线上的点到角的两边的距离相等.【例2】如图,AB=AC,D为BC中点,⊙D与AB切于E点.求证:AC与⊙D相切.4.如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC 相切于点M,与AB,AD分别相交于点E,F.求证:CD与⊙O相切.5.如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.(1)求证:AC是⊙D的切线;(2)求线段AC的长.参考答案【例1】 证明:法一:连接OD.∵AB =AC ,∴∠B =∠C.∵OB =OD ,∴∠BDO =∠B.∴∠BDO =∠C.∴OD ∥AC.∵DM ⊥AC ,∴DM ⊥OD.∴DM 与⊙O 相切.法二:连接OD ,AD. ∵AB 是⊙O 的直径,∴AD ⊥BC.∵AB =AC ,∴∠BAD =∠CAD.∵DM ⊥AC ,∴∠CAD +∠ADM =90°.∵OA =OD ,∴∠BAD =∠ODA.∴∠ODA +∠ADM =90°.即OD ⊥DM ,∴DM 是⊙O 的切线.1.(1)连接OB ,∵OA =OB ,∴∠OAC =∠OBC.∵OA ⊥OD ,∴∠AOC =90°.∴∠OAC +∠OCA =90°.∵DC =DB ,∴∠DCB =∠DBC.∵∠DCB =∠ACO ,∴∠ACO =∠DBC.∴∠DBC +∠OBC =90°.∴∠OBD =90°.∵点B 是半径OB 的外端,∴BD 与⊙O 相切.(2)设BD =x ,则CD =x ,OD =x +1,OB =OA =3,由勾股定理得:32+x 2=(x +1)2.解得x =4.∴BD =4.2.(1)连接BD ,则∠DBE =90°.∵四边形BCOE 是平行四边形,∴BC ∥OE ,BC =OE =1.在Rt △ABD 中,C 为AD 的中点,∴BC =12AD =1.∴AD =2.(2)BC 是⊙O 的切线,理由如下:连接OB ,由(1)得BC ∥OD ,且BC =OD.∴四边形BCDO 是平行四边形.又∵AD 是⊙O 的切线,∴OD ⊥AD.∴四边形BCDO 是矩形.∴OB ⊥BC ,∴BC 是⊙O 的切线.3.(1)连接OA ,OD ,∵D 为BE 的下半圆弧的中点,∴∠FOD=90°.∵AC=FC,∴∠CAF=∠AFC.∵∠AFC=∠OFD,∴∠CAF=∠OFD.∵OA=OD,∴∠ODF=∠OAF.∵∠FOD=90°.∴∠OFD+∠ODF=90°.∴∠OAF+∠CAF=90°,即∠OAC=90°.∴AC与⊙O相切.(2)∵半径R=5,EF=3,∴OF=OE-EF=5-3=2.在Rt△ODF中,DF=52+22=29.【例2】法一:连接DE,作DF⊥AC,垂足为F.∵AB是⊙D的切线,∴DE⊥AB.∵DF⊥AC,∴∠DEB=∠DFC=90°.∵AB=AC,∴∠B=∠C.∵BD=CD,∴△BDE≌△CDF.∴DF=DE.∴F在⊙D上.∴AC是⊙D的切线.法二:连接DE,AD,作DF⊥AC,F是垂足.∵AB与⊙D相切,∴DE⊥AB.∵AB=AC,BD=CD,∴∠DAB=∠DAC.∵DE⊥AB,DF⊥AC,∴DE=DF.∴F在⊙D上,∴AC与⊙D相切.4.证明:连接OM,过点O作ON⊥CD,垂足为N,∵⊙O与BC相切于M,∴OM⊥BC.∵正方形ABCD中,AC平分∠BCD,又∵ON⊥CD,OM⊥BC,∴OM=ON.∴N在⊙O上.∴CD与⊙O相切.5.(1)证明:过点D作DF⊥AC于F.∵∠ABC=90°,∴AB⊥BC.∵AD平分∠BAC,DF⊥AC,∴BD=DF.∴点F在⊙D上.∴AC是⊙D的切线.(2)在Rt△BDE和Rt△FDC中,∵BD=DF,DE=DC,∴Rt△BDE≌Rt△FDC(HL),∴EB=FC.∵AB=AF,∴AB+EB=AF+FC,即AB+EB=AC,∴AC=5+3=8.2022年中考数学复习专题---圆中阴影面积计算班级:___________姓名:___________学号:___________1.如图,直线y kx b=+经过点M(1,√3)和点N(1−,3√3),A、B是此直线与坐标轴的交点.以AB为直径作⊙C,求此圆与y轴围成的阴影部分面积.2.如图,AAAA是⊙OO的直径,CC,DD是圆上两点,且有BD�=CCDD�,连结AADD,AACC,作DDDD⊥AACC的延长线于点DD.(1)求证:DDDD是⊙OO的切线;(2)若AADD=2√3,∠AADDDD=60∘,求阴影部分的面积.(结果保留ππ)3.如图,AAAA是圆OO的直径,AACC⊥AAAA,DD为圆OO上的一点,AACC=DDCC,延长CCDD交AAAA的延长线于点DD.(1)求证:CCDD为圆OO的切线.(2)若OOFF⊥AADD,OOFF=1,30∠=o,求圆中阴影部分的面积.(结果保留ππ)OAF4.如图,⊙OO是等边ΔAAAACC的外接圆,连接AAOO并延长至点PP,且AAAA=AAPP.(1)求证:PPAA是⊙OO的切线;(2)若AAAA=2√3,求图中阴影部分的面积.(结果保留ππ和根号)5.如图,OO为等边△AAAACC的外接圆,DD为直径CCDD延长线上的一点,连接AADD,AADD=AACC.(1)求证:AADD是⊙O的切线;(2)若CCDD=6,求阴影部分的面积.6.如图,AC为圆O的直径,弦AD的延长线与过点C的切线交于点B,E为BC中点,AC= 4√3,BC=4.(1)求证:DE为圆O的切线;(2)求阴影部分面积.7.已知AB是⊙O的直径,点C是圆O上一点,点P为⊙O外一点,且OP∥BC,∠P=∠BAC.(1)求证:P A为⊙O的切线;(2)如果OP=AB=6,求图中阴影部分面积.8.如图,AAAA为⊙OO的直径,弦CCDD⊥AAAA,垂足为DD,CCDD=4√5,连接OOCC,OODD=2DDAA,FF为圆上一点,过点FF作圆的切线交AAAA的延长线于点GG,连接AAFF,AAFF=AAGG.(1)求⊙OO的半径;(2)求证:AAFF=FFGG;(3)求阴影部分的面积.9.如图,△ABC中,∠C=90º,∠ABC=2∠A,点O在AC上,OA=OB,以O为圆心,OC为半径作圆.(1)求证:AB是⊙O的切线;(2)若BC=3,求图中阴影部分的面积.10.如图,在△ABC中,∠CC=60∘,⊙OO是△ABC的外接圆,点P在直径BD的延长线上,且AB=AP.(1)求证:PA是⊙OO的切线;(2)若AB=2√3,求图中阴影部分的面积.(结果保留ππ和根号)11.如图,AB为圆O的直径,射线AD交圆O于点F,点C为劣弧BF的中点,过点C作CE⊥AD,垂足为E,连接AC(1)求证:CE是圆O的切线(2)若∠BAC=30°,AB=4,求阴影部分的面积12.如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD于G,OG:OC=3:5,AB=8.(1)求⊙O的半径;(2)点E为圆上一点,∠ECD=15º,将弧CE沿弦CE翻折,交CD于点F,求图中阴影部分的面积.13.如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=4,点D是AB的中点,连接DO并延长交⊙O于点P.(1)求劣弧PC的长(结果保留π);(2)过点P作PF⊥AC于点F,求阴影部分的面积(结果保留π).14.如图,四边形ABCD内接于圆O,对角线AC是圆O的直径,DB平分∠ADC,AC长10cm.(1)求点O到AB的距离;(2)求阴影部分的面积.15.如图,在矩形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA 的延长线交于点E,连接CE,求阴影部分的面积.16.如图,∠APB的平分线过点O,以O点为圆心的圆与PA相切于点C,DE为⊙O的直径.(1)求证:PB是⊙O的切线;(2)若∠CPO=50°,∠E=25°,求∠POD;(3)若⊙O的半径为2,CE=2√3,求阴影部分的面积.17.如图,点P在圆O外,PA与圆O相切于A点,OP与圆周相交于C点,点B与点A 关于直线PO对称,已知OA=4,∠POA=60°求:(1)弦AB的长;(2)阴影部分的面积(结果保留π).18.如图,⊙O是Rt△ABC的外接圆,直径AB=4,直线EF经过点C,AD⊥EF于点D,∠ACD=∠B.(1)求证:EF是⊙O的切线;(2)若AD=1,求BC的长;(3)在(2)的条件下,求图中阴影部分的面积.。
中考圆综合6种证明切线的模型

中考圆综合6种证明切线的模型【模型l:双切线】例1.如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.(1)求证:CE与⊙O相切;(2)若⊙O的半径为3,EF=4,求BD的长.练习1.已知:如图,AB是⊙O的直径,C是⊙O上一点,OD BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连结BE.(1)求证:BE与⊙O相切;.OE DCB A【模型2角平分线模型】例2.如图,已知AB 是⊙O 的直径,C 是⊙O 上一点,∠BAC 的平分线交⊙O 于点D ,交⊙O 的切线BE 于点E ,过点D 作DF ⊥AC ,交AC 的延长线于点F .(1)求证:DF 是⊙O 的切线;练习2.如图,AB 是O ⊙的直径,点C 在O ⊙上,CAB ∠的平分线交O ⊙于点D ,过点D 作AC 的垂线交AC的延长线于点E ,连接BC 交AD 于点F .(1)求证:ED 是O ⊙的切线;【模型3:弦切角】例3.如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.(1)求证:AC是⊙O的切线;.练习3.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CB D.(1)求证:CD是⊙O的切线;【模型4:等腰三角形】例4.如图,在Rt△ABC中,∠ACB=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长DE交BC的延长线于点F.(1)求证:BD=BF;练习4:已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O 的切线交AB于点E,交AC的延长线于点F.(1)求证:DE⊥AB;【模型5:二倍角的使用】例5.如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.(1)求证:CF为⊙O的切线;.练习5:如图,AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,过点C作⊙O的切线CF交直线AB于点F,直线DB⊥CF于点E.(1)求证:∠ABD=2∠CAB;.【模型6:垂直导角】.例6.如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO 延长线于点E,连接PB,∠EDB=∠EPB.(1)求证:PB是⊙O的切线.,弦CF与OB交于点E,过点F,A分别练习6.如图,在⊙O中,AB为直径,OC AB作⊙O的切线交于点H,且HF与AB的延长线交于点D.(1)求证:DF=DE;.。
(完整版)中考数学-圆的切线证明综合试题

专题-------圆的切线证明我们学习了直线和圆的位置关系,就出现了新的一类习题,就是证明一直线是圆的切线.在我们所学的知识范围内,证明圆的切线常用的方法有:一、若直线l 过⊙O 上某一点A ,证明l 是⊙O 的切线,只需连OA ,证明OA⊥l 就行了,简称“连半径,证垂直”,难点在于如何证明两线垂直.例1 如图,在△ABC 中,AB=AC ,以AB 为直径的⊙O 交BC 于D ,交AC 于E ,B 为切点的切线交OD 延长线于F.求证:EF 与⊙O 相切.证明:连结OE ,AD. ∵AB 是⊙O 的直径, ∴AD⊥BC. 又∵AB=BC, ∴∠3=∠4. ∴BD=DE,∠1=∠2. 又∵OB=OE,OF=OF , ∴△BOF≌△EOF(SAS ). ∴∠OBF=∠OEF. ∵BF 与⊙O 相切, ∴OB⊥BF. ∴∠OEF=900.∴EF 与⊙O 相切.说明:此题是通过证明三角形全等证明垂直的例2 如图,AD 是∠BAC 的平分线,P 为BC 延长线上一点,且PA=PD.求证:PA 与⊙O 相切.证明一:作直径AE ,连结EC. ∵AD 是∠BAC 的平分线, ∴∠DAB=∠DAC.⌒⌒∵PA=PD, ∴∠2=∠1+∠DAC. ∵∠2=∠B+∠DAB, ∴∠1=∠B. 又∵∠B=∠E, ∴∠1=∠E∵AE 是⊙O 的直径, ∴AC⊥EC,∠E+∠EAC=900. ∴∠1+∠EAC=900. 即OA⊥PA.∴PA 与⊙O 相切.证明二:延长AD 交⊙O 于E ,连结OA ,OE. ∵AD 是∠BAC 的平分线,∴BE=CE,∴OE⊥BC.∴∠E+∠BDE=900. ∵OA=OE, ∴∠E=∠1. ∵PA=PD, ∴∠PAD=∠PDA.又∵∠PDA=∠BDE,∴∠1+∠PAD=900即OA⊥PA.∴PA 与⊙O 相切说明:此题是通过证明两角互余,证明垂直的,解题中要注意知识的综合运用.例3 如图,AB=AC ,AB 是⊙O 的直径,⊙O 交BC 于D ,DM⊥AC 于M求证:DM 与⊙O 相切.证明一:连结OD. ∵AB=AC, ∴∠B=∠C.⌒⌒∵OB=OD,∴∠1=∠B.∴∠1=∠C. ∴OD∥AC. ∵DM⊥AC,∴DM⊥OD.∴DM 与⊙O 相切证明二:连结OD ,AD.∵AB 是⊙O 的直径,∴AD⊥BC.又∵AB=AC,∴∠1=∠2. ∵DM⊥AC,∴∠2+∠4=900∵OA=OD,∴∠1=∠3.∴∠3+∠4=900.即OD⊥DM.∴DM 是⊙O 的切线说明:证明一是通过证平行来证明垂直的.证明二是通过证两角互余证明垂直的,解题中注意充分利用已知及图上已知.例4 如图,已知:AB 是⊙O 的直径,点C 在⊙O 上,且∠CAB=300,BD=OB ,D 在AB 的延长线上.求证:DC 是⊙O 的切线证明:连结OC 、BC.∵OA=OC,∴∠A=∠1=∠300.∴∠BOC=∠A+∠1=600. 又∵OC=OB,∴△OBC 是等边三角形.∴OB=BC.∵OB=BD, ∴OB=BC=BD. ∴OC⊥CD. ∴DC 是⊙O 的切线.说明:此题是根据圆周角定理的推论3证明垂直的,此题解法颇多,但这种方法较好.例5 如图,AB 是⊙O 的直径,CD⊥AB,且OA 2=OD·OP.求证:PC 是⊙O 的切线.证明:连结OC∵OA 2=OD·OP ,OA=OC , ∴OC 2=OD·OP ,.OCOPOD OC 又∵∠1=∠1, ∴△OCP∽△ODC. ∴∠OCP=∠ODC. ∵CD⊥AB, ∴∠OCP=900. ∴PC 是⊙O 的切线.说明:此题是通过证三角形相似证明垂直的例6 如图,ABCD 是正方形,G 是BC 延长线上一点,AG 交BD 于E ,交CD 于F.求证:CE 与△CFG 的外接圆相切.分析:此题图上没有画出△CFG 的外接圆,但△CFG 是直角三角形,圆心在斜边FG 的中点,为此我们取FG 的中点O ,连结OC ,证明CE⊥OC 即可得解.证明:取FG 中点O ,连结OC.∵ABCD 是正方形,∴BC⊥CD,△CFG 是Rt△∵O 是FG 的中点, ∴O 是Rt△CFG 的外心. ∵OC=OG, ∴∠3=∠G,∵AD∥BC,∴∠G=∠4.∵AD=CD,DE=DE,∠ADE=∠CDE=450,∴△ADE≌△CDE(SAS)∴∠4=∠1,∠1=∠3.∵∠2+∠3=900,∴∠1+∠2=900.即CE⊥OC.∴CE与△CFG的外接圆相切二、若直线l与⊙O没有已知的公共点,又要证明l是⊙O的切线,只需作OA⊥l,A为垂足,证明OA是⊙O的半径就行了,简称:“作垂直;证半径”例7 如图,AB=AC,D为BC中点,⊙D与AB切于E点.求证:AC与⊙D相切.证明一:连结DE,作DF⊥AC,F是垂足.∵AB是⊙D的切线,∴DE⊥AB.∵D F⊥AC,∴∠DEB=∠DFC=900.∵AB=AC,∴∠B=∠C.又∵BD=CD,∴△BDE≌△CDF(AAS)∴DF=DE.∴F在⊙D上.∴AC是⊙D的切线证明二:连结DE,AD,作DF⊥AC,F是垂足.∵AB与⊙D相切,∴DE⊥AB.∵AB=AC,BD=CD,∴∠1=∠2.∴DE=DF.∴F 在⊙D 上.∴AC 与⊙D 相切.说明:证明一是通过证明三角形全等证明DF=DE 的,证明二是利用角平分线的性质证明DF=DE 的,这类习题多数与角平分线有关.例8 已知:如图,AC ,BD 与⊙O 切于A 、B ,且AC∥BD,若∠COD=900.求证:CD 是⊙O 的切线.证明一:连结OA ,OB ,作OE⊥CD,E 为垂足.∵AC,BD 与⊙O 相切, ∴AC⊥OA,BD⊥OB. ∵AC∥BD,∴∠1+∠2+∠3+∠4=1800. ∵∠COD=900,∴∠2+∠3=900,∠1+∠4=900. ∵∠4+∠5=900. ∴∠1=∠5.∴Rt△AOC∽Rt△BDO.∴.ODOCOB AC = ∵OA=OB, ∴.ODOCOA AC = 又∵∠CAO=∠COD=900, ∴△AOC∽△ODC,∴∠1=∠2.又∵OA⊥AC,OE⊥CD, ∴OE=OA. ∴E 点在⊙O 上. ∴CD 是⊙O 的切线.证明二:连结OA ,OB ,作OE⊥CD 于E ,延长DO 交CA 延长线于F.∵AC,BD 与⊙O 相切,O∵AC∥BD,∴∠F=∠BDO.又∵OA=OB,∴△AOF≌△BOD(AAS )∴OF=OD.∵∠COD=900,∴CF=CD,∠1=∠2.又∵OA⊥AC,OE⊥CD,∴OE=OA.∴E 点在⊙O 上.∴CD 是⊙O 的切线.证明三:连结AO 并延长,作OE⊥CD 于E ,取CD 中点F ,连结OF.∵AC 与⊙O 相切,∴AC⊥AO.∵A C∥BD,∴AO⊥BD.∵BD 与⊙O 相切于B ,∴AO 的延长线必经过点B.∴AB 是⊙O 的直径.∵AC∥BD,OA=OB ,CF=DF ,∴OF∥AC,∴∠1=∠COF.∵∠COD=900,CF=DF ,∴.CF CD OF ==21∴∠2=∠COF.∴∠1=∠2.∵OA⊥AC,OE⊥CD,∴OE=OA.∴E 点在⊙O 上.∴CD 是⊙O 的切线说明:证明一是利用相似三角形证明∠1=∠2,证明二是利用等腰三角形三线合一证明∠1=∠2.证明三是利用梯形的性质证明∠1=∠2,这种方法必需先证明A 、O 、B 三点共线.此题较难,需要同学们利用所学过的知识综合求解.以上介绍的是证明圆的切线常用的两种方法供同学们参考.以下是武汉市2007----2010中考题汇编:(2007中考)22.(本题8分)如图,等腰三角形ABC 中,AC =BC =10,AB =12。
证明题之圆的切线证明题学生版

中考题型训练之圆的切线证明题(有切点,连半径,正垂直;无切点,做垂直,证半径)1.如图,△ABC 内接于半圆,AB 是直径,过A 作直线MN ,若∠MAC=∠ABC .(1)求证:MN 是半圆的切线;(2)设D 是弧AC 的中点,连结BD 交AC 于G ,过D 作DE⊥AB 于E ,交AC 于F .求证:FD =FG .(3)若△DFG 的面积为4.5,且DG=3,GC=4,试求△BCG 的面积.2.如图所示,AB 是O ⊙直径,OD ⊥弦BC 于点F ,且交O ⊙于点E ,若AEC ODB ∠=∠.(1)判断直线BD 和O ⊙的位置关系,并给出证明;(2)当108AB BC ==,时,求BD 的长.3.如图,已知AB 是O ⊙的直径,点C 在O ⊙上,过点C 的直线与AB 的延长线交于点P ,AC PC =,2COB PCB ∠=∠.(1)求证:PC 是O ⊙的切线;(2)求证:12BC AB =; (3)点M 是AB 的中点,CM 交AB 于点N ,若4AB =,求MN MC 的值.4.如图, AB 是⊙O 的直径,∠BAC =30°,M 是OA 上一点,过M 作AB 的垂线交AC于点N ,交BC 的延长线于点E ,直线CF 交EN 于点F ,且∠ECF =∠E .(1)证明CF 是⊙O 的切线;(2)设⊙O 的半径为1,且AC =CE ,求MO 的长.5.如图,已知的直径垂直于弦于点,过点作交的延长线于点,连接并延长交于点,且. (1)试问:是的切线吗?说明理由;(2)请证明:是的中点; (3)若,求的长. 6、如图,在平面直角坐标系xOy 中,⊙O 交x 轴于A 、B 两点,直线FA ⊥x 轴于点A ,点D 在FA 上,且DO 平行⊙O 的弦MB ,连DM 并延长交x 轴于点C .(1)判断直线DC 与⊙O 的位置关系,并给出证明;(2)设点D 的坐标为(-2,4),试求MC 的长及直线DC 的解析式.7、已知:如图,△ABC 内接于⊙O,点D 在OC的延长线上,,∠CAD=30°.(1)求证:AD 是⊙O 的切线; (2)若OD⊥AB,BC=5,求AD 的长.8、.已知:如图,A 是O 上一点,半径OC 的延长线与过点A 的直线交于B 点,OC BC =,12AC OB =. (1)求证:AB 是O 的切线;(2)若45ACD ∠=°,2OC =,求弦CD 的长.9、已知:如图,在Rt ABC △中,90C ∠=,点O 在AB 上,以O 为圆心,OA长为半径的圆与DCAC AB ,分别交于点D E ,,且CBD A ∠=∠.(1)判断直线BD 与O 的位置关系,并证明你的结论;(2)若:8:5AD AO =,2BC =,求BD 的长.解:(1)(2)10、已知:如图,在△ABC 中,AB=AC,AE 是角平分线,BM 平分∠ABC 交AE 于点M,经过B,M 两点的⊙O 交BC 于点G,交AB 于点F,FB 恰为⊙O 的直径.(1)求证:AE 与⊙O 相切;(2)当BC=4,cosC=13时,求⊙O 的半径. 11、 已知:如图,在△ABC 中,D 是AB 边上一点,圆O 过D 、B 、C 三点,?DOC =2?ACD =90?。
证明圆的切线的七种常用方法-圆的切线证明7种方法

证明圆的切线的七种常用方法证明一条直线是圆的切线的方法及辅助线的作法1、连半径、证垂直:当直线和圆有一个公共点时,把圆心和这个公共点连接起来,然后证明直线垂直于这条半径,简称“连半径,证垂直”2、作垂直,证半径:当直线和圆的公共点没有明确时,可以过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称“作垂直,证半径”类型一、有公共点:连半径,证垂直方法1、勾股定理逆定理法证垂直1.如图,AB为⊙O的直径,点P为AB延长线上一点,点C为圆⊙O上一点,PC=8,PB =4,AB=12,求证:PC是⊙O的切线.方法2、特殊角计算法证垂直2、如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.(1)求∠P的度数;(2)求证:P A是⊙O的切线;(3)若PD=5,求⊙O的直径.方法3、等角代换法证垂直3、如图,已知Rt △ABC 中,∠C =90°,D 为BC 的中点,以AC 为直径的⊙O 交AB 于点E 。
求证:DE 是⊙O 的切线;方法4、平行线性质法证垂直4、如图,已知平行四边形OABC 的三个顶点A 、B 、C 在以O 为圆心的半圆上,过点C 作CD ⊥AB ,分别交AB 、AO 的延长线于点D 、E ,AE 交半圆O 于点F ,连接CF .且︒=∠30E ,点B 是的中点(1)判断直线DE 与半圆O 的位置关系,并说明理由;(2)求证CF=OC(2)若半圆O 的半径为6,求DC 的长.方法5 全等三角形法证垂直5、如图,AB 是⊙O 的直径,点C 、D 在⊙O 上,且四边形AOCD 是平行四边形,过点D 作⊙O 的切线,交OC 的延长线于点F ,连接BF ,求证:BF 是⊙O 的切线。
A B O D CF类型二、无公共点:做垂直,证半径方法6 角平分线的性质法证半径6.如图,在Rt △ABC 中,∠B =90°,∠BAC 的平分线交BC 于点D ,E 为AB 上的一点,DE =DC ,以D 为圆心,DB 长为半径作⊙D ,AB =5,EB =2.(1)求证:AC 是⊙D 的切线;(2)求线段AC 的长.方法7 全等三角形法证半径7.已知四边形ABCD 中,∠BAD =∠ABC =90°,CD BC AD =+,以AB 为直径的⊙O 。
初中数学--证明圆的切线方法及例题
初中数学--证明圆的切线方法及例题
证明圆的切线常用的方法有:
一、若直线l过⊙O上某一点A,证明l是⊙O的切线,只需连OA,证明OA⊥l 就行了,简称“连半径,证垂直”,难点在于如何证明两线垂直.
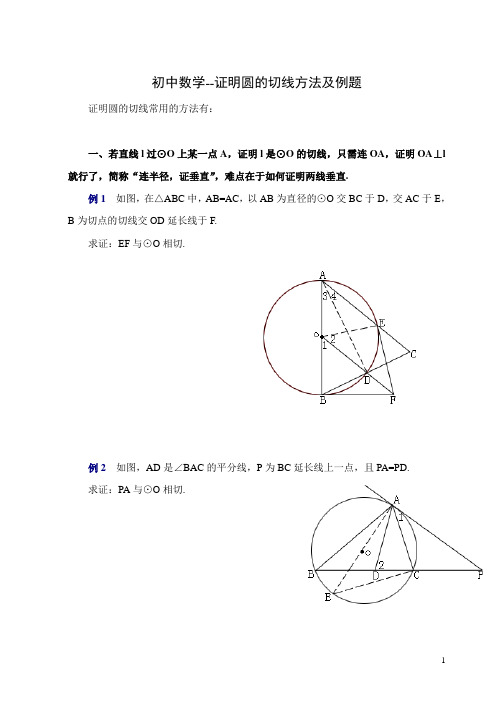
例1如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,B为切点的切线交OD延长线于F.
求证:EF与⊙O相切.
例2 如图,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD.
求证:PA与⊙O相切.
例3 如图,AB=AC,AB是⊙O的直径,⊙O交BC于D,DM⊥AC于M
求证:DM与⊙O相切.
例4 如图,已知:AB是⊙O的直径,点C在⊙O上,且∠CAB=300,BD=OB,D在AB的延长线上.
求证:DC是⊙O的切线
例5 如图,AB是⊙O的直径,CD⊥AB,且OA2=OD·OP.
求证:PC是⊙O的切线.
例6 如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F.
求证:CE与△CFG的外接圆相切.
分析:此题图上没有画出△CFG的外接圆,但△CFG是直角三角形,圆心在斜边FG的中点,为此我们取FG的中点O,连结OC,证明CE⊥OC即可得解.
二、若直线l与⊙O没有已知的公共点,又要证明l是⊙O的切线,只需作OA⊥l,A为垂足,证明OA是⊙O的半径就行了,简称:“作垂直;证半径”
例7 如图,AB=AC,D为BC中点,⊙D与AB切于E点.
求证:AC与⊙D相切.
例8 已知:如图,AC,BD与⊙O切于A、B,且AC∥BD,若∠COD=900.
求证:CD是⊙O的切线.。
李老师数学-证明圆的切线方法

李老师数学-证明圆的切线证明圆的切线常用方法总结为:方法一:“有切点,连切点,证垂直”方法二:“无切点,做垂直,证半径”方法一训练一、若直线L 过⊙O 上某一点P ,证明L 是⊙O 的切线,只需连OP ,证明OP ⊥L 即可证明L 是⊙O 的切线,简称“有切点,连切点,证垂直”。
例1 如图,在△ABC 中,AB=AC ,以AB 为直径的⊙O 交BC 于D ,交AC 于E ,B 为切点的切线交OD 延长线于F.求证:EF 与⊙O 相切.证明:连结OE ,AD.∵AB 是⊙O 的直径,∴AD ⊥BC.又∵AB=BC ,∴∠3=∠4.∴BD=DE,∠1=∠2. 又∵OB=OE ,OF=OF ,∴△BOF ≌△EOF (SAS ).∴∠OBF=∠OEF.∵BF 与⊙O 相切,∴OB ⊥BF.∴∠OEF=900.∴EF 与⊙O 相切.说明:此题是通过证明三角形全等证明垂直的⌒ ⌒例2 如图,AD 是∠BAC 的平分线,P 为BC 延长线上一点,且PA=PD.求证:PA 与⊙O 相切.证明一:作直径AE ,连结EC.∵AD 是∠BAC 的平分线,∴∠DAB=∠DAC.∵PA=PD ,∴∠2=∠1+∠DAC.∵∠2=∠B+∠DAB ,∴∠1=∠B.又∵∠B=∠E ,∴∠1=∠E∵AE 是⊙O 的直径,∴AC ⊥EC ,∠E+∠EAC=900.∴∠1+∠EAC=900.即OA ⊥PA.∴PA 与⊙O 相切.证明二:延长AD 交⊙O 于E ,连结OA ,OE.∵AD 是∠BAC 的平分线, ∴BE=CE ,∴OE ⊥BC.∴∠E+∠BDE=900.∵OA=OE ,∴∠E=∠1.∵PA=PD ,⌒ ⌒∴∠PAD=∠PDA.又∵∠PDA=∠BDE,∴∠1+∠PAD=900即OA⊥PA.∴PA与⊙O相切说明:此题是通过证明两角互余,证明垂直的,解题中要注意知识的综合运用. 例3 如图,AB=AC,AB是⊙O的直径,⊙O交BC于D,DM⊥AC于M求证:DM与⊙O相切.证明一:连结OD.∵AB=AC,∴∠B=∠C.∵OB=OD,∴∠1=∠B.∴∠1=∠C.∴OD∥AC.∵DM⊥AC,∴DM⊥OD.∴DM与⊙O相切证明二:连结OD,AD.∵AB是⊙O的直径,∴AD⊥BC.又∵AB=AC,∴∠1=∠2.∵DM⊥AC,∴∠2+∠4=900∵OA=OD,DC∴∠1=∠3.∴∠3+∠4=900.即OD ⊥DM. ∴DM 是⊙O 的切线说明:证明一是通过证平行来证明垂直的.证明二是通过证两角互余证明垂直的,解题中注意充分利用已知及图上已知.例4 如图,已知:AB 是⊙O 的直径,点C 在⊙O 上,且∠CAB=300,BD=OB ,D 在AB 的延长线上.求证:DC 是⊙O 的切线证明:连结OC 、BC.∵OA=OC ,∴∠A=∠1=∠300.∴∠BOC=∠A+∠1=600.又∵OC=OB ,∴△OBC 是等边三角形.∴OB=BC.∵OB=BD ,∴OB=BC=BD.∴OC ⊥CD. ∴DC 是⊙O 的切线. 说明:此题是根据圆周角定理的推论3证明垂直的,此题解法颇多,但这种方法较好.例5 如图,AB 是⊙O 的直径,CD ⊥AB ,且OA 2=OD ·OP.求证:PC 是⊙O 的切线.证明:连结OC∵OA 2=OD ·OP ,OA=OC ,∴OC 2=OD ·OP ,OCOP OD OC . 又∵∠1=∠1,∴△OCP ∽△ODC.∴∠OCP=∠ODC.∵CD ⊥AB ,∴∠OCP=900.∴PC 是⊙O 的切线.说明:此题是通过证三角形相似证明垂直的例6 如图,ABCD 是正方形,G 是BC 延长线上一点,AG 交BD 于E ,交CD 于F.求证:CE 与△CFG 的外接圆相切.分析:此题图上没有画出△CFG 的外接圆,但△CFG 是直角三角形,圆心在斜边FG 的中点,为此我们取FG 的中点O ,连结OC ,证明CE ⊥OC 即可得解.证明:取FG 中点O ,连结OC.∵ABCD 是正方形,∴BC ⊥CD ,△CFG 是Rt △∵O 是FG 的中点,∴O 是Rt △CFG 的外心.∵OC=OG ,∴∠3=∠G,∵AD∥BC,∴∠G=∠4.∵AD=CD,DE=DE,∠ADE=∠CDE=450,∴△ADE≌△CDE(SAS)∴∠4=∠1,∠1=∠3.∵∠2+∠3=900,∴∠1+∠2=900.即CE⊥OC.∴CE与△CFG的外接圆相切方法二训练:若直线L与⊙O没有已知的公共点,又要证明L是⊙O的切线,只需作OP⊥L,P为垂足,证明OP是⊙O的半径即可,简称:“无切点,做垂直,证半径”例7 如图,AB=AC,D为BC中点,⊙D与AB切于E点.求证:AC与⊙D相切.证明一:连结DE,作DF⊥AC,F是垂足.∵AB是⊙D的切线,∴DE⊥AB.∵DF⊥AC,∴∠DEB=∠DFC=900.∵AB=AC,∴∠B=∠C.又∵BD=CD,∴△BDE≌△CDF(AAS)∴DF=DE.∴F在⊙D上.∴AC是⊙D的切线证明二:连结DE,AD,作DF⊥AC,F是垂足.∵AB与⊙D相切,∴DE⊥AB.∵AB=AC,BD=CD,∴∠1=∠2.∵DE⊥AB,DF⊥AC,∴DE=DF.∴F在⊙D上.∴AC与⊙D相切.说明:证明一是通过证明三角形全等证明DF=DE的,证明二是利用角平分线的性质证明DF=DE 的,这类习题多数与角平分线有关.例8 已知:如图,AC ,BD 与⊙O 切于A 、B ,且AC ∥BD ,若∠COD=900. 求证:CD 是⊙O 的切线.证明一:连结OA ,OB ,作OE ⊥CD ,E 为垂足.∵AC ,BD 与⊙O 相切,∴AC ⊥OA ,BD ⊥OB.∵AC ∥BD ,∴∠1+∠2+∠3+∠4=1800.∵∠COD=900,∴∠2+∠3=900,∠1+∠4=900.∵∠4+∠5=900.∴∠1=∠5.∴Rt △AOC ∽Rt △BDO.∴OD OCOB AC =.∵OA=OB ,∴OD OCOA AC =.又∵∠CAO=∠COD=900,∴△AOC ∽△ODC ,∴∠1=∠2.又∵OA ⊥AC ,OE ⊥CD,∴OE=OA.∴E 点在⊙O 上.∴CD 是⊙O 的切线.O证明二:连结OA,OB,作OE⊥CD于E,延长DO交CA延长线于F.∵AC,BD与⊙O相切,∴AC⊥OA,BD⊥OB.∵AC∥BD,∴∠F=∠BDO.又∵OA=OB,∴△AOF≌△BOD(AAS)∴OF=OD.∵∠COD=900,∴CF=CD,∠1=∠2.又∵OA⊥AC,OE⊥CD,∴OE=OA.∴E点在⊙O上.∴CD是⊙O的切线.证明三:连结AO并延长,作OE⊥CD于E,取CD中点F,连结OF.∵AC与⊙O相切,∴AC⊥AO.∵AC∥BD,∴AO⊥BD.∵BD与⊙O相切于B,∴AO的延长线必经过点B.∴AB是⊙O的直径.∵AC∥BD,OA=OB,CF=DF,∴OF∥AC,∴∠1=∠COF.∵∠COD=900,CF=DF,∴CF CD OF ==21.∴∠2=∠COF.∴∠1=∠2.∵OA ⊥AC ,OE ⊥CD ,∴OE=OA.∴E 点在⊙O 上. ∴CD 是⊙O 的切线说明:证明一是利用相似三角形证明∠1=∠2,证明二是利用等腰三角形三线合一证明∠1=∠2.证明三是利用梯形的性质证明∠1=∠2,这种方法必需先证明A 、O 、B 三点共线.。
证明圆的切线方法

证明圆的切线方法我们学习了直线和圆的位置关系,就出现了新的一类习题,就是证明一直线是圆的切线.在我们所学的知识范围内,证明圆的切线常用的方法有:一、若直线l过⊙O上某一点A,证明l是⊙O的切线,只需连OA,证明OA ⊥l就行了,简称“连半径,证垂直”,难点在于如何证明两线垂直.例1如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,B为切点的切线交OD延长线于F.求证:EF与⊙O相切.证明:连结OE,AD.∵AB是⊙O的直径,∴AD⊥BC.又∵AB=BC,∴∠3=∠4.⌒⌒∴BD=DE,∠1=∠2.又∵OB=OE,OF=OF,∴△BOF≌△EOF(SAS).∴∠OBF=∠OEF.∵BF与⊙O相切,∴OB⊥BF.∴∠OEF=900.∴EF与⊙O相切.说明:此题是通过证明三角形全等证明垂直的例2 如图,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD. 求证:PA与⊙O相切.证明一:作直径AE,连结EC.∵AD是∠BAC的平分线,∴∠DAB=∠DAC.∵PA=PD,∴∠2=∠1+∠DAC.∵∠2=∠B+∠DAB,∴∠1=∠B.又∵∠B=∠E,∴∠1=∠E∵AE是⊙O的直径,∴AC⊥EC,∠E+∠EAC=900.∴∠1+∠EAC=900.即OA⊥PA.∴PA与⊙O相切.证明二:延长AD交⊙O于E,连结OA,OE.∵AD是∠BAC的平分线,⌒⌒∴BE=CE,∴OE⊥BC.∴∠E+∠BDE=900.∵OA=OE,∴∠E=∠1.∵PA=PD,∴∠PAD=∠PDA.又∵∠PDA=∠BDE,∴∠1+∠PAD=900即OA⊥PA.∴PA与⊙O相切说明:此题是通过证明两角互余,证明垂直的,解题中要注意知识的综合运用.例3 如图,AB=AC,AB是⊙O的直径,⊙O交BC于D,DM⊥AC于M求证:DM与⊙O相切.证明一:连结OD.∵AB=AC,∴∠B=∠C.∵OB=OD,∴∠1=∠B.∴∠1=∠C.∴OD∥AC.∵DM⊥AC,D∴DM⊥OD.∴DM与⊙O相切证明二:连结OD,AD.∵AB是⊙O的直径,∴AD⊥BC.又∵AB=AC,∴∠1=∠2.C∵DM⊥AC,∴∠2+∠4=900∵OA=OD,∴∠1=∠3.∴∠3+∠4=900.即OD⊥DM.∴DM是⊙O的切线说明:证明一是通过证平行来证明垂直的.证明二是通过证两角互余证明垂直的,解题中注意充分利用已知及图上已知.例4 如图,已知:AB是⊙O的直径,点C在⊙O上,且∠CAB=300,BD=OB,D在AB的延长线上.求证:DC是⊙O的切线证明:连结OC、BC.∵OA=OC,∴∠A=∠1=∠300.∴∠BOC=∠A+∠1=600.又∵OC=OB,∴△OBC 是等边三角形.∴OB=BC.∵OB=BD ,∴OB=BC=BD.∴OC ⊥CD. ∴DC 是⊙O 的切线. 说明:此题是根据圆周角定理的推论3证明垂直的,此题解法颇多,但这种方法较好.例5 如图,AB 是⊙O 的直径,CD ⊥AB ,且OA 2=OD ·OP.求证:PC 是⊙O 的切线.证明:连结OC∵OA 2=OD ·OP ,OA=OC ,∴OC 2=OD ·OP , OC OP OD OC . 又∵∠1=∠1,∴△OCP ∽△ODC.∴∠OCP=∠ODC.∵CD ⊥AB ,∴∠OCP=900.∴PC 是⊙O 的切线.说明:此题是通过证三角形相似证明垂直的例6 如图,ABCD 是正方形,G 是BC 延长线上一点,AG 交BD 于E ,交CD D于F.求证:CE与△CFG的外接圆相切.分析:此题图上没有画出△CFG的外接圆,但△CFG是直角三角形,圆心在斜边FG的中点,为此我们取FG的中点O,连结OC,证明CE⊥OC即可得解.证明:取FG中点O,连结OC.∵ABCD是正方形,∴BC⊥CD,△CFG是Rt△∵O是FG的中点,∴O是Rt△CFG的外心.∵OC=OG,∴∠3=∠G,∵AD∥BC,∴∠G=∠4.∵AD=CD,DE=DE,∠ADE=∠CDE=450,∴△ADE≌△CDE(SAS)∴∠4=∠1,∠1=∠3.∵∠2+∠3=900,∴∠1+∠2=900.即CE⊥OC.∴CE与△CFG的外接圆相切二、若直线l与⊙O没有已知的公共点,又要证明l是⊙O的切线,只需作OA⊥l,A为垂足,证明OA是⊙O的半径就行了,简称:“作垂直;证半径”例7 如图,AB=AC,D为BC中点,⊙D与AB切于E点.求证:AC与⊙D相切.证明一:连结DE,作DF⊥AC,F是垂足.∵AB是⊙D的切线,∴DE⊥AB.∵DF⊥AC,∴∠DEB=∠DFC=900.∵AB=AC,∴∠B=∠C.又∵BD=CD,∴△BDE≌△CDF(AAS)∴DF=DE.∴F在⊙D上.∴AC是⊙D的切线证明二:连结DE,AD,作DF⊥AC,F是垂足.∵AB与⊙D相切,∴DE⊥AB.∵AB=AC,BD=CD,∴∠1=∠2.∵DE⊥AB,DF⊥AC,∴DE=DF.∴F 在⊙D 上. ∴AC 与⊙D 相切.说明:证明一是通过证明三角形全等证明DF=DE 的,证明二是利用角平分线的性质证明DF=DE 的,这类习题多数与角平分线有关.例8 已知:如图,AC ,BD 与⊙O 切于A 、B ,且AC ∥BD ,若∠COD=900. 求证:CD 是⊙O 的切线.证明一:连结OA ,OB ,作OE ⊥CD ,E 为垂足.∵AC ,BD 与⊙O 相切,∴AC ⊥OA ,BD ⊥OB. ∵AC ∥BD ,∴∠1+∠2+∠3+∠4=1800.∵∠COD=900,∴∠2+∠3=900,∠1+∠4=900.∵∠4+∠5=900.∴∠1=∠5.∴Rt △AOC ∽Rt △BDO.∴OD OC OB AC =.∵OA=OB , ∴ODOC OA AC =. 又∵∠CAO=∠COD=900,∴△AOC ∽△ODC ,∴∠1=∠2.O又∵OA⊥AC,OE⊥CD,∴OE=OA.∴E点在⊙O上.∴CD是⊙O的切线.证明二:连结OA,OB,作OE⊥CD于E,延长DO交CA延长线于F.∵AC,BD与⊙O相切,∴AC⊥OA,BD⊥OB.∵AC∥BD,∴∠F=∠BDO.又∵OA=OB,∴△AOF≌△BOD(AAS)∴OF=OD.∵∠COD=900,∴CF=CD,∠1=∠2.又∵OA⊥AC,OE⊥CD,∴OE=OA.∴E点在⊙O上.∴CD是⊙O的切线.证明三:连结AO并延长,作OE⊥CD于E,取CD中点F,连结OF.∵AC与⊙O相切,∴AC⊥AO.∵AC∥BD,∴AO ⊥BD.∵BD 与⊙O 相切于B ,∴AO 的延长线必经过点B.∴AB 是⊙O 的直径.∵AC ∥BD ,OA=OB ,CF=DF ,∴OF ∥AC ,∴∠1=∠COF.∵∠COD=900,CF=DF ,∴CF CD OF ==21.∴∠2=∠COF.∴∠1=∠2.∵OA ⊥AC ,OE ⊥CD ,∴OE=OA.∴E 点在⊙O 上. ∴CD 是⊙O 的切线 说明:证明一是利用相似三角形证明∠1=∠2,证明二是利用等腰三角形三线合一证明∠1=∠2.证明三是利用梯形的性质证明∠1=∠2,这种方法必需先证明A 、O 、B 三点共线.此题较难,需要同学们利用所学过的知识综合求解.以上介绍的是证明圆的切线常用的两种方法供同学们参考.。
2023九年级数学下册中考专题训练——圆的切线的证明【含答案】

2023九年级数学下册中考专题训练——圆的切线的证明A AM⊙O B⊙O BD⊥AM D BD1. 如图,点是直线与的交点,点在上,垂足为,与⊙O C OC∠AOB∠B=60∘交于点,平分,.AM⊙O(1) 求证:是的切线;DC=2π(2) 若,求图中阴影部分的面积(结果保留和根号).AB⊙O AC BD⊙O OE∥AC BC E B 2. 如图,已知是的直径,,是的弦,交于,过点⊙O OE D DC BA F作的切线交的延长线于点,连接并延长交的延长线于点.DC⊙O(1) 求证:是的切线;∠ABC=30∘AB=8CF(2) 若,,求线段的长.△ABC∠B=∠C=30∘O BC O OB3. 如图,中,,点是边上一点,以点为圆心、为半径的圆A BC D经过点,与交于点.AC⊙O(1) 试说明与相切;AC=23(2) 若,求图中阴影部分的面积.ABC⊙O B C D⊙O E BC OE 4. 如图,割线与相交于,两点,为上一点,为弧的中点,BC F DE AC G∠ADG=∠AGD交于,交于,.AD⊙D(1) 求证明:是的切线;∠A=60∘⊙O4ED(2) 若,的半径为,求的长.5. 如图,, 分别是半 的直径和弦, 于点 ,过点 作半 的切线 AB AC ⊙O OD ⊥AC D A ⊙O , 与 的延长线交于点 .连接 并延长与 的延长线交于点 .AP AP OD P PC AB F(1) 求证: 是半 的切线;PC ⊙O (2) 若 ,,求线段 的长.∠CAB =30∘AB =10BF 6. 如图, 是 的直径, 是 上一点, 是 的中点, 为 延长线上一点,AB ⊙O C ⊙O D AC E OD 且 , 与 交于点 ,与 交于点 .∠CAE =2∠C AC BD H OE F(1) 求证: 是 的切线.AE ⊙O (2) 若 ,,求直径 的长.DH =9tanC =34AB 7. 如图, 是 的直径, 是 的弦,, 与 的延长线交于点 ,点 AB ⊙O AC ⊙O OD ⊥AB OD AC D 在 上,且 .E OD CE =DE(1) 求证:直线 是 的切线.CE ⊙O (2) 若 ,,.OA =23AC =3CD =8. 如图, 是的直径,弦 于点 ,点 在直径 的延长线上,AB ⊙O CD ⊥AB E G DF .∠D =∠G =30∘(1) 求证: 是 的切线.CG ⊙OCD=6GF(2) 若,求的长.AB⊙O AC D BC D EF AC9. 如图,是的直径,是弦,是的中点,过点作垂直于直线,垂E AB F足为,交的延长线于点.EF⊙O(1) 求证:是的切线.B OF⊙O3(2) 若点是的中点,的半径为,求阴影部分面积.PB⊙O B PO⊙O E F B PO BA 10. 如图,切于点,直线交于点,,过点作的垂线,垂D⊙O A AO⊙O C BC AF足为点,交于点,延长交于点,连接,.PA⊙O(1) 求证:直线为的切线;BC=6AD:FD=1:2⊙O(2) 若,,求的半径的长.AC⊙O B⊙O∠ACB=30∘CB D11. 如图,为的直径,为上一点,,延长至点,使得CB=BD D DE⊥AC E CA BE,过点作,垂足在的延长线上,连接.BE⊙O(1) 求证:是的切线;BE=3(2) 当时,求图中阴影部分的面积.AB⊙O AP⊙O A BP⊙O C12. 已知是的直径,是的切线,是切点,与交于点.∠P=35∘∠ABP(1) 如图①,若,求的度数;D AP CD⊙O(2) 如图②,若为的中点,求证:直线是的切线.Rt△ABC∠C=90∘D AB AD⊙O BC13. 如图,在中,,点在上,以为直径的与相交于点E AE∠BAC,且平分.BC⊙O(1) 求证:是的切线;∠EAB=30∘OD=3(2) 若,,求图中阴影部分的面积.⊙O PA PC PH∠APB⊙O H H 14. 如图,在中,是直径,是弦,平分且与交于点,过作HB⊥PC PC B交的延长线于点.HB⊙O(1) 求证:是的切线;HB=6BC=4⊙O(2) 若,,求的直径.AB⊙O BD⊙O BD C AB=AC AC15. 已知:是的直径,是的弦,延长到点,使,连接,过D DE⊥AC E点作,垂足为.DC=BD(1) 求证:;DE⊙O(2) 求证:为的切线.AB⊙O C⊙O D AB∠BCD=∠A16. 如图,是的直径,是上一点,在的延长线上,且.CD⊙O(1) 求证:是的切线;⊙O3CD=4BD(2) 若的半径为,,求的长.△ABC AC⊙O△ABC∠ABC⊙O17. 如图,以的边为直径的恰为的外接圆,的平分线交D D DE∥AC BC E于点,过点作交的延长线于点.DE⊙O(1) 求证:是的切线.AB=45BC=25DE(2) 若,,求的长.AB O AD∠DBC=∠A18. 如图,是半圆的直径,为弦,.BC O(1) 求证:是半圆的切线;OC∥AD OC BD E BD=6CE=4AD(2) 若,交于,,,求的长.△ABC AO⊥BC O⊙O AC D BE⊥AB 19. 如图,是等边三角形,,垂足为点,与相切于点,交AC E⊙O G F的延长线于点,与相交于,两点.AB⊙O(1) 求证:与相切;ABC8BF(2) 若等边三角形的边长是,求线段的长.AC⊙O BC⊙O P⊙O PB AB 20. 如图,是的直径,是的弦,点是外一点,连接,,∠PBA=∠C.PB⊙O(1) 求证:是的切线;OP OP∥BC OP=8⊙O22BC(2) 连接,若,且,的半径为,求的长.答案1. 【答案】(1) ,,∵∠B=60∘OB=OC是等边三角形,∴△BOC,∴∠1=∠2=60∘平分,∵OC∠AOB,∴∠1=∠3,∴∠2=∠3,∴OA∥BD,∴∠BDM=90∘,∴∠OAM=90∘是的切线.∴AM⊙O(2) ,,∵∠3=60∘OA=OC是等边三角形,∴△AOC,∴∠OAC=60∘,∵∠OAM=90∘,∴∠CAD=30∘,∵CD=2,∴AC=2CD=4,∴AD=23∴S阴影=S梯形OADC−S扇形OAC =12(4+2)×23−60⋅π×16360=63−8π3.2. 【答案】(1) 连接,OC,∵OE∥AC,∴∠1=∠ACB是的直径,∵AB⊙O,∴∠1=∠ACB=90∘,由垂径定理得垂直平分,∴OD⊥BC OD BC,∴DB=DC,∴∠DBE=∠DCE又,∵OC=OB,∴∠OBE=∠OCE即,∠DBO=∠OCD为的切线,是半径,∵DB⊙O OB,∴∠DBO=90∘,∴∠OCD =∠DBO =90∘即 ,OC ⊥DC 是 的半径,∵OC ⊙O 是 的切线.∴DC ⊙O (2) 在 中,,Rt △ABC ∠ABC =30∘ ,又 ,∴∠3=60∘OA =OC 是等边三角形,∴△AOC∴∠COF =60∘在 中,,Rt △COF tan∠COF =CF OC .∴CF =433. 【答案】(1) 连接 .OA ,∵OA =OB .∴∠OAB =∠B ,∵∠B =30∘ .∴∠OAB =30∘ 中:,△ABC ∠B =∠C =30∘ .∴∠BAC =180∘−∠B−∠C =120∘ .∴∠OAC =∠BAC−∠OAB =120∘−30∘=90∘ ,∴OA ⊥AC 是 的切线,即 与 相切.∴AC ⊙O AC ⊙O (2) 连接 .AD ,∵∠C =30∘∠OAC =90∘ .∴OC =2OA 设 的长度为 ,则 .OA x OC =2x 在 中,,.△OAC ∠OAC =90∘AC =23根据勾股定理可得:,x 2+(23)2=(2x )2解得:,(不合题意,舍去).x 1=2x 2=−2 ,∴S △OAC =12×2×23=23,S 扇形OAD =60360×π×22=23π .∴S 阴影=23−23π答:图中阴影部分的面积为 .23−23π4. 【答案】(1) 连接 .OD 为 的中点,∵E BC ,∴OE ⊥BC ,∵OD =OE ,∴∠ODE =∠OED ,∴∠AGD +∠OED =∠EGF +∠OED =90∘ ,∵∠AGD =∠ADG ,即 ,∴∠ADG +∠ODE =90∘OD ⊥AD 是 的切线.∴AD ⊙O (2) 作 于 .OH ⊥ED H ,∴DE =2DH ,∵∠ADG =∠AGD ,∴AG =AD ,∵∠A =60∘ ,∴∠ADG =60∘,∴∠ODE =30∘ ,∵OD =4 ,∴DH =32OD =23 .∴DE =2DH =435. 【答案】(1) 连接 ,OC , 经过圆心 ,∵OD ⊥AC OD O ,∴AD =CD ,∴PA =PC 在 和 中,△OAP △OCP {OA =OC,PA =PC,OP =OP,,∴△OAP ≌△OCP (SSS ) ,∴∠OCP =∠OAP 是 的切线,∵PA ⊙O .∴∠OAP =90∘,即 ,∴∠OCP =90∘OC ⊥PC 是 的切线.∴PC ⊙O (2) 是直径,∵AB ,∴∠ACB =90∘,∵∠CAB =30∘,∴∠COF =60∘ 是 的切线,,∵PC ⊙O AB =10 ,,∴OC ⊥PF OC =OB =12AB =5 ,∴OF =OC cos∠COF =10 .∴BF =OF−OB =56. 【答案】(1) 是 的中点,∵D AC ,∴OE ⊥AC ,∴∠AFE =90∘ ,∴∠E +∠EAF =90∘ ,,∵∠AOE =2∠C ∠CAE =2∠C ,∴CAE =∠AOE ,∴∠E +∠AOE =90∘ ,∴∠EAO =90∘ 是 的切线.∴AE ⊙O (2) ,∵∠C =∠B ,∵OD =OB ,∴∠B =∠ODB ,∴ODB =∠C ,∴tanC =tan∠ODB =HF DF =34 设 ,,∴HF =3x DF =4x ,∴DH =5x =9,∴x =95 ,,∴DE =365HF =275 ,,∵∠C =∠FDH ∠DFH =∠CFD ,∴△DFH ∼△CFD ,∴DF CF =FH DF,∴CF =365×365275=485 ,∴AF =CF =485设 ,OA =OD =x,∴OF =x−365 ,∵AF 2+OF 2=OA 2 ,∴(485)2+(x−365)2=x 2解得:,x =10 ,∴OA =10 直径 为 .∴AB 207. 【答案】(1) 连接 ,OC ,∵OD ⊥AB ,∴∠AOD =90∘ ,∴∠D +∠A =90∘ ,∵OA =OC ,∴∠A =∠ACO ,∵CE =DE ,∴∠ECD =∠D ,∵∠ACO +∠DCE =90∘ ,∴∠OCE =90∘ ,∴OC ⊥CE 直线 是 的切线.∴CE ⊙O (2)5【解析】(2) 连接 ,BC 是 的直径,∵AB ⊙O ,∴∠ACB =90∘ ,∴∠AOD =∠ACB ,∵∠A =∠A ,∴△ABC ∽△ADO,∴AO AC =AD AB ,∴233=AD43 ,∴AD =8 .∴CD =AD−AC =58. 【答案】(1) 连接 .OC ,,∵OC =OD ∠D =30∘ .∴∠OCD =∠D =30∘ ,∵∠G =30∘ .∴∠DCG =180∘−∠D−∠G =120∘ .∴∠GCO =∠DCG−∠OCD =90∘ .∴OC ⊥CG 又 是 的半径.∵OC ⊙O 是 的切线.∴CG ⊙O (2) 是 的直径,,∵AB ⊙O CD ⊥AB .∴CE =12CD =3 在 中,,,∵Rt △OCE ∠CEO =90∘∠OCE =30∘ ,.∴EO =12CO CO 2=EO 2+CE 2设 ,则 .EO =x CO =2x .∴(2x )2=x 2+32解得 (舍负值).x =±3 .∴CO =23 .∴FO =23在 中,△OCG ,,∵∠OCG =90∘∠G =30∘ .∴GO =2CO =43 .∴GF =GO−FO =239. 【答案】(1) 连接 ,连接 ,OD AD 点 是 的中点,∵D BC ,∴∠1=∠2 ,∵OA =OD ,∴∠2=∠3即 ,∠1=∠2=∠3 ,∴∠1=∠3 ,∴AE ∥OD ,∵AE ⊥EF ,∴OD ⊥EF 即 是 的切线.EF ⊙O(2) 点是 的中点, 半径为 ,∵B OF ⊙O 3 ,∴BF =OB =3由()可知 ,1OD ⊥EF 在 中,Rt △ODF ,∵sinF =OD OF =36=12 ,,∴∠F =30∘∠DOF =60∘故S 阴影=S △ODF −S 扇ODB=12OD ⋅DF−60∘360∘π×32=3×332−32π=32(33−π).故阴影面积为:.32(33−π)10. 【答案】(1) 如图,连接 .OB 是 的切线,∵PB ⊙O .∴∠PBO =90∘ , 于 ,∵OA =OB BA ⊥PO D ,.∴AD =BD ∠POA =∠POB 又 ,∵PO =PO .∴△PAO ≌△PBO .∴∠PAO =∠PBO =90∘ 直线 为 的切线.∴PA ⊙O (2) ,,,∵OA =OC AD =BD BC =6 .∴OD =12BC =3设 .AD =x ,∵AD:FD =1:2 ,.∴FD =2x OA =OF =2x−3在 中,由勾股定理,得 .Rt △AOD (2x−3)2=x 2+32解之得,,(不合题意,舍去).x 1=4x 2=0 ,.∴AD =4OA =2x−3=5即 的半径的长 .⊙O 511. 【答案】(1) 如图所示,连接 ,BO ,∵∠ACB =30∘ ,∴∠OBC =∠OCB =30∘,,∵DE ⊥AC CB =BD 中,,∴Rt △DCE BE =12CD =BC ,∴∠BEC =∠BCE =30∘ 中,,∴△BCE ∠EBC =180∘−∠BEC−∠BCE =120∘ ,∴∠EBO =∠EBC−∠OBC =120∘−30∘=90∘ 是 的切线.∴BE ⊙O (2) 当 时,,BE =3BC =3 为 的直径,∵AC ⊙O ,∴∠ABC =90∘又 ,∵∠ACB =30∘ ,∴AB =tan 30∘×BC =3 ,,∴AC =2AB =23AO =3 ∴S 阴影部分=S 半圆−S Rt △ABC =12π×AO 2−12AB ×BC=12π×3−12×3×3=32π−32 3.12. 【答案】(1) 是 的直径, 是 的切线,∵AB ⊙O AP ⊙O ,∴AB ⊥AP ;∴∠BAP =90∘又 ,∵∠P =35∘ ∴∠ABP =90∘−35∘=55∘(2) 如图,连接 ,,.OC OD AC 是 的直径,∵AB ⊙O (直径所对的圆周角是直角),∴∠ACB =90∘ ;∴∠ACP =90∘又 为 的中点,∵D AP (直角三角形斜边上的中线等于斜边的一半);∴AD =CD 在 和 中,△OAD △OCD {OA =OC,OD =OD,AD =CD, ,△OAD ≌△OCD (SSS ) (全等三角形的对应角相等);∴∠OAD =∠OCD 又 是 的切线, 是切点,∵AP ⊙O A ,∴AB ⊥AP ,∴∠OAD =90∘ ,即直线 是 的切线.∴∠OCD =90∘CD ⊙O13. 【答案】(1) 平分 ,∵AE ∠BAC ,∴∠CAE =∠EAD ,∵OA =OE ,∴∠EAD =∠OEA ,∴∠OEA =∠CAE ,∴OE ∥AC ,∴∠OEB =∠C =90∘ ,∴OE ⊥BC 是 的切线.∴BC ⊙O (2) ,∵∠EAB =30∘ ,∴∠EOD =60∘ ,∴∠OEB =90∘ ,∴∠B =30∘ ,∴OB =2OE =2OD =6 ,∴BE =OB 2−OE 2=33,,∴S △OEB =932S 扇形=3π2 .∴S 阴影=932−3π214. 【答案】(1) 如图,连接 .OH 平分 ,∵PH ∠APB .∴∠HPA =∠HPB ,∵OP =OH .∴∠OHP =∠HPA .∴∠HPB =∠OHP .∴OH ∥BP ,∵BP ⊥BH .∴OH ⊥BH 是 的切线.∴HB ⊙O (2) 如图,过点 作 ,垂足为 .O OE ⊥PC E ,,,∵OE ⊥PC OH ⊥BH BP ⊥BH 四边形 是矩形.∴EOHB ,.∴OE =BH =6OH =BE .∴CE =OH−4 ,∵OE ⊥PC.∴PE =EC =OH−4=OP−4在 中,,.Rt △POE OP 2=PE 2+OE 2 .∴OP 2=(OP−4)2+36 .∴OP =132 .∴AP =2OP =13 的直径是 .∴⊙O 1315. 【答案】(1) 连接 ,AD 是 的直径,∵AB ⊙O ,∴∠ADB =90∘又 ,∵AB =AC .∴DC =BD (2) 连接半径 ,OD ,,∵OA =OB CD =BD ,∴OD ∥AC ,∴∠ODE =∠CED 又 ,∵DE ⊥AC ,∴∠CED =90∘ ,即 ,∴∠ODE =90∘OD ⊥DE 是 的切线.∴DE ⊙O 16. 【答案】(1) 连接 .OC 是 的直径, 是 上一点,∵AB ⊙O C ⊙O ,即 .∴∠ACB =90∘∠ACO +∠OCB =90∘ ,,∵OA =OC ∠BCD =∠A ,∴∠ACO =∠A =∠BCD ,即 ,∴∠BCD +∠OCB =90∘∠OCD =90∘ 是 的切线.∴CD ⊙O (2) 在 中,,,,Rt △OCD ∠OCD =90∘OC =3CD =4 ,∴OD =OC 2+CD 2=5 .∴BD =OD−OB =5−3=217. 【答案】(1) 连接 ,OD 是 的直径,∵AC ⊙O,∴∠ABC =90∘ 平分 ,∵BD ∠ABC ,∴∠ABD =45∘ ,∴∠ODE =90∘ ,∵DE ∥AC ,∴∠ODE =∠AOD =90∘ 是 的切线.∴DE ⊙O (2) 在 中,,,Rt △ABC AB =45BC =25 ,∴AC =AB 2+BC 2=10 ,∴OD =5过点 作 ,垂足为 ,C CG ⊥DE G 则四边形 为正方形,ODGC ,∴DG =CG =OD =5 ,∵DE ∥AC ,∴∠CEG =∠ACB ,∴tan∠CEG =tan∠ACB ,即 ,∴CG GE =AB BC 5GE =4525解得:,GE =52 .∴DE =DG +GE =15218. 【答案】(1) 是半圆 的直径,∵AB O ,∴BD ⊥AD ,∴∠DBA +∠A =90∘ ,∵∠DBC =∠A ,即 ,∴∠DBA +∠DBC =90∘AB ⊥BC 是半圆 的切线.∴BC O (2) ,∵OC ∥AD ,∴∠BEC =∠D =90∘ ,,∵BD ⊥AD BD =6 ,∴BE =DE =3 ,∵∠DBC =∠A ,∴△BCE ∽△BAD ,即 ,∴CE BD =BE AD 46=3AD .∴AD =4.519. 【答案】(1) 过点 作 ,垂足是 .O OM ⊥AB M 与 相切于点 ,∵⊙O AC D ,∴OD ⊥AC ,∠ADO =∠AMO =90∘ 是等边三角形,,∵△ABC AO ⊥BC 是 的角平分线,∴OA ∠MAD ,,∵OD ⊥AC OM ⊥AB .∴OM =OD 与 相切.∴AB ⊙O (2) 过点 作 ,垂足是 ,连接 .O ON ⊥BE N OF ,,∵AB =AC AO ⊥BC ∴ 是 的中点,O BC ,∴OB =12BC =12×8=4 在直角 中,,,△ABC ∠ABE =90∘∠MBO =60∘ ,∴∠OBN =30∘ ,,,∵ON ⊥BE ∠OBN =30∘OB =4 ,,∴ON =12OB =2BN =42−22=23 ,∵AB ⊥BE ∴四边形 是矩形,OMBN .∴BN =OM =23 .∵OF =OM =23由勾股定理得 .NF =(23)2−22=22 .∴BF =BN +NF =23+2220. 【答案】(1) 连接 ,如图所示:OB 是 的直径,∵AC ⊙O ,∴∠ABC =90∘ ,∴∠C +∠BAC =90∘ ,∵OA =OB ,∴∠BAC =∠OBA ,∵∠PBA =∠C ,即 ,∴∠PBA +∠OBA =90∘PB ⊥OB 是 的切线.∴PB ⊙O (2) 的半径为 ,∵⊙O 22,,∴OB =22AC =42 ,∵OP ∥BC ,∴∠CBO =∠BOP ,∵OC =OB ,∴∠C =∠CBO ,∴∠C =∠BOP 又 ,∵∠ABC =∠PBO =90∘ ,∴△ABC ∽△PBO ,即 ,∴BC OB =AC OP BC 22=428 .∴BC =2。
中考数学-圆的切线证明方法

专题————---圆的切线证明我们学习了直线和圆的位置关系,就出现了新的一类习题,就是证明一直线是圆的切线。
在我们所学的知识范围内,证明圆的切线常用的方法有:一、若直线l过⊙O上某一点A,证明l是⊙O的切线,只需连OA,证明OA⊥l就行了,简称“连半径,证垂直”,难点在于如何证明两线垂直.例1 如图,AB=AC,AB是⊙O的直径,⊙O交BC于D,DM⊥AC于M,求证:DM与⊙O相切.证明一:连结OD。
∵AB=AC,∴∠B=∠C.∵OB=OD,∴∠1=∠B。
∴∠1=∠C。
∴OD∥AC。
∵DM⊥AC,∴DM⊥OD.∴DM与⊙O相切证明二:连结OD,AD。
∵AB是⊙O的直径,∴AD⊥BC。
又∵AB=AC,∴∠1=∠2.∵DM⊥AC,∴∠2+∠4=900∵OA=OD,∴∠1=∠3.∴∠3+∠4=900.即OD⊥DM.∴DM是⊙O的切线D C例2 如图,已知:AB 是⊙O 的直径,点C 在⊙O 上,且∠CAB=300,BD=OB ,D 在AB 的延长线上.求证:DC 是⊙O 的切线证明:连结OC 、BC.∵OA=OC ,∴∠A=∠1=∠300。
∴∠BOC=∠A+∠1=600.又∵OC=OB ,∴△OBC 是等边三角形.∴OB=BC. ∵OB=BD ,∴OB=BC=BD.∴OC ⊥CD.∴DC 是⊙O 的切线.例3 如图,AB 是⊙O 的直径,CD ⊥AB ,且OA 2=OD ·OP 。
求证:PC 是⊙O 的切线。
证明:连结OC∵OA 2=OD ·OP,OA=OC ,∴OC 2=OD ·OP , OC OP OD OC .又∵∠1=∠1,∴△OCP ∽△ODC 。
∴∠OCP=∠ODC 。
∵CD ⊥AB,∴∠OCP=900。
∴PC 是⊙O 的切线。
D二、若直线l与⊙O没有已知的公共点,又要证明l是⊙O的切线,只需作OA⊥l,A为垂足,证明OA是⊙O的半径就行了,简称:“作垂直;证半径”例4 如图,AB=AC,D为BC中点,⊙D与AB切于E点。
圆切线的判定与性质综合(3大类题型)(解析版)--初中数学专项训练

圆切线的判定与性质综合(3大类题型)重难点题型归纳【题型1证圆的切线-有公共点:连半径,证垂直】【题型2证圆的切线-没有公共点:作垂直,证半径】【题型3圆切线的判定与性质综合】满分必练【题型1证圆的切线-有公共点:连半径,证垂直】1(2023春•保德县校级期中)如图,△ABC中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.求证:DE是⊙O切线.【答案】见解答.【解答】证明:连接OD,∵∠BAC=2∠BAD,∠BOD=2∠BAD,∴∠BAC=∠BOD,∴OD∥AC,又∵DE⊥AC,∴∠AED=90°,∴∠ODE=∠AED=90°,∴半径OD⊥DE,∴DE是⊙O的切线.2(2022秋•大连期末)如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.求证:CD是⊙O的切线.【答案】见试题解答内容【解答】解:连OD,如图,∵∠ADE=60°,∠C=30°,∴∠A=∠ADE-∠C=60°-30°=30°,又∵OD=OA,∴∠ODA=∠A=30°,∴∠EDO=90°,所以CD是⊙O的切线.3(2022秋•龙川县校级期末)如图,OA是⊙O的半径,∠B=20°,∠AOB=70°.求证:AB是⊙O的切线.【答案】见解答.【解答】证明:∵∠AOB=70°,∠B=20°,∴∠OAB=180°-∠B-∠AOB=90°,∴OA⊥AB,∵OA是⊙O的半径,∴AB是⊙O的切线.4(2022秋•利通区期末)如图,在△ABC中,AB=AC,∠BAC=120°,点D在BC边上,⊙D经过点A和点B且与BC边相交于点E,求证:AC是⊙D的切线.【答案】见解析.【解答】证明:连接AD,∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,在⊙D中,AD=BD,∴∠BAD=∠B=30°,∴∠ADC=60°,∴∠DAC=180°-∠ADC-∠C=180°-60°-30°=90°,∴AD⊥AC,又∵DA是半径,∴AC是⊙D的切线.5(2022秋•天河区校级期末)如图,AB是⊙O的直径,AC的中点D在⊙O上,DE⊥BC于E.求证:DE是⊙O的切线.【答案】见试题解答内容【解答】证明:连接OD,∵AO=OB,D为AC的中点,∴OD∥BC,∵DE⊥BC,∴DE⊥OD,∵OD是⊙O的半径,∴DE是⊙O的切线.6(2022秋•阿瓦提县校级期末)已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB= AC,连结AC,过点D作DE⊥AC,垂足为E.求证:DE为⊙O的切线.【答案】证明过程见解答.【解答】证明:如图,连接OD.∵AB是⊙O的直径,∴∠ADB=90°,∵AB=AC,∴CD=BD,∵OA=OB,∴OD∥AC.∴∠ODE=∠CED.∵DE⊥AC,∴∠CED=90°.∴∠ODE=90°,∴OD⊥DE,∵OD是⊙O的半径,∴DE是⊙O的切线.7(2022•昭平县一模)如图,AB是⊙O的弦,OP⊥AB交⊙O于C,OC=2,∠ABC=30°.(1)求AB的长;(2)若C是OP的中点,求证:PB是⊙O的切线.【答案】见试题解答内容【解答】(1)解:连接OA、OB,如图,∵∠ABC=30°,OP⊥AB,∴∠AOC =60°,∴∠OAD =30°,∴OD =12OA =12×2=1,∴AD =3OD =3,又∵OP ⊥AB ,∴AD =BD ,∴AB =23;(2)证明:由(1)∠BOC =60°,而OC =OB ,∴△OCB 为等边三角形,∴BC =OB =OC ,∠OBC =∠OCB =60°,∴C 是OP 的中点,∴CP =CO =CB ,∴∠CBP =∠P ,而∠OCB =∠CBP +∠P ,∴∠CBP =30°∴∠OBP =∠OBC +∠CBP =90°,∴OB ⊥BP ,∴PB 是⊙O 的切线.8(2022•漳州模拟)已知:△ABC 中,AB =AC ,以AB 为直径的⊙O 交BC 于点D ,过点D 作DE ⊥AC 于点E .求证:DE 是⊙O 的切线.【答案】见试题解答内容【解答】证明:连接OD ,∵AB 为⊙O 的直径,∴AD ⊥BC ,又AB =AC ,∴BD =DC ,∵BO =OA ,∴OD ∥AC ,∴∠ODE =180°-∠AED =90°,∴DE 是⊙O 的切线.9(2022秋•芜湖期末)如图,AB 为⊙O 的直径,点C ,D 在⊙O 上,AC =CD =DB,DE ⊥AC .求证:DE 是⊙O 的切线.【答案】见解析.【解答】证明:连接OD ,∵AC =CD =DB,∴∠BOD =13×180o =60o ,∵CD =DB ,∴∠EAD =∠DAB =12∠BOD =30°,∵OA =OD ,∴∠ADO =∠DAB =30°,∵DE ⊥AC ,∴∠E =90°,∴∠EAD +∠EDA =90°,∴∠EDA =60°,∴∠EDO =∠EDA +∠ADO =90°,∴OD ⊥DE ,∵OD 是⊙O 的半径,∴DE 是⊙O 的切线.【题型2证圆的切线-没有公共点:作垂直,证半径】10(2022秋•长乐区期中)如图,在△OAB 中,OA =OB =5,AB =8,⊙O 的半径为3.求证:AB 是⊙O 的切线.【答案】证明见解析.【解答】证明:如图,过O 作OC ⊥AB 于C ,∵OA =OB ,AB =8,∴AC =12AB =4,在Rt △OAC 中,OC =OA 2-AC 2=52-42=3,∵⊙O 的半径为3,∴OC 为⊙O 的半径,∴AB 是⊙O 的切线.11(2022•八步区一模)如图,在Rt △ABC 中,∠BAC 的角平分线交BC 于点D ,E 为AB 上一点,DE =DC ,以D 为圆心,DB 的长为半径作⊙D ,AB =5,BE =3.(1)求证:AC 是⊙D 的切线;(2)求线段AC 的长.【解答】(1)证明:过点D 作DF ⊥AC 于F ;∵AB 为⊙D 的切线,∴∠B =90°,∴AB ⊥BC ,∵AD 平分∠BAC ,DF ⊥AC ,∴BD =DF ,∴AC 与⊙D 相切;(2)解:在△BDE 和△DCF 中;BD =DF DE =DC ,∴Rt △BDE ≌Rt △DCF (HL ),∴EB =FC .∵AB =AF ,∴AB +EB =AF +FC ,即AB +EB =AC ,∴AC =5+3=8.12(秋•莆田期末)如图,半圆O 的直径是AB ,AD 、BC 是两条切线,切点分别为A 、B ,CO 平分∠BCD .(1)求证:CD 是半圆O 的切线.(2)若AD =20,CD =50,求BC 和AB 的长.【解答】(1)证明:过点O 作OE ⊥CD ,垂足为点E ,∵BC是半圆O的切线,B为切点,∴OB⊥BC,∵CO平分∠BCD,∴OE=OB,∵OB是半圆O的半径,∴CD是半圆O的切线;(2)解:过点D作DF⊥BC,垂足为点F,∴∠DFB=90°,∵AD是半圆O的切线,切点为A,∴∠DAO=90°,∵OB⊥BC,∴∠OBC=90°,∴四边形ADFB是矩形,∴AD=BF=20,DF=AB,∵AD,CD,BC是半圆O的切线,切点分别为A、E、B,∴DE=AD=20,EC=BC,∵CD=50,∴EC=CD-DE=50-20=30,∴BC=30,∴CF=BC-BF=10,在Rt△CDF中,由勾股定理得:DF=DC2-CF2=502-102=206,∴AB=DF=206,∴BC的长为30,AB的长为206.【题型3 圆切线的判定与形式综合】13(2023•银川校级四模)如图△ABC中,∠ABC=90°,CD平分∠ACB交AB于点D,以点D为圆心,BD为半径作⊙D交AB于点E.(1)求证:⊙D与AC相切;(2)若AC=5,BC=3,试求AE的长.【答案】见试题解答内容【解答】(1)证明:过D 作DF ⊥AC 于F ,∵∠B =90°,∴AB ⊥BC ,∵CD 平分∠ACB 交AB 于点D ,∴BD =DF ,∴⊙D 与AC 相切;(2)解:设圆的半径为x ,∵∠B =90°,BC =3,AC =5,∴AB =AC 2-BC 2=4,∵AC ,BC ,是圆的切线,∴BC =CF =3,∴AF =AB -CF =2,∵AB =4,∴AD =AB -BD =4-x ,在Rt △AFD 中,(4-x )2=x 2+22,解得:x =32,∴AE =4-3=1.14(2022秋•五莲县期中)如图,O 为正方形ABCD 对角线上一点,以点O 为圆心,OA 长为半径的⊙O 与BC 相切于点E .(1)求证:CD 是⊙O 的切线;(2)若正方形ABCD 的边长为10,求⊙O 的半径.【答案】见试题解答内容【解答】(1)证明:连接OE ,并过点O 作OF ⊥CD .∵BC 切⊙O 于点E ,∴OE ⊥BC ,OE =OA ,又∵AC 为正方形ABCD 的对角线,∴∠ACB =∠ACD ,∴OF =OE =OA ,即:CD 是⊙O 的切线.(2)解:∵正方形ABCD 的边长为10,∴AB =BC =10,∠B =90°,∠ACB =45°,∴AC =AB 2+BC 2=102,∵OE ⊥BC ,∴OE =EC ,设OA=r,则OE=EC=r,∴OC=OE2+EC2=2r,∵OA+OC=AC,∴r+2r=102,解得:r=20-102.∴⊙O的半径为:20-102.15(2023•甘南县一模)如图,已知AB是⊙O的直径,点C在⊙O上,AD⊥DC于点D,AC平分∠DAB.(1)求证:直线CD是⊙O的切线;(2)若AB=4,∠DAB=60°,求AD的长.【答案】见试题解答内容【解答】(1)证明:连接OC,如图1所示:∵OA=OC,∴∠OAC=∠OCA,∵AC平分∠DAB,∴∠DAC=∠OAC,∴∠OCA=∠DAC,∴OC∥AD,∵AD⊥DC,∴CD⊥OC,又∵OC是⊙O的半径,∴直线CD是⊙O的切线;(2)解:连接BC,如图2所示:∵AB是⊙O的直径,∴∠ACB=90°,∵AC平分∠DAB,∠DAB=60°,∴∠DAC=∠BAC=30°,AB=2,AC=3BC=23,∴BC=12∵AD⊥DC,∴∠ADC=90°,AC=3,AD=3CD=3.∴CD=1216(2023•夹江县模拟)如图,已知AB是⊙O的直径,BC⊥AB于点B,D是⊙O上异于A、B的一个动点,连接AD,过O作OC∥AD交BC于点C.(1)求证:CD是⊙O的切线;(2)若EA=1,ED=3,求⊙O的半径.【答案】(1)见解答;(2)4.【解答】解:(1)如图,连接OD,由OD=OA得:∠OAD=∠ODA,∵OC∥AD,∴∠DOC=∠ODA,∠BOC=∠OAD,∴∠DOC=∠BOC,又∵OD=OB,OC=OC,∴△ODC≌△OBC,∴∠ODC=∠OBC,∵BC⊥AB,∴∠ODC=∠OBC=90°,又∵D在⊙O上,∴CD是⊙O的切线;(2)设⊙O的半径为x,则:OD=x,OA=x+1,∵CD是⊙O的切线,∴∠ODE=90°,在Rt△ODE中,由勾股定理得:ED2+OD2=OE2,∴32+x2=(x+1)2,解得:x=4,∴⊙O的半径为4.17(2022秋•盘山县期末)如图,已知AB是⊙O的直径,AC是⊙O的弦,过点C的直线与AB的延长线相交于点P,且AC=PC,∠P=30°.(1)求证:PC是⊙O的切线;(2)若AB=6,求PC的长.【答案】(1)证明见解析;(2)33.【解答】(1)证明:如图所示,连接OC,∵AC=PC,∠P=30°,∴∠A=∠P=30°,∴∠BOC=2∠A=60°,∴∠PCO=180°-∠P-∠POC=90°,即OC⊥PC,∵OC是⊙O的半径,∴PC是⊙O的切线;(2)解:∵AB=6且AB是⊙O的直径,∴OC=1OA=3,2在Rt△POC中,∠PCO=90°,∠P=30°,∴OP=2OC=6,∴PC=PO2-OC2=33.18(2023春•东营期末)如图,在⊙O中,PA是直径,PC是弦,PH平分∠APB且与⊙O交于点H,过H作HB⊥PC交PC的延长线于点B.(1)求证:HB是⊙O的切线;(2)若HB=4,BC=2,求⊙O的直径.【答案】见试题解答内容【解答】证明:(1)如图,连接OH,∵PH平分∠APB,∴∠HPA=∠HPB,∵OP=OH,∴∠OHP=∠HPA,∴∠HPB=∠OHP,∴OH∥BP,∵BP⊥BH,∴OH⊥BH,∴HB 是⊙O 的切线;(2)如图,过点O 作OE ⊥PC ,垂足为E ,∵OE ⊥PC ,OH ⊥BH ,BP ⊥BH ,∴四边形EOHB 是矩形,∴OE =BH =4,OH =BE ,∴CE =OH -2,∵OE ⊥PC∴PE =EC =OH -2=OP -2,在Rt △POE 中,OP 2=PE 2+OE 2,∴OP 2=(OP -2)2+16∴OP =5,∴AP =2OP =10,∴⊙O 的直径是10.19(2023•汉川市模拟)如图,AB 为⊙O 的直径,弦CD ⊥AB ,垂足为点E ,直线BF 与AD 延长线交于点F ,且∠AFB =∠ABC .(1)求证:直线BF 是⊙O 的切线;(2)若CD =12,BE =3,求⊙O 的半径.【答案】(1)证明见解析;(2)152.【解答】(1)证明:∵AC =AC ,∴∠ABC =∠ADC ,∵∠AFB =∠ABC ,∴∠ADC =∠AFB ,∴CD ∥BF ,∵CD ⊥AB ,∴AB ⊥BF ,∵OB 为⊙O 的半径.∴直线BF 是⊙O 的切线;(2)解:设⊙O 的半径为R ,连接OD ,如图,∵AB ⊥CD ,CD =12,∴CE =DE =12CD =6,∵BE =3,∴OE =R -3,在Rt △OED 中,∵OE2+DE2=OD2,∴R2=(R-3)2+62,解得:R=15 2.即⊙O的半径为15 2.20(2022秋•斗门区期末)如图,AB为⊙O的直径,P在BA的延长线上,C为圆上一点,且∠ACP=∠OBC.(1)求证:PC与⊙O相切;(2)若PA=4,PC=BC,求⊙O的半径.【答案】(1)见解析;(2)4.【解答】(1)证明:连接OC,则OC=OB,∴∠OBC=∠OCB,∵AB为⊙O的直径,∴∠ACB=90°,∴∠ACP=∠OBC,∴∠ACP=∠OCB,∴∠OCP=∠OCA+∠ACP=∠OCA+∠OCB=∠ACB=90°,∵PC经过⊙O的半径OC的外端,且PC⊥OC,∴PC与⊙O相切.(2)解:∵PC=BC,∴∠P=∠B,∵∠ACP=∠B,∴∠ACP=∠P,∴CA=PA=4,∵∠OCP=90°,∴∠ACO+∠ACP=90°,∠AOC+∠P=90°,∴∠ACO=∠AOC,∴CA=OA=OC=4.21(2023•黑龙江模拟)如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.(1)求证:DE是⊙O的切线;(2)若AB=10,BD=3,求AE的长.【答案】(1)见解析;(2)658.【解答】(1)证明:(1)连接OC ;∵AE ⊥CD ,CF ⊥AB ,又CE =CF ,∴∠1=∠2.∵OA =OC ,∴∠2=∠3,∠1=∠3.∴OC ∥AE .∴OC ⊥CD .∴DE 是⊙O 的切线.(2)解:∵OC ⊥ED ,AB =10,BD =3,∴OB =OC =5.CD =OD 2-OC 2=39,∵S △OCD =12OC ⋅CD =12OD ⋅CF ,即12×5×39=125+3 ⋅CF ,∴CF =5398,∴OF =OC 2-FC 2=658,∴AF =OA +OF =5+258=658,在Rt △AEC 和Rt △AFC 中,CE =CF ,AC =AC ,∴Rt △AEC ≌Rt △AFC (HL ),∴AE =AF =658.22(2023•宿豫区三模)如图,Rt △ABC 中,∠ACB =90°,点D 在AC 边上,以AD 为直径作⊙O 交BD 的延长线于点E ,CE =BC .(1)求证:CE 是⊙O 的切线;(2)若CD =2,BD =2,求⊙O 的半径.【答案】见试题解答内容【解答】解:(1)如图,连接OE,∵∠ACB=90°,∴∠1+∠5=90°.∵CE=BC,∴∠1=∠2.∵OE=OD,∴∠3=∠4.又∵∠4=∠5,∴∠3=∠5,∴∠2+∠3=90°,即∠OEC=90°,∴OE⊥CE.∵OE是⊙O的半径,∴CE是⊙O的切线.(2)在Rt△BCD中,∠DCB=90°,CD=2,BD=25,BC=CE=4.设⊙O的半径为r,则OD=OE=r,OC=r+2,在Rt△OEC中,∠OEC=90°,∴OE2+CE2=OC2,∴r2+42=(r+2)2,解得r=3,∴⊙O的半径为3.23(2023•东港区校级三模)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点E,点D在AB上,且以AD为直径的⊙O经过点E.(1)求证:BC是⊙O的切线;(2)当AD=3BD,且BE=4时,求⊙O的半径.【答案】(1)证明见解析;(2)3.【解答】(1)证明:连接OE,∵OA=OE,∴∠OAE=∠OEA,∵AE平分∠BAC,∴∠BAE=∠CAE,∴∠OEA=∠CAE,∴OE∥AC,∵∠C=90°,∴∠OEC =90°,∴OE ⊥BC ,∵OE 为半径,∴BC 是⊙O 切线;(2)解:∵AD =3BD ,设BD =2x ,则AD =6x ,∴AO =OD =OE =3x ,∴OB =5x ,在Rt △OBE 中,根据勾股定理得:OE 2+BE 2=OB 2,∴(3x )2+42=(5x )2,∴x =1,∴OE =3x =3,∴⊙O 半径为3.24(2023•泗县校级模拟)如图,在Rt △ABC 中,∠ACB =90°,以AB 为直径作⊙O ,在⊙O 上取一点D ,使CD =BC,过点C 作EF ⊥AD ,交AD 的延长线于点E ,交AB 的延长线于点F .(1)求证:直线EF 是⊙O 的切线;(2)若AB =10,AD =6,求AC 的长.【答案】(1)见详解;(2)45.【解答】(1)证明:连接OC ,如图,∵CD =CB,∴∠EAC =∠CAB ,∵EF ⊥AD ,∴∠EAC +∠ACE =90°,∵OC =OA ,∴∠CAB =∠OCA ,∴∠EAC =∠OCA ,∴∠ACO +∠ACE =90°,即半径OC ⊥EF ,∴EF 是⊙O 的切线;(2)解:连接BD ,交OC 于点G ,如图,∵AE ⊥EF ,OC ⊥EF ,∴AE ∥OC ,∵O 为AB 为中点,∴OG 为△ABD 中位线,∴OG=1AD=3,DG=BG,2∴DG=BG=CE,DB⊥OC,GC=OC-OG=2,∵AB=10,∴OB=5,∴BG=OB2-OG2,∴DG=BG=4,∵AE⊥EF,OC⊥EF,DB⊥OC,∴四边形DECG是矩形,∴DE=CG=2,EC=DG=4,∴AE=8,∴在△AEC中,AC=AE2+EC2=45.25(2023•荔湾区校级一模)如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.(1)求证:DE是⊙O的切线;(2)若△ABC的边长为2,求EF的长度.【答案】(1)证明见解析;(2)12.【解答】(1)证明:如图所示,连接OD,∵△ABC是等边三角形,∴∠B=∠C=60°.∵OB=OD,∴∠ODB=∠B=60°.∵DE⊥AC,∴∠DEC=90°.∴∠EDC=30°.∴∠ODE=90°.∴DE⊥OD于点D.∵点D在⊙O上,∴DE是⊙O的切线;(2)解:如图所示,连接AD,BF,∵AB为⊙O直径,∴∠AFB=∠ADB=90°.∴AF⊥BF,AD⊥BD.∵△ABC是等边三角形,∴DC=12BC=1,FC=12AC=1.∵∠EDC=30°,∴EC=12DC=12.∴EF=FC-EC=12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明圆的切线的两种类
型训练
work Information Technology Company.2020YEAR
证明圆的切线的两种类型
类型1 已知直线与圆的交点【方法】“连半径,证垂直,得切线”.“证垂直”
如图,AB=AC,AB是⊙O的直径,⊙O交BC于D,DM⊥AC于M.
求证:DM与⊙O相切.
练习1 (湖州中考改编)如图,已知P是⊙O外一点,PO交⊙O于点C,
OC=CP=2,弦AB垂直平分OC.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
练习2 (德州中考)如图,已知⊙O的半径为1,DE是⊙O的直径,过D作⊙O 的切线,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.
(1)求AD的长;
(2)BC是⊙O的切线吗?若是,给出证明,若不是,说明理由.
练习3 (临沂中考)如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
类型2 未知直线与圆的交点【方法】作垂直,证半径,得切线
如图,AB=AC,D为BC中点,⊙D与AB切于E点.求证:AC与⊙D相切.
练习4 如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙O与BC相切于点M,与AB、AD分别相交于点E、F.
求证:CD与⊙O相切.
练习5 如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB 上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
(1)求证:AC是⊙D的切线;
(2)求线段AC的长.
圆的有关计算
类型1 动态几何中弧长或扇形的面积问题
练习1 已知一个半圆形工件,未搬动前如图所示,直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50 m,半圆的直径为4 m,则圆心O所经过的路线长是______m.(结果用π表示)
练习2 如图所示,Rt△ABC的边BC位于直线l上,AC=3,∠ACB=90°,∠
A=30°,若Rt△ABC由现在的位置向右无滑动地翻转,当点A第3次落在直线l 上时,点A所经过的路线长为______.(结果用含π的式子表示)
练习3 (恩施中考)如图,在直角坐标系中放置一个边长为1的正方形ABCD ,将正方形ABCD 沿x 轴的正方向无滑动的在x 轴上滚动,当点A 离开原点后第一
次落在x 轴上时,点A 运动的路径线与x 轴围成图形的面积为(
)
A.
2π
+21 B.2π+1 C.π+1 D.π+2
1
练习4 如图所示,扇形OAB 的圆心角为60°,半径为1,将它向右滚动到扇形O ′A ′B ′的位置,点O 到O ′所经过的路线长为( )
A.π
B.34π
C.3
5
π D.2π
练习5 (日照中考)如图,正六边形ABCDEF 是边长为2 cm 的螺母,点P 是FA 延
长线上的点,在A 、P 之间拉一条长为12 cm 的无伸缩性细线,一端固定在点A ,握住另一端点P 拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P 运动的路径长为( ) A.13π cm B.14π cm C.15π cm D.16π cm
练习6 如图,边长为2的正六边形ABCDEF 在直线l 上按顺时针方向作无滑动的翻滚.
(1)当正六边形绕点F 顺时针旋转60度时,A 落在点A 1位置; (2)当点A 翻滚到点A 2的位置时,求点A 所经过的路径长.
类型2 圆中不规则图形的面积问题
(盐城中考)如图,在△ABC 中,∠BAC =90°,AB =5 cm ,AC =2 cm ,将△ABC 绕顶点C 按顺时针方向旋转45°至△A 1B 1C 的位置,求线段AB 扫过区域(图中阴影部分)的面积. 7. (泰安中考)如图7,半径为2 cm ,圆心角为90°的扇形OAB 中,分别以OA 、OB 为直径作半圆,则图中阴影部分的面积为( )
A.(
2
π
-1) cm 2 B.(
2
π
+1) cm 2
C.1 cm 2
D.
2
π
cm 2
8 (重庆中考)如图8,菱形ABCD 的对角线AC 、BD 相交于点O ,AC=8,BD=6,以AB 为直径作一个半圆,则图中阴影部分的面积为( )
A.25π-6
B.225π-6
C.625π-6
D.8
25
8-6 9 (乐山中考)如图,正方形ABCD 的边长为3,以A 为圆心,2为半径作圆弧,以D 为圆心,3为半径作圆弧.若图中阴影部分的面积分别为S 1、S 2,则S 1-S 2=______
10 (河南中考)如图,在菱形ABCD 中,AB=1,∠DAB=60°.把菱形ABCD 绕点A 顺时针旋转30°得到菱形AB ′C ′D ′,其中点C 的运动路径为CC ′,则图中阴影部分的面积为______ 11 (襄阳中考)如图,在正方形ABCD 中,AD=2,E 是AB 的中点,将△BEC 绕点B 逆时针旋转90°后,点E 落在CB 的延长线上点F 处,点C 落在点A 处.再将线段AF 绕点F 顺时针旋转90°得线段FG ,连接EF ,CG. (1)求证:EF ∥CG ;
(2)求点C ,点A 在旋转过程中形成的弧AC,弧AG 与线段CG 所围成的阴影部分的面积.。
