哈工大集合论习题课第六章树及割集习题课
ch6习题及答案

习题6解答判断题:1.二叉树中每个结点有两个子女结点,而对一般的树则无此限制,因此二叉树是树的特殊情形。
( ╳ )2.二叉树就是结点度为2的树。
( ╳ )( (哈工大2000年研究生试题)3.二叉树中不存在度大于2的结点,当某个结点只有一棵子树时无所谓左、右子树之分。
( ╳ ) (陕西省1998年自考试题)4.当k≥1时,高度为k的二叉树至多有21 k个结点。
( ╳ )5.完全二叉树的某结点若无左孩子,则它必是叶结点。
(√)(中科院软件所1997年研究生试题)6.用一维数组存放二叉树时,总是以前序遍历顺序存储结点。
( ╳ )7.若有一个结点是某二叉树子树的中序遍历序列中的最后一个结点,则它必是该子树的前序遍历序列中的最后一个结点。
( ╳ )8.存在这样的二叉树,对它采用任何次序的遍历,结果相同。
(√)(哈工大2000年研究生试题)9.中序线索二叉树的优点之一是便于在中序下查找前驱结点和后继结点。
(√)10.将一棵树转换成二叉树后,根结点没有左子树,( ╳ )(北邮1999年研究生试题。
)11.由树转换成二叉树,其根结点的右子树总是空的。
(√)12.前序遍历森林和前序遍历与该森林对应的二叉树其结果不同。
( ╳ )13.在叶子数目和权值相同的所有二叉树中,最优二叉树一定是完全二叉树。
( ╳ )14.在哈夫曼编码中,当两个字符出现的频率相同时,其编码也相同,对于这种情况应作特殊处理。
( ╳ )15.霍夫曼树一定是满二叉树。
( ╳ )16.树的度是树内各结点的度之和。
( ╳ )17.由二叉树的结点构成的集合可以是空集合。
(√)18.一棵树中的叶子结点数一定等于与其对应的二叉树中的叶子结点数。
( ╳ )选择题:19.树最适合用来表示( C )。
A.有序数据元素 B. 无序数据元素C.元素之间具有分支层次关系的数据 D. 元素之间无联系的数据20.如果结点A有3个兄弟,而且B是A的双亲,则B的度是( D )。
哈工大集合与图论习题

集合与图论习题第一章习题.画出具有个顶点地所有无向图(同构地只算一个)..画出具有个顶点地所有有向图(同构地只算一个)..画出具有个、个、个顶点地三次图..某次宴会上,许多人互相握手.证明:握过奇数次手地人数为偶数(注意,是偶数)..证明:哥尼斯堡七桥问题无解..设与是图地两个不同顶点.若与间有两条不同地通道(迹),则中是否有回路?.证明:一个连通地(,)图中≥..设是一个(,)图,δ()≥[],试证是连通地..证明:在一个连通图中,两条最长地路有一个公共地顶点..在一个有个人地宴会上,每个人至少有个朋友(≤≤).试证:有不少于个人,使得他们按某种方法坐在一张圆桌旁,每人地左、右均是他地朋友.b5E2R。
.一个图是连通地,当且仅当将划分成两个非空子集和时,总有一条联结地一个顶点与地一个顶点地边..设是图.证明:若δ()≥ ,则包含长至少是δ()地回路..设是一个(,)图,证明:()≥,则中有回路;()若≥,则包含两个边不重地回路..证明:若图不是连通图,则是连通图..设是个(,)图,试证:()δ()·δ()≤[()]([()]),若≡,,( )() δ()·δ()≤[()]·[()],若≡( ).证明:每一个自补图有或个顶点..构造一个有个顶点而没有三角形地三次图,其中≥..给出一个个顶点地非哈密顿图地例子,使得每一对不邻接地顶点和,均有≥.试求中不同地哈密顿回路地个数..试证:图四中地图不是哈密顿图..完全偶图,为哈密顿图地充分必要条件是什么?.菱形面体地表面上有无哈密顿回路?.设是一个(≥)个顶点地图.和是地两个不邻接地顶点,并且≥.证明:是哈密顿图当且仅当是哈密顿图..设是一个有个顶点地图.证明:若>δ(),则有长至少为δ()地路..证明具有奇数顶点地偶图不是哈密顿图..证明:若为奇数,则中有()个两两无公共边地哈密顿回路..中国邮路问题:一个邮递员从邮局出发投递信件,然后返回邮局.若他必须至少一次走过他所管辖范围内地每条街道,那么如何选择投递路线,以便走尽可能少地路程.这个问题是我国数学家管梅谷于年首先提出地,国外称之为中国邮路问题.p1Ean。
哈工大集合论习题

第一章 习题1.写出方程2210x x ++=的根所构成的集合。
2.下列命题中哪些是真的,哪些为假 3设有n 个集合12,,,n A A A 且121n A A A A ⊆⊆⊆⊆,试证:12n A A A ===4.设{,{}}S φφ=,试求2S?5.设S 恰有n 个元素,证明2S有2n个元素。
6.设A 、B 是集合,证明:(\)()\A B B A B B B φ=⇔=7.设A 、B 是集合,试证A B A B φ=⇔=∆8. 设A 、B 、C 是集合,证明:()()A B C A B C ∆∆=∆∆9.设A 、B 、C 为集合,证明\()(\)\A B C A B C =10.设A ,B ,C 为集合,证明: ()\(\)(\)A B C A C B C =11.设A,B,C 为集合,证明:()\(\)(\)A B C A C B C =12.设A,B,C 都是集合,若A B A C =且A B B C =,试证B=C 。
13.设A,B,C 为集合,试证:(\)\(\)\(\)A B C A B C B =14.设X Y Z ⊆⊆,证明\(\)(\)Z Y X X Z Y =15.下列命题是否成立? (1)(\)\(\)A B C A B C =(2)(\)()\AB C A B C =(3)\()()\A B C A B B = 16.下列命题哪个为真? a)对任何集合A,B,C ,若AB BC =,则A=C 。
b)设A,B,C 为任何集合,若A B A C =,则B=C 。
c)对任何集合A,B ,222A BAB =。
d)对任何集合A,B ,222A B AB =。
e)对任何集合A,B ,\22\2A BA B =。
f)对任何集合A,B ,222A BAB∆=∆。
17.设R,S,T 是任何三个集合,试证:(1)()()S T S T S T ∆=∆;(2)()()()R S T R S R T ∆⊇∆∆;(3)()()()()()R S R T R ST R S R T ∆∆⊆∆⊆∆∆;(4)()()()RS T RS R T ∆⊇∆ 18.设A 为任一集,{}IB ξξ∈为任一集族(I φ≠),证明:()()IIA B A B ξξξξ∈∈=19.填空:设A,B 是两个集合。
算法分析第六章答案

第六章1,2,3,4,5,6,7,8,12,13,15,17
1
动态规划
1. 2. 3.
多阶段过程 满足最优性原理 建立递推关系式
2
P151-1
①递推关系式(6.8)对右图成立吗?为什 么? ②递推关系式(6.8)为什么对于含有负长 度环的图不能成立?
4 1 5 2 -4 3 3 6 4 9 6 3 2 5 1 7
4 7 15 18 20 2 10 13 15 4 7 1 9 3 1
n-m=4时(j-i=4)
– – – – k=1: |W(0,0)-W(1,4)|=11 k=2: |W(0,1)-W(2,4)|=2 k=3: |W(0,2)-W(3,4)|=12 k=4: |W(0,3)-W(4,4)|=17
14
j i
j-i=0; j-i=1; j-i=2; j-i=3; j-i=4 W R
1 2 2 2 0 7
C
22 32 39
4
4+2+1 7+4+4 15+2+ 18+1+ 0 =7 =15 1=18 1=20 2 2+4+4 10+2+ 13+1+ =10 1=13 1=15 4 4+1+2 7+1+1 =7 =9 1 1+1+1 =3 1
12
递推关系式:
W(i,j) = Q(i) i=j W(i, j-1)+P(j)+Q(j) i<j C(i,j) = 0 i=j W(i, j)+min{C(i, k-1)+C(k, j)} i<j k在R(i,j-1)和R(i+1,j)中,使C(i,k-1)+C(k,j) 取最小值。 R(i,j) = k
黑龙江省哈尔滨工大学附中高考数学一轮复习 集合与逻辑单元精品练习

哈尔滨工程大学附中2014三维设计高考数学一轮单元复习精品练习:集合与逻辑本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列有关命题的说法正确的是( )A .命题“若1,12==x x 则”的否命题为:“若1,12≠=x x 则”;B .“1-=x ”是“0652=--x x ”的必要不充分条件;C .命题“01,2<-+∈∃x x R x 使得”的否定是:“01,2>-+∈∀x x R x 均有”;D .命题“若y x y x sin sin ,==则”的逆否命题为真命题;【答案】D2.下列命题中的假命题是( )A .x ∀∈R 120x -,>B .x ∀∈N 2(1)0x *,->C .0x ∃∈R,lg 01x <D .0x ∃∈R,tan 02x =【答案】B3.设集合{1,2,3,4,5}U =,{1,3,5},{2,3,5}A B ==,则图中阴影部分表示的集合是( )A .{1,2,4}B .{4}C .{3,5}D .∅【答案】A4.如果命题“非p 为真”,命题“p 且q 为假”,那么下列选项一定正确的是( )A .q 为真B .q 为假C .p 或q 为真D .p 或q 不一定为真【答案】D5.“220a b +=”是“0a =或0b =”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件【答案】A6. 2>x ”是“0)2)(1(>-+x x ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A7.命题“若x=1,则x 2-3x+2=0”以及它的逆命题,否命题和逆否命题中,真命题的个数是( )A .0B .2C .3D .4【答案】B8.集合}20{,M =,}|{M x x P ∈=,则下列关系中,正确的是( ) A .MP B .P M C . M P = D . M P ⊆ 【答案】D9.已知集合{1,0,1},{|cos ,}M N y y x x M =-==∈,则集合N 的真子集个数为( )A .3B .4C .7D .8【答案】B10.已知命题p ::若x +y ≠3,则x ≠1或y ≠2;命题q :若b 2=ac ,则a,b,c 成等比数列,下列选项中为真命题的是( )A . pB . qC . p ∧qD .(⌝p )∨q【答案】A11.设集合A={x|y=x 2-1},B={y|y=x 2-1},C={(x,y)|y=x 2-1},则下列关系错误..的是( ) A .B ∩C=Ф B .A ∩C=ФC .A ∩B=BD .A ∪B=C 【答案】D12.下列说法正确的是( )A . *N ϕ∈B . Z ∈-2C . Φ∈0D .Q ⊆2【答案】B第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.下列说法及计算不正确的是 。
图论树与割集

4)无回路,如在任意两结点之间添上一条
边,得到一个且仅一个基本回路。(n ≥ 2) 必要性:设T是树.故无回路,由(3)已证任 意两点vi与vj之间有且只有一条基本路 径,故添上一条边(vi,vj),只能得到唯 一的一条基本回路,故条件(4)成立。 充分性:设条件(4)成立,因而图无回路, 往证明图是连通的,若图不连通,则存在 两点,这两点之间不存在路径,则在这两 点之间添上一条边就不可能得到一个回路 与条件矛盾。
定理3.2 当且仅当连通无向图的每一条边均 为割边时,该图才是一棵树。 证: 必要性 设图G是一棵树, e是G的任一条边,因为 树不含回路,所以e不在回路中, 由定理 2.10知,e是割边。 充分性 设G的任一条边均为割边,则去掉 任一条边图将不连通,由定理3.1(5)知, 定理2.10 当且仅当无向图G的一条边e 图是树。
定理3.5 一个连通图至少有一棵生成树。 证: 如果连通图G无回路,根据的定义,则G本身就是 一棵生成树。 如果连通图G有回路,去掉回路的任一条边得到生 成子图G1,显然G1仍然是连通的,如果G1不含回 路,则G1就是G的生成树,否则又可去掉回路的任 一条边得到另一个生成子图,只要生成图还有回 路,就去掉回路的一条边,由于图的有限性,最 后一定得到不含回路的生成子图T,由于每次去掉 回路的一条边,并不破坏图的连通性,所以T是G 的生成树。
Kruskal算法: 设G是有n个结点,m条边(m≥n-1)的连通 图. S=Φ i=0 j=1 将所有边按照权升序排序: e1, e2, e3,… ,em S=S∪{ai} j=j+1 ai=ej i=i+1 N |S|=n-1 Y 输出S N 取ej使得 S∪{ ej}有回路? Y j=j+1 停
平凡树
哈工大电路习题答案
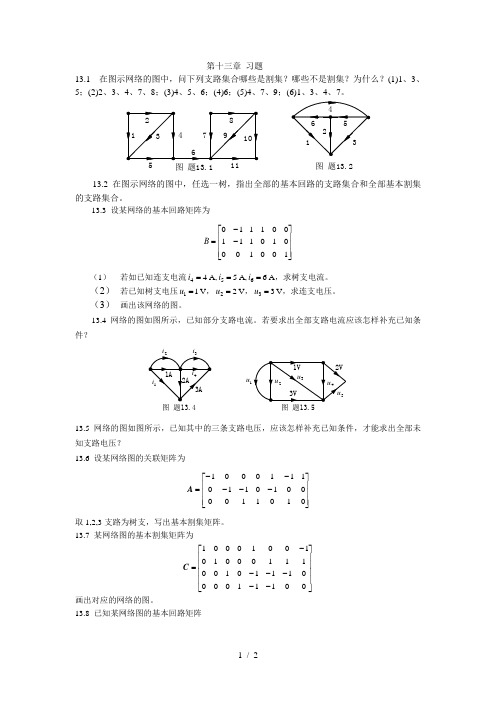
第十三章 习题13.1 在图示网络的图中,问下列支路集合哪些是割集?哪些不是割集?为什么?(1)1、3、5;(2)2、3、4、7、8;(3)4、5、6;(4)6;(5)4、7、9;(6)1、3、4、7。
图 题13.1图 题13.213.2 在图示网络的图中,任选一树,指出全部的基本回路的支路集合和全部基本割集的支路集合。
13.3 设某网络的基本回路矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=100100010111001110B(1) 若如已知连支电流44=i A,55=i A,66=i A ,求树支电流。
(2) 若已知树支电压11=u V ,22=u V ,33=u V ,求连支电压。
(3) 画出该网络的图。
13.4 网络的图如图所示,已知部分支路电流。
若要求出全部支路电流应该怎样补充已知条件?图 题13.41u 图 题13.513.5 网络的图如图所示,已知其中的三条支路电压,应该怎样补充已知条件,才能求出全部未知支路电压?13.6 设某网络图的关联矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=010110000101101110001A取1,2,3支路为树支,写出基本割集矩阵。
13.7 某网络图的基本割集矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=00111000011101001110001010010001C 画出对应的网络的图。
13.8 已知某网络图的基本回路矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=10111000011101001100001001100001B 试写出此网络的基本割集矩阵C 。
13.9 某网络有6条支路,已知3条支路的电阻分别是Ω=21R ,Ω=52R ,Ω=103R ;其余3条支路的电压分别是44=u V ,65=u V ,126-=u V 。
又知该网络的基本回路矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=110100*********001B试求全部支路电流。
13.10 图示网络的图,根据所选的树,列出独立的KCL 方程和独立的KVL 方程,并写成矩阵形式。
哈工大考研管理运筹学第六章(二)树和最小支撑树

2
3
4
三、图的最小支撑树
算法3(Prim法) 在图中找圈,并删 除其中最大边.如此进 行下去, 直至图中没有 圈止.
1 5
2
3
4
三、图的支撑树(minimum spanning tree)
三、图的最小支撑树 图G权最小的支撑树称为最小支撑树
算法1(避圈法, Kruskal法) 将边按权从小到 大依次添入图中, 若出现圈,则删去 其中最大边,直至 填满n-1条边为止(n 为顶点数)。
1 5
234ຫໍສະໝຸດ 三、图的最小支撑树算法2(破圈法) 在图中找圈,并 删除其中最大边.如 此进行下去, 直至图 中没有圈止.
二、树的性质
设T是一个点数大于3的树,则下列六个定 义是等价的:
(1)T连通且无回路;
(2)T有条边且无回路; (3)T连通且有条边; (4)T连通且每条边都是割边; (5)T的任两点间都有唯一的路相连;
(6)T无回路,但在任一对不相邻的点间 加连一条边,则构成唯一的一个回路。
三、图的支撑树(minimum spanning tree)
一、树的概念(Tree) 无圈的连通图称为树
二、树的性质
性质1 如果树T的点数不小于2,那么至少有两 个悬挂点 性质2 如果一个图G具有n个顶点,那么图G是一 个树的充分必要条件是图G不含圈且恰有n-1条边。 性质3 如果一个图G具有n个顶点,那么图G是一 个树的充分必要条件是图G是连通图且恰有n-1条边 性质4 图G是一个树的充分必要条件是任意两 个顶点恰有一条链
哈工大集合论习题课-树及割集习题课

第六章树及割集习题课1课堂例题例1设T是一棵树,T有3个度为3顶点,1个2度顶点,其余均是1度顶点.那么(1)求T有几个1度顶点(2)画出满足上述要求的不同构的两棵树.分析:对于任一棵树T ,其顶点数p和边数q的关系是:q p 1且pdeg(v) 2q ,根据这些性质容易求解.i 1解:(1)设该树T的顶点数为p,边数为q,并设树T中有x个1 度顶点.于是pdeg(v) 3 3 12 x 2q 且p 3 1 x, q p1,得x 5.i 1(2)满足上述要求的两棵不同构的无向树,如图1所示.图1例2设G是一棵树且(G) k ,证实G中至少有k个度为1项电c 证:设T 中有p个顶点,s个树叶,那么T中其余p s个顶点的度数均大于等于2,且至少有一个顶点的度大于等于k.由握手定理可得:p2q 2 p 2deg(v i) 2( p s 1) k s,有s k.i 1所以T中至少有k个树叶.习题例1假设无向图G中有p个顶点,p 1条边,那么G为树.这个命题正确吗为什么解:不正确.K3与平凡图构成的非连通图中有四个顶点三条边,显然它不是树.例2设树T中有2n个度为1的顶点,有3n个度为2的顶点,有n个度为3的顶点,那么这棵树有多少个顶点和多少条边解:设T 有p 个顶点,q 条边,那么q p 1 2n 3n n 1 6n 1deg(v) 2q 有:1 2n 2 3n 3 n 2q 2(6n 1) 12n 2,解得:n =2. v V故 q 11, p 12.例3证实恰有两个顶点度数为1的树必为一条通路.证:设T 是一棵具有两个顶点度数为1的(p,q)树,那么q p 1且p deg(V i ) 2q 2( p 1). i 1又T 除两个顶点度数为1外,其他顶点度均大于等于2,故pp 2deg(V i ) 2deg(v . 2( p 1),即i 1i 1p 2 deg(V i ) 2( p 2).1 1因此p 2个分支点的度数都恰为2,即T 为一条通路.例4画出具有4、5、6、7个顶点的所有非同构的无向树.解:4个顶点的非同构的无向树有两棵,如图 21(a),(b)所示;5个顶点的非同构的无向树有3棵,如图21(c),(d),(e)所示.(a ) (b)(c)(d)(e)图26个顶点的非同构的无向树有6棵,如图3所示图37个顶点的非同构的无向树有11棵,如图4所示.所画出的树具有6条边,因而七个顶点的度数之和应为12.由于每个顶点的度数均大于等于1,因而可产生以下七种度数序列 (d 1,d 2,L ,d 7):(1) 1111116;⑵ 1111125; (3) 1111134; (4) 1111224; (5) 1111233;(b ) 1112223; 〔7〕 1122222.在〔1〕中只有一个星形图,因而只能产生 1棵树T 1.在〔2〕, 〔3〕中有两个星形图,因而也只能各产生1棵非同构的 树,分别设为T 2,T 3.在〔4〕, 〔5〕中有三个星形图,但三个星形图是各有两个是同构 的,因而各可产生两棵非同构的树,分别设为T 4,T 5和丁6,丁7.在〔6〕中,有四个星形图,有三个是同构的,考虑到不同的排列情况,共可产生三棵非同构的树,设为 T 8,T 9,T 10O在〔7〕中,有五个星形图,都是同构的,因而可产生1棵树,设为T 11.七个顶点的所有非同构的树T 1:T 11如图2所示.例5设无向图G 是由k 〔k 边才能使G 成为一棵树解:设G 中的k 个连通分支为:T 1,T 2,L ,T k , V i T i , i 1,2,L ,k .在G 中添加边{M,v-} , i 1,2,L ,k 1 ,设所得新图为T ,那么T 连通且无回路, 因而T 为树.故所加边的条数k 1是使得G 为树的最小数目. 例6证实:任意一棵非平凡树都是偶图.分析:假设考虑一下数据结构中树〔即有向树〕的定义,那么可以很 简单地将树中的顶点按层次分类, 偶数层顶点归于顶点集V .,奇数层 顶点归于顶点集V 1 ,图G 中每条边的端点一个属于V o ,另一个属于V 1 , 而不可能存在关联同一个顶点集的边.同理,对于无向树,可以从任 何一个顶点V 出发,给该树的顶点标记奇偶性,例如,v 标记0,与v 相邻的顶点标记1,再给与标记为1的所有相邻的顶点标记0,依次类 推,直到把所有的顶点标记完为止.最后,根据树的性质证实,任何 边只可能关联V 1 〔标记为1的顶点集〕和V o 〔标记为0的顶点集〕之 间的顶点.T 2 T 3 T 4T 7 2〕棵树构成的森林,至少在G 中添加多少条T 1 T 9图4证1从任何一个顶点V出发,给该树的顶点做标记,v标记0,与V相邻的顶点标记1,然后再给与标记为1的所有顶点相邻的顶点标记0,……,依次类推,直到把所有的顶点标记完为止.下面证实:对于任何边只能关联V i (标记为1的顶点集)和V.(标记为0的顶点集)之间的顶点.不妨假设,假设某条边e关联V1中的两个顶点,设为V1和V2,又由于根据上述的标记法那么,有必至八的路P和V2至卜的路P2.设P1与P2离V1和v2最近的顶点为u ,所以,树中存在回路:V1PuP2V2eV) ,与树中无回路的性质矛盾.所以,任意边只能关联S (标记为1的顶点集)和V.(标记为0的顶点集)之间的顶点.所以,任意一棵非平凡树都是偶图.证2设T是任一棵非平凡树,那么T无回路,即T中所有回路长都是零.而零是偶数,故由偶图的判定定理可知T是偶图.例7(1) 一棵无向树有n个度数为i的顶点,i 1,2,L ,k.r)2,n3,L ,、均为数,问?应为多少(2)在(1)中,假设n,(3 r k)未知,n j(j r)均为数,问n r 应为多少k 解:(1)设T为有p个顶点,q条边无向树,那么q p 1, p R.i 1由握手定理:PPkdegV i 2q , 有degV i in i 2q 2p 2 , 即i 1i 1i 1kkin i 2p 2 2 n i 2o①i 1i 1由式①可知:kkkn〔n 2n i 2 (i 2)5 2.i 2i 2i 2(2)对于r 3,由①可知:1 k ,n r ——(2 i)n i 2 .r 2 i 1 i r例8证实:任一非平凡树最长路的两个端点都是树叶.证:设T为一棵非平凡的无向树,L V1V2L V k为T中最长的路,假设端点V1和V k中至少有一个不是树叶,不妨设V k不是树叶,即有deg(V k) 2 ,那么V k除与L上的顶点V k1相邻外,必存在V k1与V k相邻,而V k1 不在L上,否那么将产生回路.于是ML VM 1仍为T的一条比L更长的路, 这与L为最长的路矛盾.故V k必为树叶.同理,V1也是树叶.例9设无向图G中有p个顶点,q 1条边,那么G为连通图当且仅当G中无回路.证:必要性:由于G中有p个顶点,边数q p 1,又由于G是连通的,由定理可知G为树,因而G中无回路.充分性:由于G中无回路,又边数q p 1,由定理可知G为树, 所以G是连通的.例10设G是一个(p,g)图,证实:假设g p,那么G中必有回路.证:(1)设G是连通的,那么假设G中无回路,那么G是树,故q p 1与q p矛盾.故G中必有回路.(2)设G不连通,那么G中有k(k 2)个分支,G1,G2,L,G k.假设G中无回路,那么G的各个分支G(i 1,2,L ,k)中也无回路,于是各个分支都是树,所以有:q p i 1 , i 1,2,L , k.相加得:q p k(k 2) 与q p矛盾,故G中必有回路.综上所述,图G中必有回路. p例11设d1,d2,L ,d p是p个正整数,p 2,且d 2p 2.证实存在一棵顶点度数为d1&,L ,d p的树.i1证:对顶点p进行归纳证实.当p 2时,d〔d2 2 2 2 2,那么d〔d2 1 ,故以d1, d2为度数的树存在,即为一条边.p1设对任意p 1个正整数d1,d2,L a1,只要d i 2(p 1) 2,那么存i 1在一棵顶点度数为d1,d2,L ,d p1的树.p对p个正整数d;d,L ,d p ,假设有d; 2P 2 ,那么d;,d2,L ,d p中必有i1一个数为1,必有一个数大于等于2;不妨设d1 1,d p 2,因此对p 1p1个正整数d2,d3,L ,d p 1,d p 1,有d i' (d p 1) 2( p 1) 2 ,故存在一棵顶i2点度数为d2,d3,L ,d p 1,d p 1的树T.设T中u的度数为d p 1,在丁中增加一个顶点V及边{u,v},得到一个图T ,那么T为树.又T的顶点度数为d;,d2,L ,d p,故由归纳法知原命题成立例题例1 G的一条边e不包含在G的任一回路中当且仅当e是G的桥.分析:这个题给出了判断桥的充要条件,应该记住.证:必要性:设e 是连通图G 的桥,e 关联的两个顶点是u 和v . 假设e 包含在G 的一个回路中,那么除边e uv 外还有一条分别以u 和v 为端点的路,所以删去边e 后,G 仍是连通的,这与e 是桥相矛盾.充分性:假设边e 不包含在G 的任意回路中,那么连接顶点u 和v 只有 边e,而不会有其它连接u 和v 的路.由于假设连接u 和v 还有不同于边e 的路,此路与边e 就组成了一条包含边e 的回路,从而导致矛盾.所 以,删去边e 后,u 和v 就不连通了,故边e 是桥.例2设G 是连通图,满足下面条件之一的边应具有什么性质(1)在G 的任何生成树中;(2)不在G 的任何生成树中.解:(1)在G 的任何生成树中的边应为G 中的桥.(2)不在G 的任何生成树中的边应为G 中的环.例3非平凡无向连通图G 是树当且仅当的G 的每条边都是桥.证:必要性:假设T 中存在边e VM 不是桥,那么G e 仍连通,因而v,v j 之间必另有一,条(不通过e)的路.设此路为:v »向1耳2021 年刈v j , 于是G 中有回路v i e ji v i2e j2L v j ev ,这与G 是树矛盾,故G 的每条边都是 桥.充分性:只要证实G 中无回路即可.假设G 中有回路C ,那么C 中任何边都不是桥,与题设中每条边都是 桥矛盾.例4图1给出的带权图表示7个城市a,b,c,d,e, f ,g 及架起城市间直接 通信线路的预测造价,试给出一个设计方案使得各城市间能够通信且 总造价最小,要求计算出最小总造价.图1图2图3解:该题就是求图的最小生成树问题.因此,图的最小生成树即 为所求的通信线路图,如图2所示.其权即是最小总造价,其权为: (T) 1 3 4 8 9 23 48 o例7设T 是一棵树,p 2,那么(1) p 个顶点的树T 至多有多少个割点; bb 2023 15 23g3628 1617(2)p个顶点的树T有多少个桥解:(1)树的度为1的顶点(叶子)不是割点,而树至少有2 个顶点的度为1,故树至多有p 2个顶点为割点.(2)树的每一条边都是桥,故p个顶点的树有p 1个桥.例8证实或否认断言:连通图G的任意边是G的某一棵生成树的弦.答:错误.假设e是桥,那么不成立.。
图论习题课 树

环已烷 C6H12
081离散数学(60). W&M.
第十七章 平面图及图的着色
§17.1 平面图的基本概念 §17.2 欧拉公式 §17.3 平面图的判断 §17.4 平面图的对偶图 §17.5 图中顶点的着色 §17.6 地图的着色与平面图的点着色 §17.7 边着色
081离散数学(60). W&M.
证 设 C 内部有 d 条边, 则 C 内部有 d + 1 个面:
ni=2 fi = d + 1. 计算 C 内部的面的次数时, 这 d 条边每条被计算两次:
ni=2 i fi = 2d + n. 由上两式, 推得
ni=2 (i 2)fi = n 2. 同理, 对 C 的外部可推得
(c)
3
2
2
3
1
2
3
1
颜 色 的 标 涂示
色
1
13
1 23
旁
1
标2ຫໍສະໝຸດ 13数21
字
3
21 3
画
2
横
23
截
线
081离散数学(60). W&M.
例 分别用最少颜色给下面两个图着色.
(a)
081离散数学(60). W&M.
(b)
例 某校有 9 个学生: a, b, c, d, e, f, g, h, i, j, 修读 8 门课程:
4 3
21
14
2
1
4
2 3
31 31
2
32
4
2
3
1
12
3
面色数 * = 4
哈工大集合论与图论第六章作业题答案

第六章图的基本概念P习题2061.画出具有4个顶点的所有无向图(同构的只算一个)。
11个2.画出具有3个顶点的所有有向图(同构的只算一个)。
16个3.画出具有4个、6个、8个顶点的三次图。
略4.某次宴会上,许多人互相握手。
证明:握过奇数次手的人数为偶数(注意,0是偶数)。
把实际问题转化为图论问题,然后用握手定理的推论。
P习题2091.设u与v是图G的两个不同顶点。
若u与v间有两条不同的通道(迹),则G 中是否有圈?若u与v间有两条不同的通道,G中无圈若u与v间有两条不同的迹,G中有圈2.证明:一个连通的(p,q)图中q≥p-1。
数学归纳法3.设G是一个(p,q)图,且2/)2>p-q,则G是连通的。
p)(1(-6.在一个有n个人的宴会上,每个人至少有m个朋友(2≤m≤n)。
试证:有不少于m+1个人,使得他们按某种方法坐在一张圆桌旁,每人的左、右均是他的朋友。
证明:把实际问题转化为图论问题,就和下面的题一样了。
8.设G是图。
证明:若δ(G)≥2,则G包含长至少是δ(G)+1的圈。
这两个题和这个题一样的证明方法。
P习题2161.证明:若图G不是连通图,则G c 是连通图。
2.证明:每一个自补图有4n或4n+1个顶点。
P习题2281.给出一个10个顶点的非哈密顿图的例子,使得每一对不邻接的顶点u和v,均有:degu+degv≥9。
下图中任意一对不邻接的顶点u和v,均有:degu+degv≥9。
2.试求Kp中不同的哈密顿圈的个数。
(p-1)!/24.完全偶图Km,n为哈密顿图的充分必要条件是什么?10.证明具有奇数顶点的偶图不是哈密顿图。
图论-总结

第一节 图论发展概述-----了解
第二节 图的基本定义
设V是一个非空集合,V的一切二个元素所构成 子集记为P2(V),即P2(V)={A|AV且|A|=2};
2.1无向图
定(义V,1E)设称V为是一一个个无非向空图有。限集合,EP2(V),二元组 2.2 顶点的度 定义2 设v为图G=(V,E)的任一顶点,G中与v邻接的
习题
1. 2.设G是无向图,证明:若δ(G)≥m,则图中包含 长至少为m+1的圈。
3.每个自补图必有4n或4n+1个顶点(n为正整数) 4. 设A={v1,v2,…,vp},q≤p(p-1)/2。试求以V为顶 点集具有q条边的无向图的个数。 5.设m,n是正整数,则 (1) m,n满足什么条件时,Km,n是偶拉图? (2) m,n满足什么条件时,Km,n是哈密顿图? 6. 对于P个顶点的完全图Kp,则 (1)Kp一定是完全图吗? (2)Kp一定是哈密顿图吗?
第二节 生成树 2.1生成树(包含所有顶点的树)
定义1 设G=(V,E)是一个图,若G的一个生成子图T=(V,F)是 树,则称T是G的生成树。
2.2 生成树存在问题
定理1 图G有生成树的充分必要条件是G为一个连通图。
2.3 怎样求(最小)生成树(破圈法) 2.4 树的弦
定义3 设T是连通图G的生成树,G的不是T的边称为T的弦。 说明: (1) 若G是一个(p,q)连通图,T是G的生成树,则T有
个命题正确吗?为什么? 5.设树中有2n个度为1的顶点,有2n个度为2的顶,
有n个度为3的顶点,则这棵树有多少个顶点和多 少条边? 6.恰有两个顶点的度为1的树是一条通路。
第四章 平面图和图的着色
哈工大集合论习题课-第三章 关系习题课(学生)

习 题 课例1设{,,}A a b c =,给出A 上的一个二元关系,使其同时不满足自反性、反自反性、对称性、反对称和传递性的二元关系,并画出R 的关系图。
解:{(,),(,),(,),(,)}R a a b c c b a c =,关系图如图所示。
例2 设X 是一个集合,X =n ,求:1.X 上的二元关系有多少?()22n 2. X 上的自反的二元关系有多少? 3. X 上的反自反的二元关系有多少?解:因为把所有的反自反的二元关系的每个都加上对角线上的序对,就变成了自反的关系,因此,自反的与反自反的个数一样多。
即22nn-4. X 上的对称的二元关系有多少?2222n n n nn -++=,故共有222n n+个对称的关系。
5. X 上的反对称的二元关系有多少?22(32)n n n -∙6. X 上既是自反的也是反自反的二元关系的个数;(0)个7.X 上既不是自反的也不是反自反的二元关系有多少?2(2(22))n nn --解:解:可用容斥原理来计算设B 表示所有自反关系构成的集合,C 表示所有反自反关系构成的集合,则22nnB C -==。
而B C φ=,故B C B C =+,从而CC B C S B C S B C =-=--2222222222222(22)n n n n n n n n n n n ----=--=-=-于是,既不是自反的,也不是反自反关系共有22(22)n nn --个。
8.自反的且对称的关系有多少?[此结果与“反自反的且对称的关系有多少?”是一样多]即有222n n -(对角线上全去掉)9.自反的或对称的关系有多少?解:设B 表示自反关系的集合,C 表示对称关系的集合,则自反或对称关系的集合为:22222222n n n n nnB C B C B C +--=+-=+-。
10.X 上既是反自反的也是反对称的二元关系的个数为:223n n -;11.X 上既是对称的也是反对称的关系个数;解:X 上既是对称的也是反对称的关系X R I ⊆,故有2n 。
离散数学集合论哈工大答案

反之, x X ( Z \ Y ) ,则 x X 或 x Z \ Y 。 若 x X ,则由 X Y Z 有 x Y , x Z ,故 x Y \ X ,因此 x Z \ (Y \ X ) 。 若 x Z \ Y ,则 x Z 但 x Y ,故 x Y \ X ,因此 x Z \ (Y \ X ) 。从而
1
解: 2S { ,{ },{{ }},{ ,{ }}} 7.设 S 恰有 n 个元素,证明 2S 有 2n 个元素。 证明: (1)当 n=0 时, S , 2 S { }, 2S 1 20 ,命题成立。 (2)假设当 n k ( k 0, k N ) 时命题成立,即 2 S 2k ( S k 时) 。那么对 于 S1 ( S1 k 1 ) , 2S1 中的元素可分为两类,一类为不包含 S1 中某一元素 x 的 集合,另一类为包含 x 的集合。显然,这两类元素个数均为 2k 。因而 2 S1 2k 1 , 亦即命题在 n k 1 时也成立。 由(1) 、 (2) ,可证得命题在 n N 时均成立。
S T ( S T ) ( S T ) 。
反之,因为 ( S T ) ( S T ) ,故
教材习题解答
第一章 集合及其运算
P8 习题 3. 写出方程 x 2 2 x 1 0 的根所构成的集合。 解: x 2 2 x 1 0 的根为 x 1 ,故所求集合为 {1} 4.下列命题中哪些是真的,哪些为假 a)对每个集 A, A ;b)对每个集 A, A ; c)对每个集 A, A { A} ;d)对每个集 A, A A ; e)对每个集 A, A A ;f)对每个集 A, A { A} ; g)对每个集 A, A 2 A ;h)对每个集 A, A 2 A ; i)对每个集 A, { A} 2 A ;j)对每个集 A, { A} 2 A ; k)对每个集 A, 2 A ;l)对每个集 A, 2 A ; m)对每个集 A, A { A} ;n) { } ; o) {} 中没有任何元素;p)若 A B ,则 2 A 2 B q)对任何集 A, A {x | x A} ;r)对任何集 A, {x | x A} { y | y A} ; s)对任何集 A,y A y {x | x A} ; t)对任何集 A, {x | x A} { A | A A} ; 答案:假真真假真假真假真假真真假假假真真真真真 5.设有 n 个集合 A1 , A2 , , An 且 A1 A2 An A1 ,试证: A1 A2 An 证明:由 A1 A2 A4 An A1 ,可得 A1 A2 且 A2 A1 ,故 A1 A2 。 同理可得: A1 A3 A4 An 因此 A1 A2 A3 An 6.设 S { ,{ }} ,试求 2S ?
哈工大集合与图论习题

集合与图论习题第一章习题1.画出具有4个顶点的所有无向图(同构的只算一个)。
2.画出具有3个顶点的所有有向图(同构的只算一个)。
3.画出具有4个、6个、8个顶点的三次图。
4.某次宴会上,许多人互相握手。
证明:握过奇数次手的人数为偶数(注意,0是偶数)。
5.证明:哥尼斯堡七桥问题无解。
6.设u与v是图G的两个不同顶点。
若u与v间有两条不同的通道(迹),则G中是否有回路?7.证明:一个连通的(p,q)图中q ≥p-1。
8.设G是一个(p,q)图,δ(G)≥[p/2],试证G是连通的。
9.证明:在一个连通图中,两条最长的路有一个公共的顶点。
10.在一个有n个人的宴会上,每个人至少有m个朋友(2≤m≤n)。
试证:有不少于m+1个人,使得他们按某种方法坐在一张圆桌旁,每人的左、右均是他的朋友。
11.一个图G是连通的,当且仅当将V划分成两个非空子集V1和V2时,G总有一条联结V1的一个顶点与V2的一个顶点的边。
12.设G是图。
证明:若δ(G)≥ 2,则G包含长至少是δ(G)+1的回路。
13.设G是一个(p,q)图,证明:(a)q≥p,则G中有回路;(b)若q≥p+4,则G包含两个边不重的回路。
14.证明:若图G不是连通图,则G c 是连通图。
15.设G是个(p,q)图,试证:(a)δ(G)·δ(G C)≤[(p-1)/2]([(p+1)/2]+1),若p≡0,1,2(mod 4)(b) δ(G)·δ(G C)≤[(p-3)/2]·[(p+1)/2],若p≡3(mod 4)16.证明:每一个自补图有4n或4n+1个顶点。
17.构造一个有2n个顶点而没有三角形的三次图,其中n≥3。
18.给出一个10个顶点的非哈密顿图的例子,使得每一对不邻接的顶点u和v,均有degu+degv≥919.试求Kp中不同的哈密顿回路的个数。
20.试证:图四中的图不是哈密顿图。
21.完全偶图Km,n为哈密顿图的充分必要条件是什么?22.菱形12面体的表面上有无哈密顿回路?23.设G 是一个p(p ≥3)个顶点的图。
数据结构与算法课件:DS06_第5章二叉树、第6章树 习题

1.以二叉链表作为存储结构,设计算法求出 二叉树T中度为0、度为1和度为2的结点数。
【题目分析】结点计数可以在遍历中解决。 根据“访问根结点”在“递归遍历左子树” 和“递归遍历右子树”中位置的不同,而有 前序、后序和中序遍历。
∥设置三个全局变量,分别记度为2,1和叶子结点的个数 int n2,n1,n0; void Count(BinaryTreeNode<T>* t) { if(t)
【题目分析】按完全二叉树形式顺序存储二叉树时,无元素
的位置要当作“虚结点”。设虚结点取二叉树结点以外的值 (这里设为0)。设结点序号为i,则当i<=(2h-1)/2时,若其2i 和2i+1位置为虚结点,则i为叶子结点;当i>(2h-1)/2时,若i 位置不是虚结点,则必为叶子结点。
n=pow(2,h)-1; //高度为h的树的最多结点数
while(top!=0 && s[top].tag==1) //tag为1表示右子树访问过,栈顶可弹出
{ if(s[top].t->data ==x)
while(bt[n]==0) //BT足够大,且初始化为全0后再存储元素
n--;
//求出树的实际结点数
2020/9/Βιβλιοθήκη 815int Leaves(int BT[],int n)
∥计算深度为h以一维数组BT作为存储结构的二叉树的叶子结点 数,n为数组长度
{ int num=0; ∥记叶子结点数
for(i=1;i<=n;i++)
【题目分析】后序遍历最后访问根结点,当 访问到值为x的结点时,栈中所有元素均为 该结点的祖先。
void Search(BinaryTreeNode<T>* bt,T x) ∥在二叉树bt中,查找值为x的结点,并打印其所有祖先 { typedef struct
离散数学结构 第6章 集合代数

第六章集合代数1. 集合,相等,(真)包含,子集,空集,全集,幂集2. 交,并,(相对和绝对)补,对称差,广义交,广义并3. 文氏图,有穷集计数问题4. 集合恒等式(等幂律,交换律,结合律,分配律,德·摩根律,吸收律,零律,同一律,排中律,矛盾律,余补律,双重否定律,补交转换律等)学习要求1. 熟练掌握集合的子集、相等、空集、全集、幂集等概念及其符号化表示2. 熟练掌握集合的交、并、(相对和绝对)补、对称差、广义交、广义并的定义及其性质3. 掌握集合的文氏图的画法及利用文氏图解决有限集的计数问题的方法4. 牢记基本的集合恒等式(等幂律、交换律、结合律、分配律、德·摩根律、收律、零律、同一律、排中律、矛盾律、余补律、双重否定律、补交转换律)5. 准确地用逻辑演算或利用已知的集合恒等式或包含式证明新的等式或包含式6.1 集合的基本概念一.集合的表示集合是不能精确定义的基本概念。
直观地说,把一些事物汇集到一起组成一个整体就叫集合,而这些事物就是这个集合的元素或成员。
例如:方程x2-1=0的实数解集合;26个英文字母的集合;坐标平面上所有点的集合;……集合通常用大写的英文字母来标记,例如自然数集合N(在离散数学中认为0也是自然数),整数集合Z,有理数集合Q,实数集合R,复数集合C等。
表示一个集合的方法有两种:列元素法和谓词表示法,前一种方法是列出集合的所有元素,元素之间用逗号隔开,并把它们用花括号括起来。
例如A={a,b,c,…,z}Z={0,±1,±2,…}都是合法的表示。
谓词表示法是用谓词来概括集合中元素的属性,例如集合B={x|x∈R∧x2-1=0}表示方程x2-1=0的实数解集。
许多集合可以用两种方法来表示,如B也可以写成{-1,1}。
但是有些集合不可以用列元素法表示,如实数集合。
集合的元素是彼此不同的,如果同一个元素在集合中多次出现应该认为是一个元素,如{1,1,2,2,3}={1,2,3}集合的元素是无序的,如{1,2,3}={3,1,2}在本书所采用的体系中规定集合的元素都是集合。
22树

例题
例题 已知无向树T有5片树叶,2度与3度顶点各1个,其余顶 点的度数均为4,求T的阶数n,并画出满足要求的所有非同 构的无向树。 解答 设T的阶数为n, 则边数为n1,4度顶点的个数为n7。 由握手定理得
2m = 2(n1) = 51+21+31+4(n7)
解出n = 8,所以4度顶点为1个。 故T的度数列为1、1、1、1、1、2、3、4。
说明
注意:T 不一定连通,也不一定不含回路。
生成树的存在条件
定理16.3 无向图G具有生成树当且仅当G连通。 证明 必要性,显然。 充分性(破圈法)。 若G中无回路,G为自己的生成树。
若G中含圈,任取一圈,随意地删除圈上的一条边,
若再有圈再删除圈上的一条边,直到最后无圈为止。 易知所得图无圈(当然无回路)、连通且为G的生成子图, 所以为G的生成树。
在T中,u, v之间存在惟一的路径 (u,v),
则 (u,v)∪e为所要求的圈。 不同的弦对应的圈也不同是显然的。
基本回路与基本回路系统的定义
定义16.3 设T是n阶m条边的无向连通图G的一棵生成树,设e1, e2, …, emn+1为T的弦。设Cr为T添加弦er产生的G中只含弦er ,其余边均为树枝的圈,称Cr 为G的对应T的弦er 的基本回路 或基本圈,r=1, 2, …, mn+1。 称{C1, C2, …, Cmn+1}为G对应T的基本回路系统,称mn+1为G 的圈秩,记作(G)。 求基本回路的算法
例16.1
人们常称只有一个分支点,且分支点的度数为n-1的 n(n≥3)阶无向树为星形图,称唯一的分支点为星心。
例16.2
例16.2 7阶无向图有3片树叶和1个3度顶点,其余3个顶点的度 数均无1和3。试画出满足要求的所有非同构的无向树。 解答 设Ti为满足要求的无向树,则边数mi=6,于是 ∑d(vj)=12=e+3+d(v4)+d(v5)+d(v6)。 由于d(vj)≠1∧d(vj)≠3,而且d(vj)≥1且d(vj)≤6,j=4,5,6, 可知d(vj)=2,j=4,5,6。于是Ti 的度数列为 1,1,1,2,2,2,3 由度数列可知,Ti中有一个3度顶点vi,vi的邻域N(vi)中有3个 顶点,这3个顶点的度数列只能为以下三种情况之一: 1,1,2 1,2,2 2,2,2 设它们对应的树分别为T1,T2,T3。此度数列只能产生这三棵 非同构的7阶无向树。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章树及割集习题课1课堂例题例1设T是一棵树,T有3个度为3顶点,1个2度顶点,其余均是1度顶点。
则(1)求T有几个1度顶点?(2)画出满足上述要求的不同构的两棵树。
分析:对于任一棵树T,其顶点数p和边数q的关系是:q P 1且pdeg(vj 2q,根据这些性质容易求解。
i 1解:(1)设该树T的顶点数为p,边数为q,并设树T中有x个1 度顶点。
于是pdeg(v)3312 x 2q 且p 3 1 x,q p 1,得x 5。
i 1(2)满足上述要求的两棵不同构的无向树,如图1所示。
图1例2设G是一棵树且(G)k,证明G中至少有k个度为1顶点。
证:设T中有p个顶点,s个树叶,则T中其余p s个顶点的度数均大于等于2,且至少有一个顶点的度大于等于k。
由握手定理可得:p2q 2 p 2 deg(v i) 2( p s 1) k s,有s k。
i 1所以T中至少有k个树叶。
习题例1若无向图G中有p个顶点,p 1条边,则G为树。
这个命题正确吗?为什么?解:不正确。
心与平凡图构成的非连通图中有四个顶点三条边,显然它不是树。
例2设树T中有2n个度为1的顶点,有3n个度为2的顶点,有n个度为3的顶点,则这棵树有多少个顶点和多少条边?解:设T 有p 个顶点,q 条边,则q P 1 2 n 3n n 1 6n 1。
由 deg(v) 2q 有:1 2n 2 3n 3 n 2q 2(6n 1) 12n 2,解得:n =2。
v V故 q 11, p 12。
例3证明恰有两个顶点度数为1的树必为一条通路。
证:设T 是一棵具有两个顶点度数为 1的(p,q)树,则q p 1且 pdeg(V i ) 2q 2(p 1)。
i 1外,其他顶点度均大于等于2,故 p 2 deg(V i ) 2( p 1),即i 1 p 2deg(V i ) 2( p 2)。
i 1因此p 2个分支点的度数都恰为2,即T 为一条通路。
例4画出具有4、5、6、7个顶点的所有非同构的无向树。
解:4个顶点的非同构的无向树有两棵,如图 21(a),(b)所示; 5个顶点的非同构的无向树有3棵,如图21(c),(d),(e)所示。
(a ) (b) (c) (d)(e)图2 6个顶点的非同构的无向树有6棵,如图3所示图37个顶点的非同构的无向树有11棵,如图4所示。
所画出的树具有6条边,因而七个顶点的度数之和应为 12。
由 于每个顶点的度数均大于等于 1,因而可产生以下七种度数序列 (d 1,d 2,L ,d 7):(1)1111116;(2)1111125;(3)1111134 ;(4)1111224 ;(5)1111233 ;(6) 1112223; (7) 1122222。
又T 除两个顶点度数为p deg(v)i 1在(1)中只有一个星形图,因而只能产生1棵树h。
在(2), (3)中有两个星形图,因而也只能各产生1棵非同构的树,分别设为T2J3。
在(4),(5)中有三个星形图,但三个星形图是各有两个是同构的,因而各可产生两棵非同构的树,分别设为T4,T5和T6,T y。
在(6)中,有四个星形图,有三个是同构的,考虑到不同的排列情况,共可产生三棵非同构的树,设为T8,T9,T10。
在(7)中,有五个星形图,都是同构的,因而可产生1棵树,设为T11。
七个顶点的所有非同构的树T1 : T11如图2所示。
T7 T8 T9 T1o 「1图4例5设无向图G是由k(k 2)棵树构成的森林,至少在G中添加多少条边才能使G成为一棵树?解:设G中的k个连通分支为:TJ丄,T<,V i T i,i 1,2丄,k。
在G 中添加边{V i, V i 1},i 1,2丄,k 1,设所得新图为T,则T连通且无回路,因而T为树。
故所加边的条数k 1是使得G为树的最小数目。
例6证明:任意一棵非平凡树都是偶图分析:若考虑一下数据结构中树(即有向树)的定义,则可以很简单地将树中的顶点按层次分类,偶数层顶点归于顶点集V o,奇数层顶点归于顶点集V1,图G中每条边的端点一个属于V。
,另一个属于V1,而不可能存在关联同一个顶点集的边。
同理,对于无向树,可以从任何一个顶点V出发,给该树的顶点标记奇偶性,例如,v标记0,与v 相邻的顶点标记1,再给与标记为1的所有相邻的顶点标记0,依次类推,直到把所有的顶点标记完为止。
最后,根据树的性质证明,任何边只可能关联V1 (标记为1的顶点集)和V o (标记为0的顶点集)之间的顶点。
证1从任何一个顶点V出发,给该树的顶点做标记,v标记0,与V相邻的顶点标记1,然后再给与标记为1的所有顶点相邻的顶点标记 0 ,……,依次类推,直到把所有的顶点标记完为止。
下面证明:对于任何边只能关联V i (标记为1的顶点集)和V o (标 记为0的顶点集)之间的顶点。
不妨假设,若某条边e 关联V 1中的两个顶点,设为V 1和V 2,又因为 根据上述的标记法则,有V 1到v 的路R 和V 2到v 的路P 2。
设R 与P 2离w 和 v 2最近的顶点为u ,所以,树中存在回路:wRuP z V z evi ,与树中无回路 的性质矛盾。
所以,任意边只能关联V 1 (标记为1的顶点集)和V o (标 记为0的顶点集)之间的顶点。
所以,任意一棵非平凡树都是偶图。
证2设T 是任一棵非平凡树,则T 无回路,即T 中所有回路长都 是零。
而零是偶数,故由偶图的判定定理可知 T 是偶图。
例7 (1) 一棵无向树有n 个度数为i 的顶点,i 1,2,L ,k 。
n 2,匕丄,n k 均 为已知数,问n 1应为多少?(2)在(1)中,若n r (3 r k )未知,n j (j r )均为已知数,问n 「 应为多少?k解:(1)设T 为有p 个顶点,q 条边无向树,则q p 1 , p ni 1由握手定理: p p degv i 2q ,有degv iki 2q 2p 2,即 i 1 i 1 i 1k ki 1in i 2p 2 2 n i i 1 2 o由式①可知: k k kin i2 m 2 (i 2m 2 i 2 i 2i 2 (2)对于r 3,由①可知:n r(2 i )门匚 2 or 2 i 1 i r 例8证明:任一非平凡树最长路的两个端点都是树叶。
证:设T 为一棵非平凡的无向树,L V 1V 2L V k 为T 中最长的路,若 端点v 1和v k 中至少有一个不是树叶,不妨设 v k 不是树叶,即有 deg (vj 2,则V k 除与L 上的顶点V k 1相邻外,必存在v k 1与V k 相邻,而V k 1 不在 L 上,否则将产生回路。
于是 v 1L v k v k 1仍为 T 的一条比 L 更长的路, 这与 L 为最长的路矛盾。
故 v k 必为树叶。
同理,v1 也是树叶。
例9设无向图G中有p个顶点,q 1条边,则G为连通图当且仅当G中无回路。
证:必要性:因为G 中有p 个顶点,边数q p 1,又因为G 是连通的,由定理可知G 为树,因而G 中无回路。
充分性:因为G 中无回路,又边数q p 1,由定理可知G 为树,所以G 是连通的。
例10设G是一个(p,g)图,证明:若g p,则G中必有回路。
证:(1)设G 是连通的,则若G中无回路,则G是树,故q P 1与q p矛盾。
故G 中必有回路。
(2)设G 不连通,则G 中有k(k 2) 个分支,G1,G2,L ,G k 。
若G中无回路,则G的各个分支G(i 1,2,L ,k)中也无回路,于是各个分支都是树,所以有:q 口 1 ,i 1,2, L ,k。
相加得:q p k(k 2) 与q p矛盾,故G中必有回路。
综上所述,图G 中必有回路。
p例11设d1,d2,L ,d p是p个正整数,p 2,且 d 2p 2。
证明存在一棵顶点度数为d1,d2,L , d p 的树。
i 1证:对顶点p 进行归纳证明。
当p 2时,d1 d2 2 2 2 2,则d1 d? 1,故以d,?为度数的树存在,即为一条边。
p1设对任意p 1 个正整数d1, d2,L , d p 1 ,只要d i 2( p 1) 2 ,则存i1在一棵顶点度数为d1,d2,L , d p 1 的树。
p对p 个正整数d1',d2',L ,d'p,若有d i' 2 p 2 ,则d1',d2',L ,d'p中必有i1一个数为1,必有一个数大于等于2;不妨设d1' 1,d'p 2,因此对p 1p1个正整数d2' , d3' ,L ,d p'1,d'p 1,有d i'(d'p 1) 2( p 1) 2 ,故存在一棵顶i2 点度数为d2,d3,L ,d p 1,d p 1的树T。
设T中u的度数为d p 1,在T'中增加一个顶点v及边{u,v},得到一个图T ,则T为树。
又T的顶点度数为d ;d,L ,d p ,故由归纳法知原命题成立例题例1 G 的一条边e 不包含在G 的任一回路中当且仅当e 是G 的桥。
分析:这个题给出了判断桥的充要条件,应该记住。
证:必要性:设e 是连通图G 的桥,e 关联的两个顶点是u 和v 。
若e 包含在G 的一个回路中,那么除边e uv 外还有一条分别以u 和v 为端点的路,所以删去边e 后,G 仍是连通的,这与e 是桥相矛盾。
充分性:若边e 不包含在G 的任意回路中,则连接顶点u 和v 只有 边e ,而不会有其它连接u 和v 的路。
因为若连接u 和v 还有不同于边e 的路,此路与边e 就组成了一条包含边e 的回路,从而导致矛盾。
所 以,删去边e 后,u 和v 就不连通了,故边e 是桥。
例2设G 是连通图,满足下面条件之一的边应具有什么性质 ?(1) 在G 的任何生成树中;(2) 不在G 的任何生成树中。
解:(1)在G 的任何生成树中的边应为G 中的桥。
(2)不在G 的任何生成树中的边应为G 中的环。
例3非平凡无向连通图G 是树当且仅当的G 的每条边都是桥。
证:必要性:若T 中存在边e VM 不是桥,则G e 仍连通,因而 Vj 之间必另有一条(不通过e )的路。
设此路为:v V ii e ji V iz/L 即M V j , 于是G 中有回路V j e jM2e j2L V j ev ,这与G 是树矛盾,故G 的每条边都是 桥。
充分性:只要证明G 中无回路即可。
若G 中有回路C ,则C 中任何边都不是桥,与题设中每条边都是 桥矛盾。
例4图1给出的带权图表示7个城市a,b,c,d,e,仁g 及架起城市间直接 通信线路的预测造价,试给出一个设计方案使得各城市间能够通信且 总造价最小,要求计算出最小总造价。
