高频电子线路_张肃文_第5版课件__第8章
合集下载
高频电子线路 第五版 张肃文主编 学习课件(上)

2 ) 3)并联回路谐振时的谐振电阻为Rp,有:
R
p
L I S , V 与 I S同 相 , 且 达 到 最 大 值 。 CR
=
4)
ωpL R = Q p为并联振荡回路品质因数 定义: = ω pC R 因此,R p可进一步表示为: w 2 L2 1 1 L Rp = = p = Q p wp L = Q p = CR R w p C Rw 2 C 2 p Qp = Rp = R p wpC wp L
由于谐振时Z为实数,故上式必须为实数,因而分母中虚 部和分子中虚部必须相抵消。故:
ωpL R 1 = ωp L ωp RC R
进一步解得
ωp =
1 R2 2 LC L
3.2 并联谐振回路 3、品质因数:
Qp = ωp L R =
第三章 选频网络
ωp L 1 定义: = R = Q p为并联振荡回路品质因 数 R ωp C
3.1 串联谐振回路
Q=
QL =
第三章 选频网络
= Qo
ωo L
R
ω0 L R + RS + R L
可见Q L < Q
结论: ① Rs+RL使回路Q值降低,从而使谐振曲线变钝。 ②串联谐振回路通常适用于信号源内阻Rs很小(恒压 源)和负载电阻RL也不大的情况。
3.2 并联谐振回路
第三章 选频网络
L ρ = , ρ为谐振电路的特性阻抗,ρ = C R L C
1 L 1 = LC R R
QP =
ωp L
R
=
Rp
I CP = V0
I LP
1 1 = jωp CV0 = jωp CI S Q P = jQ P I S jωp C ωP C I Q ω L = V0 R + jωP L = V0 jωP L = S P P = jQ P I S jω P L
高频电子线路课件第

主要教材
高频电子线路
高等教育出版社 张肃文主编
华侨大学IC设计中心
高频电子线路学习指导与题解
高等教育出版社 张肃文主编
高频通信电子Βιβλιοθήκη 路天津理工大学 高频电子线路教研组编
教辅参考资料
华侨大学IC设计中心
1. 沈琴 非线性电子线路 高等教育出版社 2004年 2. 谢嘉奎 电子线路-非线性部分高等教育出版 2000年 3. 董在望 通信电路原理 高等教育出版 2002年 4. 张肃文 高频电子线路 高等教育出版社 1993年 5. 张凤言 电子线路基础 高等教育出版 1995年 6.高吉祥 高频电子线路 电子工业出版社 2005年 7.曾兴雯 高频电子线路 西安电子科技大学出版社 2000
无线电通信发展史
华侨大学IC设计中心
早期萌发:
古代的烽火 近代的旗语 19世纪电 磁学理论 1864麦克斯韦 电报(1837莫尔斯) 电磁场方程 电话(1876贝尔) 1887赫兹证明 电磁波的 存在
电磁波 传送信息
无线电 通信 无线电通信 实用阶段
马可尼 1895年首次百米距离通信 (意) 1901年首次横渡大西洋通信 发送设备:火花发射机、电弧发生器等 接收设备:粉末检波器
高频电子线路与无线通信系统
华侨大学IC设计中心
电信系统:传送光或电信号的系统 无线通信系统:以无线介质传送光或电信号的系统。
高频电路是通信系统, 特别是无线通信系统的基础, 是无线通信设备的重要组成部分。 各种不同类型的通信系统, 其系统组成和设备的复 杂程度都有很大不同。但是组成设备的基本电路 及其原理都是相同的, 遵从同样的规律。 本课程将 以模拟通信为重点来研究这些基本电路, 认识其规 律。 这些电路和规律完全可以推广应用到其它类 型的通信系统。
高频电子线路
高等教育出版社 张肃文主编
华侨大学IC设计中心
高频电子线路学习指导与题解
高等教育出版社 张肃文主编
高频通信电子Βιβλιοθήκη 路天津理工大学 高频电子线路教研组编
教辅参考资料
华侨大学IC设计中心
1. 沈琴 非线性电子线路 高等教育出版社 2004年 2. 谢嘉奎 电子线路-非线性部分高等教育出版 2000年 3. 董在望 通信电路原理 高等教育出版 2002年 4. 张肃文 高频电子线路 高等教育出版社 1993年 5. 张凤言 电子线路基础 高等教育出版 1995年 6.高吉祥 高频电子线路 电子工业出版社 2005年 7.曾兴雯 高频电子线路 西安电子科技大学出版社 2000
无线电通信发展史
华侨大学IC设计中心
早期萌发:
古代的烽火 近代的旗语 19世纪电 磁学理论 1864麦克斯韦 电报(1837莫尔斯) 电磁场方程 电话(1876贝尔) 1887赫兹证明 电磁波的 存在
电磁波 传送信息
无线电 通信 无线电通信 实用阶段
马可尼 1895年首次百米距离通信 (意) 1901年首次横渡大西洋通信 发送设备:火花发射机、电弧发生器等 接收设备:粉末检波器
高频电子线路与无线通信系统
华侨大学IC设计中心
电信系统:传送光或电信号的系统 无线通信系统:以无线介质传送光或电信号的系统。
高频电路是通信系统, 特别是无线通信系统的基础, 是无线通信设备的重要组成部分。 各种不同类型的通信系统, 其系统组成和设备的复 杂程度都有很大不同。但是组成设备的基本电路 及其原理都是相同的, 遵从同样的规律。 本课程将 以模拟通信为重点来研究这些基本电路, 认识其规 律。 这些电路和规律完全可以推广应用到其它类 型的通信系统。
高频电子线路(第五版)课件:锁相技术及频率合成

锁相技术及频率合成
图8.3 常用正弦鉴相器模型
锁相技术及频率合成
锁相技术及频率合成 在同频率上对两个信号的相位进行比较,可得输入信号
ui(t)的总相
式中,φi(t)是以ωrt 为参考的输入信号瞬时相位;Δωi 称为环路 的固有频差,又称起始 频差。
锁相技术及频率合成
锁相技术及频率合成
图8.4 正弦鉴相器的鉴相特性及其电路模型
锁相技术及频率合成
图8.13 一阶锁相环路的相图
锁相技术及频率合成
由图8.13可以看出,环路并不是对任意大小的固有频差 Δωi 都能进行捕捉锁定的。当 Δωi >A= AdA0 时,相轨迹与横 轴没有交点,即没有平衡点,环路失锁,如图8.13(b)所 示,这时 相点总是向右移动(若 Δωi <-A=- AdA0,则相点总是向左移动)。 当| Δωi |≤ AdA0时,相轨迹与横轴有交点,环路可以进入锁定状 态。由图8.13(a)可以看出,当| Δωi |≤ AdA0 时,相轨迹与横轴有 两个交点,环路可以进行捕捉锁定。
锁相技术及频率合成
当环路未加输入信号ui(t)时,VCO 上没有控制电压,它的 振荡频率为ωr。若将频率 ωi 恒定的输入信号加到环路上去, 固有频差(起始频差)Δ ωi = ωi - ωr,因而在接入ui(t)的 瞬间,加 到鉴相器的两个信号的瞬时相位差
锁相技术及频率合成
下面分三种情况进行讨论: (1)Δωi(t)较小,即 VCO 的固有振荡频率ωr 与输入信号频 率ωi 相差较小。 (2)Δωi较大,即ωr与ωi相差较大,使 Δωi超出环路滤波器 的通频带,但仍小于捕捉 带 Δωp。
锁相技术及频率合成 压控振荡器的输出反馈到鉴相器上,对鉴相器输出误差
高频电子线路_张肃文_第5版课件__第3章讲解

宽带非谐振放大器
有源器件 谐振回路
宽带非谐 振放大器
滤波器
3.1 概 述
高频小信号放大器的主要质量指标
1) 增益:(放大系数)
电压增益: Av
Vo Vi
功率增益: Ap
Po Pi
分贝表示: Av
20 log Vo Vi
2) 通频带:
Ap
10 log
Po Pi
3.1 概 述
高频小信号放大器的主要质量指标
不稳定状态有增益变化,中心频率偏移,通频带变窄,谐 振曲线变形,极端情况是放大器自激(主要由晶体管内反馈引 起),使放大器完全不能工作。
3.1 概 述
高频小信号放大器的主要质量指标
4) 工作稳定性:指放大器的工作状态(直流偏置)、晶体管 参数、电路元件参数等发生可能的变化时,放大器的主要特 性的稳定。
• Consider Eq. [5], for example; if we let V2 be zero, then we see that Y11 must be given by the ratio of I1 to V1.
• We therefore describe Y11 as the admittance measured at the input terminals with the output terminals short-circuited (V2 = 0).
• Admittance, conductance, and susceptance are all measured in siemens.
Admittance
• The equivalent admittance of a network consisting of a number of parallel branches is the sum of the admittances of the individual branches.
高频电子线路_张肃文_第5版课件__第8章

调频波数学表达式 (相位表达式)
a(t ) V0 cos(0t kf v (t )dt 0 )
0
t
瞬时频率 (t ) 0 kfv (t ) 瞬时相位
(t ) [0 kfv (t )]dt 0 0t kf v (t )dt 0 0
鉴频跨导
鉴频灵敏度 鉴频器的指标 鉴频频带宽度 寄生调幅抑制能力
失真和稳定性
End
• 鉴频器输出电压 与输入调频波的 瞬时频偏成正比, 其比例系数称为 鉴频跨导
图 10.1.2 鉴频特性曲线
8.2.1 瞬时频率与瞬时相位 8.2.2 调频波和调相波的 数学表示式
8.2.3 调频波和调相波的 频谱和频带宽度
0
t
(t )
t0
0
0
(t )
实轴
• 瞬时相角θ(t) 等于矢量在 t 时间内转过的 角度与初始相 角θ0 之和
调频
设调制信号为:vΩ (t), 载波信号为: v ω (t ) V0 cos(0t 0 )
∵瞬时频率与调制信号呈线性 关系,∴瞬时频率为: ω0是未调制时的载波中心频率;
调相波数学(相位)表达式
a(t ) V0 cos(0t kP v (t ) 0 )
已调相信号 a(t ) V0 cos(0t kpV cosΩt 0 )
V0 cos(0t mp cosΩt 0 )
dv (t ) 调相波频偏: Dp kp dt max
a(t ) V0{cos0t [ J 0 (mf ) 2 J 2 n (mf ) cos 2nt ]
n 1
sin 0t [2 J 2 n 1 (mf ) sin(2n 1)Ωt]}
高频电子线路课件:第一章

2f 0.7 Q0 f0
2f 0.7 BW0.7
BW0.7 BW0.1
f0 通频带:BW0.7 0.7 Q0
f0 1 1 0.7 1 BW0.7 N ( 0.7 ) Q0 2 1 0.7
BW0.1 0.1 矩形系数:K 0.1 BW0.7 0.7 1 1 N ( 0.1 ) 2 0.1 10 K 0.1 10 10 1 0.1
若 Ig 0 则输出电压相位: arctan
V0 1 归一化谐振曲线:N ( ) 2 V0 m 1
电路参数: 与串联谐振回路完全一样!
f0 通频带: BW0.7 Q0
2
矩形系数:K 0.1 10
2
N ( )
1
2
1 幅频特性
arctan
第一章 高频小信号放大器
一、概述 高频宽带放大器 高频窄带放大器 高频窄带放大器作用:
从所接收的众多电信号中,选出有用信 号并加以放大(或对已调制信号放大),而 对其它无用信号、干扰与噪声进行抑制,以 提高信号的质量和抗干扰能力。
应用:广播、电视、 通信、雷达、测量等 设备中。
主要性能指标: 增益(电压增益、功率增益) 通频带
互感耦合谐振 耦合系数:
电容耦合谐振
耦合系数:
Cm k (C1 Cm )(C2 Cm )
k
M ( L1 M )( L2 M )
Cm为耦合电容
为了简化分析和计算,假设初次级 回路完全一样,即: L L L C1 C2 C Rp1 Rp2 Rp
1 2
Cm C
R Rp
2f 0.7 BW0.7
BW0.7 BW0.1
f0 通频带:BW0.7 0.7 Q0
f0 1 1 0.7 1 BW0.7 N ( 0.7 ) Q0 2 1 0.7
BW0.1 0.1 矩形系数:K 0.1 BW0.7 0.7 1 1 N ( 0.1 ) 2 0.1 10 K 0.1 10 10 1 0.1
若 Ig 0 则输出电压相位: arctan
V0 1 归一化谐振曲线:N ( ) 2 V0 m 1
电路参数: 与串联谐振回路完全一样!
f0 通频带: BW0.7 Q0
2
矩形系数:K 0.1 10
2
N ( )
1
2
1 幅频特性
arctan
第一章 高频小信号放大器
一、概述 高频宽带放大器 高频窄带放大器 高频窄带放大器作用:
从所接收的众多电信号中,选出有用信 号并加以放大(或对已调制信号放大),而 对其它无用信号、干扰与噪声进行抑制,以 提高信号的质量和抗干扰能力。
应用:广播、电视、 通信、雷达、测量等 设备中。
主要性能指标: 增益(电压增益、功率增益) 通频带
互感耦合谐振 耦合系数:
电容耦合谐振
耦合系数:
Cm k (C1 Cm )(C2 Cm )
k
M ( L1 M )( L2 M )
Cm为耦合电容
为了简化分析和计算,假设初次级 回路完全一样,即: L L L C1 C2 C Rp1 Rp2 Rp
1 2
Cm C
R Rp
高频电子线路PPT课件

第5页/共27页
6.2 二极管大信号包络检波器
ZL
1. 大信号包络检波的工作原理
(1) 电路组成
+ + VD
ui ui
R C
由输入回路、二极管VD和RC低通滤波器组成。 - -
RC低通滤波电路有两个作用:
① 对低频调制信号uΩ来说,电容C的容抗
+ ui
1 R ,电容C相当于开路,电阻R就作为 -
3
uo
(t
)
uo uD
θ
Uim
代入有上:u式o (可t) 得 U:im
(1 3
m3a cos
t ) 3
c3oπsrd
U im
cos
maU im
cos
cos
t
UDC gUdRm cos t R
可见 uo (t ) 有两部分:直流分量 :U DC Uim cos 低频调制分量:u (t ) Um cos t
显(5然) ,底RL部越切小,割U失R分真压值越大,底部切割失真越容易产生;另外,ma
值 越越 小1连大 ,) 接原, 底如因调 部图:幅 切所一波割示般包失,为络真为了的也能取振越有出幅易效低产m地a频生U传i调。m越输制大检信,波号调后,幅的检波低波包频器络调与的制后负信级峰号低值,频U要放im求大(1:-器m的a)
☺调幅解调的分类
振幅调制
AM调制 DSB调制 SSB调制
包络检波 解调
同步检波
第2页/共27页
峰值包络检波 平均包络检波 叠加型同步检波 乘积型同步检波
☺调幅解调的方法
1. 包络检波
调幅波
t 调幅波频谱
非线形电路
ωc-Ω ωc ωc+Ω ω
6.2 二极管大信号包络检波器
ZL
1. 大信号包络检波的工作原理
(1) 电路组成
+ + VD
ui ui
R C
由输入回路、二极管VD和RC低通滤波器组成。 - -
RC低通滤波电路有两个作用:
① 对低频调制信号uΩ来说,电容C的容抗
+ ui
1 R ,电容C相当于开路,电阻R就作为 -
3
uo
(t
)
uo uD
θ
Uim
代入有上:u式o (可t) 得 U:im
(1 3
m3a cos
t ) 3
c3oπsrd
U im
cos
maU im
cos
cos
t
UDC gUdRm cos t R
可见 uo (t ) 有两部分:直流分量 :U DC Uim cos 低频调制分量:u (t ) Um cos t
显(5然) ,底RL部越切小,割U失R分真压值越大,底部切割失真越容易产生;另外,ma
值 越越 小1连大 ,) 接原, 底如因调 部图:幅 切所一波割示般包失,为络真为了的也能取振越有出幅易效低产m地a频生U传i调。m越输制大检信,波号调后,幅的检波低波包频器络调与的制后负信级峰号低值,频U要放im求大(1:-器m的a)
☺调幅解调的分类
振幅调制
AM调制 DSB调制 SSB调制
包络检波 解调
同步检波
第2页/共27页
峰值包络检波 平均包络检波 叠加型同步检波 乘积型同步检波
☺调幅解调的方法
1. 包络检波
调幅波
t 调幅波频谱
非线形电路
ωc-Ω ωc ωc+Ω ω
高频电子线路 张肃文 第5版课件第7章

检波
信号大小
工作特点
7.2.1
调幅波的数学表示式与频谱
7.2.2
调幅波中的功率关系
• 调幅波是载波振幅按照调制信号大小成线性变化的 高频振荡。 • 由于载波频率不变,所以波形疏密程度均匀一致。 • 通常传送信号(语音,音乐等)的波形复杂,包含很 多频率成分,但这些复杂波形都可以分解成许多正 弦波分量的叠加。 • 因此,为了简化分析,我们总是认为调制信号为正 弦波。 • 对(非)正弦波调制,调幅波包络线是与(非)正 弦调制信号完全相似。
2. 双边带信号 在调制过程中,将载波抑制就形成了抑制载波双边带 信号,简称双边带信号。它可用载波与调制信号相乘得到, 其表示式为
uDSB (t ) k f (t ) uc
在单一正弦信号uΩ=UΩcosΩt调制时,
uDSB (t ) kUc U cost cosct g (t ) cosct
输出没有载波分量只有边带和调制信号这些电路都要求二极管特性完全相同实际上是做不到的会加入平衡装置741742产生双边带图图741741斩波调幅器方框图斩波调幅器方框图coscos斩波调幅是将调制信号通过一个受载波频率控制的的开关电路斩波电路使调制信号输出波形被斩成周期为2载波周期的脉冲输出波形就包含频率成分及其谐波开关函数与载波周期相同图图742742斩波调幅器工作图解斩波调幅器工作图解coscos图图744744二极管二极管电桥斩电桥斩波调幅波调幅电路电路可产生可产生dsbdsbscsc如图742图图743743平衡斩波调幅及其图解平衡斩波调幅及其图解前面使用的是不对称开关电路的斩破调幅实际上更多时候使用对称开关电路形成平衡斩波调幅
u S SB(t) U 0
fc+F
t
单音调制的SSB信号波形
高频电子线路课件

第1章 绪 论
各部分作用: 各部分作用: (1)振荡器 ) 的高频振荡信号,几十千赫以上。 产生 fosc 的高频振荡信号,几十千赫以上。
调幅广播发射机的组成
(2)高频放大器 ) 多级小信号谐振放大器, 放大振荡信号, 多级小信号谐振放大器 , 放大振荡信号 , 使频率倍增 并提供足够大的载波功率。 至 fc,并提供足够大的载波功率。 (3)调制信号放大器 ) 多级放大器,前几级为小信号放大器, 多级放大器 , 前几级为小信号放大器 , 放大微音器的 电信号;后几级为功放,提供功率足够的调制信号。 电信号;后几级为功放,提供功率足够的调制信号。 (4)振幅调制器 ) 实现调幅功能, 实现调幅功能 , 将输入的载波信号和调制信号变换为 所需的调幅波信号,并加到天线上。 所需的调幅波信号,并加到天线上。
18
第1章 绪 论
1.1 无线通信系统概述
一、无线通信系统的组成
发送设备
接收设备
超外差形式
19
第1章 绪 论
1.1 无线通信系统概述
一、无线通信系统的组成 图中虚线以上部分为发送设备 发信机 图中虚线以上部分为发送设备(发信机 , 发送设备 发信机), 虚线以下部分为接收设备 收信机), 虚线以下部分为接收设备(收信机 , 接收设备 收信机 天线及天线开关为收发共用设备。 天线及天线开关为收发共用设备。 为收发共用设备 信道为自由空间。 信道为自由空间。 为自由空间 话筒和扬声器属于通信的终端设备,分别为信源和 话筒和扬声器属于通信的终端设备,分别为信源和 属于通信的终端设备 信宿。 信宿。 接收机一般都采用超外差的形式。 接收机一般都采用超外差的形式。 一般都采用超外差的形式
2
第1章 绪 论
参考书
上海交通大学张肃文高频课件

cj u
PN结呈电容效应: PN结正偏时,扩散电容cD起主要作用; PN结反偏时,势垒电容(结电容) cj起主要 作用。 在PN结反偏时经过特殊处理使cj有较大变 化范围—变容二极管 2.晶体管 场效应管 高频小功率管:高增益,低噪声,工作频率可达 几GHz。 高频大功率管:高增益,较大输出功率。
第一章 绪 论
§ 1.1 无线通信系统概述 一.无线通信系统的组成 1.通信:传输电信号。即信息的传输过程。 传输—指远距离。 信号—指声音、图像、文字等。 发展历史—从峰火台到现代通信。 通信系统:实现信息传递的系统。 2.组成:
信源
发送设备
信道
接收设备
信舍
发送设备:产生适合信道传输的信号。 信道:传递的媒介。有有线、无线、光纤之分。 接收设备:还原出原信号。
4.传播特性 指无线电信号的传播方式、传播距离和 传播特点。 无线通信的传输媒质(信道)是自由空间。 无线电信号经天线发射,由于能量被扩散、 吸收、反射、散射等现象,到接收天线时 强度大大衰减,为有效传输要选择传播方式, 传播方式的选择主要依据无线电信号的频率。 绕射传播(地波): 靠电磁波绕射传播。 长、中、短波特别是长、中波以地波传播
LR R R
LR—引线电感; cR —分布电容 LR cR越小,高频特性越好, 高频特性与制作电阻的材料、封装形式和 尺寸大小有关。
金属膜电阻比碳膜电阻高频特性好; 碳膜电阻比线绕电阻高频特性好; 表面贴装电阻比引线电阻高频特性好; 小尺寸电阻比大尺寸电阻高频特性好。 Rc 2.高频电容
c Lc c
L r c c Rp Lp
Q = ω 0L/r≫1, Rp= Rs(1+ Q2) = r (1+ Q2) Lp= L(1+ 1/Q2) ≈ L
PN结呈电容效应: PN结正偏时,扩散电容cD起主要作用; PN结反偏时,势垒电容(结电容) cj起主要 作用。 在PN结反偏时经过特殊处理使cj有较大变 化范围—变容二极管 2.晶体管 场效应管 高频小功率管:高增益,低噪声,工作频率可达 几GHz。 高频大功率管:高增益,较大输出功率。
第一章 绪 论
§ 1.1 无线通信系统概述 一.无线通信系统的组成 1.通信:传输电信号。即信息的传输过程。 传输—指远距离。 信号—指声音、图像、文字等。 发展历史—从峰火台到现代通信。 通信系统:实现信息传递的系统。 2.组成:
信源
发送设备
信道
接收设备
信舍
发送设备:产生适合信道传输的信号。 信道:传递的媒介。有有线、无线、光纤之分。 接收设备:还原出原信号。
4.传播特性 指无线电信号的传播方式、传播距离和 传播特点。 无线通信的传输媒质(信道)是自由空间。 无线电信号经天线发射,由于能量被扩散、 吸收、反射、散射等现象,到接收天线时 强度大大衰减,为有效传输要选择传播方式, 传播方式的选择主要依据无线电信号的频率。 绕射传播(地波): 靠电磁波绕射传播。 长、中、短波特别是长、中波以地波传播
LR R R
LR—引线电感; cR —分布电容 LR cR越小,高频特性越好, 高频特性与制作电阻的材料、封装形式和 尺寸大小有关。
金属膜电阻比碳膜电阻高频特性好; 碳膜电阻比线绕电阻高频特性好; 表面贴装电阻比引线电阻高频特性好; 小尺寸电阻比大尺寸电阻高频特性好。 Rc 2.高频电容
c Lc c
L r c c Rp Lp
Q = ω 0L/r≫1, Rp= Rs(1+ Q2) = r (1+ Q2) Lp= L(1+ 1/Q2) ≈ L
高频电子线路 第五版 张肃文主编 学习课件(下)

混合π参数等效电路
γ bb′是基极电阻
γ b′e是发射结电阻 γ b′c是集电结电阻
Cb′e是发射结电容 Cb′c是集电结电容 g m vb 'e 表示晶体管放大作用的 等效电流发生器 g m 称为跨导, g m = β 0 γ b 'e = I c (mA) 26(mV ) Cb′c 将输出的交流电压反馈 一部分到输入端.可能引起自激 γ bb '在共集电极电路中引起 高频反馈,降低晶体管的电流放大 系数 β0为共射极组态晶体管的低频电流放大系数
4.1 概述 4)工作稳定性:
第四章 高频小信号放大器
指在电源电压变化或器件参数变化时,其主要特性的稳定程度。 放大器不稳定的现象有哪些? 增益变化;中心频率漂移;通频带变窄;谐振曲线变形等。 常用的放大器稳定措施有哪些? 限制每级增益;选择内反馈小的晶体管;应用中和或失 配方法等稳定措施。
4.1 概述• • Nhomakorabea4.2 晶体管高频小信号等效电路和参数 第四章 高频小信号放大器 本章采用y参数系:
I1 = yV1 + yrV2 i I2 = yf V1 + yoV2
式中:
⎡I1 ⎤ ⎡ yi 即: ⎢ ⎥ = ⎢ ⎣I2 ⎦ ⎣yf
yr ⎤⎡V1 ⎤ yo ⎥⎢V2 ⎥ ⎦⎣ ⎦
I1 yi = V1 I1 V2 I yf = 2 V1 I yo = 2 V2 yr =
混合参数等效电路是基极电阻等效电流发生器表示晶体管放大作用的mvma称为跨导可能引起自激一部分到输入端将输出的交流电压反馈系数降低晶体管的电流放大高频反馈在共集电极电路中引起42晶体管高频小信号等效电路和参数422混合参数等效电路为共射极组态晶体管的低频电流放大系数第四章高频小信号放大器cbc引起的容抗相比rbc可视为开路
《高频电子线路》课件

《高频电子线路 》PPT课件
目录
• 高频电子线路概述 • 高频电子线路基础知识 • 高频电子线路中的信号传输 • 高频电子线路中的放大器 • 高频电子线路中的滤波器 • 高频电子线路中的混频器与变频
器
01
高频电子线路概述
高频电子线路的定义与特点
总结词
高频电子线路是研究高频信号传输、处理和应用的电子线路。其特点包括信号频率高、频带宽、信号传输速度快 、信号失真小等。
02
高频电子线路基础知识
高频电子线路的基本元件
电阻器
用于限制电流,调节电 压,起到分压、限流的
作用。
电容器
用于存储电荷,实现信 号的滤波、耦合和旁路
。
电感器
用于存储磁场能量,实 现信号的滤波、选频和
延迟。
晶体管
高频电子线路中的核心 元件,用于放大和开关
信号。
高频电子线路的基本电路
01
02
03
04
混频器与变频器的应用实例
混频器的应用实例
在无线通信中,混频器常用于将信号从低频转换为高频,或者将信号从高频转 换为低频。例如,在接收机中,混频器可以将射频信号转换为中频信号,便于 后续的信号处理。
变频器的应用实例
在雷达系统中,变频器可以将发射信号的频率改变,从而实现多普勒测速或者 目标识别。在电子对抗中,变频器可以用于干扰敌方雷达或者通信系统。
传输。
音频系统中的扬声器驱动电路
02
利用音频放大器将音频信号放大后驱动扬声器,实现声音的重
放。
测量仪器中的前置放大器
03
利用电压或电流放大器将微弱信号放大后传输至后续电路,实
现信号的处理和分析。
05
高频电子线路中的滤波器
目录
• 高频电子线路概述 • 高频电子线路基础知识 • 高频电子线路中的信号传输 • 高频电子线路中的放大器 • 高频电子线路中的滤波器 • 高频电子线路中的混频器与变频
器
01
高频电子线路概述
高频电子线路的定义与特点
总结词
高频电子线路是研究高频信号传输、处理和应用的电子线路。其特点包括信号频率高、频带宽、信号传输速度快 、信号失真小等。
02
高频电子线路基础知识
高频电子线路的基本元件
电阻器
用于限制电流,调节电 压,起到分压、限流的
作用。
电容器
用于存储电荷,实现信 号的滤波、耦合和旁路
。
电感器
用于存储磁场能量,实 现信号的滤波、选频和
延迟。
晶体管
高频电子线路中的核心 元件,用于放大和开关
信号。
高频电子线路的基本电路
01
02
03
04
混频器与变频器的应用实例
混频器的应用实例
在无线通信中,混频器常用于将信号从低频转换为高频,或者将信号从高频转 换为低频。例如,在接收机中,混频器可以将射频信号转换为中频信号,便于 后续的信号处理。
变频器的应用实例
在雷达系统中,变频器可以将发射信号的频率改变,从而实现多普勒测速或者 目标识别。在电子对抗中,变频器可以用于干扰敌方雷达或者通信系统。
传输。
音频系统中的扬声器驱动电路
02
利用音频放大器将音频信号放大后驱动扬声器,实现声音的重
放。
测量仪器中的前置放大器
03
利用电压或电流放大器将微弱信号放大后传输至后续电路,实
现信号的处理和分析。
05
高频电子线路中的滤波器
高频电子线路(第五版)课件:高频电路中的元器件

高频电路中的元器件
1.晶体管混合π等效模型 在分析高频小信放大器时,首先要考虑晶体管在高频时 的等效模型。图2.19是双极型 晶体管共射小信号混合π等效 模型,它反映了晶体管中的物理过程,也是分析晶体管高频 特 性的基本等效模型。
高频电路中的元器件
图2.19 晶体管混合π等效模型
高频电路中的元器件
高频电路中的元器件
高频电路中的元器件
图2.22 晶体管共发射极电路
高频电路中的元器件
高频电路中的元器件
高频电路中的元器件
图2.23 晶体管 Y 参数等效电路
高频电路中的元器件
高频电路中的元器件
4.晶体管频率特性 在分析由高频小功率管组成的交流放大电路时,其重要 的交流特性就是电路频率特 性,也就是电路所具有的频带。 电路的频率特性与高频管频率特性有着密切的关系。尽管 在上述分析中使用等效模型的概念,但实际的电路由于三极 管频率特性的限制以及输入和 输出端电容的存在,都会引起 电路频率特性的改变。同时,为了确定电路的正常工作条件, 保证模型成立,也必须对电路进行频率分析。
高频电路中的元器件
图2.11 高通电路(微分电路)
高频电路中的元器件
2.变容二极管 在高频电路中,利用二极管的电容效应,还可以制成变容 二极管。变容二极管是利用PN 结来实现的。PN 结的电容 包括势垒电容和扩散电容两部分,变容二极管主要利用的是 势垒电容。变容二极管在正常工作时处于反偏状态,其特点 是等效电容随偏置电压变化而 变化,且此时基本上不消耗能 量,噪声小,效率高。由于变容二极管的这一特点,可以将其 用 在许多需要改变电容参数的电路中,从而构成电调谐器、自 动调谐电路、压控振荡器等 电路。
② 在实际应用中可认为串联电阻Rs 是常数,但实际上Rs 是与工作电压和工作频率 有关的函数;
高频电子线路

信 源
uΩ(t)
调 制
us(t)
功 放
uc(t)
高 频 振荡波
AM 调制器示意图
调制信号:由原始信号(声音、数据、图像)转变而 来的低频信号或视频信号,以uΩ(t)或 f (t)表示。 载波:未受调制的高频振荡信号,以uc(t)表示。 已调信号:受调制后的高频振荡波,以us(t)表示
uΩ
0
t uC
Ui (s) Us (s) Ui(s)
U o (s) K u (s) U s ( s)
K (s) K (s) K u ( s) 1 K (s) F (s) 1 T (s)
闭环电压放大倍数为Ku(s)
环路增益
U i( s ) T (s) K (s) F (s) U i (s)
2.2
高频电路中的组件
1、高频振荡(谐振)回路 1)串联谐振回路 2)并联谐振回路
2、石英晶体谐振器
1 串联谐振回路 回路阻抗为:
1 1 Z S r jL r j L jC C
回路电抗:
1 X L C
谐振频率: 0
1 LC
1.2
无线通信系统的类型
可根据不同的方法来划分: (1) 按照工作频段或传输手段 有中波通信、 短波通信、 超短波通信、 微波 通信和卫星通信等。
工作频率,主要指发射与接收的射频(RF)频率。 无线通信的一个发展方向就是开辟更高的频段。
(2) 按照通信方式
只能发或只能收
既可以发也可以收 但不能同时收发
导通角
q =360 °
c
理想效率
50% 78.5%
负 载
电阻 推挽,回路 推挽 选频回路 选频回路
高频电子线路(第五版)
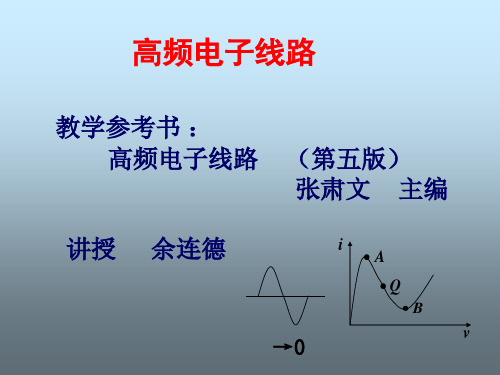
如图3.3.2
a
Vo
Y'
g ' o1
C 'o1
'
a
L1
C
2 1
Y'
L1
Gp
g 'i 2
' i2
Vo
C
' C G p
b
2 yo1 p1 yo1
p Y 'L
b
图3.3.2
图中:
2 2 2 2 g'o1 p1 go1, g'i 2 p2 gi 2 , C 'o1 p1 Co1, C 'i 2 p2 Ci 2 ,
图4.3.3
a
Ic
2 p1 g01
Gp
2 p2
gi 2
b
谐振时
A p0
Po Pi
' Gp
Pi Vi2 1 gi1
p | y | V i1 1 fe p2 g 2 2 Po Vab p2 gi 2 2 i2 G' p
2
因此
A p0 Po p12 p2 2 gi 2 | y fe |2 2 gi 2 ( A ) v0 Pi gi1 (G ' p ) 2 gi1
0
fT 1 f
2
2
1
时
则有 通常
0
fT 0 1 f
1
fT 0 f
3) 最高振荡频率 fmax
当晶体管的功率增益 AP 1 时的工作 频率--- fmax
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由于调频波和调相波的方程式相似,因此只要分析其中一 种的频谱,则对另一种也完全适用。
a(t ) V0 cos(0t mf sin Ωt) V0[cos0t cos(mf sin Ωt) sin 0t sin(mf sin Ωt)]
已调频信号
其中: cos(mf sin Ωt) J 0 (mf ) 2
(t ) 0 kfv (t )
D (t ) kfv (t )
kfvΩ (t)是瞬时频率相对于ω0的偏移,
叫瞬时频率偏移,简称频移。可表示为 Δω(t) 的最大频移,称频偏,表示为
D kf v (t ) max
t 0
调频波数学表达式 (相位 表达式)
a(t ) V0 cos(0t kf v (t )dt 0 )
4) 根据帕塞瓦尔(Parseval)定理调频波的平均功率等于各频 谱分量平均功率之和。因此,在电阻R上,调频波的平均功率 应为
V0 2 2 2 Pf [ J 0 (mf ) 2 J 2n (mf ) 2 J 2n1 (mf )] 2R n 1 n 0 2
V0 V0 2 2 [ J 0 (mf ) 2 J n (mf )] 2R 2R n 1
由于频率的变化和相位的变化都表现为总相 角的变化,因此,将调频和调相统称为调角。
因为相位是频率的积分, 故频率的变化必将 引起相位的变化, 反之亦然, 所以调频信号与调 相信号在时域特性、频谱宽度、调制与解调的原 理和实现方法等方面都有密切的联系。 角度调制与解调属于非线性频率变换, 比属 于线性频率变换的振幅调制与解调在原理和电路 实现上都要困难一些。
n 0
一、频谱
1) 单音调制时,调频波的频谱不是调制信号频谱的简单搬移, 而是由载波和无数对边带分量所组成, 它们的振幅由对应的 各阶贝塞尔函数值所确定。由教材(8.2.24)可见,奇次的上、 下边带分量振幅相等、极性相反;偶次的振幅相等、极性相 同。 2) 调制指数mf越大,具有较大振幅的边频分量就越多,见 教材图 8.2.5。这与调幅波不同,在单频信号调幅的情况下, 边频数目与调制指数无关。 3)载波分量和各边带分量的振幅均随mf变化而变化。对于某些 mf值,载频或某边频振幅为零。籍此可以测定调制指数mf。
由频偏表达式可以看出调相信号带宽随调制信号频率的升高 而增加,而调频波则不变,也把调频制叫做恒定带宽调制。
一、频谱
调制信号 v (t ) V cost
已调频信号 已调相信号
a(t ) V0 cos(0t mf sin Ωt) a(t ) V0 cos(0t mp cosΩt)
调相波数学(相位)表达式
a(t ) V0 cos(0t kP v (t ) 0 )
已调相信号 a(t ) V0 cos(0t kpV cosΩt 0 )
dv (t ) 调相波频偏: Dp kp dt max
在模拟通信方面, 调频制比调相制更加优越, 故大都采用调频制。 所以, 本章在介绍电路时, 以调频电路、 鉴频 (频率解调)电路为主题, 但由于调频信号与调相信号的内在联系, 调频可 以用调相电路间接实现,
鉴频也可以用鉴相(相位解调, 也称相位检波)电 路间接实现, 所以实际上也介绍了一些调相与鉴 相电路。
得:
D f k f V
max
• 调频波的最大相移, m k f 即调频波调制指数: f
v
0
t
(t )dt
kf V
D f
调相
以单音调制波为例 调制信号 v Ω (t ) VΩ cost 瞬时相位 (t ) 0t kpV cosΩt 0 瞬时频率 (t ) 0 kpV sin Ωt
无论调频 还是调相 调制指数 与最大频移 都满足 D m D f m f D p m p DF m F
k f V
kf V sin Ωt 0
D f kf V • 调频波的最大相移, mf 即调频波调制指数: 调相 瞬时相位 (t ) 0t kpV cosΩt 0 瞬时频率 (t ) 0 kpV sin Ωt
调频波数学(相位)表达式
a(t ) V0 cos(0t kf v (t )dt 0 )
0
t
已调频信号 a (t ) V0 cos( 0t
kf V
V0 cos(0t mf sin Ωt 0 )
调频波频偏:
sin Ωt 0 )
D kf v (t ) max
a(t ) V0{cos0t [ J 0 (mf ) 2 J 2 n (mf ) cos 2nt ]
n 1
sin 0t [2 J 2 n 1 (mf ) sin(2n 1)Ωt]}
V0 [ J 0 (mf ) cos0t 2 J 2n (mf ) cos 2nt cos0t
调频波数学表达式 (相位表达式)
a(t ) V0 cos(0t kf v (t )dt 0 )
0
t
瞬时频率 (t ) 0 kfv (t ) 瞬时相位
(t ) [0 kfv (t )]dt 0 0t kf v (t )dt 0 0
v V cosΩt
v V cosΩt
v 0 V0 cos0t
v 0 V0 cos0t
0+Dm
0–Dm
AM
FM
频谱宽度 调频波的指标
寄生调幅
抗干扰能力
载波信号 解调方式 的受控参量
解调方式 的差别
特点
用途
幅 调 度 幅 调 制 调 频 角 度 调 调 相 制 PM AM FM
n 0
J
n 1
2n
(mf ) cos 2nt
sin(mf sin t ) 2 J 2n 1 (mf ) sin(2n 1)Ωt
J n (mf ) 是以mf为参数的n阶第一类贝赛尔函数。
V0 [cos0t cos(mf sin Ωt) sin 0t sin(mf sin Ωt)]
• 调相波的最大相移, 即调相波调制指数: 得:
D p k p V
D p mp kp v (t ) max kpVΩ
以单音调制波为例 调制信号 v (t ) V cost 调频 瞬时频率 (t ) 0 kfV cosΩt
瞬时相位 (t ) 0t 调频波频偏: D f
0
t
(t )
t0
0
0
(t )
实轴
• 瞬时相角θ(t) 等于矢量在 t 时间内转过的 角度与初始相 角θ0 之和
调频
设调制信号为:vΩ (t), 载波信号为: v ω (t ) V0 cos(0t 0 )
∵瞬时频率与调制信号呈线性 关系,∴瞬时频率为: ω0是未调制时的载波中心频率;
n 1
n 0
2 J 2n 1 (mf ) sin(2n 1)t sin 0t ]
n 0
V0 {J 0 (mf ) cos0t J 2n (mf )[cos( 0 2n )t cos(0 2n )t ]}
n 1
V0 J 2n 1 (mf ){cos[0 (2n 1) ]t cos[0 (2n 1) ]t}
调频是使高频载波的瞬时频率按调制信号规律变化的一种 调制方式;调相是使高频载波的瞬时相位按调制信号规律变 化的一种调制方式。因为这两种调制都表现为高频振荡波的 总瞬时相角受到调变,故将它们统称为角度调制(简称调角) 。 d 瞬时频率 (t ) (t ) dt
瞬时相角
t t
(t ) (t )dt 0
振幅
相干解调或 频谱线性搬 频带窄 非相干解调 移频谱结构 频带利 用率高 无变化
频率
鉴频或 频谱非线性 频带宽 广播 频谱结构发 频带利 电视 频率检波 生变化属于 用不经 通信
非线性频率 济、抗 遥测 干扰性 数字 鉴相或 变换 强 通信 相位检波
相位
• 将等幅的调频信号变换成振幅 也随瞬时频率变化、既调频又 调幅的FM―AM波,就可以通 过包络检波器解调此调频信号 • 用此原理构成的鉴频器称为振 幅鉴频器 图 10.1.1 利用波形变换电路进行鉴频
0
t
t
瞬时相位偏移 相位偏移 相移
D f (t ) kf v (t )dt;
0
t
最大相移Δθf 也称调频波调制指数 mf
D f k f
v
0
t
(t )dt
max
mf
设调制信号为vΩ (t),载波信号 v ω (t ) V0 cos(0t 0 ) 调相 瞬时相位与调制信号呈线性 (t) 0t kpv (t) 0 ω0t+θ 0是未调制时的载波相位;kpvΩ (t)是瞬时相位相对 于ω0t+θ 0的偏移,叫瞬时相位偏移,简称相位偏移或相移。可 表示为 D (t ) kpv (t ) Δθ(t) 最大相移,也称调制指数,表示为
dv (t ) Dp (t ) k p dt
最大频移,即频偏:
dv (t ) Dp kp dt max
以单音调制波为例 调制信号 v Ω (t ) VΩ cost
调频
瞬时频率 (t ) 0 kfV cosΩt 瞬时相位 (t ) 0t kf V sin Ωt 0
D kp v (t ) max mp
mp为调相波调制指数
调相波数学(相位)表达式 瞬时频率 (t ) 调相波的频移:
