计算机图形学实验Koch曲线

合集下载

计算机图形学实验报告(分形图)

实验六：分形图的生成班级11信计2班学号20110502078 姓名刘昱丞分数一、实验目的理解分形图生成的基本原理，掌握几种常见的分形图生成算法，利用TurboC实现Koch 曲线和可以无穷放大的Mandelbrot Set (曼德布洛特集)生成算法。

二、实验内容1.、利用Koch 曲线生成规则，在屏幕上生成一段Koch 曲线。

2/、利用Mandelbrot Set 生成规则，在屏幕上生成可以无穷放大的Mandelbrot Set (曼德布洛特集)三、实验步骤（1）预习教材关于Koch 曲线和可以无穷放大的Mandelbrot Set (曼德布洛特集)的生成原理。

（2）仿照教材关于Koch 曲线和可以无穷放大的Mandelbrot Set (曼德布洛特集)生成算法生成算法，使用TurboC实现该算法。

（3）调试、编译、运行程序。

四、实验要求在下次实验时提交本次试验的实验报告（实验报告包括实验目的、实验内容、实验实现过程、源程序、实验结果、实验体会）。

五、实验过程( 1 ) Koch 曲线的生成规则它的构造是：迭代初始把原线段去掉中间的三分之一，代之以底边在被去线段上的等边三角形的两腰；以后每一步的迭代都是这样的重复。

从以上过程可以清楚地看出，Koch曲线（其它分形集也是如此）可以由简单的图，称为生成元，迭代产生。

在这里，Koch曲线的生成元是：六、实验代码1/、Koch曲线源程序：#include <stdio.h>#include <stdlib.h>#include <math.h>#include <conio.h>#include <graphics.h>#define rad 0.0174532925#define NUMBER 24koch(ax,ay,bx,by)int ax,ay,bx,by;{ float cx,cy,ex,ey,dx,dy,arf,le,c;c=1000; /*30000,20000,10000,5000,1000 tiao jie ci shu */if ((bx-ax)*(bx-ax)+(by-ay)*(by-ay)<c)line(ax,ay,bx,by);else{cx=ax+(bx-ax)/3;cy=ay+(by-ay)/3;ex=bx-(bx-ax)/3;ey=by-(by-ay)/3;koch((int)(ax),(int)(ay),(int)(cx),(int)(cy)); /* koch(ax,ay,cx,cy); */ koch((int)(ex),(int)(ey),(int)(bx),(int)(by));le=sqrt((ex-cx)*(ex-cx)+(ey-cy)*(ey-cy)); /* koch(ex,ey,bx,by); */ arf=atan((ey-cy)/(ex-cx));if((arf>=0 &&(ex-cx)<0)||(arf<=0 &&(ex-cx)<0))arf=arf+3.1415;dy=cy+sin(arf+3.1415/3)*le;dx=cx+cos(arf+3.1415/3)*le;koch((int)(cx),(int)(cy),(int)(dx),(int)(dy)); /*koch(cx,cy,dx,dy);*/ koch((int)(dx),(int)(dy),(int)(ex),(int)(ey)); /* koch(dx,dy,ex,ey); */ }}main(){float xa1,xb1,ya1,yb1;float xa,xb,ya,yb;float dex,dey,dx,dy;float x,y,s1,s2;int steps,k;int gdriver=DETECT,gmode;initgraph(&gdriver,&gmode,"C:\\JMSOFT\\DRV");cleardevice();setbkcolor(BLUE);/* line(400,400,600.4,540.6); */settextstyle(1,0,3);outtextxy(100,100,"Shijiazhuang University");/* koch(340,150,100,150) ; */koch(100,300,500,300) ;getch();closegraph();return 0;}输出结果为：2.、可以无穷放大的Mandelbrot Set (曼德布洛特集）源程序：#include <graphics.h>#include <conio.h>// 定义常量#define ITERATIONS 1000 // 迭代次数，越高，图像越精细#define MAXCOLOR 64 // 颜色数/////////////////////////////////////////////////// 定义复数及乘、加运算/////////////////////////////////////////////////// 定义复数struct COMPLEX{double re;double im;};// 定义复数“乘”运算COMPLEX operator * (COMPLEX a, COMPLEX b){COMPLEX c;c.re = a.re * b.re - a.im * b.im;c.im = a.im * b.re + a.re * b.im;return c;}// 定义复数“加”运算COMPLEX operator + (COMPLEX a, COMPLEX b){COMPLEX c;c.re = a.re + b.re;c.im = a.im + b.im;return c;}/////////////////////////////////////////////////// 定义颜色及初始化颜色/////////////////////////////////////////////////// 定义颜色int Color[MAXCOLOR];// 初始化颜色void InitColor(){// 使用HSL 颜色模式产生角度h1 到h2 的渐变色int h1 = 240, h2 = 30;for(int i=0; i<MAXCOLOR/2; i++){Color[i] = HSLtoRGB((float)h1, 1.0f, i * 2.0f / MAXCOLOR);Color[MAXCOLOR-1-i] = HSLtoRGB((float)h2, 1.0f, i * 2.0f / MAXCOLOR);}}/////////////////////////////////////////////////// 绘制Mandelbrot Set (曼德布洛特集)/////////////////////////////////////////////////void Draw(double fromx, double fromy, double tox, double toy){COMPLEX z, c;int x, y, k; // 定义循环变量for(x = 0; x < 640; x++){c.re = fromx + (tox - fromx) * (x / 640.0);for(y = 0; y < 480; y++){c.im = fromy + (toy - fromy) * (y / 480.0);z.re = z.im = 0;for(k = 0; k < ITERA TIONS; k++){if ( z.re * z.re + z.im * z.im > 4.0 ) break;z = z * z + c;}putpixel(x, y, (k >= ITERA TIONS) ? 0 : Color[k % MAXCOLOR]);}}}/////////////////////////////////////////////////// 主函数/////////////////////////////////////////////////void main(){// 初始化绘图窗口及颜色initgraph(640, 480);InitColor();// 初始化Mandelbrot Set(曼德布洛特集)坐标系double fromx, fromy, tox, toy;fromx = -2.1; tox = 1.1;fromy = -1.2; toy = 1.2;Draw(fromx, fromy, tox, toy);// 捕获鼠标操作，实现放大鼠标选中区域MOUSEMSG m;bool isLDown = false;int selfx, selfy, seltx, selty; // 定义选区while(!kbhit()){m = GetMouseMsg(); // 获取一条鼠标消息switch(m.uMsg){// 按鼠标中键恢复原图形坐标系case WM_MBUTTONUP:fromx = -2.1; tox = 1.1;fromy = -1.2; toy = 1.2;Draw(fromx, fromy, tox, toy);break;// 按鼠标左键并拖动，选择区域case WM_MOUSEMOVE:if (isLDown){rectangle(selfx, selfy, seltx, selty);seltx = m.x;selty = m.y;rectangle(selfx, selfy, seltx, selty);}break;// 按鼠标左键并拖动，选择区域case WM_LBUTTONDOWN:setcolor(WHITE);setwritemode(R2_XORPEN);isLDown = true;selfx = seltx = m.x;selfy = selty = m.y;rectangle(selfx, selfy, seltx, selty);// 按鼠标左键并拖动，选择区域case WM_LBUTTONUP:rectangle(selfx, selfy, seltx, selty);setwritemode(R2_COPYPEN);isLDown = false;seltx = m.x;selty = m.y;if (selfx == seltx || selfy == selty) break;// 修正选区为4:3int tmp;if (selfx > seltx) {tmp = selfx; selfx = seltx; seltx = tmp;} if (selfy > selty) {tmp = selfy; selfy = selty; selty = tmp;}if ( (seltx - selfx) * 0.75 < (selty - selfy) ){selty += (3 - (selty - selfy) % 3);selfx -= (selty - selfy) / 3 * 4 / 2 - (seltx - selfx) / 2;seltx = selfx + (selty - selfy) / 3 * 4;}else{seltx += (4 - (seltx - selfx) % 4);selfy -= (seltx - selfx) * 3 / 4 / 2 - (selty - selfy ) / 2;selty = selfy + (seltx - selfx ) * 3 / 4;}// 更新坐标系double f, t;f = fromx + (tox - fromx) * selfx / 640;t = fromx + (tox - fromx) * seltx / 640;fromx = f;tox = t;f = fromy + (toy - fromy) * selfy / 480;t = fromy + (toy - fromy) * selty / 480;fromy = f;toy = t;// 画图形Draw(fromx, fromy, tox, toy);}}getch();closegraph(); }输出结果为：。

计算机图形学_Koch雪花的分形算法实现

Koch雪花的分形算法实现1.内容介绍分形指具有多重自相似的对象，它可以是自然存在的，也可以是人造的，树木、山川、云朵、脑电图、材料断口等都是典型的分形。

分形是图形学中一门重要的理论，是最近20多年发展起来的新学科，其中Koch雪花则是分形曲线的典型代表。

本文通过对Koch雪花算法实现的详细论述与具体代码，进而分析分形的基本思想、实现方法以及实际应用等。

2.设计思想Koch雪花的实际结构为三条Koch曲线的拼接，这三条Koch曲线分别构成正三角形的三条边即可。

因此，在此详细论述Koch曲线的设计思想。

首先绘制一条线段，假设线段长度为L，则在线段L/3处至2L/3处以L/3为边长做一个正三角形，并去掉底边。

此时该图形变为四条线段，同理对每条线段继续上述步骤即可绘制出Koch曲线。

设计中的难点在于每条线段的端点坐标较难确定，根据已知的初始线段两个端点坐标，我们通过几何三角计算出每次迭代的端点坐标并进行递归即可。

如图1所示，每点的迭代算式为(x1,y1) (x3,y3)(x5,y5)(x4,y4)(x2,y2) α60°第 1 页共9 页图1 端点坐标推导计算32113211533321215333212111()()331c o s (60)31(c o s 60c o s s in 60s in )31[())]61c o s (60)31(s in 60c o s c o s 60s in )31)()]6x x x x y y y y x x L x L x x x y y y y L y L y x x y y αααααα=-+=-+=+︒+=+︒-︒=+---=+︒+=+︒+︒=+-+-在推导出每点的坐标计算后，即可通过编程实现Koch 雪花。

在程序中，首先通过初始化定义正三角形底边的两个端点坐标，然后通过计算得出顶点坐标。

对每一条边进行Koch 曲线递归绘制，最终就可以得到Koch 雪花。

Koch曲线

Koch曲線
Koch曲線是一個數學曲線，同時也是早期被描述的一種分形曲線。

它由瑞典數學家
Helge von Koch在1904年發表的一篇題為“從初等幾何構造的一條沒有切線的連續曲線”（原來的法文題目：
"Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire"）的論文中提出。

有一種Koch曲線是象雪花一樣，被稱為Koch雪花（或Koch星），它是由三條Koch曲線圍成的等邊三角形。

設想從一個線段開始，根據下列規則構造一個Koch曲線：
1．三等分一條線段；
2．用一個等邊三角形替代第一步劃分三等分的中間部分；
3．在每一條直線上，重複第二步。

Koch曲線是以上步驟地無限重複的極限結果。

Koch曲線的長度為無窮大，因為以上的變換都是一條線段變四條線段，每一條線段的長度是上一級的1/3，因此操作n步的總長度是(4/3)n：若n→∞，則總長度趨於無窮。

Koch曲線的分形維數是log 4/log 3 ≈ 1.26，其維數大於線的維數（1），小於Peano填充曲線的維數（2）。

Koch曲線是連續的，但是處處不可導的。

Koch雪花的面積是，這裡的s是最初三角形的邊長，Koch雪花的面積是原三角形面積的8/5，它成為一條無限長的邊界圍繞著一個有限的面積的幾何物件。

数学实验报告Koch雪花。

数学实验报告试验二迭代与分形练习一实验目的与要求对一个等边三角形，每条边按照Koch曲线的方式进行迭代，产生的分形图称为Koch雪花。

编制程序绘制出它的图形，并计算Koch雪花的面积，以及它的分形维数。

实验过程具体的代码如下：function plotkoch(r,k) %显示等边三角形迭代k次后的曲线图 r代表边长默认（0 0）为起点p=[(r/2) r*sin(pi/3);r 0]; %存放结点坐标，每行一个点，初始值为两结点的坐标代表边1n=1; %存放线段的数量，初始值为1A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; %用于计算新的结点for s=1:k %实现迭代过程，计算所有的结点的坐标j=0; %%以下根据线段两个结点的坐标，计算迭代后它们之间增加的三个%结点的坐标，并且将这些点的坐标按次序存暂时放到r中for i=1:n %每条边计算一次q1=p(i,:); %目前线段的起点坐标q2=p(i+1,:); %目前线段的终点坐标d=(q2-q1)/3; %j=j+1;b(j,:)=q1; %原起点存入rj=j+1;b(j,:)=q1+d; %新1点存入rj=j+1;b(j,:)=q1+d+d*A'; %新2点存入rj=j+1;b(j,:)=q1+2*d; %新3点存入rend %原终点作为下条线段的起点，在迭代下条线段时存入rn=4*n; %全部线段迭代一次后，线段数量乘4clear p %清空p ，注意：最后一个终点q2不在r中p=[b;q2]; %重新装载本次迭代后的全部结点endplot(p(:,1),p(:,2)) %显示各结点的连线图hold on; %保存图像axis equal %各坐标轴同比例p=[0 0;r 0]; %存放结点坐标，每行一个点，初始值为两结点的坐标代表边2n=1; %存放线段的数量，初始值为1A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; %用于计算新的结点for s=1:k %实现迭代过程，计算所有的结点的坐标j=0; %%以下根据线段两个结点的坐标，计算迭代后它们之间增加的三个%结点的坐标，并且将这些点的坐标按次序存暂时放到r中for i=1:n %每条边计算一次q1=p(i,:); %目前线段的起点坐标q2=p(i+1,:); %目前线段的终点坐标d=(q2-q1)/3; %j=j+1;z(j,:)=q1; %原起点存入rj=j+1;z(j,:)=q1+d; %新1点存入rj=j+1;z(j,:)=q1+d+d*A; %新2点存入rj=j+1;z(j,:)=q1+2*d; %新3点存入rend %原终点作为下条线段的起点，在迭代下条线段时存入rn=4*n; %全部线段迭代一次后，线段数量乘4clear p %清空p ，注意：最后一个终点q2不在r中p=[z;q2]; %重新装载本次迭代后的全部结点endplot(p(:,1),p(:,2)) %显示各结点的连线图hold on; %保存图像axis equal %各坐标轴同比例p=[0 0;(r/2) r*sin(pi/3)]; %存放结点坐标，每行一个点，初始值为两结点的坐标代表边3n=1; %存放线段的数量，初始值为1A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; %用于计算新的结点for s=1:k %实现迭代过程，计算所有的结点的坐标j=0; %%以下根据线段两个结点的坐标，计算迭代后它们之间增加的三个%结点的坐标，并且将这些点的坐标按次序存暂时放到r中for i=1:n %每条边计算一次q1=p(i,:); %目前线段的起点坐标q2=p(i+1,:); %目前线段的终点坐标d=(q2-q1)/3; %j=j+1;a(j,:)=q1; %原起点存入rj=j+1;a(j,:)=q1+d; %新1点存入rj=j+1;a(j,:)=q1+d+d*A'; %新2点存入rj=j+1;a(j,:)=q1+2*d; %新3点存入rend %原终点作为下条线段的起点，在迭代下条线段时存入rn=4*n; %全部线段迭代一次后，线段数量乘4clear p %清空p ，注意：最后一个终点q2不在r中p=[a;q2]; %重新装载本次迭代后的全部结点endplot(p(:,1),p(:,2)) %显示各结点的连线图hold on; %保存图像axis equal %各坐标轴同比例运行得到图像如下：k=1 k=5k=0时23 k=1时 S=234r +2312r k=2时 S=234r +2312r + 2327r k=3时 S=234r +2312r + 2327r + 243243r k=n 时 S=234r +2312r + …2(1)12133*4*()3n n r ---+2(1)233*4*()43n n r r - 每一次迭加，所产生的新三角形的边长变为上一次的13，数量为上一次的4倍. S=234+234*（3*21()3+12*221()3+……+3*(1)4n -*21()3n ）2323*(1)211[3*4*()]3n i i i -=∑曲线总面积无穷大。

Koch曲线

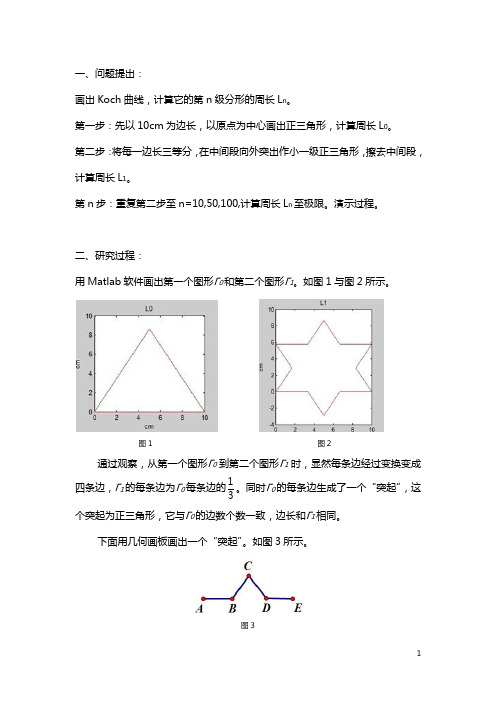
一、问题提出：画出Koch 曲线，计算它的第n 级分形的周长L n 。

第一步：先以10cm 为边长，以原点为中心画出正三角形，计算周长L 0。

第二步：将每一边长三等分，在中间段向外突出作小一级正三角形，擦去中间段，计算周长L 1。

第n 步：重复第二步至n=10,50,100,计算周长L n 至极限。

演示过程。

二、研究过程：用Matlab 软件画出第一个图形Γ0和第二个图形Γ1。

如图1与图2所示。

图1 图2通过观察，从第一个图形Γ0到第二个图形Γ1时，显然每条边经过变换变成四条边，Γ1的每条边为Γ0每条边的31。

同时Γ0的每条边生成了一个“突起”，这个突起为正三角形，它与Γ0的边数个数一致，边长和Γ1相同。

下面用几何画板画出一个“突起”。

如图3所示。

图3由图3可以看出：AE 为原来的边，取它的三分点B 、D ，在由BD 为边做出△BCD 。

C 点可以看成D 绕B 点逆时针旋转60°得到，此时B 、C 、D 确定。

设A （x 1，y ）, E （x 2，y ），则B ⎪⎭⎫ ⎝⎛-+,y x x x 3121；D ⎪⎭⎫ ⎝⎛--,y x x x 3122；设()00,y x BC =→，而⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡032123232103cos sin sin cos 121200x x x x θθθθy x ，得到()⎪⎪⎩⎪⎪⎨⎧-=-=636120120x x y x x x ，即()⎪⎪⎭⎫ ⎝⎛--=→63,61212x x x x BC 。

故用Matlab 演示过程时，在正三角形三边均取两个三分点，然后通过转轴变换移动D 至C 点，最后连接BC 、CD 即可得到图像。

同理可得，从Γn-1到Γn 的过程中，每条边经过变换变成四条边，Γn 的每条边为Γn-1每条边的31。

同时Γn-1的每条边生成了一个正三角形，它与Γn-1的边数个数一致，边长和Γn 相同。

Koch曲线

Koch 分形曲线1.1 分形原理这是一类复杂的平面曲线，可用算法描述。

从一条直线段开始，将线段中间三分之一部分用等边三角形的两条边代替，形成具有5个结点的图形(图1)；在新的图形中，又将图中每一直线段中间的三分之一部分都用一等边三角形的两条边代替，再次形成新的图形(图2)，这时，图形中共有17个结点。

这种迭代继续进行下去可以形成Koch 分形曲线。

在迭代过程中，图形中的点将越来越多，而曲线最终显示细节的多少将取决于迭代次数和显示系统的分辩率。

1.2 算法分析算法分析：考虑由直线段(2个点)产生第一个图形(5个点)的过程。

设1P 和5P 分别为原始直线段的两个端点。

现在需要在直线段的中间依次插入三个点234,,P P P 产生第一次迭代的图形(图1)。

显然，2P位于1P 点右端直线段的三分之一处， 4P 位于1P 点右端直线段的三分之二处；而3P 点的位置可以看成是由4P 点绕2P 旋转60度(逆时针方向)而得到的，故可以处理为向量24P P 经正交变换而得到向量23P P 。

算法如下：(1) 2151()/3P P P P =+-；(2) 41512()/3P P P P =+-；(3) 3242()T P P P P A =+-⨯；图2 第二次迭代图1 第一次迭代在(3)中， A 为正交矩阵：c o s s i n 33sin cos 33A ππππ⎡⎤-⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦算法根据初始数据(1P 和5P 点的坐标)，产生图1中5个结点的坐标。

结点的坐标数组形成一个5×2矩阵，矩阵的第一行为1P 的坐标，第二行为2P 的坐标，……，第五行为5P 的坐标。

矩阵的第一列元素分别为5个结点的X 坐标，第二列元素分别为5个结点的Y 坐标。

进一步考虑Koch 曲线形成过程中结点数目的变化规律。

设第k 次迭代产生结点数为k n ，第k+1次迭代产生结点数为1k n +，则k n 和1k n +之间的递推关系式为143k k n n +=-。

opengl绘制实线、虚线、kock曲线(C++)

实验四1、实验目的和要求利用OpenGL实现实线，虚线，点划线的绘制，及kock曲线。

2、实验内容1）用OpenGL程序绘制实现，虚线和点划线2）用OpenGL程序，分别以直线和正三角形为初始生成员，实现迭代次数在6次以内的kock曲线，要求用键盘交互控制迭代次数。

3、实验步骤1）相关算法及原理描述①直线的绘制在OpenGL中绘制直线通过指定直线段的端点来实现，用glVertex函数指定直线段端点的坐标位置，用glBegin/glEnd函数对包含一系列的点坐标，并利用符号常量解释这些点构成直线的方式。

②虚线的绘制绘制虚线需要先调用函数过了Enable（GL_LINE_STIPPLE）；打开划线模式。

然后，函数glLineStipple将建立用于划线的模式glLineStipple（Glint factor, GLushort pattern）；③Kock曲线Kock曲线的初始生成员是一条直线，生成规则是将直线段分为三等分，首尾两段保持不变，中间用两段等长且互成60°角的直线段代替。

这样，直线段被分成四段，每段长度都只有原来的1/3。

Kock曲线的分形维数为D=ln4/ln3≈1.26186假设原直线的首尾点是P0（x0，y0），P1（x1，y1），则新的四段直线段的五个端点坐标分别为(x0 , y0) (x0+(x1-x0)/3 , y0+(y1-y0)/3)((x1+x0)/2±(y0-y1)√3/6 , (y1+y0)/2±(x1-x0)√3/6)(x0+2(x1-x0)/3 , y0+2(y1-y0)/3) (x1 , y1)其中，第三个点坐标公式中的正负号表示中间两条心直线段处于元直线段的哪一侧。

根据这一规则迭代六次。

2）程序调试、测试与运行结果分析①直线的绘制结果②虚线的绘制结果③Kock曲线绘制结果4、实验总结这次是两个实验，先做的是直线、虚线的绘制，这要相对简单的多，直线、虚线的绘制只需要调用相应的函数即可，这个程序和上次的橡皮筋技术很像，只是线的两端点是自己指定的，不需要鼠标或键盘的确定。

Koch分形曲线

在新的图形中，有将没一直线段中间的三分之一部分都用一个等边三角形的另两边代替，得到15个结点的图形
• 每迭代一次，曲线的长度增加4/3。 • 下面是迭代5次的图形。
算法的程序设计见下页的M-文件
p=[0,0;10,0]; a=[cos(pi/3),-sin(pi/3);sin(pi/3),cos(pi/3)];
练习
• 以正三角形为基础图形，在每一个边上构造Koch曲线，得到Koch雪花。
结点 p(4:4:4*n-4,:)=q+2*d; end plot(p(:,1),p(:,2)) %插入第三组结点
算法的设计
(1) Q 1 P 1 ( p 2 P 1) / 3 ( 2 ) Q 3 P 1 2 ( P 2 P 1) / 3 ( 3 ) Q 2 Q 1 ( Q 3 Q 1) A ' ( 4 ) P 5 P 2 ; P 2 Q 1; P 3 Q 2 ; P 4 Q 3;
Koch分形曲线
一、分形的概念
• 把形态、功能和信息方面具有自相似性的对象称为分形(fractal)。 • Koch曲线是最简单的分形曲线，从一条直线段开始，将中间的三分之一部分用一个等边三角形的另两条边代替，得到5个结点的图形
（ 0, 0),( 3.3333, 0),(5.0000, 2.8868),(6.6667,0),(10.0000,0)
• 在第三步中的矩阵A为
cos A sin

3
Байду номын сангаас
sin
3
3 cos 3

• 由上面的程序，从{P1,P2}得到一个新的5 个顶点的数组{P1,P2,P3,P4,P5},就是我们的生成元，然后对每一个线段{Pi,Pi+1} 再依次进行新的生成过程，得到一个17 个顶点的数组，第n步得到4n-3个顶点……直至无限，就得到Koch曲线。

Koch曲线及Koch雪花的制作

Koch曲线及Koch雪花的制作
一、Koch曲线的制作
1．作初始元AB和生成元A-B：作线段AB，以A为中心，将点B缩放1/3、2/3得点B'、B''；再以B'为中心，将点B''逆时针旋转60°得点B'''，连折线A B' B''' B''B，得生成元A-B(左图)；
2．删除生成元A-B中四条小线段，显示出初始元线段AB，新建参数n=1，作AB→AB'、AB→B'B'''、AB→B'''B''、AB→B''B的深度为n的最终迭代，隐藏初始元及点B' 、B'''、B''，增大参数n，得Koch曲线(右图)。

二、Koch雪花的制作
1．选中Koch曲线，同时依次选中点A、B及n，创建新工具“工具#1”，调出工具脚本，将n设为自动匹配；
2．作正三角形CDE(顺时针三顶点)，若用“工具#1”依次匹配CD、DE、EC，得Koch雪花如左图，若用“工具#1” 依次匹配DC、CE、ED，得Koch反雪花如右图。

1904年科克(koch)曲线是这样的

科克(koch)曲线的
相似性维数
可以看出,科克曲线是把一条边的3等份变成4个一样长的小线段.因此设其维数为D,那么 4=3D
于是
D=log4/log3≈1.2618…
是一个非整数值.实际上,说科克曲线的维数是1有点太简单, 说它是2维又嫌太简单,那么 1.2618维可能正合适.
ห้องสมุดไป่ตู้
一正三角形每边长为1现在每边正之间13处再凸出一个小正三角形使原三角形变为六边形再在六边形的12条边上重复进行中间13处凸出一正三角形过程得到41248边形
1904年科克(koch)曲线是这样的:
一正三角形,每边长为1,现在每边正之间1/3处再凸出一个小正三角形,使原三角形变为六边形,再在六边形的12条边上重复进行中间 1/3处凸出一正三角形过程, 得到4×12 =48边形;每边的正中间还可以再在1/3处凸出一正三角形,如此一致无穷.其边缘的构造越来越精细,好象一片理想的雪花.
科克(koch)曲线一个特征:
它是一条闭合曲线,自身不交.它所包围的总面积有限永远小于第一个正三角形外接圆的面积.但其长度是无限的:因为每次变换后的长度都是原来的4/3,所以n次后的曲线长度是
(4/3)n→∞
在有限空间里有无限长的曲线,的确令人惊讶!
科克(koch)曲线另一个特征:
1904年科克(koch)曲线是这样的:
一正三角形,每边长为1,现在每边正之间1/3处再凸出一个小正三角形,使原三角形变为六边形,再在六边形的12条边上重复进行中间 1/3处凸出一正三角形过程, 得到4×12 =48边形;每边的正中间还可以再在1/3处凸出一正三角形,如此一致无穷.其边缘的构造越来越精细,好象一片理想的雪花.

图形学上机实验报告

计算机图形学上机实验报告计算机科学与技术学院班级：CS13 班学号：U姓名：指导教师：完成日期：2015/11/15实验一：kock分形雪花图案的绘制一、实验目的与要求目的：1.通过实验初步了解OPENGL。

2通过上机编程掌握OPENGL的画图机理和OPENGL。

要求：1.了解分形绘图的过程。

二、实验内容以Kock曲线为例，说明分形图形是如何生成的。

Kock曲线的初始生成元是一条直线段，生成规则是将直线段均分为三等分，首尾两端保持不变，中间用两端等长且互成60度角的直线段代替。

迭代公式如下：分别迭代1,3,6次，并记录结果。

三、实验结果实验结果图如下：3-1第一次分形3-2三次分形3-3六次分形四、体会通过这次实验了解到了分形系统的从图元到图形的形成过，分形在图形学的应用中，可以用来表示岩层、云、水、树、等。

并且亲手实现了“雪花”的分形图形。

通过迭代次数可控制图形的不同。

掌握了分形系统的形成过程。

完成了此次试验目的。

五、源程序void drawline(pt pt1, pt pt2)//绘制线{glBegin(GL_LINES);glVertex2d(pt1.x, pt1.y);glVertex2d(pt2.x, pt2.y);glEnd();}void drawkoch(pt pt1, pt pt2, int n)//n为确定的迭代次数{pt p1, p2, p3, p4, p5;glColor3f(0.0, 0.0, 0.0);p1.x = pt1.x;p1.y = pt1.y;p2.x = pt2.x;p2.y = pt2.y;if (n == 1){ drawline(p1, p2); }if (n>1){p3.x = p1.x + (-p1.x + p2.x) / 3;p3.y = p1.y + (-p1.y + p2.y) / 3;p4.x = p1.x + 2 * (-p1.x + p2.x) / 3;p4.y = p1.y + 2 * (-p1.y + p2.y) / 3;p5.x = (p4.x - p3.x) / 2 - (p4.y - p3.y)*sqrt(3.0) / 2 + p3.x;p5.y = (p4.y - p3.y) / 2 + (p4.x - p3.x)*sqrt(3.0) / 2 + p3.y;drawkoch(p1, p3, n - 1);drawkoch(p3, p5, n - 1);drawkoch(p5, p4, n - 1);drawkoch(p4, p2, n - 1);}if (n == 0)exit(0);}void display(void){glClear(GL_COLOR_BUFFER_BIT);pt p1, p2, p3;p1.x = 30;p1.y = 30;p2.x = 110;p2.y = 30;p3.x = 70;p3.y = 30 + 40 * sqrt(3.0);int n;do{//循环改变迭代次数glClear(GL_COLOR_BUFFER_BIT);printf("请输入Koch雪花的迭代次数，或输入0退出:");scanf("%d", &n);drawkoch(p1, p3, n);drawkoch(p3, p2, n);drawkoch(p2, p1, n);glFlush();} while (n != 0);}int main(int argc, char**argv){glutInit(&argc, argv);glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);glutInitWindowPosition(50, 100);glutInitWindowSize(500, 400);glutCreateWindow("KOCHCURVE");init();glutDisplayFunc(display);glutMainLoop();return 0;}实验二：星球环绕模型一、实验目的与要求目的：1.通过实验初步了解OpenGL中的深度测试缓存器算法。

电子科技大学数学实验实验报告(含详细程序和实验数据)-Koch分形雪花,计算瑞典国土,计算我国海岸线长度

Koch 分形雪花面积计算的数学实验报告2012年4月6日绘制Koch 分形雪花，分析其边数及面积规律实验内容取周长为10的正三角形为初始元。

第一步（N=1）：将边长三等分，并以中间的一份为底边构造正三角形，去掉该三角形的底边，将两腰与剩下的两份相连，得到生成元。

原三角形每条边都用生成元替换,得到具有6个凸顶点的12边形。

第二步（N=2）：对第1步得到的图形，同样将其边长三等分，并以中间的一份构造正三角形，去掉该三角形的底边，将两腰与两边的两份相连，得到生成元。

原12边形的每条边都用生成元替换，得到24个凸顶点的48边形。

如此方法，一直做下去，当∞→N 时便得到了Koch 分形雪花。

实验目的1.算法描述Koch 分形雪花2.证明Koch 分形雪花图Kn 的边数为143-⨯=n n L3.求Koch 分形雪花图Kn 的面积)(lim n N K area ∞→实验原理1. Koch 分形雪花的绘制过程与Koch 曲线的构造过程类似。

事实上，Koch 分形雪花是由三条三次Koch 曲线组成的。

Koch 曲线的构造：由一条线段产生四条线段，由n 条线段迭代一次后将产生4n 条线段，算法针对每一条线段逐步进行，将计算新的三个点。

第一个点位于线段的三分之一处，第三个点位于线段的三分之二处，第二个点以第一个点为轴心，将第一和第三个点形成的向量正向旋转ο60而得，正向旋转由正交矩阵⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-3cos 3sin 3sin3cos ππππ完成。

三条三条三次Koch 曲线由初始向量P 构造。

流程图如下：⑴)/3P －2(P + P ←Q )/3;P －(P + P ← Q 121 31211 ⑵;A ×)Q －(Q + Q ← Q T1312 ⑶．Q ← P ;Q ← P ;Q ← P ;P ← P 342312252.由于Koch分形雪花是封闭的凸多边形，所以边数=顶点数=P矩阵的行数-1。

计算机图形学实验报告旋转的Koch雪花

六.实验截图：截图一：
截图二：
对比可以看出：图形是旋转的。七.实验总结：
计算机图形学报告
旋转的 Koch 雪花
姓名：学号：专业：班级：
一.实验目的： (1).掌握 Koch 雪花的构造方法。 (2).掌握递归模式的实现方法。二.实验要求: (1)建立平面二维坐标系，原点位于屏幕客服区中心，x 轴水平 f 方向为正，y 轴垂直向上为正。 (2)以圆点为中心绘制半径为 r 的圆，与 y 轴交与p0 点，从p0 点开始，顺时针方向将圆三等分，得到p1 和p2 点。p0 p1 p2 点构成等边三角形。 (3)沿着等边三角形的三条边外侧分别绘制三段递归深度为 4，夹角为600 的 Koch 曲线，形成 Koch 雪花。三．核心算法与类型设计： Koch 曲线的构造方式是：给定一条直线 F0，将该直线三等分，并将中间的一段用以该线段为边的等边三角形的另外两边替代，得到图形。然后，再对图形中的每一小段都按上述方式修改，以至无穷，则最后得到的极限曲线。即是所有的 Koch 曲线。 Koch 曲线是典型的分形曲线，具有自相似性，这正是分形最为重要的标志。Koch 曲线的构造也决定了在计算机上绘制应该采用递归算法。在绘制 Koch 雪花时，正三角形的三条边夹角为600 ，也就是生成元存在和水平线的夹角称为生成元起始角。对于起始角α0 角的生成元，参数计算如下：直线段的长度 L：L= (bx − ax)2 + （by − ay）
2
直线段的起始角α0 ：α0 =atan
by −ay bx −ax
递归 n 次后的 Koch 曲线最小线元 d： d=L (2 ∗ (1 + cos⁡ (ѳ))n 四.实验步骤： (1).以正三角形的每条边为基，在外侧分别绘制 Koch 曲线形成 Koch 雪花。 (2).为了实现图形的旋转，采用双缓冲技术。先将图形绘制到内存设备上下文 MemDC，然后再一次型复制到显示设备上下文 pDC 上。 (3).分形函数 Fract曲线中每一段直线的长度以及边的起始角，然后调用 Fractal()函数绘制每段 Koch 曲线。 (4).Koch 函数用于在正三角形的每条边上绘制 Koch 曲线。函数的实现使用了递归模型。五.主要变量以及函数： #define PI 3.1415926 #define ROUND(a) int (a+0.5) double angle,theta,L,d,r,RotateAngle; int n; double x0,x1,x2,y0,y1,y2,ax,ay,bx,by,ex,ey; void DoubleBuffer(); void Fractal(double bx,double by,double ex,double ey); void Koch(double alpha,int n);

C++绘制Koch曲线

C++绘制Koch 曲线从一条直线段开始，将线段中间的三分之一部分用一个等边三角形的两边代替，形成山丘形图形如下图1在新的图形中，又将图中每一直线段中间的三分之一部分都用一个等边三角形的两条边代替，再次形成新的图形如此迭代，形成Koch 分形曲线。

考虑由直线段（2个点）产生第一个图形（5个点）的过程。

图1中，设1P 和5P 分别为原始直线段的两个端点，现需要在直线段的中间依次插入三个点2P ，3P ，4P 。

显然2P 位于线段三分之一处，4P 位于线段三分之二处，3P 点的位置可看成是由4P 点以2P 点为轴心，逆时针旋转600而得。

/*以下代码参考孙博文的《分形算法与程序设计:Visual C++实现》*/ #include <windows.h>#include <math.h>extern "C" WINBASEAPI HWND WINAPI GetConsoleWindow (); #define PI 3.1415926HDC hdc;void Fractal(double ax ,double ay ,double bx ,double by ){int c=100;if (((bx -ax )*(bx -ax )+(by -ay )*(by -ay ))<c){MoveToEx(hdc,ax +50,360-ay ,NULL );LineTo(hdc,bx +50,360-by );}else{double cx,cy,dx,dy,ex,ey;double l,alfa;cx=ax +(bx -ax )/3; cy=ay +(by -ay )/3;ex=bx -(bx -ax )/3; ey=by -(by -ay )/3;Fractal(ax,ay,cx,cy);Fractal(ex,ey,bx,by);l=sqrt((ex-cx)*(ex-cx)+(ey-cy)*(ey-cy));alfa=atan((ey-cy)/(ex-cx));if(alfa>=0 && (ex-cx)<0 || alfa<0 && (ex-cx)<0) alfa=alfa+PI;dx=cx+cos(alfa+PI/3)*l;dy=cy+sin(alfa+PI/3)*l;Fractal(cx,cy,dx,dy);Fractal(dx,dy,ex,ey);}}int main(){HWND hwnd = GetConsoleWindow();hdc = GetDC(hwnd);system("color 2f");Fractal(80,40,240,360);Fractal(240,360,420,100);Fractal(420,100,80,40);system("pause");}。

实验四 Koch曲线的生成11

实验四 Koch曲线生成一、实验目的1. 理解并会自己编程实现Koch曲线的画图二、实验内容和要求1.选择自己熟悉的任何编程语言, 建议使用VB,VC或JAVA。

2.创建良好的用户界面,包括菜单,参数输入区域和图形显示区域。

3.实现Koch曲线的描画。

4.将生成算法以菜单或按钮形式集成到用户界面上。

5.递归深度和生成元的初始角度等参数可以用对话框输入。

三.实验报告1．用户界面的设计思想和框图。

2．各种实现算法的算法思想。

3．算法验证例子。

4．上交源程序。

四.Koch曲线生成程序设计的步骤如下：1．创建工程名称为“Test”单文档应用程序框架（1）启动VC，选择“文件”|“新建”菜单命令，并在弹出的新建对话框中单击“工程”标签。

（2）选择MFC AppWizard(exe)，在“工程名称”编辑框中输入“Test”作为工程名称，单击“确定”按钮，出现Step 1对话框。

（3）选择“单个文档”选项，单击“下一个”按钮，出现Step 2对话框。

（4）接受默认选项，单击“下一个”按钮，在出现的Step 3～Step 5对话框中，接受默认选项，单击“下一个”按钮。

（5）在Step 6对话框中单击“完成”按钮，即完成“Test”应用程序的所有选项，随后出现工程信息对话框（记录以上步骤各选项选择情况），如图1-2所示，单击“确定”按钮，完成应用程序框架的创建。

图1-2 信息程序基本2．建立菜单2.1编辑菜单资源设计如图1-1所示的菜单项。

在工作区的ResourceView标签中，单击Menu项左边“+”，然后双击其子项IDR_MAINFRAME，并根据表1-1中的定义编辑菜单资源。

此时VC已自动建好程序框架，如图1-2所示。

表1-1菜单资源表2．2．添加消息处理函数利用ClassWizard（建立类向导）为应用程序添加与菜单项相关的消息处理函数，ClassName栏中选择CTestView，根据表1-2建立如下的消息映射函数，ClassWizard会自动完成有关的函数声明。

复绕轮包角算法

复绕轮包角算法摘要：1.复绕轮包角算法简介2.算法原理与步骤3.算法优缺点分析4.应用场景与实际案例5.总结正文：复绕轮包角算法是一种在计算机图形学中广泛应用的算法，主要用于生成复杂、美观的图案。

本文将详细介绍复绕轮包角算法的原理、优缺点以及在实际案例中的应用。

1.复绕轮包角算法简介复绕轮包角算法，又称Koch 曲线算法，是一种基于分形理论的图形生成方法。

通过对一个简单的基本图形进行迭代、变异，最终生成具有丰富细节和自相似性的复杂图案。

2.算法原理与步骤复绕轮包角算法的原理可以概括为以下几个步骤：(1) 初始化：设定初始图形，通常为一个简单的正多边形，如正三角形、正四边形等。

(2) 迭代：将图形中的每个顶点与相邻顶点连接，形成新的边。

将新边的一端固定在原顶点，另一端按照一定规律移动，形成新的顶点。

(3) 变异：在迭代过程中，对图形进行一定程度的变异，如旋转、翻转等，以增加图形的多样性和复杂性。

(4) 重复：将变异后的图形作为新的初始图形，继续进行迭代和变异，直至达到设定的迭代次数或满足特定条件。

3.算法优缺点分析优点：(1) 生成复杂图案：复绕轮包角算法能够生成具有丰富细节和自相似性的复杂图案，适用于多种计算机图形学应用场景。

(2) 简单易懂：算法原理相对简单，易于实现和理解。

缺点：(1) 计算量较大：由于需要进行多次迭代和变异，算法的计算量较大，对计算设备性能要求较高。

(2) 可控性较差：算法的生成过程具有一定的随机性，可控性相对较差，可能导致生成的图案与预期效果存在差异。

4.应用场景与实际案例复绕轮包角算法在计算机图形学领域具有广泛的应用，如分形艺术、特效制作、界面设计等。

以下为一个实际案例：在分形艺术中，利用复绕轮包角算法生成一幅具有丰富细节和自相似性的分形图案。

5.总结复绕轮包角算法是一种基于分形理论的图形生成方法，能够生成复杂、美观的图案。

尽管存在计算量较大和可控性较差等缺点，但在计算机图形学领域仍具有广泛的应用价值。

JavaScript图形实例：Koch曲线

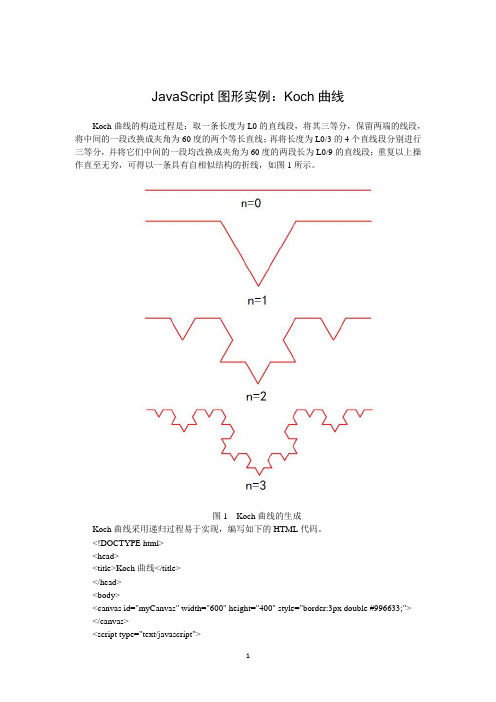
JavaScript图形实例：Koch曲线Koch曲线的构造过程是：取一条长度为L0的直线段，将其三等分，保留两端的线段，将中间的一段改换成夹角为60度的两个等长直线；再将长度为L0/3的4个直线段分别进行三等分，并将它们中间的一段均改换成夹角为60度的两段长为L0/9的直线段；重复以上操作直至无穷，可得以一条具有自相似结构的折线，如图1所示。

图1 Koch曲线的生成Koch曲线采用递归过程易于实现，编写如下的HTML代码。

<!DOCTYPE html><head><title>Koch曲线</title></head><body><canvas id="myCanvas" width="600" height="400" style="border:3px double #996633;"> </canvas><script type="text/javascript">var canvas = document.getElementById('myCanvas');var ctx = canvas.getContext('2d');var maxdepth =5;var curdepth = 0;ctx.lineWidth = 2;Koch({x:50,y:150},{x:550,y:150},Math.PI/3);function Koch(p1,p2,angle){curdepth++;if (curdepth<=maxdepth){var x1=(2*p1.x+p2.x)/3;var y1=(2*p1.y+p2.y)/3;var x3=(2*p2.x+p1.x)/3;var y3=(2*p2.y+p1.y)/3;var x2=(x3-x1)*Math.cos(angle)-(y3-y1)*Math.sin(angle)+x1;var y2=(x3-x1)*Math.sin(angle)+(y3-y1)*Math.cos(angle)+y1;Koch(p1,{x:x1,y:y1},Math.PI/3);Koch({x:x1,y:y1},{x:x2,y:y2},Math.PI/3);Koch({x:x2,y:y2},{x:x3,y:y3},Math.PI/3);Koch({x:x3,y:y3},p2,Math.PI/3);}if (curdepth>maxdepth)draw([p1,{x:x1,y:y1},{x:x2,y:y2},{x:x3,y:y3},p2]);curdepth--;}function draw(points){ctx.strokeStyle = "red";ctx.beginPath()ctx.moveTo(points[0].x,points[0].y)for(i=1;i<points.length;i++){ctx.lineTo(points[i].x,points[i].y);}ctx.closePath()ctx.stroke()}</script></body></html>在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出的Koch曲线，如图2所示。

基于Koch分形曲线方法计算中国大陆海岸线长度

基于Koch分形曲线方法计算中国大陆海岸线长度一、实验内容运用Koch分形曲线的方法来计算中国海岸线长度，分析实验结果并对此实验加以改进。

二、实验目的了解正交矩阵在几何图形绘制中的应用，掌握循环语句的常用方法。

在此过程中运用并体会坐标变换、鼠标输入数据等方法，复习读入图片及文本文件的方法。

得出计算结果后与实际的长度进行比较并分析，最后给出改进方式。

三、实验原理很显然海岸线是一种复杂但是在局部会保持与整体相似的性质，当然这也是我们可以用分形的方式来模拟出海岸线的形状进而估算出海岸线的长度的理论基础，也是数学家曼德勃罗在1967年所提出的理论。

其具体算法如下：（1）首先用鼠标读取的方式在选定的海岸线图上读出尽可能多的点；（2）然后进行Koch分形的迭代；（3）最后算出分形迭代后的图形长度。

四、实验程序（一）中国海岸线长度读取文件程序：A=imread('D:\sealine.jpg');image(A)P=ginput（二）分型计算程序：function koch(P,N)if nargin==0,P=[0 0;1 0];N=3;endn=max(size(P))-1;A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)];for k=1:Np1=P(1:n,:);p2=P(2:n+1,:);d=(p2-p1)/3;q1=p1+d;q3=p1+2*d;q2=q1+d*A';n=4*n;II=1:4:n-3;P(II,:)=p1;P(II+4,:)=p2;P(II+1,:)=q1;P(II+2,:)=q2;P(II+3,:)=q3;endplot(P(:,1),P(:,2)),axis offaxis image（三）中国海岸线长度计算程序：x=P(:,1);y=P(:,2);plot(x,y)X=diff(x);Y=diff(y);L=sum(sqrt(X.^2+Y.^2))五、实验结果及分析L（模拟海岸线长度）=17857.2794即由分形模拟出的中国海岸线长度为17857.2794千米。