水准网平差程序
高程控制网平差

i
i
i
h h V 改厕厕短的改正数, 代入上式,得:
i
i
i
V1 V2 V3 V4 W 0
W H A h1 h2 h3 h4 H B
1.附合水准路线的条件数和条件方程式组成
观测值5个,待定水准点2 个,所以条件有3个,可 以列出3个条件方程:
h1
H B h1 h2 H A 0
V 1 V 3 V 2 W a 0 V 2 V 4 V 6 W b 0 V 4 V 5 V 3 W c 0
(二)观测值权的确定:
1.各水准路线都进行了往返观测,每公里水准路线的观测中误差为 ,
则m:i
R mi2
1 4n
n i
2 i
i
式中,为测往返测高程不符值,以mm为单位;R为测段长度,以km为单位;n
H A h2 h3 h5 H D 0
H B h1 h3 h4 H C 0
一般以1个已知点为起点,其它已知点为终点,所构成的附合 水准路线为已知点数减1,这样可以列出的条件方程式为已知 水准点个数减1.
2.闭合水准路线的条件数和条件方程式的组成
从一个水准点出发,经过若干水准测段,又回到该 水准点,这样的水准路线称为闭合水准路线。
V 1 V 7 V 8 W b 0
V 2 V 8 V 7 W c 0
V 3 V 5 V 8 W d 0
V 4 V 6 V 5 W e 0
2.闭合水准路线的条件数和条件方程式的组 成
图(c)是四边形状水准网,网中有4个待定点,没有已知点, 在平差计算时,只能确定个待定水准点之间的相互关系,如 果确定一个水准点的高程,就可以确定其他点的高程。因此, 该网的必要观测是3个,观测值总数是6个,又3个多余观测, 可以列出3个条件方程。为了让所列立的条件方程式互相独 立,没个条件方程都要求有一个其他方程没有用到的观测值, 即:
测绘程序设计实验八水准网平差程序设计报告

测绘程序设计实验八水准网平差程序设计报告Pleasure Group Office【T985AB-B866SYT-B182C-BS682T-STT18】《测绘程序设计》上机实验报告(Visual C++.Net)班级:测绘0901班学号: 04姓名:代娅琴2012年4月29日实验八平差程序设计基础一、实验目的巩固过程的定义与调用巩固类的创建与使用巩固间接平差模型及平差计算掌握平差程序设计的基本技巧与步骤二、实验内容水准网平差程序设计。
设计一个水准网平差的程序,要求数据从文件中读取,计算部分与界面无关。
1.水准网间接平差模型:2.计算示例:近似高程计算:3.水准网平差计算一般步骤(1)读取观测数据和已知数据;(2)计算未知点高程近似值;(3)列高差观测值误差方程;(4)根据水准路线长度计算高差观测值的权;(5)组成法方程;(6)解法方程,求得未知点高程改正数及平差后高程值;(7)求高差观测值残差及平差后高差观测值;(8)精度评定;(9)输出平差结果。
4.水准网高程近似值计算算法5.输入数据格式示例实验代码:#pragma onceclass LevelControlPoint{public:LevelControlPoint(void);~LevelControlPoint(void);public:CString strName;trName=pstrData[0];m_pKnownPoint[i].strID=pstrData[0];m_pKnownPoint[i].H=_tstof(pstrData[1]);m_pKnownPoint[i].flag=1;trName=pstrData[i];m_pUnknownPoint[i].strID=pstrData[i];m_pUnknownPoint[i].H=0;lag=0;pBackObj=SearchPointUsingID(pstrData[0]);pFrontObj=Sear chPointUsingID(pstrData[1]);ObsValue=_tstof(pstrData[2]);ist=_tstof(pstrData[3]);trID==ID) {return &m_pKnownPoint[i];}}return NULL;}trID==ID){return &m_pUnknownPoint[i];}}return NULL;}LevelControlPoint* AdjustLevel::SearchPointUsingID(CString ID){LevelControlPoint* cp;cp=SearchKnownPointUsingID(ID);if(cp==NULL)cp=SearchUnknownPointUsingID(ID);return cp;}void AdjustLevel::ApproHeignt(void)lag!=1){pFrontObj->strID==m_pUnknownPoint[i].strID)&& m_pDhObs[j].cpBackObj->flag==1 ){ =m_pDhObs[i].cpBackObj->H - m_pDhObs[i].ObsValue;*/m_pUnknownPoint[i].H=m_pDhObs[j].cpBackObj->H + m_pDhObs[j].HObsValue;m_pUnknownPoint[i].flag=1;break;}}if(m_pUnknownPoint[i].flag!=1)pBackObj->strID==m_pUnknownPoint[i].strID)&& m_pDhObs[j].cpFrontObj->flag==1 ){ =m_pDhObs[j].cpFrontObj->H-m_pDhObs[j].HObsValue;/* m_pUnknownPoint[i].H=m_pDhObs[i].cpFrontObj->H+m_pDhObs[i].ObsValue;*/m_pUnknownPoint[i].flag=1;break;}}}}if(i==m_iUnknownPointCount-1)lag!=1)ist);p(i,i)=value;}return p;}void AdjustLevel::FormErrorEquation(CMatrix &B, CMatrix &L){(m_iDhObsCount,m_iUnknownPointCount);(m_iDhObsCount,1);for(int i=0;i<m_iDhObsCount;i++)pBackObj->strID);tmpFront=SearchPointUsingID(m_pDhObs[i].cpFrontObj->strID);trID==tmpBack->strID)trID==tmpFront->strID)bsValue-(m_pDhObs[i].cpBackObj->H-m_pDhObs[i].cpFrontObj->H);*/L(i,0)=m_pDhObs[i].HObsValue-(m_pDhObs[i].cpFrontObj->H -m_pDhObs[i].cpBackObj->H);(_T("%.3f"),L(i,0));L(i,0)=_tstof(tmp);L(i,0)=L(i,0)*1000;+=x(i,0);xt"));xt"));if()==IDCANCEL) return;CString strFileName=();setlocale(LC_ALL,"");CStdioFile sf;if(!(strFileName, CFile::modeCreate|CFile::modeWrite)) return;(LevleContent);();UpdateData(FALSE);}void CIndircLelveDlg::OnBnClickedComputelevel(){f\r\n"), [i].strID,[i].H);LevleContent+=Temp;}(_T("单位权中误差:%.1f mm\r\n"),r0*1000);LevleContent+=Temp;LevleContent+=_T("未知点高程中误差(mm):\r\n");for(int i=0;i< ;i++){();(_T("%s,%.1f\r\n"),[i].strName,Qx[i]*1000);LevleContent+=Temp;}UpdateData(false);}void CIndircLelveDlg::OnBnClickedSavelevleresult(){xt"));if()==IDCANCEL) return;CString strFileName=();setlocale(LC_ALL,"");CStdioFile sf;if(!(strFileName, CFile::modeCreate|CFile::modeWrite)) return;(LevleContent);();UpdateData(FALSE);}三、实验结果打开文件数据:平差结果:四、实验心得这从实验是我们测绘程序设计的最后一次实验,虽然这个学期我们做了好几次相关的实验,但是我却发现自己学的东西也越来越模糊,感觉很多内容都不理解。
水准网平差c++代码

水准网平差结果#include<iostream>#include<stdlib.h>#include<iomanip>#include<math.h>#define max 50Using namespace std;Class CMatrix{public:CMatrix(){row=0; column=0;}; // 默认构造函数CMatrix(int i, int j){row=i;column=j;} // 构造函数一CMatrix(constCMatrix& m); // 复制构造函数~CMatrix(void){/*cout<<"谢谢使用,矩阵所占空间以释放!"<<endl;*/} // 默认析构函数CMatrix& operator=(constCMatrix& m); // 赋值运算符bool operator==(constCMatrix& m); // 比括较运算符bool operator!=(constCMatrix& m); // 比括较运算符CMatrix operator+(constCMatrix& m); // 加运算符CMatrix operator-(constCMatrix& m); // 减运算符CMatrix& operator+=(constCMatrix& m); // 自加运算符CMatrix& operator-=(constCMatrix& m); // 自减运算符CMatrix operator-();// 取负数CMatrix& operator*(constCMatrix& m); // 乘法运算符void input(); //输入矩阵void outputMatrix(); // 输出该矩阵void setValue(int row, int column, double value) { A[row-1][column-1] = value; }// 设置(i,j)的值double getValue(int row, intcolumn)const { return A[row-1][column-1]; }// 设置行、列的值voidsetRow(constint i) { row = i; }intgetRow() const { return row; }voidsetColunm(constint i) { column = i; }intgetColumn() const { return column; }CMatrix& change(int i, int j);//交换矩阵的行CMatrix& transpose(); // 矩阵转置CMatrix& inverse(); // 矩阵求逆void find(int& f)const;// 判断该矩阵是否可用于迭代求解friend void jocabi(constCMatrix& a) ; //迭代求解void lzys(); //列主元素法求解void solve(); //可逆线性矩阵求解void qxnh(); //曲线拟合private:// 成员变量double A[max][max];int row;// 行int column;// 列};void CMatrix::input() //输入{ cout<<"开始输入矩阵值:"<<endl;int i, j;double z;for(i=0;i<row;i++){ cout<<"请输入第"<<i+1<<"行的值:"<<endl;for(j=0;j<column;j++){ cin>>z;A[i][j]=z;}}cout<<endl;};CMatrix::CMatrix(constCMatrix& m) // 复制构造函数{ int i, j;for(i=0;i<m.row;i++)for(j=0;j<m.column;j++)this->A[i][j]=m.A[i][j];};CMatrix&CMatrix::operator=(constCMatrix& m) // 赋值运算符{inti,j;for(i=0;i<row;i++){for(j=0;j<column;j++)A[i][j]=m.A[i][j];}return *this;};boolCMatrix::operator ==(constCMatrix& m) // 比括较运算符{ inti,j,k;for(i=0;i<m.row;i++){ for(j=0;j<m.column;j++)if(this->A[i][j]=m.A[i][j]) k=1;else k=0;}if(k=1) return true;else return false;};boolCMatrix::operator !=(constCMatrix& m) // 比括较运算符{ inti,j,k;for(i=0;i<m.row;i++){ for(j=0;j<m.column;j++)if(this->A[i][j]=m.A[i][j]) k=1;else k=0;}if(k=0) return true;else return false;};CMatrixCMatrix::operator+(constCMatrix& m)// 加运算符{ inti,j;if((this->row==m.row)&&(this->column==m.column)){ for(i=0;i<m.row;i++)for(j=0;j<m.column;j++)this->A[i][j]+=m.A[i][j];}else { cout<<"此两矩阵不能相加,请检查!"<<endl; }return *this;};CMatrixCMatrix::operator-(constCMatrix& m)// 减运算符{ inti,j;if((this->row==m.row)&&(this->column==m.column)){ for(i=0;i<m.row;i++)for(j=0;j<m.column;j++)this->A[i][j]-=m.A[i][j];}else { cout<<"此两矩阵不能相加,请检查!"<<endl; }return *this;};CMatrix&CMatrix::operator+=(constCMatrix& m) //自加运算符{ inti,j;for(i=0;i<m.row;i++)for(j=0;j<m.column;j++) this->A[i][j]=2*m.A[i][j];return *this;};CMatrix&CMatrix::operator-=(constCMatrix& m) //自减运算符{ inti,j;for(i=0;i<m.row;i++)for(j=0;j<m.column;j++)this->A[i][j]=m.A[i][j]-m.A[i][j];return *this;};voidCMatrix::find(int& f)const{ int i;for(i=0;i<this->row;i++)if(this->A[i][i]!=0) f=1;else f=0;};CMatrixCMatrix::operator-() // 取负数{ inti,j;for(i=0;i<this->row;i++)for(j=0;j<this->column;j++)this->A[i][j]=-this->A[i][j];return *this;};CMatrix&CMatrix::operator*(constCMatrix& m) // 乘法运算符{ inti,j,t;CMatrix n;if(this->column==m.row){for(i=0;i<this->row;i++)for(j=0;j<m.column;j++){ double sum=0.0;for(t=0;t<m.row;t++)sum+=this->A[i][t]*m.A[t][j];n.A[i][j]=sum;}}else {cerr<<"此两矩阵不能相乘,请检查!"<<endl; exit(1);}return n;};void CMatrix::outputMatrix()// 输出该矩阵{ inti,j;for(i=1;i<=row;i++){ for(j=1;j<=column;j++)cout<<A[i-1][j-1]<<" ";cout<<endl;}};CMatrix&CMatrix::transpose()// 矩阵转置{ inti,j;CMatrix m(this->column,this->row);for(i=0;i<this->row;i++)for(j=0;j<this->column;j++){ m.A[j][i]=this->A[i][j];} return m;};void jocabi(constCMatrix& a) //高斯迭代求解{ int f=1;a.find(f);if(f==0) {cerr<<"该矩阵不满足迭代求解条件!"<<endl; exit(1); }else{CMatrixx,w;x.setColunm(1);x.setRow(a.getColumn());w.setColunm(1);w.setRow(a.getColumn());int i;double z;for(i=1;i<=x.row;i++){ cout<<"请输入等式右侧的第"<<i<<"个值:";cin>>z;w.A[i-1][0]=z;}for(i=1;i<=x.row;i++){ cout<<"请输入X"<<i<<"的近似值:";cin>>z;x.setValue(i, 1, z);} i=1;while(i<=20){ int j, k;for(j=1;j<=x.row;j++){ double sum=0.0;for(k=1;k<j;k++){sum=sum-(a.A[j-1][k-1])*(x.A[k-1][0]); }for(k=j+1;k<=x.row;k++){sum=sum-(a.A[j-1][k-1])*(x.A[k-1][0]); }sum+=w.A[j-1][0];x.A[j-1][0]=sum/a.A[j-1][j-1];}i++;}for(i=1;i<=x.row;i++)cout<<"X"<<i<<" = "<<x.A[i-1][0]<<endl;}};double jdz(double a) //绝对值{ if(a>0.0) return a;else return -a;};CMatrix&CMatrix::change(int i, int j)//交换矩阵的行{ int k;double z;for(k=1;k<=this->column;k++){ z=A[i-1][k-1];A[i-1][k-1]=A[j-1][k-1];A[j-1][k-1]=z;}return *this;};void CMatrix::lzys() //列主元素法求解{ CMatrixx,w;x.setColunm(1);x.setRow(getColumn());w.setColunm(1);w.setRow(getColumn());int i;double z;for(i=0;i<row;i++){for(int j=0;j<row; j++)w.A[i][j]=0.0;}for(i=1;i<=x.row;i++)x.setValue(i, 1, 0.0);for(i=1;i<=x.row;i++){ cout<<"请输入等式右侧的第"<<i<<"个值:";cin>>z;w.A[i-1][0]=z;}i=0;while(i<x.row-1){ intj,t,h=i;for(j=i;j<x.row-1;j++){ if(jdz(A[j][i])<jdz(A[j+1][i]))h=j+1; }this->change(i+1,h+1);w.change(i+1,1);for(j=i+1;j<row;j++){ double k;k=A[j][i]/A[i][i];for(t=i;t<column;t++){A[j][t]=A[j][t]-k*A[i][t];}w.A[j][0]=w.A[j][0]-k*w.A[i][0];}i++;}if(this->A[row-1][column-1]==0){cerr<<"此矩阵对应的方程组有无穷解!"<<endl; exit(1);}i=column-1;while(i>0){ int j, t;for(j=i-1;j>=0;j--){ double k;k=A[j][i]/A[i][i];for(t=i;t>j;t--){ A[j][t]=A[j][t]-k*A[i][t]; }w.A[j][0]=w.A[j][0]-k*w.A[i][0];}i--;}int j;for(j=0;j<x.row;j++){x.A[j][0]=w.A[j][0]/this->A[j][j];}for(i=1;i<=x.row;i++)cout<<"X"<<i<<" = "<<x.A[i-1][0]<<endl; };CMatrix&CMatrix::inverse() //矩阵求逆{ if(this->row!=this->column) {cerr<<"该矩阵不符合求逆条件!"<<endl; exit(1);} else{CMatrix w;w.setColunm(this->getRow());w.setRow(getColumn());int i;for(i=0;i<row;i++){for(int j=0;j<row; j++){w.A[i][j]=0.0;}w.A[i][i]=1;}i=0;while(i<column-1){ intj,t,h=i;for(j=i;j<row-1;j++){if(jdz(A[j][i])<jdz(A[j+1][i]))h=j+1;}this->change(i+1,h+1);w.change(i+1,h+1);for(j=i+1;j<row;j++){ double k;k=A[j][i]/A[i][i];for(t=i;t<column;t++){A[j][t]=A[j][t]-k*A[i][t];w.A[j][t]=w.A[j][t]-k*w.A[i][t];}}i++;}if(this->A[row-1][column-1]==0){cerr<<"此矩阵求逆不成功,其所对应的方程组有无穷解!"<<endl; exit(1);} i=column-1;while(i>0){ int j, t;for(j=i-1;j>=0;j--){ double k;k=A[j][i]/A[i][i];for(t=i;t>j;t--){ A[j][t]=A[j][t]-k*A[i][t]; }for(t=column-1;t>=0;t--){w.A[j][t]=w.A[j][t]-k*w.A[i][t];}}i--;}intj,k;for(j=0;j<row;j++){ for(k=0;k<w.column;k++){w.A[j][k]=w.A[j][k]/this->A[j][j];} this->A[j][j]=this->A[j][j]/this->A[j][j];}return w;}}; void CMatrix::solve() //可逆线性矩阵求解{CMatrixx,w,c;x.setColunm(1);x.setRow(getColumn());w.setColunm(1);w.setRow(getColumn());c.setColunm(getColumn());c.setRow(getRow());int i;double z;for(i=1;i<=x.row;i++){ cout<<"请输入等式右侧的第"<<i<<"个值:";cin>>z;w.A[i-1][0]=z;}c.operator=(this->inverse());x.operator=(c.operator *(w));cout<<"求解结果:"<<endl;for(i=1;i<=x.row;i++)cout<<"X"<<i<<" = "<<x.A[i-1][0]<<endl;};void CMatrix::qxnh() //曲线拟合{cout<<"用矩阵曲线拟合:"<<endl;int i, j,k,t;double x, y;cout<<"请输入已知坐标点的个数:";cin>>i;CMatrix a(i,1), g(i,i) , w(i,1),c(i,i),q(i,i),p(i,i);for(j=1;j<=i;j++){ cout<<"请输入第"<<j<<"个已知点坐标(先横坐标后纵坐标):";cin>>x>>y;w.A[j-1][0]=y;g.A[j-1][0]=1.0;for(k=1;k<i;k++){ g.setValue(j,k+1,1.0);for(t=1;t<=k;t++)g.A[j-1][k]*=x;}}c=g.transpose();q=c*g;p=q.inverse();w=c*w;a=p*w;cout<<"Y="<<a.A[0][0];for(j=1;j<i;j++){ cout<<'+'<<'('<<a.A[j][0]<<')';for(k=0;k<j;k++)cout<<"*x";}cout<<endl;cout<<" 1 .求取其它点坐标 0. 退出 "<<endl; while(1){ cout<<"请选择:";cin>>k;switch(k){ case 1:{ double x, y,sum;cout<<"请输入待求点的横坐标(x):";cin>>x;y=a.A[0][0];for(j=1;j<i;j++){ sum=a.A[j][0];for(k=0;k<j;k++){sum*=x;}y+=sum;}cout<<"纵坐标:y="<<y<<endl; break;}case 0:{cerr<<"谢谢使用!"<<endl; exit(1);break;}default: cout<<"选择有误,请检查!"<<endl; break;} }};structCElvDif{double value; // 观测值double weight; // 权重long startPoint; // 起始点编号long endPoint; // 终点编号};//水准点类的设计structCLevelPoint{ // 高程平差值=高程值+高程值改正数long index; // 水准点编号double eleValue; // 高程值double dv; // 高程值改正数(初始化为0)bool isKnown; // 是否为已知点};classCElevationNet{public: // 成员函数CElevationNet(){numElvDif=0;numPoints=0;numKnPoint=0;}; // 构造函数~CElevationNet(){}; // 析构函数void input();void output();voidjsgc();intgetgz(){return numElvDif;} //返回观测值数目intgetzs(){return numPoints;} //返回总点数intgetys(){return numKnPoint;} //返回已知点数intgetws(){return numPoints-numKnPoint;} //返回未知点数double geteleValue(int i){return this->lpVec[i-1].eleValue;} //获得高程值 long getindex(int i){return lpVec[i-1].index;} //返回高程点编号void seteleValue(int i, double value){lpVec[i-1].eleValue+=value;} //修改高程值void setdv(inti,double value){this->lpVec[i-1].dv=value;} //修改改正数double getdv(int i){return lpVec[i-1].dv;} //返回改正数friend void xishu(CMatrix& B, CMatrix&X,CElevationNet A); //求取系数矩阵和未知点高程矩阵friend void quanzhen(CMatrix& Q, CElevationNet A); //求取权阵friend void l_zhen( CMatrix& l ,CMatrix& L, CElevationNet A); //求取观测值L矩阵和l阵private: // 成员变量intnumElvDif; // 高差总数intnumPoints; // 控制网中点的总数目intnumKnPoint; //控制网中已知点的数目CElvDifedVec[max]; // 观测值数组CLevelPointlpVec[max]; // 高程值数组};voidCElevationNet::input(){ inta,b,c,i;doublez,l,g;cout<<"请对已知点和未知点进行编号,注意已知点的编号应小于未知点的编号!"<<endl<<endl; cout<<"请输入控制网中水准点总数和已知点数:";cin>>a>>b;numPoints=a;numKnPoint=b;for(i=0;i<numPoints;i++){ lpVec[i].index=i+1;lpVec[i].eleValue=0.0;lpVec[i].dv=0.0;lpVec[i].isKnown=0;}for(i=0;i<numKnPoint;i++){ cout<<"请输入第"<<i+1<<"个已知点高程值:";cin>>z;lpVec[i].eleValue=z;lpVec[i].isKnown=1;}cout<<"请输入观测值个数:";cin>>c;numElvDif=c;for(i=0;i<numElvDif;i++){ cout<<"请输入第"<<i+1<<"段观测段的高差值(单位米)、长度(单位千米)、起始点编号和终点编号:"<<endl;cin>>g>>l>>a>>b;edVec[i].value=g;edVec[i].weight=l;edVec[i].startPoint=a;edVec[i].endPoint=b;}};voidCElevationNet::output(){int i;for(i=0;i<this->numPoints;i++)cout<<"编号为"<<this->lpVec[i].index<<"的点的高程值为:"<<this->lpVec[i].eleValue<<endl;for(i=0;i<this->numElvDif;i++)cout<<"观测段"<<i+1<<"的平差后的值为:"<<this->edVec[i].value<<endl;};void CElevationNet::jsgc(){ inti,j;for(i=0;i<this->numElvDif;i++){ if((lpVec[edVec[i].startPoint-1].eleValu e!=0.0)&&(lpVec[edVec[i].endPoint-1].eleVal ue==0.0)){lpVec[edVec[i].endPoint-1].eleValue=(l pVec[edVec[i].startPoint-1].eleValue)+(edVec[i].value);}elseif(lpVec[edVec[i].startPoint-1].eleValue==0 .0&&lpVec[edVec[i].endPoint-1].eleValue!=0.0){lpVec[edVec[i].startPoint-1].eleValue= (lpVec[edVec[i].endPoint-1].eleValue)-(edVe c[i].value);}}for(j=numKnPoint;j<this->numPoints;j++){if(this->lpVec[j].eleValue==0.0){for(i=0;i<this->numElvDif;i++){ if(this->edVec[i].startPoint==lpVec[ j].index&&this->lpVec[this->edVec[i].endPoi nt-1].eleValue!=0.0)this->lpVec[j].eleValue=this->lpVec[thi s->edVec[i].endPoint-1].eleValue-this->edVe c[i].value;elseif(this->edVec[i].endPoint==lpVec[j].index& &this->lpVec[this->edVec[i].startPoint-1].e leValue!=0.0){this->lpVec[j].eleValue=this->lpVec[this-> edVec[i].startPoint-1].eleValue+this->edVec [i].value;}}}//cout<<"第"<<this->lpVec[j].index<<"个点的高程近似值:"<<this->lpVec[j].eleValue<<endl;}};voidxishu(CMatrix& B, CMatrix&X,CElevationNet A){ inti,j;for(i=1;i<=B.getRow();i++)for(j=1;j<=B.getColumn();j++){ B.setValue(i,j,0);}for(i=0;i<A.numElvDif;i++){ if(A.lpVec[A.edVec[i].startPoint-1].isKn own==1&&A.lpVec[A.edVec[i].endPoint-1].isKn own==0){B.setValue(i+1,A.edVec[i].endPoint-A.numKn Point,1);}elseif(A.lpVec[A.edVec[i].startPoint-1].isKnown ==0&&A.lpVec[A.edVec[i].endPoint-1].isKnown ==1){ B.setValue(i+1,A.edVec[i].startPoint -A.numKnPoint,-1);}elseif(A.lpVec[A.edVec[i].startPoint-1].isKnown ==0&&A.lpVec[A.edVec[i].endPoint-1].isKnown ==0){ B.setValue(i+1,A.edVec[i].endPoint-A. numKnPoint,1);B.setValue(i+1,A.edVec[i].startPoint-A. numKnPoint,-1);}}for(i=0;i<X.getRow();i++)X.setValue(i+1,1,A.lpVec[A.numKnPoint+i ].eleValue);};void quanzhen(CMatrix& Q, CElevationNet A) {inti,j;double sum=0.0;for(i=0;i<A.numElvDif;i++)sum+=A.edVec[i].weight;sum=sum/A.numElvDif;for(i=1;i<=Q.getRow();i++)for(j=1;j<=Q.getColumn();j++){ Q.setValue(i,j,0);}for(i=1;i<=Q.getRow();i++)Q.setValue(i,i,sum/A.edVec[i-1].weight) ;};void l_zhen( CMatrix& l ,CMatrix& L, CElevationNet A){int i;double m;for(i=0;i<A.numElvDif;i++)L.setValue(i+1,1,A.edVec[i].value);for(i=0;i<l.getRow();i++){m=(A.lpVec[A.edVec[i].startPoint-1].ele Value+A.edVec[i].value-A.lpVec[A.edVec[i].e ndPoint-1].eleValue)*1000;l.setValue(i+1,1,m);}};void main(){CElevationNet A;A.input();A.jsgc();CMatrixB(A.getgz(),A.getws()),Q(A.getgz(),A.getgz( )),X(A.getws(),1),l(A.getgz(),1),b(A.getws( ),A.getgz()),V(A.getgz(),1);CMatrixNBB(A.getws(),A.getws()),x(A.getws(),1) ,N(A.getws(),A.getws()),L(A.getgz(),1),M(A. getws(),A.getgz()),R(A.getws(),A.getgz()),W (A.getws(),A.getgz());CMatrixvz(1,A.getgz()),vp(1,A.getgz()), p(1,1);xishu(B,X,A);quanzhen(Q,A);l_zhen(l,L,A);b.operator=(B.transpose());M.operator=(b.operator *(Q));NBB.operator=(M.operator *(B));N.operator=(NBB.inverse());R.operator=(N.operator *(b));W.operator=(R.operator *(Q));x.operator=(W.operator *(l));inti,j;for(i=A.getys()+1;i<=A.getzs();i++){A.setdv(i,(x.getValue(i-A.getys(),1)/1000));A.seteleValue(i,A.getdv(i));cout<<"平差后编号为"<<A.getindex(i)<<"的点高程值:"<<A.geteleValue(i)<<"米"<<endl;}V.operator=(B.operator *(x));V.operator-(l);for(j=0;j<V.getRow();j++)cout<<"第"<<j+1<<"段观测高差平差值为:"<<(L.getValue(j+1,1)+V.getValue(j+1,1)/100 0)<<"米"<<endl;vz.operator=(V.transpose());vp=(vz.operator *(Q));p=(vp.operator *(V));cout<<"平差后单位权中误差为:"<<"+_"<<sqrt(p.getValue(1,1)/A.getws())<<"毫米"<<endl;}。
高程平差方法 举例说明

高程平差方法举例说明引言在工程建设中不免要对高程控制网进行高精度计算,手工计算对于较为简单的控制网还可适应,但对于较为复杂、节点较多的高程控制网来讲使用手工计算容易出现误差且非常耗时,因此我们针对高程控制网的平差计算原理进行了分析,并利用这一原理结合计算机技术进行了高效的控制网平差计算。
1 平差模型的建立1. 1 平差原理下面以一个水准网的算例来说明水准网间接平差原理,水准网如图1 所示:已知A 点高程HA=237. 483m,为求B、C、D 三点的高程,进行了水准测量,观测结果为见图1, h1、h2、h3、h4、h5 分别为观测值,对应的水准路线长度为S1、S2、S3、S4、S5。
取B、C、D 三点的高程值平差值为参数,其近似值为X01、X02、X03 其中:X01=HA+h1; X02=HA+h3; X03=HA+h5 于是观测值误差方程为v:常数项l:权P:如下:其中:改正数V= 系数阵A= 参数x= 常数项l=可以解出由此可以计算出高程平差值由上可知,水准网间接平差主要分为三个步骤:(1)高程近似值的计算;(2)列立观测值的误差方程;(3)解误差方程并求高程平差值。
1. 2 常数项矩阵的问题在求近似高程时,同一个未知点的近似高程并不是唯一的一个确定值,它的值随着计算时选择的线路不同而改变,因此得出的常数项矩阵L 也并不是唯一的,在下面的程序计算里面,输入已知数据时线路的排序不同,得出的常数项矩阵L 也不同,当然最后得到的高程改正数也不一样,由于进行平差计算时设的未知数就是未知点高程的近似值,因此在最后得到的未知点的高程平差值跟计算高程近似值时选择的线路无关,只要计算正确,最终得到的高程平差值也是正确的。
这一点可以在使用程序的过程中进行检验,无论线路排序如何改变,只要数据输入正确,得到的结果是一样的。
2 平差程序设计2. 1 关于程序语言的选用考虑到本软件所要解决的问题主要是数据的处理与计算,不涉及到计算机系统底层的操作,因此选用相对简单的Visual Basic 6. 0 来进行程序的编写,使用间接平差模型,在保证计算精度的同时,一来减少了代码编写的难度,二来提高了代码执行的效率。
水准网间接平差及可视化程序设计

水准网间接平差及可视化程序设计
段艳慧;葛于祥;张晓莹;郭伟
【期刊名称】《北京测绘》
【年(卷),期】2022(36)4
【摘要】针对测量平差烦琐的矩阵运算问题,本文利用矩阵实验室(matrix laboratory,MATLAB)平台进行水准网平差、精度评价与可视化展示。
由于间接平差误差方程式建立的规律性很强,而条件平差的条件方程式的规律不够明显,本文根据间接平差的原理进行程序设计并进行实例验证,实现了水准网间接平差的程序化及可视化表达,该程序的设计与可视化界面的设计降低了误差出现的概率,极大提高了水准网平差及精度评价的速度和精度,可应用于水准网间接平差的计算中。
【总页数】5页(P488-492)
【作者】段艳慧;葛于祥;张晓莹;郭伟
【作者单位】中国矿业大学(北京)地球科学与测绘工程学院;中国矿业大学环境与测绘学院
【正文语种】中文
【中图分类】P207
【相关文献】
1.粗差探测在水准网平差程序设计中的实现
2.基于Matlab的水准网间接平差程序设计
3.浅议同一水准网条件平差与间接平差处理之异同
4.水准网条件平差粗差检测程序设计方法
5.水准网条件平差粗差检测程序设计方法
因版权原因,仅展示原文概要,查看原文内容请购买。
水准网的条件平差

目录目录 (1)观测误差 (2)摘要: (2)关键词: (2)引言 (3)1水准测量 (4)1.1水准测量的原理 .............................................................................. •1.2水准网...................................................................................... •2条件平差 .. (6)2.1 衡量精度的指标 (6)2.2条件平差的原理 .............................................................................. •3水准网的平差 .. (14)3.1必要观测与多余观测 (14)3.2条件方程 (14)3.3条件平差法方程式 (14)3.4条件平差的精度评定 (15)3.5水准网的条件平差 (18)致谢 (20)参考文献 (21)观测误差由观测者、外界环境引起的偶然误差学生:xxx 指导教师:xxx摘要:对一系列带有偶然误差的观测值,采用合理的的方法消除它们间的不符值,得出未知量的最可靠值;以及评定测量成果的精度。
关键词:偶然误差;观测值;精度引言测量工作中,要确定地面点的空间位置,就必须进行高程测量,确定地面点的高程。
几何水准测量是高程测量中最基本、最精密的一种方法。
通过测量仪器,工具等任何手段获得的以数字形式表示的空间信息,即观测量。
然而,测量是一个有变化的过程,受仪器、观测值、外界环境因素的影响,观测的结果与客观上存在的一个能反映其真正大小的数值,即真值(理论值),有一定的差异。
可以说在测量中产生误差是不可避免的。
所以,观测值不能准确得到,在测量上称这种差异为观测误差。
根据其对观测结果影响的性质,可将误差分为系统误差和偶然误差两种。
水准网平差程序设计

程序设计中的关键问题
数据处理
如何高效地读取和处理大规模数据, 避免内存占用过多或计算效率低下。
算法优化
如何优化算法以提高程序的运行效率, 减少计算时间和资源消耗。
可扩展性
如何设计程序结构,使其具有良好的 可扩展性,便于未来功能扩展和维护。
健壮性
如何提高程序的健壮性,使其能够处 理异常情况,避免因数据错误或异常 输入导致程序崩溃。
05
程序测试与验证
测试环境与测试数据
测试环境
选择合适的硬件和软件环境,确保测试结果的准确性和可靠性。
测试数据
准备充足的水准网平差数据,包括已知的控制点数据和待处理的观测数据,以覆盖各种实际情况。
测试结果分析
精度分析
01
对测试结果进行精度分析,包括闭合差、中误差等指标,评估
程序的精度水平。
效率分析
06
总结与展望
工作总结
完成了水准网平差程序设 计的需求调研和分析,明 确了程序设计的目的和功 能要求。
实现了水准网平差程序的 基本功能,包括数据导入、 平差计算、结果输出等。
ABCD
完成了程序设计方案的制 定,包括算法选择、数据 结构设计和界面设计等。
对程序进行了全面的测试 和调试,确保程序的稳定 性和正确性。
水准网平差程序设计
• 引言 • 水准网平差基础 • 水准网平差程序设计 • 水准网平差程序实现 • 程序测试与验证 • 总结与展望
目录
01
引言
目的和背景
目的
水准网平差程序设计的主要目的是对水准网进行精度分析和优化,以提高测量 数据的准确性和可靠性。
背景
随着测量技术的发展,水准网在各种工程领域中得到了广泛应用,如建筑、水 利和交通等。然而,由于测量过程中存在误差,需要对水准网进行平差处理, 以消除或减小误差的影响。
水准网间接平差程序设计

水准网间接平差程序设计水准网间接平差是测量水准网中各测站的高程值,通过观测值的处理,进行计算来消除观测误差,得到准确的高程数据。
在进行水准网间接平差程序设计时,需要考虑观测值的处理方法、具体的计算步骤、误差的传递和消除等因素。
下面将详细介绍水准网间接平差程序设计的内容。
首先,在水准网间接平差的程序设计中,需要对观测值进行处理。
观测值的处理包括检查观测数据的精度、合理性及完整性,并进行数据的筛选和滤波处理。
在这一步骤中,需要使用适当的统计方法对观测数据进行筛选,剔除异常值和明显错误的数据,保留符合要求的观测值。
接下来,在进行水准网间接平差计算之前,需要对网络进行拟合,拟合过程即将观测值与已知高程值进行比较,并进行拟合计算得到误差。
网络拟合可以使用最小二乘法进行计算,即通过最小化观测值与已知高程值的差的平方和,来求得最优拟合结果。
然后,进行水准网的平差计算。
平差计算是根据测站之间的观测关系,通过一系列的计算公式,将所有观测值联立起来,并通过方程组进行求解,得到最终的平差结果。
在这个过程中,需要进行传递误差的计算,即通过误差传递公式计算各点高程值的精度,以评估平差结果的可靠性。
最后,在完成水准网间接平差计算之后,需要对平差结果进行检查和评估。
检查结果是否符合工程要求和精度要求,评估平差的可靠性。
如果结果不符合要求,需要重新进行观测值的处理和计算。
在进行水准网间接平差程序设计时,还需要注意以下几点:1.数据的输入与输出:程序需要提供方便的数据输入和输出方式,以便用户输入观测数据,并输出平差结果。
同时,需要考虑数据的存储和传输方式,确保数据的安全和完整性。
2.程序的可扩展性:设计程序时应考虑未来可能的数据规模扩大和功能的增加。
通过模块化设计和灵活的架构,使程序能够方便地扩展和添加新的功能。
3.用户友好性:程序应提供简单易用的操作界面,提供友好的用户交互方式。
用户应能够方便地输入观测数据和设置计算参数,并能够直观地查看和分析计算结果。
测量程序设计_条件平差和间接平差

程序代码如下:
disp(‘-------水准网间接平差示例-------------’) disp(‘已知高程’) Ha = 5.015 % 已知点高程,单位m Hb = 6.016 % 已知点高程,单位m
A h2 D h1
C h6 E h7 B h4
h5
h3
disp(‘观测高差,单位m’)
L = [1.359; 2.009; 0.363; 1.012; 0.657; -0.357] disp(‘系数矩阵B’)
则: PV AT K
V P A K QA K
T
1 T
4、法方程: 将条件方程 AV+W=0代入到改正数方程V=QATK 中,则得到:
AQAT K W 0
r1 r1 r1
记作: 由于
N aa K W 0
rr
R( Naa ) R( AQAT ) R( A) r
Naa为满秩方阵, K Naa1W ( AQAT )1 ( AL A0 )
if H(1,1)+H(2,1)-H(3,1)+HA-HB==0 && H(2,1)H(4,1)==0 disp(‘检核正确') else disp(‘检核错误') end disp(‘平差后的高程值') HC = HA + H(1,1) HD = HA + H(1,1) + H(4,1)
二、间接平差的基本原理
其中l=L-d.
ˆ 设误差Δ和参数X的估计值分别为V 和 X
则有
ˆ V AX l
X0 为了便于计算,通常给参数估计一个充分接近的近似值
ˆ ˆ X X0 x
则误差方程表示为
测绘程序设计—实验八 水准网平差程序设计报告

《测绘程序设计》上机实验报告(Visual C++.Net)班级:测绘0901班学号: 04姓名:代娅琴2012年4月29日实验八平差程序设计基础一、实验目的巩固过程的定义与调用巩固类的创建与使用巩固间接平差模型及平差计算掌握平差程序设计的基本技巧与步骤二、实验内容水准网平差程序设计。
设计一个水准网平差的程序,要求数据从文件中读取,计算部分与界面无关。
1.水准网间接平差模型:2.计算示例:近似高程计算:3.水准网平差计算一般步骤(1)读取观测数据和已知数据;(2)计算未知点高程近似值;(3)列高差观测值误差方程;(4)根据水准路线长度计算高差观测值的权;(5)组成法方程;(6)解法方程,求得未知点高程改正数及平差后高程值;(7)求高差观测值残差及平差后高差观测值;(8)精度评定;(9)输出平差结果。
4.水准网高程近似值计算算法5.输入数据格式示例实验代码:#pragma onceclass LevelControlPoint{public:LevelControlPoint(void);~LevelControlPoint(void);public:CString strName;trName=pstrData[0];m_pKnownPoint[i].strID=pstrData[0];m_pKnownPoint[i].H=_tstof(pstrData[1]);m_pKnownPoint[i].flag=1;trName=pstrData[i];m_pUnknownPoint[i].strID=pstrData[i];m_pUnknownPoint[i].H=0;lag=0;pBackObj=SearchPointUsingID(pstrData[0]);pFrontObj=SearchPointUsingI D(pstrData[1]);ObsValue=_tstof(pstrData[2]);ist=_tstof(pstrData[3]);trID==ID){return &m_pKnownPoint[i];}}return NULL;}trID==ID){return &m_pUnknownPoint[i];}}return NULL;}LevelControlPoint* AdjustLevel::SearchPointUsingID(CString ID){LevelControlPoint* cp;cp=SearchKnownPointUsingID(ID);if(cp==NULL)cp=SearchUnknownPointUsingID(ID);return cp;}void AdjustLevel::ApproHeignt(void)lag!=1){pFrontObj->strID==m_pUnknownPoint[i].strID)&& m_pDhObs[j].cpBackObj->flag==1 ){ =m_pDhObs[i].cpBackObj->H - m_pDhObs[i].ObsValue;*/m_pUnknownPoint[i].H=m_pDhObs[j].cpBackObj->H + m_pDhObs[j].HObsValue;m_pUnknownPoint[i].flag=1;break;}}if(m_pUnknownPoint[i].flag!=1)pBackObj->strID==m_pUnknownPoint[i].strID)&& m_pDhObs[j].cpFrontObj->flag==1 ){ =m_pDhObs[j].cpFrontObj->H-m_pDhObs[j].HObsValue;/* m_pUnknownPoint[i].H=m_pDhObs[i].cpFrontObj->H+m_pDhObs[i].ObsValue;*/ m_pUnknownPoint[i].flag=1;break;}}}}if(i==m_iUnknownPointCount-1)lag!=1)ist);p(i,i)=value;}return p;}void AdjustLevel::FormErrorEquation(CMatrix &B, CMatrix &L){(m_iDhObsCount,m_iUnknownPointCount);(m_iDhObsCount,1);for(int i=0;i<m_iDhObsCount;i++)pBackObj->strID);tmpFront=SearchPointUsingID(m_pDhObs[i].cpFrontObj->strID);trID==tmpBack->strID)trID==tmpFront->strID)bsValue-(m_pDhObs[i].cpBackObj->H-m_pDhObs[i].cpFrontO bj->H);*/L(i,0)=m_pDhObs[i].HObsValue-(m_pDhObs[i].cpFrontObj->H - m_pDhObs[i].cpBackObj->H);(_T("%.3f"),L(i,0));L(i,0)=_tstof(tmp);L(i,0)=L(i,0)*1000;+=x(i,0);xt"));xt"));if()==IDCANCEL) return;CString strFileName=();setlocale(LC_ALL,"");CStdioFile sf;if(!(strFileName, CFile::modeCreate|CFile::modeWrite)) return;(LevleContent);();UpdateData(FALSE);}void CIndircLelveDlg::OnBnClickedComputelevel(){f\r\n"), [i].strID,[i].H);LevleContent+=Temp;}(_T("单位权中误差:%.1f mm\r\n"),r0*1000);LevleContent+=Temp;LevleContent+=_T("未知点高程中误差(mm):\r\n");for(int i=0;i< ;i++){();(_T("%s,%.1f\r\n"),[i].strName,Qx[i]*1000);LevleContent+=Temp;}UpdateData(false);}void CIndircLelveDlg::OnBnClickedSavelevleresult(){xt"));if()==IDCANCEL) return;CString strFileName=();setlocale(LC_ALL,"");CStdioFile sf;if(!(strFileName, CFile::modeCreate|CFile::modeWrite)) return;(LevleContent);();UpdateData(FALSE);}三、实验结果打开文件数据:平差结果:四、实验心得这从实验是我们测绘程序设计的最后一次实验,虽然这个学期我们做了好几次相关的实验,但是我却发现自己学的东西也越来越模糊,感觉很多内容都不理解。
Excel用于水准网平差

Excel用于水准网平差1 问题的提出在测量实践中,水准网的平差是比较常见的。
虽然现在的平差软件很多,拿来就可以用,不过研究一下水准网的计算,加深对平差的理解,对以后的工作是非常有意义的。
2 平差模型要进行水准网平差计算,需要知道以下几点要素:1、高程已知点2、高程未知点3、各段高差观测值及每段的线路长度(或测站数,用于定权)以《测量平差基础(增订本)》(以下简称“书 [1]”)第 148 页的例 4-11 为准,各个要素如下:1、高程已知点点名高程A 5.016B 6.0162、高程未知点一共有三个:P1、P2、P33、各段高差起点终点高差路线长(公里)A P1 1.3590 1.1A P2 2.0090 1.7B P1 0.3630 2.3B P2 1.0120 2.7P1 P2 0.6570 2.4P1 P3 0.2380 1.4P3 B -0.5950 2.6 书 [1]上给出了条件平差与间接平差(第 279 页)两种解法。
仔细观察就会发现:水准网按条件平差的条件比较难找(书 [1]上用了三个闭合条件和一个附和条件),而且平差步骤比较多:计算出高差改正数--〉得到高差平差值--〉计算各点的平差高程。
间接平差则相反,其误差方程很好列,而且平差结果就是各点的高程改正数,比较直接。
所以编程计算的话首选间接平差。
3 平差步骤按书 [1] 上的间接平差步骤来:1、取未知点的高程为未知数x1,x2,... x t(一共 t 个未知数)2、计算每个未知数的近似值X03、根据观测高差值列误差方程 V=BδX+L4、组成法方程NδX+U=0(N=B T PB,U=B T PL,P 为观测值的权阵)5、根据法方程解出δX,并得到 X=X0+δX这里比较麻烦的是第 2 步,即计算每个未知点的近似高程。
可以根据表2 来计算:1、扫描每段高差观测值,如一个高程已知或已获得近似高程,另一个高程未知。
那么推算出未知点的高程,并标记其为“已获得近似高程”。
通用水准网形秩亏自由网和拟稳平差程序设计
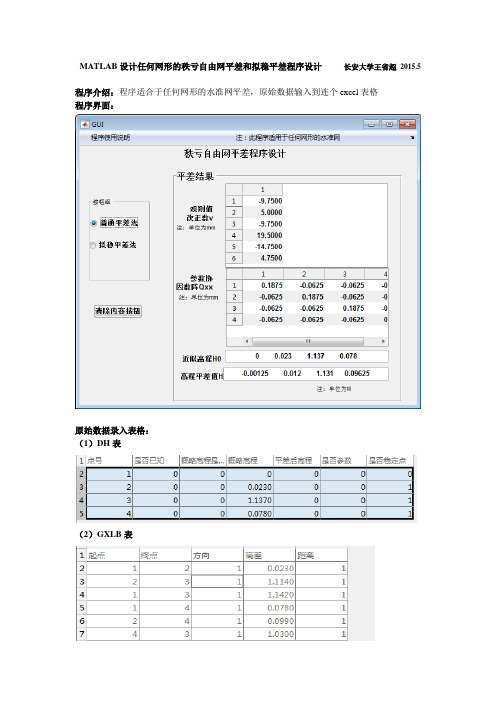
MATLAB设计任何网形的秩亏自由网平差和拟稳平差程序设计长安大学王省超2015.5程序介绍:程序适合于任何网形的水准网平差,原始数据输入到连个excel表格程序界面:原始数据录入表格:(1)DH表(2)GXLB表程序代码:function xsz=XSZ(num1,num2)%函数功能提取误差系数A[m1,n1]=size(num1);[m2,n2]=size(num2);n=0;for i=1:m1 %用来判断参数个数if num1(i,2)==1n=n+0;elsen=n+1;endendxsz=zeros(m2,n); %建立系数阵,全为零for i=1:m2 %提取系数阵q=num2(i,1);z=num2(i,2);xsz(i,z)=1;xsz(i,q)=-1;endend%---------------常数项L-------------------------------------------------------------- function l=L(num1,num2)[m1,n1]=size(num1);[m2,n2]=size(num2);l=zeros(m2,1);for i=1:m2 %计算lq=num2(i,1);z=num2(i,2);l(i,1)=num2(i,4)-num1(z,4)+num1(q,4);endl=l*1000; %把l从米换算为毫米end%-------------求平差权阵P------------------------------------------------------------ function p=P1(num1,num2)[m1,n1]=size(num1);[m2,n2]=size(num2);p=zeros(m2,m2);for i=1:m2p(i,i)=1/num2(i,5);endend%------------秩亏自由网平差--------------------------------------------------------------------- function[v,Qxx]=PTPCclear allclcglobal H1;global K1;[num1]=xlsread('DH');K=num1(:,4);K1=K';[m1,n1]=size(num1); %用来判断num1得行列[num2]=xlsread('GXLB');[m2,n2]=size(num2);A=XSZ(num1,num2) %误差方程系数r=rank(A); %矩阵的秩d=1; %秩亏数l=L(num1,num2) %误差方程常数项单位mmP=P1(num1,num2); %权N=A'*P*A %法方程系数W=A'*P*lNN=N*NN0=NN(1:r,1:r);NN_=blkdiag(inv(N0),zeros(d,d));%广义逆求逆Nm=N*NN_x=Nm*W%-----------高程平差值------H=x/1000+num1(:,4)%单位统一为MH1=H';%----精度评定-------v=A*x-l %单位mmQxx=N*NN_*N*NN_*Nmsgbox('秩亏自由网普通平差完成')%---------------拟稳平差--------------------------------------------------------------------------------------- function[v,Qxx]= NWPCclear allglobal H2;global K1;[num1]=xlsread('DH');K=num1(:,4);K1=K';;[m1,n1]=size(num1); %用来判断num1得行列[num2]=xlsread('GXLB');[m2,n2]=size(num2);A=XSZ(num1,num2) %误差方程系数r=rank(A); %矩阵的秩d=m1-r; %秩亏数l=L(num1,num2) %误差方程常数项单位mmP=P1(num1,num2); %权for i=1:m1 %找出稳定点if num1(i,7)==1f(i)=1;elsef(i)=0;endendc1=find(f==1);%找出稳定点的下标c0=find(f==0);%非稳定点下标A1=A(:,c0)A2=A(:,c1)N11=A1'*P*A1;N12=A1'*P*A2;N21=N12';N22=A2'*P*A2;M=N22-N21*inv(N11)*N12;r=rank(M);d=1;MM=M*M;M0=MM(1:r,1:r);MM_=blkdiag(inv(M0),zeros(d,d));%广义逆求逆Mm_=M*MM_;a=(A2'-N21*inv(N11)*A1')';a_=Mm_*a';b_=inv(N11)*(A1'-N12*a_);%-------结算未知数-------------------------------------------------------------x2=a_*P*l;x1=b_*P*l;x=[x1;x2]H=x/1000+num1(:,4)%单位统一为MH2=H';%------计算改正数---------------------------------------------------------------------------v=A*x-l%------计算位置参数协因数矩阵-------Qxx=[b_*P*b_' b_*P*a_';a_*P*b_' a_*P*a_']msgbox('秩亏自由网拟稳平差完成')-%-------程序界面代码----------------------------------------------------------------------------------------- function varargout = GUI(varargin)gui_Singleton = 1;gui_State = struct('gui_Name', mfilename, ...'gui_Singleton', gui_Singleton, ...'gui_OpeningFcn', @GUI_OpeningFcn, ...'gui_OutputFcn', @GUI_OutputFcn, ...'gui_LayoutFcn', [] , ...'gui_Callback', []);if nargin && ischar(varargin{1})gui_State.gui_Callback = str2func(varargin{1});endif nargout[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});elsegui_mainfcn(gui_State, varargin{:});endfunction GUI_OpeningFcn(hObject, eventdata, handles, varargin)handles.output = hObject;% Update handles structureguidata(hObject, handles);% --- Outputs from this function are returned to the command line. function varargout = GUI_OutputFcn(hObject, eventdata, handles)varargout{1} = handles.output;function radiobutton1_Callback(hObject, eventdata, handles)[v,Qxx]=PTPC;set(handles.uitable1,'Data',v);set(handles.uitable2,'Data',Qxx);global H1;set(handles.edit4,'string',num2str(H1));global K1;set(handles.edit3,'string',num2str(K1));function radiobutton2_Callback(hObject, eventdata, handles)[v,Qxx]=NWPC;set(handles.uitable1,'Data',v);set(handles.uitable2,'Data',Qxx);global H2;set(handles.edit4,'string',num2str(H2));global K1;set(handles.edit3,'string',num2str(K1));function edit1_Callback(hObject, eventdata, handles)function edit1_CreateFcn(hObject, eventdata, handles)if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');endfunction edit2_Callback(hObject, eventdata, handles)% --- Executes during object creation, after setting all properties. function edit2_CreateFcn(hObject, eventdata, handles)if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');end% --- Executes when entered data in editable cell(s) in uitable1. function uitable1_CellEditCallback(hObject, eventdata, handles)--------------------------------------------------------------------function Untitled_1_Callback(hObject, eventdata, handles)--------------------------------------------------------------------function Untitled_2_Callback(hObject, eventdata, handles)h=msgbox({'´Ë³ÌÐòÔ-ʼÊý¾ÝµÄ¼ÈëÔÚDH(µãºÅ±í)ºÍGXLB£¨¹ØϵÁбí)ÖÐ,ÒÀ¾Ý±í¸ñ˵Ã÷½øÐÐÊý¾Ý¼È룬';'ÆäÖÐ"1"±íʾÊÇ"0"±íʾ·ñ'})% ÐÞ¸Ä×ÖÌåah = get( h, 'CurrentAxes' );ch = get( ah, 'Children' );set( ch, 'FontSize', 8 );function edit3_Callback(hObject, eventdata, handles)% --- Executes during object creation, after setting all properties. function edit3_CreateFcn(hObject, eventdata, handles)if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');endfunction edit4_Callback(hObject, eventdata, handles)% --- Executes during object creation, after setting all properties. function edit4_CreateFcn(hObject, eventdata, handles)if ispc && isequal(get(hObject,'BackgroundColor'),get(0,'defaultUicontrolBackgroundColor'))set(hObject,'BackgroundColor','white');end% --- Executes on button press in togglebutton1.function togglebutton1_Callback(hObject, eventdata, handles)set(handles.edit3,'string','')set(handles.edit4,'string','')set(handles.uitable1,'data','')set(handles.uitable2,'data','')% --- Executes when entered data in editable cell(s) in uitable2. function uitable2_CellEditCallback(hObject, eventdata, handles)%--------------------------------------------------------------------function Untitled_3_Callback(hObject, eventdata, handles)function Untitled_4_Callback(hObject, eventdata, handles)。
水准网平差程序设计

水准网平差程序设计水准网平差是测绘工程中的一项重要工作,它涉及到对水准测量数据进行处理,以达到测量精度的要求。
水准网平差程序设计通常需要考虑以下几个方面:1. 程序设计的目的和意义水准网平差程序设计的主要目的是通过计算机软件对水准测量数据进行自动化处理,提高数据处理的效率和准确性。
这对于大型工程测量、城市基础设施建设、土地管理等领域具有重要意义。
2. 程序设计的基本要求- 准确性:程序需要能够准确地处理水准测量数据,减少人为误差。
- 稳定性:程序在运行过程中应具有较高的稳定性,避免因系统崩溃等原因导致数据丢失。
- 用户友好性:程序应具备良好的用户界面,使得非专业用户也能方便地使用。
- 扩展性:程序设计应考虑未来可能的功能扩展,以适应不断变化的测量需求。
3. 程序设计的理论基础水准网平差程序设计的理论基础主要包括:- 水准测量原理:了解水准测量的基本原理,包括视线高、转点高、已知点高程等概念。
- 误差理论:掌握测量误差的来源、分类及其对测量结果的影响。
- 最小二乘法:水准网平差通常采用最小二乘法进行数据处理,需要理解其数学原理和应用方法。
4. 程序设计的关键技术- 数据输入:设计高效的数据输入界面,支持多种数据格式的导入。
- 数据处理:实现数据的自动校验、筛选和处理功能。
- 平差计算:编写平差计算算法,包括闭合差计算、误差分配等。
- 结果输出:设计结果输出模块,支持多种输出格式,如文本、图表等。
5. 程序设计的实现步骤1. 需求分析:明确程序设计的目标和用户需求。
2. 系统设计:设计程序的整体架构,包括模块划分、数据流等。
3. 编码实现:根据设计文档进行编码,实现各个功能模块。
4. 测试验证:对程序进行测试,确保其准确性和稳定性。
5. 用户手册编写:编写用户手册,指导用户如何使用程序。
6. 程序设计的注意事项- 数据安全:确保程序在处理数据时的安全性,防止数据泄露。
- 异常处理:程序应能妥善处理各种异常情况,如数据格式错误、计算溢出等。
高程控制网平差

V5 X 1 X 2 l5 V6 X 2 X 3 l6
P5
P6
(一)按间接平差法对结点进行平差
2.法方程式的组成
可以看出,法方程系数矩阵的对角线元素是该 结点周围个水准路线高差观测值的权之和,非 对角线元素是两个结点间高差观测值得权的相 反数。如果两个结点间没有联测,则相应元素 为零。结点近似高程减去周围点计算该结点高 程的差值乘上水准路线权,然后求和,其值为 法方程常数项。
(四)平差计算步骤
(1)绘制水准网平差略图。 (2)水准点编号。
(3)调制已知数据和观测数据表,并按一定格式 输入到计算机。
(4)列出条件方程式和最弱点权函数,并将其系 数和闭合差输入给计算机。
(5)由计算机进行法方程组成、解算,计算高差 改正数和平差值,计算各待定结点的高程平差值, 计算单位权中误差、每千米高程中误差,计算最 弱点高程中误差。
二、高程控制网结点平差
结点平差法是由间接平差原理演变而来的一种简捷算法, 它具有算法简便、公式规律性强、结果严密等优点,便 于手算,也可编写成程序。因此,常用这种方法来平差 水准网和三角高程网。
间接平差以待定点近似高程的改正数为未知参数,以两 个高程点之间的高差为观测值,在观测值和未知值之间 列立误差方程式, 而后由误差方程式直接组成 并结算法方程。
二、高程控制网结点平差 1.按间接平差法对结点进行平差 2.按单一水准路线条件平差对各种水准路线进行平差 3.水准网结点平差算例 4.三角高程网结点平差
一、水准网条件平差
(一)水准网条件方程式的数目和组成
水准网的条件方程式个数等于多余观测的个数。用n表示水准网 中高差观测值个数,t表示必要观测值个数。在有已知水准点的 水准网,必要观测值个数等于待定点个数,在无已知水准点的 水准网中,必要观测的个数等于水准点个数减1,;用r表示多余 观测的个数,则有:
基于Matlab的水准网间接平差程序设计

基于Matlab的水准网间接平差程序设计赵亚红;周文国【摘要】设计水准网数据结构,存储在文本中,按照水准网的起点、终点、观测数据相对应关系建立矩阵,利用Matlab强大的矩阵运算功能,通过间接平差方法,按照最小二乘原理,求得任意水准网的未知点的最或然高程值,对平差结果输出存储,程序直观、简便。
并用实例验证了其正确性及通用性。
%On the basis of data structure designed, the relation of point s and lines of level net, the surveying data and the known data are st ored in the text, the matrixs were set up through the relation of the jupping -off points, end -points and the surveying data. And a program is designed in MATLAB to get the value of most probable by its strong abilty of calculating matrix, the result was output and stored. At last,the example proved the programme was right.【期刊名称】《华北科技学院学报》【年(卷),期】2011(008)003【总页数】3页(P58-60)【关键词】水准网;间接平差;Matlab【作者】赵亚红;周文国【作者单位】华北科技学院土木工程系,北京东燕郊101601;华北科技学院土木工程系,北京东燕郊101601【正文语种】中文【中图分类】P207.2水准网间接平差的的具体过程是:(1)根据水准网形进行分析,列误差方程;(2)根据误差方程系数列法方程;(3)解算法方程,求参数X及V;(4)求最或然值、精度评定。
基于VB环境下水准网平差程序设计研究

则 如果有 托个观 测值 , 总的误 差方 程 为 : 则
T r
一
^
Tr
一
T
/ r 、
分别 是 已知 观 测 数 据 输 人 、 测 数 据 信 息 提 取 、 观 未 知点 近 似 高 程 计 算 、 差 方 程 系数 矩 阵 A 和 L 生 误
成、 求解 未知参 数值 。
“
式 中
下水准 网平差程序设计研究
未知点平差后的高程最或然值 。
1 3
2 1 已知数 据输 入和 观测 数据 信 息提取 . 已知数 据按 照 一 定 的格 式 编辑 在 文本 文 档 中 , 按 行读 取到 程 序 中 , 据 输 入 后 , 序 首 先 对 已知 数 程
其 中为 每 段 高 差 的水 平 距 离
。
因 此 只要 确 定
出矩 阵 A 和矩 阵 L 就 可求 出高 程改 正值 , 而求 出 进
如果 , 点都 为未 知点 , 两 则误 差 方程 为 :
未 知点 高程 的最 或然值 。
+ 一 一 + £
,
() 2 水 准网间接平差程 序设计思路 4
高差 组成 的 误 差 方 程 的 系 数 组 成 矩 阵 A。矩 阵 L
2
A
C
3 5 .2
1 . 42
中 的元 素 则 为 相 应 的终 点 近 似 高 程 或 减 去 起 点 的 相应 近似 高程 或 已知 高程 以及 观测 高差 的值 。
2 4 求解未 知 点高程 改正值 .
3
4
5
A
B
B
如何使用四院软件进行二等水准平差

如何使用四院软件进行二等水准平差
使用软件;铁路工程精密控制测量V4.2.5
1)
2)
3) 选择项目,新建一个项目在桌面。
4)将测好的水准线路DTA文件复制到此文件中。
5)选择水准仪处理参数,设置处理参数
6) 双击水准仪处理参数,选择观测文件,打开需要平差的DTA文件。
7)点击水准仪处理参数,选择观测数据检核,设置好限差,检查文件有无超限。
8)点击水准仪处理参数,生成平差文件,将线路中控制点高程输入平差文件中保存,保存后会自动生成in1文件。
9)点击高程网平差处理,选择平差文件,选择刚保存的in1文件打开。
10)点击高程网平差处理(由于本线路中线路为附和线路,所以选择附和/环闭合差处理数据),平差结果显示未超限,则线路精度合格)。
11)点击高程网平差处理,点击平差处理(常规),线路控制点高程就出来啦。
下载链接: https:///s/1PKBYrqL0IRLCP0qY6Bg6vQ 提取码: 6i3x。
平差课程设计报告

实验一一.设计原始资料水准网周密平差及精度评定示例。
如图所示水准网,有2个已知点,3个未知点,7个测段。
各已知数据及观测值见下表(1)已知点高程H1= H2=(2)高差观测值(m)高差观测值(m)端点高差观测值测段距离序号号1-3 11-4 22-3 32-4 43-4 53-5 65-2 7(3)求各待定点的高程;3-4点的高差中误差;3号点、4号点的高程中误差。
(提示,本网可采用以测段的高差为平差元素,采用间接平差法编写程序计算。
)二、水准网间接平差思路⑴.按照网型肯定已知水准点数H1 H2,未知水准点数u ,总点数n ,必要观测数t ,多余观测数r 。
⑵.肯定参数。
为平差后能直接求得待定点高程平差值,以3个待定点高程平差值为参数。
设3,4,5点的高程平差值别离为,, 。
⑶.列立条件方程.左侧为观测值(系数为1),右边为参数和常数项,并进一步改化成误差方程,最终写成矩阵形式。
取得系数矩阵A 和常数项L⑷.列立法方程,并解求法方程。
⑸.精度评定。
计算单位权中误差的估值:评定各待定点的高程中误差: 各待定点的精度即为: 评定高程平差值的精度: 四、平差程序设计思路1、 已知数据的输入需要输入的数据包括水准网中已知点数、未知点数和这些点的点号、已知高程和高差观测值、距离观测值等。
本程序采用文件方式进行输入,文件输入的格式如下: 第一行:已知点个数、未知点个数、观测值个数 第二行:点号 (已知点在前,为支点在后) 第三行:已知高程 (顺序与上一行的点号对应)第四行起:高差观测值,依照“起点点号,终点点号,高差观测值,距离观测值”的顺序输入。
2、 平差计算进程 (1)近似高程计算。
uc PV V r PV V T T -==20ˆσ120ˆˆ20ˆˆˆˆ-==bbx x x x N Q D σσjj X X j X Q ˆˆ0ˆˆσσ±=FN F F Q F Q BB T X X T h h 1ˆˆˆˆ-==X F hT ˆˆ=(2)列立观测值的误差方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AfxGetApp()->m_pMainWnd->MessageBox( "数据文件不存在或数据文件错!", "进程. . . . . .!!!",MB_OK|MB_ICONSTOP);
//重要说明:原始数据文件中,未知点的高程可以随意输入,也可以不输入空缺, 程序自动把待定点高程赋值为 0
} for(i=ne;i<nz;i++) {
fp.ReadString(buff,MAXLINE); sscanf(buff,"%d%s%lf",&dh,ch1,&gc); dm[i]=ch1;H[i]=0; } for(i=0;i<nn;i++) { fp.ReadString(buff,MAXLINE); sscanf(buff,"%d%d%lf%lf",
教师 评语
// Gckzwpc.cpp: implementation of the CGckzwpc class. // ////////////////////////////////////////////////////////////////////// #include "stdafx.h" #include "Survey.h" #include "Gckzwpc.h" #ifdef _DEBUG #undef THIS_FILE static char THIS_FILE[]=__FILE__; #define new DEBUG_NEW #endif ////////////////////////////////////////////////////////////////////// // Construction/Destruction ////////////////////////////////////////////////////////////////////// CGckzwpc::CGckzwpc() { } CGckzwpc::~CGckzwpc() { } bool CGckzwpc::ReadData(CString filename) {
辽宁工程技术大学上机实验报告
成绩
实验名称
水准网间接平差程序设计
院系
测绘与地理 科学学院
专业
测绘工程
班级
09-1 班
姓名Βιβλιοθήκη 贺永成学号 0904070207 日期 2011.12.26
实验 目的
简述本次实验目的: 掌握用间接平差法对任意网行的水准网进行平差的算法设计以及程序编制。并采 用读文件处理数据的方法,设计水准网处理类。
W[i]+=B[k][i]*P[k]*l[k];}} invGJ(Nbb,nw); for(i=0;i<nw;i++) {
X[i]=0.0; for(k=0;k<nw;k++) {
X[i]+=Nbb[i][k]*W[k];}}} //精度评定与成果输出 void CGckzwpc::jdpd() {
n0++; j0=0; {
for(i=0;i<nn;i++) //循环高差 {
if(H[n1[i]-1]>0 && H[n2[i]-1]>0) continue; if(H[n1[i]-1]>0 && H[n2[i]-1]==0) {
H[n2[i]-1]=H[n1[i]-1]+h[i]; } if(H[n1[i]-1]==0 && H[n2[i]-1]>0) {
_exit(1); return FALSE; } fp.ReadString(buff,MAXLINE); sscanf(buff,"%d%d%d",&nz,&nw,&nn); ne=nz-nw; int dh; double gc; for(i=0;i<ne;i++) { fp.ReadString(buff,MAXLINE); sscanf(buff,"%d%s%lf",&dh,ch1,&gc); dm[i]=ch1;H[i]=gc;
实验 任务
用 C\C++编写水准网间接平差程序,并调试通过,用实测数据实算分析,并评定 精度。
实验 要求
实验 总结
1. 个人独立编写程序,原始数据存放于文本文件或数据库文件中。 2. 程序应具有通用性,即任意网形都可以平差。 3. 用实测的数据进行计算分析。 4. 评定待定点的高程精度。 本次实验的收获、体会、经验、问题和教训:
B[i] = new double [nw]; for(i=0;i<nn;i++) {
P[i]=0.0; l[i]=0.0; for(j=0;j<nw;j++)
B[i][j]=0.0; } //计算待定点的近似高程 int n0=0; //计算次数 int j0; //高程计算是否完毕?j0=0,计算完毕;j0=1,未计算完毕 for(;;) {
int i,j,k; FILE *fp; fp=fopen("out.txt","w"); VPV =0.0; for(i=0;i<nn;i++) {
V[i]=0.0; for(k=0;k<nw;k++) {
V[i]+=B[i][k]*X[k]; } V[i]+=-l[i]; VPV+=V[i]*V[i]*P[i]; ph[i]=h[i]+V[i]; } //计算验后单位权中误差 SIG0=sqrt(VPV/(nn-nw)); //计算未知参数-平差高程的自协方差 for(i=0;i<nw;i++) { DX[i]=SIG0*SIG0*Nbb[i][i]; } double **QLL,**SIGL; QLL = new double * [nn]; SIGL= new double * [nn]; for(i=0;i<nn;i++) { QLL[i] = new double [nn]; SIGL[i]= new double [nn]; } //计算观测值的平差值的中误差 QLL=B*inv(Nbb)*BT DLL=SIG0*SIG0*QLL for(i=0;i<nn;i++) {
js=(int *)malloc(n*sizeof(int));
for(k=0;k<=n-1;k++)
{
d=0.0;
for(i=k;i<=n-1;i++)
for(j=k;j<=n-1;j++)
H[n1[i]-1]=H[n2[i]-1]-h[i]; } } for(j=0;j<nz;j++) //如果有任意一个点的高程不为零,说明高程近似值计算没有 完毕,则 j0=1。 { if(H[j]==0) j0=1; } if(j0==0) break; //说明所有点的近似高程计算完毕,退出最外层的 for(;;)循环。 if(n0>nn && j0==1) { AfxMessageBox("近似高程无法计算,原始数据编排错误,程序自动终 止!"); break; }}} //形成误差方程式系数矩阵 B for(i=0;i<nn;i++) { if(n1[i]>ne) B[i][n1[i]-ne-1]=-1; if(n2[i]>ne) B[i][n2[i]-ne-1]=+1; //定权 P[i]=1/S[i]; l[i]=H[n1[i]-1]+h[i]-H[n2[i]-1]; } for(i=0;i<nw;i++) { for(j=0;j<nw;j++) { Nbb[i][j]=0.0; for(k=0;k<nn;k++) { Nbb[i][j]+=B[k][i]*B[k][j]*P[k];}}} for(i=0;i<nw;i++) { W[i]=0.0; for(k=0;k<nn;k++) {
fprintf(fp," %3d %3d %8.4lf %8.4lf %8.1lf %8.4lf %8.1lf\n", n1[i],n2[i],h[i],S[i],V[i]*1000,ph[i],SIGL[i][i]*1000);
}
fprintf(fp,"\n\n 点号
已知点名
已知高程(m)\n");
delete []SIGL;
for(i=0;i<nw;i++)
{
delete []Nbb[i];
}
delete []Nbb;
fclose(fp);
}
int CGckzwpc::invGJ(double **a,int n)
{
int *is,*js,i,j,k,l,u,v;
double d,p;
is=(int *)malloc(n*sizeof(int));
%5.1lf\n",
i+ne+1,dm[i+ne],X[i]+H[ne+i],sqrt(DX[i])*1000);
