稳恒电磁场分析与计算
合集下载
大学物理课件第11章稳恒磁场
p
已知：I、c
解：
0
B AO
0I 4a
(cos 1
cos 2 )
B
I cP
•
Ia
0 I [cos 0 cos( )]
A
4a
2
0I 4c sin
(1 cos )
2
所以 B p BAO BOB
2
方向
同理
BOB
0I 4c sin
(1 cos )
2
0I 2c sin
(1 cos )
r0
OR
dB dB
p•
dBx
X
方向
Idl r0
分析对称性、写出分量式
B
dB 0
Bx
dBx
0 4
Idl sin
r2
统一积分变量
Y
sin R r
Bx
dBx
0 4
Idl sin
r2
I Idl
O
0 IR 4r 3
dl
0 IR 4r 3
2R
r0
R x
2(
0 IR 2
R2 x2
)3
R
•
a LI
a
I
A a
•P
0 0I 5 105T S•
•T
4a R点
方向
BR BLA BLA
0 I (cos 0 cos 3 ) 0 I (cos 1 cos )
4a
4 4a 4
1.71 105T
方向 •
S点
BLA
0I 4a
(cos 0
cos
3
4
)
BLA
0I 4a
(cos
大学物理稳恒磁场小结
4R
O
R
0 I 3 B (1 ) 6R R 2
0 I
O
R
I
R
O
I
O
I
R
B
0 I B 2 4R 4 R
0 I
μ0 I
8R
2、安培定律 大小：
dF Idl B
dF
dF IdlB sin θ 方向：从 Idl 右旋到 B ，
大拇指的指向。
稳恒磁场小结
一.基本概念
1. 磁感强度大小
Fmax B qv
方向：小磁针N极在此所 指方向
pm
2. 载流线圈磁矩 P ISn m
3. 载流线圈的磁力矩 M Pm B
4.磁通量
n
I
m B dS BdS cos
二.基本实验定律
（1）首先选定回路L的绕行方向. （2）按照右手螺旋关系确定出回路的正法线方向. （3）确定通过回路的磁通量的正负. （4）确定磁通量的时间变化率的正负. （5）最后确定感应电动势的正负.
dΦ ε dt
n
L
ε 0 与回路 L绕向相反； ε 0 与回路 L绕向相同。
②感应电流 ③若为N匝
注意： 计算一段有限长载流导线在磁 场中受到的安培力时，应先将其 分割成无限多电流元，将所有电 流元受到的安培力矢量求和—矢 量积分。
B
Idl
Idl
B
L
F dF L Idl B
L
三.稳恒磁场的基本性质： 1.磁场的高斯定理：
m B dS 0
d dq d D D dS I dt dt dt
O
R
0 I 3 B (1 ) 6R R 2
0 I
O
R
I
R
O
I
O
I
R
B
0 I B 2 4R 4 R
0 I
μ0 I
8R
2、安培定律 大小：
dF Idl B
dF
dF IdlB sin θ 方向：从 Idl 右旋到 B ，
大拇指的指向。
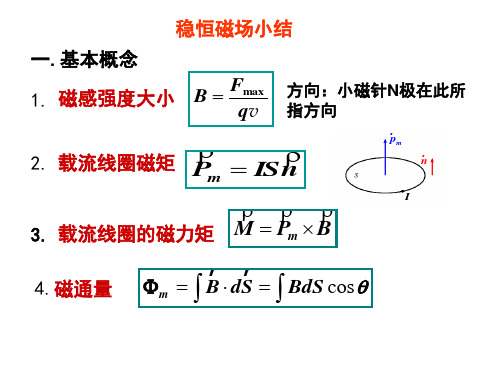
稳恒磁场小结
一.基本概念
1. 磁感强度大小
Fmax B qv
方向：小磁针N极在此所 指方向
pm
2. 载流线圈磁矩 P ISn m
3. 载流线圈的磁力矩 M Pm B
4.磁通量
n
I
m B dS BdS cos
二.基本实验定律
（1）首先选定回路L的绕行方向. （2）按照右手螺旋关系确定出回路的正法线方向. （3）确定通过回路的磁通量的正负. （4）确定磁通量的时间变化率的正负. （5）最后确定感应电动势的正负.
dΦ ε dt
n
L
ε 0 与回路 L绕向相反； ε 0 与回路 L绕向相同。
②感应电流 ③若为N匝
注意： 计算一段有限长载流导线在磁 场中受到的安培力时，应先将其 分割成无限多电流元，将所有电 流元受到的安培力矢量求和—矢 量积分。
B
Idl
Idl
B
L
F dF L Idl B
L
三.稳恒磁场的基本性质： 1.磁场的高斯定理：
m B dS 0
d dq d D D dS I dt dt dt
稳恒磁场与强度计算
B 0I 2r
I
B
Bdl 0I cos0dl
L
L2r
dl
or
0 I
2 r
dl
L
0I
L
回路绕向转向逆时针时：
B dl 0I cosdl
L
L 2r
0I
2 r
L dl 0I
与环路绕行方向成右旋关系的电流 对环流的贡献为正，反之为负。
II B
o Rr d l
L
l
如果规定
与 L 绕向成右旋关系 I 0 与 L 绕向成左旋关系 I 0
B2
0I
4R
3 2
3 0I 8R
B34 0R I(cos1cos2)
2
θ1 2 θ2
0I
O
4R
R
BB 1B 2B 3
I1 3
例 求两平行无限长直导线之间的相互作用力？
解 电流 2 处于电流 1 的磁场中
B1
0I1 2a
I1
电流 2 中单位长度上受的安培力
f12 I2B1
0I1I2 2a
电流 （运动电荷）
磁场
电流 （运动电荷）
二. 磁感应强度 B 的定义 (1) B的方向：与小磁针N 极在磁场中某点的稳定指向一致.
q
v
SN
B
F m ax
q
B
v
v//B,F0
v B ,FF m ax
(2) 带电粒子垂直 的B 方向运动时，受磁场作用力最大.
且 Fmax qv
F m a x 大小与 q , v无关 qv
极光 由于地磁场俘获带电粒子而出现的现象
绚丽多彩的极光
在地磁两极附近 由于磁感线与地面垂直 外层空间入射的带 电粒子可直接射入高空大气层内 它们和空气分子的碰撞产生 的辐射就形成了极光
大学物理下-- 稳恒磁场
2
2C Nhomakorabea dl
2
2
2B
A
BR sind
d
v
p vB
i
AC
v B dl
2
BR
0
sind
2 BR
2
讨论 本题可用补偿法求解
在AC间加一假想直导线，则 构成半圆形闭合回路，其感应 电动势为零（为什么），即
注意体积元 dV 的选取
4、位移电流的定义：
D d D I d d ds ds S S t dt
通过电场中某截面的电流等于通过该截 面的电位移通量对时间的变化率
5、反映电磁场基本性质和规律的麦克 斯韦方程组的积分形式
D ds
bc
bc 2a
v B dl
所以，线框的感应电动势为
i bc ad 4a B sin t
2
方向：顺时针
讨论：直接由电磁感应定律
d d i BS cos t dt dt 2 BS sin t 4a B sin t
r
N N B dS R2 R2 NI 0 N Bhdr N hdr R1 R1 2r 2 0 N hI R2 ln 2 R1
5. 描述稳恒磁场的两条基 本定律 （1）磁场的高斯定理
s
磁场是无源场（涡旋场） B d s 0
（2）安培环路定理 n
L i 1
L
I1
B d l I 0 i
I2
I3
用安培环路定理计算磁场的条件和方法 I i 正负的确定：规定回路环形方向，由 右手螺旋法则定出
2C Nhomakorabea dl
2
2
2B
A
BR sind
d
v
p vB
i
AC
v B dl
2
BR
0
sind
2 BR
2
讨论 本题可用补偿法求解
在AC间加一假想直导线，则 构成半圆形闭合回路，其感应 电动势为零（为什么），即
注意体积元 dV 的选取
4、位移电流的定义：
D d D I d d ds ds S S t dt
通过电场中某截面的电流等于通过该截 面的电位移通量对时间的变化率
5、反映电磁场基本性质和规律的麦克 斯韦方程组的积分形式
D ds
bc
bc 2a
v B dl
所以，线框的感应电动势为
i bc ad 4a B sin t
2
方向：顺时针
讨论：直接由电磁感应定律
d d i BS cos t dt dt 2 BS sin t 4a B sin t
r
N N B dS R2 R2 NI 0 N Bhdr N hdr R1 R1 2r 2 0 N hI R2 ln 2 R1
5. 描述稳恒磁场的两条基 本定律 （1）磁场的高斯定理
s
磁场是无源场（涡旋场） B d s 0
（2）安培环路定理 n
L i 1
L
I1
B d l I 0 i
I2
I3
用安培环路定理计算磁场的条件和方法 I i 正负的确定：规定回路环形方向，由 右手螺旋法则定出
7 稳恒磁场
讨 1）若线圈有 N 匝
论
B
N （2 x2
0 IR2
R2）32
2）x 0 B 的方向不变( I 和 B成右螺旋关系）
3） x 0 4）x R
B 0I
2R
B
0IR 2
2x3
，
B
0 IS
2π x3
比一比
I
R
ox
B
*x
B
0 IR2
（2 x2 R2）32
B
如图所示，有一长为 l , 半径为R的载流密绕直螺线管，螺 线管的总匝数为N，通有电流 I. 设把螺线管放在真空中，求 管内轴线上一点处的磁感强度.
R
o
p*
dx x
x
+++++++++++++ +
解 由圆形电流磁场公式
B
0IR 2
（2 x2 R2）3/ 2
稳恒磁场
1
x1 o p 2
x
方向：磁场中的每一点都
有一个特征方向，当试探 电荷q0沿这个方向运动时 不受力。这一特征方向定
义为磁场的方向。
稳恒磁场
直带于电v粒 子与在磁B 场组中成沿的运平动面时.
F
垂
磁场中的带电粒子速度垂直于
受力最大.
B时
F Fmax F
Fmax qv
大小： 荷无关
，该比值只取决于该点磁场的性质，与试探电
磁偶极子的磁矩： m ISen
B
0 IS 2 x3
3稳恒磁场
Hale Waihona Puke 考思考 有一根很长的载流导体直圆管，内半
径为a ，外半径为b ，电流强度为I 。电流 沿轴线方向流动，并且均匀地分布在管壁的 横截面上，空间某一点到管轴的垂直距离为 r 。（如图）。求：
（1）r < a ; (2) a < r < b ; (3) r > b 等各区域内的磁感应强度的分布。
I a br
第一步：分析磁场的分布特性，判断是否具有对称 性
第二步：选取恰当的积分回路，并规定其绕行方向
第三步：应用安培环路定理求B
例
例 无限长载流圆柱面的磁场
L1
r
IR
L2 r
0I B
2π R
oR r
解 0 r R, B d l 0 l r R, l B d l 0I
B0 B 0I
2π r
洛仑兹力
电磁合力
带电粒子磁运动
圆运动
螺线运动
螺距
第六节
现象
安培定律
积分法求磁力
例
例
例
y
一条结论
B
I
P
o
L
x
结论 任意平面载流导线在均匀磁场中 所受的力 , 与其始点和终点相同的载流直导 线所受的磁场力相同.
结论:
一条结论
在均匀的磁场中,对于任意形状的平面 载流线圈，所受磁场合力为零。
一段圆弧在其圆心处的磁场
I
θ oR
大小：B 0 I 4R
方向：按右手定则确定。
例
小结
运动电荷磁场
例
例28
本次课小结
1.毕---萨定律
2.无限长直导线磁场
3.圆电流中心磁场
大学物理磁场稳恒磁场理论1
一1820年: 将电流视为 电流元的集合 奥斯特发现电流的磁效应
求解电流磁场分布基本思路： 电流元磁场公式 磁场叠加原理 电流磁场分布
毕 — 沙定律：电流元产生磁场的规律,与点电荷电场 公式作用地位等价 I dB
P
.
r
Idl
0 Idl r dB 4r 3
讨论： 无限长直电流
讨论：
0 I B (cos 1 cos 2 ) 4a
I
1. 无限长直电流
1 0 ,
0 I B 2a
B
R,无限长半圆柱金属面通电流I，求轴线上 练习：半径
解：通电半圆柱面 电流线(无限长直电流)集合
B
R
dI
dB ' dB
I B 2a
0
2. 圆电流轴线上磁场： 2 0 IR i 0 Pm B 3 3 2 2 2 2 2 2( R x ) 2 ( R x ) 2
I 圆电流圆心处磁场： B 2R
0 0
B 0nI
电流的磁矩：
P I Sn m
第二节磁场的高斯定理和安培环路定理
2) 在垂直于导线平面内围绕电流的任意闭合路径
0 I rd LB dl LB cosdl L 2 r 0 I 2 0 d 0 I 2 若电流反向，则为 0 I
描述空间 矢量场一般方法
一. 磁场高斯定理 用场线描述场的分布 用高斯定理，环路定理揭示场的 基本性质
1.磁感应线
切向：该点 B 方向 疏密：正比于该点 B 的大小
闭合， 或两端伸向无穷远； 与载流回路互相套联； 互不相交。
特点
2. 磁通量
通过磁场中某给定面的磁感应线的总条数
求解电流磁场分布基本思路： 电流元磁场公式 磁场叠加原理 电流磁场分布
毕 — 沙定律：电流元产生磁场的规律,与点电荷电场 公式作用地位等价 I dB
P
.
r
Idl
0 Idl r dB 4r 3
讨论： 无限长直电流
讨论：
0 I B (cos 1 cos 2 ) 4a
I
1. 无限长直电流
1 0 ,
0 I B 2a
B
R,无限长半圆柱金属面通电流I，求轴线上 练习：半径
解：通电半圆柱面 电流线(无限长直电流)集合
B
R
dI
dB ' dB
I B 2a
0
2. 圆电流轴线上磁场： 2 0 IR i 0 Pm B 3 3 2 2 2 2 2 2( R x ) 2 ( R x ) 2
I 圆电流圆心处磁场： B 2R
0 0
B 0nI
电流的磁矩：
P I Sn m
第二节磁场的高斯定理和安培环路定理
2) 在垂直于导线平面内围绕电流的任意闭合路径
0 I rd LB dl LB cosdl L 2 r 0 I 2 0 d 0 I 2 若电流反向，则为 0 I
描述空间 矢量场一般方法
一. 磁场高斯定理 用场线描述场的分布 用高斯定理，环路定理揭示场的 基本性质
1.磁感应线
切向：该点 B 方向 疏密：正比于该点 B 的大小
闭合， 或两端伸向无穷远； 与载流回路互相套联； 互不相交。
特点
2. 磁通量
通过磁场中某给定面的磁感应线的总条数
稳恒电流的磁场总结汇总
1.SI J ds =⎰⎰2. 毕奥-萨伐尔定律:34Idl r dB rμπ⨯=034LI r B dl rμπ⨯=⎰3. 有限长载流导线的磁感应强度()()021021sin sin 4cos cos 4 I B z Izμθθπμββπ=-=- !!!zP 1无限长载流导线的磁感应强度 02IB zμπ=!!!4. 载流线圈在轴线上任意一点的磁感应强度()2032222IRB Rzμ=+ !!!圆心处的磁感应强度02IB Rμ=!!!5. 有限长螺线管内部任意一点的磁感应强度()021cos cos 2nIB μθθ=-无限长直螺线管内的磁感应强度 0B n I μ=!!!6. 运动电荷的磁场034q v rB rμπ⨯= 7. 磁偶极子与磁矩磁偶极子：载流线圈（任意形状）。
磁矩：m IS ISn ==其中S Sn = ，n 为面元S 的法线方向单位矢量，与I 的环绕方向成右手螺旋关系。
8. 稳恒磁场的高斯定理 0SB d s =⎰⎰9. 稳恒磁场的安培环路定理0iiLB d l Iμ=∑⎰ 两项注意:(1)虽然B的环量仅与L内的电流有关，但B本身却取决于L 内、外的所有电流。
(2) 当i I 的流动方向与L 的环绕方向成右手螺旋关系时，0i I >，反之0i I <。
10. 无限长载流圆柱体020()2()2Irr R R B Ir R rμπμπ⎧<⎪⎪=⎨⎪>⎪⎩11. 无限大载流平面的磁感应强度大小：02B μα=（其中α为面电流线密度）；方向：右手螺线关系。
12. 安培定律－磁场对载流体的作用dF Idl B =⨯13. 在一均匀外磁场中，如果一任意形状的有限平面曲线电流的平面垂直于外磁场，那么平面电流所受到的安培力的大小与由起点到终点连接而成的直线电流所受到的安培力一样，方向垂直于从起点到终点的连线。
推论：处于均匀外磁场中的任意平面闭合载流回路，所受到的安培力=0，但要受到一力矩的作用L m B =⨯处于非均匀外磁场中的闭合载流线圈受到的安培力≠0。
稳恒磁场和强度计算
磁感应强度大小定义为： B F m ax qv
单位 特斯拉 1(T )1N /A m
磁场的高斯定理
vv
Ñ 静电场： eS E d S q i/0 静电场是有源场 Ñ BvdSv磁?场：
一. 磁感应线（磁力线）
✓ 规定
(1)
方向：磁力线切线方向为磁感应强度
v B
的方向
(2)
大小：垂直
v B
Rmv mvsin
qB qB
磁场增强，运动半径减少
强磁场可约束带电粒子在一根磁场线附近 —— 横向磁约束
纵向磁约束
vv v
f
f//
f
f// 减少粒子的纵向前进速
e f//
B
f f
v
度，使粒子运动发生“反射”
应用：磁镜
B
线圈
线圈
高温等离子体
磁场：轴对称 中间弱 两边强 粒子将被束缚在磁瓶中
磁镜：类似于粒子在反射面上反射（名称之来源） 在受控热核反应中用来约束等离子体
QI nqvS r rr
dFIdlB —— 安培定律
I
r dl B
S
r
dl
vr
r B
r Id l : 电流元
磁铁
磁铁
电流
磁场
电流
磁场是从哪里来的？？？
3、电流 磁场 电流
(1).安培的“分子环流假说”
安培分子环流假说：组成磁铁的最小单元就是分子环流， 若这样一些分子环流定向地排列起来，在宏观上就会显示 出N、S极来．
安培认为： ➢ 磁现象的本质是电荷的运动 ➢ 物质的磁性来源于“分子”电 流
小结：磁极或电流之间的相互作用可归结为运动电荷之 间的相互作用，而这种相互作用是通过磁场来传递的。
大学物理第六章稳恒磁场重点内容
第六章稳恒磁场
1、主要的概念：电流强度，磁感应强度，电流元，磁感应线，磁通量，磁化和磁介质。
2、主要的了解定律：磁场叠加原理，毕奥—萨伐尔定律（推导一些特殊载流导线和运动电荷的B），磁场中的高斯定律，安培环路定律。
（了解定理的导出以及其重要的物理意义）
3、主要计算：利用毕奥—萨伐尔定律、安培环路定理计算一些特殊载流导线产生的磁感应强度；安培力和洛伦兹力的计算；磁介质中的磁化，以及应用介质中的安培环路定理计算磁场强度矢量（H）和磁感应强度（B）。
4、重点内容：毕奥—萨伐尔定律、安培环路定理、磁场力、力矩；磁介质的磁化、介质中的安培环路定理。
2．磁场方程： 磁场高斯定理：
（表明磁场是无源场）
（表明磁场是有旋场）
掌握推导过程
*通过霍尔电压可以求得磁场和电流大小。
6. 均匀磁化的B 、H 、M 关系及表面磁化电流密度与磁化强度的关系
）
（M H B 0 +=μ H M m χ= m r 1χμ+=
B 代表 H 代表 M 代表
—
——m r 0χμμ 4.载流线圈的磁矩 3.电磁相互作用 B
l Id f d ⨯=2)磁场对载流导线的安培力
⎰⨯=l
B
l Id f 3)磁场对载流线圈的作用力矩 B
m M
⨯=4)5.霍耳电压
1)安培定律。
大学物理-第三篇-第六章 稳恒磁场
v Idl I
2 首 页 上 页 下 页退 出
电流元在P点产生的磁感应强度的矢量式为 电流元在 点产生的磁感应强度的矢量式为
r r r µ 0 Idl × r0 dB = 2 4π r
整个载流导体在P点的磁感应强度则是电流元在 点产生 整个载流导体在 点的磁感应强度则是电流元在P点产生 点的磁感应强度则是电流元在 的 dB 之矢量和
=
2 R
∫ π
µ 0 IR µ 0 IR 2 = dl = 3 ∫ 4π r 2πR 2r 3
=
即
µ 0 IR 2
2( R + x )
2 2 3 2
B=
µ0
R2I
12 首 页 上 页 下 页退 出
2 (R2 + x2 )32
轴线上任一点P的磁场 轴线上任一点 的磁场
B=
B=
µ0
R2I
2 (R 2 + x2 ) 32
4 首 页 上 页 下 页退 出
2、 定律应用 由Idl×r 确定电流元在 P点的 dB 的方向 点的 向选定的坐标轴投影， 将 d B 向选定的坐标轴投影，然后分别求出
Bx = ∫ dBx
By = ∫ dBy
Bz = ∫ dBz
5 首 页 上 页 下 页退 出
（1）载流直导线的磁场： 载流直导线的磁场：
P
0
P I I
0
β 1 = 0, β 2 →
π
2
1 µI B= 2 2π a
10 首 页 上 页 下 页退 出
（2）
圆电流的磁场
r Id l
r r
dB ⊥
I R0
θ
dB/⊥
θ
dB dB // x
06 稳恒磁场复习+习题课
2 1 4a 2
L
R
a
0 I
a
L A
0 I
a
S
a
AL 两端相对于R点所对应的
1
4
2
2
AL 在R点的磁感应强度大小为
B2 sin sin 4a 2 4
l
4.载流线圈的磁矩
P NISn m
I
n S
5.电磁相互作用
1)安培定律
df Idl B
f Idl B l M Pm B
2)磁场对载流导线的安培力 3)磁场对载流线圈的作用力矩
4)磁场对运动电荷的洛仑兹力
m2
m1
2 1 4a 2
0 I
a
S
0 I
a
AL 两端相对于S点所对应的
1
4
L
2
2
R
a
AL在S点产生的磁感应强度
B2 sin sin 4a 2 4
2 1 4a 2
I1
I
A
l2
1
l1
O
I2
R
B
2
I
5
4
O点在3和4的延长线上,5离 O点可看作无限远,故:
B3 0
B4 0
3
I1
I
B5 0
A
l2
1
l1
O
I2
设1圆弧弧长l1,2圆弧弧长l2, 圆的周长为l
B1 l1 0 I 1 l 2R
B2
L
R
a
0 I
a
L A
0 I
a
S
a
AL 两端相对于R点所对应的
1
4
2
2
AL 在R点的磁感应强度大小为
B2 sin sin 4a 2 4
l
4.载流线圈的磁矩
P NISn m
I
n S
5.电磁相互作用
1)安培定律
df Idl B
f Idl B l M Pm B
2)磁场对载流导线的安培力 3)磁场对载流线圈的作用力矩
4)磁场对运动电荷的洛仑兹力
m2
m1
2 1 4a 2
0 I
a
S
0 I
a
AL 两端相对于S点所对应的
1
4
L
2
2
R
a
AL在S点产生的磁感应强度
B2 sin sin 4a 2 4
2 1 4a 2
I1
I
A
l2
1
l1
O
I2
R
B
2
I
5
4
O点在3和4的延长线上,5离 O点可看作无限远,故:
B3 0
B4 0
3
I1
I
B5 0
A
l2
1
l1
O
I2
设1圆弧弧长l1,2圆弧弧长l2, 圆的周长为l
B1 l1 0 I 1 l 2R
B2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0 Idl r dB 3 4π r
1
毕奥—萨伐尔定律
例 判断下列各点磁感强度的方向和大小.
8 2
dB 0 1、 5 点 ：
3、7点 ：dB
3
7
Idl
R
6 4
0 Idl
4π R
2
2、 4、 6、 8 点 ：
5
dB
0 Idl
4π R
0 sin 45 2
二 毕奥---萨伐尔定律应用举例
dB
0 Id l
2
B
0 IR 2π R B dl 3 0 4π r 2 0 IR
（ 2 x R ）2
2 2 3
I
o
R
x
*
B
x
B
B
0 IR
2
2 2 3
讨 论
（ 2 x R ）2 2）x 0 B 的方向不变( I 和 B 成右螺旋关系） 0 I 圆环形电流 B 3）x 0 2 R 中心的磁场 2 IR IS 0 0 4）x R B ， B 3 3 2x 2π x
d *A
R1 R2
I （ 5） I
（ 2） R
o （ 3） I R o
B0
0 I
4R
*o
B0
0 I
8R
B0
0 I
4 R2
0 I
4 R1
0 I
4π R1
三 磁偶极矩
m ISen
2
I
例2中圆电流磁感强度公 式也可写成
S
en
m
B
0 IR
2x
3
0m B e 3 n 2π x
1
P y
+
无限长载流长直导线的磁场
B
0 I
2π r
I
I
B
X
B
电流与磁感强度成右螺旋关系 半无限长载流长直导线的磁场
π 1 2 2 π
BP
0 I
4π r
I
o
r
* P
例2 圆形载流导线的磁场. 真空中 , 半径为R 的载流导线 , 通有电流I , 称圆 电流. 求其轴线上一点 p 的磁感强度的方向和大小.
2 2
1）若线圈有 N 匝
（ 2 x R ）2 2 N 0 IR
3
圆弧形电流在圆心处的磁场为什么？
I
0 I B0 2 R 2
o
R
方向： 注：仍可由右手定则判定方向！
几种典型电流体系的磁场
（ 1）
I
R B x 0 I 0 o B0 2R
I
（ 4）
0 I BA 4π d
l
2
R
2
0 nI
2
l
2
/4 R
2 1/ 2
l R
B 0nI
(2) 无限长的螺线管
（3）半无限长螺线管
B 0nI
或由 1 π , 2 0 代入
π 1 , 2 0 2
1 B 0 nI 2
0 nI cos 2 cos 1 B 2
0 I （cos1 cos 2） B sin d 4π r0 4π r0 B 的方向沿 x 轴的负方向. z D 2
0 I
2
1
B
（cos1 cos 2） 4π r0
0 I
I
无限长载流长直导线的磁场.
o
x
C
B
1 0 2 π
B
0 I
2π r0
dr
dB B
0
2
R
dr
0
2
0
dr
0 R
2
例 5 依波尔模型，氢原子中电子以速成率 v=2.2106m/s在半径为r=0.5310-8cm圆周上运动 求这电子在轨道中心所产生的磁感应强度及磁矩.
解
0 qv sin 90 B 2 4 r
7
B
+
r
- v
B
dN nS dl d B 0 qv r B 3 d N 4π r
q
r
v
B
例4 半径 为 R 的带电薄圆盘的电荷面密度 为 , 并以角速度 绕通过盘心垂直于盘面的轴转 动 ，求圆盘中心的磁感强度.
R o r
解法一
圆电流的磁场
dI
0, B 0, B
dr
向外 向内
2π 0 dI 0 dB dr 2r 2
0
2
R
0
dr
0 R
2
解法二
运动电荷的磁场
R o r
dB0
0 dqv
4π r
2
dq 2π rdr
v r
0 qv r ˆ B 2 4 r
1.60 10 2.2 10 10 13(T ) 10 2 (0.53 10 )
6
19
0m B 3 2π x
m
en
S
I
说明：只有当圆形电流的面积S很小，或场点距 圆电流很远时，才能把圆电流叫做磁偶极子.
例3* 载流直螺线管的磁场 如图所示，有一长为l , 半径为R的载流密绕直螺 线管，螺线管的总匝数为N，通有电流I. 设把螺线管 放在真空中，求管内轴线上一点处的磁感强度. o * p
R
x
dx
x
解 由圆形电流磁场公式
B
0 IR
2
2 2 3/ 2
（ 2 x R）
1
x1
o p
2
x2
x
2 2 R x dx R csc d 2 x 0 nI 2 R dx 2 2 2 2 B dB 3 / 2 R x R csc 2 2 x 1 2 R x 3 2 0 nI 2 0 nI 2 R csc d sin d B 3 3 2 1 2 1 R csc d
2
dB
0
R 2 Indx
2 3/ 2
x Rcot
讨 论
0 nI cos 2 cos 1 B 2
（1）P点位于管内轴线中点
1 π 2
l/2
cos 1 cos 2
B 0 nI cos 2
若
cos 2
l / 2
例1 载流长直导线的磁场.
dB 方向均沿
z
D
2
dz
I
z
1
r
r0
dB
* P y
r2 0 Idz sin B dB 2 CD 4π r 4π
解 dB
x 轴的负方向 0 Idz sin
x
o
C
z r0 cot , r r0 / sin 2 dz r0d / sin 0 I 2 B sin d 4π r0 1
Idl
r
B
dB
p *
o
R
I
B
dB
0 Id l
4π r
2
x
解 根据对称性分析
B Bx dB sin
Idl
R
r
x
*p
dB
cos R
o
x B
r 2 2 2 r R x 0 I cos dl
4π
l
r
2
4π r 0 I cos dl dB x 2 4π r
1 0 nI 2
B O
0 nI
x
四 运动电荷的磁场
0 Idl r 毕— 萨定律 dB 3 4 π r
j
S
dB
Idl j Sdl nSdlqv 0 nSdlqv r
4π r
3
dl
运动电荷的磁场
实用条件
q
+
r
v c v
1
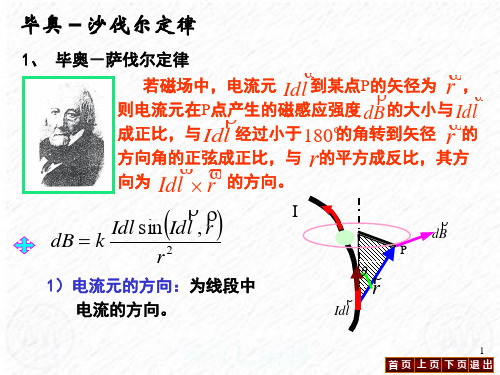
毕奥—萨伐尔定律
例 判断下列各点磁感强度的方向和大小.
8 2
dB 0 1、 5 点 ：
3、7点 ：dB
3
7
Idl
R
6 4
0 Idl
4π R
2
2、 4、 6、 8 点 ：
5
dB
0 Idl
4π R
0 sin 45 2
二 毕奥---萨伐尔定律应用举例
dB
0 Id l
2
B
0 IR 2π R B dl 3 0 4π r 2 0 IR
（ 2 x R ）2
2 2 3
I
o
R
x
*
B
x
B
B
0 IR
2
2 2 3
讨 论
（ 2 x R ）2 2）x 0 B 的方向不变( I 和 B 成右螺旋关系） 0 I 圆环形电流 B 3）x 0 2 R 中心的磁场 2 IR IS 0 0 4）x R B ， B 3 3 2x 2π x
d *A
R1 R2
I （ 5） I
（ 2） R
o （ 3） I R o
B0
0 I
4R
*o
B0
0 I
8R
B0
0 I
4 R2
0 I
4 R1
0 I
4π R1
三 磁偶极矩
m ISen
2
I
例2中圆电流磁感强度公 式也可写成
S
en
m
B
0 IR
2x
3
0m B e 3 n 2π x
1
P y
+
无限长载流长直导线的磁场
B
0 I
2π r
I
I
B
X
B
电流与磁感强度成右螺旋关系 半无限长载流长直导线的磁场
π 1 2 2 π
BP
0 I
4π r
I
o
r
* P
例2 圆形载流导线的磁场. 真空中 , 半径为R 的载流导线 , 通有电流I , 称圆 电流. 求其轴线上一点 p 的磁感强度的方向和大小.
2 2
1）若线圈有 N 匝
（ 2 x R ）2 2 N 0 IR
3
圆弧形电流在圆心处的磁场为什么？
I
0 I B0 2 R 2
o
R
方向： 注：仍可由右手定则判定方向！
几种典型电流体系的磁场
（ 1）
I
R B x 0 I 0 o B0 2R
I
（ 4）
0 I BA 4π d
l
2
R
2
0 nI
2
l
2
/4 R
2 1/ 2
l R
B 0nI
(2) 无限长的螺线管
（3）半无限长螺线管
B 0nI
或由 1 π , 2 0 代入
π 1 , 2 0 2
1 B 0 nI 2
0 nI cos 2 cos 1 B 2
0 I （cos1 cos 2） B sin d 4π r0 4π r0 B 的方向沿 x 轴的负方向. z D 2
0 I
2
1
B
（cos1 cos 2） 4π r0
0 I
I
无限长载流长直导线的磁场.
o
x
C
B
1 0 2 π
B
0 I
2π r0
dr
dB B
0
2
R
dr
0
2
0
dr
0 R
2
例 5 依波尔模型，氢原子中电子以速成率 v=2.2106m/s在半径为r=0.5310-8cm圆周上运动 求这电子在轨道中心所产生的磁感应强度及磁矩.
解
0 qv sin 90 B 2 4 r
7
B
+
r
- v
B
dN nS dl d B 0 qv r B 3 d N 4π r
q
r
v
B
例4 半径 为 R 的带电薄圆盘的电荷面密度 为 , 并以角速度 绕通过盘心垂直于盘面的轴转 动 ，求圆盘中心的磁感强度.
R o r
解法一
圆电流的磁场
dI
0, B 0, B
dr
向外 向内
2π 0 dI 0 dB dr 2r 2
0
2
R
0
dr
0 R
2
解法二
运动电荷的磁场
R o r
dB0
0 dqv
4π r
2
dq 2π rdr
v r
0 qv r ˆ B 2 4 r
1.60 10 2.2 10 10 13(T ) 10 2 (0.53 10 )
6
19
0m B 3 2π x
m
en
S
I
说明：只有当圆形电流的面积S很小，或场点距 圆电流很远时，才能把圆电流叫做磁偶极子.
例3* 载流直螺线管的磁场 如图所示，有一长为l , 半径为R的载流密绕直螺 线管，螺线管的总匝数为N，通有电流I. 设把螺线管 放在真空中，求管内轴线上一点处的磁感强度. o * p
R
x
dx
x
解 由圆形电流磁场公式
B
0 IR
2
2 2 3/ 2
（ 2 x R）
1
x1
o p
2
x2
x
2 2 R x dx R csc d 2 x 0 nI 2 R dx 2 2 2 2 B dB 3 / 2 R x R csc 2 2 x 1 2 R x 3 2 0 nI 2 0 nI 2 R csc d sin d B 3 3 2 1 2 1 R csc d
2
dB
0
R 2 Indx
2 3/ 2
x Rcot
讨 论
0 nI cos 2 cos 1 B 2
（1）P点位于管内轴线中点
1 π 2
l/2
cos 1 cos 2
B 0 nI cos 2
若
cos 2
l / 2
例1 载流长直导线的磁场.
dB 方向均沿
z
D
2
dz
I
z
1
r
r0
dB
* P y
r2 0 Idz sin B dB 2 CD 4π r 4π
解 dB
x 轴的负方向 0 Idz sin
x
o
C
z r0 cot , r r0 / sin 2 dz r0d / sin 0 I 2 B sin d 4π r0 1
Idl
r
B
dB
p *
o
R
I
B
dB
0 Id l
4π r
2
x
解 根据对称性分析
B Bx dB sin
Idl
R
r
x
*p
dB
cos R
o
x B
r 2 2 2 r R x 0 I cos dl
4π
l
r
2
4π r 0 I cos dl dB x 2 4π r
1 0 nI 2
B O
0 nI
x
四 运动电荷的磁场
0 Idl r 毕— 萨定律 dB 3 4 π r
j
S
dB
Idl j Sdl nSdlqv 0 nSdlqv r
4π r
3
dl
运动电荷的磁场
实用条件
q
+
r
v c v