高中数学必修一对数函数课件完美课件
合集下载
高一数学对数函数课件

高一数学对数函数课件
目录
• 对数函数的定义与性质 • 对数函数的运算 • 对数函数的应用 • 对数函数与其他函数的关系 • 对数函数的综合题解析
01
对数函数的定义与性质
定义与表示
总结词
对数函数是指数函数的反函数,其定义是指数函数的自变量和因变量互换位置 后得到的函数。
详细描述
对数函数的一般形式为 (y = log_{a}x)(其中 (a > 0) 且 (a neq 1)),其中 (x) 是自变量,(y) 是因变量。对数函数表示的是以 (a) 为底数,(x) 的对数。
计算机科学
在计算机科学中,对数函数常被用 于数据结构和算法设计,如二叉查 找树、哈希表等。
04
对数函数与其他函数的关 系
与指数函数的关系
指数函数和对数函数互为反函数,它 们的图像关于直线y=x对称。
对数函数和指数函数在解决实际问题 中经常一起出现,例如在计算复利、 解决声音强度问题等。
对数函数的定义是基于指数函数的, 即如果a的x次方等于N(a>0,a不等 于1),那么x叫做以a为底N的对数, 记作x=logₐN。
与三角函数的关系
对数函数和三角函数在形式上没有直接的关系,但在一些特定情况下可以相互转化 。例如,对于正弦函数和余弦函数的值可以通过对数函数进行计算。
三角函数和对数函数在解决实际问题中经常一起出现,例如在信号处理、振动分析 等领域。
对数函数和三角函数在一些数学问题中可以相互转化,例如在求解一些复杂的积分 问题时,可以将积分转化为对数函数的求解问题。
综合题类型与解题思路
01
类型三:对数方程求解
02
对数方程是常见的题型,需要掌握解对数方程的方法和步骤。
目录
• 对数函数的定义与性质 • 对数函数的运算 • 对数函数的应用 • 对数函数与其他函数的关系 • 对数函数的综合题解析
01
对数函数的定义与性质
定义与表示
总结词
对数函数是指数函数的反函数,其定义是指数函数的自变量和因变量互换位置 后得到的函数。
详细描述
对数函数的一般形式为 (y = log_{a}x)(其中 (a > 0) 且 (a neq 1)),其中 (x) 是自变量,(y) 是因变量。对数函数表示的是以 (a) 为底数,(x) 的对数。
计算机科学
在计算机科学中,对数函数常被用 于数据结构和算法设计,如二叉查 找树、哈希表等。
04
对数函数与其他函数的关 系
与指数函数的关系
指数函数和对数函数互为反函数,它 们的图像关于直线y=x对称。
对数函数和指数函数在解决实际问题 中经常一起出现,例如在计算复利、 解决声音强度问题等。
对数函数的定义是基于指数函数的, 即如果a的x次方等于N(a>0,a不等 于1),那么x叫做以a为底N的对数, 记作x=logₐN。
与三角函数的关系
对数函数和三角函数在形式上没有直接的关系,但在一些特定情况下可以相互转化 。例如,对于正弦函数和余弦函数的值可以通过对数函数进行计算。
三角函数和对数函数在解决实际问题中经常一起出现,例如在信号处理、振动分析 等领域。
对数函数和三角函数在一些数学问题中可以相互转化,例如在求解一些复杂的积分 问题时,可以将积分转化为对数函数的求解问题。
综合题类型与解题思路
01
类型三:对数方程求解
02
对数方程是常见的题型,需要掌握解对数方程的方法和步骤。
对数函数及其性质(第一课时)课件-高一上学期数学人教A版(2019)必修第一册

)
(1)A已.知cab0.3a0.4 ,A.b cB.lobga34ab,cc lBo.g0.a3 4C,b.则b(c a c )C. b Da.bc c a D.b c a
A. c b a B. a b c
C.b a c
D.b c a
例题讲练
(2)设 a log3 , b log2 3 , c log3 2 ,则(
x lxogaloyg(a ya ( 0a且 a0 且 1a),1x),也是x 也以是y以为自y 为变自量变的量函的数函(数其(中其y 中 0y, 0x , Rx ),R ), 根据根我据们我的们认的知认习知惯习,惯我,们我把们x 把 lxogaloyg中a 字y 中母字x 母, xy,对调y 对,调, 写成写y成 lyogaloxg(a 其x (中其x 中 0x, 0y, Ry ).R ).
例题讲练
【练习习 55】】
((11))已已知知ff((xx))的的定定义义域域为为[0[,10],1,] ,则函则数函数f [lof g[l1o(g31(3x)] 的x)定] 的义定域义为域___为____________._____.
22
例题讲练
(2)已知函数 y f [lg(x 1)] 的定义域为 (0,99] ,则函数 y f [log2 (x 2)] 的定义域为__________.
§4.4 对数函数及其性质 (第一课时)
人教版高中数学必修一
课堂引入:
通过前面的学习我们知道,某细胞经过 x 次分裂后,变成的细胞个数 y 2x ,
得由到一由y 个y2指x 数2x函x数x.lo由gglo22gyyy2y2对x 于对任于x意任的意lo细的g2胞细y个胞,数个对数y于,任y 我,意们我的都们细可都胞以可个通以数过通y对过,数对我运数们算运都算可 得到以得唯通到一唯过的一对的数x 与运x 之与算对之得应对到,应唯所,一以所的细以x胞细与分胞之裂分对次裂应数次,所数x以也x细可也胞以可分看以裂出看次以出数细以x胞细也个胞可数个以数y看为y成自为以变自细变胞个 量的数量函的y数函为.数自.变量的函数. 同样同地样,地根,据根指据数指与数对与数对的数关的系关,系由,y由 ayx(aax ( 0a且 a0 且 1a)可1)以可得以到得:到:
【高中数学】2023-2024学年北师大版必修第一册对数函数y=logax的图象和性质课件(22张)

例7 比较下列各题中两个数的大小:
(1)log25.3,log24.7; (2)log0.27,log0.29; (3)log3π,logπ3; (4)loga3.1,loga5.2(a>0,且a≠1).
解:(1)因为底数2>1,所以对数函数y=log2x在定义域(0,+∞) 是增函数,由5.3>4.7,得 log25.3>log24.7.
解 因为 14C 的半衰期大约是 5730 年,所以由衰减规律,
得
. 1 e5730r
2
解得
r ln 2 . 5730
因此,14C 的衰减规律服从指数型函数
ln2 t
t
C t C0e 5730 C0 2 . 5730
设发现汉谟拉比王朝字样的木炭时(1950 年),该木炭已
衰减了 t0 年,因为放射性物质的衰减速度与其质量成正比,
一、a变化对图像的影响
对数函数 y loga x ,当 a>1 时,a 的值越大,函数图像越靠 近 x 轴,当 0<a<1 时,a 的值越小,图像越靠近 x 轴.
底数互为倒数的两个对数函数图像,关于 x 轴对称.
1( .设)a.=log3π,Ab=log2 ,c=log3 ,3则
2
A.a>b>c C.b>a>c
底数互为倒数的两个对数函数图象,关于 x 轴对称.
例 8 人们早就发现了放射性物质的衰减现象,在考古工 作中,常用 14C 的含量来确定有机物的年代,已知放射性物质 的衰减服从指数规律:C(t) C0ert ,其中 t 表示衰减的时间, C0 表示放射性物质的原始质量,C(t),表示经衰减了 t 年后 剩余的质量.
(2)因为底数0<0.2<1,所以函数y=log0.2x在定义域(0,+∞)
高中数学必修1课件:2.2.2《对数函数及其性质》 (共22张PPT)

值域: R
自左向右看图象逐渐上升 在(0,+∞)上是: 增函数
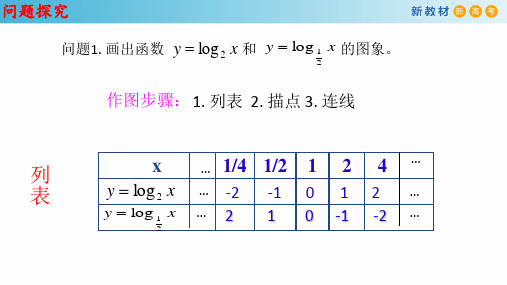
列
x … 1/4 1/2 1 2 4 …
表 y log 2 x … -2 -1 0 1 2 …
y log 1 x … 2
2
1 0 -1 -2 …
y
描
2
点
1 11
这两个函数 的图象有什
42
0 1 23 4
x 么关系呢?
连 线
-1
-2
关于x轴对称
2.2 对数函数
2.2.2 对数函数及其性质 Nhomakorabea复习回顾
1 指数函数的概念;
复 习
2 指数函数的图像与性质:
3 对数的概念和基本运算法则
对数函数的概念
一般地,函数y =
(a>0,且a≠1)
叫做对数函数.其中 x是自变量.
注意:
1.对数函数对底数的限制条件:a>0,且a≠1
2.函数的定义域是(0,+∞).
a>1
0<a<1
图y
y
象 0 (1,0)
x
0 (1,0) x
定义域 : ( 0,+∞)
性
值域 : R
过定点(1 ,0), 即当x =1时,y=0
在(0,+∞)上是增函数
质 当x>1时,y>0
当x=1时,y=0 当0<x<1时,y<0
在(0,+∞)上是减函数
当x>1时,y<0 当x=1时,y=0 当0<x<1时,y>0
作y=log2x的图象
列
x
1/4 1/2 1 2
表 y=log2x -2 -1 0 1
人教版高中数学必修一课件:2.2.2 对数函数的图像及其性质(共20张PPT)

y=0.5x 和y= log0.5x 的图象画在一个坐标内 ,观察图象的特点!
(书面作业)
•P73 2,3
19
Thank you!
要善于退,足够的退,退到不失去重 要性的地方就是解决数学问题的诀窍。
20
比较两个同底对数值的大小时:
1.观察底数是大于1还是小于1( a>1时为增函数
小
2.比较真数值的大小;
0<a<1时为减函数)
结
3.根据单调性得出结果。
14
•(3) loga5.1与 loga5.9 (a>0,且a≠1)
解: 若a>1 则函数y=log a x在区间(0,+∞)上是增函数;
∵5.1<5.9 ∴ loga5.1 < loga5.9
16
函数 yloga x,ylogb x,ylogc x,ylogd x
C 的图像如图,则 所下 示列式子中正( 确) 的
y ylogb x A .0 a b 1 c d
yloga x B .0 b a 1 d c
x
O
ylogd x C .0 d c 1 b a
2.2.2对数函数的图象与性质
y
x
o 1
1
(一)对数函数的定义 ★ 函数 y = log a x (a>0,且a≠1)叫做对数函数.
其中x是自变量, 定义域是(0,+∞)
想 对数函数解析式有哪些结构特征? 一 ①底数:a>0,且 a≠1 想 ②真数: 自变量x ? ③系数函数?(导学与评价P53) ① y log a x 2 ; ② y log 2 x 1; ③ y 2 log 8 x ; ④ yloxga(x0,且x1); ⑤ ylo5gx.
(书面作业)
•P73 2,3
19
Thank you!
要善于退,足够的退,退到不失去重 要性的地方就是解决数学问题的诀窍。
20
比较两个同底对数值的大小时:
1.观察底数是大于1还是小于1( a>1时为增函数
小
2.比较真数值的大小;
0<a<1时为减函数)
结
3.根据单调性得出结果。
14
•(3) loga5.1与 loga5.9 (a>0,且a≠1)
解: 若a>1 则函数y=log a x在区间(0,+∞)上是增函数;
∵5.1<5.9 ∴ loga5.1 < loga5.9
16
函数 yloga x,ylogb x,ylogc x,ylogd x
C 的图像如图,则 所下 示列式子中正( 确) 的
y ylogb x A .0 a b 1 c d
yloga x B .0 b a 1 d c
x
O
ylogd x C .0 d c 1 b a
2.2.2对数函数的图象与性质
y
x
o 1
1
(一)对数函数的定义 ★ 函数 y = log a x (a>0,且a≠1)叫做对数函数.
其中x是自变量, 定义域是(0,+∞)
想 对数函数解析式有哪些结构特征? 一 ①底数:a>0,且 a≠1 想 ②真数: 自变量x ? ③系数函数?(导学与评价P53) ① y log a x 2 ; ② y log 2 x 1; ③ y 2 log 8 x ; ④ yloxga(x0,且x1); ⑤ ylo5gx.
对数函数PPT课件

04 对数函数与其他函数的比 较
与指数函数的比较
指数函数和对数函数是互为反函数, 它们的图像关于直线y=x对称。
当a>1时,指数函数和对数函数都是 增函数,但它们的增长速度不同,对 数函数的增长速度更慢。
指数函数y=a^x(a>0且a≠1)的图 像总是经过点(0,1),而对数函数 y=log_a x(a>0且a≠1)的图像则 总是经过点(1,0)。
对数函数和三角函数的应用领域也不同。对数函数主要用于解决与对数运算相关的问题,如 对数的换底公式、对数的运算性质等;而三角函数则主要用于解决与三角形的边角关系、周 期性等问题相关的问题。
05 对数函数的学习方法与技 巧
学习方法
1 2 3
理解对数函数的定义
首先需要理解对数函数的基本定义,包括对数函 数的定义域、值域以及其变化规律。
对数函数ppt课件
目录
• 对数函数的定义与性质 • 对数函数的运算性质 • 对数函数的应用 • 对数函数与其他函数的比较 • 对数函数的学习方法与技巧
01 对数函数的定义与性质
定义
自然对数
以e为底的对数,记作lnx,其中e是自然对数的底数,约等于 2.71828。
常用对数
以10为底的对数,记作lgx。
当0<a<1时,指数函数和对数函数都 是减函数,但它们的下降速度也不同, 对数函数的下降速度更快。
与幂函数的比较
幂函数y=x^n(n为实数)的图像在 第一象限和第三象限都存在,而对数 函数y=log_a x(a>0且a≠1)的图像 只存在于第一象限。
幂函数的增长速度与指数和对数函数 不同,当n>0时,幂函数的增长速度 比对数函数更快;当n<0时,幂函数 的增长速度比对数函数更慢。
高中数学新人教A版必修一对数函数课件31张

- 3<a< 3).
(2)∵函数 f(x)的值域为 R,∴u=g(x)的值域应包含(0,+∞).因此
Δ=4a2-12≥0,即 a≥ 3或 a≤- 3.故实数 a 的取值范围是(-∞,- 3]∪[ 3,+∞).
(3)∵题干中命题等价于 x2-2ax+3>0 的解集为{x|x<1 或 x>3},
∴x2-2ax+3=0 的两根为 1 和 3.故 2a=1+3,即 a=2.
【解】设 f1(x)=(x-1)2,f2(x)=logax,要使当 x∈(1,2)时,不等式(x-1)2<logax
恒成立,只需函数 f1(x)=(x-1)2 在区间(1,2)上的图象在函数 f2(x)=logax 的图象
的下方即可.
当 0<a<1 时,显然不成立;
当 a>1 时,如图,
要使函数 f1(x)=(x-1)2 的图象在函数 f2(x)=logax 的图象下方,只需
且 3.2<3.6<12.96,∴a>c>b.
T 题型五简
单的反函数问题
例 5 若函数 y=f(x)是函数 y=ax(a>0,且 a≠1)的反函数,其图象经
过点( a,a),则 f(x)等于(
A.log2x
)
B.lo1x
C.
2
1
2x
【答案】B
【解析】由题意知函数 f(x)=logax 的图象经过点( a,a),
A.
2a+b
1+a
B.
2a+b
1-a
D.
C.
)
a+2b
1+a
(2)∵函数 f(x)的值域为 R,∴u=g(x)的值域应包含(0,+∞).因此
Δ=4a2-12≥0,即 a≥ 3或 a≤- 3.故实数 a 的取值范围是(-∞,- 3]∪[ 3,+∞).
(3)∵题干中命题等价于 x2-2ax+3>0 的解集为{x|x<1 或 x>3},
∴x2-2ax+3=0 的两根为 1 和 3.故 2a=1+3,即 a=2.
【解】设 f1(x)=(x-1)2,f2(x)=logax,要使当 x∈(1,2)时,不等式(x-1)2<logax
恒成立,只需函数 f1(x)=(x-1)2 在区间(1,2)上的图象在函数 f2(x)=logax 的图象
的下方即可.
当 0<a<1 时,显然不成立;
当 a>1 时,如图,
要使函数 f1(x)=(x-1)2 的图象在函数 f2(x)=logax 的图象下方,只需
且 3.2<3.6<12.96,∴a>c>b.
T 题型五简
单的反函数问题
例 5 若函数 y=f(x)是函数 y=ax(a>0,且 a≠1)的反函数,其图象经
过点( a,a),则 f(x)等于(
A.log2x
)
B.lo1x
C.
2
1
2x
【答案】B
【解析】由题意知函数 f(x)=logax 的图象经过点( a,a),
A.
2a+b
1+a
B.
2a+b
1-a
D.
C.
)
a+2b
1+a
高中数学必修一(人教版)《4.4.2 对数函数的图象和性质》课件

3
3
3
(2)因为函数 y=log1.5x 是(0,+∞)上的增函数,且 1.6>1.4,所以 log1.51.6>log1.51.4.
(3)因为 0>log70.6>log70.5,所以log170.6<log170.5,即 log0.67<log0.57.
(4)因为 log3π>log31=0,log20.8<log21=0,所以 log3π>log20.8.
(3)取中间值 1,因为 log23>log22=1=log55>log54,所以 log23>log54.
[方法技巧] 比较对数值的大小的策略
(1)比较两个底数为同一常数的对数的大小,首先要根据对数的底数来判断对 数函数的单调性,然后比较真数的大小,再利用对数函数的单调性判断.
(2)比较两个对数值的大小,对于底数是相同字母的,需要对底数进行讨论. (3)若不同底但同真,则可利用图象的位置关系与底数的大小关系解决或利用 换底公式化为同底后再进行比较. (4)若底数和真数都不相同,则常借助中间量1,0,-1等进行比较.
综上所述,当 a>1 时,原不等式的解集为{x|x>4};
当 0<a<1 时,原不等式的解集为x52<x<4
.
[方法技巧] 对数不等式的三种考查类型
(1)形如logam>logan的不等式,借助y=logax的单调性求解. (2)形如logam>b的不等式,应将b化成以a为底数的对数式的形式(b=logaab), 再借助y=logax的单调性求解. (3)形如logf(x)a>logg(x)a(f(x),g(x)>0且不等于1,a>0)的不等式,可利用换底 公式化为同底的对数进行求解,或利用函数图象求解. 提醒:底数中若含有参数,一定要注意底数大于0且不等于1,同时要注意对 底数是大于1还是大于0且小于1进行分类讨论.
4.4 对数函数(教学课件)——高中数学人教A版(2019)必修第一册(共38张PPT)

解:
(1)根据对数的运算性质,有
pH
lg[H
]
lg[H
] 1
lg
1 [H
]
.在
(0,
)
上,随着
[H
]
的增大,
1 [H
]
减小,相应地,
lg
1 [H
]
也减小,即
pH
减小.所以,随着[H
]
的
增大,pH 减小,即溶液中氢离子的浓度越大,溶液的酸性就越强.
(2)当[H] 10 7 时, pH lg10 7 7 .所以,纯净水的 pH 是 7.
对数函数的图像和性质
0 a 1
a 1
图象
定义域 值域
单调性 过定点
(0, )
R
减函数
增函数
过定点 (1,0) ,即 x 1 时, y 0
例 3 比较下列各题中两个值的大小: (1) log2 3.4 , log2 8.5 ; (2) log0.3 1.8 , log0.3 2.7 ; (3) loga 5.1 , loga 5.9 (a 0 ,且 a 1) .
例 2 假设某地初始物价为 1,每年以5% 的增长率递增,经过 t 年后的物价为 w .
(1)该地的物价经过几年后会翻一番? (2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物价 w
1 2 3 4 5 6 7 8 9 10
年数 t
0
解:
(1)由题意可知,经过 t 年后物价 w 为 w (1 5%)t ,即 w 1.05t (t [0, )) .由对
4.4 对数函数
学习目标
1.了解对数函数的概念 2.了解对数函数的单调性和特殊点 3.了解指数函数和对数函数互为反函数
对数函数的图像和性质课件人教A版高中数学必修第一册(共32张PPT)
对数函数y=log a x (a>0, a≠1)
y o1
y=logax (a>1)
x
y=logax (0<a<1) (1)定义域: (0,+∞) (2)值域:R
(3)过点(1,0), 即x=1 时, y=0
(4) a>1时, x<0,0<y<1; x>0,y>1 (4) a>1时,0<x<1,y<0; x>1,y>0
⑴定义域:
性 ⑵值域:
(0,+∞) R
质 ⑶过特殊点: 过点(1,0),即x=1时y=0 ⑷单调性 : 在(0,+∞)上是增函数 ⑷单调性:在(0,+∞)上是减函数
记忆口诀
对数函数的性质的助记口诀:
对数增减有思路, 函数图象看底数; 底数只能大于0, 等于1来也不行; 底数若是大于1, 图象从下往上增; 底数0到1之间, 图象从上往下减; 无论函数增和减, 图象都过(1,0)点.
解(2):考察函数y=log 0.3 x , ∵a=0.3< 1, ∴函数在区间(0,+∞)上是减函数; ∵1.8<2.7 ∴ log 0.3 1.8> log 0.3 2.7
例题解析
例1:比较下列各组中,两个值的大小:
(3) log a 5.1与 log a 5.9 (a>0,且a≠1)
解(3):考察函数log a 5.1与 log a 5.9 可看作函数y=log a x的 两个函值 , 对数函数的单调性取决于底数a是大于1还是小于1, 因此需要对底数a进行讨论
线
-2
y=log1/2x
关于x轴对称
问题探究
对数函数课件(共19张PPT)

即约经过4年,该放射性物质的剩留量是原来的一 半.
在②式中,对应任意一个“剩留量y”,都可求出 唯一的“经过的年数x",如果以“剩留量”作为自变量, 则依函数的定义,“经过的年数”与“剩留量”之间具 有函数关系.
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
情感目标 通过本节课学习,使学生,提升学生数学的直观想象、数学抽象、数学运算、 数学建模的核心素养
创设情境,生成问题 在在活初初动中中1,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
通常我们用x表示自变量,用y表示因变量,于是上 述的函数关系,可表示为
x=log0.84y· 一般地,函数
y=logax(a>0,且a≠1,x>0). 称为对数函数.
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
一般地,对数函数 y=logax(a>0,且a≠1)
具有下列性质: (1)定义域是(0,+∞),值域是R; (2)当x=1时,y=0,即函数的图象都经过点(1,0); (3)在其定义域内,当a>1时这个函数是增函数,
数学
基础模块(上册)
第四章 指数函数 与对数函数
4.2.4 对数函数
人民教育出版社
第四章 指数函数与对数函数 4.2.4 对数函数
在②式中,对应任意一个“剩留量y”,都可求出 唯一的“经过的年数x",如果以“剩留量”作为自变量, 则依函数的定义,“经过的年数”与“剩留量”之间具 有函数关系.
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
情感目标 通过本节课学习,使学生,提升学生数学的直观想象、数学抽象、数学运算、 数学建模的核心素养
创设情境,生成问题 在在活初初动中中1,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
通常我们用x表示自变量,用y表示因变量,于是上 述的函数关系,可表示为
x=log0.84y· 一般地,函数
y=logax(a>0,且a≠1,x>0). 称为对数函数.
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
一般地,对数函数 y=logax(a>0,且a≠1)
具有下列性质: (1)定义域是(0,+∞),值域是R; (2)当x=1时,y=0,即函数的图象都经过点(1,0); (3)在其定义域内,当a>1时这个函数是增函数,
数学
基础模块(上册)
第四章 指数函数 与对数函数
4.2.4 对数函数
人民教育出版社
第四章 指数函数与对数函数 4.2.4 对数函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5. 函数值分布:
当x=1时,y=0。 减函数
0<a<1:
0<a<1:
23.03.2022
Hale Waihona Puke 当:x>1, 图像在y轴下方; 当:x>1, 则y<0
当 0<x<1, 图像在对轴数函上数方; 当0<x<1, 则y>0;
11
图像的特征
函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占
满了整个y轴;
对数函数
2
现在有一张纸,我把这张纸对折一次就变成了两层; 我对折两次纸就变成了四层;如果我们设把纸对折的次 数为x,对折后纸的层数为y,那么,试建立y关于x的函数 关系式。
解:y 2x
提问:如果我发现对折后的纸有4层,那么我对折了多少次? 2次
如果我发现对折后的纸有8层,那么我对折了多少次? 3次
x<0, y>1
y ax
y loga x
23.03.2022
对数函数
y loga x
(0, )
(,)
a>1, 增函数 0<a<1, 减函数 a>1: x>1, y>0
0<x<1, y<0 0<a<1: x>1, y<0
0<x<1, 14
按要求回答问题 (1) y=log3 (x- 2) (2) y=log2(x2 +1)
23.03.2022
对数函数
7
Y
5
Y=X
4
3
●
2● ●
1●
-1 O -1
● ●yax(0a1) 12 3 4 5 6 ●
7X
-2
●ylogax(0a1)
23.03.2022
对数函数
8
y 2x yx
y log2 x
1
1
y (1)x 2
1 1
yx
y log 1 x
2
a>1
0<a<1
请同学们:
根据对数函数的图象描述对数函数的性质:
3. 过(1.0)点
值域: R 当x=1时,y=0。
4. 单调性: a>1时,图像上升;
增函数
0<a<1时,图像下降;
减函数
5. 函数值分布:
a>1:
a>1:
当:x>1时, 图像在y轴上方;
当x>1,
则 y>0,
当0<x<1时,图像在下方;
当0<x<1, 则y<0;
0<a<1:
0<a<1:
当:x>1, 图像在y轴下方; 当:x>1, 则y<0
对数函数
(0, )
R
(1, 0 )
减函数
当x>1, 则y<0; 当0<x<1, 则y>0:
13
名称
指数函数与对数函数对比
指数函数
对数函数
一般形式 定义域
y ax
(,)
值域 单调性
函数值 变
化情况
(0, )
a>1, 增函数 0<a<1, 减函数 a>1: x>0, y>1
x<0, 0<y<1 0<a<1: x>0, 0<y<1
……
16层呢,32层呢 … …
我们可以发现:x关于y也可以建立一个函数。
你能写出这个X关于Y的函数的关系表达式吗?
解: y 2x 指数式化对数式
23.03.2022
xlog2 y 这个就是我们要的函数关系
ylog2 x 交换X和Y,以符合习惯
对数函数
3
对数函数的定义
一般地,函数 ylo gax(a0 ,a1 ) 就叫做对数函数。x为它的自变 量,函数的定义域为 (0,).
y log5 x, y log1 x
3
以上两个函数也是对数函数!
23.03.2022
对数函数
4
我们知道,函数 y 2x 和 ylog2 x互为反函数。 提问:
函数 y a x 和 y loga x 是什么关系呢? 函数 y a x 和 y loga x 互为反函数!
23.03.2022
对数函数
5
2.利用对称性画图.
因为指数函数y=ax (0<a≠1) 与对数函数y=logax(0<a≠1)的图 象关于直线y=x对称.
23.03.2022
对数函数
6
Y
Y=ax (a>1)
5
Y=X
● 4
3
●
2
●
●
● 1●
●
●
-1 O -1
●1
2
3
● Y=logax (a>1) 4 5 6 7X
-2
23.03.2022
对数函数
16
课堂小结:
1. 对数函数是指数函数的反函数,对数 函数的定义域、值域分别为相应的指数函数的值
域和定义域,它们的图象关于y x 成轴对称.
2. 当a>1, y loga x 在 (0, ) 为增函数. 当0<a<1, y loga x 在 (0, ) 为减函数.
23.03.2022
对数函数
1
回顾指数函数图象及性质
a>1
0<a<1
图
象
1.定义域:R
2.值域:(0,+∞)
性
3.过定点(0,1),即x=0时,y=1
质 4. 当x>0时, y>1;
当x<0时,0<y<1; 5.在 R上是增函数
当x>0时,0<y<1; 当x<0时,y>1;
在R上是减函数
23.03.2022
当 0<x<1, 图像在轴上方; 当0<x<1, 则y>0;
23.03.2022
对数函数
12
对数函数图像及性质
a 1
0 a 1
图
y loga x
y loga x
象
x 1
x 1
性 质
23.03.2022
定义域: 值域: 特殊点:
单调性:
函 数值 的
分布
(0, )
R
(1, 0 )
增函数
当x>1, 则y>0; 当0<x<1, 则y<0 :
23.03.2022
对数函数
17
作业:
习题2.8 第1题.(2),(4),(6),(8). 第2题.
23.03.2022
对数函数
18
23.03.2022
对数函数
19
以下函数是对数函数吗?
23.03.2022
对数函数
9
a 1
y loga x
x 1
图像的特征
函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占满了整个y轴; 值域: R
3. 过(1.0)点
当x=1时,y=0。
4. 单调性: a>1时,图像上升;
增函数
5. 函数值分布:
a>1:
a>1:
当:x>1时, 图像在y轴上方;
当x>1, 则 y>0,
23.03.2022
当0<x<1时,图像在对数y轴函数下方;
当0<x<1, 则y<0; 10
0 a 1 y loga x
x 1
图像的特征
函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占满了整个y轴; 值域: R
3. 过(1.0)点
4. 单调性: 0<a<1时,图像下降;
(1)以上函数的定义域。
(2)以上函数如果底数为 a(a>0且a ≠1)时,函数必过那一点。
23.03.2022
对数函数
15
例二:判断下列各组数中两个 值的大小:
(1) log30.8, (2) log0.54.2, (3) loga5.9,
log33.7 log0.52.9 loga3.1 (0<a≠1)
当x=1时,y=0。 减函数
0<a<1:
0<a<1:
23.03.2022
Hale Waihona Puke 当:x>1, 图像在y轴下方; 当:x>1, 则y<0
当 0<x<1, 图像在对轴数函上数方; 当0<x<1, 则y>0;
11
图像的特征
函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占
满了整个y轴;
对数函数
2
现在有一张纸,我把这张纸对折一次就变成了两层; 我对折两次纸就变成了四层;如果我们设把纸对折的次 数为x,对折后纸的层数为y,那么,试建立y关于x的函数 关系式。
解:y 2x
提问:如果我发现对折后的纸有4层,那么我对折了多少次? 2次
如果我发现对折后的纸有8层,那么我对折了多少次? 3次
x<0, y>1
y ax
y loga x
23.03.2022
对数函数
y loga x
(0, )
(,)
a>1, 增函数 0<a<1, 减函数 a>1: x>1, y>0
0<x<1, y<0 0<a<1: x>1, y<0
0<x<1, 14
按要求回答问题 (1) y=log3 (x- 2) (2) y=log2(x2 +1)
23.03.2022
对数函数
7
Y
5
Y=X
4
3
●
2● ●
1●
-1 O -1
● ●yax(0a1) 12 3 4 5 6 ●
7X
-2
●ylogax(0a1)
23.03.2022
对数函数
8
y 2x yx
y log2 x
1
1
y (1)x 2
1 1
yx
y log 1 x
2
a>1
0<a<1
请同学们:
根据对数函数的图象描述对数函数的性质:
3. 过(1.0)点
值域: R 当x=1时,y=0。
4. 单调性: a>1时,图像上升;
增函数
0<a<1时,图像下降;
减函数
5. 函数值分布:
a>1:
a>1:
当:x>1时, 图像在y轴上方;
当x>1,
则 y>0,
当0<x<1时,图像在下方;
当0<x<1, 则y<0;
0<a<1:
0<a<1:
当:x>1, 图像在y轴下方; 当:x>1, 则y<0
对数函数
(0, )
R
(1, 0 )
减函数
当x>1, 则y<0; 当0<x<1, 则y>0:
13
名称
指数函数与对数函数对比
指数函数
对数函数
一般形式 定义域
y ax
(,)
值域 单调性
函数值 变
化情况
(0, )
a>1, 增函数 0<a<1, 减函数 a>1: x>0, y>1
x<0, 0<y<1 0<a<1: x>0, 0<y<1
……
16层呢,32层呢 … …
我们可以发现:x关于y也可以建立一个函数。
你能写出这个X关于Y的函数的关系表达式吗?
解: y 2x 指数式化对数式
23.03.2022
xlog2 y 这个就是我们要的函数关系
ylog2 x 交换X和Y,以符合习惯
对数函数
3
对数函数的定义
一般地,函数 ylo gax(a0 ,a1 ) 就叫做对数函数。x为它的自变 量,函数的定义域为 (0,).
y log5 x, y log1 x
3
以上两个函数也是对数函数!
23.03.2022
对数函数
4
我们知道,函数 y 2x 和 ylog2 x互为反函数。 提问:
函数 y a x 和 y loga x 是什么关系呢? 函数 y a x 和 y loga x 互为反函数!
23.03.2022
对数函数
5
2.利用对称性画图.
因为指数函数y=ax (0<a≠1) 与对数函数y=logax(0<a≠1)的图 象关于直线y=x对称.
23.03.2022
对数函数
6
Y
Y=ax (a>1)
5
Y=X
● 4
3
●
2
●
●
● 1●
●
●
-1 O -1
●1
2
3
● Y=logax (a>1) 4 5 6 7X
-2
23.03.2022
对数函数
16
课堂小结:
1. 对数函数是指数函数的反函数,对数 函数的定义域、值域分别为相应的指数函数的值
域和定义域,它们的图象关于y x 成轴对称.
2. 当a>1, y loga x 在 (0, ) 为增函数. 当0<a<1, y loga x 在 (0, ) 为减函数.
23.03.2022
对数函数
1
回顾指数函数图象及性质
a>1
0<a<1
图
象
1.定义域:R
2.值域:(0,+∞)
性
3.过定点(0,1),即x=0时,y=1
质 4. 当x>0时, y>1;
当x<0时,0<y<1; 5.在 R上是增函数
当x>0时,0<y<1; 当x<0时,y>1;
在R上是减函数
23.03.2022
当 0<x<1, 图像在轴上方; 当0<x<1, 则y>0;
23.03.2022
对数函数
12
对数函数图像及性质
a 1
0 a 1
图
y loga x
y loga x
象
x 1
x 1
性 质
23.03.2022
定义域: 值域: 特殊点:
单调性:
函 数值 的
分布
(0, )
R
(1, 0 )
增函数
当x>1, 则y>0; 当0<x<1, 则y<0 :
23.03.2022
对数函数
17
作业:
习题2.8 第1题.(2),(4),(6),(8). 第2题.
23.03.2022
对数函数
18
23.03.2022
对数函数
19
以下函数是对数函数吗?
23.03.2022
对数函数
9
a 1
y loga x
x 1
图像的特征
函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占满了整个y轴; 值域: R
3. 过(1.0)点
当x=1时,y=0。
4. 单调性: a>1时,图像上升;
增函数
5. 函数值分布:
a>1:
a>1:
当:x>1时, 图像在y轴上方;
当x>1, 则 y>0,
23.03.2022
当0<x<1时,图像在对数y轴函数下方;
当0<x<1, 则y<0; 10
0 a 1 y loga x
x 1
图像的特征
函数性质
1.图像位于y轴右侧;
定义域:x>0
2. 图像在y轴的投影占满了整个y轴; 值域: R
3. 过(1.0)点
4. 单调性: 0<a<1时,图像下降;
(1)以上函数的定义域。
(2)以上函数如果底数为 a(a>0且a ≠1)时,函数必过那一点。
23.03.2022
对数函数
15
例二:判断下列各组数中两个 值的大小:
(1) log30.8, (2) log0.54.2, (3) loga5.9,
log33.7 log0.52.9 loga3.1 (0<a≠1)
