Flac—土-弹性模量--地层的主要物理力学参数
理正与FLAC3D计算结果

计算说明1、计算方法1)内力计算采用弹性支点法;2)土的水平抗力系数按M法确定;3)主动土压力与被动土压力采用矩形分布模式;4)采用力法分析环形内支撑内力;5)采用"理正深基坑支护结构软件FSPW 5.2"计算,计算采用单元计算与协同计算相结合,并采用FLAC-3D进行验证;6)土层参数选取2、单元计算1)基坑分为4个区,安全等级为一级,基坑重要性系数为1.1;2)荷载:施工荷载:10kPa;地面超载:4区活动荷载为25kPa,1区、2区和3区超载按10kPa考虑;水压力;基坑外侧为常水位,内侧坑底以下0.5m。
3)基坑开挖深度:根据现场地形确定,按开挖12.50m确定;4)支撑水平刚度系数:2aTsEAKL sα=式中α取0.8,E取28000MPa,L取7.0m,sa取1.20m,s取7.0m,经计算,kT 大于800 MN/m,本计算中,取800MN/m。
5)计算过程详见附件1,其中1区选用钻孔ZK1,2区选用钻孔ZK4,3区选用钻孔ZK16,4区选用钻孔ZK5。
各区计算结果汇总如下:表2 计算结果汇总表3、协同计算1)计算方法简介协同计算采用考虑支护结构、内支撑结构及土空间整体协同作用有限元的计算方法。
有限元方程如下:([K n]+[Kz]+[Kt]){W)}={F}式中:[K n]-内支撑结构的刚度矩阵;[K z]-支护结构的刚度矩阵;[Kt]-开挖面以下桩侧土抗力的刚度矩阵;{W}-位移矩阵;{F}-荷载矩阵。
计算时采用如下简化计算方法:(1)将基坑周边分成几个计算区域,同一计算区域的支护信息相同,地质条件相同。
(2)将每一个桩或每单位长度的墙看成是一个超级的子结构,这一子结构包括桩墙,土,主动和被动土压力。
(3)将第三道锚索等效为弹性支承点,作为支承系统的一部份进行计算。
(4)单独求解(2)中的子结构,可采用单桩内力计算的一套方法,将刚度和荷载凝聚到与支锚的公共节点上,这是一个一维梁计算问题。
膨胀土边坡稳定性的FLAC分析

膨胀土边坡稳定性的FLAC分析膨胀土是一种具有显著膨胀和收缩特性的粘性土壤,常见于许多工程项目中。
然而,由于其特殊性质,膨胀土边坡的稳定性成为一个重要问题。
无数工程项目因未处理好膨胀土边坡的稳定性而遭受严重损失。
因此,膨胀土边坡稳定性的分析具有重要意义。
FLAC(Fast Lagrangian Analysis of Continua)软件是一种强大的工程分析工具,广泛应用于地质工程领域,尤其在土壤和岩土工程中发挥了重要作用。
本文将使用FLAC软件对膨胀土边坡的稳定性进行模拟分析。
膨胀土边坡的稳定性受到多种因素影响,如土壤的物理性质、边坡的几何形状和大小、降雨量、地下水等。
不稳定的膨胀土边坡可能导致滑坡、泥石流等地质灾害,给工程项目带来严重威胁。
FLAC软件在分析膨胀土边坡稳定性方面具有以下优势:考虑了土壤的物理性质,如膨胀性、收缩性、凝聚力等。
可以模拟边坡在不同工况下的稳定性,如降雨、地震、施工等。
提供了强大的后处理功能,可以对模拟结果进行详细分析和可视化。
某高速公路经过一段地形起伏较大的地区,其中部分路段的边坡由膨胀土构成。
在近年的雨季,这些边坡出现了不同程度的滑坡。
为了解决这个问题,我们使用FLAC软件对这段路段的膨胀土边坡进行稳定性分析。
建立模型:首先建立膨胀土边坡的三维模型,并确定模型的基本参数,如土壤类型、密度、含水率等。
加载条件:根据实际工况,加载包括自重、降雨、地震等外部条件。
模拟分析:使用FLAC软件对膨胀土边坡进行稳定性模拟分析。
结果分析:通过后处理功能,对模拟结果进行详细分析和可视化,得出边坡在不同工况下的稳定性状态。
针对可能出现的不稳定区域,提出相应的加固措施和优化建议。
膨胀土边坡的稳定性是工程项目中必须重视的问题。
FLAC软件在分析膨胀土边坡稳定性方面具有显著优势,可以考虑土壤的物理性质、外部加载条件,并提供了强大的后处理功能,可以直观地展示边坡的稳定性状态。
结合具体案例,使用FLAC软件进行模拟分析,可以为工程项目提供有价值的参考意见和建议。
FLAC3D在滑坡稳定性分析评价中的应用

FLAC3D在滑坡稳定性分析评价中的应用赵忠海【摘要】Taking the Gaozhi Village landslide as an example, this paper discussed the application of FLAC3D in landslide stability analysis and evaluation. The author ifrst introduced the basic principle and main process of FLAC3D, and then simulated the Gaozhi Village landslide stability under natural state and heavy rain state by Mohr-Coulomb of FLAC3D. The simulation result intuitively showed the distribution characteristics of plastic deformation and horizontal displacement of the slope in the above two conditions, and clearly showed the potential sliding surface inside the slope. According to the result of numerical simulation, the article analyzed and evaluated the landslide stability, studied and discussed the deformation and failure forms of the landslide. By analyzing the plastic deformation and displacement of slope, the author considered that the landslide is basically stable under the natural state and is unstable and likely to slide and lose its stability in the local area under the continuous high intensity rainfall state. This is consistent with the investigation and analysis. This result shows it is feasible and more simple and more intuitive and convenient to analyze and evaluate the stability of landslide by FLAC3D. Compared with the traditional limit equilibrium method, FLAC3D has the incomparable advantage.%本文以高治村滑坡为例,论述了FLAC3D在滑坡稳定性分析评价中的应用。
土体物理力学参数及其关系的试验研究

土体物理力学参数及其关系的试验研究
土体物理力学参数是指土壤在受力作用下的物理性质,包括密度、孔隙度、饱和度、渗透系数等。
这些参数对于土壤的力学性质和水文特性具有重要影响,因此对其进行试验研究具有重要意义。
密度是土壤物理力学参数中最基本的参数之一。
密度的大小直接影响土壤的强度和稳定性。
通过试验可以得出,土壤密度与土壤的孔隙度成反比关系,即密度越大,孔隙度越小。
同时,密度还与土壤的含水量有关,含水量越大,密度越小。
孔隙度是指土壤中孔隙的体积占总体积的比例。
孔隙度的大小直接影响土壤的渗透性和水分保持能力。
通过试验可以得出,孔隙度与土壤的密度成反比关系,即孔隙度越大,密度越小。
同时,孔隙度还与土壤的饱和度有关,饱和度越大,孔隙度越小。
饱和度是指土壤中孔隙中被水填满的部分所占的比例。
饱和度的大小直接影响土壤的渗透性和水分保持能力。
通过试验可以得出,饱和度与土壤的孔隙度成正比关系,即饱和度越大,孔隙度越小。
同时,饱和度还与土壤的渗透系数有关,渗透系数越大,饱和度越小。
渗透系数是指单位时间内单位面积土壤中水分通过的速率。
渗透系数的大小直接影响土壤的渗透性和水分保持能力。
通过试验可以得出,渗透系数与土壤的孔隙度成正比关系,即孔隙度越大,渗透系数越大。
同时,渗透系数还与土壤的饱和度有关,饱和度越大,渗
透系数越小。
土体物理力学参数及其关系的试验研究对于深入了解土壤的力学性质和水文特性具有重要意义。
通过试验可以得出各个参数之间的关系,为土壤的工程应用提供了科学依据。
路基施工过程变形研究的FLAC3D数值模拟

路基施工过程变形研究的FLAC3D数值模拟张宇旭【摘要】Numerical simulation analysis of the deformation characteristics in the construction process of subgrade is conducted. In different unit weight and modulus of resilience conditions of filled soil, vertical settlement and the horizontal lateral displacement in the embankment slope feet of roadbed center change with the change of the depth of fill. The deformation law are found, which guide practical engineering of the sub grade construction. The filled soil of small severe is selected or the elastic modulus is raised to improve the settlement deformation of highway under the condition of standard requirement.%对路基在施工过程中的变形特性进行数值模拟分析,研究在不同填土重度和不同填土回弹模量的条件下,路基中心处竖向沉降和路基坡脚处的水平侧向位移随路基填土高度的变化情况,在满足规范要求的条件下,尽可能的选用重度小的填土或提高路堤回弹模量,能够改善公路沉降变形.【期刊名称】《武汉工程大学学报》【年(卷),期】2011(033)006【总页数】4页(P72-75)【关键词】路基施工;FLAC3D数值模拟;沉降【作者】张宇旭【作者单位】黄石理工学院,湖北黄石435003【正文语种】中文【中图分类】U4150 引言地基沉降变形分析是土力学的重要研究课题之一.自从太沙基(Tetzaghi)的一维固结理论[1]问世以来,各国学者相继进行了土体固结沉降理论的研究,并取得了丰硕的成果,这些研究成果对实际工程建设都起到了很好的指导作用.近几年来,计算机技术的发展突飞猛进,把计算机技术应用到土力学中的计算软件也越来越多,采用有限拆分和有限元等数值计算分析地基沉降已成为现实.随着西部大开发政策的实施,西部地区的基础建设亦提上日程,兴建公路、南水北调工程、石油管线建设等项目将会日益增多,这些对沉降计算的要求也在不断提高,改进或提高沉降预测和计算方法具有重大的学术价值和社会效益[2-3].本文以西部某二级公路为例,进行路基在施工过程中的变形与数值模拟研究,对其它类似工程具有一定的工程价值.1 工程概况如图1所示,地基计算深度为50 m,分为两层,上部为回填土,厚度为10 m,下部为粘土层,厚度为40 m;路基计算宽度为200 m,填筑高度为5 m,坡度为1∶1.5,地基土分为两层,厚度为20 m,上部位粘土层,厚度8 m,下部为砂土层,厚度为12 m.具体参数见图.路堤填筑高度为4 m,分两次进行填筑.要求分析路堤填筑后土层的应力、位移状态.图1 路堤施工的几何模型Fig.1 The geometrical model of embankment construction2 模型建立基于朗格朗日法原理的FLAC(Fast Lagrangian Analysis of Continua)是一种专门用于求解岩土力学问题的程序,可用于分析有关边坡、基坑等一系列岩土工程问题.本文采用有限差分软件FLAC3D进行路堤填筑应变应力与位移的分析,有关FLAC 的基本理论见文献[4].2.1 本构模型的选取本构模型是对岩土材料力学性质特性的经验性描述,它所反映的是外荷载条件下岩、土体的应力-应变关系,因此,本构模型的选择是数值模拟的一个关键性步骤.FLAC3D具有强大的适合模拟岩土材料的本构模型,FLAC3D提供了十种基本的本构模型,分别归类到空模型、弹性模型和塑性模型中[5].事实上,一种模型不可能考虑所有影响因素,也不可能有一种模型适用于所有土体的类型和加载情况,只有当选择的本构模型与工程材料力学特性契合度较高时,其选择才是合理的.根据实际工程中土的类型及加载条件,抓住主要矛盾,选择符合实际情况的本构关系为路基工程服务具有非常重要的现实意义.本文采用的是Mohr-Coulomb模型,它需要的参数少且容易获得,基本满足工程实际需要.模拟过程中采用的不同土层的内摩擦角φ、粘聚力c值,是结合实际工程情况取值的.τf=c+σtgφ式中:τf为抗剪强度;c为粘聚力;σ为作用于剪切面上的法向应力;φ为内摩擦角.2.2 建模思路由图1可以看出,由于路堤断面具有数值方向的对称性,因此可以考虑选择对称的一半断面进行建模计算,以便减少网格数量,提高计算效率.坐标系的原点O设置在地基表面与模型对称轴的交点,水平向右为x方向,数值向上为z方向,垂直于分析平面的方向为y方向.建立的网格模型如图2.图2 模型网格建立Fig.2 The establishment of mesh model在分析时,力的边界条件:地基在自重作用下的位移已经完成,外荷载只考虑路堤土(包括等效的路面荷载)的重力作用.位移边界条件:结构模型的左右边界分别为横向固定约束,只产生竖直方向的位移;底部无任何位移故施加基地固定约束.2.3 计算参数的确定计算参数的选取如表1.表1 各土层物理力学参数Table 1 Physical and mechanical parameters of each soil土层名称ρ/(kg·m-3)c/kPaφ/(°) E/MPav回填土1 500101580.33粘土1 800202040.33在FLAC3D程序中,岩土体的变形参数采用的是剪切模量G和体积模量K,在具体计算时,需要首先采用公式(1)将变形模量转化为剪切模量和体积模量:(1)(2)2.4 初始应力的计算在路基施工前,需要将路基部分网格赋值为空模型,将地基部分的网格赋值为Mohr.由于本例中存在null模型,所以采用分阶段的弹塑性求解方法.先将Mohr 模型的凝聚力值和抗拉强度赋值为为穷大进行求解,保证在重力作用下单元不至于发生屈服,然后再将Mohr模型参数赋值为真实值,在进行求解.图3和图4为初始应力计算结束时得到的水平向应力云图和竖直向应力云图,可以发现最大竖向应力值为85.3 kPa,最大水平应力值为42.0 kPa,静止侧压力系数约为0.5,与理论计算值基本一致.图3 初始水平应力云图Fig.3 The initial horizontal stress nephogram图4 初始竖向应力云图Fig.4 The initial vertical stress nephogram2.5 施工过程模拟在进行路基施工模拟前要将初始应力计算过程中产生的节点位移和速度进行清零处理.本例中路基高度为5 m,高度方向共划分了5个单元,为了模拟路基填筑的施工过程,采用分级加载的方法激活路基单元,每次激活1 m高度的单元,相当于每次填筑高度为1 m,分5次填筑完成,每次填土进行一次求解.填筑结束后,路堤的沉降云图和水平位移云图见图5和图6.图5 填筑结束时沉降云图Fig.5 The settlement nephogram after filling图6 填筑结束时水平位移云图Fig.6 The horizontal displacement after filling 从图5和图6可以看出,路堤堆载作用引起的地基沉降最大值54.5 cm,且最大沉降位置位于路堤中心点处;最大水平位移为32.3 cm,发生在坡脚附近.由图5图6可知,在实际工程中,工程师们最关心路基中心节点和坡脚节点的变形结果.其变形结果如图7.图7 路基中心及坡脚的沉降曲线Fig.7 The settlement curve of basal slope and foundation center由图7可知,路基中心沉降曲线的斜率要大于路基坡脚水平位移曲线斜率,说明路基中心的沉降要大于路基坡脚的水平位移.3 计算结果分析3.1 路基中心沉降分析3.1.1 不同路堤填土重度对比分析计算依然选取和前文相同的数值模型和边界条件,对上部路堤填土选取了三种不同重度值进行模拟计算:γ=12 kN/m3、γ=15 kN/m3和γ=20 kN/m3.通过计算分析不同路堤填土重度对路基沉降和侧向位移的影响.图8 不同填土重度路基中心沉降曲线Fig.8 The settlement curve of foundationcenter of different filling severe图9 不同弹性模量路基中心沉降曲线Fig.9 The settlement curve of foundation center of different elastic modulus从图8可以看出,随着重度的增小,路基沉降随之减小;且重度越小,沉降曲线曲率也越缓.在填筑结束时,由γ=20 kN/m3的74.2 cm减小到γ=12 kN/m3的43.2 cm,减少了41%.因此,路堤填土重度对路堤的沉降有较大的影响,在满足规范要求的情况下,尽可能的选用重度小的填土.3.1.2 不同路堤填土模量对比分析由于填筑路堤土体的物理力学参数的差异,以及路堤施工方法的不同,在不同的路段路堤的弹性模量会有所不同.改变路堤土体的弹性模量分别进行计算,分析在路堤弹性模量不同的情况下对原有路堤沉降的影响.不同弹性模量下路基中心的沉降曲线如图9.由图9可见,随着路基弹性模量的增加,其沉降量反而较少,并且这种趋势在逐渐变缓,增大路堤模量对沉降的影响越来越小;在填筑结束时,路基中心的沉降随着路堤土体弹性模量增大的变化很不显著.从图中看出,在路堤模量为5 MPa 时,沉降量 58.2 cm,路堤模量增加到12 MPa 时,沉降量下降到52.1 cm,下降了10.4%. 因此,在路堤填筑时,适当的提高路堤模量,能够改善公路沉降变形. 3.2 路基坡脚的侧向位移分析由上文的分析可知:路基坡脚处的水平位移较大,再此仅分析在不同路基填土重度以及不同填土弹性模量情况下路基坡脚处的侧向位移.由图10和图11可知,路基坡脚侧向位移在两种情况下都比较小.3.2.1 不同路堤填土重度对比分析如图10,路基坡脚处的侧向位移随着路基填土厚度的增加而逐渐增加,达到峰值后又逐渐减小,呈凸起抛物线形;其峰值随着路基填土重度的减小而滞后,例如γ=12 kN/m3时,其峰值1.66 cm出现在填土高度为3.3 m的时候,而γ=20 kN/m3时,峰值1.82 cm出现在填土高度为2.5 m的时候.由图10还可以看出,抛物线基本随峰值对称,重度越小,抛物线的开口越大.图10 不同重度路基坡脚侧向位移曲线Fig.10 The side settlement curve of basal slope of different filling severe图11 不同弹性模量路基坡脚侧向位移曲线Fig.11 The side settlement curve of basal slope3.2.2 不同路堤填土模量对比分析如图11,路基坡脚处的侧向位移随着路基填土厚度的增加而逐渐增加,达到峰值后又逐渐减小,呈凸起抛物线形;其峰值随着路基填土弹性模量的增大而滞后,例如E=5 MPa时,其峰值2.5 cm出现在填土高度为2.5 m的时候,而E=12 MPa时,峰值1.83 cm出现在填土高度为3.1 m的时候.由图10还可以看出,在侧向位移达到峰值以后,其减小的幅度比比开始逐渐增加的幅度要大;路基填土弹性模量越大,抛物线的开口越大.4 结语a.随着重度的增小,路基中心处沉降随之减小;且重度越小,沉降曲线曲率也越缓.因此,路堤填土重度对路堤的沉降有较大的影响,在满足规范要求的情况下,尽可能的选用重度小的填土.b.随着路基弹性模量的增加,路基中心处的沉降量反而较少,并且这种趋势在逐渐变缓,增大路堤模量对沉降的影响越来越小;在填筑结束时,路基中心的沉降随着路堤土体弹性模量增大的变化很不显著.因此,在路堤填筑时,适当的提高路堤模量,能够改善公路沉降变形.c.路基坡脚处的侧向位移随着路基填土厚度的增加而逐渐增加,达到峰值后又逐渐减小,呈凸起抛物线形.d.路基坡脚处的侧向位移随着路基填土厚度的增加而逐渐增加,达到峰值后又逐渐减小,呈凸起抛物线形;其峰值随着路基填土弹性模量的增大而滞后.参考文献:[1] Alamgir M, Miura N, Proorooshasb H B, et al. Deformation analysis of soft ground reinforced by columnar inclusion[J]. Computers & Geosciences, 1996, 13(4): 267-289.[2] 殷宗泽,朱泓,吴钰.沪宁高速公路地基沉降有限元计算分析[J].水利水电科技进展,1998,18(2):22-26.[3] 吴大志,李夕兵.高速公路路基沉降计算方法[J].湖南交通科技,2001,27(4):4-6.[4] 陈育民,徐鼎平. FLAC/FLAC3D基础与工程实例[M]. 北京:中国水利水电出版社,2009.[5] 谢和平.岩石力学[M].北京:科学出版社,2004.。
基于FLAC3D对某边坡天然及地震工况下稳定性分析

基于FLAC3D对某边坡天然及地震工况下稳定性分析◎ 彭志盛 中交四航局第二工程有限公司摘 要:本文以海外某工程开挖边坡为实例,结合室内试验参数,基于RMR分类法并参考经验公式进行岩土体参数估算,进一步评估4m或6m锚杆支护的边坡在天然工况下的稳定性并在地震工况下的运用拟静力法分析其稳定性。
结果表明:采用RMR法并结合边坡实际工程地质条件,参考已有经验公式对边坡岩土体参数进行估算在实际工程中是可行的,计算结果相对保守;天然工况或地震工况条件下,采用4m或6m锚杆进行支护时,稳定性系数均满足规范中对安全系数的要求,边坡处于基本稳定状态;但安全起见,建议对该边坡采用6m锚杆进行支护。
关键词::FLAC3D;强度折减法;拟静力法;稳定性分析1.前言当前稳定性分析有定性和定量分析两类方法。
极限平衡法,极限分析法等是定量分析方法中比较常见的[1]。
无论极限平衡法或是极限分析法具因其模型简单、计算方便,在工程实践中作为首选方法进行广泛应用,但分析边坡破坏发生和发展过程方面却力有不逮[2];针对此问题,基于强度折减法理论的数值模拟软件FL AC3D通过搜索潜在滑动面及其位置可以有效解决极限平衡法的不足,计算呈现结果更加直观。
进行数值模拟计算时,参数的选取至关重要,参数选取准确与否对计算结果影响重大,而当前岩土体,尤其是岩质材料的参数取值时往往进行以下简化:以岩石(岩块)室内试验所得性质代替真实岩体。
工程实践中极少遇到未风化岩体,天然环境中的岩体受风化作用产生广泛分布的节理裂隙,影响岩体完整性,并使得真实岩体在物理力学性质上与岩块存在较大差异。
本文以某工程挖方边坡为例,对岩体材料基于更科学的方法进行取值,采用强度折减法进行天然工况及地震工况下分析边坡稳定性。
2.强度折减法强度折减法中稳定性系数即边坡达到临界状态与初始状态对应的抗剪强度之比。
岩体抗剪强度应用过程如下式所示。
式中:C d——折减后的粘聚力;φd——折减后的内摩擦角;C——折减前的粘聚力;φ——折减前的内摩擦角;F d——折减系数。
常用土层和岩石物理力学性质
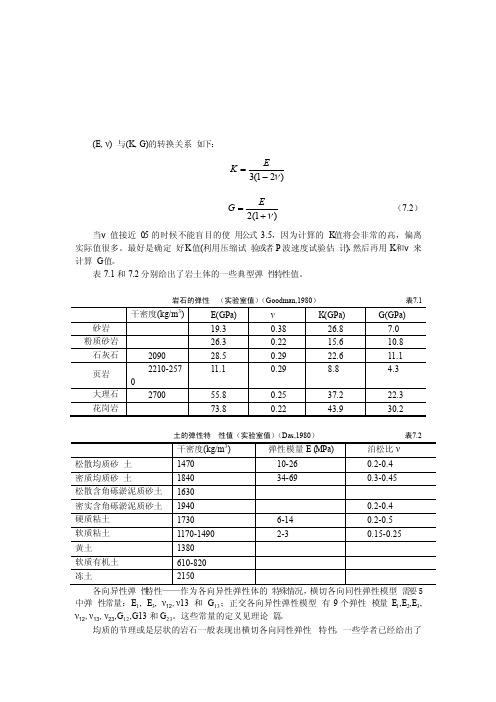
(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodm a n,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的Kf 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙 度n ,渗透系数k 以及Kf 有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数来决νC 定改变Kf 的结果。
FLAC3D在滑坡数值分析及监测预警设计中的应用

1478地下空间与工程学报第2卷料达到屈服极限时的塑性流动现象。
由于FLAC3D采用了显示差分格式和混合离散技术,可以精确的模拟材料的屈服和塑性流动。
它的三维网格可以由用户根据所模拟物体的形状进行调整,网格由若干六面体单元组成,每个单元在指定的力和边界条件下遵循指定的线性或非线性本构关系,如果单元应力使得材料发生屈服或是塑性流动,单元网格可以在大变形的计算模式下发生很大的变形‘3|。
2八字门滑坡概况八字门滑坡为一土质古滑坡,滑坡分布高程139~280m,面积12万m2,滑坡体积400万m3。
滑坡体位于侵蚀构造中低山山前斜坡,地形上前凸中平后凹,以上陡下缓的连续斜坡形态兼具三级堆积平台地貌。
滑坡体内冲沟较发育,滑坡后壁高程250m,滑坡璧较陡,坡度40。
~60。
,其剖面形态呈凹槽状。
滑坡前缘为人长江河口附近的香溪河,河道较直,受三峡库区蓄水影响,目前水位已达139m,形成了水面宽阔的库区。
滑坡体簸箕状展布于岸坡坡脚,长380m,宽100~500m,厚10—35m。
滑体主要为结构松散的崩坡积、坡积物。
滑带在上部松散堆积层与下部基岩面间连续分布,滑带物质以粉质粘土含角砾为主,颜色较杂。
滑床基岩在139m蓄水位以上主要为侏罗系下统(J,)岩层,水位以下主要为三叠系中统(T2)岩层。
目前,八字门滑坡具有发生失稳的可能性。
滑坡变形影响因素:2.1三峡水库蓄水在三峡水库蓄水175m后,滑坡的滑体大部分将处于库水位以下,地下水位强烈上升;同时在库水位145~175m变化大幅度涨落期间,地下水产生的渗透动水压力,会加剧滑坡的整体失稳。
三峡水库蓄水后即库水位调节是影响八字门滑坡稳定的最重要因素。
2.2降雨连续的降雨易使滑坡体处于饱和状态,自重不断增加,地下水的下渗,由于滑面相对隔水,上层地下水在此集中。
使滑面的强度大大降低,有可能诱发滑坡失稳。
据调查近几年来,在连续暴雨之后,在滑体中前部多次发生小型的塌滑,在滑坡后缘和边界产生裂缝。
常用岩土材料参数和岩石物理力学性质一览表
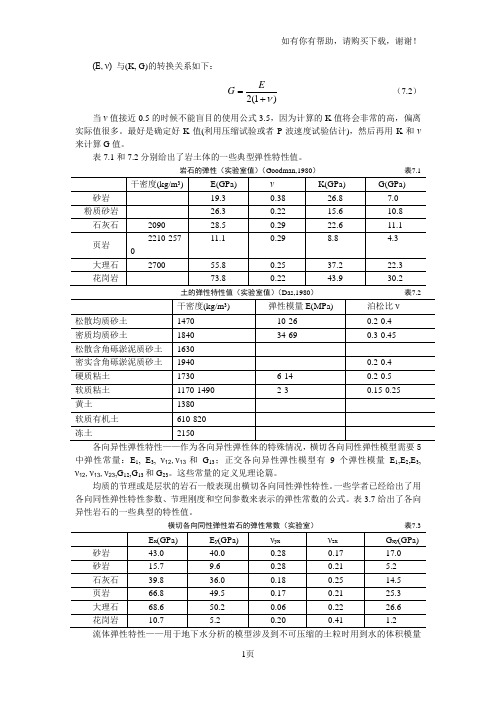
(E, ν) 与(K, G)的转换关系如下:)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
FLAC3D在地下矿山采场稳定性分析中的应用

FLAC3D在地下矿山采场稳定性分析中的应用摘要:在地下矿山生产体系中,矿体开挖的动态作业,会使得矿体应力平衡状态受到破话,在应力重新分布后,应力作用更加明显,因此对采场稳定性产生影响。
本文基于地下矿山采场失稳机理,说明FLAC3D在采场稳定性分析中的具体应用,并明确分析结论,以此为相关工作开展提供参考。
关键词:FLAC3D;矿山采场;稳定性分析FLAC3D是基于二维有限差分程序拓展而来,主要用于土质、岩石等材料三维结构受力特性模拟和塑性流动分析的软件。
基于模拟塑性破坏和塑性流动的准确分析,采用动态运动方程分析方法,能够较为快速、便捷的分析各种场景下特定材料三维结构受力情况。
在地下矿山生产中,做好采场稳定性分析,结合分析结果做好支护处理,是确保采场运行稳定、有效提升生产安全水平的基本保障。
1、地下矿山采场失稳机理1.1 采场围岩变形特性在地下矿山采场作业流程中,围岩内垂直方向的应力会明显大于水平方向应力,在顶板围岩除,拉应力作用较为显著。
而在拉应力超出极限并在继续开采作用下,必然会使得顶板及拐角部位发生裂隙现象[1]。
在支护不到位情形下,则会出现变形破坏甚至是塌落现象。
而在水平方向大于垂直方向应力时,顶板围岩则是受剪应力作用较为显著,使得围岩结构出现松动、错动或膨胀等现象,也会对造成围岩破坏,对生产运行安全产生影响。
1.2 采场失稳模式矿山采场失稳是地下矿山生产安全影响较为明显的问题,依据围岩变形特征和生产管理情况,失稳现象主要有三种模式:(1)顶板围岩局部位置为出现失稳,但矿柱能够保持稳定状态;(2)矿柱出现失稳现象,但顶板围岩依然较为稳定;(3)顶板和矿柱同时出现失稳现象。
虽然这三种模式的表现形式有所差异,但是在其中任何一种失稳现象发生时,都会由于进一步发展而造成采场整体稳定性不足,因此利用先进技术对采场进行稳定性分析,为支护设计处理提供精准参考,是生产安全管理工作需要关注的重点内容[2]。
FLAC在顺层边坡稳定性计算中的对比应用

啪 伽 啪荷载组合 啪 拗 类别
自重 自重 + 下水 地 自重 + 地震 自重 + 蓄水 自重 +蓄水 + 震 地 临时 偶然
永久荷载
W
4 5
永久荷载 偶然
间距 51 2 m, m~ 0c 延伸 长度 5m 一8m, 3 多充填 有 0 5 m ~ . m 分析软件 , 具有强 大 的计 算功 能和广 泛 的模 拟 能力 , 尤其在 大变 糙 , m的石英脉 ; ) 1 。 / WL6 。 节 理 面微 起 伏 , 糙 , 2 57EN 2 6, 粗 间距 形 问题 的分析方面 具有独 特 的优 势 。软件 提供 的针对 岩土体 3m . 1m, 5m, 和支护体系 的各 种本 构模 型 和结 构单 元更 突 出 了 F A L C的 “ 专 0 5m一 延 伸长 3m~ 闭合无 充填 。坡体 表面局 部分布 覆盖层 , 主要为崩坡 积块 碎石及 冲洪积 的含 漂砂 卵砾 石层 , 盖 覆 业” 特性 , 在国际土木工程 ( 尤其是 岩土工 程 ) 术界 和工业界 享 学
图 3 节理 裂隙及 坡面产 状赤 平投影
根 据现场勘察 结果 , 确定 各勘 探剖 面在 边坡体 中的位置 , 考
虑边坡体 实际情况 , 确定典 型计算 剖面 , 图 6 见 。
坏, 在建立边坡计算模型时基岩材料要 采用各 向异性 材料——节 理化模型 , 图 7 图 8 软弱面的搜 索采用拆 线破坏面求解 。 见 , ,
坡 的安全 稳定 提供理 论依据 , 为水 电站 的坝址选择提供决策依据。 关键 词 : 顺层边坡 ,L C, F A 显式有限差分 , 稳定性 中图分类号 :U 1 .2 T 4 3 6 文献标 识码 : A
FLAC讲义(含地下水的边坡例子)
FLAC讲义(含地下水的边坡例子)FLAC 讲义一、什么是FLAC1.1 FLAC之字义F(Fast)L(Lagrangian)A(Analysis of)C(Continua). Lagrangian相对于Eulerian为每一时阶(timestep)之位移在Lagrangian之公式中,需对网格之座标予以更新,而Eulerian之公式则不予更新。
1. 2 FLAC之运算流程1.3 FLAC 基本单元1.4 分析模式大小与RAM之关系1.5 单位1.6 正负号方向(1) 应力-正号代表张力,负号代表压力(2) 剪应力-详见下图,图中所示剪应力为正号(3) 应变-正的应变表示伸长,负的应变代表压缩(4) 剪应变-剪应变的正负号与剪应力相同(5) 孔隙压力-孔隙压力永远为正(6) 重力-正号的重力物质往下拉,负号的重力将物质往上提。
二、FLAC内建之组合律FLAC内建之组合律有:1.空洞模式(null model)使用于土壤被移除或开挖2.弹性模式3.塑性模式,包括a. Drucker -Prager modelb. Mohr-Coulomb modelc. ubiquitous-joint modeld. strain-hardening/softening modele. bilinear strain-hardening/softening modelf. double-yield modelg modified cam-clay model此外,另有选购(option)模式,包括:1. 动力模式(Dynamic Option)2. 热力模式(Thermal Option)3. 潜变模式(Creep Option)使用者另可使用FISH语言去建构独特的组合律以符合所需。
三、FLAC-以命令为输入语法请查阅相关手册四、FLAC程式之使用步骤4.1 FLAC程式使用前准备步骤步骤1:依比例画出所欲分析之资料于纸上画出地点之位置、地层资料、并简标示距离及深度资料。
FLAC 3D强度折减理论在边坡稳定分析中的应用

FLAC 3D强度折减理论在边坡稳定分析中的应用季聪;佴磊;马宏;佘小光;刘录君【摘要】FLAC3D是岩土工程中广泛应用的软件.本文主要介绍强度折减理论的基本原理,利用基于强度折减法的FLAC3D软件,对某高速公路K377+ 230 ~ K377+ 520段滑坡体进行数值模拟.计算边坡在自重作用达到初始化平衡状态时,边坡的横向与竖直方向的应力与位移,分析出边坡的破坏机制为牵引式滑坡,通过强度折减理论计算出边坡的稳定系数为0.97,由剪切应变增量云图确定边坡的滑动面.%FLAC 3D is a widely applied software in geotechnical engineering. We mainly introduce the principle of strength reduction theory. Numerical simulation on the K377 + 230 ~ k377 + 520 section of a highway has been made by FLAC 3D sofeware based on strength reduction theory. To calculate the slope lateral and vertical stress and displacement when the slope gets to the initialization equilibrium condition in dead weight function, then to analyze the result that the slope failure mechanism was retrogressive landslide; after that to calculate the slope stability coefficient as 0. 97 through the strength reduction theory, finally to determine the sliding surface by the shear strain increment chart.【期刊名称】《世界地质》【年(卷),期】2013(032)001【总页数】7页(P158-164)【关键词】FLAC3D;强度折减理论;滑动面;稳定系数【作者】季聪;佴磊;马宏;佘小光;刘录君【作者单位】中水东北勘测设计研究有限责任公司,长春130021【正文语种】中文【中图分类】P642.220 引言边坡工程是岩土工程领域的一个分支,其稳定性研究一直是个热点课题。
FLAC在基坑开挖分析中的应用_陈敏华

第28卷 增刊 岩 土 工 程 学 报 Vol.28 Supp. 2006年 11月 Chinese Journal of Geotechnical Engineering Nov., 2006 FLAC在基坑开挖分析中的应用陈敏华,陈增新,张长生(铁道科学研究院深圳研究设计院,广东 深圳 518034)摘 要:结合深圳市地铁侧某基坑支护工程实例,运用FLAC程序对基坑施工过程中的变形规律,以及对地铁的影响进行了分析;并对比现场监测结果,得到了几点关于该工程基坑变形和支护结构工作性能的结论。
关键词:基坑支护;开挖;地铁;FLAC程序中图分类号:TU463 文献标识码:A 文章编号:1000–4548(2006)S0–1437–04作者简介:陈敏华(1981–),男,广东广州人,硕士研究生,主要从事边坡稳定与软土地基方面的理论研究及其工程应用。
Application of FLAC in analysis of foundation excavationCHEN Min-hua,CHEN Zeng-xin,ZHANG Chang-sheng(Shenzhen Research and Design Institute of China Academy of Railway Sciences, Shenzhen 518034, China ) Abstract: According to the foundation excavation supporting near the subway example in Shenzhen, an analysis with FLAC program was carried out on the development of deformation for foundation pits during construction and the effect on the subway. Considering the results of in-situ monitoring, some conclusions were drawn on performance of cable and supporting piles and deformation of foundation pits.Key words: supporting of foundation pit; excavation; subway; FLAC program0 概 述近年来,在土木工程快速发展的大环境下,基坑工程设计与施工的复杂性陡增。
工程地质数值法

某路基工程施工过程数值模拟摘要本文首先对FLAC3D软件进行了介绍,简明阐述了其特点、应用范围及不足;然后结合具体路堤工程,采用FLAC3D软件对施工过程进行了模拟,生成了初始竖向和水平应力云图、第一次填筑及填筑结束时的沉降云图及水平位移云图;最后生成了路基中心点和坡脚节点的沉降曲线。
关键词:FLAC3D;数值模拟;应力云图;沉降云图;位移云图1 FLAC3D的功能与特性自R.W.Clough 1965年首次将有限元引入土石坝的稳定性分析以来,数值模拟技术在岩土工程领域获得了巨大的进步,并成功解决了许多重大工程问题。
特别是个人电脑的出现及其计算性能的不断提高,使得分析人员在室内进行岩土工程数值模拟成为可能,也使得数值模拟技术逐渐成为岩土工程研究和设计的主流方法之一。
数值模拟技术的优势在于有效延伸和扩展了分析人员的认知范围,为分析人员洞悉岩体、土体内部的破坏机理提供了强有力的可视化手段。
FLAC系列软件的出现,为岩土工程研究工作者提供了一款功能强大的数值模拟工具。
1.1 FLAC3D主要特点FLAC(Fast Lagrangian Analysis of Continua)是由Itasca公司研发推出的连续介质力学分析,是该公司旗下最知名的软件系统之一,FLAC目前已在全球七十多个国家得到广泛应用,在国际土木工程(尤其是岩土工程)学术界和工业界享有盛誉。
FLAC3D界面简洁明了,特点鲜明。
其使用特征主要表现为:命令驱动模式、专一性、开放性。
作为有限差分软件,相对于其他有限元软件,在算法上,FLAC3D 有以下几个优点:采用“混合离散法”来模拟材料的塑性破坏和塑性流动,比有限元中通常采用的“离散集成法”更准确、合理;即使模拟静态系统,也采用动态运动方程进行求解,这使得FLAC3D模拟物理上的不稳定过程不存在数值上的障碍;采用显示差分法求解微分方程。
采用FLAC3D进行数值模拟时,必须指定有限差分网格、本构关系和材料特性、边界和初始条件,这是FLAC3D求解的一般流程。
关于土体的弹性模量

关于土体的弹性模量、压缩模量与变形模量2013-05-30 15:39:28| 分类:自然科学|举报|字号订阅根据土体学推算的结果,在弹性阶段,E=Eo=Es(1-2μ^2/(1-μ))。
但在实际工程中,经常发现有弹性模量大于压缩模量的情况,并有经验说是E=(2~5)·Es,且有试验数据,但是没有理论上的推导,对试验数据也未实际去研究过。
从网络上收集这方面的论述,本篇进行简要总结,并适当修改,今后再逐步去积累这方面的经验。
论述零(关于变形模量和压缩模量的关系,土力学教材)土的变形模量和压缩模量,是判断土的压缩性和计算地基压缩变形量的重要指标。
为了建立变形模量和压缩模量的关系,在地基设计中,常需测量土的侧压力系数ξ 和侧膨胀系数μ(泊松比)。
侧压力系数ξ:是指侧向压力δx 与竖向压力δz 之比值,即:ξ =δx/δz土的侧膨胀系数μ (泊松比):是指在侧向自由膨胀条件下受压时,侧向膨胀的应变εx 与竖向压缩的应变εz 之比值,即μ=εx/εz 。
根据材料力学广义胡克定律推导求得ξ 和μ 的相互关系,ξ=μ/(1-μ)或μ=ε/(1 +ε),土的侧压力系数可由专门仪器测得,但侧膨胀系数不易直接测定,可根据土的侧压力系数,按上式求得。
在土的压密变形阶段,假定土为弹性材料,则可根据材料力学理论,推导出变形模量E0 和压缩模量Es 之间的关系。
令β=1-2u*u/(1-u),则Eo=βEs 。
当μ =0 ~0.5 时,β = 1 ~0 ,即Eo/Es 的比值在0 ~ 1 之间变化,即一般Eo 小于Es。
但很多情况下Eo/Es 都大于1。
其原因为:一方面是土不是真正的弹性体,并具有结构性;另一方面就是土的结构影响;三是两种试验的要求不同),μ、β 的理论换算值:土的种类及其对应的μ、β 值:碎石土0.15 ~0.20 ,0.95~0.90砂土0.20 ~0.25 ,0.90 ~0.83粉土0.23 ~0.31 ,0.86 ~0.726粉质粘土0.25~0.35 ,0.83 ~0.62粘土0.25 ~0.40 ,0.83 ~0.47注:以上E0 与Es 之间的关系是理论关系。
1.FLAC基本简介与本构关系

第一讲FLAC技术的基本原理和应用范围1、FLAC基本简介与本构关系1.1 FLAC程序简介FLAC(Fast Lagrangian Analysis of Continua,连续介质快速拉格朗日分析)是由Cundall和美国ITASCA公司开发出的有限差分数值计算程序,主要适用地质和岩土工程的力学分析。
该程序自1986年问世后,经不断改版,已经日趋完善。
前国际岩石力学学会主席C. Fairhurst 评价它:“现在它是国际上广泛应用的可靠程序”(1994)。
根据计算对象的形状用单元和区域构成相应的网格。
每个单元在外载和边界约束条件下,按照约定的线性或非线性应力—应变关系产生力学响应,特别适合分析材料达到屈服极限后产生的塑性流动。
由于FLAC程序主要是为岩土工程应用而开发的岩石力学计算程序,程序中包括了反映岩土材料力学效应的特殊计算功能,可解算岩土类材料的高度非线性(包括应变硬化/软化)、不可逆剪切破坏和压密、粘弹(蠕变)、孔隙介质的固—流耦合、热—力耦合以及动力学行为等,另外,程序设有界面单元,可以模拟断层、节理和摩擦边界的滑动、张开和闭合行为。
支护结构,如砌衬、锚杆、可缩性支架或板壳等与围岩的相互作用也可以在FLAC中进行模拟。
此外,程序允许输入多种材料类型,亦可在计算过程中改变某个局部的材料参数,增强了程序使用的灵活性,极大地方便了在计算上的处理。
同时,用户可根据需要在FLAC中创建自己的本构模型,进行各种特殊修正和补充。
FLAC程序建立在拉格朗日算法基础上,特别适合模拟大变形和扭曲。
FLAC采用显式算法来获得模型全部运动方程(包括内变量)的时间步长解,从而可以追踪材料的渐进破坏和垮落,这对研究工程地质问题非常重要。
FLAC程序具有强大的后处理功能,用户可以直接在屏幕上绘制或以文件形式创建和输出打印多种形式的图形。
使用者还可根据需要,将若干个变量合并在同一副图形中进行研究分析。
1.2 本构模型FLAC程序中提供了由空模型、弹性模型和塑性模型组成的十种基本的本构关系模型,所有模型都能通过相同的迭代数值计算格式得到解决:给定前一步的应力条件和当前步的整体应变增量,能够计算出对应的应变增量和新的应力条件。
