abaqus计算回弹的方法
abaqus回弹分析实例:在分析步之间传递数据

Abaqus Example Problems Guide1.5.1 Springback of two-dimensional draw bendingProducts: Abaqus/Standard Abaqus/Explicit是用explicit进行成形,然后使用standard分析回弹Problem description这个例子描述了在93年成形模拟数值会议中报道的基准测试。
这个基准包括使用三种材料描述六种问题以及两种不同的夹持力。
六个问题中的一个描述如下。
原文见Taylor等人在93年的论文。
坯料初始尺寸350*35,厚度0.78.问题本质上是个平面应变问题(垂直于模型平面的尺寸是35mm)。
夹持力是2.45kN,夹具的质量是5kg。
摩擦系数0.144坯料为低碳钢,材料为弹塑性材料,弹性为各向同性,对于塑性使用Hill 异性屈服准则。
材料的性质如下:Young's modulus = 206.0 GPaPoisson's ratio = 0.3Density = 7800.Yield stress = 167.0 MPaAnisotropic yield criterion: =1.0, =1.0402, =1.24897, =1.07895, =1.0, =1.0此例是对称问题,只取一半建模。
坯料使用一行175个一阶壳单元建模。
对称的边界条件施加到对称面上。
边界条件施加到了坯料所有的节点上以模拟平面应变的条面;建模平面外的尺寸是5mm;因此,坯料的加持力经过了粗略缩放。
成形的过程由explicit中的两个分析步完成。
坯料的加持力在第一个分析步施加。
加载使用平滑分析步,以将惯性效应最小化。
第二个分析步,通过设定冲头刚体参考点的速度冲头下行70mm。
速度使用triangular smooth step amplitude 功能施加,初始速度和最终速度都是0,峰值速度在这个过程之间。
回弹法测砼强度值的计算方法和步骤

回弹法测砼强度值的计算方法和步骤回弹法测砼强度值的计算方法和步骤在学习计算方法和步骤之前,先了解几个术语:1、测区:检测结构或构件砼抗压强度时的一个检测单元。
2、测点:在测区内进行的一个检测点。
3、测区砼强度换算值:由测区的平均回弹值和碳化深度值通过测强度曲线或查表得到的该检测单元(测区)的现龄期砼抗压强度值。
回弹法检测砼强度试用于工程结构普通砼抗压强度的检测。
砼强度值的确定分为如下几个步骤:1、回弹值测量2、碳化深度值测量3、回弹值计算4、砼强度的计算一、回弹值测量1、一般规定:结构或物件砼强度检测可采用下列两种方式,其适用范围及结构或构件数量应符合下列规定:(1)、单个检测:适用于单个结构或构件的检测。
(2)、批量检测:适用于相同的生产工艺条件下,砼强度等级相同,原材料、配合比、成型工艺、养护条件基本一致且龄期相近的同类结构或构件,按批进行检测的结构构件。
抽检数量不得少于同批构件总数的30%且不得少于10件。
2、每一结构或构件的测区应符合下列规定:(1)、每一结构或构件测区数量应不少于10个。
对某一方向尺寸小于4.5米,且另一方向尺寸小于0.3米的构件其测区数量可适当减少,但不应少于5个。
(2)、相邻两测区的间距应控制在2米以内。
测区离构件端部或施工缝边缘的距离不宜大于0.5米,且不宜小于0.2米。
(3)、测区应选在使回弹仪处于水平方向检测砼浇筑侧面,当不能满足这一要求时,可使回弹仪处于非水平方向检测砼强度浇筑侧面、表面或底面。
但回弹值需修正。
(4)、测区宜选在构件的两个对称可测面上,也可选在一个可测面上,且应均匀分布。
在构件的重要部位及薄弱部位必须布置测区,并应避开预埋件。
(5)、测区的面积不宜大于0.04㎡。
(6)、检测面应为砼表面,并应清洁平整,不应有疏松层、浮浆、油垢、涂层以及蜂窝、麻面。
必要时可用砂轮清除疏松层和杂物,且不应有残留的粉末或碎屑。
3、回弹值测定(1)、检测时,回弹仪的轴线应始终垂直于结构或构件的检测面。
abaqus计算回弹的方法

abaqus计算回弹的方法Abaqus回弹计算过程回弹分析我倒是做过两个,说下简要步骤吧,同样是仅供参考啊1.首先用?explicit做成型过程的分析,加载方式选位移加载比较好,加载的幅值选smooth step(平滑变化)2.可适当的用质量放大来加快这一准静态分析的过程3.分析完成后可用standard观察工件的回弹,具体做法是:1.Model-Copy Model2.在新复制的模型中仅留下成型件,删除其他一切无关的边界条件以及上下模,包括在Explicit中定义的接触属性3.在step模块中创建predefine field request-others-initial state-last frame/last step(导入的job名称为之前做成型分析的那个job的名称)4.删除原来所有的后续分析步,并新建一个static,general的分析步5.创建一个新的作业提交分析,并观察回弹大致就是这样吧,希望对你有用~回弹分析,从explicit导入standard计算。
先copy explicit中模型进入standard模块,然后做一下改进,删除各个part、set和surface等,只留下需要回弹分析的变形体。
删除分析步,删除接触和属性。
然后在step中建立一个static分析步骤。
设置计算为非线性。
然后定义居于前面成形结果的回弹分析,在Model Tree中打开Predefined Fields,选择 Initia作为分析步,Other最为类别,选择Initial State,然后在视窗中选择需要分析的回弹体,然后点击done,然后Edit Predefined Field,选择你成形分析的job名字。
然后一致ok下去,对称的边界哦条件还要施加。
你可以在amplitude中设置,比如说你分析步设置时间为6s,然后在amplitude中设置0,0;4,1(也就是在4秒时冲头应景达到了要求的位移,也就是液晶冲完,那么剩下的2秒就是停留的时间了),然后在另外设置一个分析步把冲头往回移就可以了小弟这些天正好在做冲压回弹,刚做成功,从simwe论坛上学了很多东西。
回弹简化计算公式

回弹简化计算公式回弹是物体在碰撞后恢复原状的能力,是一个重要的物理现象。
在实际生活中,我们经常会遇到回弹的情况,比如篮球弹起、弹簧的伸缩等。
为了更好地理解回弹现象,科学家们提出了回弹简化计算公式,用来计算物体在碰撞后的回弹情况。
回弹简化计算公式是根据能量守恒和动量守恒原理推导出来的。
在碰撞中,能量守恒意味着碰撞前后物体的总能量保持不变,动量守恒意味着碰撞前后物体的总动量保持不变。
根据这两个原理,可以推导出回弹简化计算公式。
回弹简化计算公式的一般形式为:e = (v2 v1) / (u1 u2)。
其中,e表示回弹系数,v1和v2分别表示碰撞前后物体的速度,u1和u2分别表示碰撞前后物体的速度。
在实际应用中,回弹系数e的取值范围为0到1之间。
当e=0时,表示完全非弹性碰撞,物体在碰撞后停止运动;当e=1时,表示完全弹性碰撞,物体在碰撞后以相同的速度反弹。
在实际情况中,回弹系数e的取值通常介于0和1之间,表示物体在碰撞后的部分能量损失或部分能量保持不变。
回弹简化计算公式的推导过程比较复杂,需要用到动能和动量的概念,以及一些高等数学知识。
但是,在实际应用中,我们可以通过简化计算公式来计算物体在碰撞后的回弹情况。
下面我们通过一个简单的例子来说明回弹简化计算公式的应用。
假设有两个物体A和B,它们的质量分别为m1和m2,速度分别为v1和v2。
物体A和B发生碰撞后,它们的速度分别变为u1和u2。
我们可以通过回弹简化计算公式来计算回弹系数e,进而得到物体在碰撞后的回弹情况。
首先,我们需要计算碰撞前后物体的动能和动量。
碰撞前物体A和B的总动能为:E1 = 0.5 m1 v1^2 + 0.5 m2 v2^2。
碰撞后物体A和B的总动能为:E2 = 0.5 m1 u1^2 + 0.5 m2 u2^2。
根据能量守恒原理,碰撞前后物体的总动能保持不变,即E1 = E2。
将上面的两个式子相等,可以得到:0.5 m1 v1^2 + 0.5 m2 v2^2 = 0.5 m1 u1^2 + 0.5 m2 u2^2。
abaqus 中回弹问题总结

我建议你参考A B A Q U S E x a m p l e p r o b l e m s m a n u a l 1.3.7A x i s y m m e t r i c f o r m i n g o f a c i r c u l a r c u p1.5.1 Springback of two-dimensional draw bending1.5.2 Deep drawing of a square box回弹中注意把系统改成双精度,否则有些问题是算不了的,或者显示有问题。
隐式计算回弹中的设置参考maunal中的13.5.5 Springback analysis in ABAQUS/Standard谈谈我的体会,或许对你有点帮助。
使用动力显示算法模拟成形过程,静力隐式算法分析回弹的回弹预测方法,在静力隐式求解时由于接触条件的变化,计算复杂零件的回弹收敛很困难。
为使计算收敛,大概可以从以下几个方面进行调整:1. 减小计算的步长? ?这种方法对简单形状的零件比较有效,对复杂零件来说基本上没有用。
2. 调整固定点? ?我在附图中的回弹分析中,尝试了A点固定,B点固定,C点固定三种方式。
对A,B两点固定的计算中,无论计算步长多小,都不收敛。
而在C点固定时,很快求出了结果。
所以,我觉得把固定点选在零件几何中心或回弹量对称的点上可能效果比较好。
当然,如过约束点是已经给定的可以结合第3种方法尝试。
3. 逐步去掉约束? ?把约束条件不要一次去掉,可以分几个分析步取消,也会增加收敛概率。
可能还有其它办法,这只是我做回弹分析的一点体会,希望对你有用。
我也是用了一些时间才计算出来的,重要的是多思考,多尝试。
ABAQUS常见问题汇总- 2.0版回弹分析,从explicit导入standard计算。
先copy explicit中模型进入standard模块,然后做一下改进,删除各个part、set和surface等,只留下需要回弹分析的变形体。
基于ABAQUS的板材冲压仿真及回弹分析

shell elements
beam elements
•同类型单元有很多相 同的基本特。 Elements in the same family share many basic features.
rigid elements
membrane elements
•同种类单元又有很多 变化:There are many variations within a family.
几何模型的建立
材料属性的定义
从第一次冲压成 形模型中,删除模 具、接触定义以及边 界条件等
前处理
成形步的定义 (Explicit)
回弹步的定义 (Standard)
定义表面接触 加载上步计算结果 作为初始坯料状态 定义边界条件
混凝土结构回弹方法及计算流程,终于讲清楚

混凝土结构回弹方法及计算流程,终于讲清楚回弹法检测混凝土抗压强度的基本原理:混凝土表面硬度与混凝土极限强度存在一定关系,回弹仪的弹击重锤被一定弹力打击在混凝土表面上,其回弹高度和混凝土表面硬度存在一定关系。
这样可以利用回弹仪测试混凝土表面硬度,并结合混凝土碳化深度从而间接测定混凝土强度。
然而,这种检测方式得到的结果精度较低。
不适用于表面和内容有明显质量差异的构件,结果受混凝土自身原材料、施工工艺、养护条件等众多因素影响较大。
但不可否认的是,回弹法用于检测混凝土的抗压强度已在我国得到了广泛的应用,实践证明,采用回弹法推定的混凝土抗压强值,对于处理工程质量问题具有十分重要的意义。
回弹检测方法一、回弹仪检定回弹仪检定周期为半年,当回弹仪具有下列情况之一时,应由法定计量检定机构按行业标准《回弹仪》JJG817进行检定:1、新回弹仪启用前;2、超过检定有效期限;3、数字式回弹仪数字显示的回弹值与指针直读示值相差大于1;4、经保养后,钢砧率定值不合格;5、遭受严重撞击或其他损害。
注意还有保养要求,具体详规范!回弹仪率定试验二、抽检构件数量按批进行检测的构件,抽检数量不宜少于同批构件总数的30%且构件数量不宜少于10件。
当检验批构件数量大于30个时,抽样构件数量可适当调整,但不得少于国家现行有关标准规定的最少抽样数量三、测区布置要求1、对于一般构件,测区数不宜少于10个。
可适当减少测区数,但不得少于5个的情况:受检构件数量大于30个且不需提供单个构件推定强度;受剪构件某一方向尺寸小于4.5m 且另一方向尺寸小于 0.3m 的构件;2、相邻两测区的间距不应大于2m,测区离构件端部或施工缝边缘的距离不宜大于0.5m ,且不宜小于0.2m;3、测区应选在使回弹仪处于水平方向的混凝土浇筑侧面。
当不能满足这一要求时,也可使回弹仪处于非水平方向的混凝土浇筑表面或底面;4、测区宜选在构件的两个对称可测面上,当不能布置在对称的可测面上时,也可布置在同一可测面上,且应均匀分布。
小直径厚壁管材变曲率弯曲回弹预测

第22卷㊀第3期2014年6月㊀材㊀料㊀科㊀学㊀与㊀工㊀艺MATERIALSSCIENCE&TECHNOLOGY㊀Vol 22No 3Jun.2014㊀㊀㊀㊀㊀㊀小直径厚壁管材变曲率弯曲回弹预测张㊀深,吴建军,邓良才,郭瑞超(西北工业大学现代设计与集成制造技术教育部重点实验室,西安710072)摘㊀要:为快速㊁准确地预测管材变曲率的弯曲回弹,建立变曲率弯曲回弹预测的解析模型.基于ABAQUS平台建立小直径厚壁管材变曲率弯曲成形及回弹数值模拟模型,通过试验验证了所建模拟方法的可靠性.将变曲率回弹问题转化为离散定曲率回弹问题进行研究,通过近似纯弯曲回弹实验,建立管材定曲率弯曲回弹前后半径之间的函数关系式,将变曲率弯管轴线双圆弧拟合逼近离散,针对离散化的回弹弯管进行G1连续拼接,依据轴线复杂程度,构建拼接修正函数,建立管材变曲率弯曲回弹预测解析模型.通过2个试验算例验证该解析模型能够有效预测小直径厚壁管材平面变曲率弯曲回弹.回弹的准确预测是有效控制弯管回弹缺陷的前提,用于指导后续模具型面修正,补偿回弹误差,保证弯管几何精度.关键词:管材弯曲;变曲率;回弹;预测;数值模拟;双圆弧中图分类号:TG386文献标志码:A文章编号:1005-0299(2014)03-0001-06Springbackpredictionofvariablecurvaturebendingforminordiameterthick⁃walledtubeZHANGShen,WUJianjun,DENGLiangcai,GUORuichao(TheKeyLaboratoryofContemporaryDesignandIntegratedManufacturingTechnology,NorthwesternPolytechnicalUniversity,Xiᶄan710072,China)Abstract:Topredictthespringbackofvariablecurvaturetubeformingquicklyandaccurately,mathematicanalyticmodelforspringbackpredictionofvariablecurvaturetubebendingisestablished.UsingsoftwareABAQUS,thebendingandspringbackprocessesofminordiameterthick⁃walledtubearesimulatedtorevealthespringbacklaws,andtheaccuracyandreliabilityareprovedbyexperiments.First,thespringbackofvariablecurvaturetubebendingistransformedintodiscreteconstantcurvatureproblemandthemathematicsrelationshipoftheradiusbeforeandafterspringbackcanbebuiltbytheapproximatepurebendingspringbackexperiment.Thenthetubeaxisissegmentedwithbiarc⁃curvefitting,mergedwithfirst⁃ordergeometriccontinuity,andcompensatedwithmodifiedfunctionaccordingtotheaxiscomplexity,toestablishmathematicanalyticmodelforspringbackpredictionofvariablecurvaturetubebending.Finally,thefeasibility,reliabilityandaccuracyofthemodelareproved.Thismodelisusefulforthemaintenanceofthebendingdieandwillensuretherequirementsofgeometricaccuracyofthevariablecurvaturetubebending.Keywords:tubes⁃bending;variablecurvature;springback;prediction;numericalsimulation;biarc收稿日期:2012-11-19.基金项目:西北工业大学研究生创业种子基金资助项目(Z2012039);国家自然科学基金资助项目(51075332).作者简介:张㊀深(1985-),男,博士研究生;吴建军(1963-),男,教授,博士生导师.通信作者:吴建军,E⁃mail:wujj@nwpu.edu.cn.㊀㊀以金属管材为主的中空结构,广泛应用于航空航天㊁船舶㊁车辆㊁石油化工㊁建筑及压力容器等领域[1-3];而管材零件在塑性弯曲成形工艺中将不可避免地存在回弹问题,由此造成零件的实际成形几何尺寸偏离设计要求,这已成为弯管高效精密加工技术的瓶颈.由于设计性能㊁安装空间以及轻量化等要求,管件的设计形状也变得日趋复杂[4-6],如在紧凑的飞机机身及发动机内部,管材种类及数量繁多,形状怪异复杂(包括平面变曲率构型),作用又十分重要.目前管材弯曲成形的研究主要是针对平面定曲率弯曲问题从理论㊁实验以及数值模拟等方面开展管材冷㊁热弯曲成形的相关研究工作,并结合先进的数控弯管工艺,进行数字化应用.而针对变曲率管材弯曲的回弹研究鲜有报道.A.El.Megharbel等[7]通过定量分析着重研究了应变强化理论在管材弹塑性弯曲过程中的作用规律.鄂大辛等[8]在管材弯曲变形的基本假设和简单应力状态下的线性强化材料模型的基础上,对管材弯曲进行了变形分析.在大量试验及有限元模拟的基础上,推导出管材弯曲回弹角的近似计算公式,并对影响管材弯曲回弹的变形条件和材料力学性能进行了简要分析[9].S.Mohamed等[10]通过大量钢管纯弯曲实验数据,建立能够预测钢管最终弯曲能力的神经网络模型.M.Murata等[11]利用有限元数值模拟及实验方法,重点研究了材料硬化指数对管材弯曲成形性能的影响规律.王泽康等[12]基于显/隐式弹塑性有限元仿真结合实验研究,对大口径厚壁不锈钢管数控弯曲卸载后的回弹现象进行了研究.潘昌平[13]本着理论分析与工程实际相结合的原则,采用VB6.0开发具有回弹补偿功能的弯管机控制系统,从而为薄壁管弯曲回弹的补偿提供了一条可行途径.此外,杨合团队[5,14-15]针对薄壁管塑性弯曲过程中出现的缺陷,运用能量法与有限元相结合的方法进行了大量基础研究,在预测管材弯曲过程中的失稳起皱㊁确定成形极限等方面积累了一定的研究基础,开发了基于数据库技术的数控弯管仿真系统(NCT⁃BS),对有效实现数控弯管工艺的质量控制具有重要意义.近年来,利用有限元数值模拟技术,针对难成形材料(钛合金)管材的数控弯曲进行了相关研究[16].管材种类繁多,性能要求各异,其中小直径厚壁管材(管材外径小于10mm,外径与壁厚比小于20)弯曲成形具有回弹与破裂起皱㊁截面畸变相比是主要成形缺陷的特点.本文针对小直径厚壁管材变曲率绕弯成形回弹进行研究,通过有限元数值模拟㊁相关试验研究,着重揭示变曲率管材弯曲成形回弹规律,建立快速有效预测弯曲回弹的解析模型.回弹的准确预测是有效控制弯管回弹缺陷的前提,对发展变曲率弯管精确弯曲成形技术具有重要意义.1㊀管材弯曲回弹现象管材弯曲成形过程中,管坯在外载荷作用下产生的变形由塑性变形和弹性变形组成.当外载去除后,管坯的塑性变形保留下来,而弹性变形会完全消失,使弯管的形状和尺寸发生变化而与模具尺寸不一致,称为弯曲回弹.弯管的回弹量通常用弯管的曲率变化量(ΔK)和角度变化量(Δα)来表示,如图1所示,即ΔK=1r-1rᶄ,Δα=α-αᶄ.式中:r为卸载前弯管中性层弯曲半径;rᶄ为卸载后弯管中性层弯曲半径;α为卸载前弯管的弯曲角;αᶄ为卸载后弯管的弯曲角.α′αrr′O′O图1㊀弯曲回弹弯管轴线的曲率就是针对轴线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明轴线偏离直线的程度.曲率越大,表示轴线的弯曲程度越大.曲率的倒数就是曲率半径.小直径厚壁管材变曲率弯曲过程中,弯管轴线曲率(弯曲半径)为非恒定值,连续变化.由于变曲率弯管多具有复合弯的特征,在目前的绕弯成形工艺中,只能保证轴线为外凸曲线的弯管紧贴模具成形.2㊀管材变曲率绕弯成形回弹数值模拟2.1㊀有限元模型的建立利用三维实体造型软件UGNX6.0建立小直径厚壁管材变曲率绕弯成形的三维模型,将其导入大型通用非线性有限元软件ABAQUS中,完成管材变曲率绕弯弹塑性有限元模型的建立,如图2所示.夹块管材弯曲模压块图2㊀管材变曲率绕弯成形有限元模型在该模型中,将厚壁管材视为变形体,并采用8节点六面体线性减缩积分单元C3D8R,优点是㊃2㊃材㊀料㊀科㊀学㊀与㊀工㊀艺㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第22卷㊀求解的结果精度较高,网格存在扭曲变形时分析精度不会受到较大影响且在弯曲载荷作用下不易发生剪切自锁.弯曲模及压块㊁夹块均视为离散刚体,并采用4节点四边形刚体壳单元R3D4;忽略材料各向异性,采用VonMises屈服准则,双线性硬化弹塑性模型;模具与管材间的摩擦采用库伦模型;其他模拟条件与实际物理实验条件相同;35CrMnSiA管材外径3mm,壁厚0.5mm,材料参数[17]如表1所示.表1㊀35CrMnSiA材料参数弹性模量E/GPa屈服极限σs/MPa强度极限σb/MPa泊松比μ密度ρ/(t㊃m-3)210128016200.37.82.2㊀管材变曲率绕弯成形及回弹过程有限元模拟利用ABAQUS/Explicit模块对小直径厚壁管材变曲率绕弯成形过程进行数值模拟.将变曲率管材轴线依据曲率变化规律离散成多段,在一定误差范围内用相切圆弧逼近,通过控制弯曲模刚体参考点的位置及弯曲角的方式实现管材绕弯成形模拟.初始定义第1段逼近圆弧圆心为弯曲模参考点RP1,并定义相应弯曲角,完成第一段绕弯成形;从初始成形过程分析结果文件(∗.odb)中导入有限元模型,重新定义第2段逼近圆弧圆心为弯曲模参考点RP2,同时修改相应弯曲角,在后续分析模型中对管材部件实体定义初始状态场(initialstatefield),将上一步分析的结果状态场赋给新的管材模型,完成第2段绕弯成形;以此类推完成变曲率管材绕弯成形数值模拟.利用ABAQUS/Standard分析模块,采用无模法(在成形结束时,去除模具代之以接触反力,进行迭代计算,直到接触力为零)进行管材绕弯成形外载荷去除后的回弹过程数值模拟分析.对夹块与模具夹持管材端部施加固定边界约束,以约束弯管的刚性位移,对管材部件定义初始状态场,即将管材绕弯成形应力应变场赋给新的管材模型,同时去除其他约束,完成管材绕弯成形回弹数值模拟.提取数值模拟绕弯成形回弹前后的管材轴线,与理论管材轴线(弯曲模型面中心线)进行配准对比,成形管材轴线(弯曲段长度120mm)与理论轴线最大偏差0.05mm,即偏差精度0.42mm/m,表明该方法可以准确模拟管材变曲率弯曲成形的几何位置关系.管材弯曲回弹量较大,轴线对应节点最大回弹位移偏差26.87mm,即偏差精度223.92mm/m.2.3㊀弯曲及回弹有限元模拟可靠性验证根据小直径厚壁管材变曲率绕弯成形的三维模型,加工制造出相应模具实体,将管材插入模具固定端,拧紧4个螺母以固定管材,然后施力绕弯成形,当弯管与模具型面完全贴合后,卸载作用在弯管上的力,弯管会发生回弹,如图3所示.为检验弯曲回弹的稳定性,对同一规格的多根管材进行同等时间施力加载,通过对比每根绕弯成形弯管回弹后的几何尺寸,确保弯曲回弹的稳定性.图3㊀小直径厚壁管材变曲率绕弯成形回弹使用流动式三维光学扫描仪ATOSⅡ600扫描出实际绕弯回弹后的弯管外形尺寸,提取轴线,并与数值模拟回弹弯管轴线相对比,如图4所示.可知数值模拟回弹弯管与实际弯曲成形回弹弯管外形基本吻合,轴线最大偏差2.83mm,即偏差精度23.58mm/m.表明该有限元模拟方法能够有效预测变曲率弯管回弹,同时为弯曲回弹预测模型的建立提供数值模拟试验基础.实际弯曲成形回弹弯管轴线数值模拟回弹弯管轴线回弹前理论弯管轴线图4㊀弯管数值模拟及实际绕弯成形回弹3㊀变曲率弯管成形回弹预测解析模型基于有限元模拟方法可以有效预测管材变曲率弯曲回弹,但相应工艺参数及材料性能参数的准确与否直接影响模拟精度,均需通过相应实验测得,且针对变曲率弯曲成形控制路径复杂,而使用理论解析方法求得回弹量时,通常存在众多假设,与变曲率管材绕弯成形受力方式不符,因此本㊃3㊃第3期张㊀深,等:小直径厚壁管材变曲率弯曲回弹预测文在简单力学实验的基础上,建立一种简便实用的管材变曲率弯曲回弹预测解析模型.3.1㊀近似纯弯曲回弹实验针对小直径厚壁管材35CrMnSiA(外径3mm,壁厚0.5mm),通过近似纯弯曲回弹实验[6,18],如图5所示,研究一定弯曲半径范围内的回弹性能.利用最小二乘法对弯曲回弹前后半径值进行拟合,如图6所示,建立回弹前后弯曲半径函数关系式y=0.000189x3+0.006209x2+1.319866x-2.487030.(1)式中:y为回弹后的管材弯曲半径值,mm;x为回弹前管材弯曲半径值,mm,xɪ[12.23,72.60].图5㊀管材近似纯弯曲成形回弹实验200150100501020304050607080回弹前管材弯曲半径/m m回弹后管材弯曲半径/m m实验点拟合曲线图6㊀回弹前后管材弯曲半径关系曲线3.2㊀变曲率弯管离散变曲率绕弯成形弯管轴线为外凸曲线,由于形状复杂,为便于研究其回弹问题,将变曲率弯管轴线,在误差允许范围内进行双圆弧拟合逼近[19-22],即按弯管轴线给定一系列有序形值点(节点),每相邻节点之间由2条相切圆弧段组成,两圆弧段分别通过给定的2个节点,且在节点处的切线斜率与变曲率轴线在该节点处的斜率相等.从而依据弯管轴线曲率变化规律离散成G1连续的多段圆弧.3.3㊀离散弯管回弹预测及拼接利用近似纯弯曲回弹实验结论式(1),对弯管轴线离散圆弧段进行定曲率回弹研究.在确保回弹前后各圆弧段端点处G1连续的基础上,依据拼接点处G1连续的原则,完成多段回弹圆弧段拼接,从而得到G1连续的圆弧样条,如图7所示.离散弯管轴线回弹的G 1连续拼接圆弧样条实际弯曲成形回弹弯管轴线回弹前理论弯管轴线图7㊀离散弯管回弹的G1连续拼接3.4㊀离散弯管回弹拼接修正管材弯曲成形的最后回弹形状是其整个成形历史的积累效应,而管材弯曲成形工艺与绕弯模具的几何形状㊁材料特性㊁摩擦接触等众多因素相关,且管材变曲率绕弯在整个成形过程中的受力与变形具有非对称性特点,因曲率半径的变化而产生剪切效应,其回弹问题更为复杂.一般而言,弯曲件形状越复杂,一次弯曲成形角的数量越多,弯曲时各部分相互牵制的作用力越大,由于这种叠加应力将会影响弹性势能的积累,从而导致弯管回弹量减小.离散管材弯曲回弹预测过程中假设弯曲工艺为近似纯弯曲,而实际工况下,由于各段离散弯管残余应力间的相互作用,相邻弯管在弯曲回弹过程中的相互影响不容忽视,现假设这种影响与各圆弧段弯曲半径及弧长有关,建立如下回弹预测解析模型.将理论弯管轴线离散成有限个单元,令该模具型面中心线为R,由n个单元构成初始集合R,离散回弹G1连续拼接得到的弯管轴线集合为S,则R={ririɪR3,1⩽i⩽n};S={sisiɪR3,1⩽i⩽n}.对于节点i,管材离散回弹G1连续拼接后由ri变为si,而实际管材整体回弹目标集合为P,则P={pipiɪR3,1⩽i⩽n};㊃4㊃材㊀料㊀科㊀学㊀与㊀工㊀艺㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第22卷㊀P=f(g(A),h(B))=f(R,S,h(B)).(2)式中:g(A)为与管材物性参数及成形回弹边界条件相关的函数,与R,S相关;h(B)为与离散回弹弯管轴线复杂程度相关的函数.令w=h(B),则假定式(2)变为P=R+w(S-R)⇔pi=ri+wi(si-ri),∀i,(3)式中,w为修正函数.修正函数与轴线复杂程度相关,即通过曲率变化表征,由大量模拟试验,拟合规律得到w=1max[ρi]㊃ðni=1ρiliðni=1li,i=1,2,...,n.(4)式中:ρi为圆弧段弯曲半径,li为圆弧段弧长.即通过式(3)㊁(4)对弯管轴线进行修正补偿,完成离散弯管回弹拼接修正;在保证P与R初始端点切线斜率相等的前提下,通过取点拟合样条曲线的方法,最终得到修正的光顺弯管轴线.从而完成小直径厚壁管材变曲率弯曲回弹预测解析模型(双圆弧拟合逼近离散回弹拼接修正回弹预测模型)的建立.3.5㊀算例验证针对图4所示的小直径厚壁管材变曲率绕弯成形模型,利用上述双圆弧拟合逼近离散回弹拼接修正回弹预测解析模型得到回弹预测弯管轴线a,如图8所示.轴线2与数值模拟回弹弯管轴线3最大偏差1.95mm,即偏差精度16.25mm/m;轴线2与实际弯曲回弹弯管轴线4最大偏差4.16mm,即偏差精度34.67mm/m,如图9所示.543211—回弹前理论弯管轴线2—回弹预测弯管轴线3—数值模拟回弹弯管轴线4—实际弯曲回弹弯管轴线5—离散弯管轴线回弹的G 1连续拼接圆弧样条图8㊀回弹预测弯管轴线a为进一步验证该方法的有效性,重新设计理论变曲率弯管轴线b(弯曲段长度60mm),利用该回弹预测解析模型与有限元数值模拟结果进行对比,如图10所示,回弹预测弯管轴线2与数值模拟回弹弯管轴线3最大偏差0.44mm,即偏差精度7.33mm/m,如图11所示.4321051015202530节点编号轴线偏差量/m m 数值模拟回弹弯管轴线实际弯曲回弹弯管轴线图9㊀回弹预测弯管轴线a偏差43211—回弹前理论弯管轴线2—回弹预测弯管轴线3—数值模拟回弹弯管轴线4—离散弯管轴线回弹的G 1连续拼接圆弧样条图10㊀回弹预测弯管轴线b0.40.30.20.1051015202530轴线偏差量/m m节点编号图11㊀回弹预测弯管轴线b偏差弯管轴线偏差精度均在5%以内,表明该回弹预测解析模型能够有效预测小直径厚壁管材变曲率弯曲回弹.4㊀结㊀论1)基于ABAQUS平台建立了小直径厚壁管材变曲率绕弯成形及回弹全过程三维有限元模型,并通过试验验证其可靠性.2)将变曲率弯管轴线双圆弧拟合逼近离散,借助近似纯弯曲回弹实验结论对离散弯管进行回弹预测及G1连续拼接.3)建立管材变曲率弯曲回弹预测解析模型,依据弯曲复杂程度进行拼接修正,取点拟合最终得到光顺的回弹预测弯管轴线.㊃5㊃第3期张㊀深,等:小直径厚壁管材变曲率弯曲回弹预测4)通过2个算例验证该双圆弧拟合逼近离散回弹拼接修正回弹预测解析模型能够快速合理预测小直径厚壁管材变曲率弯曲回弹.参考文献:[1]㊀温彤.管材成形技术综述[J].机械设计与制造,2006(11):77-79.WENTong.Aviewofpipeandtubeformingtechnology[J].MachineryDesign&Manufacture,2006(11):77-79.[2]㊀XIAOXT,LIAOYJ,SUNYS,etal.Studyonvar⁃yingcurvaturepush⁃bendingtechniqueofrectangularsectiontube[J].JournalofMaterialsProcessingTech⁃nology,2007,187-188:476-479.[3]㊀鄂大辛,郭学东,宁汝新.管材弯曲中应变中性层位移的分析[J].机械工程学报,2009,45(3):307-310.EDaxin,GUOXuedong,NINGRuxin.Analysisofstrainneutrallayerdisplacementintube⁃bendingprocess[J].JournalofMechanicalEngineering,2009,45(3):307-310.[4]㊀詹梅,杨合,江志强.管材弯曲成形的国内外研究现状及发展趋势[J].机械科学与技术,2004,23(12):1509-1514.ZHANMei,YANGHe,JIANGZhiqiang.Stateoftheartofresearchontubebendingprocess[J].MechanicalScienceandTechnology,2004,23(12):1509-1514.[5]㊀YANGHe,LIHeng,ZHANGZhiyong,etal.Advancesandtrendsontubebendingformingtechnologies[J].ChineseJournalofAeronautics,2012,25:1-12.[6]㊀张深.空间弯管的回弹补偿技术研究[D].西安:西北工业大学,2011.[7]㊀MEGHARBELAEI,NASSERGAEI,DOMIAYTAEI.Bendingoftubeandsectionmadeofstrain⁃hardeningmaterials[J].JournalofMaterialsProcessingTechnology,2008,203(1/2/3):372-380.[8]㊀鄂大辛,宁汝新,古涛.管材弯曲过程中的弹塑性变形分析[J].兵工学报,2009,30(10):1353-1356.EDaxin,NINGRuxin,GUTao.Analysisofelastic⁃plasticdeformationduringtube⁃bendingprocess[J].ActaArmamentarii,2009,30(10):1353-1356.[9]㊀EDaxin,HEHuahui,LIUXiaoyi,etal.Spring⁃backdeformationintubebending[J].InternationalJournalofMinerals,MetallurgyandMaterials,2009,16(2):177-183.[10]MOHAMEDS,MOHAMEDE.Neuralnetworksformodellingultimatepurebendingofsteelcirculartubes[J].JournalofConstructionalSteelResearch,2008,64(6):624-633.[11]MURATAM,KUBOKIT,TAKAHASHIK,etal.Effectofhardeningexponentontubebending[J].JournalofMaterialsProcessingTechnology,2008,201:189-192.[12]王泽康,杨合,李恒,等.大口径316L不锈钢管数控弯曲回弹规律研究[J].材料科学与工艺,2012,20(4):49-54.WANGZekang,YANGHe,LIHeng,etal.Springbacklawsoflargediameter316LstainlesssteeltubeinNCbending[J].MaterialsScienceandTechnology,2012,20(4):49-54.[13]潘昌平.管材弯曲回弹及弯管机控制系统的研究[D].长春:吉林大学,2008.[14]ZHANMei,YANGHe,HUANGLiang,etal.Springbackanalysisofnumericalcontrolbendingofthin⁃walledtubeusingnumerical⁃analyticmethod[J].JournalofMaterialsProcessingTechnology,2006,177:197-201.[15]YANGHe,YANJing,ZHANMei,etal.3Dnumeri⁃calstudyonwrinklingcharacteristicsinNCbendingofaluminumalloythin⁃walledtubeswithlargediametersundermulti⁃dieconstraints[J].ComputationalMateri⁃alsScience,2009,45(4):1052-1067.[16]JIANGZQ,YANGH,ZHANM,etal.Establishmentofa3DFEmodelforthebendingofatitaniumalloytube[J].InternationalJournalofMechanicalSciences,2010,52(9):1115-1124.[17]张深,吴建军.基于BP神经网络的管材材料参数逆向识别[J].塑性工程学报,2011,18(6):87-90.ZHANGShen,WUJianjun.Anewmethodbasedonbackpropagationneuralnetworkforidentifyingthematerialparametersoftube[J].JournalofPlasticityEngineering,2011,18(6):87-90.[18]张深,吴建军.空间弯管的回弹预测[J].航空学报,2011,32(5):953-960.ZHANGShen,WUJianjun.Spring⁃backpredictionofnon⁃planartubebending[J].ActaAeronauticaetAstronauticaSinica,2011,32(5):953-960.[19]BOLTONKM.Biarccurves[J].Computer⁃AidedDesign,1975,7(2):89-92.[20]PARKINSONDB,MORETONDN.Optimalbiarc⁃curvefitting[J].ComputerAidedDesign,1991,23(6):411-419.[21]孙家昶,郑全琳.曲线的圆弧逼近与双圆弧逼近[J].计算数学,1981,3(2):97-112.SUNJiachang,ZHENGHuilin.Onarcandbiarccurveapproximation[J].MathematicaNumericaSinica,1981,3(2):97-112.[22]王琦,郭非,王启义.圆弧样条逼近为机械零件几何轮廓的自动编程[J].机械工程学报,1998,34(2):20-25.WANGQi,GUOFei,WANGQiyi.Circulararcsplineapproximationforautoprogrammingprofilesofmachineparts[J].ChineseJournalofMechanicalEngineering,1998,34(2):20-25.(编辑㊀程利冬)㊃6㊃材㊀料㊀科㊀学㊀与㊀工㊀艺㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第22卷㊀。
混凝土强度回弹计算方法

混凝土强度回弹计算方法1. 混凝土强度的“秘密”大家好,今天我们来聊聊混凝土的强度问题。
说到混凝土,可能你脑海里浮现出的是那些大大的建筑、桥梁,甚至是你家楼下的那片水泥地面。
没错,这些都离不开混凝土的身影。
可是,你知道吗,混凝土的强度就像人一样,也需要“体检”,这体检的方法之一就是回弹法。
别担心,这可不是把混凝土送去做个健康体检,而是用一种特别的工具来测量它的强度。
1.1 回弹法的基本原理那什么是回弹法呢?简单来说,就是用一个特制的小仪器,用力戳混凝土表面,然后看它反弹的情况。
这个仪器叫做回弹仪。
你可以把它想象成一个小型的弹簧枪,弹簧的力量决定了仪器的“射程”,而混凝土的硬度则决定了弹簧的“回弹力”。
如果混凝土很坚硬,弹簧就会被压得很厉害,弹得也就越高;如果混凝土比较松软,弹簧就不会那么使劲儿,弹得也就低了。
通过这种方式,我们就能大致了解混凝土的强度了。
1.2 回弹法的具体操作说到操作,你可能会觉得复杂,但其实也很简单。
首先,拿到回弹仪后,你要确保它的表面是干净的。
然后,选一个混凝土表面比较平整的地方,避免在有裂缝或是凹凸不平的地方进行测量。
接着,把回弹仪的前端对准混凝土表面,施加一定的压力后,仪器会弹回。
注意,这个压力要均匀,不要一时用力过猛,导致测量结果不准确。
最后,记录下弹回的高度,仪器上会显示一个数值,这个数值就是混凝土的回弹值。
2. 回弹值如何解读好了,拿到回弹值后,我们接下来就得分析这个数据。
你可别以为回弹值就是最终的答案,它还得经过一番“解码”。
回弹值高说明混凝土硬度大,强度高;回弹值低,则说明混凝土比较软,强度差。
这个时候,你可能会问,怎么知道混凝土的强度是否合格呢?这就要用到标准的回弹值和实际强度之间的关系了。
2.1 回弹值和实际强度的关系回弹值和实际强度的关系不是一成不变的,它受很多因素的影响,比如混凝土的配比、养护情况等等。
一般来说,回弹值会被换算成混凝土的抗压强度,公式大致上是这样:通过回弹值查找对应的抗压强度。
基于ABAQUS的板料冲压回弹模拟研究

基于ABAQUS的板料冲压回弹模拟研究刘先兰;张文玉;伍杰;杨辉;晏恒煊【摘要】采用ABAQUS有限元分析软件,建立强度比值为1.0、0.8和0.5的几种拼焊板进行数值模拟,分析冲压成形回弹角的变化规律.结果表明:板材屈服强度为100MPa、强度比为0.5时,回弹角最小为2.0..板材强度一定时,回弹角随着强度比的增加而增加.强度比值一定时,回弹角随着板材屈服强度的增加而线性增加.【期刊名称】《锻压装备与制造技术》【年(卷),期】2016(051)005【总页数】2页(P83-84)【关键词】冲压成形;回弹;数值模拟;强度比;拼焊板【作者】刘先兰;张文玉;伍杰;杨辉;晏恒煊【作者单位】湖南工学院机械学院,湖南衡阳421002;湖南工学院机械学院,湖南衡阳421002;湖南工学院机械学院,湖南衡阳421002;湖南工学院机械学院,湖南衡阳421002;湖南工学院机械学院,湖南衡阳421002【正文语种】中文【中图分类】TG386拼焊板冲压成形技术实现了零件的高度复合化,成为实现汽车轻量化的重要途径之一[1]。
在强化车身局部强度、刚度的同时,降低了汽车的生产成本,应用前景非常广阔[2,3]。
然而,拼焊板的使用提高了冲压成形技术的难度,如冲压成形过程中的回弹、破裂和起皱等缺陷[5]。
本文通过采用ABAQUS有限元分析软件进行数值模拟,建立强度比值不同的几种拼焊板模型,分析其成形性能的影响因素,找出冲压变形规律,为生产实践提供指导。
冲压模拟过程如图1所示。
以强度分别为300MPa、200MPa和100MPa的板料,建立拼焊板三维模型的强度比值分别为1.0、0.8和0.5,杨氏模量100000MPa,泊松比0.3,摩擦系数0.05。
图1a表示冲压成形结束时冲头还未离开板材时的状态,对应板材的弯曲角度如图2a所示,即回弹前的角度;图1b表示冲压成形结束后冲头离开板材时的状态,对应板材的弯曲角度如图2b所示,即回弹后的角度。
abaqus计算回弹的方法(实用荟萃)
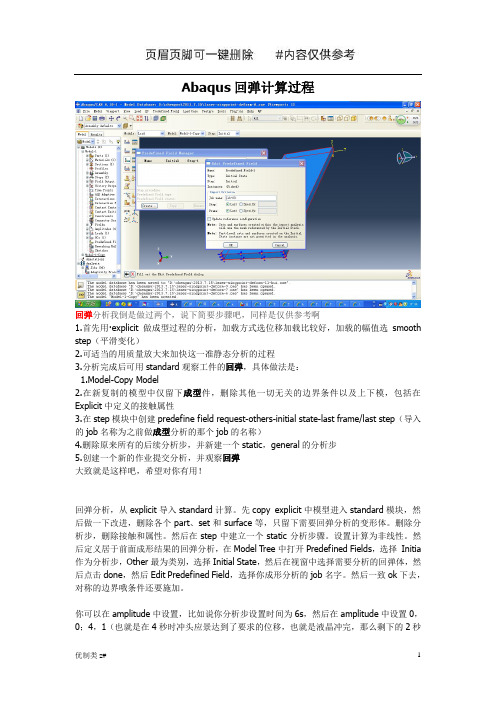
Abaqus回弹计算过程回弹分析我倒是做过两个,说下简要步骤吧,同样是仅供参考啊1.首先用·explicit做成型过程的分析,加载方式选位移加载比较好,加载的幅值选smooth step(平滑变化)2.可适当的用质量放大来加快这一准静态分析的过程3.分析完成后可用standard观察工件的回弹,具体做法是:1.Model-Copy Model2.在新复制的模型中仅留下成型件,删除其他一切无关的边界条件以及上下模,包括在Explicit中定义的接触属性3.在step模块中创建predefine field request-others-initial state-last frame/last step(导入的job名称为之前做成型分析的那个job的名称)4.删除原来所有的后续分析步,并新建一个static,general的分析步5.创建一个新的作业提交分析,并观察回弹大致就是这样吧,希望对你有用!回弹分析,从explicit导入standard计算。
先copy explicit中模型进入standard模块,然后做一下改进,删除各个part、set和surface等,只留下需要回弹分析的变形体。
删除分析步,删除接触和属性。
然后在step中建立一个static分析步骤。
设置计算为非线性。
然后定义居于前面成形结果的回弹分析,在Model Tree中打开Predefined Fields,选择Initia 作为分析步,Other最为类别,选择Initial State,然后在视窗中选择需要分析的回弹体,然后点击done,然后Edit Predefined Field,选择你成形分析的job名字。
然后一致ok下去,对称的边界哦条件还要施加。
你可以在amplitude中设置,比如说你分析步设置时间为6s,然后在amplitude中设置0,0;4,1(也就是在4秒时冲头应景达到了要求的位移,也就是液晶冲完,那么剩下的2秒就是停留的时间了),然后在另外设置一个分析步把冲头往回移就可以了小弟这些天正好在做冲压回弹,刚做成功,从simwe论坛上学了很多东西。
基于Abaqus数值模拟厚板冲压件回弹影响因素研究

由塑性原理可知,板材越厚成形件弯曲时变形抗力
越大,且弯曲时体现出来的塑性、应力分布、应变状况、
材料流动状况等也会发生较大的变化,进而体现出与薄
板不一样的回弹特性[2]。基于此,本文拟采用 Abaqus 有
限元软件对 V 形厚板冲压件的回弹过程进行数值模拟,
《模具制造》2024 年第 3 期
1.058 减小到 0.963,降低了 8.9%。
1.06
1.04
1.02
1.00
0.98
0.96
1.0
70
表面会与凹模圆角产生摩擦,增大板材外表面受到的拉
回弹量/mm
2.0
50
60
W 数值/mm
对于 V 形件而言,成形时板材流入凹模时,板材外
大,回弹数值增加的幅度明显增加。
2.5
40
(3)摩擦系数对回弹的影响。
增大到 R15mm,回弹数值达到了 2.617mm,且随着 R 角增
3.0
30
图7
从成形件变形过程及塑性成形原理分析可知,V 形
参数对成形件回弹数值会产生影响,因此,开展了各因
0.5
0.0
影响回弹的因素分析
件 R 角、凹模开口宽度、凸模成形速度、接触摩擦系数等
1.0
0.10
0.12
0.14 0.16
Z 3 个方向的旋转自由度均设置为 0,X 和 Y 方向平动自
由度也设置为 0,Z 方向运动不做约束。凸模施加位移载
(b)
图4
V 形件数值模拟结果
a——成形件应力分布云图
b——成形件应变分布云图
提取了成形件料厚分布云图,如图 5 所示。从图 5
荷,运行时间为 0.1s。网格采用四边形网格,凸模和凹模
回弹计算方法

回弹强度计算方法1.回弹法测构件强度,一个测区16个点,舍去三个最高点,三个最低点,算出10个点的平均值,然后根据碳化深度查表得出混凝土强度换算值。
如果是全面回弹,每个构件布10个或10个以上测区,采用方差法计算评定;否则按最小值法评定。
34,38,40的数据,碳化如果在1.5左右,勉强达到C30。
3+补充问题:这个透明液体是按1%配比自配的酚酞酒精溶液。
酚酞溶液测碳化深度利用的原理就是酸碱反应,酚酞作指示剂(遇碱变红,遇酸无色),二氧化碳扩散到的地方,酚酞溶液滴上去呈无色,未扩散到的地方呈红色(有碱存在)。
修改五回弹仪测定混凝土强度计算《规程JGJ/T23-2001》根据2001年颁布的《回弹法检测混凝土抗压强度技术规程》JGJ/T23-2001(J115-2001)代替1992年颁布的《回弹法检测混凝土抗压强度技术规程》JGJ/T23-92,有如下主要修改。
P119页“统一换算表”内容有部分改动(下表中的灰色部分)回弹均测区混凝土平均抗压强度换算值f(Mpa)平均碳化深度值d平均(mm)值 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.55.0 5.5 ≥620 10.3 10.1 …21 11.4 11.2 10.8 10.5 10.023 13.7 13.4 13.0 12.6 12.1 11.6 11.2 10.8 10.510.124 14.9 14.6 14.2 13.7 13.1 12.7 12.2 11.8 11.511.0 10.7 10.4 10.125 16.2 15.9 15.4 14.9 14.3 13.8 13.3 12.8 12.512.0 11.7 11.3 10.926 17.5 17.2 16.6 16.1 15.4 14.9 14.4 13.8 13.513.0 12.6 12.2 11.627 18.9 18.5 18.0 17.4 16.6 16.1 15.5 14.8 14.614.0 13.6 13.1 12.428 20.3 19.7 19.2 18.4 17.6 17.0 16.5 15.8 15.414.8 14.4 13.9 13.229 21.8 21.1 20.5 19.6 18.7 18.1 17.5 16.8 16.415.8 15.4 14.6 13.930 23.3 22.6 21.9 21.0 20.0 19.3 18.6 17.9 17.416.8 16.4 15.4 14.731 24.9 24.2 23.4 22.4 21.4 20.7 19.9 19.2 18.417.9 17.4 16.4 15.532 26.5 25.7 24.9 23.9 22.8 22.0 21.2 20.4 19.619.1 18.4 17.5 16.420.3 19.4 18.5 17.434 30.0 29.1 28.0 26.8 25.6 24.6 23.7 23.0 22.121.3 20.4 19.5 18.335 31.8 30.8 29.6 28.0 26.7 25.8 24.8 24.0 23.222.3 21.4 20.4 19.236 33.6 32.6 31.2 29.6 28.2 27.2 26.2 25.2 24.523.5 22.4 21.4 20.237 35.5 34.4 33.0 31.2 29.8 28.8 27.7 26.6 25.924.8 23.4 22.4 21.338 37.5 36.4 34.9 33.0 31.5 30.3 29.2 28.1 27.426.2 24.8 23.6 22.539 39.5 38.2 36.7 34.7 33.0 31.8 30.6 29.6 28.827.4 26.0 24.8 23.740 41.6 39.9 38.3 36.2 34.5 33.3 31.7 30.8 30.028.4 27.0 25.8 25.041 43.7 42.0 40.2 38.0 36.0 34.8 33.2 32.3 31.529.7 28.4 27.1 26.242 45.9 44.1 42.2 39.9 37.6 36.3 34.9 34.0 33.031.2 29.8 28.5 27.543 48.1 46.2 44.2 41.8 39.4 38.0 36.6 35.6 34.632.7 31.3 29.8 28.934.3 32.8 31.2 30.245 52.7 50.6 48.5 45.8 43.2 41.6 40.1 39.0 37.935.8 34.3 32.7 31.646 55.0 52.8 50.6 47.9 45.2 43.5 41.9 40.8 39.737.5 35.8 34.2 33.147 57.5 55.2 52.9 50.0 47.2 45.2 43.7 42.6 41.439.1 37.4 35.6 34.548 60.0 57.6 55.2 52.2 49.2 47.4 45.6 44.4 43.240.8 39.0 37.2 36.049 60.0 57.5 54.4 51.3 49.4 47.5 46.2 45.0 42.540.6 38.8 37.550 59.9 56.7 53.4 51.4 49.5 48.2 46.9 44.342.3 40.4 39.1P120页9-16行“构件混凝土强度推定值f推定”中的推定值计算方法有所改动:4.构件混凝土强度推定值f推定构件混凝土强度推定值是指相应于强度换算值总体分布中保证率不低于95%的强度值。
abaqus方盒拉深的有限元分析CAE

¾ Shape: Shell ¾ Type: Planar ¾ Approximate size: 0.5
点击对话框中下方的
1.1 板坯建模
3. 进入参数化建模的sketch界面,进行几何建模 点击 建立矩形边界组成的面 根据绘图窗口下方的提示输入角点坐标 回车 回车
7.1 定义板坯边界条件
只显示板坯,隐藏其他物体
双击目录树中的Loads
选择 Create Boundary Conditions Mechanical Symmetry….
Continue
选择板坯X=0的那条边
在弹出的对话框中选择 XSYMM
用相同的方法定义Y=0的那条边为YSYMM
7.2 定义凸模边界条件
本例的主要目的就是展示在Abaqus中如何应用 Explitcit 和 Implicit 来分析成形及回弹问题。
简介
几何信息(mm) : 200×200 × 0.82 的板料,凹模口尺寸为102.5 × 102.5, 四角导圆半径为
10, 凸模截面尺寸100 × 100 ,各棱边导圆半径为10.
6.1 划分板坯的网格
首先双击目录树的Parts,然后选择Blank,这时屏幕上只显示板坯。
在第一个按钮组中选择Seed Edge: By Number,定义边界上
的节点数量
选择板坯的左边和下边,点击中键确认
输入20 , 选择Done 确认 本例中单元类型采用默认的S4R单元
选择按钮Mesh Part
只显示凸模,隐藏其他物体
双击目录树中的Loads
自动计算回弹法测强度

自动计算回弹法测强度回弹法是一种常用的非破坏性试验方法,用于测量材料的强度。
该方法通过将一个小球或者一个锤头从一定高度上自由落下,然后测量其回弹高度来间接反映材料的强度,常用于金属材料、混凝土、塑料、橡胶等材料的强度测试。
回弹法的基本原理是根据能量守恒定律,当物体自由下落时,将其全部动能转化为位能,然后再通过回弹的方式重新转化为动能,最终回弹的高度与物体下落前的高度之比可以用来衡量物体的强度。
回弹法常用的仪器设备有回弹式硬度计、双回复英式震荡仪等。
回弹法测强度的基本步骤如下:1.准备工作:根据被测试材料的特性选择合适的回弹法仪器设备,包括回弹式硬度计或双回复英式震荡仪等。
同时,需要根据所测材料的特性选择合适的小球或锤头。
2.校准仪器:使用已知材料的标准样品或仪器调零盘来校准仪器,确保测量结果的准确性。
3.测试前准备:将被测试材料制成相应的试样,通常为正方形或圆形。
在测试前,需要将试样表面清洁干净,确保无杂质影响测试结果。
4.进行测试:将试样放置在平稳的台面上,确保试样表面与台面平行。
将回弹法仪器设备放置在一定高度上,确保小球或锤头直接垂直自由下落。
然后从仪器设备上使小球或锤头自由落下,记录其回弹高度。
5.重复测试:为了保证测量结果的准确性,需要重复多次测试,取其平均值作为最终结果。
6.计算并分析结果:根据回弹高度与下落高度之比的表格或曲线,可以计算出被测试材料的回弹指数或回弹硬度。
然后根据回弹指数或回弹硬度来评估材料的强度。
需要注意的是,回弹法只是一种定性评估材料强度的方法,不能直接给出物理意义上的强度数值。
因此,需要根据具体应用的要求,将回弹法测得的强度指标与其他试验方法或者标准相结合,从而得到更加准确的强度评估结果。
总结起来,回弹法是一种简单、快速、经济的材料强度测量方法。
通过回弹高度与下落高度之比的计算,可以间接反映被测试材料的强度情况。
然而在实际应用中,需要结合其他试验方法或标准来评估材料的强度,以获得更可靠的结果。
回弹计算公式范文

回弹计算公式范文回弹计算公式是指在物体碰撞后,根据碰撞之前和之后的速度、质量等因素计算出物体的回弹速度。
回弹计算公式是物理学中的重要概念之一,广泛应用于工程设计、运动学分析等领域。
本文将简要介绍回弹计算公式的基本原理以及如何应用于实际问题中。
首先,回弹计算公式基于动量守恒定律和动能守恒定律。
在碰撞过程中,物体的动量和动能在碰撞前后都不会发生改变,只是在碰撞前后的分配发生了变化。
动量守恒定律可以表示为$m_1v_1+m_2v_2=m_1v_1'+m_2v_2'$,其中$m_1$和$m_2$分别为碰撞物体1和物体2的质量,$v_1$和$v_2$分别为碰撞前两个物体的速度,$v_1'$和$v_2'$分别为碰撞后两个物体的速度。
动能守恒定律可以表示为$\frac{1}{2}m_1v_1^2 +\frac{1}{2}m_2v_2^2 = \frac{1}{2}m_1v_1'^2 +\frac{1}{2}m_2v_2'^2$,其中动能等于$\frac{1}{2}mv^2$。
为了求解回弹速度,我们可以从以上两个公式中消除$v_1'$和$v_2'$,得到如下回弹速度公式:$v_1' = \frac{(m_1 - m_2)v_1 + 2m_2v_2}{m_1 + m_2}$$v_2' = \frac{2m_1v_1 + (m_2 - m_1)v_2}{m_1 + m_2}$这些公式可以用于计算不同碰撞物体在碰撞后的回弹速度。
实际应用中,我们通常需要根据具体情况来确定各个参数的值。
例如,假设物体1质量为$m_1$,速度为$v_1$;物体2质量为$m_2$,速度为$v_2$。
根据给定的条件,可以通过上述公式计算出碰撞后物体1和物体2的回弹速度。
除了上述的基本计算公式,回弹计算还可以根据具体情况适当引入其他因素,如考虑碰撞时的能量损失等。
这种情况下,回弹计算公式会更加复杂,但原理仍然是基于动量和动能守恒定律。
回弹强度计算

回弹强度计算回弹强度计算是材料力学中的一个重要概念,也是材料工程与物理学研究中的重要参数之一。
回弹强度是指材料在经历一定压缩变形后,恢复到原始状态所需的力度。
回弹强度通常用于测定材料的弹性模量和塑性变形能力。
回弹强度的计算方法有很多种,其中比较常用的方法是通过材料的应力应变曲线来计算。
应力应变曲线是指在材料受力时,材料的应变与应力之间的关系。
这个曲线可以用力学试验来测定,通常使用压缩试验或拉伸试验。
在试验中,材料受到一定的压力或拉力,经历一定的应变,然后通过测量材料的应变和应力来确定回弹强度。
在计算回弹强度时,需要考虑材料的弹性和塑性变形。
弹性变形是指材料在受到外力时,只产生短暂的应变,当外力消失时,材料可以恢复到原来的状态。
而塑性变形是指材料在受到外力时,经历了永久性的形变,即使外力消失,材料也无法完全恢复到原来的状态。
回弹强度的计算需要考虑这两种变形的影响。
在材料的应力应变曲线中,材料受到外力时,会产生一个最大的应力点,称为屈服点。
屈服点是材料的塑性变形开始的标志,当材料受到的应力超过屈服点时,就会产生塑性变形。
在达到最大应力点后,材料会出现一定的弹性回弹,这个回弹程度可以用回弹强度来表示。
回弹强度的计算需要考虑材料的弹性模量、屈服点和最大应力点等因素。
回弹强度的计算对于材料工程和物理学研究中都具有重要的意义。
它可以用来评估材料的弹性和塑性变形能力,为材料的应用提供重要的参考。
此外,回弹强度的计算还可以用来研究材料的力学性质,为材料的性能改进提供理论基础。
回弹强度的计算是材料力学中的一个重要概念,也是材料工程与物理学研究中的重要参数之一。
回弹强度的计算方法和影响因素不同,需要根据具体情况进行分析和计算。
通过回弹强度的计算,可以评估材料的弹性和塑性变形能力,为材料的应用和性能改进提供重要的参考。
复合材料工装回弹量计算

复合材料工装回弹量计算
1.每一测区记取16点回弹值,它不包含弹击隐藏在薄薄一层水泥浆下的气孔或石子上的数值,这两种数值与该测区的正常回弹值偏差很大,很好判断。
同一测点只允许弹击一次,若重复弹击则后者回弹值高于前者,这是因为经弹击后该局部位置较密实,再弹击时吸收的能量较小从而使回弹值偏高,这种作法不允许存在。
2.测区平均回弹值计算方法同行业标准(JGJ/T23-2001)。
曾分别将每测区弹击10点,不舍弃大、小值,取其10点平均值;弹击14点,弃2大、2小值后取余下10点平均值及弹击16点弃3大、3小值后取余下10点平均值,作一统计计算,它们的离散系数分别是:0.097、0.064、0.047,以16点弃3大、3小值后取余下10点平均值为好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Abaqus回弹计算过程
回弹分析我倒是做过两个,说下简要步骤吧,同样是仅供参考啊
1.首先用·explicit做成型过程的分析,加载方式选位移加载比较好,加载的幅值选smooth step(平滑变化)
2.可适当的用质量放大来加快这一准静态分析的过程
3.分析完成后可用standard观察工件的回弹,具体做法是:
1.Model-Copy Model
2.在新复制的模型中仅留下成型件,删除其他一切无关的边界条件以及上下模,包括在Explicit中定义的接触属性
3.在step模块中创建predefine field request-others-initial state-last frame/last step(导入的job名称为之前做成型分析的那个job的名称)
4.删除原来所有的后续分析步,并新建一个static,general的分析步
5.创建一个新的作业提交分析,并观察回弹
大致就是这样吧,希望对你有用!
回弹分析,从explicit导入standard计算。
先copy explicit中模型进入standard模块,然后做一下改进,删除各个part、set和surface等,只留下需要回弹分析的变形体。
删除分析步,删除接触和属性。
然后在step中建立一个static分析步骤。
设置计算为非线性。
然后定义居于前面成形结果的回弹分析,在Model Tree中打开Predefined Fields,选择Initia 作为分析步,Other最为类别,选择Initial State,然后在视窗中选择需要分析的回弹体,然后点击done,然后Edit Predefined Field,选择你成形分析的job名字。
然后一致ok下去,对称的边界哦条件还要施加。
你可以在amplitude中设置,比如说你分析步设置时间为6s,然后在amplitude中设置0,0;4,1(也就是在4秒时冲头应景达到了要求的位移,也就是液晶冲完,那么剩下的2秒就是停留的时间了),然后在另外设置一个分析步把冲头往回移就可以了
小弟这些天正好在做冲压回弹,刚做成功,从simwe论坛上学了很多东西。
在此讲讲小弟个人经验,回报论坛:
1.在原模型中设置restart。
2.将原model,copy另取名字
3.删除不需要的instance(以回弹分析来讲只要留下欲做回弹的instance即可)
4.重设分析步,一般改用静态隐式。
(小弟把之前的分析步都删了,新建了分析步)
5.在load 模组中除去无用的边界条件,并添一个固定点或固定线。
6.在predefined field中建立initial state,选择欲做回弹的instace,job name选择原分析之odb档名(不用再加.odb),step及frame一般是选择Last.
7.再执行分析即可.
注:若想观察的是回弹量,可在initial state中勾选update reference configuration即可.
另外,多做几次,不成功的原因有时不是步骤有问题,而是自己忽略了某个小地
對於explicit至standard的回彈分析,由於通常不涉及任何接觸行為,則設定更為簡單:
1.原始分析之explicit step會在完成job後自動生成最後一個step及increment的重啟動檔。
2.將原始分析模型copy為新的後續分析模型,在assembly module中僅保留成型部件。
3.在後續分析中選擇static general為分析步,設定邊界條件防止成型件剛體運動。
4.在後續分析中為需要傳遞資料的部件定義初始狀態場,操作步驟為load module/ predefined field/ create/ 設置step 為initial/ category 選擇other/ Initial state/選擇需導入原始分析的部件/輸入原始分析job name,step及frame採預設之last。
5.提交後續分析job。
在ABAQUS/CAE中導入原始分析模型時,初始狀態場中預設的update reference configuration為不勾選,在keyword中顯示為*Import, state=yes, update=no(即不勾選update reference configuration)。
State與update的意義如下:
state=yes, update=no,可以把應變/位移和應力都導出來;後續分析中的應變、應力都為絕對值,此為預設值。
state=yes, update=yes,則不導出應變/位移,導出應力;後續分析中的應變/位移為相對值,不是絕對值,而應力是絕對值,如要觀察金屬成型後的回彈應變及位移量,可做此設定。
state=no, update=no,則後續分析中導出應變/位移,不導出應力,一般不會做此設定。
state=no, update=yes,則後續分析中應變/位移和應力都不導出來,一般不會做此設定。
用Abaqus/standard 计算回弹。
1. 在用Abaqus/Explicit 计算成形过程时,设置好Restart Request(Explicit 默认输出的,可在Step->Output->Restart Request 中定义)。
2. 成形过程计算完成后,copy model,删除模具等刚体,删除原来的step,在Load->Predefined Field 中,Step 选择Initial ,Category 选择Other ,T ype 选择Initial State, Continue 并选择型钢零件,Done. OK,这样你在Explict 中计算的结果就将作为回弹计算的状态了。
3. 这是所谓“无模法”回弹计算,不过请注意回弹过程中零件的约束条件。
约束过多,回弹不充分;约束过少,回弹不容易收敛甚至根本不收敛。
