2021届绵阳一诊

合集下载

2021年四川省绵阳市游仙区中考数学一诊试卷(含解析)

2021年四川省绵阳市游仙区中考数学一诊试卷一.选择题（共12小题）.1．下列国产车的标志中是中心对称图形的是（）A．B．C．D．2．关于x的方程（m﹣1）x2+x+m2+2m﹣3＝0的一个根是0，则m的值是（）A．7B．﹣3C．1或﹣3D．03．某口罩加工厂今年一月口罩产值达80万元，第一季度总产值达340万元，问二，三月份的月平均增长率是多少？设月平均增长率的百分数为x，则由题意可得方程为（）A．80（1+x）2＝340B．80+80（1+x）2＝340C．80（1+x）+80（1+x）2＝340D．80+80（1+x）+80（1+x）2＝3404．将抛物线y＝x2﹣4x﹣4向左平移3个单位，再向上平移3个单位，得到抛物线的表达式为（）A．y＝（x+1）2﹣13B．y＝（x﹣5）2﹣5C．y＝（x﹣5）2﹣13D．y＝（x+1）2﹣55．如图，在△ABC中，将△ABC绕着点A顺时针旋转后，得到△AB′C′，且点C′在BC上，若∠B′C′B＝52°，则∠C的度数为（）A．74°B．66°C．64°D．76°6．如图，ABCDEF是中心为原点O，顶点A，D在x轴上，半径为4的正六边形，则顶点F的坐标为（）A．（2，2）B．（﹣2，2）C．（﹣2，2）D．（﹣1，）7．如图，A、B、C三点在⊙O上，若∠ACB＝∠AOB，则∠AOB的度数是（）A．60°B．90°C．100°D．120°8．某鱼塘里养了1600条鲤鱼，若干条草鱼和800条鲢鱼，该鱼塘主通过多次捕捞试验后发现，捕捞到草鱼的频率稳定在0.5左右，则该鱼塘捞到鲢鱼的概率约为（）A．B．C．D．9．如图，矩形ABCD的边长AB＝1，BC＝2．把BC绕B逆时针旋转，使C恰好落在AD 上的点E处，线段BC扫过部分为扇形BCE．若扇形BCE正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是（）A．B．C．D．10．已知二次函数y＝ax2+bx+c与自变量x的部分对应值如表，下列说法错误的是（）x…﹣1013…y…﹣3131…A．a＜0B．方程ax2+bx+c＝﹣2的正根在4与5之间C．2a+b＞0D．若点（5，y1）、（﹣，y2）都在函数图象上，则y1＜y211．如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为点H，与BC交于点G．若BG＝4，CG＝3，则CE的长为（）A．5B．5C．5D．12．如图，函数y1＝|x2﹣m|的图象如图，坐标系中一次函数y2＝x+b的图象记为y2，则以下说法中正确的有（）①当m＝1，且y1与y2恰好有三个交点时b有唯一值为1；②当m＝4，且y1与y2只有两个交点时，b＞或﹣2＜b＜2；③当m＝﹣b时，y1与y2一定有交点：④当m＝b时，y1与y2至少有2个交点，且其中一个为（0，m）．A．1个B．2个C．3个D．4个二、填空题（共6小题）.13．平面直角坐标系中，P（x，2+y）与Q（2y，x）关于原点对称，则xy＝．14．如图，在一次游园活动中，数学小组制作了一面“赵爽弦图锣”，其中∠ABC＝90°，AC＝50cm，AB＝30cm，小明蒙上眼睛用棍子击中了锣面，他击中阴影部分的概率是．15．飞机着陆后滑行的距离s（单位：米）与滑行的时间t（单位：秒）之间的函数关系式是s＝96t﹣1.2t2，那么飞机着陆后秒停下．16．已知△ABC三边的长分别为5、12、13，那么△ABC内切圆的半径为．17．若min{a，b，c}表示a，b，c三个数中的最小值，当y＝min{x2，2x+4，12﹣x}时，则y的取值范围是．18．等边△ABC的边长为6，P是AB上一点，AP＝2，把AP绕点A旋转一周，P点的对应点为P′，连接BP′，BP′的中点为Q，连接CQ．则CQ长度的最小值是．三、解答题（共7个小题，共90分，解答应写出文字说明、证明过程或演算步骤）19．解方程：x2+2x+1＝3x+3．20．在乐善中学组织的体育测试中，小壮掷出的实心球的高度y（m）与水平距离x（m）之间的关系式是y＝﹣（x﹣3）2+，求小壮此次实心球推出的水平距离．21．疫情期间，游海中学进行了一次线上数学学情调查，九（1）班数学李老师对成绩进行分析，制作如下的频数分布表和频数分布直方图．60到70之间学生成绩尚未统计，根据情况画出的扇形图如图．请解答下列问题：类别分数段频数（人数）A60≤x＜70aB70≤x＜8016C80≤x＜9024D90≤x＜1006（1）完成频数分布表，a＝，B类圆心角＝°，并补全频数分布直方图；（2）全校九年级共有720名学生全部参加此次测试，估计该校成绩80≤x＜100范围内的学生有多少人？（3）九（1）班数学老师准备从D类优生的6人中随机抽取两人进行线上学习经验交流，已知这6人中有两名是无家长管理的留守学生，求恰好只选中其中一名留守学生进行经验交流的概率．22．如图，在平面直角坐标系中，△ABC的顶点坐标分别是A（2，4）、B（1，2）、C（5，3）．以点（0，0）为旋转中心，将△ABC顺时针旋转90°，得到△A1B1C1．（1）在坐标系中画出△A1B1C1．（2）若△ABC上有一点P（m，n），直接写出旋转后对应点P1的坐标．（3）求旋转中线段AC所经过部分的面积．23．已知关于x的一元二次方程（a﹣3）x2﹣4x+3＝0有两个不等的实根．（1）求a的取值范围；（2）当a取最大整数值时，△ABC的三条边长均满足关于x的一元二次方程（a﹣3）x2﹣4x+3＝0，求△ABC的周长．24．如图，游仙怡心月季养植园是一个矩形ABCD，AD＝32米，AB＝20米．为了便于养护与运输，养植园内留有四横四纵等宽道路，养植面积与道路面积比为7：3．（1）求道路的宽度．（2）养植区域内月季盆裁要均匀摆放，即每平方米摆放的盆数一样．每平方米最多能摆放36盆，密度越大，花的品质会下降，每盆月季的出售价也会随之降低．大棚内现在每平米有月季小盆栽10盆，每盆的出售价为5元．分析发现：每平方米每增加5盆，每盆的出售价会下降0.5元．老板准备增加养植数量，以获得最多的出售总额，那么每平米应该养植多少盆月季小盆栽才能使出售总额最多？25．如图1，O是△ABC的边BC的中点，⊙O与BC交于E、F两点，与AB相切于点D，连接AO交⊙O于点P，＝．（1）猜想AC与⊙O的位置关系，并证明你的猜想．（2）如图2，延长AO交⊙O于Q点，连接DE、DF，DQ，FQ，FQ＝，ED＝5，求DQ的长．（3）如图3，若DE＝5，连接DF、DP、PF，设DP＝x，△DPF的面积为y，求y与x 之间的函数关系式．26．如图，抛物线y＝ax2+bx+c与x轴交于A（1，0），B（5，0）两点，与y轴交于点C．抛物线顶点纵坐标为﹣4．（1）求抛物线的解析式及C点坐标．（2）如图1，过C作x轴的平行线，与抛物线交于点M，连接AM、BM，在y轴上是否存在点N，使∠ANB＝∠AMB？若存在，请求出点N的坐标；若不存在，请说明理由．（3）把线段OC绕O点顺时针旋转，使C点恰好落在抛物线对称轴上的点P处，如图2，再将线段OP绕P点逆时针旋转45°得线段PQ，请计算Q点坐标，并判断Q点在抛物线上吗？参考答案一.选择题（共12小题）.1．下列国产车的标志中是中心对称图形的是（）A．B．C．D．解：A．不是中心对称图形，不合题意；B．是中心对称图形，符合题意；C．不是中心对称图形，不合题意；D．不是中心对称图形，不合题意；故选：B．2．关于x的方程（m﹣1）x2+x+m2+2m﹣3＝0的一个根是0，则m的值是（）A．7B．﹣3C．1或﹣3D．0解：把x＝0代入方程（m﹣1）x2+x+m2+2m﹣3＝0，得m2+2m﹣3＝0，解得m＝1或﹣3．故选：C．3．某口罩加工厂今年一月口罩产值达80万元，第一季度总产值达340万元，问二，三月份的月平均增长率是多少？设月平均增长率的百分数为x，则由题意可得方程为（）A．80（1+x）2＝340B．80+80（1+x）2＝340C．80（1+x）+80（1+x）2＝340D．80+80（1+x）+80（1+x）2＝340解：设月平均增长率的百分数为x，80+80（1+x）+80（1+x）2＝340．故选：D．4．将抛物线y＝x2﹣4x﹣4向左平移3个单位，再向上平移3个单位，得到抛物线的表达式为（）A．y＝（x+1）2﹣13B．y＝（x﹣5）2﹣5C．y＝（x﹣5）2﹣13D．y＝（x+1）2﹣5解：∵y＝x2﹣4x﹣4＝（x﹣2）2﹣8，∴将抛物线y＝x2﹣4x﹣4向左平移3个单位，再向上平移3个单位，得到抛物线的表达式为y＝（x﹣2+3）2﹣8+3，即y＝（x+1）2﹣5．故选：D．5．如图，在△ABC中，将△ABC绕着点A顺时针旋转后，得到△AB′C′，且点C′在BC上，若∠B′C′B＝52°，则∠C的度数为（）A．74°B．66°C．64°D．76°解：∵将△ABC绕点A顺时针旋转后，得到△AB′C′，∴AC′＝AC，∴∠C＝∠AC′C＝∠AC′B′，∵∠B′C′B＝52°，∴∠CC′B′＝180°﹣52°＝128°，∴∠C＝∠AC′C＝∠AC′B′＝×128°＝64°，故选：C．6．如图，ABCDEF是中心为原点O，顶点A，D在x轴上，半径为4的正六边形，则顶点F的坐标为（）A．（2，2）B．（﹣2，2）C．（﹣2，2）D．（﹣1，）解：连接OF．∵∠AOF＝＝60°，OA＝OF，∴△AOF是等边三角形，∴OA＝OF＝4．设EF交y轴于G，则∠GOF＝30°．在Rt△GOF中，∵∠GOF＝30°，OF＝4，∴GF＝2，OG＝2．∴F（﹣2，2）．故选：C．7．如图，A、B、C三点在⊙O上，若∠ACB＝∠AOB，则∠AOB的度数是（）A．60°B．90°C．100°D．120°解：如图，在优弧AB上取一点D，连接AD，BD．∵∠ACB+∠ADB＝180°，∠ACB＝∠AOB＝2∠ADB，∴2∠ADB+∠ADB＝180°，∴∠ADB＝60°，∴∠AOB＝2∠ADB＝120°，故选：D．8．某鱼塘里养了1600条鲤鱼，若干条草鱼和800条鲢鱼，该鱼塘主通过多次捕捞试验后发现，捕捞到草鱼的频率稳定在0.5左右，则该鱼塘捞到鲢鱼的概率约为（）A．B．C．D．解：∵捕捞到草鱼的频率稳定在0.5左右，设草鱼的条数为x，可得：＝0.5，解得：x＝2400，∴由题意可得，捞到鲢鱼的概率为：＝；故选：D．9．如图，矩形ABCD的边长AB＝1，BC＝2．把BC绕B逆时针旋转，使C恰好落在AD 上的点E处，线段BC扫过部分为扇形BCE．若扇形BCE正好是一个圆锥的侧面展开图，则该圆锥的底面圆的半径是（）A．B．C．D．解：∵线段CE由线段BC旋转而成，BC＝2，∴BE＝BC＝2．∵AB＝1，∠BAE＝90°，∴∠AEB＝30°．∵AD∥BC，∴∠EBC＝∠AEB＝30°，∴S阴影＝＝，设围成的圆锥的底面半径为r，则2πr＝，解得：r＝．故选：A．10．已知二次函数y＝ax2+bx+c与自变量x的部分对应值如表，下列说法错误的是（）x…﹣1013…y…﹣3131…A．a＜0B．方程ax2+bx+c＝﹣2的正根在4与5之间C．2a+b＞0D．若点（5，y1）、（﹣，y2）都在函数图象上，则y1＜y2解：∵二次函数值先由小变大，再由大变小，∴抛物线的开口向下，∴a＜0，故A正确；∵x＝﹣1时，y＝﹣3，∴x＝4时，y＝﹣3，∴二次函数y＝ax2+bx+c的函数值为﹣2时，﹣1＜x＜0或3＜x＜4，即方程ax2+bx+c＝﹣2的负根在﹣1与0之间，正根在3与4之间，故B错误；∵抛物线过点（0，1）和（3，1），∴抛物线的对称轴为直线x＝，∴﹣＝＞1，∴2a+b＞0，故C正确；∵（﹣，y2）关于直线x＝的对称点为（，y2），∵＜5，∴y1＜y2，故D正确；故选：B．11．如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为点H，与BC交于点G．若BG＝4，CG＝3，则CE的长为（）A．5B．5C．5D．解：如图所示，连接EG，由旋转可得，△ADE≌△ABF，∴AE＝AF，DE＝BF，又∵AG⊥EF，∴H为EF的中点，∴AG垂直平分EF，∴EG＝FG，设CE＝x，则DE＝7﹣x＝BF，FG＝CF﹣CG＝11﹣x，∴EG＝11﹣x，∵∠C＝90°，∴Rt△CEG中，CE2+CG2＝EG2，即x2+32＝（11﹣x）2，解得x＝，∴CE的长为，故选：C．12．如图，函数y1＝|x2﹣m|的图象如图，坐标系中一次函数y2＝x+b的图象记为y2，则以下说法中正确的有（）①当m＝1，且y1与y2恰好有三个交点时b有唯一值为1；②当m＝4，且y1与y2只有两个交点时，b＞或﹣2＜b＜2；③当m＝﹣b时，y1与y2一定有交点：④当m＝b时，y1与y2至少有2个交点，且其中一个为（0，m）．A．1个B．2个C．3个D．4个解：①错误．如图1中，当直线y＝x+b与抛物线相切时，也满足条件只有三个交点．此时b≠1，故①错误．②正确．如图2中，当抛物线经过点（﹣2，0）时，0＝4﹣m，m＝4．由消去y得到x2+x+b﹣4＝0，当△＝0时，1﹣4b+16＝0，∴b＝，观察图象可知当b＞或﹣2＜b＜2时，y1与y2有两个交点．故②正确．③错误．如图3中，当b＝﹣4时，观察图象可知，y1与y2没有交点，故③错误．④正确．如图4中，当b＝4时，观察图象可知，b＞0，y1与y2至少有2个交点，且其中一个为（0，m），故④正确．故选：B．二、填空题（共6个小题，每小题4分，共24分，将答案填写在答题卡相应的横线上）13．平面直角坐标系中，P（x，2+y）与Q（2y，x）关于原点对称，则xy＝﹣8．解：∵P（x，2+y）与Q（2y，x）关于原点对称，∴，解得：，则xy＝﹣4×2＝﹣8．故答案为：﹣8．14．如图，在一次游园活动中，数学小组制作了一面“赵爽弦图锣”，其中∠ABC＝90°，AC＝50cm，AB＝30cm，小明蒙上眼睛用棍子击中了锣面，他击中阴影部分的概率是．解：∵∠ABC＝90°，AC＝50cm，AB＝30cm，∴由勾股定理得：BC＝40cm，∴S△ABC＝AB•BC＝×30×40＝600（cm2），∴S阴影＝S正方形﹣4S△ABC＝502﹣4×600＝100（cm2），∴小明蒙上眼睛用棍子击中了锣面，他击中阴影部分的概率是＝，故答案为：．15．飞机着陆后滑行的距离s（单位：米）与滑行的时间t（单位：秒）之间的函数关系式是s＝96t﹣1.2t2，那么飞机着陆后40秒停下．解：s＝96t﹣1.2t2，当t＝﹣＝＝40（秒）时，s将取到最大值，即飞机着陆后40秒停下．故答案为：40．16．已知△ABC三边的长分别为5、12、13，那么△ABC内切圆的半径为2．解：如图，圆O为△ABC内切圆，切点分别为D、E、F，连接OF、OE、OD，则OF⊥AC，OE⊥BC，OD⊥AB．由切线长定理，可知AF＝AD，CF＝CE，BD＝BE，∴OE＝OF＝CE＝CF，又∵52+122＝132，∴∠C＝90°，∴四边形FCEO为正方形，∴CE＝＝＝2．故答案为2．17．若min{a，b，c}表示a，b，c三个数中的最小值，当y＝min{x2，2x+4，12﹣x}时，则y的取值范围是y≤9．解：如图，当x＝3时y有最大值，y最大＝12﹣3＝9，故答案为y≤9．18．等边△ABC的边长为6，P是AB上一点，AP＝2，把AP绕点A旋转一周，P点的对应点为P′，连接BP′，BP′的中点为Q，连接CQ．则CQ长度的最小值是3﹣1．解：如图，取AB中点D，连接DQ，CD，AP'，∵AP＝2，把AP绕点A旋转一周，∴AP'＝2，∵等边△ABC的边长为6，点D是AB中点，∴BD＝AD＝3，CD⊥AB，∴CD＝＝＝3，∵点Q是BP'是中点，∴BQ＝QP'，又∵AD＝BD，∴DQ＝AP'＝1，在△CDQ中，CQ≥DC﹣DQ，∴CQ的最小值为3﹣1，故答案为3﹣1．三、解答题（本大题共7个小题，共90分，解答应写出文字说明、证明过程或演算步骤）19．解方程：x2+2x+1＝3x+3．解：∵x2+2x+1＝3x+3，∴（x+1）2﹣3（x+1）＝0，则（x+1）（x﹣2）＝0，∴x+1＝0或x﹣2＝0，解得x1＝﹣1，x2＝2．20．在乐善中学组织的体育测试中，小壮掷出的实心球的高度y（m）与水平距离x（m）之间的关系式是y＝﹣（x﹣3）2+，求小壮此次实心球推出的水平距离．解：令y＝0，则﹣（x﹣3）2+＝0，解得：x1＝8，x2＝﹣2（舍去），故小壮此次实心球推出的水平距离为：8米．21．疫情期间，游海中学进行了一次线上数学学情调查，九（1）班数学李老师对成绩进行分析，制作如下的频数分布表和频数分布直方图．60到70之间学生成绩尚未统计，根据情况画出的扇形图如图．请解答下列问题：类别分数段频数（人数）A60≤x＜70aB70≤x＜8016C80≤x＜9024D90≤x＜1006（1）完成频数分布表，a＝2，B类圆心角＝120°，并补全频数分布直方图；（2）全校九年级共有720名学生全部参加此次测试，估计该校成绩80≤x＜100范围内的学生有多少人？（3）九（1）班数学老师准备从D类优生的6人中随机抽取两人进行线上学习经验交流，已知这6人中有两名是无家长管理的留守学生，求恰好只选中其中一名留守学生进行经验交流的概率．解：（1）调查的总人数为：24÷50%＝48（人），∴a＝48﹣16﹣24﹣6＝2，B类圆心角的度数为360°×＝120°，故答案为2，120；补全频数分布直方图为：（2）720×＝450（人），所以估计该校成绩80≤x＜100范围内的学生有450人；（3）把D类优生的6人分别即为1、2、3、4、5、6，其中1、2为留守学生，画树状图如图：共有30个等可能的结果，恰好只选中其中一名留守学生进行经验交流的结果有16个，∴恰好只选中其中一名留守学生进行经验交流的概率为＝．22．如图，在平面直角坐标系中，△ABC的顶点坐标分别是A（2，4）、B（1，2）、C（5，3）．以点（0，0）为旋转中心，将△ABC顺时针旋转90°，得到△A1B1C1．（1）在坐标系中画出△A1B1C1．（2）若△ABC上有一点P（m，n），直接写出旋转后对应点P1的坐标．（3）求旋转中线段AC所经过部分的面积．解：（1）如图，△A1B1C1即为所求作．（2）P1（n，﹣m）．（3）线段AC所经过部分的面积＝﹣＝（OC2﹣OA2）＝•（32+52﹣22﹣42）＝，23．已知关于x的一元二次方程（a﹣3）x2﹣4x+3＝0有两个不等的实根．（1）求a的取值范围；（2）当a取最大整数值时，△ABC的三条边长均满足关于x的一元二次方程（a﹣3）x2﹣4x+3＝0，求△ABC的周长．解：（1）∵关于x的一元二次方程（a﹣3）x2﹣4x+3＝0有两个不相等的实数根，∴，解得a＜且a≠3．（2）由（1）得a的最大整数值为4；∴x2﹣4x+3＝0解得：x1＝1 x2＝3．∵△ABC的三条边长均满足关于x的一元二次方程（a﹣3）x2﹣4x+3＝0，∴①三边都为1，则△ABC的周长为3；②三边都为3，则△ABC的周长为9；③三边为1，1，3，因为1+1＜3，此情况不存在；④三边为1，3，3，则△ABC的周长为7．24．如图，游仙怡心月季养植园是一个矩形ABCD，AD＝32米，AB＝20米．为了便于养护与运输，养植园内留有四横四纵等宽道路，养植面积与道路面积比为7：3．（1）求道路的宽度．（2）养植区域内月季盆裁要均匀摆放，即每平方米摆放的盆数一样．每平方米最多能摆放36盆，密度越大，花的品质会下降，每盆月季的出售价也会随之降低．大棚内现在每平米有月季小盆栽10盆，每盆的出售价为5元．分析发现：每平方米每增加5盆，每盆的出售价会下降0.5元．老板准备增加养植数量，以获得最多的出售总额，那么每平米应该养植多少盆月季小盆栽才能使出售总额最多？解：（1）设道路宽x米，则（32﹣4x）（20﹣4x）＝32×20×，解得：x1＝1，x2＝12（不合题意舍去），故x＝1，答：道路宽为1米；（2）∵5：0.5＝10：1，故设每平方米增加10z盆，则每盆售价降低z元，出售总额为w元/m2，则：w＝（10+10z）（5﹣z）＝﹣10（z﹣2）2+90，∵10z≤36﹣10，∴z≤2.6，∴0≤z≤2.6，又∵a＝﹣10＜0，且z＝2在0≤z≤2.6内，∴每平米应该养植20盆月季小盆栽才能使出售总额最多．25．如图1，O是△ABC的边BC的中点，⊙O与BC交于E、F两点，与AB相切于点D，连接AO交⊙O于点P，＝．（1）猜想AC与⊙O的位置关系，并证明你的猜想．（2）如图2，延长AO交⊙O于Q点，连接DE、DF，DQ，FQ，FQ＝，ED＝5，求DQ的长．（3）如图3，若DE＝5，连接DF、DP、PF，设DP＝x，△DPF的面积为y，求y与x 之间的函数关系式．解：（1）结论：AC与⊙O相切，理由：过点O作OH⊥AC于H，∵⊙O与AB相切于点D，∴OD⊥AB，∵，点O是圆心，∴∠BOP＝∠COP＝90°，又∵O是BC的中点，∴AB＝AC，∴∠BAO＝∠OAC，又∵OD⊥AB，OH⊥AC，∴OD＝OH，∴OH是半径，∴AC与⊙O相切．（2）如图2中，过点Q作QN⊥CD于N，QM⊥DE交DE的延长线于M，连接QE．∵AO⊥BC，O是圆心，∴PQ是直径，∴OQ＝OF，∴FQ＝OF＝，∴FO＝，∴EF＝13，∵EC是直径，∴∠EDC＝90°，∵DE＝5∴CD＝＝＝12，∵∠QDC＝∠QOF＝45°，∴∠QDM＝∠QDN＝45°，∴＝，∴EQ＝FQ，∵QM⊥DM，QN⊥DN，∴QM＝QN，∵∠M＝∠QNF＝90°，∴Rt△QME≌Rt△QNF（HL），∴EM＝FN，∵∠M＝∠MDN＝∠DNQ＝90°，∴四边形DMQN是矩形，∵QM＝QN，∴四边形DMQN是正方形，∴DM＝DN，∴DE+DF＝DM﹣EM+DN+NF＝2DM＝17，∴DM＝DN＝，∴DQ＝DN＝．（3）如图3中，过点F作FH⊥DP交DP的延长线于H．∵∠PDF＝∠POC＝45°，∠H＝90°，∴∠HDF＝∠DFH＝45°，∴DH＝FH，DF＝FH，∵∠EDF＝∠H＝90°，∠EFP＝∠DFH＝45°，∴∠EFD＝∠PFH，∴△EFD∽△PFH，∴＝＝，∵DE＝5，∴PH＝，∴DH＝FH＝x+，∴y＝S△PDF＝•DP•FH，∴y＝×x×（x+）＝x2+x（x＞0）．26．如图，抛物线y＝ax2+bx+c与x轴交于A（1，0），B（5，0）两点，与y轴交于点C．抛物线顶点纵坐标为﹣4．（1）求抛物线的解析式及C点坐标．（2）如图1，过C作x轴的平行线，与抛物线交于点M，连接AM、BM，在y轴上是否存在点N，使∠ANB＝∠AMB？若存在，请求出点N的坐标；若不存在，请说明理由．（3）把线段OC绕O点顺时针旋转，使C点恰好落在抛物线对称轴上的点P处，如图2，再将线段OP绕P点逆时针旋转45°得线段PQ，请计算Q点坐标，并判断Q点在抛物线上吗？解：（1）设抛物线的表达式为y＝a（x﹣x1）（x﹣x2）＝a（x﹣1）（x﹣5）＝a（x2﹣6x+5），函数的对称轴为x＝3，当x＝3时，y＝a（x2﹣6x+5）＝﹣4a＝﹣4，解得a＝1，故抛物线的表达式为y＝x2﹣6x+5，当x＝0时，y＝5，故点C（0，5）；（2）存在，理由：根据点的对称性，点C（0，5），函数对称轴为x＝3，故点M（6，5），∵∠ANB＝∠AMB，则点N、M、B、A四点共圆，∵△ABM的外接圆圆心在抛物线的对称轴上，故设圆心为H（3，m），设点N（0，t），则MH＝BH，即（5﹣3）2+（m﹣0）2＝（5﹣3）2+（m﹣5）2，解得m＝3，故点H（3，3），同样HM＝HN，即（5﹣3）2+（m﹣0）2＝（0﹣3）2+（t﹣3）2，解得t＝1或5，故点N的坐标为（0，1）或（0，5），根据图象的对称性，符合条件的点N还有（0，﹣1）或（0，﹣5），故点N的坐标为（0，1）或（0，5）或（0，﹣1）或（0，﹣5）；（3）不在，理由：设函数对称轴交x轴于点D，在Rt△OPD中，OP＝OC＝5，OD＝3，则PD＝4，故P（3，4），则OP＝5，设直线PQ交x轴于点K，则KR⊥OP于点R，tan∠POD＝，在Rt△ORK中，设RK＝4x，则OR＝3x，OK＝5x，在Rt△RKP中，∠RPK＝45°，则PR＝RK＝4x，则OP＝OR+PR＝7x＝5，解得x＝，故OK＝5x＝，故点K（，0），由点P、K的坐标得，直线PK的表达式为y＝﹣7x+25，设点Q的坐标为（s，﹣7s+25），由PQ＝PO＝5得：（3﹣s）2+（4+7s﹣25）2＝25，解得s＝（不合题意值已舍去），故点Q的坐标为（，），当x＝时，y＝x2﹣6x+5＝﹣3.5≠，故点Q不在抛物线上．。

四川省绵阳市2021届高三语文第一次诊断试题(1)

四川省绵阳市2021届高三语文第一次诊断试题本试题卷分第1卷（单项选择题）和第2卷（非选择题），第一卷1至4页，第二卷4至6页，共6页，总分值150分。

考试时刻150分钟。

考生作答时，须将答案答在答题卷上，在本试题卷、草稿纸上答题无效。

考试终止后，将答题卡交回。

第一卷（单项选择题，共27分）注意事项：必需利用2B铅笔在答题卡上将所选答案对应的标号涂黑。

本部份共3大题，9小题，每题3分。

一、（12分，每题3分）一、以下词语中加点的字，读音全数正确的一项为哪一项A取缔(dì) 玩弄(nòng) 可塑性(sù) 蔫头蔫脑(yān)B坎坷（kě狙击（zǔ上档次(dàng) 扪心自问(mēn)C潜力( qián) 坊间(tāng) 骨碌(gū) 难兄难第(nán)D夹生(jiā) 量筒(liáng 胳肢窝(gé) 管窥蠡测(lí)二、以下词语中，没有错别字的一项为哪一项A、跑酷擎天柱过渡政府涸泽而鱼B、峰会手动挡健身途径代际公平C、宫阕放冷箭激浊扬清毁家信难D、窜改涨停板察颜观色蜚声文坛3、以下各句中，加点词语利用适当的一项为哪一项A、关于切外国的东西，犹如咱们关于食物一样，必需要通过自己的口腔咀嚼和胃肠运动，把它分解为精华和糟粕两部份，然后排泄糟粕，吸收精华。

B、据悉，山东省一直在酝酿起用全国高考卷；尽管最近几年来山东卷质量不断提高，但利用全国卷可大大节约人力物力财力，更利于统一考查，公平选才。

C、李克强欧洲之行的闭幕演讲，给来自欧洲政界、商界的600多名听众吃下了一枚高兴果：中国经济定会平稳运行，可不能显现有些舆论所说的硬着陆。

D、王晓峰同窗绠短汲深，做语文课代表再适合只是了，他基础知识扎实，文学功底深厚，相信他能协助语文教师把咱们班的语文学习弄得更生动活泼。

4、以下各句中，没有语病的一项为哪一项A、不管对改革有多少不同意见，对反腐有何种议论，坚持公平正义都是社会各阶级、各群体的最大公约数，也是深化改革的最大共识。

绵阳1诊(2021级)

2021级绵阳一诊物理试题二、选择题：本题共8小题，每小题6分。

在每小题给出的四个选项中，第14～17题只有一项符合题目要求，第18～21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

14. 如图所示，固定在地面上的光滑斜面足够长，一小球从斜面上某位置以沿斜面向上的初速度开始运动，则小球在运动过程中A ．速度大小和方向都不变B ．速度大小不断变化，方向不变C ．加速度大小和方向都不变化D ．加速度大小不断变化，方向不变15. 如图所示，某同学用绳子拉木箱，从静止开始沿粗糙水平路面匀加速至某一速度，在这个过程中绳子拉力大小一定A ．小于路面的摩擦力B ．大于路面的摩擦力C ．小于木箱的重力D ．大于木箱的重力16. 乘坐汽车在水平路面上转弯时，会有向外倾斜的感受，而坐高铁高速通过水平面内弯道时不会有这种感受。

这是由于转弯需要的向心力A ．坐汽车时是由人的重力和椅子对人支持力的合力提供，坐高铁时不是B ．坐高铁时是由人的重力和椅子对人支持力的合力提供，坐汽车时不是C ．坐高铁时方向是水平的，坐汽车时方向不是水平的D ．坐汽车时方向是水平的，高铁坐时方向不是水平的17. 如图所示，半径为R 的半圆轨道直径边在水平地面上，O 为圆心，A 、B 在轨道上，A 是轨道最左端，OB 与水平面夹角为60°。

在A 点正上方P 处将可视为质点的小球水平抛出，小球过B 点且与半圆轨道相切，重力加速度为g ，则小球抛出时的初速度为A ． √gRB ． √3gR2 C ． √3√3gR2 D ． √3√3gR 218. 甲、乙两汽车在同一条平直公路上同向行驶，其速度—时间图像分别如图中曲线甲和直线乙所示。

已知两车在t 1时刻并排行驶，则A ．0时刻，甲车在后，乙车在前B ．t 2时刻，甲车在前，乙车在后C ．从0到t 1时间内的某时刻，两车加速度相同D ．从t 1到t 2时间内的某时刻，两车加速度相同 19. 将一物体以某一初速度竖直向上抛出，先后经过A 、B 两点后到达最高点，然后又下落经过甲乙v t t 1 t 2 0 A O B P 60° v。

四川省绵阳市高中2021届高三第一学期第一次诊断性考试数学(理)试题含答案

nHH
nB
a opuv
／
口 3
飞·
－π
fo
、‘，／
(1)求角 C 的大小；
(2）若cosB = __!_, c = 7，求 AB 边上的高． 7 理科数学试题第 3 页（共 4 页）
20. (12分）
己知函数 f(x）是定义在R 上的奇函数，当 x<O 时， f(x）＝兰兰＋1. x
(1)求函数 f(x）的解析式： (2）若对于任意实数x，不等式 f(e勺＋ 2af(ex）二三0恒成立，求实数α的取值范围．
时cosα＝
A. _!_ 2
B. 丘二1
c. 一)一3
D. 豆1
。n+ 11.数列｛αn｝满足
一1一＝一2一一一 1 2 αn+I αn
，α2
L.
1
＝一
5
，α4＝一19
，数列｛
bn｝的前n项和为品，若bn
＝αna
n+!'
4
则便不等式
S“n
＞
一
27
成立的n的最小值为

A. 11
B. 12
c. 13
D. 14
p
极向上的活力．某公司设计方案如图，等腰今PMN 的顶点P
在半径为20m的大①0上，点 M, N在半径为lOm的小①O
上，圆心。与点P都在弦 MN的同侧．设弦 MN 与对应劣弧
所围成的弓形面积为S, LOPM 与 LOPN 的面积之和为S1,
ζMON=2α，当S1-S的值最大时，该设计方案最美，则此
2.下列函数中，既是奇函数又是增函数的是
A.y=tan.x
B.y=ln.x
C.y=x3

2021届绵阳一诊理科数学(Word版含答案)

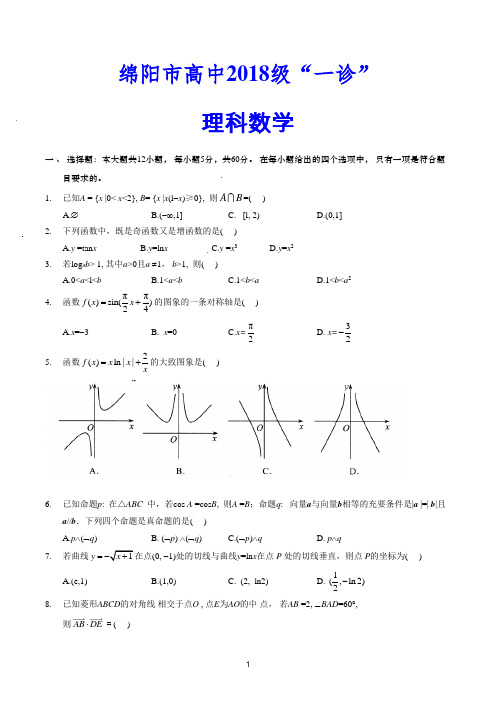
绵阳市高中2018级“一诊”理科数学一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知A = {x |0< x <2}, B = {x |x (l -x )≥0}, 则B A =( )A.∅B.(-∞,1]C. [l, 2)D.(0,1]2. 下列函数中，既是奇函数又是增函数的是( )A.y =tan xB.y =ln xC.y =x 3D.y =x 23. 若log a b > 1, 其中a >0且a ≠1， b >1, 则( )A.0<a <l<bB.1<a <bC.1<b <aD.1<b <a 24. 函数ππ()sin()24f x x =+的图象的一条对称轴是( )A.x =-3B. x =0C.x=π2D. x=32-5. 函数2()ln ||f x x x x=+的大致图象是( )6. 已知命题p : 在△ABC 中，若cos A =cos B , 则A =B ；命题q : 向量a 与向量b 相等的充要条件是|a |=| b |且a //b ．下列四个命题是真命题的是( ) A.p ∧(⌝q )B. (⌝p ) ∧(⌝q )C.(⌝p )∧qD. p ∧q7. 若曲线1y x =-+在点(0, -1)处的切线与曲线y =ln x 在点 P 处的切线垂直，则点 P 的坐标为( )A.(e,1)B.(1,0)C. (2, ln2)D. 1(,ln 2)2-8. 已知菱形ABCD 的对角线相交于点O , 点E 为AO 的中点，若AB =2, ∠BAD =60°,则AB DE ⋅＝( )A.-2B. 12-C. 72-D.129. 若a <b < 0, 则下列不等式中成立的是( )A. 11a b a <- B. 11a b b a+>+C.11b b a a -<-D. (1)(1)a b a b ->-10. 某城市要在广场中央的圆形地面设计一块浮雕，彰显城市积极向上的活力．某公司设计方案如图，等腰△PMN 的顶点P 在半径为20m 的大⊙O 上，点M , N 在半径为10m 的小⊙O 上，圆心O 与点P 都在弦MN 的同侧．设弦MN 与对应劣弧所围成的弓形面积为S , △OPM 与△OPN 的面积之和为S 1,∠MON =2α, 当S 1-S 的值最大时，该设计方案最美，则此时cos α=( ) A.12B.512- C.32D.212- 11. 数列{a n }满足21121n n n a a a ++=-,2411,59a a ==,数列{b n }的前n 项和为S n ,若b n =a n a n +1，则使不等式427n S >成立的n 的最小值为( ) A. 11 B. 12C. 13D. 1412. 若1823,23a b +==，则以下结论正确的有( ) ①b -a <1 ②112a b+> ③34ab > ④22b a > A.1个B.2个C.3个D.4个二、填空题：本大题共4小题，每小题5分，共20分．13. 已知向量a =(l, 0), b =(l, 1), 且a +λb 与a 垂直，则实数λ＝．14. 若实数x ,y 满足0,,22,x x y x y ≥⎧⎪≤⎨⎪+≥⎩则z =2x +y 的最大值为．15. 已知sin x +cos y =14, 则sin x -sin 2y 的最大值为． 16. 若函数f (x )=(x 2 +ax +2a )e x 在区间(-2, 1)上恰有一个极值点，则实数a 的取值范围为．三、解答题：共70分。

四川省绵阳市2021届高三数学第一次诊断性考试试题文（含解析）(1)

四川省绵阳市2021届高三第一次诊断性考试数学（文）试题（解析版）第I 卷（选择题，共50分）【试卷综析】本套试卷能从学科结构上设计试题，已全面覆盖了中学数学教材中的知识模块，同时，试卷突出了学科的骨干内容，集合与函数、不等式、数列、概率统计、解析几何、导数的应用等重点内容在试卷中占有较高的比例，也达到了必要的考查深度．本套试卷没有刻意追求覆盖面，还有调整和扩大的空间，注重了能力的考查，专门是运算能力，逻辑思维能力和空间想象能力的强调比较突出，实践能力和创新意识方面也在尽力表现. 一、选择题：本大题共10小题，每题5分，共50分.在每题给出的4个选项中，只有一个符合题目要求的. 【题文】一、已知集合{}{},02,0122=--=≤-∈=x x x B x Z x A 则=⋂B A ( ) A.Φ B.{}1- C.{}0 D.{}2 【知识点】集合运算. A1【答案解析】B 解析：因为A={-1，0，1}, B={-1，2}，因此=⋂B A {}1-，应选B. 【思路点拨】化简集合A 、B,从而求得A B ⋂. 【题文】二、命题"12),,0(">+∞∈∀xx 的否定是( )A."12),,0("00≤+∞∉∃x x B."12),,0("00≤+∞∈∃x xC."12),,0("≤+∞∉∀xx D."12),,0("<+∞∈∀xx 【知识点】含量词的命题的否定. A3【答案解析】B 解析：命题"12),,0(">+∞∈∀xx 的否定是"12),,0("00≤+∞∈∃x x ，应选B.【思路点拨】依照含一个量词的全称命题的否定方式写出结论.【题文】3、设各项均不为0的数列{}n a 知足)1(21≥=+n a a n n ，假设5422a a a =，那么=3a ( ) A.2 B.2 C.22 D.4 【知识点】等比数列. D3【答案解析】D 解析：由)1(21≥=+n a a n n 知数列{}n a 是以2为公比的等比数列，因为5422a a a =，因此34111122a q a q a q a ⋅=⇒=，因此=3a 4，应选D.【思路点拨】由已知条件确信数列{}n a 是等比数列，再依照5422a a a =求得1a ，进而求3a . 【题文】4、如图，正六边形ABCDEF 的边长为1，那么=⋅DB AD ( )A.3B.3-C.3D.-3 【知识点】向量的数量积. F3【答案解析】D 解析：因为,AD AB BD AB BD =+⊥,因此=⋅DB AD ()203AB BD DB AB DB BD DB BD +⋅=⋅+⋅=-=-,应选 D.【思路点拨】利用向量加法的三角形法那么，将数量积中的向量表示为夹角、模都易求的向量的数量积.【题文】五、已知53)4cos(=-x π，那么=x 2sin ( )A.2518B.2524±C.257-D.257 【知识点】二倍角公式；诱导公式. C6 C2 【答案解析】C 解析：因为53)4cos(=-x π，因此 27cos 22cos 14425x x ππ⎛⎫⎛⎫-=--=- ⎪ ⎪⎝⎭⎝⎭，即7cos 2sin 2225x x π⎛⎫-==- ⎪⎝⎭，应选C.【思路点拨】利用二倍角公式求得cos 2x π⎛⎫-⎪⎝⎭值，再用诱导公式求得sin2x 值. 【题文】六、已知y x 、知足⎪⎩⎪⎨⎧≤--≥-+≥+-0330101y x y x y x ，那么y x -2的最大值为( )A.1B.2C.3D.4 【知识点】简单的线性计划. E5【答案解析】B 解析：画出可行域如图：平移直线z=2x-y 得，当此直线过可行域中的点A （1,0）时 2x-y 有最大值2，应选B.【思路点拨】设目标函数z=2x-y ，画出可行域平移目标函数得点A （1,0）是使目标函数取得最大值的最优解. 【题文】7、在()π2,0内，使sin cosx x ≥成立的x 取值范围是( )A.⎥⎦⎤⎢⎣⎡47,4ππ B.⎥⎦⎤⎢⎣⎡45,4ππ C.⎥⎦⎤⎢⎣⎡45,0π D.⎥⎦⎤⎢⎣⎡⋃⎥⎦⎤⎢⎣⎡πππ2,474,0【知识点】三角函数不等式的解法. C1【答案解析】A 解析：当(]0,x π∈时，不等式为sinx ≥cosx ，解得,4x ππ⎡⎤∈⎢⎥⎣⎦；当(),2x ππ∈时，不等式为-sinx ≥cosx 即sinx+cosx ≤0,解得7,4x ππ⎛⎤∈ ⎥⎝⎦，综上得7,44x ππ⎡⎤∈⎢⎥⎣⎦，应选A. 【思路点拨】依照含绝对值的不等式的解法，通过讨论x 的取值范围，去掉绝对值，然后利用单位圆及三角函数线，确信结论.【题文】八、已知)(x f 的概念在()+∞,0的函数，对任意两个不相等的正数21,x x ，都有0)()(212112<--x x x f x x f x ，记5log )5(log ,2.0)2.0(,2)2(22222.02.0f c f b f a ===，那么( ) A.c b a << B.c a b << C.b a c << D.a b c << 【知识点】函数的单调性. B3【答案解析】C 解析：因为对任意两个不相等的正数21,x x ，都有0)()(212112<--x x x f x x f x ，即对任意两个不相等的正数21,x x ，都有21121212121212()()()()0x f x x f x f x f x x x x x x x x x --=<--，因此函数()()f x h x x =是()+∞,0上的减函数，因为20.220.22log 5<<，因此b>a>c,应选C.【思路点拨】构造函数()()f x h x x=，依照条件能够判定它是()+∞,0上的减函数，由此能够判定a,b,c 的大小关系.【题文】九、记函数212131)(23+-=x x x f 在()+∞,0的值域a x x g M ++=2)1()(,在()+∞∞-,的值域为N ，假设M N ⊆,那么实数a 的取值范围是( ) A.21≥a B.21≤a C.31≥a D.31≤a【知识点】函数的值域；集合关系. A1 B1【答案解析】C 解析：因为2()f x x x '=-，由()()()0,01,;f x x '>⇒∈-∞+∞由()()00,1f x x '<⇒∈，因此函数f(x)在（0,1）上单调递减，在()1,+∞上单调递增，因此M=1,3⎡⎫+∞⎪⎢⎣⎭,又N=[),a +∞，因此假设M N ⊆,那么实数a 的取值范围是31≥a ，应选C. 【思路点拨】利用导数求出函数f(x)在()+∞,0的值域M ，再求出函数g(x)的值域N,进而利用M N ⊆求得a 范围.【题文】10、已知函数⎪⎩⎪⎨⎧>≠><-=0)1,0(log 0,1)2sin()(x a a x x x x f a ，且π的图象上关于y 轴对称的点至少有3对，那么实数a 的取值范围是A.⎪⎪⎭⎫⎝⎛55,0 B.⎪⎪⎭⎫ ⎝⎛1,55 C.⎪⎪⎭⎫ ⎝⎛1,33 D.⎪⎪⎭⎫ ⎝⎛33,0 【知识点】函数的图像. B8【答案解析】A 解析：只需函数log ()(01),0a y x a x =-<<<与函数sin 1,02y x x π⎛⎫=-<⎪⎝⎭至少有3个交点，因此2log 52log a a a ->-=，因此2555a a ->⇒-<<，从而0,5a ⎛⎫∈ ⎪ ⎪⎝⎭，应选A. 【思路点拨】问题转化为函数log ()(01),0a y x a x =-<<<与函数sin 1,02y x x π⎛⎫=-<⎪⎝⎭至少有3个交点，由图像可知只需2log 52log a a a ->-=，解得a ⎛∈ ⎝⎭.第II 卷（非选择题，共100分）二、填空题：本大题5小题，每题5分，共25分. 【题文】1一、假设1tan ,3α=-则ααααcos sin 2cos 2sin 3-+= . 【知识点】已知三角函数值求三角函数式的值. C7【答案解析】35- 解析：因为1tan ,3α=-因此ααααcos sin 2cos 2sin 3-+3sin 2cos 3tan 2123cos 2sin cos 22tan 151cos 3αααααααα++-+====-----.【思路点拨】把所求化成关于正切的式子求解.【题文】1二、已知向量)0,2(),2,1(==b a ，假设b a +λ与向量)2,1(-=c 共线，那么实数=λ . 【知识点】向量共线的意义. F1【答案解析】-1 解析：因为)0,2(),2,1(==b a ，因此b a +λ=()2,2λλ+，又b a +λ与)2,1(-=共线，因此()2221λλλ-+=⇒=-.【思路点拨】依照向量的坐标运算求得b a +λ的坐标，再由b a +λ与向量)2,1(-=c 共线得关于λ的方程，解此方程即可.【题文】13、已知函数)('x f 是函数)(x f 的导函数，)0('2sin )(xf x x f +=，那么=)2('πf .【知识点】导数及其运算. B11【答案解析】-2 解析：因为)0('2sin )(xf x x f +=，因此()cos 2(0)(0)cos02(0)(0)1f x x f f f f '''''=+⇒=+⇒=-，因此()cos 2f x x '=-因此=)2('πf -2.【思路点拨】先对函数)0('2sin )(xf x x f +=求导，取得(0)f '的值，进而求出()2f π'.【题文】14、已知函数1223)(--=x x x f ，那么=+⋯+++)1110()113()112()111(f f f f . 【知识点】函数性质求函数值. B1 【答案解析】15 解析：因为1223)(--=x x x f ，因此()()()31231121121x x f x x x ----==---，因此()(1)3f x f x +-=，因此所求=310152⨯= 【思路点拨】能够发觉()(1)3f x f x +-=，因此采纳倒序相加法求解.【题文】1五、概念：若是函数)(x f y =在概念域内给定区间[]b a ,上存在)(00b x a x <<，知足ab a f b f x f --=)()()(0，那么称函数)(x f y =是[]b a ,上的“平均值函数”，0x 是它的一个均值点.例如x y =是[]2,2-上的平均值函数，0确实是它的均值点，假设函数1)(2--=mx x x f 是[]1,1-上的“平均值函数”，那么实数m 的取值范围是 .【知识点】函数中的新概念问题. B1【答案解析】(0，2) 解析：因为函数1)(2--=mx x x f 是[]1,1-上的“平均值函数”，因此存在0x )11(，-∈使21020m m mx x --=--得，1)1(10020+=⇒-=-x m m x x ，又0x )11(，-∈因此实数m 的取值范围是)20(，∈m ．【思路点拨】依照平均值函数”的概念写出m 关于0x 的函数，求此函数在（-1，1）上的值域即可. 三、解答题：本大题共6小时，共75分，解许诺写出文字说明，证明进程和演算步骤.【题文】1六、（本小题总分值12分）已知向量)cos ,(cos ),cos ,(sin wx wx n wx wx m ==，其中0>w 函数12)(-⋅=n m x f 的最小正周期为π.（1）求w 的值. （2）求函数)(x f 在⎥⎦⎤⎢⎣⎡4,6ππ上的最大值. 【知识点】向量的坐标运算;三角函数的化简求值. F2 C7 【答案解析】(1) 1=ω(2)213+ 解析：(1)=)(x f 2m·n -11cos 2cos sin 22-+⋅=x x x ωωω =)42sin(22cos 2sin πωωω+=+x x x ． ………………6分由题意知：π=T ，即πωπ=22，解得1=ω．……………………7分 (2) 由(Ⅰ)知)42sin(2)(π+=x x f ，∵6π≤x ≤4π，得127π≤42π+x ≤43π，又函数y =sin x 在[127π，43π]上是减函数，∴ )34sin(2127sin2)(max πππ+==x f …………………………10分 =213+．…………………………………………………12分【思路点拨】由向量的坐标运算能够列出关系式，求出ϖ的值，再依照解析式在概念域内求出函数的最大值. 【题文】17、（本小题总分值12分）已知函数1)2(log )(2-+-=t t t f 的概念域为D（1）求D ；（2）假设函数222)(m mx x x g -+=在D 上存在最小值2，求实数m 的值. 【知识点】函数的概念域;二次函数的最值. B1 B5【答案解析】(1) )21[，=D (2) 1=m 解析：(1) 由题知⎩⎨⎧≥->-，，0102t t 解得21<≤t ，即)21[，=D ．……………3分(2) g (x )=x 2+2mx -m 2=222)(m m x -+，此二次函数对称轴为m x -=．……4分 ① 假设m -≥2，即m ≤-2时， g (x )在)21[，上单调递减，不存在最小值；②若21<-<m ，即12-<<-m 时， g (x )在)1[m -，上单调递减，]2(，m -上递增，现在22)()(2min ≠-=-=m m g x g ，现在m 值不存在； ③m -≤1即m ≥-1时， g (x )在)21[，上单调递增，现在221)1()(2min =-+==m m g x g ，解得m =1． ………………11分综上：1=m ． ………………………………………………12分【思路点拨】由解析式成立的条件能够取得函数的概念域，再依照二次函数的性质求出m.【题文】1八、（本小题总分值12分）在ABC ∆中，c b a ,,别离是内角C B A ,,的对边，AB=5,51=∠ABC COS . （1）假设BC=4,求ABC ∆的面积ABC S ∆；（2）假设D 是边AC 的中点，且27=BD ，求边BC 的长. 【知识点】同角三角函数关系；三角形面积公式;余弦定理. C2 C8 【答案解析】(I) 46ABC S ∆= (II) 4=CB . 解析：(1) 51cos 5=∠=ABC AB ，，4BC =，又(0,)ABC π∠∈，因此562cos 1sin 2=∠-=∠ABC ABC ， ∴645624521sin 21=⨯⨯⨯=∠⋅⋅=∆ABC BC BA S ABC ．…………6分 (2) 以BC BA ，为邻边作如下图的平行四边形ABCE ，如图，则51cos cos -=∠-=∠ABC BCE ，BE =2BD =7，CE =AB =5，BCDE在△BCE 中，由余弦定理：BCE CE CB CE CB BE ∠⋅⋅-+=cos 2222．即)51(5225492-⨯⨯⨯-+=CB CB ，解得：4=CB ． ……………………………………10分【思路点拨】(1)利用同角三角函数关系求ABC ∠正弦值，再用三角形面积公式求得结论；（2）构造以BC BA ，为邻边作如下图的平行四边形ABCE ，在三角形BCE 中利用余弦定理求出边BC 长.【题文】1九、（本小题总分值12分）记公差不为0的等差数列{}n a 的前n 项和为8533,,,9,a a a S S n =成等比数列.（1）求数列{}n a 的通项公式n a 和n S ；（2）假设，⋯=+=3,2,1,2n a n c n n λ问是不是存在实数λ，使得数列{}n c 为单调递增数列？假设存在，请求出λ的取值范围，假设不存在，请说明理由.【知识点】等差数列及其前n 项和；等比数列；单调递增数列的条件. D1 D2 D3【答案解析】(1)1+=n a n ，2322n n S n =+；（2）存在实数λ，且3->λ. 解析：(1) 由832539a a a S ⋅==，，得：⎪⎩⎪⎨⎧+⋅+=+=⨯+，，)7()2()4(9223311211d a d a d a d a 解得：121==d a ，．∴ 1+=n a n ，n n n n S n 2322)12(2+=++=． …………………………………5分(2) 由题知=n c )1(2++n n λ． ………………………………………………6分假设使}{n c 为单调递增数列，则=-+n n c c 1-+++)2()1(2n n λ)]1([2++n n λ =012>++λn 对一切n ∈N *恒成立，即： 12-->n λ对一切n ∈N *恒成立， ………………………………… 10分又12)(--=n n ϕ是单调递减的, ∴ 当1=n 时，max )(n ϕ=-3，∴ 3->λ． …………………………………………………………………12分【思路点拨】(1)依照已知条件可求出等差数列的首项与公差，从而求得n a 和n S ；（2）假设数列{}n c 为单调递增数列，那么=-+n n c c 1012>++λn 对一切n ∈N *恒成立，即： 12-->n λ对一切n ∈N *恒成立，由此得λ的取值范围.【题文】20、（本小题总分值13分）已知函数e ax e x f x (1)(--=为自然对数的底数），0>a （1）假设函数)(x f 恰有一个零点，证明：1-=a aea（2）假设0)(≥x f 对任意R x ∈恒成立，求实数a 的取值集合. 【知识点】导数的应用. B12【答案解析】(1)观点析；（2）a 的取值集合为{1}.解析：(1)证明：由1)(--=ax e x f x ，得a e x f x -=')(．…………………………1分由)(x f '>0，即a e x ->0，解得x >ln a ，同理由)(x f '<0解得x <ln a ， ∴ )(x f 在(-∞，ln a )上是减函数，在(ln a ，+∞)上是增函数，于是)(x f 在a x ln =取得最小值．又∵ 函数)(x f 恰有一个零点，那么0)(ln )(min ==a f x f ， ………………… 4分即01ln ln =--a a e a ．………………………………………………………… 5分化简得：1ln 1ln 01ln -=-==--a a a a a a a a a 于是，即，， ∴ 1-=a a e a ． ………………………………………………………………… 6分 (2)解：由(Ⅰ)知，)(x f 在a x ln =取得最小值)(ln a f ，由题意得)(ln a f ≥0，即1ln --a a a ≥0，……………………………………8分令1ln )(--=a a a a h ，那么a a h ln )(-='，由0)(>'a h 可得0<a <1，由0)(<'a h 可得a >1．∴ )(a h 在(0，1)上单调递增，在(1，+∞)上单调递减，即0)1()(max ==h a h ， ∴ 当0<a <1或a >1时，h (a )<0，∴ 要使得)(x f ≥0对任意x ∈R 恒成立，.1=a ∴a 的取值集合为{1}………13分【思路点拨】依照函数的导数可判定函数的单调性,由此得函数f(x)只有一个最小值，因为函数)(x f 恰有一个零点，因此此最小值是0，从而证得结论；（1）0)(≥x f 对任意R x ∈恒成立，即函数f(x)的最小值大于或等于0，由此得关于a 的不等式，再利用导数求得结论. 【题文】2一、（本小题总分值14分）已知函数),(ln 2)(2R b a x bx x a x f ∈+-=. （1）假设1==b a ，求)(x f 点())1(,1f 处的切线方程；（2）设0≤a ，求)(x f 的单调区间；（3）设0<a ，且对任意的)2()(,0f x f x ≤>，试比较)ln(a -与b 2-的大小【知识点】导数的几何意义；导数的应用；数值大小的比较. B11 B12 E1【答案解析】(1) 2230x y --=；（2）当a =0，b ≤0时，函数)(x f 的单调递增区间是)0(∞+，；当a =0，b >0时，函数)(x f 的单调递增区间是(0，b 1)，单调递减区间是(b 1，+∞)；当0<a 时，函数)(x f 的单增区间是(0，a a b b 242--)，单减区间是(aab b 242--，+∞)．（3）ln()2a b -<-.解析：(1) 1==b a 时，x x x x f ln 21)(2+-=，xx x f 11)(+-='， ∴21)1(-=f ，1)1(='=f k ，…………………………………………2分故)(x f 点()1(1f ，)处的切线方程是2230x y --=．……………3分(2)由()()∞+∈+-=，，0ln 22x x bx x a x f ，得x bx ax x f 1)(2+-='． (1)当0=a 时，xbxx f -='1)(． ①假设b ≤0，由0>x 知0)(>'x f 恒成立，即函数)(x f 的单调递增区间是)0(∞+，．………5分 ②假设0>b ，当bx 10<<时，0)(>'x f ；当b x 1>时，0)(<'x f ．即函数)(x f 的单调递增区间是(0，b 1)，单调递减区间是(b1，+∞)．…………7分 (2) 当0<a 时，0)(='x f ，得012=+-bx ax ，由042>-=∆a b 得aa b b x a a b b x 24242221--=-+=，．显然，0021><x x ，，当20x x <<时，0)(>'x f ，函数)(x f 的单调递增，当2x x >时，0)(<'x f ，函数)(x f 的单调递减，因此函数)(x f 的单调递增区间是(0，aab b 242--)，单调递减区间是(aa b b 242--，+∞)．……9分综上所述：当a =0，b ≤0时，函数)(x f 的单调递增区间是)0(∞+，；当a =0，b >0时，函数)(x f 的单调递增区间是(0，b 1)，单调递减区间是(b1，+∞)；当0<a 时，函数)(x f 的单增区间是(0，a a b b 242--)，单减区间是(aa b b 242--，+∞)． 10分 (3)由题意知函数)(x f 在2=x 处取得最大值．由(2)知，aa b b 242--是)(x f 的唯一的极大值点，故aa b b 242--=2，整理得a b 412--=-．于是ln()(2)ln()(14)ln()14a b a a a a ---=----=-++令()ln 14(0)g x x x x =+->，那么1()4g x x '=-．令0)(='x g ，得14x =，当1(0)4x ∈，时，0)(>'x g ，)(x g 单调递增；当1()4x ∈+∞，时，0)(<'x g ，)(x g 单调递减．因此对任意0x >，)(x g ≤11()ln 044g =<，又0a ->，故()0g a -<，即041)ln(<++-a a ，即ln()142a a b -<--=-，∴ ln()2a b -<-．……………………………………………………………14分【思路点拨】（1）利用导数的几何意义)(x f 点())1(,1f 处的切线方程；（2）通过讨论a,b 的取值条件，得概念域上函数f(x)的导函数大于0或小于0的x 范围，确实是函数f(x)的增区间或减区间；（3）因为对任意的)2()(,0f x f x ≤>，因此函数)(x f 在2=x 处取得最大值．由(2)知，0<a 时，a a b b 242--是)(x f 的唯一的极大值点，故aa b b 242--=2，整理得a b 412--=-．因此ln()(2)a b ---=ln()41a a -++，利用导数判定那个式子的符号即可.。

2021级(2021届)绵阳一诊英语试题及答案

2021级(2021届)绵阳一诊英语试题及答案绵阳市高中2021 级第一次诊断性考试英语本试卷分为试题卷和答题卡两部分其中试题卷由第I卷(选择题) 和第II卷(非选择题) 组成，共12页; 答题卡共2页。

满分150分，考试时间120分钟。

注意事项:1.答题前，考生务必在答题卡上将自己的学校、班级、姓名用0.5毫米黑色签字笔填写清楚，同时用2B铅笔将考号准确填涂在“考号“栏目内。

2.选择题使用2B铅笔填涂在答题卡对应题目标号的位置上，如需改动，用橡皮擦擦干净后再选涂其它答案非选择题用0.5毫米黑色签字笔书写在答题卡的对应框内，超出答题区域书写的答案无效: 在草稿纸、试愿卷上答题无效。

3.考试结束后将答题卡收回。

第I卷(选择题，共100分)第一部分听力 (共两节，满分30分)回答听力部分时，先将答案标在试卷上。

听力部分结束前，你将有两分钟的时间将你的答案转涂到答题卡上。

第一节 (共5 小题; 每小题1.5 分，满分7.5 分)听下面5 段对话。

每段对话后有一个小题，从题中所给的A、B、C 三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10 秒钟的时间来回答有关小题并阅读下一小题。

每段对话仅读一遍。

例: How much is the shirt? A. ￡ 19.15.B. ￡ 9.18.C. ￡ 9.15. 答案是C.1. Who wants to borrow a camera?B. Jane. A. Mary.C. Alice. 2. What is the man doing?A. Attending an appointmentB. Discussing an agreement.C. Applying for aposition.3. Where are the two speakers talking?A. Ina shop.B. In a bank.C. In a cinema. 4. How long didEric stay abroad in all?A. 9 days.B. 11 days.C. 16 days. 5. Why will Mr. Rogers be off work next week? A. To make his holiday. B. To attend a wedding. C. Totravel on business.第二节 (共15小题; 每小题1.5分，满分22.5分)听下面5段对话或独白。

2021届四川省绵阳市高三第一次诊断性考试数学(理)试题word版含解析

2021届四川省绵阳市高三上学期开学考试数学（文）试题一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合}32|{<<-=x x A ，}05|{2<-∈=x x Z x B ，则=B A （） A ．}2,1{ B ．}3,2{ C ．}3,2,1{ D ．}4,3,2{ 【答案】A2.已知命题p ：01,2>+-∈∀x x R x ，则p ⌝为（）A ．01,2>+-∉∀x x R x B ．01,0200≤+-∉∃x x R x C ．01,2≤+-∈∀x x R x D ．01,0200≤+-∈∃x x R x【答案】D 【解析】试题分析：p ⌝为01,0200≤+-∈∃x x R x ，选D.考点：命题的否定【方法点睛】(1)对全称(存在性)命题进行否定的两步操作：①找到命题所含的量词，没有量词的要结合命题的含义加上量词，再进行否定；②对原命题的结论进行否定.(2)判定全称命题“∀x ∈M ，p(x)”是真命题，需要对集合M 中的每个元素x ，证明p(x)成立；要判定一个全称命题是假命题，只要举出集合M 中的一个特殊值x 0，使p(x 0)不成立即可.要判断存在性命题是真命题，只要在限定集合内至少能找到一个x ＝x 0，使p(x 0)成立即可，否则就是假命题.3.《九章算术》是我国古代内容极为丰富的一部数学专著，书中有如下问题：今有女子善织，日增等尺，七日织二十八尺，第二日、第五日、第八日所织之和为十五尺，则第九日所织尺数为（） A ．8 B ．9 C ．10 D ．11 【答案】B考点：等差数列4.若实数y x ，满足⎪⎩⎪⎨⎧≥≤+≥-010y y x y x ，则y x z +=2的最大值为（）A ．0B ．1C ．2D ．23 【答案】C 【解析】试题分析：可行域为一个三角形ABC 及其内部，其中11(0,0),(1,0),(,)22A B C ，所以直线y x z +=2过点B 时取最大值2，选C. 考点：线性规划【易错点睛】线性规划的实质是把代数问题几何化，即数形结合的思想.需要注意的是：一，准确无误地作出可行域；二，画目标函数所对应的直线时，要注意与约束条件中的直线的斜率进行比较，避免出错；三，一般情况下，目标函数的最大或最小值会在可行域的端点或边界上取得. 5.设命题p ：1)21(<x ，命题q ：1ln <x ，则p 是q 成立的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B 【解析】6.2016年国庆节期间，绵阳市某大型商场举行“购物送券”活动.一名顾客计划到该商场购物，他有三张商场的优惠券，商场规定每购买一件商品只能使用一张优惠券.根据购买商品的标价，三张优惠券的优惠方式不同，具体如下：优惠券A ：若商品标价超过100元，则付款时减免标价的10%；优惠券B ：若商品标价超过200元，则付款时减免30元；优惠券C ：若商品标价超过200元，则付款时减免超过200元部分的20%.若顾客想使用优惠券C ，并希望比使用优惠券A 或B 减免的钱款都多，则他购买的商品的标价应高于（）A ．300元B ．400元C ．500元D ．600元【答案】B 【解析】试题分析：设购买的商品的标价为x ，则(200)20%10%;(200)20%30;400,350400x x x x x x -⨯>⋅-⨯>⇒>>⇒>，选B.考点：不等式应用7.要得到函数)(2cos 32sin )(R x x x x f ∈+=的图象，可将x y 2sin 2=的图象向左平移（） A ．6π个单位 B ．3π个单位 C ．4π个单位 D ．12π个单位【答案】A 【解析】试题分析：因为()sin 2322sin(2)3f x x x x π=+=+，所以可将x y 2sin 2=的图象向左平移3=26ππ，选A.考点：三角函数图像变换【思路点睛】三角函数的图象变换，提倡“先平移，后伸缩”，但“先伸缩，后平移”也常出现在题目中，所以也必须熟练掌握.无论是哪种变形，切记每一个变换总是对字母x 而言. 函数y ＝Asin(ωx ＋φ)，x ∈R 是奇函数⇔φ＝k π(k ∈Z)；函数y ＝Asin(ωx ＋φ)，x ∈R 是偶函数⇔φ＝k π＋π2(k ∈Z)；函数y ＝Acos(ωx ＋φ)，x ∈R 是奇函数⇔φ＝k π＋π2(k ∈Z)；函数y ＝Acos(ωx ＋φ)，x ∈R 是偶函数⇔φ＝k π(k ∈Z).8.已知αθθsin 2cos sin =+，βθ2sin 22sin =，则（） A ．αβcos 2cos = B ．αβ22cos 2cos=C ．02cos 22cos =+αβD ．αβ2cos 22cos = 【答案】D9.已知定义在),0[+∞上的函数)(x f 满足)(2)1(x f x f =+，当)1,0[∈x 时，x x x f +-=2)(，设)(x f 在),1[n n -上的最大值为)(*N n a n ∈，则=++543a a a （）A ．7B ．87C ．45D ．14 【答案】A 【解析】试题分析：23412345113111111(),()2(),(2)2()1,2()2,2()4,242222222a f a f f a f f a f a f ======+======，所以3451247a a a ++=++=，选A.考点：函数性质【思路点睛】(1)运用函数性质解决问题时，先要正确理解和把握函数相关性质本身的含义及其应用方向. (2)在研究函数性质特别是奇偶性、周期、对称性、单调性、最值、零点时，要注意用好其与条件的相互关系，结合特征进行等价转化研究.如奇偶性可实现自变量正负转化，周期可实现自变量大小转化，单调性可实现去f “”，即将函数值的大小转化自变量大小关系10.在ABC ∆中，81cos =A ，4=AB ，2=AC ，则A ∠的角平分线D A 的长为（） A ．22 B ．32 C ．2 D ．1 【答案】C考点：余弦定理11.如图，矩形ABCD 中，2=AB ，1=AD ，P 是对角线AC 上一点，25AP AC =，过点P 的直线分别交DA 的延长线，AB ,DC 于N E M ,,.若DA m DM =，DC n DN =)0,0(>>n m ，则n m 32+的最小值是（） A ．56 B ．512 C ．524 D ．548【答案】C 【解析】试题分析：232555AP AC DP DA DC =⇒=+,设DP xDM yDN =+,则1x y +=，又DP mxDA ynDC =+,所以3232,15555mx ny m n==⇒+=，因此321941942423(23)()(12)(122)55555n m n m m n m n m n m n m n +=++=++≥+⋅=，当且仅当23m n =时取等号，选C.考点：向量表示，基本不等式求最值【易错点睛】在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误.12.若函数144)(234+-++=x ax x x x f 的图象恒在x 轴上方，则实数a 的取值范围是（）A ．)(2,+∞B ．)(1,+∞C ．),213(+∞-D ．),212(+∞- 【答案】A二、填空题（每题4分，满分20分，将答案填在答题纸上）13.若向量)0,1(=a ，)1,2(=b ，)1,(x c =满足条件b a -3与c 垂直，则=x . 【答案】1 【解析】试题分析：(3)0(1,1)(,1)01a b c x x -⋅=⇒-⋅=⇒= 考点：向量垂直【方法点睛】平面向量数量积的类型及求法(1)求平面向量数量积有三种方法：一是夹角公式a ·b ＝|a ||b |cos θ；二是坐标公式a ·b ＝x 1x 2＋y 1y 2；三是利用数量积的几何意义.(2)求较复杂的平面向量数量积的运算时，可先利用平面向量数量积的运算律或相关公式进行化简. 14.在公差不为0的等差数列}{n a 中，831=+a a ，且4a 为2a 和9a 的等比中项，则=5a . 【答案】13考点：等差数列 15.函数x x a x f ln )(=的图象在点))(,(22e f e 处的切线与直线x ey 41-=平行，则)(x f 的极值点是 . 【答案】e 【解析】试题分析：2(1ln )()a x f x x -'=，所以244(12)1()1a f e a e e -'==-⇒=，因此)(x f 的极值点是1ln 0,x x e -== 考点：导数几何意义，函数极值【思路点睛】(1)求曲线的切线要注意“过点P 的切线”与“在点P 处的切线”的差异，过点P 的切线中，点P 不一定是切点，点P 也不一定在已知曲线上，而在点P 处的切线，必以点P 为切点.(2)利用导数的几何意义解题，主要是利用导数、切点坐标、切线斜率之间的关系来进行转化.以平行、垂直直线斜率间的关系为载体求参数的值，则要求掌握平行、垂直与斜率之间的关系，进而和导数联系起来求解.16.)(x f 是定义在R 上的偶函数，且0≥x 时，3)(x x f =.若对任意的]32,12[+-∈t t x ，不等式)(8)3(x f t x f ≥-恒成立，则实数t 的取值范围是 .【答案】3-≤t 或1≥t 或0t = 【解析】试题分析：由题意得0x <时，3()()f x f x x =-=-，即3()||f x x =，因此33(3)8()|3|8|||3|2||f x t f x x t x x t x -≥⇒-≥⇒-≥，当0t =时，x R ∈,满足条件；当0t >时，5tx t x ≥≤-或,要满足条件，需2123150t t t t t t ⎧-≥+≤-⎪⇒≥⎨⎪>⎩或；当0t <时，5tx x t ≥-≤或,要满足条件，需2123350t t t tt t ⎧-≥-+≤⎪⇒≤-⎨⎪<⎩或；综上实数t 的取值范围是3-≤t 或1≥t 或0t = 考点：不等式恒成立【思路点睛】求参数取值范围常用的方法和思路(1)直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围； (2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.已知函数)2||,0,0)(sin()(πϕωϕω<>>+=A x A x f 的图象（部分）如图所示.（1）求函数)(x f 的解析式；（2）若），（30πα∈，且34)(=παf ，求αcos .【答案】（1）)6sin(2)(ππ+=x x f （2）6215+考点：求三角函数解析式，给值求值【方法点睛】已知函数sin()(A 0,0)y A x B ωϕω=++>>的图象求解析式(1)max min max min,22y y y y A B -+==. (2)由函数的周期T 求2,.T πωω=(3)利用“五点法”中相对应的特殊点求ϕ.18.设数列}{n a 的前n 项和为n S ，已知)(12*N n a S n n ∈-=.（1）求数列}{n a 的通项公式；（2）若对任意的*N n ∈，不等式92)1(-≥+n S k n 恒成立，求实数k 的取值范围. 【答案】（1）12-=n n a （2）)643[∞+，【解析】试题分析：（1）由和项求通项，要注意分类讨论：当1n =时，11a S =；当1n =时，11a S =解得11=a ；当2n ≥时，1n n n a S S -=-化简得12-=n n a a ；最后根据等比数列定义判断数列}{n a 为等比数列，并求出等比数列通项（2）先化简不等式，并变量分离得k ≥nn 292-，而不等式恒成立问题一般转化为对应函数最值问题，即k ≥nn 292-的最大值，而对数列最值问题，一般先利用相邻两项关系确定其增减性：令n nn b 292-=，则1112211292272+++-=---=-n nn n n nn n b b ，所以数列先增后减，最后根据增减性得最值取法：n b 的最大值是6436=b ．试题解析：(1)令111121a a S n =-==，，解得11=a ．……………………………2分由12-=n n a S ，有1211-=--n n a S ，两式相减得122--=n n n a a a ，化简得12-=n n a a （n ≥2）， ∴ 数列}{n a 是以首项为1，公比为2 的等比数列，∴ 数列}{n a 的通项公式12-=n n a ．……………………………………………6分考点：由和项求通项，根据数列单调性求最值【方法点睛】给出S n 与a n 的递推关系求a n ，常用思路是：一是利用S n －S n －1＝a n (n ≥2)转化为a n 的递推关系，再求其通项公式；二是转化为S n 的递推关系，先求出S n 与n 之间的关系，再求a n . 应用关系式a n ＝⎩⎪⎨⎪⎧S 1，n ＝1，S n －S n －1，n ≥2时，一定要注意分n ＝1，n ≥2两种情况，在求出结果后，看看这两种情况能否整合在一起. 19.在ABC ∆中，角C B A ,,所对的边分别为c b a ,,，已知12=c ，64=b ，O 为ABC ∆的外接圆圆心. （1）若54cos =A ，求ABC ∆的面积S ；（2）若点D 为BC 边上的任意一点，1134DO DA AB AC -=+，求B sin 的值. 【答案】（11442（2）552sin =B 【解析】考点：向量投影，正弦定理【思路点睛】三角函数和平面向量是高中数学的两个重要分支，内容繁杂，且平面向量与三角函数交汇点较多，向量的平行、垂直、夹角、数量积等知识都可以与三角函数进行交汇.不论是哪类向量知识与三角函数的交汇试题，都会出现交汇问题中的难点，对于此类问题的解决方法就是利用向量的知识将条件转化为三角函数中的“数量关系”，再利用三角函数的相关知识进行求解.20.已知函数x x x x f cos sin )(+=.（1）判断在)(x f 区间)3,2(上的零点个数，并证明你的结论；（参考数据：4.12≈，4.26≈）（2）若存在)2,4(ππ∈x ，使得x kx x f cos )(2+>成立，求实数k 的取值范围.【答案】（1）有且只有1个零点（2）π22<k (2)由题意等价于x x x cos sin +x kx cos 2+>，整理得x x k sin <．…………7分令x x x h sin )(=，则2sin cos )(xx x x x h -='，令x x x x g sin cos )(-=，0sin )(<-='x x x g ，∴g(x)在)24(ππ，∈x 上单调递减， …………………………………………9分 ∴0)14(22)4()(<-⨯=<ππg x g ，即0sin cos )(<-=x x x x g ， ∴0sin cos )(2<-='xx x x x h ，即x x x h sin )(=在)24(ππ，上单调递减， ……11分 ∴ππππ2242244sin)(==<x h ，即π22<k ． ………12分考点：函数零点，利用导数研究不等式有解【方法点睛】利用函数零点的情况求参数值或取值范围的方法(1)利用零点存在的判定定理构建不等式求解.(2)分离参数后转化为函数的值域(最值)问题求解.(3)转化为两熟悉的函数图象的上、下关系问题，从而构建不等式求解.21.已知函数1ln )(2-+=ax x x f ，e e x g x-=)(.（1）讨论)(x f 的单调区间；（2）若1=a ，且对于任意的),1(+∞∈x ，)()(x f x mg >恒成立，求实数m 的取值范围. 【答案】（1）a ≥0时，)(x f 的单调递增区间是)0(∞+，； 0<a 时，)(x f 的单调递增区间是)210(a-，；单调递减区间是)21(∞+-，a．（2）m ≥e 3．②当em 30<<时，令x x q x me x p x 2)(1)(=-=，．显然x me x p x 1)(-=在)1[∞+，上单调递增，∴2131)1()(min =-⨯<-==e e me p x p ．由x x q 2)(=在)1[∞+，单调递增，于是2)(min =x q ．∴min min )()(x q x p <．于是函数xme x p x 1)(-=的图象与函数x x q 2)(=的图象只可能有两种情况：若)(x p 的图象恒在)(x q 的图象的下方，此时)()(x q x p <，即0)(<'x h ，故)(x h 在)1(∞+，单调递减，又0)1(=h ，故0)(<x h ，不满足条件．若)(x p 的图象与)(x q 的图象在x>1某点处的相交，设第一个交点横坐标为x0，当)1(0x x ，∈时，)()(x q x p <，即0)(<'x h ，故)(x h 在)1(0x ，单调递减，又0)1(=h ，故当)1(0x x ，∈时，0)(<x h ．∴)(x h 不可能恒大于0，不满足条件．……9分③当m ≥e 3时，令x x me x x 21)(--=ϕ，则21)(2-+='xme x x ϕ． ∵x ∈)1(∞+，，∴21)(2-+='xme x x ϕ>2-x me ≥0123>=-⋅e e ，故x xme x x 21)(--=ϕ在x ∈)1(∞+，上单调递增，于是033211)1()(=-⨯>--=>e e me x ϕϕ，即0)(>'x h ， ∴)(x h 在)1(∞+，上单调递增，∴0)1()(=>h x h 成立．综上，实数m 的取值范围为m ≥e3．………………………………………12分考点：利用导数求函数单调区间，利用导数求参数取值范围【方法点睛】利用导数解决不等式恒成立问题的“两种”常用方法(1)分离参数法：将原不等式分离参数，转化为不含参数的函数的最值问题，利用导数求该函数的最值，根据要求得所求范围.一般地，f(x)≥a 恒成立，只需f(x)min ≥a 即可；f(x)≤a 恒成立，只需f(x)max ≤a 即可.(2)函数思想法：将不等式转化为某含待求参数的函数的最值问题，利用导数求该函数的极值(最值)，然后构建不等式求解.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）选修4-4：坐标系与参数方程以直角坐标系的原点O 为极点，x 轴非负半轴为极轴建立极坐标系，已知曲线C 的极坐标方程为θθρcos 4sin 2=.（1）求曲线C 的直角坐标方程；（2）若直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+=+=t y t x 511521（t 为参数），设点)1,1(P ，直线l 与曲线C 相交于B A ,两点，求||||PB PA +的值.【答案】（1）24y x =（2）415∴1544)(2122121=-+=-=+t t t t t t PB PA ．……………………………10分考点：极坐标方程化为直角坐标方程，直线参数方程几何意义23.（本小题满分10分）选修4-5：不等式选讲已知函数)(|1||1|)(R a a x x x f ∈+--+=.（1）若1=a ，求不等式0)(≥x f 的解集；（2）若方程()f x x =有三个实数根，求实数a 的取值范围.【答案】（1）)21[∞+-，（2）11a -<< (2)由方程x x f =)(可变形为11+--+=x x x a ．令⎪⎩⎪⎨⎧>-≤≤---<+=+--+=，，，，，，12111211)(x x x x x x x x x x h 作出图象如右． ………………………8分于是由题意可得11a -<<．…………10分考点：绝对值定义【名师点睛】含绝对值不等式的解法有两个基本方法，一是运用零点分区间讨论，二是利用绝对值的几何意义求解．法一是运用分类讨论思想，法二是运用数形结合思想，将绝对值不等式与函数以及不等式恒成立交汇、渗透，解题时强化函数、数形结合与转化化归思想方法的灵活应用，这是命题的新动向．。

四川省绵阳市2021届高三第一次诊断文综历史试题含答案

四川省绵阳市2021届高三第一次诊断试题文综历史24.两河流域、印度河流域等世界原生文明诞生地的形成空间均不过数十万平方公里，唯有中华文明的形成覆盖了长江、黄河及辽河流域的面积近300万平方公里的范围。

这凸显出中华文明形成之时便具有A.多元一体的政治格局B.以德治民的民本思想C.厉行专制的集权意识D.农耕经济的高度繁荣25.图5《废井田，开阡陌》是当代画家张友仁的作品。

他根据战国时期商鞅变法的史实创作，曾作为中学历史教材插图而广为人知。

该作品A.创作源于画家的生活实践B.能完整还原历史真实C.是对历史的一种艺术表达D.体现写意传神的特点26.北魏时期，孝文帝深叹“移风易俗,实为甚难”，南迁洛阳后，留在北方边镇民众甚至出现了鲜卑化趋势。

而在南方，新汉族较多地保存了北方汉族之文化传统，“蛮气”则显得不足。

南北民族交融的差异缘于A.区域地理环境B.经济发展水平C.汉文化影响力D.政府推行力度27.唐律规定“奴婢比之资财”，“律比畜产”，地位低下。

宋代除少数官奴婢外，私奴往往订立契约，约以时限，付以雇值，又称“女使”。

这反映了宋代A.宗法等级观念淡薄B.人身依附关系弱化C.女性政治地位提高D.雇佣劳动开始出现28.16--18世纪，“南海”是东西方贸易的集中地，中国的“朝贡贸易”规则被世界各国普遍遵守，白银产量的一半也流入中国，“南海”因此有“东方地中海”之称。

该局面的形成主要得益于A.农耕文明的发达B.郑和下西洋的推动C.海禁政策的松弛D.白银货币化的影响29.明清商人群体中常见“抱德怀才岂惮贫，广行方便方施仁。

光明正大无荣辱，留此心田荫后人”。

“处世为人做一场，要留名节与纲常"之类的劝诫。

这反映出当时A.尊富尚利意识的盛行B.社会风尚发生转变C.儒家财富观受到冲击D.商人责任意识增强30.传统观点认为，《天朝田亩制度》是对古代农民起义“均田免粮”思想的发展。

后来有学者认为，均田纲领是长期以来客家先民心理积淀的一种折射,它主要解决的是土、客矛盾, 而不是贫富悬殊的问题带有浓厚的华南乡土色彩。

2021年四川省绵阳市中考数学一诊试卷(附答案)

2021年四川省绵阳市中考数学一诊试卷一、选择题：本大题共12个小题，每小题3分，共36分.每个小题只有一个选项最符合题目要求.1. 下列各项是一元二次方程的是（）A.x−x3＝1B.2x−1＝aC.x2−x+1＝0D.x2−＝52. 下列手机手势解锁图案中，是中心对称图形的是()A. B.C. D.3. 将抛物线y＝x2平移得到抛物线y＝(x+2)2+3，下列叙述正确的是（）A.向右平移2个单位，向上平移3个单位B.向左平移2个单位，向下平移3个单位C.向右平移2个单位，向下平移3个单位D.向左平移2个单位，向上平移3个单位4. 风力发电是一种绿色可持续的能源获取方式，我国近年来在西部地区大力发展风电产业，如图的风力发电转子叶片图案绕中心旋转n∘后能与原来的图案重合，那么n的值可能是（）A.60B.90C.120D.1505. 方程x2−3x−1＝0的根的情况是（）A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法确定6. 如图，四边形ABCD是⊙O内接四边形，若∠BAC＝30∘，∠CBD＝80∘，则∠BCD的度数为（）A.50∘B.60∘C.70∘D.80∘7. 某校初2017级学生毕业时，每一位同学都将自己的照片向全班其他同学各送一张留作纪念，某班共送了1892张照片，设全班有x名学生，根据题意，列出方程应为（）A.x2＝1892B.x(x−1)＝1892C.(x−1)2＝1892D.2x(x−1)＝18928. 如图，⊙O1的直径AB长度为12，⊙O2的直径为8，∠AO1O2＝30∘，⊙O2沿直线O1O2平移，当⊙O2平移到与⊙O1和AB所在直线都有公共点时，令圆心距O1O2＝x，则x的取值范围是（）A.2≤x≤10B.4≤x≤16C.4≤x≤4D.2≤x≤89. 如图，C、D是抛物线y＝x2−x−3上在x轴下方的两点，且CD // x轴，过点C、D分别向x轴作垂线，垂足分别为B、A，则矩形ABCD周长的最大值为（）A. B. C. D.10. 如图，AB是⊙O的直径，C为⊙O上的点，把△AOC沿OC对折，点A的对应点D恰好落在⊙O上，且C、D均在直径AB上方，连接AD、BD，若AC＝4，BD＝4，则AD的长度应是（）A.12 B.10 C.8 D.611. 如图，⊙O的半径是4，A为⊙O上一点，M是⊙A上一点（M在⊙O内），过点M作⊙A切线l，且l与⊙O相交于P，Q两点，若⊙A的半径为2，当线段PQ最长时线段OM的长度为m，当线段PQ最短时线段OM的长度为n，则m−n的值是（）A.2−3B.C.2−2D.2−212. 已知P1(x1, y1)，P2(x2, y2)，…，P n(x n, y n)，…是二次函数y＝x2−2x+1图象上的一系列点，其中x1＝1，x2＝2，…，x n＝n，…，记A1＝x1+y2，A2＝x2+y3，…，A n＝x n+y n+1（n为正整数），令S＝++ +…+，则S的值是（）A. B. C. D.二、填空题：本小题共6个小题，每小题4分，共24分。