三阶幻方专项练习题
三阶幻方题目初一

三阶幻方题目初一
以下是关于三阶幻方的初一题目:
1. 什么是三阶幻方?
2. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都相等,这个和是多少?
3. 如果在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是奇数,有哪些填法?
4. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是偶数,有哪些填法?
5. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是质数,有哪些填法?
6. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是3的倍数,有哪些填法?
7. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是平方数,有哪些填法?
8. 在三阶幻方中填入数字1-9,使得每行、每列和每条对角线上的数字之和都是立方数,有哪些填法?
这些题目可以作为初一学生的练习题,通过解答这些题目,可以加深学生对三阶幻方的理解。
三阶幻方
6
28
15
例5、已知下图中,每一行、每一列对角线上3个数的乘积都相等,请填出其他的数。
1
12
6
3
例6已知下图是一个三阶幻方,每一行、每一列、每条对角线的和都等于2037,求画有“?”的格子填的数是多少。
447
?
894
练习题
1、用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
三阶幻方
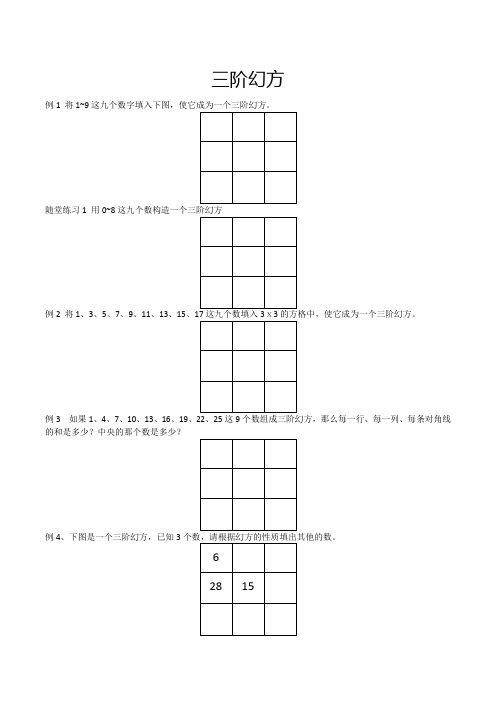
例1将1~9这九个数字填入下图,使它成为一个三阶幻方。
随堂练习1用0~8这九个数构造一个三阶幻方
例2将1、3、5、7、9、11、13、15、17这九个数填入3ⅹ3的方格中,使它成为一个三阶幻方。
例3如果1、4、7、10、13、16、19、22、25这9个数组成三阶幻方,那么每一行、每一列、每条对角线的和是多少?中央的那个数是多少?
2、用0、2、4、6、8、10、12、14、16这9个数作一个三阶幻方。
3、在空格中填数,使每一行、每一列、每条对角线的和都等于30.
5
8
4、在空格中填数,使每一行、每一列、每条对角线的和都等于30.
14
7
5、数独游戏
3
5
6
5
1
3
9
8
3
1
2
5
1
65Leabharlann 7843
4
9
1
4
8
3
1
5
7
7
5
4
2
8
9
7
1
5
8
4
9
三阶幻方练习题

三阶幻方练习题1. 幻方是一个由数字组成的方阵,每一行、每一列以及对角线上的数字之和都相等。
请计算一个三阶幻方的和。
2. 已知一个三阶幻方的行和为15,求幻方中最小的数字。
3. 一个三阶幻方的行和为33,求幻方中最大的数字。
4. 幻方的构造方法之一是使用Snellius幻方,即第一行从1开始,第二行从第二行的最后一个数字开始,依此类推。
请根据这个方法构造一个三阶幻方。
5. 请证明一个三阶幻方的数字总和是固定的。
6. 幻方中,对角线上的数字和与行和或列和相等。
请找出一个三阶幻方的对角线和。
7. 给定一个三阶幻方,其中第一行的数字为8、1、6,第三行的数字为3、5、7,求第二行中间的数字。
8. 一个三阶幻方的行和为15,且第一行的数字为4、9、2,求第三行的数字。
9. 已知一个三阶幻方的行和为15,且幻方的中心数字为5,求幻方的构造方法。
10. 请构造一个三阶幻方,使得每行、每列以及两条对角线上的数字之和都为15。
11. 幻方的数字可以是任意正整数,但通常从1开始。
请构造一个三阶幻方,其中数字从5开始。
12. 请证明一个三阶幻方中不可能有连续的三个数字构成等差数列。
13. 一个三阶幻方的行和为15,且每行的数字都是奇数,求幻方的构造方法。
14. 给定一个三阶幻方,其中第一行的数字为4、3、8,第二行的数字为9、5、1,求第三行的数字。
15. 请构造一个三阶幻方,使得每行、每列的数字之和为15,且幻方的中心数字为9。
16. 幻方的行和、列和以及对角线和都相等,这个和被称为幻和。
请证明一个三阶幻方的幻和是固定的。
17. 请构造一个三阶幻方,使得每行、每列以及两条对角线上的数字之和都为21。
18. 一个三阶幻方的行和为15,且幻方的左上角数字为1,求幻方的构造方法。
19. 请证明一个三阶幻方中,任何两个相邻的行或列的数字之和都不可能相等。
20. 一个三阶幻方的行和为15,且幻方的右上角数字为7,求幻方的构造方法。
三阶幻方练习十二题

三阶幻方练习十二题幻方是一种非常有趣的数学游戏。
在幻方中,一组数字被排列成一个正方形矩阵,并且每行、每列和对角线上的数字之和都相等。
以下是几个幻方问题的解决方案:1.构造一个三阶幻方,其中包含数字7到15.7 12 610 14 813 11 92.构造一个三阶幻方,其中包含数字3、4、5、8、9、10、13、14和15,并计算幻和。
4 9 1715 1 147 13 10幻和为30.3.使用数字3、6、9、12、15、18、21、24和27构造一个三阶幻方。
15 6 324 12 918 21 274.使用数字2、4、6、8、10、12、14、16和18构造一个三阶幻方。
16 2 126 10 148 18 45.构造一个三阶幻方,使其幻和为18.2 7 94 5 97 1 106.使用9个连续自然数构造一个三阶幻方,使每一行、每一列和每条对角线的和都为60.8 1 63 5 74 9 27.使用9个连续自然数构造一个三阶幻方,使每一行、每一列和每条对角线上的三个数字之和都为30.2 7 69 5 14 3 88.使用数字3到11填写下面的幻方,并计算幻和。
4 9 23 5 78 1 6幻和为15.9.在幻方中填写数字,使得每一行、每一列和每条对角线上的三个数字之和都为30,且数字不大于15且互不相同。
4 14 129 7 1413 3 1410.在幻方中填写数字,使得每一行、每一列和每条对角线上的三个数字之和都为30.8 1 63 5 74 9 211.在幻方中填写数字,使得每一行、每一列和每条对角线上的三个数字之和都为30.2 9 47 5 36 1 812.解决下图中的三阶幻方,找出“?”的值。
2 4 93.81 6 7的值为5.。
四年级三阶幻方题目

四年级三阶幻方题目一、三阶幻方基础概念。
1. 定义。
- 三阶幻方是一个3×3的方格阵列,将1 - 9这九个数字填入方格中,使得每行、每列以及两条对角线上的三个数字之和都相等。
这个相等的和称为幻和。
- 对于1 - 9这九个数字组成的三阶幻方,幻和为15,因为(1 +2+3+4+5+6+7+8 + 9)÷3=15。
2. 中心数的特性。
- 在三阶幻方中,中心数是关键。
中心数等于幻和除以3。
对于1 - 9组成的三阶幻方,中心数为5。
二、题目及解析。
题目1。
- 在一个三阶幻方中,已知左上角的数字是1,右上角的数字是3,请填出这个三阶幻方。
- 解析:- 因为幻和为15,所以第一行中间数为15-(1 + 3)=11,但1 - 9中没有11,说明思路错误。
由于中心数是5,那么第一行中间数为15-(1+5)=9,第三行中间数为15-(3 + 5)=7。
- 第一列中间数为15-(1+7)=7(这里与第三行中间数计算结果相同,验证了计算的合理性)。
- 第三列中间数为15-(3+9)=3。
- 所以这个三阶幻方为:begin{bmatrix}195 753 717end{bmatrix}题目2。
- 已知三阶幻方的幻和是18,求这个幻方中的中心数。
- 解析:- 根据中心数等于幻和除以3的特性,中心数为18÷3 = 6。
题目3。
- 用3、4、5、6、7、8、9、10、11构造一个三阶幻方。
- 解析:- 首先求幻和,(3 + 4+5+6+7+8+9+10+11)÷3=21。
- 中心数为21÷3 = 7。
- 然后按照与1 - 9构造幻方类似的方法,左上角先填最小数3,右上角填最大数11,则第一行中间数为21-(3+11)=7(正好是中心数,验证计算正确)。
- 第一列中间数为21-(3 + 7)=11,第三列中间数为21-(11+7)=3。
- 这个三阶幻方为:begin{bmatrix}399 876 1056end{bmatrix}题目4。
四年级三阶幻方题目

四年级三阶幻方题目一、三阶幻方基础概念。
1. 定义。
- 三阶幻方是一个3×3的矩阵,其每行、每列以及两条对角线上的数字之和都相等,这个相等的和称为幻和。
2. 幻和的计算方法。
- 对于三阶幻方,由于1 + 2+3+4+5+6+7+8+9 = 45,而三阶幻方三行(或三列)的数字之和相等,所以幻和为45÷3 = 15。
二、题目及解析。
题目1。
- 在一个三阶幻方中,已知左上角的数字是1,右上角的数字是3,求中间格的数字。
- 解析:- 设中间格数字为x。
根据三阶幻方幻和为15,先看第一行1 + a+3 = 15,可得a = 11。
再看对角线1+x + 7 = 15(因为1 - 5 - 9是一条对角线,幻和为15,所以右下角是9,那么与1和9构成对角线的中间数x = 5),解得x = 5。
题目2。
- 三阶幻方中,最上面一行中间的数字是2,最下面一行中间的数字是6,求这个幻方的幻和。
- 解析:- 设左上角数字为a,右上角数字为b。
因为幻方每行每列及对角线和相等。
第一行a+2 + b =幻和,第三行c + 6+d =幻和。
又因为中间列2 + 5+6 = 13(中间数是5,因为1 - 5 - 9是中间列常见组合满足幻和15,这里先假设幻和为15来分析数字关系)。
由于幻和相等,所以幻和为15。
再验证,设a = 4,b = 9,c = 7,d = 2,满足条件。
题目3。
- 已知三阶幻方的幻和是15,且左上角数字为2,求左下角数字。
- 解析:- 设左下角数字为x。
因为幻和为15,第一列2 + y+z = 15。
对角线2 + 5+8 = 15(中间数5,根据幻和计算中间数为15÷3 = 5)。
第三列x+w + 8 = 15。
又因为第二行y+5 + w = 15。
由幻和15可知,第一行2+7+6 = 15,所以第三列x = 4时,4+3+8 = 15。
题目4。
- 三阶幻方中,中间数是5,左上角数字是3,求右上角数字。
三阶幻方练习题。

1. 用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方2. 用0、2、4、6、8、10、12、14、16这9个数作一个三阶幻方13. 在空格中填数,使每一行,每一列、每条对角线的和都等于30.4. 用9个连续自然数组成三阶幻方,使每一行、每一列、每条对角线的和都是60□5□□□□□□3题5. 一个三阶幻方的幻和是60.这个幻方最中间的数是()。
组成幻方的9个数的和是()6.. 一个三阶幻方,最中间的数是30 ,这个幻方的幻和是()。
组成幻方的9个数的和是()7.. —个三阶幻方的幻和是45.这个幻方最中间的数是()。
组成幻方的8.. —个三阶幻方,最中间的数是8,这个幻方的幻和是(组成幻方的9个数的和是() 9.用1,234,5,6,7,8,9 写一个三阶幻方。
18、21、24、27这9个数作一个三阶幻方。
10.将6,6,6,8,8,8,10,10,10 这9个数填入幻方格中, 5.用0 — --8这9个数,做一个三阶幻方11.在空格里填数,使横竖对角线上三个数的和是2 1 . 7.使横竖对角线上三个数的和是是每行每列对角线上三个数的 用 3、6、9、12、15、12.填上其他8个数,使得方格中的9个数为9个连续自然数。
9. 有蜘蛛、蜻蜓、蝉三种昆虫共18 只,共有腿118 条。
翅膀20 对,(蜘蛛8 条腿,蜻蜓6 条腿, 2 对翅膀,蝉 6 条腿, 1 对翅膀),三种昆虫各多少只?10. 蜘蛛8 条腿,蜻蜓 6 条腿, 2 对翅膀,蝉 6 条腿, 1 对翅膀。
这三种昆虫共有21 只,有140 条腿和23 对翅膀. 求每种昆虫各几只?11. 有一个车队以每秒行 5 米的速度通过一座长200 米的大桥共用145 秒.已知每辆车长 5 米.一个车队以每秒行五米的速度通过一座长200 米的大桥共用一145 秒.已知每辆车长5 米,两车隔8 米, 这个车队有多少辆车?12. 小明步行上学,每分钟行70 米,离家12 分钟后,爸爸发现小明的文具盒忘记在家里,立即骑自行车以每分钟280 米的速度去小明,那么爸爸出发后几分钟追上小明?13. 一队中学生到某地进行军事训练,他们以每小时 5 千米的速度前进,走了 6 小时后,学校派秦老师骑自行车以每小时15 千米的速度追赶学生队伍,传达学校通知。
小学奥数三阶幻方

小学奥数三阶幻方三阶幻方三阶幻方就是将九个自然数填在3×3(三行三列)的正方形内,使每一行、每一列以及每一条对角线上的三个数的和都相等。
三阶幻方是一种特殊的数阵图。
例1将1-9这九个数填入方格,使它成为一个三阶幻方。
分析:1+2+3+4+。
+9=45所以,每行、每列、每条对角线的三个数的和是45÷3=15 9+5+1,9+4+28+6+1,8+5+2,8+4+37+6+2,7+5+36+5+4这8个式子中5出现四次,所以5一定在中心。
8、6、4、2这四个数出现三次,所以在四个角上。
816357492随堂练习1、用0-8这9个数构造一个三阶幻方。
2、将2,4,6.18填入3×3方格中,使它成为一个三阶幻方。
公式:三阶幻方中央的数=行(列)和÷3和=中央数×33、假如2、6、10、11、15、19、20、24、28能够构成一个三阶幻方,那么每行、每列、每条对角线的和是几何?中央数是几何?4、如图,这是一个三阶幻方,请填出其它数。
xxxxxxxx2324)(5)5、已知图中,每行、每列、每条对角线上3个数的乘积都相等,请填出其它的数。
6、把下图三阶幻方补充完整。
447?894练习题1、用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
2、用、2、4、6、8、10、12、14、16这9个数作一个三阶幻方。
第1题)(第2题)3、在空格中填数,使每一行、每一列、每条对角线的和是30.58第3题)(第4题)(第5题)4、在空格中填数,使每行、每列、每条对角线的和是30.5、用9个连续自然数构成三阶幻方,使每行、每列、每条对角线的和是60.6、下列图是一个三阶幻方,求?是几何。
1913第6题)(第7题)7、从1-13这13个数中选12个数填到下图,使每一横行的4个数的和相等,每一竖列的3个数的和也相等。
这时所选的12个数是哪12个数?每一行的和是多少?每一列的和是多少?。
三阶幻方练习题。

1.用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
2.用0、2、4、6、8、10、12、14、16这9个数作一个三阶幻方。
1 2题3.在空格中填数,使每一行,每一列、每条对角线的和都等于30.4. 用9个连续自然数组成三阶幻方, 使每一行、每一列、每条对角线的和都是603题5.一个三阶幻方的幻和是60.这个幻方最中间的数是 ( )。
组成幻方的9个数的和是( )6. .一个三阶幻方,最中间的数是30,这个幻方的幻和是( )。
组成幻方的9个数的和是( )7. 一个三阶幻方的幻和是45.这个幻方最中间的数是 ( )。
组成幻方的9个数的和是( )8..一个三阶幻方,最中间的数是8,这个幻方的幻和是( )。
组成幻方的9个数的和是( )9. 用1,2,3,4,5,6,7,8,9 写一个三阶幻方。
用3、6、9、12、15、18、21、24、27这9个数作一个三阶幻方。
10. 将6,6,6,8,8,8,10,10,10这9个数填入幻方格中, 5. 用0---8 这9个数,做一个三阶幻方是每行每列对角线上三个数的 和都相等。
11.在空格里填数,使横竖对角线上三个数的和是21. 7. 使横竖对角线上三个数的和是30.12.填上其他8个数,使得方格中的9个数为9个连续自然数。
9.有蜘蛛、蜻蜓、蝉三种昆虫共18只,共有腿118条。
翅膀20对,( 蜘蛛8条腿,蜻蜓6条腿,2对翅膀,蝉6条腿,1对翅膀),三种昆虫各多少只?10. 蜘蛛8条腿,蜻蜓6条腿,2对翅膀,蝉6条腿,1对翅膀。
这三种昆虫共有21只,有140条腿和23对翅膀.求每种昆虫各几只?11. 有一个车队以每秒行5米的速度通过一座长200米的大桥共用145秒.已知每辆车长5米.一个车队以每秒行五米的速度通过一座长200米的大桥共用一145秒.已知每辆车长5米,两车隔8米,这个车队有多少辆车?12. 小明步行上学,每分钟行70米,离家12分钟后,爸爸发现小明的文具盒忘记在家里,立即骑自行车以每分钟280米的速度去小明,那么爸爸出发后几分钟追上小明?13.一队中学生到某地进行军事训练,他们以每小时5千米的速度前进,走了6小时后,学校派秦老师骑自行车以每小时15千米的速度追赶学生队伍,传达学校通知。
奥数练习题之三阶幻方(含答案)-

三阶幻方同学们:在33⨯(三行三列)的正方形方格中,既不重复又不遗漏地填上1—9这9个连续的自然数,使每行、每列、每条对角线上的三个自然数的和均相等,这样的图形叫做三阶幻方。
如果在44⨯(四行四列)的正方形方格中进行填数,就要不重复,不遗漏地在44⨯方格内填上16个连续自然数,且使每行、每列、每条对角线的四个自然数之和均相等,这样的图形叫四阶幻方。
一般地,在几×几(几行几列)的方格里,既不重复又不遗漏地填上几×几个连续自然数,(注意这几×几个连续自然数不一定非要从1开始),每个数占一个格,且每行、每列、每条对角线上的几个自然数和均相等,我们把这个相等的和叫做幻和,几叫做阶,这样排成的数的图形叫做几阶幻方。
(一)思路指导与解答例1. 用1~9这九个数编排一个三阶幻方。
a bc def g hi图1 图2分析:我们先用a 、b 、c 、d 、e 、f 、g 、h 、i 分别填入九个空格内以代表应填的数。
看图(2):(1)通过审题,我们知道幻和是多少才好进行填数。
同时可以看到图(2)中,e 是一个中间数,也是关键数。
因为它分别要与第二行、第二列以及两条对角线上的另外两个数进行求和运算,结果都等于幻和;其次是三阶幻方中四个角上的数:a 、c 、g 、i 它们各自都要参加一行,一列及一条对角线的求和运算。
如果e 以及四个角上的数被确定之后,其它的数字便可以根据幻和是多少填写出来了。
(2)求幻和:幻和=++++++++÷()1234567893=÷=45315(3)选择突破口,显然是e ,看图2。
因为:a e i b e h c e g d e f ++=++=++=++=15所以:()()()()a e i b e h c e g d e f +++++++++++ =+++=1515151560也就是:()a b c d e f g h i e +++++++++⨯=360 又因为:a b c d e f g h i ++++++++=45 所以45360+⨯=e 36045⨯=-e e =5也就是说,图1中的中心方格中应填5,请注意,这个数正好是1~9这九个数中正中间的数。
2022年三阶幻方讲解和练习题

2022年三阶幻方讲解和练习题幻方起源于中国. 传说在大禹治水时,有只神龟在洛水中浮起,龟背上有奇特的图案,如右图. 人们称之为洛书.如果将龟背上的数字翻译出来,如下图.观察,你发现了什么? 观察发现,上图的每行每列,斜着的三个数之和都是15. 像这样,将九个不同的自然数填在3×3(三行三列)的正方形内,使每行、每列以及每条对角线上的三个数和都相等,这样的图形就叫三阶幻方. 三阶幻方是一种特殊的数阵图.上面的三阶幻方中,15是这个幻方的和,简称幻和. 5是幻方最中心的数字,简称中心数.三阶幻方的规律:(1)幻和= 九个数之和 ÷3; (2)中间数=幻和÷3(3)四个角上的数字 2=(3+1)÷2,8=(9+7)÷2例题1 在图中填上合适的数,使每行、每列、每一条对角线的三个数的和都相等。
巩固练习:在下图的方格中填上适合的数,使每行、每列、每一条对角线的三个数的和都等于21。
73 84 63 二、例题讲解 672159834例题2 在下图中填上适当的数,使每行、每列、每条对角线上的三个数的和都相等。
巩固练习:根据三阶幻方的特点,完成下列幻方。
例题3 在下图的每个空格中填入小于12且互不相同的九个自然数,使得每行、每列及每条对角线上的三个数之和都等于21。
巩固练习:在下列右图空着的方格内填上合适的数,使得每一横行、每一竖列和对角 线上的三个数之和都等于27。
例题4 将1~9这九个自然数填在下面图中的九个方格里,使每行、每列、两条对角线上的三个数的和都相等。
19 1410 18 812介绍杨辉法:介绍公式法:口诀:九子斜列,上下对易,左右相更,四维挺出。
想一想还有没有其他填法:第一种:816 357 492第二种:618 753 294第三种:492357816第四种:294753618第五种:672159834第六种:834159672第七种:276951438第八种:438951276巩固练习:用3-11构造一个三阶幻方课堂练习1、把4~12九个数填入方格中,使每行、每列、每一条对角线的三个数的和都相等。
三阶幻方练习题(打印版)

三阶幻方练习题(打印版)一、填空题1. 一个三阶幻方是一个3×3的方阵,其中每行、每列以及两条对角线上的数字之和都相等。
若三阶幻方的左上角数字为1,求其右下角的数字。
2. 假设一个三阶幻方的和为15,计算第二行中间的数字。
二、计算题1. 请构造一个三阶幻方,使得其每行、每列以及对角线上的数字之和为15。
2. 已知一个三阶幻方的第二行的三个数字分别为4、9、2,求出其第一行和第三行的数字。
三、推理题1. 给定一个三阶幻方,其中第一行的数字为3、5、7,第二行的中间数字为8,求出幻方的所有数字。
2. 一个三阶幻方的对角线数字之和为18,且第一行的中间数字为6,求出幻方的所有数字。
四、应用题1. 某数学竞赛中,要求参赛者构造一个三阶幻方,使得其每行、每列以及对角线上的数字之和为特定的数值。
如果这个特定的数值是18,参赛者需要构造出幻方。
2. 一个三阶幻方的每行、每列以及对角线上的数字之和为16,如果将幻方中的数字都增加2,新的幻方的和是多少?五、拓展题1. 尝试构造一个4×4的幻方,使得其每行、每列以及两条对角线上的数字之和相等。
2. 一个幻方中,数字1到9恰好各出现一次,且每行、每列以及对角线上的数字之和相等。
请说明这样的幻方存在性,并给出证明。
答案提示:- 对于填空题,需要理解幻方的基本性质,即每行、每列、每条对角线的和相等。
- 在计算题中,可以利用幻方的性质,通过已知的数字推算出未知的数字。
- 推理题需要综合运用幻方的规则和逻辑推理能力,找出所有可能的数字。
- 应用题则需要将幻方的概念应用到具体的问题中,通过计算得出答案。
- 拓展题则是对幻方概念的进一步探索,需要更高级的数学技巧和创造性思维。
注意:这些题目旨在锻炼学生的逻辑思维和数学推理能力,同时加深对幻方这一数学现象的理解。
在解答时,应遵循数学的逻辑和规则,确保答案的准确性。
