化学反应速率 化学反应速率理论
无机及分析化学二章节化学反应速率

对气体而言,C可以以p表示,如上例
v=k ·C(O2) 或v=k’·p(O2) k大小由实验测得
v2 = kc2(NO2)
3、应用反应速率方程时应注意的问题
速率方程通式: 对于反应 aA+bB=dD+eE
v=k·CAm·CBn 对于基元反应:v=k·CAa·CBb 对于非基元反应:v=k·CAm·CBn 基元反应的a.b 是方程式中的系数, 非基元反应的m.n是由实验所测数据得出 m.n可能与a.b相同,也可能不同.m=a,n=b不代 表此反应一定是基元反应
对于 H2 :1级
对于:Cl2 0.5级
对于整个反应:1.5级
反应级数与实验条件有关;如蔗糖水解 反应是二级反应,但当水为大量时,可 视为水的浓度不变,即反应对水是零级、 总反应变为一级反应。
复杂反应的反应级数求法:由实验测:
例: 298K, 3I-(aq) + S2O82-(aq)= 2SO42- + I3求k、m、n、m+n
代入 第一组(或其他组)数:
k= 0.65mol-1·min-1·L
浓度如何影响反应速率 ——影响单位体积内活化分子的总数
C(反应物)增大,单位体积内分子数增大、有 效碰撞次数增大、v增大;
活化分子总数增大但活化分子百分数f不变
单位体积内分子数 活化分子数 f
100个
8个
f=8%
浓度增大 1000个
大学化学反应速率

压力对反应速率的影响Байду номын сангаас
总结词
压力越大,反应速率越快
详细描述
在一定条件下,压力越大,气体分子 密度越大,分子之间的碰撞频率和碰 撞力度增加,从而提高了反应速率。
催化剂对反应速率的影响
总结词
催化剂可以加快或减慢反应速率
详细描述
催化剂可以改变反应的途径和能量需求,从而影响反应速率。有些催化剂可以降低活化 能,使反应更容易进行,从而提高反应速率;而有些催化剂则可能通过抑制或促进某些
课程目标
01 掌握化学反应速率的基本概念、单位和表 示方法。
02 理解影响化学反应速率的因素,如温度、 浓度、压力等。
03
学习如何通过实验测定化学反应速率,并 掌握相关的实验技能。
04
了解化学反应速率在生产和生活中的应用, 培养解决实际问题的能力。
02
化学反应速率定义
化学反应速率定义
化学反应速率是指在一定条件下,化学反应进行的快慢程度,通常用单位时间内 反应物浓度的减少或生成物浓度的增加来表示。
大学化学反应速率
• 引言 • 化学反应速率定义 • 影响化学反应速率的因素 • 化学反应速率理论 • 化学反应速率的应用 • 结论
01
引言
主题简介
化学反应速率是化学学科中的重要概 念,它描述了化学反应的快慢程度。
化学反应速率的研究有助于理解化学 反应机理、反应条件和反应过程,对 于化学工业、药物合成等领域具有重 要意义。
反应速率是化学反应动力学的重要参数,可以用来描述和比较不同化学反应的进 行速度。
反应速率的表示方法
反应速率常数
在一定温度下,反应速率与反应物的浓度无关,而与催化剂的存在、光、磁场等外部条件有关,这种速率常数称 为反应速率常数。
化学反应速率及其表示方法反应速率理论简介

二、质量作用定律
当其他条件一定时,反应物浓度越大,化学 反应的速率越快。
对有气体参加的化学反应,增大压力,反 应速率也会随之增大。
质量作用定律指出: 在一定温度下,元反应 的反应速率与反应物浓度以其化学计量数的绝 对值为幂指数的乘积成正比。
(3) 温和的催化条件:酶在常温常压下即可发 挥催化作用,温度过高会引起酶变性,失去催化 活性。
(4) 特殊的 pH:酶只能在一定的 pH 范围内发 挥催化作用,如果 pH 偏离这个范围,酶的活性就 会降低,甚至完全丧失。
对于酶的催化作用机理,一般认为是通过生成 某种中间化合物进行的。酶 E 先与底物 S 形成中间 化合物 ES,然后 ES 再进一步分解为产物 P,并释 放出酶 E。此过程可表示为:
E + S 噲垐kk1?1? ES k2 E + P
r Hm rUm=Em,2-Em,1 = (E-Em,1)(E-Em,2)
r H m=Ea-Ea'
第三节 浓度对化学反应速率的影响
一、元反应和复合反应 二、质量作用定律 三、反应级数和反应分子数
一、元反应和复合反应
反应物的微粒间直接碰撞而一步实现的化 学反应,称为元反应。
大多数化学反应要经过若干个元反应才能完 成,这类反应称为复合反应。
反应级数通常是利用实验测定的。
(二)反应分子数
反应分子数是指元反应中参加反应的微粒 的数目。元反应分为单分子反应、双分子反应 和三分子反应。
反应级数与反应分子数是两个不同的概念。 反应级数是指速率方程中浓度项的幂指数之和, 可利用实验测定,它体现了反应物浓度对反应 速率的影响,其数值可能是整数、分数或零, 也可能是负数。反应分子数是对元反应而言的, 它是由反应机理所决定的,其数值只可能是 1、 2、3 。在元反应中,反应级数和反应分子数通 常是一致的。
《有机化学》第二章 化学反应速率

1.2×10-2 = k ×(1.0)x ×(1.0)y 4.8 × 10-2 = k ×(1.0)x ×(2.0)y
以上两式相除得: y=2
该反应的速率方程为: kcA cB2
②将任何一组实验数据代入速率方程
1.2102 mol L1 S 1
k cA cB2 (1.0mol L1)(1.0mol L1)2
催化剂通过改变反 应历程,降低反应的 活化能,从而间接增 加活化分子百分数, 加快反应速率。
注:一般反应中,反应级数x、y由实验确定,x、y可以 是整数,分数 或 零。
例: 在 298.15 K 时,发生下列反应:
aA + bB
C
将不同浓度的 A,B 两种溶液混合,得到下列实验数据:
A的初始浓 度/mol·L-1
1.0
2.0 1.0
B的初始浓 度/mol·L-1
1.0
1.0 2.0
初始速率υ/ mol·L-1 ·s-1
[B] t
:物质B的浓度随时间的变化率。
二、瞬时速率
1 lim [B] B t0 t
第二节 影响反应速率的因素
一、 浓度对反应速率的影响 1.速率方程式:
一般反应: mA+nB
pC+qD
kcAx cBy
⑴速率常数k: 只与温度、催化剂有关,与浓度无关。
⑵反应级数
①定义:速率方程式中,反应物浓度的指数x、y分别称为 反应物A和B的反应级数。总反应级数 = x + y
3.质量作用定律:— 只适用于基元反应
质量作用定律:恒温下,基元反应的化学反应 速率与各反应物浓度方次的乘积成正比,反应 物浓度的方次数就等于化学反应式中各相应物 质的计量系数。
化学反应速率理论

化学反应速率理论
反应(1)为硫酸生产中的SO3的合成反应,反应(2)为合成 氨反应,都需要高温高压和催化剂的条件,而酸碱中和反应(3)在 常温常压下就能进行,且反应速率很快。
总之,反应的活化能的大小是决定反应速率的重要因素。碰撞
理论直观明了地说明了反应速率v
Ea的关系,但没有从分
子内部原子重新组合的角度去揭示活化能的物理意义。
化学反应速率理论
一、 有效碰撞理论与活化能
1918年,路易斯(Lewis)在阿仑尼乌斯研究的基础上,利用 气体分子运动论的成果,提出有效碰撞理论:化学反应发生的先决条 件是反应物分子间互相接触发生碰撞,但并不是每次碰撞都能发生化 学反应,大多数碰撞是无效的,只有相碰撞的反应物分子的能量超过 某一数值时,碰撞后才能发生反应。
化学反应速率理论
二、 过渡态理论
随着人们对原子、分子内部结构认识的深入, 1935年,艾林(Eyring)在量子力学和统计力学的 基础上提出了过渡态理论:化学反应不只是通过 反应物分子的简单碰撞就能完成的,在反应物到 生成物的转变过程中,必须经过一个中间过渡状 态,即反应物分子先形成活化络合物,然后再分 解为产物。
无机化学
化学反应速率理论
大气污染已经成为公众日益关注的环境问题,为了减少汽车尾气 的排放,可利用如下反应:
有些反应需要快速完成,而有些反应如橡胶的老化或者金属的腐 蚀,人们又常常希望它慢一些,因此只有在深入研究速率理论的基础 上了解反应机理,才能实现对反应速率和反应途径的控制。
自1889年阿仑尼乌斯提出活化分子、活化能之后,在气体分子 运动论和分子结构知识的基础上,逐渐形成有效碰撞理论和过渡态理 论两种主要的反应速率理论。
化学反应速率理论
活化分子具有较高的能量,以克服相碰撞时电子云之间的斥力, 并导致分子中旧键的断裂和新键的生成。反应速率的大小主要取决于 单位时间内有效碰撞的次数,而有效碰撞的次数不仅与活化分子的能 量、数目有关,也与反应的活化能密切相关。每个反应都有符合其特 征的活化能,在一定的温度下,反应的活化能越大、活化分子所占的 比例越小,单位时间内有效碰撞的次数越少,反应进行的速率就越慢。 反之,反应的活化能越小、活化分子所占的比例越大,反应速率就越 快。不同类型的反应,活化能差别很大,例如:
第三章 化学反应速率
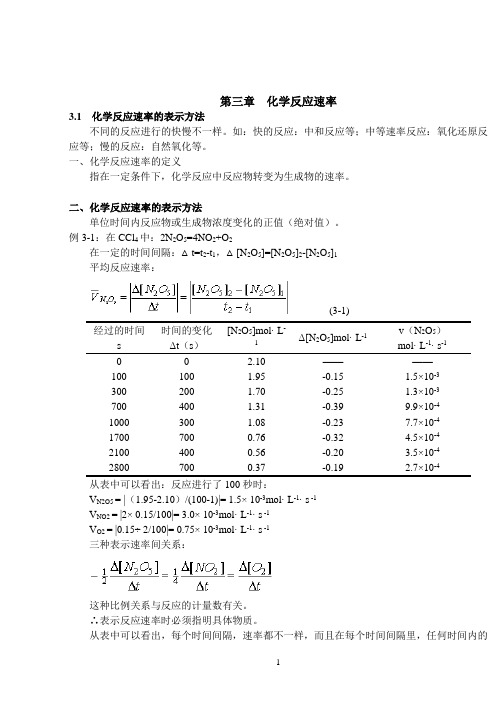
第三章化学反应速率3.1化学反应速率的表示方法不同的反应进行的快慢不一样。
如:快的反应:中和反应等;中等速率反应:氧化还原反应等;慢的反应:自然氧化等。
一、化学反应速率的定义指在一定条件下,化学反应中反应物转变为生成物的速率。
二、化学反应速率的表示方法单位时间内反应物或生成物浓度变化的正值(绝对值)。
例3-1:在CCl4中:2N2O5=4NO2+O2在一定的时间间隔:△t=t2-t1,△[N2O5]=[N2O5]2-[N2O5]1平均反应速率:(3-1)经过的时间s 时间的变化Δt(s)[N2O5]mol· L-1Δ[N2O5]mol· L-1v(N2O5)mol· L-1· s-10 0 2.10 ————100 100 1.95 -0.15 1.5×10-3300 200 1.70 -0.25 1.3×10-3700 400 1.31 -0.39 9.9×10-41000 300 1.08 -0.23 7.7×10-41700 700 0.76 -0.32 4.5×10-42100 400 0.56 -0.20 3.5×10-42800 700 0.37 -0.19 2.7×10-4从表中可以看出:反应进行了100秒时:V N2O5 = |(1.95-2.10)/(100-1)|= 1.5× 10-3mol· L-1· s -1V NO2 = |2× 0.15/100|= 3.0× 10-3mol· L-1· s -1V O2 = |0.15÷ 2/100|= 0.75× 10-3mol· L-1· s -1三种表示速率间关系:这种比例关系与反应的计量数有关。
∴表示反应速率时必须指明具体物质。
化学课件第四章、化学反应速率
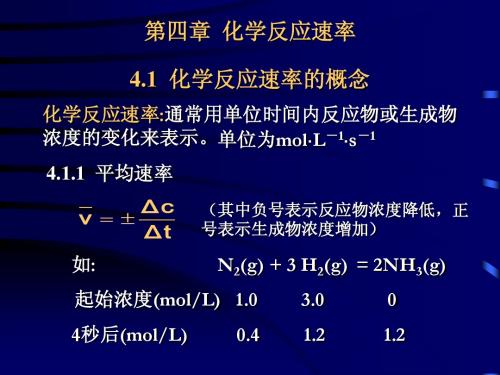
1 1 v = vNH3 = vH2 = vN2 = 0.15mol⋅L−1 ⋅ S−1 2 3
4.1.2 瞬时速率(即时速率) 瞬时速率(即时速率) 瞬时速率: 化学反应进行到某一时刻的速率. 瞬时速率: 化学反应进行到某一时刻的速率.
ν = κ ⋅ c (A)⋅ c (B)
a b
k称为速率常数,其数值为在一定条件(温度、 称为速率常数,其数值为在一定条件(温度、 催化剂) 当各反应物浓度均为1mol· 催化剂)下,当各反应物浓度均为1mol·L-1时的化 学反应速率。 值决定于反应的本性和反应温度, 学反应速率。k值决定于反应的本性和反应温度, 与反应物浓度无关。 值一般都由实验测定。 与反应物浓度无关。k值一般都由实验测定。 (a+b)称为反应总级数 (a+b)称为反应总级数
说明: (1)速率常数 的单位与反应总级数有关: 说明: (1)速率常数k的单位与反应总级数有关: 速率常数k a+b 0 1 2 反应总级数 0级 一级 二级 k的单位 mol·L mol·L-1 · S-1 S -1 L · mol-1 · S-1
(2) a+b称为反应总级数, a为反应物A的级数,b a+b称为反应总级数 a为反应物 的级数,b 称为反应总级数, 为反应物A 为反应物B的级数. 为反应物B的级数.
∆c dc v = ±lim = ± t dt ∆t→ ∆ 0
对任一化学反应: 对任一化学反应:
−ν A ⋅ A−νB ⋅ B = + Y ⋅Y +νΖ ⋅ Z ν 1 dc(A) 1 dc(B) 1 dc(Y) 1 dc(Z) v= = = = ν A dt νB dt νY dt νZ dt
化学反应速率(无机化学核心教程)

Rate of chemical reaction
作业:PP55 1,3,4,9,13
CO(g) + NO(g) == CO2(g) + 1/2 N2(g) Kθp=1.9×1060 >> 500 (298K)
常温下,此反应基本上不能进行,为什么?
CO(g) + NO(g)
3 2 1
时间变化
反应物浓 度减少
生成物浓 度增加
想一想:化学反应速度与普通物体的移动速度 有些什么相同的地方?
全程平均速度 某一点的瞬时速度
二、化学反应的平均速率和瞬时速度
平均速率 瞬时速率
△c(反应物) =- △t
dc(反应物) = -
dt
IH2O2(aq) === H2O(l) + 1/2O2(g)
E
E1 A+B+C
(1)
(2) [AC]+B
C A+B AB
[AB]+C
练习题
√1、如果催化剂能使正增加三倍,
那么必然也能使逆增加三倍。
×2、加入催化剂能使平衡常数增大。
×3、催化剂能使非自发反应变成自发反应。
三、生物催化剂——酶
酶
底物
产物(脂肪、淀粉)
特点
选择性特别高 须适当的pH、T 催化效率特别高
2.50
0
0
1.00min 2.50-2x 4x
x
c0= 2.50/5.00 = 0.500(mol/L)
lnc = - kt + lnc0
0.5mol/L
1.68x10-2s-1 60 s
N2O5的剩余浓度:c = 0.182(mol/L) ∴ N2O5的剩余量 = 0.182×5.00 = 0.910(mol) ∵ 2.50 - 2x = 0.910 ∴ x = 0.795 (mol)
化学反应速率

3 2.0×10-4
0.5×10-2
0.65×10-6
求其反应速率方程和速率常数k . 解: 设其速率方程为:v=k cm (S2O82-) ·n (I-) c
解题步骤略。
将1、2两组数据代入得:m =1; 将2、3两组数据代入得:n=1; 将m和n代入第一组数据,得:k=0.65 (L· -1· -1) mol min
温度每上升10℃,反应速率增大到原来的2~4倍。
k t+10
kt
= r = 2~4
k t+n×10 = rn kt
(4-3)
15
阿仑尼斯(Arrhenius)方程
摩尔气体常数
k = A· -Ea/RT e
速率常数 反应 温度
(4-4)
速率常数与温 度间的关系
指前因子
活化能
16
温度对反应速率的影响
对于特定化学反应:
-νA A-νBB -·· = ·· + νY Y +νz Z ·· ·· ·· ·· 其在某一时刻的反应速率为:
v= dc(A) dc(B) dc(Y) dc(Z) = = = = νAdt νBdt νYdt νZdt dξ dt
6
(4-1)
4.2 浓度对反应速率的影响
基元反应与复杂反应
k 298K 5.34 10 4 298 273 lg 4 8.2 10 2.303 8.314 298 273 k 5.9 10 3 (L mol 1 s 1 )
19
1/T
3.66×10-3
3.5×10-3
3.41×10-3
3.30×10-3
lgk
20 3.7(1/T)×10-3
第三章-化学反应速率理论

. surface
一
势 能 )面 (
1. 势能面概念的提出:
反应体系从始态经活化状态到终态,必然伴随着势能的 起伏变化,如果将这连续变化的势能标示出来,就构成了一 个如山峦起伏的势能面。如果能计算出势能面上越过某一能 垒的频率,即能计算出反应速率。
根据碰撞理论:
k PBT1/ 2eEc / RT
d ln k dT
1 2T
Ec RT 2
公 式 的
Ea
RT 2
1 2T
Ec RT 2
Ea
Ec
1 2
RT
比
EC——临界能
较
Ea——表观活化能(实验值)
由此式可知Ea与T确实有关。
Ea与Ec的异同
Ea=E活-E反——表观活化能是2个平均能量之差,是一个
正面碰撞 活化络合物 B-C键拉长
A-B成键 AB与C分离
设:x轴表示rAB,y轴表示rBC,z轴表示V, 则可得一势能面图形:
将势能面投影到一个平面图中——势能曲线 (RTP曲线)图,每条曲线是等势能线,线上数字 越大,势能越高。RTP曲线代表由A+B-C→A-B+C 的耗能最少的途径——反应坐标。
过渡态(T)能量 是所有其它中间 态能量最低的。
由R到达P点,需跨 越的最低势垒是T点
R——反应物(A+B-C)势能——势阱; T——活化络合物势能([A…B…C])——过渡态——势垒 ——鞍点; P——产物(A-B+C)势能——势阱; D——某种中间态势能(A…B…C)
化学反应速率

4.非基元反应: 反应物分子需经几步反应才能转化为生成物的反 非基元反应: 应。 例如: 例如:H2+I2 (1) I2
→ →
2HI 2I 2HI
分二步进行 (快反应) (快反应) 快反应 (慢反应) (慢反应) 慢反应
(2)2I+H2
→
速率方程V= 速率方程V= k [ I ] 2 [ H 2 ] 对于非基元反应,其反应的速率方程只有通过实验来确定。 对于非基元反应,其反应的速率方程只有通过实验来确定。
在T1、T2时, ①
Ea lg k1 = − + lg A 2.303RT1
Ea lg k 2 = − + lg A 2.303RT2
lg k 2 − lg k1 = Ea 1 1 ( − ) 2.303R T1 T2
② ②-①得:
或
k2 T 2 − T1 Ea lg ( ) = k 1 2 .303 R T1T2
例如: 例如:2N2O5=4NO2+O2
[ N 2 O 5 ]1 − [ N 2 O 5 ] 2 ∆ [ N 2O 5 ] V ( N 2O 5 ) = = t 2 − t1 ∆t
V ( NO2 ) =
V (O2 ) =
∆[ NO2 ] ∆t
∆[O2 ] ∆t
从表7 数据可知,不同时间间隔里, 从表7-1数据可知,不同时间间隔里,反应的
速率常数k 6. 速率常数k的单位与反应级数的关系 反应级数 1 2 N 0 速率方程 V= k(A) V= k(A)2 V= k(A)N V= k
k的单位
s- 1 dm3 mol-1 s (dm3 mol-1)N-1 s-2 mol dm-3 s-1
因此, 的单位,可判断出反应的级数. 因此,由k的单位,可判断出反应的级数.
影响化学反应速率的因素

影响化学反应速率的因素一、化学反应速率理论1、有效碰撞反应物分子间能发生反应的碰撞。
发生条件:①发生碰撞的分子具有较高的能量;②分子在一定方向上发生碰撞2、活化分子化学反应中,能量较高、有可能发生有效碰撞的分子。
3、活化能活化分子的平均能量与所有分子的平均能量之差。
例1:下列说法正确的是①活化分子间的碰撞一定能发生化学反应;②普通分子间的碰撞有时也能发生化学反应;③活化分子比普通分子具有较高的能量;④化学反应的实质是原子的重新组合;⑤化学反应的实质是旧化学键的断裂和新化学键的形成过程;⑥化学反应的实质是活化分子有合适取向时的有效碰撞。
例2:1918年,Lewis提出反应速率的碰撞理论:反应物分子间的相互碰撞是反应进行的必要条件,但并不是每次碰撞都能引起反应,只有少数碰撞才能发生化学反应。
能引发化学反应的碰撞称之为有效碰撞。
⑴图I是HI分解反应中HI分子之间的几种碰撞示意图,其中属于有效碰撞的是(填“A”“B”或“C”);⑵20世纪30年代,Eyring和Pelzer在碰撞理论的基础上提出了化学反应的过渡态理论:化学反应并不是通过简单的碰撞就能完成的,而是在反应物到生成物的过程红经过一个高能量的过渡态。
图Ⅱ示NO2和CO反应生成CO2和NO过程中能量变化示意图,请写出NO2和CO反应的热化学方程式:⑶过渡态理论认为,催化剂改变反应速率的原因是改变了反应的途径,对大多数反应而言主要是通过改变过渡态而导致有效碰撞所需要的能量发生变化。
请在图Ⅱ中作出NO2和CO反应时使用催化剂而使反应速率加快的能量变化示意图。
⑷进一步研究表明,化学反应的能量变化( H)与反应物和生成物的键能有关。
键能可以简单地理解为断开1mol化学键时所需吸收的能量。
下表是部分化学键的键能数据:已知白磷的燃烧热为2378.0kJ/mol,白磷完全燃烧的产物结构如图Ⅲ所示,则上表中x=二、影响化学反应速率的因素1、内因(主要因素):⑴化学键的强弱与反应速率的关系:例如:在相同条件下,F2与H2在黑暗处就能发生爆炸(反应速率非常大);Cl2与H2在光照条件下会发生爆炸(反应速率大);Br2与H2在加热条件下会发生爆炸(反应速率较大);I2与H2在较高温度时才能发生反应,同时生成HI又分解(反应速率较小)。
化学反应速率

二、反应级数和反应分子数
1.反应级数 速率方程式中各反应物浓度项指数之和
例: 某元反应
a A b B c C
反应级数 = a + b
1 dc(B) a b vB kc (A)c (B) B dt
反应级数可能因实验条件改变而发生变化 反应级数意义: ① 表示了反应速率与物质的量浓度的关系; ②零级反应表示了反应速率与反应物浓度无关 ③反应级数0~10…,是整数、分数。
2 HI( g ) H2 ( g ) I2 ( g )
10
有效碰撞的条件之一:
碰撞的分子需具备足够高的能量。 这样的分子称为活化分子
11
活化能Ea
Ea Ec E
Ec:活化分子具有的 最低能量
E:分子的平均能量
对于气相双分子反应: A(g) + B(g) →C(g)
v Ze
23
问题 :
对臭氧转变成氧的反应
2O3(g) 3O2(g)
其历程为:
O3 O+O3 O2+O (快) 2O2(慢)
适合此历程的速率方程是什么? a. kc2 (O3) c. kc(O3)2c(O2) b.kc(O3)c(O) d. kc2 (O3) c-1(O2)
24
2. 反应速率系数(k):
cA =1mol· -1 L , cB =1mol· -1 L
反应的热效应
吸热反应
放热反应
18
影响反应速率的因素
浓度对反应速率的影响 温度对反应速率的影响 催化剂对反应速率的影响
19
第三节
浓度对反应速率的影响和速率方程
一、元反应速率方程的确定—质量作用定律 在一定温度下,元反应的反应速率与反 1.质量作用定律 应物浓度以其化学计量数的绝对值为指 数的幂的乘积成正比幻灯片 31
第四章化学反应速率

(二) Arrhenius方程的应用: *测定反应的活化能 lgk = -Ea/2.303RT + lgA 1.作图法:测定不同温度下的反应速率常 数,以lgk对1/T作图,得到一条直线,直线斜率 = -Ea/2.303R 故Ea=-2.303R×(斜率)
2.计算法求Ea 因为 lgk1 = -Ea/2.303RT1 + lgA (1) lgk2 =-Ea/2.303RT2 + lgA (2) 故(2) – (1)得: lg(k2 / k1) = Ea(T2-T1) /2.303RT2T1 *求速率常数或温度 1.若已知Ea、T1、T2和k1,可求得T2温度下 的速率常数k2; 2.若已知Ea、k1、k2和T1 ,可求得另一温度 T2。
一、范托夫规则:温度每升高10K,化学反应速
率约增加到原来的2~4倍。
二、Arrhenius方程
活化能 速率系数 热力学温度
Hale Waihona Puke k = A e -Ea / RT
摩尔气体常数
指数前参量
Arrhenius方程的对数形式: lnk = -Ea / RT + lnA lgk = -Ea / 2.303RT + lgA
反应级数的确定: *首先写出该反应的速率方程式,反应级数待定; *然后固定其他反应物的浓度,只改变某一反应物 的浓度,以确定该反应物的反应级数。 序 号 1 2 3 4 起始浓度(mol⋅L-1) ⋅ 起始浓度 A 1.0×10-2 × 1.0×10-2 × 1.0×10-2 × 2.0×10-2 × B 0.5×10-3 × 1.0×10-3 × 1.5×10-3 × 0.5×10-3 × 反应速率v 反应速率 mol⋅L-1⋅min-1 ⋅ 2.5×10-7 × 5.0×10-7 × 7.5×10-7 × 1.0×10-6 ×
《普通化学》--4化学反应速率

4次碰撞 次碰撞
6次碰撞 次碰撞
8次碰撞 次碰撞
16次碰撞 次碰撞
质量作用定律指出: 在一定温度下, 质量作用定律指出: 在一定温度下,反应速 率与反应物浓度的乘积成正比。 率与反应物浓度的乘积成正比。
表明反应物浓度与反应速率之间定量关 系的数学表达式称为速率方程。 速率方程。 系的数学表达式称为速率方程
介绍一种速率方程的确定方法 — 初始速率法
对反应 NH4+(aq) + NO2-(aq)
实
1 2 3
N2(g) + 2H2O(l)
初始速率(mol dm–3·s–1)
1.35×10-7 × 2.70×10-7 × 5.40×10-7 ×
验
初始c (NH4+)
0.100 mol dm–3 0.100 mol dm–3 0.200 mol dm–3
单位时间内反应物浓度的减少或者产物浓度的 增加来表示. 增加来表示. 浓度常用mol·l-1,时间常用 ,min,h 时间常用s, 浓度常用 , 反应速率又分为平均速率(average rate)和 反应速率又分为平均速率( ) 瞬时速率(instaneous rate)两种表示方法. 瞬时速率( )两种表示方法 平均速率: 平均速率:v = △c / △t +dc(N2O 5) 瞬时速率只能用作图的方法得到: = 瞬时速率只能用作图的方法得到:v = − lim v ∆ t → t0 d
应用Arrhenius方程时,还应注意到下列问题: 方程时,还应注意到下列问题: 应用 方程时 处于方程的指数项中, 有显著影响 在室温下, 有显著影响, ● Ea处于方程的指数项中,对k有显著影响,在室温下, 值降低约80% 。 每增 加 4kJ·mol-1, k值降低约 值降低约 温度升高, 增大 一般反应温度每升高10℃ 增大, ● 温度升高,k增大,一般反应温度每升高 ℃,k将增大 将增大 2~4倍。 倍 ●根据 ln
无机化学 第二章 化学反应基本原理-化学反应速率

2.3. 3 影响化学反应速率的因素
(1)浓度对反应速率的影响 质量作用定律 law of mass action
一定温度时,基元反应的反应速率与各 反应物浓度系数次方的乘积成正比. 即基元反应
aA+dD =gG+hH
的速率方程为:
kca (A)cd (D)
此数学表达式称反应速率方程式
(mol.L-1.s-1) 0.012 0.024 0.048
求该反应的速率方程式和速率常数k .
解:与c(A)成正比,
与c(B)的平方成正比
= kc(A)c 2(B)
k = 1.2 mol-2.L2.s-1
反应级数 order of reaction
化学反应的反应速率与各反应 物浓度某次方的乘积成正比.
温度每升高10ºC,反应速率加快2~4倍
kt+10 /kt = 2~4= (温度系数)
Arrhenius (阿仑尼乌斯)公式
反应速率 k 的对数与温度 T 的倒数存在 线性关系
ln k Ea 1 lCnA Ea:活化能
RT
R:摩尔气体常数
或 ln k 2 E a ( 1 1 )A:指前因子
对D为一级
=kc-2(A)c(D)
负一级反应
=kc1/2(A)c(D)
1.5级反应
速率常数k 的量纲与反应的级数有关
级数 零级 一级 二级 三级
k 的量纲 浓度. 时间-1 时间-1 浓度-1 . 时间-1 浓度-2 . 时间-1
(2) 温度对反应速率的影响
r
r
T
T
r
r
r
T
T
T
van,t Hoff 规则
化学动力学中的反应速率理论

化学动力学中的反应速率理论在化学反应过程中,反应速率是指单位时间内反应物消失量或产物生成量与反应物浓度之积的比值。
而反应速率理论则提供了一种描述化学反应动力学的数学模型,可用于预测反应速率、反应机理和反应路径等方面的研究。
一、反应速率理论基础反应速率理论是基于化学反应物分子间碰撞的概率推导而来的。
根据亚当斯(Adams)和懦得罗夫(Guggenheim)提出的分子碰撞模型,反应物分子必须经过一定能量的阈值,才能碰撞并发生化学反应。
因此,反应速率与反应物分子碰撞的频率和碰撞能量有关。
二、反应速率常数与活化能根据反应速率理论,反应速率常数k和反应物分子碰撞的概率成正比例。
反应速率常数k的大小决定了反应速率的快慢,其大小受到反应物浓度、温度等因素的影响。
此外,反应速率理论还提出了活化能的概念。
活化能是指化学反应必须克服的能量阈值,只有高于此能量阈值,反应物分子才能进行碰撞并发生化学反应。
反应速率常数k和活化能之间有一个Arrhenius公式,可以用来描述反应速率常数的温度依赖性。
三、反应速率与反应机理的研究反应速率理论不仅可以用于预测反应速率和活化能,还可以用于研究反应机理和反应路径。
通过反应速率和温度对k和活化能的测量,可以推导出反应物子的反应路径和反应物状态的变化情况。
这对于研究复杂反应、优化催化剂以及发展新的化学反应渠道具有重要意义。
四、反应速率理论的应用反应速率理论在工业上有着广泛的应用。
例如,研究反应过程中的速率和活化能可以制定更好的催化剂。
同时,反应速率理论还有助于工业生产中的反应条件的优化,从而提高了生产效率和工艺质量。
在环境保护方面,反应速率理论也有着重要的作用,可以通过反应速率理论研究和模拟污染物的分解和去除过程。
总之,反应速率理论是描述化学反应动力学的重要理论模型,有着广泛的应用价值。
通过对反应速率、反应机理、活化能等因素的研究,可以为化学工业的发展、环境治理以及科学研究提供帮助。
无机化学:第三章 化学反应速率

第三章 化学反应的速率一、化学反应速率的概念化学反应速率是通过单位时间间隔内某反应物或某生成物浓度的变化来表示。
物质浓度的变化可以采用化学分析和仪器分析的方法测定。
单位为31mol dm s --⋅⋅,31mol dm min --⋅⋅等。
常用平均速率和瞬时速率来表示。
化学反应的瞬时速率等于时间间隔内0t ∆→时的平均速率的极限值。
表达式为0=lim t υυ∆→。
通常通过作图法来求瞬时速率,在c t -图像中,曲线上某一点切线的斜率的绝对值就是对应于该点横坐标t 的瞬时速率υ。
最有实际意义和理论意义的瞬时速率是初始速率0υ。
用反应进度定义的反应速率——对于任意一个化学反应0=B Bv B ∑,其反应速率可定义为单位体积内反应进度随时间的变化率。
表达式为1d d V tξυ=⋅ 用反应进度定义的反应速率值与物质的选择无关,也就是一个反应只有一个化学速率值,但与计量数有关。
二、化学反应速率理论——碰撞理论和过渡状态理论1、碰撞理论化学反应的发生,总要以反应物之间的接触为前提,即反应物分子之间的碰撞是有先决条件。
有效碰撞——能够发生反应的碰撞(1)能量要足够大(2)反应物分子要定向碰撞活化能和活化分子组——将具备足够能量(碰撞后足以反应)的反应物分子组,称为活化分子组。
分子组的能量要求越高,活化分子组的数量越少,这种能量要求称之为活化能,用a E 表示。
a E 在碰撞理论中,认为和温度无关。
a E →∞,活化分子组数则越少,有效碰撞分子数越小,故反应速率越慢。
分子不断碰撞,能量不断转移,因此分子的能量不断变化,故活化分子组也不是固定不变的。
但只要温度一定,活化分子组的百分数是固定的。
2、过渡状态理论(又称活化配合物理论)过度状态理论认为:反应的首要条件仍是反应物分子必须互相碰撞,但两个具有足够能量的反应物分子相互碰撞时,原来的化学键要断裂,新的化学键要形成,原子将要重新排列,经过一个过度状态,形成一种活化配合物。
专题2化学反应速率和化学平衡 第一单元 化学反应速率知识点归纳

专 题 2 化学反应速率与化学平衡第一单元 化学反应速率知识点复习一、化学反应速率的表示方法1)化学反应速率1.概念:通常用化学反应速率来衡量化学反应快慢。
2.表示方法:通常用单位时间内反应物浓度的减少或生成物浓度的增加来表示。
3.表达式若用v 表示化学反应速率,Δc 表示反应物或生成物物质的量浓度的变化(取绝对值),Δt 表示一定的时间间隔,则v =ΔcΔt。
如对于化学反应a A +b B===c C +d D ,用A 、B 、C 、D 四种物质的浓度变化来表示,则v (A)=Δc A Δt ,v (B)=Δc BΔt,v (C)=Δc CΔt,v (D)=Δc DΔt。
4.单位:常用mol·L -1·s -1或mol·L -1·min -1。
5.平均速率与瞬时速率(1)平均速率由v =ΔcΔt 求得的。
v 是在反应时间间隔Δt 内反应的平均速率。
(2)瞬时速率:①当Δt 非常小时,由v =ΔcΔt 可求化学反应在某一时刻的瞬时速率。
②通过c -t 图像,运用数学方法也可求得瞬时速率。
【注意】(1)化学反应速率,是某一时间段的平均速率而不是瞬时速率。
(2)不论是反应物还是生成物,其化学反应速率值都取正值。
(3)固体或纯液体(注意:不是溶液)的物质的量浓度可视为不变的常数,因此,一般不用固体或纯液体表示化学反应速率。
(4)同一化学反应里,用不同物质表示的反应速率可能不同,但意义相同,故描述反应速率时必须指明具体的化学物质。
①在同一个化学反应中,用不同物质表示的化学反应速率,其数值大小不一定相同,但表示的速率相同,即一种物质的速率就代表了整个化学反应的速率。
②用不同反应物表示化学反应速率时,化学反应速率之比=物质的量浓度变化之比=物质的量变化之比=化学计量数之比。
2)化学反应速率的计算与比较1.化学反应速率的计算方法 (1)定义式法利用公式v (A)=Δc AΔt 计算化学反应速率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
催化剂对反应活化能的影响
2.多相催化:
催化剂与反应物种不属于同一物相的 催化反应。 汽车尾气(NO和CO)的催化转化:
Pt(Pd, Rh) 2NO g CO g N2 g CO2 g
反应在固相催化剂表面的活性中心上 进行,催化剂分散在陶瓷载体上,其表面 积很大,活性中心足够多,尾气可与催化 剂充分接触。
活化能
(1).活化分子
分子发生有效碰撞所必须具有的最低能量若以Ec表示,则 具有等于或超过Ec能量的分子称为活化分子,能量低于Ec的 分子称为非活化分子或者普通分子。
(2).活化能
活化分子具有的平均能量 E * 与反应物分子的平均能量 之差称为反应的活化能 Ea :
E
Ea E * E
60 80 120 0.040 0.120
0.070 0.050 0.040 0.040 0.060 0.100 0.120 0.120
0.120
NO2
0.100
c /mol•L-1
0.080
0.060
0.040
N2O4
0.020 0.00 0
0
20
40
60
80
100
N2O4-NO2体系平衡的建立
Ea2
a
A+BC r Hmθ
Ea2:逆反应活化能 r Hmθ = Ea1Ea2
b
AB + C
O
反应历程
反应途径的能量变化
EⅠ-反应物(始态)势能
EⅡ-生成物(终态)势能
正反应的活化能 Ea(正) =Eac - E(Ⅰ)
逆反应的活化能 Ea(逆) =Eac - E(Ⅱ) ΔrHm= E(Ⅱ) - E(Ⅰ)= [Eac - Ea(逆)] -[Eac - Ea(正)] ΔrHm= Ea(正) - Ea(逆)
/mol•L-1 •s-1
正
正=逆
逆
t/s
可逆反应的反应速率变化示意图
(3)化学平衡: 正、逆反应速度相等时,体系所处的状态叫 做化学平衡
正 逆 0
化学平衡状态特征: (1)前提:恒温,封闭体系,可逆反应
(2)条件:正、逆反应速率相等
(3)标志:系统的组成不再随时间而变。
3 . 酶催化
酶催化:以酶为催化剂的反应。
特点:①高效
②高选择性
③条件温和
催化剂的重要性
• 从右图来看出,加入催化剂 后,正反应活化能降低的值 与逆反应括化能降低的值是 相等的。这表明,催化剂对 正、逆反应的作用是同等的, 它只加快反应速率,而不影 响化学平衡,不改变反应方 向。 有催化与天催化的反应活 • 催化剂还具有选择性,某一 化能比较 种催化剂往往只对某一种反 应起催化作用,而不能催化 其它反应。
r Gm = r Gmθ + RT lnJ J 称为反应商
如果 P,Q,Y,Z 均为气体
[ p(Y) / p θ ] y [ p( Z) / p θ ]z Jp θ p θ q [ p(P) / p ] [ p(Q) / p ]
能量
Ea无催化 催化活化配合物 Ea催化 反应物 生成物 反应历程 催化剂改变反应 途径示意图
O
例如:反应 2 H2O2(aq) → 2H2O(l) + O2(g) 无催化剂时,反应的活化能为 75. 3 kJmol1; 用 I 做催化剂时,反应的活化能为 56. 5 kJmol1; 若使用过氧化氢酶,更能把反应速率提高到 1023 倍以上。
a. b. c. d.
第二节 反应速率理论
2.2. 反应速率理论 2.2.1分子碰撞理论 只有具有足够能量的反应物分子的碰撞才有可能发 生反应。这种能够发生反应的碰撞叫有效碰撞。 那些具有足够高能量,能发生有效碰撞的分子称 为活化分子,要使普通分子成为活化分子所需最小能量 称为活化能。 发生反应的有效碰撞的分子,还必须沿着特定的 方向碰撞。
平均速率
Example 1
起始浓度/mol· L-1 2s末浓度/mol· L-1
N2 3H 2 2NH 3
2.0 1.8 3.0 2.4 0.0 0.4
c N 2 1.8 2.0 m ol L1 v N 2 0.1m ol L1 s 1 2 0s t
需要注意以下特点 :
催化剂只能通过改变反应途径来改变反应速率, 但不能改变反应的焓变(rHm)、方向和限度 在反应速率方程中,催化剂对反应速率的影响 体现在反应速率常数(k)内。对确定反应来 说,反应温度一定时,采用不同的催化剂一般 有不同的k值。
对同一个可逆反应来说,催化剂等值地降低了 正、逆反应的活化能。
(2)化学平衡的基本特征
有些化学反应逆反应比较显著。例如, 373K时, 将0.100mol无色的N2O4气体放入1L抽空的密 闭容器中,立刻出现红综色。
N2O4
时间 /s 0 20 40 C (N2O4)/(mol· L- 0.100 1) 0.000 C (NO2)/(mol· L-1)
2NO2
P(H2O) = 0.38105Pa。试计算该反应的Kc,Kp。
解: C(s) + H2O(g) CO(g) + H2(g)
4.6 7.6 7.6 平衡浓度/(10-3mol· L- - 1)) 平衡分压 - 0.38 0.63 0.63 /(105Pa) 3 1 2 1.2 10 2 mol L1 c CO c H 7 . 6 10 mol L 2 则 Kc 4.6 10 3 mol L1 c H 2O
PC = [C] RT, PD = [D]RT PY = y[Y] RT, Pz = [Z]RT z y z P Y P Z C Y C Z RT y z cd Kp c c d d P C P D C C C D 令(y + z) (c + d) = n
3.1化学反应速率
3.3.1反应速率与浓度的关系 3.3.1.1反应速率的表示方法
(1) 化学反应速率
a.反应速率定义
1.传统的定义
反应速率 是指在一定条件下单位时间内某化学反应的反应 物转化为生成物的速率,对于均匀体系的恒容反应,习惯用 单位时间内反应物浓度的减少或者产物浓度的增加来表示, 而且习惯取正值。 浓度常用mol.L-1,时间常用s,min,h,d,y. 反应速率又分为平均速率和瞬间速率两种表示方法.
例如:
O C + 生成物 (终态)
O C
O
N
活化络合物 (过渡态)
O
O C
O
O
O
N
O
+ C O O O
C N O+O C O
N
Eac
EII
(正)
Eac
Ea(逆)
EI
(正 )
Ea(
逆)
EI
EII
能量
活化配合物 A· · · B· · · C
c
Ea1
Ea1:正反应活化能
cC(g) + dD(g)
C y Y C z Z Kc c C C C d D
yY(g) + zZ(g)
P y Y P z Z Kp c P C P d D
(物质的量)浓度
n P V RT
cC(g) + dD(g)
yY(g) + zZ(g)
则:
催化剂具有选择性。
3.4 化学平衡
3.4.1可逆反应与化学平衡
1.4.1.1可逆反应与化学平衡(1)可逆反应 在同一条件下,既能向正反应方向又 能向逆反应方向进行的反应。 仅有少数的化学反应其反应物能全部转 变为生成物,亦即反应能进行到底。
Ag + Cl
2KClO3
MnO2
AgCl
2KCl + 3O2
K p Kc RT
n
平衡常数是表明化学反应限度的一种特征值。平衡常数 越大,表示正反应进行得越完全。平衡常数值与温度及反 应式的书写形式有关,但不随浓度、压力而变。
2. 书写平衡常数关系式的规则
如果反应中有固体和纯液体参加,它们 的浓度不应写在平衡关系式中 CaCO3 (s) CaO (s) + CO2 (g) Kc =c (CO2) 稀溶液中进行的反应,如有水参加,水 的浓度也不必写在平衡关系式中 Cr2O72 + H2O 2CrO42 + cCr2O7 2H c 2
p CO p H 2 0.63 10 5 Pa 5 Kp 1 . 0 10 Pa 5 p H 2O 0.38 10 Pa
2
3标准平衡常数
(1)非标准状态下的摩尔吉布斯函数变 rGm(T)
对于一化学反应:pP + qQ = yY + zZ,在恒温恒压、 任意状态下的 rGm 与标准态 rGmθ 有如下关系:
加入催化剂Br2,可以加快H2O2分解,分解 反应的机理是: 第一步 H2O2 (aq) Br2 2H (aq) O2 (g) 2Br (aq) 第二步 H2O2 (aq) 2H (aq) 2Br (aq) 2H2O(l) Br2 总反应: 2H O (aq) O (g) 2H O(l) 2 2 2 2
(4)化学平衡是动态平衡。
3.4.1.2平衡常数
1. 实验平衡常数 2. 书写平衡常数关系式的规则 3. 标准平衡常数
1. 实验平衡常数
化学平衡常数:任何可逆反应,不管反应的始 态如何,在一定温度下达平衡时,各生成物 平衡浓度幂的乘积与反应物平衡浓度幂的乘 积之比值是一个常数。以浓度表示的称为浓 度平衡常数(Kc),以分压表示的称为压力 平衡常数(Kp)。
K c 2 CrO
