九年级数学圆知识点及习题(含答案)
九年级数学: 24.1 圆的有关性质(同步练习题)( 含答案)

24.1圆的有关性质24.1.1圆1.在一个平面内,线段OA绕它固定的一个端点O__旋转一周___,__另一个端点A___所形成的图形叫做圆.这个固定的端点O叫做__圆心___,线段OA叫做__半径___.2.连接圆上任意两点间的线段叫做__弦___.圆上任意两点间的部分叫做__弧___.直径是经过圆心的弦,是圆中最长的弦.3.在同圆或等圆中,能够__互相重合___的弧叫等弧.4.确定一个圆有两个要素,一是__圆心___,二是__半径___,圆心确定__位置___,半径确定__大小___.知识点1:圆的有关概念1.以已知点O为圆心,已知长为a的线段为半径作圆,可以作( A)A.1个B.2个C.3个D.无数个2.下列命题中正确的有( A)①弦是圆上任意两点之间的部分;②半径是弦;③直径是最长的弦;④弧是半圆,半圆是弧.A.1个B.2个C.3个D.4个3.如图,图中弦的条数为( B)A.1条B.2条C.3条D.4条4.过圆上一点可以作出圆的最长弦的条数为( A)A.1条B.2条C.3条D.无数条5.如图,在四边形ABCD中,∠DAB=∠DCB=90°,则A,B,C,D四个点是否在同一个圆上?若在,说出圆心的位置,并画出这个圆.解:在,圆心是线段BD的中点.图略知识点2:圆中的半径相等6.如图,MN为⊙O的弦,∠N=52°,则∠MON的度数为( C)A.38°B.52°C.76°D.104°,第6题图),第7题图) 7.如图,AB,CD是⊙O的两条直径,∠ABC=30°,那么∠BAD=( D)A.45°B.60°C.90°D.30°8.如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.解:由ASA证△BEO≌△CFO,∴OE=OF,又∵OC=OB,∴OC+OE=OB+OF,即CE=BF9.如图,点A,B和点C,D分别在两个同心圆上,且∠AOB=∠COD.求证:∠C=∠D.解:∵∠AOB=∠COD,∴∠AOB+∠AOC=∠COD+∠AOC,即∠AOD=∠BOC,又OA=OB,OC=OD,∴△AOD≌△BOC,∴∠C=∠D10.M,N是⊙O上的两点,已知OM=3 cm,那么一定有( D)A.MN>6 cm B.MN=6 cmC.MN<6 cm D.MN≤6 cm11.如图,点A,D,G,M在半圆O上,四边形ABOC,DEOF,HMNO均为矩形.设BC=a,EF=b,NH=c,则下列各式中正确的是( B)A.a>b>c B.a=b=cC.c>a>b D.b>c>a12.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( C)A.50°B.60°C.70°D.80°,第12题图),第13题图) 13.如图是张老师出门散步时离家的距离y与时间x之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( D)14.在同一平面内,点P到圆上的点的最大距离为7,最小距离为1,则此圆的半径为__3或4___.15.如图,AB,CD为圆O的两条直径,E,F分别为OA,OB的中点.求证:四边形CEDF为平行四边形.解:∵AO=BO,E,F分别是AO和BO的中点,∴EO=FO,又CO=DO,∴四边形CEDF为平行四边形16.如图,AB是⊙O的弦,半径OC,OD分别交AB于点E,F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.解:OE=OF.证明:连接OA,OB.∵OA,OB是⊙O的半径,∴OA=OB,∴∠OBA =∠OAB.又∵AE=BF,∴△OAE≌△OBF(SAS),∴OE=OF17.如图,AB为⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E点,已知AB =2DE,∠E=18°,求∠AOC的度数.解:连接OD.∵AB为⊙O的直径,OC,OD为半径,AB=2DE,∴OC=OD=DE,∴∠DOE=∠E,∠OCE=∠ODC.又∠ODC=∠DOE+∠E,∴∠OCE=∠ODC=2∠E.∵∠E =18°,∴∠OCE=36°,∴∠AOC=∠OCE+∠E=36°+18°=54°18.如图,AB是半圆O的直径,四边形CDEF是内接正方形.(1)求证:OC=OF;(2)在正方形CDEF的右侧有一正方形FGHK,点G在AB上,H在半圆上,K在EF上.若正方形CDEF的边长为2,求正方形FGHK的面积.解:(1)连接OD,OE,则OD=OE,又∠OCD=∠OFE=90°,CD=EF,∴Rt△ODC ≌Rt△OEF(HL),∴OC=OF(2)连接OH,∵CF=EF=2,∴OF=1,∴OH2=OE2=12+22=5.设FG=GH=x,则(x+1)2+x2=5,∴x2+x-2=0,解得x1=1,x2=-2(舍去),∴S =12=1正方形FGHK24.1.2 垂直于弦的直径1.圆是__轴对称___图形,任何一条__直径___所在的直线都是它的对称轴.2.(1)垂径定理:垂直于弦的直径__平分___弦,并且__平分___弦所对的两条弧; (2)推论:平分弦(非直径)的直径__垂直___于弦并且__平分___弦所对的两条弧.3.在圆中,弦长a ,半径R ,弦心距d ,它们之间的关系是__(12a)2+d 2=R 2___.知识点1:认识垂径定理 1.(2014·毕节)如图,已知⊙O 的半径为13,弦AB 长为24,则点O 到AB 的距离是( B ) A .6 B .5 C .4 D .3,第1题图),第3题图),第4题图)2.CD 是⊙O 的一条弦,作直径AB ,使AB ⊥CD ,垂足为E ,若AB =10,CD =8,则BE 的长是( C )A .8B .2C .2或8D .3或73.(2014·北京)如图,⊙O 的直径AB 垂直于弦CD ,垂足是E ,∠A =22.5°,OC =4,则CD 的长为( C )A .2 2B .4C .4 2D .8 4.如图,在⊙O 中,直径AB ⊥弦CD 于点M ,AM =18,BM =8,则CD 的长为__24___. 知识点2:垂径定理的推论5.如图,一条公路弯道处是一段圆弧(图中的弧AB),点O 是这条弧所在圆的圆心,点C 是AB ︵的中点,半径OC 与AB 相交于点D ,AB =120 m ,CD =20 m ,则这段弯道的半径是( C )A .200 mB .200 3 mC .100 mD .100 3 m,第5题图) ,第6题图)6.如图,在⊙O 中,弦AB ,AC 互相垂直,D ,E 分别为AB ,AC 的中点,则四边形OEAD 为( C )A .正方形B .菱形C .矩形D .梯形 知识点3:垂径定理的应用7.如图是一个圆柱形输水管的横截面,阴影部分为有水部分,若水面AB 宽为8 cm ,水的最大深度为2 cm ,则输水管的半径为( C )A .3 cmB .4 cmC .5 cmD .6 cm,第7题图) ,第8题图)8.古题今解:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”这是《九章算术》中的问题,用数学语言可表述为:如图,AB 为⊙O 的直径,弦CD ⊥AB 于点E ,AE =1寸,CD =10寸,则直径AB 的长为__26___寸.9.如图是某风景区的一个圆拱形门,路面AB 宽为2米,净高5米,求圆拱形门所在圆的半径是多少米?解:连接OA.∵CD ⊥AB ,且CD 过圆心O ,∴AD =12AB =1米,∠CDA =90°.在Rt△OAD 中,设⊙O 的半径为R ,则OA =OC =R ,OD =5-R.由勾股定理,得OA 2=AD 2+OD 2,即R 2=(5-R)2+12,解得R =2.6,故圆拱形门所在圆的半径为2.6米10.如图,已知⊙O 的半径为5,弦AB =6,M 是AB 上任意一点,则线段OM 的长可能是( C )A .2.5B .3.5C .4.5D .5.5,第10题图) ,第11题图)11.(2014·黄冈)如图,在⊙O 中,弦CD 垂直于直径AB 于点E ,若∠BAD =30°,且BE =2,则CD =.12.已知点P 是半径为5的⊙O 内一点,OP =3,则过点P 的所有弦中,最长的弦长为__10___;最短的弦长为__8___.13.如图,以点P 为圆心的圆弧与x 轴交于A ,B 两点,点P 的坐标为(4,2),点A 的坐标为(2,0),则点B 的坐标为__(6,0)___.,第13题图) ,第14题图)14.如图,AB 是⊙O 的弦,AB 长为8,P 是⊙O 上一个动点(不与A ,B 重合),过点O 作OC ⊥AP 于点C ,OD ⊥PB 于点D ,则CD 的长为__4___.15.如图,某窗户是由矩形和弓形组成,已知弓形的跨度AB =3 m ,弓形的高EF =1 m ,现计划安装玻璃,请帮工人师傅求出AB ︵所在⊙O 的半径r.解:由题意知OA =OE =r ,∵EF =1,∴OF =r -1.∵OE ⊥AB ,∴AF =12AB =12×3=1.5.在Rt △OAF 中,OF 2+AF 2=OA 2,即(r -1)2+1.52=r 2,解得r =138,即圆O 的半径为138米16.如图,要把破残的圆片复制完整,已知弧上的三点A ,B ,C.(1)用尺规作图法找出BAC ︵所在圆的圆心;(保留作图痕迹,不写作法)(2)设△ABC 是等腰三角形,底边BC =8 cm ,腰AB =5 cm ,求圆片的半径R.解:(1)分别作AB ,AC 的垂直平分线,其交点O 为所求圆的圆心,图略 (2)连接AO交BC 于E.∵AB =AC ,∴AE ⊥BC ,BE =12BC =4.在Rt △ABE 中,AE =AB 2-BE 2=52-42=3.连接OB ,在Rt △BEO 中,OB 2=BE 2+OE 2,即R 2=42+(R -3)2,解得R =256,即所求圆片的半径为256cm17.已知⊙O 的半径为13 cm ,弦AB ∥CD ,AB =24 cm ,CD =10 cm ,则AB ,CD 之间的距离为( D )A .17 cmB .7 cmC .12 cmD .17 cm 或7 cm18.如图,CD 为⊙O 的直径,CD ⊥AB ,垂足为点F ,AO ⊥BC ,垂足为E ,BC =2 3. (1)求AB 的长; (2)求⊙O 的半径.解:(1)连接AC ,∵CD 为⊙O 的直径,CD ⊥AB ,∴AF =BF ,∴AC =BC.延长AO 交⊙O 于G ,则AG 为⊙O 的直径,又AO ⊥BC ,∴BE =CE ,∴AC =AB ,∴AB =BC =23 (2)由(1)知AB =BC =AC ,∴△ABC 为等边三角形,∴∠OAF =30°,在Rt △OAF 中,AF =3,可求OA =2,即⊙O 的半径为224.1.3 弧、弦、圆心角1.圆既是轴对称图形,又是__中心___对称图形,__圆心___就是它的对称中心. 2.顶点在__圆心___的角叫圆心角.3.在同圆和等圆中,相等的圆心角所对的__弧___相等,且所对的弦也__相等___. 4.在同圆或等圆中,若两个圆心角、两条弧、两条弦中,有一组量是相等的,则它们所对应的其余各组量也分别__相等___.知识点1:认识圆心角1.如图,不是⊙O 的圆心角的是( D ) A .∠AOB B .∠AOD C .∠BOD D .∠ACD,第1题图) ,第3题图)2.已知圆O 的半径为5 cm ,弦AB 的长为5 cm ,则弦AB 所对的圆心角∠AOB =__60°___.3.(2014·菏泽)如图,在△ABC 中,∠C =90°,∠A =25°,以点C 为圆心,BC 为半径的圆交AB 于点D ,交AC 于点E ,则BD ︵的度数为__50°___.知识点2:弧、弦、圆心角之间的关系4.如图,已知AB 是⊙O 的直径,C ,D 是BE ︵上的三等分点,∠AOE =60°,则∠COE 是( C )A .40°B .60°C .80°D .120°,第4题图) ,第5题图)5.如图,已知A ,B ,C ,D 是⊙O 上的点,∠1=∠2,则下列结论中正确的有( D ) ①AB ︵=CD ︵; ②BD ︵=AC ︵;③AC =BD ; ④∠BOD =∠AOC. A .1个 B .2个 C .3个 D .4个6.如图,AB 是⊙O 的直径,BC ,CD ,DA 是⊙O 的弦,且BC =CD =DA ,则∠BCD 的度数为( C )A .100°B .110°C .120°D .135°,第6题图) ,第7题图)7.如图,在同圆中,若∠AOB =2∠COD ,则AB ︵与2CD ︵的大小关系为( C ) A .AB ︵>2CD ︵ B .AB ︵<2CD ︵ C .AB ︵=2CD ︵D .不能确定8.如图,已知D ,E 分别为半径OA ,OB 的中点,C 为AB ︵的中点.试问CD 与CE 是否相等?说明你的理由.解:相等.理由:连接OC.∵D ,E 分别为⊙O 半径OA ,OB 的中点,∴OD =12AO ,OE =12BO.∵OA =OB ,∴OD =OE.∵C 是AB ︵的中点,∴AC ︵=BC ︵,∴∠AOC =∠BOC.又∵OC=OC ,∴△DCO ≌△ECO(SAS ),∴CD =CE9.如图,在⊙O 中,AB ︵=AC ︵,∠B =70°,则∠A =__40°___.,第9题图) ,第10题图)10.如图,AB 是半圆O 的直径,E 是OA 的中点,F 是OB 的中点,ME ⊥AB 于点E ,NF ⊥AB 于点F.在下列结论中:①AM ︵=MN ︵=BN ︵;②ME =NF ;③AE =BF ;④ME =2AE.正确的有__①②③___.11.如图,A ,B ,C ,D 在⊙O 上,且AB ︵=2CD ︵,那么( C )A .AB >2CD B .AB =2CDC .AB <2CDD .AB 与2CD 大小不能确定12.如图,在⊙O 中,弦AB ,CD 相交于点P ,且AC =BD ,求证:AB =CD.解:∵AC =BD ,∴AC ︵=BD ︵,∴AB ︵=CD ︵,∴AB =CD13.如图,以▱ABCD 的顶点A 为圆心,AB 为半径作圆,交AD ,BC 于E ,F ,延长BA 交⊙A 于G ,求证:GE ︵=EF ︵.解:连接AF ,∵四边形ABCD 为平行四边形,∴AD ∥BC ,∴∠GAE =∠B ,∠EAF=∠AFB.又∵AB =AF ,∴∠B =∠AFB ,∴∠GAE =∠EAF ,∴GE ︵=EF ︵14.如图,AB 是⊙O 的直径,AC ︵=CD ︵,∠COD =60°. (1)△AOC 是等边三角形吗?请说明理由; (2)求证:OC ∥BD.解:(1)△AOC 是等边三角形.理由:∵AC ︵=CD ︵,∴∠AOC =∠COD =60°.又∵OA =OC ,∴△AOC 是等边三角形(2)∵AC ︵=CD ︵,∴∠AOC =∠COD =60°,∴∠BOD =180°-(∠AOC +∠COD)=60°.∵OD =OB ,∴△ODB 为等边三角形,∴∠ODB =60°,∴∠ODB =∠COD =60°,∴OC ∥BD15.如图,在△AOB 中,AO =AB ,以点O 为圆心,OB 为半径的圆交AB 于D ,交AO 于点E ,AD =BO.试说明BD ︵=DE ︵,并求∠A 的度数.解:设∠A =x °.∵AD =BO ,又OB =OD ,∴OD =AD ,∴∠AOD =∠A =x °,∴∠ABO =∠ODB =∠AOD +∠A =2x °.∵AO =AB ,∴∠AOB =∠ABO =2x °,从而∠BOD=2x °-x °=x °,即∠BOD =∠AOD ,∴BD ︵=DE ︵.由三角形的内角和为180°,得2x +2x +x =180,∴x =36,则∠A =36°16.如图,MN 是⊙O 的直径,MN =2,点A 在⊙O 上,AN ︵的度数为60°,点B 为AN ︵的中点,P 是直径MN 上的一个动点,求PA +PB 的最小值.解:作点B 关于MN 的对称点B′.因为圆是轴对称图形,所以点B′在圆上.连接AB′,与MN 的交点为P 点,此时PA +PB 最短,ABB ′⌒所对的圆心角为90°,连接OB′,则∠AOB′=90°,∴AB ′=AO 2+OB′2=2,∴PA +PB =AB ′=2,即PA +PB 的最小值为224.1.4 圆周角1.顶点在__圆___上,并且两边和圆__相交___的角叫圆周角.2.在同圆或等圆中,__同弧___或__等弧___所对的圆周角相等,都等于这条弧所对的__圆心角___的一半.在同圆或等圆中,相等的圆周角所对的弧__相等___.3.半圆或直径所对的圆周角是__直角___,90°的圆周角所对的弦是__直径___. 4.圆内接四边形对角__互补___,外角等于__内对角___.知识点1:认识圆周角1.下列图形中的角是圆周角的是( B )2.在⊙O 中,A ,B 是圆上任意两点,则AB ︵所对的圆心角有__1___个,AB ︵所对的圆周角有__无数___个,弦AB 所对的圆心角有__1___个,弦AB 所对的圆周角有__无数___个.知识点2:圆周角定理3.如图,已知点A ,B ,C 在⊙O 上,ACB ︵为优弧,下列选项中与∠AOB 相等的是( A ) A .2∠C B .4∠B C .4∠A D .∠B +∠C,第3题图) ,第4题图)4.(2014·重庆)如图,△ABC 的顶点A ,B ,C 均在⊙O 上,若∠ABC +∠AOC =90°,则∠AOC 的大小是( C )A .30°B .45°C .60°D .70°知识点3:圆周角定理推论5.如图,已知AB 是△ABC 外接圆的直径,∠A =35°,则∠B 的度数是( C ) A .35° B .45° C .55° D .65°,第5题图),第6题图),第7题图)6.如图,CD ⊥AB 于E ,若∠B =60°,则∠A =__30°___.7.如图,⊙O 的直径CD 垂直于AB ,∠AOC =48°,则∠BDC =__24°___.8.如图,已知A ,B ,C ,D 是⊙O 上的四个点,AB =BC ,BD 交AC 于点E ,连接CD ,AD.求证:DB 平分∠ADC.解:∵AB =BC ,∴AB ︵=BC ︵,∴∠BDC =∠ADB ,∴DB 平分∠ADC知识点4:圆内接四边形的对角互补9.如图,四边形ABCD 是圆内接四边形,E 是BC 延长线上一点,若∠BAD =105°,则∠DCE 的大小是( B )A .115°B .105°C .100°D .95°,第9题图) ,第10题图)10.如图,A ,B ,C ,D 是⊙O 上顺次四点,若∠AOC =160°,则∠D =__80°___,∠B =__100°___.11.如图,▱ABCD 的顶点A ,B ,D 在⊙O 上,顶点C 在⊙O 的直径BE 上,连接AE ,∠E =36°,则∠ADC 的度数是( B )A .44°B .54°C .72°D .53°,第11题图) ,第12题图)12.(2014·丽水)如图,半径为5的⊙A 中,弦BC ,ED 所对的圆心角分别是∠BAC ,∠EAD.已知DE =6,∠BAC +∠EAD =180°,则弦BC 的弦心距等于( D )A .412B .342C .4D .3 13.如图,AB 是⊙O 的直径,点C 是圆上一点,∠BAC =70°,则∠OCB =__20°___.,第13题图),第14题图),第15题图)14.如图,△ABC 内接于⊙O ,点P 是AC ︵上任意一点(不与A ,C 重合),∠ABC =55°,则∠POC 的取值范围是__0°<∠POC <110°___.15.如图,⊙C 经过原点,并与两坐标轴分别交于A ,D 两点,已知∠OBA =30°,点A 的坐标为(2,0),则点D 的坐标为.16.如图,在△ABC 中,AB =为直径的⊙O 分别交BC ,AC 于点D ,E ,且点D 为边BC 的中点.(1)求证:△ABC 为等边三角形; (2)求DE 的长.解:(1)连接AD.∵AB 是⊙O 的直径,∴∠ADB =90°.∵点D 是BC 的中点,∴AD 是BC 的垂直平分线,∴AB =AC.又∵AB =BC ,∴AB =AC =BC ,∴△ABC 为等边三角形 (2)连接BE ,∵AB 是直径,∴∠AEB =90°,∴BE ⊥AC.∵△ABC 是等边三角形,∴AE =EC ,即E 为AC 的中点.又∵D 是BC 的中点,∴DE 是△ABC 的中位线,∴DE =12AB =12×2=117.(2014·武汉)如图,AB 是⊙O 的直径,C ,P 是AB ︵上两点,AB =13,AC =5.(1)如图①,若点P 是AB ︵的中点,求PA 的长;(2)如图②,若点P 是BC ︵的中点,求PA 的长.解:(1)连接PB.∵AB 是⊙O 的直径,P 是AB ︵的中点,∴PA =PB ,∠APB =90°,可求PA =22AB =1322(2)连接BC ,OP 交于点D ,连接PB.∵P 是BC ︵的中点,∴OP ⊥BC ,BD=CD.∵OA =OB ,∴OD =12AC =52.∵OP =12AB =132,∴PD =OP -OD =132-52=4.∵AB 是⊙O 的直径,∴∠ACB =90°,由勾股定理可求BC =12,∴BD =12BC =6,∴PB =PD 2+BD 2=42+62=213.∵AB 是⊙O 的直径,∴∠APB =90°,∴PA =AB 2-PB 2=132-(213)2=31318.已知⊙O 的直径为10,点A ,B ,C 在⊙O 上,∠CAB 的平分线交⊙O 于点D. (1)如图①,若BC 为⊙O 的直径,AB =6,求AC ,BD ,CD 的长; (2)如图②,若∠CAB =60°,求BD 的长.解:(1)∵BC 为⊙O 的直径,∴∠CAB =∠BDC =90°.在Rt △CAB 中,AC =BC 2-AB 2=102-62=8.∵AD 平分∠CAB ,∴CD ︵=BD ︵,∴CD =BD.在Rt △BDC 中,CD 2+BD 2=BC 2=100,∴BD 2=CD 2=50,∴BD =CD =52 (2)连接OB ,OD.∵AD 平分∠CAB ,且∠CAB =60°,∴∠DAB =12∠CAB =30°,∴∠DOB =2∠DAB =60°.又∵⊙O 中OB =OD ,∴△OBD 是等边三角形,∵⊙O 的直径为10,∴OB =5,∴BD =5。
人教版九年级数学复习:第二十四章 圆的知识点总结及典型例题

圆的知识点总结(一)圆的有关性质[知识归纳]1. 圆的有关概念:圆、圆心、半径、圆的内部、圆的外部、同心圆、等圆;弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧、弓形、弓形的高;圆的内接三角形、三角形的外接圆、三角形的外心、圆内接多边形、多边形的外接圆;圆心角、圆周角、圆内接四边形的外角。
2. 圆的对称性圆是轴对称图形,经过圆心的每一条直线都是它的对称轴,圆有无数条对称轴;圆是以圆心为对称中心的中心对称图形;圆具有旋转不变性。
3. 圆的确定不在同一条直线上的三点确定一个圆。
4. 垂直于弦的直径垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧;推论1(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
垂径定理及推论1 可理解为一个圆和一条直线具备下面五个条件中的任意两个,就可推出另外三个:①过圆心;②垂直于弦;③平分弦(不是直径);④平分弦所对的优弧;⑤平分弦所对的劣弧。
推论2 圆的两条平行弦所夹的弧相等。
5. 圆心角、弧、弦、弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;所对的弦的弦心距相等。
推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
此定理和推论可以理解成:在同圆或等圆中,满足下面四个条件中的任何一个就能推出另外三个:①两个圆心角相等;②两个圆心角所对的弧相等;③两个圆心角或两条弧所对的弦相等;④两条弦的弦心距相等。
圆心角的度数等于它所对的弧的度数。
6. 圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半;推论1 同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧也相等;推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径;推论3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
人教版数学九年级上册24.2《点和圆、直线和圆的位置关系》知识点+例题+练习(精品)

点、直线、圆与圆的位置关系_知识点+例题+练习1.点和圆的位置关系2.(1)点与圆的位置关系有3种.设⊙O的半径为r,点P到圆心的距离OP=d,则有:3.①点P在圆外⇔d>r4.②点P在圆上⇔d=r5.①点P在圆内⇔d<r6.(2)点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.7.(3)符号“⇔”读作“等价于”,它表示从符号“⇔”的左端可以得到右端,从右端也可以得到左端.2.确定圆的条件不在同一直线上的三点确定一个圆.注意:这里的“三个点”不是任意的三点,而是不在同一条直线上的三个点,而在同一直线上的三个点不能画一个圆.“确定”一词应理解为“有且只有”,即过不在同一条直线上的三个点有且只有一个圆,过一点可画无数个圆,过两点也能画无数个圆,过不在同一条直线上的三点能画且只能画一个圆.3.三角形的外接圆与外心(1)外接圆:经过三角形的三个顶点的圆,叫做三角形的外接圆.(2)(2)外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.(3)(3)概念说明:(4)①“接”是说明三角形的顶点在圆上,或者经过三角形的三个顶点.(5)②锐角三角形的外心在三角形的内部;直角三角形的外心为直角三角形斜边的中点;钝角三角形的外心在三角形的外部.(6)③找一个三角形的外心,就是找一个三角形的两条边的垂直平分线的交点,三角形的外接圆只有一个,而一个圆的内接三角形却有无数个.4.反证法(了解)(1)对于一个命题,当使用直接证法比较困难时,可以采用间接证法,反证法就是一个间接证法.反证法主要适合的证明类型有:①命题的结论是否定型的.②命题的结论是无限型的.③命题的结论是“至多”或“至少”型的.(2)(2)反证法的一般步骤是:(3)①假设命题的结论不成立;(4)②从这个假设出发,经过推理论证,得出矛盾;(5)③由矛盾判定假设不正确,从而肯定原命题的结论正确.5.直线和圆的位置关系(1)直线和圆的三种位置关系:①相离:一条直线和圆没有公共点.②相切:一条直线和圆只有一个公共点,叫做这条直线和圆相切,这条直线叫圆的切线,唯一的公共点叫切点.③相交:一条直线和圆有两个公共点,此时叫做这条直线和圆相交,这条直线叫圆的割线.(2)判断直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d.①直线l和⊙O相交⇔d<r②直线l和⊙O相切⇔d=r③直线l和⊙O相离⇔d>r.6.切线的性质(1)切线的性质(2)①圆的切线垂直于经过切点的半径.(3)②经过圆心且垂直于切线的直线必经过切点.(4)③经过切点且垂直于切线的直线必经过圆心.(5)(2)切线的性质可总结如下:(6)如果一条直线符合下列三个条件中的任意两个,那么它一定满足第三个条件,这三个条件是:①直线过圆心;②直线过切点;③直线与圆的切线垂直.(7)(3)切线性质的运用(8)由定理可知,若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.7.切线的判定8.(1)切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.9.(2)在应用判定定理时注意:10.①切线必须满足两个条件:a、经过半径的外端;b、垂直于这条半径,否则就不是圆的切线.11.②切线的判定定理实际上是从”圆心到直线的距离等于半径时,直线和圆相切“这个结论直接得出来的.12.③在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径,可简单的说成“无交点,作垂线段,证半径”;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线,可简单地说成“有交点,作半径,证垂直”.8.切线的判定与性质(1)切线的性质①圆的切线垂直于经过切点的半径.②经过圆心且垂直于切线的直线必经过切点.③经过切点且垂直于切线的直线必经过圆心.(2)切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.(3)常见的辅助线的:①判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;②有切线时,常常“遇到切点连圆心得半径”.9.切线长定理(1)圆的切线定义:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.(2)(2)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.(3)(3)注意:切线和切线长是两个不同的概念,切线是直线,不能度量;切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.(4)(4)切线长定理包含着一些隐含结论:(5)①垂直关系三处;(6)②全等关系三对;(7)③弧相等关系两对,在一些证明求解问题中经常用到.10.三角形的内切圆与内心(1)内切圆的有关概念:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.(2)任何一个三角形有且仅有一个内切圆,而任一个圆都有无数个外切三角形.(3)三角形内心的性质:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.11.圆与圆的五种位置关系(1)圆与圆的五种位置关系:①外离;②外切;③相交;④内切;⑤内含.如果两个圆没有公共点,叫两圆相离.当每个圆上的点在另一个圆的外部时,叫两个圆外离,当一个圆上的点都在另一圆的内部时,叫两个圆内含,两圆同心是内含的一个特例;如果两个圆有一个公共点,叫两个圆相切,相切分为内切、外切两种;如果两个圆有两个公共点叫两个圆相交.(2)圆和圆的位置与两圆的圆心距、半径的数量之间的关系:①两圆外离⇔d>R+r;②两圆外切⇔d=R+r;③两圆相交⇔R-r<d<R+r(R≥r);④两圆内切⇔d=R-r(R>r);⑤两圆内含⇔d<R-r(R>r).12.相切两圆的性质相切两圆的性质:如果两圆相切,那么连心线必经过切点.这说明两圆的圆心和切点三点共线,为证明带来了很大方便.13.相交两圆的性质(1)相交两圆的性质:(2)相交两圆的连心线(经过两个圆心的直线),垂直平分两圆的公共弦.(3)注意:在习题中常常通过公共弦在两圆之间建立联系.(4)(2)两圆的公切线性质:(5)两圆的两条外公切线的长相等;两圆的两条内公切线的长也相等.(6)两个圆如果有两条(内)公切线,则它们的交点一定在连心线上.4. 判断圆的切线的方法及应用判断圆的切线的方法有三种:(1)与圆有惟一公共点的直线是圆的切线;(2)若圆心到一条直线的距离等于圆的半径,则该直线是圆的切线;(3)经过半径外端,并且垂直于这条半径的直线是圆的切线.【例4】如图,⊙O的直径AB=4,∠ABC=30°,BC=34,D是线段BC的中点.(1)试判断点D与⊙O的位置关系,并说明理由.(2)过点D作DE⊥AC,垂足为点E,求证:直线DE是⊙O的切线.【例5】如图,已知O为正方形ABCD对角线上一点,以O为圆心,OA的长为半径的⊙O与BC相切于M,与AB、AD分别相交于E、F,求证CD与⊙O相切.【例6】如图,半圆O为△ABC的外接半圆,AC为直径,D为劣弧上一动点,P在CB 的延长线上,且有∠BAP=∠BDA.求证:AP 是半圆O 的切线.【知识梳理】1. 直线与圆的位置关系:2. 切线的定义和性质:3.三角形与圆的特殊位置关系:4. 圆与圆的位置关系:(两圆圆心距为d ,半径分别为21,r r )相交⇔2121r r d r r +<<-; 外切⇔21r r d +=;内切⇔21r r d -=; 外离⇔21r r d +>; 内含⇔210r r d -<<【注意点】与圆的切线长有关的计算.【例题精讲】例1.⊙O 的半径是6,点O 到直线a 的距离为5,则直线a 与⊙O 的位置关系为( )A .相离B .相切C .相交D .内含例 2. 如图1,⊙O 内切于ABC △,切点分别为D E F ,,.50B ∠=°,60C ∠=°,连结OE OF DE DF ,,,,则EDF ∠等于( )A .40°B .55°C .65°D .70°例3. 如图,已知直线L 和直线L 外两定点A 、B ,且A 、B 到直线L 的距离相等,则经过A 、B 两点且圆心在L 上的圆有( )A .0个B .1个C .无数个D .0个或1个或无数个例4.已知⊙O 1半径为3cm ,⊙O 2半径为4cm ,并且⊙O 1与⊙O 2相切,则这两个圆的圆心距为( ) A.1cm B.7cm C.10cm D. 1cm 或7cm例5.两圆内切,圆心距为3,一个圆的半径为5,另一个圆的半径为 例6.两圆半径R=5,r=3,则当两圆的圆心距d 满足___ ___•时,•两圆相交;•当d•满足___ ___时,两圆不外离.例7.⊙O 半径为6.5cm ,点P 为直线L 上一点,且OP=6.5cm ,则直线与⊙O•的位置关系是____例8.如图,PA 、PB 分别与⊙O 相切于点A 、B ,⊙O 的切线EF 分别交PA 、PB 于点E 、F ,切点C 在弧AB 上,若PA 长为2,则△PEF 的周长是 _.例9. 如图,⊙M 与x 轴相交于点(20)A ,,(80)B ,,与y 轴切于点C ,则圆心M 的坐标是例10. 如图,四边形ABCD 内接于⊙A ,AC 为⊙O 的直径,弦DB ⊥AC ,垂足为M ,过点D 作⊙O 的切线交BA 的延长线于点E ,若AC=10,tan ∠DAE=43,求DB 的长.【当堂检测】1.如果两圆半径分别为3和4,圆心距为7,那么两圆位置关系是( )A .相离B .外切C .内切D .相交2.⊙A 和⊙B 相切,半径分别为8cm 和2cm ,则圆心距AB 为( )A .10cmB .6cmC .10cm 或6cmD .以上答案均不对3.如图,P 是⊙O 的直径CB 延长线上一点,PA 切⊙O 于点A ,如果PA =3,PB =1,那么∠APC 等于( )A. 15B. 30C. 45D. 60O O2O14. 如图,⊙O 半径为5,PC 切⊙O 于点C ,PO 交⊙O 于点A ,PA =4,那么PC 的长等于( ) A )6 (B )25 (C )210 (D )2145.如图,在10×6的网格图中(每个小正方形的边长均为1个单位长).⊙A 半径为2,⊙B 半径为1,需使⊙A 与静止的⊙B 相切,那么⊙A 由图示的位置向左平移 个单位长.6. 如图,⊙O 为△ABC 的内切圆,∠C = 90,AO 的延长线交BC 于点D ,AC =4,DC =1,,则⊙O 的半径等于( )A. 45B. 54C. 43D. 657.⊙O 的半径为6,⊙O 的一条弦AB 长63,以3为半径⊙O 的同心圆与直线AB 的位置关系是( )A.相离B.相交C.相切D.不能确定8.如图,在ABC △中,12023AB AC A BC =∠==,°,,A ⊙与BC 相切于点D ,且交AB AC 、于M N 、两点,则图中阴影部分的面积是 (保留π).9.如图,B 是线段AC 上的一点,且AB :AC=2:5,分别以AB 、AC 为直径画圆,则小圆的面积与大圆的面积之比为_______.10. 如图,从一块直径为a+b 的圆形纸板上挖去直径分别为a 和b 的两个圆,则剩下的纸板面积是___.11. 如图,两等圆外切,并且都与一个大圆内切.若此三个圆的圆心围成的三角形的周长为18cm .则大圆的半径是______cm .12.如图,直线AB 切⊙O 于C 点,D 是⊙O 上一点,∠EDC=30º,弦EF ∥AB ,连结OC 交EF 于H 点,连结CF ,且CF=2,则HE 的长为_________.13. 如图,PA 、PB 是⊙O 的两条切线,切点分别为A 、B ,若直径AC=12cm ,∠P=60°.求弦AB 的长. 【中考连接】 一、选择题 1. 正三角形的内切圆半径为1,那么三角形的边长为( )A.2B.32C.3D.3 2.⊙O 是等边ABC △的外接圆,⊙O 的半径为2,则ABC △的边长为( )A .3B .5C .23D .253. 已知⊙O 的直径AB 与弦AC 的夹角为 30,过C 点的切线PC 与AB 延长线交于P 点.PC =5,则⊙O 的半径为 ( )A. 335 B. 635 C. 10 D. 54. AB 是⊙O 的直径,点P 在BA 的延长线上,PC 是⊙O 的切线,C 为切点,PC =26,PA =4,则⊙O 的半径等于( )A. 1B. 2C. 23D. 265.某同学制做了三个半径分别为1、2、3的圆,在某一平面内,让它们两两外O D C B ABPA OC 第3题图 第4题图 第5题图 第6题图 第8题图 第9题图 第11题图 第10题图 第12题图切,该同学把此时三个圆的圆心用线连接成三角形.你认为该三角形的形状为( )A.钝角三角形B.等边三角形C.直角三角形D.等腰三角形6.关于下列四种说法中,你认为正确的有( )①圆心距小于两圆半径之和的两圆必相交 ②两个同心圆的圆心距为零③没有公共点的两圆必外离 ④两圆连心线的长必大于两圆半径之差A.1个B.2个C.3个D.4个二、填空题 6. 如图,AB 、AC 是⊙O 的两条切线,切点分别为B 、C ,D 是优弧BC 上的一点,已知∠BAC =80°,那么∠BDC =__________度.7. 如图,AB 是⊙O 的直径,四边形ABCD 内接于⊙O ,,,的度数比为3∶2∶4,MN 是⊙O 的切线,C 是切点,则∠BCM 的度数为________.8.如图,在△ABC 中,5cm AB AC ==,cos B 35=.如果⊙O 的半径为10cm ,且经过点B 、C ,那么线段AO = cm .9.两个等圆⊙O 与⊙O ′外切,过点O 作⊙O ′的两条切线OA 、OB ,A 、B 是切点,则∠AOB = .10.如图6,直线AB 与⊙O 相切于点B ,BC 是⊙O 的直径,AC 交⊙O 于点D ,连结BD ,则图中直角三角形有 个.11.如图,60ACB ∠=°,半径为1cm 的O ⊙切BC 于点C ,若将O ⊙在CB 上向右滚动,则当滚动到O ⊙与CA 也相切时,圆心O 移动的水平距离是__________cm .12.如图, AB 与⊙O 相切于点B ,线段OA 与弦BC 垂直于点D ,∠AOB =60°,B C=4cm ,则切线AB = cm.13.如图,⊙A 和⊙B 与x 轴和y 轴相切,圆心A 和圆心B 都在反比例函数1y x =图象上,则阴影部分面积等于 .14. Rt △ABC 中,9068C AC BC ∠===°,,.则△ABC的内切圆半径r =______.15.⊙O 的圆心到直线l 的距离为d ,⊙O 的半径为r ,当d 、r 是关于x 的方程x 2-4x+m=0的两根,且直线l 与⊙O 相切时,则m 的值为_____.16.已知:⊙A 、⊙B 、⊙C 的半径分别为2、3、5,且两两相切,则AB 、BC 、CA 分别为 .17.⊙O 的圆心到直线l 的距离为d ,⊙O 的半径为r ,当d 、r 是关于x 的方程x 2-4x+m=0的两根,且直线l 与⊙O 相切时,则m 的值为_____.三、解答题18. 如图,AB 是⊙O 的弦,OA OC ⊥交AB 于点C ,过B 的直线交OC 的延长线于点E ,当BE CE =时,直线BE 与⊙O 有怎样的位置关系?请说明理由. 第3题图 第6题图 第7题图 第8题图 第10题图 第11题图 第12题图 第13题图19.如图1,在⊙O 中,AB 为⊙O 的直径,AC 是弦,4OC =,60OAC ∠=. (1)求∠AOC 的度数;(2)在图1中,P 为直径BA 延长线上的一点,当CP 与⊙O 相切时,求PO 的长;(3)如图2,一动点M 从A 点出发,在⊙O 上按A 照逆时针的方向运动,当MAO CAO S S =△△时,求动点M 所经过的弧长.第18题图。
2023年中考九年级数学高频考点提升练习--圆的综合题(含答案)
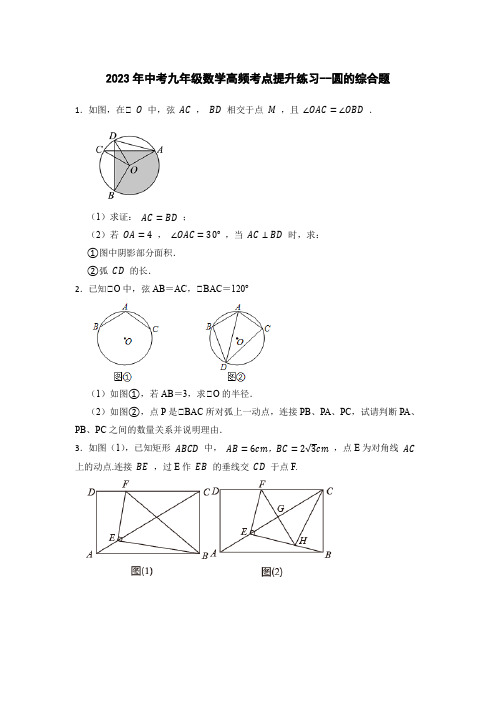
2023年中考九年级数学高频考点提升练习--圆的综合题1.如图,在⊙ O中,弦AC,BD相交于点M,且∠OAC=∠OBD.(1)求证:AC=BD;(2)若OA=4,∠OAC=30°,当AC⊥BD时,求:①图中阴影部分面积.②弧CD的长.2.已知⊙O中,弦AB=AC,⊙BAC=120°(1)如图①,若AB=3,求⊙O的半径.(2)如图②,点P是⊙BAC所对弧上一动点,连接PB、PA、PC,试请判断PA、PB、PC之间的数量关系并说明理由.3.如图(1),已知矩形ABCD中,AB=6cm,BC=2√3cm,点E为对角线AC 上的动点.连接BE,过E作EB的垂线交CD于点F.(1)探索BE与EF的数量关系,并说明理由.(2)如图(2),过F作AC垂线交AC于点G,交EB于点H,连接CH.若点E从A出发沿AC方向以2√3cm/s的速度向终点C运动,设E的运动时间为ts.①是否存在t,使得H与B重合?若存在,求出t的值;若不存在,说明理由;②t为何值时,△CFH是等腰三角形;③当CG=GH时,求△CGH的面积.4.如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.(1)求证:CD是⊙O的切线;(2)求证:⊙C=2⊙DBE.(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)5.定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,⊙ABC中,点D 是BC边上一点,连结AD,若AD2=BD⋅CD,则称点D是⊙ABC中BC边上的“好点”.(1)如图2,⊙ABC的顶点是4×3网格图的格点,请仅用直尺画出AB边上的一个“好点”.(2)⊙ABC中,BC=9,tanB=43,tanC=23,点D是BC边上的“好点”,求线段BD的长.(3)如图3,⊙ABC是⊙O的内接三角形,OH⊙AB于点H,连结CH并延长交⊙O于点D.①求证:点H是⊙BCD中CD边上的“好点”.②若⊙O的半径为9,⊙ABD=90°,OH=6,请直接写出CHDH的值.6.如图,⊙O为等边⊙ABC的外接圆,半径为2,点D在劣弧上运动(不与点A,B 重合),连接DA,DB,DC.(1)求证:DC是⊙ADB的平分线;(2)设四边形ADBC的面积为S,线段DC的长为x,试用含x的代数式表示S;(3)若点M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D 运动到每一个确定的位置,⊙DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.7.在⊙ABC中,D,E分别是⊙ABC两边的中点,如果弧DE(可以是劣弧、优弧或半圆)上的所有点都在⊙ABC的内部或边上,则称弧DE为⊙ABC的中内弧.例如,图1中弧DE是⊙ABC其中的某一条中内弧.(1)如图2,在边长为4 √3的等边⊙ABC中,D,E分别是AB,AC的中点.画出⊙ABC的最长的中内弧DE,并直接写出此时弧DE的长;(2)在平面直角坐标系中,已知点A(2 √3,6),B(0,0),C(t,0),在⊙ABC中,D,E分别是AB,AC的中点.①若t=2 √3,求⊙ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围;②请写出一个t的值,使得⊙ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值.8.如图,⊙O是⊙ABC的外接圆,AC是直径,过点O作OD⊙AB于点D,延长DO 交⊙O于点P,过点P作PE⊙AC于点E,作射线DE交BC的延长线于F点,连接PF.(1)若⊙POC=60°,AC=12,求劣弧PC的长;(结果保留π)(2)求证:OD=OE;(3)求证:PF是⊙O的切线.9.如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=32CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.(1)用关于x的代数式表示BQ=,DF=.(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.(3)当点P在点A右侧时,作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长.10.如图,⊙ABC中,⊙ACB=90°,D是边AB上一点,且⊙A=2⊙DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.(1)求证:AB是⊙O的切线;(2)若CD的弦心距为1,BE=EO,求BD的长.11.已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM 在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持⊙ABP=90°不变,BP边与直线l相交于点P.(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;(2)请利用如图1所示的情形,求证:ABPB=OMBM;(3)若AO=2 √6,且当MO=2PO时,请直接写出AB和PB的长.12.(问题情境)如图①,小区A、B位于一条笔直的道路l的同侧,为了方便A,B两个小区居民投放垃圾,现在l上建一个垃圾分类站C,使得C与A,B的距离之比为2:1.(1)(初步研究)在线段AB上作出点C,使CACB=2.如图,做法如下:第一步:过点A作射线AM,以A为圆心,任意长为半径画弧,交AM于点P1;以P1为圆心,AP1长为半径画弧,交AM于点P2;以P2为圆心,AP1长为半径画弧,交AM于点P3.第二步:连接BP3,作∠AP2C=∠AP3B,交AB于点C.则点C即为所求.请证明所作的点C满足CACB=2.(2)(深入思考)如图,点C在线段AB上,点D在直线AB外,且DADB=CACB=2.求证:DC是∠ADB的平分线.(3)(问题解决)如图,已知点A,B和直线l,点C在线段AB上,且CACB=2.用直尺和圆规完成下列作图.(保留作图痕迹,不写作法)(⊙)在直线AB上作出点E(异于点C),使EAEB=2;(⊙)在直线l上作出点F,使FAFB=2.13.在矩形ABCD中,BC=2AB,点E是对角线AC上任意一点,过点E作AD的垂线分别交AD,BC于点F,G,作FH平行AC交CD于点H.(1)证明:EF=CH.(2)连结GH交AC于点K,若AE:CK=3,求AE:EK的值.(3)作⊙FGH的外接圆⊙O,且AB=1.①若⊙O与矩形的边相切时,求CH的长.②作点E关于GH的对称点E',当E'落在⊙O上时,直接写出⊙FGH的面积。
初三有关圆的解答题及答案

初三有关圆的解答题及答案初三数学教学中,圆是一个非常重要的内容,也是经常考察的一道题型。
下面,我们来探讨一些初三有关圆的解答题及其答案。
一、相切问题问题:两个圆相切,半径分别为$r_1$和$r_2$,求它们的公切线的长度$L$。
解析:根据勾股定理,可得:$(r_1 + r_2)^2 = L^2 + (r_1 - r_2)^2$化简得:$L = 2\sqrt{r_1r_2}$答案:$L = 2\sqrt{r_1r_2}$二、切线问题问题:已知一个圆心坐标$(a, b)$,与一直线$y=k$相切,求这个圆的方程。
解析:由于圆与直线相切,所以该直线的距离等于圆的半径。
直线$y=k$与圆的距离为$|b-k|$,因此圆的方程为:$(x-a)^2 + (y-b)^2 = (b-k)^2$答案:$(x-a)^2 + (y-b)^2 = (b-k)^2$三、垂直问题问题:已知直线$y=k$和圆$(x-a)^2+(y-b)^2=r^2$相交于点$P(x_0,y_0)$,求直线$OP$的斜率,其中$O(a,b)$为圆心。
解析:首先,求点$P$的坐标。
因为$P$是圆和直线的交点,所以可以列出以下方程组:$\begin{cases} y=k \\ (x-a)^2 + (y-b)^2 = r^2 \end{cases}$将$y=k$代入第二个方程,可得:$(x-a)^2 + (k-b)^2 = r^2$将$(x,y)$代入,得到:$(x_0-a)^2 + (k-b)^2 = r^2$整理可得:$x_0 = a\pm \sqrt{r^2-(k-b)^2}$由于直线$OP$与$x$轴垂直,所以直线$OP$的斜率为$-\frac{1}{\frac{y_0-b}{x_0-a}}$。
代入$x_0$和$y_0$,即可得到答案。
答案:$-\frac{1}{\frac{y_0-b}{x_0-a}}$四、分割问题问题:一个圆$O$被圆弧$AB$和直径$CD$所分割,分别为弧$AB$和弧$BCD$。
九年级数学上册《圆》练习题及答案解析

九年级数学上册《圆》练习题及答案解析学校:___________姓名:___________班级:___________一、单选题1.下列说法正确的是()A.直径是弦,弦是直径B.过圆心的线段是直径C.圆中最长的弦是直径D.直径只有二条2.下列语句不正确的有()个.①直径是弦;①优弧一定大于劣弧;①长度相等的弧是等弧;①半圆是弧.A.1B.2C.3D.43.如图,在①O中,点B,O,C和点A,O,D分别在同一条直线上,则图中有()条弦.A.2B.3C.4D.54.下列说法正确的是()A.劣弧一定比优弧短B.面积相等的圆是等圆C.长度相等的弧是等弧D.如果两个圆心角相等,那么它们所对的弧也相等5.下列由实线组成的图形中,为半圆的是()A.B.C.D.6.下列说法正确的是()A.平分弦的直径垂直于弦B .半圆(或直径)所对的圆周角是直角C .相等的圆心角所对的弧相等D .若一条直线与一个圆有公共点,则二者相交二、填空题7.如图,已知在Rt△ABC 中,①ACB =90°,分别以AC ,BC ,AB 为直径作半圆,面积分别记为S 1,S 2,S 3,若S 3=9π,则S 1+S 2等于_____.8.如图,Rt ABC 中,90ACB ∠=︒,以点C 为圆心,BC 为半径的圆交AB 于D ,交AC 于点E ,40BCD ∠=︒,则A ∠=______.9.如图,圆中扇子对应的圆心角α(180α)与剩余圆心角β的比值为黄金比时,扇子会显得更加美观,若黄金比取0.6,则βα-的度数是__________.10.数学家赵爽在注解《周髀算经》时给出了“赵爽弦图”,如图所示,它是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,若直角三角形较短直角边长为6,大正方形的边长为10,则小正方形的边长为________.11.如图,在O 中,AB 为直径,8AB =,BD 为弦,过点A 的切线与BD 的延长线交于点C ,E 为线段BD 上一点(不与点B 重合),且OE DE =.(1)若35B ∠=︒,则AD 的长为______(结果保留π);(2)若6AC =,则DE BE=______.三、解答题12.如图,在Rt ABC 中,90ACB ∠=︒,以AC 为直径作O ,交AB 于点D ,E 为BC 的中点,连接DE 并延长交AC 的延长线于点E .(1)求证:DF 是O 的切线;(2)若2CF =,4DF =,求O 的半径.13.如图,点A ,B 分别在①DPE 两边上,且PA PB =,点C 在①DPE 平分线上.(1)连接AC ,BC ,求证:AC BC =;(2)连接AB 交PC 于点O ,若60APB ∠=︒,6PA =,求PO 的长;(3)若PO OC ,且点O 是PAB △的外心,请直接写出四边形P ACB 的形状.参考答案与解析:1.C【详解】解:A 、直径是弦,但弦不一定是直径,不符合题意;B 、过圆心的弦是直径,但线段不一定是直径,不符合题意;C 、圆中最长的弦是直径,符合题意;D 、直径有无数条,不符合题意,故选C .2.B【分析】根据圆的概念、等弧的概念、垂径定理、弧、弦直径的关系定理判断即可.【详解】解:①直径是弦,①正确;①在同圆或等圆中,优弧大于劣弧,①错误;①在同圆或等圆中,长度相等的弧是等弧,①错误;①半圆是弧,①正确;故不正确的有2个.故选:B .【点睛】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.3.B【详解】根据弦的概念,AB 、BC 、EC 为圆的弦,共有3条弦.故选B.4.B【分析】根据圆的相关概念、圆周角定理及其推论进行逐一分析判断即可.【详解】解:A.在同圆或等圆中,劣弧一定比优弧短,故本选项说法错误,不符合题意;B.面积相等的圆是等圆,故本选项说法正确,符合题意;C.能完全重合的弧才是等弧,故本选项说法错误,不符合题意;D.必须在同圆或等圆中,相等的圆心角所对的弧相等,故本选项说法错误,不符合题意.故选:B .【点睛】本题主要考查了圆周角定理及其推论、等弧、等圆、以及优弧和劣弧等知识,解题关键是理解各定义的前提条件是在同圆或等圆中.5.B【分析】根据半圆的定义即可判断.【详解】半圆是直径所对的弧,但是不含直径,故选B .【点睛】此题主要考查圆的基本性质,解题的根据熟知半圆的定义.6.B【分析】利用圆与圆的位置关系、垂径定理、圆周角定理等有关圆的知识进行判断即可【详解】A 、平分弦(不是直径)的直径垂直于弦,故本选项错误;B 、半圆或直径所对的圆周角是直角,故本选项正确;C 、同圆或等圆中,相等的圆心角所对的弧相等,故本选项错误;D 、若一条直线与一个圆有公共点,则二者相交或相切,故本选项错误,故选B .【点睛】本题考查直线与圆的位置关系,垂径定理,圆心角、弧、弦的关系,圆周角定理.能清楚的知道每个定理的条件和它对应的结论是解题的关键.7.9π.【分析】根据勾股定理和圆的面积公式,可以得到S 1+S 2的值,从而可以解答本题.【详解】解:①①ACB =90°,①AC 2+BC 2=AB 2,①S 1=π(2AC )2×12,S 2=π(2BC )2×12,S 3=π(2AB )2×12, ①S 1+S 2=π(2AC )2×12+π(2BC )2×12=π(2AB )2×12=S 3, ①S 3=9π,①S 1+S 2=9π,故答案为:9π.【点睛】本题考查勾股定理,解答本题的关键是利用数形结合的思想解答.8.20°.【分析】由半径相等得CB=CD,则①B=①CDB,在根据三角形内角和计算出①B=12(180°-①BCD)=70°,然后利用互余计算①A的度数.【详解】解:①CB=CD,①①B=①CDB,①①B+①CDB+①BCD=180°,①①B=12(180°-①BCD)=12(180°-40°)=70°,①①ACB=90°,①①A=90°-①B=20°.故答案为20°.【点睛】本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).也考查了三角形内角和定理.9.90°##90度【分析】根据题意得出α=0.6β,结合图形得出β=225°,然后求解即可.【详解】解:由题意可得:α:β=0.6,即α=0.6β,①α+β=360°,①0.6β+β=360°,解得:β=225°,①α=360°-225°=135°,①β-α=90°,故答案为:90°.【点睛】题目主要考查圆心角的计算及一元一次方程的应用,理解题意,得出两个角度的关系是解题关键.10.2【分析】在Rt①ABC中,根据勾股定理求出AC,即可求出CD.【详解】解:如图,①若直角三角形较短直角边长为6,大正方形的边长为10,①AB =10,BC =AD =6,在Rt ①ABC 中,AC 8,①CD =AC ﹣AD =8﹣6=2.故答案为:2.【点睛】本题主要考查了勾股定理,熟练掌握勾股定理是解决问题的关键.11. 149π 2539 【分析】(1)根据圆周角定理求出①AOD =70°,再利用弧长公式求解;(2)解直角三角形求出BC ,AD ,BD ,再利用相似三角形的性质求出DE ,BE ,可得结论.【详解】解:(1)①270AOD ABD ∠=∠=︒,①AD 的长704141809ππ⋅⋅==; 故答案为:149π; (2)连接AD ,①AC 是切线,AB 是直径,①AB AC ⊥,①10BC ,①AB 是直径,①90ADB ∠=︒,①AD CB ⊥,①1122AB AC BC AD ⋅⋅=⋅⋅,①245 AD=,①325 BD==,①OB OD=,EO ED=,①EDO EOD OBD ∠=∠=∠,①DOE DBO△∽△,①DO DE DB DO=,①43245DE=,①52 DE=,①325395210 BE BD DE=-=-=,①5252393910DEBE==.故答案为:25 39.【点睛】本题主要考查圆的相关知识,相似三角形的判定和性质,解直角三角形等知识,熟练掌握各性质及判定定理,正确寻找相似三角形解决问题是解题的关键.12.(1)见解析(2)3【分析】(1)连接OD、CD,由AC为①O的直径知①BCD是直角三角形,结合E为BC的中点知①CDE=①DCE,由①ODC=①OCD且①OCD+①DCE=90°可得答案;(2)设①O的半径为r,由OD2+DF2=OF2,即r2+42=(r+2)2可得r=3,即可得出答案.(1)解:如图,连接OD、CD.①AC为①O的直径,①①ADC=90°,①①CDB=90°,即①BCD是直角三角形,①E为BC的中点,①BE=CE=DE,①①CDE=①DCE,①OD=OC,①①ODC=①OCD,①①ACB=90°,①①OCD+①DCE=90°,①①ODC+①CDE=90°,即OD①DE,①DE是①O的切线;(2)解:设①O的半径为r,①①ODF=90°,①OD2+DF2=OF2,即r2+42=(r+2)2,解得:r=3,①①O的半径为3.【点睛】本题主要考查了圆切线的判定与性质,等腰三角形的性质与判定,直角三角形斜边上的中线,勾股定理等等,熟知圆切线的性质与判定是解题的关键.13.(1)证明见解析(2)(3)正方形,理由见解析【分析】(1)证明①P AC①①PBC即可得到结论;(2)根据已知条件得到①APC=①BPC=30°,OP①AB于O,求得AO=3,再利用勾股定理即可得到结论;P A B C在以O为圆心,OP为半径的圆上,再证明①APB=①PBC=①BCA=①CAP=90°,可得(3)先证明,,,OBP BPC POB根据正方形的判定定理即可得到结论.四边形APBC为矩形,再证明45,90,(1)证明:①点C在①DPE平分线上,① APC BPC ∠=∠ ,又①P A =PB ,PC =PC ,①①P AC ①①PBC (SAS );.AC BC(2)解:①,,60,PA PB APOBPO APB ①①APC =①BPC =30°,OP ①AB 于O ;①P A =6,①AO =3, 22633 3.OP(3) 解:如图,①点O 是①P AB 的外心,①OA =OB =OP ,而OP =OC , ,,,P A B C 在以O 为圆心,OP 为半径的圆上,,AB PC 为圆的直径,①①APB =①PBC =①BCA =①CAP =90°,①四边形APBC 为矩形,PC 平分,APB ∠45,APC BPC,OP OB 45,90,OBP BPC POB①四边形APBC 为正方形.【点睛】本题考查了圆的综合题,全等三角形的判定和性质,正方形的判定,圆的确定,圆周角定理,正确的识别图形是解题的关键.。
部编数学九年级上册专题24.1圆【七大题型】(人教版)(解析版)含答案

专题24.1 圆【七大题型】【人教版】【题型1 圆的概念】 (1)【题型2 圆的有关概念】 (4)【题型3 确定圆的条件】 (6)【题型4 点与圆的位置关系】 (9)【题型5 圆中角度的计算】 (12)【题型6 圆中线段长度的计算】 (15)【题型7 圆相关概念的应用】 (18)定义②:圆可以看做是所有到定点O的距离等于定长r的点的集合.【题型1 圆的概念】【例1】(2022•金沙县一模)下列说法中,不正确的是( )A.圆既是轴对称图形又是中心对称图形B.圆有无数条对称轴C.圆的每一条直径都是它的对称轴D.圆的对称中心是它的圆心【分析】利用圆的对称性质逐一求解可得.【解答】解:A.圆既是轴对称图形又是中心对称图形,正确;B.圆有无数条对称轴,正确;C.圆的每一条直径所在直线都是它的对称轴,此选项错误;D.圆的对称中心是它的圆心,正确;故选:C.【变式1-1】(2022•武昌区校级期末)由所有到已知点O 的距离大于或等于2,并且小于或等于3的点组成的图形的面积为( )A .4πB .9πC .5πD .13π【分析】根据题意、利用圆的面积公式计算即可.【解答】解:由所有到已知点O 的距离大于或等于2,并且小于或等于3的点组成的图形的面积为以3为半径的圆与以2为半径的圆组成的圆环的面积,即π×32﹣π×22=5π,故选:C .【变式1-2】(2022•杭州模拟)现有两个圆,⊙O 1的半径等于篮球的半径,⊙O 2的半径等于一个乒乓球的半径,现将两个圆的周长都增加1米,则面积增加较多的圆是( )A .⊙O 1B .⊙O 2C .两圆增加的面积是相同的D .无法确定【分析】先由L =2πR 计算出两个圆半径的伸长量,然后再计算两个圆增加的面积,然后进行比较大小即可.【解答】解:设⊙O 1的半径等于R ,变大后的半径等于R ′;⊙O 2的半径等于r ,变大后的半径等于r ′,其中R >r .由题意得,2πR+1=2πR ′,2πr +1=2πr ′,解得R ′=R +12π,r ′=r +12π;所以R ′﹣R =12π,r ′﹣r =12π,所以,两圆的半径伸长是相同的,且两圆的半径都伸长12π.∴⊙O 1的面积=πR 2,变大后的面积=π(R +12π)2,面积增加了π(R +12π)2−πR 2=R +14π,⊙O 2的面积=πr 2,变大后的面积=π(r +12π)2,面积增加了π(r +12π)2−πr 2=r +14π,∵R >r ,∴R +14π>r +14π,∴⊙O 1的面积增加的多.故选:A .【变式1-3】(2022•浙江)如图,AB 是⊙O 的直径,把AB 分成几条相等的线段,以每条线段为直径分别画小圆,设AB =a ,那么⊙O 的周长l =πa .计算:(1)把AB 分成两条相等的线段,每个小圆的周长l 2=12πa =12l ;(2)把AB 分成三条相等的线段,每个小圆的周长l 3= 13l ;(3)把AB 分成四条相等的线段,每个小圆的周长l 4= 14l ;(4)把AB 分成n 条相等的线段,每个小圆的周长l n = 1n l .结论:把大圆的直径分成n 条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的 1n .请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.【分析】把大圆的直径分成n 条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是l n =π(1n a )=1n l ,即每个小圆周长是大圆周长的1n ;根据圆的面积公式求得每个小圆的面积和大圆的面积后比较.【解答】解:(2)13l ;(3)14l ;(4)1n l ;1n ;每个小圆面积=π(12•1n a )2=14•πa 2n 2,而大圆的面积=π(12•a )2=14πa 2即每个小圆的面积是大圆的面积的1.n2【题型2 圆的有关概念】【例2】(2022•远安县期末)下列说法:①弦是直线;②圆的直径被该圆的圆心平分;③过圆内一点P的直径仅有一条;④弧是圆的一部分.其中正确的有( )A.1个B.2个C.3个D.4个【分析】根据弦,直径,弧的定义一一判断即可.【解答】解:①弦是直线,错误,弦是线段.②圆的直径被该圆的圆心平分,正确.③过圆内一点P的直径仅有一条,错误,点P是圆心时,直径有无数条.④弧是圆的一部分,正确.故选:B.【变式2-1】(2022图木舒克月考)有一个圆的半径为5,则该圆的弦长不可能是( )A.1B.4C.10D.11【分析】根据直径是圆中最长的弦,判断即可.【解答】解:∵一个圆的半径为5,∴圆中最长的弦是10,∴弦长不可能为11,故选:D.【变式2-2】(2022•嘉鱼县期末)如右图中有 1 条直径,有 4 条弦,以点A为端点的优弧有 2 条,有劣弧 2 条.【分析】根据直径、弦、优弧及劣弧的概念解答即可得.【解答】解:图中直径只有AB这1条,弦有AC、AB、CD、BC这4条,以点A为端点的优弧有ACD、ADC 这2条,劣弧有AC、AD这2条,故答案为:1、4、2、2.【变式2-3】(2022仪征市期末)如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有 4 个.【分析】解法一:过点P最长的弦是12,根据已知条件,△OAB的面积为18,可以求出AB<12,根据三角形面积可得OC=OP的长有两个整数:5,6,且OP=6是P在A或B点时,每一个值都有两个点P,所以一共有4个.解法二:根据面积可知,OA上的高为6,也就是说OA与OB互相垂直,然后算出OC长度即可.【解答】解:解法一:过O作OC⊥AB于C,则AC=BC,设OC=x,AC=y,∵AB是⊙O的一条弦,⊙O的半径为6,∴AB≤12,∵△OAB的面积为18,+y2=362y⋅x=18,则y=18x,∴x2+(18x)2=36,解得x=∴OC=4,∴4<OP≤6,∵点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.解法二:设△AOB中OA边上的高为h,则12×OAℎ=18,即12×6ℎ=18,∴h=6,∵OB=6,∴OA⊥OB,即∠AOB=90°,∴AB=OC=同理得:点P为弦AB上一动点,当OP长为整数时,OP=5或6,P点有4个.故答案为:4.【题型3 确定圆的条件】【例3】(2022•绥中县一模)小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )A.①B.②C.③D.均不可能【分析】要确定圆的大小需知道其半径.根据垂径定理知第①块可确定半径的大小.【解答】解:第①块出现两条完整的弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.故选:A.【变式3-1】(2022春•射阳县校级期末)平面直角坐标系内的三个点A(1,0)、B(0,﹣3)、C(2,﹣3) 能 确定一个圆(填“能”或“不能”).【分析】根据三个点的坐标特征得到它们不共线,于是根据确定圆的条件可判断它们能确定一个圆.【解答】解:∵B(0,﹣3)、C(2,﹣3),∴BC∥x轴,而点A(1,0)在x轴上,∴点A、B、C不共线,∴三个点A(1,0)、B(0,﹣3)、C(2,﹣3)能确定一个圆.故答案为:能.【变式3-2】(2022•西城区期末)如图,在平面直角坐标系xOy中,点A,B,C的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为 (2,1) .【分析】根据图形得出A、B、C的坐标,再连接AB,作线段AB和线段BC的垂直平分线MN、EF,两线交于Q,则Q是圆弧的圆心,最后求出点Q的坐标即可.【解答】解:从图形可知:A点的坐标是(0,2),B点的坐标是(1,3),C点的坐标是(3,3),连接AB,作线段AB和线段BC的垂直平分线MN、EF,两线交于Q,则Q是圆弧的圆心,如图,∴Q点的坐标是(2,1),故答案为:(2,1).【变式3-3】(2022•任城区校级月考)将图中的破轮子复原,已知弧上三点A,B,C.(1)画出该轮的圆心;(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求圆片的半径R.【分析】(1)根据垂径定理,分别作弦AB和AC的垂直平分线交点即为所求;(2)连接AO,OB,利用垂径定理和勾股定理可求出圆片的半径R.【解答】解:(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;(2)连接AO,OB,BC,BC交OA于D.∵BC=16cm,∴BD=8cm,∵AB=10cm,∴AD=6cm,设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,∴R2=82+(R﹣6)2,cm,解得:R=253cm.∴圆片的半径R为253【题型4 点与圆的位置关系】【例4】(2022秋•宜州区期末)如已知:如图,△ABC中,∠C=90°,AC=2cm,BC=4cm,CM是中线,以C长为半径画圆,则点A、B、M与⊙C的关系如何?【分析】点与圆的位置关系由三种情况:设点到圆心的距离为d,则当d=R时,点在圆上;当d>R时,点在圆外;当d<R时,点在圆内.【解答】解:根据勾股定理,有AB=cm);∵CA=2cm,∴点A在⊙O内,∵BC=4cm,∴点B在⊙C外;由中线定理得:CM=∴M点在⊙C上.【变式4-1】(2022春•龙湖区校级月考)⊙O的面积为25πcm2,⊙O所在的平面内有一点P,当PO =5cm 时,点P在⊙O上;当PO <5cm 时,点P在⊙O内;当PO >5cm 时,点P在⊙O外.【分析】根据圆的面积求出圆的半径,然后确定圆上点,圆内点以及圆外的到圆心的距离.【解答】解:因为圆的面积为25πcm2,所以圆的半径为5cm.当点P到圆心的距离等于5cm时,点P在⊙O上,此时OP=5cm.当点P到圆心的距离小于5cm时,点P在⊙O内,此时OP<5cm.当点P到圆心的距离大于5cm时,点P在⊙O外,此时OP>5cm.故答案分别是:PO=5cm,PO<5cm,PO>5cm.【变式4-2】(2022•广东模拟)如图,已知⊙A的半径为1,圆心的坐标为(4,3).点P(m,n)是⊙A 上的一个动点,则m2+n2的最大值为 36 .【分析】由于圆心A的坐标为(4,3),点P的坐标为(m,n),利用勾股定理可计算出OA=5,OP=这样把m2+n2理解为点P与原点的距离的平方,利用图形可得到当点P运动到射线OA上时,点P离圆点最远,即m2+n2有最大值,然后求出此时的PO长即可.【解答】解:作射线OA交⊙O于P′点,如图,∵圆心A的坐标为(4,3),点P的坐标为(m,n),∴OA5,OP=∴m2+n2是点P点圆点的距离的平方,∴当点P运动到P′处,点P离圆点最远,即m2+n2有最大值,此时OP=OA+AP′=5+1=6,则m2+n2=36.故答案为:36.【变式4-3】(2022秋•金牛区期末)如图.A(3,0).动点B到点M(3,4)的距离为1,连接BO,BO 的中点为C,则线段AC的最小值为 2 .【分析】先确定AC最小值时点B的位置:过B作BD∥AC交x轴于D,由图可知:当BD经过M时,线段BD的长最小,此时AC有最小值,根据勾股定理和三角形中位线定理可得AC的长.【解答】解:过B作BD∥AC交x轴于D,∵C是OB的中点,∴OA=AD,BD,∴AC=12∴当BD取最小值时,AC最小,由图可知:当BD经过M时,线段BD的长最小,此时AC有最小值,∵A(3,0),∴D(6,0),∵M(3,4),∴DM==5,∴BD=5﹣1=4,BD=2,即线段AC的最小值为2;∴AC=12故答案为:2.【题型5 圆中角度的计算】【例5】(2022•江宁区校级期中)如图,BD=OD,∠AOC=114°,求∠AOD的度数.【分析】设∠B=x,根据等腰三角形的性质,由BD=OD得∠DOB=∠B=x,再根据三角形外角性质得∠ADO=2x,则∠A=∠ADO=2x,然后根据三角形外角性质得2x+x=114°,解得x=38°,最后利用三角形内角和定理计算∠AOD的度数.【解答】解:设∠B=x,∵BD=OD,∴∠DOB=∠B=x,∴∠ADO=∠DOB+∠B=2x,∵OA=OD,∴∠A=∠ADO=2x,∵∠AOC=∠A+∠B,∴2x+x=114°,解得x=38°,∴∠AOD=180°﹣∠OAD﹣∠ADO=180°﹣4x=180°﹣4×38°=28°.【变式5-1】(2022•汉阳区校级月考)如图,AB是⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E.已知AB=2DE,∠AEC=25°,求∠AOC的度数.【分析】求∠AOC的度数,可以转化为求∠C与∠E的问题.【解答】解:连接OD,∵AB=2DE=2OD,∴OD=DE,又∵∠E=25°,∴∠DOE=∠E=25°,∴∠ODC=50°,同理∠C=∠ODC=50°∴∠AOC=∠E+∠OCE=75°.【变式5-2】(2022•金牛区期末)如图,AB为⊙O的直径,AD∥OC,∠AOD=84°,则∠BOC= 48° .【分析】根据半径相等和等腰三角形的性质得到∠D=∠A,利用三角形内角和定理可计算出∠A,然后根据平行线的性质即可得到∠BOC的度数.【解答】解:∵OD=OC,∴∠D=∠A,∵∠AOD=84°,(180°﹣84°)=48°,∴∠A=12又∵AD∥OC,∴∠BOC=∠A=48°.故答案为:48°.【变式5-3】(2022•大丰市月考)如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O 上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.是否存在点P,使得QP=QO;若存在,求出相应的∠OCP的大小;若不存在,请简要说明理由.【分析】点P是直线l上的一个动点,因而点P与线段AO有三种位置关系,在线段AO上,点P在OB 上,点P在OA的延长线上.分这三种情况进行讨论即可.【解答】解:①根据题意,画出图(1),在△QOC中,OC=OQ,∴∠OQC=∠OCP,在△OPQ中,QP=QO,∴∠QOP=∠QPO,又∵∠AOC=30°,∴∠QPO=∠OCP+∠AOC=∠OCP+30°,在△OPQ中,∠QOP+∠QPO+∠OQC=180°,即(∠OCP+30°)+(∠OCP+30°)+∠OCP=180°,整理得,3∠OCP=120°,∴∠OCP=40°.②当P在线段OA的延长线上(如图2)∵OC=OQ,∴∠OQP=(180°﹣∠QOC)×1①,2∵OQ=PQ,∴∠OPQ=(180°﹣∠OQP)×1②,2在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,把①②代入③得∠QOC=20°,则∠OQP=80°∴∠OCP=100°;③当P在线段OA的反向延长线上(如图3),∵OC=OQ,∴∠OCP=∠OQC=(180°﹣∠COQ)×1①,2∵OQ=PQ,∴∠P=(180°﹣∠OQP)×1②,2∵∠AOC=30°,∴∠COQ+∠POQ=150°③,∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,①②③④联立得∠P=10°,∴∠OCP=180°﹣150°﹣10°=20°.故答案为:40°、20°、100°.【题型6 圆中线段长度的计算】【例6】(2022•潮安区模拟)如图,在△ABC中,∠C=90°,AB=10.若以点C为圆心,CA长为半径的圆恰好经过AB的中点D,则⊙C的半径为( )A .B .8C .6D .5【分析】连结CD ,根据直角三角形斜边中线定理求解即可.【解答】解:如图,连结CD ,∵CD 是直角三角形斜边上的中线,∴CD =12AB =12×10=5.故选:D .【变式6-1】(2022•海港区校级自主招生)如图,圆O 的周长为4π,B 是弦CD 上任意一点(与C ,D 不重合),过B 作OC 的平行线交OD 于点E ,则EO +EB = 2 .(用数字表示)【分析】根据圆的周长公式得到OD =2,根据等腰三角形的判定和性质定理即可得到结论.【解答】解:∵⊙O 的周长为4π,∴OD =2,∵OC =OD ,∴∠C =∠D ,∵BE ∥OC ,∴∠EBD =∠C ,∴∠EBD =∠D ,∴BE =DE ,∴EO +EB =OD =2,故答案为:2.【变式6-2】(2022•龙湖区校级开学)如图,已知AB 是⊙O 的直径,C 是⊙O 上的一点,CD ⊥AB 于D ,AD <BD ,若CD =2cm ,AB =5cm ,求AD 、AC 的长.【分析】由直径AB =5cm ,可得半径OC =OA =12AB =52cm ,分别利用勾股定理计算AD 、AC 的长.【解答】解:连接OC ,∵AB =5cm ,∴OC =OA =12AB =52cm ,Rt △CDO 中,由勾股定理得:DO =32cm ,∴AD =52−32=1cm ,由勾股定理得:AC ==则AD 的长为1cm ,AC .【变式6-3】(2022秋•邗江区期中)如图,半圆O 的直径AB =8,半径OC ⊥AB ,D 为弧AC 上一点,DE ⊥OC ,DF ⊥OA ,垂足分别为E 、F ,求EF 的长.【分析】连接OD ,利用三个角是直角的四边形是矩形判定四边形DEOF 是矩形,利用矩形的对角线相等即可得到所求结论.【解答】解:连接OD .∵OC ⊥AB DE ⊥OC ,DF ⊥OA ,∴∠AOC =∠DEO =∠DFO =90°,∴四边形DEOF是矩形,∴EF=OD.∵OD=OA∴EF=OA=4.【题型7 圆相关概念的应用】【例7】(2022秋•南岗区校级期中)某中学原计划修一个半径为10米的圆形花坛,为使花坛修得更加美观,决定向全校征集方案,在众多方案中最后选出两种方案:方案A如图1所示,先画一条直径,再分别以两条半径为直径修两个圆形花坛;方案B如图2所示,先画一条直径,然后在直径上取一点,把直径分成2:3的两部分,再以这两条线段为直径修两个圆形花坛;(花坛指的是图中实线部分)(1)如果按照方案A修,修的花坛的周长是 .(保留π)(2)如果按照方案B修,与方案A比,省材料吗?为什么?(保留π)(3)如果按照方案B修,学校要求在5天内完成,甲工人承包了此项工程,甲每天能完成工程的1,他15做了1天后,发现不能完成任务,就请乙来帮忙,乙的速度是甲的2倍,乙加入后,甲的速度也提高了1,结果正好按时完成任务,若修1米花坛可得到10元钱,修完花坛后,甲,乙各得到多少钱?(π取23)【分析】(l)根据圆的周长公式:c=xd,把数据代入公式求此直径是10米的两个圆的周长即可.(2)首先根据圆的周长公式:c=元d,求出直径是4米、和6米的圆的周长和,然后与图1进行比较.(3)求出乙的钱数,再用总钱数﹣乙是钱数,可得结论.【解答】解:(1)10÷2=5(米),2π×5×2=20π(米).故答案为:20π米.=8(米),8÷2=4(米),(2)10×2=20(米),20×223=12(米),12÷2=6(米),20×323方案B花坛周长:2π(4+6)=20π(米),20π=20π,方案B与A周长一样,用的材料一样.×2×(5﹣1)×20π×10=320(元).(3)乙的钱数=115甲的钱数=20π×10﹣320=280(元),答:修完花坛后,甲,乙分别得到320元和280元.【变式7-1】(2022•南岗区期末)一个压路机的前轮直径是1.7米,如果前轮每分钟转动6周,那么这台压路机10分钟前进( )米.A.51πB.102πC.153πD.204π【分析】首先根据圆的周长公式C=πd,求出前轮的底面圆周长,然后用前轮的底面周长乘每分钟转的周数(6周),求出1分钟前进多少米,再乘工作时间10分钟即可.【解答】解:前轮的底面圆周长:π×1.7=1.7π(米),1.7π×6×10=102π(米)故选:B.【变式7-2】(2022•罗田县校级模拟)一个塑料文具胶带如图所示,带宽为1cm,内径为4cm,外径为7cm,已知30层胶带厚1.5mm,则这卷胶带长 51.81 m.(π≈3.14,结果保留4位有效数字)【分析】首先求出胶带的体积,用胶带的体积除以一米长的胶带的体积即可求得.【解答】解:4÷2=2(cm),7÷2=3.5(cm),胶带的体积是:π(3.52﹣22)•1=8.25πcm3=8.25π×10﹣6(m3),一米长的胶带的体积是:0.01×1×5×10﹣5=5×10﹣7(m3),因而胶带长是:(8.25π×10﹣6)÷(5×10﹣7)≈51.81(m).故答案为:51.81.【变式7-3】(2022•张店区期末)如图,大圆和圆的半径都分别是4cm和2cm,两圆外切于点C,一只蚂蚁由点A开始ABCDEFCGA的顺序沿着两圆圆周不断地爬行,其中各点分别是两圆周的四等分点,蚂蚁直到行走2010πcm后才停下来.则这只蚂蚁停在点 E .【分析】首先求得蚂蚁由点A开始ABCDEFCGA的顺序走一周的路线长,然后确定走2010πcm是走了多少周,即可确定.【解答】解:A开始ABCDEFCGA的顺序转一周的路径长是:8π+4π=12πcm,蚂蚁直到行走2010πcm所转的周数是:2010π÷12π=167…6π.即转167周以后又走了6πcm.从A到B得路长是:2π,再到C的路线长也是2π,从C到D,到E的路线长是2π,则从A行走6πcm 到E点.故答案是:E.。
九年级数学上册专题第14讲圆的有关性质重点、考点知识总结及练习

第14讲圆的有关性质⎧⎪⎪⎨⎪⎪⎩垂径定理弧、弦、圆心角的关系圆的有关性质圆周角定理及推论圆内接四边形的性质 知识点1垂径定理①弦和直径:(1)弦:连接圆上任意两点的线段叫做弦.(2)直径:经过圆心的弦叫做直径。
直径等于半径的两倍。
②弧:(1) 弧:圆上任意两点间的部分叫做圆弧,简称弧,用符号⌒表示,以A,B 为端点的的弧记作AB ⌒,读作弧AB.(2)半圆、优弧、劣弧:圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。
大于半圆的弧叫做优弧,优弧大于180º用三个字母表示,如 ACB .小于半圆的弧叫做劣弧,如AB 。
(3)等弧:在同圆或者等圆中能够相互重合的弧是等弧,度数或者长度相等的弧不一定是等弧。
③弦心距:(1)圆心到弦的距离叫做弦心距。
(2)圆心角、弧、弦、弦心距之间的相等关系:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的圆心角也相等,所对弦的弦心距也相等。
四者有一个相等,则其他三个都相等。
圆心到弦的垂线段的长度称为这条弦的弦心距。
④圆的性质:(1)旋转不变性:圆是旋转对称图形,绕圆心旋转任一角度都和原来图形重合;圆是中心对称图形,对称中心是圆心.在同圆或等圆中,两个圆心角,两条弧,两条弦,两条弦心距,这四组量中的任意一组相等,那么它所对应的其他各组分别相等.(2)轴对称:圆是轴对称图形,直径所在的直线是它的对称轴。
⑤垂径定理及推论:(1)垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.(2)平分弦(此弦不能是直径)的直径垂直于弦,并且平分弦所对的两条弧.(3)弦的垂直平分线过圆心,且平分弦对的两条弧.(4)平分一条弦所对的两条弧的直线过圆心,且垂直平分此弦.(5)平行弦夹的弧相等.⑥同心圆与等圆(1)同心圆:圆心相同,半径不相等的两个圆叫做同心圆。
如图一,半径为r1与半径为r2的⊙O叫做同心圆。
(图一)(2)等圆:圆心不同,半径相等的两个圆叫做等圆。
数学初三圆的试题及答案

数学初三圆的试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是圆的标准方程?A. (x-a)²+(y-b)²=r²B. x²+y²=rC. x²+y²=r²D. (x-a)²+(y-b)²=r答案:A2. 圆心为(2,3),半径为5的圆的方程是什么?A. (x-2)²+(y-3)²=25B. (x-2)²+(y-3)²=5C. x²+y²=25D. x²+y²=5答案:A3. 已知圆C的圆心为(1,1),半径为2,点P(4,3)在圆C上,那么点P 到圆心的距离是多少?A. 2B. 3C. 4D. 5答案:B4. 圆的直径是10,那么它的半径是多少?A. 5B. 10C. 20D. 15答案:A5. 圆心在原点,半径为3的圆的方程是?A. x²+y²=9B. (x-0)²+(y-0)²=3C. x²+y²=3D. (x-3)²+(y-3)²=9答案:A6. 圆的周长公式是?A. C=2πrB. C=πrC. C=2rD. C=r答案:A7. 圆的面积公式是?A. A=πr²B. A=2πrC. A=r²D. A=2r答案:A8. 圆的切线与半径垂直,那么切线与圆心的距离是多少?A. rB. 2rC. πrD. 0答案:A9. 圆的弧长公式是?A. L=rθB. L=2πrC. L=rθ/180D. L=2πrθ/360答案:D10. 圆的扇形面积公式是?A. S=1/2r²θB. S=1/2r²C. S=rθD. S=2πrθ/360答案:D二、填空题(每题4分,共20分)1. 圆心在(-2,4),半径为3的圆的方程是:(x+2)²+(y-4)²=________。
九年级数学圆知识点及习题(含答案)

九年级数学圆知识点及习题(含答案)1.圆上各点到圆心的距离都等于半径。
2.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴;圆又是中心对称图形, 圆心是它的对称中心。
3.垂直于弦的直径平分这条弦 ,并且平分弦所对的弧;平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。
4.在同圆或等圆中,如果两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量相等 ,那么它们所对应的其余各组量都分别相等。
5.同弧或等弧所对的圆周角相等 ,都等于它所对的圆心角的一半。
6.直径所对的圆周角是 90° ,90°所对的弦是直径。
7.三角形的三个顶点确定 1 个圆,这个圆叫做三角形的外接圆,三角形的外接圆的圆心叫外心,是三角形三边垂直平分线的交点。
8.与三角形各边都相切的圆叫做三角形的内切圆 ,内切圆的圆心是三角形三条角平分线的交点的交点,叫做三角形的内心。
9.圆内接四边形:顶点都在圆上的四边形,叫圆内接四边形.10.圆内接四边形对角互补,它的一个外角等于它相邻内角的对角2、与圆有关的位置关系1.点与圆的位置关系共有三种:①点在圆外 ,②点在圆上 ,③点在圆内;对应的点到圆心的距离d和半径r之间的数量关系分别为:①d > r,②d = r,③d < r.2.直线与圆的位置关系共有三种:①相交 ,②相切 ,③相离;对应的圆心到直线的距离d和圆的半径r之间的数量关系分别为:①d < r,②d = r,③d > r.3.圆与圆的位置关系共有五种:①内含 ,②相内切 ,③相交 ,④相外切 ,⑤外离;两圆的圆心距d和两圆的半径R、r(R≥r)之间的数量关系分别为:①d < R-r,②d = R-r,③ R-r < d < R+ r,④d = R+r,⑤d > R+r.4.圆的切线垂直于过切点的半径;经过直径的一端,并且垂直于这条直径的直线是圆的切线.5.从圆外一点可以向圆引 2 条切线, 切线长相等,这点与圆心之间的连线平分这两条切线的夹角。
九年级数学《圆》知识点归纳及分类训练

<<圆>>知识点归纳(1)掌握圆的有关性质和计算① 弧、弦、圆心角之间的关系:在同圆或等圆中,如果两条劣弧(优弧)、两条两个圆心角中有一组量对应相等,那么它们所对应的其余各组量也分别对应相等.② 垂径定理: 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧. 垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 弦的垂直平分线经过圆心,并且平分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.③ 在同一圆内,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半. ④ 圆内接四边形的性质:圆的内接四边形对角互补,并且任何一个外角等于它的内对角. (2)点与圆的位置关系① 设点与圆心的距离为d ,圆的半径为r ,则点在圆外d r ⇔>; 点在圆上d r ⇔=; 点在圆内d r ⇔<. ② 过不在同一直线上的三点有且只有一个圆. 一个三角形有且只有一个外接圆. ③ 三角形的外心是三角形三边垂直平分线的交点.三角形的外心到三角形的三个顶点的距离相等.(3)直线与圆的位置关系① 设圆心到直线l 的距离为d ,圆的半径为r ,则直线与圆相离d r ⇔>;直线与圆相切d r ⇔=;直线与圆相交d r ⇔<.② 切线的性质:与圆只有一个公共点;圆心到切线的距离等于半径;圆的切线垂直于过切点的半径. ③ 切线的识别:如果一条直线与圆只有一个公共点,那么这条直线是圆的切线. 到圆心的距离等于半径的直线是圆的切线.经过半径的外端且垂直与这条半径的直线是圆的切线.④ 三角形的内心是三角形三条内角平分线的交点. 三角形的内心到三角形三边的距离相等. ⑤ 切线长:圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长. ⑥ 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.(4)与圆有关的计算① 弧长公式:180n rl π= 扇形面积公式:213602n r S lr π==扇形 (其中为n 圆心角的度数,r 为半径) ② 圆柱的侧面展开图是矩形.圆柱体也可以看成是一个矩形以矩形的一边为轴旋转而形成的几何体. 圆柱的侧面积=底面周长×高 圆柱的全面积=侧面积+2×底面积③ 圆锥的侧面展开图是扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.圆锥体可以看成是由一个直角三角形以一条直角边为轴旋转而成的几何体. ④ 圆锥的侧面积=12×底面周长×母线;圆锥的全面积=侧面积+底面积能力提升(一)—— 圆中的有关概念和性质一、知识点回顾:1.确定一个圆有两要素,一是 ,二是 ,圆心确定 、半径确定 ;2.圆既是 对称图形,又是 对称图形;它的对称中心是 ,对称轴是 ,有 条对称轴。
九年级圆练习题及答案

九年级圆练习题及答案一、选择题1. 圆的半径是5,那么这个圆的直径是多少?A. 10B. 15C. 20D. 25答案:A2. 圆的周长公式是什么?A. C = πrB. C = 2πrC. C = 4πrD. C = πd答案:B3. 如果一个圆的周长是44厘米,那么它的半径是多少?A. 7厘米B. 11厘米C. 22厘米D. 无法确定答案:A4. 圆的面积公式是什么?A. A = πr²B. A = 2πrC. A = πdD. A = πd²答案:A5. 一个圆的面积是28.26平方厘米,它的半径是多少?A. 3厘米B. 4厘米C. 5厘米D. 6厘米答案:B二、填空题6. 半径为3厘米的圆的直径是______厘米。
答案:6厘米7. 一个圆的半径是4厘米,它的周长是______厘米。
答案:25.12厘米8. 圆的面积是50.24平方厘米,它的半径是______厘米。
答案:4厘米三、解答题9. 已知一个圆的半径是7厘米,求这个圆的周长和面积。
解答:根据圆的周长公式C = 2πr,代入 r = 7,得C = 2 × 3.14 × 7 = 43.96厘米。
根据圆的面积公式A = πr²,代入 r = 7,得A = 3.14 × 7²= 3.14 × 49 = 153.86平方厘米。
10. 一个圆的周长是31.4厘米,求这个圆的半径和面积。
解答:根据圆的周长公式C = 2πr,得 r = C / (2π) = 31.4 / (2 × 3.14) ≈ 5厘米。
根据圆的面积公式A = πr²,代入 r = 5,得A = 3.14 ×5² = 3.14 × 25 = 78.5平方厘米。
四、应用题11. 一个圆形花坛的半径是10米,如果沿着花坛的边缘走一圈,需要走多少米?解答:根据圆的周长公式C = 2πr,代入 r = 10,得C = 2 × 3.14 × 10 = 62.8米。
九年级圆知识点及习题(含答案)

九年级圆知识点及习题(含答案) Mathematics Review for Grade Nine: CirclesConcepts and Properties of Circles1.The distance from any point on a circle to its center is equal to the radius.2.A circle is a symmetric figure。
Any diameter is an axis of symmetry。
A circle is also a centrally symmetric figure。
with its center as the center of symmetry.3.A diameter perpendicular to a chord bisects the chord and the arc it subtends。
A diameter that bisects a chord (but is not perpendicular to it) is perpendicular to the chord and bisects the arc it subtends.4.In congruent or similar circles。
if two central angles。
two chords。
two arcs。
two chord distances from the center。
or two inscribed angles are equal。
then the other corresponding quantities are also equal.5.The central angle and the inscribed angle that subtend the same arc are equal。
初三关于圆的试题及答案

初三关于圆的试题及答案一、选择题(每题3分,共30分)1. 下列说法中,正确的是()A. 圆的直径是圆的半径的两倍B. 圆周率π是一个无限不循环小数C. 圆的周长与直径成正比例D. 圆的面积与半径的平方成正比例2. 圆的周长公式是()A. C = 2πrB. C = πdC. C = πrD. C = 2πd3. 圆的面积公式是()A. S = πr²B. S = 2πrC. S = πd²D. S = πd4. 一个圆的半径是5厘米,那么它的直径是()A. 10厘米B. 15厘米C. 20厘米D. 25厘米5. 如果一个圆的半径增加一倍,那么它的面积将增加()A. 1倍B. 2倍C. 4倍D. 8倍6. 一个圆的周长是62.8厘米,那么它的半径是()A. 10厘米B. 15厘米C. 20厘米D. 25厘米7. 圆内接四边形的对角线()A. 相等B. 垂直C. 互相平分D. 互相垂直8. 圆的直径是圆内最长的线段,这种说法()A. 正确B. 错误9. 圆的切线()A. 与半径垂直B. 与直径垂直C. 与圆心垂直D. 与圆周平行10. 圆的内切圆与外切圆的半径之和等于()A. 内切圆的半径B. 外切圆的半径C. 两圆半径之和D. 两圆半径之差二、填空题(每题3分,共30分)1. 圆的周长公式是______,面积公式是______。
2. 如果圆的半径是3厘米,那么它的周长是______厘米,面积是______平方厘米。
3. 圆的直径是半径的______倍。
4. 圆的周长与直径的比值是______。
5. 圆的面积与半径的平方的比值是______。
6. 圆的切线与半径的交点是______。
7. 圆内接四边形的对角线互相______。
8. 圆的内切圆与外切圆的半径之和等于______。
9. 圆的直径是圆内最长的线段,这种说法是______。
10. 圆的周长是圆的直径的______倍。
三、解答题(每题10分,共40分)1. 已知一个圆的半径是4厘米,求它的周长和面积。
2024~2025学年九年级数学上册期中复习——圆的基本性质学案(知识点+例题含解析)

《圆的基本性质》章节复习【要点梳理】要点一、圆的定义、性质及与圆有关的角1.圆的定义(1)线段OA绕着它的一个端点O旋转一周,另一个端点A所形成的封闭曲线,叫做圆.(2)圆是到定点的距离等于定长的点的集合.(3)不在同一条直线上的三个点确定一个圆.要点诠释:①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可;②圆是一条封闭曲线.2.点与圆的位置关系判定一个点P是否在⊙O上设⊙O的半径为,OP=,则有点P在⊙O外;点P在⊙O上;点P在⊙O内.要点诠释:点和圆的位置关系和点到圆心的距离的数量关系是相对应的,即知道位置关系就可以确定数量关系;知道数量关系也可以确定位置关系.3.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.定理2:平分弧的直径垂直平分弧所对的弦.4.与圆有关的角圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.在同圆或者等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各对量都相等.圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.在同圆或者等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.5.圆内接四边形圆内接四边形的对角互补.要点二、图形的旋转在平面内,一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转.这个定点叫做旋转中心,转过的角叫做旋转角.图形经过旋转所得的图形和原图形全等.对应点到旋转中心的距离相等.任何一对对应点与旋转中心连线所成的角度等于旋转的角度.要点三、正多边形各边相等,各内角也相等的多边形是正多边形.要点诠释:判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).正多边形的外接圆和圆的内接正多边形正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.要点四、弧长及扇形的面积圆心角为、半径为R的弧长.圆心角为,半径为R,弧长为的扇形的面积.要点诠释:(1)对于扇形面积公式,关键要理解圆心角是1°的扇形面积是圆面积的,即;(2)在扇形面积公式中,涉及三个量:扇形面积S、扇形半径R、扇形的圆心角,知道其中的两个量就可以求出第三个量.(3)扇形面积公式,可根据题目条件灵活选择使用,它与三角形面积公式有点类似,可类比记忆;(4)扇形两个面积公式之间的联系:.【典型例题】类型一、圆的基础知识1.如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行(或重合)的直线与⊙O有公共点,设OP=x,则x的取值范围是().A.-1≤x≤1B.≤x≤2C.0≤x≤2D.x>2【答案】C;【解析】如图,平移过P点的直线到P′,使其与⊙O相切,设切点为Q,连接OQ,由切线的性质,得∠OQP′=90°,∵OA∥P′Q,∴∠OP′Q=∠AOB=45°,∴△OQP′为等腰直角三角形,在Rt△OQP′中,OQ=1,OP′=2,∴当过点P且与OA平行的直线与⊙O有公共点时,0≤OP≤,当点P在x轴负半轴即点P向左侧移动时,结果相同.故答案为:0≤OP≤2.【总结升华】本题考查了直线与圆的位置关系问题.关键是通过平移,确定直线与圆相切的情况,求出此时OP的值.举一反三:【变式】如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OB平行的直线于⊙O有公共点,设P(x,0),则x的取值范围是().A.-1≤x<0或0<x≤1B.0<x≤1C.-2≤x<0或0<x≤2D.x>1【答案】∵⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,∴过点P′且与OB平行的直线与⊙O相切时,假设切点为D,∴OD=DP′=1,OP′=2,∴0<OP≤2,类型二、弧、弦、圆心角、圆周角的关系及垂径定理2.如图所示,已知在⊙O中,AB是⊙O的直径,弦CG⊥AB于D,F是⊙O上的点,且 CF CB=,BF交CG于点E,求证:CE=BE.【答案与解析】证法一:如图(1),连接BC,∵AB是⊙O的直径,弦CG⊥AB,∴ CB GB=.∵CF BC=,∴CF GB=.∴∠C=∠CBE.∴CE=BE.证法二:如图(2),作ON⊥BF,垂足为N,连接OE.∵AB是⊙O的直径,且AB⊥CG,∴ CB BG=.∵CB CF=,∴CF BC BG==.∴BF=CG,ON=OD.∵∠ONE=∠ODE=90°,OE=OE,ON=OD,∴△ONE≌△ODE,∴NE=DE.∵12BN BF=,12CD CG=,∴BN=CD,∴BN-EN=CD-ED,∴BE=CE.证法三:如图(3),连接OC交BF于点N.∵CF BC=,∴OC⊥BF.∵AB是⊙O的直径,CG⊥AB,∵BG BC=,CF BG BC==.∴BF CG=,ON OD=.∵OC=OB,∴OC-ON=OB-OD,即CN=BD.又∠CNE=∠BDE=90°,∠CEN=∠BED,∴△CNE≌△BDE,∴CE=BE.【总结升华】上述各种证明方法,虽然思路各异,但都用到了垂径定理及其推论.在平时多进行一题多解、一题多证、一题多变的练习,这样不但能提高分析问题的能力,而且还是沟通知识体系、学习知识,使用知识的好方法.举一反三:【变式】如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为()A.19B.16C.18D.20【答案】如图,延长AO交BC于点D,过O作OE⊥BC于E.则三角形ABD为等边三角形,DA=AB=BD=12,OD=AD-AO=4在Rt△ODE中,∠ODE=60°,∠DOE=30°,则DE=12OD=2,BE=BD-DE=10OE垂直平分BC,BC=2BE=20.故选D类型三、图形的旋转3.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为()A.4,30°B.2,60°C.1,30°D.3,60°【思路点拨】利用旋转和平移的性质得出,∠A′B′C=60°,AB=A′B′=A′C=4,进而得出△A′B′C是等边三角形,即可得出BB′以及∠B′A′C的度数.【答案】B;解:∵∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,∴∠A′B′C=60°,AB=A′B′=A′C=4,∴△A′B′C是等边三角形,∴B′C=4,∠B′A′C=60°,∴BB′=6-4=2,∴平移的距离和旋转角的度数分别为:2,60°.【总结升华】此题主要考查了平移和旋转的性质以及等边三角形的判定等知识,得出△A′B′C是等边三角形是解题关键.类型四、圆中有关的计算4.(2016•绵阳)如图,AB为⊙O直径,C为⊙O上一点,点D是的中点,DE⊥AC于E,DF ⊥AB于F.(1)判断DE与⊙O的位置关系,并证明你的结论;(2)若OF=4,求AC的长度.【思路点拨】(1)先连接OD、AD,根据点D是的中点,得出∠DAO=∠DAC,进而根据内错角相等,判定OD∥AE,最后根据DE⊥OD,得出DE与⊙O相切;(2)先连接BC交OD于H,延长DF交⊙O于G,根据垂径定理推导可得OH=OF=4,再根据AB是直径,推出OH是△ABC的中位线,进而得到AC的长是OH长的2倍.【答案与解析】解:(1)DE与⊙O相切.证明:连接OD、AD,∵点D是的中点,∴=,∴∠DAO=∠DAC,∵OA=OD,∴∠DAO=∠ODA,∴∠DAC=∠ODA,∴OD∥AE,∵DE⊥AC,∴DE⊥OD,∴DE与⊙O相切.(2)连接BC交OD于H,延长DF交⊙O于G,由垂径定理可得:OH⊥BC,==,∴=,∴DG=BC,∴弦心距OH=OF=4,∵AB是直径,∴BC⊥AC,∴OH∥AC,∴OH是△ABC的中位线,∴AC=2OH=8.【点评】本题主要考查了直线与圆的位置关系,在判定一条直线为圆的切线时,当已知条件中明确指出直线与圆有公共点时,通常连接过该公共点的半径,证明该半径垂直于这条直线.本题也可以根据△ODF与△ABC相似,求得AC的长.举一反三:【变式】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2.(1)求AC的长度;(2)求图中阴影部分的面积.(计算结果保留根号)【答案】解:(1)∵OF⊥AB,∴∠BOF=90°,∵∠B=30°,FO=2,∴OB=6,AB=2OB=12,又∵AB为⊙O的直径,∴∠ACB=90°,∴AC=AB=6;(2)∵由(1)可知,AB=12,∴AO=6,即AC=AO,在Rt△ACF和Rt△AOF中,∴Rt△ACF≌Rt△AOF,∴∠FAO=∠FAC=30°,∴∠DOB=60°,过点D作DG⊥AB于点G,∵OD=6,∴DG=3,+S△OFD=S△AOD=×6×3=9,∴S△ACF即阴影部分的面积是9.类型五、圆与其他知识的综合运用5.如图,△是等边三角形,是⌒上任一点,求证:ABC D BC DB DC DA+=.【答案与解析】延长DB至点E,使BE=DC,连结AE∵△ABC是等边三角形∴∠ACB=∠ABC=60°,AB=AC∴∠ADB=∠ACB=60°∵四边形ABDC是圆内接四边形∴∠ABE=∠ACD在△AEB和△ADC中,BE CDABE ACD AB AC===⎧⎨⎪⎩⎪∠∠∴△AEB≌△ADC∴AE=AD∵∠ADB=60°∴△AED是等边三角形∴AD=DE=DB+BE∵BE=DC∴DB+DC=DA.【总结升华】由已知条件,等边△ABC可得60°角,根据圆的性质,可得∠ADB=60°,利用截长补短的方法可得一个新的等边三角形,再证两个三角形全等,从而转移线段DC.本例也可以用其他方法证明.如:(1)延长DC至F,使CF=BD,连结AF,再证△ACF≌△ABD,得出AD=DF,从而DB+CD=DA.(2)在DA上截取DG=DC,连结CG,再证△BDC≌△AGC,得出BD=AG,从而DB+CD=DA.6.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是().A.3πB.6πC.5πD.4π【答案】B;【解析】阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积=扇形ABB′的面积.则阴影部分的面积是:=6π故选B.【总结升华】根据阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积=扇形ABB′的面积.即可求解.举一反三:【变式】某中学举办校园文化艺术节,小颖设计了同学们喜欢的图案“我的宝贝”,图案的一部分是以斜边长为12cm的等腰直角三角形的各边为直径作的半圆,如图所示,则图中阴影部分的面积为().A. B.72 C.36 D.72【答案】本题解法很多,如两个小半圆面积和减去两个弓形面积等.但经过认真观察等腰直角三角形其对称性可知,阴影部分的面积由两个小半圆面积与三角形面积的和减去大半圆面积便可求得,所以由已知得直角边为,小半圆半径为(cm),因此阴影部分面积为.故选C.。
九年级数学上册第二十四章圆知识点归纳超级精简版(带答案)

九年级数学上册第二十四章圆知识点归纳超级精简版单选题1、如图,点A是⊙O上一点,AB切⊙O于点A,连接OB交⊙O于点C,若∠OAC=65°,则∠B的度数是()A.40°B.50°C.45°D.55°答案:A分析:由切线的性质得到直角,再利用等腰三角形的性质求解∠O,利用直角三角形两锐角互余可得答案.解:∵AB切⊙O于点A,∴OA⊥AB,∵OA=OC,∠OAC=65°,∴∠AOC=180°−65°×2=50°,∵OA⊥AB,∴∠B=90°-∠O=40°,故选A.小提示:本题考查圆的切线的性质,等腰三角形的性质,熟悉这些性质是解题关键.2、在平面直角坐标系中,若⊙A的半径为5,A点的坐标是(4,0),P点的坐标是(0,3),则点P与⊙A的位置关系是()A.点P在⊙A内B.点P在⊙A外C.点P在⊙A上D.不能确定答案:C分析:根据两点间的距离公式求出AP的长,再与5相比较即可.解:∵点A的坐标为(4,0),点P的坐标为(0,3),∴AP=√(4−0)2+(0−3)2=5=半径,∴点P与⊙A的位置关系是:点P在⊙A上.故选:C.小提示:本题考查了勾股定理和点与圆的位置关系,熟知点与圆的三种位置关系是解答此题的关键.3、如图,斗笠是一种遮挡阳光和蔽雨的编结帽,它可近似看成一个圆锥,已知该斗笠的侧面积为550πcm2,AB是斗笠的母线,长为25cm,AO为斗笠的高,BC为斗笠末端各点所在圆的直径,则OC的值为()A.22B.23C.24D.25答案:A分析:根据圆锥的侧面积和母线可得底面圆的周长,进而可得底面圆的半径.解:∵侧面积为550π cm2,母线长为25cm,∴1×l×25=550π解得l=44π,2∵2πr=44π,∴OC=r=22,故选:A.小提示:本题考查圆锥的计算,根据侧面积和母线得到底面圆的半径是解题关键.4、已知⊙O的半径为7,AB是⊙O的弦,点P在弦AB上.若PA=4,PB=6,则OP=()A.√14B.4C.√23D.5答案:D分析:连接OA,过点O作OC⊥AB于点C,如图所示,先利用垂径定理求得AC=BC=1AB=5,然后在2RtΔAOC中求得OC=2√6,再在RtΔPOC中,利用勾股定理即可求解.解:连接OA,过点O作OC⊥AB于点C,如图所示,则AC=BC=1AB,OA=7,2∵PA=4,PB=6,∴AB=PA+PB=4+6=10,∴AC=BC=1AB=5,2∴PC=AC−PA=5−4=1,在RtΔAOC中,OC=√OA2−AC2=√72−52=2√6,在RtΔPOC中,OP=√OC2+PC2=√(2√6)2+12=5,故选:D小提示:本题考查了垂径定理及勾股定理的运用,构造直角三角形是解题的关键.5、用尺规作图作三角形的内切圆,用到了哪个基本作图()A.作一条线段等于已知线段B.作一个角等于已知角C.作一个角的平分线D.作一条线段的垂直平分线答案:C分析:根据三角形内心的定义解答.解:三角形的内切圆的圆心叫三角形的内心,是三角形三个角平分线的交点,∴用尺规作图作三角形的内切圆,用到了作角的平分线的作法,故选:C.小提示:此题考查了三角形内心的定义,正确理解定义是解题的关键.6、如图,等边△ABC中,AB=3,点D,点E分别是边BC,CA上的动点,且BD=CE,连接AD、BE交于点F,当点D从点B运动到点C时,则点F的运动路径的长度为()A .√33πB .2√33πC .√3πD .2√3π 答案:B分析:如图,作过A 、B 、F 作⊙O ,AFB⌢为点F 的轨迹,然后计算出AFB ⌢的长度即可. 解:如图:作过A 、B 、F 作⊙O ,过O 作OG ⊥AB∵等边ΔABC∴AB =BC ,∠ABC =∠C =60°∵BD =CE∴△BCE ≌△ABC∴∠BAD =∠CBE∵∠ABC =∠ABE +∠EBC =60°∴∠ABE +∠BAD =60°∴∠AFB =120°∵∠AFB 是弦AB 同侧的圆周角∴∠AOB =120°∵OG ⊥AB ,OA =OB∴∠BOG =∠AOG =12∠AOB =60°,BG =12AB =32 ∴∠OBG =30°设OB =x ,则OG =12x ∴x 2−(x 2)2=(32)2,解得x =√3或x =-√3(舍)∴AFB ⌢的长度为120∘×2√3π360∘=2√3π3. 故选B小提示:本题考查了等边三角形的性质、含30度直角三角形的性质、勾股定理以及圆周角定理,根据题意确定点F的轨迹是解答本题的关键.7、如图,点A,B,C在⊙O上,∠ACB=40°,则∠AOB的度数是()A.40°B.75°C.80°D.85°答案:C分析:直接利用圆周角定理求解.⌢,解:∵∠AOB和∠ACB都对AB∴∠AOB=2∠ACB=2×40°=80°.故选:C.小提示:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.8、已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为()A.2√5cm B.4√3cm C.2√5cm或4√5cm D.2√3cm或4√3cm答案:C分析:先画好一个圆,标上直径CD,已知AB的长为8cm,可知分为两种情况,第一种情况AB与OD相交,第二种情况AB与OC相交,利用勾股定理即可求出两种情况下的AC的长;连接AC ,AO ,∵圆O 的直径CD =10cm ,AB ⊥CD ,AB =8cm ,∴AM =12AB =12×8=4cm ,OD =OC =5cm , 当C 点位置如图1所示时,∵OA =5cm ,AM =4cm ,CD ⊥AB ,∴OM =√OA 2−AM 2=√52−42=3cm ,∴CM =OC +OM =5+3=8cm ,∴AC =√AM 2+CM 2=√42+82=4√5cm ;当C 点位置如图2所示时,同理可得OM =3cm ,∵OC =5cm ,∴MC =5−3=2cm ,在Rt △AMC 中,AC =√AM 2+CM 2=√42+22=2√5cm .故选C .小提示:本题考查垂径定理和勾股定理,根据题意正确画出图形进行分类讨论,熟练运用垂径定理是解决本题的关键.9、如图,在△ABC 中,∠ACB =90°,AC =BC ,AB =4cm ,CD 是中线,点E 、F 同时从点D 出发,以相同的速度分别沿DC 、DB 方向移动,当点E 到达点C 时,运动停止,直线AE 分别与CF 、BC 相交于G 、H ,则在点E 、F 移动过程中,点G 移动路线的长度为( )A.2B.πC.√32πD.√22π答案:D分析:由△ADE≌△CDF,推出∠DAE=∠DCF,因为∠AED=∠CEG,推出∠ADE=∠CGE=90°,推出A、C、G、D四点共圆,推出点G的运动轨迹为弧CD,利用弧长公式计算即可.解:如图,∵CA=CB,∠ACB=90°,AD=DB,∴CD⊥AB,∴∠ADE=∠CDF=90°,CD=AD=DB,在△ADE和△CDF中,{AD=CD∠ADE=∠CDFDE=DF,∴△ADE≌△CDF(SAS),∴∠DAE=∠DCF,∵∠AED=∠CEG,∴∠ADE=∠CGE=90°,∴A、C、G、D四点共圆,∴点G 的运动轨迹为弧CD ,∵AB =4,AB =√2AC ,∴AC =2√2,∴OA =OC =√2,∵DA =DC ,OA =OC ,∴DO ⊥AC ,∴∠DOC =90°,∴点G 的运动轨迹的长为90π×√2180=√2π2故选:D .小提示:本题考查等腰直角三角形的性质、轨迹、勾股定理、全等三角形的判定和性质,四点共圆等知识,解题的关键是正确探究点G 的轨迹,属于中考常考题型.10、如图,四边形ABCD 的外接圆为⊙O ,BC =CD ,∠DAC =36°,∠ACD =44°,则∠ADB 的度数为( )A .55°B .64°C .65°D .70°答案:B分析:利用圆心角、弧、弦的关系得到DC⌢=BC ⌢,再利用圆周角定理得到∠BAC =∠DAC =36°,∠ABD =∠ACD =44°,然后根据三角形内角和计算∠ADB 的度数.解:∵BC =CD ,∴DC⌢=BC ⌢, ∵∠ABD 和∠ACD 所对的弧都是AD⌢, ∴∠BAC =∠DAC =36°,∴∠BAD =∠BAC +∠DAC =72°,∵∠ABD=∠ACD=44°,∴∠ADB=180°−∠BAD−∠ABD=180°−72°−44°=64°,故选:B.小提示:本题考查了圆周角定理和圆心角、弧、弦的关系,熟练掌握圆周角定理是解决问题的关键.填空题11、如图,AB与⊙O相切于点C,AO=3,⊙O的半径为2,则AC的长为_____.答案:√5分析:根据切线的性质得到∠OCA=90°,再利用勾股定理求解即可.解:连接OC,∵AB与⊙O相切于点C,∴OC⊥AB,即∠OCA=90°,在Rt△OCA中,AO=3 ,OC=2,∴AC=√32−22=√5,所以答案是:√5.小提示:本题考查了切线的性质,勾股定理,熟练掌握切线的性质是解题关键.切线的性质:圆的切线垂直于经过切点的半径.12、三角形两边的长是3和4,第三边的长是方程x2-12x+35=0的根,则该三角形外接圆的半径为______.答案:52分析:先解一元二次方程,根据构成三角形的条件取舍,勾股定理的逆定理判定三角形为直角三角形,进而根据90度角所对的弦为直径,进而求得三角形外接圆的半径.解:x2-12x+35=0,(x−5)(x−7)=0,解得x1=5,x2=7,当x=7时,3+4=7不能构成三角形;当x=5时,32+42=25=52,∴这个三角形是斜边为5的直角三角形,,∴该三角形外接圆的半径为52所以答案是:5.2小提示:本题考查了求直角三角形的外接圆的半径,解一元二次方程,勾股定理的逆定理,直角三角形斜边上的中线等于斜边的一半,求得这个三角形是直角三角形是解题的关键.13、如图,⊙O的直径AB与弦CD相交于点P,且∠APC=45°,若PC2+PD2=32,则⊙O的半径为______.答案:4分析:过点O作OE⊥CD,连接OC,根据垂径定理可得CE=DE,根据∠APC=45°,得到EP=OE,对式子PC2+PD2=32进行变换,即可求出半径.解:设⊙O的半径为R过点O作OE⊥CD,连接OC,∴CE=DE,∵∠APC=45°,∴EP=OE,PC2+PD2=(CE+EP)2+(DE−EP)2,=CE2+2CE⋅EP+EP2+DE2−2DE⋅EP+EP2,=2CE2+2EP2,=2(CE2+EP2),=2(CE2+OE2),∴2R2=32,解得:R=4.所以答案是:4小提示:此题考查垂径定理,等腰直角三角形的性质等,把式子PC2+PD2=32进行变形是解题的关键.14、如图,正方形ABCD内接于⊙O,边长BC=√5,P为弧AD上一点且AP=1,则PC=________________.答案:3分析:连接AC,易得AC为直径,在Rt△ABC中利用勾股定理算出AC,再在Rt△ACP中利用勾股定理算出PC.解:连接AC,∵四边形ABCD是正方形,∴AB=AC=√5,∠ABC=90°,∴AC是直径.∴∠APC=90°.在Rt△ABC中,AC=√AB2+BC2=√(√5)2+(√5)2=√10,在Rt△APC中,PC=√AC2−AP2=√(√10)2−12=3.所以答案是:3.小提示:本题考查了圆的内接正多边形,直径所对的圆周角的性质,解决本题的关键是熟记并灵活运用“直径所对的圆周角是直角”.15、如图,在半径为1的扇形AOB中,∠AOB=90∘,点P是弧AB上任意一点(不与点A,B重合)OC⊥AP,OD⊥BP,垂足分别为C,D,则CD的长为________.答案:√22分析:连接AB,如图,先计算出AB=√2,再根据垂径定理得到AC=PC,BD=PD,则可判断CD为△PAB的中位线,然后根据三角形中位线定理求解.解:连接AB,如图,∵OA=OB=1,∠AOB=90°,∴AB=√2OA=√2,∵OC ⊥AP ,OD ⊥BP ,∴AC =PC ,BD =PD ,∴CD 为△PAB 的中位线,∴CD =12AB =√22. 所以答案是:√22.小提示:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了三角形的中位线定理.解答题16、在数学实验课上,小莹将含30°角的直角三角尺分别以两个直角边为轴旋转一周,得到甲、乙两个圆锥,并用作图软件Geogebra 画出如下示意图小亮观察后说:“甲、乙圆锥的侧面都是由三角尺的斜边AB 旋转得到,所以它们的侧面积相等.”你认同小亮的说法吗?请说明理由.答案:不认同,理由见详解分析:根据圆锥的侧面面积公式进行比较即可得到答案.解:甲圆锥的底面半径为BC ,母线为AB ,S 甲侧=π×BC ×AB ,乙圆锥的底面半径为AC,母线为AB,S乙侧=π×AC×AB,∵AC≠BC,∴S甲≠S乙,故不认同小亮的说法.小提示:本题考查圆锥的侧面面积,解题的关键是熟知圆锥侧面面积的计算公式.17、如图,⊙O为正五边形ABCDE的外接圆,已知CF=13BC,请用无刻度直尺完成下列作图,保留必要的画图痕迹.(1)在图1中的边DE上求作点G,使DG=CF;(2)在图2中的边DE上求作点H,使EH=CF.答案:(1)见解析(2)见解析分析:(1)连接AO并延长与CD相交,连接EF交AO延长线于M,连接BM与DE的交点即为所求作;(2)在(1)的基础上,连接BO并延长与DE相交,连接AG交BO延长线于N,连接CN并延长即可.(1)连接AO并延长与CD相交,连接EF交AO延长线于M,连接BM交DE于点G,则点G为所求作,如图1所示;理由:∵⊙O为正五边形的外接圆,∴直线AO是正五边形ABCDE的一条对称轴,点B与点E、点C与点D分别是一对对称点.∵点M在直线AO上,∴射线BM与射线EF关于直线AO对称,从而点F与点G关于直线AO对称,∴CF与DG关于直线AO对称.∴DG=CF.(2)在(1)的基础上,连接BO并延长与DE相交,连接AG交BO延长线于N,连接CN,如图2所示;小提示:本题考查了作图:无刻度直尺作图,考查了正五边形的对称性质,掌握正五边形的性质是解题的关键.18、阅读下列材料:平面上两点P1(x1,y1),P2(x2,y2)之间的距离表示为|P1P2|=√(x1−x2)2+(y1−y2)2,称为平面内两点间的距离公式,根据该公式,如图,设P(x,y)是圆心坐标为C(a,b)、半径为r的圆上任意一点,则点P适合的条件可表示为√(x−a)2+(y−b)2=r,变形可得:(x﹣a)2+(y﹣b)2=r2,我们称其为圆心为C (a,b),半径为r的圆的标准方程.例如:由圆的标准方程(x﹣1)2+(y﹣2)2=25可得它的圆心为(1,2),半径为5.根据上述材料,结合你所学的知识,完成下列各题.(1)圆心为C(3,4),半径为2的圆的标准方程为:;(2)若已知⊙C的标准方程为:(x﹣2)2+y2=22,圆心为C,请判断点A(3,﹣1)与⊙C的位置关系.答案:(1)(x−3)2+(y−4)2=25;(2)点A在⊙C的内部.分析:(1)先设圆上任意一点的坐标(x,y),根据圆的标准方程公式求解即可;(2)先根据圆的标准方程求出圆心坐标,利用两点距离公式求出点A到圆心的距离d,然后与半径r相比较,d>r,点在圆外,d=r,点在圆上,d<r,点在圆内,即可判断点A与圆的位置关系.解:(1)设圆上任意一点的坐标为(x,y),∴(x−3)2+(y−4)2=25,故答案为(x−3)2+(y−4)2=25;(2)∵⊙C的标准方程为:(x﹣2)2+y2=22,∴圆心坐标为C(2,0),∵点A(3,﹣1),AC=√(2−3)2+(0+1)2=√12+12=√2<2∴点A在⊙C的内部.小提示:本题考查两点距离公式的拓展内容,圆的标准方程,正确理解题意、熟练掌握基本知识是解题关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、圆的有关概念与性质1.圆上各点到圆心的距离都等于 半径 。
2.圆是 轴 对称图形,任何一条直径所在的直线都是它的 对称轴 ;圆又是 中心 对称图形, 圆心 是它的对称中心。
3.垂直于弦的直径平分 这条弦 ,并且平分 弦所对的弧 ;平分弦(不是直径)的 直径 垂直于弦,并且平分 弦所对的弧 。
4.在同圆或等圆中,如果两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量 相等 ,那么它们所对应的其余各组量都分别 相等 。
5.同弧或等弧所对的圆周角 相等 ,都等于它所对的圆心角的 一半 。
6.直径所对的圆周角是 90° ,90°所对的弦是 直径 。
7.三角形的三个顶点确定 1 个圆,这个圆叫做三角形的外接圆,三角形的外接圆的圆心叫 外心,是三角形 三边垂直平分线 的交点。
8.与三角形各边都相切的圆叫做三角形的 内切圆 ,内切圆的圆心是三角形 三条角平分线的交点的交点,叫做三角形的 内心 。
9.圆内接四边形:顶点都在圆上的四边形,叫圆内接四边形.10.圆内接四边形对角互补,它的一个外角等于它相邻内角的对角2、与圆有关的位置关系1.点与圆的位置关系共有三种:① 点在圆外 ,② 点在圆上 ,③ 点在圆内 ;对应的点到圆心的距离d 和半径r 之间的数量关系分别为:①d > r ,②d = r ,③d < r.2.直线与圆的位置关系共有三种:① 相交 ,② 相切 ,③ 相离 ;对应的圆心到直线的距离d 和圆的半径r 之间的数量关系分别为:①d < r ,②d = r ,③d > r.3.圆与圆的位置关系共有五种:① 内含 ,② 相内切 ,③ 相交 ,④ 相外切 ,⑤ 外离 ;两圆的圆心距d 和两圆的半径R 、r (R ≥r )之间的数量关系分别为:①d < R-r ,②d = R-r ,③ R-r < d < R+ r ,④d = R+r ,⑤d > R+r.4.圆的切线 垂直于 过切点的半径;经过 直径 的一端,并且 垂直于 这条直径 的直线是圆的切线.5.从圆外一点可以向圆引 2 条切线, 切线长 相等,这点与圆心之间的连线 平分 这两条切线的夹角。
3、与圆有关的计算1.圆的周长为 2πr ,1°的圆心角所对的弧长为 180r ,n °的圆心角所对的弧长为 180r n π ,弧长公式为180r n l π=n 为圆心角的度数上为圆半径) .2. 圆的面积为 πr 2 ,1°的圆心角所在的扇形面积为 3602r π ,n °的圆心角所在的扇形面积为S= 360n2R π⨯ = rl 21(n 为圆心角的度数,R 为圆的半径). 3.圆柱的侧面积公式:S= 2 πr l (其中为 底面圆 的半径 ,为 圆柱 的高.) 4. 圆锥的侧面积公式:S=(其中为 底面 的半径 ,为 母线 的长.)圆锥的侧面积与底面积之和称为圆锥的全面积测试题一、选择题(每小题3分,共45分)1.在△ABC 中,∠C=90°,AB =3cm ,BC =2cm,以点A 为圆心,以2.5cm 为半径作圆,则点C 和⊙A 的位置关系是( )。
A .C 在⊙A 上 B.C 在⊙A 外C .C 在⊙A 内 D.C 在⊙A 位置不能确定。
2.一个点到圆的最大距离为11cm ,最小距离为5cm,则圆的半径为( )。
A .16cm 或6cm B.3cm 或8cm C .3cm D.8cm3.AB 是⊙O 的弦,∠AOB =80°则弦AB 所对的圆周角是( )。
A .40° B.140°或40° C .20° D.20°或160°4.O 是△ABC 的内心,∠BOC 为130°,则∠A 的度数为( )。
A .130° B.60° C .70° D.80°5.如图1,⊙O 是△ABC 的内切圆,切点分别是D 、E 、F ,已知∠A = 100°,∠C = 30°,则∠DFE 的度数是( )。
A .55° B.60° C .65° D.70°6.如图2,边长为12米的正方形池塘的周围是草地,池塘边A 、B 、C 、D处各有一棵树,且AB=BC=CD=3米.现用长4米的绳子将一头羊拴在其中的一棵树上.为了使羊在草地上活动区域的面积最大,应将绳子拴在( )。
A . A 处B . B 处C .C 处D .D 处图1 图27.已知两圆的半径分别是2和4,圆心距是3,那么这两圆的位置是( )。
A .内含 B.内切 C .相交 D. 外切8.已知半径为R 和r 的两个圆相外切。
则它的外公切线长为( )。
A .R +r B.R 2+r 2C .R+r D.2Rr9.已知圆锥的底面半径为3,高为4,则圆锥的侧面积为( )。
A.10π B .12π C.15π D.20π10.如果在一个顶点周围用两个正方形和n 个正三角形恰好可以进行平面镶嵌,则n 的值是( )。
A .3B .4C .5D .611.下列语句中不正确的有( )。
①相等的圆心角所对的弧相等②平分弦的直径垂直于弦③圆是轴对称图形,任何一条直径都是它的对称轴④长度相等的两条弧是等弧A .3个 B.2个C .1个 D.4个 12.先作半径为23的第一个圆的外切正六边形,接着作上述外切正六边形的外接圆,再作上述外接圆的外切正六边形,…,则按以上规律作出的第8个外切正六边形的边长为( )。
A .7)332( B.8)332( C .7)23( D.8)23( 13.如图3,⊿ABC 中,∠C=90°,BC=4,AC=3,⊙O 内切于⊿ABC ,则阴影部分面积为( )A .12-π B.12-2π C .14-4π D.6-π14.如图4,在△ABC 中,BC =4,以点A 为圆心、2为半径的⊙A 与BC 相切于点D ,交AB 于E ,交 AC于F ,点P 是⊙A 上的一点,且∠EPF =40°,则图中阴影部分的面积是( )。
A .4-94πB .4-98πC .8-94πD .8-98π 15.如图5,圆内接四边形ABCD 的BA 、CD 的延长线交于P ,AC 、BD 交于E ,则图中相似三角形有( )。
A .2对 B.3对 C .4对 D.5对图3 图4 图5二、填空题(每小题3分,共30分)1.两圆相切,圆心距为9 cm ,已知其中一圆半径为5 cm ,另一圆半径为_____.2.两个同心圆,小圆的切线被大圆截得的部分为6,则两圆围成的环形面积为_________。
3.边长为6的正三角形的外接圆和内切圆的周长分别为_________。
4.同圆的外切正六边形与内接正六边形的面积之比为_________。
5.矩形ABCD 中,对角线AC =4,∠ACB =30°,以直线AB 为轴旋转一周得到圆柱的表面积是_________。
6.扇形的圆心角度数60°,面积6π,则扇形的周长为_________。
7.圆的半径为4cm ,弓形弧的度数为60°,则弓形的面积为_________。
8.在半径为5cm 的圆内有两条平行弦,一条弦长为6cm ,另一条弦长为8cm ,则两条平行弦之间的距离为_________。
9.如图6,△ABC 内接于⊙O,AB=AC ,∠BOC=100°,MN 是过B 点而垂直于OB 的直线,则∠ABM=________,∠CBN=________;10.如图7,在矩形ABCD 中,已知AB=8 cm ,将矩形绕点A 旋转90°,到达A ′B ′C ′D ′的位置,则在转过程 中,边CD 扫过的(阴影部分)面积S=_________。
图6 图7三、解答下列各题(第9题11分,其余每小题8分,共75分)1.如图,P 是⊙O 外一点,PAB 、PCD 分别与⊙O 相交于A 、B 、C 、D 。
(1)PO 平分∠BPD ; (2)AB=CD ;(3)OE ⊥CD ,OF ⊥AB ;(4)OE=OF 。
从中选出两个作为条件,另两个作为结论组成一个真命题,并加以证明。
2.如图,⊙O 1的圆心在⊙O 的圆周上,⊙O 和⊙O 1交于A ,B ,AC 切⊙O 于A ,连结CB ,BD 是⊙O 的直径,∠D =40°求:∠A O 1B 、∠ACB 和∠CAD 的度数。
3.已知:如图20,在△ABC 中,∠BAC=120°,AB=AC ,BC=43,以A 为圆心,2为半径作⊙A ,试问:直线BC 与⊙A 的关系如何?并证明你的结论。
4.如图,ABCD 是⊙O 的内接四边形,DP ∥AC ,交BA 的延长线于P ,求证:AD ·DC =PA ·BC 。
5.如图⊿ABC 中∠A =90°,以AB 为直径的⊙O 交BC 于D ,E 为AC 边中点,求证:DE 是⊙O 的切线。
6.如图,已知扇形OACB 中,∠AOB =120°,弧AB 长为L =4π,⊙O ′和弧AB 、OA 、OB 分别相切于点C 、D 、E ,求⊙O 的周长。
7.如图,半径为2的正三角形ABC 的中心为O ,过O 与两个顶点画弧,求这三条弧所围成的阴影部分的面积。
8.如图,ΔABC 的∠C =Rt ∠,BC =4,AC =3,两个外切的等圆⊙O 1,⊙O 2各与AB ,AC ,BC 相切于F ,H ,E ,G ,求两圆的半径。
9.如图①、②、③中,点E 、D 分别是正△ABC 、正四边形ABCM 、正五边形ABCMN 中以C 点为顶点的相邻两边上的点,且BE = CD ,DB 交AE 于P 点。
⑴求图①中,∠APD 的度数;⑵图②中,∠APD 的度数为___________,图③中,∠APD 的度数为___________;⑶根据前面探索,你能否将本题推广到一般的正n 边形情况.若能,写出推广问题和结论;若不能,请说明理由。
参考答案一、1、C 2、B 3、B 4、D 5、C 6、B 7、C 8、D9、C 10、A 11、D 12、A 13、D 14、B 15、C二、1、4 cm 或 14cm ; 2、9π; 3、32π,34π; 4、4:3;5、)3824( π;6、12+2π;7、(38π-34)cm 2;8、7cm 或1cm ; 9、65°,50°;10、16πcm 2。
三、1、命题1,条件③④结论①②, 命题2,条件②③结论①④.证明:命题1∵OE ⊥CD , OF ⊥AB, OE=OF ,∴AB=CD, PO 平分∠BPD 。
