comsol计算声子晶体算例
二组元声子晶体综合带隙算法及带隙参数规律研究

二组元声子晶体综合带隙算法及带隙参数规律研究李露露;温廷敦;韩建宁;杨鹏【摘要】在研究声子晶体能带结构的算法方面,分别使用平面波展开法和时域有限元法对声子晶体的能带结构进行计算,并将两种算法得出的禁带结果进行对比研究.根据带隙图的差异分析说明了单一方法可能的不足,同时发现了计算结果最准确的区域是通过两种算法计算所得结果的重合区域,所以使用两种方法相结合的带隙算法,讨论了二组元材料参数和填充率对禁带的影响.研究发现散射体密度与基体的密度的比值越大,禁带的宽度就越宽,散射体相比于基体,对禁带的影响更大;增大填充率时禁带宽度变宽,大到一定程度时禁带宽度变窄.【期刊名称】《科学技术与工程》【年(卷),期】2015(015)034【总页数】5页(P123-127)【关键词】声子晶体;平面波展开法;带隙;材料参数【作者】李露露;温廷敦;韩建宁;杨鹏【作者单位】中北大学理学院,太原030051;中北大学理学院,太原030051;中北大学理学院,太原030051;中北大学信息与通信工程学院,太原030051;中北大学信息与通信工程学院,太原030051【正文语种】中文【中图分类】O735声子晶体是一种新型声学功能材料,具有很多天然材料所不具备的声学特性[1],它是由M.S.Kushwsha等[2]在传统晶体和光子晶体研究的基础上提出的新课题。
近年来人们对声子晶体做了大量的研究[3—5],声波在周期性复合材料中的传播是声子晶体的主要研究方向,声子晶体的共振特性和带隙特性可以通过声波在声子晶体中的运动方程而得出,声子晶体研究的一个重要意义在于通过这些特性来控制声波在晶体中的传播[6]。
为了更好的深入研究能带结构,找到声子晶体调控声波的参数规律,需要找到一种对声子晶体能带结构设计的最好算法,该算法需具备精确度高,速度快,范围广,收敛性好等条件。
声子晶体禁带计算方面最常用的方法是平面波展开法和时域有限元法[7],有关这两种方法介绍的文献已经很多了,但对于将两者结合起来分析的文献还没有。
非对称双层薄膜型局域共振声子晶体低频隔声性能研究

2.3 附加质量块对非均匀结构影响
随后研究非对称结构薄膜上质量块的质量非均 匀分布对结构的传输性能的影响 ,下层质量块数目 为 2,上层质量块数目为 1,3 个质量块的放置位置如 图 3(b)所示,质量块所采用的材料参数均相同,且在 模拟过程中始终保持结构的总质量不变 ,仍为 936 mg。B1 结构中下层薄膜上的质量块编号为 11、12, 质量块质量均为 165 mg,上层薄膜上的质量块编号 为 2,质量块质量为 606 mg,即 m11=m12=165 mg,m2= 606 mg;B2 结构中下层薄膜上编号为 11 的质量块质 量为 606 mg,编号为 12 的质量块质量为 165 mg,上 层薄膜上的质量块编号为 2,质量为 165 mg,m12=m2 =165 mg,m11=606 mg;B3 结构中下层薄膜上编号为 11 的质量块质量为 165 mg,编号为 12 的质量块质量 为 606 mg,上层薄膜上的质量块编号为 2,质量为 165 mg,即 m11=m2=165 mg,m12=606 mg。声波的透 射系数图如图 5 所示。
图 1 非对称双层薄膜超材料的结构示意图
通过使用 FEM(COMSOL Multiphysics)进行结
构声波传输系数的研究。在研究过程中 ,采用声固
耦合模块来分析薄膜声学超材料的传输特性 ,薄膜
边界采用固定边界,计算模型中包括两个域,即空气
域和固体域,空气域中的 Helmholtz 方程为
( ) ∇
图 3 双层薄膜结构轴对称示意图
对称结构 A 的每层薄膜上均放置 1 个质量块, 且质量块均位于薄膜中心 ,即 e 1=0 mm,e 2=0 mm; 非对称结构 B 的下层薄膜上放置 2 个质量块,编号 11 的质量块位于薄膜中心位置处,编号 12 的质量块 放置在距离中心位置 6 mm 处,上层薄膜放置一个质 量块,质量块编号 2,位于薄膜中心处,即 e 11=0 mm, e 12=6 mm,e 2=0 mm;对称结构 C 的每层薄膜上均放 置 2 个质量块,编号 11 的质量块、编号 21 的质量块 均放置在薄膜中心位置处,编号 12 的质量块、编号 22 的质量块均放置在距离薄膜中心位置 6 mm 处, 即 e 11=e 21=0 mm,e 12=e 22=6 mm。所得到的有限元 模拟结果如图 4 所示。
用于超声监测压力的水凝胶声子晶体传感器

用于超声监测压力的水凝胶声子晶体传感器摘要:水凝胶是一种具有亲水性的三维凝胶,机械性质和化学性质与生物组织相似,是人类和机器之间界面的理想材料。
水凝胶声子晶体是具有特殊物理结构的超材料,通过设计可以使其具有所需的声学特性。
因此,结合超声技术,水凝胶声子晶体可以作为传感器,应用于压力的监测。
本文提出了一种可用于动物组织中超声监测压力的水凝胶声子晶体。
我们使用聚羧基甜菜碱与甲基丙烯酸羟乙酯合成出水凝胶声子晶体,并用黏附性水凝胶作为粘黏剂,将水凝胶声子晶体粘贴在生物组织上。
当生物组织运动时,水凝胶声子晶体受到压力而发生形变,物理结构改变,声学特性改变。
我们通过超声监测回波特征,就可以实现对压力的监测。
并且,由于水凝胶材料与生物组织化学性质相似,我们的水凝胶声子晶体基本不会对生物体产生危害,经过一段时间后就会降解,安全环保。
关键词:水凝胶;声子晶体;超声;可植入传感器1 引言水凝胶材料具有高含水量、机械柔性、生物相溶性、生物功能性等特点,与生物组织相似的机械性质和化学性质。
因此,水凝胶是用于人机交互的良好材料,目前已经被广泛地应用于脑机接口、神经修复术、临床设备和医疗植入物等领域,主要用于制造表皮可穿戴设备和可植入设备[1]。
水凝胶声子晶体是经过设计的具有特殊物理结构的水凝胶材料。
当这种水凝胶的物理结构发生改变时,其声学特性也会改变。
例如,北京工业大学魏瑞菊曾对基于对称性的二维声子晶体的带隙特征进行研究,发现可以通过不同方法消除声子晶体的对称性,并得到不同频率的带隙[2]。
基于此,本文研究了一种用于生物组织中通过超声监测压力的水凝胶声子晶体传感器。
我们首先对水凝胶声子晶体的声学特性进行研究,了解设计和改变其声学特性的方法,从而设计除我们所需的水凝胶声子晶体。
然后,我们研究了两种可降解可植入传感器,为我们的传感器的组成打下基础。
接着,我们选择合适的材料制备所需的水凝胶声子晶体和粘附性水凝胶。
最后,我们还在猪皮上进行了静态水压的超声监测。
声子晶体型高速公路声屏障的降噪性能

中国环境科学 2020,40(12):5493~5501 China Environmental Science 声子晶体型高速公路声屏障的降噪性能秦晓春1*,倪安辰1,韩莹1,曹林辉2,黄智华2 (1.北京交通大学土木建筑工程学院,北京 100044;2.江西赣粤高速公路股份有限公司昌九高速改扩建项目办公室,江西南昌 462000)摘要:利用高速公路改扩建工程产生的大量废旧护栏立柱,针对高速公路轮胎-路面主要噪声,建立三种二维气-固型声子晶体声屏障.利用Comsol Multiphysics计算相应的能带结构,并探究带隙的影响因素.结果表明3种形式均可以产生相应的带隙;散射体壁厚大小对于带隙宽度影响很小,但采用空心散射体可以在低频产生一条完全禁带;对散射体进行开口处理可以有效增加低频带隙宽度;当晶格填充率增大至0.5后,随着填充率增大,从高频到低频依次产生完全禁带,且带隙总宽度增大;通过仿真模拟与室内实验相结合的方式验证了声屏障的降噪特性,声屏障在带隙范围内具有良好的降噪性能,相较直立同规格复合板声屏障,低频降噪效果提升1~16dB,高频降噪效果提升1~2dB,但在1600Hz后,声子晶体声屏障降噪效果不及复合板声屏障,降噪效果受周期数影响较大.声子晶体声屏障可实现新型降噪理念与绿色环保的有机结合.关键词:交通噪声;声子晶体;声屏障;回收立柱中图分类号:X593,X707 文献标识码:A 文章编号:1000-6923(2020)12-5493-09Noise reduction performance of highway sonic crystals noise barrier. QIN Xiao-chun1*, NI An-chen1, HAN Ying1, CAO Lin-hua2, HUANG Zhi-hua2 (1.School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;2.Jiangxi Ganyue Highway Co., Ltd. Changjiu Highway Reconstruction and Expansion Project Office, Nanchang 462000, China). China Environmental Science, 2020,40(12):5493~5501Abstract:Three types of air-solid sonic crystals noise barriers were established for the tyre-road noise which is the main noise of highway by using recycled columns of the fence. Comsol Multiphysics was used to calculate the corresponding band structure and explore the influencing factors of band gaps. The results showed that the three forms can generate corresponding band gaps; the wall thickness had little effect on the band gap width, but the hollow scatterers could generate a complete band gap at low frequencies; opening treatment of the scatterers could effectively increase the low band gap width; after the lattice filling rate reached 0.5, complete band gaps were generated in order from high to low frequencies, and as the filling rate increased, the band gap overall width increased. The noise reduction characteristics of the barrier were verified through a combination of simulation and indoor experiments, the sonic crystals noise barrier had good noise reduction performance in the band gap range, compared with the aluminum alloy composite board noise barrier with the same specifications. The low-frequency noise reduction effect was increased by 1~16dB, and the high-frequency noise reduction effect was increased by 1~2dB; however, after 1600Hz, the noise reduction effect of the sonic crystals noise barrier did not outperform the composite board barrier, and the noise reduction effect was greatly affected by the number of cycles. The sonic crystal noise barrier is a promising combination of new noise reduction concepts and green environmental protection.Key words:traffic noise;sonic crystal;noise barrier;recycled column我国高速公路网络的迅猛发展极大方便了交通的出行和经济的发展,但与之相伴的噪声影响也愈加严重,成为近年来环境问题投诉的热点[1].长期处在交通噪声影响下可能会引发诸如焦虑乏力、睡眠质量下降、听力受损等一系列健康问题[2],高速公路沿线作为噪声的直接影响区域,矛盾尤为突出,控制噪声一般有3种途径:声源处控制、传播过程中控制、人耳接收处控制.声屏障作为一种末端噪声控制的形式[3],在交通领域应用最广泛,被公认为是最行之有效的措施,然而,近年来随着声屏障的大量采用,其存在的问题也逐渐显露.第一,现有的声屏障降噪缺乏针对性,不同种类的路段噪音产生的主导因素不同,特征噪声频谱也不相同[4-5],目前没有针对性的设置.第二,连续的声屏障阻碍了空气的流动,车辆在高速行驶过程中产生的持续脉动风压、以及自然环境中的风荷载会导致声屏障的使用寿命减短,无法满足安全性与稳定性[6-7],同时还会造成声泄露.第三,高大封闭的声屏障会阻碍光线,影响驾驶员的视觉, 收稿日期:2020-04-12基金项目:国家自然科学基金“面上项目”(51878039);基本科研业务费项目(2019JBM407)* 秦晓春, 副教授,**************.cn5494 中国环境科学 40卷造成孤立感, 从美学角度来看,也不利于与沿线景观的交融[8].声子晶体是具在弹性波带隙特征的周期性复合材料,它的基本特征是,带隙频率范围内的弹性波在声子晶体中传播时会被抑制[9],因此,声子晶体常被用于特定频率范围内的减振降噪.声子晶体根据带隙产生机理不同,分为Bragg散射型和局域共振型.Bragg散射型主要针对高频减振降噪,而局域共振型主要针对低频的减振降噪.目前,声子晶体已被广泛应用于航空航天、汽车潜艇、机械制造等领域[12-13].运用有限元法研究能带结构是计算效率最高、适用性最广泛的方法[14],其次,将有限元法与室内实验相结合来验证声子晶体声屏障的降噪性能也是最有效的方式[15],目前,国外已设计出多种形式的声子晶体声屏障[7,16-17].在国内,声子晶体的理论研究很多[18-20],但是对于声子晶体声屏障的实际应用研究,特别是在交通噪声防治方面,研究很少.易强等[21]对于一维声子晶体声屏障在轨道交通方面的应用进行了探索,结果表明在半封闭、全封闭声屏障上使用声子晶体,降噪效果远优于传统材质[21].张群义[22]对声屏障顶部附加了声子晶体型降噪结构,有效减少了声屏障的顶端绕射,改善了屏障后的声场分布.目前,我国尚没有声子晶体型声屏障在高速公路噪声防治的应用研究.因此,针对高速公路噪声特征,本研究提出了3种二维气-固型声子晶体声屏障,通过回收废旧钢立柱进行设计组合,并结合有限元仿真与室内实验,验证其降噪效果.旨在为高速公路噪声防治提供参考.1材料与方法1.1 高速公路噪声特性高速公路的噪声来源主要可以分为两类:一是汽车动力系统运作产生的噪声,二是车辆轮胎与路面作用而产生的噪声.其中车型、车速、路面构造是影响高速公路噪声大小与频率的3个最主要的因素[5].不同路面的轮胎-路面噪声频率分布如表1所示[4-5].Sandberg等[23]通过对轮胎与沥青路面相互作用的研究,发现轮胎-路面噪声在1000Hz附近存在共振峰,将800~1250Hz作为轮胎-路面噪声需要考虑的主要频段.我国高速公路以高等级沥青混凝土路面为主,最低限制时速为60km/h,轮胎噪声将占主要部分,因此本研究将声屏障降噪的重点放在轮胎-路面噪声部分,特别是800~1250Hz典型频段,同时针对以大型车辆或小型车辆为主的高速公路分别提出两种不同的改进方案.表1 轮胎噪声频率范围Table 1 Tire-road noise frequency range轮胎噪声频率(Hz) 车型车速沥青混凝土路面水泥混凝土路面小型车 80~120km/h 630~2000 800~2500 中型车 60~100km/h 160~1000 315~1600 大型车 60~100km/h 250~1000 315~20001.2 计算模型基于二维声子晶体模型建立声屏障,采用正方形晶格,根据Bragg散射理论[9],利用公式(1)计算相应的晶格常数大小,计算得晶格常数a=0.1715m,为方便排列选取a=0.2m.选择声阻抗差异大的材料有利于增大带隙宽度[21],因此选取高3m的回收废旧钢立柱作为散射体,插入空气基体中,具体材料参数如表2所示.3种不同的组合形式如图1所示:(Ⅰ)半径R=0.085m的空心钢管置于晶格中央,壁厚t=0.01m. (Ⅱ)将半径R=0.085m的空心钢置于晶格中央,面向道路方向开口尺寸e=0.065cm,壁厚t=0.01m.(Ⅲ)将四根半径R=0.04m的空心钢管相切组合置于晶格中央,壁厚t=0.01m.2caf=(1)式中,a为晶格常数;c为基体中声速;f为带隙中心频率(根据目标范围选取为1000Hz).HRf(2) f HR是赫姆霍兹共振频率,c f是基体声速,e是共振腔开口尺寸,r是内半径,l eq=t+0.85e是等效开口尺寸,t 是壁厚.对于薄壁结构e=2r sinα.表2材料参数Table 2 Material parameter table材料声速(m/s)密度(kg/m3) 弹性模量(N/m2)泊松比空气344 1.21钢5189 7800 2.1e11 0.31.3 基于有限元法的数值计算对于二维声子晶体,根据周期结构中波传播的Bloch定理[12],位移场u(r)可以写为下式:()()()i k rku r e u r⋅=(3)12期 秦晓春等:声子晶体型高速公路声屏障的降噪性能 5495式中:u k (r )是与声子晶体具有相同周期性的周期矢量函数;k =(k x ,k y )为波矢且被限制在第一布里渊区内;r =(x,y )为位置矢量.对单胞进行有限元网格划分,将其划分为有限个通过节点连接的单元.单个晶胞内特征方程的离散形式为: 2)=0U ω−(K M (4)式中:U 是节点位移,K 和M 分别是刚度矩阵和质量矩阵.如果单个晶胞边界上可以满足Bloch 周期条件就能保证在整个周期结构上都可以满足.将式(3)沿着周期方向施加在单个晶胞的边界上,则边界上的位移U(r )满足下式:())()i k a U r a eU r ⋅+=( (5)式中:α为晶格常数,r 为边界上节点的位置矢量.图1 (a) 空心型单胞;(b) 开口型单胞;(c) 组合型单胞;(d)第一布里渊区Fig.1 (a) Hollow type unit cell; (b) Open type unit cell; (c)Combined type unit cell; (d) First Brillouin zone结合位移边界条件(5),利用COMSOL Multiphysics 5.4©多物理场耦合有限元分析软件直接求解式(4)表示的特征值方程[16],利用计算所得的特征值来绘制对应的能带结构.采用COMSOL Multiphysics 5.4©的压力声学模块进行能带结构分析,对于3种不同单胞,能带结构计算应依据Bloch - Floquet 理论沿着第一不可约布里渊区(图1(d))的3个高对称方向ΓΧ、ΧΜ、ΜΓ进行扫描,扫描频率范围0~2500Hz,每个单胞均采用平面应变假设,将相对的两边界作为一组施加Floquet 周期性边界.采用Comsol Multiphysics 5.4©的压力声学模块进行声屏障传输特性计算,建立数值分析模型,将数值分析的结果与室内实验结果对比,可以起到相互验证的作用,以往对于声子晶体的传输计算均采用周期性边界以模拟在无限长度下的理想状态,这种方式不仅可以有效的减少网格划分数量,降低机器的运算负担提高效率,还可以表示声屏障的最佳降噪效果.将四排散射体按正方晶格周期排列在长方形波导中,上下采用连续性边界,模拟Y 方向上的无限周期,波导左侧设置背景压力场,入射波为未考虑车辆扰流的幅值为1pa 的平面波.并采用自由三角形划分网格L FEmax ≤λ/6[24].(a)无限周期传输谱(b)有限周期传输谱图2 有限元传输谱设计Fig.2 Design of FEM transmission spectrum但是现实中的声子晶体声屏障是具有有限宽度的,宽度的差异对于噪声的控制效果会产生一定影响,为了减少这种差异,同时建立与室内实验等同的有限宽度声屏障模型.将4排声屏障布置在区域中央,为了模拟半消声实验室的条件,计算区域周围由PML(完美匹配层)包裹以考虑Sommerfeld 辐射条件[7,24],采用背景压力场向区域内垂直发射未考虑车辆扰流的幅值为1pa 的平面波,模型布置与具体尺寸参数见图2.在这3种方案中,均通过插入损失(IL)来评估声屏障对噪声的控制效果(公式6).5496 中 国 环 境 科 学 40卷out 10inIL=20log (dB)P P − (6) 式中:P in 、P out 分别为声屏障插入前后的声压大小.1.4 半消声实验(a)侧视图 (b)俯视图图3 室内实验布置Fig.3 Scheme of the indoor experiment图4 (a) 空心型能带结构;(b) 开口型能带结构;(c) 组合型能带结构Fig.4 (a) Hollow type band structure; (b) Open type band structure; (c) Combined type band structure12期 秦晓春等:声子晶体型高速公路声屏障的降噪性能 5497声子晶体型声屏障作为一种新兴的方式,尚没有被纳入我国规范[11]中公路声屏障分类,国际上对于其标准化测试方法也在探索中[16-17],本文为方便与传统声屏障降噪效果进行对比,依据HJ/T90-2004声屏障测试规范及JT/T646.5-2017公路声屏障降噪效果检测方法[10-11]进行测试.实验在交通运输部环境中心(8×5×4)m 3的半消声实验室内进行,该实验室截止频率为50Hz,背景噪声为20dB.为研究二维气-固声子晶体声屏障的实际降噪效果,在半消声实验室中模拟半自由场条件,对3种回收废旧钢立柱制成的声子晶体声屏障模型进行室内半消声波动实验.在距离声屏障前1.5m 、高1.2m 处利用MHY -14324型12面体声源及HA12-AWA5870A 型功率放大器连续发射70dB(A)的白噪声,由LMS b™噪声测试分析系统测定接收端的噪声声压级,接收端的位置分别布置在屏障后d =1.5m 、3m,高1.2m 处,面向声源中心,参考点布置在声屏障正上方靠近尖劈处,分别测试声屏障安装前后声压级,测量63~5000Hz 的1/3倍频带,并采用A 计权等效声级的插入损失进行比较(公式7).实验设计如图3所示,同时声屏障的布置应靠近尖劈处,以减少绕射声可能产生的影响.这种实验布置与仿真模拟相结合的方式在近年来被大量使用,与数值模拟预测的结果有很好的吻合性[7,24]. r,b r,a IL=L L − (7) 式中:L r,b 与L r,a 为受声点安装声屏障前后的声压级,均采用A 计权等效声压级. 2 结果与讨论 2.1 能带结构沿着高对称方向(ΓΧ-ΧΜ-ΜΓ)扫描所得三种能带结构曲线如图4所示,完全带隙与方向带隙遍布在0~2500Hz 频率范围内.完全带隙(深蓝色矩形)表明弹性声波在该频段内无相对应的波矢,声波无法在该周期型结构中的任何方向进行传播[9],()Ⅰ存在两条,分别位于70~109Hz 以及801~1132Hz.低频带隙的产生主要是因为钢与空气之间的阻抗差异巨大,导致阻抗失配[16,21].而高频带隙的产生主要是因为散射体之间发生了多次Bragg 反射,从而导致相消干涉,结构的周期性起到了主导的作用.(Ⅱ)存在2条,分别位于315~502Hz 以及840~1130Hz,其中第一完全带隙的带宽显著增加,这是由于散射体开口形成赫姆霍兹共振腔,产生低频吸声共振的缘故.根据公式2(赫姆霍兹共振频率)[17]计算可得带隙中心频率为375.3Hz,与能带结构基本符合.()Ⅲ存在3条,分别位于73-118Hz 、840-910Hz 以及1410- 2175Hz.(Ⅲ)单胞填充率相较于前2个方案有所提高,导致散射体之间反射作用加强,带隙起始、终止频率升高,带隙宽度增加.而对于方向带隙,其主要存在于ΓΧ、ΧΜ方向的各频段范围内,表明在此方向声波无法传播,方向带隙同样可以起到控制噪声的作用.综上可知,带隙主要是在Bragg 散射与共振的双重作用下产生,将二者合理结合可以实现多频率范围内的减振降噪.在大型车辆居多的高速公路低频噪声会显著增加,相反小型车辆为主的高速公路高频噪声会显著增加(表1),对于这2种情况,分别采用(Ⅱ)、(Ⅲ)改进方案可以起到很好的改进作用. 2.2 能带结构影响因素采用COMS OL Multiphysics 压力声学模块.对于散射体的壁厚、开口角度大小及晶格填充率这三个因素进行研究,分析它们对于带隙的影响规律与作用机理.2.2.1 散射体壁厚 如图5所示,在(I)声屏障模型中,散射体壁厚对于起始频率、截止频率以及带隙宽度的影响不显著. 这是由于钢的声阻抗要远远大于空气,所以当声波从空气基体中传播到钢管散射体上时,会在界面上发生全反射,对于钢管内部不会产生任何的影响,声波无法在钢管内传播,钢管内空气无法响应外界的波动,因此,壁厚对于带隙宽度影响可以忽略.但是散射体在空心状态下相较实心,会增加一条低频完全禁带,这是散射体在低频产生共振的结果[17,25],这也与Morandi 等[16]关于PVC 管散射体的研究结果相类似.在实际应用中,减小散射体的壁厚,对于结构的轻便、易于加工以及材料节约、成本降低有着重要的意义,所以应适当的减小散射体壁厚.此外,采用废旧钢立柱作为散射体,“变废为宝”,相较于以铝塑、彩钢复合板为主要材料的声屏障,大幅节约了材料与施工成本.2.2.2 开口角度尺寸 开口角度对于完全禁带的影响如图6所示,在(Ⅱ)声屏障模型中,随着散射体开口角度的增大,共振带隙(第1完全禁带)的起始与终止频率均逐渐升高,带隙宽度逐渐增加,Bragg 带隙5498 中 国 环 境 科 学 40卷(第2完全禁带)宽度略微缩小.对散射体进行开口处理,使钢管内部形成赫姆霍兹共振吸声腔,声波通过散射体开口进入钢管,与开口处的空气及内部空间之间产生共振,使部分声能转换成热能,从而消耗声能,达到降噪的目的.在实际工程中,将开口处理与周期性阵列相结合,可以有效地提高声屏障的低频降噪性能,尤其适用于以大型车辆为主,低频噪声较大的高速公路.0 1 2 3 4 5 6 7 85001000 1500频率(H z )壁厚(cm)第1完全禁带第2完全禁带图5 壁厚对能带结构的影响Fig.5 The influence of wall thickness on band structure0 5 10 15 20 2530 35 40 45 50 55605001000 1500第1完全禁带第2完全禁带频率(H z )角度(°)图6 开口角度对能带结构的影响Fig.6 The influence of opening angle on band structure2.2.3 晶格填充率 对于()Ⅲ声屏障,保持晶格常数不变,通过改变散射体半径来满足不同的填充率,分析填充率对于完全禁带的影响.由图7可知,在填充率为0~0.5时,能带结构中不存在完全禁带;填充率>0.5时,高频开始出现完全禁带,且随着填充率的逐渐增加,起始频率先增加后降低,终止频率一直增加,导致带隙宽度不断加大,当填充率>0.6时,能带结构图中增加两条完全禁带,且随着填充率的增加,带隙宽度均不断加大,并且起始、终止频率均有向低频移动的趋势,当填充率达到0.785(正方晶格最大填充率)时,完全禁带数量最多,带隙宽度最宽.由此可知填充率的大小对于带隙产生有决定作用,完全禁带只有在填充率达到一定程度后才可出现,且随着填充率的增大,完全禁带先出现在高频,后出现在较低频段.随着填充率的增大,带隙总宽度明显增加.究其原因是由于刚体共振与基体间的相互作用增强而引起的,随着填充率的增加,相邻散射体之间的相互作用增强,所以完全带隙的数量与宽度增加.在实际工程中,在考虑成本与施工过程的情况下,需保证一定填充率,以满足足够范围的降噪要求,()Ⅲ对于高频轮胎-路面噪声具有较好的针对作用.0.40.50.6 0.7 0.805001000150020002500第3完全禁带第2完全禁带 第1完全禁带频率(H z )填充率图7 填充率对能带结构的影响Fig.7 The influence of filling rate on band structure2.3 降噪效果分析2.3.1 无限与有限周期仿真结果对比 为了进一步分析声子晶体声屏障降噪效果与能带结构、周期数之间的关系,将d =1.5m 时无限周期声屏障与有限周期声屏障的插入损失曲线进行对比分析.图8中,各曲线衰减域与能带结构中的带隙基本吻合,验证了能带结构计算的正确性,同时说明方向带隙也具有良好的降噪效果,甚至优于完全带隙,例如在1410~1755Hz,()Ⅰ组为ΓΧ方向带隙,而(Ⅲ)为完全带隙,而()Ⅰ组降噪效果优于()Ⅲ组.虽然方向带隙同样可以有效控制弹性波,但是其控制方向有限,而现实中波的入射方向又多种多样,因此还应尽可能多的构造完全带隙.其次,声子晶体作为周期型材料,周期数对于声波的控制效果起着至关重要的作12期秦晓春等:声子晶体型高速公路声屏障的降噪性能 5499用[9,11-12,17],一般来说,周期数越大,越接近无限周期,控制效果就越好[7,26].因此相较于无限周期条件(声屏障宽度无限长),有限宽度声屏障的插入损失曲线会有所下降,从图8中看,增加周期数可以使衰减峰向高点移动,有效提高声子晶体声屏障的降噪效果.图9中声波在经过声屏障后衰减明显.0 500 1000 1500 200020 40 60 80 100 120140 插入损失(d B )频率(Hz)I II III i ii iii图8 无限与有限周期声子晶体声屏障插入损失对比Fig.8 Comparison of the insertion loss between infinite andfinite period sonic crystals noise barriers小写罗马数字代表无限周期声屏障对于要长距离布置的高速公路声屏障来说,进行无限周期声子晶体的插入损失分析是非常必要的,便于了解声子晶体声屏障的最佳降噪效果,确定合理的周期数.图9 无限周期声屏障传输谱云图Fig.9 Transmission spectrum of infinite period noise barrier(a) 1000Hz;(b)350Hz;(c) 2000Hz2.3.2 有限周期仿真与室内实验结果对比 采用d =1.5m 时的1/3倍频程等效A 声级插入损失进行对比,由图10可知,有限元仿真与室内实验二者结果吻合良好,仿真与实验所测数据误差控制在3dB 以内,二维仿真计算忽略了地面对于声波的反射作用,声屏障顶端的部分绕射以及材料属性的差异都是造成误差的可能因素[7,15,26],尽管如此,数值结果依旧准确反映了声子晶体对于噪声的控制规律.3种声屏障在带隙范围内均有良好的降噪效果,图11中对于2种改进型,(II)在250~500Hz 的低频段中,最大插入损失可达22.5dB,较(Ⅰ)提高了4.3~19.6dB,有效提高了声屏障在低频时的表现.()Ⅲ在1100~1600Hz 间,则有效弥补了()Ⅰ的降噪性能不足,但是在1600~ 2000Hz 范围内,两者的插入损失差距不大,提升效果有限.在2000~5000Hz 范围内,3种声子晶体声屏障降噪效果均在5dB 左右波动,效果不佳.10002000 3000 4000 50000510152025插入损失(d B (A ))1/3倍频程中心频率(Hz)图10 有限周期仿真与室内实验插入损失对比 Fig.10 Comparison of the insertion loss of finite periodsimulation and indoor experiment将3种声子晶体声屏障的降噪效果与0.1m 厚铝塑复合板声屏障的进行对比,可以看出在低中频带隙范围内,声子晶体型声屏障降噪表现普遍优于复合板声屏障,特别是在(II)的低频带隙内,降噪效果提升1~16dB,但是在高频带隙内,降噪效果提升有限,在1~2dB,而在1600Hz 以后的频率范围,声子晶体声屏障的降噪效果不及复合板声屏障,究其原因是周期数主导着声子晶体声屏障的降噪效果,根据无限与有限周期仿真对比的结果,增加周期数(声屏障宽度)可以有效改善其降噪性能.声子晶体型声屏障虽具有典型弹性波带隙特征,可以有效针对特定噪声频率,但是其对于噪声的控制效果依赖于周期数,因5500 中 国 环 境 科 学 40卷此在实际工程中不适宜短距离布设.采用废旧钢立柱回收建立的声子晶体声屏障实现了绿色循环与新型降噪理念的结合,相对复合板声屏障,具有针对性好、美观性高、耐久、成本低的特点,在未来的高速公路降噪中具有广泛的应用前景,但是如何进一步减少占地面积,缩小声屏障尺寸,对多种降噪机理进行有效结合仍是将来研究需要关注的方向.(a)1000Hz(b)350Hz(c)2000Hz图11 不同频率下有限周期声屏障传输云图对比 Fig.11 Comparsion of transmission spectrum of finite periodnoise barrier at different frequency3 结论3.1 无限、有限周期声子晶体声屏障模型均可以准确反应理论能带结构.经过设计的声子晶体声屏障可以在所需降噪频段内产生相应的完全禁带,例如高速公路噪声中的250~500Hz 及800~1250Hz 主要频段,相较同规格复合板声屏障,降噪更具有针对性,声子晶体声屏障在带隙范围内,低频降噪效果提升1~16dB,高频降噪效果提升1~2dB,(Ⅱ)在低频范围效果最好,(Ⅰ)、(Ⅲ)在高频范围降噪效果提升有限,甚至不及复合板声屏障,降噪效果受周期数影响较大,实际工程中需设置足够周期以保证其降噪效果. 3.2 散射体采取空心结构,有利于在低频产生一条共振完全带隙,但是壁厚的大小对于带宽影响很小.对于散射体进行开口处理,形成共振腔,能够在低频形成一条宽带,随着开口角度的增大,低频带隙宽度增加.填充率对带隙宽度影响显著,晶格填充率>0.5时,从高频至低频依次产生完全禁带,且随着填充率的增加,带隙总宽度变大.参考文献:[1] 李 楠,冯 涛,李贤徽,等.交通噪声地图的声源反演及修正计算[J]. 中国环境科学, 2013,33(6):1081-1090.Li N, Feng T, Li X H, et al. Sources inversion and correction calculation for traffic noise mapping [J]. China Environmental Science, 2013,33(6):1081-1090.[2] 黄 婧,郭 斌,郭新彪.交通噪声对人群健康影响的研究进展 [J].北京:大学学报(医学版), 2015,47(3):555-558.Huang J, Guo B, Guo X B. Research progress on the impact of traffic noise on human health [J]. Journal of Peking University (Health Sciences), 2015,47(3):555-558.[3] 费广海,吴小萍,廖晨彦.声屏障高度对高铁(客运专线)降噪效果的影响 [J]. 中国环境科学, 2015,35(8):2539-2545.Fei G H, Wu X P, Liao C Y. The influence of sound barriers with different heights on the noise reduction effect of high -speed railway [J]. China Environmental Science, 2015,35(8):2539-2545.[4] 宋 帅.高速公路声屏障降噪效果分析及选型适用性研究 [D]. 西安:长安大学, 2014.Song S. Study on reduce the noise effect analysis and tyep selection applicability of the highway noise barrier [D]. Xian: Chang’an University, 2014.[5] 梁 艳.公路桥梁交通噪音及其控制研究 [D]. 西安:长安大学,2003.Liang Y. Research on highway bridge traffic noise and its control [D]. Xian: Chang’an University, 2003.[6]周立群,韩 健,何 宾,等.V 型减载式声屏障降噪特性的试 验研究 [J]. 噪声与振动控制, 2018,38(6):199-204.Zhou L Q, Han J, He B, et al. Experimental study on noise reduction characteristics of V -type deloading noise barriers [J]. Noise and Vibration Control, 2018,38(6):199-204.[7] Cavalieri T, Cebrecos A, Groby J P, et al. Three -dimensionalmultiresonant lossy sonic crystal for broadband acoustic attenuation: Application to train noise reduction [J]. Applied Acoustics, 2019, 46(3):1-8.[8] Peiró-Torres, M.P, Redondo J, Bravo J M, et al. Open noise barriersbased on sonic crystals. Advances in noise control in transport infrastructures [J]. Transportation Research Procedia, 2016,18:392- 398.[9] 温熙森.声子晶体 [M]. 北京:国防工业出版社, 2009.Wen X S. Phononic crystals [M]. Beijing: National Defense Industry Press, 2009.[10] JT/T 646.5-2017 公路声屏障降噪效果检测方法 [S].JT / T 646.5-2017 Detection method of noise reduction effect of highway sound barrier [S].。
压电声子晶体能带结构的有限元方法模拟

压电声子晶体能带结构的有限元方法模拟吴吉恩;胡瑞霞;邓科【摘要】基于有限元软件COMSOL Multiphysics详细介绍了压电声子晶体能带结构的计算方法,讨论了压电材料中不同分流电路对压电声子晶体能带结构的影响,分析了在能带计算过程中容易出现的几种错误,并给出相应的解决方法 .%Calculation of the band structure for piezoelectric phonons based on the finite element software COMSOL Multiphysics is introduced indetail .The effects of different shunt circuits on the band struc-ture of piezoelectric phonons are then discussed .Finally ,some common errors that are easy to occur in energy band calculation are enumerated ,and the corresponding solutions are given.【期刊名称】《吉首大学学报(自然科学版)》【年(卷),期】2018(039)003【总页数】4页(P31-34)【关键词】压电声子晶体;分流电路;能带结构;COMSOL Multiphysics【作者】吴吉恩;胡瑞霞;邓科【作者单位】吉首大学物理与机电工程学院,湖南吉首416000;吉首大学物理与机电工程学院,湖南吉首416000;吉首大学物理与机电工程学院,湖南吉首416000【正文语种】中文【中图分类】O415压电材料是能实现机械能和电能相互转换的晶体材料.自1880年法国物理学家居里兄弟发现了第一种压电材料——石英晶体后,压电材料得到了长足的发展[1].压电材料是人类声学活动中不可缺少的元器件,目前已被广泛应用于各种超声换能器.压电材料的工作方式包括主动控制和被动控制,这2种工作方式都需要给压电材料配置电路和电学器件.主动控制,需要电路中有电源/信号激励源,为系统的运作提供能量/信号,以便压电材料将电信号转换成其他信号(比如声信号).被动控制不需要电源/信号源,其工作原理类似于传感器.在处于被动控制方式的系统中,由于电路起到了分流耗散的作用,所以被动控制又被称为分流电路控制,并被应用于压电声子晶体中[2-10].在外力的作用下,压电材料因形变而产生电荷.如果在压电材料电极的两端接上分流电路,那么这些电荷将通过分流电路发生相互作用,从而把机械能转化成热能耗散掉.传统声子晶体器件的工作频率或声学特性是固定的,因此,近年来人们开始致力于带隙等声学性质可调的声子晶体的研究,如压电声子晶体,因其声学性质可通过外接分流电路来调节而备受人们青睐.众所周知,能带结构计算对研究压电声子晶体的特性至关重要,因此笔者以一维杆状压电声子晶体为例,拟基于有限元软件COMSOL Multiphysics对压电声子晶体的能带结构进行计算,并讨论压电材料中分流电路对能带的影响.1 杆状压电声子晶体的能带结构笔者设计了一种压电声子晶体杆,其单胞由压电材料和钢组成.所用的压电材料为压电陶瓷(PZT4),晶格常数a=10 mm,杆半径r=2 mm,在一个单胞中压电陶瓷和钢的长度均为2 mm,晶体杆和压电陶瓷的极化方向均沿z轴.由于压电声子晶体杆的结构在z轴方向是周期性排布的,因此在模拟实验中沿z轴方向采用周期性边界条件,而其在余方向则采用自由边界条件.压电声子晶体单胞的结构示意如图1所示,其中深灰色代表压电陶瓷,浅灰色代表钢柱.其中:图1a为开路状态;图1b压电陶瓷分流电路中只有电容;图1c分流电路处于短路状态.图1 压电声子晶体单胞结构示意Fig. 1 Schematic Model of Piezoelectric Phonon Crystal Unit Cell2 模型建立与能带计算图1所示的杆状声子晶体为三维结构,需要建立三维模型来计算其能带结构.在有限元模拟中,三维模型的计算不仅耗时多而且所需内存非常大,这给研究工作带来诸多不便.注意到杆状压电声子晶体的几何结构及其声学性质均关于中心轴(z轴)对称,因此只需建立一个二维轴对称模型来计算即可.具体建模过程如下:在COMSOL 软件中建立一个二维轴对称模型,然后选择“结构力学”模块中的“压电设备”分模块,以及该模块下的“特征频率”作为研究对象;在“全局定义”中添加参数,输入声子晶体的结构尺寸并定义波矢参数用于能带扫描;在“组件1”中的“定义”项里设置材料坐标系与空间坐标系的关系(比如,“材料xz平面系统”表示要研究的是材料的xz平面,而COMSOL中默认的研究平面是rz平面,因此需要将所研究的材料从xz平面投影到rz平面);在“几何1”中建立单胞结构图,并在“材料”中添加压电陶瓷PZT4;设置线弹性材料,选择“压力波和剪切波速度”,输入材料参数(对于该模型,纵波波速cp1=6 100 m/s,横波波速cp2=3 300 m/s,质量密度ρ=7 600 kg/m3);添加周期性边界条件,周期类型选Floquet周期,并且设kF在z方向的波矢为kz(2π/a).模型设置好后,引入静电并设置电路.静电只对压电陶瓷起作用,因此“静电”模块只需选择压电陶瓷所在区域即可(系统默认选择的区域是所有区域,这时需要手动更改).当压电陶瓷没有外接分流电路时,该模块无需手动调节其他选项.当压电陶瓷有外界分流电路时,需要添加边界“终端”和边界“接地”,即分别选中z方向的2条边(这2条边相当于薄电极).设置“终端类型”为“电路”,这里的终端作为与电路模块链接的桥梁.“显示假设方程”为(1)(1)式说明终端(电极)以Q0的形式作用于电路,即终端作为电源.Q0与电位移有关,电位移与应力应变有关,所以Q0与弹性波有关.“电路”模块只在压电陶瓷连接有分流电路的时候被启用.当启用“电路”模块时,需要在“组件1”中添加物理场,并选中“AC/DC”中的“电路”模块.电路模块无需选择材料结构或新建电路模型,所有的电学器件的连接均由节点完成.把电路模块中的“方程形式”由“研究控制”改为“稳态”,初始节点改为“接地节点1”(表示接地点,默认的节点名称为0),添加“外部I终端”(默认的节点名称为1),并将其“电势”设置为“终端电压”,这样就将静电模块与电路模块连接了起来,节点1相当于接有终端的电极.根据电路知识可知,节点0相当于接地的电极.因此,在节点0和节点1之间添加一个电容,就相当于给压电陶瓷2个电极之间接了一个电容.接下来添加一个“电容器”,其节点名称默认为0和1,多物理场的设置无需改动,网络格单元尺寸设置为特别细化.3 分流电路对能带的影响当压电声子晶体没有外接分流电路(图1a)时,能带计算无需利用电路模块和静电模块中的终端和接地,因此将其禁用,计算结果如图2a所示.从图2a可以看出,压电声子晶体在布里渊区边界产生了Bragg带隙.这是由压电陶瓷和钢的声学性质的差异引起的.当压电声子晶体接上电容(图1b)时,能带计算需要利用电路模块和静电模块中的终端和接地,因此将其启用.需要特别注意的是,由于禁用静电模块中的终端会导致电路模块中的外部I终端丢失电势信息,所以重新启用后还需重新添加电势为“终端电压”.当电容设置为20 pF时,能带计算结果如图2b所示.与图2a相比,图2b中所示的带隙已变宽,原因可参考文献[2].当压电声子晶体的外接分流电路为短路状态(图1c)时,压电陶瓷2个电极之间的电势一致,可以用电路模块使电容足够大或短路,也可以不用电路模块,只要保证2个电极的电势/电学条件一致即可.此时能带计算的结果如图2c所示.图2 压电声子晶体能带Fig. 2 Band Structures of Piezoelectric Photonic Crystals4 能带计算中常见问题在能带计算过程中可能会遇到各种各样的问题,在此列举几个典型的问题/报错,并给出相应的解决办法.网格单元尺寸设置为较细化时,接上电容的压电声子晶体的能带如图3a所示.从图3a可以看出,在低频时能带计算结果显得毫无规律.解决方法是将网格精细化.在模型较大的情况下,只针对电极(线)作精细化处理即可.图3b提示电路连接错误,解决方法是正确连接电路.图3c提示扫描错误,解决方法是将“步骤1:特征频率”中的“特征频率搜索范围”设为大于0的值.图3d提示电路不能正常工作,解决方法是将电路模块的“方程形式”由“研究控制”变更为“稳态”或其他形式.图3 计算压电声子晶体能带结构时的常见问题Fig. 3 Common Errors in Band Structure Calculation for Piezoelectric Photonic Crystals参考文献:[1] 栾桂冬,张金铎,王仁乾.压电换能器和换能器阵[M].北京:北京大学出版社,2005.[2] DEGRAEVE S,GRANGER C,DUBUS B,et al.Bragg Band Gaps Tunability in an Homogeneous Piezoelectric Rod with Periodic Electrical Boundary Conditions[J].Journal of Applied Physics,2014,115(19):194 508-194 515. [3] WILM M,KHELIF A,BALLANDRAS S,et al.Out-of-Plane Propagation of Elastic Waves in Two-Dimensional Phononic Band-Gap Materials[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2003,67(2):65 602.[4] HOU Z,WU F,LIU Y.Phononic Crystals Containing Piezoelectric Material[J].Solid State Communications,2004,130(11):745-749.[5] ZHOU H,LAN M.Band Gaps off in-Plane Waves Propagating Vertically Through Piezoelectric Phononic Crystal with Initial Stresses[J].International Journal of Control and Automation,2016,9(6):209-220.[6] GHAZARYAN K B,PILIPOSYAN D G.Interfacial Effects for Shear Waves in One Dimensional Periodic Piezoelectric Structure[J].Journal of Sound & Vibration,2011,330(26):6 456-6 466.[7] ZHOU H,LAN M.Band Gaps of SH Wave Propagating ThroughElastic/PE/PM Phonon Crystal[J].International Journal of Control and Automation,2016,9(8):281-290.[8] 陈圣兵,韩小云,郁殿龙,等.不同压电分流电路对声子晶体梁带隙的影响[J].物理学报,2010,59(1):387-392.[9] CHEN Y Y,ZHU R,BARNHART M V,et al.Enhanced Flexural Wave Sensing by Adaptive Gradient-Index Metamaterials[J].Scientific Reports,2016(6):35 048-35 058.[10] HOU Z,ASSOUAR B M.Tunable Solid Acoustic Metamaterial with Negative Elastic Modulus[J].Applied Physics Letters,2015,106(25):040 802.。
求解声子晶体Euler梁弯曲振动能带结构的一种改进传递矩阵法

求解声子晶体Euler梁弯曲振动能带结构的一种改进传递矩阵法贺静;董傲【摘要】用于计算声子晶体Euler梁弯曲振动能带结构的传递矩阵法有如下缺点:待定参数无实际物理意义、传递矩阵的计算较为繁琐以及连续性条件的应用不直接等.为解决目前存在的问题,引入Krylov函数将待定参数转化为梁端位移、转角、弯矩和剪力4个具有明确意义的参数,使处理原胞内及原胞间不同材料梁连接位置的变形和受力连续条件直接化;并由此推导了形式较为简单的传递矩阵及相应的能带结构计算方法,并通过算例验证了该方法确适用于计算声子晶体Euler梁的弯曲振动能带结构.【期刊名称】《科学技术与工程》【年(卷),期】2014(014)005【总页数】5页(P174-177,182)【关键词】声子晶体;Euler梁;改进传递矩阵法;能带结构【作者】贺静;董傲【作者单位】河海大学力学与材料学院,南京210098;河海大学力学与材料学院,南京210098【正文语种】中文【中图分类】O422.61993年M.S.Kushwsha 提出声子晶体概念[1]以来,人们对这样的可以控制和消除振动的人工材料表现出极大的研究兴趣。
声子晶体概念的提出提供了用梁来控制结构振动的新思路。
J.S.Jensen等人于2002年用试验验证了一维杆状声子晶体可以产生振动带隙[2]这一现象,这是研究梁类声子晶体梁的开端。
目前,关于声子晶体梁能带结构的计算方法主要有平面波展开法[3—5]、集中质量法[6]和传递矩阵法[7—9]等。
其中,平面波展开法和集中质量法为数值方法,其计算结果的精确程度取决于平面波数的选择和离散程度。
传递矩阵法区别于另外两种方法的是它可以获得解析关系式[10,11],在声子晶体梁能带结构计算中具有一定的优势。
文献[8]和文献[12]中所介绍的传递矩阵法(以下称为原传递矩阵法),可视为计算声子晶体梁弯曲振动能带结构的一般方法。
其关键在于利用原胞内和原胞间不同材料梁连接处的位移、转角、弯矩和剪力的连续性条件。
有限元仿真模拟在《理论声学》教学中的应用:利用散射栅实现声子晶体相空间模式调控
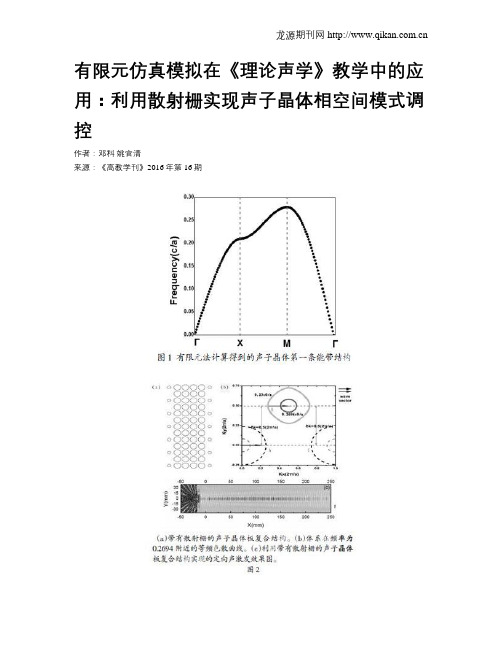
有限元仿真模拟在《理论声学》教学中的应用:利用散射栅实现声子晶体相空间模式调控作者:邓科姚官清来源:《高教学刊》2016年第16期摘要:文章以带有表面散射栅结构的声子晶体为例,探讨了计算机仿真模拟在《理论声学》教学中的应用。
基于COMSOL Multiphysics软件,利用有限元方法数值计算了表面栅声子晶体的透射性质,结果表明添加表面栅能有效实现声波的相空间调控,并以此为基础在声子晶体带隙频率范围内实现了声波的定向激发。
这种基于仿真模拟的教学模式有利于抽象概念的形象化,具有较好的教学效果。
关键词:计算机仿真教学;多物理有限元模拟;散射栅声子晶体中图分类号:G642 文献标志码:A 文章编号:2096-000X(2016)16-0072-02Abstract: Taking photonic crystals with surface scattering gratings, this paper discusses the application of computer simulation in the teaching of "Theoretical Acoustics". On the basis of COMSOL Multiphysics software, this paper works out the transmitting properties of photonic crystals with surface scattering by using the finite element method.. It is demonstrated that acoustic phase modulation can be achieved by adding scattering gratings in a sonic crystal. Based on this mechanism, directional excitation of sound wave is fully realized within the gap frequency of photonic crystals. Such an analog-simulation-based teaching mode makes the abstract concept pictorial, thus will be effective and helpful in teaching process.Keywords: computer simulation teaching; Multiphysics finite element simulation; sonic crystal with scattering grating一、概述聲波在周期性复合介质(即声子晶体)中的传播行为是《理论声学》课程中非常重要的一块教学内容。
关于comsol模拟的一些问答

1.近来用COMSOL计算光子晶体光纤的模场分布,可是不知道PML的参数如何设置,以及边界条件怎么设置,计算出来的结果不对. 实验室老板催得急,算不出来特别郁闷,不想读的心思都有了。
请用过的人帮帮忙吧:)我也是用comsol算光纤的,关于pml层的设定问题,如果不考虑损耗的话,pml层可以不设,你可以试一试就知道了,pml对模场分布基本没有影响2. COMSOL Multiphysics如何模拟带隙光子晶体光纤?要用COMSOL Multiphysics模拟带隙光子晶体光纤,也就是要加入kz,可以用如下方法:(1)用平面波模式,将模型边界条件改为电场,输入一个表达式的名字,例如E1。
(2)定义该边界表达式E1,菜单“选项>表达式>边界表达式”,选择不同的边界,分别写入该边界上电场E1的表达式,这样就能加入kz,将所需的周期性边界方程写入COMSOL Multiphysics。
3.如何准确求光子晶体光纤的限制损耗即有效折射率的虚部我在模拟PCF时,为了求其限制损耗即有效折射率的虚部,在PCF结构的外面加了PML,但是在加了PML 后,却发现光束不能约束在纤芯中了。
不知道哪里出了问题,还望各位高手给予指点,谢谢。
[attach]219885[/attach]加了PML后的结果如下:[attach]219886[/attach]我也是初学,也在做一些光子晶体的方法。
目前还不懂帮你顶顶,大家多多讨论有限元做光子?这个挺有新意,不过要注意是否适用能说一下有限元做光子为什么不合适吗?不过用FDTD做光子的还蛮多的PML的几何不对,应该是加个六边形的PML才对吧:)纤芯比外面的小,当然有可能找到外面的那个模式,多找几个模式或者将外面的区域减小应该就可以了加个圆形的就可以了PML要考虑模型的对称性,比如这个模型可以只计算1/4或者1/6楼主具体交流下怎么划分格点的?我算光子晶体光纤的模式,伪模很多阿,比如设neff=1.5附近寻找,设200个,它就给找出200个neff 出来。
声子晶体板复能带计算方法

声子晶体板复能带计算方法作者:陈圣兵张浩宋玉宝来源:《振动工程学报》2019年第03期摘要:声子晶体具有弹性波带隙,可以用于结构振动与噪声控制。
声子晶体传统能带算法一般给定波矢k在不可约布里渊区边界取值,然后求解特征频率ω,得到ω-k曲线。
因而,传统方法中波矢k只取实数,只能求解实能带。
为了求解复能带,一般需要给定频率ω,求解特征波矢k,从而得到k-ω曲线。
提出了一种参数变换方法,解决了特征波矢求解中复杂的非线性特征值问题,实现了复能带的快速求解。
最后,采用两个算例对文中算法进行了验证,包括布拉格声子晶体板和局域共振声子晶体板,研究了带隙内衰减常数随波传播方向的变化和阻尼对带隙的影响。
关键词:声子晶体; 超材料; 复能带; 参数变换中图分类号: O735; TB535; 文献标志码: A; 文章编号: 1004-4523(2019)03-0415-06DOI:10.16385/ki.issn.1004-4523.2019.03.005引言声子晶体是由两种或两种以上介质组成的具有弹性波带隙的周期性复合材料或结构。
当弹性波在声子晶体中传播时,某些频率范围内的弹性波传播将被抑制,相应的频率范围称为带隙。
由于周期性结构广泛存在于实际工程结构中,人们对周期性结构的研究有着悠久的历史[1-3]。
1992年,Sigalas和Economou研究了球形散射体埋入某一基体材料中形成的三维周期性复合介质中弹性波的传播特性,首次从理论上证实了三维周期点阵结构中存在弹性波带隙[4]。
1993年,Kushwaha等在研究镍/铝二维固体周期复合介质时第一次提出了声子晶体的概念,类比光子晶体分析了声子完全带隙在理论研究中的意义[5]。
1995年,Martínez-Sala等对西班牙马德里的一座具有两百多年历史的雕塑进行了声学特性测试,该雕塑是由直径为2.9 cm 的中空不锈钢圆柱周期性排布在一个4 m直径的圆形平台上,形成的晶格常数为10 cm,通过测试他们第一次从实验角度证实了弹性波带隙的存在[6]。
基于COMSOL的声子晶体带结构计算新方法

基于COMSOL的声子晶体带结构计算新方法付子义;王晨旭;王立国;长谷川弘治【摘要】结合声波与电磁波的物理特性,建立光子晶体与声子晶体物理量之间的联系,通过类比光子晶体能带结构的求解过程,对声子晶体能带结构进行仿真计算.以二维声子晶体为研究对象,通过重新建立数学模型,利用Born-von-karman周期性边界条件和布洛赫态,推导出声子晶体偏微分形式的本征方程,基于有限元仿真软件COMSOL Multiphysics系数偏微分模块(coefficient form PDE),求解出相应的本征频率从而求解出能带.与已有计算方法相比,该方法在适用性,难易程度等方面具有明显的优越性.【期刊名称】《软件》【年(卷),期】2018(039)012【总页数】4页(P6-9)【关键词】声子晶体;能带结构;有限元;PDE;本征方程【作者】付子义;王晨旭;王立国;长谷川弘治【作者单位】河南理工大学电气工程与自动化学院,河南焦作 454150;河南理工大学电气工程与自动化学院,河南焦作 454150;河南理工大学电气工程与自动化学院,河南焦作 454150;室兰工业大学情报电子工学系,日本室兰 0500071【正文语种】中文声子晶体是由嵌入均匀主体材料中的声波散射体组成的有限尺寸周期阵列的人造晶体。
声波与周期性排列的散射体之间的相互作用导致形成声波不能通过该结构的频带。
这种频带被称为带隙。
基于这一特性使得声子晶体具有广阔的应用前景。
声子晶体的概念是由光子晶体的概念演绎而来的,因此与光子晶体相类似的是,能带结构也是声子晶体最重要的研究内容之一。
文献[1]基于TMM方法,对声子晶体能带结构进行求解计算,但是TMM方法主要用于一维声子晶体的能带计算。
虽然结合PWE方法可用于二维情况,但计算量较大。
文献[2]基于PWE方法,但是PWE方法对于组分材料声学参数相差较大的声子晶体需要更多的计算时间和内存,而且不易给出正确结果。
声子晶体的负折射成像分析

声子晶体的负折射成像分析韩建宁;温廷敦;杨鹏;张璐;张驰【摘要】声子晶体的负折射成像已成为当今国内外研究的热点问题.首先通过分析弹性波激励声子晶体元胞的局域共振响应特性,计算了局域共振型声子晶体的带隙特性,以此为基础构建了声子晶体相应的实验模型.然后基于Comsol仿真平台,把声子晶体元胞在XY平面内排列成声子晶体板后,模拟了近场点声源通过声子晶体板的负折射声成像过程.同时计算了模拟两个理想点声源经过声子晶体板后负折射成像的特性.仿真结果表明:声子晶体能较好地分辨两个点声源所成的像,点像的最小分辨率可达到0.2λ,很好地突破了声学成像中的衍射极限.%The negative refraction imaging of phononic crystal has become a research focus at home and abroad .Localized resonant resonance characteristics of elastic wave excitation phononic crystal cell were analyzed ,and the phonon crystal band gap was calculated ,on this basis ,corresponding ex-perimental model of phononic crystal was built .Based on comsol simulation platform ,the phononic crystal cell were arranged as phononic crystal plate in XY plane ,and negative refraction acoustic im-aging process was simulated when near field acoustic source past through phononic crystal plate .Nega-tive refraction imaging characteristics was obtained when two ideal point sound source past through the phononic crystal plate .Simulation results show that phononic crystals can distinguish better the image which is made by two sound source ,the minimum resolution can reach 0 .2λ,so it can make a breakthrough in the diffraction limit of the acoustic imaging .【期刊名称】《中北大学学报(自然科学版)》【年(卷),期】2014(000)002【总页数】4页(P205-208)【关键词】声子晶体;负折射;Comsol;分辨率【作者】韩建宁;温廷敦;杨鹏;张璐;张驰【作者单位】中北大学信息与通信工程学院,山西太原030051;中北大学理学院,山西太原030051;中北大学信息与通信工程学院,山西太原030051;中北大学信息与通信工程学院,山西太原030051;中北大学信息与通信工程学院,山西太原030051【正文语种】中文【中图分类】O426.5近年来,声子晶体的负折射成像研究受到越来越多国内外学者的关注.刘正猷[1]等提出了局域共振型声子晶体具有显著不同的带隙特点,给声子晶体负折射成像提供了新思路.L.S.Chen[2]提出了只有存在部分禁带才有可能在声子晶体板中负折射成像.J.Li[3]等人用高斯光束仿真了声子晶体板的横、纵波模式负折射成像,从理论上探索了模式选择.C.Crognne[4-5]等人研究了钢柱-环氧树脂的二维声子晶体,从实验上证明了固/固式声子晶体也可以用作负折射成像.Z.Liang[6]等人提出一种具有高折射率和接近零质量密度的极端声超常材料,更激起了科学工作者的空前兴趣.声子晶体板的负折射成像具有重要的应用潜力,可以突破传统透镜的衍射极限,对细微结构实现了完美成像,极大地提高了像的分辨率.现在已知的声子晶体平板成像方法中[7],声子晶体平板实现了较好地负折射成像.本文以有限元为基础,利用有限元软件Comsol完全开放的架构和丰富的后处理功能,以二维局域共振声子晶体平板为模型进行了仿真分析,可省去人工编写代码的繁琐过程[8],得到直观的声子晶体板的声成像效果,以期更好地认识声子晶体平板实现声波完美成像和突破声学成像中衍射极限的问题.1 基本原理二维声子晶体的元胞为轴向(Z方向)厚度较小的平面薄板,外力只作用在平面内.元胞由直径为0.01 m的铅芯外面均匀地包覆0.002 m的橡胶组成散射单元(散射体),再嵌入在环氧树脂中构成.图1所示为一种二维典型正方晶格声子晶体的一个元胞[9].图1 二维局域共振型声子晶体的结构图Fig.1 Structure of two-dimensional local resonance type phononic crystal材料参数为:水,ρ水 =1 000 kg/m3,c水=1.5 ×103m/s;铅芯,ρ铅 =11 600 kg/m3,c铅 =2 160 m/s;环氧树脂,ρ环氧树脂 =1 180 kg/m3,c环氧树脂=2 680 m/s,λ环氧树脂=6 × 105N/m2,μ环氧树脂= 4 × 104N/m2; 橡胶,ρ橡胶 =1 300 kg/m3,c橡胶 =300 m/s.其中:ρ,c,λ,μ 分别表示材料的质量密度、速度以及拉美常数.如图1所示,设铅芯质量为 m铅芯,树脂质量为 m树脂,则有假设弹性波入射到声子晶体元胞中,由于声子晶体元胞之间没有耦合作用,因此对声子晶体元胞的分析就能代表整体的共振响应特性.设U1和U2分别为环氧树脂和铅芯的振幅,橡胶包覆层和铅芯的交界面为ε,根据柱坐标的应变位移关系,可知应力σr r和σrθ.[10]根据刘正猷2005年提出的简化解析模型的波动方程及边界条件[11]因此,铅芯在Z轴的振动方程将应力σrr和σrθ代入式(6)得从式(7)可求出U2/U1的比值,当入射波的频率为共振频率时,该比值出现极值点,结果如图2所示.图2 铅芯与环氧树脂位移比的变化曲线Fig.2 Displacement ratio curve of lead and epoxy resin如图2所示,当入射波频率增加到共振频率时,有效质量出现了反常行为,即表现出了负质量响应.负质量响应意味着波的指数衰减,这与声子晶体禁带一致[12].由此,可以用有效质量来确定禁带,带隙的起始频率可由共振频率确定,带隙的截止频率则可由有效质量为零的点确定.因此,当入射波频率增加到共振频率时,此时弹性波在禁带内,弹性波在该声子晶体元都不能传播,而是表现为衰逝波的形式.2 实验模型及分析根据以上所述,声子晶体元胞在XY平面内按长方形点阵周期排列成平板植入水中.近场点声源所产生的声波通过此平板,在板两界面表面经过两次负折射后,得到了一个完全由衰逝波组成的亚波长近场外部像点[13],结果如图3所示.图3(a)所示为点声源通过声子晶体板体的压力场强度分布.其中,板子的厚度d=2λ,点源与板的距离ds=0.012 5λ,λ代表水中的波长.由图3(c)可知,像点波长为0.3λ,即为亚波长成像.普通透镜由于像点不含衰逝部分而存在一个半波长的成像分辨率极限.因此,本文设计的声子晶体板分辨率要明显优于普通透镜.因为当入射波频率增加到声子晶体有效共振频率时,此时弹性波在禁带内,弹性波在该声子晶体板不能传播,而是表现为衰逝波的形式,这样点声源通过声子晶体板的传播部分将被反射掉,而且在板的另一侧就不会产生不必要的干扰,从而将点源的亚波长细节更好地传递到板子的另一侧[14].同时,这里点源与平板的距离明显小于板子的厚度,因此,近场点声源通过声子晶体的声成像过程,实现了传统声透镜难以实现的近场像难题.图3 声子晶体板的负折射声成像Fig.3 Negative refraction imaging of phononic crystal plate我们知道,点声源信号入射到声子晶体平板后,声波可通过散射性通道,到一个完全由衰逝波形成的近场亚波长像,但是在像面上实际得到的是一个具有一定面积的衍射斑.由于衍射像有一定的大小,如果两个像点之间的距离太短,就无法分辨出是两个像点.两个衍射像间所能分辨的最小间隔称为声子晶体板的衍射分辨率[15].下面模拟两个理想点声源经过声子晶体平板后成像的特性,结果如图4所示.图4 d1=0.2λ时声子晶体板的负折射声成像Fig.4 Negative refraction imaging of phononic crystal plate at d1=0.2λ图4(a)所示为两个点源通过声子晶体板体的压力场强度分布.其中:板子的厚度为d=0.2λ,两个点源之间的距离d1=0.2λ.如图4(c)所示,在像面上出现两个分离的亮斑,已完全能够辨别出这是两个不同的像点,说明由于声子晶体平板的存在,原来不分辩的两个点源变得可以分辨.3 结论本文利用有限元法研究了声子晶体局域共振型带隙特性的基本特性,以此为基础构建了声子晶体相应的实验模型.根据近场点声源通过声子晶体平板的成像过程,声子晶体板分辨率要明显优于普通透镜,实现了传统声透镜难以实现的近场成像.实验结果表明:由于声子晶体平板的存在,原来不分辩的两个点源变得可以分辨,对细微结构能够实现完美成像,极大地提高了像的分辨率,很好地突破了声学成像中的衍射极限.因此,利用声子晶体负折射成像在医学检测、工业探伤等领域有较大的应用价值.参考文献:[1]Liu Z,Zhang X,Mao Y,et al.Locally resonant sonic materials [J].Science,2000,289:1734-1736.[2]Chen L S,Kuo C H,Ye Z.Acoustic imaging and collimating by slabs of sonic crystals made from arrays of rigid cylinders in air[J].Applied Physics Letters,2004,85(6):1072-1074.[3]Li J,Liu Z,Qiu C.Negative refraction imaging of acoustic waves by a two-dimensional three-component phononic crystal[J].Physical Review B,2006,73(5):054302.[4]Croёnne C,Morvan B,Vasseur J B,et al.Analysis of elastic waves transmitted through a 2-D phononic crystal exhibiting negative refraction [J].IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control,2011,58(1):178-186.[5]Croёnne C,Manga E D,Morvan B,et al.Negative refraction of longitudinal waves in a two-dimensional solidsolid phononic crystal [J].Physical Review B,2011,83(5):054301.[6]Liang Z,Li J.Extreme acoustic metamaterial by coiling up space [J].Physical Review Letters,2012,108(11):114301.[7]覃世冬,邓芳圆,刘绍娥,等.声子晶体平板组合成像特性分析[J].振动与冲击,2012,31(17):140-144.Qin Shidong,Deng Fangyuan,Liu Shaoe,etal.The phonon crystal tablet combined imaging characteristics analysis [J].Journal of Vibration and Shock,2012,31(17):140-144.(in Chinese) [8]柯佼.含共振单元的二维多孔声子晶体带隙特性研究[D].北京:北京交通大学,2012.[9]Goffaux C,Sanchez-Dehesa J,Yeyati A L,et al.Evidence of fano-like interference phenomena in locally resonant materials[J].Phys.Rev.Lett.,2002,88(22):225502.[10]顾永伟.局域共振声子晶体的优化设计与模拟[D].上海:上海交通大学,2009.[11]Liu Z,Chan C T,Sheng P.Analytic model of phononic crystals with local resonances[J].Physical Review B,2005,71(1):014103.[12]Liu Z,Zhang X,Mao Y,et al.Locally resonant sonic materials [J].Science,2000,289:1734-1736.[13]温熙森,温激鸿,郁殿龙.声子晶体[M].北京:国防工业出版社,2009. [14]邓科.声子晶体及声超常材料的特性调控与功能设计[D].武汉:武汉大学,2010.[15]高俊丽.二维声子晶体负折射成像机理与特性研究[D].长沙:中南大学,2009.。
基于广义有限差分法的三维固体声子晶体弹性波禁带带隙分析

第35卷第1期2021年2月粉煤灰综合利用FLY ASH COMPREHENSIVE UTILIZATIONVol.35No・1Feb.2021基于广义有限差分法的三维固体声子晶体弾性波禁带带隙分析Study on Generalized Finite Difference Method for the Forbidden Bandgap Calculation of In-plane Wave in3D Solid Phononic Crystals李炉锋,汤卓超(河海大学力学与材料学院,江苏南京211100)摘要:声子晶体作为一种人工周期性结构,能够实现特定频率范围内波的屏蔽,这个频率范围被称为禁带。
目前,已有多种方法用于对能带结构的数值模拟,但多数是二维结构。
广义有限差分法(Generalized Finite Difference Method)作为一种无网格算法,具有简单易用、普适性强等特点。
本文使用广义有限差分法,对三维声子晶体能带结构进行了计算,对比不同材料及填充率所得结果,为实际工程应用提供一些指导。
关键词:三维声子晶体;广义有限差分法;能带结构中图分类号:TU755.2文献标志码:A文章编号:1005-8249(2021)01-0084-07D0I:10.19860/ki.issn1005-8249.2021.01.017LI Lufeng,TANG Zhuochao(College of Mechanics and Materials,Hohai University,Nanjing211100,China)Abstract:As an artificial periodic structure,phononic can shield waves within a certain frequency range,which is called band gap.At present, there are many methods for the numerical simulation of band structures of phononic,but most of them are two-dimensional.The generalized finite difference method as a meshless method,is simple to be used and has more general applicability.In this paper,generalized finite difference method is used in the calculation of the band structures of three-dimensional phononic crystal.The results obtained from different materials and filling rates are compared to provide some guidance for practical engineering applications.Keywords:3D phononic;generalized finite difference method;band structure0引言近几十年来,一种新型的人工周期复合结构—声子晶体受到了越来越多的关注[T]。
comsol计算声子晶体算例
信号接收点
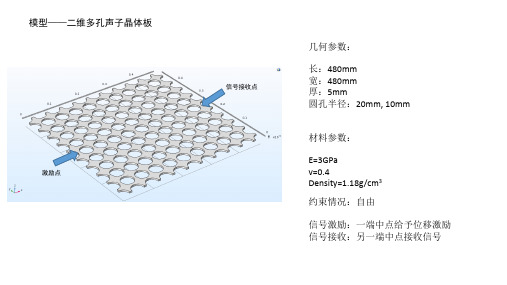
长:480mm 宽:480mm 厚:5mm 圆孔半径:20mm, 10mm
材料参数: E=3GPa v=0.4 Density=1.18g/cm3 约束情况:自由 信号激励:一端中点给予位移激励 信号接收:另一端中点接收信号
激励点
定义相关参数
新建一个工作平面创建二维图形(利用阵列、布尔操作等变换), 转换为实体后进行拉伸创建三维模型
另一端中点接收信号激励点信号接收点定义相关参数新建一个工作平面创建二维图形利用阵列布尔操作等变换转换为实体后进行拉伸创建三维模型定义材料参数设置激励点并给一个单位位移激励在对边中点设置一个域点探针接收响应在参数化扫描中设置输入频率的起始值及步长在频域设置中设置频率单位设置网格参数并划分网格计算后将结果表格输出按照以下公式计算20lg????????????????????????????????????????????????????绘制该值与频率k之间的图像即为频谱图
定义材料参数
设置激励点并给一个单位位移激励
在对边中点设置一个域点探针接收响应
在参数化扫描中设置输入频率的起始值及步长
在频域设置中设置频率单位
设置网格参数并式计算
绘制该值与频率k之间的图像即为频谱图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定义材料参数
设置激励点并给一个单位位移激励
在对边中点设置一个域点探针接收响应
在参数化扫描中设置输入频率的起始值及步长
在频域设置中设置频率单位
设置网格参数并划分网格
计算后将结果表格输出,按照以下公式计算
绘制该值与频率k之间的图像即为频谱图
模型——二维多孔声子晶体板 几何参数:
信号接收点
长:480mm 宽:480mm 厚:5mm 圆孔半径:20mm, 10mm
材料参数: E=3GPa v=0.4 Density=1.18g/cm3 约束情况:自由 信号激励:一端中点给予位移激励 信号接收:另一端中点接收信号
激励点
定义相关参数
新建一个工作平面创建二维图形(利用阵列、布尔操作等变换), 转换为实体后进行拉伸创建三维模型
