中考数学难点之动点问题
数学动点问题及练习题附答案

初中数学动点问题及练习题附参考答案专题一:建立动点问题的函数解析式函数提醒了运动变化过程中量与量之间的变化规律,是初中数学的重要容.动点问题反映的是一种函数思想,由于*一个点或*图形的有条件地运动变化,引起未知量与量间的一种变化关系,这种变化关系就是动点问题中的函数关系.则,我们怎样建立这种函数解析式呢"下面结合中考试题举例分析.一、应用勾股定理建立函数解析式。
二、应用比例式建立函数解析式。
三、应用求图形面积的方法建立函数关系式。
专题二:动态几何型压轴题动态几何特点----问题背景是特殊图形,考察问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性〔特殊角、特殊图形的性质、图形的特殊位置。
〕动点问题一直是中考热点,近几年考察探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
一、以动态几何为主线的压轴题。
〔一〕点动问题。
〔二〕线动问题。
〔三〕面动问题。
二、解决动态几何问题的常见方法有:1、特殊探路,一般推证。
2、动手实践,操作确认。
3、建立联系,计算说明。
三、专题二总结,本大类习题的共性:1.代数、几何的高度综合〔数形结合〕;着力于数学本质及核心容的考察;四大数学思想:数学结合、分类讨论、方程、函数.2.以形为载体,研究数量关系;通过设、表、列获得函数关系式;研究特殊情况下的函数值。
专题三:双动点问题点动、线动、形动构成的问题称之为动态几何问题. 它主要以几何图形为载体,运动变化为主线,集多个知识点为一体,集多种解题思想于一题. 这类题综合性强,能力要求高,它能全面的考察学生的实践操作能力,空间想象能力以及分析问题和解决问题的能力. 其中以灵活多变而著称的双动点问题更成为今年中考试题的热点,现采撷几例加以分类浅析,供读者欣赏.1 以双动点为载体,探求函数图象问题。
模型39 数轴上动点问题(解析版)-2023年中考数学重难点解题大招复习讲义-几何模型篇

1.数轴(1)数轴的概念:规定了原点、正方向、单位长度的直线叫做数轴.数轴的三要素:原点,单位长度,正方向.(2)数轴上的点:所有的有理数都可以用数轴上的点表示,但数轴上的点不都表示有理数.(一般取右方向为正方向,数轴上的点对应任意实数,包括无理数.)(3)用数轴比较大小:一般来说,当数轴方向朝右时,右边的数总比左边的数大.✮(4)数轴上两点间的距离公式:AB=X B-X A(即:右端点减左端点)✮(5)数轴上中点数公式:=+2(即:中点等于两端点相加除以2)例题精讲【例1】.如图,点A在数轴上表示的数为﹣3,点B表示的数为2,点P在数轴上表示的是整数,点P不与A、B重合,且PA+PB=5,则满足条件的P点表示的整数有___________.解:∵PA+PB=5,∴点P在A,B两点之间,A,B两点之间的整数有﹣2,﹣1,0,1,变式训练【变式1-1】.如图,点O为原点,A、B为数轴上两点,AB=15,且OA=2OB,点P从点B开始以每秒4个单位的速度向右运动,当点P开始运动时,点A、B分别以每秒5个单位和每秒2个单位的速度同时向右运动,设运动时间为t秒,若3AP+2OP﹣mBP的值在某段时间内不随着t的变化而变化,则m= 2.5或5.5.解:∵AB=15,OA=2OB,∴AO=AB=10,BO=AB=5,∴A点对应数为﹣10,B点对应数为5,设经过t秒,则AP==,OP=5+4t,BP=5+4t﹣(5+2t)=2t,当t≤15时,3AP+2OP﹣mBP=45﹣3t+10+8t﹣2mt=(5﹣2m)t+55,∴当5﹣2m=0,即m=2.5时,3AP+2OP﹣mBP的值在某段时间内不随着t的变化而变化,当t>15时,3AP+2OP﹣mBP=3t﹣45+10+8t﹣2mt=(11﹣2m)t﹣35,∴当11﹣2m=0,即m=5.5时,上式为定值﹣35,也不随t发生改变,故m为2.5或5.5.故答案为:2.5或5.5.【变式1-2】.已知数轴上两点A、B对应的数分别是6,﹣8,M、N、P为数轴上三个动点,点M从A点出发,速度为每秒2个单位,点N从点B出发,速度为M点的3倍,点P 从原点出发,速度为每秒1个单位.(1)若点M向右运动,同时点N向左运动,求多长时间点M与点N相距46个单位?(2)若点M、N、P同时都向右运动,求多长时间点P到点M,N的距离相等?(3)当时间t满足t1<t≤t2时,M、N两点之间,N、P两点之间,M、P两点之间分别有47个、37个、10个整数点,请直接写出t1,t2的值.解:(1)设运动时间为t秒,由题意可得:6+8+2t+6t=46,∴t=4,∴运动4秒,点M与点N相距46个单位;(2)设运动时间为t秒,由题意可知:M点运动到6+2t,N点运动到﹣8+6t,P点运动到t,由t=﹣8+6t可得t=1.6,当t<1.6时,点N在点P左侧,若MP=NP,则t﹣(﹣8+6t)=6+2t﹣t,解得t=(s);当t>1.6时,点N在点P右侧,若MP=NP,则﹣8+6t﹣t=6+2t﹣t,解得t=(s),∴运动s或s时,点P到点M,N的距离相等;(3)由题意可得:M、N、P三点之间整数点的多少可看作它们之间距离的大小,M、N两点距离最大,M、P两点距离最小,可得出M、P两点向右运动,N点向左运动①当t1=4s时,P在4,M在14,N在﹣32,再往前一点,MP之间的距离即包含10个整数点,NP之间有47个整数点;②当N继续以6个单位每秒的速度向左移动,P点向右运动,若N点移动到﹣33时,此时N、M之间仍为47个整数点,若N点过了﹣33时,此时N、M之间为48个整数点故t2=+4=(s),∴t1,t2的值分别为4s,s.【例2】.如图,周长为6个单位长度的圆上的六等分点分别为A,B,C,D,E,F,点A 落在2的位置,将圆在数轴上沿负方向滚动,那么落在数轴上﹣2023的点是点D.解:由图形可知,旋转一周,点B对应的数是1,点C对应的数是0,点D对应的数是﹣1,点E对应的数是﹣2,点F对应的点为﹣3,点A对应的点为﹣4,继续旋转,点B对应的点为﹣5,点C对应的点为﹣6.∵2023÷6=337…1,∴数轴上表示﹣2025的点与圆周上点D重合.故答案为:点D.变式训练【变式2-1】.在数轴上,点A,O,B分别表示﹣15,0,9,点P,Q分别从点A,B同时开始沿数轴正方向运动,点P的速度是每秒4个单位,点Q的速度是每秒1个单位,运动时间为t秒.若点P,Q,O三点在运动过程中,其中一个点恰好是另外两点为端点的线段的一个中点,则运动时间为或或秒.解:由题知,P点对应的数为:﹣15+4t,Q点对应的数为:9+t,(1)当O为PQ中点时,根据题意得15﹣4t=9+t,解得t=,(2)当P是OQ的中点时,根据题意得2(4t﹣15)=9+t,解得t=,(3)当Q是OP的中点时,根据题意得2(9+t)=4t﹣15,解得t=,故答案为:或或.【变式2-2】.如图:在数轴上A点表示数﹣3,B点示数1,C点表示数9.(1)若将数轴折叠,使得A点与C点重合,则点B与数表示的点重合;(2)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动.①若t秒钟过后,A,B,C三点中恰有一点为另外两点的中点,求t值;②当点C在B点右侧时,是否存在常数m,使mBC﹣2AB的值为定值,若存在,求m的值,若不存在,请说明理由.解:(1)AB=9﹣(﹣3)=12,12÷2=6,AB的中点表示的数为:9﹣6=3,3﹣1=2,3+2=5,则点B与5表示的点重合;(2)①由题意可知,t秒时,A点所在的数为:﹣3﹣2t,B点所在的数为:1﹣t,C点所在的数为:9﹣4t,(i)若B为AC中点,则.∴t=1;(ii)若C为AB中点,则,∴t=4;(iii)若A为BC中点,则,∴t=16,∴综上,当t=1或4或16时,A,B,C三点中恰有一点为另外两点的中点;②假设存在.∵C在B右侧,B在A右侧,∴BC=9﹣4t﹣(1﹣t)=8﹣3t,AB=1﹣t﹣(﹣3﹣2t)=4+t,mBC﹣2AB=m(8﹣3t)﹣2(4+t)=8m﹣3mt﹣8﹣2t=8m﹣8﹣(3mt+2t)=8m﹣8﹣(3m+2)t,当3m+2=0即m=时,mBC﹣2AB=8×(﹣)﹣8=﹣为定值,∴存在常数m=﹣,使mBC﹣2AB的值为定值.1.如图,将一刻度尺放在数轴上(数轴的单位长度是1cm),刻度尺上表示“0cm”“8cm”的刻度分别对应数轴上的是﹣3和x所表示的点,那么x等于()A.5B.6C.7D.8解:根据数轴可知:﹣3+8=5,故选:A.2.等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和﹣1,若△ABC绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2021次后,点B()A.对应的数是2019B.对应的数是2020C.对应的数是2021D.不对应任何数解:结合数轴,根据连续翻转可得出从原点开始,向右依次是A、B、C循环排列,2021次后共得出2022个顶点,∵2022÷3=674,∴最后一个点为C,∵最后一个点C是翻转了2021次后得到的,∴点C表示的数为2021,∴点B表示的数为2020,故选:B.3.在解决数学实际问题时,常常用到数形结合思想,比如:|x+1|的几何意义是数轴上表示数x的点与表示数﹣1的点的距离,|x﹣2|的几何意义是数轴上表示数x的点与表示数2的点的距离.结合以上知识,下列说法中正确的个数是()①若|x﹣2022|=1,则x=2021或2023;②若|x﹣1|=|x+3|,则x=﹣1;③若x>y,则|x﹣2|>|y﹣2|;④关于x的方程|x+1|+|x﹣2|=3有无数个解.A.1B.2C.3D.4解:①若|x﹣2022|=1,可得x﹣2022=±1,则则x=2021或2023;所以①说法正确;②若|x﹣1|=|x+3|,几何意义是数轴到表示数1的点和表示数3的点的距离相等的点,即可得出x=﹣1;所以②说法正确;③当y<x<0时,则|x﹣2|<|y﹣2|,所以③说法不正确;④因为|x+1|+|x﹣2|=3的几何意义是到数轴上表示﹣1的点与表示2的点的距离和等于3的点,即﹣1≤x≤2时满足题意,所以有无数个解,故④说法正确.故选:C.4.数轴上点A表示的数是﹣3,把点A向右移动5个单位,再向左移动7个单位到A′,则A′表示的数是﹣5.解:依题意得:﹣3+5﹣7=﹣5,即则A′表示的数是﹣5.故答案为:﹣5.5.数轴上点A表示﹣8,点B表示6,点C表示12,点D表示18.如图,将数轴在原点O 和点B,C处各折一下,得到一条“折线数轴”.在“折线数轴”上,动点M从点A出发,以4个单位/秒的速度沿着折线数轴的正方向运动,从点O运动到点C期间速度变为原来的一半,过点C后继续以原来的速度向终点D运动;点M从点A出发的同时,点N从点D出发,一直以3个单位/秒的速度沿着“折线数轴”负方向向终点A运动.其中一点到达终点时,两点都停止运动.设运动的时间为t秒,t=4.4时,M、N两点相遇(结果化为小数).解:当点M、N都运动到折线段O﹣B﹣C上,即t≥2时,M表示的数是×(t﹣2)=2t﹣4,N表示的数是12﹣3(t﹣2)=18﹣3t,∵M、N两点相遇时,M、N表示的数相同,∴2t﹣4=18﹣3t,解得:t==4.4,故答案为:4.4.6.如图,在一条不完整的数轴上,从左到右的点A、B、C把数轴分成①②③④四部分,点A、B、C对应的数分别是a、b、c,且ab<0.(1)原点在第②部分(填序号);(2)化简式子:|a﹣b|﹣|c﹣a|﹣|a|;(3)若|c﹣5|+(a+1)2=0,且BC=2AB,求点B表示的数.解:(1)∵点A、B、C对应的数分别是a、b、c,且ab<0,∴a<0,b>0,∴原点在点A和点B之间,又∵从左到右的点A、B、C把数轴分成①②③④四部分,∴原点在第②部分;故答案为:②(2)∵a<0,b>0,∴a﹣b<0,c>0,∴c﹣a>0,∴|a﹣b|﹣|c﹣a|﹣|a|=b﹣a﹣(c﹣a)﹣(﹣a)=b﹣a﹣c+a+a=a+b﹣c;(3)∵|c﹣5|+(a+1)2=0,又∵|c﹣5|≥0,(a+1)2≥0,∴c﹣5=0,a+1=0,∴c=5,a=﹣1,∵B对应的数是b,5>b>﹣1,∴BC=5﹣b,AB=b﹣(﹣1)=b+1,又∵BC=2AB,∴5﹣b=2×(b+1),即3b=3,解得:b=1,∴点B表示的数为1.7.已知b是最小的正整数,且(c﹣5)2与|a+b|互为相反数.(1)填空:a=﹣1,b=1,c=5;(2)若P为一动点,其对应的数为x,点P在0和2表示的点之间运动,即0≤x≤2时,化简:|x+1|﹣|x﹣1|+2|x+5|(请写出化简过程);(3)如图,a,b,c在数轴上所对应的点分别为A,B,C,在(1)的条件下,若点A 以1个单位长度/s的速度向左运动,同时,点B和点C分别以2个单位长度/s和5个单位长度/s的速度向右运动.ts后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.解:(1)依题意得,b=1,c﹣5=0,a+b=0,解得a=﹣1,c=5.故答案为:﹣1,1,5;(2)点P在0和2表示的点之间运动,即0≤x≤2时,当0≤x≤1时,x+1>0,x﹣1≤0,x+5>0,原式=x+1+x﹣1+2x+10=4x+10;当1<x≤2时,x+1>0,x﹣1>0,x+5>0,原式=x+1﹣x+1+2x+10=2x+12.综上可知,|x+1|﹣|x﹣1|+2|x+5|=4x+10或2x+12;(3)不变,理由:t秒后A点表示的数是﹣1﹣t,B点表示的数是1+2t,C的表示的数是5+5t,∵AB=1+2t﹣(﹣1﹣t)=3t+2,BC=5+5t﹣(1+2t)=3t+4,∴BC﹣AB=2,∴BC﹣AB的值不变,是2.8.数轴上有A、B、C三点,如图1,点A、B表示的数分别为m、n(m<n),点C在点B 的右侧,AC﹣AB=2.(1)若m=﹣8,n=2,点D是AC的中点.①则点D表示的数为﹣2.②如图2,线段EF=a(E在F的左侧,a>0),线段EF从A点出发,以1个单位每秒的速度向B点运动(点F不与B点重合),点M是EC的中点,N是BF的中点,在EF 运动过程中,MN的长度始终为1,求a的值;(2)若n﹣m>2,点D是AC的中点,若AD+3BD=4,试求线段AB的长.解:(1)①∵m=﹣8,n=2,∴AB=2﹣(﹣8)=10.∵AC﹣AB=2,∴AC=12,∴点C对应的数字为4,∵点D是AC的中点,∴CD=AC=6,设点D表示的数为x,∴4﹣x=6,∴x=﹣2.∴点D表示的数为﹣2.故答案为:﹣2;②设EF运动的时间为t秒,则点E对应的数字为t﹣8,点F对应的数字为t﹣8+a,∵点M是EC的中点,N是BF的中点,∴点M对应的数字为=,点N对应的数字为=,∵MN=1,∴||=1.解得:a=0或a=4,∵a>0,∴a=4;(2)设点C对应的数字为c,点D对应的是为d,∵点A、B表示的数分别为m、n(m<n),点C在点B的右侧,AC﹣AB=2,∴c=n+2,AB=n﹣m.∵点D是AC的中点,∴d=,∴AD=m=,BD=n﹣=,∵AD+3BD=4,∴=4,解得:n﹣m=3.∴AB=3.9.如图,数轴上点A,B分别表示数a,b,其中a<0,b>0.(1)若a=﹣7,b=3,求线段AB的长度及线段AB的中点C表示的数c;(2)该数轴上有另一点D表示数d.①若d=2,点D在点B的左侧,且AB=5BD.求整式2a+8b+2023的值;②若d=﹣2,且AB=5BD,能否求整式2a+8b+2023的值?若能,求出该值;若不能,说明理由.解:(1)∵a=﹣7,b=3,∴线段AB的中点C表示的数c=3﹣×(|﹣7|+3)=3﹣×10=3﹣5=﹣2;(2)①∵d=2,点D在点B的左侧,且AB=5BD,∴AB=b﹣a,BD=b﹣2,∴b﹣a=5(b﹣2),∴a+4b=10,∴2a+8b+2023=2(a+4b)+2023=2×10+2023=2043;②能求出代数式的值,∵d=﹣2,点D在点B的左侧,且AB=5BD,∴AB=b﹣a,BD=b+2,∴b﹣a=5(b+2),∴a+4b=﹣10,∴2a+8b+2023=2(a+4b)+2023=2×(﹣10)+2023=﹣20+2023=2003;10.先阅读,后探究相关的问题【阅读】|5﹣2|表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;|5+2|可以看做|5﹣(﹣2)|,表示5与﹣2的差的绝对值,也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.(1)如图,先在数轴上画出表示点4.5的相反数的点B,再把点A向左移动1.5个单位,得到点C,则点B和点C表示的数分别为﹣4.5和 3.5,B,C两点间的距离是8;(2)若点A表示的整数为x,则当x为﹣2时,|x+6|与|x﹣2|的值相等;(3)要使代数式|x+1|+|x﹣2|取最小值时,相应的x的取值范围是﹣1≤x≤2.解:(1)4.5的相反数是﹣4.5,即点B表示的数为﹣4.5;点C表示的数为5﹣1.5=3.5;B,C两点间的距离是3.5﹣(﹣4.5)=3.5+4.5=8;故答案为:﹣4.5,3.5,8;(2)∵|x+6|与|x﹣2|的值相等,∴x+6=x﹣2此种情况等式不成立,或x+6=﹣(x﹣2),x=﹣2,∴x=﹣2时,|x+6|与|x﹣2|的值相等;故答案为:﹣2;(3)∵|x+1|+|x﹣2|值最小,∴在数轴上可以看作表示x的到﹣1的距离与到2的距离和最小,∴数x只能在﹣1与2之间,包括﹣1与2两个端点,∴﹣1≤x≤2.故答案为:﹣1≤x≤2.11.如图,已知点O为数轴的原点,点A、B、C、D在数轴上,其中A、B两点对应的数分别为﹣1、3.(1)填空:线段AB的长度AB=4;(2)若点A是BC的中点,点D在点A的右侧,且OD=AC,点P在线段CD上运动.问:该数轴上是否存在一条线段,当P点在这条线段上运动时,PA+PB的值随着点P的运动而没有发生变化?(3)若点P以1个单位/秒的速度从点O向右运动,同时点E从点A以5个单位/秒的速度向左运动、点F从点B以20个单位/秒的速度向右运动,M、N分点别是PE、OF的中点.点P、E、F的运动过程中,的值是否发生变化?请说明理由.解:(1)∵A、B两点对应的数分别为﹣1、3,∴OA=1,OB=3,∴AB=OA+OB=4.故答案为:4;(2)数轴上存在一条线段,当P点在这条线段上运动时,PA+PB的值随着点P的运动而没有发生变化.理由:A、B两点对应的数分别为﹣1、3,∴OA=1,OB=3,∵点A是BC的中点,∴AC=AB=4.∴OC=AC+OA=5,∴C点对应的数为﹣5.又∵OD=AC,点D在点A的右侧,∴D点对应的数为4.设P点对应的数为x,①P点在射线CA上时,PA=﹣1﹣x,PB=3﹣x,∴PA+PB=﹣1﹣x+(3﹣x)=2﹣2x,∴PA+PB的值随着点P的运动而发生变化;②P点在线段AB上时,PA=x﹣(﹣1)=x+1,PB=3﹣x,∴PA+PB=x+1+(3﹣x)=4,∴PA+PB的值随着点P的运动没有发生变化;③P点在射线BD上时,PA=x﹣(﹣1)=x+1,PB=x﹣3,∴PA+PB=x+1+(x﹣3)=2x﹣2,∴PA+PB的值随着点P的运动而发生变化.综上,P点在线段AB上时,PA+PB的值没有发生变化,∴数轴上存在一条线段,当P点在这条线段上运动时,PA+PB的值随着点P的运动而没有发生变化;(3)在运动过程中,的值不发生变化.理由:设运动时间为t 分钟,则OP =t ,OE =5t +1,OF =20t +3,∴EF =OE +OF =25t +4,∵M 、N 分别是PE 、OF 的中点,∴EM =PM =PE =(OP +OE )=3t +,ON =OF =10t +,∴OM =OE ﹣EM =5t +1﹣(3t +)=2t +,∴MN =OM +ON =12t +2,∴.∴在运动过程中,的值不发生变化.12.如图,在数轴上,点O 表示原点,点A 表示的数为﹣1,对于数轴上任意一点P (不与点A 点O 重合),线段PO 与线段PA 的长度之比记作k (p ),即,我们称k (p )为点P 的特征值,例如:点P 表示的数为1,因为PO =1,PA =2,所以.(1)当点P 为AO 的中点时,则k (p )=1;(2)若k (p )=2,求点P 表示的数;(3)若点P 表示的数为p ,且满足p =2n ﹣1,(其中n 为正整数,且1≤n ≤7),求所有满足条件的k (p )的和.解:(1)由题意可知,当点P 为AO 的中点时点P 表示的数为,,∴,故答案为:1;(2)设点P 表示的数为x ,则PO =|x |,PA =|x ﹣(﹣1)|=|x +1|,∵k (p )=2,∴,即PO =2PA ,∴|x|=2|x+1|,∴x=2(x+1)或x=﹣2(x+1),解得:x=﹣2或;故:点P表示的数﹣2或;(3)点P表示的数为p,且满足p=2n﹣1,(其中n为正整数,且1≤n≤7),p=2n﹣1>0,此时:PO=p,PA=p﹣(﹣1)=p+1,当p=2n﹣1时∵1≤n≤7,且n为正整数,则所有满足条件的k的值分别为:(p),故所有满足条件的k的和为:=(p),令,则,②﹣①得:,∴==.13.把一根小木排放在数轴上,木棒左端点与点A重合,右端点与点B重合,数轴的单位长度为1cm,如图所示.(1)若将木棒沿数轴向右移动,当木棒的左端点移动到点B处时、它的右端点在数轴上对应的数为20;若将木棒沿数轴向左移动时,当它的右端点移动到点A处时,木棒左端点在数轴上对应的数为5,由此可得木棒的长为5cm;我们把这个模型记为“木捧摸型”;(2)在(1)的条件下,已知点C表示的数为﹣2.若木棒在移动过程中,当木棒的左端点与点C相距3cm时,求木棒的右端点与点A的距离;(3)请根据(1)的“木棒模型”解决下列问题.某一天,小字问爷爷的年龄,爷爷说:“我若是你现在那么大,你还要41年才出生;你若是我现在这么大,我就有124岁了,世界级老寿星了,哈哈!”请你画出“木棒模型”示意图,求出爷爷现在的年龄.解:(1)由图观察可知,三根木棒长是20﹣5=15(cm),则此木棒长为:15÷3=5(cm);故答案为:5cm;(2)由题可知,点A所表示的数是5+5=10,∵木棒的左端点与点C相距3cm,点C表示的数为﹣2,当左端点在点C右侧3cm时,此时木棒左端点表示的数为:﹣2+3=1,右端点表示的数为;1+5=6,木棒的右端点与A的距离为:10﹣6=4,当左端点在点C左侧3cm时,此时木棒左端点表示的数为:﹣2﹣3=﹣5,木棒的右端点表示的数为:﹣5+5=0,木棒的右端点与点A的距离=10﹣0=10,∴木棒的右端点与点A的距离为4或10;(3)由图可知,把小红与爷爷的年龄差看作木棒AB,类似爷爷是小红现在年龄时看作当B点移动到A点时,此时A点所对应的数位﹣41,因为当A点移动到B点时,此时B点所对应的数为124,所以爷爷比小红大[124﹣(﹣41)]÷3=55(岁),所以爷爷的年龄为124﹣55=69(岁),答:爷爷现在的年龄是69岁.14.对于数轴上的A,B,C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“联盟点”.例如:数轴上点A,B,C 所表示的数分别为1,3,4,此时点B是点A,C的“联盟点”.(1)若点A表示数﹣1,点B表示的数2,下列各数:,0,1,4,5所对应的点分别为C1,C2,C3,C4,C5,其中是点A,B的“联盟点”的是C2,C3,C5;(2)点A表示的数是﹣1,点B表示的数是3,P是数轴上的一个动点:①若点P在线段AB上,且点P是点A,B的“联盟点”,求此时点P表示的数;②若点P在点A的左侧,点P、A、B中有一个点恰好是其它两个点的“联盟点”,求出此时点P表示的数.解:(1)∵AC1═﹣﹣(﹣1)═,BC1═2﹣(﹣)═,∴2AC1≠BC1,∴C1不是A,B的“联盟点”.∵AC2═0﹣(﹣1)═1,BC2=2﹣0=2,∴2AC2═BC2,∴C2是A,B的“联盟点”.∵AC3═1﹣(﹣1)=2,BC3═2﹣1=1,∴AC3═2BC3,∴C3是A,B的“联盟点”.∵AC4═4﹣(﹣1)=5,BC4═4﹣2=2,∴AC4≠BC4,∴C4不是A,B的“联盟点”.∵AC5═5﹣(﹣1)=6,BC5═5﹣2=3,∴AC5═2BC5,∴C5是A,B的“联盟点”.综合上述,是点A,B的“联盟点”的是C2,C3,C5.(2)解;设点P表示的数为x,①∵P在线段AB上,∴AP=x+1,BP=3﹣x,当AP=2BP时,有x+1=2(3﹣x),解得x=,当BP=2AP时,有3﹣x=2(x+1),解得x=,综上所述,点P表示的数为,.②由题意得,AB=4,∵P在A的左侧,∴AP=﹣1﹣x,BP=3﹣x,当点A为B,P的“联盟点”时,若AB=2AP,则有4=2(﹣1﹣x),解得x=﹣3,若AP=2AB,则有﹣1﹣x=2×4,解得x=﹣9,当点B为A,P的“联盟点”时,2AB=BP,则有2×4=3﹣x,解得x=﹣5,当点P为A,B的“联盟点”时,BP=2PA,则有3﹣x=2(﹣1﹣x),解得x=﹣5,综上所述,P表示的数为﹣9,﹣3,﹣5.15.如图,点A,O,B,D在同一条直线l上,点B在点A的右侧,AB=6,OB=2,点C 是AB的中点,如图画数轴.(1)若点O是数轴的原点,则点B表示的数是2,点C表示的数是﹣1;(2)若点O是数轴的原点时,D点表示的数为x,且AD=5,求x;(3)若点D是数轴的原点,点D在点A的左侧,点A表示的数为m,且A,B,C,O 所表示的数之和等于21,求m;(4)当O是数轴的原点,动点E,F分别从A,B出发,相向而行,点E的运动速度是每秒2个单位长度,点F的运动速度是每秒1个单位长度,当EF=3时,求点A,B,E,F表示的数之和.解;(1)点B在点A的右侧,OB=2,∴点B表示的数是﹣2,故答案为:2;AB=6,点C是AB的中点,∴BC=3,∴点C表示的数是2﹣3=﹣1,故答案为:﹣1;(2)AB=6,点B在点A的右侧,点A表示的数是﹣4,AD=|﹣4﹣x|=5,x=1或x=﹣9;(3)若点D是数轴的原点,点D在点A的左侧,点A表示的数为m,∵AB=6,C是AB的中点,OB=2,∴AC=3,AO=4,∴点O表示的数是m+4,点C表示的数是m+3,点B表示的数是m+6,m+(m+6)+(m+3)+(m+4)=21,解得m=2;(4)设运动时间为t,据题意得:6﹣2t﹣t=3,解得t=1,AE=2,BF=1,点E表示的数是﹣2,点F表示的数是1,点A,B,E,F表示的数之和为:﹣4+2+(﹣2)+1=﹣3,16.如图,在数轴上点A表示数a,点B表示数b,点C表示数c,a,c满足|a+4|+(c﹣2)2=0,b是最大的负整数.(1)a=﹣4,b=﹣1,c=2.(2)若将数轴折叠,使得点A与点C重合,则点B与数﹣1表示的点重合;(3)点A,B,C开始在数轴上运动,若点A和点B分别以每秒0.4个单位长度和0.3个单位长度的速度向左运动,同时点C以每秒0.2个单位长度的速度向左运动,点C到达原点后立即以原速度向右运动,运动时间为t秒,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,请问:5AB﹣BC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求出5AB﹣BC的值.解:(1)∵|a+4|+(c﹣2)2=0,b是最大的负整数,a=﹣4,b=﹣1,c=2,故答案为:﹣4,﹣1,2;(2)AB=﹣1﹣(﹣4)=3,AC=2﹣(﹣4)=6,点B为AC的中点,故将数轴折叠,使得点A与点C重合,则点B与自身重合,故答案为:﹣1;(3)AB=3+0.4t=0.3t=3+0.1t,当C运动到原点时,t=2÷0.2=10(秒),点B运动到点A的位置,当t≤10秒时,BC=3+0.3t﹣0.2t=3+0.1t,5AB﹣B=5(3+0.1t)﹣(3+0.1t)=15+0.5t﹣3﹣0.1t=12+0.4t,5AB﹣BC的值随时间的变化而变化;当t>10时,BC=4+0.3t+0.2t=4+0.5t,5AB﹣BC=5(3+0.1t)﹣(4+0.5t)=15+0.5t﹣4﹣0.5t=11.这时5AB﹣BC的值不变.17.定义:对于数轴上的三点,若其中一个点与其他两个点的距离恰好满足2倍的数量关系.如下图,数轴上点A,B,C所表示的数分别为1,3,4,此时点B就是点A,C的一个“关联点”.(1)写出点A,C的其他三个“关联点”所表示的数:﹣2、2、7.(2)若点M表示数﹣2,点N表示数4,数﹣8,﹣6,0,2,10所对应的点分别是C1,C2,C3,C4,C5,其中不是点M,N的“关联点”是点C2.(3)若点M表示的数是﹣3,点N表示的数是10,点P为数轴上的一个动点.①若点P在点N左侧,且点P是点M,N的“关联点”,求此时点P表示的数.②若点P在点N右侧,且点P,M,N中,有一个点恰好是另外两个点的“关联点”,求此时点P表示的数.解:(1)2﹣1=1,4﹣2=2,2是A,C的一个“关联点”,设x是A,C的一个“关联点”,x﹣1=2(x﹣4)解得x=7,设y是A,C的一个“关联点”,2(1﹣y)=4﹣y解得y=﹣2,A,C的其他三个“关联点”所表示的数为:﹣2、2、7,故答案为:﹣2、2、7,(2)∵﹣2﹣(﹣8)=6,4﹣(﹣8)=12,∴C1是关联点,∵﹣2﹣(﹣6)=4,4﹣(﹣6)=10,∴C2不是关联点,∵0﹣(﹣2)=2,4﹣0=4,∴C3是关联点,∵2﹣(﹣2)=4,4﹣2=2,∴C4是关联点,∵10﹣(﹣2)=12,10﹣4=6,∴C5是关联点,故答案为:C2.(3)①若点P在点N左侧且在M的右侧,设点P表示的数为x,当2(x+3)=10﹣x解得,当x+3=2(10﹣x)解得,若点P在M点左侧,设点P表示的数为x,∴2(﹣3﹣x)=10﹣x解得x=﹣16,综上所述:P表示的数为:;②若点P在点N右侧,设点P表示的数为x,当PN=2MN时,则2×13=x﹣10解得x=36,当MN=2PN时,则13=2×(x﹣10)解得,当MP=2MN时,则x+3=2×13解得x=23,当MP=2PN时,则x+3=2×(x﹣10)解得x=23,综上所述:P表示的数为:,23.36.18.[知识背景]:数轴上,点A,点B表示的数为a,b,则A,B两点的距离表示为AB=|a﹣b|.线段AB的中点P表示的数为.[知识运用]:已知数轴上A,B两点对应的数分别为a和b,且(a﹣4)2+|b﹣2|=0,P 为数轴上一动点,对应的数为x.(1)a=4,b=2;(2)若点P为线段AB的中点,则P点对应的数x为3,若点B为线段AP的中点,则P点对应的数x为0;(3)若点A、点B同时从图中位置在数轴上向左运动,点A的速度为每秒1个单位长度,点B的速度为每秒3个单位长度,则经过122秒点B追上点A;(4)若点A、点B同时从图中位置在数轴上向左运动,它们的速度都为每秒1个单位长度,与此同时点P从表示﹣16的点处以每秒2个单位长度的速度在数轴上向右运动.经过多长时间后,点A、点B、点P三点中,其中一点是另外两点组成的线段的中点?解:(1)∵(a﹣4)2+|b﹣2|=0,∴a﹣4=0,b﹣2=0,∴a=4,b=2.故答案为4、2.(2)点A,B表示的数分别为4,2,P对应数为x,若点P为线段AB的中点,则P点对应的数x==3,若B为线段AP的中点时,则=2,解得x=0.故答案为1,0;(3)解:设经过x秒点B追上点A,(3﹣1)x=4﹣2,2x=2,x=1,答:经过1秒点B追上点A.(4)经过t秒后,点A,点B,点P三点中其中一点是另外两点的中点,t秒后,点A的位置为:4﹣t,点B的位置为:2﹣t,点P的位置为:﹣16+2t,当点A为PB的中点时,则有,2×(4﹣t)=2﹣t﹣16+2t,解得:t=,当点B为PA的中点时,则有,2×(2﹣t)=4﹣t﹣16+2t,解得:t=,当点P为BA的中点时,则有,2×(﹣16+2t)=4﹣t+2﹣t,解得:t=,答:经过秒,秒,秒后,点A,点B,点P三点中其中一点是另外两点的中点.故答案为:秒,秒,秒.19.结合数轴与绝对值的知识回答下列问题:(1)探究:①数轴上表示5和3的两点之间的距离是2.②数轴上表示﹣1和﹣4的两点之间的距离是3.③数轴上表示﹣3和5的两点之间的距离是8.(2)归纳:一般的,数轴上表示数a和数b的两点之间的距离等于|a﹣b|.(3)应用:①若数轴上表示数a的点位于﹣4与3之间,则|a+4|+|a﹣3|的值=7.②若a表示数轴上的一个有理数,且|a﹣1|=|a+3|,则a=﹣1.③若a表示数轴上的一个有理数,|a﹣1|+|a+2|的最小值是3.④若a表示数轴上的一个有理数,且|a+3|+|a﹣5|>8,则有理数a的取值范围是a>5或a<﹣3.(4)拓展:已知,如图2,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.若当电子蚂蚁P从A点出发,以4个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以3单位/秒的速度向左运动,求经过多长时间两只电子蚂蚁在数轴上相距20个单位长度,并写出此时点P所表示的数.解:(1)①5﹣3=2,故答案为:2;②(﹣1)﹣(﹣4)=3,故答案为:3;③5﹣(﹣3)=8,故答案为:8;(2)根据数轴上两点间的距离得|a﹣b|,故答案为:|a﹣b|;(3)①∵表示数a的点位于﹣4与3之间,∴|a+4|+|a﹣3|=a+4+3﹣a=7,故答案为:7;②∵|a﹣1|=|a+3|∴表示数a的点在1和﹣3之间,∴|a﹣1|=|a+3|,1﹣a=a+3,a=﹣1,故答案为:﹣1;③∵|a﹣1|+|a+2|有最小值,∴表示a的点在﹣2与1之间,∴|a﹣1|+|a+2|=1﹣a+a+2=3,故答案为:3;④|a+3|+|a﹣5|>8,当﹣3<a<5时,|a+3|+|a﹣5|=a+3+5﹣a=8,不合题意舍去;当a<﹣3时,|a+3|+|a﹣5|=﹣(a+3)+5﹣a>8,a<﹣3;当a>5时,|a+3|+|a﹣5|>8,a+3+a﹣5>8,a>5,故答案为:a<﹣3或a>5;(4)设电子蚂蚁运动x秒时,P、Q相距20个单位长度,①4x+3x+20=20+100,x=,点P表示的是4×﹣20=②4x+3x﹣20=20+100,x=20,点P表示的是4×20﹣20=60,20.将一条数轴在原点O和点B处各折一下,得到如图所示的“折线数轴”,图中点A表示﹣10,点B表示10,点C表示18.我们称点A和点C在数轴上的“友好函数”为28个单位长度.动点P从点A出发,以2单位长度/秒的速度沿着“折线数轴”向其正方向运动.当运动到点O与点B之间时速度变为原来的一半.经过点B后立刻恢复原速;同时,动点Q从点C出发,以1单位长度/秒的速度沿着“折线数轴”向其负方向运动,当运动到点B与点O之间时速度变为原来的两倍,经过O后也立刻恢复原速.设运动的时间为t秒.(1)动点P从点A运动至点C需要19秒,动点Q从点C运动至点A需要23秒;(2)P,Q两点相遇时,求出相遇点M在“折线数轴”上所对应的数;(3)是否存在t值,使得点P和点Q任“折线数轴”上的“友好距离”等于点A和点B 在“折线数轴”上的“友好距离”?若存在,求出t的值;若不存在,请说明理由.解:(1)∵点A表示﹣10,点B表示10,点C表示18,∴OA=10,BO=10,BC=8,∴动点P从点A运动至点C需要的时间是:10÷2+10÷1+8÷2=19(s),动点Q从点C运动至点A需要的时间是:10÷1+10÷2+8÷1=23(s),故答案为:19,23;(2)根据题意可知,P、Q两点在OB上相遇,P点运动到OB上时表示的数是t﹣5,Q点运动到OB上时表示的数是10﹣2(t﹣8),∴t﹣5=10﹣2(t﹣8),解得t=,∴M点表示的数是﹣5=;(3)存在t值,使得点P和点Q任“折线数轴”上的“友好距离”等于点A和点B在“折线数轴”上的“友好距离”,理由如下:∵点A表示﹣10,点B表示10,∴点A和点B在“折线数轴”上的“友好距离”是20,①当0≤t≤5时,P点在OA上,Q点在BC上,此时P点表示的数是﹣10+2t,Q点表示的数是18﹣t,∴点P和点Q任“折线数轴”上的“友好距离”为18﹣t+10﹣2t=28﹣3t,由题意可得,28﹣3t=20,解得t=;②当5<t≤8时,P点在OB上,Q点在OC上,此时P点表示的数是t﹣5,Q点表示的数是18﹣t,∴点P和点Q任“折线数轴”上的“友好距离”为18﹣t﹣t+5=23﹣2t,由题意可得,23﹣2t=20,解得t=(舍);③8<t≤13时,点P、Q都在BO上,此时PQ<10,∴此情况不符合题意;④13<t≤15时,P点在OB上,Q点在OA上,此时P点表示的数是t﹣5,Q点表示的数是t﹣13,∴点P和点Q任“折线数轴”上的“友好距离”为t﹣5+t﹣13=2t﹣18,由题意可得,2t﹣18=20,解得t=19(舍);⑤15<t≤19时,P点在BC上,Q点在OA上,此时P点表示的数是2t﹣20,Q点表示的数是t﹣13,∴点P和点Q任“折线数轴”上的“友好距离”为t﹣13+2t﹣20=3t﹣33,由题意可得,3t﹣33=20,解得t=;⑥19<t≤23时,P点在C的右侧,Q点在OA上,此时P点表示的数是2t﹣20,Q点表示的数是t﹣13,∴点P和点Q任“折线数轴”上的“友好距离”为t﹣13+2t﹣20=3t﹣33,由题意可得,3t﹣33=20,解得t=(舍);⑦t>23时,P点在C点右侧,Q点在A点左侧,PQ>20,不符合题意;综上所述:t的值为或.21.在数轴上,点M,N对应的数分别是m,n(m≠n,mn≠0),P为线段MN的中点,同时给出如下定义:如果=10,那么称M是N的“努力点”.例如:m=1,n=,M是N的“努力点”.(1)若|m﹣10|+(n+90)2=0则m=10,n=﹣90;(2)在(1)的条件下,下列说法正确的是③(填序号);①M是P的“努力点”;②M是N的“努力点”③N是M的“努力点”;④N是P的“努力点”(3)若mn<0,且P是M,N其中一点的“努力点”,求值?解:(1)∵|m﹣10|+(n+90)2=0,∴m=10,n=﹣90,故答案为:10,﹣90;(2)∵m=10,n=﹣90,∴P点对应的数是﹣40,∵||=,∴M不是P的“努力点”,故①不符合题意;∵m=10,n=﹣90,∴||=,∴M不是N的“努力点”,故②不符合题意;∵||=10,∴N是M的“努力点”,故③符合题意;∵||=,∴N是P的“努力点”,故④不符合题意;故答案为:③;(3)∵P为线段MN的中点,∴P点对应的数为,当P是M点的“努力点”时,||=10,∴=21或=﹣19,∵mn<0,∴=﹣;当P是N点的“努力点”时,||=10,∴=21或=﹣19,∵mn<0,∴=﹣19;综上所述:的值为﹣19或﹣.22.在数轴上,O为原点,点A,B对应的数分别是a,b(a≠b,ab≠0),M为线段AB的中点.给出如下定义:若OA÷OB=4,则称A是B的“正比点”;若OA×OB=4,则称A是B的“反比点”.例如a=2,时,A是B的“正比点”;a=2,b=﹣2时,A是B的“反比点”.(1)若|a+2|+(b﹣4)2=0,则M对应的数为1,下列说法正确的是③④(填序号).。
中考数学压轴题之动点问题

D C BA PQ K E D C B A 中考压轴题之动点问题1. (2011吉林)如图,梯形ABCD 中,AD ∥BC ,∠BAD =90°,CE ⊥AD 于点E ,AD =8cm ,BC =4cm ,AB =5cm .从初始时刻开始,动点P ,Q 分别从点A ,B 同时出发,运动速度均为1cm/s ,动点P 沿A -B -C -E 方向运动,到点E 停止;动点Q 沿B -C -E -D 方向运动,到点D 停止,设运动时间为x s ,△P AQ 的面积为y cm 2,(这里规定:线段是面积为0的三角形)解答下列问题:(1) 当x =2s 时,y =_____ cm 2;当x =92s 时,y =_______ cm 2. (2)当5 ≤ x ≤ 14时,求y 与x 之间的函数关系式.(3)当动点P 在线段BC 上运动时,求出154 y S 梯形ABCD 时x 的值. (4)直接写出在整个..运动过程中,使PQ 与四边形ABCE 的对角线平行的所有x 的值.2. (2007河北)如图,在等腰梯形ABCD 中,AD ∥BC ,AB =DC =50,AD =75,BC =135.点P 从点B 出发沿折线段BA -AD -DC 以每秒5个单位长的速度向点C 匀速运动;点Q 从点C 出发沿线段CB 方向以每秒3个单位长的速度匀速运动,过点Q 向上作射线QK ⊥BC ,交折线段CD -DA -AB 于点E .点P 、Q 同时开始运动,当点P 与点C 重合时停止运动,点Q 也随之停止.设点P 、Q 运动的时间是t 秒(t >0).(1)当点P 到达终点C 时,求t 的值,并指出此时BQ 的长;(2)当点P 运动到AD 上时,t 为何值能使PQ ∥DC ?(3)设射线QK 扫过梯形ABCD 的面积为S ,分别求出点E 运动到CD 、DA 上时,S 与t 的关系式;(4)△PQE 能否成为直角三角形?若能,写出t 的取值范围;若不能,请说明理由.备用图3. (2008河北)如图,在Rt ABC △中,∠C=90°,AB =50,AC =30,D ,E ,F 分别是AC ,AB ,B C 的中点.点P 从点D 出发沿折线DE -EF -FC -CD 以每秒7个单位长的速度匀速运动;点Q 从点B 出发沿BA 方向以每秒4个单位长的速度匀速运动,过点Q 作射线QK AB ⊥,交折线BC -CA 于点G .点P Q ,同时出发,当点P 绕行一周回到点D 时停止运动,点Q 也随之停止.设点P Q ,运动的时间是t 秒(0t >).(1)D F ,两点间的距离是 ;(2)射线QK 能否把四边形CDEF 分成面积相等的两部分?若能,求出t 的值.若不能,说明理由;(3)当点P 运动到折线EF FC -上,且点P 又恰好落在射线QK 上时,求t 的值;(4)连结PG ,当PG AB ∥时,请直接..写出t 的值.4. (2011山西太原)如图,在平面直角坐标系中,四边形OABC 是平行四边形.直线l 经过O 、C 两点.点A 的坐标为(8,0),点B 的坐标为(11,4),动点P 在线段OA 上从点O 出发以每秒1个单位的速度向点A 运动,同时动点Q 从点A 出发以每秒2个单位的速度沿A →B →C 的方向向点C 运动,过点P 作PM 垂直于x 轴,与折线O -C -B 相交于点M .当P 、Q 两点中有一点到达终点时,另一点也随之停止运动,设点P 、Q 运动的时间为t 秒(0t >),△MPQ 的面积为S .(1)点C 的坐标为________,直线l 的解析式为__________.(2)试求点Q 与点M 相遇前S 与t 的函数关系式,并写出相应的t 的取值范围.(3)试求题(2)中当t 为何值时,S 的值最大,并求出S 的最大值.(4)随着P 、Q 两点的运动,当点M 在线段CB 上运动时,设PM 的延长线与直线l 相交于点N .试探究:当t 为何值时,△QMN 为等腰三角形?请直接写出t 的值.B 备用图F E DC BAF E O P D C B F E O P D C B F E O P D C B 5. (2011四川重庆)如图,矩形ABCD 中,AB =6,BC =23,点O 是AB 的中点,点P 在AB 的延长线上,且BP =3.一动点E 从O 点出发,以每秒1个单位长度的速度沿OA 匀速运动,到达A 点后,立即以原速度沿AO 返回;另一动点F 从P 点出发,以每秒1个单位长度的速度沿射线P A 匀速运动,点E 、F 同时出发,当两点相遇时停止运动.在点E 、F 的运动过程中,以EF 为边作等边△EFG ,使△EFG 和矩形ABCD 在射线P A 的同侧,设运动的时间为t 秒(t ≥0).(1)当等边△EFG 的边FG 恰好经过点C 时,求运动时间t 的值;(2)在整个运动过程中,设等边△EFG 和矩形ABCD 重叠部分的面积为S ,请直接写出S 与t 之间的函数关系式和相应的自变量t 的取值范围;(3)设EG 与矩形ABCD 的对角线AC 的交点为H ,是否存在这样的t ,使△AOH 是等腰三角形?若存在,求出对应的t 的值;若不存在,请说明理由.备用图1 备用图26. (2011山东烟台)如图,在直角坐标系中,梯形ABCD 的底边AB 在x 轴上,底边CD 的端点D 在y 轴上.直线CB 的表达式为41633y x =-+,点A 、D 的坐标分别为(-4,0),(0,4).动点P 自A 点出发,在AB 上匀速运动.动点Q 自点B 出发,在折线BCD 上匀速运动,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P 运动t (秒)时,△OPQ 的面积为S (不能构成△OPQ 的动点除外).(1)求出点B 、C 的坐标;(2)求S 随t 变化的函数关系式;(3)当t 为何值时S 有最大值?并求出最大值.备用图。
九年级中考压轴——动点问题集锦

九年级中考压轴——动点问题集锦1、已知等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动。
过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点,线段MN运动的时间为t秒。
1) 当四边形MNQP为矩形时,有MN=QP,即MN在运动t秒后,线段QP的长度为3+t。
因为三角形ABC是等边三角形,所以三角形ABC的高等于边长的一半,即2根号3.因此,四边形MNQP的面积为2根号3*t平方+2t。
2) 四边形MNQP的面积为S,运动时间为t。
因为三角形ABC是等边三角形,所以三角形ABC的高等于边长的一半,即2根号3.因此,四边形MNQP的高为2根号3.由于四边形MNQP是矩形,所以MN=QP=3+t,PQ=2根号3.因此,S=PQ*MN=2根号3*(3+t)。
函数关系式为S=2根号3*t+6根号3,t的取值范围为t≥0.2、在梯形ABCD中,AD∥BC,AD=3,DC=5,AB=42,∠B=45度。
动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动。
设运动的时间为t 秒。
1) 因为三角形ABD和三角形CBD相似,所以BD=AB-AD=39.由于三角形BCD是直角三角形,所以BC=BD/根号2=39/根号2.2) 当MN∥AB时,由于三角形BMD和三角形BAC相似,所以BD/AB=MD/MN,即39/42=2t/(3+t),解XXX13秒。
3) 当△MNC为等腰三角形时,由于三角形MNC和三角形ABD相似,所以CN/AD=MN/BD,即CN/3=(3+t)/39,XXX13秒。
3、在平面直角坐标系中,四边形OABC是梯形,OA∥BC,点A的坐标为(6,0),点B的坐标为(4,3),点C在y轴的正半轴上。
动点M在OA上运动,从O点出发到A点;动点N在AB上运动,从A点出发到B点。
初三中考动点题型总结

初三中考动点题型总结
嘿,同学们!今天咱就来好好唠唠初三中考的动点题型!这动点题型啊,那可真是让咱又爱又恨呐!就好像是游戏里的大 boss,难是难,可
一旦攻克了,那成就感爆棚啊!比如说在一个直角三角形中,有一个点在边上不停移动,问你各种边长啊、角度啊之类的问题(例如:已知直角三角形ABC,直角边 AB=3,AC=4,点 P 在 BC 边上移动,问当 PA 垂直于 BC 时,PA 的长度是多少)。
动点题型就像一个神秘的宝藏盒,你永远不知道打开后会遇到什么难题!但就是这种神秘感,让我们充满了探索的欲望,不是吗!有时候一个看似简单的图形,因为动点的加入,一下子就变得超级复杂啦!就好像平静的湖面扔进了一颗石子,瞬间激起千层浪。
咱就得像侦探一样,抽丝剥茧地去分析。
想象一下,有个动点在那不停地窜来窜去,你得紧紧盯着它,看它到底想干啥(就像一个调皮的孩子在那儿捣乱,我们得想办法抓住他)。
在解决动点问题的时候,咱们得时刻保持头脑清醒,一点儿也马虎不得!要认真分析每个条件,把能用上的都用上。
画个图,仔细标注,别放过任何一个细节哟!而且,还得学会从复杂的图形中找到关键信息,这可是个技术活!就拿一个圆来说吧,上面有个点在动,看着都让人头晕(天哪,那复杂
的线条,脑袋都大了),但咱可不能怕,鼓起勇气,一点点分析,肯定能找到答案!
最后我想说,中考动点题型虽然难,但只要我们认真对待,多练习,多总结,就一定能战胜它!别被它吓倒,要相信自己的能力!我们一起加油,搞定动点题型,在中考中取得好成绩!。
几何中的动点问题:中考数学轨迹与路径

几何中的动点问题:中考数学轨迹与路径几何作为数学的一部分,一直以来被认为是高难度的学科之一,但是在实际中,几何也是生活和科学中必不可少的组成部分。
而在几何中,动点问题一直是人们感到困惑的一个问题。
在这篇文章中,我们将为大家全面介绍几何中的动点问题,以及如何在中考数学中处理轨迹和路径的问题。
一、动点问题的基本定义及特点动点问题可以简单定义为:在几何图形中,设有一个动点进行运动,如何求出该点的轨迹和路径。
动点问题是几何中的一个重要问题,具有以下特点:1. 动点问题一般是基于静态点进行分析,因此需要对静态点的性质有深刻的认识。
2. 动点问题的解决需要具备一定的数学能力和三维空间思维能力,需要较高的数学水平。
3. 动点问题结合实际进行探究,可以帮助人们更好地理解几何、物理等知识,也有益于培养人们的空间思维能力。
二、动点问题的基本应用1. 针对不同的几何图形,我们可以找到它们的动点问题:(1)直线的动点问题:一般是着眼于直线上的动点,分析其轨迹和路径;(2)圆的动点问题:针对圆上的任意一点,求其轨迹和路径;(3)曲线的动点问题:着重考虑曲线上的动点,探究它们的轨迹和路径。
2. 在实际生活中,动点问题也有很多应用:(1)公路的修建:如何建设一条曲线公路,使得大车可以顺利通过,是一个很好的动点问题实例;(2)太空飞行器飞行:在太空中,如何预测航天器的运动轨迹,需要运用动点问题的相关知识;(3)排球比赛中跑位:排球比赛中,如何控制自己的跑位,使得球能够顺利地落到自己的手中,也是一种动点问题的体现。
三、如何在中考数学中处理轨迹和路径在中考数学中,轨迹和路径的处理是重点。
我们可以通过以下方法来解决问题:1. 把动点分解成几个静止的点,结合点的特性,推导出动点刚好经过这些点时的轨迹和路径。
2. 找到一个合适的坐标系,将动点变成坐标,问题就可以转化为一个数学问题,更加便于解决。
3. 运用相关的几何定理,如垂线定理、角平分线定理等,结合动点的运动特性,解决问题。
中考数学动点问题(难)

因动点产生的三角形问题例1已知Rt △ABC 在直角坐标系内的位置如图所示,反比例函数(0)ky k x=?在第一象限内的图象与BC 边交于点D (4,m ),与AB 边交于点E (2,n ),△BDE 的面积为2. (1)求m 与n 的数量关系; (2)当tan ∠A =12时,求反比例函数的解析式和直线AB 的表达式; (3)设直线AB 与y 轴交于点F ,点P 在射线FD 上,在(2)的条件下,如果△AEO 与△EFP 相似,求点P 的坐标.例2在平面直角坐标系内,O 为原点,点A 的坐标为(1,0),点C 的坐标为(0,4),直线CM //x 轴(如图所示).点B 与点A 关于原点对称,直线y =x +b (b 为常数)经过点B ,且与直线CM 相交于点D ,联结OD .(1)求b 的值和点D 的坐标;(2)设点P 在x 轴的正半轴上,若△POD 是等腰三角形,求点P 的坐标; (3)在(2)的条件下,如果以PD 为半径的圆与圆O 外切,求圆O 的半径.例3 如图,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0). (1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S .①求S 与t 的函数关系式;②设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.练习1.如图,已知一次函数y=-x+7与正比例函数43y x=的图象交于点A,且与x轴交于点B.(1)求点A和点B的坐标;(2)过点A作AC⊥y轴于点C,过点B作直线l//y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l 交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.2.如图,在直角坐标平面内有点A(6, 0),B(0, 8),C(-4, 0),点M、N分别为线段AC和射线AB上的动点,点M以2个单位长度/秒的速度自C向A方向作匀速运动,点N以5个单位长度/秒的速度自A向B方向作匀速运动,MN交OB于点P.(1)求证:MN∶NP为定值;(2)若△BNP与△MNA相似,求CM的长;(3)若△BNP是等腰三角形,求CM的长.3.如图,已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P (0,m )是线段OC 上一动点(C 点除外),直线PM 交AB 的延长线于点D . (1)求点D 的坐标(用含m 的代数式表示); (2)当△APD 是等腰三角形时,求m 的值;(3)设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ,过点O 作直线ME 的垂线,垂足为H .当点P从O 向C 运动时,点H 也随之运动.请直接写出点H 所经过的路长(不必写解答过程).4.如图,抛物线213442y x x =--与x 轴交于A 、B 两点(点B 在点A 的右侧),与y 轴交于点C ,连结BC ,以BC 为一边,点O 为对称中心作菱形BDEC ,点P 是x 轴上的一个动点,设点P 的坐标为(m , 0),过点P作x 轴的垂线l 交抛物线于点Q .(1)求点A 、B 、C 的坐标;(2)当点P 在线段OB 上运动时,直线l 分别交BD 、BC 于点M 、N .试探究m 为何值时,四边形CQMD 是平行四边形,此时,请判断四边形CQBM 的形状,并说明理由;(3)当点P 在线段EB 上运动时,是否存在点Q ,使△BDQ 为直角三角形,若存在,请直接写出点Q 的坐标;若不存在,请说明理由.因动点产生的四边形问题例1 几何图形中的四边形存在性问题1、在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).(1)当t = 2时,AP =,点Q到AC的距离是;(2)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值.若不能,请说明理由;(4)当DE经过点C 时,请直接..写出t的值.2、如图梯形ABCD中AD∥BC,AD=CD,DE⊥BC于点E,且DE=1,AD=4, ∠B=45°.(1)直接写出BC的长;(2)直线AB以每秒0.5个单位的速度向右平移,交AD于点Q,则当直线AB的移动时间为多少秒,形成的四边形ABQP恰好为菱形?(结果精确到0.01秒);(3)AB移动的方向、速度如同第(2)题,移动时间为t秒,AB扫过梯形ABCD的面积S(用t的代数式表示,直接写出答案即可)3、如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;(2)填空:①当t为s时,四边形ACFE是菱形;②当t为s时,以A、F、C、E为顶点的四边形是直角梯形.4、已知:如图,▱ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M 作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)。
中考数学动点问题复习

中考数学动点问题复习中考数学复习(一)动点型问题一、中考专题诠释所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.“动点型问题”题型繁多、题意创新,考察学生的分析问题、解决问题的能力,内容包括空间观念、应用意识、推理能力等,是近几年中考题的热点和难点。
二、解题策略和解法精讲解决动点问题的关键是“动中求静”.从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,通过“对称、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理。
在动点的运动过程中观察图形的变化情况,理解图形在不同位置的情况,做好计算推理的过程。
在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
三、中考考点精讲考点一:建立动点问题的函数解析式(或函数图像)函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.例1 如图,动点P从点A出发,沿线段AB运动至点B后,立即按原路返回,点P在运动过程中速度不变,则以点B为圆心,线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为()A.B.C.D.对应训练1.如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是()A. B. C. D.考点二:动态几何型题目(一)点动问题.例2 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止.设运动时间为t秒,y=S△EPF,则y与t的函数图象大致是()A.B.C.D.对应训练2.如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2.设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是()A. B.C. D.(二)线动问题例3 如右图所示,已知等腰梯形ABCD,AD∥BC,若动直线l垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是()A. B.C. D.对应训练3.如图所示,在矩形ABCD中,垂直于对角线BD的直线l,从点B开始沿着线段BD匀速平移到D.设直线l被矩形所截线段EF的长度为y,运动时间为t,则y关于t的函数的大致图象是()A. B.C.D.(三)面动问题例4 如图所示:边长分别为1和2的两个正方形,其中一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形内去掉小正方形后的面积为s,那么s与t的大致图象应为()A.B.C.D.对应训练4.如图所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t,正方形除去圆部分的面积为S(阴影部分),则S与t的大致图象为()考点三:动点综合题动态问题是近几年来中考数学的热点题型,解题时需要用运动和变化的眼光去观察和研究问题,挖掘运动、变化的全过程,并特别关注运动与变化中的不变量、不变关系或特殊关系,动中取静,静中求动.(一)因动点产生的等腰三角形问题例1 如图1,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB 上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.(1)求ED、EC的长;(2)若BP=2,求CQ的长;(3)记线段PQ与线段DE的交点为F,若△PDF为等腰三角形,求BP的长.图1 备用图例2 如图1,抛物线y=ax2+bx+c经过A(-1,0)、B(3, 0)、C(0 ,3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;(3)在直线l上是否存在点M,使△MAC为等腰三角形,若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.图1例3 如图1,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.图1例4 如图1,已知一次函数y=-x+7与正比例函数43y x的图象交于点A,且与x轴交于点B.(1)求点A和点B的坐标;(2)过点A作AC⊥y轴于点C,过点B作直线l//y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA 或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.图1例5 如图1,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.(1)求y关于x的函数关系式;(2)若m=8,求x为何值时,y的值最大,最大值是多少?(3)若12ym,要使△DEF为等腰三角形,m的值应为多少?图1例 6如图1,在等腰梯形ABCD中,AD//BC,E是AB的中点,过点E作EF//BC交CD于点F,AB=4,BC=6,∠B=60°.(1)求点E到BC的距离;(2)点P为线段EF上的一个动点,过点P作PM⊥EF交BC于M,过M作MN//AB交折线ADC于N,连结PN,设EP =x.①当点N在线段AD上时(如图2),△PMN的形状是否发生改变?若不变,求出△PMN的周长;若改变,请说明理由;②当点N在线段DC上时(如图3),是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足条件的x的值;若不存在,请说明理由.图1 图2 图3例1 如图1,抛物线213442y x x =--与x 轴交于A 、B 两点(点B 在点A 的右侧),与y 轴交于点C ,连结BC ,以BC 为一边,点O 为对称中心作菱形BDEC ,点P 是x 轴上的一个动点,设点P 的坐标为(m , 0),过点P 作x 轴的垂线l 交抛物线于点Q .(1)求点A 、B 、C 的坐标;(2)当点P 在线段OB 上运动时,直线l 分别交BD 、BC 于点M 、N .试探究m 为何值时,四边形CQMD 是平行四边形,此时,请判断四边形CQBM 的形状,并说明理由;(3)当点P 在线段EB 上运动时,是否存在点Q ,使△BDQ 为直角三角形,若存在,请直接写出点Q 的坐标;若不存在,请说明理由.图1例2 如图1,抛物线233384y x x =--+与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C . (1)求点A 、B 的坐标;(2)设D 为已知抛物线的对称轴上的任意一点,当△ACD 的面积等于△ACB 的面积时,求点D 的坐标;(3)若直线l 过点E (4, 0),M 为直线l 上的动点,当以A 、B 、M 为顶点所作的直角三角形有且只有....三个时,求直线l 的解析式.图1(1)当k=-2时,求反比例函数的解析式;(2)要使反比例函数与二次函数都是y随x增大而增大,求k应满足的条件以及x的取值范围;(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.例4设直线l1:y=k1x+b1与l2:y=k2x+b2,若l1⊥l2,垂足为H,则称直线l1与l2是点H的直角线.(1)已知直线①122y x=-+;②2y x=+;③22y x=+;④24y x=+和点C(0,2),则直线_______和_______是点C的直角线(填序号即可);(2)如图,在平面直角坐标系中,直角梯形OABC的顶点A(3,0)、B(2,7)、C(0,7),P为线段OC上一点,设过B、P两点的直线为l1,过A、P两点的直线为l2,若l1与l2是点P的直角线,求直线l1与l2的解析式.图1例5 在平面直角坐标系xOy 中,抛物线22153244m my x x m m -=-++-+与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上.(1)求点B 的坐标;(2)点P 在线段OA 上,从点O 出发向点A 运动,过点P 作x 轴的垂线,与直线OB 交于点E ,延长PE 到点D ,使得ED =PE ,以PD 为斜边,在PD 右侧作等腰直角三角形PCD (当点P 运动时,点C 、D 也随之运动).①当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;②若点P 从点O 出发向点A 作匀速运动,速度为每秒1个单位,同时线段OA 上另一个点Q 从点A 出发向点O 作匀速运动,速度为每秒2个单位(当点Q 到达点O 时停止运动,点P 也停止运动).过Q 作x 轴的垂线,与直线AB 交于点F ,延长QF 到点M ,使得FM =QF ,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当点Q 运动时,点M 、N 也随之运动).若点P 运动到t 秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t 的值.图1例6 如图1,已知A 、B 是线段MN 上的两点,,,.以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,设.(1)求x 的取值范围;(2)若△ABC 为直角三角形,求x 的值; (3)探究:△ABC 的最大面积?图14=MN 1=MA 1>MB x AB=例 7如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0). (1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S .① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由; ③在运动过程中,当△MON 为直角三角形时,求t 的值.图1例8 如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0). (1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S .① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由; ③在运动过程中,当△MON 为直角三角形时,求t 的值.图1课后练习(一)一、选择题1.如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为()A.2 B.2.5或3.5 C.3.5或4.5 D.2或3.5或4.52.图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C 点,M为EF的中点,则下列结论正确的是()A.当x=3时,EC<EM B.当y=9时,EC>EMC.当x增大时,EC•CF的值增大 D.当y增大时,BE•DF的值不变3.如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD 与Rt△GEF重叠部分面积为s,则s关于t的函数图象为()A.B.C.D.4.如图,在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是()A.2 B.3 C.4 D.55.如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P 为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.(1)求当t为何值时,点Q与点D重合?(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.6.如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(-4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.(1)求直线AB的函数解析式;(2)当点P在线段AB(不包括A,B两点)上时.①求证:∠BDE=∠ADP;②设DE=x,DF=y.请求出y关于x的函数解析式;(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由.7.如图,直角梯形OABC中,AB∥OC,O为坐标原点,点A在y轴正半轴上,点C在x轴正半轴上,点B坐标为(2,2 3 ),∠BCO=60°,OH⊥BC于点H。
完整word版中考数学复习动点问题解题技巧

在运动中剖析 在静态中求解动向几何问题已成为中考试题的一大热点题型.这类试题以运动的点、线段、变化的角、图形的面积为基本条件,给出一个或多个变量,要求确定变量与其他量之间的关系,或变量在必然条件为定值时,进行相关的几何计算和综合解答,解答这类题目,一般要依照点的运动和图形的变化过程,对其不同样样状况进行分类求解,本文以一道中考题为例,谈谈此类问题的思路打破与解题反思,希望能给大家一些启示.题目 如图 1,已知点 A(2 , 0), B(0, 4),∠ AOB 的均分线交 AB 于点 C ,一动点 P 从 O 点出发,以每秒 2 个单位长度的速度,沿 y 轴向点 B 作匀速运动,过点 P 且平行于AB 的直线交 x 轴于点 Q ,作点 P 、Q 关于直线 OC 的对称点 M 、N .设点 P 运动的时间为 t(0<t<2) 秒.(1)求 C 点的坐标,并直接写出点M 、 N 的坐标(用含 t 的代数式表示) .(2)设△ MNC 与△ OAB 重叠部分的面积为 S .①试求 S 关于 t 的函数关系式; ②在直角坐标系中,画出S 关于 t 的函数图象,并回答:S 可否有最大值?若有,写出S 的最大值;若没有,请说明原由.一、研究解题思路 1.利用基础知识轻松求解 由题意不难发现第1 问是对基础知识的观察,有多种方法,考生可自行选择解法,简解 1 可经过作辅助线, 过点 C 作 CF 上 x 轴于点 F ,CE ⊥y 轴于点 E ,由题意,易知四边形 OECF 为正方形,设正方形边长为 x .由比率式求出点 C 的坐标 ( 4 , 4).33简解 2 由点 A 、B 的坐标可得直线 AB 的剖析式 y =- 2x + 4;由 OC 是∠ AOB 的均分线可得直线 OC 的剖析式 y = x ;联立方程组轻松解得点 C 的坐标 ( 4 , 4) .33关于求点 M 、N 的坐标,是对相似及对称性的观察,依照相似可得P(0,2t),Q(t ,0),依照对称性可得 M(2t , 0), N(0, t). 这样,第 1 问轻松获解.2.动静结合找界点,分类议论细演算第 2 问的第一小题中,所求函数关系式为分段函数,需要分类议论,这是本题的难点 之一; 而要点是动静结合找界点, 得出 t = 1 时重叠部分的关系会发生变化, 这是本题的难 点之二.解答时需着手画出草图,随着点M 、 N 的地址的变化,△ MNC 的地址也随之发生变化,△ MNC 与△ OAB 重叠部分的面积 S 也发生变化 .S 可能会存在两种状况: ①△ OAB 将△ MNC 全部覆盖; ②△ OAB 将△ MNC 部分覆盖; 点 M 从点 O 出发运动到点 A 时,即t = 1时重叠部分的关系会发生变化,函数关系式也随之改变.由 t = 1 这个界点确定两个范围,以此界值进行分类议论:当 0<t ≤ 1 时,点 M 在线段 OA 上,△ OAB 将△ MNC 全部覆盖,重叠部分面积为S △CMN = S 四边形 CMON -S △OMN . 结合点 C 的坐标 ( 4 , 4),可得33S △CMN =- t 2+ 2t ;当 1<t<2 时,点 M 在 OA 的延长线上,设MN 与 AB 交于点 D,△ OAB 将△ MNC 部分覆盖,则重叠部分面积为S .△CDN另一个要点是要用 t 的代数式表示 D 点的横坐标,即△ BDN 的高,这是本题的难点之三.由 M(2t , 0), N(0 , t) 可先用 t 的代数式表示直线MN 的剖析式 y=-1x+ t.2再结合直线 AB 的剖析式 y=- 2x+ 4,联立方程组,解出 D 点的横坐标为82t ,则3重叠部分面积为S△CDN=S△BDN -S△BCN1 t2 2t 83 3综上所述,t 2 2t(0 y 1)S 1 t2 2t 8 1 t 23 3由函数剖析式及其自变量的取值范围可画出函数图象,观察图象可知,当t= 1 时, S 有最大值,最大值为1.二、规范解答问题(1)如图 2,过点 C 作 CF⊥ x 轴于点 F, CE⊥y 轴于点 E,由题意,易知四边形 OECF为正方形,设正方形边长为x.∴OP= 2DQ.∵P(0,2t),∴ Q(t ,0).∵对称轴OC 为第一象限的角均分线,∴对称点坐标为:M(2t , 0), N(0 , t).(2)①当 0<t≤ 1 时,如图 3 所示,点M 在线段 OA 上,重叠部分面积为S△CMN .当1<t<2 时,如图 4 所示,点 M 在 OA 的延长线上,设 MN 与 AB 交于点 D,则重叠部分面积为 S△CDN设直线 MN 的剖析式为y= kx +b,将 M(2t , 0)、 N(0, t) 代入,得2tk b 0b t综上所述,t 2 2t(0 y 1)S1 t2 2t 8 1 t 23 3②画出函数图象,如图 5 所示:观察图象可知,当t= 1 时, S 有最大值,最大值为 1.三、解题反思1、要点的一步本题在打破第 2 问时,可否得出t= 1 时重叠部分的关系会发生变化,这是决定性的一步,否则就不知该如何分类议论,解题就难以找到前进的方向.2、解题难点解决本题的主要困难第一是分类议论,依照题意知点P 运动的时间为t(0<t<2) 秒,可以确定点肘、N 运动过程中的三类点,即起点、界点(有的题中存在多个界点)和终点,由界点值划分范围,确定分类标准(平时状况下,为了书写方便简洁,可将界点值归入动向的范围),今后进行分类计算(关于几何图形问题,平时需要依照相似、三角函数、勾股定理以及图形面积建立方程等数学模型计算).其次是重叠面积分类,当1<t<2时,我们面对的困难是如何对重叠部分的面积进行切割;如何用t 的代数式表示点 D 的横坐标;得出 S△CDN= S△BDN- S△BCN也是比较困难的;再者分类后的计算,略不注意也可能出错.3、解题收获解决此类与运动、变化相关的问题,重在运动中剖析,变化中求解.第一,要掌握运动规律,追求运动中的特别地址,在“动”中求“静” ,在“静”中研究“动”的一般规律.其次,经过研究、归纳、猜想,获得图形在运动过程中可否保留或拥有某种性质,要用运动的眼光观察出各种可能的状况分类议论,较为精确地将每种状况一一表现出来.再次,要学会将动向问题静态化,立刻动向情境化为几个静态的情境,从中搜寻两个变量间的关系,用相关字母去表示几何图形中的长度、点的坐标等,很多状况下是与三角形的相似和勾股定理等联系在一起的,在整个解题过程中,要深刻理解分类议论、数形结合、化归、相似等数学思想.。
2022年中考数学难点复习:数轴中的”动“问题(附答案解析)

2022年中考数学难点复习:数轴中的“动”问题已知数轴上三点M,O,N对应的数分别为–1,0,3,点P为数轴上任意一点,其对应的数为x.(1)求MN的长;(2)如果点P到点M、点N的距离相等,求x的值;(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.【参考答案】见试题解析【试题解析】(1)MN的长为3–(–1)=4.(2)根据题意得:x–(–1)=3–x,解得:x=1;(3)①当点P在点M的左侧时.根据题意得:–1–x+3–x=8.解得:x=–3.②P在点M和点N之间时,PN+PM=8,不合题意.③点P在点N的右侧时,x–(–1)+x–3=8.解得:x=5.∴x的值是–3或5.(4)设运动t分钟时,点P到点M,点N的距离相等,即PM=PN.点P对应的数是–t,点M对应的数是–1–2t,点N对应的数是3–3t.①当点M和点N在点P同侧时,点M和点N重合,所以–1–2t=3–3t,解得t=4,符合题意.②当点M和点N在点P异侧时,点M位于点P的左侧,点N位于点P的右侧(因为三个点都向左运动,出发时点M在点P左侧,且点M运动的速度大于点P的速度,所以点M永远位于点P的左侧),故PM=–t–(–1–2t)=t+1,PN=(3–3t)–(–t)=3–2t.所以t+1=3–2t,解得t=23,符合题意.综上所述,t的值为23或4.【方法点拨】解决动点问题最常使用的就是分类讨论了.初中数学中的分类讨论思想,是指把要研究的数学对象按照一定的标准划分为若干不同的类别,然后逐类进行研究、求解的一种数学解题思想.分类讨论解题的实质,是将整体问题化为部分问题来解决,以增加题设条件.分类讨论的原则是不重复、不遗漏,讨论的方法是逐类进行,还必须注意综合讨论的结果,以使解题步骤完整.1.把数轴上表示数2的点向右移动3个单位长度后,表示的数为A.1 B.–1 C.5 D.–52.数轴上的点A表示的数是a,当点A在数轴上向右平移了6个单位长度后得到点B,若点A和点B表示的数恰好互为相反数,则数a是A.6 B.–6 C.3 D.–33.一个点从数轴上表示–2的点开始,向右移动7个单位长度,再向左移动4个单位长度,则此时这个点表示的数是A.0 B.2 C.1 D.–14.点A在数轴上距原点5个单位长度,将点A先向左移动2个单位长度,再向右移动6个单位长度,此时点A所表示的数是A.–1 B.9C.–1或9 D.1或95.数轴上点A表示a,将点A沿数轴向左移动3个单位得到点B,设点B所表示的数为x,则x可以表示为A.a–3 B.a+3C.3–a D.3a+36.如图,数轴上点A,B表示的数分别为–40,50.现有一动点P以2个单位每秒的速度从点A向B运动,另一动点Q以3个单位每秒的速度从点B向A运动.当AQ=3PQ时,运动的时间为A.15秒B.20秒C.15秒或25秒D.15秒或20秒7.数轴上点A、B的位置如图所示,若点A向右移动2个单位得到点C,则线段BC中点所表示的数为__________.8.一只小球落在数轴上的某点P0,第一次从P0向左跳1个单位到P1,第二次从P1向右跳2个单位到P2,第三次从P2向左跳3个单位到P3,第四次从P3向右跳4个单位到P4…,若小球从原点出发,按以上规律跳了6次时,它落在数轴上的点P6所表示的数是__________;若小球按以上规律跳了2n次时,它落在数轴上的点P2n所表示的数恰好是n+2,则这只小球的初始位置点P0所表示的数是__________.9.已知小华家、小夏家、小红家及学校在同一条大路旁,一天,他们放学后从学校出发,先向南行1000m 到达小华家A处,继续向北行3000m到达小红B家处,然后向南行6000m到小夏家C处.(1)以学校以原点,以向南方向为正方向,用1个单位长度表示1000m,请你在数轴上表示出小华家、小夏家、小红家的位置;(2)小红家在学校什么位置?离学校有多远?10.如图,已知A,B两点在数轴上,点A表示的数为–10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发).(1)数轴上点B对应的数是__________.(2)经过几秒,点M、点N分别到原点O的距离相等?11.已知:数轴上点A表示的数是8,点B表示的数是–4.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左运动,动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左运动.P,Q两点同时出发.(1)经过多长时间,点P位于点Q左侧2个单位长度?(2)在点P运动的过程中,若点M是AP的中点,点N是BP的中点,求线段MN的长度.参考答案1.【参考答案】C【试题解析】把数轴上表示数2的点向右移动3个单位长度后,即2+3=5,表示的数为5,故选C.2.【参考答案】D【试题解析】由题意可得:B点对应的数是:a+6,∵点A和点B表示的数恰好互为相反数,∴a+a+6=0,解得:a=–3.故选D.3.【参考答案】C【试题解析】根据题意得:–2+7–4=1,则此时这个点表示的数是1,故选C.4.【参考答案】C【试题解析】∵点A在数轴上距原点5个单位长度,∴点A表示数–5或5,∵点A先向左移动2个单位长度,再向右移动6个单位长度,∴–5–2+6=–1,5–2+6=9,∴此时点A所表示的数是–1或9.故选C.5.【参考答案】A【试题解析】由题意得,把点A向左移动3个单位长度,即点A表示的数减小3.故B点所表示的数为a–3.故选A.6.【参考答案】D【试题解析】设运动的时间为t秒,P、Q相遇前,依题意有50–(–40)–3t=3[50–(–40)–2t–3t],解得t=15;P、Q相遇后,依题意有50–(–40)–3t=3[2t+3t–50+(–40)],解得t=20.故运动的时间为15秒或20秒.故选D.7.【参考答案】2【试题解析】根据题意知,由以上数轴知,线段BC中点所表示的数为2.故答案为:2.8.【参考答案】3,2【试题解析】由题意可得,小球从原点出发,按以上规律跳了6次时,它落在数轴上的点P6所表示的数是6÷2=3,小球按以上规律跳了2n次时,它落在数轴上的点P2n所表示的数恰好是n+2,则这只小球的初始位置点P0所表示的数是:n+2–(2n÷2)=2,故答案为:3,2.9.【试题解析】(1)因为学校是原点,向南方向为正方向,用1个单位长度表示1000m.从学校出发南行1000m到达小华家,所以点A在1处,从A向北行3000m到达小红家,所以点B在–2处,从B向南行6000m到小夏家,所以点C在4处.(2)点B是–2,所以小红家在学校的北面,距离学校2000m.10.【试题解析】(1)∵OB=3OA=30,∴B对应的数是30.故答案为:30.(2)设经过x秒,点M、点N分别到原点O的距离相等,此时点M对应的数为3x–10,点N对应的数为2x.①点M、点N在点O两侧,则10–3x=2x,解得x=2;②点M、点N重合,则3x–10=2x,解得x=10.所以经过2秒或10秒,点M、点N分别到原点O的距离相等.11.【试题解析】(1)设经过t秒,点P位于点Q左侧2个单位长度,6t–[4t+8–(–4)]=2,解得,t=7.答:经过7秒,点P位于点Q左侧2个单位长度;(2)由题意可得,经过时间t,点P表示的数为:8–6t,∵点M是AP的中点,点N是BP的中点,∴点M表示的数是:8(86)832tt +-=-,点N表示的数是:4(86)232tt -+-=-,∴MN=|(8–3t)–(2–3t)|=|8–3t–2+3t|=6,即线段MN的长度是6.。
中考复习专题之一动点问题 【含详细答案】

xAOQP By 图(3)ABC OEF ABCOD图(1) ABOE FC 图(2)动点问题 题型方法归纳动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、 相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
一、三角形边上动点1、(2009年齐齐哈尔市)直线364y x =-+与坐标轴分别交于A B 、两点,动点P Q 、同时从O 点出发,同时到达A 点,运动停止.点Q 沿线段O A 运动,速度为每秒1个单 位长度,点P 沿路线O →B →A 运动. (1)直接写出A B 、两点的坐标;(2)设点Q 的运动时间为t 秒,OPQ △的面积为S ,求出S 与t 之间 的函数关系式; (3)当485S =时,求出点P 的坐标,并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标.解:1、A (8,0) B (0,6)2、当0<t <3时,S=t2当3<t <8时,S=3/8(8-t)t提示:第(2)问按点P 到拐点B 所有时间分段分类;第(3)问是分类讨论:已知三定点O 、P 、Q ,探究第四点构成平行四边形时按已知线段身份不同分类-----①OP 为边、OQ 为边,②OP 为边、OQ 为对角线,③OP 为对角线、OQ 为边。
然后画出各类的图形,根据图形性质求顶点坐标。
2、(2009年衡阳市)如图,AB 是⊙O 的直径,弦BC=2cm , ∠ABC=60º.(1)求⊙O 的直径;(2)若D 是AB 延长线上一点,连结CD ,当BD 长为多少时,CD 与⊙O 相切;(3)若动点E 以2cm/s 的速度从A 点出发沿着AB 方向运动,同时动点F 以1cm/s 的速度从B 点出发沿BC 方向运动,设运动时间为)20)((<<t s t ,连结EF ,当t 为何值时,△BEF 为直角三角形.注意:第(3)问按直角位置分类讨论 3、(2009重庆綦江)如图,已知抛物线(1)233(0)y a x a =-+≠经过点(2)A -,0,抛物线的顶点为D ,过O 作射线O M A D ∥.过顶点D 平行于x 轴的直线交射线O M 于点C ,B 在x 轴正半轴上,连结B C . (1)求该抛物线的解析式;O M BH ACxy 图(1)O M B H A Cxy 图(2)xy M CD PQOAB PQA BC D(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线O M 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形D A O P 分别为平行四边形?直角梯形?等腰梯形?(3)若O C O B =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿O C 和B O 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.注意:发现并充分运用特殊角∠DAB=60°当△OPQ 面积最大时,四边形BCPQ 的面积最小。
2024年中考数学高频压轴题训练——圆-动点问题及参考答案
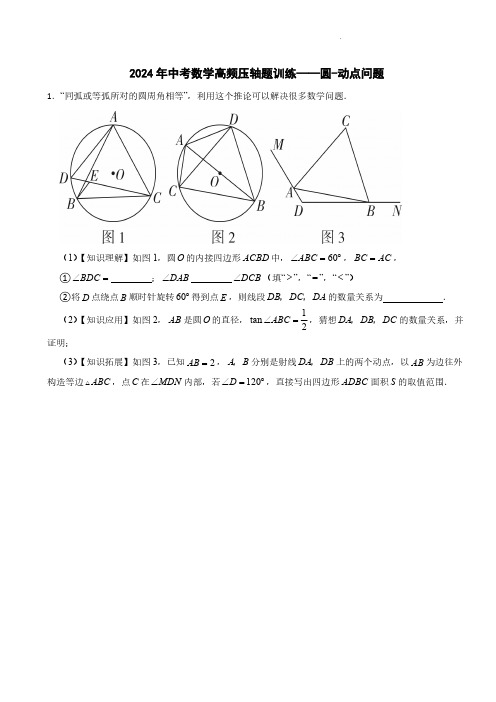
2024年中考数学高频压轴题训练——圆-动点问题1.“同弧或等弧所对的圆周角相等”,利用这个推论可以解决很多数学问题.(1)【知识理解】如图1,圆O 的内接四边形ACBD 中,60ABC ∠=︒,BC AC =,①BDC ∠=;DAB ∠DCB ∠(填“>”,“=”,“<”)②将D 点绕点B 顺时针旋转60︒得到点E ,则线段DB DC DA ,,的数量关系为.(2)【知识应用】如图2,AB 是圆O 的直径,1tan 2ABC ∠=,猜想DA DB DC ,,的数量关系,并证明;(3)【知识拓展】如图3,已知2AB =,A B ,分别是射线DA DB ,上的两个动点,以AB 为边往外构造等边ABC ,点C 在MDN ∠内部,若120D ∠=︒,直接写出四边形ADBC 面积S 的取值范围.2.如图1,对于PMN 的顶点P 及其对边MN 上的一点Q ,给出如下定义:以P 为圆心,PQ 为半径的圆与直线MN 的公共点都在线段MN 上,则称点Q 为PMN 关于点P 的内联点.在平面直角坐标系xOy 中:(1)如图2,已知点(70)A ,,点B 在直线1y x =+上.①若点(34)B ,,点(30)C ,,则在点O ,C ,A 中,点是AOB 关于点B 的内联点;②若AOB 关于点B 的内联点存在,求点B 纵坐标n 的取值范围;(2)已知点(20)D ,,点(42)E ,,将点D 绕原点O 旋转得到点F .若EOF 关于点E 的内联点存在,直接写出点F 横坐标m 的取值范围.3.在平面直角坐标系xOy 中,O 的半径为1,对于点A 和线段BC ,给出如下定义:若将线段BC 绕点A 旋转可以得到O 的弦B C ''(B C '',分别是B C ,的对应点),则称线段BC 是O 的以点A 为中心的“关联线段”.(1)如图,点112233A B C B C B C ,,,,,,的横、纵坐标都是整数.在线段112233B C B C B C ,,中,O 的以点A 为中心的“关联线段”是;(2)ABC 是边长为1的等边三角形,点()0A t ,,其中0t ≠.若BC 是O 的以点A 为中心的“关联线段”,求t 的值;(3)在ABC 中,12AB AC ==,.若BC 是O 的以点A 为中心的“关联线段”,直接写出OA 的最小值和最大值,以及相应的BC 长.4.已知:点C 为⊙O 的直径AB 上一动点,过点C 作CD ⊥AB ,交⊙O 于点D 和点E ,连接AD 、BD ,∠DBA 的角平分线交⊙O 于点F .(1)若DF =BD ,求证:GD =GB ;(2)若AB =2cm ,在(1)的条件下,求DG 的值;(3)若∠ADB 的角平分线DM 交⊙O 于点M ,交AB 于点N .当点C 与点O 重合时,AD BD DM+=;据此猜想,当点C 在AB (不含端点)运动过程中,AD BD DM +的值是否发生改变?若不变,请求其值;若改变,请说明理由.5.在平面直角坐标系xOy 中,O 的半径为1,对于ABC 和直线l 给出如下定义:若ABC 的一条边关于直线l 的对称线段PQ 是O 的弦,则称ABC 是O 的关于直线l 的“关联三角形”,直线l 是“关联轴”.(1)如图1,若ABC 是O 的关于直线l 的“关联三角形”,请画出ABC 与O 的“关联轴”(至少画两条);(2)若ABC 中,点A 坐标为(23),,点B 坐标为(41),,点C 在直线3y x =-+的图像上,存在“关联轴l ”使ABC 是O 的关联三角形,求点C 横坐标的取值范围;(3)已知A ,将点A 向上平移2个单位得到点M ,以M 为圆心MA 为半径画圆,B ,C 为M 上的两点,且2AB =(点B 在点A 右侧),若ABC 与O 的关联轴至少有两条,直接写出OC 的最小值和最大值,以及OC 最大时AC 的长.6.如图,在⊙O 中,AB 为弦,CD 为直径,且AB ⊥CD ,垂足为E ,P 为 AC 上的动点(不与端点重合),连接PD .(1)求证:∠APD =∠BPD ;(2)利用尺规在PD 上找到点I ,使得I 到AB 、AP 的距离相等,连接AD (保留作图痕迹,不写作法).求证:∠AIP+∠DAI =180°;(3)在(2)的条件下,连接IC 、IE ,若∠APB =60°,试问:在P 点的移动过程中,IC IE 是否为定值?若是,请求出这个值;若不是,请说明理由.7.在平面直角坐标系xOy 中,已知线段AB 和点P ,给出如下定义:若PA PB =且点P 不在线段AB 上,则称点P 是线段AB 的等腰顶点.特别地,当90APB ∠≥︒时,则称点P 是线段AB 的非锐角等腰顶点.(1)已知点(20)A ,,(42)B ,.①在点(40)C ,,(31)D ,,(15)E -,,(05)F ,中,是线段AB 的等腰顶点的是▲;②若点P 在直线3(0)y kx k =+≠上,且点P 是线段AB 的非锐角等腰顶点,求k 的取值范围;(2)直线33y x =-+与x 轴交于点M ,与y 轴交于点N .⊙P 的圆心为(0)P t ,,半径为,若⊙P 上存在线段MN 的等腰顶点,请直接写出t 的取值范围.8.在平面直角坐标系xOy中,⊙O的半径为1,T(0,t)为y轴上一点,P为平面上一点.给出如下定义:若在⊙O上存在一点Q,使得△TQP是等腰直角三角形,且∠TQP=90°,则称点P为⊙O的“等直点”,△TQP为⊙O的“等直三角形”.如图,点A,B,C,D的横、纵坐标都是整数.(1)当t=2时,在点A,B,C,D中,⊙O的“等直点”是;(2)当t=3时,若△TQP是⊙O“等直三角形”,且点P,Q都在第一象限,求CPOQ的值.9.综合与实践动手操作利用正方形纸片的折叠开展数学活动.探究体会在正方形折叠过程中,图形与线段的变化及其蕴含的数学思想方法.如图1,点E 为正方形ABCD 的AB 边上的一个动点,3AB =,将正方形ABCD 对折,使点A 与点B 重合,点C 与点D 重合,折痕为MN .思考探索(1)将正方形ABCD 展平后沿过点C 的直线CE 折叠,使点B 的对应点B '落在MN 上,折痕为EC ,连接DB ',如图2.①点B '在以点E 为圆心,的长为半径的圆上;②B M '=;③DB C ' 为三角形,请证明你的结论.(2)拓展延伸当3AB AE =时,正方形ABCD 沿过点E 的直线l (不过点B )折叠后,点B 的对应点B '落在正方形ABCD 内部或边上.①ABB ' 面积的最大值为;②连接AB ',点P 为AE 的中点,点Q 在AB '上,连接PQ AQP AB E ∠=∠',,则2B C PQ '+的最小值为.10.在平面直角坐标系xOy 中,过⊙T (半径为r )外一点P 引它的一条切线,切点为Q ,若0<PQ≤2r ,则称点P 为⊙T 的伴随点.(1)当⊙O 的半径为1时,①在点A(4,0),B(0,),C(1,)中,⊙O 的伴随点是▲;②点D 在直线y =x+3上,且点D 是⊙O 的伴随点,求点D 的横坐标d 的取值范围;(2)⊙M 的圆心为M(m ,0),半径为2,直线y =2x ﹣2与x 轴,y 轴分别交于点E ,F .若线段EF 上的所有点都是⊙M 的伴随点,直接写出m 的取值范围.11.定义:在平面直角坐标系xOy 中,点P 为图形M 上一点,点Q 为图形N 上一点.若存在OP OQ =,则称图形M 与图形N 关于原点O “平衡”.(1)如图,已知⊙A 是以()1,0为圆心,2为半径的圆,点()1,0C -,()2,1D -,()3,2E .①在点C ,D ,E 中,与⊙A 关于原点O “平衡”的点是;②点H 为直线y x =-上一点,若点H 与⊙A 关于原点O “平衡”,点H 的横坐标的取值范围为:;(2)如图,已知图形G 是以原点O 为中心,边长为2的正方形.⊙K 的圆心在x 轴上,半径为2.若⊙K 与图形G 关于原点O “平衡”,请直接写出圆心K 的横坐标的取值范围.12.阅读下列材料,并按要求解答相关问题:【思考发现】根据直径所对的圆周角是直角,我们可以推出“如果一条定边所对的角始终为直角,那么所有满足条件的直角顶点组成的图形是以定边为直径的圆或圆弧(直径的两个端点除外)”这一正确的结论.如图1,若AB 是一条定线段,且90APB ∠=︒,则所有满足条件的直角顶点P 组成的图形是定边AB 为直径的O (直径两端点A 、B 除外)(1)已知:如图2,四边形ABCD 是边长为8的正方形,点E 从点B 出发向点C 运动,同时点F 从点C 出发以相同的速度向点D 运动,连接AE ,BF 相交于点P .①当点E 从点B 运动到点C 的过程中,APB ∠的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请直接写出APB ∠的度数.②当点E 从点B 运动到点C 的过程中,点P 运动的路径是()A .线段;B .弧;C .半圆;D .圆③点P 运动的路经长是▲.(2)已知:如图3,在图2的条件下,连接CP ,请直接写出E 、F 运动过程中,CP 的最小值.13.对于平面内的图形1G 和图形2G ,记平面内一点P 到图形1G 上各点的最短距离为1d ,点P 到图形2G 上各点的最短距离为2d ,若12d d =,就称点P 是图形1G 和图形2G 的一个“等距点”.在平面直角坐标系xOy 中,已知点()60A ,,(0B .(1)在()30R ,,()20S ,,(1T 三点中,点A 和点B 的等距点是;(2)已知直线2y =-.①若点A 和直线2y =-的等距点在x 轴上,则该等距点的坐标为▲;②若直线y a =上存在点A 直线2y =-的等距点,求实数a 的取值范围;(3)记直线AB 为直线1l ,直线2l :33y x =-,以原点O 为圆心作半径为r 的O .若O 上有m 个直线1l 和直线2l 的等距点,以及n 个直线1l 和y 轴的等距点(0m ≠,0n ≠),求m n ≠时,求r 的取值范围.14.如图,平面上存在点P 、点M 与线段AB .若线段AB 上存在一点Q ,使得点M 在以PQ 为直径的圆上,则称点M 为点P 与线段AB 的共圆点.已知点P (0,1),点A (﹣2,﹣1),点B (2,﹣1).(1)在点O (0,0),C (﹣2,1),D (3,0)中,可以成为点P 与线段AB 的共圆点的是;(2)点K 为x 轴上一点,若点K 为点P 与线段AB 的共圆点,请求出点K 横坐标x K 的取值范围;(3)已知点M (m ,﹣1),若直线y =12x +3上存在点P 与线段AM 的共圆点,请直接写出m 的取值范围.15.如图,在ABC 中,AB BC =,30CAB ∠=︒,8AC =,半径为2的O 从点A 开始(如图1)沿直线AB 向右滚动,滚动时始终与直线AB 相切(切点为D ),当O 与ABC 只有一个公共点时滚动停止,作OG AC ⊥于点G .(1)图1中,O 在AC 边上截得的弦长AE =;(2)当圆心落在AC 上时,如图2,判断BC 与O 的位置关系,并说明理由.(3)在O 滚动过程中,线段OG 的长度随之变化,设AD x =,OG y =,求出y 与x 的函数关系式,并直接写出x 的取值范围.16.在平面直角坐标系xOy 中,给出如下定义:若点P 在图形M 上,点Q 在图形N 上,称线段PQ 长度的最小值为图形M ,N 的“近距离”,记为d(M ,N),特别地,若图形M ,N 有公共点,规定d(M ,N)=0.已知:如图,点A(2-,0),B(0,.(1)如果⊙O 的半径为2,那么d(A ,⊙O)=,d(B ,⊙O)=.(2)如果⊙O 的半径为r ,且d (⊙O ,线段AB )=0,求r 的取值范围;(3)如果C(m ,0)是x 轴上的动点,⊙C 的半径为1,使d (⊙C ,线段AB )<1,直接写出m 的取值范围.17.在平面直角坐标系xOy 中,对于点()P m n ,,我们称直线y mx n =+为点P 的关联直线.例如,点()24P ,的关联直线为24y x =+.(1)已知点()12A ,.①点A 的关联直线为;②若O 与点A 的关联直线相切,则O 的半径为;(2)已知点()02C ,,点()0.D d ,点M 为直线CD 上的动点.①当2d =时,求点O 到点M 的关联直线的距离的最大值;②以()11T -,为圆心,3为半径作.T 在点M 运动过程中,当点M 的关联直线与T 交于E ,F 两点时,EF 的最小值为4,请直接写出d 的值.18.在平面直角坐标系xOy 中,给定圆C 和点P ,若过点P 最多可以作出k 条不同的直线,且这些直线被圆C 所截得的线段长度为正整数,则称点P 关于圆C 的特征值为.k 已知圆O 的半径为2,(1)若点M 的坐标为()11,,则经过点M 的直线被圆O 截得的弦长的最小值为,点M 关于圆O 的特征值为;(2)直线y x b =+分别与x ,y 轴交于点A ,B ,若线段AB 上总存在关于圆O 的特征值为4的点,求b 的取值范围;(3)点T 是x 轴正半轴上一点,圆T 的半径为1,点R ,S 分别在圆O 与圆T 上,点R 关于圆T 的特征值记为r ,点S 关于圆O 的特征值记为.s 当点T 在x 轴正轴上运动时,若存在点R ,S ,使得3r s +=,直接写出点T 的横坐标t 的取值范围.答案解析部分1.【答案】(1)60︒;=;DC DB DA=+(2)解:在AB 上取一点E ,使ADE BDC ∠=∠,如图所示:∵AB 是圆O 的直径,1tan 2ABC ∠=,∴1tan 2AC ABC BC BC =∠⋅=,∴在Rt ACB 中,52AB BC ==,∵ BD BD =,∴DAB DCB ∠=∠,∵ADE BDC ∠=∠,∴ADE CDB ∽,∴ADAECD CB =,∴AD CB CD AE ⋅=⋅,∵ AD AD =,∴DBA DCA ∠=∠,∵ADE CDE CDB CDE ∠-∠=∠-∠,即ADC BDE ∠=∠,∴BDE CDA ∽,∴BDBECD AC =,∴BD AC CD BE ⋅=⋅,∴()AD CB AC BD CD AE CD BE CD AE BE CD AB⋅+⋅=⋅+⋅=⋅+=⋅,∴AB CD AC DB AD BC ⋅=⋅+⋅,∴122BC CD BC DB AD BC ⋅=⋅+⋅,∴5122CD DB AD ⋅=⋅+,∴5122CD DB AD =+,即2DB AD =+,故答案为:2DB AD =+.(3)解:∵A B ,分别是射线DA DB ,上的两个动点,120D ∠=︒,ABC 是等边三角形,∴四边形ADBC 的两个对角180ADB ACB ∠+∠=︒,∴构造四边形ADBC 的外接圆,∴根据四边形外接圆的性质可得:当点A 和点D 重合时,四边形ADBC 面积S 最小;当CD AB ⊥时,四边形ADBC 面积S 最大,①当点A 和点D 重合时,四边形ADBC 面积S 最小,∵CBD 时等边三角形,且2AB =,∴60CBD ∠=︒,2AB BD BC ===∴1sin 602CBD S BC BD =⋅⋅⋅= ,②当CD AB ⊥时,四边形ADBC 面积S 最大,∵CBD 时等边三角形,且2AB =,∴30ACD ∠=︒,2AC =,∴tan 233AD ACD AC =∠⋅==,∴11232322233ADC S AD DC =⋅⋅=⨯= ,∴23ADC ADBC S S == 四边形;433S <≤.2.【答案】(1)解:①O ,C ②当点B 的坐标为(0,1)时,如图,此时以BO 为半径的B 与线段OA 相切于点O ,∴点O 是OAB 关于点B 的内联点;当点B 移动到在y 轴左侧时,作图发现B 与x 轴有相交,且有一个交点不在线段OA 上,∴不再有OAB 关于点B 的内联点;当点B 的坐标为(7,8)时,以BA 为半径的B 与x 轴相切于点A ,∴点A 是OAB 关于点B 的内联点;当点B 直线x=7的右侧时,以BA 为半径的B 与x 轴相交,且有一个交点不在线段OA 上∴不再有OAB 关于点B 的内联点;综上所述,若AOB 关于点B 的内联点存在,求点B 纵坐标n 的取值范围为18n ≤≤;(2)80m 555m -≤≤≤≤或3.【答案】(1)22B C (2)解:由题意可得:当BC 是O 的以点A 为中心的“关联线段”时,则有AB C '' 是等边三角形,且边长也为1,当点A 在y 轴的正半轴上时,如图所示:设B C ''与y 轴的交点为D ,连接OB ',易得B C y ''⊥轴,∴12B D DC ''==,∴32OD ==,32==,∴OA =,∴t =;当点A 在y 轴的正半轴上时,如图所示:同理可得此时的OA =,∴t =;(3)当1min OA =时,此时BC =;当2max OA =时,此时2BC =.4.【答案】(1)证明:∵CD ⊥直径AB ,∴ BDBE =,∵DF =BD ,∴ DFBD =,∴ BEDF =,∴∠1=∠2,∴DG =BG(2)解:∠DBA 的角平分线交⊙O 于点F ,∴∠2=∠3,由(1)知,∠1=∠2,∴∠1=∠2=∠3,∵∠BCD =90°,∴∠1+∠2+∠3=90°,∴∠1=∠2=∠3=30°,∵AB 是⊙O 的直径,∴∠ADB =90°,∴∠4=90°﹣∠2﹣∠3=30°,∵AB =2,∴BD =1,在Rt △BCD 中,∠1=30°,∴BC =12BD =12,在Rt △BCG 中,∠3=30°,∴CG ==6,∴BG =2CG =33,由(1)知,DG =BG =33(3)5.【答案】(1)解:如图1,作BM ⊥x 轴,垂足为M ,根据题意AB=AE=EF=BF=,且∠EFO=∠BFM=45°,∴∠EFB=90°,∴四边形ABFE 是正方形,∴边AE ,BF 的中点所在直线就是ABC 与O 的一条“关联轴”;∵O 的半径为1,∴,且∠EFG=90°,∴四边形EFGH 是正方形,∵∠EFG+∠EFB=180°,∴B 、F 、G 三点共线,∴直线EF 是ABC 与O 的一条“关联轴”.(2)解:如图2,根据A (2,3),B (4,1),C (4,1),计算2=,故AB 不能落在圆的内部;过点A 作AN ⊥y 轴,垂足为N ,则AN=2,等于圆的直径,存在“关联轴l ”使ABC 是O 的关联三角形,此时0C x =;作点B 关于x 轴的对称点P ,此时BP=2,等于圆的直径,存在“关联轴l ”使ABC 是O 的关联三角形,此时4C x =,综上所述,点C 横坐标的范围是04C x ≤≤.(3)解:OC 的最小值为2-;OC 最大,根据勾股定理,AC=4.6.【答案】(1)证明:∵直径CD ⊥弦AB ,∴ AD BD=,∴∠APD=∠BPD ;(2)解:如图,作∠BAP 的平分线,交PD 于I ,证:∵AI 平分∠BAP ,∴∠PAI=∠BAI ,∴∠AID=∠APD+∠PAI=∠APD+BAI ,∵ AD BD=,∴∠DAB=∠APD ,∴∠DAI=∠DAB+∠BAI=∠APD+∠BAI ,∴∠AID=∠DAI ,∵∠AIP+∠DAI=180°,∴∠AIP+∠DAI=180°;(3)解:如图2,连接BI ,AC ,OA ,OB ,∵AI 平分∠BAP ,PD 平分∠APB ,∴BI 平分∠ABP ,∠BAI=12∠BAP ,∴∠ABI=12∠ABP ,∵∠APB=60°,∴∠PAB+∠PBA=120°,∴∠BAI+∠ABI=12(∠BAP+∠ABP )=60°,∴∠AIB=120°,∴点I 的运动轨迹是 AB ,∴DI=DA ,∵∠AOB=2∠APB=120°,∵AD ⊥AB ,∴ AD BD=,∴∠AOB=∠BOD=60°,∵OA=OD ,∴△AOD 是等边三角形,∴AD=AO ,∵CD 是⊙O 的直径,∴∠DAC=90°,∵CD ⊥AB ,∴∠AED=90°,∴∠AED=∠CAD ,∵∠ADC=∠ADE ,∴△ADE ∽△CDA ,∴AD DE CD AD=,∴AD 2=DE•CD ,∵DI′=DI=AD ,∴DI 2=DE•CD ,∵∠I′DE 是公共角,∴△DIE ∽△DCI ,∴2IC CD IE DI==.7.【答案】(1)解:①C(4,0),E(-1,5);②(Ⅰ)当点(40),在直线3y kx =+上时,430k +=,34k =-;(Ⅱ)当点(31),在直线3y kx =+上时,331k +=,23k =-;(Ⅲ)当点(22),在直线3y kx =+上时,232k +=,12k =-;结合图象可得3142k -≤≤-且23k ≠-;(2)解:直线333y x =-+与x 轴的交点M 坐标为()30,,与y 轴交点N 的坐标为(03,,∴tan 3NMO ∠=,∴30NMO ∠=︒,如图,作出线段MN 的垂直平分线,如图为两个临界情况:,利用待定系数法求得MN 垂直平分线解析式为y =,∴(0R -,,12230ORQ P RQ ∠=∠=︒,∴1112PR PQ ==,2222P R P Q ==,∴(10P ,(20P -,,∴t -≤<.8.【答案】(1)A 、B 、D(2)解:如图,依题意作⊙O 的“等直三角形”△TQP∴TQ=PQ ,∠TQP=90°过Q 点作MH //x 轴,交y 轴于M 点,过点P 作PH ⊥MH 于H 点∴∠TMQ=∠QHP=90°∴∠TQM+∠MTQ=∠TQM+∠HQP=90°∴∠MTQ=∠HQP∴△TMQ ≌△QHP (AAS )∴TM=QH ,MQ=HP设Q (x ,y )∴HM=MQ+QH=MQ+TM=x+3-y ,PH=MQ=x∴P (x-y+3,x+y )∵C (3,0)∴∵∴CP OQ .9.【答案】(1)BE ;3332-;等边;证明:B′D=BC CD ==,∴△DB'C 为等边三角形(2)310.【答案】(1)B ,C ;解:②如图2中,设点D 的坐标为(3)d d +,当过点D 的切线长为22r =时,OD ==由两点之间的距离公式得:OD =解得1221d d =-=-,结合图象可知,点D 的横坐标d 的取值范围是21d -≤≤-;(2)解:对于22y x =-当0y =时,220x -=,解得1x =,则点E 的坐标为(10)E ,当0x =时,2y =-,则点F 的坐标为(02)F -,⊙M 的半径为2,⊙M 的圆心为(0)M m ,24r ∴=,OM m=由题意,由以下两种情况:如图3-1中,点M 在点E 的右侧设FT 是⊙M 的切线则有两个临界位置:4FT =和点E 对应的切线长为0当4FT =时,则4OM m FT ===当点E 对应的切线长为0,即2EM =12EM m ∴=-=解得3m =结合图象得,当34m <≤时,线段EF 上的所有点都是⊙M 的伴随点②如图3-2和3-3中,点M 在点E 的左侧则有如下两个临界位置:如图3-2,设ET 是⊙M 的切线,连接MT ,则90MTE ∠=︒当4ET =时,2222245EM MT ET =+=+此时15m -=解得15m =-如图3-3,当⊙M 在直线EF 的左侧与EF 相切时,设切点为T ,连接MT∵(10)(02)E F -,,,∴12OE OF ==,∴22125EF =+=∵EF 是切线∴EF MT⊥∴90MTE FOE ∠=∠=︒∵MET FEO∠=∠∴MTE FOE~ ∴EM MTEF OF =,即22=解得EM =,即1m -=解得1m =-结合图象得,当11m -≤<-时,线段EF 上的所有点都是⊙M 的伴随点综上,m 的取值范围是11m -≤<-或34m <≤.11.【答案】(1)点C 、D ;22H x -≤≤-或22H x ≤≤(2)解: 图形G 是以原点O 为中心,边长为2的正方形,∴原点O 到正方形的最短距离是1d =,最长距离是d =,⊙K 与图形G 关于原点O “平衡”,∴原点O 到⊙K 上一点的距离1d ≤≤,⊙K 的圆心在x 轴上,半径为2,∴当⊙K 在x 轴正半轴时,圆心K 的横坐标的取值范围为:22x -≤≤+,当⊙K 在x 轴负半轴时,圆心K 的横坐标的取值范围为:22x --≤≤,综上所述,圆心K 的横坐标的取值范围22x -≤≤+或22x --≤≤.12.【答案】(1)解:①90°;②B ;③2π(2)解:413.【答案】(1)S(2,0)(2)解:①(4,0)或(8,0);②如图,设直线y a =上的点Q 为点A 和直线2y =-的等距点,连接QA ,过点Q 作直线2y =-的垂线,垂足为点C .点Q 为点A 和直线2y =-的等距点,QA QC ∴=.22QA QC ∴=.点Q 在直线y a =上,∴可设点Q 的坐标为()Q x a ,.()()22262x a a ∴-+=--⎡⎤⎣⎦.整理得2123240x x a -+-=.由题意得关于x 的方程2123240x x a -+-=有实数根.()()()212413241610a a ∴∆=--⨯⨯-=+≥.解得1a ≥-.(3)解:如图.直线l 1和直线l 2的等距点在直线l 3:33y x =-+上,直线l 1和y 轴的等距点在直线4l y =+:或33y x =+上,点O 与l 4的距离为32,点O 与l 3的距离为,点O 与l 5的距离为3,当r <时,n=0不符合题意,当r=时,m=2,n=0,符合题意,当<r <3时,m=n=2,不符合题意,当r≥3时,m=2,n=3或4,符合题意,综上所述,r=或r≥3.14.【答案】(1)C(2)解:∵P (0,1),点A (﹣2,﹣1),点B (2,﹣1).∴AP =BP ==2,如图2,分别以PA 、PB 为直径作圆,交x 轴于点K 1、K 2、K 3、K 4,∵OP=OG=1,OE∥AB,∴PE=AE=,∴OE=12AG=1,∴K1(﹣1﹣,0),k2(1﹣,0),k3(﹣1,0),k4(1+,0),∵点K为点P与线段AB的共圆点,∴﹣1﹣≤x k≤1﹣或﹣1≤x k≤1+(3)解:分两种情况:①如图3,当M在点A的左侧时,Q为线段AM上一动点,以PQ为直径的圆E与直线y=12x+3相切于点F,连接EF,则EF⊥FH,当x=0时,y=3,当y=0时,y=12x+3=0,x=﹣6,∴ON=3,OH=6,∵tan∠EHF=ON EFOH FH=36=12,设EF=a,则FH=2a,EH=a,∴OE=6﹣a,Rt △OEP 中,OP =1,EP =a ,由勾股定理得:EP 2=OP 2+OE 2,∴2221(6)a =+-,解得:a =2+(舍去)或2,∴QG =2OE =2(6﹣a )=﹣3+2,∴m≤3﹣2;②如图4,当M 在点A 的右侧时,Q 为线段AM 上一动点,以PQ 为直径的圆E 与直线y =12x+3相切于点F ,连接EF ,则EF ⊥FH ,同理得QG =3+2,∴m≥3+2,综上,m 的取值范围是m≤3﹣2或m≥3+215.【答案】(1)2(2)解:BC 与O 相切;理由:如图2,过点O 作OH BC ⊥于H ,连接OD ,∵O 与AB 相切于D ,∴OD AB ⊥,在Rt AOD 中,30BAC ∠=︒,∴24OA OD ==,∵8AC =,∴4OC =,在ABC 中,AB BC =,∴30C BAC ∠=∠=︒,在Rt OHC 中,30C ∠=︒,∴122OH OC OD ===,∴BC 与O 相切,(3)解:①当点O 在AC 的左侧时,连接OD 交AC 于F ,如备用图1,∵O 与AB 相切于D ,∴OD AB ⊥,∵OG AC ⊥,∴30FOG BAC ∠=∠=︒,在Rt FDA 中,tan FD BAC AD ∠=,∴tan 3FD AD BAC x =⋅∠=,∴23OF x =-,在Rt FOG 中,331cos 2322y OG OF FOG ⎛⎫==⋅∠=-⨯-+ ⎪ ⎪⎝⎭,即12y x =-+,此时x 的取值范围为0x ≤≤;②当点O 在AC 的右侧时,连接DO 并延长交AC 于F ,如备用图2,同①的方法得,33FD x =,∴23OF x =-,∵FD AB ⊥,∴90BAC AFD ∠+∠=︒,∴30FOG BAC ∠=∠=︒,在Rt FOG 中,331cos 2322y OG OF FOG x x ⎛⎫==⋅∠=-⨯- ⎪⎪⎝⎭,即12y x =-,此时x 的取值范围为1433x ≤≤.16.【答案】(1)0;2-(2)解:过点O 作OD ⊥AB 于点D ,∵点A(2-,0),B(0,.∴2OA OB ==,,∴4AB ==,∵1122OA OB AB OD ⋅=⋅,∴112422OD ⨯⨯=⨯⨯∴DO =,∵d (⊙O ,线段AB )=0,∴当⊙O 的半径等于OD 时最小,当⊙O 的半径等于OB 时最大,∴r r ≤≤(3)43423m -<<-17.【答案】(1)2y x =+(2)解:①当2d =时,()20D ,,设直线CD 的解析式为:y kx b =+,()02C ,,202k b b +=⎧∴⎨=⎩,解得:12k b =-⎧⎨=⎩,∴直线CD 的解析式为:y x =-+,设点M 的坐标为()2m m -+,,∴点M 的关联直线为:()212y mx m m x =-+=-+,∴点M 的关联直线经过定点()12N ,,如图2,过点O 作直线2y mx m =--+的垂线,垂足为H ,连接ON ,ON OH ∴≥,∴当点H与点N重合时,OH最大,即点O到点M的关联直线的距离最大,∴点O到点M=;2 d=②或2 3-18.【答案】(1);3(2)解:设点G是O的特征值为4的点,∴经过一点G且弦长为4(最长弦)的直线有1条,弦长为3的直线有2条,弦长为2的直线有且只有1条, 经过点G的直线被O截得的弦长的最小值为2,=,∴关于O的特征值为4的所有点都在以O为半径的圆周上,直线y x b=+分别与x,y轴交于点A、B,()0A b∴-,,()B b,,OA OB b∴==,45OBH∴∠=︒,当0b>时,线段AB与以O为半径的圆相切时,点G特征值为4,设切点为为H,连接OH,则OH=,OB∴==,b∴=,设以O 为半径的圆与y 轴正半轴的交点记为1B ,则1OB =,当线段AB 与以O 1B 时,可得b =,b ≤≤同理可求当0b <时,b ≤≤,综上,b b b ≤≤-≤(3)当372122t -≤≤+时,存在点R ,S ,使得3r s +=。
中考数学 重难点突破:初中数学动点问题7大类20小类全梳理

重难点突破:初中数学动点问题全梳理动点问题一直是中考热点题型,近几年考察探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数值、线段或面积的最值问题等,下面就此问题的常见题型作简单介绍。
题型一动点形成的面积问题1.面积公式:三角形面积用12S ah =来表示,利用未知数的代数式来表示底和高。
2.面积比等于相似比的平方:面积无法用底和高表示时,利用相似三角形的面积比等于相似比的平方来求解,只需要知道相似比和另一个三角形面积即可表示。
3.相似三角形:当面积公式和面积比等于相似比的平方不能有效解题时,利用相似三角形的比例关系求解。
角度1:利用公式法解决动点面积问题例题1:在平面直角坐标系xOy 中,抛物线2y x bx c =-++经过点30A (,)和23B (,).过点A 的直线与y 轴的负半轴相交于点C ,且1tan 3CAO ∠=.(1)求这条抛物线的表达式及对称轴;(2)连接AB 、BC ,求ABC ∠的正切值;(3)若点D 在x 轴下方的对称轴上,当ABC ADC S S ∆∆=时,求点D 的坐标.变式1:如图,在平面直角坐标系xOy 中,已知点A 的坐标为(,3)a (其中4a >),射线OA 与反比例函数12y x =的图像交于点P ,点B 、C 分别在函数12y x=的图像上,且//AB x 轴,//AC y 轴.(1)当点P 横坐标为6,求直线AO 的表达式;(2)联结BO ,当AB BO =时,求点A 坐标;(3)联结BP 、CP ,试猜想:ABP ACP S S ∆∆的值是否随a 的变化而变化?如果不变,求出ABP ACPSS ∆∆的值;如果变化,请说明理由.Oxy(备用图)Oxy解析:(1)∵反比例函数12y x=的图像经过横坐标为6的点P ,∴点P 的坐标为(6,2).设直线AO 的表达式为y kx =(0k ≠).将点P (6,2)代入y kx =,解得13k =.∴所求反比例函数的解析式为13y x =.(2)∵AB //x 轴,∴点B 纵坐标为3,将3y =代入12y x=,得4x =.∴B 坐标为(4,3).∵AB =BO ,∴224(40)(30)a -=-+-9a =.∴点A 坐标为(9,3).(3)不变.延长AB 交y 轴于点D ,延长AC 交x 轴于点E ,∴32ADO AEO S S a ∆∆==.∵点C 坐标为(a ,12a).∴6CEO S ∆=,同理6BDO S ∆=,∴ADO BDO AEO CEO S S S S ∆∆∆∆-=-,即ABO ACO S S ∆∆=.∵△ABP 与△ABO 同高,∴ABP ABO S AP S AO ∆∆=.同理ACP ACO S APS AO ∆∆=.∴1ABP ACPS S ∆∆=.即当a 变化时,ABPACPS S ∆∆的值不变,且恒为1变式2:如图,在直角坐标系中,一条抛物线与x 轴交于A 、B 两点,与y 轴交于C 点,其中(3,0)B ,(0,4)C ,点A 在x 轴的负半轴上,4OC OA =;(1)求这条抛物线的解析式,并求出它的顶点坐标;(2)联结AC 、BC ,点P 是x 轴正半轴上一个动点,过点P 作//PM BC 交射线AC 于点M ,联结CP ,若CPM ∆的面积为2,则请求出点P 的坐标;解析:(1)设这条抛物线的解析式为2(0)y ax bx c a =++≠它的顶点坐标为16(1,)3(2)过点P 作PH AC ⊥,垂足为H .∵P 点在x 轴的正半轴上,∴设0P x (,).∵A )0,1(-,∴1PA x =+.∵在Rt AOC ∆中,222OA OC AC +=;又∵14OA OC ==,∴17AC =90sin 117PH PH PHA CAO AP x ∠=︒∴∠===+ 17PH =//BP CMPM BC AB AC∴= ;300B P x (,),(,)1点P 在点B 的左侧时,3BP x =-,∴3417x -=17(3)4x CM -=∵2PCM S =△∴122CM PH ⋅⋅=,∴17(3)14(1)22417x -=解得110x .P =∴(,)2点P 在点B 的右侧时,3BP x =-,∴3417x -=17(3)4x CM -=∵2PCM S =△∴122CM PH ⋅⋅=,∴17(3)122417x -=解得1122x =+,2122x =-(不合题意,舍去)∴P (122+0).综上所述,P 的坐标为(1,0)或(122+0)角度2:利用面积比等于相似比的平方解决动点面积问题例题2:如图,已知在梯形ABCD 中,//AD BC ,5AB DC ==,4AD =.M 、N 分别是边AD 、BC 上的任意一点,联结AN 、DN .点E 、F 分别在线段AN 、DN 上,且//ME DN ,//MF AN ,联结EF .(1)如图1,如果//EF BC ,求EF 的长;(2)如果四边形MENF 的面积是ADN ∆的面积的38,求AM 的长;A BCDM NEF(图1)A BCD MNEF解析:(1)∵AD //BC ,EF //BC ,∴EF //A D .又∵ME //DN ,∴四边形EF DM 是平行四边形.∴EF =DM .同理可证,EF =AM .∴AM =DM .∵AD =4,∴122EF AM AD ===.(2)∵38ADNMENF S S ∆=四边形,∴58AME DMF ADN S S S ∆∆∆+=.即得58AME DMF ADN ADN S S S S ∆∆∆∆+=.∵ME //DN ,∴△AME ∽△AN D .∴22AME ADN S AM S AD ∆∆=.同理可证,△DM F ∽△DN A .即得22DMF ADN S DM S AD ∆∆=.设AM =x ,则4DM AD AM x =-=-.∴22(4)516168x x -+=.即得2430x x -+=.解得11x =,23x =.∴AM 的长为1或3.变式3:已知直线1l 、2l ,12//l l ,点A 是1l 上的点,B 、C 是2l 上的点,AC BC ⊥,60ABC ∠=︒,4AB =,O 是AB 的中点,D 是CB 延长线上的点,将DOC ∆沿直线CO翻折,点D 与'D 重合.(1)如图1,当点'D 落在直线1l 上时,求DB 的长;(2)延长DO 交1l 于点E ,直线'OD 分别交1l 、2l 于点M 、N .①如图2,当点E 在线段AM 上时,设x AE =,y DN =,求y 关于x 的函数解析式及其定义域;②若DON ∆的面积为323时,求AE 的长.解析:变式4:如图1,在梯形ABCD 中,//AD BC ,对角线BC AC ⊥,4AD =cm ,︒=∠45D ,3=BC cm .(1)求B ∠cos 的值;(2)点E 为BC 延长线上的动点,点F 在线段CD 上(点F 与点C 不重合),且满足ADE AFC ∠=∠,如图2,设x BE =,y DF =,求y 关于x 的函数解析式,并写出函数的定义域;(3)点E 为射线BC 上的动点,点F 在射线CD 上,仍然满足ADE AFC ∠=∠,当AFD ∆的面积为2cm 2时,求BE 的长.解析:(1)∵//AD BC ,∴ACB DAC ∠=∠.∵AC BC ⊥,∴90ACB ∠=︒.∴90DAC ∠=︒.∵45D ∠=︒,∴45ACD ∠=︒.∴AD AC =.∵4AD =,∴4AC =.∵3=BC ,∴5AB ==.∴3cos 5BC B AB ∠==.(2)∵//AD BC ,∴ADF DCE ∠=∠.∵AFC FDA FAD ∠=∠+∠,ADE FDA EDC ∠=∠+∠,又AFC ADE ∠=∠,∴FAD EDC ∠=∠.∴ADF DCE ∆~∆.∴AD DFDC CE=.在Rt ADC ∆中,222AC AD DC +=,又4==AC AD ,∴24=DC .∵x BE =,∴3-=x CE .y DF =,∴3244-=x y.22322-=x y .定义域为113<<x .(3)当点E 在BC 的延长线上,由(2)可得:ADF DCE ∆~∆,∴2)(DCAD S S DCE ADF =∆∆.∵2AFD S ∆=,4=AD ,24=DC ,∴4=∆DCE S .∵AC CE S DCE ⨯⨯=∆21,∴44)3(21=⨯-⨯BE ,∴5BE =.当点E 在线段BC 上,同理可得:44)3(21=⨯-⨯BE .∴1BE =.所以BE 的长为5或1.角度3:利用锐角三角比法解决动点面积问题例题3:已知在平面直角坐标系xoy (如图)中,抛物线212y x bx c =++经过点(4,0)A 、点(0,4)C -,点B 与点A 关于这条抛物线的对称轴对称;(1)用配方法求这条抛物线的顶点坐标;(2)联结AC 、BC ,求ACB ∠的正弦值;(3)点P 是这条抛物线上的一个动点,设点P 的横坐标为(0)m m >,过点P 作y 轴的垂线PQ ,垂足为Q ,如果QPO BCO ∠=∠,求m 的值;解析:变式5:已知在平面直角坐标系xoy 中,抛物线2(0)y ax bx c a =++>与x 轴相交于(1,0),(3,0)A B -两点,对称轴l 与x 轴相交于点C ,顶点为点D ,且ADC ∠的正切值为12.(1)求顶点D 的坐标;(2)求抛物线的表达式;(3)F 点是抛物线上的一点,且位于第一象限,联结AF ,若FAC ADC ∠=∠,求F 点的坐标.解析:(1)∵抛物线与x 轴相交于()1,0A -,()3,0B 两点,∴对称轴l :直线1x =,2AC =∵90ACD ∠=︒,1tan 2ADC ∠=,∴4CD =,∵0a >,∴()1,4D -(2)设()214y a x =--将1,0x y =-=代入上式,得,1a =所以,这条抛物线的表达为223y x x =--(3)过点F 作FH x ⊥轴,垂足为点H设()2,23F x x x --,∵FAC ADC ∠=∠,∴tan tan FAC ADC ∠=∠,∵1tan 2ADC ∠=,∴1tan 2FH FAC AH ∠==∵223FH x x =--,1AH x =+,∴223112x x x --=+解得172x =,21x =-(舍),∴79,24F ⎛⎫⎪⎝⎭巩固1:如图,在直角坐标系xOy 中,抛物线c ax ax y +-=22与x 轴的正半轴相交于点A 、与y 轴的正半轴相交于点B ,它的对称轴与x 轴相交于点C ,且OBC OAB ∠=∠,3AC =.(1)求此抛物线的表达式;(2)如果点D 在此抛物线上,DF OA ⊥,垂足为F ,DF 与线段AB 相交于点G ,且2:3:=∆∆AFG ADG S S ,求点D 的坐标.A C BO y x解析:(1)∵抛物线c ax ax y +-=22的对称轴为直线12=--=aax ,∴OC =1,OA =OC +AC =4,∴点A (4,0).∵∠OBC =∠OAB ,∴tan ∠OAB =tan ∠OBC ,∴OBOCOA OB =,∴OB OB 14=,∴OB =2,∴点B (0,2),∴⎩⎨⎧+-==,8160,2c a a c ∴⎪⎩⎪⎨⎧=-=.2,41c a ∴此抛物线的表达式为221412++-=x x y .(2)由2:3:=∆∆AFG ADG S S 得DG :FG =3:2,DF :FG =5:2,设m OF =,得m AF -=4,221412++-=m m DF ,由FG //OB ,得OA AF OB FG =,∴24m FG -=,∴2:524:)22141(2=-++-mm m ,∴01272=+-m m ,∴4,321==m m (不符合题意,舍去),∴点D 的坐标是(3,45)巩固2:如图,已知ABC ∆与BDE ∆都是等边三角形,点D 在边AC 上(不与A 、C 重合),DE 与AB 相交于点F .(1)求证:BCD DAF ∆∆∽;(2)若1BC =,设CD x =,AF y =;①求y 关于x 的函数解析式及定义域;②当x 为何值时,79BEF BCD S S ∆∆=?(1)证明:∵ABC ∆与BDE ∆都是等边三角形,∴60A C BDE ∠=∠=∠=︒∵ADF BDE C DBC ∠+∠=∠+∠,∴ADF DBC ∠=∠,∴BCD ∆∽DAF∆(2)∵BCD ∆∽DAF ∆,∴BC CDAD AF=∵1BC =,设CD x =,AF y =,∴11x x y =-,∴()201y x x x =-<<(3)解法一:∵ABC ∆与BDE ∆都是等边三角形,∴60E C ∠=∠=︒,60EBD CBA ∠=∠=︒,∴EBF CBD ∠=∠∴EBF ∆∽CBD ∆,∴BE BFBC BD=,∵BE BD =,1BC =,∴2BE BF =∵EBF ∆∽CBD ∆,79BEF BCD S S ∆∆=,∴2279BEF BCD S BE S BC ∆∆==,∴279BE BF ==,∴29AF =∴229x x -=,解得1221,33x x ==,∴当13x =或23时,79BEF BCD S S ∆∆=解法二:∵△ABC 与BDE ∆都是等边三角形,∴60E C ∠=∠=︒,60EBD CBA ∠=∠=︒,∴EBF CBD∠=∠∴EBF ∆∽CBD ∆,∵79BEF BCD S S ∆∆=,∴2279BEF BCD S BE S BC ∆∆==∵1BC =,BE BD =,∴279BD =过点B 作BH AC ⊥于点H ,∵60C ∠=︒,∴2BH =,∴16DH =,12CH =当点D 在线段CH 上时,111263CD CH DH =-=-=当点D 在线段CH 的延长线上时,112263CD CH DH =+=+=综上所述,当13x =或23时,79BEF BCD S S ∆∆=.巩固3:在矩形ABCD 中,4AB =,6AD =,点P 是射线DA 上一动点,将三角板直角顶点重合于点P ,三角板两直角边中的一边始终经过点C ,另一直角边交射线BA 于点E .(1)判断EAP ∆与PDC ∆一定相似吗?请证明你的结论;(2)设PD x =,AE y =,求y 与x 的函数关系式,并写出它的定义域;(3)是否存在这样的点P ,是EAP ∆周长等于PDC ∆周长的2倍?若存在,请求出PD 的长度;若不存在,请简要说明理由.解析:(1)△EAP ∽△PDC①当P 在AD 边上时,如图(1):∵矩形ABCD ,==90D A ∠∠ ,∴1+2=90∠∠据题意=90CPE ∠ ∴3+2=90∠∠ ,∴1=3∠∠,∴△EAP ∽△PDC ②当P 在AD 边上时,如图(2):同理可得△EAP ∽△PDC (2)若点P 在边AD 上,据题意:PD x =6PA x =-4DC =AE y=又∵△EAP ∽△PDC ,∴AE PA PD DC =,∴64y xx -=,∴22613442x x y x x -==-+()06x <<若点P 在边DA 延长线上时,据题意PD x =,则6PA x =-,4DC =,AE y =,∵△EAP ∽△PDC ,∴AE PA PD DC =,∴64y x x -=,∴()2664x x y x -=>(3)假如存在这样的点P ,使△EAP 周长等于PDC ∆的2倍①若点P 在边AD 上∵△EAP ∽△PDC ∴():6:4EAPPDCCCx =-,∴()6:42x -=,∴2x =-不合题意舍去;②若点P 在边DA 延长线上,同理得()6:42x -=,∴14x =综上所述:存在这样的点P 满足题意,此时14PD =巩固4:如图,已知抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C .(1)求这个抛物线的解析式,并写出顶点坐标;(2)已知点M 在y 轴上,OMB OAB ACB ∠+∠=∠,求点M的坐标.解析:(1)∵抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C ∴44201640c a b c a b c =-⎧⎪-+=⎨⎪++=⎩解得方程组的解为1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩∴这个抛物线的解析式为:2142y x x =--顶点为9(1,2-(2)如图:取OA 的中点,记为点N ∵OA =OC =4,∠AOC =90°∴∠ACB =45°∵点N 是OA 的中点∴ON =2又∵OB =2∴OB =ON 又∵∠BON =90°∴∠ONB =45°∴∠ACB =∠ONB∵∠OMB +∠OAB =∠ACB ∠NBA +∠OAB =∠ONB ∴∠OMB =∠NBA1°当点M 在点N 的上方时,记为M 1∵∠BAN =∠M 1AB ,∠NBA =∠OM 1B ,∴△ABN ∽△AM 1B ∴1AN ABAB AM =又∵AN =2,AB =∴110AM =又∵A (0,—4)∴1(0,6)M 2°当点M 在点N 的下方时,记为M 2,点M 1与点M 2关于x 轴对称,∴2(0,6)M -综上所述,点M 的坐标为(0,6)或(0,6)-题型二动点形成的相切问题1.直线和圆相切:圆心到直线距离等于半径构造直角三角形,利用三角比、勾股定理等来表示圆心到直线距离及半径,建立等量关系2.圆和圆相切:两圆半径和等于圆心距.利用平行线分线段成比例、勾股定理、三角比、相似等表示相关线段,建立等量关系角度4:直线与圆相切问题例题4:如图,在ABC ∆中,10,12,AB AC BC ===点E F 、分别在边BC AC 、上(点F 不与点A 、C 重合)//EF AB .把ABC ∆沿直线EF 翻折,点C 与点D 重合,设FC x =.(1)求B ∠的余切值;(2)当点D 在ABC ∆的外部时,DE DF 、分别交AB 于M 、N ,若MN y =,求y 关于x 的函数关系式并写出定义域;(3)(下列所有问题只要直接写出结果即可)以E 为圆心、BE 长为半径的E 与边AC1没有公共点时,求x 的取值范围.2一个公共点时,求x 的取值范围.3两个公共点时,求x 的取值范围.AECBFAB DGC EF 变式6:已知:矩形ABCD 中,过点B 作BG ⊥AC 交AC 于点E ,分别交射线AD 于F 点、交射线CD 于G 点,BC =6.(1)当点F 为AD 中点时,求AB 的长;(2)联结AG ,设AFG AB x S y ∆==,,求y 关于x 的函数关系式及自变量x 的取值范围;(3)是否存在x 的值,使以D 为圆心的圆与BC 、BG 都相切?若存在,求出x 的值;若不存在,请说明理由.解析:(1)∵点F 为AD 中点,且AD =BC =6,∴AF =3∵矩形ABCD 中,∠ABC =90°,BG ⊥AC 于点E ,∴∠ABE +∠EBC =90°,∠AC ∠EBC =90°∴∠ABE =∠ACB ,∴△ABF ∽△BCF ,∴ABAFBC AB =∴AB =23(2)由(1)可得△ABF ∽△BCF ∴ABAFBC AB =∵AB =x ,BC =6∴AF =62x ;同理可得:CG =x 36①当F 点在线段AD 上时DG =CG -CD =xx x x 23636-=-∴S ⊿AFG =1236213x x CG AF -=⋅。
中考热点问题”双动点问题”的处理方法复习总结(模型解析+例题精讲+真题反馈)

中考热点问题"双动点问题"的处理方法总结动点问题是中考数学必考的重难点问题,大多数同学都是“谈动色变”,选择直接放弃的更是大有人在。
解决动点问题,大家一定不要被其“动”所吓倒,我们要充分发挥空间想象能力,“动"中求“静",化“动”为“静",利用已知条件和所学知识点,寻找和所求相关的不变量和确定关系,这样,题目就化难为易了。
动点问题一般分为点动、线动和面动这三种类型,本节我们主要学习两类较难的动点问题。
一.不关联双动点问题对于不关联的双动点问题,我们采用“控制变量法",我们先控制其中一个点不动,分析另一个点运动轨迹,之后再让这个点运动起来,这样我们可以使问题更直观,思路更清晰。
我们先来看一道例题:例1.如图,RTAABC中,AC=3,AB=4,D、E分别是AB、AC上的两个动点,将AADE 沿着DE翻折,A点落在A'处,求A'C的最小值。
【简答】首先,我们固定D点不动,使E点动起来,随着E点的运动,X'始终在以D为圆心,DA为半径的圆上运动(如图1),图1只有当C、A'、D三点共线时,A z C是最短的(如图2);图2然后我们让D点也动起来,随着D点的运动,圆D的半径会发生变化,圆的半径越大,离C点就越近,因此,当D与B重合时,圆离C点的距离最近,再,移动E点,使得A,落在BC上,此时C、A,、D三定共线(如图3),CA'最小为5-4=1.图3二.多动点联动问题对于多个点运动并且是联动的这类问题,我们采用相对运动法,可以让这多个点静止,让原本的定点动起来,这样减少了动点的个数,使得问题简单化。
(原则是:让数量少的点动,让数量多的点休息)如下面这道天津中考题的最后一问。
例2.在平面直角坐标系中,四边形AOBC是矩形,点0的坐标为(0,0),点A 的坐标为(5,0),点B的坐标为(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点0,B,C的对应点分别为D,E, F.(1)如图①,当点D落在BC边上时,求点D的坐标.(2)如图②,当点D落在线段BE上时,连接AB,AD与BC交于点H.①求证:AADB义AAOB;②求点H的坐标.(3)记K为矩形AOBC对角线的交点,S^jAKDE的面积,求S的取值范围(直接写出结果即可).【简答】(1)VA(5.0), B (0.3).・.・OA=5,OB=3,..•四边形AOBC是矩形.AAC OB=3,OA BC-5,ZOBC=ZC-90°.•.•矩形ADEF是由矩形AOBC旋转得到,/.AD=AO=5.在RtAAlK中,CD V a D2+AC2 4..•.BD=BC-CD 1.AD(h3).(2)®由四边形ADEF是短形,得到ZADE=90°.•・•点D在线段BE上,:.ZADB90°,由(1)可知,AD-AO.又AB AB.ZAOB=90%ARtAADBSSRlAAOB②如图b中.由八ADB^AAOB.得到ZBAD-ZBAO.又在矩形AOBC中,OA〃BC,/.ZCBA=ZOAB,.\ZBAD=ZCBA..\BH=AH.设AH=BH=m.则HC BC-BH5-m.在RtAAHC中,VAIP-HC^AC^.ABH y..・.H(—,3).<3)要求△KDE面积的取值范围.我们只要考虑K、D,E三个点的运动情况即可.由于D、E西个点都在运动.3KDE面积的取值范围不好确定.例3.直线1外有一点D,点D到直线的距离为3,让腰长为2的等腰直角三角板ABC在直线]上滑动,则AD+CD的最小值为.【简答】由于运动是相对的,可以看做D点在直线r上运动,作点a关于直线r的对称点A'.可知当A\D、C三点共线时AD+CD 最小,最小值为A,C的长。
中考难点,圆的动点问题求解策略

中考难点,圆的动点问题求解策略近年来,初中数学动点问题在中考中出现的考点形式层出不穷,动点问题在中考数学中出现的频率非常之高,难度也非常的大。
很多考生看到动点相关问题就怕,不知道从何下手解决。
因此,很多人就常常会问动点问题会考哪些内容?怎么考等类似的问题。
为什么初中数学的动点问题对同学们来讲这么难呢?首先,动点问题本身就是一个数学难点,其次,考试中的动点问题往往结合了几何、函数等方面的知识,更是加深了题目难度。
因此,很多同学在中考复习阶段的时候会着重复习数学动点问题。
动点问题之所以会难,主要在于它能把很多知识内容结合在一起,形成不同类型的动点综合问题,如函数动点综合问题、代数动点综合问题、函数与几何动点综合问题、几何动点综合问题等,而几何动点综合问题细分的话,又可以分出四边形动点综合问题、三角形动点综合问题、与圆相关的动点综合问题等。
受疫情影响,不少初三毕业班老师担心,由于复习、预热不足,今年的中考、高考总体成绩可能会受到一定影响。
为了能更好帮助大家战胜动点类综合问题,在中考数学中取得优异的成绩,今天我们来看与圆相关的动点综合问题,期待同学加练一下。
1.(2020•泸县模拟)如图,在⊙O中,弦AB=8,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值是()A.2 B.4 C.6 D.8【解析】作OH⊥AB于H,连接OA、OD,如图,2.(2019秋•安徽期末)如图,已知⊙O的半径为5,P是直径AB的延长线上一点,BP=2,CD是⊙O的一条弦,CD=6,以PC,PD为相邻两边作平行四边形PCED,当C、D点在圆周上运动时,线段PE长的最大值为()A.24 B.22 C.20 D.18【解析】:连接OC.设CD交PE于点K,连接OK.∵四边形PCED是平行四边形,∴EK=PK,CK=DK,CD=6,∴OK⊥CD,在Rt△COK中,∵OC=5,CK=3,∴由勾股定理可求得OK=4,∵OP=OB+PB=7,∴7﹣4≤PK≤7+4,∴3≤PK≤11,∴PK的最小值为3,最大值为11,∴PE的最大值为22,故选:B.3.如图,⊙O的半径为2,弦AB的长为2√3,以AB为直径作⊙M,点C是优弧AB上的一个动点,连结AC、BC分别交⊙M于点D、E,则线段CD的最大值为()A.√3 B.2 C.2√3 -2 D.4-2√3【解析】:如图:连接OM,OB,OA,BD.则在Rt△OMB中,∵OB=2,MB=√3,∴OM=1.∵OB=2,∴∠OBM=30°.∴∠MOB=60°.连接OA.则∠AOB=120°.∴∠C=1/2∠AOB=60°.∵AB是直径,∴∠ADB=90°,∴∠CDB=90°,∴∠CBD=30°,∴CD=1/2BC,∴当BC取最大值时,CD最大.如图2,当BC是直径时,BC最大,此时点A、D重合.即BC=4.∴CD最大=2.故选:B.4.(2019•黄埔区一模)如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD的中点,过点C作CP⊥AB于点P,若CD =3,AB=8,PM=l,则l的最大值是.【解析】:方法一、延长CP交⊙O于K,连接DK,则PM=1/2DK,当DK过O时,DK最大值为8,PM=1/2DK=4,方法二、连接CO,MO,∵∠CPO=∠CMO=90°,∴C,M,O,P,四点共圆,且CO为直径(E为圆心),连接PM,则PM为⊙E的一条弦,当PM为直径时PM最大,所以PM=CO =4时PM最大.即PM max=4,故答案为:4.5.(2017•姑苏区校级二模)如图,已知线段AB=4,C为线段AB上的一个动点(不与点A,B重合),分别以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为.【解析】:如图,分别作∠A与∠B角平分线,交点为P.∵△ACD和△BCE都是等边三角形,∴AP与BP为CD、CE垂直平分线.又∵圆心O在CD、CE垂直平分线上,则交点P与圆心O重合,即圆心O是一个定点.连接OC.若半径OC最短,则OC⊥AB.又∵∠OAC=∠OBC=30°,AB=4,∴OA=OB,∴AC=BC=2,∴在直角△AOC中,OC=AC•tan∠OAC=2×tan30°=2√3/3.故答案为2√3/3.6.(2020•武汉模拟)如图,在⊙O中,弦AB=4√3,点C是弧AB上的动点(不为A,B),且∠ACB=120°,则CA+CB的最大值为.【解析】:取优弧AB中点P,连接PC,PA,PB,延长CA至M,使MA=CB,连接PM.∵弧PA=弧PB,∴PA=PB,∵∠APB+∠ACB=180°,∠ACB=120°,∴∠APB=60°,∴△APB是等边三角形,∴∠ACP=∠ABP=60°,∵∠PAM+∠PAC=180°,∠PAC+∠PBC=180°,∴∠PAM=∠PBC,∵AM=BC,AP=BP,∴△MAP≌△CBP(SAS),∴PM=PC,∵∠PCM=60°∴△MPC为等边三角形,∴PC=CM.∴CA+CB=PC,过点P作PD⊥AB连接OB,∵△PAB是等边三角形,∴PD过圆心O,∠BPD=30°,∴OB=4,当PC为圆的直径时,CA+CB的最大值为8.故答案为8.7.(2020•泸县模拟)如图,已知直线y=4/3x﹣3与x轴、y轴分别交于A,B 两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连接PA,PB,当△PAB的面积最大时,点P的坐标为.【解析】:过C作CM⊥AB于M,交x轴于E,连接AC,MC的延长线交⊙C 于D,作DN⊥x轴于N,∵直线y=4/3x﹣3与x轴、y轴分别交于A,B两点,∴A(4,0),B(0,﹣3),8.(2019秋•兴国县期末)在平面直角坐标系中,直线y=x﹣2与x轴、y轴分别交于点B、C,半径为1的⊙P的圆心P从点A(4,m)出发以每秒√2√个单位长度的速度沿射线AC的方向运动,设点P运动的时间为t秒,则当t =秒时,⊙P与坐标轴相切.【解析】:设⊙P与坐标轴的切点为D,∵直线y=x﹣2与x轴、y轴分别交于点B、C,点A(4,m),∴x=0时,y=﹣2,y=0时,x=2,x=4时,y=2,∴A(4,2),B(2,0),C(0,﹣2),∴AB=2√2,AC=2√2,OB=OC=2,∴△OBC是等腰直角三角形,∠OBC=45°,①当⊙P与x轴相切时,∵点D是切点,⊙P的半径是1,∴PD⊥x轴,PD=1,∴△BDP是等腰直角三角形,∴BD=PD=1,PB=√2,∴AP=AB﹣PB=√2,∵点P的速度为每秒√2个单位长度,∴t=1;②如图,⊙P与x轴和y轴都相切时,∵PB=√2,∴AP=AB+PB=3√2,∵点P的速度为每秒√2个单位长度,∴t=3;③当点P只与y轴相切时,∵PB=√2,∴AP=AC+PB=5√2,∵点P的速度为每秒√2个单位长度,∴t=5.综上所述,则当t=1或3或5秒时,⊙P与坐标轴相切,故答案为:1或3或5.9.(2019秋•锡山区期末)【问题发现】如图1,半圆O的直径AB=10,点P 是半圆O上的一个动点,则△PAB的面积最大值是;【问题探究】如图2所示,AB、AC、弧BC是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,弧BC所对的圆心角为60°.新区管委会想在弧BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F,即分别在弧BC、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.显然,为了快捷环保和节约成本,就要使线段PE、EF、FP之和最短(各物资站点与所在道路之间的距离、路宽均忽略不计).可求得△PEF周长的最小值为km;【拓展应用】如图3是某街心花园的一角,在扇形OAB中,∠AOB=90°,OA=12米,在围墙OA和OB上分别有两个入口C和D,且AC=4米,D 是OB的中点,出口E在弧AB上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.①出口E设在距直线OB多远处可以使四边形CODE的面积最大?最大面积是多少?(小路宽度不计)②已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元.请问:在弧AB上是否存在点E,使铺设小路CE和DE的总造价最低?若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.【解析】【问题发现】如图1,点P运动至半圆O的中点时,底边AB上的高最大,即P'O=r=5,此时△PAB的面积最大值,∴S△P'AB=1/2×10×5=25,故答案为:25;【问题探究】如图2,假设P点即为所求,分别作点P关于AB、AC的对称点P'、P'',连接PP',分别交AB、AC于点E、F,连接PE,PF,由对称性可知,PE+EF+PF=P'E+EF+FP''=P'P'',且P'、E、F、P''在一条直线上,∴P'P''即为最短距离,其长度取决于PA的长度,作出弧BC的圆心O,连接AO,与弧BC交于P,P点即为使PA最短的点,∵AB=6,AC=3km,∠BAC=60°,∴△ABC是直角三角形,∠ABC=30°,BC=3√3,∵BC所对的圆心角为60°,∴△OBC是等边三角形,∠CBO=60°,BO=BC=3√3,∴∠ABO=90°,AO=3√7,PA=3√7﹣3√3,∵∠P'AE=∠EAP,∠PAF=∠FAP'',∴∠P'AP''=2∠ABC=120°,P'A=AP'',∴∠AP'E=∠AP''F=30°,∵P'P''=2P'A•cos∠AP'E=√3P'A=3√21﹣9,∴△PEF周长的最小值为3√21﹣9;【拓展应用】①如图3﹣1,作OG⊥CD,垂足为G,延长OG交弧AB于点E′,则此时△CDE的面积最大,∵OA=OB=12,AC=4,点D为OB的中点,∴OC=8,OD=6,在Rt△COD中,CD=10,OG=4.8,∴GE′=12﹣4.8=7.2,∴出口E设在距直线OB的7.2米处可以使四边形CODE的面积最大为60平方米;②铺设小路CE和DE的总造价为200CE+400DE=200(CE+2DE),如图3﹣2,连接OE,延长OB到点Q,使BQ=OB=12,连接EQ,10.(2020•福清市模拟)如图,B,E是⊙O上的两个定点,A为优弧BE上的动点,过点B作BC⊥AB交射线AE于点C,过点C作CF⊥BC,点D在CF 上,且∠EBD=∠A.(1)求证:BD与⊙O相切;(2)已知∠A=30°.①若BE=3,求BD的长;②当O,C两点间的距离最短时,判断A,B,C,D四点所组成的四边形的形状,并说明理由.【解析】(1)证明:如图1,作直径BG,连接GE,则∠GEB=90°,∴∠G+∠GBE=90°,∵∠A=∠EBD,∠A=∠G,∴∠EBD=∠G,∴∠EBD+∠GBE=90°,∴∠GBD=90°,∴BD⊥OB,∴BD与⊙O相切;(2)解:如图2,连接AG,∵BC⊥AB,∴∠ABC=90°,由(1)知∠GBD=90°,∴∠GBD=∠ABC,∴∠GBA=∠CBD,又∵∠GAB=∠DCB=90°,∴△BCD∽△BAG,∴∠OMB=60°,∴MC=MB,∴∠MDC=∠MCD=30°=∠A,∵AB⊥BC,CD⊥BC,∴∠ABC=∠DCB=90°,∴AB∥CD,∴∠A+∠ACD=180°,∴∠BDC+∠ACD=180°,∴AC∥BD,∴四边形ABCD为平行四边形.11.(2019秋•工业园区期末)如图①,在矩形ABCD中,BC=60cm.动点P 以6cm/s的速度在矩形ABCD的边上沿A→D的方向匀速运动,动点Q在矩形ABCD的边上沿A→B→C的方向匀速运动.P、Q两点同时出发,当点P到达终点D时,点Q立即停止运动.设运动的时间为t(s),△PDQ的面积为S(cm2),S与t的函数图象如图②所示.(1)AB=cm,点Q的运动速度为cm/s;(2)在点P、Q出发的同时,点O也从CD的中点出发,以4cm/s的速度沿CD的垂直平分线向左匀速运动,以点O为圆心的⊙O始终与边AD、BC 相切,当点P到达终点D时,运动同时停止.①当点O在QD上时,求t的值;②当PQ与⊙O有公共点时,求t的取值范围.【解析】本题考查了矩形的性质,二次函数的图象及性质,切线的性质等,综合性强,解题关键是能够根据题意画出图形并能够用含字线母的代数式正确的将相关线段的长表示出来等.(1)设点Q的运动速度为a,则由图②可看出,当运动时间为5s时,△PDQ 有最大面积450,即此时点Q到达点B处,∵AP=6t,∴S△PDQ=1/2(60﹣6×5)×5a=450,∴a=6,∴AB=5a=30,故答案为:30,5;(2)①如图1,设AB,CD的中点分别为E,F,当点O在QD上时,QC=AB+BC﹣6t=90﹣6t,OF=4t,∵OF∥QC且点F是DC的中点,∴OF=1/2QC,即4t=1/2(90﹣6t),解得,t=45/7;②设AB,CD的中点分别为E,F,⊙O与AD,BC的切点分别为N,G,过点Q作QH⊥AD于H,如图2﹣1,当⊙O第一次与PQ相切于点M时,∵AH+AP=6t,AB+BQ=6t,且BQ=AH,∴HP=QH=AB=30,∴△QHP是等腰直角三角形,∵CG=DN=OF=4t,∴QM=QG=90﹣4t﹣6t=90﹣10t,PM=PN=60﹣4t﹣6t=60﹣10t,∴QP=QM+MP=150﹣20t,∵QP=√2QH,∴150﹣20t=30√2,∴t=(15-3√2)/2;如图2﹣2,当⊙O第二次与PQ相切于点M时,∵AH+AP=6t,AB+BQ=6t,且BQ=AH,∴HP=QH=AB=30,∴△QHP是等腰直角三角形,∵CG=DN=OF=4t,∴QM=QG=4t﹣(90﹣6t)=10t﹣90,PM=PN=4t﹣(60﹣6t)=10t﹣60,∴QP=QM+MP=20t﹣150,方法总结:动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
动点问题重难点知识点归纳

动点问题重难点知识点归纳
哇塞!今天我要来和大家聊聊动点问题,这可真是个让人又爱又恨的重难点呢!
你们想想看,动点就像是在数学世界里调皮捣蛋的小精灵,一会儿跑到这儿,一会儿跑到那儿,让我们这些解题的小伙伴们头疼不已。
比如说,在一个长方形的图形里,有一个点P 从长方形的一个顶点出发,沿着边按照一定的速度移动。
这时候,我们就得瞪大了眼睛,紧紧地盯着这个调皮的点P ,看看它到底跑到了哪里。
这就好像我们在玩捉迷藏,点P 藏起来了,我们得想方设法把它找出来。
还有那种在数轴上移动的点,哎呀,那更是让人眼花缭乱!就像一群小蜜蜂在数轴这条“花道”上飞来飞去。
我们得搞清楚它们的起始位置、移动方向和速度,才能算出它们最终停在哪里。
有时候,老师会给我们出一些超级难的动点问题,比如说多个动点同时移动,这简直就是一场“动点大混战”!我们得把每个动点的情况都分析清楚,就像指挥一场复杂的战斗一样。
还记得有一次,我和同桌一起研究一道动点问题,我俩都快把脑袋想破了,还是没搞明白。
我们互相争论,我说应该这样算,他说应该那样算,争得面红耳赤。
最后,还是请教了老师才弄明白。
还有啊,有些动点问题会和函数结合起来,这就像是给动点穿上了一件更复杂的“外衣”。
我们不仅要考虑动点的位置,还要想到函数的变化,这可真是太难啦!
但是,大家可别被动点问题吓倒!只要我们多做练习,多思考,就一定能把这些调皮的动点给制服。
就像孙悟空有了火眼金睛,什么妖怪都逃不过他的眼睛一样,我们也要有看穿动点问题的本领!
总之,动点问题虽然难,但只要我们不怕困难,勇敢挑战,就一定能攻克这个难关!让我们一起加油吧!。
中考数学动点问题压轴题

中考数学动点问题压轴题【典型题1】难度★★★如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PQ,设运动时间为xs,△APQ的面积为ycm2,则下列图象中能大致表示y 与x的函数关系的是()【思路分析】根据题意,分别求出两个时间段的函数关系式是解题的关键.根据题意结合图形,分情况讨论:①0≤x≤2时,根据S△APQ=AQ•AP,列出函数关系式,从而得到函数图象;②2≤x≤4时,根据S△APQ=S正方形ABCD﹣S△CP′Q′﹣S△ABQ′﹣S△AP′D列出函数关系式,从而得到函数图象,再结合四个选项即可得解.【答案解析】解:①当0≤x≤2时,∵正方形的边长为2cm,∴y =S△APQ=AQ•AP=x2;②当2≤x≤4时,y=S△APQ=S正方形ABCD ﹣S△CP′Q′﹣S△ABQ′﹣S△AP′D,=2×2﹣(4﹣x)2﹣×2×(x﹣2)﹣×2×(x﹣2)=﹣x2+2x所以,y与x之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有A选项图象符合.故选:A.【典型题2】难度★★★在边长为3 cm的正方形ABCD中,动点M自点A出发沿AB 方向,以每秒1 cm的速度运动;动点N自点A出发沿折线A —D—C—B,以每秒3 cm的速度同时出发.到达点B时两点同时停止.设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间函数关系的是().【答案解析】根据题意,作出如图所示正方形ABCD,应分三种情形:(1)当0<x≤1时,4个选项图象相同,可不作讨论;(2)当1<x≤2时,点N在边DC上点N1位置,点M在边AB 上点M1位置,AM1=x,边AM1上的高为3,.图象为从左向右上升的线段,排除选项(A)、(D);(3)当2<x≤3时,点N在边CB上点N2位置,点M在边AB 上点M2位置,如图中虚线所示.AM2=x,BN2=9-3x..图象为开口向下的抛物线上一段,排除(C),故选B.【典型题3】:难度★★★如图,已知A、B是反比例函数,图象上的两点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中箭头所示路线)匀速运动,终点为C.过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N.设矩形OMPN的面积为S,点P运动时间为t,则S与t的函数图象大致为()【答案解析】当点P在OA上运动时,S随t的增大而增大,且S与矩形边长的平方成正比,也就是与矩形的对角线OP的平方成正比,是t的二次函数,故可排除选项(B)、(D)(也可以根据点P在双曲线上运动时,矩形的面积不变,达到同样目的).当点P 在BC上运动时,S随t的增大而逐渐减小,排除选项(C).故应选A.【典型题4】难度★★★如图,在矩形ABCD中,AB=2,BC=3,动点P沿折线BCD 从点B开始运动到点D.设运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是()【思路分析】由题意当0≤x≤3时,y=3,当3<x<5时,y=×3×(5﹣x)=﹣x+.由此即可判断.【答案解析】解:由题意当0≤x≤3时,y=3,当3<x<5时,y=×3×(5﹣x)=﹣x+.故选:D.。
中考数学难点突破动点型问题例子解析版

类型一、动点问题中的特殊图形【例1】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A、B(点A在点B的左侧),与y轴交于点C(0,﹣2),OB=4OA,tan∠BCO=2.(1)求A、B两点的坐标;(2)求抛物线的解析式;(3)点M、N分别是线段BC、AB上的动点,点M从点B出发以每秒个单位的速度向点C运动,同时点N从点A出发以每秒2个单位的速度向点B运动,当点M、N中的一点到达终点时,两点同时停止运动.过点M作MP⊥x轴于点E,交抛物线于点P.设点M、点N的运动时间为t(s),当t为多少时,△PNE是等腰三角形?【答案】(1)A(﹣1,0);(2)y=x2﹣x﹣2;(3)当t=1时,△PNE是等腰三角形.【解析】(1)∵C(0,﹣2),∴OC=2,由tan∠BCO==2得OB=4,则点B(4,0),∵OB=4OA,∴OA=1,则A(﹣1,0);(2)将点A(﹣1,0)、B(4,0)代入y=ax2+bx﹣2,得:,解得:,∴抛物线解析式为y=x2﹣x﹣2;(3)设点M、点N的运动时间为t(s),则AN=2t、BM=t,∵PE⊥x轴,∴PE∥OC,∴∠BME=∠BCO,则tan∠BME=tan∠BCO,即=2,∴=,即=,则BE=t,∴OE=OB﹣BE=4﹣t,∴PE=﹣[(4﹣t)2﹣(4﹣t)﹣2]=﹣(4﹣t)2+(4﹣t)+2,①点N在点E左侧时,即﹣1+2t<4﹣t,解得t<,此时NE=AO+OE﹣AN=1+4﹣t﹣2t=5﹣3t,∵△PNE是等腰三角形,∴PE=NE,即﹣(4﹣t)2+(4﹣t)+2=5﹣3t,整理,得:t2﹣11t+10=0,解得:t=1或t=10>(舍);②当点N在点E右侧时,即﹣1+2t>4﹣t,解得t>,又且2t≤5,∴<t≤,此时NE=AN﹣AO﹣OE=2t﹣1﹣(4﹣t)=3t﹣5,由PE=NE得﹣(4﹣t)2+(4﹣t)+2=3t﹣5,整理,得:t2+t﹣10=0,解得:t=<0,舍去;或t=>,舍去;综上,当t=1时,△PNE是等腰三角形.类型二、动点问题中的计算问题【例2】如图,点A在数轴上对应的数为26,以原点O为圆心,OA为半径作优弧,使点B在O右下方,且tan∠AOB=,在优弧上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.(1)若优弧上一段的长为13π,求∠AOP的度数及x的值;(2)求x的最小值,并指出此时直线l与所在圆的位置关系;(3)若线段PQ的长为12.5,直接写出这时x的值.【答案】(1)∠POA=90°,x=;(2)当直线PQ与⊙O相切时时,此时x的值为﹣32.5;(3)满足条件的x的值为﹣16.5或31.5或﹣31.5.【解析】【分析】(1)利用弧长公式求出圆心角即可解决问题;(2)如图当直线PQ与⊙O相切时时,x的值最小.(3)由于P是优弧上的任意一点,所以P点的位置分三种情形,分别求解即可解决问题.【详解】(1)如图1中,由=13π,解得n=90°,∴∠POQ=90°,∵PQ∥OB,∴∠PQO=∠BOQ,∴tan∠PQO=tan∠QOB=,∴OQ=,∴x=;(2)如图当直线PQ与⊙O相切时时,x的值最小.在Rt△OPQ中,OQ=OP÷=32.5,此时x的值为﹣32.5;(3)分三种情况:①如图2中,作OH⊥PQ于H,设OH=4k,QH=3k.在Rt△OPH中,∵OP2=OH2+PH2,∴262=(4k)2+(12.5﹣3k)2,整理得:k2﹣3k﹣20.79=0,解得k=6.3或﹣3.3(舍弃),∴OQ=5k=31.5.此时x的值为31.5.②如图3中,作OH⊥PQ交PQ的延长线于H.设OH=4k,QH=3k.在Rt△在Rt△OPH中,∵OP2=OH2+PH2,∴262=(4k)2+(12.5+3k)2,整理得:k2+3k﹣20.79=0,解得k=﹣6.3(舍弃)或3.3,∴OQ=5k=16.5,此时x的值为﹣16.5.③如图4中,作OH⊥PQ于H,设OH=4k,AH=3k.在Rt△OPH中,∵OP2=OH2+PH2,∴262=(4k)2+(12.5﹣3k)2,整理得:k2﹣3k﹣20.79=0,解得k=6.3或﹣3.3(舍弃),∴OQ=5k=31.5不合题意舍弃.此时x的值为﹣31.5.综上所述,满足条件的x的值为﹣16.5或31.5或﹣31.5.招数三、动点问题的函数图象问题【例3】如图,已知点A是直线y=x与反比例函数(k>0,x>0)的交点,B是图象上的另一点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C (图中“→”所示路线)匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为()A.B.C.D.【答案】B【解析】试题解析:设点P的运动速度为v,分三种情况讨论:①当点P在OA上时,由于点A在直线y=x上,所以四边形OMPN为正方形,四边形OMPN的面积S=(vt)2,它的图象是抛物线的一部分;②当点P在反比例函数图象AB时,由反比例函数系数几何意义,四边形OMPN的面积S=k,它的图象是平行于t轴的直线的一部分;③当点P在BC段时,设点P运动到点C的总路程为a,则四边形OMPN的面积S=OC•(a﹣vt),由于OC,a,v都是定值,故它的图象是随t的增大而减小的直线的一部分.纵观各选项,只有B选项图形符合.故选B.。
初中数学动点问题及练习题附参考问题详解

初中数学动点问题及练习题附参考答案所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题. 关键:动中求静.数学思想:分类思想函数思想方程思想数形结合思想转化思想注重对几何图形运动变化能力的考查。
从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,通过“对称、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理。
选择基本的几何图形,让学生经历探索的过程,以能力立意,考查学生的自主探究能力,促进培养学生解决问题的能力.图形在动点的运动过程中观察图形的变化情况,需要理解图形在不同位置的情况,才能做好计算推理的过程。
在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
二期课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、实验探究等方向发展.这些压轴题题型繁多、题意创新,目的是考察学生的分析问题、解决问题的能力,容包括空间观念、应用意识、推理能力等.从数学思想的层面上讲:(1)运动观点;(2)方程思想;(3)数形结合思想;(4)分类思想;(5)转化思想等.研究历年来各区的压轴性试题,就能找到今年中考数学试题的热点的形成和命题的动向,它有利于我们教师在教学中研究对策,把握方向.只的这样,才能更好的培养学生解题素养,在素质教育的背景下更明确地体现课程标准的导向.本文拟就压轴题的题型背景和区分度测量点的存在性和区分度小题处理手法提出自己的观点.专题一:建立动点问题的函数解析式函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析.一、应用勾股定理建立函数解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动点问题 题型方法归纳动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、 相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
一、三角形边上动点1、(2009年齐齐哈尔市)直线364y x =-+与坐标轴分别交于A B 、两点,动点P Q 、同时从出发,同时到达A 点,运动停止.点Q沿线段OA 运动,速度为每秒1个单 位长度,点P 沿路线O →B →A 运动. (1)直接写出A B 、两点的坐标; (2)设点Q 的运动时间为t 秒,OPQ △的面积为S ,求出S 与t 之间的函数关系式; (3)当485S =时,求出点P 的坐标,并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标.解:1、A (8,0) B (0,6)2、当0<t <3时,S =t2当3<t <8时,S =3/8(8-t )t 提示:第(2)问按点P到拐点B所有时间分段分类;第(3)问是分类讨论:已知三定点O 、P 、Q ,探究第四点构成平行四边形时图B图B 图按已知线段身份不同分类-----①O P为边、O Q为边,②O P为边、O Q为对角线,③O P为对角线、O Q为边。
然后画出各类的图形,根据图形性质求顶点坐标。
2、(2009年衡阳市)如图,A B是⊙O的直径,弦B C=2c m,∠A B C=60º.(1)求⊙O的直径;(2)若D是A B延长线上一点,连结C D,当B D长为多少时,C D与⊙O相切;(3)若动点E以2c m/s的速度从A点出发沿着A B方向运动,同时动点F以1c m/s的速度从B点出发沿B C方向运动,设运动时间为)2)((<<tst,连结E F,当t为何值时,△B E F为直角三角形.注意:第(3)问按直角位置分类讨论3、(2009重庆綦江)如图,已知抛物线(1)20)y a x a=-+≠经过点(2)A-,0,抛物线的顶点为D,过O作射线OM AD∥.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.(1)求该抛物线的解析式;(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为()t s.问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?(3)若OC OB =,动点P 和动点Q 分别从点O 和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.注意:发现并充分运用特殊角∠D A B =60° 当△O P Q 面积最大时,四边形B C P Q的面积最小。
二、 特殊四边形边上动点4、(2009年吉林省)如图所示,菱形ABCD 的边长为6厘米,60B ∠=°.从初始时刻开始,点P 、Q同时从A 点出发,点P 以1厘米/秒的速度沿A CB →→的方向运动,点Q 以2厘米/秒的速度沿A B C D →→→的方向运动,当点Q 运动到D 点时,P 、Q 两点同时停止运动,设P 、Q 运动的时间为x 秒时,APQ △与ABC △重叠部分....的面积为y 平方厘米(这里规定:点和线段是面积为O 的三角形),解答下列问题: (1)点P 、Q 从出发到相遇所用时间是秒; (2)点P 、Q 从开始运动到停止的过程中,当APQ △是等边三角形时x 的值是 秒;(3)求y 与x 之间的函数关系式.提示:第(3)问按点Q 到拐点时间B 、C 所有时间分段分类 ; 提醒----- 高相等的两个三角O MBH A C x y图O M B H A C x y 图形面积比等于底边的比 。
5、(2009年哈尔滨)如图1,在平面直角坐标系中,点O 是坐标原点,四边形A B C O 是菱形,点A 的坐标为(3-,4),点C 在x 轴的正半轴上,直线A C 交y 轴于点M ,A B 边交y 轴于点H .(1)求直线A C 的解析式; (2)连接B M ,如图2,动点P 从点A 出发,沿折线A B C 方向以2个单位/秒的速度向终点C 匀速运动,设△P M B 的面积为S (0S ≠),点P 的运动时间为t 秒,求S 与t 之间的函数关系式(要求写出自变量t 的取值范围);(3)在(2)的条件下,当 t 为何值时,∠M P B与∠B C O 互为余角,并求此时直线O P 与直线A C 所夹锐角的正切值.注意:第(2)问按点P到拐点B所用时间分段分类;第(3)问发现∠M B C =90°,∠B C O 与∠A B M互余,画出点P 运动过程中,∠M P B =∠A B M 的两种情况,求出t 值。
利用O B ⊥A C ,再求O P 与A C 夹角正切值.6、(2009年温州)如图,在平面直角坐标系中,点A (3,0),B (33,2),C (0,2).动点D以每秒1个单位的速度从点0出发沿O C 向终点C 运动,同时动点E 以每秒2个单位的速度从点A 出发沿A B 向终点B 运动.过点E 作E F 上A B ,交B C 于点F ,连结D A 、D F .设运动时间为t 秒.(1)求∠A B C 的度数;(2)当t 为何值时,A B ∥D F ;(3)设四边形A E F D 的面积为S . ①求S 关于t 的函数关系式;②若一抛物线y =x2+m x 经过动点E ,当S <23时,求m 的取值范围(写出答案即可).注意:发现特殊性,D E ∥O A 7、(07黄冈)已知:如图,在平面直角坐标系中,四边形A B C O 是菱形,且 ∠A O C =60°,点B 的坐标是,点P 从点C 开始以每秒1个单位长度的速度在线段C B上向点B 移动,同时,点Q 从点O 开始以每秒a (1≤a ≤3)个单位长度的速度沿射线O A方向移动,设(08)t t <≤秒后,直线P Q 交O B 于点D . (1)求∠A O B 的度数及线段O A 的长;(2)求经过A ,B ,C 三点的抛物线的解析式;(3)当3,a OD ==时,求t 的值及此时直线P Q的解析式; (4)当a 为何值时,以O ,P ,Q ,D 为顶点的三角形与OAB ∆相似?当a 为何值时,以O ,P ,Q ,D 为顶点的三角形与OAB ∆不相似?请给出你的结论,并加以证明.8、(08黄冈)已知:如图,在直角梯形COAB 中,OC AB ∥,以O 为原点建立平面直角坐标系,A B C ,,三点的坐标分别为(80)(810)(04)A B C ,,,,,,点D 为线段BC 的中点,动点P 从点O 出发,以每秒1个单位的速度,沿折线OABD 的路线移动,移动的时间为t 秒.(1)求直线BC 的解析式;(2)若动点P 在线段OA 上移动,当t 为何值时,四边形OPDC 的面积是梯形COAB 面积的27?(3)动点P 从点O 出发,沿折线OABD 的路线移动过程中,设OPD △的面积为S ,请直接写出S 与t 的函数关系式,并指出自变量t 的取值范围; (4)当动点P 在线段AB 上移动时,能否在线段OA 上找到一点Q ,使四边形CQPD 为矩形?请求出此时动点P 的坐标;若不能,请说明理由.9、(09年黄冈市)如图,在平面直角坐标系x o y中,抛物线21410189y x x =--与x 轴的交点为点A ,与y 轴的交点为点B .过点B 作x 轴的平行线B C ,交抛物线于点C ,连结A C .现有两动点P ,Q 分别从O ,C 两点同时出发,点P 以每秒4个单位的速度沿O A 向终点A 移动,点Q 以每秒1个单位的速度沿C B 向点B 移动,点P 停止运动时,点Q 也同时停止运动,线段O C ,P Q 相交于点D ,过点D 作D E ∥O A ,交C A 于点E ,射线Q E 交x 轴于点F .设动点P ,Q 移动的时间为t (单位:秒) (1)求A ,B ,C 三点的坐标和抛物线的顶点的坐标;(2)当t 为何值时,四边形P Q C A 为平行四边形?请写出计算过程; (3)当0<t <92时,△P Q F 的面积是否总为定值?若是,求出此定值, 若不是,请说明理由; (4)当t 为何值时,△P Q F 为等腰三角形?请写出解答过程.提示:第(3)问用相似比的代换,得P F =O A (定值)。
第(4)问按哪两边相等分类讨论 ①P Q =P F ,②P Q =F Q ,③Q F =P F .三、 直线上动点8、(2009年湖南长沙)如图,二次函数2y ax bx c=++(0a ≠)的图象与x 轴交于A B 、两点,与y 轴相交A B DCO Py A BD COy (此y O xC N BPM A于点C .连结AC BC A C 、,、两点的坐标分别为(30)A -,、(03)C ,,且当4x =-和2x =时二次函数的函数值y 相等.(1)求实数a b c ,,的值;(2)若点M N 、同时从B 点出发,均以每秒1个单位长度的速度分别沿BA BC 、边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为t 秒时,连结MN ,将BMN △沿MN 翻折,B 点恰好落在AC 边上的P 处,求t 的值及点P 的坐标;(3)在(2)的条件下,二次函数图象的对称轴上是否存在点Q ,使得以B N Q ,,为项点的三角形与ABC △相似?如果存在,请求出点Q 的坐标;如果不存在,请说明理由.提示:第(2)问发现特殊角∠C A B =30°,∠C B A =60° 特殊图形四边形B N P M 为菱形;第(3)问注意到△A B C 为直角三角形后,按直角位置对应分类;先画出与△A B C 相似的△B N Q ,再判断是否在对称轴上。
9、(2009眉山)如图,已知直线112y x =+与y 轴交于点A ,与x 轴交于点D ,抛物线212y x bx c =++与直线交于A 、E 两点,与x 轴交于B 、C 两点,且B 点坐标为 (1,0)。
⑴求该抛物线的解析式; ⑵动点P 在x 轴上移动,当△P A E是直角三角形时,求点P 的坐标P 。
⑶在抛物线的对称轴上找一点M ,使||AM MC 的值最大,求出点M 的坐标。
