投资学6投资组合有效边界计算
证券组合的可行域和有效边界

证券组合的可行域和有效边界(一)证券组合的可行域1.两种证券组合的可行域。
如果用前述两个数字特征——期望收益率和标准差来描述一种证券,那么任意一种证券都可用在以期望收益率为纵坐标和标准差为横坐标的坐标系中的一点来表示;相应的,任何一个证券组合也可以由组合的期望收益率和标准差确定出坐标系中的一点。
这一点将随着组合的权数变化而变化,其轨迹是经过A和B的一条连续曲线,这条曲线称为证券A和证券B的组合线。
可见,组合线实际上在期望收益率和标准差的坐标系中描述了证券A和证券B所有可能的组合。
根据公式(11.1)和公式(11.2)及x A+x B=1,A、B的证券组合P的组合线由下述方程所确定:给定证券A、B的期望收益率和方差,证券A与证券B的不同的关联性将决定A、B的不同形状的组合线。
(1)完全正相关下的组合线。
在完全正相关下,ρAB=1,方程(11.5)和(11.6)变为:因为,E(r P)与x A是线性关系,而σp与x A是线性关系,所以,σp与E(r p)之间也是线性关系。
因此,证券A、B构成的组合线是连接这两点的直线(见图11-1)。
(2)完全负相关下的组合线。
在完全负相关情况下,ρAB=-l,方程(11.5)和(11.6)变为:这时,σp,与E(r p)是分段线性关系,其组合线如图11-2。
从图11-2可以看出,在完全负相关的情况下,按适当比例买入证券A和证券B可以形成一个无风险组合,得到一个稳定的收益率。
这个适当比例通过令公式(11.8)中σp=0可得:因为x A和x B均大于0,所以必须同时买入证券A和B。
这一点很容易理解,因为证券A 和B完全负相关,二者完全反向变化,因而同时买入两种证券可抵消风险。
所能得到的无风险收益率为:(3)不相关情形下的组合线。
当证券A与B的收益率不相关时,p AB=0,方程(11.5)和(11.6)变为:该方程确定的σp与E(r p)的曲线是一条经过A和B的双曲线,如图11-3所示。
几种最优投资组合在有效边界上相对位置

第56卷第4期2016年7月大连理工大学学报Journal of Dalian Universit y of Technolo gyVol.56,No.4Jul y 2016文章编号:1000-8608(2016)04-0420-07几种最优投资组合在有效边界上相对位置周伊佳, 于 波*(大连理工大学数学科学学院,辽宁大连 116024)摘要:讨论了均值-VaR ㊁均值-AVaR ㊁方差-均值比等风险-收益投资组合优化模型的最优解的有效性.基于Markowitz 均值-方差模型和有效边界理论,证明了如果各模型的最优投资组合存在,则一定位于均值-方差有效边界上.计算了各投资组合模型最优解处的均值和标准差,根据计算结果讨论了各模型的最优投资组合在有效边界上的位置.特别地,均值-VaR 模型的最优投资组合在有效边界上的位置与置信水平有关.关键词:投资组合优化模型;最优投资组合;有效边界中图分类号:O224文献标识码:Adoi :10.7511/dll g xb201604014收稿日期:2015-12-05; 修回日期:2016-03-10.基金项目:国家自然科学基金资助项目(11171051,重大计划91230103);中央高校基本科研业务费专项资金资助项目(DUT15RC (3)037).作者简介:周伊佳(1986-),女,博士生,E -mail :zhou y i j iadlut@g ;于波*(1963-),男,教授,博士生导师,E -mail :y ubo @.0 引 言20世纪50年代,Markowitz 首创了经典的投资组合理论:均值-方差(mean -variance ,M -V )投资组合优化模型[1],它奠定了现代投资组合的理论基础.在M -V 模型中方差被视为风险估计.20世纪80年代以来,随着金融市场的飞速发展及信息技术的创新,在Markowitz 投资理论框架下产生了均值-VaR (Value -at -Risk )投资组合模型.VaR ,是指在市场正常波动下以及在一定的概率水平下,于给定的置信区间内,金融资产或资产组合在未来一段时间内可能受到的最大损失[2].人们对VaR 约束下的投资组合策略的选择问题进行了研究[3-5].根据VaR 风险度量,张红兵等[6]提出多阶段资产组合选择均值-VaR 模型.王尚户等[2]利用均值-VaR 方法,提出了均值-AVaR(avera g e Value -at -Risk )模型,并在一定的置信水平下得到了投资组合的均衡理论.投资者想要获得更高的收益,就要承受更大的风险;反之要降低风险,则获得的收益也随之减少.由于风险与收益存在着这样的联系,那么只分别考虑最小风险和最大收益的投资组合决策方法往往不能较好地全面权衡收益与风险之间的关系.因此本文基于均值-方差模型的有效边界理论,研究一系列关于收益-风险的优化模型的最优投资组合,这些优化模型在某种程度上能够均衡均值与方差,即收益与风险,在一定程度上为投资者对资源做出最优的投资组合规划提供参考.1 投资组合模型首先介绍一些收益-风险投资组合优化模型及它们的最优解处的收益和标准差.1.1 均值-方差模型Markowitz 的均值-方差(M -V )模型是经典的投资组合优化模型.设在投资组合问题中,投资者选择n 种风险证券,证券的收益率向量r =(r 1r 2 r n )T,其中r i 表示第i 种证券的期望收益率;投资比例向量x =(x 1 x 2 x n )T,x i是投资第i 种证券的比例;投资组合的协方差矩阵V =(v i j )n ˑn ,其中v i j 表示第i 种证券和第j 种证券的协方差.投资组合的期望收益与方差分别为μ=r T x ,σ2=x T Vx .则M -V 投资组合模型[2]为min σ2=x T Vxs.t.r T x =μe T x =1(1)假定协方差矩阵V =(v i j )n ˑn 是正定的,根据La g ran g e 乘子法求得式(1)的最优解为[2]x *=μD(B V -1r -C V -1e )-1D(C V -1r -A V -1e )(2)式中:A =r T V -1r ,B =e T V -1e ,C =e T V -1r ,D =AB -C 2,根据定义可知,A ㊁B ㊁C ㊁D 均大于零.将式(2)代入σ2=x T Vx ,整理得到M -V 投资组合的有效边界[2]R (σ,μ)=(σ,μ)ɪR 2σ21/B -(μ-C /B )2D /B 2=1{}(3)即σ2=D -1(B μ2-2C μ+A )(4)在上式中对μ求导,可以得到模型的全局最小期望收益率为C /B ,标准差为1/B .1.2 最小化风险-收益比投资组合模型定义方差-均值比(variance -mean ratio ,VMR )模型为min σ2/μs.t.r T x =μe T x =1(5)其经济学含义是投资者在投资一定数额的资产后,平均每一单位收益所承受的风险波动.模型意在使得单位收益率下所承受的风险波动越小越好.1.3 均值-VaR 与均值-AVaR 投资组合模型VaR 在概率统计中的表达式[7]为Prob (r <VaR α[r ])=1-α(6)其中r 表示投资组合X 的收益率,α(0.5<α<1.0)为置信水平,且VaR α[r ]>0.假设不存在卖空行为,资产收益率与投资组合收益率r 均服从正态分布,即r ~N (μ,σ2),于是式(6)可变形为VaR α[r ]=z ασ-μ(7)其中z α表示标准正态分布的α分位点,则有z α=φ-1(α),φ(㊃)表示标准正态分布的分布函数[8].用VaR 代替式(1)中的方差作为目标函数,得到均值-VaR 模型[2]:min z ασ-μ=z αx T Vx -μs.t.r T x =μe T x =1(8)另外,模型(8)的边界有如下形式:R (VaRα,μ)=(VaR α,μ)ɪR 2VaR α+μz α,μæèçöø÷ɪR (σ2,μ){}根据模型(8),文献[2]中给出的均值-AVaR投资组合模型为minAVaR α=VaR αμ=z ασ-μμs.t.r T x =μe T x =1(9)显然,此模型表示投资者在投资一定数额的资产后,在给定的置信水平下,平均每一单位收益所承受的损失额,使得在单位收益率下所承受的损失额越小越好[2].2 投资组合模型解的有效性分析定理1若全局最小VMR 投资组合存在,那么它一定是均值-方差有效的.证明若VMR 模型的最优解存在,设最优投资组合为x *VMR ,对应的均值和标准差分别为μ(x *VMR )和σ(x *VMR ).如果x *VMR 不是均值-方差有效的,则存在另一个可行解x *满足μ(x *)ȡμ(x *VMR )和σ(x *)ɤσ(x *VMR ),且至少有一个为严格不等式,不妨设μ(x *)>μ(x *VMR),依据VMR 的目标函数可知VMR (x *)<VMR (x *VMR)这与x *VMR 是全局最小VMR 投资组合矛盾,因此x *VMR 是M -V 有效投资组合.Ѳ根据M -V 的有效边界理论,VMR 模型的解是有效解,则可以将式(4)代入模型(5)的目标得到min σ2μ=D -1(B μ2-2C μ+A )μ在上式中对μ求导,令0=d d μD -1(B μ2-2C μ+A )μæèçöø÷=(2D -1B μ-2D -1C )μ-D -1(B μ2-2C μ+A )μ2=D -1B μ2-D -1Aμ2得唯一的驻点μ=A /B ,继续求得二阶导数d 2(D -1(B μ2-2C μ+A ))d μ2=2D -1A μ3124 第4期周伊佳等:几种最优投资组合在有效边界上相对位置由于已知D >0,所以有D -1>0,又已知A >0,综合得到d 2VMR /d μ2>0,因此VMR 在μ=A /B 处存在唯一的最小值2D -1AB -2D -1C .类似地,可以得到下面的结论:定理2若全局最小均值-AVaR 投资组合存在,那么它一定是均值-方差有效的.证明略.根据最小均值-AVaR 模型的有效性,可以将式(4)代入模型(9)得到min AVaR α=VaR αμ=z αD -1(B μ2-2C μ+A )-μμ同样利用求导的方法,可以得到均值-AVaR模型在μ=A /C 处取得唯一最小值[2],且根据式(4)得到对应的标准差σ=A /C .另外,在置信水平α>φ(D /B )下,全局最小均值-VaR 投资组合存在,且是均值-方差有效的[9].最优投资组合对应的均值为C /B +D B z 2αB z 2α-D -1B æèçöø÷,标准差为z 2αB z 2α-D.1972年Merton[10]指出:在某一投资组合中若存在无风险证券,设无风险收益率为r f ,当且仅当此资本市场线为μ=r f +(Br f 2-2Cr f +A )σ时,资本市场线与M -V 模型的有效边界相切,设此切点为M .得到M 点的收益率为(A -Cr f )/(C -Br f ),标准差为Br f 2-2Cr f +A C -Br f,斜率为k =Br f 2-2Cr f +A .定理3设与有效边界相切的资本市场线斜率为k ,则有φ(2D /(B -C B /A ))>φ(A )>φ(k )>φ(D /B )且任取置信水平α满足α>φ(k ),全局最小均值-VaR 投资组合存在,且是均值-方差有效的.证明由于AB -C 2>C 2-CAB ,有2(AB -C 2)>AB -C AB再根据D =AB -C 2,有2D >AB -CAB ,不等式变形得到2DB -C B /A>A即φ(2D /(B -CB /A ))>φ(A ).由于无风险收益率一定满足r f <μ=C /B ,否则问题将没有意义,从而有A >Br f 2-2Cr f +A因此有φ(A )>φ(k ).再根据C -Br f >0,有B 2r f 2-2CBr f +C 2>0,且已知D =AB -C 2,B ㊁D 均大于零,因此有B 2r f 2-2CBr f +AB >D此时的斜率k =Br f 2-2Cr f +A ,故整理得到k >D /B ,有φ(k )>φ(D /B ).综上所述,对与有效边界相切的资本市场线斜率k ,有φ(2D /(B -C B /A ))>φ(A )>φ(k )>φ(D /B )成立,并且根据文献[9]知,对满足α>φ(D /B )的任意置信水平α,全局最小均值-VaR 投资组合存在,且是均值-方差有效的.Ѳ3 投资组合在有效边界上的相对位置前文中给出了各投资组合模型最优解的有效性,接下来研究各模型的最优解在有效边界上的相对位置.定理4在有效边界上,从下到上对应的投资组合为最优M -V 投资组合㊁最优VMR 投资组合与最优均值-AVaR 投资组合和切点M .证明全局最小M -V 投资组合的期望收益率为C /B ,最小VMR 投资组合的期望收益率为A /B ,两值作比较有μVMR μM-V =A /B C /B =C 2+DC 2>1因此有A /B >C /B ,即μVMR >μM -V ,则最优M -V 投资组合在最优VMR 投资组合之下.其次,均值-AVaR 投资组合的期望收益率为A /C ,与VMR 投资组合的期望收益率作比较得到224大连理工大学学报第56卷μVMR μAVAR=A /B A /C =C 2C 2+D<1因此有A /B <A /C ,故证明最优VMR 投资组合位于最优均值-AVaR 投资组合之下.再次,已知M 点的收益率为A -Cr f C -Br f,均值-AVaR 模型的最优解处的收益率为A /C ,两值作比较有μM μAVaR =A -Cr f C -Br f ㊃C A =AC -C 2r f AC -ABr f已知D =AB -C 2>0,因此μM /μAVaR >1,可见最优均值-AVaR 投资组合位于M 点之下.Ѳ根据定理4,这4种最优投资组合在有效边界上的相对位置如图1所示.图1 最优投资组合在有效边界上的相对位置Fi g .1 Relative location of o p timal p ortfolios onefficient frontier定理5设与有效边界相切的资本市场线斜率为k ,任取置信水平α满足φ(k )>α>φ(D /B )则最优均值-VaR 投资组合在切点M 之上.证明由定理3知道对任意的置信水平α满足已知条件,全局最小均值-VaR 投资组合存在,方差为z2αB z 2α-D.另外,已知M点的标准差为Br f 2-2Cr f +A C -Br f ,斜率为k =Br f 2-2Cr f +A ,则有σ2M=Br 2f -2Cr f +A C -Br fæèçöø÷2=Br f 2-2Cr f +A B 2r f 2-2BCr f +C 2=Br f 2-2Cr f +A B (Br f 2-2Cr f +A )-D =k 2Bk 2-D由于α<φ(k ),有D /z α2>D /k 2,故B -D /z 2α<B -D /k 2可以得到1/σ2VaR <1/σ2M ,即σ2VaR >σ2M ,可见最优均值-VaR 投资组合存在,且位于M 点之上.Ѳ综上,根据定理4和定理5的结论可知:在某一投资组合中存在无风险证券时,取资本市场线的斜率为k ,任取置信水平α满足φ(k )>α>φ(D /B )则各最优投资组合在有效边界上从下到上的排列依次为最优M -V 投资组合㊁VMR 投资组合㊁均值-AVaR投资组合㊁切点M 和均值-VaR 投资组合.如图2所示.图2 当置信水平满足φ(k )>α>φ(D /B )时最优投资组合的相对位置Fi g .2 Relative location of o p timal p ortfolios withthe confidence level φ(k )>α>φ(D /B )定理6设与有效边界相切的资本市场线斜率为k ,任取置信水平α满足φ(A )>α>φ(k )则最优均值-VaR 投资组合在有效边界上位于最优均值-AVaR 投资组合之上㊁M 点之下.证明由定理3知道对任意的置信水平α满足已知条件,使得全局最小均值-VaR 投资组合存在,标准差为z 2αB z 2α-D,全局最小均值-AVaR 投资组合的标准差为A /C ,两值作比较有σVaR σAVaR =z 2αB z 2α-D ㊃C A=C 2z 2αAB z 2α-AD =324 第4期周伊佳等:几种最优投资组合在有效边界上相对位置C 2z 2αC 2z 2α+D z 2α-AD由α>φ(k ),保证了分母AB z 2α-AD >0.已知φ(A )>α,故σVaR /σAVaR >1.由此可见,最优均值-VaR 投资组合位于最优均值-AVaR 投资组合之上.由于α>φ(k ),即z α>k ,有D /z α2<D /k 2,故B -D /z α2>B -D /k 2.并且已知σ2M=k 2Bk 2-D ,σ2VaR =z 2αB z 2α-D 可以得到1/σ2VaR >1/σ2M ,即σ2VaR <σ2M ,可见全局最小VaR 投资组合存在,且位于M 点之下.Ѳ综上所述,根据定理4和定理6的结论可知:在某一投资组合中存在无风险证券时,取资本市场线的斜率为k ,任取置信水平α满足φ(A )>α>φ(k )则最优M -V 投资组合㊁VMR 投资组合㊁均值-AVaR 投资组合㊁均值-VaR 投资组合和切点M 在有效边界上的排列如图3所示.图3 当置信水平满足φ(A )>α>φ(k )时最优投资组合的相对位置Fi g .3 Relative location of o p timal p ortfolios withthe confidence level φ(A )>α>φ(k )定理7任取置信水平α满足φ(2D /(B -C B /A ))>α>φ(A )则最优均值-VaR 投资组合位于最优VMR 投资组合之上㊁最优均值-AVaR 投资组合之下.证明由定理3知道对任意的置信水平α满足已知条件,全局最小均值-VaR 投资组合存在,且在此置信水平下,α<φ2D B -C B /A æèçöø÷⇔z 2α<2D B -C B /A由于2D B -C B /A =2DB /A (AB -C )=2DA /B (AB -C )(AB -C )2因此有z 2α<2D A /B (AB -C )(AB -C )2,根据D =AB -C 2将不等式变为如下的等价形式:(2AB -2CAB +D )z 2α<2D (A -CA /B )整理得到(2A -2C A /B )(B z 2α-D )<D z 2α(10)由于全局最小均值-VaR 投资组合存在,方差为z 2αB z 2α-D,全局最小VMR 投资组合的方差为D -1(2A -2C A /B ),通过两值作比较,再根据式(10)有σ2VMRσ2VaR =2A -2C A /B D z 2αB z 2α-D<1从而说明了最优VaR 投资组合位于最优VMR 投资组合之上.在置信水平α>φ(A )下,全局最小均值-VaR 投资组合的标准差为z 2αB z 2α-D,全局最小均值-AVaR 投资组合的标准差为A /C ,两值作比较有σVaR σAVaR =z 2αB z 2α-D ㊃C A=C 2z 2αAB z 2α-AD =C 2z 2αC 2z 2α+D z 2α-AD因为α>φ(A ),即z α>A ,因此σVaR /σAVaR <1,则最优均值-VaR 投资组合位于最优均值-AVaR 投资组合之下.Ѳ根据定理4和定理7得到这样的结论:在某一投资组合中存在无风险证券时,取资本市场线的斜率为k ,任取置信水平α满足φ(2D /(B -C B /A ))>α>φ(A )424大连理工大学学报第56卷则在有效边界上从下到上的排列依次为最优M -V 投资组合㊁VMR 投资组合㊁均值-VaR 投资组合㊁均值-AVaR 投资组合和切点M .如图4所示.图4 当置信水平满足φ2DB -C B /A æèçöø÷>α>φ(A )时最优投资组合的相对位置Fi g .4 Relative location of o p timal p ortfolios withthe confidence level φ2D B -C B /A æèçöø÷>α>φ(A )定理8任取置信水平α满足α>φ(2D /(B -C B /A ))则最优均值-VaR 投资组合位于最优VMR 投资组合之下㊁最优M -V 投资组合之上.证明由于在此置信水平α下,全局最小均值-VaR 投资组合存在,方差为z 2αB z 2α-D,全局最小VMR 投资组合的方差为D -1(2A -2C A /B ),且有α>φ2D B -C B /A æèçöø÷⇔z 2α>2D B -C B /A类似于定理7的证明,将不等式变形后可以得到σ2VMRσ2VaR =2A -2C A /B D z 2αB z 2α-D>1从而说明了最优VMR 投资组合位于最优均值-VaR 投资组合之上.全局最小均值-VaR 投资组合收益率为C B+D B z 2αB z 2α-D -1B æèçöø÷,M -V 投资组合收益率为C B,显然,最优均值-VaR 投资组合位于M -V 投资组合之上.Ѳ根据定理4和定理8的结论可知:在某一投资组合中存在无风险证券时,取资本市场线的斜率为k ,任取置信水平α满足α>φ(2D /(B -C B /A ))则最优M -V 投资组合㊁均值-VaR 投资组合㊁VMR 投资组合㊁均值-AVaR 投资组合和切点M 在有效边界上的排列如图5所示.图5 当置信水平满足α>φ(2DB -C B /A)时最优投资组合的相对位置Fi g .5 Relative location of o p timal p ortfolios with theconfidence level α>φ(2D B -C B /A)4 结 语本文基于均值-方差模型的有效边界理论,证明了已有的一些投资组合优化模型的最优投资组合是均值-方差有效的.通过计算各模型最优解处的均值和标准差,分析了这些最优投资组合在有效边界上的相对位置,并给出了具体图形.利用给出的图形,投资者可以对这些最优投资策略的相对保守程度有更直观的认识,从而,根据自己的投资喜好,选择适合自己的投资策略.另外,本文也指出,全局最小M -V 投资组合㊁VMR 投资组合㊁均值-AVaR 投资组合与切点M在有效边界上的相对位置是不变的.但在不同的置信水平下,最优均值-VaR 模型的投资组合在有效边界上的相对位置会发生改变.因此在利用均值-VaR 模型确定投资决策时,要将α的影响因素考虑在内.524 第4期周伊佳等:几种最优投资组合在有效边界上相对位置参考文献:[1]Markowitz H.Portfolio selection[J].The Journalof Finance,1952,7(1):77-91.[2]王尚户,张崇岐.基于均值-AVaR的投资组合均衡分析[J].广州大学学报(自然科学版),2007, 6(6):11-13.WANG Shan g-hu,ZHANG Chon g-q i.Mean-AVaRbased p ortfolio balanced anal y sis[J].Journal ofGuan g zhou Universit y(Natural Science Edition),2007,6(6):11-13.(in Chinese)[3]Alexandre G,Ba p tista A M.Economic im p licationsof usin g mean-VAR model for p ortfolio selection:acom p arison mean-variance with anal y sis[J].Journal of Economic D y namics&Control,2002, 26(7-8):1159-1193.[4]Basak S,Sha p iro A.Value-at-risk-based riskmana g ement:o p timal p olicies and asset p rices[J].Review of Financial Studies,2001,14(2):371-405.[5]Genca y R,Selcuk F,Ulu g ul y a g ci A.Hi g hvolatilit y,thick tails and extreme value theor y invalue-at-risk estimation[J].Insurance:Mathematicsand Economics,2003,33:337-356.[6]张红兵,李高明,邸涛.多阶段资产组合选择均值-VaR模型的研究[J].纺织高校基础科学学报,2005,18(2):158-161.ZHANG Hon g-bin g,LI Gao-min g,DI Tao.Stud yon mean-VaR models for multi-p eriod p ortfolioselection[J].Basic Sciences Journal of TextileUniversities,2005,18(2):158-161.(in Chinese) [7]屠新曙,王春峰.最佳均值-VaR投资组合问题的研究[J].湘潭大学自然科学学报,2002,24(2):13-17.TU Xin-shu,WANG Chun-fen g.The mean-VaRo p timum p ortfolio model[J].Natural ScienceJournal of Xian g tan Universit y,2002,24(2):13-17.(in Chinese)[8]林旭东,巩前锦.正态条件下均值-CVaR有效前沿的研究[J].管理科学,2004,17(3):52-55.LIN Xu-don g,GONG Qian-j in.Research on theefficient frontier of mean-CVaR under normaldistribution condition[J].Mana g ement Sciences inChina,2004,17(3):52-55.(in Chinese) [9]荣喜民,武丹丹,张奎廷.基于均值-VaR的投资组合最优化[J].数理统计与管理,2005,25(5):96-103.RONG Xi-min,WU Dan-dan,ZHANG Kui-tin g.Mean-VaR based p ortfolio o p timization[J].Journalof A pp lied Statistics and Mana g ement,2005,25(5):96-103.(in Chinese)[10]Merton R C.An anal y tic derivation of the efficientp ortfolio frontier[J].The Journal of Financial andQ uantitative Anal y sis,1972,7(4):1851-1872.Relative location of o p timal p ortfolios on efficient frontierZHOU Yi-j ia,YU Bo*(School of Mathematical Sciences,Dal ian Universit y of Technolo gy,Dal ian116024,China) Abstract:The validities of the o p timal solutions of reward-risk p ortfolio o p timization models are discussed,such as mean-VaR model,mean-AVaR model,mean-variance ratio model,etc..It is p roved that based on Markowitz mean-variance model and efficient frontier theor y,if the o p timal p ortfolios exist,the y must be located on the efficient frontier of mean-variance.The mean and standard deviation of these models'o p timal solutions are calculated.Accordin g to the calculated results,the relative location of the o p timal p ortfolios on the efficient frontier is discussed. Particularl y,the location of mean-VaR model's o p timal p ortfolio on the efficient frontier varies with confidence levels.Ke y words:p ortfolio o p timization model;o p timal p ortfolio;efficient frontier624大连理工大学学报第56卷。
投资组合中的可行集与有效边界问题研究剖析

投资组合中的可行集与有效边界问题研究王晓乐(常州工学院经济与管理学院,江苏常州213002)摘要:本文从从马科维茨的投资组合理论思想出发,在已有结论基础之上,利用均值方差模型分别研究了风险资产组合和引入无风险资产后各自有效边界的确定和解析表达式,随之引入CAPM模型着重分析了资本市场中,投资者如何确定投资组合来均衡收益与风险之间的关系。
文末就CAPM的有效性问题和股票收益与风险的关系这两个延伸问题进行了简单的探讨。
关键词:投资可行集有效边界CAPM模型一、引言(一)课题研究的背景面对五花八门的投资对象,大家都明白“鸡蛋不要都放在同一个篮子里”的简单道理,那么“鸡蛋”应该放在几个“篮子”里,这些“篮子”各有什么特点?在资本市场中,马科维茨的投资组合选择理论和在此基础上发展形成的CAPM模型,历来是投资者面对风险和收益决策投资组合的重要理论依据。
投资者在资本市场中,如何平衡风险与收益之间的关系,如何有效决策资产组合,这些都是关键问题。
(二)课题研究的价值投资有效组合,使资产风险合理分散化,通过充分利用数学知识,借助计量经济学的帮助,分析投资理论中的风险类型和收益模型,推导在各种风险资产组合中的可行集和有效边界,风险最小的情况下,使得投资组合获得最大利益,从而更好地服务于现代证券市场。
二、已有相关研究观点评介关于资产定价的原理和模型的研究,国内不乏众多学者。
合肥工业大学经济管理学院的邓英东教授(2004)在他的文章中评述:Markowitz的证券组合选择理论,在今天已经成为现代金融经济学的基石,人们在处理证券组合的收益-风险分析时,Markowitz理论始终是一种基本工具。
[1]东华大学理学院的陈静、胡良剑教授认为:金融决策的核心问题就是权衡证券收益与风险的问题。
[2]在论述有关CAPM模型的作用时,中国人民大学金融专业博士生导师吴晓求教授在他的文章里写道:CAPM给出了一个非常简单的结论,只有一种原因会使投资者得到更高回报,那就是投资高风险的股票。
有效组合边界分析

定义2:
• 在均值-方差分析中,如果有两个均值方差前沿组 合xP和xQ ,它们满足以下两个条件之一:(1) ~ ~ ~ ~ E(rP ) ≥ E(rQ )并且var(rP ) < var(rQ ) ;(2) ~ ~ ~ ~ E(rP ) >E(rQ )并且var(rP ) ≤var(rQ ) ,则称在均值 方差意义上xP占优于xQ 。 • 可以比较一下均值方差意义上的占优和随机占优。 可以看出,均值方差意义上的占优比随机占优更 综合的兼顾了预期收益和风险两个方面。
§6.2 均值-方差前沿组合
• 首先,市场上有N项风险资产,k=1,2, …,N ,各 ~ ~ 项资产的收益率合记为收益率向量r =( r1 , ~ ~ ~ ~ T r2 …, rN ) 。预期收益率向量记为r =(E( r1 ), ~ ~ E( r2 ), …, E(rN ))T,收益率的协方差矩阵记为 ~ ~ N ={σij}ij=1 ,其中σij=cov(ri , rj )。 ak, k=0,1, …,N,是0时期投资于第k项金融资产的资 金额,显然有ak=w,w是0时期投资者拥有的禀 赋。 xk= ak/w表示投资组合中的权重,权重向量记 为x=( x1, x2,…, xN)T,xk =1。到1时期,投资 ~ ~ ~ 者拥有的财富是w =ak(1+ rk ),即w =a T (1+ ~ r )。
涵义:
• 式中,μ是一个预期收益水平。加上系数1/2是为 了数学处理的方便,不影响优化解的结果。 • 优化模型的经济涵义是,在设定了投资组合的预 期收益水平后,要使投资组合的风险(方差)尽 可能的小。 • σP= xTx就是投资组合的方差。因为组合中的资 产是风险资产,所以σP≥0。这样,可以通过构造 拉格朗日函数来解前面的二次规划,得到xP 。
组合投资中有效边界的一些性质和模型

组合投资中有效边界的一些性质和
模型
组合投资中有效边界也称为最佳组合分配曲线,是一条用来描述投资者在投资组合中投资不同资产的最优配置线。
它显示了投资者可以在多种投资组合间选择最优的投资方案,从而获得最大的收益,并使其投资风险水平达到最低。
性质: 1、有效边界在投资组合空间中是凸的,表示投资者在获取最大收益的情况下,风险也是最小的。
2、有效边界是一维的,即只有一种投资组合可以达到最佳收益和最低风险水平。
3、有效边界是非线性的,因为它受到多重因素的影响,如资产价格波动率,资产相关性等。
模型: 1、Markowitz模型:它是组合投资理论的基础,由美国经济学家Harry Markowitz在1952年提出。
该模型假设投资者只考虑风险和收益之间的权衡,忽略其他因素,并认为投资者对风险具有一致的恐惧心理。
2、CAPM模型:该模型由William Sharpe在1964年提出,它假设市场中的投资者都是理性的,而且只关心投资组合的绝对风险和绝对收益,而不关心投资组合的相对风险和相对收益。
3、Black-Litterman模型:该模型是
Markowitz和CAPM模型的结合,由Fischer Black和Robert Litterman于1990年提出,它既考虑了投资者对风险和收益之间的权衡,又考虑了投资者对相对风险和相对收益之间的权衡。
投资学-6投资组合有效边界计算

6最优投资组合选择最优投资组合选择的过程就是投资者将财富分配到不同资产从而使自己的效用达到最大的过程。
然而,在进行这一决策之前,投资者首先必须弄清楚的是市场中有哪些资产组合可供选择以及这些资产组合的风险-收益特征是什么。
虽然市场中金融资产的种类千差万别,但从风险-收益的角度看,我们可以将这些资产分为两类:无风险资产和风险资产。
这样一来,市场中可能的资产组合就有如下几种:一个无风险资产和一个风险资产的组合;两个风险资产的组合;一个无风险资产和两个风险资产的组合。
下面分别讨论。
一、一个无风险资产和一个风险资产的组合当市场中只有一个无风险资产和一个风险资产的时候,我们可以假定投资者投资到风险资产上的财富比例为w ,投资到无风险资产上的财富比例为1-w ,这样一来,投资组合的收益就可以写为:f P r w r w r )1(-+=其中,r 为风险资产收益,这是一个随机变量;f r 为无风险资产的收益,这是一个常数。
这样,资产组合的期望收益和标准差就可以写出下述形式:f P r w r wE r E )1()()(-+=σσw P =(因为122222122)1(2)1(σσσσw w w wP -+-+=,2112122,0σσρσσ===0)其中σ为风险资产的标准差。
根据上两式,我们可以消掉投资权重,并得到投资组合期望收益与标准差之间的关系:P ff P r r E r r E σσ-+=)()( 3-1当市场只有一个无风险资产和一个风险资产时,上式就是资产组合所以可能的风险-收益集合,又称为投资组合的可行集合。
在期望收益-标准差平面上,3-1是一条直线,我们称这条直线为资本配置线。
随着投资者改变风险资产的投资权重w ,资产组合就落在资本配置线上的不同位置。
具体来说,如果投资者将全部财富都投资到风险资产上1>w ,资产组合的期望收益和方差就是风险资产的期望收益和方差,资产组合与风险资产重合。
如果投资者将全部财富都投资在无风险资产上0>w ,资产组合的期望收益和方差就是无风险资产的期望收益和方差,资产组合与无风险资产重合。
有效投资组合

当投资者能够以无风险利
率借入资金时,可能的投资
组合对应点所形成的连线就
是资本市场线,资本市场线可
以看作是所有资产,包括风
险资产和无风险资产的有效
集。资本市场线在A点与有效
投资组合曲线相切,A点就是
最优投资组合,该切点代表
了投资者所能获得的最高满
有效投资组合
•
大家已经知道,投资组合可以降低风险,
但是,任意投资组合却不一定是有效投资组
合。那么我们怎样来认识这个问题呢?
• (一)有效边界
•
根据马克维茨的投资组合理论,有效证
券组合主要包括两种性质的证券或证券组合:
一种是在同等风险条件下收益最高的证券组
合,另一种是在同等收益条件下风险最小的
证券组合。这两种证券组合的集合叫做有效
具有无风险资产的最优风险组合在什么位置?
报酬
CML:最优资本分配线
Rf
P
图中:通过无风险报酬率在纵轴的截点,我们可以画 出若干条射线。由于无风险资产和确定的有效边界, 我们选择具有最陡的坡度(即斜率最高)的资本分 配线(CML)。
报酬
资本市场线
M
Rf
P
由确定的资本分配线,所有的投资者都会沿着这条线 分配资金——无风险资产与M点的市场组合进行结合, 因为M点的市场组合对于所有投资者都具有共同期望。
那么,多种资产组合的有效集又会怎样呢?
报酬
最小方差 组合
各种资产组合
P
图中:通过给出的各种资产的机会集,我们可以确 定最小方差组合(资产组合曲线最左边的点)。
多种资产组合的有效集在什么位置?请看图:
均值-方差分析方法和投资组合有效边界模型

该理论包含两个重要内容:均值-方差分析方法和投资组合有效边界模型。
在发达的证券市场中,马科维茨投资组合理论早已在实践中被证明是行之有效的,并且被广泛应用于组合选择和资产配置。
但是,我国的证券理论界和实务界对于该理论是否适合于我国股票市场一直存有较大争议。
从狭义的角度来说,投资组合是规定了投资比例的一揽子有价证券,当然,单只证券也可以当作特殊的投资组合。
本文讨论的投资组合限于由股票和无风险资产构成的投资组合。
人们进行投资,本质上是在不确定性的收益和风险中进行选择。
投资组合理论用均值—方差来刻画这两个关键因素。
所谓均值,是指投资组合的期望收益率,它是单只证券的期望收益率的加权平均,权重为相应的投资比例。
当然,股票的收益包括分红派息和资本增值两部分。
所谓方差,是指投资组合的收益率的方差。
我们把收益率的标准差称为波动率,它刻画了投资组合的风险。
人们在证券投资决策中应该怎样选择收益和风险的组合呢?这正是投资组合理论研究的中心问题。
投资组合理论研究“理性投资者”如何选择优化投资组合。
所谓理性投资者,是指这样的投资者:他们在给定期望风险水平下对期望收益进行最大化,或者在给定期望收益水平下对期望风险进行最小化。
因此把上述优化投资组合在以波动率为横坐标,收益率为纵坐标的二维平面中描绘出来,形成一条曲线。
这条曲线上有一个点,其波动率最低,称之为最小方差点(英文缩写是MVP)。
这条曲线在最小方差点以上的部分就是著名的(马考维茨)投资组合有效边界,对应的投资组合称为有效投资组合。
投资组合有效边界一条单调递增的凹曲线。
如果投资范围中不包含无风险资产(无风险资产的波动率为零),曲线AMB是一条典型的有效边界。
A点对应于投资范围中收益率最高的证券。
如果在投资范围中加入无风险资产,那么投资组合有效边界是曲线AMC。
C点表示无风险资产,线段CM是曲线AMB的切线,M是切点。
M点对应的投资组合被称为“市场组合”。
如果市场允许卖空,那么AMB是二次曲线;如果限制卖空,那么AMB是分段二次曲线。
有效边界和最优投资组合

有效边界和最优投资组合风险偏好与⽆差异曲线不同的投资者对收益的偏好和对风险的厌恶程度是有差异的,这⼀差异的存在⽆疑会影响到他们对于投资对象的选择。
因此,我们在寻找最优投资策略时必须把投资风险、收益和投资者偏好同时加以考虑。
风险偏好相对风险⽽⾔投资者对收益的偏好,有三种类型:喜好风险型,投资者为了获得较⾼投资收益,愿意承担相对较⾼的投资风险;厌恶风险型,投资者获得⼀定投资收益时,只愿意承担相对较低的投资风险;风险中性。
⽆差异曲线投资者⽆差异曲线是指能够给投资者带来相同满⾜程度的收益与风险的不同组合。
⽆差异曲线的斜率表⽰风险和收益之间的替代率,斜率越⾼,表明为了让投资者多冒同样的风险,必须给他提供的收益补偿也应越⾼,说明该投资者越厌恶风险。
同样,斜率越低,表明该投资者厌恶风险程度较轻。
2有效边界和最优投资组合编辑现实⽣活中证券种类繁多,可以构成⽆数组合,根据马柯维茨的有效集定理,可以确定最优投资组合的⽅法。
(1)可⾏集可⾏集是指由n种证券所形成的所有组合的集合,它包括了现实⽣活中所有可能的组合。
也就是说,所有可能的组合将位于可⾏集的内部或边界上。
⼀般来说,可⾏集的形状像伞状。
(2)有效集有效集是指能同时满⾜预期收益率最⼤,风险最⼩的投资组合的集合。
对于⼀个理性投资者⽽⾔,他们都是厌恶风险⽽偏好收益的。
对于同样的风险⽔平,他们将会选择能提供最⼤预期收益率的组合;对于同样的预期收益率,他们将会选择风险最⼩的组合。
能同时满⾜这两个条件的投资组合的集合就是有效集。
有效集曲线具有如下特点:有效集是⼀条向右上⽅倾斜的曲线,它反映了“⾼收益、⾼风险“的原则;有效集是⼀条向上凸的曲线有效集曲线上不可能有凹陷的地⽅。
点击查看相关图形(3)最优投资组合最优投资组合是投资者的⽆差别曲线和有效集的切点。
有效集向上凸的特性和⽆差异曲线向下凹的特性决定了有效集和⽆差异曲线的相切点只有⼀个,也就是说最优投资组合是唯⼀的。
对于投资者⽽⾔,有效集是客观存在的,它是由证券市场决定的,⽽⽆差异曲线则是主观的,它是由投资者风险―收益偏好决定的。
投资组合之——有效边界(Efficient frontier)

.概述:有效边界是用来描述一项投资组合的风险与回报之间的关系,在以风险为横轴,预期回报率为纵轴的坐标上显示为一条曲线,所有落在这条曲线上的风险回报组合都是在一定风险或最低风险下可以获得的最大回报。
基础:1、追求收益最大化的规律特征这一特征表现在:当风险水平相当时,理性投资者都偏好预期收益较高的交易。
在可能的范围内,投资者总是选择收益率最高的资产;但是另一方面,与之相对的市场资金需求者为了自身收益最大化的要求则要选择成本最低的融资方式。
2、厌恶风险的规律特征这一特征表现在,当预期收益相当时,理性投资者总是偏好风险较小的交易。
风险越大,风险补偿额也就越高。
3、求效用最大化追求效用最大化就是要选择能带来最大满足的风险与收益的资产组合。
效用由无差异曲线表示,可供选择的最佳风险与收益组合的集合由有效益边界表示,效用曲线与有效益边界的切点就是提供最大效用的资产组合。
(1)风险厌恶的资金供应者的无差异曲线。
金融市场的无差异曲线表示在一定的风险和收益水平下,资金供应者对不同资金组合的满足程度无区别的,即同等效用水平曲线。
如下图是一组风险厌恶的资金供应者的无差异曲线。
不同水平的曲线代表着效用的大小,水平越高,效用越大,这里曲线C显然代表这最大效用。
风险厌恶投资者的无差异曲线图曲线的凸向反映着资金供应者对风险的态度,由于X轴是风险变量,Y轴是预期收益变量,因此,曲线右凸反映风险厌恶偏好。
风险厌恶者要求风险与收益成正比,曲线越陡,风险增加对收益补偿要求越高,对风险的厌恶越强烈;曲线斜度越小,风险厌恶程度越弱。
风险中性的无差异曲线为水平线,风险偏好的无差异曲线为左凸曲线。
待续...参考文献:《证券投资学》第二版第10章证券组合管理如有侵权请联系告知删除,感谢你们的配合!精品。
投资学讲义目录

投资学(现代投资理论)前言我们先考虑如下三个问题1Finance是什么?2Finance金融体系内容是什么?3投资学(现代投资理论)是什么?Finance,在中文中有这么几个意思:理财(对个人、家庭、企业、公司)、财务(企业或公司)、金融(投融资机构:基金公司,银行等)、财政(国家)等意思所以把Finance仅仅翻译成金融是不恰当的。
有三本著名的金融财务杂志(1)JFE(Journal of Financial Economics)(2)JF(Journal of Finance这是美国金融学会的)(3)RFS(Reviews of Financial Studies)有三个国际性的证书考试:(1) CFA(Chartered Financial Analyst特许金融分析师:是证券投资与管理界的一种职业资格称号,由美国“特许金融分析师学院”(ICFA)发起成立,每年在全球范围内举行资格考试。
CFA 协会主办的CFA 课程和考试被认为全球投资专业里最为严格的考试,在投资知识、专业标准及道德操守方面制定了全球准则。
CFA特许状持有人可以向其客户、雇主和同事表明他已经修读了一套严谨的专业课程,知识涵盖了广泛的投资领域,并且承诺遵守最高的职业道德准则。
因此,CFA特许状被投资业看成一个“黄金标准”,投资者也希望找到那些持有CFA特许状的专业人士,因为这一资格被认为是投资业界中具有专业技能和职业操守的承诺。
)要上万美元的考试费。
特许金融分析师 (CFA)报考条件:大四学生及以上。
取得资格所需时间(平均):3-4 年。
取得资格所需费用(不含培训):RMB18,000。
国际认可程度:高,全球投资领域通行证。
国内认可程度:高,是高端金融领域“王牌”认证,目前12000 名考生,800-1000 名持证人,2007 年考生增长57%。
薪酬水平:对投资行业薪酬状况的调查表明,雇主愿意提供高额奖金给拥有CFA特许资格认证的投资专业人士。
投资组合边界名词解释

投资组合边界名词解释
1.投资组合:是指由多种金融资产组成的投资组合,包括股票、债券、基金、外汇等。
2.风险:指投资组合的价格波动或投资回报的不确定性,也称为波动性。
风险分为系统性风险和非系统性风险。
3.收益:指投资组合的回报,包括股息、利息、资本收益等。
4.方差:指尽管平均回报相同,不同组合收益率的偏离程度,通常用
来衡量风险。
5.标准差:是方差的平方根,是一种常见的风险度量方法。
6.有效边界:是指那些实现最大收益率的组合,它们都处于风险和收
益之间的一个区域。
7.无风险资产:是指一个没有任何风险的资产,例如国债。
8.无风险利率:是指无风险资产的收益率。
9.处理方案:是指在线性规划方法中,寻找有效边界的过程。
Chapter 09 - 计算没有卖空限制的有效投资组合

c
i 1
其中 方
, cˆ
c
c
是一个N维常数列向量,
zˆ 是上左线性
程组的解。
基本定理
定理2 如果已知包络线上两个不同的组合,那
么包络线上的其他点一定是这两个已知 组合的凸组合。 通过两个包络线上的不同组合,我们可 以“重建”整个包络线。
§2 计算有效边界 -一个例子
表9.2给出一个四风险资产的投资组合,根据定理1和 2我们将寻找包络线的任务分为两步:
1、找到两个包络线上的组合; 2、通过两个已知组合“重建”包络线。
Excel提供MINVERSE()计算逆矩阵
§3 计算资本市场线
我们知道市场组合M是过无风险资产和有效边界 相切的直线的切点,根据定理1,我们知道:
第七章 没有卖空限制的有效投 资组合
主要内容
理论回顾
计算有效 边界
计算CML
§1 理论回顾
本章主要学习如何通过Excel在没有卖空限制 的条件下计算投资组合的有效边界。
基本定理
定理1 包络线上的组合可以通过下面的方程组来寻找:
zˆ E(r) cˆ
i
zi
n
zi
Z (R rf )
XT (
z1
,
z2
,,
zN
)T
N
N
N
zi zi zi
i 1
i 1
i 1
同时,资本市场线的方程为
rP
ห้องสมุดไป่ตู้
rM rf
M
P
rf
试在表9.3中计算资本市场线。
投资学(高级教程)(04)-有效投资组合

(4.1)
n
n
n
因为 ZTF = [xi (1 ) yi ] = xi (1) yi = 1
i 1
i1
i1
所以 Z 。故为凸集。证毕。
附:凹函数(定义):
对任意X、Y∈(凸集),若恒有:
f(w1X+w2Y) ≤ w1f(X)+w2f(Y) 则称 f(X) 为凹函数。(当“<”时,为严格凹函数)
同理(令h反号)可证证券组合中期望收益率同值上 升的情况。证毕。
性质6说明,当证券组合中的证券期望收益 率同值变动时,不会改变其组合期望收益率与风 险的关系。
问题:当证券组合中的证券期望收益率同值变
动时,不会改变其组合期望收益率与风险的关系, 但是否会改变原有效证券组合?换句话说,当 证券组合中的证券期望收益率同值变动时,原 (有效)证券组合是否需要调整?
所以
z2 [x+(1)y]2
故
z x+(1)y
由X、Y的任意性, 即证明了=(WTEW)1/2为凹函数。
定义4.1:一组已知的n种证券组合的“重新包装”可 以用n ×n 阶的非奇异矩阵A表示,其中
F=AF
(4.2)
重新包装的证券组合收益率、期望收益率分别为:
r*=Ar
(4.8)
有效集在空间的映射称为有效边界,为
M (R, ) min 2 W T EW,W T R R,W T F 1
(4.9)
有效集中的元素为有效证券组合,有效证券组合即指一 定投资期望收益率而风险最小的证券组合。有效集为可行 集的子集。
有效边界模型表示为:
min 2 W T EW
a' b'
投资组合值计算公式

投资组合值计算公式投资组合值是指投资者持有的所有资产的总价值。
计算投资组合值的公式可以帮助投资者了解他们的投资组合在特定时间点的价值,从而进行有效的资产配置和风险管理。
本文将介绍投资组合值的计算公式,并对其应用进行分析。
投资组合值的计算公式可以表示为:PV = ΣWi Pi。
其中,PV代表投资组合值,Wi代表第i个资产在投资组合中的权重,Pi代表第i个资产的价格。
这个公式的含义是,投资组合值等于各个资产的权重乘以其价格的总和。
在这个公式中,Wi通常表示为投资者在投资组合中持有的每个资产的比例。
例如,如果一个投资者持有股票、债券和现金,那么他们可以根据其投资金额来确定每个资产在投资组合中的权重。
假设投资者持有10000美元的股票、5000美元的债券和2000美元的现金,那么股票的权重为10000 / (10000 + 5000 + 2000) =0.555,债券的权重为5000 / (10000 + 5000 + 2000) = 0.278,现金的权重为2000 / (10000 + 5000 + 2000) = 0.167。
Pi代表每个资产的价格。
对于股票和债券,其价格可以通过市场报价来获取;对于现金,其价格可以视为1。
因此,我们可以将股票、债券和现金的价格分别表示为Pstock、Pbond和Pcash。
将权重和价格代入投资组合值的计算公式中,我们可以得到:PV = Wstock Pstock + Wbond Pbond + Wcash Pcash。
将权重和价格的具体数值代入公式中,就可以计算出投资组合的总价值。
例如,如果Wstock = 0.555,Pstock = 50,Wbond = 0.278,Pbond = 100,Wcash = 0.167,Pcash = 1,那么投资组合的总价值为:PV = 0.555 50 + 0.278 100 + 0.167 1 = 27.75 + 27.8 + 0.167 = 55.717。
均值-方差分析方法和投资组合有效边界模型。

该理论包含两个重要内容:均值-方差分析方法和投资组合有效边界模型。
在发达的证券市场中,马科维茨投资组合理论早已在实践中被证明是行之有效的,并且被广泛应用于组合选择和资产配置。
但是,我国的证券理论界和实务界对于该理论是否适合于我国股票市场一直存有较大争议。
从狭义的角度来说,投资组合是规定了投资比例的一揽子有价证券,当然,单只证券也可以当作特殊的投资组合.本文讨论的投资组合限于由股票和无风险资产构成的投资组合。
人们进行投资,本质上是在不确定性的收益和风险中进行选择。
投资组合理论用均值—方差来刻画这两个关键因素。
所谓均值,是指投资组合的期望收益率,它是单只证券的期望收益率的加权平均,权重为相应的投资比例.当然,股票的收益包括分红派息和资本增值两部分.所谓方差,是指投资组合的收益率的方差。
我们把收益率的标准差称为波动率,它刻画了投资组合的风险。
人们在证券投资决策中应该怎样选择收益和风险的组合呢?这正是投资组合理论研究的中心问题。
投资组合理论研究“理性投资者”如何选择优化投资组合。
所谓理性投资者,是指这样的投资者:他们在给定期望风险水平下对期望收益进行最大化,或者在给定期望收益水平下对期望风险进行最小化。
因此把上述优化投资组合在以波动率为横坐标,收益率为纵坐标的二维平面中描绘出来,形成一条曲线。
这条曲线上有一个点,其波动率最低,称之为最小方差点(英文缩写是MVP)。
这条曲线在最小方差点以上的部分就是著名的(马考维茨)投资组合有效边界,对应的投资组合称为有效投资组合.投资组合有效边界一条单调递增的凹曲线. 如果投资范围中不包含无风险资产(无风险资产的波动率为零),曲线AMB是一条典型的有效边界.A点对应于投资范围中收益率最高的证券。
如果在投资范围中加入无风险资产,那么投资组合有效边界是曲线AMC。
C点表示无风险资产,线段CM是曲线AMB的切线,M是切点。
M点对应的投资组合被称为“市场组合"。
如果市场允许卖空,那么AMB是二次曲线;如果限制卖空,那么AMB 是分段二次曲线。
投资组合管理第二次作业计算有效边界及CML
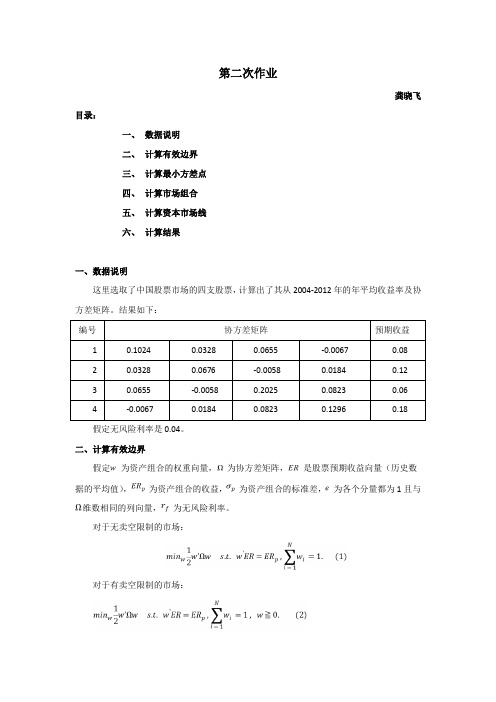
第二次作业龚晓飞目录:一、数据说明二、计算有效边界三、计算最小方差点四、计算市场组合五、计算资本市场线六、计算结果一、数据说明这里选取了中国股票市场的四支股票,计算出了其从2004-2012年的年平均收益率及协方差矩阵。
结果如下:编号协方差矩阵预期收益1 0.1024 0.0328 0.0655 -0.0067 0.082 0.0328 0.0676 -0.0058 0.0184 0.123 0.0655 -0.0058 0.2025 0.0823 0.064 -0.0067 0.0184 0.0823 0.1296 0.18假定无风险利率是0.04。
二、计算有效边界假定为资产组合的权重向量,为协方差矩阵,是股票预期收益向量(历史数据的平均值),为资产组合的收益,为资产组合的标准差,为各个分量都为1且与维数相同的列向量,为无风险利率。
对于无卖空限制的市场:对于有卖空限制的市场:对于第一个优化问题,可以使用Lagrange乘子法直接算出解的显式表达,有效前沿的表达式为:利用上面的表达式可以直接用matlab或excel画出有效前沿。
另外对第一个优化问题,可以用更加简单的方法来画有效前沿。
可以证明,给定后,可以得到与之对应的最小方差,只要赋给两个不同的值,同时得到两个相应的最小方差组合,这两个资产组合的凸组合可以形成整个有效前沿。
也就是说,假定及是两个不同的前沿组合,那么,任何其它的前沿组合都可以用来表达。
对于第二个优化问题,无法直接求得显式解,只能使用matlab或excel的二次规划函数(quadprog(H,f,A,b,Aeq,beq,lb,ub,x0))来求解出不同的所对应的最小方差,然后用这两组数据来画出有效前沿。
三、计算最小方差点以下所用记号的含义与前面相同,计算最小方差点仍然要分下面两种情况。
对于无卖空限制的市场:对于有卖空限制的市场:对于第一个优化问题,与前面一样可以使用Lagrange乘子法直接算出解的显式表达,最小方差点的收益与标准差的表达式为:上面结果也可以直接从下面表达式得到:当然上述最小方差点也可以用matlab或excel的二次规划程序来直接求解,在matlab 中所用的函数为quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6最优投资组合选择
最优投资组合选择的过程就是投资者将财富分配到不同资产从而使自己的效用达到最大的过程。
然而,在进行这一决策之前,投资者首先必须弄清楚的是市场中有哪些资产组合可供选择以及这些资产组合的风险-收益特征是什么。
虽然市场中金融资产的种类千差万别,但从风险-收益的角度看,我们可以将这些资产分为两类:无风险资产和风险资产。
这样一来,市场中可能的资产组合就有如下几种:一个无风险资产和一个风险资产的组合;两个风险资产的组合;一个无风险资产和两个风险资产的组合。
下面分别讨论。
一、一个无风险资产和一个风险资产的组合
当市场中只有一个无风险资产和一个风险资产的时候,我们可以假定投资者投资到风险资产上的财富比例为w ,投资到无风险资产上的财富比例为1-w ,这样一来,投资组合的收益就可以写为:
其中,r 为风险资产收益,这是一个随机变量;f r 为无风险资产的收益,这是一个常数。
这样,资产组合的期望收益和标准差就可以写出下述形式:
(因为122
222122)1(2)1(σσσσw w w w P -+-+=,2112122,0σσρσσ===0)
其中σ为风险资产的标准差。
根据上两式,我们可以消掉投资权重,并得到投资组合期望收益与标准差之间的关系:
P f
f P r r E r r E σσ
-+
=)()( 3-1
当市场只有一个无风险资产和一个风险资产时,上式就是资产组合所以可能的风险-收益集合,又称为投资组合的可行集合。
在期望收益-标准差平面上,3-1是一条直线,我们称这条直线为资本配置线。
随着投资者改变风险资产的投资权重w ,资产组合就落在资本配置线上的不同位置。
具体来说,如果投资者将全部财富都投资到风险资产上1>w ,资产组合的期望收益和方差就是风险资产的期望收益和方差,资产组合与风险资产重合。
如果投资者将全部财富都投资在无风险资产上0>w ,资产组合的期望收益和方差就是无风险资产的期望收益和方差,资产组合与无风险资产重合。
风险资产r 与无风险资产f r 将配置线分为三段,其中,无风险资产和风险资产之间的部分意味着投资者投资在风险资产和无风险资产上的财富都是正值;此时10<<w 。
风险资产r 的右侧的部分意味着投资者以无风险收益率借入部分资金,然后将其全部财富和借入的资金一起投资到风险资产中。
此时1>w 。
由于我们没有考虑卖空风险资产的问题,所以不存在0<w 的情况。
资本配置线的斜率等于资产组合每增加一单位标准差所增加的期望收益,即每单位额外风险的额外收益。
因此我们有时也将这一斜率称为报酬与波动性比率。
在资本配置线的推导中,我们假设投资者能以无风险收益率借入资金。
然而,在实际的资本市场中,投资者在银行的存贷利率是不同的。
一般来说,存款利率要低于贷款利率。
因此如果把存款利率视为无风险收益率,那么投资者的贷款利率就要高于无风险资产收益率。
在这种情况下,资本配置线就变为一条折线。
我们可以假设无风险资产收益率为f r ,投资者向银行贷款的利率为'
f r 。
在这种情况下,若投资者需要借入资金投资到风险资产时,
资本配置线的斜率就应该等于σ/])(['f r r E -,该斜率小于σ/])([f r r E -。
此时,在期望-收益差平面上,资本配置线就变成了如下的形状。
其中资本配置线在风险资产右侧的斜率要低于其左侧部分。
二、两个风险资产的组合
当市场中的资产是两个风险资产时,比如一只股票和一个公司债券,且投资到股票上的财富比例为w ,我们可以将该资产组合的收益写为:
此时资产组合的期望收益和标准差分别为:
其中12ρ为股票和债券收益率的相关系数。
此时,根据期望的表达式,我们可以求出投资权重为:
将其代入到标准差方程,可以得到该资产组合期望收益和标准差之间的关系式:
c r E b r E a P P P +⨯-⨯=)()(22σ 3-2
其中2
212
1122
221))
()((2r E r E a --+=
σσρσσ
当市场中存在两个风险资产的情况下,3-2描述了资产组合所有可能的期望收益和标准差的组合,当12ρ取不同的值时,上述关系是在期望收益-标准差平面中的形状也有所不同,我们对此分三种情况进行讨论。
(1)12ρ=1
在这种情况下,两个资产的收益率是完全相关的,这时,标准差变为:
在不考虑卖空或借贷的情况下,即10<<w ,标准差可写为 结合期望收益式子,可以求出
当两个风险资产完全正相关时,上式是资产组合期望收益和标准差的关系。
该式子在期望收益-标准差平面上是一条通过1点和2点的线段。
(2)12ρ=-1
在这种情况下,两个资产的收益率是完全负相关的,这时,标准差变为: 该方程对应着
再结合期望收益的表达式,可以求得资产组合期望收益和标准差之间的关系如下: 上式对应着两条斜率相反的折线,折线的一部分通过1点和E1点;另一部分则通过2点和E1点,其中E1点的坐标为(0,
2
11
221)()(σσσσ++r E r E ),为112-=ρ时资产组合可行
集内的最小方差点。
见图3-3
在完全正相关时,一种证券收益率高,另一种证券的收益率也高。
这样,在做卖空时,可以从多头(购入方)位置中获益,而从空头(销售方)位置中受损,但得利于多投资的证券。
当两种证券的收益率都低时,可以从多头中受损,而从空头中获益,投资较多的证券收益与卖空证券收益将相互抵消,投资组合的总体收益将较稳定。
在完全负相关时,一种证券收益率高,另一种证券的收益率总是相对要低。
如果卖空
高收益证券,而做多低收益证券,则投资组合的两部分都遭受损失。
另一方面,如果做多高收益证券,卖空低收益证券,则两部分都获利。
因此,在完全负相关时,投资组合的风险较高,其结果要么是“盛宴”,要么是“饥荒”。
我们总结如表6-1所示。
表6-1两证券收益率完全相关时投资组合有卖空
(3)1112<<-ρ
此时3-2在期望收益-标准差平面对应着两条双曲线。
考虑到经济意义,我们只保留双曲线在第一象限的部分。
这条双曲线的顶点E2是1112<<-ρ时资产组合可行集内的最小方差点。
从图中可看出,E 12和E 22,期望收益随方差的增大而降低,这部分的资产组合是无效的。
投资者只选择1 E 1和1E 22上的点。
例如:两个风险资产和一个无风险资产的最优投资组合的案例。
股票、债券和国库券
其中股票1和债券2之间相关系数12ρ=0.3,要得出最优风险资产组合,首先要建立1,2有效集,然后利用无风险资产建立资本配置线与有效集相切,切点即为最优风险组合所在的点。
1确定两种风险资产的比例 数学表达即为:
P
f
P P r r E S σ-=
)(=max
满足)()1()()(2111r E x r E x r E P -+= 把x1,x2求出来
2引入无风险资产C=F+P
引入效用函数2
5.0)(c c A r E U σ-=
根据f P C r y r yE r E )1()()(-+=,又有P C y σσ=。
