向量加法的运算律
2020年高中数学新教材同步必修第二册 第6章 6.2.1 向量的加法运算

6.2平面向量的运算6.2.1向量的加法运算学习目标1.理解并掌握向量加法的概念.2.掌握向量加法的三角形法则和平行四边形法则,并能熟练地运用这两个法则作两个向量的加法运算.3.了解向量加法的交换律和结合律,并能作图解释向量加法运算律的合理性.知识点一向量加法的定义及其运算法则1.向量加法的定义求两个向量和的运算,叫做向量的加法.2.向量求和的法则向量和的方法叫做向量加法的平行四边形法则位移的合成可以看作向量加法的三角形法则的物理模型,力的合成可以看作向量加法的平行四边形法则的物理模型.思考 |a +b |与|a |,|b |有什么关系?答案 (1)当向量a 与b 不共线时,a +b 的方向与a ,b 不同,且|a +b |<|a |+|b |.(2)当a 与b 同向时,a +b ,a ,b 同向,且|a +b |=|a |+|b |.(3)当a 与b 反向时,若|a |>|b |,则a +b 的方向与a 相同,且|a +b |=|a |-|b |;若|a |<|b |,则a +b 的方向与b 相同,且|a +b |=|b |-|a |. 知识点二 向量加法的运算律 向量加法的运算律交换律 a +b =b +a 结合律(a +b )+c =a +(b +c )1.0+a =a +0=a .( √ )2.AB →+BC →=AC →.( √ ) 3.AB →+BA →=0.( √ ) 4.AB →+BC →>AC →.( × ) 5.|AB →|+|BC →|=|AC →|.( × )一、向量加法法则例1(1)如图①所示,求作向量a+b.(2)如图②所示,求作向量a+b+c.→=a,然后作向量AB→=b,则向量OB→=a+b.如图③所示. 解(1)首先作向量OA(2)方法一(三角形法则)如图④所示,首先在平面内任取一点O,作向量OA→=a,再作向量AB→=b,则得向量OB→=a+b,然后作向量BC→=c,则向量OC→=(a+b)+c=a+b+c即为所求.方法二(平行四边形法则)如图⑤所示,首先在平面内任取一点O,作向量OA→=a,OB→=b,OC→=c,以OA,OB为邻边作▱OADB,连接OD,则OD→=OA→+OB→=a+b.再以OD,OC为邻边作▱ODEC,连接OE,则OE→=OD→+OC→=a+b+c即为所求.反思感悟向量加法的平行四边形法则和三角形法则的区别和联系跟踪训练1如图所示,O为正六边形ABCDEF的中心,化简下列向量.(1)OA →+OC →=________;(2)BC →+FE →=________;(3)OA →+FE →=________. 答案 (1)OB → (2)AD →(3)0解析 (1)因为四边形OABC 是以OA ,OC 为邻边的平行四边形,OB 是其对角线,故OA →+OC →=OB →.(2)因为BC →=FE →,故BC →+FE →与BC →方向相同,长度为BC →的长度的2倍,故BC →+FE →=AD →. (3)因为OD →=FE →,故OA →+FE →=OA →+OD →=0. 二、向量加法运算律的应用 例2 化简:(1)BC →+AB →;(2)DB →+CD →+BC →;(3)AB →+DF →+CD →+BC →+F A →. 解 (1)BC →+AB →=AB →+BC →=AC →. (2)DB →+CD →+BC →=BC →+CD →+DB → =(BC →+CD →)+DB →=BD →+DB →=0. (3)AB →+DF →+CD →+BC →+F A → =AB →+BC →+CD →+DF →+F A → =AC →+CD →+DF →+F A → =AD →+DF →+F A →=AF →+F A →=0.反思感悟 向量加法运算律的意义和应用原则(1)意义:向量加法的运算律为向量加法提供了变形的依据,实现恰当利用向量加法法则运算的目的.实际上,由于向量的加法满足交换律和结合律,故多个向量的加法运算可以按照任意的次序、任意的组合来进行.(2)应用原则:通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序.跟踪训练2 已知正方形ABCD 的边长等于1,则|AB →+AD →+BC →+DC →|=________. 答案 2 2解析 |AB →+AD →+BC →+DC →|=|AB →+BC →+AD →+DC →|=|AC →+AC →|=2|AC →|=2 2. 三、向量加法的实际应用例3 河水自西向东流动的速度为10 km/h ,小船自南岸沿正北方向航行,小船在静水中的速度为10 3 km/h ,求小船的实际航行速度.解 设a ,b 分别表示水流的速度和小船在静水中的速度,过平面内一点O 作OA →=a ,OB →=b ,以OA →,OB →为邻边作矩形OACB ,连接OC →,如图,则OC →=a +b ,并且OC →即为小船的实际航行速度.∴|OC →|=|a +b |2=|a |2+|b |2=20(km/h),tan ∠AOC =10310=3,∴∠AOC =60°,∴小船的实际航行速度为20 km/h ,沿北偏东30°的方向航行. 反思感悟 应用向量解决实际问题的基本步骤(1)表示:用向量表示有关量,将所要解答的问题转化为向量问题.(2)运算:应用向量加法的平行四边形法则和三角形法则,将有关向量进行运算,解答向量问题.(3)还原:根据向量的运算结果,结合向量共线、相等等概念回答原问题.跟踪训练3 如图,用两根绳子把重10 N 的物体W 吊在水平杆子AB 上,∠ACW =150°,∠BCW =120°,求A 和B 处所受力的大小.(绳子的重量忽略不计)解 如图所示,设CE →,CF →分别表示A ,B 所受的力,10 N 的重力用CG →表示,则CE →+CF →=CG →.由题意可得∠ECG =180°-150°=30°,∠FCG =180°-120°=60°. ∴|CE →|=|CG →|cos 30° =10×32=53(N), |CF →|=|CG →|cos 60° =10×12=5(N).∴A 处所受的力为5 3 N ,B 处所受的力为5 N.1.化简CB →+AD →+BA →等于( ) A.DB → B.CA → C.CD → D.DC → 答案 C解析 根据平面向量的加法运算,得CB →+AD →+BA →=(CB →+BA →)+AD →=CA →+AD →=CD →. 2.下列等式不正确的是( ) ①a +(b +c )=(a +c )+b ; ②AB →+BA →=0; ③AC →=DC →+AB →+BD →. A.②③ B.② C.① D.③ 答案 B解析 ②错误,AB →+BA →=0,①③正确. 3.在四边形ABCD 中,AC →=AB →+AD →,则( ) A.四边形ABCD 一定是矩形 B.四边形ABCD 一定是菱形 C.四边形ABCD 一定是正方形 D.四边形ABCD 一定是平行四边形 答案 D解析 由AC →=AB →+AD →知,A ,B ,C ,D 构成的四边形一定是平行四边形.4.如图,四边形ABCD 是梯形,AD ∥BC ,对角线AC 与BD 相交于点O ,则OA →+BC →+AB →+DO →等于( )A.CD →B.DC →C.DA →D.DO → 答案 B→+BC→+AB→+DO→=DO→+OA→+AB→+BC→=DA→+AB→+BC→=DB→+BC→=DC→.解析OA5.已知向量a表示“向东航行3 km”,b表示“向南航行3 km”,则a+b表示_________. 答案向东南航行3 2 km解析根据题意由于向量a表示“向东航行3 km”,向量b表示“向南航行3 km”,那么可知a+b表示向东南航行3 2 km.1.知识清单:(1)向量加法的三角形法则.(2)向量加法的平行四边形法则.(3)向量加法的运算律.2.方法归纳:数形结合.3.常见误区:向量加法的三角形法则要注意向量首尾相接,平行四边形法则要注意把向量移到共同起点.1.化简AE →+EB →+BC →等于( ) A.AB → B.BA → C.0 D.AC → 答案 D解析 AE →+EB →+BC →=AB →+BC →=AC →.2.如图,在正六边形ABCDEF 中,BA →+CD →+EF →等于( )A.0B.BE →C.AD →D.CF →答案 D解析 BA →+CD →+EF →=DE →+CD →+EF →=CE →+EF →=CF →. 3.若正方形ABCD 的边长为1,则|AB →+AD →|等于( )A.1B. 2C.3D.2 2答案 B解析 在正方形ABCD 中,AB =1,可知AC =2, 所以|AB →+AD →|=|AC →|=AC = 2.4.已知四边形ABCD 为菱形,则下列等式中成立的是( ) A.AB →+BC →=CA → B.AB →+AC →=BC →C.AC →+BA →=AD →D.AC →+AD →=DC →答案 C5.(多选)下列说法错误的有( )A.如果非零向量a 与b 的方向相同或相反,那么a +b 的方向必与a 或b 的方向相同B.在△ABC 中,必有AB →+BC →+CA →=0C.若AB →+BC →+CA →=0,则A ,B ,C 一定为一个三角形的三个顶点 D.若a ,b 均为非零向量,则|a +b |=|a |+|b | 答案 ACD解析 A 错,若a +b =0,则a +b 的方向是任意的;B 正确;C 错,当A ,B ,C 三点共线时,也满足AB →+BC →+CA →=0;D 错,|a +b |≤|a |+|b |. 6.已知AB →=a ,BC →=b ,CD →=c ,DE →=d ,AE →=e ,则a +b +c +d =________. 答案 e解析 a +b +c +d =AB →+BC →+CD →+DE →=AE →=e .7.在菱形ABCD 中,∠BAD =60°,|AB →|=1,则|BC →+CD →|=________. 答案 1解析 如图,由题意知△ABD 为等边三角形,所以|BC →+CD →|=|BD →|=|AB →|=1.8.如图,在平行四边形ABCD 中,O 是AC 和BD 的交点.(1)AB →+AD →+CD →=________; (2)AC →+BA →+DA →=________. 答案 (1)AD →(2)09.如图,已知在▱ABCD 中,O 是两条对角线的交点,E 是CD 的一个三等分点(靠近D 点),求作:(1)AO →+AC →;(2)DE →+BA →.解 (1)延长AC ,在延长线上截取CF =AO ,则向量AF →即为所求.(2)在AB 上取点G ,使AG =13AB ,则向量BG →即为所求.10.在静水中船的速度为20 m /min ,水流的速度为10 m/min ,如果船从岸边出发沿垂直于水流的航线到达对岸,求船行进的方向. 解 作出图形,如图所示.设船速v 船与岸的方向成α角, 由图可知v 水+v 船=v 实际,结合已知条件,四边形ABCD 为平行四边形, 在Rt △ACD 中,|CD →|=|AB →|=|v 水|=10 m/min , |AD →|=|v 船|=20 m/min , ∴cos α=|CD →||AD →|=1020=12,∴α=60°,从而船行进的方向与水流方向成120°角. ∴船是沿与水流方向成120°角的方向行进.11.在矩形ABCD 中,|AB →|=4,|BC →|=2,则向量AB →+AD →+AC →的长度为( ) A.2 5 B.4 5 C.12 D.6 答案 B解析 因为AB →+AD →=AC →,所以AB →+AD →+AC →的长度为AC →的模的2倍. 又|AC →|=42+22=25,所以向量AB →+AD →+AC →的长度为4 5.12.若在△ABC 中,AB =AC =1,|AB →+AC →|=2,则△ABC 的形状是( ) A.正三角形 B.锐角三角形 C.斜三角形 D.等腰直角三角形答案 D解析 以AB ,AC 为邻边作平行四边形ABDC ,∵AB =AC =1,AD =2,∴∠ABD 为直角,该四边形为正方形,∴∠BAC =90°,△ABC 为等腰直角三角形. 13.已知点G 是△ABC 的重心,则GA →+GB →+GC →=______. 答案 0解析 如图所示,连接AG 并延长交BC 于点E ,点E 为BC 的中点,延长AE 到点D ,使GE =ED ,则GB →+GC →=GD →,GD →+GA →=0,∴GA →+GB →+GC →=0.14.如图所示,已知电线AO 与天花板的夹角为60°,电线AO 所受拉力|F 1|=24 N ,绳BO 与墙壁垂直,所受拉力|F 2|=12 N.则F 1和F 2的合力为________ N.答案 12 3解析 如图,根据向量加法的平行四边形法则,得到合力F =F 1+F 2=OC →.在△OCA 中,|OA →|=24, |AC →|=12,∠OAC =60°, ∴∠OCA =90°,∴|OC →|=12 3.∴F 1与F 2的合力大小为12 3 N ,方向为与F 2成90°角,竖直向上.15.如图所示,P ,Q 是△ABC 的边BC 上两点,且BP =QC .求证:AB →+AC →=AP →+AQ →.证明 AB →=AP →+PB →,AC →=AQ →+QC →,∴AB →+AC →=AP →+PB →+AQ →+QC →.∵PB →与QC →大小相等,方向相反,∴PB →+QC →=0,故AB →+AC →=AP →+AQ →+0=AP →+AQ →.16.如图,已知D ,E ,F 分别为△ABC 的三边BC ,AC ,AB 的中点,求证:AD →+BE →+CF →=0.证明 由题意知,AD →=AC →+CD →,BE →=BC →+CE →,CF →=CB →+BF →.由平面几何知识可知,EF→=CD→,BF→=F A→,所以AD→+BE→+CF→=(AC→+CD→)+(BC→+CE→)+(CB→+BF→) =(AC→+CD→+CE→+BF→)+(BC→+CB→)=(AE→+EC→+CD→+CE→+BF→)+0=AE→+CD→+BF→=AE→+EF→+F A→=0.。
向量的加法运算及其几何意义

向量加法的性质
结合律
向量加法满足结合律,即(a+b)+c=a+(b+c), 表明向量的加法不依赖于其组合的顺序。
交换律
向量加法满足交换律,即a+b=b+a,表明向量加法 的结果与元素的组合顺序无关。
分配律
向量加法不满足分配律,即a×(b+c)不等于 a×b+a×c。
02
向量加法的几何意义
向量加法的平行四边形法则
总结词
向量加法的平行四边形法则是向量的基本加法规则之一,它 表示将两个向量首尾相接,并连接它们的起点和终点,所形 成的平行四边形的对角线向量即为这两个向量的和。
详细描述
根据平行四边形法则,向量加法满足交换律和结合律,即不 论向量的顺序如何,也不论如何分组,向量加法的结果都相 同。
向量加法的三角形法则
分配律
总结词
向量加法的分配律是指向量加法满足分配性 ,即向量加法可以分配到括号内的各个向量 上。
详细描述
分配律是向量加法的另一个重要运算律。根 据分配律,对于任意两个向量$vec{a}$和任
意标量$k$,有$k(vec{a} + vec{b}) = kvec{a} + kvec{b}$。这意味着标量可以与括
总结词
向量加法的三角形法则是向量的另一种加法规则,它表示将一个向量的起点平 移到另一个向量的终点,所形成的向量即为这两个向量的和。
详细描述
三角形法则在几何中常用于表示力的合成或速度的合成等物理现象。通过三角 形法则,可以直观地理解向量加法的几何意义,并用于解决实际问题。
向量加法的向量场意义
总结词
向量加法的向量场意义是指向量加法可以看作是向量场中点的运动变化。在向量场中,任意两点之间 的连线可以表示为向量,而这个向量的加法运算则反映了这两点之间的相对运动关系。
向量运算律

向量运算律向量是一种有方向和大小的几何对象,广泛用于数学、物理和工程等领域。
向量运算律是向量代数中的基本概念,也是进行向量运算的基础。
本文将详细介绍向量的运算律,包括交换律、结合律、分配律、加法单位元、减法单位元、数乘单位元、数乘结合律、加法逆元、数量积、平行四边形法则、三角形法则、反向量、向量的模和向量夹角。
1.交换律交换律是指对任意两个向量a和b,有a+b=b+a。
这个定律表明,向量的加法运算满足交换性质,即不依赖于其运算顺序。
2.结合律结合律是指对任意三个向量a、b和c,有(a+b)+c=a+(b+c)。
这个定律表明,向量的加法运算满足结合性质,即不依赖于其运算顺序。
3.分配律分配律是指对任意实数r和任意两个向量a和b,有(r+a)+b=r+a+b=(r+b)+a。
这个定律表明,实数与向量的加法运算满足分配性质,即实数可以分配到向量的两边。
4.加法单位元加法单位元是指对任意向量a,有u+a=a+u=a,其中u是加法单位元。
这个概念表明,加法单位元是一个与任意向量相加都保持不变的向量。
5.减法单位元减法单位元是指对任意向量a,有v-a=-a+v=a,其中v是减法单位元。
这个概念表明,减法单位元是一个与任意向量相减都保持不变的向量。
6.数乘单位元数乘单位元是指对任意实数r和任意向量a,有ra=ar=r。
这个概念表明,实数与向量的数乘运算满足数乘单位性质,即实数可以分配到向量的两边并保持不变。
7.数乘结合律数乘结合律是指对任意实数r、s和任意向量a,有(rs)a=r(sa)=s(ra)。
这个定律表明,实数的乘积可以分配到向量的两边,并且不依赖于其运算顺序。
8.加法逆元加法逆元是指对任意向量a,有-a+b=b-a。
这个概念表明,加法逆元是一个与任意向量相加都等于另一个向量的向量。
9.数量积数量积是指对任意两个向量a和b,有a·b=|a||b|cosθ,其中θ是两个向量的夹角。
这个概念表明,两个向量的数量积等于它们的模长乘积与它们夹角的余弦值之积。
【课件】向量的加法运算课件高一下学期数学人教A版(2019)必修第二册

E
C
B
c
b
D
a+b
O
乙
法二:平行四边形法则
a
A
首先在平面内任取一点O,作向量=a,=b,=c,
以OA,OB为邻边作▱OADB,连接OD,则=+=a+b.
再以OD,OC为邻边作▱ODEC,连接OE,则= + =a+b+c即为所求.
多维探究
变式1 在本例(1)条件下,求+.
1 2 +2 3 +3 4 +…+−1
= 1
[例1]
(1)如图,在△ABC中,D,E分别是AB,AC上的点,F
为线段DE延长线上一点,DE∥BC,AB∥CF,连接CD,那么
(在横线上只填一个向量):
①+=________;
+=+=
②+=________;
(3)向量加法的运算律有哪两条?
(4)|a+b|,|a|+|b|,|a|-|b|三者之间的大小有何关系?
课前小测
1.下列各式不一定成立的是( D )
A.a+b=b+a
B.0+a=a
C.+=
D.|a+b|=|a|+|b|
2. + +等于(
A.
C)
B.
C.
D.
(1) + ;
+=
(2) + ;
= = =
+ =+ =
本课小结
1.三角形法则和平行四边形法则都是求向量和的基本方法,两个法则是
统一的,当两个向量首尾相连时,常选用三角形法则;当两个向量共起点
时,常选用平行四边形法则.
2.向量的加法满足交换律,因此在进行多个向量的加法运算时,可以按照
行800 km送往C地医院,求这架飞机飞行的路程及两次位移的和.
中职数学8.2.1向量的加法

2.向量加法的运算律:
(1)证明:当 a , b 不平行时,
BC b ,则 作 AB a ,
ab ba (2)加法结合律 : (a b) c a (b c)
(1)加法交换律 :
D
a
ab
C
AC a b. 再作AD b ,连结 DC,
则四边形 ABCD 是平行四边形,
3.向量加法的平行四边形法则 :
AC AB BC a b
教材P52,练习 第 1 ,2题.
1km B 北
OA a,
AB b,
O
ab
b
OB OA AB a b,
| OB | 32 32 3 2 (km),
a
A
又 OA 与 OB的夹角是45°,所以a b 表示向 东北走 3 2km.
1.向量加法的三角形法则 :
多个向量求和
D
d
C
c
O
B
b
a
A
OD a b c d
b
A
b
b
a
B
a
于是 DC a .
因此 AD DC b a AC, 即 a b b a.
3.向量加法的平行四边形法则 :
若点A,B,D不共线,
AD b, 设 AB a ,
D
a
a b
C
以 AB, AD 为邻边作平行
A
b
四边形ABCD,
a
b
B
则对角线上的向量 AC AB BC a b
如图,填空:
(1) AB BC AC ; (2) AC CD DO AO ; (3) AC CD DA 0 .
向量加法运算及其几何意义 课件

【核心素养培优区】 【易错案例】向量的加法在向量化简中的应用 【典例】如图,在正六边形ABCDEF中, BA CD EF=( B )
A.0 B.BE C.AD D.CF
【失误案例】BA CD EF (BA AF) EF BF EF BE.
【错解分析】分析解题过程,请找出错误之处. 提示:本题错误的原因是未能结合正六边形边的关系, 得到 EF CB, 在化简的过程中代入.
【点拨】 (1)对向量加法三角形法则的两点说明 ①适用范围:任意向量. ②注意事项:(ⅰ)两个向量一定首尾相连. (ⅱ)和向量的始点是第一个向量的始点,终点是第二个 向量的终点. (ⅲ)当多个向量相加时,可以使用三角形法则.
(2)对向量加法的平行四边形法则的三点说明 ①适用范围:任意两个非零向量,且不共线. ②注意事项:(ⅰ)两个非零向量一定要有相同的始点; (ⅱ)平行四边形中的一个对角线所对应的向量为和向 量.
【变式训练】(荆州高一检测)设正六边形
ABCDEF,AB m,AE n, 则AD =________. 【解析】如图,
ED AB所 m以, 答案:n+m
AD AE ED n m.
类型三 向量加法的实际应用 【典例】长江两岸之间没有大桥的地方,常常通过轮渡 进行运输。现有一艘船从长江南岸A点出发,以5km/h的 速度向垂直于对岸的方向行驶,同时江水的速度为向东 2km/h.
列结论中,正确的是 ( ) ①a∥b;②a+b=a;③a+b=b;④|a+b|<|a|+|b|; ⑤|a+b|=|a|+|b|. A.①② B.①③ C.①③⑤ D.③④⑤
3.如图,E,F,G,H分别是梯形ABCD的边AB,BC,CD,DA的中 点,化简下列各式:
平面向量加减法口诀
向量的加法口诀: 首尾相连,首连尾,方向指向末向量。
以第一个向量的起点为起点,以第二个向量的终点为终点的向量是两向量的和向量。
二、向量的减法两向量做减法运算,图像如下图所示:向量的减法口诀: 首首相连,尾连尾,方向指向被减向量。
以第一个向量的终点为起点,以第二个向量的终点为终点的向量是两向量的差向量。
向量的学习是高一数学必修四第二章的内容,要求同学们会向量的基本运算,其中就包括加法、减法、数乘。
要求大家能根据运算法则解决基本的向量运算,学会运用图像解决向量加减法,向量的数乘等问题。
向量的相关题目难度也不是很大,只要大家认真学习,认真做好笔记,认真做做题目,总结做题规律,那么当我们遇到类似题目时就会似曾相识,做起来也很顺手,再细心点的话,得满分也没有问题。
学习方法很多,重要的事找到适合自己的方法,当然适合自己方法就是最好的方法。
附一;三角形定则解决向量加减的方法将各个向量依次首尾顺次相接,结果为第一个向量的起点指向最后一个向量的终点。
注:两个向量相减,则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。
平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣>1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上伸长为原来的λ∣倍;当∣λ∣<1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律:(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律(第一分配律):(λ+μ)a=λa+μa.数对于向量的分配律(第二分配律):λ(a+b)=λa+λb.数乘向量的消去律:① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义:已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义:两个向量的数量积(内积、点积)是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉;若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示:a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a(交换律);(λa)·b=λ(a·b)(关于数乘法的结合律);(a+b)·c=a·c+b·c(分配律);向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即:(a·b)·c≠a·(b·c);例如:(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即:由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义:两个向量a和b的向量积(外积、叉积)是一个向量,记作a×b.若a、b不共线,则a×b的模是:∣a×b∣=|a|·|b|·sin〈a,b〉;a×b的方向是:垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质:∣a×b∣是以a和b为边的平行四边形面积.。
向量的加减法及数乘运算

o·
A 的三角形法则
B
AB BC AC
ab ba (a b) c a (b c)
1. 相反向量:
与 做 记作
a长aa度的相相等反,向方量向相反的向量,叫
规定:零向量的相反向量仍是零向量。
注:(1) a a
((32))如任即 那果意: 么,向:量aaa与, b它互a相为b,反相b向反a量向a的量a, a和,0是b零向0量. 。
a
b
D
b
由作向量差的方法,
知
DB
AB
AD
a
A b
a
C B
练习u.A如uBur图,ar ,平uAuDu行r 四br边,形你A能B用CD的、ar 两br来条表对示角线Mu相uuAr交、uM于uuBr点、uMMuuCur,和且uMuuD。ur
D
C
M
b
A
r a
B
另:(1) a b a b a b
(2)若b // a(a 0),则b a是否成立?
成立
向量共线定理:
rr r r
向量a(a 0)与b共线,当且仅当有唯一一个实数,
rr
使b a.
rr
r rr r
即a与b共线
b a (a 0)
思考:1)
r a
为什么要是非零向量?
r 2) b 可以是零向量吗?
总结:
证明三点共线的方法:
AB=λBC
uuur r r uuur r r
OB a 2b,OC a 3b. 你能判断A、B、C三点之
间的位置关系吗?为什么?
C
r
r
a
b
r 3b
B
r
2b
A
6.2.3 向量的数乘运算

(3) ( x y )a ( x y )a [( x y ) ( x y )]a 2 ya
例析
例6.如图,□ 的两条对角线相交于点,且 = , = ,
用,表示,,和.
解:在□中, = + = + , = − = − .
= + 3.猜想, , 三点之间的位置关系,并证明你的猜想.
解:分别作向量,,,过点,作直线(如图).观察发现,
不论向量,怎样变化,点始终在直线上,猜想, , 三点共线.
3
事实上,因为 = − = + 2 − ( + ) = ,
(1) 5(3a 2b) 4(2b 3a ) 15a 10b 8b 12a 3a 2b;
1
1
1
(2) (a 2b ) (3a 2b ) (a b )
3
4
2
1
2
3
1
1
1
11
1
a b a b a b a b
3
3
4
2
2
2
12
3
(3)原式= 2 + 3 − − 3 + 2 − = − + 5 − 2.
2. 化简:课本练习(第16页)
(1) 5(3a 2b) 4(2b 3a );
1
1
1
(2) (a 2b ) (3a 2b ) ( a b );
3
4
2
(3) ( x y )a ( x y )a .
量.
新知探索
(完整版)平面向量的线性运算

ABabbaa a O =−→−OBA B O B a abb=−→−OB a +b ABAa +b向量的线性运算(一)1.向量的加法向量的加法:求两个向量和的运算叫做向量的加法。
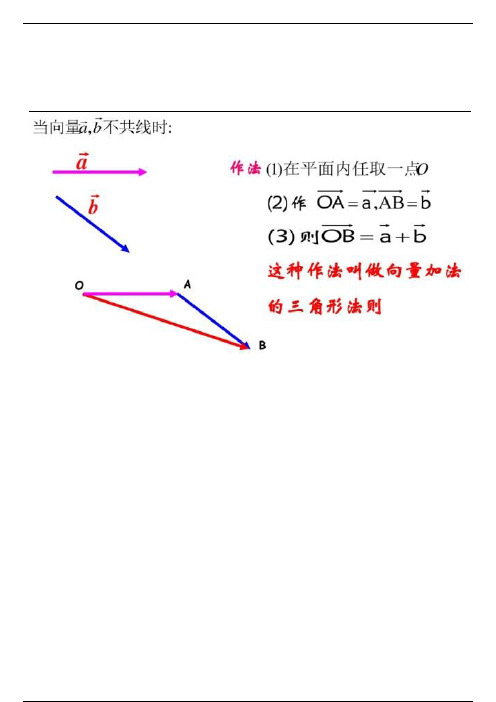
表示:→--AB −→−+BC =→--AC .规定:零向量与任一向量a ,都有00a a a +=+=.【注意】:两个向量的和仍旧是向量(简称和向量)作法:在平面内任意取一点O ,作→--OA =a →--→--OB =→--OA +→--AB a +b2.向量的加法法则(1)共线向量的加法:同向向量反向向量(2)不共线向量的加法几何中向量加法是用几何作图来定义的,一般有两种方法,即向量加法的三角形法则(“首尾相接,首尾连”)和平行四边形法则(对于两个向量共线不适应)。
三角形法则:根据向量加法定义得到的求向量和的方法,称为向量加法的三角形法则。
表示:→--AB −→−+BC=→--AC .平行四边形法则:以同一点A 为起点的两个已知向量a ,b 为邻边作平行四边形ABCD ,则以A 为起点的对角线→--AC 就是a 与b 的和,这种求向量和的方法称为向量加法的平行四边形法则。
如图,已知向量a 、b 在平面内任取一点A ,作→--AB =a ,=−→−BC b ,则向量−→−AC 叫做a与b 的和,记作a +b ,即a +b +=−→−AB =−→−BC −→−AC【说明】:教材中采用了三角形法则来定义,这种定义,对两向量共线时同样适用,当向量不共线时,向量加法的三角形法则和平行四边形法则是一致的 特殊情况:探究:(1)两相向量的和仍是一个向量;(2)当向量a 与b 不共线时,a +b 的方向不同向,且|a +b |<|a |+|b |; (3)当a 与b 同向时,则a +b 、a 、b 同向,且|a +b |=|a |+|b |,当a 与b 反向时,若|a |>|b |,则a +b 的方向与a 相同,且|a +b |=|a |-|b |;若|a |<|b |,则a +b 的方向与b 相同,且|a +b |=|b |-|a |.(4)“向量平移”:使前一个向量的终点为后一个向量的起点,可以推广到n 个向量连加3.向量加法的运算律(1)向量加法的交换律:a +b =b +a(2)向量加法的结合律:(a +b ) +c =a +(b +c ) 证明:如图:使=−→−AB a , =−→−BC b , =−→−CD c 则(a +b )+c =−→−AC +=−→−CD −→−AD ,a + (b +c )=−→−AB −→−+BD −→−=AD ,∴(a +b )+c =a +(b +c )从而,多个向量的加法运算可以按照任意的次序、任意的组合来进行例如:()()()()a b c d b d a c +++=+++;[()]()a b c d e d a c b e ++++=++++.例题:例1. O 为正六边形的中心,作出下列向量:(1)−→−OA +−→−OC (2)−→−BC +−→−FE (3)−→−OA +−→−FE例2.如图,一艘船从A 点出发以h km /32的速度向垂直于对岸的方向行驶,同时水aaab bba +ba +b ABC ABCD三角形法则平行四边形法则的流速为h km /2,求船实际航行的速度的大小与方向。
向量加法的运算律

向量加法的运算律
向量加法的运算律是指在向量空间中,向量之间的加法操作满足的规律。
向量加法的运算律包括交换律、结合律和零向量的存在性。
首先是向量加法的交换律。
对于任意向量a和b,a + b = b + a。
这意味着向量加法是满足交换律的,即加法的顺序不影响最终的结果。
这是因为向量的加法是一种可交换的运算。
其次是向量加法的结合律。
对于任意向量a、b和c,(a + b) + c = a + (b + c)。
这意味着在进行多个向量相加时,可以任意改变加法的顺序,最终结果不会改变。
这也说明向量的加法是一种满足结合律的运算。
另外,向量加法的运算律也包括零向量的存在性。
对于任意向量a,存在一个零向量0,使得a + 0 = a。
零向量是指一个模长为0的向量,它与任意向量相加都等于原向量本身。
这也意味着向量空间中存在一个单位元素,对向量加法起到类似于数字0对于加法的作用。
综上所述,向量加法的运算律包括交换律、结合律和零向量的存在性。
这些运算律是向量空间中的基本性质,对于进行向量加法运算和推导向量性质具有重要的意义。
向量加法的运算律使向量的运算更加灵活和方便,为向量空间的研究和应用提供了重要的基础。
15平面向量加减运算-学生版

待提升的知识点/题型…知识点一:向量的加法1:向量的加法(1) 求两个向量的和的运算,叫做向量的加法。
(2)已知向量a,b,在平面内任取一点A,作AB a, BC b,则向量AC叫做向量a,b的和。
记作:a b,即a b AB BC AC2 :向量的加法法则(1)三角形法则:两个向量“首尾”相接(2) 平行四边形法则:由同一点A为起点的两个已知向量a,b为邻边作平行四边形ABCD,则以A为起点的向量AC就是向量a,b 的和。
这种作两个向量和的方法叫做平行四边形法则3:向量和的特点(1)两相向量的和仍是一个向量;r r r r r r r「r「(2)当向量a与b不平行时,a +b与a,b的方向不同向,且|a + b |<|a|+|b |;(3)当向量a,b同向时,a b的方向与a,b同向,且|a b | | a | | b |当向量a,b反向时,若|a| |b|,则a b的方向与a,b同向,且|a b | |a | |b | ;若| a | | b |,则a b的方向与a,b反向,且|a b | |b | |a | ;4:向量的运算律(1)交换律:abb a ;( 2)结合律:(a b) c a (b c)说明:由于向量的加法满足交换律和结合律,对于多个向量的加法运算就可以按照任意的次序与任意的组合来进行了如:(a b) (c d) (b d) (a c);abcd e[d (ac)] (b e)(3) 实数的运算律与向量运算律比较丄…知识点二:向量的减法1向量的减法(1)用"相反向量”定义向量的减法①与a长度相同、方向相反的向量•叫做a的相反向量,记作a。
②规定:零向量的相反向量仍是零向量r r r r r r r③性质:(a) a ;a ( a) ( a) a 0如果a、b互为相反向量,则a= b,b = a,a+b = 0④向量减法的定义:向量a加上的b相反向量,叫做a与b的差.r r r r即: a b a ( b) 求两个向量差的运算叫做向量的减法.(2)用加法的逆运算定义向量的减法:向量的减法是向量加法的逆运算:若b+x = a,则x叫做a与b的差,记作a2:向量的减法法则 已知如图有a , b ,求作a(1)三角形法在平面内任取一点 uuu O ,作 OA r uuu r mu a ,OB b ,贝U BA(2)平行四边形: 在平面内任取一点uuu O ,作 OA r uuura , BOuuu uuw uuu r r则 BA BO OA a b . 知识精析、向量的加法 uuu uuruuu umr r r r r r (1) 如果 AB CD , 则 AB CD 5 (2) a (b c) (a b) cuuur uuur uuur uuuuuur AC uur uuu(3) AC CD DE AE (4) CD DA 0A . 1个B . 2个C . 3个D 4个uuu r uuur r r r r r 1-2 已知正万形 ABCD 的边长为 1, AB =a , AC =c , BC = b ,则 | a + b + c A.0 B.3 C. 72 D.2 72(一)典例分析、学一学例1-1下列各式中正确的有 ( )例 I 为()a例1-3已知正六边形 ABCDEF , O 为它的中心,若 BA a , BC b ,试用a , b 来表示向量 OE, BF,BD.(二)限时巩固,练一练1. (1) umr uuu uuu 在四边形 ABCD 中,向量 AB 、BC 、CD 的和向量是3. (2) (3) 向量(AB + MB )+( BO + BC )+ OM 化简后等于a ="向东走 4km ”,b ="向南走 3km ”,则 | a + b | == c ,DE=d ,AE3, AOB 60,则 a b且有 EB=DF 中,设 uuur r uur EC a,EA uuur r ,AD c ,则:r c 、向量的减法(一)典例分析、学一学uuu r uuu r uiur r uuu ur 例2-1如图,已知 AB a, BC b,CD c, DE d ,在图中标出已知的4个向量,并用向量r r r u uuu uuu uuu(2) AB AE a, b, c, d 表示卜列向量 (1) AD例2-2已知平行四边形 ABCD ,对角线AC 和BD 相交于点O ,下列等式成立的是(2. 如图,B 、D 在口AECF 的对角线上,UJ UUT uuur JUU UU UJU uuur UJ A. AB CD AC BD B. AB CD AC BD UU J UUT ULUT uuu UU J uuur UUT uu ur C. AB CD AC BD D. AB CD AC BD例2-3化简下列各式:① AB + BC + CA ;② AB — AC + BD — CD ;③ OA — OD + AD ; A 、1 B 、2 (二) 限时巩固、 练一练如图, 已知向量uuu r AB a 、 uuu BC r b 、 uuu CD UUJ uuuruuu uuu( 1)AB AC ; (2) A B AE ④ NQ + QP + MN — MP C 、3 D 、4 r uuu J r r r u c 、 DEd ;试用a 、b 、c 、d 表示下列向量 E结果为零向量的个数是( )D C B 三、向量的画法(一)典例分析,学一学例3-1已知向量a, b,c ;r cr r c 例3-2如图,已知向量 r r r u a 、b 、c 、d ,分别画出下列向量:1.在平行四边形ABCD中,若uuu r uuu r uuurAD a, AB b,贝U DB (用a和b表示)2. 已知向量a、b的模分别为3, 4,则| a —b |的取值范围为3. 已知I OA | =4, |OB | =8, / AOB=60 ,则 | AB | =4.uu已知OA a ,uurOBuuub ,若OA 12 ,5,且AOB 90°,则a b5•如图,在平行四边形ABCD中,已知AC BD交于点uuu O,ABr ujura, ADuur 则AO uur DO6.平行四边形ABCD中,M为DC中点, N为BC的中点. uunAB,AD b,7 .8.9. …uuuu则MN (用a , b表示).F列等式中,正确的个数是(① abba ② abbauurF列四式不能化简为AD的是(uuu uuu uuu A.( AB + CD )+ BCuuu uur uuuuC. AD + AD - BMa ④(a)C. 3a) 0uur uurB. (AD + MB)+(uuir uuu uuu D.OC -OA + CD已知AD是厶ABC的中线,试用第二部分1 .已知正方形ABCD的边长为1 ,uuiu uuuuBC +CM )uuiruuu uurAB, AD, AC表示向量uuurBD, DCuuiruuuABr uuu r a , BC b,则 a b为.uuu r uuu r 2 .在口ABCD中 , AC = a , AB = b , uuu BC =uuu uuu uuu 3.在四边形ABCD中,若AC AB ADuuu,且ABuurAD ,那么四边形ABCD为(7.如图,点 E 、 F 在平行四边形 ABCD 的对角线 uuu uurULU UUU (1)填空: BC BA =BA AF =BC AF6.如图,已知在梯形 ABCD 中,AD // BC ,点E 在边BC 上,联结 DE , AC .「士宀 uuir uuur uuu uuu(1) 填空:CD DE ______________ ; BC BA _______________ ;(2)如果把图中线段都画成有向线段 ,那么在这些有向线段所表示的向量中,试写出四个与向量 uuuBE 平行的向量是 __________________ ;uuu uur(3) 求作:AB AD .(请说明哪个向量是所求作的向量)8.已知口 ABCD 点E 是BC 边的中点,请回答下列问题:uuir ULUT ULUT uuir(1)在图中求作 AD 与DC 的和向量:AD DC = ______________ A 、矩形 B 、菱形 C 、正方形 D 、不是矩形、菱形的四边形4.已知平行四边形 ABCD , O 为平面上任意一点 UJU r uun •设 OA a ,0B r uuu r uuur u b ,OC c ,OD d ,则( r o r o 出d In d M dr 出d r uuu uuur 5.化简:(1) AB CD uuu uuir BE DE uur uuu uuur_________ ; (2) BC DA MBuuu u CMA nBD 上,且 EB = DF . uuu ULUT______ ; BC AF _________1. __________________ (1) 既有 __________ 、又有的量,叫做向量.(2) _________________ 向量的--------------------------- 也叫向量的模(或向量的长度) ______________________ 它是一个--------------------------(3)零向量:大小为 ______ ,方向_________ 的向量;记作_________.2. __________________ (1)方向 ______ 且大小的两个向量叫做相等向量.(2) ____________ 方向___________ 且大小的两个向量叫做相反向量.(3) _____________________方向的两个向量叫做平行向量.(1) 向量加法、减法的三角形法则:uuu uuu ujur ujuAB BC;AC BC(2) 向量加法、减法的平行四边形法则:uuu uuur uuu uuuAB AD;AB AD3. 向量的运算(3)向量的加法运算律:向量加法满足交换律,即:_________________________向量加法满足结合律,即:_________________________1.如图,梯形ABCD中,AD//BC , AB=CD, O为对角线AC与BD的交点,那么下列结论正确的B第6题图C . AB AD BD2•下列关于向量的运算,正确的是((A ) AB BC CA 0;(C ) AB AC CB ;D . ABAD BD)(B ) AB CB CA ;匚(D ) AB AD BD 。
【人教A版】向量的加法运算(数学)

答案uuu:r ①uuur uuur u②uur uuur
①AB DF=AB BC=AC. uuur uur uuur uuur uuur
②AD FC=AD DB=AB.
uuur
uuur
AC
AB
2.①正确,当两向量反向时,和向量的模最小为1; ②中描述的只是向量同向时的情况,故不正确,反之正 确,即③正确. 答案:①③
uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur uuur
2 DB CD BC=BC CD DB= BC CD DB=BD DB=0.
【加练·固】
在平行四边形ABCD中(如图),对角线AC,BD交于点O,
则
①
【类题·通】 利用向量解决几何问题的方法 用向量法证明几何问题的关键是把几何中的线段转化 为向量,通过向量的运算得到结论,然后把向量问题 还原为几何问题.
(1)a+0=a. ( )
uuur uuur uuur
(2) AB BA=2AB.
()
uuur uuur uuur uuur
(3) AB BD DC AC. (
)
(4)a+(b+c)=c+(a+b). ( )
提示:(1)×.两个向量的和仍然是一个向量,所以 a+0=a.
uuur uuur
【发散·拓】 向量求和的多边形法则 (1)已知n个向量,依次首尾相接,则由起始向量的起 点指向末尾向量的终点的向量即为这n个向量的和,这
uuuuur uuuuur uuuuur
称u为uuu向uuu量uur求u和uuu的uuu多r 边uuu形uur法则.即 A0A1 A1A2 A2A3
第02讲 平面向量的线性运算(3个知识点+4种题型+强化训练)解析版

第02讲 平面向量的线性运算(3个知识点+4种题型+强化训练)知识点一、向量加法1.向量加法的定义定义:求两个向量和的运算 叫做向量的加法. 对于零向量与任意向量a 规定0+a =a +0=a . 2.向量求和的法则三角形法则已知非零向量a b 在平面内任取一点A 作AB →=a BC →=b 则向量AC →叫做a 与b的和 记作a +b 即a +b =A B →+BC →=A C →.平行四边形法则已知两个不共线向量a b 作AB →=a AD →=b 以AB → AD →为邻边作▱ABCD 则对角线上的向量AC →=a +b .思考:两个向量相加就是两个向量的模相加吗?[提示] 不是 向量的相加满足三角形法则 而模相加是数量的加法. 3.向量加法的运算律 (1)交换律:a +b =b +a .(2)结合律:(a +b )+c =a +(b +c ). 知识点二、向量减法1.相反向量(1)定义:与向量a 长度相等 方向相反的向量 叫做a 的相反向量. (2)性质:①-(-a )=a .②对于相反向量有:a +(-a )=0. ③若a b 互为相反向量 则a =-b a +b =0. 2.向量的减法(1)定义:a -b =a +(-b ) 即减去一个向量相当于加上这个向量的相反向量. (2)作法:在平面内任取一点O 作OA →=a OB →=b 则向量BA →=a -b 如图所示.思考:在什么条件下|a-b|=|a|+|b|?[提示]当a b至少有一者为0或a b非零且反向时成立.知识点三、向量的数乘运算(1)定义:规定实数λ与向量a的积是一个向量这种运算叫做向量的数乘记作:λa它的长度与方向规定如下:①|λa|=|λ||a|;②当λ>0时λa的方向与a的方向相同;当λ<0时λa的方向与a的方向相反.(2)运算律:设λμ为任意实数则有:①λ(μ a)=(λμ)a;②(λ+μ)a=λa+μ a;③λ(a+b)=λa+λb;特别地有(-λ)a=λ(-a)=-(λa);λ(a-b)=λa-λb.(3)线性运算:向量的加、减、数乘运算统称为向量的线性运算向量线性运算的结果仍是向量.对于任意向量a b以及任意实数λμ1μ2恒有λ(μ1a+μ2b)=λμ1a±λμ2b.(4) 共线向量定理向量a(a≠0)与b共线的充要条件是:存在唯一一个实数λ使b=λa.思考:定理中把“a≠0”去掉可以吗?[提示]定理中a≠0不能漏掉.若a=b=0则实数λ可以是任意实数;若a=0b≠0则不存在实数λ使得b=λa.知识复习题型一、向量的加法一、单选题1.在平面四边形ABCD中下列表达式化简结果与AB相等的是()A.AC CD+B.AD DC CB++C.CA CB+--D.CB DA DC【答案】B【分析】根据平面的线性运算求得正确答案.【详解】AC C AD+=不符合题意.D++=+=符合题意.AD DC CB AC CB ABCA CB BA-=不符合题意.=+-+≠不符合题意.CB DA DC CB CA AB故选:B2.(2024下·全国·高一专题练习)下列等式不正确的是()①()()++=++;a b c a c b②0+=;AB BA③AC DC AB BD=++.A.②③B.②C.①D.③【答案】B【分析】根据向量加法的运算律判断即可.【详解】对于① ()()++=++正确;a b c a c b对于② 0+=错误;AB BA对于③ DC AB BD AB BD DC AC++=++=正确.故选:B3.(2024下·全国·高一专题练习)如图所示的方格纸中有定点O P Q E F G H则OP OQ+=()A.OE B.OF C.OG D.OH【答案】B【分析】根据平行四边形法则即可求.【详解】以OP OQ 为邻边作平行四边形 可知OF 为所作平行四边形的对角线故由平行四边形法则可知OF 对应的向量OF 即所求向量. 故选:B4.(2024下·全国·高一专题练习)已知四边形ABCD 为菱形 则下列等式中成立的是( ) A .AB BC CA += B .AB AC BC += C .AC BA AD += D .AC AD DC +=【答案】C【分析】根据菱形的性质 结合平面向量加法的运算性质进行判断即可. 【详解】对于A AB BC AC += 故A 错误;对于B 因为AB BC AC += 所以2AB AC AB BC +=+ 故B 错误; 对于C AC BA BA AC BC AD +=+== 故C 正确;对于D 因为AD DC AC += 所以2AC AD AD DC +=+ 故D 错误. 故选:C5.(2024上·河北石家庄·高一石家庄市第二十四中学校考期末)向量()AB OM BO MB +++= ( ) A .BC B .AB C .AC D .AM【答案】B【分析】利用向量加法的三角形法则及向量加法的运算律即可求解. 【详解】由()AB OM BO MB AB BO OM MB AB +++=+++= 故B 正确. 故选:B. 二、填空题6.(2024下·全国·高一专题练习)已知向量a 表示“向东航行3km” b 表示“向南航行3 km” 则a b +表示 .【答案】向东南航行32km. 【分析】根据向量加法法则分析即可.【详解】根据题意由于向量a 表示“向东航行3km” 向量b 表示“向南航行3km” 那么可知a b +表示向东南航行223332+=km. 故答案为:向东南航行32km 7.(2023·全国·高一随堂练习)化简:(1)AB BC CD ++= ; (2)AB BC CD DE EF ++++= ; (3)AB CB AC --= ; (4)12231n n A A A A A A -++⋅⋅⋅+= . 【答案】 AD AF 0 1n A A 【分析】根据向量加减法的几何意义进行运算即可. 【详解】(1)AB BC CD AC CD AD ++=+=;(2)AB BC CD DE EF AC CD DE EF ++++=+++AD DE EF AE EF AF =++=+=; (3)0AB CB AC AB BC AC AC AC --=+-=-=; (4)122311311111n n n n n n n n A A A A A A A A A A A A A A A A ----++⋅⋅⋅+=+⋅⋅⋅+==+=.故答案为:AD ;AF ;0;1n A A . 三、解答题8.(2023·全国·高一随堂练习)如果0AB BC CA ++= 那么A B C 三点是否一定是一个三角形的三个顶点? 【答案】不一定【分析】考虑A B C 三点是否共线即可回答.【详解】当A B C 三点共线也有0AB BC CA ++= 所以A B C 三点不一定是一个三角形的三个顶点.9.(2024下·全国·高一专题练习)如图 已知a 、b 、c 求作向量a b c ++.【答案】作图见解析【分析】在平面内任取一点O 作OA a = AB b = BC c = 利用平面向量加法的三角形法则可作出向量a b c ++.【详解】作法:如图所示 在平面内任取一点O 作OA a = AB b = BC c = 则OC OA AB BC a b c =++=++.题型二、向量的减法 一、单选题1.(2022上·江西·高三校联考阶段练习)对于非零向量a b “0a b +=”是“a b ∥”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】A【分析】根据相反向量一定是共线向量 共线向量不一定是相反向量可求解. 【详解】由0a b +=得0a b += 所以a b =- 则a b ∥; 由a b ∥得a 与b 方向相同或相反 模长不一定相等 所以0a b +=不一定成立所以“0a b +=”是“a b ∥”的充分不必要条件. 故选:A.2.(2023下·河北张家口·高一河北省尚义县第一中学校考阶段练习)向量AB CB DA -+=( ) A .BD B .CDC .DCD .0【答案】C【分析】根据向量的概念 以及向量加减法的运算律 即可得出答案. 【详解】由AB CB DA AB BC DA AC AD DC -+=++=-=. 故选:C.3.(2024下·全国·高一专题练习)已知,a b 为非零向量 则下列说法错误的是( ) A .若||||||a b a b +=+ 则a 与b 方向相同B .若||||||a b a b +=- 则a 与b 方向相反C .若||||||a b a b +=- 则a 与b 有相等的模D .若||||||a b a b -=- 则a 与b 方向相同 【答案】C【分析】运用向量三角不等式的取等条件求解即可.【详解】由向量三角不等式可知 只有当非零向量,a b 同向时 有||||||a b a b +=+||||||a b a b -=- 故A D 正确;只有当非零向量,a b 反向时 有||||||||b b a a +=- ||||||a b a b +=- 故B 正确 C 错误.故选:C . 二、多选题4.(2023下·湖南怀化·高一校考期中)下列各式中结果一定为零向量的是( ) A .BO OM MB ++ B .AB BC +C .C BO OB O CO +++D .AB AC BD CD -+-【答案】ACD【分析】利用向量的加法运算 结合零向量的意义逐项计算判断作答. 【详解】对于A 0O M BO M B MO OM ++=+= A 是; 对于B AB BC AC += AC 不一定是零向量 B 不是;对于C ()()000BO O OB OC CO B O C BO C O +++=+++=+= C 是; 对于D ()0AB AC BD CD AB AD AD BD AC CD -+-=+-+=-= D 是. 故选:ACD 5.若a 、b 为相反向量 且1a = 1b = 则a b += a b -= . 【答案】 0 2【分析】利用相反向量的定义结合平面向量的加、减法可求得结果. 【详解】因为a 、b 为相反向量 且1a = 1b = 则0a b += 2a b a -= 因此 0a b += 22a b a -==. 故答案为:0;2.6.(2022下·上海闵行·高一上海市七宝中学校考阶段练习)若向量a 与b 共线 且1==a b 则+=a b . 【答案】0或2【分析】由题可知a 与b 相等或互为相反向量 据此即可求a b + 【详解】向量a 与b 共线 且a b = ∴a 与b 相等或互为相反向量 当a 与b 相等时 22a a b ==+ 当a 与b 互为相反向量时 0=0a b =+. 故答案为:0或2.7.(2022·高一课时练习)如图所示 中心为O 的正八边形1278A A A A 中()11,2,,7i i i a A A i +== ()1,2,,8j j b OA j == 则25257a a b b b ++++= .(结果用i a ib 表示)【答案】6b【分析】根据向量的加减运算即可求得答案. 【详解】由题图可知 25257a a b b b ++++2356257A A A A OA OA OA =++++()()2235567OA A A OA A A OA =++++367OA OA OA =++36366OA OA OA OA b =+-==,故答案为:6b8.已知长度相等的三个非零向量,,OA OB OC 满足OA OB OC ++=0,则由A ,B ,C 三点构成的∴ABC 的形状是 三角形. 【答案】等边【详解】如图,以OA ,OB 为邻边作菱形OAFB ,则OA OB OF +=,∴OF OC +=0,∴OF =-OC . ∴O ,F ,C 三点共线. ∴四边形OAFB 是菱形, ∴CE 垂直平分AB.∴CA=CB. 同理,AB=AC.∴△ABC 为等边三角形. 四、解答题9.(2022下·河南周口·高一校考阶段练习)化简下列各式: (1)()()BA BC ED EC ---; (2)()()AC BO OA DC DO OB ++--- 【答案】(1)DA(2)0【分析】(1)根据平面向量加法和减法的运算法则化简即可得出结果; (2)首先化简出两个向量的结果 再与第三个向量进行加减运算即可求得结果. 【详解】(1)利用平面向量的加减运算法则可得()()()BA BC ED EC BA CB ED CE CA CD CA DC DA ---=+-+=-=+=(2)由平面向量的加减运算法则可得()()()()AC BO OA DC DO OB AC BA DC OD BO ++---=+-++()0BC DC BD BC BC =-+=-=题型三 、向量的数乘运算 一、单选题1.(2023·湖南岳阳·校联考模拟预测)已知向量,a b 则()()2a b a b +--=( ) A .a b + B .a b - C .3a b + D .3ab【答案】D【分析】直接由向量的线性运算即可求解.【详解】由题意()()2223a b a b a b a b a b +--=+-+=+. 故选:D.2.(2024上·河南焦作·高三统考期末)已知ABC 所在平面内一点D 满足102DA DB DC ++=则ABC 的面积是ABD △的面积的( ) A .5倍 B .4倍C .3倍D .2倍【答案】A【分析】利用平面向量的线性运算计算即可.【详解】设AB 的中点为M 因为102DA DB DC ++=所以2()CD DA DB =+ 所以4CD DM = 所以点D 是线段CM 的五等分点所以5ABC ABDCM S SDM==,所以ABC 的面积是ABD △的面积的5倍. 故选:A.3.(2023下·河南洛阳·高一河南省偃师高级中学校考阶段练习)在ABC 中 点M 是AB 的中点 N 点分AC 的比为:1:2,AN NC BN =与CM 相交于E 设,AB a AC b == 则向量AE =( )A.1132a b+B.1223a b+C.2155a b+D.3455a b+【答案】C【分析】由三点共线性质以及平面向量基本定理解方程组即可得解.【详解】由题意,,B E N三点共线所以存在Rλ∈使得()113AE AB AN AB ACλλλλ-=+-=+同理,,C E M三点共线所以存在Rμ∈使得()112AE AC AM AC ABμμμμ-=+-=+由平面向量基本定理可得1213μλλμ-⎧=⎪⎪⎨-⎪=⎪⎩解得21,55λμ==所以2155AE a b=+.故选:C.4.(2023·湖南永州·统考二模)在ABC中若1,2AB AC CA CB+=+=则ABC的面积的最大值为()A.16B.15C.14D.13【答案】D【分析】设,E F分别为,BC AB的中点结合三角形相似推出43ABC ACEFS S=四边形由题意可得1||,||12AE CF==确定四边形ACEF面积的最大值即可得答案.【详解】设,E F分别为,BC AB的中点连接EF则EF AC∥则BEF△∴BCA故14BEF ABCS S=,则34ABC ACEF S S =四边形 故43ABCACEFSS =四边形 又1,2AB AC CA CB +=+= 则21,22AB AC AE CA CB CF +==+== 故1||,||12AE CF ==当AE CF ⊥时 四边形ACEF 面积最大 最大值为1111224⨯⨯=故ABC 的面积的最大值为411343⨯=故选:D 5.(2024下·全国·高一专题练习)在ABC 中 D 为AC 上一点且满足 12AD DC =,若P 为BD 的中点 且满足 AP AB AC λμ=+,则λμ+的值是 . 【答案】23【分析】根据平面向量的线性运算计算即可. 【详解】如图因为12AD DC = 所以13AD AC =则11111112222326AP AB AD AB AC AB AC =+=+⨯=+ 所以12λ=16μ= 23λμ+=.故答案为:23.6.(2024下·全国·高一专题练习)已知矩形ABCD 中 对角线交于点O 若125,3BC e DC e == 则OC = . 【答案】12 5322e e +【分析】利用向量的线性运算可得OC 的表达形式.【详解】因为ABCD 是矩形 所以1111122222OC AC AB BC DC BC ==+=+ 所以125322OC e e =+.故答案为:125322e e +7.(2022·全国·模拟预测)在平行四边形ABCD 中 点G 在AC 上 且满足3AC AG = 若DG mAB nAD =+ 则m n -= .【答案】1【分析】利用向量线性运算求得1233DG AB AD =- 与题干对照即可求解. 【详解】()11123333DG AG AD AC AD AB AD AD AB AD =-=-=+-=- 则13m = 23n =-所以1m n -=. 故答案为:1 三、解答题8.(2024下·全国·高一专题练习)若向量x y 满足23x y a += 32x y b -= a 、b 为已知向量 求向量x y . 【答案】231313=+x a b 321313=-y a b 【分析】根据23x y a += 32x y b -= 列方程组求解. 【详解】解:由方程组2332x y ax y b +=⎧⎪⎨-=⎪⎩解得231313=+x a b 321313=-y a b .题型四、平面向量共线定理及应用一、单选题1.(2024·陕西安康·陕西省安康中学校联考模拟预测)已知平面向量a 与b 不共线 向量(),32m xa b n a x b =+=+- 若//m n 则实数x 的值为( )A .1B .13-C .1或13-D .1-或13【答案】C【分析】根据平面共线定理 由向量平行 求得x 满足满足的方程 求解即可. 【详解】由//m n 且,m n 均不为零向量 则()32,m n a x b λλλλ==+-∈R可得()132x x λλ=⎧⎨=-⎩ 则()3210x x --= 整理得23210x x 解得1x =或13x . 故选:C .2.(2024上·辽宁·高一校联考期末)已知a 与b 为非零向量,2,OA a b OB a b OC a b λμ=+=-=+ 若,,A B C 三点共线 则2λμ+=( )A .0B .1C .2D .3【答案】D【分析】根据三点共线可得向量共线 由此结合向量的相等列式求解 即得答案. 【详解】由题意知 ,,A B C 三点共线 故2,(2)(1)AB a b BC a b λμ=-=-++, 且,AB BC 共线故不妨设,(0)A k B k BC =≠ 则1(2)2(1)k k λμ=-⎧⎨-=+⎩ 所以122μλ+-=- 解得23λμ+=故选:D3.(2024下·全国·高一专题练习)已知21,e e 为两个不共线的向量 若向量12122,23a e e b e e =+=-+ 则下列向量中与向量2a b +共线的是( ) A .1252e e -+ B .12410e e +C .12104e e +D .122e e +【答案】B【分析】根据向量线性运算表示12225a b e e +=+ 然后利用共线向量基本定理求解即可. 【详解】因为向量122a e e =+ 1223b e e =-+ 所以12225a b e e +=+.又()1212410225e e e e +=+ 所以12410e e +与2a b +共线. 故选:B . 二、填空题4.(2024·全国·高三专题练习)在ABC 中 O 是边BC 的中点 AP t AO = 过点P 的直线l 交直线,AB AC 分别于,M N 两点 且,AM mAB AN nAC == 则11m n+= . 【答案】2t【分析】由三点共线的性质列式求值. 【详解】由题意:().222t t tAP t AO AB AC AB AC ==+=+ 由,,M P N 三点共线知 ()()11AP AM AN mAB nAC λλλλ=+-=+-. ()212t m t n λλ⎧=⎪⎪⎨⎪-=⎪⎩⇒ 212t m t n λλ⎧=⎪⎪⎨⎪-=⎪⎩消去λ 得112m n t+=. 故答案为:2t5.(2022上·河南·高二校联考期末)已知ABC 中 点D 在线段AB (不含端点)上 且满足()R CD xCA yCB x y =+∈, 则12x y+的最小值为 .【答案】322+/223+【分析】根据向量共线可得1x y += 即可利用基本不等式的乘“1”法求解. 【详解】∴(),R CD xCA yCB x y =+∈ 由于D 在线段AB (不含端点)上 故,,A D B 三点共线 所以1x y +=且00,x y >>则()121223322y xx y x y x y x y ⎛⎫+=++=++≥+ ⎪⎝⎭ 当且仅当2y x xy=时 即21,22x y =-=-时取等号 故12x y+有最小值322+. 故答案为:322+.6.(2024下·全国·高一专题练习)如图所示 在ABC 中 14AN NC =P 是BN 上的一点 若611AP AB mAC =+ 则实数m 的值为 .【答案】111【分析】借助共线定理的推论即可得. 【详解】因为14AN NC = 所以5AC AN = 所以6651111AP AB mAC AB mAN =+=+ 因为P B N 三点共线 所以65111m += 解得111m =.故答案为:111. 7.(2023·吉林长春·东北师大附中校考模拟预测)在ABC 中 M N 分别是边AB AC 上的点 且23AN AC =13AM AB = 点O 是线段MN 上异于端点的一点 且满足340(0)OA OB OC λλ++=≠ 则λ= .【答案】8【分析】用OA 、AN 表示出OC 、OB 从而得到6977AO AN AM λλ=+++ 再根据M O N 三点共线 得到69177λλ+=++ 解得即可. 【详解】解:因为23AN AC =13AM AB =所以()23AN OC OA =- ()13AM OB OA =- 即32OC AN OA =+ 3OB AM OA =+因为340OA OB OC λ++= 所以()333402OA AM OA AN OA λ⎛⎫++++= ⎪⎝⎭即()769AO AN AM λ+=+ 即6977AO AN AM λλ=+++ 因为M O N 三点共线 故69177λλ+=++ 解得8λ=. 故答案为:8 8.(2022下·陕西西安·高一统考期中)设,a b 是不共线的两个向量. (1)若2OA a b =- 3OB a b =+ 3OC a b =- 求证:A B C 三点共线; (2)若8a kb +与2ka b +共线 求实数k 的值. 【答案】(1)证明见解析; (2)±4.【分析】(1)要证明三点共线 即证明三点组成的两个向量共线即可. (2)由共线性质求出参数即可.【详解】(1)由2OA a b =- 3OB a b =+ 3OC a b =- 得3(2)2AB OB OA a b a b a b =-=+--=+ 3(3)242BC OC OB a b a b a b AB =-=--+=--=-因此//AB BC 且有公共点B 所以A B C 三点共线.(2)由于8a kb +与2ka b +共线 则存在实数λ 使得8(2)a kb ka b λ+=+ 即(8)(2)0k a k b λλ-+-= 而,a b 是不共线因此8020k k λλ-=⎧⎨-=⎩解得2,4k λ==或2,4k λ=-=- 所以实数k 的值是4±.9.(2024上·辽宁·高一校联考期末)如图 在ABC 中 D 是BC 上一点 G 是AD 上一点 且2AG BD DG CD== 过点G 作直线分别交,AB AC 于点,E F .(1)用向量AB 与AC 表示AD ; (2)若54AB AE = 求ACAF 和EG EF的值.【答案】(1)1233AD AB AC =+ (2)138AC AF = 1318EG EF =.【分析】(1)利用向量的线性运算求解;(2)设AC AF μ= 利用向量的线性运算和平面向量基本定理求解. 【详解】(1)2221233333AD AB BD AB BC AB BA AC AB AC =+=+=++=+.(2)因为54AB AE = 所以54AB AE =.设AC AF μ= 22122454333399189AG AD AB AC AB AC AE AF μ⎛⎫==+=+=+ ⎪⎝⎭ 因为,,G E F 三点共线 所以541189μ+= 解得138μ= 所以138AC AF =.因为48513EF EA AF AB AC =+=-+424264134859945918513EG EA AG AB AB AC AB AC AB AC ⎛⎫=+=-++=-+=-+ ⎪⎝⎭所以1318EG EF =即1318EG EF =. 10.(2024下·全国·高一专题练习)如图 在平行四边形ABCD 中 ,,AB a AD b M ==为AB 中点 N 为BD 上靠近点B 的三等分点 求证:,,M N C 三点共线.【答案】证明见解析【分析】根据三点共线要求证明//CM CN即可.【详解】∴,AB a AD b==∴BD AD AB b a=-=-.∴N是BD上靠近点B的三等分点∴11()33BN BD b a==-.∴在平行四边形中BC AD b==∴112()333CN BN BC b a b a b =-=--=--.①∴M为AB的中点∴111,()222MB a CM MC MB BC a b a b⎛⎫=∴=-=-+=-+=--⎪⎝⎭.②由①②可得32CM CN=.由向量共线定理知//CM CN.又∴CM与CN有公共点C ∴,,M N C三点共线.。
课件4:6.1.2 向量的加法

[解析] (1)如题图,由已知得四边形 DFCB 为平行四边形, 由向量加法的运算法则可知: ①A→B+D→F=A→B+B→C=A→C; ②A→D+F→C=A→D+D→B=A→B. (2)①正确,当两向量反向时,和向量的模最小为 1; ②中描述的只是向量同向时的情况,故不正确, 反之正确,即③正确.
6.1.2 向量的加法
课程标准
学法解读
1.理解向量和的定义.
1.通过学习和向量定义,培养
2.掌握向量加法的法则. 学生的数学抽象素养.
3.了解多个向量相加.
2.通过向量加法的运算,培
4.理解向量加法的运算律. 养学生的直观想象、数学运算
5.了解和向量模的不等式. 素养.
知识点 一
向量加法的定义及其运算法则
边形法 __A_→D_____为邻边作□ABCD,
则 则对角线上的向量A→C=___a_+__b____.
(3)向量 a,b 的模与 a+b 的模之间的关系: ||a|-|b||__≤____|a+b|__≤____ |a|+|b|.
思考:(1)向量求和的三角形法则中求和的两个向量的起 点与终点是怎样连接的?和向量的起点与终点是怎样的? (2)利用向量求和的三角形法则时,若向量a,b中有零向 量怎么办?若两向量共线时,能否利用三角形法则求和? (3)向量求和的平行四边形法则中“不共线”是否多余, 去掉可以吗?
(4)平行四边形法则中,求和的两个向量与和向量的起点 有什么特点?和向量是怎样产生的?
提示:(1)求和的两个向量“首尾连接”,其和向量是从 第一个向量的起点指向最后一个向量的终点的向量.
(2)对于零向量与任一向量a,规定0+a=a+0=A. 当两
向量共线时,仍可以使用三角形法则求和. (3)不可以,因为如果两个向量共线,就无法以它们为邻 边作出平行四边形,也不会产生和向量. (4)求和的两个向量与和向量共起点,和向量是以求和的 两个向量为邻边的平行四边形的对角线向量.
向量运算律

向量运算律
【原创实用版】
目录
1.向量运算律的定义
2.向量加法运算律
3.向量数乘运算律
4.向量点积运算律
5.向量运算律的应用
正文
1.向量运算律的定义
向量运算律是指在向量空间中进行的加法、数乘和点积等运算所应满足的规律。
这些规律保证了向量运算的结果是合理的,并且满足一些基本的代数性质。
2.向量加法运算律
向量加法运算律是指对于向量空间中的任意向量 a 和向量 b,它们的和仍然属于该向量空间,即 a+b 是一个向量。
具体地,对于任意两个向量 a 和 b,它们的和可以表示为 a+b,其中 a+b 的每个分量是 a 和
b 对应分量之和。
3.向量数乘运算律
向量数乘运算律是指对于向量空间中的任意向量 a 和标量 k,数乘结果仍然是一个向量。
具体地,对于任意向量 a 和标量 k,数乘结果可以表示为 ka,其中 ka 的每个分量是 a 对应分量乘以 k。
4.向量点积运算律
向量点积运算律是指对于向量空间中的任意向量 a 和向量 b,它们
的点积是一个标量。
具体地,对于任意两个向量 a 和 b,它们的点积可以表示为 a·b,其中 a·b 等于 a 和 b 对应分量之积的和。
5.向量运算律的应用
向量运算律在物理学、数学和工程学等领域有广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A5 A2 A4 A3
F
弹簧所受的拉力的合力 ?
F1 F1
F
(二)向量加法的平行四边形法则
b 已知:如图非零向量 a ,
B
a+b
C
a
a
b
A
b
D
作法: 在平面内任取一点A,作 AB= a, AD =b,以AB , AD为邻边 作平行四边形,则 AC = a + b 。 这种求向量和的方法称为向量加法的平行四边形法则。
2.2.1向量的加法
南溪中学李辉
复习
1、向量的定义 既有大小又有方母表示;
3、零向量和单位向量 长度为 0 的向量;长度为单位1的向量 4、平行向量(共线向量) 方向相同或相反的非零向量叫做平行向量. 5、相等向量 长度相等且方向相同的向量
提出问题:
a
b
A AC = a + b B C
2、方向相反
a b
A
B
C
AC = a + b
问题探究
问题1:你能说出实数运算有哪些运算律吗? 问题2:定义了一种新运算,自然要研究其运 算律问题.请类比数的加法的运算律,思考向 量的加法是否也有运算律?有哪些运算律?
(1) 交换律:
ab ba
作法: 作平行四边形ABCD ,使AB a, AD b 则 BC b,DC a ,则: AC AB BC a b
AB +(BC + CD ) = AD
练习2:求下列向量的和
(1)AB+BC+CD+DE+EF+FG= AG (2)CD+BC+AB= AD
例1、轮船从A港沿东偏北30°方向行驶了 40 n mile(海里)到达B处,再由B处沿 正北方向行驶 40 n mile到达C处,求此时轮 船与A港的相对位置 C 解:如图, 北
AB BC
AC
由此得出什么结论?
A
AB BC AC
一、向量的加法定义: 求向量和的运算,叫做向量 的 加法。
(一)向量加法的三角形法则:
b 已知:如图非零向量 a, a
b
A
C
a+b
a
b
B
作法: 在平面内任取一点A, 作 AB = a ,BC = 则向量 AC 叫做
b
a与 b
的和,即
AC AD DC b a
D
a b
C
b a
A
b a
B
(2) 结合律:
b
A
B
a
c O
C
OC OB BC (a+b)+c=_____+____=____ AC a+(b+c)=OA+_____=___ OC
向量加法的运算律
交换律: a b b a 结合律:(a b) c a (b c) 想一想
F1
1、向量加法的定义
(1)三角形法则及其推广
首尾相接 (适用于任意向量的加法)
(2)平行四边形法则
起点相同 (适用于不共线向量的加法)
2、共线向量的加法 3、向量加法的运算律
|| a | | b ||| a b || a | | b |
练习: 3、4
a+b = AB
+ BC = AC。
这种求向量和的方法称为向量加法的三角形法则。
说明:
1、向量的和仍是一个向量 2、首尾相接,由头指尾 3、不仅适用任何两个向量,而且可以推广到任 意多个向量(如下面例题)
推广:
A1 由若干条有向线段首尾相接组成的封闭的折线, 则它们的和向量为
0
如:
A 1A 2 A 2A 3 A 3A 4 A 4A 5 A 5A 1 0
答:略
B )30° D
东
A
2 | AC | | AD |2 | DC |2 (20 3) 602 40 3
例2、两个力F1、F2同时作用在一个物 体上,其中F1= 40N,方向向东, F2=30N,方向向北,求它们的合力
解:如图,
B
F2 O
C
OA表示F1, OB表示F2,以OA、OB为 邻边作平行四边形OACB,则OC表 示合力F.在Rt OAC中
2、方向相反
a
b
A
B
C AC = a + b
由此可见
ab
=
ab
=
ab
综上: a b ≤
ab
≤
ab
练习1:如图:已知平行四边形ABCD,填空
(1) (2) (3)
AB + BC =
AB + AD =
AC AC AC
AD
A
D
C
BC + AB =
B
(4) ( AB + BC)+ CD = (5)
数能进行运算,向量是否也能进行运算 呢?类比数的加法,猜想向量的加法,应 怎样定义向量的加法?
我们来看以下几个问题
1.一人从A到B,再从B按原方向到C,则两次的位移之和AB BC 是
AC
A
B
C
2.飞机从A到B,再改变方向从B到C,则两次的位移的和 AB BC 是: C A B
AC
3.船的速度为 AB ,水流的速度为 ,则两个速度的和 BC B C 是:
向量加 法
(三)方法特征
1、向量加法的三角形法则:
(1)将向量平移使得它们首尾相连 (2)和向量即是第一个向量的首指向第二个向量的尾
2、向量加法的平行四边形法则:
(1)将向量平移到同一起点 (2)和向量即以它们作为邻边平行四边形的共起点的对角线
a b
向量加 法
二、共线向量的加法: 三角形法则 1、方向相同
设 AB、 BC分别表示轮船的两次位移, 则 AC表示轮船的合位移, AC AB BC 在ADB中,ADB 90,DAB 30
| AB | 40 | DB | 20, | AD | 20 3 | DC | 20 40 60 | AC | 2 | AD | CAD 60
A | OA | F1 40 N | AC || OB | F2 30 N F合 | OC | 50 N
| AC | F2 3 设F合与F1的夹角为 , 则tan = 0.75 37 | OA | F1 4 答 : 合力大小为50 N , 方向为东偏北37
1.零向量和任一向量 a 的和为什么? 2.a b , a b 和 a b 的大小关系如何 ?
ab
a0 0a a
≤
ab
≤
ab
何时取得等号?
b 已知:如图非零向量 a, a
b
A
C
a+b
a
AC = a + b
b
B
由此可见
ab
<
ab
<
ab
1、方向相同
a
b
A AC = a + b B C
