微观经济学高鸿业版第五章课后习题答案
高鸿业《西方经济学(微观部分)》(第6版)课后习题详解(第5章 成本)

高鸿业《西方经济学(微观部分)》(第6版)第5章 成 本课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
1.表5-1是一张关于短期生产函数(),Q f L K =的产量表:表5-1 短期生产的产量表(1)在表中填空。
(2)根据(1),在一张坐标图上作出L TP 曲线,在另一张坐标图上作出L AP 曲线和MP L曲线。
(提示:为了便于作图与比较,L TP 曲线图的纵坐标的刻度单位大于L AP 曲线图和L MP 曲线图。
)(3)根据(1),并假定劳动的价格200w =,完成下面的相应的短期成本表,即表5-2。
表5-2 短期生产的成本表(4)根据表5-2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线。
(提示:为了便于作图与比较,TVC 曲线图的纵坐标的单位刻度大于AVC 曲线和曲MC 线图。
)(5)根据(2)、(4),说明短期生产曲线和短期成本曲线之间的关系。
答:(1)短期生产的产量表如表5-3所示。
表5-3 短期生产的产量表(2)根据(1)中的短期生产的产量表所绘制的L TP 曲线、L AP 曲线和L MP 曲线如图5-8所示。
图5-8 生产函数曲线(3)当200w 时,相应的短期成本表如表5-4所示。
表5-4 短期生产的成本表(4)根据(3)中的短期生产的成本表所绘制的TVC 曲线、AVC 曲线和MC 曲线如图5-9所示。
图5-9 成本曲线(5)由(2)、(4)可得边际产量和边际成本的关系为:边际成本MC 和边际产量L MP 两者的变动方向是相反的。
高鸿业微观经济学课后习题及详细答案(128页)

高鸿业微观经济学课后习题答案第1章课后习题详解1.回想你看到过或接触过的西方经济学著作。
它们各自属于本章所说的三种类别中的哪一种?答:第一类,企事业的经营管理方法和经验。
如行情研究、存货管理、产品质量控制、车间生产流程布局等内容。
著作有《现代企业财务管理》等。
第二类,对一个经济部门或经济问题的集中研究成果。
如资源经济学、商业经济学、农业经济学、石油经济学,对税收、财政和通货膨胀等问题的论述。
著作有《资源经济学》、《农业经济学》。
第三类,经济理论的研究和考察。
如微观经济学、数理经济学、福利经济学、经济思想史等。
著作有《宏观经济学》、《微观经济学》、《经济思想史》等。
2.为什么我国学员学习西方经济学的目的不同于西方?答:由于西方经济学具有双重性质,它既是资本主义的意识形态,由是资本主义市场经济的经验总结,这就决定了我国学员学习它所应持有的态度:在整个的理论体系上或整体倾向上对它持否定的态度,而在具体的内容上应该看到它的有用之处,是否真正有用还需要考虑到国情的差别,应结合我国的国情加以借鉴吸收,做到“弃其糟粕、取其精华、洋为中用”。
(1)我国学习下岗经济学的主要目的在于从中得到对我国有用的知识,即“学以致用”。
对西方经济学而言,“为艺术而艺术”的学习目标是不适用的。
因为,如果不是为了“实用”而学习,那么还不如去从事其它的活动。
“经济学”这一名词的英文来源是希腊文的名词“家庭管理”。
由此也可以看出西方经济学的“致用”的性质。
(2)既然学习西方经济学的目的是为了“致用”,那么就必须注意到它涉及对西方“致用”的两个特点:其一,它宣扬西方国家的意识形态,以便巩固西方社会的共识或凝聚力,即增加西方学者所说的“社会无形资本”;其二,它总结西方市场运行的经验,以便为改善其运行提供对策。
西方经济学之所以能够存在于西方,其原因即在于此;这就是说:它存在于西方的原因正是由于他对西方国家有用。
(3)在以上两个特点中,第一个特点显然对我国不但没有用处,反而会引起有害的作用。
高鸿业微观第五章课后习题答案

第五章成 本第一部分 教材配套习题本习题详解一、简答题1.下面表是一张关于短期生产函数Q ),(K L f 的产量表:(2)根据(1)在一张坐标图上做出TP L ,在另一张坐标图上作出AP L 曲线和MP L 曲线。
(3)根据(1),并假定劳动的价格w=200,完成下面的短期成本表。
短期生产的成本表(4和MC 曲线。
(5)根据(2)(4),说明短期生产曲线和短期成本曲线之间的关系。
解答:(1)补充完整的短期生产的产量表如表5—3所示。
2所示。
图5—1 总产量曲线 图5—2 平均产量曲线和边际产量曲线(3)补充完整的短期生产的成本表如表5—4所示。
如图5—4所示。
图5—3 总可变成本曲线图5—4 平均可变成本曲线和边际成本曲线(5)从图形可以看出,当边际产量高于平均产量时,平均产量上升,此时边际成本和平均成本下降。
当边际产量低于平均产量时,平均产量下降,此时边际成本和平均成本上升。
当边际产量上升时,边际成本下降,总产量上升,总可变成本以递减速率上升。
当边际产量等于平均产量时,边际成本等于平均成本,此时平均产量最大而平均可变成本最小。
2.假定某企业的短期成本函数是TC =Q 3-10Q 2+17Q+66,求: (1)指出该成本函数中的可变成本部分和固定成本部分;(2)写出下列函数:TVC(Q)、AC(Q)、AVC(Q)、AFC(Q)、MC(Q)。
解:(1)已知TC =Q 3-10Q 2+17Q+66,所以可变成本部分为 TVC =Q 3-10Q 2+17Q ,不变成本部分为TFC =66 。
(2) 平均成本函数为:AC =TC Q =Q 2-10Q +17+66Q平均可变成本函数为:AVC =TVCQ=Q 2-10Q+17平均不变成本函数为:AFC =TFC Q =66Q,边际成本函数为:MC(Q)=TC ′(Q)=TVC ′(Q)=3Q 2-20Q+173.下面是一张某厂商的LAC 曲线和LMC 曲线图。
西方经济学微观部分第五版高鸿业题库及答案

第一章导论一、选择题(共9个)1.经济学中的“稀缺性”是指(B)A.世界上大多数人生活在贫困中B.相对于资源的需求而言,资源总是不足的C.利用资源必须考虑下一代D.世界上的资源终将被人类消耗光2.经济物品是指(BC)A.有用的物品B.数量有限,要花费代价才能得到的物品C.稀缺的物品D.数量无限,不用付出代价就能得到的物品3.一国的生产可能性曲线以内的点表示(C)A.生产品最适度水平B.该国可利用的资源减少和技术水平降低C.失业或资源未被充分利用D.通货膨胀4.生产可能曲线的基本原理是(A)A.假定所有资源得到了充分利用B.一国资源总能被充分利用C.改进技术引起生产可能曲线向内移动D.生产可能曲线上的每一点的产品组合,对该国来说,都是最佳的5.下列那一项最可能导致生产可能性曲线向外移动(B)A.消费品生产增加,资本品生产减少B.有用性资源增加或技术进步C.通货膨胀;D.失业6.经济学中的基本选择包括(AC)A.生产什么,生产多少B.怎样生产,何时生产C.为谁生产D.以上都包括7.对某个汽车生产企业来说,下列哪一变量是外生变量(C)A.汽车的年产量B.生产线的技术水平C.消费者收入增加D.企业的人力资本管理8.下列哪一个变量属于存量( D)A.国民生产总值B.年生产能力C.居民收入D.固定资产价值9.21世纪30年代,西方经济学经历的第二次修改和补充(ACD)A.出现于1936年B.涉及垄断问题C.代表人物是凯恩斯D.为国家干预经济生活奠定了理论基础二、判断题(共1个)1.以萨缪尔森为首的新古典综合派把经济学分为微观经济学和宏观经济学。
三、解释概念(共17个)1.经济学2.欲望3.稀缺性4.选择5.机会成本6.生产可能性曲线7.经济人假定8.完全信息9.个量分析10总量分析11.静态分析12.动态分析13.实证分析14.规范分析15.常量与变量16.存量与流量17.内生变量与外生变量第一章习题答案一、选择题(共9个)题号1 2 3 4 5 6 7 8 9答案B BCC A BACC DACD二、判断题(共1个)题号 1答案√三、解释概念(共17个)(略)第二章需求、供给和均衡价格一、选择题(共18个)1.微观经济学的的基本假设条件是:(C)A.完全信息的假设B.完全竞争的假设C.合乎理性的人的假设D.边际效用递减的假设2.微观经济学的研究对象包括:(ABC)A.单个消费者B.单个厂商C.单个市场D.价格理论3.下列几组商品的交叉价格弹性为负向的有:(BD)A.面粉和大米B.汽油和汽车C.羊肉和牛肉D.CD播放机和CD4.当出租车租金下调后,对公共汽车服务的(AC) A.需求减少B.需求量增加C.需求曲线左移D.需求无法确定5.粮食市场的需求是缺乏弹性的,当粮食产量因灾害而减少时(B) A.粮食生产者的收入减少,因粮食产量下降B.粮食生产者的收入增加,因粮食价格会更大幅度上升C.粮食生产者的收入减少,因粮食需求量会大幅度减少D.粮食生产者的收入不变,因粮食价格上升与需求量减少的比率相同6.下列商品中,需求价格弹性最大的是(C)A.服装B.化妆品C.金银首饰D.食盐7.某一时期,电冰箱的供给曲线向右移动的原因可以是(B) A.电冰箱的价格下降B.生产者对电冰箱的预期价格上升C.生产冰箱的要素成本上升D.消费者的收入上升8.食盐市场的需求是缺乏弹性的,由于某种非价格因素的影响使食盐产量下降20%,在这种情况下(C) A.食盐生产者的收入减少,因为食盐产量下降20%B.食盐生产者的收入增加,因为食盐价格上升低于20%C.食盐生产者的收入增加,因为食盐价格上升超过20%D.食盐生产者的收入不变,因为食盐价格上升等于20%9.影响一种商品需求数量的因素包括(ABCD)A.商品本身的价格B.消费者的收入水平C.相关商品的价格D.消费者的偏好10.消费者预期某物品未来价格要上升,则对该物品的当前需求会(B)A.减少B.增加C.不变D.以上三种情况都有可能11.如果商品A和商品B是替代品,则A的价格下降将造成(D)A.A的需求曲线向右移动B.A的需求曲线向左移动C.B的需求曲线向右移动D.B的需求曲线向左移动12.若某行业中许多生产者生产一种标准化产品,我们可估计到其中任何一个生产者产品的需求将是(D)A.毫无弹性B.有单位弹性C.缺乏弹性或弹性较小D.富有弹性或弹性很大13.假如生产某种产品所需原料价格上升了,则这种商品(B)A.需求曲线向左移动B.供给曲线向左移动C.需求曲线向右移动D.供给曲线向右移动14.如果人们收入水平提高,则食品支出在总支出中的比重(B)A.提高B.降低C.不变D.不确定15.厂商在工资率下降的时候一般倾向于增雇工人,如果对工人的需求缺乏弹性,工资率下降将导致工资总额(A)A.减少B.不变C.增加D.无法确定16.政府为了扶持农业,对农产品规定了高于均衡价格的支持价格。
人大高鸿业版西方经济学微观部分第五章

停止营业点
AFC
0
Q
d STC SMC =
dQ
C SMC
O
L
O
Q
d STC d TVC d wL
dL
1
SMC =
=
=
=w
=w
dQ dQ dQ
dQ
MPL
五、短期生产函数和短期成本函数之间的对应关系
两点结论: 第一,MC与MPL是反向对应关系。
由于边际报酬递减规律的作用,可变要素的边际 产量MPL先上升后下降。所以,边际成本MC是先 下降,达到最低点后再上升。 第二,由边际成 本与边际产量的关系可以推知,总产量和总成本 之间也存在着对应关系,当总产量曲线上凸时, 总成本曲线下凹的,当总产量曲线下凹时,总成 本曲线是上凸的。当总产量曲线存在一个拐点时, 总成本曲线相应也有一个拐点。 ➢ 边际报酬的递增阶段对应的是边际成本的递减阶 段,边际报酬的递减阶段对应的是边际成本的递 增阶段,与边际报酬极大值相对应的是边际成本
210000
减:自有资金估算费用等(即隐含成本) 100000
所得税前的“经济利润” 减:应支付的所得税
110000 36300
第一节 短期成本分析
三、 (短期)固定成本和可变总成本
1.固定成本(fixed costs):指在短期内,使用固 定生产要素所支付的成本。
2.可变成本(variable costs):指在短期内,使用 可变生产要素所支付的成本。
Q
长期边际成本
C
LMC
LAC
0
Q
长期成本与短期成本的关系
长期成本曲线 往往称为“计 划曲线”。短 期成本曲线一 般称为“经营 曲线”。
《微观经济学》高鸿业第五版1~5章课后习题答案

微观经济学第三章1、已知一件衬衫的价格为 80 元,一份肯德鸡快餐的价格为20 元,在某消费者关于这两种商品的效用最大化的均衡点上,一份肯德鸡快餐对衬衫的边际替代率MRS 是多少?解:按照两商品的边际替代率MRS 的定义公式 , 可以将一份肯德鸡快餐对衬衫的边际替代率写成:MRS XYYX其中 : X表示肯德鸡快餐的份数 ; Y表示衬衫的件数 ;MRS, 消费者表示在维持效用水平不变的前提下增加一份肯德鸡快餐时所需要放弃的衬衫消费数量。
在该消费者实现关于这两件商品的效用最大化时,在均衡点上有MRS xy = P x / P y即有MRS xy = 20/ 80=0. 25它表明:在效用最大化的均衡点上,消费者关于一份肯德鸡快餐对衬衫的边际替代率MRS0 25为 .。
2假设某消费者的均衡如图1 9所示。
其中,横轴OX1 和纵轴OX2,分别表示商品 1和商品 2的数量,-线段AB 为消费者的预算线, 曲线 U 为消费者的无差异曲线, E 点为效用最大化的均衡点。
已知商品 1 的价格P 2 元。
1=( 1)求消费者的收入;X2220U( ) 求上品的价格P 2;A B( 3) 写出预算线的方程;E104( ) 求预算线的斜率;O1020X1(5) 求 E 点的MRS12 的值。
30解:( 1)图中的横截距表示消费者的收入全部购买商品 1 的数量为 30 单位,且已知P=2 元,所以,消费者的收入M1 =2 元× 30=60。
( 2)图中的纵截距表示消费者的收入全部购买商品 2 的数量为 20单位,且由(1)已知收入M60元,所以,商品2的价格P斜率 =-P P 23PM203元=21/2=-/ ,得2=/=( 3)由于预算线的一般形式为:P1X1+P2X2=M所以,由( 1)、( 2)可将预算线方程具体写为2X1+3X2=60。
(4)将(3)中的预算线方程进一步整理为X 2 3X20 2 3。
高鸿业版微观课后习题答案(完整版)

西方经济学(微观部分)部分课后习题答案第四章生产论1.(1)可变要素的数量可变要素的总产量可变要素的平均产量可变要素的边际产量1222212610324812448122456012126661167701048708.7509637-7(2)是;从第5单位开始2.略3.(1)TP L=-0.5L2+20L-50;AP L=-0.5L+20-50/L;MP L=-L+20(2)L=20时, TP L最大;L=10时, AP L最大;L=0时, MP L最大(3) AP L= MP L=104.(固定投入比例的生产函数)(1)此时Q=2L=3K,∴L=18,K=12(2)TC=L*P L+K*P k=12805.(1)均衡条件MP L/MPk=P L/Pk①K=2P L L/Pk②K=(P L/Pk)1/2L③K=P L L/2Pk④K=3L(2) ①K=200*21/3,L=100*21/3②K=2000,L=2000③K=5*21/3,L=10*21/3④K=1000,L=1000/36.(1)规模报酬不变(2)是7(1)a0=0;(2)略8(1)L=K=1000 ;Q=1000(2)L=K=800;Q=24009.10. 略第五章成本论1.(1)L1234567TP L103070100120130135 AP L101570/3252465/3135/7 MP L1020403020105(3)L Q TVC A VC MC1102002020 23040040/310 37060060/7 541008008 20/3 5120100025/310 61301200120/1320 71351400280/27402.略3.(1)TVC(Q)=Q3-5Q2+15Q;AFC(Q)=66(2)TVC(Q)=Q3-5Q2+15QAC(Q)=Q2-5Q+15+66/QA VC(Q)= Q2-5Q+15AFC(Q)=66/QMC(Q)=3Q2-10Q+154.Q=10时,A VC(Q)=65.(1)TFC=500;(2)TC(Q)=Q3-15Q2+100Q+500TVC(Q)= Q3-15Q2+100QAC(Q)=Q2-15Q+100+500/QA VC(Q)=Q2-15Q+1006.根据MC1=MC2求解Q1=15,Q2=257. TC(Q)=Q2/8+32TVC(Q)= Q2/8AC(Q)=Q/8+32/QA VC(Q)= Q/8MC(Q)=Q/48.(1)L=2Q(2)TC=10Q+500;AC=10+500/Q;MC=10(3)利润=Q2-4Q+1009.STC=Q3-4Q2+100Q+800SAC=Q2-4Q+100+800/QSVC=Q3-4Q2+100+800/QA VC=Q2-4Q+10010-13.略第六章完全竞争市场1.(1)Q=20(2)P<5(3)P≥5 ,Q= [4+(1.2P-2)1/2 ]/0.6P<5,Q=02.(1)P=100,Q=10,SAC=20,利润=800(2)P=4,Q=6(3)1003.(!)P=5,Q=7000(2)P=9,Q=82004.(1)P=6,Q=3900(2)处于长期均衡,数量= 78(3)P=6,Q=5600(4)处于长期均衡,数量=112(5)成本不变行业(6)34家5.(1)P=200(2)N=6006.(1)Q=20,LAC=200,利润=8000(2) 未处于长期均衡(3)Q=10,LAC=100, 利润=0(4)规模不经济7.Q=80, 利润=1608.9.10.略第七章不完全竞争的市场1.(1)MR=2(2)MR=23.根据MR=MC求解Q=20;P=854.(1)Q=2.5;P=7;TR=17.5; 利润=4.25(2)Q=10;P=4;TR=40; 利润=-52(3) 略5.Q=10;P=100;A=1006.(1)销售量3.6和4;价格84和49;总利润146 (2)P=56;Q=4; 总利润487.(1)P=138;Q=200(2)e d≈6(3)P=A-BQ=161-0.115Q或Q=(161-P)/0.1158(1)Q=8;P=72; 利润=320(2)Q=10;P=88;A=100; 利润=4809.10.11略第八章生产要素价格决定的需求方面1.2.3.4.5.略6.由W=VMP L=P*MPP L=P*dQ/dL求解:L=607.(a)由W=VMP L=P*MPP L=P*dQ/dL得L=a/2b-W/2bP由上表可知,L=79.Q=30,L=15,W=70,P=8010.L=40,q=3760,W=180第九章生产要素价格决定的供给方面1.2.3.4.5.6.7略8.(a) W=40(b) W=45(c) 由厂商和工人恰好平均承担了政府征收的10美元税款;(d)税收总额为:175009略10.准租金:由R1=TR-TVC=(P-A VC)*Q 得R1=500元经济利润:R2=TR-(TVC+TFC)得R2=100元第十章一般均衡论和福利经济学答案略第十一章市场失灵与微观经济政策1.2.3.4.5.略6.(a) Q=200,P=60,π=8000(b)由P=MC :P=20,Q=400, π=0(c)损失了40007.(a)T=43.75(b) T=62.58.(a) x=80(b) x=400, 后果:牧场因为过度放牧而在数年后一片荒芜,这就是所谓的公地问题。
高鸿业西方经济学(第五版)课后答案(微观部分齐全)
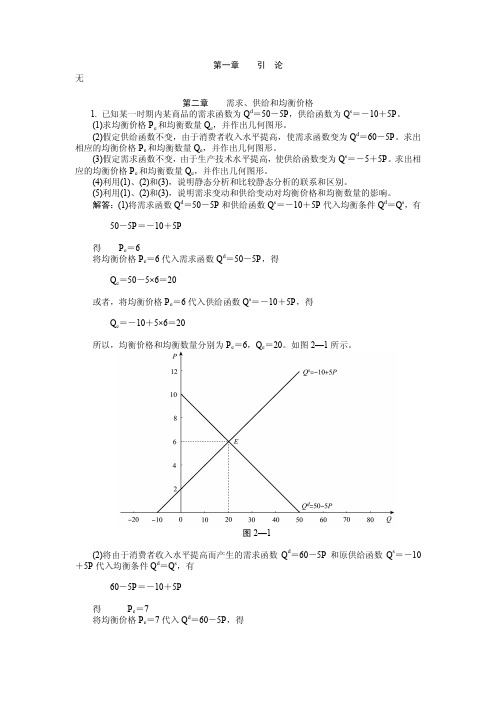
(3)根据该供给函数或供给表作出几何图形,利用几何方法求出 P=3 元时的供给的价格 点弹性。它与(2)的结果相同吗? ΔQ P1+P2 Q1+Q2 解答:(1)根据中点公式 es= · , ),有 ΔP 2 2 4 3+5 4+8 4 es= · , )= 2 2 2 3 dQ P 3 (2)由于当 P=3 时,Qs=-2+2× 3=4,所以,es= · =2·=1.5。 dP Q 4 (3)根据图 2—5,在 a 点即 P=3 时的供给的价格点弹性为 AB 6 es= = =1.5 OB 4
-
dQ i P edi=- · =3 dP Qi dQi Qi 即 =-3· (i=1,2,„,60)(1) dP P 60 Q 且 Qi= 3 (2) i=1 2 类似地,再根据题意,该市场 的商品被另外 40 个消费者购买,且每个消费者的需求的 3 价格弹性都是 6,于是,单个消费者 j 的需求的价格弹性可以写为 dQ i P edj=- · =6 dP Qj
于是,有 dQ 1 M 1 1 = - · dM 2100 2 100 进一步,可得 dQ M eM= · dM Q 1 M 1 1 = - · · 100· 2100 2 100
M 2 100
M 1 = 100 2
观察并分析以上计算过程及其结果,可以发现,当收入函数 M=aQ2(其中 a>0,为常 1 数)时,则无论收入 M 为多少,相应的需求的收入点弹性恒等于 。 2 7. 假定需求函数为 Q=MP N,其中 M 表示收入,P 表示商品价格,N(N>0)为常数。 求:需求的价格点弹性和需求的收入点弹性。 - 解答:由已知条件 Q=MP N,可得
图 2—3 (4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的 均衡状态及其特征。 也可以说, 静态分析是在一个经济模型中根据给定的外生变量来求内生 变量的一种分析方法。以(1)为例,在图 2—1 中,均衡点 E 就是一个体现了静态分析特征的 点。它是在给定的供求力量的相互作用下达到的一个均衡点。在此,给定的供求力量分别用 给定的供给函数 Qs=-10+5P 和需求函数 Qd=50-5P 表示,均衡点 E 具有的特征是:均 衡价格 Pe=6,且当 Pe=6 时,有 Qd=Qs=Qe=20;同时,均衡数量 Qe=20,且当 Qe=20 时, 有 Pd=Ps=Pe=6。 也可以这样来理解静态分析: 在外生变量包括需求函数中的参数(50, -5)以及供给函数中的参数(-10,5)给定的条件下, 求出的内生变量分别为 Pe=6 和 Qe=20。 依此类推,以上所描述的关于静态分析的基本要点,在(2)及图 2—2 和(3)及图 2—3 中 的每一个单独的均衡点 Ei (i=1,2)上都得到了体现。 而所谓的比较静态分析是考察当原有的条件发生变化时, 原有的均衡状态会发生什么变 化,并分析比较新旧均衡状态。也可以说,比较静态分析是考察在一个经济模型中外生变量 变化时对内生变量的影响,并分析比较由不同数值的外生变量所决定的内生变量的不同数 值,以(2)为例加以说明。在图 2—2 中,由均衡点 E1 变动到均衡点 E2 就是一种比较静态分 析。它表示当需求增加即需求函数发生变化时对均衡点的影响。很清楚,比较新、旧两个均 衡点 E1 和 E2 可以看到:需求增加导致需求曲线右移,最后使得均衡价格由 6 上升为 7,同 时,均衡数量由 20 增加为 25。也可以这样理解比较静态分析:在供给函数保持不变的前提 下,由于需求函数中的外生变量发生变化,即其中一个参数值由 50 增加为 60,从而使得内 生变量的数值发生变化,其结果为,均衡价格由原来的 6 上升为 7,同时,均衡数量由原来 的 20 增加为 25。 类似地,利用(3)及图 2—3 也可以说明比较静态分析方法的基本要点。 (5)由(1)和(2)可见,当消费者收入水平提高导致需求增加,即表现为需求曲线右移时, 均衡价格提高了,均衡数量增加了。 由(1)和(3)可见,当技术水平提高导致供给增加,即表现为供给曲线右移时,均衡价格 下降了,均衡数量增加了。 总之,一般地,需求与均衡价格成同方向变动,与均衡数量成同方向变动;供给与均衡 价格成反方向变动,与均衡数量成同方向变动。 2. 假定表 2—1(即教材中第 54 页的表 2—5)是需求函数 Qd=500-100P 在一定价格范围 内的需求表: 表 2—1 某商品的需求表 价格(元)
高鸿业微观经济学第五版 成本练习及答案

高鸿业微观经济学第五版成本练习及答案高鸿业微观经济学第五版成本练习及答案第五章成本理论练习一、单项选择题1、在经济学中,短期是指(d)a一年或一年以内的时期b在这一时期内所有资金投入要素均就是紧固维持不变的c在这一时期内所有资金投入要素均就是可以变动的d在这一时期内,生产者来不及调整全部生产要素的数量,至少有一种生产要素的数量是固定不变的2、在经济学中,短期和长期的分割标准就是(d)a与否可以调整产量b与否可以调整产品价格c时间长短d是否可以调整全部生产要素的数量3、在经济学中,生产的机会成本等于(d)a显性成本+隐性成本b社会成本+显性成本c财务会计成本+隐性成本da和c都对4、短期气门成本曲线随其产量减少而(a)a不断下降b不断上升c先下降再上升d先上升再下降5、某厂商生产一批产品,当生产第7个单位产品的总成本是3.5元,生产第8个单位产品总成本是4.6元,那么该厂商的边际成本是(d)a3.5元b4.6元c8.1元d1.1元6、在短期内,以下观点不恰当的一项就是(d)a总不变成本(tfc)是厂商为生产一定量的产品对不变生产要素所支付的总成本b建筑物和机器设备的折旧费属于总不变成本c总固定成本不随产量的变化而变化d当产量为零时,总固定成本也为零7、当平均成本高于边际成本时,(b)a平均值成本处在下降b平均值成本处在上升c总成本处在上升d总气门成本处在上升8、当边际成本曲线交于平均成本曲线时,下列各项不正确的是(c)a边际成本上升b平均可变成本上升c边际成本下降d总成本上升9、当边际成本曲线达到最低点时(a)a平均成本曲线呈现递减状态b平均可变成本曲线呈现递增状态c平均产量曲线达到最大值d总产量曲线达到最大值10、边际成本曲线(c)a沿着平均值总成本曲线和平均值固定成本曲线的最低点b沿着平均值气门成本曲线和平均值固定成本曲线的最低点c沿着平均值气门成本曲线和平均值成本曲线的最低点d 仅沿着平均值气门成本曲线的最低点11、当边际成本曲线上升时,其对应的平均可变成本曲线一定是(d)a上升b下降c即为不下降,也不上升d即可能将下降,又可能将上升12、当短期成本曲线以递减的速率上升时,(b)a边际成本曲线处在递增阶段b边际成本曲线处在递减阶段c边际产量曲线处在递减阶段d无法判断边际成本曲线与边际产量曲线的状态13、长期成本曲线上的各点对应的就是既定产量下的(d)a最高平均值成本b最高边际成本c平均值成本变动d最高总成本14、长期边际成本曲线呈圆形u型的原因是(c)a边际效用递减规律b边际收益递减规律c生产有规模经济向规模不经济变动d生产的一般规律15、长期成本曲线是各种产量的(a)a最高成本点的轨迹b最高平均值成本点的轨迹c最高边际成本点的轨迹d最高平均值气门成本点的轨迹16、以下关于长期边际成本曲线与长期总成本曲线之间的关系的观点恰当的就是(b)a在长期边际成本曲线下降时,长期总成本曲线以越来越快的速度下降b 在长期边际成本曲线下降时,长期总成本曲线以越来越快的速度下降c在长期边际成本曲线上升时,长期总成本曲线以越来越快的速度下降d以上均不恰当17、若某厂商的生产产量扩大1倍,而厂商生产成本的增加低于1倍,则该厂商的生产存在(a)a规模经济b规模不经济c外部性d以上均不恰当18、某日用品制造商厂单位产量所带来的边际成本大于产量增加前的平均可变成本,那么在产量增加后平均可变成本会(b)a增加b减少c维持不变d无法推论19、如某厂商的总收益为65000元,其中劳动成本为23000元,原材料成本为16500元,所有者为其他人工作可赚取14300元。
西方经济学微观部分(高鸿业_第五版)课后习题详细问题详解

第二章需求、供给和均衡价格1. 已知某一时期内某商品的需求函数为Q d=50-5P,供给函数为Q s=-10+5P。
(1)求均衡价格P e和均衡数量Q e,并作出几何图形。
(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Q d=60-5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Q s=-5+5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(4)利用(1)、(2)和(3),说明静态分析和比较静态分析的联系和区别。
(5)利用(1)、(2)和(3),说明需求变动和供给变动对均衡价格和均衡数量的影响。
解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
西方经济学微观部分(高鸿业第六版)课后习题答案

第二章需求、供给和均衡价格1. 解答:(1)将需求函数Qd=50-5P和供给函数Qs=-10+5P代入均衡条件Qd=Qs,有50-5P=-10+5P 得 Pe=6将均衡价格Pe=6代入需求函数Qd=50-5P,得Qe=50-5×6=20 或者,将均衡价格Pe=6代入供给函数Qs=-10+5P,得Qe=-10+5×6=20所以,均衡价格和均衡数量分别为Pe=6,Qe=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Qd=60-5P和原供给函数Qs=-10+5P代入均衡条件Qd=Qs,有60-5P=-10+5P 得Pe=7 将均衡价格Pe=7代入Qd=60-5P,得Qe=60-5×7=25或者,将均衡价格Pe=7代入Qs=-10+5P,得Qe=-10+5×7=25所以,均衡价格和均衡数量分别为Pe=7,Qe=25。
如图2—2所示。
图2—2(3)将原需求函数Qd=50-5P和由于技术水平提高而产生的供给函数Qs=-5+5P代入均衡条件Qd=Qs,有50-5P=-5+5P 得Pe=5.5将均衡价格Pe=5.5代入Qd=50-5P,得Qe=50-5×5.5=22.5 或者,将均衡价格Pe=5.5代入Qs=-5+5P,得Qe=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为Pe=5.5,Qe=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Qs=-10+5P和需求函数Qd=50-5P表示,均衡点E具有的特征是:均衡价格Pe=6,且当Pe =6时,有Qd=Qs=Qe=20;同时,均衡数量Qe=20,且当Qe=20时,有Pd=Ps=Pe=6。
微观经济学习题与答案(高鸿业_人大版)

第1章绪论一、单项选择题1.经济学可定义为( C )A、政府对市场制度的干预B、企业取得利润的活动C、研究如何最合理地配置稀缺资源于诸多用途D、人们靠收入生活2.经济学研究的基本问题是(D )A、怎样生产B、生产什么,生产多少C、为谁生产D、以上都包括3.说“资源是稀缺的”是指( B )A、世界上大多数人生活在贫困中B、相对于资源的需求而言,资源总是不足的C、资源必须保留给下一代D、世界上资源最终将由于生产更多的物品和劳务而消耗光4.人们在进行决策时,必须作出某种选择,这是因为(B )A、选择会导致短缺B、人们在进行决策时面临的资源是有限的C、人是自私的,所作出的选择会实现自身利益的最大化D、个人对市场的影响是微不足道的5.下列问题( C )是经济学研究不会涉及的问题A、在稀缺资源约束条件下,实现资源有效配置的方法B、如何实现中国人均收入翻两番C、中国传统文化的现代化问题D、充分就业和物价水平的稳定6.一国生产可能性曲线以内的一点表示( B )A、通货膨胀B、失业或资源没有被充分利用C、该国可利用的资源减少以及技术水平降低D、一种生产品最适度水平7.下列各项中(C )会导致一国生产可能性曲线向外移动A、失业B、通货膨胀C、有用性资源增加或技术进步D、消费品生产增加,资本物品生产下降8.下列命题中( C )不是实证经济学命题A、1982年8月联储把贴现率降到10%B、1981年失业率超过9%C、联邦所得税对中等收入家庭是不公平D、社会保险税的课税依据已超过30 000美元9.下列( B )是规范经济学的说法A、医生挣的钱比蓝领工人多B、收入分配中有太多的不公平现象C、从1999年开始,中国的物价水平基本保持稳定状态,这一现象也许会保持到2005年D、如果在20世纪80年代中期你购买了微软公司的1000股股票,现在你愿意出售的话,你肯定赚不少钱10.由市场配置资源意味着( B )A、所有的人都会得到他想要的东西B、资源的配置是由市场机制实现的C、政府能够决定谁获得多少消费品D、要得到急需的物品你只能“走后门”11.西方学者认为现代美国经济是一种( C )A、完全的自由放任经济制度B、严格的计划经济制度C、混合资本主义市场经济制度D、自给自足制度1-5 C D B B C 6-10 B C C B B11、C二、判断正误1.只有落后国家才存在资源的稀缺性和供给的短缺现象。
(全1-23章共157页)高鸿业西方经济学微观部分第五版课后习题答案
第一章引论见本书第二十三章。
第二章需求、供给和均衡价格1. 已知某一时期内某商品的需求函数为Q d=50-5P,供给函数为Q s=-10+5P。
(1)求均衡价格P e和均衡数量Q e,并作出几何图形。
(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Q d=60-5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Q s=-5+5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(4)利用(1)、(2)和(3),说明静态分析和比较静态分析的联系和区别。
(5)利用(1)、(2)和(3),说明需求变动和供给变动对均衡价格和均衡数量的影响。
解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
高鸿业第五版微观经济学课后习题答案

.2/1 于等恒 性弹点的求需的应相,少多为 M 入收论无则,时)数常为 0>a 中其( 2Qa=M 数函入收当,现发以可,果结其即程过算计上以析分并察观
:得可,步一进
:有,是于 001/M√=Q 得可 2Q 001=M 件条知以由�解 。性 弹点入收的求需的时 0046=M 入收当�求。2Q001=M 为系关数函的间之 M 入收与 Q 量数费消的品商种某于关者费消某定假 5
的出求,下件条的定给)5,01-(数参的中数函给供及以)5-,05(数参的数函求需括包量变生外在: 析分态静解理来样这以可也.eP=sP=dP
�
GO/DG=edE�有点 e 在 GO/CG=fdE�有点 f 在
GO/BG=adE�有点 a 在 :于在由理其 edE<fdE<adE 有且,的等相不是 性弹点格价的求需的点三 f.e.a 的上线曲求需性线条三于处别分:知推地便方很以可样同,法方何几的性弹点格价的求需求据根�2�
Pd
��
Q Pd � � � dE P Qd
:为写以可性弹格价的求需的计合者费消个 001 上场市该,外此 )4( )3( 且 )04……2,1=j(P/jQ6-=Pd/jQd 即 6=)Q/P(*)Pd/Qd(-=jdE :为写以可性弹格价的 求需的 j 者费消个单,是于,6 是都性弹格价的求需的者费消个每且,买购者费消个 04 外另被品商的 3/1 场市该,意题据根再,的似类相 )2( 且
�吗同相果结的�2�与它。性弹点格价的求需的时 2=P 出求法方何几用利�形图何几的应相出作表求需或数函求需该据根�3� 。性弹点格价的求需的是 2=P 求�数函求需的出给据根�2� 。性弹弧格价的求需的间之元 4 和元 2 格价出求�1� 0 5 001 4 002 3 003 2 004 1 量求需 �元�格价 表求需的品商某 �表求需的内围范格价定一在 P001-005=dQ 数函求需是 5—2 表定假 2
高鸿业微观经济学第四版四五章课后题答案

第4章 课后习题详解1.下面是一张一种可变生产要素的短期生产函数的产量表:(1)在表中填空。
(2)该生产函数是否表现出边际报酬递减如果是,是从第几单位的可变要素投入量开始的答:(1)利用短期生产的总产量(TP )、平均产量(AP )和边际产量(MP )之间的关系,可以完成对该表的填空,其结果如表4-2所示:(2)是。
由上表中数据可知,从第5单位的可变要素投入量开始出现规模报酬递减。
所谓边际报酬递减是指短期生产中一种可变要素的边际产量在达到最高点以后开始逐步下降的这样一种普遍的生产现象。
本题的生产函数表现出边际报酬递减的现象,具体地说,由表可见,当可变要素的投入量由第4单位增加到第5单位时,该要素的边际产量由原来的24下降为12。
2.用图说明短期生产函数(,)Q f L K 的TP L 曲线、AP L 曲线和MP L 曲线的特征及其相互之间的关系。
答:短期生产函数的TP L 曲线、AP L 曲线和MP L 曲线的综合图,如图4-5所示。
图4-5 生产函数曲线由图4-5可见,在短期生产的边际报酬递减规律的作用下,MP L 曲线呈现出先上升达到最高点A 以后又下降的趋势。
由边际报酬递减规律决定的MP L 曲线出发,可以方便地推导出TP L 曲线和AP L 曲线,并掌握它们各自的特征及其相互之间的关系。
关于TP L 曲线。
由于LL dTP MP dL=,所以,当MP L >0时,TP L 曲线是上升的;当MP L <0时,TP L 曲线是下降的;而当MP L =0时,TP L 曲线达最高点。
换言之,在L =L 3时,MP L 曲线达到零值的B 点与TP L 曲线达到最大值的B'点是相互对应的。
此外,在L <L 3即MP L >0的范围内,当MP L '>0时,TP L 曲线的斜率递增,即TP L 曲线以递增的速率上升;当MP L '<0时,TP L 曲线的斜率递减,即TP L 曲线以递减的速率上升;而当MP L '=0时,TP L 曲线存在一个拐点,换言之,在L =L 1时,MP L 曲线斜率为零的A 点与TP L 曲线的拐点A'是相互对应的。
微观经济学习题及答案高鸿业人大版

微观经济学习题及答案高鸿业人大版The following text is amended on 12 November 2020.第1章绪论一、单项选择题1.经济学可定义为( C )A、政府对市场制度的干预B、企业取得利润的活动C、研究如何最合理地配置稀缺资源于诸多用途D、人们靠收入生活2.经济学研究的基本问题是( D )A、怎样生产B、生产什么,生产多少C、为谁生产D、以上都包括3.说“资源是稀缺的”是指( B )A、世界上大多数人生活在贫困中B、相对于资源的需求而言,资源总是不足的C、资源必须保留给下一代D、世界上资源最终将由于生产更多的物品和劳务而消耗光4.人们在进行决策时,必须作出某种选择,这是因为( B )A、选择会导致短缺B、人们在进行决策时面临的资源是有限的C、人是自私的,所作出的选择会实现自身利益的最大化D、个人对市场的影响是微不足道的5.下列问题( C )是经济学研究不会涉及的问题A、在稀缺资源约束条件下,实现资源有效配置的方法B、如何实现中国人均收入翻两番C、中国传统文化的现代化问题D、充分就业和物价水平的稳定6.一国生产可能性曲线以内的一点表示( B )A、通货膨胀B、失业或资源没有被充分利用C、该国可利用的资源减少以及技术水平降低D、一种生产品最适度水平7.下列各项中( C )会导致一国生产可能性曲线向外移动A、失业 B、通货膨胀C、有用性资源增加或技术进步D、消费品生产增加,资本物品生产下降8.下列命题中( C )不是实证经济学命题A、1982年8月联储把贴现率降到10%B、1981年失业率超过9%C、联邦所得税对中等收入家庭是不公平D、社会保险税的课税依据已超过30 000美元9.下列( B )是规范经济学的说法A、医生挣的钱比蓝领工人多B、收入分配中有太多的不公平现象C、从1999年开始,中国的物价水平基本保持稳定状态,这一现象也许会保持到2005年D、如果在20世纪80年代中期你购买了微软公司的1000股股票,现在你愿意出售的话,你肯定赚不少钱10.由市场配置资源意味着( B )A、所有的人都会得到他想要的东西B、资源的配置是由市场机制实现的C、政府能够决定谁获得多少消费品D、要得到急需的物品你只能“走后门”11.西方学者认为现代美国经济是一种( C )A、完全的自由放任经济制度B、严格的计划经济制度C、混合资本主义市场经济制度D、自给自足制度1-5 C D B B C 6-10 B C C B B11、C二、判断正误1.只有落后国家才存在资源的稀缺性和供给的短缺现象。
西方经济学微观部分(高鸿业第六版)课后习题答案
第二章需求、供给和均衡价格1. 解答:(1)将需求函数Qd=50-5P和供给函数Qs=-10+5P代入均衡条件Qd=Qs,有50-5P=-10+5P 得 Pe=6将均衡价格Pe=6代入需求函数Qd=50-5P,得Qe=50-5×6=20 或者,将均衡价格Pe=6代入供给函数Qs=-10+5P,得Qe=-10+5×6=20所以,均衡价格和均衡数量分别为Pe=6,Qe=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Qd=60-5P和原供给函数Qs=-10+5P代入均衡条件Qd=Qs,有60-5P=-10+5P 得Pe=7 将均衡价格Pe=7代入Qd=60-5P,得Qe=60-5×7=25或者,将均衡价格Pe=7代入Qs=-10+5P,得Qe=-10+5×7=25所以,均衡价格和均衡数量分别为Pe=7,Qe=25。
如图2—2所示。
图2—2(3)将原需求函数Qd=50-5P和由于技术水平提高而产生的供给函数Qs=-5+5P代入均衡条件Qd=Qs,有50-5P=-5+5P 得Pe=5.5 将均衡价格Pe=5.5代入Qd=50-5P,得Qe=50-5×5.5=22.5 或者,将均衡价格Pe=5.5代入Qs=-5+5P,得Qe=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为Pe=5.5,Qe=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Qs=-10+5P和需求函数Qd=50-5P表示,均衡点E具有的特征是:均衡价格Pe=6,且当Pe =6时,有Qd=Qs=Qe=20;同时,均衡数量Qe=20,且当Qe=20时,有Pd=Ps=Pe=6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章1. 下面表是一张关于短期生产函数),(K L f Q 的产量表:(1) 在表1中填空 (2) 根据(1).在一张坐标图上作出TP L 曲线,在另一张坐标图上作出AP L 曲线和MP L 曲线.(3) 根据(1),并假定劳动的价格ω=200,完成下面的相应的短期成本表2. (4) 根据表2,在一张坐标图上作出TVC 曲线,在另一张坐标图上作出AVC 曲线和MC 曲线.(5) 根据(2)和(4),说明短期生产曲线和短期成本曲线之间的关系.(4)(5)边际产量和边际成本的关系,边际MC 和边际产量MP L 两者的变动方向是相反的.总产量和总成本之间也存在着对应系:当总产量TP L 下凸时,总成本TC 曲线和总可变成本TVC 是下凹的;当总产量曲线存在一个拐点时, 总成本TC 曲线和总可变成本TVC 也各存在一个拐点.平均可变成本和平均产量两者的变动方向是相反的.MC 曲线和AVC 曲线的交点与MP L 曲线和AP L 曲线的交点是对应的.2.下图是一张某厂商的LAC 曲线和LMC 曲线图.请分别在Q1和Q2的产量上画出代表最优生产规模的SAC 曲线和SMC 曲线.解:在产量Q1和Q2上,代表最优生产规模的SAC 曲线和SMC 曲线是SAC 1和SAC 2以及SMC 1和SMC 2. SAC 1和SAC 2分别相切于LAC 的A 和B SMC 1和SMC 2则分别相交于LMC 的A 1和B 1.3.假定某企业的短期成本函数是TC(Q)=Q 3-5Q 2+15Q+66: (1) 指出该短期成本函数中的可变成本部分和不变成本部分; (2) 写出下列相应的函数:TVC(Q)AC(Q)AVC(Q) AFC(Q)和MC(Q). 解(1)可变成本部分: Q 3-5Q 2+15Q不可变成本部分:66 (2)TVC(Q)= Q 3-5Q 2+15Q AC(Q)=Q 2-5Q+15+66/Q AVC(Q)= Q 2-5Q+15 AFC(Q)=66/Q MC(Q)= 3Q 2-10Q+15OMCQLMCSMC 1SAC 1SAC 2SMC 2 LACA 1B 1Q 1 Q 2长期边际成本曲线与短期成本曲线A4已知某企业的短期总成本函数是STC(Q)=0.04 Q 3-0.8Q 2+10Q+5,求最小的平均可变成本值.解: TVC(Q)=0.04 Q 3-0.8Q 2+10Q AVC(Q)= 0.04Q 2-0.8Q+10 令08.008.0=-='Q C AV 得Q=10又因为008.0>=''C AV 所以当Q=10时,6=MIN AVC5.假定某厂商的边际成本函数MC=3Q 2-30Q+100,且生产10单位产量时的总成本为1000.求:(1) 固定成本的值.(2)总成本函数,总可变成本函数,以及平均成本函数,平均可变成本函数. 解:MC= 3Q 2-30Q+100所以TC(Q)=Q 3-15Q 2+100Q+M 当Q=10时,TC=1000 =500(1) 固定成本值:500 (2) TC(Q)=Q 3-15Q 2+100Q+500TVC(Q)= Q 3-15Q 2+100Q AC(Q)= Q 2-15Q+100+500/Q AVC(Q)= Q 2-15Q+1006.某公司用两个工厂生产一种产品,其总成本函数为C=2Q 12+Q 22-Q 1Q 2,其中Q 1表示第一个工厂生产的产量,Q 2表示第二个工厂生产的产量.求:当公司生产的总产量为40时能够使得公司生产成本最小的两工厂的产量组合. 解:构造F(Q)=2Q 12+Q 22-Q 1Q 2+λ(Q 1+ Q 2-40)令⎪⎩⎪⎨⎧-===⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫=-+=∂∂=+-=∂∂=+-=∂∂3525150400204Q 2121122211λλλλQ Q Q Q FQ Q Q F Q Q F 使成本最小的产量组合为Q 1=15,Q 2=257已知生产函数Q=A 1/4L 1/4K 1/2;各要素价格分别为P A =1,P L =1.P K =2;假定厂商处于短期生产,且16=k .推导:该厂商短期生产的总成本函数和平均成本函数;总可变成本函数和平均可变函数;边际成本函数.)2(111)1(4,16:4/34/14/14/34/34/14/14/34/14/1A L P P L A L A LQ A QMP MP L A L QMP L A A QMP L A Q K L A L A LA =====∂∂∂∂==∂∂==∂∂===----所以所以因为解 由(1)(2)可知L=A=Q 2/16又TC(Q)=P A &A(Q)+P L &L(Q)+P K &16 = Q 2/16+ Q 2/16+32 = Q 2/8+32AC(Q)=Q/8+32/Q TVC(Q)= Q 2/8 AVC(Q)= Q/8 MC= Q/48已知某厂商的生产函数为Q=0.5L 1/3K 2/3;当资本投入量K=50时资本的总价格为500;劳动的价格P L =5,求: (1) 劳动的投入函数L=L(Q). (2) 总成本函数,平均成本函数和边际成本函数.当产品的价格P=100时,厂商获得最大利润的产量和利润各是多少? 解:(1)当K=50时,P K ·K=P K ·50=500,所以P K =10. MP L =1/6L -2/3K 2/3 MP K =2/6L 1/3K -1/310562613/13/13/23/2===--K L KL P P K L KL MP MP整理得K/L=1/1,即K=L.将其代入Q=0.5L 1/3K 2/3,可得:L(Q)=2Q(2)STC=ω·L (Q )+r·50 =5·2Q+500 =10Q +500 SAC= 10+500/Q SMC=10(3)由(1)可知,K=L,且已知K=50,所以.有L=50.代入Q=0.5L 1/3K 2/3, 有Q=25. 又π=TR -STC=100Q-10Q-500 =1750所以利润最大化时的 产量Q=25,利润π=17509.假定某厂商短期生产的边际成本函数为SMC(Q)=3Q 2-8Q+100,且已知当产量Q=10时的总成本STC=2400,求相应的STC 函数、SAC 函数和AVC 函数。
解答:由总成本和边际成本之间的关系。
有 STC(Q)= Q 3-4 Q 2+100Q+C= Q 3-4 Q 2+100Q+TFC2400=103-4*102+100*10+TFC TFC=800进一步可得以下函数STC(Q)= Q 3-4 Q 2+100Q+800SAC(Q)=STC(Q)/Q=Q 2-4 Q+100+800/Q AVC(Q)=TVC(Q)/Q=Q 2-4 Q+10010.试用图说明短期成本曲线相互之间的关系.解:如图,TC方倾斜的曲线.在每一个产量上,TC 曲线和TVC 曲线之间的垂直距离都等于固定的不变成本TFC. TC 曲线和TVC 曲线在同一个产量水平上各自存在一个拐点 B 和C.在拐点以前,TC 曲线和TVC 曲线的斜率是递减的;在拐点以后, TC 曲线和 TVC 曲线的斜率是递增的. AFC 曲线随产量的增加呈一直下降趋势.AVC 曲线,AC 曲线和MC 曲线均呈U 形特征.MC 先于AC 和AVC 曲线转为递增,MC 曲线和AVC 曲线相交于AVC 低点F,MC 曲线与AC AC 曲线的最低点 D.AC AVC 曲线,AFC.但永远不能相交11.试用图从短期总成本曲线推导长期总成本曲线,并说明长期总成本曲线的经济含义.如图5—4所示,假设长期中只有三种可供选择的生产规模,分别由图中的三条STC 曲线表 示。
从图5—4中看,生产规模由小到大依次为STC 1、STC 2、STC 3。
现在假定生产Q 2的产量。
长期中所有的要素都可以调整,因此厂商可以通过对要素的调整选择最优生产规模,曲线OC QSTC 1 d STC 2 STC 3LTCQ 2 Q 1 Q 3c ab图5—4 最优生产规模的选择和长期总成本曲线e以最低的总成本生产每一产量水平。
在d 、b 、e 三点中b 点代表的成本水平最低,所以长期中厂商在STC 2曲线所代表的生产规模生产Q 2产量,所以b 点在LTC 曲线上。
这里b 点是LTC 曲线与STC 曲线的切点,代表着生产Q 2产量的最优规模和最低成本。
通过对每一产量水平进行相同的分析,可以找出长期中厂商在每一产量水平上的最优生产规模和最低长期总成本,也就是可以找出无数个类似的b (如a 、c )点,连接这些点即可得到长期总成本曲线。
长期总成本是无数条短期总成本曲线的包络线。
长期总成本曲线的经济含义:LTC 曲线表示长期内厂商在每一产量水平上由最优生产规模所带来的最小的生产总成本.12. 试用图从短期平均成本曲线推导长期平均成本曲线,并说明长期平均成本曲线的经济含义.解:假设可供厂商选择的生产规模只有三种:SAC 1、SAC 2、SAC 3,如右上图所示,规模大小依次为SAC 3、SAC 2、SAC 1。
现在来分析长期中厂商如何根据产量选择最优生产规模。
假定厂商生产Q 1的产量水平,厂商选择SAC 1进行生产。
因此此时的成本OC 1是生产Q 1产量的最低成本。
如果生产Q 2产量,可供厂商选择的生产规模是SAC 1和SAC 2,因为SAC 2的成本较低,所以厂商会选择SAC 2曲线进行生产,其成本为OC 2。
如果生产Q 3,则厂商会选择SAC 3曲线所代表的生产规模进行生产。
有时某一种产出水平可以用两种生产规模中的任一种进行生产,而产生相同的平均成本。
例如生产Q 1′的产量水平,即可选用SAC 1曲线所代表的较小生产规模进行生产,也可选用SAC 2曲线所代表的中等生产规模进行生产,两种生产规模产生相同的生产成本。
厂商究竟选哪一种生产规模进行生产,要看长期中产品的销售量是扩张还是收缩。
如果产品销售量可能扩张,则应选用SAC 2所代表的生产规模;如果产品销售量收缩,则应选用SAC 1所代表的生产规模。
由此可以得出只有三种可供选择的生产规模时的LAC 曲线,即图中SAC 曲线的实线部分.在理论分析中,常假定存在无数个可供厂商选择的生产规模,从而有无数条SAC 曲线,于是便得到如图5—7所示的长期平均成本曲线,LAC 曲线是无数条SAC 曲线的包络线。
LAC 曲线经济含义:它表示厂商在长期内在每一产量水平上,通过选择最优生产规模所实现的最小的平均成本.图 最优生产规模 SAC 1 SAC 2SAC 3C 1 C 2C 3 Q 1 Q 2 Q 3 Q 2′Q 1′O CQ Q 1 O CQSAC 1SAC 2 SAC 3 SAC4SAC 5 SAC 6 SAC 7图5—7 长期平均成本曲线 Q 2 LAC13.试用图从短期边际成本曲线推导长期边际成本曲线,并说明长期边际成本曲线的经济含义.解:图中,在Q 1产量上,生产该产量的最优生产规模由SAC1曲线和SMC1曲线所代表,而PQ1既是最优的短期边际成本,又是最优的长期边际成本,即有LMC=SMC1=PQ1.同理,在Q2产量上,有LMC=SMC2=RQ2.在Q3产量上,有LMC=SMC3=SQ3.在生产规模可以无限细分的条件下,可以得到无数个类似于P,R,S 的点,将这些连接起来就得到一条光滑的LMC 曲线.LMC 曲线的经济含义:它表示厂商在长期内在每一产量水平上,通过选择最优生产规模所实现的最小的边际成本.长期边际成本曲线与短期成本曲线。
