(完整版)解三角形应用举例练习题
完整版)高考解三角形大题(30道)

完整版)高考解三角形大题(30道)1.在三角形ABC中,已知内角A,B,C的对边分别为a,b,c,且有以下等式:frac{\cos A - 2\cos C}{2c-a} = \frac{\cos B b}{\sin C}$$求该等式右侧的值,以及:2)若$\cos B=\frac{1}{4}$,$b=2$,求三角形ABC的面积S。
2.在三角形ABC中,角A,B,C的对边分别为a,b,c,已知$\sin C+\cos C=1$,求:1)$\sin C$的值;2)若$a+b=4a-8$,求边c的值。
3.在三角形ABC中,角A,B,C的对边分别为a,b,c。
1)若$\sin(A+\frac{2}{3}\pi)=2\cos A$,求角A的值;2)若$\cos A=\frac{3}{c}$,求$\sin C$的值。
4.在三角形ABC中,D为边BC上的一点,且$BD=\frac{3}{3}$,$\sin B=\frac{5}{3}$,$\cos\angleADC=\frac{\sqrt{3}}{5}$,求AD。
5.在三角形ABC中,角A,B,C的对边分别为a,b,c,已知$a=1$,$b=2$,$\cos C=-\frac{1}{4}$,求:1)三角形ABC的周长;2)$\cos(A-C)$的值。
6.在三角形ABC中,角A,B,C的对边分别为a,b,c,已知$\sin A+\sin C=\frac{1}{2}\sin B$,且$ac=\frac{1}{2}b$。
1)求a,c的值;2)若角B为锐角,求p的取值范围,其中$p=\frac{1}{5}$,$b=1$。
7.在三角形ABC中,角A,B,C的对边分别为a,b,c,且$2a\sin A=(2b+c)\sin B+(2c+b)\sin C$。
1)求角A的值;2)求$\sin B+\sin C$的最大值。
8.在三角形ABC中,角A,B,C的对边分别为a,b,c,已知$\cos 2C=-\frac{1}{4}$。
2解三角形应用举例

解三角形应用举例1.测量距离:例1.已知船在A 处测得它的南偏东︒30的海面上有一灯塔C ,船以每小时30海里的速度向东南方向航行半小时后到达B 点,于B 处看到灯塔在船的正西方向,此时船和灯塔相距_________海里演变1.某人向正东方向走x 千米后,他向右转︒150,然后朝新方向走3千米,结果他离出发点恰好3千米,那么x 的值为_________演变2.某观测站C 在城A 的南偏西20︒的方向上,由A 城出发有一条公路,走向是南偏东40︒,在C 处测得距C 为31千米的公路上B 处有一人正沿公路向A 城走去,走了20千米后,到达D 处,此时C 、D 间距离为21千米,则这人到达A 城还需走_________千米 例 2.如图,我炮兵阵地位于地面A 处,两观察所分别位于地面点C 和D 处,已知m CD 6000=,︒=∠45ACD ,︒=∠75ADC ,目标出现于地面B 处时测得︒=∠30BCD ,︒=∠15BDC ,求炮兵阵地到目标的距离。
(结果保留根号)演变 1.如图,为了测量河对岸A 、B 两点间的距离,在河的这边测得km CD 23=,︒=∠=∠30CDB ADB ,︒=∠60ACD ,︒=∠45ACB ,求A 、B 两点间的距离。
例3.一货轮航行到M 处,测得灯塔S 在货轮的北偏东15︒相距20里处,随后货轮按北偏西30︒的方向航行,半小时后,又测得灯塔在货轮的北偏东45︒,求货轮的速度演变1.如图,某海岛上一观察哨A 上午11时测得一轮船在海岛北偏东︒60的C 处,12时20分时测得船在海岛北偏西︒60的B 处,12时40分轮船到达位于海岛正西且距海岛5km 的E 港口,如果轮船始终匀速直线前行,问船速为多少?2.测量角度:例1.如图,在海岸A 处发现北偏东45︒方向,距A 1海里的B 处有一艘走私船,在A处北偏西75︒方向,距A 处2海里的C 处的我方缉私船,奉命以走私船,此时走私船正以10海里/时的速度,从B 处向北偏东30︒方向逃窜,问:辑私船沿什么方向行驶才能最快截获走私船?并求出所需时间。
解三角形应用题(2)含答案

解三角形应用题(2)1.如图,已知测速站P 到公路L 的距离PO 为40米,一辆汽车在公路L 上行驶,测得此车从点A 行驶到点B 所用的时间为2秒,并测得∠APO=600,∠BPO=300,计算此车从A 到B 的平均速度为每秒多少米(结果保留四个有效数字),并判断此车是否超过了每秒22米的限制速度。
2.如图,在小山的西侧A 处有一热气球,以30米/分钟的速度沿着与垂直方向所成夹角为30°的方向升空,40分钟后到达C 处,这时热气球上的人发现,在A 处的正东方向有一处着火点B ,十分钟后,在D 处测得着火点B 的俯角为15°,求热气球升空点A 与着火点B 的距离。
(结果保留根号,参考数据:(42615sin -=︒,42615cos +=︒,3215tan -=︒,3215cot +=︒)。
3.城市规划期间,欲拆除一电线杆AB (如图)已知距电线杆AB 水平距离14米的D 处有一大坝,背水坡CD 的坡度i=2:1,坝高CF 为2米.在坝顶C 处测得杆顶A 的仰角为30,D 、E 之间是宽为2米的人行道.试问:在拆除电线杆AB 时,为确保行人安全,是否需要将此人行道封上?请说明理由(在地面上,以点B 为圆心、以AB 为半径的圆形区域为危险区域).(732.13≈,414.12≈)B A A L O P B4.台湾“华航”客机失事后,祖国大陆海上搜救中心立即通知位于A、B两处的上海救捞人局所属专业救助轮“华意”轮、“沪救12”轮前往出事地点协助搜索。
接到通知后,“华意”轮测得出事地点C在A的南偏东60°、“沪救12”轮测得出事地点C在B的南偏东30°。
已知B在A 的正东方向,且相距100浬,分别求出两艘船到达出事地点CC可从30°升到80°.求起重机起吊的最大高度(吊钩本身的长度和所挂重物的高度忽略不计)和当起重机位置不变时使用的最大水平距离(精确到0.1米,sin80°=0.9848,cos80°=0.1736,6.如图,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时.接到气象部门通知,一台风中心正以40海里/时的速度由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均受到影响.(1)问:B处是否会受到台风的影响?请说明理由.(2)为避免受到台风的影响,该船应在多少小时内卸完货物?(供选用数据: 2 ≈1.4, 3 ≈1.7)解三角形应用题(2)答案:1.v=23.09﹥222.AB=(1500 3 +1500)米3.AB=5 3 +2﹤12 ∴不需要4.BC=100 AC=100 35.最大高度为35.5+21=56.5米最远距离为18 3 ≈31.2米6.⑴BD=160﹤200 ∴会受到⑵AE=160 3 -120∴t=(160 3 -120)÷40≈3.8小时。
第四章 §4.10 解三角形应用举例

一、单项选择题1.如图,设A,B两点在河的两岸,在点A所在河岸边选一定点C,测量AC的距离为50 m,∠ACB=30°,∠CAB=105°,则A,B两点间的距离是()A.25 2 m B.50 2 mC.25 3 m D.50 3 m2.(2024·咸阳模拟)世界上最大的球形建筑物是位于瑞典斯德哥尔摩的爱立信球形体育馆(瑞典语:Ericsson Globe),在世界最大的瑞典太阳系模型中,由该体育场代表太阳的位置,其外形像一个大高尔夫球,可容纳16 000名观众观看表演和演唱会,或14 119名观众观看冰上曲棍球.如图,某数学兴趣小组为了测得爱立信球形体育馆的直径,在体育馆外围测得AB=120 m,BC=120 m,CD=80 m,∠ABC=60°,∠BCD=120°(其中A,B,C,D四点共面),据此可估计该体育馆的直径AD大约为(结果精确到1 m,参考数据:7≈2.646)()A.98 m B.106 mC.117 m D.122 m3.如图,两座相距60 m的建筑物AB,CD的高度分别为20 m,50 m,BD为水平面,则从建筑物AB的顶端A看建筑物CD的张角∠CAD等于()A.30°B.45°C.60°D.75°4.如图,航空测量的飞机航线和山顶在同一铅直平面内,已知飞机飞行的海拔高度为10 000 m,速度为50 m/s.某一时刻飞机看山顶的俯角为15°,经过420 s后看山顶的俯角为45°,则山顶的海拔高度大约为(参考数据:2≈1.4,3≈1.7)()A .7 350 mB .2 650 mC .3 650 mD .4 650 m5.(2023·洛阳模拟)某班课外学习小组利用“镜面反射法”来测量学校内建筑物的高度.步骤如下:①将镜子(平面镜)置于平地上,人后退至从镜中能看到房顶的位置,测量出人与镜子的距离;②将镜子后移,重复①中的操作;③求建筑物高度.如图所示,前后两次人与镜子的距离分别为a 1 m ,a 2 m(a 2>a 1),两次观测时镜子间的距离为a m ,人的“眼高”为h m ,则建筑物的高度为( )A.ah a 2-a 1m B.a (a 2-a 1)h m C.(a 2-a 1)h a m D.ah 2a 2-a 1m 6.(2023·济南模拟)山东省科技馆新馆目前成为济南科教新地标(如图1),其主体建筑采用与地形吻合的矩形设计,将数学符号“∞”完美嵌入其中,寓意无限未知、无限发展、无限可能和无限的科技创新.如图2,为了测量科技馆最高点A 与其附近一建筑物楼顶B 之间的距离,无人机在点C 测得点A 和点B 的俯角分别为75°,30°,随后无人机沿水平方向飞行600米到点D ,此时测得点A 和点B 的俯角分别为45°和60°(A ,B ,C ,D 在同一铅垂面内),则A ,B 两点之间的距离为( )A .50 5 米B .150 米C .10015 米D .150 3 米二、多项选择题7.某货轮在A 处测得灯塔B 在北偏东75°方向,距离为12 6 n mile ,测得灯塔C 在北偏西30°方向,距离为8 3 n mile.货轮由A 处向正北方向航行到D 处时,测得灯塔B 在南偏东60°方向,则下列说法正确的是( )A .A 处与D 处之间的距离是24 n mileB .灯塔C 与D 处之间的距离是16 n mileC .灯塔C 在D 处的南偏西30°方向D .D 处在灯塔B 的北偏西30°方向8.(2024·重庆模拟)解放碑是重庆的地标性建筑,众多游客来此打卡拍照.现某中学数学兴趣小组对解放碑的高度进行测量,并绘制出测量方案示意图(如图所示),A 为解放碑的最顶端,B 为基座(即B 在A 的正下方),在步行街上(与B 在同一水平面内)选取C ,D 两点,测得CD的长为100 m .小组成员利用测角仪已测得∠ACB =π6,则根据下列各组中的测量数据,能计算出解放碑高度AB 的是( )A .∠BCD ,∠BDCB .∠ACD ,∠ADC C .∠BCD ,∠ACDD .∠BCD ,∠ADC三、填空题9.中国最早的天文观测仪器叫“圭表”(如图),最早装置圭表的观测台是西周初年在阳城建立的周公测景(影)台.“圭”就是放在地面上的土堆,“表”就是直立于圭的杆子,太阳光照射在表上,便在圭上成影.到了周代,使用圭表有了规范,杆子(表)规定为八尺长.用圭表测量太阳照射在竹竿上的影长,可以判断季节的变化,也能用于丈量土地.同一天内,南北两地的日影长短倘使差一寸,它们的距离就相差一千里,所谓“影差一寸,地差千里”(1尺=10寸).记“表”的顶部为A ,太阳光线通过顶部A 投影到“圭”上的点为B .同一天内,甲地日影长是乙地日影长的两倍,记甲地中直线AB 与地面所成的角为θ,且tan θ=83.则甲、乙两地之间的距离约为________千里.10.如图所示,工程师为了了解深水港码头海域海底的构造,在海平面内一条直线上的A ,B ,C 三点进行测量.已知AB =60 m ,BC =120 m ,于A 处测得水深AD =120 m ,于B 处测得水深BE =200 m ,于C 处测得水深CF =150 m ,则cos ∠DEF =______.11.台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东方向40千米处,则城市B处于危险区的时间为________小时.12.汾阳文峰塔建于明末清初,位于山西省汾阳市城区以东2公里的建昌村,该塔共十三层,雄伟挺拔,高度位于中国砖结构古塔之首.如图,某测绘小组为了测量汾阳文峰塔的实际高度AB,选取了与塔底B在同一水平面内的三个测量基点C,D,E,现测得∠BCD=30°,∠BDC =70°,∠BED=120°,BE=17.2 m,DE=10.32 m,在点C处测得塔顶A的仰角为62°,则塔高AB=________ m.(结果精确到1 m,参考数据:tan 62°≈1.88,sin 70°≈0.94,144.961 6=12.04)。
解三角形(4)---解三角形应用举例

解三角形(4)---解三角形应用举例例1、如图,设A 、B 两点在河的两岸,要测量两点之间的距离,测量者在A 的同侧,在所在的河岸边选定一点C ,测出AC 的距离是55m ,∠BAC=︒51,∠ACB=︒75.求A 、B 两点的距离(精确到0.1m )启发提问1:∆ABC 中,根据已知的边和对应角,运用哪个定理比较适当?启发提问2:运用该定理解题还需要那些边和角呢?分析:这是一道关于测量从一个可到达的点到一个不可到达的点之间的距离的问题,题目条件告诉了边AB 的对角,AC 为已知边,再根据三角形的内角和定理很容易根据两个已知角算出AC 的对角,应用正弦定理算出AB 边。
解:根据正弦定理,得ACB AB ∠sin = ABCAC ∠sin AB =ABC ACB AC ∠∠sin sin =ABC ACB ∠∠sin sin 55 = )7551180sin(75sin 55︒-︒-︒︒ =︒︒54sin 75sin 55 ≈ 65.7(m) 答:A 、B 两点间的距离为65.7米变式练习:两灯塔A 、B 与海洋观察站C 的距离都等于a km ,灯塔A 在观察站C 的北偏东30︒,灯塔B 在观察站C 南偏东60︒,则A 、B 之间的距离为多少?(画图建立数学模型。
答案:2a km )例2、如图,A 、B 两点都在河的对岸(不可到达),设计一种测量A 、B 两点间距离的方法。
分析:这是例1的变式题,研究的是两个不可到达的点之间的距离测量问题.首先需要构造三角形,所以需要确定C 、D 两点.根据正弦定理中已知三角形的任意两个内角与一边既可求出另两边的方法,分别求出AC 和BC ,再利用余弦定理可以计算出AB 的距离.解:测量者可以在河岸边选定两点C 、D ,测得CD=a ,并且在C 、D 两点分别测得∠BCA=α,∠ACD=β,∠CDB=γ,∠BDA =δ,在∆ADC 和∆BDC 中,应用正弦定理得:AC = )](180sin[)sin(δγβδγ++-︒+a = )sin()sin(δγβδγ+++a BC = )](180sin[sin γβαγ++-︒a = )sin(sin γβαγ++a 计算出AC 和BC 后,再在∆ABC 中,应用余弦定理计算出AB 两点间的距离AB =αcos 222BC AC BC AC ⨯-+ 分组讨论:还没有其它的方法呢?变式训练:若在河岸选取相距40米的C、D两点,测得∠BCA=60︒,∠ACD=30︒,∠CDB=45︒,∠BDA =60︒(画图建立数学模型。
解三角形应用举例(二)

B
80
A0
A
B0
C
已知△ABC中, BC=85mm,AB=340mm,∠C=80°,
求AC. 解:(如图)在△ABC中, 由正弦定理可得: BC sin C 85 sin 80 sin A 0.2462 AB 340 因为BC<AB,所以A为税角 , A=14°15′ ∴ B=180°-(A+C)=85°45′ 又由正弦定理: AB sin B 340 sin 85 45 AC 344.3( mm) sin C 0.9848
A0 A A0C AC ( AB BC ) AC ( 340 85) 344.3 80.7 81( mm )
答:活塞移动的距离为81mm.
解三角形应用举例
总结 实际问题 抽象概括 示意图 数学模型 推 演 理 算 实际问题的解 还原说明 数学模型的解
B
A
C
CD=BD-BC=42-28=14(m) 答:山的高度约为14米。
D
测量术语: 1 仰角,俯角 2 方向角:北偏西,南偏东 3 方位角:从正北方向顺时针旋转 到目标方向线的水平角
例 2 如图, 某渔轮在航行中不幸遇 险, 发出呼救信号. 我海军舰艇在 A处获悉后, 测出该渔轮在方位角为45 0 , 距离为10n mile的C处, 并测得渔轮正沿方位角 为105 0 的方向,以9 n mile / h的速度向小岛靠拢 .我海军舰艇立 即以21 n mile / h的速度前去营救 .求舰艇的航向和靠近 渔轮所需的时间 (角度精确到 0.10 , 时间精确到1 min).
答 舰艇应沿着方位角66.8 0 的方向航行, 经过40 min 就可靠近渔轮.
(完整版)初中解直角三角形练习题

解直角三角形练习题一、 真空题: 1、 在Rt △ABC 中,∠B =900,AB =3,BC =4,则sinA= 2、在Rt △ABC 中,∠C =900,AB =,35cm BC cm=则SinA= cosA= 3、Rt △ABC 中,∠C =900,SinA=54,AB=10,则BC =4、α是锐角,若sin α=cos150,则α= 若sin53018\=0.8018,则cos36042\=5、 ∠B 为锐角,且2cosB -1=0则∠B =6、在△ABC 中,∠C =900,∠A ,∠B ,∠C 所对的边分别为a ,b ,c ,a =9,b =12,则sinA= sinB=7、 Rt △ABC 中,∠C =900,tanA=0.5,则cotA= 8、 在Rt △ABC 中,∠C =900,若b a 32=则tanA= 9.等腰三角形中,腰长为5cm ,底边长8cm ,则它的底角的正切值是10、若∠A 为锐角,且tan 2A+2tanA -3=0则∠A = 11、Rt △ABC 中,∠A =600,c=8,则a = ,b = 12、在△ABC 中,若32=c ,b =3,则tanB= ,面积S = 13、在△ABC 中,AC :BC =1:3,AB =6,∠B = ,AC = BC = 14、在△ABC 中,∠B =900,AC 边上的中线BD =5,AB =8,则tanACB=二、选择题1、在Rt △ABC 中,各边的长度都扩大2倍,那么锐角A 的正弦、余弦值 ( )A 、都扩大2倍B 、都扩大4倍C 、没有变化D 、都缩小一半2、若∠A 为锐角,且cotA <3,则∠A ( )A 、小于300B 、大于300C 、大于450且小于600D 、大于600 3、在Rt △ABC 中,已知a 边及∠A ,则斜边应为 ( ) A 、asinA B 、A a sin C 、acosA D 、Aa cos 4、等腰三角形底边与底边上的高的比是2:3,则顶角为( ) A 、600 B 、900 C 、1200 D 、15005、在△ABC 中,A ,B 为锐角,且有sinA =cosB ,则这个三角形是( )A 、等腰三角形B 、直角三角形C 、钝角三角形D 、锐角三角形6、有一个角是300的直角三角形,斜边为1cm ,则斜边上的高为( )A 、41cmB 、21cmC 、43cmD 、23cm三、求下列各式的值1、sin 2600+cos 26002、sin600-2sin300cos3003. sin300-cos 24504. 2cos450+|32-|5. 0045cos 360sin 2+ 6. 130sin 560cos 300-7. 2sin 2300·tan300+cos600·cot300 8. sin 2450-tan 2300四、解答下列各题1、在Rt △ABC 中,∠C =900,,AB =13,BC =5, 求sinA, cosA, tanA, cotA2. 在Rt △ABC 中,∠C =900,若1312sin =A 求cosA, sinB, cosB3. 在Rt △ABC 中,∠C =900,b=17, ∠B=450,求a, c 与∠A四、根据下列条件解直角三角形。
(完整版)解三角形练习题(含答案)

一、选择题1、在△ABC中,角A、B、C的对边分别为、、,若=,则△ABC的形状为()A、正三角形B、直角三角形C、等腰三角形或直角三角形D、等腰直角三角形2、已知中,,,则角等于A. B. C. D.3、在△ABC中,a=x,b=2,B=45°,若这样的△ABC有两个,则实数x的取值范围是()A.(2,+∞) B.(0,2)C.(2,) D.()4、,则△ABC的面积等于A. B. C.或 D.或5、在中,,则角C的大小为A.300B.450C.600D.12006、的三个内角、、所对边长分别为、、,设向量,,若,则角的大小为()A. B. C. D.7、若ΔABC的内角A、B、C所对的边a、b、c满足,则ab的值为()A. B. C.1 D.8、在中,若,且,则是( )A.等边三角形B.等腰三角形,但不是等边三角形C.等腰直角三角形D.直角三角形,但不是等腰三角形9、在中,所对的边分别是且满足,则=A. B. C. D.10、若α是三角形的内角,且sin α+cos α=,则这个三角形是( ).A.等边三角形 B.直角三角形C.锐角三角形 D.钝角三角形11、在△中,,,,则此三角形的最大边长为()A. B. C. D.12、在△ABC中, 角A、B、C的对边分别为a、b、c,若(a2+c2b2)tanB=ac,则角B=()A. B. C.或 D.或13、(2012年高考(天津理))在中,内角,,所对的边分别是,已知,,则()A. B. C. D.14、已知△ABC中,=,=,B=60°,那么满足条件的三角形的个数为()A、1B、2C、3D、015、在钝角中,a,b,c分别是角A,B,C的对边,若,则最大边c的取值范围是( ) ( A. B. C. D.16、(2012年高考(上海理))在中,若,则的形状是()A.锐角三角形. B.直角三角形. C.钝角三角形. D.不能确定.17、在△ABC中,a=15,b=10, ∠A=,则()A. B. C. D.18、在△ABC中,内角A,B,C的对边分别是a,b,c,若,,则角A= ()A. B. C. D.19、()A. B. C. D.20、给出以下四个命题:(1)在中,若,则;(2)将函数的图象向右平移个单位,得到函数的图象;(3)在中,若,,,则为锐角三角形;(4)在同一坐标系中,函数与函数的图象有三个交点;其中正确命题的个数是() A.1 B.2 C.3 D.421、若△ABC的对边分别为、、C且,,,则b=()A、5B、25C、 D、22、设A、B、C是△ABC三个内角,且tanA,tanB是方程3x2-5x+1=0的两个实根,那么△ABC是()A.钝角三角形 B.锐角三角形 C.等腰直角三角形 D.以上均有可能23、设△ABC的内角A, B, C所对的边分别为a, b, c, 若, 则△ABC的形状为(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定24、在中,若,则此三角形是()A.锐角三角形 B.直角三角形 C.钝角三角形 D.任意三角形25、在△ABC中,已知A=,BC=8,AC=,则△ABC的面积为▲A.B.16 C.或16 D.或26、在△ABC中,角A,B,C所对的边长分别为a,b,c,且满足c sin A=a cos C,则sin A+sin B的最大值是( )A.1 B. C. D.3二、填空题27、在△ABC中,角A、B、C的对边分别为a、b、c, 已知A=, a=, b=1,则c= .28、已知△ABC的面积 .29、在△ABC中,角A、B、C所对的对边分别为a、b、c,若,则A= 。
高中数学 第二章 解三角形 3 解三角形的实际应用举例 第1课时 距离和高度问题练习(含解析)北师大

距离和高度问题A 级 基础巩固一、选择题1.海上有A 、B 两个小岛相距10海里,从A 岛望C 岛和B 岛成60°的视角,从B 岛望C 岛和A 岛成75°的视角,则B 、C 间的距离是(D )A .103海里B .106海里C .52海里D .56海里[解析]如图,由正弦定理得 BCsin60°=10sin45°,∴BC =5 6.2.学校体育馆的人字形屋架为等腰三角形,如图,测得AC 的长度为4 m ,∠A =30°,则其跨度AB 的长为( D )A .12 mB .8 mC .3 3 mD .4 3 m[解析] 在△ABC 中,已知可得BC =AC =4,∠C =180°-30°×2=120°,所以由余弦定理得AB 2=AC 2+BC 2-2AC ·BC cos120°=42+42-2×4×4×⎝ ⎛⎭⎪⎫-12=48,∴AB =43(m).3.如图所示,为测一树的高度,在地面上选取A ,B 两点,从A 、B 两点分别测得树尖的仰角为30°,45°,且A ,B 两点之间的距离为60 m ,则树的高度为( A )A .(30+303)mB .(30+153)mC .(15+303)mD .(15+153)m[解析] 由正弦定理可得60sin45°-30°=PBsin30°,PB =60×12sin15°=30sin15°.h =PB ·sin45°=30sin15°·sin45°=(30+303)(m).4.甲船在湖中B 岛的正南A 处,AB =3 km ,甲船以8 km/h 的速度向正北方向航行,同时乙船从B 岛出发,以12 km/h 的速度向北偏东60°方向驶去,则行驶15分钟时,两船的距离是( B )A .7 kmB .13 kmC .19 kmD .10-3 3 km[解析] 由题意知AM =8×1560=2,BN =12×1560=3,MB =AB -AM =3-2=1,所以由余弦定理得MN 2=MB 2+BN 2-2MB ·BN cos120°=1+9-2×1×3×(-12)=13,所以MN =13km.5.如图所示,已知两座灯塔A 和B 与海洋观察站C 的距离都等于a (km),灯塔A 在观察站C 的北偏东20°,灯塔B 在观察站C 的南偏东40°,则灯塔A 与灯塔B 的距离为( B )A .a (km)B .3a (km)C .2a (km)D .2a (km)[解析]在△ABC 中,∠ACB =180°-(20°+40°)=120°. ∵AB 2=AC 2+BC 2-2AC ·BC cos120°=a 2+a 2-2a 2×(-12)=3a 2,∴AB =3a (km).6.在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30°、60°,则塔高为( A )A .4003米B .40033米C .20033米D .2003米[解析] 解法一:如图,设AB 为山高,CD 为塔高,则AB =200,∠ADM =30°,∠ACB =60°,∴BC =200tan30°=20033,AM =DM tan30°=BC tan30°=2003.∴CD =AB -AM =4003.解法二:如图AB 为山高,CD 为塔高. 在△ABC 中,AC =ABsin60°=40033, 在△ACD 中,∠CAD =30°,∠ADC =120°. 由正弦定理CD sin ∠CAD =ACsin ∠ADC .∴CD =40033×1232=4003(米).二、填空题7.一只蜘蛛沿正北方向爬行x cm 捕捉到一只小虫,然后向右转105°,爬行10 cm 捕捉到另一只小虫,这时它向右转135°爬行回它的出发点,则x =1063cm.[解析] 如图,由题意知,∠BAC =75°,∠ACB =45°.∠B =60°,由正弦定理,得x sin ∠ACB =10sin B,∴x =10sin ∠ACB sin B =10×sin45°sin60°=1063.8.如图所示,设A 、B 两点在河的两岸,一测量者在A 所在的河岸边选定一点C ,测出AC 的距离为50 m ,∠ACB =45°,∠CAB =105°后,就可以计算A 、B 两点的距离为50 2 m.[解析] 因为∠ACB =45°,∠CAB =105°, 所以∠ABC =30°, 根据正弦定理可知:AC sin ∠ABC =ABsin ∠ACB,即50sin30°=ABsin45°,解得AB =50 2 m.三、解答题9.海面上相距10海里的A 、B 两船,B 船在A 船的北偏东45°方向上,两船同时接到指令同时驶向C 岛,C 岛在B 船的南偏东75°方向上,行驶了80分钟后两船同时到达C 岛,经测算,A 船行驶了107海里,求B 船的速度.[解析] 如图所示,在△ABC 中,AB =10,AC =107,∠ABC =120°由余弦定理,得AC 2=BA 2+BC 2-2BA ·BC ·cos120°即700=100+BC 2+10BC ,∴BC =20,设B 船速度为v ,则有v =2043=15(海里/小时).即B 船的速度为15海里/小时.10.在某某世博会期间,小明在中国馆门口A 处看到正前方上空一红灯笼,测得此时的仰角为45°,前进200米到达B 处,测得此时的仰角为60°,小明身高1.8米,试计算红灯笼的高度(精确到1 m).[解析] 由题意画出示意图(AA ′表示小明的身高).∵AB =200,∠CA ′B ′=45°,∠CB ′D ′=60°, ∴在△A ′B ′C 中,A ′B ′sin ∠A ′CB ′=B ′Csin45°,∴B ′C =A ′B ′sin45°sin15°=200×226-24=200(3+1).在Rt △CD ′B ′中,CD ′=B ′C ·sin60°=100(3+3),∴CD =1.8+100(3+3)≈475(米). 答:红灯笼高约475米.B 级 素养提升一、选择题1.一货轮航行到M 处,测得灯塔S 在货轮的北偏东15°,与灯塔S 相距20海里,随后货轮按北偏西30°的方向航行30分钟后,又测得灯塔在货轮的东北方向,则货轮的速度为( B )A .20(2+6)海里/时B .20(6-2)海里/时C .20(6+3)海里/时D .20(6-3)海里/时[解析] 设货轮航行30分钟后到达N 处,由题意可知∠NMS =45°,∠MNS =105°, 则∠MSN =180°-105°-45°=30°.而MS =20, 在△MNS 中,由正弦定理得MN sin30°=MSsin105°,∴MN =20sin30°sin105°=10sin 60°+45°=10sin60°cos45°+cos45°sin45°=106+24=10(6-2).∴货轮的速度为10(6-2)÷12=20(6-2)(海里/时).2.如图所示,在山底A 处测得山顶B 的仰角∠CAB =45°,沿倾斜角为30°的山坡向山顶走1 000米到达S 点,又测得山顶仰角∠DSB =75°,则山高BC 为( D )A .500 2 mB .200 mC .1 000 2 mD .1 000 m[解析] ∵∠SAB =45°-30°=15°,∠SBA =∠ABC -∠SBC =45°-(90°-75°)=30°, 在△ABS 中,AB =AS ·sin135°sin30°=1 000×2212=1 0002,∴BC =AB ·sin45°=1 0002×22=1 000(m). 3.一船向正北航行,看见正西方向有相距10 n mlie 的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°方向上,另一灯塔在船的南偏西75°方向上,则这艘船的速度是每小时( C )A .5 n mlieB .5 3 n mlieC .10 n mlieD .10 3 n mlie[解析] 如图,依题意有∠BAC =60°,∠BAD =75°,∴∠CAD =∠CDA =15°,从而CD =CA =10, 在Rt △ABC 中,求得AB =5,∴这艘船的速度是50.5=10(n mlie/h).4.要测量底部不能到达的东方明珠电视塔的高度,在黄浦某某岸选择甲、乙两观测点,在甲、乙两点分别测得塔顶的仰角分别为45°,30°,在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°,甲、乙两地相距500米,则电视塔在这次测量中的高度是( D )A .1002米B .400米C .2003米D .500米[解析] 由题意画出示意图,设高AB =h , 在Rt △ABC 中,由已知BC =h ,在Rt △ABD 中,由已知BD =3h ,在△BCD 中,由余弦定理BD 2=BC 2+CD 2-2BC ·CD ·cos∠BCD 得3h 2=h 2+5002+h ·500,解之得h =500(米).二、填空题5.某地电信局信号转播塔建在一山坡上,如图所示,施工人员欲在山坡上A 、B 两点处测量与地面垂直的塔CD 的高,由A 、B 两地测得塔顶C 的仰角分别为60°和45°,又知AB 的长为40米,斜坡与水平面成30°角,则该转播塔的高度是4033米.[解析] 如图所示,由题意,得∠ABC =45°-30°=15°,∠DAC =60°-30°=30°. ∴∠BAC =150°,∠ACB =15°,∴AC =AB =40米,∠ADC =120°,∠ACD =30°, 在△ACD 中,由正弦定理,得CD =sin ∠CAD sin ∠ADC ·AC =sin30°sin120°·40=4033.6.如图,一辆汽车在一条水平的公路上向正东行驶,到A 处时,测量公路南侧远处一山顶D 在东偏南15°的方向上,行驶5 km 后到达B 处,测得此山顶在东偏南30°的方向上,仰角为15°,则此山的高度CD 等于5(2-3)km.[解析] 在△ABC 中,∠A =15°,∠ACB =30°-15°=15°, 所以BC =AB =5.又CD =BC ·tan∠DBC =5×tan15°=5×tan(45°-30°)=5(2-3).三、解答题7.(2018·全国卷Ⅰ理,17)在平面四边形ABCD 中,∠ADC =90°,∠A =45°,AB =2,BD =5.(1)求cos ∠ADB ; (2)若DC =22,求BC .[解析] (1)在△ABD 中,由正弦定理得BD sin ∠A =ABsin ∠ADB ,即5sin 45°=2sin ∠ADB ,所以sin ∠ADB =25.由题设知,∠ADB <90°, 所以cos ∠ADB =1-225=235. (2)由题设及(1)知,cos ∠BDC =sin ∠ADB =25. 在△BCD 中,由余弦定理得BC 2=BD 2+DC 2-2BD ·DC ·cos∠BDC =25+8-2×5×22×25=25, 所以BC =5.8.某人在M 汽车站的北偏西20°的方向上的A 处,观察到点C 处有一辆汽车沿公路向M 站行驶.公路的走向是M 站的北偏东40°.开始时,汽车到A 的距离为31千米,汽车前进20千米后,到A 的距离缩短了10千米.问汽车还需行驶多远,才能到达M 汽车站?[解析] 由题画出示意图如图所示,设汽车前进20千米后到达B 处,在△ABC 中,AC =31,BC =20,AB =21.由余弦定理得cos C =AC 2+BC 2-AB 22AC ·BC =2331,则sin C =12331,所以sin ∠MAC =sin(120°-C )=sin120°cos C -cos120°sin C =35362.在△MAC 中,由正弦定理得MC =AC ·sin∠MAC sin ∠AMC =3132×35362=35,从而MB =MC -BC =15.即汽车还需行驶15千米才能到达M汽车站.。
解三角形应用举例

B C
α β
A
D
BC AB = sin(α β ) sin(90 + β )
BC sin(90 + β ) BC cos β = 所以,AB = sin(α β ) sin(α β )
解RtABD, 得 BC cos β sin α BD = AB sin ∠BAD = sin(α β ) 28 cos 30 sin 60 = sin(60 30 ) = 42(m)
视 线
N 仰角 俯角
水平线
方位角 60度
目标方向线
视 线
二、例 题 讲 解
例2、如图,要测底部不能到达的烟囱的高 ,从与烟囱底部在 、如图,要测底部不能到达的烟囱的高AB, 间的距离是12m.已知测角仪器高 已知测角仪器高1.5m,求烟囱的高。 求烟囱的高。 , 间的距离是 求烟囱的高 β = 60° CD间的距离是 已知测角仪器高 想一想 图中给出了怎样的一个 几何图形?已知什么, 几何图形?已知什么, 求什么? 求什么?
a sin β AC = sin(α β ) a sin α sin β AB = AE + h = AC sin α + h = +h sin(α β )
ห้องสมุดไป่ตู้
练习: 在山顶铁塔上B处测得地面 练习 在山顶铁塔上 处测得地面 上一点A的俯角 的俯角α= ° 上一点 的俯角 = 60° ,在塔底 C处测得 处的俯角 =30°。已 处测得A处的俯角 处测得 处的俯角β= ° 知铁塔BC部分的高为 部分的高为28m,求出 知铁塔 部分的高为 , 山高CD. 山高 分析:根据已知条件, 分析:根据已知条件,应该设 法计算出AB或 的长 法计算出 或AC的长 解:在⊿ABC中, 中 ∠BCA=90°+β, ° ∠ABC=90°-α, ∠BAC=α° β, ∠BAD=α.根据正弦定理, 根据正弦定理, 根据正弦定理
解三角形应用题(7)含答案

H G F D C BA45°30°C A 解三角形应用题(7)1.如图,自卸车厢的一个侧面是矩形ABCD ,AB =3米,BC =0.5米,车厢底部离地面1.2米,卸货时,车厢倾斜的角度θ=60°,问此时车厢的最高点A 离地面多少米?(精确到1米)2.如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45º降为30º,已知原滑滑板AB 的长为5米,点D 、B 、C 在同一水平地面上. ⑴改善后滑滑板会加长多少?(精确到0.01)⑵若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?说明理由 (参考数据: 2 =1.414, 3 =1.732,6 =2.449 )3.如图,A 城气象台测得台风中心从A 城正西方向300千米B 处以每小时107 千米的速度向北偏东60°的BF 方向移动,距台风中心200千米的范围内为受台风影响的区域(1)问A 城是否会受这次台风的影响?并说明理由(2)若A 城受到这次台风的影响,那么A 城遭受这次影响的时间有多少长?4.如图,在气象站台A 的正西方向240km 的B 处有一台风中心,该台风中心以每小时20km 的速度沿北偏东60°的BD 方向移动,在距离台风中心130km 内的地方都要受到其影响。
⑴台风中心在移动过程中,与气象台A 的最短距离是多少?⑵台风中心在移动过程中,气象台将受台风的影响,求台风影响气象台的时间会持续多长?北60o东DC BAA P东北4560 5.今年五、六月份,我省各地、市普遭暴雨袭击,水位猛涨.某市抗洪抢险救援队伍在B 处接到报告:有受灾群众被困于一座遭水淹的楼顶A 处,情况危急!救援队伍在B 处测得A 在B 的北偏东600的方向上(如图所示),队伍决定分成两组:第一组马上下水游向A 处就人,同时第二组从陆地往正东方向奔跑120米到达C 处,再从C 处下水游向A 处救人,已知A 在C 的北偏东300的方向上,且救援人员在水中游进的速度均为1米/秒.在陆地上奔跑的速度为4米/秒,试问哪组救援队先到A 处?请说明理由(参考数据 3 =1.732)6.如图,甲船在港口P 的北偏西60°方向,距港口80海里的A 处,沿AP 方向以12海里/时的速度驶向港口P .乙船从港口P 出发,沿北偏东45°方向匀速驶离港口P ,现两船同时出发,2小时后乙船在甲船的正东方向.求乙船的航行速度.(精确到0.1海里/时,参考数据: 3 ≈1.73, 2 ≈1.41)7.在一次课题学习课上,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB 表示窗户,且AB=2米,BCD 表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD 的最小夹角α为18.6°,最大夹角β为64.5°.请你根据以上数据,帮助小明同学计算出遮阳蓬中CD 的长是多少米?(结果保留两个有效数字)(参考数据sin18.6°=0.32,tan18.6°=0.34,sin64.5°8.如图,沿水库拦水坝的背水坡将坝顶加宽2米,由原来的背水坡坡角为30°改建成坡度为i=1:2.5,已知坝高6米,坝长50米,求完成这项工程需要多少方土?(参考数据:3 ≈1.73,2 ≈1.41)9.某森林管理处雇用两架直升飞机向森林喷洒农药,两机从同一地点A出发,甲机沿东北方向以20km/h的速度飞行,乙机沿南偏东30°方向以20 2 km/h的速度飞行,3小时后,乙机发现有部分药品误放在甲机上了,而此时,乙机只能沿北偏东15°方向追赶甲机,则乙机应以怎样的速度飞行,才能赶上甲机?10.如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度i=1∶ 3 ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45,在山坡的坡顶D处测得铁架顶端A的仰角为60°.(1)求小山的高度;(2)求铁架的高度.( 3 ≈1.73,精确到0.1米)11.在湖水高出水面50米的山顶A处,望见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,其在湖中的像的俯角为60°,试求飞艇离湖面的高度。
(完整版)解三角形练习题及答案

第一章解三角形一、选择题1.己知三角形三边之比为5∶7∶8,则最大角与最小角的和为().A.90°B.120°C.135°D.150°2.在△ABC中,下列等式正确的是().A.a∶b=∠A∶∠B B.a∶b=sin A∶sin BC.a∶b=sin B∶sin A D.a sin A=b sin B3.若三角形的三个内角之比为1∶2∶3,则它们所对的边长之比为( ).A.1∶2∶3 B.1∶3∶2C.1∶4∶9 D.1∶2∶34.在△ABC中,a=5,b=15,∠A=30°,则c等于( ).A.25B.5C.25或5D.10或55.已知△ABC中,∠A=60°,a=6,b=4,那么满足条件的△ABC的形状大小 ( ).A.有一种情形B.有两种情形C.不可求出D.有三种以上情形6.在△ABC中,若a2+b2-c2<0,则△ABC是( ).A.锐角三角形B.直角三角形C.钝角三角形D.形状不能确定7.在△ABC中,若b=3,c=3,∠B=30°,则a=( ).A.3B.23C.3或23D.28.在△ABC中,a,b,c分别为∠A,∠B,∠C的对边.如果a,b,c成等差数列,∠B=30°,△ABC的面积为23,那么b=().A.231+B.1+3C.232+D.2+39.某人朝正东方向走了x km后,向左转150°,然后朝此方向走了3 km,结果他离出发点恰好3km,那么x的值是( ).A.3B.23C.3或23D.310.有一电视塔,在其东南方A处看塔顶时仰角为45°,在其西南方B处看塔顶时仰角为60°,若AB=120米,则电视塔的高度为( ).A .603米B .60米C .603米或60米D .30米 二、填空题11.在△ABC 中,∠A =45°,∠B =60°,a =10,b = .12.在△ABC 中,∠A =105°,∠B =45°,c =2,则b = .13.在△ABC 中,∠A =60°,a =3,则C B A c b a sin sin sin ++++= . 14.在△ABC 中,若a 2+b 2<c 2,且sin C =23,则∠C = . 15.平行四边形ABCD 中,AB =46,AC =43,∠BAC =45°,那么AD = .16.在△ABC 中,若sin A ∶sin B ∶sin C =2∶3∶4,则最大角的余弦值= .三、解答题17. 已知在△ABC 中,∠A =45°,a =2,c =6,解此三角形.18.在△ABC 中,已知b =3,c =1,∠B =60°,求a 和∠A ,∠C .19. 根据所给条件,判断△ABC 的形状.(1)a cos A =b cos B ;(2)A a cos =B b cos =Cc cos .20.△ABC 中,己知∠A >∠B >∠C ,且∠A =2∠C ,b =4,a +c =8,求a ,c 的长.第一章 解三角形参考答案一、选择题1.B解析:设三边分别为5k ,7k ,8k (k >0),中间角为, 由cos =k k k k k 85249-64+25222⨯⨯=21,得 =60°,∴最大角和最小角之和为180°-60°=120°.2.B 3.B4.C5.C6.C7.C8.B解析:依题可得:⎪⎪⎩⎪⎪⎨⎧︒︒30cos 2-+=23=30sin 212=+222ac c a b ac b c a ⇒⎪⎩⎪⎨⎧ac ac c a b ac b c a 3-2-)+(=6=2=+22 代入后消去a ,c ,得b 2=4+23,∴b =3+1,故选B .9.C10.A二、填空题11.56.12.2.13.23.解析:设A a sin =B b sin =C c sin =k ,则C B A c b a +sin +sin sin ++=k =A a sin =︒60sin 3=23. 14.32π.15.43.16.-41.三、解答题17.解析:解三角形就是利用正弦定理与余弦定理求出三角形所有的边长与角的大小.解法1:由正弦定理得sin C =26sin 45°=26·22=23. ∵c sin A =6×22=3,a =2,c =6,3<2<6, ∴本题有二解,即∠C =60°或∠C =120°,∠B =180°-60°-45°=75°或∠B =180°-120°-45°=15°.故b =Aa sin sin B ,所以b =3+1或b =3-1, ∴b =3+1,∠C =60°,∠B =75°或b =3-1,∠C =120°,∠B =15°.解法2:由余弦定理得b 2+(6)2-26b cos 45°=4,∴b 2-23b +2=0,解得b =3±1. 又(6)2=b 2+22-2×2b cos C ,得cos C =±21,∠C =60°或∠C =120°,所以∠B =75°或∠B =15°.∴b =3+1,∠C =60°,∠B =75°或b =3-1,∠C =120°,∠B =15°.18.解析:已知两边及其中一边的对角,可利用正弦定理求解. 解:∵B b sin =Cc sin , ∴sin C =b B c sin ⋅=360sin 1︒⋅=21. ∵b >c ,∠B =60°,∴∠C <∠B ,∠C =30°,∴∠A =90°.由勾股定理a =22+c b =2,即a =2,∠A =90°,∠C =30°.19.解析:本题主要考查利用正、余弦定理判断三角形的形状.(1)解法1:由余弦定理得a cos A =b cos B ⇒a ·(bc a c b 2222-+)=b ·(acc b a 2222+-)⇒a 2c 2-a 4-b 2c 2+b 4=0, ∴(a 2-b 2)(c 2-a 2-b 2)=0,∴a 2-b 2=0或c 2-a 2-b 2=0,∴a =b 或c 2=a 2+b 2.∴△ABC 是等腰三角形或直角三角形.解法2:由正弦定理得sin A cos A =sin B cos B⇒sin 2A =sin 2B⇒2∠A =2∠B 或2∠A =-2∠B ,∠A ,∠B ∈(0,)⇒∠A =∠B 或∠A +∠B =2π, ∴△ABC 是等腰三角形或直角三角形.(2)由正弦定理得a =2R sin A ,b =2R sin B ,c =2R sin C 代入已知等式,得A A R cos sin 2=BB R cos sin 2=C C R cos sin 2, ∴A A cos sin =B B cos sin =CC cos sin , 即tan A =tan B =tan C .∵∠A ,∠B ,∠C ∈(0,π),∴∠A =∠B =∠C,∴△ABC 为等边三角形.20.解析:利用正弦定理及∠A =2∠C 用a ,c 的代数式表示cos C ;再利用余弦定理,用a ,c 的代数式表示cos C ,这样可以建立a ,c 的等量关系;再由a +c =8,解方程组得a ,c . 解:由正弦定理A a sin =Cc sin 及∠A =2∠C ,得 C a 2sin =C c sin ,即C C a cos sin 2⋅=Cc sin , ∴cos C =ca 2. 由余弦定理cos C =abc b a 2222-+, ∵b =4,a +c =8,∴a +c =2b ,∴cos C =)()(c a a c c a a +-4++222=)())((c a a c a c a +4+3-5=a c a 43-5, ∴c a 2=ac a 43-5, 整理得(2a -3c )(a -c )=0,∵a ≠c ,∴2a =3c . 又∵a +c =8,∴a =524,c =516.。
解直角三角形在实际生活中的应用

解直角三角形在实际生活中的应用山东 李浩明在现实生活中, 有许多和解直角三角形有关的实际问题,如航海航空、建桥修路、测量技术、图案设计等,解决这类问题其关键是把具体问题抽象成“直角三角形”模型,利用直角三角形的边角关系以及勾股定理来解决.下面举例说明,供大家参考.一、航空问题例1.(2008年桂林市)汶川地震后,抢险队派一架直升飞机去A 、B 两个村庄抢险,飞机在距地面450米上空的P 点,测得A 村的俯角为30︒,B 村的俯角为60︒(如图1).求A 、B1.414 1.732==)分析:要求A 、B 两个村庄间的距离,由题意知AB =PB ,在Rt △PBC 中,可求得60PBC ∠=︒,又因为PC =450,所以可通过解直角三角形求得PB.解:根据题意得:30A ∠=︒,60PBC ∠=︒,所以6030APB ∠=︒-︒,所以A P B A ∠=∠,所以AB =PB .在Rt BCP ∆中,90,60C PBC ∠=︒∠=︒,PC =450,所以PB=450sin 60==︒.所以520AB PB ==≈(米) 答:A 、B 两个村庄间的距离为520米. 二、测量问题例2.(2008年湛江市)如图2所示,课外活动中,小明在离旗杆AB 10米的C 处,QB CP A 45060︒30︒图1用测角仪测得旗杆顶部A 的仰角为40︒,已知测角仪器的高CD =1.5米,求旗杆AB 的高(精确到0.1米) .分析:要求AB 的高,由题意知可知CD=BE ,先在Rt △ADE 中求出AE 的长,再利用AB=BE +AE 求出AB 的长.解:在Rt △ADE 中,tan ∠ADE =DEAE. ∵DE =10,∠ADE =40︒.∴AE =DE tan ∠ADE =10tan 40︒≈100.84⨯=8.4. ∴AB =AE +EB =AE +DC =8.4 1.59.9+=.答:旗杆AB 的高为9.9米. 三、建桥问题例4.(2008年河南)如图所示,A 、B 两地之间有一条河,原来从A 地到B 地需要经过DC ,沿折线A →D →C →B 到达,现在新建了桥EF ,可直接沿直线AB 从A 地到达B 地.一直BC =11km ,∠A =45°,∠B =37°.桥DC 和AB 平行,则现在从A 地到达B 地可比原来少走多少路程?(结果精确到0.1km .参考数据: 1.412≈,sin37°≈0.60,cos37°≈0.80). 分析:要求现在比原来少走多少路程,就需要计算两条路线路程之差,如图构造平行四边形DCBG ,将两条路线路程之差转化为AD DG AG +-,作高线DH ,将△ADG 转化为两个直角三角形,先在在Rt DGH △中求DH 、GH ,再在Rt ADH △中求AD 、AH,此题即可得解.解:如图,过点D 作DH AB ⊥于H ,DG CB ∥交AB 于G .DC AB ∥,∴四边形DCBG 为平行四边形.∴DC GB =,11GD BC ==.∴两条路线路程之差为AD DG AG +-. 在Rt DGH △中,sin37110.60 6.60DH DG =⋅≈⨯=, cos37110.808.80GH DG =⋅⨯≈≈.在Rt ADH △中,1.41 6.609.31AD =⨯≈≈.6.60AH DH =≈.∴(9.3111)(6.608.80)AD DG AG +-=+-+≈即现在从A 地到B 地可比原来少走约4.9km . 四、图案设计问题例4.(2008年上海市)“创意设计”公司员工小王不慎将墨水泼在一张设计图纸上,导致其中部分图形和数据看不清楚(如图4所示).已知图纸上的图形是某建筑物横断面的示意图,它是以圆O 的半径OC 所在的直线为对称轴的轴对称图形,A 是OD 与圆O 的交点.由于图纸中圆O 的半径r 的值已看不清楚,根据上述信息(图纸中1:0.75i =是坡面CE 的坡度),求r 的值.分析:要求圆O 的半径r 的值,需在直角三角形ODH 中来解决,而已知的条件太少,需要先在直角三角形CEH 中,根据条件5CE =、坡面CE 的坡度1:0.75i =求出EH 、CH ,然后在直角三角形ODH 中利用勾股定理列出方程,从而求出r 的值.解:由已知OCDE ⊥,垂足为点H ,则90CHE ∠=.图41:0.75i =,43CH EH ∴=. 在Rt HEC △中,222EH CH EC +=.设4CH k =,3(0)EH k k =>,又5CE =,得222(3)(4)5k k +=,解得1k =.∴3EH =,4CH =.∴7DH DE EH =+=,7OD OA AD r =+=+,4OH OC CH r =+=+. 在Rt ODH △中,222OH DH OD +=,∴222(4)7(7)r r ++=+. 解得83r =.航海中的安全问题船只在海上航行,特别要注意安全问题,这就需要运用数学知识进行有关的计算,以确保船只航行的安全性.请看下面两例.例1 (深圳市)如图1,某货船以24海里/时的速度将一批重要物资从A 处运往正东方向的M 处,在点A 处测得某岛C 在北偏东60的方向上.该货船航行30分钟后到达B 处,此时再测得该岛在北偏东30的方向上,已知在C 岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.分析:问题的关键是弄清方位角的概念,过点C 作CD ⊥AB 于D ,然后通过解直角三角形求出CD 的长,通过列方程解决几何问题也是一种常用方法.解:由已知,得AB=24×21=12,∠CAB=90°-60°=30°,∠CBD=90°-30°=60°,所以∠C=30°,所以∠C=∠CAB ,所以CB=AB=12.在Rt △CBD 中,sin ∠CBD=CB CD ,所以CD=CB ·sin ∠CBD=12×3623=.∵936> 所以货船继续向正东方向行驶无触礁危险.例2 如图2,一艘渔船在A 处观测到东北方向有一小岛C ,已知小岛C 周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B 处,在B 处测得小岛C 在北偏东60°方向上,这时渔船改变航线向正东(即BD )方向航行,这艘渔船是否有进入养殖场的危险?分析:先将实际问题转化为解直角三角形的问题.可有如下两种方法求解. 解法一:如图3,过点B 作BM ⊥AH 于M ,则BM//AF.所以∠ABM=∠BAF=30°. 在Rt △BAM 中,AM=21AB=5,BM=35. 过点C 作CN ⊥AH 于点N ,交BD 于K. 在Rt △BCK 中,∠CBK=90°-60°=30°. 设CK=x ,则BK=3x.在Rt △CAN 中,因为∠CAN=90°-45°=45°,所以AN=NC.所以AM+MN=CK+KN. 又NM=BK ,BM=KN ,所以x+35=5+3x.解得x=5. 因为5>4.8,所以渔船没有进入养殖场的危险.解法二:如图4,过点C 作CE ⊥BD 于E.所以CE//GB//FA. 所以∠BCE=∠GBC=60°,∠BCA=∠FAC=45°. 所以∠BCA=∠BCE-∠ACE=60°-45°=15°. 又∠BAC=∠FAC-∠FAB=45°-30°=15°,D图2图3图4所以∠BCA=∠BAC.所以BC=AB=10.在Rt △BCE 中,CE=BC ·cos ∠BCE=BC ·cos60°=10×21=5. 也5>4.8,所以渔船没有进入养殖场的危险.实际中的仰角和俯角问题在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.计算原理:视线、水平线、物体的高构成直角三角形,已知仰角、俯角和另一边,利用解直角的知识就可以求出物体的高度.梳理总结:⑴仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的;可巧记为“上仰下俯”.在测量物体的高度时,要善于将实际问题抽象为数学问题.⑵在测量山的高度时,要用“化曲为直”的原则把曲的山坡“化整为零地分成一些小段,把每一小段山坡长近似地看作直的,测出仰角求出每一小段山坡对应的高,再把每部分高加起来,就得到这座山的高度.例1 (成都)如图2,甲、乙两栋高楼的水平距离BD 为90米,从甲楼顶部C 点测得乙楼顶部A 点的仰角α为30︒,测得乙楼底部B 点的俯角β为60︒,求甲乙两栋高楼各有多高?(计算过程和结果都不取近似值.分析:过点C 作CE ⊥AB 于点E, 在Rt △BCE 和Rt △ACE 中, BE 和AE 可用含CE(即为水平距离)的式子表示出来,从而求得两楼的高.解:作CE ⊥AB 于点E,∵CE ∥DB,CD ∥AB,且∠CDB=090,∴四边形BECD 是矩形. ∴CD=BE,CE=BD.图 1 E图2在Rt △BCE 中, ∠β=060,CE=BD=90米. ∵,tan CEBE=β∴BE=CE 39060tan 90tan 0=⨯=⋅β(米). ∴CD=BE=390(米).在Rt △ACE 中, ∠α=030,CE=90米. ∵ ,tan CEAE=α∴AE=CE 330339030tan 90tan 0=⨯=⨯=⋅α(米). ∴AB=AE+BE=3120390330=+(米). 答:甲楼高为390米,乙楼高为3120米.反思:仰角和俯角问题是解直角三角形中的常见题型,作辅助线构造直角三角形(一般同时得到两个直角三角形)并解之是解决这类问题的常用方法.例2 (乐山)如图3,小山上有一棵树.现有测角仪和皮尺两种测量工具,请你设计一种测量方案,在山脚水平地面上测出小树顶端A 到水平地面的距离AB .要求:⑴画出测量示意图;⑵写出测量步骤(测量数据用字母表示); ⑶根据(2)中的数据计算AB .分析:要测量底步不能到达的物体的高度,要转化为双直角三角形问题,测量方案如图2,计算的关键是求 AE,可设AE=x,则在Rt △AGF 和 Rt △AEF 中, 利用三角函数可得αtan x HE =,βtan x EF = ,再根据HE-FE=CD=m 建立方程即可. 解:(1)测量图案(示意图)如图4所示(2)测量步骤:第一步:在地面上选择点C 安装测角仪,测得此时树尖A 的仰角AHE α=∠;第二步:沿CB 前进到点D ,用皮尺量出C D ,之间的距离CD m =;AB图3AE F H CDB图4第三步:在点D 安装测角仪,测得此时树尖A 的仰角AFE β=∠; 第四步:用皮尺测出测角仪的高h . (3)计算: 令AE=x,则,tan HE x =α得αtan x HE =,又,tan EF x =β得βtan xEF =, ∵HE-FE=HF=CD=m, ∴,tan tan m xx =-βα 解得αββαtan tan tan tan -⋅=m x ,∴AB=.tan tan tan tan h m +-⋅αββα反思:在多个直角三角形中一定要认真分析各条线段之间的关系(包括三角函数关系、相等关系),运用方程求解,有时可起到事半功倍之效.快乐套餐:1.(泰安)如图5,一游人由山脚A 沿坡角为30的山坡AB 行走600m ,到达一个景点B ,再由B 沿山坡BC 行走200m 到达山顶C ,若在山顶C 处观测到景点B 的俯角为45,则山高CD 等于 (结果用根号表示)2.(安徽)如图6,某幢大楼顶部有一块广告牌CD ,甲乙两人分别在相距8米的A 、B 两处测得D 点和C 点的仰角分别为45°°和60°,且A 、B 、E 三点在一条直线上,若BE=15米,求这块广告牌的高度.(1.73,计算结果保留整数)ABCD图5第19题图EDCB A450600图6参考答案:1. (300 .2. ∵AB=8,BE=15,∴AE=23,在Rt△AED中,∠DAE=45°,∴DE=AE=23.在Rt△BEC中,∠CBE=60°,∴CE=BE·tan60°=CD=CE-DE=23≈2.95≈3.即这块广告牌的高度约为3米.。
解三角形应用题(4)含答案

CB DA2023 解三角形应用题(4)1.如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在她家北偏东60度500m 处,那么水塔所在的位置到公路的距离AB 是( ). A.250m B.D. 2.如图2,AC 是电杆AB 的一根拉线,测得BC=6米,∠ACB=52°, 则拉线AC 的长为( ) A.︒526sin 米 B. ︒526tan 米 C. 6·cos 52°米 D. ︒526cos 米 3.测量一座楼房的高度: (1)已知楼AB 高6m,在A 处测得对面一座楼房顶部的仰角为45°,底部的俯角为30°,则CD 高度为 。
(2)将(1)中的“AB=6m ”改为“BC 间距为10m ”,则AB= CD=(3)已知楼AB 高10m,在A 处测得对面一座楼房顶部的仰角为45°,到B 处后测得对面楼顶的仰角为60°,则CD 高度为 ,两楼间距为 。
(4)建筑物AB 的高度为30m,欲测量对面的一低层建筑物CD 的高度(如图)站在顶端测得对面小楼底和楼顶的俯角分别为45°和30°,则两楼间距为 , 建筑物CD 的高度为 .(5)从A 处测得点D 的俯角为45°,从B 处测得点D 的仰角为30°,且AB=20m,则CD= 。
4.如图,山顶建有一座铁塔,塔高30m CD =,某人在点A 处测得塔底C 的仰角为20,塔顶D 的仰角为23,求此人距CD 的水平距离AB .(参考数据:sin 200.342≈,cos 200.940≈,tan 200.364≈,sin 230.391≈,cos 230.921≈,tan 230.424≈)5.某地震救援队探测出某建筑物废墟下方点C 处有生命迹象,已知废墟一侧地面上两探测点A 、B 相距 3 米,探测线与地面的夹角分别是30°和 60°(如图),试确定生命所在点C 的深度.(结果精确到0.1 1.41 1.73≈≈)BC第3题(1.2)第3题(3)BDCCBAD第3题(4)DC 第3题(5)东 ABC ┐第2题6.如图,A 、B 两地间有座山,汽车原来从A 地到B 地须往C 地沿折线A-C-B 行驶,现开通隧道后,汽车直接沿AB 行驶,已知按原路行驶需行驶(10+5√2)km,∠A=30°,∠B=45°,问隧道开通后,汽车从A 地到B 地可以比原来少走多少路?(精确到0.1km,√2≈1.41,√3≈1.73)7.6月以来,我省普降大雨,时有山体滑坡灾害发生。
2024届新高考数学复习:专项(解三角形的综合运用大题)历年好题练习(附答案)

2024届新高考数学复习:专项(解三角形的综合运用大题)历年好题练习1.[2023ꞏ新课标Ⅰ卷]已知在△ABC中,A+B=3C,2sin (A-C)=sin B.(1)求sin A;(2)设AB=5,求AB边上的高.2.△ABC中,sin2A-sin2B-sin2C=sin B sin C.(1)求A;(2)若BC=3,求△ABC周长的最大值.3.[2023ꞏ新课标Ⅱ卷]记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC面积为3,D为BC的中点,且AD=1.(1)若∠ADC=π3,求tan B;(2)若b2+c2=8,求b,c.4.[2022ꞏ新高考Ⅰ卷,18]记△ABC的内角A,B,C的对边分别为a,b,c,已知cos A 1+sin A=sin 2B1+cos 2B.(1)若C=2π3,求B;(2)求a2+b2c2的最小值.5.[2023ꞏ全国乙卷(理)]在△ABC 中,已知∠BAC =120°,AB =2,AC =1. (1)求sin ∠ABC ;(2)若D 为BC 上一点,且∠BAD =90°,求△ADC 的面积.6.[2023ꞏ河北石家庄模拟]在①cos C =217 ,②a sin C =c cos ⎝⎛⎭⎫A -π6 ,这两个条件中任选一个,补充在下面问题中的横线处,并完成解答.问题:△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,B =π3 ,D 是边BC 上一点,BD =5,AD =7,且________,试判断CD 和BD 的大小关系________.注:如果选择多个条件分别解答,按第一个解答计分.7.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,设(sin B -sin C )2=sin 2A -sin B sin C . (1)求A ;(2)若2 a +b =2c ,求sin C .8.[2022ꞏ全国乙卷(理),17]记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin C sin (A -B )=sin B sin (C -A ).(1)证明:2a 2=b 2+c 2;(2)若a =5,cos A =2531 ,求△ABC 的周长.参考答案1.答案解析:方法一 (1)在△ABC 中,A +B =π-C ,因为A +B =3C ,所以3C =π-C ,所以C =π4 . 因为2sin (A -C )=sin B ,所以2sin (A -π4 )=sin (3π4 -A ),展开并整理得2 (sin A -cos A )=22 (cos A +sin A ), 得sin A =3cos A ,又sin 2A +cos 2A =1,且sin A >0,所以sin A =31010 .(2)由正弦定理BCsin A =AB sin C ,得BC =AB sin C ×sin A =522×31010 =35 ,由余弦定理AB 2=AC 2+BC 2-2AC ꞏBC cos C ,得52=AC 2+(35 )2-2AC ꞏ35 cos π4 , 整理得AC 2-310 AC +20=0, 解得AC =10 或AC =210 ,由(1)得,tan A =3>3 ,所以π3 <A <π2 ,又A +B =3π4 ,所以B >π4 ,即C <B ,所以AB <AC ,所以AC =210 ,设AB 边上的高为h ,则12 ×AB ×h =12 ×AC ×BC sin C ,即5h =210 ×35 ×22 ,解得h =6,所以AB 边上的高为6.方法二 (1)在△ABC 中,A +B =π-C ,因为A +B =3C ,所以3C =π-C ,所以C =π4 . 因为2sin (A -C )=sin B ,所以2sin (A -C )=sin [π-(A +C )]=sin (A +C ),所以2sin A cos C -2cos A sin C =sin A cos C +cos A sin C , 所以sin A cos C =3cos A sin C , 易得cos A cos C ≠0,所以tan A =3tan C =3tan π4 =3,又sin A >0,所以sin A =332+12 =31010 . (2)由(1)知sin A =31010 ,tan A =3>0,所以A 为锐角,所以cos A =10,所以sin B =sin (3π4 -A )=22 (cos A +sin A )=22 ×(1010 +31010 )=255 ,由正弦定理AC sin B =ABsin C ,得AC =AB ꞏsin Bsin C =5×25522=210 ,故AB 边上的高为AC ×sin A =210 ×31010 =6.2.答案解析:(1)由正弦定理和已知条件得BC 2-AC 2-AB 2=AC ꞏAB .① 由余弦定理得BC 2=AC 2+AB 2-2AC ꞏAB cos A .②由①②得cos A =-12 .因为0<A <π,所以A =2π3 .(2)由正弦定理及(1)得AC sin B =AB sin C =BCsin A =23 ,从而AC =23 sin B ,AB =23 sin (π-A -B )=3cos B -3 sin B .故BC +AC +AB =3+3 sin B +3cos B =3+23 sin ⎝⎛⎭⎫B +π3 . 又0<B <π3 ,所以当B =π6 时,△ABC 周长取得最大值3+23 . 3.答案解析:(1)因为D 为BC 的中点,所以S △ABC =2S △ADC =2×12 ×AD ×DC sin ∠ADC =2×12 ×1×DC ×32 =3 , 解得DC =2,所以BD =DC =2,a =4.因为∠ADC =π3 ,所以∠ADB =2π3 .在△ABD 中,由余弦定理,得c 2=AD 2+BD 2-2AD ꞏBD cos ∠ADB =1+4+2=7,所以c =7 .在△ADC 中,由余弦定理,得b 2=AD 2+DC 2-2AD ꞏDC ꞏcos ∠ADC =1+4-2=3,所以b =3 .在△ABC 中,由余弦定理,得cos B =c 2+a 2-b 22ac =7+16-32×4×7=5714 ,所以sin B =1-cos 2B =2114 .(2)因为D 为BC 的中点,所以BD =DC .因为∠ADB +∠ADC =π,所以cos ∠ADB =-cos ∠ADC ,则在△ABD 与△ADC 中,由余弦定理,得AD 2+BD 2-c 22AD ꞏBD =-AD 2+DC 2-b 22AD ꞏDC , 得1+BD 2-c 2=-(1+BD 2-b 2),所以2BD 2=b 2+c 2-2=6,所以BD =3 ,所以a =23 .在△ABC 中,由余弦定理,得cos ∠BAC =b 2+c 2-a 22bc =8-122bc =-2bc ,所以S △ABC =12 bc sin ∠BAC =12 bc 1-cos 2∠BAC=12 bc 1-⎝⎛⎭⎫-2bc 2=12 b 2c 2-4 =3 ,解得bc =4.则由⎩⎪⎨⎪⎧bc =4b 2+c 2=8 ,解得b =c =2. 4.答案解析:(1)由已知条件,得sin 2B +sin A sin 2B =cos A +cos A cos 2B .所以sin 2B =cos A +cos A cos 2B -sin A sin 2B =cos A +cos (A +2B )=cos [π-(B +C )]+cos [π-(B +C )+2B ]=-cos (B +C )+cos [π+(B -C )]=-2cos B cos C ,所以2sin B cos B =-2cos B cos C , 即(sin B +cos C )cos B =0.由已知条件,得1+cos 2B ≠0,则B ≠π2 ,所以cos B ≠0,所以sin B =-cos C =12 .又0<B <π3 ,所以B =π6 .(2)由(1)知sin B =-cos C >0,则B =C -π2 ,所以sin A =sin (B +C )=sin (2C -π2 )=-cos 2C .由正弦定理,得a 2+b 2c 2 =sin 2A +sin 2B sin 2C =cos 22C +cos 2Csin 2C =(1-2sin 2C )2+(1-sin 2C )sin 2C =2+4sin 4C -5sin 2C sin 2C=2sin 2C +4sin 2C -5≥22sin 2C ꞏ4sin 2C -5=42 -5,当且仅当sin 2C =22 时,等号成立,所以a 2+b 2c 2 的最小值为42 -5. 5.答案解析:(1)如图,由余弦定理得BC 2=AB 2+AC 2-2AB ꞏAC ꞏcos ∠BAC =22+12+2×2×1×12 =7,得BC =7 .方法一 由正弦定理ACsin ∠ABC =BC sin ∠BAC ,得sin ∠ABC =1×327=2114 .方法二 由余弦定理得cos ∠ABC =AB 2+BC 2-AC 22AB ꞏBC =4+7-12×2×7 =5714 , 所以sin ∠ABC =1-cos 2∠ABC =21 .(2)方法一 由sin ∠ABC =2114 ,得tan ∠ABC =35 ,又tan ∠ABC =DA AB =DA 2 ,所以DA =235 ,故△ADC 的面积为12 DA ꞏAC ꞏsin (120°-90°)=12 ×235 ×1×12 =3 .方法二 △ABC 的面积为12 AC ꞏAB ꞏsin ∠BAC =12 ×1×2×32 =32 ,S △ADC S △BAD=12AC ꞏAD ꞏsin ∠CAD12AB ꞏAD ꞏsin ∠BAD =sin 30°2×sin 90° =14 ,故△ADC 的面积为15 S △ABC =15 ×3 =3.6.答案解析:设AB =x ,在△ABD 中由余弦定理可得:49=x 2+25-2ꞏx ꞏ5ꞏcos π3 =x 2+25-5x , 即x 2-5x -24=0,解得x =8. 方案一 选条件①.由cos C =217 得sin C =277 , ∵A +B +C =π,∴sin A =sin (B +C )=32 ×217 +12 ×277 =5714 ,在△ABC 中由正弦定理可得:BC 5714 =8277,解得:BC =10,∴CD =BD =5. 方案二 选条件②.由正弦定理可得:a =2R sin A ,c =2R sin C ,代入条件a sin C =c cos ⎝⎛⎭⎫A -π6 得:sin A sin C =sin C ꞏ⎝⎛⎭⎫32cos A +12sin A =32 cos A sin C +12 sin A sin C ,∴12 sin A sin C =3cos A sin C ,因为A 为三角形内角,所以tan A =3 ,故A =π3 , 所以△ABC 为等边三角形,所以BC =8,∴CD =3,所以CD <BD .7.答案解析:(1)由已知得sin 2B +sin 2C -sin 2A =sin B sin C ,故由正弦定理得b 2+c 2-a 2=bc .由余弦定理得cos A =b 2+c 2-a 22bc =12 . 因为0°<A <180°,所以A =60°.(2)由(1)知B =120°-C ,由题设及正弦定理得2 sin A +sin (120°-C )=2sin C ,即62 +3 cos C +12 sin C =2sin C ,可得cos (C +60°)=-2.由于0°<C <120°,所以sin (C +60°)=22 ,故 sin C =sin (C +60°-60°)=sin (C +60°)cos 60°-cos (C +60°)sin 60°=6+2 .8.答案解析:(1)证明:∵sin C sin (A -B )=sin B sin (C -A ),∴sin C sin A cos B -sin C cos A sin B =sin B sin C cos A -sin B cos C sin A , ∴sin C sin A cos B =2sin B sin C cos A -sin B cos C sin A . 由正弦定理,得ac cos B =2bc cos A -ab cos C .由余弦定理,得a 2+c 2-b 22 =b 2+c 2-a 2-a 2+b 2-c 22. 整理,得2a 2=b 2+c 2.(2)由(1)知2a 2=b 2+c 2.又∵a =5,∴b 2+c 2=2a 2=50.由余弦定理,得a 2=b 2+c 2-2bc cos A ,即25=50-5031 bc ,∴bc =312 .∴b +c =b 2+c 2+2bc =50+31 =9, ∴a +b +c =14.故△ABC 的周长为14.。
2020高二数学人教A必修5练习:1.2.1 解三角形的实际应用举例 Word版含解析

课时训练3解三角形的实际应用举例一、测量中的距离问题1.有一长为10 m的斜坡,倾斜角为60°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长的长度(单位:m)是()A.5B.5√3C.10√3D.10答案:D解析:如图,在Rt△ABC中,AC=10,∠ACB=60°.∴AB=5√3,BC=5,在Rt△ABD中,∠ADB=30°,∴BD=15.∴CD=BD-BC=10.2.(2015福建宁德五校联考,14)一艘船以15 km/h的速度向东航行,船在A处看到灯塔B在北偏东60°处;行驶4 h后,船到达C处,看到灯塔B在北偏东15°处,这时船与灯塔的距离为km.答案:30√2解析:根据题意画出图形,如图所示,可得B=75°-30°=45°,在△ABC中,根据正弦定理得,ACsinB =BCsin∠BAC,即22=BC12,∴BC=30√2 km,即此时船与灯塔的距离为30√2 km.3.(2015福建厦门高二期末,15)如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A 城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是千米.答案:24解析:由已知得CD=21,BC=31,BD=20,在△BCD 中,由余弦定理得cos ∠BDC=212+202-3122×21×20=-17. 设∠ADC=α,则cos α=17,sin α=4√37. 在△ACD 中,由正弦定理,得AC=21sinαsin60°=24.二、测量中的高度与角度问题4.如图,D ,C ,B 三点在地面同一直线上,DC=a ,从C ,D 两点测得A 点的仰角分别是β,α(α<β),则A 点距离地面的高度AB 等于( )A.asinαsinβsin(β-α) B.asinαsinβcos(α-β) C.asinαcosβsin(β-α) D.acosαsinβcos(α-β)答案:A解析:在△ACD 中,∠DAC=β-α,DC=a ,∠ADC=α,由正弦定理得AC=asinαsin(β-α), ∴在Rt △ACB 中,AB=AC sin β=asinαsinβsin(β-α).5.运动会开幕式上举行升旗仪式,在坡度15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10√6 m(如图所示),则旗杆的高度为( ) A.10 m B.30 mC.10√3 mD.10√6 m答案:B解析:如图所示,由题意知∠AEC=45°,∠ACE=180°-60°-15°=105°,∴∠EAC=180°-45°-105°=30°,由正弦定理知CE sin ∠EAC=AC sin ∠CEA,∴AC=CE·sin∠CEAsin∠EAC=20√3(m),∴在Rt△ABC中,AB=AC·sin∠ACB=30(m).∴旗杆的高度为30 m.6.当甲船位于A处时获悉,在其正东方向相距20 n mile的B处有一艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距10 n mile C处的乙船,乙船立即朝北偏东θ角的方向沿直线前往B处救援,则sin θ的值等于()A.√217B.√22C.√32D.5√714答案:D解析:根据题目条件可作图如图:在△ABC中,AB=20,AC=10,∠CAB=120°,由余弦定理有BC2=AB2+AC2-2AB·AC cos∠CAB=202+102-2×20×10cos 120°=700,∴BC=10√7.再由正弦定理得ABsin∠ACB =BCsin∠CAB,∴sin∠ACB=AB·sin∠CAB=20×sin120°10√7=√217.又0°<∠ACB<90°,∴cos∠ACB=2√7,∴sin θ=sin(30°+∠ACB)=sin 30°cos∠ACB+cos 30°sin∠ACB=1×2√7+√3×√21=5√7.7.某海岛周围38 n mile有暗礁,一轮船由西向东航行,初测此岛在北偏东60°方向,航行30 n mile后测得此岛在东北方向,若不改变航向,则此船触礁的危险(填“有”或“无”).答案:无解析:由题意在△ABC中,AB=30 n mile,∠BAC=30°,∠ABC=135°,∴∠ACB=15°. 由正弦定理,得BC=AB sin ∠ACB·sin ∠BAC=30sin15°·sin 30°=6-24=15(√6+√2).在Rt △BDC 中,CD=√22BC=15(√3+1)>38.∴无触礁的危险.8.如图,在一个特定时段内,以点E 为中心的7海里以内海域被设为警戒水域.点E 正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A 北偏东45°且与点A 相距40√2海里的位置B ,经过40分钟又测得该船已行驶到点A 北偏东45°+θ(其中sinθ=√2626,0°<θ<90°)且与点A 相距10√13海里的位置C. (1)求该船的行驶速度(单位:海里/小时);(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由. 解:(1)因为AB=40√2,AC=10√13,∠BAC=θ,sin θ=√26,0°<θ<90°,所以cos θ=√1-(√2626)2=5√2626.由余弦定理得BC=√AB 2+AC 2-2AB ·AC ·cosθ=10√5,所以该船的行驶速度为v=10√523=15√5(海里/小时).(2)设直线AE 与BC 的延长线相交于点Q. 在△ABC 中,由余弦定理得 cos ∠ABC=AB 2+BC 2-AC 22AB ·BC=√2)2√5)2√13)22×402×105=3√1010,所以sin ∠ABC=√1-cos 2∠ABC =√1-910=√1010. 在△ABQ 中,由正弦定理得AQ=ABsin∠ABCsin(45°-∠ABC)=40√2×√101022×21010=40.因为AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.过点E作EP⊥BC于点P,则EP为点E到直线BC的距离.在Rt△QPE中,PE=QE·sin∠PQE=QE·sin∠AQC=QE·sin(45°-∠ABC)=15×√55=3√5<7.故该船会进入警戒水域.(建议用时:30分钟)1.如图,已知两座灯塔A和B与海岸观察站C的距离相等,灯塔A在观察站C的北偏东40°,灯塔B 在观察站C的南偏东60°,则灯塔A在灯塔B的()的位置.A.北偏东10°B.北偏西10°C.南偏东10°D.南偏西10°答案:B解析:由图可知,∠ACB=180°-(40°+60°)=80°.又∵AC=BC,∴∠A=∠CBA=12(180°-80°)=50°.∵CE∥BD,∴∠CBD=∠BCE=60°,∴∠ABD=60°-50°=10°.∴灯塔A在灯塔B的北偏西10°的位置.2.如图所示,为测一树的高度,在地面上选取A,B两点(点A,B与树根部在同一直线上),从A,B两点分别测得树尖的仰角为30°,45°,且A,B两点之间的距离为60 m,则树的高度为()A.(30+30√3) mB.(30+15√3) mC.(15+30√3) mD.(15+3√3) m答案:A解析:设树高为h,则由题意得√3h-h=60,∴h=√3-1=30(√3+1)=(30√3+30)(m).3.一艘客船上午9:30在A处,测得灯塔S在它的北偏东30°,之后它以32 n mile/h的速度继续沿正北方向匀速航行,上午10:00到达B处,此时测得船与灯塔S相距8√2 n mile,则灯塔S在B处的()A.北偏东75°B.东偏南75°C.北偏东75°或东偏南75°D.以上方位都不对答案:C解析:根据题意画出示意图,如图,由题意可知AB=32×12=16,BS=8√2,∠A=30°.在△ABS中,由正弦定理得ABsinS =BSsinA,sin S=ABsinABS=16sin30°8√2=√22,∴S=45°或135°,∴B=105°或15°,即灯塔S在B处的北偏东75°或东偏南75°.4.一货轮航行到M处,测得灯塔S在货轮的北偏东15°方向,与灯塔S相距20 n mile,随后货轮按北偏西30°的方向航行3 h后,又测得灯塔在货轮的东北方向,则货轮的速度为()A.103(√6+√2) n mile/hB.103(√6−√2) n mile/hC.103(√6+√3) n mile/hD.103(√6−√3) n mile/h答案:B解析:如图,设货轮的时速为v,则在△AMS中,∠AMS=45°,∠SAM=105°,∠ASM=30°,SM=20,AM=3v.由正弦定理得3vsin30°=20sin105°,即v=206sin105°=103(√6−√2)(n mile/h).5.某人站在山顶向下看一列车队向山脚驶来,他看见第一辆车与第二辆车的俯角差等于他看见第二辆车与第三辆车的俯角差,则第一辆车与第二辆车的距离d1与第二辆车与第三辆车的距离d2之间的关系为()A.d1>d2B.d1=d2C.d1<d2D.不能确定大小答案:C解析:如图,B,C,D分别是第一、二、三辆车所在的位置,由题意可知α=β.在△PBC中,d1sinα=PBsin∠PCB,在△PCD中,d2sinβ=PDsin∠PCD,∵sin α=sin β,sin∠PCB=sin∠PCD,∴d1d2=PBPD.∵PB<PD,∴d1<d2.6.如图,某人于地面上C处观察一架迎面飞来的飞机在A处的仰角为30°,过1 min后到B再测得仰角为45°,如果该飞机以450 km/h的速度沿水平方向飞行,则飞机的高度为 km.答案:15(√3+1)4解析:如图,∠DCA=60°,∠DCB=45°,设飞机高为h,则BD=h,AD=√3h.又AB=450×160=7.5,由AD-BD=AB得√3h-h=7.5.∴h=√3-1=15(√3+1)4.7.一船以24 km/h的速度向正北方向航行,在点A处望见灯塔S在船的北偏东30°方向上,15 min后到点B处望见灯塔在船的北偏东75°方向上,则船在点B时与灯塔S的距离是 km.答案:3√2解析:如图,由条件知,AB=24×1560=6(km).在△ABS中,∠BAS=30°,AB=6,∠ABS=180°-75°=105°,∴∠ASB=45°.由正弦定理,得BSsin30°=ABsin45°,∴BS=6sin30°sin45°=3√2.8.海上一观测站测得方位角为240°的方向上有一艘停止待修的商船,在商船的正东方有一艘海盗船正向它靠近,速度为90 n mile/h.此时海盗船距观测站10√7 n mile,20 min后测得海盗船距观测站20 n mile,再过min,海盗船到达商船.答案:403解析:如图,设开始时观测站、商船、海盗船分别位于A,B,C处,20 min后,海盗船到达D处,在△ADC 中,AC=10√7,AD=20,CD=30,由余弦定理,得cos∠ADC=AD2+CD2-AC22AD·CD =400+900-7002×20×30=12.∴∠ADC=60°,在△ABD中,由已知,得∠ABD=30°,∠BAD=60°-30°=30°,∴BD=AD=20,2090×60=403(min).9.如图,某货轮在A 处看灯塔B 在货轮的北偏东75°方向,距离为12√6 km,在A 处看灯塔C 在货轮的北偏西30°方向,距离为8√3 km,货轮由A 处向正北航行到D 处时,再看灯塔B 在北偏东120°方向,求:(1)A 处与D 处的距离; (2)灯塔C 与D 处的距离.解:(1)在△ABD 中,∠ADB=60°,∠B=45°,由正弦定理得AD=AB ·sinB sin ∠ADB=12√6×√2232=24(km).∴A 处与D 处的距离为24 km .(2)在△ACD 中,由余弦定理得CD 2=AD 2+AC 2-2AD ·AC cos 30°,解得CD=8√3(km).∴灯塔C 与D 处的距离为8√3 km .。
1.2解三角形应用举例(一)

1.2解三角形应用举例(一)班级_______姓名________ 1、自动卸货汽车的车厢采用液压机构,设计时需要计算油泵顶杆BC的长度,已知车箱的最大仰角是60°,油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的夹角为6°20′,AC长为1.40m,计算BC的长(精确到0.01m)。
2、如图,在山脚A测得山顶P的仰角为,α沿倾斜角为β的斜坡向上走a米到B,在B处测得山顶P的仰角为,γ求证:山高sin sin().sin()ahαγβγβ-=-3、勘探队员朝一座山行进,在前后两处观察山顶的仰角分别是29°和38°,两个观察点之间的距离是200m,求此山的高度。
4、飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔20 250m,速度为1 000km/h,飞行员先看到山顶的俯角为18°30′,经过150s后又看到山顶的俯角为81°,求山顶的海拔高度(精确到1 m)。
5、测山上石油钻井的井架BC 的高,从山脚A 测得AC=65.3m ,塔顶B 的仰角a 是25°25′。
已知山坡的倾斜角β是17°38′,求井架的高BC 。
6、在△ABC 中,根据下列条件,求三角形的面积S (精确到0.01cm 2):(1)已知 45,33,28===B cm c cm a ;(2)已知cm a C A 36,5.66,8.32=== ;(3)已知三边的长分别为cm c cm b cm a 71,61,54===。
7、证明三角形的面积公式AC B a S sin sin sin 212=8、有一块四边形土地的形状如图所示,它的三条边的长分别是50m ,60m ,70m ,两个内角是127°和132°,求四边形的面积(精确到0.01m 2)。
9、货轮在海上以35n mile/h 的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为148°的方向航行。
(完整版)三角形中几何计算、解三角形实际应用举例
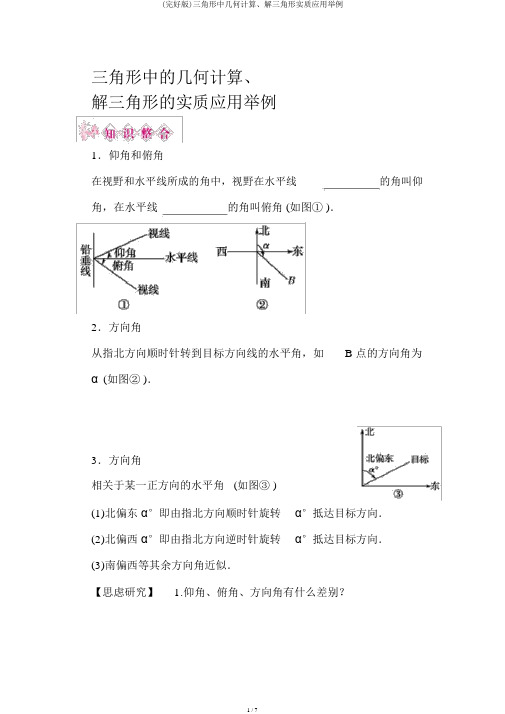
三角形中的几何计算、解三角形的实质应用举例1.仰角和俯角在视野和水平线所成的角中,视野在水平线的角叫仰角,在水平线的角叫俯角 (如图① ).2.方向角从指北方向顺时针转到目标方向线的水平角,如 B 点的方向角为α(如图② ).3.方向角相关于某一正方向的水平角(如图③ )(1)北偏东α°即由指北方向顺时针旋转α°抵达目标方向.(2)北偏西α°即由指北方向逆时针旋转α°抵达目标方向.(3)南偏西等其余方向角近似.【思虑研究】 1.仰角、俯角、方向角有什么差别?以平面几何图形为背景,求解相关长度、角度、面积、最值和优化等问题,往常是转变到三角形中,利用正、余弦定理加以解决.在解决某些详细问题时,常先引入变量 (如边长、角度等 ),而后把要解的三角形的边或角用所设变量表示出来,再利用正、余弦定理列出方程,解之.以平面几何图形为背景,求解相关长度、角度、面积、最值和优化等问题,往常是转变到三角形中,利用正、余弦定理加以解决.在解决某些详细问题时,常先引入变量 (如边长、角度等 ),而后把要解的三角形的边或角用所设变量表示出来,再利用正、余弦定理列出方程,解之.如右图, D 是直角△ ABC 斜边 BC 上一点, AB=AD,记∠ CAD=,∠ ABC=β.(1)证明: sin+cos 2β=0;(2)若 AC= 3 DC,求β的值.【变式训练】 1.如图,在四边形ABCD 中,已知 AD⊥ CD,AD =10,AB=14,∠ BDA= 60°,∠ BCD= 135°,则 BC 的长为________.求距离问题要注意:(1)选定或确立要创立的三角形,要第一确立所求量所在的三角形,若其余量已知则直接解;如有未知量,则把未知量放在另一确立三角形中求解.(2)确立用正弦定理仍是余弦定理,假如都可用,就选择更便于计算的定理.例题 2.如下图,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15 2海里 /小时,在甲船从 A 岛出发的同时,乙船从 A 岛正南 40 海里处的 B 岛1出发,朝北偏东θtanθ=2的方向作匀速直线航行,速度为10 5海里 /小时.(1)求出发后 3 小时两船相距多少海里?(2)求两船出发后多长时间距离近来?近来距离为多少海里?丈量高度问题一般是利用地面上的观察点,经过丈量仰角、俯角等数据计算物体的高度,这种问题一般用到立体几何知识,先把立体几何问题转变为平面几何问题,再经过解三角形加以解决.例题 3,如图,丈量河对岸的塔形建筑 AB,A 为塔的顶端, B 为塔的底端,河两岸的地面上随意一点与塔底端 B 处在同一海拔水平面上,现给你一架测角仪 (能够丈量仰角、俯角和视角 ),再给你一把尺子 (能够丈量地面上两点间距离 ),图中给出的是在一侧河岸地面 C 点测得仰角∠ ACB=,请设计一种丈量塔建筑高度 AB 的方法 (此中测角仪支架高度忽视不计,计算结果可用丈量数据所设字母表示 ).【变式训练】3. A、B 是海平面上的两个点,相距800 m,在A 点测得山顶C 的仰角为 45°,∠ BAD=120°,又在 B 点测得∠ ABD=45°,此中 D 是点 C 到水平面的垂足,求山高 CD.丈量角度问题也就是经过解三角形求角问题,求角问题能够转变为求该角的函数值.假如是用余弦定理求得该角的余弦,该角简单确立,假如用正弦定理求得该角的正弦,就需要议论解的状况了.例题 4,在海岸A处,发现北偏东45°方向,距离A处(3-1) n mile的 B 处有一艘走私船,在 A 处北偏西 75°的方向,距离 A 处 2 n mile 的 C 处的缉私船受命以 10 3 n mile/h 的速度追截走私船.此时,走私船正以 10 nmile/h 的速度从 B 处向北偏东 30°方向逃跑,问缉私船沿什么方向能最快追上走私船?【变式训练】 4.如下图,甲船以每小时302海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西 105°方向的 B1处,此时两船相距20海里.当甲船航行20分钟抵达 2 处时,A乙船航行到甲船的北偏西120°方向的 B2处,此时两船相距 10 2海里,问乙船每小时航行多少海里?1.解三角形的一般步骤(1)剖析题意,正确理解题意分清已知与所求,特别要理解应用题中的相关名词、术语,如坡度、仰角、俯角、方向角等.(2)依据题意画出表示图.(3)将需求解的问题归纳到一个或几个三角形中,经过合理运用正弦定理、余弦定理等相关知识正确求解.演算过程中,要算法精练,计算正确,并作答.(4)查验解出的答案能否拥有实质意义,对解进行弃取.2.解斜三角形实质应用举例(1)常有几种题型丈量距离问题、丈量高度问题、丈量角度问题、计算面积问题、航海问题、物理问题等.(2)解题时需注意的几个问题①要注意仰角、俯角、方向角等名词,并能正确地找出这些角;②要注意将平面几何中的性质、定理与正、余弦定理联合起来,发现题目中的隐含条件,才能顺利解决.从近两年的高考试题来看,利用正弦定理、余弦定理解决与丈量、几何计算相关的实质问题是高考的热门,一般以解答题的形式考察,主要考察计算能力和剖析问题、解决实质问题的能力,常与解三角形的知识及三角恒等变换综合考察.1.(2012 ·江西卷 )E,F 是等腰直角△ ABC 斜边 AB 上的三平分点,则tan∠ECF= ()16233A.27B.3C. 3D.42.(2012 ·陕西卷 )如图, A,B 是海面上位于东西方向相距5(3+ 3 )海里的两个观察点,现位于 A 点北偏东 45°, B 点北偏西 60°的 D 点有一艘轮船发出求救信号,位于 B 点南偏西 60°且与 B 点相距 20 3 海里的C点的营救船立刻前去营救,其航行速度为 30 海里 / 时,该营救船抵达 D 点需要多长时间?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解三角形应用举例练习题
一、选择题
1.某人向正东方向走x km后,他向右转150°,然后朝新方向走3 km,结果他离出发点恰好 3 km,那么x的值为()
A.3B.2 3
C.23或 3 D.3
2.已知船A在灯塔C北偏东85°且到C的距离为2km,船B在灯塔C西偏北25°且到C的距离为3km,则A,B两船的距离为()
A.23km B.32km
C.15km
D.13km
3.已知△ABC的三边长a=3,b=5,c=6,则△ABC的面积是()
A.14 B.214
C.15 D.215
4.两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为()
A.a km B.3a km
C.2a km D.2a km
5.已知△ABC中,a=2、b=3、B=60°,那么角A等于()
A.135°B.90°
C.45°D.30°
6.一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°方向上,另一灯塔在船的南偏西75°方向上,则这艘船的速度是每小时()
A.5海里B.53海里
C.10海里D.103海里
二、填空题
7.(2010~2011·醴陵二中、四中期中)已知A、B两地的距离为10km,BC两地的距离为20km,经测量∠ABC=120°,则AC两地的距离为________km.
8.如图,为了测量河的宽度,在一岸边选定两点A,B,望对岸的标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m,则河的宽度是__________.
9.
(2011·北京朝阳二模)如图,一艘船上午800在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午830到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距42n mile,则此船的航行速度是________n mile/h.
三、解答题
10.如图,为了测量河
对岸A,B两点间的距离,在河的这边测得CD=
3
2km,∠ADB=∠CDB=30°,∠ACD=
60°,∠ACB=45°,求A、B两点间的距离.。
