三维函数图像练习
标题-2018-2019学年高中新三维一轮复习数学浙江专版:课时跟踪检测(十一) 函数的图象
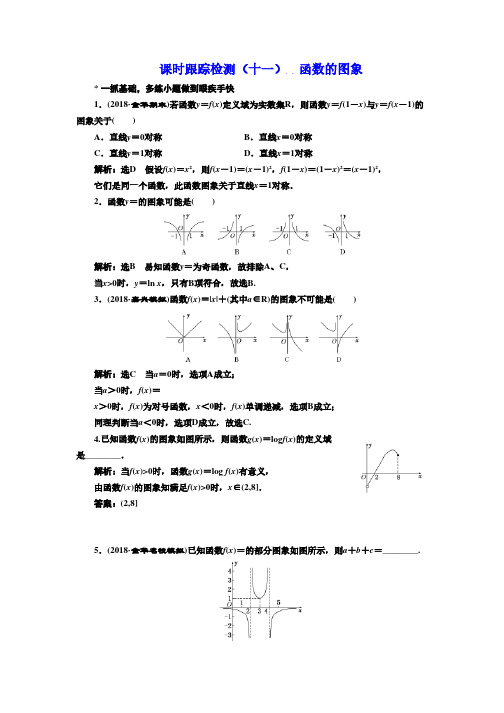
课时跟踪检测(十一)函数的图象*一抓基础,多练小题做到眼疾手快1.(2018·金华期末)若函数y=f(x)定义域为实数集R,则函数y=f(1-x)与y=f(x-1)的图象关于( )A.直线y=0对称 B.直线x=0对称C.直线y=1对称D.直线x=1对称解析:选D 假设f(x)=x2,则f(x-1)=(x-1)2,f(1-x)=(1-x)2=(x-1)2,它们是同一个函数,此函数图象关于直线x=1对称.2.函数y=的图象可能是( )解析:选B 易知函数y=为奇函数,故排除A、C,当x>0时,y=ln x,只有B项符合,故选B.3.(2018·嘉兴模拟)函数f(x)=|x|+(其中a∈R)的图象不可能是( )解析:选C 当a=0时,选项A成立;当a>0时,f(x)=x>0时,f(x)为对号函数,x<0时,f(x)单调递减,选项B成立;同理判断当a<0时,选项D成立,故选C.4.已知函数f(x)的图象如图所示,则函数g(x)=log f(x)的定义域是________.解析:当f(x)>0时,函数g(x)=log f(x)有意义,由函数f(x)的图象知满足f(x)>0时,x∈(2,8].答案:(2,8]5.(2018·金华名校模拟)已知函数f(x)=的部分图象如图所示,则a+b+c=________.解析:由图象知2,4是y=ax2+bx+c的两根,又由二次函数y=ax2+bx+c的对称性和图象知顶点为(3,1),故解得则a+b+c=-3.答案:-3*二保高考,全练题型做到高考达标1.(2018·桂林一调)函数y=(x3-x)2|x|的图象大致是( )解析:选B 由于函数y=(x3-x)2|x|为奇函数,故它的图象关于原点对称,当0<x<1时,y<0;当x>1时,y>0,故选B.2.下列函数f(x)图象中,满足f>f(3)>f(2)的只可能是( )解析:选D 因为f >f(3)>f(2),所以函数f(x)有增有减,排除A,B.在C中,f <f(0)=1,f(3)>f(0),即f <f(3),排除C,选D.3.(2018·宁波模拟)在同一个坐标系中画出函数y=a x,y=sin ax的部分图象,其中a>0且a≠1,则下列所给图象中可能正确的是( )解析:选D 当a>1时,y=sin ax的周期小于2 À,排除A、C,当0<a<1时,y=sin ax的周期大于2 À,故选D.4.(2017·台州期中)函数y=的大致图象如图所示,则( )A.a∈(-1,0) B.a∈(0,1)C.a∈(-∞,1) D.a∈(1,+∞)解析:选B 当x=0时,y=0,故a≠0,当x>0 时,y=>0恒成立,即a>-x2恒成立,所以a>0,所以y==≤,当且仅当x=时取等号,由图知,当x>0时,函数取得最大值时相应的x的值小于1,∴0<<1,∴0<a<1.5.已知函数f(x)的定义域为R,且f(x)=若方程f(x)=x+a有两个不同实根,则a的取值范围为( )A.(-∞,1) B.(-∞,1]C.(0,1) D.(-∞,+∞)解析:选A x≤0时,f(x)=2-x-1,0<x≤1时,-1<x-1≤0,f(x)=f(x-1)=2-(x-1)-1.故x>0时,f(x)是周期函数,如图所示.若方程f(x)=x+a有两个不同的实数根,则函数f(x)的图象与直线y=x+a有两个不同交点,故a<1,即a的取值范围是(-∞,1).6.(2018·稽阳联考)函数f(x)=的图象如图所示,则a+b+c=________.解析:由图象可求得直线的方程为y=2x+2,又函数y=log c的图象过点(0,2),将其坐标代入可得c=,所以a+b+c=2+2+=.答案:7.(2018·金华名校联考)已知函数f(x)=若直线y=m与函数y=f(x)的图象交于四点,且四点的横坐标从左至右分别是x1,x2,x3,x4,则z=(x1-1)(x2-1)(x3-1)(x4-1)的取值范围是________.解析:作出直线y=m和函数f(x)的图象如图所示,由题意知x1<1,x2<1,且|log2(1-x1)|=|log2(1-x2)|,即log2(1-x1)=-log2(1-x2),得0=log2(1-x1)+log2(1-x2)=log2(1-x1)(1-x2),∴(x1-1)(x2-1)=1.易知x3,x4>1,结合f(x)=-(x-3)2+5(1≤x≤5)的图象关于直线x=3对称,得=3,x3∈[1,3),则(x3-1)(x4-1)=(x3-1)(6-x3-1)=-x+6x3-5=-(x3-3)2+4∈[0,4),故z=(x1-1)(x2-1)(x3-1)(x4-1)∈[0,4).答案:[0,4)8.(2018·宁波模拟)已知函数f(x)=x的图象与函数y=g(x)的图象关于直线y=x对称,令h(x)=g(1-|x|),则关于h(x)有下列命题:①h(x)的图象关于原点对称;②h(x)为偶函数;③h(x)的最小值为0;④h(x)在(0,1)上为减函数.其中正确命题的序号为________.(将你认为正确的命题的序号都填上)解析:g(x)=log x,∴h(x)=log(1-|x|),∴h(x)=得函数h(x)的大致图象如图所示,故正确命题序号为②③.答案:②③9.已知函数f(x)=(1)在如图所示给定的直角坐标系内画出f(x)的图象;(2)写出f(x)的单调递增区间;(3)由图象指出当x取什么值时f(x)有最值.解:(1)函数f(x)的图象如图所示.(2)由图象可知,函数f(x)的单调递增区间为[-1,0],[2,5].(3)由图象知当x=2时,f(x)min=f(2)=-1,当x=0时,f(x)max=f(0)=3.10.已知函数f(x)=2x,x∈R.(1)当m取何值时方程|f(x)-2|=m有一个解?两个解?(2)若不等式f2(x)+f(x)-m>0在R上恒成立,求m的取值范围.解:(1)令F(x)=|f(x)-2|=|2x-2|,G(x)=m,画出F(x)的图象如图所示.由图象看出,当m=0或m≥2时,函数F(x)与G(x)的图象只有一个交点,原方程有一个解;当0<m<2时,函数F(x)与G(x)的图象有两个交点,原方程有两个解.(2)令f(x)=t(t>0),H(t)=t2+t,因为H(t)=2-在区间(0,+∞)上是增函数,所以H(t)>H(0)=0.因此要使t2+t>m在区间(0,+∞)上恒成立,应有m≤0,即所求m的取值范围为(-∞,0].*三上台阶,自主选做志在冲刺名校1.(2017·台州期中)偶函数f(x)、奇函数g(x)的图象分别如图①②所示,若方程:f(f(x))=0,f(g(x))=0,g(g(x))=2,g(f(x))=2的实数根的个数分别为a,b,c,d,则a+b+c+d =( )A.16 B.18C.20 D.22解析:选D 逐个考察下列方程.(1)f(f(x))=0,根的个数分析如下:令f(x)=0解得x=0,-,,再分别令f(x)=0,-,,解的个数分别为3,0,0,共3个,所以a=3;(2)f(g(x))=0,根的个数分析如下:令f(x)=0解得x=0,-,,再分别令g(x)=0,-,,解的个数分别为3,3,3,共9个,所以b=9;(3)g(g(x))=2,根的个数分析如下:令g(x)=2解得x=1,-,,再分别令g(x)=1,-,解的个数分别为3,3,共6个,所以c=6;(4)g(f(x))=2,根的个数分析如下:令g(x)=2解得x=1,-,再分别令f(x)=1,-,解的个数分别为2,2,共4个,所以d=4;∴a+b+c+d=3+9+6+4=22.2.已知函数f(x)的图象与函数h(x)=x++2的图象关于点A(0,1)对称.(1)求f(x)的解析式;(2)若g(x)=f(x)+,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.解:(1)设f(x)图象上任一点P(x,y),则点P关于(0,1)点的对称点P′(-x,2-y)在h(x)的图象上,即2-y=-x-+2,∴y=f(x)=x+(x≠0).(2)g(x)=f(x)+=x+,g′(x)=1-.∵g(x)在(0,2]上为减函数,∴1-≤0在(0,2]上恒成立,即a+1≥x2在(0,2]上恒成立,∴a+1≥4,即a≥3,故实数a的取值范围是[3,+∞).。
三维函数的作图[大全]
![三维函数的作图[大全]](https://img.taocdn.com/s3/m/02c6be4676232f60ddccda38376baf1ffc4fe397.png)
实验七 三维函数的作图一、实验目的及意义熟练掌握Plot3D ,ListPlot3D ,ParametricPlot3D 等各种绘制三维图形的函数,了解其众多的可选参数,注意与二维绘图的异同。
了解使用外部函数绘制三维图形。
从中感受到Mathematica 绘制图形的强大功能及图形的美妙之处二、实验内容1、掌握二元函数的作图方法,注意各种参数的正确选用;2、掌握三维参数曲线及曲面的作图;3、使用外部函数绘制三维图形;(1)改进的三维参数式绘图函数;(2)柱面参数式;(3)球面参数式;(4)曲线生成的旋转曲面;4、简单图形动画的演示;5、了解一下声音的制作与播放。
三、本次实验中可能用到的函数或命令<<Graphics`ParametricPlot3D`,<<Graphics`SurfaceOfRevolution`,<<Graphics`Graphics3D`,Export ,Import ,Plot3D ,ListPlot3D ,ParametricPlot , ,CylindricalPlot3D ,SphericalPlot3D ,SurfaceOfRevolution ,Animation ,ShowAnimation ,Play ,ListPlay ,Contour ,Shadow四、实验步骤a) 进入Mathematica 的运行环境;b) 各种简单三维图形的绘制;c) 三维参数图形的绘制;d) 三维外部函数的使用;e) 如实记录相关内容,如果结果过多,可以有针对性的记录一些;f) 关闭Mathematica,关机,把键盘及桌椅归理清楚;g) 根据记录结果书写实验报告,并浅谈本次实验的心得体会。
说明:由于本次内容过多,命令长而不好记,容易出错,大家在输入时一定要小心,最好使用Ctrl+K 来帮助输入。
希望同学们一定要结合教材上相关内容来做本次的演示实验。
最新最常见的18个三维图形练习

练习NO.14
参考文献与网址:练习NO.15
标题:大学生究竟难在哪?—创业要迈五道坎2004年3月23日练习NO.16
(一)上海的经济环境对饰品消费的影响
2、价格“适中化”
(一)上海的经济环境对饰品消费的影响练习NO.17
2.www。cer。net/artide/2003082213089728。shtml。
创业首先要有“风险意识”,要能承受住风险和失败。还要有责任感,要对公司、员工、投资者负责。务实精神也必不可少,必须踏实做事;
练习NO.18
最常见的
练习NO.01
练习NO.02
练习NO.03
练习NO.04
练习NO.05
练习NO.06
练习NO.07
练习NO.08练习NO.9源自练习NO.10练习NO.11
自制性手工艺品。自制饰品其实很简单,工艺一点也不复杂。近两年来,由于手机的普及,自制的手机挂坠特别受欢迎。练习NO.12
(二)对“碧芝”自制饰品店的分析练习NO.13
CAD三维练习图
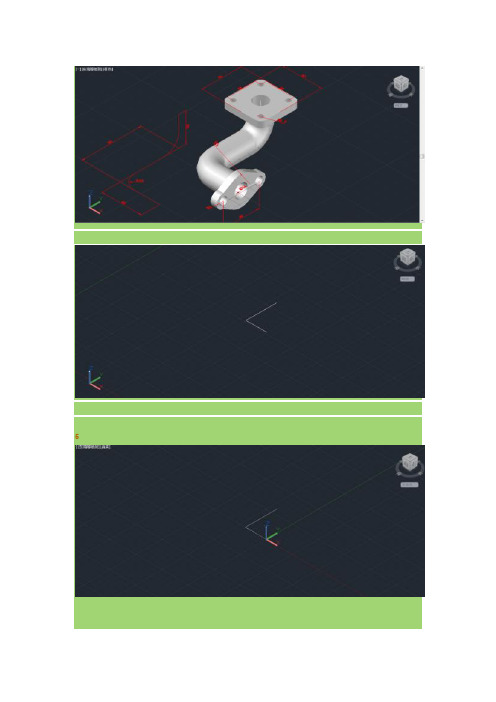
56,画完多段线,再把坐标沿Y轴旋转90度,在多段线端点上绘制一个半径为15的园。
7,画一条辅助线,端点是r15园的原点,沿Y轴长为18,在这条线端点处绘制出一个R4和R7的园。
8,利用对象捕捉的捕捉切点命令绘制出R15和R7的相切线,再用镜像命令沿两个圆的圆心把线段复制另一侧。
9,重复镜像命令把R7,R4和两条切线沿X轴复制到另一侧!10,用修剪把不需要的线全部剪掉(如果在三维图修剪不了的话,就按命令旋转P投影命令,确定再选择V视图确定,就可以修剪了)。
修剪完,用面域,创建面域!11.再着色!下一步在坐标处绘制R7的圆(此圆为轴孔部分)外轴部分没有给出尺寸,那我们就把R7的圆使用偏移命令向往偏移3就绘制出另一个圆了!12,下一步使用差集命令,用外面的大面减去中间两个小圆形成两个孔!1413,下一步用拉伸命令选择面拉伸,选择方向D,沿Z轴拉伸-6个单位,重复拉伸命令,选择中间R7和R10的圆进行拉伸,选择路径P,点击多段线就形成以上图像,14,使用刚才用的差集命令,做出中间轴孔!收起回复•这步具体是怎样?我弄了好久都弄吧出来中建的孔2012-8-10 07:51回复•2012-8-10 11:43回复•2012-8-10 14:33回复••••很嗨很耐看15.把图转为二维之后,把图旋转到此位置,利用实体编辑里拉伸面命令(此命令为拉伸面命令,不是之前的拉伸命令)选择路径P沿多段线进行拉伸!16拉伸完毕,把轴沿y轴旋转90度,用矩形命令画长宽均为40的矩形,倒R5的角,进行拉伸,高度6。
17,在长方体沿两边中点画一条辅助线,用移动命令选择长方体的中点,把长方体移动到圆轴圆心。
18,在长方体中点绘制R7的园,拉伸使其与轴孔重合,使用差集去除不要的部分!19,四个小孔圆心距离为28,利用尺寸画出第一个圆,20,对第一个圆进行拉伸,高度为6,使用移动命令把圆柱下移到长方体表面,21,使用镜像命令,把第一个圆柱沿长方体Y轴俩个中点进行复制,22.重复镜像命令,把两个圆柱沿长方体X轴两个中点进行复制!23,最后使用差集用大面减去四个小圆,形成四个孔,最后着色完成!我这个方法比较麻烦,我刚学会,希望能和大家分享!!!希望大家不要见笑!快累死我了收起回复•121109173:2012-6-29 15:53回复•2013-1-16 11:12回复•••热血赤峰小枪回复••收起回复•很抱歉的告诉你,我公司用04的07的都画出来了!我看视频学习是09的!我2012-6-29 20:58回复•2012-7-2 10:13回复•很嗨很耐看:回复@hehao1320:是不是那两条多段线?如果是的话,这两条线不用合并!t2012-7-2 22:11回复•2012-7-3 08:24回复•••Mr_zhang87回复••cht0221回复••张塞亚SRX2收起回复•谢谢••LOVE820065221回复••阿伊西代鲁回复••收起回复•很嗨很耐看:说句实在话,用快捷命令我不怎么会!我一般用快捷命令栏,打开对象捕捉命令栏选择捕捉原点,再选择圆柱就能找到中心点了!2012-7-2 22:09回复•2012-7-2 22:14回复•••很麻甩的麻甩佬回复•回复••收起回复•为什么我第14步拉深轴孔做不出来,请赐教2012-7-3 13:38回复•2012-7-3 22:54回复•2012-7-4 09:46回复•很嗨很耐看:回复@431179555:就是另一端有么?有的话就是这一端你没有选择大的区域哦X••431179555回复@很嗨很耐看:我画到这里就成这样了郁闷啊怎么差集都不行啊收起回复•并集再差集2012-7-6 22:36回复•2012-7-6 22:41回复•回复••回复••学习画一下回复••回复•回复••收起回复•对呀,笛卡尔坐标系2分钟全搞定••收起回复•在图层哪里改变线条颜色至你需要的颜色,在转至体着色就搞定了•汉服同袍•胜利之鹫收起回复•老师~~你挖坟~••二介平民求高手给解决瑕疵问题。
[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]
![[Matlab绘图][三维图形][三维曲线基本函数+三维曲面+其他三维图形]](https://img.taocdn.com/s3/m/3e3fb127657d27284b73f242336c1eb91a373395.png)
[Matlab绘图][三维图形][三维曲线基本函数+三维曲⾯+其他三维图形]1.绘制三维图形的基本函数最基本的三维绘图函数为plot3;plot3与plot⽤法⼗分相似,调⽤格式:plot(x1,y1,z1,选项1,x2,y2,z2,选项2,...,xn,yn,zn,选项n)当x,y,z是同维向量时,则x,y,z,对应元素构成⼀条三维曲线;当x,y,z是同维矩阵时,则以x,y,z对应列元素绘制三维曲线,曲线条数等于矩阵列数。
例:程序如下:t=0:pi/50:2*pi;x=8*cos(t);y=4*sqrt(2)*sin(t);z=-4*sqrt(2)*sin(t);plot3(x,y,z,'p');title('Line in 3-D Space');text(0,0,0,'origin');xlabel('x'),ylabel('y'),zlabel('z');grid; 运⾏结果:2.三维曲⾯2.1平⾯⽹格坐标矩阵的⽣成 绘制z=f(x,y)所代表的三维曲⾯图,先要在xy平⾯选定⼀个矩形区域,假定矩形区域D=[a,b]*[c,d],然后将[a,b]在x⽅向分成m份,将[c,d]在y⽅向分成n份,由各划分点分别作平⾏于两坐标轴的直线,将区域D分成m*n个⼩矩形,⽣成代表每⼀个⼩矩形顶点坐标的平⾯⽹格坐标矩阵,最后利⽤有关函数绘图。
产⽣平⾯区域内的⽹格坐标矩阵有两种⽅法: 1.利⽤矩阵运算⽣成、x=a:dx:b;y=(c:dy:d)';X=ones(size(y))*x;Y=y*ones(size(x));语句执⾏后,矩阵X的每⼀⾏都是向量x,⾏数等于向量y的元素个数,矩阵Y的每⼀列都是向量y,列数等于向量x的元素个数。
于是对于矩阵X,Y来说,它们位置(i,j)上的元素值(X(i,j),Y(i,j))就是所要形成的平⾯⽹格在位置(i,j)上的X,Y坐标。
初中八年级数学上册专项总结训练(三维立体学习法)-八秋07-函数的概念、正比例函数-教师版.doc

初中数学备课组 教师 班级 初二 学生 日期上课时间教学内容:函数的概念 正比例函数函数的概念 一、知识点 1. 变量与常量在问题研究过程中,可以取不同数值的量叫做变量,保持数值不变的量叫做常量. 2. 函数的定义在某个变化过程中有两个变量x 和y ,如果在x 的允许取值范围内,变量y 随着x 的变化而变化,它们存在确定的依赖关系,那么变量y 叫做变量x 的函数,x 叫做自变量。
3. 函数的定义域与函数值函数的自变量允许取值的范围叫做这个函数的定义域. 如果y 是x 的函数,那么对于x 在定义域内取定的一个值a ,变量y 的对应值叫做当x a =时的函数值.符号“()y f x =”表示y 是x 的函数,f 表示y 随x 变化而变化的规律. 二、例题讲解例1 物体所受的重力与它的质量之间有如下的关系:G mg =,其中,m 表示质量,G 表示重力,9.8g =牛/千克,物体所受的重力G 是不是它的质量m 的函数?解:物体所受的重力G 随它的质量m 的变化而变化,由G mg =可知,这两个变量之间存在确定的依赖关系,所以物体所受的重力G 是它的质量m 的函数.例2 汽车的速度为50千米/时,写出汽车匀速运动时行驶的路程y (千米)关于时间x (时)的函数解析式及定义域.分析: 本题依据公式“路程=时间X速度”列出数量关系,因为时间为非负数,所以定义域为0x ≥. 解:函数解析式为50y x =,定义域为0x ≥. 例3 求下列函数的定义域:(1)23y x =+; (2)11y x =-; (3)21y x =+. 解:(1)对于整式23x +,无论x 取什么实数,它都有意义,所以函数23y x =+的定义域是一切实数;(2)对于分式11x -,当1x =时,它没有意义.所以函数11y x =-的定义域是1x ≠; (3)对于二次根式21x +,当12x ≥-时,它有意义,所以函数21y x =+的定义 域是12x ≥-.说明:求函数的定义域应该根据解析式的特征进行思考. 例4 已知()321xf x x =-+,求12f ⎛⎫- ⎪⎝⎭的值. 分析:函数与函数值是不同的概念.函数是指两个变量之间的某种关系,而函数值指的是当自变量取某一数值时,函数的一个对应值.求12f ⎛⎫- ⎪⎝⎭的值,就是当12x =-时,求321xy x =-+的值,只需要把12x =-代入后计算即可. 解:131322.241212f ⎛⎫⨯- ⎪⎛⎫⎝⎭-==- ⎪⎝⎭⎛⎫-⨯-+ ⎪⎝⎭例5 等腰三角形的周长等于20cm ,请写出这个等腰三角形的底边长()x cm 和腰长()y cm 之间的解析式. 分析 根据周长的定义,得220x y +=,整理得20220,2xy x y -=-=, 即 1102y x =-+.函数解析式就是一个等式,求函数解析式时,有时可以利用一些现成的等式或公式,比如周长公式、面积公式等等.答案:1102y x =-+ 说明:1. 变量2x +是不是变量x 的函数?解: 对于代数式2x +,给定x 的一个值,可以求出这个代数式的一个值.所以2x +与x 有着确定的依赖关系,可以把变量2x +看做y .由函数的概念:在某个变化过程中有两个变量x 和y ,如果在x 的允许取值范围内,变量y 随着x 的变化而变化,它们之间存在确定的依赖关系,那么变量y 叫做变量x 的2. 对于“()f x ”中的“f ”怎样理解?答:记号“()f x ”表示“y 是x 的函数”,这个记号比较抽象,“f ”并不是表示一个变量,()f x 也不是表示“f ”与“x ”的积,而是指明在变化过程中的自变量为x ,用f 表示变量y 随着x 的变化而变化的规律;在同时研究几个函数时,应选用不同字母表示不同函数变量间相互依赖的变化规律,如()()g x h x 、等,以免引起混乱.三、 巩固练习1. 说出下列变化过程中,哪些量是常量,哪些量是变量,变量之间是函数关系吗? (1)正方形的周长C 与它的边长a ;(2)银行一年定期存款的本金x 元与利息y 元; (3)等腰三角形顶角的度数x 与底角的度数y ; (4)长方形的宽一定时,其长与面积; (5)等腰三角形的底边长与面积;(6)关系式y x=中的y 与x .答案:(1)变量是周长C 与边长a ,是函数关系;(2)变量是本金x 元与利息y 元,是函数关系; (3)变量是顶角的度数x 与底角的度数y ,是函数关系;(4)变量是长方形的宽与面积,是函数关系; (5)变量是等腰三角形的底边长与面积,不是函数关系;(6)变量是y 与x ,不是函数关系. 2. 写出下列个函数的定义域;(1)2y x =-; (2)1y x =+;答案: 一切实数 答案:1x ≥- (3)234y x x =+-; (4)11y x =-;答案:一切实数 答案:1x ≠(5)1y x x =+; (6)2x y x =- 答案:0x ≠ 答案:0x ≥≠且x 23. 在ABC V 中,它的底边长是a ,底边上的高是h ,则三角形面积12S ah=,当a 为定长时,在此式子中( A ).A. S 、h 是变量,a 是常量B. ,,S h a 是变量,12是常量 C. ,a h 是变量,1,2S 是常量 D. S 是变量,1,,2a h是常量 4. 下列函数中,自变量的取值范围是113x <<的是( D ).A. 131x y x -=- B. 311x y x -=- C.131x y x -=- D. 11131y x x =+-- 5. 如果()9f x x x =-+,那么()3f =___3-____.6. 已知()234x f x x +=+,则()0f =___34____,()2f=____52814+_____. 7. 若12y x y -=+,则y 用x 的代数式表示为y =___211x x+-___.8. 设某种电报收费标准是每个字0.1元,写出电报费y (元)与字数x (个)之间的函数关系式,并求自变量x 的取值范围.答案:()0.10y x x x =≥且是整数 提高题1. 若函数2221x x y x --=-,则与函数值0y =对应的x 的值是( D ). A. 1x =-或2x = B. 1x =或2x =- C. 1x =-且2x = D. 2x = 2. 把一块边长为20厘米的正方形铁皮,四角各截去边长为x 厘米的小正方形后折成一个无盖盒子,则盒子的容积V (立方厘米)关于自变量x (厘米)的函数解析式为__()2202V x x =-__,定义域为_010x <<_. 3. 洗衣机在洗衣的过程中经历了进水、清洗、排水等过程.下图能反映洗衣机工作时的水量y (升)与时间x (分)之间关系的图像大致是( C )A. B. c. D..正比例函数 一、知识点1. 正比例函数的概念如果两个变量的每一组对应值的比值是一个非零常数,那么称两个变量成正比例.用数学符号语言记为yk x =或()0y kx k =≠.解析式形如()0y kx k =≠的函数叫做正比例函数,其中,常数k 叫做比例系数,正比例函数y kx =的定义域是一切实数.2. 正比例函数的图像和基本性质 函数名称 解 析 式图 像性质正比例函数()0y kx k =≠1.图像为过原点和点()1,k 的一条直线.2. 当0k >时,直线过第一、三象限.3. 当0k <时,直线过第二、四象限.1. 当0k >时,y 的值随着x 的增大而增大.2. 当0k <时,y 的值随着x 的增大而减小.yXy XyXyX二、例题 例1 若函数()31m y m x -=-是正比例函数,则m =_________,函数的图像经过_________象限.分析 由正比例函数的解析式可知,31m -=,所以4m =.把4m =代入函数解析式,得3y x =,再由正比例函数的性质,得到它的图像经过第一、三象限. 解:4m =,图像经过第一、三象限. 例2 若y 与21x +成正比例,且函数图像经过点()3,1A -,求y 与x 的函数解析式. 分析 由y 与21x +成正比例,可以设()()210y k x k =+≠.再把点A 的坐标()3,1-代入函数解析式,即可求出k 的值,这种求函数解析式的方法叫做待定系数法.解: Q y 与21x +成正比例,∴ 设()()210y k x k =+≠.把点A()3,1-代入,得15k =-,()1215y x ∴=-+例3 已知点()11,x y 和()22,x y 在正比例函数()2y k x =-的图像上,当12x x >时,12y y <,那么k 的取值范围是多少? 分析 由条件当12x x >时,12y y <,联系正比例函数的图像和性质,可知函数值y 随着x 的值增大而减小,即比例系数小于零.解 :由题意,函数值y 的值随着x 的值增大而减小,0,2k k ∴<<例4 直角三角形的一条直角边是6,写出它的面积y 关于另一条直角边x 的函数关系式并画出这个函数的图像.解:由直角三角形的面积公式,得162x y⨯=.()30y x x ∴=>说明:由于直角三角形的边长为正数,在画函数图像时要特别注意自变量x 的取值范围,因为定义域为0x >,此时函数图像为一条射线,并且要除去端点.1. 如何理解正比例函数的性质:当0k >时,y 随着x 的值增大而逐渐增大,当0k <时,y 随着x 的值增大而逐渐减小?4212yX答:从解析式来看,当0k >时,若12x x <,由不等式的性质有12kx kx <,即12y y <;当0k <时,若12x x <由不等式的性质有12kx kx >,即12y y >;也可以结合正比例函数的图像去理解:当0k >时,从左往右看,直线上的点的横坐标从小到大逐渐变化,点的位置随着从低到高逐渐变化,说明此时函数值y 相应地从小到大逐渐变化.当0k <时类似.2. 学习函数的性质要掌握的一个重要数学思想是“数形结合”,学会利用函数的图像直观的研究函数的性质.三、 巩固练习 1. 填空:(1)如果正比例函数的图像过点(1,-2),那么它的解析式是_2y x =-__;函数的图像经过第__二、四__象限.(2)正比例函数2y x =-的图像上一点横坐标为2,纵坐标是__-4___, 函数值随x 的值增大而__减小___. (3)由图写直线PO 的解析式:___34y x =___. (4)某函数具有下列两条性质:① 它的图像是经过 原点(0,0)的一条直线;② y 的值随x 的值增大而增大.请你举出一个满足上述条件的函数:____2y x =_(答案不唯一)___. 2. 选择:(1)下列函数中,正比例函数的是( B )A.3y x =B. 32y x =-C. 213x y += D. 2y x =(2)下列各点中,在直线2y x =上的点有( A ).A.2,12⎛⎫- ⎪ ⎪⎝⎭ B. ()2,2- C. ()5,10D. ()2,1-(3)函数y kx =的图像经过点(1,4),那么()2y k x=-的图像经过第( B )象限.A. 一、三B. 二、四C. 一、二D. 三、四 3. 已知y 是x 的正比例函数,当2x =时,12y =(1)求y 与x 的函数解析式;P-3/2-20yX(2)求当3x =时,y 的值;(3)在直角坐标系内画出该函数的图像. 答案:(1)14y x =;(2)34y =;(3)略 4. 正比例函数2112y k x k ⎛⎫=++- ⎪⎝⎭的图像经过第二、四象限,求函数的解析式.答案:12y x =-5. 已知3y -与x 成正比例函数,且它的图像经过点(2,7) (1)求y 与x 的函数解析式; (2)求当4x =时,y 的值; (3)求当3y =-时,x 的值.答案:(1)23y x =+; (2)11; (3)-3 6. 如果28my mx -=是正比例函数,而且对于它的每一组非零的对应值(),x y ,有0xy <.求m 的值.答案:-37. 小明早上骑自行车离开家去学校,下图反映了小明离开家的距离y (米)与时间x (分)之间的关系.根据图像回答:(1) 小明家与学校的距离是___3000__米;(2) 小明骑自行车的平均速度是___200___米/分; (3) 写出小明汽车途中,离开家的距离y (米)与时间x (分)的函数关系式及定义域:___()200015y x x =≤≤___.提高题1. 正比例函数y kx =的图像上有一点A ,过点A 向x 轴作垂线,垂足为点B ,点B 的坐标为(2,0).若三角形OAB 的面积为6,试求k 的值. 答案:3或-32. 已知正比例函数的自变量x 减小2时,对应的函数值增加4.求该正比例函数的解析式. 答案:2y x =-y (米)x(分)1510530003. 已知点()()122,,1,A y B y -是正比例函数y kx =的图像上的两个点.若12y y >,试判断k 的取值范围. 答案:0k <家庭作业一、 填空题: 1. 若()21m y m x=+是正比例函数,则m =___1___.2. 已知函数()33g x x=-,则()2g =___3___. 3. 在直角坐标系中,若点(),4M x -和点()3,N y 关于x 轴对称,则x y +=_7__.4. 如果正比例函数3xy =的图像过点()6,k ,那么k =___2___. 5. 已知矩形的周长为12,若矩形一边长为x ,面积为y ,则y 与x 的函数关系式及定义域是__()2606y x x x =-+<<___.6. 若等腰三角形顶角的度数为y ,底角的度数为x ,则y 与x 的函数关系式及定义域是__()1802090y x x =-<<___.7. 若等腰三角形的周长是20cm ,腰长与底边长分别是ycm 和xcm ,那么y 与x 的函数关系式为__102xy =-__,定义域为__010x <<__. 8. 若()25y a x b =+-+是正比例函数,且其图像恰为第二、四象限的角平分线,则a b +=__2__. 9. 若等腰梯形的周长为20cm ,上底长ycm ,底角为30,腰长xcm ,则y 与x 的函数关系式为__23102y x +=-__. 10. 若y 与x 成正比例,且当4x =时,3y =-则当32x =时,y =__62-___. 二、选择题11. 若()2,P x y 是1P 关于y 轴的对称点,而点1P 在第三象限内,则( A ) A. 0,0x y >> B. 0,0x y >< C. 0,0x y << D. 0,0x y <> 12. 若点()111,P x y 与()222,P x y 在同一个正比例函数的图像上,则( D )A. 1212x x y y +=+;B. 1212x x y y -=-;C.1212y y x x =; D. 1221x y x y =. 13. 平面直角坐标系中有点()4,3A -,那么点A 到x 轴的距离是( A )A. 3 ;B. -3 ;C. 4 ;D. -4. 14. 点()11,A x y 与()11,B y y 之间的距离是( A )A. 11x y -;B. 112x y - ;C. 2211x y +;D. 22112x y +; 15. 下列问题中,两个变量成正比例的是( D ) A. 三角形的面积一定,它的底边与底边上的高; B. 等边三角形的面积与它的高;C. 长方形的一边长确定,它的周长与另一边长;D. 商品的价格确定时,销售额与销售量;E. 点到横坐标的距离确定时,它的纵坐标与横坐标;F. 商品的价格确定时,利润与成本. 三、 简答题16. 求下列函数的定义域:(1)322612y x x x =--+; (2)27y x =-;答案:一切实数 答案:72x ≥(3)126x y x +=-; (3)2143x y x+=-. 答案:126x x ≥-≠且 答案:143x <17. 已知()225f x x =-+,求()()5+13f f a f a ⎛⎫- ⎪⎝⎭、、.答案:5539f ⎛⎫-=-⎪⎝⎭;()225f a a =-+;2243a a --+ 18. 已知正比例函数23y x =-. (1) 当x 取何值时,3y >-; (2) 当x 取何值时,3y =-; (3) 当x 取何值时,3y <-; (4) 画出图像,并结合图像说明理由. 答案:(1)()()999;2;3(4)222x x x <=>略四、综合题已知函数()0y kx k =≠的图像与函数34y x =的图像关于y 轴对称,依照要求画图,并完成以下各 (1) 在函数34y x =的图像上取一点A (横坐标为4),点A 的坐标是__()4,3__;设点A 关于y 轴对称的点为A ’,那么A ’的坐标是__()4,3-__;(2) 过原点和点A ’画直线OA ’,它与直线34y x =关于y 轴对称吗?___对称____; (3) 如果在函数34y x =的图像上选取另一点B ,点B 关于y 轴对称的点B ’在直线OA ’上吗? ________在_______;(4) 已知函数()0y kx k =≠的图像与函数34y x =的图像关于y 轴对称,那么k 的值是多少? _____34y x =-____.y=3x/442-224y (米)x(分)-2-40。
2018-2019学年高中新三维一轮复习理数江苏专版课件:

- 1≤ x≤ 1, 解得 1 x≠ 2且 x≠ - , 2
1 即- 1≤ x≤ 1 且 x≠- , 2
1 1 所以所求函数的定义域为- 1,- ∪- , 1. 2 2
1 1 答案:-1,- ∪- ,1 2 2
f x+1 3.若函数 y=f(x)的定义域是[1,2 019],则函数 g(x)= 的 x-1 定义域是 ________.
解得 0≤ x<1
或 1<x≤ 2 018.故函数 g(x)的定义域为[0,1)∪(1, 2 018].
答案:[0,1)∪(1,2 018]
4.(2018· 南京师范大学附中模拟)函数 f(x)= 定义域是 ________.
log 1 2x- 3的
2
Hale Waihona Puke 3 解析:由题意得 log 1 (2x- 3)≥ 0⇒0<2x-3≤ 1⇒ <x≤ 2,即 2
2
函数
3 f(x)的定义域是 , 2. 2
3 答案: ,2 2
[小题体验]
1.(2018· 常州期末 )函数 y= 1- x+ lg(x+ 2)的定义域为 ________.
1- x≥ 0, 解析:由题意可得 x+ 2> 0,
解得-2<x≤1,故所求函数
的定义域为(-2,1].
答案:(-2,1]
2.已知 f( x)=x-1,则 f(2)=________.
1 3 + 5f = +1,则函数 x x
f(x)的解析式为________.
1 3 1 解析: 用 代替 3f(x)+ 5f = + 1 中的 x, x x x
得
1 3f + 5f(x)= 3x+ 1, x
《三维设计》高考数学(苏教,理科)大一轮配套课时跟踪检测20 函数y=Asin(ωx+φ)的图像及三角函数模型

课时跟踪检测(二十) 函数y =A sin(ωx +φ)的图像及三角函数模型的简单应用 第Ⅰ组:全员必做题1.函数y =A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)在闭区间[-π,0]上的图像如图所示,则ω=____________.2.将函数y =2sin π3x 的图像上每一点向右平移1个单位长度,再将所得图像上每一点的横坐标扩大为原来的π3倍(纵坐标保持不变),得函数y =f (x )的图像,则f (x )的解析式为____________.3.已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,0≤φ<2π)在R 上的部分图像如图所示,则f (2 013)=________.4.(2014·苏北四市调研)已知函数f (x )=sin ωx +π3(ω>0),若f π6=f π2,且f (x )在区间π6,π2上有最大值,无最小值,则ω=________.5.(2013·镇江12月统考)在矩形ABCD 中,AB ⊥x 轴,且矩形ABCD 恰好能完全覆盖函数y =a sin ax (a ∈R ,a ≠0)的一个完整周期图像,则当a 变化时,矩形ABCD 周长的最小值为________.6.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y =a +A cos ⎣⎡⎦⎤π6(x -6)(x =1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为________℃.7.已知函数f (x )=2sin ⎝⎛⎭⎫2x -π4+1. (1)求它的振幅、最小正周期、初相; (2)画出函数y =f (x )在⎣⎡⎦⎤-π2,π2上的图像.8.已知函数f (x )=23sin ⎝⎛⎭⎫x 2+π4cos ⎝⎛⎭⎫x 2+π4-sin(x +π). (1)求f (x )的最小正周期;(2)若将f (x )的图像向右平移π6个单位,得到函数g (x )的图像,求函数g (x )在区间[0,π]上的最大值和最小值.第Ⅱ组:重点选做题1.(2013·盐城三调)将函数y =sin(2x +φ)(0≤φ<π)的图像向左平移π6个单位长度后,所得的函数恰好是偶函数,则φ的值为________.2.为迎接夏季旅游旺季的到来,少林寺单独设置了一个专门安排游客住宿的客栈,寺庙的工作人员发现为游客准备的一些食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:①每年相同的月份,入住客栈的游客人数基本相同;②入住客栈的游客人数在2月份最少,在8月份最多,相差约400人; ③2月份入住客栈的游客约为100人,随后逐月递增直到8月份达到最多. (1)试用一个正弦型三角函数描述一年中入住客栈的游客人数与月份之间的关系; (2)请问哪几个月份要准备400份以上的食物?答 案第Ⅰ组:全员必做题1.解析:因为T =2π3,所以ω=2πT =3.答案:32.解析:函数y =2sin π3x 向右平移1个单位长度得y =2sin π3(x -1)=2sin ⎝⎛⎭⎫π3x -π3,将所得图像上每一点的横坐标扩大为原来的π3倍(纵坐标保持不变),则y =2sin ⎝⎛⎭⎫π3·3πx -π3, 即y =2sin ⎝⎛⎭⎫x -π3. 答案:y =2sin ⎝⎛⎭⎫x -π3 3.解析:由图知A =5,T =12,从而ω=π6,φ=π6,则f (x )=5sin ⎝⎛⎭⎫π6x +π6, 故f (2 013)=f (9)=-532.答案:-5324.解析:由题意f ⎝⎛⎭⎫π3=1,即ω·π3+π3=π2+2k π,k ∈Z ,所以ω=12+6k ,k ∈Z. 又π3<2πω,所以0<ω<6,故ω=12. 答案:125.解析:根据题意,设矩形ABCD 的周长为c ,则c =2(AB +AD )=4|a |+4π|a |≥8π,当且仅当a =±π时取等号.答案:8π6.解析:依题意知,a =28+182=23,A =28-182=5,∴y =23+5cos ⎣⎡⎦⎤π6(x -6), 当x =10时,y =23+5cos ⎝⎛⎭⎫π6×4=20.5. 答案:20.57.解:(1)振幅为2,最小正周期T =π,初相为-π4.(2)图像如图所示.8.解:(1)因为f (x )=3sin ⎝⎛⎭⎫x +π2+sin x =3cos x +sin x =2⎝⎛ 32cos x +⎭⎫12sin x =2sin ⎝⎛⎭⎫x +π3, 所以f (x )的最小正周期为2π.(2)∵将f (x )的图像向右平移π6个单位,得到函数g (x )的图像,∴g (x )=f ⎝⎛⎭⎫x -π6 =2sin ⎣⎡⎦⎤⎝⎛⎭⎫x -π6+π3=2sin ⎝⎛⎭⎫x +π6. ∵x ∈[0,π],∴x +π6∈⎣⎡⎦⎤π6,7π6, ∴当x +π6=π2,即x =π3时,sin ⎝⎛⎭⎫x +π6=1,g (x )取得最大值2. 当x +π6=7π6,即x =π时,sin ⎝⎛⎭⎫x +π6=-12,g (x )取得最小值-1. 第Ⅱ组:重点选做题1.解析:函数y =sin(2x +φ)(0≤φ<π)的图像向左平移π6个单位后,得y =sin ⎝⎛⎭⎫2x +π3+φ, 则π3+φ=(2k +1)π2. 又0≤φ<π,所以φ的值为π6.答案:π62.解:(1)设该函数为f (x )=A sin(ωx +φ)+B (A >0,ω>0,0<|φ|<π),根据条件①,可知这个函数的周期是12;由②可知,f (2)最小,f (8)最大,且f (8)-f (2)=400,故该函数的振幅为200;由③可知,f (x )在[2,8]上单调递增,且f (2)=100,所以f (8)=500.根据上述分析可得,2πω=12,故ω=π6,且⎩⎪⎨⎪⎧ -A +B =100,A +B =500,解得⎩⎪⎨⎪⎧A =200,B =300.根据分析可知,当x =2时f (x )最小, 当x =8时f (x )最大, 故sin ⎝⎛⎭⎫2×π6+φ=-1, 且sin ⎝⎛⎭⎫8×π6+φ=1. 又因为0<|φ|<π,故φ=-5π6.所以入住客栈的游客人数与月份之间的关系式为f (x )=200sin ⎝⎛⎭⎫π6x -5π6+300. (2)由条件可知,200sin ⎝⎛⎭⎫π6x -5π6+300≥400,化简,得sin ⎝⎛⎭⎫π6x -5π6≥12⇒2k π+π6≤π6x -5π6≤2k π+5π6,k ∈Z , 解得12k +6≤x ≤12k +10,k ∈Z . 因为x ∈N *,且1≤x ≤12, 故x =6,7,8,9,10.即只有6,7,8,9,10五个月份要准备400份以上的食物.。
【三维设计】高中数学 教师用书 第1部分 第二章 2.4.1 函数的零点课件 新人教版B版必修1

(3)法一:当 x≥0 时, 令 f(x)=0,得 x+1=0, 解得 x=-1,与 x≥0 矛盾; 当 x<0 时,令 f(x)=0,得 x-1=0, 解得 x=1,与 x<0 矛盾. 所以函数 f(x)=xx+-11,,xx≥<00, 没有零点.
[思路点拨] 根据二次方程根的分布画出相应的函数图 象,数形结合建立关于a的不等式组.
[精解详析] 令 f(x)=ax2-2(a+1)x+a-1,依题意知,函 数 f(x)有两个零点,且一个零点大于 2,一个零点小于 2.
∴f(x)的大致图象如图所示:
(4 分)
则 a 应满足af>20<,0, 或af<2>0,0,
第 2. 2.4.
二4
1
章
函 数
函 数
与
的
函方
零
数程
点
理解教材新知 把握热点考向 应用创新演练
考点一 考点二 考点三
给定一元二次函数y=x2+2x-3,ቤተ መጻሕፍቲ ባይዱ图象如下:
问题1:方程x2+2x-3=0的根是什么? 提示:方程的根为-3,1.
问题2:函数的图象与x轴的交点是什么? 提示:交点为(-3,0),(1,0). 问题3:方程的根与交点的横坐标有什么关系? 提示:相等. 问题4:通过图象观察,在每一个交点附近,两侧函数 值符号有什么特点? 提示:在每一交点两侧函数值符号异号.
法二:∵f(0)=c,∴ac=af(0)<0,
∴af>00<,0,
或a<0, f0>0.
可知无论哪种情况,抛物线 y=ax2+bx+c 与 x 轴都有
函数三角数列立体几何562

高考数学练习 (562)函数三角数列立体几何1.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是 ( )A .36πB .12πC .33πD .433π2.对实数a 和b ,定义运算“⊗”:,1,,1.a ab a b b a b -≤⎧⊗=⎨->⎩设函数()()()222fx x x x =-⊗-,x ∈R.若函数()y f x c =-的图象与x 轴恰有两个公共点,则c 的取值范围是( )A .()3,21,2⎛⎫-∞-- ⎪⎝⎭B .(]3,21,4⎛⎫-∞---⎪⎝⎭C .111,,44⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭D .311,,44⎛⎫⎡⎫--+∞ ⎪⎪⎢⎝⎭⎣⎭3.若函数b 3bx 6x )x (f 3+-=在)1,0(内有极小值,则实数b 的取值范围是 ( )A .)1,0(B .)1,(-∞C .),0(∞+D .)21,0(4.已知函数2sin 2tan y x x =- ,则( ) A .函数最小值是-1,最大值是0 B .函数最小值是-4,无最大值 C .函数无最小值,最大值是0 D .函数最小值是-4,最大值是05.已知函数()f x 的定义域为[3,)-+∞, 且(6)(3)2f f =-=,'()f x 为()f x 的导函数,函数'()fx 的图象如右图所示.若正数a,b正视图俯视图侧视图满足(2)2f a b +<,则32b a +-的取值范围是( )A . 3(,3)2-B .9(,)(3,)2-∞-+∞ C .9(,3)2- D .3(,)(3,)2-∞-+∞6.在数列}{n a 中,若点),(n a n 在经过点(5,3)的定直线l 上,则数列}{n a 的前9项和S 9= .7.函数1,(10)()cos ,(0)2x x f x x x π+-≤<⎧⎪=⎨-≤≤⎪⎩的图象与坐标轴所围成的封闭图形的面积为8.已知函数()||.f x x a =-不等式()3f x ≤的解集为{|15}x x -≤≤ (1)求实数a 的值;(2)若c c x f x f 4)5()(2-≥++对一切实数x 恒成立,求实数c 的取值范围。
最常见的24个三维图形练习.docx
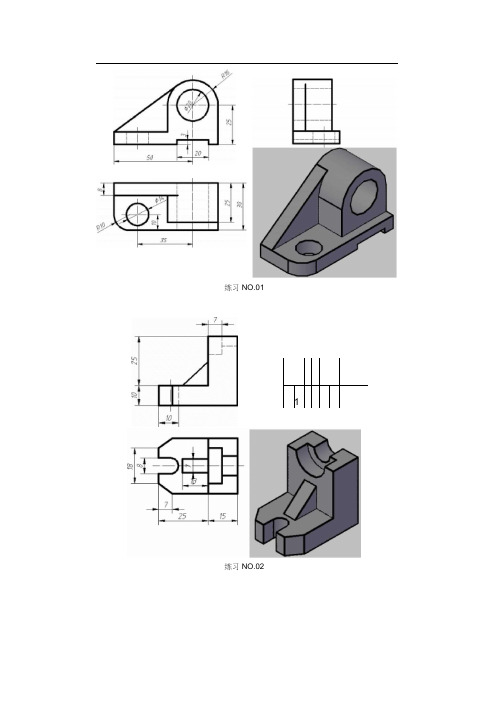
练习NO.01-1 练习NO.02? 2 ?最常见的24个三维图形练习效果及尺寸练习NO.04练习NO.03最常见的24个三维图形练习效果及尺寸? 342练习NO.06练习NO.05———I_ I—3020 16---------------------------- -----------------------------------------------------------i I? 4 ? 最常见的24个三维图形练习效果及尺寸练习NO.07、08练习NO.09最常见的24个三维图形练习效果及尺寸? 5 ?练习NO.10练习N0.11? 6 ? 最常见的24个三维图形练习效果及尺寸练习N0.12^^练习N0.13最常见的24个三维图形练习效果及尺寸? 7 ?R926--------- H练习N0.14练习N0.15? 8 ? 最常见的24个三维图形练习效果及尺寸485t20练习N0.16R3练习N0.17最常见的24个三维图形练习效果及尺寸? 9 ?练习N0.19? 10 ?最常见的24个三维图形练习效果及尺寸∈3O坊练习NO.20RlIII2枫5去除斛颛,⅛H练习N0.21最常见的24个三维图形练习效果及尺寸练习NO.22 J ⅛练习NO.23? 12 ? 最常见的24个三维图形练习效果及尺寸练习NO.24。
Matlab实训5-三维图形的绘制

例 在xy平面内选择区域[-8,8]×[-8,8],绘制4种三维曲面图。 程序如下:
[x,y]=meshgrid(-8:0.5:8); z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps); subplot(2,2,1); mesh(x,y,z); title('mesh(x,y,z)') subplot(2,2,2); meshc(x,y,z); title('meshc(x,y,z)') subplot(2,2,3); meshz(x,y,z) title('meshz(x,y,z)') subplot(2,2,4); surf(x,y,z); title('surf(x,y,z)')
例 画多条曲线观察函数Z=(X+Y).^2. 程序如下
x=-3:0.1:3;y=1:0.1:5; [X,Y]=meshgrid(x,y); Z=(X+Y).^2; plot3(X,Y,Z)
plot3(X1,Y1,Z1,选项),通过 选项 指定曲 线和点的属性,选项的取值与plot介绍的相 同。 plot3(...,'PropertyName',PropertyValue ,...),利用指定的属性绘制图形。 h = plot3(...),绘制图形并返回图形句柄, h 为一个列向量,每个元素对应图像中每个 对象的句柄。
图形修饰处理
1. 视点处理
MATLAB提供了设置视点的函数view,其调用格式为: view(az,el)
其中az为方位角,即表示视点在xOy平面投影点与y轴 负方向之间的夹角;el为仰角,即视点与xOy平面的夹 角,它们均以度为单位。系统缺省的视点定义为方位 角-37.5°,仰角30°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三维曲线
plot3函数与plot函数用法十分相似,其调用格式为:
plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n)
其中每一组x,y,z组成一组曲线的坐标参数,选项的定义和plot函数相同。
当x,y,z是同维向量时,则x,y,z 对应元素构成一条三维曲线。
当x,y,z是同维矩阵时,则以x,y,z对应列元素绘制三维曲线,曲线条数等于矩阵列数。
例绘制三维曲线。
程序如下:
t=0:pi/100:20*pi;
x=sin(t);
y=cos(t);
z=t.*sin(t).*cos(t);
plot3(x,y,z);
title('Line in 3-D Space');
xlabel('X');ylabel('Y');zlabel('Z');
三维曲面
1.产生三维数据
在MATLAB中,利用meshgrid函数产生平面区域内的网格坐标矩阵。
其格式为:
x=a:d1:b; y=c:d2:d;
[X,Y]=meshgrid(x,y);
语句执行后,矩阵X的每一行都是向量x,行数等于向量y的元素的个数,矩阵Y的每一列都是向量y,列数等于向量x的元素的个数。
2.绘制三维曲面的函数
surf函数和mesh函数的调用格式为:
mesh(x,y,z,c):画网格曲面,将数据点在空间中描出,并连成网格。
surf(x,y,z,c):画完整曲面,将数据点所表示曲面画出。
一般情况下,x,y,z是维数相同的矩阵。
x,y是网格坐标矩阵,z是网格点上的高度矩阵,c 用于指定在不同高度下的颜色范围。
例绘制三维曲面图z=sin(x+sin(y))-x/10。
程序如下:
[x,y]=meshgrid(0:0.25:4*pi); %在[0,4pi]×[0,4pi]区域生成网格坐标
z=sin(x+sin(y))-x/10;
mesh(x,y,z);
axis([0 4*pi 0 4*pi -2.5 1]);
此外,还有带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。
其用法与mesh类似,不同的是meshc还在xy平面上绘制曲面在z轴方向的等高线,meshz还在xy平面上绘制曲面的底座。
例在xy平面内选择区域[-8,8]×[-8,8],绘制4种三维曲面图。
程序如下:
[x,y]=meshgrid(-8:0.5:8);
z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps);
subplot(2,2,1);
mesh(x,y,z);
title('mesh(x,y,z)')
_hotinko1_新浪博客
色彩处理
1.颜色的向量表示
MATLAB除用字符表示颜色外,还可以用含有3个元素的向量表示颜色。
向量元素在[0,1]范围取值,3个元素分别表示红、绿、蓝3种颜色的相对亮度,称为RGB三元组。
2.色图
色图(Color map)是MATLAB系统引入的概念。
在MATLAB中,每个图形窗口只能有一个色图。
色图是m×3 的数值矩阵,它的每一行是RGB三元组。
色图矩阵可以人为地生成,也可以调用MATLAB提供的函数来定义色图矩阵。
3.三维表面图形的着色
三维表面图实际上就是在网格图的每一个网格片上涂上颜色。
surf函数用缺省的着色方式对网格片着色。
除此之外,还可以用shading命令来改变着色方式。
shading faceted命令将每个网格片用其高度对应的颜色进行着色,但网格线仍保留着,其shading flat命令将每个网格片用同一个颜色进行着色,且网格线也用相应的颜色,从而使得图形表面显得更加光滑。
shading interp命令在网格片内采用颜色插值处理,得出的表面图显得最光滑。
颜色是黑色。
这是系统的缺省着色方式
例3种图形着色方式的效果展示。
程序如下:
[x,y,z]=sphere(20);
colormap(copper);
subplot(1,3,1);
surf(x,y,z);
axis equal
subplot(1,3,2);
surf(x,y,z);shading flat;
axis equal
subplot(1,3,3);
surf(x,y,z);shading interp;
axis equal
光照处理
MATLAB提供了灯光设置的函数,其调用格式为:
light('Color',选项1,'Style',选项2,'Position',选项3)
光照处理后的球面。
程序如下:
[x,y,z]=sphere(20);
subplot(1,2,1);
surf(x,y,z);axis equal;
light('Posi',[0,1,1]);
shading interp;
hold on;
plot3(0,1,1,'p');text(0,1,1,' light');
subplot(1,2,2);
surf(x,y,z);axis equal;
light('Posi',[1,0,1]);
shading interp;
hold on;
plot3(1,0,1,'p');text(1,0,1,' light');
图形的裁剪处理
例4-22 绘制三维曲面图,并进行插值着色处理,裁掉图中x和y都小于0部分。
程序如下:
[x,y]=meshgrid(-5:0.1:5);
z=cos(x).*cos(y).*exp(-sqrt(x.^2+y.^2)/4);
surf(x,y,z);shading interp;
pause %程序暂停
i=find(x<=0&y<=0);
z1=z;z1(i)=NaN;
surf(x,y,z1);shading interp;
为了展示裁剪效果,第一个曲面绘制完成后暂停,然后显示裁剪后的曲面。
动画制作
MATLAB提供getframe、moviein和movie函数进行动画制作。
1.getframe函数
getframe函数可截取一幅画面信息(称为动画中的一帧),一幅画面信息形成一个很大的列向量。
显然,保存n幅图面就需一个大矩阵。
2.moviein函数
moviein(n)函数用来建立一个足够大的n列矩阵。
该矩阵用来保存n幅画面的数据,以备播放。
之所以要事先建立一个大矩阵,是为了提高程序运行速度。
3.movie函数
movie(m,n)函数播放由矩阵m所定义的画面n次,缺省时播放一次。
例
绘制了peaks函数曲面并且将它绕z轴旋转。
程序如下
[X,Y,Z]=peaks(30);
surf(X,Y,Z)
axis([-3,3,-3,3,-10,10])
axis off;
shading interp;
colormap(hot);
m=moviein(20); %建立一个20列大矩阵
for i=1:20
view(-37.5+24*(i-1),30) %改变视点
m(:,i)=getframe; %将图形保存到m矩阵
end
movie(m,2); %播放画面2次。
