matlab 程序 晶粒长大
lammps多晶al的晶粒尺寸

lammps多晶al的晶粒尺寸LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) 是一个经典分子动力学软件包,被广泛用于模拟材料的原子尺度行为。
在本文中,我们将讨论使用LAMMPS模拟多晶Al材料时,晶粒尺寸的影响。
晶粒尺寸是材料的重要性质之一,对材料的力学性能、导电性能、热传导性能等起着重要作用。
在多晶材料中,晶粒尺寸的大小和分布直接影响材料的宏观性能。
因此,研究晶粒尺寸对材料性能的影响具有重要意义。
通过LAMMPS模拟多晶Al材料,我们可以控制晶粒尺寸,以研究晶粒尺寸对材料性能的影响。
首先,我们需要构建一个多晶Al的模型。
可以采用随机堆积的方法生成具有所需晶粒尺寸的模型。
通过设置晶粒的种子原子数目,可以控制晶粒尺寸的大小。
在模拟过程中,我们可以通过改变种子原子数目来改变晶粒尺寸。
在模拟过程中,我们需要设置模拟的温度、压力和时间步长等参数。
温度的选择要考虑到Al的熔点和实际应用条件。
压力的选择要符合实际应用条件。
时间步长的选择要保证模拟的稳定性和准确性。
通过调节这些参数,我们可以得到不同晶粒尺寸下材料的力学性能、热传导性能等信息。
通过LAMMPS模拟多晶Al材料,我们可以得到晶粒尺寸对材料性能的影响。
例如,随着晶粒尺寸的增大,材料的强度可能会降低,而塑性可能会增加。
这是因为大尺寸晶粒中的晶界和位错数量相对较少,导致材料的位错运动更加容易,从而增加了材料的塑性。
另外,晶粒尺寸的增大还可能导致材料的热传导性能降低,因为大尺寸晶粒中的晶界会散射热传导的载流子。
除了晶粒尺寸,材料的取向分布也会对材料性能产生影响。
通过LAMMPS模拟,我们可以研究不同晶粒尺寸下的取向分布情况,并分析其对材料性能的影响。
例如,晶粒尺寸较大时,取向分布可能更加随机,导致材料的力学性能和热传导性能均相对较差。
通过LAMMPS模拟多晶Al材料,我们可以控制晶粒尺寸,研究其对材料性能的影响。
MATLAB中常见问题的解决方法总结

MATLAB中常见问题的解决方法总结MATLAB是一种强大的数值计算和科学编程环境,被广泛应用于工程、科学研究和数据分析等领域。
然而,在使用MATLAB的过程中,我们常常会遇到各种各样的问题。
本文将总结一些常见问题,并提供相应的解决方法,以帮助读者更好地使用MATLAB。
1. 内存溢出问题在处理大规模数据或者运行占用内存较大的程序时,经常会遇到内存溢出的问题。
为了解决这个问题,可以尝试以下几种方法:- 使用循环代替矢量化操作:矢量化操作可能会导致内存占用过高,特别是在处理大型数据时。
通过将操作改为循环形式,可以减少内存的使用。
- 释放不必要的变量:在程序运行过程中,需要及时释放不再使用的变量。
可以使用clear命令清除不再需要的变量,并使用pack命令压缩内存空间。
- 增加系统虚拟内存:可以通过增加系统的虚拟内存来扩大MATLAB的可用内存空间。
在Windows系统中,可以通过“计算机属性-高级系统设置-高级-性能-设置-高级-虚拟内存-更改”来进行设置。
2. 代码运行速度慢问题当我们需要处理大量数据或者进行复杂的计算时,可能会遇到MATLAB代码运行速度慢的问题。
以下是一些优化代码运行速度的方法:- 矢量化操作:在MATLAB中,矢量化操作可以显著提高代码的执行速度。
矢量化操作意味着使用矩阵运算代替循环操作,这样可以充分利用MATLAB的内置优化工具。
- 预分配数组空间:在使用循环操作时,应该预先为数组分配足够的空间。
预分配数组空间可以避免因为MATLAB动态调整数组大小而导致的运行速度下降。
- 使用函数而不是脚本:在MATLAB中,函数比脚本通常执行得更快。
将代码封装成函数可以提高代码的复用性和执行效率。
- 使用编译器:对于一些复杂的计算和循环操作,可以使用MATLAB的JIT 编译器来提高代码的执行速度。
可以使用命令"mex -g"将MATLAB代码转换为C 或Fortran源代码,并进行编译。
matlab编程要点

matlab编程要点Matlab编程是一种高级的计算机编程语言和环境,常用于科学计算、工程仿真、数据分析和可视化。
它的优势在于简单易学、语法直观、丰富的函数库以及强大的矩阵运算能力。
在进行Matlab编程时,有一些重要的要点需要注意,下面将详细介绍。
1. 合理使用变量:在编程过程中,变量是存储和处理数据的基本单位。
在Matlab 中,变量的命名应该具有清晰明确的意义,遵循一定的命名规则,以提高代码的可读性。
同时,还要注意变量的声明和初始化,避免未定义或者未初始化的变量引发错误。
2. 利用向量化操作:Matlab的矩阵运算功能十分强大,利用向量和矩阵的操作可以大大简化编程过程。
向量化能够提高运算的速度,并且更加简洁明了。
因此,在编程过程中,应尽量使用矩阵和向量的操作,避免使用循环等低效的操作。
3. 熟悉常用函数库:Matlab提供了丰富的函数库,包括数值计算、优化、统计、线性代数、图像处理等领域的函数。
熟悉和理解这些函数的使用方法,可以大大简化编程过程,提高编程效率。
4. 错误处理与调试:在编程过程中,难免会出现错误或者异常情况。
这时候,需要采取一些措施,便于定位和解决问题。
Matlab提供了强大的调试工具,可以单步执行代码、查看变量的值等。
合理利用这些调试工具,可以快速定位问题所在,并进行修复。
5. 合理的代码布局和注释:良好的代码布局和注释对于代码的可读性和可维护性非常重要。
在编程时,要注意适当缩进代码,使用空行和注释来分割不同功能的代码块。
同时,添加清晰明了的注释,对代码进行解释和说明,方便阅读和理解。
6. 避免重复代码:在编程过程中,应该尽量避免写重复的代码。
重复代码不仅会增加代码量,还会造成维护上的不便。
可以将重复的代码抽象出来,封装成函数或者脚本,提高代码的复用性和可维护性。
7. 性能优化与向量化:在Matlab编程中,有时候需要处理大规模的数据或者复杂的算法。
为了提高程序的运行效率,可以考虑使用一些性能优化技巧,如减少内存开销、并行计算、矩阵预分配、利用稀疏矩阵等。
如何优化Matlab代码的运行速度

如何优化Matlab代码的运行速度在科学计算和数据分析领域,Matlab是一个被广泛使用的编程语言和环境。
然而,由于其解释性的特点,Matlab的执行效率并不是很高。
为了提高Matlab代码的运行速度,我们可以采取一系列优化措施。
本文将介绍一些常见的Matlab代码优化技巧,以提高程序的执行效率。
1. 向量化操作Matlab在处理矩阵和向量运算时效率非常高。
因此,我们应尽量避免使用显式的循环结构。
可以尝试将循环转化为向量操作,使用点乘、点除等运算符,以减少循环次数,提高计算速度。
例如,对于两个向量的元素级别的运算,可以使用“.*”和“./”运算符,而不是显式地使用循环。
2. 预分配变量内存空间在Matlab中,数组的大小是可以动态调整的。
然而,频繁地增加数组的大小会导致额外的内存分配和拷贝操作,从而降低程序的执行效率。
为了避免这种性能损失,我们可以在循环之前预先分配足够的内存空间。
这样一来,Matlab就不需要进行内存分配和拷贝操作,从而提高了程序的执行速度。
3. 使用适当的数据结构在Matlab中,使用适当的数据结构可以提高程序的执行效率。
例如,使用稀疏矩阵代替密集矩阵可以减少存储空间和计算量。
另外,使用cell数组可以在不同的数据类型之间进行存储和访问,从而提高程序的灵活性和执行效率。
4. 减少内存访问和拷贝Matlab中的内存访问和拷贝操作是比较耗时的。
为了提高程序的执行效率,我们可以尽量避免频繁地进行内存访问和拷贝操作。
例如,在循环中可以将局部变量提到循环外,以减少重复的内存访问和拷贝。
5. 使用Matlab编译器Matlab提供了一个编译器(MEX)来将Matlab代码转化为可执行的机器代码。
使用MEX编译器可以显著提高Matlab代码的执行效率。
通过编译,我们可以使用机器级别的优化和并行化技术,从而提高程序的运行速度。
6. 使用并行计算Matlab中的并行计算工具箱可以有效地利用多核处理器的计算能力,提高程序的执行速度。
晶体生长计算软件FEMAG系列之晶体生长方法介绍

可扩展性
软件具有开放性和可扩展性, 用户可以根据需要添加新的材 料属性和边界条件。
图形界面
提供友好的图形界面,方便用 户进行模型建立、参数设置和 结果分析。
软件应用领域
半导体晶体生长
用于研究半导体晶体生长过程中的物理和化学行 为,优化晶体质量和性能。
光学晶体生长
用于研究光学晶体的生长过程,优化晶体光学性 能和加工工艺。
增强可视化功能
为了更好地帮助用户理解和分析计算结果,FEMag软件将 增加更强大的可视化功能,如3D图形界面、实时渲染等, 使用户能够更直观地查看和操作计算结果。
拓展应用领域和范围
扩大应用领域
随着晶体生长研究的不断发展,FEMag软件的应用领域将不 断扩大。未来,FEMag软件将不仅应用于传统的晶体生长研 究,还将拓展到其他相关领域,如材料科学、化学、生物学 等。
该软件通过建立数学模型,模拟晶体生长过程中各 种因素对晶体形态、结构和性能的影响。
FEMag软件提供了丰富的材料属性和边界条件设置 ,支持多种晶体结构和生长条件。
软件特点
01
02
03
04
高效计算
采用有限元方法进行数值计算 ,能够快速求解大规模的晶体 生长问题。
精确模拟
能够模拟晶体生长过程中的温 度场、浓度场、应力场等物理 场,以及化学反应过程。
专业和深入。
与实验结果的比较
FEMag与实验的一致性
FEMag软件在模拟晶体生长方面取得了与实验结果高度一致的结果。通过对比实验和模拟数据,可以验证 FEMag软件的准确性和可靠性,进一步推动其在晶体生长研究中的应用。
实验验证的局限性
尽管FEMag软件与实验结果具有较好的一致性,但实验验证仍然存在局限性。实验条件和参数的微小变化可能 会对结果产生显著影响,而模拟结果可能无法完全反映这些细微差异。因此,将实验和模拟结果相结合,进行综 合分析是更为可靠的方法。
matlab程序优化的常用方法

matlab程序优化的常用方法
Matlab程序优化的常用方法有许多种,其中包括以下几种:
1. 向量化:使用向量和矩阵来代替循环,可以大大提高程序的执行速度。
2. 预分配变量空间:在循环前预先分配变量空间,避免程序在循环中频繁开辟空间。
3. 避免过多的变量复制:减少变量的复制次数,可以减少内存占用和运行时间。
4. 注意变量类型:使用更加高效的变量类型,如uint8和int8,可以减少内存占用和提高程序运行速度。
5. 减少I/O操作:尽量减少文件读写和图形绘制的操作,可以提高程序的执行速度。
6. 利用矩阵运算:使用矩阵运算代替单个数值的运算,可以大大提高程序的运行速度。
7. 简化代码逻辑:简化代码逻辑和减少冗余计算,可以提高程序的
运行速度和减少内存占用。
8. 选择最优算法:选择最优算法可以使程序更加高效,并且减少程序的执行时间。
9. 并行计算:使用并行计算可以提高程序的执行速度,尤其是在大规模数据处理和计算中。
10. 利用Matlab工具箱:Matlab提供了许多工具箱,如优化工具箱和图像处理工具箱等,可以减少程序的开发时间和提高程序的执行效率。
一维粒子扩散过程代码matlab -回复

一维粒子扩散过程代码matlab -回复一维粒子扩散过程是指在一维空间中,粒子由高浓度区域向低浓度区域移动的过程。
这个过程可以用扩散方程进行建模和描述。
在本文中,将介绍如何使用Matlab编写一维粒子扩散过程的代码,并逐步解释每一步。
起初,我们需要定义一维空间的尺寸和时间步长。
在这个例子中,我们假设一维空间的尺寸为L,时间步长为dt。
matlabL = 10; 一维空间尺寸dt = 0.01; 时间步长然后,我们需要定义初始条件和边界条件。
在这个例子中,我们假设初始浓度分布是一个高斯分布,边界条件为周期性边界,即当粒子到达一维空间的边界时会从另一边进入。
matlabN = 100; 粒子数x = linspace(0, L, N); 一维空间均匀分布的点c0 = exp(-(x - L/2).^2); 初始浓度分布为高斯分布c = c0; 当前浓度分布周期性边界条件c(1) = c(end);c(end) = c(1);接下来,我们需要定义扩散系数D,它描述了粒子在单位时间内从高浓度区域向低浓度区域扩散的速率。
在这个例子中,我们假设扩散系数是一个常数。
matlabD = 0.1; 扩散系数然后,我们可以使用扩散方程来模拟粒子扩散的过程。
扩散方程可以写成以下形式:matlabdc = D * (circshift(c,1) - 2*c + circshift(c,-1)) / (dx^2);c = c + dc * dt;在这个方程中,dc表示浓度变化率,circshift函数用于实现周期性边界条件,dx表示一维空间中相邻两个点的间距。
最后,我们需要设置模拟的总时间和输出间隔,并在每一个输出步骤中绘制当前的浓度分布。
matlabtTotal = 10; 总时间tOutput = 0.1; 输出间隔nSteps = round(tTotal / dt); 总步数nOutputSteps = round(tOutput / dt); 输出步数figure;for i = 1:nStepsdc = D * (circshift(c,1) - 2*c + circshift(c,-1)) / (dx^2);c = c + dc * dt;if mod(i,nOutputSteps) == 0plot(x,c);axis([0 L 0 max(c0)]);xlabel('Position');ylabel('Concentration');title(['Diffusion Process at Time = ' num2str(i*dt)]);drawnow;endend通过以上的简单步骤,我们就可以使用Matlab编写一维粒子扩散过程的代码。
金属热锻过程再结晶与晶粒长大演化的数值模拟

金属热锻过程再结晶与晶粒长大演化的数值模拟金属热锻是一种常用的金属加工方法,通过在高温下施加力量对金属进行塑性变形,从而改变金属的形状和性能。
在热锻过程中,金属会发生再结晶和晶粒长大现象,这对最终产品的性能具有重要影响。
本文将介绍金属热锻过程中再结晶和晶粒长大的数值模拟方法及其应用。
首先,我们需要了解再结晶和晶粒长大的基本概念。
再结晶是指在金属加工中,由于高温和变形应力的作用,原初晶粒消失并重新形成新的晶粒的过程。
晶粒长大是指由于温度升高,晶界扩散速度加快,晶粒间的界面发生改变,导致晶粒尺寸增大的过程。
数值模拟方法是理解金属热锻过程再结晶和晶粒长大现象的重要手段之一、下面将结合两个典型模拟方法介绍这方面的研究工作。
一种常用的数值模拟方法是有限元法。
该方法基于对金属材料的形变进行建模,并采用热力学和动力学方程对再结晶和晶粒长大过程进行模拟。
具体而言,首先需要通过实验或已有的数据确定金属材料的本构方程和热力学参数。
然后,将金属材料的几何形状进行离散化处理,建立起有限元模型。
接下来,在模拟过程中考虑金属材料的应变变形、应力分布和温度变化等因素,并结合再结晶和晶粒长大的机制进行模拟计算。
最后,通过数值分析软件对结果进行处理和分析,以获得相关的热锻参数和金属材料的结构演化规律。
另一种常用的数值模拟方法是细胞自动机法。
该方法是一种离散动力学模拟方法,通过对金属材料的离散单元进行建模,模拟材料的宏观变形和微观结构演化。
具体而言,首先需要将金属材料的微观结构进行离散化处理,将其划分为多个细胞单元。
然后,根据所选取的再结晶或晶粒长大模型,设置相应的细胞状态和演化规则。
细胞状态可以包括晶粒尺寸、晶粒形状、晶界能等参数。
通过迭代计算,细胞自动机将自动地模拟金属材料的形变和结构演化过程,得到材料的再结晶和晶粒长大的过程和结果。
以上介绍的是金属热锻过程再结晶和晶粒长大数值模拟的两种常用方法。
这些模拟方法能够提供对金属材料微观结构演化的深入认识,并为优化热锻工艺提供理论指导和技术支持。
解决MATLAB中常见问题的技巧和方法

解决MATLAB中常见问题的技巧和方法MATLAB是一种高级编程语言和数值计算环境,被广泛应用于工程、科学和数学等领域。
然而,在使用MATLAB的过程中,可能会遇到一些常见的问题,这些问题可能会降低编程效率和准确性。
本文将介绍一些解决MATLAB中常见问题的技巧和方法,以帮助用户更好地应对挑战。
第一,解决MATLAB速度慢的问题。
在使用MATLAB时,我们可能会遇到速度慢的情况,这对于大规模数据处理和复杂计算任务来说是一个常见问题。
为了解决这个问题,我们可以采取以下措施:1. 合理利用向量和矩阵运算。
MATLAB在处理向量和矩阵运算时具有高效的内建函数,因此我们应该尽量避免使用循环,并使用矩阵和向量的索引和运算进行计算。
2. 使用适当的数据类型。
MATLAB提供了多种数据类型,如单精度浮点数(single)、双精度浮点数(double)和整数(integers)等。
根据需求选择适当的数据类型可以提高计算效率。
3. 避免频繁的内存分配和拷贝。
在循环中频繁地重新分配内存或复制数据会导致性能下降。
我们可以提前分配好足够的内存空间,并尽量重复利用已经分配的内存。
第二,解决MATLAB图形绘制问题。
图形绘制是MATLAB的一个重要功能,但在实际应用中可能会遇到一些问题,如图形显示不清晰、图例显示不正确等。
为了解决这些问题,我们可以尝试以下做法:1. 增加图形分辨率。
通过设置图形的分辨率,可以提高图形的清晰度。
可以使用“dpi”命令设置分辨率,如“dpi(300)”可以将分辨率设置为300dpi。
2. 调整坐标轴范围和刻度。
使用“xlim”和“ylim”命令可以调整坐标轴的范围,并使用“xticks”和“yticks”命令来设置刻度。
这样可以确保图形显示完整且刻度清晰。
3. 使用适当的图形对象。
MATLAB提供了多种图形对象,如线图(plot)、散点图(scatter)和条形图(bar)等。
根据需要选择适当的图形对象可以更好地呈现数据。
提高MATLAB编程效率的技巧和方法

提高MATLAB编程效率的技巧和方法MATLAB是一种广泛应用于科学计算和工程领域的编程语言和环境。
它的功能强大且易于使用,但在大型项目或复杂计算过程中,编程效率的提升对于节约时间和资源是至关重要的。
因此,本文将介绍一些提高MATLAB编程效率的技巧和方法,以帮助用户更高效地开发和调试代码。
1. 使用向量化操作在MATLAB中,向量化操作是一种重要的优化技术。
它通过避免循环,对整个向量或矩阵进行操作,从而减少了代码的执行时间。
与使用循环逐个元素处理相比,向量化操作可以显着提高计算速度。
例如,用矩阵乘法代替循环相乘可以提高计算速度。
2. 预分配矩阵空间在循环中频繁增加矩阵大小会导致执行时间的增加,因为MATLAB需要重新分配内存空间。
为了避免这种情况,我们可以在进入循环之前预先分配矩阵所需的空间。
这样,MATLAB就可以直接在已分配的空间中进行操作,而不需要重新分配内存,从而提高编程效率。
3. 使用合适的数据类型选择合适的数据类型也可以提高MATLAB编程效率。
对于大型矩阵或数组,使用适当的数据类型(比如单精度浮点型)可以减少内存占用和计算时间。
此外,在处理整数运算时,使用整数数据类型而不是浮点数类型的运算也会提高效率。
4. 避免重复计算在编写MATLAB代码时,避免重复计算可以提高效率。
如果某个计算结果在后续的代码中被多次使用,可以将其保存在一个变量中,而不是每次使用时重新计算。
这样可以节省计算时间,并且使代码更清晰易读。
5. 合理利用MATLAB的并行计算能力MATLAB具有并行计算的能力,可以利用多核处理器的计算能力来加速计算过程。
通过使用parfor循环替代普通的for循环,以及使用parallel computing toolbox中的函数,可以将代码并行化。
这样可以将计算任务拆分为多个子任务,并同时在多个处理器上执行,从而提高编程效率。
6. 使用适当的数据结构选择适当的数据结构对于提高MATLAB编程效率也非常重要。
matlab 腐蚀、膨胀、开运算、闭运算

《深度探讨:Matlab中的腐蚀、膨胀、开运算和闭运算》在图像处理领域,腐蚀、膨胀、开运算和闭运算是常用的图像处理技术。
它们可以帮助我们对图像进行形态学处理,从而对图像进行特定的操作和增强。
本文将从简单入手,深入探讨Matlab中的腐蚀、膨胀、开运算和闭运算的原理、应用和个人观点。
1. 腐蚀腐蚀是一种图像形态学处理操作,其主要作用是“侵蚀”目标的边界。
在Matlab中,可以使用im erode函数来进行腐蚀操作。
腐蚀操作可以帮助我们去除图像中的细小细节或者连接目标,使得图像中的目标变得更加清晰和突出。
腐蚀操作的核心思想在于利用一个结构元素对图像进行扫描,当结构元素与图像相交时,输出图像的对应像素值将取决于结构元素中的最小像素值。
2. 膨胀相对于腐蚀,膨胀是一种图像形态学处理操作,其主要作用是“膨胀”目标的边界。
在Matlab中,可以使用im dilate函数来进行膨胀操作。
膨胀操作可以帮助我们连接图像中的细小裂缝或者增强目标的边界,使得图像中的目标变得更加完整和饱满。
膨胀操作的核心思想在于利用一个结构元素对图像进行扫描,当结构元素与图像相交时,输出图像的对应像素值将取决于结构元素中的最大像素值。
3. 开运算开运算是腐蚀操作和膨胀操作的结合,其主要作用是先进行腐蚀操作,然后进行膨胀操作。
在Matlab中,可以使用im open函数来进行开运算。
开运算可以帮助我们去除图像中的噪声或者平滑图像中的目标,使得图像中的目标更加清晰和稳定。
开运算的核心思想在于先利用腐蚀操作去除细小细节,然后利用膨胀操作连接目标。
4. 闭运算闭运算是膨胀操作和腐蚀操作的结合,其主要作用是先进行膨胀操作,然后进行腐蚀操作。
在Matlab中,可以使用im close函数来进行闭运算。
闭运算可以帮助我们填充图像中的小洞或者平滑图像中的目标边界,使得图像中的目标更加完整和稳定。
闭运算的核心思想在于先利用膨胀操作连接裂缝,然后利用腐蚀操作去除小洞。
MATLAB编程技巧与调试方法

MATLAB编程技巧与调试方法MATLAB是一种强大的科学计算软件,广泛应用于各个领域的数据分析、模拟和可视化等工作中。
本文将介绍一些MATLAB编程的技巧和调试方法,以帮助读者更高效地使用这一工具。
一、MATLAB编程技巧1. 使用函数:将代码封装为函数可以使代码更加模块化和可读性更高。
通过定义输入和输出参数,可以使函数的使用更加灵活,方便复用。
2. 合理使用向量化操作:MATLAB对向量化操作的支持非常好,使用向量化操作可以大大提高代码的执行效率。
尽量避免使用循环,而是使用矩阵运算或者数组操作。
3. 避免不必要的内存分配:MATLAB中的变量赋值和内存分配操作比较耗时。
尽量避免在循环中频繁地进行变量赋值和内存分配,可以通过预分配内存的方式提高代码的执行效率。
4. 使用MATLAB自带的函数和工具箱:MATLAB提供了丰富的函数库和工具箱,包括信号处理、优化、数据拟合等。
合理使用这些函数和工具箱可以简化代码的编写过程,提高编程效率。
5. 使用好MATLAB的文档和帮助文档:MATLAB提供了详细的文档和帮助文档,可以通过查阅文档快速地获取到所需的函数和用法。
合理利用这些资源可以提高编程效率。
二、MATLAB调试方法1. 使用断点:断点是调试的常用方法之一。
在代码中设置断点后,运行程序时会在断点处暂停执行,可以逐步调试程序,并观察变量的取值和函数的调用情况。
2. 输出调试信息:在程序中通过disp函数输出一些关键的中间结果或者调试信息,帮助我们了解程序的执行流程和数据的变化情况。
3. 遵循自上而下的调试原则:当程序出现问题时,可以从程序的开头逐行调试,一步一步地找到问题所在。
这样可以减少调试的复杂性,缩小问题的范围。
4. 使用MATLAB的调试工具:MATLAB提供了包括调试器、变量查看器和堆栈跟踪器等在内的多种调试工具。
通过熟练掌握这些工具的使用,可以更方便地进行程序的调试和分析。
5. 分模块调试:当程序很大或者比较复杂时,可以将程序划分为多个模块进行调试。
matlab程序优化的常用方法

matlab程序优化的常用方法MATLAB是一款广泛应用于科学计算和工程计算的软件。
由于其灵活性和易用性,可以用于许多领域的研究,如信号处理、图像处理、数值计算、控制系统等。
但是,随着数据量和问题复杂度的增加,MATLAB程序的运行效率会变得越来越低,这时需要使用一些优化方法来提高程序的性能。
以下是MATLAB程序优化的常用方法:1. 向量化:MATLAB是一种向量化的语言,使用向量化的操作可以极大地提高程序的性能。
向量化可以避免使用循环,减少 MATLAB 内置函数的调用次数,从而提高程序的效率。
例如,使用矩阵运算来代替循环,使用向量化的函数来代替 for 循环等。
2. 预分配:在运行一个循环时,MATLAB 会动态分配内存来存储结果。
如果在循环中多次分配内存,程序的运行时间会很慢。
因此,在循环之前预分配足够的内存是非常重要的。
可以使用 MATLAB 的函数repmat, zeros 或 ones 来预分配内存。
3. 函数调用:MATLAB 的函数调用很方便,但是,函数调用也会带来一定的开销。
因此,减少函数调用次数可以提高程序的效率。
可以将一些简单的操作放在主程序中,而不是使用函数来实现。
4. 编译程序:MATLAB的编译器可以将MATLAB代码编译成本地机器代码,从而提高程序的执行速度。
可以使用 MATLAB 的编译器将程序编译成可执行文件或者 MEX 文件。
5. 矩阵分解:在大规模矩阵计算中,矩阵分解可以大大提高程序的效率。
常用的矩阵分解方法包括奇异值分解(SVD)、QR 分解、LU 分解等。
6. 并行计算:MATLAB支持并行计算,可以使用并行计算工具箱来将计算分配到多个 CPU 或 GPU 上,从而提高程序的效率。
7. 代码优化工具:MATLAB的代码优化工具可以帮助识别并提高程序性能问题,可以使用优化工具箱中的函数来诊断 MATLAB 代码的性能问题,从而找到性能瓶颈并优化代码。
综上所述,以上是MATLAB程序优化的常用方法,通过优化程序可以提高程序的性能和效率,使得程序在处理大量数据和复杂问题时更加高效。
区域生长算法原理及MATLAB实现

区域⽣长算法原理及MATLAB实现1. 基于区域⽣长算法的图像分割原理数字图像分割算法⼀般是基于灰度值的两个基本特性之⼀:不连续性和相似性。
前⼀种性质的应⽤途径是基于图像灰度的不连续变化分割图像,⽐如图像的边缘。
第⼆种性质的主要应⽤途径是依据实现指定的准则将图像分割为相似的区域。
区域⽣长算法就是基于图像的第⼆种性质,即图像灰度值的相似性。
1.1 基本公式令R表⽰整幅图像区域,那么分割可以看成将区域R划分为n个⼦区域R1,,R2,......Rn的过程,并需要满⾜以下条件:a: U(Ri) = R;b: Ri是⼀个连通区域,i=1,2,3,......n;c: Ri ∩ Rj = 空集,对于任何的i,j;都有i≠j;d: P(Ri) = Ture, 对i=1,2,......n;e: R(Pi U Rj) = False, i≠j;正如“区域⽣长”的名字所暗⽰的:区域⽣长是根据⼀种事先定义的准则将像素或者⼦区域聚合成更⼤区域的过程,并且要充分保证分割后的区域满⾜a~e的条件。
1.2 区域⽣长算法设计思路区域⽣长算法的设计主要由以下三点:⽣长种⼦点的确定,区域⽣长的条件,区域⽣长停⽌的条件。
种⼦点的个数根据具体的问题可以选择⼀个或者多个,并且根据具体的问题不同可以采⽤完全⾃动确定或者⼈机交互确定。
区域⽣长的条件实际上就是根据像素灰度间的连续性⽽定义的⼀些相似性准则,⽽区域⽣长停⽌的条件定义了⼀个终⽌规则,基本上,在没有像素满⾜加⼊某个区域的条件的时候,区域⽣长就会停⽌。
在算法⾥⾯,定义⼀个变量,最⼤像素灰度值距离reg_maxdist.当待加⼊像素点的灰度值和已经分割好的区域所有像素点的平均灰度值的差的绝对值⼩于或等于reg_maxdist时,该像素点加⼊到已经分割到的区域。
相反,则区域⽣长算法停⽌。
在种⼦店1的4邻域连通像素中,即2、3、4、5点,像素点5的灰度值与种⼦点的灰度值最接近,所以像素点5被加⼊到分割区域中,并且像素点5会作为新的种⼦点执⾏后⾯的过程。
图像分析软件计算金属晶粒大小

茹 5 1
采用正火工艺改善热煨弯管性能
四川石 油天 然气建 设工程有 限责任公司 ( 成都 6 0 1 ) 王学军 1 2 3
管道热煨 弯管是长输管道 中重要的管道元件 ,
一
( )加 工工艺 热煨 弯管加工 的参数 :推制 2 温度为 9 0~9 0 2 6 ℃,推制 速度为 3 mm/ n 5 mi ,喷 淋冷却 水量为 1 m / 。热处理 工艺为 :装炉温 度 6 h
为 室 温 ,升 温 速 度 ≤ l O h 3 ℃/ ,保 温 温 度 (9 ± 50
般采用中频感应加 热弯管工艺制造大角度弯管 ,
制作工艺过程是淬火 +高温 回火。此过程中淬火温 度若控制不严格 ,会导致其性能指标达不到要求 , 采用正火工艺能够解决热煨弯管的性能偏差问题。
2 )℃ ,保温时间4 m n 0 0 i,空冷。
图像分析软件计算金属晶粒大小
7 10 2 中 电投 宁夏青铜 峡铝业股 份有限公 司 ( 5 1 0 ) 王 刚
云 内动 力股份有 限公司
( 云南 昆明
6 0 2 ) 潘亮 星 5 2 4
刘星舟
利 用 金 相 显微 镜 和 配 套 的 图像分 析处 理 软 件 ,
之一 ,依次点取该线与其贯穿的晶界线的交点坐标 。 图2 所示为I gJ 件的P i eet n功能及其获得 mae.  ̄ on S l i s t co 的交点坐标数据。并将对每条线获得的交点坐标数据
》
—r —’
-’
>
_
图像分析处理软件与普通数据处理软件Ex e等结 cl 合起来 ,利用定量金相理论 ,实现 了晶粒大小的较 快计算 ,同时无需 另购其他软件。 ( )利 用图像分析软件 ( ma e为例 ), 1 以I g J 在原始金相 照片上标定和设置标 尺 ,并设置一定的
提高Matlab技术使用效率的10个技巧

提高Matlab技术使用效率的10个技巧引言:Matlab作为一种高级的技术计算软件,广泛应用于科学计算、数据分析和数字信号处理等领域。
然而,在日常使用过程中,有时候我们可能会感觉到Matlab的运行速度较慢,或者对某些功能不够熟悉,从而影响了我们的工作效率。
本文将介绍10个提高Matlab技术使用效率的技巧,希望能够帮助读者更好地使用Matlab。
一、向量化操作在Matlab中,向量化操作是一种可以显著提高代码运行效率的技巧。
向量是Matlab中的基本数据结构之一,通过将循环操作改为向量操作,可以大幅减少代码的执行时间。
例如,假设有一个长度为100的向量x,我们需要对每个元素进行平方操作,可以使用如下代码:x = 1:100;y = x.^2;通过使用向量操作,可以一次性对整个向量进行操作,而不需要使用for循环逐个元素计算,从而提高运行效率。
二、使用矩阵代替循环除了向量化操作,使用矩阵代替循环也是提高Matlab代码效率的常用技巧。
循环操作在Matlab中是比较耗时的,可以通过使用矩阵操作来减少循环次数,从而提高代码执行效率。
例如,假设有一个3行4列的矩阵A,我们需要计算每行元素的平均值,可以使用如下代码:A = [1 2 3 4; 5 6 7 8; 9 10 11 12];avg = mean(A, 2);通过使用矩阵操作,可以一次性对每行元素进行计算,并返回结果向量avg。
三、使用预分配内存动态内存分配是Matlab中比较耗时的操作之一,可以通过提前预分配内存来减少内存分配和释放的次数,从而提高代码执行效率。
预分配内存可以使用zeros、ones等函数来实现,例如:n = 1000;X = zeros(n, n);通过提前预分配内存,可以避免在循环中多次动态分配内存的操作,从而提高代码运行效率。
四、避免重复计算在Matlab中,重复计算是一种较为常见的低效操作。
为了避免重复计算,可以使用局部变量或者缓存结果的方式。
动态再结晶二次开发
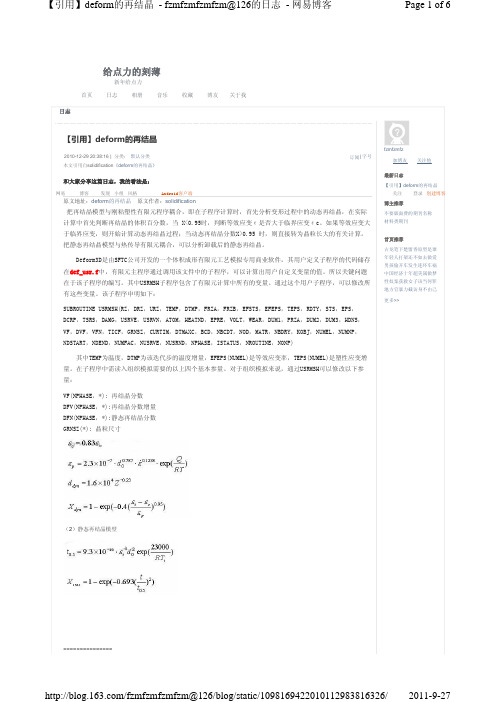
于临界应变,则开始计算动态再结晶过程;当动态再结晶分数X>0.95 时,则直接转为晶粒长大的有关计算。
把静态再结晶模型与热传导有限元耦合,可以分析卸载后的静态再结晶。
Deform3D是由SFTC公司开发的一个体积成形有限元工艺模拟专用商业软件,其用户定义子程序的代码储存 在def_usr.f中,有限元主程序通过调用该文件中的子程序,可以计算出用户自定义变量的值。所以关键问题 在于该子程序的编写。其中USRMSH子程序包含了有限元计算中所有的变量。通过这个用户子程序,可以修改所 有这些变量。该子程序申明如下:
fzmfzmfz 加博友
关注他
最新日志 【引用】deform的再结晶
关注 登录 创建博客 博主推荐 不要版面费的期刊名称 材料类期刊
首页推荐
古龙笔下楚留香原型是谁 年轻人打架还不如去做爱 男孩偷开车发生连环车祸 中国经济十年超美属做梦 性奴案获救女子该当何罪 地方官暴力截访身不由己
更多>>
(2)静态再结晶模型
================================================= 引言 高温成形过程中,金属将发生动态和静态再结晶,产生新的晶粒这种微观组织的演变在很大程度上决定了产品的宏观力学性能 [1,2]利用热加工过程控制晶 粒大小,细化微观组织,是提高产品力学性能的重要手段因此,研究材料在热成形过程中宏观力 学行为和微观组织的变化,揭示其相互之间的关系,并依据优化工 艺参数、设计塑性成形工艺和锻后冷却方案,这对解决目 前的工艺问题,提高产品质量是很有意义的,同时也是变形过程全面模拟的前沿课题[3] 有限元数值模拟技术是随着物理模拟设备的完善以及计算机技术的发展而发展起来的鉴于有限元法是目前唯一能对塑性加工过 程给出全面且较为精确数值解的分析方法,本文对材料组织性能所进行的数值模拟均采用该分析方法 数值模拟软件是求解塑性加工问题的一个基本工具现在市场上已有许多成熟的用于金属塑性加工的商业软件如 DEFORM, MSC.MARC,MSC.SUPERFORM,Dynaform等,但这些软件都只进行宏观变形和温度的分析计算,没有考虑宏观与微观耦 合,不具备微观组织演化的模拟和预测功能,或者只具有简单的预测能力,其模型并不一定适合于所考察的问题本文通过对 Deform3D二次开发,将适合于 材料的组织模型与成形的热力耦合计算结合,模拟热成形过程中的组织演化 1 模型建立 材料在热塑性变形中除了应力和应变的变化外,还要发生复杂的微观组织变化,即动态再结晶、静态再结晶、晶粒生长等研究 表明,再结晶的晶粒尺寸和再结晶晶粒百分比,除了和原始晶粒尺寸与微量元素含量有关外,主要取决于变形及冷却过程的温 度、应变和应变速率 由于热成形过程的复杂性,很难进行现场测试,而在实验室进行研究,只能得到简单条件下的显微组织与宏观热力参数间的定 量关系图1给出了用有限元模拟材料热变形过程中微观组织演化的计算流程 在实验室通过热力模拟试验,可以获得材料的准经验数学模型,其经验模型大都是通过试验数据回归获得Avrami形式的数学 模型在对有限元软件开发过程中,将组织模型离散,在每一迭代步中计算,其计算过程如图2所示
matlab膨胀函数

matlab膨胀函数
MATLAB膨胀函数(dilate)是一个用于图像处理的函数,它可以在图像上执行形态学膨胀运算。
该函数可以改变图像的结构,从而改变图像的效果。
2. MATLAB膨胀函数的用法
MATLAB膨胀函数的语法如下:
B = imdilate(A, se, padding, corner_option)
其中,A是输入图像,se是形态元素的数组,padding 是指定是否使用填充,corner_option指定如何处理图像的角点,B是输出图像。
例如:
B = imdilate(A, [1,1,1;1,1,1;1,1,1], 'same', 'corner');
表示使用3×3的结构元素对图像A进行膨胀,使用相同的填充方式,并使用“角”操作处理图像角点,得到输出图像B。
3. MATLAB膨胀函数的应用
MATLAB膨胀函数可以用于图像分割、物体轮廓提取、图像增强等图像处理操作。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
76. if L(x,y)~=0 %如果格点不在边界区域则开始模拟
77.
78. %---------------------如果选取点为晶粒格点---------------------
79. if L(x,y)~=-1 %如果选取点为晶粒格点
135.
136. %后处理1开始---------------每interval_save_jpg次MCS后存储图形矩阵---------------%
137. if rem(step,interval_save_jpg)==0
138. figure1=figure('visible','off','PaperPosition',[3.067 9.28 14.81 11.1],'PaperSize',[20.98 29.68]);
119. set_probability=rand();
120. if exp(-(change_BG_energy-BG_energy)/T)>=set_probability
121. L(x,y)=temp_Q;
89. diff_grain_count=diff_grain_count+1;
90. diff_ss(diff_grain_count,1)=ss(ii,1);
91. diff_ss(diff_grain_count,2)=ss(ii,2);
51. 1 0
52. 1 1]; %便于随即选取所选格点周围相邻的一个格点
53.
54.
55.%开始CAS模拟
56.for step=1:step_num
57.
58. step %显示MCS进程
59.
60. rand_l=randperm(Ln^2);
95. same_grain_count=same_grain_count+1;
96. end
97. if L(ss(ii,1), ss(ii,2))==-1
98. pore_count=pore_count+1;
99. end
100. end
101. end
102. total_grain_count=diff_grain_count+same_grain_count;
41.temp_L(2:Ln+1,2:Ln+1)=L;
42.L=temp_L;
43.Ln=Ln+2; %此时L边长Ln=Ln+2
44.
45.s=[-1 -1
46. -1 0
47. -1 1
48. 0 -1
49. 0 1
50. 1 -1
8.stastics_data=zeros(step%存储每interval_stastics次MCS后的平均晶粒尺寸和相对密度,存储格式为(MCS,grain count,average area,average diameter,relative density)
84. same_grain_count=0; %计数所选晶粒格点L(x,y)周围与之相同的晶粒格点数
85. diff_ss=zeros(8,3); %存储所选晶粒格点L(x,y)周围与之不同的晶粒格点坐标及其取向度值
113.
114. if change_BG_energy<=BG_energy
115. L(x,y)=temp_Q;
116. end
117.
118. if change_BG_energy>BG_energy
128. %---------------------如果选取点为晶粒格点---------------------
129.
130. end %对应于如果格点不在边界区域则开始模拟
131.
132. end %对应于随机选取格点
133.
134. %========================================================后处理过程========================================================
142. if V_pore==0
143. jpg_name=strcat(num2str(step),'_','Ln=',num2str(Ln-2),'_','Q=',num2str(Q),'_','T=',num2str(T),'_','J1=',num2str(J1),'.jpg');
69. x=Ln;
70. y=fix(rand_l(i)/Ln);
71. else
72. x=rem(rand_l(i),Ln);
73. y=fix(rand_l(i)/Ln)+1;
74. end
34. y=fix(rand_l(i)/Ln)+1;
35. end
36. rand_Q=randperm(Q);
37. L(x,y)=rand_Q(1); %标识晶粒区域
38.end
39.
40.temp_L=zeros(Ln+2); %标识边界区域标示为0,便于后续处理
9.
10.
11.%烧结模拟过程参数赋值
12.T=1; %温度参数
13.J1=1; %晶界能
14.
15.
16.%初始结构的格点赋值
17.rand_l=randperm(Ln^2);
18.for i=1:Ln^2*V_pore
19. if rem(rand_l(i),Ln)==0
20. x=Ln;
21. y=fix(rand_l(i)/Ln);
22. else
23. x=rem(rand_l(i),Ln);
24. y=fix(rand_l(i)/Ln)+1;
25. end
26. L(x,y)=-1; %标识孔洞区域
61.
62. for i=1:Ln^2 %随机选取格点
63.
64. %if rem(i,1000)==0 %显示选取格点进程
65. % i
66. %end
67.
68. if rem(rand_l(i),Ln)==0 %把rand_l(i)转换成实际坐标L(x,y)
139. axes1 = axes('Layer','top','YDir','reverse','Parent',figure1);
140. axis(axes1,[0.5 Ln-2+0.5 0.5 Ln-2+0.5]);
141. image1 = image('CData',L(2:Ln-2+1,2:Ln-2+1),'CDataMapping','scaled','XData',[1 Ln],'YData',[1 Ln],'Parent',axes1);
27.end
28.for i=(Ln^2*V_pore+1):Ln^2
29. if rem(rand_l(i),Ln)==0
30. x=Ln;
31. y=fix(rand_l(i)/Ln);
32. else
33. x=rem(rand_l(i),Ln);
103.
104. if diff_grain_count~=0 %如果所选晶粒格点L(x,y)周围有与之不同的晶粒格点
105.
106. BG_energy=J1*diff_grain_count; %BG_energy为格点所处晶界能
92. diff_ss(diff_grain_count,3)=L(ss(ii,1),ss(ii,2));
93. end
94. if L(ss(ii,1), ss(ii,2))==L(x,y)
122. end
123. end
124.
125. end %对应于如果所选晶粒格点L(x,y)周围有与之不同的晶粒格点
126.
127. end %对应于如果选取点为晶粒格点
2.Ln=200; %格点边长
3.L=zeros(Ln); %格点矩阵
4.Q=120; %总取向数
5.step_num=500; %MC总步数
6.interval_save_jpg=20; %图形存储间隔
7.interval_stastics=2; %晶粒平均参数和相对密度统计间隔
80.
81. ss=s+[x y; x y; x y; x y; x y; x y; x y; x y]; %存储所选晶粒格点L(x,y)周围格点坐标
82.
83. diff_grain_count=0; %计数所选晶粒格点L(x,y)周围与之不同的晶粒格点数
110. rand_ll=randperm(length(diff_ss_2));
111. temp_Q=diff_ss_2(rand_ll(1));
112. change_BG_energy=J1*(total_grain_count-length(find(diff_ss_1==temp_Q)));
