四川省绵阳南山中学2018-2019学年高一下学期入学考试数学试题(解析版) (1)
四川省绵阳南山中学2018-2019年度初升高自主招生数学试题(含答案)
18.一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水.任意转动这个正方体,则水 面在容器中的形状可以是 :(1) 三角形;(2)长方形;(3)正方形;(4)正六边形.其中正确的结论是 ____________.(把你认为正确的序号都填上) 三.解答题:本大题共 7 个小题,共 90 分.解答应写出文字说明、证明过程或演算步骤.
由此还可以对某些函数的增减性进行判断和证明。
如:证明函数 f (x) 2 (x 0) 是减函数. x
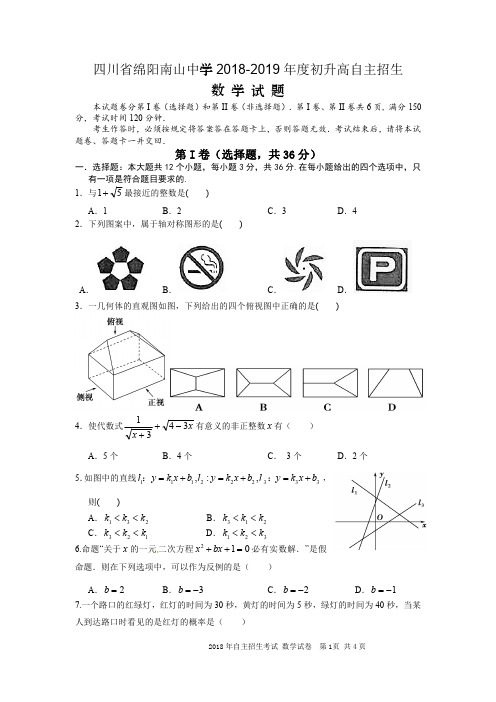
证明:假设 x1 x2 ,且 x1 0, x2 0,
f
(x1)
f
(x2 )
2 x1
2 x2
2(x2 x1) x1x2
∵ x1 x2 ,且 x1 0, x2 0,
2018 年自主招生考试 数学试卷 第 3页 共 4 页
20.(本小题满分 12 分) 为了落实“全民阅读活动”,从某学校初一学生中随机抽取了 100 名学生,获得了他们一
周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
组号
分组
频数
1
0 x2
6
2
2 x4
8
故 从 该 校 随 机 选 取 一 名 学 生 , 估 计 其 该 周 课 外 阅 读 时 间 少 于 12 小 时 的 概 率 为
0.9.
……………(8 分)
(3)样本中的 100 名学生该周课外阅读时间的平均数在第 4 组
…………(12 分)
(每小问 4 分。重点在估计二字上,规范酌情扣分)
4.使代数式 1 4 3x 有意义的非正整数 x 有( ) x3
2018-2019学年四川省绵阳市南山中学高一下学期期中数学试题(解析版)

2018-2019学年四川省绵阳市南山中学高一下学期期中数学试题一、单选题1.设a b c d R ∈、、、,且a bc d ><,,则下列结论中正确的是( ) A .a c b d +>+ B .a c b d ->-C .ac bd >D .a bd c> 【答案】B【解析】利用不等式性质判断或者举反例即可. 【详解】对A,当1,0,2,4a b c d ====时a c b d +<+不满足对B,因为,a b c d ><则a d b c +>+⇒a c b d ->-成立.故B 正确. 对C,当1,0,1,2a b c d ===-=时不满足ac bd >,故不成立. 对D,当3,2,1,2a b c d ====时不满足,故不成立. 故选:B 【点睛】本题主要考查了不等式的性质运用等,属于基础题型. 2.等差数列{a n }中,a 1+a 5=10,a 4=7,则数列{a n }的公差为 A .1 B .2C .3D .4【答案】B【解析】∵a 1+a 5=10,a 4=7,∴⇒d =23.若四边形ABCD 满足AD u u u v =BC uuu v 且|AD u u u v |=|AB u u u v|,则四边形ABCD 的形状是( )A .等腰梯形B .矩形C .正方形D .菱形【答案】D【解析】由AD BC =u u u r u u u r ,利用向量相等的意义可得:四边形ABCD 是平行四边形.又|AD u u u r|=|AB u u u r|,即可得出.【详解】∵AD BC =u u u v u u u v ,∴AD P BC ,∴四边形ABCD 为平行四边形,又|AD u u u v |=|AB u u u v|, ∴AD =AB ,∴四边形ABCD 为菱形.故选D. 【点睛】本题考查了向量相等、平行四边形与菱形的定义,考查了推理能力与计算能力,属于基础题.4.在ABC V 中,sin sin A C =,则ABC V 是( ) A .直角三角形 B .等腰三角形C .锐角三角形D .等腰直角三角形 【答案】B【解析】由正弦定理角化边可直接得到结果. 【详解】 由正弦定理得:22a c R R=,即a c =,ABC ∆∴为等腰三角形. 故选:B . 【点睛】本题考查正弦定理边角互化判断三角形形状的问题,属于基础题. 5.已知AD 为ABC V 的中线,则AD u u u r等于( )A .AB AC +u u u r u u u rB .AB AC -u u u r u u u rC .1122AB AC -u u ur u u u rD .1122AB AC +u u ur u u u r【答案】D【解析】根据平面向量线性运算可直接求得结果. 【详解】AD Q 为ABC ∆中线,2AB AC AD ∴+=u u u r u u u r u u u r,即1122AD AB AC =+u u u r u u u r u u u r .故选:D . 【点睛】本题考查平面向量线性运算问题,属于基础题. 6.已知数列{}n a 满足130n n a a ++=,243a =-,则{}n a 的前10项和等于( ) A .106(13)---B .101(13)9-- C .103(13)-- D .103(13)-+【答案】C【解析】试题分析:设由题设可知数列是公比为,首项是的等比数列.故其前项和为,应选C.【考点】等比数列的定义及前项和的运用.7.若()2,3a =v ,()4,7b =-v ,则a v 在b v 方向上的投影为( )A 3B 13C 65D 65【答案】C【解析】先求得两向量的数量积,再求得向量b r的模,代入公式求解.【详解】a r 在b r 方向上的投影为()2224376556547a b b ⨯-+⨯⋅===-+r rr 故选:C 【点睛】本题主要考查向量投影的定义及求解的方法,公式与定义两者要灵活运用. 8.如果33log log 4m n +≥,那么m n +的最小值为( ) A .4 B .3C .9D .18【答案】D【解析】先由对数的运算法则得出()333log log log m n mn +=,再利用基本不等式性质可求出最小值. 【详解】解:∵()333log log log 4m n mn +=≥, ∴43mn ≥,又由已知条件隐含着0m >,0n >,故422318m n mn +≥≥=,当且仅当9m n ==时取到最小值. 所以m n +的最小值为18. 故选:D 【点睛】本题考查了对数的运算法则、基本不等式的性质,属于基础题.9.在△ABC 中,sin A =34,a =10,则边长c 的取值范围是( ) A .15(,)2+∞ B .(10,+∞) C .(0,10) D .40(0,]3【答案】D【解析】由正弦定理得sin 104040sin sin (0,]3sin 334a C c C C A ===∈ ,选D. 10.已知等差数列{}n a 的前n 项和为55,5,15n S a S ==,则数列11n n a a +⎧⎫⎨⎬⎩⎭的前100项和为A .100101B .99101C .99100D .101100【答案】A【解析】设等差数列{a n }的首项为a 1,公差为d. ∵a 5=5,S 5=15,∴1145{545152a d a d +=⨯+=⇒11{1a d ==⇒a n =n. ∴11n n a a +⋅=()11+n n =111n n -+, S 100=112⎛⎫- ⎪⎝⎭+1123⎛⎫- ⎪⎝⎭+…+11100101⎛⎫- ⎪⎝⎭=1-1101=100101.11.在ABC V 中角,,A B C 的对边分别为,,,a b c 若2A+C =B ,1,a=b =则ABC S ∆等于( )A. BCD .2【答案】C【解析】根据已知等式利用内角和定理求出B 的度数,确定出sin B 的值,再由a 与b 的值,利用正弦定理求出sin A 的值,确定出A 的度数,进而确定出C 的度数,即可求出sin C 的值.【详解】∵A +C =2B ,A +B +C =180°, ∴B =60°,∵a =1,bsin B, ∴由正弦定理sin a A =sin b B 得:sin A =asin B b1=12, ∵a <b ,∴A <B =60°,∴A =30°,即C =90°,则sin C =1.所以11=sin 122ABC S ab C ∆=⨯ 故选:C. 【点睛】此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键. 12.已知0<b<1+a ,若关于x 的不等式(x -b )2>(ax )2的解集中的整数恰有3个,则( ) A .-1<a<0 B .0<a<1 C .1<a<3 D .3<a<6【答案】C【解析】由22()()x b ax ->,整理可得(1-2a )2x -2bx+2b >0,由于该不等式的解集中的整数恰有3个,则有1-2a <0,此时2a >1,而0<b<1+a ,故a>1,由不等式222(1)2a x bx b -+-<0解得222222,2(1)2(1)b ab b ab x a a ---+<<--即111b bx a a -<<<-+要使该不等式的解集中的整数恰有3个,那么-3<1b a --<-2,由1b a --<-2得-b<-2(a -1),则有a<2b+1,即a<2b +1<12a ++1,解得a<3,由-3<1ba --得3a -3>b>0,解得a>1,则1<a<3.二、填空题 13.数列9271,1,,,57--⋅⋅⋅的一个通项公式为________.【答案】13(1)21n nn --⋅- 【解析】根据数列各项所满足的规律可写出结果. 【详解】()01311211-=-⋅⨯-Q ,()12311221=-⋅⨯-,()239315231-=-⋅⨯-,()3427317241=-⋅⨯-, ∴一个通项公式为:()13121n nn --⋅-.故答案为:()13121n nn --⋅-. 【点睛】本题考查根据数列中的项写出通项公式的问题,关键是能够准确找到数列中的项所满足的变化规律. 14.不等式2103x x+≤-的解集为________. 【答案】1,,(3,)2⎛⎤-∞-+∞ ⎥⎝⎦U 【解析】根据分式不等式的求解方法可直接求得结果. 【详解】 由2103x x +≤-得:()()213030x x x ⎧+-≤⎨-≠⎩,解得:12x ≤-或3x >, ∴不等式2103x x +≤-的解集为()1,3,2⎛⎤-∞-+∞ ⎥⎝⎦U .故答案为:()1,3,2⎛⎤-∞-+∞ ⎥⎝⎦U .【点睛】本题考查分式不等式的求解,易错点是忽略分母不为零的要求,造成求解错误. 15.太湖中有一小岛C ,沿太湖有一条正南方向的公路,一辆汽车在公路A 处测得小岛在公路的南偏西15°的方向上,汽车行驶1 km 到达B 处后,又测得小岛在南偏西75°的方向上,则小岛到公路的距离是________ km.【答案】3 6【解析】如图所示,过C作CD⊥AB,垂足为D,∠A=15°,∠CBD=75°,AB=1km,△ABC中,BC=sin15sin60,△CBD中,CD=BCcos15°=1sin302sin60=3km.故填3.16.如图所示,半圆的直径AB=2,O为圆心,C是半圆上不同于A,B的任意一点,若P为半径OC上的动点,则(PAu u u v+PBu u u v)·PCuuu v的最小值是________.【答案】12-【解析】试题分析:因为点O是线段AB的中点,所以向量PA PB+u u u r u u u r=2POu u u r.所以()?PA PB PC+u u u r u u u r u u u r=2PO PC⋅u u u r u u u r.又因为向量,PO PCu u u r u u u r是互为相反向量.所以2PO PC⋅u u u r u u u r=-2PO PCu u u r u u u r=-22(1)2()PO PO PO PO-=--u u u r u u u r u u u r u u u r=2112[()]24PO--u u u r12≥-.所以填12-.【考点】1.向量的求和运算.2.向量的数量积.3.最值问题.三、解答题17.已知ar,br,cr在同一平面内,且()1,2a=r.(1)若||25c=r//c ar r,求cr;(2)若5||b=r()()22a b a b+⊥-r r r r,求ar与br的夹角.【答案】(1)(2,4)c =r 或(2,4)c =--r(2)π.【解析】(1)设(),c x y =r,根据//c a r r ,得到 20x y -=,再根据||c =r方程组求解.(2)根据22a b a b +⊥-rrrr,得到(2)(2)0a b a b +⋅-=r r ,结合2||5a =r,||2b =,求得a b ⋅rr ,再求夹角. 【详解】(1)设(),c x y =r ,//c a r r Q ,(1,2)a =r ,∴20x y -=,∴2y x =,∵||c =r=∴2220x y +=,即22420x x +=, ∴24x y =⎧⎨=⎩,或24x y =-⎧⎨=-⎩∴(2,4)c =r或(2,4)c =--r. (2)∵22a b a b +⊥-rrrr, ∴(2)(2)0a b a b +⋅-=r r,∴222320a a b b +⋅-=r r r r , 即222||32||0a a b b +⋅-=rr r r又∵2||5a =r,225||4b ==r, ∴5253204a b ⨯+⋅-⨯=rr ,∴52a b ⋅=-rr ,∵||a =r||2b =r∴5cos 1||||a ba b θ-⋅===-⋅r r r r∵[]0,θπ∈,∴θπ=. 【点睛】本题主要考查平面向量的基本运算,还考查了运算求解的能力,属于中档题.18.已知数列{}n a 的前n 项和为n S ,且22n S n n =+,*n N ∈,数列{}n b 满足24log 3n n a b =+,*n N ∈.(1)求n a 和n b 的通项公式; (2)求数列{n n a b ⋅}的前n 项和n T .【答案】(1)21n b n =-;(2)(45)25nn T n =-+【解析】试题分析:(1)求数列{}n a 的通项公式主要利用()()111{2n n n S n a S S n -==-≥求解,分情况求解后要验证1n =是否满足2n ≥的通项公式,将求得的{}n a 代入24log 3,n n a b =+整理即可得到n b 的通项公式;(2)整理数列{}n n a b ⋅的通项公式得()141?2n n n a b n -=-,依据特点采用错位相减法求和试题解析:(1)∵2*2,n S n n n N =+∈,∴当1n =时,113a S ==. 当2n ≥时,2212[2(1)(1)]41n n n a S S n n n n n -=-=+--+-=-. ∵1n =时,13a =满足上式,∴*41,n a n n N =-∈.又∵*24log 3,n n a b n N =+∈,∴2414log 3n n b -=+,解得:12n n b -=. 故41,n a n =-,12n n b -=,*n N ∈. (2)∵41,n a n =-,12n n b -=,*n N ∈∴1122n n n T a b a b a b =+++L 01213272(45)2(41)2n n n n --=⨯+⨯++-⨯+-⨯L ①12123272(45)2(41)2n n n T n n -=⨯+⨯++-⨯+-⨯L ②由①-②得:1213424242(41)2n nn T n --=+⨯+⨯++⨯--⨯L12(12)34(41)2(54)2512n n n n n --=+⨯--⨯=-⨯--∴(45)25nn T n =-⨯+,*n N ∈.【考点】1.数列通项公式求解;2.错位相减法求和【方法点睛】求数列{}n a 的通项公式主要利用11a S =,()12n n n a S S n -=-≥分情况求解后,验证1a 的值是否满足()12n n n a S S n -=-≥关系式,解决非等差等比数列求和问题,主要有两种思路:其一,转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解(即分组求和)或错位相减来完成,其二,不能转化为等差等比数列的,往往通过裂项相消法,倒序相加法来求和,本题中()141?2n n n a b n -=-,根据特点采用错位相减法求和19.在ABC V 中,角A ,B ,C 的对边分别为a 、b 、c ,且满足(2)cos cos a b C c B -=⋅,ABC V 的面积S =7c =.(1)求角C ; (2)求a ,b 的值. 【答案】(1)3C π=(2)8a =,5b =或5a =,8b =【解析】(1)利用正弦定理边化角,结合两角和差正弦公式整理可求得cos C ,进而得到结果;(2)利用三角形面积公式和余弦定理可构造方程组求得结果. 【详解】(1)由正弦定理得:()2sin sin cos sin cos A B C C B -=, 即()sin cos sin cos sin sin 2sin cos C B B C B C A A C +=+==,()0,A π∈Q ,sin 0A ∴≠,1cos 2C ∴=, ()0,C π∈Q ,3C π∴=.(2)由11sin sin 2234S ab C ab ab π====得:40ab =…①, 由余弦定理得:()2222222cos 349c a b ab C a b ab a b ab =+-=+-=+-=…②, 由①②得:8a =,5b =或5a =,8b =. 【点睛】本题考查解三角形的相关知识,涉及到正弦定理边角互化的应用、余弦定理和三角形面积公式的应用等知识,属于常考题型.20.已知()f x 是定义在[1,1]-上的奇函数且单调递增,(1)1f =.(1)解不等式:1121f x f x ⎛⎫⎛⎫+< ⎪ ⎪-⎝⎭⎝⎭; (2)若2()21f x t at ≤-+对所有[1,1]x ∈-,[1,1]a ∈-恒成立,求实数t 的取值范围.【答案】(1)3,12⎡⎫--⎪⎢⎣⎭;(2)(]{}[),202,-∞-+∞U U 【解析】(1)根据函数的单调性和定义域可得到不等式组,解不等式组求得结果; (2)根据函数单调性可将问题转化为()220g a t at =-≥对[]1,1a ∈-恒成立的问题,进而可知()min 0g a ≥;分别讨论0t =、0t >和0t <三种情况,构造不等式求得结果.【详解】(1)()f x Q 为定义在[]1,1-上的增函数,∴由1121f x f x ⎛⎫⎛⎫+< ⎪ ⎪-⎝⎭⎝⎭得:111211111121x x x x ⎧-≤+≤⎪⎪⎪-≤≤⎨-⎪⎪+<⎪-⎩,解得:312x -≤<-, ∴不等式1121f x f x ⎛⎫⎛⎫+< ⎪ ⎪-⎝⎭⎝⎭的解集为3,12⎡⎫--⎪⎢⎣⎭. (2)()f x Q 为定义在[]1,1-上的增函数且()11f =,()1f x ∴≤,∴要使()221f x t at ≤-+对所有[]1,1x ∈-,[]1,1a ∈-恒成立,只需2211t at -+≥对[]1,1a ∈-恒成立,即220t at -≥恒成立.设()22g a t at =-,则只需()0g a ≥恒成立,即()min 0g a ≥. 当0t =时,()0g a =,满足题意;当0t >时,()g a 在[]1,1-上单调递减,则()()2min 120g a g t t ==-≥,解得:2t ≥; 当0t <时,()g a 在[]1,1-上单调递增,则()()2min 120g a g t t =-=+≥,解得:2t ≤-. 综上所述:t 的取值范围为(]{}[),202,-∞-+∞U U .【点睛】本题考查利用函数的单调性求解函数不等式、恒成立问题的求解问题;求解恒成立问题的关键是能够将问题转化为函数最值的求解问题;易错点是在求解函数不等式时忽略函数定义域的要求,造成求解错误.。
四川省绵阳市南山中学实验学校2018-2019学年高一数学12月月考试题(无答案)

四川省绵阳市南山中学实验学校2018-2019学年高一数学12月月考试题(无答案)本试卷分为试题卷和答题卡两部分,其中试题卷由第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)组成,共4页;答题卡共4页.满分100分,考试时间100分钟.注意事项:1.答题前,考生务必将自己的学校、班级、姓名用0.5毫米黑色签字笔填写清楚,同时用2B 铅笔将考号准确填涂在“考号”栏目内.2.选择题使用2B 铅笔填涂在答题卡对应题目标号的位置上,如需改动,用橡皮擦擦干净后再选涂其它答案;非选择题用0.5毫米黑色签字笔书写在答题卡的对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.3.考试结束后将答题卡收回.第Ⅰ卷(选择题,共48分)一.选择题:本大题共12小题,每小题4分,共48分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.设全集{1,2,3,4,5}U =,集合{}4,3,1=M ,则=M C U ( ) A .{1,3}B .{2,5}C .{3,5}D .{4,5} 2.=+0000160sin 10cos 20cos 10sin ()A .23-B .23C .21-D .21 3.函数)1ln(21++-=x xy 的定义域为( ) A .{}21<<-x x B .{}2<x x C .{}21≤≤-x x D .{}1->x x 4.对于任意0>a 且1≠a ,函数3)1(log )(+-=x x f a 的图象必经过点( )A .(4,2)B .(2,4)C .(2,3)D .(3,2)5.扇形的周长为cm 8,面积为24cm ,则扇形的圆心角的弧度数为()A .2B .2πC .π2 D.46.要得到函数sin 34xy π⎛⎫=- ⎪⎝⎭的图象,只需将sin 3xy =的图象( )A .向左平移4π个单位 B .向右平移4π个单位C .向左平移34π个单位 D.向右平移34π个单位7.设12log 3a =,1sin 2=b ,232=c ,则( )A..a b c <<B.c b a <<C.c a b <<D.b a c <<8.已知2tan =θ,则=+θθ2sin 22cos ( ) A.51 B.57C.1D.599.已知1052==b a ,则=+b a 11( )A .21B .2CD .110.函数y=ln e 1--x x 的图象大致是( )A .B .C .D .11.已知函数34)(x x x f +=,则不等式0)12sin 2(>-x f ,),π0(∈x 的解集为( )A .⎪⎭⎫ ⎝⎛26ππ,B .⎪⎭⎫ ⎝⎛323ππ,C .⎪⎭⎫ ⎝⎛12512ππ, D .⎪⎭⎫ ⎝⎛⋃⎪⎭⎫ ⎝⎛πππ,12512,0 12.已知M 是函数)2sin(221)(1ππ-+⎪⎭⎫ ⎝⎛=-x x f x 在区间[]42,-上的所有零点之和,则M 的值为() A .4 B .6 C .8 D .10第Ⅱ卷(非选择题,共52分)二.填空题:本大题共4小题,每小题3分,共12分.把答案直接填在答题卡中的横线上.13.已知幂函数f (x )=a x 的图象过点11(,)24,则log 8a = . 14.已知⎪⎭⎫ ⎝⎛∈ππα,2,534sin =⎪⎭⎫ ⎝⎛+πα,则αcos 的值___________. 15.若函数()f x 是R 上的偶函数,且对任意的R x ∈有)2()2(-=+x f x f ,当[]2,0∈x 时,22)(x x f =,则)2019(f 的值为 .16.给出下列命题,其中正确的序号是__________________.(写出所有正确命题的序号) ①正切函数x y tan =在定义域内是增函数; ②函数)4cos()4sin()(ππ+⋅+=x x x f 是偶函数; ③8π=x 是函数)452sin()(π+=x x f 的一条对称轴方程; ④若βα,是第一象限角,且βα>,则βαsin sin >;⑤若α是第三象限角,则2cos 2cos2sin 2sinαα+取值的集合为{}0,2-.三.解答题:本大题共4小题,每小题10分,共40分.解答应写出文字说明、证明过程或演算步骤.17.已知集合⎭⎬⎫⎩⎨⎧≤≤=4281x x A ,B ={x |1<x <5},C ={x |m ﹣1≤x ≤2m } (1)求B A ⋂,B A ⋃;(2)若C C B =⋂,求实数m 的取值范围.18.已知函数R x x x f ∈+=),62sin(3)(π.(1)求函数的最小正周期及单调递增区间;(2)若⎥⎦⎤⎢⎣⎡∈2,0πx ,求函数的最值及对应的x 的值.19.某企业一天中不同时刻的用电量y (万千瓦时)关于时间t (小时,024t ≤≤)的函数()y f t =近似满足()sin()f t A t B ωϕ=++,(0,0,0)A ωϕπ>><<.下图是函数()y f t =的部分图象(0t =对应凌晨0点).(1)根据图象,求A ,ω,ϕ,B 的值;(2)由于当地冬季雾霾严重,从环保的角度,既要控制火力发电厂的排放量,电力供应有限;又要控制企业的排放量,于是需要对各企业实行分时拉闸限电措施.已知该企业某日前半日能分配到的供电量()g t (万千瓦时)与时间t (小时)的关系可用线性函数模型()225(012)g t t t =-+≤≤模拟.当供电量小于该企业的用电量时,企业就必须停产.初步预计停产时间在中午11点到12点间,为保证该企业既可提前准备应对停产,又可尽量减少停产时间,请从这个初步预计的时间段开始,用二分法帮其估算出精确到15分钟的停产时间段.20.已知函数)10(1)(≠>-=a a a a x f xx 且. (1)判断函数)(x f 的奇偶性,并证明;(2)若0)1(>f ,不等式0)4()(2>-++x f bx x f 在R x ∈上恒成立,求实数b 的取值范围; (3)若23)1(=f 且)(21)(22x mf a a x h x x -+=在[)+∞∈,1x 上最小值为2-,求m 的值.。
四川省绵阳南山中学2018-2019学年高二下学期入学考试数学(文)试题(含精品解析)

设抛物线方程x2=-2py(p>0),将点C代入抛物线方程得p=2,
∴抛物线方程为x2=-4y,行车道总宽度AB=6m,
∴将x=3代入抛物线方程,y=-2.25m,
∴限度为
则车辆通过隧道的限制二次模型的实际应用,解题的关键是理解题意.
不喜欢吃零食
20
30
50
总计
50
50
100
附:K2= ,
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
k0
2.072
2.706
3.841
5.024
6.635
根据以上数据,你有多大把握认为“喜欢吃零食与性别有关”( )
A. 以上B. 以上C. 以上D. 以上
【答案】A
【解析】
【分析】
根据公式计算卡方,再对照数据作判断.
三、解答题(本大题共6小题,共70.0分)
17.为了加强中学生实践、创新和团队建设能力的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表,解答下列问题:
(注: = , = -b )
6.以椭圆 的右焦点为圆心,且与双曲线 的渐近线相切的圆的方程是()
A.
B.
C.
D.
【答案】D
【解析】
试题分析:椭圆右焦点 ,双曲线渐近线 ,即
,故选D.
考点:1、圆的方程;2、直线与圆锥曲线.
7.某校举行演讲比赛,9位评委给选手 打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现有一个数字(茎叶图中的 )无法看清,若统计员计算无误,则数字 应该是()
四川省绵阳南山中学2018-2019学年高二下学期入学考试数学(文)试题(解析版)

四川省绵阳南山中学2018-2019学年高二下学期入学考试数学(文)试题一、选择题(本大题共12小题,共60.0分)1.直线x-y+1=0的倾斜角为()A. B. C. D.【答案】B【解析】【分析】先根据方程求斜率,再求倾斜角.【详解】根据题意,设该直线的倾斜角为θ,(0°≤θ<180°)直线方程x-y+1=0,其斜率k=1,有tanθ=k=1,解可得θ=45°,故选:B.【点睛】本题考查直线斜率与倾斜角,考查基本分析求解能力,属基础题.2.经过点A(3,2),且与直线平行的直线方程为()A. B.C. D.【答案】B【解析】试题分析:设直线方程为,因为经过点A(3,2),所以,所以直线方程为。
考点:直线方程的求法;直线平行的条件。
点评:与Ax+By+C=0平行的直线可深为:Ax+By+C1=0(C1≠C)。
与Ax+By+C=0垂直的直线可设为:Bx-Ay+C1=0。
3.已知,应用秦九韶算法计算时的值时,的值为()A. 27B. 11C. 109D. 36【答案】D【解析】由秦九韶算法可得1故答案选4.南山中学膳食中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:根据表中数据,采用分层抽样的方法抽取的20人中,喜欢吃甜品的男、女生人数分别是()A. 1,6B. 2,12C. 2,4D. 4,16【答案】B【解析】【分析】先确定抽样比例,再根据抽样比例确定结果.【详解】根据题意,得;抽取20人组成样本时的抽样比例是,∴样本中喜欢吃甜食的男生人数是10×=2,女生人数是60×=12.故选:B.【点睛】本题考查分层抽样,考查基本分析求解能力,属基础题.5.一位妈妈记录了孩子6至9岁的身高(单位:cm),所得数据如下表:年龄身高由散点图可知,身高与年龄之间的线性回归方程为,预测该孩子10岁时的身高为A. 154B. 153C. 152D. 151【答案】B【解析】试题分析:根据题意,由表格可知,身高y与年龄x之间的线性回归直线方程为,那么可知回归方程必定过样本中心点,即为(7,131)代入可知,=65,预测该学生10岁时的身高,将x=10代入方程中,即可知为153,故可知答案为B考点:线性回归直线方程点评:主要是考查了线性回归直线方程的回归系数的运用,属于基础题。
四川省绵阳市南山中学2018-2019学年高一下学期入学考试数学试题(Word版含答案)

1 2 3 4 5 6 7 8 9 10 11 12 213 14 15 16 17 180.50 1.5143.532.54.5yt四川省绵阳市南山中学2018-2019学年高一下学期入学考试数学试题(Word 版含答案)一、选择题(本大题共10小题,每题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.若P ={x|x <1},Q ={x|x >-1},则( )A .∁R P ⊆QB .Q ⊆P C.P ⊆Q D .Q ⊆∁R P 2.已知23)2cos(=+ϕπ,且||ϕ<2π,则=ϕtan ( )A. 33-B. 33C. 3-D. 3 3.下列函数中,既是偶函数又在(0,)+∞上单调递增的函数是( ) A.3y x = B.1y x =+ C.21y x =-+ D.2xy -=5.函数()2xf x e x =+-的零点所在的一个区间是( )A.(-2,-1)B.(-1,0)C.(0,1)D.(1,2) 6. 已知直线)0(<=a a x 与函数x x xx y y y y10,2,21,31==⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=的图像依次交与A,B,C,D 四点,则这四个点从上到下的排列次序是( )A. A 、B 、C 、DB. B 、C 、A 、DC. B 、A 、C 、DD. C 、A 、B 、D 7.某研究小组在一项实验中获得一组关于y 、t 之间的数据,将其整理得到如图所示的散点图,下列函数中,最能近似刻画y 与t 之间关系的是( ) A .y =2t B .y =2t 2 C .y =t 3D .y =log 2t8.若函数()(01)xxf x ka a a a -=->≠且在(,)-∞+∞上既是奇函数又是增函数,则函数()log ()a g x x k =+的图像是( )A B C D9.若函数y = f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x 轴向左平移2π个单位长度,沿y 轴向下平移1个单位长度,得到函数y =21sin x 的图象,则函数y=f(x)是( ) A. y=12π2sin 21+⎪⎭⎫ ⎝⎛+x B. y =12π2sin 21+⎪⎭⎫⎝⎛-xC. y =14π2sin 21+⎪⎭⎫ ⎝⎛+xD. y =14π2sin 21+⎪⎭⎫⎝⎛-x10.在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数()f x 的图象恰好通过*(N )n n ∈个整点,则称函数()f x 为n 阶整点函数.有下列函数 ①1()f x x x =+(0)x > ② 3()g x x = ③1()()3x h x = ④()ln x x ϕ= 其中是一阶整点函数的是( )A .①②③④B .①③④C .④D .①④二、填空题(本大题共5小题,每题4分,共20分)11.已知角α的终边经过点()8,6cos 60oP m --且cos α45=-,则m 的值为_______. 12.设函数⎩⎨⎧>-≤=-)1(,log 1)1(,2)(21x x x x f x 则满足2)(≤x f 的x 的取值范围是______________.13.已知=)(αf )360tan()180tan()90sin()180tan()270sin()180sin(αααααα-++--- ,则)631(π-f 的值为______. 14.若函数()y f x =是定义域为R 的奇函数,且对于任意x ∈R ,有(3)()f x f x +=-,若(1)1f =, tan 2α=,则)cos sin 2005(ααf 的值为 . 15.关于函数xxx f a-+=11log )((a>0且a ≠1)下列说法: ①)(x f 的定义域是()1,1-;② 当a>1时,使0)(>x f 的x 的取值范围是()0,1-; ③ 对定义域内的任意x ,)(x f 满足)()(x f x f -=-; ④ 当0<a<1时,如果1021<<<x x ,则)()(21x f x f <;其中正确结论的序号是 .(填上你认为正确的所有结论序号)三、解答题(本大题共4小题,共40分.解答应写出文字说明、证明过程或演算步骤) 16.已知A={x|-1<x≤3},B={x|m≤x<1+3m}. (1)当m=1时,求A ∪B ;(2)若B ⊆C R A ,求实数m 的取值范围.17.有时可用函数⎪⎩⎪⎨⎧>--≤-+=)6(,44.4)6(,ln 151.0)(x x x x x a a x f 描述学习某知识的掌握程度,其中x 表示某知识的学习次数(x ∈N +),)(x f 表示对该知识的掌握程度,正实数a 与知识有关. (1) 证明:当x ≥7时,掌握程度的增加量)()1(x f x f -+总是下降;(2) 根据经验,甲、乙、丙对应的a 的取值区间分别为(115,121],(121,127],(127,133].当学习某知识6次时,掌握程度是85%,请确定相应的.(已知数据)18.如图是函数)2,0,0)(sin()(πϕωϕω<>>+=A x A x f 的部分图像,(1)求函数)(x f 的解析式; (2)当)0,2(π-∈x 时,求函数的值域.19.设函数())f x x a R =+∈. (1)若1a =,求()f x 的值域;(2)若不等式()2f x ≤对[8,3]x ∈--恒成立,求实数a 的取值范围.参考答案数学试题(答案)一、选择题: 1-5.ACBCC 6-10.ADCBD 二、填空题: 11.21 12.[)+∞,0 13.23 14.-1 15.①③17.解:(1)当x ≥7时,)4)(3(4.)()1(--=-+x x o x f x f …………………(2分)而当x ≥7时,函数)4)(3(--=x x y 单调递增,且0)4)(3(>--x x 故)()1(x f x f -+单调递减.……………………(4分)∴当x ≥7时,掌握程度的增加量)()1(x f x f -+总是下降. …………………(5分) (2)由题可知当x=6时,=)(x f 85.06ln151.0=-+a a ,整理可得05.06e a a=-,解得:0.1236*50.206*105.005.0==-=e e a …………………(8分)而123.0∈(121,127],由此可知,该是乙.…………………(10分) 18.解:(1)由图可知:A=3,2)6(32πππ=--=T 即π=T , ∴πωπ==2T ,则2=ω所以)2sin(3)(φ+=x x f ………………(2分)又由图可知:)0,6(π-是五点作图法中的第一点∴2* 0)6(=+-φπ即3πφ=……………………(4分)∴)32sin(3)(π+=x x f ……………………(5分)(2)由(1)知:)32sin(3)(π+=x x f∵)0,2(π-∈x 则 33232πππ<+<-x …………………(7分) ∴23)32sin(1-<+≤πx 即233)32sin(3<+≤-πx ……………(9分)∴函数)(x f 在)0,2(π-∈x 上的值域是⎪⎪⎭⎫⎢⎣⎡-233,3.…………………(10分) 19.解:(1)1a =时()f x x =+)1(≤x ,令 01≥-=x t 则 21x t =-,∴()2215()1(0)24y f x t t t t ⎛⎫==-+=--+≥ ⎪⎝⎭…………………(3分)∴45≥y 即函数)(x f 的值域是⎪⎭⎫⎢⎣⎡+∞,45.…………………(5分) (2)令t =)38(-≤≤-x 则)32(12≤≤-=t t x ,2()1y f x t at ==-++, 不等式()2f x ≤对[8,3]x ∈--恒成立212t at ⇔-++≤对[2,3]t ∈恒成立1a t t⇔≤+对[2,3]t ∈恒成立…………………(7分)令1()g t t t=+,[2,3]t ∈ 则函数)(t g 在[]3,2上是一个增函数, ∴min 5()(2)2g t g ==……………(9分) ∴min 5()2a g t ≤=即a 的取值范围为5,2⎛⎤-∞ ⎥⎝⎦.…………………(10分)。
2018-2019学年四川省绵阳市南山中学高一(下)入学数学试卷(3月份)解析版

2018-2019学年四川省绵阳市南山中学高一(下)入学数学试卷(3月份)一、选择题(本大题共12小题,共48.0分)1.满足A∪{1,-1}={1,0,-1}的集合A共有()A. 2个B. 4个C. 8个D. 16个2.角α的终边上一点的坐标为(sin,cos),则tan2α=()A. B. C. D.3.三个数0.76,60.7,log0.76的大小关系为()A. B. C. D.4.设向量=(2,4)与向量=(x,6)共线,则实数x=()A. 2B. 3C. 4D. 65.可以写成①+;②-;③-;④-.其中正确的是()A. ①②B. ②③C. ③④D. ①④6.已知f(x)是偶函数,对任意的a,b∈[0,+∞)都有<,若f(lg x)>f(1),则x的取值范围是()A. B. ∪ C. D. ∪7.若sinα=,α∈(-,),则cos()=()A. B. C. D.8.函数>,>,<的图象如图所示,则函数y=A cos(ωx+φ)的递减区间是()A. ∈B. ∈C. ∈D. ∈9.函数f(x)=,的零点个数为()A. 2B. 3C. 4D. 510.函数y=a|x|+1(a>0且a≠1),x∈[-k,k],k>0的图象可能为()A.B.C.D.11.已知函数y=f(x)在(0,3)上是增函数,函数y=f(x+3)是偶函数,则f(),f(),f(2)的大小关系()A. B. C. D.12.函数y=f(x)的定义域为D,且f(x)同时满足以下条件:①f(x)在D上是单调递增或单调递减函数;②存在闭区间[a,b]⊊D(其中a<b),使得当x∈[a,b]时,f(x)的取值集合也是[a,b].那么,我们称函数y=f(x)(x∈D)是闭函数.若f(x)=k+是闭函数,则实数k的取值范围是()A. B. C. D.二、填空题(本大题共4小题,共12.0分)13.若f(x)=是奇函数,则a=______.14.在正方形ABCD中,E是DC边的中点,且=,=,则=______.15.已知函数f(x)=,,>,若直线y=m与函数y=f(x)的图象有三个不同交点的横坐标依次为x1,x2,x3,则x1+x2+x3的取值范围是______.16.给出下列五个命题:①函数y=f(x),x∈R的图象与直线x=a不可能有两个不同的交点;②函数y=log2x2与函数y=2log2x是相同函数;③对于指数函数y=2x与幂函数y=x2,存在x0,当x>x0时,有2x>x2成立;④对于函数y=f(x),x∈[a,b],若有f(a)•f(b)<0,则f(x)在(a,b)内有零点;其中正确的序号是______.三、解答题(本大题共4小题,共40.0分)17.已知集合A为函数f(x)=得定义域,B={x∈R|y=lg(x-4)}.(1)求集合A,B;(2)已知集合C={x|1-m≤x≤m-1},若集合C⊆(A∪B),求实数m的取值范围.18.经市场调查,某种商品在过去50天的销售量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N).前30天价格为g(t)=t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).(1)写出该种商品的日销售额S与时间t的函数关系;(2)求日销售额S的最大值.19.已知函数f(x)=•(),其中向量=(sin x,-cos x),=(sin x,-3cos x),=(-cos x,sin x),x∈R.(1)若f(α)=,<<,求cos2α的值;(2)不等式|f(x)-m|<2在x∈[,]上恒成立,求实数m的取值范围.20.已知函数f(x)=,g(x)=f(2x).(1)判断函数f(x)在区间(-1,+∞)上的单调性,并用定义证明;(2)g(x-1)+g(3-2x)<0,求实数x的取值集合;(3)若函数F(x)=g(x)-2x-m存在零点,求实数m的取值范围.答案和解析1.【答案】B【解析】解:根据题意,集合可能为{0}、{0,1}、{0,-1}、{0,1,-1},共有4个;故选:B.根据题意,分析可得,集合A中必须有元素0,可能含有元素1或-1,由此列举可得全部可能的集合A,即可得答案.本题考查集合并集的性质,关键是由并集的定义,分析得到集合A中必须有的元素和可能有的元素.2.【答案】A【解析】解:∵α的终边上一点的坐标为(sin,cos),即(,-)∴tanα==-,则tan2α===,故选:A.根据三角函数的定义求出tanα,利用正切的倍角公式进行计算即可.本题主要考查三角函数值的计算,结合三角函数的定义以及倍角公式是解决本题的关键.比较基础.3.【答案】D【解析】解:由对数函数y=log0.7x的图象和性质可知:log0.76<0由指数函数y=0.7x,y=6x的图象和性质可知0.76<1,60.7>1∴log0.76<0.76<60.7故选:D.从而得到结论.本题主要考查指数函数,对数函数的图象和性质,在比较大小中往往转化为函数的单调性或图象分面来解决.4.【答案】B【解析】解;因为向量=(2,4)与向量=(x,6)共线,所以4x=2×6,解得x=3;故选:B.利用向量共线的充要条件得到坐标的关系求出x.本题考查了向量共线的坐标关系;如果两个向量向量=(x,y)与向量=(m,n)共线,那么xn=ym.5.【答案】D【解析】解:∵①+=;②-=;③-=;④-=.因此其中正确的是①④.故选:D.利用向量的运算法则即可判断出.本题考查了向量的原式法则,属于基础题.6.【答案】C【解析】解:由于f(x)是偶函数,对任意的a,b∈[0,+∞)都有,则偶函数f(x)在[0,+∞)递减,则f(lgx)>f(1),即为f(|lgx|)>f(1),即有|lgx|<1,即-1<lgx<1,则<x<10.故选:C.f(lgx)>f(1),即为f(|lgx|)>f(1),由单调性,即可得到,再解不等式即可得到解集.本题考查函数的奇偶性和单调性的运用:解不等式,考查对数不等式的解法,考查运算能力,属于中档题.7.【答案】A【解析】解:∵sinα=,α∈(-),∴cosα==,∴cos ()=-(cosα-sinα)=-.故选:A.由已知利用同角三角函数基本关系式可求cosα的值,进而根据两角和的余弦函数公式,特殊角的三角函数值即可计算得解.本题主要考查了同角三角函数基本关系式,两角和的余弦函数公式,特殊角的三角函数值在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.8.【答案】C【解析】解:由“五点法”可知解得ω=2,φ=-,由图象可知A=1,则函数y=cos(2x-),由2k,k∈Z解得k∈Z故选:C.利用函数图象求出A ,利用五点法得到,求出ω,φ,结合余弦函数的单调性求出函数的递减区间.本题是基础题,考查三角函数的图象求函数的解析式,掌握五点法作图,函数的基本性质,是9.【答案】A【解析】解:函数f(x)=,可得当x≤0时,x2+2x-3=0,解得x=1(舍去)或x=-3;当x>0时,-2+lnx=0,解得x=e2,函数有2个零点.故选:A.利用分段函数分别求解函数的零点即可.本题考查分段函数的应用,函数的零点的求法,考查计算能力.10.【答案】C【解析】解:函数y=a|x|+1(a>0且a≠1),x∈[-k,k],k>0.函数是偶函数,排除A;函数y=a|x|+1>1,排除B;a>1时,x>0函数是增函数,C 不满足题意,D不满足题意;当a∈(0,1)时,x>0函数是减函数,C 满足题意,D不满足题意;故选:C.利用函数的奇偶性排除选项,通过a的范围,利用函数的性质判断选项即可.本题考查函数的图象的判断,考查分类讨论思想的应用,函数的奇偶性以及函数的单调性,是判断函数图象的常用方法.11.【答案】A【解析】解:根据题意,函数y=f(x+3)是偶函数,则函数f(x)的图象关于直线x=3对称,则f ()=f(),f()=f (),又由函数y=f(x)在(0,3)上是增函数,则f()<f(2)<f (),则有f ()<f(2)<f(),故选:A.根据题意,由函数的奇偶性的性质分析可得函数f(x)的图象关于直线x=3对称,进而可得f ()=f(),f ()=f(),结合函数的单调性分析可得答案.本题考查函数的奇偶性与单调性的综合应用,注意分析f(x)的对称性,属于基础题.12.【答案】B【解析】解:根据题意,f(x)=k+,有x+2≥0,易得f(x)为增函数,若f(x)=k+为闭函数,则存在闭区间[a,b],满足,即a、b是方程k+=x的两根,令t=,则t≥0,则原方程等价于k+t=t2-2,变形可得t2-t-k-2=0,若方程k+=x有两根,则t2-t-k-2=0有两个非负的实根,设g(t)=t2-t-k+2则有,解可得-<k≤-2,即k的取值范围为(-,-2] 故选:B.根据题意,分析易得f(x)=k+在其定义域上为增函数,结合闭函数的定义分析可得,即a、b是方程k+=x的两根,令t=,则原方程等价于k+t=t2-2,变形可得t2-t-k-2=0,分析易得t2-t-k-2=0有两个非负的实根,设g(t)=t2-t-k+2,则有,解可得t的取值范围,即可得答案.本题考查函数与方程的关系,涉及函数单调性的判定与应用,属于基础题.13.【答案】【解析】解:∵f(x)是奇函数,∴f(x)=-f(-x),∴=∴=,解得a=.根据奇函数的性质,f(x)=-f(-x),代入f(x)的解析式,得到等式即可求出a的值.本题主要考查奇函数的性质,根据f(x)=-f(-x)列出式子即可解得a的值,本题比较基础.14.【答案】-【解析】解:∵正方形ABCD中,E是DC边的中点,且=,=,∴=+=+=-=-.故答案为:-.由题意可得=+=+=,把=,=代入化简可得结果.本题主要考查平面向量基本定理,两个向量的加减法的法则,以及其几何意义,属于基础题.15.【答案】(2,2017)【解析】解:作出函数f(x)的图象,则当0<x<1时,函数f(x)关于x=对称,若直线y=m与函数y=f(x)三个不同交点的横坐标依次为x1,x2,x3,且x1<x2<x3,则0<m<1,且x1,x2关于x=对称,则x1+x2=1,由log2016x=1,得x=2016,则1<x3<2016,则2<x1+x2+x3<2017,即x1+x2+x3的取值范围是(2,2017),故答案为:(2,2017).作出函数f(x)的图象,利用函数的对称性以及对数函数的图象和性质进行求解即可.本题主要考查分段函数的应用,考查了函数图象的作法及应用及函数零点与函数图象的有关系,利用数形结合是解决本题的关键.属于中档题.16.【答案】①③【解析】解:①根据函数的定义可得:函数y=f(x),x∈R的图象与直线x=a不可能有两个不同的交点,正确;②函数y=log2x2与函数y=2log2x的定义域不同,前者的定义域为{x|x∈R,x≠0},后者的定义域为{x|x>0},因此不是相同函数;③对于指数函数y=2x与幂函数y=x2,存在x0,当x>x0时,有2x>x2成立,例如取x0=5满足条件,因此正确;④对于函数y=f(x),x∈[a,b],若有f(a)•f(b)<0,则f(x)在(a,b)内不一定有零点,例如取函数f(x)=,a=2,b=4,满足条件,但是在(a,b)内无零点.综上正确的为①③.故答案为:①③.①根据函数的定义即可判断出正误;②函数y=log2x2与函数y=2log2x的定义域不同,不是相同函数;③例如取x0=5满足条件,可得正确;④f(x)在(a,b)内不一定有零点,例如取函数f(x)=,a=2,b=4,满足条件,但是在(a,b)内无零点.本题考查了函数的定义及其性质、函数零点存在定理、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.17.【答案】解:(1)根据题意,函数f(x)=,有4-2x>0,解可得x<2,则A=(-∞,2),y=lg(x-4),有x-4>0,解可得x>4,则B=(4,+∞);(2)由(1)的结论,A=(-∞,2),B=(4,+∞);则A∪B=(-∞,2)∪(4,+∞),C={x|1-m≤x≤m-1},集合C⊆(A∪B),分2种情况讨论:当1-m>m-1,即m<1时,C=∅,满足C⊆(A∪B),当1-m≤m-1,即m≥1时,若C⊆(A∪B),必有m-1<2或1-m>4,解可得1≤m<3,综合可得:m<3.【解析】(1)根据题意,对于函数f(x)=,有4-2x>0,解可得x的取值范围,即可得集合A,对于(2)由(1)的结论,求出集合A∪B,按C是否为空集分2种情况讨论,求出m的取值范围,综合即可得答案.本题考查集合的包含关系的应用,涉及函数的解析式的计算,属于基础题.18.【答案】解:(1)当1≤t≤30时,由题知f(t)•g(t)=(-2t+200)•()=-t2+40t+6000,当31≤t≤50时,由题知f(t)•g(t)=45(-2t+200)=-90t+9000,所以日销售额S与时间t的函数关系为S=;(2)当1≤t≤30,t∈N时,S=-(t-20)2+6400,当t=20时,S max=6400元;当31≤t≤50,t∈N时,S=-90t+9000是减函数,当t=31时,S max=6210元.∵6210<6400,则S的最大值为6400元.【解析】(1)根据销售额等于销售量乘以售价得S与t的函数关系式,此关系式为分段函数;(2)求出分段函数的最值即可.考查学生根据实际问题选择函数类型的能力.理解函数的最值及其几何意义的能力.19.【答案】解:(1)f(x)=•()=(sin x,-cos x)•(sin x-cos x,sin x-3cos x)=sin2x-2sin x cosx+3cos2x=1-sin2x+2cos2x=2+cos2x-sin2x=2+sin(2x+),若f(α)=,则2+sin(2α+)=,即sin(2α+)=,由<<∴-<2α<-,即-<2α+<,则cos(2α+)=,则cos2α=cos[(2α+)-]=cos(2α+)cos+sin(2α+)sin=(-)+×(-)=.(2)∵不等式|f(x)-m|<2在x∈[,]上恒成立,∴-2<f(x)-m<2,即f(x)-2<m<f(x)+2在x∈[,]上恒成立,当x∈[,],则2x∈[,π],2x+∈[π,],则当2x+=π时,f(x)取得最大值,最大值为f(x)=2,当2x+=时,f(x)取得最小值,最小值为f(x)=2+sin=2-,则><,得0<m<4-,即实数m的取值范围是(0,4-).【解析】(1)根据向量数量积的公式以及辅助角公式进行化简,结合两角和差的余弦公式进行转化计算即可.(2)利用不等式恒成立,利用参法分离法转化为最值问题即可.本题主要考查不等式恒成立问题,结合向量数量积的公式,利用辅助角公式进行化简,结合两角和差的余弦公式以及参数分离法转化求最值是解决本题的关键.20.【答案】解:(1)根据题意,f(x)==1-,在(-1,+∞)上为增函数,证明:设-1<x1<x2,则f(x1)-f(x2)=(1-)-(1-)=-=,又由-1<x1<x2,则(x1+1)>0,(x2+1)>0,(x1-x2)<0,则f(x1)-f(x2)<0,故函数f(x)在(-1,+∞)上为增函数,(2)根据题意,g(x)=f(2x)=,则g(-x)==-()=-g(x),函数g(x)为奇函数,设t=2x,则t>0,t=2x在R上为增函数,y=g(t)在(0,+∞)上为增函数,则y=g(x)在R上为增函数,g(x-1)+g(3-2x)<0⇒g(x-1)<-g(3-2x)⇒g(x-1)<g(2x-3)⇒x-1<2x-3,解可得x>2,即实数x的取值集合为(2,+∞);(3)函数F(x)=g(x)-2x-m存在零点,即方程-2x=m有根,则m=1--2x=-[()+(2x+1)]+2,又由()+(2x+1)≥2=2,故m≤2-2,即m的取值范围为m≤2-2.【解析】(1)根据题意,函数的解析式变形可得f(x)==1-,设-1<x1<x2,由作差法分析可得结(2)根据题意,分析可得g(x)为奇函数且在其定义域上为增函数,据此可得g(x-1)+g(3-2x)<0⇒g(x-1)<-g(3-2x)⇒g(x-1)<g(2x-3)⇒x-1<2x-3,解可得x的取值范围,即可得答案;(3)函数F(x)=g(x)-2x-m 存在零点,即方程-2x=m有根,变形可得m=1--2x=-[()+(2x+1)]+2,结合基本不等式的性质分析m的取值范围,即可得答案.本题考查函数的单调性以及奇偶性的综合应用,涉及复合函数的单调性以及方程与函数的关系,属于综合题.。
四川省绵阳市南山中学2018-2019学年高一上学期期中考试数学试题 Word版含解析

四川省绵阳市南山中学2018-2019学年高一(上)期中数学试卷一、选择题(本大题共12小题,共48.0分) 1.已知集合M ={x ∈N |x 2-1=0},则有( ) A. {}1M ∈ B. 1M -∈C. {}1,1M -⊆D. {1,-0,{}1}1M ⋂= 【答案】D 【解析】 【分析】求出集合M ,由此能求出结果.【详解】解:由集合{}2M N |10{1}x x =∈-==,知: 在A 中,{1}M ⊆,故A 错误; 在B 中,1M -∉,故B 错误; 在C 中,{1,1}M -⊇,故C 错误; 在D 中,{1,0,1}M {1}-=,故D 正确. 故选:D .【点睛】本题考查命题真假的判断,考查元素与集合的关系、集合与集合的关系等基础知识,考查运算求解能力,是基础题.2.已知函数f (x )=2x 的反函数为y =g (x ),则g (12)的值为( ) A. 1- B. 1C. 12D. 2【答案】A 【解析】 【分析】由已知函数解析式求得x ,再把x 与y 互换可得原函数的反函数,取12x =得答案.【详解】解:∵由()2x y f x ==,得2log x y = ∴原函数的反函数为2()log g x x =, 则211log 122g ⎛⎫==-⎪⎝⎭. 故选:A .【点睛】本题考查函数的反函数的求法,是基础题.3.在用二次法求方程3x +3x -8=0在(1,2)内近似根的过程中,已经得到f (1)<0,f (1.5)>0,f (1.25)<0,则方程的根落在区间( ) A. ()1,1.25 B. ()1.25,1.5 C. ()1.5,2D. 不能确定【答案】B 【解析】 【分析】根据函数的零点存在性定理,由f (1)与f (1.5)的值异号得到函数f (x )在区间(1,1.5)内有零点,同理可得函数在区间(1.25,1.5)内有零点,从而得到方程0833=-+x x 的根所在的区间.【详解】解:∵f (1)<0,f (1.5)>0,∴在区间(1,1.5)内函数()338xf x x =+-存在一个零点 又∵f (1.5)>0,f (1.25)<0,∴在区间(1.25,1.5)内函数()338x f x x =+-存在一个零点, 由此可得方程0833=-+x x 的根落在区间(1.25,1.5)内, 故选:B .【点睛】本题给出函数的一些函数值的符号,求相应方程的根所在的区间.着重考查了零点存在定理和方程根的分布的知识,考查了学生分析解决问题的能力,属于基础题.4.下列函数中,在其定义域内既为奇函数且又为增函数的是( ) A. ()1f x x=-B. ()3f x x =C. ()f x x =D.()332x xf x -+=【答案】B 【解析】 【分析】根据函数奇偶性和单调性的性质分别进行判断即可. 【详解】解:A .函数是奇函数,在定义域上不是单调函数 B .函数是奇函数,在(-∞,+∞)上是增函数,满足条件. C .)()(x f x f =-,函数是偶函数,不满足条件. D .)()(x f x f =-,函数是偶函数,不满足条件. 故选:B .【点睛】本题主要考查函数奇偶性和单调性的判断,要求熟练掌握常见函数的单调性和奇偶性.5.设P 是平面内的动点,AB 是两个定点,则属于集合{P |PA =PB }的点组成的图形是( ) A. 等腰三角形B. 等边三角形C. 线段AB 的垂直平分线D. 直线AB【答案】C 【解析】 【分析】利用集合与线段的垂直平分线点性质即可得出结论.【详解】解:P 是平面内的动点,AB 是两个定点,则属于集合{P|PA=PB}的点组成的图形是线段AB 的垂直平分线. 故选:C .【点睛】本题考查了集合与线段的垂直平分线点性质,考查了推理能力与计算能力,属于基础题.6.已知a =log 20.3,b =20.1,c =0.21.3,则a ,b ,c 的大小关系是( ) A. a b c <<B. c a b <<C. b c a <<D.a cb <<【答案】D 【解析】 【分析】根据指数函数与对数函数单调性得到a ,b ,c 的取值范围,即得到它们的大小关系. 【详解】解:由对数和指数的性质可知,0.10 1.302log 0.3022100.20.21a b c a c b =<=>=<=<=∴<<,,,故选:D .【点睛】本题考查对数的性质,考查指数的性质,考查比较大小,在比较大小时,若所给的数字不具有相同的底数,需要找一个中间量,把要比较大小的数字用不等号连接起来.7.若3a=5b=225,则1a +1b=( ) A.12B. 14C. 1D. 2【答案】A 【解析】 【分析】先化对数式,再由换底公式可得结果. 【详解】解:35225a b ==35log 225,log 225a b ∴==则225225225111log 3log 5log 152a b +=+== 故选:A .【点睛】本题主要考查了指数与对数运算性质及对数的换底公式的简单应用,属于基础试题8.已知f (x )=()202(0)xx log x x ≤⎧⎪>⎨⎪⎩,若f (a )+f (1)=12,则a =( )A. 1B. 1-或11-【答案】D 【解析】 【分析】直接利用分段函数以及函数值转化求解即可. 【详解】解:211(1)log 10,()(1)()22f f a f f a ==+=∴=可得:0,122a a ≤⎧⎪⎨=⎪⎩或20,1log 2a a >⎧⎪⎨=⎪⎩,解得1a =-或a =D .【点睛】本题考查分段函数的应用,函数值的求法,考查分类讨论思想以及计算能力.9.如图中阴影部分的面积S 是h 的函数(其中0≤h ≤H ),则该函数的大致图象为( )A. B. C.D.【答案】D 【解析】 【分析】利用排除法求解.首先确定当h H =时,阴影部分面积为0,排除A 与B ,又由当2Hh =时,阴影部分的面积小于整个半圆面积的一半,排除C ,从而得到答案D . 【详解】解:∵当h H =时,对应阴影部分的面积为0, ∴排除A 与B ; ∵当2Hh =时,对应阴影部分的面积小于整个区域面积的一半,且随着h 的增大,S 随之减小,减少的幅度不断变小, ∴排除C . 从而得到答案D . 故选:D .【点睛】此题考查了函数问题的实际应用.注意排除法在解选择题中的应用,还要注意数形结合思想的应用.10.已知函数f (x )的定义域是R ,则实数a 的取值范围是 A. a >13 B. –12<a ≤0C. –12<a <0D. a ≤13【答案】B 【解析】 【分析】根据分母不为零列不等式,再根据不等式恒成立转化实数a 的满足条件,解得结果. 【详解】2a 30x ax +-≠由题意得恒成立,因此a =0或()2430a a a ≠⎧⎨∆=-⨯-<⎩,可得a =0或–12<a <0,即–12<a ≤0,故选B .【点睛】本题考查函数定义域以及不等式恒成立,考查转化化简与求解能力.11.已知函数f (x )=x +2x ,g (x )=x +ln x ,f (x )=x +12x 的零点分别为321,,x x x ,则321,,x x x 的大小关系为( ) A. 321x x x >>B. 231x x x >>C. 321x x x >>D.231x x x >>【答案】B 【解析】 【分析】将函数的零点问题转化为对应函数图象交点横坐标的问题,利用数形结合思想求解.【详解】解:在同一直角坐标系中,作出1234,2,ln ,x y x y y x y =-===图象,如图观察图象可知,函数()()()122,ln ,xf x xg x x x f x x x =+=+=+的零点分别为123,,x x x ,满足231,x x x >> 故选:B .【点睛】本题考查函数零点的求法,属于基础题目.12.设函数f (x )g (x )=ln (ax 2-3x +1),若对任意的x 1∈[0,+∞),都存在x 2∈R ,使得f (x 1)=g (x 2)成立,则实数a 的最大值为( ) A. 2 B.94C. 4D.92【答案】B 【解析】 【分析】先求函数f (x )值域,再根据题意得g (x )值域所需满足的条件,最后根据二次函数图象确定实数a 满足的条件,即得结果.【详解】解:设()()2ln 31g x ax x =-+的值域为A ,∵()1f x =[0,+∞)上的值域为(],0-∞, ∴(],0-∞⊆A ,∴()231h x ax x =-+至少要取遍(0,1]中的每一个数,又()01h =∴实数a 需要满足a ≤0或0940a a >⎧⎨=-≥⎩解得94a ≤. ∴故选:B .【点睛】本题考查函数值域以及二次函数性质,是中档题,解题时要认真审题,注意函数性质的合理运用.二、填空题(本大题共4小题,共12.0分) 13.若幂函数y =f (x )的图象经过点(9,13),则f (25)的值是______. 【答案】15【解析】幂函数()y f x =的图象经过点19,3⎛⎫ ⎪⎝⎭,设幂函数(),fx x αα=为常数,119,32αα∴=∴=-,故()()()11221,25255f x x f --===,故答案为15.14.函数213log (23)y x x =+-的单调增区间为 . 【答案】()--3∞,【解析】试题分析:,3x <-或1x >,在3x <-时递减,在1x >时递增,又13log y u =单调递减,所以原函数单调减区间是(,3)-∞-.考点:函数的单调性.【名师点晴】本题考查复合函数的单调性,函数(),y g t t M =∈,()t h x =,()t h x =的值域为N ,且N M ⊆,则复合函数(())y g h x =的单调性与(),()g t h x 的关系是:(),()g t h x 同增或同减时,(())y g h x =是单调递增,当(),()g t h x 的单调性相反时,(())y g h x =是单调递减.求函数的单调区间必先求函数的定义域,象本题由得3x <-或1x >,然后在区间(,3)-∞-和(1,)+∞上分别研究其单调性即可.15.关于x 的方程2015x =235aa+-有实数根,则实数a 的取值范围为______. 【答案】(-23,5) 【解析】 【分析】先求2015xy =的值域,再解不等式得结果.【详解】解:设2015xy =,则y 的值域为(0,+∞),即3220,(32)(5)0.,5.53a a a a a ∴+⎛⎫<∴+-<∈- ⎪-⎝⎭【点睛】本题考查了指数函数的值域,分式不等式的解法,属于基础题.16.给出下列五个命题:①函数f (x )=2a 2x -1-1的图象过定点(12,-1); ②已知函数f (x )是定义在R 上的奇函数,当x ≥0时,f (x )=x (x +1),若f (a )=-2则实数a =-1或2. ③若log a12>1,则a 的取值范围是(12,1); ④若对于任意x ∈R 都f (x )=f (4-x )成立,则f (x )图象关于直线x =2对称; ⑤对于函数f (x )=ln x ,其定义域内任意x 1≠x 2都满足f (122x x +)≥()()122f x f x + 其中所有正确命题的序号是______. 【答案】③④⑤ 【解析】 【分析】由指数函数的图象的特点解方程可判断①;由奇函数的定义,解方程可判断②;由对数不等式的解法可判断③;由函数的对称性可判断④;由对数函数的运算性质可判断⑤.【详解】解:①函数21()21x f x a -=-,则1()12f =,故①错误;②因为当0≥x 时, ()(1)0f x x x =+≥,且(1)2f =,所以由函数f (x )是定义在R 上的奇函数得(1)2()1f f a a -=-=∴=-,故②错误; ③若1log 12a>,可得112a >>,故③正确; ④因为)4()(x f x f -=,则f (x )图象关于直线x=2对称,故④正确;⑤对于函数()()12121212ln ln ()ln ,ln ln 2222f x f x x x x x x x f x x f ++++⎛⎫==≥==⎪⎝⎭当且仅当12x x =取得等号,其定义域内任意12x x ≠都满足()1212()22f x f x x x f ++⎛⎫≥⎪⎝⎭,故⑤正确.故答案为:③④⑤.【点睛】本题考查函数的单调性、奇偶性和对称性、凹凸性,以及函数图象,考查运算能力和推理能力,属于中档题.三、解答题(本大题共4小题,共40.0分) 17.已知集合A ={x |x 2-4x +3≤0},B ={x |log 2x >1}, (I )求A∩B,(∁R B )∪A;(II )若{x |1<x <a }⊆A ,求实数a 的取值范围.【答案】(Ⅰ)A ∩B ={x |2<x ≤3},(∁R B )∪A ={x |x ≤3}.(Ⅱ)a ≤3. 【解析】 【分析】(Ⅰ)先解不等式得集合A ,B ,再根据交集、补集、并集定义求结果,(II )根据子集为空集与非空分类讨论,解得结果.【详解】解:(Ⅰ){}{}22|430{|13},|log 1{|2}A x x x x x B x x x x =-+≤=≤≤=>=>则{|23},{|2}R AB x xC B x x =<≤=≤,(){|3}R C B A x x =≤(Ⅱ)若{|1}x x a <<=∅,即1a ≤,满足条件, 若{|1}x x a <<≠∅,则需1313a a a >≤∴<≤,综上3≤a .【点睛】本题考查集合交并补运算以及解不等式,考查基本运算求解能力,属基础题.18.某种树苗栽种时高度为A(A 为常数)米,栽种n 年后的高度记为f(n).经研究发现f(n)近似地满足 f(n)=9nA a bt +,其中232t -=,a ,b 为常数,n∈N,f(0)=A .已知栽种3年后该树木的高度为栽种时高度的3倍.(1)栽种多少年后,该树木的高度是栽种时高度的8倍; (2)该树木在栽种后哪一年的增长高度最大.【答案】(1)栽种9年后,该树木的高度是栽种时高度的8倍;(2)第5年的增长高度最大. 【解析】试题分析:(1)由题中所给条件()()033f A f A =,=,运用待定系数法不难求出18a b =,=,进而确定出函数9f(n)+18n A t+⨯,其中2-3t 2=.由()8f n A =,运用解方程的方法即可求出9n =,问题得解; (2)由前面(1)中已求得9f(n)=18nAt +⨯,可表示出第n 年的增长高度为()(1)f n f n ∆=--=1991818n n A A t t --+⨯+⨯,这是一个含有较多字母的式子,这也中本题的一个难点,运用代数化简和整体思想可得:n172(1)1+64t +8(t+1)n A t t --∆=,观察此式特征能用基本不等式的方法进行求它的最值,即:n 172(1)1+64t +8(t+1)n A t t--≤,成立的条件为 当且仅当n1164t n t-=时取等号,即可求出5n =.试题解析: (1)由题意知()()033f A f A =,=. 所以9=A {9=3A 1b 4Aa b A a ++解得18a b =,=. 4分所以9f(n)+18nA t +⨯,其中2-3t 2=. 令()8f n A =,得9=8A 18nA t +⨯,解得n1t 64=,所以9n =.所以栽种9年后,该树木的高度是栽种时高度的8倍. 6分 (2)由(1)知9f(n)=18nAt+⨯. 第n 年的增长高度为()(1)f n f n =--=1991818n n A At t --+⨯+⨯. 9分所以11112172(1)72(1)(18)(18)18(1)64n n n n n n At t At t t t t t t -------∆+⨯+⨯+++== n 172(1) =1+64t +8(t+1)n A t t--12分≤当且仅当n1164t n t -=,即2(21)-31264n -=时取等号,此时5n =. 所以该树木栽种后第5年的增长高度最大. 14分 考点:1.待定系数法求解;2.函数的最值;3.基本不等式的运用19.已知函数()f x 是二次函数,且满足()()()01,125f f x f x x =+-=+;函数()()01x g x a a a =>≠且.(1)求()f x 的解析式; (2)若()124g =,且()g f x k ⎡⎤≥⎣⎦对[]1,1x ∈-恒成立,求实数k 的取值范围. 【答案】(1)2()41f x x x =++(2)【解析】试题分析:(1)用待定系数法设()f x 的解析式,由已知条件可求得三个系数;(2)由()f x 的解析式可得当[]1,1x ∈-时()f x 的值域,由()124g =可得的解析式,由的单调性可得的最小值,由()g f x k ⎡⎤≥⎣⎦可得.试题解析:(1)设()()20f x mx bx c m =++≠.()()20 1.1f c f x mx bx ==∴=++.()()()()2211111f x f x m x b x mx bx ∴+-=++++---22 5.mx m b x =++=+ 1,4m b ∴==.()241f x x x ∴=++.(2)()()24121112...422x x g a a g f x ++⎛⎫⎡⎤==∴=∴= ⎪⎣⎦⎝⎭()f x 开口向上,对称轴2x =-.()f x ∴在[]1,1-上单调递增,()()max 16f x f ∴==.()6min12g f x ⎛⎫⎡⎤∴= ⎪⎣⎦⎝⎭,611264.k ⎛⎫∴≤=⎪⎝⎭. 考点:二次函数的值域、指数函数的单调性.【易错点晴】本题主要考查了二次函数图象与性质及指数函数的单调性的阴功,其中第一问主要考查待定系数求二次函数,由题中的条件很容易求出函数的解析式;第二问由()124g =求出的解析式,只要注意()f x 的值域和的单调性很容易求出[]1,1x ∈-时的值域,这样的能求.本题也是围绕着函数的性质来进行考查的,着重了值域的考查,难度中等.20.已知函数f (x )=log m33x x -+(m >0且m ≠1), (I )判断f (x )的奇偶性并证明; (II )若m=12,判断f (x )在(3,+∞)的单调性(不用证明); (III )若0<m <1,是否存在β>α>0,使f (x )在[α,β]的值域为[log m m (β-1),log m (α-1)]?若存在,求出此时m 的取值范围;若不存在,请说明理由.【答案】(Ⅰ)f (x)是奇函数(Ⅱ)见解析(Ⅲ)204⎛⎫ ⎪ ⎪⎝⎭,.【解析】 【分析】(Ⅰ)先求定义域,再判断()f x -与f (x )关系,最后根据奇偶性定义作判断与证明,(Ⅱ)根据单调性定义进行判断,(Ⅲ)先根据单调性确定方程组,转化为一元二次方程有两正根,再根据二次方程实根分布列方程,最后解不等式组得结果. 【详解】解:(Ⅰ)f (x )是奇函数;证明如下: 由303x x -+>解得x <-3或x >3, 所以f (x )的定义域为(-∞,-3)∪(3,+∞),关于原点对称. ∵()3333mm x x f x log log x x --+-==-+-=()13()3m x log f x x -+=--, 故f (x )为奇函数/(Ⅱ)任取x 1,x 2∈(3,+∞)且x 1<x 2,()()1212123333mm x x f x f x log log x x ---=-++=()()()()12123333m x x log x x -++-,∵(x 1-3)(x 2+3)-(x 1+3)(x 2-3)<0,∴(x 1-3)(x 2+3)<(x 1+3)(x 2-3), 即()()()()121233133x x x x -++-<,当m =12时,()()()()12112233033x x log x x -++-<,即f (x 1)<f (x 2). 故f (x )在(3,+∞)上单调递减.(Ⅲ)由(Ⅱ)知,当0<m <1时,f (x )在[α,β]上单调递减.假设存在β>α>0,使f (x )在[α,β]的值域为[log m m (β-1),log m (α-1)].则有()()313313m m m m log log m log log m αααβββ-⎧=-⎪+⎪⎨-⎪=-+⎪⎩,∴()()313313m m αααβββ-⎧=-⎪+⎪⎨-⎪=-+⎪⎩.所以α,β是方程()313x m x x -=-+的两正根, 整理得mx 2+(2m -1)x -3m +3=0在(0,+∞)有2个不等根α和β. 令h (x )=mx 2+(2m -1)x -3m +3,则h (x )在(0,+∞)有2个零点,()010*********m h m m m h m ⎧⎪⎪⎪--⎨⎪⎪-⎛⎫-⎪ ⎪⎝⎭⎩<<.>,>,<,解得0m <,故m 的取值范围为0⎛ ⎝⎭.【点睛】本题考查函数奇偶性、单调性以及一元二次方程实根分布,考查数形结合思想方法以及等价转化思想方法,考查综合综合分析与求解能力,属难题.。
2018-2019学年四川省绵阳市南山中学高一下学期4月月考数学试题(解析版)

2018-2019学年四川省绵阳市南山中学高一下学期4月月考数学试题一、单选题 1.数列1111,,,261220,……的一个通项公式是( ) A .1(2)n a n n =+B .12(21)n a n n =-C .111n a n n =-+ D .11n a n=-【答案】C【解析】用通项公式去求数列的项,有不符合的就排除. 【详解】 A 中113a =,不合,B 中2112a =,不合;D 中10a =,不合, C 中111n a n n =-+时,12341111,,,261220a a a a ====,符合.故选:C. 【点睛】本题考查数列的通项公式,已知数列的前几项,选择通项公式,可以代入检验.2.在△ABC 中,角C 为90°,AB u u u r =(k,1).AC uuu r =(2,3)则k 的值为( )A .5B .-5C .32D .-3 2【答案】A【解析】:∵()AB k,1=u u u r .()AC 2,3=u u u r则 (22)90?02(2)605BC k C AC BC k k -∠=︒∴∴-+∴u u u v u u u v u Q u u v =,===故选A .3.在ABC V 中,角A ,B ,C 所对的边分别为a ,b ,c ,若60751B C a =︒=︒=,,,则b =( )A .B .14C D .12【答案】C【解析】由正弦定理可求解. 【详解】由题意45A =︒,由sin sin a b A B =得sin 1sin 60sin sin 452a Bb A ⨯︒===︒. 故选:C. 【点睛】本题考查正弦定理,掌握正弦定理是解题基础.利用正弦定理可解决两类问题 1.已知两角及其中一角的对边,如A ,B ,a ①由A +B +C =180°,求出C ; ②根据正弦定理,得sin a A =sin b B 及sin aA =sin c C,求出边b ,c 2. 已知两边及其中一边所对的角,如a ,b ,A ①根据正弦定理,经讨论求B ;②求出B 后,由A +B +C =180°,求出C ; ③再根据正弦定理sin aA =sin c C,,求出边c . 也可以根据余弦定理,列出以边c 为元的一元二次方程c 2-(2b cos A )c +(b 2-a 2)=0,根据一元二次方程的解法,求边c ,然后应用正弦定理或余弦定理,求出B ,C4.在△ABC 中,已知|AB u u u r |=1,|BC uuu r ,CA u u u r =2,则AB u u u r .AC uuur =( )A .12B .1C D .-1【答案】B【解析】由题在ABC V 中,已知|AB u u u r|=1,|BC uuu r |=, CA 2,=u u u v 可知ABC V 为直角三角形,且,3A π∠= 则1AB AC AB AC cos 12 1.2A u u u v u u u v u u u v u u u v ⋅=⋅∠=⨯⨯=故选B.5.在等差数列{}n a 中,已知16101596a a a a +++=,则9102a a -=( ) A .20 B .22C .24D .26【答案】C【解析】用基本量法,全部用首项1a 和公差d 表示. 【详解】16101511111591442896a a d a d a a d a d a a a =++++++=++++=,∴1724a d +=,∴91011122(8)(9)724a a a d a d a d -=+-+=+=. 故选:C. 【点睛】本题考查等差数列的通项公式,考查基本量计算,解题时可把已知式,求值式都用首项和公差表示即可得出结论,本题也可能等差数列的性质计算,可减少计算量. 6.如图,四边形ABCD 是正方形,延长CD 至点E ,使得DE CD =.若点P 为线段DC 上的点,CP PD =.且AP mAE nAB =+u u u r u u u r u u u r,则m n -=( )A .1B .12C .1-D .12-【答案】D【解析】选取,AB AD u u u r u u u r为基底,其他向量都用基底表示,可得.【详解】由题意P 是CD 中点,12AP AD DP AD AB =+=+u u u r u u u r u u u r u u u r u u u r ,()()mAE nAB m AD DE nAB m AD CD nAB +=++=++u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r ()m AD AB nAB =-+u u u r u u u r u u u r ()mAD n m AB =+-u u u r u u u r ,∵AP mAE nAB =+u u u r u u u r u u u r ,∴112m n m =⎧⎪⎨-=⎪⎩,解得132m n =⎧⎪⎨=⎪⎩,∴12m n -=-. 故选:D. 【点睛】本题考查平面向量基本定理,解题时选取基底,用基底表示其他向量进行运算即可. 7.若()()3a b c b c a bc +++-=,且sin 2sin cos A B C =,那么ABC V 是( ) A .直角三角形 B .等边三角形 C .等腰三角形D .等腰直角三角形【答案】D 【解析】【详解】解析:由题设可得2222221cos ,223b c a b c a bc A A bc π+-+-=⇒==⇒=由题设可得222222cos 202a b c a b C a b b c b c ab+-=⇒=⇒-=⇒=,即该三角形是等边三角形,应选答案B .8.已知周长为12的钝角ABC V 的三边长是公差为d (公差大于0)的等差数列,则公差d 的取值范围是( ) A .(0,2) B .(0,4)C .(1,2)D .(2,4)【答案】C【解析】由等差数列性质得出中间的边长,再由公差表示出最长边和最短边,然后由余弦定理得出不等关系,同时注意三边需能构成三角形. 【详解】设三边长为,,m d m m d -+,则312m d m m d m -+++==,4m =, 三角形最大内角记为α,三角形是钝角三角形,则222(4)4(4)cos 024(4)40444d d d d d d α⎧-+-+=<⎪⨯⨯-⎪⎪->⎨⎪-+>+⎪⎪⎩, 解得12d <<. 故选:C. 【点睛】本题考查等差数列的性质,考查余弦定理.解题中要注意三线段能构成三角形必须满足两较小线段长度之和大于最长的线段长.9.校运动会开幕式上举行升旗仪式,旗杆正好处在坡度为15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为m (如图所示),旗杆底部与第一排在一个水平面上.若国歌时长为50s ,升旗手匀速升旗的速度为( )A .0.4m /sB .0.6m /sC .0.8m /sD .1m /s【答案】B【解析】在AEC ∆中由正弦定理求得AC ,然后在直角ABC ∆中求得旗杆AB 的高度,可得升旗的速度. 【详解】由题意301545AEC ∠=︒+︒=︒,1801560105ACE ∠=︒-︒-︒=︒,∴30EAC ∠=︒, 在AEC ∆中由sin sin AC ECAEC EAC=∠∠,所以sin 106sin 30203sin EC AEC AC EAC ∠︒===∠,在直角ABC ∆中,3sin 6020330AB AC =︒==, ∴300.6(/)50t m s ==. 故选:B. 【点睛】本题考查解三角形应用,在三角形中由已知条件确定选用正弦定理还是用余弦定理是解题关键.10.在△ABC 中, a,b,c 分别为A,B,C 的对边,若2,a b a csin B sinAsinC a c c+-==+ a=6,则△ABC 的外接圆的面积( ) A .12π B .24π C .36π D .48π 【答案】A【解析】由题设及正弦定理,根据2,sin B sinAsinC =可得2,b ac = 又a b a ca c c+-=+,可得22ac bc a c +=-,将2,b ac =代入可得2221,0,,223b c a cosA AA bc ππ+-==<<∴=Q设ABC V 的外接圆半径为,R 则由正弦定理可得2,23,sin 3a R R A ==∴= 故ABC V 的外接圆面积为212.R ππ= 故选A.11.在△ABD 中,AB=2,AD=22,E ,C 分别在线段AD,BD 上,且AE=13AD .BC=34BD,AC BE ⋅u u u r u u u r =113则∠A=( )A .4π B . 3πC .23π D .3 4π【答案】D 【解析】【详解】根据题意,()3313AC AB AB BC BD AB AD AB AB AD,4444=+=+=+-=+u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v1BE AE AB AD AB,3=-=-u u u v u u u v u u u v u u u v u u u v22131112AC BE AB AD AD AB AB AD AD AB 443443⎛⎫⎛⎫∴⋅=+-=-+-⋅ ⎪⎪⎝⎭⎝⎭u u u v u u u v u u u v u u u v u u u v u u u v u u uv u u u v u u u v u u u v(22112222AD AB AD AB 1134,443=-⨯+⨯-⋅=⇒⋅=-u u uv u u u v u u u v u u u vAD AB 23cos ,0,,24AD ABA A A u u u v u u u v u u u Q v u u u v ππ⋅∴∠==-<<∴=⋅ 故选D.12.在ABC V 中,a ,b ,c 分别为A ,B ,C 的对边,O 为ABC V 的外心,33AB BC AC +=,sin (cos 3)cos sin 0C A C A +=.若,(,)AO x AB y AC x y R =+∈u u u r u u u r u u u r ,则xy=( )A .1B .1-C 3D .3【答案】B【解析】由两角和的正弦公式及诱导公式可得sin B C =,从而有b =,代入3AB BC AC +=得三边关系,然后用余弦定理求得ABC ∠,设一边长BC a =,这样AB AC ⋅uu u r uuu r可表示,对AO x AB y AC =+u u u r u u u r u u u r .分别与,AB AC u u u r u u u r 点乘,可得,x y 的方程组,求得,x y . 【详解】由sin (cos cos sin 0C A C A +=得sin cos cos sin C A C A C +=,即sin()C A C +=,∴sin B C =,即b =,代入3AB BC AC +=,有AB BC =,设AB BC a ==则AC =,由余弦定理222cos2BAC ∠==,30BAC ︒∠=, 由2AO AB xAB yAC AB ⋅=+⋅u u u r u u u r u u u r u u u r u u u r,(,)x y R ∈,得221()cos302AB xAB y AC AB =+⋅︒u u ur u u u r u u u r u u u r , 2221322a xa ya =+,∴有1322x y =+, 同理由2,(,)AO AC xAB AC yAC x y R ⋅=⋅+∈u u u r u u u r u u u r u u u r u u u r ,得33322x y =+,于是可得11x y =-=,.∴1xy=-. 故选:B. 【点睛】本题考查平面向量的数量积,考查平面向量的线性运算.考查两角和的正弦公式、诱导公式,考查正弦定理和余弦定理,考查知识点较多.其中三角形外心的向量性质一定要注意:O 是ABC ∆外心,则212AB AO AB ⋅=u u u r u u u r u u u r .本题属于中档题.二、填空题13.已知向量(1,2),(1,0)a b ==r r ,点()()0,13,5C D ,,若λ为实数,()//a b CD λ+u u u r r r,则λ=_____.【答案】12【解析】由向量平行的坐标表示可计算. 【详解】由题意(1,2)λλ+=+r ra b ,(3,4)CD =u u u r ,∵()//a b CD λ+u u u rr r,∴4(1)6λ+=,12λ=. 故答案为:12. 【点睛】本题考查向量平行的坐标运算,属于基础题.14.在ABC V 中,60,3A a b ︒∠===,则ABC V 解的情况是_____(填“无解”、“一解”或“两解”). 【答案】无解【解析】由正弦定理确定. 【详解】由正弦定理得sin sin 14b A B a ===>,无解. 故答案为:无解. 【点睛】本题考查用正弦定理解三角形,判断解的个数,可以由正弦定理求出角的正弦,由正弦值来判断角的个数,同时注意大边对大角的性质即可.15.设△ABC 的内角A,B,C 所对边的长分别是a,b,c,且b=3,c=1,A=2B .则a 的值为_______【答案】【解析】在ABC V 中,231a bA B b c sinA sinBQ ,=,,,=== 可得3,2a sinBcosB sinB= 整理得6a cosB =,∴由余弦定理可得21962a a a a+-=⨯∴=, ,故答案为16.在△ABC 中,角A 是B,C 的等差中项,∠BAC 的平分线交BC 于点D,若AB=4,且AD u u u r =1AC 4u u u r +λAB u u u r(λ∈R)则AD 的长为_______【答案】33【解析】因为角B 是,A C 的等差中项,,3B π∴=又因B D C ,,三点共线,所以有131,44,λλ+=∴= ,如图,过点D 分别作AC AB ,的平行线交AB AC ,于点M N ,,则13 44AN AC AM AB ==u u u v u u u v u u u u v u u u v,, ABC QV 中,3A A π∠=∠, 的平分线交BC 于D ,AMDN ∴是菱形,4333AB AN AM AD =∴==∴=Q ,,. 故答案为3【点睛】本题考查向量在几何中的应用,考查学生的计算能力,其中确定3==AN AM 是解题的关键.三、解答题17.已知等差数列{}n a 满足125310,4a a a a +==+. (1)求{}n a 的通项公式;(2)记{}n a 的前n 项和为n S ,若122k k S a a +<+,求正整数k 的值. 【答案】(1)22n a n =+(2)1k =.【解析】(1)求出公差d 和首项1a 可得通项公式;(2)求出和n S ,代入不等式122k k S a a +<+可化为k 的二次不等式,解之可得,只是要注意*k N ∈. 【详解】 解:(1)32152,1053a d a a a -==+=-, 即1110a a d ++=,所以14a =, 所以42(1)22n a n n =+-=+. (2)212(1)423,22n k k n n S n n n S a a +-=+⨯=+<+, 即2(1)3(1)2(22)6k k k +++<++,即260k k +-<,32k ∴-<<,又因为k 是正整数,所以1k =.【点睛】本题考查等差数列的通项公式和前n 项和公式,方法是基本量法.属于基础题.18.已知平面向量34,55a ⎛⎫= ⎪⎝⎭r,||2b =r ,a 与b 夹角为4π. (1)求向量a r在b r方向上的投影;(2)求a b -r r 与a b +rr 夹角的余弦值.【答案】(1)2;(2) 5. 【解析】试题分析:(1)由向量数量积的几何意义可求向量a r在b r方向上的投影; (2)由向量夹角公式可求a r -b r 与a r +b r的夹角的余弦值 试题解析:(1)|a r|=|(34,55)|=1 ∴向量a r 在b r 方向上的投影为a r cosθ=a ?b b r r r(2)cos<a r -b r ,a r +b r>=()()a b a b a ba br r r r rr r r -+-+ |a r -b r|2=|a r|2+|b r|2-2ab rr =12,|ab -r r |=2. |a b +rr|2=|a r|2+|b r|2+2ab rr =52,|a b+r r (a b -rr)(a b +rr)=a r2-b r2=12 cos<,a b a b -+r r r r >=()()a b a b a b a b r r r r r r r r -+-+19.在ABC ∆中,边a ,b ,c 分别是角A ,B ,C 的对边,且满足cos (3)cos b C a c B =-.(1)求cos B ;(2)若ABC ∆的面积为b =ABC ∆的周长.【答案】(1)cosB=13;(2) 8+【解析】试题分析:(1)利用正弦定理把题设等式中的边换成角的正弦,进而利用两角和公式化简整理求得cos B 的值.(2)由 3及△ABC 的面积为,可得 12ac = ,可求ABC V 的周长再由余弦定理可得22 40a c += ,由此求得边a c , 的值.试题解析:(1)由正弦定理,sinBcosC=(3sinA-sinC)cosB即sin(B+C)=3sinAcosB,sinA=3sinAcosB(sinA>0)所以cosB=13.3,S=12,所以ac=12 由余弦定理,cosB=222a c b 2ac +-=()22a c 2ac b 2ac+--=13所以.【点睛】本题以三角形为载体,主要考查了正弦定理、余弦定理的运用,考查两角和公式.考查了学生综合分析问题和解决问题的能力,属于中档题.20.已知四边形ABCD 内接于圆O .(1)若60,10,6,4ABC AB BC CD ︒∠====,求AD ;(2)若1,4AC BC ADB π==∠=,求22AD DC +的取值范围. 【答案】(1)6AD =(2)22[4,6)AD DC +∈【解析】(1)在ABC V 中,由余弦定理求得AC ,在ADC V 中,再用余弦定理可求得AD ;(2)由圆周角定理得4ACB π∠=,ABC V 中由余弦定理得AB ,再由余弦定理得ABC ∠,从而得ADC ∠,在ADC V 中,应用正弦定理,并令ACD θ∠=,则22AD DC +可表示为θ的三角函数,由两角和与差的正弦公式、二倍角公式化为一个角的一个三角函数形式,由(0,)3π∈θ可求得取值范围.【详解】解(1)ABCD 四点共圆,所以ABC ADC π∠+∠=.在ABC V 中,由余弦定理得2222cos AC AB BC AB BC ABC =+-⋅∠, 所以276AC =.在ADC V 中,由余弦定理得2222cos AC AD DC AD DC ADC =+-⋅∠.所以6AD =.(2),44ADB ACB ππ∠=∴∠=Q ,ABC V 中由余弦定理得,2222cos AB AC BC AC BC ACB =+-⋅∠,所以22212,cos 22AB BC AC AB ABC AB BC +-=∠===⋅ 所以2,33ABC ADC ππ∠=∠=.在ADC V 中,由正弦定理得sin sin sin AC AD CD ADC ACD CAD ===∠∠∠所以,AD ACD CD CAD =∠=∠, 令ACD θ∠=,则3CAD πθ∠=-,2222)3AD DC πθθ⎡⎤⎛⎫+=+- ⎪⎢⎥⎝⎭⎣⎦2210sin 6cos cos θθθθ=+-264sin cos θθθ=+-8(2cos 22)θθ=-+84sin 26πθ⎛⎫=-+ ⎪⎝⎭. 50,,2,3666ππππθθ⎛⎫⎛⎫∈∴+∈ ⎪ ⎪⎝⎭⎝⎭Q , 1sin 2,162πθ⎛⎫⎛⎤∴+∈ ⎪ ⎥⎝⎭⎝⎦, 22[4,6)AD DC ∴+∈.【点睛】本题考查正弦定理、余弦定理解三角形,考查三角函数二倍角公式和两角和与差的正弦公式,考查正弦函数性质.解三角形问题要关注正弦定理、余弦定理、三角形内角和定理、三角形面积公式,要适时、适度进行“角化边”或“边化角”,要抓住能用某个定理的信息.一般地,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式,则考虑用正弦定理;以上特征都不明显时,则两个定理都有可能用到.。
四川省绵阳中学2018-2019学年高一下学期第三次月考数学试题 含解析

绵阳中学高2018级高一下期第三学月考试数学试题一、选择题:本大题共12小题,每题4分,共48分. 1.若,,a b c ∈R 且a b >,则下列不等式成立的是( ) A. 22ac bc > B.11a b< C.b a a b< D.||1||1a bc c >++【答案】D 【解析】 【分析】利用作差法对每一个选项逐一判断分析.【详解】选项A, 222()0,ac bc a b c -=-≥所以a ≥b,所以该选项错误;选项B, 11b a a b ab--=,符合不能确定,所以该选项错误; 选项C, ()()b a b a b a a b ab+--=,符合不能确定,所以该选项错误;选项D,0||1||1||1a b a b c c c --=>+++,所以||1||1a bc c >++,所以该选项正确. 故选:D【点睛】本题主要考查实数大小的比较,意在考查学生对该知识的理解掌握水平和分析推理能力.2.若,a b 是互相垂直的单位向量且()(3)a b a b λ+⊥+,则λ=( ) A. 3 B. -3C. 1D. -1【答案】B【解析】 【分析】由向量垂直的数量积表示化简求解.【详解】由题得22()(3)=+3+1+3a b a b a b a b λλλ+⋅+⋅rrrrrrrr ()=+3+0=0=-3.λλ∴,故选:B【点睛】本题主要考查向量垂直的数量积表示,考查数量积的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力.3.已知数列{}n a 为等比数列,且12a =,58a =,则3a =( ) A. 5 B. 4±C. 4D. -4【答案】C 【解析】 【分析】利用等比中项的性质求解.【详解】由题得231532816,4a a a a ==⨯=∴=±.因为等比数列的奇数项同号,所以34a =. 故选:C【点睛】本题主要考查等比数列的性质和等比中项的应用,意在考查学生对这些知识的理解掌握水平和分析推理能力.4.下列4个命题中,两直线,a b ,平面α:①若a b ∥,则a 平行于经过b 的任何平面;②若直线a ∥平面α,则a 与α内任一直线平行;③若a α,b α,则a b ∥;④a b ∥,a α,α⊄b ,则b α.正确命题个数为( ) A. 0 B. 1C. 2D. 3【答案】B 【解析】 【分析】利用空间直线和平面的位置关系对每一个命题逐一判断得解.【详解】①若a b ∥,则a 平行于经过b 的任何平面,是错误的,因为a,b 有可能在一个平面内; ②若直线a ∥平面α,则a 与α内任一直线平行,是错误的,因为a 与α内任一直线平行或异面; ③若a α,b α,则a b ∥,是错误的,因为a 和b 可能平行,相交或异面; ④a b ∥,a α,α⊄b ,则b α.是正确的; 故选:B【点睛】本题主要考查空间直线和平面的位置关系,意在考查学生对这些知识的理解掌握水平和分析推理能力.5.已知变量,x y 满足约束条件10040x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩,则2z x y =+的最大值为( )A. 8B. 7C. 6D. 4【答案】B 【解析】 【分析】先画出满足约束条件1040x x y x y ⎧⎪-⎨⎪+-⎩………的平面区域,然后求出目标函数z x y =+取最大值时对应的最优解点的坐标,代入目标函数即可求出答案.【详解】满足约束条件1040x x y x y ⎧⎪-⎨⎪+-⎩………的平面区域如下图所示:作直线0:20l x y +=把直线向上平移可得过点(1,3)时2x y +最小 当1x =,3y =时,2z x y =+取最大值 7, 故答案为 7.【点睛】本题考查的知识点是简单线性规划,其中画出满足约束条件的平面区域,找出目标函数的最 优解点的坐标是解答本题的关键.6.圆台上底半径为2,下底半径为6,母线长为5,则圆台的体积为( ) A. 40π B. 52π C. 50πD.2123π 【答案】B【解析】 【分析】作出圆台的轴截面,由圆台的上、下底面半径分别为2,6,构造直角三角形,结合母线长 为5,由勾股定理求出圆台的高.再求圆台的体积. 【详解】作出圆台的轴截面如图所示:上底面半径2MD =,下底面半径6NC =,过D 做DE 垂直NC , 则624EC =-= 由5CD = 故3DE = 即圆台的高为3,所以圆台的体积为2213(26523V πππ=⋅⋅⋅+⋅+=.故选:B .【点睛】本题考查的知识点是旋转体及其体积的计算,圆台的几何特征,其中画出轴截面,将空间问题转化为平面问题是解答的关键.7.已知{}n a 是正项等比数列且2754a a a ⋅=,4a 与62a 的等差中项为18,则5a =( ) A. 2 B. 4C. 8D. 16【答案】C 【解析】 【分析】由题得到关于1,a q 的方程组,解方程组即得1,a q 的值,再求5a 得解.【详解】由题得641113511141236,,220a q a q a q a q a q a q q ⎧⋅=⎪+=∴==⎨⎪>⎩.所以451282a =⋅=. 故选:C【点睛】本题主要考查等比数列的性质和等差中项的应用,意在考查学生对这些知识的理解掌握水平和分析推理能力.8.已知||1,||1a b ==,a 与b 夹角为3π,则a b -与b 的夹角为( ) A. 60︒ B. 90︒C. 120︒D. 150︒【答案】C 【解析】 【分析】先求出||a b -,再代向量的夹角公式求解即可.【详解】由题得||1a b -==r r ,所以a b -与b 的夹角为11()12cos =112||||a b a b a b α--⋅==-⋅-⋅r r r r r r, 所以两向量的夹角为120︒. 故选:C【点睛】本题主要考查向量的夹角的求法,考查平面向量的数量积的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力.9.关于x 的不等式0ax b ->的解集为(,1)-∞,则关于x 的不等式(2)()0x ax b -+>的解集为( )A. ()12, B. ()12-, C. (,1)(2,)-∞-+∞ D. (,1)(2,)-∞⋃+∞【答案】C 【解析】由已知0a b =>,不等式()(2)0ax b x +->为(1)(2)0a x x +->,所以1x <-或2x >,故选C .10.点O 为ABC △所在平面内一点,,||||AB AC OA OB OA OC AO AB AC λ⎛⎫⋅=⋅=+ ⎪⎝⎭则ABC △的形状为( )A. 直角三角形B. 等腰三角形C. 等腰直角三角形D. 等边三角形【答案】B 【解析】 【分析】由,OA OB OA OC ⋅=⋅得OA 和BC 垂直,由||||AB AC AO AB AC λ⎛⎫=+ ⎪⎝⎭得到OA 是∠BAC 的角平分线,综合即可判断△ABC 的形状. 【详解】,)0OA OB OA OC OA OB OC OA CB ⋅=⋅∴⋅-=⋅=(,所以OA BC ⊥.||||AB AC AO AB AC λ⎛⎫=+ ⎪⎝⎭∴AO 在∠BAC 的角平分线上,所以AO 既在BC 边的高上,也是∠BAC 的平分线, 所以△ABC 是等腰三角形. 故选:B【点睛】本题主要考查平面向量的加法法则和减法法则的几何应用,意在考查学生对这些知识的理解掌握水平和分析推理能力.11.在ABC △中,2a =,sin()sin 2B Ca A B c +⋅+=⋅,则ABC △周长的最大值为( ) A. 8 B. 7C. 6D. 5【答案】C 【解析】 【分析】先由sin()sin2B C a A B c +⋅+=⋅得到A=3π,再利用基本不等式求b+c 的最大值,即得三角形周长的最大值.【详解】由题得sin cos ,2Aa C c ⋅=⋅所以sin sin sin cos ,2AA C C ⋅=⋅所以sin cos ,2sin cos cos 2222A A A AA =∴=,因为(0,),cos 0,222A Aπ∈∴≠所以1sin =223A A π∴=,.由余弦定理得22224=2cos b c bc A b c bc +-=+-,所以22())43434b c b c bc ++=+≤+⋅(, 当且仅当b=c=2时取等. 所以4,6b c a b c +≤∴++≤. 故选:C【点睛】本题主要考查正弦定理余弦定理解三角形,考查基本不等式求最值,意在考查学生对这些知识的理解掌握水平和分析推理能力.12.己知等差数列{}n a 的公差为-1,前n 项和为n S ,若357,,a a a 为某三角形的三边长,且该三角形有一个内角为120︒,则n S 的最大值为( )A. 25B. 40C. 50D. 45【答案】D 【解析】 【分析】利用已知条件,结合余弦定理,转化求解数列的和,然后求解n S 的最大值.【详解】等差数列{}n a 的公差为1-,357,,a a a 为某三角形的三边长,且该三角形有一个内角为120︒,可得:35277225a a a a a =++, 得11(4)(9)0a a --=,所以14a =(舍)或19a =, 2(1)199(1)22n n n n nS n --+=+⋅-=.所以n=9或n=10时, 故n S 的最大值为910==45S S . 故选:D .【点睛】本题主要考查等差数列的性质和等差数列的前n 项和及其最值,意在考查学生对这些知识的理解掌握水平和分析推理能力.二、填空题:本大题共4小题,每小题3分,共12分.13.若数列{}n a 的前n 项和为21n S n =+,则通项公式为__________.【答案】()()2,121,2n n a n n ⎧=⎪=⎨-≥⎪⎩【解析】 【分析】利用()12n n n a S S n -=-≥ 求解,但要注意验证n=1时11a S = 是否成立.【详解】当n=1时,112a S == ;()()2211111n n S n S n n +=+∴=++≥又()12n n n a S S n -=-≥()212n a n n ∴=-≥ ,111a S =≠ ∴()()2,121,2n n a n n ⎧=⎪=⎨-≥⎪⎩【点睛】本题考查利用数列前n 项和求数列通项公式,属于基础题目,解题中需要注意利用公式()12n n n a S S n -=-≥求解出的通项公式需要验证n=1时,是否满足题目条件.14.如图,已知PQ 为O 的一条弦,且4PQ PO ⋅=,则||PQ =__________.【答案】【解析】 【分析】过点O 作OA ⊥PQ,垂足为A. 则PA=AQ ,再利用平面向量的数量积和三角函数求解.【详解】,过点O 作OA ⊥PQ,垂足为A. 则PA=AQ.因为4PQ PO ⋅=,所以2||1||||cos ||||||4||2PA PQ PO OPQ PQ PO PQ PO ∠=⋅==, 所以||22PQ =故答案为:【点睛】本题主要考查直线和圆的位置关系,考查平面向量的数量积的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力.15.已知矩形的周长为16,矩形绕它的一条边旋转360︒形成一个圆柱的侧面积的最大值为__________. 【答案】32π 【解析】分析】利用矩形的周长公式、基本不等式的性质、圆柱的侧面积计算公式即可得出. 【详解】如图所示,设矩形的长与宽分别为a ,b . 则2216a b +=,即8a b +=. ∴8…,当且仅当4a b ==时取等号.解得16ab …. ∴旋转形成的圆柱的侧面积221632a b πππ==…. ∴旋转形成的圆柱的侧面积的最大值为32π.故答案为:32π.【点睛】本题考查了基本不等式求最值、圆柱的侧面积计算公式,属于基础题.16.有三条棱互相平行的五面体,其三视图如图所示,则该五面体外接球的体积为__________.【答案】3【解析】【分析】先作出三视图对应的原几何体,再求几何体外接球的半径,再求几何体外接球的体积.【详解】由题得几何体原图是如图所示的直三棱柱ABC-EFG,D,H分别是AB,EF中点,O点时球心,所以OH=52,1522HF EF ==,所以R ==所以几何体外接球的体积为343π⋅⋅故答案为:3【点睛】本题主要考查三视图还原几何体,考查几何体外接球的体积的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力.三、解答题:本大题共4个小题,共40分,解答应写出文字说明,证明过程或演算步骤.17.在三棱柱111ABC A B C -中,E 、F 、G 、H 分别AB 、AC 、11A B 、11A C 的中点,求证:(1)B 、C 、H 、G 四点共面;(2)平面1EFA BCHG ∥.【答案】(1)证明见解析;(2)证明见解析.【解析】试题分析:(1)要证明四点共面,只需证//GH BC ,根据中位线,有11////GH B C BC ,所以四点共面;(2)利用中位线,易证1//,//EF BC A F BG ,所以平面1EFA 平面BCHG .试题解析:(1)∵ G H ,分别为1111 A B AC ,中点,∴11GHB C , ∵三棱柱111AB A B C 中,11BC B C ,∴GH B ,∴ B C H G ,,,四点共面.…………………………5分(1)∵ E F ,分别为 AB AC ,中点,∴EF BC ∥,∴11EF BC B C GH ,又∵ E G ,分别为三棱柱侧面平行四边形11AA B B 对边11AB A B ,中点, ∴四边形1A EBG 为平行四边形,1A E BG ,∴平面1EFA 中有两条直线1A E EF ,分别与平面BCHG 中的两条直线BG ,BC 平行, ∴平面1EFA BCHG 平面.………………………………12分考点:证明四点共面及面面平行.18.某单位建造一间背面靠墙的房屋,地面面积为302m ,房屋正面每平方米造价为1500元,房屋侧面每平方米造价为900元,屋顶造价为5800元,墙高为3米,且不计算背面和地面的费用,问怎样设计房屋能使总造价最低?最低总造价是多少?【答案】房屋正面长为6m ,侧面宽为5m 时,总造价最低为59800元.【解析】【分析】令房屋地面的正面长为x m ,侧面宽为y m ,总造价为z 元,求出z 的表达式,再利用基本不等式求最低造价.【详解】令房屋地面的正面长为x m ,侧面宽为y m ,总造价为z 元,则30x y ⋅=,1500390065800450054005800z x y x y =⋅+⋅+=++,∵45005400229003054000x y +≥=⨯=⨯⨯=,∴45005400580054000580059800z x y =++≥+=,当且仅当4500540030x y x y =⎧⎨⋅=⎩即65x y =⎧⎨=⎩时取等号, 答:房屋正面长6m ,侧面宽为5m 时,总造价最低为59800元.【点睛】本题主要考查基本不等式的应用,意在考查学生对这些知识的理解掌握水平和分析推理能力.19.设数列{}n a 的前n 项和为n S 且344n n S a =-.(1)求{}n a 的通项公式;(2)令2211log log n n n b a a +=⋅,若{}n b 的前n 项和为n T ,且n T m <恒成立,求m 的取值范围. 【答案】(1)4n n a =;(2)14m ≥. 【解析】【分析】(1)利用项和公式求{}n a 的通项公式;(2)先化简得11141n n ⎛⎫=- ⎪+⎝⎭,再利用裂项相消求解. 【详解】(1)令1n =,则111113444S a a S a =-⎧∴=⎨=⎩,, 当2n ≥时,344n n S a =-,①11344n n S a --=-,②①-②得:1344n n n a a a -=-,∴14n n a a -=,即14n n a a -=, ∴数列{}n a 为14a =,公比为4的等比数列,∴1144n n n a a -==(2)12211log 4log 422(1)n n n b n n +==⋅⋅+11141n n ⎛⎫=- ⎪+⎝⎭, ∴111111111422311n T n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-+- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦11141n ⎛⎫=- ⎪+⎝⎭()41n n =+, ∵1111414n T n ⎛⎫=-< ⎪+⎝⎭且n T m <恒成立, ∴14m ≥ 【点睛】本题主要考查项和公式求通项,考查裂项相消求和,意在考查学生对这些知识的理解掌握水平和分析推理能力.20.ABC ∆中,,,a b c 分别是角,,A B C 所对的边且2sin 3tan c B a A =.(1)求222b c a+的值; (2)若1a =,当角A 最大时,求ABC ∆的面积.【答案】(1)4;(2)4. 【解析】【分析】(1)利用正弦定理和余弦定理化简即得解;(2)先求出A 最大时,3cos 4A ≥,再求出b,c 和sinA ,再求ABC ∆的面积.【详解】(1)∵sin 2sin 3tan 3cos A c B a A a A⋅=⋅=⋅, ∴2sin cos 3sin c B A a A ⋅⋅=⋅,∴2cos 3c b A a a ⋅⋅=⋅, ∴2222232b c a cb a bc+-⋅=, ∴2224b c a +=,∴2224b c a+=; (2)1a =时,22244b c a +==, ∵2223cos 22b c a A bc bc+-==且2224bc b c ≤+=, ∴3cos 4A ≥, ∴当角A 最大时,3cos 4A =,此时sin A = 224b c b c b c ⎧+=⇒==⎨=⎩∴11sin 2244ABC S bc A =⋅==. 【点睛】本题主要考查正弦定理余弦定理解三角形,考查三角形的面积的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2019学年四川省绵阳市南山中学高一(下)入学数学试卷(3月份)一、选择题(本大题共12小题,共48.0分)1.满足A∪{1,-1}={1,0,-1}的集合A共有()A. 2个B. 4个C. 8个D. 16个2.角α的终边上一点的坐标为(sin,cos),则tan2α=()A. B. C. D.3.三个数0.76,60.7,log0.76的大小关系为()A. B. C. D.4.设向量=(2,4)与向量=(x,6)共线,则实数x=()A. 2B. 3C. 4D. 65.可以写成①+;②-;③-;④-.其中正确的是()A. ①②B. ②③C. ③④D. ①④6.已知f(x)是偶函数,对任意的a,b∈[0,+∞)都有<,若f(lg x)>f(1),则x的取值范围是()A. B. ∪ C. D. ∪7.若sinα=,α∈(-,),则cos()=()A. B. C. D.8.函数>,>,<的图象如图所示,则函数y=A cos(ωx+φ)的递减区间是()A. ∈B. ∈C. ∈D. ∈9.函数f(x)=,的零点个数为()A. 2B. 3C. 4D. 510.函数y=a|x|+1(a>0且a≠1),x∈[-k,k],k>0的图象可能为()A.B.C.D.11.已知函数y=f(x)在(0,3)上是增函数,函数y=f(x+3)是偶函数,则f(),f(),f(2)的大小关系()A. B. C. D.12.函数y=f(x)的定义域为D,且f(x)同时满足以下条件:①f(x)在D上是单调递增或单调递减函数;②存在闭区间[a,b]⊊D(其中a<b),使得当x∈[a,b]时,f(x)的取值集合也是[a,b].那么,我们称函数y=f(x)(x∈D)是闭函数.若f(x)=k+是闭函数,则实数k的取值范围是()A. B. C. D.二、填空题(本大题共4小题,共12.0分)13.若f(x)=是奇函数,则a=______.14.在正方形ABCD中,E是DC边的中点,且=,=,则=______.15.已知函数f(x)=,,>,若直线y=m与函数y=f(x)的图象有三个不同交点的横坐标依次为x1,x2,x3,则x1+x2+x3的取值范围是______.16.给出下列五个命题:①函数y=f(x),x∈R的图象与直线x=a不可能有两个不同的交点;②函数y=log2x2与函数y=2log2x是相同函数;③对于指数函数y=2x与幂函数y=x2,存在x0,当x>x0时,有2x>x2成立;④对于函数y=f(x),x∈[a,b],若有f(a)•f(b)<0,则f(x)在(a,b)内有零点;其中正确的序号是______.三、解答题(本大题共4小题,共40.0分)17.已知集合A为函数f(x)=得定义域,B={x∈R|y=lg(x-4)}.(1)求集合A,B;(2)已知集合C={x|1-m≤x≤m-1},若集合C⊆(A∪B),求实数m的取值范围.18.经市场调查,某种商品在过去50天的销售量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N).前30天价格为g(t)=t+30(1≤t≤30,t∈N),后20天价格为g (t)=45(31≤t≤50,t∈N).(1)写出该种商品的日销售额S与时间t的函数关系;(2)求日销售额S的最大值.19.已知函数f(x)=•(),其中向量=(sin x,-cos x),=(sin x,-3cos x),=(-cos x,sin x),x∈R.(1)若f(α)=,<<,求cos2α的值;(2)不等式|f(x)-m|<2在x∈[,]上恒成立,求实数m的取值范围.20.已知函数f(x)=,g(x)=f(2x).(1)判断函数f(x)在区间(-1,+∞)上的单调性,并用定义证明;(2)g(x-1)+g(3-2x)<0,求实数x的取值集合;(3)若函数F(x)=g(x)-2x-m存在零点,求实数m的取值范围.第2页,共8页答案和解析1.【答案】B【解析】解:根据题意,集合可能为{0}、{0,1}、{0,-1}、{0,1,-1},共有4个;故选:B.根据题意,分析可得,集合A中必须有元素0,可能含有元素1或-1,由此列举可得全部可能的集合A,即可得答案.本题考查集合并集的性质,关键是由并集的定义,分析得到集合A中必须有的元素和可能有的元素.2.【答案】A【解析】解:∵α的终边上一点的坐标为(sin,cos),即(,-)∴tanα==-,则tan2α===,故选:A.根据三角函数的定义求出tanα,利用正切的倍角公式进行计算即可.本题主要考查三角函数值的计算,结合三角函数的定义以及倍角公式是解决本题的关键.比较基础.3.【答案】D【解析】解:由对数函数y=log0.7x的图象和性质可知:log0.76<0由指数函数y=0.7x,y=6x的图象和性质可知0.76<1,60.7>1 ∴log0.76<0.76<60.7故选:D.由对数函数的图象和性质,可得到log0.76<0,再指数函数的图象和性质,可得0.76<1,60.7>1从而得到结论.本题主要考查指数函数,对数函数的图象和性质,在比较大小中往往转化为函数的单调性或图象分面来解决.4.【答案】B【解析】解;因为向量=(2,4)与向量=(x,6)共线,所以4x=2×6,解得x=3;故选:B.利用向量共线的充要条件得到坐标的关系求出x.本题考查了向量共线的坐标关系;如果两个向量向量=(x,y)与向量=(m,n)共线,那么xn=ym.5.【答案】D【解析】解:∵①+=;②-=;③-=;④-=.因此其中正确的是①④.故选:D.利用向量的运算法则即可判断出.本题考查了向量的原式法则,属于基础题.6.【答案】C【解析】解:由于f(x)是偶函数,对任意的a,b∈[0,+∞)都有,则偶函数f(x)在[0,+∞)递减,则f(lgx)>f(1),即为f(|lgx|)>f(1),即有|lgx|<1,即-1<lgx<1,则<x<10.故选:C.由于f(x)是偶函数,对任意的a,b∈[0,+∞)都有,则偶函数f(x)在[0,+∞)递减,f(lgx)>f(1),即为f(|lgx|)>f(1),由单调性,即可得到,再解不等式即可得到解集.本题考查函数的奇偶性和单调性的运用:解不等式,考查对数不等式的解法,考查运算能力,属于中档题.7.【答案】A【解析】解:∵sinα=,α∈(-),∴cosα==,∴cos()=-(cosα-sinα)=-.故选:A.由已知利用同角三角函数基本关系式可求cosα的值,进而根据两角和的余弦函数公式,特殊角的三角函数值即可计算得解.本题主要考查了同角三角函数基本关系式,两角和的余弦函数公式,特殊角的三角函数值在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.8.【答案】C【解析】解:由“五点法”可知解得ω=2,φ=-,由图象可知A=1,则函数y=cos(2x-),由2k,k∈Z解得k∈Z故选:C.利用函数图象求出A ,利用五点法得到,求出ω,φ,结合余弦函数的单调性求出函数的递减区间.本题是基础题,考查三角函数的图象求函数的解析式,掌握五点法作图,函数的基本性质,是解好本题的关键.9.【答案】A【解析】解:函数f(x)=,可得当x≤0时,x2+2x-3=0,解得x=1(舍去)或x=-3;当x>0时,-2+lnx=0,解得x=e2,函数有2个零点.故选:A.利用分段函数分别求解函数的零点即可.本题考查分段函数的应用,函数的零点的求法,考查计算能力.10.【答案】C【解析】解:函数y=a|x|+1(a>0且a≠1),x∈[-k,k],k>0.函数是偶函数,排除A;函数y=a|x|+1>1,排除B;a>1时,x>0函数是增函数,C 不满足题意,D不满足题意;当a∈(0,1)时,x>0函数是减函数,C 满足题意,D不满足题意;故选:C.利用函数的奇偶性排除选项,通过a的范围,利用函数的性质判断选项即可.第4页,共8页本题考查函数的图象的判断,考查分类讨论思想的应用,函数的奇偶性以及函数的单调性,是判断函数图象的常用方法.11.【答案】A【解析】解:根据题意,函数y=f(x+3)是偶函数,则函数f(x)的图象关于直线x=3对称,则f ()=f (),f()=f (),又由函数y=f(x)在(0,3)上是增函数,则f()<f(2)<f(),则有f ()<f(2)<f(),故选:A.根据题意,由函数的奇偶性的性质分析可得函数f(x)的图象关于直线x=3对称,进而可得f()=f(),f ()=f(),结合函数的单调性分析可得答案.本题考查函数的奇偶性与单调性的综合应用,注意分析f(x)的对称性,属于基础题.12.【答案】B【解析】解:根据题意,f(x)=k+,有x+2≥0,易得f(x)为增函数,若f(x)=k+为闭函数,则存在闭区间[a,b],满足,即a、b是方程k+=x的两根,令t=,则t≥0,则原方程等价于k+t=t2-2,变形可得t2-t-k-2=0,若方程k+=x有两根,则t2-t-k-2=0有两个非负的实根,设g(t)=t2-t-k+2则有,解可得-<k≤-2,即k的取值范围为(-,-2]故选:B.根据题意,分析易得f(x)=k+在其定义域上为增函数,结合闭函数的定义分析可得,即a、b是方程k+=x的两根,令t=,则原方程等价于k+t=t2-2,变形可得t2-t-k-2=0,分析易得t2-t-k-2=0有两个非负的实根,设g(t)=t2-t-k+2,则有,解可得t的取值范围,即可得答案.本题考查函数与方程的关系,涉及函数单调性的判定与应用,属于基础题.13.【答案】【解析】解:∵f(x)是奇函数,∴f(x)=-f(-x),∴=∴=,解得a=.故答案为:.根据奇函数的性质,f(x)=-f(-x),代入f(x)的解析式,得到等式即可求出a的值.本题主要考查奇函数的性质,根据f(x)=-f(-x)列出式子即可解得a的值,本题比较基础.14.【答案】-【解析】解:∵正方形ABCD中,E是DC边的中点,且=,=,∴=+=+=-=-.故答案为:-.由题意可得=+=+=,把=,=代入化简可得结果.本题主要考查平面向量基本定理,两个向量的加减法的法则,以及其几何意义,属于基础题.15.【答案】(2,2017)【解析】解:作出函数f(x)的图象,则当0<x<1时,函数f(x)关于x=对称,若直线y=m与函数y=f(x)三个不同交点的横坐标依次为x1,x2,x3,且x1<x2<x3,则0<m<1,且x1,x2关于x=对称,则x1+x2=1,由log2016x=1,得x=2016,则1<x3<2016,则2<x1+x2+x3<2017,即x1+x2+x3的取值范围是(2,2017),故答案为:(2,2017).作出函数f(x)的图象,利用函数的对称性以及对数函数的图象和性质进行求解即可.本题主要考查分段函数的应用,考查了函数图象的作法及应用及函数零点与函数图象的有关系,利用数形结合是解决本题的关键.属于中档题.16.【答案】①③【解析】解:①根据函数的定义可得:函数y=f(x),x∈R的图象与直线x=a不可能有两个不同的交点,正确;②函数y=log2x2与函数y=2log2x的定义域不同,前者的定义域为{x|x∈R,x≠0},后者的定义域为{x|x>0},因此不是相同函数;③对于指数函数y=2x与幂函数y=x2,存在x0,当x>x0时,有2x>x2成立,例如取x0=5满足条件,因此正确;④对于函数y=f(x),x∈[a,b],若有f(a)•f(b)<0,则f(x)在(a,b)内不一定有零点,例如取函数f(x)=,a=2,b=4,满足条件,但是在(a,b)内无零点.综上正确的为①③.故答案为:①③.①根据函数的定义即可判断出正误;②函数y=log2x2与函数y=2log2x的定义域不同,不是相同函数;③例如取x0=5满足条件,可得正确;④f(x)在(a,b)内不一定有零点,例如取函数f(x)=,a=2,b=4,满足条件,但是在(a,b)内无零点.本题考查了函数的定义及其性质、函数零点存在定理、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.17.【答案】解:(1)根据题意,函数f(x)=,有4-2x>0,解可得x<2,则A=(-∞,2),y=lg(x-4),有x-4>0,解可得x>4,则B=(4,+∞);(2)由(1)的结论,A=(-∞,2),B=(4,+∞);则A∪B=(-∞,2)∪(4,+∞),C={x|1-m≤x≤m-1},集合C⊆(A∪B),分2种情况讨论:当1-m>m-1,即m<1时,C=∅,满足C⊆(A∪B),当1-m≤m-1,即m≥1时,若C⊆(A∪B),必有m-1<2或1-m>4,解可得1≤m<3,综合可得:m<3.【解析】(1)根据题意,对于函数f(x)=,有4-2x>0,解可得x的取值范围,即可得集合A,对于y=lg(x-4),有x-4>0,解可得x的取值范围,即可得集合B;(2)由(1)的结论,求出集合A∪B,按C是否为空集分2种情况讨论,求出m的取值范围,综合即可得答案.本题考查集合的包含关系的应用,涉及函数的解析式的计算,属于基础题.18.【答案】解:(1)当1≤t≤30时,由题知f(t)•g(t)=(-2t+200)•()=-t2+40t+6000,当31≤t≤50时,由题知f(t)•g(t)=45(-2t+200)=-90t+9000,所以日销售额S与时间t的函数关系为S=;(2)当1≤t≤30,t∈N时,S=-(t-20)2+6400,当t=20时,S max=6400元;当31≤t≤50,t∈N时,S=-90t+9000是减函数,当t=31时,S max=6210元.第6页,共8页∵6210<6400,则S的最大值为6400元.【解析】(1)根据销售额等于销售量乘以售价得S与t的函数关系式,此关系式为分段函数;(2)求出分段函数的最值即可.考查学生根据实际问题选择函数类型的能力.理解函数的最值及其几何意义的能力.19.【答案】解:(1)f(x)=•()=(sin x,-cos x)•(sin x-cos x,sin x-3cos x)=sin2x-2sin x cosx+3cos2x=1-sin2x+2cos2x=2+cos2x-sin2x=2+sin(2x+),若f(α)=,则2+sin(2α+)=,即sin(2α+)=,由<<∴-<2α<-,即-<2α+<,则cos(2α+)=,则cos2α=cos[(2α+)-]=cos(2α+)cos+sin(2α+)sin=(-)+×(-)=.(2)∵不等式|f(x)-m|<2在x∈[,]上恒成立,∴-2<f(x)-m<2,即f(x)-2<m<f(x)+2在x∈[,]上恒成立,当x∈[,],则2x∈[,π],2x+∈[π,],则当2x+=π时,f(x)取得最大值,最大值为f(x)=2,当2x+=时,f(x)取得最小值,最小值为f(x)=2+sin=2-,则><,得0<m<4-,即实数m的取值范围是(0,4-).【解析】(1)根据向量数量积的公式以及辅助角公式进行化简,结合两角和差的余弦公式进行转化计算即可.(2)利用不等式恒成立,利用参法分离法转化为最值问题即可.本题主要考查不等式恒成立问题,结合向量数量积的公式,利用辅助角公式进行化简,结合两角和差的余弦公式以及参数分离法转化求最值是解决本题的关键.20.【答案】解:(1)根据题意,f(x)==1-,在(-1,+∞)上为增函数,证明:设-1<x1<x2,则f(x1)-f(x2)=(1-)-(1-)=-=,又由-1<x1<x2,则(x1+1)>0,(x2+1)>0,(x1-x2)<0,则f(x1)-f(x2)<0,故函数f(x)在(-1,+∞)上为增函数,(2)根据题意,g(x)=f(2x)=,则g(-x)==-()=-g(x),函数g(x)为奇函数,设t=2x,则t>0,t=2x在R上为增函数,y=g(t)在(0,+∞)上为增函数,则y=g(x)在R上为增函数,g(x-1)+g(3-2x)<0⇒g(x-1)<-g(3-2x)⇒g(x-1)<g(2x-3)⇒x-1<2x-3,解可得x>2,即实数x的取值集合为(2,+∞);(3)函数F(x)=g(x)-2x-m存在零点,即方程-2x=m有根,则m=1--2x=-[()+(2x+1)]+2,又由()+(2x+1)≥2=2,故m≤2-2,即m的取值范围为m≤2-2.【解析】(1)根据题意,函数的解析式变形可得f(x)==1-,设-1<x1<x2,由作差法分析可得结论;(2)根据题意,分析可得g(x)为奇函数且在其定义域上为增函数,据此可得g(x-1)+g(3-2x)<0⇒g(x-1)<-g(3-2x)⇒g(x-1)<g(2x-3)⇒x-1<2x-3,解可得x的取值范围,即可得答案;(3)函数F(x)=g(x)-2x-m存在零点,即方程-2x=m有根,变形可得m=1--2x=-[()+(2x+1)]+2,结合基本不等式的性质分析m的取值范围,即可得答案.本题考查函数的单调性以及奇偶性的综合应用,涉及复合函数的单调性以及方程与函数的关系,属于综合题.第8页,共8页。
