蝴蝶形态分析分解
蝴蝶.pptx

科学研究领域贡献和应用前景
科学研究贡献
蝴蝶作为生物学研究的对象,为科学家提供了丰富的实验材 料。通过研究蝴蝶的生态学、行为学、生理学等方面,可以 揭示昆虫乃至其他生物的生存策略和进化规律。
蝴蝶的寿命因种类和环境而异,一般来说,小型蝴蝶的寿命较短,而大 型蝴蝶的寿命相对较长。在适宜的环境条件下,蝴蝶可以活数周至数月 之久。
成虫行为
成虫期蝴蝶主要进行觅食、交配和产卵等活动,以完成生命周期的延续 。它们通过吸食花蜜等甜味物质来维持生命活动,并寻找合适的交配对 象进行繁殖。
03
蝴蝶在生态系统中作用和价值 评估
蝴蝶的体型呈长圆柱形,分为 头、胸、腹三部分,身体相对
纤细。
触角特征
蝴蝶的触角通常为棒状或锤状 ,细长且底部略有加粗,具有
灵敏的嗅觉功能。
腿部结构
蝴蝶的足部发达,前足退化, 中足和后足用于行走和抓握,
末端有爪和爪垫。
翅膀形态与颜色多样性
1 2 3
翅膀形态
蝴蝶拥有两对翅膀,翅膀形态多样,通常前翅较 后翅略大,翅面覆有鳞片,形成各种斑纹。
动。
栖息地选择
02
蝴蝶喜欢栖息在环境优美的地方,如花园、丛林、草地等,这
些地方有丰富的花蜜和寄主植物供其取食和繁殖。
迁徙习性
03
部分蝴蝶种类具有迁徙习性,为了寻找更适宜的生存环境,它
们会跨越数千公里进行迁徙。
种类鉴别与分布区域
种类鉴别
蝴蝶的种类繁多,鉴别主要依据体型、翅膀形态及颜色等 特征。专业的蝴蝶分类学家还会结合生殖器结构等细微特 征进行鉴别。
探究教案:了解不同形态的蝴蝶及其生活习性

探究教案:了解不同形态的蝴蝶及其生活习性。
一、蝴蝶的形态特点蝴蝶的身体由头、胸、腹三部分组成。
头部含有复眼、触角、口器等器官,复眼可以看到周围光线强度的变化,触角则承担着嗅觉和味觉的作用。
蝴蝶的胸部则长有六条腿和两个翅膀,翅膀上有各种花纹,不同品种的蝴蝶翅膀上的花纹也不相同。
最后是蝴蝶的腹部,其中含有蝴蝶生殖器官。
二、蝴蝶的生命周期蝴蝶的生命周期一般分为四个阶段,分别是卵、幼虫、蛹和成虫。
卵是蝴蝶的最初阶段,卵大小不一,形状各异,其中也有根据不同品种而异。
在卵孵化后,就会孵化出幼虫。
幼虫是蝴蝶的吃货阶段,它们需要通过吃叶子长大。
在吃了一段时间后,幼虫会停下来,蜕皮,直到脱去皮壳,变成一只蛹。
蛹是蝴蝶的躯体重组时间,昆虫躯体发生巨大变化的过程就是在蛹内完成的。
这个过程称为“化蛹成蝶”,即从一个不知变化的生物到变成为一只美丽的蝴蝶。
经过一个固定的时间成虫会从蛹里钻出来。
三、蝴蝶的生存习性1、食性蝴蝶是植食性昆虫,主要以植物茎、叶、花、果实为食。
由于体型较小,所以喜欢采食花蜜,也是许多植物传播花粉的主要载体之一。
2、趋光性蝴蝶具有强烈的趋光性,喜欢飞翔在光线充足的区域。
蝴蝶的视觉系统非常灵敏,能够准确地感知外界的光照变化,并根据变化轨迹行反应。
3、繁殖行为蝴蝶并没有集结在一起组成共同生活的社群,它们的繁殖行为也颇为奇特,有很多种蝴蝶是具有严格的单配偶关系的。
4、逃避机制蝴蝶在面对危险时,常常会采取突然飞起或快速向远处飞行的方式逃避。
蝴蝶的翅膀上还具有类似于眼睛的花纹,这种花纹在遭受威胁时可以强化蝴蝶的逃避效果。
本次任务旨在让我们了解蝴蝶的形态特点、生命周期和生存习性,从而更好地认识这些美丽的昆虫。
蝴蝶在自然界里有着重要的生态作用,我们也应该在观赏它们的美丽之余,对它们的生存条件做出更多的努力,保护它们,共同维护自然生态的平衡。
认识蝴蝶身体结构分解

樺斑蝶
紅紋鳳蝶
淡小紋青斑蝶
大白斑蝶
無尾鳳蝶
認識大白斑蝶
幼蟲 蛹
食草 成蟲
認識淡小紋青斑蝶
幼蟲 蛹
食草 成蟲
認識無尾鳳蝶
卵
幼蟲
蛹
成蟲
認識紅紋鳳蝶
幼蟲 蛹
食草 成蟲
認識樺斑蝶
卵
幼蟲
蛹
成蟲
蝴蝶的習性
交配 曝曬
飛舞 吸蜜
如何保護自己
卵卵(產分(體於散積葉產小背卵) ) 蛹(保擬警護態戒色) )
謝謝觀賞
認識蝴蝶身體結構
卵的型態
• 球型-------大鳳蝶、無尾鳳蝶…等。 • 砲彈型----紋白蝶…等。 • 梭型-------台灣黃蝶、端紅蝶…等。 • 雞蛋型----大白斑蝶、圓翅紫斑…等。 • 橄欖型----樺斑蝶…等。
蝴蝶幼蟲的身體構造圖
蛹的構造圖
成蟲的身體結構圖
認識校園的蝴蝶
猜幼蟲
• 夜間活動
蝴蝶的天敵
早期的台灣人
把蝴蝶翅膀做成拼貼畫
蝴蝶為我,我為蝴蝶
• 三零年代,蝴蝶用他的身體養活了許多 台灣人,如今台灣經濟蓬勃發展,卻忘 了他曾經對我們人類的貢獻,現代雖然 我們已經不需要靠他來賺錢了,但是我 們卻還能利用他來觀測環境污染的程度, 站在尊重生命的立場上,我們更應該一 起來保護他
幼蟲(保擬警以護態戒量色取) 勝) ) 成蟲(擬裝警氣態死戒味)色驅)散)小朋友你遇到源自險會如何保護自己蛾與蝶的不同
蝶
• 幼蟲較為挑食,只吃 特定的食草,只有少 數一兩種有毒性
• 化蛹
• 成蟲的觸鬚為棍棒狀 且末端膨大
• 日間活動
蛾
• 幼蟲比較不挑食有些 甚至為肉食姓,多數 有毒性
蝴蝶的结构特征

蝴蝶的结构特征蝴蝶是昆虫中的一种美丽的生物,它们以其独特的结构特征而闻名于世。
蝴蝶的结构特征可以从外部形态、触角、翅膀和口器等方面来进行描述。
外部形态:蝴蝶的外部形态呈现出一种鲜艳多彩的外观。
它们的身体可以分为头部、胸部和腹部三个部分。
头部有一对复眼,复眼可以同时看到前方和两侧的景象,使蝴蝶能够快速察觉到危险。
头部中央有一对触角,触角具有嗅觉功能,可以帮助蝴蝶寻找花蜜和寄主植物。
蝴蝶的胸部有三对足,可以帮助它们在空中飞行和站立。
腹部则是蝴蝶的消化、排泄和繁殖器官的所在地。
触角:蝴蝶的触角非常敏感,可以帮助它们感知周围的环境。
触角的形状和长度因蝴蝶的种类而异,但一般都比较细长。
触角上布满了感觉毛,这些毛可以接收空气中的化学物质,并将其转化为蝴蝶能够理解的信息。
通过触角,蝴蝶可以感知到食物、伴侣和危险等信息。
翅膀:蝴蝶的翅膀是其最为明显的特征之一。
蝴蝶的翅膀通常呈现出丰富多样的颜色和图案,这些颜色和图案有助于它们进行保护伪装和求偶展示。
蝴蝶的翅膀由透明的薄膜和覆盖在其上的鳞片构成。
鳞片的颜色来自于翅膀中的色素和结构性颜色。
翅膀的主要功能是帮助蝴蝶进行飞行,蝴蝶通过翅膀的摆动产生空气动力学的升力,从而实现飞行。
口器:蝴蝶的口器呈卷曲状,称为吸管式口器。
蝴蝶通过吸管式口器来获取花蜜和其他液体食物。
蝴蝶的口器由两个长度不等的齿轮状器官组成,这两个器官可以分开或合并,用于吸取花蜜。
蝴蝶的口器也可以用于吸取水分和营养液。
除了上述结构特征之外,蝴蝶还具有其他一些特殊的结构。
比如,蝴蝶的瞳孔可以放大或缩小,使其在不同的光线条件下能够看清周围的环境。
此外,蝴蝶的翅膀上还有一些特殊的结构,如鳞片和毛发,这些结构有助于蝴蝶进行保护伪装和体温调节。
总结起来,蝴蝶的结构特征包括外部形态、触角、翅膀和口器等方面。
这些特征使蝴蝶能够适应不同的环境和生活方式,并展示出其独特的美丽。
通过对蝴蝶结构特征的研究,我们可以更好地了解蝴蝶的生态习性和进化历程。
蝴蝶形态分析分解

更多黄金投资知识请关注微信公众平台:goldinvestor早在1935年有个叫h.m.gartley的人出了一本书,叫《股市利润》(“profits in the stock market”),这是一本关于形态技术分析的书,其最为精华的部分在第222页讨论了一个最佳时间与价格的形态,这个形态是非常的强大和有效,后来这个形态被命名为gartley222,这是以人的名字做为形态的名称。
现在网上一般流行一本电子书名为:价值连城的精确短线交易技术—gartley“222”。
这就是根据《股市利润》里面的内容整理的。
之后scott m.carney在1999年出版了一本叫《和谐的交易》("the harmonic trader")的书,这还是一本形态分析和交易的书, carney在书的第3部分在讨论了gartley222后介绍和详细讨论了蝴蝶形态( butterfly ),蝴蝶形态分为牛市蝴蝶形态和熊市蝴蝶形态,蝴蝶形态的基础就是gartley222,丰富了gartley形态的内涵和内容。
到现在为止,scott m.carney,已经出版了三本关于蝴蝶形态的书籍了,我只看过《和谐交易》这本,其中两本想必会更精彩,另两本书名好似为《harmonic trading of the financial markets: volume two》,《harmonic trading of the financial markets: volume one》。
蝴蝶理论的基础与大众所知的波浪理论有着同样的理论基础:黄金分割率,也就是斐波纳奇数例。
larry pesavento所写的《 fibonacci ratios with pattern recognition》是一本关于黄金分割率介绍和应用的书。
在后面我会给出黄金回调位与目标位的关系。
蝴蝶理论与大众所熟悉的波浪理论有着同样的理论基础:黄金分割率,也就是斐波纳奇数。
加特力形态(蝴蝶形态)

加特力形态(蝴蝶形态)二十世纪前叶美国形态技术分析的先驱H.M.Gartley早在1935年就已推出震撼投资界的形态分析力作《股市利润》(“Profits in the Stock Market”),以每本1,500美元的天价限量售出1,000册,以当时正处于经济大萧条时期美国的购买力,这本书可以买到三辆全新的福特汽车!全书厚达700多页,其最为精华的部分出现在第222页,这就是被誉为具备最佳时间与价格形态的短线交易技术Gartley“222”!该项技术原理其实相当简单,以一个上升的“222”形态为例,首先价格出现一轮回升(由X点升至A点),然后展开由A、B、C、D四点所组成的回调,结构上必须满足这样的比率:AD=(0.618)AX,D=B+C-A,如此一来便构成完美的Gartley"222"价格形态,可以在D点买进,分享短期的突破性上升。
近日沪深股市不乏类似的经典范例,其中凤凰股份(600679)的“222”形态竟然精确到完美无暇(D点的最低价竟然一分不差!),随后的大幅飚升更令人叹为观止。
Gartley基本价格形态之一、二H.M.Gartley的经典价格形态自1935年面世至今逾六十载仍历久常新,其极其看重价格与时间同时呈现和谐比例的价格形态内涵每时每刻都在投资市场上重复演绎着,并且不断被后继者发展创新,但基本结构一直未变。
著名的“蝴蝶转向”形态就是由知名的技术分析专家Larry Pesavento在数十年投资生涯中将Gartley“222”形态发挥得淋漓尽致的硕果,我们将结合沪深股市个股的实际走势,对Gartley 最著名的十种基本价格形态逐一倾力推介,务求与投资者分享经典形态分析的精华。
Gartley基本价格形态一是由A、B、C、D四点所构成的之字型结构所体现(Gartley基本价格形态二结构相同,方向相反),其中AB线与CD线在60%的情况下无论是价格升幅还是所运行时间均趋于相等,同时BC线回调AB线升幅的0.618至0.786之间,当AB线升势较为强劲的情况下,BC线可能仅回调AB线的0.382,另外,在40%的情况下,当CD线运行期间若出现跳空缺口或很宽的价格波幅时,可以预期CD线的升幅将相当于AB线的1.27或1.618。
对称的蝴蝶知识点归纳总结

对称的胡蝶知识点归纳总结1. 前言胡蝶是昆虫界的一类小型、精美且颜色斑斓的生物。
它们自然界中的奇特秀丽和对称性屡屡令人赞叹不已。
本文将对胡蝶的对称性进行归纳总结,包括胡蝶的身体结构、翅膀图案以及生活习性等方面,旨在援助读者更好地理解和观览这些秀丽的昆虫。
2. 胡蝶的身体结构与对称性胡蝶身体由头部、胸部和腹部组成。
在头部,胡蝶有复眼和感觉器官,复眼呈扇形排列,具有较强的视觉能力。
胸部是胡蝶的主要运动器官,它们有六条细长的腿,每条腿末端有爪状结构,可以援助胡蝶攀爬和停留在花朵上。
胡蝶的腹部有消化器官和排泄器官。
胡蝶的对称性主要体此刻它们对称的身体结构,例如,两只翅膀以及身体的左右两侧都呈现对称外形。
这种对称性有助于胡蝶在空中飞行时保持平衡,并使得它们从遥处能够更容易被其他动物或观察者识别。
3. 胡蝶翅膀的对称图案胡蝶的翅膀是它们最引人注目标特征之一,翅膀通常由许多小而有规律的图案组成。
这些图案通常是对称的,以吸引配偶或作为威慑天敌的手段。
胡蝶翅膀的对称图案可分为垂直对称和旋转对称两种类型。
垂直对称即翅膀两侧关于中轴线对称,常见的例子有斑马蝶、凤蝶等。
而旋转对称即图案盘绕一其中心点旋转对称,常见的例子有孔雀蝶、剑角蝶等。
此外,胡蝶的翅膀上屡屡出现光学迷彩图案。
这些图案通过仿效花朵或其他环境中的外形和颜色,使胡蝶在自然界中更难被探测到。
这种对称图案也为胡蝶提供了保卫的机会,使它们更容易逃离天敌的追捕。
4. 胡蝶的生活习性与对称性的干系胡蝶的生活习性与其外貌的对称性密切相关。
胡蝶通常在花朵上寻找花蜜作为主要食物来源,并通过吸取花蜜传播花粉,起到授粉的作用。
胡蝶与花朵之间的干系是一种共生干系,它们互相依存,通过对称性可以更好地匹配。
胡蝶的对称性还与其生殖行为有关。
雄性胡蝶通常会通过翅膀上的图案吸引雌性胡蝶。
一些探究表明,胡蝶翅膀上的对称图案与雌性选择密切相关,对称图案越完美,雌性越容易对其产生爱好,这可能是由于对称表明胡蝶的健康和繁殖能力。
蝴蝶外形结构

蝴蝶外形结构蝴蝶,美丽的昆虫,拥有独特的外形结构。
它的身体呈纺锤形,由头部、胸部和腹部组成。
让我们一起来探索蝴蝶的外形结构吧!1. 头部:蝴蝶的头部是它身体的前端,也是它的感觉器官的聚集地。
头部有一对大而复杂的复眼,复眼可以感知光线的强弱和方向。
此外,蝴蝶的头部还有一对触角,触角上有许多感受味道和触觉的感受器。
这些触角能帮助蝴蝶寻找食物和伴侣。
2. 胸部:蝴蝶的胸部位于头部的后面,是它的主要运动器官。
胸部有三对足,每只足上都有细小的刺毛,可以帮助蝴蝶抓住物体。
蝴蝶的胸部还有两对翅膀,翅膀是蝴蝶最醒目的特征之一。
蝴蝶的翅膀通常呈现出各种鲜艳的颜色和花纹,这些颜色和花纹有助于它们吸引伴侣和迷惑天敌。
3. 腹部:蝴蝶的腹部位于胸部的后面,是它的消化、排泄和繁殖器官的所在地。
蝴蝶的腹部有一对触角状的生殖器,雄性蝴蝶的触角状生殖器较长,而雌性蝴蝶的触角状生殖器较短。
蝴蝶的腹部还有一对呼吸管,用来进行呼吸和排泄废物。
蝴蝶的外形结构与其生活方式密切相关。
蝴蝶的翅膀不仅仅是用来飞行的工具,它们还起到了保护和欺骗的作用。
一些蝴蝶的翅膀上有与环境相似的花纹,这使它们能够更好地隐藏在植物中,避免被天敌发现。
还有一些蝴蝶的翅膀上有明亮的颜色和鲜艳的花纹,这些颜色和花纹可以吸引伴侣,用于繁殖。
蝴蝶的复杂的外形结构使它们能够适应各种环境和生存方式。
它们在花丛中飞舞,采集花蜜;它们在草地上翩翩起舞,与伴侣共度美好时光。
无论是什么样的蝴蝶,它们都以美丽的外形和独特的结构吸引了无数人的目光。
总结一下,蝴蝶的外形结构由头部、胸部和腹部组成。
头部有复眼和触角,用于感知环境和寻找食物。
胸部有足和翅膀,用于运动和吸引伴侣。
腹部有触角状生殖器和呼吸管,用于繁殖和呼吸排泄。
蝴蝶的外形结构与其生活方式密切相关,使它们能够适应各种环境和生存方式。
无论是什么样的蝴蝶,它们的美丽外形都让人为之倾倒。
蝴蝶的生命史与形态特征

教育价值:蝴蝶的美丽和独特性使 其成为重要的教育素材,有助于提 高公众的环保意识
添加标题
添加标题
添加标题
添加标题
科学研究:蝴蝶在生物学、生态学 等领域具有重要的研究价值
经济价值:蝴蝶在旅游业、摄影业 等领域具有经济价值,保护蝴蝶有 助于促进相关产业的发展
开展宣传教育:提高公众对 蝴蝶保护的认识和意识
蛹期的作用:蝴 蝶在蛹期内进行 内部器官的改造 和发育,为成虫 阶段做准备
蛹期的时长:不 同种类的蝴蝶, 蛹期的时长也不 同,通常为几天 到几个月不等
蝴蝶的成虫期是生命周期中最活跃 的阶段
成虫期的蝴蝶寿命通常较短,一般 在几周至几个月之间
添加标题
添加标题
添加标题
添加标题
成虫期的蝴蝶会进行交配、产卵等 活动
成虫期:蛹羽化后,蝴蝶破茧而出,开始 新的生活
蝴蝶的幼虫期通常持续数 周至数月
幼虫期的蝴蝶以植物为食, 部分种类会危害农作物
幼虫期结束后,蝴蝶会进 入蛹期,准备化蛹成蝶
幼虫期的蝴蝶具有明显的 形态特征,如翅膀未发育
完全,身体柔软等
蛹期的定义:蝴 蝶发育过程中的 一个阶段,介于 幼虫和成虫之间
蛹期的特征:蛹 的外形多样,颜 色各异,有的具 有保护色
光明女神闪蝶: 世界上最美丽的 蝴蝶,数量稀少, 分布在南美洲
亚历山大鸟翼蝶: 世界上最大的蝴 蝶,分布在东南 亚地区
蓝闪蝶:颜色鲜 艳,数量稀少, 分布在南美洲
金斑喙凤蝶:中 国特有的珍稀蝴 蝶,分布在华南 地区
蝴蝶的生态习性
蝴蝶的食物来源主要 是花蜜和花粉
蝴蝶通过吸食花蜜来 获取能量
蝴蝶在花朵上停留时, 会沾上花粉,帮助花
建立自然保护区:为蝴蝶提 供适宜的生存环境
蝴蝶的形态特征及变化过程

蝴蝶的形态特征及变化过程蝴蝶是节肢动物门、昆虫纲、鳞翅目、锤角亚目的总称,全世界大约有14000多种,大部分分布在美洲,尤其在亚马逊河流域品种最多。
中国有1200种。
蝴蝶-般色彩鲜艳。
身上有好多条纹,色彩较丰富,翅膀和身体有各种花斑。
蝴蝶的形态特征包括: :1.成虫体表及翅上被有鳞片,口器虹吸式。
2.触角只有两种形状:头部有一对棒状或锤状触角。
3.蝴蝶的体型大多为中至大型,有2对膜质的翅。
体躯长圆柱形,分为头、胸.腹三部分。
蝴蝶的变化过程是一个典型的完全变态过程,包括四个阶段:1.卵期:蝴蝶的卵一般为圆形或椭圆形,表面有蜡质壳,防止水分蒸发,一端有细孔,是精子进入的通路。
不同品种的蝴蝶,其卵的大小差别很大。
蝴蝶一般将卵产于幼虫喜食的植物叶面上,为幼虫准备好食物。
2.幼虫期:幼虫孵化出后,主要就是进食,要吃掉大量植物叶子,幼虫的形状多样,多为肉虫,少数为毛虫。
幼虫成熟后要变成蛹,幼虫一般在植物叶子背面隐蔽的地方,用几条丝将自己固定住,之后直接化蛹,无茧。
3.蛹期:蛹期的幼虫会蜕变为蛹,通常会将幼虫藏在树叶的后面,用一根线将自己綁起来,然后就会变成没有茧的蛹。
4.成虫期:在成虫开始羽化的时候,蛹的头、胸和后背都会出现一个十字状的裂口,然后它的前肢伸展开来,把它的褶皱的翅膀和隆起的肚子从茧里拖出来。
但成虫成熟后,从蛹中破壳钻出,需要-定的时间使翅膀干燥变硬,这时的蝴蝶无法躲避天敌,属于危险期。
蝴蝶与蛾类的主要区别是蝴蝶头部有一对棒状或锤状触角,蛾的触角形状多样。
以上内容仅供参考,如需更多信息,建议查阅相关文献或咨询昆虫学家。
蝴蝶基本结构

蝴蝶基本结构蝴蝶是昆虫中一类美丽的生物,其独特的外形和翅膀的色彩吸引了许多人的注意。
蝴蝶的基本结构包括头部、胸部和腹部,以及两对翅膀。
下面我们来详细了解一下蝴蝶的基本结构。
首先是蝴蝶的头部。
蝴蝶的头部相对较小,呈圆形或椭圆形。
头部上有一对大而复杂的复眼,复眼由许多小眼组成,可以提供广角视野。
此外,蝴蝶的头部还有一对触角,触角可以感知周围的环境和寻找食物。
触角的末端有许多感受器,可以帮助蝴蝶感知气味和温度变化。
接下来是蝴蝶的胸部。
蝴蝶的胸部呈椭圆形,由三个节组成,分别是前胸、中胸和后胸。
胸部上有三对足,用于行走和附着在植物上。
蝴蝶的胸部还有一对前翅,前翅通常比后翅大。
前翅的形状和色彩各异,是蝴蝶最引人注目的部分之一。
蝴蝶的前翅上有许多细小的鳞片,这些鳞片使得蝴蝶的翅膀看起来丰富多彩。
最后是蝴蝶的腹部。
蝴蝶的腹部较长且柔软,由十个左右的节组成。
腹部上有一对后翅,后翅形状和颜色通常与前翅相似,但稍小一些。
蝴蝶的后翅上也有许多细小的鳞片,这些鳞片使得蝴蝶的翅膀更加华丽。
蝴蝶的腹部还有一对触角状的结构,称为尾触角,尾触角可以用来识别异性或同种蝴蝶。
除了基本的头部、胸部和腹部结构,蝴蝶的翅膀也是其独特之处。
蝴蝶的翅膀由独特的鳞片构成,这些鳞片有不同的形状、大小和颜色。
这些鳞片可以使蝴蝶的翅膀呈现出各种各样的花纹和色彩,供蝴蝶用于吸引异性、迷惑捕食者或融入环境中。
蝴蝶通过振动翅膀来飞行,翅膀的振动频率和幅度可以控制蝴蝶的飞行方向和速度。
总的来说,蝴蝶的基本结构包括头部、胸部和腹部,以及两对翅膀。
蝴蝶的头部有复眼和触角,可以感知周围的环境。
胸部有足和前翅,用于行走和飞行。
腹部有后翅和尾触角,用于飞行和识别。
蝴蝶的翅膀则是其最引人注目的部分,通过鳞片的形状和颜色展现出美丽的花纹和色彩。
蝴蝶的基本结构使其成为大自然中一道独特的风景线,也为我们带来了无尽的惊喜和美好的体验。
汇市蝴蝶原理实战分析讲解(一至四)和实战案例分析(1--41)

炒股票吧 file:///C|/Documents and Settings/Administrator/桌面/新建文件夹 (4)/汇市蝴蝶原理实战分析讲解1.htm[2010-9-2 2:04:24]
汇市蝴蝶原理实战分析讲解
下图是我在2007年7月31日通过蝴蝶形态做的美元兑瑞郎1小时图图表分析
这是一个典型的已知X、A、B、C、D点,预测翻转走势的分析。美元兑瑞郎小时图走势显示X、A、B、C、D各点脉络清 晰。B点针对XA段菲薄纳奇回调满足0.50。C点针对AB段菲薄纳奇回调满足0.786。D点针对BC段菲薄纳奇回调满足1.618。 即AB=CD(0.786/1.618)。以上回调比例均满足BAT形态比例关系。由此判断出D点位置后,我们可以初步预测行情即将发生 翻转。而随后美元兑瑞郎也应验了前期的预测,走势产生中幅下跌。
wwwwww.t.otoppccfafa.c.coomm
炒股票吧 file:///C|/Documents and Settings/Administrator/桌面/新建文件夹 (4)/汇市蝴蝶原理实战分析讲解1.htm[2010-9-2 2:04:24]
汇市蝴蝶原理实战分析讲解
早在1935年有个叫hmgartley的人出了一本书叫股市利润profitsinthestockmarket这是一本关于形态技术分析的书全书厚达700多页以每本1500美元的天价限量售出1000册以当时正处于经济大萧条时期美国的购买力这本书可以买到三辆全新的福特汽车其最为精华的部分在第222页讨论了一个最佳时间与价格的形态这个形态是非常的强大和有效后来这个形态被命名为gartley222这是以人的名字做为形态的名称
wwwwww.t.otoppccfafa.c.coomm
形态学辨认记录

形态学辨认记录蝴蝶,是一种美丽的昆虫,常常在花丛中翩翩起舞。
它们的翅膀有着绚丽多彩的花纹,令人赞叹不已。
下面我将以人类的视角,详细描述蝴蝶的形态特征。
蝴蝶的身体由头部、胸部和腹部组成。
头部前端有一对复眼,复眼能够感知光线和运动,帮助蝴蝶寻找食物和探索世界。
头部上方还有一对触角,触角的末端有感受器,可以感知气味。
蝴蝶靠触角来辨别花朵的芳香以及同类的信息。
蝴蝶的胸部很宽大,胸部上有三对细长的腿,腿上有细小的毛发。
这些腿可以帮助蝴蝶在花间穿梭,并且还能感知风的方向和强度。
胸部上方还有一对前翅和一对后翅,这些翅膀是蝴蝶最引人注目的特征。
蝴蝶的翅膀由细小的鳞片组成,这些鳞片有着不同的颜色和形状。
当阳光照射在翅膀上时,鳞片会反射出美丽的光芒。
蝴蝶的翅膀有很多种不同的花纹和颜色,有些蝴蝶的翅膀上甚至有眼状斑纹,这些花纹和斑纹能够迷惑天敌,起到保护的作用。
蝴蝶的翅膀还有一个特殊的结构,那就是翅膀上的脉络。
脉络是蝴蝶翅膀内部支撑和连接鳞片的重要结构,它们像血管一样运输营养和氧气。
脉络的形状和分布也有助于蝴蝶在空中飞行时保持稳定。
除了形态特征外,蝴蝶的行为也十分有趣。
它们喜欢在花间飞舞,吸取花蜜作为食物。
蝴蝶的飞行速度非常快,翅膀的拍动频率高达几十次每秒。
有些蝴蝶还会进行迁徙,长途飞行跨越数千公里,这是它们生命中令人惊叹的旅程。
蝴蝶是大自然的艺术品,它们的形态特征和行为都展现了生命的奇妙和多样性。
我们应该保护和珍视这些美丽的昆虫,让它们在我们的世界中继续舞动。
希望我的形态学辨认记录能够带给您一些关于蝴蝶的新见解,让您更加了解这些迷人的生物。
蝴蝶形态特点

蝴蝶形态特点蝴蝶是昆虫中的一种,具有独特的形态特点。
蝴蝶的形态特点主要包括身体结构、翅膀形状和颜色等方面。
下面将从这三个方面对蝴蝶的形态特点进行详细解释,并符合标题中心扩展下描述。
一、身体结构蝴蝶的身体结构主要由头部、胸部和腹部组成。
头部有一对复眼、一对触角和一张口器,复眼能看到周围的环境,触角则能感知气味和触觉。
胸部有三对腿和一对翅膀,腿用于行走和附着,翅膀则是蝴蝶最具特色的部分。
腹部主要包含消化系统、生殖系统和呼吸系统等内部器官。
二、翅膀形状蝴蝶的翅膀呈扇形,由一个大的前翅和一个小的后翅组成。
前翅比后翅稍大,形状多样,可以是圆形、椭圆形、尖状等。
翅膀的边缘通常是波浪状或锯齿状的,这样的形状有助于增加蝴蝶的飞行稳定性。
此外,翅膀上还有许多细小的鳞片,这些鳞片可以反射光线,使蝴蝶呈现出丰富多彩的色彩。
三、翅膀颜色蝴蝶的翅膀颜色非常丰富多样,可以是红色、橙色、黄色、绿色、蓝色、紫色等各种颜色的组合。
这些颜色并非是由色素所产生的,而是由翅膀上的鳞片反射光线的结果。
蝴蝶的翅膀颜色对其生存具有重要意义,有些蝴蝶的翅膀颜色可以起到伪装的作用,使其融入周围的环境,以躲避捕食者的攻击;而有些蝴蝶的翅膀颜色则鲜艳夺目,用于吸引异性或警示捕食者。
蝴蝶的形态特点使其成为自然界中一道美丽的风景线。
无论是在花园中、田野里还是森林中,蝴蝶的身姿都能引起人们的注意。
蝴蝶的形态特点不仅让它们具有了独特的外观,还使其具备了适应环境和生存的能力。
蝴蝶的翅膀形状可以使其在飞行时更加灵活和稳定。
蝴蝶的翅膀呈扇形,这种形状使得蝴蝶能够在空气中产生足够的升力,从而保持飞行的稳定性。
此外,翅膀上的波浪状或锯齿状的边缘也能减小空气阻力,提高蝴蝶的飞行效率。
蝴蝶的翅膀颜色也起到了重要的作用。
蝴蝶的翅膀颜色多种多样,既有鲜艳夺目的颜色,也有暗淡隐蔽的颜色。
这些颜色有助于蝴蝶在不同的环境中生存。
有些蝴蝶的翅膀颜色可以使其融入周围的环境,使得捕食者很难察觉到它们的存在,从而提高了蝴蝶的生存几率。
蝴蝶的进化过程解析

蝴蝶的进化过程解析蝴蝶是一类美丽的昆虫,它们的进化过程多样而有趣。
从最早的蛹化昆虫到现在的蝶类,经历了漫长的进化过程。
本文将以蝴蝶的进化过程为标题,探讨蝴蝶的起源、形态演化以及适应环境的进化。
一、起源与进化历程蝴蝶的起源可以追溯到距今约2亿年前的白垩纪晚期。
最早的蝴蝶是一类原始昆虫,它们的外形与今天的蝴蝶相差甚远。
这些原始蝴蝶的翅膀呈灰褐色,没有明显的花纹和色彩。
它们的飞行能力有限,主要依靠跳跃和滑翔来移动。
随着时间的推移,蝴蝶逐渐经历了一系列的进化过程。
它们的翅膀逐渐变得宽大而轻盈,身体也变得细长。
这使得蝴蝶能够更加灵活地飞行。
同时,蝴蝶的翅膀上开始出现各种各样的花纹和色彩,这为它们在繁殖、求偶和捕食中起到了重要的作用。
二、形态演化与适应环境蝴蝶的翅膀是它们最引人注目的特征之一。
蝴蝶的翅膀由透明的薄膜和覆盖在上面的鳞片组成。
这些鳞片可以反射和散射光线,使蝴蝶展现出丰富多样的颜色。
这些颜色不仅仅是美丽的装饰,还可以用于迷惑天敌或吸引异性。
在进化过程中,蝴蝶的翅膀形态也发生了很大的变化。
有些蝴蝶的翅膀呈现出鲜艳的颜色和复杂的花纹,这些特征使它们能够更好地融入环境中。
例如,一些蝴蝶的翅膀上有与花朵相似的斑纹和色彩,这使它们能够在花丛中更好地伪装自己,以便于捕食和逃避天敌。
蝴蝶的触角也是它们适应环境的重要特征之一。
蝴蝶的触角上布满了感觉细胞,可以帮助它们感知周围的气味和风向。
这样,蝴蝶可以准确地找到花朵和其他食物源,同时也可以避开危险的地方。
触角的长度和形状也因物种而异,这使得不同的蝴蝶能够适应不同的环境。
三、适应性进化与生存竞争蝴蝶的进化过程中,适应环境是一个非常重要的驱动力。
在不同的环境中,蝴蝶通过进化来适应不同的生存条件。
例如,在丛林中生活的蝴蝶通常具有较深的颜色和复杂的花纹,这使它们能够更好地隐藏在树叶和花朵中。
而在开阔地区生活的蝴蝶则通常具有较浅的颜色和简单的花纹,以适应阳光的照射和视觉上的对比。
化蝶的过程.具体几个过程比如成蛹,蜕变标题一类的谢谢啦

化蝶的过程.具体几个过程比如成蛹,蜕变标题一类的谢谢啦蝴蝶的变化过程如下:蝴蝶的寿命一般只有一年.蝴蝶的一生是从卵开始的.卵的形状各不相同,有的是球形的、有的是炮弹形、有的是甜瓜形的等.这是蝴蝶的第一个生长阶段——卵.一段时间后,毛毛虫就从卵里孵化出来了,它先吃掉卵壳,再去吃植物并迅速长大,每隔一段时间,毛毛虫就要蜕皮一次,换上更宽松的表皮.一般来说毛毛虫要蜕四次皮,这是蝴蝶的幼年时期,为第一个发育阶段——幼虫.毛毛虫长大之后,就会选择地点,吐丝固定身体,蜕皮化成蛹,这是蝴蝶的第三个发育阶段——蛹.蛹一般经过数天就变成了蝴蝶,也叫成虫,蝴蝶成虫的主要任务就是产卵,第二年卵又发育成幼虫、蛹、成虫,就这样蝴蝶在大自然中一代代延续下来.在生长的各个阶段,它的身体都发生了明显的变化,这个过程就叫变态.简单:蝴蝶是属於完全变态的昆虫,它的一生要经过四个时期,即卵、幼虫、蛹、成虫期,每个时期的形态差异相当大.具体:蝶类生活在距今几万年的远古时代,卵和幼虫以及蛹的阶段占据了蝴蝶一生的几乎全部时间~之所以属于蝶类,是因为在蝴蝶的一生几乎是在等待和希冀中度过的,即将结束之际才回蜕变成成为真正的蝴蝶,拥有着巨大的美丽的却是脆弱的翅膀,在夕阳中幸福而绝望地跳着属于它们的舞蹈飞翔在天空中.蝴蝶的一生,只有仅仅的一天是以蝶的形态存在的.蝴蝶就一定要在这一天之中找到那些可以和之厮守余生的同类,它们疯狂相爱,并且还要完成繁衍后代的责任.一天相对于广漠的宇宙而言是那么短暂和微不足道,一天对于深深相爱的伴侣又是多么的残忍和令人绝望.一天的爱情虽然短暂却又是是那么的满足,因为这一天等于它们的永远!有些蝴蝶还来不及找到它们所爱的同类,就必须死去;它们还来不及告诉那些也许近在咫尺的朋友们.但是找到它们赋予毕生所爱的伴侣时,它们又是如何幸福的相互依偎走向永恒呢?蝴蝶是多么热爱他们热爱活着的一切,哪怕是黑暗、痛苦、遥遥无期的绝望的等待,都必须死去.是的,蝴蝶必须按时死去,庞大的翅膀和纤细的身躯从很高很高的天空中飘落,至极的美丽是那么丰盈,又是那么纷繁而厚重.蝴蝶飞舞着找寻着一个安全的一个安全的地方产下自己的卵,然后她利用最后的精力拼命的飞舞着,仿佛这样可以冲破属于化蝶的命运!没多久耗尽所有力气的美丽蝴蝶终于犹如一片枯叶般坠落尘埃.经过若干时日那些受精卵已经孵化成为一群细小软弱而又丑陋的毛虫,他们一经破卵而出就开始迅速的进食,因为他们知道自己的命运.拼命的吃,张开嘴,使劲咽着,将胃里塞满食物!拼命的睡.为的是有一天能像他们的父母一样继续在那美丽的天空翱翔的梦.就这样毛虫开始迎来了自己的第一次蜕皮.蜕皮意味着蝴蝶生长完成了第一阶段.蜕皮的过程是痛苦的,就像在经历死亡.毛虫拼命挣扎着扭动自己的身体,拼命挣脱着他那已经没有任何积极意义的旧皮.虽然蜕皮是那么的痛苦,但是毛虫必须坚持.因为如果蜕皮失败将意味着它将永远变不成一只真正的蝴蝶.它感到周身剧烈的疼痛,整个身体就像要裂成碎片,像无数把锋利的刀插在它身上.毛虫即将出来了,只剩最后一点,只见它用尽全身的力气一挣,毛虫那丑陋的旧皮就永远地离它而去了,现在的毛虫得到了一件新衣服虽然不是很美丽但是已经不象刚刚出世的时候那么软弱细小了.毛虫经历了一次死亡.它变得不那么怕疼了,表皮变得更加鲜艳和坚硬了,同时也变得迟钝和麻木.却没有人会知道毛虫的内部变得更加柔软也更加敏感了.它的体重不断增长,这完全是它努力吃努力睡的结果,毛虫清醒地知道它还要经历几次这样的过程,最终,会成为一只蝴蝶,一只绝顶美丽的蝴蝶.每一次蜕皮后的毛虫都比从前更大也更美,它背部的花纹形状越来越怪异,颜色也越来越鲜艳.最终,当毛虫蜕去最后一层旧皮时,背上的图案竟在美丽中略显狰狞,这令到毛虫不安同时也令它激动不已.是的,它是一只经历了许多次痛苦的蝴蝶的幼虫,尽管还没有谁知道它会是一只蝴蝶.有过了一些日子,这时毛虫的身体渐渐变得有些僵硬,它知道那种无法抵挡的变化正悄悄在它体内发生着,毛虫无法抑制内心的激动,它终于做了一只安安静静的蛹.毛虫变成了一只蛹,不能动,不能睁开双眼.它在羽化.羽化的过程是幸福的,尽管从蛹的外表看不出什么变化,但在蛹的内部,毛虫的的确确在成为一只真正的蝴蝶.但是毛虫知道,一旦它变成一只蝴蝶它就要死去,必须死去,它们以蝴蝶的形态存在于世只能有一天,这是蝶类永远不可能改变的命运,虽然它依旧渴望着.毛虫是在接近拂晓时咬破了它的蛹,湿漉漉地爬了出来,这个过程比你想像的要艰难得多.还好,毛虫有了那么多次蜕皮的经验,这次总算让自己完整地爬了出来.它慢慢展开它的翅膀,随着阳光的照射,翅膀慢慢平滑美丽.它终于变成一只美丽的蝴蝶.这时它发现自己的翅膀竟然是那么美丽.色彩缤纷的斑点,在晨光中闪着奇异而变幻莫测的光泽,像星。
美术ppt课件蝴蝶

蝴蝶在雕塑中的表现
材料选择
空间关系
雕塑家根据作品的主题和风格选择合 适的材料,如铜、石、木等,以呈现 蝴蝶的多维度质感。
雕塑家通过蝴蝶与其他物体的空间关 系,营造出深远的意境,引导观者的 视线和情感。
形态塑造
雕塑家通过巧妙的雕刻技艺,塑造出 蝴蝶的优美形态,突出其轻盈、灵动 的特点,使观者感受到蝴蝶的生命力 。
的幼虫会以植物的叶子为食。
蝴蝶的分布地区
01
蝴蝶在全球范围内都有分布,从 热带到温带都有它们的身影。
02
在我国,蝴蝶主要分布在南方地 区,因为南方地区的气候条件更 适合蝴蝶的生长和繁衍。
CHAPTER 02
蝴蝶的种类与分类
蝴蝶的种类介绍
蝴蝶种类繁多,根据不同的分类标准, 可以分为不同的种类。常见的分类方式 有按形态特征和生态环境等分类。其中 ,按形态特征分类将蝴蝶分为凤蝶、粉
理解和感悟。
CHAPTER 04
蝴蝶的文化意义
蝴蝶在中国文化中的意义
01
02
03
蝴蝶与梦境
在中国古代文学中,蝴蝶 常被用作梦境和现实的象 征,如庄周梦蝶的故事。
蝴蝶与爱情
在中国的传统艺术中,蝴 蝶常被用来象征忠贞不渝 的爱情,如梁山伯与祝英 台化蝶的故事。
蝴蝶与美丽
在中国的传统美学中,蝴 蝶被视为美丽的化身,常 被用作装饰图案和工艺品 的元素。
膀而著名。
蝴蝶的分类方法
根据形态特征分类
根据蝴蝶的形态特征进行分类是最常见的分类方式。主要依据包括蝴蝶的触角 、翅膀、腿等部位的形态和结构。通过这些特征的不同,可以将蝴蝶分为不同 的种类。
根据生态环境分类
根据蝴蝶所生活的环境和习性进行分类。例如,可以将蝴蝶分为森林蝶、草地 蝶、沼泽蝶等。这种分类方式有助于了解蝴蝶的生活习性和生态关系。
蝴蝶形态系列..
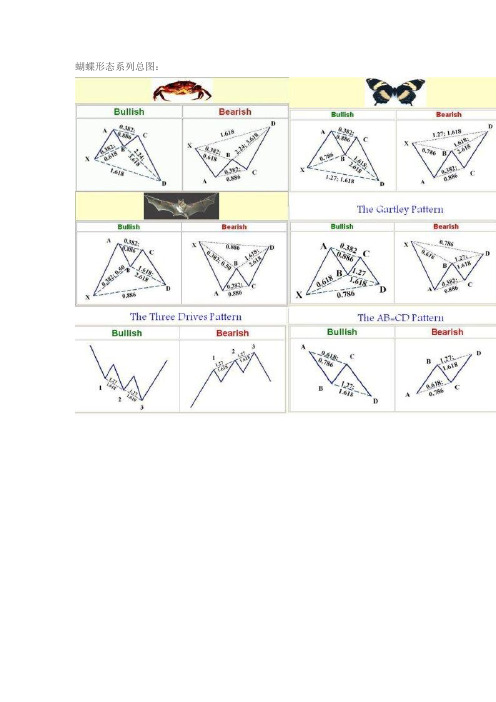
蝴蝶形态系列总图:5-0模式:0X代表真实下跌的一段;X代表先前下跌段的低点。
在快速反弹至A点之后,继续原来下跌趋势直到在低于X的某处:AB在艾略特波浪理论中——称作失败的3浪或5浪。
B点在XA的回调扩展位在1.13-1.618之间;这个失败的推动浪完成之后,随后的BC反弹(rally to)至AB回撤扩展位的1.618—2.24之间。
同样,BC针对AB的这个回撤扩展比率是该5-0结构定义要求的,如果连1.618都达不到,这就不是个有效的5-0结构。
似乎也有AB=CD形态,另外要注意形态中类似平行四边形这样的对称形态。
蝴蝶形态:由布莱斯·吉尔摩首先发现,他是澳大利亚的一个交易者,制作了波浪交易软件;该软件是第一个使用包括菲波纳齐数字在内的所有神秘数字的计算机软件,就是在这种开创性探索研究中最终导致了蝴蝶形态的发现。
该软件分析每一个波段和比率,并按照波段和比率在某一位置的聚集程度,把市场形态定为1-10级。
10级形态意味着10个波段和比率在同一时间和价格上汇集在一起。
当波浪10级如果失败时,通常表明市场会继续在原来的趋势方向上运行。
蝴蝶形态中,CD通常是AB同向影射(投影)的1.272~1.618倍;D点通常在XA价格扩展位的1.27~1.618倍处,其中1.27是最重要的比例关系。
这里得强调,蝴蝶形态是一种失败的Gartley形态,如果CD>2.618XA,则蝴蝶形态失败,这时可能演变成螃蟹或者其它形态,但也可能是原趋势的继续……做股票最怕碰到深海“螃蟹”形态,CD脚伸得太长,以至于通常会认为是新的趋势的开始(CD是BC回撤扩展的2.618、3.14以及3.618)。
而“蝴蝶”形态的极点也就是CD是BC投影的2.618以内,止损挺重要;Scott Carney在2001年发现该形态;AB能回撤XA的0.886而非平常的0.382~0.618倍;CD在XA 价格回撤扩展的1.618倍处,通常会有强烈反转形态出现。
介绍蝴蝶的知识点总结

介绍蝴蝶的知识点总结一、蝴蝶的形态特征蝴蝶的身体通常分为头、胸部和腹部三部分。
其头部有触角和复眼,胸部有三对腿,腹部有生殖器官。
蝴蝶两对翅膀上有许多小鳞片,因为它的飞翔和生活习性,翅膀色彩鲜艳多样是蝴蝶最为吸引人的地方。
蝴蝶翅膀上的花纹不仅美丽,而且具有诱捕异性、抵御天敌等功能。
二、蝴蝶的生活习性蝴蝶通常在温暖湿润的环境中生活,它们喜欢在花丛中飞舞,采食花粉和花蜜。
蝴蝶的生命周期通常包括卵、幼虫、蛹和成虫四个阶段。
在整个生命周期中,蝴蝶的食性和飞行能力都会发生变化,这也是蝴蝶生态系统中重要的一环。
三、蝴蝶的繁殖方式蝴蝶的繁殖方式主要通过交配产卵完成。
雌蝶通常会在植物上产下一粒粒卵,这些卵在适宜的环境下会孵化成为幼虫。
蝴蝶的繁殖周期与其生活环境有直接关系,通常会在适宜的气候和养分条件下进行繁殖。
四、蝴蝶的分类与分布根据蝴蝶的形态特征、生活习性和分布区域等因素,蝴蝶可以被分为不同属、种。
蝴蝶种类繁多,其分布地区也非常广泛,大多数蝴蝶都生活在热带和亚热带地区,但也有一些蝴蝶种类分布在寒带地区。
在世界各地,不同种类和属的蝴蝶都有其独特的分布区域。
五、蝴蝶的生态功能蝴蝶在生态系统中有着重要的功能。
首先,蝴蝶是植物的传粉者之一,它们会在花丛中采食花粉和花蜜,而在这个过程中会将花粉带给其他植物,促进了植物的繁殖。
其次,蝴蝶是一些天敌昆虫和鸟类的食物来源,为维持生态平衡做出了贡献。
在世界各地,因为人类活动和气候变化等原因,蝴蝶的数量和种类都受到了一定的影响。
因此,保护蝴蝶生态环境和采取有效的保护措施变得尤为重要,这不仅有助于维持生态平衡,同时也有利于人类的可持续发展。
希望通过不断的研究和保护工作,蝴蝶能够在自然界中继续繁衍生息,为我们的世界增添更多的色彩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
更多黄金投资知识请关注微信公众平台:goldinvestor早在1935年有个叫h.m.gartley的人出了一本书,叫《股市利润》(“profits in the stock market”),这是一本关于形态技术分析的书,其最为精华的部分在第222页讨论了一个最佳时间与价格的形态,这个形态是非常的强大和有效,后来这个形态被命名为gartley222,这是以人的名字做为形态的名称。
现在网上一般流行一本电子书名为:价值连城的精确短线交易技术—gartley“222”。
这就是根据《股市利润》里面的内容整理的。
之后scott m.carney在1999年出版了一本叫《和谐的交易》("the harmonic trader")的书,这还是一本形态分析和交易的书, carney在书的第3部分在讨论了gartley222后介绍和详细讨论了蝴蝶形态( butterfly ),蝴蝶形态分为牛市蝴蝶形态和熊市蝴蝶形态,蝴蝶形态的基础就是gartley222,丰富了gartley形态的内涵和内容。
到现在为止,scott m.carney,已经出版了三本关于蝴蝶形态的书籍了,我只看过《和谐交易》这本,其中两本想必会更精彩,另两本书名好似为《harmonic trading of the financial markets: volume two》,《harmonic trading of the financial markets: volume one》。
蝴蝶理论的基础与大众所知的波浪理论有着同样的理论基础:黄金分割率,也就是斐波纳奇数例。
larry pesavento所写的《 fibonacci ratios with pattern recognition》是一本关于黄金分割率介绍和应用的书。
在后面我会给出黄金回调位与目标位的关系。
蝴蝶理论与大众所熟悉的波浪理论有着同样的理论基础:黄金分割率,也就是斐波纳奇数。
larry pesavento 编写的《 fibonacci ratios with pattern recognition》是一本关于黄金分割率的介绍和应用的书,对理解蝴蝶理论有着很大的意义。
蝴蝶理论只要讨论了六种形态,包括:1、crab螃蟹;2、butterfly蝴蝶;3、bat蝙蝠;4、gartly;5、three drives;6、ab=cd。
下面是这六种形态的标准图形,每一种都包括牛市(bullish)和熊市(bearish)的划分。
1、crab螃蟹2、butterfly蝴蝶3、bat蝙蝠4、gartly5、three drives6、ab=cd五种形态所对应的完美回调位,好多时候可能会有一些偏差,给出的回调位都是一些完美的回调价位,在实践中,只能无限接近这个价位,不能过分要求符合。
这些数字是如何看的呢比如对于gartley这个形态来说,当我们知道了ab=0.447xa,而且初步确认了bc=0.500ab的时候,我们预定的d点的目标位为bc的两倍,也就是对应表格中的ab=cd(0.500/2.000),这里面包括了两个d点价位的测量方法,一则是通过ab=cd来测量,另一则是利用cd=2.00bc来测量,很多时候,这两种测量的结果都是相当接近的,在往下我会给出事例。
在《股市利润》这本书上介绍的更多是关于目标位到达后的一个反转走势,因为外国很多股票都是可以做空的,而股票下跌也提供了极好的赚钱机会,但目前中国还没有实行这样的制度,传闻的中融资融券就是这样的一个概念,不知如何才能实现。
蝴蝶走势过程图:本身追求的就是到达d点后的下跌利润,或者是下跌目标到达后的上涨利润,而在中国,在这个形态中,有两次赚钱的机会,第一次就是潜在的c点得到确认后,可以赚取c到d这一段空间的利润,在潜在的c点做多,这一技术的判断可能通过k线理论或其它技术来分析。
说到这点,令我想起了《专业投机原理》所介绍的2b买入法则,真的有异曲同工之妙,这在很大程度上说明了一点,好多理论技术都是相通的。
万变不离其宗呀!而第二次机会就是在看涨图形中的,下跌到了目标位后,反转做多。
上图是一个熊市的图形,牛市看多的正好相反。
而对d点到达目标位后是否反转的判断,最重要的是根据k线理论和回调价位,形态的和谐来判断。
一般来说,到达d点后,经常性会有一些明显的信号出现的,1.极端的价格行为。
也就是说会收到大阴线或大阳线之类的。
2.跳空缺口。
3.特定的k线形态。
比如十字星,长上影线,长下影线,收盘价最高,或收盘价最低。
每一个局部顶点或低点都会有上面所说的某一种或3种都有的特征。
下一篇文章我会简单地说一下黄金分割率的情况。
蝴蝶理论的结构基础是斐波拉契数列。
斐波拉契数列包括下列数字:1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597……直至无限。
构成斐波拉契数字系列的基础非常简单,由1,2,3开始,产生无限数字系列,而3,实际上为1与2之和,以后出现的一系列数字,全部依照上述简单的原则,两个连续出现的相邻数字相加,等于一个后面的数字。
例如3加5等于8,5加8等于13,8加13等于21,……直至无限。
表面看来,此一数字系列很简单,但背后却隐藏着无穷的奥妙。
这个数列被称为斐波拉契数列。
这个数列有如下特性:1.任何相列的两个数字之和都等于后一个数字,例如:1 + 1 = 2;2 + 3 = 5;5 + 8 = 13;144 + 233 = 377;2.除了最前面3个数(1,2,3),任何一个数与后一个数的比率接近0.618,而且越往后,其比率越接近0.618:例如:3 ÷ 5 = 0.6;8 ÷ 13 = 0.618;21 ÷ 34 = 0.618;3.除了首3个数外,任何一个数与前一个数的比率,接近1.618。
有趣的是,1.618的倒数是0.618。
例如:13 ÷ 8 = 1.625;21 ÷ 13 = 1.615;34 ÷ 21 = 1.619;通过对各种图形的分析,发现存在着几个相当重要的回调位,最重要的有0.618,1.618,0.786,1.27次要的点位有0.382,0.5,1.0,2.0.2.24,2.618,3.14,这些黄金分割点位是构成蝴蝶理论的基础,但作为蝴蝶理论最重要的一点还是形态的和谐。
而上面的黄金数字都不是凭空说出来的,都是有来源的。
我们大家知道的黄金分割率是0.618,那么0.618的平方0.382,0.618的开方就是0.786,或者通过下面会更清晰。
1.000 =根号1 =1.0001.272 =根号1.618 =0.7861.414 =根号2 =0.7071.618 =根号2.618 =0.6182.000 =根号4 =0.52.236 =根号5 =0.447这些都是一一对应关系的。
而通过对数以千计的图形的分析,本人觉得1.618是一个非常重要的,而且是经常出现的黄金目标位。
无论是相对于crab,butterfly,或者bat,gartly 形态来说都好,1.618都是一个极其重要的目标位,好多时候都是在这个回调位发生转势的,无论是在股票市场,还是期货,外汇,黄金都可以找到极多的例子,我将1.618当成是一个极限,也就是各种回调目标位的收敛目标位。
下面我再详细地来说一下各种形态需要注意的问题,这些都是比较重要的。
一.ab=cd上图的四个数字是一一对应的,也就是0.786/1.27,0.618/1.618这样的对应关系。
1.ab 必须等于 cd的长度 , 公差0.152.时间上ab和cd的形成差不多一样3.a必须是最高或最低点4.角的形态必须明显的对称5.c必须在ab的0.618到0.718 之间,这是书中的介绍,但好多实例说明,c在0.382-0.786上都可以的。
6.d必须在ab的1.27到1.618 之间,这也是书中的介绍,但事实上,d可以去到1.27-2.24这个范围上的。
7.在好的市场,也就是强势市场,d的目标是1.618,最大可以去到2.618。
二.bat形态是一个蝙蝠形态,也是gartley形态的扩展,也就是说是满足回调比例的第二个目标形态。
这一形态应该注意的问题包括有:1.b小于0.618ax, 最好是0.5或0.382 ax2.d点必须是0.886xa3.d点的反弹必须要超越1.618bc的长度4.等待d点的转折点确认后才入场三.butterfly这一形态的目标位是最多的,也是相当重要的,它基本上包括了所有的形态结果一眼看上去,这两个形态与gartley的很相似,但两者有本质的区别,gartley形态中,d 点是不会超过x点的,但在butterfly形态中,d点是要超过x点的,这是一个比较直观的本质区别。
应该注意的几点包括:1.普通出现在顶/底2.d点通常是趋势后的最高点/最低点3.ab=<cd. cd大过或等于ab4.入场在反弹形成后5.蝴蝶形态里,a点是最高/最低点6.c点在ab中间7. 牛市,d点在最低点。
熊市,d点是最高点8.特有的固定形态是很重要的。
四.crab形态是各种蝴蝶形态发展的最终形态,也是最高级别形态。
虽然这幅图一眼看上去与前面的很相似,但只要细细比较一下,就会发展有很多不一样的地方了。
crab形态应该注意的问题:1.d相等于1.618ax2.d点的反弹普通在2.24, 2.618,3.14, 3.618 bc的长度3.形态确认后,在d点入场,必须把止损调到最小程度五.gartley形态可以说是所有蝴蝶形态中最经典的形态了,在好多书上介绍为“222”形态,与这个比较相似,只是“222”形态不太关注b点,也就是说只要ab的长度不超过xa就可以了,而gartley对b点的要求是比较严格的。
1. xa的长度必须是最大的2.d差不多是0.786xa3.d点不会超越x点4.ab必须差不多在0.618xa5.c点必须在ab之间6.d点要超越b点7.ab等于cd8.在d点抢反弹,止损必须超越x点9.最好的入场点在反弹确认形成后10.d点的反弹跟xa线很相似在技术分析领域中,讲究的是价,量,时,空.这些名词意思大家都明白,但实际应用起来却是非常非常困难的.就如平时所说的,以时间换空间,究竟是用多少的时间来换多大的空间呢?没有人能明白.就如万物之中确实存在着时间周期,但时间周期到底是怎么的一种神秘的事物,也没有人能给一个详细的解说.在时间周期这一方面上.人们以往所提倡的就是k线的数目就是代表时间的多少.我从数以千计的图形中得出一个结论,在所有的价格中,收盘价是最有效的,也是最能反映出市场真实情况的一个价位.我在思考时间周期的问题就是归于为收盘价的问题.我的一个观点就是:在上涨行情中,只有收盘价比前一天高才算是真正的一天,同样地,在下跌行情中,只有收盘价低于前一天,才算是完整的一天.蝴蝶原理的可贵之处是其存在的客观性。
