分式复习PPT课件

合集下载

分式-复习课件-(共34张PPT)

x2
1 x2
2
9
变: 已知 x2 – 3x+1=0 ,求 x2+
x
x
的1x2值. 的1x2 值.
变:已知 x+ 1=3 ,求
x
x2 /x2 的值. x4+x2+1 /x2
1
x2
1 x2
1
两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母。
用符号语言表达： a c ac b d bd
27xy2
-2(a-b)2 -8(b-a)3
关键找出分子和分母的公因式
m2+4m+4
(3)
m2 - 4
关键找出分母的
2.通分
最简公分母
(1) x 与 y (2)
6a2b
9ab2c
a-1
6
a2+2a+1 与 a2-1
约分与通分的依据都是: 分式的基本性质
整体代入法化简思想：
【【例例11】】已已知知：：1x
a0 1
an
1
an
(a 0)
(1)(3)3 1 (3)3
1 27
(2)(3a)2 b2 (a2b2 )3 解：原式= 32 a2b2 a6b6
6、用科学记数法表示：
例： 0.00065 6.5104
(1) 0.000030
3.0 105
7、约分
:
例(1)
6x2y 12 xy 2
(2) x 1 2x 1 3x 2 x 1 1 x x 1
复习回顾一:
1.解分式方程的思路是：
分式方程
去分母
整式方程
2.解分式方程的一般步骤

分式复习课教学课件(两课时)

4.分式的混合运算的顺序是先乘方、再乘除、后加减，如有括号，先算括号内。注意：分式运算的结果要化为最简分式。
小试牛刀：
a b c 2b , , 12a 1、分式 2b 3a 2 4ab 的最简公分母是 1 1 1 1 1 , , 2 , 2 2、分式 , x x 1 x 1 x 1 x 2 x 的最简公分母是 1
一展身手：
1.不改变分式的值，使下列分式的分子与分母的最高次项的系数是正数：
x (1) 2 1 x
(2)
y y (3) 2 y y
2
2 x 2 x 3
2.不改变分式的值，把下列各式的分子与分母中最高次项的系数都化为正整数。
1 1 a 2 (1) 1 a 3
a 0.2a (2) 2 3 a 0.3a
2
3、若将分式 a、b的值分别扩大为原来的2倍，则分式的值为（） 1 A．扩大为原来的2倍 B．缩小为原来的 2 C．不变 D．缩小为原来的 1
ab (a 、 b 均为正数）中的字母 ab
4 2 x2 4 1 m 3x 1 , , , (a b), , 4、下列各式中， 3x 2 2 y 3 x2
( A B 1) x (2 A B 5) 0
A B 1 0 2 A B 5 0
A 2 解得： B 1
例６、某工程要求限期完成，甲队独做正好按期完成，乙队独做则要误期3天，现甲、乙两队合做2天后，余下的工程由乙队独做，正好按期完成，问该工程限期多少天？例７、正在修建的西塔（西宁～塔尔寺）高速公路上，有一段工程，若甲、乙两个工程队单独完成，甲工程队比乙工程队少用10天；若甲、乙两队合作，12天可以完成．若设甲单独完成这项工程需要x天．则根据题意，可列方程为 _______________-

第三章整理《分式》(复习)ppt课件

顺水速=静水速+水流速逆水速=静水速-水流速
设是水流速为xkm/ h
则水为 20 + x)km/ h 顺速 (
逆速 (20 - x)km/ h 水为
72 48 = 20 + x 20 − x
A．扩大3倍 B．扩大9倍C．扩大4倍D．不变扩大3 扩大9 扩大4
3、填空： x ( x − y ) = ( x − 2
y)
x + xy
x+y
例1：化简求值：
a−2 a −1 a−4 ( 2 − 2 )÷ a + 2a a + 4a + 4 a + 2 2 其中a满足：a + 2a − 1 = 0
1. 若分式
A、 A、x≠-1 C、x≠2 、
若有意义，应满足（若有意义，则x应满足（ B ）应满足
B、 ≠-1且 B、x ≠-1且x ≠2 D、x ≠-1或x ≠2 、或
x −4 ( x + 1)( x − 2)
若值为0，应满足（若值为，则x应满足（ B ）应满足
A、x=2 、 C、、
1km
中点 18km }
xkm / h
甲 A
乙 B
甲走了总共20km 甲走了总共
设乙的速度 xkm / h 则甲的速度( x + 0.5)km / h
20 18 = x + 0.5 x
1、一项工程，若甲队单独做，恰好在规定的日期、一项工程，若甲队单独做，完成，若乙队单独做要超过规定日期3天完成天完成；完成，若乙队单独做要超过规定日期天完成；现在先由甲、乙合做2天在先由甲、乙合做天，剩下的工程再由乙队单独也刚好在规定日期完成，做，也刚好在规定日期完成，问规定的日期是多少天？少天？ 1 甲每天的工作量 x 设天甲x

分式复习优质课市公开课一等奖省优质课获奖课件

1 x2 2x 1
3
x 2x2
2 1
2 x2 1 4x 4
x2
4 (π
x)2
第4页
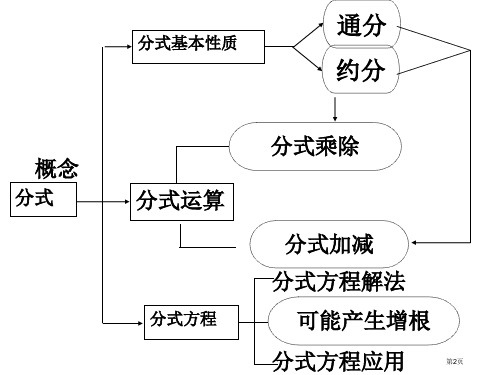
2.分式基本性质:
分式分子和分母都乘以（或除以）同一个不等于0整式，分式值不变.
A AM A AM
,
(其中M是不等于0整式)
B BM B BM
第5页
1.以下式子
（1） a x a （1 2）
b x b1
n ；na ,a 0
b ； a 1
ab
（3） x y x； y（4）
xy xy
ba ab ca ac
中正确是
（）
A 、1个 B 、2 个 C、 3 个 D、 4 个
第9页
4b、值若分将别分扩式大为a原ab来b (2a倍、，b均则为分正式数值）为中（字）母a、
A．扩大为原来2倍 B．缩小为原来 1
C．不变
D．缩小为原来 2
x2 y2
B、 x y2
y2 x2 C、 x y
x2 y2 D、 x 2 y xy 2
第13页
1.计算：
第14页
第15页
5. a2 b2 (1 a2 b2 )
a2b ab2
2ab
6. x 3 (x 2 5 )
x2
x2
第16页
3.化简并求值：
x2
x2
2x
x2
x 1 4x 4
x y z
4.分式
,
,
5b2c 10a 2b 2ac
最简公分母是
；
3
y
x 2 y y 3 , xy x 2
最简公分母是
.
第11页
4.什么是最简分式？一个分式分子和分母没有公因式时叫做最

数学中考专题复习分式市公开课一等奖课件名师大赛获奖课件

分式有意义的条件：分母不为零
分式值为零的条件：分子等于零且分母不等于零
例题：当 x 1 =______时，分式 x2 1 的值为0。
x 1
x2 1 0
分析：
x 1 0
x 1 x 1
2．分分式式的的基基本本性性质质：
表达式：AB＝AB× ×M M，AB＝AB÷ ÷M M(M 是不等于 0 的整式)．约分：把分式的分子与分母中的公因式约去，叫做分式的约分．通分：利用分式的基本性质，使分子和分母同时乘以适当的整式，不改变分式的值，把异分母化成同分母的分式，这样的分式变形叫做分式的通分．
的
值代入求值。
解析：原式=
(x x
1 1
1 ) x 1
x2
x2 1 4x 4
x2 x 1
(x 1)(x 1) (x 2)2
x 1 x2
当 x 1 时，上式= 2 （错解）
发现：x可以取除1、-1、2以外的任意整数
正解：当 x 3 时，上式=4
例3：先化简，再求值：3mm2
3 6m
(m
x2 x2 xy xy y2 x y
y2 x y
原式=
x2 x y
x
y
方法2
xx22
((xx y)
xx yy
x2 (x y)(x y)
x y
x y
x2 (x2 y2) x y
y2 x y
例2：先化简
(1
1) x 1
x2
4x x2 1
4
，然后选一个你喜欢的整数作为
x
2
m
5
2
)
，其中
m 是方程
x 2 3x 1 0的根。

第3节分式-中考数学一轮知识复习PPT课件

3．通分：
(1)定义：把几个异分母的分式化为同___分__母__分式的过程叫做分式的通分．通分的关键是确定各分母的_最__简__公___分__母__．
(2)确定最简公分母的方法： ①取各分母系数的最小公倍数，作为最简公分母的系数；取各分母所有因式的最高次幂的积，作为最简公分母的因式． ②若分母是多项式，则应先把各个分母分解因式，再确定最简公分母．温馨提示
2．分式有、无意义和值为 0 的条件：条件
分式AB 有意义
__B__≠_0__
分式AB 无意义
__B_＝__0__
分式AB 的值为 0
__A_＝__0__且 B≠0
3.最简分式：分子与分母没有_公__因__式__的分式．
分式的基本性质
1．基本性质：分式的分子与分母都_乘__或___除__以___同一个不等
B．缩小 10 倍
C．是原来的23
D．不变
☞命题点3 分式的运算 A
1 x＋1
8．(2020·随州)x2－2 4
1 ÷x2－2x
的计
算结果为( B )
A.x＋x 2
B．x＋2x2
C．x－2x2
2 Dx（x＋2）
☞命题点4 分式的化简及求值(8年7考)
9.(2018·广东 18 题 6 分)先化简，再求值：
6．(2020·花都区一模)计算：x＋x 1 ＋x＋1 1 =___1__．
7．(12020·黄冈)计算：x2－y y2 ÷1－x＋x y 的结果是_____x_－__y____．
8．(2020·东莞一模)先化简：1＋a2－1 1
a ÷a－1
，
请在－1，0，1，2，3 当中选一个合适的数代入求值．
3

初中数学《分式》课件(同步+复习+名师=精选课件)

（４）当x ＝-３时，
x 4 ∴当x = 2时分式的值为零。 x2
2
x 2 4 (3) 2 4 x2 3 2 5
1.填空:
(1)当 x≠2
1 x 时,分式 4 x 8 有意义;
时,分式
(2)当
x=3
3 x 9 x 2 的值是零;
Байду номын сангаас
xa (3)当x=2时,分式 x b 没有意义,则 b= -2
七年级
（下册）
义务教育教科书
学科网
1、下列代数式中，哪些是整式？哪些是分式？
3 4
2
b 3 2a
y -1 x
m( n p ) 7
4 5b c
m 7
x 2 xy y 2 2 x 1

a 1 2、对于分式 2a
（1）当a=1时，求分式的值（2）当a取何值时，分式无意义？当a取何值时，分式有意义？（3）当a取何值时，分式值为零？
2 y 1 x
4 5b c
3
m 7 m 7
x xy y 2 x 1
2
2

整式有: 分式有:
3 2 b 3 2 a 1
m( n p ) 7
3

4 5b c
x 2 xy y 2 2 x 1
b 分式分母中的字母能取任何实数吗？ a
为什么？分式
2x 3 中的字母x呢？ x2
:
我们已经知道:
2 3 16 36
= =
25 3 5
=
10 15
;
4 9
16 4 36 4
=
这是根据分数的基本性质：
分数的分子与分母都乘以或除以同一个不等于零的数，分数的值不变．

《分式方程复习》课件

详细描述
在金融和经济领域，分式方程可以用来描述和预测市场行为、投资回报和成本效益分析等。在交通领域，分式方程可以用来解决交通流量和路线规划问题。在工程领域，分式方程可以用来描述机械运动、热传导和电路等问题。
04 分式方程的解题技巧
转化思想
总结词
转化思想是将复杂问题转化为简单问题，将未知问题转化为已知问题的一种解题策略。
详细描述
分式方程与整式方程的主要区别在于分母中是否含有未知数。分式方程的分母中含有未知数，而整式方程的分母中不含有未知数。此外，分式方程的解法通常需要更多的技巧和注意事项，例如需要处理分母为零的情法
01
02
03
04
直接求解法
通过对方程进行化简，直接求出方程的解。
详细描述
在解分式方程时，通过对方程进行适当的变形和转化，可以将分式方程转化为整式方程或更容易解决的形式，从而简化解题过程。
整体思想
总结词
整体思想是从整体角度出发，将问题看作一个整体，从而简化问题的一种解题策略。
详细描述
在解分式方程时，可以将方程中的某些项看作一个整体，通过对方程进行整体变形和运算，从而简化解题过程。
代数方法
总结词
代数方法是利用代数性质和定理，对方程进行变形和求解的一种解题策略。
VS
详细描述
在解分式方程时，可以利用代数性质和定理，如乘法分配律、合并同类项等，对方程进行变形和简化，从而找到方程的解。
05 分式方程的易错点分析
概念理解不清
总结词
概念理解不清晰
详细描述
分式方程的基本概念和定义是解题的基础，如果对分式方程的概念理解不清晰，会导致解题思路出现偏差，甚至无法正确列出方程。

第16章分式复习课件PPT

Байду номын сангаас
ag贵宾会注册
[单选,A1型题]上尿路结石形成的因素与下列哪项无关（）A.饮食结构中肉类过多B.长期卧床不起C.尿中枸橼酸增多D.肾小管酸中毒E.饮食结构中纤维素过少 [填空题]电气化铁路接触网停电检修时，禁止向停电区放行（）及动车组。司机发现不符合此项规定时，应立即降下受电弓并（）。 [多选]关于航空运输市场的含义下列说法正确的是()A.航空运输市场是一种特定的市场B.是航空运输产品和服务交易的场所C.是指航空运输产品供求关系的总和D.是在一定时空条件下对航空运输产品和服务需求的总和E.供求关系的无法测量的市场 [单选]以下哪种药物抑制胃酸分泌最弱A．奥美拉唑B．法莫替丁C．兰索拉唑D．雷尼替丁E．硫糖铝 [单选]脑栓塞的临床表现不正确的是（）。A.患者较年轻B.多有风湿性心瓣膜病史C.起病急骤D.多有脑膜刺激征E.可有偏瘫失语 [单选]医疗单位使用毒性药品，每张处方不得超过（）A.2日常用量B.3日常用量C.2日极量D.3日极量E.7日常用量 [单选]通信记录装置功能失效或者时钟误差（）分钟，为通信一类障碍。A.1分钟B.2分钟C.3分钟D.5分钟 [单选]以下关于合同分析作用的说法，错误的是（）。A.分析合同漏洞，解释争议内容B.分析合同风险，制定风险对策C.分解合同工作并落实合同责任D.进行图纸交底，简化合同管理工作 [判断题]经常项目下的个人外汇业务按照可兑现原则管理，资本项目下的个人外汇业务按照可兑换进程管理。A.正确B.错误 [单选,A2型题,A1/A2型题]下列出血性疾病中，属于凝血功能异常的是（）A.过敏性紫癜B.维生素C缺乏症C.血小板减少性紫癜D.新生儿出血症E.遗传性毛细血管扩张症 [单选]充分利用原材料，做到物尽其用，这是职业道德中（）的要求A、讲究公德B、发对浪费C、钻研业务D、尽职尽责 [单选,A1型题]乳腺癌患者乳腺皮肤出现“酒窝征”的原因是（）。A.肿瘤侵犯了胸大肌B.肿瘤侵犯了Cooper韧带C.瘤细胞堵塞了局部皮下淋巴管D.肿瘤侵犯了周围腺体E.肿瘤侵犯了局部皮肤 [单选,A1型题]下列除哪项外都是得神的表现（）A.两目精彩B.面色荣润C.肌肉不削D.面色潮红E.运动自如 [单选,A1型题]下列哪组药物属于辛温解表药（）A.荆芥、防风、蔓荆子B.藁本、牛蒡子、辛夷C.紫苏、香薷、白芷D.白芷、桂枝、葛根E.麻黄、羌活、桑叶 [单选,A1型题]佝偻病肺脾气虚型的治法是()A.温脾助运B.健脾益肺，调和营卫C.补肾填精D.补肾壮骨E.平肝潜阳 [单选,A1型题]患者男，20岁。骨盆骨折合并尿道损伤，术后两个月，现排尿困难，应给予（）A.导尿B.少饮水C.膀胱造瘘D.尿道探子扩张尿道E.给予利尿剂 [填空题]煤在高温炼焦时，配合煤中的硫约有（）转入到煤气中。 [单选]治疗上消化道出血脾不统血证，应首选方剂是（）A.归脾汤B.独参汤C.泻心汤D.十灰散E.四味回阳饮 [名词解释]拖延比赛 [单选]下列除哪一项外，都与温病的发病有密切关系？（）A.感受外邪B.正气强弱及邪正力量的对比C.失治、误治D.外界环境中的自然因素 [单选]关于雌激素的作用，下列说法正确的是（）。A.促进水、钠排泄B.抑制输卵管蠕动C.使阴道上皮角化现象消失D.使子宫颈黏液分泌增多而稀薄E.对下丘脑和垂体仅产生负反馈作 [单选,A2型题,A1/A2型题]下列是协调活动的重要手段和依据准则的为（）A.规章制度B.行政法规C.基本法D.刑法E.民法 [单选,A1型题]低肾素性高血压降压首选（）A.利尿剂或钙离子通道阻滞剂B.β受体阻滞剂C.肼苯达嗪D.血管紧张素转换酶抑制剂E.利血平 [多选]施工现场配水管网布置应符合下列原则是（）。A.在保证不间断供水的情况下，管道铺设越短越好B.施工期间各段管网应固定C.主要供水管线采用枝状，孤立点可设环状D.尽量利用已有的或提前修建的永久管道E.管径要经过计算确定 [单选,A2型题,A1/A2型题]首次发现病毒的科学家是（）。A.琴纳B.郭霍C.巴斯德D.伊凡诺夫斯基E.吕文虎克 [单选]无限大容量电力系统是指（）。A.电源系统容量无限大B.当用户供电系统短路时，系统容量近似不变C.当用户供电系统短路时，系统输出电压近似不变。D.当用户供电系统短路时，系统输出功率不变 [填空题]橄榄球中“斯克兰”的英文名（）。 [单选,A型题]属于胞内寄生菌的肠道杆菌是（）A.痢疾杆菌B.大肠杆菌C.伤寒杆菌D.肺炎杆菌E.变形杆菌 [单选]心室颤动时，首次直流电除颤用（）A.100JB.150JC.200JD.300JE.360J或以上 [单选]在软土地基上建斜坡结构防波堤，堤心抛石有挤淤要求、抛石顺序应（）。A.沿堤横断面从一端向另一端抛B.沿堤纵断面从一段的一端向另一端抛C.沿堤的横断面从中间向两侧抛D.沿堤断面全面平抛 [单选]在药品标签上必须印有规定标识的是（）A.贵重药品B.自费药品C.处方药D.非处方药品E.内服药品 [问答题,简答题]心电图的测量方法 [名词解释]Fab(Fragmentantigenbinding) [单选,A型题]现行中华人民共和国药典颁布使用的版本为A、1990年版B、1993年版C、1995年版D、1998年版E、2000年版 [单选]偃旗息鼓“偃”的意思是：（）A.摘下B.收起C.停止D.放倒 [单选]思科IOS命令ipnatinsidesourcestatic10.1.1.5172.35.16.5的作用是什么（）。A.为所有外部nat创建一个全局的地址池B.为内部的静态地址创建动态的地址池C.为所有内部本地pat创建了动态源地址转换D.为内部本地地址和内部全局地址创建一对一的映射关系E.映射一个内部源地址到一 [单选,A2型题,A1/A2型题]CT显示器所表现的亮度信号的等级差别称为（）A.CT值标度B.矩阵C.窗宽D.窗位E.灰阶 [单选]下列哪项不是队列研究的特点（）A.可以直接计算发病率B.多用于罕见病C.多数情况下要计算人年发病率D.每次调查能研究几种疾病E.因素可分为几个等级，以便计算剂量反应关系 [单选]某企业生产甲产品，属于可比产品，上年实际平均单位成本为300元，上年实际产量为1800件，本年实际产量为1000件，本年实际平均单位成本为298元，则本年甲产品可比产品成本降低额为()元。A.1000B.2000C.3000D.0 [问答题,论述题]一个优秀的团队应具备哪些特征？

分式中考经典总复习课件

状元备课
)
--
=-1
+
-
-
D.
=
+
+
B.
解析:应用分式的基本性质时,要注意“都”与“同”这两个字的含义,
-
-(-) -
,
=
=- .
避免犯只乘分子或只乘分母的错误.D项中 +
+
+
答案:D
规律方法探究
命题点1
命题点2
命题点3
命题点 3
【例 3】
命题点4
分式的约分与通分
0.
考点二
分式的基本性质
分式的分子与分母同乘(或除以)一个不等于零的整式,分式的

×
÷
值不变.用式子表示是: = × , = ÷(其中 M 是不等于 0 的整
式).
基础自主导学
考点梳理
状元备课
自主测试
考点三分式的约分与通分
1.约分
分式约分:利用分式的基本性质,约去分式的分子、分母中的
答案:C
状元备课
规律方法探究
命题点1
命题点2
命题点3
命题点4
3+5
5
1
无意义,则当
−
=0
-1
3-2 2-
变式训练若分式
3+5
解析:由
无意义,可得 x=1,
-1
5
1
5
1
由
−
=0,得
−
=0,
3-2 2-
3-2 2-1
5
1
即
=
,
3-2
2-1
所以 5(2m-1)=3m-2.

分式中考总复习原创课件

2.下列分式中不是最简分式的是( )
C
全体实数
x≠2
x≠±2
4.计算：(1) (2)
3.计算：
x－2
a4b4
解：原式
解：原式
解：原式
(3)
5．已知 ,当x＝________时，A＝0；当x＝________时，A无意义．
解：(1) (2)由已知，得x=1或2，但x不能取1，所以x=2. 当x=2时, .
8．已知求的值．
解：由已知，得y－x=4xy，x－y=－4xy.原式=另解：原式=
第一章数与式第3课分式
1.分式的有关概念： (1)如果A，B分别是整式，并且B中含有________，那么式子叫做分式． (2)当B________时，分式 (A，B分别是整式)有意义．
2.分式的基本性质：分式的分子与分母乘(或除以)同一个________的整式，分式的值__________．用式子表示为或 (C≠____)，其中A，B，C均为整式．
【变式2】计算：
解：原式
【考点3】分式的化简求值
【例3】先化简，再求值：在0，1，2，这三个数中选一个合适的代入求值．
解：
根据分式的意义，x≠0，x≠2,所以x取1，当x=1时,原式= .
【变式3】已知（ ),求的值
－2
2
提示:先化简原式= ，当A=0时，分子x+2=0.解得x=－2.当A无意义时，分母x－2=0，解得x=2.
6.计算：（1）
解：原式
解：原式
（2）
7．已知(1)化简A；(2)当x满足不等式1≤x＜3，且x为整数时，求A的值．
字母,B≠ 0
3.分式的运算： (1)加、减同分母； (2)乘、除化简．

八年级数学下册第八章分式复习课件(PPT)

2
2 2m 2 x a1 b 2 a 2 m x 1 ab 4. 化简：（2） 2 5.计算：（1） x 1 m b 4 2am 2b 2 x a 1
．

a ( a b)
2(a b) 2 m a (m 2)( m 2)
1 例1. 在函数 y 中，自变量x的取值范围是（A） x2 A． x 2 B． x 2 C． x≤2 D． ≥—2 x
列分式方程解应用题
列分式方程解应用题的一般步骤
1、审题； 2、设未知数；
3、找出能表示题目全部含意的相等关系，列出分式方程； 4、解分式方程；
5、验根：先检验是否有增根，再检查是否合符题意；
6、写出答案。
常见题型及相等关系
1、行程问题：
基本量之间的关系：
路程=速度 X 速度，即s=vt
解：设规定日期为x天，根据题意得
4 x 1 x x6
解得 x=12, 经检验，x=12是原方程的解。答：规定日期是12天。
小结
列分式方程解应用题的一般步骤
1、审题； 2、设未知数；
3、找出能表示题目全部含意的相等关系，列出分式方程； 4、解分式方程；
5、验根：先检验是否有增根，再检查是否合符题意；
想一想
x y 探究：⑴当x、y满足什么条件时，分式的值为0. x 1
解：x y 0且x 1 0 所以x y且x 1, y 1
分式方程
100 60 20 v 20 v
像这样，分母里含有未知数的方程叫做分式方程.
解分式方程的思路是：
分式方程
去分母
3.
4.
x 2 (2) 1 x 1 3x 3

浙教版七年级下册5分式课件

D.
3-m
13.下列各式中，正确的是（ D ）
A.
a+m b+m
=
a b
C.ab-1
ac-1
=
b-1 c-1
BD..xaax2+---byyb2==0x+1y
谢谢
时扩大2倍，则分式的值____不__变_；
x2
2.把分式中的分子、分母的x，y同时
扩大2倍，则分y式的值___是__本__来__的___2；倍
3.分式乘除法的法则
a c ac b d bd
a c a d ad b d b c bc
计算（1）2a2b3（ 3ab ） 6ab2 4ab2
（2）x2
6x x 1
9
3 x x2 1
4.（1）同分母分式的加减法法则：
a b ab cc c
计算：
（1）a 4b 2a-b ab ab
（2）（xy
2 1 y）2
（1y
x2 x）2
4.（2）异分母分式的加减法法则：
步骤：1.找公分母；2.通分；3.转化为同分母分式，再加减。
计算
（1） a b 8ab3 6a2b
C（（．xx
1）2 1）2
x2
D．x2 1
2、分式的基本性质
分式的分子与分母都乘以（或除以）同一个不等于零的整式，分式的值不变。
即：AB =
A●M B●M
A A÷M B = B÷M
（M≠0）
应用一分子、分母系数化整
应用二最高次项的系数都化为正数
应用三化简分式
1. x 中的分子、分母的x，y同 x+y
（1）当
x2
x 时x（，分x -式2）x 2 有意义；

分式和分式方程(复习)课件

2 2 2
最简公分母的确定
如果分母是单项式时，最简公分母是：①系数取最小公倍数；②字母取所有字母；③字母的次数取所有字母的最高次幂。如果分母是多项式时，应该先考虑分解因式，再确定最简公分母。 1 3 2 例： )通分：与 (1 、 3 2 ax 2b x 3cx x2 x 1 ( 2)通分：2 与 2 x 2x x 4x 4
解：方程两边都乘以 4得： x
2
（x 2) a ( x 2)
2
2
若方程有增根，只能是 2或x 2 x 将x 2和x 2分别代入整式方程可得： a 16或a 16
m 1 1、关于x的方程 1 x 1 x 2 1 有增根-1，求m
2、若方程
增根的定义
增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方 ······ 程的根. ··· 使最简公分母值为零的根产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根, 而不是分式方程的根.···· ····
x2 a x2 例：若关于x的方程 2 x2 x 4 x2 有增根，求a的值。
ab 1 1 解：由已知可得 3, 即 3(1), ab a b 1 1 1 1 同理得： 4(2), 5 b c c a 1 1 1 6 a b c 1 1 原式 ab bc ac 6 abc
分式方程
概念：分母中含有未知数的有理方程，叫做分式方程。解分式方程的步骤：将分式方程转化为整式方程（方程两边同时乘以最简公分母）解整式方程检验（验根）写出方程的解
解分式方程易错点分析
一、去分母时常数漏乘最简公分母 2 x 1 例1、解方程： 2 x 3 3 x 二、去分母时，分子是多项式不加括号 5 3 x 例2、解方程： 2 0 x 1 x 1 三、方程两边同时除以可能为零的整式 3x 2 3x 2 例3、解方程： x4 x3

人教版八年级上册数学第十五章分式章末复习课件

检验：当x=
35 时 6
6 ，（2x+5）（2x-5）≠
0
因此，x=
35 6
是原方程的解.
达标检测
1. 当x__=_5__时，分式
1 无意义；当
x5
x__=_-_1_时，分式
x2 1 x2 3x 2
的值为0.
2.把分式
a
ab
b
中的a和b都扩大10倍，那么
分式的值（ C ）
A.扩大为原来的2倍
解：方程两边同乘以x2+x，得
5x+2=3x 解得 x = -1
检验：当x=-1时， x2+x=0
因此，x=-1不是原方程的解，方程无解.
（2）22xx-5
-
2 2x
5
=1．
解：方程两边同乘以（2x+5）（2x-5），得
2x（2x+5）-2（2x-5）=（2x+5）（2x-5）
解得 x = 35
1 x
1 y
3 ，则分式
2x 3xy 2 y x 2xy y
的值为多少？
解：分子分母同除以xy，得
2 3 y
2 x
1 x
1
y
2
3
3 2 3
3
1 2 1
y
x
1 x
1
y
2
3 2
5
6. A、B两地相距80公里，一辆公共汽车从A地驶出3 小时后，一辆小汽车也从A地出发，它的速度是公共汽车的3倍.已知小汽车比公共汽车迟20分钟到达B地，求两车的速度.
加减法： a c ad bc
bd
bd
乘除法： a • c ac
b d bd

分式总复习上课课件

(2) (4)
x2 1 x2 1 ( x 1)( x 1) ( x 1)( x 1) 2 x 1 2 x 1 x 2x 1 x 1 ( x 1)
分式的乘除法其实就是约分的过程
你能完成下列计算吗？
0
1 1 （） 1 3.14 3 ( ) 2
有意义，则B≠0
A 分式 B
x 1
A 0 B 0
1 变式3：分式 x 1 的值可以为0吗？
不
行
1 变式1：当 _____ x 1 时, x - 1 的值为正数.
1 正正”或“负”)数. 变式2：分式 x 1 值为___(“
x2 x2 变式3：若 2 值为负数，则 x满足________ x 1 1 变式4：若 x为整数，且 x - 1为整数，求 x 的值.

2a (a 2) a2 (a 2)(a 2) (a 2)(a 2)
答案必须是最简分式
1 a2
学过分式运算后，老师出了一道题“化简小明的做法是：
x3 2 x 2 x2 x 4
”
小亮的做法是：
小芳的做法是：
x3 2 x 2 x2 x 4 ( x 3)( x 2) x 2 2 2 x 4 x 4 x2 x 6 x 2 x2 4 x2 8 2 x 4
中
考
链
接
x 2 1 x是不等式组 1 4 若，则原式的值又是多少？其中的整数解，求式子的值原式的值能否等于 . 在x 0 ，，2 三个数中选一个合适的 ,代入求值 . . 再选取一个你喜欢的数 , 代入求值 . 1？说明理由 2( x 1) 4

分式综合复习上课课件

二、分式方程的应用：
例、甲、乙两地相距19千米，王刚从甲地去乙地，先步行了7千米，然后改骑自行车，共用了2小时到达乙地，已知王刚骑自行车的速度是步行速度的4倍，求他步行的速度和骑自行车的速度。解：设步行的速度是 x 千米/小时，则骑自行车的速度为 4x 千米/小时。根据题意，得
7 19 7 2 x 4x
值为零？
m2 9 例：当 m 取何值时，分式有意义？ m3
解：由 m – 3 ≠0，得 m≠3。所以当 m≠3 时，分式有意义；由 m2 – 9 =0，得 m=±3。而当 m=3 时，分母 m – 3 =0，分式没有意义，故应舍去，所以当 m= - 3时，分式的值为零。
当分式的分母不等于零时，分式有意义；当分式的分子等于零，而分母不等于零时，分式的值为零。
4、分式的加减法：同分母的分式相加减，分母不变，把分子相加减；异分母的分式相加减，先通分，化为同分母的分式，然后再按同分母分式的加减法则进行计算。
5、分式方程是分母中含有未知数的方程：解分式方程的基本思想是把分式方程转化为整式方程，其一般步骤是：去分母，解整式方程，验根。
专题总结
一、分式的意义：
第三章分式综合复习
授课教师
第三章
本章学习目标
分式
分式的意义
分式方程的应用
典型习题剖析
1.能熟练背诵分式、分式方程、分式的基本性质、分式乘除法运算法则、分式加减法法则等基本概念。 2.会进行分式的约分、通分和加减混合运算。 3.会解可化为一元一次方程的分式方程并检验分式方程的根。 4.能解决一些与分式、分式方程有关的实际问题。
则 k 的值是多少？
当堂练习
一、当 x 取什么值时，分式（1）有意义？