曲柄滑块机构分析
曲柄滑块机构运动分析

曲柄滑块机构运动分析一、相关参数在图1所示的曲柄滑块机构中,已知各构件的尺寸分别为mm l 1001=,mm l 3002=,s rad /101=ω,试确定连杆2和滑块3的位移、速度和加速度,并绘制出运动线图。
图1 曲柄滑块机构二、数学模型的建立1、位置分析为了对机构进行运动分析,将各构件表示为矢量,可写出各杆矢所构成的封闭矢量方程。
C S l l =+21将各矢量分别向X 轴和Y 轴进行投影,得sin sin cos cos 22112211=+=+θθθθl l S l l C(1)由式(1)得 ⎪⎪⎭⎫ ⎝⎛-=2112sin arcsin l l θθ 2211cos cos θθl l S C +=2、速度分析将式(1)对时间t 求导,得速度关系C v l l l l =--=+222111222111sin sin 0cos cos θωθωθωθω (2)将(2)式用矩阵形式来表示,如下所示 ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-1111122222cos sin . 0 cos 1 sin θθωωθθl l v l l C (3) 3、加速度分析将(2)对时间t 求导,得加速度关系⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-1111111222222222222sin cos 0 sin 0 cos 0 cos 1 sin θωθωωωθωθωαθθl l v l l a l l C C三、计算程序1、主程序%1.输入已知数据clear;l1=0.1;l2=0.3;e=0;hd=pi/180;du=180/pi;omega1=10;alpha1=0;%2.曲柄滑块机构运动计算for n1=1:721theta1(n1)=(n1-1)*hd;%调用函数slider_crank计算曲柄滑块机构位移、速度、加速度[theta2(n1),s3(n1),omega2(n1),v3(n1),alpha2(n1),a3(n1)]=slider_crank(theta1(n1),omega1,alp ha1,l1,l2,e);endfigure(1);n1=0:720;subplot(2,3,1)plot(n1,theta2*du);title('连杆转角位移线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角位移/\circ');grid onsubplot(2,3,2)plot(n1,omega2);title('连杆角速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角速度/rad\cdots^{-1}');grid onsubplot(2,3,3)plot(n1,alpha2);title('连杆角加速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角加速度/rad\cdots^{-2}');grid onsubplot(2,3,4)plot(n1,s3);title('滑块位移线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块位移/\m');grid onsubplot(2,3,5)plot(n1,v3);title('滑块速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块速度/m\cdots^{-1}');grid onsubplot(2,3,6)plot(n1,a3);title('滑块加速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块加速度/m\cdots^{-2}');grid on2、子程序function[theta2,s3,omega2,v3,alpha2,a3]=slider_crank(theta1,omega1,alpha1,l1,l2,e);%计算连杆2的角位移和滑块3的线位移s3=l1*cos(theta1)+l2*cos(theta2);theta2=asin((e-l1*sin(theta1))/l2);%计算连杆2的角速度和滑块3的线速度A=[l2*sin(theta2),1;-l2*cos(theta2),0];B=[-l1*sin(theta1);l1*cos(theta1)];omega=A\(omega1*B);omega2=omega(1);v3=omega(2);%计算连杆2的角加速度和滑块3的线加速度At=[omega2*l2*cos(theta2),0;omega2*l2*sin(theta2),0];Bt=[-omega1*l1*cos(theta1);-omega1*l1*sin(theta1)];alpha=A\(-At*omega+alpha1*B+omega1*Bt);alpha2=alpha(1);a3=alpha(2);四、程序运行结果与分析图2 运动规律曲线图从仿真曲线可以看出,当曲柄以w1=10rad/s匀速转动时,连杆的转角位移变化X围大约在-20~20度之间,在90°或270°有极值,呈反正弦变化趋势;连杆的角速度变化X围大约在-3.3~3.3rad/s,在0°或180°有极值,成反余弦变化趋势;连杆角加速度变化X围大约在-35~35rad/s2,在90°或270°有极值,呈正弦变化趋势。
曲柄(导杆)滑块机构设计分析正文.

目录1 引言1.1 选题的依据及意义·························································································(1)1.2 国内外研究概况及发展趋势··········································································(2)1.3 论文主要工作·······························································································(3)2 曲柄(导杆)滑块机构简介····································································(4)3 曲柄(导杆)滑块机构的运动学分析3.1 曲柄导杆滑块机构的运动分析······································································(5)3.1.1 机构装配的条件····················································································(6)3.1.2 建立数学模型·························································································(6)3.1.3 计算机辅助分析及其程序设计······························································(9)3. 2曲柄滑块机构的运动分析3.2.1 机构装配的条件·····················································································(25)3.2.2 建立数学模型·······················································································(25)3.2.3 计算机辅助分析及其程序设计·····························································(27)4 曲柄(导杆)滑块机构实验台装置设计4. 1 实验台结构·································································································(40)4.2 实验台硬件操作说明···················································································(41)4.3 用SolidWorks 2006实现实验台的立体图形················································(42)总结·········································································································(46)参考文献·········································································································(47)致谢·········································································································(48)1 引言1.1 选题的依据及意义1.曲柄(导杆)滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
曲柄滑块机构的结构

工作原理
当曲柄绕固定轴转动 时,通过连杆带动滑 块做往复直线运动。
通过改变曲柄的转速 和转向,可以控制滑 块的往复运动速度和 方向。
曲柄的长度和安装位 置可以改变滑块的行 程长度和方向。
应用领域
内燃机
曲柄滑块机构广泛应用于内燃机的活塞运动,通过曲柄的转动使活塞 进行往复运动,实现内燃机的吸气、压缩、做功和排气过程。
可能是由于润滑不良、部件磨损或异物卡住引起 的。应检查润滑状况,清洁机构并更换磨损部件。
异响
可能是由于部件松动、润滑不良或部件损坏引起 的。应检查紧固件和润滑状况,必要时更换损坏 部件。
精度下降
可能是由于部件磨损、松动或导轨弯曲引起的。 应检查并调整部件的精度,必要时更换磨损部件 或修正导轨。
谢谢观看
热处理工艺
总结词
热处理工艺能够显著提高材料的机械性能,是曲柄滑块机构优化的重要环节。
详细描述
热处理工艺包括淬火、回火、表面淬火和化学热处理等。淬火可以提高材料的硬度和强度,回火则可以改善材料 的韧性和降低内应力。表面淬火可以强化材料表面的硬度,提高耐磨性。化学热处理可以改变材料表面的化学成 分,提高耐腐蚀性和疲劳强度。
曲柄滑块机构的结构
目录
• 曲柄滑块机构简介 • 曲柄滑块机构类型 • 曲柄滑块机构的设计 • 曲柄滑块机构的优化 • 曲柄滑块机构的维护与保养
01
曲柄滑块机构简介
定义与特点
定义
曲柄滑块机构是一种将曲柄的回 转运动转化为滑块的往复直线运 动的机构。
特点
结构简单,工作可靠,能实现精 确的直线运动,且运动范围较大 ,因此在各种机械装置中得到广 泛应用。
总结词
当曲柄绕机架转动时,导杆仅作直线往复运动的曲柄滑块机构。
1.分析曲柄滑块机构机架长度及滑块偏置尺寸运动参数的影响。

1.分析曲柄滑块机构机架长度及滑块偏置尺寸运动参数的影响。
曲柄滑块机构是一种常见的转动运动转化为往复运动的机构。
机架长度和滑块偏置尺寸对该机构的运动参数有较大的影响。
首先,机架长度会影响机构的行程和速度。
机架长度越长,滑块往复运动的行程也就越大,同时速度也就越慢。
反之,机架长度越短,滑块往复运动的行程越小,速度也就越快。
因此,在实际设计中,应根据所需的行程和速度来选择合适的机架长度。
其次,滑块偏置尺寸会影响滑块的加速度和最大速度。
滑块偏置越大,滑块启动时的加速度就越大,最大速度也就越大。
但是,滑块偏置过大会导致机构的冲击振动较大,影响机构的稳定性和工作寿命。
因此,在实际设计中,应根据机构的要求选择合适的滑块偏置尺寸。
总的来说,机架长度和滑块偏置尺寸都是影响曲柄滑块机构运动参数的重要因素,在设计时需要综合考虑。
需要根据机构所要求的行程、速度、稳定性和工作寿命等方面的要求进行合理设计。
曲柄滑块机构分析

Fx
A
60
B Fy
求解过程:
第一步:以曲柄1为研究对象进行受力分析,如图 所示:
X方向:F21*cos(60)+Fx+F=0 Y方向:Fy+F21*sin(60)=0 转矩平衡方程:F*OA-F21*OB*sin(60)=0 三个未知量,三个方程,则可求解得到F21,即 曲柄对连杆的作用力。
7
F4 F’x
D.其他情况
13
扩展1:曲柄滑块机构
M B
A C
D
14
扩展2:当杆长发生变化时,弹簧力会发生什 么变化?
D
F
D
F
200 100 B
A
C
500 100 B
A
C
D
F
200 100 B
A
C
15
课后作业2:教材P77,课后习题4
图2-128所示为曲柄导杆机构。已知曲柄长为 a=100mm,曲柄回转中心A与导杆摆动中心C的 距离为b=200mm。曲柄以ω=36(°)/s的角速 度匀速转动。 (1)试建立该曲柄导杆机构的虚拟样机模型。 (2)仿真机构的虚拟样机模型,并测量获取导杆 角度、角速度和角加速度的变化规律; (3)试根据仿真分析结果,计算求取机构的行程 速比系数
16
课后作业1:教材P77,课后习题5
在图2-129所示的对心曲柄滑块机构,已知曲柄为 100cmx10cmx5cm的钢质杆,连杆为200cmx10cmx5cm的用在曲柄上的 驱动力矩为M1=20N.m。 (1)试建立该曲柄滑块机构的虚拟样机模型; (2)请仿真机构的虚拟样机模型,并测量获取滑块3在0s-20s运 动时间内的位移、速度和加速度的变化规律。
曲柄滑块机构分析
曲柄滑块机构滑块速度计算

曲柄滑块机构滑块速度计算1. 曲柄滑块机构概述哎,大家好,今天咱们聊聊一个跟机械有关的玩意儿——曲柄滑块机构。
这听起来有点高大上,但其实它就像个机械界的小明星,常常在各种机器中大显身手。
简单来说,这个机构的主要功能就是把旋转的运动转化为直线的运动,听起来很简单吧?其实背后可是有一套复杂的运算呢!曲柄、滑块,各种零部件一起合作,像是在跳一支优雅的舞蹈,真是让人忍不住想拍手叫好。
1.1 机构的组成部分首先,我们得知道这个机构里都有什么。
最主要的有三个角色:曲柄、滑块和连杆。
曲柄就像是个大老板,负责旋转;滑块则是个勤勤恳恳的小员工,负责移动;而连杆嘛,就像是个好朋友,把它们俩紧紧联系在一起。
想象一下,如果没有连杆的帮助,曲柄和滑块就像两条平行线,永远无法相遇。
哎呀,这场舞蹈可就没法演下去了。
1.2 运动的过程好了,假设曲柄开始转动,滑块就会在导轨上来回移动。
这个过程中,滑块的速度可不是固定的哦,它会随着曲柄的转动而变化。
想象一下,滑块就像是乘坐过山车,随着曲柄的旋转,它的速度也是时快时慢,简直惊心动魄!所以,咱们得计算出滑块的速度,才能更好地控制整个机构的运行。
2. 滑块速度的计算说到计算,这可是个关键的环节。
咱们得用到一些公式,不用担心,这里没有高深的数学,咱们简单易懂地来。
首先,我们要知道曲柄的转动角度和半径。
假设曲柄的长度是R,转动角度是θ,那滑块的线速度V可以通过公式来计算。
用公式表示,就是 V = R * ω,其中ω是角速度,听起来复杂,其实就是曲柄转动的快慢。
2.1 角速度的理解说到角速度,其实就像是你骑自行车,越快转动脚踏板,车速自然就上来了。
对于我们的曲柄也是一样,转得快,滑块就移动得快。
再者,曲柄的旋转角度和滑块的移动距离也是有关系的,比如说转动一圈,滑块可能就往前走了一大段,这个就是“距离与角度”的关系,简单又形象。
2.2 速度变化的因素不过,滑块的速度可不是一成不变的哦!它会随着曲柄的转动位置而变化。
曲柄滑块机构运动分析与力学计算

一、运动分析
S = Q sin R L ∴ ≈ Q cos ∴ = = ∴ = a
= L
R sin
+
L cos
−
R
cos ) + sin
α α
= ~
− →
L cos
cos
β β
)
R (1 −
α
= R sin =
L (1 −
β
= R L
β
= cos 1 − sin 1 2
λ
(1 − cos 2 α
cos
2 α 2 α )
)
(1 −
α α
λ
λ (1 −
cos
( 1 − cos dS = = dt
λ (1 −
= 2 α
)
dS d α + 1 2 ⋅
ω R sin
2
α
+
1 4
λ
⋅ 2
sin
2 α
σc =
g
设计时扭矩要照此要求
Q
转动副的摩擦 (轴颈摩擦)
力分析
r r r R21 = N 21 + F21
2 2 N 21 + F21 = N 21 1 + f 2
全反力 R21 =
N
Q
R21 − Q = 0 M d − R21 ⋅ ρ = 0
或
M d − F21 ⋅ r = 0
F21 ⋅ r f ρ= = R21 1+ f
→ R21 ⋅ ρ = F21 ⋅ r
Md
ω12
1
O N21
曲柄滑块机构的结构
曲拐轴式曲柄滑块机构便于实现可调行程 且结构较简单,但由于曲柄悬伸,受力情
况较差,因此主要在中、小型机械压力机 上应用。
偏心齿轮工作时只传递扭矩,弯矩由芯轴承受,因此 偏心齿轮的受力比曲轴简单些,芯轴只承受弯矩,受
力情况也比曲轴好,且刚度较大。此外,偏心齿轮的
铸造比曲轴锻造容易解决,但总体结构相对复杂些。
为了保证滑块的运动精度,滑块的导向面应尽量长 ,因而滑块的高度要足够高,滑块高度与宽度的比 值,在闭式单点压力机上约为1.08~1.32 ,在开式压力机上则高达1.7左右。
滑块还应该越轻越好,质量轻的滑块上升时消耗的 能量小,可以减少滑块停止在上止点位置时的制动 力。
滑块还应有足够的强度,小型压力机的滑块常用HT200铸造。中 型压力机的滑块常用HT200或稀土球铁铸造,或用Q235钢板 焊接而成。
所以,偏心齿轮驱动的曲柄及滑块机构常用于大中型 压力机。
滑块与导轨结构
压力机上的滑块是一个箱形结构,它的上部与连杆连接,下面开有“ T”形槽或模柄孔,用以安装模具的上模。
滑块在曲柄连杆的驱动下,沿机身导轨上下往复运动,并直接承受上 模传来的工艺反力。
为了保证滑块底平面和工作台上平面的平行度,保 证滑块运动方向与工作台面的垂直度,滑块的导向 面必须与底平面垂直。(下平面的平面度,导向面的 平面度,下平面对导向面的垂直度,导向面对母线 的直线度)
综上所述,机身变形对冲压工艺的影响是至关重要的,必须给予重视 。不同刚度的压力机,在同样的工作负荷下,刚度小的变形大,刚度
大的变形小;而对同一台压力机,工作负荷越大,变形也越大。这是 在选择压力机时必须考虑的因素。
曲柄滑块机构的运动分析
S
R 1
cos
2
第二章 通用压力机-曲柄滑块机构

柱面连接的连杆滑块结构
• 销子与连杆孔有间隙,工作行程 时,柱面接触,传递载荷。 • 回程时销子承受滑块的重量和脱 模力。 • 柱面加工困难。
三点传力的柱销式连杆结构
• 柱销中部增加了一个支承面, • 柱销的弯矩和剪力减小, • 柱销的直径减小。
柱塞导向的连杆结构
• 连杆通过导向柱塞5与滑块连接; • 偏心齿轮为浸油式润滑,减少齿 轮磨损,降低噪声。 • 加长了滑块的导向长度,提高了 压力机的运动精度。 • 中大型压力机广泛应用。
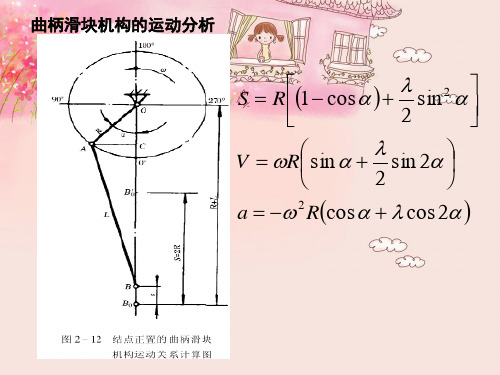
曲柄滑块机构的运动分析
• 结点正置曲柄滑块机构运动简图中, OA 是曲柄,O点是曲柄的旋转中心。 • AB 为连杆,A 点是曲柄和连杆的连结 点。 • • B 点为连杆与滑块的连结点。 曲柄长度为 R,也称为曲柄半径,连 杆长度为 L,λ= R/L 称为连杆系数 连杆系数。 连杆系数 • 对于通用压力机,λ一般为 0.1~0.2。 一般为 ~
• 滑块有铸造箱形结构、 铸造整体结构和钢板焊接结构; • 四周设有导向面,为了保证滑块运动方向与工作台的垂直度 ,滑块的导向面必须与底平面垂直。 • 导轨和滑块的导向面应保持一定的间隙,而且能进行调节。 • 为了保证滑块的导向精度,滑块的导向面应该足够长,滑块 高度和宽度的比值,在开式压力机上达1.7左右,在单点闭式 压力机上达 1.08~1.32。
s = R[(1 − cos α ) + λ 4 (1 − cos 2α )]
曲柄转角和滑块位移的关系
• 曲轴转角α与滑块行程 s的关系式为
s = R[(1 − cos α ) + λ 4 (1 − cos 2α )]
• 在实际工作中,往往根据工作行程 sP ,求 出相应的曲柄转角αP。
cos α p = 1 − c 1 + λ − cλ
曲柄滑块机构运动分析与力学计算

sin( ) sin cos cos sin sin 1 2 sin 2 sin cos
(sin sin 2 )
2
M1
PAB R(sin
2
sin 2 )在下死点
0
PR(sin sin 2 )
2
M1(P, , R, L)
设计(公称压力)行程Sg ;设计(公称压力)角 g
Q
N
Q
Md
12
O
R21
1 2
N21
F21
以轴颈中心为圆心,为半径作的圆称为摩擦圆,
为摩擦圆半径。
三、实际机构扭矩计算
理想机构:不计弹性变形;不计配合间隙 不计摩擦;不计惯性力
sin (RA RB )
L
M
' 2
PAB
m2
m2 RA R sin( )
PAB 2
R0
PAB 2
R0
PAB R0
1 1 2 s in 2
2
s in 2 1 (1 c os 2 )
2
c os 1 1 2 (1 c os 2 )
4
S R(1 c os ) L 1 2 (1 c os 2 )
4
R (1 c os )
L R
1 4
(1 c os 2 )
R (1 c os )
PAB
P
sin(90 ) sin(90 )
PAB
P
coscos 源自由于在下死点附近,,很小M 2 PAB RA R0 R sin PAB P
当 0, 0
M 2 PRA R0 R sin
P R A
R0
RRA
L
RB
R L
曲柄滑块机构特点

曲柄滑块机构特点
曲柄滑块机构是一种机械结构,常用于减速器、变速器等领域。
其特点包括:
1. 分离式机构:曲柄滑块机构将动力通过曲柄和滑块之间的摩擦传递,使得发动机输出的转速与传动速度分离,提高了传动效率。
2. 高精度:曲柄滑块机构采用了高精度的齿轮设计,使得传动精度高,能够实现快速、准确的转速控制。
3. 高效率:曲柄滑块机构能够将动力高效地传递到车轮,提高了车辆的燃油经济性和行驶里程。
4. 适应性强:曲柄滑块机构可以适应不同的发动机转速和输出要求,能够在不同的行驶状态和路况下保持稳定的性能和可靠性。
5. 易于维护:曲柄滑块机构结构简单,制造和维护成本较低,使得其易于维护和修理。
曲柄滑块机构具有分离式机构、高精度、高效率、适应性强和易于维护等特点,是一种应用广泛的机械结构。
曲柄滑块机构的仿真分析图

六. 曲柄滑块机构的运动仿真分析图
图13 曲柄滑块机构的仿真模型图
图14 曲柄滑块机构整体运动仿真的的路径图像
图15 曲柄滑块机构的曲柄扫过的路径图像
图16 曲柄滑块机构的连杆的路径图像
图17 曲柄滑块机构的滑块及切刀的路径图像
图18 曲柄滑块机构的极限位置点扫过的路径图像
图19 滑块(切刀)的位移图像
图20 滑块(切刀)的速度图像
图21 滑块(切刀)的加速度图像
图22 主动曲柄的位移图像
图23 主动曲柄的速度图像
图24 主动曲柄的加速度图像
图25 连杆的位移图像
图26 连杆的速度图像
图27 连杆的加速度图像
通过对曲柄滑块机构的仿真分析,了解了所设计的曲柄滑块机构的运动模型以及各个杆件的运动路径,曲柄的匀速圆周运动,通过连杆带动曲柄做上下往复运动,以满足切刀的上下往复运动。
通过对滑块(切刀)以及连杆、曲柄的位移、速度、加速度的图像分析可得,此方案能够满足所设计的要求。
曲柄滑块机构的运动分析及应用解读

机械原理课程机构设计实验报告题目:曲柄滑块机构的运动分析及应用小组成员与学号:刘泽陆(********)陈柯宇(11071177)熊宇飞(11071174)张保开(11071183)班级:1107172013年6月10日摘要 (3)曲柄滑块机构简介 (4)曲柄滑块机构定义 (4)曲柄滑块机构的特性及应用 (4)曲柄滑块机构的分类 (8)偏心轮机构简介 (9)曲柄滑块的动力学特性 (10)曲柄滑块的运动学特性 (11)曲柄滑块机构运行中的振动与平衡 (14)参考文献 (15)组员分工 (15)摘要本文着重介绍了曲柄滑块机构的结构,分类,用途,并进行了曲柄滑块机构的动力学和运动学分析,曲柄滑块机构的运动学特性分析,得出了机构压力表达式,曲柄滑块机构的运动特性分析,得出了滑块的位移、速度和加速度的运动表达式。
最后,对曲柄滑块机构运动中振动、平衡稳定性等进行了总结。
关键字:曲柄滑块动力与运动分析振动与平稳性ABSTRACTThe paper describes the composition of planar linkage, focusing on the structure, classification, use of a slider-crank mechanism and making the dynamic and kinematic analysis, kinematics characteristics of the crank slider mechanism analysis for a slider-crank mechanism, on one hand , we obtain the drive pressure of the slider-crank mechanism ,on the other hand,we obtain the expression of displacement, velocity and acceleration of movement. Finally, the movement of the vibration and balance stability of the crank slider mechanism are summarized.曲柄滑块机构简介曲柄滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
曲柄滑块机构运动分析的简便图解法

曲柄滑块机构运动分析的简便图解法曲柄滑块机构是利用多轴关节间通过曲柄滑块机构建立位置联系,实现传动的一类机构。
它包括曲柄轴、滑块和接头、从而实现曲线运动、往复运动、轮廓曲线运动等。
本文主要介绍一种简便的图解法,可用于分析曲柄滑块机构的运动规律。
首先是基本要素的分析,曲柄滑块机构的基本要素有曲柄轴、滑块、接头。
曲柄轴是一种用于变换位置信息的轴,它能够把位置信息传递到滑块上,使滑块形成对应的位置。
滑块能够和曲柄轴之间建立有限的接触,从而使曲柄轴把位置信息传送给接头,形成所需的运动。
其次是图解法的原理及步骤。
曲柄滑块机构的根本是控制曲柄轴运动,它的运动规律是由曲柄轴的运动控制的,而曲柄轴的运动规律是由曲柄滑块机构的特征决定的。
采用图解法可以较容易地描述出曲柄滑块机构的运动规律,从而更好地分析机构的运动特性。
图解法的基本步骤是:第一步,先确定曲柄滑块机构的结构形式,并在平面图中绘制出一个曲柄滑块机构;第二步,在机构结构图中标注它各铰接节点的位置(如轴中心点、滑块中心点等);第三步,当曲柄轴的角度发生变化时,按照基于运动的结构的原理,推算出曲柄滑块机构各连接节点的运动情况,用椭圆形表示滑块的运动轨迹;第四步,根据所得的滑块的运动轨迹的轮廓,进行有关的计算分析,可以得出某些变量与角度的规律,用于描述曲柄滑块机构的运动规律。
综上所述,图解法不仅可以帮助人们更好地理解曲柄滑块机构的运动规律,而且可以有效地解决机构设计问题。
通过图解法可以快速、准确地推导出机构的各种运动要求,从而为曲柄滑块机构的设计提供可靠的理论依据。
结论:图解法是一种利用机构特性计算分析曲柄滑块机构运动规律的简便方法,它既可以提供有效的分析手段,又可以帮助机构设计人员更好地理解机构的运动。
图解法不仅复杂性较小且易于实施,而且其结果可以用于机构的设计和调试。
第二节 曲柄滑块机构的运动与受力特点-新模板做的

学习内容 1、了解运动和受力公式,此部分了解分析的方法, 已经有了更好的算法,此部分了解一下即可。 2、重点理解压力机许用负荷图是如何得出的,对 L/O/G/O 于选择压力机有什么意义。
这一部分具体推导参见课 本
一、曲柄滑块机构的运动分 析 1、滑块位移与曲柄转角的关系
dt d dt
d
.
ddຫໍສະໝຸດ Rsin 2sin
2
2Rcos cos2 4
压力机滑块位移、速度和加速度曲线
❖ 运动原理: Vmax= ±ωR = ±2πnR/60 = ±πns/60 s-滑块行程, n-转 速, R-曲轴半径
❖ 滑块的运动速度是变化→要求速度恒定的工艺不完全合适
5
二、曲柄滑块机构受力分析 1、连杆与导轨受力分析
FAB F / cos Q F tan
FAB F
Q F sin a
二、曲柄滑块机构受力分析
(2)曲轴受扭矩
ML
FR (sin
a
2
sin
2a)
•F一定时,曲轴所受扭 矩随a值增大而增大;
•ML一定时,变形抗力F 随a值增大而减小;
•临界角(标称压力角)ag
3、压力机许用负荷图
ML恒定
F M gL (sin a sin 2a)1
1
1
1 2 sin2
采用幂级数展开,并取近似得:
s
R(1
cos
)
4
1
cos2
3
2、 滑块速度与曲柄转角的关系
滑块速度:
v d(2R s) ds ds . d . ds
dt
dt d dt d
Rsin sin 2
曲柄滑块机构及曲柄导杆机构的运动规律

曲柄滑块机构及曲柄导杆机构的运动规律
曲柄滑块机构和曲柄导杆机构都是常见的机械传动机构之一,其运动规律如下:
1. 曲柄滑块机构的运动规律
曲柄滑块机构由曲柄、连杆和滑块组成。
当曲柄转动时,连杆带动滑块做直线往复运动。
曲柄的转动是匀速的,而滑块的速度则是变化的。
具体来说,滑块在前半周期内加速,后半周期内减速,且滑块的最大速度出现在过渡点处。
2. 曲柄导杆机构的运动规律
曲柄导杆机构由曲柄、连杆和导杆组成。
与曲柄滑块机构相比,曲柄导杆机构的特点是滑块被曲柄改为了导杆,使得滑块的运动方式发生了变化。
当曲柄转动时,导杆在导轨上做往复运动,同时连杆也产生了往复运动。
曲柄的转动是匀速的,导杆的速度也是变化的。
具体来说,导杆在前半周期内减速,后半周期内加速,且导杆的最大速度出现在过渡点处。
总之,曲柄滑块机构和曲柄导杆机构的运动规律都是由曲柄的匀速转动和连杆的往复运动所决定的。
不同的是,曲柄滑块机构中滑块的运动方式为直线往复运动,而曲柄导杆机构中导杆的运动方式为沿导轨做往复运动。
曲柄滑块机构运动分析的简便图解法

曲柄滑块机构运动分析的简便图解法曲柄滑块机构是由曲柄、滑块、连接杆和钢杆等部件组成的动力学机构,它在工业上广泛应用于汽车、火车、舰船、压电等领域。
曲柄滑块机构的运动分析对汽车,火车等交通工具的运行安全,以及机械制造、检测等技术的发展具有重要意义。
这里,将介绍一种简单而有效的图解法来分析曲柄滑块机构的运动。
首先,我们需要进行示意图的绘制,这里添加了所有重要的装配元件,包括滑块、连接杆和钢杆等,还有两个表示运动轨迹的圆圈。
其次,我们可以基于这个图示,使用数学公式来分析曲柄滑块机构的运动。
一般情况下,滑块的运动轨迹是一个椭圆形,有关椭圆形轨迹的数学描述如下:$$x^2/a^2+y^2/b^2=1$$这里,a和b是椭圆形的两个顶点,这两个顶点表示滑块的最大水平和最大竖直距离。
当给定滑块的运动轨迹的长短半轴时,利用上述方程可以求出滑块的具体位置。
第三,需要计算曲柄滑块机构的速度和加速度。
通过观察图示,可以看出滑块运动圆心角θ的变化,引入θ的偏微分即可求出滑块的速度:$$V=frac {dtheta}{dt}$$而加速度可以用偏微分的第二次求得:$$A=frac {d^2theta}{dt^2}$$最后,可以利用斯特拉汀佐夫公式计算曲柄滑块机构的动偶比。
斯特拉汀佐夫公式是一个关于曲柄滑块机构的复杂的统计公式,它把滑块的输入力和转动角度等变量都连接起来,可以求出机构的总动偶比:$$I_{tot}=sum^n_{i=1}I_icdot K_i$$其中,I_i是单个机件的动偶比,K_i是分动偶比。
以上,就是使用简便图解法分析曲柄滑块机构运动的步骤,通过这个方法,可以快速得出曲柄滑块机构的运动参数,如滑块的速度和加速度、机构的动偶比等,从而更加方便的完成机构的参数设计和性能分析。
此外,简单的图示法还可以用于曲柄滑块机构运动的其他分析,比如由动力学方程求解滑块的位置和力学量,以及计算曲柄滑块机构的振动响应等问题。
例如,可以利用Euler-Lagrange方程求解曲柄滑块机构的运动方程组。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械工程郑佳文学号:1508520102 任务:根据杆长判断机构类型,模拟仿真曲柄滑块机构运动,并绘制滑块速度及加速度图像。
源代码:
clear all
clc
l1=4,l2=10,e=0,w1=10;
if(e==0) & (l1>l2)
% load handel
% sound(y,Fs)
disp('当e=0时,l1需小于l2。
不满足杆长条件,请重新输入l1,l2,e的值')
elseif((e~=0)&(l1+e>l2))
% load handel
% sound(y,Fs)
disp('当e~=0时,l1+e需小于l2。
不满足杆长条件,请重新输入l1,l2,e的值') else
end
fai=linspace(0,2*pi);
for i=1:10:length(fai)
JGT2(fai(i),l1,l2,e,w1)
end
%%%%%%%%%%%计算滑块速度并绘制图像
figure (2)
fai=0:0.01:2*pi;
v=-l1.*sin(fai).*w1-(l2^2-(l1.*sin(fai)-e). ^2).^(-0.5)*(l1^2).*(l1.*sin(fai)-e).*sin(f ai).*cos(fai).*w1;
plot(fai,v,'-b')
title('滑块角度-速度图像')
xlabel('角度\phi/°')
ylabel('速度/m/s')
figure (3)
A=- l1.*cos(fai) -
(l1^2.*cos(fai).^2)./(l2^2 - (e -
l1.*sin(fai)).^2).^(1/2) - (l1.*sin(fai).*(e - l1.*sin(fai)))./(l2^2 - (e -
l1.*sin(fai)).^2).^(1/2) ...
- (l1^2.*cos(fai).^2.*(e -
l1.*sin(fai)).^2)./(l2^2 - (e -
l1.*sin(fai)).^2).^(3/2);
plot(fai,A,'-b')
title('滑块角度-加速度图像')
xlabel('角度\phi/°') ylabel('速度/m/s')
结果图:
-2
2
468
10
12
14
滑块位移图像
角度φ/°
滑块位移/
m
0123
4567
滑块角度-速度图像
角度φ/°
速度/m /s
0123
4567
-6
-5-4-3-2-1012
3滑块角度-加速度图像
角度 /°
速度/m /s。
