曲柄滑块机构的运动学分析
曲柄滑块机构运动分析的简便图解法

曲柄滑块机构运动分析的简便图解法以《曲柄滑块机构运动分析的简便图解法》为标题,本文主要介绍了曲柄滑块机构运动分析的具体方法,特别提出了一种简便的图解法。
曲柄滑块机构是机械领域中一种重要的结构,它的分析及控制对工业发展至关重要。
由于它的运动路径复杂多变,因此,曲柄滑块机构的运动分析一直是一个重要的科学问题。
过去,曲柄滑块机构运动分析采用大量的数学分析方法,然而,这种方法并不适用于实际应用,原因是数学模型太复杂,而且计算量也很大。
因此,有必要开发新的运动分析方法,使之能够更加简便有效地分析出曲柄滑块机构的运动状态。
经过多年的探索,我们发现,采用简便的图解法,可以很容易地实现曲柄滑块机构运动分析。
一般来说,简便图解法采用操作角度分析方法,其步骤如下:首先,画出机构图,标注出每个构件的尺寸及运动角度;其次,查表求出每个构件的位置关系;然后,用构件位置关系相互抵消,解出运动关系;最后,根据运动关系,求出机构的运动状态。
经过这样的计算,我们就可以获得机构的完整运动状态,从而使曲柄滑块机构的运动分析变得更加简单有效。
另外,通过不断完善运动分析方法,我们还可以使曲柄滑块机构运动分析变得更加精确。
例如,可以引入曲率半径、摩擦力等参数,将机构的运动分析变得更加准确和准确的。
总的来说,本文主要介绍了曲柄滑块机构运动分析的简便图解法,提出了一种基于操作角度分析的新方法,可以快速有效地分析出曲柄滑块机构的运动状态。
同时,随着技术的发展,我们可以继续开发更加准确的运动分析方法,从而更好地控制机构的运动状态。
以上就是本文关于曲柄滑块机构运动分析的简便图解法的全部内容,希望本文可以为广大机械领域的朋友们提供帮助。
曲柄(导杆)滑块机构设计分析正文.

目录1 引言1.1 选题的依据及意义·························································································(1)1.2 国内外研究概况及发展趋势··········································································(2)1.3 论文主要工作·······························································································(3)2 曲柄(导杆)滑块机构简介····································································(4)3 曲柄(导杆)滑块机构的运动学分析3.1 曲柄导杆滑块机构的运动分析······································································(5)3.1.1 机构装配的条件····················································································(6)3.1.2 建立数学模型·························································································(6)3.1.3 计算机辅助分析及其程序设计······························································(9)3. 2曲柄滑块机构的运动分析3.2.1 机构装配的条件·····················································································(25)3.2.2 建立数学模型·······················································································(25)3.2.3 计算机辅助分析及其程序设计·····························································(27)4 曲柄(导杆)滑块机构实验台装置设计4. 1 实验台结构·································································································(40)4.2 实验台硬件操作说明···················································································(41)4.3 用SolidWorks 2006实现实验台的立体图形················································(42)总结·········································································································(46)参考文献·········································································································(47)致谢·········································································································(48)1 引言1.1 选题的依据及意义1.曲柄(导杆)滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
曲柄滑块机构运动规律实验报告

(1.17)
对摆角β可以利用幂级数展开的 Maclaurin 公式
arcsin
得到摆角的近似模型。粗略一些,可以取
3
6
, 1
(1.18)
1 sin
而必要时,可以取
r l
(1.19)
r r3 2 sin 3 sin 3 l 6l
(1.20)
r cos l
r2 2 1 sin 2l 2
(1.16)
r sin 2 r 3 sin 2 sin 2 r sin 2l 4l 3
从(1.16)出发,又可得近似加速度
r cos2 r 3 (sin2 2 2sin2 cos2) a2 r cos 3 l 4l
(1.11)
d 2 1 r 2 sin 2 dt l
( 1.23)
且 r=100nm l=3r=300nm ω=240 转/min. 以 a 代表角加速度实际值,以 a1,a2 代表角加速度近似值利用公式(1.11)、(1.23)、 (1.24)编制 MATLAB 的 M 文件吗 m1_1.m; function m1_1(t) ..............................................................................................................建立函数变量 r=100;l=300;w=240/60*2*pi; ...............................................................................................................赋值已知条件 a=-r*w^2*sin(t).*(l^2-r^2)./((l^2-r^2*sin(t).^2).^(3/2)) .....................................................................................................编写角加速度公式方程 a1=-w^2*r/l*sin(t) .............................................................................................编写近似角加速度公式方程一 a2=-w^2*(r/l*sin(t)+r^3/(2*l^3).*(sin(t).^3-sin(2*t).*cos(t))) .................................................................................................编写近似角加速度公式方程二 然后在命令窗口输入 m1_1([0:pi/12:pi]) 可得如表 1.1 所列出的一些相应数据; θ/rad 0 1π/12 2π/12 3π/12 4π/12 5π/12 6π/12 7π/12 8π/12 9π/12 10π/12 11π/12 π a(θ/s^2) 0 -48.9857 -97.6175 -144.1871 -184.6798 -213.0328 -223.3237 -213.0328 -184.6798 -144.1871 -97.6175 -48.9857 -0.0000 a1(θ/s^2) 0 -54.4948 -105.2758 -148.8824 -182.3430 -203.3772 -210.5516 -203.3772 -182.3430 -148.8824 -105.2758 -54.4948 -0.0000 a2(θ/s^2) 0 -49.0482 -97.9650 -144.7468 -184.8755 -212.4053 -222.2489 -212.4053 -184.8755 -144.7468 -97.9650 -49.0482 -0.0000
曲柄滑块机构及曲柄导杆机构的运动规律

曲柄滑块机构及曲柄导杆机构的运动规律
曲柄滑块机构和曲柄导杆机构都是常用的机构形式,在工业制造、机械设计等领域得到广泛应用。
它们的运动规律分别如下:
1. 曲柄滑块机构的运动规律
曲柄滑块机构由曲柄、连杆和滑块组成。
在机构运动过程中,曲柄转动,驱动连杆做直线往复运动,滑块则沿着滑道做往复运动。
曲柄滑块机构的运动规律可以简单描述为:曲柄绕定点转动时,连杆和滑块做往复直线运动。
具体来说,曲柄绕定点O转动一个角度θ,连杆就会做往复直线运动,滑块也沿着滑道做同样的往复运动。
2. 曲柄导杆机构的运动规律
曲柄导杆机构由曲柄、连杆和导杆组成。
在机构运动过程中,曲柄转动,驱动连杆做直线往复运动,导杆则做垂直于连杆方向的往复运动。
曲柄导杆机构的运动规律可以简单描述为:曲柄绕定点转动时,连杆做往复直线运动,导杆垂直于连杆方向做往复运动。
具体来说,曲柄绕定点O转动一个角度θ,连杆就会做往复直线运动,导杆则沿着垂直于连杆方向的轨迹做同样的往复运动。
总之,曲柄滑块机构和曲柄导杆机构都是常用的机构形式,它们的运动规律基于曲柄的旋转和连杆的直线往复运动,滑块或导杆则随之做相应的往复运动。
这些机构在工业制造、机械设计等领域有着广泛的应用。
曲柄滑块机构运动分析

曲柄滑块机构运动分析一、相关参数在图1所示的曲柄滑块机构中,已知各构件的尺寸分别为mm l 1001=,mm l 3002=,s rad /101=ω,试确定连杆2和滑块3的位移、速度和加速度,并绘制出运动线图。
图1 曲柄滑块机构二、数学模型的建立1、位置分析为了对机构进行运动分析,将各构件表示为矢量,可写出各杆矢所构成的封闭矢量方程。
将各矢量分别向X 轴和Y 轴进行投影,得0sin sin cos cos 22112211=+=+θθθθl l S ll C(1) 由式(1)得2、速度分析将式(1)对时间t 求导,得速度关系C v l l l l =--=+222111222111sin sin 0cos cos θωθωθωθω(2) 将(2)式用矩阵形式来表示,如下所示⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-1111122222cos sin . 0 cos 1 sin θθωωθθl l v l lC(3) 3、加速度分析将(2)对时间t 求导,得加速度关系三、计算程序1、主程序%1.输入已知数据clear;l1=0.1;l2=0.3;e=0;hd=pi/180;du=180/pi;omega1=10;alpha1=0;%2.曲柄滑块机构运动计算for n1=1:721theta1(n1)=(n1-1)*hd;%调用函数slider_crank计算曲柄滑块机构位移、速度、加速度[theta2(n1),s3(n1),omega2(n1),v3(n1),alpha2(n1),a3(n1)]=slider_crank(theta1(n1),omega1,alpha1,l1,l2,e); endfigure(1);n1=0:720;subplot(2,3,1)plot(n1,theta2*du);title('连杆转角位移线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角位移/\circ');grid onsubplot(2,3,2)plot(n1,omega2);title('连杆角速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角速度/rad\cdots^{-1}');grid onsubplot(2,3,3)plot(n1,alpha2);title('连杆角加速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('连杆角加速度/rad\cdots^{-2}');grid onsubplot(2,3,4)plot(n1,s3);title('滑块位移线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块位移/\m');grid onsubplot(2,3,5)plot(n1,v3);title('滑块速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块速度/m\cdots^{-1}');grid onsubplot(2,3,6)plot(n1,a3);title('滑块加速度运动线图');xlabel('曲柄转角\theta_1/\circ');ylabel('滑块加速度/m\cdots^{-2}');grid on2、子程序function[theta2,s3,omega2,v3,alpha2,a3]=slider_crank(theta1,omega1,alpha1,l1,l2,e);%计算连杆2的角位移和滑块3的线位移s3=l1*cos(theta1)+l2*cos(theta2);theta2=asin((e-l1*sin(theta1))/l2);%计算连杆2的角速度和滑块3的线速度A=[l2*sin(theta2),1;-l2*cos(theta2),0];B=[-l1*sin(theta1);l1*cos(theta1)];omega=A\(omega1*B);omega2=omega(1);v3=omega(2);%计算连杆2的角加速度和滑块3的线加速度At=[omega2*l2*cos(theta2),0;omega2*l2*sin(theta2),0];Bt=[-omega1*l1*cos(theta1);-omega1*l1*sin(theta1)];alpha=A\(-At*omega+alpha1*B+omega1*Bt);alpha2=alpha(1);a3=alpha(2);四、程序运行结果及分析图2 运动规律曲线图从仿真曲线可以看出,当曲柄以w1=10rad/s匀速转动时,连杆的转角位移变化范围大约在-20~20度之间,在90°或270°有极值,呈反正弦变化趋势;连杆的角速度变化范围大约在-3.3~3.3rad/s,在0°或180°有极值,成反余弦变化趋势;连杆角加速度变化范围大约在-35~35rad/s2,在90°或270°有极值,呈正弦变化趋势。
曲柄滑块机构运动分析与力学计算

一、运动分析
S = Q sin R L ∴ ≈ Q cos ∴ = = ∴ = a
= L
R sin
+
L cos
−
R
cos ) + sin
α α
= ~
− →
L cos
cos
β β
)
R (1 −
α
= R sin =
L (1 −
β
= R L
β
= cos 1 − sin 1 2
λ
(1 − cos 2 α
cos
2 α 2 α )
)
(1 −
α α
λ
λ (1 −
cos
( 1 − cos dS = = dt
λ (1 −
= 2 α
)
dS d α + 1 2 ⋅
ω R sin
2
α
+
1 4
λ
⋅ 2
sin
2 α
σc =
g
设计时扭矩要照此要求
Q
转动副的摩擦 (轴颈摩擦)
力分析
r r r R21 = N 21 + F21
2 2 N 21 + F21 = N 21 1 + f 2
全反力 R21 =
N
Q
R21 − Q = 0 M d − R21 ⋅ ρ = 0
或
M d − F21 ⋅ r = 0
F21 ⋅ r f ρ= = R21 1+ f
→ R21 ⋅ ρ = F21 ⋅ r
Md
ω12
1
O N21
偏置曲柄滑块机构的运动学分析

研究生课程论文科目:是否进修生?是□ 否■偏置曲柄滑块机构的运动学分析摘要:综合利用函数法和矢量法,在ADAMS软件中对偏置式曲柄滑块机构进行了仿真和运动分析。
首先,通过函数法对偏置式曲柄滑块机构的运动特性进行分析,根据矢量法建立机构的运动学矩阵方程。
然后,介绍了ADAMS在偏置曲柄滑块机构运动学及动力学分析中的应用。
通过对偏置曲柄滑块进行仿真和分析,得到其运动曲线。
该方法的仿真形象直观,测量方便,在机械系统运动学特性分析中具有一定的应用价值。
关键词:偏置曲柄滑块;ADAMS;仿真;运动学Abstract: The article analyzes the simulation and kinetic characteristic of deflection slider-crank mechanism by the function and the vector method in ADAMS.The kinematic equation of the deflection slider-crank mechanism is established by vector method. The application of ADAMS in kinematics analysis of slider-crank mechanism is presented. The motion and dynamic curves of offset slider-crank by ADAMS/View is obtained. In the method, simulation is authentic, visualized and convenient in measurement. The result shows that the method is efficient and useful in the kinematic characteristics analysis of mechanism.Keyword: offset slider-crank mechanism ; ADAMS; simulation ; kinematic0.引言平面连杆机构是由若干个构件用低副(转动副、移动副)连接组成的平而机构,它不仅在众多工农业机械和工程机械中得到广泛应用,还应用于人造卫星太阳能板的展开机构、机械手的传动机构等。
五种方法对曲柄滑块机构切割器运动学分析

幼儿园大班疫情学习计划一、学习目标1. 让幼儿在疫情期间保持学习的连续性和积极性,不因不能上学而丧失学习的动力和兴趣;2. 帮助幼儿掌握一定的学习内容,提高他们的认知水平和学习能力;3. 培养幼儿的自主学习能力和合作精神,提高他们的综合素质。
二、学习内容1. 语言表达:乐观向上的表达,通过故事、诗歌、游戏等形式培养幼儿的语言表达能力,培养他们的乐观情绪;2. 数学概念:让幼儿在生活中感知和认识数字、形状、大小、长度等数学概念,培养他们对数学的兴趣和好奇心;3. 绘画创作:通过观察和感知,让幼儿自由地表达自己对世界的观察和理解,培养他们的艺术创造力;4. 实践活动:通过游戏、手工制作等活动,培养幼儿的动手能力和创造力,丰富他们的生活经验;5. 社交能力:培养幼儿的社会适应能力和团队协作意识,促进他们的个性发展。
三、学习方法1. 亲子学习:鼓励家长和幼儿一起参与学习,通过家庭教育增进亲子关系,培养家庭共同学习的氛围;2. 线上学习:利用网络资源,为幼儿提供各种学习内容,如网络课程、教学视频等,帮助幼儿在家中继续学习;3. 自主学习:鼓励幼儿主动观察、思考和探索,培养他们的自主学习能力和独立思考能力;4. 互助学习:鼓励幼儿之间相互学习和交流,培养他们的合作精神和团队意识。
四、学习环境1. 创设良好的学习环境,包括家庭、幼儿园和社区等多个层面;2. 家庭学习环境:家长要创造良好的学习氛围,提供适宜的学习空间和资源,让幼儿在家中能够愉快地学习;3. 幼儿园学习环境:幼儿园要利用各种途径向家长传达学习内容,同时为幼儿提供线上学习服务和学习指导;4. 社区学习环境:社区要支持和配合学校,在社区内为幼儿提供学习资源和学习活动,让幼儿在社区中也能获取学习帮助和资源。
五、学习活动1. 语言表达:通过诗歌朗诵、趣味故事讲解等学习活动,让幼儿在欢乐中提高语言表达能力;2. 数学概念:通过数学游戏、形状分类等学习活动,让幼儿在愉快的氛围中感知和认知数学概念;3. 绘画创作:通过绘画比赛、手工DIY等活动,让幼儿展现自己的创造力和想象力;4. 实践活动:通过生活实践、家务劳动等活动,让幼儿在生活中学以致用,培养他们的实践能力;5. 社交能力:通过角色扮演、小组讨论等活动,培养幼儿的社交能力和团队协作意识。
曲柄滑块机构运动分析与力学计算

sin( ) sin cos cos sin sin 1 2 sin 2 sin cos
(sin sin 2 )
2
M1
PAB R(sin
2
sin 2 )在下死点
0
PR(sin sin 2 )
2
M1(P, , R, L)
设计(公称压力)行程Sg ;设计(公称压力)角 g
Q
N
Q
Md
12
O
R21
1 2
N21
F21
以轴颈中心为圆心,为半径作的圆称为摩擦圆,
为摩擦圆半径。
三、实际机构扭矩计算
理想机构:不计弹性变形;不计配合间隙 不计摩擦;不计惯性力
sin (RA RB )
L
M
' 2
PAB
m2
m2 RA R sin( )
PAB 2
R0
PAB 2
R0
PAB R0
1 1 2 s in 2
2
s in 2 1 (1 c os 2 )
2
c os 1 1 2 (1 c os 2 )
4
S R(1 c os ) L 1 2 (1 c os 2 )
4
R (1 c os )
L R
1 4
(1 c os 2 )
R (1 c os )
PAB
P
sin(90 ) sin(90 )
PAB
P
coscos 源自由于在下死点附近,,很小M 2 PAB RA R0 R sin PAB P
当 0, 0
M 2 PRA R0 R sin
P R A
R0
RRA
L
RB
R L
曲柄滑块机构的运动分析及应用解读

机械原理课程机构设计实验报告题目:曲柄滑块机构的运动分析及应用小组成员与学号:刘泽陆(********)陈柯宇(11071177)熊宇飞(11071174)张保开(11071183)班级:1107172013年6月10日摘要 (3)曲柄滑块机构简介 (4)曲柄滑块机构定义 (4)曲柄滑块机构的特性及应用 (4)曲柄滑块机构的分类 (8)偏心轮机构简介 (9)曲柄滑块的动力学特性 (10)曲柄滑块的运动学特性 (11)曲柄滑块机构运行中的振动与平衡 (14)参考文献 (15)组员分工 (15)摘要本文着重介绍了曲柄滑块机构的结构,分类,用途,并进行了曲柄滑块机构的动力学和运动学分析,曲柄滑块机构的运动学特性分析,得出了机构压力表达式,曲柄滑块机构的运动特性分析,得出了滑块的位移、速度和加速度的运动表达式。
最后,对曲柄滑块机构运动中振动、平衡稳定性等进行了总结。
关键字:曲柄滑块动力与运动分析振动与平稳性ABSTRACTThe paper describes the composition of planar linkage, focusing on the structure, classification, use of a slider-crank mechanism and making the dynamic and kinematic analysis, kinematics characteristics of the crank slider mechanism analysis for a slider-crank mechanism, on one hand , we obtain the drive pressure of the slider-crank mechanism ,on the other hand,we obtain the expression of displacement, velocity and acceleration of movement. Finally, the movement of the vibration and balance stability of the crank slider mechanism are summarized.曲柄滑块机构简介曲柄滑块机构定义曲柄滑块机构是铰链四杆机构的演化形式,由若干刚性构件用低副(回转副、移动副)联接而成的一种机构。
曲柄滑块机构运动分析的简便图解法

曲柄滑块机构运动分析的简便图解法曲柄滑块机构是一种具有复杂运动特性的机械系统,它在许多机械系统中起着重要的作用,能够提供有效的运动和力学参数。
因此,对曲柄滑块机构的正确分析和计算尤为重要。
近年来,研究人员们不断提出了各种新的方法来分析曲柄滑块机构的运动特性,如矩阵方法、积分方法等。
但是,这些方法都比较复杂,容易出错。
鉴于此,为了更简单地分析曲柄滑块机构的运动特性,本文提出了一种基于简单图解法的曲柄滑块机构运动分析方法。
首先,简单图解法用图形化的方式表示曲柄滑块机构的工作原理,可以清楚地展示曲柄滑块机构的运动特性,从而更容易理解它的工作原理及特性。
其次,在基于简单图解法的曲柄滑块机构运动分析中,需要考虑曲柄与滑块的结构参数,即弹性参数、刚度参数以及惯性参数等,以及滑块动力学输入信号,如外加载荷、内力和外力等。
根据这些参数和动力学信号,我们可以通过图解法求解曲柄滑块机构的运动特性,从而计算曲柄滑块的运动参数,如瞬时位置、速度、加速度等。
此外,基于简单图解法的曲柄滑块机构运动分析具有一定的普适性,可以用于分析各种类型的曲柄滑块机构,如拉伸曲柄滑块机构、蜗杆曲柄滑块机构、压簧曲柄滑块机构等。
因此,本文提出的基于简单图解法的曲柄滑块机构运动分析方法,对于分析各种曲柄滑块机构的运动特性具有重要的意义。
本文证明了简单图解法可以有效地分析曲柄滑块机构的运动特性,从而计算曲柄滑块机构的运动参数。
本文给出的分析过程,可以用来计算各种类型的曲柄滑块机构的运动特性,从而帮助工程师设计和优化曲柄滑块机构。
综上所述,本文提出的简单图解法分析曲柄滑块机构的运动特性是一种有效的方法,可以帮助工程师正确计算曲柄滑块机构的运动参数,从而更好地提高机械设备的工作效率和性能。
通过对简单图解法分析曲柄滑块机构运动特性的研究,可以为未来对曲柄滑块机构运动分析方法的设计和优化提供重要的参考和借鉴。
总之,简单图解法可以有效地分析曲柄滑块机构的运动特性和运动参数,是机械分析中非常有用的一种方法,有助于提高机械设备的性能和效率。
曲柄滑块机构结构
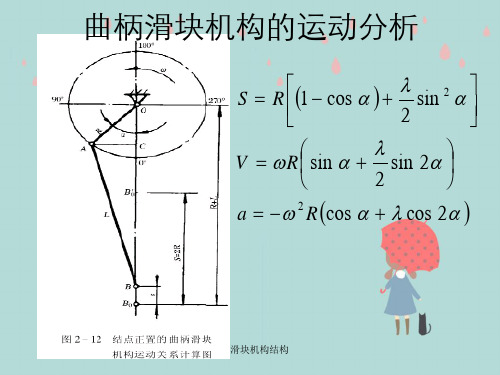
曲柄滑块机构结构
• 不同形式的机身承载能力有差异,工艺用 途也不一样。
• 双柱可倾式机身便于从机身背部卸料,有 利于冲压工作的机械化与自动化。但随着 压力机速度的提高和气动顶推装置的普及, 可倾式机身的作用将逐渐变小。
• 升降台式机身可以在较大范围内改变压力 机的装模高度,运用工艺范围较广,但其 承载能力较小。
• 除了增大导向长度来保证滑块的运动精度外, 导轨的形式也是影响滑块运动精度的一个重要 因素。导轨的形式有多种。在开式压力机上, 目前绝大多数采用成双对称布置的90°V形 导轨。
曲柄滑块机构结构
如下图所示的矩形导轨是开式压力机上较理 想的形式,其导向精度高,而摩擦损失小, 只是间隙调整比V形导轨难些。目前,国内 外高性能压力机均采用这一形式。
曲柄滑块机构结构
• 压力机的工作台、垫板及滑块,在负荷状态下, 如果出现如下图所示那样的挠度,平面度就会被 严重破坏,尤其在双动或双点压力机中,这一点 特别明显。
• 这种变形会造成模具的安装面和垫板上平面以及 滑块下平面接触不紧密,引起模具变形。
• 对于冲裁工艺,在冲裁终了时,压力机各受力部 件突然卸载,机身变形恢复,会使凸模以很高的 速度冲入凹模刃口内较大的深度,结果加速了模 具的磨损,降低了模具寿命和冲裁件质量,并且 产生较大的振动和噪声。
曲柄滑块机构的受力分析
曲柄滑块机构结构
曲柄滑块机构结构
曲柄滑块机构的结构
驱动形式: 主要为曲轴式、曲拐式和偏心齿轮式。 a、曲轴式:
曲柄半径是固定的,曲柄行程不可调。 b、曲拐式:
行程可调,但悬臂结构使受力情况较差。 c、偏心齿轮式:
受力状况较好,刚度较大,适用于大、中型压 力机。
曲柄滑块机构结构
曲柄滑块机构运动分析的简便图解法

曲柄滑块机构运动分析的简便图解法曲柄滑块机构是利用多轴关节间通过曲柄滑块机构建立位置联系,实现传动的一类机构。
它包括曲柄轴、滑块和接头、从而实现曲线运动、往复运动、轮廓曲线运动等。
本文主要介绍一种简便的图解法,可用于分析曲柄滑块机构的运动规律。
首先是基本要素的分析,曲柄滑块机构的基本要素有曲柄轴、滑块、接头。
曲柄轴是一种用于变换位置信息的轴,它能够把位置信息传递到滑块上,使滑块形成对应的位置。
滑块能够和曲柄轴之间建立有限的接触,从而使曲柄轴把位置信息传送给接头,形成所需的运动。
其次是图解法的原理及步骤。
曲柄滑块机构的根本是控制曲柄轴运动,它的运动规律是由曲柄轴的运动控制的,而曲柄轴的运动规律是由曲柄滑块机构的特征决定的。
采用图解法可以较容易地描述出曲柄滑块机构的运动规律,从而更好地分析机构的运动特性。
图解法的基本步骤是:第一步,先确定曲柄滑块机构的结构形式,并在平面图中绘制出一个曲柄滑块机构;第二步,在机构结构图中标注它各铰接节点的位置(如轴中心点、滑块中心点等);第三步,当曲柄轴的角度发生变化时,按照基于运动的结构的原理,推算出曲柄滑块机构各连接节点的运动情况,用椭圆形表示滑块的运动轨迹;第四步,根据所得的滑块的运动轨迹的轮廓,进行有关的计算分析,可以得出某些变量与角度的规律,用于描述曲柄滑块机构的运动规律。
综上所述,图解法不仅可以帮助人们更好地理解曲柄滑块机构的运动规律,而且可以有效地解决机构设计问题。
通过图解法可以快速、准确地推导出机构的各种运动要求,从而为曲柄滑块机构的设计提供可靠的理论依据。
结论:图解法是一种利用机构特性计算分析曲柄滑块机构运动规律的简便方法,它既可以提供有效的分析手段,又可以帮助机构设计人员更好地理解机构的运动。
图解法不仅复杂性较小且易于实施,而且其结果可以用于机构的设计和调试。
实验数学八:曲柄滑块机构的运动规律

目录
CONTENTS
• 曲柄滑块机构简介 • 曲柄滑块机构的运动特性 • 曲柄滑块机构的建模与仿真 • 曲柄滑块机构的设计优化 • 曲柄滑块机构的实验研究
01 曲柄滑块机构简介
曲柄滑块机构的基本概念
曲柄滑块机构是一种常见的机械机构 ,由曲柄、滑块和机架组成。曲柄通 常固定在机架上,滑块通过导轨或轴 承与曲柄相连,实现往复运动。
1 2 3
曲柄滑块机构的基本运动规律
曲柄滑块机构是由曲柄、滑块和机架组成的平面 连杆机构,其运动规律包括曲柄的旋转运动和滑 块的往复直线运动。
曲柄滑块机构的运动周期
曲柄滑块机构的运动周期是指完成一个完整的往 复直线运动所需的时间,通常由曲柄的长度和转 速决定。
曲柄滑块机构的运动轨迹
滑块的往复直线运动轨迹取决于曲柄的长度和转 速,可以通过调整曲柄长度和转速来改变轨迹。
曲柄滑块机构可以通过改变曲柄的长 度、角度或滑块的行程等参数,实现 不同的运动规律和功能。
曲柄滑块机构的应用领域
01
曲柄滑块机构广泛应用于各种机 械系统中,如冲压机、压铸机、 剪切机等。
02
在汽车制造领域,曲柄滑块机构 常被用于发动机的配气机构和曲 轴连杆机构中,实现气门的开闭 和活塞的往复运动。
设计一个用于实现大范围运动的曲柄 滑块机构,通过经验法和实验法进行 机构设计和优化。
实例二
设计一个用于实现高速传动的曲柄滑 块机构,通过仿真法模拟机构的运动 过程和特性,并进行实验验证。
05 曲柄滑块机构的实验研究
曲柄滑块机构的实验设备
实验台
用于固定和安装曲柄滑块机构 ,确保机构在实验过程中稳定
02
比较不同参数的影 响
第二节 曲柄滑块机构的运动与受力特点-新模板做的

学习内容 1、了解运动和受力公式,此部分了解分析的方法, 已经有了更好的算法,此部分了解一下即可。 2、重点理解压力机许用负荷图是如何得出的,对 L/O/G/O 于选择压力机有什么意义。
这一部分具体推导参见课 本
一、曲柄滑块机构的运动分 析 1、滑块位移与曲柄转角的关系
dt d dt
d
.
ddຫໍສະໝຸດ Rsin 2sin
2
2Rcos cos2 4
压力机滑块位移、速度和加速度曲线
❖ 运动原理: Vmax= ±ωR = ±2πnR/60 = ±πns/60 s-滑块行程, n-转 速, R-曲轴半径
❖ 滑块的运动速度是变化→要求速度恒定的工艺不完全合适
5
二、曲柄滑块机构受力分析 1、连杆与导轨受力分析
FAB F / cos Q F tan
FAB F
Q F sin a
二、曲柄滑块机构受力分析
(2)曲轴受扭矩
ML
FR (sin
a
2
sin
2a)
•F一定时,曲轴所受扭 矩随a值增大而增大;
•ML一定时,变形抗力F 随a值增大而减小;
•临界角(标称压力角)ag
3、压力机许用负荷图
ML恒定
F M gL (sin a sin 2a)1
1
1
1 2 sin2
采用幂级数展开,并取近似得:
s
R(1
cos
)
4
1
cos2
3
2、 滑块速度与曲柄转角的关系
滑块速度:
v d(2R s) ds ds . d . ds
dt
dt d dt d
Rsin sin 2
曲柄滑块机构运动分析的简便图解法

曲柄滑块机构运动分析的简便图解法曲柄滑块机构是由曲柄、滑块、连接杆和钢杆等部件组成的动力学机构,它在工业上广泛应用于汽车、火车、舰船、压电等领域。
曲柄滑块机构的运动分析对汽车,火车等交通工具的运行安全,以及机械制造、检测等技术的发展具有重要意义。
这里,将介绍一种简单而有效的图解法来分析曲柄滑块机构的运动。
首先,我们需要进行示意图的绘制,这里添加了所有重要的装配元件,包括滑块、连接杆和钢杆等,还有两个表示运动轨迹的圆圈。
其次,我们可以基于这个图示,使用数学公式来分析曲柄滑块机构的运动。
一般情况下,滑块的运动轨迹是一个椭圆形,有关椭圆形轨迹的数学描述如下:$$x^2/a^2+y^2/b^2=1$$这里,a和b是椭圆形的两个顶点,这两个顶点表示滑块的最大水平和最大竖直距离。
当给定滑块的运动轨迹的长短半轴时,利用上述方程可以求出滑块的具体位置。
第三,需要计算曲柄滑块机构的速度和加速度。
通过观察图示,可以看出滑块运动圆心角θ的变化,引入θ的偏微分即可求出滑块的速度:$$V=frac {dtheta}{dt}$$而加速度可以用偏微分的第二次求得:$$A=frac {d^2theta}{dt^2}$$最后,可以利用斯特拉汀佐夫公式计算曲柄滑块机构的动偶比。
斯特拉汀佐夫公式是一个关于曲柄滑块机构的复杂的统计公式,它把滑块的输入力和转动角度等变量都连接起来,可以求出机构的总动偶比:$$I_{tot}=sum^n_{i=1}I_icdot K_i$$其中,I_i是单个机件的动偶比,K_i是分动偶比。
以上,就是使用简便图解法分析曲柄滑块机构运动的步骤,通过这个方法,可以快速得出曲柄滑块机构的运动参数,如滑块的速度和加速度、机构的动偶比等,从而更加方便的完成机构的参数设计和性能分析。
此外,简单的图示法还可以用于曲柄滑块机构运动的其他分析,比如由动力学方程求解滑块的位置和力学量,以及计算曲柄滑块机构的振动响应等问题。
例如,可以利用Euler-Lagrange方程求解曲柄滑块机构的运动方程组。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
****** 曲柄滑块机构的运动学分析 *******'
SC=input(' 输入滑块行程的均值(mm) SC = '); P=input(' 输入曲柄轴心至滑销最远距离(mm) P = ');
E=input(' 输入机构偏心距的均值(mm) E = '); RL=input(' 输入曲柄与连杆长度比的均值 RL = '); DR=input(' 输入曲柄长度偏差(mm) DR = '); DL=input(' 输入连杆长度偏差(mm) DL = '); DE=input(' 输入机构偏心距偏差(mm) DE = '); N=input(' 输入曲柄转速(r/min) N = ');
L=sqrt((P-SC)^2-E^2)/(1-RL);
fprintf(1,' 连杆长度的均值(mm) L = %3.6f \n',L)
R=RL*L;
fprintf(1,' 曲柄长度的均值(mm) R = %3.6f \n',R)
CR=DR/3;CL=DL/3;CE=DE/3;
EL=E/L;
fprintf(1,' 偏心距与连杆长度比的均值(mm) EL = %3.6f \n',EL)
fprintf(1,' 曲柄长度的标准离差(mm) CR = %3.6f \n',CR)
fprintf(1,' 连杆长度的标准离差(mm) CR = %3.6f \n',CL)
fprintf(1,' 偏心距的标准离差(mm) CE = %3.6f \n',CE)
W=pi*N/30;
fprintf(1,' 曲柄的角速度(mm) W = %3.6f \n',W)
CRL=sqrt((R*CL)^2+(L*CR)^2)/L^2;
fprintf(1,' 曲柄与连杆长度比的标准离差 CRL = %3.6f \n',CRL)
CEL=sqrt((E*CL)^2+(L*CE)^2)/L^2;
fprintf(1,' 偏心距与连杆长度比的标准离差 CEL = %3.6f \n',CEL)
theta=0:10:360;
hd=theta.*pi/180;
% 计算滑块位移、速度、加速度的均值
S=R.*(1-cos(hd)-EL.*sin(hd)+0.5.*RL.*sin(hd).^2);
V=R.*W.*(sin(hd)-EL.*cos(hd)+0.5.*RL.*sin(2.*hd));
A=R.*W^2.*(cos(hd)+EL.*sin(hd)+RL.*cos(2.*hd));
figure(1);
subplot(1,3,1);
plot(theta,S,'r')
title('\bf \mus 线图')
subplot(1,3,2);
plot(theta,V,'k')
title('\bf \muv 线图')
xlabel('\bf 曲柄转角\theta(度)')
subplot(1,3,3);
plot(theta,A,'b')
title('\bf \mua 线图')
% 计算滑块位移、速度、加速度的标准离差
CS=sqrt((1-cos(hd)+(0.5.*RL.*sin(hd)-EL).*sin(hd)).^2.*CR^2+(0.5.*(CR L.*sin(hd)).^2-CEL^2).^2.*(R.*sin(hd)).^2);
CV=W.*sqrt((sin(hd)-EL.*cos(hd)+0.5.*RL.*sin(2.*hd)).^2.*CR^2+(0.5.*( CRL.*sin(hd)).^2-(CEL.*cos(hd)).^2)*R^2);
CA=W^2.*sqrt((cos(hd)+EL.*sin(hd)+RL.*cos(2.*hd)).^2.*CR^2+(R.*CRL.*s in(hd)).^2+(RL.*CEL.*cos(2.*hd)).^2);
figure(2);
subplot(1,3,1);
plot(theta,CS,'r')
title('\bf \sigmas 线图')
subplot(1,3,2);
plot(theta,CV,'k')
title('\bf \sigmav 线图')
xlabel('\bf 曲柄转角\theta(度)')
subplot(1,3,3);
plot(theta,CA,'b')
title('\bf \sigmaa 线图')
% 计算滑块位移、速度、加速度的偏差
DS=3.*CS;DV=3.*CV;DA=3.*CA;
% 计算滑块位移、速度、加速度的最大值和最小值
SM=S+DS;SN=S-DS;
VM=V+DV;VN=V-DV;
AM=A+DA;AN=A-DA;
% 计算滑块位移、速度、加速度的差值
SD=2.*DS;VD=2.*DV;AD=2.*DA;
figure(3);
subplot(1,3,1);
plot(theta,SD,'r')
title('\bf \Deltas 线图')
subplot(1,3,2);
plot(theta,VD,'k')
title('\bf \Deltav 线图')
xlabel('\bf 曲柄转角\theta(度)')
subplot(1,3,3);
plot(theta,AD,'b')
title('\bf \Deltaa 线图')。
