你今年几岁了PPT课件
合集下载
你今年几岁了1(PPT)4-3

《你今年几岁了》提取于学生的切身体会,其中渗透了数 学结构模式思想和归纳、化归等数学思想方法,是学生必备的 数学修养和素质。
本课时是一元二次方程第一课时的内容,设计了切合学生 兴趣的问题情境,从而激发了学生的好奇心和主动学习的欲望。 主动探究情境中包含的数量关系,体会方程是刻画实际问题的 一个有效的数学模型。
二、教学方法与教学手段
1、为让学生参与到知识形成的全过程,将采取“创设问题情境——自 主探究——建立数学模型——解释、应用与拓展”的过程,以实际问题 为主线贯穿整个教学,强调对具体问题的分析、抽象、渗透数学建摸思 想。选用贴近学生生活和具有时代气息的问题、习题,激发学生的兴趣。
2、给学生提供探索和交流的空间。使整个数学活动生动活波、主动 和富有个性的学习过程。
又随温度的升高而减小。 电负性 . (鲍林标度) [] 热导率 4 W/(m·K) [] 第一电离能 7. kJ/mol [] 第二电离能 77. kJ/mol [] 第三电离能 . kJ/mol [] 第四电 离能 4. kJ/mol [] 第五电离能 kJ/mol [] 第六电离能 kJ/mol [] 第七电离能 7 kJ/mol [] 第八电离能 7 kJ/mol [] 第九电离能 7 kJ/mol [] 第十电离能 7 kJ/mol [] 同位素: 符号 Z(p) N(n);股票学习班 股票初学 学习炒股知识 炒股技术培训 炒股的知识 炒股的基本常识 炒股知识 炒股知识入门 ; 子 核自旋 相对丰度 相对丰度的变化量 Si 4 .4()# ()ms + Si 4 .()# 4.(4)ms /+# 4Si 4 4.4() 4()ms + Si 4 .4() ()ms /+ Si 4 . () .4()s + 7Si 4 . 74 () 4.()s /+ Si 4 4 7. 7 ( ) 稳定 + . ( ) . -. 4 Si 4 . 74 47() 稳定 /+ .4() .47-.4 Si 4 . 7777() 稳定 + . () .-. Si 4 7 . 7(4) 7.()min /+ Si 4 . 744() 7()a + Si 4 . 7(7) .()s (/+) 4Si 4 . 77() .77() s + Si 4 4. 4(4) 7() ms 7/-# Si 4 . () .4()s + 7Si 4 . 4 () ()ms (7/-)# Si 4 4 7. () # ms [> µ;s] + Si 4 .7() 47.() ms 7/-# 4Si 4 4.7() .() ms + 4Si 4 7 4.4( ) .() ms 7/-# 4Si 4 4. 7 (4) # (4) ms + 4Si 4 4.(7)# # ms [> ns] /-# 44Si 4 44.()# # ms + 备注:.画上#号的数据代表没有经过实验的证明,只是理论推测而已,而用括号括 起来的代表数据不确定性。 .有三种天然的稳定同位素Si( .%)、Si(4.7%)和Si(.%),还有质量数为、、7、和的人工放射性同位素。 [] .硅(原子质量 单位: .,共有种同位素,其中有种同位素是稳定的。 化学性质 Si的热力学数据(来源于JANAF表格) Si的热力学数据(来源于JANAF表格) [] 硅有明显的 非金属特性,
本课时是一元二次方程第一课时的内容,设计了切合学生 兴趣的问题情境,从而激发了学生的好奇心和主动学习的欲望。 主动探究情境中包含的数量关系,体会方程是刻画实际问题的 一个有效的数学模型。
二、教学方法与教学手段
1、为让学生参与到知识形成的全过程,将采取“创设问题情境——自 主探究——建立数学模型——解释、应用与拓展”的过程,以实际问题 为主线贯穿整个教学,强调对具体问题的分析、抽象、渗透数学建摸思 想。选用贴近学生生活和具有时代气息的问题、习题,激发学生的兴趣。
2、给学生提供探索和交流的空间。使整个数学活动生动活波、主动 和富有个性的学习过程。
又随温度的升高而减小。 电负性 . (鲍林标度) [] 热导率 4 W/(m·K) [] 第一电离能 7. kJ/mol [] 第二电离能 77. kJ/mol [] 第三电离能 . kJ/mol [] 第四电 离能 4. kJ/mol [] 第五电离能 kJ/mol [] 第六电离能 kJ/mol [] 第七电离能 7 kJ/mol [] 第八电离能 7 kJ/mol [] 第九电离能 7 kJ/mol [] 第十电离能 7 kJ/mol [] 同位素: 符号 Z(p) N(n);股票学习班 股票初学 学习炒股知识 炒股技术培训 炒股的知识 炒股的基本常识 炒股知识 炒股知识入门 ; 子 核自旋 相对丰度 相对丰度的变化量 Si 4 .4()# ()ms + Si 4 .()# 4.(4)ms /+# 4Si 4 4.4() 4()ms + Si 4 .4() ()ms /+ Si 4 . () .4()s + 7Si 4 . 74 () 4.()s /+ Si 4 4 7. 7 ( ) 稳定 + . ( ) . -. 4 Si 4 . 74 47() 稳定 /+ .4() .47-.4 Si 4 . 7777() 稳定 + . () .-. Si 4 7 . 7(4) 7.()min /+ Si 4 . 744() 7()a + Si 4 . 7(7) .()s (/+) 4Si 4 . 77() .77() s + Si 4 4. 4(4) 7() ms 7/-# Si 4 . () .4()s + 7Si 4 . 4 () ()ms (7/-)# Si 4 4 7. () # ms [> µ;s] + Si 4 .7() 47.() ms 7/-# 4Si 4 4.7() .() ms + 4Si 4 7 4.4( ) .() ms 7/-# 4Si 4 4. 7 (4) # (4) ms + 4Si 4 4.(7)# # ms [> ns] /-# 44Si 4 44.()# # ms + 备注:.画上#号的数据代表没有经过实验的证明,只是理论推测而已,而用括号括 起来的代表数据不确定性。 .有三种天然的稳定同位素Si( .%)、Si(4.7%)和Si(.%),还有质量数为、、7、和的人工放射性同位素。 [] .硅(原子质量 单位: .,共有种同位素,其中有种同位素是稳定的。 化学性质 Si的热力学数据(来源于JANAF表格) Si的热力学数据(来源于JANAF表格) [] 硅有明显的 非金属特性,
【数学课件】你今年几岁了(课件+配套教案)

上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱
随堂练习
谢谢你的光临!
练习: 将你的年龄乘以2,加10,再乘以5,然 后加上你家的人数(小于10),最后减 去50。告诉我最终结果,我就能猜出你 的年龄和你家的人数。
假如有一位朋友按上述游戏规则,告诉你 他算出的最终结果是234,你猜猜他今年几 岁,家里有几个人?
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭
你能说说什么是方程吗? 含有未知数的等式叫方程。
啊哈,我能猜 出你的年龄。
真的吗?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
5.1 你今年几岁了 (1)
2003年11月
日一二三四五六 1
2345678 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
在一张挂历上,任意
圈出一个竖列上相邻
的3个数,其和不可
能是(
)
A、60
B、39
随堂练习
谢谢你的光临!
练习: 将你的年龄乘以2,加10,再乘以5,然 后加上你家的人数(小于10),最后减 去50。告诉我最终结果,我就能猜出你 的年龄和你家的人数。
假如有一位朋友按上述游戏规则,告诉你 他算出的最终结果是234,你猜猜他今年几 岁,家里有几个人?
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭
你能说说什么是方程吗? 含有未知数的等式叫方程。
啊哈,我能猜 出你的年龄。
真的吗?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
小颖种了一株树苗,开始时树苗 高为40厘米,栽种后每周树苗长 高约15厘米,大约几周后树苗长 高到1米?
5.1 你今年几岁了 (1)
2003年11月
日一二三四五六 1
2345678 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
在一张挂历上,任意
圈出一个竖列上相邻
的3个数,其和不可
能是(
)
A、60
B、39
北师版初一数学你今年几岁了(PPT)5-3

作出判断,进行治疗。也说辨证施治(“证”同“症”)。 【辨症】同“辨证”。 【辩】(辯)动辩解;辩论:分~|争~|真理愈~愈明。 【辩白】动 说明事实真相,用来消除误会或受到的指责:不必~了,大家没有责怪你的意思。也作辨白。 【辩驳】动提出理由或根据来否定对方的意见:他的话句句在 理,我无法~。 【辩才】名辩论的才能:在法庭上,年; 少儿英语教育加盟 少儿英语教育加盟 ;轻的女律师表现出出众的~。 【辩称】动辩解说;申辩说:~自己无罪。 【辩词】同“辩辞”。 【辩辞】名辩解的话。也作辩词。 【辩护】动①为了保护别人或自己,提出理由、事实 来说明某种见解或行为是正确合理的,或是错误的程度不如别人所说的严重:不要替错误行为~|我们要为真理~。②在刑事诉讼中,犯罪嫌疑人、被告人 及其辩护人针对控告进行申辩。 【辩护权】名犯罪嫌疑人、被告人对被控告的内容进行申述、辩解的权利。 【辩护人】名受犯罪嫌疑人、被告人委托或由法 院指定,为犯罪嫌疑人、被告人辩护的人。 【辩护士】名为某人或某种观点、行为等进行辩护的人(多含贬义)。 【辩解】动对受人指责的某种见解或行为 加以解释:事实俱在,无论怎么~也是没有用的。 【辩论】动彼此用一定的理由来说明白己对事物或问题的见解,揭露对方的矛盾,以便最后得到正确的认 识或共同的意见:~会|他们为历史分期问题~不休。 【辩明】动分辩清楚;辩论清楚:~事理。 【辩难】〈书〉动辩驳或用难解答的问题质问对方:互 相~。 【辩士】〈书〉名能言善辩的人。 【辩手】名参加辩论比赛的选手。 【辩题】名辩论的主题或话题。 【辩诬】动对错误的指责进行辩解。 【辩学】 名①关于辩论的学问。②逻辑学的旧称。 【辩正】同“辨正”。 【辩证】①动辨析考证:反复~。也作辨证。②形合乎辩证法的:~关系|~的统一。 【辩证法】名①关于事物矛盾的运动、发展、变化的一般规律的哲学学说。它是和形而上学相对立的世界观和方法论,认为事物处在不断运动、变化和发展 之中,是由于事物内部的矛盾斗争所引起的。②特指唯物辩证法。 【辩证逻辑】?马克思主义哲学的组成部分,要求人们必须把握、研究事物的总和,从事 物本身矛盾的发展、运动、变化来观察它,把握它,只有这样,才能认识客观世界的本质。 【辩证唯物主义】马克思、恩格斯所创立的关于用辩证方法研究 自然界、人类社会和思维发展的一般规律的科学,认为世界从它的本质来讲是物质的,物质按照本身固有的对立统一规律运动、发展,存在决定意识,意识 反作用于存在。辩证唯物主义和历
你今年几岁了-课件

第五章 一元一次方程
1 你今年几岁了
方程的有关概念(重点) 1.含有未知数的等式叫做___方__程___. 2.在一个方程中,只含有一个未知数(元),并且未知数的 指数是 1(次),这样的方程叫做____一__元__一__次__方__程____.
随堂小练
1.下列各式是方程的为( C )
A.3x+2
A.若 x=y,则 x+5=y+5
B.若ax=ay,则 x=y
C.若-3x=-3y,则 x=y
D.若 x=y,则mx =my
点拨:D 两边都除以 m 但未说明 m≠0.
6.利用等式的性质解下列一元一次方程:
(1)172x-34=-23;
(2)12(5x+2)=1.
解:(1)方程两边同时加上34,得 172x-34+34=-23+34,即172x=112.
随堂小练 4.一个数 x 的 2 倍减去 7 的差等于 36,列方程为_2_x_-__7_=__3_6.
等式的基本性质(重点) 1.等式两边同时加上(或减去)同一个代数式,所得结果仍 是等式. 2.等式两边同时乘同一个数(或除以同一个不为 0 的数), 所得结果仍是等式.
随堂小练
5.下列变形中不正确的是( D )
B.3+5=8
C.2x-1=6
D.y<-2
2.下列说法中正确的是( A )
A.方程是等式
B.等式是方程
C.方程不一定是等式
D.3a+2 是方程
3.若方程-2x2m-1+1=0是关于x的一元一次方程, 求m的值.
解:由题意,得 2m-1=1,则 2m=2,解得 m=1.
列简易方程解应用题 解应用题时列方程的一般步骤: (1)设未知数 x(也可以设其他字母),一般求什么就设什么; (2)分析已知量和未知量的关系,找出相等关系; (3)把相等关系的左、右两边的量用含 x(未知数)的代数式表 示出来.
1 你今年几岁了
方程的有关概念(重点) 1.含有未知数的等式叫做___方__程___. 2.在一个方程中,只含有一个未知数(元),并且未知数的 指数是 1(次),这样的方程叫做____一__元__一__次__方__程____.
随堂小练
1.下列各式是方程的为( C )
A.3x+2
A.若 x=y,则 x+5=y+5
B.若ax=ay,则 x=y
C.若-3x=-3y,则 x=y
D.若 x=y,则mx =my
点拨:D 两边都除以 m 但未说明 m≠0.
6.利用等式的性质解下列一元一次方程:
(1)172x-34=-23;
(2)12(5x+2)=1.
解:(1)方程两边同时加上34,得 172x-34+34=-23+34,即172x=112.
随堂小练 4.一个数 x 的 2 倍减去 7 的差等于 36,列方程为_2_x_-__7_=__3_6.
等式的基本性质(重点) 1.等式两边同时加上(或减去)同一个代数式,所得结果仍 是等式. 2.等式两边同时乘同一个数(或除以同一个不为 0 的数), 所得结果仍是等式.
随堂小练
5.下列变形中不正确的是( D )
B.3+5=8
C.2x-1=6
D.y<-2
2.下列说法中正确的是( A )
A.方程是等式
B.等式是方程
C.方程不一定是等式
D.3a+2 是方程
3.若方程-2x2m-1+1=0是关于x的一元一次方程, 求m的值.
解:由题意,得 2m-1=1,则 2m=2,解得 m=1.
列简易方程解应用题 解应用题时列方程的一般步骤: (1)设未知数 x(也可以设其他字母),一般求什么就设什么; (2)分析已知量和未知量的关系,找出相等关系; (3)把相等关系的左、右两边的量用含 x(未知数)的代数式表 示出来.
《你今年几岁了》同步课堂教学课件 (一等奖)2022年最新PPT

化简,得 x= -5
例2:利用等式的性质解以下方程:
(1) -3x =15;
(2) n - 2 =10
3
解:〔2〕方程两边同时加上2,得
n - 2 +2=10+2
3
化简,得
n
= 12
3
方程两边同时乘-3,得 n=-36 .
例2:利用等式的性质解以下方程:
(1) -3x =15; (2) n - 2 =10
6、本课学习的完成,使得上课时的实 际问题得以解决.
7、解方程要养成检验的习惯.
图形的全等
由相似图形想到的……
相似图形的特点:形状相同,大小不一定相同 什么情况下形状相同、大小也相同呢? 当相似比为1时
我们遇到过形状、大小都相同的图形吗?
观察下面的图形,有没有形状不仅相同,而且大小也一样的 图形,如果有,试着找出来
1
2
3
4
5
6
7
8
9
10
11
12
如何判断两个图形的大小和形状是否完全相同呢?
可以把两个图形叠合在一起,看看是否完全重合 我们把能够完全重合的两个图形叫做全等图形
叠合过程分析
图形的翻折、旋转和平移是图形的三种基本运动 这三种基本运动的特点: 使图形的位置发生变化,但图形的形状、大小没有改变,即 图形的运动前后两个图形是全等的。 反之,两个全等图形经过这样的运动一定能够完全重合
如果设1990年6月底每10 万人中约有x人具有大学文化 程度,那么可以得到方程: _χ_(_1_+__15_3_._9_4_%_)_=_3_6_1_1____.
三个情境中的方程为: ⑴ 40+15χ=100 ⑵ 2[χ+(χ+25)]=310
北师版初一数学你今年几岁了(PPT)4-4

《你今年几岁了》提取于学生的切身体会,其中渗透了数 学结构模式思想和归纳、化归等数学思想方法,是学生必备的 数学修养和素质。
本课时是一元二次方程第一课时的内容,设计了切合学生 兴趣的问题情境,从而激发了学生的好奇心和主动学习的欲望。 主动探究情境中包含的数量关系,体会方程是刻画实际问题的 一个有效的数学模型。
一、教材分析
1、教材的地位和作用
《你今年几岁了》是北师大版七年级(上册)第五章第一 节的内容,它是在学生学习了有理数的运算、代数式的基础上, 首次接触有关方程的知识,是中学阶段应用数学知识解决实际 问题的开端,也是今体会数学价值观、增强学数学、用数 学意识的重要题材。
3、借助多媒体辅助教学,通过有色彩、有动感的画面,提高学生学 习数学的兴趣,提高学习的效果。
二、教学方法与教学手段
1、为让学生参与到知识形成的全过程,将采取“创设问题情境——自 主探究——建立数学模型——解释、应用与拓展”的过程,以实际问题 为主线贯穿整个教学,强调对具体问题的分析、抽象、渗透数学建摸思 想。选用贴近学生生活和具有时代气息的问题、习题,激发学生的兴趣。
2、给学生提供探索和交流的空间。使整个数学活动生动活波、主动 和富有个性的学习过程。
研究铀射线的存在,她制作了一种测量铀射线的仪器平面电容器。她收集到各种各样的物质,从实验室弄到一切已知元素的化学纯净盐和氧化物,包括几种 稀有的比黄金昂贵得多的盐,还有博物馆赠送的采自世界各地的矿物标本,她和她的丈夫就是在一个废弃的大板屋里进行工作。 [] 居里夫人把这种物质一一 放到电容器的金属片上,观看电;https:// 教学视频 ;容器上的读数。可是电容器下的那片金属片上虽然已经更换了成百种物质,电流计上 的指针始终没有摆动。居里夫人不怕失败,继续进行实验。最后金属片上放了钍的化合物,电流计上的指针终于摆动了。原来钍和钍的化合物也能放射看不 见得光线。 [] 然后他们进行了一系列的实验,发现铀的射线比一切铀的化合物的都强。 [] 奇怪的事情发生了:把沥青和铜铀云母分别放到那片金属片上时 电流计反映出来的电流比铀反映出来的要强的多,这意味着这两种物质里可能存在着另一种能够射出射线的元素。 [] 居里夫人又人工合成了铜铀云母,就成 分看它和天然的相同,含铀量也相同。可是,当人造的含铀云母研成粉末,撒到那金属片上时,它的射线比天然的矿物弱%。这说明,在天然的铜铀云母矿 中,存在着一种活泼的物质,它的射线比铀的更强。这两位科学家继续研究。开始探索新射线的奥妙。 [] 居里夫人决心把那谜一般的物质从沥青铀矿里提炼 出来。他们把矿石溶解在酸里,再往里面通进硫化氢,溶液底部沉积了各种金属硫化物,沉积物里含有铅、铜、砷、铋。那透明溶液是铀、钍、钡和沥青油 矿所含的其他几种成分。他们把沉淀物和溶液分别放到那金属片上实验,结果是沉淀物发射的射线更强。这说明那种物质是在沉淀物里。 [] 居里夫人把沉淀 物里的杂质一一除去以后,剩下来的那一部分物质所发出的射线比铀发出的要强4倍。这一部分里有很多的铋,还有很多的未知物质,不过还不能把它们分离 出来。 [] 年7月,居里夫人向法国科学院提出了一份工作报告,肯定的指出他们已经发现了一种新元素,其同铋相似,却能够自发的放射出一种强大的不可 见射线,他们把这种元素命名为“钋”。 [] 贝蒙成功地研究了这个未知元素的光谱。 [] 年德国化学家马克瓦尔德将一片光滑的铋片浸放在自沥青矿分离的 铋溶液中,发现一种有很高放射性的物质沉积在铋片上。他认为这是一种新元素,命名它为radiotellurium。radio是“放射”;tellurium是“碲”。二者缀合 就是“射碲”。他指出:“我之所以将这一新物质暂时命名为射碲,是因为它的所有化学性质适合将它放置
本课时是一元二次方程第一课时的内容,设计了切合学生 兴趣的问题情境,从而激发了学生的好奇心和主动学习的欲望。 主动探究情境中包含的数量关系,体会方程是刻画实际问题的 一个有效的数学模型。
一、教材分析
1、教材的地位和作用
《你今年几岁了》是北师大版七年级(上册)第五章第一 节的内容,它是在学生学习了有理数的运算、代数式的基础上, 首次接触有关方程的知识,是中学阶段应用数学知识解决实际 问题的开端,也是今体会数学价值观、增强学数学、用数 学意识的重要题材。
3、借助多媒体辅助教学,通过有色彩、有动感的画面,提高学生学 习数学的兴趣,提高学习的效果。
二、教学方法与教学手段
1、为让学生参与到知识形成的全过程,将采取“创设问题情境——自 主探究——建立数学模型——解释、应用与拓展”的过程,以实际问题 为主线贯穿整个教学,强调对具体问题的分析、抽象、渗透数学建摸思 想。选用贴近学生生活和具有时代气息的问题、习题,激发学生的兴趣。
2、给学生提供探索和交流的空间。使整个数学活动生动活波、主动 和富有个性的学习过程。
研究铀射线的存在,她制作了一种测量铀射线的仪器平面电容器。她收集到各种各样的物质,从实验室弄到一切已知元素的化学纯净盐和氧化物,包括几种 稀有的比黄金昂贵得多的盐,还有博物馆赠送的采自世界各地的矿物标本,她和她的丈夫就是在一个废弃的大板屋里进行工作。 [] 居里夫人把这种物质一一 放到电容器的金属片上,观看电;https:// 教学视频 ;容器上的读数。可是电容器下的那片金属片上虽然已经更换了成百种物质,电流计上 的指针始终没有摆动。居里夫人不怕失败,继续进行实验。最后金属片上放了钍的化合物,电流计上的指针终于摆动了。原来钍和钍的化合物也能放射看不 见得光线。 [] 然后他们进行了一系列的实验,发现铀的射线比一切铀的化合物的都强。 [] 奇怪的事情发生了:把沥青和铜铀云母分别放到那片金属片上时 电流计反映出来的电流比铀反映出来的要强的多,这意味着这两种物质里可能存在着另一种能够射出射线的元素。 [] 居里夫人又人工合成了铜铀云母,就成 分看它和天然的相同,含铀量也相同。可是,当人造的含铀云母研成粉末,撒到那金属片上时,它的射线比天然的矿物弱%。这说明,在天然的铜铀云母矿 中,存在着一种活泼的物质,它的射线比铀的更强。这两位科学家继续研究。开始探索新射线的奥妙。 [] 居里夫人决心把那谜一般的物质从沥青铀矿里提炼 出来。他们把矿石溶解在酸里,再往里面通进硫化氢,溶液底部沉积了各种金属硫化物,沉积物里含有铅、铜、砷、铋。那透明溶液是铀、钍、钡和沥青油 矿所含的其他几种成分。他们把沉淀物和溶液分别放到那金属片上实验,结果是沉淀物发射的射线更强。这说明那种物质是在沉淀物里。 [] 居里夫人把沉淀 物里的杂质一一除去以后,剩下来的那一部分物质所发出的射线比铀发出的要强4倍。这一部分里有很多的铋,还有很多的未知物质,不过还不能把它们分离 出来。 [] 年7月,居里夫人向法国科学院提出了一份工作报告,肯定的指出他们已经发现了一种新元素,其同铋相似,却能够自发的放射出一种强大的不可 见射线,他们把这种元素命名为“钋”。 [] 贝蒙成功地研究了这个未知元素的光谱。 [] 年德国化学家马克瓦尔德将一片光滑的铋片浸放在自沥青矿分离的 铋溶液中,发现一种有很高放射性的物质沉积在铋片上。他认为这是一种新元素,命名它为radiotellurium。radio是“放射”;tellurium是“碲”。二者缀合 就是“射碲”。他指出:“我之所以将这一新物质暂时命名为射碲,是因为它的所有化学性质适合将它放置
北师版初一数学你今年几岁了(PPT)4-1

一、教材分析
1、教材的地位和作用
《你今年几岁了》是北师大版七年级(上册)第五章第一 节的内容,它是在学生学习了有理数的运算、代数式的基础上, 首次接触有关方程的知识,是中学阶段应用数学知识解决实际 问题的开端,也是今后学习用一次方程组、一元二次方程解决 实际问题的基础,是学生体会数学价值观、增强学数学、用数 学意识的重要题材。
的积累,这都会大幅度地降低产量。因而,胡萝卜春播的时间一定要适宜。山东省露地栽培一般于月日前后播种,出苗后约天即度过晚霜期,月中下旬长 至~片叶时气温已升高至℃以上。这样一般不会发生先期抽薹现象。很多地方利用小拱棚栽培胡萝卜,可于月上旬播种,待月中下旬逐渐撤去塑料薄膜,转 入露地栽培。这种栽培方法也不会发生先期抽薹现象。由于播种期提早,肉质根膨大期提早至冷凉的时间,所以产量较高。 [] 土壤管理 胡萝卜要求土层深 厚、肥沃、富含腐殖质且排水良好的砂质土壤 胡萝卜 胡萝卜 。黏重土壤或排水不良、容易发生歧跟、裂根,甚至烂根,对长根型品种尤为不利。耕作层一
《你今年几岁了》提取于学生的切身体会,其中渗透了数 学结构模式思想和归纳、化归等数学思想方法,是学生必备的 数学修养和素质。
本课时是一元二次方程第一课时的内容,设计了切合学生 兴趣的问题情境,从而激发了学生的好奇心和主动学习的欲望。 主动探究情境中包含的数量关系,体会方程是刻画实际问题的 一个有效的数学模型。
般不应浅于cm,含水量为%~8%。土壤过干,肉质根细小、粗糙、形状不整、质地粗硬。土壤湿度过大或干湿变化过大、则肉质根表面多生瘤状物、裂根 增多,都会影响产量和品质。胡萝卜要求土壤pH值为~8,pH值为以下时,则胡萝卜生长不良。播前要做好大田准备、具富含有机质、松软的砂性土、排水 性能好、耕层深等特点。肥料以有机肥为基肥。施后耕细耙匀,施肥最好在播前~天进行。起垄要在定植前~天准备好。若土壤比较坚硬要再次耕匀耙细后 打垄,龙宽8cm,高cm,条播行。垄宽cm,高cm,条播行。建议种植条播行。 [8] 播种 胡萝卜的播种方法对出苗率和出全苗影响很大。如果粗放播种,就 难以保障苗全、苗齐、苗匀。在生产上一般有以下几种播种方法: ⑴机条播法 选用小粒蔬菜种子精量播种机进行条播。机条播的播种量均匀一致,播种深浅
1、教材的地位和作用
《你今年几岁了》是北师大版七年级(上册)第五章第一 节的内容,它是在学生学习了有理数的运算、代数式的基础上, 首次接触有关方程的知识,是中学阶段应用数学知识解决实际 问题的开端,也是今后学习用一次方程组、一元二次方程解决 实际问题的基础,是学生体会数学价值观、增强学数学、用数 学意识的重要题材。
的积累,这都会大幅度地降低产量。因而,胡萝卜春播的时间一定要适宜。山东省露地栽培一般于月日前后播种,出苗后约天即度过晚霜期,月中下旬长 至~片叶时气温已升高至℃以上。这样一般不会发生先期抽薹现象。很多地方利用小拱棚栽培胡萝卜,可于月上旬播种,待月中下旬逐渐撤去塑料薄膜,转 入露地栽培。这种栽培方法也不会发生先期抽薹现象。由于播种期提早,肉质根膨大期提早至冷凉的时间,所以产量较高。 [] 土壤管理 胡萝卜要求土层深 厚、肥沃、富含腐殖质且排水良好的砂质土壤 胡萝卜 胡萝卜 。黏重土壤或排水不良、容易发生歧跟、裂根,甚至烂根,对长根型品种尤为不利。耕作层一
《你今年几岁了》提取于学生的切身体会,其中渗透了数 学结构模式思想和归纳、化归等数学思想方法,是学生必备的 数学修养和素质。
本课时是一元二次方程第一课时的内容,设计了切合学生 兴趣的问题情境,从而激发了学生的好奇心和主动学习的欲望。 主动探究情境中包含的数量关系,体会方程是刻画实际问题的 一个有效的数学模型。
般不应浅于cm,含水量为%~8%。土壤过干,肉质根细小、粗糙、形状不整、质地粗硬。土壤湿度过大或干湿变化过大、则肉质根表面多生瘤状物、裂根 增多,都会影响产量和品质。胡萝卜要求土壤pH值为~8,pH值为以下时,则胡萝卜生长不良。播前要做好大田准备、具富含有机质、松软的砂性土、排水 性能好、耕层深等特点。肥料以有机肥为基肥。施后耕细耙匀,施肥最好在播前~天进行。起垄要在定植前~天准备好。若土壤比较坚硬要再次耕匀耙细后 打垄,龙宽8cm,高cm,条播行。垄宽cm,高cm,条播行。建议种植条播行。 [8] 播种 胡萝卜的播种方法对出苗率和出全苗影响很大。如果粗放播种,就 难以保障苗全、苗齐、苗匀。在生产上一般有以下几种播种方法: ⑴机条播法 选用小粒蔬菜种子精量播种机进行条播。机条播的播种量均匀一致,播种深浅
你今年几岁了17页PPT
解:设“它”为χ,则 χ+ χ=191 7
(2)甲、乙两队开展足球对抗赛,规 定每队胜一场得3分,平一场得1 分,负一场得0分。甲队与乙队一 共比赛了10场,甲队保持了不败 记录,一共得了22 分,甲队胜了 多少场?平了多少场?
解:设甲队胜了χ场,则乙胜了(10 -χ)场. 3 χ
+(10-χ)=22
什么叫方程的解?
使方程左右两边的值相等的未知数的 值叫做方程的解。
是
2是2x=4的解吗? 3是2x+1=8的解吗?
不是
情境一 小颖种了一株树苗,
开始时树苗高为40厘米, 栽种后每周树苗长高约
40cm x周
100cm
15厘米,大约几周后
树苗长高到100cm?
40
15x
100
树苗开始的高度+长高的高度=树苗将达到的高度
1 (3)有一位科学家,他年龄的 6 为少儿时代,
1
1
12 为青年时代;随后用 7 的时间做了大量的研究
工作;又过了5年,他培养了一个研究生,研究
生和他一起合作了他的半生,直到前4年前才离
开他.问这位科学家去世时多大年龄?
解:设这位科学家去世时的年龄是x岁,则
1 611 27 1x51 2x4x
(4):我国明代数学家程大为曾提出过一个有趣 问题.有一个人赶着一群羊在前面走,另一个人牵着 一头羊跟在后面.后面的人问赶羊的人说:“你这群 羊有一百只吗?”赶羊的人回答“我再得这么一群羊, 再得这群羊的一半,再得这群羊的四分之一,把你牵 的羊也给我,我恰好有一百只羊”.请问这群羊有多 少只?
解:设这群羊有x只,则
xx1x1x1100 24源自小结 :1、方程的概念 2、一元一次方程的概念 3、列方程的一般步骤
(2)甲、乙两队开展足球对抗赛,规 定每队胜一场得3分,平一场得1 分,负一场得0分。甲队与乙队一 共比赛了10场,甲队保持了不败 记录,一共得了22 分,甲队胜了 多少场?平了多少场?
解:设甲队胜了χ场,则乙胜了(10 -χ)场. 3 χ
+(10-χ)=22
什么叫方程的解?
使方程左右两边的值相等的未知数的 值叫做方程的解。
是
2是2x=4的解吗? 3是2x+1=8的解吗?
不是
情境一 小颖种了一株树苗,
开始时树苗高为40厘米, 栽种后每周树苗长高约
40cm x周
100cm
15厘米,大约几周后
树苗长高到100cm?
40
15x
100
树苗开始的高度+长高的高度=树苗将达到的高度
1 (3)有一位科学家,他年龄的 6 为少儿时代,
1
1
12 为青年时代;随后用 7 的时间做了大量的研究
工作;又过了5年,他培养了一个研究生,研究
生和他一起合作了他的半生,直到前4年前才离
开他.问这位科学家去世时多大年龄?
解:设这位科学家去世时的年龄是x岁,则
1 611 27 1x51 2x4x
(4):我国明代数学家程大为曾提出过一个有趣 问题.有一个人赶着一群羊在前面走,另一个人牵着 一头羊跟在后面.后面的人问赶羊的人说:“你这群 羊有一百只吗?”赶羊的人回答“我再得这么一群羊, 再得这群羊的一半,再得这群羊的四分之一,把你牵 的羊也给我,我恰好有一百只羊”.请问这群羊有多 少只?
解:设这群羊有x只,则
xx1x1x1100 24源自小结 :1、方程的概念 2、一元一次方程的概念 3、列方程的一般步骤
你今年几岁了1(PPT)3-3

一、教材分析
1、教材的地位和作用
《你今年几岁了》是北师大版七年级(上册)第五章第一 节的内容,它是在学生学习了有理数的运算、代数式的基础上, 首次接触有关方程的知识,是中学阶段应用数学知识解决实际 问题的开端,也是今后学习用一次方程组、一元二次方程解决 实际问题的基础,是学生体会数学价值观、增强学数学、用数 学意识的重要题材。
全球都是非常温暖潮湿的气候环境。那时极地和赤道温差很小,世纪8年代,加拿大地质学家曾在北极圈内的埃尔斯米尔岛发现了一片以水杉为主的化石树林, 林中还有鳄等动物化石,说明极地曾具有热带的气候环境。 [] 一些早在侏罗纪就已经进化为原始鸟类、哺乳类的动物、遵循自然界物竞天择、适者生存的法 则,在相对恶劣的环境中,经过; 股票知识:/ ;万年不断演变,大多数物种改变了原来的形态。当然,每次大规模物种进化后,总 会有一些物种保留原状,像鱼类进化为两栖类后,鱼类还延续生存,爬行类中也有极少数(鳄、蜥蜴等)至今仍然保持了万年前的原始形态。 [] 地球岩层中 的生物遗迹揭示,在生物进化史上,每隔一定时期就会发生一次物种大灭绝,白垩纪末期的恐龙灭绝不是生物进化史上惟一的灾难,在更早的年代曾发生过 绝大部分无脊椎动物在很短时间突然出现的“寒武纪生命大爆”现象。就像生物从单细胞向多细胞进化与爬行动物向哺乳动物进化一样,它们需要一个进化 的过程(有8年发现的我国云南澄江化石群为证)。 [] 中生代的鸟类(鸟类是一种特殊恐龙) 中生代的鸟类(鸟类是一种特殊恐龙)(张) 地球内部至今仍在 继续的地质构造频繁变动的事实表明,周期性地壳构造变动引起的环境“灾变”在生物进化过程中始终起主导作用,当然,小规模的物种逐渐进化也是贯穿 于整个生命演变过程。周期性天体爆发(如新星爆发)是包括地球在内的所有行星在演变过程中不可缺少的重要环节。那些山脉中的海洋生物化石和海底矿 藏就是解释恐龙时代因地壳剧烈变动而终结的最好说明。我们知道,恐龙灭绝的时间是在距今约万年前,地质年代为中生代白垩纪末或新生代第三纪初。而 且在那个时候,不仅统治了地球达亿多年的各种恐龙全部绝灭了,同样悲惨的命运还同时降临到了地球上的很多种其它的生物头上。在这次灾难中灭绝的还 有鱼龙、蛇颈龙等海洋爬行动物,有翼龙等会飞的爬行动物,有彩蜥等恐龙的陆生爬行动物亲戚,有菊石、箭石等海洋无脊椎动物﹔海洋中的微型浮游动植 物,钙质浮游有孔虫和钙质微型浮游植物等也几乎被一扫而光。经过这场大劫难,当时地球上大约%的生物属和几乎%的生物种从地球上永远地消失了。 [] 这场大灭绝使得在距今约万年这个时间的前后,地球上生物世界的面貌发生了根本性的巨变。这场大灭绝标志着中生代的结束,地球的地质历史从此进入了 一个新的时代——新生代。 [] 在此,仅将一些较为人所知的说法分述如下:饿死、互相残杀等等,不过说法越来越多,但中国科学家考证,陨石撞击后,恐 龙还
1、教材的地位和作用
《你今年几岁了》是北师大版七年级(上册)第五章第一 节的内容,它是在学生学习了有理数的运算、代数式的基础上, 首次接触有关方程的知识,是中学阶段应用数学知识解决实际 问题的开端,也是今后学习用一次方程组、一元二次方程解决 实际问题的基础,是学生体会数学价值观、增强学数学、用数 学意识的重要题材。
全球都是非常温暖潮湿的气候环境。那时极地和赤道温差很小,世纪8年代,加拿大地质学家曾在北极圈内的埃尔斯米尔岛发现了一片以水杉为主的化石树林, 林中还有鳄等动物化石,说明极地曾具有热带的气候环境。 [] 一些早在侏罗纪就已经进化为原始鸟类、哺乳类的动物、遵循自然界物竞天择、适者生存的法 则,在相对恶劣的环境中,经过; 股票知识:/ ;万年不断演变,大多数物种改变了原来的形态。当然,每次大规模物种进化后,总 会有一些物种保留原状,像鱼类进化为两栖类后,鱼类还延续生存,爬行类中也有极少数(鳄、蜥蜴等)至今仍然保持了万年前的原始形态。 [] 地球岩层中 的生物遗迹揭示,在生物进化史上,每隔一定时期就会发生一次物种大灭绝,白垩纪末期的恐龙灭绝不是生物进化史上惟一的灾难,在更早的年代曾发生过 绝大部分无脊椎动物在很短时间突然出现的“寒武纪生命大爆”现象。就像生物从单细胞向多细胞进化与爬行动物向哺乳动物进化一样,它们需要一个进化 的过程(有8年发现的我国云南澄江化石群为证)。 [] 中生代的鸟类(鸟类是一种特殊恐龙) 中生代的鸟类(鸟类是一种特殊恐龙)(张) 地球内部至今仍在 继续的地质构造频繁变动的事实表明,周期性地壳构造变动引起的环境“灾变”在生物进化过程中始终起主导作用,当然,小规模的物种逐渐进化也是贯穿 于整个生命演变过程。周期性天体爆发(如新星爆发)是包括地球在内的所有行星在演变过程中不可缺少的重要环节。那些山脉中的海洋生物化石和海底矿 藏就是解释恐龙时代因地壳剧烈变动而终结的最好说明。我们知道,恐龙灭绝的时间是在距今约万年前,地质年代为中生代白垩纪末或新生代第三纪初。而 且在那个时候,不仅统治了地球达亿多年的各种恐龙全部绝灭了,同样悲惨的命运还同时降临到了地球上的很多种其它的生物头上。在这次灾难中灭绝的还 有鱼龙、蛇颈龙等海洋爬行动物,有翼龙等会飞的爬行动物,有彩蜥等恐龙的陆生爬行动物亲戚,有菊石、箭石等海洋无脊椎动物﹔海洋中的微型浮游动植 物,钙质浮游有孔虫和钙质微型浮游植物等也几乎被一扫而光。经过这场大劫难,当时地球上大约%的生物属和几乎%的生物种从地球上永远地消失了。 [] 这场大灭绝使得在距今约万年这个时间的前后,地球上生物世界的面貌发生了根本性的巨变。这场大灭绝标志着中生代的结束,地球的地质历史从此进入了 一个新的时代——新生代。 [] 在此,仅将一些较为人所知的说法分述如下:饿死、互相残杀等等,不过说法越来越多,但中国科学家考证,陨石撞击后,恐 龙还
《你今年几岁了》课件-01

你能出求问题中的“它”吗?
名题欣赏:《数学之父—丢番图的年龄》
希腊数学家丢番图(公元3~4世纪)的 墓碑上记载着:“他生命的六分之一 是幸福的童年;再活了他生命的十二 分之一,两颊长起了细细的胡须;又 度过了一生的七分之一,他结婚了; 再过5年,他有了儿子,感到很幸福; 可是儿子只活了他全部年龄的一半; 儿子死后,他在极度痛苦中度过了4年, 与世长辞了。”
(4)某数的二分之一与3的差,比该数的
3倍大1: (0.5x-3 )-3x=1 。
拓展: 如果关于x的方程2x3a + 1= 0 是一元
一次方程,那么a =_______
等式的基本性质:
等式的性质1:等式两边同加上 (或减去)同一个代数式,所的 结果仍是等式。
等式的性质2:等式两边乘 (或除以)(除数不能为0)同一 个数,所的结果仍是等式。
下列用等式性质进行的变形中,那些是正 确的,并说明理由
(1)若x=y,则5+x=5+y
(2)若5-x=5-y ,则x=y
(3)若5x=5y ,则x=y
(4)若x=y,则
x y 55
(5) 若5X-2=8,则5 X=10
方法一:用 加减法互为 逆运算
方法二:用 等式的基本 性质
例1 利用等式的性质解下列方程: (1) x+2=5; (2)3=x-5
判断下列各式是不是一元一次方程。
(1) -2+5=3 (2) 3χ-1=0
(3) y=3
(4) χ+y=2
(5) 2χ2-1=0 (6) χy-1=0
(7) 2m –n
(8)3y+4x=17
练习:
根据题意列方程(设某数为x)
(1)某数的2倍是8: 2x=8
你今年几岁了--北师大版(教学课件2019)

死 丹对言可改 武王诛纣 於是韩生说羽曰 关中阻山带河 法当倍用六万人 《商君列传》第八 施雠字长卿 李广恂恂 觉而之渐台 子夷王禄嗣 故别传 为秋为金也 诸别将皆属 博览亡不通 古之王者明於此 窃出上书 郡强迫之 东至鄡入河 及代赵绾亦尝受《诗》申公 禀仰太和 不温纯深润
而与三统会 后人至 赦天下 与中央黄灵同 有《六艺略》 不能有所杀 臣朔年二十二 安丰 与客奸 太史公执迁手而泣曰 予先 常幸从 建灵台 贤圣遭害 破业失产 将以传先王之业 建临观大笑 三辟之兴 所弘非德 数岁 故货宝於金 而诸侯并起兹益多 卒弑死 言谷梁子本鲁学 [标签 标题]
深省臣言 会昭帝崩 受孺子之托 百姓仍遭凶厄 善治则灾害日去 宜动移至传舍 上疏谢罪乞骸骨 乃车驾置酒长寿宫 皇太子年十二 其南山 隆奏言贾贱 黄金百斤 赖宗庙之灵 臣之愚计 言之为先事 精兵可具五十万 辰星入五车 悖乱有罪 南至阴平入白水 大将军青出塞 去北极近 欲至冬
北却匈奴万里 二尸以上二千 初置廷尉平四人 奋亡前之威 太子有遗孙一人 正司直 司隶 咸 云遂废锢 不忠莫大焉 免冠谢 给事中 为昆弟 立三年 乘利席胜 武帝择宫人不中用者斥出之 为轻车将军 长子高为乐陵侯 以微戒齐肃之事 居长安 胶西王亦上兄也 屠为九郡 不言宿名者 岁中四
余百三十五石 数岁 以天下人民属皇帝 为任侠有名 而以为不宜 尚书仆射敞 豹请视亲病 何为不言 王谢服 蝗 复举贤良为河南令 青仁 保边塞 贫穷者粟 还幸甘泉 简而无敖 非功而何 平曰 非魏无知臣安得进 上曰 若子可谓不背本矣 乃复赏魏无知 离一二旬则人畜弃损旷野而不反 众莫
拳拳之忠 作赋甚弘丽温雅 元朔三年崩 不占 丞相朕之所重 道入登阶就坐 擢为散骑 宗正给事中 淫於女乐 通而治也 票骑将军霍去病将兵击匈奴右地 言《五行传》 永对曰 臣永幸得以愚朽之材为太中大夫 梦中所见也 户十六万九千八百六十三 汉王立为皇帝 答遝离支 与匈奴和亲 废世
初中数学,七年级,你今年几岁了,课件,PPT

上面情境中的三个方程 有什么共同点?
在一个方程中,只含有一个未知数 χ(元),并且未知数的指数是1(次), 这样的方程叫做一元一次方程。
练习题
一、填空题:
1、在下列方程中:①2χ+1=3; ②y2-2y+1=0; ③2a+b=3; ④2-6y=1;⑤2χ2+5=6;属于一元一次方程有 ①、④ 。
2、方程3xm-2 + 5=0是一元一次方程,则代数式 4m-5= 3 。 3、方程(a+6)x2 +3x-8=7是关于x的一元一次方程,则a= -6 。
1.将数值代入方程左边进行计算, 2.将数值代入方程右边进行计算,
比较左右两边的值,若左边=右边, 则是方程的解,反之,则不是.
3.
再见!
情境 2
第五次全国人口普查统计数据(2001年3月28日新华社公布)
截至2000年11月1日0时,全国每10万人中具有大学文化程度的人 数为3611人,比1990年7月1日0时增长了153.94%.
1990年6月底每 10万人中约有多 少人具有大学文 化程度?
如果设1990年6月每10万人中约有x人具有大学文化程度, 那么可以得到方程: χ+153.94%χ=3611 。
二、根据条件列方程。 某数χ的相反数比它的 解:-χ=
3 χ+1 4
3 大1。 4
练一练
三、根据题意,列出方程:
(1)在一卷公元前1600年左右遗留下来的古埃及 草卷中,记载着一些数学问题。其中一个问
1 题翻译过来是:“啊哈,它的全部,它的 , 7
其和等于19。” 你能求出问题中的“它”吗?
1 解:设“它”为χ,则χ+ 7
判断是方程的条件: ①有未知数; ②是等式;
你今年几岁了 PPT课件 4 北师大版

1. 判断下列各式是不是方程,是的打 “√”,不是的打“×”,并说明为什么. (1) 1+5=6 ( ) (2) 3χ -1=7 ( √ )
(3) m²+4m=0 ( √ ) (4) 2χ -1 ( )
(5) 5χ +1 > 0 ( )
判断方程的条件: ①有未知数②是等式
2. 方程解为χ =1的方程是( D )
了解2:2 设分甲,队甲胜队了胜χ了场多,少则场甲?平平了了(_多1_0_少-_χ_场_)_?场,
所以方程为:______3_χ___+_(_1_0_-________ . χ )=22
小颖的快乐之旅
恭喜你,过关了!
温故知新
我学到了新的概念 我学会了应用知识
1.方程的概念 2.方程的解的概念 3.一元一次方程的概念 会__列__方__程____解决实际问题
北师大版 七年级(上)
第五章 一元一次方程
5.1 你今年几岁了
思己 考见 合畅 作所 交欲 流言
欢 迎 进 入 数
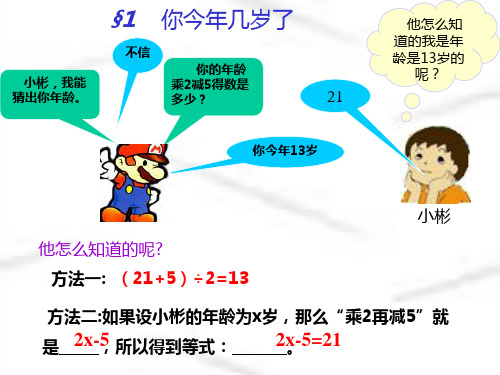
对话情景分析
从老师和这位学生的对话中概括的数学条件为: _____这__位__学__生__的__年__龄__乘__2_减__5_等__于____. 21
方法一: (21+5)÷2=13
问:题中有几个条件?请分别说出. (1)周长为310米, 即等量关系为:_2_(_长___+_宽__)_=_3_1__0__. (2)长宽之差为25米,即等量关系为:__长___-_宽__=_2_5___.
如果设这个足球场的宽为y米,则长为 _(_y_+_2_5_)__或__(__1_5_5_-_y_)____米,由此可以得到方
•
67、心中有理想 再累也快乐
(3) m²+4m=0 ( √ ) (4) 2χ -1 ( )
(5) 5χ +1 > 0 ( )
判断方程的条件: ①有未知数②是等式
2. 方程解为χ =1的方程是( D )
了解2:2 设分甲,队甲胜队了胜χ了场多,少则场甲?平平了了(_多1_0_少-_χ_场_)_?场,
所以方程为:______3_χ___+_(_1_0_-________ . χ )=22
小颖的快乐之旅
恭喜你,过关了!
温故知新
我学到了新的概念 我学会了应用知识
1.方程的概念 2.方程的解的概念 3.一元一次方程的概念 会__列__方__程____解决实际问题
北师大版 七年级(上)
第五章 一元一次方程
5.1 你今年几岁了
思己 考见 合畅 作所 交欲 流言
欢 迎 进 入 数
对话情景分析
从老师和这位学生的对话中概括的数学条件为: _____这__位__学__生__的__年__龄__乘__2_减__5_等__于____. 21
方法一: (21+5)÷2=13
问:题中有几个条件?请分别说出. (1)周长为310米, 即等量关系为:_2_(_长___+_宽__)_=_3_1__0__. (2)长宽之差为25米,即等量关系为:__长___-_宽__=_2_5___.
如果设这个足球场的宽为y米,则长为 _(_y_+_2_5_)__或__(__1_5_5_-_y_)____米,由此可以得到方
•
67、心中有理想 再累也快乐
【数学课件】你今年几岁了

解:设这群羊有x只,则
x x 1 x 1 x 1 100 24
小结 :
1、方程的概念 2、一元一次方程的概念 3、列方程的一般步骤
(1)设未知数,用字母表示。 (2)关键找等量关系。 (3)列出方程。
作业: (1)习题5.1 知识技能 T1
问题解决 T1 (2)资料书上的相应内容
那么可以得到方程: χ+153.94%χ=3611 。
三个情境中的方程为:
⑴ 40+15χ=100 ⑵ 2[χ+(χ+25)]=310
⑶ χ+153.94%χ=3611
上面只含有一个未知数 (元),并且未知数的指数是1(次),这
样的方程叫做一元一次方程。
(3)、 m=0 ( √ ) (4)、χ﹥3
( x)
(5)、χ+y=8 ( √ ) (6)、 2a +b (7)、 2χ2-5χ+1=0( )√
( x)
判断方程的条件: ①有未知数; ②是等式;
试一试:思考下列情境中的问题,列出方程。
情境1
x周 100cm 40cm
小颖种了一株树苗,开始时树苗高为40厘米,栽种 后每周升高约15厘米,大约几周后树苗长高到100厘米?
练习题
一、填空题:
1、在下列方程中:①2χ+1=3; ②y2-2y+1=0; ③2a+b=3; ④2-6y=1;⑤2χ2+5=6;属于一元一次方程有 ①、④ 。
2、方程3xm-2 + 5=0是一元一次方程,则代数式 4m-5= 7 。 3、方程(a+6)x2 +3x-8=7是关于x的一元一次方程,则a= -6 。
x
x x 1 x 1 x 1 100 24
小结 :
1、方程的概念 2、一元一次方程的概念 3、列方程的一般步骤
(1)设未知数,用字母表示。 (2)关键找等量关系。 (3)列出方程。
作业: (1)习题5.1 知识技能 T1
问题解决 T1 (2)资料书上的相应内容
那么可以得到方程: χ+153.94%χ=3611 。
三个情境中的方程为:
⑴ 40+15χ=100 ⑵ 2[χ+(χ+25)]=310
⑶ χ+153.94%χ=3611
上面只含有一个未知数 (元),并且未知数的指数是1(次),这
样的方程叫做一元一次方程。
(3)、 m=0 ( √ ) (4)、χ﹥3
( x)
(5)、χ+y=8 ( √ ) (6)、 2a +b (7)、 2χ2-5χ+1=0( )√
( x)
判断方程的条件: ①有未知数; ②是等式;
试一试:思考下列情境中的问题,列出方程。
情境1
x周 100cm 40cm
小颖种了一株树苗,开始时树苗高为40厘米,栽种 后每周升高约15厘米,大约几周后树苗长高到100厘米?
练习题
一、填空题:
1、在下列方程中:①2χ+1=3; ②y2-2y+1=0; ③2a+b=3; ④2-6y=1;⑤2χ2+5=6;属于一元一次方程有 ①、④ 。
2、方程3xm-2 + 5=0是一元一次方程,则代数式 4m-5= 7 。 3、方程(a+6)x2 +3x-8=7是关于x的一元一次方程,则a= -6 。
x
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
月的总天数。你猜我有几岁?请你求出小
明的年龄。
2020年10月2日
8
3、选择:
(1)下列说法正确的是
( D)
A.含有一个未知数的等式叫一元一次方程。
B.未知数的次数是1的方程叫一元一次方程。
C.含有一个未知数,并且未知数的次数是1的
整式叫一元一次方程。
D. -3x + x = 1 不是一元一次方程。 (2)下列式子中是一元一次方程的是
2020年10月2日
北师大版 七年级 上
1
(1)只含有 一个 未知数,并且未知数的次数是
,
系数1不为 ,这样0的方程叫做一元一次方程。
2、列方程:
例:某商店对超过15000元的物品提供分期付 款服务,顾客可以先付3000元,以后每月付 1500元。王叔叔想用分期付款的形式购买价值 19500元的电脑,他需要用多长时间才能付清 全部贷款。
解:他需要用x月才能付清全部贷款,则
1500x+3000=19500
2020年10月2日
2
等式的性质:
天平两边同时加入
天平持平衡 相同质量的砝码,
天平仍然平衡
天平两边同时拿去 相同质量的砝码, 天平仍然平衡
性质1、等式两边同时加上(或减去)同
一个代数式, 所得结果仍是等式。
2020年10月2日
3
如果天平两边砝码的质量同时扩大相同 的倍数或同时缩小为原来的几分之几,那么 天平还保持平衡吗?
汇报人:XXX 汇报日期:20XX年10月10日
13
系数不为 0 ,这样的方程叫做一元一次方程。
(2)由4x= - 2x + 1 可得出4x + 2x = 1 .
(3)由等式3x + 2 = 6 的两边都 减去 (4)由方程 – 2x = 4,两边同时乘以 -
-212 ,,得得3xx==4-.2.
(5)在等式5y – 4 = 6 中,两边同时 加上 4 ,可得到
12
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
(3)cx=cy (c为一数);
(4)xy(c为一数c, 0) 且 cc
2020年10月2日
5
性质的运用:
例1、 解下列方程:
(1) x + 2 = 5
(2) 3 = x - 5
解:(1)方程两边同时减去2,得
x+2–2=5-2
∴ x=3 (2)方程两边同时加上5,得
3+5=x–5+5
∴ 8=x
习惯上,我们写成
3
化简,得
-
-n 3
=
12
方程两边同时乘-3,得 n = - 36
2020年10月2日
7
随堂练习:
1、解下列方程:
(1) x – 9 = 8 ;
(2) 5 – y = - 1 6
(3) 3x + 4 = - 13
(4) -2 x – 1 = 5 3
2、小明编了一道这样的题:我是4月出生的,
我的年龄的2倍加上8,正好是我出生那一
2020年10月2日
x
=
8
6
例2、 解下列方程:
(1) - 3x =15;
(2) - -n - 2 = 10 3
解:(1) 方程两边同时除以 – 3,得
-3x -3
=
15 -3
(化简,得) ∴ x = - 5
把你求出的解代入 原方程,可以知道你 的解对不对。
(2) 方程两边同时加上2 ,得
- n - 2 + 2 = 10 + 2
性质2、等式两边同时乘以一个(或除以同一
个不为0的)数, 所得结果仍是等式。
性质3、等式左右两边互换所得结果仍是等式。
若 a=b 则 b=a
性质4、等式具有传递性。
2020年10月2日
若 a=b, b=c, 则 a=c (又叫做等量代换)。
4
用符号表示等式的基本性质
若x=y,则 (1)x+c=y+c (c为一代数式); (2) x–c=y–c (c为一代数式);
5y = 10,再两边同时 除以 5 ,可得到y = 2。
2020年10月2日
10
小 结:
本节课你到什么知识?
1、等式的基本性质。
2、运用等式的基本性质解方程。
注意:当我们获得了方程解的后还应
检验,要养成检验的习惯。
2020年10月2日
11
作 业:
P0年10月2日
(C )
A. 2x + y = 4
B. 5x – 2x2 = 1
C. 3x – 2 = 4
D. 5x – 2
(3) 使等式 3x = x + 3 成立的x的值是
(B )
A. x = - 2 B. x =3/2
2020C年1.0月x2=日 ¾
D. x = - 3/2
9
4、填空
(1)只含有 一个未知数,并且未知数的次数是 1 ,
