控制系统的数学模型23控制系统的结构图与信号流图.ppt
合集下载
控制系统结构图与信号流图

第四节
控制系统结构图与信号流图
1
提纲:
❖ 一 、控制系统的结构图 ❖ 二、控制系统的信号流图 ❖ 三、控制系统的传递函数
2
引言:
求系统的传递函数时,需要对微分方程组 或经拉氏变换后的代数方程组进行消元。而 采用结构图或信号流图,更便于求取系统的 传递函数,还能直观地表明输入信号以及各 中间变量在系统中的传递过程。因此,结构 图和信号流图作为一种数学模型,在控制理 论中得到了广泛的应用。
J s2 Bs
(f)
Eb (s) Kesm (s) (g)
c
(s)
1
i
m
(s)
(h)
图2-27 式(2.80)(e)~(h)子方程框图
10
按系统中各元件的相互关系,分清各输入量和输出量, 将各结构图正确地连接起来(图2-28)。
图2-28 位置随动系统结构图
11
略去La,系统结构图如图2-29所示:
8
Ia
(s)
U
a (s) La s
Eb (s) Ra
(2.80)(a)
e(s) r(s)c(s)
(b)
Us(s) Kse(s)
(c)
Ua (s) KaU s (s)
(d)
图2-27 式(2.80)(a)~(d)子方程框图
9
M d (s) KmIa (s) (e)
m(s)
M d(s) M L(s)
3
一 、控制系统的结构图
(一 )结构图的概念 图2-24 RC网络的微分方程式为:
1
ur Ri C idt
uc
1 C
idt
也可写为:
uc
1 C
ห้องสมุดไป่ตู้ idt
控制系统结构图与信号流图
1
提纲:
❖ 一 、控制系统的结构图 ❖ 二、控制系统的信号流图 ❖ 三、控制系统的传递函数
2
引言:
求系统的传递函数时,需要对微分方程组 或经拉氏变换后的代数方程组进行消元。而 采用结构图或信号流图,更便于求取系统的 传递函数,还能直观地表明输入信号以及各 中间变量在系统中的传递过程。因此,结构 图和信号流图作为一种数学模型,在控制理 论中得到了广泛的应用。
J s2 Bs
(f)
Eb (s) Kesm (s) (g)
c
(s)
1
i
m
(s)
(h)
图2-27 式(2.80)(e)~(h)子方程框图
10
按系统中各元件的相互关系,分清各输入量和输出量, 将各结构图正确地连接起来(图2-28)。
图2-28 位置随动系统结构图
11
略去La,系统结构图如图2-29所示:
8
Ia
(s)
U
a (s) La s
Eb (s) Ra
(2.80)(a)
e(s) r(s)c(s)
(b)
Us(s) Kse(s)
(c)
Ua (s) KaU s (s)
(d)
图2-27 式(2.80)(a)~(d)子方程框图
9
M d (s) KmIa (s) (e)
m(s)
M d(s) M L(s)
3
一 、控制系统的结构图
(一 )结构图的概念 图2-24 RC网络的微分方程式为:
1
ur Ri C idt
uc
1 C
idt
也可写为:
uc
1 C
ห้องสมุดไป่ตู้ idt
自动控制原理第二章 胡寿松ppt课件

—线性定常二阶微分方程式
4、消去中间变量i(t),整理后得整:理版课件
22
第二章 控制系统数学模型
例2、 设一弹簧、质量块、阻
尼器组成的系统如图所示,
当外力F(t)作用于系统时,系 F(t) 统将产生运动。试写出外力
F(t)与质量块的位移y(t)之间
m
的微分方程。
解:
f
1、确立入-出,入-F(t),出—y(t); 2、根据牛顿定律,∑F=ma;
limsF(s)存在 f(0)lifm (t)lism (F s)
s
t 0
s
(6)终值定理
若: L[f(t)]F(s)
f( )lifm (t)lism (F s)
t
s 0
整理版课件
7
第二章 控制系统数学模型
例2、求下列函数的拉氏变换。
(1)f(t)2(1cot)(s2)f(t)sin5(t() 3)f (t)tnet
L[
d
2
dt
f (t) 2
]
s
2
F
(s)
L [ d n f ( t ) ] s n F ( s )整理版课件
5
dt n
第二章 控制系统数学模型
(2)积分性质
若: L[f(t)]F(s)
L [ f(t)d] t1 sF (s)1 s f(t)dt t0
当初始条件为0,则有:
L[
f
(t )dt ]
1 - 311 1 14 s 2s 1s 2 s 1s 2
f(t) L 1 [f(t) ](t) e t 4 e 2 t
整理版课件
16
第二章 控制系统数学模型
例 6 求F(s)s(s2ss11)的拉氏反变换
4、消去中间变量i(t),整理后得整:理版课件
22
第二章 控制系统数学模型
例2、 设一弹簧、质量块、阻
尼器组成的系统如图所示,
当外力F(t)作用于系统时,系 F(t) 统将产生运动。试写出外力
F(t)与质量块的位移y(t)之间
m
的微分方程。
解:
f
1、确立入-出,入-F(t),出—y(t); 2、根据牛顿定律,∑F=ma;
limsF(s)存在 f(0)lifm (t)lism (F s)
s
t 0
s
(6)终值定理
若: L[f(t)]F(s)
f( )lifm (t)lism (F s)
t
s 0
整理版课件
7
第二章 控制系统数学模型
例2、求下列函数的拉氏变换。
(1)f(t)2(1cot)(s2)f(t)sin5(t() 3)f (t)tnet
L[
d
2
dt
f (t) 2
]
s
2
F
(s)
L [ d n f ( t ) ] s n F ( s )整理版课件
5
dt n
第二章 控制系统数学模型
(2)积分性质
若: L[f(t)]F(s)
L [ f(t)d] t1 sF (s)1 s f(t)dt t0
当初始条件为0,则有:
L[
f
(t )dt ]
1 - 311 1 14 s 2s 1s 2 s 1s 2
f(t) L 1 [f(t) ](t) e t 4 e 2 t
整理版课件
16
第二章 控制系统数学模型
例 6 求F(s)s(s2ss11)的拉氏反变换
2-3 控制系统的结构图与信号流图

其中,节点又分为三种:
输入节点(源节点):只有输出支路的节点。 混合节点:既有输入支路,又有输出支路的节点。 输出节点(阱点或汇点):只有输入支路的节点。
17:19 28
② 信号流图中常用术语 (ⅰ)、通道(通路):从一个节点开始,沿支路箭头方向 穿过各相连支路的路径。 开通道:通道与任何一个节点只相交一次。 闭通道(回环):通路的终点回到起点,而通道与任何其它节 点只相交一次。“自环”即闭通道的一种特殊情况。 前向通道:从源点开始到汇点结束的开通道。
H1 G1 1/ G1 1/ G2
17:19
G2
(2) 同时进行串联、并联
26
G 1G2 1/G1+1/G2+H1 (3)系统的C(S)/ R(S)
G1G2 ———————— 1+ G1+G2+G1G2H
C(s) G1(s)G2(s) —— = —————————————— R(s) 1+ G1(s)+G2(s)+G1(s)G2(s)H(s)
C ( S ) G3 G4 G1G2 R( S ) 1 G2G3 H
方法2:B移动到A (略)
17:19 25
例题6 试利用结构图等效变换原则,简化下述结构图,并求取系统 的C(S)/ R(S)。
R(S)
H(S)
A
G1(S)
BC
C(S)
G2(S)
解:(1) 同时将B处相加点前移、C处分支点后移:
17:19 18
⑸ 分支点的移动:移动原则同“⑷相加点的移动”。 ① 前往后移
X1
G(S)
X2 X1
X1
G(S)
X2 X1
1/ G(S)
② 后往前移
X1
G(S)
输入节点(源节点):只有输出支路的节点。 混合节点:既有输入支路,又有输出支路的节点。 输出节点(阱点或汇点):只有输入支路的节点。
17:19 28
② 信号流图中常用术语 (ⅰ)、通道(通路):从一个节点开始,沿支路箭头方向 穿过各相连支路的路径。 开通道:通道与任何一个节点只相交一次。 闭通道(回环):通路的终点回到起点,而通道与任何其它节 点只相交一次。“自环”即闭通道的一种特殊情况。 前向通道:从源点开始到汇点结束的开通道。
H1 G1 1/ G1 1/ G2
17:19
G2
(2) 同时进行串联、并联
26
G 1G2 1/G1+1/G2+H1 (3)系统的C(S)/ R(S)
G1G2 ———————— 1+ G1+G2+G1G2H
C(s) G1(s)G2(s) —— = —————————————— R(s) 1+ G1(s)+G2(s)+G1(s)G2(s)H(s)
C ( S ) G3 G4 G1G2 R( S ) 1 G2G3 H
方法2:B移动到A (略)
17:19 25
例题6 试利用结构图等效变换原则,简化下述结构图,并求取系统 的C(S)/ R(S)。
R(S)
H(S)
A
G1(S)
BC
C(S)
G2(S)
解:(1) 同时将B处相加点前移、C处分支点后移:
17:19 18
⑸ 分支点的移动:移动原则同“⑷相加点的移动”。 ① 前往后移
X1
G(S)
X2 X1
X1
G(S)
X2 X1
1/ G(S)
② 后往前移
X1
G(S)
自动控制原理-第二章-控制系统的数学模型—结构图-信号流图-传递函数

(1)单位脉冲 (2)单位阶跃 (3)单位斜坡 (4)单位加速度 (5)指数函数 (6)正弦函数 (7)余弦函数
f (t)
(t)
1(t )
t t2 2
e at
sin t cos t
F (s)
1
1s 1 s2 1 s3
1 (s a)
(s2 2) s (s2 2)
2.2 线性定常微分方程的求解 拉普拉斯反变换:部分分式展开法
时域 差分方程
解析式模型
状态方程
复域
传递函数 结构图-信号流图
图模型
频域 频率特性
数学模型是一个反应变量之间关系的表达式,在不同的域中有不同的表现形式!
1.引言
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表 达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(例如阶跃信号、单位脉冲信号、正弦信 号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s2
2Tj
s
1)
i 1
j 1
适用于 频域分
析
3.2 传递函数的基本概念 传递函数的标准形式
K:增益
K*=根轨迹增益
K与K*的关系:
两者关系
m
zj
K K*
j 1 n
pi
i 1
3.3 典型环节及其传递函数
一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见 的几种形式有:
Y (s)
R(s)
Y (s)
f (t)
(t)
1(t )
t t2 2
e at
sin t cos t
F (s)
1
1s 1 s2 1 s3
1 (s a)
(s2 2) s (s2 2)
2.2 线性定常微分方程的求解 拉普拉斯反变换:部分分式展开法
时域 差分方程
解析式模型
状态方程
复域
传递函数 结构图-信号流图
图模型
频域 频率特性
数学模型是一个反应变量之间关系的表达式,在不同的域中有不同的表现形式!
1.引言
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表 达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(例如阶跃信号、单位脉冲信号、正弦信 号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s2
2Tj
s
1)
i 1
j 1
适用于 频域分
析
3.2 传递函数的基本概念 传递函数的标准形式
K:增益
K*=根轨迹增益
K与K*的关系:
两者关系
m
zj
K K*
j 1 n
pi
i 1
3.3 典型环节及其传递函数
一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见 的几种形式有:
Y (s)
R(s)
Y (s)
自动控制原理控制系统的结构图

比较点后移
R(s)
G(s)
比较点前移
+
Q(s)
C(s)
R(s)
+
C(s) G(s)
比较点后移
Q(s)
R(s)
+
C(s) G(s)
Q(s)
C(s) R(s)G(s) Q(s)
[R(s) Q(s) ]G(s) G(s)
R(s)
C(s) G(s)
+
Q(s)
G(s)
C(s) [R(s) Q(s)]G(s)
R(s)G(s) Q(s)G(1s6 )
(5)引出点旳移动(前移、后移)
引出点前移
R(s)
G(s)
分支点(引出点)前移
C(s) C(s)
引出点后移
R(s)
G(s)
R(s)
分支点(引出点)后移
R(s)
G(s)
C(s)
G(s)
C(s)
C(s) R(s)G(s)
G(s) R(s)
C(s) R(s)
将 C(s) E(s)G(s) 代入上式,消去G(s)即得:
E(s) R(s)
1
H
1 (s)G(s)
1
1 开环传递函数
31
N(s)
+ E(s)
++
C(s)
R(s)
G1(s)
G2 (s)
-
B(s)
H(s)
(1)
打开反馈
C(s) R(s)
1
G(s) H (s)G(s)
前向通路传递函数 1 开环传递函数
注意:进行相加减旳量,必须具有相同旳量纲。
X1 +
+
X1+X2 R1(s)
自动控制原理:第二章--控制系统数学模型全

TaTLma KJe K
dMdML m dtdt
L
Tm
Ra J K eKm
——机电时间常数(秒);
Ta
La Ra
—电动机电枢回路时间常数 (秒)
若输出为电动机的转角q ,则有
TaTm
d 3q
dt 3
Tm
d 2q
dt 2
dq
dt
1 Ke
ua
Tm J
ML
TaTm J
dM L dt
—— 三阶线性定常微分方程 9
(1)根据克希霍夫定律可写出原始方程式
((23))式消LuLCcdd中去(titd)i中2d是utRc间2(中Cti1)变间C1量iR变dCti量idd后udt,ct,(t它)u输r与u(入tc输)(输t)出出uu微rc((tt)分)有方如程下式关系
或
T1T2
d 2uc (t) dt 2
T2
duc (t) dt
扰动输入为负载转矩ML。 (1)列各元件方程式。电动机方程式为:
TaTm
d 2w
dt 2
测输T速Km出发td为d电wt电测压机速w 反 K馈1e系ua数
Tm J
M反L馈 电TaJT压m
dM L dt
ua Kae ut Ktw e ur ut 12
(2)消去中间变量。从以上各式中消去中间变
量ua,e,ut,最后得到系统的微分方程式
线性(或线性化)定常系统在零初始条件下, 输出量的拉氏变换与输入量的拉氏变换之比 称为传递函数。
令线C性(s定)=常L[c系(t统)],由R下(s)述=Ln阶[r(微t)]分,方在程初描始述条:件为零
时[[aab,nnmbssdmdn进mt+ndn+dt行acmmbn(tm拉-r1)-(s1t氏ns)-am1变n+-1b1+…m换dd…1t+,nndd+1a1t得mm1bcs1(11到+ts)r+a关(t0b)]于0C]的RD(sM的s的a(()分s1s(分))=代sdbd为母)t1子为数cd传d多(tt多传方)r递项(项t程递函)式a式0函数c。b(0数tr) (t)
《自动控制原理》课件第二章

Cen idRd
Ld
d id dt
ud
(2-4)
当略去电动机的负载力矩和粘性摩擦力矩时,机械运动
微分方程式为
M GD2 d n 375 d t
(2-5)
式中,M为电动机的转矩(N·m); GD2为电动机的飞轮矩
(N·m2)。当电动机的励磁不变时,电动机的转矩与电枢电
流成正比,即电动机转矩为
M=Cmid
称为相似量。如式(2-1)中的变量ui、uo分别与式(2-3)中的变
量f(t)、y(t)为对应的相似量。
2.1.2 线性定常微分方程求解及系统运动的模态 当系统微分方程列写出来后,只要给定输入量和初始条
件,便可对微分方程求解,并由此了解系统输出量随时间变 化的特性。
若线性定常连续系统的微分方程模型的一般表示形式为 y(n)(t)+a1y(n-1)(t)+···+any(t)=b0u(m)(t)+b1u(m-1)(t)+…+bmu(t)
x0
( x x0 )2
当增量x-x0很小时,略去其高次幂项,则有
y
y0
f (x)
f (x0)
d f (x) dx
x0
(x x0)
令Δy=y-y0=f(x)-f(x0),Δx=x-x0,K=(df(x)/dx)|x0,则线性
化方程可简记为Δy=KΔx。这样,便得到函数y=f(x)在工作
点A附近的线性化方程为y=Kx。
图2-4 小偏差线性化示意图
对于有两个自变量x1、x2的非线性函数f(x1,x2),同样 可在某工作点(x10,x20)附近用泰勒级数展开为
y
f (x1 ,x2 )
f
控制系统的结构图与信号流图
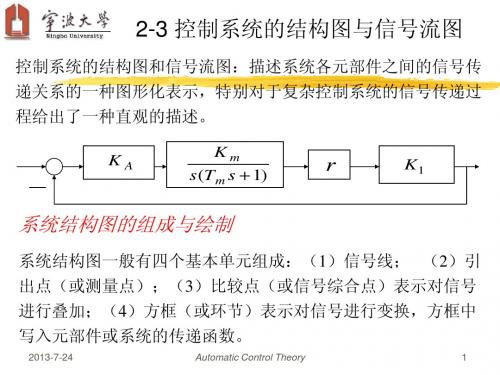
2-3 控制系统的结构图与信号流图
控制系统的结构图和信号流图:描述系统各元部件之间的信号传 递关系的一种图形化表示,特别对于复杂控制系统的信号传递过 程给出了一种直观的描述。
KA
Km s (T m s 1)
r
K1
系统结构图的组成与绘制
系统结构图一般有四个基本单元组成:(1)信号线; (2)引 出点(或测量点);(3)比较点(或信号综合点)表示对信号
Automatic Control Theory 2
M s C M U a (s )
2013-7-24
绳轮传动机构: L( s ) r m ( s )
测量电位器:
E (s)
E 2 ( s ) K 1 L( s )
M s (s)
CM
U a (s )
E1 ( s )
m (s) L (s )
2013-7-24 Automatic Control Theory 14
•回路 起点和终点同在一个节点上,而且信号通过每个节点不多 于一次的闭合通路(单独回路)。 •不接触回路 回路之间没有公共节点时,该回路称为不接触回路。
信号流图的绘制
(1)由微分方程绘制信号流图: RC串联电路的信号流图
u r (t ) i1 (t ) R1 u c (t ) u c (t ) i (t ) R2 1 i2 (t ) dt i1 (t ) R1 u1 (t ) C i1 (t ) i2 (t ) i (t )
之间的所有传递函数之乘积,记为 H(s)
开环传递函数:反馈引入点断开时,输入端对应比较器输出 E(s)
到输入端对应的比较器的反馈信号 B(s) 之间所有传递函数的乘 积,记为GK(s), GK(s)=G(s)H(s) E (s) C (s)
控制系统的结构图和信号流图:描述系统各元部件之间的信号传 递关系的一种图形化表示,特别对于复杂控制系统的信号传递过 程给出了一种直观的描述。
KA
Km s (T m s 1)
r
K1
系统结构图的组成与绘制
系统结构图一般有四个基本单元组成:(1)信号线; (2)引 出点(或测量点);(3)比较点(或信号综合点)表示对信号
Automatic Control Theory 2
M s C M U a (s )
2013-7-24
绳轮传动机构: L( s ) r m ( s )
测量电位器:
E (s)
E 2 ( s ) K 1 L( s )
M s (s)
CM
U a (s )
E1 ( s )
m (s) L (s )
2013-7-24 Automatic Control Theory 14
•回路 起点和终点同在一个节点上,而且信号通过每个节点不多 于一次的闭合通路(单独回路)。 •不接触回路 回路之间没有公共节点时,该回路称为不接触回路。
信号流图的绘制
(1)由微分方程绘制信号流图: RC串联电路的信号流图
u r (t ) i1 (t ) R1 u c (t ) u c (t ) i (t ) R2 1 i2 (t ) dt i1 (t ) R1 u1 (t ) C i1 (t ) i2 (t ) i (t )
之间的所有传递函数之乘积,记为 H(s)
开环传递函数:反馈引入点断开时,输入端对应比较器输出 E(s)
到输入端对应的比较器的反馈信号 B(s) 之间所有传递函数的乘 积,记为GK(s), GK(s)=G(s)H(s) E (s) C (s)
控制系统的信号流图

-
R2 (s)
R1(s)
R1(s) R2(s)
-
R2 (s)
R1(s)
R1(s) R2(s)
-
R2 (s)
Υ1 +
+
Υ1+Υ2
Υ1
Υ3 Υ1-Υ2+Υ3
-
Υ2
Υ2
16:00
8
(4)分支点(引出点)Branch Point 表示信号测量或引出的位置
R(s)
P(s)
G1(s)
G2 (s)
C(s)
P(s) 图2-16 分支点示意图
G1
H2 G2
H1
C(s)
G3
G4
H3
H2
1 G4
G1
G2
G3 a G4 b
H3 H1
6 变换技巧二:作用分解
同一个变量作用于两个加项点,或者是两个变量 作用于同一个方框,可以把这种作用分解成两个 单独的回路,用以化解回路之间的相互交连。一 般适用于反馈通道。
16:00
39
例5
G4
作用分解
R(s)
U0
(s)
1 C1s
I3(s)
I
2
(
s)
U
0
(
s) U R2
2
(s)
1
U2 (s) C2s I2 (s)
16:00
19
各环节方框图
I1
(s
)
U1
(
s)
U R1
0
(
s)
I3 (s) I1(s) I2 (s)
U0
(s)
1 C1s
I3(s)
I
2
(
R2 (s)
R1(s)
R1(s) R2(s)
-
R2 (s)
R1(s)
R1(s) R2(s)
-
R2 (s)
Υ1 +
+
Υ1+Υ2
Υ1
Υ3 Υ1-Υ2+Υ3
-
Υ2
Υ2
16:00
8
(4)分支点(引出点)Branch Point 表示信号测量或引出的位置
R(s)
P(s)
G1(s)
G2 (s)
C(s)
P(s) 图2-16 分支点示意图
G1
H2 G2
H1
C(s)
G3
G4
H3
H2
1 G4
G1
G2
G3 a G4 b
H3 H1
6 变换技巧二:作用分解
同一个变量作用于两个加项点,或者是两个变量 作用于同一个方框,可以把这种作用分解成两个 单独的回路,用以化解回路之间的相互交连。一 般适用于反馈通道。
16:00
39
例5
G4
作用分解
R(s)
U0
(s)
1 C1s
I3(s)
I
2
(
s)
U
0
(
s) U R2
2
(s)
1
U2 (s) C2s I2 (s)
16:00
19
各环节方框图
I1
(s
)
U1
(
s)
U R1
0
(
s)
I3 (s) I1(s) I2 (s)
U0
(s)
1 C1s
I3(s)
I
2
(
控制系统的结构图与信号流图.ppt

-
C2s
1 I1(s) - 1 u(s)
R1
I (s) C1s
1 R2C2s +1
uo (s)
ui (s)
-
-1
R1
R1C2 s
1 u(s)
C1s
1 R2C2s +1
uo (s)
ui (s) -
14:45
1
- R1
R1C2 s
1 u(s)
C1s
1 R2C2s +1
uo (s)
ui (s) -
1 R1C1s + 1
u1 ( s )
[
I1 ( s)
I2
(s)]
1 sC1
I
2
(
s)
u1(s) uC R2
(s)
uC
(s)
I2
(s)
1 sC2
i1 R1 u1 R2 i2
ur
1 sC1
1 sC2
uc
14:45
有变量相减,说明存在反馈和比较,比较后的信号一 般是元件的输入信号,所以将上页方程改写如下相乘 的形式:
等效变换: 被变换部分的输入量和输出量 之间的数学关系,在变换前后 保持不变。
14:45
(1)串联
R(s)
两个F(环s) 节串C联(s) 的R等(s)效变换:C1(s)C(s)
G1(s)
RG(s2()GsG)11((ss))GC2(1s()s)CG(Gs2()s1)(s)C(s) G2(s)
不是串C联1(s!)=R(s)G1(s也) 不是串联!
- 1/R2 UC(s)
I2(s)1/sC2
C2s
1 I1(s) - 1 u(s)
R1
I (s) C1s
1 R2C2s +1
uo (s)
ui (s)
-
-1
R1
R1C2 s
1 u(s)
C1s
1 R2C2s +1
uo (s)
ui (s) -
14:45
1
- R1
R1C2 s
1 u(s)
C1s
1 R2C2s +1
uo (s)
ui (s) -
1 R1C1s + 1
u1 ( s )
[
I1 ( s)
I2
(s)]
1 sC1
I
2
(
s)
u1(s) uC R2
(s)
uC
(s)
I2
(s)
1 sC2
i1 R1 u1 R2 i2
ur
1 sC1
1 sC2
uc
14:45
有变量相减,说明存在反馈和比较,比较后的信号一 般是元件的输入信号,所以将上页方程改写如下相乘 的形式:
等效变换: 被变换部分的输入量和输出量 之间的数学关系,在变换前后 保持不变。
14:45
(1)串联
R(s)
两个F(环s) 节串C联(s) 的R等(s)效变换:C1(s)C(s)
G1(s)
RG(s2()GsG)11((ss))GC2(1s()s)CG(Gs2()s1)(s)C(s) G2(s)
不是串C联1(s!)=R(s)G1(s也) 不是串联!
- 1/R2 UC(s)
I2(s)1/sC2
自动控制理论邹伯敏PPT第二章

等其它模型均由它而导出 状态变量描述 状态方程是这种描述的最基本形式
建立系统数学模型的方法
实验法:人为施加某种测试信号,记录基本输出响应。
解析法:根据系统及元件各变量之间所遵循的基本物理
定律,列写处每一个元件的输入-输出关系式。
2019/11/2
第二章 控制系统的数学模型
2
自动控制理论
第一节 列写系统微分方程的一般方法
即
Gs C Rssb a00ssm n b a1 1ssm n 1 1
bm 1sbm an1san
Gs就是系统的传递函数。
( 2-30)
其中 C, sLCt;RsLRt它们之间的传
方框图表示。
2019/11/2
第二章 控制系统的数学模型
15
自动控制理论
由式(2-17)减式(2-15),式(2-17)减式(2-15)后得
iBRNdd t u1 E GC 1
( 2-19) ( 2-20)
式(2-19)、(2-20)均为增量方程,它们描述了发电机在平衡点 A处受到△u1作用后的运动过程。对增量方程式而言,磁化曲线的坐 标原点不是在O点,而是移到A点。因而发电机的初始条件仍为零。 式中N为励磁绕组的匝数。
n0
1 Ce
EG
(n0为电动机的空载转速)
(2-9 )
测速发电机
输入量是电动机的转速n,输出量是测速发电机的电压Ufn ,假设 测速发电机的磁场恒定不变,则Ufn与n成线性关系即有
2019/11/2
第二章 控制系统的数学模型
11
自动控制理论
而
ufn an
(2-10)
ue ug-ufn
(2-11)
建立系统数学模型的方法
实验法:人为施加某种测试信号,记录基本输出响应。
解析法:根据系统及元件各变量之间所遵循的基本物理
定律,列写处每一个元件的输入-输出关系式。
2019/11/2
第二章 控制系统的数学模型
2
自动控制理论
第一节 列写系统微分方程的一般方法
即
Gs C Rssb a00ssm n b a1 1ssm n 1 1
bm 1sbm an1san
Gs就是系统的传递函数。
( 2-30)
其中 C, sLCt;RsLRt它们之间的传
方框图表示。
2019/11/2
第二章 控制系统的数学模型
15
自动控制理论
由式(2-17)减式(2-15),式(2-17)减式(2-15)后得
iBRNdd t u1 E GC 1
( 2-19) ( 2-20)
式(2-19)、(2-20)均为增量方程,它们描述了发电机在平衡点 A处受到△u1作用后的运动过程。对增量方程式而言,磁化曲线的坐 标原点不是在O点,而是移到A点。因而发电机的初始条件仍为零。 式中N为励磁绕组的匝数。
n0
1 Ce
EG
(n0为电动机的空载转速)
(2-9 )
测速发电机
输入量是电动机的转速n,输出量是测速发电机的电压Ufn ,假设 测速发电机的磁场恒定不变,则Ufn与n成线性关系即有
2019/11/2
第二章 控制系统的数学模型
11
自动控制理论
而
ufn an
(2-10)
ue ug-ufn
(2-11)
控制工程-234页PPT

可加性: f(x 1 x 2 ) f(x 1 ) f(x 2 )
齐次性: f(x)f(x)
或: f(x 1 x 2 ) f( x 1 ) f( x 2 )
30.09.2019
25
第二章 数学模型
非线性系统
用非线性微分方程描述的系统。非线性系统不 满足叠加原理。
30.09.2019
37
第二章 数学模型
实例:液位系统的线性化
Ad dH t(t)H(t)qi(t) 节流阀
解:稳态时:
qi(t)
qi0qo0, H0qi0
H(t)
节流阀
非线性项 H (t) 的泰勒展开为:
液位系统 qo(t)
H H 0 d dH H H 0(H H 0) 2 1 !d d 2 H 2H H 0(H H 0)2
数学模型应能反映系统内在的本质特征,同时
应对模型的简洁性和精确性进行折衷考虑。
30.09.2019
3
第二章 数学模型
对控制系统的哪些部分建模
被控对象
干扰/破坏
执行器 传感器
目标任务
控制器
干扰
干扰/破坏
执行器
建模的三个要素
建立数学模型 获取参数 验证模型
传感(感知)
干扰/破坏
干扰/破坏
fC
(t)
C
d dt
xo
(t)
30.09.2019
11
第二章 数学模型
m d d2 2txo(t)C d dxto(t)Ko(tx )fi(t)
式中,m、C、K通常均为常数,故机械平移系 统可以由二阶常系数微分方程描述。
显然,微分方程的系数取决于系统的结构参数, 而阶次等于系统中独立储能元件(惯性质量、 弹簧)的数量。
自动控制原理控制系统的结构图

I1(s)
I2 (s)
CR1s
7
i2
C
i
i1 R1
ui
R2
uo
(3)
I(s) I1(s) I2 (s)
I2 (s)
I (s)
I1(s)
(4)U o (s) R2 I (s)
I (s)
Uo (s)
R2
8
(1)Ui (s)
(3)
- Uo(s)
I2 (s)
(2)
1
I1(s)
I1(s)
I2 (s)
- Uo (s)
(d)
将图(b)和(c)组合起来即得到图(d),图(d)为该 一阶RC网络的方框图。
11
2.3.3 系统结构图的等效变换和简化
为了由系统的方框图方便地写出它的闭环传递函 数,通常需要对方框图进行等效变换。
方框图的等效变换必须遵守一个原则,即: 变换前后各变量之间的传递函数保持不变
在控制系统中,任何复杂系统的方框图都主要由 串联、并联和反馈三种基本形式连接而成。
u
o
idt c
对其进行拉氏变换得:
I (s)
U
o
(s)
U
i (s)
I (s) sC
U R
o
(s)
(1) (2)
10
I (s)
U
o
(s)
U
i (s)
I (s) sC
U R
o
(s)
(1) (2)
Ui (s)
I(s)
(b)
Uo (s)
I(s)
(c)
Uo (s)
Ui (s)
I(s)
Uo (s)
自动控制原理胡寿松(课堂PPT)

G2(s)G4(s)
G3(s)H(s) G4(s)H(s)
C(s) G5 (s)
3
R(s) G 1 ( s ) G 3 ( s ) G 2 ( s ) G 4 ( s )
C(s) G5 (s)
G 3 ( s ) G 4 ( s ) H ( s )
4
R(s)
1
G 1 ( s ) G 3 ( s ) G 2 ( s ) G 4 ( s ) 1G3(s)G4(s)H(s)
函数确定。 r (t )
1 e(t) 1/ s
1
c(t)
1
22
信号流图常用的名词术语
➢源节点(输入节点):只有信号输出支路的节点。
➢阱节点(输出节点):只有信号输入支路的节点。
C(s) G5 (s)
5
C R ( (s s) ) G 1 1 (s G )G 3 3 (( ss )) G G 4 2 (( ss ))H G 4 (( ss ))G 5(s) 6
21
• 信号流图的组成及性质
信号流图是以点和有向线段,描述系统的组成、结构、信号传 递关系的图形。它完全表述了一个系统。
C(s)
1G2(s)G3(s)H2(s) G4(s)
H3(s)/G2(s) H1(s)
G2(s)G3(s)G4(s) 1G2(s)G3(s)H2(s)
C(s)
H3(s)/G2(s) H1(s)
G1(s)
G 2(s)G 3(s)G 4(s)
C(s)
1G 2(s)G 3(s)H 2(s)G 3(s)G 4(s)H 3(s)
1
§2-3 控制系统的结构图与信号流图
1.系统结构图的组成和绘制 2.结构图的等效变换和简化 3.信号流图的组成和性质 4.信号流图的绘制 5.梅逊增益公式 6.闭环系统的传递函数
G3(s)H(s) G4(s)H(s)
C(s) G5 (s)
3
R(s) G 1 ( s ) G 3 ( s ) G 2 ( s ) G 4 ( s )
C(s) G5 (s)
G 3 ( s ) G 4 ( s ) H ( s )
4
R(s)
1
G 1 ( s ) G 3 ( s ) G 2 ( s ) G 4 ( s ) 1G3(s)G4(s)H(s)
函数确定。 r (t )
1 e(t) 1/ s
1
c(t)
1
22
信号流图常用的名词术语
➢源节点(输入节点):只有信号输出支路的节点。
➢阱节点(输出节点):只有信号输入支路的节点。
C(s) G5 (s)
5
C R ( (s s) ) G 1 1 (s G )G 3 3 (( ss )) G G 4 2 (( ss ))H G 4 (( ss ))G 5(s) 6
21
• 信号流图的组成及性质
信号流图是以点和有向线段,描述系统的组成、结构、信号传 递关系的图形。它完全表述了一个系统。
C(s)
1G2(s)G3(s)H2(s) G4(s)
H3(s)/G2(s) H1(s)
G2(s)G3(s)G4(s) 1G2(s)G3(s)H2(s)
C(s)
H3(s)/G2(s) H1(s)
G1(s)
G 2(s)G 3(s)G 4(s)
C(s)
1G 2(s)G 3(s)H 2(s)G 3(s)G 4(s)H 3(s)
1
§2-3 控制系统的结构图与信号流图
1.系统结构图的组成和绘制 2.结构图的等效变换和简化 3.信号流图的组成和性质 4.信号流图的绘制 5.梅逊增益公式 6.闭环系统的传递函数
《自动控制原理》-胡寿松-002-自动控制原理-第二章ppt

3
2-0 预备知识—牢记一些典型时域数学模型
1.电容 2 .电感 3弹簧弹性力 4 阻尼器 5 牛顿定律 6 电机 7 二阶方程的通解
4
§2.1 傅里叶变换与拉普拉斯变换
▪ 傅里叶 变换 自学
5
拉氏变换及其性质
1.定义 X (s) x(t )est dt 0 记 X(s) = L[x(t)]
24
2.2 时域模型 - 微分方程
2.2.1. 建立系统或元件微分方程的步骤
I. 确定元件输入量和输出量
II. 根据物理或化学定律,列出元件的原始方 程
III. 在可能条件下,对各元件的原始方程进行 适当简化,略去一些次要因素或进行线性 化处理
IV. 消去中间变量,得到描述元件输入和输出 关系的微分方程
t
0
t
0
t0
0
t
A
解: x(t) = x1(t) + x2(t) =A1(t) A1(t t0 )
X (s) A A et0s A (1 et0s )
ss
s
13
例2-7 求e at 的拉氏变换。
解:
X (s) eat est dt
1
e(as)t
1
0
as
0 sa
X (s) L 1(t )eat 1 sa 例2-8 求e 0.2 t 的拉氏变换。 解:
论: (1) D(s) = 0无重根。
16
X (s) c1 c2
cn
n
ci
(s p1 ) (s p2 )
(s pn ) i1 (s pi )
式中ci 是待定常数,称为X(s)在极点si 处的留数。
ci
lim(s
2-0 预备知识—牢记一些典型时域数学模型
1.电容 2 .电感 3弹簧弹性力 4 阻尼器 5 牛顿定律 6 电机 7 二阶方程的通解
4
§2.1 傅里叶变换与拉普拉斯变换
▪ 傅里叶 变换 自学
5
拉氏变换及其性质
1.定义 X (s) x(t )est dt 0 记 X(s) = L[x(t)]
24
2.2 时域模型 - 微分方程
2.2.1. 建立系统或元件微分方程的步骤
I. 确定元件输入量和输出量
II. 根据物理或化学定律,列出元件的原始方 程
III. 在可能条件下,对各元件的原始方程进行 适当简化,略去一些次要因素或进行线性 化处理
IV. 消去中间变量,得到描述元件输入和输出 关系的微分方程
t
0
t
0
t0
0
t
A
解: x(t) = x1(t) + x2(t) =A1(t) A1(t t0 )
X (s) A A et0s A (1 et0s )
ss
s
13
例2-7 求e at 的拉氏变换。
解:
X (s) eat est dt
1
e(as)t
1
0
as
0 sa
X (s) L 1(t )eat 1 sa 例2-8 求e 0.2 t 的拉氏变换。 解:
论: (1) D(s) = 0无重根。
16
X (s) c1 c2
cn
n
ci
(s p1 ) (s p2 )
(s pn ) i1 (s pi )
式中ci 是待定常数,称为X(s)在极点si 处的留数。
ci
lim(s
2-4 控制系统的结构图与信号流图
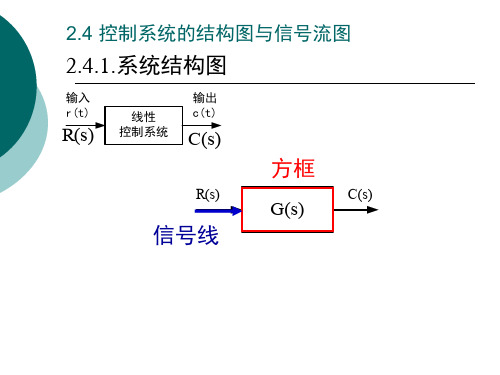
其中r(t),n(t)为系统的输入,c(t)为系统的输出, K0,K1,T,τ均为常数,要求: 1.绘制系统的结构图 C ( s) 2.求传递函数
(t ) K1n(t ) x1 (t ) r (t ) c
( s)
R( s)
2005年1月10日
用梅逊公式求下图所示系统在R(s) 和 N(s) 同时作用下的输出C(s)
R( s)
G1 ( s ) G2 ( s )
N (s) C (s)
G1G2 G2 (1 G1 ) 1 G1 G2 G1G2 C ( s) R( s ) N ( s) 1 G1 G2 2G1G2 1 G1 G2 2G1G2
2.4.3 闭环控制系统的传递函数 N(s)
1 1
2 1 G2G3 H 2
P2 H4
例2.4.2 已知系统结构图如图,试求传递函数
H4(s) R(s) H1(s) + C(s)
G1(s) +
G2(s) H2(s) H3(s)
G3(s)
C (s) P 11 P 22 R( s)
G1G2G3 H 4 (1 G2G3 H 2 ) 1 H 3 H 4 G1G2G3 H 3 G2G3 H 2 G1H1 G2G3 H 2 H 3 H 4 G1G2G3 H1H 2
当H(s)=1时,为单位反馈系统,此时
Gc (s)G p (s) C ( s) ( s ) R(s) 1 Gc (s)G p (s)
R(s)+
N(s) Gc(s) 控制器 +
-
对扰动输入的传递函数
D ( s) G p ( s) 1 Gc (s)G p (s) H (s)
(t ) K1n(t ) x1 (t ) r (t ) c
( s)
R( s)
2005年1月10日
用梅逊公式求下图所示系统在R(s) 和 N(s) 同时作用下的输出C(s)
R( s)
G1 ( s ) G2 ( s )
N (s) C (s)
G1G2 G2 (1 G1 ) 1 G1 G2 G1G2 C ( s) R( s ) N ( s) 1 G1 G2 2G1G2 1 G1 G2 2G1G2
2.4.3 闭环控制系统的传递函数 N(s)
1 1
2 1 G2G3 H 2
P2 H4
例2.4.2 已知系统结构图如图,试求传递函数
H4(s) R(s) H1(s) + C(s)
G1(s) +
G2(s) H2(s) H3(s)
G3(s)
C (s) P 11 P 22 R( s)
G1G2G3 H 4 (1 G2G3 H 2 ) 1 H 3 H 4 G1G2G3 H 3 G2G3 H 2 G1H1 G2G3 H 2 H 3 H 4 G1G2G3 H1H 2
当H(s)=1时,为单位反馈系统,此时
Gc (s)G p (s) C ( s) ( s ) R(s) 1 Gc (s)G p (s)
R(s)+
N(s) Gc(s) 控制器 +
-
对扰动输入的传递函数
D ( s) G p ( s) 1 Gc (s)G p (s) H (s)
控制系统的结构图与信号流图107页PPT

控制系统的结构图与信号流图
6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
Байду номын сангаас
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
1
0
、
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
Байду номын сангаас
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
1
0
、
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
X(s)
(2)方框:表示对信号进行的数学变换,方框内的函 数为元件或系统的传递函数。
X(s)
Y(s)
G(s)
11:07
5
第二章 控制系统的数学模型
(3)比较点(综合点、相加点):表示对两个以上的信号 进行加减运算,加号常省略,负号必须标出;进行相加减 的量,必须具有相同的量纲。
(4)引出点:表示信号引出或测量的位置,同一位置引 出的信号大小和性质完全相同。
X2(s)
X3(s) X2(s)
引出点前移
G(s)
X3(s) X2(s)
X1(s) + -
X 3(s)
G(s)
X2(s)
X 1(s)
X3(s)
比较点后移
G(s) G(s)
+ X2(s) -
移动的支路上乘以它所扫过方框内的传函。
11:07
15
第二章 控制系统的数学模型
X1(s)
G(s)
X2(s)
一 结构图的组成和绘制
控制系统的结构图是表示系统各元件特性、系统结构和 信号流向的图示方法。
定义:将方块图中各时间域中的变量用其拉氏
变换代替,各方框中元件的名称换成各元件的传 递函数,这时方框图就变成了动态结构图,简称结 构图,即传递函数的几何表达形式。
11:07
3
第二章 控制系统的数学模型
例1 引入闭环控制后的直流电机转速控制系统
X1(s) G(s)
X2(s)
X3(s) X1(s)
引出点后移
1
G(s) X3(s) X1(s)
X1(s)
G(s) +
X3(s)
-
X1(s)
+
G(s) X3(s)
1-
X2(s) G(s)
X 2 (s)
比较点前移
移动的支路上乘以它所扫过方框内的传函的倒数。
11:07
16
第二章 控制系统的数学模型
解:利用复阻抗的概念及元件特性可得每一元件的输 入量和输出量之间的关系如下:
I1 ( s)
ur
(s) u1(s) R1
u1
I
2
(s) (s)
[I1(s) I2
u1(s) uC R2
(s)] (s)
1 sC1
uC
(s)
I2
(s)
1 sC2
i1 R1 u1 R2 i2
ur
1 sC1
1 sC2
11:07
18
第二章 控制系统的数学模型
2 变换思路
(1)用最少的步骤将系统结构图化成由三 种基本结构组成的图形,然后通过串联和并 联变换化简信号通道,通过反馈回路变换化 简回路(记住公式)。
(2)通过比较点和引出点的移动(向同类移 动,并利用可交换性法则),解除回路之间互 相交连的部分,从而简化结构图。
uc
11:07
10
第二章 控制系统的数学模型
有变量相减,说明存在反馈和比较,比较后的信号一 般是元件的输入信号,所以将上页方程改写如下相乘 的形式:
I1
(s)
ur
(s) u1(s) R1
u1
I
2
(s) (s)
[I1(s) I2
u1(s) uC R2
(s)] (s)
1 sC1
uC
(s)
I2
(s)
1 sC2
11:07
[ur
(
s)
u1
(
s)
]
1 R1
I1 ( s)
[ I1 ( s) [u1 ( s)
I
2
(s)]
1 sC1
uC
(s)]
1 R2
u1 ( s ) I 2 (s)
I
2
(s)
1 sC2
uC (s)
11
第二章 控制系统的数学模型
绘制每一元件的结构图,并把相同变量连接起来,得 到系统的结构图。
11:07
19
第二章 控制系统的数学模型
变换技巧
• 变换技巧一:向同类移动 引出点向引出点移动,比较点向比较
点移动。移动后再将它们合并,以减少结 构图中引出点和比较点的数目。一般适用 于前向通道。
11:07
Ur(s) -
1/R1 I1(s)
U1(s)
-I2(s) 1/sC1
U1(s)
- 1/R2 I2(s) 1/sC2 UC(s)
UC(s)
11:07
12
第二章 控制系统的数学模型
二 结构图的等效变换
变换方法
1 三种典型结构的变换 2 比较点和引出点的移动变换 3 相邻引出点的处理 4 相邻比较点的处理
第二章 控制系统的数学模型
第二章 控制系统的数学模型
第三节 控制系统的结构图 与信号流图
11:07
1
第二章 控制系统的数学模型
本节内容
➢结构图的组成和绘制 ➢结构图的等效变换→求系统传递函数 ➢信号流图的组成和绘制 ➢MASON公式→求系统传递函 ➢闭环系统有关数传函的一些基本概念
11:07
2
第二章 控制系统的数学模型
(2)
R
ui
iC
uo
(a)
绘制每一元件的结构图,并把相同变量连接起来,得
到系统的结构图。
11:07
Ui(s) 1/R I(s) 1/sC Uo(s) Uo(s)
8
第二章 控制系统的数学模型
例2:绘制两级RC网络的结构图。
i1
ur
R1 u1
1 sC1
R2 i2
1 sC2
uc
11:07
9
第二章 控制系统的数学模型
11:07
6
第二章 控制系统的数学模型
结构图的绘制
例1 画出RC电路的结构图。
R
ui
iC
uo
一(阶aR)C网络
11:07
7
第二章 控制系统的数学模型
解:利用复阻抗的概念及元件特性可得每一元件的输
入量和输出量之间的关系如下:
R: I (s) Ui (s) Uo (s) (1)
R
C:
Uo (s)
I (s) sC
+Vcc
电网电压
电
可
ur
压
控
u
放 大
uk
硅 功
ua
uf - 器
放
n
M
负载
G 测速发电机
原理示意图
扰动
P
电位器
ur u
uf -
电压 放大器
uk
可控硅 放大器
ua 直流 电动机
n
11:07
测速机 职能方块图
4
第二章 控制系统的数学模型
结构图的组成
(1)信号线:带有箭头的直线,箭头表示信号的流向, 在直线旁边标有信号的时间函数或象函数。一条信 号线上的信号处处相同。
11:07
13
1 三种典型结构直接进行变换
串联
G1 G2
等 效方 框
G1 G2
(a)
并联
G1 G2 +
反馈
G +H
G1 +G2
(b)
G 1 +GH
(c)
第二章 控制系统的数学模型
2 引出点和比较点的移动变换
原则:保持移动前后封闭域输入输出关系不变。
X1(s)
G(s)
X2(s)
X1(s)
G(s)
3 相邻引出点可互换位置、可合并
ab
ba
4 相邻比较点可互换位置、可合并
a b
a b
11:07
17
第二章 控制系统的数学模型
需要说明的两点:
1 变换目的:是为了得到系统的传递函数。 与传递函数的代数运算等价,通过代数运算 也可以得到同样的结果。
❖在走投无路时,记住等效代数化简是最根本的 方法,它可以解决你在图形变换法中解决不了的 各种疑难问题。
(2)方框:表示对信号进行的数学变换,方框内的函 数为元件或系统的传递函数。
X(s)
Y(s)
G(s)
11:07
5
第二章 控制系统的数学模型
(3)比较点(综合点、相加点):表示对两个以上的信号 进行加减运算,加号常省略,负号必须标出;进行相加减 的量,必须具有相同的量纲。
(4)引出点:表示信号引出或测量的位置,同一位置引 出的信号大小和性质完全相同。
X2(s)
X3(s) X2(s)
引出点前移
G(s)
X3(s) X2(s)
X1(s) + -
X 3(s)
G(s)
X2(s)
X 1(s)
X3(s)
比较点后移
G(s) G(s)
+ X2(s) -
移动的支路上乘以它所扫过方框内的传函。
11:07
15
第二章 控制系统的数学模型
X1(s)
G(s)
X2(s)
一 结构图的组成和绘制
控制系统的结构图是表示系统各元件特性、系统结构和 信号流向的图示方法。
定义:将方块图中各时间域中的变量用其拉氏
变换代替,各方框中元件的名称换成各元件的传 递函数,这时方框图就变成了动态结构图,简称结 构图,即传递函数的几何表达形式。
11:07
3
第二章 控制系统的数学模型
例1 引入闭环控制后的直流电机转速控制系统
X1(s) G(s)
X2(s)
X3(s) X1(s)
引出点后移
1
G(s) X3(s) X1(s)
X1(s)
G(s) +
X3(s)
-
X1(s)
+
G(s) X3(s)
1-
X2(s) G(s)
X 2 (s)
比较点前移
移动的支路上乘以它所扫过方框内的传函的倒数。
11:07
16
第二章 控制系统的数学模型
解:利用复阻抗的概念及元件特性可得每一元件的输 入量和输出量之间的关系如下:
I1 ( s)
ur
(s) u1(s) R1
u1
I
2
(s) (s)
[I1(s) I2
u1(s) uC R2
(s)] (s)
1 sC1
uC
(s)
I2
(s)
1 sC2
i1 R1 u1 R2 i2
ur
1 sC1
1 sC2
11:07
18
第二章 控制系统的数学模型
2 变换思路
(1)用最少的步骤将系统结构图化成由三 种基本结构组成的图形,然后通过串联和并 联变换化简信号通道,通过反馈回路变换化 简回路(记住公式)。
(2)通过比较点和引出点的移动(向同类移 动,并利用可交换性法则),解除回路之间互 相交连的部分,从而简化结构图。
uc
11:07
10
第二章 控制系统的数学模型
有变量相减,说明存在反馈和比较,比较后的信号一 般是元件的输入信号,所以将上页方程改写如下相乘 的形式:
I1
(s)
ur
(s) u1(s) R1
u1
I
2
(s) (s)
[I1(s) I2
u1(s) uC R2
(s)] (s)
1 sC1
uC
(s)
I2
(s)
1 sC2
11:07
[ur
(
s)
u1
(
s)
]
1 R1
I1 ( s)
[ I1 ( s) [u1 ( s)
I
2
(s)]
1 sC1
uC
(s)]
1 R2
u1 ( s ) I 2 (s)
I
2
(s)
1 sC2
uC (s)
11
第二章 控制系统的数学模型
绘制每一元件的结构图,并把相同变量连接起来,得 到系统的结构图。
11:07
19
第二章 控制系统的数学模型
变换技巧
• 变换技巧一:向同类移动 引出点向引出点移动,比较点向比较
点移动。移动后再将它们合并,以减少结 构图中引出点和比较点的数目。一般适用 于前向通道。
11:07
Ur(s) -
1/R1 I1(s)
U1(s)
-I2(s) 1/sC1
U1(s)
- 1/R2 I2(s) 1/sC2 UC(s)
UC(s)
11:07
12
第二章 控制系统的数学模型
二 结构图的等效变换
变换方法
1 三种典型结构的变换 2 比较点和引出点的移动变换 3 相邻引出点的处理 4 相邻比较点的处理
第二章 控制系统的数学模型
第二章 控制系统的数学模型
第三节 控制系统的结构图 与信号流图
11:07
1
第二章 控制系统的数学模型
本节内容
➢结构图的组成和绘制 ➢结构图的等效变换→求系统传递函数 ➢信号流图的组成和绘制 ➢MASON公式→求系统传递函 ➢闭环系统有关数传函的一些基本概念
11:07
2
第二章 控制系统的数学模型
(2)
R
ui
iC
uo
(a)
绘制每一元件的结构图,并把相同变量连接起来,得
到系统的结构图。
11:07
Ui(s) 1/R I(s) 1/sC Uo(s) Uo(s)
8
第二章 控制系统的数学模型
例2:绘制两级RC网络的结构图。
i1
ur
R1 u1
1 sC1
R2 i2
1 sC2
uc
11:07
9
第二章 控制系统的数学模型
11:07
6
第二章 控制系统的数学模型
结构图的绘制
例1 画出RC电路的结构图。
R
ui
iC
uo
一(阶aR)C网络
11:07
7
第二章 控制系统的数学模型
解:利用复阻抗的概念及元件特性可得每一元件的输
入量和输出量之间的关系如下:
R: I (s) Ui (s) Uo (s) (1)
R
C:
Uo (s)
I (s) sC
+Vcc
电网电压
电
可
ur
压
控
u
放 大
uk
硅 功
ua
uf - 器
放
n
M
负载
G 测速发电机
原理示意图
扰动
P
电位器
ur u
uf -
电压 放大器
uk
可控硅 放大器
ua 直流 电动机
n
11:07
测速机 职能方块图
4
第二章 控制系统的数学模型
结构图的组成
(1)信号线:带有箭头的直线,箭头表示信号的流向, 在直线旁边标有信号的时间函数或象函数。一条信 号线上的信号处处相同。
11:07
13
1 三种典型结构直接进行变换
串联
G1 G2
等 效方 框
G1 G2
(a)
并联
G1 G2 +
反馈
G +H
G1 +G2
(b)
G 1 +GH
(c)
第二章 控制系统的数学模型
2 引出点和比较点的移动变换
原则:保持移动前后封闭域输入输出关系不变。
X1(s)
G(s)
X2(s)
X1(s)
G(s)
3 相邻引出点可互换位置、可合并
ab
ba
4 相邻比较点可互换位置、可合并
a b
a b
11:07
17
第二章 控制系统的数学模型
需要说明的两点:
1 变换目的:是为了得到系统的传递函数。 与传递函数的代数运算等价,通过代数运算 也可以得到同样的结果。
❖在走投无路时,记住等效代数化简是最根本的 方法,它可以解决你在图形变换法中解决不了的 各种疑难问题。
