21.3二次根式的加减法(优秀课件)
合集下载
二次根式的加减PPT课件

1+912+1102
人教版 九年级上
第十九章 生活用电
第1节 家庭电路
课堂导练
3.下图是家庭电路的组成,请填出各组成部分的名称。
①__电__能__表__;②_总__开__关__;③_保__险__装__置__;④_三__孔__插__座__; ⑤__火__线____;⑥__零__线____;⑦___地__线___。
19 见习题
15 C
答案显示
1.同类二次根式:将几个二次根式化成_最__简__二__次__根__式___, 如果被开方数__相__同____,那么这样的二次根式称为同类 二次根式.
2.二次根式的加减,与整式的加减类似,关键是将 _同__类__二__次__根__式_ 合 并 . 其 步 骤 为 先 将 二 次 根 式 化 为 最__简__二__次__根__式__,再将同类二次根式合并.
课后训练
13.(2020·常州)请以笔画线代替导线,将三孔插座、开关控 制的电灯接入电路。 解:如图所示。
课堂导练
【点拨】开关应安装在火线上,当断开开关时,用电器与 火线断开,不会发生触电事故; 空气开关“跳闸”后,电 流无法形成通路,故家庭电路整体上处于断路状态;零线、 地线和大地间的电压都是0 V,用试电笔分别接触零线与 地线时,氖管都不发光,所以试电笔不能辨别零线与地线, 但试电笔可以辨别火线和零线。 【答案】火;断路;不能
【答案】会;44
课后训练
1.下列各式中,与 2 是同类二次根式的是( C ) A. 3 B. 4 C. 8 D. 12
2.下列二次根式中,与 a 是同类二次根式的是( C ) A. a2 B. 2a C. 4a D. 4+a
3.下列二次根式中,与 20是同类二次根式的是( B )
21.3 二次根式的加减(47张ppt)

全解全习
典例精析
第3节 二次根式 的加减
【答案】B 【解题关键】能合并的,就是同类二次根式,反 之亦然.所以判断能否合并的关键就要把它们化 为最简二次根式.
全解全习
典例精析
第3节 二次根式 的加减
全解全习
典例精析
第3节 二次根式 的加减
【思路分析】按照二次根式加减运算的步骤, 先把各个二次根式化为最简二次根式,再合 并同类二次根式即可.
全解全习
新知预习
第3节 二次根式 的加减
3.二次根式加减运算的步骤:(1)先把各个二次根式化为 最简二次根式;(2)再把同类二次根式__合__并____. 4.二次根式的混合运算(与整式的混合运算类似):先算 __乘__方____,再算__乘__除____,最后算__加__减____,同级运算按 照_从__左__到__右___的顺序依次进行,有括号的要先算括号里面 的.还需注意的是,能运用_运__算__律__和__乘__法__公__式___的,要运 用运算律和乘法公式简化计算.
全解全习
当堂练习
第3节 二次根式 的加减
全解全习
当堂练习
第3节 二次根式 的加减
全解全习
当堂练习
第3节 二次根式 的加减
全解全习
当堂练习
第3节 二次根式 的加减
观察上面结果,直接写出=____________. 利用以上提供的方法化简下式:
全解全习
当堂练习
第3节 二次根式 的加减
全解全习
典例精析
第3节 二次根式 的加减
知识点1 二次根式的加减 【例1】下列二次根式不能与 合并的是( )
全解全习
典例精析
第3节 二次根式 的加减
【思路分析】将所给的二次根式 化为最简二 次根式是 =3 ,能与它合并的必须是同类 二次根式,即化为最简二次根式后的被开方数必 须是3,把所给各选项化为最简二次根式即可判 断.
九年级数学上册_21.3二次根式的加减第一课时课件_人教新课标版

m 1
27
4.如果最简二次根式
5
与
mn
是同类二次根式,求m、n 的值.
二次根式的加减法
合并同类二次根式:
6 3 3 3 (6 3) 3 9 3
6 36 2
合并同类项:
6ab+3ab=(6+3)ab=9ab 2+6ab3= 6ab
2 2 2 2
6 3 6 2 5 2 3 3
d
课堂小结
1、判断同类二次根式的关键是什么? (1)化成最简二次根式, (2)被开方数相同,根指数相同(都等于2) 2、二次根式加减运算的步骤: (1)把各个二次根式化成最简二次根式 (2)把各个同类二次根式合并.
(3)不是同类二次根式的不能合并.
(2)被开方数相同,根指数相同(都等于2) 1.下列各式中,哪些是同类二次根式?
1 1 (1) 2 ; (2) 75 ; (3) ; ( 4) ; (5) 3; 50 27 2 a 3 ( 6) 8ab ; (7)6b ; (8) 12 a 12b . 3 2b
1、下面给出4组根式(其中b>0)
(6 3 3 3 ) (6 2 5 2 ) 9 3 11 2
思考:二次根式的加减的一般步骤.
(1)把各个二次根式化成最简二次根式
(2)把各个同类二次根式合并.
下列计算哪些正确,哪些不正确?
⑴
⑵ ⑶ ⑷
3 2 5
(不正确) (不正确) (不正确) (正确) (不正确) a 0
人教新版九年级上
§21.3 二次根式的加减 (1)
一、观察下列单项式有什么共同特征。
-a2b
称为同类项
5a2b
2a2b
27
4.如果最简二次根式
5
与
mn
是同类二次根式,求m、n 的值.
二次根式的加减法
合并同类二次根式:
6 3 3 3 (6 3) 3 9 3
6 36 2
合并同类项:
6ab+3ab=(6+3)ab=9ab 2+6ab3= 6ab
2 2 2 2
6 3 6 2 5 2 3 3
d
课堂小结
1、判断同类二次根式的关键是什么? (1)化成最简二次根式, (2)被开方数相同,根指数相同(都等于2) 2、二次根式加减运算的步骤: (1)把各个二次根式化成最简二次根式 (2)把各个同类二次根式合并.
(3)不是同类二次根式的不能合并.
(2)被开方数相同,根指数相同(都等于2) 1.下列各式中,哪些是同类二次根式?
1 1 (1) 2 ; (2) 75 ; (3) ; ( 4) ; (5) 3; 50 27 2 a 3 ( 6) 8ab ; (7)6b ; (8) 12 a 12b . 3 2b
1、下面给出4组根式(其中b>0)
(6 3 3 3 ) (6 2 5 2 ) 9 3 11 2
思考:二次根式的加减的一般步骤.
(1)把各个二次根式化成最简二次根式
(2)把各个同类二次根式合并.
下列计算哪些正确,哪些不正确?
⑴
⑵ ⑶ ⑷
3 2 5
(不正确) (不正确) (不正确) (正确) (不正确) a 0
人教新版九年级上
§21.3 二次根式的加减 (1)
一、观察下列单项式有什么共同特征。
-a2b
称为同类项
5a2b
2a2b
《二次根式的加减法》优质课件

通过化简根式,将复杂的二次根式加 减法转化为简单的加减运算。
练习题与答案解析
题目1
计算$\sqrt{18} + \sqrt{72}$
答案
$3\sqrt{2} + 6\sqrt{2} = 9\sqrt{2}$
解析
首先化简根式,$\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}$,$\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}$,然后进行加法运算,$3\sqrt{2} + 6\sqrt{2} = 9\sqrt{2}$。
二次根式具有非负性,其他根式则没有此性质。
易错点
在进行二次根式的加减运算时,容易忽略二次根式的非负性,导致结果错误。
03
典型例题解析与练习
简单例题解析
01
题目
计算$\sqrt{12} + \sqrt{27}$
02 03
解析
首先化简根式,$\sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3}$, $\sqrt{27} = \sqrt{9 \times 3} = 3\sqrt{3}$,然后进行加法运算, $2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}$。
拓展阅读材料推荐
《数学简史》
一本介绍数学发展史的书 籍,其中涵盖了二次根式 的重要性和应用。
《数学之美》
一本介绍数学在各个领域 中的应用的书籍,包括二 次根式在物理学和经济学 中的应用。
《数学杂志》
一本学术期刊,上面有许 多关于二次根式的论文和 研究文章,可以深入了解 该领域的最新进展。
05
总结回顾与展望未来
《二次根式的加减》课件

VS
详细描述
在进行二次根式的加减运算时,有时需要 对二次根式进行合并或简化。学生在合并 或简化过程中,容易出错,导致计算结果 错误。例如,将$sqrt{5} + sqrt{2}$错误 地合并为$sqrt{7}$,或将$sqrt{4} sqrt{9}$错误地简化为$3 - 2$。
PART 05
练习与巩固
2023 WORK SUMMARY
《二次根式的加减》 ppt课件
REPORTING
目录
• 二次根式的加减概述 • 二次根式的加减运算方法 • 二次根式的加减运算实例 • 二次根式的加减易错点解析 • 练习与巩固
PART 01
二次根式的加减概述
二次根式的加减定义
定义
二次根式的加减运算是指将具有 相同被开方数的二次根式进行合 并或分离的过程。
计算
$(sqrt{5} + 2sqrt{2})(sqrt{5} 2sqrt{2})$
计算
$(sqrt{3} + sqrt{2})^{2}$
计算
$(sqrt{5} - sqrt{3})^{2}$
综合练习题
解方程
$3sqrt{2}x = 4sqrt{3}x$
解方程
$(sqrt{3} + sqrt{2})x = 5$
THANKS
感谢观看
REPORTING
解方程
$(sqrt{5} - sqrt{3})x^{2} - (sqrt{5} + sqrt{3})x = 0$
解方程组
${begin{array}{l}sqrt{2}x - sqrt{6}y = 4 sqrt{3}x + sqrt{5}y = 7 end{array}$
《二次根式的加减》二次根式PPT教学课件(第2课时)

试卷下载: .
/shiti/
教案下载: .
/jiaoan/
ppt论坛: . .cn
ppt课件: .
/kejian/
语文课件: .
/kejian/yuwen/ 数学课件: .
/kejian/shuxue/
英语课件: .
/kejian/yingyu/ 美术课件: .
/kejian/meishu/
科学课件: .
1
2
4 2 + 6 2 × 6 × 500 = 2 2 + 3 2 × 6 × 500
= 5 2 × 6 × 500
= 5000 3 3 .
答:这段路基的土石方为5000 32
链接中考
(2021•包头)若x= 2 + 1,则代数式x2-2x+2的值为( C )
A.7
B.4
x2-2x+2=(x-1)2+1
= 3
B.
3
2
6
2
3
2
3
的结果是(
2
C )
C. 3
D.2 3
预习检测
2.计算( 80+ 20)× 5的结果是( D )
A.6
B.2 5
( 80+ 20)× 5
= (4 5+2 5)× 5
= 6 5× 5
= 30
C.2 10
D.30
新知讲解
长方形的长为 2 + 5,宽为 6,它的面积是多少?
长方形的面积=( 2 + 5) × 6
=2−
3
2
3
易错提示
与有理数、实数运算一样,在混合运算中先乘除,后加减;
对于(1):先算乘,再化简,若有相同的二次根式进行合并,
/shiti/
教案下载: .
/jiaoan/
ppt论坛: . .cn
ppt课件: .
/kejian/
语文课件: .
/kejian/yuwen/ 数学课件: .
/kejian/shuxue/
英语课件: .
/kejian/yingyu/ 美术课件: .
/kejian/meishu/
科学课件: .
1
2
4 2 + 6 2 × 6 × 500 = 2 2 + 3 2 × 6 × 500
= 5 2 × 6 × 500
= 5000 3 3 .
答:这段路基的土石方为5000 32
链接中考
(2021•包头)若x= 2 + 1,则代数式x2-2x+2的值为( C )
A.7
B.4
x2-2x+2=(x-1)2+1
= 3
B.
3
2
6
2
3
2
3
的结果是(
2
C )
C. 3
D.2 3
预习检测
2.计算( 80+ 20)× 5的结果是( D )
A.6
B.2 5
( 80+ 20)× 5
= (4 5+2 5)× 5
= 6 5× 5
= 30
C.2 10
D.30
新知讲解
长方形的长为 2 + 5,宽为 6,它的面积是多少?
长方形的面积=( 2 + 5) × 6
=2−
3
2
3
易错提示
与有理数、实数运算一样,在混合运算中先乘除,后加减;
对于(1):先算乘,再化简,若有相同的二次根式进行合并,
华师版九年级数学 21.3 二次根式的加减(学习、上课课件)

第21章 二次根式
21.3 二次根式的加减
学习目标
1 课时讲解 同类二次根式
二次根式的加减 二次根式的混合运算
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
感悟新知
知识点 1 同类二次根式
知1-讲
1. 同类二次根式 与整式中同类项相类似,我们把像3 a、-2 a与
4 a这样的几个二次根式,称为同类二次根式 .
(3-2 2)]100(3-2 2)=1100×(3-2 2)=3-2 2.
感悟新知
4-1. 计算:
(1) 3×( 6+ 8); 解:原式= 18+ 24=3 2+2 6;
(2)(4 3-3 6)÷2 3; 原式=4 3×2 1 3-3 6×2 1 3=2-32 2;
(3)( 6+2)×( 6- 3);
感悟新知
知1-练
例 1 [中考·凉山州] 下列根式中,不能与 3 合并的是( )
A.
1 3
B. 3 3
C.
2 3
D. 12
解题秘方:紧扣“同类二次根式”的定义中的两个
条件进行识别 .
感悟新知
知1-练
解:首先把选项中每个根式化成最简二次根式,然后找出 被开方数不是3的二次根式 .
13=
1= 3
1× 3×
(2)(5 15+ 35)÷ 15.
原式=5 15+
3 5 ×
115=5
15×115+
35×115=5+15=256.
感悟新知
知3-练
例 4 计算: (1)( 2+ 3- 6)2-( 2- 3- 6)2; (2)(1+ 2- 3)(1- 2+ 3); (3)(3+2 2)100(3-2 2)101. 解题秘方:紧扣“乘法公式”和“幂的运算法则” 的特征进行计算.
21.3 二次根式的加减
学习目标
1 课时讲解 同类二次根式
二次根式的加减 二次根式的混合运算
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
感悟新知
知识点 1 同类二次根式
知1-讲
1. 同类二次根式 与整式中同类项相类似,我们把像3 a、-2 a与
4 a这样的几个二次根式,称为同类二次根式 .
(3-2 2)]100(3-2 2)=1100×(3-2 2)=3-2 2.
感悟新知
4-1. 计算:
(1) 3×( 6+ 8); 解:原式= 18+ 24=3 2+2 6;
(2)(4 3-3 6)÷2 3; 原式=4 3×2 1 3-3 6×2 1 3=2-32 2;
(3)( 6+2)×( 6- 3);
感悟新知
知1-练
例 1 [中考·凉山州] 下列根式中,不能与 3 合并的是( )
A.
1 3
B. 3 3
C.
2 3
D. 12
解题秘方:紧扣“同类二次根式”的定义中的两个
条件进行识别 .
感悟新知
知1-练
解:首先把选项中每个根式化成最简二次根式,然后找出 被开方数不是3的二次根式 .
13=
1= 3
1× 3×
(2)(5 15+ 35)÷ 15.
原式=5 15+
3 5 ×
115=5
15×115+
35×115=5+15=256.
感悟新知
知3-练
例 4 计算: (1)( 2+ 3- 6)2-( 2- 3- 6)2; (2)(1+ 2- 3)(1- 2+ 3); (3)(3+2 2)100(3-2 2)101. 解题秘方:紧扣“乘法公式”和“幂的运算法则” 的特征进行计算.
二次根式加减ppt课件

答案及解析
计算
化简
$sqrt{27} + sqrt{3} = 3sqrt{3} + sqrt{3} = 4sqrt{3}$
$2sqrt{3} - sqrt{2} = sqrt{3} - sqrt{2}$
比较大小
$sqrt{25} = 5$,因为 $5 > 3$,所以 $sqrt{25} > 3$
判断正误
01
02
03
识别同类二次根式
首先需要识别出表达式中 的同类二次根式,即具有 相同被开方数的二次根式 。
合并同类二次根式
将同类二次根式进行合并 ,即将它们的系数相加减 ,根号下的被开方数保持 不变。
举例说明
将表达式中的 $sqrt{2}$ 和 $sqrt{2}$ 合并为 $2sqrt{2}$。
$sqrt{8} + sqrt{18} = 2sqrt{2} + 3sqrt{2} = 5sqrt{2}$,不等于 $2sqrt{2}$,所以判 断为错。
THANKS
感谢观看
sqrt{2}}{sqrt{2} times sqrt{2}} = frac{sqrt{6}}{2}$。
二次根式的化简技巧
利用平方差公式
对于形如 $sqrt{a^2 - b^2}$ 的表达式,可以利 用平方差公式进行化简。
利用完全平方公式
对于形如 $sqrt{a + b}$ 或 $sqrt{a - b}$ 的表达 式,可以利用完全平方公式进行化简。
二次根式的加减法规则
总结词
掌握二次根式的加减法规则是进行运 算的关键。
详细描述
二次根式的加减法需先将各项化为最 简二次根式,然后合并同类二次根式 。
九年级上数学《21.3 二次根式的加减》课件
回顾旧知
抢答
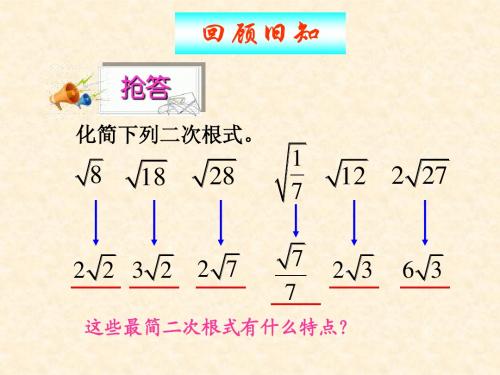
化简下列二次根式。
8
18
28
1 7
12 2 27
2 2 3 2
2 7
7 7
2 3
6 3
这些最简二次根式有什么特点?
新课导入
有一个三角形,它的两边长分别为 20 和 5 , 如果该三角形的周长为 9 5 ,你能求出第三边吗?
提示 根据三角形的周长公式 C = a+ b+ c 求解。
?
a 20
答:35 秒后△PBQ 的面积为 35 cm2 , PQ的距离为 5 7 cm 。
例题
计算
8 3 6 8 6 3 6
8 6 3 6
注意
4 3 3 2
(1)加减与乘除的混合运算,先乘除, 后加减,使难点分散。 (2)在运算中,对于各根式不一定要先 化简,而是先乘除,进行约分,达到化简的 目的,但最后结果一定要化简。
【情感态度与价值观】
利用规定准确计算和化简的严谨的科 学精神。 经过探索二次根式的重要结论,发展 学生观察、分析、发现问题的能力。
教学重难点
二次根式化简为最简二次根式以及二 次根式的判定。
二次根式的加减、乘除、乘方等运算 规律。 由整式运算知识迁移到含二次根式的 运算。
我们可以这样来计算
一化
二找
三合并
例题
解答
如图所示的 Rt△ABC中,∠B=90°,点 P 从点 B 开始沿 BA 边以 1 cm/s 的速度向点 A 移动。同时, 点 Q 也从点 B 开始沿 BC 边以 2 cm/s 的速度向点 C 移动。问:几秒后△PBQ 的面积为 35 cm2 ?PQ 的 距离是多少厘米?(结果用最简二次根式)
抢答
化简下列二次根式。
8
18
28
1 7
12 2 27
2 2 3 2
2 7
7 7
2 3
6 3
这些最简二次根式有什么特点?
新课导入
有一个三角形,它的两边长分别为 20 和 5 , 如果该三角形的周长为 9 5 ,你能求出第三边吗?
提示 根据三角形的周长公式 C = a+ b+ c 求解。
?
a 20
答:35 秒后△PBQ 的面积为 35 cm2 , PQ的距离为 5 7 cm 。
例题
计算
8 3 6 8 6 3 6
8 6 3 6
注意
4 3 3 2
(1)加减与乘除的混合运算,先乘除, 后加减,使难点分散。 (2)在运算中,对于各根式不一定要先 化简,而是先乘除,进行约分,达到化简的 目的,但最后结果一定要化简。
【情感态度与价值观】
利用规定准确计算和化简的严谨的科 学精神。 经过探索二次根式的重要结论,发展 学生观察、分析、发现问题的能力。
教学重难点
二次根式化简为最简二次根式以及二 次根式的判定。
二次根式的加减、乘除、乘方等运算 规律。 由整式运算知识迁移到含二次根式的 运算。
我们可以这样来计算
一化
二找
三合并
例题
解答
如图所示的 Rt△ABC中,∠B=90°,点 P 从点 B 开始沿 BA 边以 1 cm/s 的速度向点 A 移动。同时, 点 Q 也从点 B 开始沿 BC 边以 2 cm/s 的速度向点 C 移动。问:几秒后△PBQ 的面积为 35 cm2 ?PQ 的 距离是多少厘米?(结果用最简二次根式)
《二次根式的加减》课件

二次根式的化简方法
学习如何化简复杂的二次根式,通过变形和简化步骤,简化二次根式的形式, 使其更加简洁和易于计算。
二次根式乘法原理
了解和应用二次根式的乘法原理,掌握乘法的规则和技巧,使用乘法原理计和应用二次根式的除法原理,掌握除法的规则和方法,使用除法原理计 算和简化二次根式的表达式。
二次根式的加法原理
探索和应用二次根式的加法原理,了解加法的规则和技巧,用加法原理合并 或简化二次根式的表达式。
二次根式的减法原理
研究和应用二次根式的减法原理,掌握减法的规则和方法,通过减法原理合并或简化二次根式的表达式。
二次根式加减法的综合运用
将之前学习的加法和减法原理综合应用于解决实际问题,通过综合运用掌握二次根式加减法在实际情境中的应 用。
《二次根式的加减》PPT 课件
在本课件中,我们将探索如何定义和求解二次根式,掌握化简、乘法、除法 以及加减法的原理和综合运用,并探讨二次根式在数学和实际生活中的应用。
二次根式的定义和求解
本节将介绍二次根式的概念和如何求解二次根式的具体步骤。掌握二次根式的定义和求解方法,为后续的学习 打下坚实基础。
《二次根式的加减》课件

《二次根式的加减》
知识回顾
最简二次根式:满足以下两个条件的二次根式,叫做
最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式 .
二次根式化成最简二次根式的
1.分:利用分解因数或分解因式的方法把被开方
数的分子、分母都化成质因数(或最简因式)的
幂的乘积的形式.
2.移:把能开得尽方的因数(或因式)分母
中的因式移到根号外时,要注意依旧写在分母的
位置上.
3.化:化去被开方数中的分母.
4.约:约分,化为最简二次根式.
下列二次根式中,最简二次根式是( C )
A. 24
B.
63 2
解析:A选项 24 = 2 6.
B选项 63 2 = ab 6.
C选项
被开方数相乘除.
被开方数不变.
结果化为最简
先化为最简二次根式,
二次根式.
再合并同类二次根式.
化简
例 计算:
(1) 80 − 45.
(2) 9 + 25.
解:(1) 80 − 45 = 4 5 − 3 5 = 5.
(2) 9 + 25 = 3 + 5 = 8 .
注意:一定要将不能开方的数字和
C. 18
B.
1 3
= .
3 3
D. 9=3.
D. 9
2.下列各式不成立的是( C ).
A. 18 −
C.
8
9
=
2
3
2+ =2
解析:B选项中
7
3
2
2
3
8+ 18
2
=
B.
8+ 18
知识回顾
最简二次根式:满足以下两个条件的二次根式,叫做
最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式 .
二次根式化成最简二次根式的
1.分:利用分解因数或分解因式的方法把被开方
数的分子、分母都化成质因数(或最简因式)的
幂的乘积的形式.
2.移:把能开得尽方的因数(或因式)分母
中的因式移到根号外时,要注意依旧写在分母的
位置上.
3.化:化去被开方数中的分母.
4.约:约分,化为最简二次根式.
下列二次根式中,最简二次根式是( C )
A. 24
B.
63 2
解析:A选项 24 = 2 6.
B选项 63 2 = ab 6.
C选项
被开方数相乘除.
被开方数不变.
结果化为最简
先化为最简二次根式,
二次根式.
再合并同类二次根式.
化简
例 计算:
(1) 80 − 45.
(2) 9 + 25.
解:(1) 80 − 45 = 4 5 − 3 5 = 5.
(2) 9 + 25 = 3 + 5 = 8 .
注意:一定要将不能开方的数字和
C. 18
B.
1 3
= .
3 3
D. 9=3.
D. 9
2.下列各式不成立的是( C ).
A. 18 −
C.
8
9
=
2
3
2+ =2
解析:B选项中
7
3
2
2
3
8+ 18
2
=
B.
8+ 18
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
2
ppt课件
14
2.在下列各组根式中,是同类二次根式的
是( B )
A . 2, 12
B. 2 , 1
2
C. 4ab, ab2 D. a1, a1
3. 与 12 是同类二次根式的是( D )
A.
32 B.
24 C.
125 D. 6 1
27
4.如果最简二次根式 2 mn2 与
是同类二次根式,求m、n 的值. ppt课件
(2) 27 12 45 (3) 25x 16x 9x
4
ppt课件
11
ห้องสมุดไป่ตู้
二次根式加减运算的步骤: (1)把各个二次根式化成最简二次根式
(2)把各个同类二次根式合并. 注意:不是同类二次根式的二次根式
(如 2 与 3 )不能合并
练习 1.判断:下列计算是否正确?为什么?
1 2 3 5 ; 2 2 2 2 2 ;
3
8
ppt课件
18
1.同类二次根式的定义?
2.二次根式加减运算的步骤? 3.如何合并同类二次根式?
合并同类二次根式与合并同类项类似.
ppt课件
19
此课件下载可自行编辑修改,此课件供参考! 部分内容来源于网络,如有侵权请与我联系删除!感谢你的观看!
(2)两列火车分别运煤2x吨和3y吨,问这两
列火车共运多少?_(__2_x___+__3_y__)_吨__
以下问题你能用同样的方法计算吗?
(1)3 32 3 (2)3 a2 a
ppt课件
6
(1)3 32 3 (2)3 a2 a
几个二次根式化成最简二次根式后, 如果被开方数相同,这几个二次根式就 叫做同类二次根式.
mn
15
练习
5.计算:
1 528718
2 8 4 12
2
3 3( 12 1 )
27
42 9x6 x2x 1
3
4
x
ppt课件
16
例3 计算: (1)( 21)( 21) ; (2)( a2b)(a2b) .
ppt课件
17
练习: 计算:
(1) 24 1 2 2 1 6,
2
38
(2)( 32 0.52 1)( 1 75)
8
(1)说出 2 5 的三个同类二次根式;
(2)试举出一组同类二次根式.
(3)下列各式中哪些是同类二次根式?
2, 7,51, 1, 3,28 a3b ,6 ba,32
5027 3
2 b
ppt课件
9
例1:计算 3 2 32 23 3
解: (3原 222 式 )(3 33)
22 3
ppt课件
10
例2 : 计算 (1) 50 32
3 818 49235
2
ppt课件
12
1、下列计算正确吗?
4 6 10
10 7 3
2 2 4
2 32 3
ppt课件
13
彗眼识真: 下列计算哪些正确,哪些不正确?
⑴ 3 2 5 (不正确)
⑵ a ba b (不正确) ⑶ a b ab (不正确)
⑷ aaba(ab) a (正确)
⑸ 1 3a1 2a a a0(不正确)
分母含有二次根式
如:2 () 3
被开方数含有小数或分数
如:1或 0.2()
分子分母可约分 2 如:a 2 ()
2a
ppt课件
3
判断下列各式中哪些是最简二次根式, 哪些不是?为什么?
(1) 3a2b (2) 1.5ab (3) x2 y2 (4) a b
ppt课件
4
练习:把下列二次根式化为最简二次根式。
3 32 2
2
4 818 12
ppt课件
7
例题解析
例1: 下列各式中,哪些是同类二次根式?
12
48
18
50
23 43 32 52
1
32
2 2 42
2
45
35
1 1
3
23 3
注意:判断一组式子是否为同类二次根式,只需看
化为最简二次根式后的被开方数是否相同,与最简二
次根式前面的因式和符号pp无t课件关.
ppt课件
1
复习回顾:二次根的乘除 二次根式的乘法法则 a ba(b a0,b0)
二次根式的除法法则 积的算术平方根的性质
a a(a0,b0) bb
a ba b(a0,b0)
商的算术平方根的性质
a a(a0,b0) bb
ppt课件
2
最简二次根式的两个条件:
(1)被开方数不含分母; (2)被开方数中不含能开得尽方的因数或因式;
(1) 24
(2) 2 5
3
(3) 125a3
(4) 2
(5) 1 8
(6) 3 3 5
(7) 0.4 (8 ) 18 b 2
a
(9) 3 24
(10) 1 2 1
(11) 3 2 5
ppt课件
5
(1)两列火车分别运煤2x吨和3x吨,问这两
列火车共运多少?2__x__+__3__x_=__5__x__吨
