导数与微分PPT教学课件
合集下载
《导数与微分》ppt课件

求 求导方法:
y
(1)求出函数的增量
B
M T
y f (x0 x) f (x0 )
Mo A αφ
x0
△y dy △x X0+△x x
2、作出比值: y
x
y
3、求出 x 0 时 x 的极限。
二、可导与连续的关系
函数在点 x0
连续,指
lim y 0
x0
存在。
,可导是
lim
x0
y x
定理:如果y=f(x) 在点x0处可导,则它在点x0 处一定连续。
9 5
k
1___ k
1 25
切线方程y x ____ y 1 x 25
例:一球在斜面上向上滚动,已知在t(s)时球与 起始位置的距离是s(t) 3t t2, 求初速度、何时 开始下滚? 解:v(t) s' (t) 3 2t ___ t 0 v(0) 3m / s 当v 0时开始下滚, 3 2t 0 t 1.5s
数
u,对v, 应y 增量 u, v, y
y (u u)(v v) uv uv vu u v
y u v v u u v
x
x x x
y ' (uv)' uv' u 'v
例: 例1、2、3、4 p26
例:求y x sin x cosx 的导数 x cosx sin x
x
2!
y ' lim y nx n1 x0 x
即: (x n )' nxn1
对于n为任意实数时,上式也成立。
例7:正弦函数 y sin x 的导数
y sin(x x) sin x 2cos(x x) sin x
2
《高数四导数与微分》课件

以通过对弦的长度进行微分得到。
微分在近似计算中的应用
泰勒级数展开
微分可以用来将一个复杂的函数 展开成泰勒级数,从而可以用简 单的多项式来近似复杂的函数。 这在近似计算中非常有用。
误差估计
通过微分,可以估计函数值近似 值的误差大小。例如,在求函数 在某一点的近似值时,可以通过 微分来估计误差的大小。
常数函数的导数
对于常数函数y=c,其导 数为dy/dx=0。
幂函数的导数
对于函数y=x^n,其导数 为dy/dx=nx^(n-1)。
指数函数的导数
对于函数y=a^x,其导数 为dy/dx=a^x*ln(a)。
对数函数的导数
对于函数y=log_a(x),其 导数为dy/dx=(1/x*ln(a)) 。
复合函数的导数
01 复合函数求导法则
对于复合函数y=f(g(x)),其导数为 dy/dx=(dy/du)*(du/dx)。
02 链式法则
对于复合函数y=f(g(x)),其导数为 dy/dx=(dy/du)*(du/dx)。
03 幂函数的链式法则
对于幂函数u=g(x)=x^n,其导数为 du/dx=nx^(n-1)。
导数的几何意义
总结词
导数的几何意义是切线的斜率,即函 数图像上某一点处的切线与x轴正方向 的夹角的正切值。
详细描述
对于可导函数f(x),其在任意点x处的 导数f'(x)表示函数图像上该点处的切 线斜率。具体来说,当函数在某点x处 可导时,该点的切线斜率即为f'(x)。
导数的物理意义
总结词
导数的物理意义是描述物理量随时间变化的速率,如速度、加速度等。
THANKS
感谢观看
03
高等数学导数与微分ppt

h 则 tanα = 500
h
dα = 1 ⋅ 1 ⋅140 故sec α = 2 , ∴ d t 2 500
2
两边对 t 求导 500 1 dh dα 2 = 2 2 sec α ⋅ sec α = 1+ tan α 500 dt dt dh 已知 = 140 , 且h = 500 时, tanα = 1 , dt h=500 ( rad/ m ) in
若上述参数方程中 则由它确定的函数 利用新的参数方程
二阶可导, 二阶可导 且 可求二阶导数 . , 可得 dy ψ′(t ) : = G(t) = dx ϕ′(t )
x = ϕ(t )
d2 y d d = (G(t )) = (G(t )) dx 2 d x dx dt dt ψ′′(t )ϕ′(t ) −ψ′(t )ϕ′′(t ) = ϕ′(t ) ′2 (t ) ϕ
( x −1)( x − 2) 例6. 求 y = 的导数. 的导数 ( x − 3)( x − 4)
可以验证
′ u′( x) (ln | u( x) |) = u( x)
先两边取对数
1 ln y = [ ln(x −1) + ln(x − 2)− ln( x − 3) − ln( x − 4)] 2
由直线的点斜式公式, 由直线的点斜式公式, 得椭圆在点 处的切线方程
化简后得
注意 : 已知
×
t f ′′(t )
x = f ′(t ) d2 y 例如, 例如 y = t f ′(t ) − f (t ) , 且 f ′′(t ) ≠ 0, 求 2 . dx
dy dy / dt = 解: = dx dx / dt
r
πR (h− x)
导数与微分PPT优秀课件

x x0
当 f(x0)0 时,曲线 f ( x ) 在 M 0 的法线方程为
1 yf(x0)f(x0)(xx0).
而当 f(x0)0时,曲线 f ( x ) 在 M 0 的法线方程为
x x0 (即法线平行y轴).
前页 后页 结束
例3 求函数 y 的x 2导数
解: (1)求增量:
yf(x x )f(x )
2.2.5 隐函数和由参数方程确定的函数的导数
1. 隐函数的导数
隐函数即是由 F(x, y)所确定的函数,其求导方法就是把y 看成x的函数,方程两端同时对x求导,然后解出 y 。
例9 求方程 eyx2yex0所确定的函数的导数
解: 方程两端对x求导得
eyy (2 x y x 2y ) e x 0
x0 x
lim f ( x0 x) f ( x0 )
x0
x
y
y f (x) N
y
M
T
x P
O
x 0 x0 x x
前页 后页 结束
例2 产品总成本的变化率
设某产品的总成本C是产量Q的函数,即C=C(Q ),当产
量Q 从Q 0 变到 Q0 Q 时,总成本相应地改变量为
C C ( Q 0 Q ) C ( Q 0 )
定理3.1 y = f (x)在x =x0可导的充分必要条件是 y = f (x)在x=x0 的左、右导数存在且相等.
前页 后页 结束
三、导数的几何意义
当自变量x 0 从变化到 x0 x 时,曲线y=f(x)
上的点由M0(x0, f(x0)).变到M (x 0 x ,f(x 0 x )).
x
即
(tanx)sec2x
类似可得(cotx)csc2x
当 f(x0)0 时,曲线 f ( x ) 在 M 0 的法线方程为
1 yf(x0)f(x0)(xx0).
而当 f(x0)0时,曲线 f ( x ) 在 M 0 的法线方程为
x x0 (即法线平行y轴).
前页 后页 结束
例3 求函数 y 的x 2导数
解: (1)求增量:
yf(x x )f(x )
2.2.5 隐函数和由参数方程确定的函数的导数
1. 隐函数的导数
隐函数即是由 F(x, y)所确定的函数,其求导方法就是把y 看成x的函数,方程两端同时对x求导,然后解出 y 。
例9 求方程 eyx2yex0所确定的函数的导数
解: 方程两端对x求导得
eyy (2 x y x 2y ) e x 0
x0 x
lim f ( x0 x) f ( x0 )
x0
x
y
y f (x) N
y
M
T
x P
O
x 0 x0 x x
前页 后页 结束
例2 产品总成本的变化率
设某产品的总成本C是产量Q的函数,即C=C(Q ),当产
量Q 从Q 0 变到 Q0 Q 时,总成本相应地改变量为
C C ( Q 0 Q ) C ( Q 0 )
定理3.1 y = f (x)在x =x0可导的充分必要条件是 y = f (x)在x=x0 的左、右导数存在且相等.
前页 后页 结束
三、导数的几何意义
当自变量x 0 从变化到 x0 x 时,曲线y=f(x)
上的点由M0(x0, f(x0)).变到M (x 0 x ,f(x 0 x )).
x
即
(tanx)sec2x
类似可得(cotx)csc2x
高数导数与微分PPT课件

例1、设 y 2x5 sin x, 求 y和 y(0).
解: y 10x4 cos x, y 40x3 sin x,
y 120x2 cos x, y(0) 1
第15页/共36页
机动 目录 上页 下页 返回 结束
三、求导法则
(1) 函数的和、差、积、商的求导法则
设u u( x), v v( x)可导,则
100!
练习2、设 f (x) x 1,用导数的定义求f (2).
解: f (2) lim f ( x) f (2) lim
x2 x 2
x2
lim 1 1 x2 x 1 1 2
x 11 x2
第7页/共36页
机动 目录 上页 下页 返回 结束
6、导数的几何意义
f ( x0 )表示曲线 y f ( x)在点 M ( x0 , f ( x0 ))处切线
(1)(u v) u v,
(2)(cu) cu(c是常数),
(3)(uv) uv uv, [u( x) v( x)] u( x) v( x);
(4)
u v
uv v2
uv
(v
0)
.
u( x)
v(
x
)
u( x) v( x)
.
第16页/共36页
机动 目录 上页 下页 返回 结束
dy
则
dy dx
dt dx
(t) ; (t )
dt
d2y dx2
d( dy ) dx
dx
d ( (t)) dt (t)
dx
dt
第23页/共36页
机动 目录 上页 下页 返回 结束
例4、设
y
f
(
x
)
解: y 10x4 cos x, y 40x3 sin x,
y 120x2 cos x, y(0) 1
第15页/共36页
机动 目录 上页 下页 返回 结束
三、求导法则
(1) 函数的和、差、积、商的求导法则
设u u( x), v v( x)可导,则
100!
练习2、设 f (x) x 1,用导数的定义求f (2).
解: f (2) lim f ( x) f (2) lim
x2 x 2
x2
lim 1 1 x2 x 1 1 2
x 11 x2
第7页/共36页
机动 目录 上页 下页 返回 结束
6、导数的几何意义
f ( x0 )表示曲线 y f ( x)在点 M ( x0 , f ( x0 ))处切线
(1)(u v) u v,
(2)(cu) cu(c是常数),
(3)(uv) uv uv, [u( x) v( x)] u( x) v( x);
(4)
u v
uv v2
uv
(v
0)
.
u( x)
v(
x
)
u( x) v( x)
.
第16页/共36页
机动 目录 上页 下页 返回 结束
dy
则
dy dx
dt dx
(t) ; (t )
dt
d2y dx2
d( dy ) dx
dx
d ( (t)) dt (t)
dx
dt
第23页/共36页
机动 目录 上页 下页 返回 结束
例4、设
y
f
(
x
)
导数与微分(高等数学)市公开课获奖课件省名师示范课获奖课件
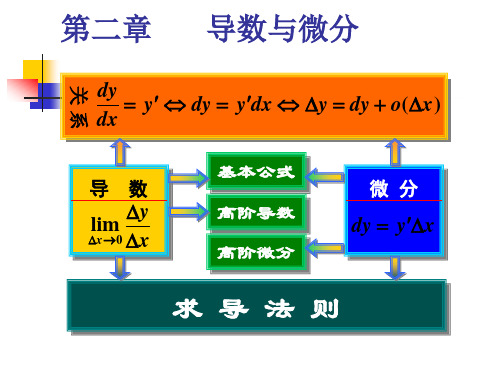
k dy 1 3t 2 dx t1 2t
t 1
2 1 2
于是所求旳切线方程为 y =-x
例题:设
x ln(1 t 2 ) ,求 d 2 y
y t arctan t
dx2
(6) 对数求导法
先在方程两边取对数,然后利用隐函数旳求导措施 求出导数.
合用范围:
函数相乘和幂指函数 u(x)v(x)的情形.
两边对x求导数,得
1 y
y
1 2
1 x 1
1 x2
x
1 3
x
1
4
,
y
1 2
y
1 x 1
x
1
2
x
1 3
x
1
4
1 2
(x 1)(x (x 3)(x
2) 4)
1 x 1
x
1
2
x
1 3
x
1
4
.
首页 上页 下页
(7)抽象函数旳求导法则
1.y f (x2 ),求y
2.y f (x2 ),求y
1.已知f (x) xex ,求f (1)
2.已知y ln(1 x),求y
3.已知y xex ,求y(0)
练习:P51 2(1) (4) (5)
上页 下页
8、微分
(1)微分旳定义
设函数y f ( x)在某区间内有定义 , x0及x0 x 在这区间内, 如果
y f ( x0 x) f ( x0 ) A x o(x) 成立(其中A是与x无关的常数),则称函数y f ( x)
一般地,可得 y( n ) e x .
n 例 求 y sin x 旳
阶导数.
解
导数与微分课件

导数和微分都与函数的局部性质 有关,它们都可以用来研究函数 的单调性、极值和曲线的形状等
。
导数与微分的区别
导数主要关注函数在某一点的变化率,而微分则更关注函数在某一点附近的局部变 化趋势。
导数是函数值的增量之比,而微分则是函数值增量的近似值。
导数是一种数学运算,可以通过求导公式或法则进行计算;而微分则是一种近似计 算方法,常常用于近似计算函数的值。
总结词
函数单调性与导数正负相关
详细描述
如果函数在某区间内的导数大于0,则函数在此区间内单调递增;如果导数小于 0,则函数单调递减。导数的正负可以判断函数的增减性。
极值与导数
总结词
导数变化与极值点的关系
详细描述
函数极值点处的一阶导数为0,但一阶导数为0的点不一定是极值点。需要进一步 判断二阶导数的正负来确定是否为极值点。
公式
$f'(x) = lim_{Delta x to 0} frac{Delta y}{Delta x}$
解释
其中$Delta y = f(x + Delta x) - f(x)$,表 示函数在$x$处的变化量,$Delta x$表示 自变量的变化量。
导数的几何意义
总结词
导数的几何意义是切线的斜率, 表示函数图像在该点的切线。
二项式定理
对于多项式函数,可以使 用二项式定理进行近似计 算。
泰勒级数
将函数展开成泰勒级数, 可以用来近似计算函数的 值。
误差估计
导数与误差
导数可以用来估计函数值 的误差大小。
微分中值定理
利用微分中值定理,可以 估计函数在某区间的变化 量。
误差传播
在误差传播过程中,可以 利用微分知识来估计误差 的大小。
第2章:导数与微分-PPT课件

n f ( x ) x ( n N ) 在 x a处的导数 . 例2. 求函数
解:
xn an f (x) f (a) lim f (a) lim xa x a x a xa
2 n 3 a x lim ( x n 1 a xn2 an1)
二、导数的定义
) 在点 x 0 的某邻域内有定义 , 定义1 设函数 y f (x
若
x x0
y lim f (x) f (x0) lim
x x0
x 0 x
y f( x ) f( x ) 0 xxx 0
存在,则称函数 f ( x ) 在点 x 0 处可导,并称此极限为 y f (x ) 在点 x 0 的导数. 记作: dy d f (x) ; y xx0 ; f (x x x 0); dx x x0 dx 0
时) (当
切线 MT 的斜率
C M
T
lim tan k tan
o x 0
x x
f( x ) f( x ) 0 割线 M N 的斜率 tan x x0 f( x ) f( x ) 0 k lim x x0 x x 0
f( t ) f( t ) 0 瞬时速度 v lim t t0 t t0
若上述极限不存在,就说函数f (x)在点x0不可导。 y , 也称 f ( x) 在 x 的导数为无穷大 . 若 lim 0 x 0 x 若函数在开区间 I 内每点都可导,就称函数在I 内可导. 此时导数值构成的新函数称为导函数. 记作:
y ;
注意:
f ( x) ;
dy ; dx
f( x 5x )f( x ) f( x h )f( x ) =5 f ( x ) f (x0 h) f (x0 ) 0 0 0 0 ( 1 )l i m lim 5 l i m 0 h 0 h0 h x 0 h x
《导数与微分§》课件

《导数与微分§》PPT课件
本课程介绍导数与微分的基本概念、计算方法以及几何和物理意义,深入而 生动地带你领略微积分的奥妙。
导数的定义与计算
1
导数公式的推导
2
通过推导,揭示导数计算的原理和方
法。
3
导数的几何意义与物理意义
4
深入理解导数在几何和物理问题中的 应用。
导数的概念与定义
探索导数的本质与含义,为后续学习 打下基础。
导数计算的基本方法
掌握导数计算的常用技巧和规则。
常见函数的导数公式
幂Hale Waihona Puke 数的导数公式掌握幂函数的导数计算规则,用于解决相关 问题。
对数函数的导数公式
理解对数函数的导数特性,解决涉及对数的 导数问题。
指数函数的导数公式
学习指数函数的导数性质和计算方法,应用 于实际情境。
三角函数的导数公式
探索三角函数的导数规律,应用于各种题型 中。
1
微分的几何意义与物理意义
2
深入探讨微分在几何和物理中的应用
与解释。
3
高阶微分的概念及其应用
4
理解高阶微分的定义和应用,拓展微 分的深度应用。
微分的定义与计算
学习微分的含义和计算方法,以及与 导数的关系。
微分的应用:求函数的极值与 最值
应用微分求解函数的极值和最值问题, 解决实际应用难题。
高阶导数与导函数
高阶导数的概念
了解高阶导数的定义及其在求解复杂函数中的 作用。
高阶导数的计算方法
掌握高阶导数计算的技巧与步骤,提升问题解 决能力。
导函数的概念与计算方法
深入研究导函数的定义和求解思路,加深理解。
导函数与原函数的关系
探索导函数与原函数之间的联系与性质,为进 阶探索打下基础。
本课程介绍导数与微分的基本概念、计算方法以及几何和物理意义,深入而 生动地带你领略微积分的奥妙。
导数的定义与计算
1
导数公式的推导
2
通过推导,揭示导数计算的原理和方
法。
3
导数的几何意义与物理意义
4
深入理解导数在几何和物理问题中的 应用。
导数的概念与定义
探索导数的本质与含义,为后续学习 打下基础。
导数计算的基本方法
掌握导数计算的常用技巧和规则。
常见函数的导数公式
幂Hale Waihona Puke 数的导数公式掌握幂函数的导数计算规则,用于解决相关 问题。
对数函数的导数公式
理解对数函数的导数特性,解决涉及对数的 导数问题。
指数函数的导数公式
学习指数函数的导数性质和计算方法,应用 于实际情境。
三角函数的导数公式
探索三角函数的导数规律,应用于各种题型 中。
1
微分的几何意义与物理意义
2
深入探讨微分在几何和物理中的应用
与解释。
3
高阶微分的概念及其应用
4
理解高阶微分的定义和应用,拓展微 分的深度应用。
微分的定义与计算
学习微分的含义和计算方法,以及与 导数的关系。
微分的应用:求函数的极值与 最值
应用微分求解函数的极值和最值问题, 解决实际应用难题。
高阶导数与导函数
高阶导数的概念
了解高阶导数的定义及其在求解复杂函数中的 作用。
高阶导数的计算方法
掌握高阶导数计算的技巧与步骤,提升问题解 决能力。
导函数的概念与计算方法
深入研究导函数的定义和求解思路,加深理解。
导函数与原函数的关系
探索导函数与原函数之间的联系与性质,为进 阶探索打下基础。
导数与微分的定义通用课件

导数与微分的定义通用课件
目录
• 导数定义与性质 • 微分定义与性质 • 导数与微分的关系 • 导数与微分在各领域的应用 • 导数与微分常见问题解析
01
导数定义与性质
导数的定义
导数的定义
导数描述了函数在某一点处的切线斜率,是函数 值随自变量变化的速率。
符号表示
用 f'(x) 表示函数 f 在 x 处的导数。
单调性与极值综合问题
掌握如何结合单调性和极值解决综合问题的方法。
THANK YOU
感谢各位观看
导数的性质
线性性质
若 c 是常数,f 和 g 是可导函数,则 (c * f)' = c * f' 和 (f + g)' = f' + g'。
链式法则
若 u = g(x) 是可导函数,y = f(u) 是可导函数,则 (f ∘ g)' = f'(g(x)) * g'(x)。
乘积法则
若 f 和 g 是可导函数,则 (fg)' = f'g + fg'。
03
导数与微分的关系
导数是微分的商
导数定义为函数在某一点的变化率, 即函数在这一点上切线的斜率,用微 分除以自变量的增量得到。
导数表示函数在某一点附近的小范围 内变化的速度或趋势,是微分的一种 数学表达。
导数与微分的应用
01
导数在经济学中用于研究边际 成本、边际收益和边际利润等 概念,帮助理解经济行为的变 化趋势和最优决策。
详细描述
在物理学中,导数和微分被用于描述物体的速度、加速度、温度变化、电磁场等物理量随时间或空间 的变化规律。例如,在经典力学中,物体的速度和加速度可以通过导数和微分来计算;在热力学中, 温度的变化率可以用导数来描述。
目录
• 导数定义与性质 • 微分定义与性质 • 导数与微分的关系 • 导数与微分在各领域的应用 • 导数与微分常见问题解析
01
导数定义与性质
导数的定义
导数的定义
导数描述了函数在某一点处的切线斜率,是函数 值随自变量变化的速率。
符号表示
用 f'(x) 表示函数 f 在 x 处的导数。
单调性与极值综合问题
掌握如何结合单调性和极值解决综合问题的方法。
THANK YOU
感谢各位观看
导数的性质
线性性质
若 c 是常数,f 和 g 是可导函数,则 (c * f)' = c * f' 和 (f + g)' = f' + g'。
链式法则
若 u = g(x) 是可导函数,y = f(u) 是可导函数,则 (f ∘ g)' = f'(g(x)) * g'(x)。
乘积法则
若 f 和 g 是可导函数,则 (fg)' = f'g + fg'。
03
导数与微分的关系
导数是微分的商
导数定义为函数在某一点的变化率, 即函数在这一点上切线的斜率,用微 分除以自变量的增量得到。
导数表示函数在某一点附近的小范围 内变化的速度或趋势,是微分的一种 数学表达。
导数与微分的应用
01
导数在经济学中用于研究边际 成本、边际收益和边际利润等 概念,帮助理解经济行为的变 化趋势和最优决策。
详细描述
在物理学中,导数和微分被用于描述物体的速度、加速度、温度变化、电磁场等物理量随时间或空间 的变化规律。例如,在经典力学中,物体的速度和加速度可以通过导数和微分来计算;在热力学中, 温度的变化率可以用导数来描述。
第三章 导数与微分 《经济数学》PPT课件

CHAPTER
03
第3章 导数与 微分
PART
03
3.1
导数
导数是数学中的一个分支——微积分的两个基本概念之一,它
表示一个函数的因变量相对于自变量的变化的快慢程度,即因变 量关于自变量的变化率.事物总是在不断地运动和变化的,而描述 这种运动和变化离不开变化率,导数就是对现实生活中各种各样 的变化率的一种统一的数学抽象.导数是微积分以及实际生活中 应用极其广泛的概念,其应用范围包括函数性态的描述、曲线的 描绘、最优化问题的讨论以及变化率的分析等.
,
即函数在点x=0处的右导数不存在,所以函数f(x)在点x=0处的导
数不存在.
3. 1. 5
高阶导数
在本小节中,我们将讨论一个量的变化率的变化率.这样的变化率 有很多种,例如,汽车的加速度是它的速度关于时间的变化率,而 速度本身又是路程关于时间的变化率.如果路程的单位是千米,时 间的单位是小时,那么速度(路程关于时间的变化率)的单位是千 米/小时,而加速度(速度的变化率)的单位则是千米/小时2.
上述有关变化率的变化率的问题,在经济上是常用的.例如,在通 货膨胀时期,你可以听到经济部门的报告指出,“尽管通货膨胀率 在增长,但其增长速度在减缓”,就是指物价在上涨,但已经不比 以前那样增长得快了.
3. 1. 5
高阶导数
1) 高阶导数的概念 ➢ 设函数y=f(x)关于x的变化率由其导函数f '(x)给出.类似地,函数f
3.2 1 微分的定义
关于微分定义的几点说明: ➢ (1)函数的微分dy是Δx的一次函数,它不仅与Δx有关,而且与x也
有关.函数的微分dy与Δy只差一个比Δx高阶的无穷小,它是Δy的 主要部分,所以也称微分dy是函数改变量Δy的线性主部. ➢ (2)若函数y=f(x)在x处的改变量Δy可以表示成Δx的线性函数 k(x)Δx与一个比Δx高阶的无穷小之和Δy=k(x)Δx+o(Δx),则称 函数y=f(x)在点x处可微. ➢ (3)由于自变量x的微分dx=(x)'Δx=Δx,故dx可理解为自变量x的 改变量Δx.于是dy=f '(x)Δx=f '(x)dx,即函数的微分等于函数的 导数乘上自变量的微分.
03
第3章 导数与 微分
PART
03
3.1
导数
导数是数学中的一个分支——微积分的两个基本概念之一,它
表示一个函数的因变量相对于自变量的变化的快慢程度,即因变 量关于自变量的变化率.事物总是在不断地运动和变化的,而描述 这种运动和变化离不开变化率,导数就是对现实生活中各种各样 的变化率的一种统一的数学抽象.导数是微积分以及实际生活中 应用极其广泛的概念,其应用范围包括函数性态的描述、曲线的 描绘、最优化问题的讨论以及变化率的分析等.
,
即函数在点x=0处的右导数不存在,所以函数f(x)在点x=0处的导
数不存在.
3. 1. 5
高阶导数
在本小节中,我们将讨论一个量的变化率的变化率.这样的变化率 有很多种,例如,汽车的加速度是它的速度关于时间的变化率,而 速度本身又是路程关于时间的变化率.如果路程的单位是千米,时 间的单位是小时,那么速度(路程关于时间的变化率)的单位是千 米/小时,而加速度(速度的变化率)的单位则是千米/小时2.
上述有关变化率的变化率的问题,在经济上是常用的.例如,在通 货膨胀时期,你可以听到经济部门的报告指出,“尽管通货膨胀率 在增长,但其增长速度在减缓”,就是指物价在上涨,但已经不比 以前那样增长得快了.
3. 1. 5
高阶导数
1) 高阶导数的概念 ➢ 设函数y=f(x)关于x的变化率由其导函数f '(x)给出.类似地,函数f
3.2 1 微分的定义
关于微分定义的几点说明: ➢ (1)函数的微分dy是Δx的一次函数,它不仅与Δx有关,而且与x也
有关.函数的微分dy与Δy只差一个比Δx高阶的无穷小,它是Δy的 主要部分,所以也称微分dy是函数改变量Δy的线性主部. ➢ (2)若函数y=f(x)在x处的改变量Δy可以表示成Δx的线性函数 k(x)Δx与一个比Δx高阶的无穷小之和Δy=k(x)Δx+o(Δx),则称 函数y=f(x)在点x处可微. ➢ (3)由于自变量x的微分dx=(x)'Δx=Δx,故dx可理解为自变量x的 改变量Δx.于是dy=f '(x)Δx=f '(x)dx,即函数的微分等于函数的 导数乘上自变量的微分.
导数与微分 PPT

lim v(xx)v(x)
x 0
所以 [ u ( x ) v ( x ) ] u ( x ) v ( x ) u ( x ) v ( x )
(3)
u(x) v(x)
u(x)v(xv)2 (xu)(x)v(x)
(v(x)0)
特别地,当u(x)c ( c为常数)时,有
[c(vx)]cv(x)
x
x
(3)取极限,求得导数
f
(x0)
lim ylim f(x0 x)f(x0)
x x 0
x 0
x
例2.1.1 求函数 yc ( c为常数)的导数 y
解: 利用导数定义求:
因为 ycc0
所以 lim ylim cc0
x 0x x 0 x
即 (c) 0
例2.1.2 求函数 ysinx的导数 y 及 y(0)
定理2.2.1 设函数u(x) 和v( x)
数
u(x)v(x)
, u(x) 以及v ( x )
(v(x)0)
在x点 处可导,那u么(x)函v(x)
x
在 处也可导,且
(1) [ u ( x ) v ( x ) ] u ( x ) v ( x )
推广: 若 u1 (x), u2 (x), ,un(x) 在 x处都可导,则
lim
lim 1
x 0 x0
x x 0
f(0)
lim f(x)f(0 )lis m ixn 01 x 0 x0 x x 0
于是
f(0) f(0)1
即知 f (0)1
例2.1.4
设函数y
x2,
x 0 ,求 f (x) .
sinx, x 0
解:当 x 0时,f(x)(x2)2x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定理:设y f (u), u (x), 若 (x)在x点处可导,
f (u)在相应的u点处可导,
则y f[ (x)]在x点处可导,且y f (u)(x)
即函数y对中间变量u求导f (u)乘中间变量u对
自变量x求导 (x)。
导数与微分
注:复合函数求导法则的关键在于: (1) 将复合函数分解成若干个基本初等函数; (2) 分别求出这些函数的导数并相乘; (3) 将所设中间变量还原
x x(t)
y
y(t)
t
求导公式:y(x) y(t) x(t)
例8:求下列参数方程给出的函数的导数
(1)
x ln(1 t)
y
arctgt
y(x)
y(t) x(t)
(arctgt) (ln(1 t))
1 1t 2
1 1t
1t 1 t2
导数与微分
x a(t sin t)
(2)
导数与微分
例9 求下列函数的微分 (1) y ln ln x
y (ln ln x) 1 (ln x) 1
ln x
x ln x
dy 1 dx x ln x
导数与微分
一、导数的概念
1.自变量的增量:x x x0, x x0 x 2.函数的增量: y f (x0 x) f (x0 ) 3.导数的定义:
f
( x0
)
lim
x0
y x
lim x0
f (x0
x) x
f (x0 )
一般地:
f (x) lim f (x x) f (x) (导函数)
cos t sin t sin t cos t
k y |t0 1 又t 0时x 0, y 1
切线方程为:y 1 1 (x 0) y x 1
导数与微分
五、函数的微分
1.微分的定义:设函数y=f(x)在点x0处可导, 是自
变量x的增量,则称
为函数f(x)在x0处关
于x的微分.记为: ,即 dy f (x0 )x
u=-x f (x) (x) f (x), f (x) f (x) f (x) f (x) 故f (x)是奇函数 同理可证奇函数的导数是偶函数。
导数与微分
• 3.隐函数求导法则: 隐函数:由含x,y的方程F(x,y)=0给出的函数称 为隐函数。有些方程,可以从中解出y,将y表示成 x的显函数的形式。如:
导数与微分
(3) x y y x
ln x y ln y x , y ln x x ln y
yln x y ln y x y
x
y
y(ln x x ) ln y y
y
x
y y(x ln y y) x( y ln x x)
导数与微分
• 注:对一些较复杂的乘积,商或根式函数求导时, 可利用先取对数后求导的方法计算
导数与微分
例7:求下列函数的导数
(1) y x x
ln y x ln x,
1 y ln x x 1
y
x
y x x (1 ln x).
(2) y xsin x
ln y ln xsinx sin x ln x
1 y cos x ln x sin x
y
x
y xsinx (cos x ln x sin x ) x
线斜率即 f (x0 )
x0
若切点为 k t则g曲 线f (在x0 )
的
切线方程为(x0:, y0 )
x x0
法线方程为:y y0 f (x0 )(x x0 )
y
y0
1 (x f (x0 )
x0 )
导数与微分
例2:求曲线y ax在(0,1)点处的切线和法线方程
解:k f (0) (a x ) (a x ln a) |x0 ln a 切线方程为:
2.函数可微的条件:
定理: 函数y=f(x)在x点可微的充分必要条件是 y=f(x)在x点处可导.
即:函数可微 存在,则函数可导且 反之,函数可导,既 存在,则 函数可微.
, 从而
导数与微分
y f (x), dy f (x)x 对于函数y x, dy dx (x)x x x dx 即自变量的增量等于自变量的微分,从而函 数的微分的一般公式可写成: dy f (x)dx
导数与微分
例4 求下列函数的导数
(1) y ln tgx, 令 : y ln u, u tgx
y (ln u) (tgx) 1 sec2 x ctgx sec2 x u
(2)
y
3
1
2x2
,令
:
y
1
u3
,u
1
2x2
y
(u
1 3
)
1 2x2
y
1
(u
2 3
)
(4x)
4
x
3
3 3 1 2x2
利用复合函数求导法则对y求导再乘 y 得到一个含
y的方程,最后从新方程y中 解出 y
导数与微分
• 例6:求下列函数的导数
(1) y x sin y 0 解:y 1 sin y y 0 y(1 sin y) 1
y 1
1 sin y
导数与微分
(2) y xey 1 求y(0)
y (ln u) (arctgv) ( x )
1 1 1 u 1 v2 2 x
1
2 x (1 x)arctg x
y(1) 1
导数与微分
(5)
y
2cos
1 x
令
:
y
2u ,u
cos
v, v
1 x
y
(2u
)
(cos
v)
(
1 x
)
2u
ln
2
(
sin
v)
(
1 x2
)
ln
2
2cos
1 x
x2
sin
1
ln
x
导数与微分
(3)y x 1 x 1
y ( x 1) x 1
(x 1)(x 1) (x 1)(x 1) (x 1)2
x 1 x 1 (x 1)2
2 (x 1)2
导数与微分
(4) y x(x 1)(x 2)(x n),求y(0)
解法1:利用导数的定义计算
y(0) lim f (x) f (0) lim x(x 1)(x 2)(x n) 0
h0
h
lim f (x0 h) f (x0 ) lim f (x0 h) f (x0 )
h0
h
h0
h
f (x0 ) f (x0 ) 2 f (x0 )
导数与微分
二、导数的物理和几何意义
1.物理意义: s(x) 表示运动物体瞬时速度即:
2.几何意v 义s:(t) 表示曲线y=f(x)在x0处的切
y 1=lna( x 0 ) y lna x 1 法线方程为:
y 1 1 (x 0) y x 1
ln a
ln a
导数与微分
三、基本求导公式:
1(. c) 0, 3 .(xn ) nxn1
5. (ex ) ex
2 .(x ) x 1
4 .(a x ) a x ln a
6.
(log
y
a(1
cos
t)
y y(t) a(1 cos t) a sin t ctg t x(t) a(t sin t) a(1 cos t) 2
x et sin t
(3)
y
et
cos
t
求在t 0处的切线方程
y
y(t)=(et cos t)= et x(t) (et sin t) et
cos t et sin t sin t et cos t
1 x3 (4) y 3 1 x3
解:ln
y
ln( 1 1
x3 1
x3 )3
1 ln 3
1 x3 1 x3
1 [ln(1 3
x3) ln(1 x3)]
1 y
y
1 3
3x2
( 1
x3
3x2 1 x3
)
2x2 1 x6
y
3
1 1
x3 x3
2x2 1 x6
导数与微分
5.参数方程求导法则
由参数方程给出的函数 :
1 x2
导数与微分
15 .(arccos x) 1
.
1 x2
16
.(arctgx)
1 1 x2
17.
(arcctgx)
1
1 x
2
18
.(
1 xLeabharlann )1 x219. ( x ) 1 2x
导数与微分
• 四、求导法则 • 若u=u(x),v=v(x)在x处可导,则
(u v) u v
(u v) uv uv
x0 x 0
x0
x
(1)(2)(n) (1)n n!
解法2:令, f (x) (x 1)(x 2)(x n),则y xf (x)
y (x) f (x) xf (x) f (x) xf (x)
y(0) f (0) 0 (1)(2)(n) (1)n n!
导数与微分
2.复合函数求导
导数与微分
(3) y ln cos ex ,令 : y ln u,u cos v, v ex y (ln u) (cos v) (ex )
1 ( sin v) ex u
ex
sin ex cos ex
extgex
导数与微分
(4) y ln arctg x,求y(1) 令 : y ln u,u arctgv, v x
f (u)在相应的u点处可导,
则y f[ (x)]在x点处可导,且y f (u)(x)
即函数y对中间变量u求导f (u)乘中间变量u对
自变量x求导 (x)。
导数与微分
注:复合函数求导法则的关键在于: (1) 将复合函数分解成若干个基本初等函数; (2) 分别求出这些函数的导数并相乘; (3) 将所设中间变量还原
x x(t)
y
y(t)
t
求导公式:y(x) y(t) x(t)
例8:求下列参数方程给出的函数的导数
(1)
x ln(1 t)
y
arctgt
y(x)
y(t) x(t)
(arctgt) (ln(1 t))
1 1t 2
1 1t
1t 1 t2
导数与微分
x a(t sin t)
(2)
导数与微分
例9 求下列函数的微分 (1) y ln ln x
y (ln ln x) 1 (ln x) 1
ln x
x ln x
dy 1 dx x ln x
导数与微分
一、导数的概念
1.自变量的增量:x x x0, x x0 x 2.函数的增量: y f (x0 x) f (x0 ) 3.导数的定义:
f
( x0
)
lim
x0
y x
lim x0
f (x0
x) x
f (x0 )
一般地:
f (x) lim f (x x) f (x) (导函数)
cos t sin t sin t cos t
k y |t0 1 又t 0时x 0, y 1
切线方程为:y 1 1 (x 0) y x 1
导数与微分
五、函数的微分
1.微分的定义:设函数y=f(x)在点x0处可导, 是自
变量x的增量,则称
为函数f(x)在x0处关
于x的微分.记为: ,即 dy f (x0 )x
u=-x f (x) (x) f (x), f (x) f (x) f (x) f (x) 故f (x)是奇函数 同理可证奇函数的导数是偶函数。
导数与微分
• 3.隐函数求导法则: 隐函数:由含x,y的方程F(x,y)=0给出的函数称 为隐函数。有些方程,可以从中解出y,将y表示成 x的显函数的形式。如:
导数与微分
(3) x y y x
ln x y ln y x , y ln x x ln y
yln x y ln y x y
x
y
y(ln x x ) ln y y
y
x
y y(x ln y y) x( y ln x x)
导数与微分
• 注:对一些较复杂的乘积,商或根式函数求导时, 可利用先取对数后求导的方法计算
导数与微分
例7:求下列函数的导数
(1) y x x
ln y x ln x,
1 y ln x x 1
y
x
y x x (1 ln x).
(2) y xsin x
ln y ln xsinx sin x ln x
1 y cos x ln x sin x
y
x
y xsinx (cos x ln x sin x ) x
线斜率即 f (x0 )
x0
若切点为 k t则g曲 线f (在x0 )
的
切线方程为(x0:, y0 )
x x0
法线方程为:y y0 f (x0 )(x x0 )
y
y0
1 (x f (x0 )
x0 )
导数与微分
例2:求曲线y ax在(0,1)点处的切线和法线方程
解:k f (0) (a x ) (a x ln a) |x0 ln a 切线方程为:
2.函数可微的条件:
定理: 函数y=f(x)在x点可微的充分必要条件是 y=f(x)在x点处可导.
即:函数可微 存在,则函数可导且 反之,函数可导,既 存在,则 函数可微.
, 从而
导数与微分
y f (x), dy f (x)x 对于函数y x, dy dx (x)x x x dx 即自变量的增量等于自变量的微分,从而函 数的微分的一般公式可写成: dy f (x)dx
导数与微分
例4 求下列函数的导数
(1) y ln tgx, 令 : y ln u, u tgx
y (ln u) (tgx) 1 sec2 x ctgx sec2 x u
(2)
y
3
1
2x2
,令
:
y
1
u3
,u
1
2x2
y
(u
1 3
)
1 2x2
y
1
(u
2 3
)
(4x)
4
x
3
3 3 1 2x2
利用复合函数求导法则对y求导再乘 y 得到一个含
y的方程,最后从新方程y中 解出 y
导数与微分
• 例6:求下列函数的导数
(1) y x sin y 0 解:y 1 sin y y 0 y(1 sin y) 1
y 1
1 sin y
导数与微分
(2) y xey 1 求y(0)
y (ln u) (arctgv) ( x )
1 1 1 u 1 v2 2 x
1
2 x (1 x)arctg x
y(1) 1
导数与微分
(5)
y
2cos
1 x
令
:
y
2u ,u
cos
v, v
1 x
y
(2u
)
(cos
v)
(
1 x
)
2u
ln
2
(
sin
v)
(
1 x2
)
ln
2
2cos
1 x
x2
sin
1
ln
x
导数与微分
(3)y x 1 x 1
y ( x 1) x 1
(x 1)(x 1) (x 1)(x 1) (x 1)2
x 1 x 1 (x 1)2
2 (x 1)2
导数与微分
(4) y x(x 1)(x 2)(x n),求y(0)
解法1:利用导数的定义计算
y(0) lim f (x) f (0) lim x(x 1)(x 2)(x n) 0
h0
h
lim f (x0 h) f (x0 ) lim f (x0 h) f (x0 )
h0
h
h0
h
f (x0 ) f (x0 ) 2 f (x0 )
导数与微分
二、导数的物理和几何意义
1.物理意义: s(x) 表示运动物体瞬时速度即:
2.几何意v 义s:(t) 表示曲线y=f(x)在x0处的切
y 1=lna( x 0 ) y lna x 1 法线方程为:
y 1 1 (x 0) y x 1
ln a
ln a
导数与微分
三、基本求导公式:
1(. c) 0, 3 .(xn ) nxn1
5. (ex ) ex
2 .(x ) x 1
4 .(a x ) a x ln a
6.
(log
y
a(1
cos
t)
y y(t) a(1 cos t) a sin t ctg t x(t) a(t sin t) a(1 cos t) 2
x et sin t
(3)
y
et
cos
t
求在t 0处的切线方程
y
y(t)=(et cos t)= et x(t) (et sin t) et
cos t et sin t sin t et cos t
1 x3 (4) y 3 1 x3
解:ln
y
ln( 1 1
x3 1
x3 )3
1 ln 3
1 x3 1 x3
1 [ln(1 3
x3) ln(1 x3)]
1 y
y
1 3
3x2
( 1
x3
3x2 1 x3
)
2x2 1 x6
y
3
1 1
x3 x3
2x2 1 x6
导数与微分
5.参数方程求导法则
由参数方程给出的函数 :
1 x2
导数与微分
15 .(arccos x) 1
.
1 x2
16
.(arctgx)
1 1 x2
17.
(arcctgx)
1
1 x
2
18
.(
1 xLeabharlann )1 x219. ( x ) 1 2x
导数与微分
• 四、求导法则 • 若u=u(x),v=v(x)在x处可导,则
(u v) u v
(u v) uv uv
x0 x 0
x0
x
(1)(2)(n) (1)n n!
解法2:令, f (x) (x 1)(x 2)(x n),则y xf (x)
y (x) f (x) xf (x) f (x) xf (x)
y(0) f (0) 0 (1)(2)(n) (1)n n!
导数与微分
2.复合函数求导
导数与微分
(3) y ln cos ex ,令 : y ln u,u cos v, v ex y (ln u) (cos v) (ex )
1 ( sin v) ex u
ex
sin ex cos ex
extgex
导数与微分
(4) y ln arctg x,求y(1) 令 : y ln u,u arctgv, v x
