数学分析简明教程答案20
数学分析简明教程答案

第十一章 广义积分§11.1 无穷限广义积分1. 求下列无穷积分的值: (1)⎰+∞-2211dx x ; (2)⎰+∞+22)1(1dx x x ;(3))0(02>⎰+∞-a dx xe ax ;(4))0(sin 0>⎰+∞-a bxdx eax;. (5)⎰∞++021dx x x; (6))0,()()(022>+++⎰+∞q p q x p x dx.解 (1)3ln 21)31ln 11(ln 21lim 11lim 112222=-+-=-=-+∞→+∞→+∞⎰⎰A A dx x dx x A A A . (2)2ln 21)2ln 1(ln 21lim )1(1lim )1(1221212=++=+=++∞→+∞→∞+⎰⎰AA dx x x dx x x A A A . (3)a211a 21limlim222=-==-+∞→-+∞→+∞-⎰⎰)(e dx e x dx ex ax A Aax A ax . (4)设⎰+∞-=0sin bxdx e I ax )0(>a ,则)cos sin 1(lim sin lim 000⎰--+∞→-+∞→+-=⎰=A ax A ax A Aax A dx bx e a b bx e a bxdx e I)sin cos (lim 002⎰--+∞→+-=A ax A axA bxdx e b bx e a bI ab a b bxdx eab a b bxdx e a b a b axA axA 22202220222sin sin lim -=-=-=⎰⎰∞+--+∞→,所以 ,22ba bI +=. (5)作变换y x =,则有⎰+++-+--++=+=+⎰⎰dy y y y y y y y y y y dy y y dx x x )21)(21()21(22)21(221212222422 ⎰⎰-+++-+-=)22(21)(2121)21(42222y y d y y y y d ⎰⎰+++++++-)22(2121)21)21(42222y dyy y y y d C y y y y y y +++-++++-=)]12arctan()12[arctan(222121ln 4222C x x x x x xy +++-+++-=)]12arctan()12[arctan(221)21(ln 4222, 所以,)]12arctan()12[arctan(221)21(ln 421222++-+++-=+⎰A A A A A dx x x A)(22)22(22+∞→=+→A πππ,即,π22102=+⎰∞+dx xx . (6) 由于当q p =时,用⎰+=n n x a dxI )(22的地推公式,p x dxp p x x p p x dx q x p x dx +++=+=++⎰⎰2222222121)())((C pxp p p x x p +++=arctan 21212所以,时,0>=q ppp p A p p p A A p p x dx A AA 4)arctan 2121(lim )(lim2022π=++=++∞→+∞→⎰, 当q p ≠时,由于⎰⎰⎰+-+-=++--=++dx p x q x q p q x p x dx q p q p q x p x dx )11(1))(()(1))((222222C pxp q x q q p +--=)arctan 1arctan 1(1, 所以,当q p ≠时,⎰⎰+=+++∞→+∞A A q x dx q x p x dx 02022)(lim ))(( )(2)arctan 1arctan 1(1limq p pq p A p q A q q p A +=--=+∞→π两种情况下,即只要0,>q p ,就有⎰+∞+=++022)(2))((q p pq q x p x dx π. 2. 讨论下列积分的收敛性: (1)⎰+∞+0341x dx ;(2)⎰+∞+031arctan dx x x;(3)⎰∞+121sindx x;(4)⎰+∞+0dx xx sin 11;(5)⎰+∞+022sin 1dx xx x; (6))0,(10>+⎰∞+m n dx xx nm; (7)⎰∞++-0 1242x x dxx ;(8)⎰+∞+13211dx xx ;(9))0(02≥⎰+∞-p dx e x x ;(10)⎰+∞1ln dx x xp; (11)⎰∞+12ln dx x xn (n 是正整数); (12)⎰∞+02sin dx xx; (13)⎰+∞+01cos dx x axn ; (14)⎰+∞+-+1]11)11[ln(dx x x ;(15)⎰+∞+1)1sin 1ln(cos dx xx ;(16)⎰∞+-⎪⎪⎭⎫ ⎝⎛-0dx x x 1222sin 1ln 1. 解 (1)111lim 3434=++∞→x xx ,所以积分⎰+∞+0341x dx 收敛.(2)21arctan lim 32π=++∞→x x x x x ,故所求积分收敛.(3)111sin lim1sin lim 2222==+∞→+∞→x x xx x x ,因此所求积分收敛. (4)0≥∀x ,有011sin 11>+≥+x x x ,且+∞=+=+=++∞→+∞→+∞⎰⎰)1ln(lim 1lim 10A x dx x dxA A A 0,即⎰+∞+01xdx发散,由比较判别法知⎰+∞+0x x dx sin 1发散.(5)0≥∀x ,有01sin 1222>+≥+x x x x x ,而11lim 2=++∞→x xx x ,无穷积分⎰+∞+021dx x x 发散,由比较判别法知⎰+∞+022sin 1dx xx x发散. (6)因为11lim=++∞→nnx x x ,所以, 当1>-m n ,即1+>m n 时,⎰∞++01dx x x nm收敛;当1≤-m n ,即1+≤m n 时,⎰∞++01dx xx nm发散. (7) 11lim 2422=+-+∞→x x x x x ,所以积分收敛.(8)1111lim11lim 323235=+=++∞→+∞→x xx xx x ,所以积分收敛.(9) 因为 =+==++∞→++∞→-+∞→x px x p x xpx ex p e x e x x 122)2(lim lim )(lim 0])[()1)(2(lim ][=-++=-+∞→x p p x ex p p p p , 所以无穷积分收敛.(10) 若1>p ,则可以选取00>ε,使得10>-εp ,由于0ln limln lim 0==+∞→-+∞→εεx xxx x X pp x ,所以⎰+∞1ln dx xxp 收敛; 若1≤p ,则当e x ≥时,p p x x x 1ln ≥,而⎰+∞11dx x p 发散,由比较判别法,⎰+∞1ln dx xx p 发散.从而,⎩⎨⎧≤>⎰∞+.时发散时收敛1p ,,1p ,ln 1dx x x p (11)由于012)1(22lim ln 2lim ln lim ln lim 2121121223=-⋅====+∞→-+∞→+∞→+∞→x n n x x n x x xx x x n x n x n x , 所以无穷积分⎰∞+12ln dx x xn 收敛. (12) 因为xxx x x x x 22cos 2122cos 1sin 2-=-=,而 21)0sin 2(sin 212cos 0≤-=⎰A xdx A,对一切0>A 成立,x21在[1,+)∞单调下降,且当+∞→x 时趋于0,由Dirichlet 判别法⎰+∞122cos dx xx收敛,又⎰+∞12x dx 发散,所以⎰∞+02sin dx x x 发散(0=x 是可去间断点). (13)当1>n 时,由于n nx x ax +≤+111cos ,而⎰+∞+011dx x n 收敛,所以⎰+∞+01cos dx xax n 收敛,故这时不论R a ∈是哪个常数,⎰+∞+01cos dx xaxn均绝对收敛. 当10≤<n 时,若0≠a ,则由于aaA a axdx A 1sin 1cos 0≤=⎰,而n x +11在),0[+∞单调递减,且当+∞→x 时趋于0,由Dirichlet 判别法知,无穷积分收敛,但由于)1(22cos )1(211cos 1cos 2nn n nx ax x x ax x ax +++=+≥+, 则由于⎰+∞+0)1(21dx x n 发散,同样由Dirichlet 判别法知⎰+∞+0)1(22cos dx x ax n 收敛,故⎰∞++021cos dx xax n 发散,由比较判别法知⎰∞++012cos dx x ax n 发散,故这时无穷积分条件收敛. 当10≤<n 且0=a 时,无穷积分为⎰+∞+011dx xn发散. 当0=n 时,无穷积分为⎪⎪⎩⎪⎪⎨⎧=+∞=≠==+∞→+∞→+∞→∞+⎰⎰,02A lim ,0sin 21lim 2cos lim 2cos A A 00a a aA adx ax dx ax A A ,不存在, 故这时,不论a 为何常数,积分发散.当0<n 时,若0=a ,无穷积分为⎰+∞+011dx x n发散.以下假设0≠a ,0820>=∃a πε,N K A ∈∃>∀,0,使得A a a k >-42ππ且142≤⎪⎪⎭⎫ ⎝⎛-na a k ππ,这时 0424282)44(421cos επππππππ==+≥+⎰+-a a a dx xax a a k aa k n, 由Cauchy 收敛原理,⎰+∞+01cos dx x axn 发散. 综上,积分⎰+∞+01cos dx x axn当0>n 时绝对收敛;当10≤<n 且0≠a 时条件收敛;其他时候发散.(14) 因为)1(21))1(11(1)1(21111)11ln(2222xo x x o x x x o x x x x +=+--+-=+-+,所以,⎰+∞+-+1]11)11[ln(dx xx 收敛.(15) 因为xx x xx x x x 1)1sin 1ln(cos lim)1sin 1ln(cos lim +=++∞→+∞→ 11sin1cos 1sin1cos lim )1)(1sin 1(cos )1(1cos )1(1sin lim222=+-=-+-+--=+∞→+∞→x x x x xx x x x x x x x , 所以,⎰+∞+1)1sin 1ln(cos dx xx 发散.(16)因为12sin 1212≤-≤x ,所以,2ln 2sin 1ln 012≤⎪⎪⎭⎫⎝⎛-≤-x .因此,21221222ln 2sin 1ln 12sin 1ln 1x x x x x ≤⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫⎝⎛---, 而⎰+∞122ln dx x 收敛,所以⎰∞+-⎪⎪⎭⎫⎝⎛-0dx x x 1222sin 1ln 1收敛(0=x 是可去间断点). 3.讨论下列无穷积分的收敛性(包括绝对收敛或条件收敛): (1)⎰∞+1dx xx2cos ; (2)⎰+∞1dx x xcos ; (3)⎰+∞1cos dx xx p ; (4)⎰∞++0100cos dx x xx ;(5)⎰+∞2sin ln ln ln xdx xx. 解 (1)xxx x x x x 22cos 2122cos 1cos 2+=+=, 由于⎰+∞121dx x 发散,而⎰+∞1dx xx 22cos 收敛(Dirichlet 判别法),因此,⎰∞+1dx x x 2cos 发散.(2)由Dirichlet 判别法知⎰+∞1dx xxcos 收敛,但由于x x x x 2cos cos ≥,而由(1),⎰∞+1dx x x2cos 发散,故由比较判别法知⎰∞+1cos dx x x 发散,因而⎰+∞1dx xx cos 条件收敛.(3)1>p 时,由于p p x x x 1cos ≤对一切),1[+∞∈x 成立,所以⎰+∞1cos dx x x p绝对收敛.10≤<p 时,用Dirichlet 判别法知⎰+∞1dx xxp cos 收敛,但由于 pp p px x x x x x x 22cos 21cos cos 2+=≥,同样用Dirichlet 判别法知⎰+∞122cos dx x xp 收敛,而⎰+∞121dx x p 发散,故由比较判别法知⎰∞+1cos dx x x p发散,所以这时⎰+∞1cos dx x xp条件收敛. 0=p 时,⎰+∞1cos xdx 发散.0<p 时,亦发散(用Cauchy 收敛原理即可).所以,⎰+∞1cos dx xxp 当1>p 时绝对收敛;10≤<p 时条件收敛;0≤p 时发散. (4)⎰⎰∞+∞++=+11100cos 100cos dx x x x x dx x x x ,由于⎰+∞1cos dx x x 收敛,100+x x 单调递减有界,故由Abel 判别法,⎰∞++1100cos dx x x x 收敛,从而⎰∞++0100cos dx x xx 也收敛,但)100(22cos )100(2100cos 100cos 2+++=+≥+x xx x x x x x x xx ,同样⎰∞++0)100(22cos dx x x x 收敛,但⎰∞++0)100(2dx x x发散,所以⎰∞++0100cos dx x x x 发散.因此,⎰∞++0100cos dx x xx 条件收敛.(5)⎰⎰+∞+∞=22ln ln ln ln sin sin ln ln ln dx x x x x xdx x x,用Dirichlet 判别法知⎰+∞2ln sin dx xx 收敛,而由于)(0ln ln ln +∞→→x xx ,因而xx ln ln ln 有界,且由于23)(ln 2ln ln 2ln ln ln x x xx x -=⎪⎪⎭⎫⎝⎛,当2e e x ≥小于零,故当2e e x ≥时,xx ln ln ln 单调递减,由Abel 判别法,⎰+∞2sin ln ln ln xdx xx收敛.但xx x x x x x x x x x ln 22cos )ln (ln ln 2ln ln sin ln ln ln sin ln ln ln 2-=≥, 同样用Abel 判别法,⎰∞+2ln 22cos ln ln dx xx x 收敛,而⎰∞+2ln 2ln ln dx xx 发散(当x 充分大时,xx x 1ln ln ln ≥),故⎰∞+22sin ln ln ln xdx x x 发散,由比较判别法,dx x x x ⎰∞+2sin ln ln ln 发散,无穷积分⎰+∞2sin ln ln ln xdx xx条件收敛. 4.设)()()(x g x h x f ≤≤,+∞<≤x a ,)(,x h 在任意有限区间],[A a 可积,又⎰+∞adx x f )(和⎰+∞adx x g )(收敛.求证⎰+∞adx x h )(收敛.证明 由于)()()(x g x h x f ≤≤,+∞<≤x a ,所以,)()()()(0x f x g x f x h -≤-≤,+∞<≤x a ,又⎰+∞adx x f )(和⎰+∞adx x g )(收敛,故⎰+∞-adx x f x g )]()([也收敛,因而由比较判别法,⎰+∞-adx x f x h )]()([收敛.而)()]()([)(x f x f x h x h +-=, 所以,dx x f x f x h dx x h aa⎰⎰+∞+∞+-=)}()]()({[)(收敛.5. 证明定理11.2,并举例说明其逆是不成立的.证明 定理11.2 若⎰+∞adx x f )(收敛,则⎰+∞adx x f )(收敛.证法1、由于⎰+∞adx x f )(收敛,有无穷限积分的Cauchy 原理,0A ,0>∃>∀ε,当A A A >''',时,有ε<⎰'''A A )(dx x f ,从而当A A A >''',时,有ε<≤⎰⎰''''''A A A A dx x f dx x f )()(,同样由无穷积分的Cauchy 收敛原理,知⎰+∞adx x f )(收敛.证法2、由于),[,)()()(∞+∈≤≤-a x x f x f x f ,由第4题结论知,⎰+∞adx x f )(收敛.其逆是不成立的.例如,3(2)题中积分⎰+∞1dx xxcos 收敛,但⎰∞+1cos dx x x 发散. 6. 若)(x f 在),[∞+a 上单调下降,且积分⎰+∞adx x f )(收敛,求证:0)(lim =+∞→x xf x .证明 由于⎰+∞adx x f )(收敛,故依)(x f 在),[∞+a 上单调下降知,),[∞+∈∀a x ,有0)(≥x f ,否则,若),[0∞+∈∃a x ,使0)(0<x f ,则01x x >∀,有0)()(01<≤x f x f ,因而0x b >∀,有)+∞→∞-→-+≤+=⎰⎰⎰⎰b x b x f dx x f dx x f dx x f dx x f bax abx x a())(()()()()(000, 与⎰+∞adx x f )(收敛相矛盾.由无穷积分的Cauchy 收敛原理00>∃>∀A ,ε,当A A ,A >'''时,有2)(A A ε<⎰'''dx x f ,所以,当A 2>x 时,有2)(2ε<⎰xxdt t f ,由⎰<⇒<≤x x x xf dt t f x f x 2)(2)()(2εε,因此,0)(lim =+∞→x xf x .7. 设)(x f 在),0[+∞上一致连续,并且积分⎰+∞)(dx x f 收敛.证明0)(lim =+∞→x f x .如果仅仅知道积分⎰+∞)(dx x f 收敛,以及)(x f 在),0[+∞上连续,0)(≥x f ,是否仍有0)(lim =+∞→x f x ?证明 证法1、由)(x f 在),0[+∞上一致连续,0 0>∃>∀δε,(不妨设εδ≤),当),0[,21∞+∈x x ,δ≤-21x x 时,2)()(21ε<-x f x f ,又由⎰+∞)(dx x f 收敛,对上述0>δ,,0>∃N ,当N x x >21,时,有2)(221δ<⎰x xdx x f .N x >∀,取N x x >21,,使得21x x x <<,且δ=-12x x ,则由⎰⎰⎰⎰+-==21212121)()()()()(x x x x x x x x dt t f dt t f dt x f dt x f x f δ22)()()(22121δδε+<+-≤⎰⎰x x x x dt t f dt t f x f ,所以,当N x >时,εδε≤+<22)(x f ,因此,0)(lim =+∞→x f x .证法2、假设0)(lim ≠+∞→x f x ,则00>∃ε,0>∀A ,存在与A 有关的A x >0,使00)(ε≥x f .不妨设00)(ε≥x f ,由)(x f 在),0[+∞上一致连续,0>∃δ,当a x x ≥''',,且δ<''-'x x 时,2)()(0ε<''-'x f x f .故当),(00δδ+-∈x x x 时,2)()(00ε<-x f x f ,所以,22)()(00εε≥->x f x f ,因此δεδδ000)(≥⎰+-x x dx x f ,与⎰+∞)(dx x f 收敛矛盾,从而0)(lim =+∞→x f x .如果仅仅知道积分⎰+∞)(dx x f 收敛,以及)(x f 在),0[+∞上连续非负,则0)(lim =+∞→x f x 不成立.例如⎪⎪⎩⎪⎪⎨⎧-++⋃∈===∞=+,其他线性,,]211,21[]21,0[,0,),2,1(,1)(11 n n n n n x n n x x f则121)(10==∑⎰∞=+∞n n dx x f ,即⎰+∞0)(dx x f 收敛,显然)(x f 在),0[+∞上连续非负,但)(lim x f x +∞→不存在.8. 设⎰+∞adx x f )(与⎰+∞'adx x f )(收敛,求证:0)(lim =+∞→x f x .证明 由于⎰+∞'adx x f )(收敛,因而,))()((lim )(lim )('lima f x f t f dt t f x xa x xax -==+∞→+∞→+∞→⎰存在,因而)(lim x f x +∞→存在,设l x f x =+∞→)(lim ,若0≠l ,不妨设0>l ,则a A >∃0且00>A ,当0201,A A A A >>时,02)(>>lx f .又⎰+∞a dx x f )(收敛,故0>∀ε,a A >∃1且01>A ,当11,A A A A >''>'时,有ε<⎰'''AAdx x f )(.令},m ax {10A A A =,则当AA >'时,A A >'2,因此以下二式同时成立:ε<>'⎰''A A dx x f lA f 2)(,2)(.故022)(22>'=>⎰⎰''''A ldx l dx x f A A A A , 所以,ε<'A l2,但这是矛盾的,因此0)(lim =+∞→x f x .9.设)(x f 单调下降趋于0, )(x f '在),0[∞+连续.求证:⎰+∞'02sin )(xdx x f收敛.证明⎰⎰⎰+∞→+∞→+∞='='AA AA x xdf xdx x f xdx x f 020202)(sin limsin )(limsin )(⎰⎰+∞+∞→=-=022sin )(]2sin )(sin )([lim xdx x f xdx x f A A f A A ,由于0>∀A ,1)12(cos 212sin 0≤--=⎰A xdx A,由Dirichlet 判别法,⎰+∞02sin )(xdx x f 收敛,因而⎰+∞'02sin )(xdx x f 收敛.10.设)(x f 和)(x g 是定义在),[∞+a 上的函数,且在任何有限区间],[A a 上可积.证明:若⎰+∞adx x f )(2与⎰+∞adx x g )(2收敛,则⎰+∞+adx x g x f 2)]()([与⎰+∞adx x g x f )()(也收敛.证明 由于)]()([21)()(22x g x f x g x f +≤及)()(x g x f 在任何有限区间],[A a 上可积,⎰+∞adx x f )(2与⎰+∞adx x g )(2收敛,由比较判别法知⎰+∞adx x g x f )()(收敛,因而⎰+∞adx x g x f )()(收敛.又)()()(2)()]()([222x g x g x f x f x g x f ++=+,所以⎰+∞+adx x g x f 2)]()([也收敛.11.证明:(1)设)(x f 在),0[∞+连续,且k x f x =+∞→)(lim ,则)0(ln ])0([)()(0>>-=-⎰+∞a b abk f dx x bx f ax f ; (2)若上述条件k x f x =+∞→)(lim 改为⎰+∞a dx xx f )(存在)0(>a ,则)0.(ln )0()()(0>>=-⎰+∞a b abf dx x bx f ax f . 证明(1)当+∞<∆<<δ0时,积分 ⎰⎰⎰⎰⎰∆∆∆∆∆-=-=-b b a a dz zz f dz z z f dx x bx f dx x ax f dx x bx f ax f δδδδδ)()()()()()( ⎰⎰⎰⎰∆∆∆∆--=b a b a b a b a z dzf z dz f dz zz f dz z z f )()()()(ηξδδδδ ),(ln )(ln )(∆≤≤∆≤≤-=b a b a abf a b f ηδξδηξ,所以,⎰⎰∆+∞→∆+∞-=-δdx xbx f ax f dx x bx f ax f )()(lim )()(0ab f f a b f a b f ln )](lim )(lim [)ln )(ln)((lim 00ηξηξδδ+∞→∆→→+∞→∆-=-=++由于+→0δ时,+→0ξ;+∞→∆时,∞→+η,所以abk f a b f f dx x bx f ax f ln ])0([ln )](lim )(lim [)()(0-=-=-+∞→∆→∆+⎰ηξδδ. (2) 用(1),当+∞<∆<<δ0时,有⎰⎰⎰∆∆∆-=-δδδb a b a dz zz f dz z z f dx x bx f ax f )()()()( )()(ln )(δξδξb a dz zz f a b f b a ≤≤-=⎰∆∆,令+∞→∆→+,0δ取极限,由于⎰+∞a dx x x f )(存在,故)(0)(+∞→∆→⎰∆∆b a dz zz f ,所以,abf dx x bx f ax f ln )0()()(0=-⎰+∞.§11.2 瑕积分1. 下列积分是否收敛?若收敛求其值. (1)⎰210cot xdx ;(2)⎰1ln xdx ;(3)⎰-axa dx 0;(4)⎰-11dx xx. 解 (1) +∞=-=++→→⎰)sin ln 21sin (ln lim cot lim 0210ηηηηxdx ,所以,⎰210cot xdx 发散.(2)1)1ln (lim )ln (lim ln lim 01101-=+--=-=+++→→→⎰⎰ηηηηηηηηηdx x x xdx ,所以⎰1ln xdx收敛, 且⎰-=11ln xdx .(3)a a dt t t xa dx aa 2)(22lim lim 0=-=-=-⎰⎰++→-→ηηηηη,所以⎰-a xa dx0收敛,且⎰=-aa xa dx2. (4)ηηηηηηηη-→-→-→⎪⎭⎫ ⎝⎛+-=+=-+++⎰⎰1020102220101arctan lim )1(2lim 1lim t t t dt t t dx xx2)1(1arctanπηηηη=---=,所以dx x x ⎰-11收敛 ,且其值为2π. 2.讨论下列积分的收敛性: (1)dx xx ⎰123sin ;(2)⎰-1032)1(x x dx ;(3)⎰-1021ln dx x x;(4)⎰2022cos sin πx x dx; (5)⎰1ln dx x p;(6)⎰-20cos 1πdx xxm; (7)⎰10ln x dx ;(8)⎰πsin xdx ;(9)⎰1ln xdx xα;(10)⎰---111ln dx xx x q p ;(11)⎰20tan πdx x ; (12)⎰20sin ln cos πxdx x .解(1)因为2123231sin xxx xx =≤,]1,0(∈∀x ,由dx x⎰11收敛及比较判别法,知 dx xx ⎰123sin 收敛.(2)⎰⎰⎰-+-=-12132210321032)1()1()1(x x dx x x dx x x dx ,]21,0(∈x 时,32332322)211(1)1(1xdxx x x =-≤-,由于⎰2103232dx x收敛,可得⎰-21032)1(x x dx 收敛 ;]1,21(∈x 时,33323214)1(211)1(1xdx x x x -=-⎪⎭⎫⎝⎛≤-,由于dx x⎰-2103314收敛,可得⎰-12132)1(x x dx 收敛,所以⎰-1032)1(x x dx 收敛.(3)⎰-1021ln dx x x 只有瑕点1,0==x x 是可去奇点.因为当210≤<x 时, x x x ln 341ln 2-≤-成立,故由比较判别法知⎰-1021ln dx x x收敛(绝对收敛).(4)12sin 4lim cos sin 1lim 2202220==++→→x x x x x x x ,所以,⎰2022cos sin πxx dx 发散. (5)若0<p ,则由于)0(0ln +→→x x p知0=x 是可去间断点, 而1=x 是瑕点 ,这时由于)1()1(~)]1(1ln[ln -→--+=x x x xp pp,故当01<<-p 时,⎰1ln dx x p收敛,1-≤p 时,发散.若0=p ,则是常义积分11=⎰dx 存在.当0>p 时, 1=x 是可去间断点, 而0=x 是瑕点,由于0ln lim 21=+→px xx ,所以⎰1ln dx x p收敛.(6)mm x xx x 2sin 2cos 12=-, 当2≤m 时,+→0x 时该式极限为0或21存在,故这时0=x 不是瑕点,这是常义积分.当2>m 时, 由于21cos 1lim 20=--→+mm x x x x ,所以, 当12<-m 即32<<m 时,瑕积分⎰-2cos 1πdx x xm收敛,当12≥-m 即3≥m 时发散. (7)1ln 1)1(lim 1=---→xx x ,所以⎰10ln x dx 发散. (8)⎰⎰⎰+=ππππ22sin sin sin xdx x dx xdx ,因为1sin 1lim 210=+→xxx , 1sin 1)(lim 21=--→xx x ππ,所以⎰20sin πxdx ,⎰ππ2sin xdx 均收敛,故⎰πsin xdx 收敛.(9)当0>α时,由于0ln lim 0=+→x x x α,故是常义积分.当0=α时,1))1(ln (lim ln lim ln 011-=---==++→→⎰⎰εεεεεεxdx xdx ,所以积分收敛.当01<<-α时 ,00>∃ε,使101000<+-<⇒->->εαεα,而()0ln lim ln lim 000=-=++→+-→x x x x x x x εαεα,所以,⎰1ln xdx xα收敛.当 1-≤α 时,+∞==++→-→x x x xx x ln lim ln lim 0αα,由1≥-α知,⎰1ln xdx x α发散.(10) 当q p =时被积函数为0,故积分值为0.由于在相差一个负号的意义下,qp ,对称,故可只考虑q p >的情形.这时,)1(ln ln 111-=-----qp q q p x xx x x x ,若1>q ,则0=x 不是瑕点,因而积分为常义积分,积分值存在. 若1<q ,则被积函数为)1(ln 11---qp qx xx . ① 当11<-q 即0>q 时,故00>∃ε,使110<+-εq ,而⎰+-110εq x dx 收敛,xx ln 0ε单调增加(在)1,0(),且当+→0x 时趋于0,故由此得xx ln 0ε有界,因而由Abel 判别法知dx x x q ⎰-101ln 1收敛,又1--qp x 在)1,0(单调增加且有界,故知⎰---101)1(ln 1dx x xx q p q 即⎰---111ln dx xx x q p 收敛.② 当11>-q 即 0<q 时, 01>∃ε,使111>--εq ,因而)1(ln 11)1(ln 11111-=------q p q qp q x xx x x x x εε, 而 +∞=--→+)1(ln 1lim 10q p x x x x ε,故有10<<δ,当δ<<x 0时,1)1(ln 11>--qp x xx ε,因而1111)1(ln 1ε---->-q qp q xx x x ,所以积分 ⎰---1011ln dx x x x q p 发散. ③ 当11=-q 时,即0=q 时,由于当]21,0(∈x 时,0ln <x 而1121-≥-⎪⎭⎫⎝⎛--q p qp x ,故当]21,0(∈x 时,⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛≥---121ln 1)1(ln 1qp qp x x x x x ,由于 -∞=-==++→→⎰⎰)ln ln 2ln (ln lim ln 1lim ln 10210210εεεεdx xx dx x x发散,故由比较判别法,⎰--21)1(ln 1dx x xx qp 发散,因而⎰--10)1(ln 1dx x x x q p 发散.若1=q ,积分为⎰--10)1(ln 1dx x x qp ,这时0)1(ln 1lim 0=--→+q p x x x,故0=x 不是瑕点,积分是常义积分,因而存在.综上,瑕积分⎰---111ln dx xx x q p 当0>>q p 时收敛,q p >且0≤q 时发散;对称地,瑕积分⎰---111ln dx xx x q p 当0>>p q 时收敛,p q >而0≤p 时发散;q p =时,亦收敛.(11)解法1、令t x =tan ,则2tan t x =,2arctan t x =,dt ttdx 412+=,且当0=x 时,0=t ;2π=x 时,+∞=t .瑕积分⎰⎰∞++=0422012tan dt tt dx x π化为了无穷积分.由于212lim 422=++∞→t t t t , 故广义积分⎰∞++04212dt tt 收敛,即⎰20tan πdx x 收敛. 解法2、由于1sin )2sin()2(lim tan )2(lim 212212=--=---→→x x x x x x x πππππ,所以⎰20tan πdx x收敛.(12)由于0sin ln cos lim 0=+→x x x x ,故⎰20sin ln cos πxdx x 收敛.实际上,1)cos sin ln sin (lim sin ln cos lim sin ln cos 202020-=--==⎰⎰⎰++→→πεεπεεπεεxdx xdx x xdx x .3.判别敛散性: (1)⎰∞+-⎪⎭⎫ ⎝⎛-12111ln dx x ; (2)⎰+∞--01dx e x x p ;(3)⎰∞+0)(arctan dx x x pq; (4)⎰+∞+0)1ln(dx xx p;(5)⎰+∞1ln x x dxq p ;(6)⎰+∞+0qp xx dx; (7)⎰+∞--032)2()1(x x x dx ;(8)⎰∞-0ln dx x e x .解(1)⎰⎰⎰∞+--∞+-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-221212112111ln 11ln 11ln dx x dx x dx x ,对⎰⎰∞+∞+-⎪⎭⎫ ⎝⎛--=⎪⎭⎫ ⎝⎛-2222111ln 11ln dx x dx x ,由于122111lim )11ln(lim 33222=⋅-=⎥⎦⎤⎢⎣⎡--+∞→+∞→x x x x x x x ,所以,⎰∞+-⎪⎭⎫ ⎝⎛-22111ln dx x 收敛. 对⎰⎰⎰⎰--=--=⎪⎭⎫ ⎝⎛--2122121222121)1ln(ln 21ln 11ln dx x xdx dx x x dx x ,前一项为定积分,后一项以1=x 为瑕点.由于⎰⎰⎰-++=-2121212)1ln()1ln()1ln(dx x dx x dx x ,前一项为常义积分,而对后一项,由于0)1ln()1(lim 211=--+→x x x ,故⎰-21)1ln(dx x 收敛,因此⎰⎪⎭⎫ ⎝⎛--212111ln dx x 收敛,最后知道⎰∞+-⎪⎭⎫ ⎝⎛-12111ln dx x 收敛.(2)当1≥p 时,⎰+∞--01dx e x x p 是一无穷积分,收敛.当1<p 时,⎰⎰⎰+∞----+∞--+=111101dx e x dx e x dx e x x p x p x p ,后者为无穷积分收敛;对于前者,由于1)(lim 110=---→+x p px e x x,所以当11<-p ,即10<<p 时,⎰--11dx e x x p 收敛,当11≥-p ,即0≤p 时,⎰--11dx e xxp 发散.从而,当0>p 时,⎰+∞--01dx e x x p 收敛,当0≤p 时发散.(3)由于当0→x 时,x x →arctan ,所以当p q >时,pq pq x x x -~)(arctan ,)0(+→x ;p q =时,1)(arctan lim 0=+→pqx x x .故当p q ≥时,上述积分只是无穷积分而无瑕点.若1>p 且p q ≥,由qpp q x x x ⎪⎭⎫⎝⎛≤21)(arctan π≤x p 1)2(πq,收敛;若10≤<p 且p q ≥,则由)1(1)(arctan ≥≥x xx x pp q ,发散; 若0=p 且p q ≥时,当x 充分大时,)1(1)(arctan ≥≥x xx pq这时无穷积分发散; 若0<p 且p q ≥时,显然发散.当p q <时,积分可分为⎰⎰∞++110)(arctan )(arctan dx x x dx x x p qp q ,对于前者,pqx x )(arctan 与qp x -1是同阶无穷大量,故当10<-<q p ,即1+<<q p q 时收敛,而当1≥-q p 即1+≥q p 时发散.对于后者,同样在1>p 时收敛,1≤p 时发散.综上,当1+<<q p q 且1>p 时积分收敛,当p q <而1≤p 时积分发散. 因此,当1>≥p q 或1+<<q p q 且1>p 时积分收敛,其他情况发散.即当11+<<q p 时积分收敛,其他情况积分发散.(4)⎰⎰⎰+∞+∞+++=+11)1ln()1ln()1ln(dx xx dx xx dx xx ppp,因为1)1ln(lim 1=+-→+xx x pp x ,故前一积分当11<-p 即2<p 时收敛,当2≥p 时发散.而对后一积分,若1>p ,则00>∃ε,使得10>-εp ,且0)1ln(lim 0=++∞→εxx x ,故当x 充分大时,001)1ln(1)1ln(εεε--<+=+p p p x x x x x x ,由比较判别法,积分收敛.当1≤p 时,x x x p1)1ln(≥+(1-≥e x 时),所以这时积分发散. 因此,当21<<p 时,原积分收敛,否则发散. (5)⎰⎰⎰+∞+∞+=2211ln ln ln xx dxx x dx x x dx q p q p q p , 对于前者,因为0ln 1)1(lim 211=-+→xx x qp x ,故总是收敛的; 对于后者,1>p 或1=p 而1>q 时收敛,其他发散.故⎰+∞1ln x x dxq p 当1>p 或1=p 而1>q 时收敛,对于其他情况均发散.(6)⎰⎰⎰+∞+∞+++=+1100qp q p q p x x dx x x dx x x dx , 若q p =,则前者要求1<=q p 收敛,后者要求1>=q p 收敛,故这时积分发散.由q p ,的对称性,只需考虑q p >的情况.对于前者由)1(11+=+-qp q q p x x x x ,故当1<q 时收敛,1≥q 时发散.而对于后者,由于)1(11p q p q p x x x x -+=+,故当1>p 时收敛,1≤p 时发散.故⎰+∞+0qp xx dx当1>p 且1<q 或1<p 且1>q 时收敛,其他情况下均发散. (7)⎰⎰⎰--+--=--∞+2321322103232)2()1()2()1()2()1(x x x dx x x x dx x x x dx⎰⎰+∞--+--+33232332)2()1()2()1(x x x dx x x x dx由于332321)2()1(lim =--+→x x x xx , 1)2()1()1(lim32321=---→x x x x x ,33231221)2()1(2lim=---→x x x x x , 1)2()1(1lim 3234=--+∞→x x x xx ,以上四个积分均收敛,故原积分收敛.(8)令t x =-,则-∞=x 时,+∞=t ,当0=x 时,0=t 仍记t 为x .⎰⎰⎰⎰⎰+∞--+∞-∞+-∞-+==-=11ln ln ln ln ln xdx e xdx e xdx e xdx e dx x e x xxxx.由于当x 充分大时,21ln xx ex≤-,而⎰+∞121dx x 收敛,故⎰+∞-1ln xdx e x收敛,又0ln lim 0=-→+x e x x x ,故⎰-1ln xdx e x 亦收敛,所以⎰⎰+∞-∞-=00ln ln xdx e dx x e x x 收敛.4.讨论下列积分的收敛性与绝对收敛性: (1)⎰+∞2sin dx x ;(2)⎰∞+0sin dx x x q p,其中0>p ; (3))0(1sin 0≥+⎰∞+q dx xxx qp ; (4)⎰∞++0)1sin(dx xx x n . 解 (1)由于0sin lim 0=+→xx x ,所以0=x 不是瑕点,由Dirichlet 判别法,无穷积分⎰+∞sin dx xx 收敛,因此,⎰⎰⎰⎰+∞+∞→+∞→+∞→===00002sin 21sin lim 212sin limsin lim2dt ttdt t t t dtt dx x A A A A AA所以,⎰+∞2sin dx x 收敛.但xx xxx xx 22cos 21sin sin 2-=≥,由于⎰+∞121dx x发散,同样用Dirichlet 判别法知⎰+∞122cos dx xx 收敛,故⎰+∞-1)22cos 21(dx xx x发散,由比较判别法知⎰∞+1sin dx xx 发散,因而⎰∞+0sin dx xx 发散,但⎰⎰⎰+∞→+∞→+∞→==A A AA AA dt tt dt t tdx x 002sin lim 212sin limsin lim不存在,故⎰+∞2sin dx x 发散,因而⎰+∞2sin xdx 条件收敛.(2)⎰⎰⎰∞+∞++=1100sin sin sin dx xx dx x x dx x x q pq p q p,先考虑⎰10sin dx x x q p ,由于pp x x ~sin )0(+→x ,所以q p x x sin 与p q x-1是同阶变量)0(+→x ,从而当1<-p q 时,即1+<p q 时该积分收敛,1+≥p q 时积分发散.且由于0sin ≥qpxx ,故是绝对收敛的. 再看⎰⎰⎰∞+-+∞+-∞+==1111111sin 11sin sin dt xtp dt t p x t x t dx x x pq p p q pqp ,故当011>-+p q 时,即1>+p q 时积分收敛,否则发散.且当1>q 时绝对收敛,11≤<-q p 条件收敛.所以当p q p +<<-11时,积分收敛,否则发散. 当p q +<<11时绝对收敛,11≤<-q p 时条件收敛.(3)⎰⎰⎰∞+∞++++=+11001sin 1sin 1sin dx xx x dx x x x dx x xx q pq p q p , 先考虑积分⎰+11sin dx x x x q p ,由于111sin lim 1sin lim 010=+=+++→--→q x q p p x xx x x x x x ,所以积分⎰+11sin dx x xx qp 仅当11<--p 即2->p 时收敛,且是绝对收敛的,而当2-≤p 时发散.再考虑积分⎰∞++11sin dx x x x qp ,若q p ≥,则1>∀A ,必存在正整数N ,使A N >+42ππ,且当42ππ+≥N x 时,恒有311>+q p x x .于是对42ππ+='N A ,22ππ+=''N A ,有 62sin 311sin =>+⎰⎰''''''A A A A qp xdx dx x x x ,由Canchy 收敛原理,积分⎰∞++11sin dx x xx qp 发散.若1-<q p ,取0>ε,使1-<+q p ε,即1>--εp q ,由于0sin 1lim sin 1lim =+=++∞→--+∞→εεxxx x x x x xq q x q p p q x ,所以,积分⎰∞++11sin dx x xx qp 绝对收敛.现设q p q <≤-1.先证⎰∞++11sin dx x x x qp 发散.事实上,此时,可取10>A ,使当A x ≥0时,3111>++qp xx ,故有 +∞=≥+=+⎰⎰⎰∞+∞++∞+00sin 31sin 11sin 1A A q p A qp dx x xdx x x xx dx x x x , 从而⎰∞++11sin dx xx x qp 发散.再证⎰∞++11sin dx x xx qp 收敛.若0=q ,则01<≤-p 此时积分⎰⎰∞+∞+=+11sin 211sin xdx x dx xx x pq p 收敛;若0>q ,由于[]0)1()()1(21<+--='+-q qp q p x x p q p x x x (当x 充分大时),故当x 充分大时,函数qpxx +1单调递减趋于0,而2cos 1cos sin 1≤-=⎰A xdx A有界,故积分⎰∞++11sin dx x xx qp 收敛.于是,得到⎰∞++01sin dx xxx qp 当2->p 且1+>p q 时绝对收敛;当2->p ,1+<<p q p 时条件收敛,其他情况发散.(4)当0≤n 时,积分是发散的当0>n 时,先考虑积分⎰∞++a n dx xx x )1sin( ()1>a .由于 ⎰⎰∞+∞+-+-=+a n a n dx xx x x x dx xx x )11()1sin()11()1sin(22,。
数值分析简明教程 - 课后答案
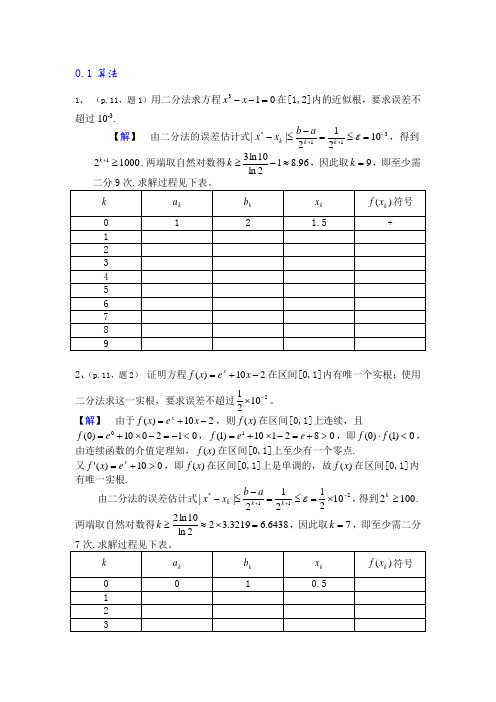
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数值分析简明教程第二版(王超能)习题答案24页全解word版[1]
![数值分析简明教程第二版(王超能)习题答案24页全解word版[1]](https://img.taocdn.com/s3/m/b6157a37168884868762d65e.png)
数值分析简明教程第二版(王超能)习题答案24页全解0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数学分析简明教程第二版第二篇课后答案

第二章 函数§1 函数概念1.证明下列不等式: (1) y x y x -≥-;(2) n n x x x x x x +++≤+++ 2121;(3) )(2121n n x x x x x x x x +++-≥++++ . 证明(1)由 y y x y y x x +-≤+-=)(,得到y x y x -≤-,在该式中用x 与y 互换,得到 x y x y -≤-,即y x y x --≥-,由此即得,y x y x -≥-.(2)当2,1=n 时,不等式分别为212111,x x x x x x +≤+≤,显然成立. 假设当k n =时,不等式成立,即 k k x x x x x x +++≤+++ 2121,则当1+=k n 时,有121121121121121)()(+++++++++=++++≤++++≤++++=++++k k k k k k k k k k x x x x x x x x x x x x x x x x x x x x有数学归纳法原理,原不等式成立.(3)n n n x x x x x x x x x x x x +++-≥++++=++++ 212121)( )(21n x x x x +++-≥ . 2.求证bb aa ba b a +++≤+++111.证明 由不等式 b a b a +≤+,两边加上)(b a b a ++后分别提取公因式得,)1()()1(b a b a b a b a +++≤+++,即bb aa ba b ba a ba b a ba b a +++≤+++++=+++≤+++111111.3.求证22),max(ba b a b a -++=; 22),min(ba b a b a --+=. 证明 若b a ≥,则由于b a b a -=-,故有22),max(b a b a a b a -++==,22),min(b a b a b b a --+==, 若b a <,则由于)(b a b a --=-,故亦有22),max(b a b a b b a -++==,22),min(ba b a a b a --+==, 因此两等式均成立.4.已知三角形的两条边分别为a 和b ,它们之间的夹角为θ,试求此三角形的面积)(θs ,并求其定义域.解 θθsin 21)(ab s =,定义域为开区间),0(π. 5.在半径为r 的球内嵌入一内接圆柱,试将圆柱的体积表为其高的函数,并求此函数的定义域.解 设内接圆柱高为x ,则地面半径为422x r r -=',因而体积)4(222x r x x r V -='=ππ,定义域为开区间)2,0(r .6.某公共汽车路线全长为km 20,票价规定如下:乘坐km 5以下(包括km 5)者收费1元;超过km 5但在km 15以下(包括km 15)者收费2元;其余收费2元5角. 试将票价表为路程的函数,并作出函数的图形.解 设路程为x ,票价为y ,则⎪⎩⎪⎨⎧≤<≤<≤<=.2015,5.2,155,2,50,1x x x y函数图形见右图.7.一脉冲发生器产生一个三角波.若记它随时间t 的变化规律为)(t f ,且三个角分别有对应关系0)0(=f ,20)10(=f ,0)20(=f ,求)200()(≤≤t t f ,并作出函数的图形.解 ⎩⎨⎧≤<-≤≤=.2010,240,100,2)(t t t t t f函数图形如右图所示.8.判别下列函数的奇偶性:(1)12)(24-+=x x x f ; (2)x x x f sin )(+=; (3)22)(x e x x f -=;(4))1lg()(2x x x f ++=.解(1)定义域为),(∞+-∞,由于),(∞+-∞∈∀x ,有),(∞+-∞∈-x ,且有)(121)(2)()(2424x f x x x x x f =-+=--+-=-,即得12)(24-+=x x x f 是偶函数. (2)定义域为),(∞+-∞,由于),(∞+-∞∈∀x ,有),(∞+-∞∈-x ,且有)()sin (sin )sin()()(x f x x x x x x x f -=+-=--=-+-=-,因此,x x x f sin )(+=是奇函数.(3)定义域为),(∞+-∞,由于),(∞+-∞∈∀x ,有),(∞+-∞∈-x ,且有)()()(222)(2x f e x e x x f x x ==-=----,即22)(x e x x f -=是偶函数.(4)定义域为),(∞+-∞,由于),(∞+-∞∈∀x ,有),(∞+-∞∈-x ,且有,)()1lg(11lg)1lg())(1lg()(2222x f x x x x x x x x x f -=++-=++=++-=-++-=-因此,)1lg()(2x x x f ++=是奇函数.9.判别下列函数是否是周期函数,若是,试求其周期: (1)2cos )(x x f =; (2)3sin 22cos )(x x x f +=; (3)x x f 4cos )(π=;(4)x x f tan )(=.解(1)不是.若为周期函数,设周期为T ,则R x ∈∀,有)()(x f T x f =+,即22cos )cos(x T x =+,移项并使用三角公式化简得,0)2sin()2sin(222=+++T Tx T Tx x ,由R x ∈的任意性知道这是不可能的,故2cos )(x x f =不是周期函数.(2)是.周期为ππ4212=和ππ6312=的最小公倍数π12. (3)是.周期是842=ππ.(4)定义域是使0tan ≥x 的一切x 的取值,即},2{)(Z k k x k x f D ∈+<≤=πππ,由于)(f D x ∈∀,必有)(f D x ∈+π,且)(tan )tan()(x f x x x f ==+=+ππ,因此x x f tan )(=是周期函数,周期为π.10.证明21)(xxx f +=在),(∞+-∞有界. 证明 实际上,),(∞+-∞∈∀x ,都有21112111)(2222=++⋅≤+=+=xx x x x x x f , 由定义,21)(xxx f +=在),(∞+-∞有界. 11.用肯定语气叙述函数无界,并证明21)(x x f =在)1,0(无界. 解 叙述:若X x M M ∈∃>∀,0,使得M x f M >)(,则称函数)(x f 在X 无界.0>∀M ,要使M x x f >=21)(,只须Mx 1<,取)1,0(11∈+=M x M ,则有M M x x f MM >+==11)(2,所以21)(x x f =在)1,0(无界. 12.试证两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,一个奇函数和一个偶函数的乘积是奇函数.证明 设)(,)(x g x f 是定义于X 偶函数,)(,)(x x h ϕ是定义于X 奇函数.则由于以下事实)()()()(x g x f x g x f =--,)()()]()][([)()(x x h x x h x x h ϕϕϕ=--=--, )()()]()[()()(x h x f x h x f x h x f -=-=--,知两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,一个奇函数和一个偶函数的乘积是奇函数.13.设)(x f 为定义在),(∞+-∞内的任何函数,证明)(x f 可分解成奇函数和偶函数之和.证明 由于)(x f 的定义域为),(∞+-∞,故)(,),(x f x -∞+-∞∈∀有意义. 令2)()()(x f x f x g -+=,2)()()(x f x f x h --=,则)(x g 是偶函数,)(x h 是奇函数,且有)()()(x h x g x f +=.14.用肯定语气叙述:在),(∞+-∞上 (1) )(x f 不是奇函数; (2) )(x f 不是单调上升函数; (3) )(x f 无零点; (4) )(x f 无上界.解 (1)),(0∞+-∞∈∃x ,使得)()(00x f x f -≠-,则)(x f 在),(∞+-∞不是奇函数;(2)),(,21∞+-∞∈∃x x ,虽然21x x <,但)()(21x f x f >,则)(x f 在),(∞+-∞不是单调上升函数;(3)),(∞+-∞∈∀x ,均有0)(≠x f ,则)(x f 在),(∞+-∞无零点;(4)),(,),(∞+-∞∈∃∞+-∞∈∀b x b ,使得b x f b >)(,则)(x f 在),(∞+-∞无上界.§2 复合函数与反函数1.设xxx f +-=11)(,求证x x f f =))((. 证明 ()x f 定义域为1-≠x 的一切实数,因此1-≠∀x ,有()()()()x xx x x xx x x x x x f x f x f f =+-++++-+=+-++--=+-=11111111111111.2.求下列函数的反函数及其定义域: (1) +∞<<⎪⎭⎫⎝⎛+=x x x y 1,121; (2) ()+∞<<∞--=-x e e y x x,21; (3) ⎪⎩⎪⎨⎧+∞<<≤≤<<∞-=.x x x x x y x 4,2,41,,1,2解(1)变形为0122=+-yx x ,解得12-+=y y x ,由于()+∞∈∀=⋅⋅≥⎪⎭⎫ ⎝⎛+=,1,11221121x xx x x y 成立,因此函数⎪⎭⎫ ⎝⎛+=x x y 121,+∞<<x 1的反函数为()∞+∈-+=,1,12x x x y .(2)变形得,0122=--xxye e,解出1244222++=++=y y y y e x,即()1ln 2++=y y x ,因此原来函数的反函数为()∞+∞-∈++=,,)1ln(2x x x y .(3)当1<<∞-x 时,1,<<∞-=y y x ,当41≤≤x 时,161,≤≤=y y x ,而当+∞<<x 4时,16,log 2>=y y x .所以反函数为⎪⎩⎪⎨⎧+∞<<≤≤<<∞-=.x x x x x x y 16,log ,161,,1,2定义域为()+∞∞-,.3.设()x f ,()x g 为实轴上的单调函数,求证))((x g f 也是实轴上的单调函数. 证明 设()x f ,()x g 为实轴上的单调增函数,即()2,1,,=+∞∞-∈∀i x i ,且,21x x < 有()()()()2121,x g x g x f x f ≤≤,因此))(())((21x g f x g f ≤,即))((x g f 也是单调增函数.同理可证:当()x f ,()x g 为实轴上的单调减函数时,))((x g f 也是单调增函数;当()x f 为增函数,而()x g 为减函数或()x f 为减函数,而()x g 为增函数时,))((x g f 均为减函数.因此,()x f ,()x g 为实轴上的单调函数时,))((x g f 也是实轴上的单调函数. 4.设()⎩⎨⎧>≤--=.0,,0,1x x x x x f ()⎩⎨⎧>-≤=.0,,0,2x x x x x g , 求复合函数))((x g f ,))((x f g .解 有复合函数的定义,立即可得⎩⎨⎧>-≤--=,0,1,0,1))((2x x x x x g f ()⎪⎩⎪⎨⎧>-≤≤----<<∞-+-=.0,,01,1,1,1))((22x x x x x x x f g5.设21)(xx x f +=,求))((x f f f n次.解 2222221111)(1)())((xx x xx xx f x f x f f +=+++=+=,归纳法假设21))((kx xx f f f k +=次, 则有222)1(111)1()))((())((kx x kx xkx xf x f f f f x f f f k k +++=+==+ 次次2)1(1xk x ++=,依归纳法原理,知21))((nxx x f f f n +=次.6.设x x x f --+=11)(,试求))((x f f f n次.解 ⎪⎩⎪⎨⎧>≤≤--<-=1,2,11,2,1,2)(x x x x x f , ⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤≤--<-=21,2,2121,4,21,2))((x x x x x f f ,归纳法假设 ⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤≤-<-=----111121,2,2121,2,21,2))((k k k kk k x x x x x f f f 次,则当1+=k n 时,有⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤≤-<-==++,21,2,2121,2,21,2)))((())((1)1(kk k k k k k x x x x x f f f f x f f f 次次 所以,⎪⎪⎪⎩⎪⎪⎪⎨⎧>≤≤-<-=----.次111121,2,2121,2,21,2))((n n n n n n x x x x x f f f 7.设x x f -=11)(,求))((x f f ,)))(((x f f f ,))(1(x f f . 解 x x f -=11)(定义域1≠x 的一切实数,)(11))((x f x f f -=要求1)(≠x f 且1≠x ,因此xxxx f x f f -=--=-=11111)(11))((,0≠x 且1≠x ; ))((11)))(((x f f x f f f -=要求1))((≠x f f 且0≠x ,1≠x ,因此x xx x f f x f f f =--=-=111))((11)))(((,21≠x ,0≠x 且1≠x ; )(111))(1(x f x f f -=要求1≠x 且1)(1≠x f ,因此 xx x f x f f 1)1(11)(111))(1(=--=-=,0≠x 且1≠x .§3 初等函数1.对下列函数分别讨论函数的定义域和值域,奇偶性,周期性,有界性,并作出函数的图形:(1) x y =;(2) ][x x y -=;(3) x y tan =; (4) )2(x x y -=;(5) x y 2sin =;(6) x x y cos sin +=.解(1)定义域),(∞+-∞=D ,值域),0[)(∞+=X f ,是偶函数,无界非周期函数; (2)定义域),(∞+-∞=D ,值域)1,0[)(=X f ,既非奇函数也非偶函数,是周期为1的有界周期函数;(1)题图 (2)题图(3)定义域),(∞+-∞=D ,值域),()(∞+-∞=X f ,是偶函数,无界非周期函数; (4)定义域]2,0[=D ,值域]1,0[)(=X f ,既非奇函数也非偶函数,是有界非周期函数;(3)题图 (4)题图(5)定义域),(∞+-∞=D ,值域]1,0[)(=X f ,是偶函数,是周期为π的有界周期函数;(6)定义域),(∞+-∞=D ,是偶函数.由于x x x x x y 2sin 1cos sin 2cos sin 222+=++=,所以212≤≤y ,并注意到0≥y ,得到函数的值域]2,1[)(=X f ,因而是有界函数.因为)(cos sin sin cos )2cos()2sin()2(x y x x x x x x x y =+=-+=+++=+πππ,所以函数x x y cos sin +=是周期为2π的周期函数.2.若已知函数)(x f y =的图形,作函数)(1x f y =,)(2x f y -=,)(3x f y --=的图形,并说明321,,y y y 的图形与y 的图形的关系.解 由于⎩⎨⎧<-≥==0)(,)(,0)(,)()(1x f x f x f x f x f y ,故其图形是将函数)(x f y =的图形在x轴上方部分的不动,在x 轴下方的部分绕x 轴旋转180后即得;)(2x f y -=的图形是将函数)(x f y =的图形绕y 轴旋转 180后得到的;)(3x f y --=的图形是将函数)(x f y =的图形在坐标平面内绕坐标原点旋转 180后得到的.3.若已知函数)(x f ,)(x g 的图形,试作函数])()()()([21x g x f x g x f y -±+=的图形,并说明y 的图形与)(x f 、)(x g 图形的关系.解 由于)}(),(max{)()(,)(,)()(,)(])()()()([21x g x f x g x f x g x g x f x f x g x f x g x f =⎩⎨⎧<≥=-++,)}(),(min{)()(,)(,)()(,)(])()()()([21x g x f x g x f x f x g x f x g x g x f x g x f =⎩⎨⎧<≥=--+, 因而极易由函数)(x f ,)(x g 的图形作出两函数])()()()([21x g x f x g x f y -±+=的图形,也知其关系.4. 作出下列函数的图形:(1) x x y sin =;(2) xy 1sin=. 解 图形如下.(1)题图 (2)题图5.符号函数⎪⎩⎪⎨⎧<-=>==,0,1,0,0,0,1sgn x x x x y试分别作出x sgn ,)2sgn(x ,)2sgn(-x 的图形.解x sgn )2sgn(x)2sgn(-x6.作出下列函数的图形: (1) x y cos sgn =;(2) ⎥⎦⎤⎢⎣⎡-=22][x x y .解(1)(2)数学分析续论A 卷复习资料一. 计算题1. 求函数3311(,)f x y x y y x=+在点(0,0)处的二次极限与二重极限. 解: 333311(,)sinf x y x y x y y x ==,因此二重极限为0. 因为33011x x y y x →+与33011y x y y x→+均不存在,故二次极限均不存在。
数学分析简明教程答案(尹小玲 邓东皋)第一二章

5.在半径为r得瑟球内嵌入一内接圆柱,试将圆柱的体积表示为其高的函数,并求此函数 的定义域。
h2 解:设其高为h, 那么圆柱的底面半径为R r ; 于是圆柱体积 4 2 V R h
2
hr 2
4
h3
由于圆柱为球的内接圆柱,故有h (0, 2r ).
-2-
6.某公交车路线全长为20 Km, 票价规定如下:乘坐5 Km以下(包含5 Km)者收费1元;超过 5 Km但在15 Km以下(包含15Km)者收费2元;其余收费2元5角。试将票价表示成路线的 函数,并作出函数的图像。 解:设y为票价,x为路程,则有 1 y ( x) 2 2.5 它的函数图像如下: x (0,5] x (5,15] . x (15, 20]
画图板作图
7.一脉冲发生器产生一个三角波,若记它随时间t的变化规律为f (t ), 且三个角分别对应关 系f (0) 0, f (10) 20, f (20) 0, 求f (t )(0 t 20), 并作出函数的图形。 解:由题意可知所求函数为: 2t f (t ) 40 2t 其函数图像为:
2 2 2 2
(2). x1 x2 xn x1 x2 xn ; 证明:使用数学归纳法; i.对于x, y , 总有 x y xy, 于是有 x 2 x y y x 2 2 xy y 2 ; 整理后可得 x y x y ,即当n 2时所证成立。 ii.假设当n k时所证不等式也成立,即 x1 x2 xk x1 x2 xk . iii.当n k 1时,取y x1 x2 xk , 于是有: x1 x2 xk xk 1 y xk 1 y xk 1 x1 x2 xk xk 1 x1 x2 xk xk 1 即当n k 1时所证不等式也成立。 那么由数学归纳法可知题证成立。
数值分析简明教程第二版课后习题答案(供参考)

0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数学分析简明教程答案(尹小玲 邓东皋)

第九章 再论实数系§1 实数连续性的等价描述2211.{}({},{})1(1).1; sup 1,inf 0;(2)[2(2)]; sup ,inf ;1(3),1,(1,2,); sup ,inf 2;1(4)[1(1)]; n n n n n n n n n n k k n n n n x x x x x x nx n x x x k x k x x k n x n ++∞-∞=-===+-=+∞=-∞==+==+∞=+=+- 求数列的上下确界若无上下确界则称,是的上下确界: sup 3,inf 0;(5) sup 2,inf 1;12(6)cos ; sup 1,inf .132n n n n n n n n x x x x x n n x x x n π=====-===-+2.(),(1)sup{()}inf (); (2)inf{()}sup ().(1)sup{()},.,();.0,()..,();.x Dx Dx Dx Dx Df x D f x f x f x f x A f x i x D f x A ii x D f x A i x D f x A ii εεε∈∈∈∈∈-=--=-=-∀∈-≤∀>∃∈->-∀∈≥-∀>设在上定义求证:证明:设即有对有 对使得 于是有对有 对0,().inf (),inf (),sup{()}inf ()x Dx Dx Dx Dx D f x A A f x A f x f x f x ε∈∈∈∈∃∈<-+-==--=-使得 那么即因此有成立。
(2)inf{()},.,();.0,()..,();.0,().sup (),sup (),x Dx Dx DB f x i x D f x B ii x D f x B i x D f x B ii x D f x B B f x A f x εεεε∈∈∈=-∀∈-≥∀>∃∈-<+∀∈≤-∀>∃∈>---==-设即有对有 对使得 于是有对有 对使得 那么即因此有inf{()}sup ()x Dx Df x f x ∈∈-=- 成立。
数学分析简明教程答案

第二十一章曲线积分与曲面积分§1 第一型曲线积分与曲面积分1.对照定积分的基本性质写出第一型曲线积分和第一型曲面积分的类似性质。
解:第一型曲线积分的性质:1(线性性)设⎰L ds z y x f ),,(,⎰L ds z y x g ),,(存在,21,k k 是实常数,则[]ds z y x g k z y x f kL ⎰+),,(),,(21存在,且[]ds z y x g k z y x f k L⎰+),,(),,(21⎰⎰+=LLds z y x g kds z y x f k ),,(),,(21;2l ds L=⎰1,其中l 为曲线L 的长度;3(可加性)设L 由1L 与2L 衔接而成,且1L 与2L 只有一个公共点,则⎰Lds z y x f ),,(存在⇔⎰1),,(Lds z y x f 与⎰2),,(L ds z y x f 均存在,且=⎰Lds z y x f ),,(⎰1),,(L ds z y x f +⎰2),,(L ds z y x f ;4(单调性)若⎰L ds z y x f ),,(与⎰L ds z y x g ),,(均存在,且在L 上的每一点p 都有),()(p g p f ≤则⎰⎰≤L L ds p g ds p f )()(;5若⎰L ds p f )(存在,则⎰L ds p f )(亦存在,且≤⎰ds p f L)(⎰Ldsp f )(6(中值定理)设L 是光滑曲线,)(p f 在L 上连续,则存在L p ∈0,使得l p f ds p f L)()(0=⎰,l 是L 的长度;第一型曲面积分的性质: 设S 是光滑曲面,⎰⎰S ds p f )(,⎰⎰S ds p g )(均存在,则有1(线性性)设21,k k 是实常数,则[]⎰⎰+Sds p g k p f k)()(21存在, 且[]⎰⎰+Sds p g k p f k )()(21⎰⎰⎰⎰+=SSds p g k ds p f k )()(21;2s ds S=⎰1, 其中s 为S 的面积;3(可加性)若S 由1S ,2S 组成21S S S =,且1S ,2S 除边界外不相交,则⎰⎰Sds p f )(存在⇔⎰⎰1)(S ds p f 与⎰⎰2)(S ds p f 均存在,且⎰⎰Sds p f )(=⎰⎰1)(S ds p f +⎰⎰2)(S ds p f4 (单调性)若在S 上的的每一点p 均有),()(p g p f ≤则⎰⎰⎰⎰≤SSds p g ds p f )()(;5⎰⎰S ds p f )(也存在,且≤⎰⎰Sdsp f )(⎰⎰Sds p f )(;6 (中值定理)若)(p f 在S 上连续,则存在S p ∈0,使得使得s p f ds p f S⎰⎰=)()(0,其中s 为S 的面积。
《数值分析简明教程》(第二版)王能超课后习题答案

532 a= = 0.9726 547 b = 285 = 0.05 2 ( f , ϕ1 ) = 369321.5 ,解之得 5696 ,∴ y = 0.9726 + 0.05 x .
yn = yn −1 + hf ( xn −1 , yn −1 ) = yn −1 + h ⋅ ( axn −1 + b)
故 yn −1 = yn −2 + h ⋅ ( axn − 2 + b)
LL y1 = y0 + h ⋅ ( ax0 + b)
将上组式子左右累加,得
yn = y0 + ah( x0 + L + xn −2 + xn −1 ) + nhb = ah(0 + h + 2h L + ( n − 2) h + (n − 1) h) + nhb
第一章 题 12 给定节点 x0 = −1 , x1 = 1 , x2 = 3 , x3 = 4 ,试分别对下列函数导出拉格朗日插 值余项: (1) (1) (2) (2) 解 (1) f
(4)
f ( x) = 4 x3 − 3 x + 2 f ( x) = x 4 − 2 x3 ( x) = 0 ,
1.5
5 ≈ × 9
8 8 5 8 + × + × 2 2 3 9 4 + ( 0 + 1) 9 3 4+− + 1 4+ + 1 5 5 = 3.141068 .
数值分析简明教程第二版课后习题答案(供参考)
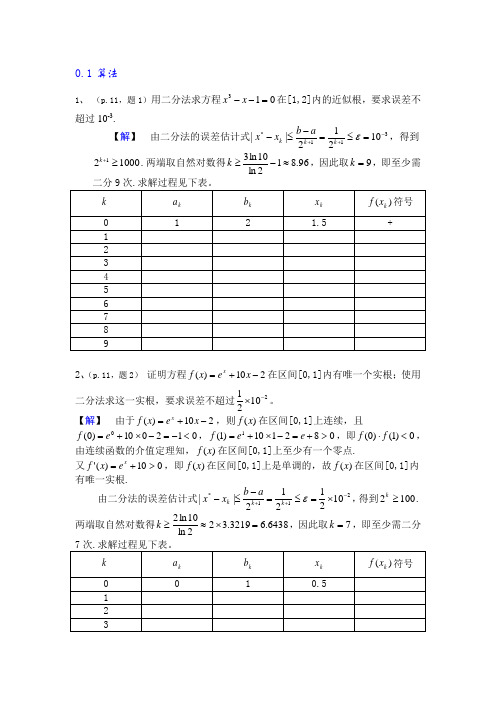
0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=-K x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=-K x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=-K x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数学分析简明教程答案(尹小玲 邓东皋)

即
un vn un vn .
n 1 n 1 n 1
D
4.设级数 un 各项是正的, 把级数的项经过组合而得到的新级数 U n ,即
n 1 n 1
U n 1 ukn 1 ukn 2 ukn1 , n 0,1, 2, , 其中k0 0, k0 k1 k2 kn kn 1 . 若级数 U n收敛,证明原来的级数也收敛。
(2)
n 1
1 4n 2 1
1 1 1 2 n 1 2n 1 2n 1
1 1 1 1 1 1 1 1 lim 1 2 n 3 3 5 5 7 2n 1 2n 1 1 1 1 lim 1 . 2 n 2n 1 2
n
于是可得 Sn 由于 r 1,因此有
r
n 1
n
r cos x r 2 . 1 r 2 2r cos x
2.讨论下列级数的敛散性: (1) n ; n 1 2n 1
lim
n 1 0, 故原级数发散。 n 2n 1 2 由于级数 lim cos
第十章 数项级数
§1 级数问题的提出
1.证明:若微分方程xy '' y ' xy 0有多项式解 y a0 a1 x a2 x 2 an x n ; 则必有ai 0, i 1, 2, , n. 证明:若y a0 a1 x a2 x 2 an x n 微分方程的一个解, 那么 y ' a1 2a2 x 3a3 x 2 nan x n 1 y '' 2a2 6a3 x n(n 1)an x n 2 ; 于是可得 xy '' 2a2 x 6a3 x 2 n(n 1)an x n 1 xy a0 x a1 x 2 a2 x 3 an x n 1. 因此可知 xy '' y ' xy a1 (4a2 a0 ) x (9a3 a1 ) x 2 (n 2 an an 2 ) x n 1 an x n 0 那么由多项式相等可知有 a1 0 2 n an an 2 0 a 0 n 递推可知有ai 0, i 1, 2, , n成立。 n 2.
数学分析简明教程解答(尹小玲 邓东皋)第一二章

ab
a b ab
1 a b 1 a b ab
由于
a b 2 ab
a (1 b ) b (1 a )
a
b
,因此
1 a b ab
(1 b )(1 a ) 1 a 1 b
a b a b ab a b 2 ab a b . 1 a b 1 a b ab 1 a b ab 1 a 1 b
函数,并作出函数的图像。
解:设y为票价,x为路程,则有
它的函数图像如下:
1 y(x) 2
2.5
x (0,5] x (5,15] . x (15, 20]
画图板作图
7.一脉冲发生器产生一个三角波,若记它随时间t的变化规律为f (t),且三个角分别对应关 系f (0) 0, f (10) 20, f (20) 0,求f (t)(0 t 20),并作出函数的图形。 解:由题意可知所求函数为:
2
22
ii.当a b时 a b a b a b a b b min(a,b);
22
22
当a b时 a b a b a b b a a min(a,b).
2
2
22
于是有 max(a,b) a b a b ,min(a,b) a b a b 成立。
解:设其高为h, 那么圆柱的底面半径为R r2 h2 ;于是圆柱体积 4
V R2h
hr2 h3 4
由于圆柱为球的内接圆柱,故有h (0, 2r).
-2-
6.某公交车路线全长为20Km, 票价规定如下:乘坐5Km以下(包含5Km)者收费1元;超过
5Km但在15Km以下(包含15Km)者收费2元;其余收费2元5角。试将票价表示成路线的
数学分析简明教程答案

第十章 数项级数§1 级数问题的提出1.证明:若微分方程0=+'+''xy y y x 有多项式解n n x a x a x a a y ++++= 2210,则必有),,2,1(0n i a i ==.证明 由多项式解nn x a x a x a a y ++++= 2210得1232132-++++='n n x na x a x a a y , 22432)1(1262--++++=''n n x a n n x a x a a y .从而 134232)1(1262--++++=''n n x a n n x a x a x a y x , 且 111232210+---++++++=n n n n n n x a x a x a x a x a x a xy .将上述结果代入微分方程0=+'+''xy y y x ,得342231201)16()9()4(x a a x a a x a a a ++++++0)(11122=++++++---n n n n n n n x a x a x a n a .比较系数得递推公式如下:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧===+=+=+=--.0,0,0,09,04,012231201n n n n a a a n a a a a a a由此解得0210=====n a a a a ,因而),,2,1,0(0n i a i ==.2.试确定系数 ,,,,10n a a a ,使n n nx a∑∞=0满足勒让德方程0)1(2)1(2=++'-''-y l l y x y x .解 设nn nx ay ∑∞==,则11-∞=∑='n n n xna y ,22)1(-∞=∑-=''n n nx an n y ,故∑∑∑∞=∞=-∞=----=--=''-2222222)1()1()1()1()1(n n n n n n n n n x a n n xa n n xa n n x y x ,∑∑∞=∞=--=-='-111222n n n n n n x na xna x y x ,∑∑∞=∞=+=+=+0)1()1()1(n n n n nn x a l l x a l l y l l .将上述结果代入勒让德方程0)1(2)1(2=++'-''-y l l y x y x ,得y l l y x y x )1(2)1(02++'-''-=∑∑∑∑∞=∞=∞=∞=-++----=01222)1(2)1()1(n n n n nn n nn n n n x a l l x na x a n n xa n n∑∑∑∑∞=∞=∞=∞=+++---++=0122)1(2)1()1)(2(n n n n nn n nn n nn x a l l x na x a n n x a n n .比较系数,得递推公式如下:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+++++-=+++--=++-=++-=++++-.,0)1)(2()1)((,0)1()))(1((,012)3)(2(,06)2)(1(,02)1(211423120n n n n a n n a n l n l na n a n l n l a a l l a a l l a a l l 由此解得⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧++++-+-+--=⨯⨯⨯++--=⨯+--=⨯+--=-++++-+--=⨯⨯++-=⨯+--=+-=+,)!12()2()4)(2)(1()32)(12()1(,2345)4)(2)(1)(3(45)4)(3(,23)2)(1(,)!2()12()3)(1()42)(22()1(,234)3)(1()2(34)3)(2(,2)1(112135130202402a k k l l l l k l k l a a l l l l a l l a a l l a a k k l l l l k l k l a a l l l l a l l a a l l a k k k k从而可以得到⎥⎦⎤⎢⎣⎡-+++-+--+=∑∞=1200)!2()12()1()42)(22()1(k k k x k k l l l k l k l a a y⎥⎦⎤⎢⎣⎡+++-+-+--++∑∞=+11211)!12()2()2)(1()32)(12()1(k k k x k k l l l k l k l a x a .其中10,a a 取任何常数.§2 数项级数的收敛性及其基本性质1.求下列级数的和: (1)∑∞=+-1)15)(45(1n n n ; (2)∑∞=-12141n n;(3)∑∞=---1112)1(n n n ; (4)∑∞=-1212n nn ; (5)1,sin 1<∑∞=r nx rn n;(6)1,cos 1<∑∞=r nx rn n.解(1)由于⎪⎭⎫⎝⎛+--=+-15145151)15)(45(1n n n n ,故)15)(45(11161611+-++⨯+⨯=n n S n ⎪⎭⎫ ⎝⎛+--++-+-=1514511116161151n n )(51151151∞→→⎪⎭⎫ ⎝⎛+-=n n , 所以级数的和51=S . (2)由于⎪⎭⎫⎝⎛+--=-121121211412n n n ,故)(21121121121121513131121∞→→⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛+--++-+-=n n n n S n .所以级数的和21=S . (3)322111212)1(11111=⎪⎭⎫ ⎝⎛--=⎪⎭⎫⎝⎛-=--∞=∞=--∑∑n n n n n .(4)12221222121111-=⎪⎭⎫ ⎝⎛-=-∑∑∑∑∞=∞=∞=∞=n nn nn n n n nn n ,因此欲求原级数的和,只需计算级数∑∞=122n n n 即可.对级数∑∞=122n n n ,设其部分和n n n S 2226242232++++= ,则 14322222226242221++-++++=n n n nn S , 故1432222222222212121+-+++++=-=n n n n n n S S S 1432222121212121+-⎪⎭⎫ ⎝⎛+++++=n n n112222112112121+---⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+=n n n . 从而221lim =∞→n n S ,即4lim =∞→n n S ,因此原级数31412221211=-=-=-∑∑∞=∞=n n n n n n . (5)由于级数的部分和kx rS nk kn sin 1∑==,故[]x k x k r x kx rxS r nk k nk k n )1sin()1sin(cos sin 2cos 21111-++==∑∑=+=+x k r x k rnk k nk k )1sin()1sin(1111-++=∑∑=+=+kx rrkx r n k kn k k sin sin 1212∑∑-=+=+=)sin ()sin )1sin((21nx r S r x r x n r S n n n n -+-++=+,从中解得xr r xn r nx r x r S n n n cos 21)1sin(sin sin 212-++-+=++.又由于当∞→n 时,0)1sin(,0sin 1122→≤+→≤++++n n n n r x n r r nx r ,故xr r xr S n n cos 21sin lim 2-+=∞→, 因此xr r xr nx r n n cos 21sin sin 21-+=∑∞=.(6)级数的部分和kx rS nk kn cos 1∑==,从而[]x k x k r x kx rxS r nk k nk k n )1cos()1cos(cos cos 2cos 21111-++==∑∑=+=+x k r x k rnk k nk k )1cos()1cos(1111-++=∑∑=+=+kx rrkx r n k kn k k cos cos 1212∑∑-=+=+=)cos 1()cos )1cos((21nx r S r x r x n r S n n n n -++-++=+,从中解得x r r r x r x r r r x n r nx r x r S n n n n n cos 21cos cos 21)1cos(cos cos lim lim 222212-+-=-+-+-+=++∞→∞→. 因此x r r r x r nx r n ncos 21cos cos 221-+-=∑∞=. 2.讨论下列级数的敛散性: (1)∑∞=-112n n n; (2)∑∞=⎪⎭⎫ ⎝⎛+13121n nn; (3)∑∞=+112cosn n π;(4)∑∞=+-1)13)(23(1n n n ; (5)∑∞=+++1)1()1(1n n n n n .解(1)由于通项)(02112∞→≠→-n n n ,故原级数发散. (2)由于∑∑∞=∞=⎪⎭⎫ ⎝⎛=112121n nn n ,∑∑∞=∞=⎪⎭⎫⎝⎛=113131n nn n 均收敛,故原级数收敛.(3)由于通项)(010cos 12cos ∞→≠=→+n n π,故原级数发散.(4)由于⎪⎭⎫⎝⎛+--=+-13123131)13)(23(1n n n n ,从而部分和)13)(23(1741411+-++⨯+⨯=n n S n ⎪⎭⎫ ⎝⎛+--++-+-=131231714141131n n)(31131131∞→→⎪⎭⎫ ⎝⎛+-=n n , 因而原级数收敛.(5)由于⎪⎪⎭⎫⎝⎛+-=+-+=+++11111)1()1(1n n n n nn n n n n ,从而∞→n 时, 111111131212111→+-=+-++-+-=n n n S n ,故原级数收敛.3.证明定理10.2.定理10.2 若级数∑∞=1n n u ,∑∞=1n nv收敛,则级数)(1n n nv u±∑∞=也收敛,且∑∑∑∞=∞=∞=±=±111)(n n n n n n nv u v u.证明 设∑∑==='=nk k nnk kn v S uS 11,,则由已知条件知,存在有限数s s ',,使得 s v S s u S nk k n nn nk k n n n '=='==∑∑=∞→∞→=∞→∞→11lim lim ,lim lim , 设级数)(1n n nv u±∑∞=的部分和数列为n μ,则)()(111∞→'±→'±=±=±=∑∑∑===n s s S S v u v u nn nk k nk k nk k k n μ, 所以)(1n n nv u±∑∞=也收敛,且∑∑∑∞=∞=∞=±=±111)(n n n n n n n v u v u .4.设级数∑∞=1n nu各项是正的,把级数的项经过组合而得到新级数∑∞=1n nU,即,2,1,0,1211=+++=++++n u u u U n n n k k k n ,其中 <<<<<<=+12100,0n n k k k k k k ,若∑∞=1n nU收敛,证明原来的级数也收敛.证明 设∑∑====nk k n nk kn U uS 11,σ,则n nk k n U U U U +++==∑= 211σ)()(21112121k k k k u u u u u u +++++++=++ n n n n k k k k S u u u =+++++++--)(2111 .由于∑∞=1n nU收敛,故}{n σ有界,即{n k S }有界,即存在0>M ,使得N n ∈∀,都有M S n k ≤.又由于∑∞=1n nu是正项级数,故M S S n k n ≤≤,而且{n S }单调上升,由单调有界原理可知,原级数∑∞=1n nu收敛.§3 正项级数1.判别下列级数的收敛性: (1)∑∞=+121n nn ;(2)∑∞=--1122)12(1n n n ; (3)∑∞=--112n n nn ; (4)∑∞=12sinn nπ;(5))1(111>+∑∞=a a n n; (6)∑∞=11n nnn;(7)nn n ∑∞=⎪⎭⎫⎝⎛+1121;(8)[]∑∞=+1)1ln(1n nn ;(9)∑∞=-+12)1(2n nn; (10)∑∞=13sin2n nn π;(11)∑∞=-+15sin ))1(3(n nn n π;(12)∑∞=11!2sin n nn ; (13)∑∞=⎪⎭⎫ ⎝⎛-11cos 1n n n ; (14)∑∞=11cos n n ; (15)∑∞=⎪⎪⎭⎫ ⎝⎛+111ln 1n n n ; (16)∑∞=+12)1ln(n n n ; (17)∑∞=11arcsin 1sin n n n ; (18)∑∞=12arctan n nn π;(19)∑∞=⎪⎪⎭⎫ ⎝⎛-+1111n n ; (20)∑∞=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫⎝⎛+122111n n .解(1)∑∞=+121n nn .由于111lim2=+∞→nnn n ,而∑∞=11n n 发散,所以级数∑∞=+121n nn 发散.(2)∑∞=--1122)12(1n n n .对任意正整数n ,都成立关系式nn n n 2121222212)12(1≤≤---, 而级数∑∞=1222n n 收敛,由比较判别法知,原级数收敛. (3)∑∞=--112n n n n .由于02112lim ≠=--∞→n n n n ,所以级数∑∞=--112n n nn 发散.(4)∑∞=12sin n nπ.由于ππ=∞→n n n 212sinlim,而∑∞=121n n 收敛,故∑∞=12sin n nπ收敛. (5)∑∞=+111n n a .由于1>a ,故n nn a a a ⎪⎭⎫ ⎝⎛=<+1111,而∑∞=⎪⎭⎫⎝⎛11n na 收敛,由比较判别法知,级数∑∞=+111n na收敛. (6)∑∞=11n n n n .由于11lim 11lim ==∞→∞→n n n n n nn n ,而∑∞=11n n 发散,故∑∞=11n n nn 发散.(7)nn n ∑∞=⎪⎭⎫ ⎝⎛+1121.由于10121lim 121lim <=+=⎪⎭⎫ ⎝⎛+∞→∞→n n n n n n ,故级数nn n ∑∞=⎪⎭⎫⎝⎛+1121收敛.(8)[]∑∞=+1)1ln(1n nn .由于10)1ln(1lim )1ln(1lim <=+=⎪⎪⎭⎫ ⎝⎛+∞→∞→n n n n nn ,故原级数收敛.(9)∑∞=-+12)1(2n nn. 方法1因为∑∑∑∞=∞=-∞=-+=-+11112)1(212)1(2n n n n n n nn ,而∑∞=-1121n n 和∑∞=-12)1(n n n 均收敛,故∑∞=-+12)1(2n nn收敛. 方法2 由于n n n 232)1(2≤-+对一切n 都成立,而∑∞=123n n 收敛,故∑∞=-+12)1(2n nn 收敛.(10)∑∞=13sin2n nnπ.由于πππ=⋅=⎪⎭⎫ ⎝⎛∞→∞→nn n n n nn n n 3123sin2lim 323sin2lim,而∑∞=⎪⎭⎫ ⎝⎛132n n收敛,故原级数收敛.(11)∑∞=-+15sin))1(3(n nnn π.由于4)1(3≤-+n,因此,若∑∞=15sin 4n nn π收敛,则原级数收敛.考虑级数∑∞=15sin4n nnπ,由于πππ=⋅=⎪⎭⎫ ⎝⎛∞→∞→nn nn n n nn n 5145sin4lim 545sin4lim,且∑∞=⎪⎭⎫ ⎝⎛154n n收敛,故∑∞=15sin4n nn π收敛,因而原级数收敛.(12)∑∞=11!2sin n nn .由于!1!2sin n n n ≤,而∑∞=1!1n n 收敛,因而原级数收敛.(13)∑∞=⎪⎭⎫ ⎝⎛-11cos 1n n n .由于21121sin 2lim 11cos 1lim22==⎪⎭⎫ ⎝⎛-∞→∞→n n n n n n n ,而∑∞=11n n发散,因而原级数发散.(14)∑∞=11cos n n .由于011cos lim ≠=∞→n n ,由级数收敛的必要条件知,原级数发散. (15)∑∞=⎪⎪⎭⎫ ⎝⎛+111ln 1n n n .由于1111ln lim 111ln 1lim 23=⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛+∞→∞→nn n n n n n ,而∑∞=1231n n 收敛,故原级数收敛.(16)∑∞=+12)1ln(n n n .由于0)1ln(lim 1)1ln(1lim 232=+=+∞→∞→n n n n n n n ,而级数∑∞=1231n n 收敛,故原级数收敛.(17)∑∞=11arcsin 1sin n n n .由于111arcsin 1sin lim2=∞→n n n n ,而级数∑∞=121n n收敛,故原级数收敛.(18)∑∞=12arctan n nn π.由于极限ππ=∞→n n n n n 22arctanlim,而对于级数∑∞=12n nn ,根据1212lim <=∞→nn n n ,故由根式判别法知,级数∑∞=12n nn 收敛,因而原级数收敛. (19)∑∞=⎪⎪⎭⎫ ⎝⎛-+1111n n .对通项进行分子有理化可得 )1(21)1(2111211111111111+>+=+>++=++=-+n n n nn n n n n n n , 由于∑∞=+1)1(21n n 发散,故原级数发散.(20)∑∞=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛+122111n n .由于422212111n n n +=-⎪⎭⎫⎝⎛+,而级数∑∑∞=∞=14121,2n n n n 均收敛,因而原级数收敛.2.判别下列级数的敛散性:(1)∑∞=1!n nn n ;(2)∑∞=12ln n nnn ; (3)∑∞=12!n n nn n ;(4)∑∞=13!n n nnn ;(5)∑∞=1!n n nne n ;(6)∑∞=⎪⎭⎫ ⎝⎛+121n nn n n ;(7)212312nn n n ∑∞=⎪⎭⎫ ⎝⎛-+; (8)∑∞=++1212)3(n n nn n n ;(9))0()1()1)(1(12≥+++∑∞=x x x x x n nn; (10)+⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅+⋅⋅+107419753741753415313. 解(1)∑∞=1!n n n n .由于11lim !)!1()1(lim 1>=⎪⎭⎫⎝⎛+=++∞→+∞→e n n n n n n n n n n n ,所以∑∞=1!n n n n 发散. (2)∑∞=12ln n nnn .由于 121ln 1ln 1lim 21lim ln )1ln(21lim 2ln 2)1ln()1(lim 1<=⎪⎪⎪⎪⎭⎫ ⎝⎛++⋅+=⎪⎭⎫ ⎝⎛++=++∞→∞→∞→+∞→n n n n n n n nn n n n n n n n n n n , 根据达朗贝尔判别法知,原级数收敛.(3)∑∞=12!n n n n n .由于121lim 22!)1(2)!1(lim 11<=⎪⎭⎫⎝⎛+=++∞→++∞→e n n n n n n n n n n n n n ,故∑∞=12!n n n n n 收敛. (4)∑∞=13!n n n n n .由于131lim 33!)1(3)!1(lim 11>=⎪⎭⎫⎝⎛+=++∞→++∞→e n n n n n n n n nn n n n ,故∑∞=13!n n n n n 发散. (5)∑∞=1!n n nne n .这个级数不能用达朗贝尔判别法和柯西判别法判别,也不能用拉阿比判别法判别,但由斯特林公式可知)10(2!12<<⎪⎭⎫⎝⎛=θπθnn e e n n n ,因而πππθθn e n ne e e n n ne n n n n n nn n222!1212>=⎪⎭⎫⎝⎛=,通项的极限不为0,由级数收敛的必要条件知原级数∑∞=1!n n nne n 发散.(6)∑∞=⎪⎭⎫ ⎝⎛+121n n n n n .因为101)(lim 1lim 22<=+=⎪⎭⎫ ⎝⎛+∞→∞→n n n n n n n n n n n ,故∑∞=⎪⎭⎫ ⎝⎛+121n n n n n 收敛. (7)∑∞=⎪⎭⎫⎝⎛-+122312n n n n .由于1322312lim2312lim 2<=-+=⎪⎭⎫⎝⎛-+∞→∞→n n n n n n n n ,由柯西判别法知,原级数收敛.(8)∑∞=++1212)3(n n nn n n .由于)(031)3()3(222212∞→→+=+++n nn n n n n n n n n n n,因此,如果级数∑∞=+122)3(n n n n n n 收敛,则原级数也收敛.考虑级数∑∞=+122)3(n n nn n n ,由于1313lim)3(lim 222<=+=+∞→∞→nn nn n n n nn n n ,故它收敛,因而原级数也收敛.(9))0()1()1)(1(12≥+++∑∞=x x x x x n nn.当0=x 时,级数显然收敛;当0>x 时,由于⎪⎩⎪⎨⎧>=<<=+=+++++++∞→++∞→.1,0,1,21,10,1lim )1()1)(1()1()1)(1(lim 12121x x x x x x x x x x x x x x n n n n n n n 因而∑∞=+++12)1()1)(1(n nnx x x x 收敛,因此原级数对一切0≥x 收敛. (10) +⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅+⋅⋅+107419753741753415313.级数的一般项)23(741)12(753-⋅⋅+⋅⋅=n n u n ,由于1321332lim )23(741)12(753)13(741)32(753lim lim1<=++=-⋅⋅+⋅⋅+⋅⋅+⋅⋅=∞→∞→+∞→n n n n n n u u n n nn n , 因而原级数收敛.3.判别级数的敛散性:(1)∑∞=1ln 1n nn;(2)∑∞=1ln )(ln 1n nn ; (3)∑∞=1ln 21n n;(4)∑∞=1ln 31n n;(5)∑∞=131n n;(6)∑∞=13n nn;(7)∑∞=1ln n p n n(p 是任意实数); (8)∑∞=2ln 1n pnn (p 是任意实数). 解(1)∑∞=1ln 1n nn.当9≥n 时2ln >n ,故当9≥n 时2ln 11n n n <,而∑∞=121n n收敛,由比较判别法知,原级数收敛.(2)∑∞=1ln )(ln 1n n n .由于)ln(ln ln 1)(ln 1n n n n =,且)()ln(ln ∞→+∞→n n ,故存在N ,当N n >时2)ln(ln >n ,从而2)ln(ln n n n >,即当N n >时,2ln )(ln n n n>,而级数∑∞=121n n收敛,故原级数收敛.(3)∑∞=1ln 21n n.方法1 由于n n n u u n n n n n n n n n nn 112lim 12lim 12121lim 1lim 11ln 11ln )1ln(ln 1-=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+∞→⎪⎭⎫ ⎝⎛+∞→+∞→+∞→, 该极限为型极限,由L 'hospital 法则得 12ln 11112ln 2lim112lim22111ln 11ln <=-⎪⎭⎫ ⎝⎛-+⋅⋅=-⎪⎭⎫ ⎝⎛+∞→⎪⎭⎫ ⎝⎛+∞→nn nn n n n n , 由Raabe 判别法知,原级数发散.方法2 由于n enn=<ln ln 2,所以n n 121ln >,而级数∑∞=11n n发散,由比较判别法知,原级数∑∞=1ln 21n n发散.(4)∑∞=1ln 31n n.由于13ln 13lim 1lim )11ln(1>=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛-+∞→+∞→n n n n n n u u n ,由Raabe 判别法知,原级数收敛.一般地,对)0(11ln >∑∞=a an n,当e a ≤<0时,对一切N n ∈,n e a n n =<ln ln 成立,所以n a n11ln ≥,从而∑∞=1ln 1n n a 发散;当e a >时,由于1ln 1lim 1>=⎪⎪⎭⎫ ⎝⎛-+∞→a u u n n n n ,由Raabe 判别法知,级数∑∞=1ln 1n na收敛.(5)∑∞=131n n.由于+∞=∞→n n n ln lim,所以存在0>N ,当N n >时,有3ln 2ln >n n ,即n n ln 23ln >,从而23n n>,故2131n n <,而∑∞=121n n 收敛,故∑∞=131n n 收敛. (6)∑∞=13n nn.由于+∞=∞→n n n ln lim,所以存在0>N ,当N n >时,有3ln 3ln >n n ,即n n ln 33ln >,从而33n n>,故213n n n <,而∑∞=121n n 收敛,故∑∞=13n n n 收敛.(7)∑∞=1ln n p n n (p 是任意实数).由于当3>n 时,p p n nn ln 1<,所以若∑∞=11n p n 发散,则原级数必发散,而1≤p 时∑∞=11n p n 发散,因而1≤p 时,原级数∑∞=1ln n p nn发散.当1>p 时,由于21211111)1(11)1(1ln 11ln 11ln ln p x p x x p tdt p dt t t dt t t p p x p x p xp-+---=-=⋅=--+--⎰⎰⎰, 因而211)1(1ln ln limp dx x x dt t t p xp x -==⎰⎰∞+∞→,利用柯西积分判别法知,原级数收敛. (8)∑∞=2ln 1n p n n (p 是任意实数).当1>p 时,由于p p n n n 1ln 1<且∑∞=21n p n收敛,故原级数收敛;当1=p 时,由于)2ln(ln )ln(ln ln ln 1ln 122-==⎰⎰x t d t dt t t x x,因而+∞==⎰⎰∞+∞→dx xx dt t t x x 22ln 1ln 1lim ,由柯西积分判别法知,原级数发散;当1<p 时,由于n n n n p ln 1ln 1>,而∑∞=2ln 1n n n 就是前面1=p 时的级数,已证得它发散,因而原级数发散.4.利用Taylor 公式估算无穷小量的阶,从而判别下列级数的收敛性:(1)∑∞=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-111n pn n e ;(2)∑∞=⎥⎦⎤⎢⎣⎡3cos 1ln n pn π; (3)∑∞=+--+111ln)1(n p n n n n ; (4)∑∞=++-+142)(n b n n a n .解(1)∑∞=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-111n pn n e .令xx x f ⎪⎭⎫⎝⎛+=11)(,则⎪⎭⎫ ⎝⎛+=x x x f 11ln )(ln ,从而⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+⎪⎭⎫ ⎝⎛+='1111ln 1111111ln )()(2x x x x x x x x f x f x , 因此⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=-⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛+-∞→∞→∞→1111ln 11lim 11111ln 11lim111lim 2200n n n n nn n n nn e n n nn nn ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛++-⎪⎭⎫ ⎝⎛+=∞→1113121111lim 3322n n n n n n n nn ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++-+⎪⎭⎫ ⎝⎛+=∞→332213121)1(111lim n n n n n n n nn 22113121)1(11lim 2e e n n n n n n nn =⋅=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++-+⎪⎭⎫ ⎝⎛+=∞→ . 该极限为有限数,因而nn e ⎪⎭⎫⎝⎛+-11与n 1是同阶无穷小量,由于∑∞=11n p n当1>p 时收敛,1≤p 时发散,因而原级数∑∞=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-111n pn n e 当1>p 时收敛,1≤p 时发散.(2)∑∞=⎥⎦⎤⎢⎣⎡3cos 1ln n pn π.由于 ⎪⎭⎫ ⎝⎛+===n n n nππππ22tan 1ln 21sec ln 21sec ln cos 1ln⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+-=n n nπππ2222tan 2)(tan tan 21 , 故21cos 1ln lim 22ππ=⎥⎦⎤⎢⎣⎡∞→nn n ,这是一个有限数,从而n πcos 1ln 与21n 是同阶无穷小量,因此原级数∑∞=⎥⎦⎤⎢⎣⎡3cos 1ln n pn π与∑∞=121n p n的收敛性一致,所以当12>p 即21>p 时,原级数收敛,而当12≤p 即21≤p 时,原级数发散.(3)∑∞=+--+111ln)1(n p n n n n .由于0)1(>-+pn n ,011ln <+-n n ,故原级数是负项级数,又由于⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛++=+---+121ln 1111ln)1()1(n n n n n n n pp ⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+-⎪⎪⎭⎫ ⎝⎛++=111211n n n n p,故11ln)1(+--+n n n n p与121+p n 是同阶无穷小量,因而当112>+p ,即0>p 时,原级数收敛,0≤p 时,原级数发散.(4)∑∞=++-+142)(n b n n a n .因为42242)(bn n a n b n n a n b n n a n ++++++-+=++-+))(()12(2422b n n a n b n n a n ba n a ++++++++-+-=,因而当21=a 时,上式与231n 是同阶无穷小量,故原级数收敛;当21≠a 时,上式与211n 是同阶无穷小量,故原级数发散.5.讨论下列级数的收敛性:(1)∑∞=2)(ln 1n pn n ; (2)∑∞=⋅⋅2ln ln ln 1n n n n ; (3))0(ln ln )(ln 121>∑∞=+σσn nn n ;(4)∑∞=2)ln (ln )(ln 1n qpn n n . 解(1)∑∞=2)(ln 1n p n n .令函数px x x f )(ln 1)(=,则该函数在),2[+∞非负、连续且单调下降.当1=p 时,由于+∞=-==∞→∞→∞→⎰⎰))2ln(ln )(ln(ln lim ln ln 1lim ln 1lim 22x t d t dt t t x x x xx ,因而原级数发散.当1≠p 时,由于⎰⎰⎰-∞→∞→∞→==x px xp x xx t d t dt t t dt t f 222ln )(ln lim )(ln 1lim )(lim()p p x x p--∞→--=11)2(ln )(ln 11lim⎪⎩⎪⎨⎧>-<∞+=-.1,1)2(ln ,1,1p p p p因而由柯西积分判别法知,当1<p 时级数发散,当1>p 时级数收敛.综上可知,级数∑∞=2)(ln 1n pn n 在1>p 时收敛,在1≤p 时发散.(2)∑∞=⋅⋅2ln ln ln 1n nn n .根据级数通项nu ,可令函数x x x x f ln ln ln 1)(⋅⋅=,则)2(),(≥=n n f u n 且)(x f 在),2[+∞非负、连续且单调下降,由于⎰⎰⎰∞→∞→∞→==x x xx x x t d tt d t t dt t f 222ln ln ln ln 1lim ln ln ln ln 1lim )(lim[]+∞=-=∞→2ln ln ln ln ln ln lim x x .由柯西积分判别法知,原级数发散.(3))0(ln ln )(ln 121>∑∞=+σσn nn n .由于+∞=∞→n n ln ln lim ,故当n 充分大时,1ln ln >n ,因而σσ++≤11)(ln 1ln ln )(ln 1n n n n n ,由(1)知∑∞=+21)(ln 1n n n σ收敛,从而原级数收敛.(4)∑∞=2)ln (ln )(ln 1n qpn n n . 当1=p 时,由于⎰⎰∞+∞+=22)ln(ln )ln (ln 1)ln (ln ln 1x d x dx x x x q q,故1>q 时级数收敛,1≤q 时级数发散.当1>p 时,令)0(21>+=σσp ,则qq p n n n n n n n n u )ln (ln )(ln )(ln 1)ln (ln )(ln 11σσ+==, 由于+∞=∞→qn n n )ln (ln )(ln lim σ,故存在0>N ,任意N n >时,1)ln (ln )(ln >qn n σ,从而σ+<1)(ln 1n n u n ,而由(1)知∑∞=+11)(ln 1n n n σ收敛,从而原级数收敛. 当1<p 时,令)0(21>-=σσp ,则qq p n n n n n n n n u )ln (ln )(ln )(ln )ln (ln )(ln 11σσ-==, 由于+∞→q n n )ln (ln )(ln σ,从而当n 充分大时,1)ln (ln )(ln >qn n σ,从而σ-≥1)(ln 1n n u n ,而由(1)知∑∞=-11)(ln 1n n n σ发散,因此原级数发散. 综上可知,原级数∑∞=2))(ln(ln )(ln 1n qp n n n 的收敛情况是:当1>p 或1,1>=q p 时收敛,当1<p 或1,1≤=q p 时发散.6.利用拉阿比判别法研究下列级数的收敛性.(1)∑∞=⎥⎦⎤⎢⎣⎡-1!)!2(!)!12(n pn n (p 是实数);(2))0,0(1!)1()1(1>>-++∑∞=βααααβn n n n .解(1)级数∑∞=⎥⎦⎤⎢⎣⎡-1!)!2(!)!12(n pn n 的通项pn n n u ⎥⎦⎤⎢⎣⎡-=!)!2(!)!12(,因而根据二项展开式得⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛++⋅-=⎪⎪⎭⎫⎝⎛-∞→+∞→1!)!12(!)!22(!)!2(!)!12(lim 1lim 1p n n n n n n n n n u u n []pp p n p n n n n n n n n )12()22()12(lim 11222lim +-++=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛++=∞→∞→()()[]1)2()2(22)2()2()12(lim11+++-++⋅++=--∞→ p p p p p pn n p n n p n n n []2)12()12()2(lim 1pn n p n p p p n =+-++=-∞→ . (上式也可以在第二个等式处将1222++n n 化为1211++n 直接使用二项展开式),所以当12>p 即2>p 时,原级数收敛,当12<p即2<p 时,原级数发散. 当2=p 时,Raabe 判别法失效,此时,由于对一切n ,222221)12(1111211n n n n n nn n u u nn n θμλ++=⎥⎦⎤⎢⎣⎡++-++=⎪⎭⎫ ⎝⎛++=+令, 即1,1==μλ而且1≤n θ,因而根据高斯判别法知,原级数发散.(2))0,0(1!)1()1(1>>-++∑∞=βααααβn n n n .根据原级数的通项知ββαααααα)1()()1()!1(1!)1()1(1++++⋅-++=+n n n nn n u u n n βββαα⎪⎭⎫⎝⎛+++=+++=n n n nn n n 111)()1)(1(, 因而αααββ+--⎪⎭⎫⎝⎛++=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛+++=⎪⎪⎭⎫ ⎝⎛-∞→∞→+∞→n n n n n n n n n u u n n n n nn 11)1(lim 1111lim 1lim 1βαααβ+-=+--⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+++=∞→1111)1(lim nn n n n n ,所以当11>+-βα,即βα<时级数收敛;当11<+-βα,即βα>时级数发散.当βα=时,Raabe 判别法失效,此时由于⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+-++++=⎪⎭⎫ ⎝⎛+++=+221112)1(11111n n n n n n n n u u n n αααααα⎪⎭⎫⎝⎛⋅++++-++++++-++=2211)(2)1()1()()1(1n n n n n n n n n n n ααααααααα 22)1(1)(2)1()1(111n n n n n n n n n θμλαααα++=⎥⎦⎤⎢⎣⎡⋅++++-+++=令 , 即1,1==μλ而且显然n θ有界,因而根据高斯判别法可知,原级数发散.7.已知两正项级数∑∞=1n nu和∑∞=1n nv发散,问),max (1∑∞=n n nv u,∑∞=1),min(n n n v u 两级数的收敛性如何?答 级数),max (1∑∞=n n nv u一定发散.事实上,0),m ax (≥≥n n n u v u ,而∑∞=1n n u 发散,故),max (1∑∞=n n nv u发散.∑∞=1),min(n n n v u 可能收敛,也可能发散.例如∑∑∞=∞=---+112)1(1,2)1(1n nn n 均发散,但由于0),min(=n n v u 对一切n 都成立,故∑∞=1),min(n n nv u收敛.8.若正项级数∑∞=1n n a 收敛,证明:02lim21=+++∞→nna a a nn .证明 设正项级数∑∞=1n na的部分和n n a a a S +++= 21,则下述两式成立:121121)2()1(--++-+-=+++n n a a n a n S S S , (*)n n na na na nS +++= 21, (**)用(**)减去(*)得n n n na a a S S S nS +++=+++-- 211212)(,两端同时除以n 可得nna a a n S S S nS nn n +++=+++-- 211212)(,即nna a a n S S S S n S n nn n n +++=++++--- 211212)1(,由于正项级数∑∞=1n na收敛,因而n n S ∞→lim 存在,假设s S n n =∞→lim ,根据收敛数列的算术平均数构成的新数列收敛,且与原数列极限相等可知,s nS S S nn =+++∞→ 21lim,因此0)1(lim 2lim12121=-=⎪⎭⎫⎝⎛++++--=+++-∞→∞→s s n S S S S n S n n na a a n n n n n n ,从而结论成立.9.设⎪⎪⎩⎪⎪⎨⎧===≠=,,2,1,1,,2,1,,12222 k k a k k n n a k n求证:(1)∑∞=1n na收敛;(2) 0lim ≠∞→n n na .证明(1)由于∑∞=121n n 收敛,故∑∑∞≠=∞≠==22,12,11k n n k n n n na 收敛,而∑∑∞=∞==12112k k kk a 收敛,从而∑∑∞≠=∞=+22,11kn n nk k aa收敛,即∑∞=1n na收敛.(2)考虑n na 的一个子列}{22k a k ,则11lim lim 2222==∞→∞→kka k n k n ,即0lim ≠∞→n n na . 10. 设0>n a ,且l a a nn n =+∞→1lim,求证l a n n n =∞→lim .反之是否成立?证明 令10=a ,构造数列⎭⎬⎫⎩⎨⎧=-1}{n n n a a u ,则}{n u 的前n 项的几何平均数可构成一个新数列,由于新数列收敛且与数列}{n u 极限相同,故11111lim lim lim++∞→+∞→+∞→===n n n n n n nn n u u u u a a ln n n n n n n n n n n n n a a a a a a a a a a ∞→+++∞→+-+∞→==⋅⋅=lim 1lim lim 1111011211 , 因而结论成立.反之不真,反例如级数∑∞=-+12)1(2n nn,由于21232)1(22121→≤-+=≤=nn n n n n n a , 故21lim =∞→n n n a ,而 613221,231223************=⋅==⋅=++--m m m m m m m m a a a a , 从而21lim1≠+∞→nn n a a ,因此反之结论不一定成立.11.利用级数收敛的必要条件证明:(1)0)!(lim 2=∞→n n n n ;(2))1(0)!2(lim!>=∞→a a n n n .证明(1)0)!(lim 2=∞→n n n n .考虑级数∑∞=12)!(n nn n ,由于 )(011111∞→→⎪⎭⎫⎝⎛++=+n n n u u nn n , 故级数∑∞=12)!(n n n n 收敛,因而0)!(lim 2=∞→n n nn . (2))1(0)!2(lim !>=∞→a a n n n .考虑级数∑∞=1!)!2(n n an ,由于)(0)12)(22(!1∞→→++=+n a n n u u nn n n , 所以级数∑∞=1!)!2(n n a n 收敛,因而)1(0)!2(lim !>=∞→a a n n n . 12.设0≥n a ,且数列}{n na 有界,证明级数∑∞=12n na收敛.证明 由数列}{n na 有界知,存在0>M ,对N n ∈∀,都有M na n ≤,从而nMa n ≤,进一步可得222n M a n≤,又由于∑∞=121n n收敛,因而由比较判别法知,级数∑∞=12n n a 收敛.13.设正项级数∑∞=1n na收敛,证明∑∞=+11n n n a a 也收敛.证明 由于对任意n ,1+n n a a )(211++≤n n a a 均成立,而级数∑∞=1n n a 和级数∑∞=+11n n a 均收敛,从而级数)(11∑∞=++n n na a也收敛,由比较判别法知,级数∑∞=+11n n n a a 收敛.14.设l a n n =∞→lim ,求证:(1)当1>l 时,∑∞=11n a nn 收敛; (2)当1<l 时,∑∞=11n a nn发散. 问1=l 时会有什么结论?证明(1)当1>l 时,令021>-=l ε,则由l a n n =∞→lim 知,存在N ,N n >∀时,有12121>+=--=->l l l l a n ε,从而当N n >时,2111+<l a n n n ,而∑∞=+1211n l n 收敛,故原级数收敛.(2)当1<l 时,令021>-=lε,则由l a n n =∞→lim 知,存在M ,M n >∀时,有12121<+=-+=+<l l l l a n ε,从而当M n >时2111+>l a n n n ,而∑∞=+1211n l n 发散,故原级数发散.当1=l 时,考虑级数∑∞=2)(ln 1n pn n ,由于nnp pn n n ln ln ln 1)(ln +=,令nnp a n ln ln ln 1+=,则1lim =∞→n n a ,此即为本题1=l 的情形,但由第5题(1)知,该级数在1>p 时收敛,1≤p 时发散,从而当1=l 时,级数∑∞=11n a nn 可能收敛也可能发散.§4 一般项级数1.讨论下列级数的收敛性:(1)∑∞=+-1100)1(n nn n;(2)∑∞=12sin ln n n n n π; (3)∑∞=++++-1131211)1(n nnn ;(4)∑∞=-+-2)1()1(n nnn ; (5))1(sin 21+∑∞=n n π;(6)∑∞=--12)1(3)1(n n n n ;(7))0()1(1>-∑∞=p n n pn; (8)2sin 311πn n n∑∞=; (9)∑∞=-12cos )1(n nnn; (10)∑∞=-12sin )1(n nn n;(11))0(sin)1(1≠-∑∞=x nxn n ; (12)∑∞=+-12)1()1(n n n n; (13)++--+++--++--1111131131121121n n ; (14))0(1)1(11>+-∑∞=+a a an n nn ;(15)∑∞=⎪⎭⎫ ⎝⎛+11sin n n n n ; (16)∑∞=⋅12sin sin n n n n .解(1)∑∞=+-1100)1(n nn n.令100)(+=x x x f ,则2)100(2100)(+-='x x x x f ,显然当100>x 时0)(≤'x f ,即)(x f 单调下降并趋向于0.由于级数前有限项的值不影响该级数的敛散性,因而由Leibniz 判别法知原交错级数收敛.(2)∑∞=12sin ln n n nn π.由于⎩⎨⎧∈-=-∈==+++,,12,)1(,,2,02sin 1Z k k n Z k k n n k π 舍去偶数项,原级数∑∑∞=+∞=---=11112)12ln()1(2sin ln k k n k k n n n π变成交错级数.令x xx f ln )(=,则2ln 1)(xxx f -=',显然当3≥x 时0)(<'x f ,即)(x f 单调下降并趋向于0.因而从第3项开始,数列⎭⎬⎫⎩⎨⎧n n ln 单调下降并趋向于0,故n 取奇数时该数列也是单调下降并趋向于0的,由Leibniz 判别法知,原交错级数收敛.(3)∑∞=++++-1131211)1(n nnn .由于数列的前n 项的算术平均数构成的新数列极限与原数列极限相等,故根据数列⎭⎬⎫⎩⎨⎧n 1单调递减趋向于0知,数列⎭⎬⎫⎩⎨⎧++++n n 131211 单调递减趋向于0,又因为原级数是一个交错级数,由Leibniz 判别法知原交错级数收敛.(4)∑∞=-+-2)1()1(n nn n .由于⎪⎪⎪⎭⎫ ⎝⎛+--=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+---=-+⋅-=-+-2311)1(1)1(1)1()1(11)1()1()1(nO n n n O n n nn n nn n n nnn ,而级数∑∞=-2)1(n nn及∑∞=2231n n收敛,但级数∑∞=21n n发散,因而原级数发散. (5))1(sin 21+∑∞=n n π.由于)1(sin )1())1(sin()1sin(222n n n n n n n -+-=-++=+ππππnn n ++-=1sin)1(2π,又由于⎭⎬⎫⎩⎨⎧++n n 1sin 2π单调下降趋于0,故由Leibniz 判别法知原级数收敛. (6)∑∞=--12)1(3)1(n n n n .由于∑∑∞=∞=-=-112)1(313)1(n nn nn n 收敛,故原级数绝对收敛,因而自身收敛.(7))0()1(1>-∑∞=p n n p n .由于pn 1单调递减趋向于0,根据Leibniz 判别法知原级数收敛.进一步可知:当10≤<p 时级数条件收敛,当1>p 时级数绝对收敛.(8)2sin 311πn n n ∑∞=.由于n n n 312sin31≤π,而∑∞=131n n 收敛,故原级数收敛且绝对收敛.(9)∑∞=-12cos )1(n nnn.由于 n k nk 2cos 1sin 24cos 1sin 22cos 1sin 22cos 1sin 21+++=∑=))12sin()12(sin()3sin 5(sin )1sin 3(sin --+++-+-=n n 1sin )12sin(-+=n ,故1sin 11sin 21sin )12sin(2cos 1≤-+=∑=n k nk ,即∑∞=12cos n n 的部分和数列有界,而数列⎭⎬⎫⎩⎨⎧n 1单调趋于0,由Dirichlet 判别法知级数∑∞=12cos n n n 收敛,即∑∞=-12cos )1(n n n n 收敛,从而原级。
数值分析简明教程课后习题答案

比较详细的数值分析课后习题答案0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数值分析简明教程(第二版)课后习题答案

0.1算法1、 (p.11,题1)用二分法求方程013=--x x 在[1,2]内的近似根,要求误差不超过10-3.【解】 由二分法的误差估计式311*10212||-++=≤=-≤-εk k k a b x x ,得到100021≥+k .两端取自然对数得96.812ln 10ln 3≈-≥k ,因此取9=k ,即至少需2、(p.11,题2) 证明方程210)(-+=x e x f x在区间[0,1]内有唯一个实根;使用二分法求这一实根,要求误差不超过21021-⨯。
【解】 由于210)(-+=x e x f x ,则)(x f 在区间[0,1]上连续,且012010)0(0<-=-⨯+=e f ,082110)1(1>+=-⨯+=e e f ,即0)1()0(<⋅f f ,由连续函数的介值定理知,)(x f 在区间[0,1]上至少有一个零点.又010)('>+=x e x f ,即)(x f 在区间[0,1]上是单调的,故)(x f 在区间[0,1]内有唯一实根.由二分法的误差估计式211*1021212||-++⨯=≤=-≤-εk k k a b x x ,得到1002≥k .两端取自然对数得6438.63219.322ln 10ln 2=⨯≈≥k ,因此取7=k ,即至少需二分0.2误差1.(p.12,题8)已知e=2.71828…,试问其近似值7.21=x ,71.22=x ,x 2=2.71,718.23=x 各有几位有效数字?并给出它们的相对误差限。
【解】有效数字:因为11102105.001828.0||-⨯=<=- x e ,所以7.21=x 有两位有效数字; 因为12102105.000828.0||-⨯=<=- x e ,所以71.22=x 亦有两位有效数字;因为3310210005.000028.0||-⨯=<=- x e ,所以718.23=x 有四位有效数字;%85.17.205.0||111=<-=x x e r ε; %85.171.205.0||222=<-=x x e r ε; %0184.0718.20005.0||333=<-=x x e r ε。
数学分析简明教程答案

第十章 数项级数§1 级数问题的提出1.证明:若微分方程0=+'+''xy y y x 有多项式解n n x a x a x a a y ++++= 2210,则必有),,2,1(0n i a i ==.证明 由多项式解nn x a x a x a a y ++++= 2210得1232132-++++='n n x na x a x a a y , 22432)1(1262--++++=''n n x a n n x a x a a y .从而 134232)1(1262--++++=''n n x a n n x a x a x a y x , 且 111232210+---++++++=n n n n n n x a x a x a x a x a x a xy .将上述结果代入微分方程0=+'+''xy y y x ,得342231201)16()9()4(x a a x a a x a a a ++++++0)(11122=++++++---n n n n n n n x a x a x a n a .比较系数得递推公式如下:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧===+=+=+=--.0,0,0,09,04,012231201n n n n a a a n a a a a a a由此解得0210=====n a a a a ,因而),,2,1,0(0n i a i ==.2.试确定系数 ,,,,10n a a a ,使n n nx a∑∞=0满足勒让德方程0)1(2)1(2=++'-''-y l l y x y x .解 设nn nx ay ∑∞==,则11-∞=∑='n n n xna y ,22)1(-∞=∑-=''n n nx an n y ,故∑∑∑∞=∞=-∞=----=--=''-2222222)1()1()1()1()1(n n n n n n n n n x a n n xa n n xa n n x y x ,∑∑∞=∞=--=-='-111222n n n n n n x na xna x y x ,∑∑∞=∞=+=+=+0)1()1()1(n n n n nn x a l l x a l l y l l .将上述结果代入勒让德方程0)1(2)1(2=++'-''-y l l y x y x ,得y l l y x y x )1(2)1(02++'-''-=∑∑∑∑∞=∞=∞=∞=-++----=01222)1(2)1()1(n n n n nn n nn n n n x a l l x na x a n n xa n n∑∑∑∑∞=∞=∞=∞=+++---++=0122)1(2)1()1)(2(n n n n nn n nn n nn x a l l x na x a n n x a n n .比较系数,得递推公式如下:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+++++-=+++--=++-=++-=++++-.,0)1)(2()1)((,0)1()))(1((,012)3)(2(,06)2)(1(,02)1(211423120n n n n a n n a n l n l na n a n l n l a a l l a a l l a a l l 由此解得⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧++++-+-+--=⨯⨯⨯++--=⨯+--=⨯+--=-++++-+--=⨯⨯++-=⨯+--=+-=+,)!12()2()4)(2)(1()32)(12()1(,2345)4)(2)(1)(3(45)4)(3(,23)2)(1(,)!2()12()3)(1()42)(22()1(,234)3)(1()2(34)3)(2(,2)1(112135130202402a k k l l l l k l k l a a l l l l a l l a a l l a a k k l l l l k l k l a a l l l l a l l a a l l a k k k k从而可以得到⎥⎦⎤⎢⎣⎡-+++-+--+=∑∞=1200)!2()12()1()42)(22()1(k k k x k k l l l k l k l a a y⎥⎦⎤⎢⎣⎡+++-+-+--++∑∞=+11211)!12()2()2)(1()32)(12()1(k k k x k k l l l k l k l a x a .其中10,a a 取任何常数.§2 数项级数的收敛性及其基本性质1.求下列级数的和: (1)∑∞=+-1)15)(45(1n n n ; (2)∑∞=-12141n n;(3)∑∞=---1112)1(n n n ; (4)∑∞=-1212n nn ; (5)1,sin 1<∑∞=r nx rn n;(6)1,cos 1<∑∞=r nx rn n.解(1)由于⎪⎭⎫⎝⎛+--=+-15145151)15)(45(1n n n n ,故)15)(45(11161611+-++⨯+⨯=n n S n ⎪⎭⎫ ⎝⎛+--++-+-=1514511116161151n n )(51151151∞→→⎪⎭⎫ ⎝⎛+-=n n , 所以级数的和51=S . (2)由于⎪⎭⎫⎝⎛+--=-121121211412n n n ,故)(21121121121121513131121∞→→⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛+--++-+-=n n n n S n .所以级数的和21=S . (3)322111212)1(11111=⎪⎭⎫ ⎝⎛--=⎪⎭⎫⎝⎛-=--∞=∞=--∑∑n n n n n .(4)12221222121111-=⎪⎭⎫ ⎝⎛-=-∑∑∑∑∞=∞=∞=∞=n nn nn n n n nn n ,因此欲求原级数的和,只需计算级数∑∞=122n n n 即可.对级数∑∞=122n n n ,设其部分和n n n S 2226242232++++= ,则 14322222226242221++-++++=n n n nn S , 故1432222222222212121+-+++++=-=n n n n n n S S S 1432222121212121+-⎪⎭⎫ ⎝⎛+++++=n n n112222112112121+---⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+=n n n . 从而221lim =∞→n n S ,即4lim =∞→n n S ,因此原级数31412221211=-=-=-∑∑∞=∞=n n n n n n . (5)由于级数的部分和kx rS nk kn sin 1∑==,故[]x k x k r x kx rxS r nk k nk k n )1sin()1sin(cos sin 2cos 21111-++==∑∑=+=+x k r x k rnk k nk k )1sin()1sin(1111-++=∑∑=+=+kx rrkx r n k kn k k sin sin 1212∑∑-=+=+=)sin ()sin )1sin((21nx r S r x r x n r S n n n n -+-++=+,从中解得xr r xn r nx r x r S n n n cos 21)1sin(sin sin 212-++-+=++.又由于当∞→n 时,0)1sin(,0sin 1122→≤+→≤++++n n n n r x n r r nx r ,故xr r xr S n n cos 21sin lim 2-+=∞→, 因此xr r xr nx r n n cos 21sin sin 21-+=∑∞=.(6)级数的部分和kx rS nk kn cos 1∑==,从而[]x k x k r x kx rxS r nk k nk k n )1cos()1cos(cos cos 2cos 21111-++==∑∑=+=+x k r x k rnk k nk k )1cos()1cos(1111-++=∑∑=+=+kx rrkx r n k kn k k cos cos 1212∑∑-=+=+=)cos 1()cos )1cos((21nx r S r x r x n r S n n n n -++-++=+,从中解得x r r r x r x r r r x n r nx r x r S n n n n n cos 21cos cos 21)1cos(cos cos lim lim 222212-+-=-+-+-+=++∞→∞→. 因此x r r r x r nx r n ncos 21cos cos 221-+-=∑∞=. 2.讨论下列级数的敛散性: (1)∑∞=-112n n n; (2)∑∞=⎪⎭⎫ ⎝⎛+13121n nn; (3)∑∞=+112cosn n π;(4)∑∞=+-1)13)(23(1n n n ; (5)∑∞=+++1)1()1(1n n n n n .解(1)由于通项)(02112∞→≠→-n n n ,故原级数发散. (2)由于∑∑∞=∞=⎪⎭⎫ ⎝⎛=112121n nn n ,∑∑∞=∞=⎪⎭⎫⎝⎛=113131n nn n 均收敛,故原级数收敛.(3)由于通项)(010cos 12cos ∞→≠=→+n n π,故原级数发散.(4)由于⎪⎭⎫⎝⎛+--=+-13123131)13)(23(1n n n n ,从而部分和)13)(23(1741411+-++⨯+⨯=n n S n ⎪⎭⎫ ⎝⎛+--++-+-=131231714141131n n)(31131131∞→→⎪⎭⎫ ⎝⎛+-=n n , 因而原级数收敛.(5)由于⎪⎪⎭⎫⎝⎛+-=+-+=+++11111)1()1(1n n n n nn n n n n ,从而∞→n 时, 111111131212111→+-=+-++-+-=n n n S n ,故原级数收敛.3.证明定理10.2.定理10.2 若级数∑∞=1n n u ,∑∞=1n nv收敛,则级数)(1n n nv u±∑∞=也收敛,且∑∑∑∞=∞=∞=±=±111)(n n n n n n nv u v u.证明 设∑∑==='=nk k nnk kn v S uS 11,,则由已知条件知,存在有限数s s ',,使得 s v S s u S nk k n nn nk k n n n '=='==∑∑=∞→∞→=∞→∞→11lim lim ,lim lim , 设级数)(1n n nv u±∑∞=的部分和数列为n μ,则)()(111∞→'±→'±=±=±=∑∑∑===n s s S S v u v u nn nk k nk k nk k k n μ, 所以)(1n n nv u±∑∞=也收敛,且∑∑∑∞=∞=∞=±=±111)(n n n n n n n v u v u .4.设级数∑∞=1n nu各项是正的,把级数的项经过组合而得到新级数∑∞=1n nU,即,2,1,0,1211=+++=++++n u u u U n n n k k k n ,其中 <<<<<<=+12100,0n n k k k k k k ,若∑∞=1n nU收敛,证明原来的级数也收敛.证明 设∑∑====nk k n nk kn U uS 11,σ,则n nk k n U U U U +++==∑= 211σ)()(21112121k k k k u u u u u u +++++++=++ n n n n k k k k S u u u =+++++++--)(2111 .由于∑∞=1n nU收敛,故}{n σ有界,即{n k S }有界,即存在0>M ,使得N n ∈∀,都有M S n k ≤.又由于∑∞=1n nu是正项级数,故M S S n k n ≤≤,而且{n S }单调上升,由单调有界原理可知,原级数∑∞=1n nu收敛.§3 正项级数1.判别下列级数的收敛性: (1)∑∞=+121n nn ;(2)∑∞=--1122)12(1n n n ; (3)∑∞=--112n n nn ; (4)∑∞=12sinn nπ;(5))1(111>+∑∞=a a n n; (6)∑∞=11n nnn;(7)nn n ∑∞=⎪⎭⎫⎝⎛+1121;(8)[]∑∞=+1)1ln(1n nn ;(9)∑∞=-+12)1(2n nn; (10)∑∞=13sin2n nn π;(11)∑∞=-+15sin ))1(3(n nn n π;(12)∑∞=11!2sin n nn ; (13)∑∞=⎪⎭⎫ ⎝⎛-11cos 1n n n ; (14)∑∞=11cos n n ; (15)∑∞=⎪⎪⎭⎫ ⎝⎛+111ln 1n n n ; (16)∑∞=+12)1ln(n n n ; (17)∑∞=11arcsin 1sin n n n ; (18)∑∞=12arctan n nn π;(19)∑∞=⎪⎪⎭⎫ ⎝⎛-+1111n n ; (20)∑∞=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫⎝⎛+122111n n .解(1)∑∞=+121n nn .由于111lim2=+∞→nnn n ,而∑∞=11n n 发散,所以级数∑∞=+121n nn 发散.(2)∑∞=--1122)12(1n n n .对任意正整数n ,都成立关系式nn n n 2121222212)12(1≤≤---, 而级数∑∞=1222n n 收敛,由比较判别法知,原级数收敛. (3)∑∞=--112n n n n .由于02112lim ≠=--∞→n n n n ,所以级数∑∞=--112n n nn 发散.(4)∑∞=12sin n nπ.由于ππ=∞→n n n 212sinlim,而∑∞=121n n 收敛,故∑∞=12sin n nπ收敛. (5)∑∞=+111n n a .由于1>a ,故n nn a a a ⎪⎭⎫ ⎝⎛=<+1111,而∑∞=⎪⎭⎫⎝⎛11n na 收敛,由比较判别法知,级数∑∞=+111n na收敛. (6)∑∞=11n n n n .由于11lim 11lim ==∞→∞→n n n n n nn n ,而∑∞=11n n 发散,故∑∞=11n n nn 发散.(7)nn n ∑∞=⎪⎭⎫ ⎝⎛+1121.由于10121lim 121lim <=+=⎪⎭⎫ ⎝⎛+∞→∞→n n n n n n ,故级数nn n ∑∞=⎪⎭⎫⎝⎛+1121收敛.(8)[]∑∞=+1)1ln(1n nn .由于10)1ln(1lim )1ln(1lim <=+=⎪⎪⎭⎫ ⎝⎛+∞→∞→n n n n nn ,故原级数收敛.(9)∑∞=-+12)1(2n nn. 方法1因为∑∑∑∞=∞=-∞=-+=-+11112)1(212)1(2n n n n n n nn ,而∑∞=-1121n n 和∑∞=-12)1(n n n 均收敛,故∑∞=-+12)1(2n nn收敛. 方法2 由于n n n 232)1(2≤-+对一切n 都成立,而∑∞=123n n 收敛,故∑∞=-+12)1(2n nn 收敛.(10)∑∞=13sin2n nnπ.由于πππ=⋅=⎪⎭⎫ ⎝⎛∞→∞→nn n n n nn n n 3123sin2lim 323sin2lim,而∑∞=⎪⎭⎫ ⎝⎛132n n收敛,故原级数收敛.(11)∑∞=-+15sin))1(3(n nnn π.由于4)1(3≤-+n,因此,若∑∞=15sin 4n nn π收敛,则原级数收敛.考虑级数∑∞=15sin4n nnπ,由于πππ=⋅=⎪⎭⎫ ⎝⎛∞→∞→nn nn n n nn n 5145sin4lim 545sin4lim,且∑∞=⎪⎭⎫ ⎝⎛154n n收敛,故∑∞=15sin4n nn π收敛,因而原级数收敛.(12)∑∞=11!2sin n nn .由于!1!2sin n n n ≤,而∑∞=1!1n n 收敛,因而原级数收敛.(13)∑∞=⎪⎭⎫ ⎝⎛-11cos 1n n n .由于21121sin 2lim 11cos 1lim22==⎪⎭⎫ ⎝⎛-∞→∞→n n n n n n n ,而∑∞=11n n发散,因而原级数发散.(14)∑∞=11cos n n .由于011cos lim ≠=∞→n n ,由级数收敛的必要条件知,原级数发散. (15)∑∞=⎪⎪⎭⎫ ⎝⎛+111ln 1n n n .由于1111ln lim 111ln 1lim 23=⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫ ⎝⎛+∞→∞→nn n n n n n ,而∑∞=1231n n 收敛,故原级数收敛.(16)∑∞=+12)1ln(n n n .由于0)1ln(lim 1)1ln(1lim 232=+=+∞→∞→n n n n n n n ,而级数∑∞=1231n n 收敛,故原级数收敛.(17)∑∞=11arcsin 1sin n n n .由于111arcsin 1sin lim2=∞→n n n n ,而级数∑∞=121n n收敛,故原级数收敛.(18)∑∞=12arctan n nn π.由于极限ππ=∞→n n n n n 22arctanlim,而对于级数∑∞=12n nn ,根据1212lim <=∞→nn n n ,故由根式判别法知,级数∑∞=12n nn 收敛,因而原级数收敛. (19)∑∞=⎪⎪⎭⎫ ⎝⎛-+1111n n .对通项进行分子有理化可得 )1(21)1(2111211111111111+>+=+>++=++=-+n n n nn n n n n n n , 由于∑∞=+1)1(21n n 发散,故原级数发散.(20)∑∞=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛+122111n n .由于422212111n n n +=-⎪⎭⎫⎝⎛+,而级数∑∑∞=∞=14121,2n n n n 均收敛,因而原级数收敛.2.判别下列级数的敛散性:(1)∑∞=1!n nn n ;(2)∑∞=12ln n nnn ; (3)∑∞=12!n n nn n ;(4)∑∞=13!n n nnn ;(5)∑∞=1!n n nne n ;(6)∑∞=⎪⎭⎫ ⎝⎛+121n nn n n ;(7)212312nn n n ∑∞=⎪⎭⎫ ⎝⎛-+; (8)∑∞=++1212)3(n n nn n n ;(9))0()1()1)(1(12≥+++∑∞=x x x x x n nn; (10)+⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅+⋅⋅+107419753741753415313. 解(1)∑∞=1!n n n n .由于11lim !)!1()1(lim 1>=⎪⎭⎫⎝⎛+=++∞→+∞→e n n n n n n n n n n n ,所以∑∞=1!n n n n 发散. (2)∑∞=12ln n nnn .由于 121ln 1ln 1lim 21lim ln )1ln(21lim 2ln 2)1ln()1(lim 1<=⎪⎪⎪⎪⎭⎫ ⎝⎛++⋅+=⎪⎭⎫ ⎝⎛++=++∞→∞→∞→+∞→n n n n n n n nn n n n n n n n n n n , 根据达朗贝尔判别法知,原级数收敛.(3)∑∞=12!n n n n n .由于121lim 22!)1(2)!1(lim 11<=⎪⎭⎫⎝⎛+=++∞→++∞→e n n n n n n n n n n n n n ,故∑∞=12!n n n n n 收敛. (4)∑∞=13!n n n n n .由于131lim 33!)1(3)!1(lim 11>=⎪⎭⎫⎝⎛+=++∞→++∞→e n n n n n n n n nn n n n ,故∑∞=13!n n n n n 发散. (5)∑∞=1!n n nne n .这个级数不能用达朗贝尔判别法和柯西判别法判别,也不能用拉阿比判别法判别,但由斯特林公式可知)10(2!12<<⎪⎭⎫⎝⎛=θπθnn e e n n n ,因而πππθθn e n ne e e n n ne n n n n n nn n222!1212>=⎪⎭⎫⎝⎛=,通项的极限不为0,由级数收敛的必要条件知原级数∑∞=1!n n nne n 发散.(6)∑∞=⎪⎭⎫ ⎝⎛+121n n n n n .因为101)(lim 1lim 22<=+=⎪⎭⎫ ⎝⎛+∞→∞→n n n n n n n n n n n ,故∑∞=⎪⎭⎫ ⎝⎛+121n n n n n 收敛. (7)∑∞=⎪⎭⎫⎝⎛-+122312n n n n .由于1322312lim2312lim 2<=-+=⎪⎭⎫⎝⎛-+∞→∞→n n n n n n n n ,由柯西判别法知,原级数收敛.(8)∑∞=++1212)3(n n nn n n .由于)(031)3()3(222212∞→→+=+++n nn n n n n n n n n n n,因此,如果级数∑∞=+122)3(n n n n n n 收敛,则原级数也收敛.考虑级数∑∞=+122)3(n n nn n n ,由于1313lim)3(lim 222<=+=+∞→∞→nn nn n n n nn n n ,故它收敛,因而原级数也收敛.(9))0()1()1)(1(12≥+++∑∞=x x x x x n nn.当0=x 时,级数显然收敛;当0>x 时,由于⎪⎩⎪⎨⎧>=<<=+=+++++++∞→++∞→.1,0,1,21,10,1lim )1()1)(1()1()1)(1(lim 12121x x x x x x x x x x x x x x n n n n n n n 因而∑∞=+++12)1()1)(1(n nnx x x x 收敛,因此原级数对一切0≥x 收敛. (10) +⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅+⋅⋅+107419753741753415313.级数的一般项)23(741)12(753-⋅⋅+⋅⋅=n n u n ,由于1321332lim )23(741)12(753)13(741)32(753lim lim1<=++=-⋅⋅+⋅⋅+⋅⋅+⋅⋅=∞→∞→+∞→n n n n n n u u n n nn n , 因而原级数收敛.3.判别级数的敛散性:(1)∑∞=1ln 1n nn;(2)∑∞=1ln )(ln 1n nn ; (3)∑∞=1ln 21n n;(4)∑∞=1ln 31n n;(5)∑∞=131n n;(6)∑∞=13n nn;(7)∑∞=1ln n p n n(p 是任意实数); (8)∑∞=2ln 1n pnn (p 是任意实数). 解(1)∑∞=1ln 1n nn.当9≥n 时2ln >n ,故当9≥n 时2ln 11n n n <,而∑∞=121n n收敛,由比较判别法知,原级数收敛.(2)∑∞=1ln )(ln 1n n n .由于)ln(ln ln 1)(ln 1n n n n =,且)()ln(ln ∞→+∞→n n ,故存在N ,当N n >时2)ln(ln >n ,从而2)ln(ln n n n >,即当N n >时,2ln )(ln n n n>,而级数∑∞=121n n收敛,故原级数收敛.(3)∑∞=1ln 21n n.方法1 由于n n n u u n n n n n n n n n nn 112lim 12lim 12121lim 1lim 11ln 11ln )1ln(ln 1-=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+∞→⎪⎭⎫ ⎝⎛+∞→+∞→+∞→, 该极限为型极限,由L 'hospital 法则得 12ln 11112ln 2lim112lim22111ln 11ln <=-⎪⎭⎫ ⎝⎛-+⋅⋅=-⎪⎭⎫ ⎝⎛+∞→⎪⎭⎫ ⎝⎛+∞→nn nn n n n n , 由Raabe 判别法知,原级数发散.方法2 由于n enn=<ln ln 2,所以n n 121ln >,而级数∑∞=11n n发散,由比较判别法知,原级数∑∞=1ln 21n n发散.(4)∑∞=1ln 31n n.由于13ln 13lim 1lim )11ln(1>=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛-+∞→+∞→n n n n n n u u n ,由Raabe 判别法知,原级数收敛.一般地,对)0(11ln >∑∞=a an n,当e a ≤<0时,对一切N n ∈,n e a n n =<ln ln 成立,所以n a n11ln ≥,从而∑∞=1ln 1n n a 发散;当e a >时,由于1ln 1lim 1>=⎪⎪⎭⎫ ⎝⎛-+∞→a u u n n n n ,由Raabe 判别法知,级数∑∞=1ln 1n na收敛.(5)∑∞=131n n.由于+∞=∞→n n n ln lim,所以存在0>N ,当N n >时,有3ln 2ln >n n ,即n n ln 23ln >,从而23n n>,故2131n n <,而∑∞=121n n 收敛,故∑∞=131n n 收敛. (6)∑∞=13n nn.由于+∞=∞→n n n ln lim,所以存在0>N ,当N n >时,有3ln 3ln >n n ,即n n ln 33ln >,从而33n n>,故213n n n <,而∑∞=121n n 收敛,故∑∞=13n n n 收敛.(7)∑∞=1ln n p n n (p 是任意实数).由于当3>n 时,p p n nn ln 1<,所以若∑∞=11n p n 发散,则原级数必发散,而1≤p 时∑∞=11n p n 发散,因而1≤p 时,原级数∑∞=1ln n p nn发散.当1>p 时,由于21211111)1(11)1(1ln 11ln 11ln ln p x p x x p tdt p dt t t dt t t p p x p x p xp-+---=-=⋅=--+--⎰⎰⎰, 因而211)1(1ln ln limp dx x x dt t t p xp x -==⎰⎰∞+∞→,利用柯西积分判别法知,原级数收敛. (8)∑∞=2ln 1n p n n (p 是任意实数).当1>p 时,由于p p n n n 1ln 1<且∑∞=21n p n收敛,故原级数收敛;当1=p 时,由于)2ln(ln )ln(ln ln ln 1ln 122-==⎰⎰x t d t dt t t x x,因而+∞==⎰⎰∞+∞→dx xx dt t t x x 22ln 1ln 1lim ,由柯西积分判别法知,原级数发散;当1<p 时,由于n n n n p ln 1ln 1>,而∑∞=2ln 1n n n 就是前面1=p 时的级数,已证得它发散,因而原级数发散.4.利用Taylor 公式估算无穷小量的阶,从而判别下列级数的收敛性:(1)∑∞=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-111n pn n e ;(2)∑∞=⎥⎦⎤⎢⎣⎡3cos 1ln n pn π; (3)∑∞=+--+111ln)1(n p n n n n ; (4)∑∞=++-+142)(n b n n a n .解(1)∑∞=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-111n pn n e .令xx x f ⎪⎭⎫⎝⎛+=11)(,则⎪⎭⎫ ⎝⎛+=x x x f 11ln )(ln ,从而⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+⎪⎭⎫ ⎝⎛+='1111ln 1111111ln )()(2x x x x x x x x f x f x , 因此⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=-⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛+-∞→∞→∞→1111ln 11lim 11111ln 11lim111lim 2200n n n n nn n n nn e n n nn nn ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛++-⎪⎭⎫ ⎝⎛+=∞→1113121111lim 3322n n n n n n n nn ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++-+⎪⎭⎫ ⎝⎛+=∞→332213121)1(111lim n n n n n n n nn 22113121)1(11lim 2e e n n n n n n nn =⋅=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++-+⎪⎭⎫ ⎝⎛+=∞→ . 该极限为有限数,因而nn e ⎪⎭⎫⎝⎛+-11与n 1是同阶无穷小量,由于∑∞=11n p n当1>p 时收敛,1≤p 时发散,因而原级数∑∞=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-111n pn n e 当1>p 时收敛,1≤p 时发散.(2)∑∞=⎥⎦⎤⎢⎣⎡3cos 1ln n pn π.由于 ⎪⎭⎫ ⎝⎛+===n n n nππππ22tan 1ln 21sec ln 21sec ln cos 1ln⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+-=n n nπππ2222tan 2)(tan tan 21 , 故21cos 1ln lim 22ππ=⎥⎦⎤⎢⎣⎡∞→nn n ,这是一个有限数,从而n πcos 1ln 与21n 是同阶无穷小量,因此原级数∑∞=⎥⎦⎤⎢⎣⎡3cos 1ln n pn π与∑∞=121n p n的收敛性一致,所以当12>p 即21>p 时,原级数收敛,而当12≤p 即21≤p 时,原级数发散.(3)∑∞=+--+111ln)1(n p n n n n .由于0)1(>-+pn n ,011ln <+-n n ,故原级数是负项级数,又由于⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛++=+---+121ln 1111ln)1()1(n n n n n n n pp ⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+-⎪⎪⎭⎫ ⎝⎛++=111211n n n n p,故11ln)1(+--+n n n n p与121+p n 是同阶无穷小量,因而当112>+p ,即0>p 时,原级数收敛,0≤p 时,原级数发散.(4)∑∞=++-+142)(n b n n a n .因为42242)(bn n a n b n n a n b n n a n ++++++-+=++-+))(()12(2422b n n a n b n n a n ba n a ++++++++-+-=,因而当21=a 时,上式与231n 是同阶无穷小量,故原级数收敛;当21≠a 时,上式与211n 是同阶无穷小量,故原级数发散.5.讨论下列级数的收敛性:(1)∑∞=2)(ln 1n pn n ; (2)∑∞=⋅⋅2ln ln ln 1n n n n ; (3))0(ln ln )(ln 121>∑∞=+σσn nn n ;(4)∑∞=2)ln (ln )(ln 1n qpn n n . 解(1)∑∞=2)(ln 1n p n n .令函数px x x f )(ln 1)(=,则该函数在),2[+∞非负、连续且单调下降.当1=p 时,由于+∞=-==∞→∞→∞→⎰⎰))2ln(ln )(ln(ln lim ln ln 1lim ln 1lim 22x t d t dt t t x x x xx ,因而原级数发散.当1≠p 时,由于⎰⎰⎰-∞→∞→∞→==x px xp x xx t d t dt t t dt t f 222ln )(ln lim )(ln 1lim )(lim()p p x x p--∞→--=11)2(ln )(ln 11lim⎪⎩⎪⎨⎧>-<∞+=-.1,1)2(ln ,1,1p p p p因而由柯西积分判别法知,当1<p 时级数发散,当1>p 时级数收敛.综上可知,级数∑∞=2)(ln 1n pn n 在1>p 时收敛,在1≤p 时发散.(2)∑∞=⋅⋅2ln ln ln 1n nn n .根据级数通项nu ,可令函数x x x x f ln ln ln 1)(⋅⋅=,则)2(),(≥=n n f u n 且)(x f 在),2[+∞非负、连续且单调下降,由于⎰⎰⎰∞→∞→∞→==x x xx x x t d tt d t t dt t f 222ln ln ln ln 1lim ln ln ln ln 1lim )(lim[]+∞=-=∞→2ln ln ln ln ln ln lim x x .由柯西积分判别法知,原级数发散.(3))0(ln ln )(ln 121>∑∞=+σσn nn n .由于+∞=∞→n n ln ln lim ,故当n 充分大时,1ln ln >n ,因而σσ++≤11)(ln 1ln ln )(ln 1n n n n n ,由(1)知∑∞=+21)(ln 1n n n σ收敛,从而原级数收敛.(4)∑∞=2)ln (ln )(ln 1n qpn n n . 当1=p 时,由于⎰⎰∞+∞+=22)ln(ln )ln (ln 1)ln (ln ln 1x d x dx x x x q q,故1>q 时级数收敛,1≤q 时级数发散.当1>p 时,令)0(21>+=σσp ,则qq p n n n n n n n n u )ln (ln )(ln )(ln 1)ln (ln )(ln 11σσ+==, 由于+∞=∞→qn n n )ln (ln )(ln lim σ,故存在0>N ,任意N n >时,1)ln (ln )(ln >qn n σ,从而σ+<1)(ln 1n n u n ,而由(1)知∑∞=+11)(ln 1n n n σ收敛,从而原级数收敛. 当1<p 时,令)0(21>-=σσp ,则qq p n n n n n n n n u )ln (ln )(ln )(ln )ln (ln )(ln 11σσ-==, 由于+∞→q n n )ln (ln )(ln σ,从而当n 充分大时,1)ln (ln )(ln >qn n σ,从而σ-≥1)(ln 1n n u n ,而由(1)知∑∞=-11)(ln 1n n n σ发散,因此原级数发散. 综上可知,原级数∑∞=2))(ln(ln )(ln 1n qp n n n 的收敛情况是:当1>p 或1,1>=q p 时收敛,当1<p 或1,1≤=q p 时发散.6.利用拉阿比判别法研究下列级数的收敛性.(1)∑∞=⎥⎦⎤⎢⎣⎡-1!)!2(!)!12(n pn n (p 是实数);(2))0,0(1!)1()1(1>>-++∑∞=βααααβn n n n .解(1)级数∑∞=⎥⎦⎤⎢⎣⎡-1!)!2(!)!12(n pn n 的通项pn n n u ⎥⎦⎤⎢⎣⎡-=!)!2(!)!12(,因而根据二项展开式得⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛++⋅-=⎪⎪⎭⎫⎝⎛-∞→+∞→1!)!12(!)!22(!)!2(!)!12(lim 1lim 1p n n n n n n n n n u u n []pp p n p n n n n n n n n )12()22()12(lim 11222lim +-++=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛++=∞→∞→()()[]1)2()2(22)2()2()12(lim11+++-++⋅++=--∞→ p p p p p pn n p n n p n n n []2)12()12()2(lim 1pn n p n p p p n =+-++=-∞→ . (上式也可以在第二个等式处将1222++n n 化为1211++n 直接使用二项展开式),所以当12>p 即2>p 时,原级数收敛,当12<p即2<p 时,原级数发散. 当2=p 时,Raabe 判别法失效,此时,由于对一切n ,222221)12(1111211n n n n n nn n u u nn n θμλ++=⎥⎦⎤⎢⎣⎡++-++=⎪⎭⎫ ⎝⎛++=+令, 即1,1==μλ而且1≤n θ,因而根据高斯判别法知,原级数发散.(2))0,0(1!)1()1(1>>-++∑∞=βααααβn n n n .根据原级数的通项知ββαααααα)1()()1()!1(1!)1()1(1++++⋅-++=+n n n nn n u u n n βββαα⎪⎭⎫⎝⎛+++=+++=n n n nn n n 111)()1)(1(, 因而αααββ+--⎪⎭⎫⎝⎛++=⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛+++=⎪⎪⎭⎫ ⎝⎛-∞→∞→+∞→n n n n n n n n n u u n n n n nn 11)1(lim 1111lim 1lim 1βαααβ+-=+--⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+++=∞→1111)1(lim nn n n n n ,所以当11>+-βα,即βα<时级数收敛;当11<+-βα,即βα>时级数发散.当βα=时,Raabe 判别法失效,此时由于⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+-++++=⎪⎭⎫ ⎝⎛+++=+221112)1(11111n n n n n n n n u u n n αααααα⎪⎭⎫⎝⎛⋅++++-++++++-++=2211)(2)1()1()()1(1n n n n n n n n n n n ααααααααα 22)1(1)(2)1()1(111n n n n n n n n n θμλαααα++=⎥⎦⎤⎢⎣⎡⋅++++-+++=令 , 即1,1==μλ而且显然n θ有界,因而根据高斯判别法可知,原级数发散.7.已知两正项级数∑∞=1n nu和∑∞=1n nv发散,问),max (1∑∞=n n nv u,∑∞=1),min(n n n v u 两级数的收敛性如何?答 级数),max (1∑∞=n n nv u一定发散.事实上,0),m ax (≥≥n n n u v u ,而∑∞=1n n u 发散,故),max (1∑∞=n n nv u发散.∑∞=1),min(n n n v u 可能收敛,也可能发散.例如∑∑∞=∞=---+112)1(1,2)1(1n nn n 均发散,但由于0),min(=n n v u 对一切n 都成立,故∑∞=1),min(n n nv u收敛.8.若正项级数∑∞=1n n a 收敛,证明:02lim21=+++∞→nna a a nn .证明 设正项级数∑∞=1n na的部分和n n a a a S +++= 21,则下述两式成立:121121)2()1(--++-+-=+++n n a a n a n S S S , (*)n n na na na nS +++= 21, (**)用(**)减去(*)得n n n na a a S S S nS +++=+++-- 211212)(,两端同时除以n 可得nna a a n S S S nS nn n +++=+++-- 211212)(,即nna a a n S S S S n S n nn n n +++=++++--- 211212)1(,由于正项级数∑∞=1n na收敛,因而n n S ∞→lim 存在,假设s S n n =∞→lim ,根据收敛数列的算术平均数构成的新数列收敛,且与原数列极限相等可知,s nS S S nn =+++∞→ 21lim,因此0)1(lim 2lim12121=-=⎪⎭⎫⎝⎛++++--=+++-∞→∞→s s n S S S S n S n n na a a n n n n n n ,从而结论成立.9.设⎪⎪⎩⎪⎪⎨⎧===≠=,,2,1,1,,2,1,,12222 k k a k k n n a k n求证:(1)∑∞=1n na收敛;(2) 0lim ≠∞→n n na .证明(1)由于∑∞=121n n 收敛,故∑∑∞≠=∞≠==22,12,11k n n k n n n na 收敛,而∑∑∞=∞==12112k k kk a 收敛,从而∑∑∞≠=∞=+22,11kn n nk k aa收敛,即∑∞=1n na收敛.(2)考虑n na 的一个子列}{22k a k ,则11lim lim 2222==∞→∞→kka k n k n ,即0lim ≠∞→n n na . 10. 设0>n a ,且l a a nn n =+∞→1lim,求证l a n n n =∞→lim .反之是否成立?证明 令10=a ,构造数列⎭⎬⎫⎩⎨⎧=-1}{n n n a a u ,则}{n u 的前n 项的几何平均数可构成一个新数列,由于新数列收敛且与数列}{n u 极限相同,故11111lim lim lim++∞→+∞→+∞→===n n n n n n nn n u u u u a a ln n n n n n n n n n n n n a a a a a a a a a a ∞→+++∞→+-+∞→==⋅⋅=lim 1lim lim 1111011211 , 因而结论成立.反之不真,反例如级数∑∞=-+12)1(2n nn,由于21232)1(22121→≤-+=≤=nn n n n n n a , 故21lim =∞→n n n a ,而 613221,231223************=⋅==⋅=++--m m m m m m m m a a a a , 从而21lim1≠+∞→nn n a a ,因此反之结论不一定成立.11.利用级数收敛的必要条件证明:(1)0)!(lim 2=∞→n n n n ;(2))1(0)!2(lim!>=∞→a a n n n .证明(1)0)!(lim 2=∞→n n n n .考虑级数∑∞=12)!(n nn n ,由于 )(011111∞→→⎪⎭⎫⎝⎛++=+n n n u u nn n , 故级数∑∞=12)!(n n n n 收敛,因而0)!(lim 2=∞→n n nn . (2))1(0)!2(lim !>=∞→a a n n n .考虑级数∑∞=1!)!2(n n an ,由于)(0)12)(22(!1∞→→++=+n a n n u u nn n n , 所以级数∑∞=1!)!2(n n a n 收敛,因而)1(0)!2(lim !>=∞→a a n n n . 12.设0≥n a ,且数列}{n na 有界,证明级数∑∞=12n na收敛.证明 由数列}{n na 有界知,存在0>M ,对N n ∈∀,都有M na n ≤,从而nMa n ≤,进一步可得222n M a n≤,又由于∑∞=121n n收敛,因而由比较判别法知,级数∑∞=12n n a 收敛.13.设正项级数∑∞=1n na收敛,证明∑∞=+11n n n a a 也收敛.证明 由于对任意n ,1+n n a a )(211++≤n n a a 均成立,而级数∑∞=1n n a 和级数∑∞=+11n n a 均收敛,从而级数)(11∑∞=++n n na a也收敛,由比较判别法知,级数∑∞=+11n n n a a 收敛.14.设l a n n =∞→lim ,求证:(1)当1>l 时,∑∞=11n a nn 收敛; (2)当1<l 时,∑∞=11n a nn发散. 问1=l 时会有什么结论?证明(1)当1>l 时,令021>-=l ε,则由l a n n =∞→lim 知,存在N ,N n >∀时,有12121>+=--=->l l l l a n ε,从而当N n >时,2111+<l a n n n ,而∑∞=+1211n l n 收敛,故原级数收敛.(2)当1<l 时,令021>-=lε,则由l a n n =∞→lim 知,存在M ,M n >∀时,有12121<+=-+=+<l l l l a n ε,从而当M n >时2111+>l a n n n ,而∑∞=+1211n l n 发散,故原级数发散.当1=l 时,考虑级数∑∞=2)(ln 1n pn n ,由于nnp pn n n ln ln ln 1)(ln +=,令nnp a n ln ln ln 1+=,则1lim =∞→n n a ,此即为本题1=l 的情形,但由第5题(1)知,该级数在1>p 时收敛,1≤p 时发散,从而当1=l 时,级数∑∞=11n a nn 可能收敛也可能发散.§4 一般项级数1.讨论下列级数的收敛性:(1)∑∞=+-1100)1(n nn n;(2)∑∞=12sin ln n n n n π; (3)∑∞=++++-1131211)1(n nnn ;(4)∑∞=-+-2)1()1(n nnn ; (5))1(sin 21+∑∞=n n π;(6)∑∞=--12)1(3)1(n n n n ;(7))0()1(1>-∑∞=p n n pn; (8)2sin 311πn n n∑∞=; (9)∑∞=-12cos )1(n nnn; (10)∑∞=-12sin )1(n nn n;(11))0(sin)1(1≠-∑∞=x nxn n ; (12)∑∞=+-12)1()1(n n n n; (13)++--+++--++--1111131131121121n n ; (14))0(1)1(11>+-∑∞=+a a an n nn ;(15)∑∞=⎪⎭⎫ ⎝⎛+11sin n n n n ; (16)∑∞=⋅12sin sin n n n n .解(1)∑∞=+-1100)1(n nn n.令100)(+=x x x f ,则2)100(2100)(+-='x x x x f ,显然当100>x 时0)(≤'x f ,即)(x f 单调下降并趋向于0.由于级数前有限项的值不影响该级数的敛散性,因而由Leibniz 判别法知原交错级数收敛.(2)∑∞=12sin ln n n nn π.由于⎩⎨⎧∈-=-∈==+++,,12,)1(,,2,02sin 1Z k k n Z k k n n k π 舍去偶数项,原级数∑∑∞=+∞=---=11112)12ln()1(2sin ln k k n k k n n n π变成交错级数.令x xx f ln )(=,则2ln 1)(xxx f -=',显然当3≥x 时0)(<'x f ,即)(x f 单调下降并趋向于0.因而从第3项开始,数列⎭⎬⎫⎩⎨⎧n n ln 单调下降并趋向于0,故n 取奇数时该数列也是单调下降并趋向于0的,由Leibniz 判别法知,原交错级数收敛.(3)∑∞=++++-1131211)1(n nnn .由于数列的前n 项的算术平均数构成的新数列极限与原数列极限相等,故根据数列⎭⎬⎫⎩⎨⎧n 1单调递减趋向于0知,数列⎭⎬⎫⎩⎨⎧++++n n 131211 单调递减趋向于0,又因为原级数是一个交错级数,由Leibniz 判别法知原交错级数收敛.(4)∑∞=-+-2)1()1(n nn n .由于⎪⎪⎪⎭⎫ ⎝⎛+--=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+---=-+⋅-=-+-2311)1(1)1(1)1()1(11)1()1()1(nO n n n O n n nn n nn n n nnn ,而级数∑∞=-2)1(n nn及∑∞=2231n n收敛,但级数∑∞=21n n发散,因而原级数发散. (5))1(sin 21+∑∞=n n π.由于)1(sin )1())1(sin()1sin(222n n n n n n n -+-=-++=+ππππnn n ++-=1sin)1(2π,又由于⎭⎬⎫⎩⎨⎧++n n 1sin 2π单调下降趋于0,故由Leibniz 判别法知原级数收敛. (6)∑∞=--12)1(3)1(n n n n .由于∑∑∞=∞=-=-112)1(313)1(n nn nn n 收敛,故原级数绝对收敛,因而自身收敛.(7))0()1(1>-∑∞=p n n p n .由于pn 1单调递减趋向于0,根据Leibniz 判别法知原级数收敛.进一步可知:当10≤<p 时级数条件收敛,当1>p 时级数绝对收敛.(8)2sin 311πn n n ∑∞=.由于n n n 312sin31≤π,而∑∞=131n n 收敛,故原级数收敛且绝对收敛.(9)∑∞=-12cos )1(n nnn.由于 n k nk 2cos 1sin 24cos 1sin 22cos 1sin 22cos 1sin 21+++=∑=))12sin()12(sin()3sin 5(sin )1sin 3(sin --+++-+-=n n 1sin )12sin(-+=n ,故1sin 11sin 21sin )12sin(2cos 1≤-+=∑=n k nk ,即∑∞=12cos n n 的部分和数列有界,而数列⎭⎬⎫⎩⎨⎧n 1单调趋于0,由Dirichlet 判别法知级数∑∞=12cos n n n 收敛,即∑∞=-12cos )1(n n n n 收敛,从而原级。
数学分析课本-习题及答案第二十章

第十章 曲线积分一、证明题1.证明:若函数f 在光滑曲线L:x=x(t),y=y(t)(β≤≤αt )上连续,则存在点()L y ,x 00∈,使得,()⎰L ds y ,x f =()L y ,x f 00∆其中L ∆为L 的长。
二、计算题1.计算下列第一型曲线积分:(1) ()⎰+Lds y x ,其中L 是以0(0,0),A(1,0)B(0,1)为顶点的三角形; (2) ()⎰+L 2122ds y x ,其中L 是以原点为中心,R 为半径的右半圆周;(3) ⎰L xyds ,其中L 为椭圆22a x +22by =1在第一象限中的部分; (4) ⎰L ds y ,其中L 为单位圆22y x +=1;(5)()⎰++L 222ds z y x ,其中L 为螺旋线x=acost,y=asinr, z=bt(π≤≤2t 0)的一段;(6) ⎰L xyzds ,其中L 是曲线x=t,y=3t 232,z=2t 21 ()1t 0≤≤的一段; (7) ⎰+L 22ds z y 2,其中L 是222z y x ++=2a 与x=y 相交的圆周.2.求曲线x=a,y=at,z=2at 21(0a ,1t 0>≤≤)的质量,设其线密度为az 2=ρ, 3.求摆线x=a(t -sint),y=a(1-cost)(π≤≤t 0)的重心,设其质量分布是均匀的.4.若曲线以极坐()θρ=ρ()21θ≤θ≤θ表示,试给出计算()⎰Lds y ,x f 的公式.并用此公式计算下列曲线积分.(1)⎰+L y x ds e 22,其中L 为曲线ρ=a ⎪⎭⎫ ⎝⎛π≤θ≤40的一段; (2)⎰L xds ,其中L 为对数螺线θ=ρx ae (x>0)在圆r=a 内的部分. 5.设有一质量分布不均匀的半圆弧,x=rcos θ,y=rsin θ(π≤θ≤0),其线密度θ=ρa (a 为常数),求它对原点(θ,0)处质量为m 的质点的引力.6.计算第二型曲线积分:(1) ⎰-Lydx xdy ,其中L 为本节例2的三种情形; (2)()⎰+-L dy dx y a 2,其中L 为摞线x=a(t-sint),y=a(1-cost)(π≤≤2t 0)沿t 增加方向的一段; (3)⎰++-L 22y x ydy x dx ,其中L 为圆周222a y x =+,依逆时针方向; (4)⎰+L xdy sin ydx ,其中L 为y=sinx(π≤≤x 0) 与x 轴所围的闭曲线,依顺时针方向;(5)⎰++Lzdz ydy xdx ,其中L 为从(1,1,1)到(2,3,4)的直线段. 7.质点受力的作用,力的反方向指向原点,大小与质点离原点的距离成正比,若质点由(a,0)沿椭圆移动到(0,b),求力所作的功.8.设质点受力的作用,力的方向指向原点,大小与质点到xy 平面的距离成反比,若质点沿直线x=at,y=bt,z=ct(0c ≠) 从M(a,b,c)到N(2a,2b,2c),求力所作的功.9.计算沿空间曲线的第二型曲线积分:(1)⎰L xyzddz ,其中L 为x 2+y 2+z 2=1与y=z 相交的圆,其方向按曲线依次经过1,2,7,8卦限;(2) ()()()⎰-+-+-L 222222dz y x dy x z dx z y ,其中L 为球面x 2+y 2+z 2=1在第一卦限部分的边界线,其方向按曲线依次经过xy 平面部分,yz 平面部分和zx 平面部分.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f (P0 ) 2
d r
(
P
,
P0
)
2
f ( p0 ) ( )2 22
2 8
f ( p0 ) 0.
(2) 若在 上 f (P) g(P) ,即 P0 ,使 f (P0 ) g(P0 ) . 不妨设 f (P0 ) g(P0 ) ,
由此得 f (P0 ) g(P0 ) 0. 由于 f , g 在 上连续,因而函数 f (P) g(P) 在 上连续,因而在 P0
i 1
i 1
令d
max{
1i n
i的直径}
0,
按积分的定义,
n
n
D
f ( p)d
lim d 0 i 1
f
(
pi ) i
lim
d 0
i 1
g( pi ) i
D
g( p)d
.
性质(6)为积分中值定理: 设 D 是有界闭区域(因而是连通的), f (P) 在 D 上连续,则存在
P0 D ,使得 f (P)d f (P0 ) D ,其中 D 表示 D 的面积.
b
f (x)dx
d
g( y)dy.
a
c
a
c
a
c
D
5.若 f (x, y) 在 D 上可积,那么 f (x, y) 在在 D 上是否可积?考察函数
f
(x,
y)
1, 1,
若x, y都是有理数 若x, y至少有一个是无理数
在[0,1] [0,1] 上的积分.
第二十章 重 积 分
§1 重积分的概念
1.证明性质(4),性质(6).
证明 性质(4)为单调性:若 f 与 g 都在 D 可积,且在 D 的每点 P 都有 f (P) g(P) ,则
f (P)d g(P)d .
D
D
事实上, f 与 g 的 Rimann 和有以下关系:
n
n
f ( pi ) i g( pi ) i ,
D
n
lim (
0 i 1
d c
f (i )g( y)dy)xi
D
f (x)g( y)dxdy.
由定积分的定义即得
b d
(
ac
f
(x)g( y)dy)dx
f
(x)g( y)dxdy.
D
即
f (x)g( y)dxdy
b
dx
d
f (x)g( y)dy
b
( f (x)
d g( y)dy)dx
n
i1
m
mijxiy j
j1
n i1
d c
f
(i )g( y)dyxi
n i1
m
M ijxiy j ,
j1
当
max{
1i n
ij的直径}
0
时
,
m1iaxn{xi} 0. 由 于 f (x)g( y) 在 矩 形 区 域
1 j m
D [a,b] [c, d ]上可积,上式左右两端当 0 时有公共极限值 f (x)g( y)dxdy.因此由夹迫性
(2) 若在 的任何区域 上,有 f ( p)d= g( p)d ,则在 上有, f ( p) g( p).
证明:不妨设 是可度量的平面图形, f , g 在 上连续.
(1) 若在 上 f ( p) 0, 且 f ( p) 0, 则存在一点 P0 , 使 f ( p0 ) 0.
2D
,
D
表示 D 的面积.
把
D
分成 n
个 区 域 1, 2,, n ,
使
d
m
显
然
f (P)
在 i
上的振幅
i
2D
.
所以
n
i i
i 1
2D
D
2
.
故 f (P) 在 D 上可积.
3.设 是可度量的平面图形或空间立体, f , g 在 上连续,证明:
(1) 若在 上 f ( p) 0, 且 f ( p) 0, 则 f ( p)d 0;
连续,故对
f (P0 ) g(P0 ) 0, 2
0
,当
r(P,
P0
)
2
时,有
f (P) g(P) ( f (P0 ) g(P0 ))
f (P0 ) g(P0 ) . 2
即有
f (P) g(P) f (P0 ) g(P0 ) . 2
设
{P
:
r(P,
P0
)
2
}
,这时
[ f (P) g(P)]d
由于
f
在
上连续,
因
而
对
f ( P0 ) 2
0,
0, P
, r(P,
P0
)
2
,
就
有
f (P)
f (P0 )
f (P0 ) ,即有 f (P) 2
f (P0 ) . 2
由可加性,有
f (P)d
r
(
P
,
P0
)
2
f (P)d
{r
(
P
,
P0
)
2
}
f
(P)d
r
(
P
,
P0
)
2
f (P)d
,即
f ( p)d f ( p0 ) D .
D
2.证明有界闭区域上的连续函数必可积.
证 明 在 有 界 闭 区 域 D 上 的 连 续 函 数 f (P) 必 定 是 一 致 连 续 的 , 故
0,
0, P1 , P2
D ,只要 r( p1, p2 )
,就有
f (P1 )
f (P2 )
y)dxdy
b a
f
d
( x)dx c
g( y)dy.
D
证明: 用平行坐标轴的直线网 a x0 x1 x2 xn b, c y0 y1 y2 ym d ,
将 D 分 为 m n 个 小 矩 形 ij [xi1, xi ] [ y j1, y j ]. 记 f (x)g( y) 在 ij 的 上 下 确 界 分 别 为
M ij , mij ,任取 i [xi1, xi ], 则
mijy j
yj y j1
f
(i )g( y)dy
M ijy j ,
对 j 求和得
i 1,2,, n, j 1,2,, m.
m
mijy j
j 1
d c
f
(i )g( y)dy
m
M ijy j ,
j 1
i 1,2,, n.
乘以 xi 后再对 i 求和,得
f
( P0
)
g ( P0
)
(
)
2
0.
2
2
即 f ( p)d g( p)d ,矛盾. 所以在 上 f (P) g(P).
4.设 f (x) 在[a,b] 可积, g( y) 在[c, d ]可积,则 f (x)g( y) 在矩形区域 D [a,b] [c, d ] 上可积,且
f
(x)g(
D
事实上,设 M 与 m 是连续函数 f (P) 在有界闭区域 D 上的最大值与最小值,即: P D ,
f (P)d
m f (P) M . 所以, m D f ( p)d M D ,即 m D
D
D
M .
f (P)d
由 有 界 闭 区 域 上 的 连 续 函 数 的 介 值 定 理 , 存 在 P0 D , 使 得 f (P0 ) D D
