高中数学三角函数练习题
高中数学三角函数专项练习题(含答案)

高中数学三角函数专项练习题(含答案)一、填空题1.设函数()f x 是定义在实数集R 上的偶函数,且()()2f x f x =-,当[0,1]x ∈时,3()f x x =,则函数()|cos |()g x x f x π=-在15,22⎡⎤-⎢⎥⎣⎦上所有零点之和为___________.2.如图所示,一竖立在地面上的圆锥形物体的母线长为4,一只小虫从圆锥的底面圆上的点P 出发,绕圆锥爬行一周后回到点P 处,若该小虫爬行的最短路程为43,则这个圆锥的体积为___________.3.已知三棱锥S ABC -中,SA SB SC ==,ABC 是边长为4的正三角形,点E ,F 分别是SC ,BC 的中点,D 是AC 上的一点,且EF SD ⊥,若3FD =,则DE =___________. 4.已知函数()2sin()f x x ωφ=+(0>ω,||φπ<)的部分图象如图所示,()f x 的图象与y 轴的交点的坐标是(0,1),且关于点(,0)6π-对称,若()f x 在区间14(,)333ππ上单调,则ω的最大值是___________.5.已知函数()sin 2sin 23f x x x a π⎛⎫=+++ ⎪⎝⎭同时满足下述性质:①若对于任意的()()()123123,0,,4,x x x f x f x f x π⎡⎤∈+⎢⎥⎣⎦恒成立;②236f a π⎛⎫- ⎪⎝⎭,则a 的值为_________.6.在角1θ,2θ,3θ,…,29θ的终边上分别有一点1P ,2P ,3P ,…,29P ,如果点k P 的坐标为()()()sin 15,sin 75k k-+,129k ≤≤,k ∈N ,则12329cos cos cos cos θθθθ+++⋅⋅⋅+=______7.已知ABC 为等边三角形,点G 是ABC 的重心.过点G 的直线l 与线段AB 交于点D ,与线段AC 交于点E .设AD AB λ=,AE AC μ=,则11λμ+=__________;ADE 与ABC 周长之比的取值范围为__________.8.如图,在边长为2的正方形ABCD 中,M ,N 分别为边BC ,CD 上的动点,以MN 为边作等边PMN ,使得点A ,P 位于直线MN 的两侧,则PN PB ⋅的最小值为______.9.已知空间单位向量1e ,2e ,3e ,4e ,1234123421+=+=+++=e e e e e e e e ,则13⋅e e 的最大值是___________.10.在平面直角坐标系xOy 中,已知直线2y x =+与x 轴,y 轴分别交于M ,N 两点,点P 在圆22()2x a y -+=上运动.若MPN ∠恒为锐角,则实数a 的取值范围是________.二、单选题11.已知函数()()sin cos sin cos 0f x x x x x ωωωωω=++->,则下列结论错误的是( )①1ω=时,函数()f x 图象关于π4x =对称;②函数()f x 的最小值为-2;③若函数()f x 在π,04⎡⎤-⎢⎥⎣⎦上单调递增,则(]03ω∈,;④1x ,2x 为两个不相等的实数,若()()124f x f x +=且12x x -的最小值为π,则2ω=. A .②③B .②④C .①③④D .②③④12.已知函数()|sin |(0)f x x ωω=>在区间,53ππ⎡⎤⎢⎥⎣⎦上单调递减,则实数ω的取值范围为( ) A .5,32⎡⎤⎢⎥⎣⎦B .30,2⎛⎤ ⎥⎝⎦C .8,33⎡⎤⎢⎥⎣⎦D .50,4⎛⎤ ⎥⎝⎦13.已知函数()2sin()0,02f x x πωϕωϕ⎛⎫=+><< ⎪⎝⎭,且有()02f ()()1g x f x =-的图象在()0,2π内有5个不同的零点,则ω的取值范围为( )A .5571,2424⎛⎤ ⎥⎝⎦B .5571,2424⎛⎫ ⎪⎝⎭C .4755,2424⎛⎫ ⎪⎝⎭D .4755,2424⎛⎤ ⎥⎝⎦14.已知函数()()sin f x x ωφ=+π0,02ωφ⎛⎫><< ⎪⎝⎭在π5π,88⎛⎫ ⎪⎝⎭上单调,且π3π088f f ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭,则π2f ⎛⎫⎪⎝⎭的值为( ) A .22B .1C .1-D .22-15.在ABC 中,,E F 分别是,AC AB 的中点,且32AB AC =,若BEt CF <恒成立,则t 的最小值为( ) A .34B .78C .1D .5416.已知双曲线22413y x -=的左右焦点分别为1F ,2F ,点M 是双曲线右支上一点,满足120MF MF →→⋅=,点N 是线段12F F 上一点,满足112F N F F λ→→=.现将12MF F △沿MN 折成直二面角12F MN F --,若使折叠后点1F ,2F 距离最小,则λ=( )A .15B .25C .35D .4517.如图,长方形ABCD 中,152AB =,1AD =,点E 在线段AB (端点除外)上,现将ADE 沿DE 折起为A DE '.设ADE α∠=,二面角A DE C '--的大小为β,若π2αβ+=,则四棱锥A BCDE '-体积的最大值为( )A .14B .23C 151-D 51-18.在三棱锥A BCD -中,5,2,2AC AD AB CD BC BD ======接球的半径为( ) A 210B 210C 25D .519.()sin()(0)f x x ωφφ=+>的部分图象如图所示,设P 是图象的最高点,A ,B 是图象与x 轴的交点,若tan 2APB ∠=-,则ω的值为( )A .4π B .3π C .2π D .π20.在ABC 中,若22sin cos 1A B +=,则8cos AB BCBC A AC+的取值范围为( )A .)43,8⎡⎣B .)43,7⎡⎣C .()7,8D .()0,43三、解答题21.将函数2sin 3y x =+的图象上所有点的横坐标缩短到原来的12倍,纵坐标不变,再将所得的图象向右平移3π个单位长度后得到函数()f x 的图象. (1)写出函数()f x 的解析式;(2)若,36x ππ⎡⎤∈-⎢⎥⎣⎦时,22()2()()1g x f x mf x m =-+-,求()g x 的最小值min ()g x .22.已知1l ,2l ,3l 是同一平面内自上而下的三条不重合的平行直线.(1)如图1,如果1l 与2l 间的距离是1,2l 与3l 间的距离也是1,可以把一个正三角形ABC 的三顶点分别放在1l ,2l ,3l 上,求这个正三角形ABC 的边长.(2)如图2,如果1l 与2l 间的距离是1,2l 与3l 间的距离是2,能否把一个正三角形ABC 的三顶点分别放在1l ,2l ,3l 上,如果能放,求BC 和3l 夹角θ的正切值并求该正三角形边长;如果不能,试说明理由.(3)如果边长为2的正三角形ABC 的三顶点分别在1l ,2l ,3l 上,设1l 与2l 间的距离为1d ,2l 与3l 间的距离为2d ,求12d d ⋅的取值范围.23.将函数()sin 2g x x =3向左平移4π个单位长度,得到函数()y f x =的图象,设函数()()()h x f x g x =+. (1)对函数()h x 的解析式;(2)若对任意,,2παβπ⎡⎤∈⎢⎥⎣⎦,不等式()()a h h b αβ≤-≤恒成立,求b a -的最小值;(3)若26x h t π⎛⎫-= ⎪⎝⎭在[)0,2π内有两个不同的解1x ,2x ,求()12cos x x -的值(用含t 的式子表示).24.在①ABC ∆面积2ABC S ∆=,②6ADC π∠=这两个条件中任选一个,补充在下面问题中,求AC .如图,在平面四边形ABCD 中,34ABC π∠=,BAC DAC ∠=∠,______,24CD AB ==,求AC .25.已知函数22()cos sin 3sin cos 3f x a x a x x x =-+-,其中a R ∈. (Ⅰ)当1a =时,求函数()f x 的对称中心;(Ⅱ)若函数()f x 的最小值为4-,求实数a 的值.26.已知ABC ∆的外接圆...2,内角A ,B ,C 的对边分别为a ,b ,c ,又向量()sin sin ,m A C b a =--,2sin sin n A C B ⎛⎫=+ ⎪ ⎪⎝⎭,且m n ⊥. (1)求角C ;(2)求三角形ABC 的面积S 的最大值并求此时ABC ∆的周长. 27.在ABC ∆中,角,,A B C 的对边分别为,,a b c . 已知10sin 2C =(1)若4a =,210c =ABC ∆的面积; (2)若ABC ∆91522213sin sin sin 16A B C +=,求c 的值.28.已知函数22()sin 22sin 26144f x x t x t t ππ⎛⎫⎛⎫=---+-+ ⎪ ⎪⎝⎭⎝⎭,,242x ππ⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭,最小值为()g t .(1)求当1t =时,求8f π⎛⎫⎪⎝⎭的值;(2)求()g t 的表达式; (3)当112t -≤≤时,要使关于t 的方程2()9g t k t =-有一个实数根,求实数k 的取值范围.29.已知函数()()2cos 3sin cos 1f x xx x =+-.(1)求函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值;(2)若()85f x =-,2,3x ππ⎡⎤∈⎢⎥⎣⎦,求cos2x 的值;(3)若函数()()0y f x ωω=>在区间,62ππ⎡⎤⎢⎥⎣⎦上是单调递增函数,求正数ω的取值范围.30.函数f (x )=A sin (2ωx +φ)(A >0,ω>0,|φ|<2π)的部分图象如图所示 (1)求A ,ω,φ的值;(2)求图中a ,b 的值及函数f (x )的递增区间; (3)若α∈[0,π],且f (α)=2,求α的值.【参考答案】一、填空题1.7 21282π37 4.115.06.07. 3 213,32⎡⎢⎣⎦8.14- 9735+ 10.71a 或4a二、单选题 11.B 12.A 13.A 14.D 15.B 16.C 17.A 18.A 19.C 20.A 三、解答题21.(1)2()2sin 233f x x π⎛⎫=-+ ⎪⎝⎭;(2)22min21,47()1,4128(32312m m m g x m m m m m ⎧-+≤⎪⎪=-<<+⎨⎪⎪-++≥+⎩ 【解析】(1)根据函数图象的变换规律即可求得()f x 的解析式;(2)令()t f x =可求得则()[1,3f x ∈+,设22()21M t t mt m =-+-,[1,3t ∈,通过定区间讨论对称轴4mt =的三种情况()M t 的单调性,进而可确定最小值的情况. 【详解】(1)将函数2sin 3y x =+的图象上所有点的横坐标缩短到原来的12倍,可得2sin 23y x =+得图象,再向右平移3π个单位长度得2()2sin 232sin 2333f x x x ππ⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎝⎭⎝⎭. (2)∵,36x ππ⎡⎤∈-⎢⎥⎣⎦,242,333x πππ⎡⎤-∈--⎢⎥⎣⎦,则()[1,3f x ∈+, 令()t f x =,则设22()21M t t mt m =-+-,[1,3t ∈+, ①当14m≤,即4m ≤时,函数()M t在[1,3上单调递增, ∴22min ()(1)211M t M m m m m ==-+-=-+;②当134m<<412m <<+ 函数()M t 在1,4m ⎛⎫ ⎪⎝⎭上单调递减,在,34m ⎛ ⎝上单调递增,∴2min 7()148m M t M m ⎛⎫==- ⎪⎝⎭;③当34m≥+12m ≥+()M t在[1,3+上单调递减,∴2min ()(3(323M t M m m ==-++∴综上有22min21,47()1,4128(32312m m m g x m m m m m ⎧-+≤⎪⎪=-<<+⎨⎪⎪-++≥+⎩. 【点睛】本题考查三角函数图象的变换,考查二次函数在三角函数中的应用,考查定区间动轴的最值取值情况,难度较难.22.(1)2 ;(2)能放,tan θ=;(3)(]0,1 【解析】 【分析】(1)根据,A C 到直线2l 的距离相等,可得2l 过AC 的中点M ,2l AC ⊥,从而求得边长2AC AM =的值.(2)假设能放,设边长为a ,BC 与3l 的夹角θ,不妨设060θ<≤,可得sin 2a θ=,()sin 601a θ-=,两式相比化简可得sin θa 的值,从而得出结论. (3)利用两角和差的正弦、余弦公式化简()124sin 60sin d d θθ⋅=-为()2sin 2301θ+-,再根据正弦函数的定义和值域求出12d d ⋅的取值范围. 【详解】 (1),A C 到直线2l 的距离相等,∴2l 过AC 的中点M , ∴2l AC ⊥, ∴边长22AC AM ==(2)假设能放,设边长为a ,BC 与3l 的夹角θ, 由对称性,不妨设060θ<≤, ∴sin 2a θ=,()sin 601a θ-=,两式相比可得:()sin 2sin 60θθ=-,即sin sin θθθ-,2sin θθ∴=,tan θ∴=,sin θ∴=,故边长a ==, 综上可得,能放.(3)()1214sin 60sin 4sin sin 2d d θθθθθ⎫⋅=-=-⎪⎪⎝⎭()1cos 2222sin 23012θθθ⎫+=-=+-⎪⎪⎝⎭. 060θ<≤,30230150θ∴<+≤,()1sin 23012θ≤+≤, 所以()02sin 23011θ≤+-≤, 又10d >,20d >,所以(]120,1d d ⋅∈. 【点睛】本题是一道考查三角函数应用的题目,解题的关键是掌握等边三角形的性质以及三角函数的恒等变换,属于中档题.23.(1)()2sin 23h x x π⎛⎫=+ ⎪⎝⎭(2)4;(3)()212cos 12tx x -=-【解析】(1)将()g x⇒2y x =;再向左平移4π个单位长度⇒()24f x x π⎛⎫=+ ⎪⎝⎭,最后代入()h x ,得答案;(2)对()h x 在,2x ππ⎡⎤∈⎢⎥⎣⎦,由内到外求出值域,因为()()a h h b αβ≤-≤恒成立,所以max b m ≥,min a m ≤,整理得答案;(3)表示26x h π⎛⎫- ⎪⎝⎭并化简,由1x ,2x 是2sin x t =在[)0,2π内有两个不同的解,所以12x x π+=或123x x π+=,因需求()12cos x x -,所以分别表示12x x -并代入,利用诱导公式和二倍角公式化简,将式子中22sin x 换成t 得答案. 【详解】(1)将函数()sin 2g x x =得到函数2y x =的图象,再将2y x =的图象向左平移4π个单位长度得到函数()y f x =,所以()224f x x x π⎛⎫=+= ⎪⎝⎭,又()()()h x f x g x =+,所以()sin 222sin 23h x x x x π⎛⎫==+ ⎪⎝⎭;(2)当,2x ππ⎡⎤∈⎢⎥⎣⎦时,472,333x πππ⎛⎫⎛⎫+∈ ⎪ ⎪⎝⎭⎝⎭,所以sin 21,3x π⎡⎛⎫+∈-⎢ ⎪⎝⎭⎣⎦,所以2sin 22,3x π⎛⎫⎡+∈- ⎪⎣⎝⎭, 令()()m h h αβ=-,因为()()a h h b αβ≤-≤恒成立,所以max 2b m ≥=,min 2a m ≤=-2a -≥所以4b a -≥即b a -的最小值为4;(3)法一:因为2sin 22sin 26263x x h x πππ⎡⎤⎛⎫⎛⎫-=-+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,所以1x ,2x 是2sin x t =在[)0,2π内有两个不同的解, 所以12x x π+=或123x x π+=, 所以1222x x x π-=-或12232x x x π-=-所以()()22212221cos 2sin 12sin 1122t x x x x -=-=-=-;法二:①当t >0时,不妨设12x x <,则有1202x x ππ<<<<,所以1cos x =2cos x =②当0t <时,不妨设12x x <,则有1232x x πππ<<<<2,所以1cos x 2cos x = ③当0=t 时,显然有10x =,2x π=,所以()2121212cos cos cos sin sin 12t x x x x x x -=+=-.【点睛】本题考查了由三角函数图像的伸缩平移变换表示解析式,给定定义域求三角函数值域,不等式恒成立问题,还考查了函数零点问题,充分体现了数学中转化与划归思想,属于难题. 24.见解析 【解析】选择①:利用三角形面积公式和余弦定理可以求接求出AC 的长;选择②:在ABC ∆,ACD ∆中,分别运用正弦定理,可以求接求出AC 的长; 【详解】 解:选择①:113sin 2sin 2224ABC S AB BC ABC BC π∆=⋅⋅⋅∠=⋅⋅⋅=所以BC = 由余弦定理可得2222cos AC AB BC AB BC ABC =+-⋅⋅∠482220⎛=+-⨯⨯=⎝⎭所以AC==选择②设BAC CADθ∠=∠=,则04πθ<<,4BCAπθ∠=-,在ABC∆中sin sinAC ABABC BCA=∠∠,即23sin sin44ACππθ=⎛⎫-⎪⎝⎭所以sin4ACπθ=⎛⎫-⎪⎝⎭在ACD∆中,sin sinAC CDADC CAD=∠∠,即4sinsin6ACπθ=所以2sinACθ=.所以2sinsin4πθθ=⎛⎫-⎪⎝⎭,解得2sin cosθθ=,又04πθ<<,所以sinθ=,所以2sinACθ==【点睛】本题考查了正弦定理、余弦定理、三角形面积公式,考查了数学运算能力.25.(Ⅰ)(,3),.122kk Zππ-+-∈(Ⅱ)12a=或12a=-【解析】(Ⅰ)当1a=时,根据二倍角公式、辅助角公式化简函数,根据正弦函数的性质可得.(Ⅱ)将函数化简为()sin()f x A x bωϕ=++的形式,分类讨论可得.【详解】解:(Ⅰ)当1a=时,22()cos sin cos3f x x x x x=-+-cos2232sin(2)36x x xπ=-=+-()2sin(2)36f x xπ∴=+-由2,6x k k Zππ+=∈得:,122kx k Zππ=-+∈()f x∴的对称中心为(,3),.122kk Zππ-+-∈(Ⅱ)22()cos sin sin cos 3f x a x a x x x =-+-()cos 2sin 23f x a x x ∴=-()2sin(2)36f x a x π∴=+- 1sin(2)16x π-≤+≤ 当0a >时,232sin(2)3236a a x a π--≤+-≤- 则有234a --=- 解得12a = 当0a =时,min ()3f x =-,不合题意当0a <时,232sin(2)3236a a x a π-≤+-≤-- 则有234a -=-解得12a =- 综上 12a ∴=或12a =-. 【点睛】本题主要考查三角函数的图象和性质,利用三角公式将函数进行化简是解决本题的关键,要求熟练掌握三角函数的图象和性质,属于中档题.26.(1) 3C π=. (2) max S = 【解析】【分析】(1)由0m n m n ⊥⇒⋅=,利用坐标表示化简,结合余弦定理求角C (2)利用(1)中222c a b ab =+-,应用正弦定理和基本不等式,即可求出面积的最大值,此时三角形为正三角即可求周长.【详解】(1)∵0m n m n ⊥⇒⋅=,∴()())sin sin sin sin sin 0A C A C b a B -+-=,且2R =)22022a c b a R R ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭, 化简得:222c a b ab =+-.由余弦定理:2222cos c a b ab C =+-,∴12cos 1cos 2C C =⇒=, ∵0C π<<,∴3C π=.(2)∵()22222sin 6a b ab c R C +-===,∴2262a b ab ab ab ab =+-≥-=(当且仅当a b =时取“=”)1sin 2S ab C ==≤所以,max S =ABC ∆为正三角形,此时三角形的周长为 【点睛】本题主要考查了利用数量积判断两个平面向量的垂直关系,正弦定理,余弦定理,基本不等式,属于中档题.27.(1)2)c =【解析】【分析】(1)先根据sin 2C =sin C 与cos C ,再利用余弦定理求出b 边,最后利用1sin 2ABC S ab C ∆=求出答案; (2)利用正弦定理将等式化为变得关系,再利用余弦定理化为2c 与ab 的关系式,再结合面积求出c 的值.【详解】解:(1)因为sin 2C = 所以2101cos 12sin 122164C C =-=-⨯=-.又()0,C π∈,所以sin C =.因为4a =,c =2222cos c a b ab C =+-, 所以214016244b b ⎛⎫=+-⨯⨯- ⎪⎝⎭, 解得4b =,所以11sin 4422ABC S ab C ∆==⨯⨯= (2)因为22213sin sin sin 16A B C +=,由正弦定理,得2221316a b c +=. 又2222cos a b ab C c +-=,所以283c ab =.又1sin 2ABC S ab C ∆=,得18ab =,所以248c =,所以c = 【点睛】 本题考查正余弦定理解三角形,属于基础题.28.(1)4-(2)22515421()611282(1)t t t g t t t t t t ⎧⎛⎫-+<- ⎪⎪⎝⎭⎪⎪⎛⎫=-+-≤≤⎨ ⎪⎝⎭⎪⎪-+>⎪⎩(3)--22∞⋃+∞(,)(,) 【解析】【分析】 (1)直接代入计算得解;(2)先求出1sin(2)[,1]42x π-∈-,再对t 分三种情况讨论,结合二次函数求出()g t 的表达式;(3)令2()()9h t g t k t =-+,即2()(6)t 10h t k =-++有一个实数根,利用一次函数性质分析得解.【详解】(1)当1t =时,2()sin 22sin 2444f x x t x ππ⎛⎫⎛⎫=---- ⎪ ⎪⎝⎭⎝⎭,所以48f π⎛⎫=- ⎪⎝⎭. (2)因为[,]242x ∈ππ,所以32[,]464x πππ-∈-,所以1sin(2)[,1]42x π-∈- 2()[sin(2)]614f x x t t π=---+([,]242x ∈ππ) 当12t <-时,则当1sin(2)42x π-=-时,2min 5[()]54f x t t =-+ 当112t -≤≤时,则当sin(2)4x t π-=时,min [()]61f x t =-+ 当1t >时,则当sin(2)14x π-=时,2min [()]82f x t t =-+ 故22515421()611282(1)t t t g t t t t t t ⎧⎛⎫-+<- ⎪⎪⎝⎭⎪⎪⎛⎫=-+-≤≤⎨ ⎪⎝⎭⎪⎪-+>⎪⎩(3)当112t -≤≤时,()61g t t =-+,令2()()9h t g t k t =-+即2()(6)t 10h t k =-++ 欲使2()9g t kt =-有一个实根,则只需1()02(1)0h h ⎧-≤⎪⎨⎪≥⎩或1()02(1)0h h ⎧-≥⎪⎨⎪≤⎩ 解得-2k ≤或2k ≥.所以k 的范围:--22∞⋃+∞(,)(,). 【点睛】本题主要考查三角函数的范围的计算,考查二次函数的最值的求法和方程的零点问题,意在考查学生对这些知识的理解掌握水平和分析推理能力,属于中档题.29.(I )1-;(II;(III )10,3⎛⎤ ⎥⎝⎦ 【解析】【分析】 将()f x 整理为2sin 26x π⎛⎫+ ⎪⎝⎭;(I )利用x 的范围求得26x π+的范围,结合sin x 的图象可求得最值;(II )利用()85f x =-可求得sin 26x ;结合角的范围和同角三角函数关系可求得cos 26x π⎛⎫+ ⎪⎝⎭;根据cos 2cos 266x x ππ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦,利用两角和差余弦公式可求得结果;(III )利用x 的范围求得26x πω+的范围,从而根据sin x 单调递增区间构造出关于ω的不等式组,解不等式组再结合0>ω即可得到结果.【详解】()2cos 2cos 12cos 22sin 26f x x x x x x x π⎛⎫=+-=+=+ ⎪⎝⎭ (I )0,2x π⎡⎤∈⎢⎥⎣⎦ 72,666x πππ⎡⎤∴+∈⎢⎥⎣⎦[]2sin 21,26x π⎛⎫∴+∈- ⎪⎝⎭ ()f x ∴在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值为:1- (II )由题意得:82sin 265x π⎛⎫+=- ⎪⎝⎭ 4sin 265x π⎛⎫∴+=- ⎪⎝⎭ 2,3x ππ⎡⎤∈⎢⎥⎣⎦ 3132,626x πππ⎡⎤∴+∈⎢⎥⎣⎦ 3cos 265x π⎛⎫∴+= ⎪⎝⎭ cos 2cos 2cos 2cos sin 2sin 666666x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫∴=+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦341552=⨯(III )()2sin 26f x x πωω⎛⎫=+ ⎪⎝⎭ ,62x ππ⎡⎤∈⎢⎥⎣⎦时,2,6366x πωπππωωπ⎡⎤+∈++⎢⎥⎣⎦ 2622362k k ππωππωππππ⎧+≤+⎪⎪∴⎨⎪+≥-⎪⎩,k Z ∈,解得:12362k k ωω⎧≤+⎪⎨⎪≥-⎩,k Z ∈ 0ω>,可知当0k =时满足题意,即103ω<≤ω∴的取值范围为:10,3⎛⎤ ⎥⎝⎦【点睛】本题考查正弦型函数的值域求解、单调性应用、三角恒等变换公式应用、同角三角函数关系等问题.关键是能够利用二倍角公式和辅助角公式将函数化为()sin A x ωϕ+的形式,从而通过整体对应的方式来研究函数的值域和性质.30.(1)π2,1,6A ωϕ===;(2)7π,112a b =-=,递增区间为()πππ,π36k k k Z ⎡⎤-+∈⎢⎥⎣⎦;(3)π24或7π24. 【解析】【分析】(1)利用函数图像可直接得出周期T 和A ,再利用=2T πω,求出ω, 然后利用待定系数法直接得出ϕ的值.(2)通过第一问求得的值可得到()f x 的函数解析式,令()=0f x ,再根据a 的位置确定出a 的值;令0x =得到的函数值即为b 的值;利用正弦函数单调增区间即可求出函数的单调增区间.(3)令()f α=0απ,即可求得α的取值. 【详解】解:(1)由图象知A =2,34T =512π-(-3π)=912π, 得T =π, 即22πω=2,得ω=1, 又f (-3π)=2sin[2×(-3π)+φ]=-2, 得sin (-23π+φ)=-1, 即-23π+φ=-2π+2k π, 即ω=6π+2k π,k ∈Z , ∵|φ|<2π, ∴当k =0时,φ=6π, 即A =2,ω=1,φ=6π; (2)a =-3π-4T =-3π-4π=-712π,b =f (0)=2sin6π=2×12=1, ∵f (x )=2sin (2x +6π), ∴由2k π-2π≤2x +6π≤2k π+2π,k ∈Z , 得k π-3π≤x ≤k π+6π,k ∈Z , 即函数f (x )的递增区间为[k π-3π,k π+6π],k ∈Z ;(3)∵f (α)=2sin (2α+6π)即sin (2α+6π) ∵α∈[0,π],∴2α+6π∈[6π,136π], ∴2α+6π=4π或34π, ∴α=24π或α=724π.【点睛】关于三角函数图像需记住:两对称轴之间的距离为半个周期;相邻对称轴心之间的距离为半个周期; 相邻对称轴和对称中心之间的距离为14个周期. 关于正弦函数单调区间要掌握: 当2,222x k k ππωϕππ⎡⎤+∈-+⎢⎥⎣⎦时,函数单调递增; 当32+,222x k k ππωϕππ⎡⎤+∈+⎢⎥⎣⎦时,函数单调递减.。
高中数学(三角函数)练习题及答案

第一章 三角函数一、选择题 1.已知为第三象限角,则2α所在的象限是(). A .第一或第二象限B .第二或第三象限 C .第一或第三象限D .第二或第四象限 2.若sin θcos θ>0,则θ在(). A .第一、二象限B .第一、三象限 C .第一、四象限D .第二、四象限 3.sin3π4cos 6π5tan ⎪⎭⎫ ⎝⎛3π4-=(). A .-433B .433C .-43D .43 4.已知tan θ+θtan 1=2,则sin θ+cos θ等于(). A .2B .2C .-2D .±2 5.已知sin x +cos x =51(0≤x <π),则tan x 的值等于(). A .-43B .-34C .43D .34 6.已知sin >sin ,那么下列命题成立的是(). A .若,是第一象限角,则cos >cos B .若,是第二象限角,则tan >tan C .若,是第三象限角,则cos >cos D .若,是第四象限角,则tan>tan7.已知集合A ={|=2k π±3π2,k ∈Z },B ={|=4k π±3π2,k ∈Z },C = {γ|γ=k π±3π2,k ∈Z },则这三个集合之间的关系为( ). A .A ⊆B ⊆C B .B ⊆A ⊆C C .C ⊆A ⊆B D .B ⊆C ⊆A8.已知cos(+)=1,sin =31,则sin的值是().A .31B .-31C .322D .-3229.在(0,2π),使sin x >cos x 成立的x 取值围为(). A .⎪⎭⎫ ⎝⎛2π ,4π∪⎪⎭⎫ ⎝⎛4π5 ,πB .⎪⎭⎫⎝⎛π ,4πC .⎪⎭⎫ ⎝⎛4π5 ,4πD .⎪⎭⎫ ⎝⎛π ,4π∪⎪⎭⎫ ⎝⎛23π ,4π510.把函数y =sin x (x ∈R )的图象上所有点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的21倍(纵坐标不变),得到的图象所表示的函数是(). A .y =sin ⎪⎭⎫ ⎝⎛3π - 2x ,x ∈R B .y =sin ⎪⎭⎫ ⎝⎛6π + 2x ,x ∈RC .y =sin ⎪⎭⎫ ⎝⎛3π + 2x ,x ∈RD .y =sin ⎪⎭⎫ ⎝⎛32π + 2x ,x ∈R二、填空题11.函数f (x )=sin 2x +3tan x 在区间⎥⎦⎤⎢⎣⎡3π4π ,上的最大值是.12.已知sin =552,2π≤≤π,则tan =. 13.若sin ⎪⎭⎫ ⎝⎛α + 2π=53,则sin ⎪⎭⎫⎝⎛α - 2π=.14.若将函数y =tan ⎪⎭⎫ ⎝⎛4π + x ω(ω>0)的图象向右平移6π个单位长度后,与函数y =tan ⎪⎭⎫ ⎝⎛6π + x ω的图象重合,则ω的最小值为.15.已知函数f (x )=21(sin x +cos x )-21|sin x -cos x |,则f (x )的值域是. 16.关于函数f (x )=4sin ⎪⎭⎫ ⎝⎛3π + 2x ,x ∈R ,有下列命题:①函数 y = f (x )的表达式可改写为y =4cos ⎪⎭⎫ ⎝⎛6π - 2x ;②函数 y =f (x )是以2π为最小正周期的周期函数; ③函数y =f (x )的图象关于点(-6π,0)对称; ④函数y =f (x )的图象关于直线x =-6π对称. 其中正确的是______________. 三、解答题17.求函数f (x )=lgsin x +1cos 2-x 的定义域.18.化简:(1))-()+(-)++()+()-(-)++(-αααααα︒︒︒︒180cos cos 180tan 360tan sin 180sin ;(2))-()+()-()++(πcos πsin πsin πsin n n n n αααα(n ∈Z ).19.求函数y =sin ⎪⎭⎫ ⎝⎛6π - 2x 的图象的对称中心和对称轴方程.20.(1)设函数f (x )=xax sin sin +(0<x <π),如果 a >0,函数f (x )是否存在最大值和最小值,如果存在请写出最大(小)值;(2)已知k <0,求函数y =sin 2x +k (cos x -1)的最小值.参考答案一、选择题 1.D解析:2k π+π<<2k π+23π,k ∈Z ⇒k π+2π<2α<k π+43π,k ∈Z .2.B解析:∵sin θcos θ>0,∴sin θ,cos θ同号.当sin θ>0,cos θ>0时,θ在第一象限;当sin θ<0,cos θ<0时,θ在第三象限.3.A解析:原式=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-3πtan 6πcos 3πsin =-433. 4.D解析:tan θ+θtan 1=θθcos sin +θθsin cos =θθcos sin 1=2,sin cos =21. (sin θ+cos θ)2=1+2sin θcos θ=2.sin +cos =±2.5.B解析:由得25cos 2x -5cos x -12=0. 解得cos x =54或-53. 又0≤x <π,∴sin x >0. 若cos x =54,则sin x +cos x ≠51,∴cos x =-53,sin x =54,∴tan x =-34.6.D 解析:若,是第四象限角,且sin >sin ,如图,利用单位圆中的三角函数线确定,的终边,故选D .7.B解析:这三个集合可以看作是由角±3π2的终边每次分别旋转一周、两周和半周所得到的角的集合.8.B解析:∵cos(+)=1, ∴+=2k π,k ∈Z . ∴=2k π-.∴sin =sin(2k π-)=sin(-)=-sin =-31.9.C解析:作出在(0,2π)区间上正弦和余弦函数的图象,解出两交点的横坐标4π和45π,由图象可得答案.本题也可用单位圆来解.⎩⎨⎧1=cos +sin 51=cos +sin 22x x x x (第6题`)10.C解析:第一步得到函数y =sin ⎪⎭⎫ ⎝⎛+3πx 的图象,第二步得到函数y =sin ⎪⎭⎫ ⎝⎛+3π2x 的图象.二、填空题 11.415. 解析:f (x )=sin 2 x +3tan x 在⎥⎦⎤⎢⎣⎡3π4π ,上是增函数,f (x )≤sin 23π+3tan 3π=415. 12.-2. 解析:由sin =552,2π≤≤π⇒cos =-55,所以tan =-2.13.53. 解析:sin ⎪⎭⎫ ⎝⎛α + 2π=53,即cos =53,∴sin ⎪⎭⎫⎝⎛α - 2π=cos =53.14.21.解析:函数y =tan ⎪⎭⎫ ⎝⎛4π+x ω(ω>0)的图象向右平移6π个单位长度后得到函数y =tan ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛4π+6π-x ω=tan ⎪⎭⎫ ⎝⎛ωω6π-4π+x 的图象,则6π=4π-6πω+k π(k ∈Z ), ω=6k +21,又ω>0,所以当k =0时,ωmin =21. 15.⎥⎦⎤⎢⎣⎡221 ,-. 解析:f (x )=21(sin x +cos x )-21|sin x -cos x |=⎩⎨⎧)<()(x x x x x x cos sinsin cos ≥sincos 即f (x )等价于min{sin x ,cos x },如图可知,f (x )max =f ⎪⎭⎫ ⎝⎛4π=22,f (x )min =f (π) =-1.16.①③.解析:①f (x )=4sin ⎪⎭⎫ ⎝⎛+3π2x =4cos ⎪⎭⎫ ⎝⎛--3π22πx=4cos ⎪⎭⎫ ⎝⎛+-6π2x=4cos ⎪⎭⎫ ⎝⎛-6π2x .②T =22π=π,最小正周期为π.③令 2x +3π=k π,则当 k =0时,x =-6π, ∴ 函数f (x )关于点⎪⎭⎫ ⎝⎛0 6π-,对称. ④令 2x +3π=k π+2π,当 x =-6π时,k =-21,与k ∈Z 矛盾. ∴ ①③正确. 三、解答题17.{x |2k π<x ≤2k π+4π,k ∈Z }. 解析:为使函数有意义必须且只需⎪⎩⎪⎨⎧-② 0 ≥1 cos 2①>0 sin x x先在[0,2π)考虑x 的取值,在单位圆中,做出三角函数线. 由①得x ∈(0,π),由②得x ∈[0,4π]∪[47π,2π]. 二者的公共部分为x ∈⎥⎦⎤⎝⎛4π0,.所以,函数f (x )的定义域为{x |2k π<x ≤2k π+4π,k ∈Z }. 18.(1)-1;(2)±αcos 2. (第15题)(第17题)解析:(1)原式=αααααα cos cos tan tan sin sin -+--=-ααtan tan =-1.(2)①当n =2k ,k ∈Z 时,原式=)-()+()-()++(π2 cos π2sin π2sin π2sin k k k k αααα=α cos 2.②当n =2k +1,k ∈Z 时,原式=])+-([])++([])+-([]+)++([π12 cos π12sin π12sin π12sin k k k k αααα=-αcos 2.19.对称中心坐标为⎪⎭⎫⎝⎛0 ,12π + 2πk ;对称轴方程为x =2πk +3π(k ∈Z ). 解析:∵y =sin x 的对称中心是(k π,0),k ∈Z ,∴令2x -6π=k π,得x =2πk +12π. ∴所求的对称中心坐标为⎪⎭⎫⎝⎛0 ,12π + 2πk ,k ∈Z .又y =sin x 的图象的对称轴是x =k π+2π, ∴令2x -6π=k π+2π,得x =2πk +3π. ∴所求的对称轴方程为x =2πk +3π(k ∈Z ). 20.(1)有最小值无最大值,且最小值为1+a ;(2)0. 解析:(1) f (x )=x a x sin sin +=1+xa sin ,由0<x <π,得0<sin x ≤1,又a >0,所以当sin x =1时,f (x )取最小值1+a ;此函数没有最大值.(2)∵-1≤cos x ≤1,k <0, ∴k (cos x -1)≥0, 又 sin 2x ≥0,∴当 cos x =1,即x =2k (k ∈Z)时,f (x )=sin 2x +k (cos x -1)有最小值f (x )min =0.。
高中数学三角函数练习题含答案

高中数学三角函数练习题含答案一、填空题1.已知在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且6a =,点O 为其外接圆的圆心.已知·15BO AC =,则当角C 取到最大值时ABC 的面积为______2.在长方体1111ABCD A B C D -中,13AB =,5AD =,112AA =,过点A 且与直线CD 平行的平面α将长方体分成两部分.现同时将两个球分别放入这两部分几何体内,则在平面α变化的过程中,这两个球的半径之和的最大值为___________.3.已知三棱锥S ABC -中,SA SB SC ==,ABC 是边长为4的正三角形,点E ,F 分别是SC ,BC 的中点,D 是AC 上的一点,且EF SD ⊥,若3FD =,则DE =___________. 4.平行六面体1111ABCD A B C D -的各棱长均相等,1160BAD DAA A AB ∠=∠=∠=,直线1AC ⋂平面1A BD E =,则异面直线1D E 与AD 所成角的余弦值为_________.5.已知函数()233cos sin cos 2f x x x x =+-,给出下列结论:①函数()f x 的最小正周期为π;②函数12y f x π⎛⎫=+ ⎪⎝⎭是偶函数;③函数()f x 关于点()026k k Z ππ⎛⎫-∈⎪⎝⎭,成中心对称;④函数()f x 在3,22ππ⎡⎤⎢⎥⎣⎦上是减函数.其中正确的结论是_______.(写出所有正确结论的序号)6.已知向量a ,b ,c 满足0a b c ++=,()()0a b a c -⋅-=,||9b c -=,则||||||a b c ++的最大值是___________.7.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示.将函数()y f x =的图象向右平移4π个单位,得到()y g x =的图象,则下列有关()f x 与()g x 的描述正确的有___________(填序号).①()2sin 23g x x π⎛⎫=- ⎪⎝⎭;②方程()()360,2f x g x x π⎫⎛⎫+∈ ⎪⎪⎝⎭⎭所有根的和为712π; ③函数()y f x =与函数()y g x =图象关于724x π=对称.8.在ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,且23,3a A π==.若mb nc +(0,0m n >>)有最大值,则nm的取值范围是__________. 9.已知当()0,x π∈时,不等式2cos 23sin 20cos 4sin 1x x x x +-≤--的解集为A ,若函数()()()sin 0f x x =+<<在x A ∈上只有一个极值点,则ϕ的取值范围为______.10.已知P 是直线34130x y ++=上的动点,PA ,PB 是圆()()22111x y -+-=的切线,A ,B 是切点,C 是圆心,那么四边形PACB 面积的最小值是________.二、单选题11.设函数()211f x x =-,()122x f e x --=,()31sin 23f x x π=,99i ia =,0i =、1、2、、99.记()()()()()()10219998k k k k k k k I f a f a f a f a f a f a =-+-++-,1k =、2、3,则( ) A .123I I I << B .321I I I << C .132I I I <<D .213I I I <<12.如图,设1F ,2F 是双曲线()22210xy a a-=>的左、右焦点,过点2F 作渐近线的平行线交另外一条渐近线于点A ,若12AF F △的面积为54,离心率满足12e <<,则双曲线的方程为( )A .2215x y -=B .2214x y -=C .2213x y -=D .2212x y -=13.已知函数()()sin f x x ωφ=+π0,02ωφ⎛⎫><< ⎪⎝⎭在π5π,88⎛⎫ ⎪⎝⎭上单调,且π3π088f f ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭,则π2f ⎛⎫⎪⎝⎭的值为( ) A 2B .1 C .1- D .214.已知函数()()3log 911x f x x+=-,下列说法正确的是( )A .()f x 既不是奇函数也不是偶函数B .()f x 的图象与sin y x =有无数个交点C .()f x 的图象与2y =只有一个交点D .()()21f f -<-15.如图,长方形ABCD 中,152AB =,1AD =,点E 在线段AB (端点除外)上,现将ADE 沿DE 折起为A DE '.设ADE α∠=,二面角A DE C '--的大小为β,若π2αβ+=,则四棱锥A BCDE '-体积的最大值为( )A .14B .23C 151-D 51-16.高斯是世界四大数学家之一,一生成就极为丰硕,以他的名字“高斯”命名的成果达110个,属数学家中之最.对于高斯函数[]y x =,[]x 表示不超过实数x 的最大整数,如[]1.71=,[]1.22-=-,{}x 表示x 的非负纯小数,即{}[]x x x =-.若函数{}1log a y x x=-+(0a >且1a ≠)有且仅有3个零点,则实数a 的取值范围为( ) A .(]3,4B .()3,4C .[)3,4D .[]3,417.已知函数()sin os 0(c f x x a x a ωω=+>且0>ω),周期2T π<,()33f π()f x 在6x π=处取得最大值,则ω的最小值为( )A .11B .12C .13D .1418.在ABC 中,若22sin cos 1A B +=,则8cos AB BCBC A AC+的取值范围为( )A .)43,8⎡⎣B .)43,7⎡⎣C .()7,8D .(0,4319.已知函数()()sin 302f x x πϕϕ⎛⎫=-<≤ ⎪⎝⎭在0,4⎡⎤⎢⎥⎣⎦π上单调递增,现有如下三个结论:①ϕ的最小值为3π;②当ϕ取得最大值时,将函数()f x 的图像向左平移18π个单位后,再把曲线上各点的横坐标伸长到原来的2倍,得到函数()g x 的图像,则132g π⎛⎫= ⎪⎝⎭;③函数()f x 在[]0,2π上有6个零点. 则上述结论正确的个数为( ) A .0B .1C .2D .320.在ABC 中,2AB =,,D E 分别是边AB ,AC 的中点,CD 与BE 交于点O ,若OC =,则ABC 面积的最大值为( )AB .C .D .三、解答题21.已知函数()cos f x x =.(1)若,αβ为锐角,()f αβ+= 4tan 3α=,求cos2α及tan()βα-的值;(2)函数()(2)3g x f x =-,若对任意x 都有2()(2)()2g x a g x a ≤+--恒成立,求实数a 的最大值;(3)已知3()()()=2f f f αβαβ+-+,,(0,)αβπ∈,求α及β的值.22.已知函数()()()()2cos +2cos 02f x x x x πϕϕϕϕ⎛⎫=+++<< ⎪⎝⎭.(1)求()f x 的最小正周期;(2)若13f π⎛⎫= ⎪⎝⎭,求当()2f x =时自变量x 的取值集合.23.已知函数2()2sin cos ()f x x x x a a R =-++∈,且(0)f = (1)求a 的值;(2)若()f x ω在[0,]π上有且只有一个零点,0>ω,求ω的取值范围.24.已知函数()()2sin 24sin 206x x x f πωωω⎛⎫=--+> ⎪⎝⎭,其图象与x 轴相邻的两个交点的距离为2π. (1)求函数()f x 的解析式;(2)若将()f x 的图象向左平移()0m m >个长度单位得到函数()g x 的图象恰好经过点,03π⎛-⎫ ⎪⎝⎭,求当m 取得最小值时,()g x 在7,612ππ⎡⎤-⎢⎥⎣⎦上的单调区间. 25.已知函数()2sin cos cos2x x x x f =+. (1)求()f x 的最小正周期及单调递减区间; (2)求()f x 在区间0,4π⎡⎤⎢⎥⎣⎦上的最大值和最小值.26.已知函数 2()sin 2cos 1f x x m x =--- [0,]2x π∈()1若()f x 的最小值为 - 3,求m 的值;()2当2m =时,若对任意 12,[0,]2x x π∈ 都有()()12124f x f x a -≤-恒成立,求实数a 的取值范围.27.已知向量a ,b 满足2sin ,6sin 4a x x π⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭,cos ,2cos 4b x x π⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭,函数()()f x a b x R =⋅∈.(1)求()f x 的单调区间;(2)已知数列()2*11224n n a n f n N ππ⎛⎫=-∈ ⎪⎝⎭,求{}n a 的前2n 项和2n S . 28.已知函数()sin 23cos2f x x x =+.(1)求函数()f x 的最小正周期及对称中心坐标; (2)若02πα-<<,()1f α=,求sin 2α的值.29.函数()sin()f x A x ωϕ=+(其中0,0,||2A πωϕ>><)的部分图象如图所示,把函数()f x 的图像向右平移4π个单位长度,再向下平移1个单位,得到函数()g x 的图像.(1)当17,424x ππ⎡⎤∈⎢⎥⎣⎦时,求()g x 的值域(2)令()=()3F x f x -,若对任意x 都有2()(2)()20F x m F x m -+++≤恒成立,求m 的最大值30.在锐角△ABC 中,a 、b 、c 分别为角A 、B 、C 所对的边,且32sin a c A = (Ⅰ)确定角C 的大小: (Ⅱ)若c =,且△ABC 的面积为,求a +b 的值.【参考答案】一、填空题1.2.165383 4.565.①②③6.3+37.①③8.1,22⎛⎫ ⎪⎝⎭9.2(0,)(,)33πππ⋃10二、单选题 11.D 12.B 13.D 14.C 15.A 16.C 17.C 18.A 19.C 20.C 三、解答题21.(1)72cos 2,tan()2511αβα=--=;(2)265-;(3)3παβ== 【解析】 【分析】(1)根据同角三角函数的关系和二倍角的余弦公式可求得cos2α的值,利用二倍角的正切公式、同角三角函数的基本关系以及两角差的正切公式可求解tan()βα-的值;(2)由余弦函数的有界性求得()g x 的值域,再将不等式分离参数,并令()1t g x =-,可得1a t t ≤+对[5,3]t ∈--恒成立.易知函数1y t t=+在[5,3]t ∈--单调递增,求出其最小值,则可得265a ≤-,从而求得a 的最大值; (3)利用和差化积公式(需证明)以及二倍角公式,将该式化简,配凑成22(2coscos)sin 0222αβαβαβ+---+=,再结合,(0,)αβπ∈,即可求出α及β的值.【详解】 解:(1)4tan 3α=,且α为锐角, 4sin 5α∴=,3cos 5α=,22tan 24tan 21tan 7ααα==--则227cos 2cos sin 25ααα=-=-,又()cos()f αβαβ+=+=,αβ为锐角,sin()αβ∴+=,tan()2αβ+=-, tan()tan[()2]βααβα∴-=+-242()tan()tan 227241tan()tan 2111(2)()7αβααβα---+-===+++-⨯-; (2)()(2)3cos 23[4,2]g x f x x =-=-∈--,2()(2)()2g x a g x a ≤+--对任意x 恒成立,即2()2()2(()1)g x g x g x a -+≤-对任意x 恒成立, 令()1[5,3]t g x =-∈--,211t a t t t+∴≤=+对[5,3]t ∈--恒成立,又函数1y t t=+在[5,3]t ∈--单调递增,∴当5t =-时,min 126()5t t +=-,265a ∴≤-,则a 的最大值为265-; (3)3()()()2f f f αβαβ+-+=, 即3cos cos cos()2αβαβ+-+= , cos cos()22αβαβα+-=+coscossinsin2222αβαβαβαβ+-+-=-,cos cos()22αβαββ+-=-coscos+sinsin2222αβαβαβαβ+-+-=,cos cos 2coscos22αβαβαβ+-∴+=,又2cos()2cos12αβαβ++=-,232coscos2cos 12222αβαβαβ+-+∴-+=, 则24cos 4coscos10222αβαβαβ++--+=, 22(2coscos)1cos 0222αβαβαβ+---+-=, 即22(2coscos)sin 0222αβαβαβ+---+=,2cos cos 022sin 02αβαβαβ+-⎧-=⎪⎪∴⎨-⎪=⎪⎩,又0απ<<,0βπ<<, 3παβ∴==.【点睛】本题考查了同角三角函数间的关系,两角和与差的三角函数公式,二倍角余弦和正切公式,不等式恒成立问题,考查了运算能力和转化能力,属于综合性较强的题.22.(1)π;(2)12x x k ππ⎧=-+⎨⎩或()4x k k Z ππ⎫=+∈⎬⎭【解析】 【分析】(1)由辅助角公式可得()f x 2sin 2216x πϕ⎛⎫=+++ ⎪⎝⎭,再求周期即可;(2)由13f π⎛⎫= ⎪⎝⎭求出12πϕ=,再解方程2sin 2123x π⎛⎫++= ⎪⎝⎭即可.【详解】解:(1)()()()()2cos 2cos f x x x x ϕϕϕ=++++()()2cos21x x ϕϕ=++++2sin 2216x πϕ⎛⎫=+++ ⎪⎝⎭,则()f x 的最小正周期为2T ππω==.(2)因为13f π⎛⎫= ⎪⎝⎭,所以2sin 221136ππϕ⎛⎫⨯+++= ⎪⎝⎭,即()526k k Z πϕπ+=∈, 解得()5212k k Z ππϕ=-∈. 因为02πϕ<<,所以12πϕ=.因为()2f x =,所以2sin 2123x π⎛⎫++= ⎪⎝⎭,即1sin 232x π⎛⎫+= ⎪⎝⎭,则2236x k πππ+=+或()52236x k k Z πππ+=+∈, 解得12x k ππ=-+或()4x k k Z ππ=+∈.故当()2f x =时,自变量x 的取值集合为12x x k ππ⎧=-+⎨⎩或()4x k k Z ππ⎫=+∈⎬⎭.【点睛】本题考查了三角恒等变换,重点考查了解三角方程,属中档题.23.(1)a =(2)15,36⎡⎫⎪⎢⎣⎭【解析】 【分析】(1)利用降次公式、辅助角公式化简()f x 表达式,利用(0)f =a 的值. (2)令()0f x ω=,结合x 的取值范围以及三角函数的零点列不等式,解不等式求得ω的取值范围. 【详解】(1)2()2sin cos f x x x x a =-++sin 2x x a =+2sin 23x a π⎛⎫=++- ⎪⎝⎭(0)f =(0)2sin3f a π∴=+=即a =(2)令()0f x ω=,则sin 203x πω⎛⎫+= ⎪⎝⎭,[0,]x π∈,2,2333πππωπω⎡⎤∴+∈+⎢⎥⎣⎦,()f x 在[0,]π上有且只有一个零点,223πππωπ∴+<,1536ω∴<, ω∴的取值范围为15,36⎡⎫⎪⎢⎣⎭. 【点睛】本小题主要考查三角恒等变换,考查三角函数零点问题,考查化归与转化的数学思想方法,属于基础题.24.(1)()23f x x π⎛⎫=+ ⎪⎝⎭(2)单调增区间为,612ππ⎡⎤--⎢⎥⎣⎦,57,1212ππ⎡⎤⎢⎥⎣⎦;单调减区间为5,1212ππ⎡⎤-⎢⎥⎣⎦. 【解析】 【分析】(1)利用两角差的正弦公式,降幂公式以及辅助角公式化简函数解析式,根据其图象与x 轴相邻的两个交点的距离为2π,得出周期,利用周期公式得出1ω=,即可得出该函数的解析式;(2)根据平移变换得出()223m x x g π⎛⎫=++ ⎪⎝⎭,再由函数()g x 的图象经过点,03π⎛⎫- ⎪⎝⎭,结合正弦函数的性质得出m 的最小值,进而得出()223g x x π⎛⎫=+ ⎪⎝⎭,利用整体法结合正弦函数的单调性得出该函数在7,612ππ⎡⎤-⎢⎥⎣⎦上的单调区间.【详解】解:(1)()2sin 24sin 26x x x f πωω⎛⎫=--+ ⎪⎝⎭11cos22cos24222xx x ωωω-=--⨯+32cos22x x ωω=+23x πω⎛⎫=+ ⎪⎝⎭由已知函数()f x 的周期T π=,22ππω=,1ω=∴()23f x x π⎛⎫=+ ⎪⎝⎭.(2)将()f x 的图象向左平移()0m m >个长度单位得到()g x 的图象∴()223m x x g π⎛⎫=++ ⎪⎝⎭,∵函数()g x 的图象经过点,03π⎛⎫- ⎪⎝⎭22033m ππ⎡⎤⎛⎫⨯-++= ⎪⎢⎥⎝⎭⎣⎦,即sin 203m π⎛⎫-= ⎪⎝⎭∴23m k ππ-=,k Z ∈∴26k m ππ=+,k Z ∈ ∵0m >,∴当0k =,m 取最小值,此时最小值为6π此时,()223g x x π⎛⎫=+ ⎪⎝⎭. 令7612x ππ-≤≤,则2112336x πππ≤+≤ 当22332x πππ≤+≤或32112236x πππ≤+≤,即当612x ππ-≤≤-或571212x ππ≤≤时,函数()g x 单调递增 当232232x πππ≤+≤,即51212x ππ-≤≤时,函数()g x 单调递减. ∴()g x 在7,612ππ⎡⎤-⎢⎥⎣⎦上的单调增区间为,612ππ⎡⎤--⎢⎥⎣⎦,57,1212ππ⎡⎤⎢⎥⎣⎦;单调减区间为5,1212ππ⎡⎤-⎢⎥⎣⎦. 【点睛】本题主要考查了由正弦函数的性质确定解析式以及正弦型函数的单调性,属于中档题.25.(1)最小正周期π;单调递减区间是5,88k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈(2)最大值和最小值和1.【解析】(1)利用二倍角的正弦公式的逆用公式以及两角和的正弦公式的逆用公式化简得()24f x x π⎛⎫+ ⎪⎝⎭,再根据周期公式可得周期,利用正弦函数的递减区间可得()f x 的递减区间;(2)利用正弦函数的性质可求得结果.【详解】(1)因为()sin 2cos 224x f x x x π⎛⎫=+=+ ⎪⎝⎭. 所以()f x 的最小正周期22T ππ==. 由3222242k x k πππππ+≤+≤+,得588k x k ππππ+≤≤+, 所以()f x 的单调递减区间是5,88k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈. (2)因为0,4x π⎡⎤∈⎢⎥⎣⎦,所以32,444x πππ⎡⎤+∈⎢⎥⎣⎦.所以当242x ππ+=,即8x π= 当244x ππ+=或34π,即0x =或4x π=时,函数取得最小值1.所以()f x 在区间0,4⎡⎤⎢⎥⎣⎦π和1. 【点睛】本题考查了二倍角的正弦公式,考查了两角和的正弦公式,考查了正弦型函数的周期公式,考查了求三角函数的单调区间和最值,属于基础题.26.(1)1m =;(2)13[,)8a ∈+∞ 【解析】【分析】(1)将函数化为2()cos 2cos 2f x x m x =--,设cos [0,1]t x =∈,将函数转化为二次函数,利用二次函数在给定的闭区间上的最值问题的解法求解.(2) 对任意 12,[0,]2x x π∈ 都有()()12124f x f x a -≤-恒成立, 等价于12max 1()()24f x f x a -≤-,然后求出函数()f x 的最值即可解决. 【详解】(1)2()cos 2cos 2f x x m x =--,[0,]2x π∈ 令 cos [0,1]t x =∈, 设222()22()2g t t mt t m m =--=---,①0m <,则min g(0)2()3g t ==-≠-,②01m ≤≤,则2min )3(2t m g =--=-,∴1m =± ∴1m =③1m ,则min g(1)21()3g m t ==--=-,∴1m =.(舍)综上所述:1m =.(2)对任意12,[0,]2x x π∈都有()()12124f x f x a -≤-恒成立, 等价于12max 1()()24f x f x a -≤-, 2m =,∴2g()(2)6t t =--,[0,1]t ∈max ()g(0)2f x ==-,min ()g(1)5f x ==-12max ()(25)()3f x f x =---=-∴ 1234a -≥,∴ 138a ≥, 综上所述:13[,)8a ∈+∞. 【点睛】本题考查三角函数中的二次“型”的最值问题,和双参恒成立问题,属于中档题.27.(1)单调增区间为7,1212k k ππππ⎡⎤--⎢⎥⎣⎦,k Z ∈,单调减区间为5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦,k Z ∈;(2))22n n + 【解析】【分析】(1)由向量数量积的坐标运算可得()2sin 222sin 23f x a b x x x π⎛⎫=⋅=-=+ ⎪⎝⎭, 再利用三角函数单调区间的求法即可得解;(2)由题意可得()()22222221234212n S n n ⎤=-+-+⋅⋅⋅+--⎦,又()()2221241n n n --=-+,则)2442434n S n n =--⨯-⨯-⋅⋅⋅-+,再利用等差数列求和公式即可得解.【详解】解:(1)向量a ,b 满足2sin 4a x x π⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭,cos 4b x x π⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭,函数()2sin 222sin 23f x a b x x x π⎛⎫=⋅=-=+ ⎪⎝⎭, 由2222232k x k πππππ-≤+≤+,可得71212k x k ππππ-≤≤-,k Z ∈, 解得()f x 的单调增区间为7,1212k k ππππ⎡⎤--⎢⎥⎣⎦,k Z ∈; 单调减区间为5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦,k Z ∈. (2)因为22112sin 2244n n a n f n n ππππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,所以()()22222221234212n S n n ⎤=-+-+⋅⋅⋅+--⎦, 又()()2221241n n n --=-+, )2442434n S n n --⨯-⨯-⋅⋅⋅-+,所以())2234122n n n S n n --+==+.【点睛】本题考查了三角函数单调区间的求法及数列中捆绑求和,属中档题.28.(1)最小正周期为π,对称中心坐标为(),026k k Z ππ⎛⎫-∈ ⎪⎝⎭;(2)12-. 【解析】【分析】(1)利用辅助角公式先将函数()y f x =的解析式化简,然后利用周期公式计算出函数()y f x =的最小正周期,令()23x k k Z ππ+=∈,解出x 的表达式可得出对称中心坐标;(2)由()1f α=得出1sin 232πα⎛⎫+= ⎪⎝⎭,结合角α的范围求出α的值,代入sin 2α并结合诱导公式求出sin 2α的值.【详解】(1)()1sin 222sin 222f x x x x x ⎛⎫== ⎪ ⎪⎝⎭2sin 2cos cos 2sin 2sin 2333x x x πππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭, 所以,函数()y f x =的最小正周期为22ππ=, 令()23x k k Z ππ+=∈,解得()26k x k Z ππ=-∈, 因此,函数()y f x =的对称中心坐标为(),026k k Z ππ⎛⎫-∈ ⎪⎝⎭; (2)()2sin 213f παα⎛⎫=+= ⎪⎝⎭,得1sin 232πα⎛⎫+= ⎪⎝⎭, 02πα-<<,22333πππα∴-<+<,236ππα∴+=,得26πα=-, 因此,1sin 2sin sin 662ππα⎛⎫=-=-=- ⎪⎝⎭. 【点睛】本题考查三角函数的周期和对称中心,考查三角函数求值,解三角函数问题首先就是要将三角函数解析式化简,在求值时,要利用已知角来配凑未知角,借助同角三角函数的基本关系以及两角和差公式进行计算,考查计算能力,属于中等题.29.(1)1,02⎡⎤--⎢⎥⎣⎦(2)265- 【解析】【分析】(1)根据图象的最低点求得A 的值,根据四分之一周期求得ω的值,根据点7,112π⎛⎫- ⎪⎝⎭求得ϕ的值,由此求得函数()f x 的解析式,进而根据图象平移变换求得()g x 的解析式,并由此求得17,424x ππ⎡⎤∈⎢⎥⎣⎦时()g x 的值域.(2)先求得()f x 的值域,由此求得()F x 的值域.令()[4,2]t F x =∈--对题目所给不等式换元,根据二次函数的性质列不等式组,解不等式组求得m 的取值范围,由此求得m 的最大值. 【详解】(1)根据图象可知171,4123A T ππ==- 2,2,()sin(2)T f x x Tππωϕ∴=∴===+ 代入7,112π⎛⎫- ⎪⎝⎭得,7sin 1,2,63k k Z ππϕϕπ⎛⎫+=-=+∈ ⎪⎝⎭, ||,0,23k ππϕϕ<∴==()sin 23f x x π⎛⎫∴=+ ⎪⎝⎭ 把函数()f x 的图像向右平移4π个单位长度,再向下平移1个单位,得到函数()g x ()sin 21sin 21436g x x x πππ⎛⎫⎛⎫⎛⎫∴=-+-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 设26t x π=-,则5,34t ππ⎡⎤∈⎢⎥⎣⎦, 此时sint ⎡⎤∈⎢⎥⎣⎦,所以值域为1,0⎡⎤⎢⎥⎣⎦. (2)由(1)可知()sin 2[1,1]3f x x π⎛⎫=+∈- ⎪⎝⎭ ()()3[4,2]F x f x =-∈--对任意x 都有2()(2)()20F x m F x m -+++≤恒成立令()[4,2]t F x =∈--,2()(2)2h t t m t m =-+++,是关于t 的二次函数,开口向上则max ()0h t ≤恒成立而()h t 的最大值,在4t =-或2t =-时取到最大值则(2)0(4)0h h -≤⎧⎨-≤⎩,4(2)(2)2016(2)(4)20m m m m -+-++≤⎧⎨-+-++≤⎩, 解得103265m m ⎧≤-⎪⎪⎨⎪≤-⎪⎩所以265m ≤-,则m 的最大值为265-. 【点睛】 本小题主要考查由三角函数图像求三角函数的解析式,考查三角函数图像变换,考查不等式恒成立问题,考查化归与转化的数学思想方法,属于中档题.30.(Ⅰ) 3π(Ⅱ)5 【解析】【详解】试题分析:(12sin sin A C A =即可得sin C =60C =︒(2)∵1sin 2S ab C ==a b + 试题解析:解:(12sin sin A C A =,∵,A C 是锐角,∴sin C =60C =︒.(2)∵1sin 2S ab C ==6ab = 由余弦定理得222222cos ()3()187c a b ab C a b ab a b =+-=+-=+-=∴5a b +=点睛:在解三角形问题时多注意正余弦定理的结合运用,正弦定理主要用在角化边和边化角上,而余弦定理通常用来求解边长。
高中数学三角函数专项练习题(含答案)

高中数学三角函数专项练习题(含答案)一、填空题1.设函数()f x 是定义在实数集R 上的偶函数,且()()2f x f x =-,当[0,1]x ∈时,3()f x x =,则函数()|cos |()g x x f x π=-在15,22⎡⎤-⎢⎥⎣⎦上所有零点之和为___________.2.设函数()sin f x x π=,()21g x x x =-+,有以下四个结论.①函数()()y f x g x =+是周期函数: ②函数()()y f x g x =-的图像是轴对称图形: ③函数()() y f x g x =⋅的图像关于坐标原点对称: ④函数()()f x yg x =存在最大值 其中,所有正确结论的序号是___________.3.在长方体1111ABCD A B C D -中,13AB =,5AD =,112AA =,过点A 且与直线CD 平行的平面α将长方体分成两部分.现同时将两个球分别放入这两部分几何体内,则在平面α变化的过程中,这两个球的半径之和的最大值为___________.4.已知四棱锥P ABCD -的顶点均在球O 的球面上,底面ABCD 是正方形,AB =120APB ∠=︒,当AD AP ⊥时,球O 的表面积为______.5.在锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若2cos b a a C -=,则ac的取值范围是______.6.在角1θ,2θ,3θ,…,29θ的终边上分别有一点1P ,2P ,3P ,…,29P ,如果点k P 的坐标为()()()sin 15,sin 75k k-+,129k ≤≤,k ∈N ,则12329cos cos cos cos θθθθ+++⋅⋅⋅+=______7.关于函数())cos sin f x x x x =+①其表达式可写成()cos 26f x x π⎛⎫=+ ⎪⎝⎭;②直线12x π=-是曲线()y f x =的一条对称轴;③()f x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增;④存在0,2πα⎛⎫∈ ⎪⎝⎭使()()3f x f x αα+=+恒成立.其中正确的是______(填写正确的番号). 8.已知当()0,x π∈时,不等式2cos 23sin 20cos 4sin 1x x x x +-≤--的解集为A ,若函数()()()sin 0f x x =+<<在x A ∈上只有一个极值点,则ϕ的取值范围为______.9.已知空间单位向量1e ,2e ,3e ,4e ,1234123421+=+=+++=e e e e e e e e ,则13⋅e e 的最大值是___________.10.如图,在棱长为1的正方体1111ABCD A B C D -中,若点P 是棱上一点,则满足1222PA PC +=的点P 有__________个.二、单选题11.已知()1,0A -,()3,0B ,P 是圆22:45O x y +=上的一个动点,则sin APB ∠的最大值为( ) A 3B 5C 3D 512.已知函数()|sin |(0)f x x ωω=>在区间,53ππ⎡⎤⎢⎥⎣⎦上单调递减,则实数ω的取值范围为( ) A .5,32⎡⎤⎢⎥⎣⎦B .30,2⎛⎤ ⎥⎝⎦C .8,33⎡⎤⎢⎥⎣⎦D .50,4⎛⎤ ⎥⎝⎦13.在ABC 中,角,,A B C 所对应的边分别为,,a b c ,设ABC 的面积为S ,则24Sa bc+的最大值为( ) A 2 B 3C 3D 214.已知1F ,2F 分别是椭圆2222:1(0)x yE a b a b+=>>的左、右焦点,若在椭圆E 上存在点M ,使得12MF F △的面积等于2122sin b F MF ∠,则椭圆E 的离心率e 的取值范围为( )A .3⎡⎫⎪⎢⎪⎣⎭B .3⎛ ⎝⎦C .122⎛ ⎝⎦D .2⎡⎫⎪⎢⎪⎣⎭15.已知ABC 的内角分别为,,A B C ,23cos 12A A =,且ABC 的内切圆面积为π,则AB AC ⋅的最小值为( ) A .6B .8C .10D .1216.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭,3B π=,则a c +的取值范围是( )A .3,32⎛⎤⎥ ⎝⎦B .3,32⎛⎤⎥⎝⎦C .3,32⎡⎤⎢⎥⎣⎦D .3,32⎡⎤⎢⎥⎣⎦17.如图,将矩形纸片ABCD 折起一角落()EAF △得到EA F '△,记二面角A EF D '--的大小为π04θθ⎛⎫<< ⎪⎝⎭,直线A E ',A F '与平面BCD 所成角分别为α,β,则( ).A .αβθ+>B .αβθ+<C .π2αβ+>D .2αβθ+>18.已知函数()*()cos 3f x x πωω⎛⎫=+∈ ⎪⎝⎭N ,若函数()f x 图象的相邻两对称轴之间的距离至少为4π,且在区间3(,)2ππ上存在最大值,则ω的取值个数为( ) A .4B .3C .2D .119.设点()11,P x y 在椭圆22182x y +=上,点()22,Q x y 在直线280x y +-=上,则2121x x y y -+-的最小值是( )A .21B 3C .31D .220.将方程23sin cos 3x x x =的所有正数解从小到大组成数列{}n x ,记()1cos n n n a x x +=-,则122021a a a ++⋅⋅⋅+=( )A .3B .2C .3D .2三、解答题21.已知1l ,2l ,3l 是同一平面内自上而下的三条不重合的平行直线.(1)如图1,如果1l 与2l 间的距离是1,2l 与3l 间的距离也是1,可以把一个正三角形ABC 的三顶点分别放在1l ,2l ,3l 上,求这个正三角形ABC 的边长.(2)如图2,如果1l 与2l 间的距离是1,2l 与3l 间的距离是2,能否把一个正三角形ABC 的三顶点分别放在1l ,2l ,3l 上,如果能放,求BC 和3l 夹角θ的正切值并求该正三角形边长;如果不能,试说明理由.(3)如果边长为2的正三角形ABC 的三顶点分别在1l ,2l ,3l 上,设1l 与2l 间的距离为1d ,2l 与3l 间的距离为2d ,求12d d ⋅的取值范围.22.已知函数 f (x )=a (|sin x |+|cos x |)﹣sin2x ﹣1,a ∈R . (1)写出函数 f (x )的最小正周期(不必写出过程); (2)求函数 f (x )的最大值;(3)当a =1时,若函数 f (x )在区间(0,k π)(k ∈N*)上恰有2015个零点,求k 的值.23.已知函数()2sin 2cos 3f x x a x =+-.(1)当1a =时,求该函数的最大值;(2)是否存在实数a ,使得该函数在闭区间0,2π⎡⎤⎢⎥⎣⎦上的最大值为1?若存在,求出对应a的值;若不存在,试说明理由. 24.已知函数1()1xf x x-=+. (1)证明函数()f x 在(1,)-+∞上为减函数;(2)求函数ln (tan )y f x =的定义域,并求其奇偶性;(3)若存在(,)42ππ,使得不等式(tan )tan 0f x a x +≤能成立,试求实数a 的取值范围.25.将函数()4sin cos 6g x x x π⎛⎫=+ ⎪⎝⎭的图象向左平移02πϕϕ⎛⎫<≤ ⎪⎝⎭个单位长度后得到()f x 的图象.(1)若()f x 为偶函数,求ϕ;(2)若()f x 在7,6ππ⎛⎫ ⎪⎝⎭上是单调函数,求ϕ的取值范围. 26.已知向量 22(2,22()),(,)22a xb ωϕ=+=,其中0,02πωϕ><<.函数()f x a b =⋅的图象过点()1,2B ,点B 与其相邻的最高点的距离为4.(Ⅰ)求函数()f x 的单调递减区间; (Ⅱ)计算()()()12...2017f f f +++的值;(Ⅲ)设函数()()1g x f x m =--,试讨论函数()g x 在区间 [0,3] 上的零点个数. 27.已知ABC ∆的三个内角A ,B ,C 的对边分别为a ,b ,c ,函数()()2sin cos sin f x x A x A =-+,且当512x π=时,()f x 取最大值. (1)若关于x 的方程()f x t =,0,2x π⎛⎫∈ ⎪⎝⎭有解,求实数t 的取值范围;(2)若5a =,且43sin sin 5B C +=,求ABC ∆的面积. 28.已知函数()()2cos 3sin cos 1f x xx x =+-.(1)求函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值;(2)若()85f x =-,2,3x ππ⎡⎤∈⎢⎥⎣⎦,求cos2x 的值;(3)若函数()()0y f x ωω=>在区间,62ππ⎡⎤⎢⎥⎣⎦上是单调递增函数,求正数ω的取值范围.29.已知函数()()sin ,f x A x x R ωϕ=+∈(其中0,0,02A πωϕ>><<)的图象如图所示:(1)求函数()f x 的解析式及其对称轴的方程;(2)当0,2x π⎡⎤∈⎢⎥⎣⎦时,方程()23f x a =-有两个不等的实根12,x x ,求实数a 的取值范围,并求此时12x x +的值.30.函数()sin()16f x A x πω=-+(0,0A ω>>)的最大值为3, 其图象相邻两条对称轴之间的距离为2π, (1)求函数()f x 的解析式;(2)设π(0,)2α∈,则()22f α=,求α的值【参考答案】一、填空题1.72.②④3.165384.28π5.⎝⎭6.07.②③8.2(0,)(,)33πππ⋃9 10.18二、单选题 11.D 12.A 13.A 14.A 15.A 16.A 17.A 18.C 19.D 20.C 三、解答题21.(1)2 ;(2)能放,tan θ=;(3)(]0,1 【解析】(1)根据,A C 到直线2l 的距离相等,可得2l 过AC 的中点M ,2l AC ⊥,从而求得边长2AC AM =的值.(2)假设能放,设边长为a ,BC 与3l 的夹角θ,不妨设060θ<≤,可得sin 2a θ=,()sin 601a θ-=,两式相比化简可得sin θa 的值,从而得出结论. (3)利用两角和差的正弦、余弦公式化简()124sin 60sin d d θθ⋅=-为()2sin 2301θ+-,再根据正弦函数的定义和值域求出12d d ⋅的取值范围. 【详解】 (1),A C 到直线2l 的距离相等,∴2l 过AC 的中点M , ∴2l AC ⊥, ∴边长22AC AM ==(2)假设能放,设边长为a ,BC 与3l 的夹角θ, 由对称性,不妨设060θ<≤, ∴sin 2a θ=,()sin 601a θ-=,两式相比可得:()sin 2sin 60θθ=-,即sin sin θθθ-,2sin θθ∴=,tan 2θ∴=,sin θ∴=,故边长a ==, 综上可得,能放.(3)()1214sin 60sin 4sin sin 2d d θθθθθ⎫⋅=-=-⎪⎪⎝⎭()1cos 2222sin 23012θθθ⎫+=-=+-⎪⎪⎝⎭. 060θ<≤,30230150θ∴<+≤,()1sin 23012θ≤+≤, 所以()02sin 23011θ≤+-≤, 又10d >,20d >,所以(]120,1d d ⋅∈. 【点睛】本题是一道考查三角函数应用的题目,解题的关键是掌握等边三角形的性质以及三角函数的恒等变换,属于中档题.22.(1)最小正周期为π.(2)见解析(3)k =1008.(1)由题意结合周期函数的定义直接求解即可;(2)令t ,t ∈[1,则当0,2x π⎡⎤∈⎢⎥⎣⎦时,()()2f x t at t μ==-,当,2x π⎛⎤∈π ⎥⎝⎦时,()()22f x v t t at ==+-,易知()()t v t μ≤,分类比较()1v 、v的大小即可得解;(3)转化条件得当且仅当sin2x =0时,f (x )=0,则x ∈(0,π]时,f (x )有且仅有两个零点,结合函数的周期即可得解. 【详解】(1)函数 f (x )的最小正周期为π. (2)∵f (x )=a (|sin x |+|cos x |)﹣sin2x ﹣1=sin2x ﹣1=(sin2x +1),令t =t ∈[1],当0,2x π⎡⎤∈⎢⎥⎣⎦时,()()(21f x t at t t μ==-≤≤,当,2x π⎛⎤∈π ⎥⎝⎦时,()()(221f x v t t at t ==+-≤≤,∵()()()2222220t v t at t t at t μ-=--+-=-+≤即()()t v t μ≤.∴()()(){}max max max 1,f x v t v v ==,∵()11v a =-,v,∴当1a ≤-()f x 最大值为1a -;当1a >-()f x .(3)当a =1时,f (x )sin 21x -,若f (x )=0sin 21x =+即22sin 22sin 2sin x x x =+,∴当且仅当sin2x =0时,f (x )=0,∴x ∈(0,π]时,f (x )有且仅有两个零点分别为2π,π, ∴2015=2×1007+1, ∴k =1008. 【点睛】本题考查了三角函数的综合问题,考查了分类讨论思想和转化化归思想,属于难题. 23.(1)1-;(2)存在,且2a =. 【解析】 【分析】(1)将1a =代入函数()y f x =的解析式,得出()()2cos 11f x x =---,由1cos 1x -≤≤结合二次函数的基本性质可得出该函数的最大值;(2)换元[]cos 0,1t x =∈,将问题转化为二次函数()222t at g t -+-=在区间[]0,1上的最大值为1,然后分0a ≤、01a <<和1a ≥三种情况讨论,利用二次函数的基本性质求出函数()222t at g t -+-=在区间[]0,1上最大值,进而求得实数a 的值.【详解】(1)当1a =时,()()22sin 2cos 3cos 11f x x x x =+-=---,1cos 1x -≤≤,当cos 1x =时,该函数取得最大值,即()max 1f x =-;(2)()22sin 2cos 3cos 2cos 2x a x x a x f x =+-=-+-,当0,2x π⎡⎤∈⎢⎥⎣⎦时,设[]cos 0,1t x =∈,设()222t at g t -+-=,[]0,1t ∈,二次函数()y g t =的图象开口向下,对称轴为直线t a =.当0a ≤时,函数()y g t =在[]0,1上单调递减,所以0=t 时,()()max 021g t g ==-≠,0a ∴≤不符合题意;当1a ≥时,函数()y g t =在[]0,1上单调递增,所以1t =时,()()max 1231g t g a ==-=,2a ∴=满足1a ≥;当01a <<时,函数()y g t =在[]0,a 上单调递增,在(],1a 上单调递减, ∴当t a =时,()()2max 21g t g a a ==-=,a ∴=01a <<.综上,存在2a =符合题意. 【点睛】本题考查二次型余弦函数的最值,将问题转化为二次函数的最值来求解是解题的关键,第二问要对二次函数图象的对称轴与区间的位置关系进行分类讨论,结合二次函数的单调性求解,考查分类讨论思想的应用,属于中等题.24.(1)证明见解析;(2),,44k k k Z ππππ⎛⎫-++∈ ⎪⎝⎭,奇函数;(3)(,3-∞-. 【解析】(1)利用单调性定义证明即可.(2)根据条件可得tan 1tan 1x x <⎧⎨>-⎩,其解集即为函数的定义域,可判断定义域关于原点对称,再根据奇偶性定义可判断函数的奇偶性. (3)令tan t x =,考虑101tat t-+<+在()1,+∞上有解即可,参变分离后利用基本不等式可求实数a 的取值范围. 【详解】(1)11x ∀>-,21x ∀>-,12x x <, 又()()()122212121211()()11112x x x x f x f x x x x x ----=-+-=+++, 因为11x >-,21x >-,12x x <,故110x +>,210x +>,120x x -<, 故12())0(f x f x ->即12()()f x f x >,所以函数()f x 在(1,)-+∞上为减函数.(2)((ln t )n )a y f x =的x 满足的不等关系有:1tan 01tan xx->+即()()1tan tan 10x x +-<,故tan 1tan 1x x <⎧⎨>-⎩,解得,44k x k k Z ππππ-+<<+∈,故函数的定义域为,44k k ππππ⎛⎫-++ ⎪⎝⎭,k Z ∈,该定义域关于原点对称.令()((ln ta )n )F x f x = 又()()()tan tan tan()tan tan 11ln lnln 11x xx x xF x f -+--===--+()()()tan ln x f F x =-=-,故ln (tan )y f x =为奇函数.(3)令tan t x =,因为(,)42x ππ∈,故1u >.故在(,)42ππ上不等式(tan )tan 0f x a x +≤能成立即为存在1t >,使得101tat t-+≤+,所以()11t a t t -≤+在()1,+∞上能成立, 令1s t =-,则0s >且()21121323t s t t s s s s-==+++++,由基本不等式有2s s+≥s 时等号成立, 所以()131t t t -≤=-+,当且仅当1t 时等号成立, 故()11t y t t -=+的最大值为3-,所以a的取值范围为(,3-∞-. 【点睛】本题考查与正切函数、对数函数有关的复合函数的性质的讨论,此类问题常用换元法把复合函数性质的讨论归结为常见函数性质的讨论,本题较综合,为难题. 25.(1)6π=ϕ;(2),62ππϕ⎡⎤∈⎢⎥⎣⎦【解析】 【分析】(1)根据三角恒等变换对()4sin cos 6g x x x π⎛⎫=+ ⎪⎝⎭化简变形为()2sin 216g x x π⎛⎫=+- ⎪⎝⎭,然后可得到图象左移之后的函数()2sin 2216f x x ϕπ⎛⎫=++- ⎪⎝⎭,利用三角函数偶函数的性质即可求出ϕ;(2)先求出2222,22662x πππϕπϕπϕ⎛⎫++∈++++ ⎪⎝⎭,再根据ϕ的范围求出26πϕ+和22πϕ+的范围,从而根据单调性列出关于ϕ的不等式,解之即可求得结果. 【详解】(1)()()14sin sin 21cos 22g x x x x x x ⎫=-=--⎪⎪⎝⎭ 2sin 216x π⎛⎫=+- ⎪⎝⎭, ∴()2sin 2216f x x ϕπ⎛⎫=++- ⎪⎝⎭. 又()f x 为偶函数,则()262k k Z ππϕπ+=+∈,02πϕ<≤,∴6π=ϕ; (2)7,6x ππ⎛⎫∈ ⎪⎝⎭,∴2222,22662x πππϕπϕπϕ⎛⎫++∈++++ ⎪⎝⎭.02πϕ<≤,∴72,666πππϕ⎛⎫+∈ ⎪⎝⎭,32,222πππϕ⎛⎫+∈ ⎪⎝⎭()f x 在7,6ππ⎛⎫ ⎪⎝⎭是单调函数,∴26202ππϕπϕ⎧+≥⎪⎪⎨⎪<≤⎪⎩, ∴,62ππϕ⎡⎤∈⎢⎥⎣⎦. 【点睛】本题考查三角恒等变换、三角函数的图象变换及性质,以及基本的运算能力和逻辑推理能能力,综合性较强,属于有一定难度的中档题.26.(Ⅰ)[41,43]k k ++,k Z ∈;(Ⅱ)2018;(Ⅲ)详见解析.【解析】【分析】(Ⅰ)由数量积的坐标运算可得f (x ),由题意求得ω4π=,再由函数f (x )的图象过点B (1,2)列式求得φ.则函数解析式可求,由复合函数的单调性求得f (x )的单调递增区间;(Ⅱ)由(Ⅰ)知,f (x )=1+sin 2x π,可得f (x )是周期为4的周期函数,且f (1)=2,f (2)=1,f (3)=0,f (4)=1.得到f (1)+f (2)+f (3)+f (4)=4. 进一步可得结论;(Ⅲ)g (x )=f (x )﹣m ﹣12sinx m π=-,函数g (x )在[0,3]上的零点个数,即为函数y =sin 2x π的图象与直线y =m 在[0,3]上的交点个数.数形结合得答案.【详解】(Ⅰ)∵a =(2,2cos2(ωx +φ)),b =(22,22-), ∴f (x )222222a b =⋅=⨯-⨯cos2(ωx +φ)=1﹣cos2(ωx +φ)), ∴f (x )max =2,则点B (1,2)为函数f (x )的图象的一个最高点. ∵点B 与其相邻的最高点的距离为4,∴242πω=,得ω4π=. ∵函数f (x )的图象过点B (1,2),∴1222cos πϕ⎛⎫-+= ⎪⎝⎭,即sin2φ=1. ∵0<φ2π<,∴φ4π=.∴f (x )=1﹣cos2(44x ππ+)=1+sin 2x π, 由322222k x k πππππ+≤≤+,得4143k x k +≤≤+,k Z ∈. ()f x ∴的单调递减区间是[41,43]k k ++,k Z ∈.(Ⅱ)由(Ⅰ)知,f (x )=1+sin 2x π,∴f (x )是周期为4的周期函数,且f (1)=2,f (2)=1,f (3)=0,f (4)=1. ∴f (1)+f (2)+f (3)+f (4)=4.而2017=4×504+1,∴f (1)+f (2)+…+f (2017)=4×504+2=2018;(Ⅲ)g (x )=f (x )﹣m ﹣12sinx m π=-,函数g (x )在[0,3]上的零点个数, 即为函数y =sin 2x π的图象与直线y =m 在[0,3]上的交点个数.在同一直角坐标系内作出两个函数的图象如图:①当m >1或m <﹣1时,两函数的图象在[0,3]内无公共点;②当﹣1≤m <0或m =1时,两函数的图象在[0,3]内有一个共点;③当0≤m <1时,两函数的图象在[0,3]内有两个共点.综上,当m >1或m <﹣1时,函数g (x )在[0,3]上无零点;②当﹣1≤m <0或m =1时,函数g (x )在[0,3]内有1个零点;③当0≤m <1时,函数g (x )在[0,3]内有2个零点.【点睛】本题考查三角函数中的恒等变换应用,考查数量积的坐标运算,体现了数形结合的解题思想方法,是中档题.27.(1)(;(2 【解析】【分析】(1)利用两角和差的正弦公式整理()f x 可得:()sin(2)A f x x =-,再利用已知可得:522122A k πππ⨯-=+(k Z ∈),结合已知可得:3A π=,求得:(0,)2x π∈时,sin(2)13x π<-≤,问题得解.(2)利用正弦定理可得:sin sin )+=+B C b c ,结合sin sin B C +=可得:8+=b c ,对a 边利用余弦定理可得:2222cos a b c bc A =+-,结合已知整理得:13=bc ,再利用三角形面积公式计算得解.【详解】解:(1)()2sin()cos sin f x x A x A =-+2sin()cos sin[()]x A x x x A =-+--2sin()cos sin cos()cos sin()x A x x x A x x A =-+---sin cos()cos sin()x x A x x A =-+-sin(2)x A =-.因为()f x 在512x π=处取得最大值, 所以522122A k πππ⨯-=+,k Z ∈, 即2,3A k k Z ππ=-+∈. 因为(0,)A π∈,所以3A π=, 所以()sin(2)3f x x π=-. 因为(0,)2x π∈,所以22(,)333x πππ-∈-所以sin(2)13x π<-≤,因为关于x 的方程()f x t =有解,所以t 的取值范围为(. (2)因为5a =,3A π=,由正弦定理sin sin sin b c a B C A ==于是sin sin )+=+B C b c .又sin sin B C +=,所以8+=b c . 由余弦定理得:2222cos a b c bc A =+-,整理得:2225=+-b c bc ,即225()3643=+-=-b c bc bc ,所以13=bc ,所以1sin 2ABC S bc A ∆== 【点睛】本题主要考查了两角和、差的正弦公式应用,还考查了三角函数的性质及方程与函数的关系,还考查了正弦定理、余弦定理的应用及三角形面积公式,考查计算能力及转化能力,属于中档题.28.(I )1-;(II ;(III )10,3⎛⎤ ⎥⎝⎦ 【解析】【分析】 将()f x 整理为2sin 26x π⎛⎫+ ⎪⎝⎭;(I )利用x 的范围求得26x π+的范围,结合sin x 的图象可求得最值;(II )利用()85f x =-可求得sin 26x ;结合角的范围和同角三角函数关系可求得cos 26x π⎛⎫+ ⎪⎝⎭;根据cos 2cos 266x x ππ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦,利用两角和差余弦公式可求得结果;(III )利用x 的范围求得26x πω+的范围,从而根据sin x 单调递增区间构造出关于ω的不等式组,解不等式组再结合0>ω即可得到结果.【详解】()2cos 2cos 12cos 22sin 26f x x x x x x x π⎛⎫=+-=+=+ ⎪⎝⎭ (I )0,2x π⎡⎤∈⎢⎥⎣⎦ 72,666x πππ⎡⎤∴+∈⎢⎥⎣⎦[]2sin 21,26x π⎛⎫∴+∈- ⎪⎝⎭ ()f x ∴在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值为:1- (II )由题意得:82sin 265x π⎛⎫+=- ⎪⎝⎭ 4sin 265x π⎛⎫∴+=- ⎪⎝⎭ 2,3x ππ⎡⎤∈⎢⎥⎣⎦ 3132,626x πππ⎡⎤∴+∈⎢⎥⎣⎦ 3cos 265x π⎛⎫∴+= ⎪⎝⎭ cos 2cos 2cos 2cos sin 2sin 666666x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫∴=+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦341552=⨯(III )()2sin 26f x x πωω⎛⎫=+ ⎪⎝⎭ ,62x ππ⎡⎤∈⎢⎥⎣⎦时,2,6366x πωπππωωπ⎡⎤+∈++⎢⎥⎣⎦ 2622362k k ππωππωππππ⎧+≤+⎪⎪∴⎨⎪+≥-⎪⎩,k Z ∈,解得:12362k k ωω⎧≤+⎪⎨⎪≥-⎩,k Z ∈ 0ω>,可知当0k =时满足题意,即103ω<≤ω∴的取值范围为:10,3⎛⎤ ⎥⎝⎦【点睛】本题考查正弦型函数的值域求解、单调性应用、三角恒等变换公式应用、同角三角函数关系等问题.关键是能够利用二倍角公式和辅助角公式将函数化为()sin A x ωϕ+的形式,从而通过整体对应的方式来研究函数的值域和性质.29.(1)()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,()62k x k Z ππ=+∈;(2)522a ≤<,3π. 【解析】【分析】(1)根据图像得A=2,利用412562T πππω=-=,求ω值,再利用6x π=时取到最大值可求φ,从而得到函数解析式,进而求得对称轴方程;(2)由0,2x π⎡⎤∈⎢⎥⎣⎦得72,666x πππ⎡⎤+∈⎢⎥⎣⎦,方程f (x )=2a ﹣3有两个不等实根转为f (x )的图象与直线y =2a ﹣3有两个不同的交点,从而可求得a 的取值范围,利用图像的性质可得12x x +的值.【详解】(1)由图知,2,A =4156242=T ππππω=-=,解得ω=2,f(x)=2sin(2x+φ), 当6x π=时,函数取得最大值,可得2sin 226πϕ⎛⎫⨯+= ⎪⎝⎭,即sin 13πϕ⎛⎫+= ⎪⎝⎭, 2,32k k Z ππϕπ+=+∈,解得2,6k k Z πϕπ=+∈ ,又(0,)2πϕ∈所以6π=ϕ, 故()2sin 26f x x π⎛⎫=+ ⎪⎝⎭, 令262x k πππ+=+则()62k x k Z ππ=+∈, 所以()f x 的对称轴方程为()62k x k Z ππ=+∈; (2)70,2,2666x x ππππ⎡⎤⎡⎤∈∴+∈⎢⎥⎢⎥⎣⎦⎣⎦,所以方程()23f x a =-有两个不等实根时,()y f x =的图象与直线23y a =-有两个不同的交点,可得1232,a ≤-<522a ∴≤<, 当0,2x π⎡⎤∈⎢⎥⎣⎦时,()()12f x f x =,有122266x x πππ+++=, 故123x x π+=.【点睛】 本题考查由y =A sin (ωx +φ)的部分图象确定函数解析式,考查函数y =A sin (ωx +φ)的图象及性质的综合应用,属于中档题.30.(1)()2sin(2) 1.6f x x π=-+;(2)3π. 【解析】【详解】(1)由三角函数性质得,最大值为A+1=3,∴A=2, 周期2222πππωω⨯==⇒=,∴f (x )=2sin (2x-6π)+1(2)π(0,)2α∈,f (2α)=2 ∴2sin (22α⨯-6π)+1=2,得sin (α-6π)=12,α=3π。
高三数学三角函数练习大题经典22套

三角函数(三)1、在△ABC 中,AC=3,sinC=2sinA.(1)求AB 的值。
(2)求sin(2A -4π)的值。
2、设△ABC 的内角A 、B 、C 所以的边长分别为a,b,c ,3cos cos 5a Bb A C -=,(1)tan cot A B 的值。
(2)tan()A B -的最大值。
3、在△ABC中,5cos13B=-,4cos5C=.(I)sin A的值;(II)设△ABC的面积S△ABC=332,求BC的长。
4、设△ABC的内角A、B、C的对边分别为,,a b c,且A=60°,c=3b。
求(I)ac的值;(II)cot cotB C+的值.三角函数(四)1、在△ABC 中ambmc 分别为角A 、B 、C 的对的边长,a = ,tantan 422A B C++=,2sin sin cos 2AB C =。
求A 、B 及a 、c .2、在△ABC 中,内角A 、B 、C 对边的边长分别为,,a b c ,已知2,3c C π==(I )若S △ABC ,a b .(II )若sin sin()2sin 2C B A A +-=,求△ABC 的面积。
3、设锐角△ABC的内角A、B、C的对边分别为,,a b c,2sina b A=.(I)求角B的大小;(II)求cos sinA C+的取值范围。
4、在△ABC中,1tan4A=,3tan5B=,(I)求角C的大小;(II)若△ABC三角函数(五)1、已知△ABC的内角A、B及其对边,a b满足cot cot,a b a A b B+=+求内角C.2、△ABC中,D为BC上的一点,BD=33,5sin13B=,3cos5ADC∠=,求AD.3、在△ABC 中,角A 、B 、C 所对的边分别为,,a b c ,已知1cos 24C =-. (I )求sin C 的值;(2)当2,2sin sin a A C ==时,求b c 及的长。
高中数学三角函数练习题及答案解析(附答案)

高中数学三角函数练习题及答案解析(附答案)一、选择题1.探索如图所呈现的规律,判断2 013至2 014箭头的方向是()图1-2-3【解析】观察题图可知0到3为一个周期,则从2 013到2 014对应着1到2到3.【答案】 B2.-330是()A.第一象限角 B.第二象限角C.第三象限角 D.第四象限角【解析】-330=30+(-1)360,则-330是第一象限角.【答案】 A3.把-1 485转化为+k360,kZ)的形式是()A.45-4360 B.-45-4360C.-45-5360 D.315-5360【解析】-1 485=-5360+315,故选D.【答案】 D4.(2019济南高一检测)若是第四象限的角,则180-是() A.第一象限的角 B.第二象限的角C.第三象限的角 D.第四象限的角【解析】∵是第四象限的角,k360-90k360,kZ,-k360+180180--k360+270,kZ,180-是第三象限的角.【答案】 C5.在直角坐标系中,若与的终边互相垂直,则与的关系为()A.=+90B.=90C.=+90-k360D.=90+k360【解析】∵与的终边互相垂直,故-=90+k360,kZ,=90+k360,kZ.【答案】 D二、填空题6.,两角的终边互为反向延长线,且=-120,则=________. 【解析】依题意知,的终边与60角终边相同,=k360+60,kZ.【答案】k360+60,kZ7.是第三象限角,则2是第________象限角.【解析】∵k360+180k360+270,kZk180+90k180+135,kZ当k=2n(nZ)时,n360+90n360+135,kZ,2是第二象限角,当k=2n+1(nZ)时,n360+270n360+315,nZ2是第四象限角.【答案】二或四8.与610角终边相同的角表示为________.【解析】与610角终边相同的角为n360+610=n360+360+250=(n+1)360+250=k360+250(kZ,nZ).【答案】k360+250(kZ)三、解答题9.若一弹簧振子相对平衡位置的位移x(cm)与时间t(s)的函数关系如图所示,图1-2-4(1)求该函数的周期;(2)求t=10.5 s时该弹簧振子相对平衡位置的位移.【解】(1)由题图可知,该函数的周期为4 s.(2)设本题中位移与时间的函数关系为x=f(t),由函数的周期为4 s,可知f(10.5)=f(2.5+24)=f(2.5)=-8(cm),故t=10.5 s时弹簧振子相对平衡位置的位移为-8 cm.图1-2-510.如图所示,试表示终边落在阴影区域的角.【解】在0~360范围中,终边落在指定区域的角是0或315360,转化为-360~360范围内,终边落在指定区域的角是-4545,故满足条件的角的集合为{|-45+k36045+k360,kZ}.11.在与530终边相同的角中,求满足下列条件的角.(1)最大的负角;(2)最小的正角;(3)-720到-360的角.【解】与530终边相同的角为k360+530,kZ.(1)由-360<k360+530<0,且kZ可得k=-2,故所求的最大负角为-190.(2)由0<k360+530<360且kZ可得k=-1,故所求的最小正角为170(3)由-720k360+530-360且kZ得k=-3,故所求的角为-550.。
高中数学三角函数公式练习(答案)

高中数学三角函数公式练习(答案)1.sin(29π/6)的值为()A。
-1133B。
-C。
D。
2222答案】C解析】考点:任意角的三角函数2.已知sin(α-π/4)=7/√5301,cos2α=71/2525,sinα=5/13,求cosα的值。
A。
-/6662B。
-1025/4433C。
-727/5555D。
5555/2553答案】D解析】考点:两角和与差的三角函数,二倍角公式3.cos690°的值为()A。
-1133B。
C。
-2222D。
-答案】C解析】考点:三角函数的诱导公式4.tan(π/3)的值为()A。
-33B。
C。
3D。
-333答案】C解析】考点:三角函数的求值,诱导公式5.若-π<β<α<π,且cos(β+π/4)=5/√5301,则cos(α+β)的值为()A。
-B。
-3399C。
D。
-答案】C解析】考点:诱导公式,三角函数的化简求值。
6.若角 $\alpha$ 的终边在第二象限且经过点 $P(-1,3)$,则$\sin\alpha$ 等于 $\dfrac{3}{2}$。
7.$\sin7^\circ\cos37^\circ-\sin83^\circ\cos53^\circ$ 的值为$-\dfrac{1}{3}$。
8.已知 $\cos(-x)=\dfrac{\sqrt{3}}{2}$,那么 $\sin2x=-\dfrac{1}{2}$。
9.已知 $\sin\dfrac{5\pi}{2}+\alpha=\dfrac{1}{23}$,则$\cos2\alpha=-\dfrac{5}{9}$。
10.已知 $\sin(\dfrac{\pi}{2}+a)=\dfrac{1}{27}$,则$\cos2a=-\dfrac{1}{9}$。
11.已知点 $P(\tan\alpha,\cos\alpha)$ 在第三象限,则角$\alpha$ 在第二象限。
12.已知 $\alpha$ 是第四象限角,$\tan\alpha=-\dfrac{5}{22}$,则 $\sin\alpha=-\dfrac{12}{13}$。
高中数学三角函数练习题附答案

高中数学三角函数练习题附答案一、填空题1.已知函数()f x 在R 上可导,对任意x 都有()()2sin f x f x x --=,当0x ≤时,()1f x '<-,若π2π()33f t f t t ⎛⎫⎛⎫≤-- ⎪ ⎪⎝⎭⎝⎭,则实数t 的取值范围为_________2.在ABC 中,AB =BC =1cos 7BAC ∠=,动点D 在ABC 所在平面内且2π3BDC ∠=.给出下列三个结论:①BCD △②线段AD 的长度只有最小值,无最大值,且最小值为1;③动点D 的轨迹的长度为8π3.其中正确结论的序号为______.3.在长方体1111ABCD A B C D -中,13AB =,5AD =,112AA =,过点A 且与直线CD 平行的平面α将长方体分成两部分.现同时将两个球分别放入这两部分几何体内,则在平面α变化的过程中,这两个球的半径之和的最大值为___________.4.已知点A 为直线:3l y x =上一点,且A 位于第一象限,点()10,0B ,以AB 为直径的圆与l 交于点C (异于A ),若60CBA ∠≥,则点A 的横坐标的取值范围为___________.5.在ABC 中,角A ,B ,C 所对的边长分别为a ,b ,c ,D 为边BC 上的一点,若6c =,b =sin BAD ∠=,cos BAC ∠=,则AD =__________.6.在ABC 中,AB BC ≠,O 为ABC 的外心,且有AB BC AC +=,sin (cos cos sin 0C A A A +=,若AO x AB y AC =+,,x y R ∈,则2x y -=________.7.△ABC 中,角A ,B ,C 所对的三边分别为a ,b ,c ,c =2b ,若△ABC 的面积为1,则BC 的最小值是________ .8.已知函数()sin cos f x x x =+,()sin cos g x x x =:①函数()f x 的图象关于点(,0)4π对称;②函数|()|g x 的最小正周期是2π;③把函数f (2x )图象上所有点向右平移8π个单位长度得到的函数图象的对称轴与函数y=()g x 图象的对称轴完全相同;④函数1()()y f x g x =--在R 上的最大值为2.则以上结论正确的序号为_______________9.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示.将函数()y f x =的图象向右平移4π个单位,得到()y g x =的图象,则下列有关()f x 与()g x 的描述正确的有___________(填序号).①()2sin 23g x x π⎛⎫=- ⎪⎝⎭;②方程()()360,2f x g x x π⎫⎛⎫+∈ ⎪⎪⎝⎭⎭所有根的和为712π;③函数()y f x =与函数()y g x =图象关于724x π=对称. 10.已知1OB →=,,A C 是以O 为圆心,220BA BC →→⋅=,设平面向量OA →与OB →的夹角为θ(π04θ≤≤),则平面向量OA →在BC →方向上的投影的取值范围是_____.二、单选题11.已知双曲线2221(0)y x b b-=>的左、右焦点分别为1F ,2F ,过点2F 作直线l 交双曲线的右支于A ,B 两点.若11||::3:3:2AB AF BF =,则双曲线的离心率为( ) A 33B 2C .113D .1112.已知无穷项实数列{}n a 满足: 1a t =, 且 14111n n n a a a +=--, 则( ) A .存在1t >, 使得20111a a = B .存在0t <, 使得20211a a =C .若2211a a =, 则21a a =D .至少有2021个不同的t , 使得20211a a =13.在ABC 中,角,,A B C 所对应的边分别为,,a b c ,设ABC 的面积为S ,则24Sa bc+的最大值为( ) A 2B 3C 3D 214.《九章算术》卷五“商功”:今有刍甍,下广3丈,袤4丈;上袤2丈,无广;高1丈.其描述的是下图的一个五面体,底面ABCD 是矩形,4AB =,3BC =,2EF =,//EF 底面ABCD 且EF 到底面ABCD 的距离为1.若DE AE BF CF ===,则该刍甍中点F 到平面EBC 的距离为( )A .15B .35C 10D 2515.已知函数()sin 22cos f x x x =-,下列说法错误的是( ) A .函数()f x 是周期函数 B .6x π=是函数()f x 图象的一条对称轴C .函数()f x 的增区间为()72,266k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z D .函数()f x 3316.已知函数()()cos 333f x a x x a ππ⎛⎫⎛⎫=--∈ ⎪ ⎪⎝⎭⎝⎭R 是偶函数.若将曲线()2y f x =向左平移12π个单位长度后,再向上平移1个单位长度得到曲线()y g x =,若关于x 的方程()g x m =在70,12π⎡⎤⎢⎥⎣⎦有两个不相等实根,则实数m 的取值范围是( )A .[]0,3B .[)0,3C .[)2,3D .)21,3⎡⎣17.已知函数()()3log 911x f x x+=-,下列说法正确的是( )A .()f x 既不是奇函数也不是偶函数B .()f x 的图象与sin y x =有无数个交点C .()f x 的图象与2y =只有一个交点D .()()21f f -<-18.设点()11,P x y 在椭圆22182x y +=上,点()22,Q x y 在直线280x y +-=上,则2121x x y y -+-的最小值是( )A .21B 3C .31D .219.设函数()cos 2sin f x x x =+,下述四个结论: ①()f x 是偶函数; ②()f x 的最小正周期为π; ③()f x 的最小值为0;④()f x 在[]0,2π上有3个零点 其中所有正确结论的编号是( ) A .①②B .①②③C .①③④D .②③④20.已知1sin ,sin ,sin ,222a x x b x ωωω⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,其中0>ω,若函数1()2f x a b =⋅-在区间(,2)ππ内有零点,则实数ω的取值可能是( )A .18B .14C .12D .34三、解答题21.已知1l ,2l ,3l 是同一平面内自上而下的三条不重合的平行直线.(1)如图1,如果1l 与2l 间的距离是1,2l 与3l 间的距离也是1,可以把一个正三角形ABC 的三顶点分别放在1l ,2l ,3l 上,求这个正三角形ABC 的边长.(2)如图2,如果1l 与2l 间的距离是1,2l 与3l 间的距离是2,能否把一个正三角形ABC 的三顶点分别放在1l ,2l ,3l 上,如果能放,求BC 和3l 夹角θ的正切值并求该正三角形边长;如果不能,试说明理由.(3)如果边长为2的正三角形ABC 的三顶点分别在1l ,2l ,3l 上,设1l 与2l 间的距离为1d ,2l 与3l 间的距离为2d ,求12d d ⋅的取值范围.22.如图,甲、乙两个企业的用电负荷量y 关于投产持续时间t (单位:小时)的关系()y f t =均近似地满足函数()sin()(0,0,0)f t A t b A ωϕωϕπ=++>><<.(1)根据图象,求函数()f t 的解析式;(2)为使任意时刻两企业用电负荷量之和不超过9,现采用错峰用电的方式,让企业乙比企业甲推迟(0)m m >小时投产,求m 的最小值.23.已知函数2()232sin cos ()f x x x x a a R =-++∈,且(0)3f = (1)求a 的值;(2)若()f x ω在[0,]π上有且只有一个零点,0>ω,求ω的取值范围.24.已知()sin ,2cos a x x =,()2sin ,sin b x x =,()f x a b =⋅ (1)求()f x 的解析式,并求出()f x 的最大值;(2)若0,2x π⎡⎤∈⎢⎥⎣⎦,求()f x 的最小值和最大值,并指出()f x 取得最值时x 的值.25.如图,长方形ABCD 中,2,3AB BC ==,点,,E F G 分别在线段,,AB BC DA (含端点)上,E 为AB 中点,⊥EF EG ,设AEG θ∠=.(1)求角θ的取值范围;(2)求出EFG ∆周长l 关于角θ的函数解析式()f θ,并求EFG ∆周长l 的取值范围. 26.已知函数22()cos sin 23sin cos 3f x a x a x a x x =-+-,其中a R ∈. (Ⅰ)当1a =时,求函数()f x 的对称中心; (Ⅱ)若函数()f x 的最小值为4-,求实数a 的值.27.为丰富市民的文化生活,市政府计划在一块半径为200m ,圆心角为0120的扇形地上建造市民广场,规划设计如图:内接梯形ABCD 区域为运动休闲区,其中A ,B 分别在半径OP ,OQ 上,C ,D 在圆弧PQ 上,CD //AB ;上,CD //AB ;OAB ∆区域为文化展区,AB 长为3域,且CD 长不得超过200m.(1)试确定A ,B 的位置,使OAB ∆的周长最大?(2)当OAB ∆的周长最长时,设2DOC θ∠=,试将运动休闲区ABCD 的面积S 表示为θ的函数,并求出S 的最大值.28.设函数2()cos sin 2f x x a x a =-+++(a ∈R ). (1)求函数()f x 在R 上的最小值;(2)若不等式()0f x <在[0,]2π上恒成立,求a 的取值范围;(3)若方程()0f x =在(0,)π上有四个不相等的实数根,求a 的取值范围.29.函数()sin()16f x A x πω=-+(0,0A ω>>)的最大值为3, 其图象相邻两条对称轴之间的距离为2π, (1)求函数()f x 的解析式;(2)设π(0,)2α∈,则()22f α=,求α的值30.函数f (x )=A sin (2ωx +φ)(A >0,ω>0,|φ|<2π)的部分图象如图所示 (1)求A ,ω,φ的值;(2)求图中a ,b 的值及函数f (x )的递增区间; (3)若α∈[0,π],且f (α)=2,求α的值.【参考答案】一、填空题1.π6∞⎛⎤- ⎥⎝⎦,2.①③3.165384.)133,⎡++∞⎣5.46.4333- 738.②③④ 9.①③10.2525⎡⎢⎣⎦二、单选题 11.A12.D 13.A 14.C 15.B 16.C 17.C 18.D 19.B 20.D 三、解答题21.(1)2 ;(2)能放,tan θ=;(3)(]0,1 【解析】 【分析】(1)根据,A C 到直线2l 的距离相等,可得2l 过AC 的中点M ,2l AC ⊥,从而求得边长2AC AM =的值.(2)假设能放,设边长为a ,BC 与3l 的夹角θ,不妨设060θ<≤,可得sin 2a θ=,()sin 601a θ-=,两式相比化简可得sin θa 的值,从而得出结论. (3)利用两角和差的正弦、余弦公式化简()124sin 60sin d d θθ⋅=-为()2sin 2301θ+-,再根据正弦函数的定义和值域求出12d d ⋅的取值范围. 【详解】 (1),A C 到直线2l 的距离相等,∴2l 过AC 的中点M , ∴2l AC ⊥, ∴边长22AC AM ==(2)假设能放,设边长为a ,BC 与3l 的夹角θ, 由对称性,不妨设060θ<≤, ∴sin 2a θ=,()sin 601a θ-=,两式相比可得:()sin 2sin 60θθ=-,即sin sin θθθ-,2sin θθ∴=,tan θ∴=,sin θ∴=,故边长3a==,综上可得,能放.(3)()1214sin60sin4sin sin2d dθθθθθ⎫⋅=-=-⎪⎪⎝⎭()1cos2222sin23012θθθ⎫+=-=+-⎪⎪⎝⎭.060θ<≤,30230150θ∴<+≤,()1sin23012θ≤+≤,所以()02sin23011θ≤+-≤,又10d>,2d>,所以(]120,1d d⋅∈.【点睛】本题是一道考查三角函数应用的题目,解题的关键是掌握等边三角形的性质以及三角函数的恒等变换,属于中档题.22.(1)()sin462f t tππ⎛⎫=++⎪⎝⎭;(2)4【解析】【分析】(1)由212Tπω==,得ω,由53A bb A+=⎧⎨-=⎩,得A,b,代入(0,5),求得ϕ,从而即可得到本题答案;(2)由题,得()()cos()cos8966f t m f t t m tππ⎡⎤⎛⎫++=+++≤⎪⎢⎥⎣⎦⎝⎭恒成立,等价于cos()cos166t m tππ⎡⎤⎛⎫++≤⎪⎢⎥⎣⎦⎝⎭恒成立,然后利用和差公式展开,结合辅助角公式,逐步转化,即可得到本题答案.【详解】(1)解:由图知212Tπω==,6πω∴=又53A bb A+=⎧⎨-=⎩,可得41bA=⎧⎨=⎩()sin46f t tπϕ⎛⎫∴=++⎪⎝⎭,代入(0,5),得22kπϕπ=+,又0ϕπ<<,2πϕ∴=所求为()sin462f t tππ⎛⎫=++⎪⎝⎭(2)设乙投产持续时间为t小时,则甲的投产持续时间为()t m+小时,由诱导公式,企业乙用电负荷量随持续时间t 变化的关系式为:()sin 4cos 4626f t t t πππ⎛⎫=++=+ ⎪⎝⎭同理,企业甲用电负荷量变化关系式为:()cos ()46f t m t m π⎡⎤+=++⎢⎥⎣⎦两企业用电负荷量之和()()cos ()cos 866f t m f t t m t ππ⎡⎤⎛⎫++=+++ ⎪⎢⎥⎣⎦⎝⎭,0t ≥依题意,有()()cos ()cos 8966f t m f t t m t ππ⎡⎤⎛⎫++=+++≤ ⎪⎢⎥⎣⎦⎝⎭恒成立即cos ()cos 166t m t ππ⎡⎤⎛⎫++≤⎪⎢⎥⎣⎦⎝⎭恒成立 展开有cos 1cos sin sin 16666m t m t ππππ⎡⎤⎛⎫⎛⎫⎛⎫+-≤ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦恒成立cos 1cos sin sin cos 66666m t m t A t πππππϕ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+-=+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦其中,A =cos 16cos m Aπϕ⎛⎫+ ⎪⎝⎭=,sin 6sin m A πϕ=1A ∴=≤整理得:1cos 62m π⎛⎫≤- ⎪⎝⎭解得2422363k m k πππππ⎛⎫+≤≤+ ⎪⎝⎭即124128k m +≤≤+ 取0k =得:48m ≤≤ m ∴的最小值为4. 【点睛】本题主要考查根据三角函数的图象求出其解析式,以及三角函数的实际应用,主要考查学生的分析问题和解决问题的能力,以及计算能力,难度较大. 23.(1)a =(2)15,36⎡⎫⎪⎢⎣⎭【解析】 【分析】(1)利用降次公式、辅助角公式化简()f x表达式,利用(0)f =a 的值. (2)令()0f x ω=,结合x 的取值范围以及三角函数的零点列不等式,解不等式求得ω的取值范围. 【详解】(1)2()2sin cos f x x x x a =-++sin 2x x a =+2sin 23x a π⎛⎫=++- ⎪⎝⎭(0)f =(0)2sin3f a π∴=+=即a =(2)令()0f x ω=,则sin 203x πω⎛⎫+= ⎪⎝⎭,[0,]x π∈,2,2333πππωπω⎡⎤∴+∈+⎢⎥⎣⎦,()f x 在[0,]π上有且只有一个零点,223πππωπ∴+<,1536ω∴<, ω∴的取值范围为15,36⎡⎫⎪⎢⎣⎭. 【点睛】本小题主要考查三角恒等变换,考查三角函数零点问题,考查化归与转化的数学思想方法,属于基础题.24.(1)()f x 214x π⎛⎫=-+ ⎪⎝⎭1.(2)0x =时,最小值0.38x π=1. 【解析】 【分析】(1)利用数量积公式、倍角公式和辅助角公式,化简()f x ,再利用三角函数的有界性,即可得答案; (2)利用整体法求出32444x πππ-≤-≤,再利用三角函数线,即可得答案. 【详解】(1)()22sin 2sin cos f x x x x =+1cos2sin2x x =-+214x π⎛⎫=-+ ⎪⎝⎭∴sin 214x π⎛⎫-≤ ⎪⎝⎭,()f x ∴1.(2)由(1)得()214f x x π⎛⎫=-+ ⎪⎝⎭,∵0,2x π⎡⎤∈⎢⎥⎣⎦,32444x πππ∴-≤-≤.sin 2124x π⎛⎫≤-≤ ⎪⎝⎭,∴当244x ππ-=-时,即0x =时,()f x 取最小值0.当242x ππ-=,即38x π=时,()f x 1. 【点睛】本题考查向量数量积、二倍角公式、辅助角公式、三角函数的性质,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意整体法的应用.25.(1)[,]63ππ(2)1sin cos ()sin cos f θθθθθ++=,[,]63ππθ∈,EFG ∆周长l 的取值范围为1)]【解析】(1)结合图像可得当点G 位于D 点时,角θ取最大值,点F 位于C 点时,BEF ∠取最大值,角θ取最小值,在直角三角形中求解即可. (2)在Rt ΔEAG 中,求出1cos EG θ=,在Rt ΔEBF 中,求得1sin EF θ=,在Rt ΔGEF 中,根据勾股定理得222FG EF EG =+,从而可得111()cos sin sin cos f θθθθθ=++,通分可得1sin cos ()sin cos f θθθθθ++=,令sin cos t θθ=+,借助三角函数的性质即可求解.【详解】(1)由题意知,当点G 位于D 点时,角θ取最大值,此时tan θ=02πθ<<,所以max 3πθ=当点F 位于C 点时,BEF ∠取最大值,角θ取最小值, 此时=3BEF π∠,所以min 236πππθ=-=故所求θ的取值集合为[,]63ππ(2)在Rt ΔEAG 中,cos AE EG θ=,1AE =,所以1cos EG θ= 在Rt ΔEBF 中,cos cos()2BE BEF EF πθ∠=-=,1BE =,所以1sin EF θ= 在Rt ΔGEF 中,有勾股定理得222FG EF EG =+2222222211sin cos 1sin cos sin cos sin cos θθθθθθθθ+=+== 因为[,]63ππθ∈,所以sin 0,cos 0θθ,1sin cos FG θθ=所以111()cos sin sin cos f EG EF FG θθθθθ=++=++ 所以1sin cos ()sin cos f θθθθθ++=,[,]63ππθ∈令sin cos t θθ=+,则21sin cos 2t θθ-=所以22(1)211t l t t +==-- 因为[,]63ππθ∈,57[,]41212πππθ+∈,所以sin()4πθ+∈所以sin cos )4t πθθθ=+=+∈所以EFG ∆周长l 的取值范围为1)] 【点睛】本题考查了三角函数的在平面几何中的应用,主要考查了辅助角公式以及换元法求三角函数的值域,属于中档题. 26.(Ⅰ)(,3),.122k k Z ππ-+-∈(Ⅱ)12a =或12a =- 【解析】(Ⅰ)当1a =时,根据二倍角公式、辅助角公式化简函数,根据正弦函数的性质可得. (Ⅱ)将函数化简为()sin()f x A x b ωϕ=++的形式,分类讨论可得. 【详解】解:(Ⅰ)当1a =时,22()cos sin cos 3f x x x x x =-+-cos 2232sin(2)36x x x π=-=+-()2sin(2)36f x x π∴=+-由2,6x k k Z ππ+=∈ 得:,122k x k Z ππ=-+∈ ()f x ∴的对称中心为(,3),.122k k Z ππ-+-∈(Ⅱ)22()cos sin sin cos 3f x a x a x x x =-+-()cos 2sin 23f x a x x ∴=-()2sin(2)36f x a x π∴=+-1sin(2)16x π-≤+≤当0a >时,232sin(2)3236a a x a π--≤+-≤-则有234a --=- 解得12a =当0a =时,min ()3f x =-,不合题意当0a <时,232sin(2)3236a a x a π-≤+-≤--则有234a -=-解得12a =-综上 12a ∴=或12a =-.【点睛】本题主要考查三角函数的图象和性质,利用三角公式将函数进行化简是解决本题的关键,要求熟练掌握三角函数的图象和性质,属于中档题.27.(1)OA 、OB 都为50m ;(2)8sin 64sin cos S θθθθ=-+;0,6πθ⎛⎤∈ ⎥⎝⎦;最大值为2625(8m +. 【解析】 【分析】对于(1),设OA m =,OB n =,m ,n (0,200)∈,在△OAB 中,利用余弦定理可得22222cos3AB OA OB OA OB π=+-⋅⋅,整理得222m n mn =++,结合基本不等式即可得出结论;对于(2),当△AOB 的周长最大时,梯形ACBD 为等腰梯形,过O 作OF ⊥CD 交CD 于F ,交AB 于E ,则E 、F 分别为AB ,CD 的中点,利用已知可表示出相关线段;然后利用梯形的面积公式可知,8sin 64sin cos S θθθθ=-+ ,0,6πθ⎛⎤∈ ⎥⎝⎦,令()8sin 64sin cos f θθθθθ=-+0,6πθ⎛⎤∈ ⎥⎝⎦,,结合导数,确定函数的单调性,即可求出S 的最大值. 【详解】解:(1)设OA m =,OB n =,m ,n (0,200)∈,在OAB ∆中,22222cos3AB OA OB OA OB π=+-⋅⋅,即222m n mn =++.所以22222()3()()()44m n m n mn m n m n +=+-+-=+.所以m n 100+,当且仅当m n 50==时,m n +取得最大值, 此时OAB ∆周长取得最大值.答:当OA 、OB 都为50m 时,OAB ∆的周长最大. (2)当AOB ∆的周长最大时,梯形ABCD 为等腰梯形.如上图所示,过O 作OF CD ⊥交CD 于F ,交AB 于E ,则E 、F 分别为AB 、CD 的中点, 所以DOE θ∠=.由CD 200,得0,6πθ⎛⎤∈ ⎥⎝⎦.在ODF ∆中,DF 200sin θ=,OF 200cos θ=. 又在AOE ∆中,OE OAcos253π==,故EF 200cos 25θ=-.所以1(503400sin )(200cos 25)2S θθ=-625(38sin )(8cos 1)θθ=-625(838sin 64sin cos 3)θθθθ=-+,0,6πθ⎛⎤∈ ⎥⎝⎦.令()838sin 64sin cos 3f θθθθθ=-+0,6πθ⎛⎤∈ ⎥⎝⎦,()838cos 64cos 216sin 64cos 26f πθθθθθθ'⎛⎫=--+=-++ ⎪⎝⎭,0,6πθ⎛⎫∈ ⎪⎝⎭.又16sin 6y πθ⎛⎫=-+ ⎪⎝⎭及cos 2y θ=在0,6πθ⎛⎤∈ ⎥⎝⎦上均为单调递减函数,故()f θ'在0,6πθ⎛⎤∈ ⎥⎝⎦上为单调递减函数.因1()1640623f π⎫'=-⨯>⎪⎪⎝⎭,故()0f θ'>在0,6πθ⎛⎤∈ ⎥⎝⎦上恒成立, 于是,()f θ在0,6πθ⎛⎤∈ ⎥⎝⎦上为单调递增函数.所以当6πθ=时,()f θ有最大值,此时S 有最大值为625(8153)+. 答:当6πθ=时,梯形ABCD 面积有最大值,且最大值为2625(8153)m +.【点睛】本题主要考查了余弦定理、基本不等式以及导数的应用,在(2)中得到()838sin 64sin cos 3f θθθθθ=-+()16sin 64cos 26f πθθθ'⎛⎫=-++ ⎪⎝⎭,结合函数在公共区间上,减函数+减函数等于减函数,从而确定()f θ'在0,6πθ⎛⎤∈ ⎥⎝⎦上为单调递减函数.属于难题.28.(1)2min2,2;()1,22;422,2.a af x a a a a >⎧⎪⎪=-++-≤≤⎨⎪+<-⎪⎩(2)(,1)a ∈-∞-(3)12a -<<-【解析】 【分析】(1)通过换元法将函数变形为二次函数,同时利用分类讨论的方法求解最大值; (2)恒成立需要保证max ()0f x <即可,对二次函数进行分析,根据取到最大值时的情况得到a 的范围;(3)通过条件将问题转化为二次函数在给定区间上有两个零点求a 的范围,这里将所有满足条件的不等式列出来,求解出a 的范围. 【详解】解:(1)令sin x t =,[1,1]t ∈-,则2()()1f x g t t at a ==+++,对称轴为2a t =-. ①12a -<-,即2a >,min ()(1)2f x g =-=. ②112a -≤-≤,即22a -≤≤,2min ()()124a a f x g a =-=-++.③12a->,即2a <-,min ()(1)22f x g a ==+. 综上可知,2min2,2;()1,22;422,2.a af x a a a a >⎧⎪⎪=-++-≤≤⎨⎪+<-⎪⎩ (2)由题意可知,max ()0f x <,2()()1f xg t t at a ==+++,[0,1]t ∈的图象是开口向上的抛物线,最大值一定在端点处取得,所以有(0)10,(1)220,g a g a =+<⎧⎨=+<⎩故(,1)a ∈-∞-. (3)令sin x t =,(0,)x π∈.由题意可知,当01t <<时,sin x t =有两个不等实数解,所以原题可转化为2()10g t t at a =+++=在(0,1)内有两个不等实数根.所以有201,24(1)0,12(0)10,(1)220,a a a a g a g a ⎧<-<⎪⎪⎪∆=-+>⇒-<<-⎨⎪=+>⎪=+>⎪⎩【点睛】(1)三角函数中,形如2()sin sin f x a x b x c =++或者2()cos cos f x a x b x c =++都可以采用换元法求解函数最值;(2)讨论二次函数的零点的分布,最好可以采用数形结合的方法解决问题,这样很大程度上减少了遗漏条件的可能.29.(1)()2sin(2) 1.6f x x π=-+;(2)3π.【解析】 【详解】(1)由三角函数性质得,最大值为A+1=3,∴A=2, 周期2222πππωω⨯==⇒=,∴f (x )=2sin (2x-6π)+1 (2)π(0,)2α∈,f (2α)=2∴2sin (22α⨯-6π)+1=2,得sin (α-6π)=12,α=3π30.(1)π2,1,6A ωϕ===;(2)7π,112a b =-=,递增区间为()πππ,π36k k k Z ⎡⎤-+∈⎢⎥⎣⎦;(3)π24或7π24. 【解析】 【分析】(1)利用函数图像可直接得出周期T 和A ,再利用=2Tπω,求出ω,然后利用待定系数法直接得出ϕ的值.(2)通过第一问求得的值可得到()f x 的函数解析式,令()=0f x ,再根据a 的位置确定出a 的值;令0x =得到的函数值即为b 的值;利用正弦函数单调增区间即可求出函数的单调增区间.(3)令()f α=0απ,即可求得α的取值.【详解】解:(1)由图象知A =2,34T =512π-(-3π)=912π, 得T =π, 即22πω=2,得ω=1, 又f (-3π)=2sin[2×(-3π)+φ]=-2, 得sin (-23π+φ)=-1,即-23π+φ=-2π+2k π, 即ω=6π+2k π,k ∈Z , ∵|φ|<2π,∴当k =0时,φ=6π, 即A =2,ω=1,φ=6π;(2)a =-3π-4T =-3π-4π=-712π,b =f (0)=2sin 6π=2×12=1,∵f (x )=2sin (2x +6π),∴由2k π-2π≤2x +6π≤2k π+2π,k ∈Z ,得k π-3π≤x ≤k π+6π,k ∈Z ,即函数f (x )的递增区间为[k π-3π,k π+6π],k ∈Z ;(3)∵f (α)=2sin (2α+6π)即sin (2α+6π) ∵α∈[0,π],∴2α+6π∈[6π,136π], ∴2α+6π=4π或34π,∴α=24π或α=724π.【点睛】关于三角函数图像需记住: 两对称轴之间的距离为半个周期; 相邻对称轴心之间的距离为半个周期;相邻对称轴和对称中心之间的距离为14个周期.关于正弦函数单调区间要掌握:当2,222x k k ππωϕππ⎡⎤+∈-+⎢⎥⎣⎦时,函数单调递增;当32+,222x k k ππωϕππ⎡⎤+∈+⎢⎥⎣⎦时,函数单调递减.。
高中数学三角函数练习题含答案
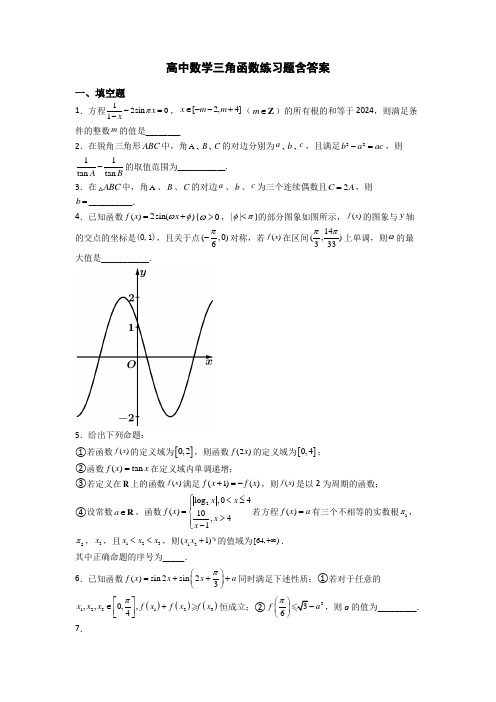
高中数学三角函数练习题含答案一、填空题1.方程12sin 01x xπ-=-,[2,4]x m m ∈--+(m ∈Z )的所有根的和等于2024,则满足条件的整数m 的值是________2.在锐角三角形ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且满足22b a ac -=,则11tan tan A B-的取值范围为___________. 3.在ABC 中,角A 、B 、C 的对边a 、b 、c 为三个连续偶数且2C A =,则b =__________.4.已知函数()2sin()f x x ωφ=+(0>ω,||φπ<)的部分图象如图所示,()f x 的图象与y 轴的交点的坐标是(0,1),且关于点(,0)6π-对称,若()f x 在区间14(,)333ππ上单调,则ω的最大值是___________.5.给出下列命题:①若函数()f x 的定义域为[]0,2,则函数(2)f x 的定义域为[]0,4; ②函数()tan f x x =在定义域内单调递增;③若定义在R 上的函数()f x 满足(1)()f x f x +=-,则()f x 是以2为周期的函数;④设常数a ∈R ,函数2log ,04()10,41x x f x x x ⎧<≤⎪=⎨>⎪-⎩若方程()f x a =有三个不相等的实数根1x ,2x ,3x ,且123x x x <<,则312(1)x x x +的值域为[64,)+∞.其中正确命题的序号为_____.6.已知函数()sin 2sin 23f x x x a π⎛⎫=+++ ⎪⎝⎭同时满足下述性质:①若对于任意的()()()123123,0,,4,x x x f x f x f x π⎡⎤∈+⎢⎥⎣⎦恒成立;②236f a π⎛⎫- ⎪⎝⎭,则a 的值为_________.7.在锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若2cos b a a C -=,则ac的取值范围是______.8.已知正四棱柱1111ABCD A B C D -中,2AB =,13AA =.若M 是侧面11BCC B 内的动点,且AM MC ⊥,则1A M 的最小值为__________.9.已知函数()cos()(0,0,0)f x A x A ωϕωϕπ=->><<的部分图像如图所示,设函数()266g x f x f x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则()g x 的值域为___________.10.已知函数()2log ,0,0x x f x x x >⎧=⎨-≤⎩,函数()g x 满足以下三点条件:①定义域为R ;②对任意x ∈R ,有()()2g x g x π+=;③当[]0,x π∈时,()sin .g x x =则函数()()y f x g x =-在区间[]4,4ππ-上零点的个数为__________个.二、单选题11.已知ABC 中,角,,A B C 的对边分别为,,a b c .若2222224cos 4sin 33a B b A b c +=-,则cos A 的最小值为( )A 2B 7C 7D .3412.已知30.4tan(1),tan0.1,a b c πππ=+-==,则( ).A .b c a <<B .c a b <<C .a c b <<D .a b c <<13.若函数sin 2y x =与()sin 2y x ϕ=+在0,4π⎛⎫⎪⎝⎭上的图象没有交点,其中()0,2ϕπ∈,则ϕ的取值范围是( )A .[),2ππB .,2ππ⎡⎤⎢⎥⎣⎦C .(),2ππD .,214.《九章算术》卷五“商功”:今有刍甍,下广3丈,袤4丈;上袤2丈,无广;高1丈.其描述的是下图的一个五面体,底面ABCD 是矩形,4AB =,3BC =,2EF =,//EF 底面ABCD 且EF 到底面ABCD 的距离为1.若DE AE BF CF ===,则该刍甍中点F 到平面EBC 的距离为( )A .15B .35C 10D 2515.已知函数2()log f x x =,函数()g x 满足以下三点条件:①定义域为R ;②对任意x ∈R ,有()2()g x g x π+=;③当[0,]x π∈时,()sin g x x =.则函数()()y f x g x =-在区间[0,4]π上的零点个数为( )A .5B .6C .7D .816.已知函数()sin 22cos f x x x =-,下列说法错误的是( ) A .函数()f x 是周期函数 B .6x π=是函数()f x 图象的一条对称轴C .函数()f x 的增区间为()72,266k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z D .函数()f x 3317.已知双曲线22413y x -=的左右焦点分别为1F ,2F ,点M 是双曲线右支上一点,满足120MF MF →→⋅=,点N 是线段12F F 上一点,满足112F N F F λ→→=.现将12MF F △沿MN 折成直二面角12F MN F --,若使折叠后点1F ,2F 距离最小,则λ=( )A .15B .25C .35D .4518.已知函数()sin os 0(c f x x a x a ωω=+>且0>ω),周期2T π<,()33f π()f x 在6x π=处取得最大值,则ω的最小值为( )A .11B .12C .13D .1419.设点()11,P x y 在椭圆22182x y +=上,点()22,Q x y 在直线280x y +-=上,则2121x x y y -+-的最小值是( )A .21B 3C .31D .220.设函数()sin cos f x a x b x ωω=+()0ω>在区间,62ππ⎡⎤⎢⎥⎣⎦上单调,且2236f f f πππ⎛⎫⎛⎫⎛⎫==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,当12x π=时,()f x 取到最大值4,若将函数()f x 的图象上各点的横坐标伸长为原来的2倍得到函数()g x 的图象,则函数()3y g x x π=-+零点的个数为( ) A .4B .5C .6D .7三、解答题21.将函数2sin 3y x =+的图象上所有点的横坐标缩短到原来的12倍,纵坐标不变,再将所得的图象向右平移3π个单位长度后得到函数()f x 的图象. (1)写出函数()f x 的解析式;(2)若,36x ππ⎡⎤∈-⎢⎥⎣⎦时,22()2()()1g x f x mf x m =-+-,求()g x 的最小值min ()g x .22.已知向量(1,0)a =,(sin 2,1)b x =--,(2sin ,1)c x =+,(1,)d k =(,)x k R ∈. (1)若[,]x ππ∈-,且()//a b c +,求x 的值; (2)对于()11,m x y =,()22,n x y =,定义12211(,)2S m n x y x y =-.解不等式1(,)2S b c >; (3)若存在x ∈R ,使得()()a b c d +⊥+,求k 的取值范围. 23.已知函数2()23sin 2sin cos ()f x x x x a a R =-++∈,且(0)3f =. (1)求a 的值;(2)若()f x ω在[0,]π上有且只有一个零点,0>ω,求ω的取值范围.24.已知函数()()2sin 24sin 206x x x f πωωω⎛⎫=--+> ⎪⎝⎭,其图象与x 轴相邻的两个交点的距离为2π. (1)求函数()f x 的解析式;(2)若将()f x 的图象向左平移()0m m >个长度单位得到函数()g x 的图象恰好经过点,03π⎛-⎫ ⎪⎝⎭,求当m 取得最小值时,()g x 在7,612ππ⎡⎤-⎢⎥⎣⎦上的单调区间.25.某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角ΔABC 和以BC 为直径的半圆拼接而成,点P 为半圈上一点(异于B ,C ),点H 在线段BC 上,且满足CH AB ⊥.已知90ACB ∠=︒,1dm AB =,设ABC θ∠=.(1)为了使工艺礼品达到最佳观赏效果,需满足ABC PCB ∠=∠,且CA CP +达到最大.当θ为何值时,工艺礼品达到最佳观赏效果;(2)为了工艺礼品达到最佳稳定性便于收藏,需满足60PBA ∠=︒,且CH CP +达到最大.当θ为何值时,CH CP +取得最大值,并求该最大值.26.已知函数22()cos sin 23sin cos 3f x a x a x a x x =-+-,其中a R ∈. (Ⅰ)当1a =时,求函数()f x 的对称中心;(Ⅱ)若函数()f x 的最小值为4-,求实数a 的值.27.已知(1,sin )a x =,(1,cos )b x =,(0,1)e =,且(cos sin )[1,2]x x -∈. (1)若()//a e b +,求sin cos x x 的值;(2)设()()f x a b me a b =⋅+⋅-,m R ∈,若()f x 的最大值为12-,求实数m 的值.28.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,cos 222cos 20C C ++=. (1)求角C 的大小;(2)若2b a =,ABC ∆的面积为2sin sin 2A B ,求sin A 及c 的值. 29.已知函数()()sin ,f x A x x R ωϕ=+∈(其中0,0,02A πωϕ>><<)的图象如图所示:(1)求函数()f x 的解析式及其对称轴的方程;(2)当0,2x π⎡⎤∈⎢⎥⎣⎦时,方程()23f x a =-有两个不等的实根12,x x ,求实数a 的取值范围,并求此时12x x +的值.30.已知函数()()()24sin sin cos sin cos sin 142x f x x x x x x π⎛⎫=+++-- ⎪⎝⎭.(1)求函数()f x 的最小正周期; (2)若函数()()()12122g x f x af x af x a π⎡⎤⎛⎫=+---- ⎪⎢⎥⎝⎭⎣⎦在,42ππ⎡⎤-⎢⎥⎣⎦的最大值为2,求实数a 的值.【参考答案】一、填空题1.1008或10092.⎛ ⎝⎭3.104.115.③④ 6.0 7.⎝⎭89.9[,4]4-10.6二、单选题 11.C 12.D 13.A 14.C 15.A 16.B 17.C 18.C 19.D 20.D 三、解答题21.(1)2()2sin 233f x x π⎛⎫=-+ ⎪⎝⎭;(2)22min21,47()1,4128(32312m m m g x m m m m m ⎧-+≤⎪⎪=-<<+⎨⎪⎪-++≥+⎩ 【解析】(1)根据函数图象的变换规律即可求得()f x 的解析式;(2)令()t f x =可求得则()[1,3f x ∈+,设22()21M t t mt m =-+-,[1,3t ∈,通过定区间讨论对称轴4mt =的三种情况()M t 的单调性,进而可确定最小值的情况. 【详解】(1)将函数2sin 3y x =+的图象上所有点的横坐标缩短到原来的12倍,可得2sin 23y x =+得图象,再向右平移3π个单位长度得2()2sin 232sin 2333f x x x ππ⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎝⎭⎝⎭. (2)∵,36x ππ⎡⎤∈-⎢⎥⎣⎦,242,333x πππ⎡⎤-∈--⎢⎥⎣⎦,则()[1,3f x ∈+, 令()t f x =,则设22()21M t t mt m =-+-,[1,3t ∈+, ①当14m≤,即4m ≤时,函数()M t在[1,3上单调递增, ∴22min ()(1)211M t M m m m m ==-+-=-+;②当134m<<412m <<+ 函数()M t 在1,4m ⎛⎫ ⎪⎝⎭上单调递减,在,34m ⎛ ⎝上单调递增,∴2min 7()148m M t M m ⎛⎫==- ⎪⎝⎭;③当34m≥+12m ≥+()M t在[1,3+上单调递减,∴2min ()(3(323M t M m m ==-++∴综上有22min21,47()1,4128(32312m m m g x m m m m m ⎧-+≤⎪⎪=-<<+⎨⎪⎪-++≥+⎩. 【点睛】本题考查三角函数图象的变换,考查二次函数在三角函数中的应用,考查定区间动轴的最值取值情况,难度较难. 22.(1)6π-或56π-(2)5,,66x k k k Z ππππ⎛⎫∈++∈ ⎪⎝⎭(3)[]5,1k ∈--【解析】 【分析】(1)由题()sin 1,1a b x +=--,由()//a b c +可得()sin 12sin x x -=-+,进而求解即可; (2)由题意得到()()()1,sin 22sin sin 2S b c x x x =-++=,进而求解即可; (3)由()()a b c d +⊥+可得()()0a b c d +⋅+=,整理可得k 关于x 的函数,进而求解即可 【详解】(1)由题,()sin 1,1a b x +=--,因为()//a b c +,所以()sin 12sin x x -=-+,则1sin 2x =-,因为[,]x ππ∈-,所以6x π=-或65x π=-(2)由题,()()()1,sin 22sin sin 2S b c x x x =-++=, 因为1(,)2S b c >,所以1sin 2x >, 当[]0,x π∈时,566x ππ<<, 因为sin y x =是以π为最小正周期的周期函数, 所以5,,66x k k k Z ππππ⎛⎫∈++∈ ⎪⎝⎭(3)由(1)()sin 1,1a b x +=--,由题,()3sin ,1c d x k +=++, 若()()a b c d +⊥+,则()()()()()sin 13sin 10a b c d x x k +⋅+=-+-+=, 则()22sin 2sin 4sin 15k x x x =+-=+-, 因为[]sin 1,1x ∈-,所以[]5,1k ∈-- 【点睛】本题考查共线向量的坐标表示,考查垂直向量的坐标表示,考查解三角函数的不等式23.(1)a =(2)15,36⎡⎫⎪⎢⎣⎭【解析】 【分析】(1)利用降次公式、辅助角公式化简()f x 表达式,利用(0)f =a 的值. (2)令()0f x ω=,结合x 的取值范围以及三角函数的零点列不等式,解不等式求得ω的取值范围. 【详解】(1)2()2sin cos f x x x x a =-++sin 2x x a =+2sin 23x a π⎛⎫=++- ⎪⎝⎭(0)f =(0)2sin3f a π∴=+=即a =(2)令()0f x ω=,则sin 203x πω⎛⎫+= ⎪⎝⎭,[0,]x π∈,2,2333πππωπω⎡⎤∴+∈+⎢⎥⎣⎦,()f x 在[0,]π上有且只有一个零点,223πππωπ∴+<,1536ω∴<, ω∴的取值范围为15,36⎡⎫⎪⎢⎣⎭. 【点睛】本小题主要考查三角恒等变换,考查三角函数零点问题,考查化归与转化的数学思想方法,属于基础题.24.(1)()23f x x π⎛⎫=+ ⎪⎝⎭(2)单调增区间为,612ππ⎡⎤--⎢⎥⎣⎦,57,1212ππ⎡⎤⎢⎥⎣⎦;单调减区间为5,1212ππ⎡⎤-⎢⎥⎣⎦. 【解析】 【分析】(1)利用两角差的正弦公式,降幂公式以及辅助角公式化简函数解析式,根据其图象与x 轴相邻的两个交点的距离为2π,得出周期,利用周期公式得出1ω=,即可得出该函数的解析式;(2)根据平移变换得出()223m x x g π⎛⎫=++ ⎪⎝⎭,再由函数()g x 的图象经过点,03π⎛⎫- ⎪⎝⎭,结合正弦函数的性质得出m 的最小值,进而得出()223g x x π⎛⎫=+⎪⎝⎭,利用整体法结合正弦函数的单调性得出该函数在7,612ππ⎡⎤-⎢⎥⎣⎦上的单调区间.【详解】解:(1)()2sin 24sin 26x x x f πωω⎛⎫=--+ ⎪⎝⎭11cos22cos24222xx x ωωω-=--⨯+32cos22x x ωω=+23x πω⎛⎫=+ ⎪⎝⎭由已知函数()f x 的周期T π=,22ππω=,1ω=∴()23f x x π⎛⎫=+ ⎪⎝⎭.(2)将()f x 的图象向左平移()0m m >个长度单位得到()g x 的图象∴()223m x x g π⎛⎫=++ ⎪⎝⎭,∵函数()g x 的图象经过点,03π⎛⎫- ⎪⎝⎭22033m ππ⎡⎤⎛⎫⨯-++= ⎪⎢⎥⎝⎭⎣⎦,即sin 203m π⎛⎫-= ⎪⎝⎭∴23m k ππ-=,k Z ∈∴26k m ππ=+,k Z ∈∵0m >,∴当0k =,m 取最小值,此时最小值为6π此时,()223g x x π⎛⎫=+ ⎪⎝⎭. 令7612x ππ-≤≤,则2112336x πππ≤+≤当22332x πππ≤+≤或32112236x πππ≤+≤,即当612x ππ-≤≤-或571212x ππ≤≤时,函数()g x 单调递增当232232x πππ≤+≤,即51212x ππ-≤≤时,函数()g x 单调递减. ∴()g x 在7,612ππ⎡⎤-⎢⎥⎣⎦上的单调增区间为,612ππ⎡⎤--⎢⎥⎣⎦,57,1212ππ⎡⎤⎢⎥⎣⎦;单调减区间为5,1212ππ⎡⎤-⎢⎥⎣⎦.【点睛】本题主要考查了由正弦函数的性质确定解析式以及正弦型函数的单调性,属于中档题.25.(1)π6θ=(2)当π12θ=,CH CP +【解析】(1)设ABC PCB θ∠=∠=,则在直角ΔABC 中,sin AC θ=,cos BC θ=,计算得到2sin sin 1AC CP θθ+=-++,计算最值得到答案.(2)计算sin cos CH θθ=⋅,得到πsin 23CH CP θ⎛⎫+=+ ⎪⎝⎭.【详解】(1)设ABC PCB θ∠=∠=,则在直角ΔABC 中,sin AC θ=,cos BC θ=. 在直角ΔPBC 中,2cos cos cos cos PC BC θθθθ=⋅=⋅=, sin sin cos sin cos PB BC θθθθθ=⋅=⋅=.22sin cos sin 1sin AC CP θθθθ+=+=+-2sin sin 1θθ=-++,π0,3θ⎛⎫∈ ⎪⎝⎭,所以当1sin 2θ=,即π6θ=,AC CP +的最大值为54. (2)在直角ΔABC 中,由1122ABC S CA CB AB CH ∆=⋅=⋅,可得sin cos sin cos 1CH θθθθ⋅==⋅.在直角ΔPBC 中,πsin 3PC BC θ⎛⎫=⋅- ⎪⎝⎭ππcos sin cos cos sin 33θθθ⎛⎫=⋅- ⎪⎝⎭,所以1sin cos cos sin 2CH CP θθθθθ⎫+=+-⎪⎪⎝⎭,π0,3θ⎛⎫∈ ⎪⎝⎭,所以211sin 2sin cos 22CH CP θθθθ+=-11πsin 22sin 2423θθθ⎛⎫==+ ⎪⎝⎭所以当π12θ=,CH CP + 【点睛】本题考查了利用三角函数求最值,意在考查学生对于三角函数知识的应用能力. 26.(Ⅰ)(,3),.122k k Z ππ-+-∈(Ⅱ)12a =或12a =- 【解析】(Ⅰ)当1a =时,根据二倍角公式、辅助角公式化简函数,根据正弦函数的性质可得. (Ⅱ)将函数化简为()sin()f x A x b ωϕ=++的形式,分类讨论可得.【详解】解:(Ⅰ)当1a =时,22()cos sin cos 3f x x x x x =-+-cos 2232sin(2)36x x x π=-=+- ()2sin(2)36f x x π∴=+- 由2,6x k k Z ππ+=∈ 得:,122k x k Z ππ=-+∈ ()f x ∴的对称中心为(,3),.122k k Z ππ-+-∈(Ⅱ)22()cos sin sin cos 3f x a x a x x x =-+-()cos 2sin 23f x a x x ∴=-()2sin(2)36f x a x π∴=+- 1sin(2)16x π-≤+≤ 当0a >时,232sin(2)3236a a x a π--≤+-≤- 则有234a --=- 解得12a = 当0a =时,min ()3f x =-,不合题意当0a <时,232sin(2)3236a a x a π-≤+-≤--则有234a -=-解得12a =- 综上 12a ∴=或12a =-. 【点睛】本题主要考查三角函数的图象和性质,利用三角公式将函数进行化简是解决本题的关键,要求熟练掌握三角函数的图象和性质,属于中档题.27.(1)0 (2)32【解析】【分析】(1)通过()//a e b +可以算出()(1,sin 1)//1,cos cos sin 1x x x x +⇒=+,移项、两边平方即可算出结果.(2)通过向量的运算,解出()()f x a b me a b =⋅+⋅-,再通过最大值根的分布,求出m 的值.【详解】(1)通过()//a e b +可以算出()(1,sin 1)//1,cos cos sin 1x x x x +⇒=+,即2cos sin 1(cos sin )112sin cos 1sin cos 0x x x x x x x x -=⇒-=⇒-=⇒=故答案为0.(2)()1sin cos (sin cos )f x x x m x x =++-,设()cos sin x x t t ⎡-=∈⎣,22112sin cos sin cos 2t x x t x x --=⇒=,22113()()1222t g t f x mt t mt -==+-=--+,即213(),22g t t mt t ⎡=--+∈⎣的最大值为12-; ①当11m m -≤⇒≥-时,max 1313()(1)2222g x g m m ==--+=-⇒=(满足条件);②当11m m <-≤⇒<-时,222max 1311()()22222g x g m m m m =-=-++=-⇒=-(舍);③当m m -><max 131()2222g x g m ==-⨯-=-⇒= 故答案为32m =【点睛】 当式子中同时出现sin cos ,sin cos ,sin cos x x x x x x +-时,常常可以利用换元法,把sin cos x x 用sin cos ,sin cos x x x x +-进行表示,但计算过程中也要注意自变量的取值范围;二次函数最值一定要注意对称轴是否在规定区间范围内,再讨论最后的结果.28.(1)34C π=(2)sin A =1c = 【解析】【分析】(1)化简等式,即可求出角C .(2)利用角C 的余弦公式,求出c 与a 的关系式,再由正弦定理求出角A 的正弦值,再结合面积公式求出c 的值.【详解】(1)∵cos 220C C ++=,∴22cos s 10C C +=+,即)210C +=,∴cos C = 又()0,C π∈,∴34C π=. (2)∵2222222cos 325c a b ab C a a a =+-=+=,∴c =,即sin C A =,∴sinA C =∵1sin 2ABC S ab C ∆=,且in sin ABC S A B ∆=,∴1sin sin 22ab C A B =,∴sin sin sin ab C A B= 2sin sin c C C ⎛⎫= ⎪⎝⎭1c =. 【点睛】本题考查利用解三角形,属于基础题.29.(1)()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,()62k x k Z ππ=+∈;(2)522a ≤<,3π. 【解析】【分析】(1)根据图像得A=2,利用412562T πππω=-=,求ω值,再利用6x π=时取到最大值可求φ,从而得到函数解析式,进而求得对称轴方程;(2)由0,2x π⎡⎤∈⎢⎥⎣⎦得72,666x πππ⎡⎤+∈⎢⎥⎣⎦,方程f (x )=2a ﹣3有两个不等实根转为f (x )的图象与直线y =2a ﹣3有两个不同的交点,从而可求得a 的取值范围,利用图像的性质可得12x x +的值.【详解】(1)由图知,2,A =4156242=T ππππω=-=,解得ω=2,f(x)=2sin(2x+φ), 当6x π=时,函数取得最大值,可得2sin 226πϕ⎛⎫⨯+= ⎪⎝⎭,即sin 13πϕ⎛⎫+= ⎪⎝⎭,2,32k k Z ππϕπ+=+∈,解得2,6k k Z πϕπ=+∈ ,又(0,)2πϕ∈所以6π=ϕ, 故()2sin 26f x x π⎛⎫=+ ⎪⎝⎭, 令262x k πππ+=+则()62k x k Z ππ=+∈, 所以()f x 的对称轴方程为()62k x k Z ππ=+∈; (2)70,2,2666x x ππππ⎡⎤⎡⎤∈∴+∈⎢⎥⎢⎥⎣⎦⎣⎦, 所以方程()23f x a =-有两个不等实根时,()y f x =的图象与直线23y a =-有两个不同的交点,可得1232,a ≤-<522a ∴≤<, 当0,2x π⎡⎤∈⎢⎥⎣⎦时,()()12f x f x =,有122266x x πππ+++=, 故123x x π+=.【点睛】 本题考查由y =A sin (ωx +φ)的部分图象确定函数解析式,考查函数y =A sin (ωx +φ)的图象及性质的综合应用,属于中档题.30.(1) 2T π=;(2)2a =-或6a =【解析】【分析】(1)根据二倍角公式进行整理化简可得()2sin f x x =,从而可得最小正周期;(2)将()g x通过换元的方式变为21112y t at a =-+--,1t ≤;讨论对称轴的具体位置,分别求解最大值,从而建立方程求得a 的值.【详解】(1)()2221cos sin cos sin 12f x x x x x π⎡⎤⎛⎫=-++-- ⎪⎢⎥⎝⎭⎣⎦ ()222sin sin 12sin 12sin x x x x =++--=∴最小正周期2T π=(2)()1sin2sin cos 12g x a x a x x a =+--- 令sin cos x x t -=,则()22sin 21sin cos 1x x x t =--=-22221111122242a a y t at a t at a t a ⎛⎫∴=-+--=-+-=--+- ⎪⎝⎭sin cos 4t x x x π⎛⎫=-=- ⎪⎝⎭由42x ππ-≤≤得244x πππ-≤-≤ 1t ≤①当2a <a <-当t =max 122y a ⎫=--⎪⎭由1222a ⎫--=⎪⎭,解得()817a ==->-)②当12a ≤,即2a -≤时 当2a t =时,2max 142a y a =- 由21242a a -=得2280a a --=,解得2a =-或4a =(舍去) ③当12a >,即2a >时 当1t =时,max 12a y =-,由122a -=,解得6a = 综上,2a =-或6a =【点睛】本题考查正弦型函数最小正周期的求解、利用二次函数性质求解与三角函数有关的值域问题,解题关键是通过换元的方式将所求函数转化为二次函数的形式,再利用对称轴的位置进行讨论;易错点是忽略了换元后自变量的取值范围.。
高中数学三角函数测试卷(答案解析版)

高中数学三角函数测试卷(答案解析版)高中数学三角函数测试卷(答案解析版)一、选择题1. 假设α是锐角,sinα=0.6,那么sin(90°-α)的值是多少?解析:根据三角函数的互余关系,sin(90°-α) = cosα = √(1 - sin²α) = √(1 - 0.6²) = 0.8。
答案:0.82. 已知tanα = 3/4,sinα的值为多少?解析:由tanα = sinα/cosα可得sinα = tanα × cosα = 3/4 × 4/5 = 3/5。
答案:3/53. 已知sinα = 1/2,cosβ = 3/5,α和β都是锐角,则sin(α+β)的值是多少?解析:根据两角和的公式,sin(α+β) = sinα × cosβ + cosα × sinβ = (1/2) × (3/5) + √(1 - (1/2)²) × √(1 - (3/5)²) = 3/10 + √(3/10 × 7/10) = 3/10 + √(21/100) = 3/10 + 3√21/10√10 = (3 + 3√21)/10。
答案:(3 + 3√21)/10二、填空题4. 在锐角三角形ABC中,已知∠A=30°,BC=6,AC=10,则AB 等于多少?解析:根据正弦定理,AB/AC = sin∠B/sin∠A,代入已知条件得到AB/10 = sin∠B/sin30°,即AB = 10×sin∠B/sin30°。
由∠B + ∠C = 90°可得∠B = 90° - ∠A - ∠C = 90° - 30° - 60° = 0°。
因此,AB =10×sin0°/sin30° = 0/0 = 0。
高中数学《三角函数图像》练习题

三角函数的图像与性质(文科)姓名 号数一、选择题1.若函数cos()3y x πω=+(0)ω>的图象相邻两条对称轴间距离为2π,则ω等于 . A .12B .12C .2D .42.将函数sin()()6yx x R π=+∈的图象上所有的点向左平行移动4π个单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为A .5sin(2)()12y x x R π=+∈ B .5sin()()212x y x R π=+∈C .sin()()212x y x R π=-∈D .5sin()()224x y x R π=+∈3.将函数sin y x =的图象向左平移(02)ϕϕπ≤≤个单位后,得到函数sin()6yx π=-的图象,则ϕ等于( ) A .6πB .76πC .116πD .56π4.将函数的图象上所有点的横坐标伸长到原来的倍(纵坐标不变),再将所得的图象向左平移个单位,得到的图象对应的解析式是 ( )A .B . C. D.5.要得到函数y = sin (2x -3π)的图象,只要将函数y = sin2x 的图象 ( ) A .向左平行移动3π个单位 B .向右平行移动3π个单位C .向左平行移动6π个单位 D .向右平行移动6π个单位6在(0,2π)内,使sin x >cos x 成立的x 的取值范围是A.(4π,2π)∪(π,4π5)B.(4π,π)C.(4π,4π5) D.(4π,π)∪(4π5,2π3) 7已知函数y =tan (2x +ϕ)的图象过点(12π,0),则ϕ可以是 A.-6πB.6πC.-12π D.12π8把函数y =cos (x +3π4)的图象向左平移4个单位,所得的函数为偶函数则ϕ的最小值是 A.3π4B.3π2 C.3π D.3π5 9为了得到函数y =sin (2x -6π)的图象,可以将函数y =cos2x 的图象 A.向右平移6π个单位长度 B.向右平移3π个单位长度 C.向左平移6π个单位长度D.向左平移3π个单位长度 10对于函数y =sin(132π-x ),下面说法中正确的是 ( ) (A) 函数是周期为π的奇函数 (B) 函数是周期为π的偶函数 (C) 函数是周期为2π的奇函数 (D) 函数是周期为2π的偶函数二、填空题11,函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间12设函数f (x )=A +B sin x ,若B <0时,f (x )的最大值是23,最小值是-21,则A =_______, B =_______.13如图,给出函数y = f (x ) = A sin (ωx + ϕ) (其中A>0,ω>0,|ϕ|<2π) 的图象的一段,则函数f (x )的解析式为______________________.三、解答题14.已知函数f(x)=sin 2x+3xcosx+2cos 2x,x ∈R.(I )求函数f(x)的最小正周期和单调增区间;(Ⅱ)函数f(x)的图象可以由函数y=sin2x(x ∈R)的图象经过怎样的变换得到?。
高中三角函数练习题及答案

高中三角函数练习题及答案1. 题目1. 已知直角三角形ABC,∠C=90°,边AC=5cm,边BC=12cm。
求∠A和∠B的正弦值、余弦值和正切值。
2. 已知正弦函数y=sin(x)的图像上点P的坐标为(Px, Py),其中Py=1/2。
求点P的横坐标Px的可能值。
3. 已知直角三角形ABC,∠B=30°,边AC=4cm。
求∠A的正弦值、余弦值和正切值。
4. 已知余弦函数y=cos(x)的图像上点Q的坐标为(Qx, Qy),其中Qy=-1/2。
求点Q的横坐标Qx的可能值。
2. 答案1. ∠A的正弦值为sin(A) = AC / BC = 5 / 12 ≈ 0.417,余弦值为cos(A) = BC / AC = 12 / 5 =2.4,正切值为tan(A) = sin(A) / cos(A) ≈ 0.174;∠B的正弦值为 sin(B) = BC / AC = 12 / 5 = 2.4,余弦值为cos(B) = AC / BC = 5 / 12 ≈ 0.417,正切值为 tan(B) = sin(B) / cos(B) ≈ 2.289。
2. 根据正弦函数的定义,sin(x)的取值范围是[-1, 1]。
已知Py=1/2,因此横坐标Px的可能值为[-π/6, π/6],即Px的取值范围是[-30°, 30°]。
3. ∠A的正弦值为sin(A) = BC / AC = √3 / 2 ≈ 0.866,余弦值为cos(A) = AC / BC = 2 / √3 ≈ 1.155,正切值为 tan(A) = sin(A) / cos(A) ≈ 0.75。
4. 根据余弦函数的定义,cos(x)的取值范围是[-1, 1]。
已知Qy=-1/2,因此横坐标Qx的可能值为[2π/3, 4π/3],即Qx的取值范围是[120°, 240°]。
以上是高中三角函数练题及答案。
高中数学三角函数专题练习题及答案

高中数学三角函数专题练习题及答案1. 试计算下列各函数值:(1)tan(π/4)(2)csc(3π/2)(3)sec(0)(4)cot(5π/3)解答:(1)tan(π/4) = sin(π/4) / cos(π/4) = 1 / 1 = 1(2)csc(3π/2) = 1 / sin(3π/2) = 1 / -1 = -1(3)sec(0) = 1 / cos(0) = 1 / 1 = 1(4)cot(5π/3) = cos(5π/3) / sin(5π/3) = -1/2 / (-√3/2) = 1 / √32. 已知直角三角形中,一锐角的正弦值为1/2,则该锐角的值是多少?解答:设该锐角为θ,则sinθ = 1/2。
根据反正弦函数的定义,θ = arcsin(1/2) = π/6。
3. 在锐角三角函数中,sinx和cosx经过哪个变换可以得到cosx和sinx的值?sinx和cosx经过变换x → x + π/2可以得到cosx和sinx的值。
4. 给定cosx = -1/3,且x在第四象限,求sinx的值。
解答:根据余弦函数的定义可知,sinx = √(1 - cos²x) = √(1 - (-1/3)²) = √(1 - 1/9) = √(9/9 - 1/9) = √8/3 = (2√2)/3。
5. 已知tanx = -√3,且x在第三象限,求secx和cotx的值。
解答:根据正切函数的定义可知,secx = 1/cosx,cotx = 1/tanx。
又由于sin²x + cos²x = 1,可以得到cosx = 1/√(1 + tan²x) = 1/√(1 + (-√3)²) = 1/√(1 + 3) = 1/2。
因此,secx = 1/(1/2) = 2,cotx = 1/(-√3) = -√3/3。
6. 已知sinx + 3cosx = 0,求tanx的值。
高中数学三角函数题目及答案

高中数学三角函数题目及答案一、填空题1.$\\sin 30° = \\underline{\\hspace{1cm}}$2.$\\cos 60° = \\underline{\\hspace{1cm}}$3.$\\tan 45° = \\underline{\\hspace{1cm}}$二、选择题1.已知直角三角形的斜边长为10,其中一个锐角的正弦值等于$\\frac{1}{2}$,则此角的度数是: A. 30° B. 45°C. 60°D. 90°2.若$\\sin \\theta = \\frac{3}{5}$,$\\theta$为锐角,则$\\cos \\theta =$ A. $\\frac{4}{5}$ B. $\\frac{3}{4}$ C. $\\frac{3}{5}$ D. $\\frac{5}{4}$3.若$\\tan \\alpha = \\sqrt{3}$,$\\alpha$为锐角,则$\\cot \\alpha =$ A. −1 B. $\\frac{\\sqrt{3}}{2}$ C. $-\\sqrt{3}$ D. $\\frac{1}{\\sqrt{3}}$三、计算题1.求解$\\sin 45° \\cdot \\cos 45° - \\sin 30° \\cdot\\cos 60°$2.求解$\\frac{\\sin^2 30° + \\cos^2 30°}{\\sin 60°\\cos 30°}$四、简答题1.说明余切的定义及其在三角函数中的关系。
2.如何利用正弦定理和余弦定理解决三角形的不全等问题?五、综合题已知直角三角形ABC中,$\\angle B = 90°$,AA=6,AA=8,求角A的大小。
六、答案1.$\\sin 30° = \\frac{1}{2}$ $\\cos 60° =\\frac{1}{2}$ $\\tan 45° = 1$1. C. 60°2. A. $\\frac{4}{5}$3. C. $-\\sqrt{3}$1.$\\sin 45° \\cdot \\cos 45° - \\sin 30° \\cdot\\cos 60° = \\frac{1}{2}$2.$\\frac{\\sin^2 30° + \\cos^2 30°}{\\sin 60° \\cos30°} = 1$1.余切的定义为正切的倒数,即$\\cot \\theta =\\frac{1}{\\tan \\theta}$。
高中三角函数专题练习题及答案

高中三角函数专题练习题及答案一、填空题1.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .角B 为钝角.设△ABC 的面积为S ,若()2224bS a b c a =+-,则sin A +sin C 的最大值是____________.2.已知函数()sin()(0,)R f x x ωϕωϕ=+>∈在区间75,126ππ⎛⎫⎪⎝⎭上单调,且满足73124f f ππ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭.有下列结论: ①203f π⎛⎫= ⎪⎝⎭; ②若5112f π⎛⎫= ⎪⎝⎭,则函数()f x 的最小正周期为π;③ω的取值范围为(]0,4;④函数()f x 在区间[)0,2π上最多有6个零点. 其中所有正确结论的编号为________. 3.若函数()sin12xf x x π=+,则(1)(2)(3)(2021)f f f f +++⋯⋯+=__________4.已知()()()cos sin 3cos 0f x x x x ωωωω=+>,如果存在实数0x ,使得对任意的实数x ,都有()()()002016f x f x f x π≤≤+成立,则ω的最小值为___________.5.log sin()3y x ππ=+的单调增区间为________.6.意大利著名画家、数学家、物理学家达芬奇在他创作《抱银貂的女子》时思考过这样一个问题:固定项链的两端,使其在重力的作用下自然下垂,那么项链所形成的曲线是什么?这就是著名的悬链线问题,连接重庆和湖南的世界第一悬索桥——矮寨大桥就采用了这种方式设计.经过计算,悬链线的函数方程为()e e cos 2x xh x -+=,并称其为双曲余弦函数.若()()cos sin cos cos sin cos h h m θθθθ+≥-对0,2πθ⎡⎤∀∈⎢⎥⎣⎦恒成立,则实数m 的取值范围为______.7.已知向量a ,b ,c 满足0a b c ++=,()()0a b a c -⋅-=,||9b c -=,则||||||a b c ++的最大值是___________.8.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示.将函数()y f x =的图象向右平移4π个单位,得到()y g x =的图象,则下列有关()f x 与()g x 的描述正确的有___________(填序号).①()2sin 23g x x π⎛⎫=- ⎪⎝⎭;②方程()()360,2f x g x x π⎫⎛⎫+∈ ⎪⎪⎝⎭⎭所有根的和为712π; ③函数()y f x =与函数()y g x =图象关于724x π=对称. 9.1643年法国数学家费马曾提出了一个著名的几何问题:已知一个三角形,求作一点,使其到这个三角形的三个顶点的距离之和为最小.它的答案是:当三角形的三个角均小于120°时,所求的点为三角形的正等角中心(即该点与三角形的三个顶点的连线段两两成角120°),该点称为费马点.已知ABC 中,其中60A ∠=︒,1BC =,P 为费马点,则PB PC PA +-的取值范围是__________.10.已知函数()2log ,0,0x x f x x x >⎧=⎨-≤⎩,函数()g x 满足以下三点条件:①定义域为R ;②对任意x ∈R ,有()()2g x g x π+=;③当[]0,x π∈时,()sin .g x x =则函数()()y f x g x =-在区间[]4,4ππ-上零点的个数为__________个.二、单选题11.已知函数()21ln e 1xf x x -⎛⎫=+ ⎪+⎝⎭,a ,b ,c 分别为ABC 的内角A ,B ,C 所对的边,且222446,a b c ab +-=则下列不等式一定成立的是( ) A .()()sin cos f A f B ≤ B .f (cos A )≤f (cos B ) C .f (sin A )≥f (sin B ) D .f (sin A )≥f (cos B )12.已知点P 是曲线e 3xy =+α为曲线在点P 处的切线的倾斜角,则α的取值范围是( )A .0,6π⎛⎤ ⎥⎝⎦B .,62ππ⎡⎫⎪⎢⎣⎭C .,63ππ⎡⎤⎢⎥⎣⎦D .0,3π⎛⎤ ⎥⎝⎦13.《九章算术》卷五“商功”:今有刍甍,下广3丈,袤4丈;上袤2丈,无广;高1丈.其描述的是下图的一个五面体,底面ABCD 是矩形,4AB =,3BC =,2EF =,//EF 底面ABCD 且EF 到底面ABCD 的距离为1.若DE AE BF CF ===,则该刍甍中点F 到平面EBC 的距离为( )A .15B .35C 10D 2514.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若cos cos sin sin()sin B C AA C bc C ⎛⎫++= ⎪⎝⎭,3B π=,则a c +的取值范围是( ) A .33⎝ B .332⎛ ⎝C .33⎡⎤⎢⎥⎣ D .332⎡⎢⎣15.已知函数2()log f x x =,函数()g x 满足以下三点条件:①定义域为R ;②对任意x ∈R ,有()2()g x g x π+=;③当[0,]x π∈时,()sin g x x =.则函数()()y f x g x =-在区间[0,4]π上的零点个数为( )A .5B .6C .7D .816.已知双曲线22413y x -=的左右焦点分别为1F ,2F ,点M 是双曲线右支上一点,满足120MF MF →→⋅=,点N 是线段12F F 上一点,满足112F N F F λ→→=.现将12MF F △沿MN 折成直二面角12F MN F --,若使折叠后点1F ,2F 距离最小,则λ=( )A .15B .25C .35D .4517.已知函数()sin sin()f x x x π=+,现给出如下结论:①()f x 是奇函数;②()f x 是周期函数;③()f x 在区间(0,)π上有三个零点;④()f x 的最大值为2.其中所有正确结论的编号为( ) A .①③B .②③C .②④D .①④18.已知三棱锥A BCD -中,4AB BC BD CD AD =====,二面角A BD C --的余弦值为13,点E 在棱AB 上,且3BE AE =,过E 作三棱锥A BCD -外接球的截面,则所作截面面积的最小值为( ) A .103πB .3πC .3π D 319.()sin()(0)f x x ωφφ=+>的部分图象如图所示,设P 是图象的最高点,A ,B 是图象与x 轴的交点,若tan 2APB ∠=-,则ω的值为( )A .4π B .3π C .2π D .π20.在锐角ABC 中,三内角,,A B C 的对边分别为,,a b c ,且2sin a b C =,则tan tan tan A B C ++的最小值为( )A .2B .4C .6D .8三、解答题21.将函数2sin 3y x =+的图象上所有点的横坐标缩短到原来的12倍,纵坐标不变,再将所得的图象向右平移3π个单位长度后得到函数()f x 的图象. (1)写出函数()f x 的解析式;(2)若,36x ππ⎡⎤∈-⎢⎥⎣⎦时,22()2()()1g x f x mf x m =-+-,求()g x 的最小值min ()g x .22.如图,四边形ABCD 是某市中心一边长为4百米的正方形地块的平面示意图. 现计划在该地块上划分四个完全相同的直角三角形(即Rt ,Rt ,Rt ABF BCG CDH 和Rt DAE ),且在这四个直角三角形区域内进行绿化,中间的小正方形修建成市民健身广场,为了方便市民到达健身广场,拟修建4条路,AE ,BF ,CG DH . 已知在直角三角形内进行绿化每1万平方米的费用为10a 元,中间小正方形修建广场每1万平方米的费用为13a 元,修路每1百米的费用为a 元,其中a 为正常数.设FAB θ∠=,0,4πθ⎛⎫∈ ⎪⎝⎭.(1)用θ表示该工程的总造价S ;(2)当cos θ为何值时,该工程的总造价最低? 23.已知函数()cos f x x x =,()sin g x x =,0,2x π⎡⎤∈⎢⎥⎣⎦.(1)求证:()()f x g x ≤;(2)若()ax g x bx <<在0,2π⎛⎫⎪⎝⎭上恒成立,求a 的最大值与b 的最小值.24.已知函数2211()cos sin cos sin 22f x x x x x =+-.(1)求()f x 的单调递增区间;(2)求()f x 在区间,82ππ⎡⎤-⎢⎥⎣⎦的最大值和最小值.25.已知函数2()23sin 2sin cos ()f x x x x a a R =-++∈,且(0)3f =. (1)求a 的值;(2)若()f x ω在[0,]π上有且只有一个零点,0>ω,求ω的取值范围.26.如图,在ABC ∆中,90,3,1ABC AB BC ︒∠===,P 为ABC ∆内一点,90BPC ︒∠=.(1)若3PC =,求PA ; (2)若120APB ︒∠=,求ABP ∆的面积S . 27.已知函数1()1xf x x-=+. (1)证明函数()f x 在(1,)-+∞上为减函数;(2)求函数ln (tan )y f x =的定义域,并求其奇偶性;(3)若存在(,)42ππ,使得不等式(tan )tan 0f x a x +≤能成立,试求实数a 的取值范围.28.设函数2()cos sin 2f x x a x a =-+++(a ∈R ). (1)求函数()f x 在R 上的最小值;(2)若不等式()0f x <在[0,]2π上恒成立,求a 的取值范围;(3)若方程()0f x =在(0,)π上有四个不相等的实数根,求a 的取值范围.29.已知函数2()2cos 23cos f x x x x =+. (Ⅰ)求()f x 的单调递增区间;(Ⅱ)若()f x 在区间,6m π⎡⎤-⎢⎥⎣⎦上的值域为[]0,3,求m 的取值范围.30.函数f (x )=A sin (2ωx +φ)(A >0,ω>0,|φ|<2π)的部分图象如图所示 (1)求A ,ω,φ的值;(2)求图中a ,b 的值及函数f (x )的递增区间; (3)若α∈[0,π],且f (α)2α的值.【参考答案】一、填空题1.982.①②④ 3.30324.140325.(2,2)(Z)36k k k ππππ-++∈6.12,1⎡⎤⎣⎦7.3310+31038.①③9.3⎡⎫⎪⎢⎪⎣⎭10.6二、单选题 11.D 12.A 13.C 14.A 15.A 16.C 17.A 18.B 19.C20.D 三、解答题21.(1)2()2sin 233f x x π⎛⎫=-+ ⎪⎝⎭;(2)22min21,47()1,4128(32312m m m g x m m m m m ⎧-+≤⎪⎪=-<<+⎨⎪⎪-++≥+⎩ 【解析】(1)根据函数图象的变换规律即可求得()f x 的解析式;(2)令()t f x =可求得则()[1,3f x ∈+,设22()21M t t mt m =-+-,[1,3t ∈,通过定区间讨论对称轴4mt =的三种情况()M t 的单调性,进而可确定最小值的情况. 【详解】(1)将函数2sin 3y x =+的图象上所有点的横坐标缩短到原来的12倍,可得2sin 23y x =+得图象,再向右平移3π个单位长度得2()2sin 232sin 2333f x x x ππ⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎝⎭⎝⎭. (2)∵,36x ππ⎡⎤∈-⎢⎥⎣⎦,242,333x πππ⎡⎤-∈--⎢⎥⎣⎦,则()[1,3f x ∈+, 令()t f x =,则设22()21M t t mt m =-+-,[1,3t ∈+, ①当14m≤,即4m ≤时,函数()M t在[1,3上单调递增, ∴22min ()(1)211M t M m m m m ==-+-=-+;②当134m<<412m <<+ 函数()M t 在1,4m ⎛⎫ ⎪⎝⎭上单调递减,在,34m ⎛ ⎝上单调递增,∴2min 7()148m M t M m ⎛⎫==- ⎪⎝⎭;③当34m≥+12m ≥+()M t在[1,3+上单调递减,∴2min ()(3(323M t M m m ==-++∴综上有22min21,47()1,4128(32312m m m g x m m m m m ⎧-+≤⎪⎪=-<<+⎨⎪⎪-++≥+⎩. 【点睛】本题考查三角函数图象的变换,考查二次函数在三角函数中的应用,考查定区间动轴的最值取值情况,难度较难.22.(1)()16(13sin 6sin cos )S a θθθθ=+-,0,4πθ⎛⎫∈ ⎪⎝⎭;(2)当3cos 4θ=时,()16()S af θθ=取得最小值 【解析】(1)根据题意可知4sin BF θ=,4cos AF θ=,进而求得Rt ABFS 与EFGH S 正方形再求得总造价S 即可.(2)由(1)有()16(13sin 6sin cos )S a θθθθ=+-,再求导分析函数的单调性与最值即可.【详解】(1)在Rt ABF 中,FAB θ∠=,4AB =,所以4sin BF θ=,4cos AF θ=. 由于Rt ,Rt ,Rt ABF BCG CDH 和Rt DAE 是四个完全相同的直角三角形,所以4sin AE BF CG DH θ====,4(cos sin )EF FG GH HE θθ====-,所以Rt114cos 4sin 8sin cos 22ABFS AF BF θθθθ=⋅⋅=⨯⨯=, 2224(cos sin )16(12sin cos )EFGH S EF θθθθ==-=-正方形.所以()48sin cos 1016(12sin cos )1344sin S a a a θθθθθθ=⨯⨯+-⨯+⨯⨯16[20sin cos (12sin cos )13sin ]a θθθθθ=+-⨯+ 16(13sin 6sin cos )a θθθ=+-,0,4πθ⎛⎫∈ ⎪⎝⎭. (2)由(1)记()13sin 6sin cos f θθθθ=+-,0,4πθ⎛⎫∈ ⎪⎝⎭.则22232()cos 6(cos sin )12cos cos 612(cos )(cos )43f θθθθθθθθ'=--=-++=--+. 令()0f θ'=,因为0,4πθ⎛⎫∈ ⎪⎝⎭,所以3cos 4θ=或2cos 3θ=-(舍).记03cos 4θ=,所以当0(0,)θθ∈时,()0f θ'<,()f θ单调递减; 当0(,)4πθθ∈时,()0f θ'>,()f θ单调递增. 所以当3cos 4θ=时,()f θ取得极小值,也是最小值, 又0a >,所以当3cos 4θ=时,()16()S af θθ=取得最小值. 【点睛】本题主要考查了三角函数在几何中的运用,同时也考查了求导分析函数最值的方法,属于难题. 23.(1)答案见解析;(2)a 最大值为2π,b 的最小值为1. 【解析】 【分析】(1)构建函数()cos sin h x x x x =-,通过导数研究函数()h x 在0,2π⎡⎤⎢⎥⎣⎦单调性并计算最值,可得结果.(2)构造函数()sin M x x cx =-,通过分类讨论的方法,0c ≤,1c ≥和01c <<,利用导数判断函数()M x 的单调性,并计算最值比较,可得结果. 【详解】(1)由()()()cos sin h x f x g x x x x =-=- 所以()'cos sin cos sin h x x x x x x x =--=-. 又0,2x π⎡⎤∈⎢⎥⎣⎦,()'sin 0h x x x =-≤,所以()h x 在区间上0,2π⎡⎤⎢⎥⎣⎦单调递减.从而()()00h x h ≤=,()()f x g x ≤. (2)当0x >时,“()ax g x <”等价于“sin 0x ax ->” “()g x bx <”等价于“sin 0x bx -<”.令()sin M x x cx =-,则()'cos M x x c =-,当0c ≤时,()0M x >对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立.当1c ≥时,因为对任意0,2x π⎛⎫∈ ⎪⎝⎭,()'cos 0M x x c =-<,所以()M x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递减.从而()()00M x M <=对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立.当01c <<时,存在唯一的00,2x π⎛⎫∈ ⎪⎝⎭,使得()'cos 0M x x c =-=.()M x 与()'M x 在区间0,2π⎛⎫⎪⎝⎭上的情况如下:因为在区间0上是增函数, 所以()()000M x M >=.进一步,“()0M x >对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立”当且仅当1022M c ππ⎛⎫=-≥ ⎪⎝⎭,即20c π<≤,综上所述: 当且仅当2c π≤时,()0M x >对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立; 当且仅当1c ≥时,()0M x <对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立.所以,若()ax g x bx <<对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立,则a 最大值为2π,b 的最小值为1. 【点睛】本题考查导数的综合应用,关键在于构建函数,化繁为简,同时掌握分类讨论的思想,考验分析问题的能力以及计算能力,属中档题.24.(1)3,88k k ππππ⎡⎤-++⎢⎥⎣⎦,()k Z ∈;(2)()max f x =,()min 12f x =- 【解析】 【分析】(1)直接利用三角函数的恒等变换,把三角函数变形成正弦型函数.进一步求出函数的单调区间.(2)直接利用三角函数的定义域求出函数的最值. 【详解】 解:(1)2211()cos sin cos sin 22f x x x x x =+-11()cos 2sin 222f x x x ∴=+()24f x x π⎛⎫∴=+ ⎪⎝⎭ 令222242k x k πππππ-+≤+≤+,()k Z ∈解得388k x k ππππ-+≤≤+,()k Z ∈ 即函数的单调递增区间为3,88k k ππππ⎡⎤-++⎢⎥⎣⎦,()k Z ∈(2)由(1)知n ()224f x x π⎛⎫=+ ⎪⎝⎭ ,82x ππ⎡⎤∈-⎢⎥⎣⎦ 520,44x ππ⎡⎤∴+∈⎢⎥⎣⎦所以当242x ππ+=,即8x π=时,()max f x = 当5244x ππ+=,即2x π=时,()min 12f x =- 【点睛】本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的单调性的应用,利用函数的定义域求三角函数的值域.属于基础型.25.(1)a =(2)15,36⎡⎫⎪⎢⎣⎭【解析】【分析】(1)利用降次公式、辅助角公式化简()f x 表达式,利用(0)f =a 的值.(2)令()0f x ω=,结合x 的取值范围以及三角函数的零点列不等式,解不等式求得ω的取值范围.【详解】(1)2()2sin cos f x x x x a =-++sin 2x x a =+2sin 23x a π⎛⎫=++- ⎪⎝⎭(0)f =(0)2sin 3f a π∴=+=即a =(2)令()0f x ω=,则sin 203x πω⎛⎫+= ⎪⎝⎭, [0,]x π∈,2,2333πππωπω⎡⎤∴+∈+⎢⎥⎣⎦, ()f x 在[0,]π上有且只有一个零点, 223πππωπ∴+<,1536ω∴<, ω∴的取值范围为15,36⎡⎫⎪⎢⎣⎭. 【点睛】本小题主要考查三角恒等变换,考查三角函数零点问题,考查化归与转化的数学思想方法,属于基础题.26.(1;(2 【解析】【分析】(1)求出12BP ==,,36CBP ABP ππ∠=∠=,ABP ∆中由余弦定理即可求得PA ;(2)设PBA α∠=,利用正弦定理表示出()sin120sin 60AB PB =︒︒-α,求得tan α=,利用面积公式即可得解.【详解】(1)在ABC ∆中,90,1ABC AB BC ︒∠===,2AC =P 为ABC ∆内一点,90BPC ︒∠=,PC =,所以12BP =, CBP ∆中,由余弦定理得:2221cos 22BP BC PC CBP BP BC +-∠==⋅ 所以,36CBP ABP ππ∠=∠=ABP ∆中,由余弦定理得:AP==; (2)120APB ︒∠=,设0,,90,602PBA PBC PAB π⎛⎫∠=α∈∠=︒-α∠=︒-α ⎪⎝⎭, 在Rt PBC ∆中,sin sin PB BC =⋅α=α,在PBA ∆中,由正弦定理()sin120sin 60AB PB =︒︒-α,即()sin 2sin 60α=︒-α,sin sin α=α-α,所以tan α=sin PB α==ABP ∆的面积11sin 22S AB PB α=⋅==. 【点睛】 此题考查解三角形,对正余弦定理的综合使用,涉及两角差的正弦公式以及同角三角函数关系的使用,综合性较强.27.(1)证明见解析;(2),,44k k k Z ππππ⎛⎫-++∈ ⎪⎝⎭,奇函数;(3)(,3-∞-. 【解析】(1)利用单调性定义证明即可.(2)根据条件可得tan 1tan 1x x <⎧⎨>-⎩,其解集即为函数的定义域,可判断定义域关于原点对称,再根据奇偶性定义可判断函数的奇偶性.(3)令tan t x =,考虑101t at t-+<+在()1,+∞上有解即可,参变分离后利用基本不等式可求实数a 的取值范围.【详解】(1)11x ∀>-,21x ∀>-,12x x <, 又()()()122212121211()()11112x x x x f x f x x x x x ----=-+-=+++, 因为11x >-,21x >-,12x x <,故110x +>,210x +>,120x x -<,故12())0(f x f x ->即12()()f x f x >,所以函数()f x 在(1,)-+∞上为减函数.(2)((ln t )n )a y f x =的x 满足的不等关系有:1tan 01tan x x->+即()()1tan tan 10x x +-<, 故tan 1tan 1x x <⎧⎨>-⎩,解得,44k x k k Z ππππ-+<<+∈, 故函数的定义域为,44k k ππππ⎛⎫-++ ⎪⎝⎭,k Z ∈,该定义域关于原点对称. 令()((ln ta )n )F x f x =又()()()tan tan tan()tan tan 11ln ln ln 11x x x x xF x f -+--===--+ ()()()tan ln x f F x =-=-,故ln (tan )y f x =为奇函数.(3)令tan t x =,因为(,)42x ππ∈,故1u >. 故在(,)42ππ上不等式(tan )tan 0f x a x +≤能成立即为 存在1t >,使得101t at t-+≤+,所以()11t a t t -≤+在()1,+∞上能成立, 令1s t =-,则0s >且()21121323t s t t s s s s-==+++++,由基本不等式有2s s+≥s 时等号成立, 所以()131t t t -≤=-+,当且仅当1t 时等号成立, 故()11t y t t -=+的最大值为3-,所以a的取值范围为(,3-∞-. 【点睛】本题考查与正切函数、对数函数有关的复合函数的性质的讨论,此类问题常用换元法把复合函数性质的讨论归结为常见函数性质的讨论,本题较综合,为难题.28.(1)2min 2,2;()1,22;422,2.a a f x a a a a >⎧⎪⎪=-++-≤≤⎨⎪+<-⎪⎩(2)(,1)a ∈-∞-(3)12a -<<-【解析】【分析】(1)通过换元法将函数变形为二次函数,同时利用分类讨论的方法求解最大值; (2)恒成立需要保证max ()0f x <即可,对二次函数进行分析,根据取到最大值时的情况得到a 的范围;(3)通过条件将问题转化为二次函数在给定区间上有两个零点求a 的范围,这里将所有满足条件的不等式列出来,求解出a 的范围.【详解】解:(1)令sin x t =,[1,1]t ∈-,则2()()1f x g t t at a ==+++,对称轴为2a t =-. ①12a-<-,即2a >,min ()(1)2f x g =-=. ②112a -≤-≤,即22a -≤≤,2min ()()124a a f x g a =-=-++. ③12a ->,即2a <-,min ()(1)22f x g a ==+. 综上可知,2min 2,2;()1,22;422,2.a a f x a a a a >⎧⎪⎪=-++-≤≤⎨⎪+<-⎪⎩ (2)由题意可知,max ()0f x <,2()()1f x g t t at a ==+++,[0,1]t ∈的图象是开口向上的抛物线,最大值一定在端点处取得,所以有(0)10,(1)220,g a g a =+<⎧⎨=+<⎩故(,1)a ∈-∞-. (3)令sin x t =,(0,)x π∈.由题意可知,当01t <<时,sin x t =有两个不等实数解,所以原题可转化为2()10g t t at a =+++=在(0,1)内有两个不等实数根.所以有201,24(1)0,12(0)10,(1)220,a a a a g a g a ⎧<-<⎪⎪⎪∆=-+>⇒-<<-⎨⎪=+>⎪=+>⎪⎩【点睛】(1)三角函数中,形如2()sin sin f x a x b x c =++或者2()cos cos f x a x b x c =++都可以采用换元法求解函数最值;(2)讨论二次函数的零点的分布,最好可以采用数形结合的方法解决问题,这样很大程度上减少了遗漏条件的可能.29.(Ⅰ) (),,36ππππ⎡⎤-+∈⎢⎥⎣⎦k k k Z (Ⅱ) 62ππ≤≤m 【解析】【分析】(Ⅰ)利用二倍角的正弦公式、二倍角的余弦公式以及两角和与差的正弦公式将函数()f x化为π2sin 216x ⎛⎫++ ⎪⎝⎭,利用正弦函数的单调性解不等式,可得到函数()f x 的递增区间; (Ⅱ) 要使得()f x 在π,6m ⎡⎤-⎢⎥⎣⎦上的值域为[]0,3,即πsin 26x ⎛⎫+ ⎪⎝⎭在π,3m ⎡⎤-⎢⎥⎣⎦上的值域为112⎡⎤-⎢⎥⎣⎦,,可得7 2266m πππ≤+≤,从而可得结果. 【详解】(Ⅰ)()22f x cos x =+πcos212sin 216x x x ⎛⎫=+=++ ⎪⎝⎭, 由()222,262k x k k Z πππππ-≤+≤+∈得(),36k x k k Z ππππ-≤≤+∈所以,()f x 的单调递增区间是(),,36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ (Ⅱ)由(Ⅰ)知()π2sin 216f x x ⎛⎫=++ ⎪⎝⎭. 因为π,6x m ⎡⎤∈-⎢⎥⎣⎦,所以π2,2666x m ππ⎡⎤+∈-+⎢⎥⎣⎦. 要使得()f x 在π,6m ⎡⎤-⎢⎥⎣⎦上的值域为[]0,3,即πsin 26x ⎛⎫+ ⎪⎝⎭在π,3m ⎡⎤-⎢⎥⎣⎦上的值域为112⎡⎤-⎢⎥⎣⎦,. 所以72266m πππ≤+≤,即62m ππ≤≤. 【点睛】本题主要考查二倍角公式、辅助角公式的应用以及三角函数的单调性、三角函数的值域,属于中档题. 函数sin()y A x ωϕ=+的单调区间的求法:若0,0A ω>>,把x ωϕ+看作是一个整体,由22k x ππωϕ+≤+≤()322k k Z ππ+∈求得函数的减区间,2222k x k πππωϕπ-+≤+≤+求得增区间.30.(1)π2,1,6A ωϕ===;(2)7π,112a b =-=,递增区间为()πππ,π36k k k Z ⎡⎤-+∈⎢⎥⎣⎦;(3)π24或7π24. 【解析】【分析】(1)利用函数图像可直接得出周期T 和A ,再利用=2T πω,求出ω,然后利用待定系数法直接得出ϕ的值.(2)通过第一问求得的值可得到()f x 的函数解析式,令()=0f x ,再根据a 的位置确定出a 的值;令0x =得到的函数值即为b 的值;利用正弦函数单调增区间即可求出函数的单调增区间.(3)令()f α=0απ,即可求得α的取值. 【详解】解:(1)由图象知A =2,34T =512π-(-3π)=912π, 得T =π, 即22πω=2,得ω=1, 又f (-3π)=2sin[2×(-3π)+φ]=-2, 得sin (-23π+φ)=-1, 即-23π+φ=-2π+2k π, 即ω=6π+2k π,k ∈Z , ∵|φ|<2π, ∴当k =0时,φ=6π, 即A =2,ω=1,φ=6π; (2)a =-3π-4T =-3π-4π=-712π, b =f (0)=2sin 6π=2×12=1, ∵f (x )=2sin (2x +6π), ∴由2k π-2π≤2x +6π≤2k π+2π,k ∈Z , 得k π-3π≤x ≤k π+6π,k ∈Z , 即函数f (x )的递增区间为[k π-3π,k π+6π],k ∈Z ;(3)∵f (α)=2sin (2α+6π)即sin (2α+6π) ∵α∈[0,π],∴2α+6π∈[6π,136π], ∴2α+6π=4π或34π,∴α=24π或α=724π. 【点睛】关于三角函数图像需记住:两对称轴之间的距离为半个周期;相邻对称轴心之间的距离为半个周期; 相邻对称轴和对称中心之间的距离为14个周期. 关于正弦函数单调区间要掌握: 当2,222x k k ππωϕππ⎡⎤+∈-+⎢⎥⎣⎦时,函数单调递增; 当32+,222x k k ππωϕππ⎡⎤+∈+⎢⎥⎣⎦时,函数单调递减.。
完整版)高中三角函数测试题及答案

完整版)高中三角函数测试题及答案高一数学必修4第一章三角函数单元测试班级:__________ 姓名:__________ 座号:__________评分:__________一、选择题:共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
(48分)1、已知$A=\{\text{第一象限角}\}$,$B=\{\text{锐角}\}$,$C=\{\text{小于90°的角}\}$,那么$A$、$B$、$C$ 关系是()A.$B=A\cap C$B.$B\cup C=C$C.$A\cap D$D.$A=B=C$2、将分针拨慢5分钟,则分钟转过的弧度数是A。
$\frac{\pi}{3}\sin\alpha-\frac{2}{3}\cos\alpha$ B。
$-\frac{\pi}{3}$C。
$\frac{\pi}{6}$D。
$-\frac{\pi}{6}$3、已知 $\tan\alpha=-5$,那么 $\tan\alpha$ 的值为A。
2B。
$\frac{1}{6164}$C。
$-\frac{1}{6164}$D。
$-\frac{2}{3}$4、已知角 $\alpha$ 的余弦线是单位长度的有向线段,那么角 $\alpha$ 的终边()A。
在 $x$ 轴上B。
在直线 $y=x$ 上C。
在 $y$ 轴上D。
在直线 $y=x$ 或 $y=-x$ 上5、若 $f(\cos x)=\cos 2x$,则 $f(\sin 15^\circ)$ 等于()A。
$-\frac{2}{3}$B。
$\frac{3}{2}$C。
$\frac{1}{2}$D。
$-\frac{1}{2}$6、要得到 $y=3\sin(2x+\frac{\pi}{4})$ 的图象只需将$y=3\sin 2x$ 的图象A。
向左平移 $\frac{\pi}{4}$ 个单位B。
向右平移 $\frac{\pi}{4}$ 个单位C。
高中三角函数专题练习题(附答案)

高中三角函数专题练习题(附答案)一、填空题1.在ABC 中,AB =BC =1cos 7BAC ∠=,动点D 在ABC 所在平面内且2π3BDC ∠=.给出下列三个结论:①BCD △②线段AD 的长度只有最小值,无最大值,且最小值为1;③动点D 的轨迹的长度为8π3.其中正确结论的序号为______.2.已知单位向量1e ,2e 与非零向量a 满足12322e e +≤()120a e e ⋅-≤,则()1232a e e a⋅+的最大值是______.3.若,,44x y ππ⎡⎤∈-⎢⎥⎣⎦,a ∈R ,且33sin 204sin cos 0x x a y y y a ⎧+-=⎨++=⎩,则()cos 2x y +=______(提示:sin y x =在,22x ππ⎡⎤∈-⎢⎥⎣⎦上严格增函数) 4.△ABC 中,角A ,B ,C 所对的三边分别为a ,b ,c ,c =2b ,若△ABC 的面积为1,则BC 的最小值是________ .5.已知向量a ,b ,c 满足0a b c ++=,()()0a b a c -⋅-=,||9b c -=,则||||||a b c ++的最大值是___________.6.已知函数()2sin 16f x x πω⎛⎫=-- ⎪⎝⎭,其中0>ω,若()f x 在区间(4π,23π)上恰有2个零点,则ω的取值范围是____________.7.已知函数()sin cos f x x x =+,()sin cos g x x x =:①函数()f x 的图象关于点(,0)4π对称;②函数|()|g x 的最小正周期是2π;③把函数f (2x )图象上所有点向右平移8π个单位长度得到的函数图象的对称轴与函数y=()g x 图象的对称轴完全相同;④函数1()()y f x g x =--在R 上的最大值为2.则以上结论正确的序号为_______________8.平面向量a ,b ,c 满足1a a b c =-==,()222b ac b c b a c +⋅+-=⋅+,1a b b a b b cb⋅+=+⋅,则()2b c-=______.9.在三棱锥P ABC -中,4AB BC ==,8PC =,异面直线PA ,BC 所成角为π3,AB PA ⊥,AB BC ⊥,则该三棱锥外接球的表面积为______.10.已知函数()cos()(0,0,0)f x A x A ωϕωϕπ=->><<的部分图像如图所示,设函数()266g x f x f x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则()g x 的值域为___________.二、单选题11.已知双曲线2221(0)y x b b-=>的左、右焦点分别为1F ,2F ,过点2F 作直线l 交双曲线的右支于A ,B 两点.若11||::3:3:2AB AF BF =,则双曲线的离心率为( ) A .333B .2C .113D .1112.《九章算术》卷五“商功”:今有刍甍,下广3丈,袤4丈;上袤2丈,无广;高1丈.其描述的是下图的一个五面体,底面ABCD 是矩形,4AB =,3BC =,2EF =,//EF 底面ABCD 且EF 到底面ABCD 的距离为1.若DE AE BF CF ===,则该刍甍中点F 到平面EBC 的距离为( )A .15B .35C 10D 2513.在锐角ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,S 为ABC 的面积,且()222S a b c =--,则222b c bc+的取值范围为( )A .4359,1515⎛⎫ ⎪⎝⎭B .4322,15⎡⎫⎪⎢⎣⎭C .5922,15⎡⎫⎪⎢⎣⎭D .)22,⎡+∞⎣14.如图,将矩形纸片ABCD 折起一角落()EAF △得到EA F '△,记二面角A EF D '--的大小为π04θθ⎛⎫<< ⎪⎝⎭,直线A E ',A F '与平面BCD 所成角分别为α,β,则( ).A .αβθ+>B .αβθ+<C .π2αβ+>D .2αβθ+>15.如图,在正方体ABCD EFGH -中,P 在棱BC 上,BP x =,平行于BD 的直线l 在正方形EFGH 内,点E 到直线l 的距离记为d ,记二面角为A l P --为θ,已知初始状态下0x =,0d =,则( )A .当x 增大时,θ先增大后减小B .当x 增大时,θ先减小后增大C .当d 增大时,θ先增大后减小D .当d 增大时,θ先减小后增大16.在ABC 中,60BAC ∠=,3BC =,且有2CD DB =,则线段AD 长的最大值为( ) A 13B .2 C 31 D .317.在三棱锥S ABC -中,侧棱SA ,SB ,SC 两两垂直,且2SA SB SC +==.设SA x =,该三棱锥的表面积为函数()y f x =,以下判断正确的是( ) A .()f x 为常数 B .()f x 有极小值 C .()f x 有极大值D .()f x 是单调函数18.设点()11,P x y 在椭圆22182x y +=上,点()22,Q x y 在直线280x y +-=上,则2121x x y y -+-的最小值是( )A .212+B .3C .312+D .219.函数()sin()0,||2f x x πωϕωϕ⎛⎫=+>≤ ⎪⎝⎭,已知,06π⎛⎫- ⎪⎝⎭为()f x 图象的一个对称中心,直线1312x π=为() f x 图象的一条对称轴,且() f x 在1319,1212ππ⎡⎤⎢⎥⎣⎦上单调递减.记满足条件的所有ω的值的和为S ,则S 的值为( ) A .125 B .85C .165D .18520.在ABC 中,2AB =,,D E 分别是边AB ,AC 的中点,CD 与BE 交于点O ,若OC 3OB =,则ABC 面积的最大值为( )A .3B .33C .63D .93三、解答题21.在海岸A 处,发现北偏东45︒方向,距离A 为31-海里的B 处有一艘走私船,在A 处北偏西75︒方向,距离A 为2海里的C 处有一艘缉私艇奉命以103海里/时的速度追截走私船,此时,走私船正以10海里/时的速度从B 处向北偏东30方向逃窜.(1)问C 船与B 船相距多少海里?C 船在B 船的什么方向? (2)问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.22.函数()()3sin 03f x x πωω⎛⎫=+> ⎪⎝⎭在一个周期内的图象如图所示,A 为图象的最高点,B ,C 为图象与x 轴的交点,ABC ∆为等边三角形.将函数()f x 的图象上各点的横坐标变为原来的π倍后,再向右平移23π个单位,得到函数()y g x =的图象.(Ⅰ)求函数()g x 的解析式;(Ⅱ)若不等式()23sin 324x m g x m π-⋅-≤+对任意x ∈R 恒成立,求实数m 的取值范围.23.已知函数()cos f x x x =,()sin g x x =,0,2x π⎡⎤∈⎢⎥⎣⎦.(1)求证:()()f x g x ≤;(2)若()ax g x bx <<在0,2π⎛⎫⎪⎝⎭上恒成立,求a 的最大值与b 的最小值.24.已知函数2()23sin 2sin cos ()f x x x x a a R =-++∈,且(0)3f =. (1)求a 的值;(2)若()f x ω在[0,]π上有且只有一个零点,0>ω,求ω的取值范围. 25.如图所示,在平面四边形ABCD 中,1,2,AB BC ACD ==∆为正三角形.(1)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,若sin(2)3sin A C C +=,求角B 的大小; (2)求BCD ∆面积的最大值.26.如图,在ABC ∆中,90,3,1ABC AB BC ︒∠===,P 为ABC ∆内一点,90BPC ︒∠=.(1)若32PC =,求PA ; (2)若120APB ︒∠=,求ABP ∆的面积S .27.已知函数()()sin 0,2f x t x t πωϕϕ⎛⎫=+>< ⎪⎝⎭,()f x 的部分图像如图所示,点()0,3N ,,02M π⎛⎫- ⎪⎝⎭,,4P t π⎛⎫⎪⎝⎭都在()f x 的图象上.(1)求()f x 的解析式;(2)当,2x ππ⎡⎤∈-⎢⎥⎣⎦时,()3f x m -≤恒成立,求m 的取值范围.28.已知向量()cos sin ,sin a m x m x x ωωω=-,()cos sin ,2cos b x x n x ωωω=--,设函数()()2n f x a b x R =⋅+∈的图象关于点,112π⎛⎫⎪⎝⎭对称,且()1,2ω∈ (I )若1m =,求函数()f x 的最小值;(II )若()4f x f π⎛⎫≤ ⎪⎝⎭对一切实数恒成立,求()y f x =的单调递增区间.29.已知函数())2cos cos 1f x xx x =+-.(1)求函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值;(2)若()85f x =-,2,3x ππ⎡⎤∈⎢⎥⎣⎦,求cos2x 的值;(3)若函数()()0y f x ωω=>在区间,62ππ⎡⎤⎢⎥⎣⎦上是单调递增函数,求正数ω的取值范围.30.已知a ,b ,c 分别为ABC 三个内角A ,B ,C 的对边,S 为ABC 的面积,()222sin SB C a c +=-. (1)证明:2A C =;(2)若2b =,且ABC 为锐角三角形,求S 的取值范围.【参考答案】一、填空题1.①③2 3.145.3+36.742ω<<或91322ω<≤.7.②③④8.229.80π 10.9[,4]4-二、单选题 11.A 12.C 13.C 14.A 15.C 16.C 17.A 18.D 19.A 20.C 三、解答题21.(1)=BC C 船在B 船的正西方向;(2)缉私艇沿东偏北30才能最快追上走私船. 【解析】(1)在ABC 中根据余弦定理计算BC ,再利用正弦定理计算ABC ∠即可得出方位; (2)在BCD △中,利用正弦定理计算BCD ∠,再计算BD 得出追击时间. 【详解】解:(1)由题意可知1=AB ,2AC =,120BAC ∠=︒, 在ABC 中,由余弦定理得:2222cos1206BC AB AC AB AC =+-︒=,BC ∴,由正弦定理得:sin sin AC BCABC BAC=∠∠,即2sin ABC∠解得:sin ABC ∠=, 45ABC ∴∠=︒,C ∴船在B 船的正西方向.(2)由(1)知=BC 120DBC ∠=︒, 设t 小时后缉私艇在D 处追上走私船,则10BD t =,CD =,在BCD △10sin tBCD∠, 解得:1sin 2BCD ∠=, 30BCD ∴∠=︒,BCD ∴△是等腰三角形,10t ∴=,即t =∴缉私艇沿东偏北30【点睛】本题考查了正余弦定理解三角形,以及解三角形的实际应用,考查转化能力和运算能力,属于中档题.22.(Ⅰ)()12g x x =(Ⅱ)2,23⎡⎤-⎢⎥⎣⎦【解析】 【分析】(Ⅰ)利用等边三角形的性质,根据已知,可以求出函数的周期,利用正弦型函数的最小正周期公式求出ω,最后根据正弦型函数图象的变换性质求出()y g x =的解析式; (Ⅱ)根据函数()y g x =的解析式,原不等式等价于23cos 3cos 10x m x m +++≥在x ∈R 恒成立,利用换元法,构造二次函数,分类讨论进行求解即可. 【详解】(Ⅰ)点A ABC ∆为等边三角形,所以三角形边长为2,所以24T πω==,解得2πω=,所以()23f x x ππ⎛⎫+ ⎪⎝⎭,将函数()f x 的图象上各点的横坐标变为原来的π倍后,得到()123h x x π⎛⎫=+ ⎪⎝⎭,再向右平移23π个单位,得到()12g x x =.(Ⅱ)()22g x x x ππ⎛⎫-=-= ⎪⎝⎭,所以()223sin 233cos 3cos x g x x m x π⋅-=--,原不等式等价于23cos 3cos 10x m x m +++≥在x ∈R 恒成立. 令cos x t =,[]1,1t ∈-,即23310t mt m +++≥在[]1,1t ∈-上恒成立.设()2331t t mt m ϕ=+++,对称轴2m t =-, 当12m-≤-时,即2m ≥时,()1240m ϕ-=-+≥,解得2m ≤,所以2m =;当12m-≥时,即2m ≤-时,()1440m ϕ=+≥,解得1m ≥-(舍); 当112m -<-<时,即22m -<<时,231024m m m ϕ⎛⎫-=-++≥ ⎪⎝⎭,解得223m -≤<.综上,实数m 的取值范围为2,23⎡⎤-⎢⎥⎣⎦.【点睛】本题考查了正弦型函数的图象变换和性质,考查了利用换元法、构造法解决不等式恒成立问题,考查了数学运算能力.23.(1)答案见解析;(2)a 最大值为2π,b 的最小值为1. 【解析】 【分析】(1)构建函数()cos sin h x x x x =-,通过导数研究函数()h x 在0,2π⎡⎤⎢⎥⎣⎦单调性并计算最值,可得结果.(2)构造函数()sin M x x cx =-,通过分类讨论的方法,0c ≤,1c ≥和01c <<,利用导数判断函数()M x 的单调性,并计算最值比较,可得结果. 【详解】(1)由()()()cos sin h x f x g x x x x =-=- 所以()'cos sin cos sin h x x x x x x x =--=-. 又0,2x π⎡⎤∈⎢⎥⎣⎦,()'sin 0h x x x =-≤,所以()h x 在区间上0,2π⎡⎤⎢⎥⎣⎦单调递减.从而()()00h x h ≤=,()()f x g x ≤. (2)当0x >时,“()ax g x <”等价于“sin 0x ax ->” “()g x bx <”等价于“sin 0x bx -<”.令()sin M x x cx =-,则()'cos M x x c =-,当0c ≤时,()0M x >对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立.当1c ≥时,因为对任意0,2x π⎛⎫∈ ⎪⎝⎭,()'cos 0M x x c =-<,所以()M x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递减.从而()()00M x M <=对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立.当01c <<时,存在唯一的00,2x π⎛⎫∈ ⎪⎝⎭,使得()'cos 0M x x c =-=.()M x 与()'M x 在区间0,2π⎛⎫⎪⎝⎭上的情况如下:因为在区间0上是增函数, 所以()()000M x M >=.进一步,“()0M x >对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立”当且仅当1022M c ππ⎛⎫=-≥ ⎪⎝⎭,即20c π<≤,综上所述: 当且仅当2c π≤时,()0M x >对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立; 当且仅当1c ≥时,()0M x <对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立.所以,若()ax g x bx <<对任意0,2x π⎛⎫∈ ⎪⎝⎭恒成立,则a 最大值为2π,b 的最小值为1. 【点睛】本题考查导数的综合应用,关键在于构建函数,化繁为简,同时掌握分类讨论的思想,考验分析问题的能力以及计算能力,属中档题.24.(1)a =(2)15,36⎡⎫⎪⎢⎣⎭【解析】 【分析】(1)利用降次公式、辅助角公式化简()f x 表达式,利用(0)f =a 的值. (2)令()0f x ω=,结合x 的取值范围以及三角函数的零点列不等式,解不等式求得ω的取值范围. 【详解】(1)2()2sin cos f x x x x a =-++sin 2x x a =+2sin 23x a π⎛⎫=++- ⎪⎝⎭(0)f =(0)2sin3f a π∴=+=即a =(2)令()0f x ω=,则sin 203x πω⎛⎫+= ⎪⎝⎭,[0,]x π∈,2,2333πππωπω⎡⎤∴+∈+⎢⎥⎣⎦,()f x 在[0,]π上有且只有一个零点,223πππωπ∴+<,1536ω∴<, ω∴的取值范围为15,36⎡⎫⎪⎢⎣⎭. 【点睛】本小题主要考查三角恒等变换,考查三角函数零点问题,考查化归与转化的数学思想方法,属于基础题.25.(1)23B π=;(21. 【解析】 【分析】(1)由正弦和角公式,化简三角函数表达式,结合正弦定理即可求得角B 的大小;(2)在ABC ∆中,设,ABC ACB αβ∠=∠=,由余弦定理及正弦定理用,αβ表示出CD .再根据三角形面积公式表示出∆BCD S ,即可结合正弦函数的图像与性质求得最大值. 【详解】 (1)由题意可得:sin2cos cos2sin 3sin A C A C C +=∴()22sin cos cos 12sin sin 3sin A A C A C C +-=整理得sin (cos cos sin sin )sin A A C A C C -= ∴sin cos()sin A A C C += ∴sin cos sin A B C -= ∴sin 1cos sin 2C c B A a =-=-=- 又(0,)B π∈ ∴23B π=(2)在ABC ∆中,设,ABC ACB αβ∠=∠=,由余弦定理得:22212212cos 54cos AC αα=+-⨯⨯=-,∵ACD ∆为正三角形, ∴2254cos CD C A α=-=, 在ABC ∆中,由正弦定理得:1sin sin ACβα=, ∴sin sin AC βα=, ∴sin sin CD βα=,∵()222222(cos )1sin sin 54cos sin CD CD CD ββααα=-=-=--2(2cos )α=-,∵BAC β<∠,∴β为锐角,cos 2cos CD βα=-, 12sin sin 233BCD S CD CD ππββ∆⎛⎫⎛⎫=⨯⨯⨯+=+ ⎪ ⎪⎝⎭⎝⎭1cos sin 2CD ββ=+,1cos )sin sin 223πααα⎛⎫=-+=- ⎪⎝⎭, ∵(0,)απ∈∴当56πα=时,()max 1BCD S ∆=. 【点睛】本题考查了三角函数式的化简变形,正弦定理与余弦定理在解三角形中的应用,三角形面积的表示方法,正弦函数的图像与性质的综合应用,属于中档题.26.(1;(2 【解析】 【分析】(1)求出12BP ==,,36CBP ABP ππ∠=∠=,ABP ∆中由余弦定理即可求得PA ;(2)设PBA α∠=,利用正弦定理表示出()sin120sin 60AB PB =︒︒-α,求得tan α=,利用面积公式即可得解. 【详解】(1)在ABC ∆中,90,1ABC AB BC ︒∠===,2AC =P 为ABC ∆内一点,90BPC ︒∠=,PC =,所以12BP =,CBP ∆中,由余弦定理得:2221cos 22BP BC PC CBP BP BC +-∠==⋅所以,36CBP ABP ππ∠=∠=ABP ∆中,由余弦定理得:AP==; (2)120APB ︒∠=,设0,,90,602PBA PBC PAB π⎛⎫∠=α∈∠=︒-α∠=︒-α ⎪⎝⎭,在Rt PBC ∆中,sin sin PB BC =⋅α=α, 在PBA ∆中,由正弦定理()sin120sin 60AB PB=︒︒-α,即()sin 2sin 60α=︒-α,sin sin α=α-α,所以tan α=sin PB α==ABP ∆的面积11sin 22S AB PB α=⋅==. 【点睛】此题考查解三角形,对正余弦定理的综合使用,涉及两角差的正弦公式以及同角三角函数关系的使用,综合性较强.27.(1)()22sin 33x f x π⎛⎫=+ ⎪⎝⎭;(2)[]1,0-【解析】 【分析】(1)由三角函数图像,求出,,t ωϕ即可;(2)求出函数()f x m -的值域,再列不等式组32m m +≥⎧⎪⎨≤⎪⎩.【详解】解:(1)由()f x 的图象可知34424T πππ⎛⎫=--= ⎪⎝⎭,则3T π=, 因为23T ππω==,0>ω,所以23ω=,故()2sin 3t x f x ϕ⎛⎫=+ ⎪⎝⎭.因为,02M π⎛⎫- ⎪⎝⎭在函数()f x 的图象上,所以sin 023f t ππϕ⎛⎫⎛⎫-=-+= ⎪ ⎪⎝⎭⎝⎭, 所以()3k k Z πϕπ-+=∈,即()3k k Z πϕπ=+∈,因为2πϕ<,所以3πϕ=.因为点(N 在函数()f x 的图象上,所以()0sin 3f t π==解得2t =,故()22sin 33x f x π⎛⎫=+ ⎪⎝⎭.(2)因为,2x ππ⎡⎤∈-⎢⎥⎣⎦,所以22,3333x πππ⎡⎤+∈-⎢⎥⎣⎦,所以2sin 33x π⎡⎤⎛⎫+∈⎢⎥ ⎪⎝⎭⎣⎦,则()2f x ≤.因为()33f x m -≤-≤,所以()3m f x m ≤+, 所以32m m +≥⎧⎪⎨⎪⎩10m -≤≤.故m 的取值范围为[]1,0-. 【点睛】本题考查了利用三角函数图像求解析式,重点考查了三角函数值域的求法,属中档题.28.(Ⅰ)1()22,31234k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ 【解析】 【分析】化简()f x 解析式可得()()22n f x x ωϕ=-+;根据图象关于,112π⎛⎫ ⎪⎝⎭可求得n ;(Ⅰ)若1m =,则()()21f x x ωϕ=-+,从而可得函数最小值;(Ⅱ)利用4x π=为对称轴,,112π⎛⎫ ⎪⎝⎭为对称中心可得()*642T T k k N π=+⋅∈,根据周期和ω的范围可求得ω;将,112π⎛⎫ ⎪⎝⎭代入解析式可求得()314f x x π⎛⎫=-+ ⎪⎝⎭,将34x π-整体放入正弦函数的单调递增区间中,解出x 的范围即可. 【详解】由题意得:()()22cos sin 2sin cos 2n f x m x x n x x ωωωω=--++()sin 2cos 2222n n n x m x x ωωωϕ=-+=-+ 其中cos ϕ=sin ϕ=图象关于点,112π⎛⎫⎪⎝⎭对称 12n ∴=,解得:2n =()()21f x x ωϕ∴=-+(Ⅰ)若1m =,则()()21f x x ωϕ=-+()min 1f x ∴=(Ⅱ)()4f x f π⎛⎪≤⎫ ⎝⎭对一切实数恒成立 ()max 4f x f π⎛⎫∴= ⎪⎝⎭()*412642T T k k N πππ∴-==+⋅∈,即:()()*223212T k N k ππω==∈+ ()3212k ω∴=+,又()1,2ω∈ 32ω∴=()2sin3cos31f x x m x ∴=-+,又图象关于点,112π⎛⎫⎪⎝⎭对称2sin cos 111244f m πππ⎛⎫∴=-+= ⎪⎝⎭,解得:2m =()2sin 32cos31314f x x x x π⎛⎫∴=-+=-+ ⎪⎝⎭令232242k x k πππππ-+≤-≤+,k Z ∈,解得:2212343k k x ππππ-+≤≤+,k Z ∈ ()f x ∴的单调递增区间为:()22,31234k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ 【点睛】本题考查三角函数图象与性质的综合应用问题,涉及到根据三角函数的性质求解函数解析式的求解、三角函数最值的求解、单调区间的求解问题.29.(I )1-;(II ;(III )10,3⎛⎤ ⎥⎝⎦【解析】 【分析】将()f x 整理为2sin 26x π⎛⎫+ ⎪⎝⎭;(I )利用x 的范围求得26x π+的范围,结合sin x 的图象可求得最值;(II )利用()85f x =-可求得sin 26x ;结合角的范围和同角三角函数关系可求得cos 26x π⎛⎫+ ⎪⎝⎭;根据cos 2cos 266x x ππ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦,利用两角和差余弦公式可求得结果;(III )利用x 的范围求得26x πω+的范围,从而根据sin x 单调递增区间构造出关于ω的不等式组,解不等式组再结合0>ω即可得到结果. 【详解】()2cos 2cos 12cos 22sin 26f x x x x x x x π⎛⎫=+-=+=+ ⎪⎝⎭(I )0,2x π⎡⎤∈⎢⎥⎣⎦ 72,666x πππ⎡⎤∴+∈⎢⎥⎣⎦[]2sin 21,26x π⎛⎫∴+∈- ⎪⎝⎭()f x ∴在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值为:1-(II )由题意得:82sin 265x π⎛⎫+=- ⎪⎝⎭ 4sin 265x π⎛⎫∴+=- ⎪⎝⎭2,3x ππ⎡⎤∈⎢⎥⎣⎦ 3132,626x πππ⎡⎤∴+∈⎢⎥⎣⎦ 3cos 265x π⎛⎫∴+= ⎪⎝⎭ cos 2cos 2cos 2cos sin 2sin 666666x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫∴=+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦341552=⨯(III )()2sin 26f x x πωω⎛⎫=+ ⎪⎝⎭,62x ππ⎡⎤∈⎢⎥⎣⎦时,2,6366x πωπππωωπ⎡⎤+∈++⎢⎥⎣⎦2622362k k ππωππωππππ⎧+≤+⎪⎪∴⎨⎪+≥-⎪⎩,k Z ∈,解得:12362k k ωω⎧≤+⎪⎨⎪≥-⎩,k Z ∈ 0ω>,可知当0k =时满足题意,即103ω<≤ω∴的取值范围为:10,3⎛⎤ ⎥⎝⎦【点睛】本题考查正弦型函数的值域求解、单调性应用、三角恒等变换公式应用、同角三角函数关系等问题.关键是能够利用二倍角公式和辅助角公式将函数化为()sin A x ωϕ+的形式,从而通过整体对应的方式来研究函数的值域和性质. 30.(1)见解析;(2)2⎫⎪⎪⎝⎭【解析】 【分析】(1)利用三角形面积公式表示S ,结合余弦定理和正弦定理,建立三角函数等式,证明结论,即可.(2)结合三角形ABC 为锐角三角形,判定tanC 的范围,利用tanC 表示面积,结合S 的单调性,计算范围,即可. 【详解】(1)证明:由()222sin S B C a c +=-,即222sin SA a c=-, 22sin sin bc A A a c∴=-,sin 0A ≠,22a c bc ∴-=, 2222cos abc bc A =+-,2222cos a c b bc A ∴-=-, 22cos b bc A bc ∴-=,2cos b c A c ∴-=,sin 2sin cos sin B C A C ∴-=,()sin 2sin cos sin A C C A C ∴+-=,sin cos cos sin sin A C A C C ∴-=, ()sin sin A C C ∴-=,A ,B ,()0,C π∈,2A C ∴=.(2)解:2A C =,3B C π∴=-,sin sin3B C ∴=.sin sin a b A B=且2b =,2sin2sin3Ca C∴=, ()212sin2sin 2sin2sin 2tan2tan 4tan 4sin 32sin 2sin2cos cos2sin tan2tan 3tan tan tan C C C C C C C S ab C C C C C C C C C CC C∴======+++--,ABC 为锐角三角形,20,230,20,2A C B C C ππππ⎧⎛⎫=∈ ⎪⎪⎝⎭⎪⎪⎛⎫∴=-∈⎨ ⎪⎝⎭⎪⎪⎛⎫∈⎪⎪⎝⎭⎩,,64C ππ⎛⎫∴∈ ⎪⎝⎭,tan C ⎫∴∈⎪⎪⎝⎭, 43tan tan S CC=-为增函数, 2S ⎫∴∈⎪⎪⎝⎭.【点睛】考查了正弦定理,考查了余弦定理,考查了三角形面积公式,考查了函数单调性判定,难度偏难.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学第一次月考试题一.选择题(每题5分,共60分)1.函数的最小正周期是( ))62sin(2π+=x y A . B . C . D .π4π2π2π2.=( )sin 300 A . B C .- D 12123.如图,在直角坐标系xOy 中,射线OP 交单位圆O 于点P ,若∠AOP =θ,则点P 的坐标是( )A .(cos θ,sin θ)B .(-cos θ,sin θ)C .(sin θ,cos θ)D .(-sin θ,cos θ)4.如果=-5,那么tan α的值为( )sin α-2cos α3sin α+5cos αA .-2B .2C.D .-231623165.函数的图象的一条对称轴方程是())252sin(π+=x y A . B .C .D .2π-=x 4π-=x 8π=x 45π=x 6.将函数y =sin(x -)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再π3将所得的图象向右平移个单位,得到的图象对应的解析式是( )π3A .y =sin xB .y =sin(x -)1212π2C .y =sin(x -)D .y =sin(2x -)12π6π67.已知是第二象限角,且,则( )α4tan =-3αA . B .C . D .4sin =-5α4sin =5α3cos =5α4cos =-5αhe8.已知,且,则=( )3cos +=25πθ⎛⎫⎪⎝⎭3,22ππθ⎛⎫∈ ⎪⎝⎭tan θA . B .-C .D .-434334349.已知函数f (x )=2sin(ωx +φ)(ω>0,|φ|<)的部分图象如图所示,则函数f (x )一π2个单调递增区间是( )A. B.[-7π12,5π12][-7π12,-π12]C. D.[-π4,π6][11π12,17π12]10.函数y=cos 2x –3cosx+2的最小值是()A .2B .0C .D .64111.函数y =cos(ωx +φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,A ,B 分别为最高点与最低点,并且两点间的距离为2,则该函数图象的一条对称轴方程为( )2A .x = B .x = C .x =1 D .x =22ππ212.设ω>0,函数y =sin(ωx +)+2的图象向右平移个单位后与原图象重合,则π34π3ω的最小值是( )A. B. C. D .3234332二.填空题(每题5分,共20分) 13.函数的单调递增区间是_____________________________________)x sin(y -=14.已知sin α+2cos α=0,则2sin αcos α-cos 2α的值是________. 15.、、的大小顺序是 1tan 2tan 3tan 16.函数的图象为,则如下结论中正确的序号是_____ π()3sin 23f x x ⎛⎫=-⎪⎝⎭C ①、图象关于直线对称; C 11π12x =②、图象关于点对称; C 2π03⎛⎫⎪⎝⎭,③、函数在区间内是增函数; ()f x π5π1212⎛⎫-⎪⎝⎭,④、由的图角向右平移个单位长度可以得到图象.3sin 2y x =π3C 二.解答题 17.(10分)已知角终边上一点P (-4,3),求的值α)29sin()211cos()sin()2cos(απαπαπαπ+---+18.(12分)已知的最大值为,最小值为。
求函数cos3(0)y a b x b =->3212-的周期、最值,并求取得最值时的之值;并判断其奇偶性。
4sin(3)y a bx =-x19.(12分)已知函数f (x )=cos(2x -),x ∈R .2π4(1)求函数f (x )的最小正周期和单调递增区间.(2)求函数f (x )在区间[-,]上的最小值和最大值,并求出取得最值时x 的值.π8π220.(12分)函数f 1(x )=A sin(ωx +φ)(A >0,ω>0,|φ|<)的一段图象过点(0,1),如π2图所示.(1)求函数f 1(x )的表达式;(2)把f 1(x )的图象向右平移个单位长度得到f 2(x )的图象,求f 2(x )取得最大值时xπ4的取值.21.(12分)某同学用“五点法”画函数f (x )=A sin(ωx +φ)(ω>0,|φ|<)在某一个周π2期内的图象时,列表并填入部分数据,如下表:ωx +φ0π2π3π22πx π35π6Asin(ωx +φ)05-5(1)请将上表数据补充完整,并直接写出函数f (x )的解析式;(2)将y =f (x )图象上所有点向左平移个单位长度,得到y =g (x )图象,求y =g (x )π6的图象离原点O 最近的对称中心.22.(12分)如图为一个观览车示意图,该观览车半径为4.8 m ,圆上最低点与地面距离为0.8 m,60秒转动一圈,图中OA 与地面垂直,以OA 为始边,逆时针转动θ角到OB ,设B 点与地面距离为h .(1)求h 与θ间关系的函数解析式;(2)设从OA 开始转动,经过t 秒到达OB ,求h 与t 间关系的函数解析式.参考答案一.选择题1-5.CDADA 6-10.BBCDB 11.C12.C二.填空题13. 14.-1 15.3+2,+2,22k k k Z ππππ⎡⎤∈⎢⎥⎣⎦tan1>tan 2>tan 316.①②③三.解答题17.3-418.由题意得,解得3+=21-=-2a b a b ⎧⎪⎪⎨⎪⎪⎩1=2=1a b ⎧⎪⎨⎪⎩ =-2sin 3y x 周期;此时,此时;23T π=max =2y 2=-+,63x k k Z ππ∈min =-3y 2=+,63x k k Z ππ∈因为定义域为,而所以为奇函数R ()()()-=-2sin -3=2sin 3=-f x x x f x 19.解:(1)因为f (x )=cos(2x -),所以函数f (x )的最小正周期为T ==π.2π42π2由-π+2k π≤2x -≤2k π(k ∈Z ),得-+k π≤x ≤+k π(k ∈Z ),故函数π43π8π8f (x )的单调递增区间为[-+k π,+k π](k ∈Z ).3π8π8(2)因为f (x )=cos(2x -)在区间[-,]上为增函数,在区间[,]上为2π4π8π8π8π2减函数,又f (-)=0,f ()=,f ()=cos(π-)=-cos =-1,所以π8π82π22π42π4函数f (x )在区间[-,]上的最大值为,此时x =;最小值为-1,此时x =.π8π22π8π220.解:(1)由图知,T =π,于是ω==2.将y =A sin2x 的图象向左平移,得2πT π12y =A sin(2x +φ)的图象,于是φ=2×=.将(0,1)代入y =A sin(2x +),得A =2.π12π6π6故f 1(x )=2sin(2x +).π6(2)依题意,f 2(x )=2sin[2(x -)+]π4π6=-2cos(2x +),π6当2x +=2k π+π(k ∈Z ),即x =k π+(k ∈Z )时,π65π12y max =2.此时x 的取值为{x |x =k π+,k ∈Z }.5π1221.解:(1)根据表中已知数据,解得A =5,ω=2,φ=-,数据补全如下表:π6ωx +φ0π2π3π22πxπ12π37π125π613π12A sin(ωx +φ)5-5且函数表达式为f (x )=5sin(2x -).π6(2)由(1)知f (x )=5sin(2x -),因此g (x )=5sin[2(x +)-]=5sin(2x +)π6π6π6π6因为y =sin x 的对称中心为(k π,0),k ∈Z .令2x +=k π,k ∈Z ,解得x =-,k ∈Z .π6k π2π12即y =g (x )图象的对称中心为(-,0),k ∈Z ,其中离原点O 最近的对称中心为k π2π12(-,0).π1222.解:(1)由题意可作图如图.过点O 作地面平行线ON ,过点B 作ON 的垂线BM 交ON 于M点.当θ>时,∠BOM =θ-.π2π2h =|OA |+0.8+|BM |=5.6+4.8sin(θ-);π2当0≤θ≤时,上述解析式也适合.π2(2)点A 在⊙O 上逆时针运动的角速度是,π30∴t 秒转过的弧度数为t ,π30∴h =4.8sin(t -)+5.6,t ∈[0,+∞).π30π2。
