比焓与比熵定义及区别
解读“焓”与“熵”

编年史 @ 制冷原理
曹小军 2014-6-7
以生成物的焓小于反应物的焓。 2. 如果单纯通过热传递来改变物体的内能,内能的变化可以用传递热量的多少来度量,这时物体内 能的增加(或减少)量△U 就等于外界吸收(或对外界放出)热量 Q 的数值,即△U=Q。 3. 在做功和热传递同时存在的过程中,物体内能的变化,则要由做功和所传递的热量共同决定。在 这种情况下,物体内能的增量△U 就等于从外界吸收的热量 Q 和对外界做功 W 之和。即△U=W+Q 能量守恒定律: 能量既不能凭空产生,也不能凭空消失,它只能从一种形式转化为另一种形式,或者从一个物体 转移到另一个物体,在转移和转化的过程中,能量的总量不变。 能量的多样性: 物体运动具有机械能、分子运动具有内能、电荷具有电能、原子核内部的运动具有原子能等等, 可见,在自然界中不同的能量形式与不同的运动形式相对应。 不同形式的能量转化: “摩擦生热”是通过克服摩擦力做功将机械能转化为内能;水壶中的水沸腾时水蒸气对壶盖做功 将壶盖顶起,表明内能转化为机械能;电流通过电热丝做功可将电能转化为内能。 。 。这些实例说明了 不同形式的能量之间可以相互转化,且这一转化过程是通过做功来完成的。 能量守恒的意义: 1.能的转化与守恒是分析解决问题的一个极为重要的方法,它比机械能守恒定律更普遍。例如物体在 空中下落受到阻力时,物体的机械能不守恒,但包括内能在内的总能量守恒。 2. 能量守恒定律是 19 世纪自然科学中三大发现之一,也庄重宣告了第一类永动机幻想的彻底破灭。 3.能量守恒定律是认识自然、改造自然的有力武器,这个定律将广泛的自然科学技术领域联系起来。 第一类永动机 不消耗任何能量却能源源不断地对外做功的机器。 其不可能存在,因为违背的能量守恒定律。 热力学第二定律 热力学第二定律有几种表述方式: 克劳修斯表述:热量可以自发地从温度高的物体传递到较冷的物体,但不可能自发地从温度低的物体 传递到温度高的物体; 开尔文-普朗克表述:不可能从单一热源吸取热量,并将这热量变为功,而不产生其他影响。 熵表述:随时间进行,一个孤立体系中的熵总是不会减少。——“熵”的引入 熵在热力学中是表征物质状态的参量之一,通常用符号 S 表示。在经典热力学中,可用增量定义为 dS=(dQ/T),式中 T 为物质的热力学温度;dQ 为熵增过程中加入物质的热量。有了熵的概念,热力学 第二定律可以从数学上表述为熵增加原理, 他揭示了自然界中这样的一个事实: 在一个可逆的过程中, 系统的熵越大,就越接近平衡状态,虽然此间能量的数量不变,但可供利用或者是转化的能量却是越 来越少。 意义: 在可逆微变化过程中,熵的变化等于系统从热源吸收的热量与热源的热力学温度之比,可用于度 量热量转变为功的程度。 在不可逆微变化过程中,实际发生的过程总使整个系统的熵值增大,此即熵增原理,熵的增加就 意味着有效能量的减少,一定的能量就被转化成了不能再做功的无效能量。 就这样,热力学第一定律阐明了热在转化过程中各种能量总是保持不变的规律,熵增加原理则定 量地揭示出宏观过程的方向性和限度,两个定律相互交织,构成了一幅完整的图画,使人们对热现象 的能量转化过程的基本特征有了全面的认识。 关系
焓,比焓,熵

焓:1、焓是一个热力学系统中的能量参数。
原理物体中所有分子做热运动的动能和分子势能和分子、原子内部所具有的能量等的总和叫做物体的热力学能,也叫做内能。
热力学能与动能、势能一样,是物体的一个状态量。
初中我们学过,改变物体内能的方式有两个:做功和热传递。
一个物体,如果它跟外界不发生热交换,也就是它既没有吸收热量也没有放出热量,则外界对其做功等于其热力学能的增量:ΔU1=W如果物体对外界做功,则W为负值,热力学能增加量ΔU1也为负值,表示热力学能减少。
如果外界既没有对物体做功,物体也没有对外界做功,那么物体吸收的热量等于其热力学能的增量:ΔU2=Q如果物体放热,则Q为负值,热力学能增加量ΔU2也为负值,表示热力学能减少。
一般情况下,如果物体跟外界同时发生做功和热传递的过程,那么物体热力学能的增量等于外界对物体做功加上物体从外界吸收的热量,即:ΔU=ΔU1+ΔU2=Q+W因为热力学能U是状态量,所以:ΔU=ΔU末态-ΔU初态=Q+W上式即热力学第一定律的表达式。
化学反应都是在一定条件下进行的,其中以恒容与恒压最为普遍和重要。
在密闭容器内的化学反应就是恒容过程。
因为系统体积不变,而且只做体积功(即通过改变物体体积来对物体做功,使物体内能改变,如在针管中放置火柴头,堵住针头并压缩活塞,火柴头会燃烧)(这里很多人质疑为什么体积不变还做体积功,我解释一下,做功的形式有很多种,有的功不通过体积改变的形式来实现,比如电流做功,但是气体只能做体积功,因为是恒容过程,所以体积功为零,并不是说只做体积功就是说这个过程做功了,只是为了说明W=0)所以W=0,代入热一定律表达式得:ΔU=Q它表明恒容过程的热等于系统热力学能的变化,也就是说,只要确定了过程恒容和只做体积功的特点,Q就只决定于系统的初末状态。
在敞口容器中进行的化学反应就是恒压过程。
所谓恒压是指系统的压强p等于环境压强p外,并保持恒定不变,即p=p外=常数。
由于过程恒压且只做体积功,所以:W=W体积=-p外(V2-V1)=-(p2V2-p1V1)其中W为外界对系统做的功,所以系统对外做功为负。
工程热力学公式

工程热力学公式一、基本状态参数相关公式1.温度(T):-热力学温度(开尔文温度,K)与摄氏温度(℃)的关系:T(K)= t(℃)+273.15。
2.压力(p):-绝对压力、表压力和真空度的关系:-绝对压力= 大气压力+ 表压力;-绝对压力-大气压力= 真空度。
3.比体积(v):-质量为m 的物质,体积为V,则比体积v = V/m。
二、热力学第一定律相关公式1.闭口系统能量方程:- ΔU = Q - W,其中ΔU 是系统内能的变化,Q 是系统吸收的热量,W 是系统对外所做的功。
2.开口系统稳定流动能量方程:- ΔH + Δ(1/2mc²)+ gΔz = Q - Ws,其中ΔH 是焓的变化,m 是质量流量,c 是流体流速,g 是重力加速度,z 是高度,Q 是系统吸收的热量,Ws 是轴功。
三、热力学第二定律相关公式1.克劳修斯不等式:- ℃(dQ/T)≤0,对于可逆循环取等号,对于不可逆循环取小于号。
其中dQ 是微元热量,T 是热力学温度。
2.熵的定义式:- dS = dQ/T,其中dS 是熵的微元变化,dQ 是可逆过程中的微元热量,T 是热力学温度。
3.孤立系统熵增原理:- ΔSiso≥0,孤立系统的熵永不减少,对于可逆过程熵不变,对于不可逆过程熵增加。
四、理想气体状态方程及相关公式1.理想气体状态方程:- pV = nRT,其中p 是压力,V 是体积,n 是物质的量,R 是通用气体常数,T 是热力学温度。
2.比焓(h)、比内能(u)和比熵(s)的计算:-对于理想气体,比焓h = u + pv,其中u 是比内能,p 是压力,v 是比体积。
-比内能u = CvT,其中Cv 是定容比热,T 是热力学温度。
-比熵s = Cvln(T/T0) + Rln(v/v0),其中T0 和v0 是参考状态的温度和比体积,Cv 是定容比热,R 是通用气体常数。
五、卡诺循环相关公式1.卡诺循环热效率:- ηc = 1 - T2/T1,其中ηc 是卡诺循环热效率,T1 是高温热源温度,T2 是低温热源温度。
焓与熵的定义

焓与熵的定义引言焓和熵是热力学中两个重要的概念。
它们描述了物质在热力学过程中的性质和变化。
本文将对焓和熵的定义进行全面详细、完整且深入的阐述,以便更好地理解和应用这些概念。
焓的定义焓(enthalpy)是热力学中一个重要的状态函数,通常用符号H表示。
焓可以理解为系统的内能和对外界做功之间的关系。
焓的定义如下:H = U + PV其中,H表示焓,U表示系统的内能,P表示系统的压强,V表示系统的体积。
焓的单位通常是焦耳(J)或卡路里(cal)。
焓的定义可以通过对焓的微分形式进行推导得到:dH = dU + PdV + VdP根据热力学第一定律,系统的内能变化等于系统所吸收的热量与对外界做的功之和:dU = δQ - δW将上式代入焓的微分形式中,可以得到焓的微分形式表达式:dH = δQ - δW + PdV + VdP根据热力学第二定律,对于可逆过程,系统的熵变可以表示为:δQ = TdS将上式代入焓的微分形式中,可以得到焓的微分形式的另一种表达式:dH = TdS - δW + PdV + VdP通过以上推导,我们可以看出焓的定义与系统的内能、压强、体积和熵之间有着密切的关系。
熵的定义熵(entropy)是热力学中一个重要的状态函数,通常用符号S表示。
熵可以理解为系统的混乱程度或无序程度。
熵的定义如下:S = k ln W其中,S表示熵,k表示玻尔兹曼常数,W表示系统的微观状态数。
熵的单位通常是焦耳/开尔文(J/K)或卡路里/开尔文(cal/K)。
熵的定义可以通过对熵的微分形式进行推导得到:dS = δQ / T其中,dS表示熵的微分,δQ表示系统吸收的热量,T表示系统的温度。
根据热力学第二定律,对于可逆过程,可以得到:dS = dQ / T通过以上推导,我们可以看出熵的定义与系统吸收的热量和温度之间有着密切的关系。
焓与熵的关系焓和熵之间存在着一定的关系。
根据焓和熵的定义,可以得到焓和熵的关系式如下:dH = TdS + VdP上式表明,在恒温恒压条件下,焓的变化等于系统吸收的热量与温度的乘积,再加上系统的体积和压强的乘积。
名词解释比焓

名词解释比焓
比焓是描述系统热力学状态的物理量,表示在常压下单位质量的物质所具有的能量与其温度之间的关系。
比焓是由内能和流动能组成的,内能是物质微观粒子间相互作用所产生的能量,而流动能则是物质流动所携带的能量。
比焓的计算公式为H = U + PV,其中H表示比焓,U表示内能,P 表示压强,V表示体积。
比焓在热力学过程中起着重要的作用,它可以用来描述物质在温度变化或压强变化下的能量变化情况。
比焓的改变量可以通过测量温度和压强的变化来确定,从而可以了解系统在吸热或放热过程中的能量变化情况。
比焓的单位通常是焦耳/千克(J/kg)或卡/克(cal/g)。
在化学工程和能源工程等领域,比焓常用于计算物质的热平衡、传热、传质等过程,并在工程实践中具有重要的应用价值。
蒸汽的参数

蒸汽的参数全文共四篇示例,供读者参考第一篇示例:蒸汽是指水在受热后产生的气态水蒸气,它是一种无色、无味、无臭的气体。
在自然界中,蒸汽是一种极为常见的状态,我们可以在煮水时看到涌泉腾腾的蒸汽冒出,也可以在洗澡时感受到热气弥漫在浴室里。
蒸汽在工业生产、能源利用、环境保护等方面都具有重要的作用。
蒸汽有许多重要的参数,这些参数主要是用来描述和评估蒸汽的性质和性能的。
其中最重要的参数包括压力、温度、比容、热容和焓等。
下面我们就来逐一介绍这些参数:1. 压力:蒸汽的压力是指蒸汽对其容器或周围环境施加的压力。
蒸汽的压力通常以帕斯卡(Pa)或大气压(atm)为单位。
蒸汽的压力与其温度有直接的关系,在常压下,水的沸点温度为100摄氏度,所对应的是标准大气压(1atm)的蒸汽压力。
2. 温度:蒸汽的温度是指蒸汽的热量水平,通常以摄氏度(℃)或开尔文(K)为单位。
蒸汽的温度与其压力密切相关,随着温度的升高,蒸汽的压力也会增加,这是由于热量增加导致蒸汽分子速度增加而产生的结果。
3. 比容:蒸汽的比容是指单位质量的蒸汽所占的体积大小,通常以立方米/千克(m³/kg)为单位。
比容与密度的倒数成正比,即比容越大,密度越小。
蒸汽的比容随着温度和压力的变化而变化,一般情况下比容随温度升高而增大。
4. 热容:蒸汽的热容是指单位质量的蒸汽吸收或释放的热量,通常以焦尔/千克-开尔文(J/kg-K)为单位。
热容是描述物质温度变化时需要吸收或释放的热量大小的重要参数,它与物质本身的热性质有关。
5. 焓:蒸汽的焓是用来描述蒸汽的热力状态的参数,通常表示为单位质量的蒸汽所具有的内能和功的总和,以焦耳/千克(J/kg)为单位。
蒸汽的焓随着温度和压力的变化而变化,它能够反映蒸汽的热力特性和能量状况。
综上所述,蒸汽的压力、温度、比容、热容和焓是描述和评估蒸汽性质和性能的重要参数,它们之间具有密切的关系,并且随着蒸汽的物理状态和热力特性的变化而变化。
焓和熵的介绍

焓(enthalpy),符号H,是一个系统的热力学参数。
定义一个系统内: H = U + pV 式子中"H"为焓,U为系统内能,p为其压强,V则为体积。
焓不是能量,仅具有能量的量纲,它没有明确的物理意义。
焓有下述一些特性: 焓的绝对值无法求得,使用配分函数求出的焓值也不是绝对值。
焓是系统的容量性质,与系统内物质的数量成正比。
焓是一个状态函数,也就是说,系统的状态一定,焓是值就定了。
单位质量的物质所含有的热量叫作焓. "系统的状态一定,焓值也确定了。
" 焓是代表流动工质沿着流动方向往前方传递的总能量(内能、推动功、动能、势能)中,直接取决于热力状态的那部分能量。
举例:单位时间内锅炉主蒸汽的热焓-(锅炉给水的热焓+排污水的热焓)/单位时间内进炉煤的低位发热值,就是锅炉的效率啊。
引用焓的概念,可使热工计算大为简单,对借助于图解法来研究工质的热力过程更为方便。
熵的说明:热量是工质与外界存在温差时所传递的能量,则温度T是传热的推动力,只要工质与外界有微小的温差就能传热,于是相应地也应有某一状态参数的变化来标志有无传热,这个状态参数定名为熵。
根据熵的变化,可以判断工质在可逆过程中是吸热、放热,还是绝热。
熵的更重要的作用是用以恒量过程的不可逆程度。
如:蒸汽经过节流孔板,喷嘴等处可以理解为等熵绝热过程的。
焓是单位物质所含能量的多少!汽轮机中就是一个焓降的过程,焓降的过程就是对外做功的过程!实际上,哪怕效率非常高的机组,焓降也不会很高,我们为什么不能让焓降更大呢?这就引出了熵,霍金语:“熵是一种新的世界观” 熵的多少代表了我们利用这些能量所需要付出代价的多少。
焓降的过程伴随着熵增,当焓降到一定程度,熵会增到一定程度,也就说我们利用这些能所需要的代价越来越高,熵增到一定程度,需要付出的代价已经不划算利用这些能源了!熵是一种代价,它决定了我们不能靠能量守恒定律而尽情挥霍能源。
举例,同样参数的汽轮机,背压机组能发电20-30MW,凝气机组能发电100MW,因为我们建立了真空,付出了循环水的“代价”熵描述热力学系统的重要态函数之一。
关于焓和熵的概念

熵和焓的概念(2008-11-22 15:23:21)转载标签:杂谈解释 1、焓是物体的一个热力学能状态函数。
在介绍焓之前我们需要了解一下分子热运动、热力学能和热力学第一定律: 1827年,英国植物学家布朗把非常细小的花粉放在水面上并用显微镜观察,发现花粉在水面上不停地运动,且运动轨迹极不规则。
起初人们以为是外界影响,如振动或液体对流等,后经实验证明这种运动的的原因不在外界,而在液体内部。
原来花粉在水面运动是受到各个方向水分子的撞击引起的。
于是这种运动叫做布朗运动,布朗运动表明液体分子在不停地做无规则运动。
从实验中可以观察到,布朗运动随着温度的升高而愈加剧烈。
这表示分子的无规则运动跟温度有关系,温度越高,分子的无规则运动就越激烈。
正因为分子的无规则运动与温度有关系,所以通常把分子的这种运动叫做分子的热运动。
在热学中,分子、原子、离子做热运动时遵从相同的规律,所以统称为分子。
既然组成物体的分子不停地做无规则运动,那么,像一切运动着的物体一样,做热运动的分子也具有动能。
个别分子的运动现象(速度大小和方向)是偶然的,但从大量分子整体来看,在一定条件下,他们遵循着一定的统计规律,与热运动有关的宏观量——温度,就是大量分子热运动的统计平均值。
分子动能与温度有关,温度越高,分子的平均动能就越大,反之越小。
所以从分子动理论的角度看,温度是物体分子热运动的平均动能的标志(即微观含义,宏观:表示物体的冷热程度)。
分子间存在相互作用力,即化学上所说的分子间作用力(范德华力)。
分子间作用力是分子引力与分子斥力的合力,存在一距离r0使引力等于斥力,在这个位置上分子间作用力为零。
分子引力与分子斥力都随分子间距减小而增大,但是斥力的变化幅度相对较大,所以分子间距大于r0时表现为引力,小于r0时表现为斥力。
因为分子间存在相互作用力,所以分子间具有由它们相对位置决定的势能,叫做分子势能。
分子势能与弹簧弹性势能的变化相似。
物体的体积发生变化时,分子间距也发生变化,所以分子势能同物体的体积有关系。
焓和熵
p v T
工质的状态参数 与质量无关
锅炉热平衡计算 与工质质量有关
焓
系统
广延参数 与质量有关
p,v,T
1kg工质
在电站锅炉给水系统中,工质源源不 断的进入系统。对于1kg工质来说,进入 系统的能量除了这1kg工质本身的内能外, 还有这1kg工质从后面获得的推动功pv,因 此1kg工质进入系统的总能量为u+pv,我 们把u+pv定义为比焓即h=u+pv,等式两边 都乘以质量m即H=U+pV,H就是焓。考虑 到锅炉给水系统的连续运作,随工质转移 的能量等于焓,故在计算锅炉热平衡时更 广泛的使用焓H。
持续抽气 p外1’
持续抽气 p外2’
1’状态 p内1’
2’状态 p内2’ dx 活塞面积为A
活塞面积为A
p
1
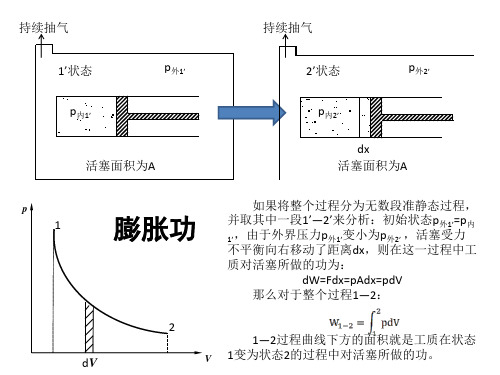
膨胀功
如果将整个过程分为无数段准静态过程, 并取其中一段1’—2’来分析:初始状态p外1’=p内 1’,由于外界压力p外1’变小为p外2’ ,活塞受力 不平衡向右移动了距离dx,则在这一过程中工 质对活塞所做的功为: dW=Fdx=pAdx=pd—2过程曲线下方的面积就是工质在状态 1变为状态2的过程中对活塞所做的功。
推动功
系统
活塞面积为A
系统 ∆x p,v,T
活塞面积为A
p,v,T
气缸是一个系统,工质从 系统外流入推动活塞做功
气缸是一个系统,工质从 系统外流入推动活塞做功
工质通过管道进入气缸时,设工质的状态为p,v,T,活塞面积为A,活塞 移动距离为∆x,那么工质对活塞所做的推动功为F ∆x=pA∆x=pV=mpv 推动功:1千克工质的推动功pv
熵
T
2
定义式:
ds
理想气体比热、内能、焓和熵分析

理想⽓体⽐热、内能、焓和熵分析理想⽓体的⽐热和热量为了计算在状态变化过程中的吸热量和放热量,我们引⼊了⽐热容的概念。
⼀、⽐热容的定义⽐热容与我们前⾯所讲过的⽐容、⽐内能、⽐焓、⽐功等参数类似,它是⼀个⽐参数,那么它的⼴延参数就是热容,所以在讲⽐热容之前我们先看⼀下热容。
1.热容热容指的是物体在⼀定的准静态过程中,温度升⾼或降低1K 时吸收或放出的热量,⽤符号C 表⽰。
根据热容的定义,我们可以得到:若⼯质在⼀定的准静态过程中,温度变化了△T ,过程中热量为Q ,那么这个过程中的⽐热为:Q C T=? ⽽物体的⽐热容是随温度变化的,并不是⼀个常数,我们上⾯的表⽰⽅法仅仅表⽰的是⼯质在这⼀过程中的平均⽐热容,若我们精确的表⽰⼯质在某⼀温度处的热容,则:QC dT δ=单位为J/K2.⽐热容⽤符号c 表⽰,⽐热容是热容的⽐参数。
⽐参数是⼴延参数与质量的⽐值。
所以⽐热容的定义为:1kg 物体在⼀定的准静态过程中温度升⾼或降低1K 时吸收或放出的热量。
C q c m dTδ== 单位:J/(kgK)这个⽐容⼜叫⽐质量热容,除了⽐质量热容外,热容还有两种⽐参数,分别是容积⽐热和摩尔⽐热。
容积⽐热⽤符号c ’表⽰,指的是1Nm 3⼯质在⼀定的准静态过程中温度升⾼或降低1K 时吸收或放出的热量。
单位为J/( Nm3K)。
摩尔⽐热⽤符号Mc 表⽰,指的是1mol ⼯质在⼀定的准静态过程中温度升⾼或降低1K 时吸收或放出的热量。
单位为J/( molK)。
三个⽐容之间的关系:'Mc M c Vm c =?=?⼆、理想⽓体的⽐热热量是过程参数,其数值的⼤⼩与所进⾏的热⼒过程有关,同样⽐热也是过程参数,也与⼯质所进⾏的热⼒过程有关,不同热⼒过程的⽐热值也是不相同的。
在我们⼯程热⼒学的研究范围中,最常⽤到的⽐热有两种:⼀个是定容过程的⽐热,⼀个是定压过程的⽐热。
定容过程:整个热⼒过程中⼯质的容积保持不变。
⽐如固定容器中的⽓体被加热。
关于焓和熵的概念

关于焓和熵的概念熵和焓的概念(2008-11-22 15:23:21)转载标签:杂谈解释1、焓是物体的一个热力学能状态函数。
在介绍焓之前我们需要了解一下分子热运动、热力学能和热力学第一定律:1827年,英国植物学家布朗把非常细小的花粉放在水面上并用显微镜观察,发现花粉在水面上不停地运动,且运动轨迹极不规则。
起初人们以为是外界影响,如振动或液体对流等,后经实验证明这种运动的的原因不在外界,而在液体内部。
原来花粉在水面运动是受到各个方向水分子的撞击引起的。
于是这种运动叫做布朗运动,布朗运动表明液体分子在不停地做无规则运动。
从实验中可以观察到,布朗运动随着温度的升高而愈加剧烈。
这表示分子的无规则运动跟温度有关系,温度越高,分子的无规则运动就越激烈。
正因为分子的无规则运动与温度有关系,所以通常把分子的这种运动叫做分子的热运动。
在热学中,分子、原子、离子做热运动时遵从相同的规律,所以统称为分子。
既然组成物体的分子不停地做无规则运动,那么,像一切运动着的物体一样,做热运动的分子也具有动能。
个别分子的运动现象(速度大小和方向)是偶然的,但从大量分子整体来看,在一定条件下,他们遵循着一定的统计规律,与热运动有关的宏观量——温度,就是大量分子热运动的统计平均值。
分子动能与温度有关,温度越高,分子的平均动能就越大,反之越小。
所以从分子动理论的角度看,温度是物体分子热运动的平均动能的标志(即微观含义,宏观:表示物体的冷热程度)。
分子间存在相互作用力,即化学上所说的分子间作用力(范德华力)。
分子间作用力是分子引力与分子斥力的合力,存在一距离r0使引力等于斥力,在这个位置上分子间作用力为零。
分子引力与分子斥力都随分子间距减小而增大,但是斥力的变化幅度相对较大,所以分子间距大于r0时表现为引力,小于r0时表现为斥力。
因为分子间存在相互作用力,所以分子间具有由它们相对位置决定的势能,叫做分子势能。
分子势能与弹簧弹性势能的变化相似。
理想气体比热、内能、焓和熵分析

理想气体的比热和热量为了计算在状态变化过程中的吸热量和放热量,我们引入了比热容的概念。
一、比热容的定义比热容与我们前面所讲过的比容、比内能、比焓、比功等参数类似,它是一个比参数,那么它的广延参数就是热容,所以在讲比热容之前我们先看一下热容。
1.热容热容指的是物体在一定的准静态过程中,温度升高或降低1K 时吸收或放出的热量,用符号C 表示。
根据热容的定义,我们可以得到:若工质在一定的准静态过程中,温度变化了△T ,过程中热量为Q ,那么这个过程中的比热为:Q C T=∆ 而物体的比热容是随温度变化的,并不是一个常数,我们上面的表示方法仅仅表示的是工质在这一过程中的平均比热容,若我们精确的表示工质在某一温度处的热容,则:QC dT δ=单位为J/K2.比热容用符号c 表示,比热容是热容的比参数。
比参数是广延参数与质量的比值。
所以比热容的定义为:1kg 物体在一定的准静态过程中温度升高或降低1K 时吸收或放出的热量。
C q c m dTδ== 单位:J/(kgK)这个比容又叫比质量热容,除了比质量热容外,热容还有两种比参数,分别是容积比热和摩尔比热。
容积比热用符号c ’表示,指的是1Nm 3工质在一定的准静态过程中温度升高或降低1K 时吸收或放出的热量。
单位为J/( Nm 3K)。
摩尔比热用符号Mc 表示,指的是1mol 工质在一定的准静态过程中温度升高或降低1K 时吸收或放出的热量。
单位为J/( molK)。
三个比容之间的关系:'Mc M c Vm c =⋅=⋅二、理想气体的比热热量是过程参数,其数值的大小与所进行的热力过程有关,同样比热也是过程参数,也与工质所进行的热力过程有关,不同热力过程的比热值也是不相同的。
在我们工程热力学的研究范围中,最常用到的比热有两种:一个是定容过程的比热,一个是定压过程的比热。
定容过程:整个热力过程中工质的容积保持不变。
比如固定容器中的气体被加热。
定压过程:整个热力过程中工质的压力保持不变。
熵与焓

熵shang释义1:物理学上指热能除以温度所得的商,标志热量转化为功的程度。
2: 科学技术上用来描述、表征体系混乱度的函数。
亦被社会科学用以借喻人类社会某些状态的程度。
3:熵是生物亲序,是行为携灵现象。
科学家已经发明了测量无序的量,它称作熵,熵也是混沌度,是内部无序结构的总量。
英译entropy熵指的是体系的混乱的程度,它在控制论、概率论、数论、天体物理、生命科学等领域都有重要应用,在不同的学科中也有引申出的更为具体的定义,是各领域十分重要的参量。
熵由鲁道夫·克劳修斯(Rudolf Clausius)提出,并应用在热力学中。
后来克劳德·艾尔伍德·香农(Claude Elwood Shannon)第一次将熵的概念引入到信息论中来。
历史1850年,德国物理学家鲁道夫·克劳修斯首次提出熵的概念,用来表示任何一种能量在空间中分布的均匀程度,能量分布得越均匀,熵就越大。
一个体系的能量完全均匀分布时,这个系统的熵就达到最大值。
在克劳修斯看来,在一个系统中,如果听任它自然发展,那么,能量差总是倾向于消除的。
让一个热物体同一个冷物体相接触,热就会以下面所说的方式流动:热物体将冷却,冷物体将变热,直到两个物体达到相同的温度为止。
克劳修斯在研究卡诺热机时,根据卡诺定理得出了对任意循环过程都都适用的一个公式:dS=(dQ/T)。
对于绝热过程Q=0,故S≥0,即系统的熵在可逆绝热过程中不变,在不可逆绝热过程中单调增大。
这就是熵增加原理。
由于孤立系统内部的一切变化与外界无关,必然是绝热过程,所以熵增加原理也可表为:一个孤立系统的熵永远不会减少。
它表明随着孤立系统由非平衡态趋于平衡态,其熵单调增大,当系统达到平衡态时,熵达到最大值。
熵的变化和最大值确定了孤立系统过程进行的方向和限度,熵增加原理就是热力学第二定律。
1948年,香农在Bell System Technical Journal上发表了《通信的数学原理》(A Mathematical Theory of Communication)一文,将熵的概念引入信息论中。
理想气体的内能、焓、比热容、熵

pV=nRT
n
V Vi i1
亚美格定律—理想气体混合物的容积等于各组成气体分容积之和
(amagat 's law)
对某一组成气体i,按分压力及分容积分别列出 其状态方程式,则有:
piVniRT pVi niRT
对比二式,有: p i V i pV
即组成气体的分压力与混合物压力之比,等于组 成气体的分容积与混合物容积之比。
dv v
dsdhTvdpcp0dTTvdpcp0dTTRg
dp p
dscv0dTTRg
dvvcv0dppdvvRg
dvvcv0dppcp0
dv
v
s
cv0
ln
T2 T1
Rg
ln
v2 v1
s
c
p0
ln
T2 T1
R g ln
p2 p1
s
c v 0 ln
p2 p1
c p 0 ln
v2 v1
T
M m m 1 m 2 m n n 1 M 1 n 2 M 2 n iM n
nn
n
又得: M y 1 M 1 y 2 M 2 y n M n
n
M yi Mi
i1
混合物的折合气体常数为:
R Rg M
R R gi M i
即得:R g R ( y 1 M 1 y 2 M 2 y n M n )
对定容过程dv=0
q v T u v dT
c v d q v T T u v
同样用 qdhvdp可得定压过程dp=0:
qp
h T
dT p
cp
qp
dT
h Tp
3
理想气体内能变化(Δu)的计算: 按定容过程(constant volume process):
焓和熵的介绍

焓(enthalpy),符号H,是一个系统的热力学参数。
定义一个系统内: H = U + pV 式子中"H"为焓,U为系统内能,p为其压强,V则为体积。
焓不是能量,仅具有能量的量纲,它没有明确的物理意义。
焓有下述一些特性: 焓的绝对值无法求得,使用配分函数求出的焓值也不是绝对值。
焓是系统的容量性质,与系统内物质的数量成正比。
焓是一个状态函数,也就是说,系统的状态一定,焓是值就定了。
单位质量的物质所含有的热量叫作焓. "系统的状态一定,焓值也确定了。
" 焓是代表流动工质沿着流动方向往前方传递的总能量(内能、推动功、动能、势能)中,直接取决于热力状态的那部分能量。
举例:单位时间内锅炉主蒸汽的热焓-(锅炉给水的热焓+排污水的热焓)/单位时间内进炉煤的低位发热值,就是锅炉的效率啊。
引用焓的概念,可使热工计算大为简单,对借助于图解法来研究工质的热力过程更为方便。
熵的说明:热量是工质与外界存在温差时所传递的能量,则温度T是传热的推动力,只要工质与外界有微小的温差就能传热,于是相应地也应有某一状态参数的变化来标志有无传热,这个状态参数定名为熵。
根据熵的变化,可以判断工质在可逆过程中是吸热、放热,还是绝热。
熵的更重要的作用是用以恒量过程的不可逆程度。
如:蒸汽经过节流孔板,喷嘴等处可以理解为等熵绝热过程的。
焓是单位物质所含能量的多少!汽轮机中就是一个焓降的过程,焓降的过程就是对外做功的过程!实际上,哪怕效率非常高的机组,焓降也不会很高,我们为什么不能让焓降更大呢?这就引出了熵,霍金语:“熵是一种新的世界观” 熵的多少代表了我们利用这些能量所需要付出代价的多少。
焓降的过程伴随着熵增,当焓降到一定程度,熵会增到一定程度,也就说我们利用这些能所需要的代价越来越高,熵增到一定程度,需要付出的代价已经不划算利用这些能源了!熵是一种代价,它决定了我们不能靠能量守恒定律而尽情挥霍能源。
举例,同样参数的汽轮机,背压机组能发电20-30MW,凝气机组能发电100MW,因为我们建立了真空,付出了循环水的“代价”熵描述热力学系统的重要态函数之一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【热寂论的敌论--"热环论"】
恩格斯曾多次指出:"放射到太空中去的热一定有可能通过某种途径转变为另一种运动形式,在这种运动形式中,它能够重新集结和活动起来"。我们通过长期对熵理论的研究,提出了"热环论"(又可称"热动论"),完成了恩格斯的遗愿。
可压缩流体的静力学方程,即势焓(势能+焓)平衡规律(另文)指出,在引力场中,相同质量的流质其拥有的势焓值均为同一常数,这就意味着当流质势能大时其焓值小(温度低),相反,当势能小时其焓值大(温度高),如果星体中心的势焓值比外围低时,引力将迫使外围低温区热量向中心高温区传导转移,以趋于势焓平衡。又根据热辐射定律可知,热辐射仅由温度决定,不受引力影响(另文证明)。上述两类因素是热循环的动力,即热量在引力的帮助下从低温3k传导至高温亿万 k(太空中或星体内部都存在着温度梯度这个客观事实),再以辐射的方式逸散到太空中去,就这样循环往复以至无穷,这就"热环论"描述的现象。以白矮星为例,白矮星内部无热源为何能发光呢?,原来星体引力能从太空云集低温热能。任何星体与太空间都存在着相反的热循环转移过程,即使是具有内部热源的星体也叠加着上述热循环过程,这是宇宙生机勃勃、永不死寂的真谛!
焓不是能量,仅具有能量的量纲,它没有明确的物理意义,同熵一样,用H表示
热力学能(U):一个系统内能量的总和(分子的平均动能,转动能,振动能,分子间势能,原子间键能,电子运动能,核内离子间核能等)。
把所研究的一个反应过程的所有参与因素看作一个系统,这个系统在反应前有一个上述的热力学能U1,反应后变为U2。
【分熵的特点】
熵概念源于卡诺热机循环效率的研究,是以热温商的形式而问世的,当计算某体系发生状态变化所引起的熵变总离不开两点,一是可逆过程;二是热量的得失,故总熵概念摆脱不了热温商这个原始外衣。当用状态数来认识熵的本质时,我们通过研究发现,理想气体体系的总微观状态数受宏观的体积、温度参数的控制,进而得到体系的总熵等于体积熵与温度熵之和(见有关文章),用分熵概念考察体系的熵变化,不必设计什么可逆路径,概念直观、计算方便(已被部分专家认可),因而有利于教和学。
1.地球内部的放射性元素蜕变放热,即原子能;
2.地球在形成初期带来的热量。我们对上述解释的看法是,如果是第一种,有三种情况:
①地热温度呈外低内高按一定梯度的分布,那热源必在地心,这不就是原子弹吗?后果不堪设想;
②矿物分布通常遵循"物以类聚"的原则,如果地球内部的放射性元素分布(热源)与地热分布一致?显然这不合
“焓”具体是多少。
焓变>0 系统经历了吸热反应。
焓变<0 系统经历了放热反应。
可逆过程的熵增等于该过程吸收的热量于温度的比值;焓的定义是该工质的内能与推动功的总和。焓可以在某种程度上表征工质做功能力。而熵微观上表征物质内部分子混乱程度。熵增分为熵流和熵产。熵流表示由于与系统与外界传热引起的熵增,熵产表示不可逆产生的熵增。熵和焓在工程上应用都极为广泛。熵主要涉及的是热二律,焓则多为热一律。两者都是状态量。
【电冰箱不能实现熵的减少】
克劳修斯把熵增原理表述为:"热量不能自动地从低温物体传向高温物体",这给人们一个错觉,外界做功使热量从低温物体传到高温物体,或者说使等温体变成不等温体,就意味着发生熵减。这种认识是偏面的,以绝热房间内放一工作的电冰箱为例,冰箱内温度变低,冰箱外的房间内温度变高,许多人把这外界做功而拉开温差的现象叫做熵减,并解释将发电厂一并考虑在内,总体上仍是熵增。这种看法是错误的,仅就室内的冰箱内外来说,如果考虑了电流的热效应,这个室内的总熵变化只增不减(不信可计算一下)。外界做功不能使绝热系统内的熵减少,不论是电能、机械能等非热能做功(通常不能避免热效应)都不能使绝热系统内的熵减少,所以说,我们认为熵增原理准确的表述应为:"在等势面上,绝热系统内的熵永不减少"。
【熵减应分为绝对熵减和相对熵减两类】
人们过去认识的熵减,其机理是流出系统的熵流大于系统内的熵产生(对开放系统),习惯上称流入系统的负熵流大于系统内熵产生,从系统内外一并考察总熵变化仍大于零,服从熵增原理,换句话说,此处熵减是以彼处熵增为代价的,故这类熵减应叫相对熵减。而引力在引力方向能拉开温差,把低温区的热量自动地转移到高温区,经计算表明这是熵减!这并不伴随引力的削弱(引力是物质的固有的性质),也不以任何地方或形式的熵增为代价,所以说这种熵减是绝对熵减,是不服从熵增原理的。
构造一种情况使得反应前后(甚至反应的过程中)系统的压强保持不变。反应前后系统的体积会有一个变化量。反应前后系统的能量变化中有一部分用来做功改变系统体积。这部分能量值为系统的压强乘以体积变化量(可正可负可零)=[P*(V2-V1)]
定义系统有一个 “焓变” = (U2-U1)+ P*(V2-V1)
【熵计算公式介绍】
1、克劳修斯首次从宏观角度提出熵概念,其计算公式为:S=Q/T ,(计算熵差时,式中应为△Q)
2、波尔兹曼又从微观角度提出熵概念,公式为:S=klnΩ,Ω是微观状态数,通常又把S当着描述混乱成度的量。
3、笔者针对Ω不易理解、使用不便的现状,研究认为Ω与理想气体体系的宏观参量成正比,即:Ω(T)=(T/εT)3/2 , Ω(V)=V/εV,得到理想气体的体积熵为SV=klnΩv=klnV,温度熵为ST=klnΩT=(3/2)klnT ,计算任意过程的熵差公式为△S=(3/2)kln(T'/T)+kln(V'/V),这微观与宏观关系式及分熵公式,具有易于理解、使用方便的特点,有利于教和学,可称为第三代熵公式。
ds=δq/T
即在微元可逆过程中工质比熵的增加等于单位质量工质所吸收的热量除以工质的热力学温度所得的商。比熵s同比体积v一样是工质的状态参数。
比焓定义类似;
熵是随机热运动状态的几率大小的量度,也就是热运动的混乱程度或无序度,一般都是看它的改变量,用S表示
工程热力学中规定:系统吸收热量的值为正,系统放出热量的值为负。
在可逆过程中,系统与外界交换的热量的计算公式与功的计算公式具有相同的形式。对于微元可逆过程,单位质量工质与外界交换的热量可以表示为
δq=Tds
式中,s称为比熵,单位为J/ (kg·K) 或 kJ/ (kg·K)。比熵的定义为
【熵与宇宙模型】
目前流行的大爆炸理论仍然是崇尚热寂的,只不过换个说法而已,该理论认为:对于一个静态的体系(或宇宙中的局部空间)熵仍趋于最大值,但膨胀的(看着气体膨胀)宇宙会拉大温差,宇宙根本不能达到平衡态,所以宇宙不会出现热寂。举个通俗的例子,一池塘清水,有污水不断向池里流入,水质面临恶化,如果外界又不断地向池中加入清水,且加入清水的量远多于污水,毫无疑问这池水永远是清水(设池塘容积可增加)。熵增原理是在忽略引力作用时得到的规律,而在研究宇宙熵变时引力就不能忽视,所以笔者认为大爆炸理论对熵的解释是错误的,不论宇宙是膨胀、收缩或静态,宇宙都不会进入热寂,因为星体引力具有减熵的能力,而高温星体向太空辐射光和热,这是熵增过程,这两种相反的热流将永恒的对峙着,实现熵和热的大环流,所以说,即使是有限的宇空也永远不会出现热寂。仍用上述例子,一池塘清水,有污水不断向池里流入,但池塘有自净功能,有能力处理流入的污中,所以水质不会恶化。
熵现在不仅是一个热力学概念,而且它的研究领域已经设计到哲学、生命学、信息学等领域用来解释一些现象。。。。
【地热特点及来源】
地下热能储量巨大,相当于全球煤炭储量的1.7亿倍。有人估算,以当今全世界耗能总量计算,即使全部使用地热能,4100万年后才能使地球内部的温度下降 1℃。地热的特点呈内高外低分布,我们认为(另有论文)它遵循"可压缩流体的静力学方程",即势焓(势能+焓)平衡规律,当地内势焓低于地表势焓时,重力具有云集地表低温热能向地心转移的机制,地热是永恒存在的能源。关于地热来源问题,目前人们尚无准确定论,主要有两种解释:
【熵减和永动机的关系】
许多人都认为发现了熵减就等于说能制造出第二类永动机,这种看法是一种误解,解释如下:在宇宙中只有星体引力能导致熵减,当星体外部势焓大于内部势焓时, 星体具有向引力中心云集热量的功能,实现了热量自动地从低温区转移到高温区,对于温度比较高的星体,又以辐射的形式向外释放能量,故星体具有永动机的性质,但星体不能人工制造,更无法利用这一原理造出一台机器,从单一热源(大气或水中)吸热获得机械能,所以说存在熵减并不能制造出永动机。假设人工能造出第二类永动机,那一定是熵减过程,熵减和永动机就是这种特殊的关系。
熵定律是科学定律之最,这是爱因斯坦的观点。我们知道能源与材料、信息一样,是物质世界的三个基本要素之一,而在物理定律中,能量守恒定律是最重要的定律,它表明了各种形式的能量在相互转换时,总是不生不灭保持平衡的。在等势面上,熵增原理反映了非热能与热能之间的转换具有方向性,即非热能转变为热能效率可以100%,而热能转变成非热能时效率则小于100%(转换效率与温差成正比),这种规律制约着自然界能源的演变方向,对人类生产、生活影响巨大;在重力场中,热流方向由体系的势焓(势能+焓)差决定,即热量自动地从高势焓区传导至低势焓区,当出现高势焓区低温和低势焓区高温时,热量自动地从低温区传导至高温区,且不需付出其它代价,即绝对熵减过程。显然熵所描述的能量转化规律比能量守恒定律更重要,通俗地讲:熵定律是"老板",决定着企业的发展方向,而能量守恒定律是"出纳",负责收支平衡,所以说熵定律是自然界的最高定律。
上述三代熵公式,使用的物理量从形式上看具有"直观→抽象→直观"的特点,我们认为这不是概念游戏,是对熵概念认识的一次飞跃。
【熵流是什么】
熵流是普里戈津在研究热力学开放系统时首次提出的概念(普里戈津是比利时科学家,因对热力学理论有所发展,获得1977年诺贝尔化学奖),普氏的熵流概念是指系统与外界交换的物质流及能量流。我们认为这个定义不太精辟,这应从熵的本质来认识它,不错物质流一定是熵的载体,而能量流则不一定,能量可分热能和非热能〔如电能、机械能、光能(不是热辐射)〕,当某绝热系统与外界交换非热能(发生可逆变化)时,如通电导线(超导材料)经过绝热系统内,对体系内熵没有影响,准确地说能量流中只有热能流(含热辐射)能引人熵流(对非绝热系统)。对于实际情形,非热能作用于系统发生的多是不可逆过程,会有热效应产生,这时系统出现熵增加,这只能叫(有原因的)熵产生,而不能叫熵流的流入,因能量流不等于熵流,所以不论什么形式的非热能流都不能叫熵流,更不能笼统地把能量流称为熵流。
