矩形、菱形练习题
矩形菱形练习题

矩形一、性质1、下列性质中,矩形具有而平行四边形不一定具有的是( )A 、对边相等B 、对角相等C 、对角线相等D 、对边平行 2.在矩形ABCD 中,∠AOD=130°,则∠ACB=__ _3.已知矩形的一条对角线长是8cm ,两条对角线的一个交角为60°,则矩形的周长为______4. 矩形的一内角平分线把矩形的一条边分成3和5两部分,则该矩形的周长是___________.5.形的两条对角线的夹角是60°,一条对角线与矩形短边的和为15,那么矩形对角线的长为_______,短边长为_______.6矩形ABCD 被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm , 对角线是13cm ,那么矩形的周长是____________7在矩形ABCD 中, 对角线交于O 点,AB=0.6, BC=0.8, 那么△AOB 的面积为_________; 周长为_________.8一个矩形周长是12cm, 对角线长是5cm, 那么它的面积为_______________9在△ABC 中, AM 是中线, ∠BAC=90︒, AB=6cm, AC=8cm, 那么AM 的长为____________. 10角三角形斜边上的高与中线分别是5cm 和6cm ,则它的面积为___11.,在Rt △ABC 中,BD 为斜边AC 上的中线,若∠A=35°,那么∠DBC= 。
12图所示,矩形ABCD 中,AE ⊥BD 于E ,∠BAE=30°,BE=1cm ,那么DE 的长为_____13图,矩形ABCD 中,AC 与BD 交于O 点,BE ⊥AC 于E ,CF ⊥BD 于F. 求证:BE=CF.14图,△ABC 中,∠ACB=900,点D 、E 分别为AC 、AB 的中点,点F 在BC 延长线上,且∠CDF=∠A ,求证:四边形DECF 是平行四边形;15知:如图,在△ABC 中,∠BAC ≠90° ∠ABC=2∠C ,AD ⊥AC ,交BC 或CB 的延长线D 。
初三矩形菱形经典练习题

矩形的性质与判定1.(1)矩形的定义中有两个条件:一是 ,二是 .(2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .2.下列说法错误的是( ). A 、矩形的对角线互相平分B 、矩形的对角线相等 C 、有一个角是直角的四边形是矩形 D 、有一个角是直角的平行四边形叫做矩形 3.矩形的对角线把矩形分成的三角形中全等三角形一共有( ). A 、2对 B 、4对 C 、6对 D 、8对4.已知矩形的一条对角线长为10cm ,两条对角线的一个交角为120°,则矩形的边长分别为______cm , cm , cm , cm .5、已知:如图 ,矩形 ABCD 中,AB 长8 cm ,对角线比AD 边长4 cm .求AD 的长及点A 到BD 的距离AE 的长.6、 下列各句判定矩形的说法是否正确?为什么?(1)有一个角是直角的四边形是矩形; ( ) (2)有四个角是直角的四边形是矩形; ( ) (3)四个角都相等的四边形是矩形; ( ) (4)对角线相等的四边形是矩形; ( ) (5)对角线相等且互相垂直的四边形是矩形; ( ) (6)对角线互相平分且相等的四边形是矩形; ( ) (7)对角线相等,且有一个角是直角的四边形是矩形; ( ) (8)一组邻边垂直,一组对边平行且相等的四边形是矩形;( ) (9)两组对边分别平行,且对角线相等的四边形是矩形. ( ) 7.工人师傅做铝合金窗框分下面三个步骤进行:⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB =CD ,EF =GH ; ⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ;⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,根据的数学道理是: ;8.矩形的两条对角线的夹角为60°,对角线长为15cm ,较短边的长为( ).(A)12cm (B)10cm (C)7.5cm (D)5cm9、如图,矩形ABCD 中,AC 与BD 交于O 点,BE AC ⊥于E ,CF BD ⊥于F 。
4.3~4.4矩形,菱形的性质及判定练习

4.3~4.4矩形,菱形的性质及判定练习1.菱形、矩形的有关概念矩形:有一个角是直角的平行四边形叫做矩形.菱形:有一组邻边相等的平行四边形叫做菱形.温馨提醒:(1)矩形、菱形具有平行四边形的一切性质;(2)依据矩形的性质,得出直角三角形具有的性质斜边上的中线等于斜边的一半;(3)矩形、菱形既是轴对称图形又是中心对称图形;3.菱形、矩形的判定矩形的判定方法:①有一个角是直角的平行四边形是矩形.②有三个角是直角的四边形是矩形.③对角线相等的平行四边形是矩形.菱形的判定方法:①有一组邻边相等的平行四边形是菱形;②四条边都相等的四边形是菱形;③对角线互相垂直的平行四边形是菱形;温馨提示:(1)矩形的对角线是矩形比较常用的性质,当对角线的夹角中,有一个角为60度时,则构成一个等边三角形;在判定矩形时,要注意利用定义或对角线来判定时,必须先证明此四边形为平行四边形,然后再找一个角为直角或对角线相等。
很多同学容易忽视这个问题。
(2)在利用菱形的判定时,也要注意所要证明的四边形是不是平行四边形,而你用的判定定理需不需要证明它是平行四边形,有对角线时,通常考虑利用对角线互相垂直的平行四边形是菱形来证明,否则一般不利用此定理。
(3)两条对角线相等的四边形不一定是矩形,必须加上平行四边形这个条件;对角线相互垂直的四边形不一定是菱形,必须加上平行四边形这个条件。
5.面积、角度、线段等计算问题S 菱形=12l l ·l 2(l 1、l 2为菱形对角线长) 连对角线,矩形、菱形就可得到特殊三角形(如等腰三角形、直角三角形),因此,解矩形、菱形问题时,要注意特殊三角形性质的运用。
利用全等三角形解决问题。
跟踪训练:一、填空题:1.矩形的定义:____________________________的平行四边形叫做矩形。
2.矩形的性质:矩形是一个特殊的平行四边形,它具有四边形和平行四边形的所有性质;矩形的四个角______________; 矩形的对角线______________; 矩形是轴对称图形,它的对称轴是______________。
矩形菱形正方形练习题和答案

一、性质1、下列性中.矩形具有而质平行四边形不一定具有的是()A 、对边相等B 、对角相等C 、对角线相等D 、对边平行2 .在矩形ABCD 中.NAOD=130°.则NACB=__3 .已知矩形的一条对角线长是8cm.两条对角线的一个交角为60°.则矩形的周长为4 .矩形ABCD 被两条对角线分成四个小三角形.如果四个小三角形的周长的和是86cm.对角线是13cm.那么矩形的周长是5 .如图所示.矩形ABCD 中.AE ,BD 于E.Nk BAE=30°.BE=1cm.那么DE 的长为 6、直角三角形斜边上的高与中线分别是5cm 和6cm.则它的面积为7、已知.在Rt△ABC 中出口为斜边AC 上的中线.若NA=35°.那么NDBC 二。
8、如图.矩形ABCD 中.AC 与8口交于。
点.BELAC 于E.CFLBD 于F.求证:BE=CF. 9 .如口图.△ABC 中.NACB=90度.点D 、E 分别为AC 、AB 矩形的习题精选AB的中点.点F在BC延长线上.且/CDF=NA.求证:四边形DECF是平行四边形;10.已知:如图.在aABC中.NBACW90°NABC=2NC.AD±AC.交BC或CB的延长线D。
试说明:DC=2AB.11、在4ABC中.NC=90O.AC=BC.AD=BD.PE^AC于点E.PFLBC于点F。
求证:DE=DF二、判定1、下列检查一个门框是否为矩形的方法中正确的是(C)A.测量两条对角线.是否相等B.测量两条对角线.是否互相平分他用曲尺测量门框的三个角.是否都是直角口.用曲尺测量对角线.是否互相垂直2、平行四边形ABCD.E是CD的中点.4人8£是等边三角形.求证:四边形ABCD是矩形3、在平行四边形ABCD中.对角线AC、BD相交于O.EF过点O.且AF,BC. 求证:四边形AFCE是矩形4、平行四边形ABCD中.对角线AC、8口相交于点。
矩形菱形练习题及答案

矩形 【2 】.菱形常识考点:懂得并控制矩形的剖断与性质,并能应用所学常识解决有关问题. 精典例题:【例1】如图,已知矩形ABCD 中,对角线AC.BD 订交于点O,AE ⊥BD,垂足为E,∠DAE ∶∠BAE =3∶1,求∠EAC 的度数.剖析:本题充分应用矩形对角线把矩形分成四个等腰三角形的根本图形进行求解. 解略,答案450.例1图E ODC BA例2图FE DCB A例3图【例2】如图,已知菱形ABCD 的边长为3,延伸AB 到点E,使BE =2AB,贯穿连接EC 并延伸交AD 的延伸线于点F,求AF 的长.剖析:本题应用菱形的性质,联合平行线分线段成比例的性质定理,可使问题得解. 解略,答案AF =4.5.【例3】如图,在矩形ABCD 中,M 是BC 上的一动点,DE ⊥AM,垂足为E,3AB =2BC,并且AB.BC 的长是方程02)2(2=+--k x k x 的两根.(1)求k 的值;(2)当点M 分开点B 若干时,△ADE 的面积是△DEM 面积的3倍?请解释来由. 剖析:用韦达定理树立线段AB.AC 与一元二次方程系数的关系,求出k . 略解:(1)由韦达定理可得AB +BC =2-k ,AB ·BC =k 2,又由BC =23AB 可消去AB,得出一个关于k 的一元二次方程0123732=+-k k ,解得1k =12,2k =31,因AB +BC =2-k >0,∴k >2,故2k =31应舍去. (2)当k =12时,AB +BC =10,AB ·BC =k 2=24,因为AB <BC,所以AB =4,BC =6,由DEM AED S S ∆∆=3可得AE =3EM =43AM.易证△AED ∽△MBA 得MB AE =AMAD ,设AE =a 3,AM =a 4,则MB =22a ,而AB 2+BM 2=AM 2,故2421644a a =+,解得2a =2,MB =22a =4.即当MB =4时,DEM AED S S ∆∆=3.评注:本题将几何问题从“形”向“数”转化,这类分解题既有几何证实中的剖析和推理,又有代数式的灵巧变换.盘算,其解题进程层次较多,步骤较庞杂,书写进程也要增强练习.摸索与创新:【问题一】如图,四边形ABCD 中,AB =6,BC =35-,CD =6,且∠ABC =1350,∠BCD =1200,你知道AD 的长吗?剖析:这个四边形是一个不规矩四边形,应将它补割为规矩四边形才便于求解. 略解:作AE ⊥CB 的延伸线于E,DF ⊥BC 的延伸线于F,再作AG ⊥DF 于G ∵∠ABC =1350,∴∠ABE =450 ∴△ABE 是等腰直角三角形又∵AB =6,∴AE =BE =3 ∵∠BCD =1200,∴∠FCD =600 ∴△DCF 是含300的直角三角形 ∵CD =6,CF =3,DF =33 ∴EF =3)35(3+-+=8 由作图知四边形AGFE 是矩形 ∴AG =EF =8,FG =AE =3从而DG =DF -FG =32 在△ADG 中,∠AGD =900∴AD =22DG AG +=1264+=76=192【问题二】把矩形ABCD 沿BD 折叠至如上图所示的情况,请你猜想四边形ABDE 是什问题一图GD问题二图么图形,并证实你的猜想.剖析与结论:本题依据题设并联合图形猜想该四边形是等腰梯形,应用对称及全等三角形的有关常识易证.跟踪练习:一.填空题:1.若矩形的对称中间到双方的距离差为4,周长为56,则这个矩形的面积为.2.已知菱形的锐角是600,边长是20cm,则较短的对角线长是cm.3.如图,矩形ABCD 中,O 是对角线的交点,若AE ⊥BD 于E,且OE ∶OD =1∶2,AE =3cm,则DE =cm.4.如图,P 是矩形ABCD 内一点,PA =3,PD =4,PC =5,则PB =.5.如图,在菱形ABCD 中,∠B =∠EAF =600,∠BAE =200,则∠CEF =.第3题图E O DC BA第4题图543P D CBA 第5题图FEBA二.选择题:6.在矩形ABCD 的各边AB.BC.CD.DA 上分离取点E.F.G.H,使EFGH 为矩形,则如许的矩形( )A.仅能作一个B.可以作四个C.一般情况下不可作D.可以作无限多个7.如图,在矩形ABCD 中,AB =4cm,AD =12cm,P 点在AD 边上以每秒1 cm 的速度从A 向D 活动,点Q 在BC 边上,以每秒4 cm 的速度从C 点动身,在CB 间往返活动,二点同时动身,待P 点到达D 点为止,在这段时光内,线段PQ 有( )次平行于AB. A.1 B.2 C.3 D.4••第7题图QPDCB第8题图GFE DCBA8.如图,已知矩形纸片ABCD 中,AD =9cm,AB =3cm,将其折叠,使点D 与点B 重合,那么折叠后DE 的长和折痕EF 的长分离是( ) A.4cm.10cm B.5cm.10cmC.4cm.32cmD.5cm.32cm9.给出下面四个命题:①对角线相等的四边形是矩形;②对角线互相垂直的四边形是菱形;③有一个角是直角且对角线互相等分的四边形是矩形;④菱形的对角线的平方和等于边长平方的4倍.个中准确的命题有( ) A.①②B.③④C.③D.①②③④10.平行四边形四个内角的等分线,假如能围成一个四边形,那么这个四边形必定是( ) A.矩形 B.菱形 C.正方形 D.等腰梯形 三.解答题:11.如图,在矩形ABCD 中,F 是BC 边上一点,AF 的延伸线交DC 的延伸线于点G,DE ⊥AG 于E,且DE =DC,依据上述前提,请在图中找出一对全等三角形,并证实你的结论.第11题图GFEDCBA第12题图 EBA第13题图C12.如图,在△ABC 中,∠ACB =900,CD 是AB 边上的高,∠BAC 的等分线AE 交CD 于F,EG ⊥AB 于G,求证:四边形GECF 是菱形.13.如图,以△ABC的三边为边在BC的统一侧分离作三个等边三角形,即△ABD.△BCE.△ACF.请答复下列问题(不请求证实):(1)四边形ADEF是什么四边形?(2)当△ABC知足什么前提时,四边形ADEF是矩形?(3)当△ABC知足什么前提时,以A.D.E.F为极点的四边形不消失?跟踪练习参考答案一.填空题:3;5.2001.180;2.20cm;3.3;4.2提醒:4题过点P作矩形任一边的垂线,应用勾股定理求解;5题贯穿连接AC,证△ABE≌△ACF得AE=AF,从而△AEF是等边三角形.二.DDBBA三.解答题:11.可证△DEA≌△ABF12.略证:AE等分∠BAC,且EG⊥AB,EC⊥AC,故EG=EC,易得∠AEC=∠CEF,∵CF =EC,EG=CF,又因EG⊥AB,CD⊥AB,故EG∥CF.四边形GECF是平行四边形,又因EG=FG,故GECF是菱形.13.(1)平行四边形;(2)∠BAC=1500;(3)当∠BAC=600时,以A.D.E.F为极点的四边形不消失.。
九年级中考临考专题训练:矩形、菱形(含答案)

2021中考临考专题训练:矩形、菱形一、选择题1. 下列说法,正确的个数有 ()①正方形既是菱形又是矩形;②有两个角是直角的四边形是矩形;③菱形的对角线相等;④对角线互相垂直平分且相等的四边形是正方形.A.1个B.2个C.3个D.4个2. 已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为()A.2B.2C.4D.23. (2020·四川甘孜州)如图,菱形ABCD中,对角线AC,BD相交于点O,E 为AB的中点.若菱形ABCD的周长为32,则OE的长为( )A.3 B.4 C.5 D.64. 如图所示,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象的大致形状是()5. (2020·黄冈)若菱形的周长为16,高为2,则菱形两邻角的度数之比为()A.4∶1 B.5∶1 C.6∶1 D.7∶16. (2020·广州)如图5,矩形ABCD的对角线AC、BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为( )C DFE OBA图5 A .485 B .325 C .245 D .1257. (2020·泰安)如图,矩形ABCD 中,AC ,BD 相交于点O ,过点B 作BF ⊥AC 交CD 于点F ,交AC 于点M ,过点D 作DE ∥BF 交AB 于点E ,交AC 于点N ,连接FN ,EM .则下列结论:① DN ﹦BM ;②EM ∥FN ;③AE ﹦FC ;④当AO ﹦AD 时,四边形DEBF 是菱形.其中,正确结论的个数是( ) A .1个 B .2个 C . 3个 D .4个AB CDEFOMN 8. (2020·达州)如图,∠BOD =45°,BO=DO ,点A 在OB 上,四边形ABCD 是矩形,连接AC 、BD 交于点E ,连接OE 交AD 于点F .下列4个判断:①OE 平分∠BOD ;②OF=BD ;③DF=AF ;④若点G 是线段OF 的中点,则△AEG 为等腰直角三角形.正确判断的个数是( ) A.4 B.3 C.2 D.1二、填空题9. 如图,矩形ABCD 的对角线AC 与BD 相交于点O ,∠ADB=30°,AB=4,则OC= .10. 如图,矩形ABCD 中,AC ,BD 交于点O ,M ,N 分别为BC ,OC 的中点.若DCA B F EOMN=4,则AC的长为.11. 如图,菱形ABCD的边长为10 cm,DE⊥AB,sin A=,则这个菱形的面积= cm2.12. 如图,矩形ABCD的面积是15,边AB的长比AD的长大2,则AD的长是________.13. 如图,在菱形ABCD中,E、F分别是AD、BD的中点,若EF=2,则菱形ABCD的周长为________.14. (2020·四川甘孜州)如图,有一张长方形纸片ABCD,AB=8cm,BC=10cm,点E为CD上一点,将纸片沿AE折叠,BC的对应边B'C'恰好经过点D,则线段DE的长为__________cm.15. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE.如果∠ADB =30°,则∠E=________度.16. 如图,在矩形纸片ABCD中,AB=6,BC=10.点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A 恰落在线段BF 上的点H 处.有下列结论:①∠EBG =45°;②△DEF ∽△ABG ;③S △ABG =32S △FGH ;④AG +DF =FG . 其中正确的是______________.(把所有正确结论的序号都选上)三、解答题17. 如图,将等腰三角形ABC 绕顶点B 按逆时针方向旋转α到△A 1BC 1的位置,AB 与A 1C 1相交于点D ,AC 与A 1C 1,BC 1分别交于点E ,F . (1)求证:△BCF ≌△BA 1D ;(2)当∠C=α时,判断四边形A 1BCE 的形状,并说明理由.18. 如图,对折矩形纸片ABCD ,使AB 与DC 重合,得到折痕MN ,将纸片展平;再一次折叠,使点D 落到MN 上的点F 处,折痕AP 交MN 于E ;延长PF 交AB 于G .求证: (1)△AFG ≌△AFP ; (2)△APG 为等边三角形.19. 如图,在四边形ABCD 中,BD 为一条对角线,AD ∥BC ,AD=2BC ,∠ABD=90°,E 为AD 的中点,连接BE. (1)求证:四边形BCDE 为菱形;(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.20. 如图,在平行四边形ABCD中,点O是边BC的中点,连接DO并延长,交AB的延长线于点E,连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)若∠A=50°,则当∠BOD=°时,四边形BECD是矩形.21. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD、CE交于点F.(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.22. 如图,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和点G,H.(1)求证:△PHC≌△CFP;(2)证明四边形PEDH和四边形PFBG都是矩形,并直接写出它们面积之间的关系.23. 如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,将△ABE沿BE折叠得到△FBE,且点F落在矩形ABCD的内部,连接AF,BF,EF,过点F作GF⊥AF交AD于点G,设ADAE=n.(1)求证:AE=GE;(2)当点F落在AC上时,用含n的代数式表示ADAB的值;(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.24. 如图,在菱形ABCD中,AB=5,sin∠ABD=55,点P是射线BC上一点,连接AP交菱形对角线BD于点E,连接EC.(1)求证:△ABE≌△CBE;(2)如图①,当点P在线段BC上时,且BP=2,求△PEC的面积;(3)如图②,当点P在线段BC的延长线上时,若CE⊥EP,求线段BP的长.2021中考临考专题训练:矩形、菱形-答案一、选择题1. 【答案】B2. 【答案】C3. 【答案】B【解析】本题考查了菱形的性质和直角三角形斜边上的中线性质.∵四边形ABCD 是菱形,∴AB =BC =CD =DA .∵菱形ABCD 的周长为32,∴AB =8.∵AC ⊥BD ,E 为AB 的中点,∴OE =AB =4.故选B .4. 【答案】C 【解析】本题考查菱形的性质、相似三角形的性质、函数的图象和二次函数的图象和性质. 解题思路:设AC 、BD 交于点O ,由于点P 是菱形ABCD的对角线AC 上一动点,所以0<x <2.当0<x <1时,△AMN ∽△ABD ⇒APAO =MN BD ⇒x 1=MN 1⇒MN =x ⇒y =12x 2.此二次函数的图象开口向上,对称轴是x =0,此时y 随x 的增大而增大. 所以B 和D 均不符合条件.当1<x <2时,△CMN∽△CBD ⇒CP CO =MN BD ⇒2-x 1=MN 1⇒MN =2-x ⇒y =12x(2-x)=-12x 2+x.此二次函数的图象开口向下,对称轴是x =1,此时y 随x 的增大而减小. 所以A 不符合条件.综上所述,只有C 是符合条件的.5. 【答案】B【解析】本题考查了菱形的性质及锐角三角函数等知识.由菱形的周长为16可得其边长为4,而高为2,即转化为已知某一直角三角形的斜边为4,一直角边为2,求该直角三角形的锐角.由sin α=2142,可得锐角α=30°,所以该菱形的两邻角为150°和30°,两邻角之比5∶1,因此本题选B . 6. 【答案】C【解析】本题考查了矩形的性质,由勾股定理可得AC=10,再由矩形的对角线相等且互相平分的性质可得,OA=OD=5. △ABD 的面积为24,OA 为△ABD 的中线,由中线等分面积可得,△AOD 的面积为12.再由等面积法即可得OE+EF 的值.过程如下:∵AOE EOD AOD S S S ∴111222OA OE OD EF 即11551222OE EF ,∴OE+EF=245,因此本题选C .7. 【答案】D【解析】本题考查了矩形的性质、三角形全等的条件与性质、等边三角形的条件与性质、平行四边形的条件与性质以及菱形的判定方法,因为四边形ABCD 是矩形,所以AB=CD ,AD=BC ,AD ∥BC ,所以∠DAN=∠BCM.因为BF ⊥AC ,DE ∥BF ,所以DE ⊥AC ,即∠AND=∠CMB=90°,所以△ADN ≌△CBM ,所以DN=BM ,∠AND=∠CBM ,则△ADE ≌△CBF ,所以AE=CF 、DE=BF ,所以NE=MF ,即①②③都是正确的,由AE=CF 、AB=CD ,所以BE=DF ,所以四边形AEBF 是平行四边形. 因为四边形ABCD 是矩形,所以AO=DO ,因为当AO ﹦AD 时,AO=DO=AO ,所以△ADO 是等边三角形,所以∠AND=∠BDE=30°,所以∠BDE=∠ABD=30°,所以DE=BE ,所以四边形DEBF 是菱形,则④也是正确的,因此本题选D . 8. 【答案】A【解析】由矩形的性质可知:BE=DE=BD ,∠OAD=∠BAD=90°,在△ODE 和△OBE 中,BO=DO ,BE=DE ,OE=OE ,所以△ODE ≌△OBE ,∠OED=∠OEB=90°,∠OBD=∠ODB=67.5°,∠BOE=∠DOE=22.5°,故①正确;在R t △AOD 中,∠BOD=45°,∴OA=AD ,在R t △ABD 中,∠BAD=90°,∠OBD=67.5°,所以∠BDA=22.5°,在△BDA 和△FOA 中,∠BDA=∠FOA ,OA=AD ,∠OAD=∠BAD=90°,所以△BDA ≌△FOA ,所以OF=BD ,故②正确;如答图,过点F 作FQ ⊥OD 于点Q ,由角平分线的性质得AF=FQ ,由题可知∠ADO=45°,所以△FDQ 是等腰直角三角形即DF=AF ,故③正确;如答图,AG=OG=OF ,所以OG=DE ,由题意可得△OAG ≌△DAE ,所以∠OAG=∠DAE ,AG=AE ,又由∠OAG +∠GAF=90°可得∠GAE=90°,所以△GAE 是等腰直角三角形,故④正确.二、填空题9. 【答案】4 [解析]由题意可知,四边形ABCD 为矩形,则AC=BD ,OC=AC.已知∠ADB=30°,故在Rt △ABD 中,BD=2AB=8,∴AC=BD=8,OC=AC=4.10. 【答案】1611. 【答案】60[解析]菱形的面积可以用边长×高,即AB ×DE 计算,在Rt △ADE中,∵AD=10,sin A=,∴DE=6,∴菱形的面积为60 cm 2.12. 【答案】3【解析】本题主要考查了一元二次方程的实际应用问题. 设AD =x ,由题知,AB =x +2,又∵矩形ABCD 的面积为15,则x(x +2)=15,得到x 2+2x -15=0,解得,x 1=-5(舍) , x 2=3,∴AD =3.13. 【答案】16 【解析】∵E ,F 分别是AD ,BD 的中点,∴AB =2EF =4,∴菱形ABCD 周长是4AB =16.14. 【答案】5【解析】本题考查了矩形的性质,轴对称的性质,勾股定理.∵长方形纸片ABCD ,AB =8,BC =10,∴AB '=8,AD =10,B 'C '=10.在R t △ADB '中,由勾股定理,得DB '=6.∴DC '=4. 设DE =x ,则CE =C 'E =8-x .在R t △C 'DE 中,由勾股定理,得DE 2=EC '2+DC '2GQD C AB F E O即x 2=(8-x )2+42.∴x =5.即线段DE 的长为5cm .461088-x x 108C'B'D A BCE15. 【答案】15 【解析】如解图,连接AC.∵四边形ABCD 是矩形,∴AD =BC ,AC =BD ,又∵AB =BA ,∴△DAB ≌△CBA(SSS ),∴∠ACB =∠ADB =30°,∵CE =BD ,∴AC =CE ,∴∠E =∠CAE =12∠ACB =15°.解图16. 【答案】①③④ 【解析】由折叠的性质得,∠CBE =∠FBE ,∠ABG =∠FBG ,∴∠EBG =∠FBE +∠FBG =12×90°=45°,故①正确;由折叠的性质得,BF =BC =10,BA =BH =6,∴HF =BF -BH =4,AF =BF 2-BA 2=102-62=8,设GH =x ,则GF =8-x ,在Rt △GHF 中,x 2+42=(8-x)2,∴x =3,∴GF =5,∴AG =3,同理在Rt △FDE 中,由FD 2=EF 2-ED 2,得ED =83,EF =103,∴EDFD =43≠AB AG =2,∴△DEF 与△ABG 不相似,故②不正确;S △ABG =12×3×6=9,S △FGH =12×3×4=6,∴S △ABG S △FGH =96=32,故③正确;∵AG =3,DF =AD -AF =2,∴FG=5,∴AG +DF =FG =5,故④正确.综上,答案是①③④.三、解答题17. 【答案】解:(1)证明:∵△ABC 是等腰三角形,B 是顶点, ∴AB=BC ,∠A=∠C ,∵将等腰三角形ABC 绕顶点B 按逆时针方向旋转α到△A 1BC 1的位置, ∴A 1B=AB=BC ,∠A 1=∠A=∠C ,∠A 1BD=∠CBC 1.在△BCF 与△BA 1D 中,∴△BCF≌△BA1D.(2)四边形A1BCE是菱形.理由如下:∵将等腰三角形ABC绕顶点B按逆时针方向旋转α到△A1BC1的位置,∴∠A1=∠A,∵∠ADE=∠A1DB,∴∠AED=∠A1BD=α,∵∠AED=∠C=α,∴A1E∥BC.∵∠AED=∠A1=α,∴A1B∥CE.∴四边形A1BCE是平行四边形,又∵A1B=BC,∴四边形A1BCE是菱形.18. 【答案】证明:(1)∵对折矩形纸片ABCD,使AB与CD重合,得到折痕MN,∴MN∥AB,M,N分别为AD,BC中点,由平行线的性质可知PF=GF.由折叠的性质得∠PF A=∠GF A=90°,∴△AFG≌△AFP(SAS).(2)∵△AFG≌△AFP,∴AP=AG,∠2=∠3.又∵∠2=∠1,∴∠1=∠2=∠3.又∵∠1+∠2+∠3=90°,∴3∠2=90°,∴∠2=30°,∠P AG=2∠2=60°,∴△APG 为等边三角形.19. 【答案】解:(1)证明:∵E为AD的中点,AD=2BC,∴BC=ED,∵AD∥BC,∴四边形BCDE是平行四边形,∵∠ABD=90°,AE=DE,∴BE=ED,∴四边形BCDE是菱形.(2)∵AD∥BC,AC平分∠BAD,∴∠BAC=∠DAC=∠BCA,∴BA=BC=1,∵AD=2BC=2,∴sin∠ADB=,∴∠ADB=30°,∴∠DAC=∠BAD=30°,∠ADC=2∠ADB=60°.∴∠ACD=90°.在Rt△ACD中,AD=2,CD=1,∴AC=.20. 【答案】解:(1)证明:∵平行四边形ABCD,∴AE∥DC,∴∠EBO=∠DCO,∠BEO=∠CDO,∵点O是边BC的中点,∴BO=CO,∴△EBO≌△DCO(AAS),∴EO=DO,∴四边形BECD是平行四边形.(2)100[解析]若四边形BECD为矩形,则BC=DE,BD⊥AE,又AD=BC,∴AD=DE.根据等腰三角形的性质,可知∠ADB=∠EDB=40°,故∠BOD=180°-∠ADE=100°.21. 【答案】(1)证明:∵△ADE 是由△ABC 绕点A 沿顺时针方向旋转而得,∴AD =AB ,AE =AC ,∠BAC =∠DAE ,(1分)∵AB =AC ,∴AD =AB =AE =AC ,∠EAC =∠DAB ,在△AEC 和△ADB 中∵⎩⎨⎧AD = AE∠EAC =∠DAB AB =AC,∴△AEC ≌△ADB(SAS ).(3分)(2)解:当四边形ADFC 是菱形时,AC =DF ,AC ∥DF ,∴∠BAC =∠ABD ,又∵∠BAC =45°,∴∠ABD =45°,(5分)又∵△ADE 是由△ABC 绕点A 沿顺时针方向旋转而得,∴AD =AB ,∴∠DAB =90°,(6分)又∵AB =2,由勾股定理可得:BD =AD 2+AB 2=2AB =22,在菱形ADFC 中,DF =AD =AB =2,∴BF =BD -DF =22-2.(8分)22. 【答案】(1)证明:∵四边形ABCD 是矩形,∴DC ∥AB ,AD ∥BC ,∠DCB =90°.(1分) ∵EF ∥AB ,GH ∥AD ,∴EF ∥CD ,GH ∥BC ,∴四边形PFCH 是矩形,(2分)∴∠PHC =∠PFC =90°,PH =CF ,HC =PF ,(3分)∴△PHC ≌△CFP(SAS ).(4分)(2)证明:(1)由(1)知AB ∥EF ∥CD ,AD ∥GH ∥BC ,∴四边形PEDH 和四边形PGBF 都是平行四边形,∵四边形ABCD 是矩形,∴∠D =∠B =90°,∴四边形PEDH 和四边形PGBF 都是矩形,∴S 矩形PEDH =S 矩形PGBF .(8分)【解法提示】同(1)证法一样可得,△ACD ≌△CAB ,△APE ≌△PAG ,△PHC ≌△CFP ,∴S △ACD -S △AEP -S △PCH =S △CAB -S △PGA -S △CFP ,∴S 四边形PEDH =S 四边形PFBG .23. 【答案】(1)证明:由折叠性质得AE =FE ,∴∠EAF =∠EF A ,∵GF ⊥AF ,∴∠EAF +∠FGA =∠EF A +∠EFG =90°,∴∠FGA =∠EFG ,∴EG =EF ,∴AE =GE ;(2)解:如解图①,当点F 落在AC 上时,设AE =a ,则AD =na ,解图①由对称性得BE ⊥AF ,∴∠ABE +∠BAC =90°,∵∠DAC +∠BAC =90°,∴∠ABE =∠DAC ,又∵∠BAE =∠D =90°,∴△ABE ∽△DAC , ∴AB DA =AE DC ,∵AB =DC ,∴AB 2=AD ·AE =na ·a =na 2,∵AB >0,∴AB =na ,∴AD AB =na na=n ; (3)解:若AD =4AB ,则AB =n 4a , 如解图②,当点F 落在线段BC 上时,EF =AE =AB =a .解图②此时n 4a =a ,∴n =4,∴当点F 落在矩形内部时,n >4.∵点F 落在矩形的内部,点G 在AD 上,∴∠FCG <∠BCD ,∴∠FCG <90°.①若∠CFG =90°,则点F 落在AC 上,由(2)得AD AB =n ,即4AB AB =n ,∴n =16;②如解图③,若∠CGF =90°,则∠CGD +∠AGF =90°,解图③∵∠F AG +∠AGF =90°,∴∠CGD =∠F AG =∠ABE .∵∠BAE =∠D =90°,∴△ABE ∽△DGC ,∴AB DG =AE DC ,∵DG =AD -AE -EG =na -2a =(n -2)a ,∴AB ·DC =DG ·AE ,即(n 4a )2=(n -2)a ·a ,解得n 1=8+42,n 2=8-42<4(不合题意,舍去).综上所述,当n =16或n =8+42时,以点F ,C ,G 为顶点的三角形是直角三角形.24. 【答案】(1)证明:∵四边形ABCD 是菱形,∴AB =BC ,∠ABE =∠CBE .在△ABE 和△CBE 中,AB =BC ,∠ABE =∠CBE ,BE =BE ,∴△ABE ≌△CBE (SAS);(2)解:如解图①,连接AC 交BD 于点O ,分别过点A 、E 作BC 的垂线,垂足分别为点H 、F ,解图①∵四边形ABCD 是菱形,∴AC ⊥BD ,∵AB =5,sin ∠ABD =55,∴AO =OC =5,∴BO =OD =25, ∴AC =25,BD =45, ∵12AC ·BD =BC ·AH ,即12×25×45=5AH ,∴AH =4,∵AD ∥BC ,∴△AED ∽△PEB , ∴AE PE =AD BP, ∴AE +PE PE =AD +BP BP ,即AP PE =5+22=72,∴AP =72PE ,又∵EF ∥AH ,∴△EFP ∽△AHP ,∴EF AH =PE AP ,∴EF =PE AP ·AH =PE 72PE×4=87,∴S △PEC =12PC ·EF =12×(5-2)×87=127;(3)解:如解图②,连接AC 交BD 于点O ,解图②∵△ABE ≌△CBE ,CE ⊥PE ,∴∠AEB =∠CEB =45°,∴AO =OE =5,∴DE =OD -OE =25-5=5,BE =3 5. ∵AD ∥BP ,∴△ADE ∽△PBE ,∴AD BP =DE BE ,∴5BP=535,∴BP=15.。
菱形、矩形判定性质练习题

菱形性质与判定练习题1. 已知菱形ABCD中, 对角线AC与BD交于点O, ∠BAD=120°, AC=4, 则该菱形的面积是()A.16B.16C.8D.82.菱形的周长为4, 一个内角为60°, 则较短的对角线长为()A. 2B.C. 1D.3.菱形的周长为8cm, 高为1cm, 则该菱形两邻角度数比为()A. 3: 1B. 4: 1C. 5: 1D. 6: 14.如图, 菱形ABCD中, AB=15, ∠ADC=120°, 则B.D两点之间的距离为()A. 15B.C. 7.5D.5.如图, 菱形ABCD的周长是16, ∠A=60°, 则对角线BD的长度为()A. 2B.C. 4D.6. 已知菱形的两条对角线长分别为2cm, 3cm, 则它的面积是_________cm2.7. 如图, 菱形ABCD的对角线AC、BD相交于点O, 且AC=8, BD=6, 过点O作OH丄AB, 垂足为H, 则点0到边AB的距离OH=_________.8.如图, 菱形ABCD的边长是2cm, E是AB的中点, 且DE丄AB, 则菱形ABCD的面积为cm2.6题图7题图8题图9题图9. 如图, 在菱形ABCD中, 对角线AC与BD相交于点O, AB=13, AC=10, 过点D作DE∥AC交BC的延长线于点E, 则△BDE的周长为_________.10. 如图, 已知菱形ABCD的一个内角∠BAD=80°, 对角线AC.BD相交于点O, 点E在AB上且BE=BO, 则∠BEO= _________度.11.如图, 活动菱形衣架的边长均为16cm, 若墙上钉子间的距离AB=BC=16cm, 则∠1=度.10题图13题14题图15题图12. 已知菱形的一个内角为60°, 一条对角线的长为, 则另一条对角线的长为_________.13. 如图, 两个全等菱形的边长为1米, 一机器人由A点开始按A—B—C—D—E—F—C—G—A的顺序沿菱形的边循环运动, 行走2009米停下, 则这个微型机器人停在_____点.14. 如图, P为菱形ABCD的对角线上一点, PE⊥AB于点E, PF⊥AD于点F, PF=3cm, 则P点到AB的距离是____ cm.15. 已知: 菱形ABCD中, ∠B=60°, AB=4, 则以AC为边长的正方形ACEF的周长为______.16. 已知菱形的周长为40cm, 两条对角线之比为3: 4, 则菱形的面积为_________cm2.17. 已知菱形的周长是52cm, 一条对角线长是24cm, 则它的面积是_________cm2.18.如图, 菱形ABCD的对角线的长分别为2和5, P是对角线AC上任一点(点P不与点A、C重合), 且PE∥BC交AB 于E, PF∥CD交AD于F, 则阴影部分的面积是_________.17题图18题图19题图19. 如图: 菱形ABCD中, AB=2, ∠B=120°, E是AB的中点, P是对角线AC上的一个动点, 则PE+PB的最小值是_________.20. 如图: 点E、F分别是菱形ABCD的边BC.CD上的点, 且∠EAF=∠D=60°, ∠FAD=45°, 则∠CFE=度. 21.如图所示, 在菱形ABCD中, ∠ABC=60°, DE∥AC交BC的延长线于点E.求证:DE= BE.22. 如图, 在菱形ABCD中, ∠A=60°, AB=4, O为对角线BD的中点, 过O点作OE⊥AB, 垂足为E.(1)求∠ABD的度数;(2)求线段BE的长.23. 如图, 四边形ABCD是菱形, BE⊥AD.BF⊥CD, 垂足分别为E、F.(1)求证:BE=BF;(2)当菱形ABCD的对角线AC=8, BD=6时, 求BE的长.24. 如图, 在菱形ABCD中, P是AB上的一个动点(不与A.B重合), 连接DP交对角线AC于E连接BE.(1)证明: ∠APD=∠CBE;(2)若∠DAB=60°, 试问P点运动到什么位置时, △ADP的面积等于菱形ABCD面积的, 为什么?25. 如图所示, 在矩形ABCD中, AB=4cm, BC=8cm、点P从点D出发向点A运动, 同时点Q从点B出发向点C运动, 点P、Q的速度都是1cm/s.(1)在运动过程中, 四边形AQCP可能是菱形吗?如果可能, 那么经过多少秒后, 四边形AQCP是菱形?(2)分别求出菱形AQCP的周长、面积.矩形的性质与判定【知识要点:】1. 矩形的定义: 有一个角是直角的平行四边形是矩形(矩形是特殊的平行四边形)。
初二数学菱形、矩形复习题(含答案)

初二数学菱形、矩形复习题矩形:定义:有一个是直角的平行四边形是矩形性质:判定:菱形:定义:有一组邻边相等的平行四边形是菱形性质:判定:1.如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为____________2.如图,在矩形ABCD中,AB=3,AD=4,点P在AB上,PE⊥AC于E,PF⊥BD于F,则PE+PF 等于________3.如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=8,则DE的长度是_______________4.如图,E,F分别是矩形ABCD边AD、BC上的点,且△ABG,△DCH的面积分别为15和20,则图中阴影部分的面积为________________5.若菱形两条对角线长分别为6和8,则这个菱形的面积为________________6.若菱形的周长为16,两邻角度数之比为1:2,则该菱形的面积为_________________7.如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有________________8.如果矩形一条较短的边是5,两条对角线的夹角是60°,则对角线长是.9.Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为.10.如图,四边形ABCD为矩形,H、F分别为AD、BC边的中点,四边形EFGH为矩形,E、G 分别在AB、CD边上,则图中四个直角三角形面积之和与矩形EFGH的面积之比为.11.如图,在矩形ABCD中,AD=5,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于.12.如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为.13.如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是;若将△ABP的PA边长改为,另两边长度不变,则点P到原点的最大距离变为.14.如图,在菱形ABCD中,AD=8,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为.15.如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则BG= .16.下列命题:①矩形的对角线互相平分且相等;②对角线相等的四边形是矩形;③菱形的每一条对角线平分一组对角;④一条对角线平分一组对角的平行四边形是菱形.其中正确的命题为(注:把你认为正确的命题序号都填上)17.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足(关系)时,四边形EFGH为矩形.18.如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=6,AF=BF,则四边形BCDE的面积是.19.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点D是斜边AB上任意一点,DE⊥AC,DF⊥BC,垂足分别是点E、F,点Q是EF的中点,则线段DQ长的最小值等于.20.如图,矩形ABCD中,AB=20cm,BC=4cm,点P从A 开始沿折线A﹣B﹣C﹣D以4cm/s的速度运动,点Q从C开始沿CD边以1cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s),当t= 时,四边形APQD也为矩形.21.如图,在菱形ABCD中,∠BAD=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是.(把所有正确结论的序号都填在横线上)①OG=AB;②与△EGD全等的三角形共有5个;③S四边形CDGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.22.如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是.23.如图,已知四边形ABCD是平行四边形,并且∠A=∠D.(1)求证:四边形ABCD为矩形;(2)点E是AB边的中点,F为AD边上一点,∠1=2∠2,若CE=4,CF=5,求DF的长.24.已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC 的平行线与CE的延长线交于点F,连接DF.(1)求证:AF=DC;(2)请问:AD与CF满足什么条件时,四边形AFDC是矩形,并说明理由.25.如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.(1)求证:四边形DEBF是菱形;(2)请判断四边形AGBD是什么特殊四边形?并加以证明.26.如图,四边形ABCD中,AB=AC=AD,BC=CD,锐角∠BAC的角平分线AE交BC于点E,AF 是CD边上的中线,且PC⊥CD与AE交于点P,QC⊥BC与AF交于点Q.求证:四边形APCQ 是菱形.27.矩形ABCD中,E是CD上一点,且AE=CE,F是AC上一点FH⊥AE于H,FG⊥CD于G,求证:FH+FG=AD.28.如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB 于点H.(1)求证:四边形AGPH是矩形;(2)在点P在运动过程中,GH是否存在最小值?若存在,请求出,若不存在,请说明理由.29.如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P (点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE.(1)求证:四边形AEPQ为菱形;(2)当点P在何处时,菱形AEPQ的面积为四边形EFBQ面积的一半?30.在△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC交AD于E,交AC于G,GF⊥BC 于F,连接EF.(1)如图1,求证:四边形AEFG是菱形;(2)如图2,若E为BG的中点,过点E作EM∥BC交AC于M,在不添加任何辅助线的情况下,请直接写出图2中是CM长倍的所有线段.31.阅读下面短文:如图①,△ABC是直角三角形,∠C=90°,现将△ABC补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个矩形ACBD和矩形AEFB(如图②)解答问题:(1)设图②中矩形ACBD和矩形AEFB的面积分别为S1、S2,则S1S2(填“>”“=”或“<”).(2)如图③,△ABC是钝角三角形,按短文中的要求把它补成矩形,那么符合要求的矩形可以画个,利用图③把它画出来.(3)如图④,△ABC是锐角三角形且三边满足BC>AC>AB,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出个,利用图④把它画出来.(4)在(3)中所画出的矩形中,哪一个的周长最小?为什么?32.如图1,菱形ABCD中,点E、F分别为AB、AD的中点,连接CE、CF.(1)求证:CE=CF;(2)如图2,若H为AB上一点,连接CH,使∠CHB=2∠ECB,求证:CH=AH+AB.33.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.34.将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;(2)若AB=8,AD=4,求四边形DHBG的面积.35.如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.(1)求证:四边形ABCF是矩形;(2)若EA=EG,求证:ED=EC.36.如图1,平行四边形ABCD,DE⊥AB.垂足E在BA的延长线上,BF⊥DC,垂足F在DC 的延长线上.(1)求证:四边形BEDF是矩形;(2)如图2,若M、N分别为AD、BC的中点,连接EM、EN、FM、FN,求证:四边形EMFN 是平行四边形.37.如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;(2)如图1,当点G和点M、C不重合时,求证:DG=DN.参考答案矩形:定义:有一个是直角的平行四边形是矩形性质:判定:菱形:定义:有一组邻边相等的平行四边形是菱形性质:1.如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为__________【解答】解:∵四边形ABCD是矩形,∴AB=DC,BC=AD,OA=OC=OB=OD,AD∥BC,∴∠EDO=∠FBO,.∵矩形ABCD的周长为20cm,∴BC+DC=10cm,∵EF⊥AC,∴CE=CF,在△ODE和△OBF中,,∴△ODE≌△OBF(ASA),∴DE=BF,∴△CDE的周长=DE+CE+DC=BF+CF+DC=BC+DC=10cm.2.如图,在矩形ABCD中,AB=3,AD=4,点P在AB上,PE⊥AC于E,PF⊥BD于F,则PE+PF 等于______【解答】解:方法一:设AP=x,PB=3﹣x.∵∠EAP=∠EAP,∠AEP=∠ABC;∴△AEP∽△ABC,故=①;同理可得△BFP∽△DAB,故=②.①+②得=,∴PE+PF=.方法二:(面积法)如图,作BM⊥AC于M,则BM==,∵S△AOB=S△AOP+S△POB,∴•AO•BM=•AO•PE+•OB•PF,∵OA=OB,∴PE+PF=BM=.3.如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=8,则DE的长度是______________【解答】解:∵四边形ABCD是矩形,∴∠ADC=90°,AC=BD=8,OA=OC=AC=4,OB=OD=BD=4,∴OC=OD,∴∠ODC=∠OCD,∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,∴∠EDC=22.5°,∠EDA=67.5°,∵DE⊥AC,∴∠DEC=90°,∴∠DCE=90°﹣∠EDC=67.5°,∴∠ODC=∠OCD=67.5°,∴∠ODC+∠OCD+∠DOC=180°,∴∠COD=45°,∴OE=DE,∵OE2+DE2=OD2,∴2DE2=OD2=16,∴DE=2.4.如图,E,F分别是矩形ABCD边AD、BC上的点,且△ABG,△DCH的面积分别为15和20,则图中阴影部分的面积为_____________【解答】解:连接EF,∵S△ABF=S△EBF∴S△EFG=S△ABG=15;同理:S△EFH=S△DCH=20∴S阴影=S△EFG+S△DCH=15+20=35.5.若菱形两条对角线长分别为6和8,则这个菱形的面积为________________【解答】解:菱形的面积为:×6×8=24.6.若菱形的周长为16,两邻角度数之比为1:2,则该菱形的面积为___________【解答】解:如图,∵两邻角度数之比为1:2,两邻角和为180°,∴∠ABC=60°,∠BAD=120°,∵周长为16,∴边长AB=4,∴菱形的对角线AC=4,BD=2×4sin60°=4,∴面积=AC•BD=×4×4=8.7.如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S△EOD;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称图形.其中正确的结论有___________【解答】解:①正确∵E、F分别是OA、OC的中点.∴AE=OE.∵S△ADE=×AE×OD=×OE×OD=S△EOD∴S△ADE=S△EOD.②正确∵四边形ABCD是菱形,E,F分别是OA,OC的中点.∴EF⊥OD,OE=OF.∵OD=OD.∴DE=DF.同理:BE=BF∴四边形BFDE是菱形.③正确∵菱形ABCD的面积=AC×BD.∵E、F分别是OA、OC的中点.∴EF=AC.∴菱形ABCD的面积=EF×BD.④不正确由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.⑤正确∵EF⊥OD,OE=OF,OD=OD.∴△DEO≌△DFO.∴△DEF是轴对称图形.∴正确的结论有四个,分别是①②③⑤8.如果矩形一条较短的边是5,两条对角线的夹角是60°,则对角线长是10 .【解答】解:如图,在矩形ABCD中,AO=BO,∵AC、BD的夹角是60°,∴△ABO是等边三角形,∴AO=AB=5,∴对角线AC=2AO=2×5=10.故答案为:10.9.Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为.【解答】解:由题意知,四边形AFPE是矩形,∵点M是矩形对角线EF的中点,则延长AM应过点P,∴当AP为直角三角形ABC的斜边上的高时,即AP⊥BC时,AM有最小值,此时AM=AP,由勾股定理知BC==5,∵S△ABC=AB•AC=BC•AP,∴AP==,∴AM=AP=.10.如图,四边形ABCD为矩形,H、F分别为AD、BC边的中点,四边形EFGH为矩形,E、G 分别在AB、CD边上,则图中四个直角三角形面积之和与矩形EFGH的面积之比为1:1 .【解答】解:连接HF,∵四边形ABCD为矩形,∴AD=BC,AD∥BC,∠D=90°∵H、F分别为AD、BC边的中点,∴DH=CF,DH∥CF,∵∠D=90°,∴四边形HFCD是矩形,∴△HFG的面积是CD×DH=S矩形HFCD,即S△HFG=S△DHG+S△CFG,同理S△HEF=S△BEF+S△AEH,∴图中四个直角三角形面积之和与矩形EFGH的面积之比是1:1,故答案为:1:1.11.如图,在矩形ABCD中,AD=5,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于.【解答】解:连接FH、EG;∵AF=CG=2,AE=CH=4﹣1=3,∠A=∠C=90°,∴△AEF≌△CHG,S△AEF=S△CHG=3;同理可证:△FHD≌△GEB,S△FHD=S△GEB=1.5;∴FH=EG,EF=GH,即四边形EFHG是平行四边形;且S平行四边形=S矩形﹣2S△AEF﹣2S△FHD=11;过P作EF、GH的垂线,交EF于M,GH于N;则S△EFP+S△GHP=EF(PM+PN)=EF•MN=S▱EFHG=.故答案为:.12.如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为.【解答】解:∵四边形ABCD是矩形,点G是DF的中点,∴AG=DG,∴∠ADG=∠DAG,∵AD∥BC,∴∠ADG=∠CED,∴∠AGE=∠ADG+∠DAG=2∠CED,∵∠AED=2∠CED,∴∠AED=∠AGE,∴AE=AG=4,在Rt△ABE中,AB===.故答案为:.13.如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是1+;若将△ABP的PA边长改为,另两边长度不变,则点P到原点的最大距离变为1+.【解答】解:取AB的中点M,连OM,PM,在Rt△ABO中,OM==1,在等边三角形ABP中,PM=,无论△ABP如何运动,OM和PM的大小不变,当OM,PM在一直线上时,P距O最远,∵O到AB的最大值是AB=1,此时在斜边的中点M上,由勾股定理得:PM==,∴OP=1+,将△AOP的PA边长改为,另两边长度不变,∵22+22=,∴∠PBA=90°,由勾股定理得:PM==,∴此时OP=OM+PM=1+.故答案为:1+,1+.14.如图,在菱形ABCD中,AD=8,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为4.【解答】解:连接BD,DE,∵四边形ABCD是菱形,∴B、D关于直线AC对称,∴DE的长即为PE+PB的最小值,∵ABC=120°,∴∠BCD=60°,∴△BCD是等边三角形,∵E是BC的中点,∴DE⊥BC,CE=BC=×8=4,∴DE===4.故答案为:4.15.如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则BG= 5 .【解答】解:∵AG∥BD,BD=FG,∴四边形BGFD是平行四边形,∵CF⊥BD,∴CF⊥AG,又∵点D是AC中点,∴BD=DF=AC,∴四边形BGFD是菱形,设GF=x,则AF=13﹣x,AC=2x,∵在Rt△ACF中,∠CFA=90°,∴AF2+CF2=AC2,即(13﹣x)2+62=(2x)2,解得:x=5,即BG=5.故答案是:5.16.下列命题:①矩形的对角线互相平分且相等;②对角线相等的四边形是矩形;③菱形的每一条对角线平分一组对角;④一条对角线平分一组对角的平行四边形是菱形.其中正确的命题为①③④(注:把你认为正确的命题序号都填上)【解答】解:①矩形的对角线互相平分且相等;故正确;②对角线相等的四边形是矩形,不能正确判定,故错误;③菱形的每一条对角线平分一组对角,这是菱形的一条重要性质,故正确;④一条对角线平分一组对角的平行四边形是菱形,故正确.故答案为:①③④.17.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足AB=AD (关系)时,四边形EFGH为矩形.【解答】解:∵四边形ABCD是矩形,∴∠A=90°.∵AE=AF,∴∠AFE=∠AEF=45°.又∵EH⊥EF,FG⊥EF∴∠GFB=∠HED=45°,∴△DHE和△BGF都是等腰直角三角形.如果四边形EFGH是矩形,则EH=FG,∴ED=FB又∵AE=AF,∴AD=AB.故答案是:AD=AB.18.如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=6,AF=BF,则四边形BCDE的面积是18.【解答】解:∵AF=BF,即F为AB的中点,又DE垂直平分AC,即D为AC的中点,∴DF为三角形ABC的中位线,∴DE∥BC,DF=BC,又∠ADF=90°,∴∠C=∠ADF=90°,又BE⊥DE,DE⊥AC,∴∠CDE=∠E=90°,∴四边形BCDE为矩形,∵BC=6,∴DF=BC=3,在Rt△ADF中,∠A=30°,DF=3,∴tan30°=,即AD=3,∴CD=AD=3,则矩形BCDE的面积S=CD•BC=18.故答案为:18.19.如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点D是斜边AB上任意一点,DE⊥AC,DF⊥BC,垂足分别是点E、F,点Q是EF的中点,则线段DQ长的最小值等于 2.4 .【解答】解:∵在△ABC中,∠ACB=90°,AC=6,BC=8,∴AB=10,连接CD,∵DE⊥AC,DF⊥BC,∴四边形EDFC是矩形,∴EF=CD,∠EDF=90°,∵点Q是EF的中点,∴DQ=EF=CD,当CD最小时,则DQ最小,根据垂线段最短可知当CD⊥AB时,则CD最小,∴DQ=EF=CD=×=2.4,故答案为:2.4.20.如图,矩形ABCD中,AB=20cm,BC=4cm,点P从A 开始沿折线A﹣B﹣C﹣D以4cm/s的速度运动,点Q从C开始沿CD边以1cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s),当t= 4 时,四边形APQD也为矩形.【解答】解:根据题意,当AP=DQ时,四边形APQD为矩形.此时,4t=20﹣t,解得t=4(s).故答案是:4.21.如图,在菱形ABCD中,∠BAD=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是①④.(把所有正确结论的序号都填在横线上)①OG=AB;②与△EGD全等的三角形共有5个;③S四边形CDGF>S△ABF;④由点A、B、D、E构成的四边形是菱形.【解答】解:∵四边形ABCD是菱形,∴AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,∴∠BAG=∠EDG,△ABO≌△BCO≌△CDO≌△AOD,∵CD=DE,∴AB=DE,在△ABG和△DEG中,,∴△ABG≌△DEG(AAS),∴AG=DG,∴OG是△ACD的中位线,∴OG=CD=AB,①正确;∵AB∥CE,AB=DE,∴四边形ABDE是平行四边形,∵∠BCD=∠BAD=60°,∴△ABD、△BCD是等边三角形,∴AB=BD=AD,∠ODC=60°,∴OD=AG,四边形ABDE是菱形,④正确;∴AD⊥BE,由菱形的性质得:△ABG≌△BDG≌△DEG,在△ABG和△DCO中,,∴△ABG≌△DCO(SAS),∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG,②不正确;∵OB=OD,AG=DG,∴OG是△ABD的中位线,∴OG∥AB,OG=AB,∴△GOD∽△ABD,△ABF∽△OGF,∴△GOD的面积=△ABD的面积,△ABF的面积=△OGF的面积的4倍,AF:OF=2:1,∴△AFG的面积=△OGF的面积的2倍,又∵△GOD的面积=△AOG的面积=△BOG的面积,∴S四边形ODGF=S△ABF;不正确;正确的是①④.故答案为:①④.22.如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.【解答】解:∵五边形ABCDE是正五边形,∴AB∥CE,AD∥BC,∴四边形ABCF是平行四边形,又∵AB=BC=CD=DE=EA,∴四边形ABCF是菱形,∴AC⊥BF,∴OB2+OC2=BC2,∵AC=2OC,BF=2OB,∴AC2+BF2=(2OC)2+(2OB)2=4OC2+4OB2=4BC2,又∵BC=CD,∴AC2+BF2=4CD2.故答案为:AC2+BF2=4CD2.23.如图,已知四边形ABCD是平行四边形,并且∠A=∠D.(1)求证:四边形ABCD为矩形;(2)点E是AB边的中点,F为AD边上一点,∠1=2∠2,若CE=4,CF=5,求DF的长.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠A+∠D=180°,又∠A=∠D,∴∠A=∠D=90°,∴平行四边形ABCD为矩形;(2)解:延长DA,CE交于点G,∵四边形ABCD是矩形,∴∠DAB=∠B=90°,AD∥BC,∴∠GAE=90°,∠G=∠ECB,∵E是AB边的中点,∴AE=BE,在△AGE和△BCE中,,∴△AGE≌△BCE(AAS),∴AG=BC,若CE=4,CF=5,设DF=x,根据勾股定理得:CD2=CF2﹣DF2=CG2﹣DG2,即52﹣x2=82﹣(5+x)2,解得:x=,即DF=.24.已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC 的平行线与CE的延长线交于点F,连接DF.(1)求证:AF=DC;(2)请问:AD与CF满足什么条件时,四边形AFDC是矩形,并说明理由.【解答】(1)证明:∵AF∥BC,∴∠AFE=∠DCE,又∵E为AD的中点,∴AE=DE,在△AEF和△DEC中,,∴△AEF≌△DEC(AAS),∴AF=DC;(2)解:当AD=CF时,四边形AFDC是矩形;理由如下:由(1)得:AF=DC且AF∥DC,∴四边形AFDC是平行四边形,又∵AD=CF,∴四边形AFDC是矩形(对角线相等的平行四边形是矩形).25.如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.(1)求证:四边形DEBF是菱形;(2)请判断四边形AGBD是什么特殊四边形?并加以证明.【解答】(1)证明:∵四边形ABCD是平行四边形∴AB∥CD且AB=CD,AD∥BC且AD=BCE,F分别为AB,CD的中点,∴BE=AB,DF=CD,∴BE=DF,∴四边形DEBF是平行四边形在△ABD中,E是AB的中点,∴AE=BE=AB=AD,而∠DAB=60°∴△AED是等边三角形,即DE=AE=AD,故DE=BE∴平行四边形DEBF是菱形.(2)解:四边形AGBD是矩形,理由如下:∵AD∥BC且AG∥DB∴四边形AGBD是平行四边形由(1)的证明知AD=DE=AE=BE,∴∠ADE=∠DEA=60°,∠EDB=∠DBE=30°故∠ADB=90°∴平行四边形AGBD是矩形.26.如图,四边形ABCD中,AB=AC=AD,BC=CD,锐角∠BAC的角平分线AE交BC于点E,AF 是CD边上的中线,且PC⊥CD与AE交于点P,QC⊥BC与AF交于点Q.求证:四边形APCQ 是菱形.【解答】证明:∵AC=AD,AF是CD边上的中线,∴∠AFC=90°,∴∠ACF+∠CAF=90°,∵∠ACF+∠PCA=90°,∴∠PCA=∠CAF,∴PC∥AQ,同理:AP∥QC,∴四边形APCQ是平行四边形.∵AF∥CP,AE∥CQ,∴∠EPC=∠PAF=∠FQC,∵AB=AC,AE平分∠BAC,∴CE=BE=CB(等腰三角三线合一),∵AF是CD边上的中线,∴CF=CD,∵CB=DC,∴CE=CF,∵PC⊥CD,QC⊥BC,∴∠ECP+∠PCQ=∠QCF+∠PCQ=90°,∴∠PCE=∠QCF,∴△PEC≌△QFC(AAS),∴PC=QC,∴四边形APCQ是菱形.27.矩形ABCD中,E是CD上一点,且AE=CE,F是AC上一点FH⊥AE于H,FG⊥CD于G,求证:FH+FG=AD.【解答】证明:连接EF,如图所示:∵FH⊥AE于H,FG⊥CD于G,∴△ACE的面积=△AEF的面积+△CEF的面积=AE•FH+CE•FG,∵AE=CE,∴△ACE的面积=CE(FH+FG),又∵四边形ABCD是矩形,∴AD⊥CD,∴△ACE的面积=CE•AD,∴FH+FG=AD.28.如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB 于点H.(1)求证:四边形AGPH是矩形;(2)在点P在运动过程中,GH是否存在最小值?若存在,请求出,若不存在,请说明理由.【解答】(1)证明∵AC=9 AB=12 BC=15,∴AC2=81,AB2=144,BC2=225,∴AC2+AB2=BC2,∴∠A=90°.∵PG⊥AC,PH⊥AB,∴∠AGP=∠AHP=90°,∴四边形AGPH是矩形;(2)存在.理由如下:连结AP.∴GH=AP.∵当AP⊥BC时AP最短.∴9×12=15•AP.∴AP=.29.如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P (点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE.(1)求证:四边形AEPQ为菱形;(2)当点P在何处时,菱形AEPQ的面积为四边形EFBQ面积的一半?【解答】(1)证明:∵EF∥AB,PQ∥AC,∴四边形AEPQ为平行四边形,∴∠BAD=∠EPA,∵AB=AC,AD平分∠CAB,∴∠CAD=∠BAD,∴∠CAD=∠EPA,∴EA=EP,∴四边形AEPQ为菱形.(2)解:P为EF中点,即AP=AD时,S菱形AEPQ=S四边形EFBQ∵四边形AEPQ为菱形,∴AD⊥EQ,∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴EQ∥BC,又∵EF∥AB,∴四边形EFBQ为平行四边形.作EN⊥AB于N,如图所示:则S菱形AEPQ=EP•EN=EF•EN=S四边形EFBQ.30.在△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC交AD于E,交AC于G,GF⊥BC 于F,连接EF.(1)如图1,求证:四边形AEFG是菱形;(2)如图2,若E为BG的中点,过点E作EM∥BC交AC于M,在不添加任何辅助线的情况下,请直接写出图2中是CM长倍的所有线段.【解答】(1)证明:∵AD⊥BC,GF⊥BC,∴∠ADF=∠GFC=90°,∴AE∥GF,在△ABG和△FBG中,,∴△ABG≌△FBG,∴AG=FG,∵∠FBG+∠BED=90°,∵∠BED=∠AEG,∴∠FBG+∠AEG=90°,∵∠ABG+∠AGE=90°,∵∠ABG=∠FBG,∴∠AEG=∠AGE,∴AE=AG,∴AE=FG,∴四边形AEFG是平行四边形,∵AE=AG∴四边形AEFG是菱形.(2)解:∵四边形AEFG是菱形,∴AE=AG,∵BE=EG,∠BAG=90°,∴AE=BE=EG,∴△AEG是等边三角形,∴∠AGE=60°,在RT△ABG中,∵∠ABG=30°,∴AB=AG,∵∠C=30°,∴BC=2AB,∴BE=GE,EF∥AC,EM∥BC,∴BF=FC,CM=GM,在RT△AEM中,∵∠AME=∠C=30°,∠GEM+∠GME=60°,∴∠GEM=∠GME=30°,∴EG=AG=GM=CM,∵EM∥FC,EF∥CM,∴四边形EFCM是平行四边形,∴AB=BF=CF=EM=CM,∴是CM长倍的所有线段有AB、BF、CF、EM.31.阅读下面短文:如图①,△ABC是直角三角形,∠C=90°,现将△ABC补成矩形,使△ABC的两个顶点为矩形一边的两个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个矩形ACBD和矩形AEFB(如图②)解答问题:(1)设图②中矩形ACBD和矩形AEFB的面积分别为S1、S2,则S1= S2(填“>”“=”或“<”).(2)如图③,△ABC是钝角三角形,按短文中的要求把它补成矩形,那么符合要求的矩形可以画 1 个,利用图③把它画出来.(3)如图④,△ABC是锐角三角形且三边满足BC>AC>AB,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出 3 个,利用图④把它画出来.(4)在(3)中所画出的矩形中,哪一个的周长最小?为什么?【解答】解:(1)=(2)1(3)3(4)以AB为边长的矩形周长最小,设矩形BCED,ACHQ,ABGF的周长分别为L1,L2,L3,BC=a,AC=b,AB=c.易得三个矩形的面积相等,设为S,∴L1=+2a;L2=+2b;L3=+2c.∵L1﹣L2=2(a﹣b)而a﹣b>0,ab﹣s>0,ab>0∴L1﹣L2>0,∴L1>L2,同理可得L2>L3∴以AB为边长的矩形周长最小.32.如图1,菱形ABCD中,点E、F分别为AB、AD的中点,连接CE、CF.(1)求证:CE=CF;(2)如图2,若H为AB上一点,连接CH,使∠CHB=2∠ECB,求证:CH=AH+AB.【解答】(1)证明:∵四边形ABCD是菱形,∴∠B=∠D,AB=BC=CD=AD,∵点E、F分别为AB、AD的中点,∴BE=AB,DF=AD,∴BE=DF,在△BCE和△DCF中,,∴△BCE≌△DCF(SAS),∴CE=CF;(2)证明:延长BA与CF,交于点G,∵四边形ABCD是菱形,∴∠B=∠D,AB=BC=CD=AD,AF∥BC,AB∥CD,∴∠G=∠FCD,∵点F分别为AD的中点,且AG∥CD,∴AG=AB,∵△BCE≌△DCF,∴∠ECB=∠DCF,∵∠CHB=2∠ECB,∴∠CHB=2∠G,∵∠CHB=∠G+∠HCG,∴∠G=∠HCG,∴GH=CH,∴CH=AH+AG=AH+AB.33.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.【解答】(1)证明:在△ABC和△ADC中,,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,在△ABF和△ADF中,,∴△ABF≌△ADF(SAS),∴∠AFD=∠AFB,∵∠AFB=∠CFE,∴∠AFD=∠CFE;(2)证明:∵AB∥CD,∴∠BAC=∠ACD,又∵∠BAC=∠DAC,∴∠CAD=∠ACD,∴AD=CD,∵AB=AD,CB=CD,∴AB=CB=CD=AD,∴四边形ABCD是菱形;(3)当EB⊥CD时,即E为过B且和CD垂直时垂线的垂足,∠EFD=∠BCD,理由:∵四边形ABCD为菱形,∴BC=CD,∠BCF=∠DCF,在△BCF和△DCF中,,∴△BCF≌△DCF(SAS),∴∠CBF=∠CDF,∵BE⊥CD,∴∠BEC=∠DEF=90°,∴∠BCD+∠CBE=∠CDF+∠EFD,∴∠EFD=∠BCD.34.将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;(2)若AB=8,AD=4,求四边形DHBG的面积.【解答】解:(1)四边形DHBG是菱形.理由如下:∵四边形ABCD、FBED是完全相同的矩形,∴∠A=∠E=90°,AD=ED,AB=EB.在△DAB和△DEB中,,∴△DAB≌△DEB(SAS),∴∠ABD=∠EBD.∵AB∥CD,DF∥BE,∴四边形DHBG是平行四边形,∠HDB=∠EBD,∴∠HDB=∠HBD,∴DH=BH,∴▱DHBG是菱形.(2)由(1),设DH=BH=x,则AH=8﹣x,在Rt△ADH中,AD2+AH2=DH2,即42+(8﹣x)2=x2,解得:x=5,即BH=5,∴菱形DHBG的面积为HB•AD=5×4=20.35.如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.(1)求证:四边形ABCF是矩形;(2)若EA=EG,求证:ED=EC.【解答】证明:(1)∵AB∥CD,且FC=AB,∴四边形ABCF为平行四边形,∵∠B=90°,∴四边形ABCF是矩形;(2)∵EA=EG,∴∠EAG=∠EGA=∠FGC,∵四边形ABCF为矩形,∴∠AFC=∠AFD=90°,∴∠D+∠DAF=∠FGC+∠ECD=90°,∴∠D=∠ECD,∴ED=EC.36.如图1,平行四边形ABCD,DE⊥AB.垂足E在BA的延长线上,BF⊥DC,垂足F在DC 的延长线上.(1)求证:四边形BEDF是矩形;(2)如图2,若M、N分别为AD、BC的中点,连接EM、EN、FM、FN,求证:四边形EMFN 是平行四边形.【解答】证明:(1)∵平行四边形ABCD,∴AB∥CD,∴∠ABF+∠F=180°,∠FDE+∠E=180°,∵DE⊥AB.BF⊥DC,∴∠E=90°,∠F=90°,∴∠ABF=90°,∠FDE=90°,∴四边形BEDF是矩形;(2)∵平行四边形ABCD,四边形BEDF是矩形,∴∠NBF+∠BCF=90°,∠EDM+∠ADC=90°,AD∥BC,AD=BC,BF=DE,∴∠ADC=∠BCF,∴∠NBF=∠MDE,∵M、N分别为AD、BC的中点,∴BN=DM,在△BNF与△DME中∴△BNF≌△DME(SAS),∴EM=FN,同理可得:EN=MF,∴四边形EMFN是平行四边形.37.如图1,在Rt△ABC中,∠ACB=90°,点D是边AB的中点,点E在边BC上,AE=BE,点M是AE的中点,联结CM,点G在线段CM上,作∠GDN=∠AEB交边BC于N.(1)如图2,当点G和点M重合时,求证:四边形DMEN是菱形;(2)如图1,当点G和点M、C不重合时,求证:DG=DN.【解答】证明:(1)如图2中,∵AM=ME.AD=DB,∴DM∥BE,∴∠GDN+∠DNE=180°,∵∠GDN=∠AEB,∴∠AEB+∠DNE=180°,∴AE∥DN,∴四边形DMEN是平行四边形,∵DM=BE,EM=AE,AE=BE,∴DM=EM,∴四边形DMEN是菱形.(2)如图1中,取BE的中点F,连接DM、DF.由(1)可知四边形EMDF是菱形,∴∠AEB=∠MDF,DM=DF,∴∠GDN=∠AEB,∴∠MDF=∠GDN,∴∠MDG=∠FDN,∵∠DFN=∠AEB=∠MCE+∠CME,∠GMD=∠EMD+∠CME,、在Rt△ACE中,∵AM=ME,∴CM=ME,∴∠MCE=∠CEM=∠EMD,∴∠DMG=∠DFN,∴△DMG≌△DFN,∴DG=DN.。
矩形_菱形的性质及判定专项练习习题精选

M N OD CBA 矩形,菱形的性质及判定专项练习1.在下列命题中,真命题是()A.两条对角线相等的四边形是矩形B.两条对角线互相垂直的四边形是菱形C.两条对角线互相平分的四边形是平行四边形D.两条对角线互相垂直且相等的四边形是正方形2.已知菱形的两条对角线长为10cm 和24cm, 那么这个菱形的周长为______________, 面积为_______________.3.将两张长10cm 宽3cm 的长方形纸条叠放在一起, 使之成60度角, 那么重叠部分的面积的最大值为________________. 4.一个菱形面积为80, 周长为40, 那么两条对角线长度之和为__________. 5.顺次连接一个特殊四边形的中点, 得到一个菱形. 那么这个特殊四边形是___________. 6.如图,矩形ABCD 的对角线相交于点O ,OF ⊥BC ,CE ⊥BD ,OE :BE=1:3,OF=4,求∠ADB 的度数和BD 的长。
7.如图所示,矩形ABCD 中,M 是BC 的中点,且MA ⊥MD ,若矩形的周长为36cm ,求此矩形的面积。
8.折叠矩形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,如图,若AB=2,BC=1,求AG 。
9.已知:如图,平行四边形ABCD 的四个内角的平分线分别相交于点E ,F ,G ,H ,求证:四边形EFGH 是矩形。
OFEDCBAGEDCBA10.如图,在矩形ABCD 中,E 是AD 上一点,F 是AB 上一点,EFCE ,且,2EFCE DEcm ,矩形ABCD 的周长为16cm ,求AE 与CF 的长.11.如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,(1),画出△AOB 平移后的三角形,其平移的方向为射线AD 的方向,平移的距离为线段AD 的长。
(2)观察平移后的图形,除了矩形ABCD 外还有哪一种特殊的平行四边形?并给出证明。
矩形和菱形的性质与判定经典例题练习

、用中学习:
1.如图,周长为68的矩形ABCD被分成7个全等的矩形,则矩形ABCD勺面积为()
形的较小的内角是度.
精讲精练
例1如图,在矩形ABCD中,AC、BD相较于点O,AE平分.BAD交BC于E,若
.
变式:已知矩形ABCD中,如图2,对角线AC、BD相交于O,AE丄BD于E,若∠DAE:
∠BAE=3:1,则∠EAC=.
例2、如图,在矩形ABCD中,AB=3,AD=4 ,P是AD上的动点,PE_AC于E,PF_BD于F,求PE+PF的值。
D.75°
【探究三】直角三角形斜边上的中线性质
1、根据矩形对角线性质可得到直角三角形斜边上的中线性质:
2、归纳我们已学过的直角三角形的性质:
角:
边:
斜边上的中线:
边与角:
练一练:1、已知直角三角形的周长为14,斜边上的中线长为3.则直角三角形的面积为()
A.5 B.6 C.7 D.8
2、如果一个直角三角形斜边上的中线与斜边上的高所夹的锐角为34°那么这个直角三角
第一课时一一矩形的性质
矩形的性质:
边
角
对角线
对称性
练一练:
1矩形的两条对角线把矩形分成个等腰三角形•
2、矩形具有而平行四边形不具有的性质是()
A对角线互相平分B•两组对边分别相等C•相邻两角互补D•对角线相等
3.已知E是矩形ABCD的Байду номын сангаасBC的中点,那么SUed=S矩形ABCD()
1
6
E,且CE=DE若AB=2AD,贝q∠ADE等于()
中考复习《矩形、菱形、正方形》测试题(含答案)
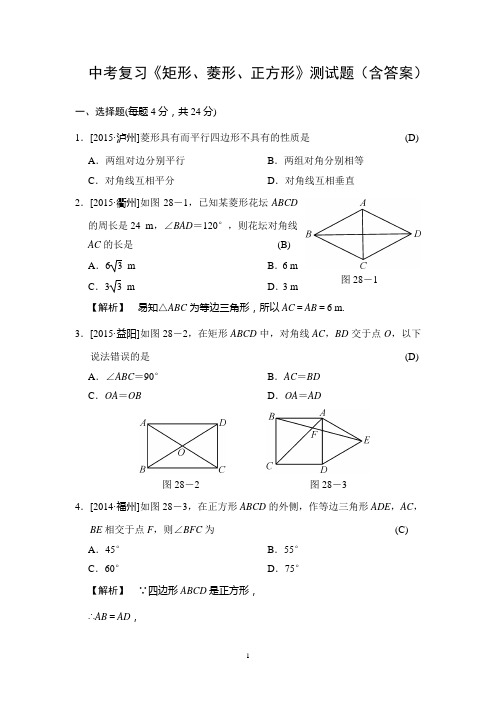
中考复习《矩形、菱形、正方形》测试题(含答案)一、选择题(每题4分,共24分)1.[2015·泸州]菱形具有而平行四边形不具有的性质是(D) A.两组对边分别平行B.两组对角分别相等C.对角线互相平分D.对角线互相垂直2.[2015·衢州]如图28-1,已知某菱形花坛ABCD的周长是24 m,∠BAD=120°,则花坛对角线AC的长是(B)A.6 3 m B.6 m图28-1 C.3 3 m D.3 m【解析】易知△ABC为等边三角形,所以AC=AB=6 m.3.[2015·益阳]如图28-2,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是(D) A.∠ABC=90°B.AC=BDC.OA=OB D.OA=AD图28-2 图28-34.[2014·福州]如图28-3,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为(C) A.45°B.55°C.60°D.75°【解析】∵四边形ABCD是正方形,∴AB=AD,又∵△ADE 是等边三角形, ∴AE =AD =DE ,∠DAE =60°, ∴AB =AE ,∴∠ABE =∠AEB ,∠BAE =90°+60°=150°, ∴∠ABE =(180°-150°)÷2=15°, 又∵∠BAC =45°, ∴∠BFC =45°+15°=60°.5.[2015·临沂]如图28-4,四边形ABCD 为平行四边形,延长AD 到E ,使DE =AD ,连结EB ,EC ,DB .添加一个条件,不能使四边形DBCE 成为矩形的是 (B) A .AB =BEB .BE ⊥DCC .∠ADB =90°D .CE ⊥DE【解析】 因为四边形ABCD 为平行四边形,所以AD 綊BC ,因为DE =AD ,所以DE 綊BC所以四边形EDBC 为平行四边形,A .假若AB =BE ,因为AB =BE ,AD =DE ,BD =BD ,所以△ADB ≌△EDB ,所以∠BDE =90°,所以四边形EDBC 为矩形; B .假若BE ⊥DC ,可得四边形EDBC 为菱形;C .假若∠ADB =90°,所以∠EDB =90°,所以四边形EDBC 为矩形;D .假若CE ⊥DE ,所以∠DEC =90°,所以四边形EDBC 为矩形,故选B. 6.[2015·日照]小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件①AB =BC ,②∠ABC =90°,③AC =BD ,④AC ⊥BD 中选两个作为补充条件,使▱ABCD 成为正方形(如图28-5)现有下列四种选法,你图28-4图28-5认为其中错误的是(B)A.①②B.②③C.①③D.②④【解析】此题考查正方形的判定,即在▱ABCD的基础上,需要再同时具备矩形和菱形的特征.①是菱形的特征;②是矩形的特征;③是矩形的特征,④是菱形的特征.而B中都是矩形的特征,故选B.二、填空题(每题4分,共20分)7.[2015·铜仁]已知一个菱形的两条对角线长分别为6 cm和8 cm,则这个菱形的面积为__24__cm2.8.[2014·衡阳]如图28-6,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为__10__.9.[2015·上海]已知E是正方形ABCD的对角线AC上一点,图28-6 AE=AD,过点E作AC的垂线,交边CD于点F,那么∠F AD=__22.5__度.10.[2014·淄博]已知▱ABCD,对角线AC,BD相交于点O,请你添加一个适当的条件,使▱ABCD成为一个菱形.你添加的条件是__AB=BC或AC⊥BD等__.11.[2014·资阳]如图28-7,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为__6__.图28-7【解析】如答图,连结BD,DE,∵四边形ABCD是正方形,∴点B与点D关于直线AC对称,∴DE的长即为BQ+QE的最小值,∵DE=BQ+QE=5,∴△BEQ周长的最小值=DE+BE=5+1=6.三、解答题(共20分)12.(10分)[2015·安顺]如图28-8,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于图28-8F.(1)求证:AE=DF;(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.证明:(1)∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形,∴AE=DF;(2)若AD平分∠BAC,四边形AEDF是菱形,理由如下:∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形,∵AD平分∠BAC,∴∠EAD=∠F AD,∵AE∥DF,∴∠EAD=ADF,∠DAF=∠FDA,∴AF=DF,∴平行四边形AEDF为菱形.13.(10分)[2015·青岛]已知:如图28-9,在△ABC中,AB =AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.(1)求证:△ABD≌△CAE;图28-9(2)连结DE ,线段DE 与AB 之间有怎样的位置和数量关系?请证明你的结论. 解:(1)证明:∵AB =AC ,AD 是BC 边上的中线, ∴AD ⊥BC ,BD =CD . ∵AE ∥BC ,CE ⊥AE , ∴四边形ADCE 是矩形, ∴AD =CE .在Rt △ABD 与Rt △CAE 中, ⎩⎪⎨⎪⎧AD =CE ,AB =CA ,∴△ABD ≌△CAE (HL );(2)DE ∥AB ,DE =AB .证明如下: 如答图所示,∵四边形ADCE 是矩形, ∴AE =CD =BD ,AE ∥BD , ∴四边形ABDE 是平行四边形, ∴DE ∥AB ,DE =AB .14.(10分)[2014·扬州]如图28-10,已知Rt △ABC ,∠ABC =90°,先把△ABC 绕点B 顺时针旋转90°后至△DBE ,再把△ABC 沿射线AB 平移至△FEG ,DE ,FG 相交于点H .(1)判断线段DE ,FG 的位置关系,并说明理由; (2)连结CG ,求证:四边形CBEG 是正方形. 解:(1)DE ⊥FG ,理由如下:由题意得∠A =∠EDB =∠GFE ,∠ABC =∠DBE =90°,第13题答图图28-10∴∠BDE+∠BED=90°.∴∠GFE+∠BED=90°,∴∠FHE=90°,即DE⊥FG;(2)证明:∵△ABC沿射线AB平移至△FEG,∴CB∥GE,CB=GE.∴四边形CBEG是平行四边形.∵∠ABC=∠GEF=90°,∴四边形CBEG是矩形.∵BC=BE,∴四边形CBEG是正方形.15.(10分)[2015·南京]如图28-11,AB∥CD,点E,F分别在AB,CD上,连结EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.(1)求证:四边形EGFH是矩形;(2)小明在完成(1)的证明后继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD交于点P,Q,得到四边形MNQP.此时,他猜想四边形MNQP是菱形,请在下列框图中补全他的证明思路.小明的证明思路由AB∥CD,MN∥EF,易证四边形MNQP是平行四边形,要证▱MNQP是菱形,只要证MN=NQ.由已知条件__FG平分∠CFE__,MN∥EF,可证NG=NF,故只要证GM=FQ,即证△MEG≌△QFH,易证__GE=FH__,__∠GME =∠FQH__.故只要证∠MGE=∠QFH.易证∠MGE=∠GEF,∠QFH=∠EFH,__∠GEF=∠EFH__,即可得证.图28-11解:(1)证明:∵EH平分∠BEF.∴∠FEH=12∠BEF,∵FH平分∠DFE,∴∠EFH=12∠DFE,∵AB∥CD,∴∠BEF+∠DFE=180°,∴∠FEH+∠EFH=12(∠BEF+∠DFE)=12×180°=90°,又∵∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°-(∠FEH+∠EFH)=180°-90°=90°,同理可证,∠EGF=90°,∵EG平分∠AEF,∴∠FEG=12∠AEF,∵EH平分∠BEF,∴∠FEH=12∠BEF,∵点A,E,B在同一条直线上.∴∠AEB=180°,即∠AEF+∠BEF=180°.∴∠FEG+∠FEH=12(∠AEF+∠BEF)=12×180°=90°,即∠GEH=90°.∴四边形EGFH是矩形;(2)本题答案不唯一,下列解法供参考.例如,FG平分∠CFE;GE=FH;∠GME =∠FQH;∠GEF=∠EFH.16.(6分)[2015·资阳]若顺次连结四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是(D) A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形17.(10分)如图28-12,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;…;按此规律继续下去,则四边形A2B2C2D2的周长是__20__;四边形A2 016B2 016C2 016D2 016的周长是__521 005__.图28-12。
矩形、菱形、正方形辅导练习题

1矩形、菱形、正方形测试题 姓名: 成绩:一选择题1、矩形具有而一般平行四边形不具有的性质是( ).A 、 对角线相等B 、 对边相等C 、 对角相等D 、 对角线互相平分2、下列对矩形的判定:“(1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(4)有四个角是直角的四边形是矩形;(5)四个角都相等的四边是矩形;(6)对角线相等,且有一个直角的四边形是矩形;(7)一组邻边垂直,一组对边平行且相等的四边形是矩形;(8)对角线相等且互相垂直的四边形是矩形”中,正确的个数有( ) A 、3 个 B 、4个 C 、5个 D 、6个3、下列性质中,菱形具有而矩形不一定具有的性质是( )A 对边平行且相等B 对角线互相平分C 内角和等于外角和D 每一条对角线所在直线都是对称轴4、下列条件中,能判定一个四边形为菱形的条件是( )A 、对角线互相平分的四边形B 、对角线互相垂直且平分的四边形C 、对角线相等的四边形D 、对角线相等且互相垂直的四边形5、已知四边形ABCD 是平行四边形,下列结论中不一定正确的是( )A 、AB=CDB 、AC=BDC 、当AC ⊥BD 时,它是菱形 D 、当∠ABC=90°时,它是矩形6、正方形具有而矩形不一定具有的性质是( )。
A .四个角都是直角B .对角线互相平分C .对角线相等D .对角线互相垂直7、正方形具有而菱形不一定具有的性质是( )。
A 、对角线相等B 、对角线互相垂直平分C 、四条边相等D 、一条对角线平分一组对角8、下列条件中不能判定四边形是正方形的条件是( )。
A 、对角线互相垂直且相等的四边形B 、一条对角线平分一组对角的矩形C 、对角线相等的棱形D 、对角线互相垂直的矩形9、下列命题中,假命题是( )。
A 、四个内角都相等的四边形是矩形B 、四条边都相等的平行四边形是正方形C 、既是菱形又是矩形的四边形是正方形D 、对角线互相垂直的平行四边形是菱形10、在四边形ABCD 中,O 是对角线的交点,能判定四边形是正方形的条件是( )。
中考数学专项训练 矩形、菱形与正方形(含解析)

矩形、菱形与正方形一、选择题1.矩形具有而菱形不具有的性质是()A.两组对边分别平行 B.对角线相等C.对角线互相平分D.两组对角分别相等2.如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是()A.矩形 B.菱形 C.正方形D.梯形3.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于()A.B.C.D.4.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=()A. cm B. cm C. cm D. cm5.如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有()A.1个B.2个C.3个D.4个二、填空题6.若菱形的两条对角线分别为2和3,则此菱形的面积是.7.在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .8.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= .9.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是.10.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的序号是(把你认为正确的都填上).三、解答题(共40分)11.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.12.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.13.如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.14.如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,(1)的值为;(2)求证:AE=EP;(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.矩形、菱形与正方形参考答案与试题解析一、选择题1.矩形具有而菱形不具有的性质是()A.两组对边分别平行 B.对角线相等C.对角线互相平分D.两组对角分别相等【考点】矩形的性质;菱形的性质.【分析】根据矩形与菱形的性质对各选项分析判断后利用排除法求解.【解答】解:A、矩形与菱形的两组对边都分别平行,故本选项错误;B、矩形的对角线相等,菱形的对角线不相等,故本选项正确;C、矩形与菱形的对角线都互相平分,故本选项错误;D、矩形与菱形的两组对角都分别相等,故本选项错误.故选B.【点评】本题考查了矩形的性质,菱形的性质,熟记两图形的性质是解题的关键.2.如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是()A.矩形 B.菱形 C.正方形D.梯形【考点】旋转的性质;矩形的判定.【分析】根据旋转的性质可得AE=CE,DE=EF,再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF是平行四边形,然后利用等腰三角形三线合一的性质求出∠ADC=90°,再利用有一个角是直角的平行四边形是矩形解答.【解答】解:∵△ADE绕点E旋转180°得△CFE,∴AE=CE,DE=EF,∴四边形ADCF是平行四边形,∵AC=BC,点D是边AB的中点,∴∠ADC=90°,∴四边形ADCF是矩形.故选:A.【点评】本题考查了旋转的性质,矩形的判定,主要利用了对角线互相平分的四边形是平行四边形,有一个角是直角的平行四边形是矩形的判定方法,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.3.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于()A.B.C.D.【考点】勾股定理;菱形的性质;矩形的性质.【分析】首先由菱形的四条边都相等与矩形的四个角是直角,即可得到直角△ABM中三边的关系.【解答】解:∵四边形MBND是菱形,∴MD=MB.∵四边形ABCD是矩形,∴∠A=90°.设AB=x,AM=y,则MB=2x﹣y,(x、y均为正数).在Rt△ABM中,AB2+AM2=BM2,即x2+y2=(2x﹣y)2,解得x=y,∴MD=MB=2x﹣y=y,∴==.故选:C.【点评】此题考查了菱形与矩形的性质,以及直角三角形中的勾股定理.解此题的关键是注意数形结合思想与方程思想的应用.4.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=()A. cm B. cm C. cm D. cm【考点】菱形的性质;勾股定理;解直角三角形.【分析】先求出菱形的边长,然后利用面积的两种表示方法求出DH,在Rt△DHB中求出BH,然后得出AH,利用tan∠HAG的值,可得出GH的值.【解答】解:∵四边形ABCD是菱形,对角线AC=8cm,BD=6cm,∴AO=4cm,BO=3cm,在Rt△AOB中,AB==5cm,∵BD×AC=AB×DH,∴DH=cm,在Rt△DHB中,BH==cm,则AH=AB﹣BH=cm,∵tan∠HAG===,∴GH=AH=cm.故选:B.【点评】本题考查了菱形的性质、解直角三角形及三角函数值的知识,注意菱形的面积等于对角线乘积的一半,也等于底乘高.5.如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有()A.1个B.2个C.3个D.4个【考点】正方形的性质.【分析】根据四边形ABCD是正方形及CE=DF,可证出△ADE≌△BAF,则得到:①AE=BF,以及△ADE 和△BAF的面积相等,得到;④S△AOB=S四边形DEOF;可以证出∠ABO+∠BAO=90°,则②AE⊥BF一定成立.错误的结论是:③AO=OE.【解答】解:∵四边形ABCD是正方形,∴CD=AD∵CE=DF∴DE=AF∴△ADE≌△BAF∴AE=BF(故①正确),S△ADE=S△BAF,∠DEA=∠AFB,∠EAD=∠FBA∵S△AOB=S△BAF﹣S△AOF,S四边形DEOF=S△ADE﹣S△AOF,∴S△AOB=S四边形DEOF(故④正确),∵∠ABF+∠AFB=∠DAE+∠D EA=90°∴∠AFB+∠EAF=90°∴AE⊥BF一定成立(故②正确).假设AO=OE,∵AE⊥BF(已证),∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),∵在Rt△BCE中,BE>BC,∴AB>BC,这与正方形的边长AB=BC相矛盾,∴,假设不成立,AO≠OE(故③错误);故错误的只有一个.故选:A.【点评】本题考查了正方形的四条边都相等,每一个角都是直角的性质,全等三角形的判定与性质,综合题但难度不大,求出△ADE≌△BAF是解题的关键,也是本题的突破口.二、填空题6.若菱形的两条对角线分别为2和3,则此菱形的面积是 3 .【考点】菱形的性质.【分析】菱形的面积是对角线乘积的一半,由此可得出结果即可.【解答】解:由题意,知:S菱形=×2×3=3,故答案为:3.【点评】本题考查了菱形的面积两种求法:(1)利用底乘以相应底上的高;(2)利用菱形的特殊性,菱形面积=×两条对角线的乘积;具体用哪种方法要看已知条件来选择.7.在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= 5 .【考点】含30度角的直角三角形;矩形的性质.【分析】根据矩形的性质,可以得到△AOB是等边三角形,则可以求得OA的长,进而求得AB的长.【解答】解:∵四边形ABCD是矩形,∴OA=OB又∵∠AOB=60°∴△AOB是等边三角形.∴AB=OA=AC=5,故答案是:5.【点评】本题考查了矩形的性质,正确理解△AOB是等边三角形是关键.8.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= 20°.【考点】旋转的性质;矩形的性质.【分析】根据矩形的性质得∠B=∠D=∠BAD=90°,根据旋转的性质得∠D′=∠D=90°,∠4=α,利用对顶角相等得到∠1=∠2=110°,再根据四边形的内角和为360°可计算出∠3=70°,然后利用互余即可得到∠α的度数.【解答】解:如图,∵四边形ABCD为矩形,∴∠B=∠D=∠BAD=90°,∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′,∴∠D′=∠D=90°,∠4=α,∵∠1=∠2=110°,∴∠3=360°﹣90°﹣90°﹣110°=70°,∴∠4=90°﹣70°=20°,∴∠α=20°.故答案为:20°.【点评】本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了矩形的性质.9.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是10 .【考点】轴对称﹣最短路线问题;正方形的性质.【分析】由正方形性质的得出B、D关于AC对称,根据两点之间线段最短可知,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,进而利用勾股定理求出即可.【解答】解:如图,连接DE,交AC于P,连接BP,则此时PB+PE的值最小.∵四边形ABCD是正方形,∴B、D关于AC对称,∴PB=PD,∴PB+PE=PD+PE=DE.∵BE=2,AE=3BE,∴AE=6,AB=8,∴DE==10,故PB+PE的最小值是10.故答案为:10.【点评】本题考查了轴对称﹣最短路线问题,正方形的性质,解此题通常是利用两点之间,线段最短的性质得出.10.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的序号是①②④(把你认为正确的都填上).【考点】正方形的性质;全等三角形的判定与性质;等边三角形的性质.【专题】压轴题.【分析】根据三角形的全等的知识可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据线段垂直平分线的知识可以判断③的正误,利用解三角形求正方形的面积等知识可以判断④的正误.【解答】解:∵四边形ABCD是正方形,∴AB=AD,∵△AEF是等边三角形,∴AE=AF,在Rt△ABE和Rt△ADF中,,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∵BC=DC,∴BC﹣BE=CD﹣DF,∴CE=CF,∴①说法正确;∵CE=CF,∴△ECF是等腰直角三角形,∴∠CEF=45°,∵∠AEF=60°,∴∠AEB=75°,∴②说法正确;如图,连接AC,交EF于G点,∴AC⊥EF,且AC平分EF,∵∠CAF≠∠DAF,∴DF≠FG,∴BE+DF≠EF,∴③说法错误;∵EF=2,∴CE=CF=,设正方形的边长为a,在Rt△ADF中,AD2+DF2=AF2,即a2+(a﹣)2=4,解得a=,则a2=2+,S正方形ABCD=2+,④说法正确,故答案为:①②④.【点评】本题主要考查正方形的性质的知识点,解答本题的关键是熟练掌握全等三角形的证明以及辅助线的正确作法,此题难度不大,但是有一点麻烦.三、解答题(共40分)11.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.【考点】矩形的判定;全等三角形的判定与性质.【专题】证明题.【分析】(1)根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明△AEF和△DEC全等,根据全等三角形对应边相等可得AF=CD,再利用等量代换即可得证;(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形,再根据一个角是直角的平行四边形是矩形,可知∠ADB=90°,由等腰三角形三线合一的性质可知必须是AB=AC.【解答】解:(1)BD=CD.理由如下:依题意得AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AEF和△DEC中,,∴△AEF≌△DEC(AAS),∴AF=CD,∵AF=BD,∴BD=CD;(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,∵AB=AC,BD=CD(三线合一),∴∠ADB=90°,∴▱AFBD是矩形.【点评】本题考查了矩形的判定,全等三角形的判定与性质,平行四边形的判定,是基础题,明确有一个角是直角的平行四边形是矩形是解本题的关键.12.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.【考点】菱形的判定与性质;三角形中位线定理.【分析】从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以是菱形;∠BCF是120°,所以∠EBC为60°,所以菱形的边长也为4,求出菱形的高面积就可求.【解答】(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC,又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC,∴四边形BCFE是平行四边形,又∵BE=FE,∴四边形BCFE是菱形;(2)解:∵∠BCF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴菱形的边长为4,高为2,∴菱形的面积为4×2=8.【点评】本题考查菱形的判定和性质以及三角形中位线定理,以及菱形的面积的计算等知识点.13.如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.【考点】正方形的性质;全等三角形的判定与性质.【专题】证明题.【分析】(1)根据正方形的性质可得AB=AD,∠BAE=∠D=90°,再根据同角的余角相等求出∠ABE=∠DAF,然后利用“角边角”证明△ABE和△DAF全等,再根据全等三角形的证明即可;(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,然后与(1)相同.【解答】(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,∵在△ABE和△DAF中,,∴△ABE≌△DAF(ASA),∴AF=BE;(2)解:MP与NQ相等.理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,∵AB∥CD,AD∥BC,∴四边形AMPF与四边形BNQE是平行四边形,∴AF=PM,BE=NQ,∵在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,∵在△ABE和△DAF中,,∴△ABE≌△DAF(ASA),∴AF=BE;∴MP=NQ.【点评】本题考查了正方形的性质,全等三角形的判定与性质,主要利用了正方形的四条边都相等,每一个角都是直角的性质,同角的余角相等的性质,利用三角形全等证明相等的边是常用的方法之一,要熟练掌握并灵活运用.14.如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,(1)的值为;(2)求证:AE=EP;(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.【考点】正方形的性质;全等三角形的判定与性质;平行四边形的判定.【分析】(1)由正方形的性质可得:∠B=∠C=90°,由同角的余角相等,可证得:∠BAE=∠CEF,根据同角的正弦值相等即可解答;(2)在BA边上截取BK=BE,连接KE,根据角角之间的关系得到∠AKE=∠ECP,由AB=CB,BK=BE,得AK=EC,结合∠KAE=∠CEP,证明△AKE≌△ECP,于是结论得出;(3)作DM⊥AE于AB交于点M,连接ME、DP,易得出DM∥EP,由已知条件证明△ADM≌△BAE,进而证明MD=EP,四边形DMEP是平行四边形即可证出.【解答】(1)解:∵四边形ABCD是正方形,∴∠B=∠D,∵∠AEP=90°,∴∠BAE=∠FEC,在Rt△ABE中,AE==,∵sin∠BAE==sin∠FEC=,∴=,解法二:由上得∠BAE=∠FEC,∵∠BAE=∠FEC,∠B=∠DCB,∴△ABE∽△ECF,∴=,(2)证明:在BA边上截取BK=BE,连接KE,∵∠B=90°,BK=BE,∴∠BKE=45°,∴∠AKE=135°,∵CP平分外角,∴∠DCP=45°,∴∠ECP=135°,∴∠AKE=∠ECP,∵AB=CB,BK=BE,∴AB﹣BK=BC﹣BE,即:AK=EC,由第一问得∠KAE=∠CEP,∵在△AKE和△ECP中,,∴△AKE≌△ECP(ASA),∴AE=EP;(3)答:存在.证明:作DM⊥AE交AB于点M,则有:DM∥EP,连接ME、DP,∵在△ADM与△BAE中,,∴△ADM≌△BAE(ASA),∴MD=AE,∵AE=EP,∴MD=EP,∴MD EP,∴四边形DMEP为平行四边形.【点评】此题考查了相似三角形的判定与性质,全等三角形的判定与性质以及正方形的性质等知识.此题综合性很强,图形比较复杂,解题的关键是注意数形结合思想的应用与辅助线的准确选择.。
矩形与菱形同步练习

6.1-6.2 矩形与菱形一、精心选一选(每小题3分,共30分)1.已知一矩形的周长是24cm ,相邻两边之比是1:2,那么这个矩形的面积是…………( ) A .24cm 2B .32cm 2C .48cm 2D .128cm 22.矩形具有而一般的平行四边形不具有的特征是…………………………………( ) A .对角线相等B .对边相等C .对角相等D .对角线互相平分3.下列图形既是轴对称图形,又是中心对称图形的是……………………………………( ) A .矩形B .直角三角形C .等腰三角形D .平行四边形4.下列条件中,不能判定四边形ABCD 是菱形的是………………………………………( ) A .□ ABCD 中,AB =BC B .□ ABCD 中,AC ⊥BD C .□ ABCD 中,AC =BDD .□ ABCD 中,AC 平分∠BAD5.若直角三角形中两直角边的长分别为12和5,则斜边上的中线是……………………( ) A .13B .6C .6.5D .6.5或66.菱形和矩形都具有的性质是 ……………………………………………………………( ) A .对角线相等B .对角线互相平分C .对角线平分一组对角D .对角线互相垂直7.已知:如图,在矩形ABCD 中,DE ⊥AC,∠ADE=21∠CDE,那么∠BDC 等于…………( ) A .60°B .45°C .30°D .22.5°8.已知菱形的边长和一条对角线的长均为2cm ,则菱形的面积为………………………( )A .23cmB .24cmC2D .29.菱形相邻两角的比为1:2,那么菱形的对角线与边长的比为…………………………( ) A .1:2:3 B .1:2:1C .1:3:2D .1:3:110.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB =3,折叠后,点C 落在AD 边上的C 1 处,并且点B 落在EC 1边上的B 1处.则BC 的长为( ) A .3B .2C .3D .32CB AD二、专心填一填(每小题3分,共30分)11.若矩形的一条角平分线分一边为3cm 和5cm 两部分,则矩形的周长为 . 12.如图,四边形ABCD 是平行四边形,使它成为矩形的条件可以是 . 13.若矩形短边长4cm ,两对角线的夹角为60度,则对角线长是 cm .14.如图,在菱形ABCD 中,∠BAD =80度,AB 的垂直平分线交对角线AC 于点F ,E 为垂足,连接DF ,则∠CDF 的度数为 .(第12题图) (第14题图) (第16题图) (第17题图)15.顺次连结对角线互相垂直的四边形各边中点所得的四边形是 . 16.如图,一斜坡AB 的中点为D ,BC =1,CD =1.5,则斜坡的坡长 . 17.如图,在扇形中,∠AOB =90度,OA=5,C 是弧AB 上一点,且CD ⊥OB ,CE ⊥OA ,垂足分别为点D 、E ,则DE = .18.菱形OABC在平面直角坐标系中的位置如图所示,45AOC OC ∠==°,B 的坐标为 .19.如图,一活动菱形衣架中,菱形的边长均为16cm ,若墙上钉子间的距离16cm AB BC ==, 则1=∠ 度.(第18题图) (第19题图) (第20题图)20.如图,两张宽为1cm 的矩形纸条交叉叠放,其中重叠部分部分是四边形ABCD,已知∠BAD=30°则重叠部分的面积是 cm 2. 三、耐心做一做(本题有5小题,共40分)21.(本题6分)已知:如图所示,在矩形ABCD 中,AF =BE .求证:DE =CF .1A B CA D CB22.(本题8分)如图 ,ABCD 是菱形,对角线AC 与BD 相交于O ,306ACD BD ∠==°,.(1)求证:△ABD 是正三角形; (2)求 AC 的长(结果可保留根号).23.(本题8分)如图,在矩形ABCD 中,AC 与BD 相交于一点O ,AE 平分∠BAD,若∠EAO=15°,求∠BOE 的度数.O DCBA。
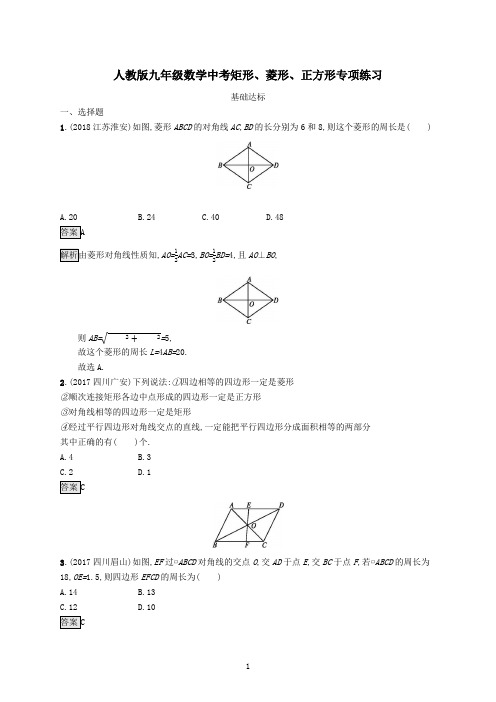
人教版九年级数学中考矩形、菱形、正方形专项练习及参考答案
人教版九年级数学中考矩形、菱形、正方形专项练习基础达标一、选择题1.(2018江苏淮安)如图,菱形ABCD 的对角线AC ,BD 的长分别为6和8,则这个菱形的周长是( )A.20B.24C.40D.48,AO=12AC=3,BO=12BD=4,且AO ⊥BO ,则AB=√AA 2+AA 2=5, 故这个菱形的周长L=4AB=20. 故选A.2.(2017四川广安)下列说法:①四边相等的四边形一定是菱形②顺次连接矩形各边中点形成的四边形一定是正方形 ③对角线相等的四边形一定是矩形④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分其中正确的有( )个. A.4 B.3C.2D.13.(2017四川眉山)如图,EF 过▱ABCD 对角线的交点O ,交AD 于点E ,交BC 于点F ,若▱ABCD 的周长为18,OE=1.5,则四边形EFCD 的周长为( ) A.14 B.13C.12D.104.(2018贵州遵义)如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为()A.10B.12C.16D.18PM⊥AD于点M,交BC于点N.则四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,×2×8=8,∴S△DFP=S△PBE=12∴S阴影=8+8=16,故选C.5.(2017山东枣庄)如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=A(x<0)的图象经过顶点B,则k的值为()AA.-12B.-27C.-32D.-366.(2018江苏无锡)如图,已知点E是矩形ABCD的对角线AC上的一动点,正方形EFGH的顶点G,H都在边AD上,若AB=3,BC=4,则tan ∠AFE的值()A.等于37B.等于√33C.等于34D.随点E位置的变化而变化EF∥AD,∴∠AFE=∠FAG,△AEH∽△ACD,∴AAAA =AAAA=34.设EH=3x,AH=4x,∴HG=GF=3x,∴tan∠AFE=tan∠FAG=AA AA =3A3A+4A=37.故选A.二、填空题7.(2018湖南株洲)如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为..5四边形ABCD是矩形,∴AC=BD=10,BO=DO=12BD,∴OD=12BD=5,∵点P,Q分别是AO,AD的中点,∴PQ是△AOD的中位线,∴PQ=12DO=2.5.8.(2018广东广州)如图,若菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,则点C的坐标是.-5,4)菱形ABCD的顶点A,B的坐标分别为(3,0),(-2,0),点D在y轴上,∴AB=5,∴AD=5,∴由勾股定理知:OD=√AA2-AA2=√52-32=4,∴点C的坐标是(-5,4).9.(2018湖北武汉)以正方形ABCD的边AD为边作等边三角形ADE,则∠BEC的度数是.150°1,图1∵四边形ABCD为正方形,△ADE为等边三角形,∴AB=BC=CD=AD=AE=DE,∠BAD=∠ABC=∠BCD=∠ADC=90°,∠AED=∠ADE=∠DAE=60°,∴∠BAE=∠CDE=150°,又AB=AE,DC=DE,∴∠AEB=∠CED=15°,则∠BEC=∠AED-∠AEB-∠CED=30°.如图2,图2∵△ADE是等边三角形,∴AD=DE,∵四边形ABCD是正方形,∴AD=DC,∴DE=DC,∴∠CED=∠ECD,∴∠CDE=∠ADC-∠ADE=90°-60°=30°,∴∠CED=∠ECD=1(180°-30°)=75°,同理∠BEA=∠ABE=75°,2∴∠BEC=360°-75°×2-60°=150°.三、解答题10.如图,在菱形ABCD 中,对角线AC 与BD 交于点O.过点C 作BD 的平行线,过点D 作AC 的平行线,两直线相交于点E.(1)求证:四边形OCED 是矩形;(2)若CE=1,DE=2,则ABCD 的面积是多少?四边形ABCD 是菱形,∴AC ⊥BD , ∴∠COD=90°. ∵CE ∥OD ,DE ∥OC ,∴四边形OCED 是平行四边形,又∠COD=90°,∴平行四边形OCED 是矩形.(1)知,平行四边形OCED 是矩形,则CE=OD=1,DE=OC=2.∵四边形ABCD 是菱形, ∴AC=2OC=4,BD=2OD=2, ∴菱形ABCD 的面积为12AC ·BD=12×4×2=4. 能力提升一、选择题1.下列说法中,正确的个数为( )①对顶角相等;②两直线平行,同旁内角相等; ③对角线互相垂直的四边形为菱形;④对角线互相垂直平分且相等的四边形为正方形.A.1B.2C.3D.4对顶角相等,故①正确;②两直线平行,同旁内角互补,故②错误;③对角线互相垂直且平分的四边形为菱形,故③错误; ④对角线互相垂直平分且相等的四边形为正方形,故④正确,故选B .2.(2018山东枣庄)如图,在矩形ABCD 中,点E 是边BC 的中点,AE ⊥BD ,垂足为F ,则tan ∠BDE 的值是( )A.√24B.14C.13D.√23四边形ABCD 是矩形,∴AD=BC ,AD ∥BC , ∵点E 是边BC 的中点, ∴BE=12BC=12AD , ∴△BEF ∽△DAF , ∴AA AA =AA AA =12, ∴EF=12AF , ∴EF=13AE ,∵点E 是边BC 的中点, ∴由矩形的对称性得:AE=DE , ∴EF=13DE ,设EF=x ,则DE=3x , ∴DF=√AA 2-AA 2=2√2x , ∴tan ∠BDE=AAAA =2√2A =√24.故选A.3.如图,在Rt △ABC 中,∠C=90°,AC=BC=6cm,点P 从点A 出发,沿AB 方向以每秒√2 cm 的速度向终点B 运动;同时,动点Q 从点B 出发沿BC 方向以每秒1 cm 的速度向终点C 运动,将△PQC 沿BC 翻折,点P 的对应点为点P'.设Q 点运动的时间为t s,若四边形QPCP'为菱形,则t 的值为( )A.√2B.2C.2√2D.3PP',交BC于N点,过P作PM⊥AC,垂足为M.若运动t s时四边形QPCP'为菱形,则PQ=PC,PN⊥BC,四边形PMCN为矩形,BQ=t,AP=√2t,PM=NC=t,∴QC=2t,∴BC=BQ+QC=t+2t=3t=6cm,∴t=2,故选B.4.(2018河南)如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1 cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为()图1图2A.√5B.2D.2√5C.52D作DE⊥BC于点E由题图2可知,点F由点A到点D用时为a s,△FBC的面积为a cm2.∴AD=a.DE·AD=a.∴12∴DE=2.当点F从D到B时,用√5s,∴BD=√5.Rt△DBE中,BE=√AA2-AA2=√(√5)2-22=1,∵ABCD是菱形,∴EC=a-1,DC=a.Rt△DEC中,a2=22+(a-1)2,.解得a=52故选C.5.(2017广东)如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是()A.①③B.②③C.①④D.②④二、填空题6.(2018山东潍坊)如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x 轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C'D'的位置,B'C'与CD相交于点M,则点M的坐标为.)-1,√33,连接AM ,∵将边长为1的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB'C'D', ∴AD=AB'=1,∠BAB'=30°, ∴∠B'AD=60°,在Rt △ADM 和Rt △AB'M 中,∵{AA =AA ',AA =AA ,∴Rt △ADM ≌Rt △AB'M (HL), ∴∠DAM=∠B'AM=12∠B'AD=30°, ∴DM=AD tan ∠DAM=1×√33=√33, ∴点M 的坐标为(-1,√33).三、解答题 7.如图所示,在△ABC 中,点O 是AC 边上的一个动点,过O 作直线MN ∥BC ,设MN 交∠ACB 的平分线于点E ,交∠ACB 的外角平分线于点F.(1)求证:OE=OF ;(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论.MN ∥BC ,∴∠OEC=∠BCE.又∠OCE=∠BCE ,∴∠OEC=∠OCE ,∴OE=OC.同理可证OF=OC ,∴OE=OF.O 运动到AC 中点时,四边形AECF 是矩形.证明:∵CE ,CF 分别是∠ACB 的内,外角平分线.∴∠OCE+∠OCF=12(∠ACB+∠ACD )=12×180°=90°,即∠ECF=90°,又∵OE=OF ,∴当O 点运动到AC 中点时,OA=OC ,四边形AECF 是矩形.8.(2018贵州遵义)如图,正方形ABCD的对角线交于点O,点E,F分别在AB,BC上(AE<BE),且∠EOF=90°,OE,DA的延长线交于点M,OF,AB的延长线交于点N,连接MN.(1)求证:OM=ON;(2)若正方形ABCD的边长为4,E为OM的中点,求MN的长.四边形ABCD是正方形,∴OA=OB,∠DAO=45°,∠OBA=45°,∴∠OAM=∠OBN=135°,∵∠EOF=90°,∠AOB=90°,∴∠AOM=∠BON,∴△OAM≌△OBN(ASA),∴OM=ON.,过点O作OH⊥AD于点H,∵正方形的边长为4,∴OH=HA=2,∵E为OM的中点,∴HM=4,则OM=√22+42=2√5,由(1)知OM=ON,∴MN=√2OM=2√10.。
菱形、矩形习题

菱形、矩形习题菱形1.如图1,在菱形ABCD 中,AB=5,∠BCD=120°,则△ABC 的周长等于()A.20B.15C.10D.52.如图2,在菱形ABCD 中,对⾓线AC 与BD 相交于点O ,OE ⊥AB ,垂⾜为E ,若∠ADC=130°,则∠AOE 的⼤⼩为()A.75°B.65°C.55°D.50°3.如图3,在菱形ABCD 中,∠A=110°,E,F 分别是边AB 和BC 的中点,EP ⊥CD 于点P,则∠FPC=( ) A.35° B.45° C.50° D.55°4.如图4,在菱形ABCD 中,AB =5,对⾓线AC =6.若过点A 作AE ⊥BC ,垂⾜为E ,则AE 的长为______.5.如图5,在菱形ABCD 中,∠ABC=60°,E 为AB 的中点,P 为对⾓线BD 上任意⼀点,AB=4,PA+PE 的最⼩值为()A.4B.2C.32D.336.如图6,在菱形ABCD 的边长是6,∠ABC=60°,点E 、F 、G 是BC 、CD 、BD 上的任意⼀点,则EG+FG 的最⼩值是()A.33B.2C.23D.67.如图,在平⾏四边形ABCD 中,AE 、CF 分别是∠BAD 和∠BCD 的平分线.添加⼀个条件,仍⽆法判断四边形AECF 为菱形的是()A.AE=AFB.EF ⊥ACC.∠B=60°D.AC 是∠EAF 的平分线8.如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于点D ,AE 平分∠BAC ,分别于BC 、CD 交于E 、F ,EH ⊥AB 于H ,连接FH ,求证:四边形CFHE 是菱形.9.如图,已知△ABC ,按如下步骤作图:①分别以A ,C 为圆⼼,⼤于21AC 的长为半径画弧,两弧交于P ,Q 两点;②作直线PQ ,分别交AB ,AC 于点E ,D ,连接CE ;③过C 作CF ∥AB 交PQ 于点F ,连接AF .(1)求证:△AED ≌△CFD ; (2)求证:四边形AECF 是菱形.10.如图,平⾏四边形ABCD 中,AB=2,AD=1,∠ADC=60°,将平⾏四边形ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点D'处,折痕交CD 边于点E.(1)求证:四边形BCED ′是菱形;(2)若点P 是直线l 上的⼀个动点,请计算PD '+PB 的最⼩值.11.如图,两张宽度相等的纸条叠放在⼀起,重叠部分构成四边形ABCD.(1)求证:四边形ABCD 是菱形;(2)若纸条宽3cm ,∠ABC=60°,求四边形ABCD 的⾯积.矩形1.若四边形ABCD 的对⾓线互相平分,要使它变为矩形,需要添加的条件是( )A.AB=CDB.AD=BCC.∠AOB=45°D.∠ABC=90°2.如图,在矩形ABCD 中,AB=6cm ,点E ,F 分别是边BC ,AD 上⼀点,将矩形ABCD 沿EF 折叠,使点C 、D 分别落在点C '、D '处.若C 'E ⊥AD ,则EF 的长为_____cm .3.矩形具有⽽⼀般平⾏四边形不具有的性质是( )A.对⾓相等B.对⾓线相等C.对边相等D.对⾓线互相平分4.如图,P 是矩形ABCD 的对⾓线AC 的中点,E 是AD 的中点.若AB=6,AD=8,则四边形ABPE 的周长为()A.14 B.16C.17D.185.矩形⼀个⾓的平分线分矩形⼀边为1cm 和3cm 两部分,则这个矩形的⾯积为_____.6.在△ABC 中,AB=6,AC=8,BC=10,P 为边BC 上⼀动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最⼩值为______.7.如图左,在矩形ABCD 中,AD=2AB,点M 、N 分别在AD 、BC 上,连接BM 、DN.若四边形MBND 是菱形,则MDAM 等于() 8.如右上图,在矩形ABCD 中,AB=10 , BC=5 .若点M 、N 分别是线段ACAB 上的两个动点,则BM+MN 的最⼩值为______.9.下列四边形:①对⾓线互相平分的四边形;②对⾓线相等的四边形;③对⾓线相等的平⾏四边形;④对⾓线互相平分且相等的四边形.其中⼀定是矩形的个数是( )A.1个B.2个C.3个D.4个10.如图,顺次连接四边形ABCD 各边中点得四边形EFGH ,要使四边形EFGH 为矩形,应添加的条件是()A.AB ∥DCB.AC=BDC.AC ⊥BDD.AB=DC11.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE ,求证:四边形BCDE 是矩形.12.如图,将平⾏四边形ABCD 的边AB 延长⾄点E ,使BE=AB ,连接DE ,EC ,DE 交BC 于点O .(1)求证:△ABD ≌△BEC ;(2)连接BD ,若∠BOD=2∠A ,求证:四边形BECD 是矩形.13.已知:点E 是矩形ABCD 的对⾓线BD 上的⼀点,且BE=BC ,AB=3,BC=4,点P 是EC 上的⼀动点,且PQ ⊥BC 于点Q ,PR ⊥BD 于点R.(1)如图1,当点P 为线段EC 中点时,易证:PR+PQ=512. (2)如图2,当点P 为线段EC 上的任意⼀点(不与点E 、点C 重合)时,其它条件不变,则(1)中的结论是否仍然成⽴?若成⽴,请给予证明;若不成⽴,请说明理由.(3)如图3,当点P 为线段EC 延长线上的任意⼀点时,其它条件不变,则PR 与PQ 之间⼜具有怎样的数量关系?请直接写出你的猜想.【菱形、矩形适应性训练】1.⼩敏不慎将⼀块平⾏四边形玻璃打碎成如图的四块,为了能在商店配到⼀块与原来相同的平⾏四边形玻璃,他带了两块碎玻璃,其编号应该是( )A.①,②B.①,④C.③,④D.②,③2.已知菱形的周长为40cm ,⼀条对⾓线长为16cm,则该菱形的⾯积是________.3.下列命题:①四边都相等的四边形是菱形;②两组邻边分别相等的四边形是菱形;③对⾓线互相垂直的平⾏四边形是菱形;④对⾓线相等的四边形是菱形;⑤⼀条对⾓线平分⼀组对⾓的平⾏四边形是菱形.其中正确的是_____.(填序号)4.如图,点E 、F 、G 、H 分别是任意四边形ABCD 中AD ,BC ,BD ,CA 的中点,当四边形ABCD 的边⾄少满⾜条件__________时,四边形EGFH 是菱形.5.如图,在△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针⽅向旋转得到的,连接BE、CF相交于点D.(1)求证:BE=CF;(2)当四边形ACDE为菱形时,求BD的长.6.如图,BD是△ABC的⾓平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.(1)请判断四边形EBGD的形状,并说明理由;※(2)若∠ABC=30°,∠C=45°,ED=2,点H是BD上的⼀个动点,求HG+HC的最⼩值.7.如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对⾓线的所有平⾏四边形ADCE中,DE的最⼩值是_____________.8.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F 处,过点F作FG∥CD,交AE于点G 连接DG.(1)求证:四边形DEFG为菱形; (2)若CD=8,CF=4,求DECE的值.第14题图EBCD9.如图,在△ABC中,点O是边AC上⼀个动点,过点O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外⾓平分线于点F.(1)求证:OE=OF; (2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.10.已知点P是矩形ABCD边AB上的任意⼀点(与点A、B不重合).(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取⼀点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的⼤⼩关系,并说明你的理由;※(3)如图③,分别在AD、BC上取点F、C′,使得∠APF=∠BPC′,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△PBC′沿PC′翻折得到△PEC′,连接FC′,取FC′的中点H,连接GH、EH,试问(2)中的结论还成⽴吗?请说明理由.11.在菱形ABCD和正△BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.(1)如图1,当点G在BC边上时,猜想PG与PC的关系,并证明.(提⽰:延长GP交CD于点E)※(2)如图2,当点F在AB的延长线上时,线段PC、PG还满⾜(1)中的结论吗?写出你的猜想,并给与证明;※(3)如图3,当点F在CB的延长线上时,线段PC、PG⼜有怎样的数量关系,直接写出你的猜想,不必证明.正⽅形1.正⽅形具有⽽矩形不⼀定具有的性质是( )A.四个⾓都相等B.四条边相等C.对⾓线相等D.对⾓线互相平分则CF 的长为_____.3.如图,边长为6的⼤正⽅形中有两个⼩正⽅形.若两个⼩正⽅形的⾯积分别为21S S ,,则1S +2S 的值为() A.16 B.17 C.18 D.194.如图,将正⽅形纸⽚ABCD 折叠,使边AB ,CB 均落在对⾓线BD 上,得折痕BE 、BF ,则∠EBF 的⼤⼩为______.5.如图,点E 在正⽅形ABCD 的对⾓线AC 上,且EC=2AE ,直⾓△FEG 的两直⾓边EF 、EG 分别交BC 、DC 于点M 、N .若正⽅形ABCD 的变长为a ,则重叠部分四边形EMCN 的⾯积为______.6.如图,E ,F 是正⽅形ABCD 的边AD 上两个动点,满⾜AE =DF .连接CF 交BD 于G ,连接BE 交AG 于点H .若正⽅形的边长为2,则线段DH 长度的最⼩值是_____.7.如图,正⽅形ABCD 中,∠DAC 的平分线交DC 于点E .若P 、Q 分别是AD 和AE 上的动点,A.2B.4C.6D.88.如图,在正⽅形ABCD 中,对⾓线AC 、BD 相交于点O ,E 、F 分别在OD ,OC 上,且DE=CF ,连接DF 与AE 的延长线交DF 于点M .求证:AM ⊥DF .9.如图①,已知在正⽅形ABCD中,点P是对⾓线BD上⼀点,点E在AD的延长线上,且且PA=PE,PE交CD于F.(1)证明:PC=PE;(2)求∠CPE的度数;(3)如图2,把正⽅形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.10.如图,已知平⾏四边形ABCD中,对⾓线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三⾓形.(1)求证:四边形ABCD是菱形; (2)若∠AED=2∠EAD,求证四边形ABCD是正⽅形.11.在正⽅形地块内修两条笔直的道路,把正⽅形分成形状相同且⾯积相等的四部分,道路宽度忽略不计.请设计三种不同的⽅案,在给出的三张正⽅形图纸上分别画出来,并简述绘图步骤.12.正⽅形ABCD和正⽅形CEFG,连接BF,DF,点P为线段DF的中点,连接GP.(1)如图1,若点E、G分别在边BC、CD上,猜想BF与GP的关系,并证明.(2)如图2,在图1的基础上将正⽅形CEFG绕点C旋转,(1)中的结论是否仍成⽴?若成⽴,请给出证明;若不成⽴,说明理由.【正⽅形习题训练】1.在□ABCD中,AB=10,BC=14,E、F分别为边BC、AD上的点,若四边形AECF为正⽅形,则AE的长为()A.7 B.4或10C.5或9D.6或82.如图,边长分别为4和8的两个正⽅形ABCD和CEFG并排放在⼀起,连结BD并延长交EG2 C.2 D.1于点T,交FG于点P,则GT=() A.2 B.23.如图,正⽅形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正⽅形,则△DBF 的⾯积为_______.4.如图,E是边长为1的正⽅形ABCD的对⾓线BD上⼀点,且BE=BC,P为CE上任意⼀点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是()A.B.C.D.5.如图,在正⽅形ABCD中,E、F分别是AD,DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正⽅形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP 与NQ是否相等?并说明理由.6.如图,在△ABC 中,点O是AC边上的⼀个动点,过点O作直线MN∥BC,设MN交∠BCA 的⾓平分线于点E,交∠BCA的外⾓∠ACD平分线于点F.(1)试说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.(3)当点O运动到何处,且△ABC满⾜什么条件时,四边形AECF是正⽅形?并说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《矩形与菱形》素质基础训练
班级______________ 姓名______________ 学号______________
一、精心选一选(每小题3分,共30分)
1、已知一矩形的周长是24cm,相邻两边之比是1:2,那么这个矩形的面积是()m2。
A.24 B.32 C.48 D.128
2、矩形具有而一般的平行四边形不具有的特征是()。
A.对角线相等B.对边相等 C.对角相等 D.对角线互相平分
3、下列图形既是轴对称图形,又是中心对称图形的是()。
A.矩形B.直角三角形C.等腰三角形D.平行四边形4、下列条件中,不能判定四边形ABCD是菱形的是()。
A.□ABCD中,AB=BC B.□ABCD中,AC⊥BD C.□ABCD中,AC=BD D.□ABCD中,AC平分∠BAD 5、若直角三角形中两直角边的长分别为12和5,则斜边上的中线是()。
A、13 B、6 C、6.5 D、6.5或6
6、菱形和矩形都具有的性质是……………………………()
A.对角线相等B.对角线互相平分
C.对角线平分一组对角D.对角线互相垂直
7、已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=
1∠CDE,那么∠BDC
2 Array
等于()。
A.60°B.45°C.30°D.22.5°
8、已知菱形的边长和一条对角线的长均为2cm,则菱形的面积为()。
A.2
4cm C.2
3cm B.2
23cm
3cm D.2
9、菱形相邻两角的比为1:2,那么菱形的对角线与边长的比为()A.1:2:3 B.1:2:1 C.1:3:2 D.1:3:1
10、将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=3,折叠后,点C落在AD
边上的C1处,并且点B落在EC1边上的B1处.则
BC的长为()。
A.3B.2 C.3 D.3
2
二、专心填一填(每小题3分,共30分)
11.若矩形的一条角平分线分一边为3cm和5cm两部分,则矩形的周长为.
12.如图,四边形ABCD是平行四边形,使它成为矩形的条件可以是.
13.矩形短边长4cm,两对角线的夹角为60度,则对角线长是cm.
14.如图,在菱形ABCD中,∠BAD=80度,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数为.
(第12题图)(第14题图)(第16题图)(第17题图)
C
B
A
D
15.顺次连结对角线互相垂直的四边形各边中点所得的四边形是 .
16.如图,一斜坡AB 的中点为D ,BC =1,CD =1.5,则斜坡的坡长 .
17.如图,在扇形中,∠AOB =90度,OA=5,C 是弧AB 上一点,且CD ⊥OB ,CE ⊥OA ,垂足分别为点D 、E ,则DE = . 18.菱形OABC 在平面直角坐标系中的位置如图所
示,452AOC OC ∠==°,,则点B 的坐标为 .
19.如图,一活动菱形衣架中,菱形的边长均为16cm ,若墙上钉子间的距离16cm AB BC ==, 则1=∠ 度.
20.如图,两张宽为1cm 的矩形纸条交叉叠放,其中
重叠部分部分是四边形ABCD ,已知∠BAD=30°则重
叠部分的面积是 cm 2.
三、耐心做一做(本题有5小题,共40分)
21.(本题6分)已知:如图所示,在矩形ABCD 中,AF =BE .
求证:DE =CF .
A
D
C
B
F E
22.(本题8分)如图,ABCD是菱形,对角
线AC与BD相交于点O,306
∠==
°,.
ACD BD
(1)求证:△ABD是正三角形;(2)求AC的长.
23.(本题10分)已知,一张矩形纸片ABCD的边长分别为9cm 和3cm,把顶点A和C叠合在一起,得折痕EF(如图).(1)猜想四边形AECF是什么四边形,并证明你的猜想.(2)求折痕EF的长.
2010年永嘉县八年级数学(下)素质基础训练(十)参考答案
一、选择题
二、填空题
11、22cm或26m
12、AC=BD或∠ABC=90度(或其他三个角也可以)
13、8
14、60度
15、矩形
16、1:22
17、5
18、(2+1,1)
19、120度
20、2
三、解答题
21、略
22、(1)略
(2)AC=63
23、75度
24、(2)平行四边形,两组对边分别相等的四边形是平行四边形。
(3)矩形,有一个为直角的平行四边形为矩形。
25、(1)菱形,可证四边形AECF的四边相等。
(2)10
【注:本卷由桥头中学蔡秋莲老师(664268)命题、瓯北三中陈建义老师(679002)审阅,各题可能有不同的正确解法,仅供参考。
】。
