三角形一边平行线的知识总结及试题
三角形一边的平行线-知识讲解

三角形一边的平行线-知识讲解本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March三角形一边的平行线 知识讲解责编:常春芳【学习目标】1、掌握三角形一边的平行线性质定理及推论;判定定理及推论;以及平行线分线段成比例定理的推导与应用;2、了解三角形的重心的意义和性质并能应用它解题;3、经历运用分类思想针对图形运动的不同位置分别探究的过程,初步领略运用运动观点、化归和分类讨论等思想进行数学思考的策略.【要点梳理】要点一、三角形一边的平行线性质定理及推论1.性质定理:平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例.2.推论:平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.要点诠释:(1)主要的基本图形:分A 型和X 型;A 型 X 型(2)常用的比例式:,,AD AE AD AE DB EC DB EC AB AC AB AC=== 3.三角形的重心:三角形三条中线的交点叫做三角形的重心.要点诠释:(1)重心的性质:三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的二倍.(2)重心的画法:两条中线的交点.要点二、三角形一边的平行线判定定理及推论1.判定定理:如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.2.推论:如果一条直线截三角形两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.要点诠释:判断平行线的条件中,只能是被截的两条直线的对应线段成比例(被判断的平行线本身不能参与作比例).要点三、平行线分线段成比例定理1.性质定理:两条直线被三条平行的直线所截,截得的对应线段成比例.2.平行线等分线段定理:两条直线被三条平行的直线所截,如果在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.要点诠释:(1)平行线等分线段定理是平行线分线段成比例定理的特例;(2)平行线分线段成比例没有逆定理;(3) 由于平行线分线段成比例定理中,平行线本身没有参与作比例,因此,有关平行线段的计算问题通常转化到“A”、“X”型中.【典型例题】类型一、三角形一边的平行线性质定理1. 如图已知直线截△ABC三边所在的直线分别于E、F、D三点且AD=BE.求证:EF:FD=CA:CB.【答案与解析】过D 作DK ∥AB 交EC 于K 点.则,, 即 又∵AD=BE ,∴.【总结升华】运用三角形一边的平行线性质定理,即只要有平行线就可推出对应线段成比例.举一反三【变式】如图,在⊿ABC, DG ∥EC, EG ∥BC,求证:2AE AB AD =⋅【答案】∵DG ∥EC,∴AD AG AE AC=, ∵EG ∥BC,∴AE AG AB AC =, ABC DEG∴AD AE AE AB=, 即2AE AB AD =⋅.2.已知,△ABC 中,G 是三角形的重心, AG ⊥GC ,AG=3,GC=4,求BG 的长.【答案与解析】延长BG 交AC 于点D,∵G 是三角形的重心,∴点D 是线段AC 的中点,又∵AG ⊥GC ,AG=3,GC=4,∴AC=5,即DG=, ∵BG:GD=2:1.∴BG=5.【总结升华】三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的二倍.类型二、三角形一边的平行线判定定理3. 如图,AM 是△ABC 的中线,P 是AM 上任意一点,BP 、CP 的延长线分别交AC 、AB 于E 、D 两点.求证:DE ∥BC.GB C A【答案与解析】延长AM到H,使HM=MP,连接BH、CH∵BM=MC∴四边形BPCH是平行四边形∵BH∥CD,CH∥BE在△ABH和△ACH中,有,∴DE∥BC【总结升华】平行线所截得的对应线段成比例,而两条平行线中的线段与所截得的线段不成比例.举一反三【变式】如图,在△ABC(AB>AC)的边AB上取一点D,在边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P,求证:BP BD CP CE.【答案】过点C作CF∥AB交DP于点F,∵CF∥AB,∴∠ADE=∠EFC∵AD=AE,∴∠ADE=∠AED=∠FEC∴∠EFC=∠FEC∴CF=CE∵CF∥AB∴BP BD CP CF=,即BP BD CP CE=.类型三、平行线分线段成比例定理4. 如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,,求证:EF∥DC.【答案与解析】证明:∵DE∥BC,∴=,∵=,∴=,∴=,∴EF∥DC.【总结升华】本题考查了平行线分线段成比例.注意找准对应关系,以防错解.举一反三【变式】如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为()A.12B. 2C.25D.35【答案】D提示:∵AG=2,GB=1,∴AB=AG+BG=3,∵直线l1∥l2∥l3,∴=,。
三角形一边的平行线(二)

第3讲三角形一边的平行线(二)知识框架本讲主要讲解三角形一边平行线判定定理及推论,以及平行线分线段成比例定理;重点是理清该判定定理及其推论之间的区别和联系,难点是灵活运用本节的三个定理及两个推论,并理解和掌握“作平行线”这一主要的作辅助线的方法,为学习相似三角形的性质和判定做好准备.3.1 三角形一边的平行线判定定理及推论我们来讨论三角形一边平行线性质定理的逆命题是否正确.如图,在ABC△中,点D、E分别在边AB、AC上,如果AD AEDB EC=,那么DE//BC吗?解析:要肯定上述问题结论的正确,只要证明有一个平行四边形的相对两边分别在直线DE和BC上.如图,过点C作平行于AB的直线CF,交直线DE于点F,得四边形BCFD.证明:∵CF//AB∵AD AECF EC=(三角形一边平行线性质定理的推论)又∵AD AE DB EC=∵ AD ADCF DB=,得CF DB=.由CF//DB,CF DB=,可知四边形BCFD是平行四边形∵ DF//BC,即DE//BC.根据比例的性质可知,在关系式∵AD AEDB EC=、∵AD AEAB AC=、∵BD CEAB AC=中,由其中一个可推出其余两个.因此,以关系式∵、∵、∵之一为已知条件,都可推出DE//BC.这样,就得到以下定理:三角形一边的平行线判定定理如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.如图,如果点D 、E 分别在边AB 、AC 的延长线或反向延长线上,且具备条件∵、∵、∵之一,那么也可以用上述同样的方法推出DE //BC .由此由得到:三角形一边的平行线判定定理的推论 如果一条直线截三角形两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.思考:如图,点D 、E 分别在边AB 、AC 上,如果DE ADBC AB=,那么能否得到DE //BC ,为什么?例1. 如图,在ABC △中,点D 、E 分别在边AB 、AC 上,根据下列条件,试判断DE 与BC是 否平行. (1)3cm AD =,4cm DB =, 1.8cm AE =, 2.4cm CE =; (2)6cm AD =,9cm BD =,4cm AE =,10cm AC =; (3)8cm AD =,16cm AC =,6cm AE =,12cm AB =;(4)2AB BD =,2AC CE =.例2. 如图,::1:3AM MB AN NC ==,则:MN BC =__________.例1题图 例2题图例题分析例3. 如图,ABC △中,E 点在边AB 上,F 点在边AC 上,下列命题中不正确的是( )(A )若EF //BC ,则AE AFEB FC=; (B )若AE AFEB FC=,则EF //BC ; (C )若EF //BC ,则AE EFAB BC=;(D )若AE EFAB BC=,则EF //BC . 例4. 如图,点D 、F 在ABC △的边AB 上,点E 在边AC 上,且DE //BC ,AF ADAD AB=.求证:EF //DC .例5. 点D 、E 分别在ABC △的边AB 、AC 上,且DE //BC ,以DE 为一边作平行四边形DEFG ,延长BG 、CF 交于点H ,连接AH ,求证:AH //EF .例6.如图,M为AB的中点,EF//AB,联结EM、FM分别交AF、BE于点C和点D.求证:CD//AB.例7.如图,在菱形ABCD中,点E、F分别在边BC、CD上,BAF DAE∠=∠,AE与BD交于点G,又DF AD FC DF=.求证:四边形BEFG是平行四边形.3.2 平行线分线段成比例定理如图,已知ABC△,直线1l与边AB、AC分别相交于点D、E,直线2l与边AB、AC分别相交于点F、G,12////l l BC.那么所截得的线段是否成比例?解析:对于这个问题,只需讨论DF EGFB GC=是否成立即可.证明:如图,过点D作直线AC的平行线'l,设直线'l与BC、2l分别交于点'C、'G,则'DG EG=,''G C GC=.利用三角形一边的平行线的性质定理和等量代换,可得DF EGFB GC=.根据上述结论,在利用比例的性质,可知截得的线段成比例.如图,将ABC△的三边AB AC BC、、改为三条直线,则上述结论表述为:直线DB与EC被三条平行的直线所截,截得的对应线段成比例.于是得到:平行线分线段成比例定理两条直线被三条平行线所截,截得的对应线段成比例.如图5,当直线2l过DB中点M,即DM MB=时,则EN NC=.也就是说:两直线被三条平行线所截,如果在一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.这是平行线分线段成比例定理的特例,也称为平行线等分线段定理.例1.如图,1l//2l//3l,3AB=,8AC=,10DF=,则EF的长为__________.例1题图知识精讲例题分析例2. 如图,直线1l 、2l 、3l 分别交直线4l 于点A 、B 、C ,交直线5l 于点D 、E 、F ,且1l //2l //3l .已知3AB =,5AC =,9DF =,则EF 的长为________.例3. 如图,ABC △中,90C ∠=︒,四边形EDFC 为内接正方形,5AC =,3BC =,则:AE DF =___________.例2题图 例3题图例4. 命题“梯形ABCD 中,AD //BC ,点E 、F 在AB 、CD 上,且::AE EB DF FC =,则EF //BC ”是__________命题.(填“真”或“假”) 例5. 已知线段a 、b 、c ,求作线段x ,使::a b c x =.例6. 如图,AB 、CD 、EF 都垂直于直线l ,12AB =,7EF =,:2:3BD DF =,求CD 的长.例7. 如图,ABC △中,M 为BC 中点,O 为AM 上一点,BO 的延长线交AC 于点D ,CO的延长线交AB 于点E ,PQ //BC ,且PQ 过点O 与AB 、AC 分别交于点P 和点Q .求证:(1)PO OQ =;(2)DE //BC .例8. 如图,在等腰梯形ABCD 中,AB //CD ,两对角线AC 和BD 相交于点O ,过点O 作EF//AB ,且10EF =,若:1:3AE ED =,求梯形ABCD 中位线的长.例9. 如图,已知点A 、C 、E 和点B 、F 、D 分别是O ∠两边上的点,且AB //ED ,BC//EF .求证:AF //CD .例10.如图,M、N分别是ABC△两边AB、AC的中点,P是MN上任一点,延长BP、CP交AC、AB于K、H,求AH AKHB KC+的值.例11.如图,矩形ABCD中,AC、BD相交于点O,OE BC⊥于点E.(1)连接DE交OC于点F,作FG BC⊥于点G,求证:点G是线段BC的一个三等分点;(2)请你仿照(1)的作法,在原图上作出BC的一个四等分点(要求保留作图痕迹,可不写作法及证明过程).3.3 课堂检测1. 如图,ABC △中,点D 、E 分别在边AB 、AC 上,已知=3AD ,5AB =,2AE =,43EC =,由此判断DE 和BC 的位置关系是__________,理由是_________________________.2. 在ABC △中,直线DE 交AB 于点D ,交AC 于点E ,以下能推出DE //BC 的条件是( )(A )23AB AD =,12EC AE =; (B )23AD AB =,23DE BC =;(C )23AD DB =,23CE AE =; (D )43AD AB =,43AE EC =.3. 在ABC △中,点D 、E 分别在边AB 和BC 上,2AD =,3DB =,10BC =,要使DE//AC ,则BE =__________. 4. 如图,ABC △中,DE //BC ,AF ADDF DB=,求证:EF //CD .5. 如图,已知AD //BE //CF ,它们依次交直线1l 、2l 于点A 、B 、C 和点D 、E 、F .(1)如果6AB =,10BC =,8EF =,求DE 的长; (2)如果:3:5DE EF =,24AC =,求AB 、BC 的长.6. 如图,平行四边形ABCD 中,AC 、BD 相交于点O ,2AB =,3BC =,1AF =,BA的延长线交OF 的延长线于点E ,求AE .7. 如图,在ABC △中,点E 、F 分别在AB 、AC 上,且EF //BC ,D 为BC 的中点,ED 、FD 的延长线分别交AC 、AB 的延长线于点H 、点G ,连接HG ,求证:EF //GH .8. 如图1,在菱形ABCD 中,点G 是CD 边上的一点,联结BG 交AC 于F ,过F 作FH//CD 交BC 于H ,可以证明结论FH FGAB BG=成立(不必证明). (1)如图2,上述条件中,若点G 在CD 的延长线上,其他条件不变时,结论FH FGAB BG=是否仍成立?若成立,请给出证明;若不成立,请说明理由;(2)在(1)的条件下,若已知4AB =,60ADC ∠=︒,9CG =,求线段BG 与FG 的长.BC=,在线段AB上9.如图,矩形ABCD中,对角线AC、BD相交于点O,4AB=,3取一点P,过点P作AC的平行线交BC于点E,连接EO,并延长交AD于点F,连接PF.(1)求证:PF//BD;(2)设的AP长为x,PEF△的面积为y,求y与x的函数关系式,并写出它的定义域.3.4 课后作业1. 在A ∠的一边上顺次有B 、C 两点,在另一边上顺次有D 、E 两点,下列条件能判断BD //CE 的个数是().(1)3cm AB =,4cm BC =, 1.8cm AD =, 2.2cm DE =; (2):2:3AB AD =, 1.8cm AE =, 1.2cm AC =; (3)5cm AB =,6cm BC =, 4.4cm AE =, 2.4cm DE =; (4)10cm AB =,15cm AC =,10cm BD =,15cm EC =. (A )1个;(B )2个;(C )3个;(D )4个2.ADE △中,点B 和点C 分别在AD 、AE 上,且2AB BD =,2AC CE =,则:BC DE =_______.3. 已知点D 、E 分别是ABC △的边AB 、AC 的反向延长线上的点,如果25AD AB =, 当=AEAC_______时,BD //CE . 4. 如图,在ABC △中,点D 、E 、F 分别在AC 、AB 、BC 上,且3DE =, 4.5BF =,25AD AE AC AB ==.求证:EF //AC .5. 如图,在梯形ABCD 中,EF //AB //CD ,两对角线AC 和BD 相交于点O ,且分别与EF相交于点M 、N ,下列比例式中正确的是( )(A )AO BO ABCO DO CD ==; (B )AM BN MNCM DN AB ==; (C )AE AB BF DE CD CF==;(D )BD AC ABDN CM MN==. 6. 如图,1l //2l ,:2:5AF FB =,:4:1BC CD =,则不成立的是( )(A ):2:1AE EC =; (B ):2:5FG GD =; (C ):2:5GF FD =;(D ):1:2AG BC =第5题图 第6题图7. 如图,直线1l //2l //3l ,若5cm AB =,8cm BC =,2cm EG =,3cm GF =,求线段DE 与GC 的长.8. 如图,已知线段AB ,在线段AB 上求作一点C ,使得:1:2AC BC =.9. 如图,ABC △中,90C ∠=︒,点G 是三角形的重心,8AB =. (1)求GC 的长;(2)过点G 的直线MN //AB ,交AC 于点M ,交BC 于点N ,求MN 的长.AB10. 如图,E 、F 、G 、H 分别是四边形ABCD 各边的点,且AE FD EB AF ⋅=⋅,BG HC GC DH ⋅=⋅,连接EH 、GF 相交于点O .求证:OE GO FO OH ⋅=⋅.11. 如图,D 是线段BC 上一点,且23BD DC =,CE 交AB 于点F ,:1:3AE ED =, 求:AF BF 的值.12. 梯形ABCD 中,点E 在AB 上,点F 在CD 上,且AD a =,BC b =.(1)如图(a ),如果点E 、F 分别为AB 、CD 的中点,求证:EF //BC 且2a bEF +=; (2)如图(b ),如果AE DF mEB FC n==,判断EF 和BC 是否平行,并证明你的结论,并用a 、b 、m 、n 的代数式表示EF .图(a ) 图(b )。
九年级同步第3讲:三角形一边的平行线(二)-教师版

例题解析否平行.【答案】(1)平行;(2)平行;(3)不平行;(4)平行. 【解析】(1)处 长 3,可推知平行;DB CE 4根据线段大小和位置关系,得 AD BD, AE CE,空空 1,可推知平行. BD CE【总结】考查三角形一边平行线判定定理的内容,根据比例性质进行相关变形应用.【例 2】如图, AM: MB AN : NC 1:3,则 MN: BC 【难度】★ 【答案】1:4 .【解析】由 AM: MB AN:NC 1:3,根据三角形一边平行线的判定定理,可知 MN //BC ,根据三角形一边平行线 的性质定理和比例的合比性,可得 MN : BC AN : AC 1:4.【总结】考查三角形一边平行线性质定理及其判定定理,先判定再应用.(2) CE (3)AD ABAD AE 2AC AE 6, CD"可推知平行;BD CE 3 2AE 3—— —,不相等,可推知不平行;3 AC 8【例1】在ABC 中,点D 、E 分别在边 AB 、AC 上,根据下列条件,试判断 DE 与BC 是(1) AD 3cm, DBAE 1.8cm, CE 2.4cm ; (2) AD BDAE 4cm, AC 10cm ; (3) AD 8cm, AC16cm,AE6cm, AB12cm ;(4)AB AC则配BA【难度】★ 【答案】5.3AP BP 3【斛析】由 ,由比例合比性,可得AM BN 8可知MN//AB, MN PM 5 . BA AP 3【总结】考查三角形一边平行线性质定理及其判定定理,先判定再应用.【例4】如图, ABC 中,E 点在边AB 上,F 点在边AC 上,下列命题中不正确的是B 、C 选项都可由三角形一边平行线性质定理及其判定定理可判定正确,项不符合定理判定内容.【总结】考查三角形一边平行线性质定理及其判定定理的内容.【例3】如图, PMN 中,点A 、B 分别在MP 和NP 的延长线上,且AP AMBP BN(A)(B) AE AF若EF // BC ,贝U ————EB FC什 AE AF 若————,贝U EF // BCEB FC(C) (D)一 AE EFEF 〃 BC ,则把 EFAB BCAE EF 皿 “————,贝U EF 〃 BC AB BC【例5】如图,点D 、F 在 ABC 的边AB 上, 点E 在边AC 上,且DE 〃 BC ,空AD求证:EF 〃DC. 【答案】略. 【解析】证明: Q DE//BC , 又Q AF AD ADABAF ADAD DB AE AC 'AE EC则处处 AB ACEF // DC .AD AB根据三角形一边平行线的判定定理的推论,根据三角形一边平行线的性质定理,可得 【解析】A 、 AP BP 3 - --- -- , PM PN 5【总结】考查三角形一边平行线性质定理及其判定定理, 行判定应用. AO【例6】如图,四边形ABCD 中,AC 、BD 相交于点。
三角形一边的平行线-平行线分线段成比例定理

探索与思考
如果DE // FG // BC,那么DF EG ? FB GC
D
E
FM G
B
N
C
过点D作DN∥EC交 FG、BC于点M、N, 得到A字型
注意:这是不能得到与 DE、FG、BC有关的比例 线段。
DF EG DF EG FB GC FB GC DB EC DB EC
知识点回顾
1、三角形一边的平行线的性质定理的内容是什么? 平行于三角形一边的直线截其他两边所在
的直线,截得的对应线段成比例.
知识点回顾 2、三角形一边的平行线的判定定理的内容是什么? 如果一条直线截三角形的两边所得的对应线段 段成比例,那么这条直线平行于三角形的第三边.
AD DE AB BC
如图,已知线段AB, 在线段AB上 求作一点C,使AC : CB 1: 2.
A
B
例题1 已知:如图 l1 // l2 // l3 ,AB=3,AC=8,
DF=10.求DE,EF.
D l1
B
E
l2Biblioteka CFl3例题2、已知线段 a, b, c.求作线段 x, 使a : b c : x.
a
b
c
试一试:已知线段 a, b, c.求作线段 x, 使ax bc.
想一想:若已知a、b、c作第四比例项d,下列作法正确的是_
两条直线被三条平行的直线所截,如果 在一条直线上截得的线段相等,那么在另 一条直线上截得的线段也相等。
定理的应用:
如果DA //
BE
//
CF,那么 DE EF
AB
__B_C___,
AC BC
DF
中考数学《相似三角形》知识点及练习题

相似三角形一. 知识梳理1.平行线分线段成比例定理定理:两条直线被三条平行线所截,所得的对应线段成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
2.相似三角形定义:三角对应相等、三边对应成比例的两个三角形叫做相似三角形。
相似比:相似三角形对应边的比叫做相似比。
3.相似三角形的判定平行法:平行于三角形一边的直线和其他两边相交,所得的三角形与原三角形相似。
两角法:两角分别相等的两个三角形相似。
边角法:两边成比例且夹角相等的两个三角形相似。
三边法:三边对应成比例的两个三角形相似。
4.相似三角形的性质①相似三角形的对应角相等,对应边成比例;②相似三角形对应边上高的比,对应边上中线的比与对应角平分线的比都等于相似比;③相似三角形周长的比等于相似比;④相似三角形面积的比等于相似比的平方。
5.位似图形定义:如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心。
这时的相似比又叫位似比6. 黄金分割:点C 把线段AB 分成两条线段AC 和BC,如果ACBC AB AC =,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比. 1:618.0215:≈-=AB AC 二.课后作业1.下列图形中不一定属于相似形的是( )A.两个圆B.两个等边三角形C.两个正方形D.两个矩形2.如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )A. 1∶16B. 1∶4C. 1∶6D. 1∶23.已知△ABC ∽△DEF ,且AB:DE=1:2,则△ABC 的周长与△DEF 的周长之比( )A.1:2B.1:4C.2:1D.4:14.如图,给出下列条件:其中,不能单独判定△ABC∽△ACD 的条件为( )A.∠B=∠ACDB.∠ADC=∠ACBC.AC CD =AB BCD.AC AD =AB AC5.如图,DE ∥BC ,且AD=2,BD=5,则△ADE 与△ABC 的相似比为( )A.2:5B.5:2C.2:7D.7:26.如图,在△ABC 中,DE ∥BC ,AD=2,AE=3,BD=4,则AC=( ) A.7 B.8 C.9 D.10 E A D CB A BC DE7.已知△ABC ∽△DEF ,且它们的周长之比为1:2,那么它们的相似比为 。
三角形一边平行线性质定理题型+答案详解

基础知识点三角形一边的平行线性质定理:平行于三角形一边的直线截其他两边所在直线,截得的对应线段成比例。
如图(1),若DE//BC ,则AD AE DB EC =或AD AE AB AC =或DB CEAB AC =如图(2),若DE//BC ,则AB AC AE AD =或AB AC EB DC =或EA DAEB DC=EDE(2)(1)CBADC BA三角形一边的平行线性质定理推论:平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例。
如图(1)已知:△ABC 中,点D 、E 分别在AB 、AC 上,且DE//BC ,则AD DE AEAB BC AC==; 如图(2)已知:△ABC 中,点D 、E 分别在CA 、BA 的延长线上,且DE//BC ,则AB BC ACAE DE AD==. EDE(2)(1)CBADC BA同高(或等高)的两个三角形的面积之比等于对应底边的比(2)(1)DCBADCBA如图(1):ABD ADCS BDSDC =如图(2):若AD//BC,则ADC ABCS ADSBC=三角形重心(三中线交点):三角形的重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍。
1、三角形三条中线交于一点,三角形三条中线的交点叫做三角形的重心。
2、三角形的重心到一个顶点的距离,等于它到这个顶点对边中点距离的两倍。
例题解析如图,在ABC ∆中,DE //BC ,下列各式中错误的是( ). A.AD AB AE AC = B.BD EC AD AE = C.AD DE DB BC = D.AE DEAC BC =答案:C变式:如图,已知在ABC ∆中,DE //BC ,EF //CD ,那么下列线段的比中与AEAC相等的有( )个。
①AF AB②AF AD ③FD FB④ADABA.0B.1C.2D.3答案:C,①和④例题讲解:在△ABC 中,DE//BC ,DE 与AB 相交于D ,与AC 相交于E 。
七年级下册数学三角形基本知识以及平行线练习

三角形知识点一、三角形相关概念1.三角形的概念: 由不在同一直线上的三条线段首尾顺次连结所组成的图形叫做三角形要点:①三条线段;②不在同一直线上;③首尾顺次相接.2.三角形的表示:通常用三个大写字母表示三角形的顶点,如用A、B、C表示三角形的三个顶点时,此三角形可记作△ABC,其中线段AB、BC、AC是三角形的三条边,∠A、∠B、∠C分别表示三角形的三个内角.3.三角形中的三种重要线段: 三角形的角平分线、中线、高线是三角形中的三种重要线段.(1)三角形的角平分线:三角形一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.注意:①三角形的角平分线是一条线段,可以度量,而角的平分线是经过角的顶点且平分此角的一条射线.②三角形有三条角平分线且相交于一点,这一点一定在三角形的内部.③三角形的角平分线画法与角平分线的画法相同,可以用量角器画,也可通过尺规作图来画.(2)三角形的中线:在一个三角形中,连结一个顶点和它的对边中点的线段叫做三角形的中线.注意:①三角形有三条中线,且它们相交三角形内部一点.②画三角形中线时只需连结顶点及对边的中点即可.(3)三角形的高线:从三角形一个顶点向它的对边作垂线,顶点和垂足间的限度叫做三角形的高线,简称三角形的高.注意:①三角形的三条高是线段②画三角形的高时,只需要向对边或对边的延长线作垂线,连结顶点与垂足的线段就是该边上的高.知识点二、三角形三边关系定理①三角形两边之和大于第三边,故同时满足△ABC三边长a、b、c的不等式有:a+b>c,b+c>a,c+a>b.②三角形两边之差小于第三边,故同时满足△ABC三边长a、b、c的不等式有:a>b-c,b>a-c,c>b-a.注意:判定这三条线段能否构成一个三角形,只需看两条较短的线段的长度之和是否大于第三条线段即可知识点三、三角形的稳定性三角形的三边确定了,那么它的形状、大小都确定了,三角形的这个性质就叫做三角形的稳定性.例如起重机的支架采用三角形结构就是这个道理.知识点四、三角形的内角结论1:三角形的内角和为180°.表示:在△ABC中,∠A+∠B+∠C=180°结论2:在直角三角形中,两个锐角互余.注意:①在三角形中,已知两个内角可以求出第三个内角如:在△ABC中,∠C=180°-(∠A+∠B)②在三角形中,已知三个内角和的比或它们之间的关系,求各内角.如:△ABC中,已知∠A:∠B:∠C=2:3:4,求∠A、∠B、∠C的度数.知识点五、三角形的外角1.意义:三角形一边与另一边的延长线组成的角叫做三角形的外角.2.性质:①三角形的一个外角等于与它不相邻的两个内角的和.②三角形的一个外角大于与它不相邻的任何一个内角.③三角形的一个外角与与之相邻的内角互补3.外角个数过三角形的一个顶点有两个外角,这两个角为对顶角(相等),可见一个三角形共有六个外角.六、多边形①多边形的对角线2)3(nn条对角线;②n边形的内角和为(n-2)×180°;③多边形的外角和为360°一、选择题:1.下列可能是n边形内角和的是()A、300°B、550°C、720°D、960°2.若一个多边形的内角和与外角和相加是1800°,则此多边形是( )A、八边形B、十边形C、十二边形D、十四边形3.多边形每一个内角都等于150°,则此多边形一个顶点发出的对角线有()A、7条B、8条C、9条D、10条4.小李家装修地面,已有正三角形形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则小李不应购买的地砖形状是( )A、正方形B、正六边形C、正八边形D、正十二边形二、填空题:1.一个多边形中,它的内角最多可以有个锐角。
三角形及平行线+综合训练课件2024-2025学年北师大版数学八年级上册

1 ×54°=117°.
2
3.△ABC 中,∠C=80°,点D,E分别是△ABC 边AC,BC上的点,点P是一 动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠ɑ.
(1)若点P在边AB上,且∠ɑ=50°,如图①,则∠1+∠2=________. (2)若点P在边AB上运动,如图②,则∠ɑ,∠1,∠2之间的关系为
(2)∠1+∠2=80°+∠α 点拨:如图②,连接CP, ∵∠1是△CDP的外角, ∴∠1=∠DCP+∠DPC, 同理可得,∠2=∠ECP+∠EPC,∴∠1+∠2=∠ACB+∠DPE=80°+∠α. (3)∠1=80°+∠2+∠α,理由如下: 如图③,∵在△CDM中,∠1=∠C+∠CMD,在△EMP中,∠CMD=∠2+∠α, ∴∠1=∠C+∠2+∠α, 即∠1=80°+∠2+∠α.
则∠ADC=____°,∠DAC=____°; ②如图1,若∠B=∠BAD,∠ADC=∠C, 则∠B=____°,∠C=_____°,∠DAC=______°;
图1
一题多设问
如图,在△ABC中,∠C>∠B,点D是BC上一点(点D不与点B,C重合), 连接AD.(1)若AD平分∠BAC.
③如图2,过点A作AE⊥BC于点E, 若∠B=40°,∠C=60°,则∠DAE=__ °.
C
E
DP
B
图1
链接真题
拓展探究:(3)如图2,敏学小组画出了点P,E分别在线段DB,
AB延长线上时的情形,其余条件不变,提出如下问题. A
请从下面A,B两题中任选一题作源自答.我选择题.A.画
∠DPE的角平分线,交AD的延长线
于点F.请在图2中补全图形,并直 接写出∠AFP的度数.B.请直接写
CA
D
三角形一边平行线的知识总结及试题

一、本节知识点汇总: 1. 比例线段的有关概念: 在比例式::中,、叫外项,、叫内项,、叫前项,a b cda b c d a d b c a c ==()b 、d 叫后项,d 叫第四比例项,如果b=c ,那么b 叫做a 、d 的比例中项。
把线段AB 分成两条线段AC 和BC ,使AC 2=AB ·BC ,叫做把线段AB 黄金分割,C 叫做线段AB 的黄金分割点。
2. 比例性质: ①基本性质:a b c dad bc =⇔= ②合比性质:±±a b c d a b b c dd =⇒=③等比性质:……≠……a b c d m n b d n a c m b d n ab===+++⇒++++++=()0 3.平行线分线段成比例定理:两条直线被三条平行的直线所截,截得的对应线段成比例. 用符号语言表示:AD ∥BE ∥CF,,,AB DE BC EF AB DEBC EF AC DF AC DF∴===. 4.平行线等分线段定理:两条直线被三条平行的直线所截,如果在一直线上所截得的线段相等,那么在另一直线上所截得的线段也相等. 用符号语言表示:AD BE CF AB BC DE EF ⎫⇒=⎬=⎭.5. 三角形一边平行线判定定理 如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.6.三角形一边的平行线判定定理推论 如果一条直线截三角形两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.EC23.1——23.3比例线段单元测试班级_______姓名________学号________分数________一、填空1.已知线段b 是线段a 、c 的比例中项,且a =9,c =4,则b = .2.线段AB =6cm ,点P 在线段AB 上,且AP 是是AB 与BP 的比例中项,则PB =_______cm . 3.△ABC 与△A 1B 1C 1中32111111===C B BC C A AC B A AB ,若AB +AC +BC =40cm ,则△A 1B 1C 1的周长是__________.4.在比例尺为1︰1000000的地图上,AB 两地的图上距离是3.4厘米,则AB 两地的实际距离是____________千米. 5.已知832=-b b a ,则______=ba. 6.已知:在ABC ∆中,点D 、E 分别在AB 、AC 上,且DE ∥BC ,AB =6,AD =2,EC =3,则AE = .7.已知:点D 、E 分别在⊿ABC 的边AB 、AC 的反向延长线上,且DE ∥BC ,15,32==BC AB AD ,则DE = .8.如图,在梯形ABCD 中,AD ∥BC ,AC 、BD 相交于点O .若S △AOD =4,S △AOB =6,则S △BOC =_________.9.如图,l 1∥l 2∥l 3 , AB =2,AC =5,DF =10,则DE = . 10.如图,AM ∶MB =AN ∶NC=1∶3,则MN ∶BC = .11.如图,在ΔABC 中,AM 是中线,G 是重心,GD ∥BC ,交AC 于D .若BC =6,则GD = .12.如图,AD ∥EF ∥BC ,AD =13厘米、BC =18厘米,AE ︰EB =2︰3,则EF = .(第13题)(第12题)(第11题)L3MMBABCC第10题第11题第12题13.如图,△ABC 中有菱形ANPN ,如果21=MB AM ,则BC BP =_________. 14.如图,在□ABCD 中,EF ∥AB ,32=EA DE ,EF =4,则CD 的长为________.15.已知平行四边形ABCD 中,E 为AD 的中点,AF ∶BF=2∶5,则_____=GCAG.二、选择题:16.如图,下列各组线段中不能说明DE ∥BC 的是 ( ) (A)AD =6,BD =4,AE =2.4,CE =1.6; (B )AD =4,AB =6,DE =2,BC =3; (C )AD =4,AB =6,AE =2,AC =3;(D )BD =2,AB =6,CE =1,AC =3.17.已知线段a 、b 、c ,求作线段x ,满足bx=ac ,下列哪种作法满足要求的是( )18.如图,在□ABCD 中,E 是AD 上一点,连接CE 并延长交BA 于F ,则下列结论中错误的是 ( )(A )∠AEF =∠DEC ; (B )FA ﹕CD =AE ﹕BC ; (C )FA ﹕AB =FE ﹕EC ; (D )AB =DC .19.点P 是线段AB 的黄金分割点,且AB =4,则AP 的长是 ( ) (A )252-; (B )526-; (C )252-或526-;(D )以上结论都不对. 三、解答题:20.如图,在△ABC 中,DE ∥BC ,AB = 4,AC = 8,DB = AE ,求AE 的值。
4-三角形一边平行线判定定理

1.已知:如图,点D,F在 的边AB上,点E在边AC上,且DE//BC, ,求证:EF∥DC .
2.如图,在平行四边形ABCD中,E是AB的中点,在AD上截取AF=FD,EF交AC于点G.求的值.
3.如图,已知在△ABC中,点D、E、F分别在AB、BC、CA上,且,CF=CE.求证:四边形CFDE是菱形。
三、练习
1.梯形两底分别为m、n,过梯形的对角线的交点,引平行于底边的直线被两腰所截得的线段长为( )
(A) (B) (C) (D)
2.如图,AD是△ABC的中线,E是AC边上的三等分点,BE交AD于点F.则AF:FD为( )
3.如图,梯形ABCD的中位线MN与对角线BD、AC分别相交于点E、F,若AD:BC=1:3.则EF:MN等于( ).
一、基础知ቤተ መጻሕፍቲ ባይዱ点
1、三角形一边平行线判定定理如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.
如果D ,E分别在AB,AC的延长线上时,或在反向延长线上时,以上结论同样成立.
2、三角形一边的平行线判定定理推论如果一条直线截三角形两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
4、如图,在△ABC中,点D是AC的中点,3BE=2EC,AE与BD相交于点F.求DF:BF的值.
5.如图4,点O为△ABC的中线AD上任意一点,BO、CO的延长线分别交AC、AB于点E、F,连结EF,且 。求证:EF∥BC.
6、如图,D、E分别为△ABC的AB和AC上的点,且BC的延长线于F点,且求证:DB=EC.
4.如图,BD、CE是△ABC的中线,P、Q分别是BD、EC的中点.则PQ:BC等于( )
三角形一边平行线判定定理完整题型+答案

基础知识点三角形一边平行线的判定定理:如果一条直线截三角形两边所得的对应线段成比例,那么这条直线平行于三角形的第三边。
(由成比例得平行)A如图,若EC AE DB AD =(或AC AE AB AD =或ACEC AB BD =),则DE//BCD EB C三角形一边平行线的判定定理的推论:如果一条直线截三角形两边的延长线(这两条延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于第三边。
若CE AC BD AB =(或AE AC AD AB =或AC EC AD BD =) 若AC AE AB AD =(或EC AE BD AD =或CEAC BD AB =) 则DE//BC 则DE//BC例题解析例题解析:在△ABC 中,点D 、E 在边AB 、AC 上,根据下列给定的条件,试判断DE 与BC 是否平行? 并说明理由.(1)AD=3cm ,DB=4cm ,AE=1.8cm ,CE=2.4cm ;(2)AD=6cm ,BD=9cm ,AE=4cm ,AC=10cm;答案:(1)是;(2)不是.变式:在△ABC 中,点D 、E 在边AB 、AC 上,根据下列给定的条件,试判断DE 与BC 是否平行? 并说明理由.(1)AD=8cm ,AC=16cm ,AE=6cm ,AB=12cm;(2)AB=3BD ,AE=32AC;(3)AB=2BD ,AC=2CE.答案:(1)不是;(2)是;(3)是.例题解析:如图,点D 、E 分别在AB 、AC 上,以下能推得DE//BC 的条件是( )。
A.AD:AB=DE:BCB.AD:DB=DE:BCC.AD:DB=AE:ECD.AE:AC=AD:DB 答案:解析:∵AD:DB=AE:EC ,∴DE//BC ,故选:C .变式:在△ABC 中,点D 、E 分别在边AB 、AC 上,下列条件中不能判定DE//BC 的是( )。
A.= B.= C.= D.=解析:∵=,∴DE//BC ,选项A 不符合题意;∵=,∴DE//BC ,选项B 不符合题意; ∵=,∴DE//BC ,选项C 不符合题意;=,DE//BC 不一定成立,选项D 符合题意.故选:D .例题解析:已知:如图,点D ,F 在△ABC 的边AB 上,点E 在边AC 上,且DE//BC ,ABAD AD AF =,求证:EF//DC. 解答:证明:∵DE//BC ,∴AC AE AB AD =, ∵AB AD =,∴AC AD =,∴ADAC =,∴EF//DC.变式:如图,在△ABC 中,EF//CD ,DE//BC 。
三角形一边平行线判定定理完整题型+答案

基础知识点三角形一边平行线的判定定理:如果一条直线截三角形两边所得的对应线段成比例,那么这条直线平行于三角形的第三边。
(由成比例得平行)A如图,若EC AE DB AD =(或AC AE AB AD =或ACEC AB BD =),则DE//BCD EB C三角形一边平行线的判定定理的推论:如果一条直线截三角形两边的延长线(这两条延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于第三边。
若CE AC BD AB =(或AE AC AD AB =或AC EC AD BD =) 若AC AE AB AD =(或EC AE BD AD =或CEAC BD AB =) 则DE//BC 则DE//BC例题解析例题解析:在△ABC 中,点D 、E 在边AB 、AC 上,根据下列给定的条件,试判断DE 与BC 是否平行? 并说明理由.(1)AD=3cm ,DB=4cm ,AE=1.8cm ,CE=2.4cm ;(2)AD=6cm ,BD=9cm ,AE=4cm ,AC=10cm;答案:(1)是;(2)不是.变式:在△ABC 中,点D 、E 在边AB 、AC 上,根据下列给定的条件,试判断DE 与BC 是否平行? 并说明理由.(1)AD=8cm ,AC=16cm ,AE=6cm ,AB=12cm;(2)AB=3BD ,AE=32AC;(3)AB=2BD ,AC=2CE.答案:(1)不是;(2)是;(3)是.例题解析:如图,点D 、E 分别在AB 、AC 上,以下能推得DE//BC 的条件是( )。
A.AD:AB=DE:BCB.AD:DB=DE:BCC.AD:DB=AE:ECD.AE:AC=AD:DB 答案:解析:∵AD:DB=AE:EC ,∴DE//BC ,故选:C .变式:在△ABC 中,点D 、E 分别在边AB 、AC 上,下列条件中不能判定DE//BC 的是( )。
A.= B.= C.= D.=解析:∵=,∴DE//BC ,选项A 不符合题意;∵=,∴DE//BC ,选项B 不符合题意; ∵=,∴DE//BC ,选项C 不符合题意;=,DE//BC 不一定成立,选项D 符合题意.故选:D .例题解析:已知:如图,点D ,F 在△ABC 的边AB 上,点E 在边AC 上,且DE//BC ,ABAD AD AF =,求证:EF//DC. 解答:证明:∵DE//BC ,∴AC AE AB AD =, ∵AB AD =,∴AC AD =,∴ADAC =,∴EF//DC.变式:如图,在△ABC 中,EF//CD ,DE//BC 。
九年级数学相似三角形知识点总结及例题讲解

1. 平行线分线段成比例定理
例.
已知 l 1∥ l 2∥ l 3,
A Dl
B El
: 三条平行线截两条直线
1 2
, 所得的 对应线段成比 .
C
Fl
可得 AB
DE AB 或
DE 等.
BC EF AC DF
2. 推论 : 平行于三角形一边的直线截其它两边
3
( 或两边的延长线 ) 所得的对应线段成比例 .
注意 :(1) 此性质的证明运用了“设 k 法” ,这种方法是有关比例计算,变形中一种常用方法.
(2) 应用等比性质时,要考虑到分母是否为零.
(3)
可利用分式性质将连等式的每一个比的前项与后项同时乘以一个数,再利用等比性质也成立.
知识点三:黄金分割
1) 定义 :在线段 AB 上,点 C 把线段 AB 分成两条线段 AC 和 BC(AC>BC ),如果 AC AB
ad bc
(两外项的积等于两内项积)
2. 反比性质:
ac bd
bd a c ( 把比的前项、后项交换 )
3. 更比性质 ( 交换比例的内项或外项 ) :
ac bd
a b ,(交换内项 ) cd d c ,(交换外项 ) ba d b .(同时交换内外项 ) ca
4. 合比性质
a
:
c
bd
ab b
cd (分子加(减)分母 , 分母不变)
例 4、矩形 ABCD 中, BC=3AB , E、F,是 BC 边的三等分点,连结 AE 、 AF 、AC ,问图中是否存在非全 等的相似三角形?请证明你的结论。
二、如何应用相似三角形证明比例式和乘积式
例 5、△ ABC 中,在 AC 上截取 AD ,在 CB 延长线上截取 BE ,使 AD=BE ,求证: DF AC=BC FE
三角形一边的平行线(解析版)

三角形一边的平行线【知识梳理】1、三角形一边的平行线性质定理平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例. 如图,已知ABC ∆,直线//l BC ,且与AB 、AC 所在直线交于点D 和点E ,那么AD AEDB EC=.2、三角形一边的平行线性质定理推论平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例. 如图,点D 、E 分别在ABC ∆的边AB 、AC 上, //DE BC ,那么DE AD AE BC AB AC ==.3、三角形的重心定义:三角形三条中线交于一点,三条中线交点叫三角形的重心.性质:三角形重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍. 4、三角形一边的平行线判定定理如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边. 5、三角形一边的平行线判定定理推论如果一条直线截三角形的两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.如图,在ABC ∆中,直线l 与AB 、AC 所在直线交于点D 和点E ,如果AD AEDB EC=那么l //BC .6、平行线分线段成比例定理两条直线被三条平行的直线所截,截得的对应线段成比例. 如图,直线1l //2l //3l ,直线m 与直线n 被直线1l 、2l 、3l 所截,那么DF EGFB GC=.7、平行线等分线段定理两条直线被三条平行的直线所截,如果一条直线上截得的线段相等,那么另一条直线上截得的线段也相等.【考点剖析】 一.三角形的重心(共13小题)1.(2023•青浦区一模)三角形的重心是( ) A .三角形三条角平分线的交点 B .三角形三条中线的交点C .三角形三条边的垂直平分线的交点D .三角形三条高的交点【分析】根据三角形的重心概念作出回答,结合选项得出结果. 【解答】解:三角形的重心是三角形三条中线的交点. 故选:B .【点评】考查了三角形的重心的概念.三角形的外心是三角形的三条垂直平分线的交点;三角形的内心是三角形的三条角平分线的交点.2.(2023•奉贤区一模)在△ABC 中,AD 是BC 边上的中线,G 是重心.如果AD =6,那么线段DG 的长是 .BCD E FG【分析】根据重心的性质三角形的重心到一顶点的距离等于到对边中点距离的2倍,直接求得结果.【解答】解:∵三角形的重心到顶点的距离是其到对边中点的距离的2倍,∴DG=AG=2.故答案为:2.【点评】本题考查的是三角形的重心,熟知心到顶点的距离与重心到对边中点的距离之比为2:1是解题的关键.3.(2022秋•杨浦区期末)如图,△ABC中,∠BAC=90°,点G是△ABC的重心,如果AG=4,那么BC 的长为.【分析】延长AG交BC于点D,根据重心的性质可知点D为BC的中点,且AG=2DG=4,则AD=6,再根据直角三角形斜边的中线等于斜边的一半即可求解.【解答】解:如图,延长AG交BC于点D.∵点G是△ABC的重心,AG=4,∴点D为BC的中点,且AG=4,∴DG=2,∴AD=AG+DG=6,∵△ABC中,∠BAC=90°,AD是斜边的中线,∴BC=2AD=12.故答案为12.【点评】本题考查了三角形重心的定义及性质,三角形的重心是三角形三边中线的交点,重心到顶点的距离与重心到对边中点的距离之比为2:1.同时考查了直角三角形的性质.4.(2022秋•青浦区校级期末)如图,已知在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E,如果CB=10,则线段GE的长为()A.B.C.D.【分析】因为点G是△ABC的重心,根据三角形的重心是三角形三条中线的交点以及重心的性质:重心到顶点的距离与重心到对边中点的距离之比是2:1,可知点D为BC的中点,,根据GE⊥AC,可得∠AEG=90°,进而证得△AEG∽△ACD,从而得到,代入数值即可求解.【解答】解:如图,连接AG并延长交BC于点D.∵点G是△ABC的重心,∴点D为BC的中点,,∵CB=10,∴,∵GE⊥AC,∴∠AEG=90°,∵∠C=90°,∴∠AEG=∠C=90°,∵∠EAG=∠CAD(公共角),∴△AEG∽△ACD,∴,∵,∴,∴,∴.故选:D.【点评】本题考查了相似三角形的判定和性质,三角形的重心的定义及其性质,熟练运用三角形重心的性质是解题的关键.5.(2021秋•松江区期末)如图,已知点G是△ABC的重心,那么S△BCG:S△ABC等于()A.1:2B.1:3C.2:3D.2:5【分析】连接AG延长交BC于点D,由G是重心可得D是BC的中点,所以S△ABD=S△ACD,S△BG=S△CDG,又由重心定理可AG=2GD,则2S△BGD=S△ABG,进而得到3S△BDG=S△ABC,即可求解.【解答】解:连接AG延长交BC于点D,∵G是△ABC的重心,∴D是BC的中点,∴S△ABD=S△ACD,S△BDG=S△CDG,∵AG=2GD,∴2S△BDG=S△ABG,∴3S△BGD=S△ABD,∴3S△BDG=S△ABC,∴S△BDG:S△ABC=1:3,故选:B.【点评】本题考查三角形的重心,熟练掌握三角形重心定理,利用等底、等高三角形面积的特点求解是解题的关键.6.(2022秋•杨浦区校级期末)如图,G是△ABC的重心,延长BG交AC于点D,延长CG交AB于点E,P、Q分别是△BCE和△BCD的重心,BC长为6,则PQ的长为.【分析】连接DE,由G是△ABC的重心,可证DE是△ABC的中位线,从而可求出DE的长.延长EP交BC 于F点,连接DF,利用三角形重心的定义和性质得到EP=2PF,DQ=2QF,再证明△FPQ∽△FED得到即可.【解答】解:连接DE,延长EP交BC于F点,连接DF,如图,∵G是△ABC的重心,∴D、E分别是AB、AC的中点,∴DE是△ABC的中位线,∴.∵P点是△BCE的重心,∴F点为BC的中点,EP=2PF,∵Q点是△BCD的重心,∴点Q在中线DF上,DQ=2QF,∵∠PFQ=∠EFD,,∴△FPQ∽△FED,∴,∴,故答案为:1.【点评】本题考查了三角形的重心,三角形的中位线,相似三角形的判定与性质.三角形的重心是三角形三边中线的交点;重心到顶点的距离与重心到对边中点的距离之比为2:1.7.(2022秋•徐汇区期末)在Rt△ABC中,∠B=90°,∠BAC=30°,BC=1,以AC为边在△ABC外作等边△ACD,设点E、F分别是△ABC和△ACD的重心,则两重心E与F之间的距离是.【分析】取AC中点O,连接OB、OD、BD、EF.根据含30度角的直角三角形的性质求出AC=2BC=2,利用勾股定理得出AB=,根据等边三角形的性质得出CD=AD=AC=2,∠CAD=60°,那么∠BAD=∠BAC+∠CAD=90°,利用勾股定理求出BD=.然后证明△EOF∽△BOD,得出EF=BD=.【解答】解:如图,取AC中点O,连接OB、OD、BD、EF.在Rt△ABC中,∠B=90°,∠30°,BC=1,∴AC=2BC=2,AB===,∵△ACD是等边三角形,∴CD=AD=AC=2,∴∠CAD=60°,∴∠BAD=∠BAC+∠CAD=90°,∴BD===.∵点E、F分别是△ABC和△ACD的重心,∴==,又∠EOF=∠BOD,∴△EOF∽△BOD,∴===,∴EF=BD=.故答案为:.【点评】本题考查了相似三角形的判定与性质,含30度角的直角三角形的性质,等边三角形的性质,三角形重心的定义与性质,掌握重心到顶点的距离与重心到对边中点的距离之比为2:1是解题的关键.8.(2022秋•黄浦区月考)已知点G是△ABC的重心,那么S△ABG:S△ABC=.【分析】三角形的重心是三角形三边中线的交点,重心到顶点的距离与重心到对边中点的距离之比为2:1,由此即可计算.【解答】解:延长AG交BC于D,∵点G是△ABC的重心,∴BD=CD,AG:DG=2:1,∴AG:AD=2:3,∴S△ABG:S△ABD=2:3,∵S△ABD:S△ABC=1:2,∴S△ABG:S△ABC=1:3.故答案为:1:3.【点评】本题考查三角形的重心,关键是掌握三角形重心的性质.9.(2023•金山区一模)如图,△ABC为等腰直角三角形,∠A=90°,AB=6,G1为△ABC的重心,E为线段AB上任意一动点,以CE为斜边作等腰Rt△CDE(点D在直线BC的上方),G2为Rt△CDE的重心,设G1、G2两点的距离为d,那么在点E运动过程中d的取值范围是.【分析】分别求出d的最小值和最大值,即可得到d的取值范围.【解答】解:当E与B重合时,G1与G2重合,此时d最小为0,当E与A重合时,G1G2最大,连接并延长AG1交BC于H,连接并延长DG2交AC于K,连接HK,过G2作G2T⊥AH于T,如图:∵G1为等腰直角三角形ABC的重心,∴H为BC中点,∴∠AHB=∠AHC=90°,∴△ABH和△ACH是等腰直角三角形,∴BH=CH=AH==3,∵AG1=2G1H,∴AG1=2,G1H=,∵G2是为等腰Rt△CDE的重心,∴K为AC中点,∴∠AKD=∠CKD=90°,∠AKH=∠CKH=90°,∴∠AKD+∠AKH=180°,∴D,K,H共线,∵AK=CK=DK=AC=AB=3=HK,∴G2K=DK=1,G2D=DK﹣G2K=2,∴G2H=G2K+HK=4,∵TG2∥ED,∴====,即==,∴TG2=2,TH=2,∴TG1=TH﹣G1H=,∴G1G2==,∴G1G2最大值为,∴G1G2的范围是0≤G1G2≤,故答案为:0≤d≤.【点评】本题考查三角形的重心,涉及等腰直角三角形的性质及应用,解题的关键是掌握三角形重心的性质.10.(2023•松江区一模)已知△ABC,P是边BC上一点,△P AB、△P AC的重心分别为G1、G2,那么的值为.【分析】由重心的性质:重心到顶点的距离与重心到对边中点的距离之比为2:1,得到△AG1G2∽△ADE,推出△AG1G2的面积:△ADE的面积=4:9,而△ADE的面积=×△ABC的面积,即可解决问题.【解答】解:延长AG1交PB于D,延长AG2交PC于E,∵△PAB、△PAC的重心分别为G1、G2,∴AG1:AD=AG2:AE=2:3,D是PB中点,E是PC中点,∵∠G1AG2=∠DAE,∴△AG1G2∽△ADE,∴△AG1G2的面积:△ADE的面积=4:9,∵D是PB中点,E是PC中点,∴△ADE的面积=×△ABC的面积,∴的值为.故答案为:.【点评】本题考查三角形的重心,三角形的面积,相似三角形的判定和性质,关键是掌握三角形重心的性质.11.(2022秋•徐汇区期中)已知点G是等腰直角三角形ABC的重心,AC=BC=6,那么AG的长为.【分析】根据三角形的重心到顶点的距离等于到对边中点的距离的2倍解答即可.【解答】解:∵G是等腰直角△ABC的重心,AC=BC=6,∴CD=BC=3,由勾股定理得:AD==3,∴AG=×=2,故答案为:2.【点评】本题考查了三角形的重心,熟记三角形的重心到顶点的距离等于到对边中点的距离的2倍是解题的关键.12.(2018•宝山区校级自主招生)G为重心,DE过重心,S△ABC=1,求S△ADE的最值,并证明结论.【分析】设AD=mAB,AE=nAC,由G为△ABC重心得=3,再由当==时,有最大值,则mn有最小值,而无论D、E任何移动,mn,即可求出S△ADE的最值.【解答】解:S△ADE的最大值为,最小值为.证明:假设△ABC面积为S1,△ADE面积为S2,设AD=mAB,AE=nAC,∵G为△ABC重心,∴=3,∴S2=AD•AE•sinA=mAB•nAC•sinA=mnS1,当==时,有最大值,则mn有最小值,而无论D、E任何移动,mn,∴S1≤S2≤S1,∴S△ADE的最大值为,最小值为.【点评】本题主要考查了三角形重心的性质,解决此题的关键是根据G为△ABC重心得到=3.13.(2019秋•嘉定区校级月考)如图,点G是△ABC的重心,过点G作EF∥BC,分别交AB、AC于点E、F,且EF+BC=7.2cm,求BC的长.【分析】如果连接AG并延长,交BC于点P,由三角形的重心的性质可知AG=2GP,则AG:AP=2:3.又EF∥BC,根据相似三角形的判定可知△AGF∽△APC,得出AF:AC=2:3,最后由EF∥BC,得出△AEF∽△ABC,从而求出EF:BC=AF:AC=2:3,结合EF+BC=7.2cm来求BC的长度.【解答】解:如图,连接AG并延长,交BC于点P.∵G为△ABC的重心,∴AG=2GP,∴AG:AP=2:3,∵EF过点G且EF∥BC,∴△AGF∽△APC,∴AF:AC=AG:AP=2:3.又∵EF∥BC,∴△AEF∽△ABC,∴==.又EF+BC=7.2cm,∴BC=4.32cm.【点评】本题主要考查了三角形的重心的性质,相似三角形的判定及性质.三角形三边的中线相交于一点,这点叫做三角形的重心.重心到顶点的距离等于它到对边中点距离的两倍.平行于三角形一边的直线截其它两边,所得三角形与原三角形相似.相似三角形的三边对应成比例.二.平行线分线段成比例(共1914.(2022秋•徐汇区期末)在△ABC中,点D、E分别在边AB和BC上,AD=2,DB=3,BC=10,要使DE∥AC,那么BE必须等于.【分析】此题主要考查了平行线分线段成比例定理的逆定理,根据题意得出要使DE∥AC,必须即可得出BE的长.【解答】解:∵在△ABC中,点D、E分别在边AB和BC上,AD=2,DB=3,BC=10,∴要使DE∥AC,∴,∴,解得:BE=6.故答案为:6.【点评】此题主要考查了平行线分线段成比例定理的逆定理,根据题意得出要使DE∥AC,必须是解决问题的关键.15.(2022秋•闵行区期末)如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、C、E和点B、D、F,如果AC:CE=3:1,BF=10,那么DF等于()A.B.C.D.【分析】由AB∥CD∥EF,可得出=,代入AC=3CE,BF=10,即可求出DF的长.【解答】解:∵AB∥CD∥EF,∴=,即=,∴DF=.故选:C.【点评】本题考查了平行线分线段成比例,牢记“三条平行线截两条直线,所得的对应线段成比例”是解题的关键.16.(2023•宝山区一模)在△ABC中,点D、E分别在边AB、AC上,如果AD:BD=1:3,那么下列条件中能判断DE∥BC的是()A.=B.=C.=D.【分析】如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边,进而可得出结论.【解答】解:∵AD:BD=1:3,∴,∴当时,,∴DE∥BC,故A选项能够判断DE∥BC;而C,B,D选项不能判断DE∥BC.故选:A.【点评】本题主要考查了由平行线分线段成比例来判定两条直线是平行线的问题,能够熟练掌握并运用.17.(2022秋•嘉定区校级期末)如果点H、G分别在△DEF中的边DE和DF上,那么不能判定HG∥EF 的比例式是()A.DH:EH=DG:GF B.HG:EF=DH:DEC.EH:DE=GF:DF D.DE:DF=DH:DG【分析】根据平行线分线段成比例定理判断即可.【解答】解:A、当DH:EH=DG:GF,即=时,HG∥EF,本选项不符合题意;B、当HG:EF=DH:DE∥EF,本选项符合题意;C、当EH:DE=GF:DF,即=时,HG∥EF,本选项不符合题意;D、当DE:DF=DH:DG,即=时,HG∥EF,本选项不符合题意;故选:B.【点评】本题考查的是平行线分线段成比例定理成比例定理,灵活运用定理、找准对应关系是解题的关键.18.(2023•徐汇区一模)如图,a∥b∥c,若,则下面结论错误的是()A.B.C.D.【分析】已知a∥b∥c,根据平行线分线段成比例定理,对各项进行分析即可.【解答】解:由,得==,故A不符合题意;∵a∥b∥c,∴==,故B不符合题意;根据已知条件得不出=,故C符合题意;由=,得==,故D不符合题意;故选:C.【点评】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.19.(2021秋•嘉定区期末)如图,已知AB∥CD∥EF,AC:AE=3:5,那么下列结论正确的是()A.BD:DF=2:3B.AB:CD=2:3C.CD:EF=3:5D.DF:BF=2:5【分析】根据平行线分线段成比例定理判断即可.【解答】解:∵AB∥CD∥EF,∴BD:DF=AC:CE=3:2,A选项错误,不符合题意;AB:CD的值无法确定,B选项错误,不符合题意;CD:EF的值无法确定,C选项错误,不符合题意;DF:BF=CE:AE=2:5,D选项正确,符合题意;故选:D.【点评】本题考查的是平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例,灵活运用定理、找准对应关系是解题的关键.20.(2023•长宁区一模)如图,AD∥BE∥CF,已知AB=5,DE=6,AC=15,那么EF的长等于.【分析】由AD∥BE∥CF,可得=,即=,可解得DF=18,从而EF=DF﹣DE=12.【解答】解:如图:∵AD∥BE∥CF,∴=,∵AB=5,DE=6,AC=15,∴=,解得DF=18,∴EF=DF﹣DE=18﹣6=12,故答案为:12.【点评】本题考查平行线分线段成比例,解题的关键是掌握平行线分线段成比例定理,列出比列式.21.(2023•松江区一模)如图,已知直线AD∥BE∥CF,如果=,DE=3,那么线段EF的长是.【分析】根据平行线分线段成比例解答即可.【解答】解:∵AD∥BE∥CF,∴=,∵DE=3,∴=,∴EF=,故答案为:.【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.22.(2022秋•松江区月考)如图,在△ABC中,点D在AB上,点E在AC上,且DE∥BC,AD=3,AB =4,AC=6,求EC.【分析】根据平行线分线段成比例定理列出比例式,把已知数据代入计算即可.【解答】解:∵DE∥BC,∴=,即=,解得:AE=,∴EC=AC﹣AE=6﹣=.【点评】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.23.(2022秋•松江区月考)如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.(1)求EC的值;(2)求证:AD•AG=AF•AB.【分析】(1)由平行可得=,可求得AC,且EC=AC﹣AE,可求得EC;(2)由平行可知==,可得出结论.【解答】(1)解:∵DE∥BC,∴=,又=,AE=3,∴=,解得AC=9,∴EC=AC﹣AE=9﹣3=6;(2)证明:∵DE∥BC,EF∥CG,∴==,∴AD•AG=AF•AB.【点评】本题主要考查平行线分线段成比例的性质,掌握平行线分线段所得线段对应成比例是解题的关键.24.(2023•崇明区一模)四边形ABCD中,点F在边AD上,BF的延长线交CD的延长线于E点,下列式子中能判断AD∥BC的式子是()A.=B.=C.=D.=【分析】根据各个选项中的条件和图形,利用相似三角形的判定和性质、平行线的判定,可以判断哪个选项符合题意.【解答】解:当时,无法判断AD∥BC,故选项A不符合题意;当=时,∠AFB=∠DFE,则△AFB∽△DFE,故∠ABF=∠DEF,AB∥CD,但无法判断AD∥BC,故选项B不符合题意;当时,无法判断AD∥BC,故选项C不符合题意;当时,∠FED=∠BEC,则△FED∽△BEC,故∠EFD=∠EBC,可以判断判断AD∥BC,故选项D符合题意;故选:D.【点评】本题考查平行线分线段成比例、平行线的判定、相似三角形的判定和性质,解答本题的关键是明确题意,利用数形结合的思想解答.25.(2022秋•杨浦区校级期末)如图,已知AB∥CD∥EF,AD:AF=3:5,BE=24,那么BC的长等于()A.4B.C.D.8【分析】根据平行线分线段成比例得到,即可求出BC.【解答】解:∵AB∥CD∥EF,∴,∵BE=24,∴,解得:.故选:C.【点评】本题考查了平行线分线段成比例;熟练掌握三条平行线截两条直线,所得的对应线段成比例是本题的关键.26.(2022秋•浦东新区期末)如图,DF∥AC,DE∥BC,下列各式中正确的是()A.B.C.D.【分析】根据平行线分线段成比例定理逐个判定即可.【解答】解:A.∵DE∥BC,∴=,∴=,故本选项符合题意;B.∵DF∥AC,∴=,故本选项不符合题意;C.∵DE∥BC,∴=,∴=,即=,故本选项不符合题意;D.∵DE∥BC,DF∥AC,∴,,∴=,故本选项不符合题意;故选:A.【点评】本题考查了平行线分线段成比例定理和比例的性质,能根据平行线分线段成比例定理得出正确的比例式是解此题的关键.27.(2022秋•青浦区校级期末)如图,已知直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,AB=6,BC=3,DF=12,则DE=.【分析】根据平行线分线段成比例,即可进行解答.【解答】解:∵l1∥l2∥l3,∴,即,∵DF=12,∴DE+DE=12,解得:DE=8.故答案为:8.【点评】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.掌握平行线分线段成比例是解题关键.28.(2022•宝山区二模)已知:如图,点D、E、F分别在△ABC的边AB、AC、BC上,DF∥AC,BD=2AD,AE=2EC.(1)如果AB=2AC,求证:四边形ADFE是菱形;(2)如果AB=AC,且BC=1,联结DE,求DE的长.【分析】(1)根据菱形的判定方法解答即可;(2)根据相似三角形的判定和性质解答即可.【解答】(1)证明:∵BD=2AD,AE=2EC,∴=,∵DF∥AC,∴=,∴=,∴EF∥AB,又∵DF∥AC,∴四边形ADFE是平行四边形,∵AB=2AC,AE=AC,∴AE=AB,∴AD=AE,∵四边形ADFE是平行四边形,∴四边形ADFE是菱形;(2)如图,在△ADE和△ACB中,∠A是公共角,===,===,∴△ADE∽△ACB,∵BC=1,∴DE=.【点评】本题主要考查了菱形的判定和相似三角形的判定和性质,熟练掌握这些判定定理和性质定理是解答本题的关键.29.(2021秋•杨浦区校级月考)如图,点D为△ABC中内部一点,点E、F、G分别为线段AB、AC、AD 上一点,且EG∥BD,GF∥DC.(1)求证:EF∥BC;(2)当,求的值.【分析】(1)先根据相似比的性质得出=,=,故可得出=,由此即可得出结论;(2)先根据EF∥BC得出∠AEF=∠ABC,再由DG∥BD得出∠AEG=∠ABD,故可得出∠GEF=∠DBC,同理可得,∠GEF=∠DBC,故可得出△EGF∽△BDC根据相似三角形面积的比等于相似比的平方即可得出结论.【解答】(1)证明:∵EG∥BD,∴=,∵GF∥DC,∴=,∴=,∴EF∥BC;(2)解:∵EF∥BC,∴∠AEF=∠ABC,∵EG∥BD,∴∠AEG=∠ABD,∴∠AEF﹣∠AEG=∠ABC﹣∠AED,即∠GEF=∠DBC,同理可得,∠GEF=∠DBC,∴△EGF∽△BDC,∵,∴==,∴=()2=.【点评】熟知相似三角形对应边的比等于相似比,面积的比等于相似比的平方是解答此题的关键.30.(2021秋•宝山区校级月考)如图,已知直线l1、l2、l3分别截直线l4于点A、B、C,截直线l5于点D、E、F,且l1∥l2∥l3.(1)如果AB=4,BC=8,EF=12,求DE的长.(2)如果DE:EF=2:3,AB=6,求AC的长.【分析】(1)由平行线分线段成比例定理得出比例式,即可得出DE的长;(2)由平行线分线段成比例定理得出比例式,求出BC的长,即可得出AC的长.【解答】解:(1)∵l1∥l2∥l3.∴==,∴DE=EF=6;(2)∵l1∥l2∥l3.∴=,∴BC=AB=×6=9,∴AC=AB+BC=6+9=15.【点评】本题考查了平行线分线段成比例定理;熟练掌握平行线分线段成比例定理,并能进行推理计算是解决问题的关键.31.(2022秋•奉贤区期中)如图,已知直线l1∥l2∥l3,直线AC和DF被l1、l2、l3所截.若AB=3cm,BC =5cm,EF=4cm.(1)求DE、DF的长;(2)如果AD=40cm,CF=80cm,求BE的长.【分析】(1)利用平行线分线段成比例定理求解;(2)过点A作AK∥DF交BE于点J,交CF于点K,则AD=JE=FK=40cm.求出BJ,可得结论.【解答】解:(1)∵l1∥l2∥l3,∴=,∴=,∴DE=(cm),∴DF=DE+EF=4+=(cm).(2)如图,过点A作AK∥DF交BE于点J,交CF于点K,则AD=JE=FK=40cm.∴CK=CF﹣FK=40cm,∵BJ∥CK,∴=,∴=,∴BJ=15cm,∴BE=BJ+JE=15+40=55cm.【点评】本题考查平行线分线段成比例定理,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.32.(2022秋•浦东新区校级月考)如图,已知点A、C、E和点B、F、D分别是∠O两边上的点,且AB∥ED,BC∥EF,AF、BC交于点M,CD、EF交于点N.(1)求证:AF∥CD;(2)若OA:AC:CE=3:2AM=1,求线段DN的长.【分析】(1)根据平行线分线段成比例定理,由AB∥DE得到OA•OD=OE•OB,由BC∥EF得到OC•OF=OE •OB,所以OA•OD=OC•OF,即=,于是可判断AF∥CD;(2)先利用BC∥EF得到==,则可设OB=5x,BF=4x,再由AF∥CD得到==,==,所以FD=6x,接着由FN∥BC得到==,于是可设DN=3a,则CN=2a,然后证明四边形MFNC为平行四边形得到MF=CN=2a,最后利用=得到=,求出a从而得到DN的长.【解答】(1)证明:∵AB∥DE,∴=,即OA•OD=OE•OB,∵BC∥EF,∴=,即OC•OF=OE•OB,∴OA•OD=OC•OF,即=,∴AF∥CD;(2)解:∵OA:AC:CE=3:2:4,∴OC:CE=5:4,∵BC∥EF,∴==,设OB=5x,则BF=4x,∵AF∥CD,∴==,==∴FD=OF=×9x=6x,∵FN∥BC,∴===,设DN=3a,则CN=2a,∵FN∥CM,MF∥CN,∴四边形MFNC为平行四边形,∴MF=CN=2a,∵=,即=,解得a=1,∴DN=3a=3.【点评】本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.【过关检测】一、单选题A.4【答案】C【分析】根据平行线分线段成比例得到35BC ADBE AF==,即可求出BC.【详解】解:∵AB CD EF∥∥,∴35 BC ADBE AF==,∵24 BE=,∴3 245 BC=,解得:725 BC=.故选:C【点睛】本题考查了平行线分线段成比例;熟练掌握三条平行线截两条直线,所得的对应线段成比例是本题的关键.九年级校考期中)在ABC中,分别在ABC的边【答案】A【分析】根据平行线分线段成比例定理对各个选项进行判断即可.【详解】解:A、AD DEAB BC=,不能判定DE BC∥,故A符合题意;B、∵AD AE AB AC=,∴DE BC∥,故B不符合题意;C、∵AED C∠=∠,∴DE BC∥,故C不符合题意;D、∵AD AE BD EC=,∴DE BC∥,故D不符合题意.故选:A.【点睛】本题主要考查了平行线分线段成比例定理,平行线的判定,如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.九年级单元测试)在ABC中,点【答案】B【分析】根据题目的已知条件画出图形,然后利用平行线分线段成比例解答即可.【详解】如图:∵DE∥AC,AE:EB=3:2,∴32 AE CDEB BD==∴23BD CD =∵DF AB ∥, ∴23AF BD FC CD == 故选:B【点睛】本题考查了平行线分线段成比例,熟练掌握平行线分线段成比例这个基本事实是解题的关键. 在ABC 的边 【答案】A【分析】根据平行线分线段成比例可得47AE AD AC AB ==,则可以推出当47AF AE AD AC ==,即37DF AD =时,EF CD ∥.【详解】解:DE BC ∥,43AD DB =,∴44437AE AD AD AC AB AD DB ====++,∴当47AF AE AD AC ==时,EF CD ∥,此时74377DF AD AF AD AD −−===,故A 选项符合题意; B ,C ,D 选项均不能得出EF CD ∥.故选A .【点睛】本题考查平行线分线段成比例,解题的关键是掌握“如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边”.5.(2023·上海浦东新·校考一模)如图,点D 、E 分别在AB 、AC 上,以下能推得DE BC ∥的条件是( )A .::AD AB DE BC =B .::AD DB DE BC = C .::AD DB AE EC =D .::AE AC AD DB =【答案】C 【分析】平行于三角形一边的直线截其他两边或延长线,所得的对应线段成比例.如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.【详解】解:设DE BC ∥,那么AD AB AE AC AD DB AE EC DB AB EC AC ===::,::,::,选项A 、B 、D 、不符合平行线分段成比例定理.如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.∵AD DB AE EC =::,∴DE BC ∥.故选:C .【点睛】此题主要考查平行线分线段成比例,解答此题的关键的是明确哪些对应线段成比例.学生初学,容易出错.九年级校考期中)在ABC 中,点【答案】B【分析】利用如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边可对各选项进行判断即可.【详解】当AD AE DB EC =或AD AE AB AC =时, DE BC ∥, 当AD AE DB EC =时,可得23AE EC =,当AD AE AB AC =时,可得25AE AC =, 即23AE EC =或25AE AC =.所以B 选项是正确的,故选:B .【点睛】本题考查了平行线分线段成比例定理,熟练掌握和灵活运用相关知识是解题的关键.二、填空题 7.(2022秋·上海嘉定·九年级校考期中)在ABC 中,点D 、E 分别在线段AB 、AC 的延长线上,DE 平行于BC ,1AB =,3BD =,2AC =,那么AE =___________.【答案】8【分析】根据平行线分线段陈比例定理求解即可.【详解】∵DE AB ∥ ∴AB AC AD AE = ∵1AB =,3BD =,2AC =,∴124AE =∴8AE =故答案为:8.【点睛】此题考查了平行线分线段陈比例定理,解题的关键是掌握平行线分线段陈比例定理.8.(2022春·上海普陀·九年级校考期中)如图,ABCD Y 中,E 是边AD 的中点,BE 交对角线AC 于点F ,那么:AFE FEDC S S 四边形的值为____.【答案】15/0.2【分析】证明12AF EF AE CF BF BC ===,推出24BCF ABF AEF S S S ==,设AEF S m =,则2ABF S m =,4CBF S m =,求出四边形FEDC 的面积,可得结论.【详解】解:∵四边形ABCD 是平行四边形,∴AD BC =,AD BC ∥,∴AF EF AE CF BF BC ==, ∵ E 是边AD 的中点,∴1122AE DE AD BC ===,∴12AF EF AE CF BF BC ===, ∴24BCF ABF AEF S S S ==,设AEF S m =,则2ABF S m =,4S m , ∴6ACB ADC S S m ==, ∴65FECD S m m m =−=四边形, 1::55AFE FECD S S m m ==四边形; 故答案为:15.【点睛】本题考查相似三角形的判定和性质,平行四边形的性质等知识,解题的关键是掌握平行线分线段成比例定理,属于中考常考题型.9.(2022秋·上海黄浦·九年级统考期中)如图,AD 、BC 相交于点O ,点E 、F 分别在BC 、AD 上,AB CD EF ∥∥,如果6CE =,4EO =,5BO =,6AF =,那么AD = ___________.【答案】10【分析】利用平行线分线段成比例定理得到EO FO BO AO =,EO FO CE DF =,求得4893FO AF ==,4DF =即可解决问题.【详解】解:∵AB CD EF ∥∥,EO FO BO AO =,EO FO CE DF =,∵4EO =,5BO =,∴45FO AO =, ∵6AF =,∴4893FO AF ==,∵6CE =,∴8436DF =,∴4DF =,∴6410AD AF DF =+=+=.故答案为:10.【点睛】本题考查平行线分线段成比例定理,解题的关键是灵活运用所学知识解决问题.10.(2022秋·上海奉贤·九年级校联考期中)如图,四边形ABCD 中,AD BC EF ∥∥,如果3810AE AB CD ===,,,则CF 的长是________.【答案】254【分析】根据平行线分线段成比例得出AE DF AB CD =,求出154DF =,即可得出答案. 【详解】∵AD BC EF ∥∥, ∴AE DF AB CD =, ∵3810AE AB CD ===,,, ∴3810DF =, 解得:154DF =, ∴15251044CF CD DF =−=−=, 故答案为:254.【点睛】本题考查平行线分线段成比例,正确得出比例线段是解题的关键. 11.(2022秋·上海宝山·九年级统考期中)在ABC 中,点D 、E 分别在直线AB 、AC 上,如果DE BC ∥,1AB =,2AC =,3AD =,那么CE =________.【答案】4【分析】根据平行线分线段陈比例定理求解即可.【详解】解:作如下图:∵DE BC ∥,∴AB AC AD AE =, ∵1AB =,2AC =,3AD =,∴123AE =,∴6AE =,∴624CE AE AC =−=−=,故答案为:4.【点睛】此题考查了平行线分线段陈比例定理,解题的关键是掌握平行线分线段陈比例定理.。
初二数学平行线分线段成比例定理讲义及练习

平行线分线段成比例定理一、主要知识点1.平行线分线段成比例定理,三条平行线截两条直线,所得的对应线段成比例.2.三角形一边平行线的性质定理(即平行线分线段成比例定理的推论):平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.3.三角形一边的平行线的判定定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.4.三角形一边的平行线的性质定理2(即课本例6):平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形三边对应成比例。
二、重点剖析1.平行线分线段成比例定理,是研究相似的最重和最基本的理论,同时,它也是直接证明线段成比EFBC=, 可以说成“上比下等于上比下"DEAB=, 可以说成“上比全等于上比全"又∵43=EC AE ∴ 73=AC AE ∴73=DC EG极 EG=3X , DC=7X (X>0),则∵32=DC BD ∴ DB=x x DC 31473232=⨯= ∴9143314==x xEG BD10例3求证分析 BC//FE 证明:∵则例4 分别连结E ,DB 分析:首先观察证明:∵点评 (1(3 例5 求证分析 例6 分析在△②—①得-AB AD BF BC 例7 如图11,AD BF ⊥AD 的延长线于交BC 的延长线于M 求证:AE=EM分析 要证AE=EM,可延长BF 交AC 证明:延长BF 交AC ∴△ABF ≌△ANF8. 图,GB AF l l 52,//21=,BC=4CD , 91011AE 1213① 求证ME=NF② 当EF 向上平移 图(2)各个位置其他条件不变时, ①的结论是否成立,请证明你的判断。
[练习与测试参考解答或提示]1.215;2.18cm ; 3.52,35; 4.9:4; 5.9; 6.10,18; 7.9:1; 8.2; 9.6 10.提示,过D 作DH//AC 交BG 于H 点,则DH AEGD AG =,DHEC BD BC =,又AE=EC ,BD=AB,即可得结论。
七年级下册三角形-平行线-轴对称-整式知识点总结及习题

第七章生活中的轴对称(知识点总结)一,基本概念1.轴对称图形,对称轴如果一个图形沿着某条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
轴对称图形不一定只有一条对称轴,但至少有一条。
2.轴对称对于两个图形,如果沿一条直线对折后,它们能完全的重合,那么称这两个图形关于这条直线对称,也称这两个图形成轴对称。
3.轴对称和对称轴图形中的对称轴是直线,而不是线段和射线。
4.轴对称的性质:1)对应点所连的线段被对称轴垂直平分;2)对应线段相等,4.角平分的性质:角平分线上的点到这个角的两边的距离相等。
5.垂直平分线:垂直并且平分一条线段的直线叫做这条线段的垂直平分线。
6.垂直平分线的性质:线段垂直平分线上的点到这条线段两个端点的距离相等。
7.等腰三角形:有两边相等的三角形叫做等腰三角形。
8.等腰三角形性质:1)等腰三角是轴对称图形;2)等腰三角形顶角的平分线、底边上的中线,底边上的高重合(三线合一),它们所在的直线都是等腰三角形的对称轴。
3)等腰三角形的两个底角相等。
(注意:等腰三角形的性质常用于说明两线段相等或两角相等)9.等腰三角形的判定方法:1)有两个角相等的三角形是等腰三角形(等角对等边);2) 有两条边相等的三角形是等腰三角形(等边对等角)。
10.等边三角形:三边都相等的三角形是等边三角形,也叫正三角形。
11.等边三角形的性质:1)等边三角形的三个内角均为600; 2)等边三角形的三边相等。
12.镜子成像的特点:1) 物体与镜子平行时:左右互换是关键,物与像成轴对称,简单可以看反面。
;2)物体与镜面垂直时:像的方向与物体的方向上下颠倒。
第五章三角形(知识点总结)1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
用“△”表示三角形,以A、B、C为顶点的三角形记作“△ABC”。
2三角形的三边关系:三角形任意两边之和大于第三边,三角形任意两边之差小于第三边。
初三数学第4讲:三角形一边的平行线判定定理

教学内容一、知识要点:1、三角形一边的平行线判定定理:如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边。
数学表达:如图,直线DE 截△ABC 得两边AB 、AC ,若①AD AEDB EC=,②AD AEAB AC =,③BD ECAB AC=中之一为已知条件,则DE DE∥∥BCED CBA2、三角形一边的平行线判定定理推论:如果一条直线截三角形两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边。
数学表达:若点D 、E 分别在射线AB 、AC 上,如图(1)或分别在他们的方向延长线上如图(2),且具备上述条件①、②、③之一,则D E ∥BC.EDCBAEDC B A牛刀小试:1、如图,△ABC 中,点D 、E 分别在边AB 、AC 上。
判断在下列条件下能否推出D E ∥BC,为什么?为什么? (1)23AD DB =,AE=2,AE=2,,AC=3 (2)25AD AB =,25DEBC = (3)23AD DB =,53AC CE =EDCBA2、△ABC 中,直线DE 交AB 于点D ,交AC 于点E ,那么能推出D E ∥BC 的条件是(的条件是( )) A 、AB3=AD 2,EC1=AE 2 B B、、AD 2=AB3,DE2=BC 3 C 、AD 2=DB3,CE 2=AE3D D、、AD 3=AB4,AE 3=EC4二、典型例题例1、如图EF ∥BC ,31=ACAF ,BF=4,FD=2,求证:EF ∥AD A D E F B C 例2、如图所示,、如图所示,M M 为AB 的中点,的中点,EF EF EF∥∥AB,AB,连接连接EM EM、、FM FM,分别交,分别交AF AF、、BE 于点C 、D ,连接CD CD。
求证:求证:CD CD CD∥∥AB.分析:判定两直线平行的方法一般有四种:(1)通过“三线八角”的相等或互补判定两直线平行;(2)通过三角形、梯形中位线定理判定两直线平行;(3)通过平行四边形的判定间接证平行;(4)通过比例线段证平行。
三角形一边的平行线-知识讲解

三角形一边的平行线-知识讲解在几何学中,三角形是一种简单且常见的图形。
三角形有各种性质和特点,其中之一是它们的边可以被称为平行线。
在本文中,我们将深入探讨三角形的一边的平行线及其相关概念。
一、平行线的定义在几何学中,当两条直线在同一平面上并且永远不相交时,这两条直线被称为平行线。
平行线具有如下性质:1. 任意平面上的直线和平行于该直线的其他直线之间都是平行关系。
2. 平行线之间的距离始终保持相等。
二、三角形的边三角形是由三条线段组成的,我们将这些线段称为三角形的边。
三角形的边可分为三类:1. 底边:三角形底部的水平边被称为底边,通常为最长的一边。
2. 左边:与底边不相交的边被称为左边。
3. 右边:与底边不相交的边被称为右边。
三、三角形一边的平行线我们经常遇到的情况是,三角形的一边与另一直线平行。
在这种情况下,我们可以得到一些重要的结论。
首先,如果三角形的两边分别与一条直线平行,那么这两边之间的边也将平行于该直线。
这个性质被称为平行线穿过三角形。
其次,如果在一个三角形中,一个边与一条直线平行,那么这个三角形的另外两个对边也将平行于该直线。
这些性质使得我们能够利用平行线的关系来推断出三角形内部的一些特征。
四、平行线的应用平行线的应用非常广泛,下面我们将介绍一些常见且实用的应用。
1. 相似三角形:当一个直线与一个三角形的两边平行时,根据平行线的性质,我们可以得出这个三角形与原始三角形相似的结论。
这种关系在解决几何问题和图形比例时非常有用。
2. 三角形判定:在解决三角形问题时,如果我们知道一个三角形的两边平行,我们可以推断出该三角形是等腰三角形或等腰直角三角形。
这可以大大简化问题的解决过程。
3. 垂直角关系:当两条直线互相垂直时,它们与平行线的关系密切相关。
通过利用平行线的性质,我们可以推断出垂直角之间的关系,进而解决垂直角相关的几何问题。
五、总结在几何学中,平行线是一种常见且重要的概念。
三角形的一边平行于直线时,我们可以得到一些实用的结论。
2022-2023学年上海九年级数学上学期同步精讲精练第3讲 三角形一边的平行线(解析版)
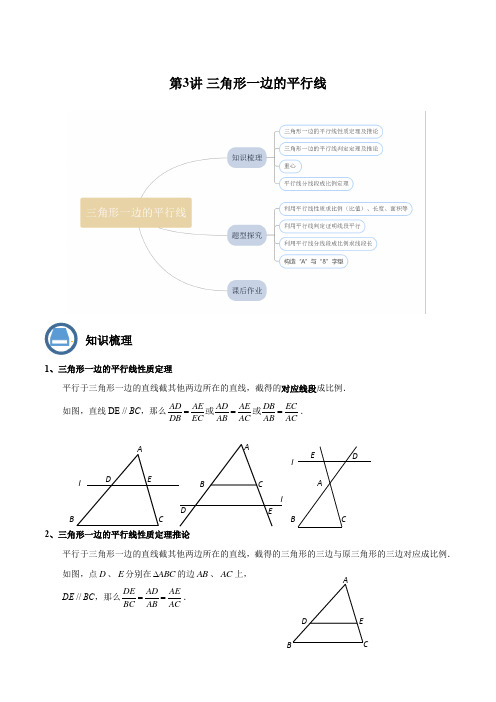
第3讲 三角形一边的平行线1、三角形一边的平行线性质定理平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例. 如图,直线DE // BC,那么AD AE AD AE DB ECDB EC AB AC AB AC===或或.2、三角形一边的平行线性质定理推论平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例. 如图,点D 、E 分别在ABC ∆的边AB 、AC 上, DE // BC ,那么DE AD AEBC AB AC==.知识梳理lA BCDEABCDEABCDE ll ABCDE3、三角形的重心定义:三角形三条中线交于一点,三条中线交点叫三角形的重心.性质:三角形重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍.4、三角形一边的平行线判定定理如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.5、三角形一边的平行线判定定理推论如果一条直线截三角形的两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.6、平行线分线段成比例定理ABCDEABCDEABCDE两条直线被三条平行的直线所截,截得的对应线段成比例. 如图,直线1l //2l //3l ,直线m 与直线n 被直线1l 、2l 、3l所截,那么DF EGFB GC.7、平行线等分线段定理两条直线被三条平行的直线所截,如果一条直线上截得的线段相等,那么另一条直线上截得的线段也相等.题型探究BCD E FG题型一、利用平行线性质求比例(比值)、长度、面积等【例1】如图,在ABC∆中,//DE BC,18AB=,12AC=,6BD=,求CE.【答案】4.【解析】BD CEAB AC=,代入可得:=4CE.【例2】如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交DC的延长线于点F,AB=2,BE=3EC,那么DF的长为.【答案】83.【解析】∵四边形ABCD为平行四边形,∴DC=AB=2,又∵CF∥AB,∴13CF CEAB BE==,∴CF=23,则DF=2+CF= 83.【例3】如图,在ABC∆中,CD平分ACB∠,//DE BC,5AC=厘米,3:5ADAB=,求DE的长.【答案】2cm . 【解析】//DE BC ,35AE AD AC AB ∴==. 由5AC cm =,代入可求得:32AE cm CE cm ==,. 又//DE BC ,EDC DCB ∴∠=∠.又CD 平分ACB ∠, ECD DCB ∴∠=∠. ECD EDC ∴∠=∠, 2DE CE cm ∴==.【例4】如图,在△ABC 中,点G 是△ABC 的重心,过点G 作DE ∥AC 分别交AB 、BC 于点D 、E ,过点D 作DF ∥BC 交AC 于点F ,如果DF=4,那么BE= .【答案】8.【解析】∵点G 是△ABC 的重心,DE ∥AC ,∴2BE BDCE AD==,由题意可得,四边形CEDF 为平行四边形,则DF=CE=4,∴BE=2CE=8.【例5】如图,已知在ABC ∆中,//DE BC ,//EF AB ,2AE CE =,6AB =,9BC =,求四边形BDEF 的周长.【答案】16. 【解析】2AE CE =,2133AE CE AC AC ∴==,.又//DE BC ,//EF AB ,2133AD AE EF CE AB AC AB AC ∴====,,四边形BDEF 为平行四边形. 代入可求得:62DE EF ==,,()2=16BDEF C DE EF ∴=+四边形.【例6】如图,在ABC ∆中,AB AC >,AD BC ⊥于点D ,点F 是BC 中点,过点F 作BC 的垂线交AB 于点E ,:3:2BD DC =,则:BE EA =.【答案】5:1.【解析】由:3:2BD DC =,BF FC =, 即得:32BF FD BF FD +=-,可得:51BF FD =.又AD BC ⊥,EF BC ⊥, EF ∴//AD ,::5:1BE EA BF FD ∴==.【例7】如图,在等腰ABC ∆中,AB=AC ,AD 、BE 分别是边BC 、AC 上的中线,AD 与BE 交于点F ,若BE=6,FD=3,则ABC ∆的面积.【答案】97.【解析】∵点F 是△ABC 的重心,∴AF BFFD EF==2,∴AF=2FD=6,AD=9,BF=4, 又∵AB=AC ,AD 是边BC 上的中线,∴AD 垂直于BC,∴由勾股定理得,BD=CD=7,∴S △ABC =11279=9722BC AD ⨯⨯=⨯⨯. 题型二、利用平行线判定证明线段平行【例8】如图,ABC ∆中,E 点在边AB 上,F 点在边AC 上,下列命题中不正确的是( )(A )若EF //BC ,则AE AFEB FC =(B )若AE AFEB FC =,则EF //BC (C )若EF //BC ,则AE EFAB BC =(D )若AE EFAB BC =,则EF //BC 【答案】D【解析】A 、B 、C 选项都可由三角形一边平行线性质定理及其判定定理可判定正确,D 选 项不符合定理判定内容.故选:B.【例9】如图,点D 、F 在ABC ∆的边AB 上,点E 在边AC 上,且DE //BC ,AF ADAD AB =.求证:EF //DC .AB CEFA BCDEFGH【答案】见解析.【解析】证明://DE BC , AD AE DB EC ∴=, 则AD AEAB AC =. 又AF AD AD AB =,AF AEAD AC ∴=, ∴EF //DC . 【例10】点D 、E 分别在ABC ∆的边AB 、AC 上,且DE //BC ,以DE 为一边作平行四边形DEFG ,延长BG 、CF 交于点H ,连接AH ,求证:AH //EF . 【答案】略. 【解析】证明:DE //BC , DE AEBC AC∴=. 又四边形DEFG 为平行四边形, //DE FG DE FG ∴=,. FG HF BC HC ∴=, AE HF AC HC ∴=, AE HFEC FC∴=, ∴AH //EF .题型三、利用平行线分线段成比例求线段长【例11】如图,1l //2l //3l ,3AB =,8AC =,10DF =, 求DE 、EF 的长.【答案】152544DE EF ==,. 【解析】根据平行线分线段成比例定理和比例的合比性,可得AB DE AC DF =,代入求得154DE =,则ABCDE F B CA DEF254EF DF DE=-=.【例12】如图,直线1l、2l 、3l 分别交直线4l 于点A 、B、C,交直线5l于点D、E、F,且1l//2l// 3l.已知3AB=,5AC=,9DF=,求DE、EF的长.【答案】271855DE EF==,.【解析】根据平行线分线段成比例定理和比例的合比性,可得AB DEAC DF=,代入求得275DE=,则185EF DF DE=-=.题型四、构造“A”与“8”字型【例13】如图,在梯形ABCD中,AD∥BC,AD=3,BC=9,AB=6,CD=4.若EF∥BC,且EF=7,求AE和DF的长.(用两种方法解决)【答案】AE=4,DF=83;【解析】方法1:如图,过点A作AG∥CD,交EF于点H,交BC于点G,易得FH=CG=AD=3,AG=CD=4,∴EH=EF-FH=4,BG=BC-CG=6,∵EF∥BC,∴46AE EHAB AG==,∴DF AECD AB=,∴AE=4,DF=83.方法2:延长BA、CD交于点Q,可得AD∥EF∥BC,∴13AQ QD ADQB QC BC===,∴AQ=12AB=3,QD=12DC =2,CBADEFABDCE F∵AD ∥EF ,∴37AD QA QD EF QE QF ===,∴QE=7,QF=143,∴AE=7-3=4,DF=QF-QD=83.【例14】如图,D 是线段BC 上一点,且23BD DC =,CE 交AB 于点F ,:1:3AE ED =,求:AF BF 的值.【答案】2:15.【解析】过点A 作//AM BC 交CF 的延长线于点M , 根据三角形一边平行线的性质定理, 则有13AM AE DC ED ==. 又23BD DC =,即()23BC DC DC -=.可得25DC BC =, 则215AM BC =. 由//AM BC 可得:::2:15AF BF AM BC ==.举一反三1.ABC ∆中,直线DE 交AB 于点D ,交AC 于点E ,以下能推出DE //BC 的条件是( )A .23AB AD =,12EC AE = B .23AD AB =,23DE BC =C .23AD DB =,23CE AE = D .43AD AB =,43AE EC = 【答案】A【解析】根据比例的性质,可知只有A 选项中满足2AB AEBD EC ==,根据三角形一边平行线的判定定理可知A 选项正确,其它都不满足.2.(2021•醴陵市模拟)如图,直线123////l l l ,直线AC 和DF 被1l ,2l ,3l 所截,如果2AB =,3BC =,2EF =,那么DE 的长是( )A .2B .43C .1D .34【答案】B【解析】解:直线123////l l l ,∴AB DEBC EF=, 2AB =,3BC =,2EF =,∴232DE=, 43DE ∴=, 故选:B .3.(2021•松北区模拟)如图,ABC ∆中,//DE BC ,//GF AC ,下列式子错误的是( )A .AG CFBG BF=B .AD AE AB AC=C .GM AEMF EC=D .FC AGDM DG=【答案】C 【解析】解://DE BC ,//GF AC ,ADE ABC ∴∆∆∽,BGF BAC ∆∆∽,DGM DAE ∆∆∽,且四边形MECF 是平行四边形.∴AG CFBG BF=,AD AEAB AC=,ME AGDM DG=,ME FC=.∴FC AGDM DG=.所以ABD正确,C 错误.4.(2021•温岭市模拟)如图,////AB CD EF,AF与BE相交于点G,且2AG=,1GD=,5DF=,则:(BC CE=)A.3:5B.1:3C.5:3D.2:3【答案】A【解析】解:////AB CD EF,∴21355BC ADCE DF+===.故选:A.5.在ABC∆中,点D、E分别在边AB和BC上,2AD=,3DB=,10BC=,要使DE//AC,则BE=.【答案】6.【解析】根据三角形一边平行线的判定定理,要得到DE//AC,则必有DB BEAB BC=,即3=2+310BE,即可求得6BE=.6.如图,ABC∆中,DE//BC,AF ADDF DB=,求证:EF//CD.【答案】略.【解析】证明:DE//BC,AD AEDB EC∴=.又AF ADDF DB=,AF AEDF EC∴=.∴EF//CD.7.如图,已知AD//BE//CF,它们依次交直线1l、2l于点A、B、C和点D、E、F.AB CD EFABCPQ(1)如果6AB =,10BC =,8EF =,求DE 的长; (2)如果:3:5DE EF =,24AC =,求AB 、BC 的长.【答案】(1)245;(2)915AB BC ==,.【解析】(1)根据平行线等分线段成比例定理,则有DE AB EF BC =,代入可求得245DE = (2)根据平行线等分线段成比例定理,则有35AB DE BC EF ==, 根据比例的合比性,则有38AB AC =,代入可得9AB =,15BC AC AB =-= 8.如图,在平行四边形ABCD 中,点E 在边DC 上,若:1:2DE EC =,则:BF BE =.【答案】3:5.【解析】:1:2DE EC =,可知23CE CE CD AB ==,由//CE AB ,可知32BF AB EF CE ==,故:3:5BF BE =. 9.如图,ABC ∆中,在BC 上取一点P ,CA 上取一点Q ,使得BP : PC = 2 : 5,CQ : QA = 3 : 4,AP 与BQ 交于点R ,则AR : RP =______.【答案】14:3.【解析】过点P 作//PD BQ 交AC 于D , 根据三角形一边平行线性质定理,则有AR AQPR QD=, 25BP QD PC DC ==,又CQ : QA = 3 : 4,令4AQ a =, 则3CQ a =,2677QD CQ a ==,由此即可得:6::4:14:37AR RP AQ QD a a ===.A B CD E F10.如图,在梯形ABCD中,//AD BC,3AD=,5BC=,E、F是两腰上的点,//EF AD,:1:2AE EB=,求EF的长.【答案】113.【解析】过点A作//AH DC交BC于H,交EF于G,则有32CH FG AD BH====,,又//EG BH,可得:13EG AEBH AB==,解得:23EG=,故113EF EG GF=+=.课后作业1.(2020年•黄浦区一模)如图1,点D、E分别在△ABC的两边BA、CA的延长线上,下列条件能判定ED ∥BC的是().(A)AD DEAB BC=;(B)AD AEAC AB=;DRQPCBA(C )AD AB DE BC ⋅=⋅; (D )AD AC AB AE ⋅=⋅.【答案】D【解析】根据三角形一边的平行线判定定理以及推论,如果AD AE AD AE DB ECDB EC AB AC AB AC ===或或,那么直线DE // BC ,逐一验证可得A 、B 、C 均不正确,故选:D.2.如图,点F 是▱ABCD 的边CD 上一点,直线BF 交AD 的延长线于点E ,则下列结论错误的是( )A.AB DF EA ED = B.FB EF BC ED = C.BE BF ED BC = D.AEBCBE BF =【答案】C【解析】【解答】解:∵四边形ABCD 是平行四边形, ∴CD ∥AB ,AD ∥BC ,CD=AB ,AD=BC ,∴ABDFEA ED =,故A 符合题意; ∴FB EF AD DE =,∴FB EFBC ED =,故B 符合题意; ∴EF BF ED BC =,故C 不符合题意; ∴AE AD BE BF =,∴AEBC BE BF =,故D 符合题意. 故答案为:C .3.(2020年•浦东新区一模)]如图,已知直线123,,l l l 分别交直线4l 于点A ,B ,C ,交直线5l于点D ,E ,F ,且123l l l ∥∥,若AB=4,AC=,,DF=9,则DE 的长为 ( )A.5B.6C.7D.8【答案】B【解析】∵123l l l ∥∥,AB=4,AC=,,DF=9,∴4=69AB DE DEAC DF=即,∴DE=6.故选B. 4.(2020年•徐汇区一模)如图,EF CD AB ////,2=AC ,5=AE ,5.1=BD ,那么下列结论正确的是( )(A )415=DF ; (B )415=EF ; (C )415=CD ; (D )415=BF .【答案】D【解析】∵EF CD AB ////,2=AC ,5=AE ,5.1=BD ,所以2 1.5=5AC BD AE BFBF =即,∴BF=154.故选D.5.(2021•洪泽区二模)如图,123////l l l ,AC 交1l 、2l 、3l 分别于A 、B 、C ,且6AC =,4BC =,DF 交1l 、2l 、3l 分别于D 、E 、F ,则DEEF= .【答案】12【解析】解:6AC =,4BC =,A B C D EF(第7题图)2AB AC BC ∴=-=, 123////l l l ,∴12DE AB EF BC ==, 故答案为:12. 6.(2020年•吉林中考)如图,AB ∥CD ∥EF .若12AC CE =,BD =5,则DF = .【答案】10【解析】∵AB ∥CD ∥EF , ∴12AC BD CE DF ==,∴DF =2BD =2×5=10. 故答案为10.7.(2020年•虹口区一模)如图4,在梯形AEFB 中,AB ∥EF ,AB =6,EF =10,点C 、D 分别在边AE 、BF上且CD ∥AB ,如果AC=3CE ,那么CD 长为 .【答案】9【解析】如图所示,过点B 作BN ∥AE 交EF 于点N ,交CD 于点M,∵AB ∥EF ∥CD ,BN ∥AE ,∴四边形AENB 为平行四边形,∴EN=CM=AB=6,FN=10-6=4,又∵DM ∥FN ,∴34AC MD AE FN ==,所以MD=3,则CD=3+6=9.8.(2020年•静安区一模)在△ABC 中,边BC 、AC 上的中线AD 、BE 相交于点G ,AD =6,那么AG= . 【答案】4【解析】∵边BC 、AC 上的中线AD 、BE 相交于点G ,∴点G 为△ABC 的重心,∴AG :AB=2:3,∵AD=6,∴AG=4.9.如图,在△ABC 中,若BD ∶DC=CE ∶EA=2∶1,AD 与BE 交于F,则AF ∶FD= .【答案】3:4【解析】过点D 作DH ∥BE 交AC 于点H , ∴2EH BD HC DC ==,∴EH=23CE ,∵BD ∶DC=CE ∶EA=2∶1,∴AE=12CE=34EH ,∴34AF AE DF EH ==.10.(2019年•长宁区月考)如图,平行四边形ABCD 中,点E 在CD 上,点F 在CD 的延长线上,AF 交BD 于点O ,交BC 于点G ,且DF:CD=DE:EC, 求:OE ∥BC【答案】见解析.【解析】∵四边形ABCD 为平行四边形,∴AB=CD,AB ∥CD ,∴DF OD AB OB =,即DF ODCD OB=,又∵DF:CD=DE:EC,∴DE ODEC OB=,∴OE ∥BC. 11.(2020秋•浦东新区期中)如图,已知////AD BE CF ,它们依次交直线1l 、2l 于点A 、B 、C 和点D 、EGF ODCBAE、F.(1)如果6AB=,8BC=,21DF=,求DE的长;(2)如果:2:5DE DF=,9AD=,14CF=,求BE的长.【答案】(1)DE=9;(2)BE=11.【解析】解:(1)////AD BE CF,∴DE ABDF AC=,6AB=,8BC=,21DF=,∴6 2168 DE=+,9DE∴=.(2)过点D作//DG AC,交BE于点H,交CF于点G,则9CG BH AD===,1495GF∴=-=,//HE GF,∴HE DEGF DF=,:2:5DE DF=,5GF=,∴2 55 HE=,2 HE∴=,9211BE∴=+=.12.(2019秋•黄浦区期中)如图,已知在ABC∆中,//EF CD,3AF=,5AD=,4AE=.(1)求CE 的长; (2)当253AB =时,求证://DE BC .【答案】(1)CE =38;(2)证明过程见解析. 【解析】解:(1)//EF CD ,∴AF AEAD AC=, 3AF =,5AD =,4AE =,∴345AC=, 解得:203AC =, 4AE =,208433CE AC AE ∴=-=-=; (2)253AB =,5AD =,4AE =,203AC =, ∴35AD AE AB AC ==, A A ∠=∠,ADE ABC ∴∆∆∽,ADE B ∴∠=∠,//DE BC ∴.13.(2019年•上海课时练习)梯形ABCD 中,点E 在AB 上,点F 在CD 上,且AD a =,BC b =. (1)如图(a ),如果点E 、F 分别为AB 、CD 的中点,求证:EF //BC 且2a bEF +=; (2)如图(b ),如果AE DF mEB FC n==,判断EF 和BC 是否平行,并证明你的结论,并用a 、b 、m 、n 的代数式表示EF .【答案】(1)见解析;(2)平行,an bm EF m n +=+. 【解析】(1)证明:过点F 作//MN AB 交AD 延长线于点M ,交BC 于点N ,则四边形ABNM 为平行四边形,AB MN AM BN ∴==,.F 为CD 中点,由平行可得F 为MN 中点,即12FN MN =,DM CN =.E 为AB 中点,1122BE AB MN NF ∴===.由//MN AB ,∴四边形EBNF 为平行四边形,//EF AB ∴且EF AM BN ==. 即()()()111222EF AM BN a DM b CN a b =+=++-=+. (2)证明:过点F 作//MN AB 交AD 延长线于点M ,交BC 于点N ,则四边形ABNM 为平行四边形,AB MN AM BN ∴==,.由//DM CN ,DM MF DF CN FN CF ∴==.AE DF EB FC =,AE MF EB FN ∴=,AB MN EB FN ∴=,EB FN ∴=.由//MN AB ,∴四边形EBNF 为平行四边形.//EF AB ∴且EF AM BN ==.由DM DF m CN FC n ==,可得AM a m b BN n -=-,即EF a m b EF n -=-, 解得:an bm EF m n +=+.A B C D E FA BC D E F。
(精品)数学讲义九年级同步第2讲:三角形一边的平行线(一) - 教师版

三角形一边的平行线是九年级数学上学期第一章第二节的内容,本讲主要讲解三角形一边平行线性质定理及推论,重点是掌握该定理及其推论,分清该定理及其推论之间的区别和联系,难点是理解该定理和推论的推导过程中所蕴含的分类讨论思想和转化思想,并认识“A”字型和“X”字形这两个基本图形,为后面学习相似三角形奠定基础.1、三角形一边的平行线性质定理平行于三角形一边的直线截其他两边所在的直线,截得的对应线段成比例.如图,已知ABC∆,直线//l BC,且与AB、AC所在直线交于点D和点E,那么AD AEDB EC=.三角形一边的平行线(一)内容分析知识结构模块一:三角形一边的平行线性质定理知识精讲【例1】如图,在ABC∆中,15AB=,10AC=,//DE BC,6BD=,求CE.【难度】★【答案】4.【解析】BD CEAB AC=,代入可得:=4CE.【总结】考查三角形一边平行线的性质定理.【例2】阳光通过窗口照在教室内,在地面上留下2.7米宽的亮区(如图).已知亮区一边到窗下的墙角距离8.7CE=米,窗口 1.8AB=米,求窗口底边离地面的高BC.【难度】★【答案】5.8m.【解析】射入的光线平行,则有AB DEAC CE=,代入可求得:5.8AC m=,4BC AC AB m=-=.【总结】考查三角形一边平行线性质定理的应用,在路灯、太阳光线中经常用到.【例3】在ABC∆中,点D、E分别在AB、AC的反向延长线上,//DE BC,若:2:3AD AB=,12EC=厘米,则AC=.【难度】★【答案】7.2cm.【解析】由//DE BC,可得23AE ADAC AB==,故53ECAC=,代入求得7.2AC cm=.【总结】考查三角形一边平行线的性质定理和比例合比性的综合应用.例题解析2/ 25【例4】如图在ABC ∆中,CD 平分ACB ∠,//DE BC ,5AC =厘米,3:5ADAB=,求DE 的长.【难度】★ 【答案】2cm . 【解析】//DE BC ,35AE AD AC AB ∴==. 由5AC cm =,代入可求得:32AE cm CE cm ==,. 又//DE BC ,EDC DCB ∴∠=∠.又CD 平分ACB ∠, ECD DCB ∴∠=∠. ECD EDC ∴∠=∠, 2DE CE cm ∴==.【总结】本题中涉及一个基本图形,平行线与角平分线一起会产生等腰三角形,同时应用三角形一边平行线的性质定理.【例5】如图,已知在ABC ∆中,//DE BC ,//EF AB ,2AE CE =,6AB =,9BC =,求四边形BDEF 的周长.【难度】★ 【答案】16. 【解析】2AE CE =,2133AE CE AC AC ∴==,. 又//DE BC ,//EF AB ,2133AD AE EF CE AB AC AB AC ∴====,,四边形BDEF 为平行四边形. 代入可求得:62DE EF ==,, ()2=16BDEF C DE EF ∴=+四边形.【总结】考查三角形一边平行线性质定理的综合应用.【例6】如图,在ABC∆中,10AB=,8AC=,点D在直线AB上,过点D作//DE BC交直线AC与点E.如果4BD=,求AE的长.【难度】★★【答案】245或565.【解析】(1)D在线段AB上时,6AD AB BD=-=,由//DE BC,可得:AD AEAB AC=,代入可得:245AE=;(2)D在线段AB延长线上时,14AD AB BD=+=,由//DE BC,可得:AD AEAB AC=,代入可得:565AE=;(3)D在线段AB反向延长线上的情况不存在.【总结】题目中的点是在直线或者射线上时,要注意仔细看题,考虑多解情况的出现.【例7】如图,在ABC∆中,AB AC>,AD BC⊥于点D,点F是BC中点,过点F作BC 的垂线交AB于点E,:3:2BD DC=,则:BE EA=.【难度】★★【答案】5:1.【解析】由:3:2BD DC=,BF FC=,即得:32BF FDBF FD+=-,可得:51BFFD=.又AD BC⊥,EF BC⊥,EF∴//AD,::5:1BE EA BF FD∴==.【总结】考查三角形一边平行线性质定理的综合应用.4/ 25【例8】如图,已知////AB CD EF ,14OA =,16AC =,8CE =,12BD =,求OB 、DF 的长.【难度】★★ 【答案】212OB =,6DF =. 【解析】由////AB CD EF ,OA OBAC BD ∴=. 代入可得:141221162OB ⨯==. 同时根据比例的合比性,可得:OA AC OB BD AC BD ++=,即OC ODAC BD=, 又根据平行,可得:OC ODCE DF=, AC BDCE DF∴=.代入求得:812616DF ⨯==. 【总结】考查三角形一边平行线定理的变形应用,实际上,任意两条直线被三条平行线所截得的线段对应成比例.【例9】如图,已知ABC ∆是边长为2的等边三角形,//DE BC ,:3:4ECD BCD S S ∆∆=,求EC 的长.【难度】★★【答案】12.【解析】∵ECD 和BCD 为等高三角形,故34ECD BCD S DE BC S ==,由//DE BC ,2BC =,ABC ∆为等边三角形, 可知ADE 也为等边三角形,∴32DE =,∴31222EC AC AE =-=-=. 【总结】平行于等边三角形一边截得的三角形也是等边三角形.【例10】如图,P为ABCD对角线BD上任意一点.求证:PQ PI PR PS=.【难度】★★【答案】略.【解析】证明:四边形ABCD为平行四边形,////AB CD AD BC∴,,////RB DI SD BQ∴,.根据三角形一边平行线的性质定理,则有PI PD PS PR PB PQ==,PQ PI PR PS∴⋅=⋅.【总结】初步认识相似三角形中的“X”字型,一个图形中存在往往不只一个,可用来进行等比例转化.【例11】如图,在平行四边形ABCD中,CD的延长线上有一点E,BE交AC于点F,交AD于点G.求证:2BF FG EF=.【难度】★★【答案】略.【解析】证明:四边形ABCD为平行四边形,////AB CD AD BC∴,,////AB CE AG BC∴,.根据三角形一边平行线的性质定理,则有:EF CF BF BF AF FG==,∴2BF FG EF=.【总结】初步认识相似三角形中的“X”字型,一个图形中存在往往不只一个,可用来进行等比例转化.6/ 25【例12】如图,点C 在线段AB 上,AMC ∆和CBN ∆都是等边三角形.求证:(1)MD AMDC CN =;(2)MD EB ME DC =.【难度】★★ 【答案】略. 【解析】证明:(1)AMC ∆和CBN ∆是等边三角形,60ACM NCB AMC ∴∠=∠=∠=︒.∵点C 在线段AB 上,18060MCN ACM NCB AMC ∴∠=︒-∠-∠=︒=∠.//AM CN ∴,∴MD AMDC CN =. (2)同(1)易证得//CM BN ,则有ME MCEB NB=.AMC ∆和CBN ∆是等边三角形,MC AM NB CN ∴==,,MD MEDC EB∴=, ∴MD EB ME DC =. 【总结】初步认识相似三角形中的“X ”字型,一个图形中存在往往不只一个,可用来进行等比例转化.【例13】如图,ABC ∆的面积是10,点D 、E 、F (与A 、B 、C 是不同的点)分别位于 AB 、BC 、CA 各边上,而且2AD =,3DB =,如果ABE ∆的面积和四边形DBEF 的面积相等,求ABE ∆的面积.【难度】★★★ 【答案】6. 【解析】连结DE ,由ABEDBEF S S =四边形,可得ADFAEFSS=,两三角形同底,可得两三角形等高,故//DE AC ,根据平行于三角形一边的直线性质定理,可得:35BD BE AB BC ==,故35ABE ABC S BE S BC ==,求得3=10=65ABES⨯. 【总结】注意等高(同底)三角形面积比等于底边(高)之比.8 / 25【例14】如图,在ABC ∆中,6BC =,42AC =,45C ∠=︒,在BC 边上有一动点P ,过P 作//PD AB 与AC 相交于于点D ,联结AP ,设BP x =,APD ∆的面积为y .(1)求y 与x 之间的函数关系式,并指出自变量x 的取值范围; (2)P 点是否存在这样的位置,使APD ∆的面积是APB ∆的面积的23?若存在,求出BP 的长;若不存在,请说明理由.【难度】★★★【答案】(1)()212063y x x x =-+<<;(2)存在,2BP =.【解析】(1)过点P 作PE AC ⊥于点E . 由BP x =,可得:6PC x =-, 又45C ∠=︒,故()22622PE CE PC x ===-. 又//PD AB ,故BP ADBC AC=,代入可得223AD x =,故()()2112221620622233y PE AD x x x x x =⋅=⋅-⋅=-+<<. (2)过点A 作AF BC ⊥于点F . 由4542C AC ∠=︒=,可得4AF CF ==, 故122ABPSAF BP x =⋅=, ∵APD ∆的面积是APB ∆面积的23, ∴2122233y x x x =-+=⨯,解得:2x =,即2BP =.【总结】考查三角形中一边平行线性质的综合应用,同时在题目中,注意对于特殊角的利用.FE1、三角形一边的平行线性质定理推论平行于三角形一边的直线截其他两边所在的直线,截得的三角形的三边与原三角形的三边对应成比例.如图,点D 、E 分别在ABC ∆的边AB 、AC 上,//DE BC,那么DE AD AEBC AB AC==.2、三角形的重心定义:三角形三条中线交于一点,三条中线交点叫三角形的重心.性质:三角形重心到一个顶点的距离,等于它到这个顶点对边中点的距离的两倍.【例15】如图,D 、E 分别是ABC ∆的边AB 、AC 上的点,且//DE BC . (1)如果2DE =,6BC =,3AD =,求AB 的长; (2)如果2DE =,6BC =,8BD =,求AD 、AB 的长;(3)如果35AD BD =,求DEBC的值. 【难度】★【答案】(1)9;(2)412AD AB ==,;(3)38.【解析】(1)∵//DE BC ,13AD DE AB BC ==,9AB =; (2)∵//DE BC ,∴13AD DE AD BD BC ==+,∴4AD =,∴12AB AD BD =+=;(3)∵//DE BC ,∴33358DE AD BC AB ===+. 【总结】考查三角形一边平行线的性质定理.模块二:三角形一边的平行线性质定理推论知识精讲例题解析10 / 25【例16】如图,BE 、CF 是ABC ∆的中线,交于点G .求证:12GE GF GB GC ==.【难度】★ 【答案】略.【解析】证明:过点F 作//FD BE 交AC 于点D . F 是AB 中点, D ∴是AE 中点,故12DF AD BE AE ==, 又E 是AC 中点,//FD EG ,12GF DE GC CE ∴==,23EG CE FD CD ==,即()2132EG EG BG =+,整理得:12GE GF GB GC ==. 【总结】考查三角形重心性质的证明,通过一个中点作对边的平行线即可.【例17】已知小智的身高是 1.6CD =米,他在路灯下的影长2DE =米,小智与路灯灯杆的底部B 的距离为3DB =米,则路灯灯泡A 距地面的高度AB =米.【难度】★ 【答案】4.【解析】∵//AB CD ,∴22235CD DE AB BE ===+,∴4AB m =. 【总结】考查三角形一边平行线定理的实际应用.【例18】如图,一根直立于水平地面的木杆AB 在灯光下形成影子,当木杆绕点A 按逆时针 反向旋转直至到达地面时,影子的长度发生变化.设AB 垂直于地面时的影子为AC (假 定AC AB >),影子的最大值为m ,最小值为n ,有下列结论:① m AC >;②m=AC ;③n AB =;④影子的长度先增大后减小.其中正确的序号是.【难度】★★ 【答案】①③④.【解析】木杆绕点A 逆时针旋转时,当AB 与BC 光线垂直 时,m 最大,则m AC >,①成立,②不成立;最小值 为AB 与AC 重合,故③成立;由上可知,影子长度先增大后减小,故④成立.【总结】找准临界值,注意进行思维分析.Da Nb Qx c P M xNa Qcb P M cNxQa b P M cN b Qa x PM 【例19】已知:MN // PQ ,a b ≠,c x ≠,则满足关系式bcx a=的图形是( )A .B .C .D .【难度】★★ 【答案】C【解析】交叉相乘,满足ax bc =的是C 选项. 【总结】考查三角形一边平行线性质的简单应用.【例20】如图,ABC ∆中,//DE BC ,3AE =,4DE =,2DF =,5CF =,求EC 的长. 【难度】★★ 【答案】92EC =. 【解析】//DE BC ,25DE DF AE BC CF AC ∴===,即3235EC =+,求得:92EC =.【总结】相似三角形中“A ”字型和“X ”字型的综合应用,可得到相等比例关系式.【例21】如图,在平行四边形ABCD 中,点E 在边DC 上,若:1:2DE EC =,则:BF BE =.【难度】★★ 【答案】3:5.【解析】:1:2DE EC =,可知23CE CE CD AB ==,由//CE AB ,可知32BF AB EF CE ==,故:3:5BF BE =. 【总结】初步认识相似三角形中的“X ”字型.12 / 25【例22】如图,在ABC ∆中,6BC =,G 是ABC ∆的重心,过G 作边BC 的平行线交AC 于点H ,求GH 的长.【难度】★★ 【答案】2.【解析】连结AG 并延长交BC 于点D ,根据重心的定义,可知D 为BC 中点,则132DC BC ==,根据重心的性质,又//GH DC ,可得:23GH AG DC AD ==,求得2GH =.【总结】考查三角形重心的性质.【例23】如图,已知////AB CD EF .AB m =,CD n =,求EF 的长.(用m 、n 的代数式表示).【难度】★★【答案】mnm n+.【解析】由////AB CD EF ,则有EF CF EF BFAB BC CD BC==,,即1EF EF m n +=,得mnEF m n =+.【总结】考查相似三角形中“X ”字型的综合应用,得到比例关系.【例24】如图,E 为平行四边形ABCD 的对角线AC 上一点,13AE EC =,BE 的延长线交CD的延长线于点G ,交AD 于点F ,求:BF FG 的值.【难度】★★ 【答案】1:2.【解析】由//AF BC ,可得13AF AE BC EC ==,即13AF AD =, 故12AF FD =,由//AB DG ,可得:::1:2BF FG AF FD ==.【总结】考查相似三角形中“X ”字型的综合应用,得到比例关系.D【例25】如图,12//l l ,:2:5AF FB =,:4:1BC CD =,求:AE EC 的值. 【难度】★★ 【答案】2:1.【解析】由12//l l ,得:25AG AF BD FB ==,又:4:1BC CD =,可得21AG CD =,故::2:1AE EC AG CD ==.【总结】考查相似三角形中“X ”字型的综合应用,得到比例关系.【例26】如图,在梯形ABCD 中,//AD BC ,对角线AC 、BD 交于点O ,点E 在AB 上,且//EO BC ,已知3AD =,6BC =.求EO 的长.【难度】★★ 【答案】2.【解析】由//AD BC ,可得:3162AO AD CO BC ===,故13AO AC =,由//EO BC ,13EO AO BC AC ==,求得2EO =. 【总结】相似三角形中“A ”字型和“X ”字型的综合应用,可得到相等比例关系式.【例27】如图,在梯形ABCD 中,//AD BC ,3AD =,5BC =,E 、F 是两腰上的点,且//EF AD ,:1:2AE EB =,求EF 的长.【难度】★★ 【答案】113.【解析】过点A 作//AH DC 交BC 于H ,交EF 于G , 则有32CH FG AD BH ====,,又//EG BH ,可得:13EG AE BH AB ==,解得:23EG =,故113EF EG GF =+=. 【总结】两条直线被三条平行线所截得的线段长对应成比例.G H14 / 25MFEDCBA 【例28】如图,在ABC ∆中,D 是BC 边上的一点,:3:1BD DC =,G 为AD 的中点,联结BG 并延长AC 交于E ,求:EG GB 的值.【难度】★★ 【答案】1:7.【解析】过点D 作//DF BE 交AC 于F .此时则有14DF CF DC BE CE BC ===,又G 为AD 中点,根据平行可得:12GE DF =,故18GE BE =,即18EG EG GB =+,可得:1:7EG GB =.【总结】构造平行线,构造比例线段是解决这类问题的根本.【例29】已知点D 是ABC ∆的BC 边上的一点,13CD BC =,E 是AD 的中点,BE 的延长线交AC 于F ,求:AF AC 的值.【难度】★★ 【答案】2:5.【解析】过点D 作//DM BF 交AC 于点M .∵13CD BC =,∴13CM CD CF BC ==,∴12CM MF =. 又E 为AD 中点,//DM BF , ∴F 为AM 中点,即AF FM =,∴:2:5AF FC =.【总结】考查三角形一边平行线的性质定理,通过构造平行线等比例转化即可得出答案.F【例30】如图,路灯A 的高度为7米,在距离路灯正下方B 点20米处有一墙壁CD ,CD BD ⊥, 如果身高为1.6米的学生EF 站立在线段BD 上(EF BD ⊥,垂足为F ,EF CD <),他的影子的总长度为3米,求该学生到路灯正下方B 点的距离FB 的长.【难度】★★★【答案】818m 或18m【解析】(1)影子全部在地面上时, 设点E 在地面的投影为点M , 则有3FM =.由EF BD ⊥,AB BD ⊥,可得//EF AB ,则有EF FMAB BM =, 代入可求得:1058BM m =,则818FB BM FM m =-=. (2)影子部分在地面,部分在墙面上时,如图,根据同一时刻同一地点任何物体影长与其 高度比值相同,设墙上部分影长ND x =,则有3DF x =-,17FB x =+,则有ND GD AB GB =, 即720x GD GD =+,可得207xGD x=-, 又根据//ND EF ,可得ND GD EF GF =,即207201.637xx x x xx-=+--, 整理即得:210110x x +-=, 解得:()12111x x ==-,舍.故18FB m =.【总结】影长问题,注意同一时刻同一地点任何物体影长与其高度比值相同,有障碍物时,障碍物上的影长仍满足这个条件,注意进行分类讨论.EFNG16 / 25GH FEDCBAFE D CBA【例31】如图,平行四边形ABCD 中,点E 、F 分别在AB 、AD 上,EF 交AC 于点G ,若:2:3AE EB =,:1:2AF AD =,求:AG AC 的值.【难度】★★★ 【答案】2:9.【解析】延长FE 交CB 的延长线于点H .∵//AF BH ,∴23AF AE BH EB ==. 又:1:2AF AD =,故可得:227AF AF CH AF BH ==+,∵//AF CH ,∴27AG AF GC CH ==,故:2:9AG AC =. 【总结】构造与所求线段相关的“A ”字型或“X ”字型,比例转化.【例32】如图,在ABC ∆中,设D 、E 是AB 、AC 上的两点,且BD CE =,延长DE 交BC的延长线于点F ,:3:5AB AC =,12cm EF =,求DF 的长.【难度】★★★ 【答案】20cm .【解析】过点D 作//DH AC 交BC 于H ,则有35BD AB DH AC ==,又BD CE =,则有35CE DH =,由//CE DH ,得35EF CE DF DH ==,代入计算得:125320DF cm =⨯÷=. 【总结】作平行线,构造出与所求线段相关的“A ”字型或“X ”字型,比例转化.G FEDCBA G FEDCBA【例33】如图,已知ABC ∆中,点D 、E 分别在边AB 、AC 上,且:3:2AD DB =,:1:2AE EC =,直线ED 和CB 的延长线交于点F ,求:FB FC .【难度】★★★ 【答案】1:3.【解析】过点B 作//BG FE 交AC 于G . 根据三角形一边平行线的性质定理,可得: 32AE AD EG DB ==,又:1:2AE EC =,故13EG EC =,由//BG FE ,可得:::1:3FB FC EG EC ==.【总结】作平行线,构造出与所求线段相关的“A ”字型或“X ”字型,比例转化.【例34】已知:在ABC ∆中,D 、E 是BC 上的两点,且//AD EG ,EG 交AC 于F ,交BA 的延长线于G ,若2EF EG AD +=.求证:AD 是ABC ∆的中线.【难度】★★★ 【答案】略.【解析】证明://AD EG , AD BD EF CEEG BE AD CD ∴==,. BE CEEG AD EF AD BD CD∴=⋅=⋅,.2EF EG AD +=, 2BE CE BD CD∴+=. 则有11BE CEBD CD-=-, BE BD CD CEBD CD --∴=. 即DE DEBD CD=. BD CD ∴=.即AD 是ABC ∆的中线.【总结】考查三角形一边平行线的性质定理,注意根据题目条件灵活进行比例转换,将条件转化到同一个量,得出结论.18 / 25【习题1】如图,在ABC ∆,//DE BC ,DE 与边AB 、AC 分别交于点D 、E . (1)已知6AD =,8BD =,4AE =,求CE 、AC 的长;(2)已知:2:5AE AC =,10AB =,求AD 的长.【难度】★ 【答案】(1)162833AE CE ==,;(2)4. 【解析】(1)∵//DE BC ,∴AE AD CE DB =,∴163CE =; (2)∵//DE BC ,:2:5AE AC =,∴25AD AE AB AC ==,∴4AD =.【总结】考查三角形一边平行线的性质.【习题2】如图,//EF AB ,//DE BC ,下列各式正确的是()(A )AD BF BD CF = (B )AE CEED BC =(C )AE BDEC AD=(D )AD ABED BC=【难度】★ 【答案】A【解析】根据三角形边平行线的性质进行比例线段转化可 知A 选项正确;B 、C 、D 错误.【总结】考查三角形一边平行线的性质的应用.【习题3】如图,菱形ADEF 内接于ABC ∆,16AB =,14BC =,12AC =,求BE 的长. 【难度】★ 【答案】8.【解析】根据三角形一边平行线的性质,DE BE EF CEAC BC AB BC==,, 即有1DE EF AC AB +=,可解得菱形边长487DE AD ==,故647BD AB AD =-=,BE BDBC BA=,∴8BE =. 【总结】考查三角形一边平行线的性质的综合应用.随堂检测GMDCBA【习题4】如图,P 是ABC ∆的中线AD 上一点,//PE AB ,//PF AC .求证:BE CF =.【难度】★★ 【答案】略.【解析】证明://PE AB ,//PF AC ,BE AP CF APBD DA DC DA ∴==,, BE CFBD DC ∴=, 又BD CD =,BE CF ∴=.【总结】考查三角形一边平行线的性质的综合应用,用固定线段的比值作为中间量.【习题5】如图,在ABC ∆中,//DE BC ,且:2:3AD AB =,求:EO EB 的值. 【难度】★★ 【答案】2:5.【解析】由//DE BC ,可得23DE AD BC AB ==,则23EO DE BO BC ==,根据比例的合比性,可得:2:5EO EB =.【总结】找准图形中的“A ”字型和“X ”字型进行比例线段的转化构造.【习题6】在ABC ∆中,AB AC =,如果中线BM 与高AD 相交于点G ,求AGAD. 【难度】★★【答案】23.【解析】AB AC AD BC =⊥,,BD CD ∴=.即D 为BC 中点,M 为AC 中点, G ∴为ABC ∆重心,23AG AD ∴=. 【总结】考查重心的意义和性质,先证明再利用性质.20 / 25NE GH F M D CBA【习题7】如图ABC ∆,点D 、E 分别在BC 、AC 上,BE 平分ABC ∠,//DE BA .如果24CE =,26AE =,45AB =,求DE 和CD 的长.【难度】★★ 【答案】1085DE =,129665CD =. 【解析】根据三角形一边平行线的性质,可得DE CEAB AC=, ∴452410824265AB CE DE AC ⋅⨯===+.由BE 平分ABC ∠,则有ABE DBE ∠=∠,由//DE BA ,可得:DEB ABE ∠=∠,即DEB DBE ∠=∠,故1085BD DE ==,进而可得:CD CE BD AE =,∴129665BD CE CD AE ⋅==. 【总结】考查三角形一边平行线的性质定理的应用,同时考查平行线与角平分线一起出现会产生等腰三角形的基本图形.【习题8】如图,梯形ABCD 中,//////DC EF GH AB ,30AB cm =,10CD cm =,::2:3:4DE EG GA =,求EF 与GH 的长度.【难度】★★★ 【答案】13019099EF cm GH cm ==,.【解析】过点C 作//CP DA 分别交EF 、GH 、AB 于 点M 、点N 、点P ,则易得四边形DAPC 为平行 四边形.则10EM GN AP DC cm ====,20PB cm =.由//FM BP ,可得:29FM CM DE PB CP DA ===,代入可得:409FM cm =,1309EF EM FM cm =+=. 由//NH PB ,可得:59NH CN DG PB CP DA ===,代入可得:1009NH cm =,1909GH GN NH cm =+=. 【总结】夹在平行线间的线段对应成比例.M N P【作业1】已知线段a、m、n,且ax mn=,求作x,作法正确的是()(A)(B)(C)(D)【难度】★【答案】C【解析】考查三角形一边平行线的性质定理,变形即为a nm x=,可知C选项满足题意.【总结】考查三角形一边平行线的性质定理,进行简单的变形应用,可知线段错位相乘满足题意的即为所求选项.【作业2】如图,ABC∆中,AB ACBE EC=,53ABAC=,//DE AC,求:AB BD的值.【难度】★【答案】8:5.【解析】由AB ACBE EC=,53ABAC=,可得53BEEC=,根据比例的合比性质,可得58BEBC=,由//DE AC,可得::8:5AB BD BC BE==.【总结】考查三角形一边平行线性质的综合应用.课后作业22 / 25NEFMDCB A 【作业3】如图,////AB EF CD ,2AB =,8CD =,:1:5AE EC =,求EF 的长度. 【难度】★★ 【答案】3EF =.【解析】过点B 作//BN AC 交EF 于点M ,交CD 于点N . ∵////AB EF CD ,∴四边形AEMB 、ACNB 、ECNM 都为平行四边形,∴2CN EM AB ===,且有FM BMDN BN =. :1:5AE EC =,16BM AE BN AC ∴==. 16FM BM ND BN ∴==/ ∵6ND CD CN =-=, ∴1FM =,3EF EM FM ∴=+=.【总结】三条平行线被两条直线所截,将其中一条直线平移,放到同一个三角形中解答.EGFMDCBA E G FMDCBA 【作业4】平行四边形ABCD ,E 是AB 的中点,在直线AD 上截取2AF FD =,EF 交AC于G ,求AGGC 的值.【难度】★★【答案】25或23.【解析】(1)当点F 在AD 上时,如图. 过点E 作//EM BC 交AC 于点M , 由E 为AB 中点,则M 为AC 中点, 四边形ABCD 为平行四边形,//AD BC AD BC ∴=,.又2AF FD =, 223AF AF AF AD BC EM ∴===. 由//AF EM , 43AG AF GM EM ∴==,42105AG AG GC GM AM ∴===+. (2)当点F 在AD 延长线上时,如图, 过点E 作//EM BC 交AC 于点M , 由E 为AB 中点,则M 为AC 中点, 四边形ABCD 为平行四边形,//AD BC AD BC ∴=,.又2AF FD =, 22AF AF AF AD BC EM ∴===. 由//AF EM , 4AG AF GM EM∴==4263AG AG GC GM AM ∴===+. 【总结】注意题目中的关键词语,在直线上,由此要进行分类讨论,根据三角形一边平行线的性质构造“A ”字型、“X ”字型即可.24 / 25【作业5】如图,////AB EF DC ,已知20AB =,80CD =,求EF 的长. 【难度】★★ 【答案】16【解析】由////AB EF DC ,可得:BF EF BC CD =,CF EFBC AB=,则有1EF EFAB CD+=,代入计算得16EF =. 【总结】考查三角形一边平行线性质的综合应用,利用比例线段之间的关系构造等式求解.【作业6】如图,在ABC ∆中,D 是边BC 上一点,//DF AB ,//DE CA .(1)求证:AE CFEB FA =; (2)如果2CF =,5AC =,6AB =,求AE 、DE 的长. 【难度】★★【答案】(1)略;(2)1235AE DE ==,. 【解析】(1)证明://DE CA ,AE CDEB DB ∴=, 又//DF AB , CD CFDB FA∴=,AE CFEB FA∴=. (2)解:由(1)可得AE CFEB FA=, 根据比例的合比性质,得:AE CFAB AC=, 代入可解得:621255AE ⨯==, 由//DE CA ,//DF AB , 可知四边形AEDF 为平行四边形,即得:3DE AF AC CF ==-=.【总结】考查三角形一边平行线性质的综合应用,进行比例线段转化.【作业7】如图,在平行四边形ABCD 中,E 是AD 上一点,CE 与BD 相交于点O ,CE 与BA 的延长线相交于点G ,已知2DE AE =,10CE =,求GE 和CO 的长.【难度】★★★【答案】56GE CO ==,.【解析】四边形ABCD 是平行四边形, //AD BC AD BC ∴=,.又2DE AE =,13GE AE AE GC BC AD ∴===,23EO DE OC BC ==, 即13GE GE EC =+,23EC CO CO -=,代入即可求得56GE CO ==,.【总结】考查利用三角形一边平行线的性质构造“A ”字型和“X ”字型,进行比例线段的综合应用.【作业8】如图, //DE BC ,3ADE S ∆=,18CBD S ∆=,求ABC S ∆. 【难度】★★★ 【答案】27. 【解析】设BDES a =,则有3AED BEDS AE SBE a==,318ABD CBDS AD a SCD +==,由DE //BC ,可知AE ADBE CD=, 则有3318aa +=,整理得23540a a +-=,解得6a =, 由此361827ABCADEBDEDBCS SSS=++=++=.【总结】考查三角形一边的平行线定理,以及等高三角形面积比等于其底边之比的知识点的灵活运用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、本节知识点汇总: 1. 比例线段的有关概念: 在比例式
::中,、叫外项,、叫内项,、叫前项,a b c
d
a b c d a d b c a c ==()b 、
d 叫后项,d 叫第四比例项,如果b=c ,那么b 叫做a 、d 的比例中项。
把线段AB 分成两条线
段AC 和BC ,使AC 2
=AB ·BC ,叫做把线段AB 黄金分割,C 叫做线段AB 的黄金分割点。
2. 比例性质: ①基本性质:
a b c d ad bc =⇔= ②合比性质:±±a b c d a b b c d
d =⇒=
③等比性质:
……≠……a b c d m n b d n a c m b d n a b
===+++⇒++++++=()0 3.平行线分线段成比例定理:
两条直线被三条平行的直线所截,截得的对应线段成比例. 用符号语言表示:
ΘAD ∥BE ∥CF,
,,AB DE BC EF AB DE
BC EF AC DF AC DF
∴===
. 4.平行线等分线段定理:
两条直线被三条平行的直线所截,如果在一直线上所截得的线段相等,那么在另一直线上所截得的线段也相等. 用符号语言表示:
AD BE CF AB BC DE EF ⎫
⇒=⎬=⎭
P P .
5. 三角形一边平行线判定定理 如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边.
6.三角形一边的平行线判定定理推论 如果一条直线截三角形两边的延长线(这两边的延长线在第三边的同侧)所得的对应线段成比例,那么这条直线平行于三角形的第三边.
E
C
23.1——23.3比例线段单元测试
班级_______姓名________学号________分数________
一、填空
1.已知线段b 是线段a 、c 的比例中项,且a =9,c =4,则b = .
2.线段AB =6cm ,点P 在线段AB 上,且AP 是是AB 与BP 的比例中项,则PB =_______cm . 3.△ABC 与△A 1B 1C 1中3
2
111111===C B BC C A AC B A AB ,若AB +AC +BC =40cm ,则△A 1B 1C 1
的周长是__________.
4.在比例尺为1︰1000000的地图上,AB 两地的图上距离是3.4厘米,则AB 两地的实际距离是____________千米. 5.已知
832=-b b a ,则______=b
a
. 6.已知:在ABC ∆中,点D 、E 分别在AB 、AC 上,且DE ∥BC ,AB =6,AD =2,EC =3,则AE = .
7.已知:点D 、E 分别在⊿ABC 的边AB 、AC 的反向延长线上,且DE ∥BC ,15,3
2
==BC AB AD ,则DE = .
8.如图,在梯形ABCD 中,AD ∥BC ,AC 、BD 相交于点O .若S △AOD =4,S △AOB =6,则S △BOC =_________.
9.如图,l 1∥l 2∥l 3 , AB =2,AC =5,DF =10,则DE = . 10.如图,AM ∶MB =AN ∶NC=1∶3,则MN ∶BC = .
11.如图,在ΔABC 中,AM 是中线,G 是重心,GD ∥BC ,交AC 于D .若BC =6,则GD = .
12.如图,AD ∥EF ∥BC ,AD =13厘米、BC =18厘米,AE ︰EB =2︰3,则EF = .
(第13题)(第12题)(第11题)
L3
M
M
B
A
B
C
C
第10题
第11题
第12题
13.如图,△ABC 中有菱形ANPN ,如果2
1
=MB AM ,则BC BP =_________. 14.如图,在□ABCD 中,EF ∥AB ,3
2
=EA DE ,EF =4,则CD 的长为________.
15.已知平行四边形ABCD 中,E 为AD 的中点,AF ∶BF=2∶5,则_____=GC
AG
.
二、选择题:
16.如图,下列各组线段中不能说明DE ∥BC 的是 ( ) (A
)AD =6,BD =4,AE =2.4,CE =1.6; (B )AD =4,AB =6,DE =2,BC =3; (C )AD =4,AB =6,AE =2,AC =3;
(D )BD =2,AB =6,CE =1,AC =3.
17.已知线段a 、b 、c ,求作线段x ,满足bx=ac ,下列哪种作法满足要求的是( )
18.如图,在□ABCD 中,E 是AD 上一点,连接CE 并延长交BA 于F ,则下列结论中错误的是 ( )
(A )∠AEF =∠DEC ; (B )FA ﹕CD =AE ﹕BC ; (C )FA ﹕AB =FE ﹕EC ; (D )AB =DC .
19.点P 是线段AB 的黄金分割点,且AB =4,则AP 的长是 ( ) (A )252-; (B )526-; (C )252-或526-;(D )以上结论都不对. 三、解答题:
20.如图,在△ABC 中,DE ∥BC ,AB = 4,AC = 8,DB = AE ,
求AE 的值。
第13题 第14题 第16题
第15题 C
B
E
D
A
第(5)题
21.如图:□ABCD ,P 为对角线BD 上的点,过点P 作一直线分别交BA 、BC 的延长线于Q 、R ,交CD 、AD 于S 、I ,求证:PQ ·PI=PR ·PS .
22.如图,已知点D 、E 在△ABC 的边AB 、AC 上,且DE ∥BC,以DE 为一边作平行四边形DEFG,延长BG 、CF 交于点H,连接AH,求证:AH ∥EF.
H
B
C
G
A F
E
D
23.如图,AD 为△ABC 的角平分线,BF ⊥AD 的延长线于点F ,AM ⊥AD 于A 交BC 的延长线于M ,FC 的延长线交AM 于E . 求证:AE =EM .
四、拓展训练:在△ABC 中,D 、E 是BC 、AB 上的点,AD 、CE 相交于点F .DE 、BF 相交于点O .GH ∥BC ,且过点O 于AD 、CE 交于K 、P . 求证:OP =PH .。
