PID自适应控制学习与Matlab仿真
智能控制作业_模糊自适应PID控制

模糊自适应PID 控制的Matlab 仿真设计研究姓名:陈明学号:201208070103班级:智能1201一、 模糊控制思想、PID 控制理论简介:在工业生产过程中,许多被控对象受负荷变化或干扰因素很多基于模糊自适应控制理论, 设计了一种模糊自适应PID 控制器, 具体介绍了这种PID 控制器的控制特点及参数设计规则, 实现PID 控制器的在线自整定和自调整。
通过matlab 软件进行实例,仿真表明, , 提高控制系统实时性和抗干扰能力,易于实现.便于工程应用。
1.1 模糊控制的思想:应用模糊数学的基本理论和方法, 控制规则的条件、操作用模糊集来表示、并把这些模糊控制规则以及有关信息, 诸如PID 控制参数等作为知识存入计算机知识库, 然后计算机根据控制系统的实际情况(系统的输入, 输出) , 运用模糊推理。
1.2 PID 算法:u(t)=k p * e(t)+k i * ∫e(t)t 0dt +k d *de(t)dt= k p *e(t)+ k i *∑e i (t) + k d * e c (t)其中, u (t) 为控制器输出量, e(t) 为误差信号, e c (t)为误差变化率, k p , k i , k d 分别为比例系数、积分系数、微分数。
然而,课本中,为了简化实验难度,只是考虑了kp ,ki 参数的整定。
1.3 模糊PID 控制器的原理图:二、基于Matlab的模糊控制逻辑模块的设计关于模糊逻辑的设计,主要有隶属函数的编辑,参数的选型,模糊规则导入,生成三维图等观察。
2.1 模糊函数的编辑器的设定:打开matlab后,在命令窗口输入“fuzzy”,回车即可出现模糊函数编辑器,基本设置等。
基于课本的实验要求,我选的是二输入(e, e c)二输出(k p ,k i)。
需要注意的是,在命名输入输出函数的时候,下标字母需要借助下划线的编辑,即e_c 能够显示为e c。
2.2四个隶属函数的N, Z, P 函数设定:在隶属函数的设定中,N 选用的是基于trimf(三角形隶属函数) , Z是基于zmf(Z型隶属函数),P是基于smf(S型隶属函数)。
自适应模糊PID控制器的设计与仿真

自适应模糊PID控制器的设计与仿真自适应模糊PID控制器是一种结合了模糊控制和PID控制的自适应控制器,它能够在系统的不同工况下根据实际需求对PID参数进行自适应调整,从而使得系统具有更好的动态性能和稳定性。
本文将介绍自适应模糊PID控制器的设计思路和仿真过程。
1.设计思路1.1系统建模首先需要对待控制的系统进行建模,得到系统的数学模型。
这可以通过实验数据或者理论分析来完成。
一般情况下,系统的数学模型可以表示为:$G(s)=\frac{Y(s)}{U(s)}=\frac{K}{s(Ts+1)}$其中,K是系统的增益,T是系统的时间常数。
1.2设计模糊控制器接下来需要设计模糊控制器,包括模糊规则、模糊集和模糊运算等。
模糊控制器的输入是系统的误差和误差的变化率,输出是PID参数的调整量。
1.3设计PID控制器在模糊控制器的基础上,设计PID控制器。
PID控制器的输入是模糊控制器的输出,输出是控制信号。
1.4设计自适应机制引入自适应机制,根据系统的性能指标对PID参数进行自适应调整。
一般可以采用Lyapunov函数进行系统性能的分析和优化。
2.仿真过程在仿真中,可以使用常见的控制系统仿真软件,如MATLAB/Simulink 等。
具体的仿真过程如下:2.1设置仿真模型根据系统的数学模型,在仿真软件中设置仿真模型。
包括系统的输入、输出、误差计算、控制信号计算等。
2.2设置模糊控制器根据设计思路中的模糊控制器设计,设置模糊控制器的输入和输出,并设置模糊规则、模糊集和模糊运算等参数。
2.3设置PID控制器在模糊控制器的基础上,设置PID控制器的输入和输出,并设置PID参数的初始值。
2.4设置自适应机制设置自适应机制,根据系统的性能指标进行PID参数的自适应调整。
2.5运行仿真运行仿真,观察系统的响应特性和PID参数的变化情况。
根据仿真结果可以对设计进行调整和优化。
3.结果分析根据仿真结果,可以分析系统的稳定性、动态性能和鲁棒性等指标,并对设计进行调整和改进。
PID控制算法的MATLAB仿真研究

目录一、课程设计的目的和要求.............................................. - 3 -二、课程设计的基本内容及步骤 ..................................... - 3 -三、设计过程...................................................................... - 4 -四、小结............................................................................. - 11 - 参考资料................................................................................ - 11 -一、课程设计的目的和要求1.目的(1)通过本课程设计进一步巩固PID算法基本理论及数字控制器实现的认识和掌握,归纳和总结PID控制算法在实际运用中的一些特性。
(2)熟悉MATLAB语言及其在控制系统设计中的应用,提高学生设计控制系统程序的能力。
2.要求通过查阅资料,了解PID算法的研究现状和研究领域,充分理解设计内容对PID算法的基本原理与运用归纳和总结,并独立完成设计实验和总结报告。
二、课程设计的基本内容及步骤1.任务的提出采用带纯滞后的一阶惯性环节作为系统的被控对象模型,传递函数为G(s)= Ke−τd s,其中各参数分别为K=30,T f=630,τd=60。
对PID控制算法的仿1+T f s真研究可以从以下四个方面展开。
(1)PID控制器调节参数K p、K I、K D的整定。
PID参数的整定对控制系统能否得到较好的控制效果是至关重要的,PID参数的整定方法有很多种,可采用理论整定法(如ZN法)或者实验确定法(如扩充临界比例度、试凑法等),也可采用模糊自适应参数整定、遗传算法参数整定等新型的PID 参数整定方法。
模糊PID控制器设计及MATLAB仿真_李健

图 1 模糊 PID 控制结构图
PID 参 数 模 糊 自 整 定 是 先 找 出 PID 控 制 器 的 3 个 参 数 Kp、 Ki 和 Kd 与偏差 e 和偏差变化率 ec 之间的模糊关系, 在运行中 通过不断检测 e 和 ec,根据模糊控制规则来对 3 个参量进行在
线修改 ,以 满 足 不 同 e 和 ec 对 控 制 器 参 数 的 不 同 要 求 ,从 而 使
起较大的超调 。 微 分 系 数 Kd 影 响 系 统 的 动 态 特 性 ,Kd 越 大 ,越
能抑制偏差变化,但过大会延长调节时间,降低抗干扰能力。
根 据 参 数 Kp、Ki、Kd 对 系 统 输 出 特 性 的 影 响 情 况 ,可 归 纳 出 系统在被控过程中对于不同的偏差和偏差变化率 , 参数 Kp、Ki、 Kd 的自整定原则:
摘要 将模糊控制器和 PID 控制器结合在一起,构造了一个模糊 PID 控制器,利用模糊推理的方法调整 PID 控制器的参数, 并利用 MATLAB 的 SUMLINK 工具箱,对系统进行仿真,仿真结果表明模糊 PID 控制器能使系统达到满意的控制效果。 关键词:PID 控制器,模糊控制,MATLAB,SIMULINK,系统仿真
1.3 模糊控制算法的确立
PID 参数的整定必须考虑到在不同时刻 3 个参数的作 用 以
及相互之间的互联关系。 模糊自整定 PID 是在 PID 算法的基础
上通过计算当前系统误差 e 和误差变化 ec,利用模糊规则 进 行
模糊推理,查询模糊矩阵表进行参数调整。 参数修正公式:
'
Kp =Kp +(e,ec)p
被控对象具有良好的动、静态性能。
1.2 PID 控制器的确立
通常,PID 控制器的控制算式为:
基于MATLAB的自适应模糊PID控制系统计算机仿真

摘要: 在分析自适应模糊控制及 HIJ 参数变化对系统性能影响的基础上 K 提出在动态过程中对 HIJ 参数进行整定。 仿真研究表 明 K 控制质量得到了提高 。 关键词: 模糊 HIJ 控制; 自适应; 仿真 E19F1G; 中图分类号: 9HCB&$ B 文献标识码: 1
&
E19F1G 简介
E19F1G 软件于 &B?/ 年由美国的 E)82W",X7 公司推出 K 该软件使用简单、方便 。自 &BBC 年以来 K E)82W",X7 公司相继推出了 E19F1G /$ . 、 E19F1G /$ %、 E19F1GD$ %、 E19F1G <$ . 等版本。本文在 E19Z F1G<$ . 基础上 K 介绍如何利用 RIE4FI’[ 和 \4]]^ 工具箱构造某模糊控制系统的结构框图和进行仿真研 究的方法及步骤。 &$ & 模糊逻辑工具箱 模糊逻辑工具箱 @ 0+PP-#";3:8""#Q"_ A 提供了模糊逻辑控制器及系统设计的各种途径。工具箱提供了生成 和编辑模糊推理系统 @ \IR A 常用的工具函数 K 如 *6W037, )OO5),, )OOM0, )OO,+##6, 768037, W,386037 等 K 它包括了产
!"#$ %& ()*+),-
’"$ & %../
安徽工业大学学报 ($ "0 1*2+3 4*356,738- "0 96:2*"#";-
第 %& 卷 第 & 期 %../ 年 &月
神经网络PID 控制策略及其Matlab 仿真研究.

神经网络PID 控制策略及其Matlab 仿真研究赵娟平(沈阳化工学院,辽宁,沈阳 110142 )摘要:本文讨论了神经网络PID 控制策略,利用神经网络的自学习能力进行PID控制参数的在线整定,并使用Matlab 软件进行了仿真研究。
仿真结果表明,神经网络PID 控制器参数调整简单,具有很高的精度和很强的适应性,可以获得满意的控制效果。
关键词:神经网络,BP 网络,PID ,参数整定,仿真中图分类号:TP183 文献标识码:ANeural Network PID control and its Matlab Simulation researchJuanPing Zhao(ShenYang institute of chemical industry, LiaoNing, ShenYang 110142 )Abstract: This paper discusses the nerve network PID control strategy, makes use of the study ability of the nerve network to turning the PID control parameters, and proceeds the simulation research using matlab software. From the simulation results, it is can be shown that Neural Network PID controller have the higher accuracy and stronger adaptability, and can get satisfied control result.Key word: neural network, BP neural network, PID, parameter turning, simulation1.引言PID 控制由于其具有直观性好、实现简单、可靠性高以及强鲁棒性等优点,在工业控制中得到广泛的应用,尤其适用于建立了精确数学模型的确定性系统。
单神经元自适应 PID 控制器及其仿真研究论文

单神经元自适应 PID 控制器及其仿真研究摘要:随着科学技术的不断发展和进步,被控对象变得越来越复杂,传统的pid控制器对时变系统和非线性系统往往得不到较好的控制效果。
本文重点研究了单神经元自适应pid控制器,分析了学习规则,并对控制对象的跟踪特性做出了仿真研究。
仿真结果表明,这种控制器不但具有pid控制的优点而且还具有自适应特点,具有良好的控制性能。
关键词:单神经元;pid;自适应;仿真【中图分类号】g4201.单神经元自适应pid控制器单神经元作为构成神经网络的基本单位,具有自学习和自适应能力,而且结构简单易于计算。
而传统的pid控制器也具有结构简单、调整方便和参数整定与工程指标联系密切等特点。
若将这两者结合,则可以在一定程度上解决传统pid控制器不易在线实时整定参数、难于对一些复杂过程和参数慢时变系统进行有效控制的不足。
用神经元实现的自适应pid控制器的结构框图如图1-1所示:单神经元控制系统的结构如图1所示。
图中转换器的输入为设定值r(k)和输出y(k),转换器的输出为神经元学习所需要的状态量x1,x2,x3,k为神经元的比例系数。
神经元自适应控制器的控制算法为:单神经元的控制算法中的权系数wi(k)可以通过自学习功能进行自适应调整,单神经元自适应pid控制器正是通过对加权系数的调整来实现自适应、自学习功能的。
加权系数的调整可以采用不同的学习规则,从而构成不同的控制算法。
2、单神经元自适应pid控制器学习规则2.1 有监督hebb学习规则对于有监督的hebb学习规则由于加权系数wi(k)和神经元的输入、输出和输出偏差三者的相关函数有关,因此采用有监督hebb 学习算法时有(1-12)(1-13)根据无监督的hebb学习规则的推导,可以得到(1-14)同样为保证这种单神经元自适应控制学习算法的收敛性和鲁棒性,将其规范化处理后可得式(1-15)。
(1-15)(1-16)其中,,,(1-17),是输出误差信号,分别表示比例、积分、微分的学习速率。
基于MATLAB的自适应模糊PID控制系统计算机仿真

GENG i Ru ( i g agP oic l cdmyo u ev inadh印 啦 IfrEet n rd c , ab 500 O ̄a Heo j n rv i a e f prio n l l i n n aA S s 0Io l r i P ou t H ri 109 , i ) co c s n n
12 SMU IK工具箱 . I LN
1 MA L B 简 介 T
M TA A L B软 件 于 18 9 4年 由美 国 的 Ma w rs t ok 公 h
交 互式 的模 型 输 入 与仿 真环 境 SM LN IU IK工具 箱是 M T A A L B软件 的扩 展 , 要用 于 动 态 系统 的仿 主 真 。它 的 WID WS中提供 了建 立 系统 模 型所 需 的 NO 大部分 类 型方块 。用户 只需用 鼠标器 选择 所需模块 在模 型窗 口上 “ 出” 型 ( 画 模 双击 任 何模 块 , 即可 打开
收 稿 日期 :20 o6—0 0 6— 7 作 者 简 介 :耿 瑞 (9 8 , ,02年 毕业 于 黑 龙 江 大 学 电 子 工 程 学 17 一)男 20
Ab ta t Ba e n te a ay i f s l a a t e f zy c nr la d te ifu n e o I c nr lp rmee sr c : s d o h n lss o ef— d p i u z o t v o n h nl e c fP D o to a a tr
r sa c d c t sta i me o a k o t lq ai mp v . e e rh i iae t s t d C ma e c n r u t i r e n h t h h n o l y o d
pid控制器matlab仿真

pid控制器matlab仿真PID控制是最早发展的自动控制策略之一,PID控制系统由比例单元(P)、积分单元(I)和微分单元(D)组成。
具有简单易懂,使用中不需精确的系统模型等先决条件,因而成为应用最为广泛的控制器。
PID控制的参数自动调整是通过智能化调整或自校正、自适应算法来实现。
当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。
即当我们不完全了解一个系统和被控对象,或不能通过有效的测量手段来获得系统参数时,最适合用PID控制技术。
PID控制,实际中也有PI和PD控制。
PID控制器就是根据系统的误差,利用比例、积分、微分计算出控制量进行控制的。
本文首先从PID理论出发,建立模型,讨论系统的稳定性,快速性,准确性。
利用MATLAB对PID控制的参数进行仿真,设计不同的参数,以使系统满足所要求的性能指标。
2、控制领域有一个很重要的概念是反馈,它通过各种输出值和它们各自所需值的实时比较的度量―各种误差,再以这些误差进行反馈控制来减少误差。
这样形成的因果链是输入、动态系统、输出、测量、比较、误差、输入构成的一个环路,因而也构成了包含原动态系统在内的一个新的动态闭环系统。
采用反馈的基本原因是要在不确定性存在的条件下达到性能目标。
许多情况下,对于系统的了解是不全面的,或者可用的模型是基于许多简化的假设而使它们变得不透彻。
系统也可能承受外界干扰,输出的观测常受噪声干扰。
有效的反馈能减少这些不确定性的影响,因为它们可以补偿任何原因引起的误差。
反馈概括了很广泛的概念,包括当前系统中的许多回路、非线性和自适应反馈,以及将来的智能反馈。
广义的讲,反馈可以作为描述和理解许多复杂物理系统中发生的循环交互作用的方式。
在实际的过程控制和运动控制系统中,PID占有相当的地位,据统计,工业控制中PID 类控制器占有90%以上。
基于matlab的智能PID控制器设计和仿真毕业设计论文

基于MATLAB的智能PID控制器设计与仿真摘要在工业生产中应用非常广泛的是PID控制器,是最早在经典控制理论基础上发展起来的控制方法,应用也十分广泛。
传统的PID控制器原理十分简单,即按比例、积分、微分分别控制的控制器,但是他的核心也是他的难点就是三个参数(比例系数Kp、积分系数Ki、微分系数Kd)的整定。
参数整定的合适,那么该控制器将凭借结构简单、鲁棒性好的优点出色的完成控制任务,反之则达不到人们所期望的控制效果。
人工神经网络模拟人脑的结构和功能而形成的信息处理系统,是一门十分前沿高度综合的交叉学科,并广泛应用于工程领域。
神经网络控制是把自动控制理论同他模仿人脑工作机制的数学模型结合起来,并拥有自学习能力,能够从输入—输出数据中总结规律,智能的处理数据。
该技术目前被广泛应用于处理时变、非线性复杂的系统,并卓有成效。
关键词自适应PID控制算法,PID控制器,神经网络Design and simulation of Intelligent PID Controllerbased on MATLABAbstractPID controller ,the control method which is developed on the basis of classical control theory, is widely used in industrial production.The Principle of traditional PID controller is very simple, which contains of the proportion, integral, differential three component, but its core task and difficulties is three parameter tuning(proportional coefficient Kp, integral coefficient Ki and differential coefficient KD).If the parameter setting is suitable, the controller can accomplish the control task with the advantages of simple structure and good robustness;but on the contrary, it can not reach the desired control effect which we what.Artificial neural network , the formation of the information processing system which simulate the structure and function of the human brain , is a very high degree of integration of the intersection of disciplines, and widely used in the field of engineering. Neural network control ,combining automatic control theory and the imitate mathematical model of the working mechanism of human brain , has self-learning ability, and can summarize the law of the input-output data , dealing with data intelligently .This technique has been widely used in the process of time-varying, nonlinear and complex system, and it is very effective.Key W ord:Adaptive PID control algorithm,PID controller,Neural network目录摘要 (I)Abstract (II)第一章绪论 (1)1.1 课题研究背景及意义 (1)第二章 PID控制器 (2)2.1 PID控制原理 (2)2.2常规PID控制器的算法理论 (3)2.2.1 模拟PI D控制器 (3)2.2.2 数字P I D控制算法 (3)2.2.3常规PID控制的局限 (5)2.2.4 改进型PID控制器 (5)第三章人工神经网络 (8)3.1 人工神经网络的原理 (8)3.2神经网络PID控制器 (8)3.2.1神经元PID控制器 (8)3.2.2 单神经元自适PID应控制器 (9)3.3 BP神经网络参数自学习的PID控制器 (12)第四章MATAB仿真 (16)4.1 仿真过程 (16)第五章结论与展望 (24)致谢 (25)参考文献 (25)华东交通大学毕业设计(论文)第一章绪论1.1 课题研究背景及意义在工业生产中应用非常广泛的是PID控制器,是最早在经典控制理论基础上发展起来的控制方法,应用也十分广泛。
单神经元自适应PID控制 Hebb学习规则 matlab仿真 增量式PID 控制规律

实验一、单神经元自适应PID 控制一、实验目的1、熟悉单神经元PID 控制器的原理。
2、通过实验进一步掌握有监督的Hebb 学习规则及其算法仿真。
二、实验内容利用单神经元实现自适应PID 控制器,对如下二阶对象进行控制,在MATLAB 环境中进行仿真。
被控对象为:y(k)=0.368y(k-1)+0.26y(k-2)+0.1u(k-1)+0.632u(k-2) 三、实验原理线性神经网络是最简单的一种神经元结构,它不同于感知器,其函数是一线性函数,因此神经元的输出可以是任意值。
我们可以用它实现增量PID 控制器的功能,误差为神经元的输入,权系数为PID 控制系数,由于神经网络可以用在线学习对权系数进行实时修改,所以使得PID 控制具有了自适应功能。
PID 控制器的增量公式为一个3输入的线性神经元的计算公式为k 为神经元的比例系数,w i 为神经元权系数,x i 为神经元输入,u 为神经元的输出。
神经元的学习方法可以采用Hebb 学习规则。
有监督的Hebb 学习算法规范法处理后为3131111222333()()()()(1)()()(1)()()()()(1)()()()()(1)()()()()i i ii i i i i p d k k k u k u k k k x k k k u k e k x k k k u k e k x k k k u k e k x k ωωωωωωηωωηωωη=='==-++=++=++=+∑∑ 四、实验步骤1、编写程序实现单神经元的自适应PID 控制器,输入信号为单位阶跃信号。
单神经元控制的各参考参数为0.12,0.40,0.35,0.40p i d k ηηη====2、修改输入信号为()0.5(sin 4)r t sign t π=,进行上述试验。
3、改变被控制对象为如下几种情况,进行上述试验。
模型1:y(k)=0.368y(k-1)+0.264y(k-2)+u(k-1)+0.632u(k-2))2()(211---+-⨯+-+=∆k k k d k k P K i k e e e k e e k e k u )(332211x w x w x w k u ++=∆模型2:y(k)=0.368y(k-1)+0.264y(k-2)+gu(k-1)+0.632u(k-2)g=1+0.1*sin(0.01k)五、问题讨论神经网络学习算法的收敛速度与自适应控制效果的关系,收敛过程与学习规则中学习系数选取的关系。
自适应模糊PID控制系统及其MATLAB仿真

争 ・ ・ ・ ・ ・ ・ ・ ・ ・ 争 夺 夺 夺 夺 夺 争 夺 争
文 献标 识码 : A
文章 编号 : 7 - 6 (0 10-040 1 1 84 21)503- 6 7 2
第1 0卷
第 5期
漯河职 业技 术学院 学报
J u a fLu h cto a c n lg le e o r lo o eVo ain lTe h oo yColg n
Vo .1 No. 1 0 5
Sp 2 1 e . 01
21 0 1年 9月
d i1 . 9 9 ji n 1 7 -8 4 2 1 . 5 0 5 o :0 3 6 / .s . 6 17 6 .0 0 . 1 s 1
摘
要 : 据 自适 应 PD控 制 系统 的 结 构 和 原 理 , 究 M T A 根 I 研 A L B仿 真 工具 箱及 仿 真 方 法 , 并给 出仿 真 实例 和 分
析 结果。将 自适应技术和 PD控制技术相结合 , 以辅助软件 M T A I 借 A L B有力地验证 了这一技 术的优 势。
定 , 据专 家或 者操作 者 的手 动控制 经验 总结 出来 的一 即根
系列 控制 规则 也 即模 糊 控制 规 则 表 。模 糊 控 制 规则 一 般 具有 如下 形式 :
系统相 结合 , 构建 自适 应 模 糊 PD控 制 系统 , 用 模糊 推 I 运 理, 实现 对 PD参 数 的 实 时调 整 , 了验 证 自适 应 技术 对 I 为 PD控 制 的改进 , I 文章 通过 M T A A L B的 S LN I IK模块 对 MU
自适应模糊PID控制器的设计与仿真

毕业论文(设计) 题目自适应模糊PID控制器的设计与仿真学生姓名*******学号*******院系*******专业电气工程与自动化指导教师*******二O一一年五月二十五日目录1引言 (1)1.1 PID简介 (1)1.2 模糊控制简介 (2)1.3 本文研究的目的和意义 (2)1.4 本文的内容与安排 (3)2国内外现状 (3)3 MATLAB工具箱简介 (4)3.1 MATLAB 系统的应用 (4)3.2 Simlulink工具箱 (4)3.3 模糊逻辑工具箱 (5)3.4 MATLAB环境下的SIMULINK的应用 (5)3.4.1 MATLAB 环境中启动SIMULINK 的方法 (5)3.4.2打开SIMULINK 模型窗口的方法 (5)3.4.3 SIMULINK 仿真基本步骤 (5)4自适应模糊PID控制器的设计 (6)4.1 自适应模糊PID控制器的性能要求 (6)4.2 PID控制的理论基础 (6)4.3 模糊控制原理 (9)4.4 模糊PID控制系统结构及原理 (10)4.5 PID控制器参数自整定原则 (10)4.6 各变量隶属度函数的确定 (11)4.7 建立模糊规则表 (13)5 利用MATLAB对模糊PID控制系统进行仿真 (18)5.1建立系统结构仿真框图 (18)5.2 仿真结果分析 (19)6结论 (22)参考文献 (23)ABSTRACT (25)致谢 (26)附录 (27)自适应模糊PID控制器的设计与仿真摘要:本文在参数自适应模糊PID控制器的基础上,利用模糊推理的方法实现了对PID参数的在线自动整定,并且在MATLAB软件下将该控制器在某系统中的应用进行了研究,仿真结果表明,参数自适应模糊PID控制能使系统达到满意的控制效果,对进一步应用研究具有较大的参考价值。
关键词:自适应;PID控制器;模糊PID;MATLAB仿真1引言1.1 PID简介PID,(Proportional Integral Derivative)控制是目前工业上应用最广泛深入的控制方法。
Fuzzy自整定PID控制器设计及其MATLAB仿真

关键词 :I PD控制 ; 自适应 ; 模糊控制 ; 仿真
中图分类号 :F 7 . T 23 4 文献标识码 : A
在工业控制过程 中经常会碰到大滞后 、 时变 的、 非线性的复杂系统 , 其中有的参数未知或缓慢 变化 ; 的带有延时和随机干扰 ; 有 有的无法获得较
制器 , 常见结构如图 1 所示 。
维普资讯
第26 期 20年 月 0卷第1 3
. .
Ju a o S eyn stt o eoat a E g er g orl f h nagI tu f rnui l ni ei n 沈阳n i e A 学报 c n n 航空工业学院
规则组织控制决策表 , 然后 由该表决定控制量的 大小。将模糊控制和 PD控制两者结合起来 , I 扬
长避短 , 既具有模糊控制灵活、 适应性强的优点, 又具有数与 I I
e e 之间的模糊关 系, 和 c 在运行中通过不断检测 e
摘
要: 针对常规 P I D控制器不能在线进行 参数 自整定 的问题 , 结合模糊 控制技 术 , 出了一种 提
模糊 自整定 PD参数 的方法 , I 运用 M T A A L B进行仿 真研究表 明, 该模糊 自整定 PD控制器既具有 I PD控制器高精度 的优点 , I 又具有模糊控制器快速 、 性强的特点 , 被控对 象具有 良好 的动 、 适应 使
精确的数学模型或模型非常粗糙。对上述这些系 统, 如果使用常规 的 PD控制器 , I 则较难整定 PD I
参数 , 因而 比较难达到预期效果。模糊控制器是
一
种近年来发展起来的新型控制器, 其优点是不
图 1 自适 应 模 糊 PD控 制 器 结 构 I
pid控制及其matlab仿真-详细

在MATLAB中搭建仿真模型,验证PID控制器对复杂系统的控制 效果。
PID控制器的参数优化
参数优化方法
采用智能优化算法(如遗传算法、粒子群算法等)对PID 控制器参数进行优化,以进一步提高控制性能。
01
MATLAB实现
在MATLAB中编写优化算法程序,通过 Simulink仿真模型进行测试和验证。
积分控制
02
03
微分控制
通过累积输入信号的变化量来控 制输出信号,以减小输出信号的 误差。
通过预测输入信号的变化趋势来 控制输出信号,以减小输出信号 的超调和响应时间。
PID控制器的参数整定
比例系数
影响控制器的增益,比例系数越 大,控制器的增益越大,输出信 号变化越快。
积分系数
影响积分控制的强度,积分系数 越大,积分控制作用越强,误差 减小越快。
温度控制系统中的应用
温度控制系统是PID控制器的另一个重要应用领域。在工 业和科学实验中,温度控制对于保持恒定的实验条件和产 品质量至关重要。
PID控制器用于温度控制系统的目的是通过自动调节加热 元件的功率或冷却介质的流量,将温度维持在设定的范围 内。
PID控制器通过比较温度传感器的实际测量值与期望值之 间的误差,来调整加热元件或冷却介质的控制信号,以减 小误差并实现稳定的温度控制。
pid控制及其 matlab仿真-详细
目 录
• PID控制理论简介 • MATLAB仿真环境介绍 • PID控制器在MATLAB中的实现 • PID控制器的性能分析 • PID控制器的应用实例 • 结论与展望
01
CATALOGUE
PID控制理论简介
单神经元自适应PID控制器实验报告
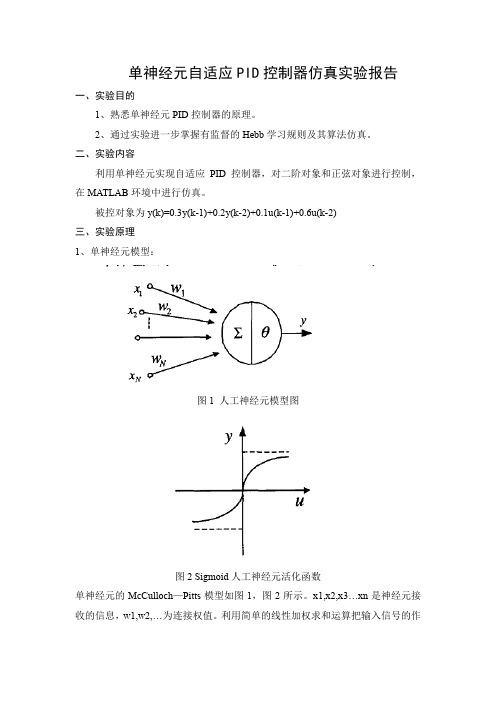
单神经元自适应PID控制器仿真实验报告一、实验目的1、熟悉单神经元PID控制器的原理。
2、通过实验进一步掌握有监督的Hebb学习规则及其算法仿真。
二、实验内容利用单神经元实现自适应PID控制器,对二阶对象和正弦对象进行控制,在MATLAB环境中进行仿真。
被控对象为y(k)=0.3y(k-1)+0.2y(k-2)+0.1u(k-1)+0.6u(k-2)三、实验原理1、单神经元模型:图1 人工神经元模型图图2 Sigmoid人工神经元活化函数单神经元的McCulloch—Pitts模型如图1,图2所示。
x1,x2,x3…xn是神经元接收的信息,w1,w2,…为连接权值。
利用简单的线性加权求和运算把输入信号的作用结合起来构成净输入input=∑w j x j−θ。
此作用引起神经元的状态变化,而神经元的输出v是其当前状态的激活函数。
2、神经经网络的有监督Hebb学习规则学习规则是修改神经元之间连接强度或加权系数的算法,使获得的知识结构适应周围环境的变化。
两个神经元同时处于兴奋状态或同时处理抑制状态时,它们之间的连接强度将得到加强,当一个神经元兴奋而另一个抑制时,它们之间的连接强度就应该减弱。
这一论述的数学描述被称为Hebb学习规则。
在学习过程中,网络根据实际输出与期望输出的比较,进行联接权系数的调整,将期望输出称导师信号是评价学习的标准。
这样,就得到了有监督的Hebb学习规则如果用oi表示单元i的输出,oj表示单元j的输出Wij表示单元j到单元i的连接加权系数,di表示网络期望目标输出,η为学习速率,则神经网络有监督的Hebb学习规则下式所示。
∆w ij(k)=η[di(k)−oi(k)]oi(k)oj(k)(1) 3.基于单神经元的PID控制单神经元控制系统的结构如图3所示。
图中转换器的输人为设定值r(k)和输出y(k),转换器的输出为神经元学习所需要的状态量x1,x2,x3,K为神经元的比例系数。
图3 单神经元自适应控制器结构图单神经元自适应控制器是通过对加权系数的调整来实现自适应、自组织功能的,权系数的调整是按有监督的Hebb规则实现的。
模糊PID控制系统设计及MATLAB仿真

相比传统的PID控制系统,基于Matlab的模糊PID控制系统具有更好的适应性 和鲁棒性。在面对具有非线性、时变等特点的被控对象时,模糊PID控制系统可 以更好地实现精确控制。仿真结果表明,该方法在改善系统的动态性能和稳态精 度方面均具有显著的优势。
然而,基于Matlab的模糊PID控制系统仍然存在一些问题需要进一步研究和 解决。例如,针对不同的被控对象,如何自适应地调整模糊PID控制器的参数仍 然是一个亟待解决的问题。此外,如何进一步提高模糊PID控制系统的鲁棒性和 自适应性也是未来研究的重要方向。
模糊PID控制系统设计及MATLAB仿 真
01 引言
03 参考内容
目录
02
模糊PID控制系统设 计
摘要:本次演示主要介绍了模糊PID控制系统的设计方法及其在MATLAB环境 下的仿真过程。首先,阐述了模糊PID控制系统的基本原理和设计流程,并通过 一个实际案例加以说明。接下来,介绍了MATLAB仿真的基本原理和实施步骤,并 展示了仿真结果。最后,总结了本次演示的主要内容,并指出了未来的研究方向。
(4)设计控制表:根据模糊规则和控制要求,计算出各模糊变量的控制表。
(5)设计去模糊化器:去模糊化器的作用是将模糊量转换为精确量,以便 输出到被控对象。
3、设计案例
以一个简单的温度控制系统为例,介绍模糊PID控制系统的设计应用。该系 统的输入为温度误差和温度变化率,输出为加热器的控制信号。首先,确定输入 输出变量,定义相应的模糊变量。然后,根据控制要求和系统特性制定模糊规则, 并计算出各模糊变量的控制表。最后,设计去模糊化器,将模糊量转换为精确量, 输出加热器的控制信号。通过这样的设计流程,可以实现对该温度控制系统的数学计算软件,它可以用于各种控制系统仿真的工 具。在MATLAB中,可以使用Simulink模块进行系统建模和仿真。Simulink提供 了丰富的库和工具箱,可以方便地构建各种类型的控制系统模型,并对系统进行 仿真和分析。
模糊自适应PID控制方法研究与仿真

应用模 糊控 制算 法来实 现对 PD参数 的 自动 整定是 一种 比较有效 的解 决方 案 ,即利用 模糊 推理 规则 ,用 实 测 I
ቤተ መጻሕፍቲ ባይዱ
值与设 定 值问 的误 差 以及 误差 变化 率作 为系统 的输入 ,对 PD调节器 的 K 、K 、K I P I D参 数进 行调 整 ,从 而 实
现对控 制对 象 的实时控 制 _ 。其控 制系统 结构 图如 图 1 2 J 所示 。
图 1 模 糊 自适 应 PD控 制 器 结 构 图 I
[ 关键词]模 糊 自适应 ;PD控制 ;Maa 仿 真 I tb l
[ 中图分类号]T 232 P7 .
[ 文献标识码 ]A
[ 文章编号]10 —18 (0 10 0 4 —0 0 8 7 X 2 1)2— 0 5 4
在 许 多实 际的工业 过程 中 ,由于普遍 存 在的非 线性 、参 数 时变性 和模型 的不确 定性 ,使 得 常规 的 PD控 I
Ap . 01 r2 1
模 糊 自适 应 PD控 制方 法 研究 与仿 真 I
李春 光 ,孙朝 霞
( 门理工学 院计算 机科学 与技 术系 ,福建厦 门 3 12 ) 厦 6 04
【 摘 要]对于非 线性 、时变性 的系统来讲 .传统 PD控制难 以达到 满意效果 。利用 模糊推 理的方 法 I
过 程 中 ,不 断检测 误差 e 与误 差变 化率 e,根据模糊 控制 策略对 K 、K 、K c P I D进行 在线 修正 ,从 而满 足不 同
自适应模糊PID控制器的设计及MATLAB仿真

自适应模糊PID控制器的设计及MATLAB仿真宋超;曹翱;温家玺【摘要】自适应模糊PID控制利用PID参数整定经验来使模糊控制器自动整定参数,从而达到满意效果.在参数自适应模糊PID控制器的基础上,利用模糊推理的方法实现了对PID参数的在线自动整定,并且在MATLAB软件下将该控制器在某系统中的应用进行了研究.仿真结果表明,参数自适应模糊PID控制能使系统达到良好的控制效果,对进一步应用研究具有较大的参考价值.【期刊名称】《现代制造技术与装备》【年(卷),期】2018(000)007【总页数】3页(P203-205)【关键词】自适应;PID;控制器;模糊;PID;控制器;MATLAB;仿真【作者】宋超;曹翱;温家玺【作者单位】长安大学工程机械学院,西安 710064;长安大学工程机械学院,西安710064;长安大学工程机械学院,西安 710064【正文语种】中文PID控制是经典控制中用于过程控制最有效的策略之一,常规PID控制具有结构简单、技术成熟、稳定性好以及参数调整方便等优点,广泛应用工业控制中。
但常规PID控制难以解决被控对象数学模型复杂、非线性以及时变不确定性等系统问题,而自适应模糊PID控制可以有效解决此问题[1]。
自适应模糊PID控制指把模糊控制技术与常规PID控制技术相融合,实现在线对PID参数的最优整定[2]。
本文依靠MATLAB/sIMULINK的模糊逻辑工具箱的Fuzzy Logic Controller与常规PID Controller结合,设计了一种在线整定模糊PID控制器,并通过sIMULINK对自适应模糊PID控制和常规PID仿真结果对比,自适应模糊PID控制适应参数变化,动态响应较好。
1 常规PID控制原理常规的PID控制系统是将偏差的比例、积分和微分通过合成,对被控对象进行控制。
系统结构如图1所示。
图1 常规PID控制框图图1中,r(t)为输入信号,e(t)为偏差信号,μ(t)为控制信号,y(t)为被控系统输出信号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PID自适应控制学习与Matlab仿真0 引言在P ID控制中,一个关键的问题便是P I D参数整定。
传统的方法是在获取对象数学模型的基础上,根据某一整定原则来确定PID参数。
然而实际的工业过程往往难以用简单的一阶或二阶系统来描述,且由于噪声、负载扰动等因素的干扰,还可以引起对象模型参数的变化甚至模型结构的政变。
这就要求在P I D 控制中。
不仅PID参数的整定不依赖于对象数学模型,而PID参数能在线阐整,以满足实时控制的要求。
1 自适应控制的概念及分类控制系统在设计和实现中普通存在着不确定性,主要表现在:①系统数学模型与实际系统间总是存在着差别,即所谓系统具有末建模的动态特性;②系统本身结构和参数是未知的或时变的;③作用在系统上的扰动往往是随机的,且不可量测;④系统运行中,控制对象的特性随时间或工作环境改变而变化,且变化规律往往难以事先知晓。
为了解决控制对象参数在大范围变化时,一般反馈控制、一般优控制和采用经典校正方法不能解决的控制问题。
参照在日常生活中生物能够遏过自觉调整本身参数改变自己的习性,以适应新的环境特性。
为此,提出自适应控制思想。
自适应控制的概念所谓自适应控制是指对于控制对象的动态信息了解得不够充分对周围环境变化尚掌握不够明确的情况下控制系统对控制器的参数进行积极的自动调节。
自适应控制方法应该做到:在系统远行中,依靠不断采集控制过程信息,确定被控对象的当前实际工作状态,优化性能准则,产生自适应控制规律,从而实时地调整控制器结构或参数,使系统始终自动地工作在最优或次最优的运行状态下。
作为较完善的自适应控制应该具有以下三方面功能:(1)系统本身可以不断地检测和处理理信息,了解系统当前状态。
(2)进行性能准则优化,产生自适应校制规律。
(3)调整可调环节(控制器),使整个系统始终自动运行在最优或次最优工作状态。
自适应控制是现代控制的重要组成部分,它同一般反馈控制相比较有如下突出特点:(1) 一般反馈控制主要适用于确定性对象或事先确知的对象,而自适应控制主要研究不确定对象或事先难以确知的对象。
(2) 一般反馈控制具有强烈抗干扰能力,即它能够消除状态扰动引起的系统误差,而自适应控制因为有辨识对象和在线修改参数的能力,因而能消除状态扰动引起的系统误差,而且还能消除系统结构扰动引起的系统误差。
(3) 一般反馈控制系统的设计必须事先掌握描述系统特性的数学模型及其环境变化状况,而自适应控制系统设计则很少依赖数学模型全部,仅需要较少的验前知识,但必须设计一套自适应算法,因而将更多地依靠计算机技术实现。
(4) 自适应控制是更复杂的反馈控制,它在一般反调控制的基础上增加了自适应控制机构或辨识器,还附加一个可调系统。
自适应控制系统的基本结构与分类通常,自适应控制系统的基本结构有两种形式,即前馈自适应控制和反馈自适应控制。
1.2.1 前馈自适应控制结构前馈自适应控制亦称开环自适应控制,它借助对作用于过程信号的测量。
并通过自适应机构按照这些测量信号改变控制器的状态,从而达到改变系统特性的目的。
没有“内”闭环反馈信号而实现控制器参数是前馈自适应控制的突出特点。
图1 前馈自适应控制结构图这种结构类似于一般扰动的复合控制,所不同的是增添了自适应机构和可调控制器。
1950年,增益调度的前馈自适应控制方案被首次用于飞机。
在此,增益被设计为可观测信号的前置量,以描述运行状态,被计算参数以特性曲线表的形式存储在计算机中,以便同控制器参数适配来控制运行状态。
前馈自适应控制由于可预先知其过程状态和无须对可观测过程的输入和输出信号进行辨识。
因此能够快速反应过程变化是该结构方案的优点。
其缺点是,忽略了不可观测信号、干扰和意料之外的过程状态变化,且大量参数存储必须有许多操作,从而限制—厂该方法的使用。
1.2.2 反馈自适应控制结构如果过程品质变化不能直接由外过程信号测量确定,则可采用图中控制方案。
这是应用最广泛的自适应控制结构,其特点如下:(1) 过程特性或信号变化可借助测量各内控制回路信号进行观测。
(2) 除基本回路反馈外,自适应机构还将形成附加反馈级。
(3) 闭环信号流通道能产生非线性第二反馈级。
图2 反馈自适应控制结构1.2.3自适应控制系统的发展及应用自适应控制系统的设计始终围绕着解决给定对象(过程)下,寻求控制方案和控制器的合理结构与参数,并考虑控制器远行于包括工作点的整个工作范围。
对于确定性的控制对象常采用经典控制方案:开环控制、反馈控制、补偿控制和最优控制,控制器的结构和参数一般是固定的。
对于不确定性的控制对象由于经典控制方案不能圆满解决控制任务而迫使人们寻求新的控制方案,并出现了可调控制器。
控制器参数的自动调整最早出现于1940年,当时的自适应控制仅被定义为控制器所具有的按照过程动态和静态特性调整本身参数的能力。
在此期间,飞机自适应控制器的设计对自适应控制研究产生了巨大的影响。
早在20世纪50年代未,由于飞行控制的需要,美国麻省理工学院(MIT)的怀特克(whztaker)教授首先提出了飞机自动驾驶仪的模型参考自适应控制方案,称为MIT方案。
这时因现代控制理论向不成熟和计算机技术的限制。
1957年用自动驾驶仪试验时随着飞机失事而失败。
直到20世纪70年代,这一方法才重新兴起。
1960年至1970年间,控制理论(如状态空间和稳定性理论)得到了发展,从而为自适应控制设计提供了有效服务。
并注入了新技术(对偶控制、白适应控制递推方法及模型辨识与参数估计)。
1962年首次成功地实现了利用过程计算机进行直接数字式控制。
1963年罗马尼亚学者波被夫提出了超稳定性理论、随即法国学者兰道把这—理论引用到模型参考自适应控制中。
在1966年德国学者帖克斯(Park)提出了用李雅普诺夫第二法推导自适应算法,以保证自适应系统全局渐进稳定。
1973年由瑞典学者阿斯待罗姆和威特马克首先提出自校正调节器,并在造纸厂获得成功。
此后,自适应控制技术真正转入成功实用阶段。
1974年吉尔巴待和温斯顿(Gilbart and Wiston)利用模型参考自适应控制使一种光学跟踪望远镜精度提高了5倍以上,同年博里森和西丁(borrisom and Hedquist)在200kW的矿石破碎机中采用自校正控制,使产量提高约l0%,而且也改进了动态性能。
进入20世纪80年代后,随着数字机件性能价格比的迅速改善和微机脚用技术的个断提高、普及,自适应控制如鱼得水,更显示出了应用活力。
1982年第一台工业数字式自适应拉制器进入市场;1986年约有15个公司出售工业过程数字自校正装置或自适应控制器。
与此同时,自适应控制技术再度对航空、航天机器入、舰船驾驶以及现代武器系统产生了极大约吸引力,并获得了具体应用。
在航空方面,自适应控制首次成功地解决了高性能飞机的自适应自动驾驶仪问题。
除此,可借助鲁棒直接自适应控制重构故障后的飞行控制系统;利用飞行员自适应驾驶模型研究和预测新机飞行操纵品质,通过自适应控制技术实现空中飞行模拟和采用自校正控制技术设计飞机刹车防滑控制规律等。
在航天领城内,自适应控制为飞船姿态调节和跟踪、卫星跟踪望远镜安装和使用,以及空间环境模拟等必不可少的关键技术。
在高新技术密集的现代武器系统上,自适应控制是极其重要的一个方面。
以导弹武器系统为例,可以说所有类型的导弹(无论是一般导弹或是遥控导弹,近距小型导弹还是中远程战术导弹)的自动驾驶仪都实现了自适应体制,而对于反舰导弹来说,应用自适应控制技术尤其具有特殊价值和意义。
2 PID自适应控制PID控制是最早发展起来的控制策略之一。
由于其算法简单、鲁棒性好,参数容易调整和可靠性高,而被广泛用于工业量测系统及工业过程控制,尤其适用于确定性控制系统,对于自适应控制系统亦是理想的控制器选择对象。
近年来,出现了许多新型PID控制器,如参数自适应PID控制器,基于非参数模型的自适应PID控制器,是人们一直寻求PID控制器自动整定技术的结果,同时为自适应控制的实际应用开辟了新途径。
PID控制的原理和特点PID控制器问世至今已有近70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。
当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。
即当我们不完全了解一个系统和被控对象,或不能通过有效的测量手段来获得系统参数时,最适合用PID控制技术。
PID控制器就是根据系统的误差,利用比例、积分、微分计算出控制量进行控制的。
PID控制器是一种具有固定结构形式的线性控制器,其原理如图3所示。
图3 PID控制器结构比例控制(P)是一种最简单的控制方式。
其控制器的输出与输入误差信号成比例关系。
它是按比例反应系统的偏差,系统一旦出现了偏差,比例调节立即产生调节作用用以减少偏差。
积分(I)控制使控制器的输出与输入误差信号的积分成正比关系。
积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。
积分作用的强弱取决与积分时间常数Ti。
加入积分调节可使系统稳定性下降,动态响应变慢。
微分(D)控制器使输出与输入误差信号的微分成正比关系。
在控制器中仅引入“比例”项往往是不够的,比例项的作用仅是放大误差的幅值,而目前需要增加的是“微分项”,它能预测误差变化的趋势,从而避免了被控量的严重超调。
微分作用反映系统偏差信号的变化率,具有预见性,能预见偏差变化的趋势,因此能产生超前的控制作用,在偏差还没有形成之前,已被微分调节作用消除。
PID控制器的参数整定PID控制器的参数整定是控制系统设计的核心内容。
它是根据被控过程的特性确定PID 控制器的比例系数、积分时间和微分时间的大小。
PID控制器参数整定的方法很多,概括起来有两大类:一是理论计算整定法。
它主要是依据系统的数学模型,经过理论计算确定控制器参数。
这种方法所得到的计算数据未必可以直接用,还必须通过工程实际进行调整和修改。
二是工程整定方法,它主要依赖工程经验,直接在控制系统的试验中进行,且方法简单、易于掌握,在工程实际中被广泛采用。
PID控制器参数的工程整定方法,主要有临界比例法、反应曲线法和衰减法。
三种方法各有其特点,其共同点都是通过试验,然后按照工程经验公式对控制器参数进行整定。
但无论采用哪一种方法所得到的控制器参数,都需要在实际运行中进行最后调整与完善。
现在一般采用的是临界比例法。
利用该方法进行 PID控制器参数的整定步骤如下:(1) 首先预选择一个足够短的采样周期让系统工作;(2) 仅加入比例控制环节,直到系统对输入的阶跃响应出现临界振荡,记下这时的比例放大系数和临界振荡周期;(3) 在一定的控制度下通过公式计算得到PID控制器的参数。
