信号与系统作业1
2011年12月考试信号与系统第一次作业

2011年12⽉考试信号与系统第⼀次作业2011年12⽉考试信号与系统第⼀次作业⼀、单项选择题(共9题、总分18分、得分18分)1. 连续信号f(t) 与δ(t?t0)的乘积,即 f(t)*δ(t?t0)=( )(本题分数:2 分,本题得分:2分。
)A、B、C、D、题⽬信息难度: 2正确答案: B解题⽅案:2. 已知f(t),为求f(t0?at) 应按下列哪种运算求得正确结果?(式中t0,a 都为正值) (本题分数:2 分,本题得分:2A、f(-at)左移t0B、f(-at) 右移t0C、f(at) 左移t0/aD、f(at)右移t0/a题⽬信息难度: 2正确答案: D解题⽅案:3. 已知 f(t),为求f(t0-at) 应按下列哪种运算求得正确结果?(式中t0,a 都为正值) (本题分数:2 分,本题得分:2A 、B 、f(at) 右移t 0C 、f(at) 左移t 0/aD 、f(-at) 右移t 0/a题⽬信息难度: 3 正确答案: D 解题⽅案:A 、两个周期信号之和必为周期信号;B 、⾮周期信号⼀定是能量信号;C 、能量信号⼀定是⾮周期信号;D 、两题⽬信息难度: 3 正确答案: C 解题⽅案:5. 信号f1(t),f2(t)波形如图所⽰,设f(t)=f1(t)*f2(t),则f(0)为()(本题分数:2 分,本题得分:2 分。
)A 、1B 、2C 、3D 、4题⽬信息难度:4 正确答案: B解题⽅案:卷积的图解法计算。
如直接⽤卷积定义式更加简单。
6. 积分∫?∞te ?2t δ(τ)&DifferentialDτ等于() (本题分数:2 分,本题得分:2 分。
)A 、B、C、D、题⽬信息难度: 4正确答案: B解题⽅案:冲激信号的性质(本题分数:2 分,本题得分:2分。
)A、0B、1C、2D、3题⽬信息难度: 4正确答案: D解题⽅案:利⽤卷积的定义式计算8. 线性时不变连续系统的数学模型是() (本题分数:2 分,本题得分:2分。
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
信号与系统第1-3章习题

卷积 y(t) u (t 2) et u( t 1) 等于________________。 信号 x(n) cos(3 n / 5) 2sin(2 n / 3) 的基波周期为_______________。
sin 2t 2 ( t )dt _________。 t
(1) 确定该系统的单位冲激响应; (2) 画出系统方框图。 56、已知信号 f (t ) t[u(t) u(t 2)] ,试确定该信号的奇分量和偶分量。 57、已知系统的冲激响应 h(t ) u(t 1) u(t 2) ,激励 f(t ) u(t 1) u(t 2) ,求系统的零 状态响应 y(t)。 58、已知 f 1 2t 的波形如题图 58 所示,画出 f t 的波形,并写出 f t 的表达式。
d x1 (t ) 作 dt
6
54、什么叫稳定系统?一个因果稳定的离散时间 LTI 系统应满足什么条件? 55、考虑一因果的 LTI 系统,y(t)为系统输出,x(t)为系统输入,其微分方程为:
d 2 y (t ) dy (t ) 3dx(t ) 4 3 y (t) x(t ) 2 dt dt dt
j / 4
的直角坐标式为_____________________。
信号 x(t ) 2 cos(10t 1) sin( 4t 1) 的基波周期为_____________________。
4
25、 26、 27、
t
e ( )d _________。
(2t ) __________________。
B
1
-4 -3 -2 -1 0
t
信号与系统第一章习题及作业(1,2)

(2)(余弦序列是否为周期信号,取决于2л/Ω0是正整 (余弦序列是否为周期信号,取决于 Ω 有理数还是无理数。) 数、有理数还是无理数。) 因此, 因此, 2л/Ω0=2л·7/8л=7/4=N/m Ω =2л·7/8л 所以基波周期为N=7; 所以基波周期为N=7; N=7
因为2л/Ω =16л 为无理数, (4) 因为 Ω0=16л,为无理数,则此信号不是周期 信号. 信号. (5) 因为周期信号在[-∞,+∞]的区间上,而本题的重 因为周期信号在[ ∞,+∞]的区间上, 的区间上 复区间是[0, +∞],则此信号为非周期信号 则此信号为非周期信号, 复区间是[0, +∞],则此信号为非周期信号,
f(n) 1 0 3 6 … n
9、判断是否为线性系统?为什么? 、判断是否为线性系统?为什么?
( 3) ( 5) (7 )
y( t ) = ln y( t 0 ) + 3t 2 f ( t ) y( t ) = y( t 0 ) + f 2 ( t ) y( t ) = sin t ⋅ f ( t )
8、一个连续时间系统的输入-输出关系为 、一个连续时间系统的输入 输出关系为
1 t+T y ( t ) = T [ f ( t ) ] = ∫ T2 f (τ )d τ T t− 2 试确定系统是否为线性的?非时变的?因果的? 试确定系统是否为线性的?非时变的?因果的?
解:积分系统是线性的,因此系统是线性系统。 积分系统是线性的,因此系统是线性系统。
sin ω 0 tε ( t )
sin ω 0 ( t − t 0 )ε ( t )tt0 Nhomakorabeat
sin ω 0 tε ( t − t 0 )
信号与系统理论及应用 习题 - 第1章 -作业参考答案

1
t
1.5 写出如题图所示信号的解析表达式。
X1(t) E
0
(1)
2
t
X2(t) 1 0 -1
(2)
1
2
t
X3(t)
0
2T
4T
6T
8T
t
(3)
X4(n)
1
(4)
-2
-1
0
1
2
n
(1) x1 (t )
E (t 2)[u(t ) u(t 2)] 2
(2) x2 (t ) [u(t ) u(t 1)] [u(t 1) u(t 2)] (3) x3 (t ) e sin
t o
1 (t ) 2
(6) (9)
d t d [e (t )] (t ) '(t ) dt dt
0
et sin t (t 1)dt 0
(11)
1
1
(t 2 4)dt 0
1.7 已知 x(t)的波形如题图所示, 试画出 x(3-2t)、 x(3-t) 、 x(2t)、 x(t/2)的波形图。
1.14 请求出下面两个信号的 Nyquist 频率(即信号的最高频率)。
1. x1 (t ) cos(500 2 t ) sin(400 2 t ) 2. x2 (t ) cos(600 2 t ) sin(300 2 t ) 答:1. cos sin
答:
x(3-t) 1
0 -1
1
2
3
t
x(2t) 1
1
x(t/2)
0 -1
1
2
信号与系统练习题——第1-3章

信号与系统练习题——第1-3章信号与系统练习题(第1-3章)一、选择题1、下列信号的分类方法不正确的是(A )A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、连续信号和离散信号2、下列离散序列中,哪个不是周期序列? (D )A 、165()3cos()512f k k ππ=+ B 、2211()5cos()712f k k ππ=+ C 、33()9sin()5f k k π= D 、433()7sin()45f k k π=+ 3、下列哪一个信号是周期性的?(C )。
A 、()3cos 2sin f t t t π=+;B 、()cos()()f t t t πε=;C 、()sin()76f k k ππ=+; D 、1()cos()53f k k π=+。
4、周期信号()sin6cos9f t t t =+的周期为(D )A 、πB 、2πC 、12π D 、23π5、周期信号()sin3cos f t t t π=+的周期为(C )。
A 、πB 、2πC 、无周期D 、13π 6、以下序列中,周期为5的是(D ) A. 3()cos()58f k k π=+ B. 3()sin()58f k k π=+ C. 2()58()j k f k eπ+= D. 2()58()j k f k e ππ+=7、下列说法正确的是(D )A 、两个周期信号()x t ,()y t 的和信号()()x t y t +一定是周期信号B 、两个周期信号()x t ,()y t 的周期分别为2()()x t y t +是周期信号C 、两个周期信号()x t ,()y t 的周期分别为2和π,则信号()()x t y t +是周期信号D 、两个周期信号()x t ,()y t 的周期分别为2和3,则信号()()x t y t +是周期信号8、下列说法不正确的是(A )A 、两个连续周期信号的和一定是连续周期信号B 、两个离散周期信号的和一定是离散周期信号C 、连续信号()sin(),(,)f t t t ω=∈-∞+∞一定是周期信号D 、两个连续周期信号()x t ,()y t 的周期分别为2和3,则信号()()x t y t +是周期信号9、(52)f t -是如下运算的结果(C )A 、(2)f t -右移5B 、(2)f t -左移5C 、(2)f t -右移25 D 、(2)f t -左移25 10、将信号()f t 变换为(A )称为对信号()f t 的平移。
信号与系统答案1
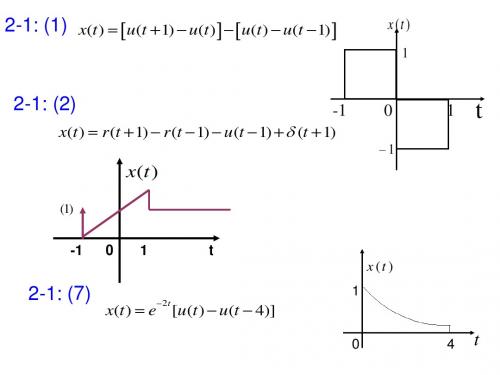
∫
∞
e jω0t [δ (t +T) δ (t T)]dt = e jω0 (T ) e jω0 (T )
= 2 j sin(ω0T)
2-5: (4)
x(t)
2 0 2 3 5
t
2 -1 0
x(t+1)
1 2 4
t
2 -3 0
x(t/3+1)
3 6 12
t
2-9:
x(t) = et [u(t 1) u(t 2)] + tδ (t 3), 求 (1) (t), x '(t) x ∵x(t) = et [u(t 1) u(t 2)] + 3δ (t 3)
3-31:
5 1 y[k ] y[k 1] + y[k 2] = x[k ], y(1) = 0, y(2) = 1, 6 6 x[k ] = u[k ]
根据单位脉冲响应的定义,应满足方程 解: (1) 根据单位脉冲响应的定义 应满足方程: 应满足方程 5 1 h[k ] h[k 1] + h[k 2] = δ [k ] 6 6 第一步:求等效初始条件 第一步 求等效初始条件 :
t
3-4 已知离散时间 系统,输入 x1[k ] = δ [k 1] 时,输出 已知离散时间LTI系统 输入 输出; 系统 输出
1 k 1 y1[k ] = ( ) u[k 1], 求当输入x2 [k ] = 2δ [k ] + u[k ]时系统响应y2 [k ]. 2
x2 [k ] = 2 x1[k + 1] +
2-13:(3)
x[3k ]
2 1 1
2
k
-1 0 1 2
2-13:(4)
第二次信号与系统作业答案

下半年信号与系统作业1一、判断题:1.拉普拉斯变换满足线性性。
正确2.拉普拉斯变换是连续时间系统进行分析的一种方法。
正确 3.冲击信号的拉氏变换结果是一个常数。
正确 4.单位阶跃响应的拉氏变换称为传递函数。
错误二、填空题1.如果一个系统的幅频响应是常数,那么这个系统就称为 全通系统 。
2.单位冲击信号的拉氏变换结果是 ( 1 ) 。
3.单位阶跃信号的拉氏变换结果是 (1 / s) 。
4.系统的频率响应和系统的传递函数之间的关系是把传递函数中的s 因子用j ω 代替后的数学表达式。
5.从数学定义式上可以看出,当双边拉氏变换的因子s=j ω时,双边拉氏变换的就变成了傅立叶变换的定义式,所以双边拉氏变换又称为 广义傅立叶变换 。
6、单边拉普拉斯变换(LT)的定义式是:.7、双边拉普拉斯变换(LT)的定义式是:.三、计算题 1. 求出以下传递函数的原函数 1)F (s )=1/s 解:f (t)=u(t) 2)F(s)=11+s 解:f (t)=e -tu(t)3)F(s)=)1(12-s s解:F(S)=)1(12-s s =)1)(1(1+-s s s =)1(5.0-s +)1(5.0+s -s1F(t)=0.5e-tu(t)+ 0.5e -t u(t)-U(t)2.根据定义求取单位冲击函数和单位阶跃函数的拉氏变换。
解:L[δ(t)]= ⎰+∞∞-δ(t) e -st dt=1L[u(t)]= ⎰+∞∞-u(t) e -stdt=⎰+∞∞- e -st dt=s13、已知信号)(t f 是因果信号其拉氏变换为F (s )=21s,试求)0(f =? )0(f =lim 0→t )(t f =lim ∞→s S ·F(s)=lim∞→s 2ss =0 4、已知信号)(t f 是因果信号其拉氏变换为F (s )=)100010()10)(2(2++++s s s s s ,试求)(∞f =? 由终值定理)(∞f =lim 0→s SF(s)=lim→s s)100010()10)(2(2++++s s s s s =0.025、求)()(3t u t t f =的拉氏变换答:L[)(t f ]=46s(Re(s)>0)一、判断题(1)如果x(n)是偶对称序列,则X(z)=X(z -1)。
信号与系统练习题——第1-3章

信号与系统练习题(第1-3章)一、选择题1、下列信号的分类方法不正确的是(A )A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、连续信号和离散信号 2、下列离散序列中,哪个不是周期序列? (D ) A 、165()3cos()512f k k ππ=+ B 、2211()5cos()712f k k ππ=+C 、33()9sin()5f k k π= D 、433()7sin()45f k k π=+ 3、下列哪一个信号是周期性的?(C )。
A 、()3cos 2sin f t t t π=+;B 、()cos()()f t t t πε=;C 、()sin()76f k k ππ=+; D 、1()cos()53f k k π=+。
4、周期信号()sin6cos9f t t t =+的周期为(D )A 、πB 、2πC 、12π D 、23π 5、周期信号()sin3cos f t t t π=+的周期为(C )。
A 、πB 、2πC 、无周期D 、13π 6、以下序列中,周期为5的是(D )A. 3()cos()58f k k π=+ B. 3()sin()58f k k π=+ C.2()58()j k f k eπ+= D. 2()58()j k f k eππ+=7、下列说法正确的是(D )A 、两个周期信号()x t ,()y t 的和信号()()x t y t +一定是周期信号B 、两个周期信号()x t ,()y t 的周期分别为2()()x t y t +是周期信号C 、两个周期信号()x t ,()y t 的周期分别为2和π,则信号()()x t y t +是周期信号D 、两个周期信号()x t ,()y t 的周期分别为2和3,则信号()()x t y t +是周期信号 8、下列说法不正确的是(A )A 、两个连续周期信号的和一定是连续周期信号B 、两个离散周期信号的和一定是离散周期信号C 、连续信号()sin(),(,)f t t t ω=∈-∞+∞一定是周期信号D 、两个连续周期信号()x t ,()y t 的周期分别为2和3,则信号()()x t y t +是周期信号 9、(52)f t -是如下运算的结果(C )A 、(2)f t -右移5B 、(2)f t -左移5C 、(2)f t -右移25 D 、(2)f t -左移2510、将信号()f t 变换为(A )称为对信号()f t 的平移。
信号与系统练习题1

.一、单项选择题:14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为() A .400rad /s B 。
200 rad /s C 。
100 rad /s D 。
50 rad /sf如下图(a)所示,其反转右移的信号f1(t) 是()15、已知信号)(tf如下图所示,其表达式是()16、已知信号)(1tA、ε(t)+2ε(t-2)-ε(t-3)B、ε(t-1)+ε(t-2)-2ε(t-3)C、ε(t)+ε(t-2)-ε(t-3)D、ε(t-1)+ε(t-2)-ε(t-3)17、如图所示:f(t)为原始信号,f1(t)为变换信号,则f1(t)的表达式是()A、f(-t+1)B、f(t+1)C、f(-2t+1)D、f(-t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是( )19。
信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为( )A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ,则该系统是()>-系统的系统函数.已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示,该系统微分方程的特征根是( )A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示,则系统的输入应当是( )A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC. )(t fD.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差 2A 、1-eB 、3eC 、3-e D 、1 27.信号〔ε(t)-ε(t -2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28.已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae 2--+,则其2个特征根为( )A 。
2018年9月份考试信号与系统第一次作业

2014年9月份考试信号与系统第一次作业一、单项选择题(本大题共100分,共 40 小题,每小题 2.5 分)1. 已知 f(t),为求f(t0-at) 应按下列哪种运算求得正确结果?(式中t,a都为正值)()。
A.B. f(at) 右移t0 C. f(at) 左移t/a D. f(-at) 右移t/a2. 系统函数H(s)与激励信号X(s)之间是()。
A. 反比关系 B. 无关系C. 线性关系D. 不确定3. 下列论断正确的为()。
A. 两个周期信号之和必为周期信号; B. 非周期信号一定是能量信号; C. 能量信号一定是非周期信号; D. 两个功率信号之和仍为功率信号。
4. 序列的正确图形是()A.B.C.D.5. 已知某系统的系统函数为H(s),唯一决定该系统单位冲激响应h(t)函数形式的是() A. H(s)的零点 B. H(s)的极点 C. 系统的输入信号 D. 系统的输入信号与H(s)的极点6. 信号波形如图所示,设,则为()A. 1B. 2C. 3D. 47. 某信号的频谱密度函数为则f(t) =()。
A.B.C.D.8. 积分等于()A.B.C.D.9. 积分等于()A.B.C.D.10. 信号波形如图所示,设,则为()A. 0B. 1C. 2D. 311. 信号和分别如图(a)和图(b)所示,已知,则的傅里叶变换为()A.B.C.D.12. f(5-2t)是如下运算的结果————————() A. f(-2t)右移5B. f(-2t)左移5C. f(-2t)右移5/2D. f(-2t)左移5/213. 图(b)中与图(a)所示系统等价的系统是()A.B.C.D.14. 若系统的起始状态为0,在x(t)的激励下,所得的响应为———() A. 强迫响应 B. 稳态响应 C. 暂态响应 D. 零状态响应15. 已知信号的傅里叶变换<mml:math xmlns:mml="/1998/Math/MathML" xmlns:m="/officeDocument/2006/math"><mml:mrow ><mml:mi>F</mml:mi><mml:mo>(</mml:mo><mml:mi>j</mml:mi><mml:mi>&omega ;</mml:mi><mml:mo>)</mml:mo><mml:mo>=</mml:mo><mml:mi>δ</mml:mi ><mml:mo>(</mml:mo><mml:mi>ω</mml:mi><mml:mo>−</mml:mo><m ml:msub><mml:mrow><mml:mi>ω</mml:mi></mml:mrow><mml:mrow><mml:m n>0</mml:mn></mml:mrow></mml:msub><mml:mo>)</mml:mo></mml:mrow></mml: math>,则为()A.<mml:math xmlns:mml=" /1998/Math/MathML" xmlns:m=" /officeDocument/2006/math"><mml:mact ionactiontype="link"><mml:mrow><mml:mfrac><mml:mrow><mml:mn>1</mml:mn></ mml:mrow><mml:mrow><mml:mn>2</mml:mn><mml:mi>π</mml:mi></mml:mrow></mml:mfrac><mml:msup><mml:mrow><mml:mi>e</mml:mi ></mml:mrow><mml:mrow><mml:mi>j</mml:mi><mml:msub><mml:mrow><mml:mi>w </mml:mi></mml:mrow><mml:mrow><mml:mn>0</mml:mn></mml:mrow></mml:msub ><mml:mi>t</mml:mi></mml:mrow></mml:msup></mml:mrow></mml:math>B.<mml:math xmlns:mml=" /1998/Math/MathML" xmlns:m=" /officeDocument/2006/math"><mml:mact ionactiontype="link"><mml:mrow><mml:mfrac><mml:mrow><mml:mn>1</mml:mn></ mml:mrow><mml:mrow><mml:mn>2</mml:mn><mml:mi>π</mml:mi></mml:mrow></mml:mfrac><mml:msup><mml:mrow><mml:mi>e</mml:mi ></mml:mrow><mml:mrow><mml:mo>−</mml:mo><mml:mi>j</mml:mi><mml:msub><mml:mrow><mml:mi>w</mml:mi></mm l:mrow><mml:mrow><mml:mn>0</mml:mn></mml:mrow></mml:msub><mml:mi>t</m ml:mi></mml:mrow></mml:msup></mml:mrow></mml:math>C.<mml:math xmlns:mml=" /1998/Math/MathML" xmlns:m=" /officeDocument/2006/math"><mml:mact ionactiontype="link"><mml:mrow><mml:mfrac><mml:mrow><mml:mn>1</mml:mn></ mml:mrow><mml:mrow><mml:mn>2</mml:mn><mml:mi>π</mml:mi></mml:mrow></mml:mfrac><mml:msup><mml:mrow><mml:mi>e</mml:mi ></mml:mrow><mml:mrow><mml:mi>j</mml:mi><mml:msub><mml:mrow><mml:mi>w </mml:mi></mml:mrow><mml:mrow><mml:mn>0</mml:mn></mml:mrow></mml:msub ><mml:mi>t</mml:mi></mml:mrow></mml:msup><mml:mi>ξ</mml:mi><mml:mrow><mml:mo>(</mml:mo><mml:mi>t</mml:mi><mml:mo>)</mml :mo></mml:mrow></mml:mrow></mml:math>D.<mml:math xmlns:mml=" /1998/Math/MathML" xmlns:m=" /officeDocument/2006/math"><mml:mact ionactiontype="link"><mml:mrow><mml:mfrac><mml:mrow><mml:mn>1</mml:mn></ mml:mrow><mml:mrow><mml:mn>2</mml:mn><mml:mi>π</mml:mi></mml:mrow></mml:mfrac><mml:msup><mml:mrow><mml:mi>e</mml:mi ></mml:mrow><mml:mrow><mml:mo>−</mml:mo><mml:mi>j</mml:mi><mml:msub><mml:mrow><mml:mi>w</mml:mi></mm l:mrow><mml:mrow><mml:mn>0</mml:mn></mml:mrow></mml:msub><mml:mi>t</m ml:mi></mml:mrow></mml:msup><mml:mi>ξ</mml:mi><mml:mrow><mml:mo>(</mml:mo><mml:mi>t</mml:mi><mml:mo>)</mml :mo></mml:mrow></mml:mrow></mml:math>16. 离散信号f(n)是指()A. n的取值是连续的,而f(n)的取值是任意的信号B. n的取值是离散的,而f(n)的取值是任意的信号C. n的取值是连续的,而f(n)的取值是连续的信号D. n的取值是连续的,而f(n)的取值是离散的信号17. 连续信号与的卷积,即()A. f(t)B. f(t-t) C.D.18. 信号的拉氏变换及收敛域为()A.B.C.D.19. 若序列f(n)的图形如图(a)所示,那么f(-n+1)的图形为图(b)中的()A.B.C.D.20. 的拉氏反变换为()A.B.C.D.21. 若周期信号 f(t)是时间 t的奇函数,则其三角形傅里叶级数展开式中只含( )。
电子科技大学14秋《信号与系统》在线作业1答案

B.
C.
D.
?
正确答案:A
5.题目及选项如下:
A.
B.
C.
D.
?
正确答案:B
6.题目及选项如下:
A.
B.
C.
D.
?
正确答案:C
7.题目及选项如下:
A.
B.
C.
D.
?
正确答案:D
8.题目及选项如下:
A.
B.
C.
D.
?
正确答案:C
9.题目及选项如下:
A.
B.
C.
D.
?
正确答案:D
10.零输入相应是()。
3.在变换域中解差分方程时,首先要对差分方程两端进行Z变换。A.错误B来自正确?正确答案:B
4. H(s)的零点和极点中仅极点决定了h(t)的函数形式。
A.错误
B.正确
?
正确答案:B
5.从信号频谱的连续性和离散性来考虑,周期信号的频谱是连续的。
A.错误
B.正确
?
正确答案:A
B.虚偶函数的傅里叶级数中不包含正弦项,只可能包含直流项和余弦项
C.实奇函数的傅里叶技术中不包含余弦项和直流项,只可能包含正弦项
D.实奇谐函数的傅里叶级数中只可能包含基波和奇次谐波的正弦、余弦项,而不包含偶次谐波项
?
正确答案:ACD
3.连续时间周期信号的频谱特点有()。
A.连续性
B.离散性
C.谐波性
A.全部自由响应
B.部分自由相应
C.部分零状态相应
D.全响应与强迫响应之差
?
正确答案:B
二,多选题
1.系统的性质有( )。
A.记忆性
北交《信号与系统》在线作业一【标准答案】

北交《信号与系统》在线作业一-0005
试卷总分:100 得分:100
一、单选题 (共 10 道试题,共 30 分)
1.欲使信号通过系统后只产生相位变化,则该系统一定是()。
A.高通滤波网络
B.带通滤波网络
C.全通网络
D.最小相移网络
答案:C
2.某信号的频谱是周期的离散谱,则对应的时域信号为()。
A.连续的周期信号
B.连续的非周期信号
C.离散的非周期信号
D.离散的周期信号
答案:D
3.如果一连续时间二阶系统的系统函数H(s)的共轭极点在虚轴上,则它的h(t)应是()。
A.指数增长信号
B.指数衰减振荡信号
C.常数
D.等幅振荡信号
答案:D
4.周期矩形脉冲序列的频谱的谱线包络线为()。
A.δ函数
B.Sa函数
C.ε函数
D.无法给出
答案:B
5.Sa[π(t-4)]δ(t-4)等于()。
A.δ(t-4)
B.sinπ(t-4)
C.1
D.0
答案:A
6.卷积δ(t)*f(t)*δ(t)的结果为()。
A.δ(t)
B.δ(2t)
C.f(t)
D.f(2t)。
信号与系统1

1.(10分)已知某LTI 系统的阶跃响应)()(t u e t g t ⋅=-,求当输入信号t e t f 2)(= )(∞<<-∞t 时系统的零状态响应)(t y f ? 解: 根据零状态线性有:)()()()('t u e t t g t h t ⋅-==-δ 所以有:t t f e t u e t t h t f t y 2*)]()([)(*)()(⋅-==-δt t t e t u e e 22*)(⋅-=-t t e e 2231-=t e 232=2. (10分)已知)(t f 的傅立叶变换为)(w F ,求下列信号的频谱函数。
(1))(1t f =)(*)(t f t f +)(t f (2))(2t f = )(at tf解: 根据傅里叶变换的时域卷积定理有:F()(*)(t f t f ) = )(2w F所以:]1)([)()()()(21+⋅=+=w F w F w F w F w F根据傅里叶变换的尺度变换特性有: F[)(at f ]=)(1aw F a 所以根据傅里叶变换的频域微分特性有: dwa w dF j a w F )(1)(2⋅=3. (10分)已知一因果线性时不变系统,其输入输出关系用下列微分方程表示,)()(2)(3)('''t x t y t y t y =++求该系统的系统函数)(s H 及冲激响应)(t h ? 解:对微分方程两端做拉氏变换有: )()(2)(3)(2s X s Y s sY s Y s =++ 所以有:231)()()(2++==s s s X s Y s H 则:)(][)(2t u e e t h t t ⋅-=--4. (10分)如下图所示电路,若激励为)(]23[)(32t u e e t e t t ⋅+=--,求响应)(2t u ,并指出暂态分量和稳态分量?解: 电路的S 域模型如右下图所示:则有:)(2221)(2s E s s s U ⋅++= 又知)3)(2(1353223)(+++=+++=s s s s s s E ,代入上式有: 312112)3)(1(13521)(2+⋅++=+++=s s s s s s U 则:)(]212[)(32t u e e t u t t ⋅-=--暂态分量为:)(]212[3t u e e t t ⋅---稳态分量为:05. (10分)某离散系统如下图所示,求该系统的系统函数)(z H 及单位序列响应)(n h ?解: 由系统模拟框图可得:)(5.0)(5.1)()(21z Y z z Y z z F z Y ---+= 从而有:E(s))5.05.15.05.111)()()(2221+-=+-==--z z z z z z F z Y z H 对)(z H 求逆Z 变换:21125.05.1)(22---=+-=z zz z z z z z H所以:)(])21(2[)(n u n h n ⋅-=1.(10分)如下图所示,该系统由多个子系统组成,各子系统的冲激响应分别为:)()(),1()(),()(321t t h t t h t u t h δδ-=-==,求:(1) 复合系统的冲激响应h (t );(2) 若)()(t u t f =,求复合系统的零状态响应)(t y ?解: (1)根据复合系统的特性有:)(*)(*)()()(3211t h t h t h t h t h += )]([*)1(*)()(t t t u t u δδ--+= )1()(--=t u t u(2))(*)]1()([)(*)()(t u t u t u t h t f t y --==)1()1()(---=t u t t tu2.(10分)若描述系统的微分方程为)(17)(7)(6)(5)(22t f dt t df t y dt t dy dtt y d +=++,且)(t f =)(t u e t -,2)0(1)0('==--y y ,,求系统的零输入响应)(t y x 和零状态响应)(t y f ?解: 系统特征方程为:0652=++λλ则特征根为λ1 = -2,λ2 = -3 所以t t x e A e A t y 3221)(--+= 0≥t将2)0(1)0('==--y y ,代入上式有:4521-==A A ,t t x e e t y 3245)(---= 0≥t对微分方程两端做拉氏变换(起始状态为0)有:)()177()(6)(5)(2s F s s Y s sY s Y s f f f ⋅+=++ 所以3223151165)177()(2+-+-+=+⋅+++=s s s s s s s s Y ft t t f e e e t y 32235)(-----= 0≥t3.(10分)已知某连续系统的频率响应特性为⎩⎨⎧<>-=0,0,)(ωωω j j j H ,计算系统对激励)cos()(0t t f ω=的零状态响应y (t )?解:)]()([)()()()(00w w w w j H jw F j H j Y -++⋅=⋅=δδπωωω )]()([00w w j w w j --+=δδπ )]()([00w w w w j --+=δδπ 所以:)sin()(0t w t y =4.(10分)下图为某线性时不变连续系统的模拟框图,求: (1)系统函数)(s H ; (2)写出系统的微分方程?解: 由系统模拟框图可得:)()(3)(2)(2s Y s s sY s Y s F =--整理得:)()()23(2s F s Y s s =++ 所以231)()()(2++==s s s F s Y s H 系统的微分方程为:)()(2)(3)(22t f t y dt t dy dtt y d =++1. (10分)一线性非时变因果连续时间系统的微分方程为)('t y +2)(t y =)(t f ,当其输入信号为)(t f =)(t u -)2(-t u ,用时域分析法求系统的零状态响应)(t y ?解: 由系统微分方程得系统函数为:21)(+=s s H对)(s H 求拉氏逆变换有:)()(2t u e t h t ⋅=- 所以有:)(*)]2()([)(*)()(2t u e t u t u t h t f t y t ---== )(*)2()(*)(22t u e t u t u e t u t t ----=)2(21)(21)2(22-⋅--⋅-=---t u e t u e t t 2.(10分)求下图所示信号的频谱函数)(w F ? 解: 对信号)(t f 求两次导数有: )2(2)1(4)(2)(''-+--=t t t t f δδδ对)(''t f 作傅里叶变换有: F[)(''t f ] = jw jw e e 2242--+- 根据傅里叶变换的时域微分特性有:F[)(''t f ] =)()(2w F jw所以:22)(242)(jw e e w F jwjw --+-=3.(10分)已知连续系统)(s H 的零极分布图如下图所示,且H(∞)=2,求系统函数)(s H 及系统的单位冲激响应)(t h ?解: 由)(s H 的零极分布图可得:)3)(1()2()(++-=s s s ks s H ,又知H(∞)=2,则2=k所以 )3)(1()2(2)(++-=s s s s s H对)(s H 作拉氏逆变换:315132)3)(1(6122)3)(1()2(2)(+-++=+++-=++-=s s s s s s s s s s H 从而 )(]153[)(2)(3t u e e t t h t t ⋅-+=--δ4.(10分)已知一线性非时变因果连续时间系统的微分方程为 )(t y ''+7)('t y +10)(t y =)(2't f +)(3t f求系统函数)(s H ,单位冲激响应)(t h ,并判断系统的稳定性。
奥鹏2020年6月福师《信号与系统》在线作业一_3.doc

1.信号f(t)=Sa(100t)的最低抽样率等于( )。
A.100/πB.π/100C.100D.1/100【参考答案】: A2.下列描述正确的是()。
A.信号f(t)反折,则其相应的频谱F(jω)也反折B.信号f(t)在时间轴上扩展2倍,则其相应的频谱在ω轴上也扩展2倍C.信号f(t)在时间轴上平移2,则其相应的频谱在ω轴上也平移2D.信号f(t)为时限信号,则其相应的频谱也是频带有限的【参考答案】: A3.函数f(s)=1/s+1/(s+1)逆变换的初值等于( )。
A.0B.1C.2D.3【参考答案】: C4.单位序列响应h(n)=2u(n)的系统是( )系统。
A.因果及稳定B.非因果及稳定C.因果及非稳定D.非因果及非稳定【参考答案】: C5.单位序列响应h(n)=u(n)/n的系统是( )系统。
A.因果及稳定B.非因果及稳定C.因果及非稳定D.非因果及非稳定【参考答案】: C6.在一个周期内绝对可积是周期信号频谱存在的( )条件。
A.充分B.必要C.充要D.以上答案都不正确【参考答案】: B7.一个矩形脉冲信号,当脉冲幅度提高一倍,脉冲宽度扩大一倍,则其频带宽度较原来频带宽度()。
A.缩小一倍B.扩大一倍C.不变D.不能确定【参考答案】: A8.函数f(s)=(s+6)/[(s+2)*(s+5)]逆变换的初值等于( )。
A.1B.0C.6D.2【参考答案】: A9.信号f(t)=Asin(500πt)cos(2000πt)的归一化功率等于( )。
A.A*A/2B.A*A/4C.1/4D.以上答案都不正确【参考答案】: B10.零输入响应是( )。
A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差【参考答案】: B11.信号f(t)=Acos(200πt)cos(2000πt)的归一化功率等于( )。
A.A*A/2B.A*A/4C.1/4D.以上答案都不正确【参考答案】: B12.单位序列响应h(n)是指离散系统的激励为( ) 时,系统的零状态响应。
信号与系统第一章习题

(2)
1 2,为时变系统
X
图解说明
xt
1
x t
经系统 1 2
O 1t
O
右移1
2t
x t 1 12 O1
第 17 页
3t
xt
xt 1
1
右移1 1
经系统
x t 1 1 2
O 1t
O 1 2t
O
2
4t
X
例1-7
第 18
页
系统的输入为x(t),输出为y(t),系统关系如下,判断系统是否
是因果系统。
X
例1-6
第 16
页
判断系统 yt x t 是否为线性时不变系统?
2
此系统的作用是展宽输入系统的信号,一切变换都是 对t而言
xt
经系统, t t 2
x t 2
时移, t t0
x t t0 2
(1)
xt 时移, t t0
xt t0
经系统, t t 2
x
t 2
t0
X
例1-5
第 14
页
判断方程 yt x2t 描述的系统是否为线性系统?
在检验一个系统的线性时,重要的是要牢记:系统必须 同时满足可加性和齐次性。
设x1t, x2t为两个输入信号
先经系统
x1t y1t x12 t
x2 t y2 t x22 t
再线性运算
ay1t by2t ax12t bx22t
2
1
O 1 2 3t
d f 6 2t
dt
1
(1) (1)
3
O 12
t
(2)
对信号的波形进行微分变换时, 应注意在函数的跳变点处会出 现冲激信号。
信号与系统答案西北工业大学段哲民信号与系统1_3章答案
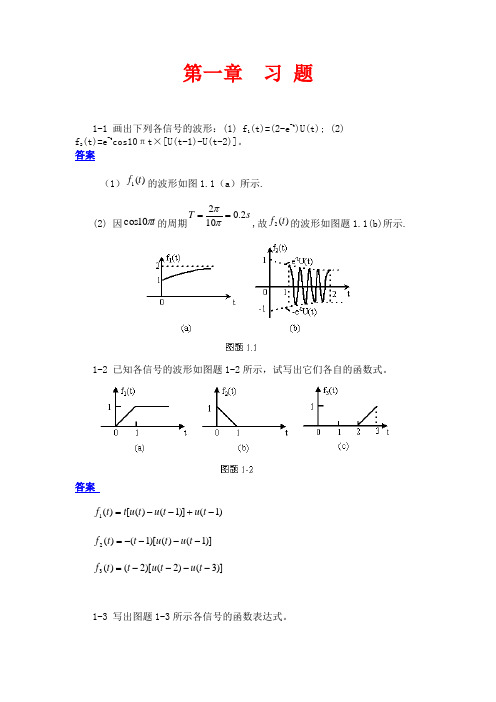
第一章 习 题1-1 画出下列各信号的波形:(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。
答案(1))(1t f 的波形如图1.1(a )所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示,试写出它们各自的函数式。
答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。
答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形:(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。
答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号,若是周期信号,求其周期T 。
信号与系统实验一、二
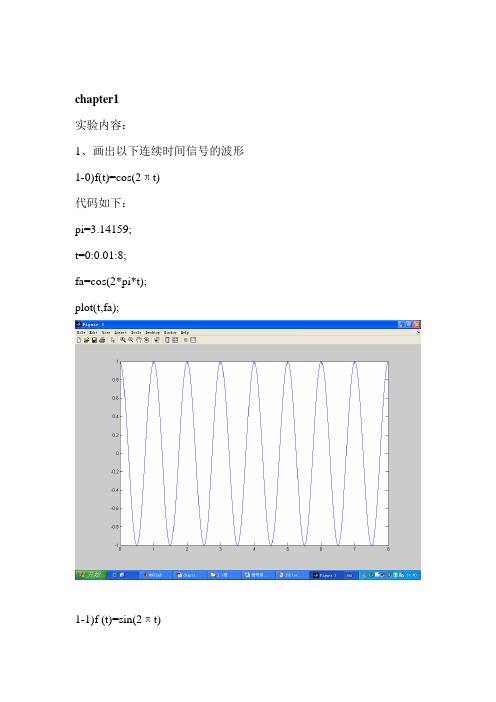
chapter1实验内容:1、画出以下连续时间信号的波形1-0)f(t)=cos(2πt)代码如下:pi=3.14159;t=0:0.01:8;fa=cos(2*pi*t);plot(t,fa);1-1)f (t)=sin(2πt)代码如下:pi=3.14159;t=0:0.01:8;fa=sin(2*t*pi); plot(t,fa);2-0)f (t)=Sa(t/π) 代码如下:pi=3.14159;t=0:0.01:8;fa=sinc(t/pi); plot(t,fa);3-0)f (t)=2[u(t 3)- u(t 5)] 代码如下:t=-1:0.01:10;ft=2*((t>=3)-(t>=5)); plot(t,ft);axis([-1,10,0,3]);4-1)f (t)=e t 代码如下:t=0:0.01:10; ft=exp(t);plot(t,ft);4-2)f (t)=e-t u(t) 代码如下:t=0:0.01:10;f1=(t>=0);f2=exp(-t);plot(t,f1.*f2);5-0)f(t)=2e j(π/4)t,画出实部、虚部、模和相角的波形代码如下:t=0:0.01:10;ft=2*exp(j*(pi/4)*t);h=real(ft); %实部g=imag(ft); %虚部r=abs(ft); %模a=angle(ft); %相角subplot(2,2,1),plot(t,h),title('实部') subplot(2,2,3),plot(t,g),title('虚部') subplot(2,2,2),plot(t,r),title('模')subplot(2,2,4),plot(t,a),title('相角')7)f (t) = u(t)代码如下:t=-1:0.01:5ft=(t>=0);plot(t,ft);axis([-1,5,0,1.5]);8)f (t) =δ(t)代码如下:t=-1:0.01:5;ft=(t>=0)-(t>=0.1); plot(t,ft);axis([-1,1,0,1.1]);9)f9为周期矩形信号,其幅度从-1 到1,占空比为75% 代码如下:pi=3.14159;t=-10:0.01/pi:10;ft=square(t,75);plot(t,ft);2、信号本身运算画出f1(t)为宽度是4,高为1,斜度为0.5 的三角脉冲,然后画出f1(-t),f1(2t),f1(2-2t)的波形以及f1(t)的微分和积分波形。
信号与系统第一次作业

信号与系统第⼀次作业信号与系统上半年作业11、什么是离散时间信号?周期信号?答:如果信号仅在⼀些离散的点具有确定的数值,则称其为离散信号。
周期信号:瞬时幅值随时间重复变化的信号称为周期信号。
2、什么是模拟信号?数字信号?答:模拟信号:模拟信号是指信息参数在给定范围内表现为连续的信号。
数字信号:数字信号指幅度的取值是离散的,幅值表⽰被限制在有限个数值之内。
3、举例说明什么是能量信号与功率信号?给出数学模型。
答:能量信号:信号在时间区间(-∞,∞)内的能量为有限值,⽽在时间区间(-∞,∞)内的平均功率p=0,这样的信号称为能量信号。
功率信号:信号在时间区间(-∞,∞)内的能量为∞,但在⼀个周期(-T/2,T/2)内的平均功率为有限值,这样的信号称为功率信号。
4、试判断下列信号是否为周期信号。
若是,确定其周期。
解:(1)f 1(t )中两个⼦信号sin3t 和cos π t 的周期分别为它们不存在公倍数,是⾮周期信号,或者说周期为∞。
(2) f 2(t )中三个⼦信号的周期分别为它们的最⼩公倍数是1740π,所以f 2(t )是周期为1740π的周期信号。
ππ5829123==T ,815151622ππ==T ,342321ππ==T dtt f E dt t f P ??-∞→-∞→??222222)(lim )(1lim τττττττs 321π=T s22=T5、给出单位阶跃信号的数学描述,图⽰,和性质。
单位阶跃信号(跳变信号,t=0时发⽣跳变)性质:切除性单位阶跃信号U (t )具有使任意⽆时限信号f (t )变为因果信号的功能,即将f (t )乘以U (t ) ,所得f (t )U (t )即为因果信号。
6、给出单位门信号的数学描述,图⽰,和性质。
性质:截取性单位门信号G τ(t )具有使任意⽆时限信号f (t )变为时限信号的功能,即将f (t )乘以G τ(t ) ,所得f (t )G τ(t )即为时限信号><=0100)(t t t U (0)0U -=><==0)(00)()()(t t f t t U t f t y )2()2()(τττ--+=t U t U t G ,1τ门宽为门⾼为7、给出单位冲击信号的数学描述,图⽰,和主要性质。
奥鹏地大21年春季 《信号与系统》在线作业一.doc

1.f(k)=sin3k是()。
A.周期信号B.非周期信号C.不能表示信号D.以上都不对【参考答案】: B2.以线性常系数微分方程表示的连续时间系统的自由响应取决于()A.系统函数极点B.系统函数零点C.激励极点D.激励零点【参考答案】: A3.某系统的输入为f(t),输出为y(t),且y(t)=3f(t),则该系统是()A.线性非时变系统B.线性时变系统C.非线性非时变系统D.非线性时变系统【参考答案】: B4.信号f(4-3t)是()A.f(3t)右移4B.f(3t)左移4/3C.f(-3t)左移4D.f(-3t)右移4/3【参考答案】: D5.离散线性时不变系统的单位序列响应h(n)为()A.输入为单位冲激信号的零状态响应B.输入为单位阶跃信号的响应C.系统的自由响应D.系统的强迫响应【参考答案】: A6.函数f(s)=(s+6)/[(s+2)*(s+5)]逆变换的终值等于( )。
A.1B.0C.6D.2【参考答案】: B7.信号f(t)与δ(t)的卷积等于( )。
A.f(t)B.δ(t)C.f(t)δ(t)D.0【参考答案】: A8.信号的时宽与频宽之间的关系是()。
A.正比关系B.反比关系C.平方关系D.没有关系【参考答案】: B9.在一个周期内绝对可积是周期信号频谱存在的( )条件。
A.充分B.必要C.充要D.以上都不对【参考答案】: B10.某系统的系统函数为H(s),若同时存在频响函数H(jw),则该系统必须满足条件()。
A.时不变系统B.因果系统C.稳定系统D.线性系统【参考答案】: C11.模拟离散系统的三种基本部件是什么()。
A.加法器B.乘法器C.积分器D.减法器【参考答案】: ABC12.下列系统中,()不是可逆系统。
A.y[n]=nx[n]B.y[n]=x[n]x[n-1]C.y(t)=x(t-4)D.y(t)=cos[x(t) ]【参考答案】: ABD13.时域是实偶函数,其傅氏变换不可能是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统作业1
1、什么是离散时间信号?周期信号?
答:如果信号仅在一些离散的点具有确定的数值,则称其为离散信号。
周期信号:瞬时幅值随时间重复变化的信号称为周期信号。
2、什么是模拟信号?数字信号?
答:模拟信号:模拟信号是指信息参数在给定范围内表现为连续的信号。
数字信号:数字信号指幅度的取值是离散的,幅值表示被限制在有限个
数值之内。
3、举例说明什么是能量信号与功率信号?给出数学模型。
答:能量信号:信号在时间区间(-∞,∞)内的能量为有限值,而在时间区间
(-∞,∞)内的平均功率p=0,这样的信号称为能量信号。
功率信号:信号在时间区间(-∞,∞)内的能量为∞,但在一个周期(-T/2,
T/2)内的平均功率为有限值,这样的信号称为功率信号。
4、试判断下列信号是否为周期信号。
若是,确定其周期。
解:(1)f 1(t )中两个子信号sin3t 和cos π t 的周期分别为
它们不存在公倍数,是非周期信号,或者说周期为∞。
(2) f 2(t )中三个子信号的周期分别为
它们的最小公倍数是1740π,所以f 2(t )是周期为1740π 的周期信号。
5、给出单位阶跃信号的数学描述,图示,和性质。
单位阶跃信号(跳变信号,t=0时发生跳变)
π
π5829
123==T ,815151622ππ==T ,342321ππ==T )291sin()1516cos()23sin(
)()2(cos 3sin )()1(21t C t B t A t f t t t f ++=+=πdt
t f E dt t f P ⎰⎰-
∞→-∞→∆∆222222)(lim )(1
lim τττττττ
s 321π
=T s
22=T ⎩⎨
⎧><=0
100)(t t t U
性质:切除性
单位阶跃信号U (t )具有使任意无时限信号f (t )变为因果信号的功能,即将f (t )乘以U (t ) ,所得f (t )U (t )即为因果信号。
6、给出单位门信号的数学描述,图示,和性质。
性质:截取性
单位门信号G τ(t )具有使任意无时限信号f (t )变为时限信号的功能,即将f (t )乘以G τ(t ) ,所得f (t )G τ(t )即为时限信号
7、给出单位冲击信号的数学描述,图示,和主要性质。
(0)0U -=⎩⎨⎧><==0)(0
0)()()(t t f t t U t f t y ⎪⎩⎪⎨⎧<
<-=其余0221)(τττt t G )
2
()2()(τ
ττ--+=t U t U t G ,1
τ门宽为门高为
8、求下列表达式值
0()lim ()lim ()1
t dt f t dt f t dt ττδ∞
∞∞
-∞
-∞-∞
→→===⎰
⎰⎰(1)定义
⎩⎨
⎧≠=∞=0
00)(t t t δ且面积
1
)()(00==⎰⎰
+
-
∞
∞
-dt t dt t δδ001
()lim ()lim ()
t f t G t τττδτ
→→==3
2
(1)(3)(2) (2)(23)(12)t t dt t t t dt δδ∞
∞
-∞
-∞
+++-⎰⎰且
9、画出 f (t )=sgn(cos2πt )的波形。
10、 给出抽样信号的数学描述,图示,和特点。
答:抽样信号是指利用抽样序列s(t)从连续信号f(t).中“抽取”一系列离散样值而得的离散信号。
特点: 1.
3
3
311
(1) (3)(2)(3)()(03)() 1.5
22
t t dt t t dt t dt δδδ∞
∞
∞-∞-∞-∞+=+⨯=+⨯=⎰⎰⎰2
22
221(2) (23)(12)(23)[2()]2111 =(23)[2()](23)()222111117 =(23)()22228
t t t dt t t t dt
t t t dt t t t dt
t dt δδδδδ∞
∞
-∞-∞∞∞-∞-∞∞-∞++-=++--++-=++⨯-+⨯+⨯-=
⎰⎰⎰⎰⎰()⎩⎨
⎧<->==0
cos2 10cos2 1)2sgn(cos )(t t t t f πππ)( sin )(∞<<-∞=t t
t t f 偶函数
)()(t Sa t Sa =-
2.
3.
4
5.
11、已知f (1-2t)如图所示,试画出f (t)的波形。
折叠→展缩→时移
1
)(
lim
,1
)(
,0
=
=
=
→
t
Sa
t
Sa
t
t
即
Λ,3,2,1
,
,0
)(=
±
=
=n
n
t
t
Saπ
π
π
=
=⎰
⎰∞∞-
∞
dt
t
t
dt
t
t sin
,
2
sin
)(
lim=
±∞
→
t
Sa
t
)
2
1(t
f-)2
1(t
f+
−
−→
−折叠
)
1(
)
2
1
2
1(
1t
f
t
f+
=
⨯
+
−
−→
−倍
展宽
12、 什么是线性系统?用公式说明。
线性系统:能同时满足比例性与叠加性的系统。
13、 若T [f (t )]=af (t )+b =y (t ),问该系统是否为线性系统。
解:
而
显然
故系统为非线性系统。
14、 什么是系统的时不变特性?
)
()11(1
t f t f =-+−−→−右时移)()()()()()( ),()(221122112211t y k t y k t f k t f k t y t f t y t f +→+→→b
t f k t f k a t f k t f k T ++=+)]()([)]()([22112211)]
([)]([)()(22112211t f T k t f T k t y k t y k +=+2
12
21122
11)]()([])([])([bk bk t f k t f k a b t af k b t af k +++=+++=)
()()]()([22112211t y k t y k t f k t f k T +≠+
15、什么是冲激响应与阶跃响应?
答:当激励为单位冲激函数时,电路的零状态响应称为单位冲激响应,简称冲激响应。
当激励为单位阶跃函数时,电路的零状态响应称为单位阶跃响应,简称阶跃响应。
16、给出卷积积分公式。
