第5讲 差分方程模型
差分方程模型的基本概念

预测经济趋势
通过建立差分方程模型,可以对 未来的经济趋势进行预测,帮助 决策者制定相应的经济政策。
评估经济政策
差分方程模型可以用来评估不同 经济政策的实施效果,为政策制 定者提供参考依据。
在物理学中的应用
描述振动现象
差分方程模型可以用来描述物体的振动规律,如弹簧振荡、单摆 等。
预Байду номын сангаас波动传播
在声学和波动理论中,差分方程模型可以用来描述波动传播的规 律,如声波、电磁波等。
可以采用动态模型来反映数据的变化趋势,减少时间滞后的影 响。
可以利用大数据技术来处理大规模的数据集,提高模型的预测 精度和稳定性。
可以尝试优化参数估计方法,例如采用全局优化算法或贝叶斯 推断等方法,以提高参数估计的准确性和稳定性。
THANKS FOR WATCHING
感谢您的观看
确定差分关系
根据时间序列数据的特性,确定合适的差分关系,以描述数据的变化规律。差分关系通常表示为变量在不同时间 点的变化量或变化率。
建立差分方程模型
根据变量和参数建立模型
根据确定的变量和参数,建立差分方程模型,以描述变量的变化规律。
验证模型的适用性
建立差分方程模型后,需要验证模型的适用性,确保模型能够准确描述实际问题的变化规律。
Python
使用Python的数值计算库,如NumPy和 SciPy,求解差分方程。
Mathematica
使用Mathematica的符号计算和数值计算功 能求解差分方程。
04 差分方程模型的应用
在经济学中的应用
描述经济周期
差分方程模型可以用来描述经济 活动的周期性变化,如经济增长、 通货膨胀、就业率等的时间序列 数据。
5第五讲 典型模型方程-波动方程的差分格式

得到 高阶精度的Runge-Kutta方法,其步骤相同。如四阶精度的Runge-Kutta方法
若采用二阶空间差分格式,则其 提高时间导数的差分精度。
, Runge-Kutta方法仅
Comments
• 高阶精度的差分格式需要更多的计算资源和推
导计算的复杂性。 • 一般情况下,二阶精度的差分格式能提供足够 的精度。 • 对于一维波动方程,二阶精度的显格式如 Lax-Wendroff格式在计算资源消耗少的情 况下能给出很好的数值解。隐格式在相对较小 的时间步长情况下,计算中可能导致一些不稳 定解,且需要存储中间时间层上的值和求解方 程组,消耗较多的计算资源,不一定是最优的 原则。
为了使其为稳定差分方法,修正如下
:
因此,此差分方程不一定总相容于PDE,当 则相容,为条件相容。
t 0, x 0 x
t 0, x 0
2
t
0
?
时,v保持为常数,
Lax差分方法的耗散性和色散性分析
当v不为1时,耗散性很强。
理解下图???
Euler差分方法(如下)不稳定
其辐角误差为:
因此相对相位误差(relative phase shift error)(见图4.3)为:
因此,当
1 e 1 e
leading phase error lagging phase error
solution : u ( x, t ) sin[6 ( x ct )]
(4-2)
泰勒展开:
n n 1 u u 在 j 处展开, j 在 u n j 处展开,
utt j 在 utt nj 处展开,相减后 泰勒展开:
n 1
(4.57)式两式相减,并整理得:
(完整版)差分方程模型(讲义)

差分方程模型一. 引言数学模型按照离散的方法和连续的方法,可以分为离散模型和连续模型。
1. 确定性连续模型1) 微分法建模(静态优化模型),如森林救火模型、血管分支模型、最优价格模型。
2) 微分方程建模(动态模型),如传染病模型、人口控制与预测模型、经济增长模型。
3) 稳定性方法建模(平衡与稳定状态模型),如军备竞赛模型、种群的互相竞争模型、种群的互相依存模型、种群弱肉强食模型。
4) 变分法建模(动态优化模型),如生产计划的制定模型、国民收入的增长模型、渔业资源的开发模型。
2. 确定性离散模型1) 逻辑方法建模,如效益的合理分配模型、价格的指数模型。
2) 层次分析法建模,如旅游景点的选择模型、科研成果的综合评价模型。
3)图的方法建模,如循环比赛的名次模型、红绿灯的调节模型、化学制品的存放模型。
4)差分方程建模,如市场经济中的蛛网模型、交通网络控制模型、借贷模型、养老基金设置模型、人口的预测与控制模型、生物种群的数量模型。
随着科学技术的发展,人们将愈来愈多的遇到离散动态系统的问题,差分方程就是建立离散动态系统数学模型的有效方法。
在一般情况下,动态连续模型用微分方程方法建立,与此相适应,当时间变量离散化以后,可以用差分方程建立动态离散模型。
有些实际问题既可以建立连续模型,又可建立离散模型,究竟采用那种模型应视建模的目的而定。
例如,人口模型既可建立连续模型(其中有马尔萨斯模型Malthus、洛杰斯蒂克Logistic模型),又可建立人口差分方程模型。
这里讲讲差分方程在建立离散动态系统数学模型的的具体应用。
二. 差分方程简介在实际中,许多问题所研究的变量都是离散的形式,所建立的数学模型也是离散的,譬如,像政治、经济和社会等领域中的实际问题。
有些时候,即使所建立的数学模型是连续形式,例如像常见的微分方程模型、积分方程模型等。
但是,往往都需要用计算机求数值解。
这就需要将连续变量在一定的条件下进行离散化,从而将连续型模型转化为离散型模型。
差分方程模型

差分方程模型
周家全
对连续型变化的问题而言, 常常可建立微分方程模型. 而对离散状态转移的问题, 则可建立差分方程模型. 差分方 程与常微分方程有很多类似的性质和结论.首先引入差分的 概念.
1 差分定义及其性质
定义 设函数 y = y(x) 在等距节点 xi = x0 + ih ( i = 0,1, , n)
对于一般的差分方程 xn+2 + axn+1 + bxn = f 来讲, 其平衡 点的稳定性问题可以同样给出. 二阶方程的上述结果可以推
广到 n 阶线性差分方程, 即稳定平衡点的条件是特征根: n
次代数方程的根 λi (i = 1, 2, , n) 均有| λi |< 1.
4 经济学中的蛛网模型
1. 提出问题 在自由竞争的社会中, 很多领域会出现循环波动的现象. 在经济领域中, 可以从自由集市上某种商品的价格变化看到 如下现象:在某一时期, 商品的上市量大于需求, 引起价格 下跌, 生产者觉得该商品无利可图, 转而经营其它商品;一
解
Δf (0) = f (0.5) − f (0) = 0.75 ,
-2-
洛阳理工学院数学建模竞赛培训教案
Δf (0.5) = f (1) − f (0.5) = 1.25
周家全
Δ2 f (0)= Δ(Δf (0)) = Δf (0.5) − Δf (0) = 1.25 − 0.75 = 0.5
计算较多点的差分可按差分表进行, 容易看出表中每一 个需要计算的差分值分别等于其左侧的数减去左上侧的 数.每个点 xi 处的各阶差分位于与主对角线平行的斜线上.
(I) 先求解对应的特征方程
a0λn + a1λn−1 + + a0 = 0
第五章 差分方程模型

第五章 差分方程模型在第四章中,我们利用微分方程方法研究了一些连续变化的变量。
如果将变量离散化,即可得到相应的差分方程模型,为了方便不熟悉差分方程的读者,先对本章用到的差分方程的知识作一简略介绍。
5.1差分方程简介一、差分方程及其通解以t 表示时间,规定t 只取非负整数。
0=t 表示第一周期初,1=t 表示第二周期初等。
记t y 为变量y 在时刻t 时的取值,则称t t t y y y -=∆+1为的一阶差分,称t t t t t t t y y y y y y y +-=∆-∆=∆∆=∆+++12122)(为y t 的二阶差分。
类似地,可以定义y t 的n 阶差分t n y ∆。
由t 、t y 及t y 的差分给出的方程称为t y 差分方程,其中含t y 的最高阶差分的阶数称为该差分方程的阶。
差分方程也可以写成不显含差分的形式。
例如,二阶差分方程02=+∆+∆t t t y y y 也可改写成012=+-++t t t y y y 。
满足差分方程的序列t y 称为此差分方程的解。
类似于微分方程情况,若解中含有的独立常数的个数等于差分方程的阶数时,则称此解为该差分方程的通解。
若解中不含任意常数,则称此解为满足某些初值条件的特解,例如,考察两阶差分方程: 02=++t t y y 易见t y t 2sin π=与t y t 2cos π=均是它的特解,而t c t c y t 2cos 2sin 21ππ+=则为它的通解,其中1c ,2c 为两个任意常数。
类似于微分方程,称差分方程)()()()(110t b y t a y t a y t a t n n t n t =+++-++ (1) 为n 阶线性差分方程,当0)(≠t b 时称其为n 阶非齐次线性差分方程,而0)()()(110=+++-++t n n t n t y t a y t a y t a (2) 称为方程(1)对应的齐次线性差分方程。
差分方程模型

(1)设 k 时段商品数量为 xk ,其价格为 yk ,这里把时间 离散化为时段,一个时期相当于商品的一个生产周期。 (2)同一时段的商品价格取决于该时段商品的数量,称
yk f ( xk )
为需求函数。出于对自由经济的理解,商品的数量越多,其 价格就越低。故可以假设需求函数为一个单调递减函数。 (3) 下一时段的商品数量由上一时段的商品价格决定,
lim x x0,所以 P 若P 0 是稳定点,则应有 k k 0 点稳定的条件是
1
同理 P 0 点不稳定的条件是
1
4、模型修正
在上述模型的基础上,对供应函数进行改进。下面在决 定商品的生产数量 xk 1时,不仅考虑前一时期的价格 yk ,而 y k y k 1 x g ( ) ,在 P 且考虑了价格 yk 1 ,取 k 1 0 附近取线性近 2 似,则有
若特征方程有k重复根 i ,则方程(2)的通解为
(c1 ck t k 1 ) t cost (c1 ck t k 1 ) t sint
3.求非齐次方程的一个特解yt ,若 yt 为齐次方程的通 解,则非齐次方程的通解为 yt yt 。 对特殊形式的特解 b(t )可以使用待定系数法求非齐次方 qk ( t ) 程的特解。例如 b(t ) bt pk (t ), pk (t ) 为t的k次多项式时可以证 t b 明:若b不是特征根,则方程(1)有形如 qk (t ) 的特解, 也是t的k次多项式;若b是r重特征根,则方程(1)有形如 bt t r 1qk (t ) 的特解。进而可以用待定系数法求出 qk (t ) ,从 而得到方程(1)的一个特解。
图1和图2中的折线 P1 P2 , P2 P3 ,形如蛛网,故把这种 模型称为蛛网模型。在进行市场经济分析中,f 取 决于消费者对某种商品的需求程度及其消费水平, g 取决于生产者的生产、管理等能力。 当已知需求函数和供应函数之后,可以根据 f 和 g 的性质判断平衡点 P0 的稳定性。当 | x1 x0 | P0 的稳定性取决于 f 和 g 在点 P0 的斜率, 较小时, 即当
数学模型(差分方程)

定义为
X ( z ) Z [ x(k )] x(k ) z k
k 0 k
其中z是复变量,因此级数 x(k ) z 的收敛域为某个圆的外部。
k 0
X ( z)
的Z反变换记作 x(k ) Z 1[ X ( z)]
(k )
1.几个常用离散函数的变换
一部分为当月新生的,而由题设知当月新生的兔子对数等于上上月
兔子对数,所以
h(n) h(n 1) h(n 2), n 3 h(1) h(2) 1
一、常系数线性齐次差分方程的求解方法-解析法 形如
h(n) a1h(n 1) a2h(n 2) ak h(n k ) 0 (n k , k 1,) (1)
h(n) h(n 1) 3h(n 2) 5h(n 3) 2h(n 4) 0 ( n 4,5, )
的特解 . 解:该差分方程对应的特征方程为
x 4 x3 3x 2 5 x 2 0
x 其根为:1 x2 x3 1, x4 2 ,所以
令l k N
特别地 Z[ x(k 1)] z[ X ( z) X (0)] 证 : Z[ x(k N )] x(k N ) z
k 0 N
l l 0
k
x(l ) z
l N
l N
z
N
=z [ x(l ) z x(l ) z l ] z N [ X ( z ) x(k ) z k ]
差分方程的通解为:
t
mi
重根,则该
h(n) h1 (n) h2 (n) ht (n) hi (n)
差分方程模型PPT课件

回到全国竞赛题。这里提出了新的问题: (1)潜伏期病人如何描述? (2)死亡病人在模型中的描述。 (3)需要考虑人口的迁移影响,如何描述? (4)如何控制疾病的蔓延?
问题的图示
b O
a
d
d
利用简单的几何关系即得到 yk1 f ( yk ), y1 b
例2:按年龄分组的种群增长模型。
问题考虑两个要点:增长和人口分布 人口分布:对于连续问题,可以利用分布函数和 密度函数描绘。
我们也可以利用离散的方法描述人口分布。把t时
刻人口从小到大分为n组,第k 组人数xk(t),则离 散人口分布可以利用向量
试从中国的实际情况和人口增长的上述特点出发, 参考附录2中的相关数据(也可以搜索相关文献和 补充新的数据),建立中国人口增长的数学模型, 并由此对中国人口增长的中短期和长期趋势做出 预测;特别要指出你们模型中的优点与不足之处。
附录1 《国家人口发展战略研究报告》 附录2 人口数据(《中国人口统计年鉴》中的部 分数据)及其说明
差分方程建模:设第k天病人所占比例为i(k),健 康人数量为s(k),则第k天病人数量变化为
Ni(k 1) Ni(k) s(k)Ni(k) Ni(k)
第k天健康人数量变化为
Ns(k 1) Ns(k) s(k)Ni(k)
把两个式子化简即得到差分方程组。
差分方程和微分方程的建模过程没有差异,差别 在于:变化率和的意义不同。
一阶线性差分方程组的稳定性: 设一阶线性差分方程组的解为{Xk}, 而受扰动解为 {Yk}。记扰动误差为
k X k Yk 则扰动误差满足
k1 A k
对任意初始扰动0,k0的充分必要条件为
( A) 1
这就是差分方程的稳定性条件。
差分方程模型

问题:
若k n,则
y C1 y1 C2 y2 Ck yk 一定是通解吗?
定理7:如果
y1 (x),y2 (x), ,yn (x) 是
方程(1)的n个线性无关的特解, 那么
y C1 y1 C2 y2 Cn yn 就是方程(1)的通解.
注:由差分的定义及性质可知,差分方程的 不同定义形式之间可以相互转换。 如y x 5 4 y x 3 3 y x 2 2 0是三阶差分方程;
y x y x 1 0,虽然含有三阶差分,
3
但实际上是二阶差分方 程,
由于该方程可以化为 y x 3 3 y x 2 3 y x 1 1 0因此它是二阶差分方程 ,
nx ( n1)
(公式)
2.差分的四则运算法则
(1)(Cy x ) Cy x (C为常数)
(2)( y x z x ) y x z x
3 yx z x yx1z x z x yx yx z x z x1yx
y x z x y x y x z x z x 1y x y x 1z x 4 z z x z x 1 z x z x 1 x
差分方程及差分方程模型
一、差分的概念及性质 二、差分方程的概念 三、线性差分方程解的结构
四、一阶常系数线性差分方程
五、差分方程模型
一、差分的概念及性质
1.差分的定义
设 函 数 f ( x ).当x取 非 负 整 数 时 , y 函数值可以排成一个列 : 数 f (0),f (1), ,f ( x ),f ( x 1), 将之简记为 y 0,y1,y 2, ,y x,y x 1 , 称 函 数 的 改 变 量x 1 y x 为 函 数 的 差 分 , y y 也 称 为 一 阶 差 分 , 记 Δ y x y x 1 y x . 为
差分方程模型

设特解为 an D 代入 D 0.5D 0.1 得 D 0.2 , 于是所求通解 an c(0.5) n 0.2 例3 (养老金) 解: 齐次特征方程 设特解 an D
an1 1.01an 1000
1.01 0,
* an c(1.01) n.
代入原方程得 D 100000
例 4 求非齐次差分方程
* 对应齐次方程的通解为 an c1 2n c2 n 2n
的通解
f (n) 2 中, 2 是2 重根, 设特解为
n
an A n 2 2 n
n 2 n1
代入
得 A 1 2 方法2 (化齐) :
故通解为 an c1 2 c2 n 2 n 2
Fn Fn 1 Fn 2 F1 F2 1
解:差分方程的特征方程为 x 2 x 1 0 特征根
x1
n
1 5 1 5 , x2 2 2
n
1 5 1 5 Fn c1 c2 2 2
n
2(an1 4an2 4an3 ) 2 2n1 相减得 an 6an1 12an2 8an3 0 特征方程 3 62 12 8 0 特征根 2 为三重根, 通解为:
an 4an1 4an2 2n
an c1 2n c2 n 2n c3n 2 2n
x k b1 x k 1 b2 x k 2 bk 0
称为差分方程的特征方程,其根称为特征根。 定理1(单根)若特征方程恰有k个相异的特 x1 , x2 ,, x 征根 , k 则差分方程的通解为
an c x c x ck x
差分方程模型蛛网模型混沌理论

三、 符号说明
1.
N i (t ) —— t
时刻 i 龄鱼的数量, i 1, 2, 3,4;
k N i(0 ) ——第 k 年初 i 龄鱼的数量, i 1, 2, 3,4; 2.
N i(1k ) ——第 k 年底 i 龄鱼的数量, i 1 , 2 , 3 , 4 ;
3. r ——鱼的自然死亡率; 4. c ——4 龄鱼的平均产卵量; 5. M i —— i 龄鱼的平均重量, i 1, 2, 3,4;
对于3,4龄鱼,在第8个月末数量
2 ( r b3 ) (k ) (k 3 N 31 N 30 ) e 2 N ( k ) N ( k ) e ( r b4 ) 3 40 41
在后4个月,对于3、4龄鱼,只有死亡率起作用,因而
{
Fn Fn1 Fn2 F F2 1 1
Fn 称为fibonacci数列。
差分方程模型
对于k阶差分方程 F( n; xn, xn-1, … , xn-k ) = 0 若有xn = x (n), 满足 F(n; x(n), x(n - 1) , … , x(n -k )) = 0, 则称xn = x (n)是差分方程(4-6)的解, 包含k个任 意常数的解称为(4-6)的通解, x0, x1, … , xk-1为已 知时称为(4-6)的初始条件,通解中的任意常数都 由初始条件确定后的解称为(4-6)的特解. (4-6)
a n 2a n 1 1 an 1
例2 设第一月初有雌雄各一的一对小兔,假定两 月长成 成兔,同时(即第三月)开始每月初产雌 雄各一的一 对小兔,新增小兔也按此规律繁殖, 设共有对,试建 立关于第n月末兔子对数的差分方程。
解: 因第n月末的兔子包括两部分,一部分为上月留下 的,另一部分为当月新生的,而由题设当月生的小兔 数等于前月末的兔数。故
差分方程

第八讲 差分方程模型一、差分方程介绍规定t 只取非负整数。
记为变量在t 点的取值,则称t y y t t t y y y −=Δ+1为的一阶向前差分,简称差分,称Δ为的二阶差分。
类似地,可以定义的阶差分。
t y t t t t t y t t y y y y y y +−=Δ−Δ=ΔΔ=+++12122)(t y t y n t ny Δ由及的差分给出的方程称为的差分方程,其中含的最高阶差分的阶数称为该差分方程的阶。
差分方程也可以写成不显含差分的形式。
例如,二阶差分方程也可改写成t y t 、t y t y t y 02=+Δ+Δt t t y y y 012=+−++t t t y y y 。
满足一差分方程的序列称为差分方程的解。
类似于微分方程情况,若解中含有的独立常数的个数等于差分方程的阶数时,称此解为该差分方程的通解。
若解中不含任意常数,则称此解为满足某些初值条件的特解。
t y 称如下形式的差分方程)(110t b y a y a y a t n t n t n =+++−++L (1) 为阶常系数线性差分方程,其中是常数,n n a a a ,,,10L 00≠a 。
其对应的齐次方程为0110=+++−++t n t n t n y a y a y a L (2)容易证明,若序列与均为(2)的解,则也是方程(2)的解,其中为任意常数。
若是方程(2)的解,是方程(1)的解,则也是方程(1)的解。
)1(t y )2(t y )2(2)1(1t tt y c y c y +=21,c c )1(t y )2(t y )2()1(t t t y y y +=方程(1)可用如下的代数方法求其通解: (I )先求解对应的特征方程(3)00110=+++−a a a n nL λλ(II )根据特征根的不同情况,求齐次方程(2)的通解。
(i )若特征方程(3)有n 个互不相同的实根n λλ,,1L ,则齐次方程(2)的通解为t n n t c c λλ++L 11 (为任意常数)n c c ,,1L (ii )若λ是特征方程(3)的重根,通解中对应于k λ的项为t k k tc c λ)(11−++L ,),,1(k i c i L =为任意常数。
差分方程模型应用

金融市场预测
自回归移动平均模型(ARMA)
01
通过差分方程刻画时间序列数据的自相关和移动平均特性,用
于金融市场价格波动的预测。
自回归条件异方差模型(ARCH)
02
应用差分方程描述金融时间序列数据的波动率聚类现象,提高
波动率预测的精度。
随机波动率模型(SV)
03
将波动率视为随机过程,通过差分方程刻画其动态特性,用于
将差分方程模型应用于计算机视觉领域,如目标跟踪、人脸识别、 三维重建等。
06
差分方程求解方法及数值计 算技巧
解析法求解差分方程
迭代法
通过逐步代入的方式,求解差分方程的解, 适用于简单的一阶或二阶差分方程。
特征根法
通过求解差分方程的特征根,进而得到通解的方法 ,适用于线性常系数差分方程。
变换法
通过适当的变换,将差分方程转化为易于求 解的形式,如z变换等。
数值法求解差分方程
欧拉法
一种简单的数值求解方 法,通过逐步逼近的方 式得到差分方程的数值 解。
龙格-库塔法
一种高精度的数值求解 方法,通过多步迭代和 加权平均的方式提高求 解精度。
线性多步法
利用已知多个点的信息 来构造高阶逼近式,从 而提高求解精度和稳定 性。
编程实现和案例分析
01
Python编程实现
金融衍生品定价和风险管理。
03
差分方程模型在物理学中应 用
振动与波动现象描述
振动现象建模
差分方程模型可用于描述物体的振动现象,如弹簧振子、单摆等。通过差分方程,可以分析振动的周期性、振幅、 频率等特性。
波动现象建模
差分方程模型也可用于描述波动现象,如声波、光波等。通过差分方程,可以研究波的传播速度、波长、波幅等 参数。
差分方程模型介绍

结果分析:Xk= pXk-1 + qXk-2
∗ 以k=0时X0=M代入,递推n次可得n年后本息为
xn = (1 + r ) M
n
∗ 例2 污水处理厂每天可将处理池的污水浓度降低一个固 定比例q,问多长时间才能将污水浓度降低一半? ∗ 记第k天的污水浓度为Ck,则第k+1天的污水浓度为 Ck+1=(1q)Ck, k=0,1,2,···· 从k=0开始递推n次得
模型及其求解
∗ 记一棵植物春季产种的平均数为C,种子能活过一个冬天的 (1岁种子)比例为b,活过一个冬天没有发芽又活过一个冬天 的(2岁种子)比例仍为b,1岁种子发芽率a1,2岁种子发芽 率a2。 ∗ 设C,a1,a2固定,b是变量,考察能一直繁殖的条件 ∗ 记第k年植物数量为Xk,显然Xk与Xk-1,Xk-2有关,由Xk-1决 定的部分是 a1bCXk-1,由Xk-2决定的部分是 a2b(1-a1)bCXk-2
• 用矩阵表示
x1 (k + 1) 0.6 0.2 0.1 x1 (k ) x2 (k + 1) = 0.3 0.7 0.3 x2 ( k ) x (k + 1) 0.1 0.1 0.6 x ( k ) 3 3
λ1,2 < 1, xk → 0(k → ∞)
λ 1, 2 > 1, x k → ∞ ( k → ∞ )
第三章_差分方程模型

第三章 差分方程模型§1、 差分方程设有未知序列{}k y ,称0),,,;(1=++n k k k y y y k F (1)为n 阶差分方程。
若有)(k y y k =,满足0))(,),1(),(;(=++n k y k y k y k F则称)(k y y k =是差分方程(1)的解,包含n 个任意常数的解称为(1)的通解, 当110,,,-n y y y 为已知时,称其为(1)的初始条件,通解中的任意常数都由初始条件确定后的解称为(1)的特解。
[例1] 设第一月初有雌雄各一的一对小兔,假定两月后长成成兔,同时即第三月开始每月初产雌雄各一的一对小兔,新增小兔也按此规律繁殖。
设第k 月末共有k y 对兔子,试建立关于k y 的差分方程。
[解] 因为第2+k 月末的兔子包括两部分,一部分为上月留下的,另一部分为当月新生的,而由题设当月生的小兔数等于前月末的兔数,所以有⎩⎨⎧==+=++1,01012y y y y y k k k 这是著名的裴波那契数列。
[例2] 汉诺塔问题将k 个大小不同的圆盘依其半径大小依次套在桩A 上,大的在下,小的在上。
现将此k 个盘移到空桩B 或C 上,但要求一次只能移动一个盘且移动过程中,始终保持大盘在下,小盘在上,移动过程中桩A 也可利用。
设移动k 个盘的次数为k y ,试建立k y 的差分方程。
[解] 先将桩A 上的k 个大小不同的圆盘按题设要求移到C 上,这需要移动k y 次,再将A 上的最大盘移到B 上,这需要移动一次,最后将C 上的k 个盘按要求移到B 上,这又需要移动k y 次。
所以,差分方程为⎩⎨⎧=+=+01201y y y k k§2、 差分方程的解法一.常系数线性齐次差分方程形如 0110=+++-++k n n k n k y a y a y a ——(1)其中n a a a ,,,10 为常数,且0,00≠≠n a a ,称为n 阶常系数齐次线性差分方程。
copy-第五讲 差分方程模型
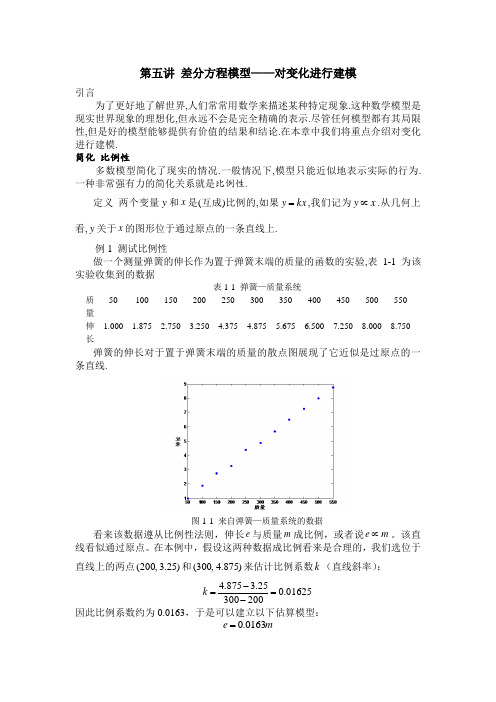
第五讲 差分方程模型——对变化进行建模引言为了更好地了解世界,人们常常用数学来描述某种特定现象.这种数学模型是现实世界现象的理想化,但永远不会是完全精确的表示.尽管任何模型都有其局限性,但是好的模型能够提供有价值的结果和结论.在本章中我们将重点介绍对变化进行建模. 简化 比例性多数模型简化了现实的情况.一般情况下,模型只能近似地表示实际的行为.一种非常强有力的简化关系就是比例性.定义 两个变量y 和x 是(互成)比例的,如果kx y =,我们记为x y ∝.从几何上看,y 关于x 的图形位于通过原点的一条直线上.例1 测试比例性做一个测量弹簧的伸长作为置于弹簧末端的质量的函数的实验,表1-1为该实验收集到的数据表1-1 弹簧—质量系统 质量50 100 150 200 250 300 350 400450 500 550 伸长1.000 1.8752.7503.2504.375 4.8755.6756.5007.2508.000 8.750 弹簧的伸长对于置于弹簧末端的质量的散点图展现了它近似是过原点的一条直线.图1-1 来自弹簧—质量系统的数据看来该数据遵从比例性法则,伸长e 与质量m 成比例,或者说m e ∝。
该直线看似通过原点。
在本例中,假设这两种数据成比例看来是合理的,我们选位于直线上的两点)25.3,200(和)875.4,300(来估计比例系数k (直线斜率):01625.020030025.3875.4=--=k因此比例系数约为0.0163,于是可以建立以下估算模型:m e 0163.0=然后把表示该模型的直线图形重叠画到散点图上,以考察模型对这些数据的拟合效果。
从图中可以看出这个简化的比例模型是合理的。
图1-2来自弹簧—质量系统的数据和比例性模型直线对变化进行建模对变化进行建模的一个非常有用的范例就是:未来值=现在值+变化人们往往希望从现在知道的东西加上精心观测到的变化来预测未来。
数学建模方法之差分方程模型

数学建模方法之差分方程模型差分方程模型是数学建模中常用的一种方法,它基于差分方程来描述问题,并用差分方程来求解问题。
所谓差分方程,是指用差分代替微分的方程,它是一种离散的模型。
在实际问题中,很多情况下,并不能直接通过微分方程来描述问题,而差分方程模型则可以通过离散化的方法来近似地描述问题。
差分方程模型的优点之一是可以适用于离散化的数据,对于实际问题的离散化模型建立是非常有帮助的。
差分方程模型的另一个优点是可以通过数值方法来求解,不需要进行繁琐的解析推导,因此适用于复杂问题的求解。
差分方程模型的基本形式为:yn+1 = fn(yn, yn-1, ..., yn-k)其中,yn表示第n个时刻的解,fn是一个给定的函数,表示通过前k个时刻的解来计算第n+1个时刻的解。
这个方程是离散的,通过已知的初始条件来逐步递推获得结果。
差分方程模型的适用范围非常广泛,可以用于描述和预测各种动态过程。
例如,差分方程模型可以用来描述人口增长模型、生态系统模型、传染病模型等等。
在这些例子中,差分方程模型可以通过已知的数据和初始条件来预测未来的发展趋势。
差分方程模型的建立步骤主要包括以下几个方面:1.确定问题的描述和目标:明确问题的背景和目标,确定需要建立差分方程模型的原因和用途。
2.确定模型的变量和参数:根据实际问题,确定需要用到的变量和参数。
3.确定差分方程的形式和函数:根据问题的特点和要求,选择合适的差分方程形式和函数。
这部分需要结合实际问题和数学方法来确定。
4.确定初始条件和边界条件:确定差分方程模型的初始条件和边界条件。
这部分是求解差分方程的前提条件。
5.差分方程的求解和分析:通过数值方法求解差分方程,得到数值解,并对结果进行分析和解释。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一 差分方程模型 二 差分方程解法 三 差分方程的平衡点及稳定性 四 建模案例 五 用Matlab求解差分方程问题
一 差分方程模型
对一数列{an},把数列中的an和前面的ai(0<=i<n)关
联起来的方程叫差分方程,也叫递推关系。
例:设第一月初有雌雄各一的一对小兔。假定两月 后长成成兔,同时从第三个月开始每月初产雌雄各 一对一对小兔,新增小兔也按次规律繁殖。设第n月 末共有Fn对兔子,试建立关于Fn的差分方程。
3 一阶非线性差分方程的平衡点及稳定性 考察一阶非线性差分方程xk+1=f(xk) (7) 的平衡点的稳定性。其平衡点x*由x=f(x)解出。 将(7)的右端在x*点做泰勒展开,只取一次项 ,则(7)可以近似为:
x k 1f'(x *x k ) (x * ) f(x *) (8) x*也是(8)的平衡点。线性方程(8) 的平衡 点 的 稳 定 性 讨 论 同 ( 1 ) , 而 当 |f ’(x*)|≠1 时 ( 7 )与(8)的平衡点的稳定性相同。从而有: 当|f ’(x*)|<1时,方程(7)的平衡点是稳定的; 当|f ’(x*)|>1时,方程(7)的平衡点是不稳定的 。
(2) 重根 若差分方程(1)的特征方程Xk+b1xk-
1+…+bk=0的相异特征根x1,x2,…,xt ,重数依次为 m1,m2,…,mt, m1+m2+…+mt=k,则差分方程的通 解为
m 1
m 2
m t
a n c1jnj 1x1nc2jnj 1x2 n ... ctn jj 1xtn
j 1
2. 二阶线性差分方程的平衡点及稳定性 考察二阶线性差分方程xk+a1xk+1+a2xk+2=0 (4) 在平衡点x*=0的稳定性。为求(4)的通解,先写 出他的特征方程
2a1a20
记它的根为λ1,λ2,则(4)的通解可以表示为
xk c11k c2k2
,其中常数c1,c2由初始条件x0,x1确定,从而可知 ,当且仅当|λ1|<1, |λ2|<1时方程(4)的平衡点是 稳定的。
返回
三、差分方程的平衡点及稳定性
1. 一阶线性常系数差分方程的平衡点及稳定 性
一阶线性常系数差分方程 xk+1+axk=b,k=0,1,2,…(1)
x b 1 a
k
的平衡点由x+ax=b解得,为
,当
时,若xkx*,则x*是稳定的。
方程(1)的平衡点的稳定性问题可以通过变
量代换转换为齐次方程
xk+1+axk=0,k=0,1,2… (2)
鱼群数据为:
(1) 各年龄组鱼的自然死亡率为0.8(1/年),其 平均重量分别为5.07,11.55,17.86,22.99(g); (2) 1龄鱼和2龄鱼不产卵,产卵期间,平均每条4 龄鱼产卵量为1.109╳105(个),3龄鱼为其一半 ;
(3) 卵孵化的成活率为1.22╳1011/(1.22╳1011+n )(n为产卵总量);
问题描述如下: 如何实现可持续捕获(即每年开始捕捞时渔场 中各年龄组鱼群不变),并在此前提下得到最 高收获量; 合同要求某渔业公司在5年合同期满后鱼群的生 产能力不能受到太大破坏,承包时各年龄组鱼 群数量为122,29.7,10.1,3.29(╳109条)。 在固定努力量的捕捞方式下,问该公司应采取 怎样的捕捞策略,才能使总收获量最高。
的平衡点x*=0的稳定性问题。而对于方程(2), 其解可以表示为
xk=(-a)kx0, k=1,2,… (3) 所以当且仅当|a|<1时,方程(2)(从而方程(1 ))的平衡点是稳定的。
对于n维向量x(k)和n╳n常数矩阵A构成的 方程组
x(k+1)+Ax(k)=0 其平衡点稳定的条件是A的特征根 λi,I=1,2,…,均有|λi|<1。
(1). 引入变量 X=(X1,X2,X3,X4)T 为鱼群数向量; α---单位时间的自然死亡率; c----年存活率,c=1-0.8=0.2; k----单位时间4龄鱼的捕捞强度系数; β--- 孵 化 卵 成 活 率 , β=1.22╳1011/ ( 1.22╳1011+n); m---4龄鱼的平均产卵量,m为1.109╳105(个 ),3龄鱼为其一半。
2. 常系数线性非齐次差分方程的解法 形如an+b1an-1+b2an-2+…+bkan-k=f(n)(1)(其中bi为 常 数 , bk≠0,n>=k,f(n) ≠0) 的 差 分 方 程 , 称 为 {an}的k阶常系数线性非齐次差分方程。 非齐次差分方程的通解等于对应的齐次差分方程 的通解加上非齐次差分方程的一个特解。
返回
四、建模案例--最优捕鱼策略
问题简介 生态学原理:对可再生资源的开发策略应为在可持
续收获的前提下追求最大经济效益。 考虑4个年龄组:1龄鱼,2龄鱼,3龄鱼,4龄鱼的
某鱼类。该鱼类在每年后4个月产卵繁殖。因而 捕捞只能在前8个月进行。每年投入的捕捞能力 不变,单位时间捕捞量与各年龄组鱼群条数的比 例称为捕捞强度系数。且只能捕捞3、4龄鱼,两 个捕捞强度系数比为0.42:1。即为固定努力量 捕捞。
j 1
j 1
(3) 共轭复根
若差分方程(1)的特征方程Xk+b1xk-1+…+bk=0
有一对共x3,…,xk,则差分方程的通解为,
a n c 1n cn o c 2n s sn i c n 3 x 3 n . .c k x .k n
其中 22,arc tan
解:因为第n月末的兔子包括两部分,一部分为上月 留下的,另一部分为当月新生的,而由题设当月生 的小兔等于前月末的兔子数,所以有 Fn=Fn-1+ Fn-2 ,F1=F2=1.返回
二 差分方程解法
1. 常系数线性齐次差分方程的解法 形 如 an+b1an-1+b2an-2+…+bkan-k=0 ( 1 ) ( 其 中 bi 为 常 数,bk≠0,n>=k.)的差分方程,称为{an}的k阶常系数 线性齐次差分方程。 Xk+b1xk-1+…+bk=0为上述差分方程的特征方程,其 根称为特征根。 解分为三种情况: (1) 单根 若差分方程(1)的特征方程Xk+b1xk-1+…+bk=0有k 个 相 异 的 特 征 根 x1,x2,…,xk , 则 an=c1x1n+c2x2n+…+ckxkn是一个通解,其中ci为常数, 由初始条件a0=u0,a1=u1,…,ak-1=uk-1可确定一个满足初 始条件的特解。
