第六章习题
第六章 计划习题

第六章计划一.单项选择题1.根据计划的明确性,可以把计划分类为( )。
A.长期计划和短期计划B.战略性计划和战术性计划C.具体性计划和指导性计划D.程序性计划和非程序性计划2.财务计划和人事计划与业务计划的关系描述不正确的是( )。
A.财务计划和人事计划是为业务计划服务的B.财务计划和人事计划是围绕着业务计划展开的C.业务计划研究如何从资本的提供和利用上促进业务活动的有效进行D.人事计划分析如何为业务规模的维持或扩大提供人力资源的保证3.拟定和选择行动计划不包括( )内容。
A.拟定可行动计划B.评估计划C.修改计划D.选定计划4.( )的计划是有效率的。
A.能得到最大的剩余B.能实现目标C.成本等于收益D.详细二.填空题1.目标管理是美国管理学家( )于1954年提出的。
2.实践中计划组织实施行之有效的方法主要有( )、( )和( )。
3.滚动计划法是一种( )。
4.滚动计划法的具体做法是,( )。
5.目标管理是一种程序,使一个组织中的上下各级管理人员会同一起来制订共同的目标,确定彼此的成果责任,并以此项责任来作为( )。
6.决策是计划的前提,计划是决策的( )。
7.计划是将决策实施所需完成的活动任务进行( )上的分解,以便将其具体地落实到组织中的不同部门和个人。
8.根据综合性标准,可以把计划分为( )和( )。
9.根据( )标准,可以把计划分为业务计划,财务计划,人事计划。
10.所有层次的、不同职能的管理人员都要做计划工作,这反映了计划的( )性;同时计划工作要求纵向层次性和横向协作性,这反映了计划工作的( )性。
三.多项选择题1.把战略性计划所确定的目标在时间和空间两个维度展开,( )A.具体地规定了组织的各个部门在目前到未来的各个较短的时期阶段应该从事何种活动B.从事该种活动应达到何种要求C.为各组织成员在近期内的行动提供了依据D.保证了组织目标的实现2.实践中对计划组织实施行之有效的方法主要有( )等方法。
第六章 品种法 习题

第六章品种法二、判断分析题1.生产特点和管理要求对产品成本计算的影响,主要表现在成本计算对象的确定上。
分析:2.成本计算对象是区分产品成本计算基本方法的主要标志。
分析:3.单步骤生产由于工艺过程不能间断,因而只能按产品的品种计算成本。
分析:4.由于每个工业企业最终都必须按照产品品种算出产品成本,因此,品种法是成本计算方法中的最基本方法。
分析:5.一般情况下,品种法的成本计算期与生产周期是一致的。
分析:6.单件生产是指根据需用单位的要求,生产个别的、特定的产品,这种产品的品种一般较多,而且很少重复生产。
分析:7.品种法一般适用于计算大量大批多步骤生产的产品成本。
分析:8.分类法的适用与否与产品的生产类型有着直接的联系。
分析:9.联产品必须采用分类法计算成本。
分析:10.用分类法计算出的类内各种产品的成本具有一定的假定性。
分析:11.主、副产品在分离前应合为一类产品计算成本。
分析:12.副产品在与主产品分离后,还需要单独进行加工的,应按其分离后继续加工的生产特点和管理的要求单独计算成本。
分析:13.系数分配法是运用系数分配计算类内各规格产品成本的一种方法,系数一经确定,在一定时期内应稳定不变。
分析:三、单项选择题1.区分各种成本计算基本方法的主要标志是()。
A.成本计算对象B.成本计算日期C.间接费用的分配方法D.完工产品与在产品之间分配费用的方法2.品种法的成本计算期与()是不一致的,一般是按月进行的。
A.生产周期B.会计核算期C.会计分期D.生产日期3.产品成本计算的分类法适用于()。
A.品种、规格繁多的产品B.可以按照一定标准分类的产品C.品种、规格繁多,而且可以按照产品结构、所用原材料和工艺过程的不同划分为若干类别的产品D.只适用于大批大量生产的产品4.按照系数比例分配同类产品中各种产品成本的方法()。
A.是一种完工产品和月末在产品之间分配费用的方法B.是一种单独的产品成本计算方法C.是一种简化的分类法D.是一种分配间接费用的方法5.一般适用于分离后不再加工,而且价格波动不大的联产品成本计算方法是()。
第六章、七章、八章课后习题答案

第六章课后练习题1、三通公司拟发行5年期、利率6%、面额1000元债券一批;预计发行总价格为550元,发行费用率2%;公司所得税率33%。
要求:试测算三通公司该债券的资本成本率。
参考答案:可按下列公式测算:=1000*6%*(1-33%)/550*(1-2%)=7.46%2、四方公司拟发行优先股50万股,发行总价150万元,预计年股利率8%,发行费用6万元。
要求:试测算四方公司该优先股的资本成本率。
参考答案:可按下列公式测算:其中:=8%*150/50=0.24=(150-6)/50=2.88=0.24/2.88=8.33%3、五虎公司普通股现行市价为每股20元,现准备增发8万份新股,预计发行费用率为5%,第一年每股股利1元,以后每年股利增长率为5%。
要求:试测算五虎公司本次增发普通股的资本成本率。
参考答案:可按下列公式测算:=1/19+5%=10.26%4、六郎公司年度销售净额为28000万元,息税前利润为8000万元,固定成本为3200万元,变动成本为60%;资本总额为20000万元,其中债务资本比例占40%,平均年利率8%。
要求:试分别计算该公司的营业杠杆系数、财务杠杆系数和联合杠杆系数。
参考答案:可按下列公式测算:DOL=1+F/EBIT=1+3200/8000=1.4DFL=8000/(8000-20000*40%*8%)=1.09DCL=1.4*1.09=1.535、七奇公司在初创时准备筹集长期资本5000万元,现有甲、乙两个备选筹资方案,有关资料如下表:筹资方式筹资方案甲筹资方案乙筹资额(万元)个别资本成本率(%)筹资额(万元)个别资本成本率(%)长期借款公司债券普通股800120030007.08.514.0110040035007.58.014.0合计5000 —5000 —要求:试分别测算该公司甲、乙两个筹资方案的综合资本成本率,并据以比较选择筹资方案。
参考答案:(1)计算筹资方案甲的综合资本成本率:第一步,计算各种长期资本的比例:长期借款资本比例=800/5000=0.16或16% 公司债券资本比例=1200/5000=0.24或24%普通股资本比例 =3000/5000=0.6或60%第二步,测算综合资本成本率:Kw=7%*0.16+8.5%*0.24+14%*0.6=11.56%(2)计算筹资方案乙的综合资本成本率:第一步,计算各种长期资本的比例:长期借款资本比例=1100/5000=0.22或22% 公司债券资本比例=400/5000=0.08或8%普通股资本比例 =3500/5000=0.7或70%第二步,测算综合资本成本率:Kw=7.5%*0.22+8%*0.08+14%*0.7=12.09%由以上计算可知,甲、乙两个筹资方案的综合资本成本率分别为11.56%、12.09%,可知,甲的综合资本成本率低于乙,因此选择甲筹资方案。
第六章++课后习题+参考答案

第6章完全垄断市场下的价格与产量课后习题参考答案一、单选题1.对完全垄断厂商来说(C)。
A.提高价格一定能够增加收益B.降低价格一定会减少收益C.提高价格未必能增加收益,降低价格未必减少收益D.以上都不对解析:完全垄断市场上,厂商的总收益TR曲线是先增加后减少。
因此,对完全垄断厂商来说,提高价格未必能增加收益,降低价格未必减少收益。
选C。
2.垄断厂商利润极大时,(C)。
A.P=MR=MCB.P>MR=ACC.P>MR=MCD.P>MC=AC解析:垄断厂商定价时遵循利润最大化原则,此时有边际收益等于边际成本MR=MC,而当垄断厂商利润极大时,价格P显然高于边际成本MC。
3.垄断利润或者说超额利润(A)。
A.不是一种成本,因为它不代表生产中使用的资源所体现的替换成本B.不能为垄断者在长期中所获取,因为价格在最优产出水平上必须等于长期平均成本C.为保证资本继续进入该行业所必需D.能为完全竞争者和垄断者一样在长期中获取解析:BCD选项均有明显错误。
垄断利润或者说超额利润不是一种成本,选A。
4.在短期,完全垄断厂商(D)。
A.无盈余B.取得最大利润C.发生亏损D.以上任何一种情况都有可能出现解析:完全垄断厂商在短期均衡点上可能获得超额利润,可能只获得正常利润,还可能发生亏损。
因此选D。
5.在完全垄断厂商的最好或最优产量处(D)。
A.P=MCB.P=SAC的最低点的值C.P最高D.MR=MC解析:根据利润最大化原则,边际收益等于边际成本MR=MC时的价格和产量是最优的。
因此选D。
二、简答题1.成为垄断者的厂商可以任意定价,这种说法对吗?这种说法不正确。
从理论上讲,垄断者是价格的制定者,其产品没有替代品,其他厂商无法进入垄断行业,厂商是产品唯一的卖者。
然而在实际上,如果垄断厂商定价过高,购买量就会下降,从而使总收益和利润下降;其他厂商如看到有丰厚的利润,尽管没有替代品,但相似的替代品总是会生产的,因而垄断厂商如果定价过高,会使自己产品失去销路,市场被相似替代品夺去;国家也会对垄断厂商的定价加以控制,有些国家会通过制定反垄断法,规定最高限价,还可用征税等办法加以控制。
第六章 计划习题

第六章计划一.单项选择题1.根据计划的明确性,可以把计划分类为( )。
A.长期计划和短期计划B.战略性计划和战术性计划C.具体性计划和指导性计划D.程序性计划和非程序性计划2.财务计划和人事计划与业务计划的关系描述不正确的是( )。
A.财务计划和人事计划是为业务计划服务的B.财务计划和人事计划是围绕着业务计划展开的C.业务计划研究如何从资本的提供和利用上促进业务活动的有效进行D.人事计划分析如何为业务规模的维持或扩大提供人力资源的保证3.拟定和选择行动计划不包括( )内容。
A.拟定可行动计划B.评估计划C.修改计划D.选定计划4.( )的计划是有效率的。
A.能得到最大的剩余B.能实现目标C.成本等于收益D.详细二.填空题1.目标管理是美国管理学家( )于1954年提出的。
2.实践中计划组织实施行之有效的方法主要有( )、( )和( )。
3.滚动计划法是一种( )。
4.滚动计划法的具体做法是,( )。
5.目标管理是一种程序,使一个组织中的上下各级管理人员会同一起来制订共同的目标,确定彼此的成果责任,并以此项责任来作为( )。
6.决策是计划的前提,计划是决策的( )。
7.计划是将决策实施所需完成的活动任务进行( )上的分解,以便将其具体地落实到组织中的不同部门和个人。
8.根据综合性标准,可以把计划分为( )和( )。
9.根据( )标准,可以把计划分为业务计划,财务计划,人事计划。
10.所有层次的、不同职能的管理人员都要做计划工作,这反映了计划的( )性;同时计划工作要求纵向层次性和横向协作性,这反映了计划工作的( )性。
三.多项选择题1.把战略性计划所确定的目标在时间和空间两个维度展开,( )A.具体地规定了组织的各个部门在目前到未来的各个较短的时期阶段应该从事何种活动B.从事该种活动应达到何种要求C.为各组织成员在近期内的行动提供了依据D.保证了组织目标的实现2.实践中对计划组织实施行之有效的方法主要有( )等方法。
近代史-第六章 练习题

第六章中华民族的抗日战争一.单项选择题1.1931年9月18日,日本关东军在中国( A )市郊柳条湖爆破铁路,制造借口向中国军队进攻。
“九·一八”事变后,日军迅即侵占我国东北三省。
A.沈阳B.长春C.大连D.旅顺2.1932年1月28日,日军向上海闸北中国驻军进攻,中国爱国将领蒋光鼐、蔡廷锴率领( B )奋起抵抗,发动了一二八淞沪抗战。
A.第二十九军B.第十九路军C.第二十六路军D.第二十五军3、不属于中国共产党1942年开展的整风运动内容的是(C )A、反对主观主义B、反对宗派主义C、反对官僚主义D、反对党八股4.1935年8月1日,中共驻共产国际代表团发表( B ),呼吁一致抗日。
A.《停止内战一致抗日》B.《为抗日救国告全国同胞书》C.《停战议和一致抗日》D.《反日反蒋的初步协定》5.1935年12月,中国共产党确定抗日民族统一战线政策的会议是( B )A.遵义会议B.瓦窑堡会议C.洛川会议D.晋绥干部会议6、1937年9月,国共第二次合作实现的根本原因是(C )A、西安事变的推动B、美英的支持C、民族矛盾突出D、中共的努力争取7、在抗日战争的战略防御阶段,国民党军队在正面战场上取得胜利的战役是( A )A.台儿庄战役B.桂南战役C.枣宜战役D.中条山战役8、毛泽东在《论持久战》中指出,中国抗日战争取得胜利最关键的阶段是( B )A.战略防御阶段B.战略相持阶段C.战略反攻阶段D.战略决战阶段9、国民党的片面抗战路线和共产党的全面抗战路线,最根本的区别是BA、要不要抗战B、依靠什么力量抗战C、抗战应走怎样的道路D、是正面战场抗战还是敌后战场抗战10、1938年,国民党声明:“此次抗战,为国家民族存亡所系,人人皆应献出生命,以争取国家民族之生存……然抗战之胜利惟望一个信仰、一个领袖、一个政府。
”以上材料表明国民党(D)A、愿意加强国共合作力度,团结抗日B、决定发动全民族的抗战C、总结以前战事,以利再战D、政策重心由对外转向对内11、抗战进入相持阶段后,蒋介石集团投降反共倾向增长,但又不放弃抗日,不与共产党彻底决裂。
第六章 练习题+答案
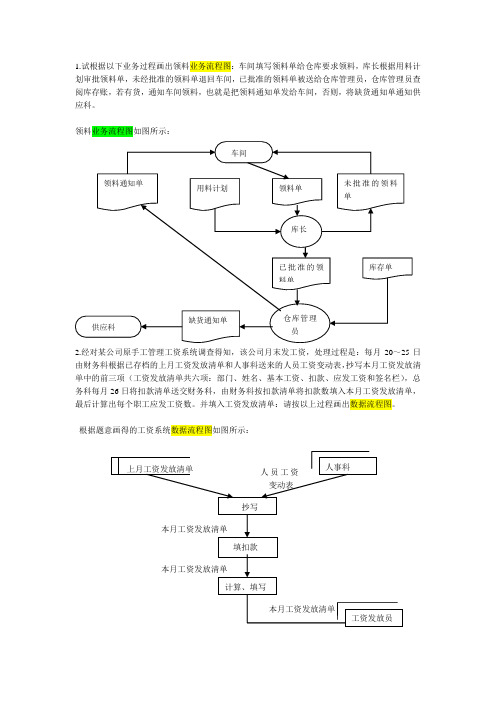
1.试根据以下业务过程画出领料业务流程图:车间填写领料单给仓库要求领料,库长根据用料计划审批领料单,未经批准的领料单退回车间,已批准的领料单被送给仓库管理员,仓库管理员查阅库存账,若有货,通知车间领料,也就是把领料通知单发给车间,否则,将缺货通知单通知供应科。
领料业务流程图如图所示:2.经对某公司原手工管理工资系统调查得知,该公司月末发工资,处理过程是:每月20~25日由财务科根据已存档的上月工资发放清单和人事科送来的人员工资变动表,抄写本月工资发放清单中的前三项(工资发放清单共六项:部门、姓名、基本工资、扣款、应发工资和签名栏),总务科每月26日将扣款清单送交财务科,由财务科按扣款清单将扣款数填入本月工资发放清单,最后计算出每个职工应发工资数。
并填入工资发放清单:请按以上过程画出数据流程图。
根据题意画得的工资系统数据流程图如图所示:3.某货运站的收费标准如下:若收件地点在本省,则快件每公斤6元,慢件每公斤4元;若收件地点在外省,则在25公斤以内(包括25公斤)快件每公斤8元,慢件每公斤6元;如果超过25公斤时,快件每公斤10元,慢件每公斤8元。
试绘制确定收费标准的判断表。
收费标准决策表如下:4.某企业的成品库存业务流程描述如下:入库时,成品库保管员按车间送来的入库单登记库存台帐,发货时,发货员根据销售科送来的发货通知单将成品出库并发货,同时填写三份出库单,其中一份交成品库保管员,由他按此出库单登记库存台帐,出库单的另外两联分别送销售科和会计科。
试按以上业务过程画出业务流程图。
(15分)企业的成品库存业务流程图如下:5.某商场pos系统的前台管理的程序是:1、由各柜台开出购物收款单,在POS 上录入收款单并检查,出收款传票(打印小票);2、据传票和现金或信用卡进行收款处理,并出发货单去柜台领回商品,另一方面出销售流水记录;3、对销售流水帐进行分类后出收款分类表交财务,并出销售分类账;4、每日进行销售汇总和审核以对柜组考核,并给出日出库明细账和进销存日报表中的销售情况。
第六章 新自测练习题

第六章社会主义初级阶段理论(章节自测练习题)一、单项选择题:1.一切从我国的实际出发,我国最大的实际就是( D )A.底子薄,人口多,资源相对不足 B.生产力不发达,教育科技落后C.社会制度不健全、不完善 D.现在处在并将长期处于社会主义初级阶段2.社会主义初级阶段在各方面先进和落后的并存,是我国基本国情的重要特点,它决定了社会主义初级阶段的发展具有的总的基本特征是:(A)A.逐步摆脱不发达状态,基本实现社会主义现代化的历史阶段B.由农业国逐步转变为工业国的历史阶段C.由经济文化发展不平衡逐步变为缩小差距的历史阶段D.由自然经济半自然经济占很大比重,逐步转变为经济市场化程度较高的历史阶段3.邓小平指出:"社会主义究竟是个什么样子,苏联搞了很多年,也并没有搞清楚,可能列宁的思路比较好,搞了个新经济政策,但是最后苏联模式僵化了",列宁新经济政策关于社会主义的思路之所以"比较好"是因为:( B )A.提出了比较系统的社会主义建设纲领B.根据俄国的实际情况来探索社会主义建设的道路C.为俄国找到一种比较成熟的社会主义发展模式D.按照马克思恩格斯关于未来的设想来建设社会主义4. 第一次提出我国社会主义制度还处于初级阶段是( A )A.1981. 6 党的十一届六中全会通过的《关于建国以来党的若干历史问题的决议》B.1982 . 9党的十二大政治报告C.1986 十二届六中全会的《中共中央关于社会主义精神文明建设指导方针的决议》D.1987 年党的十三大政治报告5.第一次全面系统地论述社会主义初阶阶段理论是党的( B )A.十二大B.十三大C. 十四大D. 十五大6.党的十五大首次全面系统地概括了( A )A.初级阶段的基本特征B.初级阶段的基本纲领C.初级阶段的基本路线D.初级阶段的基本经验7.我国是从( C)进入社会主义初级阶段的。
A.1949年新中国成立B.1976年粉碎“四人帮”后C.1956年基本完成生产资料公有制的社会主义改造后D.1978年改革开放后8.正式提出党在社会主义初级阶段的基本路线:领导和团结全国各族人民,以经济建设为中心,坚持四项基本原则,坚持改革开放,自力更生,艰苦创业,为把我国建设成为富强, 民主,文明的社会主义现代化国家而奋斗.是( C )A.1982 党的十二大B.1986 年十二届六中全会C.1987 年党的十三大D.1992 年党的十四大9.把"和谐"与"富强民主文明"一起写入了社会主义初级阶段基本路线的是( B )A.2002 年党的十六大通过的党章B.2007 年党的十七大通过的党章C.1992 年 9 月党的十四大通过的党章D.1997 年党的十五大通过的党章10.社会主义初级阶段是不可逾越的,这主要取决于( B )A.市场经济的不可逾越性B.生产力发展的不可逾越性C.生产关系发展的不可逾越性D.文化传统的不可逾越性11.1981年党的十一届六中全会通过《关于建国以来党的若干历史问题的建议》对我国社会主要矛盾作了规范的表述:“社会主义改造完成以后,我国所要解决的主要矛盾,是人民日益增长的物质文化需要同落后的社会生产之间的矛盾。
第六章练习册习题

第六章三相交流电路习题1.是非题()(1)三相对称电动势任一瞬间的代数和为零。
()(2)三相四线制供电,中性线的作用是保证负载不对称时,相电流对称。
()(3)在同一电源作用下,负载作星形连接时的线电压等于作三角形连接时的线电压。
()(4)在三相功率计算式cosL LP Iϕ中,ϕ是指线电压与线电流之间的相位差。
()(5)三相对称交流电路中,负载消耗的功率与负载的连接方式无关。
()(6)当三相负载作星形连接时,负载越接近对称,中性线上的电流就越小。
()(7)一台三相电动机,每个绕组的额定电压是220V,现在三相电源的线电压是380V,则这台电动机的绕组应连成三角形。
()(8)一台三相电动机,每个绕组的额定电压是220V,若三相电源的线电压是220V,则这台电动机的绕组应连成星形。
()(9)两根相线间的电压叫做相电压。
()(10)只要在线路中安装熔断器,不论其规格如何,电路都能正常工作。
()(11)为保证机床操作者的安全,机床照明灯的电压应选36V以下。
()(12)三相交流电源是由频率、有效值、相位都相同的三个单相交流电源按一定的方式组合起来的。
2.填空题(1)U、V、W是三相交流发电机的三个绕组,它们的电阻不计,每相绕组产生的感应电动势可表示为e1=314sin314t V,e2=314sin(314t-120°) V,e3=314sin(314t+120°) V。
负载由三个相同的白炽灯组成,电路连接如图所示,若白炽灯正常发光,可知白炽灯的额定电压是_____________。
(2)三相对称负载作星形连接时,UYP=_________UYL,且IYP=________IYL,此时中性线电流为___________。
(3)三相对称负载作三角形连接时,U∆P=_________U∆L,且I∆P=________I∆L各线电流比相应的相电流_________度。
(4)工厂中一般动力电源电压为___________,照明电源电压为__________。
第六章 练习题

第六章练习题一、选择题1. 利用乃奎斯特稳定性判据判断系统的稳定性时,Z P N=-中的Z表示意义为()(2001.23真题)A.开环传递函数零点在S左半平面的个数B.开环传递函数零点在S右半平面的个数C.闭环传递函数零点在S右半平面的个数D.闭环特征方程的根在S右半平面的个数【答案】D【知识点】第六章【解析】该题考查考生乃奎斯特稳定性判据。
答案为D。
2. 关于劳斯—胡尔维茨稳定性判据和乃奎斯特稳定性判据,以下叙述中正确的是()(2001.24真题)A.劳斯—胡尔维茨判据属代数判据,是用来判断开环系统稳定性的B.乃奎斯特判据属几何判据,是用来判断闭环系统稳定性的C.乃奎斯特判据是用来判断开环系统稳定性的D.以上叙述均不正确【答案】B【知识点】第六章【解析】该题考查考生关于劳斯—胡尔维茨稳定性判据和乃奎斯特稳定性判据。
答案为B 。
3. 一单位反馈系统的开环传递函数为G s K s s K ()()=+,则该系统稳定的K 值范围为( )(2001.26真题)A.K >0B.K >1C.0<K <10D. K >-1【答案】A【知识点】第六章【解析】该题考查考生劳斯稳定判据。
闭环传递函数为:()K sK s K s G ++=+211,特征方程为:02=++K sK s列劳斯表:S 2 1 KS 1 KS 0 K由劳斯稳定判据可得:想要系统稳定,必须满足K >0。
答案为A 。
4. 以下性能指标中不能反映系统响应速度的指标为( )(2001.28真题)A.上升时间t rB.调整时间t sC.幅值穿越频率ωcD.相位穿越频率ωg【答案】D【知识点】第六章【解析】该题考查考生反映系统响应速度的指标。
上升时间tr ,调整时间ts和幅值穿越频率c均能反映系统响应的速度,所以,答案为D。
5.在设计控制系统时,稳定性判断( )(2002.15真题)A.不必判断B.绝对必要C.有时是必要的D.根据系统而定【答案】B【知识点】第六章【解析】该题考查考生稳定性的概念。
高等数学课后答案-第六章-习题详细解答

习 题 6—11、在平行四边形ABCD 中, 设−→−AB =a , −→−AD =b . 试用a 和b 表示向量−→−MA 、−→−MB 、−→−MC 、−→−MD , 其中M 是平行四边形对角线的交点.解: 由于平行四边形的对角线互相平分, 所以a +b −→−−→−==AM AC 2, 即 -(a +b )−→−=MA 2, 于是 21-=−→−MA (a +b ).因为−→−−→−-=MA MC , 所以21=−→−MC (a +b ). 又因-a +b −→−−→−==MD BD 2, 所以21=−→−MD (b -a ). 由于−→−−→−-=MD MB , 所以21=−→−MB (a -b ).2、若四边形的对角线互相平分,用向量方法证明它是平行四边形.证: =,BM =,∴=+=+BM =与 平行且相等,结论得证.3、 求起点为)1,2,1(A ,终点为)1,18,19(--B 的向量→AB 与12AB −−→-的坐标表达式.解:→AB =j i k j i 2020)11()218()119(--=-+--+--={20,20,0}--, 12AB −−→-={10,10,0}4、 求平行于a ={1,1,1}的单位向量.解:与a 平行的单位向量为{}1,1,131±=±a a .5、在空间直角坐标系中,指出下列各点在哪个卦限?(1,1,1),A - (1,1,1),B -(1,1,1),C -- (1,1,1).D -- 解: A:Ⅳ; B:Ⅴ; C:Ⅷ; D:Ⅲ.6、 求点),,(z y x M 与x 轴,xOy 平面及原点的对称点坐标.解:),,(z y x M 关于x 轴的对称点为),,(1z y x M --,关于xOy 平面的对称点为),,(2z y x M -,关于原点的对称点为),,(3z y x M ---.7、已知点A(a, b, c), 求它在各坐标平面上及各坐标轴上的垂足的坐标(即投影点的坐标). 解:分别为),0,0(),0,,0(),0,0,(),,0,(),,,0(),0,,(c b a c a c b b a .8、过点(,,)P a b c 分别作平行于z 轴的直线和平行于xOy 面的平面,问它们上面的点的坐标各有什么特点?解:平行于z 轴的直线上面的点的坐标:x a,y b,z R ==∈;平行于xOy 面的平面上的点的坐标为 z c,x,y R =∈.9、求点P (2,-5,4)到原点、各坐标轴和各坐标面的距离.解:到原点的距离为x y 轴的距离为到z10、 求证以)1,3,4(1M 、)2,1,7(2M 、)3,2,5(3M 三点为顶点的三角形是一个等腰三角形. 解:222212(74)(13)(21)14M M =-+-+-=,222223(57)(21)(32)6M M =-+-+-= 222213(45)(32)(13)6M M =-+-+-=,即1323M M M M =,因此结论成立.11、 在yoz 坐标面上,求与三个点A(3, 1, 2), B(4, -2, -2), C(0, 5, 1)等距离的点的坐标. 解:设yoz 坐标面所求点为),,0(z y M ,依题意有||||||MC MB MA ==,从而222)2()1()30(-+-+-z y 222)2()2()40(++++-=z y222)2()1()30(-+-+-z y联立解得2,1-==z y ,故所求点的坐标为)2,1,0(-.12、 z 轴上,求与点A(-4, 1, 7), 点B(3, 5,-2)等距离的点. 解:设所求z 轴上的点为),0,0(z ,依题意:222)7()10()40(-+-++z 222)2()50()30(++-+-=z ,两边平方得914=z ,故所求点为)914,0,0(.13、 求λ使向量}5,1,{λ=a 与向量}50,10,2{=b 平行. 解:由b a //得5051012==λ得51=λ.14、 求与y 轴反向,模为10的向量a 的坐标表达式. 解:a =j j 10)(10-=-⋅={0,10,0}-.15、求与向量a ={1,5,6}平行,模为10的向量b 的坐标表达式. 解:}6,5,1{6210==a a a ,故 {}6,5,16210100±=±=a b .16、 已知向量6410=-+a i j k ,349=+-b i j k ,试求: (1)2+a b ; (2)32-a b .解:(1) 264102(349)1248i a b i j k i j k j k +=-+++-=+-; (2)323(6410)2(349)=122048a b =i j k i j k i j k --+-+--+.17、已知两点A 和(3,0,4)B ,求向量AB 的模、方向余弦和方向角.解: 因为(1,1)AB =-, 所以2AB =,11cos ,cos 22αβγ===-,从而π3α=,3π4β=,2π3γ=.18、设向量的方向角为α、β、γ.若已知其中的两个角为π3α=,2π3β=.求第三个角γ. 解: π3α=,2π3β=,由222cos cos cos 1αβγ++=得21cos 2γ=.故π4γ=或3π4.19、 已知三点(1,0,0)=A ,(3,1,1)B ,(2,0,1)C ,求:(1)BC 与CA 及其模;(2)BC 的方向余弦、方向角;(3)与BC 同向的单位向量.解:(1)由题意知{}{}23,01,111,1,0,BC =---=--{}{}12,00,011,0,1,CA =---=-- 故 2,2==BC CA .(2)因为{}1,1,0,=--BC 所以,由向量的方向余弦的坐标表示式得:cos 0αβγ===,方向角为:3,42ππαβγ===.(3)与BC 同向的单位向量为:oa =⎧⎫=⎨⎬⎩⎭BCBC .20、 设23,23,34,m i j k n i j k p i j k =++=+-=-+和23a m n p =+-求向量在x 轴上的投影和在y 轴上的分向量.解:2(23)3(23)(34)5114a i j k i j k i j k i j k =++++---+=+-.故向量a 在x 轴上的投影5=x a ,在y 轴上的投影分量为11y a j =.21、一向量的终点为点B(-2,1,-4),它在x 轴,y 轴和z 轴上的投影依次为3,-3和8,求这向量起点A 的坐标.解:设点A 为(x, y, z ),依题意有:84,31,32=---=-=--z y x , 故12,4,5-==-=z y x ,即所求的点A (-5, 4,-12).22、 已知向量a 的两个方向余弦为cos α=72 ,cos β=73, 且a 与z 轴的方向角是钝角.求cos γ. 解:因222cos cos cos 1,αβγ++=22223366cos 1cos 77497γγ=-==±故()—(),,又γ是钝角,所以76cos -=γ.23、设三力1232234F ,F ,F i j i j k j k =-=-+=+作用于同一质点,求合力的大小和方向角.解: 合力123(2)(234)()F F F F i k i j k j k =++=-+-+++323i j k =-+,因此,合力的大小为|F |=合力的方向余弦为,222cos ,cos 223cos -===βγα因此παγβ===-习 题 6—21、 {}0,0,1=a ,{}0,1,0=b ,)1,0,0(=c ,求⋅a b ,c a ⋅,c b ⋅,及a a ⨯,b a ⨯,c a ⨯,c b ⨯. 解:依题意,i a =,j b =,k c =,故0=⋅=⋅j i b a ,0=⋅=⋅k i c a ,0=⋅=⋅k j c b .0=⨯=⨯i i a a ,k j i b a =⨯=⨯,j k i c a -=⨯=⨯,i k j c b =⨯=⨯.2、 }}{{1,2,2,21,1==b a ,,求b a ⋅及b a ⨯ .a 与b的夹角余弦. 解:(1)121221⋅=⨯+⨯+⨯=a b 6, 112221⨯==i j ka b }{3,3,0-.(2)cos a b a b a b θ++==3、 已知 π5,2,,3∧⎛⎫=== ⎪⎝⎭a b a b ,求23a b -解:()()2232323-=-⋅-a b a b a b 22412976=-⋅+=a a b b ,∴ 23-=ab4、 证明下列问题:1)证明向量}{1,0,1=a 与向量}{1,1,1-=b 垂直. 2) 证明向量c 与向量()()a c b b c a ⋅-⋅垂直. 证:1)01110)1(1=⨯+⨯+-⨯=⋅b a ,^π(,)2a b ∴=,即a 与b 垂直. 2) [()()]⋅-⋅⋅a c b b c a c [()()]=⋅⋅-⋅⋅a c b c b c a c ()[]=⋅⋅-⋅c b a c a c 0=[()()]∴⋅-⋅⊥a c b b c a c .5、 求点)1,2,1(M 的向径OM 与坐标轴之间的夹角.解:设OM 与x 、y 、z 轴之间的夹角分别为γβα,,,则211)2(11cos 22=++==α,22cos ==β, 21cos ==γ. 3π=∴α, 4π=β, 3π=γ.6、 求与k j i a ++=平行且满足1=⋅x a 的向量x .解:因x a //, 故可设{}λλλλ,,==a x ,再由1=⋅x a 得1=++λλλ,即31=λ,从而⎭⎬⎫⎩⎨⎧=31,31,31x .7、求与向量324=-+a i j k ,2=+-b i j k 都垂直的单位向量.解:=⨯=xy z x y zij kc a b a a a b b b 324112=--i j k =105+j k,||10==c 0||∴=c c c=.⎫±+⎪⎭j8、 在顶点为)2,1,1(-A 、)2,6,5(-B 和)1,3,1(-C 的三角形中,求三角形ABC 的面积以及AC 边上的高BD .解:{0,4,3},{4,5,0}AC AB =-=-,三角形ABC 的面积为,22516121521||21222=++=⨯=AB C A S ||||21,5)3(4||22BD S ==-+= ||521225BD ⋅⋅= .5||=∴BD9、 已知向量≠0a ,≠0b ,证明2222||||||()⨯=-⋅a b a b a b .解 2222||||||sin ()∧⨯=⋅a b a b ab 222||||[1cos ()]∧=⋅-a b ab 22||||=⋅a b 222||||cos ()∧-⋅a b ab 22||||=⋅a b 2().-⋅a b10、 证明:如果++=0a b c ,那么⨯=⨯=⨯b c c a a b ,并说明它的几何意义.证: 由++=0a b c , 有()++⨯=⨯=00a b c c c , 但⨯=0c c ,于是⨯+⨯=0a c b c ,所以⨯=-⨯=⨯b c a c c a . 同理 由()++⨯=0a b c a , 有 ⨯=⨯c a a b ,从而 ⨯=⨯=⨯b c c a a b .其几何意义是以三角形的任二边为邻边构成的平行四边形的面积相等.11、 已知向量23,3=-+=-+a i j k b i j k 和2=-c i j ,计算下列各式:(1)()()⋅-⋅a b c a c b (2)()()+⨯+a b b c (3)()⨯⋅a b c (4)⨯⨯a b c 解: (1)()()8(2)8(3)⋅-⋅=---+=a b c a c b i j i j k 824--j k .(2) 344,233+=-++=-+a b i j k b c i j k ,故()()+⨯+a b b c 344233=-=-i jk--j k . (3)231()231(2)(85)(2)11311312-⨯⋅=-⋅-=--+⋅-=-=--i jk a b c i j i j k i j 2. (4)由(3)知85,()851120⨯=--+⨯⨯=--=-i jka b i j k a b c 221++i j k .习 题 6—31、已知)3,2,1(A ,)4,1,2(-B ,求线段AB 的垂直平分面的方程. 解:设),,(z y x M 是所求平面上任一点,据题意有|,|||MB MA =()()()222321-+-+-z y x ()()(),412222-+++-=z y x化简得所求方程26270x y z -+-=.这就是所求平面上的点的坐标所满足的方程, 而不在此平面上的点的坐标都不满足这个方程,所以这个方程就是所求平面的方程.2、 一动点移动时,与)0,0,4(A 及xOy 平面等距离,求该动点的轨迹方程.解:设在给定的坐标系下,动点),,(z y x M ,所求的轨迹为C ,则(,,)M x y z C MA z ∈⇔= 亦即z z y x =++-222)4( 0)4(22=+-∴y x 从而所求的轨迹方程为0)4(22=+-y x .3、 求下列各球面的方程:(1)圆心)3,1,2(-,半径为6=R ; (2)圆心在原点,且经过点)3,2,6(-;(3)一条直径的两端点是)3,1,4()5,32(--与;(4)通过原点与)4,0,0(),0,3,1(),0,0,4(- 解:(1)所求的球面方程为:36)3()1()2(222=-+++-z y x (2)由已知,半径73)2(6222=+-+=R ,所以球面方程为49222=++z y x(3)由已知,球面的球心坐标1235,1213,3242=-=-=+-==+=c b a , 球的半径21)35()31()24(21222=++++-=R ,所以球面方程为: 21)1()1()3(222=-+++-z y x(4)设所求的球面方程为:0222222=++++++l kz hy gx z y x因该球面经过点)4,0,0(),0,3,1(),0,0,4(),0,0,0(-,所以⎪⎪⎩⎪⎪⎨⎧=-=++=+=08160621008160k h g g l 解之得⎪⎪⎩⎪⎪⎨⎧=-=-==2210k g h l∴所求的球面方程为0424222=+--++z y x z y x .4、将yOz 坐标面上的抛物线22y z =绕z 旋转一周,求所生成的旋转曲面的方程. 解:222x y z +=(旋转抛物面) .5、将zOx 坐标面上的双曲线12222=-c z a x 分别绕x 轴和z 轴旋转一周,求所生成的旋转曲面的方程.解: 绕x 轴旋转得122222=+-c z y a x 绕z 轴旋转得122222=-+cz a y x .6、指出下列曲面的名称,并作图:(1)22149x z +=;(2)22y z =;(3)221x z += ;(4)22220x y z x ++-=; (5)222y x z +=;(6)22441x y z -+=;(7)221916x y z ++=;(8)222149x y z -+=-;(9)1334222=++z y x ;(10)2223122z y x +=+.解: (1)椭圆柱面;(2) 抛物柱面;(3) 圆柱面;(4)球面;(5)圆锥面;(6)双曲抛物面;(7)椭圆抛物面;(8)双叶双曲面;(9)为旋转椭球面;(10)单叶双曲面.7、指出下列方程在平面解析几何和空间解析几何中分别表示什么图形? (1)1+=x y ;(2)422=+yx ;(3)122=-y x ;(4)22x y =.解:(1)1+=x y 在平面解析几何中表示直线,在空间解析几何中表示平面; (2)422=+y x 在平面解析几何中表示圆周,在空间解析几何中表示圆柱面; (3)122=-y x 在平面解析几何中表示双曲线,在空间解析几何中表示双曲柱面;(4)y x22=在平面解析几何中表示抛物线,在空间解析几何中表示抛物柱面.8、 说明下列旋转曲面是怎样形成的?(1)1994222=++z y x ;(2)14222=+-z y x (3)1222=--z y x ;(4)222)(y x a z +=- 解:(1)xOy 平面上椭圆19422=+y x 绕x 轴旋转而成;或者 xOz 平面上椭圆22149+=x z 绕x 轴旋转而成(2)xOy 平面上的双曲线1422=-y x 绕y 轴旋转而成;或者 yOz 平面上的双曲线2214-=y z 绕y 轴旋转而成(3)xOy 平面上的双曲线122=-y x 绕x 轴旋转而成;或者 xOz 平面上的双曲线221x z -=绕x 轴旋转而成 (4)yOz 平面上的直线a y z +=绕z 轴旋转而成或者 xOz 平面上的直线z x a =+绕z 轴旋转而成.9、 画出下列各曲面所围立体的图形:(1)012243=-++z y x 与三个坐标平面所围成;(2)42,42=+-=y x x z 及三坐标平面所围成; (3)22=0,(0)=1z z =a a >,y =x,x +y 及0x =在第一卦限所围成;(4)2222,8z x y z x y =+=--所围. 解:(1)平面012243=-++z y x 与三个坐标平面围成一个在第一卦限的四面体; (2)抛物柱面24z x =-与平面24x y +=及三坐标平面所围成;(3)坐标面=0z 、0x =及平面(0)z =a a >、y=x 和圆柱面22=1x +y 在第一卦限所围成; (4)开口向上的旋转抛物面22z x y =+与开口向下的抛物面228z x y =--所围.作图略.习 题 6—41、画出下列曲线在第一卦限内的图形(1)⎩⎨⎧==21y x ;(2)⎪⎩⎪⎨⎧=---=0422y x y x z ;(3)⎪⎩⎪⎨⎧=+=+222222a z x ay x解:(1)是平面1x =与2y =相交所得的一条直线; (2)上半球面z 与平面0x y -=的交线为14圆弧; (3)圆柱面222x y a +=与222x z a +=的交线.图形略.2、分别求母线平行于x 轴及y 轴而且通过曲线⎪⎩⎪⎨⎧=-+=++0162222222y z x z y x 的柱面方程.解:消去x 坐标得16322=-z y ,为母线平行于x 轴的柱面;消去y 坐标得:162322=+z x ,为母线平行于y 轴的柱面.3、求在yOz 平面内以坐标原点为圆心的单位圆的方程(任写出三种不同形式的方程).解:⎩⎨⎧==+0122x z y ;⎩⎨⎧==++01222x z y x ; ⎪⎩⎪⎨⎧=+=++1122222z y z y x .4、试求平面20x -=与椭球面222116124x y z ++=相交所得椭圆的半轴与顶点.解:将椭圆方程22211612420x y z x ⎧++=⎪⎨⎪-=⎩化简为:221932y z x ⎧+=⎪⎨⎪=⎩,可知其为平面2=x 上的椭圆,半轴分别为3,3,顶点分别为)3,0,2(),3,0,2(),0,3,2(),0,3,2(--.5 、将下面曲线的一般方程化为参数方程(1)2229x y z y x ⎧++=⎨=⎩; (2)⎩⎨⎧==+++-04)1()1(22z z y x解:(1)原曲线方程即:⎪⎩⎪⎨⎧=+=199222z x xy ,化为⎪⎪⎪⎩⎪⎪⎪⎨⎧=≤≤==tz t t y t x sin 3)20(cos 23cos 23π;(2))20(0sin 3cos 31πθθθ≤≤⎪⎪⎩⎪⎪⎨⎧==+=z y x .6、求螺旋线⎪⎩⎪⎨⎧===θθθb z a y a x sin cos 在三个坐标面上的投影曲线的直角坐标方程.解:⎩⎨⎧==+0222z a y x ;⎪⎩⎪⎨⎧==0sin x b z a y ;⎪⎩⎪⎨⎧==0cosy b z a x .7、指出下列方程所表示的曲线(1)222253⎧++=⎨=⎩x y z x (2)⎩⎨⎧==++13094222z z y x ;(3)⎩⎨⎧-==+-3254222x z y x ; (4)⎩⎨⎧==+-+408422y x z y ; (5)⎪⎩⎪⎨⎧=-=-0214922x z y . 解:(1)圆; (2)椭圆; (3)双曲线; (4)抛物线; (5)双曲线.8、 求曲线⎩⎨⎧==-+30222z x z y 在xOy 面上的投影曲线方程,并指出原曲线是何种曲线.解:原曲线即:⎩⎨⎧=-=3922z x y ,是位于平面3=z 上的抛物线,在xOy 面上的投影曲线为⎩⎨⎧=-=0922z x y9、 求曲线 ⎪⎩⎪⎨⎧==++211222z z y x 在坐标面上的投影. 解:(1)消去变量z 后得,4322=+y x 在xOy 面上的投影为,04322⎪⎩⎪⎨⎧==+z y x 它是中心在原点,半径为23的圆周.(2)因为曲线在平面21=z 上,所以在xOz 面上的投影为线段.;23||,021≤⎪⎩⎪⎨⎧==x y z (3)同理在yOz 面上的投影也为线段..23||,21≤⎪⎩⎪⎨⎧==y x z10、 求抛物面x z y =+22与平面 02=-+z y x 的交线在三个坐标面上的投影曲线方程.解: 交线方程为⎩⎨⎧=-+=+0222z y x x z y ,(1)消去z 得投影,004522⎩⎨⎧==-++z x xy y x(2)消去y 得投影2252400x z xz x y ⎧+--=⎨=⎩,(3)消去x 得投影22200y z y z x ⎧++-=⎨=⎩.习 题 6—51、写出过点()3,2,10M 且以{}1,2,2=n 为法向量的平面方程. 解:平面的点法式方程为()()()032212=-+-+-z y x .2、求过三点()()()01,0,0,1,0,0,0,1C B A 的平面方程.解:设所求平面方程为0=+++d cz by ax ,将C B A ,,的坐标代入方程,可得d c b a -===,故所求平面方程为1=++z y x .3、求过点()1,0,0且与平面1243=++z y x 平行的平面方程. 解:依题意可取所求平面的法向量为}2,4,3{=n ,从而其方程为()()()0120403=-+-+-z y x 即 2243=++z y x .4、求通过x 轴和点(4, -3, -1)的平面的方程.解:平面通过x 轴, 一方面表明它的法线向量垂直于x 轴, 即A =0; 另一方面表明它必通过原点, 即D =0. 因此可设这平面的方程为By +Cz =0.又因为这平面通过点(4, -3, -1), 所以有-3B -C =0, 或C =-3B . 将其代入所设方程并除以B (B 0), 便得所求的平面方程为y -3z =0.5、求过点)1,1,1(,且垂直于平面7=+-z y x 和051223=+-+z y x 的平面方程.解:},1,1,1{1-=n }12,2,3{2-=n 取法向量},5,15,10{21=⨯=n n n所求平面方程为化简得:.0632=-++z y x6、设平面过原点及点)1,1,1(,且与平面8x y z -+=垂直,求此平面方程.解: 设所求平面为,0=+++D Cz By Ax 由平面过点)1,1,1(知平0,A B C D +++=由平面过原点知0D =,{1,1,1},n ⊥- 0A B C ∴-+=,0A C B ⇒=-=,所求平面方程为0.x z -=7、写出下列平面方程:(1)xOy 平面;(2)过z 轴的平面;(3)平行于zOx 的平面;(4)在x ,y ,z 轴上的截距相等的平面.解:(1)0=z ,(2)0=+by ax (b a ,为不等于零的常数), (3)c y = (c 为常数), (4) a z y x =++ (0)a ≠.8、 求平行于0566=+++z y x 而与三个坐标面所围成的四面体体积为1的平面方程.解: 设平面为,1=++c z b y a x ,1=V 111,32abc ∴⋅=由所求平面与已知平面平行得,611161c b a ==化简得,61161c b a ==令tc t b t a t c b a 61,1,6161161===⇒===代入体积式 11111666t t t ∴=⋅⋅⋅ 1,6t ⇒=±,1,6,1===∴c b a 或1,6,1,a b c =-=-=-所求平面方程为666x y z ++=或666x y z ++=-.9、分别在下列条件下确定n m l ,,的值:(1)使08)3()1()3(=+-+++-z n y m x l 和016)3()9()3(=--+-++z l y n x m 表示同一平面; (2)使0532=-++z my x 与0266=+--z y lx 表示二平行平面; (3)使013=+-+z y lx 与027=-+z y x 表示二互相垂直的平面.解:(1)欲使所给的二方程表示同一平面,则:168339133-=--=-+=+-l n n m m l 即: ⎪⎩⎪⎨⎧=-+=-+=-+092072032n l m n l m ,解之得 97=l ,913=m ,937=n . (2)欲使所给的二方程表示二平行平面,则:6362-=-=m l ,所以4-=l ,3=m . (3)欲使所给的二方程表示二垂直平面,则:7230l ++=所以: 57l=-.10、求平面011=-+y x 与083=+x 的夹角; 解:设011=-+y x 与083=+x 的夹角为θ,则cos θ ∴ 4πθ=.11、 求点(2,1,1)到平面2240x y z +-+=的距离. 解:利用点到平面的距离公式可得933d ===.习 题 6—61、求下列各直线的方程:(1)通过点)1,0,3(-A 和点)1,5,2(-B 的直线; (2) 过点()1,1,1且与直线433221-=-=-z y x 平行的直线. (3)通过点)3,51(-M 且与z y x ,,三轴分别成︒︒︒120,45,60的直线; (4)一直线过点(2,3,4)-A ,且和y 轴垂直相交,求其方程. (5)通过点)2,0,1(-M 且与两直线11111-+==-z y x 和01111+=--=z y x 垂直的直线; (6)通过点)5,3,2(--M 且与平面02536=+--z y x 垂直的直线.解:(1)所求的直线方程为:015323-=-=++z y x 即:01553-=-=+z y x ,亦即01113-=-=+z y x . (2)依题意,可取L 的方向向量为{}4,3,2=s ,则直线L 的方程为413121-=-=-z y x . (3)所求直线的方向向量为:{}⎭⎬⎫⎩⎨⎧-=︒︒︒21,22,21120cos ,45cos ,60cos ,故直线方程为: 132511--=+=-z y x . (4)因为直线和y 轴垂直相交,所以交点为),0,3,0(-B 取{2,0,4},BA s −−→==所求直线方程.440322-=+=-z y x (5)所求直线的方向向量为:{}{}{}2,1,10,1,11,1,1---=-⨯-,所以,直线方程为:22111+==-z y x . (6)所求直线的方向向量为:{}5,3,6--,所以直线方程为: 235635x y z -++==--.2、求直线1,234x y z x y z ++=-⎧⎨-+=-⎩的点向式方程与参数方程.解 在直线上任取一点),,(000z y x ,取10=x ,063020000⎩⎨⎧=--=++⇒z y z y 解2,000-==z y .所求点的坐标为)2,0,1(-,取直线的方向向量{}{}3,1,21,1,1-⨯=s k j i kji34312111--=-=,所以直线的点向式方程为:,321041-+=--=-z y x 令102,413x y z t --+===--则所求参数方程: .3241⎪⎩⎪⎨⎧--=-=+=tz ty tx3、判别下列各对直线的相互位置,如果是相交的或平行的直线求出它们所在的平面,如果相交时请求出夹角的余弦.(1)⎩⎨⎧=-+=+-0623022y x z y x 与⎩⎨⎧=-+=--+01420112z x z y x ;(2)⎪⎩⎪⎨⎧--=+==212t z t y tx 与142475x y z --+==-. 解:(1)将所给的直线方程化为标准式为:4343223z y x =-=--43227-=--=-z y x 234234-==-- ∴二直线平行.又点)0,43,23(与点(7,2,0)在二直线上,∴向量⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧--0,45,2110,432,237平行于二直线所确定的平面,该平面的法向量为:{}{}19,22,50,45,2114,3,2--=⎭⎬⎫⎩⎨⎧⨯-,从而平面方程为:0)0(19)2(22)7(5=-+---z y x ,即0919225=++-z y x .(2)因为121475-≠≠-,所以两直线不平行,又因为0574121031=--=∆,所以两直线相交,二直线所决定的平面的法向量为{}{}{}1,1,35,7,412,1--=-⨯-,∴二直线所决定的平面的方程为:330x y z -++=.设两直线的夹角为ϕ,则cos ϕ==4、判别下列直线与平面的相关位置: (1)37423z y x =-+=--与3224=--z y x ;(2)723zy x =-=与8723=+-z y x ; (3)⎩⎨⎧=---=-+-01205235z y x z y x 与07734=-+-z y x ;(4)⎪⎩⎪⎨⎧-=+-==4992t z t y t x 与010743=-+-z y x .解(1) 0)2(3)2()7(4)2(=-⨯+-⨯-+⨯-,而017302)4(234≠=-⨯--⨯-⨯,所以,直线与平面平行.(2) 0717)2(233≠⨯+-⨯-⨯,所以,直线与平面相交,且因为772233=--=,∴直线与平面垂直. (3)直线的方向向量为:{}{}{}1,9,51,1,22,3,5=--⨯-, 0179354=⨯+⨯-⨯,所以直线与平面平行或者直线在平面上;取直线上的点)0,5,2(--M ,显然点在)0,5,2(--M 也在平面上(因为4(2)3(5)70⨯--⨯--=),所以,直线在平面上.(4)直线的方向向量为{}9,2,1-, 097)2(413≠⨯+-⨯-⨯∴直线与平面相交但不垂直.5、验证直线l :21111-=-=-z y x 与平面π:032=--+z y x 相交,并求出它的交点和交角. 解: 032111)1(2≠-=⨯-⨯+-⨯∴直线与平面相交.又直线的参数方程为:⎪⎩⎪⎨⎧+=+=-=t z t y tx 211设交点处对应的参数为0t ,∴03)21()1()(2000=-+-++-⨯t t t ∴10-=t ,从而交点为(1,0,-1). 又设直线l 与平面π的交角为θ,则:21662111)1(2sin =⨯⨯-⨯+-⨯=θ,∴6πθ=.6、确定m l ,的值,使: (1)直线13241zy x =+=-与平面0153=+-+z y lx 平行; (2)直线⎪⎩⎪⎨⎧-=--=+=135422t z t y t x 与平面076=-++z my lx 垂直.解:(1)欲使所给直线与平面平行,则须:015334=⨯-⨯+l 即1l =-. (2)欲使所给直线与平面垂直,则须:3642=-=m l ,所以:8,4-==m l .7、求下列各平面的方程: (1)通过点)1,0,2(-p ,且又通过直线32121-=-=+z y x 的平面; (2)通过直线115312-+=-+=-z y x 且与直线⎩⎨⎧=--+=---052032z y x z y x 平行的平面; (3)通过直线223221-=-+=-z y x 且与平面0523=--+z y x 垂直的平面;(4). 求过点(2,1,0)M 与直线2335x t y t z t =-⎧⎪=+⎨⎪=⎩垂直的平面方程.解:(1)因为所求的平面过点)1,0,2(-p 和)2,0,1(-'p ,且它平行于向量{}3,1,2-,所以要求的平面方程为:03331212=--+-z y x , 即015=-++z y x .(2)已知直线的方向向量为{}{}{}2,1,11,2,13,1,5--⨯-=,∴平面方程为:2311510315x y z -++--=,即3250x y z +--= (3)所求平面的法向量为{}{}{}13,8,11,2,32,3,2-=-⨯-,∴平面的方程为:0)2(13)2(8)1(=--+--z y x ,即09138=+--z y x .(4).所求平面的法向量为{}2,3,1,则平面的方程为:2(2)3(1)(0)0x y z -+-+-=, 即 2370x y z ++-=.8、求点(4,1,2)M 在平面1x y z ++=上的投影.解: 过点(4,1,2)M 作已知平面的垂线,垂线的方向向量就是已知平面的法向量(1,1,1),所以垂线方程为412111x y z ---==,此垂线与已知平面的交点即为所求投影.为了求投影,将垂线方程化为参数方程412x t y t z t =+⎧⎪=+⎨⎪=+⎩,代入平面方程求得2t =-,故投影为(2,1,0)-. 9、求点)1,3,2(-p 到直线⎩⎨⎧=++-=++-0172230322z y x z y x 的距离.解:直线的标准方程为:2251211-+==-z y x 所以p 到直线的距离 1534532025)2(1212392292421243222222===-++-+--+-=d .10、设0M 是直线L 外一点,M 是直线L 上一点,且直线的方向向量为s ,试证:点0M 到直线L 的距离为d =.证:设0M M 与L 的夹角为θ,一方面由于0sin d M M θ=;另一方面,00sin M M s M M s θ⨯=,所以d =.11、求通过平面0134=-+-z y x 和025=+-+z y x 的交线且满足下列条件之一的平面: (1)通过原点; (2)与y 轴平行;(3)与平面0352=-+-z y x 垂直. 解: (1)设所求的平面为:0)25()134(=+-++-+-z y x z y x λ 欲使平面通过原点,则须:021=+-λ,即21=λ,故所求的平面方程为 0)25()134(2=+-++-+-z y x z y x 即:0539=++z y x .(2)同(1)中所设,可求出51=λ.故所求的平面方程为 0)25()134(5=+-++-+-z y x z y x 即:031421=-+z x .(3)如(1)所设,欲使所求平面与平面0352=-+-z y x 垂直,则须:0)3(5)51()4(2=-++--+λλλ从而3=λ,所以所求平面方程为05147=++y x .12、求直线⎩⎨⎧=++-=--+0101z y x z y x 在平面0=++z y x 上的投影直线的方程.解:应用平面束的方法.设过直线⎩⎨⎧=++-=--+0101z y x z y x 的平面束方程为0)1()1(=++-+--+z y x z y x λ即01)1()1()1(=-++-+-++λλλλz y x这平面与已知平面0=++z y x 垂直的条件是01)1(1)1(1)1(=⋅+-+⋅-+⋅+λλλ,解之得1-=λ代入平面束方程中得投影平面方程为10y z --=,所以投影直线为⎩⎨⎧=++=--001z y x z y .13、请用异于本章第五节例7的方法来推导点到平面的距离公式.证:设),,(0000z y x P 是平面π:0+++=Ax By Cz D 外的一点,下面我们来求点0P 到平面π的距离. 过0P 作平面π的垂线L :000x x y y z z A B C---==,设L 与平面π的交点为(,,)P x y z ,则P 与0P 之间的距离即为所求.因为点(,,)P x y z 在L 上,所以000x x Aty y Bt z z Ct-=-=-=⎧⎪⎨⎪⎩,而(,,)P x y z 在平面π上,则000()()()0A x At B y Bt C z Ct D ++++++=000222Ax By Cz A B t DC ⇒=-+++++,故000222Ax By Cz Dd t A B C+++===++=.习 题 6—7飞机的速度:假设空气以每小时32公里的速度沿平行y 轴正向的方向流动,一架飞机在xoy 平面沿与x 轴正向成π6的方向飞行,若飞机相对于空气的速度是每小时840公里,问飞机相对于地面的速度是多少?解:如下图所示,设OA 为飞机相对于空气的速度,AB 为空气的流动速度,那么OB 就是飞机相对于地面的速度.840cos 840sin 4203420,3266OA i j i j AB j ππ=⋅+⋅=+=所以, 24203452,(420856.45OB i j OB =+=≈千米/小时.复习题A一 、判断正误:1、 若c b b a ⋅=⋅且≠0b ,则c a =; ( ⨯ )解析 c b b a ⋅-⋅=)(c a b -⋅=0时,不能判定=b 0或c a =.例如i a =,j b =,k c =,有⋅=⋅=0a b b c ,但c a ≠.2、 若c b b a ⨯=⨯且≠0b ,则c a =; ( ⨯ )解析 此结论不一定成立.例如i a =,j b =,)(j i c +-=,则k j i b a =⨯=⨯,k j i j c b =+-⨯=⨯)]([,c b b a ⨯=⨯,但c a ≠.3 、若0=⋅c a ,则=0a 或=0c ; ( ⨯ ) 解析 两个相互垂直的非零向量点积也为零.4、 a b b a ⨯-=⨯. ( √ ) 解析 这是叉积运算规律中的反交换律.二、选择题:1 、 当a 与b 满足( D )时,有b a b a +=+;(A)⊥a b ; (B)λ=a b (λ为常数); (C)a ∥b ; (D)⋅=a b a b .解析 只有当a 与b 方向相同时,才有a +b =a +b .(A)中a ,b 夹角不为0,(B),(C)中a ,b 方向可以相同,也可以相反.2、下列平面方程中,方程( C )过y 轴;图6-1 空所流动与飞机飞行速度的关系(A) 1=++z y x ; (B) 0=++z y x ; (C) 0=+z x ; (D) 1=+z x . 解析 平面方程0=+++D Cz By Ax 若过y 轴,则0==D B ,故选C .3 、在空间直角坐标系中,方程2221y x z --=所表示的曲面是( B );(A) 椭球面; (B) 椭圆抛物面; (C) 椭圆柱面; (D) 单叶双曲面.解析 对于曲面2221y x z --=,垂直于z 轴的平面截曲面是椭圆,垂直于x 轴或y 轴的平面截曲面是开口向下的抛物线,根据曲面的截痕法,可以判断曲面是椭圆抛物面.4、空间曲线⎩⎨⎧=-+=5,222z y x z 在xOy 面上的投影方程为( C );(A)722=+y x ; (B)⎩⎨⎧==+5722z y x ; (C) ⎩⎨⎧==+0722z y x ;(D)⎩⎨⎧=-+=0222z y x z解析 曲线⎩⎨⎧==+5722z y x 与xOy 平面平行,在xOy 面上的投影方程为⎩⎨⎧==+0722z y x .5 、直线11121-+==-z y x 与平面1=+-z y x 的位置关系是( B ). (A) 垂直; (B) 平行; (C) 夹角为π4; (D) 夹角为π4-.解析 直线的方向向量s ={2,1,-1},平面的法向量n ={1,-1,1},n s ⋅=2-1-1=0,所以,s ⊥n ,直线与平面平行.三、填空题:1、若2=b a ,π()2=a,b ,则=⨯b a 2 ,=⋅b a 0 ; 解 =⨯b a b a sin()a,b π22=2,=⋅b a b a cos()a,b π22=0.2、与平面062=-+-z y x 垂直的单位向量为 }2,1,1{66-±; 解 平面的法向量 n ={1,-1,2}与平面垂直,其单位向量为0n =411++=6,所以,与平面垂直的单位向量为}2,1,1{66-±.3、过点)2,1,3(--和)5,0,3(且平行于x 轴的平面方程为 057=-+z y ;解 已知平面平行于x 轴,则平面方程可设为 0=++D Cz By ,将点 (-3,1,-2)和(3,0,5)代入方程,有{20,50,B C D C D -+=+= ⇒ 7,51,5B D C D ⎧=-⎪⎨⎪=-⎩得 05157=+--D Dz Dy ,即 057=-+z y .4、过原点且垂直于平面022=+-z y 的直线为z yx -==20; 解 直线与平面垂直,则与平面的法向量 n ={0,2,-1}平行,取直线方向向量s =n ={0,2,-1},由于直线过原点,所以直线方程为z yx -==20 .5、曲线⎩⎨⎧=+=1,222z y x z 在xOy 平面上的投影曲线方程为 ⎩⎨⎧==+.0,1222z y x解: 投影柱面为 1222=+y x ,故 ⎩⎨⎧==+0,1222z y x 为空间曲线在xOy 平面上的投影曲线方程.四、解答题:1、 已知}1,2,1{-=a ,}2,1,1{=b ,计算(a) b a ⨯; (b) ()()-⋅+2a b a b ; (c) 2b a -;解: (a) b a ⨯=211121-kj i 1,3}5,{--=. (b) {2,4,2}{1,1,2}{1,5,0}2a b -=--=-,1,3}{2,{1,1,2}2,1}{1,-=+-=+b a , 所以()()-⋅+2a b a b 7}3,1,2{}0,5,1{=-⋅-=.(c) 1}3,{0,{1,1,2}2,1}{1,--=--=-b a ,所以2b a -10)19(2=+=.2、已知向量21P P 的始点为)5,2,2(1-P ,终点为)7,4,1(2-P ,试求:(1)向量21P P 的坐标表示; (2)向量21P P 的模;(3)向量21P P 的方向余弦; (4)与向量21P P 方向一致的单位向量.解: (1) }2,6,3{}57),2(4,21{21-=-----=P P ;74926)3(222==++-=;(3) 21P P 在z y x ,,三个坐标轴上的方向余弦分别为362cos ,cos ,cos 777αβγ=-==;(4)k j i k j i 7276737263)(21++-=++-==P P.3、设向量{}1,1,1=-a ,{}1,1,1=-b ,求与a 和b 都垂直的单位向量.解: 令{}1110,2,2111=⨯=-=-i j kc a b,01⎧==⎨⎩c c c ,故与a 、b都垂直的单位向量为0⎧±=±⎨⎩c .4、向量d垂直于向量]1,3,2[-=a和]3,2,1[-=b ,且与]1,1,2[-=c的数量积为6-,求向量d解: d垂直于a与b ,故d平行于b a⨯,存在数λ使()b a d⨯=λ⨯-=]1,3,2[λ]3,2,1[-]7,7,7[λλλ--=因6-=⋅c d,故6)7(1)7()1(72-=-⨯+-⨯-+⨯λλλ, 73-=λ]3,3,3[-=∴d.5、求满足下列条件的平面方程:(1)过三点)2,1,0(1P ,)1,2,1(2P 和)4,0,3(3P;(2)过x 轴且与平面025=++z y x 的夹角为π3. 解 (1)解1: 用三点式.所求平面的方程为0241003211201210=---------z y x ,即01345=+--z y x . 解2:}1,1,1{-=}2,1,3{-=,由题设知,所求平面的法向量为k j i kj in 452131113121--=--=⨯=P P P P , 又因为平面过点)2,1,0(1P ,所以所求平面方程为0)2(4)1(5)0(=-----z y x ,即01345=+--z y x .解3: 用下面的方法求出所求平面的法向量},,{C B A =n ,再根据点法式公式写出平面方程也可. 因为3121,P P P P ⊥⊥n n ,所以{0,320,A B C A B C +-=-+=解得A C A B 4,5-=-=,于是所求平面方程为0)2(4)1(5)0(=-----z A y A x A ,即 01345=+--z y x .(2)因所求平面过x 轴,故该平面的法向量},,{C B A =n 垂直于x 轴,n 在x 轴上的投影0=A ,又平面过原点,所以可设它的方程为0=+Cz By ,由题设可知0≠B (因为0=B 时,所求平面方程为0=Cz 又0≠C ,即0=z .这样它与已知平面025=++z y x 所夹锐角的余弦为π1cos 32=≠=,所以0≠B ),令C B C'=,则有0='+z C y ,由题设得 22222212)5(10121503cos ++'++⨯'+⨯+⨯=πC C , 解得3='C 或13C '=-,于是所求平面方程为03=+z y 或03=-z y .6、 一平面过直线⎩⎨⎧=+-=++04,05z x z y x 且与平面01284=+--z y x 垂直,求该平面方程;解法1: 直线⎩⎨⎧=+-=++04,05z x z y x 在平面上,令x =0,得 54-=y ,z =4,则(0,-54,4)为平面上的点.设所求平面的法向量为n =},,{C B A ,相交得到直线的两平面方程的法向量分别为 1n ={1,5,1},2n ={1,0,-1},则直线的方向向量s =1n ⨯2n =101151-kj i ={-5,2,-5},由于所求平面经过直线,故平面的法向量与直线的方向向量垂直,即⋅n s ={-5,2,-5}•},,{C B A =C B A 525-+-=0,因为所求平面与平面01284=+--z y x 垂直,则}8,4,1{},,{--⋅C B A =C B A 84--=0,解方程组{5250,480,A B C A B C -+=--= ⇒ 2,5,2A CBC =-⎧⎪⎨=-⎪⎩ 所求平面方程为 0)4()54(25)0(2=-++---z C y C x C ,即012254=+-+z y x .解法2: 用平面束(略)7、求既与两平面1:43x z π-=和2:251x y z π--=的交线平行,又过点(3,2,5)-的直线方程.解法1:{}11,0,4=-n ,{}22,1,5=--n ,{}124,3,1s =⨯=---n n ,从而根据点向式方程,所求直线方程为325431x y z +--==---,即325431x y z +--==. 解法2:设{},,s m n p =,因为1⊥s n ,所以40m p -=;又2⊥s n ,则250m n p --=,可解4,3m p n p ==,从而0p ≠.根据点向式方程,所求直线方程为32543x y z p p p +--==,即325431x y z +--==. 解法3:设平面3π过点(3,2,5)-,且平行于平面1π,则{}311,0,4==-n n 为3π的法向量,从而3π的方程为1(3)0(2)4(5)0x y z ⋅++⋅--⋅-=,即4230x z -+=.同理,过已知点且平行于平面2π的平面4π的方程为25330x y z --+=.故所求直线的方程为423025330x z x y z -+=⎧⎨--+=⎩.8、 一直线通过点)1,2,1(A ,且垂直于直线11231:+==-z y x L ,又和直线z y x ==相交,求该直线方程;解: 设所求直线的方向向量为{,,}m n p =s ,因垂直于L ,所以320m n p ++=;又因为直线过点)1,2,1(A ,则所求直线方程为 p z n y m x 121-=-=-,联立121,①,②320,③x y z m n p x y z m n p ---⎧==⎪⎨==⎪++=⎩由①,令λ=-=-=-p z n y m x 121,则有⎪⎩⎪⎨⎧+=+=+=,1,2,1p z n y m x λλλ代入方程②有{12,11,m n m p λλλλ+=++=+ 可得p m =,代入③解得p n 2-=, 因此,所求直线方程为112211-=--=-z y x .9、 指出下列方程表示的图形名称:(a) 14222=++z y x ;(b) z y x 222=+;(c) 22y x z +=;(d) 022=-y x ;(e) 122=-y x ; (f) ⎩⎨⎧=+=222z y x z .解: (a) 绕y 轴旋转的旋转椭球面.(b) 绕z 轴旋转的旋转抛物面. (c) 绕z 轴旋转的锥面. (d) 母线平行于z 轴的两垂直平面:y x =,y x -=. (e) 母线平行于z 轴的双曲柱面. (f) 旋转抛物面被平行于XOY 面的平面所截得到的圆,半径为2,圆心在(0,0,2)处.10、求曲面22z x y =+与222()z x y =-+所围立体在xOy 平面上的投影并作其图形.解: 将所给曲面方程联立消去z ,就得到两曲面交线C 的投影柱面的方程122=+y x ,所以柱面与xOy 平面的交线⎩⎨⎧==+'01:22z y x C 所围成的区域221+≤x y 即为曲面22z x y =+与222()z x y =-+所围立体在xOy 平面上的投影(图略).复习题B1、设4=a ,3=b ,()6π=a,b ,求以2+a b 和3-a b 为邻边的平行四边形的面积.解:(2)(3)326A =+⨯-=⨯-⨯+⨯-⨯a b a b a a a b b a b b325=-⨯-⨯=-⨯a b a b a b 15sin()543302=⋅=⨯⨯⨯=a b a,b .2、设(3)(75)+⊥-a b a b ,(4)(72)-⊥-a b a b ,求()a,b . 解: 由已知可得:(3)(75)0+⋅-=a b a b ,(4)(72)0-⋅-=a b a b 即 22715160-+⋅=a b a b ,2278300+-⋅=a b a b .这可看成是含三个变量a 、b 及⋅a b 的方程组,可将a 、b 都用⋅a b 表示,即==a b 1cos()22⋅⋅===⋅a b a b a,b a b a b ,()3π=a,b .3、求与}3,2,1{-=a 共线,且28=⋅b a 的向量b .解 由于b 与a 共线,所以可设}3,2,{λλλλ-==a b ,由28=⋅b a ,得28}3,2,{}3,2,1{=-⋅-λλλ, 即2894=++λλλ,所以2=λ,从而}6,4,2{-=b .4、 已知}0,1,1{},2,0,1{=-=b a ,求c ,使b c a c ⊥⊥,且6=c .解法1: 待定系数法.设},,{z y x =c ,则由题设知0,0=⋅=⋅b c a c 及6=c ,所以有①20②③6x z ⎧-=⎪=由①得2xz = ④,由②得x y -= ⑤,将④和⑤代入③得62)(222=⎪⎭⎫⎝⎛+-+x x x ,解得2,4,4±==±=z y x ,于是 }2,4,4{-=c 或}2,4,4{--=c .解法2: 利用向量的垂直平行条件,因为b c a c ⊥⊥,,所以c ∥b a ⨯.设λ是不为零的常数,则k j i k j i b a c λλλλλ+-=-=⨯=22011201)(,因为6=c ,所以6]1)2(2[2222=+-+λ,解得2±=λ,所以}2,4,4{-=c 或{4,4,2}=--c .解法3: 先求出与向量b a ⨯方向一致的单位向量,然后乘以6±.k j i kji b a +-=-=⨯22011201,31)2(2222=+-+=⨯b a ,故与b a ⨯方向一致的单位向量为}1,2,2{31-.于是}1,2,2{36-±=c ,即}2,4,4{-=c 或}2,4,4{--=c .5、求曲线222x y R x y z ⎧+=⎨++=⎩的参数式方程.解: 曲线参数式方程是把曲线上任一点(,,)P x y z 的坐标,,x y z 都用同一变量即参数表示出来,故可令cos ,sin x R t y R t ==,则(cos sin )z R t t =-+.6、求曲线22:2z L x y x⎧⎪=⎨+=⎪⎩xOy 面上及在zOx 面上的投影曲线的方程.解: 求L 在xOy 面上的投影的方程,即由L 的两个方程将z 消去,即得L 关于xOy 面的投影柱面的方程222x y x +=则L 在xOy 面上的投影曲线的方程为2220x y xz ⎧+=⎨=⎩. 同理求L 在zOx 面上的投影的方程,即由L 的两个方程消去y ,得L 关于zOx 面的投影柱面的方程z =L 在zOx面上的投影曲线方程为0z y ⎧=⎪⎨=⎪⎩.7、已知平面π过点0(1,0,1)M -和直线1211:201x y z L ---==,求平面π的方程. 解法1: 设平面π的法向量为n ,直线1L 的方向向量1(2,0,1)=s ,由题意可知1⊥n s ,(2,1,1)M 是直线1L 上的一点,则0(1,1,2)M M =在π上,所以0MM ⊥n ,故可取10MM =⨯n s (1,3,2)=--.则所求平面的点法式方程为1(1)3(0)2(1)0x y z ⋅-+⋅--⋅+=,即3230x y z +--=为所求平面方程.解法2: 设平面π的一般方程为0Ax By Cz D +++=,由题意可知,π过点0(1,0,1)M -,故有0A C D -+=, (1)在直线1L 上任取两点12(2,1,1),(4,1,2)M M ,将其代入平面方程,得20A B C D +++=, (2)420A B C D +++=, (3)由式(1)、(2)、(3)解得3,2,3B A C A D A ==-=-,故平面π的方程为3230x y z +--=.解法3: 设(),,M x y z 为π上任一点.由题意知向量0M M 、01M M 和1s 共面,其中()12,1,1M 为直线1L 上的点,1(2,0,1)=s 为直线1L 的方向向量.因此0011()0M M M M ⨯⋅=s ,故平面π的方程为1012110110201x y z --+--+=,即3230x y z +--=为所求平面方程.8、求一过原点的平面π,使它与平面0:π4830x y z -+-=成4π角,且垂直于平面1:π730x z ++=. 解: 由题意可设π的方程为0Ax By Cz ++=,其法向量为(,,)A B C =n ,平面0π的法向量为0(1,4,8)=-n ,平面1π的法向量为1(7,0,1)=n ,由题意得00||cos 4||||π⋅=⋅n n n n ,即=(1) 由10⋅=n n ,得70A C +=,将7C A =-代入(12=,解得20,B A =或10049B A =-,则所求平面π的方程为2070x y z +-= 或 491003430x y z --=.9、求过直线1L :0230x y z x y z ++=⎧⎨-+=⎩且平行于直线2L :23x y z ==的平面π的方程.解法1: 直线1L 的方向向量为1=s 111(4,1,3)213==---i j k,直线2L 的对称式方程为632x y z==,方向向量为2(6,3,2)=s ,依题意所求平面π的法向量1⊥n s 且2⊥n s ,故可取12=⨯n s s ,则413(7,26,18)632=--=-i j kn ,又因为1L 过原点,且1L 在平面π上,从而π也过原点,故所求平面π的方程为726180x y z -+=.解法2: 设所求平面π为 (23)0x y z x y z λ+++-+=,即(12)(1)(13)0x y z λλλ++-++=, 其法向量为(12,1,13)λλλ=+-+n ,由题意知2⊥n s ,故26(12)3(1)2(13)0λλλ⋅=++-++=n s ,得1115λ=-,则所求平面π的方程为726180x y z -+=.另外,容易验证230x y z -+=不是所求的平面方程.10、求过直线L :⎩⎨⎧=+-+=+-+0185017228z y x z y x 且与球面1222=++z y x 相切的平面方程解: 设所求平面为 ()018517228=+-+++-+z y x z y x λ,即 (15)(288)(2)170x y z λλλλ+++-+++=,由题意:球心)0,0,0(到它的距离为1,即1)2()828()51(17222=--+++++λλλλ解得:89250-=λ 或 2-=λ 所求平面为:42124164387=--z y x 或 543=-y x11、求直线L :11111--==-z y x 在平面π:012=-+-z y x 上投影直线0L 的方程,并求直线0L 绕y 轴旋转一周而成的曲面方程.解: 将直线L :11111--==-z y x 化为一般方程 ⎩⎨⎧=-+=--0101y z y x ,设过直线L 且与平面π垂直的平面方程为()011=-++--y z y x λ,则有02)1(1=+--λλ,即2λ=-,平面方程为0123=+--z y x ,这样直线0L 的方程⎩⎨⎧=-+-=+--0120123z y x z y x 把此方程化为:⎩⎨⎧--==)1(221y z yx ,因此直线0L 绕y 轴旋转一周而成的曲面方程为:22221(2)(1)2x z y y ⎛⎫+=+-- ⎪⎝⎭即 0124174222=-++-y z y x .12、求过点)1,0,3(-A 且平行于平面1π:3450x y z --+=,又与直线1:2x L =1111y z -+=-相交的直线L 的方程.解法1: 用点向式方程.因为直线L 平行于平面1π,故直线L 的方向向量},,{p n m =s 垂直于平面1π的法向量}1,4,3{--=n ,从而得043=--p n m ①,又直线1L 的方向向量为}1,1,2{-=s ,)1,1,0(-B 是直线1L 上一点,)1,0,3(-A 是直线L 上一点,根据题设:直线L 与直线1L 相交,所以1s,s 及AB 共面,因此1()2110312m n pAB ⨯⋅=-=-s s ,即0=-+-p n m ②,将①和②联立解得p n p m 4,5-=-=,由此得145p n m =-=-,于是所求直线方程为11453-=-=-+z y x .。
马原第六章 练习题

马原第六章练习题(总6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第六章社会主义的发展及其规律一、单选题1.科学社会主义的直接理论来源是( B )世纪欧洲空想社会主义思潮世纪初欧洲空想社会主义理论世纪法国唯物主义和无神论世纪德国古典哲学2.无产阶级革命和无产阶级专政的第一次尝试是( A )年巴黎工人起义和由此建立的巴黎公社世纪40年代英国宪章运动及法、德、意工人运动年俄国的“二月革命”年列宁领导的十月革命和由此建立的第一个无产阶级专政的国家政权3.无产阶级政党的组织原则是( C )A.民主制B.集中制C.民主集中制D.高度统一原则4.社会主义民主的本质是( D )A.公正B.平等C.共同富裕D.人民当家做主5.经济政治发展的不平衡是资本主义的绝对规律,由此得出结论:社会主义可能首先在少数或者甚至在单独一个资本主义国家内获得胜利。
提出这一著名论断的是( C )A.马克思B.恩格斯C.列宁D.斯大林6..社会主义实现由空想到科学发展的标志是( A )A.《共产党宣言》的发表B.“共产主义同盟”的建立C.空想社会主义理想的破灭D.无产阶级革命的胜利7.马克思说:“暴力是每一个孕育着新社会的旧社会的助产婆”,这说明( B ) A.暴力革命是无产阶级革命的唯一形式 B.暴力革命是无产阶级革命的主要形式 C.暴力革命与和平发展互相排斥 D.暴力革命与和平发展可以相互取代8. 科学社会主义之所以能够超越空想社会主义,是因为把争取社会主义的斗争建立在( A )。
A.科学的思想体系上B.社会发展客观规律的基础上C.批判空想社会主义上D.共产主义者同盟上9.社会主义社会发展生产力的根本目的是( C )。
A.建立多种所有制形式B.实行多种分配方式C.消灭剥削和消除两极分化,最终达到共同富裕 D.巩固共产党的领导10.科学社会主义创立的理论基础是(C)A.英国古典政治经济学 B.德国古典哲学C.唯物史观和剩余价值学说 D.空想社会主义学说11.社会主义政治制度的基本特征是坚持(C)A.马克思主义的指导 B.共产党的领导C.无产阶级专政 D.社会主义方向12.资本主义必然被社会主义所代替的主要依据是(D)A.现代无产阶级日益壮大和觉醒B.个别企业有组织的生产与整个社会生产无政府状态之间的矛盾C.无产阶级与资产阶级斗争的尖锐化D.生产的社会化与资本主义私人占有制之间的矛盾13.无产阶级革命之所以能取得胜利,其根本保证是(A)A.无产阶级政党的正确领导 B.取得国家政权C.人民群众的革命积极性的极大提高 D.建立革命统一战线14.无产阶级反对资产阶级的斗争中,最具决定意义的是(D)A.理论斗争 B.议会斗争 C.经济斗争 D.政治斗争15.无产阶级革命的发生,归根结底是( A )A.由生产力发展水平决定的B.由生产关系的性质决定的C.由被统治阶级的意愿决定的D.由统治阶级的倒行逆施决定的16.科学社会主义的核心内容是( A )A.无产阶级专政和社会主义民主B.唯物史观C.无产阶级专政D.剩余价值学说17.下列观点中,错误的是( D )A.国际共产主义运动当今正处在低潮时期B.社会主义必然取代资本主义C.社会主义取代资本主义是一个长期的曲折的过程D.社会主义在若干国家的严重挫折改变了资本主义必然灭亡的命运18.资本主义必然被社会主义所代替的主要依据是( D )A.现代无产阶级日益壮大和觉醒B.个别企业有组织的生产与整个社会生产无政府状态之间的矛盾C.无产阶级与资产阶级斗争的尖锐化D.生产的社会化与资本主义私人占有制之间的矛盾19.列宁对社会主义革命学说的重大贡献是( C )A.提出了新经济政策 B.提出了战时共产主义政策C.提出了社会主义革命将首先在一国或数国取得胜利的理论D.提出了利用国家资本主义过渡社会主义的理论20.经济文化相对落后的国家可以先于发达资本主义国家进人社会主义,其根本原因是( A )A.革命的客观形势和条件所决定的B.经济文化相对落后的国家具有较高的精神文明C.它是以高度社会化的资本主义大生产作为社会主义革命的物质前提的D.社会主义生产关系可以在旧社会的内部孕育生长起来21.马克思所说未来社会的第一阶段是指( D ) A.社会主义革命时期B.向社会主义过渡时期C.社会主义初级阶段D.社会主义社会22.列宁提出社会主义可能在一国或数国首先胜利的理论依据是( B )A.资本主义必须灭亡B.帝国主义时代资本主义政治经济发展不平衡的规律C.资本主义国家无产阶级与资产阶级的规律D.生产关系必须适应生产力发展要求的规律23.科学社会主义创立的理论依据是( C )A.空想社会主义学说B.德国古典哲学C.唯物史观和剩余价值学说D.英国古典政治经济学24.社会主义各个阶段的划分最终应以( A )A. 生产力的发展为标准 B.生产关系为标准C.生产资料的公有制程度为标准 D. 以阶级斗争为标准25.社会主义从理论到实践的飞跃,具体途径是( C )A.通过改革和革命实现的B.通过对人民群众的教育和灌输实现的C.实践D.通过无产阶级革命实现的二、多项选择题世纪空想社会主义代表人物是( ACE )A.圣西门 B.黑格尔 C.欧文 D.费尔巴哈 E.傅立叶2.经济文化相对落后的国家社会主义建设的艰巨性和长期性,这是由于( ABCE )A.生产力发展状况的制约 B.经济基础和上层建筑的制约C.国际环境的严峻挑战 D.社会主义还只是一种理想E.对社会主义道路探索和对社会主义建设规律的认识是一个长期的艰苦的过程3.社会主义的主要特征有( ABCD )A.剥削制度的消灭和在生产资料所有制上坚持以公有制为主体B.按劳分配C.大力发展社会主义市场经济D.实行无产阶级专政4.经济文化相对落后的国家建设社会主义之所以是长期和艰巨的,是因为( ABCD )A..商品经济不发达,生产力落后B.封建主义传统长,缺乏近代民主的传统C..社会主义国家从诞生之日起,就处在资本主义世界的包围之中,受到资本主义列强的遏制和扼杀D.马克思主义执政党对社会主发展道路和建设规律的探索是一个过程5.我国社会主义初级阶段的含义是( BC )A.我国还处在社会主义过渡的新时期B.我国已经是社会主义社会C.我国的社会主义还处在初级阶段D.我国正处于向共产主义过渡的新时期6.社会主义发展史上的两次飞跃是(AD )A.社会主义由空想到科学的发展B.早期空想社会主义到空想平均共产主义的发展C.空想平均共产主义到批判的空想社会主义的发展D.社会主义由理论到实践7.邓小平把社会主义的本质概括为( ABD )A.解放生产力,发展生产力B.消灭剥削,消除两极分化C.允许一部分人先富起来D.最终达到该天赋有8.社会主义的国家制度采取( AB )A.人民当家做主享有充分广泛民主权利的国体B.民主共和国形式的政体C.人民当家做主享有充分广泛民主权利的政体D.民主共和国形式的国体9.要探索符合本国国情的社会主义发展道路,就要( ABC )A.以马克思主义理论为指导B.从本国国情出发C.吸收一切人类文明成果D.以发达国家为样板10.马克思主义政党的劳动核心作用主要体现在( ABC )A.社会主义革命中B.社会主义建设中C.改革开放事业中D.自发的群众运动中11.社会主义发展道路多样性的原因( ABC )A.各个国家的生产力和社会发展状况有不同的特点B.历史文化传统的差异性C.时代和实践是不断发展的D.领导人的领导风格和意愿不同12.从资本主义社会向社会主义社会过渡必须具备的条件是( ABCD )A.有无产阶级政党的领导 B.夺取了资产阶级的国家政权C.实行生产资料公有制 D.建立无产阶级政权的政府E.生产力高度发达13.从资本主义社会向社会主义社会过渡必须具备的条件是( ABD )A.有无产阶级政党的领导 B.夺取了资产阶级的国家政权C.实行生产资料公有制 D.建立无产阶级政权的政府E.生产力高度发达14.东欧剧变、苏联解体给我们的深刻教训有( ABCD )A.必须坚持社会主义道路B.必须坚持共产党的领导C.必须坚持马克思主义的主导地位D.必须坚决抵制各种资本主义思想的侵袭15.下列各项属于实现社会主义自我发展与完善的成功经验的有( ABC )A.以发展着的马克思主义理论为指导B.选择正确的改革方式与步骤C.妥善处理改革、发展与稳定的关系D.完全按照发达国家模式发展16.下列各项关于空想社会主义理论的说法正确的有( ABCD )A.是一种批评、否定资本主义的思潮B.反映、代表了早期无产阶级意识和利益C.看到了资本主义必然灭亡的命运D.只揭示了资本主义必然灭亡的经济根源17.空想社会主义不是成熟的社会革命的理论,是因为( BCD )A.没有彻底否定资本主义制度B.没有揭示资本主义必然灭亡的经济根源C.没有看到埋葬资本主义的力量D.没有找到实现理想社会的现实道路18.社会主义革命的实践超越了马克思、恩格斯当年的预想,不是在生产社会化程度最高的资本主义国家首先实现,而是在经济文化相对落后的国家首先取得胜利。
No3.第6章习题及答案

2) 对于 FH→E,由于有 F→E,则为多余的:
-4-
第六章习题答案
5
F2={ E→G,G→E,F→E,F→G,H→E,H→G }
3) 在 F2 中的 F→E 和 F→G 以及 H→E 和 H→G 之一是多余的,则为:
R 属于______ NF。
答案:AB,2
-1-
第六章习题答案
2
二、选择题:
1.在二元关系模式 R(U,F)中,X、Y 都是单一属性,如果 X→Y,则 R 一定可以达到( )
A.2NF B. 3NF C. BCNF D. 4NF
答案:D
2.在关系模式 )
F3={ E→G,G→E,F→G, H→G }
F3={ E→G,G→E,F→G, H→E }
F3={ E→G,G→E,F→E, H→E }
F3={ E→G,G→E,F→E, H→G }
3).设有关系模式 R(A,B,C,D),其上的函数依赖集:F={A→C,C→A,B→AC,D→AC},试计算: A)(AD)+; B)F的最小等价依赖集F‘; C)R 的关键字; 答案: 1) 令X={AD},X(0)={AD},X(1)={ACD},X(2)={ACD},故(AD)+={ACD}。 2)
第六章习题答案
1
《数据库系统概论》第 6 章习题答案
题型:
1、填空题: 10 题 2、选择题: 10 题 2、综合题: 3 题
一、填空
1. 与 1NF 相比,2NF 消除了非主属性对候选关键字的_________。
答案:部分函数依赖
2.与 2NF 相比,3NF 消除了非主属性对候选关键字的_________。
第六章 习题

一、选择题(易)1 调频信号的频偏量与 。
( )A .调制信号的频率有关B .调制信号的振幅有关C .调制信号的相位有关 答案:B(中)2 调相信号的最大相移量与 。
( )A .调制信号的频率有关B .调制信号的振幅成正比C .调制信号的相位有关 答案:B(中)3 调频信号必须工作在 。
( )A .中波波段B .短波波段C .超短波波段 答案:C(易)4 调频信号解调是 。
( )A .用检波器B .先检波后鉴频C .先鉴频后检波 答案:C(中)5 对分频器描述正确的是 。
( )A .分频器是振荡器的一种,为了实现分频,工作状态应当是非常不稳定的B .分频器是振荡器的一种,为了实现分频,工作状态应当是非常稳定的C .都不对 答案:C(中)6 下面的说法 是正确的。
( )A .PM 波的相位随u Ω而变,但频率不变化B .FM 波的相位随u Ω而变,但频率不变化C .PM 波与FM 波的频率都变化,但变化规律不相同 答案:C(易)7 调频波的灵敏度为 。
( )A .ωΩ B .U ωΩC .ω 答案:B(中)8 若载波c cm c =cos u U t ω,调制信号=cos u U t ΩΩΩ,则FM 波的最大ω = 。
( )A .f m ΩB .f k U ΩC .f k U ΩΩ 答案:A(中)9 若载波c cm c =cos u U t ω,调制信号=cos u U t ΩΩΩ,则FM 波的表达式为 。
( )A .()cos(sin )FM cm c f u t U t m t ω=+ΩB .()cos(-sin )FM cm c f u t U t m t ω=ΩC .()cos(-cos )FM cm c f u t U t m t ω=Ω 答案:C(中)10 若载波c cm c =cos u U t ω,调制信号=cos u U t ΩΩΩ,则PM 波的表达式为 。
( )A .()cos(sin )PM cm c P u t U t m t ω=+ΩB .p ()cos(-sin )PM cm c u t U t m t ω=ΩC .p ()cos(-cos )PM cm c u t U t m t ω=Ω 答案:A(中)11 若调频发射机和调幅发射机采用同一型号的功放管,则调频机的实际输出功率比调幅机的实际输出功率 。
第六章 习题

课后习题一、判断题1.固定股利支付率政策,能使股利与公司盈余紧密结合,以体现多盈多分、少盈少分的原则。
()2.成长中的企业,一般采用低股利政策;处于经营收缩期的企业,则可能采用高股利政策。
()3.由于发放股票股利后,增加了市场流通的股票股数,从而使每位股东所持股票的市场价值总额增加。
()4.一个新股东要想取得本期股利,必须在除权日之前购入股票,否则即使持有股票也无权领取股利。
()5.资本公积和盈余公积均可用于转增资本和弥补亏损。
()6.财务风险大、资金结构不合理的企业追加投资时,应尽可能从企业内部融资,以调整资金结构降低风险。
()7.企业发放股票股利将使同期每股盈余下降。
()8.股份有限公司利润分配的一个主要特点是,提取任意盈余公积在支付优先股股利之后但在分配普通股股利之前。
()9.股东为防止控制权稀释,往往希望公司提高股利支付率。
()10.企业不能用资本发放股利,但可以在没有累计盈余的情况下提取盈余公积金。
()11.只要公司拥有足够现金,就可以发放现金股利。
()12.弥补亏损可由税前利润、税后利润和盈余公积弥补。
()13.按照利润分配的积累优先原则,企业税后利润分配,不论什么条件下均应优先提取法定公积金。
()14.如果发放股票股利的比例大于股价下降的比例,股东就可得到收益。
()15.股份公司的股利分配政策遵循“无利不分”的原则,公司当年无盈利就不能支付股利。
()二、单项选择题1.极易造成股利的支付与企业盈余相脱节的股利政策是()。
A.固定股利政策B.剩余股利政策C.固定股利支付率政策D. 正常股利加额外股利政策2.上市公司提取法定盈余公积达到注册资本的()时,可不再提取法定盈余公积金。
A.15%B.25%C.40%D.50%3.公司为了稀释流通在外的本公司股票价格,对股东支付股利的形式采用()。
A.现金股利B.财产股利C.负债股利D.股票股利4.体现“多盈多分”、“少盈少分”的股利政策是()。
第六章 习题及答案

A、运动战
B、阵地战
C、地雷战
D、敌后游击
战争
7、1938年9月至11月,中国共产党在延安举行了扩大的六届六中全会,
在这次全会上,毛泽东明确地提出了( )这个命题。
A、抗日民主根据地建设
B、马克思主义中国化
C、中国共产党自身建设
D、抗日民族统一战线
9、
8、1941年5月,毛泽东做了( )的报告,整风运动首先在党的高
五、论述 1、为什么说中国的抗日战争是神圣的民族解放战争? 2、为什么说中国共产党是中国人民抗日战争的中流砥柱? 3、怎样评价国民党政府在抗日战争中执行的路线和正面战场的地位与 作用? 4、为什么说中国人民抗日战争是弱国战胜强国的范例?其基本经验是什 么? 论述题答案: 1、为什么说中国的抗日战争是神圣的民族解放战争?
2、国民党五届三中全会是第二次国共合作初步形成的标志。
3、抗战初期,国民党正面战场大溃退的主要原因在于它实行了消极抗
日积极反共的方针。
4、土地革命是民主革命的主要内容,抗日战争是民主革命的重要时
期,因此抗战时期也必须开展土地革命,没收地主阶级的土地,分给无
地或少地的农民。
5、抗战爆发后,英美政府采取了坚决支援中国抗战的立场。
B、《中国革命和中国共
产党》
C、《新民主主义论》
D、《改造我们的学
习》Βιβλιοθήκη E、《论持久战》9、中国人民的抗日战争得到了世界许多国家及其人民的支持和援助,
它们有( )
A、苏联
B、美国
C、英国
D、加拿大
E、
法国
10、抗日战争胜利的基本经验有(
)
A、民族团结是力量的源泉
B、民族精神是奋进的动力
第六章 课后练习答案

第六章具体经济业务的核算课后习题答案习题一(一)计算题1、目的:练习所有者权益各项目的构成及相互关系的确定。
资料:利和股份公司所属A公司200×年年初所有者权益总额为2 318 000元,年内接受某投资人的实物投资800 000元,接受现金投资260 000元,用资本公积金转增资本120 000元。
要求:计算年末公司的所有者权益总额是多少?解答:期末的所有者权益= 期初的所有者权益+ 本期增加的所有者权益- 期末所有者权益。
利和股份公司所属A公司年末的所有者权益= 2 318 000 +(800 000 + 260 000)= 3 378 000(元)2、目的:练习权责发生制与收付实现制假设下企业损益额的确定。
资料:利和股份公司200×年6月发生下列业务:(1)销售商品520 000元,其中400 000元当即收款,存入银行;另120 000元尚未收到。
(2)收到上个月提供劳务的款项100 000元存入银行。
(3)用银行存款支付本月的水电费7 200元。
(4)用现金30 000元预付下半年的房租。
(5)用银行存款6 000元支付本季度银行借款利息(其中本月2 000元)。
(6)本月提供劳务获得收入48 000元,款项未收到。
(7)按照合同规定预收客户的订货款200 000元,存入银行。
(8)本月负担年初已付预收款的产品本月销售,价款280 000元。
(9)本月负担的修理费5 000元(款项在下个月支付)。
要求:分别按收付实现制和权责发生制计算公司本月的收入、费用和利润各是多少,并对两种原则下确定的经营成果进行简要说明。
根据题意做如下的解答:(1)收付实现制:收入= 400 000 + 100 000 + 200 000 = 700 000(元)费用= 7 200 + 30 000 + 6 000 = 43 200(元)利润= 700 000 – 43 200 = 656 800(元)(2)权责发生制:收入= 520 000 +48 000 + 280 000 = 848 000(元)费用= 7 200 + 2 000 + 5 000 = 14 200(元)利润= 848 000 – 14 200 = 833 800(元)(二)业务题1.目的:练习有关资金筹集业务的核算。
大学物理第六章课后习题答案

第六章 静电场中的导体与电介质 6 -1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近,则导体B 的电势将( )(A ) 升高 (B ) 降低 (C ) 不会发生变化 (D ) 无法确定 分析与解 不带电的导体B 相对无穷远处为零电势。
由于带正电的带电体A 移到不带电的导体B 附近时,在导体B 的近端感应负电荷;在远端感应正电荷,不带电导体的电势将高于无穷远处,因而正确答案为(A )。
6 -2 将一带负电的物体M 靠近一不带电的导体N ,在N 的左端感应出正电荷,右端感应出负电荷。
若将导体N 的左端接地(如图所示),则( )(A ) N 上的负电荷入地 (B )N 上的正电荷入地(C ) N 上的所有电荷入地 (D )N 上所有的感应电荷入地分析与解 导体N 接地表明导体N 为零电势,即与无穷远处等电势,这与导体N 在哪一端接地无关。
因而正确答案为(A )。
6 -3 如图所示将一个电量为q 的点电荷放在一个半径为R 的不带电的导体球附近,点电荷距导体球球心为d ,参见附图。
设无穷远处为零电势,则在导体球球心O 点有( )(A )d εq V E 0π4,0== (B )dεq V d εq E 020π4,π4== (C )0,0==V E(D )R εq V d εq E 020π4,π4==分析与解 达到静电平衡时导体内处处各点电场强度为零。
点电荷q 在导 体球表面感应等量异号的感应电荷±q′,导体球表面的感应电荷±q′在球心O 点激发的电势为零,O 点的电势等于点电荷q 在该处激发的电势。
因而正确答案为(A )。
6 -4 根据电介质中的高斯定理,在电介质中电位移矢量沿任意一个闭合曲面的积分等于这个曲面所包围自由电荷的代数和。
下列推论正确的是( )(A ) 若电位移矢量沿任意一个闭合曲面的积分等于零,曲面内一定没有自由电荷(B ) 若电位移矢量沿任意一个闭合曲面的积分等于零,曲面内电荷的代数和一定等于零(C ) 若电位移矢量沿任意一个闭合曲面的积分不等于零,曲面内一定有极化电荷(D ) 介质中的高斯定律表明电位移矢量仅仅与自由电荷的分布有关 (E ) 介质中的电位移矢量与自由电荷和极化电荷的分布有关分析与解 电位移矢量沿任意一个闭合曲面的通量积分等于零,表明曲面 内自由电荷的代数和等于零;由于电介质会改变自由电荷的空间分布,介质中的电位移矢量与自由电荷与位移电荷的分布有关。
第六章 固定资产习题

第六章固定资产习题一、名词解释1.固定资产 2.原始价值 3.净值 4.固定资产净残值 5.固定资产折旧 6.双倍余额递减法 7.融资租赁二、单项选择题1.在建工程发生减值应计入()。
A.在建工程成本 B.管理费用 C.营业外支出 D.长期待摊费用2.某企业购入一台需要安装的设备,取得的增值税专用发票上注明的设备买价为60 000元,增值税款为10 200元,支付的运输费为1 200元。
设备安装时领用工程用材料物资价值1 500元,购进该批材料物资时支付的增值税额为255元,设备安装时支付有关人员薪酬2 500元,该项固定资产的成本为()。
A.60 000元 B.62 700元 C.65 200元 D.75 655元3.企业采用出包方式购建固定资产,按合同规定预付的工程款,应通过( )账户核算.A.预付账款B.应付账款C.固定资产D.在建工程4.生产经营期间固定资产报废清理的净损失应计入( ).A.营业外支出B.管理费用C.资本公积D.长期待摊费用5.对于建造固定资产的借款利息,在固定资产达到预定可使用状态之前发生的,应借记( )科目.A.管理费用B.财务费用C.在建工程D.固定资产6.某企业对生产线进行扩建。
该生产线原价为1000万元,已提折旧300万元.扩建生产线时发生扩建支出800万元,同时扩建时处理废料发生变价收入50万元。
该生产线新的原价应为( )万元.A.1750 B.1800 C.1500 D.14507.企业对固定资产计提减值准备,应( ).A.按单项资产计提B.按资产类别计提C.按全部资产计提D.企业根据实际情况自行决定8.企业对某固定资产进行扩建,该固定资产原价为200000元,已提折旧36000元,扩建时发生支出90000元,同时在扩建时发生残料变价收入4000元,该固定资产的原价应为( )元.A.164000B.200000C.250000D.2860009.融资租入的固定资产( ).A.由出租方计提折旧B.由承租方计提折旧C.由租赁双方协商确定哪一方计提折旧D.双方均需计提折旧10.以非货币性交易换入的固定资产,其入账价值按( )确定.A.固定资产换出方的账面价值B.同类或类似固定资产的市场价格C.双方协议的价值D.固定资产换入方换出资产的账面价值加上应支付的相关税费11.企业有设备一台,原价100000元,预计净残值4000元,预计可使用年限5年.按双倍余额递减法计提折旧,则第2年应计提折旧为( )元.A.19200B.20000C.24000D.2464012.企业有设备一台,原价100000元,预计净残值4000元,预计可使用年限5年.按年数总和法计提折旧,则第2年应计提折旧为( )元.A.18133 B.19200 C.25600 D.2666713.企业融资租赁的固定资产占企业资产总额比例大于30℅的,应按租赁开始日租赁资产的( )作为租入资产的入账价值.A.原账面价值B.最低租赁付款额C.最低租赁付款额的现值D.原账面价值与最低租赁付款额的现值两者中较低者三、多项选择题1.下列属于固定资产的有()。
近代史第六章 习题(含答案)

第六章中华民族的抗日战争重要知识点1.日本发动灭亡中国的侵略战争2.中国人民奋起抗击日本侵略者3.抗日战争的正面战场4.抗日战争的中流砥柱5.抗日战争的胜利及其意义练习题一、选择题(一)单选题1.毛泽东明确地提出“马克思主义的中国化”这个命题是在中国共产党的( )A.二大B.七大C.六届六中全会D.八七会议2.近代以来中国第一次取得反侵略完全胜利的战争是()A.中法战争B.甲午战争C.抗日战争D.抗美援朝战争3.全国抗战爆发后,国民党正面战场取得的第一个大的胜利是()A.平型关战役B.枣宜战役C.豫湘桂战役D.台儿庄战役4.全国抗战爆发后,共产党领导的敌后战场取得的第一个大的胜利是()A.平型关伏击战B.台儿庄战役C.百团大战D.淞沪会战5.1927年日本召开“东方会议”,制定了()A.《对华政策纲要》B.《昭和十二年度对华作战计划》C.《反共产国际协定》D.《大陆政策》6.抗日战争进入相持阶段的时间是()A.1937年7月B.1938年5月C.1938年10月D.1941年12月7.1936年,东北各抗日武装统一为()A.东北抗日联军B.东北义勇军C.东北人民革命军D.抗日游击队8.抗日战争进入相持阶段后,日本帝国主义对国民党采取的政策是()A.军事打击为主,政治诱降为辅B.政治诱降为主,军事打击为辅C.军事打击和政治诱降齐头并进D.政治诱降取代军事进攻9.1939年1月,国民党确定“防共、限共、溶共、反共”方针的会议是()A.国民党五届三中全会B.国民党五届五中全会C.国民党五届六中全会D.国民党临时全国代表大会10.日本开始实施变中国为其独占殖民地的事件是()A.“九一八”事变B.华北事变C.皇姑屯事变D.卢沟桥事变11.确立毛泽东思想为全党的指导思想的会议是()A.遵义会议B.瓦窑堡会议C.洛川会议D.中共七大12.面对日军的大举侵略,蒋介石在1931年7月的方针是()A.“绝对不抵抗”B.“以华制华”C.“自强之术,必先练兵”D.“攘外必先安内”13.延安整风运动的最主要任务是()A.反对主观主义以整顿学风B.反对宗派主义以整顿党风C.反对党八股以整顿文风D.反对官僚主义以整顿作风14.1941年中共中央批准颁布的、全面体现党关于根据地建设基本方针的是()A.《论持久战》B.《关于若干历史问题的决议》C.《陕甘宁边区施政纲领》D.《停战议和一致抗日通电》15.中国人民抗日战争取得完全胜利的标志是()A.1945年8月14日,日本政府表示接受波茨坦公告B.1945年8月15日,日本天皇发表终战诏书C.1945年9月2日,日本向同盟国投降签字D.1945年10月25日,中国收回被日本占领的台湾及澎湖列岛16.标志以国共合作为基础的抗日民族统一战线正式形成的是()A.西安事变的和平解决B.国民党五届三中全会确定实行联共政策C.国民党公布了合作宣言和蒋介石发表承认中共合法地位的谈话D.7月17日,周恩来,秦邦宪等在庐山同蒋介石、张冲等进行谈判17.毛泽东在《论持久战》中分析交战的中日双方存在着相互矛盾的特点是()A.敌强我弱;敌退步我进步;敌小国我大国;敌寡助我多助B.抗日战争是持久战,最后胜利是中国的C.战争要经过战略防御、战略相持、战略反攻D.中国是正义战争,日本是侵略战争18.在新民主主义革命时期,曾以“团结的大会,胜利的大会”载入中国共产党史册的一次具有最重要意义的会议是()A.瓦窑堡会议B.六届六中全会C.党的“七大”D.洛川会议19.抗日战争时期,中国共产党解决农民问题的基本政策是()A.土地国有B.没收地主土地C.减租减息D.按人口平均分配土地20.抗日战争时期,国民党第二次反共高潮达到顶点的标志是()A.晋西事变B.陇东事变C.平江惨案D.皖南事变21.毛泽东比较完整阐明新民主主义基本理论、纲领和政策的著作是()A.《论反对日本帝国主义的策略》B.《新民主主义论》C.《中国共产党在民族战争中的地位》D.《抗日游击战争的战略问题》22.下列关于抗战历史意义的表述,不恰当的是()A.是中国人民近百年来第一次取得的反对帝国主义侵略斗争的完全胜利B.增强了全国人民的自尊心和自信心C.是世界反法西斯战争的重要组成部分D.结束了中国半殖民地半封建社会的历史23.中国共产党领导的民主政权实行“三三制”原则是()A.解放战争时期B.抗日战争时期C.土地革命时期D.大革命时期24.最早为中国抗日战争提供援助的国家是()A美国B英国C法国D苏联25.1938年5月,毛泽东发表的论述抗日战争发展规律的著作是()A.《论反对日本帝国主义的策略》B.《论持久战》C.《中国共产党在民族战争中的地位》D.《抗日游击战争的战略问题》26.标志着中国人民抗日救亡运动新高潮的到来的是()A.第十九路军抗战B.卢沟桥抗战C.华北事变D.一二九运动27.中国共产党内反复出现“左”、右倾错误的思想认识根源是()A.经验主义B.宗派主义C.官僚主义D.主观主义28.抗战后期,国民党军队遭到大溃败的战役是()A.长沙会战B.豫湘桂战役C.淞沪会战D.武汉会战29.1937年8月,中国共产党制定《抗日救国十大纲领》的会议是()A.瓦窑堡会议B.中共七大C.洛川会议D.中共扩大的六届六中全会30.中国共产党在抗日民族统一战线中必须坚持独立自主原则的实质是()A.力争中国共产党对抗日战争的领导权B.扩充自己的军事实力C.防止国民党顽固派的反共政策D.独自抗击日本侵略者参考答案1.C2.C3.D4.A5.A6.C7.A8.B9.B 10.A 11.D 12.D 13.A 14.C 15.D 16.C 17.A 18.C 19.C 20.D 21.B 22.D 23.B 24.D 25.B 26.D27.D 28.B 29.C 30.A(二)多选题1.1938年9月至11月,中国共产党在延安举行的扩大的六届六中全会,会议纠正了王明的右倾错误是()A.一切经过统一战线B.轻视共产党领导的游击战争C.关门主义D.一切服从统一战线2.延安整风运动是一场伟大的思想解放运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章
思考题
1、考虑伺服阀的动态时,如何用频率法分析系统的动态特性?
2、有哪些因素影响系统的稳态误差?
3、在电液伺服系统中为什么要增大电气部分的增益,减小液压部分的增益?
4、开环增益、穿越频率、系统频宽之间有什么关系?
5、未加校正的液压伺服系统有什么特点?
6、为什么电液伺服系统一般都要加校正装置,在电液位置伺服系统中加滞后校正、速度与加速度校正、压力反馈和动压反馈校正的主要目的是什么?
7、电液速度控制系统为什么一定要加校正,加滞后校正和加积分校正有什么不同?
8、在力控制系统中负载刚度对系统特性有何影响?影响了哪些参数?
9、力控制系统和位置控制系统对伺服阀的要求有什么不同?为什么?
习题
1、如下图所示液压位置伺服系统,已知:
mA s m K q ⋅⨯=-/102036,
rad m D m /10536-⨯=,rad m n /1003.02-⨯=,m V K f /50=,s rad h /100=ω,225.0=h ξ。
求
1)系统临界稳定状态时的放大器增益a K 多少?
2)幅值裕量为dB 6时的a K 为多少?
3)系统作s m /1022-⨯等速运动时的位置误差为多少?伺服阀零漂mA I d 6.0=∆时引起的静差
为多少?
图1 电液位置伺服系统
2、有一稳定的电液位置伺服系统,其速度放大系数s K v /120
=,为了保证稳态精度的要求需将速度放大系数提高到s /1100,求滞后校正网络的传递函数。
3、有一振动台,其方块图如下图所示。
已知系统参数为:s rad h /140=ω,2.0=h ξ,
A s m K sv ⋅⨯=-/10432,V A K a /1012-⨯=,m V K f /102.12⨯=,22101m A p -⨯=。
求
1)、不加加速度反馈校正时的系统增益裕量g K 和闭环频宽b ω。
2)、将系统开环阻尼比提高到3.0=h ξ的加速度反馈系数fa K 和系统增益裕量g K 和闭环频宽b ω。
液压振动台方块图
4、有一速度控制系统,其原理方块图如下图所示。
已有系统参数为:电液伺服阀固有频率s rad sv /340=ω,阻尼比7.0=sv ξ,流量增益A s m K sv ⋅⨯=-/105.332,液压固有频率s rad h /183=ω,阻尼比2.0=h ξ,测速机增益rad s V K fv /19.0⋅=,液压马达排量rad m D m /1063.136-⨯=。
求稳定裕量dB K g 6=,ο87=γ时积分放大器增益为多少?
速度控制系统方块原理图。
