密置层原子堆积模型
最紧密堆积模型堆积密度
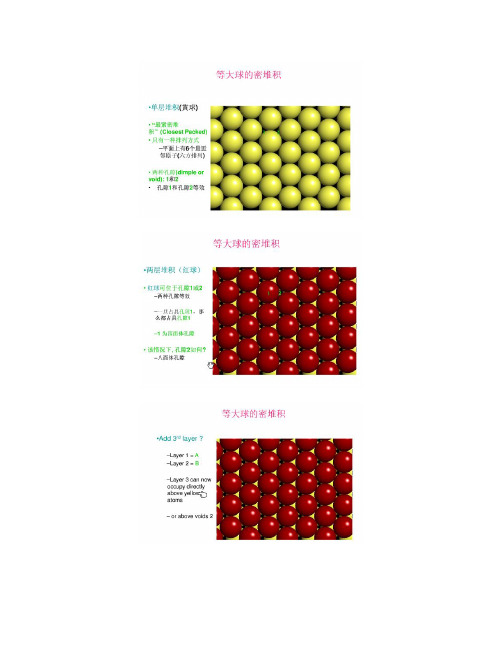
六方紧密堆积等大球体密置层堆积的两种基本型式之一。
其圆球的配位数为12,空间利用率为74.05%,晶胞内原子数为2,密置层按两层重复,即ABABAB……的方式重复堆积,其第三层的球心投影位置与第一层的重复,第四层与第二层重复,其余依此类推。
由于在这种堆积中可以划分出六方原始格子,故称为六方最密堆积。
其密置层平行于{0001}。
镁、锇、锌等的晶体结构即属此种堆积,故又称为镁型。
六方(最密)堆积空间利用率的证明晶胞参数a=b ,c=2/3 倍√6 倍a,α =β=90度γ=120度即一四棱柱,底面是以a为边长,一内角120度的菱形,高是c。
空间利用率74.05%,和立方面心最密的利用率一样。
证明 1 每个晶胞里有2个球,边长0.5a2 c是以a为边长的证四面体的高的2倍由此得出空间利用率74.05%实验5 14种布拉维格子和球体紧密堆积一、一、实验目的:加深对14种布拉维格子和球体紧密堆积原理的理解。
二、基本原理1. 布拉维格子只在单位平行六面体的八个角顶上分布有结点的空间格子,称为原始格子(Primitive lattice,符号P),在单位平行六面体的体中心还有一个结点时,则构成体心格子(Body-centered lattice,符号I)。
如果在某一对面的中心各有一个结点时,称为单面心格子(One-face-centered lattice),(001)面上有心的格子为底心格子或称C心格子(End-centered lattice, Base-centeredlattice or C-centered lattice,符号C),当(100)面或(010)面上有心时,分别称为A心格子(A-centered lattice,符号A)和B心格子(B-centered lattice,符号B)。
如果在所有三对面的中心都有结点时,称为面心格子或全面心格子(Face-centered lattice or All-face-centered lattice,符号F)。
3.1金属原子的堆积方式

镁 型
… ABAB
2
Mg、Zn、 Ti
12
74%
铜 型
…AB CABC …
4
Cu、Ag、 Au、Pb
12
74%
合金是指由两种或两种以上的金属或 金属与非金属经熔炼、烧结或其他方法组 合而成并具有金属特性的物质 。
合金一般是将各组分熔合成均匀的 液体,再经冷凝而制得的。
合金的特性:
1)具有超导性质的合金,如Nb3Ge,Nb3Al, Nh3Sn,V3Si,NbN等
非密置层
配位数:4
密置层
配位数:6
二.金属原子在三维空间的堆积方式(4种)
简单立方:Po
体心立方:钠、钾、铬、钼、钨
面心立方(最密堆积):金、银、铜、铅
六方堆积(最密堆积):锌、钛、镁
简单立方堆积
体心立方堆积
面心立方最密堆积
六方最密堆积
第二层对第一层来讲最紧密的堆积方式是将球对准 1,3,5 位。(或对准 2,4,6 位,其情形是一样的)
A
ABC ABC 形式的堆积,
为什么是面心立方堆积?
我们来加以说明。
C B A
堆积 模型
命 名
表示 符号
晶胞
每个晶 采纳这种堆积 胞所含 的典型金属 原子数
配 位 数
空间 利用 率
非 密 置 层
简单立 方堆积
—
Байду номын сангаас
—
1
Po
6
52%
体心立 方堆积
钾 型
—
2
Na、K、 Cr、Mo、W
8
68%
六方 堆积 密 置 层 面心立 方堆积
2)具有特殊电学性质的金属间化合物,如 InTe-PbSe,GaAs-ZnSe等在半导体材料用 3)具有强磁性的合金物,如稀土元素(Ce, La,Sm,Pr,Y等)和Co的化合物,具有 特别优异的永磁性能
《金属晶体的原子堆积模型》名师教案

金属晶体的原子堆积模型一、核心思想学生发展核心素养倡导培养学生的科学精神和学会学习的能力,那么以课堂为载体、将核心素养的培养内化到学生学习过程中是我们每节课的追求目标。
为实现培养学生能力和突破教学重难点的双重目标,本节课通过开展活动探究式教学,让学生“动手做、动眼看、动口议、动笔写、动脑思”,加强学生自主探究活动,培养他们的理性思维能力、批判质疑精神和勇于探究精神,真正体现学生的主体地位。
二、教学内容分析1教材分析本节课是鲁科版选修三第三章第一节第二课时的内容,第三章的主题是物质的聚集状态与物质性质,旨在让学生通过本章的学习,了解四种基础晶体类型,能从晶体结构的视角认识物质的性质,进一步形成有关物质结构的概念。
2价值分析(1)学科价值:在教材中承上启下,帮助学生了解金属晶体的原子堆积模型;(2)应用价值:能够判断金属晶体的晶胞类型;(3)学生发展价值:从微观角度认识世界。
3学情分析(1)知识层面:学生已初步了解分子晶体、原子晶体的定义及结构特点。
(2)能力层面:有学习热情,有一定的探究能力、分析思维能力和自主学习能力,主动探究能力有待提升。
(3)可能遇到的问题:语言表达能力不足、不会表达或化学用语不规范;知识迁移运用能力不足,分析问题、解决问题的能力有待提高。
三、教学目标分析1课程目标(1)了解金属晶体的四种基本堆积模型:简单立方堆积、体心立方堆积、六方最密堆积和面心立方最密堆积。
(2)认识四种基本堆积模型的晶胞、能判断金属原子的配位数及四种堆积方式的空间利用率的计算。
2学生核心素养目标(1)科学精神:理性思维能力、严谨求知的态度,勇于探究的精神。
(2)自主发展:乐学善学、学习方法的习得,信息意识。
3方法目标(1)通过观察和制作堆积模型训练学生的空间想象能力和动手能力。
(2)通过小组合作培养学生的合作互助意识。
四、教学重点和难点1教学重点:金属原子在三维空间的四种堆积方式2教学难点:四种堆积方式晶胞、配位数、原子利用率的区别五、教学方法活动探究式学习六、设计思想本节课的设计思想如下,逐步开展三个思考与交流活动以及4个探究环节、梯度螺旋化上升,符合学生认知规律。
金属晶体的四种堆积模型总结

金属晶体的四种堆积模型总结Metal crystals can be classified into four main stacking models: Close-packed cubic (FCC), Close-packed hexagonal (HCP), Body-centered cubic (BCC), and Simple cubic (SC). These models represent different ways in which metal atoms arrange themselves in a crystal lattice. Close-packed cubic structures have atoms arranged in layers of repeating ABCABC... pattern, giving them high packing efficiency.金属晶体可以分为四种主要的堆积模型:密堆立方(FCC)、密堆六方(HCP)、体心立方(BCC)和简单立方(SC)。
这些模型代表了金属原子在晶格中排列的不同方式。
密堆立方结构中,原子按照重复ABCABC...模式排列在不同层中,使得具有较高的填充效率。
Close-packed hexagonal structures, on the other hand, consist of layers with an ABAB... stacking sequence. This type of arrangement gives rise to a compact structure with a hexagonal unit cell. Body-centered cubic structures have atoms arranged in a simple cubic lattice with an additional atom at the center of the cube. This arrangement provides good mechanical properties due to thepresence of the central atom, which enhances the strength of the crystal lattice.另一方面,密堆六方结构由具有ABAB...堆叠序列的层组成。
晶体堆积模型

认识晶体第二课时三、晶体结构堆积模型(金属键、离子键、范德华力均没有方向性,所以组成金属晶体、离子晶体、分子晶体的微粒服从紧密堆积堆积原理,降低体系能量,使晶体变得比较稳定)1、等径圆球的密堆积①等径圆球在一列上紧密堆积的方式只有一种,所有的圆球都在一条直线上排列②等径圆球在一个平面上最紧密堆积的方式只有一种,每个等径圆球与周围其它6个球接触,形成层称为密置层③类型:金属晶体结构为等径原子密堆积 A3型最密堆积(六方最密堆积)ABABA1型最密堆积(面心立方最密堆积)ABCABCA2型密堆积(体心立方密堆积)配位数:在密堆积中,一个原子或离子周围所邻接的原子或离子的数目A3型最密堆积配位数12 同层6 上下层各3A1型最密堆积配位数12 同层6 上下层各32、非等径圆球的密堆积①离子晶体可视作非等径圆球密堆积,大球先按一定方式做等径圆球密堆积,小球再填充在大球所形成的空隙中。
NaCl、ZnS是A1型最密堆积②分子晶体,原子以共价键形成分子,分子再以分子间作用力形成晶体,由于范德华力没有方向性和饱和性,故此分子尽可能采取紧密堆积,但分子的排列方式与分子的形状有关③原子晶体堆积方式:不服从紧密堆积方式原因:共价键具有方向性和饱和性,因此就决定了一个原子周围的其它原子数目不仅是有限的而且堆积方向是一定的,所有不是密堆积晶体的特性和晶体结构的堆积模型1.下列关于晶体和非晶体的本质区别的叙述中正确的是( )A.是否具有规则几何外形的固体 B.是否具有固定组成的物质C.是否具有美观对称的外形 D.内部基本构成微粒是否按一定规律做周期性重复排列2.下列说法错误的是( )A.同一物质有时可以是晶体,有时可以是非晶体B.区分晶体和非晶体最可靠的科学方法是确定有没有固定熔点C.雪花是水蒸气凝华得到的晶体D.溶质从溶液中析出可以得到晶体3.关于晶体的自范性,下列叙述正确的是( )A.破损的晶体能够在固态时自动变成规则的多面体B.缺角的氯化钠晶体在饱和NaCl溶液中慢慢变为完美的立方体块C.圆形容器中结出的冰是圆形的体现了晶体的自范性D.由玻璃制成规则的玻璃球体现了晶体的自范性4.下列途径不能得到晶体的是( )A.熔融态SiO2快速冷却 B.熔融态SiO2热液缓慢冷却C.FeCl3蒸气冷凝 D.CuSO4饱和溶液蒸发浓缩后冷却5.将晶体分为离子晶体、金属晶体、原子晶体和分子晶体的本质标准是( )A.基本构成的微粒种类 B.晶体中最小重复结构单元的种类C.微观粒子的密堆积种类 D.晶体内部微粒的种类及微粒间相互作用的种类6.下列叙述正确的是( )A.任何晶体中,若含有阳离子也一定含有阴离子 B.离子晶体中可能含有共价键C.离子晶体中只含有离子键不含有共价键 D.分子晶体中只存在分子间作用力,不含有其他化学键7.金属原子在二维空间里的放置有下图所示的两种方式,下列说法不正确的是( )A.图a为密置 B.图b为非密置层 C.图a配位数为6 D.图b配位数为68.(2019·邢台一中月考)(1)在下列物质中,__________(填序号,下同)是晶体,______________是非晶体。
几种常见的晶体模型

Ⅱ. 体心立方堆积
密置层的堆积方式
第一层 :
第二层 :对第一层来讲最紧密的堆积方式是将球对准 1,3,5 位。 ( 或对准 2,4,6 位,其情形是一样的 )
6 5 4
3
6 5 4
3
A
,
1
2
1
2
B
关键是第三层,对第一、二层来说,第三层可以有两 种最紧密的堆积方式。
Ⅲ.六方最密堆积
第一种: 将第三层球对准第一层的球
几种常见的晶体模型
1.原子晶体
2.分子晶体
3.离子晶体 离子晶体中的配位数是指一个离子周围最邻近 的异电性离子的 因素、键性因素。
F
几种碳酸盐的热分解温度和阳离子半径
碳酸盐 热分解温度 /℃ 阳离子半径 /pm MgCO3 402 66 CaCO3 900 99 SrCO3 1172 112 BaCO3 1360 135
金属阳离子的半径越小,分解温度越小。
4.石墨晶体
石墨晶体中,既有共价键, 又有金属键,还有范德华 力。
思考:石墨为什么会导电?
5.常见金属晶体的原子堆积模型
二维平面堆积方式
I 型 II 型
非密置层
行列对齐四球一空 非最紧密排列
密置层
行列相错三球一空 最紧密排列
三维空间堆积方式
Ⅰ.
简单立方堆积
A
1 6 5
2
3 4
B
A B
于是每两层形成一个周期, 即 AB AB 堆积方式,形成 六方堆积。
A
配位数 12 ( 同层 6,上下层各 3 )
Ⅳ:面心立方最密堆积
第三层的另一种排列方
式,是将球对准第一层的 2
,4,6 位,不同于 AB 两
2-密堆积
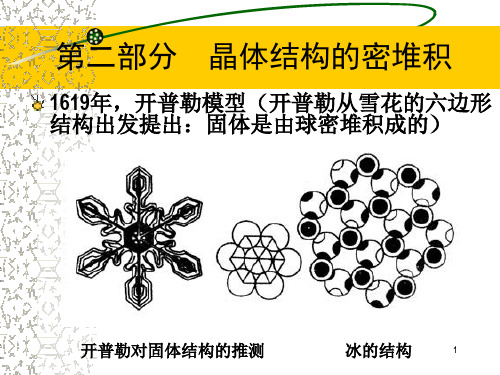
S a a sin 60 3 a2 2
平行六面体的高:
h 2边长为a的四面体高
2 6 a 2 6 a
3
3
20
V晶胞
3 a2 2 6 a
2
3
2a3 8 2r3
V球
2
4
3
r3
(晶胞中有2个球)
V球 V晶胞 100% 74.05%
21
22
23
隙上方,其排列方式与第一层相同,但与第
二层错开,形成ABAB…堆积。这种堆积方式
可以从中划出一个六方单位来,所以称为六
方最密堆积(A3)。
9
三维等径圆球的堆积(A3)
能量较低 密置层
A B A B A
B
A
10
A3最密堆积形成的六方晶胞
A3最密堆积形成后, 从中可以划分 出什么晶胞? 六方晶胞.
11
47
(4)六方ZnS晶胞图
48
六方ZnS
(1)六方晶系,简单六方晶胞 (2)Z=1 (3)Zn2+和S2- 六方最密堆积周期|AaBb|。 (4)配位数4:4。 (6)2s:0 0 0,2/3 1/3 1/2;
2Zn:0 0 5/8,2/3 1/3 1/8。
49
(5) CsCl型:
(1)立方晶系,简单立方晶胞。 (2)Z=1。 (3)Cs+,Cl-,离子键。 (4)配位数8:8。 (5) Cs+离子位于简单立方点阵的阵点上
3 30
A2型密堆积图片
31
金刚石型堆积(A4)
配位数为4,空间利用率为
34.01%,不是密堆积。这
种堆积方式的存在因为原
子间存在着有方向性的共
六方最密堆积PPT课件

精选ppt课件最新
7
4、金属晶体结构具有金属光泽和颜色
▪ 由于自由电子可吸收所有频率的光,然后很 快释放出各种频率的光,因此绝大多数金属 具有银白色或钢灰色光泽。而某些金属(如 铜、金、铯、铅等)由于较易吸收某些频率 的光而呈现较为特殊的颜色。
▪ 当金属成粉末状时,金属晶体的晶面取向杂 乱、晶格排列不规则,吸收可见光后辐射不 出去,所以成黑色。
B
三维空间里密置层的 金属原子的堆积方式
(1) ABAB… 堆积方式
(2) ABCABC…
堆积方式
俯视图
2
1
3
6
4
5
2
1
3
6
4
5
AB▪ Biblioteka 二层小球的球心对准第一层的 1、3、5 位 (▽)或对准 2、4、6 位(△)。
▪ 关键是第三层,对第一、二层来说,第三层 可以有两种最紧密的堆积方式。
(3)ABAB…堆积方式
精选ppt课件最新
28
▪ (3)体心立方晶胞平均占有的原子数目:
1 8
×8
+
1=
2
活动与探究3 三维空间里密置层金属原子的堆积方式
▪ 将密置层的小球在一个平面上黏合在一起, 再一层一层地堆积起来(至少堆4层),使 相邻层上的小球紧密接触,有哪些堆积方式?
▪ 注意:堆积方式的周期性、稳定性
A
A
B
金属容易导热,是由于自由电子运动时与金 属离子碰撞把能量从温度高的部分传到温度低 的部分,从而使整块金属达到相同的温度。
精选ppt课件最新
6
3、金属晶体结构与金属延展性的关系
【讨论3】金属为什么具有较好的延展性?
原子晶体受外力作用时,原子间的位移必 然导致共价键的断裂,因而难以锻压成型, 无延展性。而金属晶体中由于金属离子与自 由电子间的相互作用没有方向性,各原子层 之间发生相对滑动以后,仍可保持这种相互 作用,因而即使在外力作用下,发生形变也 不易断裂。
堆积模型

b
a
a
例2、现有甲、乙、丙(如图)三种晶体, 试写出甲、乙二晶体的化学式和丙晶体中 C和D的个数比。
例3、晶体硼的基本结构单元都是由 硼原子组成的正二十面体,其中含有20个等 边三角形的面和一定数目的顶角,每个顶角 各有一个硼原子,如图所示。
回答: (1)键角 ; (2)晶体硼中的 硼原子数_______; (3)B–B键__条?
三、晶体结构的基本单元----晶胞
1、晶胞
(1)晶胞:从晶体中“截取”出来的最小 的结构重复单元。是能够反映晶体结构特 征的基本重复单位。 (2)晶胞一定是一个平行六面体,其三条边 的长度不一定相等.也不一定互相垂内; 晶胞的形状和大小由具体晶体的结构所决 定。
(3)整个晶体就是晶胞按其周期性在二维空 间重复排列而成的。这种排列必须是晶胞 的并置堆砌。所谓并置堆砌是指平行六面 体之间没有任何空隙,同时,相邻的八个 平行六面体均能共顶点相连接。
2. 常见三种密堆积的晶胞 面心立方晶胞----A1型
体心立方晶胞----A2型
六方晶胞----A3型
一刀得面,两刀得棱, 三刀得点
3.晶胞中微粒数的计算
晶胞抽取的计算原则
①顶点:由8个小立方体共有,所以为1/8
②棱上:由4个小立方体共有,所以为1/4 ③面心:由2个小立方体共有,所以为1/2
二、晶体结构的堆积方式
在金属晶体、离子晶体和分子晶体的结构中,金 属键、离子键和分子间相互作用均没有方向性, 因此都趋向于使金属原子、离子或分子吸引尽可 能多的其他原子、离子或分子分布于周围,并以 密堆积的方式降低体系的能量,使晶体变的比较 稳定。
1、等径圆球的密堆积
在一个平面上进行最紧密堆积只有一种,即只 有当每个等径圆球与周围其他六个球相接触时, 才能做到最紧密堆积。
金属晶体的堆积模型

精品课件
金属晶体原子平面排列方式有几种?
探究
2 1A3
4
2
1
3
A
6
4
5
配位数为4 非密置层
精品课件
配位数为6 密置层
非密置层层层堆积情况1: 相邻层原子在同一直线上的堆积
金属晶体的堆积方式──简单立方堆积
精品课件
简单立方堆积
配位数:6 晶胞含金属原子数 1
例: (Po) 精品课件
精品课件
2).立方面心结构 立方面心结构的配位数=12(即每个圆球有12个最
近的邻居,同一层有六个,上一层三个,下一层三 个)。立方密堆积中可以取出一个立方面心的单位 来,每个单位中有四个圆球,球心的位置是000;0 1/2 1/2;1/2 0 1/2;1/2 1/2 0。
等径圆球的最紧密堆积方式,在维持每个球的周围 的情况等同的条件下,就只有上述两种,它们的空 间利用率最高(74.05%)。
精品课件
立方体边长=a';
立方体对角线=
a';
四面体边长=
a';
精品课件
精品课件
设圆半径为R,晶胞棱长为a,晶胞面对角
线长
则
晶胞体
积
立方面心晶胞中含4个圆球,每个球体积
为:
立方最密堆积虽晶胞大小不同,每个晶胞中 含球数不同。但计算得到空间占有率相同。
精品课件
而体心立方堆积(bcp)则空间占有率低一些。 体对角线长为 晶胞体积 体心立方晶胞含2个球
精品课件
2、某些金属晶体(Cu、Ag、Au)的原子按面心 立方的形式紧密堆积,即在晶体结构中可以 划出一块正立方体的结构单元,金属原子处 于正立方体的八个顶点和六个侧面上,试计 算这类金属晶体中原子的空间利用率。
化学:3.3.2金属晶体原子堆积模型PPT课件(新人教版选修3)

配位数 12 。 ( 同层 6,上下层各 3 ) ,空 间利用率为74%
12
6
3
54
下图是此种六方 紧密堆积的前视图
A
B A B A
3.六方最密堆积--镁型
第二种是将第三层球对准 第一层的 2,4,6 位,不 同于 AB 两层的位置,这是 C 层。
12 63
54
12
6
3
54
12
6
3
54
第四层再排 A,
A
于是形成 ABC ABC
三层一个周期。 得
C
到面心立方堆积。
B
12
A
6
3
C
54
B
A
配位数 12 。 ( 同层 6, 上下层各 3 ) 此种立方紧密堆积的前视图
④面心立方最密堆积:铜型
C B A
镁型
铜型
金属晶体的两种最密堆积方式
堆积 采纳这种堆 模型 积的典型代
表
简单 Po (钋) 立方
钾型 K、Na、Fe (bcp)
镁型 Mg、Zn、Ti (hcp)
空间 利用
率 52%
68%
74%
配位数
6 8 12
铜型 Cu, Ag, Au 74% 12 (ccp)
晶胞
小结:三种晶体类型与性质的比较
晶体类型
概念
作用力
构成微粒 熔沸点
物 理 硬度 性 质 导电性
原子晶体
分子晶体
金属晶体
相邻原子之间以共价 键相结合而成具有空
间网状结构的晶体
分子间以范德 华力相结合而
成的晶体
通过金属键形成的 晶体
共价键
范德华力
金属晶体堆积模型及计算公式
A
3
5
6
8
7
1
2
4
3
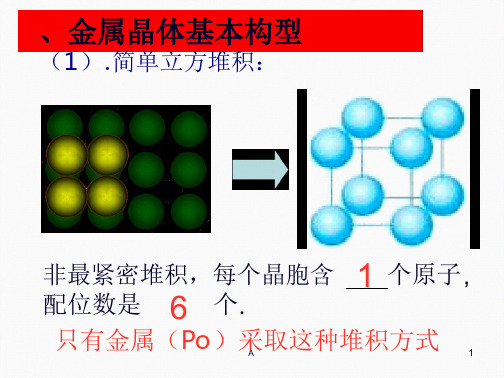
这种堆积晶胞是一个体心立方,每个晶胞含
2 个原子,属于非密置层堆积,配位数
8 为
,许多金属(如 Na、K、Fe等)采取这种堆
积方式。
A
4
空间利用率的计算
(2)体心立方:在立方体顶
点的微粒为 8个晶胞共享,处 于体心的金属原子全部属于 该晶胞。
微粒数为: 8×1/8 + 1 = 2
空间利用率:
4×4л r3/3
= 74.05%
(2 ×1.414r)
3 A
8
堆积方式及性质小结
简单立 方堆积
体心立方 堆积
六方最
密堆积
面心立方
最密堆积
简单立方
体心立方 六方
面心立方
52%
68%
74% 74%
A
6
Po
8
Na 、K、Fe
12 Mg 、Zn 、Ti
12 Cu 、 Ag、Au
9
A
10
小结:三种晶体类型与性质的比较
A
5
1200
平行六面体
每个晶胞含 2 个原子
A
6
铜型(面心立方紧密堆积)
7
1 9
6
8 2
3
5
4
12
10
11
这种堆积晶胞属于最密置层堆集,配位数
为 12 ,许多金属(如 Cu、Ag、Au等)采取这
种堆积方式。
A
7
(3)面心立方:在立方体顶点的微粒为 8个
晶胞共有,在面心的为 2个晶胞共有。
微粒数为: 8×1/8 + 6 ×1/2 = 4
