1.2独立性检验的基本思想及其初步应用
高中数学:1.2《独立性检验的基本思想及其初步应用》复习教案

1.2独立性检验的基本思想及其初步应用教学目标:1理解独立性检验的基本思想2、会从列联表、柱形图、条形图直观判断吸烟与患癌有关。
3、了解随机变量K2的含义。
教学重点:理解独立性检验的基本思想。
教学难点;1、理解独立性检验的基本思想、2、了解随机变量K2的含义。
教学过程:一、引入:从问题“吸烟是否与患肺癌有关系”引出独立性检验的问题,并借助样本数据的列联表,柱形图,和条形图的展示,使学生直观感觉到吸烟和患肺癌可能会有关系。
但这种结论能否推广到总体呢?要回答这个问题,就必须借助于统计理论来分析。
二、独立性检验就是检验两个分类变量是否有关的一种统计方法:用字母表示吸烟与患肺癌的列联表:不患肺癌患肺癌合计不吸烟 a b a+b吸烟 c d c+d合计a+c b+d a+b+c+d样本容量 n=a+b+c+d假设H0 : 吸烟与患肺癌没有关系。
则吸烟者中不患肺癌的的比例应该与不吸烟者中相应的比例差不多,即:()()()()()()()220a ca c d c ab ad bc a b c dad bc n ad bc k a b c d a c b d n a b c d≈⇒+≈+⇒-≈++--=++++=+++因此 : 越小, 说明吸烟与患肺癌之间关系越弱.构造随机变量 其中()()2781721489874916.635⨯⨯≈⨯⨯⨯≥≈≥2020220202若H 成立,则K 应该很小. 把表中数据代入公式9965777549-422099K =56.632在H 成立的情况下.统计学家估算出如下概率P K 0.01即在H 成立的情况下,K 的值大于6.635的概率非常小.如果K 6.635,就断定H 不成立,出错的可能性有多大?出现K =56.6326.635 的概率不超过1% .因此,我们有99%的把握认为"吸烟与患肺癌有关系."三、作业:预习17页。
1.2独立性检验的基本思想及其初步应用(第二课时)。
《独立性检验的基本思想及其初步应用》PPT课件

0.05 3.841
0.025 5.024
0.010 0.005 6.635 7.879
0.001 10.828
K2的观测值为k
如果 k k0,就以 (1 P(K 2 k0 )) 100%的把握
认为“X与Y有关系”;而这种判断有可能出错,出
错的概率不会超过 P(K 2 k0 )。
7
例如 :
1如果k 10.828,就有99.9%把握认为" X与Y有
❖ 试用你所学过的知识进行分析,能否在犯错 误的概率不超过0.005的前提下,认为“喜欢 体育还是文娱与性别有关系”?
体育 文娱 总计
男生 21 23 44
女生 6 29 35
总计 27 52 79
16
[思路探索] 可用数据计算 K2,再确定其中的具体关系. 解 判断方法如下: 假设 H0“喜欢体育还是喜欢文娱与性别没有关系”,若 H0 成立, 则 K2 应该很小. ∵a=21,b=23,c=6,d=29,n=79, ∴k=a+bcn+add-ab+cc2b+d =21+237×9×6+212×9×29-212+3×66×223+29≈8.106.
12
例4:为研究不同的给药方式(口服与注射)和药的效果(有效 与无效)是否有关,进行了相应的抽样调查,调查的结果列 在表中,根据所选择的193个病人的数据,能否作出药的效果 和给药方式有关的结论?
口服 注射 合计
有效 58 64 122
无效 40 31 71
合计 98 95 193
P(k≥k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
1.2独立性检验的基本思想及其初步应用

试用图形判断服用药和患病之间是否有关系?
解析:相应的等高条形图如下:
从图形可以看出,服用药的样本中患病的比例明显低于 没有服用药的样本中患病的比例,因此可以认为:服用药和 患病之间有关系.
独立性检验方法——K2公式
在调查的480名男士中有38名患有色盲,520名女 士中有6名患有色盲,能否在犯错误的概率不超过0.001的前 提下认为性别与患色盲有关系? 分析:
4.下面是一个2×2列联表: x1 x2 总计 y1 a 2 b y2 21 25 46 总计 73 27 100
则表中a、b的值分别为( C ) A.94、96 C.52、54 B.52、50 D.54、52
5.性别与身高列联表如下: 男 女 总计 高(165 cm以上) 37 6 43 矮(165 cm以下) 4 13 17 总计 41 19 60
作出2×2列联表 → 计算随机变量K2的值 → 对照临界值作出结论 解析:根据题目所给的数据作出如下的列联表:
色盲 不色盲 总计
男
女 总计
38
6 44
442
514 956
480
520 1 000
根据列联表中所给的数据可以得: a=38,b=442,c=6,d=514,a+b=480,c+d= 520,a+c=44,b+d=956,n=1 000.
3.独立性检验. 利用随机变量K2来判断“两个分类变量有关系”的方法 定义 称为独立性检验.
nad-bc2 公式 K2=_____________________ a+bc+da+cb+d ,其中n=______________. a+b+c+d
①根据实际问题的需要确定容许推断“两个分类变量有 临界值 k0 .② 关系”犯错误概率的上界α,然后查表确定 ________ k________ ≥k0 利用公式计算随机变量K2的 ________ , 观测值 k .③如果 具体 就推断“X与Y有关系”,这种推断犯错误的概率不超过 步骤 α;否则,就认为在犯错误的概率不超过α的前提下不能 推断“X与Y有关系”,或者在样本数据中没有发现足够 证据支持结论“X与Y有关系”.
1.2独立性检验的基本思想及其初步应用课件人教新课标

类型二 由K2进行独立性检验 例2 对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病 人进行3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如下 表所示.
心脏搭桥手术 血管清障手术
总计
又发作过心脏病 39 29 68
未发作过心脏病 总计
157
196
167
196
324
392
试根据上述数据比较这两种手术对病人又发作过心脏病的影响有没有差别. 解 假设病人又发作过心脏病与做过心脏搭桥手术还是血管清障手术没 有关系,由表中数据得a=39,b=157,c=29,d=167,a+b=196,c +d=196,a+c=68,b+d=324,n=392, 由公式得K2的观测值
解答
达标检测
1.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下列
联表:
喜欢程度
男
女
总计
爱好
40
20
60
不爱好
20
30
50
总计
60
50
110
nad-bc2 由 K2=a+bc+da+cb+d算得,
110×40×30-20×202 k= 60×50×60×50 ≈7.8,
12345
附表:
12345
解析 答案
5.“全国文明城市”称号是最有价值的城市品牌,某市为创建第五届“全 国文明城市”,开展了“创建文明城市人人有责”活动.为了了解哪些人 更关注“创城”活动,随机抽取了年龄在10~70岁之间的100人进行调 查,并按年龄绘制如下频数散布表.
年龄(岁) [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]
1.2独立性检验的基本思想及其初步应用课件人教新课标

因此,
|ad-bc|越小,说明吸烟与患肺癌之间关系越弱; |ad-bc|越大,说明吸烟与患肺癌之间关系越强.
为了使不同样本容量的数据有统一的评判 标准,基于上述分析,我们构造一个随机变量:
K2 =
n(ad - bc)n
(a + b)(c + d)(a + c)(b + d)
其中n=a+b+c+d为样本容量.
48 121 208 223 193 165 42
(I)将各组的频率填入表中;
(II)根据上述统计结果,计算灯管使用寿命不足 1500小时的频率.
解答
分组
频数 频率
[500,9 [900, 00) 1100)
48 121 0.048 0.121
[1100, 1300)
208 0.208
[1300, 1500)
P(k2>k) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 0.455 0.708 1.323 2.072 2.706 3.84 5.024 6.635 7.879 10.83
(2)利用K2公式,计算随机变量K2的观测值k.
(3)如果k>k0,就推断“X与Y有关系”,这 种推断犯错误的概率不超过a;否则,就认为在犯 错误的概率不超过a的前提下不能推断“X与Y有关 系”.
k=
16.373 > 6.635
3891048 665 772
所以有99%的把握认为”秃顶与患心脏病有关”.
解答
根据题目所得数据得到列联表:
秃顶 不秃顶
总计
患心脏病 214 451 665
人教A版高中数学选修1-2《一章 统计案例 1.2 独立性检验的基本思想及其初步应用》精品课件_33

解:根据题目所给数据得到如下列联表:
患心脏病 不患心脏病 总计
秃顶
214
ቤተ መጻሕፍቲ ባይዱ不秃顶
451
总计
665
175
389
597
1048
772
1437
根据列联表中的数据,得到
K 2 1437 (214597 175 451)2 16.373 6.635. 3891048 665 772
案 例:某医疗机构为了了解呼吸道疾病与吸 烟是否有关,进行了一次抽样调查,共调查了 515个成年人,其中吸烟者220人,不吸烟者 295人。
调查结果:吸烟的220人中有37人患呼吸道疾 病,183人未患呼吸道疾病;不吸烟的295人中 有21人患病,274人未患病。
根据这些数据,能否断定:患呼吸道疾 病与吸烟有关?
(2)求k值 (3)下结论
5
8
3
2
6
1
4
5
9
8
(1)如果k 10.828,就有99.9%的把握认为" X 与Y有关系" (2)如果k 7.879,就有99.5%的把握认为" X 与Y有关系"
(3)如果k 6.635,就有99%的把握认为" X 与Y有关系"
(4)如果k 5.024,就有97.5%的把握认为" X 与Y有关系"
练习3:为了调查胃病是否与生活规律有关,在某地对540名40岁以上 的人进行了调查,结果是:患胃病者生活不规律的共60人,患胃病者 生活规律的共20人,未患胃病者生活不规律的共260人,未患胃病者生 活规律的共200人. (1)根据以上数据列出2×2列联表; (2)能够以99%的把握认为40岁以上的人患胃病与否和生活规律有关 系吗?为什么?
1.2独立性检验的基本思想及其初步应用

(2)若饮用干净水得病的有5人,不得病的有50人;饮用不干净水得病的 有9人,不得病的有22人.按此样本数据分析这种传染病是否与饮用水有 关,并比较两种样本在反映总体时的差异.
解 依题意得2×2列联表如下所示:
得病
不得病
干净水
5
50
不干净水
9
22
总计
14
72
此时,K2
的观测值
86×5×22-50×92 k= 14×72×55×31 ≈5.785.
2.下面是一个2×2列联表:
y1
y2
总计
x1
a
21
73
x2
8
25
33
总计
b
46
则表中a、b处的值分别为( C )
A.94,96
B.52,50
C.52,60
D.54,52
解析 ∵a+21=73,∴a=52,b=a+8=52+8=60.
1 23
1 23
3.为了判断高中学生的文理科选修是否与性别有关系,随机调查了50名 学生,得到如下2×2列联表:
文
有兴趣
138
73
无兴趣
98
52
总计
Hale Waihona Puke 236125总计 211 150 361
代入公式得K2的观测值 k=3612×36×13182×5×522-117×3×159082≈1.871×10-4. ∵1.871×10-4非常小,∴可以认为学生选报文、理科与对外语的兴趣无关.
达标检测
1 23
1.在研究吸烟与患肺癌的关系中,通过收集数据、整理分析数据得“吸 烟与患肺癌有关”的结论,并且在犯错误的概率不超过0.01的前提下认 为这个结论是成立的,下列说法中正确的D是( ) A.100个吸烟者中至少有99人患有肺癌 B.1个人吸烟,那么这个人有99%的概率患有肺癌 C.在100个吸烟者中一定有患肺癌的人 D.在100个吸烟者中可能一个患肺癌的人也没有 解析 独立性检验的结果与实际问题有差异,即独立性检验的结论是一 个数学统计量,它与实际问题中的确定性存在差异.
独立性检验
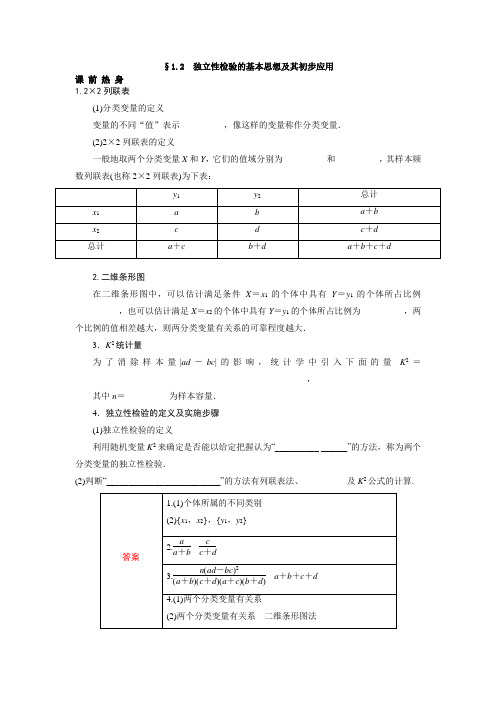
§1.2独立性检验的基本思想及其初步应用课前热身1.2×2列联表(1)分类变量的定义变量的不同“值”表示__________,像这样的变量称作分类变量.(2)2×2列联表的定义一般地取两个分类变量X和Y,它们的值域分别为__________和__________,其样本频数列联表(也称2×2列联表)为下表:2.二维条形图在二维条形图中,可以估计满足条件X=x1的个体中具有Y=y1的个体所占比例__________,也可以估计满足X=x2的个体中具有Y=y1的个体所占比例为__________,两个比例的值相差越大,则两分类变量有关系的可靠程度越大.3.K2统计量为了消除样本量|ad-bc|的影响,统计学中引入下面的量K2=_____________________________________________________,其中n=__________为样本容量.4.独立性检验的定义及实施步骤(1)独立性检验的定义利用随机变量K2来确定是否能以给定把握认为“________________”的方法,称为两个分类变量的独立性检验.(2)判断“__________________________”的方法有列联表法、__________及K2公式的计算.名师讲解一般地,假设两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(也称为2×2列联表)为下表:若要推断的论述为H1:“X与Y有关系”.可以按如下步骤判断H1成立的可能性.(1)通过二维条形图,可以粗略地判断两个分类变量是否有关系,但是这种判断无法精确地给出所得结论的可靠程度.在二维条形图中,可以估计满足条件X=x1的个体中具有Y=y1的个体所占比例为aa+b,也可以估计满足条件X=x2的个体中具有Y=y1的个体所占的比例为cc+d,两个比例的值相差越大,H1成立的可能性就越大.(2)可以利用独立性检验来考察两个分类变量是否有关系,并且能较精确地给出这种判断的可靠程度,具体的做法是:根据数据代入公式K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)求出随机变量K2的观测值k,其值越大,说明X与Y有关系的可能性越大,当得到的观测数据a、b、c、d都不小于5时,可以得到以下结论用于确定X与Y的可信程度:①如果k>10.828,有99.9%的把握认为X与Y有关系.②如果k>7.879,就有99.5%的把握认为X与Y有关系.③如果k>6.635,就有99%的把握认为X与Y有关系.④如果k>5.024,就有97.5%的把握认为X与Y有关系.⑤如果k>3.841,就有95%的把握认为X与Y有关系.⑥如果k>2.706,就有90%的把握认为X与Y有关系.⑦如果k≤2.706,就认为没有充分的证据显示X与Y有关系.典例剖析题型一概念辨析例1在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是()A.如果K2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病C.若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推理出现错误D.以上三种说法都不正确误区警示题中所说的“有99%的把握认为吸烟与患肺病有关”是指统计上的关系,而不是因果关系,也不能认为99%是指某人患有肺病的概率.变式训练1下列说法正确的个数为()①对事件A与B的检验无关,说明两事件互不影响;②事件A与事件B关系越密切,K2的值就越大;③K2的大小是判断事件A与B是否相关的唯一数据;④若判断两事件A与B相关,则A发生B一定发生.A.1B.2C.3D.4例2打鼾不仅影响别人休息,而且可能与患某种疾病有关.下表是一次调查所得的数据,试问:每晚都打鼾与患心脏病有关吗?用图表分析.变式训练2在500人身上试验某种血清预防感冒的作用,把一年中的记录与另外500个未用血清的人作比较,结果如下:题型三利用K2公式进行独立性检验例3在研究某种新措施对猪白痢的防治效果问题时,得到以下数据:试问新措施对防治猪白痢是否有效果?分析对于新措施对防治猪白痢是否有效果?可以计算K2的值与临界值进行比较,作出判断.规律技巧虽然二维条形图也能判断新措施对防治猪白痢是否有效果,但不能给出它们关系这一结论的可靠程度,因而我们常用K2公式解答问题.变式训练3调查者询问了72名大学生在购买食品时是否观看营养说明得到下表所示的数据,从表中数据分析看不看说明书与大学生的性别之间有没有关系.题型四独立性检验的应用例4下表是某地区的一种传染病与饮用水的调查表:(1)这种传染病是否与饮用水的卫生程度有关,请说明理由;(2)若饮用干净水得病5人,不得病50人,饮用不干净水得病9人,不得病22人.按此样本数据分析这种疾病是否与饮用水有关,并比较两种样本在反映总体时的差异.变式训练4现有两种治疗运动员膝关节损伤的药方,为了比较两药方的疗效收集的数据如下表:(2)哪种药方疗效好?技能演练基础强化1.下列关于K2的说法正确的是()A.K2在任何相互独立问题中都可以用来检验有关还是无关B.K2的值越大,两个事件的相关性越大C.K2是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合D.K2的观测值的计算公式为K2=n(ad-bc)(a+b)(c+d)(a+c)(b+d)2.下面是一个2×2列联表则表中aA.94、96B.52、50 C.52、54 D.54、52 3.观察下列各图,其中两个分类变量x,y之间关系最强的是()4.考察棉花种子经过处理跟生病之间的关系得到如下表数据:A .种子经过处理跟是否生病有关B .种子经过处理跟是否生病无关C .种子是否经过处理决定是否生病D .以上都是错误的 5.分类变量x 和y 的列联表如下,则( )A.ad -bc C .(ad -bc )2越大,说明x 与y 的关系越强 D .(ad -bc )2越小,说明x 与y 的关系越强 6.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:A .99%B .95%C .90%D .无充分依据7.某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表:k =50(13×20-10×7)220×30×23×27≈4.844,因为k >3.841,所以确定主修统计专业与性别有关系,那么这种判断出错的可能性为__________.8.某大学在研究性别与职称(分正教授,副教授)之间是否有关系,你认为应该收集的数据是__________.能力提升9.利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅下表来确定断言“X 和Y有关系”的可信度.如果k>5.024,那么就有把握认为“X和Y有关系”的百分比为__________.1011.在对人们休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动,你能否判断性别与休闲方式是否有关系?品味高考12.(2010·新课标)为了调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:(1)(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关;(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由?附:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )。
独立性检验的基本思想及其初步应用习题及答案

数学·选修1-2(人教A版)1.2 独立性检验的基本思想及其初步应用►达标训练1.在研究两个分类变量之间是否有关时,可以粗略地判断两个分类变量是否有关的是( )A.散点图B.等高条形图C.2×2列联表D.以上均不对答案:B2.在等高条形图形图中,下列哪两个比值相差越大,要推断的论述成立的可能性就越大( )A.aa+b与dc+d B.ca+b与ac+dC.aa+b与cc+d D.aa+b与cb+c答案:C3.对分类变量X与Y的随机变量K2的观测值k,说法正确的是( )A.k越大,“X与Y有关系”可信程度越小B.k越小,“X与Y有关系”可信程度越小C.k越接近于0,“X与Y无关”程度越小D.k越大,“X与Y无关”程度越大答案:B4.下面是一个2×2列联表:则表中a、b的值分别为( )A.94、96 B.52、50C.52、54 D.54、52答案:C5.性别与身高列联表如下:那么,检验随机变量K2的值约等于( )A.0.043 B.0.367C.22 D.26.87答案:C6.给出列联表如下:根据表格提供的数据,估计“成绩与班级有关系”犯错误的概率约是( )A .0.4B .0.5C .0.75D .0.85答案:B►素能提高1.在调查中发现480名男人中有38名患有色盲,520名女人中有6名患有色盲,下列说法中正确的是( )A .男人、女人中患有色盲的频率分别为0.038、0.006B .男人、女人患色盲的概率分别为19240、3260C .男人中患色盲的比例比女人中患色盲的比例大,患色盲是与性别有关的D .调查人数太少,不能说明色盲与性别有关解析:男人患色盲的比例为38480,比女人中患色盲的比例6520大,其差值为⎪⎪⎪⎪⎪⎪⎪⎪38480-6520≈0.067 6,差值较大. 答案:C2.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男 女 总计 爱好 40 20 60 不爱好 20 30 50 总计 60 50 110由K 2=算得, K 2=≈7.8.附表:P(K2≥k0)0.0500.0100.001k0 3.841 6.63510.828参照附表,得到的正确结论是( )A.有99%以上的把握认为“爱好该项运动与性别有关”B.有99%以上的把握认为“爱好该项运动与性别无关”C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”答案:A3.若由一个2×2列联表中的数据计算得K2=4.013,那么在犯错误的概率不超过0.05的前提下认为两个变量______(填“有”或“没有”)关系.答案:有4.(2013·韶关二模)以下四个命题:①在一次试卷分析中,从每个试室中抽取第5号考生的成绩进行统计,是简单随机抽样;②样本数据:3,4,5,6,7的方差为2;③对于相关系数r,|r|越接近1,则线性相关程度越强;④通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下列联表:男女总计走天桥402060走斑马线203050总计6050110由K2=可得,K2==7.8,则有99%以上的把握认为“选择过马路方式与性别有关”,其中正确的命题序号是________.答案:②③④附表P(K2≥k0)0.050.0100.001k03.8416.63510.8285.某学校为了调查喜欢语文学科与性别的关系,随机调查了一些学生情况,具体数据如下表:类别性别不喜欢语文喜欢语文男1310女720为了判断喜欢语文学科是否与性别有关系,根据表中的数据,得到K2的观测值k=≈4.844,因为k≥3.841,根据下表中的参考数据:P(K2≥k0)0.500.400.250.150.100.050.0250.010.0050.001k00.4550.7081.3232.0722.7063.8415.0246.6357.87910.828 判定喜欢语文学科与性别有关系,那么这种判断出错的可能性为________.答案:5%6.某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(满分100分)如下表若单科成绩85以上(含85分),则该科成绩优秀.解析:(1)2×2列联表为(单位:人):(2)根据题(1)中表格的数据计算,能否在犯错误的概率不超过0.005的前提下认为学生的数学成绩与物理成绩之间有关系?参数数据:①假设有两个分类变量X和Y,它们的值域分别为(x1,x2)和(y1,y2),其样本频数列联表(称为2×2列联表)为:则随机变量K2=,其中n=a+b+c+d为样本容量;②独立检验随机变量K2的临界值参考表如下:P(K2≥k0)0.500.400.250.150.10k00.4550.708 1.323 2.072 2.706P(K2≥k0)0.050.0250.0100.0050.001k0 3.841 5.024 6.6357.87910.828 解析:根据列联表可以求得K2的观测值k=≈8.802>7.879.在犯错误的概率不超过0.005的前提下认为:学生的数学成绩与物理成绩之间有关系.7.2013年3月14日,CCTV财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象.为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相混凝土耐久性达标混凝土耐久性不达标总计使用淡化海砂25530使用未经淡化海砂151530 总计402060的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?解析:提出假设H0:使用淡化海砂与混凝土耐久性是否达标无关.根据表中数据,求得K2的观测值k==7.5>6.635.查表得P(K2≥6.635)=0.010.∴能在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关.(2)若用分层抽样的方法在使用淡化海砂的样本中抽取了6个,现从这6个样本中任取2个,则取出的2个样本混凝土耐久性都达标的概率是多少?解析:用分层抽样的方法在使用淡化海砂的样本中抽取6个,其中应抽取“混凝土耐久性达标”的为2530×6=5,“混凝土耐久性不达标”的为6-5=1,“混凝土耐久性达标记”为A 1,A 2,A 3,A 4,A 5”;“混凝土耐久性不达标”的记为B .在这6个样本中任取2个,有以下几种可能:(A 1,A 2),(A 1,A 3),(A 1,A 4),(A 1,A 5),(A 1,B ),(A 2,A 3),(A 2,A 4),(A 2,A 5),(A 2,B ),(A 3,A 4),(A 3,A 5),(A 3,B ),(A 4,A 5),(A 4,B )(A 5,B ),共15种.设“取出的2个样本混凝土耐久性都达标”为事件A ,它的对立事件A 为“取出的2个样本至少有1个混凝土耐久性不达标”,包含(A 1,B ),(A 2,B ),(A 3,B ),(A 4,B ),(A 5,B ),共5种可能.∴P (A )=1-P (A )=1-515=23.即取出的2个样本混凝土耐久性都达标的概率是23.8.某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.左下表是甲流水线样本频数分布表,右下图是乙流水线样本的频率分布直方图.(1)根据上表数据作出甲流水线样本的频率分布直方图;解析:甲流水线样本的频率分布直方图如下:(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率;解析:由题表知甲样本中合格品数为8+14+8=30,由题图知乙样本中合格品数为(0.06+0.09+0.03)×5×40=36,故甲样本合格品的频率为3040=0.75,乙样本合格品的频率为3640=0.9.据此可估计从甲流水线任取1件产品,该产品恰好是合格品的概率为0.75.从乙流水线任取1件产品,该产品恰好是合格品的概率为0.9.(3)由以上统计数据完成下面2×2列联表,能否在犯错误的概率不超过0.1的前提下认为产品的包装质量与两条自动包装流水线的选择有关?甲流水线 乙流水线 合计 合格品 a = b = 不合格品 c = d =合计n =附表: P (K 2≥k 0) 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 02.0722.7063.8415.0246.6357.87910.828(参考公式:K 2=,其中n =a +b +c +d )解析:2×2列联表如下:甲流水线 乙流水线 合计 合格品 a =30 b =36 66 不合格品 c =10 d =4 14合计4040n =80∵K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)=80×(120-360)266×14×40×40≈3.117>2.706.∴在犯错误的概率不超过0.1的前提下认为产品的包装质量与两条自动包装流水线的选择有关.►品味高考1.为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下:解析:调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中需要帮助的老年人的比例的估计值为70500=14%.(2)能否在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关?解析:K2的观测值k=500×(40×270-30×160)2200×300×70×430≈9.967,由于9.967>6.635所以在犯错误的概率不超过0.01的前提下认为该地区的老年人是否需要帮助与性别有关.(3)根据(2)的结论,能否提出更好的调查办法来估计该地区的老年人中需要志愿者提供帮助的老年人的比例?说明理由.解析:由于(2)的结论知,该地区的老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好.附:K2=P(K2≥k0)0.0500.0100.001k0 3.841 6.63510.8282.某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分为5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图所示的频率分布直方图.(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;解析:由已知得,样本中有25周岁以上组工人60名,25周岁以下组工人40名.所以,样本中日平均生产件数不足60件的工人中,25周岁以上组工人有60×0.05=3(人),记为A1,A2,A3;25周岁以下组工人有40×0.05=2(人),记为B1,B2.从中随机抽取2名工人,所有的可能结果共有10种,它们是:(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).其中至少有1名“25岁以下组”工人的可能结果共有7种,它们是:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2).故所求的概率P=7 10.(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?附:K2=P(K2≥k0)0.1000.0500.0100.001k0 2.706 3.841 6.63510.828解析:由频率分布直方图可知,在抽取的100名工人中,“25周岁以上组”中的生产能手60×0.25=15(人),“25周岁以下组”中的生产能手40×0.375=15(人),据此可得2×2列联表如下:生产能手非生产能手合计25周岁以上组15456025周岁以下组152540合计3070100因为1.79<2.706,所以没有90%的把握认为“生产能手与工人所在年龄组有关”.。
人教A版高中数学选修1-2课件:1.2独立性检验的基本思想及其初步应用 (共39张PPT)

梅青中学
高二备课组
1.2×2列联表
(1) 分 类 变 量 : 变 量 的 不 同 “ 值 ” 表 示 个 体 所 属 的
不同类别 ________,像这类变量称为分类变量.
(2)2×2列联表 假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和 {y1,y2},其样本频数列联表(也称为2×2列联表)为 变 量 x1 x2 总 计 表. y1 a c a+c y2 b d b+d 总 计 a+b c+d a+b+c+d
像上表这样列出的两个分类变量的 __________ 频数表 称为列联
在列联表中,如果两个分类变量没有关系,则应满足ad-
bc≈0.因此|ad-bc|越小,说明两个分类变量之间关系越弱; |ad -bc|越大,说明两个分类变量之间关系越强.
2.独立性检验 为了使不同样本容量的数据有统一的评判标准,我们构造
独立性检验 【例2】 某大学餐饮中心为了解新生的饮食习惯,在全校
一年级学生中进行了抽样调查,调查结果如下表所示:
学 生 喜欢甜品 60 10 70 不喜欢甜品 20 10 30 合 计 80 20 100
南方学生 北方学生 合 计
根据表中数据,问是否有 95%的把握认为“南方学生和北 方学生在选用甜品的饮食习惯方面有差异”?
关系很大; 如果 K2 的值比较小,则说明二者之间关系不明 显.
2.某大型企业人力资源部为了研究企业员工工作态度和 对待企业改革态度的关系,经过调查得到如下列联表: 态 度 积极支持企业改革 不太支持企业改革 总计 32 63 95 工作一般 86 103 189 总 计 根据列联表,能否在犯错误的概率不超过 0.005 的前提下 认为工作态度与对待企业改革态度之间有关系?
1.2独立性检验的基本思想及其初步应用课件人教新课标1

d)
P(K 2 k0 ) 0.50 0.40 0.5 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k0
0.445 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
男生 女生 合计
喜欢足球 不喜欢足球 合计
问题7:这组数据采集于我们班这个小范围内, 为了使得结论更客观、更可靠,我们应该做何改 进?
独立性检验的基本思想
反证法
独立性检验
目标
两种 情况
理论 根据
证明结论成立(只有一种)
H0 : 结论成立; H1:结论的反面成立;
矛盾双方不可能同时成立 但是有且只有一个成立
判断分类变量A与B之间是否有关 结果有两种可能:有关或无关
H0 : A与B无关(独立); H1:A与B有关;
在一次实验中,小概率事件几 乎是不可能产生的
1.2 独立性检验的基本思想及应用
问题导入,激发兴趣
有人说:吸烟有害
健康!吸烟会引发肺癌.
另一些人说:吸烟
不影响健康.理由是,有
的吸烟老人却很长寿。
这两种观点哪个正
确呢?
用数据说话
初步探索,展示内涵
为了调查吸烟与患肺癌是否有联系,某像 类机这 变构样 量列 的随出 频机的 数调两 表查个 ,了分 称 9965人,得到了下表中的数据(单位:人) 为列联表。
操作 步骤
(1)假设H 0的反面H1成立;
(1)原假设H
成立;
0
(2)计算K 2的值;
(2)推到出矛盾,从而H1不成立; (3)确定临界值k(0 如何确定?);
(3)由H1不成立,说明H 0成立.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)在假设条件下,计算构造的随机变量K2,如果由观测数据 计算得到的K2很大,则在一定程度上说明假设不合理.
(3)根据随机变量K2的含义,可以通过(2)式评价假设不合理 的程度,由实际计算出的k>6.635,说明假设不合理的程度约为 99%,即“两个分类有关系”这一结论成立的可信程度约为99%.
反证法原理与独立性检验原理
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
独立性检验的定义
上面这种利用随机变量K2来确定在多大 程度上可以认为“两个分类变量有关系”的 方法,称为两个分类变量的独立性检验。
例1.在500人身上试验某种血清预防感冒作用,把他们 一P(年χ≥x中0) 的0.5感0 冒0.4记0 录0.与25 另0.1外5 500.100名0未.05用0血.02清5 0的.01人0 的0.0感05 冒0.0记01 录作x0 比较0.4,55结0.7果08如1.3表23所2.0示72。2.7问06:3.该841种5血.02清4 6能.63否5 起7.8到79 预10.防828 感冒的作用?
99.9%把握认 为A与B有关
K 2 6.635
1%把握认为A与B无 关
99%把握认 为A与B有关
K 2 2.706 10%把握认为 A与B无关
90%把握认 为A与B有关
K 2.706 2 没有充分的依据显示A与B有关,但也不能显示A与B无关
独立性检验的步骤
第一步:H0: 吸烟和患肺癌没有关系
未感冒
感冒
合计
使用血清
258
242
500
未使用血清
216
284
500
合计
474
526
1000
解:设H0:感冒与是否使用该血清没有关系。
因当H0成立时,χ2≥6.635的概率约为0.01,故有99%的把握认 为该血清能起到预防感冒的作用。
独立性检验的基本思想: 类似于数学上的反证法,对“两个分类变量有关系” 这一结论成立的可信程度的判断: (1)假设该结论不成立,即假设结论“两个分类变量 没有关系”成立.
根据这些数据能否断定:患肺癌与 吸烟有关吗?
-5-
知识梳理
列2×2联
为了研究这个问题,我们将上述问题用下表表表示:
不患肺癌 患肺癌 总计
不吸烟 7775
42
7817
吸烟
2099
49
2148
总计
9874
91
9965
在不吸烟者中患病的比重是 0.54% 在吸烟者中患病的比重是 2.28%
知识梳理
通过图形直观判断
(1)
作为检验在多大程度上可以认为“两个变量 有关系”的标准 。
独立性检验
解:H0:吸烟和患病之间没有关系
不患肺癌 患肺癌 总计
不吸烟 2099
49
7817
吸烟
7775
42
2148
总计
9874
91
9965
通过公式计算
通过查阅下表确定临界值:
P(K 2 k) 0.10 0.05 0.025 0.010 0.005 0.001
P(k2≥k0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
K 2 10.828
0.1%把握认 为A与B无关
k
2.706 3.841 5.024 6.635 7.879 10.828
这个值到底能告诉我们什么?
已知在H0 成立的情况下,
即在 H0 成立的情况下K,2 大于6.635概率非常 小,近似为0.010 现在的K 2 =56.632的观测值远大于6.635,出现 这样的观测值的概率不超过0.010。 故有99%的把握认为H0不成立,即有99%的把握认为 “患病与吸烟有关系”。但这种判断会犯错误, 犯错误的概率不超过0.010
1.2独立性检验的基本思想及其初步应用
对于性别变量,其取值为男和女两种.
这种变量的不同“值”表示个体所属的不 同类别,像这类变量称为分类变量.
生活中的分类变量
是否吸烟,宗教信仰,国籍…
我们常常关心两个分类变量之间是否有关 系。例如吸烟与患肺癌是否有关系?性别 是否与喜欢学习数学有关系?
某肿瘤研究所为了了解患肺癌与吸烟是 否有关,进行了一次抽样调查,共调查了 9965人,其中吸烟者2148人,不吸烟者7817 人,调查结果是:吸烟的2148人中49人患肺 癌, 2099人不患肺癌;不吸烟的7817人中 42人患肺癌, 7775人不患肺癌。
不患肺癌
患肺癌
总计
第二步:列出2×2列联表
不吸烟
a
b
a+b
吸烟
c
d
c+d
总计
ቤተ መጻሕፍቲ ባይዱ
a+c
b+d
a+b+c+d
第三步:计算: K 2
n(ad bc)2
(a b)(c d )(a c)(b d )
第四步:查对临界值表,作出判断。
P( ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
在假设H0下,如果推
出一个矛盾,就证
明了H0不成立.
在假设H0 下,如果出 现一个与H0相矛盾 的小概率事件,就
推断H0 不成立,且
该推断犯错误的概 率不超过这个小概 率.
-19-
知识梳理 双击自测 1 2 3 4
1.下列结论正确的画“√”,错误的画“×”.
(1)事件X,Y关系越密切,则由观测数据计算得到的K2的观测
总计
a+c
b+d
a+b+c+d
如果:吸烟与患肺癌没有关系,则在吸烟者中不患肺癌的比例 应该与不吸烟者中相应的比例差不多,即
b d 得 ad bc 0 ab cd
|ad-bc|越小,说明吸烟与患肺癌之间关系越弱;
|ad-bc|越大,说明吸烟与患肺癌之间关系越强。
知识梳理
独立性检验
为了使不同样本容量的数据有统一的评判标准,基 于上述分析,我们构造一个随机变量
-6-
等高 条形图
不患病 比例
患病 比例
上述结论能判断吸烟与患病有关吗?
从上面数据和图形可以看出吸烟和患肺癌有关
这种判断是否可靠,我们能够有多大的 把握认为“吸烟与患肺癌有关呢”?
吸烟
患肺癌
知识梳理
假设H0:吸烟和患病之间没有关系, 列出2×2列联表
不患肺癌
患肺癌
总计
不吸烟
a
b
a+b
吸烟
c
d
c+d
