进位反馈移位寄存器的状态图
《数字逻辑设计》第9章 寄存器与计数器

基本寄存器(Registers) 移位寄存器(Shift Registers) 计数器(Counters) 节拍发生器(Beat Generator)
Registers
一个n 位寄存器由 n 个触发器构成,能存放 n 位二进制数。 各种触发器均能构成寄存器,用 D 触发器最简单。
D3 = Y3Y2Y1 +Y3Y2 +Y3Y1
0
C3
1 D3
0
C2
1 D2
0
C1
1 D1
= Y3Y2Y1 +Y3Y2Y1
CP
Rd D2 = Y2Y1 +Y2Y1
D1 = Y1
+
+
Y3 Y1 Y3 Y3 Y1 Y2 Y1 Y2 Y1 Y2 Y2
Next-state equations
Y1n+1 = D1 Y2n+1 = D2 Y3n+1 = D3
4
Q
Clr CE
D
En
4 Load CLK
写入 ClrN=1, Load=1, clk↓
Q3Q2Q1Q0=D3D2D1D0
读出
En=0
Q3Q2Q1Q0=D3D2D1D0
Register Transfers
Parallel Adder with Accumulator X=X+Y
xn
Q’
Q
CE
D
xi
D2 Q2
D1 Q1
D0 Q0
Serial out (SO)
CE
CE
CE
CE
Shift Clock
数字电子技术基础第四章习题及参考答案

数字电子技术基础第四章习题及参考答案第四章习题1.分析图4-1中所示的同步时序逻辑电路,要求:(1)写出驱动方程、输出方程、状态方程;(2)画出状态转换图,并说出电路功能。
CPY图4-12.由D触发器组成的时序逻辑电路如图4-2所示,在图中所示的CP脉冲及D作用下,画出Q0、Q1的波形。
设触发器的初始状态为Q0=0,Q1=0。
D图4-23.试分析图4-3所示同步时序逻辑电路,要求:写出驱动方程、状态方程,列出状态真值表,画出状态图。
CP图4-34.一同步时序逻辑电路如图4-4所示,设各触发器的起始状态均为0态。
(1)作出电路的状态转换表;(2)画出电路的状态图;(3)画出CP作用下Q0、Q1、Q2的波形图;(4)说明电路的逻辑功能。
图4-45.试画出如图4-5所示电路在CP波形作用下的输出波形Q1及Q0,并说明它的功能(假设初态Q0Q1=00)。
CPQ1Q0CP图4-56.分析如图4-6所示同步时序逻辑电路的功能,写出分析过程。
Y图4-67.分析图4-7所示电路的逻辑功能。
(1)写出驱动方程、状态方程;(2)作出状态转移表、状态转移图;(3)指出电路的逻辑功能,并说明能否自启动;(4)画出在时钟作用下的各触发器输出波形。
CP图4-78.时序逻辑电路分析。
电路如图4-8所示:(1)列出方程式、状态表;(2)画出状态图、时序图。
并说明电路的功能。
1C图4-89.试分析图4-9下面时序逻辑电路:(1)写出该电路的驱动方程,状态方程和输出方程;(2)画出Q1Q0的状态转换图;(3)根据状态图分析其功能;1B图4-910.分析如图4-10所示同步时序逻辑电路,具体要求:写出它的激励方程组、状态方程组和输出方程,画出状态图并描述功能。
1Z图4-1011.已知某同步时序逻辑电路如图4-11所示,试:(1)分析电路的状态转移图,并要求给出详细分析过程。
(2)电路逻辑功能是什么,能否自启动?(3)若计数脉冲f CP频率等于700Hz,从Q2端输出时的脉冲频率是多少?CP图4-1112.分析图4-12所示同步时序逻辑电路,写出它的激励方程组、状态方程组,并画出状态转换图。
实验8移位寄存器实验报告

实验8移位寄存器实验报告移位寄存器实验报告(⼀)实验原理移位寄存器是⽤来寄存⼆进制数字信息并且能进⾏信息移位的时序逻辑电路。
根据移位寄存器存取信息的⽅式可分为串⼊串出、串⼊并出、并⼊串出、并⼊并出4种形式。
74194是⼀种典型的中规模集成移位寄存器,由4个RS 触发器和⼀些门电路构成的4位双向移位寄存器。
该移位寄存器有左移,右移、并⾏输⼊数据,保持及异步清零等5种功能。
有如下功能表 CLRN CLK S1 S0 × × × × 1 1 0 11 00 0 ⼯作状态 0 × 清零 1 0 保持1 ↑并⾏置数,Q 为ABCD 1↑串⾏右移,移⼊数据位为SRS11↑串⾏左移,移⼊数据位为SLS11↑保持(⼆)实验框图时钟脉冲输⼊串⾏输⼊并⾏输⼊ABCD清零输⼊模式控制输⼊并⾏输出QA 、QB 、QC 、QD74194移位寄存器(三)实验内容1.按如下电路图连接电路⼗个输⼊端,四个输出端,主体为74194.2.波形图参数设置:End time:2us Grid size:100ns波形说明:clk:时钟信号; clrn:置0s1s0:模式控制端 sl_r:串⾏输⼊端abcd:并⾏输⼊ qabcd:并⾏输出结论:clrn优先级最⾼,且低有效⾼⽆效;s1s0模式控制,01右移,10左移,00保持,11置数重载;sl_r控制左移之后空位补0或补1。
3.数码管显⽰移位(1)电路图(2)下载验证管脚分配:a,b,c,d:86,87,88,89 bsg[3..0]:99,100,101,102 clk:122 clk0:125 clrn:95 q[6..0]:51,49,48,47,46,44,43 s0,s1:73,72sl_r:82,83结论:下载结果与仿真结果⼀致,下载正确。
第5章 数字逻辑基础(4)

F1
1D
Fn-1
C1 Q
1. 环形计数器 1) 电路组成 (以四位环形计数器为例)
f
F0 1D CP 1D F1 1D F2 1D F3
C1 Q
C1
Q
C1
Q
C1 Q
特点: 将串行输出端 和串行输入端 相连.
2)环形计数器状态图
1000 0001 0100 0010 1110 1101 0111 1011 1100 1001 0110 0011 0101 0000 1010 1111
Q2 Q3 Q0Q1 00
00 01 01 11 10
1
1
f=Q0Q1Q2
&
11
10
F0
F1 Q 1D Q Q 1D
F2 Q Q 1D
F3 Q
(3) 画逻辑图
CP
f
1D
C1 Q
C1
C1
C1 Q
4) 用MSI构成的能自启动环形计数器 •如输出均为0,则通 74194 SRG4 过 DSR移入1,进入 SB 0 0 1 SA 1 } M 3 有效 循环;否则经 过移位, 总会将1移 CP C4 1→/2← 到Q3处,电路进入 1 R 置数状态,置入1000, ≥1 DSR 进入有效循环状态 1,4D
1100
1110
0010
1001
0100
1010
0001
0011
0111
1111
0101
1011
0110
1101
3) 用中规模集成移位计数器构成扭环形计数器 74194
1 B S 0 A
S
SRG4
0 1
Q0Q1Q2Q3
FCSR原理及其VHDL语言的实现

法。 工作过程如下:
( 1) 计算整数和: Ρn =
∑q a
k
r
∑∑q a
j
r- 1
i
i- j
2 - m r- 1 2 , 0 ≤- p ≤ q 且 q 为奇数。 如果 p
i
r
n- k
+ m n- 1。
i= 0 j = 0
k= 1
和 q 互素, 那么 a 有周期 T = o rdq ( 2) 。 特殊的, 如果 T = 5 ( q) ( Υ为欧拉函数) , 即 2 为模 q 的本原根, 那么该序列达到 他的最大周期。 由欧拉函数的性质可知, 此时 5 ( q) = q - 1。 称其为连接数为 q 的最大周期 FCSR 序列, 或 l 序列。 由于在 FCSR 中, 初始状态、移位寄存器级数、抽头 数目、抽头位置的变化都会产生不同的序列, 因此可以通 过设计参数可变的 FCSR 发生器来生成周期更长的伪随
lib ra ry ieee; u se ieee 1 std _ log ic_ 11641a ll; u se w o rk 11com ponen ts1a ll; en tity l_ seq is po rt (clk, reset: in std _ log ic; p rn: in std_ log ic_ vecto r ( 9 dow n to 0) ; sel: in std_ log ic_ vecto r ( 9 dow n to 0) ; q: ou t std_ log ic) ; end; a rch itectu re behavio r of l_ seq is signa l ci_ n s, fback: std _ log ic_ vecto r ( 9 dow n to 0) ; signa l rr, rq: std _ log ic_ vecto r ( 3 dow n to 0) ; signa l co 1, co 2: std _ log ic; signa l sum 1: std _ log ic_ vecto r ( 2 dow n to 0) ; signa l add _ a , sum 2: std _ log ic_ vecto r ( 3 dow n to 0) ; beg in u0: d _ ff po rt m ap ( sum 2 ( 0) , clk, reset, p rn ( 0) , ci_ n s ( 0) ) ; gen1: fo r i in 1 to 9 genera te m id_ d: d _ ff po rt m ap (ci_ n s ( i- 1) , clk, reset, p rn ( i) , ci_ n s ( i) ) ; end genera te gen1; gen2: fo r i in 0 to 9 genera te fback ( i) < = ci_ n s ( i) and sel ( i) ; end genera te gen2; u1: fadd10_ 4 po rt m ap (fback, co 1, sum 1) ; add _ a ( 3) < = co 1; add _ a ( 2 dow n to 0) < = sum 1; rr ( 3) < = co 2; rr ( 2 dow n to 0) < = sum 2 ( 3 dow n to 1) ; u2: fadd4 po rt m ap (add _ a, rq, co 2, sum 2) ; u3: reg4 po rt m ap ( rr, clk, rq ) ;
寄存器和移位寄存器(共15张PPT)

第2页,共15页。
寄存器的结构特点
Q0 Q0
FF0 1D C1 R
Q1 Q1
FF1 1D C1 R
Q2 Q2
FF2 1D C1 R
Q3 Q3
FF3 1D C1 R
D0 CP CR D1
D2
D3
各触发器均为 D 功能且并行使用。
1 个触发器能存放 1 位二进制数码,因此 N 个触 发器可构成 N 位寄存器。
(1) 用同步置零端或置数端获得 N 进制计数器 。这时应根据 SN-1 对应的二进制代码写反馈函数。
4 位寄存器 理解寄存器和移位寄存器的作用和工作原理。
翻转是否同步分有:同步计数器和异步计数器 理解寄存器和移位寄存器的作用和工作原理。
M1 M0 = 01 时,右移功能。 和状态转换真值表,然后由此分析时序逻 按计数进制分有:二进制计数器、十进制计数器和任意进制计数器;
。计数器除了用于计数外,还常用于分频、定 每输入一个移位脉冲,移位寄存器中的数码依次向左移动 1 位。
6.4 寄存器和移位寄存器
主要要求:
理解寄存器和移位寄存器的作用和工作原理。 了解集成移位寄存器的应用。
第1页,共15页。
一、寄存器
RQe0g~isQte3r,是同用时于输存出放的二,进这制种数输码出。方式称
并行输出。
DQ00 Q0 QD11 Q1 QD22 Q2 QD33 Q3
4 位 寄
FF0 1D C1 R
有关。时序逻辑电路的工作状态由触发器存
储和表示。
第9页,共15页。
时序逻辑电路按时钟控制方式不同分为同步时序逻 辑电路和异步时序逻辑电路。前者所有触发器的时 钟输入端 CP 连在一起,在同一个时钟脉冲 CP 作用
若干典型的时序逻辑集成电路

FF0 FF1 FF2 FF3
0 00 0
Q0n+1=DSI Q1n+1 = Q0n Q2n+1 =Qn1 Q3n+1 =Qn2
1CP 后 1 2CP 后 1 3CP 后 0 4CP 后 1
10 0 0 1 10 0 0 11 0 1 01 1
1011 DSI CP
FF0 Q0 FF1 Q1 FF2 Q2 FF3
D1
1R R
D2 1S C1
D2
1R R
D3 1S C1
D3
1R R
CP
CR
Q0
Q1
Q2
Q3
74HCT194 的功能表
输入
输出
清 控制信 串行输
零号
入
时
并行输入
CR
S1
S0
右 移
左 移
钟 CP
DI0
DI1
DI2
DI3
Q
n1 0
Q1n1Q
2n1Q
n1 3
行
DSR DSL
L ×× × × × × × × × L L L L1
H LL×× H LHL × H LHH× HHL× L H HL × H H HH× ×
×
×
×
×
×
Q 0n
Q1n
Q
n 2
Q
n 3
2
↑ ↑
× ×
× ×
× ×
× ×
L H
Q
n 0
Q 0n
Q1n Q1n
Q
n 2
Q
n 2
3 4
↑
×
×
×
×
Q1n
Q
(整理)寄存器说明图表.
一、McBsp概述McBSP是TI公司生产的数字信号处理芯片的多通道缓冲串行口。
McBSP是在标准串行接口的基础之上对功能进行扩展,因此,具有与标准串行接口相同的基本功能。
它可以和其他DSP器件、编码器等其他串口器件通信。
它具有普通串口的以下特点:(1)全双工通信;(2)拥有两级缓冲发送和三级缓冲接收数据寄存器,允许连续数据流传输;(3)为数据发送和接收提供独立的帧同步脉冲和时钟信号;(4)能够与工业标准的解码器、模拟接口芯片(AICs)和其他串行A/D和D/A设备直接连接;(5)支持外部移位时钟或内部频率可编程移位时钟。
(6)128个通道用于接收传送。
(7)支持A-bis(8)接口直接连接工业标准的多媒体数字信号编解码器,A/D、D/A和模拟芯片。
此外,McBSP还具有以下特殊功能:(1)可以与IOM-2、SPI、AC97等兼容设备直接连接;(2)支持多通道发送和接收,每个串行口最多支持128通道;(3)串行字长度可选,包括8、12、16、20、24和32位;(4)支持μ-Law和A-Law数据压缩扩展;(5)进行8位数据传输时,可以选择LSB或MSB为起始位;(6)帧同步脉冲和时钟信号的极性可编程;(7)内部时钟和帧同步脉冲的产生可编程,具有相当大的灵活性。
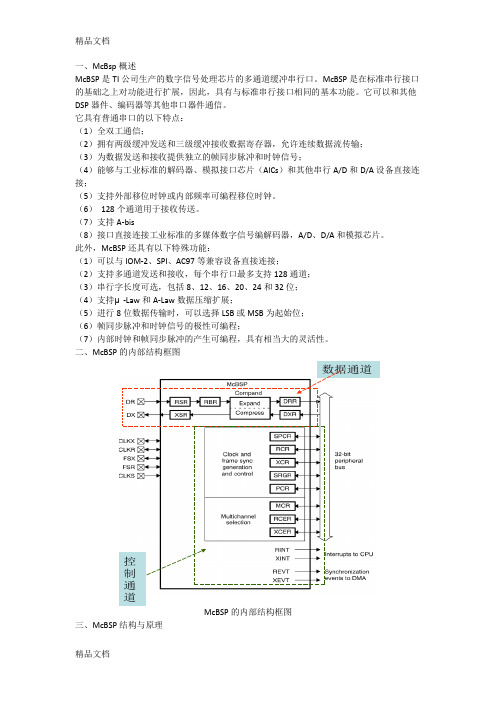
二、McBSP的内部结构框图McBSP的内部结构框图三、McBSP结构与原理数据通道控制通道四、McBsp数据压缩功能。
图1-1 DXR数据发送寄存器图1-2 XSR数据发送移位寄存器表1-2 数据发送移位寄存器(XSR)位段说明图1-3 DRR数据接收寄存器表1-3 数据接收寄存器(DRR)位段说明图1-4 RBR数据接收缓存寄存器表1-4 数据接收缓存寄存器(RBR)位段说明图1-5 RSR数据接收移位寄存器表1-5 数据接收移位寄存器(RSR)位段说明图1-6 SPCR串口控制寄存器表1-6 串口控制寄存器(SPCR)位段说明图1-7 RCR接收控制寄存器表1-7 接收控制寄存器(RCR)位段说明图1-8 XCR发送控制寄存器表1-8 发送控制寄存器(XCR)位段说明图1-9 SRGR采样率发生控制寄存器表1-9采样率发生控制寄存器(SRGR)位段说明图1-10 MCR多通道控制寄存器表1-10多通道控制寄存器(MCR)位段说明图1-11 RCER接收通道使能寄存器表1-11 接收通道使能寄存器(RCER)位段说明图1-12 XCER发送通道使能寄存器表1-12 发送通道使能寄存器(XCER)位段说明图1-13 RCERE增强的接收通道使能寄存器0-3表1-13 增强的接收通道使能寄存器(RCERE)位段说明图1-14 XCERE增强的发送通道使能寄存器0-3 表1-14 增强的发送通道使能寄存器(RCERE)位段说明图1-15 PCR引脚控制寄存器表1-15 引脚控制寄存器(PCR)位段说明自定义数据结构1.数据接收三级缓存寄存器状态表1-16数据接收三级缓存寄存器状态段说明2.PC串口使能表1-16 PC串口使能段说明***********************华丽的分割线***********************************。
