拉曼散射理论
larman定律

larman定律
摘要:
1.拉曼定律的背景和定义
2.拉曼效应的原理
3.拉曼光谱的应用领域
4.我国在拉曼光谱技术的研究和发展
5.拉曼光谱技术的未来展望
正文:
拉曼定律,又称拉曼散射定律,是印度物理学家钱德拉·拉曼于1928 年提出的。
该定律描述了光通过物质时,光线的散射现象。
根据拉曼定律,当光通过物质时,散射光中的一部分与入射光的频率相同,另一部分则与入射光的频率不同,这种现象被称为拉曼效应。
拉曼效应是一种非弹性散射现象,它使得物质对光的吸收和散射产生光谱,这种光谱被称为拉曼光谱。
拉曼光谱的原理是,当光束照射到物质上时,物质中的分子振动产生拉曼散射。
拉曼散射光与入射光之间的频率差与物质的性质有关,因此可以通过测量拉曼光谱来分析物质的结构和性质。
拉曼光谱具有很高的结构特异性,因此被广泛应用于化学、物理、生物医学、环境监测等领域。
在我国,拉曼光谱技术的研究和发展取得了显著成果。
自20 世纪50 年代开始,我国科学家就对拉曼光谱技术进行了系统研究,并取得了一系列重要成果。
近年来,我国在拉曼光谱技术领域的研究不断深入,不仅在理论研究方面取得了突破,而且在实际应用中也取得了显著成果。
例如,拉曼光谱技术被
成功应用于材料分析、生物医学诊断、环境监测等多个领域。
未来,拉曼光谱技术将继续保持稳定的发展趋势。
随着技术的不断进步,拉曼光谱仪器的性能将得到进一步提高,测量速度和灵敏度将得到显著改善。
此外,拉曼光谱技术在新领域的应用也将不断拓展,如在生物医学领域的个体化医疗、在环境监测领域的实时在线监测等。
相干拉曼散射

相干拉曼散射相干拉曼散射是一种非弹性散射现象,它是指当光线与物质相互作用时,光的频率发生变化的过程。
相干拉曼散射的研究在物理学、化学和生物学等领域有着广泛的应用。
相干拉曼散射的基本原理是光与物质之间的相互作用。
当光线照射到物质上时,部分光被散射,其中一部分光的频率发生了变化。
这种频率变化是由于光与物质之间的相互作用导致的。
相干拉曼散射可以通过测量散射光的频率变化来研究物质的结构、性质和反应等。
相干拉曼散射的频率变化是由物质分子的振动引起的。
物质分子在光的作用下会发生振动,这些振动会导致散射光的频率发生变化。
相干拉曼散射的频率变化与物质的振动频率有关,通过测量散射光的频率变化可以获得物质的振动信息。
相干拉曼散射的应用非常广泛。
在物理学领域,相干拉曼散射被用于研究材料的结构和性质。
通过测量散射光的频率变化,可以获得材料的振动信息,从而了解材料的结构和性质。
在化学领域,相干拉曼散射被用于分析化学物质的成分和反应过程。
通过测量散射光的频率变化,可以获得化学物质的振动信息,从而确定化学物质的成分和反应过程。
在生物学领域,相干拉曼散射被用于研究生物分子的结构和功能。
通过测量散射光的频率变化,可以获得生物分子的振动信息,从而了解生物分子的结构和功能。
相干拉曼散射的研究还有一些挑战和困难。
首先,相干拉曼散射的信号很弱,需要使用高灵敏度的光学设备进行测量。
其次,相干拉曼散射的信号还会受到背景噪声的干扰,需要进行信号处理和噪声抑制。
此外,相干拉曼散射的理论模型复杂,需要进行数值计算和模拟分析。
相干拉曼散射的发展和应用为我们深入了解物质的结构和性质提供了重要的手段。
通过测量散射光的频率变化,我们可以获得物质的振动信息,从而揭示物质的内在规律。
相干拉曼散射的研究还有很多潜在的应用,可以用于材料的表征、化学反应的研究、生物分子的分析等领域。
相干拉曼散射是一种非弹性散射现象,通过测量散射光的频率变化可以研究物质的结构、性质和反应等。
拉曼光谱拉曼谱是以印度物理学家拉曼(C.V.Raman)命名的一种散射光谱

拉曼光谱拉曼谱是以印度物理学家拉曼(C.V.Raman)命名的一种散射光谱.1928年拉曼和克利希南(K.S.Krishnan)在研究单色光在液体中散射时,不仅观察到与入射光频率相同的瑞利散射,而且还发现有强度很弱,与入射光频率不同的散射光谱.同年,前苏联的曼迭利斯塔姆和兰兹贝尔格在石英的散射中也观察到了这一现象.这种新谱线对应于散射分子中能级的跃迁,为研究分子结构提供了一种重要手段,引起学术界极大兴趣,拉曼也因此荣获1930年的诺贝尔物理学奖.但由于拉曼光谱很弱,受当时光源和检测手段的限制,它的发展曾停滞了一段时期.19世纪60年代激光技术的出现使拉曼光谱得以迅速发展,再加上近年来发展的高分辨率的单色仪和高灵敏度的光电检测系统,使拉曼光谱学进入崭新的阶段,应用领域遍及物理、化学、生物、医学等.利用各种类型的材料作为散射物质,几乎都可能得到相应的拉曼谱.这种新型的实验技术正日益显示其重要意义。
通过实验了解激光拉曼光谱仪的基本结构与工作原理;了解拉曼散射的原理及其在现代科学研究中的作用;测量典型的CCl4拉曼散射谱。
一、实验原理当一束单色光入射在固、液或气态介质上时,从介质中有散射光向四面八方射出.散射光中较强的是瑞利散射,其频率与入射光频率ν0相同,其强度和数量级约为入射光强的10-4~10-3.除瑞利散射外还有拉曼散射,拉曼散射的散射光频率ν与入射光频率相比有明显的变化,即ν=ν0±|Δν|,其强度数量级约为瑞利散射的10-8-10-6,最强的也只是瑞利散射的10-3.瑞利线ν0长波一侧出现的散射线ν=ν0-|Δν|称为斯托克斯(Stokes)线,又称为红伴线;把短波一侧出现的ν=ν0+|Δν|称为反斯托克斯(anti-Stokes)线,又称紫伴线.斯托克斯线比反斯托克斯线通常要强一些.散射光频率ν相对于入射光频率ν0的偏移,即拉曼光谱的频移Δν,是拉曼谱的一个重要特征量.散射线的±|Δν|相对于瑞利线是对称的,而且这些谱线的频移Δν不随入射光频率而变化,只决定于散射物质的性质.换句话说,在不同频率单色光的入射下都能得到类似的拉曼谱.拉曼散射是由分子振动,固体中的光学声子等元激发与激发光相互作用产生的非弹性散射。
拉曼效应

定理定律
1930年诺贝尔物理学奖授予当时正在印度加尔各答大学工作的拉曼(SirChandrasekhara Venkata Raman, 1888——1970年),以表彰他研究了光的散射和发现了以他的名字命名的定律。
在光的散射现象中有一特殊效应,和X射线散射的康普顿效应类似,光的频率在散射后会发生变化。“拉曼散 射”是指一定频率的激光照射到样品表面时,物质中的分子与光子发生能量转移,振动态(例如:原子的摆动和 扭动,化学键的摆动和振动)发生不同方式和程度的改变,然后散射出不同频率的光。频率的变化决定于散射物 质的特性,不同种类的原子团振动的方式是独一的,因此可以产生与入射光频率有特定差值的散射光,其光谱就 称为“指纹光谱”,可以照此原理鉴别出组成物质的分子的种类。这是拉曼在研究光的散射过程中于1928年发现 的。在拉曼和他的合作者宣布发现这一效应之后几个月,苏联的兰兹伯格(ndsberg)和曼德尔斯坦 (L.Mandelstam)也独立地发现了这一效应,他们称之为联合散射。拉曼光谱是入射光子和分子相碰撞时,分子 的振动能量或转动能量和光子能量叠加的结果,利用拉曼光谱可以把处于红外区的分子能谱转移到可见光区来观 测。因此拉曼光谱作为红外光谱的补充,是研究分子结构的有力武器。
(1)Material checks: inorganic and organic contaminations, stress材料 (2)Corrosions products: identification of different oxides腐蚀 (3)Carbon: diamond -CVD and natural,amorphous carbon,carbon fibres碳 (4)Adsorbates on catalysts and electrode surfaces催化剂和电极表面 (5)Forensic: detection & identification of drugs, explosives, fabrics etc.适于法庭 (6)Mineralogy and Gemmology: characterisation,inclusions,purity宝石学 (7)Art: identification of materials and paintings, (restauration!) (建筑物等)修复,修缮) 艺术品
拉曼光谱的基本原理和应用

拉曼光谱的基本原理和应用拉曼光谱是物理学中的一种光谱分析技术,由印度物理学家拉曼于1928年首次发明并应用于物质分析领域,被誉为光谱分析技术中的“黄金标准”。
它是一种非破坏性的、非接触的分析方法,通过记录分子或晶格振动产生的光散射谱,来确定样品的化学成分和分子结构等信息。
本文将对拉曼光谱的基本原理和应用进行介绍。
1. 基本原理拉曼散射现象,是指当激发光通过物质后,和物质分子(原子)作用,从而使部分光子散射并改变波长和能量的现象。
其中有经典理论和量子理论两种解释方式。
经典理论认为,当入射光作用于分子时,分子会处于一种较稳定的振动状态(低频振动状态),此时来自光的能量被吸收到分子内部,并在其振动中被存储。
当入射光继续辐照分子时,它将对分子中的电荷作用,使分子从初始振动状态转移到不同的振动状态,从而引起辐射吸收和耗散。
这个过程中,散射出来的光子波长与入射光子波长略有不同,这种现象被称为拉曼散射。
量子理论则通过分子内部电子能级的变化来解释拉曼散射。
当光子入射到分子中时,分子内部的电子受到激发,从一个能量级跃迁到另一个高能级状态。
接着,这些高能态电子再从高能级态回到低能级态时,向周围外沿部分辐射自身的能量,并使辐射光的波长发生变化,形成了拉曼散射光谱。
无论是通过经典理论还是通过量子理论来解释拉曼散射,其实质都是把激发光子的能量转换成分子振动的能量,从而实现对分子结构和物质成分的分析。
2. 应用(1)化学分析拉曼光谱在化学分析领域中得到了广泛应用。
它可以快速、准确地确定化合物的成分和结构,对于分析固态、液态、气态样品均可适用。
例如,在制药领域中,分析拉曼光谱可以帮助研究人员了解样品的物质成分和结构,从而更好地控制生产过程和最终成品的质量。
(2)生化学分析拉曼光谱技术在生命科学、医学、环境保护、食品安全等领域也有广泛应用。
通过对生物分子的拉曼光谱进行分析,可以帮助我们研究生物分子的组成、形态、稳定性、相互作用等信息。
拉曼的原理及应用

拉曼的原理及应用拉曼散射现象拉曼散射是一种非弹性散射现象,是由分子或晶体中的分子振动引起的。
通过拉曼散射,我们可以得到关于分子结构和动力学信息的宝贵数据。
拉曼散射是基于拉曼效应的,即当光通过样品时,与样品中的分子相互作用,波长会发生改变,从而产生散射光谱信号。
拉曼的原理拉曼效应是由印度物理学家拉曼于1928年首次观察到的,他发现光散射时发生了频率变化。
这种变化是由于光与样品中的分子相互作用后,分子的振动状态改变所导致的。
拉曼散射的原理可以通过光的电磁波动理论解释。
当光与分子相互作用时,光的能量可以转移给分子内部的振动模式,这会导致散射光的频率发生变化。
拉曼散射光分为两类:被称为斯托克斯线的低频移光和被称为反斯托克斯线的高频移光。
斯托克斯线的频率低于入射光的频率,而反斯托克斯线的频率高于入射光的频率。
这种频率的变化可以用拉曼散射光谱来观察和测量。
拉曼的应用拉曼散射技术广泛应用于许多领域,包括化学、生物、材料科学、环境科学等。
以下是拉曼的一些主要应用:•材料分析:拉曼散射可以用于材料的标识和鉴定。
由于不同材料的分子结构和振动模式不同,它们在拉曼散射光谱中显示出特定的峰位和频率。
通过分析样品的拉曼散射光谱,我们可以确定材料的成分和结构。
•化学反应动力学:拉曼散射可以用于研究化学反应的动力学过程。
通过测量反应物和产物在反应过程中的拉曼光谱变化,我们可以了解反应的中间步骤和反应速率。
•医学诊断:拉曼散射技术可以用于医学诊断。
通过分析人体组织和体液中的拉曼光谱,我们可以检测到与健康状态和疾病相关的变化。
拉曼光谱可以用于早期癌症诊断、血液分析和药物代谢研究等领域。
•环境监测:拉曼散射可以用于环境监测和检测。
通过分析大气中的颗粒物和有机物的拉曼光谱,我们可以了解大气污染物的来源和浓度。
拉曼散射还可以用于水质检测和土壤分析等环境领域。
•表面增强拉曼光谱:表面增强拉曼光谱(SERS)是一种利用金属纳米颗粒增强拉曼信号的技术。
拉曼光谱的原理

拉曼光谱的原理
拉曼光谱是一种分析材料的非常重要的光谱技术。
它利用拉曼散射现象来研究物质的分子结构和化学成分。
拉曼散射是指物质被光激发后,发生的光的频率改变的现象。
当入射光与物质相互作用时,一部分光会发生弹性散射,即光的频率保持不变。
然而,少量的光会发生非弹性散射,出射光的频率发生改变。
这种频率的改变称为拉曼散射频移。
拉曼光谱的原理基于拉曼散射导致的频移现象。
当入射光与物质发生相互作用时,入射光的一部分会被样品中的分子散射。
根据量子力学和振动理论,物质分子的振动和旋转会导致散射光的频率发生改变。
这种频率的改变与物质的化学组成和结构有关,因此可以通过测量散射光的频率变化来分析样品。
为了测量拉曼光谱,首先需要一个激光源。
激光光束通过透镜聚焦到样品上,与物质相互作用后,散射光被收集并传递到光谱仪中。
光谱仪中包含光栅和光电探测器。
光栅可以将散射光按照频率进行分离,使得不同频率的散射光可以被准确地测量。
光电探测器可以将光能转化为电信号,进而获得光谱图。
通过分析拉曼光谱图,可以得到物质的分子振动信息。
拉曼光谱可以提供许多有用的信息,例如分子的结构、功能基团、化学键以及样品的杂质。
此外,拉曼光谱还可以用于判别不同物质之间的差异,实现物质的快速鉴定和定量分析。
综上所述,拉曼光谱是一种基于拉曼散射的光谱技术,通过测
量散射光的频率变化来分析物质的化学组成和结构。
拉曼光谱具有非常广泛的应用领域,包括化学、材料科学、生物医学等。
拉曼散射经典物理解释

拉曼散射经典物理解释
拉曼散射是一种非弹性光散射过程,具体指入射光与拉曼介质相互作用时,散射光相较于入射光在频率上会有所不同。
经典理论解释了拉曼散射的实验现象:光波在介质中产生周期性电场、角频率为ω0,介质分子以ωj振动、极化率也有同频率的振动,可以计算介质
的感应电偶极矩的振动。
介质的感应电偶极矩振动,不仅有ω0项、还有(ω0±ωj)项,这就是Raman散射。
虽然Raman光的出现可以用经典光的
二次谐波解释,但经典理论无法说明为什么Stokes光比anti-Stokes光更强。
以上信息仅供参考,如果还有疑问,建议查阅物理专业书籍或咨询物理学家。
SERS(表面增强拉曼散射)理论

SERS 的物理类模型物理类模型致力于阐释金属表面局域场的增强,它的主要代表包括表面电磁增强模型和镜像场模型。
1、表面电磁增强模型(Electromagnetic Enhancemant Model ,简记为EM )表面电磁增强模型[5~7]又可称为表面等离子体共振模型,它认为一个吸附在金属表面的分子的诱发偶极矩是通过金属椭球由入射场和散射场共同产生的。
对于椭球比光波波长小的情况,在频率与偶极表面等离子体共振时,散射场比入射场大,这可以看作是椭球外部空间的场密度的影响。
因此拉曼散射场会与金属颗粒的强散射场引起的金属颗粒表面的等离子体振荡发生共振,这种共振的结果使振荡分子产生了非常大的能量。
如图2-1所示,把一个可以看成经典电偶极子的分子放在球形金属颗粒外的r ' 处,以频率为ω0的平面波照射,分子偶极子会产生频率为ω的拉曼散射,其偶极矩为:),(),(00ωαωr E r P P •'=' (2-1)这里的α'是分子的拉曼极化率而P E 包括两部分:),(),(),(000ωωωr E r E r E LM i P '+'=' (2-2)其中i E 是入射场的场强,LM E 是用Lorenz-Mie 理论计算获得的散射场场强。
在观察点r 处与拉曼散射相关的电场由下式给出),(),(),(ωωωr E r E r E sc dip R +=(2-3)图2-1 纳米颗粒表面增强散射示意图其中,dip E 是球形颗粒不存在时振荡偶极子P 发射的场,sc E 是由球形颗粒产生的必须满足频率ω的边值问题的散射场。
拉曼散射的强度R I 是远场振幅R E 的平方:2/)ex p(),(lim r ikr r E I R kr R ω ∞→=,增强因子G 定义为0R R I I G =,其中0R I 是在金属球形颗粒不存在时的拉曼强度。
那么在小颗粒的限制下,增强因子可由下式给出:[]230333033303)(3)1/()1/()(3i n n r g a r i r g a g a r i i n n g a i G ⋅+'+'-'+'-⋅+=(2-4) 这里的i 指入射场在r '处的偏振态,也就是()i E r E i 00,='ω,r r n ''=/ ,g和g 0是表达式()()21+-εε在ω和ω0处的值,其中ε是胶体颗粒与周围物质的复合介电函数的比值。
第六章受激拉曼散射与受激布
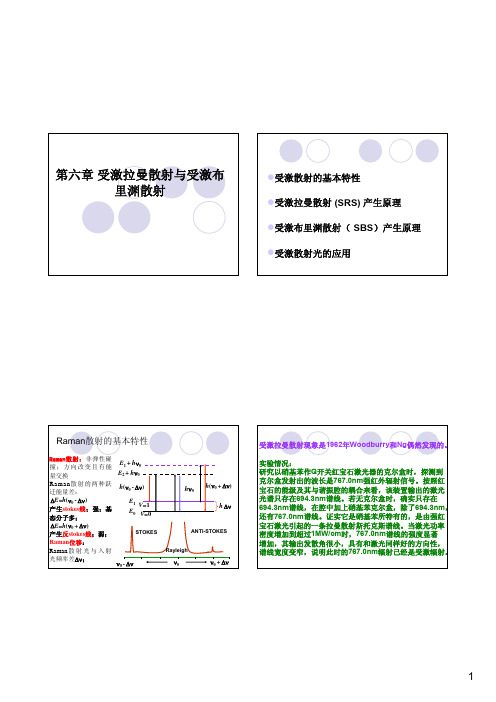
相位共轭的应用
6
SBS用于相位共轭
休斯公司的Mangir等采用布里渊振荡级和 放大级量级组合,振荡级产生共轭种子信 号较弱但有优异的相位共轭保真度,放大 级可以将共轭信号放大并转换绝大部分的 泵浦能量(70%)。利用此装置,得到能 量为4.5J的1.05微米波长的输出,保真度优 于85%。
λ
4
获得优异近场保真度的SBS相位共轭输出
hν0
h(ν0 + Δν) h Δν
ANTI-STOKES Rayleigh
ν0
ν0 + Δν
1
1、受激散射的基本特性
背景:高强度激光产生,许多基于激光与物质相互作用的 受激过程被陆续发现。
2、受激散射主要特征:
高的输出强度:SRS及SBS的强度可以达到入射激光强度同样的 量级,甚至更高 应用:拉曼频移器(高压氢池) 好的方向性:前向或背向的受激散射输出的发散角与入射激光的 发散角有关,可以优于毫弧度,甚至达到衍射极限 高阶散射:受激散射中存在斯托克斯散射和反斯托克斯散射分别 低于或者高于入射激光的频率。增大入射激光强度,选取有大的 散射介面的介质或增加所用介质的长度,可以得到更高阶斯托克 斯散射和反斯托克斯的受激散射。 相位共轭特性:受激散射光场的相位特性(或波阵面特性)与入 射激光的相位特性(或波阵面特性)具有共轭关系。 应用:畸变补偿技术(在SBS过程特别突出)
SRS理论
前向受激拉曼散射是最重要和应用最广的一种SRS,入 射光场和激发的斯托克斯光场都沿正Z轴方向传播。 斯托克斯光场在介质中传播:I s = I sn [exp(gI l L) − 1]
SRS具有增益特性,SRS输出始于泵浦光场作用下从量子噪声。 周围环境中不存在真空,根据量子力学的测不准原理,在真空中 不断产生着虚实粒子对并互相湮灭。这些粒子的产生会造成噪音。 Isn为噪声输入分子的一个振动模具有的增益因子g~10-9cm/W, 当强度为109W/cm2的泵浦激光在介质中传输25cm后,可以得到 gIL=25,从泵浦光转换至斯托克斯光的转换效率为1%。人们将 gIL=25作为SRS产生的指数增益阈值。
光的散射与拉曼效应

光的散射与拉曼效应光是一种电磁波,它在空气中传播时经常会发生散射现象。
散射是光线在遇到微观颗粒或分子时改变传播方向的过程。
而拉曼效应则是光与物质相互作用时,光波发生频率和能量的改变。
这两种现象起初似乎相互无关,但事实上它们之间存在着一定的联系。
首先,让我们先来了解一下光的散射现象。
光在传播过程中,当遇到气体、液体或固体中微小分子或颗粒时,便会发生散射。
散射的过程中,光线会改变原本的传播方向,并通过多次散射形成分散的光束。
光的散射与物体的大小和颗粒的浓度有关。
当物体的尺寸远远大于光的波长时,散射现象几乎不会发生。
而当物体的尺寸接近或小于光的波长时,光就会被散射出去,从而产生可见的光散射现象。
光的散射现象在日常生活中也很容易观察到,比如,在晴朗的天空中,我们可以看到散射光使天空呈现蓝色。
这是因为当太阳光透过大气层时,会与气体分子发生散射。
而气体分子对不同波长的光有不同的散射效应,而蓝色光的波长比较短,被散射得更强烈,所以我们看到的天空是蓝色的。
此外,夕阳的红色更为明显,是因为夕阳的光经过较长的传播距离后,大部分蓝光已经散射消失了,只有红光较强烈的情况下才能到达我们的眼睛。
接下来,让我们探讨一下拉曼效应。
拉曼效应是由印度籍物理学家拉曼在1928年发现的一种光与物质相互作用的现象。
它是指当光线与物质相互作用后,光波的频率和能量发生变化。
具体来说,拉曼效应主要表现为散射光的频率发生了位移,而且位移的大小与物质相互作用的类型和分子的结构有关。
拉曼效应的物理机制可以通过分析分子的振动行为来解释。
当光与物质相互作用时,光的能量可以激发物质内部的分子振动。
这种分子振动会导致散射光的频率发生变化,其中一部分光会发生频移,称为斯托克斯散射;而另一部分光则发生频率上升,称为反斯托克斯散射。
斯托克斯散射和反斯托克斯散射的频移量取决于物质的分子振动频率。
拉曼效应在科学研究和实际应用中有着广泛的应用。
从科学角度来看,拉曼效应提供了一种非常有效的手段来研究物质的结构和振动行为。
拉曼光谱拉曼光谱分析

引言概述:拉曼光谱是一种非侵入性的光谱分析技术,可以用来研究物质的化学成分、结构和分子间相互作用等信息。
通过测量样品与激发光相互作用后反散射光的频移,可以得到样品的拉曼光谱图谱。
拉曼光谱具有快速、灵敏和无需样品处理等优势,因此在化学、材料科学、生物医学和环境科学等领域被广泛应用。
正文内容:一、理论基础1. 拉曼散射原理:介绍拉曼光谱的基本原理,包括应力引起的拉曼散射和分子振动引起的拉曼散射。
2. 基本理论模型:介绍拉曼光谱的基本理论模型,包括简谐振动模型和谐振子模型等。
二、仪器设备1. 激发光源:介绍常用的激发光源,如激光器和光纤激光器等,以及它们的特点和选择。
2. 光谱仪:介绍常用的拉曼光谱仪,包括激光外差光谱仪和光纤光谱仪等,以及它们的原理和优缺点。
3. 采样系统:介绍拉曼光谱的采样系统,包括反射式、透射式和光纤探头等,以及它们的适用范围和操作注意事项。
三、数据处理与分析1. 光谱预处理:介绍光谱预处理的方法,包括光谱平滑、噪声抑制和基线校正等,以提高数据质量和减少干扰。
2. 谱图解析:介绍拉曼光谱谱图的解析方法,包括峰拟合、峰识别和谱图比较等,以确定样品的化学成分和结构信息。
3. 定量分析:介绍拉曼光谱的定量分析方法,包括多元线性回归和主成分分析等,以快速准确地测量样品的含量和浓度。
四、应用领域1. 化学分析:介绍拉曼光谱在化学分析中的应用,包括有机物和无机物的定性和定量分析,以及催化剂和原位反应研究等。
2. 材料科学:介绍拉曼光谱在材料科学中的应用,包括纳米材料、多晶材料和聚合物等的表征和结构分析。
3. 生物医学:介绍拉曼光谱在生物医学中的应用,包括体液中代谢产物和蛋白质的检测,以及癌症和药物代谢研究等。
4. 环境科学:介绍拉曼光谱在环境科学中的应用,包括土壤和水体中有机物和无机物的检测,以及大气污染和环境污染物的监测等。
五、发展前景与挑战1. 发展前景:介绍拉曼光谱在未来的发展前景,包括高灵敏度和高分辨率的光谱仪、纳米尺度的光学探针和超快激光技术等。
相干拉曼散射

相干拉曼散射相干拉曼散射是一种光学散射现象,指的是当激光束与物质相互作用时,入射光子与分子或晶体的振动模式相互耦合,发生能量和动量的转移,导致散射光中出现与入射光具有特定频移的拉曼散射光子。
相干拉曼散射是一种非弹性散射过程,相比于非弹性散射,它具有更高的灵敏度和更强的信号强度,因此在光谱分析、材料表征、生物医学和环境监测等领域有着广泛的应用。
相干拉曼散射的原理可以通过量子力学的耦合振动理论来解释。
当入射光束与分子或晶体相互作用时,光子与分子的振动模式相互耦合,形成一个共振态。
这个共振态又可以通过一个新的振动模式的形式表达出来,这个新的振动模式被称为拉曼振动。
在相干拉曼散射中,入射光子的能量和动量转移到拉曼振动上,从而产生拉曼散射光子。
相干拉曼散射的频移是由入射光子的能量差和拉曼振动的振动频率决定的。
具体来说,拉曼散射光子的频移等于入射光子的频率减去拉曼振动的频率。
这个频移可以用来研究物质的结构、化学键的性质和分子的振动模式等信息。
通过测量拉曼散射光子的频移,并进行光谱分析,可以获取物质的拉曼光谱,从而实现对物质的非破坏性分析和表征。
相干拉曼散射具有许多优点,使得它成为一种重要的光谱分析技术。
首先,相比于其他光谱分析技术,相干拉曼散射无需对样品进行特殊处理,也无需添加外部试剂,能够直接对样品进行分析。
其次,相干拉曼散射具有很高的灵敏度,可以检测到非常低浓度的物质,甚至可以实现单分子的检测。
此外,相干拉曼散射还具有非常高的选择性,可以通过选择合适的激光波长和拉曼散射光子的频移范围,来实现对不同物质的分析和区分。
相干拉曼散射广泛应用于许多领域。
在材料科学中,相干拉曼散射可用于研究材料的晶体结构、晶格动力学和相变等性质。
在化学分析中,相干拉曼散射可以用来鉴定分子的化学组成和结构,以及研究化学反应的动力学过程。
在生物医学领域,相干拉曼散射可以用于体液和组织的分析,实现疾病的早期诊断和治疗监测。
在环境监测中,相干拉曼散射可以用来检测水体和空气中的污染物,实现环境污染的监测和预警。
拉曼光谱的物理学原理

拉曼光谱的物理学原理拉曼光谱是一种重要的光谱分析技术,其物理学原理关乎着我们对物质本质的了解。
本文将从拉曼散射现象的原理入手,探讨拉曼光谱的物理学原理,以及其在实际应用中的价值和意义。
一、拉曼散射现象的原理拉曼效应是指当光线通过物质时,由于分子或晶格的振动引起光子的频率改变,产生散射现象的一种物理现象。
此种散射光称为拉曼散射光,拉曼效应是物质所具有的一种固有属性。
根据波动光学理论,光在不同介质中传播时,取决于介质的折射率。
而物质振动对于电磁波频率的改变,会引起散射光的频率发生变化,导致散射光成为一束由反射光波振幅不同频率组成的复合光。
对于波长为λ的入射光,分子的散射光中一部分波长为λ+delta_λ,另一部分波长为λ-delta_λ,其中delta_λ是分子振动的频率引起的光的频移量。
这种散射就是拉曼散射现象。
二、拉曼光谱的物理学原理拉曼散射光产生的频率偏移量非常小,通常只有以千万分之一为单位,观测起来非常困难。
为了解决这个问题,通常采用拉曼光谱仪来进行研究。
拉曼光谱仪的主要构成部分包括激光器、单色器、样品架和检测器。
激光器产生出单色、单频和高亮度的激光光束,经过单色器过滤后入射到样品上。
当激光光束与样品中的分子振动相互作用时,就会产生拉曼散射光,单色器通过过滤,只让频率与入射光不同的拉曼散射光进入检测器中进行测量。
具体而言,拉曼光谱的物理学机理主要包括三个方面:光学散射、分子振动、以及化学键的振动。
其中,光学散射是指入射光与样品分子相互作用,而导致的光散射现象。
分子振动是指分子在吸收或者发射光子时,所产生的一个固有特性振动行为。
至于化学键的振动,则是指不同化学键在化学反应中所产生的振动行为,使得单个的化学键的振动和内部谐振频率纷杂交错。
总体来说,拉曼光谱的物理机理比较复杂,其基本特征是能够提供大量的关于样品分子的信息,可以判断样品的种类、结构、化学键和组成。
因此,这种技术被广泛应用于世界范围内的各种科学和工程领域。
拉曼散射实验

拉曼散射实验拉曼散射实验是一种基于拉曼效应的实验方法,通过观察被分子或晶格散射后的光谱变化,可以得到有关分子结构和振动信息的重要数据。
本文将从物理定律出发,详细解读拉曼散射实验的准备、过程和应用,并分析其在其他专业角度上的价值。
拉曼散射实验主要涉及的定律是拉曼散射效应,该效应由印度物理学家拉曼于1928年发现。
该效应是指光线与物质相互作用时,入射光子能量的一部分被物质吸收,然后以不同能量重新辐射出去。
这导致散射光谱发生频移,即拉曼散射光谱。
拉曼散射谱包含了一些与物质的分子振动和转动状态有关的信息,因此在材料学、化学、生物学等领域有广泛的应用。
进行拉曼散射实验前,需要准备以下设备和材料:激光器、分光仪、光学器件、样品以及探测器等。
首先,选择合适的激光器,一般采用连续波激光器,如氩离子激光器或二极管激光器等。
然后,通过光学装置将激光束聚焦到样品上,样品可以是气体、液体或固体。
在拉曼散射实验中,通常选用单色仪、光栅或光纤进行光谱分析。
最后,使用探测器记录被散射光子的能量和强度信息。
在拉曼散射实验过程中,首先要对激光进行调节,确保其在样品上的聚焦度和功率适中。
然后,使用分光仪等光学器件收集样品散射回来的光线,并将其分离成不同波长的光谱。
这些光谱会呈现出不同的拉曼散射峰,每个峰对应着不同的振动模式。
通过分析这些峰的频率差异和强度变化,可以了解样品的分子结构和振动特性。
实验过程中需要注意排除其他干扰因素,如背景散射或荧光现象。
拉曼散射实验在许多领域有广泛的应用。
首先,在材料科学中,拉曼散射可以用来研究材料的结构、相变、应力等。
例如,通过分析拉曼散射谱,可以确定材料中的晶格结构、相对含量和纯度等。
其次,在化学领域,拉曼光谱可以用来研究分子的化学键、化学反应动力学等。
此外,拉曼光谱还可以用于生物医学研究,如检测生物分子、细胞成分的变化,甚至用于癌症和药品研究。
除了应用价值外,拉曼散射实验还在其他专业角度上具有重要意义。
光纤受激拉曼散射的理论模型

l h ia o be u 【 d a e I u r f e T e t e l h wa n t n l e wi p m e l h i e s y u a o t l i ts d u l- m c w v i q a z i r h So s i t s o o l r a g h p I t b . k g ye t d t u p d i tn ni t l i ef h g t tb s s
Co a e wi h o mp r d t ec mmo o p i g v e u t n,t i e u f nh de o idt e h sc l c a im o S ht nc u l wa e q a o n i h s q a o a mb d e h p y ia me h n s f RSmu hb t i c e-
atn t . efrt a t ua on Th i s pe kof ed u e h m p dwa es i e ot e on e i h t o bl- u e v h f dt hes o dpe kw h np t a e umpe i h n e iyicra e The dlg titnst n e s d
i tt na o t e q a 0 wa c ic e c wi p r n. e d s t a n e rt n ry u o hg —re So e to mi i u t e u t 1 s o i n e t e e me tB s e icni r e e eg jmp f ihod r tk s o . ao b h i1 n d h x i i tp
tn i ha ha e lngt a s isoni p ia b rwa e uo . ce ua o r cl m p ov dt a rt ok s e st t t y c ng sao t n m s i o tc l e sd d e Th q t ndie t i r e h tt f s he r n i f d i y hei St e
拉曼散射

拉曼光谱产生的基本原理
拉曼散射是光照射到物质上发生的非 弹性散射所产生的。单色光束的入射光光 子与分子相互过程中,光子与分子间没有能 量交换 ,光子只改变运动方向而不改变频 率 ,这种散射过程称为瑞利散射。而在非弹 性碰撞过程中,光子与分子之间发生能量交 换 ,光子不仅仅改变运动方向, 同时光子的 一部分能量传递给分子 ,或者分子的振动和 转动能量传递给光子 ,从而改变了光子的频 率 ,这种散射过程称为拉曼散射。
E
拉曼散射谱线的强度与诱导偶极矩成正比。
二硫化碳的振 动及其极化度 的变化
退偏振比(去偏振度)
由于激光是线偏振光,而大多数的有机分子是各向异性 的,在不同方向上的分子被入射光电场极化程度是不同的。 在红外中只有单晶和取向的高聚物才能测量出偏振,而在激 光拉曼光谱中,完全自由取向的分子所散射的光也可能是偏
激光拉曼谱仪比用汞弧灯作光源的经典拉曼光谱仪具有明显 的优点: (1)被激发的拉曼谱线比较简单,易于解析; (2)灵敏度高,样品用量少,普通拉曼光谱液体样品需 50ml左右,而激光拉曼光谱只要1l即可,固体0.5 g,气 体只要1011个分子; (3)激光是偏振光,测量偏振度比较容易。
2. 制样技术及放置方式 拉曼实验用的样品主要是溶液(以水溶液为主),固体(包括纤维)。
Raman光谱仪
Raman 光谱仪主要由光源、外光路系统、样品池、单色器、信号处理输出系 统五部分组成。
1. 激光光源
激光是原子或分子受激辐射产生的。激光和普通光源 相比,具有以下几个突出的优点:
(1)具有极好的单色性。
(2) 具有极好的方向性。 拉曼光谱仪中最常用的是He-Ne气体激光器。
Ar+激光器是拉曼光谱仪中另一个常用的光源。 由于激光的这些特点,它是 拉曼散射光谱的理想光源,
拉曼散射强度计算公式

拉曼散射强度计算公式拉曼散射是一种用于研究物质分子结构和动力学的非常重要的光谱技术。
通过测量样品受到的激发光和散射光的能量差,可以推断出样品分子的振动和旋转状态,从而获得样品的结构信息。
在拉曼散射实验中,我们常常需要计算拉曼散射的强度,以便定量分析样品的特性。
拉曼散射强度的计算公式是基于散射截面和散射强度的关系。
散射截面是指单位面积内散射光子被散射的概率。
而散射强度则是指单位时间内散射光通过单位面积的能量。
由于拉曼散射是一种非常弱的现象,因此我们常常使用微扰理论来计算散射截面。
在拉曼散射实验中,我们通常使用激光作为激发光源。
激光的能量可以用光子的能量来表示,即E = hc/λ,其中E为光子的能量,h 为普朗克常数,c为光速,λ为光波长。
当激光照射到样品上时,一部分光子会被样品吸收,而另一部分光子会被样品散射出来。
被散射出来的光子的波长通常会发生变化,这就是拉曼散射。
根据微扰理论,拉曼散射的散射截面可以用下面的公式来计算:σ = (4π^4/3) * ((n^4-1)/(n^4+2))^2 * (λ^4/NA^2) * |α|^2 * Γ(ω)其中,σ为散射截面,n为样品的折射率,λ为激光的波长,NA为阿伏伽德罗常数,α为样品的极化率,Γ(ω)为散射光的谱线形状函数。
在这个公式中,第一项是与样品的折射率有关的项,它表示了激光在样品中传播时的衰减情况。
第二项是与样品的极化率有关的项,它表示了样品分子的振动和旋转状态对散射强度的影响。
第三项是与激光的波长有关的项,它表示了不同波长的激光对散射强度的影响。
最后一项是谱线形状函数,它描述了散射光的频率分布情况。
通过计算散射截面,我们可以得到拉曼散射的强度。
散射强度可以用下面的公式来表示:I = (σ * I0 * λ^4)/(16π^2 * r^2 * c)其中,I为散射强度,I0为激光的强度,r为样品与探测器之间的距离,c为光速。
由于拉曼散射强度非常弱,因此在实际测量中常常需要使用灵敏的探测器和放大器来增强信号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拉曼散射理论
当考虑拉曼散射,大家可以想一想物理两种方法之一:经典的波函数或量子粒子解释。
在古典波解释,光被认为是电磁辐射,其中包含一个振荡电场,随着通过它的极化的分子相互作用。
极化是通过与电场相互作用的电子云的能力来确定。
例如,软分子如苯往往是强大的拉曼散射而像水更难分子往往是相当微弱的拉曼散射。
拉曼散射解释图R-2的比较
当考虑量子粒子解释,光被认为是一个光子它撞击分子,然后inelasticaly飞散。
在此解释的散射光子的数量成比例的键的大小。
例如,分子具有大π键如苯倾向于散射大量的光子,而水与小单键往往是非常弱拉曼散射。
图的R-2示出了这两种方法的视觉比较。
当导出拉曼效应,它通常是最容易通过考虑上的弹簧上的简单双原子分子作为质量(如图R-3)其中 m 表示原子质量,x表示位移开始与经典解释,并K表示的粘结强度。
图R-3双原子分子作为一种大众在春天
当使用该近似,该分子的位移可以通过使用胡克定律如待表达
公式R-1
通过更换降低的质量(M1M2 / [M1 + M2])与μ和总位移(X1 + X2)其中 q,方程可以简化为,
方程的R-2
通过解这个方程对于 q,我们得到,
方程的R-3
其中νm是分子振动并且被定义为,
方程的R-4
从方程的R-3和R-4,显而易见的是,在分子振动与频率成比例的粘结强度和反比于降低的质量余弦图案。
由此我们可以看到,每个分子将具有不仅由分子中的原子数,但也个别键的特性来确定它自己的独特的振动签名。
通过拉曼效应,这些振动频率可由于这样的事实,一个分子的polorizabilityα,是位移,q的函数来测量。
当入射光与分子相互作用时,它诱导一个偶极矩,P,等于该分子的polorizability和电场入射光源的产物。
这可表示为,
方程的R-5
其中,E o为强度和νo为电场的频率使用小振幅近似,polorizability可谓位移的线性函数,
方程的R-6
当与方程的R-3和R-5的结果在合并,
方程的R-7
在等式的R-7中,我们看到,有从该分子的相互作用与入射光2所得的效果。
第一效果被称为瑞利散射,它是主导作用并导致在入射光的频率没有改变。
第二个效果是拉曼散射分量和时扩大到,
方程的R-8
现在,我们已经使用了经典的波函数产生的拉曼效应,我们可以用量子粒子的解释,以更好地可视化的流程和确定的其他信息。
如在量子解释前面讨论的,拉曼效应被描述为一个光子的非弹性散射掉的分子键。
从图的R-4中所示的查布隆斯基图中,我们可以看到,这将导致从入射的光子激发所述分子成一个虚拟能量状态。
图R-4雅布隆斯基图表代表
量子能量转换为瑞利和拉曼散射
发生这种情况时,有三种不同的可能的结果。
首先,这种分子可以回落到基态放松,放出的能量相当于一个光子入射光子的; 这是一种弹性的过程,并且再次被称为瑞利散射。
其次,这种分子可以放松到一个真实的声子的状态,放出一个光子比入射的光子的能量少; 这就是所谓的斯托克斯位移拉曼散射。
第三个可能的结果是,分子已经处于兴奋状态的声子,很高兴到一个更高的虚拟状态,然后再放松回落到基态发射比入射光子多能量的光子; 这就是所谓的反斯托克斯拉曼散射。
由于这样的事实,大部分分子将在室温下的基态中找到,有低得多的概率,一个光子将反斯托克斯散射。
其结果是,大多数的拉曼测量来执行仅考虑斯托克斯位移光。
