天津大学 场论初步
场论课件
x
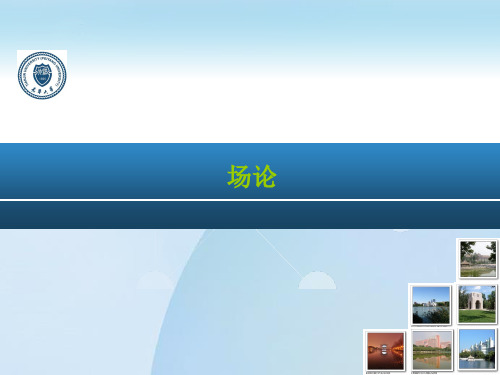
f (r ) y f ( r ) z f (r ) , f (r ) y r z r f (r ) f (r ) f (r ) grad f (r ) j k i z P y z x r 1 f (r ) ( x i y j z k ) o r y 1 x f (r ) r f (r ) r 0 r
由于
div r div( x i y j z k ) 3 xyz xyz grad grad e e ( yz i xz j xy k )
所以 n (3 , 2 , 2) 3 2 2 方向余弦为 cos , cos , cos 17 17 17 u u u 而 yz 9, 6, 6 M M x y M z M
u 所以 n
M
u u u ( cos cos cos ) x y z
在任一点M(x, y, z)的散度为
证明: 由奥-高公式 A d S P d y d z Q d z d x Rdx d y
S S
P Q R ( )dv x y z
又由中值定理得
P Q R P Q R V ( ) dV x y z x y z M *
指向数量场 在点 M 处的法向量,
M
u(M) 增大的一方.
u C
矢量场 grad u 称为由数量场u产生的梯度场. 注:
运算公式
(2) (Cu) Cu
(4) (uv) uv vu
u vu uv (5) ( ) v v2
例3.
处矢径 r 的模 , 试证
数学分析ch14-5场论初步

曲面
f (x, y, z) c (常数)
称为 f 的等值面。若 f x , f y , f z 不同时为零,那么 n
等值面上的一个单位法向量,并且有
f grad f 及 grad f f n 。
n
n
fxi fy j fzk 为
fx2 fy2 fz2
这说明, f 在一点的梯度方向与它的等值面在这点的一个法线方 向相同,这个法线方向就是 f 的方向导数取到最大值 grad f 的方向, 于是,沿着与梯度方向相同的方向, f 的函数值增加最快。而沿着与 梯度方向相反的方向, f 的方向导数取到最小值 grad f ,于是,沿 着与梯度方向相反的方向,函数值减少最快。
如果 为一张封闭曲面,定向为外侧。那么 0说明从曲面内 的流出量大于流入量,此时在 内必有产生流体的源头(源); 0 说明从曲面内的流出量小于流入量,此时在 内必有排泄流体的漏 洞(汇)。
要判断场中一点 M (x, y, z) 是否为源或汇,以及源的“强弱”或汇
的“大小”,可以作一张包含 M 的封闭曲面 (定向为外侧),考察
为场中的定向曲面,称曲面积分
a dS
为向量场 a 沿指定侧通过曲面的通量。
设 M 为这个场中任一点。称
P (M ) Q (M ) R (M )
x
y
z
为向量场 a 在 M 点的散度,记为 diva(M ) 。
定义 14.5.1 设
a(x, y, z) P(x, y, z)i Q(x, y, z) j R(x, y, z)k ,
其中 vx , vy , vz 具有连续偏导数。设 M 0 (x0 , y0 , z0 ) 是场中一点。如果在 M 0
点有旋涡,流体以角速度 旋转(这里 在旋涡的轴线上,且方向与
天津大学2018年考研复试大纲

并对用户调查及访谈、用户模型建立及行为分析、可用性研究方法等具备较扎实的基础。
二、考试内容及比例
1. 工业设计历史沿革及设计理念的发展:20%
2. 工业设计的内涵:10%
3. 工业设计中人-物-环境-社会关系的协调方法:20%
4. 人机界面设计:10%
5. 设计调查的基本特点 10%
6. 用户认知行为研究 15%
基因工程
数据库、计算机组成原理及计算 机网络
数据结构、算法基础与面向对象 程序设计 先秦诸子哲学 科学技术哲学 中国近现代史 科学社会主义理论
生命科学学院 海洋科学与技术学院
生物学 海洋科学 海洋技术 海洋环境科工程(专业学位)
电子与通信工程(专业学位) 计算机技术(专业学位)
医学科学与工程基础
课程编号:50101
课程名称:力学综合
力学学科按一级学科进行复试,其中主要包括一般力学,固体力学,流体力学等三个专业的
内容。考生可以按自己的需求进行选择
一、考试的总体要求 · 一般力学: 考察学生对理论力学基本概念、基本理论和基本方法的掌握程度。要求运用力学的基本理论 和基本方法熟练进行研究对象的受力分析、静力学合成与平衡问题求解;运动分析、各运动 量的求解;动力学分析及动力学综合问题的求解。 · 固体力学: 能运用材料力学知识分析解决工程结构模型简单的强度、刚度问题。 · 流体力学: 对流体力学的基本物理现象、基本概念和基本定律有正确的理解。对具体的流体问题能正确 判断流体及运动的基本类型。 二、考试的内容: · 一般力学: 1)静力学:受力分析、物系的平衡问题。 2)运动学:点的合成运动、刚体的平面运动及运动学综合应用问题。 3)动力学:应用普遍定理求解动力学问题中的力和运动综合问题。 · 固体力学: 1)了解常用材料拉、压、扭下的基本力学性能和测试方法; 2)能熟练地作出杆件在各种变形下的内力图,计算其应力及变形,并进行强度和刚度分析。 3)能利用材料力学的基本知识计算基本组合变形问题的应力及变形,并应用第三或第四强度 理论进行校核 · 流体力学: 1) 流体的基本方程:连续性方程、运动方程、能量方程。 2) Navier-Stokes 方程组精确解:平行平板间的定常流动等。 3) 层流边界层:边界层微分方程、边界层厚度、边界层动量积分关系式。 三、试卷题型及比例 计算、理论分析题为主,有少量选择、填空题 四、 考试形式及时间 考试形式:笔试。考试时间:1.5 小时。
79-2场论初步
散度(Divergence) 散度
定义2 定义 设向量场 A( x , y , z ) ∈ C 1 ( )
则 A( x, y, z) = P( x, y, z) i + Q( x, y, z) j + R( x, y, z) k
的散度定义为
3
P Q R div A = + + = A x y z
12
定理4 定理 设G ∈ R 是单连域,A(M)∈C (G), 是单连域,
3
1
则以下四个命题等价: 则以下四个命题等价: 等价
是无旋场, A 是无旋场,即 rot A = × A = O; 沿G内任意简单闭曲线 C 的环量 内任意简单闭曲线
∫ A ds = ∫ Pdx + Qdy + Rdz = 0
c c
是一保守场,即在G内线积分 A是一保守场,即在 内线积分
∫
( B)
( A)
与路径无关; A ds 与路径无关;
13
是一有势场,即在G内存在 A是一有势场,即在 内存在 u , 使 du = Pdx + Qdy + Rdz .
以下我们只对定理4的 空间的情况 空间的情况定理 以下我们只对定理 的2D空间的情况定理 4′ 作证明.它可以看作是 公式的推论. 作证明 它可以看作是 Green 公式的推论
B
P
Q
17
若如右图两曲线除 A,B 两点外还有其它交点 两点外还有其它交点, 则 外还有其它交点 可从A出发另作一条曲线 可从 出发另作一条曲线 弧ARB, 使其与弧 APB和 和 均不相交, 弧 AQB 均不相交 从而
B
P
Q R
A
于是证得了线积分只与始终点有关, 于是证得了线积分只与始终点有关,而与 与路径无关. 与路径无关
高等数学(2017高教五版)课件场论初步(工科类)

被吸收 M0 , 则
在点 A
S div A( M 0 ) 是流量对体积 V 的变化率,
A dS .
A
M 0 的流量密度.
量的流体流出这一点, 则称这一点
若
称这点为 “汇”. 若在每一点都有
则称 . div A 0, 为 “无源场” A
为 V 上的一个向量场.
R Q P R Q P F ( x, y, z ) i + j+ k y z z x x y 为 A 的旋度. A F 是由向量场 派生出来的一个向量
例如电力线、
注 场的性质是它本身的属性, 和坐标系的引进无关. 引入或选择某种坐标系是为了便于通过数学方法来 进行计算和研究它的性质.
§4 场论初步
场的概念
梯度场
散度场
旋度场
管量场与有势场
梯度场
在第十七章§3 中我们已经介绍了梯度的概念, 是由数量函数 它
u( x , 所定义的向量函数 y, z )
( u v ) u v .
( u v ) u(v ) (u)v .
特别地有 3. 若
(u2 ) 2u(u) . r ( x , y , z ) , ( x , y , z ) , 则 d dr .
f f (u) , u u( x , y, z ) , 则 f f ( u) u . f f ( u1 , u2 ,, um ) , ui ui ( x , y , z ) , m f f ui . i 1 ui
§4 场论初步
场的概念
梯度场
散度场
旋度场
2017天津大学各院系专业考研复习资料汇总_研途宝考研
2017天津大学各院系专业考研专业课资料汇总_研途宝考研
天大2017考研复习也慢慢步入正轨,而市面上很多关于天大考研各专业复习资料参差不齐,考研备考的成果则是我们选择了使用什么样的复习资料,选对了复习资料无疑能让我们的备考工作事半功倍,因此,研途宝思博天大考研网整理了天津大学各院系专业的考研资料,给大家考研专业课真题资料的选择提供参考。
天大专业课考研辅导推荐:
对于考研辅导班,人云亦云。
但复习进度慢、基础比较低的同学,选择报考辅导班是非常有必要的。
目前,针对天津大学最实效的四大考研辅导班主要有:
2017天津大学考研VIP高辅班
2017天津大学考研专业课无忧通关班
2017天津大学考研专业课VIP全科班
2017天津大学考研专业课一对一全程班
欢迎加入2017天津大学考研群:310523834,群内将及时提供最新考研信息、备考复习指导、考研真题资料下载及学长学姐一对一答疑等。
更多天津大学考研参考书目、考研真题、考研报录比、考研大纲、考研录取分数线、考研招生简章、考研招生目录等考研信息,请直接去研途宝思博天大考研官网查看。
第03讲预备知识-场论1

e3
顺时针为负
置换符号说明: i、j 、k取值不同值时, εijk取1 或-1(6个),其余分量(21个)为零。即:
e2 e1 逆时针为正
ε 123 = ε 231 = ε 312 = 1
ε 132 = ε 213 = ε 321 = −1
置换法则:任意2个自由指标对换后差一个负号 正负取值规律:按右图中,逆时针取值为正,顺时针取值为负。
a = ax i + a y j + az k
任意一点M的矢径 矢径微分
r = xi + yj + z k
M z y o x
a
dr = dxi + dyj + dzk
dr × a = 0
r
叉积为零:
这就是向量线的微分方程(Differential Equation) 在直角坐标系(System Of Rectangular Coordinates)当中表示为
可以列表表示:
e1
′ e1
e2
e3
α 11 α12 α13 α 21 α22 α23
α 31 α 32 α 33
ei′ = α ij e j ei = α ji e ′j
e′ 2
′ e3
上述关系可简写为:
同理,老坐标的单位向量可用新坐标的单位向量表示:
根据上述单位向量的性质和关系可导出:
ei ⋅ e j = e′ ⋅ e′j i
a ⋅ bc = (a ⋅ b)c = (b ⋅ a )c = c (a ⋅ b)
ab ⋅ cd = a (b ⋅ c )d = (b ⋅ c )ad = ad (c ⋅ b) c ⋅ ab ⋅ d = (c ⋅ a )(b ⋅ d ) = (b ⋅ d )(c ⋅ a )
天津大学XXXX级新生辩论赛策划书共12页文档

天津大学新生辩论赛策划书天津大学学生会一.活动背景诸社百团,唯我辩扬!天大学子,快意辩场!辩论,汉语艺术与思想逻辑的完美结合,如今正在大学校园里兴起,学生参与的积极性越来越高。
天津大学,一所工科类学校,同月们以理工科的严谨与扎实,充分发挥才思,踊跃的参与到辩论赛中。
作为全校最大的学生组织,天津大学学生会一直积极的筹办着各种校级辩论赛,让同学们在大学里能够感受辩论参与辩论。
现在,正值一批新生怀着梦想走进北洋园,为了让新生们能快速融入学校,感受校园文化氛围,,我校学生会积极筹办天津大学新生辩论赛,并且得到了老师们的大力支持,同学们的积极响应,各项准备工作都在有条不紊的进行中。
为了能让比赛举办的更好,我校学生会正在积极联系校外赞助,希望得到商家们的支持。
二.活动目的及意义为了让新生了解辩论赛,更多地参与辩论赛,锻炼我们天大学子的思维能力以及语言表达能力,增强我校凝聚力,培养同学们的团队合作精神,使学生成为有激情的高素质人才,我校举办此次辩论赛以促进我校学生辩论事业的发展。
这次活动,我校会与商家合作,共同创办这次新生辩论赛。
辩论赛经过班、院级的成功举办,它已经在同学心目中产生了积极有益的影响,有良好的学生基础,这次校级辩论赛定会产生广泛影响,使大一新生们又好又快的融入到校园文化氛围中。
同时,这种影响范围广的活动比能让主办方的知名度得到很大提升,也会让赞助的商家达到想要的最佳宣传效果。
三.活动对象本次新生辩论赛参赛选手是11级新生,所以活动的主要对象是大一新生。
另外,此次活动还将面向全校师生,天津市其他高校的同学和老师,社会上爱辩论的、关注辩论的各阶层人士。
四.宣传方式校内宣传1.前期宣传1)悬挂灯箱布地点:鹏翔门口,学五,大活,七里台,。
时间:十月十五日至活动结束。
内容:XX杯新生辩论赛;新生辩论赛揭幕战。
活动信息,赞助商家。
辩题,双方班级。
2)海报地点:鹏翔公寓各宿舍楼;七里台宿舍区公告栏;图书馆时间:十月十五日至活动结束。
场论初步

yz zx,
函数u在点M处最大的方向导数和它的方向。
梯度的性质:
1 grad (u v ) gradu gradv; 2 grad (u v ) ugradv vgradu; 3 gradf (u ) f (u ) gradu.
2、散度
设有一个稳定流动的流体速度场
Ax dx Ay dy Az dz
C
可以改写为以下形式:
C S
其物理意义是:向量场 A 沿闭曲线C的环量等于
展布在以C为边界的曲面S上每一点绕法线的旋 度之和。
A( P) l ds rot A( P) ndS.
Green公式,Guass公式,Stokes公式之 间的关系
S V
奥-高公式的物理意义:向量场通过闭曲面的总 流量等于闭曲面所围成的体内的每一点的散度的 总和。
奥-高公式表述了流量和散度之间的关系。流 量刻画的是向量场的整体性质,而散度刻画 的是向量场的局部性质。此二者之间存在密 切关系。
3 3 3 例2、求向量场 A( x , y , z ) x i y j z k
设 l (cos , cos , cos ) 是射线l的单位向
量,则 f f f f ( , , ) (cos , cos , cos ) l x y z gradf ( P ) l gradf ( P ) l cos gradf ( P ) cos .
结论:梯度方向是函数f(x,y,z)在点P变化率最 大的方向,即函数值增加或减少最快的方向。
等值面:曲面f(x,y,z)=C(C为常数)称为等值面。
场f(x,y,z)中过点 P0 ( x0 , y0 , z0 ) 有且仅有一 个等值面,等值面在 P0 的法线方程为
张量分析及场论

u
w
v
图 1.1、矢量加法的平行四边形法则
W | F || u | cos
其中 F 、| u |分别表示矢量 F 、 u 的大小,θ表示矢量 F 与矢量 u 之间的夹角,这就 定义了一种称为点积的运算。
点积的定义: 设 u ,v 为两个任意不为零的矢量, 设| u |, | v |分别为其大小 (也称为模) 。 θ为这两个矢量之间的夹角,则 u 与 v 的点积为
张 量 分 析 及 场 论 Tensor Analysis and Field Theory
刘长根第一章 张量代数 ..................................................................................................................... 1 §1.1 点积、矢量分量及记号 ij .......................................................................................... 1 1.2 记号 ijk 、矢积(叉乘)、 关系 ........................................................................ 5 1.3、坐标变换 ...................................................................................................................... 9 1.4、并矢、张量 ................................................................................................................ 12 1.5 张量的代数运算 ........................................................................................................... 14 1.6 张量识别定理(商判则) ........................................................................................... 16 1.7、二阶张量 .................................................................................................................... 17 1.8、张量举例 .................................................................................................................... 21 习题一 ................................................................................................................................. 36 第二章 正交曲线坐标系中的张量分析与场论 ................................................................. 39 2.1、矢量函数、及其导数与微分 .................................................................................... 39 2.2 场 ................................................................................................................................... 43 2.3、曲线坐标 .................................................................................................................... 45 2.4、标量场的方向导数、梯度 ........................................................................................ 49 2.5、矢量场的通量、散度、奥高定理 ............................................................................ 53 2.6、矢量场的环量、旋度、斯托克斯公式 .................................................................... 56 2.7、哈密顿算子 ................................................................................................................ 58 2.8、基矢量对坐标的导数及其应用 ................................................................................ 62 2.9、几种重要的场 ............................................................................................................ 69 习题二 ................................................................................................................................. 75 第三章 一般曲线坐标系中的张量分析初步 ....................................................................... 77 3.1、曲线坐标,基矢量,度量张量 ................................................................................ 77 3.2、克里斯托弗尔符号及其性质 .................................................................................... 80 3.3、协变导数,逆变导数 ................................................................................................ 82
数学分析22.4场论初步(含习题及参考答案)

第二十二章 曲面积分4 场论初步一、场的概念概念:若对全空间或其中某一区域V 中每一点M ,都有一个数量(或向量)与之对应,则称V 上给定了一个数量场(或向量场).温度场和密度场都是数量场. 若数量函数u(x,y,z)的偏导数不同时为0, 则满足方程u(x,y,z)=c(常数)的所有点通常是一个曲面.曲面上函数u 都取同一个值时,称为等值面,如温度场中的等温面.重力场和速度场都是向量场. 设向量函数A(x,y,z)在三坐标轴上投影分别为:P(x,y,z), Q(x,y,z), R(x,y,z), 则A(x,y,z)=(P(x,y,z), Q(x,y,z), R(x,y,z)), 其中P , Q, R 为定义区域上的数量函数,且有连续偏导数.设向量场中的曲线L 上每点M 处的切线方向都与向量函数A 在该点的方向一致,即P dx =Q dy =Rdz, 则称曲线L 为向量场A 的向量场线. 如, 电力线、磁力线等都是向量场线.二、梯度场概念:梯度是由数量函数u(x,y,z)定义的向量函数grad u=⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂z u y u x u ,,, 且grad u 的方向是使lu∂∂达到最大值的方向, 其大小为u 在这个方向上的方向导数. 所以可定义数量场u 在点M 处的梯度grad u 为在M 处最大的方向导数的方向,及大小为在M 处最大方向导数值的向量. 因为方向导数的定义与坐标系的选取无关,所以梯度定义也与坐标系选取无关. 由梯度给出的向量场,称为梯度场. 又数量场u(x,y,z)的等值面u(x,y,z)=c 的法线方向为⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂z u y u x u ,,, 所以 grad u 的方向与等值面正交, 即等值面法线方向. 引进符号向量: ▽=⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂z y x ,,. 将之视为运算符号时, grad u=▽u.基本性质:若u,v 是数量函数, 则 1、▽(u+v)=▽u+▽v ;2、▽(uv)=u(▽v)+(▽u)v. 特别地▽u 2=2u(▽u);3、若r=(x,y,z), φ=φ(x,y,z), 则d φ=dr ▽φ;4、若f=f(u), u=u(x,y,z), 则▽f=f ’(u)▽u ;5、若f=f(u 1,u 2,…,u n ), u i =u i (x,y,z) (i=1,2,…,n), 则▽f=i ni iu u f∑=∇∂∂1. 证:1、▽(u+v)=⎪⎪⎭⎫ ⎝⎛∂+∂∂+∂∂+∂z v u y v u x v u )(,)(,)(=⎪⎪⎭⎫⎝⎛∂∂+∂∂∂∂+∂∂∂∂+∂∂z v z u y v y u x v x u ,, =⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂z u y u x u ,,+⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂z v y v x v ,,=▽u+▽v. 2、▽(uv)=⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂z uv y uv x uv )(,)(,)(=⎪⎪⎭⎫⎝⎛∂∂+∂∂∂∂+∂∂∂∂+∂∂z v u v z u y v u v y u x v u v x u ,,=⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂z v u y v u x v u,,+⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂v z u v y u v x u ,,=u ⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂z v y v x v ,,+⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂z u y u x u ,,v=u(▽v)+(▽u)v. 当u=v 时,有▽u 2=▽(uv)=u(▽v)+(▽u)v =2u(▽u).3、∵dr=dx+dy+dz, ▽φ=⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂z y x ϕϕϕ,,, ∴dr ▽φ=(dx+dy+dz)⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂z y x ϕϕϕ,,=dz z dy y dx x ∂∂+∂∂+∂∂ϕϕϕ=d φ. 4、∵▽f=⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂z f y f x f ,,=⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂z u du df y u du df x u du df ,,, 又▽u=⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂z u y u x u ,,, f ’(u)=du df, ∴f ’(u)▽u=⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂z u y u x u du df ,,=⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂z u du df y u du df x u du df ,,=▽f. 5、▽f =⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂z f y f x f ,,=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛∂∂∂∂⎪⎪⎭⎫ ⎝⎛∂∂∂∂⎪⎪⎭⎫ ⎝⎛∂∂∂∂∑∑∑===n i i i n i i i n i i i z u u f y u u f x u u f 111,,=∑=⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂∂∂∂∂∂∂ni i i i i i i z u u f y u u f x u u f 1,,=∑=⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂∂∂n i i i i iz u y u x u u f1,,=i n i iu u f∑=∇∂∂1.例1:设质量为m 的质点位于原点, 质量为1的质点位于M(x,y,z), 记OM=r=222z y x ++, 求rm的梯度. 解:rm∇=⎪⎭⎫ ⎝⎛-r z r y r x r m ,,2.注:若以r 0表示OM 上的单位向量,则有r m∇=02r rm -, 表示两质点间引力方向朝着原点, 大小是与质量的乘积成正比, 与两点间的距离的平方成反比. 这说明引力场是数量函数r m 的梯度场. 所以称rm为引力势.三、散度场概念:设A(x,y,z)=(P(x,y,z), Q(x,y,z), R(x,y,z))为空间区域V 上的向量函数, 对V 上每一点(x,y,z), 定义数量函数D(x,y,z)=zRy Q x P ∂∂+∂∂+∂∂, 则 称D 为向量函数A 在(x,y,z)处的散度,记作D(x,y,z)=div A(x,y,z).设n 0=(cos α, cos β, cos γ)为曲面的单位法向量, 则=n 0dS 就称为曲面的面积元素向量. 于是得高斯公式的向量形式:⎰⎰⎰VdivAdV =⎰⎰⋅SdS A .在V 中任取一点M 0, 对⎰⎰⎰VdivAdV 应用中值定理,得⎰⎰⎰VdivAdV =div A(M*)·△V=⎰⎰⋅SdS A , 其中M*为V 中某一点,于是有div A(M*)=VdSA S∆⋅⎰⎰. 令V 收缩到点M 0(记为V →M 0) 则M*→M 0, 因此div A(M 0)=VdSA SM V ∆⋅⎰⎰→0lim.因⎰⎰⋅SdS A 和△V 都与坐标系选取无关,所以散度与坐标系选取无关.由向量场A 的散度div A 构成的数量场,称为散度场.其物理意义:div A(M 0)是流量对体积V 的变化率,并称它为A 在点M 0的流量密度.若div A(M 0)>0, 说明在每一单位时间内有一定数量的流体流出这一点,则称这一点为源.反之,若div A(M 0)<0, 说明流体在这一点被吸收,则称这点为汇. 若向量场A 中每一点皆有div A=0, 则称A 为无源场.向量场A 的散度的向量形式为:div A=▽·A.基本性质:1、若u,v 是向量函数, 则▽·(u+v)=▽·u+▽·v ; 2、若φ是数量函数, F 是向量函数, 则▽·(φF)=φ▽·F+F ·▽φ;3、若φ=φ(x,y,z)是一数量函数, 则▽·▽φ=222222zy x ∂∂+∂∂+∂∂ϕϕϕ.证:1、记u(P 1(x,y,z),Q 1(x,y,z),R 1(x,y,z)), v(P 2(x,y,z),Q 2(x,y,z),R 2(x,y,z)), 则▽·(u+v)=zR R y Q Q x P P ∂+∂+∂+∂+∂+∂)()()(212121 =⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂+⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂z R y Q x P z R y Q x P 222111=▽·u+▽·v. 2、▽·(φF)=z R y Q x P ∂∂+∂∂+∂∂)()()(ϕϕϕ=zR z R y Q y Q x P x P ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂ϕϕϕϕϕϕ =φ⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂z R y Q x P +(P ,Q,R)⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂z y x ϕϕϕ=φ▽·F+F ·▽φ. 3、∵▽φ=⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂z y x ϕϕϕ,,, ∴▽·▽φ=⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂z z y y x x ϕϕϕ=222222zy x ∂∂+∂∂+∂∂ϕϕϕ.注:算符▽的内积▽·▽常记作△=▽·▽=222222zy x ∂∂+∂∂+∂∂,称为拉普拉斯算符, 于是有▽·▽φ=△φ.例2:求例1中引力场F=⎪⎭⎫⎝⎛-r z r y r x r m,,2所产生的散度场.解:∵r 2=x 2+y 2+z 2, ∴F=3222)(z y x m ++-(x,y,z),▽·F=-m ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂333r z z r y y r x x =0.注:由例2知,引力场内每一点处的散度都为0(除原点处外).四、旋度场概念:设A(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))为空间区域V 上的向量函数, 对V 上每一点(x,y,z), 定义向量函数F(x,y,z)=⎪⎪⎭⎫⎝⎛∂∂-∂∂∂∂-∂∂∂∂-∂∂y P x Q x R z P z Q y R ,,, 称之为向量函数A 在(x,y,z)处的旋度, 记作rot A.设(cos α,cos β,cos γ)是曲线L 的正向上的单位切线向量t 0的方向余弦, 向量ds =(cos α,cos β,cos γ)ds= t 0dl 称为弧长元素向量. 于是有 斯托克斯公式的向量形式:⎰⎰SdS rotA ·=⎰Lds A ·.向量函数A 的旋度rot A 所定义的向量场,称为旋度场.在流量问题中,称⎰L A ·为沿闭曲线L 的环流量. 表示流速为A 的不可压缩流体在单位时间内沿曲线L 的流体总量,反映了流体沿L 时的旋转强弱程度. 当rot A=0时,沿任意封闭曲线的环流量为0,即流体流动时不成旋涡,这时称向量场A 为无旋场.注:旋度与坐标系的选择无关. 在场V 中任意取一点M 0,通过M 0作平面π垂直于曲面S 的法向量n 0, 且在π上围绕M 0作任一封闭曲线L, 记L 所围区域为D ,则有⎰⎰SrotA ·=⎰⎰DdS n rotA 0·=⎰LA ·. 又由中值定理有 ⎰⎰DdS n rotA 0·=(rotA ·n 0)M*μ(D)=⎰LA ·, 其中 μ(D)为区域D 的面积, M*为D 中的某一点. ∴(rotA ·n 0)M*=)(·D A Lμ⎰.当D 收缩到点M 0(记作D →M 0)时, 有M*→M 0, 即有 (rotA ·n 0)0M =)(·limD A LMD μ⎰→ .左边为rot A 在法线方向上的投影,即为旋度的另一种定义形式. 右边的极限与坐标系的选取无关,所以rot A 与坐标系选取无关.物理意义:⎰⎰DdS n rotA 0·=(rotA ·n 0)M*μ(D)=⎰LA ·, 表明向量场在曲面边界线上的切线投影对弧长的曲线积分等于向量场旋度的法线投影在曲面上对面积的曲面积分. 即流体的速度场的旋度的法线投影在曲面上对面积的曲面积分等于流体在曲面边界上的环流量.刚体旋转问题:设一刚体以角速度ω绕某轴旋转,则角速度向量ω方向沿着旋转轴,其指向与旋转方向的关系符合右手法则,即右手拇指指向角速度ω的方向,其它四指指向旋转方向. 若取定旋转轴上一点O 作为原点,则刚体上任一点P 的线速度v 可表示为v=ω×r, 其中r=OP 是P 的径向量. 设P 的坐标为(x,y,z),便有r=(x,y,z),设ω(ωx ,ωy ,ωz ), ∴v=(ωy z-ωz y,ωz x-ωx z,ωx y-ωy x), ∴rot v=(2ωx ,2ωy ,2ωz )=2ω或ω=21rot v.即线速度向量v 的旋度除去21, 就是旋转的角速度向量ω. 也即 v 的旋度与角速度向量ω成正比.基本性质:rot A=▽×A. 1、若u,v 是向量函数, 则 (1)▽×(u+v)=▽×u+▽×v ;(2)▽(u ·v)=u ×(▽×v)+v ×(▽×u)+(u ·▽)v+(v ·▽)u ; (3)▽·(u ×v)=v ·(▽×u)-u ·(▽×v);(4)▽×(u ×v)=(v ·▽)u-(u ·▽)v+(▽·v)u-(▽·u)v.2、若φ是数量函数, A 是向量函数, 则▽×(φA)=φ(▽×A)+▽φ×A.3、若φ是数量函数, A 是向量函数, 则 (1)▽·(▽×A)=0, ▽×▽φ=0,(2)▽×(▽×A)=▽(▽·A)-▽2A =▽(▽·A)-△A.证:1、记u(P 1(x,y,z),Q 1(x,y,z),R 1(x,y,z)), v(P 2(x,y,z),Q 2(x,y,z),R 2(x,y,z)),则(1)▽×(u+v)=⎪⎪⎭⎫⎝⎛∂+∂-∂+∂∂+∂-∂+∂∂+∂-∂+∂yP P xQ Q xR R zP P zQ Q yR R )()(,)()(,)()(212121212121=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂-∂∂∂∂-∂∂y P xQ xR zP zQ yR 111111,,+⎪⎪⎭⎫⎝⎛∂∂-∂∂∂∂-∂∂∂∂-∂∂y P x Q x R z P z Q yR 222222,,=▽×u+▽×v. (2)∵▽(u ·v)=▽(P 1P 2+Q 1Q 2+R 1R 2)=⎪⎪⎭⎫⎝⎛∂++∂∂++∂∂++∂z R R Q Q P P y R R Q Q P P x R R Q Q P P )(,)(,)(212121212121212121 = ⎝⎛∂∂+∂∂+∂∂+∂∂+∂∂+∂∂,122112211221x RR x R R x Q Q x Q Q x P P x P P,122112211221y RR y R R y Q Q y Q Q y P P y P P ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂⎪⎭⎫∂∂+∂∂+∂∂+∂∂+∂∂+∂∂z R R z R R z Q Q z Q Q z P P z P P 122112211221.又u ×(▽×v)=u ×⎪⎪⎭⎫⎝⎛∂∂-∂∂∂∂-∂∂∂∂-∂∂y P x Q x R z P z Q yR 222222,, = ⎝⎛∂∂+∂∂-∂∂-∂∂,21212121xRR z P R y P Q xQ Q ⎪⎪⎭⎫∂∂+∂∂-∂∂-∂∂∂∂+∂∂-∂∂-∂∂z Q Q y R Q x R P z P P x R P z P P y P R x Q R 2121212121212121,. v ×(▽×u)= ⎝⎛∂∂+∂∂-∂∂-∂∂,12121212xR R zP R yP Q xQ Q ⎪⎪⎭⎫∂∂+∂∂-∂∂-∂∂∂∂+∂∂-∂∂-∂∂z Q Q y R Q x R P z P P x R P z P P y P R x Q R 1212121212121212,. (u ·▽)v=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂z R y Q x P 111v =⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂+∂∂+∂∂∂∂+∂∂+∂∂z R R y R Q x R P z Q R y Q Q x Q P z P R y P Q x P P 212121212121212121,,(v ·▽)u=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂+∂∂+∂∂∂∂+∂∂+∂∂z R R yR Q xR P zQ R yQ Q xQ P zP R yP Q xP P 121212121212121212,,; ∴▽(u ·v)=u ×(▽×v)+v ×(▽×u)+(u ·▽)v+(v ·▽)u. (3)∵▽·(u ×v)=▽·(Q 1R 2-R 1Q 2,R 1P 2-P 1R 2,P 1Q 2-Q 1P 2) =zP Q Q P y R P P R xQ R R Q ∂-∂+∂-∂+∂-∂)()()(212121212121=y P R y R P y R P y P R x R Q x Q R x Q R x R Q ∂∂-∂∂-∂∂+∂∂+∂∂-∂∂-∂∂+∂∂1221122112211221zQP z P Q z P Q z Q P ∂∂-∂∂-∂∂+∂∂+12211221.又v ·(▽×u)=v ·⎪⎪⎭⎫⎝⎛∂∂-∂∂∂∂-∂∂∂∂-∂∂y P xQ xR zP zQ yR 111111,,=yP R xQ R xR Q zP Q zQ P yR P ∂∂-∂∂+∂∂-∂∂+∂∂-∂∂121212121212;u ·(▽×v)=yPR x Q R x R Q z P Q z Q P yR P ∂∂-∂∂+∂∂-∂∂+∂∂-∂∂212121212121;∴▽·(u ×v)=v ·(▽×u)-u ·(▽×v).(4)∵▽×(u ×v)=▽×(Q 1R 2-R 1Q 2,R 1P 2-P 1R 2,P 1Q 2-Q 1P 2)=⎪⎪⎭⎫⎝⎛∂-∂-∂-∂∂-∂-∂-∂∂-∂-∂-∂y Q R R Q x R P P R x P Q Q P z Q R R Q z R P P R y P Q Q P )()(,)()(,)()(212121212121212121212121= ⎝⎛∂∂+∂∂+∂∂-∂∂-∂∂-∂∂-∂∂+∂∂,1221122112211221zP R zR P zR P zP R yQ P yP Q yP Q yQ P,1221122112211221x QP x P Q x P Q x Q P z R Q z Q R z Q R z R Q ∂∂+∂∂+∂∂-∂∂-∂∂-∂∂-∂∂+∂∂⎪⎪⎭⎫∂∂+∂∂+∂∂-∂∂-∂∂-∂∂-∂∂+∂∂y R Q y Q R y Q R y R Q x P R x R P x R P x P R 1221122112211221; 又(v ·▽)u=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂+∂∂+∂∂∂∂+∂∂+∂∂z R R yR Q xR P zQ R yQ Q xQ P zP R yP Q xP P 121212121212121212,,; (u ·▽)v=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂∂∂+∂∂+∂∂∂∂+∂∂+∂∂z R R y R Q x R P z Q R y Q Q x Q P z P R y P Q xP P 212121212121212121,,;(▽·v)u=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂z R y Q xP 222u =⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂+∂∂+∂∂∂∂+∂∂+∂∂z R R y Q R x P R z R Q y Q Q x P Q z R P y Q P xP P 212121212121212121,,; (▽·u)v=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂+∂∂+∂∂∂∂+∂∂+∂∂z R R yQ R xP R zR Q yQ Q xP Q zR P yQ P xP P 121212121212121212,,; ∴▽×(u ×v)=(v ·▽)u-(u ·▽)v+(▽·v)u-(▽·u)v. 2、记φ=φ(x,y,z), A=A(P(x,y,z),Q(x,y,z),R(x,y,z)), 则▽×(φA)=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂-∂∂∂∂-∂∂y P xQ xR zP zQ yR )()(,)()(,)()(ϕϕϕϕϕϕ=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂+∂∂∂∂-∂∂-∂∂+∂∂∂∂-∂∂-∂∂+∂∂P yyP Q xxQ R xxR P zzP Q zzQ R yyR ϕϕϕϕϕϕϕϕϕϕϕϕ,,=φ⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂-∂∂∂∂-∂∂y P xQ x R zP z Q yR ,,+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂-∂∂∂∂-∂∂P yQ xR xP zQ zR yϕϕϕϕϕϕ,,=φ(▽×A)+▽φ×A.3、记φ=φ(x,y,z), A=A(P(x,y,z),Q(x,y,z),R(x,y,z)), 则(1)▽·(▽×A)=▽·⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂-∂∂∂∂-∂∂y P xQ x R zP z Q yR ,,=⎪⎪⎭⎫⎝⎛∂∂-∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂y P x Q z x R z P y z Q y R x=⎪⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎪⎭⎫ ⎝⎛∂∂∂∂y P z x Q z x R y z P y z Q x y R x =⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂+⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎪⎭⎫ ⎝⎛∂∂∂∂z Q x x Q z y P z z P y x R y y R x =0. ▽×▽φ=▽×⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂z y x ϕϕϕ,,=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎪⎭⎫ ⎝⎛∂∂∂∂⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂⎪⎪⎭⎫ ⎝⎛∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂∂∂x y y x z x x z y z z y ϕϕϕϕϕϕ,,=0. (2)▽×(▽×A)=▽×⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂-∂∂∂∂-∂∂y P xQ x R zP z Q yR ,,= ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂-⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂-⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂-⎪⎪⎭⎫ ⎝⎛∂∂-∂∂∂∂z Q y R y x R z P x y P x Q x z Q y R z x R z P z y P x Q y ,, =⎪⎪⎭⎫ ⎝⎛∂∂∂+∂∂-∂∂-∂∂∂∂∂∂+∂∂-∂∂-∂∂∂∂∂∂+∂∂-∂∂-∂∂∂z y Q y R x R z x P y x P x Q z Q y z R x z R z P y P x y Q 222222222222222222,,; 又▽(▽·A)=▽⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂z R yQ xP=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂∂z R y Q x P z z R y Q x P y z R y Q x P x ,,, =⎪⎪⎭⎫⎝⎛∂∂+∂∂∂+∂∂∂∂∂∂+∂+∂∂∂∂∂∂+∂∂∂+∂∂222222222222,,z R y z Q x z P z y R y Q x y P x z R y x Q x P ; ▽2A=△A=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂∂+∂∂+∂∂∂+∂∂+∂∂222222222222222222,,z R y R x R z Q y Q x Q z P y P x P ;∴▽×(▽×A)=▽(▽·A)-▽2A =▽(▽·A)-△A.五、管量场与有势场概念:对无源场A ,即div A=0,由高斯公式知,此时沿任何闭曲面的曲面积分都为0,这样的向量场称为管量场. 因为 在向量场A 中作一向量管,即由向量线围成的管状曲面, 用断面S 1, S 2截它,以S 3表示所截出的管的表面,即得到 由S 1, S 2, S 3围成的封闭曲面S ,于是有⎰⎰⋅SdS A =⎰⎰⋅外侧1S dS A +⎰⎰⋅外侧2S dS A +⎰⎰⋅外侧3S dS A =0. 又由向量线与曲面S 3的法线正交知,⎰⎰⋅外侧3S dS A =0.∴⎰⎰⋅外侧1S dS A +⎰⎰⋅外侧2S dS A =0, 即⎰⎰⋅内侧1S dS A +⎰⎰⋅外侧2S dS A . 等式说明,流体通过向量管的任意断面流量相同,∴称场A 为管量场. 如例2,由梯度rm ∇所成的引力场F 是管量场.概念:对无旋场A ,即rot A=0,由斯托克斯公式知,这时在空间单连通区域内沿任何封闭曲线的曲线积分都等于0,该向量场称为有势场. 因为当rot A=0时,由定理22.7推得此时空间曲线积分与路线无关, 且有u(x,y,z), 使得du=Pdx+Qdy+Rdz, 即grad u=(P ,Q,R), u 称为势函数. 所以,若向量场A 的旋度为0,则必存在某势函数u ,使得grad u=A. 这也是一个向量场是某个数量场的梯度场的充要条件. 例1中引力势u=r m 就是势函数. ∴▽u=F=-⎪⎭⎫⎝⎛r z r y r x r m ,,2. 又▽×▽u ≡0, ∴▽×F=0, 它也是引力场F 是有势场的充要条件.若向量场A 既是管量场,又是有势场,则称其为调和场.例2中的引力场F 就是调和场. 若A 是一个调和场,则必有 ▽·A=0, ▽u=A. 显然▽·▽u=▽2u=△u=0, 即必有势函数u 满足222222z uy u x u ∂∂+∂∂+∂∂=0, 这时称函数u 为调和函数. 习题1、若r=222z y x ++, 计算▽r, ▽r 2, ▽r1, ▽f(r), ▽r n (n ≥3). 解:∵x r ∂∂=r x , y r ∂∂=r y , z r ∂∂=r z, ∴▽r=⎪⎭⎫ ⎝⎛r z r y r x ,,=r1(x,y,z); 记u=r 2=x 2+y 2+z 2, ∵x u ∂∂=2x, y u ∂∂=2y, zu ∂∂=2z, ∴▽r 2=▽u=2(x,y,z);记v=r1, ∵x v ∂∂=-3r x , y v ∂∂=-3r y , z v∂∂=-3rz , ∴▽r 1=▽v=31r -(x,y,z);∵x f ∂∂=f ’(r)r x , y f ∂∂=f ’(r)ry , z f∂∂=f ’(r)r z , ∴▽f(r)=f ’(r)r 1(x,y,z); ∴▽r n =nr n-1⎪⎭⎫ ⎝⎛r z r y r x ,,=nr n-2(x,y,z), (n ≥3).2、求u=x 2+2y 2+3z 2+2xy-4x+2y-4z 在O(0,0,0), A(1,1,1), B(-1,-1,-1)处的梯度,并求梯度为0的点. 解:∵x u ∂∂=2x+2y-4, y u ∂∂=4y+2x+2, zu∂∂=6z-4,∴在O(0,0,0), grad u=(-4,2,-4); 在A(1,1,1), grad u=(0,8,2); 在B(-1,-1,-1), grad u=(-8,-4,-10);又由2x+2y-4=0, 4y+2x+2=0, 6z-4=0, 解得x=5, y=-3, z=32, ∴在(5,-3,32), |grad u|=0.3、证明梯度的基本性质1~5. 证:见梯度的基本性质.4、计算下列向量场A 的散度与旋度:(1)A=(y 2+z 2,z 2+x 2,x 2+y 2);(2)A=(x 2yz,xy 2z,xyz 2);(3)A=⎪⎪⎭⎫⎝⎛++xy z zx y yz x . 解:(1)∵P=y 2+z 2, Q=z 2+x 2, R=x 2+y 2; ∴div A=x ∂∂(y 2+z 2)+y ∂∂(z 2+x 2)+z ∂∂(x 2+y 2)=0;又y ∂∂(x 2+y 2)-z ∂∂(z 2+x 2)=2y-2z; z ∂∂(y 2+z 2)-x∂∂(x 2+y 2)=2z-2x; x∂∂(z 2+x 2)-y ∂∂(y 2+z 2)=2x-2y. ∴rot A=2(y-z,z-x,x-y).(2)∵P=x 2yz, Q=xy 2z, R=xyz 2; ∴div A=x ∂∂(x 2yz)+y ∂∂(xy 2z)+z∂∂(xyz 2)=6xyz ;又y ∂∂(xyz 2)-z ∂∂(xy 2z)=x(z 2-y 2); z ∂∂(x 2yz)-x∂∂(xyz 2)=y(x 2-z 2); x∂∂(xy 2z)-y ∂∂(x 2yz)=z(y 2-x 2). ∴rot A=(x(z 2-y 2),y(x 2-z 2),z(y 2-x 2)).(3)A=⎪⎪⎭⎫ ⎝⎛++xy z zx y yz x . ∵P=yz x , Q=zxy, R=xy z ;∴div A=⎪⎪⎭⎫ ⎝⎛∂∂yz x x +⎪⎭⎫ ⎝⎛∂∂zx y y +⎪⎪⎭⎫ ⎝⎛∂∂xy z z =xyzx yz 111++; 又⎪⎪⎭⎫ ⎝⎛∂∂xy z y -⎪⎭⎫ ⎝⎛∂∂zx y z =22xy z xz y -; ⎪⎪⎭⎫ ⎝⎛∂∂yz x z -⎪⎪⎭⎫ ⎝⎛∂∂xy z x =22yz x y x z-; ⎪⎭⎫ ⎝⎛∂∂zx y x -⎪⎪⎭⎫ ⎝⎛∂∂yz x y =z x y z y x 22-. ∴rot A=⎪⎪⎭⎫⎝⎛---x y y x z x x z y z z y xyz 222222,,1.5、证明散度的基本性质1~3. 证:见散度的基本性质.6、证明旋度的基本性质1~3. 证:见旋度的基本性质.7、证明:场A=(yz(2x+y+z),zx(x+2y+z),xy(x+y+2z))是有势场并求其势函数.证:P=yz(2x+y+z), Q=zx(x+2y+z), R=xy(x+y+2z),y ∂∂[xy(x+y+2z)]-z∂∂[zx(x+2y+z)]=x 2+2xy+2xz-x 2-2xy-2xz=0; z ∂∂[yz(2x+y+z)]-x∂∂[xy(x+y+2z)]=2xy+y 2+2yz-2xy-y 2-2yz=0; x∂∂[zx(x+2y+z)]-y ∂∂[yz(2x+y+z)]=2xz+2yz+z 2-2xz-2yz-z 2=0.∴对空间任一点(x,y,z)都有rot A=(0,0,0)=0i+0j+0k=0, ∴A 是有势场. 由d[xyz(x+y+z)]=yz(2x+y+z)dx+xz(x+2y+z)dy+xy(x+y+2z)dz 知, 其势函数为u(x,y,z)=xyz(x+y+z)+C.8、若流体流速A=(x 2,y 2,z 2), 求单位时间内穿过81球面x 2+y 2+z 2=1, x>0,y>0,z>0的流量.解:设S 为所给81球面,S 1, S 2, S 3分别是S 在三个坐标面上的投影, 则 所求流量为:⎰⎰⋅SdS n A 0+⎰⎰⋅11S dS n A +⎰⎰⋅22S dS n A +⎰⎰⋅33S dS n A =⎰⎰⎰⎪⎭⎫ ⎝⎛球体81V divAdV=⎰⎰⎰++Vdxdydz z y x )(2=⎰⎰⎰++103202sin )cos sin sin cos (sin 2dr r d d ϕϕθϕθϕϕθππ=⎰⎥⎦⎤⎢⎣⎡++2021)sin (cos 421πθθθπd =83π.注:其中n 0, n 1, n 2, n 3分别是S, S 1, S 2, S 3的单位法矢,显然有A|n i (i=1,2,3),∴A ·n i =0,从而⎰⎰⋅iS i dS n A =0 (i=1,2,3), 于是所求流量为:⎰⎰⋅SdS n A 0=83π.9、设流速A=(-y,x,c) (c 为常数),求环流量: (1)沿圆周x 2+y 2 =1, z=0;(2)沿圆周(x-2)2+y 2 =1, z=0.解:(1)圆周x 2+y 2 =1, z=0的向径r 适合方程r=costi+sintj+0k(0≤t ≤2π). ∵A ·dr=(-sinti+costj+ck)·(-sinti+costj+0k)dt=dt, ∴所环流量为⎰⋅c dr A =⎰π20dt =2π.(2)圆周(x-2)2+y 2 =1, z=0的向径r=(2+cost)i+sintj+0k (0≤t ≤2π); ∵A ·dr=[-sinti+(2+cost)j+ck]·(-sinti+costj+0k)dt=(2cost+1)dt, ∴所环流量为⎰⋅c dr A =⎰+π20)1cos 2(dt t =2π.。
天津大学自然辩证法重点

★★★★★1.如何理解自然辩证法定义:自然辩证法是马克思主义关于自然和科学技术发展的一般规律、人类认识和改造自然的一般方法以及科学技术与人类社会相互作用的理论体系;是对以科学技术为中介和手段的人与自然、社会的相互关系的概括、总结。
自然辩证法是马克思主义自然辩证法,是马克思主义理论的重要组成部分。
性质:自然辩证法是一门自然科学、社会科学与思维科学相交叉的哲学性质的马克思主义理论学科。
它站在世界观、认识论和方法论的高度上,从整体上研究和考察包括天然自然和人工自然在内的自然的存在和演化的规律,以及人通过科学技术活动认识自然和改造自然的普遍规律;研究作为中介的科学技术的性质和发展规律;研究科学技术和人类社会之间相互关系的规律。
自然辩证法具有综合性、交叉性和哲理性的特点。
研究内容:马克思主义自然观、马克思主义科学技术观、马克思主义科学技术方法论和马克思主义科学技术社会论,构成了马克思主义自然辩证法的重要理论基石。
★★★★★2.如何理解中国马克思主义科学技术观中国马克思主义科学技术观是自然辩证法中国化发展的最新形态,是中国共产党人集体智慧的结晶,是对毛泽东、邓小平、江泽民、胡锦涛等的科学技术思想的概括和总结,是他们科学技术思想的理论升华和飞跃,是他们科学技术思想的凝练和精髓。
包括科学技术的功能观、战略观、人才观、和谐观和创新观的基本内容,体现出时代性、实践性、科学性、创新性、自主性、人本性等特征,建设中国特色的创新型国家,是中国马克思主义科学技术观的具体体现。
中国马克思主义科学技术观,是马克思主义科学技术观与中国具体科学技术实践相结合的产物,是马克思主义科学技术论的重要组成部分。
★★★★★3.创新型国家建设中国马克思主义科学技术观为人们认识和改造自然,促进科学技术与自然、社会的和谐发展和创新型国家建设提供了重要的思想武器。
建设中国特色的创新型国家,是中国马克思主义科学技术观的具体体现;提高自主创新能力是中国特色的创新型国家建设的核心;国家创新体系建设是中国特色的创新型国家建设的关键。
矢量分析与场论 天津大学 流体力学基础

(2) 梯度的性质:从(2.7)式我们可以得到梯度的 两个重要性质:
1) 方向导效等于梯度在该方向的投影,即有:
2) 数量场中每一点处的梯度,垂直于过该点的等值面,且 指向函数u(M)增大的方向.
函数,记作:
A=A(t)
(1.1)
这时,矢量A在直角坐标系中的三个坐标(即它在三个坐标轴上的投
影),显然都是 t 的数性函数:
依此,就可以写出矢量A酌坐标表示式:
2.矢端曲线
为了能用图形来直观地表示矢性因数A)的变化状态, 把A的的起点取在坐标原点.这样,当 t 变化时,矢 量A(t)的终点就描绘出一条曲线);这条曲线叫矢性函 数A的的矢端曲线,亦叫做矢性函数A(t)的图形.
因梯度具有上述性质,它是数量场中的一个重要概念.如果我们把数量 场中每一点的梯度与场中之点一一对应起来,就得到一个矢量场,称为 由此数量场产生的梯度场.
(3) 哈米尔顿(Hamllton)算子.为了方便,我们引入一个矢段微分算子
叫做哈米尔顿算子.记号▽是一个微分运算符号,但同时又要当 作矢量看待.其运算规则是:
值函数u=u(M),当取定了oxyz坐标系以后,成为点M的坐标(x,y,z)的函数
一个数量场,可以用一个函数来表示.
在数量场中,为了宣观地研究物理量M在场中的分布状况,需要考察 场中有相同物理量的点,也就是使u(M)取相同数的点值的各点。
这个方程,一般在几伺上表示一曲而,这个曲面,称为数员场的等 值面.例如温度场中的等值面,就是由温度相同的点所组成的等温面; 电位场中的等值面,就是由电位相同的点须组成的等位面。
2.1场

2014年5月11日星期日
华北科技学院基础部
23
《场论初步》
§2.1
场
正点电荷的电场线
2014年5月11日星期日
负点电荷的电场线
华北科技学院基础部 24
《场论初步》
§2.1
场
两等量正点电荷 的电场线分布
2014年5月11日星期日
两等量异号点电荷 的电场线分布
场
例3:已知数量场 u
xy , 求场中与直线 x 2 y 4 0 c , 设切点为 ( x , y )
0 0
相切的等值线方程。 解:数量场的等值线为 xy
从而有
x0 y0 c x0 2 y0 4 0 c 1 2 x0 2
解之得 x0 2, y0 1, c 2
《场论初步》
§2.1 《场论初步》
场
第二章
场 论
1
2014年5月11日星期日
华北科技学院基础部
《场论初步》
§2.1
场
教 学 内 容
第一节 第二节 第三节 第四节 第五节
2014年5月11日星期日
场 数量场的方向导数和梯度 矢量场的通量及散度 矢量场的环量及旋度 几种重要的矢量场
华北科技学院基础部 2
或者说:场是一定空间范围内连续分布的客体.
Maxwell是第一个使用场的科学家.
场有两个显著特点:
1.场是客观存在的. 2.场可以随时间和空间发生变化.
2014年5月11日星期日
华北科技学院基础部
4
《场论初步》
§2.1
场
根据物理量的性质,分为数量场和矢量场。 数量场(标量场):物理量是数量。如温度场,电 位场,密度场等。 矢量场:物理量是矢量。比如力场,速度场,电磁
天津大学《工程光学》学习指南

第一章几何光学的基本定律和成像概念一.教学要求通过本章4课时的授课,应使学生掌握几何光学的基本定律(光的直线传播定律、独立传播定律、反射定律和折射定律),光的全反射性质,费马原理、马吕斯定律以及二者与几何光学基本定律之间的关系;明确完善成像概念和相关表述;会熟练应用符号规则进行单个折射球面的光线光路计算,掌握单个折射球面和反射球面的成像公式,包括物像位置、垂轴放大率β、轴向放大率α、角放大率γ、拉赫不变量等公式及其各量的物理意义,并推广到共轴球面系统的成像计算。
二.重点难点1.几何光学的基本定律光是一种电磁波,它在介质中的传播规律可概括为以下四个基本定律:直线传播定律,独立传播定律、反射定律和折射定律。
4个定律的内容、实例和适用条件。
折射率的概念。
费马原理和马吕斯定律从另外的角度描述了光在介质中的传播规律,它们与几何光学的四个基本定律是完全等价的,可以相互推导证明。
2.成像的基本概念与完善成像条件光学系统的作用之一是对物体成像。
若一个物点对应的一束同心光束,经光学系统后仍为同心光束,该光束的中心即为该物点的完善像点。
物体上每个点经光学系统后所成完善像点的集合就是该物体经光学系统后的完善像。
物所在的空间称为物空间,像所在的空间称为像空间,物像空间的范围均为(-∞,+∞)。
物像有虚实之分,由实际光线相交所形成的物或像为实,由光线的延长线相交所形成的物或像为虚。
【其中物像空间和物像虚实的判断是难点】光学系统成完善像应满足以下三个条件之一:1)入射波面是球面波时,出射波面也是球面波。
2)入射是同心光束时,出射光也是同心光束。
3)物点及其像点之间任意两条光路的光程相等。
3.几何光学中的符号规则和单个折射球面的光线光路计算为保持几何光学公式的一致性和讨论问题的方便,特确定了如下的符号规则:1)光线的传播方向由左向右。
沿轴线段以折射面顶点为原点度量,若与光线的传播方向相同,其值为正,反之为负;2)垂轴线段以光轴为基准,在光轴以上为正,光轴以下为负;3)光线与光轴的夹角用由光轴转向光线形成的锐角度量,顺时针为正,逆时针为负;4)光线与法线的夹角用由光线转向法线形成的锐角度量,顺时针为正,逆时针为负;5)光轴与法线的夹角用由光轴转向法线形成的锐角度量,顺时针为正,逆时针为负;6)折射面间隔从前一面的顶点到后一面的顶点,与光线的传播方向相同,其值为正,反之为负。
天津大学场论初步

第二十四页,编辑于星期一:四点 三十九分。
第二十五页,编辑于星期一:四点 三十九分。
第二十六页,编辑于星期一:四点 三十九分。
第二十七页,编辑于星期一:四点 三十九分。
第二十八页,编辑于星期一:四点 三十九分。
第二十九页,编辑于星期一:四点 三十九分。
第九页,编辑于星期一:四点 三十九分。
第十页,编辑于星期一:四点 三十九分。
第十一页,编辑于星期一:四点 三十九分。
第十二页,编辑于星期一:四点 三十九分。
第十三页,编辑于星期一:四点 三十九分。
第十四页,编辑于星期一:四点 三十九分。
第十五页,编辑于星期一:四点 三十九分。
第十六页,编辑于星期一:四点 三十九分。
第一页,编辑于星期一:四点 三十九分。
第二页,编辑于星期一:四点 三十九分。
第三页,编辑于星期一:四点 三十九分。
第四页,编辑于星期一:四点 三十九分。
第五页,编辑于星期一:四点 三十九分。
第六页,编辑于星期一:四点 三十九分。
第七页,编辑于星期一:四点 三十九分。
第十七页,编辑于星期一:四点 三十九分。
第十八页,编辑于星期一:四点 三十九分。
第十九页,编辑于星期一:四点 三十九分。
第二十页,编辑于星期一:四点 三十九分。
第二十一页,编辑于星期一:四点 三十九分。
第二十二页,编辑于星期一:四点 三十九分。
第二十三页,编辑于星期一:四点 三十九分。
