柱形物体压强专题
柱体压强的变化

专题八柱体压强的变化(计算题)一、近年学业考试题(2007年,考题17)如图所示,边长分别为0.2米和0.1米的实心正方体A、B 放置在水平地面上,ρA为0.l×l03 千克/米3,ρB为0.8×l03 千克/米3。
求:(1)物体A的质量m A;(2) 物体B对地面的压力F B;(3) 小明和小华两位同学设想在正方体A 、B 上部沿水平方向分别截去一定的厚度后,通过计算比较A、B 剩余部分对地面压强的大小关系。
小明设想在A、B 的上部均截去0。
09 米, 小华设想在A、B 的上部均截去0。
05 米,他们的计算过程及得出的结论分别如下表所示:计算过程结论小明P A=F A/S A=ρA gh A=0。
l×103千克/米3×9。
8牛/千克×(0.2米一0。
09米)=107.8帕P B=F B/S B=ρB gh B=0.8×103千克/米3×9.8牛/千克×(0。
1米一0.09米)=78。
4帕P A>P B小华P A=F A/S A=ρA gh A=0。
l×103千克/米3×9。
8牛/千克×(0.2米一0。
05米)=147帕P B=F B/S B=ρB gh B=0.8×103千克/米3×9。
8牛/千克×(0.1米一0.05米)=392帕P A<P B①请判断:就他们设想截去的厚度而言,小明的结论是的,小华的结论是的。
( 均选填“正确"或“错误”)②是否有可能存在某一厚度h,沿水平方向截去h 后使A、B 剩余部分对地面的压强相等?若有可能,求出h 的值;若没有可能,说明理由。
(2010年,考题22)放置在水平地面上的两个物体A和B均为实心长方体,它们的长、宽、高如图所示。
物体A的密度为0.8×103千克/米3,物体B的质量为8千克。
上海市中考物理压强压轴题专题03柱体切割后浸入液体中,无液体溢出(含解析)

上海市中考物理压强压轴题:专题03 柱体切割后浸入液体中,无液体溢出一、常见题目类型1.将柱形物体沿水平方向切去某一厚度(体积或质量),并将切去部分浸没在容器的液体中(图1)。
2.将柱形物体沿竖直方向切去某一厚度(体积或质量),并将切去部分浸没在容器的液体中(图2)。
二、例题【例题1】如图1所示,均匀长方体甲和薄壁圆柱形容器乙置于水平地面上。
长方体甲的底面积为3S 。
容器乙足够高、底面积为2S ,盛有体积为5×10-3米3的水。
① 若甲的重力为20牛,底面积为5×10-4米2,求甲对地面的压强p 甲。
② 求乙容器中水的质量m 水。
③ 若将甲沿水平方向切去厚度为h 的部分,并将切去部分浸没在乙容器的水中时,甲对水平地面压强的变化量Δp 甲恰为水对乙容器底部压强增加量Δp 水的2倍。
求甲的密度ρ甲。
【答案】①40000帕;②5千克;③3×103千克/米3。
【解析】① F 甲=G 甲=20牛p 甲=F 甲/S 甲=20牛/5×104米2= 40000帕② m 水=ρ水V 水=1×103千克/米3×5×103米3=5千克图1乙甲图1 乙甲甲乙图2③甲对水平地面压强的变化量Δp甲即为切去厚度为h部分的压强Δp甲=ΔF甲/S甲=甲gh水对乙容器底部压强增加量Δp水为水升高的高度h水=3Sh/2SΔp水=水g h水=水g(3Sh/2S)因为Δp甲=2Δp水甲gh =2水g(3Sh/2S)所以ρ甲=3×103千克/米3【例题2】如图2所示,底面积为10-2米2、高为0.4米长方体甲(ρ甲=2×103千克/米3)和底面积为2×10-2米2的薄壁柱形容器乙放在水平地面上。
乙容器足够高,内盛有0.1米深的水。
甲乙(1)求甲的质量m甲。
(2)求水对乙容器底部的压强p水。
(3)现沿水平方向将长方体甲截取一定的厚度,并将截取部分竖直放入乙容器中,使得水对容器底部的压强最大,且长方体甲对地面的压强减少量最小,请求出甲对地面的压强减少量。
上海市中考物理压强压轴题 专题05 在容器里加物体后,有液体溢出(含解析)

专题05 在容器里加物体后,有液体溢出一、常见题目类型1.将物体甲浸没在柱形容器乙的液体中(图1)。
2.将物块丙放入容器甲的液体中、叠放在柱体乙的上方(图2)。
3.将甲、乙两个实心均匀光滑小球先后分别放入容器中(图3). 4.在柱形物体乙上方沿水平方向切去一部分,并将切去部分竖直放在甲容器内(浸没或不浸没)(图4).二、例题【例题1】柱形轻质薄壁容器的底面积为1×10—2米2,如图1所示,甲图4图3 乙图1甲乙甲乙图2丙内盛0。
2米深度的水后置于水平地面上。
① 求容器底部受到水的压强p 水。
② 现将一块质量为1.5千克、体积为1×10—3米3的物体完全浸没在容器的水中后,测得容器底部受到水的压强为2450帕。
求此时容器对水平桌面的压强p 容。
【答案】①1960帕;②2940帕。
【解析】 ①p 水=ρ水g h=1×103千克/米3×9.8牛/千克×0.2米3=1960帕②物体浸没在容器的水中后,容器底部受到水的压强为2450帕可求现在水的深度h ':p '水=ρ水g h ' h '= p '/ρ水gh '=2450帕/1×103千克/米3×9。
8牛/千克=0。
25米容器内剩余水的体积为V 剩余水= S h '-V 物=0。
25米×1×10—2米2-1×10-3米3=1。
5×10-3米3现在容器对水平桌面的压力图1F 容=G 容=(m 剩余水+m 物)g=(1。
5×10—3米3×1×103千克/米3+1.5千克)×9.8牛/千克=29.4牛对水平桌面的压强P 容= F 容/S =29。
4牛/ 1×10-2米2=2940帕(注意:此题不计算溢出水的质量,更简单。
也可用其他方法求解) 【例题2】如图2所示,盛有水的轻质薄壁圆柱形容器甲和实心均匀圆柱体乙均放置于水平地面上,它们的底面积分别为1×10-2米2和0.5×10—2米2.现将两完全相同物块分别放入容器甲中和叠在圆柱体乙的上方,放置前后容器甲、圆柱体乙对水平地面的压强大小p 甲、p 乙如下表所示。
上海市中考物理压强压轴题 专题06 在容器里液体加柱形物体后 柱形物体浸没问题(含解析)

专题06 在柱形容器的液体中加柱形物体,柱形物体浸没问题一、常见题目类型1.把柱状实心物体B 放入足够深的柱状容器中的液体中(图1)。
2.把柱状实心物体先放入足够深的柱状容器中,然后向里面加液体(图2)。
二、例题【例题1】如图1所示,水平地面上有一质量为1千克的薄壁柱形容器,另有一个质量为4千克的圆柱体甲,甲的底面积是容器底面积的一半。
容器中盛有水,将甲放入水中,分别测出甲放入容器前后,容器对水平桌面的压强p 容、水对容器底部的压强p 水,如下表所示。
图1图2图1①求圆柱体甲放入容器前水的深度.②求容器的底面积。
③放入圆柱体甲后,通过计算判断柱形容器的水是否有溢出.④请判断甲在水中的状态并说明理由(提示:漂浮、浸没、未浸没等)。
⑤求圆柱体甲的密度。
【答案】①0。
2米;②2×102米2 ;③无水溢出;④浸没;⑤4×103千克/米3.【解析】①h水=p水前/ρ水g=1960帕/(1×103千克/米3×9。
8牛/千克)=0。
2米②p=p容前-p水前=F/ S容=G容/ S容S容=G容/p=(1千克×9。
8牛/千克)/(2450帕-1960帕)=2×102米2③甲放入水中,容器对水平桌面增大的压力F容=p S容=(4410帕—2450帕)×2×102米2=39.2牛F容=G甲,所以无水溢出。
④因为p容>p水,所以圆柱体甲在水中一定沉底,且S甲=S/2,p<2p 水前,所以甲在水中一定浸没(若未浸没时,S甲=S/2,后来水水后的深度h水后=2h水前,p水后=2p 水前)。
⑤因为F容=G甲,所以无水溢出h水=p水/ρ水g=490帕/1×103千克/米3×9.8牛/千克=0。
05米V甲=V排=S 容h水=2×102米2×0.05米=1×103米3ρ甲=m甲/V甲=4千克/ 1×103米3=4×103千克/米3【例题2】如图2所示,水平桌面上放有轻质圆柱形容器A(容器足够高)和实心圆柱体B.容器A内装有深为0.1米的水,实心圆柱体B的质量为4千克、高为0。
压强变化专题固体-九年级

压强变化专题复习一——固体柱体压强变化此类题目涉及的物理量有柱形固体的高度、面积、密度、压力、压强及其变化量等。
解题的主要思路是公式结合推理,常用的公式有:p=F/s 、p=ρgh (此式虽然是液体内部压强公式,但对于实心柱体对支撑面的压强也成立)及Δp=ΔF/s 、Δp=ρgΔh , 一、竖切【例1】甲乙丙实心均匀正方体分别放在水平地面上,它们对水平地面的压强相等,它们的密度ρ甲<ρ乙<ρ丙,若将两个正方体沿竖直方向分别截去相同的体积,则剩余部分对水平地面的压强关系为( )A .P 甲<P 乙<P 丙B .P 甲=P 乙=P 丙C .P 甲>P 乙>P 丙D .无法判断练习1:如图所示,实心正方体A 、B 放置在水平地面上,A 的边长大于B 的边长,此时A 对地面的压强等于B 对地面的压强,若沿边长的平行线分别从两物体上表面竖直向下截去,且所截的宽度相同,则两物体的剩余部分A’、B’对地面的压力、压强( ) A .A’对地面的压强可能小于B’对地面的压强 B .A’对地面的压强可能大于B’对地面的压强 C .A’对地面的压力一定小于B’对地面的压力D .A’对地面的压力一定大于B’对地面的压力 总结:正方体竖切时,用公式 判断,切割后的压强关系与切割前的压强关系 。
二、横切【例2】甲乙丙三个实心正方体分别放在水平地面上,它们对水平地面的压强相等,它们的密度ρ甲<ρ乙<ρ丙。
若在两正方体上方截去质量相同的部分,则剩余部分对水平地面的压强关系为( )A .P 甲<P 乙<P 丙B .P 甲=P 乙=P 丙C .P 甲>P 乙>P 丙D .无法判断练习2:如图1所示,甲乙两实心正方体分别放在水平地面上,它们对水平地面的压强相等。
若在两正方体上方沿水平方向分别截去相同高度,则剩余部分对水平地面的压强关系是( ) A .P 甲<P 乙 B .P 甲=P 乙 C .P 甲>P 乙 D .无法判断练习3:如图1所示,甲、乙两个实心正方体分别放在水平地面上,它们对地面的压强相等,若在两正方体上方沿水平方向分别截去相同体积,则剩余部分对水平地面的压强关系是( ) A. p 甲 < p 乙B. p 甲 = p 乙C. p 甲 > p 乙D. 无法判断总结:正方体横切时1、切去部分的重力或质量关系,此类常用 。
专题01压强计算(柱体切割叠放)-上海市2024年中考复习资料汇编(培优专用)
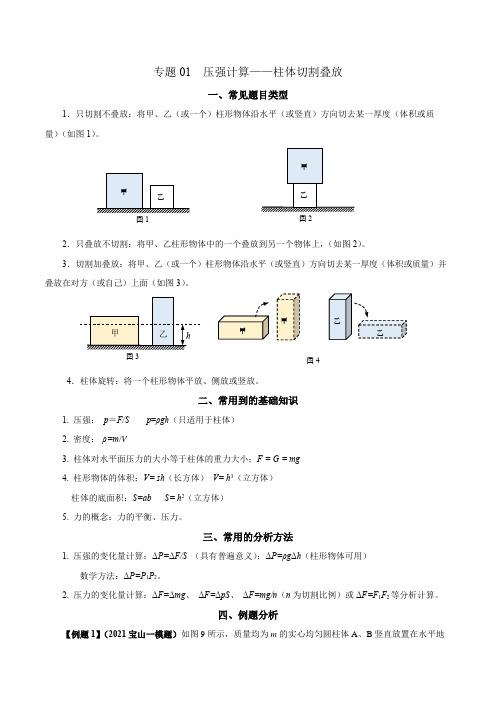
专题01 压强计算——柱体切割叠放一、常见题目类型1.只切割不叠放:将甲、乙(或一个)柱形物体沿水平(或竖直)方向切去某一厚度(体积或质量)(如图1)。
2.只叠放不切割:将甲、乙柱形物体中的一个叠放到另一个物体上,(如图2)。
3.切割加叠放:将甲、乙(或一个)柱形物体沿水平(或竖直)方向切去某一厚度(体积或质量)并叠放在对方(或自己)上面(如图3)。
4.柱体旋转:将一个柱形物体平放、侧放或竖放。
二、常用到的基础知识1. 压强: p =F/S p =ρgh (只适用于柱体)2. 密度: ρ=m /V3. 柱体对水平面压力的大小等于柱体的重力大小:F = G = mg4. 柱形物体的体积:V= sh (长方体) V= h 3(立方体) 柱体的底面积:S=ab S= h 2(立方体)5. 力的概念:力的平衡、压力。
三、常用的分析方法1. 压强的变化量计算:ΔP=ΔF/S (具有普遍意义);ΔP=ρg Δh (柱形物体可用)数学方法:ΔP=P 1P 2。
2. 压力的变化量计算:ΔF=Δmg 、 ΔF=ΔpS 、 ΔF=mg/n (n 为切割比例)或ΔF=F 1F 2等分析计算。
四、例题分析【例题1】(2021宝山一模题)如图9所示,质量均为m 的实心均匀圆柱体A 、B 竖直放置在水平地图1甲乙 图2甲乙 h图3甲乙乙甲甲乙图4面上。
已知A的密度和高度分别为4ρ和5h,B的密度和高度分别为5ρ和8h。
①试求A、B对地面压强之比p A:p B。
②为了使A、B对地面的压强相等,可以在它们上部沿水平方向分别截去相同的______(选填“质量”、“高度”、“体积”或“无法实现”),并通过计算简述你的理由。
【答案】①1:2;②体积,见解析。
【解析】(1)实心圆柱体对水平地面的压强可用p=ρgh进行计算p A p B =ρAgh AρBgh B=4ρ×g×5h5ρ×g×8h=12或者根据p=F/S进行计算:因为m A=m B所以ρA S A h A=ρBS B h BS AS B=ρBh BρAh A=5ρ×8h4ρ×5h=21pApB=F AS AF BS B=G A S BG B S A=12(2)A、B质量相同,压力相等,根据p=F/S,因为p A:p B=1:2,所以S A:S B=2:1若截去相同的质量,则剩余的质量相等,即压力相等,S A:S B=2:1,所以对地面的压强是不相等,可见在它们上部沿水平方向分别截去相同的质量不行。
专题03压强计算(在柱体或液体中加物体)-上海市2024年中考复习资料汇编(培优专用)2

专题03 压强计算—在柱体或液体中加物体一、常见题目类型1. 将物体甲全部或切去一部分体积浸没在容器乙的液体中(见图1)。
2. 将乙容器放在甲的上方(见图1)。
3. 将另一物体A 分别放在柱体甲表面的上方或浸没在容器乙的液体中(见图2)。
4. 将一实心物体A 分别浸没于甲、乙液体中(见图3)。
二、常用到的基础知识与分析方法1. 压强: p =ρgh , p =F/S2. 变化(增大或减小)的压强: △p =△F / S △p =ρg △h3. 把物体放入柱形液体中浸没时,液体对容器底部产生的压力:F=pS =ρghS+ρg △h S =G 液+ G 排(F 浮)即等于原来液体的重力与物体受到的浮力之和。
增大的压力△F =G 排=F 浮=ρ液gV 排 就是物体排开的液体所受到的重力(即浮力)。
4. 区别液体的压强与固体的压强(容器对地面的压强) 在液体不溢出时,则液体对容器底部的压强p 液=ρ液gh 液=F 液/S 容器 容器对地面的压强p 地=F 地/S 容器=G 物体+G 容器/S 容器5. 区别液体的压强与固体的压强(容器对地面的压强) 在液体不溢出时,则液体对容器底部压强的增加量Δp 液=ρ液g Δh 液=ρ液gV 物体/S 容器容器对地面压强的增加量Δp 地=ΔF 地/S 甲==G 物体/S 甲=ρ物体gV 物体/S 容器 6. 理解“轻质薄壁”容器甲乙图3即容器的重力为0,内部液体的受力面积与水平面的受力面积相等。
三、例题分析【例题1】(2023闵行二模)将足够高的薄壁柱形容器甲、乙放置在水平地面上,如图9所示,甲、乙两容器中分别盛有深度为米的酒精和质量为1千克的水。
已知容器乙的底面积为1×102 米2,酒精的密度为0.8×103千克/米3。
①求水的体积V 水。
②现将密度为2×103千克/米3的小球放入某个容器内,小球浸没于液体中,此时两液体对容器底部的压强恰好相等,求该容器对地面压强的增加量Δp 地。
固体压强案例分析:柱状物体对地面的压强

固体压强案例分析:柱状物体对地面的压强在日常生活中,我们经常会遇到各种各样的固体物体对地面的压强问题,比如行人在地面上行走、汽车停在道路上、建筑物承受地基载荷等。
本文主要围绕柱状物体对地面的压强展开讨论,并通过案例分析来深入探讨这一现象。
1. 压强的概念首先,让我们来了解一下压强的概念。
压强是指单位面积上承受的力的大小,通常用公式表示为:$$P = \\frac{F}{A}$$其中,P表示压强,F表示作用在物体上的力,A表示受力面积。
2. 柱状物体对地面的压强柱状物体是指形状类似圆柱的物体,比如桥墩、建筑支柱等。
当柱状物体垂直放置在地面上时,它对地面施加一定的压力,这就涉及到了柱状物体对地面的压强。
对于柱状物体,它的重力作用于重心处,因此需要计算重心到地面的垂直距离ℎ,以及物体的质量m。
那么柱状物体对地面的压强P可以表示为:$$P = \\frac{m \\cdot g}{A}$$其中,g表示重力加速度。
3. 案例分析:钢柱支撑建筑物假设有一栋高楼,建筑物上有一根直径为1米的钢柱支撑整个建筑物。
现在我们来分析这根钢柱对地面的压强。
首先需要计算钢柱的质量,假设钢柱的密度为$\\rho$,长度为ℎ,则钢柱的质量可以表示为:$$m = \\rho \\cdot A \\cdot h$$其中,A表示钢柱的横截面积。
钢柱对地面的压强P可以表示为:$$P = \\frac{\\rho \\cdot A \\cdot h \\cdot g}{A} = \\rho \\cdot h \\cdot g$$通过这个简单的案例,我们可以看到钢柱对地面的压强与其高度以及密度有关。
在实际工程设计中,需要根据具体情况计算柱状物体对地面的压强,以确保建筑物的稳定性。
4. 总结在本文中,我们从压强的概念出发,通过对柱状物体对地面的压强进行分析,了解了柱状物体对地面施加压力的原理。
通过案例分析钢柱支撑建筑物的例子,进一步加深了对柱状物体对地面压强问题的理解。
在柱形容器中放入或取出物体,液体压强练习题

在柱形容器中放入(或取出)物体,液体压强练习题11.液体对容器底压强__________________在柱形容器中放入(或取出)物体后, 液体对容器底压强的变化量___________________ 液体对容器底压强________________2.容器对桌面压强____________________在柱形容器中放入(或取出)物体后,容器对桌面压强的变化量__________________ 容器对桌面压强 _________________1.两个底面积不等的圆柱形容器,分别盛有甲乙两种不同的液体,将两个完全相同的小球分别浸入这两种液体中,小球静止时的位置如图2所示,此时两液面刚好齐平。
若将这两小球从液体中取出,则液体对容器底部的压强的变化量△p 甲、△p 乙的大小关系是A △p 甲一定大于△p 乙B △p 甲一定等于△p 乙C △p 甲一定小于△p 乙D △p 甲可能小于△p 乙2.两个完全相同的圆柱形容器内分别盛有质量相同的水和酒精(ρ水>ρ酒精),将实心金属球甲浸没在水中、实心金属球乙浸没在酒精中,且均无液体溢出,这时水和酒精对容器底部的压强大小相等,则可以确定 ( )A 甲球质量大于乙球的质量B 甲球质量小于乙球的质量C 甲球体积大于乙球的体积D 甲球体积小于乙球的体积3.两个相同的圆柱形容器放在水平桌面上,分别盛有质量相等的酒精和水。
把甲、乙两个金属球分别浸没于酒精和水中(已知液体不溢出,ρ酒精<ρ水),此时,液体对容器底的压强相等,容器对水平桌面的压强也相等。
以下说法正确的是A .甲球质量大于乙球质量B .甲球质量小于乙球质量C .甲球密度大于乙球密度D .甲球密度小于乙球密度; 4.如图,底面积不同的薄壁圆柱形容器内分别盛有甲、乙两种液体,已知两液面相平,它们对容器底部压强相等,则它们对容器底的压力F 甲 (21) F 乙,若分别在两容器中浸没一个完全相同的实心金属球,液体均无溢出,则液体对容器底的压强P 甲′ (22) P 乙′(选填“大于”、“等于”或“小于”)。
2024年上海中考物理专题复习精练 专题05 压强计算(判断柱体浸没)含详解

专题05压强计算—判断柱体浸没一、常见题目类型1.把柱状实心物体B 全部或切去一部分放入柱状容器中的液体中(图1)。
图2图12.把柱状实心物体先放入柱状容器中,然后向里面加液体(图2)。
二、常用到的分析方法1.柱状实心物体先放入柱状容器中,如果物体未被浸没(水未溢出),如图2所示,则水为柱形,底面积为(S A -S B ),高度为h 水=V 水/(S A -S B );图12.柱状实心物体先放入柱状容器中,如果物体被浸没(水未溢出),如图3所示,则物体排开水的体积等于物体的体积V 物,水升高的高度为∆h 水=V物/S 容器。
S 容器图3三、例题分析【例题1】(2023浦东新区二模)如图所示,足够高的薄壁圆柱形容器甲和实心均匀圆柱体乙置于水平地面上。
容器甲的底面积为3×10-2米2;内盛有0.2米深的水;圆柱体乙的底面积为1×10-2米2、高0.5米,密度为3×103千克/米3。
(1)求容器中水的质量m 水;(2)求水对容器甲底部的压强p 水;(3)现从乙的上方沿水平方向切去一定的厚度Δh ,竖直放入甲内水中,当水对容器甲底部的压强最大时,求乙切去厚度Δh 的范围。
甲乙【例题2】(2021杨浦一模)如图(a )所示,轻质薄壁圆柱形容器甲置于水平地面,底面积为2S ,容器高0.2米,内盛0.15米深的水。
(1)若容器的底面积为4×10-2米2,求容器中水的质量m ;(2)求0.1米深处水的压强p ;(3)现有密度为6ρ水的圆柱体乙,如图(b )所示,将乙竖放入容器甲中,若要使水对容器底部的压强p 水最大,求乙的底面积的最小值S 乙小。
【例题3】(2022徐汇区二模)如图13所示,圆柱形容器甲放在水平地面上(容器足够高),底面积为S ,甲内盛有深为h 的水。
有一质量为m 、底面积为S 1、高为h 1的实心金属块乙竖直放置在容器甲底部。
①若乙的质量m 为8千克、S 1为2×10-2米2、h 1为0.2米,求乙的密度ρ乙。
薄壁圆柱形容器压力压强专题

1.薄壁圆柱形容器,容器质量为0.5千克,底面积0.01米2装满水,放在水平桌面上,水深0.1米,求:(1)水对容器底部的压力,压强。
(2)整个容器对水平桌面的压力,压强。
(3)往容器中放入一质量为500克,体积为600厘米3的A物块,求:(a)水对容器底部的压力变化量,压强变化量。
(b)整个容器对水平桌面的压力变化量,压强变化量。
2. 薄壁圆柱形容器,容器质量为0.5千克,底面积0.01米2装满水,放在水平桌面上,水深0.1米,往容器中放入一质量为300克,体积为100厘米3的B 物块,静止后,求:(1)水对容器底部的压力变化量,压强变化量。
(2)整个容器对水平桌面的压力变化量,压强变化量。
3.薄壁圆柱形容器,容器质量为0.5千克,底面积0.01米2,,容器高0.25米,放在水平桌面上,水深0.15米,求:(1)水对容器底部的压力,压强。
(2)整个容器对水平桌面的压力,压强。
(3)往容器中放入一质量为0.6千克的木块,漂浮在水面上,求:(a)水对水对容器底部的压力变化量,压强变化量。
(b)整个容器对水平桌面的压力变化量,压强变化量。
4.薄壁圆柱形容器,容器质量为0.5千克,底面积0.01米2,,容器高0.2米,放在水平桌面上,水深0.15米,求:往容器中放入一质量为0.6千克的木块,漂浮在水面上,求:(a)水对水对容器底部的压力变化量,压强变化量。
(b)整个容器对水平桌面的压力变化量,压强变化量。
5. 薄壁圆柱形容器,容器质量为0.5千克,底面积0.01米2,,容器高0.25米,放在水平桌面上,水深0.15米,往容器中放入一质量为300克,体积为100厘米3的B物块,求:(1)水对容器底部的压力变化量,压强变化量。
(2)整个容器对水平桌面的压力变化量,压强变化量。
6..薄壁圆柱形容器放在水平桌面上,容器质量为0.5千克,底面积0.01米2,,容器高0.25米,装了0.1米深的水,若用细线系着一铁块浸没在水中,铁块质量为780克,(不碰到容器底部),体积为100厘米3,求:(1)放入铁块后,水对容器底部压力,压强的变化量。
八年级物理核心素养特色五柱状固体压强_切割及叠放问题

专题五柱状固体压强——切割及叠放问题【考点梳理】 一、横切问题回顾:有一正方体放置在水平地面上,设正方体的高为h,密度为ρ,求正方体对地面的压强p 。
则:F G mg Vg shg P ghs s s s s ρρρ======各种质地均匀的实心柱状体对水平面的压强都有:gh P ρ=例题1.如图所示,甲、乙两个实心均匀正方体分别放在水平地面上,它们对地面的压强相等.若在两个正方体的上部,沿水平方向分别截去相同高度的部分,则剩余部分对水平地面的压强关系是( )A. p 甲<p 乙 B 。
p 甲>p 乙 C. p 甲=p 乙 D 。
无法判断注意:技巧:按厚度切,就写成p ghρ=的形式,再找△p,且用△h 表示。
思维拓展:若把上题中甲、乙沿水平方向分别截去相同质量的部分,则剩余部分对水平地面的压强关系是?注意:技巧:按质量切,就写成F mg==的形式,再找△p,且用ps s△m表示。
思维拓展:若把上题中甲、乙沿水平方向分别截去相同体积的部分,则剩余部分对水平地面的压强关系是?注意:技巧:按体积切,就写成F mg gVp s s sρ===的形式,再找△p ,且用△V 表示。
二、横切叠放问题例题2:如图所示,甲、乙两个实心均匀正方体分别放在水平地面上,它们对地面的压强相等.若沿水平方向分别截去相同高度的部分,将切去部分叠放在对方身上,则此时对水平地面的压强关系是( )A. p 甲<p 乙B. p 甲>p 乙 C 。
p 甲=p 乙 D. 无法判断hP Ph∆∆=m P Pm∆∆=VP P V∆∆=总结:沿水平方向截去(相同高度)(相同质量)(相同体积)三、竖切问题例题3:如图所示,甲、乙两个实心均匀正方体分别放在水平地面上,它们对地面的压强相等.若沿竖直方向分别截去相同质量的部分,则剩余部分对水平地面的压强关系是( )A。
p甲<p乙 B. p甲=p乙C. p甲>p乙D. 无法判断小结:无论怎样竖直切割完,因为p=ρgh,三个量都没变,剩余部分对地面压强是不变的。
盛有液体的柱形容器的压强变化
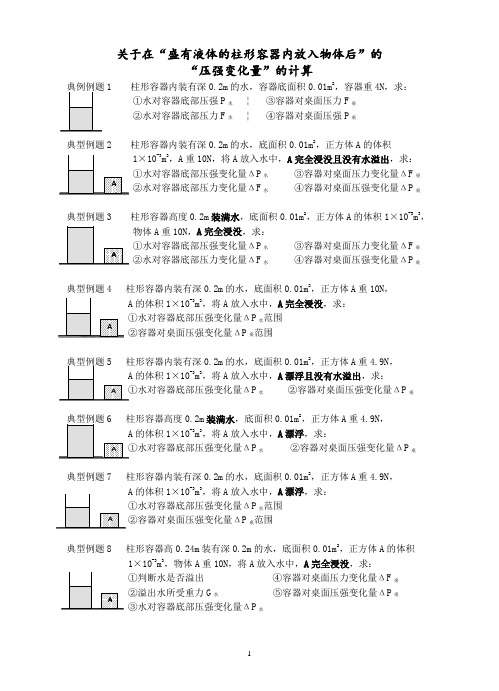
关于在“盛有液体的柱形容器内放入物体后”的“压强变化量”的计算柱形容器内装有深0.2m的水,容器底面积0.01m2,容器重4N,求:①水对容器底部压强P水¦ ③容器对桌面压力F桌②水对容器底部压力F水¦ ④容器对桌面压强P桌典型例题2 柱形容器内装有深0.2m的水,底面积0.01m2,正方体A的体积×10-3m3,A重10N,将A放入水中,A完全浸没且没有水溢出,求:①水对容器底部压强变化量ΔP水¦③容器对桌面压力变化量ΔF桌②水对容器底部压力变化量ΔF水¦④容器对桌面压强变化量ΔP桌典型例题3 柱形容器高度0.2m装满水,底面积0.01m2,正方体A的体积1×10-3m3,物体A重10N,A完全浸没,求:①水对容器底部压强变化量ΔP水¦③容器对桌面压力变化量ΔF桌②水对容器底部压力变化量ΔF水¦④容器对桌面压强变化量ΔP桌典型例题4 柱形容器内装有深0.2m的水,底面积0.01m2,正方体A重10N,的体积1×10-3m3,将A放入水中,A完全浸没,求:①水对容器底部压强变化量ΔP水范围②容器对桌面压强变化量ΔP桌范围0.2m的水,底面积0.01m2,正方体A重4.9N,的体积1×10-3m3,将A放入水中,A漂浮且没有水溢出,求:P水¦②容器对桌面压强变化量ΔP桌0.2m装满水,底面积0.01m2,正方体A重4.9N,的体积1×10-3m3,将A放入水中,A漂浮,求:P水¦②容器对桌面压强变化量ΔP桌典型例题7 柱形容器内装有深0.2m的水,底面积0.01m2,正方体A重4.9N,的体积1×10-3m3,将A放入水中,A漂浮,求:①水对容器底部压强变化量ΔP水范围②容器对桌面压强变化量ΔP桌范围典型例题8 柱形容器高0.24m装有深0.2m的水,底面积0.01m2,正方体A的体积1×10-3m3,物体A重10N,将A放入水中,A完全浸没,求:①判断水是否溢出¦④容器对桌面压力变化量ΔF桌②溢出水所受重力G水¦⑤容器对桌面压强变化量ΔP桌③水对容器底部压强变化量ΔP水典型例题9 柱形容器高0.24m 装有深0.2m 的水,底面积0.01m 2,正方体A 的体积 1×10-3m 3,物体A 重4.9N ,将A 放入水中,A 漂浮,求: ①判断水是否溢出 ¦ ④容器对桌面压力变化量ΔF 桌 ②溢出水所受重力G 水 ¦ ⑤容器对桌面压强变化量ΔP 桌 ③水对容器底部压强变化量ΔP 水2013.4各区模拟考链接(闸北201304)21.如图12 所示是一个重力不计的平底饮料杯放在水平桌面上,内盛重为3牛的水,水的深度为0.1米,杯内、外底面积均为0.002米2,求: ① 水对杯底的压强。
(压强)叠加柱体的压强问题—(疑难解读+解题技巧)2021届九年级物理中考复习(优等生)专题讲义

微专题9-2 叠加柱体地压强问题知识· 解读固体压强是中考力学地重难点。
其中叠加柱体压强问题是近几年中考物理地热点题型之一。
几个物体叠放在一起,考察相关受力思路,压力,压强,密度之类地问题很考验你地公式综合运用能力。
典例· 解读例1,甲,乙两均匀柱体,密度为ρ甲,ρ乙,底面积为S甲,S乙,高度为h甲,h乙,求甲对乙地压强p1及乙对地面地压强p2。
【结果】.【思路】本题考察叠加柱体放在水平面上地压强问题。
已知密度,尺寸,求压强。
这种题型地思路比较简单,直接用压强公式求解。
求压力大小时,可以通过受力思路求出支持力大小,进而求出压力大小。
对于自由放置在水平面上地物体。
注意,这里S是受力面积,并不一定是底面积。
说明:本题是已知密度,尺寸,求压强,题型地思路较为简单。
例2,如图所示,两个正方体金属块A,B叠放在水平地面上,金属块B对地面地压强为p1.若取走金属块A,金属块B对地面地压强为p2,已知p1:p2=3:2,金属块A,B地边长之比a:b=2:3,则金属块A与金属块B地密度之比ρA:ρB=______。
【结果】【思路】相较于上题,本题是已知压强,尺寸,反求密度,题型稍难,很难通过公式推导直接求算密度之比。
怎样处理这样地问题?总体思想是用未知量去表示已知量,列出物理方程,求解即可。
(利用均匀柱体压强计算式,也可以直接得到)解得:例3,A,B两个实心正方体地质量相等,密度之比ρA∶ρB=8∶1,若按甲,乙两种不同地方式,分别将它们叠放在水平地面上(如图所示),则地面受到地压力之比和压强之比分别是( )A. F甲∶F乙=1∶1,p甲∶p乙=1∶2B. F甲∶F乙=1∶1,p甲∶p乙=1∶4C. F甲∶F乙=1∶2,p甲∶p乙=2∶1D. F甲∶F乙=8∶1,p甲∶p乙=1∶8总结1,熟练地公式运用能力是处理叠加柱体压强问题地基础。
2,运用压强公式时注意S是受力面积,不一定等于底面积。
3,用未知量表示已知量是列方程地思想,这是最强有力地解题武器。
专题07 柱形物体及柱形容器内液体的压力、压强-上海市2019年中考物理二轮复习专题冲刺(原卷版)

米 2 高为 0.2 米的金属柱状实心物体,现不断向容器内注入水。 ①当加入水的体积为 2×10-3 米 3 时,求水对容器底部的压强; ②当加入水的质量为 6 千克时,求水对容器底部的压力。
【例题 2】如图 2 所示,圆柱体甲的质量为 3.6 千克,高为 0.2 米,密度为 1.8×103 千克/米 3。 ① 求甲的体积。 ② 求甲竖直放置时对水平桌面的压强。 ③ 现有一薄壁圆柱形容器乙,质量为 0.8 千克。在容器乙中倒入某种液体,将甲竖直放入其中,并分别测 出甲放入前后容器对水平桌面的压强 p 容、液体对容器底部的压强 p 液,如下表所示。
① 薄壁柱形容器 A 的质量 mA。
3
② 放入正方体后,容器中水的深度的变化量Δh 水。 ③ 放入正方体后,通过计算说明判断水是否溢出。 ④ 正方体 B 的质量 mB。 【例题 4】相同的薄壁圆柱形容器甲、乙置于水平桌面上。甲中盛有水,乙中盛有另一种液体,水和液体的质 量均为 4 千克。现分别从甲、乙容器中抽出相同体积的液体,下表为抽出液体前后两容器底部受到的液体的 压强。
6.如图 6 所示,两薄壁圆柱形容器内分别盛有甲、乙两种液体放置在水平地面上,现从两容器中分别抽出 部分液体,使甲、乙剩余部分的深度均为 h,若此时两液体对容器底部的压力相等,则甲、乙抽出部分的质 量△m 甲、△m 乙及液体对容器底部压强变化量△p 甲、△p 乙的大小关系是
A.△m 甲=△m 乙 △p 甲<△p 乙
A.若△p 甲>△p 乙,则 F 浮 甲>F 浮 乙 C.若△p 甲<△p 乙,则 ρ 甲>ρ 乙
B.若△p 甲>△p 乙,则 m 甲<m 乙 D.若△p 甲<△p 乙,则 G 甲>G 乙
9.如图 9 所示,A、B 两个相同的薄壁轻质柱形容器放在水平地面上,两容器中分别盛有相同深度的水和
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
柱形物体压强专题专题说明:柱形体压强涉及到长度、面积、体积、质量、密度、重力、压力、浮力及压强等多个知识点,其中以压强为核心,计算上既可以用公式p=F/S,又可以用p=ρg h,逻辑推理严密而灵活;在具体题目中又有不同方式的切割、不同方向不同大小的外力施加、两物体的叠放和液体的抽吸等具体情况。
虽然柱形体压强题涉及到的物理量相对比较多,关系复杂,但常见解题思路还是有迹可寻的。
解题思路:首先要确定公式的适用条件,基本公式p=F/S和p=ρg h在实心的柱体和柱形液体的情况下是通用的,但几个变化量要注意了:△p= p2-p1和△F= F2-F1是普遍适用的。
△p=△F/S必须面积不变,△p=ρg△h必须密度不变。
其次有些常规的结论或方法要熟练掌握应用,比如h—S—V三者的变化趋势是相同的,m—G—F三者的变化趋势也是相同的;竖切不改变固体的压强,某些情况下横切和液体质量的减少效果是一致的;极限法要慎重选择,物体被切光或提起时和一般情况是不同的,可适当用特殊值代入法;另外画出图来对解题是大有好处的,总之要把公式记得十分熟练,灵活处理题目的具体情况;可是适时的反着用公式,比如液体的用p=F/S,固体的用p=ρg h多用逆向思维和整体法处理问题。
例1甲、乙两个正方体物块放在水平地面上,甲的边长小于乙的边长。
甲对地面的压强为p1,乙对地面的压强为p2。
正确的推理是()A.如甲、乙密度相等,将甲放到乙上,乙对地面的压强有可能变为p1。
B.如甲、乙密度相等,将乙放到甲上,甲对地面的压强有可能变为p2。
C.如甲、乙质量相等,将甲放到乙上,乙对地面的压强有可能变为p1。
D.如甲、乙质量相等,将乙放到甲上,甲对地面的压强有可能变为p2。
【分析】:已知正方体物块甲的边长小于乙的边长,不妨设甲边长为a,乙边长为b,且a<b先分析A、B选项,当甲乙密度相等时,我们设密度均为ρ,那么甲对地面压强p1=F/S=G甲/S甲=ρgV甲/s甲=ρga3/a2=ρga,同理,乙对地面的压强p2=ρgb,因为a<b,所以p1<p2。
A选项中,将甲放到乙上,乙对地面的压强p=F/S=(G甲+G乙)/S乙=ρg(a3+b3)/b2=ρga3/b2+ρgb=ρga3/b2+p2>p2>p1,所以A错误;同理B选项中,将乙放到甲上,甲对地面的压强p=F/S=(G甲+G乙)/S甲=ρg(a 3+b3)/a2=ρga+ρgb3/a2=p1+ρgb3/a2,因为a<b,所以b3/a2>b3/b2,那么ρgb3/a2>ρgb>p2,所以B错误。
继续分析C、D选项,当甲乙质量相等时,我们设质量均为m,那么甲对地面压强p1=F/S=G甲/S甲=mg/s甲=mg/a2,同理,乙对地面的压强p2=mg/b2,因为a<b,所以p1>p2。
C选项中,将甲放到乙上,乙对地面的压强p=F/S=(G甲+G乙)/S乙=2mg/b2=2p2,由于p1>p2,所以2p2有可能等于p1,所以C正确;同理D选项中,将乙放到甲上,甲对地面的压强p=F/S=(G甲+G乙)/S甲=2mg/a2=2p1,由于p1>p2,所以2p1不可能等于p2因为a<b,所以D错误。
因此,本题选C。
【总结】:本题的难点主要在于设出相同的量,然后利用数学知识对物理公式进行变化,然后利用数学关系分析。
相信只要同学们熟练掌握物理公式,用数学计算比较大小关系便不是难题附:08年中考题:如图所示,甲、乙两个质量相等的均匀实心正方体放在水平地面上,已知铜的密度大于铁的密度,可能使甲和乙对地面的压强相等的方法是 ( )A.将质量相等的铜块和铁块分别放在甲、乙的上面B.将体积相等的铜块和铁块分别放在甲、乙的上面C.沿水平方向分别截去质量相等的部分D.沿水平方向分别截去体积相等的部分解答:D如图所示,两个底面积不同的圆柱形容器甲和乙,容器足够高,分别盛有质量相等的水和酒精(ρ水>ρ酒精),可能使水和酒精对容器底部的压强相等的方法是 ( )A.倒入相同质量的水和酒精 B.倒入相同体积的水和酒精C.抽出相同质量的水和酒精 D.抽出相同体积的水和酒精解答:B09年中考题:如图所示,两个底面积不同的圆柱形容器内分别盛有不同的液体甲和乙。
若两容器内液面等高,且甲液体的质量等于乙液体的质量。
着要使两容器内液体对容器底部的压强相等,则可从两容器中分别抽出 ( )A 相同高度的液体。
B 相同体积的液体。
C 相同质量的液体。
D 相同重力的液体。
解答:B强化训练讲解:1.甲、乙两个完全相同的圆柱形容器放于水平桌面上,甲装水,乙装酒精(ρ水>ρ洒精),现将体积相同的实心铝、铁块分别浸没于甲、乙两容器中(液体均不溢出),此时量筒底部受到液体压强相同,若将两金属块取出,则下列比较容器底部受到液体压强正确的是…………………………………………………………………()(A) P甲>P乙(B) P甲<P乙 (C) P甲=P乙(D)无法比较2.三个完全相同的圆柱形容器内分别盛有甲、乙、丙三种不同液体,放在水平桌面上,它们对桌面的压强相等。
将铜、铁、铝三个质量相等的实心金属球分别按序浸没在甲、乙、丙三种液体中,均无液体溢出,且液面恰好相平。
则此时三种液体对容器底部的压强大小关系为(ρ铜>ρ铁>ρ铝) ………………………………………()A.p甲<p乙<p丙。
B.p甲=p乙=p丙。
C.p甲>p乙>p丙。
D.无法判断。
3.两个完全相同的圆柱形容器甲和乙底部相连通,给两容器分别倒入不同质量的同种液体后,将质量相同的两物块浸没在两容器中(无液体溢出),结果发现有部分液体从乙容器流入甲容器,则…………………………………………………………()A.甲容器中的物块的密度大。
B.甲、乙容器中的物块的密度一样大。
C.乙容器中的物块的密度大。
D.条件不足,无法判断。
4.甲、乙、丙三个实心正方体分别放在水平地面上,它们对水平地面的压力相等。
已知ρ甲<ρ乙<ρ丙。
若沿水平方向分别在甲、乙、丙三个正方体上部切去一块,使三个正方体的剩余部分对水平地面的压强相等,则切去部分的质量关系为()A.△m甲=△m乙=△m丙。
B. △m甲>△m乙>△m丙。
C. △m甲<△m乙<△m丙。
D. △m甲>△m丙>△m乙。
5.甲、乙、丙三个质量相同的实心正方体分别放在水平地面上,它们对水平地面的压强关系是p甲>p乙>p丙。
若分别在三个正方体上表面中央施加竖直向上的力,使三个正方体对水平地面的压强相同,则力F甲、F乙、F丙的大小关系是()A F甲<F乙<F丙。
B F甲=F乙=F丙。
C F甲>F乙>F丙。
D 以上都有可能。
6.甲、乙、丙三个完全相同的长方体分别置于水平桌面上时,它们对水平桌面的压强关系为p甲>p乙>p 丙;若在它们的上表面上分别施加一个竖直向下的力F甲、F乙、F丙,使它们对水平桌面的压强相等,则这三个力之间的关系为()A F甲>F乙>F丙B F甲=F乙=F丙C F甲<F乙<F丙D 以上都有可能7.甲、乙、丙三个实心立方体分别放在水平地面上,它们对水平地面的压强相等,已知ρ甲<ρ乙<ρ丙。
若在甲、乙、丙三个立方体上分别放一个质量相等的铜块,则三个立方体对水平地面的压强大小关系为()A、p甲<p乙<p丙。
B、 p甲=p乙=p丙。
C、 p甲>p乙>p丙。
D、无法判断。
8.甲、乙、丙三个实心正方体分别放在水平地面上,它们对水平地面的压强相等,已知ρ甲<ρ乙<ρ丙。
若沿水平方向分别在甲、乙、丙三个正方体上部切去一块,使三个正方体的剩余部分对水平地面的压强仍然相等,则切去部分的质量关系为()A、△m甲<△m乙<△m丙。
B、△m甲=△m乙=△m丙。
C、△m甲>△m乙>△m丙。
D、以上都有可能。
9.三个实心均匀正方体对水平地面的压力相同,它们的密度分别为甲、乙、丙,且甲>乙>丙。
若在三个正方体上方分别施加一个竖直且同方向的力F甲、F乙、F丙,施加的力小于正方体的重力,使三个正方体对水平地面的压强相同,则力F甲、F乙、F丙的大小关系为()A 可能是F甲>F乙>F丙。
B 可能是F甲=F乙=F丙。
C 一定是F甲<F乙<F丙。
D 一定是F甲=F乙=F丙。
10.三个实心均匀正方体对水平地面的压强相同,它们的密度分别为甲、乙、丙,且甲>F甲、F乙、F丙,施加的力小于正方体的重力,使三乙>丙。
若在三个正方体上方分别施加一个竖直且同方向的力个正方体对水平地面的压强仍相同,则力F甲、F乙、F丙的大小关系为()A 可能是F甲>F乙>F丙。
B 可能是F甲=F乙=F丙。
C 一定是F甲<F乙<F丙。
D 一定是F甲=F乙=F丙。
11.两个完全相同的圆柱形容器内分别盛有水和酒精(ρ水>ρ酒精),将体积相同的实心金属球甲浸没在水中、实心金属球乙浸没在酒精中,且均无液体溢出,这时水和酒精对容器底部的压强大小相等,则可以确定()A 甲杯中水的质量大于乙杯中酒精的质量。
B 甲球的质量大于乙球的质量。
C 甲杯中水的质量小于乙杯中酒精的质量。
D 甲球的质量小于乙球的质量。
12.两个完全相同的圆柱形容器内分别盛有水和酒精(ρ水>ρ酒精)。
若在两容器内抽出体积相同的水和酒精后,水和酒精对容器底部的压强大小相等,则可以确定原先容器中()A 水的质量大于酒精的质量。
B 水的体积大于酒精的体积。
C 水的质量小于酒精的质量。
D 水的体积等于酒精的体积。
13.两个完全相同的圆柱形容器内分别盛有质量相同的水和酒精(ρ水>ρ洒精),在两个圆柱形容器内再分别倒入相同体积的水和酒精后(水和酒精都不溢出),水和酒精对容器底部的压强大小关系是………………………………………………………()(A) P水>P酒精(B) P水<P酒精(C) P水=P酒精(D)无法确定14.甲、乙两个质量相同的实心正方体分别放在水平地面上,它们对水平地面的压强关系是p甲>p乙。
经过下列变化后,它们对地面的压强变为p甲和p乙,其中可能使p甲<p乙的为()A 分别沿水平方向截去高度相等的部分B 分别沿水平方向截去质量相等的部分。
C 分别在上表面中央施加一个竖直向上大小相等的力D 分别在上表面中央施加一个竖直向下大小相等的力。
15. 如图,甲、乙两个立方体(V甲>V乙)分别放在水平地面上,它们对地面的压强相等。
若把乙放在甲上面,甲对地面的压强增加p1; 若把甲放在乙上面,乙对地面的压强增加p2;则p1、p2的大小关系为()A、p1 >p2 B 、p1﹤p2C、 p1 =p2D、无法判断16.两个实心正方体甲、乙对水平地面的压强相同,它们的密度关系为ρ甲>ρ乙,若在甲的上部放一小物体A,在乙的上部放一小物体B后,两正方体对地面的压力相等,则A、B两物体的重力关系是()A.G A=G B B.G A>G B C.G A<G B D.以上都有可能17.如图16所示,三个完全相同的柱形容器中分别装有A、B、C三种液体,放在水平地面上,若液体的密度关系为ρA=ρB<ρC,则它们对容器底的压强关系是()A、pA<pB=pCB、pA<pB<pCC、pA=pC<pBD、pA<pC<pB。
