matlab随机数生成方法

合集下载

matlab中的rand用法

matlab中的rand用法随机数在计算机科学和数学领域中被广泛使用，其中MATLAB是一种常用的科学计算软件。

在MATLAB中，rand函数是生成随机数的一种常用方法。

本文将介绍MATLAB中rand函数的用法以及一些相关的概念。

一、rand函数的基本用法在MATLAB中，rand函数可用于生成一个0到1之间的均匀分布的随机数。

它的基本语法如下：rand这将生成一个0到1之间的随机数。

例如，运行以下代码：x = rand将会得到一个0到1之间的随机数，例如0.4572。

如果需要生成一个范围在a到b之间的随机数，可以使用如下语法：x = a + (b-a)*rand其中，a和b为给定的数值。

例如，如果想生成一个范围在10到20之间的随机数，可以运行以下代码：x = 10 + (20-10)*rand这将生成一个范围在10到20之间的随机数。

二、rand函数的应用举例1. 生成随机向量在MATLAB中，可以使用rand函数生成一个随机向量。

例如，如果想生成一个长度为n的随机向量，可以运行以下代码：x = rand(1, n)其中，n为给定的整数。

这将生成一个长度为n的随机向量。

2. 生成随机矩阵同样地，可以使用rand函数生成一个随机矩阵。

例如，如果想生成一个m行n 列的随机矩阵，可以运行以下代码：x = rand(m, n)这将生成一个m行n列的随机矩阵。

3. 生成服从正态分布的随机数除了生成均匀分布的随机数，还可以使用randn函数生成服从正态分布的随机数。

它的基本语法如下：x = mu + sigma*randn其中，mu和sigma为给定的数值。

例如，如果想生成一个均值为0，标准差为1的正态分布随机数，可以运行以下代码：x = randn这将生成一个服从标准正态分布的随机数。

4. 生成随机整数有时候，我们需要生成一个随机整数而不是小数。

可以使用randi函数来实现这个目的。

例如，如果想生成一个范围在a到b之间的随机整数，可以运行以下代码：x = randi([a,b])其中，a和b为给定的整数。

matlab rand用法

matlab rand用法Matlab是一种基于数学计算的软件，专为科学家和工程师设计。

Rand是Matlab用来生成随机数的函数之一，它可以产生均匀分布的伪随机数。

下面就来介绍一下Matlab rand函数的用法。

使用rand函数生成随机数rand函数可以生成从0到1之间的随机数，输出是一个double类型的向量或矩阵。

以下是rand函数的使用方式：1.生成一个1 × 1 的随机数:rand2.生成一个1 × 3的随机数：rand(1,3)3.生成一个3 × 3的随机数矩阵：rand(3,3)4.使用rand函数生成一定数量的随机数：rand(1,1000)在rand函数中，第一个参数代表行数，第二个参数代表列数。

如果省略列数，则rand函数默认生成一行随机数。

在生成随机数之前，可以使用rand('seed',s)函数来设定随机数生成器的种子，以确保每次都能得到相同的随机数序列。

使用randn函数生成正态分布的随机数randn函数可以生成服从正态分布的随机数，输出是一个double类型的向量或矩阵。

以下是randn函数的使用方式：1.生成一个1 × 1的随机数：randn2.生成一个1 × 3的随机数：randn(1,3)3.生成一个3 × 3的随机数矩阵：randn(3,3)4.使用randn函数生成一定数量的随机数：randn(1,1000)在使用randn函数时，也可以像rand函数一样使用randn('seed',s)函数来设定随机数生成器的种子。

如果需要生成均值为m，标准差为s的正态分布随机数，可以使用 m + s * randn()。

总结在Matlab中，使用rand函数可以生成均匀分布的伪随机数，使用randn函数可以生成服从正态分布的随机数。

需要注意的是，在生成随机数之前可以使用rand('seed',s)或randn('seed',s)来设定随机数生成器的种子，以确保每次都能得到相同的随机数序列。

matlab中随机数生成

matlab中随机数生成无题在MATLAB中，我们可以使用随机数生成函数来生成各种类型的随机数。

这些随机数可以用于模拟实验、数据分析、算法测试等方面。

在这篇文章中，我将介绍一些常用的随机数生成函数，并给出一些实际应用的例子。

一、rand函数rand函数用于生成0到1之间均匀分布的随机数。

例如，我们可以使用rand函数来模拟抛硬币的结果，生成0或1的随机数，其中0表示正面，1表示反面。

下面是一个示例代码：```matlabresult = rand(1, 100); % 生成100个0到1之间的随机数heads = sum(result < 0.5); % 统计正面的次数tails = sum(result >= 0.5); % 统计反面的次数fprintf('正面的次数：%d\n', heads);fprintf('反面的次数：%d\n', tails);```二、randn函数randn函数用于生成服从标准正态分布（均值为0，方差为1）的随机数。

这在统计学中经常用到。

我们可以使用randn函数来模拟一组身高数据，然后计算平均身高和标准差。

下面是一个示例代码：```matlabheights = randn(1, 1000) * 10 + 170; % 生成1000个身高数据，均值为170，标准差为10average_height = mean(heights); % 计算平均身高std_height = std(heights); % 计算标准差fprintf('平均身高：%f\n', average_height);fprintf('身高标准差：%f\n', std_height);```三、randi函数randi函数用于生成指定范围内的整数随机数。

例如，我们可以使用randi函数来模拟投掷骰子的结果，生成1到6之间的整数随机数。

matlab中0-1的随机数

在matlab中生成0-1之间的随机数是一种常见的操作，可以通过内置的随机数生成函数来实现。

生成0-1之间的随机数在模拟实验、统计分析、机器学习等方面具有重要的应用，因此掌握在matlab中生成0-1随机数的方法对于数据科学和工程领域的研究人员来说是非常重要的。

1. 使用rand函数生成均匀分布的随机数在matlab中可以使用rand函数来生成均匀分布的随机数，其语法为：```matlabr = rand(m, n)```其中m 和n 分别表示生成随机数的维度，m 表示行数，n 表示列数。

rand函数生成的随机数范围在0-1之间，且满足均匀分布。

2. 使用randn函数生成正态分布的随机数除了生成均匀分布的随机数外，matlab还可以使用randn函数来生成正态分布的随机数，其语法为：```matlabr = randn(m, n)```其中 m 和 n 同样表示生成随机数的维度，randn函数生成的随机数满足标准正态分布，即均值为0，方差为1。

3. 控制随机数的种子在生成随机数时，可以通过控制随机数的种子来保证生成的随机数是可重复的。

在matlab中可以使用rng函数来控制随机数的种子，其语法为：```matlabrng(seed)```其中 seed 表示随机数的种子，通过设置相同的种子可以确保每次生成的随机数是一样的。

在matlab中生成0-1之间的随机数有多种方法，包括使用rand函数生成均匀分布的随机数，使用randn函数生成正态分布的随机数，以及通过控制随机数的种子来保证随机数的可重复性。

这些方法为研究人员在数据分析和模拟实验中提供了便利，对于提高工作效率和保证实验结果的可靠性具有重要意义。

在实际应用中，生成0-1之间的随机数通常用于模拟实验、统计分析、概率建模、机器学习算法等领域。

通过生成符合特定分布的随机数，可以更好地模拟实际场景，并进行有效的数据分析与处理。

在matlab中，生成0-1之间的随机数的应用十分广泛，具有很高的实用价值。

matlab 概率密度

matlab 概率密度（原创实用版）目录一、引言二、MATLAB 中生成随机数的方法1.使用概率密度函数2.使用 rand 函数三、MATLAB 中绘制概率密度图的方法1.使用 hist 函数2.使用 ksdensity 函数3.使用 plot 函数四、总结正文一、引言在 MATLAB 中，概率密度函数常用于生成随机数和绘制概率密度图。

本文将介绍两种在 MATLAB 中生成随机数的方法以及三种绘制概率密度图的方法。

二、MATLAB 中生成随机数的方法1.使用概率密度函数在 MATLAB 中，可以使用概率密度函数生成随机数。

假设我们要生成一个在区间 [a, b] 内均匀分布的随机数，可以按照以下步骤操作：```matlabfunction r = rJYFB(a, b, varargin)rrand(varargin:)(b - a) / (b - a);end```调用该函数时，可以像 rand 函数那样指定维数，从而产生一个随机数组。

例如：```matlabJYFB(3, 4) % 生成一个 3-4 之间均匀分布的随机数rJYFB(3, 4, 1000, 1) % 生成一个 1000x1 的随机数组，其元素在 3-4 之间均匀分布```2.使用 rand 函数除了使用概率密度函数，还可以直接使用 rand 函数生成随机数。

例如，生成一个在区间 [a, b] 内均匀分布的随机数，可以执行以下操作：```matlaba = 3;b = 4;r = rand(a, b);```三、MATLAB 中绘制概率密度图的方法1.使用 hist 函数hist 函数可以用于计算概率密度，并根据给定的数据绘制概率密度图。

例如，假设我们有一组数据 y，可以使用以下代码绘制概率密度图：```matlabdatarandn(10000, 1); % 生成 10000 个正态分布的随机数[y, x] = hist(data, 100); % 统计数据，将数据分为 100 个区间yy / length(data) / mean(diff(x)); % 计算概率密度bar(x, y, 1); % 使用 bar 画图，最后的 1 是画 bar 图每条 bar 的宽度，默认```2.使用 ksdensity 函数ksdensity 函数可以直接计算概率密度，并绘制概率密度图。

如何用matlab生成随机数函数

如何⽤matlab⽣成随机数函数1. MATLAB 函数 rand产⽣在区间 (0, 1)的均匀随机数，它是平均分布在 (0,1)之间。

⼀个称为seed的值则是⽤来控制产⽣随机数的次数。

均匀随机数函数的语法为rand(n),rand(m,n)，其结果分别产⽣⼀矩阵含n×n个随机数和⼀矩阵含m×n的随机数。

注意每次产⽣随机数的值都不会⼀样，这些值代表的是随机且不可预期的，这正是我们⽤随机数的⽬的。

我们可利⽤这些随机数代⼊算式中，来表⽰某段讯号的不规则振幅或是某个事件出现的机率。

均匀随机数其值平均的分布于⼀区间的特性可以从其统计密度函数(probabilitydensity function, PDF)说明。

从其PDF分布类似长条图的分布，可以看出其每⼀个随机数值出现的机率皆相同，所以它被称为均匀随机数。

见以下的例⼦：>> rand(1,6) % 第⼀次使⽤随机数产⽣器ans =0.2190 0.0470 0.6789 0.6793 0.9347 0.3835>>hist(ans) % 看看长条图的长相>>plot(ans) % ⽐较上个图与这个图有何差异？何者能代表不规则数据的分布>> rand(1,6) % 第⼆次使⽤随机数产⽣器，注意每次产⽣的随机数值皆不同ans =0.5194 0.8310 0.0346 0.0535 0.5297 0.6711因为每次随机数产⽣的值皆不同，如果因为验证算式需要确定所使⽤的随机数值是相同的，可以利⽤seed这个选项，⽤以设定使⽤计算随机数产⽣器的起始值，其语法为rand('seed',n)，n的规定是。

其中n=0有特别意义是使⽤第⼀次产⽣随机数值的起始值(=931316785)，其它的n 值即是所使⽤起始值。

如果使⽤相同的起始值，则随机数值会⼀样，因为随机数的计算是依据起始值。

matlab中1-10之间的随机数

一、介绍MATLAB是一种用于数学计算、分析、可视化和算法开发的高级技术计算语言和交互环境。

它包括用于管理和操作数组、函数、绘图和数据的工具。

在MATLAB中，我们可以轻松地生成随机数。

二、生成指定范围内的随机数如果我们想在MATLAB中生成1到10之间的随机数，可以使用rand 函数。

该函数可以生成0到1之间的均匀分布的随机数。

我们可以通过乘以9并加1来将其映射到1到10之间。

```matlabrandom_number = rand() * 9 + 1;```三、生成多个随机数如果我们想生成多个1到10之间的随机数，可以使用rand函数的矢量化功能。

我们可以指定要生成的随机数的数量，并将其存储在数组中。

```matlabrandom_numbers = rand(1, 10) * 9 + 1;```四、生成整数随机数如果我们想生成1到10之间的整数随机数，可以使用randi函数。

该函数可以生成指定范围内的均匀分布的随机整数。

```matlabinteger_random_number = randi([1, 10], 1);```五、生成多个整数随机数如果我们想生成多个1到10之间的整数随机数，可以使用randi函数的矢量化功能。

```matlabinteger_random_numbers = randi([1, 10], 1, 10);```六、生成服从特定分布的随机数除了生成均匀分布的随机数之外，MATLAB还提供了生成服从其他分布的随机数的功能。

比如我们可以使用randn函数生成服从标准正态分布的随机数。

```matlabnormal_random_number = randn();```七、设置随机数种子在生成随机数时，我们可以通过设置随机种子来控制随机数的生成。

这在需要重现随机实验结果时很有用。

我们可以使用rng函数来设置随机数种子。

```matlabrng(123); 设置随机数种子为123random_number = rand() * 9 + 1;```八、应用举例生成随机数在模拟实验、随机抽样、加密算法等领域有着广泛的应用。

产生正态分布随机数的matlab方法random

产生正态分布随机数的matlab方法random在Matlab中生成正态分布随机数有多种方法，下面将介绍其中几种常用的方法，并对它们进行全面评估。

1. 使用randn函数生成正态分布随机数- randn函数是Matlab中用于生成符合标准正态分布的随机数的函数。

- 该方法的优点是简单易用，一行代码就可以生成所需的随机数序列。

- 但是，这种方法生成的随机数序列可能不够随机，存在一定的偏差。

2. 使用Box-Muller变换生成正态分布随机数- Box-Muller变换是一种经典的生成正态分布随机数的方法，通过均匀分布的随机数生成正态分布的随机数。

- 这种方法生成的随机数更加符合正态分布的特性，具有更好的随机性和分布性。

- 但是，实现Box-Muller变换需要一定的数学基础和编程技巧，相对复杂一些。

3. 使用truncated normal distribution生成截尾正态分布随机数- 有时候我们需要生成一定范围内的正态分布随机数，这时可以使用truncated normal distribution方法。

- 这种方法可以有效地控制生成的随机数范围，使其符合实际应用需要的要求。

- 但是，对于一些特殊情况，需要考虑truncated normal distribution生成的随机数是否符合实际问题的分布需求。

总结回顾：在Matlab中生成正态分布随机数有多种方法，每种方法都有各自的优点和局限性。

根据实际需求，选择合适的方法是非常重要的。

在编写程序时，需要根据具体情况综合考虑随机性、分布性和实际应用需求，选择最合适的方法来生成正态分布随机数。

个人观点和理解：在实际编程中，生成符合实际需求的随机数是非常重要的。

对于正态分布随机数的生成，需要考虑到数据的随机性和分布特性，才能更好地应用于实际问题中。

也要注意选择合适的方法，并在实际应用中进行验证和调整，以确保生成的随机数符合实际需求。

正态分布是自然界和社会现象中广泛存在的一种分布形式，它具有许多重要的统计特性，如均值、标准差和形态等。

matlab 给定范围的随机数

matlab 给定范围的随机数
在MATLAB 中，可以使用`rand` 函数生成0 到1 之间的随机数。

如果要生成指定范围内的随机数，可以使用以下方法：
1. 使用`rand` 生成0 到1 之间的随机数，然后通过线性变换将其映射到指定的范围。

例如，要生成1 到10 之间的随机数，可以使用以下代码：
matlab
range_min = 1;
range_max = 10;
random_num = range_min + (range_max - range_min) * rand;
2. 使用`randi` 函数生成指定范围内的整数。

例如，要生成1 到10 之间的随机整数，可以使用以下代码：
matlab
range_min = 1;
range_max = 10;
random_num = randi([range_min, range_max]);
请注意，上述代码中的范围是闭区间，即包含范围的两个端点。

如果要生成的范围是半开区间或开区间，请根据需要对代码进行适当的调整。

matlab随机数生成方法

R = chi2rnd(V)
R = chi2rnd(V
,m)
R = chi2rnd(V ,m,n)
六．期望为 MU 的指数随机数（即 Exp
1
MU
R = exprnd(MU)
R = exprnd(MU,m)
随机数）： R = exprnd(MU,m,n)
七．自由度为 V1， V2 的 F 分布随机数： R = frnd(V1，V2) R = frnd(V1， V2,m)
如果你安装了统计工具箱（Statistic Toolbox)，除了这两种基本分布外，还可以用 Matlab 部函数生成符合下面这些分布的随机数。 3．unifrnd() 和 rand()类似，这个函数生成某个区间均匀分布的随机数。基本语法 unifrnd(a,b,[M,N,P,...]) 生成的随机数区间在(a,b)，排列成 M*N*P... 多维向量。如果只写 M，则生成 M*M 矩阵；如果参数为[M,N]可以省略掉方括号。一些例子： unifrnd(-2,3,5,1) %生成 5 个随机数排列的列向量，一般用这种格式 unifrnd(-2,3,5) %生成 5 行 5 列的随机数矩阵 unifrnd(-2,3,[5,4]) %生成一个 5 行 4 列的随机数矩阵 %注：上述语句生成的随机数都在(-2,3)区间. 生成的随机数大致的分布。
R = geornd(P) （生成参数为 P 的几何随机数） R = geornd(P,m) （生成参数为 P 的 × m 个几何随机数）
１ R = geornd(P,m,n) （生成参数为 P 的 m 行 n 列的 m × n 个几何随机数）例如 (1) R = geornd(1./ 2.^(1:6)) ( 生成参数依次为 1/2,1/2^2,到 1/2^6 的 6 个几何随机数) (2) R = geornd(0.01,[1 5]) (生成参数为 0.01 的（１行５列）5 个几何随机数).

Matlab产生随机数

Matlab产⽣随机数介绍：Matlab产⽣随机数在有些时候是⾮常必要的，⽐如在产⽣某个范围的随机数进⾏相关的测试等；函数命令介绍：1、rand:rand(n):产⽣0到1之间的n阶随机数⽅阵；rand(m,n):产⽣0到1之间的m⾏n列的随机数矩阵；2、randn:此函数命令是产⽣⽩噪声的（均值为0，⽅差为1）randn(n):产⽣0到1之间的n阶随机数⽅阵；randn(m,n):产⽣0到1之间的m⾏n列的随机数矩阵；两者的区别：rand是0-1均匀分布；randn是产⽣⽩噪声的；3、randint:randint(m,n,[1 N]):产⽣m⾏n列的1到N之间的整数型的随机数（有重复），与randint(m,n,N+1)效果相同；4、randperm:randperm(n):产⽣1到n的之间的整数型的⽆重复的随机排列，利⽤它可以得到⽆重复的随机数；betarnd 贝塔分布的随机数⽣成器binornd ⼆项分布的随机数⽣成器chi2rnd 卡⽅分布的随机数⽣成器exprnd 指数分布的随机数⽣成器frnd f分布的随机数⽣成器gamrnd 伽玛分布的随机数⽣成器geornd ⼏何分布的随机数⽣成器hygernd 超⼏何分布的随机数⽣成器lognrnd 对数正态分布的随机数⽣成器nbinrnd 负⼆项分布的随机数⽣成器ncfrnd ⾮中⼼f分布的随机数⽣成器nctrnd ⾮中⼼t分布的随机数⽣成器ncx2rnd ⾮中⼼卡⽅分布的随机数⽣成器normrnd 正态（⾼斯）分布的随机数⽣成器poissrnd 泊松分布的随机数⽣成器raylrnd 瑞利分布的随机数⽣成器trnd 学⽣⽒t分布的随机数⽣成器unidrnd 离散均匀分布的随机数⽣成器unifrnd 连续均匀分布的随机数⽣成器weibrnd 威布尔分布的随机数⽣成器。

Matlab中的随机数生成与随机模拟

Matlab中的随机数生成与随机模拟在科学研究、工程领域和现代计算机技术的工作中，随机数生成和随机模拟是非常重要的工具和方法。

Matlab作为一种强大的数值计算环境和编程语言，提供了丰富的工具包和函数库，可以帮助我们进行随机数生成和随机模拟的工作。

在本文中，我们将探讨Matlab中的随机数生成方法、常见的随机分布函数及其应用以及一些相关的技巧和注意事项。

Matlab提供了多种方法来生成随机数。

最常见的方法是使用rand函数，该函数可以生成一个[0,1)之间的均匀分布的随机数。

例如，当我们执行rand语句时，Matlab会生成一个随机数，如0.8467。

我们可以通过传递参数来生成多个随机数，例如rand(1,1000)将生成一个包含1000个随机数的向量。

除了rand函数，Matlab还提供了其他一些常见的随机数生成函数。

例如，randn函数可以生成符合标准正态分布的随机数。

这些随机数具有均值为0，方差为1的特性。

我们可以使用randn(1,1000)来生成一个包含1000个符合标准正态分布的随机数的向量。

除了均匀分布和正态分布外，Matlab还提供了其他一些常见的随机分布函数，例如指数分布、伽马分布、泊松分布等。

以指数分布为例，我们可以使用exprnd函数生成符合指定参数lambda的随机数。

例如，exprnd(1,1,1000)将生成一个包含1000个符合参数lambda为1的指数分布的随机数的向量。

在随机模拟中，我们可以使用这些随机分布函数来模拟实际问题。

以蒙特卡洛方法为例，它是一种基于随机模拟的数值计算方法。

在蒙特卡洛方法中，我们通过随机生成大量的样本来模拟实际问题，并根据这些样本进行数值计算和推理，从而得到问题的近似解。

Matlab提供了强大的工具和函数来支持蒙特卡洛模拟。

例如，我们可以使用rand函数来生成随机样本，并利用这些样本进行数值计算。

如果我们想模拟一个投掷硬币的实验，通过设定rand函数生成的随机数大于0.5为正面，小于0.5为反面，我们可以模拟多次投掷，从而获得正反面出现的概率。

Matlab中的随机数生成与分布拟合技巧

Matlab中的随机数生成与分布拟合技巧在科学研究和工程应用中，我们常常需要使用随机数生成和分布拟合技巧来解决各种问题。

Matlab作为一款强大的科学计算软件，提供了一系列方便的函数和工具，可以帮助我们快速、准确地处理随机数和分布相关的任务。

本文将介绍一些常用的Matlab函数和技巧，以及它们在随机数生成和分布拟合中的应用。

一、随机数生成在Matlab中，我们可以使用rand和randn函数快速生成服从均匀分布和正态分布的随机数序列。

rand函数可以生成0到1之间的均匀分布的随机数，例如：```matlabrandom_numbers = rand(100,1);```上述代码将生成一个100行1列的随机数矩阵。

如果我们需要生成服从其他均匀分布的随机数，可以利用rand函数生成0到1之间的随机数，然后利用线性变换将其映射到目标分布区间。

例如，如果我们需要生成一个在区间[2,5]上均匀分布的随机数，可以使用如下代码：```matlaba = 2;b = 5;random_numbers = a + (b-a)*rand(100,1);```其中a和b分别为所需区间的上下界。

同样，randn函数可以生成服从均值为0、标准差为1的正态分布的随机数序列。

例如：```matlabrandom_numbers = randn(100,1);```与均匀分布类似，如果我们需要生成服从其他正态分布的随机数，也可以通过线性变换来实现。

假设我们需要生成一个均值为m，标准差为s的正态分布随机数，可以使用如下代码：```matlabm = 10;s = 2;random_numbers = m + s*randn(100,1);```其中m和s分别为所需正态分布的均值和标准差。

二、分布拟合在实际问题中，我们经常需要将一组实验数据与某种理论概率分布进行拟合，以揭示数据背后的规律。

在Matlab中，可以利用hist函数快速绘制直方图，并借助一些函数进行分布拟合。

Matlab中的随机数生成方法与应用案例

Matlab中的随机数生成方法与应用案例引言：随机数在数学、统计学和计算机科学等领域中具有重要的应用价值。

在大数据分析、模拟实验以及密码学等领域，随机数生成方法的选择和应用至关重要。

Matlab作为一种常用的科学计算软件，提供了多种随机数生成方法和函数。

本文将介绍Matlab中常用的随机数生成方法，以及如何在实际应用中选择合适的方法来满足需求。

一、Matlab中的随机数生成方法1. 均匀分布随机数生成方法Matlab中的`rand`函数可以生成一个0到1之间的均匀分布的随机数。

该函数返回的随机数是一个矩阵，可以通过设定参数来控制矩阵的大小。

```matlabx = rand(1, 100); % 生成一个1行100列的矩阵，每个元素在0到1之间```2. 高斯分布随机数生成方法Matlab中的`randn`函数可以生成服从均值为0，方差为1的标准正态分布的随机数。

该函数返回的随机数也是一个矩阵，大小也可以通过参数进行控制。

```matlabx = randn(1, 100); % 生成一个1行100列的矩阵，每个元素满足标准正态分布```3. 二项分布随机数生成方法Matlab中的`binornd`函数可以生成二项分布的随机数。

该函数需要指定实验次数和成功概率，并返回符合二项分布的随机数。

```matlabx = binornd(10, 0.5); % 进行10次实验，每次成功的概率为0.5，返回符合二项分布的随机数```4. 泊松分布随机数生成方法Matlab中的`poissrnd`函数可以生成泊松分布的随机数。

该函数需要指定均值，并返回符合泊松分布的随机数。

```matlabx = poissrnd(5); % 均值为5的泊松分布随机数```5. 均匀整数分布随机数生成方法Matlab中的`randi`函数可以生成指定范围内的均匀分布的整数随机数。

该函数需要指定随机数的范围和生成的矩阵大小。

matlab产生随机数的方法

matlab产生随机数的方法第一种方法是用random语句，其一般形式为y=random('分布的英文名',A1,A2,A3,m,n)，表示生成m行n列的m×n个参数为(A1,A2,A3)的该分布的随机数。

例如:(1)R=random('Normal',0,1,2,4):生成期望为0,标准差为1的(2行4列)2×4个正态随机数(2)R=random('Poisson',1:6,1,6):依次生成参数为1到6的(1行6列)6个Poisson随机数第二种方法是针对特殊的分布的语句：一．几何分布随机数（下面的P，m都可以是矩阵）R=geornd(P)（生成参数为P的几何随机数）R=geornd(P,m)（生成参数为P的×m个几何随机数）１R=geornd(P,m,n)（生成参数为P的m行n列的m×n个几何随机数）例如(1)R=geornd(1./2.^(1:6))(生成参数依次为1/2,1/2^2,到1/2^6的6个几何随机数)(2)R=geornd(0.01,[15])(生成参数为0.01的（１行５列）5个几何随机数).二．Beta分布随机数R=betarnd(A,B)（生成参数为A,B的Beta随机数）R=betarnd(A,B,m)（生成×m个数为A,B的Beta随机数）１R=betarnd(A,B,m,n)（生成m行n列的m×n个数为A,B的Beta随机数）.三．正态随机数R=normrnd(MU，SIGMA)（生成均值为MU，标准差为SIGMA的正态随机数）R=normrnd(MU，SIGMA,m)（生成1×m个正态随机数）R=normrnd(MU，SIGMA,m,n)（生成m行n列的m×n个正态随机数）例如(1)R=normrnd(0,1,[15])生成5个正态(0,1)随机数(2)R=normrnd([123;456],0.1,2,3)生成期望依次为[1,2,3;4,5,6],方差为0.1的2×3个正态随机数．四．二项随机数：类似地有R=binornd(N,P)R=binornd(N,P,m)R=binornd(N,p,m,n)例如n=10:10:60;r1=binornd(n,1./n)或r2=binornd(n,1./n,[1 6])（都生成参数分别为11),L,(60,)的６个二项随机数．(10,1060五．自由度为V的χ2随机数：R=chi2rnd(V)R=chi2rnd(V R=chi2rnd(V,m),m,n)六．期望为MU的指数随机数（即Exp随机数）：1MUR=exprnd(MU)R=exprnd(MU,m)R=exprnd(MU,m,n)七．自由度为V1，V2的F分布随机数：R=frnd(V1，V2)R=frnd(V1，V2,m)R=frnd(V1，V2,m,n)八．Γ(A,λ)随机数：R=gamrnd（A,lambda）R=gamrnd（A,lambda,m)R=gamrnd （A,lambda,m,n)九．超几何分布随机数：R=hygernd(N,K,M)R=hygernd(N,K,M,m)R=hygernd(N,K,M,m,n)十．对数正态分布随机数R=lognrnd(MU，SIGMA)R=lognrnd(MU，SIGMA,m)R=lognrnd(MU，SIGMA,m,n)十一．负二项随机数：R=nbinrnd(r,p)R=nbinrnd(r,p,m)R=nbinrnd(r,p,m,n)十二．Poisson随机数：R=poissrnd(lambda)R=poissrnd(lambda,m)R=poissrnd(lambda,m,n)例如，以下3种表达有相同的含义：lambda=2;R=poissrnd(lambda,1,10)（或R=poissrnd(lambda,[110])或R=poissrnd(lambda(ones(1,10)))十三．Rayleigh随机数：R=raylrnd(B)R=raylrnd(B,m)R=raylrnd(B,m,n)十四．V个自由度的t分布的随机数：R=trnd(V)R=trnd(V,m)R=trnd(V,m,n)42十五．离散的均匀随机数：R=unidrnd(N)R=unidrnd(N,m)R=unidrnd(N,m,n)十六．[A,B]上均匀随机数R=unifrnd(A,B)R=unifrnd(A,B,m)R=unifrnd(A,B,m,n)例如unifrnd(0,1:6)与unifrnd(0,1:6,[16])都依次生成[0,1]到[0,6]的６个均匀随机数．:十七．Weibull随机数R=weibrnd(A,B)R=weibrnd(A,B,m)R=weibrnd(A,B,m,n)MATLAB中产生高斯白噪声的两个函数MATLAB中产生高斯白噪声非常方便，可以直接应用两个函数，一个是WGN，另一个是AWGN。

matlab 任意分布随机数生成函数

matlab 任意分布随机数生成函数Matlab是一种常用的数学软件，它提供了各种函数来生成随机数。

其中包括生成符合任意分布的随机数的函数。

本文将介绍一些常用的Matlab函数，用于生成服从不同分布的随机数。

我们来介绍一种常见的分布——均匀分布。

均匀分布是指在一定的范围内，随机变量的取值概率是相等的。

在Matlab中，可以使用`rand`函数来生成服从均匀分布的随机数。

例如，要生成一个介于0和1之间的随机数，可以使用以下代码：```x = rand;```如果要生成一个介于a和b之间的随机数，可以使用以下代码：```x = a + (b-a)*rand;```接下来，我们来介绍一种常见的分布——正态分布。

正态分布又称为高斯分布，是一种在统计学中非常重要的分布。

在Matlab中，可以使用`randn`函数来生成服从标准正态分布（均值为0，标准差为1）的随机数。

例如，要生成一个服从标准正态分布的随机数，可以使用以下代码：```x = randn;```如果要生成一个服从均值为mu，标准差为sigma的正态分布的随机数，可以使用以下代码：```x = mu + sigma*randn;```除了均匀分布和正态分布，Matlab还提供了许多其他常见的分布生成函数。

例如，可以使用`randi`函数来生成服从离散均匀分布的随机整数。

例如，要生成一个介于a和b之间的随机整数，可以使用以下代码：```x = randi([a, b]);```如果要生成一个服从泊松分布的随机整数，可以使用`poissrnd`函数。

例如，要生成一个服从参数为lambda的泊松分布的随机整数，可以使用以下代码：```x = poissrnd(lambda);```Matlab还提供了许多其他分布的生成函数，包括二项分布、负二项分布、指数分布、伽马分布等等。

使用这些函数可以方便地生成符合不同分布的随机数。

除了生成单个随机数，Matlab还提供了生成随机矩阵的函数。

matlab生成随机数函数

matlab生成随机数函数1. MA TLAB 函数 rand产生在区间 (0, 1)的均匀随机数，它是平均分布在 (0,1)之间。

一个称为seed的值则是用来控制产生随机数的次数。

均匀随机数函数的语法为rand(n),rand(m,n)，其结果分别产生一矩阵含n×n个随机数和一矩阵含m×n的随机数。

注意每次产生随机数的值都不会一样，这些值代表的是随机且不可预期的，这正是我们用随机数的目的。

我们可利用这些随机数代入算式中，来表示某段讯号的不规则振幅或是某个事件出现的机率。

均匀随机数其值平均的分布于一区间的特性可以从其统计密度函数(probabilitydensity function, PDF)说明。

从其PDF分布类似长条图的分布，可以看出其每一个随机数值出现的机率皆相同，所以它被称为均匀随机数。

见以下的例子：>> rand(1,6) % 第一次使用随机数产生器ans =0.2190 0.0470 0.6789 0.6793 0.9347 0.3835>>hist(ans) % 看看长条图的长相>>plot(ans) % 比较上个图与这个图有何差异？何者能代表不规则数据的分布>> rand(1,6) % 第二次使用随机数产生器，注意每次产生的随机数值皆不同ans =0.5194 0.8310 0.0346 0.0535 0.5297 0.6711因为每次随机数产生的值皆不同，如果因为验证算式需要确定所使用的随机数值是相同的，可以利用seed这个选项，用以设定使用计算随机数产生器的起始值，其语法为rand('seed',n)，n的规定是。

其中n=0有特别意义是使用第一次产生随机数值的起始值(=931316785)，其它的n值即是所使用起始值。

如果使用相同的起始值，则随机数值会一样，因为随机数的计算是依据起始值。

请看以下的例子：>> rand('seed',0) % 将随机数值的起始值重设，相当于是第一次产生随机数值>>rand('seed') % 显示现在使用的 seed 值=931316785ans =931316785>> rand(2,3) % 注意随机数值的上下限介于 [0,1] 区间ans =0.2190 0.6789 0.93470.0470 0.6793 0.3835>> rand('seed') % 显示再产生随机数值所用的seed=412659990ans =412659990>> rand('seed',0)>> rand(1,6)ans =0.2190 0.0470 0.6789 0.6793 0.9347 0.3835>> rand('seed',100) % 设定随机数值的起始值=100>> rand('seed')ans =100>> rand(2,5)ans =0.2909 0.0395 0.3671 0.5968 0.92530.0484 0.5046 0.9235 0.8085 0.3628如果需要产生随机数值不是介于[0,1]区间，可以采用以下步骤将随机数值从[0,1]区间转换到其它区间。

matlab中随机数生成 -回复

matlab中随机数生成-回复Matlab中的随机数生成是一项强大且常用的功能，它允许我们生成任意分布和范围内的随机数。

在这篇文章中，我们将逐步探讨如何在Matlab 中生成随机数，并讨论其一些应用。

首先，让我们研究一下如何生成一个随机数。

在Matlab中，我们可以使用rand函数来生成0到1之间的一个均匀分布的随机数。

它的语法如下：r = rand;这里，r将会是一个0到1之间的一个随机数。

我们可以将rand函数与其他数学运算符（+，-，*，/等）一起使用，以生成具有特定范围的随机数。

例如，要生成一个在给定范围内的随机整数，我们可以执行以下步骤：Step 1: 定义范围的下限和上限：lower = 1;upper = 10;Step 2: 计算范围内的随机整数：r = lower + randi(upper-lower);这里，randi函数用于生成一个在给定范围内的随机整数。

接下来，让我们来讨论如何生成符合特定分布的随机数。

Matlab提供了一系列的函数来生成符合不同分布的随机数。

其中一些常见的分布函数包括正态分布、均匀分布、指数分布等。

要生成符合正态分布的随机数，我们可以使用randn函数。

以下是生成一些符合正态分布的随机数的示例代码：mu = 0;sigma = 1;r = mu + sigma * randn(1, 100);这里，mu代表均值，sigma代表标准差。

randn函数将生成一个大小为1x100的数组，其中包含由给定的均值和标准差定义的正态分布的随机数。

对于均匀分布，我们可以使用unifrnd函数。

以下是生成一个范围在0到1之间的随机数的示例代码：r = unifrnd(0, 1, 1, 100);这里，unifrnd函数将生成一个大小为1x100的数组，其中包含由给定范围定义的均匀分布的随机数。

在Matlab中，还有许多其他用于生成各种分布随机数的函数，如exppdf 函数用于生成符合指数分布的随机数，gamrnd函数用于生成符合伽马分布的随机数等。

rand在matlab中的用法

rand在matlab中的用法
Rand是Matlab中的一个函数，用于生成随机数。

它可以用于各种情况，例如生成随机矩阵、向量、数组等。

Rand函数可以通过以下方法使用：
1. 基本用法：生成随机数
a = rand();
其中a是一个0到1之间的随机数。

2. 生成随机矩阵
a = rand(n,m);
其中n和m是矩阵的行数和列数。

这将生成一个大小为n×m的矩阵，其中每个元素都是0到1之间的随机数。

3. 生成随机向量
a = rand(1,n);
其中n是向量的长度。

这将生成一个大小为1×n的向量，其中每个元素都是0到1之间的随机数。

4. 生成随机整数
a = randi(n);
其中n是要生成的整数的最大值。

这将生成一个0到n之间的随机整数。

除此之外，还有其他与rand函数有关的函数，例如randn、randperm等。

randn函数用于生成正态分布的随机数，randperm函数用于生成随机排列。

总之，rand函数是Matlab中一个非常有用的工具，可以用于各种随机化应用。

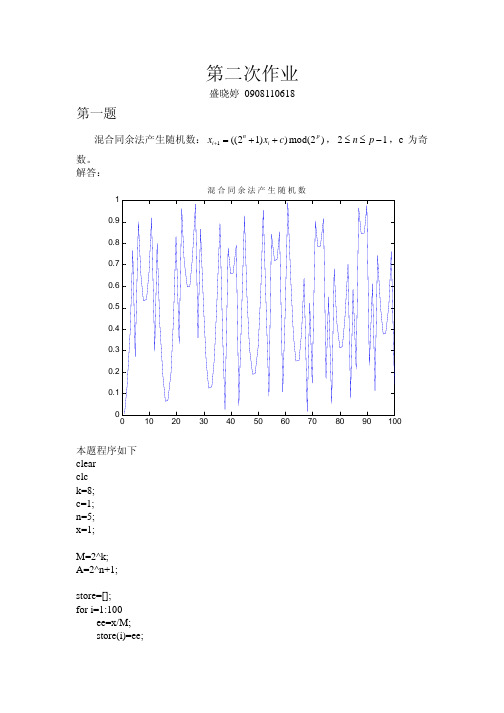
生成随机数的MATLAB程序

混合同余法产生随机数 1
0.9
0.8
0.7
0.6
0.5 0.4 0.3 0.2 0.1
0 0 10 20 30 40 50 60 70 80 90 100
本题程序如下 clear clc k=8; c=1; n=5; x=1;
M=2^k; A=2^n+1;
store=[]; for i=1:100
ee=x/M; store(i)=ee;
%=======将逆 M 序列的幅值变为 a 和-a a=5; %a 为指定的幅值 I=IM.*a*2; I=I-a;
figure(3) stairs(1:n,I) axis([0,n,-a-1,a+1]) title('幅值为 a 的逆 M 序列') xlabel('时序脉冲')
%=======产生逆 M 序列============== s=zeros(1,length(M)); %s 为方波序列 s(1)=1; for i=2:n
s(i)=~s(i-1); end
IM=xor(M,s);
figure(2) stairs(1:n,IM) axis([0,n,0,1.5]) title('逆 M 序列') xlabel('时序脉冲')
C6
C7
C8
C9
此处设 x 的初始值为[0 1 0 1 1 0 1 1 1]; a=5
M序列 1.5
1
0.5
0
0
5 10 15 20 25 30 35 40 45 50
时序脉冲
逆 M序列 6
4
2
0
-2
-4
-6
0

matlab随机数生成方法

matlab中的rand用法

matlab rand用法

matlab中随机数生成

matlab中0-1的随机数

matlab 概率密度

如何用matlab生成随机数函数

matlab中1-10之间的随机数

产生正态分布随机数的matlab方法random

matlab 给定范围的随机数

matlab随机数生成方法

Matlab产生随机数

Matlab中的随机数生成与随机模拟

Matlab中的随机数生成与分布拟合技巧

Matlab中的随机数生成方法与应用案例

matlab产生随机数的方法

matlab 任意分布 随机数生成函数

matlab生成随机数函数

matlab中随机数生成 -回复

rand在matlab中的用法

生成随机数的MATLAB程序

matlab 任意分布随机数生成函数