使用Matlabcftool工具箱对图像进行拟合
用MATLAB(高版本) cftool拟合多条曲线

听说你想要用cftool作出这样的东西?楼上有人说用cftool-v1,不过很绝望比较新的版本都完全无法使用这个功能了。
反正我的R2016a不行。
我也是在问遍没有可靠的解法后自己无意间摸索出来的,完全原创,希望对大家有帮助!转载请注明原出处和原作者!这里我们以RLC串联谐振需要在同一个坐标里画出频率特性的XC,XL,Z曲线为例,首先敲出坐标数据如下(请手动无视i数据):然后运行,转到了cftool界面如下:首先我们拟合xc-f曲线(这是个反函数曲线),然后点:文件——generate code然后你看到了这个:保存一下,然后点运行,这里就有点GAY了,说什么参数不足,但是没事,你鼠标点一下“键入运行代码那一行然后变成了下面这个样子”,再点运行图标。
然后会跳出一个窗口,就是下面这个玩意儿,注意观察的话,你会发现他的曲线颜色和你一般的直接从cftool里点print to figure曲线颜色不一样!我们要的就是这个效果!保留上面这个窗口,回答cftool依次把剩下的xl-f曲线,z-f曲线按照上面的步骤操作,得到三个窗口。
接下来是见证奇迹的时候了!进到每个窗口把属性编辑器打开,像酱紫:然后你看到下面这一幕:没错,刚才的单个独立窗口合并到了一起变成了三个标签!接下来就是把任何两个标签里的曲线复制到余下哪一个,比如我们把figure1,figure2里的曲线都弄到figure3里:选中figure2曲线——右击复制(千万不要用ctrl+c,不信你可以看一下会发生什么。
)——到figure3里右击粘贴(同样的道理,不要Ctrl+v),现在看到你要的了吧!对figure1实行同样的操作,然后就得到了:剩下的就是用属性编辑器编辑成你要的样子了!声明一下,如果直接从cftool里print to figure三次然后再复制粘贴是不行的,应为根本无法实现曲线的复制粘贴,他产生的结果会和上面你用Ctrl+c复制Ctrl+v粘贴产生同样的效果,根本不是我们想要的!重复一遍,我也是在问遍没有可靠的解法后自己无意间摸索出来的,完全原创,完全野路子,希望对大家有帮助!转载请注明原出处和原作者!谢谢!吐槽一下知乎的回答编辑板块渣渣。
用MATLAB(高版本)cftool拟合多条曲线

用MATLAB(高版本)cftool拟合多条曲线听说你想要用cftool作出这样的东西?楼上有人说用cftool-v1,不过很绝望比较新的版本都完全无法使用这个功能了。
反正我的R2016a不行。
我也是在问遍没有可靠的解法后自己无意间摸索出来的,完全原创,希望对大家有帮助!转载请注明原出处和原作者!这里我们以RLC串联谐振需要在同一个坐标里画出频率特性的XC,XL,Z曲线为例,首先敲出坐标数据如下(请手动无视i数据):然后运行,转到了cftool界面如下:首先我们拟合xc-f曲线(这是个反函数曲线),然后点:文件——generate code然后你看到了这个:保存一下,然后点运行,这里就有点GAY了,说什么参数不足,但是没事,你鼠标点一下“键入运行代码那一行然后变成了下面这个样子”,再点运行图标。
然后会跳出一个窗口,就是下面这个玩意儿,注意观察的话,你会发现他的曲线颜色和你一般的直接从cftool里点print to figure曲线颜色不一样!我们要的就是这个效果!保留上面这个窗口,回答cftool依次把剩下的xl-f曲线,z-f曲线按照上面的步骤操作,得到三个窗口。
接下来是见证奇迹的时候了!进到每个窗口把属性编辑器打开,像酱紫:然后你看到下面这一幕:没错,刚才的单个独立窗口合并到了一起变成了三个标签!接下来就是把任何两个标签里的曲线复制到余下哪一个,比如我们把figure1,figure2里的曲线都弄到figure3里:选中figure2曲线——右击复制(千万不要用ctrl+c,不信你可以看一下会发生什么。
)——到figure3里右击粘贴(同样的道理,不要Ctrl+v),现在看到你要的了吧!对figure1实行同样的操作,然后就得到了:剩下的就是用属性编辑器编辑成你要的样子了!声明一下,如果直接从cftool里print to figure三次然后再复制粘贴是不行的,应为根本无法实现曲线的复制粘贴,他产生的结果会和上面你用Ctrl+c复制Ctrl+v粘贴产生同样的效果,根本不是我们想要的!重复一遍,我也是在问遍没有可靠的解法后自己无意间摸索出来的,完全原创,完全野路子,希望对大家有帮助!转载请注明原出处和原作者!谢谢!吐槽一下知乎的回答编辑板块渣渣。
MATLAB拟合函数使用说明

MATLAB拟合函数使用说明MATLAB是一种强大的数学计算和数据分析软件,其中的拟合函数可以用来对实验数据进行拟合以获得一个数学模型,进而预测和分析数据。
使用MATLAB进行数据拟合可以帮助我们理解数据的规律和趋势,进行预测和决策。
在MATLAB中,有多种不同的拟合函数可以使用,包括线性拟合、多项式拟合、非线性拟合等。
下面将对其中几种常用的拟合函数进行介绍,并说明如何使用这些函数进行数据拟合。
1. 线性拟合:使用polyfit函数可以进行线性拟合。
该函数的基本语法为:```p = polyfit(x, y, n)```其中x和y是待拟合的数据,n是拟合多项式的次数。
函数返回一个多项式系数向量p,可以用polyval函数将该多项式应用于其他数据进行预测。
2. 多项式拟合:在MATLAB中,可以使用polyfitn函数进行多项式拟合。
该函数的基本语法为:```p = polyfitn(x, y, n)```其中x和y是待拟合的数据,n是拟合多项式的次数。
函数返回一个多项式系数向量p,可以用polyvaln函数将该多项式应用于其他数据进行预测。
3. 非线性拟合:MATLAB提供了curve fitting toolbox工具箱,其中的cftool函数可以进行非线性拟合。
使用cftool函数可以通过交互界面进行拟合,也可以通过脚本进行自定义拟合。
该工具箱提供了多种非线性模型,如指数模型、对数模型、幂函数模型等。
在进行拟合之前,首先需要准备好待拟合的数据。
常见的方式是将数据存储在一个数组或矩阵中,然后将数组或矩阵传递给拟合函数进行处理。
拟合函数的参数列表中各个参数的选择对拟合结果有一定的影响,一般情况下需要根据具体问题选择合适的参数。
例如,在多项式拟合中,选择合适的拟合多项式的次数n可以避免过度拟合或欠拟合的问题。
进行数据拟合后,可以使用plot函数将原始数据和拟合结果进行可视化比较。
此外,还可以使用拟合结果进行预测,通过polyval或polyvaln函数将拟合多项式应用于其他数据,得到预测结果。
cftool的应用

Matlab非线性拟合工具箱cftool本文来自: MATLAB爱好者论坛作者: admin日期: 2009-6-3 11:06 阅读: 4361人打印收藏Matlab, cftool, 非线性, 工具箱, 拟合一、单一变量的曲线逼近Matlab有一个功能强大的曲线拟合工具箱 cftool ,使用方便,能实现多种类型的线性、非线性曲线拟合。
下面结合我使用的 Matlab R2007b 来简单介绍如何使用这个工具箱。
假设我们要拟合的函数形式是 y=A*x*x + B*x, 且A>0,B>0 。
1、在命令行输入数据:》x=[110.3323 148.7328 178.064 202.8258033 224.7105 244.5711 262.908 280.0447 296.204 311.5475];》y=[5 10 15 20 25 30 35 40 45 50];2、启动曲线拟合工具箱》cftool3、进入曲线拟合工具箱界面“Curve Fitting tool”(1)点击“Data”按钮,弹出“Data”窗口;(2)利用X data和Y data的下拉菜单读入数据x,y,可修改数据集名“Data set name”,然后点击“Create data set”按钮,退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的曲线图;(3)点击“Fitting”按钮,弹出“Fitting”窗口;(4)点击“New fit”按钮,可修改拟合项目名称“Fit name”,通过“Data set”下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:Custom Equations:用户自定义的函数类型Exponential:指数逼近,有2种类型, a*exp(b*x) 、 a*exp(b*x) + c*exp(d*x) Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1*cos(x*w) + b1*sin(x*w) Gaussian:高斯逼近,有8种类型,基础型是 a1*exp(-((x-b1)/c1)^2)Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preservingPolynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree~Power:幂逼近,有2种类型,a*x^b 、a*x^b + cRational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思)Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是 a1*sin(b1*x + c1) Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)选择好所需的拟合曲线类型及其子类型,并进行相关设置:——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口,有“Linear Equations线性等式”和“General Equations构造等式”两种标签。
CFTOOL

Matlab非线性拟合工具箱cftool一、单一变量的曲线逼近Matlab有一个功能强大的曲线拟合工具箱cftool ,使用方便,能实现多种类型的线性、非线性曲线拟合。
下面结合我使用的Matlab R2007b 来简单介绍如何使用这个工具箱。
假设我们要拟合的函数形式是y=A*x*x + B*x, 且A>0,B>0 。
1、在命令行输入数据:》x=[110.3323 148.7328 178.064 202.8258033 224.7105 244.5711 262.908 280.0447 296.204 311.5475];》y=[5 10 15 20 25 30 35 40 45 50];2、启动曲线拟合工具箱》cftool3、进入曲线拟合工具箱界面“Curve Fitting tool”(1)点击“Data”按钮,弹出“Data”窗口;(2)利用X data和Y data的下拉菜单读入数据x,y,可修改数据集名“Data set name”,然后点击“Create data set”按钮,退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的曲线图;(3)点击“Fitting”按钮,弹出“Fitting”窗口;(4)点击“New fit”按钮,可修改拟合项目名称“Fit name”,通过“Data set”下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:Custom Equations:用户自定义的函数类型Exponential:指数逼近,有2种类型,a*exp(b*x) 、a*exp(b*x) + c*exp(d*x)Fourier:傅立叶逼近,有7种类型,基础型是a0 + a1*cos(x*w) + b1*sin(x*w) Gaussian:高斯逼近,有8种类型,基础型是a1*exp(-((x-b1)/c1)^2)Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~ Power:幂逼近,有2种类型,a*x^b 、a*x^b + cRational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思)Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是a1*sin(b1*x + c1) Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)选择好所需的拟合曲线类型及其子类型,并进行相关设置:——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口,有“Linear Equations线性等式”和“General Equations构造等式”两种标签。
matlab如何实现曲线拟合?matlab做曲线拟合的教程

matlab如何实现曲线拟合?matlab做曲线拟合的教程Matlab是⼀个很强⼤的数据处理软件,是⼈们进⾏数据分析的得⼒助⼿。
⼀般我们做社会调研或科学研究时,会得到很多实验
数据。
当需要研究两个变量之间的关系时,经常要⽤到曲线拟合。
曲线拟合不仅能给出拟合后的关系式,还能⽤图形直观的展现出变量之间的关系。
其实⽤matlab做曲线拟合很便捷,下⾯将以两个变量(y=f(x))为例详细介绍:
1、运⾏Matlab软件。
在⼯作空间中存⼊变量的实验数据。
具体如下:可以直接⽤矩阵来存放数据,直接在命令窗⼝输⼊
x=[数据x1,数据x2,...,数据xn];
y=[数据y1,数据y2,...,数据yn];
当数据较多时,可以从excel,txt等⽂件中导⼊。
2、把数据存⼊⼯作空间后,在命令窗⼝中输⼊cftool,回车运⾏。
3、在这个拟合⼯具窗⼝的左边,选择变量,即分别选择x,y。
4、选择拟合的曲线类型,⼀般是线性拟合,⾼斯曲线,平滑曲线等,根据需要选择。
选择完后会⾃动完成拟合,并且给出拟合函数表达式。
5、点击菜单栏中的“file”,选择“print to figure"进⾏画图。
6、在图形窗⼝中,可以对图形显⽰模式进⾏修改,如添加标题,坐标名称等。
7、最后得到⽐较完整的图形曲线。
点击”file"中的“save"进⾏保存。
注意事项:x和y的数据个数应该⼀致。
Matlab拟合工具箱CFtool使用指南
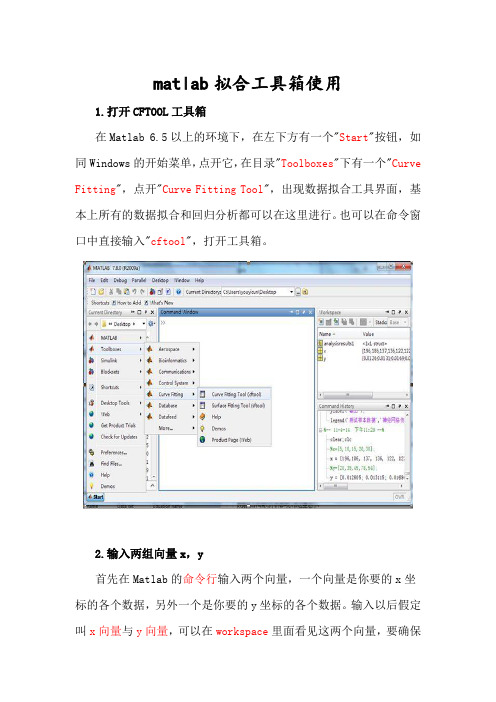
matlab拟合工具箱使用1.打开CFTOOL工具箱在Matlab 6.5以上的环境下,在左下方有一个"Start"按钮,如同Windows的开始菜单,点开它,在目录"Toolboxes"下有一个"Curve Fitting",点开"Curve Fitting Tool",出现数据拟合工具界面,基本上所有的数据拟合和回归分析都可以在这里进行。
也可以在命令窗口中直接输入"cftool",打开工具箱。
2.输入两组向量x,y首先在Matlab的命令行输入两个向量,一个向量是你要的x坐标的各个数据,另外一个是你要的y坐标的各个数据。
输入以后假定叫x向量与y向量,可以在workspace里面看见这两个向量,要确保这两个向量的元素数一致,如果不一致的话是不能在工具箱里面进行拟合的。
例如在命令行里输入下列数据:x = [196,186, 137, 136, 122, 122, 71, 71, 70, 33];y = [0.012605; 0.013115; 0.016866; 0.014741; 0.022353;0.019278; 0.041803; 0.038026; 0.038128; 0.088196];3.选取数据打开曲线拟合共工具界面,点击最左边的"Data..."按钮,出现一个Data对话框,在Data Sets页面里,在X Data选项中选取x向量,Y Data选项中选取y向量,如果两个向量的元素数相同,那么Create data set按钮就激活了,此时点击它,生成一个数据组,显示在下方Data Sets列表框中。
关闭Data对话框。
此时Curve Fitting Tool窗口中显示出这一数据组的散点分布图。
4.拟合曲线(幂函数power)。
点击Fitting...按钮,出现Fitting对话框,Fitting对话框分为两部分,上面为Fit Editor,下面为Table of Fits,有时候窗口界面比较小,Fit Editor部分会被收起来,只要把Table of Fits 上方的横条往下拉就可以看见Fit Editor。
使用MATLAB曲线拟合工具箱做曲线拟合(2013)

使用 MATLAB 曲线拟合工具箱做曲线拟合在实际的工程应用领域和经济应用领域中,人们往往通过实验或者观测得到一些数据, 为了从这些数据中找到其内在的规律性, 也就是求得自变量和因变量之间的近似函数关系表 达式。
这类问题可以归结曲线拟合。
1.MATLAB 曲线拟合工具箱简介MATLAB 做曲线拟合可以通过内建函数或者拟合工具箱(Curve Fitting Toolbox )。
这个 工具箱集成了用MATLAB 建立的图形用户界面(GUIs )和 M 文件函数。
利用这个工具箱 可以进行参数拟合(当想找出回归系数以及他们背后的物理意义的时候就可以采用参数拟 合),或者通过采用平滑样条或者其他各种插值方法进行参数拟合(当回归系数不具有物理 意义并且不在意他们的时候,就采用非参数拟合)。
利用这个界面,可以快速地在简单易用 的环境中实现许多基本的曲线拟合。
2.实际例子应用数学模型书上关于汽车刹车距离模型,建立的模型如下:2 1 d t v kv=+ 其中v 是汽车速度, 1 t 是反应时间,按大多数人平均取 0.75 秒,d 是刹车距离。
交通部 门提供了一组刹车的距离实际数据如表1 所示(刹车距离括号内为最大值)。
表 1车速(英尺 秒)29.3 44 58.7 73.3 88 102.7 1173 刹车距离 (英尺) 42(44) 73.5(78) 116(124) 173(186) 248(268) 343(372) 464(506) 利用表 1 的数据,我们拟合在 MATLAB 的 command window 里输入:>>v=[29.3 44 58.7 73.3 88 102.7 117.3];>>d1=[42 73.5 116 173 248 343 464];>>cftool %cftool 是打开拟合工具箱的命令;则跳出曲线拟合工具箱的界面如图 1 所示, 如果输入数据非常大, 并且每次输入有困难, 可以新建一个 M 文件,依次输入上述命令行,保存之后执行,同样可以进入曲线拟合工具 箱界面。
打开matlab拟合工具箱
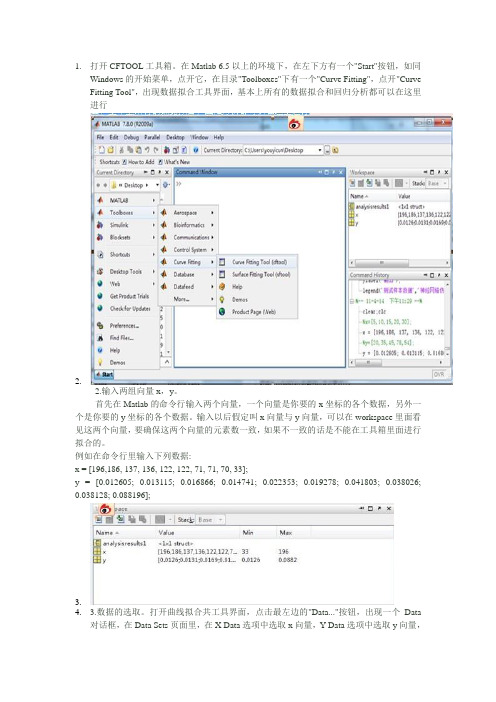
1.打开CFTOOL工具箱。
在Matlab 6.5以上的环境下,在左下方有一个"Start"按钮,如同Windows的开始菜单,点开它,在目录"Toolboxes"下有一个"Curve Fitting",点开"Curve Fitting Tool",出现数据拟合工具界面,基本上所有的数据拟合和回归分析都可以在这里进行2.2.输入两组向量x,y。
首先在Matlab的命令行输入两个向量,一个向量是你要的x坐标的各个数据,另外一个是你要的y坐标的各个数据。
输入以后假定叫x向量与y向量,可以在workspace里面看见这两个向量,要确保这两个向量的元素数一致,如果不一致的话是不能在工具箱里面进行拟合的。
例如在命令行里输入下列数据:x = [196,186, 137, 136, 122, 122, 71, 71, 70, 33];y = [0.012605; 0.013115; 0.016866; 0.014741; 0.022353; 0.019278; 0.041803; 0.038026;0.038128; 0.088196];3.4. 3.数据的选取。
打开曲线拟合共工具界面,点击最左边的"Data..."按钮,出现一个Data对话框,在Data Sets页面里,在X Data选项中选取x向量,Y Data选项中选取y向量,如果两个向量的元素数相同,那么Create data set按钮就激活了,此时点击它,生成一个数据组,显示在下方Data Sets列表框中。
关闭Data对话框。
此时Curve Fitting Tool 窗口中显示出这一数据组的散点分布图5.6.7.4.曲线拟合(幂函数power)。
点击Fitting...按钮,出现Fitting对话框,Fitting对话框分为两部分,上面为Fit Editor,下面为Table of Fits,有时候窗口界面比较小,Fit Editor部分会被收起来,只要把Table of Fits 上方的横条往下拉就可以看见Fit Editor。
Matlab拟合工具箱CFtool使用指南

matlab拟合工具箱使用1.打开CFTOOL工具箱在Matlab 6.5以上的环境下,在左下方有一个"Start"按钮,如同Windows的开始菜单,点开它,在目录"Toolboxes"下有一个"Curve Fitting",点开"Curve Fitting Tool",出现数据拟合工具界面,基本上所有的数据拟合和回归分析都可以在这里进行。
也可以在命令窗口中直接输入"cftool",打开工具箱。
2.输入两组向量x,y首先在Matlab的命令行输入两个向量,一个向量是你要的x坐标的各个数据,另外一个是你要的y坐标的各个数据。
输入以后假定叫x向量与y向量,可以在workspace里面看见这两个向量,要确保这两个向量的元素数一致,如果不一致的话是不能在工具箱里面进行拟合的。
例如在命令行里输入下列数据:x = [196,186, 137, 136, 122, 122, 71, 71, 70, 33];y = [0.012605; 0.013115; 0.016866; 0.014741; 0.022353;0.019278; 0.041803; 0.038026; 0.038128; 0.088196];3.选取数据打开曲线拟合共工具界面,点击最左边的"Data..."按钮,出现一个Data对话框,在Data Sets页面里,在X Data选项中选取x向量,Y Data选项中选取y向量,如果两个向量的元素数相同,那么Create data set按钮就激活了,此时点击它,生成一个数据组,显示在下方Data Sets列表框中。
关闭Data对话框。
此时Curve Fitting Tool窗口中显示出这一数据组的散点分布图。
4.拟合曲线(幂函数power)。
点击Fitting...按钮,出现Fitting对话框,Fitting对话框分为两部分,上面为Fit Editor,下面为Table of Fits,有时候窗口界面比较小,Fit Editor部分会被收起来,只要把Table of Fits上方的横条往下拉就可以看见Fit Editor。
曲线拟合工具箱 CFtool 使用简介 CFtool简介

曲线拟合工具箱CFtool使用简介一、CFtool简介Matlab有一个功能强大的曲线拟合工具箱cftool,使用方便,能实现多种类型的线性、非线性曲线拟合。
它的使用简介如下(Matlab R2011b中)。
假设我们要拟合的函数形式是 y=A*x*x + B*x, 且A>0, B>0 。
1.在命令行输入数据:x=[110.3323 148.7328 178.064 202.8258033 224.7105 244.5711 262.908 280.0447 296.204 311.5475];y=[5 10 15 20 25 30 35 40 45 50];2.启动曲线拟合工具箱:cftool3.进入曲线拟合工具箱界面“Curve Fitting tool”:1)利用X data和Y data的下拉菜单读入数据x,y,这时会自动画出数据集的曲线图,注意右侧的Auto fit选项;2)通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:(1)Custom Equations:用户自定义的函数类型(2)Exponential:指数逼近,有2种类型, a*exp(b*x) 、 a*exp(b*x) + c*exp(d*x)(3)Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1*cos(x*w) + b1*sin(x*w)(4)Gaussian:高斯逼近,有8种类型,基础型是 a1*exp(-((x-b1)/c1)^2) (5)Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving(6)Polynomial:多形式逼近,有9种类型,linear polynomial、quadratic polynomial、cubic polynomial以及4-9th degree polynomial (7)Power:幂逼近,有2种类型,a*x^b 、a*x^b + c(8)Rational:有理数逼近,分子(Numerator)、分母(Denominator)共有的类型是linear rational、quadratic rational、cubic rational、4-5th degree rational;此外,分子(Numerator)还包括constant型(9)Smoothing Spline:平滑样条逼近(10)Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是a1*sin(b1*x + c1)(11)Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)3)选择好所需的拟合曲线类型及其子类型,并进行相关设置:——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口,有“Linear Equations线性等式”和“General Equations构造等式”两种标签。
matlab数据拟合-有图有例子-一看就会教学教材

m a t l a b数据拟合-有图有例子-一看就会Matlab CFTool使用简介:单一变量的曲线逼近Matlab有一个功能强大的曲线拟合工具箱 cftool ,使用方便,能实现多种类型的线性、非线性曲线拟合。
下面结合我使用的 Matlab R2007b 来简单介绍如何使用这个工具箱。
假设我们要拟合的函数形式是 y=A*x*x + B*x, 且A>0,B>0 。
1、在命令行输入数据:》x=[你的X轴数据];》y=[你的Y轴数据];》cftool可以将上面三个行建立一个M文件,以便后面进行数据拟合时可以直接使用,点击运行即可进入曲线拟合工具箱界面“Curve Fitting tool”(1)点击“Data”按钮,弹出“Data”窗口;(2)利用X data和Y data的下拉菜单读入数据x,y,可修改数据集名“Data set name”,然后点击“Create data set”按钮,退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的曲线图;(3)点击“Fitting”按钮,弹出“Fitting”窗口;(4)点击“New fit”按钮,可修改拟合项目名称“Fit name”,通过“Data set”下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:•Custom Equations:用户自定义的函数类型•Exponential:指数逼近,有2种类型, a*exp(b*x) 、 a*exp(b*x) + c*exp(d*x)•Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1*cos(x*w) + b1*sin(x*w)•Gaussian:高斯逼近,有8种类型,基础型是 a1*exp(-((x-b1)/c1)^2) •Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving•Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~•Power:幂逼近,有2种类型,a*x^b 、a*x^b + c•Rational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型•Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思)•Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是a1*sin(b1*x + c1)•Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)•选择好所需的拟合曲线类型及其子类型,并进行相关设置:•——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;•——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口,有“Linear Equations线性等式”和“General Equations构造等式”两种标签。
Matlab拟合工具箱CFtool使用指南

matlab拟合工具箱使用之阳早格格创做正在Matlab 6.5以上的环境下,正在左下圆有一个"Start"按钮,如共Windows的启初菜单,面启它,正在目录"Toolboxes"下有一个"Curve Fitting",面启"Curve Fitting Tool",出现数据拟合工具界里,基原上所有的数据拟合战返回分解皆不妨正在那里举止.也不妨正在下令窗心中直交输进"cftool",挨启工具箱.2.输进二组背量x,y最先正在Matlab的下令止输进二个背量,一个背量是您要的x坐目标各个数据,其余一个是您要的y坐目标各个数据.输进以去假定喊x背量与y背量,不妨正在workspace内里瞅睹那二个背量,要保证那二个背量的元素数普遍,如果纷歧致的话是不克不迭正在工具箱内里举止拟合的.比圆正在下令止里输进下列数据:x = [196,186, 137, 136, 122, 122, 71, 71, 70, 33];y = [0.012605; 0.013115; 0.016866; 0.014741; 0.022353; 0.019278; 0.041803; 0.038026; 0.038128; 0.088196];挨启直线拟合共工具界里,面打最左边的"Data..."按钮,出现一个Data对于话框,正在Data Sets页里里,正在X Data选项中采用x背量,Y Data选项中采用y背量,如果二个背量的元素数相共,那么Create data set按钮便激活了,此时面打它,死成一个数据组,隐现正在下圆DataSets列表框中.关关Data对于话框.此时Curve Fitting Tool窗心中隐现出那一数据组的集面分集图.4.拟合直线(幂函数power).面打Fitting...按钮,出现Fitting对于话框,Fitting对于话框分为二部分,上头为Fit Editor,底下为Table of Fits,偶我间窗心界里比较小,Fit Editor部分会被支起去,只消把Table of Fits上圆的横条往下推便不妨瞅睹Fit Editor.正在Fit Editor内里面打New Fit按钮,此时其下圆的各个选框被激活,正在Data Set选框中选中刚刚才建坐的xy数据组,而后正在Type of fit选框中采用拟合大概返回典型,各个典型的拟合大概返回相映的分别是:Custom Equations 用户自定义函数Expotential e指数函数Fourier 傅坐叶函数,含有三角函数Gaussian 正态分集函数,下斯函数Interpolant 插值函数,含有线性函数,移动仄衡等典型的拟合Polynomial 多项式函数Power 幂函数Rational 有理函数(不太领会,不怎么用过)Smooth Spline ??(光润插值大概者光润拟合,不太领会)Sum of sin functions正弦函数类Weibull 威布我函数(出用过)正在那个Type of fit选框中采用佳符合的典型,并选佳符合的函数形式.于是面打Apply按钮,便启初举止拟合大概者返回了.此时正在Curve Fitting Tool窗心上便会出现一个拟合的直线.那便是所要的截止.正在上头的例子中,采用sum of sin functions中的第一个函数形式,面打Apply按钮,便不妨瞅睹拟合得到的正弦直线.正在Fitting对于话框中的Results文原框中隐现有此次拟合的主要统计疑息,主要有General model of sin1:....... (函数形式)Coefficients (with 95% conffidence range) (95%致疑区间内的拟合常数)a1=... ( ... ...) (等号后里是仄衡值,括号里是范畴)....Godness of fit: (统计截止)SSE: ... (圆好)Rsquared: ... (决断系数,不知讲干什么的)Adjusted Rsquared: ... (矫正后的决断系数,怎么样矫正的不得而知)RMSE: ... (尺度好)上头的例子中通过拟合得到的函数末尾为6.拟合分解(Analysis).其余要道的是,如果念把那个拟合的图像导出的话,正在Curve Fitting Tool窗心的File菜单下选Print to Figure,此时弹出一个新的图像窗心,内里是您要导出的图像,正在那个figure窗心的File菜单里再选Export,采用佳符合的要领,普遍是jpeg,采用佳路径,面打OK便不妨了.出去的图像不妨正在Word等编写环境中使用,便已几道了.要建改图像的本量,如数据面的大小、颜色等等的,只需要正在对于象上面左键,便好已几不妨找到了.其余使用步调去举止直线拟合:p=polyfit(xdata,ydata,n) n为采用的要领a=polyval(p,xdata) 举止直线拟合后估计所得到得值不妨将拟合直线与源直线绘出去:plot(xdata,ydata,'b*',xdata,a,'r')legend('ydata','fit');。
matlab拟合命令

matlab拟合命令Matlab是一种非常流行的科学计算软件,它可以用来进行各种数学计算、数据分析和可视化等操作。
其中,拟合命令是Matlab中非常重要的一个功能,它可以帮助我们对数据进行拟合,得到一个符合实际情况的模型。
本文将详细介绍Matlab中的拟合命令。
一、Matlab中的拟合命令简介在Matlab中,有多种拟合命令可供选择,包括polyfit、fit、cftool 等。
这些命令都可以用来对数据进行拟合,但具体使用方法和适用范围略有不同。
1. polyfit命令polyfit是Matlab中最简单和最基础的拟合命令之一。
它可以用来对一组数据进行多项式拟合,并返回多项式系数。
其基本语法如下:p = polyfit(x, y, n)其中x和y分别是待拟合数据的自变量和因变量数组,n表示要进行多项式拟合的次数。
2. fit命令fit命令比polyfit更加灵活和强大,它可以用来对各种类型的函数进行非线性拟合,并返回最优参数值。
其基本语法如下:f = fit(x, y, model)其中x和y同样表示待拟合数据的自变量和因变量数组,model表示要拟合的函数模型,可以是Matlab内置的函数模型,也可以是自定义的函数模型。
3. cftool命令cftool是Matlab中一个交互式工具箱,它可以用来进行各种类型的拟合,并可视化显示拟合结果。
使用cftool命令时,用户需要先打开cftool工具箱界面,在界面中选择要进行拟合的数据和函数模型,并设置相应参数。
最后点击“fit”按钮即可得到拟合结果。
二、多项式拟合多项式拟合是最基本的数据拟合方法之一,在Matlab中可以使用polyfit命令进行多项式拟合。
其基本思路是通过一条多项式曲线来逼近原始数据点,使得曲线与原始数据点之间的误差最小。
1. 一次多项式拟合一次多项式拟合即为线性拟合,在Matlab中可以使用polyfit命令进行。
其基本语法如下:p = polyfit(x, y, 1)其中x和y分别为待拟合数据的自变量和因变量数组,1表示进行一次多项式(即直线)拟合。
cftool拟合函数

cftool拟合函数cftool是MATLAB中的一个工具箱,可以用于拟合函数。
拟合函数是指通过一些已知的数据点,找到一个函数,使得这个函数能够最好地描述这些数据点的分布规律。
cftool可以帮助我们找到这个函数,并且可以对这个函数进行可视化展示。
使用cftool拟合函数的步骤如下:1. 准备数据我们需要准备一些数据。
这些数据可以是实验数据、观测数据或者是模拟数据。
这些数据应该是有一定规律的,我们需要通过这些数据来找到一个函数,使得这个函数能够最好地描述这些数据的规律。
2. 打开cftool在MATLAB中,我们可以通过输入cftool来打开cftool工具箱。
在cftool中,我们可以选择不同的拟合函数类型,比如多项式、指数函数、对数函数等等。
我们还可以选择不同的拟合算法,比如最小二乘法、最大似然法等等。
3. 导入数据在cftool中,我们可以通过导入数据来进行拟合。
我们可以将数据从MATLAB的工作区中导入,也可以从文件中导入。
在导入数据之后,我们可以对数据进行可视化展示,以便更好地理解数据的分布规律。
4. 拟合函数在cftool中,我们可以选择不同的拟合函数类型,并且可以对这些函数进行参数调整。
在拟合函数之后,我们可以对拟合结果进行可视化展示,以便更好地理解拟合结果。
5. 评估拟合结果在cftool中,我们可以对拟合结果进行评估。
我们可以查看拟合函数的拟合优度、残差分布等等。
这些评估结果可以帮助我们判断拟合函数的拟合效果,并且可以帮助我们进一步优化拟合函数。
6. 导出拟合结果在cftool中,我们可以将拟合结果导出到MATLAB的工作区中,以便我们在MATLAB中进一步分析和处理数据。
我们还可以将拟合结果导出为图片或者PDF文件,以便我们在论文或者报告中使用。
cftool是一个非常方便的工具箱,可以帮助我们快速地找到一个函数,使得这个函数能够最好地描述我们的数据。
通过cftool,我们可以更好地理解数据的分布规律,并且可以更好地进行数据分析和处理。
MATLAB中如何直接曲线拟合

MATLAB中如何直接曲线拟合,而不使用cftool的GUI界面(这里使用的版本是MATLAB 2009a)我们知道在MATLAB中有个很方便的曲线拟合工具:cftool最基本的使用方法如下,假设我们需要拟合的点集存放在两个向量X和Y中,分别储存着各离散点的横坐标和纵坐标,则在MATLAB中直接键入命令cftool(X,Y) 就会弹出Curve Fitting Tool的GUI界面,点击界面上的fitting即可开始曲线拟合。
MATLAB提供了各种曲线拟合方法,例如:Exponential, Fourier, Gaussing, Interpolant, Polynomial, Power, Rational, Smoothing Spline, Sum of Functions, Weibull等,当然,也可以使用Custom Equations.cftool不仅可以绘制拟合后的曲线、给出拟合参数,还能给出拟合好坏的评价参数(Goodness of fit)如SSE, R-square, RMSE等数据,非常好用。
但是如果我们已经确定了拟合的方法,只需要对数据进行计算,那么这种GUI的操作方式就不太适合了,比如在m文件中就不方便直接调用cftool。
MATLAB已经给出了解决办法,可以在cftool中根据情况生成特定的m文件,让我们直接进行特定的曲线拟合并给出参数。
具体方法在帮助文件的如下文档中" \ Curve Fitting Toolbox \ Generating M-files From Curve Fitting Tool " ,以下简单举例说明:以双色球从第125期到第145期蓝球为Y值:Y=[12 15 4 1 7 11 5 7 1 6 16 1 1 14 2 12 9 13 10 12 11];X=1:1:21;cftool(X,Y);点击Fitting选择最常用的多项式拟合(Polynomial),选择3次多项式拟合(cubic),然后就会出现如下拟合图形:然后在Curve Fitting Tool窗口中点击" \ File \ Generate M-file " 即可生成能直接曲线拟合的m函数文件,其中使用的拟合方法就是刚才使用的三次多项式拟合,文件中这条语句证明了这一点:ft_ = fittype('poly3');保存该m文件(默认叫做createFit.m),调用方法和通常的m文件一样,使用不同的X和Y值就能拟合出不同的曲线。
matlab中cftool的用法

matlab中cftool的用法MATLAB中cftool的用法MATLAB中的cftool是一个交互式的拟合工具,用于在实验数据中拟合各种曲线模型。
下面是cftool的一些用法以及详细的讲解。
1. 打开cftool工具在MATLAB命令窗口中直接输入cftool,即可打开cftool工具。
2. 导入数据在cftool工具中,可以通过多种方式导入数据:•在工具栏点击”File”->“Import Data”,选择需要导入的数据文件;•直接在工具栏中点击”New Session”,手动输入数据。
3. 选择拟合模型在导入数据后,可以在左侧的”Fit”选项卡中选择需要的拟合模型。
cftool提供了多种常见的拟合模型,如线性、二次、指数等。
4. 拟合数据在选择了拟合模型后,可以点击”Fit”按钮对数据进行拟合。
cftool会自动计算出最佳拟合曲线,并在图像中展示出来。
5. 优化拟合模型参数如果觉得拟合效果还不够理想,可以在”Fit”选项卡中调整拟合模型的参数。
点击”Options”按钮,可以进入参数调整界面。
通过修改参数,可以优化拟合效果。
6. 验证拟合模型在进行参数优化后,可以点击”Go”按钮验证拟合模型的效果。
cftool会将拟合曲线与原始数据进行比较,给出拟合优度和拟合误差等评估指标。
7. 导出拟合模型当对拟合模型满意后,可以将其导出,进一步在MATLAB中应用。
在cftool工具上方的菜单栏中,点击”File”->“Export Model”,选择导出模型的格式和保存路径。
导出后的模型可以在其他MATLAB代码中加载和使用。
以上就是MATLAB中cftool的主要用法和讲解,通过这个交互式的拟合工具,可以方便地进行各种曲线拟合操作。
8. 调整数据范围在cftool工具中,可以通过调整数据范围来改善拟合效果。
在”Fit”选项卡的下方有一个”Data Range”选项,可以设置需要使用的数据范围。
Matlab的CFtool工具箱在浮选尾矿灰分与图像灰度曲线拟合中的应用

Matlab的CFtool工具箱在浮选尾矿灰分与图像灰度曲线拟
合中的应用
高鹏
【期刊名称】《选煤技术》
【年(卷),期】2015(000)001
【摘要】为解决数据处理过程中工作量繁重的问题,在获取浮选尾矿灰分数据与图像灰度数据的基础上,利用Matlab的CFtool工具箱对其进行曲线拟合,并对拟合结果进行验证,建立二者对应的函数关系.结果表明:CFtool工具箱能很好地对数据进行处理,大大减轻了设计人员的工作量,且数据拟合的准确性很高.
【总页数】4页(P67-70)
【作者】高鹏
【作者单位】中煤科工集团唐山研究院有限公司,河北唐山063012;河北省煤炭洗选工程技术研究中心,河北唐山063012
【正文语种】中文
【中图分类】TD948.9
【相关文献】
1.Matlab曲线拟合工具箱在地基沉降预测模型中的应用 [J], 高艳平;王杰
2.Matlab系统辨识工具箱在煤泥浮选过程辨识建模中的应用 [J], 刘兆田;李敬敬;何旭;施心陵
3.MATLAB工具箱在软磁材料单位损耗曲线拟合中的应用 [J], 范隽宏;程汉湘
4.MATLAB曲线拟合工具箱在发动机特性拟合中的应用 [J], 黄兵锋;解方喜;傅佳宏
5.MATLAB曲线拟合工具箱在发动机特性拟合中的应用 [J], 黄兵锋;解方喜;傅佳宏;
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使用Matlab cftool工具箱对图像进行拟合
Matlab提供了强大的工具箱系统,利用工具箱进行各种操作简单快捷。
此处介绍使用cftool(Curve Fitting Tool)进行图像拟合操作。
网上有很多关于图像拟合的代码,但是如果照着运行不是上传代码的通知有所保留,就是环境不同无法运行,即使千方百计做出来,也难以举一反三,攻克其他的难题。
使用cftool工具箱的流程如下:假定对X-Y坐标下的一组散点进行拟合,如
A=[4 5 9 15 17 29 40 50 79];
B=[14 19 39 40 70 100 140 290 400];
在Command界面输入如下两组数组,A代表X坐标的数值,B代表Y坐标下的数值。
输入cftool回车。
如图:
可以打开cftool主界面
单击Data选项框,设定X Data为A,Y Data为B,如图:
可见Preview栏中自动绘制出了散点图。
并且选择Create data set选项框,此时散点图会被复制到
cftool主界面中。
单击Fitting选项框,弹出Fitting界面,在Fitting Editor选项框中选择New Fit。
如图产生如下效果:
此处只需按照需求更改Type of fit以及下面备选框中的曲线名称。
Type of fit中有如下选项:Polynomial(线性拟合),Exponential(指数函数拟合),Fourier(傅里叶函数拟合)等等。
此处先选择Polynomial一次线性拟合。
在备选框中选择linear Polynomial。
单击Apply。
返回cftool主界面,会产生如下效果:拟合成的曲线被绘制为红色,大功告成。
在Fitting界面中的Results框图中,可看到如下结果:
Linear model Poly1:
f(x) = p1*x + p2
Coefficients (with 95% confidence bounds):
p1 = 5.267 (4.236, 6.298)
p2 = -21.57 (-58.93, 15.79)
Goodness of fit:
SSE: 6633
R-square: 0.9542
Adjusted R-square: 0.9477
RMSE: 30.78
给定了函数的参数,即拟合函数为f(x) = 5.267*x -21.57。
Goodness of fit意思为拟合度。
R-square意思为函数相关系数的平方,Adjusted R-square意思为系统调整后的相关系数。
RMSE为均方根误差。
此处R-square值越接近1,表示取下拟合程度越高,反之拟合状况越差。
想得到较高的拟合度可以改变Type of fit 以及备选框中的曲线名称,一一进行拟合,选取拟合程度最高的曲线。
如选择Exponential下的a*exp(b*x)曲线类型,操作如上得到如下图像和拟合值:
General model Exp1:
f(x) = a*exp(b*x)
Coefficients (with 95% confidence bounds):
a = 46.07 (15.24, 76.9)
b = 0.02815 (0.01843, 0.03788)
Goodness of fit:
SSE: 1.496e+004
R-square: 0.8967
Adjusted R-square: 0.882
RMSE: 46.24
(注:素材和资料部分来自网络,供参考。
请预览后才下载,期待你的好评与关注!)。
